第10天—四边形专题:中点四边形&中位线定理及其应用
中考数学几何模型专题专题十—经典模型
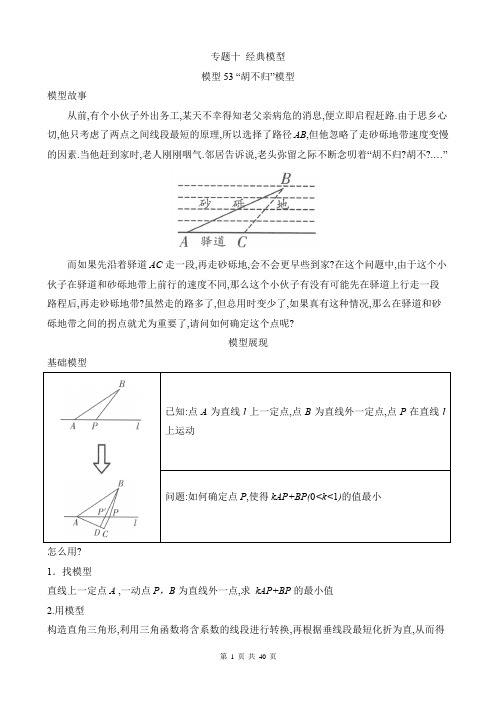
专题十经典模型模型53 “胡不归”模型模型故事从前,有个小伙子外出务工,某天不幸得知老父亲病危的消息,便立即启程赶路.由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了路径AB,但他忽略了走砂砾地带速度变慢的因素.当他赶到家时,老人刚刚咽气.邻居告诉说,老头弥留之际不断念叨着“胡不归?胡不?.…”而如果先沿着驿道AC走一段,再走砂砾地,会不会更早些到家?在这个问题中,由于这个小伙子在驿道和砂砾地带上前行的速度不同,那么这个小伙子有没有可能先在驿道上行走一段路程后,再走砂砾地带?虽然走的路多了,但总用时变少了,如果真有这种情况,那么在驿道和砂砾地带之间的拐点就尤为重要了,请问如何确定这个点呢?模型展现基础模型怎么用?1.找模型直线上一定点A ,一动点P,B为直线外一点,求kAP+BP的最小值2.用模型构造直角三角形,利用三角函数将含系数的线段进行转换,再根据垂线段最短化折为直,从而得到线段和最小值,最后运用锐角三角函数求解即可 模型分析如图,求这类带有系数的折线最值问题,通常我们都是将折线转化成为线段,再利用两点之间线段最短或垂线段最短求解,该模型就是利用了垂线段最短的性质,具体解题步骤如下: 一找:找带有系数k 的线段kAP ;二构:在点B 异侧,构造以线段AP 为斜边的直角三角形; ①以定点A 为顶点作①CAP ,使得sin ①P AC =h ; ①过动点P 作垂线构造Rt ①P AC ; 三转化:化折为直,将kAP 转化为PC ;四求解:使得hAP +BP =PC +BP ,利用“垂线段最短”转化为求BD 的长度.拓展延伸熟记特殊角的锐角三角函数值,kAP +BP 中系数k 发生变化时,所构造的直角三角形也会发生变化,同学们需要牢记特殊角度的正弦值:01sin 30 =2,0sin 60,0sin 45 =2,03sin 375,04sin 53 5例1如图, 在①ABC 中,AC =6,①A =30°,点D 是AB 边上一动点,(点拨:两定点A 、C ,动点D ,含特殊角30°)则12AD CD 的最小值为_________(点拨:线段数量关系的最小值,考虑“胡不归”)考什么?直角三角形的性质,30°,60°角的锐角三角函数值,垂线段最短.思路点拨哪条线段带有系数,就以它为斜边构造直角三角形,使得其中一锐角的正弦值恰好与系数相等.例2如图, 在平行四边形ABCD中,①DAB=45°,(点拨:特殊角)AB=6,BC=2,P为CD边上的一动点,则22PB PD(点拨:线段数量关系出现,且0<k<1,模型出现)的最小值为_____________考什么?平行四边形的性质,直角三角形的性质,45°角的锐角三角函数值,垂线段最短。
《四边形的认识》教学反思范文(通用7篇)

《四边形的认识》教学反思范文(通用7篇)《四边形的认识》教学反思范文(通用7篇)作为一名到岗不久的人民教师,我们需要很强的课堂教学能力,通过教学反思能很快的发现自己的讲课缺点,来参考自己需要的教学反思吧!以下是小编帮大家整理的《四边形的认识》教学反思范文(通用7篇),欢迎大家借鉴与参考,希望对大家有所帮助。
《四边形的认识》教学反思1《四边形》一课是一节概念课,同时这又是一节操作性很强的课,学生通过操作能进一步理解、巩固概念。
这一教学内容教材安排了两个例题:例1是借助于涂颜色的活动,让学生从众多的图形中区分出四边形,并感悟到四边形有四条直直的边和四个角。
例2让学生通过观察、量一量、折一折、比一比等数学活动把四边形进行分类,对不同的四边形各自的特性有所了解。
在这节课中,我做得比较好的地方有:1、关注生活经验,提供感性材料。
学生生活的世界和所接触的事物大都和数学中的“空间与图形”有关,生活经验是发展学生空间观念的宝贵资源。
学生在生活中已经接触过很多图形,对四边形也不陌生。
因此,本节课以学生熟悉的图形为教学素材,目的就是联系学生的生活经验,丰富他们对图形特别是四边形的感性认识,并从整体上感知自己生活中的四边形。
既使学生感觉到数学来源于生活,又使他们对数学产生浓厚兴趣和亲切感。
2、在小组合作的过程中发挥学生的集体智慧。
小组合作的优点之一就是学生之间能互相启发,从不同的角度来解决问题。
在认识了四边形后,我安排的教学环节是让学生小组讨论将图形分分类。
在这里,学生的思维被充分的展开了,出现了许多情况:有根据角分的、有根据边分的、有根据是否是对称图形分的、还有根据对边是否相等来分的。
尤其是有根据是否是对称图形分的情况,学生能将新知识与已有知识进行联系,这虽然是一位同学的想法,却给了更多同学一启示。
在讨论的过程中,学生还培养了说的能力和听的能力,一举多得。
针对课堂上学生的实际反应,我觉得存在着以下几点不足,需要自己不断努力:1、在这次教学中,前面几个环节的教学是教师引导学生去获取知识,但是在分类这一环节中没有给学生足够的思考时间和发表自己看法的空间,过多地牵制了学生的思维,使得有几种不错的分类方法没能在课堂上得到展示。
《四边形》精品教案

《四边形》精品教案教学内容四边形。
(教材第79~82页)教学目标1.直观感知四边形,能区分和辨认四边形,进一步认识长方形和正方形的特征,知道它们的角都是直角。
2.通过找一找、围一围、涂一涂、剪一剪等活动,培养学生的观察、比较和抽象概括的能力。
3.通过情景图和生活中的事物,感受生活中的四边形无处不在,激发学生的学习兴趣。
重点难点重点:认识四边形。
难点:长方形和正方形的特征。
教具学具课件、方格纸、直尺。
教学过程一创设情境,激趣导入师:图形是一个美丽的世界,我们的生活中存在许多漂亮的图案都是由图形组成的,今天我们就一起走进图形的世界。
二探究体验,经历过程1.教学例1。
师:把你认为是四边形的图形圈出来,在小组里说一说四边形有什么特点。
(课件出示:教材第79页例1)学生观察这些四边形,在小组里讨论交流四边形的特点;教师巡视了解情况。
师:你认为四边形有什么特点呢?生:四边形都有4条直的边。
生:四边形都有4个角。
师:你能在方格纸上自己画出一个四边形吗?学生尝试画四边形;教师巡视了解情况,指导个别有困难的学生。
组织学生交流展示;画图正确的学生给予表扬鼓励。
2.教学例2。
师:仔细观察下面的长方形和正方形,说说有什么特点。
跟小组同学说一说。
(课件出示:教材第80页例2)学生进行小组活动;教师巡视了解情况。
师:把你的发现跟大家说一说吧!生1:长方形的对边是相等的。
生2:正方形的4条边都相等。
生3:长方形和正方形都有4个直角。
……只要学生回答合理就要给予肯定并鼓励。
【设计意图:充分利用学生观察、操作的实践活动。
组织学生进行探索,进一步认识长方形和正方形的特点】三总结提升师:你学会了什么?(知道了长方形的特点:对边相等,四个角都是直角;正方形的特点:四条边相等,四个角都是直角)【设计意图:课末总结帮助学生对课堂知识进行梳理,回顾知识点的同时学会数学思考的方法】四课堂作业新设计A类判断。
(对的在括号里画“√”,错的画“✕”)(1)长方形的对边相等,四个角都是直角。
九年级数学中考专题(空间与图形)-第九讲《四边形(一)》课件(北师大版)

B
C
E
体验中考
1.(06常州)已知:如图,在四边形ABCD AO CO, 中,AC与BD相交与点O,AB∥CD, 求证:四边形ABCD是平行四边形.
A O B C D
体验中考
2.(06大连西岗)如图,ABCD中, AE⊥BD于E,CF⊥BD于F. 求证:AE = CF
A F E B D
典型例题
E 变式1:顺次连结矩形四边中点所得的四边形是菱形. D 变式2:顺次连结菱形四边中点所得的四边形是矩形. G H 变式3:顺次连结正方形四边中点所得的四边形 是正方形. B F 变式4:顺次连结等腰梯形四边中点所得的四边形 A 是菱形. 变式5:若AC=BD,AC⊥BD,则四边形EFGH是正方形. 变式6:在四边形ABCD中,若AB=CD,E、F、G、H分别为AD、BC、 BD、AC的中点,求证:EFGH是菱形. C 变式7:如图:在四边形ABCD中, M D E为边AB上的一点,△ADE和△ Q BCE都是等边三角形,P、Q、M、 N N分别是AB、BC、CD、DA边上 的中点,求证:四边形PQMN是菱形. B A E P
二、选择题: 1、若□ABCD的周长为28,△ABC的周长为17cm,则AC的长 为( ) A、11cm B、5.5cm C、4cm D、3cm 2、如图,□ABCD和□EAFC的顶点D、E、F、B在同一条直 线上,则下列关系中正确的是( ) C A、DE>BF B、DE=BF D C、DE<BF D、DE=FE=BF E F B
C
典型例题
例3 已知如图,在△ABC中,∠C=900,点M在BC上, 且BM=AC,点N在AC上,且AN=MC,AM和BN相交于 P,求∠BPM的度数.
分析:条件给出的是线段的等量关系,求的却是角的度数,为此,我们由条件中 的直角及相等的线段,可联想到构造等腰直角三角形,从而应该平移AN. 证明:过M作ME∥AN,且ME=AN,连结NE、BE,则四边形AMEN是平行四 边形,得NE=AM,ME∥AN,AC⊥BC ∴ME⊥BC在△BEM和△AMC中, ME=CM,∠EMB=∠MCA=900,BM=AC ∴△BEM≌△AMC A ∴BE=AM=NE,∠1=∠2, ∠3=∠4,∠1+∠3=90° 1 ∴∠2+∠4=90 ° ,且BE=NE N P ∴△BEN是等腰直角三角形 3 C B ∴∠BNE=45 ° ∵AM∥NE M ∴∠BPM=∠BNE =45 ° 2
2020年中考数学二轮复习压轴专题四边形(含解析)

《四边形》1.【习题再现】课本中有这样一道题目:如图1,在四边形ABCD中,E,F,M分别是AB,CD,BD的中点,AD=BC.求证:∠EFM =∠FEM.(不用证明)【习题变式】(1)如图2,在“习题再现”的条件下,延长AD,BC,EF,AD与EF交于点N,BC与EF 交于点P.求证:∠ANE=∠BPE.(2)如图3,在△ABC中,AC>AB,点D在AC上,AB=CD,E,F分别是BC,AD的中点,连接EF并延长,交BA的延长线于点G,连接GD,∠EFC=60°.求证:∠AGD=90°.【习题变式】解:(1)∵F,M分别是CD,BD的中点,∴MF∥BP,,∴∠MFE=∠BPE.∵E,M分别是AB,BD的中点,∴ME∥AN,,∴∠MEF=∠ANE.∵AD=BC,∴ME=MF,∴∠EFM=∠FEM,∴∠ANE=∠BPE.(2)连接BD,取BD的中点H,连接EH,FH.∵H,F分别是BD和AD的中点,∴HF∥BG,,∴∠HFE=∠FGA.∵H,E分别是BD,BC的中点,∴HE∥AC,,∴∠HEF=∠EFC=60°.∵AB=CD,∴HE=HF,∴∠HFE=∠EFC=60°,∴∠A GF=60°,∵∠AFG=∠EFC=60°,∴△AFG为等边三角形.∴AF=GF,∵AF=FD,∴GF=FD,∴∠FGD=∠FDG=30°,∴∠AGD=60°+30°=90°.2.(1)问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合),连接AD,过点A作AE⊥AD,并满足AE=AD,连接CE.则线段BD和线段CE的数量关系是BD=CE,位置关系是BD⊥CE.(2)探索:如图2,当D点为BC边上一点(不与点B,C重合),Rt△ABC与Rt△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE.试探索线段BD2、CD2、DE2之间满足的等量关系,并证明你的结论;(3)拓展:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=3,CD=1,请直接写出线段AD的长.解:(1)问题:在Rt△ABC中,AB=AC,∴∠B=∠ACB=45°,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),故答案为:BD=CE,BD⊥CE;(2)探索:结论:DE2=BD2+CD2,理由是:如图2中,连接EC.∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,在△ABD和△ACE中,∵,∵△BAD≌△CAE(SAS),∴BD=CE,∠B=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=45°+45°=90°,∴DE2=CE2+CD2,∴DE2=BD2+CD2;(3)拓展:如图3,将AD绕点A逆时针旋转90°至AG,连接CG、DG,则△DAG是等腰直角三角形,∴∠ADG=45°,∵∠ADC=45°,∴∠GDC=90°,同理得:△BAD≌△CAG,∴CG=BD=3,Rt△CGD中,∵CD=1,∴DG===2,∵△DAG是等腰直角三角形,∴AD=AG=2.3.如图1,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.(1)BE和DG的数量关系是BE=DG,BE和DG的位置关系是BE⊥DG;(2)把正方形ECGF绕点C旋转,如图2,(1)中的结论是否还成立?若成立,写出证明过程,若不成立,请说明理由;(3)设正方形ABCD的边长为4,正方形ECGF的边长为3,正方形ECGF绕点C旋转过程中,若A、C、E三点共线,直接写出DG的长.解:(1)BE=DG.BE⊥DG;理由如下:∵四边形ABCD和四边形CEFG为正方形,∴CD=BC,CE=CG,∠BCE=∠DCG=90°,在△BEC和△DGC中,,∴△BEC≌△DGC(SAS),∴BE=DG;如图1,延长GD交BE于点H,∵△BEC≌△DGC,∴∠DGC=∠BEC,∴∠DGC+∠EBC=∠BEC+∠EBC=90°,∴∠BHG=90°,即BE⊥DG;故答案为:BE=DG,BE⊥DG.(2)成立,理由如下:如图2所示:同(1)得:△DCG≌△BCE(SAS),∴BE=DG,∠CDG=∠CBE,∵∠DME=∠BMC,∠CBE+∠BMC=90°,∴∠CDG+∠DME=90°,∴∠DOB=90°,∴BE⊥DG;(3)由(2)得:DG=EB,分两种情况:①如图3所示:∵正方形ABCD的边长为4,正方形ECGF的边长为3,∴AC⊥BD,BD=AC=AB=4,OA=OC=OB=AC=2,CE=3,∴AE=AC﹣CE=,∴OE=OA﹣AE=,在Rt△BOE中,由勾股定理得:DG=BE==;②如图4所示:OE=CE+OC=2+3=5,在Rt△BOE中,由勾股定理得:DG=BE==;综上所述,若A、C、E三点共线,DG的长为或.4.如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点D从点C出发,沿CA方向匀速运动,速度为2cm/s;同时,动点E从点A出发,沿AB方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.设点D,E运动的时间是t(s)(0<t<5).过点D作DF⊥BC于点F,连接DE,EF.(1)t为何值时,DE⊥AC?(2)设四边形AEFC的面积为S,试求出S与t之间的关系式;(3)是否存在某一时刻t,使得S四边形AEFC:S△ABC=17:24,若存在,求出t的值;若不存在,请说明理由;(4)当t为何值时,∠ADE=45°?解:(1)∵∠B=90o,AB=6 cm,BC=8 cm,∴AC===10(cm),若DE⊥AC,∴∠EDA=90°,∴∠EDA=∠B,∵∠A=∠A,∴△ADE∽△ABC,∴=,即:=,∴t=,∴当t=s时,DE⊥AC;(2)∵DF⊥BC,∴∠DFC=90°,∴∠DFC=∠B,∵∠C=∠C,∴△CDF∽△CAB,∴=,即=,∴CF=,∴BF=8﹣,BE=AB﹣AE=6﹣t,∴S=S△ABC﹣S△BEF=×AB•BC﹣×BF•BE=×6×8﹣×(8﹣t)×(6﹣t)=﹣t2+t;(3)若存在某一时刻t,使得S四边形AEFC:S△ABC=17:24,根据题意得:﹣t2+t=××6×8,解得:t1=,t2=(不合题意舍去),∴当t=s时,S四边形AEFC:S△ABC=17:24;(4)过点E作EM⊥AC与点M,如图所示:则∠EMA=∠B=90°,∵∠A=∠A,∴△AEM∽△ACB,∴==,即==,∴EM=t,AM=t,∴DM=10﹣2t﹣t=10﹣t,在Rt△DEM中,当DM=ME时,∠ADE=45°,∴10﹣t=t,∴t=∴当t=s时,∠ADE=45°.5.我们定义:如果两个等腰三角形的顶角相等,且项角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如图(1),△ABC与△ADE都是等腰三角形,其中∠BAC=∠DAE,则△ABD≌△ACE(SAS)(1)熟悉模型:如图(2),已知△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,求证:BD=CE;(2)运用模型:如图(3),P为等边△ABC内一点,且PA:PB:PC=3:4:5,求∠APB 的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以BP为边构造等边△BPM,这样就有两个等边三角形共顶点B,然后连结CM,通过转化的思想求出了∠APB的度数,则∠APB的度数为150 度;(3)深化模型:如图(4),在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC =45°,求BD的长.(1)证明:∵∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE;(2)解:以BP为边构造等边△BPM,连接CM,如图(3)所示:∵△ABC与△BPM都是等边三角形,∴AB=BC,BP=BM=PM,∠ABC=∠PBM=∠BMP=60°,∴∠ABC﹣∠PBC=∠PBM﹣∠PBC,即∠ABP=∠CBM,在△ABP和△CBM中,,∴△ABP≌△CBM(SAS),∴AP=CM,∠APB=∠CMB,∵PA:PB:PC=3:4:5,∴CM:PM:PC=3:4:5,∴PC2=CM2+PM2,∴△CMP是直角三角形,∴∠PMC=90°,∴∠CMB=∠BMP+∠PMC=60°+90°=150°,∴∠APB=150°,故答案为:150;(3)解:过点A作EA⊥AD,且AE=AD,连接CE,DE,如图(4)所示:则△ADE是等腰直角三角形,∠EAD=90°,∴DE=AD=4,∠EDA=45°,∵∠ADC=45°,∴∠EDC=45°+45°=90°,在Rt△DCE中,CE===,∵∠ACB=∠ABC=45°,∴∠BAC=90°,AB=AC,∵∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE=.6.(1)某学校“学习落实”数学兴趣小组遇到这样一个题目如图,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO =2:1,求AB的长经过数学小组成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2)请回答:∠ADB=75 °,AB=3(2)请参考以上解决思路,解决问题:如图3在四边形ABCD中对角线AC与BD相交于点0,AC⊥AD,AO=,∠ABC=∠ACB =75°,BO:OD=2:1,求DC的长解:(1)如图2中,过点B作BD∥AC,交AO的延长线于点D,∵BD∥AC,∴∠ADB=∠OAC=75°.∵∠BOD=∠COA,∴△BOD∽△COA,∴==2,.又∵AO=,∴OD=2AO=2,∴AD=AO+OD=3.∵∠BAD=30°,∠ADB=75°,∴∠ABD=180°﹣∠BAD﹣∠ADB=75°=∠ADB,∴AB=AD=3;故答案为75,3.(2)如图3中,过点B作BE∥AD交AC于点E.∵AC⊥AD,BE∥AD,∴∠DAC=∠BEA=90°.∵∠AOD=∠EOB,∴△AOD∽△EOB,∴===2.∵BO:OD=1:3,∵AO=,∴EO=2,∴AE=3.∵∠ABC=∠ACB=75°,∴∠BAC=30°,AB=AC,∴AB=2BE.在Rt△AEB中,BE2+AE2=AB2,即(4BE2)2+BE2=(2BE)2,解得:BE=3,∴AB=AC=6,AD=在Rt△CAD中,AC2+AD2=CD2,即62+()2=CD2,解得:CD=(负根已经舍弃).7.正方形ABCD中,AB=4,点E、F分别在AB、BC边上(不与点A、B重合).(1)如图1,连接CE,作DM⊥CE,交CB于点M.若BE=3,则DM= 5 ;(2)如图2,连接EF,将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;再将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;依此操作下去…,①如图3,线段EF经过两次操作后拼得△EFD,其形状为等边三角形,在此条件下,求证:AE=CF;②若线段EF经过三次操作恰好拼成四边形EFGH,(3)请判断四边形EFGH的形状为正方形,此时AE与BF的数量关系是AE=BF;(4)以1中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.解:(1)如图1中,∵四边形ABCD是正方形,∴∠B=∠DCM=90°,∵BE=3,BC=4,∴CE===5,∵DM⊥EC,∴∠DMC+∠MCE=90°,∠MCE+∠CEB=90°,∴∠DMC=∠CEB,∵BC=CD,∴△BCE≌△CDM(AAS),∴DM=EC=5.故答案为5.(2)如题图3,由旋转性质可知EF=DF=DE,则△DEF为等边三角形.故答案为等边三角形.(2)①四边形EFGH的形状为正方形,此时AE=BF.理由如下:依题意画出图形,如答图1所示:连接EG、FH,作HN⊥BC于N,GM⊥AB于M.由旋转性质可知,EF=FG=GH=HE,∴四边形EFGH是菱形,由△EGM≌△FHN,可知EG=FH,∴四边形EFGH的形状为正方形.∴∠HEF=90°∵∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3.∵∠3+∠4=90°,∠2+∠3=90°,∴∠2=∠4.在△AEH与△BFE中,,∴△AEH≌△BFE(ASA)∴AE=BF.故答案为正方形,AE=BF.(4)利用①中结论,易证△AEH、△BFE、△CGF、△DHG均为全等三角形,∴BF=CG=DH=AE=x,AH=BE=CF=DG=4﹣x.∴y=S正方形ABCD﹣4S△AEH=4×4﹣4×x(4﹣x)=2x2﹣8x+16.∴y=2x2﹣8x+16(0<x<4)∵y=2x2﹣8x+16=2(x﹣2)2+8,∴当x=2时,y取得最小值8;当x=0时,y=16,∴y的取值范围为:8≤y<16.8.已知:如图1,在平面直角坐标系中,长方形OABC的顶点B的坐标是(6,4).(1)直接写出A点坐标( 6 ,0 ),C点坐标(0 , 4 );(2)如图2,D为OC中点.连接BD,AD,如果在第二象限内有一点P(m,1),且四边形OADP的面积是△ABC面积的2倍,求满足条件的点P的坐标;(3)如图3,动点M从点C出发,以每钞1个单位的速度沿线段CB运动,同时动点N 从点A出发.以每秒2个单位的速度沿线段AO运动,当N到达O点时,M,N同时停止运动,运动时间是t秒(t>0),在M,N运动过程中.当MN=5时,直接写出时间t的值.解:(1)∵四边形OABC是长方形,∴AB∥OC,BC∥OA,∵B(6,4),∴A(6,0),C(0,4),故答案为:6,0,0,4;(2)如图2,由(1)知,A(6,0),C(0,4),∴OA=6,OC=4,∵四边形OABC是长方形,∴S长方形OABC=OA•OC=6×4=24,连接AC,∵AC是长方形OABC的对角线,∴S△OAC=S△ABC=S长方形OABC=12,∵点D是OC的中点,∴S△OAD=S△OAC=6,∵四边形OADP的面积是△ABC面积的2倍,∴S四边形OADP=2S△ABC=24,∵S四边形OADP=S△OAD+S△ODP=6+S△ODP=24,∴S△ODP=18,∵点D是OC的中点,且OC=4,∴OD=OC=2,∵P(m,1),∴S△ODP=OD•|m|=×2|m|=18,∴m=18(由于点P在第二象限,所以,m小于0,舍去)或m=﹣18,∴P(﹣18,1);(3)如图3,由(2)知,OA=6,OC=4,∵四边形OABC是长方形,∴∠AOC=∠OCB=90°,BC=6,由运动知,CM=t,AN=2t,∴ON=OA﹣AN=6﹣2t,过点M作MH⊥OA于H,∴∠OHM=90°=∠AOC=∠OCB,∴四边形OCMH是长方形,∴MH=OC=4,OH=CM=t,∴HN=|ON﹣CM|=6﹣2t﹣t|=|6﹣3t|,在Rt△MHN中,MN=5,根据勾股定理得,HN2=MN2﹣MH2,∴|6﹣3t|2=52﹣42=9,∴t=1或t=3,即:t的值为1或3.9.综合与实践问题情境数学课上,李老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB =2,PC=3.你能求出∠APB的度数吗?(1)小敏与同桌小聪通过观察、思考、讨论后,得出了如下思路:思路一:将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP',求出∠APB的度数;思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP',求出∠APB的度数.请参考以上思路,任选一种写出完整的解答过程.类比探究(2)如图2,若点P是正方形ABCD外一点,PA=3,PB=1,,求∠APB的度数.拓展应用(3)如图3,在边长为的等边三角形ABC内有一点O,∠AOC=90°,∠BOC=120°,则△AOC的面积是.解:(1)思路一,如图1,将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP',则△ABP'≌△CBP,AP'=CP=3,BP'=BP=2,∠PBP'=90°∴∠BPP'=45°,根据勾股定理得,,∵AP=1,∴AP2+P'P2=1+8=9,又∵P'A2=32=9,∴AP2+P'P2=P'A2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'+∠BPP'=90°+45°=135°.思路二、同思路一的方法.(2)如图2,将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP'.则△ABP'≌△CBP,,BP'=BP=1,∠PBP'=90°∴∠BPP'=45°,根据勾股定理得,,∵AP=3,∴AP2+P'P2=9+2=11,又∵,∴AP2+P'P2=P'A2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'﹣∠BPP'=90°﹣45°=45°.(3)如图,将△ABO绕点B顺时针旋转60°,得到△BCE,连接OE.则△BAO≌△BCE,∠AOB=∠BEC=360°﹣90°﹣120°=150°,∵△BOE是等边三角形,∴∠BEO=∠BOE=60°,∴∠OEC=90°,∠OEC=120°﹣60°=60°,∴sin60°==,设EC=k,OC=2k,则OA=EC=k,∵∠AOC=90°,∴OA2+OC2=AC2,∴3k2+4k2=7,∴k=1或﹣1(舍弃),∴OA=,OC=2,∴S△AOC=•OA•OC=××2=.故答案为.10.如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,BP=BE.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.(1)求证:∠BAP=∠BGN;(2)若AB=6,BC=8,求;(3)如图2,在(2)的条件下,连接CF,求tan∠CFM的值.(1)证明:如图1中,∵四边形ABCD是矩形,∴∠ABC=90°,∴∠BAP=∠APB=90°∵BP=BE,∴∠APB∠BEP=∠GEF,∵MN垂直平分线段AP,∴∠GFE=90°,∴∠BGN+∠GEF=90°,∴∠BAP=∠BGN.(2)解:∵四边形ABCD是矩形,∴∠BAD=∠ABP=90°,AD∥BC,AD=BC=8,∴BD===10,∵AD∥BC,∴∠DAE=∠APB,∵∠APB=∠BEP=∠DEA,∴∠DAE=∠DEA,∴DA=DE=8,∴BE=BP=BD﹣DE=10﹣8=2,∴PA===2,∵MN垂直平分线段AP,∴AF=PF=,∵PB∥AD,∴===,∴PE=PA=,∴EF=PF﹣PE=﹣=,∴==.(3)解:如图3中,连接AM,MP.设CM=x.∵四边形AB CD是矩形,∴∠ADM=∠MCP=90°,AB=CD=6,AD=BC=8,∵MN垂直平分线段AP,∴MA=MP,∴AD2+DM2=PC2+CM2,∴82+(6﹣x)2=62+x2,∴x=,∵∠PFM=∠PCM=90°,∴P,F,M,C四点共圆,∴∠CFM=∠CPM,∴tan∠CFM=tan∠CFM===.11.在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB=8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.请你回答:(1)在图①中,中线AD的取值范围是1<AD<7 .(2)应用上述方法,解决下面问题①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.解:(1)延长AD到点E,使AD=DE,连接BE,如图①所示:∵点D是BC边上的中点,∴BD=CD,在△A DC和△EDB中,,∴△ADC≌△EDB(SAS),∴AC=EB=6,在△ABE中,AB﹣BE<AE<AB+BE,∴8﹣6<AE<8+6,即2<AE<14,∴1<AD<7,故答案为:1<AD<7;(2)①延长ED到点N,使ED=DN,连接CN、FN,如图②所示:∵点D是BC边上的中点,∴BD=CD,在△NDC和△EDB中,中,,∴△NDC≌△EDB(SAS),∴BE=CN=4,∵DF⊥DE,ED=DN,∴EF=FN,在△CFN中,CN﹣CF<FN<CN+CF,∴4﹣2<FN<4+2,即2<FN<6,∴2<EF<6;②CE⊥ED;理由如下:延长CE与DA的延长线交于点G,如图③所示:∵点E是AB中点,∴BE=AE,∵∠BCD=150°,∠ADC=30°,∴DG∥BC,∴∠GAE=∠CBE,在△GAE和△CBE中,,∴△GAE≌△CBE(ASA),∴GE=CE,AG=BC,∵BC=CF,DF=AD,∴CF+DF=BC+AD=AG+AD,即:CD=GD,∵GE=CE,12.如图,在平行四边形ABCD中,AB⊥AC,对角线AC、BD相交于点O,将直线AC绕点O 顺时针旋转一个角度α(0°<α≤90°),分别交线段BC、AD于点E、F,已知AB=1,,连接BF.(1)如图①,在旋转的过程中,请写出线段AF与EC的数量关系,并证明;(2)如图②,当α=45°时,请写出线段BF与DF的数量关系,并证明;(3)如图③,当α=90°时,求△BOF的面积.解:(1)AF=CE;理由如下:∵四边形ABCD是平行四边形,∴AD∥BC,AO=CO,∴∠FAO=∠ECO,∴在△AFO与△CEO中,,∴△AFO≌△CEO(ASA),(2)BF=DF;理由如下:∵AB⊥AC,∴∠BAC=90°,∴AC===2,∵四边形ABCD是平行四边形,∴BO=DO,AO=CO=AC=1,∴AB=AO,又∵AB⊥AC,∴∠AOB=45°,∵α=45°,∠AOF=45°,∴∠BOF=∠AOB+∠AOF=45°+45°=90°,∴EF⊥BD,∵BO=DO,∴BF=DF;(3)∵AB⊥AC,∴∠CAB=90°,∴∠CAB=∠AOF=α=90°,∴AB∥EF,∵四边形ABCD是平行四边形,∴AF∥BE,∴四边形ABEF是平行四边形,∴AB=EF=1,由(1)得:△AFO≌△CEO,∴OF=OE=EF=,由(2)得:AO=1,∵AB∥EF,AO⊥EF,∴S△BOF=S△AOF=AO•OF=×1×=.13.综合与实践(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.请写出∠AEB的度数及线段AD,BE之间的数量关系,并说明理由.(2)类比探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.填空:①∠AEB的度数为90°;②线段CM,AE,BE之间的数量关系为AE=BE+2CM.(3)拓展延伸在(2)的条件下,若BE=4,CM=3,则四边形ABEC的面积为35 .解:(1)∠AEB=60°,AD=BE,理由如下:∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°.∴∠ACD=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴∠ADC=∠BEC.AD=BE,∵△DCE为等边三角形,∴∠CDE=∠CED=60°.∵点A,D,E在同一直线上,∴∠ADC=120°.∴∠BEC=120°.∴∠AEB=∠BEC﹣∠CED=60°.(2)猜想:①∠AEB=90°,②AE=BE+2CM.理由如下:∵△ACB和△DCE均为等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°.∴∠ACD=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴AD=BE,∠ADC=∠BEC.∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°.∵点A,D,E在同一直线上,∴∠ADC=135°.∴∠BEC=135°.∴∠AEB=∠BEC﹣∠CED=90°.∵CD=CE,CM⊥DE,∴DM=ME.∵∠DCE=90°,∴DM=ME=CM.∴AE=AD+DE=BE+2CM.故答案为:90°,AE=BE+2CM;(3)由(2)得:∠AEB=90°,AD=BE=4,∵△DCE均为等腰直角三角形,CM为△DCE中DE边上的高,∴CM⊥AE,DE=2CM=6,∴AE=AD+DE=4+6=10,∴四边形ABEC的面积=△ACE的面积+△ABE的面积=AE×CM+AE×BE=×10×3+×10×4=35;故答案为:35.14.如图,正方形OABC的边长为8,P为OA上一点,OP=2,Q为OC边上的一个动点,分别以OP\PQ为边在正方形OABC内部作等边三角形OPD和等边三角形PQE.(1)证明:DE=OQ;(2)直线ED与OC交于点F,点Q在运动过程中.①∠EFC的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由;②连结AE,求AE的最小值.(1)证明:如图1中,∵△OPD和△PQE是等边三角形,∴PO=PD,PQ=PE,∠OPD=∠QPE=60°,∴∠OPQ=∠DPE,∴△OPQ≌△DPE(SAS),∴DE=OQ.(2)①∵△OPQ≌△DPE,∴∠EDP=∠POQ=90°,∵∠DOP=∠ODP=60°∴∠FDO=∠FDO=30°,∴∠EFC=∠FOC+∠FDO=60°.②如图2中,当点Q与点C重合时,以PQ为边作正三角形PQM.∵∠EFC=60°为定值,点E的运动路径为线段DM,过点P作PH⊥EA,垂足为H,∴当AE⊥DE时,AE的值最小∵∠PDE=∠DEH=∠PHE=90°,∴四边形PDEH是矩形,∴∠DPH=90°,EH=PD=2,∴EH=DP=2,在△PHA中,∠AHP=90°,∠HPA=30°∴AH=PA=3,∴AE=EH+AH=2+3=5.15.我们把对角线互相垂直的四边形叫做垂直四边形.(1)如图1,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂直四边形吗?请说明理由;(2)如图2,四边形ABCD是垂直四边形,求证:AD2+BC2=AB2+CD2;(3)如图3,Rt△ABC中,∠ACB=90°,分别以AC、AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,BC=3,求GE长.(1)解:四边形ABCD是垂直四边形;理由如下:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂直四边形;(2)证明:设AC、BD交于点E,如图2所示:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得:AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+DE2+CE2,∴AD2+BC2=AB2+CD2;(3)解:连接CG、BE,如图3所示:∵正方形ACFG和正方形ABDE,∴AG=AC,AB=AE,CG=AC=4,BE=AB,∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∵∠AEC+∠CEB+∠ABE=90°,∴∠ABG+∠CEB+∠ABE=90°,即CE⊥BG,∴四边形CGEB是垂直四边形,由(2)得,CG2+BE2=BC2+GE2,∵AC=4,BC=3,∴AB===5,BE=AB=5,∴GE2=CG2+BE2﹣BC2=(4)2+(5)2﹣32=73,∴GE=.。
中考专题复习四边形

基础知识点练习:1.如果一个多边形的边数增加一条,那么这个多边形的内角和增加,外角和增加.2.已知一个多边形的内角和是它的外角和的3倍,那么这个多边形的边数是_________.3.平行四边形ABCD的周长是18,三角形ABC的周长是14,则对角线AC的长是.4.已知平行四边形ABCD的面积为4,O为两对角线的交点,则△AOB的面积是___________.(一)例题讲解例1 等腰△ABC中AB=AC,D为BC上的一动点,DE∥AC,DF∥AB,则DE+DF是否随D点变化而变化?若不变化请证明.例2. 如图,在ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F ,求证:S △ABF=S平行四边形ABCD.例3如图,已知在□ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.求证:四边形GEHF是平行四边形.例4.如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P•从A开始沿AD边向D以1cm/s 的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,•问t为何值时.四边形PQCD是平行四边形.例5.图,△ABC中,AB=AC,延长BC至D,使CD=BC,点E在边AC上,以CE、CD为邻边作□CDFE,过点C作CG∥AB 交EF与点G.连接BG、DE.(1)∠ACB与∠GCD有怎样的数量关系?请说明理由.(2)求证:△BCG≌△DCE.练习1如图,在ABCD中,对角线AC、BD相交于点O,E、F•是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形()A. OE=OFB. DE=BFC. ∠ADE=∠CBFD. ∠ABE=∠CDFAB D CEF2如图,在ABCD 中,已知对角线AC 和BD 相交于点O ,△AOB•的周长为15, AB =6,那么对角线AC +BD =_______. 矩形、菱形、正方形1.在下列命题中,正确的是( )A .一组对边平行的四边形是平行四边形B .有一个角是直角的四边形是矩形C .有一组邻边相等的平行四边形是菱形D .对角线互相垂直平分的四边形是正方形 2.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,若OA =2,则BD 的长为( ) A .4 B .3 C .2 D .13.如图在菱形ABCD 中,对角线AC BD ,相交于点O E ,为AB 的中点,且OE a =,则菱形ABCD 的周长为( )A .16aB .12aC .8aD .4a4.在右图的方格纸中有一个菱形ABCD (A 、B 、C 、D 四点均为格点),若方格纸中每个最小正方形的边长为1,则该菱形的面积为5.如图在矩形ABCD 中,对角线AC BD ,交于点O ,已知120 2.5AOD AB ∠==,,则AC 的长为. (一)例题讲解例1已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE CG =,连接BG 并延长交DE 于F .(1)求证:BCG DCE △≌△;(2)将DCE △绕点D 顺时针旋转90得到DAE '△,判断四边形E BGD '是什么特殊四边形?并说明理由.例2如图,在四边形ABCD 中,点E 是线段AD 上的任意一点(E 与A D ,不重合),G F H ,,分别是 BE BC CE ,,的中点.(1)证明四边形EGFH 是平行四边形;(2)在(1)的条件下,若EF BC ⊥,且12EF BC =,证明平行四边形EGFH 是正方形.1.对角线互相垂直平分的四边形是( )A .平行四边形、菱形B .矩形、菱形C .矩形、正方形D .菱形、正方形D B O A A B C D O A B DA B C DA B CD E F E ' GB G A E FH D C2.顺次连接菱形各边中点所得的四边形一定是( )A.等腰梯形B.正方形C.平行四边形D.矩形3.如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是( ) A .当AB=BC 时,它是菱形 B .当AC ⊥BD 时,它是菱形C .当∠ABC=900时,它是矩形 D .当AC=BD 时,它是正方形4.如图,在ABC △中,点E D F ,,分别在边AB ,BC ,CA 上,且DE CA ∥,DF BA ∥.下列四个判断中,不正确...的是( ) A .四边形AEDF 是平行四边形B .如果90BAC ∠=,那么四边形AEDF 是矩形C .如果AD 平分BAC ∠,那么四边形AEDF 是菱形D .如果AD BC ⊥且AB AC =,那么四边形AEDF 是正方形5.如图,四边形ABCD 为矩形纸片.把纸片ABCD 折叠,使点B 恰好落在CD 边的中点E 处,折痕为AF .若6CD =,则AF 等于( ) A .43.33 C .42.86.如图,矩形ABCD 的周长为20cm ,两条对角线相交于O 点,过点O 作AC 的垂线EF ,分别交AD BC ,于E F ,点,连结CE ,则CDE △的周长为( ) A .5cm B .8cm C .9cm D .10cm7.如图,矩形ABCD 中,O 是AC 与BD 的交点,过O 点的直线EF 与AB CD ,的延长线分别交于E F ,.(1)求证:BOE DOF △≌△;(2)当EF 与AC 满足什么关系时,以A E C F ,,,为顶点的四边形是菱形?证明你的结论.8.如图,在△ABC 中,点O 是AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交 ∠BCA 的角平分线于点E ,交∠BCA 的外角平分线于点F . (1)求证:EO =FO ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.9.如图,将边长为8cm 的正方形ABCD 的四边沿直线l 向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A 所经过的路线的长是________cm .第3题 D A A F C D B E 第4 题B FC E D A 第5题 A O B E 第6题 F D OCBEAA BCE F M NOFE MD CB A10如图,先将一矩形ABCD 置于直角坐标系中,使点A 与坐标系的原点重合,边AB 、AD 分别落在x 轴、y 轴上(如图①所示),•再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图②所示),若AB =4,BC =3,则图①和图②中,点B 的坐标为________,点C 的坐标为______.11如图,四边形ABCD 是矩形,E 是AB 上一点,且DE =AB ,过C 作CF ⊥DE ,垂足为F . (1)猜想:AD 与CF 的大小关系;(2)请证明上面的结论.12 已知:如图,D是△ABC 的边。
四边形解题技巧专题中点问题作业ppt

中点在平行四边形中的应用
总结词
矩形中点性质
详细描述
矩形的对角线相等且互相平分,中点到矩形四个顶点的距离相等,利用这一性质可以解决关于矩形中点的问题。
中点在矩形中的应用
菱形中点性质
总结词
菱形的对角线互相垂直且平分,中点到菱形四个顶点的距离相等,利用这一性质可以解决关于菱形中点的问题。
详细描述
中点在菱形中的应用
中点问题经典例题解析
03
VS
平行四边形中点应用例题是解决中点问题的重要题型之一,通过证明两个三角形全等,得到对应边相等,从而得出中点结论。
详细描述
平行四边形中点应用例题通常涉及两个三角形,其中一个是平行四边形,另一个是三角形或平行四边形。通过证明这两个三角形全等,可以得出对应边相等,从而得出中点结论。在证明全等时,通常需要利用平行四边形的性质和全等三角形的判定方法。
总结词
平行四边形中点应用例题
总结词
矩形中点应用例题通常涉及矩形的对角线,通过对角线平分矩形得到两个全等的三角形,从而得出中点结论。
详细描述
矩形中点应用例题通常涉及两个全等的三角形,通过证明这两个三角形全等,可以得出对应边相等,从而得出中点结论。在证明全等时,通常需要利用矩形的性质和对角线平分矩形的性质。
菱形中点应用练习题
中点问题易错点及注意事项
05
1
中点应用常见的错误及解决办法
2
3
四边形中点与中位线概念不同,中点是四边形两边中点的连线,而中位线是四边形两对角线中点的连线。
混淆中点与中位线的概念
中点四边形是指以四边形的各边中点为顶点的四边形,其具有平行四边形的性质,但并不总是平行四边形。
未掌握中点四边形的性质
中考专题复习中点四边形ppt(共17张PPT)

D
D1
C3
C2
C1
B3 B2
C
A D2 O
D3
A1
A3
A2
B1
B
3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE相交于点G, 则可得结论:
①AF=DE ②AF⊥DE(不须证明) ⑴如图②,若点E,F不是正方形ABCD的边BC,CD的中点,但满足CE=DF则上面 的结论①②是否仍然成立?(请直接回答“成立”或“不成立”)
A
H
D
E
G
B
F
C
问题4:
依次连接怎样一个四边形四边中点的图形是菱形?
连接对角线相等的四边形四条边中点得到的四边形
是菱形
问题5:
依次连接菱形四边中点得到的四边形是什么四边形?
已D求A证知的::中四如点边图,形,EAEF、GFH、是G矩H、形。H分别是D 菱形ABGCD四条边CAB、BC、CD、 依⑶中依2依求∴依∴∴∴已使⑶中求依依2∴求⑶中①C∴依 求5D_∴求使_、 、、四 E四 E四 四 四)1次如的次次证次知四如的证次次证如的A次证证四_AFF连连 如F_边边边边边矩1是=连 图 哪 连 连 : 连 : 边 图 哪 : 连 连 : 图 哪 连: : 边_=的接接 图形形形形形形_D△接④一接接四接如形④一四接接四④一接 四四形_A中对对 ,AEEEEEE,_怎,种菱怎边普图E,种边怎怎边,种怎 边边ECBFFFFF_点②角角 四FF矩=CGGGGG_样在,形样形通,在,形样样形在,样 形形GG6,A线线 边的形HHHHH一(并四一平(并一一(并一EEEEEEHHF的的的的的以相相 形中FFFFF、是是⊥个写边个行写个个写个222GGGGG周周周周周此等等)))A位F矩矩D四出中四四出四四出四HHHHHB、长长长长长类E的的的的的线是是是是是形形CD边证点边边证边边证边(G为为为为为推不四 四基基基D)平平矩菱平,,形明得形形明形形明形、面22222,须边边础础础矩行行形形行应应四过到四四过四四过四00000H积四证形形上上上形四四。。四添添边程的边边程边边程边分为边明四四,,,,边边边加加中。四中中。中中。中别1形)条条连连连正形形形的的,点边点点点点点是A边边接接接方。。。条条A的形的得的的的等1中中AAA1形B件件图是图到图图图腰、EEE1点点是是和和和C形什形的形形形梯B得得11EEE是么是四是是是形D、到到FFF1矩四菱边菱正菱A,,,C若若若的的的B形边形形形方形1点 点 点C面四四、?形?是?形?DMMM积边边D四什??。。,,,1NNN是形形条分么,,,PPP_是是边别四,,,_QQQ菱菱_A是边分分分_B形形_A形别别别、_B_?为为为B、_C四AAAB、EEEC边,,,C、EEE形DFFFC,,,A、FFFD2DDDD、B,,,AAAA2DC的DDDA2的的的中的D中中中2点中的点点点,点面,,,请请请,积先先先A_2判判判_、_断断断_B_2四 四 四_、_边边边_C四形形形2、边MMMDNNN形2PPPA分QQQ2是是是别01矩矩矩是0B形形形A210,,,B菱菱菱110形形形、C,,,2B正正正011方方方C01形形形D、2,,,等等等0C11腰腰腰0D的梯梯梯1、面形形形积
三年级上册数学四边形的认识说课稿范文

三年级上册数学四边形的认识说课稿三年级上册数学四边形的认识说课稿范文在教学工作者开展教学活动前,常常要根据教学需要编写说课稿,是说课取得成功的前提。
我们该怎么去写说课稿呢?以下是小编收集整理的三年级上册数学四边形的认识说课稿范文,欢迎大家分享。
三年级上册数学四边形的认识说课稿篇1一、说教材说课内容:西师版四年级下册第97—98页中的平行四边形的知识。
二、教学内容的地位、作用和意义。
平行四边形的这节课是在学生已经直观认识平行四边形,初步掌握了长方形、正方形、三角形的特征,认识了平行与相交的基础上,通过一系列的探究活动继续认识平行四边形,了解对边分别平行和对边相等的特征,并认识平行四边形的底和高。
这部分的内容是以后学习了平行四边形面积的基础,有利于提高学生动手能力,进一步发展学生对“图形与空间”的学习兴趣。
三、说目标1、知识与技能目标。
(1)通过观察和操作等活动理解平行四边形的概念及其特征。
(2)通过操作活动认识平行四边形的底和高,会画高。
2、情感态度与价值观目标。
(1)让学生感受图形与生活的密切联系,在探索中感受到成功的乐趣。
(2)进一步发展学生的空间观念。
培养学生实践能力、观察能力、分析能力。
四、说教学重难点重点:认识平行四边形的特征。
认识平行四边形的底和高。
难点:作平行四边形的高,明白底与高的对应关系。
五、说教法和学法。
(一)说教法:根据本节课的教材内容特点,为了更有效地突出重点,突破难点,按照学生的认知规律,遵循教师为主导、学生为主体的指导思想,教法中采用观察、操作为主,多媒体演示为辅。
教学中,引导学生操作和思考,适时运用多媒体课件化静为动,使学生始终处于主动探索问题的积极状态,从而培养学习生的思维能力。
(二)说学法根据自主性和差异性原则,利用实际生活中的图形,让学生在“观察→操作→交流→总结→应用”的学习过程中,自主参与知识的发生、发展和形成的过程。
使获取新知识的过程水到渠成,增强学生学习的成就感及自信心,从而培养浓厚的学习兴趣。
中考数学总复习-四边形专题模块-矩形的性质及判定讲义教师版

知识点 A 要求 B 要求C要求矩形 会识别矩形掌握矩形的概念、判定和性质,会用矩形的性质和判定解决简单问题 会运用矩形的知识解决有关问题1.矩形的定义:有一个角是直角的平行四边形叫做矩形. 2.矩形的性质矩形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质: ① 边的性质:对边平行且相等. ② 角的性质:四个角都是直角.③ 对角线性质:对角线互相平分且相等.④ 对称性:矩形是中心对称图形,也是轴对称图形.直角三角形斜边上的中线等于斜边的一半.直角三角形中,30︒角所对的边等于斜边的一半.点评:这两条直角三角形的性质在教材上是应用矩形的对角线推得,用三角形知识也可推得. 3.矩形的判定判定①:有一个角是直角的平行四边形是矩形. 判定②:对角线相等的平行四边形是矩形. 判定③:有三个角是直角的四边形是矩形.重点:掌握矩形的性质,并学会应用. 难点:理解矩形的特殊性.关键:把握平行四边形的演变过程,迁移到矩形概念与性质上来,明确矩形是特殊的平行四边形.一、矩形的判定【例1】 在矩形ABCD 中,点H 为AD 的中点,P 为BC 上任意一点,PE HC ⊥交HC 于点E ,PF BH⊥交BH 于点F ,当AB BC ,满足条件 时,四边形PEHF 是矩形【考点】矩形的性质和判定 【题型】填空 【难度】2星 【关键词】 【解析】省略【答案】2BC AB =例题精讲重、难点中考要求中考要求矩形的性质 及判定【例2】 如图,在四边形ABCD 中,90ABC BCD ∠=∠=︒,AC BD =,求证:四边形ABCD 是矩形.CDB A【考点】矩形的性质和判定 【题型】解答 【难度】2星 【关键词】 【解析】省略【答案】∵90ABC BCD ∠=∠=︒,∴AB ∥CD在Rt ABC ∆和Rt DCB ∆中BC CBAC BD =⎧⎨=⎩∴Rt ABC ∆≌Rt DCB ∆ (HL )∵AB CD =,∴四边形ABCD 是平行四边形 ∵AC BD =,∴四边形ABCD 是矩形【巩固】 矩形具有而平行四边形不具有的性质为( )A .对角线相等B .对角相等C .对角线互相平分D .对边相等【考点】矩形的性质和判定 【题型】选择 【难度】1星 【关键词】 【解析】省略 【答案】A【例3】 如图,已知在四边形ABCD 中,AC DB ⊥交于O ,E 、F 、G 、H 分别是四边的中点,求证四边形EFGH 是矩形.HG OFEDCB A【考点】矩形的性质和判定 【题型】解答 【难度】2星 【关键词】 【解析】省略【答案】∵E 、F 、G 、H 分别是四边的中点∴EF 、GH 为中位线∴EF GH BD ∥∥且12EF GH BD ==∴四边形EFGH 为平行四边形∴四边形EFGH 是矩形.【巩固】 如图,在平行四边形ABCD 中,M 是AD 的中点,且MB MC =,求证:四边形ABCD 是矩形.MCDB A【考点】矩形的性质和判定 【题型】解答 【难度】2星 【关键词】 【解析】省略【答案】∵四边形ABCD 是平行四边形,∴AB CD =, 180A D ∠+∠=︒∵M 是AD 的中点,∴AM MD =在ABM ∆和CDM ∆中AM DM MB MC AB CD =⎧⎪=⎨⎪=⎩∴ABM ∆≌CDM ∆ (SSS ),∴A D ∠=∠ ∴90A ∠=︒,∴四边形ABCD 是矩形【例4】 如图,平行四边形ABCD 中,AQ 、BN 、CN 、DQ 分别是DAB ∠、ABC ∠、BCD ∠、CDA ∠的平分线,AQ 与BN 交于P ,CN 与DQ 交于M ,证明:四边形PQMN 是矩形.NMQPDCBA【考点】矩形的性质和判定 【题型】解答 【难度】4星 【关键词】 【解析】省略【答案】∵四边形ABCD 为平行四边形∴AB CD ∥,AD BC ∥∵AQ 、BN 分别是DAB ∠、ABC ∠的平分线 ∴180BAD ABC ∠+∠=︒ ∴90QPN ∠=︒同理90PQM QMN MNP ∠=∠=∠=︒ ∴四边形PQMN 是矩形.【例5】 如图,在ABC ∆中,D 是BC 边上的一点,E 是AD 的中点,过A 点作BC 的平行线交CE 的延长线于点F ,且AF BD =,连结BF . ⑴ 求证:BD CD =.⑵ 如果AB AC =,试判断四边形AFBD 的形状,并证明你的结论.FED CB A【考点】矩形的性质和判定 【题型】解答 【难度】3星【关键词】2009年,安顺市中考 【解析】省略【答案】⑴ ∵AF BC ∥,AFE DCE ∠=∠E 是AD 的中点,∴AE DE = ∵AFE DCE AE DE AEF DEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AEF DEC ∆∆≌ ∴AF DC =,∵AF BD = ∴BD CD =(2)四边形AFBD 是矩形∵AB AC =,D 是BC 的中点(利用全等) ∴AD BC ⊥ ∴90ADB ∠=︒∵AF BD =,AF BC ∥∴四边形AFBD 是平行四边形 又90ADB ∠=︒∴四边形AFBD 是矩形.【巩固】 如图,在ABC ∆中,点D 是AC 边上的一个动点,过点D 作直线MN BC ∥,若MN 交BCA ∠的平分线于点E ,交BCA ∠的外角平分线于点F (1)求证:DE DF =(2)当点D 运动到何处时,四边形AECF 为矩形?请说明理由!NMFEDCBA【考点】矩形的性质和判定 【题型】解答 【难度】3星 【关键词】 【解析】省略【答案】⑴证明:ED DC DF DC ==,⑵当D 为AC 的中点时,四边形AECF 为矩形【例6】 如图所示,在Rt ABC ∆中,90ABC ∠=︒,将Rt ABC ∆绕点C 顺时针方向旋转60︒得到DEC ∆点E在AC 上,再将Rt ABC ∆沿着AB 所在直线翻转180︒得到ABF ∆连接AD .⑵ 连接BE 并延长交AD 于G 连接CG ,请问:四边形ABCG 是什么特殊平行四边形?为什么?AB CDGEF【考点】矩形的性质和判定,菱形的性质和判定 【题型】解答 【难度】3星【关键词】2009年,襄樊市中考 【解析】省略【答案】⑴ Rt DEC ∆是由Rt ABC ∆绕C 点旋转60︒得到∴AC DC =,60ACB ACD ∠=∠=︒ ∴ACD ∆是等边三角形 ∴AD DC AC ==又∵Rt ABF ∆是由Rt ABC ∆沿AB 所在 直线翻转180︒得到∴AC AF =,90ABF ABC ∠=∠=︒ ∴180FBC ∠=︒∴点F 、B 、C 三点共线 ∴AFC ∆是等边三角形 ∴AF FC AC ==∴AD DC FC AF === ∴四边形AFCD 是菱形. ⑵ 四边形ABCG 是矩形.由⑴可知:ACD ∆是等边三角形,DE AC ⊥于E ∴AE EC =,又∵AG BC ∥∴EAG ECB ∠=∠,AGE EBC ∠=∠ ∴AEG CEB ∆∆≌,∴AG BC =∴四边形ABCG 是平行四边形,而90ABC ∠=︒ ∴四边形ABCG 是矩形.【巩固】 如图,在ABCD 中,AE BC ⊥于E ,AF CD ⊥于F ,AEF ∆的两条高相交于M ,20AC =,16EF =,求AM 的长.MF E DC BAGMF E DC BA【考点】平行四边形的性质和判定,矩形的性质和判定,三角形的三线五心 【题型】解答 【难度】6星 【关键词】【解析】过C 作CG AD ⊥于G ,连接EG 、FG .∵AE BC ⊥,FM AE ⊥,∴FM ∥EC∴四边形EMFC 为平行四边形,∴MF EC = 又∵AE BC ⊥,CG AD ⊥且BC ∥AD ∴90EAG AGC GCE AEC ∠=∠=∠=∠=︒ ∴四边形AGCE 为矩形∴EC AG =,EG AC =,∴MF AG = 又∵MF ∥AG∴四边形AGFM 为平行四边形,∴GF AM = ∵AM EF ⊥,∴GF EF ⊥,即90GFE ∠=︒∴GF =∴12AM =【答案】12【例7】 已知,如图矩形ABCD 中,延长CB 到E ,使CE AC =,F 是AE 中点.求证:BF DF ⊥.ABCE FDBCM【考点】矩形的性质和判定,等腰三角形的性质和判定 【题型】解答 【难度】4星 【关键词】【解析】延长BF 交AD 于M ,连结DB .∵四边形ABCD 是矩形,∴AD BC AD BC AC BD ==∥,, ∴M EBF ∠=∠,∵F 是AE 中点,∴AF EF =,在AFM △和EFB △中, ∵M EBF MFA BFE AF EF ∠=∠∠=∠=,,∴AFM EFG ∆∆≌.∴AM BE =,MF BF =,∴AD AM BC BE CE DM +=+== ∵CE AC AC BD ==,,∴DM DB = ∵MF BF =,∴BF DF ⊥【答案】见解析板块二、矩形的性质及应用【例8】 如图,在矩形ABCD 中,点E 是BC 上一点,AE AD =,DF AE ⊥,垂足为F .线段DF 与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明。
专题10 四边形-2017年中考数学试题分项版解析汇编(解析版)

专题10:四边形一、选择题1.(2017北京第6题)若正多边形的一个内角是150°,则该正多边形的边数是( )A . 6B . 12C . 16D .18【答案】B .【解析】试题分析:设多边形的边数为n ,则有(n -2)×180°=n ×150°,解得:n =12.故选B .考点:多边形的内角与外角2. (2017河南第7题)如图,在ABCD 中,对角线AC ,BD 相交于点O ,添加下列条件不能..判定ABCD 是菱形的只有( )A .AC BD ⊥B .AB BC = C .AC BD = D .12∠=∠【答案】C .考点:菱形的判定.3. (2017湖南长沙第10题)如图,菱形ABCD 的对角线BD AC ,的长分别为cm cm 8,6,则这个菱形的周长为( )A .cm 5B .cm 10C .cm 14D .cm 20【答案】D【解析】试题分析:根据菱形的对角线互相垂直,可知OA =3,OB =4,根据勾股定理可知AB =5,所以菱形的周长为4×5=20.故选:D考点:菱形的性质4. (2017湖南长沙第12题)如图,将正方形ABCD 折叠,使顶点A 与CD 边上的一点H 重合(H 不与端点D C ,重合),折痕交AD 于点E ,交BC 于点F ,边AB 折叠后与边BC 交于点G ,设正方形ABCD 的周长为m ,CHG ∆的周长为n ,则mn 的值为( ) A .22 B .21 C .215- D .随H 点位置的变化而变化【答案】B【解析】试题分析:设正方形ABCD 的边长为2a ,正方形的周长为m =8a ,设CM =x ,DE =y ,则DM =2a -x ,EM =2a -y ,∵∠EMG =90°,∴∠DME +∠CMG =90°.∵∠DME +∠DEM =90°,∴∠DEM =∠CMG ,又∵∠D =∠C =90°△DEM ∽△CMG , ∴CG CM MG DM DE EM ==,即22CG x MG a x y a y==-- ∴CG =(2)(2)=,x a x x a y CG MG y y--= △CMG 的周长为CM +CG +MG =24ax x y-在Rt △DEM 中,DM 2+DE 2=EM 2即(2a -x )2+y 2=(2a -y )2整理得4ax -x 2=4ay∴CM +MG +CG =2444ax x ay a y y-===n . 所以12n m = 故选:B .考点:1、正方形,2、相似三角形的判定与性质,3、勾股定理5. (2017山东临沂第7题)一个多边形的内角和是外角和的2倍,这个多边形是( )A .四边形B .五边形C .六边形D .八边形【答案】C【解析】试题分析:根据多边形的外角和为360°,可知其内角和为720°,因此可根据多边形的内角和公式(n -2)·180°=720°,解得n =6,故是六边形.故选:C考点:多边形的内外角和6. (2017山东临沂第12题)在ABC V 中,点D 是边BC 上的点(与B 、C 两点不重合),过点D 作DE AC ∥,DF AB ∥,分别交AB ,AC 于E 、F 两点,下列说法正确的是( )A .若AD BC ⊥,则四边形AEDF 是矩形B .若AD 垂直平分BC ,则四边形AEDF 是矩形C .若BD CD =,则四边形AEDF 是菱形D .若AD 平分BAC ∠,则四边形AEDF 是菱形【答案】D【解析】试题分析:根据题意可知:DE AC ∥,DF AB ∥,可得四边形AEDF 是平行四边形.若AD ⊥BC ,则四边形AEDF 是平行四边形,不一定是矩形;选项A 错误;若AD 垂直平分BC ,则四边形AEDF 是菱形,不一定是矩形;选项B 错误;若BD =CD ,则四边形AEDF 是平行四边形,不一定是菱形;选项C 错误;若AD 平分∠BAC ,则四边形AEDF 是菱形;正确.故选:D考点:特殊平行四边形的判定7. (2017山东青岛第7题)如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,AE ⊥BC ,垂足为E ,3=AB ,AC =2,BD =4,则AE 的长为( )A .23B .23C .721D .7212 【答案】D考点:1、平行四边形的性质,2、勾股定理,3、面积法求线段长度8. (2017四川泸州第11题)如图,在矩形ABCD 中,点E 是边BC 的中点,AE BD ⊥,垂足为F ,则tan BDE ∠的值是 ( )A .24B .14C .13D .23【答案】A .【解析】试题分析:由AD ∥BC 可得△ADF ∽△EBF ,根据相似三角形的性质可得AD AF DF EB EF BF== ,因点E 是边BC 的中点且AD =BC ,所以AD AF DF EB EF BF ===2,设EF =x ,可得AF =2x ,在Rt △ABE 中,由射影定理可得BF =2x ,再由AD AF DF EB EF BF ===2可得DF =22x ,在Rt △DEF 中,tan BDE ∠=2422EF x DF x == ,故选A . 9. (2017江苏苏州第10题)如图,在菱形CD AB 中,60∠A =,D 8A =,F 是AB 的中点.过点F 作F D E ⊥A ,垂足为E .将F ∆AE 沿点A 到点B 的方向平移,得到F '''∆A E .设P 、'P 分别是F E 、F ''E 的中点,当点'A 与点B 重合时,四边形CD 'PP 的面积为A .283B .243C .323D .3238-【答案】A .【解析】试题分析:作,,DH AB PK AB FL AB ⊥⊥⊥在菱形CD AB 中,60∠A =,D 8A =,F 是AB 的中点 423,3AF EF EL ∴==∴=,P 是F E 的中点,32PK ∴= 43DH = 1373322PP CD ∴-= 高为4 7382832S ∴=⨯=L K H故答案选A .考点:平行四边形的面积,三角函数. 10.(2017江苏苏州第7题)如图,在正五边形CD AB E 中,连接BE ,则∠ABE 的度数为A .30B .36C .54D .72【答案】B .【解析】试题分析:∠ABE =3601=3652︒⨯︒ 故答案选B . 考点:多边形的外角,等腰三角形的两底角相等11.(2017浙江台州第10题) 如图,矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上,BE BF =,将,AEH CFG ∆∆分别沿,EH FG 折叠,当重叠部分为菱形且面积是菱形ABCD 面积的116时,则AE EB 为 ( )A . 53B .2C . 52D .4 【答案】A考点:1、菱形的性质,2、翻折变换(折叠问题)二、填空题1.(2017天津第17题)如图,正方形ABCD 和正方形EFCG 的边长分别为3和1,点G F ,分别在边CD BC ,上,P 为AE 的中点,连接PG ,则PG 的长为 .【答案】5.【解析】试题分析:连结AC ,根据正方形的性质可得A 、E 、C 三点共线,连结FG 交AC 于点M ,因正方形ABCD 和正方形EFCG 的边长分别为3和1,根据勾股定理可求得EC =FG =2,AC =32,即可得AE =22,因P 为AE 的中点,可得PE =AP =2,再由正方形的性质可得GM =EM =22,FG 垂直于AC ,在Rt △PGM 中,PM =322,由勾股定理即可求得PG =5.2.(2017福建第15题)两个完全相同的正五边形都有一边在直线l 上,且有一个公共顶点O ,其摆放方式如图所示,则AOB ∠等于 度.【答案】108【解析】∵五边形是正五边形,∴每一个内角都是108°,∴∠OCD =∠ODC =180°-108°=72°,∴∠COD =36°,∴∠AOB =360°-108°-108°-36°=108°.D C3.(2017广东广州第16题)如图9,平面直角坐标系中O 是原点,OABC 的顶点,A C 的坐标分别是()()8,0,3,4,点,D E 把线段OB 三等分,延长,CD CE 分别交,OA AB 于点,F G ,连接FG ,则下列结论:①F 是OA 的中点;②OFD ∆与BEG ∆相似;③四边形DEGF 的面积是203;④453OD =;其中正确的结论是 .(填写所有正确结论的序号)【答案】①③【解析】试题分析:如图,分别过点A 、B 作AN OB ⊥ 于点N ,BM x ⊥ 轴于点M在OABC 中,(80)(34)(114)137A C B OB ∴= ,,,,,D E 、 是线段AB 的三等分点, 12OD BD ∴= ,CB OF ODF BDC ∴∆∆111222OF OD OF BC OA BC BD ∴==∴==, F ∴ 是OA 的中点,故①正确.(34)5C OC OA ∴=≠ ,,OABC ∴ 不是菱形.,DOF COD EBG ODF COD EBG ∴∠≠∠=∠∠≠∠=∠(40)17,F CF OC CFO COF ∴=<∴∠>∠ ,,DFO EBG ∴∠≠∠故OFD ∆ 和BEG ∆ 不相似.则②错误;由①得,点G 是AB 的中点,FG ∴ 是OAB ∆ 的中位线1137,22FG OB FG OB ∴== D E 、 是OB 的三等分点,1373DE ∴= 1118416222OAB S OB AN OA BM ∆=⋅=⋅=⨯⨯= 解得:1162AN OB= ,DF FG ∴ 四边形DEGH 是梯形()551202121223DEGF DE FG h S OB h OB AN -∴==⋅=⋅=四边形 则③正确 113733OD OB == ,故④错误. 综上:①③正确.考点: 平行四边形和相似三角形的综合运用4.(2017广东广州第11题)如图6,四边形ABCD 中,0//,110AD BC A ∠=,则B ∠=___________.【答案】70°【解析】试题分析:两直线平行,同旁内角互补,可得:B ∠=180°-110°=70°考点:平行线的性质5.(2017山东临沂第18题)在ABCD Y 中,对角线AC ,BD 相交于点O .若4AB =,10BD =,3sin 5BDC ∠=,则ABCD Y 的面积是 .【答案】24【解析】试题分析:作OE ⊥CD 于E ,由平行四边形的性质得出OA =OC ,OB =OD =12BD =5,CD =AB =4,由sin ∠BDC =35,证出AC ⊥CD ,OC =3,AC =2OC =6,得出▱ABCD 的面积=CD •AC =24. 故答案为:24.考点:1、平行四边形的性质,2、三角函数,3、勾股定理6.(2017山东青岛第13题)如图,在四边形 ABCD 中,∠ABC =∠ADC =90°,E 为对角线AC 的中点,连接BE 、ED 、BD ,若∠BAD =58°,则∠EBD 的度数为__________度.【答案】32 【解析】 试题分析:如下图由∠ABC =∠ADC =90°,E 为对角线AC 的中点,可知A ,B ,C ,D 四点共圆,圆心是E ,直径AC 然后根据圆周角定理由∠BAD =58°,得到∠BED =116°,然后根据等腰三角形的性质可求得∠EBD =32°. 故答案为:32.考点:1、圆周角性质定理,2、等腰三角形性质7.(2017山东滨州第16题)如图,将矩形ABCD 沿GH 对折,点C 落在Q 处,点D 落在AB 边上的E 处,EQ 与BC 相交于点F .若AD =8,AB =6,AE =4,则△EBF 周长的大小为___________.ABCDHQGFE【答案】8.【解析】由折叠的性质可得DH =EH ,设AH =x ,则DH =EH =8-x ,在Rt △AEH 中,根据勾股定理可得2224(8)x x +=- ,解得x =3,即可得AH =3,EH =5;根据已知条件易证△AEH ∽△BFE ,根据相似三角形的性质可得AH AE EH BE BF EF == ,即3452BF EF ==,解得BF =83 ,EF =103,所以△EBF 的周长为2+83+103=8. 8.(2017江苏宿迁第15题)如图,正方形CD AB 的边长为3,点E 在边AB 上,且1BE =.若点P 在对角线D B 上移动,则PA +PE 的最小值是 .【答案】10.9.(2017辽宁沈阳第16题)如图,在矩形ABCD 中,53AB BC ==,,将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ,点A 落在矩形ABCD 的边CD 上,连接CE ,则CE 的长是 .【答案】3105. 【解析】试题分析:如图,过点C 作MN ⊥BG ,分别交BG 、EF 于点M 、N ,根据旋转的旋转可得AB =BG =EF =CD =5,AD =GF =3,在Rt △BCG 中,根据勾股定理求得CG =4,再由1122BCG S BC CG BG CM =⋅=⋅ ,即可求得CM =125 ,在Rt △BCM 中,根据勾股定理求得BM =22221293()55BC CM -=-=,根据已知条件和辅助线作法易知四边形BENMW 为矩形,根据矩形的旋转可得BE =MN =3,BM =EN =95,所以CN =MN -CM =3-125=35,在Rt △ECN 中,根据勾股定理求得EC =22223990310()()55255CN EN +=+==.考点:四边形与旋转的综合题.10.(2017江苏苏州第18题)如图,在矩形CD AB 中,将C ∠AB 绕点A 按逆时针方向旋转一定角度后,C B 的对应边C ''B 交CD 边于点G .连接'BB 、CC ',若D 7A =,CG 4=,G ''AB =B ,则CC '='BB (结果保留根号).【答案】745. 【解析】试题分析:连接AG ,设DG =x ,则 G=4+x ''AB =B在'Rt AB G ∆ 中,22492(4)1x x x +=+⇒= ,则5,7AB BC =='254974'55CC BB +∴==考点:旋转的性质 ,勾股定理 .11. (2017山东菏泽第11题)菱形ABCD 中, 60=∠A ,其周长为cm 24,则菱形的面积为____2cm . 【答案】183. 【解析】试题分析:如图,连接BD ,作DE ⊥AB ,已知菱形的周长为cm 24,根据菱形的性质可得AB =6;再由 60=∠A ,即可判定△ABD 是等边三角形;求得DE =33,所以菱形的面积为:6×33=183.12. (2017浙江湖州第13题)已知一个多边形的每一个外角都等于72,则这个多边形的边数是 . 【答案】5考点:多边形的外角和三、解答题1. (2017北京第20题) 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》) 请根据上图完成这个推论的证明过程.证明:()ADC ANF FGC NFGD S S S S ∆∆∆=-+矩形,ABC EBMF S S ∆=-矩形(____________+____________). 易知,ADC ABC S S ∆∆=,_____________=______________,______________=_____________. 可得NFGD EBMF S S =矩形矩形.【答案】,,,AEF CFM ANF AEF FGC CFM S S S S S ∆∆∆∆∆;;S . 【解析】试题分析:由矩形的对角线的性质,对角线把矩形分成两个面积相等的三角形计算即可. 本题解析:由矩形对角线把矩形分成两个面积相等的两部分可得:(),()ADC ANF FGC ABC AEF FMC NFGD EBMF S S S S S S S S ∆∆∆∆∆=-+=-+矩形矩形 ,∴,,ADC ABC ANF AEF FGC FMC S S S S S S ∆∆∆∆∆∆=== , ∴NFGD EBMF S S =矩形矩形 . 考点:矩形的性质,三角形面积计算.2. (2017北京第22题)如图,在四边形ABCD 中,BD 为一条对角线,0//,2,90AD BC AD BC ABD =∠=,E 为AD 的中点,连接BE .(1)求证:四边形BCDE 为菱形;(2)连接AC ,若AC 平分,1BAD BC ∠=,求AC 的长. 【答案】(1)证明见解析.(2)3. 【解析】试题分析:(1)先证四边形是平行四边形,再证其为菱形;(2)利用等腰三角形的性质,锐角三角函数,即可求解.本题解析:(1)证明:∵E 为AD 中点,A D =2BC ,∴BC =ED , ∵AD ∥BC , ∴四边形ABCD 是平行四边形,∵AD =2BE , ∠ABD =90°,AE =DE ∴BE =ED , ∴四边形ABCD 是菱形.(2)∵AD ∥BC ,AC 平分∠BAD ∴∠BAC =∠DAC =∠BCA ,∴BA =BC =1, ∵AD =2BC =2,∴sin ∠ADB =12,∠ADB =30°, ∴∠DAC =30°, ∠ADC =60°.在RT △ACD 中,AD =2,CD =1,AC = 3 .考点:平行线性质,菱形判定,直角三角形斜边中线定理.3. (2017天津第24题)将一个直角三角形纸片ABO 放置在平面直角坐标系中,点)0,3(A ,点)1,0(B ,点)0,0(O .P 是边AB 上的一点(点P 不与点B A ,重合),沿着OP 折叠该纸片,得点A 的对应点'A .(1)如图①,当点'A 在第一象限,且满足OB B A ⊥'时,求点'A 的坐标; (2)如图②,当P 为AB 中点时,求B A '的长;(3)当030'=∠BPA 时,求点P 的坐标(直接写出结果即可).【答案】(1)点A ’的坐标为(2,1);(2)1;(3)3333(,)22--或2333(,)22- . 【解析】试题分析:(1)因点)0,3(A ,点)1,0(B ,可得OA =3 ,OB =1,根据折叠的性质可得△A ’OP ≌△AOP ,由全等三角形的性质可得OA ’=OA =3,在Rt △A ’OB 中,根据勾股定理求得'A B 的长,即可求得点A的坐标;(2)在Rt △AOB 中,根据勾股定理求得AB =2,再证△BOP 是等边三角形,从而得∠OPA =120°.在判定四边形OPA ’B 是平行四边形,根据平行四边形的性质即可得B A '的长; 试题解析:(1)因点)0,3(A ,点)1,0(B , ∴OA =3 ,OB =1.根据题意,由折叠的性质可得△A ’OP ≌△AOP .∴OA ’=OA =3,由OB B A ⊥',得∠A ’BO =90°.在Rt △A ’OB 中,22''2A B OA OB =-=, ∴点A ’的坐标为(2,1). (2) 在Rt △AOB 中,OA =3 ,OB =1, ∴222AB OA OB =+= ∵当P 为AB 中点, ∴AP =BP =1,OP =12AB =1. ∴OP =OB =BP , ∴△BOP 是等边三角形 ∴∠BOP =∠BPO =60°, ∴∠OPA =180°-∠BPO =120°. 由(1)知,△A ’OP ≌△AOP ,∴∠OPA ’=∠OPA =120°,P ’A =PA =1,又OB =PA ’=1,∴四边形OPA ’B 是平行四边形. ∴A ’B =OP =1. (3)3333(,)22--或2333(,)22- .4. (2017福建第24题)如图,矩形ABCD 中,6,8AB AD ==,,P E 分别是线段AC 、BC 上的点,且四边形PEFD 为矩形.(Ⅰ)若PCD ∆是等腰三角形时,求AP 的长; (Ⅱ)若2AP =,求CF 的长.【答案】(Ⅰ)AP 的长为4或5或145;(Ⅱ)CF =324【解析】试题分析:(Ⅰ)分情况CP =CD 、PD =PC 、DP =DC 讨论即可得;(Ⅱ)连结PF 、DE ,记PF 与DE 的交点为O ,连结OC ,通过证明△ADP ∽△CDF ,从而得34CF CD AP AD == ,由AP =2 ,从而可得CF =324. 试题解析:(Ⅰ)在矩形ABCD 中,AB =6,AD =8,∠ADC =90°,∴DC =AB =6, AC =22AD DC + =10;要使△PCD 是等腰三角形,有如下三种情况: (1)当CP =CD 时,CP =6,∴AP =AC -CP =4 ;(2)当PD =PC 时,∠PDC =∠PCD ,∵∠PCD +∠PAD =∠PDC +∠PDA =90°,∴∠PAD =∠PDA ,∴PD =PA ,∴PA =PC ,∴AP =2AC,即AP =5;(3)当DP =DC 时,过D 作DQ ⊥AC 于Q ,则PQ =CQ ,∵S △ADC =12 AD ·DC =12AC ·DQ ,∴DQ =245AD DC AC = ,∴CQ =22185DC DQ -= ,∴PC =2CQ =365 ,∴AP =AC -PC =145. 综上所述,若△PCD 是等腰三角形,AP 的长为4或5或145;(Ⅱ)连结PF 、DE ,记PF 与DE 的交点为O ,连结OC ,∵四边形ABCD 和PEFD 都是矩形,∴∠ADC =∠PDF =90°,即∠ADP +∠PDC =∠PDC +∠CDF ,∴∠ADP =∠CDF ,∵∠BCD =90°,OE =OD ,∴OC =12 ED ,在矩形PEFD 中,PF =DE ,∴OC =12PF ,∵OP =OF =12PF ,∴OC =OP =OF ,∴∠OCF =∠OFC ,∠OCP =∠OPC ,又∵∠OPC +∠OFC +∠PCF =180°,∴2∠OCP +2∠OCF =180°,∴∠PCF =90°,即∠PCD +∠FCD =90°,在Rt △ADC 中,∠PCD +∠PAD =90°,∴∠PAD =∠FCD ,∴△ADP ∽△CDF ,∴34CF CD AP AD == ,∵AP =2 ,∴CF =324.5. (2017广东广州第24题)如图13,矩形ABCD 的对角线AC ,BD 相交于点O ,COD ∆关于CD 的对称图形为CED ∆.(1)求证:四边形OCED 是菱形;(2)连接AE ,若6cm AB =,5BC cm =. ①求sin EAD ∠的值;②若点P 为线段AE 上一动点(不与点A 重合),连接OP ,一动点Q 从点O 出发,以1/cm s 的速度沿线段OP 匀速运动到点P ,再以1.5cm /s 的速度沿线段PA 匀速运动到点A ,到达点A 后停止运动.当点Q 沿上述路线运动到点A 所需要的时间最短时,求AP 的长和点Q 走完全程所需的时间.【答案】(1)详见解析;(2)①2sin 3EAD ∠= ②32AP =和Q 走完全程所需时间为32s 【解析】(2)①连接OE ,直线OE 分别交AB 于点F ,交DC 于点GCOD ∆ 关于CD 的对称图形为CED ∆,OE DC DC AB ∴⊥ ,OF AB EF AD ∴⊥在矩形ABCD 中,G 为DC 的中点,且O 为AC 的中点OG ∴ 为CAD ∆ 的中位线 52OG GE ∴==同理可得:F 为AB 的中点,532OF AF ==, 22223593()22AE EF AF ∴=+=+= 32sin sin 932EAD AEFEAD AEF ∠=∠∴∠=∠==②过点P 作PM AB ⊥ 交AB 于点MQ ∴ 由O 运动到P 所需的时间为3s由①可得,23AM AP = ∴ 点O 以1.5/cm s 的速度从P 到A 所需的时间等于以 1/cm s 从M 运动到A 即:11OP PA OP MA t t t OP MA =+=+=+ Q ∴ 由O 运动到P 所需的时间就是OP +MA 和最小.如下图,当P 运动到1P ,即1PO AB 时,所用时间最短. 3t OP MA ∴=+=在11Rt APM ∆ 中,设112,3AM x APx == 2222211115(3)=(2)+()22AP AM PM x x =+∴ 解得:12x = 32AP ∴= 32AP ∴=和Q 走完全程所需时间为32s考点:菱形的判定方法;构造直角三角形求三角函数值;确定极值时动点的特殊位置6. (2017山东青岛第24题)(本小题满分12分)已知:Rt △EFP 和矩形ABCD 如图①摆放(点P 与点B 重合),点F ,B (P ),C 在同一条直线上,AB =EF =6cm ,BC =FP =8cm ,∠EFP =90°。
《四边形》教案(10篇)

《四边形》教案(10篇)《四边形》教案 1一、教学内容:第34-36页四边形.二、教学目标:1.直观感知四边形,能区分和辨认四边形,知道四边形的特征。
进一步认识长方形和正方形,知道它们的角都是直角。
2.通过画一画、找一找、拼一拼等活动,培养学生的观察比较和概括抽象的能力,发展空间想象能力。
3.通过情境图和生活中的事物进入课堂,感受生活中的四边形无处不在,进一步激发学生的学习兴趣。
三、教学重点:认识四边形的共同特点,分辨不同四边形的的不同之处。
四、教具、学具:例2的四边形组图每生一份、钉子板、投影仪、三角尺、剪刀、小棒等。
五、设计理念:在实际情景中丰富学生对四边形的认识,关注学生的学习过程,培养学生动手能力以及合作与交流的能力,发展空间观念和创新意识;激发学生对数学学习的'兴趣。
六、教学过程:(一)、出示主题图:1、师:这是哪儿?在这幅图中你能发现哪些图形?(学生从中找一找图形,一边看一边汇报。
)2.师:大家真能干!在我们的校园中,同学们发现了这么多的图形,看来啊,图形在我们生活中无处不在。
这节课我们来认识其中的一个图形──四边形,你们愿意和它成为好朋友吗?(板书课题:四边形)(二)、初步感知,发现特征1.师:同学们,你想像中的四边形应该是什么样的?(指名回答,让学生充分发表意见。
)2、师:四边形到底是什么样的图形呢?今天我们进一步来研究。
看,数学王国里有这么多的图形(做一做第2题)。
把你认为是四边形的涂上相同的颜色,同桌互相检查评价。
请学生上台展示。
3.师:观察,我们找出的“四边形”有什么共同的特征吗?(在小组内说一说,学生汇报、互相交流。
)师根据学生的汇报,结合图形得出:像这样有四条直直的边围成,有四个角的图形就是四边形,教师板书。
师:看着这么多的四边形,现在你能说说到底什么样的图形是四边形?4.生活中我们见过许多四边形,现在又知道了四边形的特点,你能不能说一说生活中哪些物体表面的形状是四边形的。
九年级数学中考专题(空间与图形)-第十讲《四边形(二)》课件(北师大版)

能力训练
10、如图,在矩形ABCD中,AB=4cm,AD=12cm, P点在AD边上以每秒1 cm的速度从A向D运动,点Q在 BC边上,以每秒4 cm的速度从C点出发,在CB间往返 运动,二点同时出发,待P点到达D点为止,在这段时 间内,线段PQ有( )次平行于AB. A、1 B、2 C、3 D、4 A D P Q B C
参考答案
18、略证:延长AP与EF相交于点H,连结PC, 因为BD是对角线,易证PA=PC,∠1=∠2,根 据PE⊥BC于E,PF⊥DC于F,知PECF为矩形, PC=EF,且∠DAH=∠FPH,又因为∠1=∠2 =∠3,所以在△PHF中,∠FPH+∠3=∠4+ ∠1=90°,所以△PHF为直角三角形,故 AP⊥EF.
A
D G B E F C
能力训练
16、如图,以△ABC的三边为边在BC的同一侧分别作 三个等边三角形,即△ABD、△BCE、△ACF.请回答下 列问题(不要求证明): (1)四边形ADEF是什么四边形? (2)当△ABC满足什么条件时,四边形ADEF是矩形? (3)当△ABC满足什么条件时,以A、D、E、F为顶点 的四边形不存在? E F D
E
A A`
D
D` C C`
B
B`
能力训练
8、四边形ABCD的对角线AC、BD相交于点O,给出以 下题设条件:①AB=BC=CD=DA;②AO=BO=CO= DO;③AO=CO,BO=DO,AC⊥BD;④AB=BC, CD=DA.其中能判断它是正方形的题设条件是 (把正确的序号填在横线上).
四边形解题技巧专题中点问题作业ppt

四边形的边长和角度关系
对角线分成的两个三角形相似
在四边形中,对角线将四边形分成两个三角形,这两个三角形是相似的。
对角线平分
在凸四边形中,对角线平分四个内角;在凹四边形中,对角线平分四个外角。
四边形的对称性和面积计算
对称性
四边形可以具有轴对称性或中心对称性。轴对称四边形是关 于一条直线对称的,中心对称四边形是关于一个点对称的。
详细描述
1. 构造直角三角形: 利用矩形的性质,通 过连接对角线或构造 直角三角形来寻找中 点之间的关系。
2. 利用中位线定理: 直角三角形的斜边中 线等于斜边的一半。 即如果一个三角形是 直角三角形
3. 解题时要注意:在 解决矩形中点问题时 ,要关注图形中的隐 含条件,如角度、线 K YOU.
2. 利用中位线定理:平 行四边形的中位线等于 它的一半,即如果一个 四边形是平行四边形, 那么它的中位线等于它 的两条对角线的一半。
3. 解题时要注意:在解 决平行四边形中点问题 时,要关注图形中的隐 含条件,如角度、线段 长度等。
矩形中点问题例题
总结词:矩形中点问 题主要涉及矩形的性 质和直角三角形的中 位线定理,通过构造 直角三角形或利用中 位线定理进行求解。
2023
四边形解题技巧专题-中点 问题作业
目录
• 四边形基本知识回顾 • 中点问题解题技巧 • 中点问题经典例题解析 • 中点问题解题策略总结
01
四边形基本知识回顾
四边形的定义和性质
定义
四边形是由四条直线段连接的封闭图形。
性质
四边形具有凸性和凹性,其中凸四边形具有最小内角和最大外角,凹四边形 具有最大内角和最小外角。
矩形中点问题
总结词
矩形中点问题主要涉及矩形的性质和直角三角形中的 中位线定理,通过中点连接可以证明两对相等的线段 ,从而得到矩形。
人教版初中数学中考总复习:特殊的四边形--知识讲解(基础)
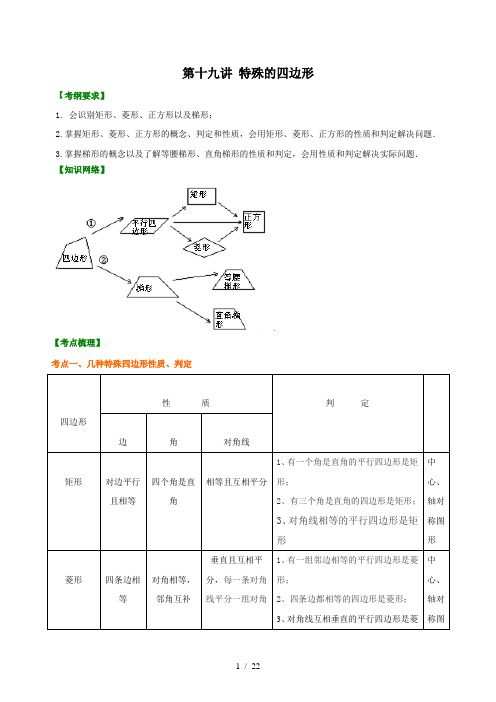
第十九讲特殊的四边形【考纲要求】1. 会识别矩形、菱形、正方形以及梯形;2.掌握矩形、菱形、正方形的概念、判定和性质,会用矩形、菱形、正方形的性质和判定解决问题.3.掌握梯形的概念以及了解等腰梯形、直角梯形的性质和判定,会用性质和判定解决实际问题.【知识网络】【考点梳理】考点一、几种特殊四边形性质、判定四边形性质判定边角对角线矩形对边平行且相等四个角是直角相等且互相平分1、有一个角是直角的平行四边形是矩形;2、有三个角是直角的四边形是矩形;3、对角线相等的平行四边形是矩形中心、轴对称图形菱形四条边相等对角相等,邻角互补垂直且互相平分,每一条对角线平分一组对角1、有一组邻边相等的平行四边形是菱形;2、四条边都相等的四边形是菱形;3、对角线互相垂直的平行四边形是菱中心、轴对称图形.形正方形四条边相等四个角是直角相等、垂直、平分,并且每一条对角线平分一组对角1、邻边相等的矩形是正方形2、对角线垂直的矩形是正方形3、有一个角是直角的菱形是正方形4、对角线相等的菱形是正方形中心、轴对称图形等腰梯形两底平行,两腰相等同一底上的两个角相等相等1、两腰相等的梯形是等腰梯形;2、在同一底上的两个角相等的梯形是等腰梯形;3、对角线相等的梯形是等腰梯形.轴对称图形【要点诠释】矩形、菱形、正方形都是特殊的平行四边形,它们具有平行四边形的一切性质.考点二、梯形1.解决梯形问题常用的方法:(1)“平移腰”:把梯形分成一个平行四边形和一个三角形(图1);(2)“作高”:使两腰在两个直角三角形中(图2);(3)“平移对角线”:使两条对角线在同一个三角形中(图3);(4)“延腰”:构造具有公共角的两个三角形(图4);(5)“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形(图5).图1 图2 图3 图4 图5【要点诠释】解决梯形问题的基本思想和方法就是通过添加适当的辅助线,把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决.在学习时注意它们的作用,掌握这些辅助线的使用对于学好梯形内容很有帮助.2.特殊的梯形1)等腰梯形:两腰相等的梯形叫做等腰梯形.性质:(1)等腰梯形的同一底边上的两个角相等;等腰梯形的两条对角线相等.(2)同一底边上的两个角相等的梯形是等腰梯形.(3)等腰梯形是轴对称图形,它的对称轴是经过两底中点的一条直线.2)直角梯形:有一个角是直角的梯形叫做直角梯形.考点三、中点四边形相关问题1.中点四边形的概念:把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.2.若中点四边形为矩形,则原四边形满足条件对角线互相垂直;若中点四边形为菱形,则原四边形满足条件对角线相等;若中点四边形为正方形,则原四边形满足条件对角线互相垂直且相等.【要点诠释】中点四边形的形状由原四边形的对角线的位置和数量关系决定.【典型例题】类型一、特殊的平行四边形的应用1. 在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.(1)如图①,试判断四边形EGFH的形状,并说明理由;(2)如图②,当EF⊥GH时,四边形EGFH的形状是;(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是;(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.【思路点拨】中点四边形的形状由原四边形的对角线的位置和数量关系决定.【答案与解析】(1)四边形EGFH是平行四边形;证明:∵平行四边形ABCD的对角线AC、BD交于点O,∴点O是平行四边形ABCD的对称中心;∴EO=FO,GO=HO;∴四边形EGFH是平行四边形;(2)菱形;(提示:菱形的对角线垂直平分)(3)菱形;(提示:当AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2))(4)四边形EGFH是正方形;证明:∵AC=BD,∴平行四边形ABCD是矩形;又∵AC⊥BD,∴平行四边形ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;∵EF⊥GH,∴∠GOF=90°;∴∠BOG=∠COF;∴△BOG≌△COF(ASA);∴OG=OF,∴GH=EF;由(3)知四边形EGFH是菱形,又EF=GH,∴四边形EGFH是正方形.【总结升华】主要考查了平行四边形、菱形、矩形、正方形的判定和性质以及全等三角形的判定和性质;熟练掌握各特殊四边形的联系和区别是解答此类题目的关键.2.动手操作:在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小明同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB 的方法得到菱形AECF(见方案二).(1)你能说出小颖、小明所折出的菱形的理由吗?(2)请你通过计算,比较小颖和小明同学的折法中,哪种菱形面积较大?【思路点拨】(1)、要证所折图形是菱形,只需证四边相等即可.(2)、按照图形用面积公式计算S=30和S=35.21,可知方案二小明同学所折的菱形面积较大. 【答案与解析】(1)小颖的理由:依次连接矩形各边的中点所得到的四边形是菱形, 小明的理由:∵ABCD 是矩形, ∴AD ∥BC ,则∠DAC=∠ACB , 又∵∠CAE=∠CAD ,∠ACF=∠ACB , ∴∠CAE=∠CAD=∠ACF=∠ACB , ∴AE=EC=CF=FA , ∴四边形AECF 是菱形. (2)方案一:S 菱形=S 矩形-4S △AEH =12×5-4×12×6×52=30(cm )2, 方案二:设BE=x ,则CE=12-x , ∴AE=22BE AB +=225x +由AECF 是菱形,则AE 2=CE 2∴x 2+25=(12-x )2, ∴x=11924, S 菱形=S 矩形-2S △ABE =12×5-2×12×5×11924≈35.21(cm )2, 比较可知,方案二小明同学所折的菱形面积较大.【总结升华】本题考查了矩形的性质和菱形的判定,以及图形面积的计算与比较. 举一反三:【变式】如图,点O 是矩形ABCD 的中心,E 是AB 上的点,沿CE 折叠后,点B 恰好与点O 重合,若BC=3,则折痕CE 的长为 ( ).A.B.C.4 D.5【答案】A.类型二、梯形的应用3.(•黄州区校级模拟)如图,△ABC中,∠BAC=90°,延长BA至D,使AD=AB,点E、F分别是边BC、AC的中点.(1)判断四边形DBEF的形状并证明;(2)过点A作AG∥BC交DF于G,求证:AG=DG.【思路点拨】(1)利用梯形的判定首先得出四边形DBEF为梯形,进而得出四边形HFEB是平行四边形,得出BE=FD进而得出答案;(2)利用四边形DBEF为等腰梯形,得出∠B=∠D,利用AG∥BG,∠B=∠DAG,得出答案.【答案与解析】(1)解:四边形DBEF为等腰梯形,理由如下:如图,过点F作FH∥BC,交AB于点H,∵FH∥BC,点F是AC的中点,点E是BC的中点,∴AH=BH=AB,EF∥AB,显然EF<AB<AD,∴EF≠AD,∴四边形DBEF为梯形,∵AD=AB,∴AD=AH,∴CA是DH的中垂线,∴DF=FH,∵FH∥BC,EF∥AB,∴四边形HFEB是平行四边形,∴FH=BE,∴BE=FD,故四边形DBEF为等腰梯形;(2)证明:∵四边形DBEF为等腰梯形,∴∠B=∠D,∵AG∥BG,∠B=∠DAG,∴∠D=∠DAG,∴AG=D G.【总结升华】此题主要考查了等腰梯形的判定以及其性质和平行四边形的判定与性质等知识,得出BE=FD 是解题关键.举一反三:【变式】如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,则CE的长为().C. 2.5D.2.3A.22B. 231类型三、特殊四边形与其他知识结合的综合运用4. (•北京)在▱ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.【思路点拨】(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE 是平行四边形,再根据矩形的判定,可得答案;(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.【答案与解析】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.∵BE∥DF,BE=DF,∴四边形BFDE是平行四边形.∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形;(2)解:∵四边形ABCD是平行四边形,∴AB∥DC,∴∠DFA=∠FAB.在Rt△BCF中,由勾股定理,得BC===5,∴AD=BC=DF=5,∴∠DAF=∠DFA,∴∠DAF=∠FAB,即AF平分∠DAB.【总结升华】本题考查了平行四边形的性质,利用了平行四边形的性质,矩形的判定,等腰三角形的判定与性质,利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键.5.已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.【思路点拨】(1)根据菱形的对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠1=∠ACD,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM,再根据等腰三角形三线合一的性质可得CE=DE,然后求出CD的长度,即为菱形的边长BC的长度;(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G,然后证明∠1=∠G,根据等角对等边的性质可得AM=GM,再利用“角角边”证明△CDF和△BGF 全等,根据全等三角形对应边相等可得GF=DF,最后结合图形GM=GF+MF即可得证.【答案与解析】(1)解:∵四边形ABCD是菱形,∴AB∥CD,∴∠1=∠ACD,∵∠1=∠2,∴∠ACD=∠2,∴MC=MD,∵ME⊥CD,∴CD=2CE,∵CE=1,∴CD=2,∴BC=CD=2;(2)证明:如图,∵F为边BC的中点,∴BF=CF=12BC,∴CF=CE,在菱形ABCD中,AC平分∠BCD,∴∠ACB=∠ACD,在△CEM和△CFM中,∵CE CFACB ACDCM CM=⎧⎪∠=∠⎨⎪=⎩,∴△CEM≌△CFM(SAS),∴ME=MF,延长AB交DF于点G,∵AB∥CD,∴∠G=∠2,∵∠1=∠2,∴∠1=∠G,∴AM=MG,在△CDF和△BGF中,∵2GBFG CFDBF CF∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CDF≌△BGF(AAS),∴GF=DF,由图形可知,GM=GF+MF,∴AM=DF+ME.【总结升华】本题考查了菱形的性质,全等三角形的判定与性质,等角对等边的性质,作出辅助线构造出全等三角形是解题的关键.6 . 如图,己知ABC的顶点B、C为定点,A为动点(不在直线BC上).是点B关于直线AC的对称点,是点C关于直线AB的对称点.连结、、、.(1)猜想线段与'的数量关系,并证明你的结论;(2)当点A运动到怎样的位置时,四边形为菱形?这样的位置有几个?请用语言对这样的位置进行描述;(不用证明)(3)当点A在线段BC的垂直平分线l(BC的中点及到BC的距离为的点除外)上运动时,判断以点B、C、、为顶点的四边形的形状,画出相应的示意图.(不用证明)【思路点拨】本题考查轴对称的基本性质,综合考查菱形、正方形、等腰梯形的判定.在运动变化过程中,认识图形之间的内在联系.【答案与解析】(1)猜想:BC′=CB′∵B′是点B关于直线AC的对称点∴AC垂直平分B B′∴BC= CB′同理BC= BC′∴B C′=C B′(2)要使BCB′C′是菱形,根据菱形的性质,对角线互相垂直平分∵B′是点B关于直线AC的对称点,C′是点C关于直线AB的对称点∴AC垂直平分B B′,AB垂直平分C C′,∴B B′、C C′应该同时过A点∴∠BAC=90°∴只要AB⊥AC即可满足要求,这样的位置有无数个.(3)如图,当A是BC的中点时,没有形成四边形;当A到BC时,∵l是BC的垂直平分线,∴∠ACB=∠ABC=30°,∴∠BAC=120°,∴∠BOC=60°,∴BC=C B′= B′C′=B C′.∴BC B′C′为菱形,当BC的中点及到BC BC的点除外时,∵∠BOC= B′O C′,OB=OC O B′=O C′,∴∠OBC=∠OCB=∠O B′C′=∠O C′B′,∴BC∥B′C′.∵B C′不平行C B′,B C′=C B′,四边形BC B′ C′为等腰梯形.【总结升华】本题可以很好的培养观察推理能力,按照要求画出图形可以更清楚的解题.举一反三:【变式】(2012•襄阳)如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.(1)求证:梯形ABCD是等腰梯形;(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求出此时菱形AECD的面积.【答案】(1)证明:∵AD∥BC,∴∠DEC=∠EDA,∠BEA=∠EAD,又∵EA=ED,∴∠EAD=∠EDA,∴∠DEC=∠AEB,又∵EB=EC,∴△DEC≌△AEB,∴AB=CD,∴梯形ABCD是等腰梯形.(2)当AB⊥AC时,四边形AECD是菱形.证明:∵AD∥BC,BE=EC=AD,∴四边形ABED和四边形AECD均为平行四边形.∴AB=ED,∵AB⊥AC,∴AE=BE=EC,∴四边形AECD是菱形.过A作AG⊥BE于点G,∵AE=BE=AB=2,∴△ABE是等边三角形,∴∠AEB=60°,∴AG=3,∴S菱形AECD=EC•AG=2×3=23.第十九讲特殊的四边形一、选择题1.(•天水)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和BC′F的周长之和为()A.3 B.4 C.6 D.82.如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF面积为( ).A.4 B.6 C.8 D.103.如图所示,在矩形ABCD中,AB=3,AD=4,P是AD上的一点,PE⊥AC,垂足为E,PF⊥BD,垂足为F,则PE+PF的值为( ).A.B.C.2 D.第3题第4题4.如图,E、F、G、H分别是四边形ABCD四条边的中点,要使EFGH为矩形,四边形应该具备的条件是().A.一组对边平行而另一组对边不平行B.对角线相等C.对角线相互垂直 D.对角线互相平分5.如图,正方形ABCD中,O是对角线AC、BD的交点,过O点作OE⊥OF分别交AB、BC于E、F,若AE=4,CF=3,则EF等于().A.7B.5C.4D.3第5题第6题6.如图,在矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为().A.15° B.18° C.36° D.54°二、填空题7.(春•西城区期末)直角△ABC中,∠BAC=90°,D、E、F分别为AB、BC、AC的中点,已知DF=3,则AE= .8. 如图,菱形ABCD中,于E,于F,,则等于___________.9. 正方形ABCD中,E为BC上一点,BE=,CE=,P在BD上,则PE+PC的最小值可能为__________.10.如图,M为正方形ABCD中BC边的中点,将正方形折起,使点A与M重合,设折痕为EF,若正方形的面积为64,则△AEM的面积为____________.11.如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC 于F,则线段EF长度的最小值是_______________.第10题第11题第12题12.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=23,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为________.三、解答题13.如图1,图2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.(1)如图1,当点E在AB边的中点位置时:①猜想DE与EF满足的数量关系是__________;②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是__________;③请证明你的上述两个猜想.(2)如图2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时 DE 与EF有怎样的数量关系.14. 如图,在梯形ABCD中,AD//BC,AB=CD=3cm,∠A=120°,BD⊥CD,(1)求BC、AD的长度;(2)若点P从点B开始沿BC边向点C以2cm/秒的速度运动,点Q从点C开始沿CD边向点D以1cm/秒的速度运动,当P、Q分别从B、C同时出发时,写出五边形ABPQD的面积S与运动时间t之间的关系式,并写出t的取值范围(不包含点P在B、C两点的情况);(3)在(2)的前提下,是否存在某一时刻t,使线段PQ把梯形ABCD分成两部分的面积比为1:5?若存在,求出t的值;若不存在,请说明理由.15. (•青岛模拟)已知正方形ABCD的边长为a,两条对角线AC、BD相交于点O,P是射线AB上任意一点,过P点分别作直线AC、BD的垂线PE、PF,垂足为E、F.(1)如图1,当P点在线段AB上时,PE+PF的值是否为定值?如果是,请求出它的值;如果不是,请加以说明.(2)如图2,当P点在线段AB的延长线上时,求PE﹣PF的值.16.如图,十三个边长为正整数的正方形纸片恰好拼成一个大矩形(其中有三个小正方形的边长已标出字母x,y,z).试求满足上述条件的矩形的面积最小值.【答案与解析】一.选择题1.【答案】C.【解析】将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,∵∠ABE+∠EBF=∠C′BF+∠EBF=90°∴∠ABE=∠C′BF在△BAE和△BC′F中,∴△BAE≌△BC′F(ASA),∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3,△ABE和△BC′F的周长=2△ABE的周长=2×3=6.故选:C.2.【答案】C.3.【答案】A.4.【答案】C.5.【答案】B.【解析】可证△OEB≌△OFC,则EB=FC=3,AE=BF=4,32346.【答案】B.【解析】由题意∠ADE=54°,∠CDE=36°,∠DCE=54°,∠BDE=54°-36°=18°.二.填空题7.【答案】3.【解析】如图,∵在直角△ABC中,∠BAC=90°,D、F分别为AB、AC的中点,∴DF是△ABC的中位线,∴DF=BC.又∵点E是直角△ABC斜边BC的中点,∴AE=BC,∵DF=3,∴DF=AE.故填:3.8.【答案】60°.9.【答案】.10.【答案】10.【解析】提示:设AE=x=EM ,BE=8-x,MB=4,在Rt△BEM中由勾股定理解得x=5,从而算出面积.11.【答案】125.【解析】连接PC.∵PE⊥AC,PF⊥BC,∴∠PEC=∠PFC=∠C=90°;又∵∠ACB=90°,∴四边形ECFP是矩形,∴EF=PC,∴当PC最小时,EF也最小,即当CP⊥AB时,PC最小,∵AC=4,BC=3,∴AB=5,∴12AC•BC=12AB•PC,∴PC=125.∴线段EF长的最小值为125;故答案是:125.12.【答案】3+3.【解析】首先由已知AD∥BC,∠ABC=90°点E是BC边的中点,推出四边形ABED是矩形,所以得到直角三角形CED,所以能求出CD和DE,又由△DEF是等边三角形,得出DF,由直角三角形AGD可求出AG、DG,进而求得FG,再证△AGD≌△BGF,得到BF=AD,从而求出△BFG的周长.三.综合题13.【解析】(1)①DE=EF;②NE=BF;③∵四边形ABCD为正方形,∴AD=AB,∠DAB=∠ABC=90°,∵N,E分别为AD,AB中点,∴AN=DN=12AD,AE=EB=12AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,又∵∠ADE+∠AED=90°,∴∠FEB=∠ADE,又∵AN=AE,∴∠ANE=∠AEN,又∵∠A=90°,∴∠ANE=45°,∴∠DNE=180°-∠ANE=135°,又∵∠CBM=90°,BF平分∠CBM,∴∠CBF=45°,∠EBF=135°,∴△DNE≌△EBF(ASA),∴DE=EF,NE=BF.(2)在DA上截取DN=EB(或截取AN=AE),连接NE,则点N可使得NE=BF.此时DE=EF.证明方法同(1),证△DNE≌△EBF.14.【解析】(1)在Rt△BCD中,CD=3cm,∠C=60°, ∴∠DBC=30°,∴BC=2CD=6cm.由已知得:梯形ABCD是等腰梯形,∴∠ABC=∠C=60°,∴∠ABD=∠ABC-∠DBC=30°.∵AD∥BC,∴∠ADB=∠DBC=30°,∴∠ABD=∠ADB,∴AD=AB=3cm.(2)当P、Q分别从B、C同时出发运动t秒时,BP=2t,CQ=t, ∴PC=6-2t,过Q作QE⊥BC于E,则QE=CQsin60°=32t,∴S梯形ABCD-S△PCQ=2734-34(6-2t)t=34(2t2-6t+27)(0<t<3).(3)存在时刻t,使线段PQ把梯形ABCD分成两部分的面积比为1:5.∵S梯形ABCD=2734,S△ABD=12×3×32×3,∴S△ABD=13×S梯形ABCD,∴五边形ABPQD的面积不可能是梯形ABCD面积的16.∴S△PCQ:S五边形ABPQD=1:5,即S五边形ABPQD=56S梯形ABCD∴34(2t2-6t+27)=56×2734,整理得:4t2-12t+9=0,∴t=32,即当t=32秒时,PQ把梯形ABCD分成两部分的面积比为1:5.15.【解析】解:(1)是定值,∵四边形ABCD为正方形,∴AC⊥BD.∵PF⊥BD,∴PF∥AC,同理PE∥BD.∴四边形PFOE为矩形,故PE=OF.又∵∠PBF=45°,∴PF=BF.∴PE+PF=OF+FB=OB=acos45°=a.(2)∵四边形ABCD为正方形,∴AC⊥BD.∵PF⊥BD,∴PF∥AC,同理PE∥BD.∴四边形PFOE为矩形,故PE=OF.又∵∠PBF=45°,∴PF=BF.∴PE﹣PF=OF﹣BF=OB=acos45°=a.16.【解析】已有三个小正方形的边长为x,y,z,我们通过x,y,z表示其余正方形的边长依次填在每个正方形中,它们是x+y,x+2y,x+3y,4y,x+7y,2x+y,2x+y+z,4x+4y-z,4x+4y-2x及5x-2y+z.因矩形对边相等,所以得11x+3y=7x+16y-z及8x+8y-3z=6x+5y+z.化简上述的两个方程得到z=13y-4x,4z=2x+3y,消去z得18x=49y.因为18与49互质,所以x、y的最小自然数解是x=49,y=18,此时z=38.以x=49,y=18,z=38代入矩形长、宽的表达式11x+3y及8x+8y-3z,得长、宽分别为593和422.此时得最小面积值是593×422=250246.。
中点四边形教案

《探究中点四边形形状》教案教学目标:1.知识与技能:(1)了解中点四边形的概念;(2)利用三角形中位线定理证明中点四边形是平行四边形,理解特殊的平行四边形的中点四边形的特征;(3)理解中点四边形的形状与原四边形的对角线的关系。
2. 过程与方法:(1)经历观察、猜想、证明中点四边形是平行四边形的过程熟练运用三角形中位线定理;(2)经历由一般到特殊的思维进程,发现并证明特殊的平行四边形的中点四边形的特征;3.情感态度与价值观:(1)通过数学活动培养学生观察、猜想、证明的探索精神;(2)通过小组讨论活动,培养学生合作的意识。
教学重点:1、任意四边形的中点四边形形状的判定和证明;2、特殊平行四边形的中点四边形形状的判定和证明。
教学难点:影响中点四边形形状的主要因素的分析和概括。
教学过程:一、复习旧知,情境引入1、回顾三角形中位线性质定理。
2、问题1:出示问题:一块白铁皮零料形状如图,工人师傅要从中裁出一块平行四边形白铁皮,并使四个顶点分别落在原白铁皮的四条边上,可以如何裁?(学生思考、讨论、分析,想出解决办法)师:你能证明吗?生:已知:如图,点E、F、G、H分别是四边形ABCD各边中点。
求证:四边形EFGH为平行四边形。
(学生可连接AC,也可连接AC、BD)二、探索活动1、中点四边形的定义:顺次连接四边形各边中点所得的四边形叫做中点四边形。
2、结合引例得出结论:任意一个四边形的中点四边形,都为平行四边形。
问题2:观察这个图形,平行四边形EFGH各边与什么有关?各个内角又与什么有关?在问题2的基础上,完成下列三个探究。
探究1:四边形对角线满足什么条件时,它的中点四边形是矩形?探究2:四边形对角线满足什么条件时,它的中点四边形是菱形形?探究3:四边形对角线满足什么条件时,它的中点四边形是正方形形?学生四人小组合作探究并得出结论:(1)中点四边形的形状与原四边形的有密切关系;(2)只要原四边形的两条对角线,就能使中点四边形是菱形;(3)只要原四边形的两条对角线,就能使中点四边形是矩形;(4)要使中点四边形是正方形,原四边形要符合的条件是。
特殊的平行四边形专题(题型详细分类)
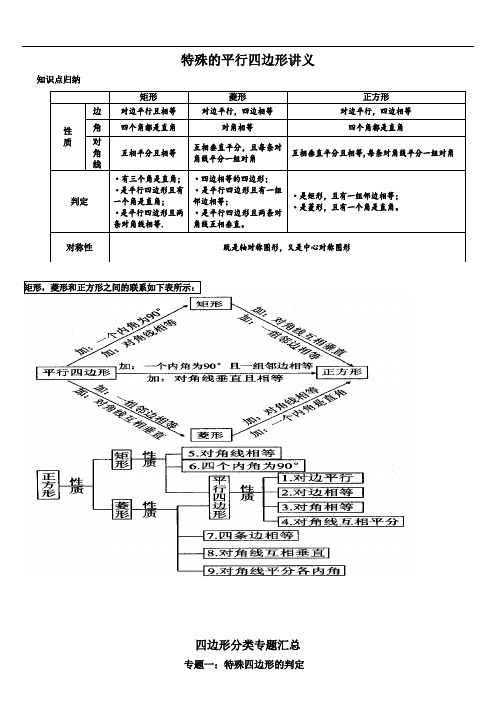
特殊的平行四边形讲义知识点归纳矩形,菱形和正方形之间的联系如下表所示:四边形分类专题汇总专题一:特殊四边形的判定矩形 菱形 正方形 性 质 边 对边平行且相等 对边平行,四边相等 对边平行,四边相等角 四个角都是直角 对角相等 四个角都是直角 对角线互相平分且相等 互相垂直平分,且每条对角线平分一组对角 互相垂直平分且相等,每条对角线平分一组对角 判定 ·有三个角是直角; ·是平行四边形且有一个角是直角; ·是平行四边形且两条对角线相等. ·四边相等的四边形;·是平行四边形且有一组邻边相等;·是平行四边形且两条对角线互相垂直。
·是矩形,且有一组邻边相等; ·是菱形,且有一个角是直角。
对称性 既是轴对称图形,又是中心对称图形【知识点】1.平行四边形的判定方法:(1)______________ (2)______________ (3)______________ (4)______________ (5)______________2.矩形的判定方法:(1)______________ (2)______________ (3)______________3.菱形的判定方法:(1)______________ (2)______________ (3)______________4.正方形的判定方法:(1)______________ (2)______________ (3)______________5.等腰梯形的判定方法:(1)______________ (2)______________ (3)______________【练一练】一.选择题1.能够判定四边形ABCD是平行四边形的题设是().A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠DC.AB=CD,AD=BC D.AB=AD,CB=CD2.具备下列条件的四边形中,不能确定是平行四边形的为().A.相邻的角互补 B.两组对角分别相等C.一组对边平行,另一组对边相等 D.对角线交点是两对角线中点3.下列条件中,能判定四边形是平行四边形的条件是( )A.一组对边平行,另一组对边相等B.一组对边平行,一组对角相等C.一组对边平行,一组邻角互补D.一组对边相等,一组邻角相等4.如下左图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是().A.若AO=OC,则ABCD是平行四边形;B.若AC=BD,则ABCD是平行四边形;C.若AO=BO,CO=DO,则ABCD是平行四边形;D.若AO=OC,BO=OD,则ABCD是平行四边形5.不能判定四边形ABCD是平行四边形的条件是()A.AB=CD,AD=BC B.AB∥CD,AB=CDC.AB=CD,AD∥BC D.AB∥CD,AD∥BC6.四边形ABCD的对角线AC,BD相交于点O,能判断它为矩形的题设是()A.AO=CO,BO=DO B.AO=BO=CO=DOC.AB=BC,AO=CO D.AO=CO,BO=DO,AC⊥BD7.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD8.在四边形ABCD中,O是对角线的交点,下列条件能判定这个四边形是正方形的是()A、AC=BD,AB∥CD,AB=CDB、AD∥BC,∠A=∠CC、AO=BO=CO=DO,AC⊥BDD、AC=CO,BO=DO,AB=BC9.在下列命题中,真命题是()A.两条对角线相等的四边形是矩形B.两条对角线互相垂直的四边形是菱形C.两条对角线互相平分的四边形是平行四边形D.两条对角线互相垂直且相等的四边形是正方形 10.在下列命题中,正确的是( )A 一组对边平行的四边形是平行四边形B 有一个角是直角的四边形是矩形C 有一组邻边相等的平行四边形是菱形D 对角线互相垂直平分的四边形是正方形 11.如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是( ) A .当AB=BC 时,它是菱形 B .当AC ⊥BD 时,它是菱形 C .当∠ABC=900时,它是矩形 D .当AC=BD 时,它是正方形12.如图,在ABC △中,点E D F ,,分别在边AB ,BC ,CA 上,且DE CA ∥,DF BA ∥.下列四个判断中,不正确...的是( ) A .四边形AEDF 是平行四边形B .如果90BAC ∠=,那么四边形AEDF 是矩形C .如果AD 平分BAC ∠,那么四边形AEDF 是菱形D .如果AD BC ⊥且AB AC =,那么四边形AEDF 是菱形 13.下列条件中不能判定四边形是正方形的条件是( )。
小学三四年级奥数10天精选练习分阶推进 附名师解析

奥数四年级10天精选练习 分阶推进第一天1. 如图,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)【分析】四边形面积为大等腰直角三角形减去小等腰直角三角形.四边形面积为()2273220-÷=. 2.(第二届走美试题)如下图,一块边长为180厘米的正方形铁片,四角各被截去一个边长为40厘米的小正方形铁片,现在要从剩下的铁片中剪出一块完整的正方形铁片来,剪出的正方形面积最大为 __平方厘米.【分析】2(180-402)10000⨯=(180-402)4022000⨯⨯÷=所以最大的正方形面积为:100002000418000+⨯=平方厘米.3. 如图,ABCD 是一个长方形,E 点在CD 延长线上.已知5AB =,12BC =,且三角形AFE 的面积等于20,那么三角形CFE 的面积等于多少?CFD EBA【分析】三角形ABE 面积为:()1302AB BC ⨯⨯=则三角形ABF面积为:302010-=且三角形ABF和三角形CFD的面积和为长方形ABCD面积的一半,则三角形FCD面积为301020-=.可得2AFFD=.则三角形EFD面积为202=40+=.⨯,三角形CFE面积为:4020604.如图23—2,(l)A→B→D有种不同的路线(A点不得重复);(2)A→D,有种不同的路线(A点不得重复).【分析】(l)依据乘法原理:A→B→D:3×2=6种。
依据加法原理。
①A直达D:2种。
(上方和下方)②经过AC:1种。
③经过B:3×2=6种2+1+6=9种。
答:(l)6种。
(2)9种。
5.从1-400的所有自然数中,不含有数字3的自然数有多少个?【分析】方法一:1~9:含3的有:1个10~99:个位数是3:9;十位数是3:9;注意33计算过两遍。
100~199:个位是3的:10;十位是3:9;200~299:个位是3的:10;十位是3:9;300~399:100个含3一共有:1+9+9+10+9+10+9+100=157∴不含3:400-157=243个方法二:按位数分类:一位数有:1,2,4,5,6,7,8,9,共8个二位数有:首位有8种,各位有9种,一共种三位数有:百位有1,2共2种,其余各位为9中,一共是种,加上400一共是163种。
中考数学复习----《中点四边形》知识点总结与专项练习题(含答案解析)

中考数学复习----《中点四边形》知识点总结与专项练习题(含答案解析)知识点总结1.中点四边形的定义:将任意四边形各条边的中点顺次连接起来得到的四边形叫做中点四边形。
2.中点四边形的判定:①任意四边形的中点四边形是平行四边形。
②对角线相互垂直的四边形的中点四边形是矩形。
(菱形的中点四边形是矩形)③对角线相等的四边形的中点四边形是菱形。
(矩形的中点四边形是菱形)④对角线相互垂直且相等的四边形的中点四边形是正方形。
(正方形的中点四边形是正方形)练习题1、(2022•玉林)若顺次连接四边形ABCD各边的中点所得的四边形是正方形,则四边形ABCD的两条对角线AC,BD一定是()A.互相平分B.互相垂直C.互相平分且相等D.互相垂直且相等【分析】根据三角形中位线定理得到所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是正方形,那么邻边互相垂直且相等,选择即可,【解答】解:如图,∵E、F、G、H分别是AB、BC、CD、AD的中点,∴EH∥FG∥BD,EF∥AC∥HG,∴四边形EFGH是平行四边形,∵四边形EFGH是正方形,即EF⊥FG,FE=FG,∴AC⊥BD,AC=BD,故选:D.2、(2022•德阳)如图,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA 边上的中点,则下列结论一定正确的是()A.四边形EFGH是矩形B.四边形EFGH的内角和小于四边形ABCD的内角和C.四边形EFGH的周长等于四边形ABCD的对角线长度之和D.四边形EFGH的面积等于四边形ABCD的面积的【分析】根据三角形中位线定理可得四边形EFGH是平行四边形,进而逐一判断即可.【解答】解:A.如图,连接AC,BD,在四边形ABCD中,∵点E,F,G,H分别是AB,BC,CD,DA边上的中点,∴EH∥BD,EH=BD,FG∥BD,FG=BD,∴EH∥FG,EH=FG,∴四边形EFGH是平行四边形,故A选项错误;B.∵四边形EFGH的内角和等于360°,四边形ABCD的内角和等于360°,故B选项错误;C.∵点E,F,G,H分别是AB,BC,CD,DA边上的中点,∴EH=BD,FG=BD,∴EH+FG=BD,同理:EF+HG=AC,∴四边形EFGH的周长等于四边形ABCD的对角线长度之和,故C选项正确;D.四边形EFGH的面积不等于四边形ABCD的面积的,故D选项错误.故选:C.。
《四边形的初步认识》教研评课稿(10月)

《四边形的初步认识》教研评课稿(10月) 尊敬的各位领导、老师:大家好!今天有幸聆听了袁平老师执教的《四边形的初步认识》一课,收益匪浅,老师根据学生爱表现这一心理特征,精心为同学们准备了形式多样的练习,通过有效的练习,及时了解学生的掌握情况,同学们个个都表现的棒棒的。
下面我谈一下自己的一些粗浅的想法。
一、激发兴趣,引发思考。
袁老师引导学生回顾所学图形有哪些,为新知的学习做好知识上的铺垫,从而引出新课的学习。
探讨式的课堂真正的体现了新课标所提出的“学生是课堂学习的主人”,怎么样的图形是四边形?探讨式的课堂,真正的体现了,新课标所提出的,学生是课堂学习的主人,二、体现了课堂的组织者,引导者。
袁老师从已有经验开始,直接引入,尝试领悟。
很多时候我们喜欢创设一些情景去展开新课,事实上,有些课可以更简洁一些,比如这节课,袁老师开门见山地引入课题,然后让学生画一个大大的四边形,接着静静地思考怎样地图形是四边形?这样既快速地集中了学生的注意力又使抽象数学概念变得直观形象。
三、主动辨析,积极参与,深入了解。
在丰富多彩的活动中,小学生具有好奇,好动的特点,而数学知识本身又是枯燥,抽象的,要使学生掌握数学知识,就必须符合儿童的自身的特点。
在这节课中,范老师让学生通过画一画,圈一圈,分一分,找一找,说一说,剪一剪,猜一猜等多种活动中获得新知,整节课学生都处于主动积极的状态中,不仅培养了学生的动手能力和观察能力,而且还使学生养成了善于思考,乐于动脑的好习惯。
四、活动设计开放性。
袁老师创造广阔的思维空间,学生能在开放的活动中发挥自己的想象力,培养创新意识,实践能力,是本节课的教学目标之一。
通过把四边形分类的活动,进一步感受到了四边形的细微差别之处,有的学生按照是不是直角分,有的学生按照直角的多少分,有的学生按照对边是不是相等分,这些多角度的分法,正是学生活跃思维的体现。
五、学生通过猜信封里的图形是什么图形是课堂中又一个高潮,学生在潜移默化中深化对长方形和正方形地认识,这对学生的空间思维能力,数学想象能力有非常大帮助以及促进作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中点四边形&中位线定理及其应用知识要点1.三角形中位线:连结三角形两边中点的线段。
注意:三角形的中位线有3条。
2.三角形中位线定理:三角形中位线平行于第三边且等于第三边的一半。
推论:过三角形一边的中点作另一边的平行线,必平分第三边。
3.梯形的中位线是连结梯形两腰中点的线段注意:(1)不是连结两底中点,是连接两腰的中点;(2)梯形的中线是唯一的 4.梯形的中位线定理:梯形的中位线平行于两底,并且等于两底和的一半 推论:过梯形一腰的中点,作底边的平行线,必平分另一腰。
有关中点证明的几种方法发散:例1.已知:如图1,在梯形ABCD 中,AB//CD ,以AD 、AC 为边作□ACED , DC 的延长线交EB 于F 。
求证:EF = FB 。
本题证法较多,关键是如何添加辅助线,主要方法如下。
(1) 延长EC ,交AB 于点G (如图2); 小结(2) 延长EC ,交BA 的延长线于点G (如图3); (3) 连结AE ,交CD 于点G (如图4);(4) 过点E 作EG ⊥AB ,分别交DF 、AB 于G 、H (如图5);(5) 过点E 作EG//CD ,交AD 的延长线于G (如图6); 构造梯形中线 (6) 过点F 作FG//AD ,交AB 于G (如图7); (7) 过点F 作FG//AC ,交AB 于G (如图8);(8) 过点B 作BG//AD ,交CF 的延长线于,连结EG (如图9)。
构造平行四边形(图2) (图3) (图4) (图5)(图6) (图7) (图8) (图9)构造三角形中位线构造全等三角形B A FE DCGBA FE DCGB AFE DCGB A FE DCG BAFE DCGBAFE D CGBAFE DCGBAF E DC G H BAFE DC〖注〗重点研究图2、3、4、5的证法,其他图形的证法仅提一提,以培养学生的发散思维能力。
例2.已知:如图10,在△ABC 中,AB=AC ,E 是AB 的中点,延长AB 到D ,使BD=AB 。
求证:CD=2CE 。
证法一:取AC 的中点F ,连结BF (如图11)。
证法二:过点B 作BF//CE ,交AC 的延长线于F (如图12)。
证法三:延长CE 到F ,使EF=CE ,连结FA 、FB (如图13)。
(图10)(图11) (图12) (图13) 例3.已知:如图14,在△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,E 是BC 的中点。
求证:AB=2DE分析:(1) 要证AB=2DE ,只需证等于AB 一半的线段等于DE 或等于DE 的2倍的线段等于AB 。
(2) 找等于AB 一半的线段有三种方法:一是只取AB 的中点,但这不利于问题的证明; (图14) 二是构造以AB 为斜边的直角三角形中线(因为条件中有垂直),再证此中线长等于DF ; 三是构造以AB 为第三边某三角形的中位线,再证此中位线等于DE 。
证法一:取AB 的中点F ,连结DF 、EF (如图15)。
(以下证明略)证法二:取AC 的中点F ,连结DF 、EF (如图16)。
(以下证明略) (图15) (图16)ABCDEABCDEFABCDEFA B CDE ABC D E FA B CDE FABCDEF课堂练习1.顺次连结四边形各边中点所得的四边形是 ; 2.顺次连结平行四边形各边中点所得的四边形是 ; 3.顺次连结矩形各边中点所得的四边形是 ; 4.顺次连结菱形各边中点所得的四边形是 ; 5.顺次连结正方形各边中点所得的四边形是 ; 6.顺次连结梯形各边中点所得的四边形是 。
7.顺次连结直角梯形各边中点所得的四边形是 。
8.顺次连结等腰梯形各边中点所得的四边形是 。
9.顺次连结对角线 的四边形各边中点所得的四边形是菱形; 10.顺次连结对角线 的四边形各边中点所得的四边形是矩形; 11.顺次连结对角线 的四边形各边中点所得的四边形是正方形。
12.已知△ABC 的周长为1,连结△ABC 的三边中点构成第二个三角形,•再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( ) A 、20081 B 、20091C 、220081D 、220091 13.如图所示,已知四边形ABCD ,R ,P 分别是DC ,BC 上的点,E ,F 分别是AP ,RP 的中点,当点P 在BC 上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减少 C .线段EF 的长不变 D .线段EF 的长不能确定14. 如图1,在四边形ABCD 中,E 、F 分别为AC 、BD 的中点,则EF 与AB +CD 的关系是 A .2EF AB CD =+ B. 2EF AB CD >+ C. 2EF AB CD <+ D. 不确定FED CBA15. 如上图2,四边形ABCD 中,AD=BC ,F 、E 、G 分别是AB 、CD 、AC 的中点,若∠DAC=200,∠ACB=600,则∠FEG= .16. 如上图3,M 、P 分别为△ABC 的AB 、AC 上 的点,且AM=BM ,AP=2CP ,BP 与CM 相交于N ,已知PN=1,则PB 的长为 ( ) A. 2 B. 3 C .4 D. 5 17. 如上图4,在△ABC 中,AD 平分∠BAC ,BD ⊥AD ,DE ∥AC ,交AB 于E ,若AB=5,则DE 的长为 . 18.如上图5,把长为8cm 的长方形对折,按图中的虚线剪出一个梯形并打开,则打开后的梯形中位线长为cm.19.已知梯形的中位线长16cm ,梯形的一条对角线把中位线分成两条线段,这两条线段的差是4cm,则梯形上底长是 cm.20.如下图1,△ABC 中,AD 、BE 是中线且交于G ,那么ABC BDG S S △△=.21.如上图2,梯形ABCD 中,AD∥BC,EF 为中位线,G 为BC 上任一点,如果S △GEF =22cm 2,那么梯形的面积是 cm 2.22.如上图3,DE 是△ABC 的中位线,F 是DE 的中点,BF 的延长线交AC 于H ,则AH ∶HE 等于( )A .1∶1B .2∶1C .1∶2D .3∶223、梯形的面积是242cm ,高为6cm ,那么它的中位线长为( )A 、8cmB 、30cmC 、4cmD 、18cm24.已知:如图,AD 是△ABC 的中线,E 是AD 的中点,AE 的延长线交AC 于F 。
求证:BE = 3EF 。
25.已知:如图,在四边形ABCD 中,AB=CD ,E 、F 分别是AD 、BC 的中点,延长BA 、CD ,分别交FE 的延长线于M 、N 。
求证:∠BMF=∠CNF 。
A BCDE FCB AF DE M N26、如图,△ABO与△CDO均为等腰三角形,且∠BAO=∠DCO=90°,M为BD的中点,MN⊥AC,试探究MN与AC的数量关系,并说明理由。
27、在△ABC与△BDE中,∠ABC=∠BDE=90°,BC=DE,AC=BE,M.N分别是AB.BD 的中点,连接MN交CE于点K(1)如图-1,当C.B.D共线,AB=2BC时,探究CK与EK之间的数量关系,并证明;(2)如图-2,当C.B.D不共线,AB≠2BC时,(1)中的结论是否成立,若成立,请证明;若不成立,请说明理由;(3)将题目中的条件“∠ABC=∠BDE=90°,BC=DE,AC=BE”都去掉,再添加一个条件,写出一个类似的对一般三角形都成立的问题(画出图形,写出已知和结论,不用证明)28、如图,在△ABC中,AD平分∠BAC,AD=AB,CM⊥AD于M. 求证:AB+AC=2AM29、如图20,在△ABC中,∠ABC=2∠C,AD平分∠BAC,过BC的中点M作ME⊥AD,交BA的延长线于E,交AD的延长线于F. 求证:12BE BD.30、如图,已知△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=900,如图(a),连接DE,设M为DE的中点.(1)求证:MB=MC;(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图(b)的位置,试问MB=MC是否成立?并证明其结论.课后练习:1、.如图-1,在Rt△ABC 中,∠ACB=90°,∠BAC=60°,(1)将Rt△ABC绕点A逆时针旋转90°,得到Rt△AC'B',直线BB'交直线CC'于点D,连接AD. 探究:AD与BB'之间的关系,并说明理由。
(2)如图-2,若将Rt△ABC绕点A逆时针旋转任意角度,其他条件不变,还有(1)的结论吗?为什么?2、如图1 ,正三角形ABO与正三角形CDO有一个公共点O,N为AB的中点,M为CD 的中点,P为BD的中点,且A、O、C三点共线,⑴求出∠MPN的度数;⑵当正三角形CDO绕点O旋转一定的角度,如图2,其他条件不变,⑴中的结论成立吗?说明理由;⑶如图3,若把⑵中“正三角形ABO与正三角形CDO”改为等腰三角形ABO与CDO,其中AO=OB,OC=OD,∠ABO=∠CDO=α”,探究∠MPN与α的数量关系;。
