自动控制原理学生实验:二阶开环系统的频率特性曲线
实验三 系统频率特性曲线的绘制及系统分析

《自动控制原理》实践报告实验三系统频率特性曲线的绘制及系统分析熟悉利用计算机绘制系统伯德图、乃奎斯特曲线的方法,并利用所绘制图形分析系统性能。
一、实验目的1.熟练掌握使用MATLAB软件绘制Bode图及Nyquist曲线的方法;2.进一步加深对Bode图及Nyquist曲线的了解;3.利用所绘制Bode图及Nyquist曲线分析系统性能。
二、主要实验设备及仪器实验设备:每人一台计算机奔腾系列以上计算机,配置硬盘≥2G,内存≥64M。
实验软件:WINDOWS操作系统(WINDOWS XP 或WINDOWS 2000),并安装MATLAB 语言编程环境。
三、实验内容已知系统开环传递函数分别为如下形式, (1))2)(5(50)(++=s s s G (2))15)(5(250)(++=s s s s G(3)210()(21)s G s s s s +=++ (4))12.0)(12(8)(++=s s s s G (5)23221()0.21s s G s s s s ++=+++ (6))]105.0)125.0)[(12()15.0(4)(2++++=s s s s s s G 1.绘制其Nyquist 曲线和Bode 图,记录或拷贝所绘制系统的各种图形; 1、 程序代码: num=[50];den=conv([1 5],[1 2]); bode(num,den)num=[50];den=conv([1 5],[1 2]); nyquist(num,den)-80-60-40-20020M a g n i t u d e (d B)10-210-110101102103-180-135-90-450P h a s e (d e g )Bode DiagramFrequency (rad/sec)-1012345-4-3-2-11234Nyquist DiagramReal AxisI m a g i n a r y A x i s2、 程序代码: num=[250];den=conv(conv([1 0],[1 5]),[1 15]); bode(num,den)num=[250];den=conv(conv([1 0],[1 5]),[1 15]);-150-100-5050M a g n i t u d e (d B )10-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)nyquist(num,den)3、 程序代码: num=[1 10];den=conv([1 0],[2 1 1]); bode(num,den)-150-100-50050100M a g n i t u d e (d B)10-210-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.10-15-10-551015System: sys Real: -0.132Imag: -0.0124Frequency (rad/sec): -10.3Nyquist DiagramReal AxisI m a g i n a r y A x i snum=[1 10];den=conv([1 0],[2 1 1]); nyquist(num,den)-25-20-15-10-5-200-150-100-5050100150200Nyquist DiagramReal AxisI m a g i n a r y A x i s-100-5050100M a g n i t u d e (d B )10-210-110101102-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)4、 程序代码: num=[8];den=conv(conv([1 0],[2 1]),[0.2 1]); bode(num,den)-18-16-14-12-10-8-6-4-20-250-200-150-100-50050100150200250Nyquist DiagramReal AxisI m a g i n a r y A x i snum=[8];den=conv(conv([1 0],[2 1]),[0.2 1]); nyquist(num,den)5、 程序代码: num=[1 2 1]; den=[1 0.2 1 1]; bode(num,den)num=[1 2 1];den=[1 0.2 1 1]; nyquist(num,den)-40-30-20-10010M a g n i t u d e (d B )10-210-110101102-360-270-180-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)-2.5-2-1.5-1-0.500.51 1.5-3-2-1123Nyquist DiagramReal AxisI m a g i n a r y A x i s-100-5050100M a g n i t u d e (d B )10-210-110101102-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)6、 num=[2 4];den=conv(conv([1 0],[2 1]),[0.015625 0.05 1]); bode(num,den)num=[2 4];den=conv(conv([1 0],[2 1]),[0.015625 0.05 1]); nyquist(num,den)2.利用所绘制出的Nyquist 曲线及Bode 图对系统的性能进行分析:(1)利用以上任意一种方法绘制的图形判断系统的稳定性; 由Nyquist 曲线判断系统的稳定性,Z=P-2N 。
自动控制原理频率特性曲线讲解
100
ω
-20db
90 o
--40db
180 o
[-40]
振荡环节L(ω)
返回
L(ω)
二阶微分L(ω)
180o
40db
90o
20db
0o
0db
1
0.1
-20db
20lg 2 1 2
[40]
10
20 lg 2
100
ω
G(s) 0.25s2 s 1
--40db
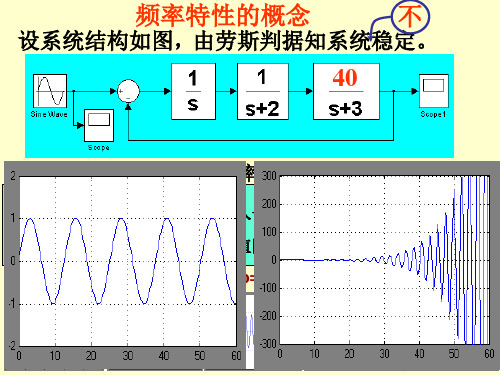
频率特性的概念
不
设系统结构如图,由劳斯判据知系统稳定。
40
给系统输入一个幅值不变频率不断增大的正弦,曲线如下:
给稳定的系统输入一个正弦,其稳态输出是与输入
结论:
同频率的正弦,幅值随ω而变,相角也是ω的函数。
Ar=1 ω=0.5 ω=1
ω=2
ω=2.5
ω=4
绘制L(ω)曲线例题
例题:绘制开环对数幅频渐近特性曲线 解:开环传递函数为
斜率: -40 -20 -40
返回
说明: r(t)=δ(t), 所以,系统稳定
C( )=0
时域稳定曲线
返回
说明: r(t)=δ(t), 所以,系统不稳定
C( )=
时域不稳定曲线
返回
对数坐标系
返回
倒置的坐标系
返回
返回
L(ω)
积分环节L(ω)
40db 20db 0db -20db
[-20] 0.1 0.2
-20db -90
--40db
-114.7
-93.7 -137.5
-180
返回
例题1:绘制
G(s)
自动控制原理实验报告四

自动控制原理实验报告实验时间:201X年X 月X 日 地点:XXXX 实验报告人(签名):倪马 同组实验人(签名):1 实验名称:线性系统的频域分析2 实验目的:(1)掌握二阶开环系统的对数频率特性、幅相频率特性、实频特性和虚频特性;(2)掌握欠阻尼二阶闭环系统中的自然频率、阻尼比对开环参数幅值穿越频率、相位裕度的影响,以及幅值穿越频率和相位裕度的计算;(3)掌握二阶开环系统对数频率特性曲线和幅相频率特性曲线的特点及绘制方法。
3 实验内容:(1)根据实验讲义上模拟电路图和接线要求,在LabACTn 自控/计控原理实验机的对应接口上连接好线路;(2)根据实验讲义的具体要求进行“运行”操作,并观察实验曲线,根据曲线计算对应参数——一阶惯性环节的转折频率、二阶闭环系统的谐振频率r ω&谐振峰值)(r L ω,改变被测系统的各项电路参数,画出其系统模拟电路图。
4 实验步骤 4.1 实验操作4.1.1 一阶惯性环节的频率特性曲线惯性环节的频率特性测试电路见图3-2-1,改变被测系统的各项电路参数,画出其系统模拟电路图,及频率特性曲线,並计算和测量其转折频率,填入实验报告。
一阶惯性环节的转折频率:T /1=ω图3-2-1 惯性环节的频率特性测试电路图3-2-1电路的增益K=1,惯性时间常数 T=0.1,转折频率:s /1rad .0/1==T ω 实验内容及步骤(1)构造模拟电路:按图3-2-1安置短路套及插孔连线。
(2)运行、观察、记录:① 选择系统的频域分析/一阶惯性环节频率特性曲线,将弹出频率特性扫描点设置表,用户可在…频率特性扫描点‟设置表中根据需要填入各个扫描点角频率,设置完后,点击《确认》后,将弹出…频率特性曲线‟实验界面,点击《开始》,即可按表中规定的角频率值,按序自动产生多种频率信号,画出频率特性曲线。
② 测试结束后(约五分钟),将显示被测系统的对数幅频、相频特性曲线(伯德图)和幅相曲线(奈奎斯特图),界面“显示选择”选择了“伯德图”。
自动控制原理实验实验指导书

自动控制原理实验目录实验一二阶系统阶跃响应(验证性实验) (1)实验三控制系统的稳定性分析(验证性实验) (9)实验三系统稳态误差分析(综合性实验) (15)预备实验典型环节及其阶跃响应一、实验目的1.学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。
2.学习典型环节阶跃响应测量方法,并学会由阶跃响应曲线计算典型环节传递函数。
二、实验内容搭建下述典型环节的模拟电路,并测量其阶跃响应。
1.比例(P)环节的模拟电路及其传递函数示于图1-1。
2.惯性(T)环节的模拟电路及其传递函数示于图1-2。
3.积分(I)环节的模拟电路及其传递函数示于图1-3。
4. 比例积分(PI)环节的模拟电路及其传递函数示于图1-4。
5.比例微分(PD)环节的模拟电路及其传递函数示于图1-5。
6.比例积分微分(PID)环节的模拟电路及其传递函数示于图1-6。
三、实验报告1.画出惯性环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的模拟电路图,用坐标纸画出所记录的各环节的阶跃响应曲线。
2.由阶跃响应曲线计算出惯性环节、积分环节的传递函数,并与由模拟电路计算的结果相比较。
附1:预备实验典型环节及其阶跃响应效果参考图比例环节阶跃响应惯性环节阶跃响应积分环节阶跃响应比例积分环节阶跃响应比例微分环节阶跃响应比例积分微分环节阶跃响应附2:由模拟电路推导传递函数的参考方法1. 惯性环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:整理得进一步简化可以得到如果令R 2/R 1=K ,R 2C=T ,则系统的传递函数可写成下面的形式:()1KG s TS =-+当输入r(t)为单位脉冲函数时 则有输入U 1(s)=1输出U 2(s)=G(s)U 1(s)= 1KTS-+由拉氏反变换可得到单位脉冲响应如下:/(),0t TK k t e t T-=-≥ 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)= 11K TS s-+由拉氏反变换可得到单位阶跃响应如下:/()(1),0t T h t K e t -=--≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2323R R C T R R =+2Cs12Cs-(s)U R10-(s)U 21R R +-=12212)Cs (Cs 1(s)U (s)U )(G R R R s +-==12212)Cs 1((s)U (s)U )(G R R R s +-==由拉氏反变换可得到单位斜坡响应如下:/()(1),0t T c t Kt KT e t -=--≥2. 比例微分环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:(s)(s)(s)(s)(s)U100-U U 0U 2=1R1R23(4)CSU R R '''---=++由前一个等式得到 ()1()2/1U s U s R R '=- 带入方程组中消去()U s '可得1()1()2/11()2/12()1134U s U s R R U s R R U s R R R CS+=--+由于14R C〈〈,则可将R4忽略,则可将两边化简得到传递函数如下: 2()23232323()(1)1()11123U s R R R R R R R R G s CS CS U s R R R R R ++==--=-++如果令K=231R R R +, T=2323R R C R R +,则系统的传递函数可写成下面的形式:()(1)G s K TS =-+当输入r(t)为单位脉冲函数时,单位脉冲响应不稳定,讨论起来无意义 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)=(1)K TS S-+由拉氏反变换可得到单位阶跃响应如下:()(),0h t KT t K t δ=+≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2(1)K TS S -+由拉氏反变换可得到单位斜坡响应如下:(),0c t Kt KT t =+≥实验一 二阶系统阶跃响应(验证性实验)一、实验目的研究二阶系统的两个重要参数阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
实验二 二阶系统的模拟及频率特性测试

实验二 二阶系统的模拟及频率特性测试一、实验目的1. 学会二阶系统的模拟方法,研究系统参数n ω和ξ对阶跃响应指标的影响;2. 学习频率特性测试仪的使用方法;3. 学会系统频率特性测试方法。
二、实验设备1. 自动控制原理试验箱一台;2. 双踪示波器一台;3. 频率特性测试仪一台;4. 万用表一块。
三、实验内容及步骤1. 二阶系统的阶跃响应按图2-1接线,传递函数222()()()2nn nC s G s R s s s ωξωω==++,其中110R K R =、111T R C =、222T R C =、n ω=112n T ξω=。
取1212120.1(1010)T T T s R R K C C F μ=====Ω==,,则在00.5(10)R K ξ==Ω取时,110n Tω==,观测二阶系统的阶跃响应曲线。
2. 测试二阶系统的频率响应特性方法与步骤:(1)按图2-1先接成二阶系统,并观测阶跃响应。
接上频率特性测试仪,如图2-2 所示。
(2)先测试转折频率 1.592(10/)f H z rad s ω==时对应的幅值R 和相角ϕ。
设定频率 1.592FREQ clear EN TER →→→;设定前面板状态w aveform ~,d e l a y 0.1s ,inputrang AUTO ,int errator AUTO ,display mod e R 、ϕ,sw eep o ff 。
按sin gle 键,从显示窗读取对应 1.592f H z =的R 和ϕ的值。
(3)系统参数不变。
采用单次步进测量,记录f 由0.1Hz 到15Hz ,步长为0.5Hz的R 和ϕ的值。
设定最大频率 m ax 15.0f clear EN TER →→→;设定最小频率 m in 0.1f clear EN TER →→→;设定步长(0.5Hz )/0.5Lin F step clear EN TER →∆→→→; 设定前面板状态 sw eep Lin →∆,其他与(2)同。
自动控制原理实验——二阶系统的动态过程分析

实验二二阶系统的动态过程分析一、 实验目的1. 掌握二阶控制系统的电路模拟方法及其动态性能指标的测试技术。
2. 定量分析二阶系统的阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
3. 加深理解“线性系统的稳定性只与其结构和参数有关,而与外作用无关”的性质。
4. 了解和学习二阶控制系统及其阶跃响应的Matlab 仿真和Simulink 实现方法。
二、 实验内容1. 分析典型二阶系统()G s 的ξ和n ω变化时,对系统的阶跃响应的影响。
2. 用实验的方法求解以下问题:设控制系统结构图如图2.1所示,若要求系统具有性能:%20%,1,p p t s σσ===试确定系统参数K 和τ,并计算单位阶跃响应的特征量d t ,r t 和s t 。
图2.1 控制系统的结构图3. 用实验的方法求解以下问题:设控制系统结构图如图2.2所示。
图中,输入信号()r t t θ=,放大器增益AK 分别取13.5,200和1500。
试分别写出系统的误差响应表达式,并估算其性能指标。
图2.2 控制系统的结构图三、实验原理任何一个给定的线性控制系统,都可以分解为若干个典型环节的组合。
将每个典型环节的模拟电路按系统的方块图连接起来,就得到控制系统的模拟电路图。
通常,二阶控制系统222()2nn nG ssωξωω=++可以分解为一个比例环节、一个惯性环节和一个积分环节,其结构原理如图 2.3所示,对应的模拟电路图如图2.4所示。
图2.3 二阶系统的结构原理图图2.4 二阶系统的模拟电路原理图图2.4中:()(),()()r cu t r t u t c t==-。
比例常数(增益系数)21RKR=,惯性时间常数131T R C=,积分时间常数242T R C=。
其闭环传递函数为:12221112()1()(1)crKU s TTKKU s T s T s K s sT TT==++++(0.1) 又:二阶控制系统的特性由两个参数来描述,即系统的阻尼比ξ和无阻尼自然频率n ω。
自动控制原理实验报告
实验一典型环节的模拟研究及阶跃响应分析1、比例环节可知比例环节的传递函数为一个常数:当Kp 分别为,1,2时,输入幅值为的正向阶跃信号,理论上依次输出幅值为,,的反向阶跃信号。
实验中,输出信号依次为幅值为,,的反向阶跃信号,相对误差分别为1.8%,2.2%,0.2%.在误差允许范围内可认为实际输出满足理论值。
2、 积分环节积分环节传递函数为:〔1〕T=0.1(0.033)时,C=1μf(0.33μf),利用MATLAB ,模拟阶跃信号输入下的输出信号如图:与实验测得波形比较可知,实际与理论值较为吻合,理论上时的波形斜率近似为时的三倍,实际上为,在误差允许范围内可认为满足理论条件。
3、 惯性环节惯性环节传递函数为:K = R f /R 1,T = R f C,(1) 保持K = R f /R 1= 1不变,观测秒,秒〔既R 1 = 100K,C = 1μf ,μf 〕时的输出波形。
利用matlab 仿真得到理论波形如下:时t s 〔5%〕理论值为300ms,实际测得t s =400ms 相对误差为:〔400-300〕/300=33.3%,读数误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近。
时t s 〔5%〕理论值为30ms,实际测得t s =40ms 相对误差为:〔40-30〕/30=33.3% 由于ts 较小,所以读数时误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近(2) 保持T = R f s 不变,分别观测K = 1,2时的输出波形。
K=1时波形即为〔1〕中时波形K=2时,利用matlab 仿真得到如下结果:t s 〔5%〕理论值为300ms,实际测得t s =400ms相对误差为:〔400-300〕/300=33.3% 读数误差较大K 理论值为2,实验值, 相对误差为〔〕/2=5.7%if i o R RU U -=1TS K)s (R )s (C +-=与理论值较为接近。
自动控制原理5.3 系统开环频率特性

[20 ]的 斜
率线。
20lgK
0
[ 20 ]
1
§5-3 系统开环频率特性
j
lim b0 sm a0 sn
s j
lim b0 a0 snm
s j
lim
b0 a0 nm
[(n
m)
2
]
0[(n m) ] 2
j
0
以确定Байду номын сангаас角度 收敛于原点
§5-3 系统开环频率特性
3. 确定幅相曲线与实轴的交点:
令Im[Gk ( j)] 0,求得,代入Re[Gk ( j)]中即可
s 20lgK为水平线。所以此时
L() 20lg K 20lg 20lg K 20 lg
顺序斜率迭加法(续)
§5-3 系统开环频率特性
当 1时,L() 20lg K,而 20 lg为 1处
过0db的[20 ]的斜率线。
因此低频起
始段为在
1处过
(n
m)
1、 0的起始段:
lim
0
G
j
lim
0
(
K
j
)
K
lim
0
(
)
2
υ =2
j
υ =3
K 0
υ =0
起始段只取决于和K。
不同,起始段的差异很大。
υ =1
§5-3 系统开环频率特性
开环幅相频率特性的绘制(续)
2、 的终止段:
lim G
得到曲线与实轴的交点。
自动控制原理实验4

七、注意事项
1、 若只使用其中某一个运算放大器,则其
余的运算放大器必须接成比例环节,不允许
输入端和输出端悬空,以避免损坏运算放大
器;
2、所有导线使用前须用万用表测通断 3、调零
方法1:李沙育图形示波器设置
CH1接输入,CH2接输出
示波器设置
示波器设置
示波器设置
示波器设置
格式设置成XY
示波器设置
方法2:
示波器设置
CH1,CH2的波形调成一样大
一阶惯性环节频率特性
4、二阶系统的频率特性测量 (1)用MATLAB求出该二阶系统频率特性, 绘制幅频曲线和相频曲线; (2)连接示波器:将正弦波端子与Ui和示波 器通道CH1相连接,实验电路UO与示波器通道 CH2相连接; (3)输入正弦波信号,通过示波器观测输入 输出正弦波曲线并调节正弦波频率,绘制该二 阶系统的幅频曲线和相频曲线,并与仿真结果 相比较; 3.根据二阶系统的理论计算,选择频率测试 点ω,填写下表。
二阶系统频率特性
五、实验报告要求:
1.
2.
3.
1. 整理表4.2、表4.3中的实验数据,在半对 数坐标纸上作出被测系统的对数幅频特性和 相频特性。 2. 参考相频特性,对对数幅频特性采用折线 近似,从而确定被测系统的参数(转折频率、 阻尼比、开环放大倍数),与实验时所设置 的原始参数进行比较。 3.讨论李沙育图形法测试频率特性的精度。
实 验 四
典型系统的频率特性测试
一、实验目的:
1.掌握测量典型一阶系统和二阶 系统频率特性曲线的方法; 2.通过本实验进一步理解频率特性 的物理意义。
二、实验仪器:
1.自控系统教学模拟机 XMN-2 1台; 2.数字示波器 TDS1002B 1台;
自动控制原理 开环系统的频率特性—典型环节非最小相

频率特性
G
j
1
2 n2
j2
n
幅频特性
A G j
1
2 n2
2
2
n
2
不变!
相频特性
2
G
j
arctan
1
n 2
n2
A
1
2 n2
2
2
n
2
2
arctan
1
n 2
n2
2
arctan
1
n 2
n2
2
180 arctan
n
2 n2
1
0 A 1, 0
1 n
第四象限
不变!
0 ~ 90
Ts 1 频率特性 G j Tj 1
L 20 lg A 20 lg 1 T 22 180 arctanT
不变!
180 ~ 90
上页
L dB
40
20
3dB
0
0.1
12
180
0.5s 1
90 0 90
0.5s 1 0.5s 1
20
10
100
上页
7
11/22/2013
4,振荡环节
Gs
n2 s2 2ns n2
s2
1 n2 2
n s 1
频率特性
G
j
1
2 n2
1 j2
n
幅频特性
A G j
1
1
2 n2
2
2
n
2
不变!
相频特性
2
G
j
arctan
1
n 2Biblioteka n2A 11
实验二二阶系统的阶跃响应及频率特性

实验二二阶系统的阶跃响应及频率特性实验简介:通过本实验学生能够学习二阶系统的频率响应和幅频特性的测试方法,对实验装置和仪器的调试操作,具备对实验数据、结果的处理及其与理论计算分析比较的能力。
适用课程:控制工程基础实验目的:A 学习运算放大器在控制工程中的应用及传递函数的求取。
B 学习二阶系统阶跃响应曲线的实验测试方法。
C 研究二阶系统的两个重要参数ζ、ωn对阶跃瞬态响应指标的影响。
D 学习频率特性的实验测试方法。
E 掌握根据频率响应实验结果绘制Bode图的方法。
F 根据实验结果所绘制的Bode图,分析二阶系统的主要动态特性(MP ,ts)。
面向专业:机械类实验性质:综合性/必做知 识 点:A《模拟电子技术》课程中运算放大器的相关知识;B《数字电子技术》课程中采样及采样定理的相关知识;C《机械工程控制基础》课程中,传递函数,时域响应, 频率响应三章的内容。
学 时 数:2设备仪器:XMN-2自动控制原理学习机,CAE-98型微机接口卡,计算机辅助实验系统2.0软件,万用表。
材料消耗:运算放大器,电阻,电容,插接线。
要 求:实验前认真预习实验指导书的实验内容,完成下述项目, 做实验时交于指导教师检查并与实验报告一起记入实验成绩。
B推导图2所示积分放大器的输出输入时域关系和传递函数。
C 推导图3所示加法和积分放大器的输出输入时域关系(两输入单输出)和S<1>.写出op1,op2,op9,0p6对应的微分方程组(4个方程)。
<2>.画出系统方框图。
<3>.用方框图化简或方程组联立消元的方法求取实验电路所示系统的传递函数,写出求解过程。
和ζ。
<4>.求取该系统的ωn实验地点:教一楼327室实验照片:实验装置及仪器。
武汉大学《自动控制原理》实验报告

2016〜2017学年第一学期〈〈自动控制原理》实验报告年级:2014级班号:姓名:He学号:成绩:教师:实验设备及编号:实验同组人名单:实验地点:电气工程学院自动控制原理实验室实验时间:2016年10月目录:实验一典型环节的电路模拟 (3)一、实验目的................................................................. 3..二、实验内容................................................................. 3..三、实验电路图及参数.......................................................... 3.四、实验分析 ................................................................ 1.0五、实验思考题............................................................... 1.1实验二二阶系统的瞬态响应. (12)一、实验目的................................................................. 1.2二、实验设备................................................................. 1.2三、实验电路图及其传递函数................................................... 1.2四、实验结果及相应参数 (14)五、实验分析................................................................. 1.6六、实验思考题............................................................... 1.6实验五典型环节和系统频率特性的测量 (17)一、实验目的................................................................. 1.7二、实验设备................................................................. 1.7三、传递函数•模拟电路图及波特图 ............................................. 1.7四、实验思考题 (22)实验六线性定常系统的申联校正 (24)一、实验目的 (24)二、实验设备 (24)三、实验电路图及其实验结果 (24)四、实验分析 (28)五、实验思考题 (28)实验七单闭环直流调速系统 (29)一、实验目的 (29)二、实验设备 (29)三、P ID参数记录表及其对应图像.............................................. .3.0四、P ID控制参数对直流电机运行的影响 (37)实验一典型环节的电路模拟一、 实验目的1. 熟悉THKKL-B 型模块化自控原理实验系统及“自控原理软件”的使用;2. 熟悉各典型环节的阶跃响应特性及其电路模拟;3. 测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
二阶系统的频率响应与频率特性测量
实验四二阶系统的频率响应与频率特性测量一、实验目的1.掌握频率特性的实验测试方法,进一步理解频率特性的物理意义2.掌握根据频率响应实验结果绘制Bode图的方法3.根据二阶系统的Bode图,确定系统的数学模型4.掌握二阶系统的频域指标与时域指标的对应关系二、实验仪器与设备1.自动控制原理学习机2.计算机(安装自动控制原理实验系统)3.万用表及接线三、实验原理1.输入、输出波形直接测试法如图4-1所示,给定的被测对象是一个稳定的系统。
由实验系统提供正弦信号,每选择一个频率,即可利用实验系统获得输入、输出随时间变化的曲线,取输出稳定后同周期的输入、输出曲线如图4-2。
图4-1 测量被控系统的频率响应图4-2 稳定后系统的输入输出曲线幅频特性)(2)(2)(ωωωmmXYjG=相频特性oTtjG360)(⨯∆-=∠ω2.李沙育图形法取被测对象某一选定频率下的输入信号x (t )和输出信号y (t )(去掉不稳定部分),利用实验系统做X-Y 图,得到一个椭圆图形,如图4-3所示。
图4-3 李沙育图形幅频特性:)(2)(2)(ωωωm m X Y j G =相频特性:如图4-3,椭圆长轴在第一、三象限,()()()ωωωφm 01-2Y 2Y sin=若椭圆长轴在第二、四象限,()()()ωωωφm 01-o 2Y 2Y sin-180=随着角频率的增加,大多数情况下椭圆逆时针运动,表明输出信号Y (t )滞后于输入信号X (t ),相位的计算结果要添加一个负号,如果椭圆顺时针运动,Y (t )超前于X (t ),计算结果为正。
幅值取两倍是为了便于测量。
3.测试频率的选取选取合适的实验测试频率范围是准确确定系统频率特性的关键。
控制系统多为低通滤波器,在频率很低时,系统的输出能够复现输入信号,通常,取被测对象转折频率的1/10作为起始测试频率,若对象模型未知,则先确定最大测试频率,方法是先测出输入信号频率为0时输出的幅值Y (0),逐渐增大输入信号频率,直至输出幅值Y m 为Y (0)/(50-100),此时频率便可确定为最大测试频率,测试频率可以在0与max ω之间选取若干点。
自动控制原理-控制系统的频率特性实验报告
肇庆学院工程学院 自动控制原理实验报告_12 _年级_ 电气一班 组员:王园园、李俊杰 实验日期 2014/6/9 姓名:李奕顺 学号:2130 老师评定___________ 实验四:控制系统的频率特性一、实验原理1.被测系统的方块图:见图4-1图4-1 被测系统方块图系统(或环节)的频率特性G (j ω)是一个复变量,可以表示成以角频率ω为参数的幅值和相角:) G(j ω) G(j ω) G(j ω= (4—1)本实验应用频率特性测试仪测量系统或环节的频率特牲。
图4-1所示系统的开环频率特性为:) E(j ω) B(j ω)E(j ω)B(j ω) E(j ω) B(j ω) (j ωG ) (j ωG 21==⋅(4—2)采用对数幅频特性和相频特性表示,则式(4—2)表示为:)E(j ω)B(j ωlg20) )H(j ω (j ωG ) (j ωG 20lg 21=⋅) E(j ωlg 20) B (j ωlg 20-= (4—3)) E(j ω) B(j ω)E(j ω)B(j ω) H(j ω) (j ωG ) (j ωG 21-==(4—4)将频率特性测试仪内信号发生器产生的超低频正弦信号的频率从低到高变化,并施加于被测系统的输人端[r(t)],然后分别测量相应的反馈信号[b(t)]和误差信号[e(t)]的对数幅值和相位。
频率特性测试仪测试数据经相关运算器后在显示器中显示。
根据式(4—3)和式(4—4)分别计算出各个频率下的开环对数幅值和相位,在半对数座标纸上作出实验曲线:开环对数幅频曲线和相频曲线。
根据实验开环对数幅频曲线画出开环对数幅频曲线的渐近线,再根据渐近线的斜率和转角频确定频率特性(或传递函数)。
所确定的频率特性(或传递函数)的正确性可以由测量的相频曲线来检验,对最小相位系统而言,实际测量所得的相频曲线必须与由确定的频率特牲(或传递函数)所画出的理论相频曲线在一定程度上相符,如果测量所得的相位在高频(相对于转角频率)时不等于- 90°(q-p)[式中p和q分别表示传递函数分子和分母的阶次],那么,频率特性(或传递函数)必定是一个非最小相位系统的频率特性。
自动控制原理学生实验:二阶开环系统的频率特性曲线

实验三 二阶开环系统的频率特性曲线一.实验要求1.研究表征系统稳定程度的相位裕度γ和幅值穿越频率c ω对系统的影响。
2.了解和掌握欠阻尼二阶开环系统中的相位裕度γ和幅值穿越频率c ω的计算。
3.观察和分析欠阻尼二阶开环系统波德图中的相位裕度γ和幅值穿越频率ωc ,与计算值作比对。
二.实验内容及步骤本实验用于观察和分析二阶开环系统的频率特性曲线。
由于Ⅰ型系统含有一个积分环节,它在开环时响应曲线是发散的,因此欲获得其开环频率特性时,还是需构建成闭环系统,测试其闭环频率特性,然后通过公式换算,获得其开环频率特性。
自然频率:TiT K=n ω 阻尼比:KT Ti21=ξ (3-2-1) 谐振频率:221ξωω-=n r 谐振峰值:2121lg20)(ξξω-=r L (3-2-2)计算欠阻尼二阶闭环系统中的幅值穿越频率ωc 、相位裕度γ: 幅值穿越频率: 24241ξξωω-+⨯=n c (3-2-3)相位裕度: 424122arctan)(180ξξξωϕγ++-=+=c(3-2-4)γ值越小,Mp%越大,振荡越厉害;γ值越大,Mp%小,调节时间ts 越长,因此为使二阶闭环系统不致于振荡太厉害及调节时间太长,一般希望:30°≤γ≤70° (3-2-5)本实验所构成的二阶系统符合式(3-2-5)要求。
被测系统模拟电路图的构成如图1所示。
图1 实验电路本实验将数/模转换器(B2)单元作为信号发生器,自动产生的超低频正弦信号的频率从低到高变化(0.5Hz~16Hz ),OUT2输出施加于被测系统的输入端r (t),然后分别测量被测系统的输出信号的开环对数幅值和相位,数据经相关运算后在虚拟示波器中显示。
实验步骤:(1)将数/模转换器(B2)输出OUT2作为被测系统的输入。
(2)构造模拟电路:安置短路套及测孔联线表同笫3.2.2 节《二阶闭环系统的频率特性曲线测试》。
(3)运行、观察、记录:① 将数/模转换器(B2)输出OUT2作为被测系统的输入,运行LABACT 程序,在界面的自动控制菜单下的线性控制系统的频率响应分析-实验项目,选择二阶系统,就会弹出虚拟示波器的界面,点击开始,实验开始后,实验机将自动产生0.5Hz~16H 等多种频率信号,等待将近十分钟,测试结束后,观察闭环对数幅频、相频曲线和幅相曲线。
自动控制原理实验

第二部分控制理论实验一典型环节的电路模拟与软件仿真一、实验目的1.熟悉并掌握THBCC-1型信号与系统·控制理论及计算机控制技术实验平台及上位机软件的使用方法。
2.熟悉各典型环节的电路传递函数及其特性,掌握典型环节的电路模拟与软件仿真研究。
3.测量各典型环节的阶跃响应曲线,了解参数变化对其动态特性的影响。
二、实验设备1.THBCC-1型信号与系统·控制理论及计算机控制技术实验平台2.PC机1台(含上位机软件) 37针通信线1根3.双踪慢扫描示波器1台(可选)三、实验内容1.设计并组建各典型环节的模拟电路;2.测量各典型环节的阶跃响应,并研究参数变化对其输出响应的影响;3.在上位机界面上,填入各典型环节数学模型的实际参数,据此完成它们对阶跃响应的软件仿真,并与模拟电路测试的结果相比较。
四、实验原理自控系统是由比例、积分、惯性环节等按一定的关系连接而成。
熟悉这些惯性环节对阶跃输入的响应,对分析线性系统将是十分有益。
在附录中介绍了典型环节的传递函数、理论上的阶跃响应曲线和环节的模拟电路图。
五、实验步骤1.熟悉实验台,利用实验台上的模拟电路单元,构建所设计的(可参考本实验附录)并连接各典型环节(包括比例、积分、比例积分、比例微分、比例积分微分以及惯性环节)的模拟电路。
待检查电路接线无误后,接通实验台的电源总开关,并开启±5V,±15V直流稳压电源。
2.对相关的实验单元的运放进行调零(令运放各输入端接地,调节调零电位器,使运放输出端为0V)注意:积分、比例积分、比例积分微分实验中所用到的积分环节单元)不需要锁零(令积分电容放电)时,需将锁零按钮弹开,使用锁零按扭时需要共地,则需要把信号发生器的地和电源地用导线相连。
3.测试各典型环节的阶跃响应,并研究参数变化对输出响应的影响1) 不用上位机时,将实验平台上 “阶跃信号发生器”单元的输出端与相关电路的输入端相连,选择“正输出”然后按下按钮,产生一个阶跃信号(用万用表测试其输出电压,并调节电位器,使其输出电压为“1”V ,用示波器x-t 显示模式观测该电路的输入与输出曲线如果效果不好要做新做则只要按一下锁零开关对电容放电,在重新做即可。
自动控制原理_卢京潮_利用开环频率特性分析系统的性能

自动控制原理_卢京潮_利用开环频率特性分析系统的性能自动控制原理是指通过对系统采集的输入与输出信号进行比较,利用控制器对系统进行调节,实现对所控对象的自动调整的一种技术。
其中,开环控制是一种最基本的控制方式,其通过直接将控制量输入到被控对象中,实现对系统的控制。
而开环频率特性分析则是通过对开环控制系统进行频率特性分析,来评估系统的性能。
开环频率特性分析主要包括幅频特性分析和相频特性分析。
首先,幅频特性分析是指通过改变输入信号的频率,观察输出信号的幅值变化,从而分析系统的频率响应。
在开环控制系统中,通过改变输入信号的频率,可以得到系统的频率特性曲线,即Bode图。
Bode图包括幅频特性曲线和相频特性曲线两部分。
幅频特性曲线反映了系统对不同频率的输入信号的放大或衰减程度。
它是由系统的增益裕度和截止频率决定的。
增益裕度表示系统对输入信号幅值的放大倍数,而截止频率则表示系统能够传递的最高频率。
通过幅频特性曲线的分析,可以判断系统的稳定性和频率特性,以及对各个频率成分的衰减程度。
相频特性分析是指通过改变输入信号的频率,观察输出信号与输入信号之间的相位差,从而分析系统的相位特性。
相频特性曲线反映了系统对不同频率输入信号的相位差变化。
通过相频特性曲线的分析,可以得出系统响应的相位裕度和相角裕度。
相位裕度表示系统对输入信号相位变化的响应程度,相角裕度则表示系统能够承受的相位变化范围。
通过对开环控制系统的幅频特性和相频特性进行分析,可以对系统的性能进行评估。
常用的评估指标包括频率响应曲线的特征参数,如增益裕度、相位裕度、截止频率等。
增益裕度和相位裕度越大,说明系统对干扰和变化的抑制能力越强,系统的稳定性越好。
截止频率则表示了系统对高频信号的响应能力。
通过频率特性分析,可以对系统进行合理的调整和优化,确保系统具有足够的控制能力和稳定性。
总之,利用开环频率特性分析系统的性能,可以为控制系统的设计和调整提供指导。
通过分析系统的幅频特性和相频特性,可以评估系统的稳定性、频率响应特性和抑制能力,从而实现对系统的优化和改进。
自动控制原理学生实验:二阶开环系统的频率特性曲线

实验三 二阶开环系统的频率特性曲线一.实验要求1.研究表征系统稳定程度的相位裕度γ和幅值穿越频率c ω对系统的影响。
2.了解和掌握欠阻尼二阶开环系统中的相位裕度γ和幅值穿越频率c ω的计算。
3.观察和分析欠阻尼二阶开环系统波德图中的相位裕度γ和幅值穿越频率ωc ,与计算值作比对。
二.实验内容及步骤本实验用于观察和分析二阶开环系统的频率特性曲线。
由于Ⅰ型系统含有一个积分环节,它在开环时响应曲线是发散的,因此欲获得其开环频率特性时,还是需构建成闭环系统,测试其闭环频率特性,然后通过公式换算,获得其开环频率特性。
自然频率:TiT K=n ω 阻尼比:KT Ti21=ξ (3-2-1) 谐振频率:221ξωω-=n r 谐振峰值:2121lg20)(ξξω-=r L (3-2-2)计算欠阻尼二阶闭环系统中的幅值穿越频率ωc 、相位裕度γ: 幅值穿越频率: 24241ξξωω-+⨯=n c (3-2-3)相位裕度: 424122arctan)(180ξξξωϕγ++-=+=c(3-2-4)γ值越小,Mp%越大,振荡越厉害;γ值越大,Mp%小,调节时间ts 越长,因此为使二阶闭环系统不致于振荡太厉害及调节时间太长,一般希望:30°≤γ≤70° (3-2-5)本实验所构成的二阶系统符合式(3-2-5)要求。
被测系统模拟电路图的构成如图1所示。
图1 实验电路本实验将数/模转换器(B2)单元作为信号发生器,自动产生的超低频正弦信号的频率从低到高变化(0.5Hz~16Hz ),OUT2输出施加于被测系统的输入端r (t),然后分别测量被测系统的输出信号的开环对数幅值和相位,数据经相关运算后在虚拟示波器中显示。
实验步骤:(1)将数/模转换器(B2)输出OUT2作为被测系统的输入。
(2)构造模拟电路:安置短路套及测孔联线表同笫3.2.2 节《二阶闭环系统的频率特性曲线测试》。
(3)运行、观察、记录:① 将数/模转换器(B2)输出OUT2作为被测系统的输入,运行LABACT 程序,在界面的自动控制菜单下的线性控制系统的频率响应分析-实验项目,选择二阶系统,就会弹出虚拟示波器的界面,点击开始,实验开始后,实验机将自动产生0.5Hz~16H 等多种频率信号,等待将近十分钟,测试结束后,观察闭环对数幅频、相频曲线和幅相曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 二阶开环系统的频率特性曲线
一.实验要求
1.研究表征系统稳定程度的相位裕度γ和幅值穿越频率c ω对系统的影响。
2.了解和掌握欠阻尼二阶开环系统中的相位裕度γ和幅值穿越频率c ω的计算。
3.观察和分析欠阻尼二阶开环系统波德图中的相位裕度γ和幅值穿越频率ωc ,与计算值作比对。
二.实验内容及步骤
本实验用于观察和分析二阶开环系统的频率特性曲线。
由于Ⅰ型系统含有一个积分环节,它在开环时响应曲线是发散的,因此欲获得其开环频率特性时,还是需构建成闭环系统,测试其闭环频率特性,然后通过公式换算,获得其开环频率特性。
自然频率:T iT
K
=
n ω 阻尼比:KT Ti
2
1=
ξ (3-2-1) 谐振频率:
2
21ξωω-=n r 谐振峰值:2
121lg
20)(ξ
ξω-=r L (3-2-2)
计算欠阻尼二阶闭环系统中的幅值穿越频率ωc 、相位裕度γ: 幅值穿越频率: 24241ξξωω-+⨯
=n c (3-2-3)
相位裕度: 4
24122arctan
)(180ξξξωϕγ++-=+=c
(3-2-4)
γ值越小,Mp%越大,振荡越厉害;γ值越大,Mp%小,调节时间ts 越长,因此为使
二阶闭环系统不致于振荡太厉害及调节时间太长,一般希望:
30°≤γ≤70° (3-2-5)
本实验所构成的二阶系统符合式(3-2-5)要求。
被测系统模拟电路图的构成如图1所示。
图1 实验电路
本实验将数/模转换器(B2)单元作为信号发生器,自动产生的超低频正弦信号的频率从低到高变化(0.5Hz~16Hz ),OUT2输出施加于被测系统的输入端r (t),然后分别测量被测系统的输出信号的开环对数幅值和相位,数据经相关运算后在虚拟示波器中显示。
实验步骤:
(1)将数/模转换器(B2)输出OUT2作为被测系统的输入。
(2)构造模拟电路:安置短路套及测孔联线表同笫3.2.2 节《二阶闭环系统的频率特性曲线测试》。
(3)运行、观察、记录:
① 将数/模转换器(B2)输出OUT2作为被测系统的输入,运行LABACT 程序,在界面
的自动控制菜单下的线性控制系统的频率响应分析-实验项目,选择二阶系统,就会弹出虚拟示波器的界面,点击开始,实验开始后,实验机将自动产生0.5Hz~16H 等多种频率信号,等待将近十分钟,测试结束后,观察闭环对数幅频、相频曲线和幅相曲线。
② 待实验机把闭环频率特性测试结束后,再在示波器界面左上角的红色‘开环’或‘闭
环’字上双击,将在示波器界面上弹出‘开环/闭环’选择框,点击确定后,示波器界面左上角的红字,将变为‘开环’然后再在示波器界面下部‘频率特性’选择框点击(任一项),在示波器上将转为‘开环’频率特性显示界面。
可点击界面下方的“频率特性”选择框中的任意一项进行切换,将显示被测系统的开环对数幅频、相频特性曲线(伯德图)和幅相曲线(奈奎斯特图)。
③幅值穿越频率ωc ,相位裕度γ的测试:
在开环对数幅频曲线中,用鼠标在曲线L(ω)=0 处点击一下,待检测完成后,就可以根据‘十字标记’测得系统的幅值穿越频率ωc ,见图3-2-6 (a );同时还可在开环对数相频曲线上根据‘十字标记’测得该系统的相位裕度γ。
实验结果与式(3-2-3)和(3-2-4)的理论计算值进行比对。
④ 改变惯性环节开环增益:改变运算模拟单元A3的输入电阻R=10K 、4K 、2K 。
Ti=1(C1=2u ),T=0.1(C2=1u )( R 減小(ξ減小))。
改变惯性环节时间常数:改变运算模拟单元A3的反馈电容C 2=1u 、2u 、3u 。
Ti=1(C1=2u ),K=25(R=4K ),(C 2增加 (ξ減小))。
改变积分环节时间常数:改变运算模拟单元A3的反馈电容C 1=1u 、2u 。
T=0.1(C2=1u ),K=25(R=4K ) ,(C1減小(ξ減小))。
重新观测结果,界面上方将显示该系统用户点取的频率点的ω、L 、φ、Im 、Re 、谐振频率ωr ,谐振峰值L(ωr )等相关数据,填入实验报告。
三.实验数据及数据处理
实验条件: 12R=10K ,C =2F,C =1F,μμΩ侧得开环频率特性曲线如下图
图2: 幅频特性曲线
图3: 幅相特性曲线
图4: 相频特性曲线
取点前数据表 取点后数据表
实验条件: 12R=4K ,C =2F,C =1F,μμΩ测得波形图如下所示:
图5:幅频特性曲线 图6:相频特性曲线 图7:幅相特性曲线
取点前数据表 取点后数据表
实验条件: 12R=2K ,C =2F,C =1F,μμΩ侧得开环频率特性曲线如下图
图8:幅频特性曲线 图9:相频特性曲线 图10: 幅相特性曲线
取点前数据表 取点后数据表
实验条件: 12R=4K ,C =2F,C =2F,μμΩ测得波形图如下所示:
图11: 幅频特性 图12:相频特性 图13: 幅相特性
取点前数据表 取点后数据表
实验条件: 12R=4K ,C =2F,C =3F,μμΩ测得波形图如下所示:
图14: 幅频特性 图15: 相频特性 图16: 幅相特性
取点前数据表 取点后数据表
实验条件: 12R=4K ,C =1F,C =1F,μμΩ测得波形图如下所示:
图17幅频特性 图18相频特性 图19: 幅相特性
取点前数据表 取点后数据表。
