用GAAA求解TSP问题

合集下载

数学建模之求解TSP问题的遗传算法

求解TSP问题的遗传算法实现邱文（湖北工业大学机械学院，湖北，武汉，120131055）摘要：本文应用遗传算法（GA）解决TSP（travel salesman problem）问题，在此采用基于对各个城市访问顺序的编码方案，同时在探讨影响GA性能的遗传算子的基础上，介绍了可以改善解的质量的倒位算子。

最后通过在VC++6.0上运行该算法的程序得到问题的最优解。

关键词：遗传算法（GA）TSP问题倒位算子最优解Genetic Algorithm for Solving TSP ProblemsQiu Wen(School of Science, Hubei University of Technology, Hubei, Wuhan,120131055）Abstract:This paper apply genetic algorithm to solve TSP(travel salesman problems) problem .The encoding scheme based on sequence of each city .During the same time , on the studying of the performance of genetic algorithm which based on the genetic operators , we introduce an inversion operator to improve the quality of solution .Keywords: genetic algorithm (GA); TSP problem; inversion optimal solution1引言TSP问题（Traveling Salesman Problems 可描述为：已知n个城市之间的相互距离，现有一推销员必须遍历这n个城市，并且每个城市只能访问一次，最后又必须返回出发城市。

TSP问题用GA方法求解

程序一：主程序%TSP问题（又名：旅行商问题，货郎担问题）遗传算法通用matlab程序%D是距离矩阵，n为种群个数%参数a是中国31个城市的坐标%C为停止代数，遗传到第C代时程序停止,C的具体取值视问题的规模和耗费的时间而定%m为适应值归一化淘汰加速指数,最好取为1,2,3,4,不宜太大%alpha为淘汰保护指数,可取为0~1之间任意小数,取1时关闭保护功能,建议取0.8~1.0之间的值%R为最短路径,Rlength为路径长度function [R,Rlength]=geneticTSP(D,a,n,C,m,alpha)[N,NN]=size(D);farm=zeros(n,N);%用于存储种群for i=1:nfarm(i,:)=randperm(N);%随机生成初始种群endR=farm(1,:);subplot(1,3,1)scatter(a(:,1),a(:,2),'x')pause(1)subplot(1,3,2)plotaiwa(a,R)pause(1)farm(1,:)=R;len=zeros(n,1);%存储路径长度fitness=zeros(n,1);%存储归一化适应值counter=0;while counterfor i=1:nlen(i,1)=myLength(D,farm(i,:));%计算路径长度endmaxlen=max(len);minlen=min(len);fitness=fit(len,m,maxlen,minlen);%计算归一化适应值rr=find(len==minlen);R=farm(rr(1,1),:);%更新最短路径FARM=farm;%优胜劣汰，nn记录了复制的个数nn=0;for i=1:nif fitness(i,1)>=alpha*randnn=nn+1;FARM(nn,:)=farm(i,:);endendFARM=FARM(1:nn,:);[aa,bb]=size(FARM);%交叉和变异while aaif nn<=2nnper=randperm(2);elsennper=randperm(nn);endA=FARM(nnper(1),:);B=FARM(nnper(2),:);[A,B]=intercross(A,B);FARM=[FARM;A;B];[aa,bb]=size(FARM);endif aa>nFARM=FARM(1:n,:);%保持种群规模为nendfarm=FARM;clear FARMcounter=counter+1endRlength=myLength(D,R);subplot(1,3,3)plotaiwa(a,R)程序二：计算邻接矩阵%输入参数a是中国31个城市的坐标%输出参数D是无向图的赋权邻接矩阵function D=ff01(a)[c,d]=size(a);D=zeros(c,c);for i=1:cfor j=i:cbb=(a(i,1)-a(j,1)).^2+(a(i,2)-a(j,2)).^2;D(i,j)=bb^(0.5);D(j,i)=D(i,j);endend程序三：计算归一化适应值%计算归一化适应值的子程序function fitness=fit(len,m,maxlen,minlen)fitness=len;for i=1:length(len)fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.0001))).^m;end程序四：交叉和变异的子程序%交叉算法采用的是由Goldberg和Lingle于1985年提出的PMX(部分匹配交叉) function [a,b]=intercross(a,b)L=length(a);if L<=10%确定交叉宽度W=9;elseif ((L/10)-floor(L/10))>=rand&&L>10W=ceil(L/10)+8;elseW=floor(L/10)+8;endp=unidrnd(L-W+1);%随机选择交叉范围，从p到p+Wfor i=1:W%交叉x=find(a==b(1,p+i-1));y=find(b==a(1,p+i-1));[a(1,p+i-1),b(1,p+i-1)]=exchange(a(1,p+i-1),b(1,p+i-1));[a(1,x),b(1,y)]=exchange(a(1,x),b(1,y));endfunction [x,y]=exchange(x,y)temp=x;x=y;y=temp;程序五: 计算路径的子程序%该路径长度是一个闭合的路径的长度function len=myLength(D,p)[N,NN]=size(D);len=D(p(1,N),p(1,1));for i=1:(N-1)len=len+D(p(1,i),p(1,i+1));end程序六：用于绘制路径示意图的程序function plotaiwa(a,R)scatter(a(:,1),a(:,2),'x')hold onplot([a(R(1),1),a(R(31),1)],[a(R(1),2),a(R(31),2)])hold onfor i=2:length(R)x0=a(R(i-1),1);y0=a(R(i-1),2);x1=a(R(i),1);y1=a(R(i),2);xx=[x0,x1];yy=[y0,y1];plot(xx,yy)hold onend。

第17章基于GA的TSP求解

第十七章
MATLAB优化算法案例分析与应用
第17章基于GA的TSP求解
第十七章
MATLAB优化算法案例分析与应用
•17.1 旅行商问题分析
旅行商问题（Traveling Salesman Problem，简称TSP），也称货郎担问题，是数学领域中的著名问题之一。 TSP问题已经被证明是一个NP-hard问题，由于TSP问题代表一类组合优化问题，因此对其近似解的研究一直是算法设计的一个重要问题。该问题的求解算法主要分为两类。一类是与问题特征相关的启发式搜索算法。主要有动态规划法、分支界定法等。另一类是独立于问题的智能优化算法，如模拟退火法、禁忌搜索法、蚁群算法、遗传算法、粒子群算法等。本文将基于遗传算法进行 TSP问题的求解。
17.3.2 基于遗传算法的TSP算法框架
遗传算法求解TSP的基本步骤如下：（1）种群初始化。个体编码方法有二进制编码和实数编码，在解决TSP问题过程中个体编码方法为实数编码。对于TSP问题，实数编码为1-n的实数的随机排列，初始化的参数有种群个数M、染色体基因个数N（即城市的个数）、迭代次数C、交叉概率Pc、变异概率Pm。（2）适应度函数。在TSP问题中，对于任意两个城市之间的距离 D i, j 已知，每个染色体（即n个城市的随机排列）可计算出总距离，因此可将一个随机全排列的总距离的倒数作为适应度函数，即距离越短，适应度函数越好，满足TSP要求。（3）选择操作。遗传算法选择操作有轮盘赌法、锦标赛法等多种方法，本程序采用基于适应度比例的选择策略，即适应度越好的个体被选择的概率越大，同时在选择中保存适应度最高的个体。（4）交叉操作。遗传算法中交叉操作有多种方法。本程序中对于个体，随机选择两个个体，在对应位置交换若干个基因片段，同时保证每个个体依然是1-n的随机排列，防止进入局部收敛。（5）变异操作。本程序中对于变异操作，随机选取个体，同时随机选取个体的两个基因进行交换以实现变异操作。

遗传算法（GA）解决TSP问题

遗传算法（GA）解决TSP问题遗传算法解决TSP问题遗传算法遗传算法的基本原理是通过作⽤于染⾊体上的基因寻找好的染⾊体来求解问题，它需要对算法所产⽣的每个染⾊体进⾏评价，并基于适应度值来选择染⾊体，使适应性好的染⾊体有更多的繁殖机会，在遗传算法中，通过随机⽅式产⽣若⼲个所求解问题的数字编码，即染⾊体，形成初始种群；通过适应度函数给每个个体⼀个数值评价，淘汰低适应度的个体，选择⾼适应度的个体参加遗传操作，经过遗产操作后的个体集合形成下⼀代新的种群，对这个新的种群进⾏下⼀轮的进化。

TSP问题TSP问题即旅⾏商问题，经典的TSP可以描述为：⼀个商品推销员要去若⼲个城市推销商品，该推销员从⼀个城市出发，需要经过所有城市后，回到出发地。

应如何选择⾏进路线，以使总的⾏程最短。

从图论的⾓度来看，该问题实质是在⼀个带权完全⽆向图中，找⼀个权值最⼩的哈密尔顿回路。

遗传算法解决TSP问题概念介绍：种群 ==> 可⾏解集个体 ==> 可⾏解染⾊体 ==> 可⾏解的编码基因 ==> 可⾏解编码的分量基因形式 ==> 遗传编码适应度 ==> 评价的函数值（适应度函数）选择 ==> 选择操作交叉 ==> 编码的交叉操作变异 ==> 可⾏解编码的变异遗传操作：就包括优选适应性强的个体的“选择”；个体间交换基因产⽣新个体的“交叉”；个体间的基因突变⽽产⽣新个体的“变异”。

其中遗传算法是运⽤遗传算⼦来进⾏遗传操作的。

即：选择算⼦、变异算⼦、交叉算⼦。

遗传算法的基本运算过程（1）种群初始化：个体编码⽅法有⼆进制编码和实数编码，在解决TSP问题过程中个体编码⽅法为实数编码。

对于TSP问题，实数编码为1-n的实数的随机排列，初始化的参数有种群个数M、染⾊体基因个数N（即城市的个数）、迭代次数C、交叉概率Pc、变异概率Pmutation。

（2）适应度函数：在TSP问题中，对于任意两个城市之间的距离D(i,j)已知，每个染⾊体（即n个城市的随机排列）可计算出总距离，因此可将⼀个随机全排列的总距离的倒数作为适应度函数，即距离越短，适应度函数越好，满⾜TSP要求。

遗传算法(GA)在旅行商问题(TSP)中的应用

遗传算法（GA）在旅行商问题（TSP）中的应用旅行推销员问题（Traveling Saleman Problem，TSP）又被译为旅行商问题，简称为TSP，是最基本的路由问题，问题是在寻找从起点单一的旅客，所有给出需求点之后，最后回到最小路径成本的起源。

最早的旅行商问题数学规划是由Dantzig（1959）等提出。

文章通过遗传算法及三交换启发交叉（THGA），较好的解决了点数较多时最优解的查询，算法结构简明，可用于大规模点阵的最优路径问题。

标签：遗传算法；最优路径；旅行商问题；C++指针1 概述“旅行商问题”常被称为“旅行推销员问题”，指的是需要有一个推销员拜访多个地点，如何找到时间来访问每个地点，然后返回到最短路径的起点。

规则是简单的，但增加了位置的数量后，解决极为复杂。

以42个地点举例，以确定是否要列出所有最好的旅游路线，然后计算总路径大，几乎难以计数。

多年来全球数学家竭尽全力，试图找到一个高效的算法。

在文章中，基于遗传算法寻求TSP 问题的更优解决。

2 遗传算法介绍2.1 遗传算法的机理在遗传算法中，优化问题的解决方案被称为个体，它可表示为染色体或基因串。

染色体通常可以表示为一个简单的字符串或数字串，这个过程称为编码处理。

算法随机生成一定数量的个体。

在每一代均可以被评估，并通过计算获得适应度值。

之后个体和群体组成的下一代。

这个过程是通过交配（crossover）和突变（mutation）来实现。

根据一项新的个体适应选择，这个过程被重复：每个个体进行评价，计算两个个体的适合度进行交配，然后突变，形成第三代。

周而复始，直到终止条件出现。

2.2 遺传算法的实施步骤（1）选择一个编码；给出一个有N个染色体的出事群体pop，t：=1。

（2）对群体pop（t）中每一个染色体计算它的适应函数fi=fitness（popi（t））。

（3）若停止的规则满足，则算法会停止；否则，计算概率，i=1，2，…，N，并以概率的分布（9）从pop（t）随机选染色体来构成一个新种群NewPOP（t+1）={popi（t）1j=1，2，…，N}（4）通过交配得到一个拥有N个染色体的CrossPOP（t+1）。

遗传算法求解TSP问题的实现与改进

遗传算法求解TSP问题的实现与改进作者：周春辉胡适军文元桥来源：《软件导刊》2013年第02期摘要：旅行商问题（Traveling Salesman Problem，简称TSP）已经被证明为NP难题。

通过应用遗传算法求解TSP问题，给出了遗传算法中各算子的实现方法，并用遗传算法（Genetic Algorithm，简称GA）和穷举法分别求解了15个城市的TSP问题，结果表明，遗传算法具有明显的优越性。

引入模拟退火的思想对遗传算法的变异算子进行改进，并求解了50个城市的TSP，得到了满意的结果。

关键词：遗传算法；TSP；模拟退火中图分类号：TP312 文献标识码：A 文章编号：16727800（2013）0020055030 引言本文在分析遗传算法的基础之上求解TSP问题，并与穷举法所得结果进行比较。

表明了遗传算法在求解此问题上的优越性。

针对遗传算法的不足，结合模拟退火思想对遗传算法进行改进，取得了理想的试验结果。

1 算法设计TSP问题的模型是简单而易于描述的。

实际应用中，像印刷电路板工艺这样的应用可能是和模型比较接近的。

但是模型中的城市之间的距离代表的是某个解的耗费，实际中不一定是欧氏距离，有可能点与点之间的耗费需要另外用权值给出。

而且在实际中，两个城市之间的消耗不一定是对称的，例如乘船到另一城市和返回的费用可能是不同的。

这里对TSP问题模型进行简化，在500×500的平面内随机生成了一些点，用它们来代表城市。

假设每个城市和其它任意一个城市之间都以欧氏距离直接相连。

1.1 遗传算法的总体框架遗传算法的简单通用的特点，主要是指其主要框架简单通用，可以说是万变不离其中。

其基本结构可以概括为：①初始化种群；②对种群每个个体进行评估；③选择（竞争生存机会）；④变化（重组、杂交与变异）；⑤如不满足终止条件，转②；否则结束。

其中变化算子的设计是最重要的，既要考虑保留种群在演化中产生的好的基因，又不能使种群过早地局限于某个局部。

TSP的几种求解方法及其优缺点

TSP的几种求解方法及其优缺点一、什么是TSP问题旅行商问题，简称TSP，即给定n个城市和两两城市之间的距离，要求确定一条经过各城市当且仅当一次的最短路线。

其图论描述为：给定图G=（V，A），其中V为顶点集，A 为各顶点相互连接组成的边集，设D=（dij）是由顶点i和顶点j之间的距离所组成的距离矩阵，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短距离。

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，⋯，n）；2）非对称旅行商问题（dij≠dji，ϖi，j=1，2，3，⋯，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

若对于城市V={v1，v2，v3，⋯，v n}的一个访问顺序为T={t1，t2，t3，⋯，t i，⋯，t n}，其中t i∈V（i=1，2，3，⋯，n），且记t n+1=t1，则旅行商问题的数学模型为：minL=。

TSP是一个典型的组合优化问题，并且是一个NP完全难题，是诸多领域内出现的多种复杂问题的集中概括和简化形式，并且已成为各种启发式的搜索、优化算法的间接比较标准。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

但是，由于构造型算法优化质量较差，迄今为止已开发了许多性能较好的改进型搜索算法，主要有：1）模拟退火算法2）禁忌搜索算法3）Hopfield神经网络优化算法4）蚁群算法5）遗传算法6）混合优化策略2.1模拟退火算法方法1）编码选择：采用描述TSP解的最常用的一种策略——路径编码。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SW AP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

GA-TSP

i<n and child[i]!=0:
i += 1
if i>=n:
break
child[i] = temp[j]
i += 1
j += 1
temp = copy.copy(mother)
for i in range(begin,end+1):
child[i] = father[i]
temp.remove(child[i])
i = 1
j = 1
distance[i][j] = int(line[j])
fp.close()
return distance,n
def randRout(n):
"""
随机产生一个以 0 城市为开头的路线
input:
n: int,城市个数
n: int,城市个数
output:
l: int,闭合路径的长度
"""
l = 0
for i in range(-1,n-1):
l += distance[rout[i]][rout[i+1]]
return l
def cross(father,mother,n):
"""
交叉规则：随机一段，保留father该段的gene，并将mother中剩余的gene按顺序填入
input:
father: 列表，亲代路径1
mother：列表，亲代路径2
for i in range(n):
line = fp.readline().split()

佳点集遗传算法求解安徽十七的TSP问题

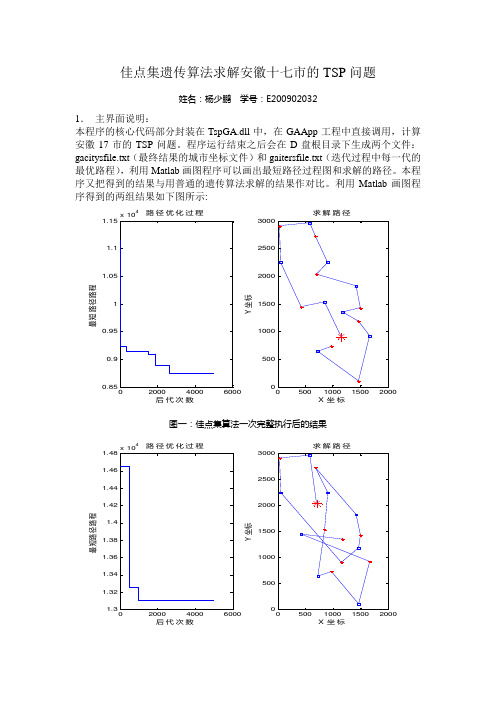
佳点集遗传算法求解安徽十七市的TSP 问题姓名：杨少鹏学号：E2009020321．主界面说明：本程序的核心代码部分封装在TspGA.dll 中，在GAApp 工程中直接调用，计算安徽17市的TSP 问题。

程序运行结束之后会在D 盘根目录下生成两个文件：gacitysfile.txt （最终结果的城市坐标文件）和gaitersfile.txt （迭代过程中每一代的最优路程），利用Matlab 画图程序可以画出最短路径过程图和求解的路径。

本程序又把得到的结果与用普通的遗传算法求解的结果作对比。

利用Matlab 画图程序得到的两组结果如下图所示:0.850.90.9511.051.11.154后代次数最短路径路程路径优化过程50010001500200025003000Ｘ坐标Ｙ坐标求解路径图一：佳点集算法一次完整执行后的结果1.31.321.341.361.381.41.421.441.461.484后代次数最短路径路程路径优化过程50010001500200025003000Ｘ坐标Ｙ坐标求解路径图二：普通遗传算法一次完整执行后的结果2. 动态链接库说明1）gacode.h 算法中所需结构体的定义，包括SYCoordinate、SYCity、SYCityDistance、SYRouter2）gacode.cpp 算法中所有功能函数的实现，主要包括InitialGA、CountCityDistance、CreateCityRouter2opt、CountTotalDistance、CreateFitnessofPop、SelectPop、CrossoverPop、Crossover、MutationPop、OneIterGACompution等等。

后面将分别介绍这些功能函数的作用。

3）MainFrm.cpp流程控制函数的实现，该函数是GACompution。

后面将详细介绍该函数的流程。

3.流程控制函数和功能函数的介绍(主要部分)流程控制函数GACompution控制循环的迭代和结束，其主要代码如下：UINT GACompution(LPVOID pParam){int totalgen = GetTotalGeneration(); //获取遗传算法的迭代总代数int nowiter = 0;while( nowiter <= totalgen && nowiter >= 0 ) //判断迭代次数是否大于迭代总代数，大于则停止计算{nowiter = OneIterGACompution(); //进行一代计算，包括竞争选择、交叉和变异}}下面是一些重要的功能函数的说明：OneIterGACompution() 最重要的功能函数是，它完成一代的计算，包括竞争选择、交叉和变异，在gacode.cpp中实现，其主要代码如下int OneIterGACompution(){CreateFitnessofPop(FITNESS_MODE); //为每个染色体计算评价函数SelectPop(); //群体竞争选择CrossoverPop(CROSSOVER_MODE); //种群交叉MutationPop(MUTATION_MODE); //种群变异NowGenNumber++; //当前代数递增return NowGenNumber;}CreateFitnessofPop() 对群体中的每个染色体计算适应函数/评价函数，采用基于序的计算方法。

遗传算法解决TSP问题

算法设计技巧与分析题目遗传算法解决TSP问题学院电子工程学院专业智能科学与技术学生姓名教师姓名摘要根据TSP 问题的特征信息并借鉴邻域搜索算法的有关思想，提出了一种基于近邻策略的TSP 问题求解算法，该算法首先依据TSP 问题的特殊性求出相应的近邻模式，再将近邻模式用于初始种群的生成，而后在进化过程中随机引入这类模式。

该算法可以大大缩短遗传进程，提高进化效率。

通过仿真实验，验证了该算法的有效性，并且随着城市数目的增加其优越性更为明显。

关键字：近邻策略；遗传算法；旅行商问题1.引言遗传算法（Genetic Algorithm ，GA ）是一种借鉴生物界中自然选择和进化机制发展起来的随机、自适应全局搜索算法，由Holland 教授于1975 年提出。

Goldberg 总结了一种统一的最基本的遗传算法的形式SGA （Simple Genetic Algorithms ）。

SGA 在选定了染色体编码方案后，随机生成初始群体，再通过选择、交叉、变异三种遗传算子的作用对种群不断实行优化，直至找到问题的最优解或近似最优解。

遗传算法具有很强的全局搜索能力，但是对于大型旅行商问题（TSP ），它存在收敛速度过慢的缺点。

TSP 是一个著名的NP 难的组合优化问题，对称TSP 问题可描述为：给定n 个城市和每两个城市之间的距离，求一条经过所有城市一次且仅一次的长度最短的回路。

TSP 问题的数学表述：寻找一条遍历n 个城市的最短路径，或者说搜索到自然数集X={1，2，3，…，n}（X 中元素表示对n 个城市的编号）的一个全排列π（X ）={v1，v2，…，vn}，使Td = （vi ，vi +1）+d （v1，vn ）n −1i=1取最小值，式中的d（vi，vi+1）表示城市vi到城市vi+1的距离。

对于n 个城市的TSP，其所有的旅程路线组合数目是（n-1）! /2。

当城市数目n 增加时，可能的路径数将呈指数级增长。

应用GA和PSO算法求解10城市TSP问题

应用GA 和PSO 算法求解10城市TSP问题1 问题描述旅行团计划近期在城市A 、B 、C 、D 、E 、F 、G 、H 、I 和J 共10个城市间进行一次周游旅行，为了尽量节省旅行开支，希望能找到一条里程数最少或相对较少的旅行路线。

问题1，给定10个城市之间的公路里程如表1所示，并要求使用GA 算法求解优化问题。

问题2，与问题1数据相同，要求使用PSO 算法求解优化问题。

2 使用GA 算法求解2.1 算法描述(1) 编码和适应度函数分别用1-10表示城市A-J ，然后采用自然数编码方式为TSP 问题编码，例如，旅程（1 6 2 8 9 10 5 7 3 4）表示从城市A 出发分别经过了F-B-H-I-J-E-G-C-D 的一次旅行。

每一个问题的解及算法中的个体都可以计算相应的距离。

那么种群中的最小距离和最大距离也相应的可以确定。

选择种群个数为50。

根据种群中个体的距离并考虑使用自适应的标定方法，定义如下的适应度函数， 2i )-x 1()(种群最小距离种群最大距离种群最小距离距离--=i x f使用此适应度函数的后面的乘方次数可以调整来改变淘汰速度。

这里选择2，表示淘汰速度比较适中。

(2) 定义算子选择算子，根据适应度函数的大小进行选择。

计算每个个体被选中的概率∑==Ni ii i x f x f x p 1)()()(，以各个个体所分配到的概率值作为其遗传到下一代的概率，基于这些概率用赌盘选择法来产生下一代群体。

交叉算子，采用部分映射交叉(Partially Mapped Crossover, PMX)方法实现算法交叉。

首先选取选需要交叉的区间段，然后确定区间段的映射关系，接下来交换区间段的遗传信息，此时未换部分的遗传信息会出现不合法的情况，因此根据将未换部分按映射关系进行交换。

交叉率为0.9。

变异算子，把一个染色体中的两个基因的交换作为变异算法。

在算法中随机的产生一个染色体中需要交换的两个基因的位置，将这两个基因进行交换来实现变异。

用于TSP的自适应贪婪GA算法

第３９卷　第６期２０１２年６月计算机科学Ｃｏｍｐｕｔｅｒ　ＳｃｉｅｎｃｅＶｏｌ．３９Ｎｏ．６Ｊｕｎｅ　２０１２到稿日期：２０１１－０７－２４　返修日期：２０１１－１１－２４本文受软件开发环境国家重点实验室开放课题（ＳＫＬＳＤＥ－２０１１ＫＦ－０４）及国家高技术研究发展计划（８６３计划）（２００９ＡＡ０４３３０３）资助。

陈张和（１９８７－），男，硕士生，主要研究方向为智能算法、非经典逻辑及应用，Ｅ－ｍａｉｌ：ｃｈｅｎｚｈａｎｇｈｅ２０１２＠ｇｍａｉｌ．ｃｏｍ；洪　龙（１９５２－），男，博士，教授，主要研究方向为人工智能、非经典逻辑及应用、计算机系统结构；钱建屹（１９８７－），男，硕士生，主要研究方向为计算机网络。

用于ＴＳＰ的自适应贪婪ＧＡ算法陈张和１　洪　龙１，２　钱建屹１（南京邮电大学计算机学院　南京２１０００３）１　（软件开发环境国家重点实验室　北京１００１９１）２摘　要　ＴＳＰ问题是一个典型的组合优化问题，很多现实生活中的问题都可以归结为ＴＳＰ问题，ＧＡ算法是一种典型的优化算法。

通过对ＧＡ算法要点的分析，提出了一种自适应贪婪ＧＡ算法，以解决ＴＳＰ问题。

自适应适应度函数的各种定义、定理，确保了算法的正确性。

通过平均复制的方法进行选择操作，使得算法不会过早地陷入局部最优。

通过建立基于哈密顿回路的双向环贪婪插入算子进行交叉操作，确保了算法收敛的高效性。

最后通过实例的计算分析及与传统ＧＡ算法的比较，说明了所提出的自适应贪婪ＧＡ算法在ＴＳＰ研究中能够更好地发挥作用。

关键词　自适应适应度函数，平均复制，双向环贪婪插入中图法分类号　ＴＰ３０１．６文献标识码　Ａ　Ａｄａｐｔｉｖｅ　Ｇｒｅｅｄｙ　ＧＡ　Ａｌｇｏｒｉｔｈｍ　ｆｏｒ　ＴＳＰＣＨＥＮ　Ｚｈａｎｇ－ｈｅ１　ＨＯＮＧ　Ｌｏｎｇ１，２　ＱＩＡＮ　Ｊｉａｎ－ｙｉ　１（Ｃｏｌｌｅｇｅ　ｏｆ　Ｃｏｍｐｕｔｅｒ，Ｎａｎｊｉｎｇ　Ｕｎｉｖｅｒｓｉｔｙ　ｏｆ　Ｐｏｓｔｓ　＆Ｔｅｌｅｃｏｍｍｕｎｉｃａｔｉｏｎｓ，Ｎａｎｊｉｎｇ　２１０００３，Ｃｈｉｎａ）１（Ｓｔａｔｅ　Ｋｅｙ　Ｌａｂｏｒａｔｏｒｙ　ｏｆ　Ｓｏｆｔｗａｒｅ　Ｄｅｖｅｌｏｐｍｅｎｔ　Ｅｎｖｉｒｏｎｍｅｎｔ，Ｂｅｉｊｉｎｇ　１００１９１，Ｃｈｉｎａ）２　Ａｂｓｔｒａｃｔ　ＴＳＰ　ｉｓ　ａ　ｔｙｐｉｃａｌ　ｃｏｍｂｉｎａｔｏｒｉａｌ　ｏｐｔｉｍｉｚａｔｉｏｎ　ｐｒｏｂｌｅｍ，ａｎｄ　ｍａｎｙ　ｒｅａｌ　ｌｉｆｅ　ｐｒｏｂｌｅｍｓ　ｃａｎ　ａｔｔｒｉｂｕｔｅｄ　ｔｏ　ｔｈｅ　ＴＳＰ．ＧＡ　ｉｓ　ａ　ｔｙｐｉｃａｌ　ｏｐｔｉｍｉｚａｔｉｏｎ　ａｌｇｏｒｉｔｈｍ．Ａｎａｌｙｚｉｎｇ　ＧＡ’ｓ　ｉｍｐｏｒｔａｎｔ　ｐｏｉｎｔｓ，ａ　ａｄａｐｔｉｖｅ　ｇｒｅｅｄｙ　ＧＡ　ｗａｓ　ｐｒｏｐｏｓｅｄ　ｔｏ　ｓｏｌｖｅＴＳＰ．Ｄｅｆｉｎｉｔｉｏｎｓ　ａｎｄ　ｔｈｅｏｒｅｍｓ　ｏｎ　ａｄａｐｔｉｖｅ　ｆｉｔｎｅｓｓ　ｆｕｎｃｔｉｏｎ　ｅｎｓｕｒｅ　ｔｈｅ　ｃｏｒｒｅｃｔｎｅｓｓ　ｏｆ　ｔｈｅ　ａｌｇｏｒｉｔｈｍ．Ａｌｇｏｒｉｔｈｍ　ｄｏｅｓ　ｎｏｔｐｒｅｍａｔｕｒｅｌｙ　ｆａｌｌ　ｉｎｔｏ　ｌｏｃａｌ　ｏｐｔｉｍｕｍ　ｂｅｃａｕｓｅ　ｏｆ　ａｖｅｒａｇｅ　ｒｅｐｌｉｃａｔｉｏｎ　ｍｅｔｈｏｄ　ｆｏｒ　ｓｅｌｅｃｔ　ｏｐｅｒａｔｉｏｎｓ．Ａｌｇｏｒｉｔｈｍ　ｃａｎ　ｂｅ　ｅｆｆｉ－ｃｉｅｎｔｌｙ　ｃｏｎｖｅｒｇｅｄ　ｂｙ　ｅｓｔａｂｌｉｓｈｉｎｇ　ｂｉｄｉｒｅｃｔｉｏｎａｌ　ｒｉｎｇ　ｇｒｅｅｄ　ｉｎｓｅｒｔ　ｏｐｅｒａｔｏｒ　ｂａｓｅｄ　ｏｎ　Ｈａｍｉｌｔｏｎｉａｎ　ｔｗｏ－ｗａｙ　ｌｏｏｐ　ｃｉｒｃｕｉｔ　ｆｏｒｃｒｏｓｓ　ｏｐｅｒａｔｉｏｎ．Ｆｉｎａｌｌｙ，ｔｈｅ　ｃａｌｃｕｌａｔｉｏｎ　ａｎｄ　ａｎａｌｙｓｉｓ　ｏｆ　ｔｈｅ　ｅｘａｍｐｌｅ　ａｎｄ　ｔｈｅ　ｃｏｍｐａｒｉｓｏｎ　ｗｉｔｈ　ｔｈｅ　ｔｒａｄｉｔｉｏｎａｌ　ＧＡ　ａｌｇｏ－ｒｉｔｈｍ　ｓｈｏｗ　ｔｈａｔ　ｔｈｅ　ｐｒｏｐｏｓｅｄ　ＧＡ　ａｌｇｏｒｉｔｈｍ　ｃａｎ　ｐｌａｙ　ｂｅｔｔｅｒ　ｒｏｌｅ　ｉｎ　ＴＳＰ　ｓｔｕｄｙ．Ｋｅｙｗｏｒｄｓ　Ａｄａｐｔｉｖｅ　ｆｉｔｎｅｓｓ　ｆｕｎｃｔｉｏｎ，Ａｖｅｒａｇｅ　ｃｏｐｙ，Ｂｉｄｉｒｅｃｔｉｏｎａｌ　ｇｒｅｅｄ　ｉｎｓｅｒｔ　１　引言遗传算法是美国Ｍｉｃｈｉｇａｎ大学的Ｊ．Ｈｏｌｌａｎｄ教授于１９７５年提出的。

TSP的几种求解方法及其优缺点

一、什么是TSP问题旅行商问题，简称TSP，即给定n个城市和两两城市之间的距离，要求确定一条经过各城市当且仅当一次的最短路线。

其图论描述为：给定图G=（V，A），其中V为顶点集，A为各顶点相互连接组成的边集，设D=（dij）是由顶点i和顶点j之间的距离所组成的距离矩阵，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短距离。

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，⋯，n）；2）非对称旅行商问题（dij≠dji，ϖi，j=1，2，3，⋯，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

但是，由于构造型算法优化质量较差，迄今为止已开发了许多性能较好的改进型搜索算法，主要有：1）模拟退火算法2）禁忌搜索算法3）Hopfield神经网络优化算法4）蚁群算法5）遗传算法6）混合优化策略模拟退火算法方法1）编码选择：采用描述TSP解的最常用的一种策略——路径编码。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SWAP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

TSP的几种求解方法及其优缺点

其图论描述为：给定图G=（V，A），其中V 为顶点集，A为各顶点相互连接组成的边集，设D=（dij）是由顶点i和顶点j之间的距离所组成的距离矩阵，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短距离。

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，，n）；2）非对称旅行商问题（dij≠dji，i，j=1，2，3，，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

若对于城市V={v1，v2，v3，，v n}的一个访问顺序为T={t1，t2，t3，，t i，，t n}，其中t i∈V（i=1，2，3，，n），且记t n+1=t1，则旅行商问题的数学模型为：minL=。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SWAP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

基于遗传算法（GA）的多变量旅行商问题（TSP）

基于遗传算法（GA）的多变量旅行商问题（TSP）MTSPV_GA可变多个旅行商问题（M - TSP）遗传算法（GA）找到了（附近）的M - TSP的变化（即具有最佳的解决方案可变数量的推销员）设立GA在搜索的最短路径（最小距离为推销员需要前往每个城市一次，并返回其起始位置）摘要：1。

每个业务员一套独特的城市，并完成回城的路线，他开始从2。

每个城市访问过的一个业务员输入：XY（浮动）是一个城市位置的NX2矩阵，其中N是城市数量DMAT（浮动）是NxN的矩阵点的距离或成本点MIN_TOUR（标量整数）是任何推销员的最低游览长度POP_SIZE（标量整数）人口规模（应该是能被4整除）NUM_ITER（标量整数）是算法运行所需的迭代数如果真正SHOW_PROG（标量逻辑）显示GA进展SHOW_RES（标量逻辑）的GA结果显示，如果为true输出：OPT_RTE（整型数组）是由算法发现的最佳途径OPT_BRK（整型数组）是路线破发点的名单（这些指定的指数到用来获取个人业务员路线路线）MIN_DIST（标浮动）由推销员走过的总距离路由/断点详情：如果有10个城市和3个推销员，一个可能的途径/休息组合可能是：RTE = [5 6 9 1 4 2 8 10 3 7]，brks = [3 7]两者合计，这些代表的解决方案[5 6 9] [1 4 2 8] [10 3 7]指定为如下3推销员路线：。

业务员1旅游城市5到6日至9日，回到5。

业务员2旅游城市1至4日至2日至8回1。

业务员3旅游城市10至3日至7回10function varargout = mtspv_ga(xy,dmat,min_tour,pop_size,num_iter,show_prog,show_ res)% MTSPV_GA Variable Multiple Traveling Salesman Problem (M-TSP) Genetic Algorithm (GA)% Finds a (near) optimal solution to a variation of the M-TSP (that has a% variable number of salesmen) by setting up a GA to search for the% shortest route (least distance needed for the salesmen to travel to% each city exactly once and return to their starting locations)%% Summary:% 1. Each salesman travels to a unique set of cities and completes the% route by returning to the city he started from% 2. Each city is visited by exactly one salesman%% Input:% XY (float) is an Nx2 matrix of city locations, where N isthe number of cities% DMAT (float) is an NxN matrix of point to point distances or costs% MIN_TOUR (scalar integer) is the minimum tour length for any of the salesmen% POP_SIZE (scalar integer) is the size of the population (should be divisible by 4)% NUM_ITER (scalar integer) is the number of desired iterations for the algorithm to run% SHOW_PROG (scalar logical) shows the GA progress if true% SHOW_RES (scalar logical) shows the GA results if true %% Output:% OPT_RTE (integer array) is the best route found by the algorithm% OPT_BRK (integer array) is the list of route break points (these specify the indices% into the route used to obtain the individual salesman routes)% MIN_DIST (scalar float) is the total distance traveled by the salesmen%% Route/Breakpoint Details:% If there are 10 cities and 3 salesmen, a possible route/break% combination might be: rte = [5 6 9 1 4 2 8 10 3 7], brks = [3 7]% Taken together, these represent the solution [5 6 9][1 4 2 8][10 3 7],% which designates the routes for the 3 salesmen as follows:% . Salesman 1 travels from city 5 to 6 to 9 and back to 5% . Salesman 2 travels from city 1 to 4 to 2 to 8 and back to 1% . Salesman 3 travels from city 10 to 3 to 7 and back to 10%% Example:% n = 35;% xy = 10*rand(n,2);% min_tour = 3;% pop_size = 40;% num_iter = 5e3;% a = meshgrid(1:n);% dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),n,n);% [opt_rte,opt_brk,min_dist] = mtspv_ga(xy,dmat,min_tour,pop_size,num_iter,1,1);%% Author: Joseph Kirk%Email:*******************% Release: 1.1% Release Date: 9/21/08% Process Inputs and Initialize Defaultsnargs = 7;for k = nargin:nargs-1switch kcase 0xy = 10*rand(40,2);case 1N = size(xy,1);a = meshgrid(1:N);dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),N,N); case 2min_tour = 3;case 3pop_size = 80;case 4num_iter = 5e3;case 5show_prog = 1;case 6show_res = 1;otherwiseendend% Verify InputsN = size(xy,1);[nr,nc] = size(dmat);if N ~= nr || N ~= ncerror('Invalid XY or DMAT inputs!')endn = N;% Sanity Checksmin_tour = max(1,min(n,round(real(min_tour(1))))); pop_size = max(8,8*ceil(pop_size(1)/8));num_iter = max(1,round(real(num_iter(1))));show_prog = logical(show_prog(1));show_res = logical(show_res(1));% Initialize the Populationspop_rte = zeros(pop_size,n); % population of routespop_brk = cell(pop_size,1); % population of breaksfor k = 1:pop_sizepop_rte(k,:) = randperm(n);pop_brk{k} = randbreak();endtmp_pop_rte = zeros(8,n);tmp_pop_brk = cell(8,1);new_pop_rte = zeros(pop_size,n);new_pop_brk = cell(pop_size,1);% Select the Colors for the Plotted Routesclr = hsv(floor(n/min_tour));% Run the GAglobal_min = Inf;total_dist = zeros(1,pop_size);dist_history = zeros(1,num_iter);if show_progpfig = figure('Name','MTSPV_GA | Current Best Solution','Numbertitle','off');endfor iter = 1:num_iter% Evaluate Each Population Member (Calculate Total Distance)for p = 1:pop_sized = 0;p_rte = pop_rte(p,:);p_brk = pop_brk{p};salesmen = length(p_brk)+1;rng = [[1 p_brk+1];[p_brk n]]';for s = 1:salesmend = d + dmat(p_rte(rng(s,2)),p_rte(rng(s,1)));for k = rng(s,1):rng(s,2)-1d = d + dmat(p_rte(k),p_rte(k+1));endendtotal_dist(p) = d;end% Find the Best Route in the Population[min_dist,index] = min(total_dist);dist_history(iter) = min_dist;if min_dist < global_minglobal_min = min_dist;opt_rte = pop_rte(index,:);opt_brk = pop_brk{index};salesmen = length(opt_brk)+1;rng = [[1 opt_brk+1];[opt_brk n]]';if show_prog% Plot the Best Routefigure(pfig);for s = 1:salesmenrte = opt_rte([rng(s,1):rng(s,2) rng(s,1)]);plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:));title(sprintf(['Total Distance = %1.4f, Salesmen = %d, ' ... 'Iterations = %d'],min_dist,salesmen,iter));hold onendhold offendend% Genetic Algorithm Operatorsrand_grouping = randperm(pop_size);for p = 8:8:pop_sizertes = pop_rte(rand_grouping(p-7:p),:);brks = pop_brk(rand_grouping(p-7:p)); dists = total_dist(rand_grouping(p-7:p)); [ignore,idx] = min(dists);best_of_8_rte = rtes(idx,:);best_of_8_brk = brks{idx};rte_ins_pts = sort(ceil(n*rand(1,2)));I = rte_ins_pts(1);J = rte_ins_pts(2);for k = 1:8 % Generate New Solutionstmp_pop_rte(k,:) = best_of_8_rte;tmp_pop_brk{k} = best_of_8_brk;switch kcase 2 % Fliptmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J)); case 3 % Swaptmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]); case 4 % Slidetmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]); case 5 % Change Breakstmp_pop_brk{k} = randbreak();case 6 % Flip, Change Breakstmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J)); tmp_pop_brk{k} = randbreak();case 7 % Swap, Change Breakstmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]); tmp_pop_brk{k} = randbreak();case 8 % Slide, Change Breakstmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]);tmp_pop_brk{k} = randbreak();otherwise % Do Nothingendendnew_pop_rte(p-7:p,:) = tmp_pop_rte;new_pop_brk(p-7:p) = tmp_pop_brk;endpop_rte = new_pop_rte;pop_brk = new_pop_brk;endif show_res% Plotsfigure('Name','MTSPV_GA | Results','Numbertitle','off'); subplot(2,2,1);plot(xy(:,1),xy(:,2),'k.');title('City Locations');subplot(2,2,2);imagesc(dmat(opt_rte,opt_rte));title('Distance Matrix');salesmen = length(opt_brk)+1;subplot(2,2,3);rng = [[1 opt_brk+1];[opt_brk n]]';for s = 1:salesmenrte = opt_rte([rng(s,1):rng(s,2) rng(s,1)]);plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:));title(sprintf('Total Distance = %1.4f',min_dist));hold on;endsubplot(2,2,4);plot(dist_history,'b','LineWidth',2)title('Best Solution History');set(gca,'XLim',[0 num_iter+1],'YLim',[0 1.1*max([1 dist_history])]);end% Return Outputsif nargoutvarargout{1} = opt_rte;varargout{2} = opt_brk;varargout{3} = min_dist;end% Generate Random Set of Breaksfunction breaks = randbreak()salesmen = ceil(floor(n/min_tour)*rand);num_brks = salesmen - 1;dof = n - min_tour*salesmen; % degrees of freedomaddto = ones(1,dof+1);for kk = 2:num_brksaddto = cumsum(addto);endcum_prob = cumsum(addto)/sum(addto);num_adjust = find(rand < cum_prob,1)-1;spaces = ceil(num_brks*rand(1,num_adjust));adjust = zeros(1,num_brks);for kk = 1:num_brksadjust(kk) = sum(spaces == kk);endbreaks = min_tour*(1:num_brks) + cumsum(adjust);endend。

tsp问题有几种方案

TSP问题有几种方案引言TSP（Traveling Salesman Problem，旅行商问题）是指给定一系列城市和每对城市之间的距离，找出一条最短路径，使得旅行商可以从起始城市出发，经过每个城市恰好一次，最后回到起始城市。

TSP问题是一个经典的组合优化问题，在计算机科学和运筹学领域被广泛研究。

本文将介绍TSP问题的几种解决方案。

1. 暴力法暴力法是最简单直接的解决TSP问题的方法。

该方法通过枚举所有可能的路径，并计算每个路径的总距离，最后找出最短路径。

但是，由于TSP问题的解空间随着城市数量的增加呈指数级增长，因此暴力法的时间复杂度非常高，不适用于大规模的问题。

2. 穷举法穷举法是改进的暴力法，通过剪枝操作减少了暴力法的时间复杂度。

穷举法一般使用深度优先搜索（DFS）或广度优先搜索（BFS）算法来遍历解空间，并在搜索过程中记录当前路径的总距离。

当搜索到目标节点时，更新最短路径。

穷举法的时间复杂度仍然很高，但相比暴力法有所改善。

3. 动态规划动态规划是一种常用的解决TSP问题的方法。

动态规划通过将原问题划分为若干子问题，并记录每个子问题的最优解，从而通过计算较小规模的问题得到整体问题的最优解。

具体来说，动态规划中的状态转移方程可以表示为：dp[S][i] = min(dp[S-{i}][j] + d[j][i])，其中 S 表示已经访问过的城市集合，i 表示当前城市，j 表示 i 的上一个访问的城市。

通过迭代计算出 dp[S][i]，最后找出使得 dp[S][i] + d[i][0] 最小的 i 值作为最优路径的终点。

4. 贪心算法贪心算法是一种启发式算法，它通过贪心地选择当前最优解来逐步构建整体问题的解。

在TSP问题中，贪心算法每一步都选择离当前城市最近的未访问过的城市，直到遍历完所有城市。

然而，贪心算法并不能保证得到最优解，因为局部最优解并不一定是全局最优解。

5. 遗传算法遗传算法是一种演化算法，模拟生物进化的过程来寻找最优解。

用遗传算法解决货郎担问题

用遗传算法解决货郎担问题SC10023033 何岸泓摘要：货郎担问题也叫旅行商问题，即TSP问题。

TSP问题是一个组合优化问题。

该问题可以被证明具有NPC计算复杂性。

TSP问题属于易于描述但难于解决的著名难题之一，至今世界上还有不少人在研究它。

在实际运用中，由于TSP问题的复杂度极高，运用面极广，故任何对TSP问题的突破都将受到关注，传统的穷举法在TSP问题中无法实施，而GA算法由于其高度的适应性，近年来受到广泛的关注，本文将试图使用GA算法解决TSP问题，并在文末附上算法结果。

关键字：TSP，货郎担问题，遗传算法，GA，计算机仿真一背景介绍遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

该算法由密歇根大学的约翰·霍兰德和他的同事于二十世纪六十年代在对细胞自动机进行研究时率先提出。

在二十世纪八十年代中期之前，对于遗传算法的研究还仅仅限于理论方面。

随着计算机计算能力的发展和实际应用需求的增多，遗传算法逐渐进入实际应用阶段。

1989年，纽约时报作者约翰·马科夫写了一篇文章描述第一个商业用途的遗传算法--进化者（Evolver）之后，越来越多种类的遗传算法出现并被用于许多领域中，财富杂志500强企业中大多数都用它进行时间表安排、数据分析、未来趋势预测、预算、以及解决很多其他组合优化问题。

遗传算法的发展大致可分为以下几个时期：1）萌芽期：50年代后期至70年代初期；2）成长期：70年代初期至80年代末期；3）发展期：90年代至今；1）萌芽期50年代后期，一些生物学家着手采用电子计算机模拟生物的遗传系统，尽管这些工作纯粹是研究生物现象，但其中已使用现代遗传算法的一些标识方式。

直到1965年，德国的L.Rechenberg等人正式提出进化策略的方法，当时的进化策略只有一个个体，而且进化操作也只有变异一种。

TSP的几种求解方法及其优缺点

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，⋯，n）；2）非对称旅行商问题（dij≠dji，ϖi，j=1，2，3，⋯，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SW AP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

TSP的几种求解方法及其优缺点

旅行商问题可分为如下两类：1）对称旅行商问题（dij=dji，Πi，j=1，2，3，⋯，n）；2）非对称旅行商问题（dij≠dji，ϖi，j=1，2，3，⋯，n）。

非对称旅行商问题较难求解，我们一般是探讨对称旅行商问题的求解。

因此，快速、有效地解决TSP有着重要的理论价值和极高的实际应用价值。

二、主要求解方法基于TSP的问题特性，构造型算法成为最先开发的求解算法，如最近邻点、最近合并、最近插入、最远插入、最近添加、贪婪插入等。

2）SA状态产生函数的设计：对于基于路径编码的SA状态产生函数操作，可将其设计为：①互换操作（SW AP）；②逆序操作（INV）；③插入操作（INS）。

3）SA状态接受函数的设计：min{1，exp（-△/t）}>random[0，1]准则是作为接受新状态的条件最常用的方案，其中△为新旧状态的目标值差，t为”温度”。

用GAAA求解TSP问题

数学建模之求解TSP问题的遗传算法

TSP问题用GA方法求解

第17章 基于GA的TSP求解

遗传算法（GA）解决TSP问题

遗传算法(GA)在旅行商问题(TSP)中的应用

遗传算法求解TSP问题的实现与改进

TSP的几种求解方法及其优缺点

GA-TSP

佳点集遗传算法求解安徽十七的TSP问题

遗传算法解决TSP问题

应用GA和PSO算法求解10城市TSP问题

用于TSP的自适应贪婪GA算法

TSP的几种求解方法及其优缺点

TSP的几种求解方法及其优缺点

基于遗传算法（GA）的多变量旅行商问题（TSP）

tsp问题有几种方案

用遗传算法解决货郎担问题

TSP的几种求解方法及其优缺点

TSP的几种求解方法及其优缺点

第17章基于GA的TSP求解