山东省泰安市2012届高三第一次高考模拟 理科数学(2012泰安一模)
2012年普通高等学校招生全国统一考试模拟试题(山东卷,理数).pdf

2012年普通高等学校招生全国统一考试模拟试题(山东卷) 数学(理科) 考生注意事项: 答题前,务必在试题卷?答题卡规定填写自己的姓名?座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名?座位号是否一致.务必在答题卡背面规定的地方填写姓名和座位号后两位. 答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号. 答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整?笔迹清晰.作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答,超出书写的答案无效,在试题卷?草稿纸上答题无效. 考试结束后,务必将试题卷和答题卡一并上交. 参考公式: 椎体体积,其中为椎体的底面积,为椎体的高. 若(x,y),(x,y)…,(x,y)为样本点,为回归直线,则 , , 说明:若对数据适当的预处理,可避免对大数字进行运算. 第Ι卷(共60分)选择题:本大题共12小题,没小题5分,共60分.在每小题给出的四个选项中只有一项是符合题目要求的. 1.已知集合,,则=( ) A. B. C. D. 2.设复数,,则在复平面内对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.对于函数,下列命题中正确的是( ) A. B. C. D. 4.已知点的坐标满足条件 那么的取值范围是( ) A.B. C. D. 5.若,则是成立的( ) A.充分必要条件 B.充分不必要条件 C.必要不充分条件 D.既非充分也非必要条件 6.将函数的图象向右平移个单位长度得到图象,若的一条对称轴是直线则的一个可能取值是( ) A. B. C. D. 7.有人收集了春节期间平均气温与某取暖商品销售额的有关数据如下表: 平均气温()销售额(万元)20232730根据以上数据,用线性回归的方法,求得销售额与平均气温之间线性回归方程的系数.则预测平均气温为时该商品销售额为( ) A.万元 B.万元 C.万元 D.万元 8.已知分别是双曲线的左?右焦点,过且平行于轴 的直线交双曲线的渐近线两点.若为锐角三角形,则该双曲线的离心率的取值范围是( ) A. B. C. D. 9.已知,若那么与在同一坐标系内的图象可能是( ) A.B. C.D. 10.已知,( ) A.奇函数 B.偶函数 C.非奇非偶函数D.既奇且偶函数 11.某几何体的三视图如图所示,该几何体的体积是( ) A.B. C.D. 12.已知向量,.若实数与向量满足,则可以是( ) A.B. C.D.第Ⅱ卷(共90分)一?填空题.本大题共4小题,每小题4分,共16分. 13.已知程序框图如右,则输出的=. 14.的展开式中的常数项是 .(用数字作答) 15.设曲线在点(1,1)处的切线与x轴的交点的横坐标为,令,则的值为 16.已知函数,若对于任意的,恒成立,则的取值范围是______. 三?解答题:本大题共6小题,共74分. 17.(本小题满分12分) 已知函数,. (1)求的零点; (2)求的最大值和最小值. 18.(本小题满分12分) 一个口袋中装有大小相同的2个白球和3个黑球. (1)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率; (2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的分布列与期望. 19.(本小题满分12分) 已知正方形的边长为2,.将正方形沿对角线折起,使,得到三棱锥,如图所示. (1)当时,求证:; (2)当二面角的大小为时,求二面角的正切值. 20.(本小题满分12分)已知数列的前项和,; (1)求的值; (2)求数列的通项公式; (3)令,,试比较与的大小,并予以证明. 21.(本小题满分12分) 如图所示,在平面直角坐标系上放置一个边长为的正方形,此正方形沿轴滚动(向左或向右均可),滚动开始时,点位于原点处,设顶点的纵坐标与横坐标的函数关系是,该函数相邻两个零点之间的距离为. (1)写出的值并求出当时,点运动路径的长度; (2)写出函数的表达式;研究该函数的性质并填写下面表格: 函数性质结 论奇偶性单调性递增区间递减区间零点(3)试讨论方程在区间上根的个数及相应实数的取值范围. 22.(本小题满分14分) 设双曲线的渐近线为,焦点在轴上且实轴长为1.若曲线上的点到双曲线的两个焦点的距离之和等于,并且曲线:(是常数)的焦点在曲线上. (1)求满足条件的曲线和曲线的方程; (2)过点的直线交曲线于点?(在轴左侧),若,求直线的倾斜角.2012年普通高等学校招生全国统一考试模拟试题答案(山东卷) 数学(理科) 选择题(本大题共12小题,每小题5分,共60分) 1-5 DDBDC 6-11 AACCADD 二.填空题:(本大题共4小题,每小题4分,共16分) 13.9 14.-20 15.-2 16. 三.解答题:(本大题共6小题,共74分) 17.解法一: (1)解:令,得 , 所以,或. 由 ,,得; 由 ,,得. 综上,函数的零点为或. (2)解:. 因为,所以. 当,即时,的最大值为; 当,即时, 的最小值为. 解法二: (1)解:. 令,得 . 因为,所以. 所以,当,或时,. 即 或时,. 综上,函数的零点为或. (2)解:由(1)可知, 当,即时,的最大值为; 当,即时, 的最小值为. 18.解:(1)采取放回抽样方式,从中摸出两个球,两球恰好颜色不同,也就是说从5个球中摸出一球,若第一次摸到白球,则第二次摸到黑球;若第一次摸到黑球,则第二次摸到白球. 因此它的概率P是: (2)设摸得白球的个数为ξ,则ξ=0,1,2? 的分布列为: ξ012P 19.(1)证明:根据题意,在中,,, 所以,所以. 因为是正方形的对角线, 所以. 因为, 所以. (2)解法1:由(1)知,,如图,以为原点,,所在的直线分别为轴,轴建立如图的空间直角坐标系, 则有,,,. 设,则,. 又设面的法向量为, 则即 所以,令,则. 所以. 因为平面的一个法向量为, 且二面角的大小为, 所以,得. 因为,所以. 解得.所以. 设平面的法向量为,因为, 则,即 令,则. 所以. 设二面角的平面角为, 所以. 所以. 所以二面角的正切值为. 解法2:折叠后在△中,, 在△中,. 所以是二面角的平面角, 即. 在△中,, 所以. 如图,过点作的垂线交延长线于点, 因为,,且, 所以平面. 因为平面,所以. 又,且,所以平面. 过点作作,垂足为,连接, 因为,,所以平面. 因为平面,所以. 所以为二面角的平面角. 在△中,,,则,, 所以. 在△中,,所以 在△中,. 所以二面角的正切值为. 20.解析:(I)在中,令n=1,可得,即 当时, , . . 又数列是首项和公差均为1的等差数列.于是. (II)由(I)得,所以 由①-②得 于是确定的大小关系等价于比较的大小 由 可猜想当证明如下: 21.解:(1),; (2); 函数性质结 论奇偶性偶函数单调性递增区间,递减区间,零点,(3)(i)易知直线恒过原点; 当直线过点时,,此时点到直线的距离为,直线 与曲线相切,当时,恒在曲线之上, (ii)当直线与曲线相切时,由点到直线 的距离为,,此时点到直线的距离为,直线 与曲线相离; (iii)当直线与曲线相切时,由点到直线 的距离为,,此时点到直线的距离为, 直线与曲线相交于两个点; ()当直线过点时,,此时点到直线的距离为,直线与曲线相交于两个点; 点到直线的距离为,直线与曲线相交于两个点; ()当时,直线与曲线有且只有5个交点; ()当时,直线与曲线有且只有1个交点; 因为函数的图像关于轴对称, 故综上可知: (1)当时,方程只有1实数根; (2)当时,方程有3个实数根; (3)当时,方程有5个实数根; (4)当或时,方程有7个实数根; (5)当时,方程有9个实数根; (6) 当时,方程有11个实数根. 22.解:⑴双曲线满足:, 解得 则,于是曲线的焦点., 曲线是以.为焦点的椭圆,设其方程为, 解得,即:, 依题意,曲线的焦点为, 于是,所以,曲线 ⑵由条件可设直线的方程为, 由得,,由求根公式得:,, 由得,于是,解得,由图知,,直线的倾斜角为 A B C D O A B C D O y x z A B C D O H K。
山东省泰安市高考第一次模拟考试数学理试题

山东省泰安市高考第一次模拟考试数学理试题姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)若集合,,则=()A .B .C . 或D . 或2. (2分) (2016高二下·民勤期中) i是虚数单位,复数 =()A . 1+2iB . 2+4iC . ﹣1﹣2iD . 2﹣i3. (2分)投掷两枚骰子,所得点数之和记为x,那么X=4表示的随机实验结果是()A . 一枚是3点,一枚是1点B . 两枚都是2点C . 两枚都是4点D . 一枚是3点,一枚是1点或两枚都是2点4. (2分)在中,已知,且,则=()A .C .D .5. (2分)若点A的坐标为(3,2),F为抛物线y2=2x的焦点,点P是抛物线上的一动点,则|PA|+|PF|取得最小值时,点P的坐标是()A . (0,0)B . (1,1)C . (2,2)D .6. (2分) (2017高一上·湖州期末) 将函数y=sin(x﹣)图象上所有的点(),可以得到函数y=sin (x+ )的图象.A . 向左平移单位B . 向右平移单位C . 向左平移单位D . 向右平移单位7. (2分)盒中装有大小形状都相同的5个小球,分别标以号码1,2,3,4,5,从中随机取出一个小球,其号码为偶数的概率是()A .B .C .8. (2分) (2018高一下·北京期中) 下列命题中,正确命题的个数是()①有三个公共点的两个平面重合②梯形的四个顶点在同一平面内③三条互相平行的直线必共面④四条线段顺次首尾相接,构成平面图形A . 0B . 1C . 2D . 39. (2分) (2018高二下·大连期末) 已知,函数满足:恒成立,其中是的导函数,则下列不等式中成立的是()A .B .C .D .10. (2分)点P是双曲线左支上的一点,其右焦点为,若M为线段FP的中点, 且M到坐标原点的距离为,则双曲线的离心率e的取值范围是()A .B .C .D .11. (2分) (2016高一下·黔东南期末) 已知某几何体的正(主)视图,侧(左)视图和俯视图均为边长为1的正方形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为()A . 4πB . 3πC . 2πD . π12. (2分) (2019高一上·珠海期中) 已知函数,对于任意,且,均存在唯一实数,使得,且,若关于的方程有4个不相等的实数根,则的取值范围是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)(2018·延边模拟) 已知实数满足,则的最小值是________.14. (1分) (2018高一下·福州期末) ________.15. (1分) (2016高三上·珠海模拟) 在(1﹣3x)6的展开式中,x2的系数为________.(用数字作答)16. (1分)(2017·黄冈模拟) 如图,在△ABC中,,点D在线段AC上,且AD=2DC,BD= ,则cosC=________.则三角形ABC的面积为________.三、解答题 (共7题;共70分)17. (10分)已知数列{an}中,a1=2,n∈N* , an>0,数列{an}的前n项和为Sn ,且满足an+1= .(1)求{Sn}的通项公式;(2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列.①求b3;②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.18. (10分)(2014·天津理) 如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(1)证明:BE⊥DC;(2)求直线BE与平面PBD所成角的正弦值;(3)若F为棱PC上一点,满足BF⊥AC,求二面角F﹣AB﹣P的余弦值.19. (10分)随着互联网经济逐步被人们接受,网上购物的人群越来越多,网上交易额也逐年增加,某地一建设银行连续五年的网银交易额统计表,如表所示:年份x20122013201420152016网上交易额y(亿元)567810经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,工作人员将上表的数据进行了处理,t=x﹣2011,z=y﹣5,得到如表:时间代号t12345z01235(1)求z关于t的线性回归方程;(2)通过(1)中的方程,求出y关于x的回归方程;(3)用所求回归方程预测到2020年年底,该地网银交易额可达多少?(附:在线性回归方程 = x+ 中,,)20. (10分) (2017高二上·靖江期中) 在平面直角坐标系xOy中,如图,已知椭圆C: +y2=1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=﹣3分别交于点M、N.(1)设直线AP、PB的斜率分别为k1,k2,求证:k1•k2为定值;(2)求线段MN长的最小值;(3)当点P运动时,以MN为直径的圆是否经过某定点?请证明你的结论.21. (10分)(2018·广元模拟) 已知函数在其定义域内有两个不同的极值点.(1)求的取值范围;(2)证明:22. (10分)设椭圆C1:(a>b>0)的一个顶点与抛物线C2:x2=4y的焦点重合,F1 , F2分别是椭圆的左、右焦点,离心率e=,过椭圆右焦点F2的直线与椭圆C交于M,N两点.(Ⅰ)求椭圆C的方程;(Ⅱ)是否存在直线,使得•=﹣2,若存在求出直线的方程;若不存在,说明理由.23. (10分)(2018·河北模拟) 选修4-5:不等式选讲已知函数.(1)求不等式的解集;(2)若正数,满足,求证:.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共70分) 17-1、17-2、18-1、18-2、18-3、19-1、19-2、19-3、20-1、20-2、20-3、21-1、21-2、22-1、23-1、23-2、。
山东省泰安市高三一模(数学理)(word版)

泰安市高三第一轮复习质量检测数 学 试 题(理科)一、选择题:本大题共12个小题。
每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
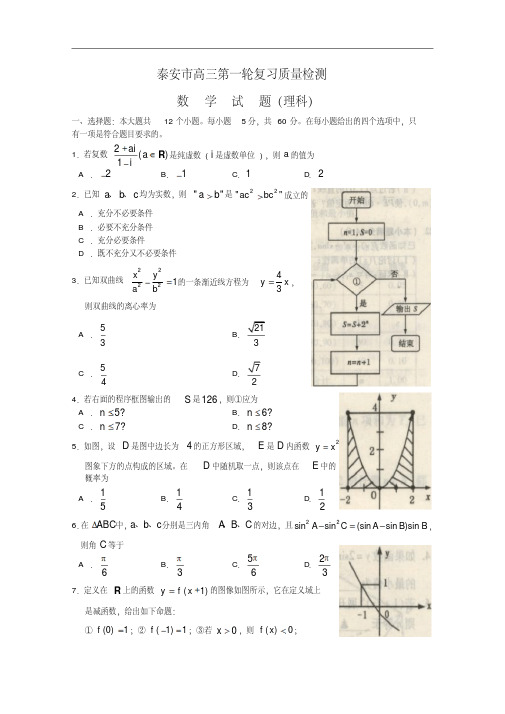
1.若复数2()1aia i+∈-R 是纯虚数(i 是虚数单位),则a 的值为 A .2- B .1- C .1 D .22.已知a b c 、、均为实数,则""a b >是22""ac bc >成立的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分又不必要条件3.已知双曲线22221x y a b-=的一条渐近线方程为43y x =,则双曲线的离心率为A .53 BC .54D4.若右面的程序框图输出的S 是126,则①应为 A .5?n ≤ B .6?n ≤ C .7?n ≤ D .8?n ≤5.如图,设D 是图中边长为4的正方形区域,E 是D 内函数2y x = 图象下方的点构成的区域。
在D 中随机取一点,则该点在E 中的 概率为 A .15B .14C .13D .126.在ABC ∆中,a b c 、、分别是三内角A B C 、、的对边,且22sin sin (sin sin )sin A C A B B -=-,则角C 等于A .6π B .3π C .56π D .23π 7.定义在R 上的函数(1)y f x =+的图像如图所示,它在定义域上 是减函数,给出如下命题:①(0)1f =;②(1)1f -=;③若0x >,则()0f x <;④若0x <,则()1f x >。
其中正确的命题是A .②③B .①④C .②④D .①③8.如图,在棱长均为1的三棱锥S ABC -中,E 为棱SA 的中点,F 为ABC ∆的中心,则直线EF 与平面ABC 所成角的正切值是 A.B .1CD.29.定义在R 上的函数()f x 满足()()()2(,),(1)2,f x y f x f y xy x y f +=++∈=R 则(2)f -等于 A .2B .3C .6D .910.已知非零向量,a b 满足:2=||||a b ,若函数3211()32f x x x x =++⋅||a a b 在R 上有极值,设向量,a b 的夹角为θ,则cos θ的取值范围为 A .[1[,1]2B .1(,1]2C .1[1,]2- D .1[1,)2-11.如果直线1y kx =+与圆2240x y kx my +++-=交于M N 、两点,且M N 、关于直线0x y +=对称,则不等式组 10,0,0,kx y kx my y -+≥-≤≥表示的平面区域的面积是A .14B .12C .1D .212.某钢厂的年产量由1990年的40万吨增加到2000年的50万吨,如果按照这样的年增长率计算,则该钢厂2010年的年产量约为A .60万吨B .61万吨C .63万吨D .64万吨二、填空题:本大题共4个小题,每小题4分,共16分。
山东省泰安市高三数学第一次高考模拟 理(泰安一模)

山东省泰安市2012届高三第一次模拟考试数 学 试 题(理)2012.03一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 为实数,则“a b <1”是“0<a <b1”的 A.充分而不必要条件 B.必要而不充分条件 C.充分条件D.既不充分也不必要条件2.已知i 是虚数单位,则i i+-221等于 A.i -B.iC.i 5354- D.i -54 3.过点A (2,3)且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x ] C.032=+-y xD.052=+-y x4.设{}{}R x y y Q R x x y y P x∈==∈+-==,2,,12,则 A.Q P ⊆B.P Q ⊆C.Q P C R ⊆D.P C Q R ⊆5.+=≠=,0,且⊥,则向量与的夹角为 A.30° B.60°C.120°D.150°6.函数x xy cos 1⋅=在坐标原点附近的图象可能是7.设偶函数()x f 满足()()042≥-=x x x f ,则不等式()2-x f >0的解集为 A.{x x <2-或x >}4B.{x x <0或x >}4C.{x x <0或x >}6D.{x x <2-或x >}28.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程x y53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位; ③线性回归方程a x b yˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0 B.1 C.2 D.39.正方体ABCD —A 1B 1C 1D 1中,CC 1与面BDA 1所成角的余弦值是A.32 B.33 C.32 D.36 10.执行如图所示的程序框图,输出的S 值为 A.3 B.—6 C.10 D.15-11.已知(){}1,1,≤≤=Ωy x y x ,A 是曲线2x y =与21x y =围成的区域,若向区域Ω上随机投一点P ,则点P 落入区域A 的概率为 A.31 B.41 C.81 D.121 12.函数()(a x y a 13l o g -+=>0,且)1≠a 的图象恒过定点A ,若点A 在直线01=++ny mx 上(其中m ,n >0),则nm 21+的最小值等于 A.16 B.12 C.9 D. 8二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置.13.431⎪⎭⎫ ⎝⎛-x x 展开式中常数为 ▲ .14.一个棱锥的三视图如图所示,则这个棱锥的体积为▲ .15.函数()()ϕω+=x A x f sin (ϕω,,A 为常数,A >0,ω>0)的部分图象如图所示,则⎪⎭⎫⎝⎛6πf 的值是 ▲ . 16.F 1、F 2为双曲线C :12222=-by a x (a >0,b >0)的焦点,A 、B 分别为双曲线的左、右顶点,以F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M ,且满足∠MAB=30°,则该双曲线的离心率为 ▲ .三、解答题:本大题共6个小题满分74分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 17.(本小题满分12分)已知数列{}n a 是等差数列,满足.13,542==a a 数列{}n b 的前n 项和是T n ,且.3=+n n b T (1)求数列{}n a 及数列{}n b 的通项公式; (II )若n n n b a c ⋅=,试比较n c 与1+n c 的大小.18.(本小题满分12分)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且满足.cos cos cos 2B c C b B a += (I )求角B 的大小;(II )求函数()⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=62cos 4sin 22ππA A A f 的最大值及取得最大值时的A 值.19.(本小题满分12分)在三棱锥P —ABC 中,PB ⊥平面ABC ,AB ⊥BC ,AB=PB=2,BC=23,E 、F 、G 分别为PC 、AC 、PA 的中点. (I )求证:平面BCG ⊥平面PAC ;(II )在线段AC 上是否存在一点N ,使PN ⊥BE ?证明你的结论. 20.(本小题满分12分)为缓解某路段交通压力,计划将该路段实施“交通银行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:(I )作出被调查人员年龄的频率分布直方图;(II )若从年龄在[)[)35,25,25,15的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通银行”的人数为ξ,求随机变量ξ的分布列和数学期望.21.(本小题满分12分)已知椭圆12222=+by a x (a >b >0)与抛物线x y 42=有共同的焦点F ,且两曲线在第一象限的交点为M ,满足.35=MF (I )求椭圆的方程;(II )过点P (0,1)的直线l 与椭圆交于A 、B 两点,满足25-=⋅PB PA ,求直线l 的方程.22.(本小题满分14分)已知函数()().ln 122x a x a x x f ++-=(I )当2=a 时,求曲线()x f y =在点()()1,1f 处的切线方程; (II )求函数()x f 的单调区间;(III )若对任意()2,3--∈a 及[]3,1∈x 时,恒有()x f ma -<1成立,求实数m 的取值范围.。
山东省泰安市2012届高三第一次高考模拟(英语)(2012泰安一模)

山东省泰安市2012届高三第一次高考模拟(英语)(2012泰安一模)2012.03本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷l至10页。
第II卷11至12页。
满分为150分。
考试用时120分钟。
第I卷(三部分,共105分)注意事项:1.答题前,考生在答题卡和试卷规定位置务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题纸各题目的指定位置。
答题时不能使用涂改液、胶带纸或修正带。
第一部分听力(共两节,满分30分)第一节(共5小题,每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有。
个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置;听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.How much will the woman lend the man?A.£7.B.£9.C.£5.2.What are the two speakers talking about?A.Foreign languages.B.A novel.C.A film.3.What will they do tonight?A.Play music.B.Dance.C.Hear music.4.What can you learn from the dialogue?A.Jim is Frank’brother.B.Jim is Frank’s teacher.C.Jim is Frank’s friend.5.What is wanted in the ad?A.Waiter.B.Waitress.c.Cook.第二节(共15小题)听下面5段对话或独白。
山东省泰安市2012届高三基本能力第一次高考模拟(2012泰安一模)

山东省泰安市2012届高三第一次模拟考试基本能力试题2012.03 注意事项:1.本试卷分第一部分和第二部分两部分。
满分100分,考试时间为120分钟。
按考生实际得分的60%计入总分。
2.考生务必在试卷和答题卡上用黑色签字笔或蓝黑钢笔清楚填写姓名、准考证号,并用2B铅笔在答题卡上正确涂写准考证号。
3.本试卷全部为选择题,由机器阅卷,答案必须全部涂在答题卡上。
考生应将代表正确答案的小方格涂黑。
注意试题题号和答题卡上编号一一对应,不能错位。
答案需要更改时,必须将原选项用橡皮擦干净,再重新选择。
答案写在试卷上一律不得分。
第一部分(共70分)共70小题,每小题1分。
在每题给出的四个选项中,只有一个选项最符合题目要求。
春节是中国最盛大、最热闹、最重要的一个古老传统节日,是农历新年的开始。
2012年是一个闰年,龙年。
据此完成1~10题。
1.下面有关闰年的说法,不正确的是A.公历闰年一年的天数是366天B.判定公历闰年的简单计算方法是年份能被4整除C.农历的闰年有13个月,增加的一个月称为闰月D.闰年是为弥补人为历法规定造成的年度天数与地球实际公转周期的时间差而设立的2.在2012年的迎新春晚会上,人们以民乐合奏《金蛇狂舞》来庆祝龙年的到来。
对这首乐曲,以下描述正确的是A.表现了在节日夜晚赛龙舟的热闹场面 B.它用陕北民歌做素材C.它运用了鱼咬尾的创作手法D.它是一首北方风格的吹打乐曲3.作为十二生肖的龙,在中国神话中是一种神异动物,是九种动物合而为一,具有九不像之形象。
西方也有传说中的龙,下面图片所示不具有中国龙特点的是4.为增添春节喜庆气氛,植物学家可以在冬天培育出盛开的莲花,这其中包含的哲理是A.人们可以认识规律,并改造规律B.不同季节,规律有不同的表现C.矛盾具有特殊性,问题不同解决的方法就不同D.实践是有意识、有目的的能动性的活动5.右图所示的红山玉龙产生于新石器时代,距今5000年左右,曾有“中华第一龙”的称誉,下面说法正确的是①玉器、瓷器、丝绸在唐代开始被销往世界各地②玉器还被赋予丰富的内涵,象征伦理道德③完璧归赵、固若金汤都是与玉有关的成语④C型状的红山玉龙属于工艺美术的范畴A.①② B.②④C.①③ D.③④6.中华五千年文明和教育的发展密切相关,唐朝教育在当时处于世界先进水平,其主要表现是A.兴办私学,普及教育B.书院林立,学风活跃C.完备学校体制,确立专业教育D.完善科举制度,推动教育事业7.2012年春运期间,铁路客户服务中心开通了网上售票方式,在一定程度上缓解了火车站售票压力。
2012年山东高考理科数学试题及答案

2012年普通高等学校招生全国统一考试(山东卷)理科数学第I 卷(共60分)一、 选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1 若复数x 满足z(2-i)=11+7i(i 为虚数单位),则z 为 A 3+5i B 3-5i C -3+5i D -3-5i 解析:i ii i i i z 535)1114(7225)2)(711(2711+=++-=++=-+=.答案选A。
另解:设),(R b a bi a z ∈+=,则i i a b b a i bi a 711)2(2)2)((+=-++=-+ 根据复数相等可知72,112=-=+a b b a ,解得5,3==b a ,于是i z 53+=。
2 已知全集U ={0,1,2,3,4},集合A={1,2,3,},B={2,4} ,则(CuA )U B 为A {1,2,4}B {2,3,4}C {0,2,4}D {0,2,3,4}解析:}4,2,0{)(},4,0{==B A C A C U U Y 。
答案选C 。
3 设a >0 a ≠1 ,则“函数f(x)= a x 在R 上是减函数 ”,是“函数g(x)=(2-a) 3x 在R 上是增函数”的A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件解析:p :“函数f(x)= a x 在R 上是减函数 ”等价于10<<a ;q :“函数g(x)=(2-a) 3x 在R 上是增函数”等价于02>-a ,即,20<<a 且a ≠1,故p 是q 成立的充分不必要条件. 答案选A 。
(4)采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,……,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷A ,编号落入区间[451,750]的人做问卷B ,其余的人做问卷C.则抽到的人中,做问卷B 的人数为(A )7 (B ) 9 (C ) 10 (D )15解析:采用系统抽样方法从960人中抽取32人,将整体分成32组,每组30人,即30=l ,第k 组的号码为930)1(+-k ,令750930)1(451≤+-≤k ,而z k ∈,解得2516≤≤k ,则满足2516≤≤k 的整数k 有10个,故答案应选C 。
山东省泰安市2012届高三第一次高考模拟理综试题(2012泰安一模)

山东省泰安市2012届高三第一次模拟考试理科综合试题2012.03 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共16页,满分240分,考生用时150分钟。
考试结束后,将本试卷、答题卡和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在答题卡和答题纸规定的地方。
第I卷(必做题,共87分)注意事项:1.每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑,如需改动,用橡皮擦干净以后,再涂写其他答案标号。
不涂答题卡,只答在试卷上不得分。
2.第I卷共20小题,1~13题,每小题4分;14~20题,每小题5分,共87分。
可能用到的相对原子质量:H l C 12 N 14 O 16 Na 23 Fe 56 Cu 64 Ba 137一、选择题(本题包括1 3小题。
每小题只有一个选项符合题意)1.端粒存在于真核生物染色体的末端,是由DNA序列及其相关的蛋白质所组成的复合体。
端粒酶是一种逆转录酶,由蛋白质和RNA构成。
由此可知,属于核膜、端粒和端粒酶共同点的是A.都存在于所有生物细胞中B.都含有C、H、O、N、P等化学元素C.都与遗传信息的传递无关D.都含有遗传物质2.右图是物质进出细胞方式的概念图。
下列分析正确的是A.①方式表示协助扩散B.⑤、⑥两种方式的共同特点是都需要载体C.③、④两种方式都与细胞膜的流动性有关D.质壁分离实验中蔗糖进入细胞的方式为④3.下列关于植物激素的说法正确的是A.单侧光照使植物弯曲生长时,背光侧生长素浓度比向光侧低B.探究不同浓度生长素类似物对插条生根影响时.应选不同种的植物材料C.用赤霉素多次喷洒水稻植株后,将导致产量降低D.种子在浸泡过程中,用适量的乙烯处理可解除休眠而萌发4.动物细胞中的一类基因是维持基本生命活动的。
在各种细胞中都处于活动状态。
另一类基因是选择性表达的基因。
右图是能产生A抗体的细胞。
关于该细胞中三个基因的开闭状态,下列说法正确的是A.其中有一个处于活动状态。
2012年山东泰安市高考模拟题(数学)

2012年高考数学模拟题一、选择题:本大题12个小题,每小题5分,共60分在每小题给山的四个选项中只有一项是符合题目要求的.1.已知集合{}{}等于则N M ,R x x y y N R x y y M x ∈==∈==,|,,2|2 ( ) A.()∞+,0 B.[)∞+,0 C.{}42, D.()(){}16442,,, 2.复数11z i=-(i 是虚数单位)在复平面上对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限3.给出如下四个命题:①若“p 且q ”为假命题,则p 、q 均为假命题;②命题“若a b >,则221a b >-”的否命题为“若a b ≤,则221a b ≤-”; ③“2,11x x ∀∈+≥R ”的否定是“2,11x x ∃∈+≤R ”;④在△ABC 中,“A B >”是“sin sin A B >”的充要条件.其中不正确...的命题的个数是( )A .4B .3C .2D .1 4. 下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是 ( )A.①②B.②③C.②④D.①③5. 为了了解某校高三学生的视力情况,随机抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道后5组频数和为62,设视力在4.6到4.8之间的学生数为a ,最大频率为0.32,则a 的值为( )A .64B .54C .48D .276. 已知直线l ⊥平面α,直线m ⊂平面β,给出下列命题:①α∥β⇒l ⊥m ②α⊥β⇒l ∥m ③l ∥m ⇒α⊥β ④l ⊥m ⇒α∥β 其中正确命题的序号是 ( )A. ①②③B. ②③④C. ①③D. ②④ 7.如果执行如图的程序框图,那么输出的值是( ) A.2010B.-1C.12D.28.从四棱锥S —ABCD 的八条棱中任取两条,其中抽到两条棱成异面直线的概率为( ) A .17B .12C .27D .479. 如下图,有一直角墙角,两边的长度足够长,在P 处有一棵树与两墙的距离分别是(012),4am a m <<,不考虑树的粗细,现在用16m 长的篱笆,借助墙角围成一个矩形的花圃ABCD 。
山东省泰安市高三数第一次高考模拟考试(理)新人教
已知函数 f (x)
x
a
x ln a ,其中 a
(1,e]
( Ⅰ) 讨论 f (x) 的单调性;
( Ⅱ) 求证:对 x1, x2 [ 1,1] ,都有 | f ( x1 ) f ( x2 ) | e 2 。
泰安市高三第一轮复习质量检测
数学参考答案及评分标准(理科)
一、选择题: ( 每小题 5 分,共 60 分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D B A B C B B C A D A C
b1
椭圆的方程为 x 2 y 2 1 ……………………………………………………
3分
4
( Ⅱ ) 当直线 l 的斜率存在时,设其斜率为 k ,则 l 的方程为: y k( x 1)
x2 y2 1 4 y k( x 1)
(4k 2 1) x2 8k 2 x 4 k 2 4 0
P ( x1, y1), Q (x2 , y2 )
二、填空题: ( 每小题 4 分,共 16 分)
13 .
14 .
3
三、解答题:
15 . 5 16 . y2
3x’
17.解:(Ⅰ) f ( x) (1 cos2x)2 2cos 2 x 1
cos2 2x
sin( x)sin( x)
4
4
sin( x)cos( x)
4
4
2cos 2 2x
2cos 2 2 x 2cos 2x ………………………………… 4 分
形, AB BC 2CD 。 ( Ⅰ) 在线段 BE 上是否存在一点 F ,使 CF // 平面 ADE ? ( Ⅱ) 求证:平面 ADE 平面 ABE ; ( Ⅲ) 求二面角 A DE B 的正切值。
泰安一模试题理科数学

泰安一模试题理科数学————————————————————————————————作者:————————————————————————————————日期:泰安市高三第一轮复习质量检测 数学试题(理科) 2013.3一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}{}1,1,124x A B x =-=≤<,则A B ⋂等于A.{}1,0,1-B.{}1C.{}1,1-D.{}0,1 2.复数311i i -+(i 为虚数单位)的模是 A.5 B.22 C.5 D.83.如果椭机变量()()21,,310.4N P ζσζ---≤≤-=且,则()1P ζ≥等于A.0.4B.0.3C.0.2D.0.1 4.下列结论错误..的是 A.命题“若2340x x --=,则4x =”的逆否命题为“若24,340x x x ≠--≠则”B.“4x =”j “2340x x --=”的充分条件C.命题“若0m >,则方程20x x m +-=有实根”的逆命题为真命题D.命题“若220m n +=,则00m n ==且”的否命题是“若220.00m n m n +≠≠≠则或”5.若程序框图如图所示,则该程序运行后输出k 的值是A.4B.5C.6D.76.当4x π=时,函数()()()sin 0f x A x A ϕ=+>取得最小值,则函数34y f x π⎛⎫=- ⎪⎝⎭是 A.奇函数且图像关于点,02π⎛⎫⎪⎝⎭对称B.偶函数且图像关于点(),0π对称C.奇函数且图像关于直线2x π=对称D.偶函数且图像关于点,02π⎛⎫ ⎪⎝⎭对称 7.在2ABC AB ∆∠=中,A=60,且ABC ∆的面积为32,则BC 的长为 A.3 B.3 C.7 D.78.已知()1,6,2a b a b a ==⋅-=则向量a b 与的夹角为A.2πB.3πC.4πD. 6π 9.若,,0,a b R ab ∈>且则下列不等式中,恒成立的是 A.2a b ab +≥ B.112a b ab+> C.2b a a b +≥ D.222a b ab +> 10.设函数()()3402f x x x a a =-+<<有三个零点1x 、x 2、x 3,且123,x x x <<则下列结论正确的是A.11x >-B.20x <C.32x >D.201x <<11.直线()2110x a y +++=的倾斜角的取值范围是 A.0,4π⎡⎤⎢⎥⎣⎦ B.3,4ππ⎡⎤⎢⎥⎣⎦ C.0,,42πππ⎡⎤⎛⎫⋃ ⎪⎢⎥⎣⎦⎝⎭ D.3,,424ππππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭12.设奇函数()[]1,1f x -在上是增函数,且()11f -=-,若函数,()221f x t at ≤-+对所有的[]1,1x ∈-都成立,则当[]1,1a ∈-时t 的取值范围是 A.22t -≤≤B.1122t -≤≤ C.202t t t ≤-=≥或或 D.11022t t t ≤-=≥或或 二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置.13.从集合{}1,2,3,4,5中随机选取3个不同的数,这个数可以构成等差数列的概率为 ▲ .14.二项式6213x x ⎛⎫+ ⎪⎝⎭的展开式中,常数项等于 ▲ (用数字作答).15.已知矩形ABCD 的顶点都在半径为5的球O 的球面上,且8,23AB BC ==,则棱锥O ABCD -的体积为 ▲ .16.设双曲线221x y m n+=的离心率为2,且一个焦点与抛物线28x y =的焦点相同,则此双曲线的方程为 ▲ .三、解答题:17.(本小题满分12分)设等比数列{}n a 的前n 项和为,415349,,,n S a a a a a =-成等差数列.(I )求数列{}n a 的通项公式;(II )证明:对任意21,,,k k k R N S S S +++∈成等差数列.18.(本小题满分12分)已知()sin ,,3,cos ,, 2.334x x m A A n f x m n f π⎛⎫⎛⎫⎛⎫===⋅= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭且 (1)求A 的值;(II )设α、()()30780,,3,3,cos 21725f f πβαπβπαβ⎡⎤⎛⎫∈+=-=-+ ⎪⎢⎥⎣⎦⎝⎭求的值.19.(本小题满分12分)如图在多面体ABCDEF 中,ABCD 为正方形,ED ⊥平面ABCD ,FB//ED ,且AD=DE=2BF=2.(I )求证:AC EF ⊥;(II )求二面角C —EF —D 的大小;(III )设G 为CD 上一动点,试确定G 的位置使得BG//平面CEF ,并证明你的结论.20.(本小题满分12分)某产品按行业生产标准分成6个等级,等级系数ξ依次为1,2,3,4,5,6,按行业规定产品的等级系数5ξ≥的为一等品,35ξ≤<的为二等品,3ξ<的为三等品.若某工厂生产的产品均符合行业标准,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下;(I )以此30件产品的样本来估计该厂产品的总体情况,试分别求出该厂生产原一等品、二等品和三等品的概率;(II )已知该厂生产一件产品的利润y (单位:元)与产品的等级系数ζ的关系式为1,32,354,5y ξξξ<⎧⎪=≤<⎨⎪≥⎩,若从该厂大量产品中任取两件,其利润记为Z ,求Z 的分布列和数学期望.21.(本小题满分13分) 已知椭圆221:1164y x C +=,椭圆C 2以C 1的短轴为长轴,且与C 1有相同的离心率. (I )求椭圆C 2的方程;(II )设直线l 与椭圆C 2相交于不同的两点A 、B ,已知A 点的坐标为()2,0-,点()00,Q y 在线段AB 的垂直平分线上,且4QA QB ⋅=,求直线l 的方程.22.(本小题满分13分)已知函数()()()()201,10.x f x ax bx c e f f =++==且(I )若()f x 在区间[]0,1上单调递减,求实数a 的取值范围;(II )当a=0时,是否存在实数m 使不等式()224141x f x xe mx x x +≥+≥-++对任意x R ∈恒成立?若存在,求出m 的值,若不存在,请说明理由.1。
山东省泰安一中2012年普通高考理科综合仿真化学试题---最后一考

泰安一中2012年普通高考理科综合化学仿真试题本试卷分第I卷和第II卷两部分,共12页,满分240分。
考试用时150分钟。
答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在试卷和答题卡规定的位置。
考试结束后,将本试卷和答题卡一并交回。
第I卷(必做,共87分)注意事项:1.第I卷共20小题。
第1~13题每小题4分,第14~20题每小题5分,共87分。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不涂在答题卡上,只答在试卷上不得分。
以下数据可供答题时参考:(略)相对原子质量:(略)一、选择题(本题包括13小题,每小题只有一个选项符合题意)7.下列说法中,不正确的是A.原子最外层电子数比次外层电子数多的元素一定位于第周期B.从氟到碘,单质与氢气发生化合反应越来越难C.14C和14N两种核素的质量数相同,中子数也相同D.离子化合物中可能含有共价键,但共价化合物中一定不含离子健8.下列说法或做法正确的是A.苯、乙醇、四氯化碳都是重要有机溶剂,都可用于提取碘水中的碘单质B.在强碱性溶液中,[Al(OH)4]-、HCO3-、Na+、Ca2+可能同时大量共存C.铁船底镶嵌锌块,构成原电池,锌作负极,以防船体被腐蚀D.用量筒量取10.mL 1.0mol/L的盐酸于100mL溶液瓶中,加水稀释至刻度,可制得0.1mol/L 的盐酸9.下列离子方程式书写正确的A.少量Cl2通入FeBr2溶液中:2Fe2++Cl22Fe3++2Cl-B.硫酸溶液中逐滴加入氢氧化钡溶液,至溶液恰好呈中性:Ba2++OH-+SO24-+H+BaSO4↓+H2OC.澄清石灰水中加入盐酸:Ca(OH)2+2H+2H2O+Ca2+D.向AlCl3溶液中滴加过量氨水:Al3++4NH3·H2O [Al(OH)4]-+4NH4+10.下列实验能达到预期目的的是A.将含有SO2的CO2气体通过足量的饱和Na2CO3溶液以除去SO2B.用石墨作电极,电解Mg(NO3)2、Cu(NO3)2的混合溶液,确定铜和镁瓣金属活动性强弱C.称取19.0g氯化亚锡(SnCl2),用100mL蒸馏水溶解,配制1.0mol/LSnCl2溶液D.测定NaCl和NaF溶液的pH值,确定F、Cl两元素非金属性的强弱11.美国探测发现,在土卫六上的碳氢化合物储量是地球上的几百倍。
山东省泰安市2012届高考数学第一次模拟 理 (2012泰安一模)新人教A版

山东省泰安市2012届高三第一次模拟考试数 学 试 题(理)2012.03一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 为实数,则“1<ab ”是“ba 10<<”的 A.充分而不必要条件 B.必要而不充分条件 C.充分条件D.既不充分也不必要条件【答案】B【解析】b a 10<<,所以⎪⎩⎪⎨⎧<>>100ab b a ,所以“1<ab ” 是“b a 10<<”的必要而不充分条件,选B.2.已知i 是虚数单位,则i i+-221等于 A.i - B.iC.i 5354- D.i -54 【答案】A 【解析】i ii i i i i i -=-=-+--=+-55)2)(2()2)(21(221,选A. 3.过点A (2,3)且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x C.032=+-y xD.052=+-y x【答案】A【解析】法一:设所求直线方程为02=+-C y x ,将点A 代入得,062=+-C ,所以4=C ,所以直线方程为042=+-y x ,选A.法二:直线052=-+y x 的斜率为2-,设所求直线的斜率为k ,则21=k ,代入点斜式方程得直线方程为)2(213-=-x y ,整理得042=+-y x ,选A. 4.设{}{}R x y y Q R x x y y P x∈==∈+-==,2,,12,则 A.Q P ⊆B.P Q ⊆C.Q P C R ⊆D.P C Q R ⊆【答案】C【解析】{}{}1,12≤=∈+-==y y R x x y y P ,{}{}0,2>=∈==y y R x y y Q x ,所以}1{>=y y P C R ,所以Q P C R ⊆,选C.5.若b a c a b +=≠=,02,且a c ⊥,则向量a 与b 的夹角为 A.30° B.60° C.120°D.150°【答案】C【解析】因为a c ⊥,所以0)(=•+=•a b a a c ,即02=•+b a a .所以2a b a -=•,所以向量a 与b 的夹角的余弦值212cos 22-=-=•=aa ba b a θ,所以0120=θ,选C.6.函数x xy cos 1⋅=在坐标原点附近的图象可能是【答案】A【解析】函数为奇函数,所以B 不正确,,定义域中没有0≠x ,所以D 不正确,当20π<<x 时,函数值为正,所以C 不正确,答案选A.7.设偶函数()x f 满足()()042≥-=x x x f ,则不等式()2-x f >0的解集为 A.{x x <2-或x >}4B.{x x <0或x >}4C.{x x <0或x >}6D.{x x <2-或x >}2【答案】B【解析】当2≥x 时,()0824)2(22>-=--=-x x x f ,解得4>x ,此时不等式的解为4>x ,当2<x 时,()04)2(2)2(2>-=--=-=-x x x f x f ,所以0<x ,此时不等式的解为0<x ,综上,不等式的解集为}40{><x x x 或,选B. 8.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程x y53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位; ③线性回归方程a x b yˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0 B.1 C.2 D.3 本题可以参考独立性检验临界值表()kK P ≥20.5 0.40 0.25 0.15 0.10 0.05 0.25 0.10 0.005 0.001 k0.4550.7081.3232.0722.7063.8415.0246.5357.87910.828【答案】B【解析】①③④正确,②回归方程x y53ˆ-=,当变量x 增加一个单位时,y 平均减少5个单位,所以错误,所以错误的个数有1个,答案选B.9.正方体ABCD —A 1B 1C 1D 1中,CC 1与面BDA 1所成角的余弦值是 A.32 B.33 C.32 D.36 【答案】D 【解析】10.执行如图所示的程序框图,输出的S 值为A.3B.—6C.10D.15-【答案】C【解析】第一次循环为:2,1,1=-==i S i ,第二次循环为:3,341,2==+-==i S i ,第三次循环为:4,693,3=-=-==i S i ,第四次循环为:5,10166,4==+-==i S i ,第五次循环条件不成立,输出10=S ,答案选C.11.已知(){}1,1,≤≤=Ωy x y x ,A 是曲线2x y =与21x y =围成的区域,若向区域Ω上随机投一点P ,则点P 落入区域A 的概率为 A.31 B.41 C.81 D.121 【答案】D【解析】本题为几何概率.区域Ω的面积为422=⨯.区域A 的面积为313132)3132()(1032310221=-=-=-⎰x x dx x x ,所以点P 落入区域A 的概率为121431==P ,选D.12.函数()(a x y a 13log -+=>0,且)1≠a 的图象恒过定点A ,若点A 在直线01=++ny mx 上(其中m ,n >0),则nm 21+的最小值等于 A.16 B.12C.9D. 8【答案】D【解析】令13=+x ,得2-=x ,此时1-=y ,所以图象过定点A )1,2(--,点A 在直线01=++ny mx ,所以12=+--n m ,即12=+n m .8424442)(21=+≥++=++n m m n n m n m )(,当且仅当nmm n 4=,即m n 2=时取等号,此时21,41==n m ,选D.二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置.13.431⎪⎭⎫ ⎝⎛-x x 展开式中常数为 .【答案】4-【解析】二项展开式为k kk k k k k k kkk x C x x C xx C T )1()1()1()(412431244341-=-=-=----+,所以当04-12=k ,即3=k 时,为常数项,所以常数项为4-.14.一个棱锥的三视图如图所示,则这个棱锥的体积为 .【答案】12【解析】由三视图可知,这是一个底面为矩形,两侧面和底面垂直的四棱锥,底面矩形长4宽为3,四棱锥的高为3,所以四棱锥的体积为1234331=⨯⨯⨯,答案为12.15.函数()()ϕω+=x A x f sin (ϕω,,A 为常数,A >0,ω>0)的部分图象如图所示,则⎪⎭⎫⎝⎛6πf 的值是 ▲ .【答案】26 【解析】由图象可知2=A ,431274πππ=-=T ,所以ϖππ2==T ,2=ϖ,所以()()ϕ+=x x f 2sin 2,2-67sin 21272sin 2127=⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛+⨯=⎪⎭⎫ ⎝⎛ϕπϕππf ,所以16sin =⎪⎭⎫⎝⎛+ϕπ,所以3πϕ=,所以()⎪⎭⎫ ⎝⎛+=32sin 2πx x f ,2623232sin 2362sin 2)6(=⨯=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+⨯=ππππf . 16.F 1、F 2为双曲线C :12222=-by a x (a >0,b >0)的焦点,A 、B 分别为双曲线的左、右顶点,以F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M ,且满足∠MAB=30°,则该双曲线的离心率为 .【答案】【解析】由⎪⎩⎪⎨⎧=+=222c y x x ab y ,解得⎩⎨⎧==b y a x ,即交点M 的坐标),(b a ,连结MB ,则AB MB ⊥,即ABM ∆为直角三角形,由∠MAB=30°得33230tan 0===a b AB MB ,即2234,332a b a b ==,所以2222237,34a c a a c ==-,所以321,372==e e ,所以双曲线的离心率321=e .三、解答题:本大题共6个小题满分74分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 17.(本小题满分12分)已知数列{}n a 是等差数列,满足.13,542==a a 数列{}n b 的前n 项和是T n ,且.3=+n n b T (1)求数列{}n a 及数列{}n b 的通项公式; (II )若n n n b a c ⋅=,试比较n c 与1+n c 的大小. 【答案】18.(本小题满分12分)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且满足.cos cos cos 2B c C b B a += (I )求角B 的大小;(II )求函数()⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=62cos 4sin 22ππA A A f 的最大值及取得最大值时的A 值. 【答案】19.(本小题满分12分)在三棱锥P —ABC 中,PB ⊥平面ABC ,AB ⊥BC ,AB=PB=2,BC=23,E 、F 、G 分别为PC 、AC 、PA 的中点.(I )求证:平面BCG ⊥平面PAC ;(II )在线段AC 上是否存在一点N ,使PN ⊥BE ?证明你的结论.【答案】20.(本小题满分12分)为缓解某路段交通压力,计划将该路段实施“交通银行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:(I )作出被调查人员年龄的频率分布直方图;(II )若从年龄在[)[)35,25,25,15的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通银行”的人数为ξ,求随机变量ξ的分布列和数学期望. 【答案】21.(本小题满分12分)已知椭圆12222=+by a x (a >b >0)与抛物线x y 42=有共同的焦点F ,且两曲线在第一象限的交点为M ,满足.35=MF (I )求椭圆的方程;(II )过点P (0,1)的直线l 与椭圆交于A 、B 两点,满足25-=⋅PB PA ,求直线l 的方程. 【答案】22.(本小题满分14分)已知函数()().ln 122x a x a x x f ++-=(I )当2=a 时,求曲线()x f y =在点()()1,1f 处的切线方程; (II )求函数()x f 的单调区间;(III )若对任意()2,3--∈a 及[]3,1∈x 时,恒有()x f ma -<1成立,求实数m 的取值范围.【答案】。
山东省泰安市高考数学第一次模拟 文 (泰安一模)新人教A版

山东省泰安市2012届高三第一次模拟考试数 学 试 题(文)2012.03一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 为实数,则“a b <1”是“0<a <b1”的 A.充分而不必要条件 B.必要而不充分条件 C.充分条件D.既不充分也不必要条件【答案】B【解析】b a 10<<,所以⎪⎩⎪⎨⎧<>>100ab b a ,所以“1<ab ” 是“b a 10<<”的必要而不充分条件,选B.2.已知i 是虚数单位,则ii+-221等于 A.i - B.i -54 C.i 5354-D.i【答案】A 【解析】i i i i i i i i -=-=-+--=+-55)2)(2()2)(21(221,选A. 3.过点A (2,3)且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x ] C.032=+-y xD.052=+-y x【答案】A【解析】法一:设所求直线方程为02=+-C y x ,将点A 代入得,062=+-C ,所以4=C ,所以直线方程为042=+-y x ,选A.法二:直线052=-+y x 的斜率为2-,设所求直线的斜率为k ,则21=k ,代入点斜式方程得直线方程为)2(213-=-x y ,整理得042=+-y x ,选A. 4.设{}{}R x y y Q R x x y y P x∈==∈+-==,2,,12,则 A.Q P ⊆B.P Q ⊆C.Q P C R ⊆D.P C Q R ⊆【答案】C【解析】{}{}1,12≤=∈+-==y y R x x y y P ,{}{}0,2>=∈==y y R x y y Q x,所以}1{>=y y P C R ,所以Q P C R ⊆,选C.5.已知向量()()k ,1,1,2-==,若()-⊥2,则k 等于 A.6 B.—6 C.12D.—12【答案】C【解析】因为()b a a -⊥2,所以()02=-∙,即0=∙-,所以0)2()5(22=+--k ,解得12=k ,选C.6.函数x y 2log =的图象大致是【答案】A【解析】函数⎩⎨⎧<->==0),(log 0,log log 222x x x x x y ,所以函数图象为A.7.设偶函数()x f 满足()()042≥-=x x x f ,则不等式()2-x f >0的解集为 A.{x x <2-或x >}4B.{x x <0或x >}4C.{x x <0或x >}6D.{x x <2-或x >}2【答案】B【解析】当2≥x 时,()0824)2(22>-=--=-x x x f ,解得4>x ,此时不等式的解为4>x ,当2<x 时,()04)2(2)2(2>-=--=-=-x x x f x f ,所以0<x ,此时不等式的解为0<x ,综上,不等式的解集为}40{><x x x 或,选B. 8.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程x y53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位; ③线性回归方程a x b yˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0 B.1 C.2 D.3【答案】B【解析】①③④正确,②回归方程x y53ˆ-=,当变量x 增加一个单位时,y 平均减少5个单位,所以错误,所以错误的个数有1个,答案选B.9已知βα,是两平面,n m ,是两直线,则下列命题中不正确...的是 A.若,m n m α⊥,//则α⊥mB.若,,βα⊥⊥m m 则βα//C.若,α⊥m 直线m 在面β内,则βα⊥D. 若n m =⋂βαα,//,则n m // 【答案】D【解析】选项D 中,直线m 与平面β的位置关系没有确定,所以n m ,的关系不确定,所以选项D ,不正确。
山东省泰安一模数学试题及答案(理)

山东省泰安一模数学试题及答案(理) 高三第一轮复质量检测数学试题(理科)第I卷一、选择题:本大题共12小题,每小题5分。
共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={-10.-9.…。
2},集合B={y | y=2x-3.x∈A},则A∩B等于()。
A。
{-10.-9.…。
-1}B。
{-1}C。
{-1.0 (2)D。
{0 (2)2.若(1-2i)z=5i,则z的值为()。
A。
3B。
5C。
3+2iD。
5+2i3.在各项均为正数的等比数列{an}中,a6=3,则a4+a8()。
A。
有最小值6B。
有最大值6C。
有最大值9D。
有最小值34.下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x与相应的生产能耗y的几组对应数据:x | 1 | 2 | 3 | 4 | 5 |y | 18.5 | 28.9 | 38.3 | 47.7 | 57.1 |根据上表可得回归方程y=9.4x+9.1,则表中m的值为()。
A。
27.9B。
25.5C。
26.9D。
265.阅读右侧程序框图,运行相应程序,则输出i的值为()。
i = 0while i < 5:if i % 3 == 0:i += 2elif i % 3 == 1:i += 3else:i += 1print(i)A。
3B。
4C。
5D。
66.将函数f(x)=sin(2x+π/3)的图像向右平移π/6个单位,得到函数g(x)的图像,则下列说法不正确的是()。
A。
g(x)的周期为πB。
g(π/3)=f(0)C。
x=π/6是g(x)的一条对称轴D。
g(x)为奇函数7.以F(0.2√2)为焦点的抛物线C的准线与双曲线x-y=2相交于M、N两点,若△MNF为正三角形,则抛物线C的标准方程为()。
A。
y2=26xB。
y2=46xC。
x2=46yD。
x2=26y8.a=∫2(-cosx)dx,则ax+2ax2的展开式中项的系数为()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省泰安市2012届高三第一次模拟考试数 学 试 题(理)2012.03一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 为实数,则“1<ab ”是“ba 10<<”的A.充分而不必要条件B.必要而不充分条件C.充分条件D.既不充分也不必要条件【答案】B【解析】b a 10<<,所以⎪⎩⎪⎨⎧<>>100ab b a ,所以“1<ab ” 是“b a 10<<”的必要而不充分条件,选B.2.已知i 是虚数单位,则i i +-221等于A.i -B.iC.i 5354-D.i -54【答案】A 【解析】i i i i i i ii -=-=-+--=+-55)2)(2()2)(21(221,选A.3.过点A (2,3)且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x C.032=+-y xD.052=+-y x【答案】A【解析】法一:设所求直线方程为02=+-C y x ,将点A 代入得,062=+-C ,所以4=C ,所以直线方程为042=+-y x ,选A.法二:直线052=-+y x 的斜率为2-,设所求直线的斜率为k ,则21=k ,代入点斜式方程得直线方程为)2(213-=-x y ,整理得042=+-y x ,选A.4.设{}{}R x y y Q R x x y y P x∈==∈+-==,2,,12,则 A.Q P ⊆B.P Q ⊆C.Q P C R ⊆D.P C Q R ⊆【答案】C【解析】{}{}1,12≤=∈+-==y y R x x y y P ,{}{}0,2>=∈==y y R x y y Qx ,所以}1{>=y y P C R ,所以Q P C R ⊆,选C.5.若b a c +=≠=,0,且a c ⊥,则向量a 与b 的夹角为 A.30° B.60° C.120° D.150°【答案】C【解析】因为a c ⊥,所以0)(=∙+=∙a b a a c0=∙+b a .所以b a =∙,所以向量a 与b的夹角的余弦值21cos -==∙=b a θ,所以0120=θ,选C.6.函数x xy cos 1⋅=在坐标原点附近的图象可能是【答案】A【解析】函数为奇函数,所以B 不正确,,定义域中没有0≠x ,所以D 不正确,当20π<<x 时,函数值为正,所以C 不正确,答案选A.7.设偶函数()x f 满足()()042≥-=x x x f ,则不等式()2-x f >0的解集为 A.{x x <2-或x >}4 B.{x x <0或x >}4C.{x x <0或x >}6D.{x x <2-或x >}2【答案】B【解析】当2≥x 时,()0824)2(22>-=--=-x x x f ,解得4>x ,此时不等式的解为4>x ,当2<x 时,()04)2(2)2(2>-=--=-=-x x x f x f ,所以0<x ,此时不等式的解为0<x ,综上,不等式的解集为}40{><x x x 或,选B. 8.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程x y 53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位;③线性回归方程a x b yˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0B.1C.2D.3本题可以参考独立性检验临界值表()k KP ≥20.5 0.40 0.25 0.15 0.10 0.05 0.25 0.10 0.005 0.001k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.535 7.879 10.828【答案】B【解析】①③④正确,②回归方程x y53ˆ-=,当变量x 增加一个单位时,y 平均减少5个单位,所以错误,所以错误的个数有1个,答案选B.9.正方体ABCD —A 1B 1C 1D 1中,CC 1与面BDA 1所成角的余弦值是 A.32 B.33 C.32 D .36【答案】D 【解析】10.执行如图所示的程序框图,输出的S 值为A.3B.—6C.10D.15-【答案】C【解析】第一次循环为:2,1,1=-==i S i ,第二次循环为:3,341,2==+-==i S i ,第三次循环为:4,693,3=-=-==i S i ,第四次循环为:5,10166,4==+-==i S i ,第五次循环条件不成立,输出10=S ,答案选C.11.已知(){}1,1,≤≤=Ωy x y x ,A 是曲线2xy =与21x y =围成的区域,若向区域Ω上随机投一点P ,则点P 落入区域A 的概率为 A.31B.41C.81 D.121【答案】D【解析】本题为几何概率.区域Ω的面积为422=⨯.区域A 的面积为313132)3132()(103231221=-=-=-⎰x x dx x x ,所以点P 落入区域A 的概率为121431==P ,选D.12.函数()(a x y a 13l o g -+=>0,且)1≠a 的图象恒过定点A ,若点A 在直线01=++ny mx 上(其中m ,n >0),则nm 21+的最小值等于A.16B.12C.9D. 8【答案】D【解析】令13=+x ,得2-=x ,此时1-=y ,所以图象过定点A )1,2(--,点A 在直线01=++ny mx ,所以012=+--n m ,即12=+n m .8424442)(21=+≥++=++nm m n n m nm )(,当且仅当nm mn 4=,即m n 2=时取等号,此时21,41==n m ,选D.二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置.13.431⎪⎭⎫⎝⎛-x x 展开式中常数为 .【答案】4-【解析】二项展开式为kkk kk kk kkkk xC xxC xx C T )1()1()1()(412431244341-=-=-=----+,所以当04-12=k ,即3=k 时,为常数项,所以常数项为4-.14.一个棱锥的三视图如图所示,则这个棱锥的体积为 .【答案】12【解析】由三视图可知,这是一个底面为矩形,两侧面和底面垂直的四棱锥,底面矩形长4宽为3,四棱锥的高为3,所以四棱锥的体积为1234331=⨯⨯⨯,答案为12.15.函数()()ϕω+=x A x f sin (ϕω,,A 为常数,A >0,ω>0)的部分图象如图所示,则⎪⎭⎫⎝⎛6πf 的值是 ▲.【答案】26【解析】由图象可知2=A ,431274πππ=-=T ,所以ϖππ2==T ,2=ϖ,所以()()ϕ+=x x f 2s in 2,2-67sin 21272sin 2127=⎪⎭⎫⎝⎛+=⎪⎭⎫⎝⎛+⨯=⎪⎭⎫⎝⎛ϕπϕππf ,所以16sin =⎪⎭⎫⎝⎛+ϕπ,所以3πϕ=,所以()⎪⎭⎫ ⎝⎛+=32si n2πx x f ,2623232sin 2362sin 2)6(=⨯=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+⨯=ππππf .16.F 1、F 2为双曲线C :12222=-by ax (a >0,b >0)的焦点,A 、B 分别为双曲线的左、右顶点,以F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M ,且满足∠MAB=30°,则该双曲线的离心率为 .【答案】【解析】由⎪⎩⎪⎨⎧=+=222c y x x ab y ,解得⎩⎨⎧==b y a x ,即交点M 的坐标),(b a ,连结MB ,则AB MB ⊥,即ABM ∆为直角三角形,由∠MAB=30°得33230tan 0===ab AB MB ,即2234,332a ba b ==,所以2222237,34a ca ac ==-,所以321,372==e e,所以双曲线的离心率321=e .三、解答题:本大题共6个小题满分74分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 17.(本小题满分12分)已知数列{}n a 是等差数列,满足.13,542==a a 数列{}n b 的前n 项和是T n ,且.3=+n n b T (1)求数列{}n a 及数列{}n b 的通项公式; (II )若n n n b a c ⋅=,试比较n c 与1+n c 的大小. 【答案】18.(本小题满分12分)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且满足.cos cos cos 2B c C b B a += (I )求角B 的大小;(II )求函数()⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=62cos 4sin 22ππA A A f 的最大值及取得最大值时的A 值. 【答案】19.(本小题满分12分)在三棱锥P —ABC 中,PB ⊥平面ABC ,AB ⊥BC ,AB=PB=2,BC=23,E 、F 、G 分别为PC 、AC 、PA 的中点.(I )求证:平面BCG ⊥平面PAC ;(II )在线段AC 上是否存在一点N ,使PN ⊥BE ?证明你的结论.【答案】20.(本小题满分12分)为缓解某路段交通压力,计划将该路段实施“交通银行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:(I)作出被调查人员年龄的频率分布直方图;(II)若从年龄在[)[),15的被调查者中各随机选取两人进行追踪调查,记选中的4 252535,,人中不赞成“交通银行”的人数为ξ,求随机变量ξ的分布列和数学期望. 【答案】21.(本小题满分12分) 已知椭圆12222=+by ax (a >b >0)与抛物线x y 42=有共同的焦点F ,且两曲线在第一象限的交点为M ,满足.35=MF(I )求椭圆的方程;(II )过点P (0,1)的直线l 与椭圆交于A 、B 两点,满足25-=⋅PB PA ,求直线l 的方程.【答案】22.(本小题满分14分)已知函数()().ln 122x a x a x x f ++-=(I )当2=a 时,求曲线()x f y =在点()()1,1f 处的切线方程; (II )求函数()x f 的单调区间;(III )若对任意()2,3--∈a 及[]3,1∈x 时,恒有()x f ma -<1成立,求实数m 的取值范围.【答案】。
