2008年 四川省成都市七中外地生招生考试数学试卷
2008年四川省成都市高中阶段教育学校统一招生考试数学试卷及答案(word)

某某市二00八年高中阶段教育学校统一招生考试试卷(含某某市初三毕业会考)数学全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
A 卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷为选择题,第Ⅱ为其它类型的题。
第Ⅰ卷(选择题,共30分)注意事项:1. 第Ⅰ卷共2页。
答第Ⅰ卷前,考生务必将自己的某某、某某号、考试科目涂写在试卷和答题卡上。
考试结束,监考人员将试卷和答题卡一并收回。
2. 第Ⅰ卷全是选择题。
各题均有四个选项,只有一项符合题目要求。
每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动骼橡皮摖干净后,再先涂其他答案,选择题的答案不能答在试卷上。
请注意机读答题卡的横竖格式。
A 卷(共100分)一、选择题。
(每小题3分,共30分)1.2cos45°的值等于(A )22(B )2(C )42(D )22 2.化简(-3x 2)·2x 3的结果是(A )-6x 5(B )-3x 5(C )2x 5(D )6x 53.奥运会火炬传递以“和谐之旅”为主题,以“点燃激情 传递梦想”为口号进行,其传递总路程约为1370000千米,这个路程用科学记数法表示为×104千米×105千米×105千米×106千米4.用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是(A)4 (B)5 (C)6 (D)75.下列事件是必然事件的是(A)打开电视机,任选一个频道,屏幕上正在播放天气预报(B)到电影院任意买一X电影票,座位号是奇数(C)在地球上,抛出去的篮球会下落(D)掷一枚均匀的骰子,骰子停止转动后偶数点朝上x 中,自变量x的取值X围是6.在函数y=3(A)x≥- 3 (B)x≤- 3 (C)x≥3 (D )x≤ 37.如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是(A)∠B=∠E,BC=EF (B)BC=EF,AC=DF(C)∠A=∠D,∠B=∠E (D)∠A=∠D,BC=EF8.一交通管理人员星期天在市中心的某十字路口,对闯红灯的人次进行统计,根据上午7∶00 ~ 12∶00中各时间段(以1小时为一个时间段)闯红灯的人次,制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别为(A)15,15 (B)10,15 (C)15,20 (D)10,209. 如图,小红同学要用纸板制作一个高4cm ,底面周长是6πcm 的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是(A )12πcm 2 (B )15πcm 2 (C )18πcm 2 (D )24πcm 210. 有下列函数:①y = - 3x ;②y = x – 1:③y = - x1 (x < 0);④y = x2 + 2x + 1.其中当x 在各自的自变量取值X 围内取值时,y 随着x 的增大而增大的函数有(A )①② (B )①④ (C )②③ (D )③④第Ⅱ卷(非选择题,共70分)注意事项:1. A 卷的第Ⅱ卷和B 卷共10页,用蓝、黑钢笔或圆珠笔直接答在试卷上。
成都七中2008年外地生招生考试物理试题

成都七中2008年外地生招生考试物理试题考试时间:100分钟满分100分说明:1、本试卷分为第Ⅰ卷(选择题)第Ⅱ卷(非选择题)两部分,第Ⅰ卷1-5页,第Ⅱ卷6-7页。
2、答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目用铅笔填写在答题卡上,第小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦净后,选涂其它答案,不能答在试卷上。
3、将Ⅱ卷的答案写在试卷上规定的地方。
第Ⅰ卷一、单项选择题(每小题只有一个选项符合题意,每题1.5分,共27分)1、在我国古代学者沈括的著作《梦溪笔谈》中有如下记载:“若鸢飞空中,其影随鸢而移;或中间为空隙所束,则影与鸢遂相违,鸢东则影西,鸢西则影东。
”意思是说:若鹞鹰在空中飞翔,它的影子随鹞鹰而动;如鹞鹰和影子中间被窗户孔隙所约束,影子与鹞鹰作相反方向移动,鹞鹰向东则影子向西移,鹞鹰向西则影子向东移。
这描述的是光的(A)A、直线传播现象B、折射现象C、干涉现象D、衍射现象2、如图P是位于水平的粗糙桌面上的物体。
用跨过定滑轮的轻绳将P与小盘相连,小盘内有砝码,小盘和砝码的总质量为m。
在P运动的过程中,若不计空气阻力,则关于在水平方向受到的作用力与相应的施力物体,下列说法正确的是(B)A、拉力和摩擦力,施力物体是地球和桌面B、拉力和摩擦力,施力物体是绳和桌面C、重力mg和摩擦力,施力物体是地球和桌面D、重力mg和摩擦力,施力物体是绳和桌面3、16世纪末,伽得略用实验和推理,推翻了已在欧洲流行了近两千年的亚里士多德关于力和运动的理论,开启了物理学发展的新纪元。
在以下说法中,与亚里士多德观点相反的是(D)A、四匹马拉的车比两匹马拉的车跑得快;这说明,物体受的力越大,速度就越大B、一个运动的物体,如果不再受力了,它总会逐渐停下来;这说明,静止状态才是物体长不受力时的“自然状态”C、两物体从同一高度自由下落,较重的物体下落较快D、一个物体维持匀速直线运动,不需要力4、在电源电压不变的情况下,为使正常工作的电热器在单位时间内产生的热量增加一倍,下列措施可行的是(B)A、剪去一半的电阻丝B、并联一根相同的电阻丝C、串联一根相同的电阻丝D、使电热器两端的电压增大一倍5、某一网络电路中的部分电路如图所示,已知I=3A,I1=2A,R1=10Ω,R2=5Ω,R3=30Ω,则下列结论正确的是(B)A、通过R3的电流为0.5A,方向从a→bB、通过R3的电流为0.5A,方向从b→aC、通过电流表的电流为0.5A,电流表“+”接线柱在右边D、通过电流表的电流为1.5A,电流表“+”接线柱在左边6、如图所示,物体A靠在竖直墙面上,在力F作用下,A、B保持静止。
成都七中外地生招生考试数学试题(答案)

成都七中2015年外地生招生考试数学试题考试时间:120分钟 满分:150分注意:请将答案涂写在答题卡上,本试卷作答无效。
一、单项选择题(本大题共10小题,每题6分,共60分)1、已知等腰△ABC 的面积为1,其中∠A=120°,则△ABC 内切圆的面积为A. 18B. 54C. 9D. 272如图所示,两对角线长分别为4和2的菱形围绕其中心旋转90︒,可以围成一个四角星(其各边用实线标注),则该四角星的周长为A. 3B. 3C. 3D. 33、已知1x =,则4242x x +=+A.3B.4C. 4+D. 8+4、某三棱锥的三视图如右图所示,则该三棱锥的最长棱长为A. B. C. D.45、设x 、y 为实数,则代数式22245425x xy y x y ++-+-的最小值是A.-8B.8C.0D.-106、已知6x y z w ≤≤≤≤,则方程18x y z w +++=的正整数解的个数为 A.5 B. 6 C.7 D.87、定义分子为1且分母为正整数的分数为单位分数,把1分拆成若干个不同的单位分数之和。
如:1=156113211101901721561421301111216121++++++++++++n m ,其中m n ≤。
设1x m ≤≤,1y n ≤≤,则21x y x +++的最小值为 A. 232 B. 52 C. 87 D. 343 8、若一个两位数平方的末两位恰好等于其本身,则这样的两位数有( )个A.2B.3C.4D.59、设p 、q 为不相等的正整数,且关于x 的方程20x px q -+=和20x qx p -+=的根都是正整数,则p q -= A.1 B.2 C.3 D.410、在正方形ABCD 所在平面上的直线l 满足下列条件:正方形ABCD 的四个顶点到直线l 的距离只取两个值,其中的一个值是另一个值的3倍,这样的直线l 的条数为A.4B.8C.12D.16二、填空题(本大题共4小题,每题7分,共28分)11、在四边形ABCD 中, BC=8,CD=19,AD=10,∠A=∠B=60°,则AB=______12、如右图,点E 、F 分别是正方形ABCD 的边BC 、CD 上的点,而△ABE 、△ECF 、△FDA 的面积分别为2、3、4,那么△AEF 的面积为______13、函数24y x mx m =++的图像被x 轴所截的最大值为_______14、已知[]x 表示不超过x 的最大整数,如[]π=3. []3=3,那么=________ 三、填空题(本大题共4小题,每题8分,共32分) 15、已知.10.33=,即10.30.030.003.....3=+++,等式两边同乘 3.则有10.90.090.00=+++,也即.10.9=,借鉴上述操作,若有222221111.....61234π=++++,那么++++222271513111…=_________16、在四边形ABCD 中,∠DAC=98°,∠DBC=82°,∠BCD=70°,BC=AD ,则∠ACD=____17、方程x xx x =-+-111的解为________18、已知o 为△ABC 的外心,有AB=2,AC=4,则AO ·BC 的最小值为_______四、解答题(本大题共2小题,19题14分,20题16分,共30分)19、如图正方形OABC 的顶点O 在坐标原点,且OA 边和AB 边所在直线的解析式分别为34y x =和42533y x =-+,D 、E 分别为OC 、AB 的中点,P 为OA 边上一动点(点P 与点O 不重合),连接DE 和CP ,交点为Q(1)求证:Q 为△COP 的外心(2)求正方形OABC 的边长(3)当圆Q 与AB 相切时,求点P 的坐标20、若存在正常数L ,对某一函数图像上任意不同两点111(,)P x y ,222(,)P x y ,有不等式1212y y L x x -≤-恒成立,则称该函数为李氏函数,L 为该函数的李氏系数。
2008年四川省成都七中育才学校(东区)衔接班招生数学试卷(一)

2008年四川省成都七中育才学校(东区)衔接班招生数学试卷(一)2008年四川省成都七中育才学校(东区)衔接班招生数学试卷(一)一、选择题1.(3分)(2011•高邮市模拟)分数单位是的所有真分数的和应是()32.(3分)在三角形ABC中,AF=FG=GB,AE=ED=DC,则阴影部分的面积占三角ABC面积的().C D.3.(3分)下面说法正确有()(1)把一根长2米的绳子,平均截成5段,每段占全长的;(2)公元2100年有366天;(3)分数一定小于(a、b均为非零自然数);(4)因为1.6÷0.3=16÷3=5…1,所以1.6除以0.3的余数是1;(5)五年级的三好生人数占五年级学生人数的45%,六年级三好生人数占六年级学生人数的55%,五年级的三好4.(3分)如图图形中,由正方体展开而得到的图形有()个.5.(3分)在长度分别为1,2,3,4,5,6,7,8,9的线段各1条,从中选出若干条组成正方形,那么不同的选二、填空题6.(3分)3400平方厘米=_________平方分米;1.4时=_________分;3.05立方米=_________立方分米;24千克=_________吨.7.(3分)300千克海水可以制盐6千克,要制300千克的盐,需要海水_________吨.8.(3分)一台拖拉机,4小时耕地5公顷,这台拖拉机每公顷需要耕_________小时,每小时可以耕_________公顷地.9.(3分)时针速度是分钟速度的_________,分针速度是钞针速度的_________.10.(3分)如图是一个正五边形,它的每个角均为_________度.11.(3分)用1,2,3,4,5这5个数字组成一个五位数,使得这个五位数的任意相邻数字的和都是质数.这个五位数最小是_________.12.(3分)从1~6中选出5个数填入□中,使得算式:□×(□﹣□)×(□﹣□)的积尽可能的大,这个最大值是_________.13.(3分)用“+、﹣、×、÷、”将19、20、21、22组成24:_________.14.(3分)如图是一个周长为50的长方形纸片,A、B两点分别是长和宽的中点.将此长方形沿图中的虚线撕成甲、乙两张.如果甲的周长是48,那么乙的周长是_________.15.(3分)蜗牛从一个枯井往上爬,白天向上爬110厘米,夜里向下滑40厘米,若要在第6天的白天爬到井口,这口井最多深_________厘米.16.(3分)甲、乙两个数的和是23.126,如果把甲数的小数点向左移动一位,得到的数为乙数的3倍,则甲数是_________.17.(3分)如图,ABCD是正方形,DE为3厘米,梯形BCDE的面积比三角形ABE的面积大24平方厘米,则梯形EDCB的面积为_________平方厘米.18.(3分)用三张数字卡片:1、5、9,一共可以组成_________个不同的自然数.19.(3分)张师傅开车去送货,在起点处他看见路边的里程碑上的两位数为AB千米,1小时后他看见里程碑上的两位数为:BA千米,又过1小时,看见里程碑上的数为三位数,且恰好是第一个里程碑上的两位数中间加上一个0:AOB千米.张师傅的车速为每小时_________千米.20.(3分)一个正方形,它对角线长5厘米,这个正方形的面积是_________平方厘米.21.(3分)把一个长6厘米,宽5厘米,高4厘米的长方体切成3个大小一样的小长方体后,它表面积至少要增加_________平方厘米.22.(3分)一个两位数去除2008,余数是34,这样的两位数有_________个.23.(3分)在梯形ABCD中,BE=2EC,CF=2AF,阴影部分的面积为3平方厘米,则梯形的面积为_________平方厘米.24.(3分)用5个相同的长方形一个大长方形,大长方形的周长是66厘米,则每个小长方形的周长是_________厘米.25.(3分)(2013•吴中区)六年级某班学生中有的学生年龄为13岁,有的学生年龄为12岁,其余学生年龄为11岁,这个班学生的平均年龄是_________岁.26.(3分)如图中,一共有_________个三角形.27.(3分)在右边的算式中,不同的字代表不同的数字,相同的字代表相同的数字.“成都七嘉祥”代表的六位数的最小值是_________.三、计算题28.计算:①4050﹣6030÷_________=3900②3×6+33×66+333×666=③1﹣+﹣+﹣=④方程:10.1﹣17X=1.86﹣15解是X=⑤1÷(2÷3)÷(3÷4)÷(4÷5)÷…÷(19÷20)=⑥3×(3+)+3.4×=29.脱式计算:(1)7.6×2008.4+(2008.4+12.5)×2.4(2)5÷[(0.13×+1÷400)×].四、解答题30.在5.12汶川特大地震中,有16个爱心人士一共收养了27个灾区孤儿,其中收养1个孤儿的爱心人士与收养2~3个孤儿的爱心人士一样多,求收养3个孤儿的爱心人士有多少人?31.一次数学竞赛中,某校获奖同学的总平均分为80分.其中8名获一等奖的同学的平均分为95分,有2名获三等奖同学的平均分为70分,其余的同学获二等奖,平均分为75分,该校这次竞赛中获二等奖的同学的人数有多少?32.一辆速度为每小时72千米的汽车,向正前方向的一个回音壁驶去,鸣笛后4.5秒钟才听到回声,己知声音在空气中的速度是每秒钟340米,听到回声时汽车离回音壁还有多远?33.在黑、白棋子一堆,其中黑子的3倍与白子的5倍相等;如果每次取出黑子7个,白子5个,若干次后,黑子还剩下13个,白子还剩下3个,求这堆棋子一共有多少个?34.甲、乙、丙、丁四人从同一地点出发都去某地,甲先走了一段时间,然后乙、丙、丁三人一起同时出发,经过6小时后,乙追上甲;经过9小时后,丙追上甲;经过12小时后,丁追上甲.己知乙每小时行27千米,丙每小时行23千米,那么丁每小时行多少千米?2008年四川省成都七中育才学校(东区)衔接班招生数学试卷(一)参考答案与试题解析一、选择题1.(3分)(2011•高邮市模拟)分数单位是的所有真分数的和应是()3分数单位是中间一个是的真分数有、、、、、、+++++=32.(3分)在三角形ABC中,AF=FG=GB,AE=ED=DC,则阴影部分的面积占三角ABC面积的().C D.EFG=AEG=三角形ABD=EFG=×××三角形三角形BDG=ABD=三角形BDG=×三角形ABC=面积的:+=EFG=AEG=三角形三角形ABD=三角形×××ABC=BDG=三角形BDG=×三角形三角形面积的:+=面积的.3.(3分)下面说法正确有()(1)把一根长2米的绳子,平均截成5段,每段占全长的;(2)公元2100年有366天;(3)分数一定小于(a、b均为非零自然数);(4)因为1.6÷0.3=16÷3=5…1,所以1.6除以0.3的余数是1;(5)五年级的三好生人数占五年级学生人数的45%,六年级三好生人数占六年级学生人数的55%,五年级的三好)分数和,所以题中每段占全长的是错误的;<,所以分数一定小于4.(3分)如图图形中,由正方体展开而得到的图形有()个.5.(3分)在长度分别为1,2,3,4,5,6,7,8,9的线段各1条,从中选出若干条组成正方形,那么不同的选二、填空题6.(3分)3400平方厘米=34平方分米;1.4时=84分;3.05立方米=3050立方分米;24千克=0.024吨.7.(3分)300千克海水可以制盐6千克,要制300千克的盐,需要海水15吨.,8.(3分)一台拖拉机,4小时耕地5公顷,这台拖拉机每公顷需要耕0.8小时,每小时可以耕 1.25公顷地.9.(3分)时针速度是分钟速度的,分针速度是钞针速度的.;60=故答案为:,10.(3分)如图是一个正五边形,它的每个角均为108度.11.(3分)用1,2,3,4,5这5个数字组成一个五位数,使得这个五位数的任意相邻数字的和都是质数.这个五位数最小是14325.12.(3分)从1~6中选出5个数填入□中,使得算式:□×(□﹣□)×(□﹣□)的积尽可能的大,这个最大值是64.13.(3分)用“+、﹣、×、÷、”将19、20、21、22组成24:(19+21)÷20+22或(21﹣19)×22﹣20.14.(3分)如图是一个周长为50的长方形纸片,A、B两点分别是长和宽的中点.将此长方形沿图中的虚线撕成甲、乙两张.如果甲的周长是48,那么乙的周长是23.15.(3分)蜗牛从一个枯井往上爬,白天向上爬110厘米,夜里向下滑40厘米,若要在第6天的白天爬到井口,这口井最多深460厘米.16.(3分)甲、乙两个数的和是23.126,如果把甲数的小数点向左移动一位,得到的数为乙数的3倍,则甲数是22.38.×=22.3817.(3分)如图,ABCD是正方形,DE为3厘米,梯形BCDE的面积比三角形ABE的面积大24平方厘米,则梯形EDCB的面积为44平方厘米.18.(3分)用三张数字卡片:1、5、9,一共可以组成26个不同的自然数.19.(3分)张师傅开车去送货,在起点处他看见路边的里程碑上的两位数为AB千米,1小时后他看见里程碑上的两位数为:BA千米,又过1小时,看见里程碑上的数为三位数,且恰好是第一个里程碑上的两位数中间加上一个0:AOB千米.张师傅的车速为每小时45千米.20.(3分)一个正方形,它对角线长5厘米,这个正方形的面积是12.5平方厘米.21.(3分)把一个长6厘米,宽5厘米,高4厘米的长方体切成3个大小一样的小长方体后,它表面积至少要增加80平方厘米.22.(3分)一个两位数去除2008,余数是34,这样的两位数有3个.23.(3分)在梯形ABCD中,BE=2EC,CF=2AF,阴影部分的面积为3平方厘米,则梯形的面积为20.25平方厘米.S(S×24.(3分)用5个相同的长方形一个大长方形,大长方形的周长是66厘米,则每个小长方形的周长是30厘米.,则小长方形的长就是×=925.(3分)(2013•吴中区)六年级某班学生中有的学生年龄为13岁,有的学生年龄为12岁,其余学生年龄为11岁,这个班学生的平均年龄是12岁.×××﹣)26.(3分)如图中,一共有23个三角形.27.(3分)在右边的算式中,不同的字代表不同的数字,相同的字代表相同的数字.“成都七嘉祥”代表的六位数的最小值是102586.三、计算题28.计算:①4050﹣6030÷40.2=3900②3×6+33×66+333×666=③1﹣+﹣+﹣=④方程:10.1﹣17X=1.86﹣15解是X=⑤1÷(2÷3)÷(3÷4)÷(4÷5)÷…÷(19÷20)=⑥3×(3+)+3.4×=+1﹣()﹣(××××…;+﹣﹣+1﹣(﹣﹣(﹣+1﹣+1﹣1+﹣﹣+,X=÷÷…,××××…3+×××+×+××+129.脱式计算:(1)7.6×2008.4+(2008.4+12.5)×2.4(2)5÷[(0.13×+1÷400)×].÷××××]四、解答题30.在5.12汶川特大地震中,有16个爱心人士一共收养了27个灾区孤儿,其中收养1个孤儿的爱心人士与收养2~3个孤儿的爱心人士一样多,求收养3个孤儿的爱心人士有多少人?31.一次数学竞赛中,某校获奖同学的总平均分为80分.其中8名获一等奖的同学的平均分为95分,有2名获三等奖同学的平均分为70分,其余的同学获二等奖,平均分为75分,该校这次竞赛中获二等奖的同学的人数有多少?32.一辆速度为每小时72千米的汽车,向正前方向的一个回音壁驶去,鸣笛后4.5秒钟才听到回声,己知声音在空气中的速度是每秒钟340米,听到回声时汽车离回音壁还有多远?33.在黑、白棋子一堆,其中黑子的3倍与白子的5倍相等;如果每次取出黑子7个,白子5个,若干次后,黑子还剩下13个,白子还剩下3个,求这堆棋子一共有多少个?34.甲、乙、丙、丁四人从同一地点出发都去某地,甲先走了一段时间,然后乙、丙、丁三人一起同时出发,经过6小时后,乙追上甲;经过9小时后,丙追上甲;经过12小时后,丁追上甲.己知乙每小时行27千米,丙每小时行23千米,那么丁每小时行多少千米?参与本试卷答题和审题的老师有:林清涛;xuetao;sdlcx;杜爱占;WX321;zhuyum;wl;71ssk;彭辉;浩淼;张倩;苏卫萍;nywhr;旭日芳草;似水年华;zhangx;王亚彬;dgdyq;忘忧草;1075493;彭京坡;王庆(排名不分先后)菁优网2014年5月4日。
2008年四川省成都市高中统一招生考打印k4

2008年成都市高中阶段教育学校统一招生考试试卷(地震无听力)(含成都市初三毕业会考)全卷分A卷和B卷。
A卷满分100分,B卷满分50分。
考试时间120分钟。
A卷分A卷I和A卷II,A卷I为选择题,A卷II为其他类型的题。
A卷I答案务必填在答题卡上;A卷II及B卷答案务必全部写在试卷上。
请注意答题卡的横竖格式。
A卷(共100分)A卷I(选择题90分)注意事项:1.A卷I共6页,在答A卷I前,考生务必将自己的姓名、准考证号、考试科目涂写在试卷和答题卡上。
考试结束时,监考人员将试卷和答题卡一并收回。
2.每小题选出答案后,用2B铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
第一部分基础知识运用(共50小题,计50分)一、选择填空(共30小题,计30分)A)从各题的A、B、c三个选项中,找出和画线部分意思相同或相近、并能替换画线部分的选项。
(共5分)1. A few minutes later,Paul an d Nancy got to Center Street by bus.A.ran to B.arrived at C.went to2. Sam looks strong,but actually he is not in good health.A.in fact B.in all C.in general3. I found a supermarket close to my new house.A.in front of B.far from C.next to4. After the vacation, all the students returned to the schoo1.A.gave back B.sent back C.went back5. Peter told me he loves China and he wants to travel all over China.A.around B.through C.inB) 从各题的A、B、c三个选项中选择正确答案。
08年招生统数学试卷2

某某市2008年高级中等教育学校招生统一考试数学试卷一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.-2的绝对值等于( ).A .2B .-2C .±2D .212.下列轴对称图形中,对称轴条数最多的是( ).3.以下所给的数值中,为不等式-2x +3<0的解的是( ).A .-2B .-1C .23D .24.某校初三·一班6名女生的体重(单位:kg )为:353638404242则这组数据的中位数等于( ). A .38B .39C .40D .425.2008年8月8日,五环会旗将在“鸟巢”高高飘扬, 会旗上的五环(如图)间的位置关系有( ).A .相交或相切B .相交或内含C .相交或相离D .相切或相离6.“5·12”汶川大地震使某某也遭受了重大损失,社会各界踊跃捐助.据新华社讯,截止到6月22日12时,我国收到社会各界捐款、捐物共计467.4亿元.把467.4亿元用科学记数法表示为( ).A .4.674×1011 元B .4.674×1010 元C .4.674×109 元D .4.674×108 元7.已知,如图,∠1=∠2=∠3=55°,则∠4的度数等于( ). A .115°B .120° C .125°D .135°8.若关于x 的多项式x 2-px -6含有因式x -3,则实数p 的值为( ). A .-5B .5C .-1D .19.某几何体的三视图如下所示,则该几何体可以是( ).10.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为().11.二次函数y=ax2 +bx+c的部分对应值如下表:利用二次函数的图象可知,当函数值y<0时,x的取值X围是().A.x<0或x>2B.0<x<2C.x<-1或x>3D.-1<x<312.如图,O是边长为1的正△ABC的中心,将△ABC绕点O逆时针方向旋转180°,得△A1B1C1,则△A1B1C1与△ABC重叠部分(图中阴影部分)的面积为().A.33B.43C.63D.83二、填空题:本大题共6个小题,每小题4分,共24分.将答案直接填写在题中横线上.13.3×(-31)=.14.函数xxy2+=中,自变量x的取值X围是.15.如图是由若干个边长为1的小正方形组成的网格,在图中作出将五角星ABCDE向其东北方向平移23个单位的图形.16.质地均匀的正四面体骰子的四个面上分别写有数字2,3,4,5,投掷这个正四面体两次,则第一次底面上的数字能够整除第二次底面上的数字的概率是.x-3 -2 -1 0 1 2 3 4 5y12 5 0 -3 -4 -3 0 5 1217.如图,AB 是圆O 的直径,弦AC 、BD 相交于点E ,若 ∠BEC =60°,C 是BD⌒的中点,则tan ∠ACD =. 18.△ABC 中,∠C =90°,AB =1,tan A =43,过AB 边上一点P 作PE ⊥AC 于E ,PF ⊥BC 于F ,E 、F 是垂足,则EF 的 最小值等于.三、解答题:本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤.19.(本题共2个小题,每小题8分,共16分)(1)计算:(-2-2 +31)×86-20080÷sin45°.(2)计算:)1111()12(22122+---+⋅-+m m m m m m m .20.(本题满分12分)某面粉批发商通过统计前48个星期的面粉销售量(单位:吨),销售量 18.5≤x <19.519.5≤x <20.520.5≤x <21.521.5≤x <22.522.5≤x <23.523.5≤x <24.5合计 划记频数67 9 12 8 6 48(1)在图1、图2中分别画出频数分布直方图和频数折线图;(2)试说明这位面粉批发商每星期进面粉多少吨比较合适(精确到0.1吨)?21.(本题满分12分)已知如图,点A (m ,3)与点B (n ,2)关于直线y =x 对称,且都在反比例函数x ky =的图象上,点D 的坐标为(0,-2).(1)求反比例函数的解析式;(2)若过B 、D 的直线与x 轴交于点C ,求sin ∠DCO 的值.60︒E OA BDC22.(本题满分12分)A 、B 两地相距176 km ,其间一处因山体滑坡导致连接这两地的公路受阻.甲、乙两个工程队接到指令,要求于早上8时,分别从A 、B 两地同时出发赶往滑坡点疏通公路.10时,甲队赶到立即开始作业,半小时后乙队赶到,并迅速投入“战斗”与甲队共同作业,此时甲队已完成了工程量的241.(1)若滑坡受损公路长1 km ,甲队行进的速度是乙队的23倍多5 km ,求甲、乙两队赶路的速度;(2)假设下午4点时两队就完成公路疏通任务,胜利会师.那么若只由乙工程队疏通这段公路时,需要多少时间能完成任务?23.(本题满分12分)青年企业家X 敏准备在北川禹里乡投资修建一个有30个房间供旅客住宿的旅游度假村,并将其全部利润用于灾后重建.据测算,若每个房间的定价为60元∕天,房间将会住满;若每个房间的定价每增加5元∕天时,就会有一个房间空闲.度假村对旅客住宿的房间将支出各种费用20元∕天·间(没住宿的不支出).问房价每天定为多少时,度假村的利润最大?24.(本题满分12分)如图,⊙O 的直径AB 为10 cm , 弦AC 为6 cm ,∠ACB 的平分线交AB 于E ,交⊙O 于D . 求弦AD 、CD 的长.25.(本题满分14分)如图,矩形ABCD 中,AB = 8,BC = 10,点P 在矩形的边DC 上由D 向C 运动.沿直线AP 翻折△ADP ,形成如下四种情形.设DP =x ,△ADP 和矩形重叠部分(阴影)的面积为y .(1)如图丁,当点P 运动到与C 重合时,求重叠部分的面积y ;(2)如图乙,当点P 运动到何处时,翻折△ADP 后,点D 恰好落在BC 边上?这时重叠部分的面积y 等于多少?(3)阅读材料:已知锐角α≠45°,tan 2α是角2α的正切值,它可以用角α的正切值tan α来表示,即2)(tan 1tan 22tan ααα-=(α≠45°).根据上述阅读材料,求出用x 表示y 的解析式,并指出x 的取值X 围.(提示:在图丙中可设∠DAP =α)一、填空题1~6.AADBCB 7~12.CDABDC 二、填空题13.-114.x ≥-2且x ≠015.图形如右 16.16517.3318.2512三、解答题19.(1)原式=221212)3141(÷-⨯+-=21212121⨯-⨯=0.(2)原式=)1)(1()1(1)1(4)1(2122+---+-+⋅-+m m m m m m m m m=)1)(1(2)1)(1(2+--+-m m m m m =)1(2)1)(1()1(2+=+--m m m m .20.(1)(2)由频数折线图,得(19×6+20×7+21×9+22×12+23×8+24×6)÷48=1035÷48=21.5625, 所以这位面粉批发商每星期进面粉21.6吨比较合适.21.(1)∵A (m ,3)与B (n ,2)关于直线y =x 对称, ∴m =2,n =3, 即 A (2,3),B (3,2).于是由 3=k ∕2,得k =6.因此反比例函数的解析式为xy 6=. (2)设过B 、D 的直线的解析式为y =kx +b .∴2=3k +b ,且 -2=0·k +b .解得k =34,b =-2.故直线BD 的解析式为y =34x -2.∴当y =0时,解得x =.即C (,0),于是OC =,DO =2. 在Rt △OCD 中,DC =5.225.122=+. ∴sin ∠DCO =545.22==DC DO . 说明:过点B 作BE ⊥y 轴于E ,则 BE = 3,DE = 4,从而 BD = 5,sin ∠DCO = sin ∠DBE =54.22.(1)甲队行进了2小时,乙队行进了2.5小时. 设乙队的速度为x ,则甲队为x +5. 由题意得方程2.5x +(x +5)×2+1=176. 整理得 5.5x =165,解得x =30. ∴x +5=×30+5=50.即甲队赶路的速度为50 km ∕h ,乙队赶路的速度为30 km ∕h . (2)设若由乙队单独施工,需x 小时才能完成.则由题意有 6×(21241÷)+5.5×x 1=1.解得x =11.即乙队单独做,需要11小时才能完成任务.23.设每天的房价为60+5x 元,则有x 个房间空闲,已住宿了30-x 个房间. 于是度假村的利润y =(30-x )(60+5x )-20(30-x ),其中0≤x ≤30. ∴y =(30-x )·5·(8+x )=5(240+22x -x 2)=-5(x -11)2 +1805.因此,当x =11时,y 取得最大值1805元,即每天房价定为115元∕间时,度假村的利润最大.法二 设每天的房价为x 元,利润y 元满足)56030)(20(---=x x y =84046512-+-x x (60≤x ≤210,是5的倍数).法三 设房价定为每间增加x 元,利润y 元满足 )530)(2060(x x y --+==120022512++-x x (0≤x ≤150,是5的倍数).24.∵AB 是直径,∴∠ACB =90°.在Rt △ABC 中,BC =2222610-=-AC AB = 8(cm ). ∵CD 平分∠ACB ,∴AD⌒=BD ⌒,进而AD =BD .于是在Rt △ABD 中,得AD =BD =22AB = 52(cm ). 过E 作EF ⊥AC 于F ,EG ⊥BC 于G ,F 、G 是垂足,则四边形CFEG 是正方形.设EF =EG =x ,由三角形面积公式,得21AC ·x +21BC ·x =21AC ·BC ,即21×6·x +12×8×x =12×6×8,解得x =724. ∴CE =2x =7224. 由△ADE ∽△CBE ,得DE :BE =AE :CE =AD :BC , 即DE :BE =AE :7224=52:8, 解得AE =730,BE =AB -AE =10-730=740,∴DE =7225.因此CD =CE +DE =7224+7225= 72(cm ). 答:AD 、CD 的长依次为52cm ,72cm .说明:另法一 求CD 时还可以作CG ⊥AE ,垂足为G ,连接OD . 另法二 过A 作AF ⊥CD 于F ,则△ACF 是等腰直角三角形.25.(1)由题意可得∠DAC =∠D ′AC =∠ACE ,∴AE =CE . 设AE =CE =m ,则BE =10-m .在Rt △ABE 中,得m 2 =82 +(10-m )2,m =8.2.∴重叠部分的面积y =21·CE ·AB =21×8.2×8=32.8(平方单位).另法 过E 作EO ⊥AC 于O ,由Rt △ABC ∽Rt △EOC 可求得EO . (2)由题意可得△DAP ≌△D ′AP , ∴AD ′=AD =10,PD ′=DP =x .在Rt △ABD ′中,∵AB =8,∴BD ′=22810 = 6,于是CD ′=4. 在Rt △PCD ′中,由x 2 =42 +(8-x )2,得x =5.此时y =21·AD ·DP =21×10×5=25(平方单位).表明当DP =5时,点D 恰好落在BC 边上,这时y =25. 另法 由Rt △ABD ′∽Rt △PCD ′可求得DP .(3)由(2)知,DP =5是甲、丙两种情形的分界点.G当0≤x ≤5时,由图甲知y =S △AD ′P =S △ADP =21·AD ·DP =5x .当5<x <8时,如图丙,设∠DAP =α,则∠AEB =2α,∠FPC =2α.在Rt △ADP 中,得 tan α=10xAD DP =.根据阅读材料,得 tan2α=2210020)10(1102x x x x -=-⋅. 在Rt △ABE 中,有BE =AB ∕tan2α=2100208x x -=x x 5)100(22-.同理,在Rt △PCF 中,有CF =(8-x )tan2α=2100)8(20x x x --.∴△ABE 的面积S △ABE =21·AB ·BE =21×8×x x 5)100(22-=x x 5)100(82-.△PCF 的面积S △PCF =21·PC ·CF =21(8-x )×2100)8(20x x x --=22100)8(10x x x --. 而直角梯形ABCP 的面积为S 梯形ABCP =21(PC +AB )×BC =21(8-x +8)×10=80-5x .故重叠部分的面积y =S 梯形ABCP -S △ABE -S △PCF=80-5x -x x 5)100(82--22100)8(10xx x --. 经验证,当x =8时,y =32.8适合上式. 综上所述,当0≤x ≤5时,y =5x ;当5<x ≤8时,y =80-5x -x x 5)100(82--22100)8(10x x x --.2008年高级中等教育学校招生统一考试数学试卷一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.32-的倒数等于( ).A .32B .32-C .23D .23-2.下列各式中,计算正确的是( ). A .5a 2-2a 2 =3B .2a +3b =5ab C .(2xy 2)2 =4x 2y 4D .6mn ÷3n =3m3.下列四个几何体的三视图是同一个图形的是( ).4.据报道,“5·12”汶川大地震使得李白纪念馆刹那间墙倾屋摧,满目疮痍.经过抢救,包括71件顶级国宝在内的4000余件馆藏文物(价值约2 010 000 000元)全部从危房中救出,并被安全转移.将数字2 010 000 000用科学记数法可表示为( ).A .2.01×107B .2.01×108C .2.01×109D .2×1095.在奔驰、宝马、丰田、三菱等汽车标志图形中,为中心对称图形的是( ).6.如图,△ABC 中,延长边AB 、CA 构成∠1、∠2,若∠C =55°, 则∠1+∠2=( ).A .125°B .235°C .250°D .305°7.如图,把一X 矩形纸片ABCD 沿对角线BD 折叠,BC 交AD 于O .给出下列结论:①BC 平分∠ABD ;②△ABO ≌△CDO ;③ ∠AOC =120°;④△BOD 是等腰三角形.其中正确的结论有( ).A .①③B .②④C .①②D .③④8.某某市笔试科目 语文 数学 英语 物理 化学 满分值15015015010080若把表中各笔试科目满分值按比例绘成扇形统计图,则表示数学学科的扇形的圆心角为(结果保留3个有效数字)( ).A .85.7°B .86°C .42.7°D .43°9.若实数m ,n 满足2m +3n =0 且 4m +n -10=0,则过点P (m ,n )的反比例函数的解析式为( ).A .x y 61=B .x y 61-=C .x y 6=D .xy 6-=10.如图,△ABC 中 ,∠C =90°,∠A =30°,BD 是∠ABC 的平 分线,设△ABD 、△BCD 的面积分别为S 1、S 2,则S 1:S 2 =( ).A .2:1B .2:1C .3:2D .2:311.如图,正方形ABCD 中,DE =2AE ,DF =CF ,则sin ∠BEF =( ). A .410B .810C .10103D .31 12.抛物线bx x y 2322+=与x 轴的两个不同交点是O 和A ,顶点B 在直线y =kx 上,若△OAB 是等边三角形,则b =( ).A .±3B .±3C .33±D .31± 二、填空题:本大题共6个小题,每小题4分,共24分.将答案直接填写在题中横线上. 13.︱-2︱=.14.若1)1(2-=-a a ,则实数a 的取值X 围是.15.如图,⊙O 的弦AB 、CD 互相平行,E 、F 分别是圆周上 两点,则∠BEC +∠AFD =度.16.抛掷两枚均匀的正方体骰子(它们的六个面分别标有数字 1,2,3,4,5,6),骰子朝上的面的数字分别为a ,b ,则a +b = 6的概率为.17.“5·12”汶川大地震使不少建筑物受损.某地一 水塔地震时发生了严重沉陷(未倾斜).如图,已知地震 前,在距该水塔30米的A 处测得塔顶B 的仰角为60°; 地震后,在A 处测得塔顶B 的仰角为45°,则该水塔沉 陷了米.(,3≈1.7321,2≈1.4142)18.连接抛物线y =ax 2(a ≠0)上任意四点所组成的四边形可能是(填写所有正确选项的序号).①菱形;②有三条边相等的四边形;③梯形;④平行四边形.三、解答题:本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤.19.(本题共2个小题,每小题8分,共16分)(1)计算:6)273482()31()21()3(120÷-+--÷--π.(2)化简:)111()1111(22aa a a a ---÷++-.20.(本题满分12分)已知反比例函数x m y 5-=的图象有一支在第一象限.(1)求常数m 的取值X 围;(2)若它的图象与函数y =x 的图象一个交点的纵坐标为2,求当-2<x <-1时,反比例函数值y 的取值X 围.21.(本题满分12分)某图书馆为了了解读者的需求情况,某天对读者借阅的所有图书类别 少儿类 科技类 文艺类 体育类 其他 数量(本) 20 80 40 比例10%25%40%(1)补全上表,并求当天共借阅了多少本图书?(2)若用一个统计图描述当天借阅的各类图书所占比例的情况,你认为最好选用什么统计图?作出你所选用的统计图;(3)试根据调查结果,给该图书馆的采购部提一条合理化建议.22.(本题满分12分)华联商场预测某品牌衬衫能畅销市场,先用了8万元购入这种衬衫,面市后果然供不应求,于是商场又用了17.6万元购入第二批这种衬衫,所购数量是第一批购入量的2倍,但单价贵了4元.商场销售这种衬衫时每件定价都是58元,最后剩下的150件按定价的八折销售,很快售完.试求:(1)第一次购买这种衬衫的单价是多少? (2)在这两笔生意中,华联商场共赢利多少元?23.(本题满分12分)如图,P A 、PB 是⊙O 的切线,A 、 B 为切点,连结AO 并延长交⊙O 于C ,交PB 的延长线于D .(1)找出图中所有的相似三角形,并证明你的结论(不再添加辅助线); (2)若P A =2+2,∠P = 45︒,求图中阴影部分的面积.24.(本题满分12分)如图,在□ABDO 中,已知A 、 D 两点的坐标分别为A (3,3),D (23,0).将□ABDO 向左平移3个单位,得到四边形A ′B ′D ′O ′.抛物线C 经过点A ′、B ′、D ′.(1)在图中作出四边形A ′B ′D ′O ′,并写出它的四个顶点坐标;(2)在抛物线C 上是否存在点P ,使△ABP 的面积恰好为四边形A ′B ′D ′O ′的面积的一半?若存在,求出点P 的坐标;若不存在,说明理由.25.(本题满分14分)(1)已知△ABC 是等腰直角三角形,现分别以它的直角边BC 、斜边AB 为边向外作正方形BCEF 、ABMN ,如图甲,连接MF ,延长CB 交MF 于D .试观测DF 与DM 的长度关系,你会发现.(2)如果将(1)中的△ABC 改为非等腰的直角三角形,其余作法不变,如图乙,这时D 点还具有(1)的结论吗?请证明你的判断.(3)如果将(1)中的△ABC 改为锐角三角形,仍以其中的两边分别向外作正方形,如图丙,则应在图中过B 点作△ABC 的线,它与MF 的交点D 恰好也具有(1)的结论.请证明在你的作法下结论的正确性.一、填空题1~6.DCDCBB7~12.BADACA 二、填空题13.214.a ≥115.18016.6117.21.96 18.②③ 三、解答题19.(1)原式=6)3938(3411÷-+-÷=6334÷--=221-.(2)原式=)1()1(11122-+-÷--++a a a a a a a =)1(11222--÷-a a a a =-2a 2. 20.(1)∵反比例函数的图象有一支在第一象限,∴m -5>0,即m >5. 因此m 的取值X 围为m >5. (2)由题意可知,反比例函数xm y 5-=的图象经过点(2,2), ∴ 2×2=m -5,得 m =9,∴xy 4=. 当x =-2时,y =-2;当x =-1时,y =-4.故根据反比例函数图象知,当-2<x <-1时,y 的取值X 围是-4<x <-2. 21.(1)∵20÷10%=200,∴ 这天共借了200本.类别 少儿类 科技类 文艺类 体育类 其他 数量(本) 20 50 80 40 10 比例10%25%40%20%5%(2)最好选用扇形统计图,图如右: (3)建议:可多采购些文艺类书籍.22.(1 第一批 第二批 单价 x x +4 总价 80000176000 数量x800004176000+x 有x 80000×2 =4+x .解得x =40,此即为第一批购入衬衫的单价. (2)由(1)知,第一批购入了 80000÷40=2000件. 在这两笔生意中,华联商场共赢利为2000×(58-40)+(2000×2-150)×(58-44)+150×(58×0.8-44)=90260元. 答:第一批购入这种衬衫的单价为40元,两笔生意中华联商场共赢利90260元. 23.(1)△OBD ∽△P AD .证明∵P A 、PB 是⊙O 的切线,∴OA ⊥P A ,OB ⊥PB ,∴∠OAP =∠OBD =90°. 又∠D =∠D ,∴△OBD ∽△P AD .(2)∵∠P =45°,∴∠DOB =45°,∴△OBD 、△P AD 均是等腰直角三角形, 从而PD =2P A ,BD =OB . 又∵P A =2+2,P A =PB ,∴BD =OB =PD -PB =2P A -P A =(2-1)P A =(2-1)(2+2)=2.故S 阴影=S △OBD -S 扇形=23604521BD BD OB ⋅-⋅⋅π=2812221⨯-⨯⋅π=41π-.24.(1)作出平移后的四边形A ′B ′D ′O ′如右.顶点坐标分别为A ′(0,3)、B ′(23,3)、D ′(3,0)、O ′(-3,0).(2)由题意可设抛物线C 的解析式为y = ax 2 + bx +3,则⎪⎩⎪⎨⎧+⋅+⋅=+⋅+⋅=,33)3(0,332)32(322b a b a 解得a =33,b =-2.∴抛物线C 的解析式为y =33x 2-2x +3. ∵四边形A ′B ′D ′O ′是平行四边形, ∴它的面积为O ′D ′×OA ′=23×3=6.假设存在点P ,则△ABP 的面积为3.设△ABP 的高为h ,则 21×AB ×h =21×23×h =3,得 h =3.即点P 到AB 的距离为3,∴P 点的纵坐标为0或23. ∴当P 的纵坐标为0时,即有 0=33x 2-2x +3,解得x 1 =x 2 =3. 当P 的纵坐标为23时,即有23=33x 2-2x +3,解得631-=x ,632+=x . 因此存在满足条件的点P ,坐标为(3,0),(63-,23),(63+,23).25.(1)DF =DM .(2)仍具有(1)的结论,即DF =DM .证明:延长CD ,过M 作MP ⊥CD ,交于P ,P 为垂足. ∵∠MBP +∠ABC =90°,∠BAC +∠ABC =90°, ∴∠MBP =∠BAC .又∠ACB =∠MPB =90°,AB =BM , ∴△ABC ≌△BMP ,从而BC =MP .∵BC=BF,∴BF=MP.又∠PDM=∠BDF,∠DPM=∠DBF,∴△DBF≌△DPM,∴DF=DM.(3)高.证明:如图,延长GD,过M、F作GD的垂线垂足为P、Q.∵∠MBP+∠BMP=90°,∠ABG+∠MBP=90°,∴∠BMP=∠ABG.又∠MPB=∠AGB=90°,AB=BM,∴△ABG≌△BMP,∴MP=BG.同理△FQB≌△BGC,∴FQ=BG,∴MP=FQ.∵∠FDQ=∠MDP,∠FQD=∠MPD=90°,∴△FDQ≌△MDP,进而DF=DM.说明过F作FH∥BM交BD的延长线于H.通过证明△ABC≌△HFB得HF=AB=BM,进而证明△BDM≌△HFD,得出D是FM的中点.。
成都七中2009年外地生招生考试数学、物理、英语有答案【2】

成都七中2008年外地生招生考试数学试题考试时间120分钟 满分150分注:请将选择题的正确选项填涂到季度卡上一、选择题(每小题只有一个正确答案,共10个小题,满分60分)1、已知三个整数a,b,c 的和为奇数,那么abc c b a 2222+-+ ( )A 、一定是非零偶数B 、等于零C 、一定为奇数D 、可能是奇数,也可能是偶数。
2、已知3 2c b a 1abc 222=++=++=c b a ,,, 则111111-++-++-+b ca a bc c ab 的值是( ) A 、1 B 、21- C 、2 D 、32-3、设02=+-q px x 的二实根为βα,,而以22βα,为根的二次方程仍是02=+-q px x ,则数对),(q p 的个数是( )A 、2B 、3C 、4D 、04、设函数543222-----=k k kx x y 的最大值为M ,为使M 最大,k= ( )A 、-1B 、1C 、-3D 、35、若132=-x x ,则=+--+200872129234x x x x ( )A 、2011B 、2010C 、2009D 、20086、已知坐标原点O 和点)-2,A(2,B 是坐标轴上的一点,若AOB ∆是等腰三角形,则这样的点B 一共有多少个 ( )A 、4B 、5C 、6D 、87、如图:有六个面积为1的正方形组成的长方形,其中有A 、B 、C 、D 、E 、F 、G 7个点,以这7个点为顶点,并且面积为1的三角形有 ( )A 、11个B 、12个C 、13个D 、14个8、锐角ABC ∆的三边两两不等,D 是BC 边上的一点,︒=∠+∠90C BAD ,则AD 一定过ABC ∆的 ( ) A 、垂心 B 、内心 C 、外心 D 、重心9、有纯农药一桶,倒出20L 后用水补满,然后又倒出10L ,再用水补满,这时,桶中纯农药与水的容积之比为3:5,则桶的容积为( )A 、30B 、40C 、50D 、60 A B CD EF G10、如图,直线4321//////l l l l ,相邻两条平行线间的距离都等于1,若正方形ABCD 的四个顶点分别在四条直线上,则它的面积等于( )A 、4B 、5C 、24D 、25二、填空题(每小题6分,满分48分)11、如图正方形的每一个面上都有一个自然数,已知相对的两个面上二数之和都相等,若13、9、3的对面的书分别为a,b,c,则 =---++bc ac ab c b a 222 12、已知等边ABC ∆外有一点P ,设P 到BC 、CA 、AB 的距离分别为321h ,h ,h ,且63h2-h1=+h ,那么等边ABC ∆的面积为13、Rt ABC ∆中,︒=∠90C ,若sinA 和sinB 是方程022=--k x x 的两个根,则k=14、在ABC ∆中,2AC =,D 是AB 的中点,E 是CD 上一点,CD 31ED =, 若AE CE AB CE ⊥=且31,则BC= 15、方程22323=--+x x 的解为16、在正八边形中,与所有边均不平行的对角线有 条17、若正整数n 恰好有4个正约数,则称n 为奇异数,例如6、8、10都是奇异数,那么在27、42、69、111、125、137、343、899、3599、7999这10个正整数中奇异数有 个18、如图,MN 是半圆O 的半径,A 是半圆的一个三等分点,B 是中点,P 是直径MN 上的点,若PB AP +的最小值为22厘米, 则圆的半径r = 厘米1l 2l 3l 4l A B C D 3913三、解答题(每小题14分,满分42分)19、(1)已知抛物线3)3(2--+=x m mx y )0(>m 与x 轴交于点)0,(1x A ,)0,(2x B )21(x x <与y 轴交于点C 且AB=4,圆M 过A 、B 、C 三点,求扇形MAC 的面积S 。
2008年中考数学试题及答案解析
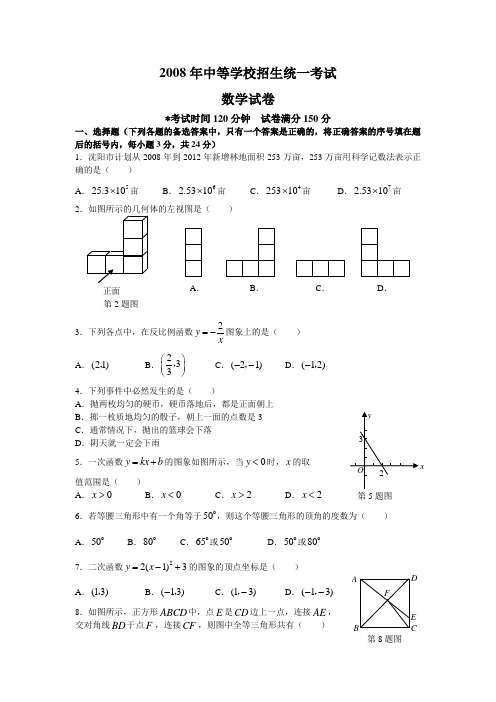
2008年中等学校招生统一考试数学试卷*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分)1.沈阳市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( ) A .525.310⨯亩B .62.5310⨯亩C .425310⨯亩D .72.5310⨯亩2)3.下列各点中,在反比例函数2y x=-图象上的是()A .(21),B .233⎛⎫⎪⎝⎭,C .(21)--,D .(12)-,4.下列事件中必然发生的是( )A .抛两枚均匀的硬币,硬币落地后,都是正面朝上B .掷一枚质地均匀的骰子,朝上一面的点数是3C .通常情况下,抛出的篮球会下落D .阴天就一定会下雨5.一次函数y kx b =+的图象如图所示,当0y <时,x 的取 值范围是( ) A .0x > B .0x <C .2x >D .2x <6.若等腰三角形中有一个角等于50,则这个等腰三角形的顶角的度数为( ) A .50B .80C .65或50D .50或807.二次函数22(1)3y x =-+的图象的顶点坐标是( )A .(13),B .(13)-,C .(13)-,D .(13)--, 8.如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE , 交对角线BD 于点F ,连接CF ,则图中全等三角形共有( )正面第2题图A .B .C .D .第5题图xADCEFB第8题图A .1对B .2对C .3对D .4对二、填空题(每小题3分,共24分)9.已知A ∠与B ∠互余,若70A ∠=,则B ∠的度数为 . 10.分解因式:328m m -= .11.已知ABC △中,60A ∠=,ABC ∠,ACB ∠的平分线交于点O ,则BOC ∠的度数为 .12.如图所示,菱形ABCD 中,对角线AC BD ,相交于点O ,若再补 充一个条件能使菱形ABCD 成为正方形,则这个条件是 (只填一个条件即可). 13.不等式26x x -<-的解集为 .14.如图所示,某河堤的横断面是梯形ABCD ,BC AD ∥,迎水坡AB 长13米,且12tan 5BAE ∠=,则河堤的高BE 为 米.15.观察下列图形的构成规律,根据此规律,第8第15题图16.在平面直角坐标系中,点A 的坐标为(11),,点B 的坐标为(111),,点C 到直线AB 的距离为4,且ABC △是直角三角形,则满足条件的点C 有 个.三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.计算:101(1)52-⎛⎫π-+-+- ⎪⎝⎭18.解分式方程:1233xx x=+--.19.先化简,再求值:222()()2y x y x y x y ++---,其中13x =-,3y =.第1个 ……第2个 第3个 第4个ADC BO 第12题图 B C DA 第14题图20.如图所示,在66⨯的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形,如图①中的三角形是格点三角形. (1)请你在图①中画一条直线将格点三角形分割成两部分,将这两部分重新拼成两个不同的格点四边形,并将这两个格点四边形分别画在图②,图③中; (2)直接写出这两个格点四边形的周长.四、(每小题10分,共20分)21.如图所示,AB 是O 的一条弦,OD AB ⊥,垂足为C ,交O 于点D ,点E 在O 上.(1)若52AOD ∠=,求DEB ∠的度数;(2)若3OC =,5OA =,求AB 的长.22.小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局. (1)一次出牌小刚出“象”牌的概率是多少?(2)如果用A B C ,,分别表示小刚的象、虎、鼠三张牌,用1A ,1B ,1C 分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.图① 第20题图图②图③第21题图 小刚 小明A 1B 1C 1A B C 第22题图23.在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ; (2)请你将表格补充完整:(3)请从下列不同角度对这次竞赛成绩的结果进行分析:①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩;③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩. 六、(本题12分)24.一辆经营长途运输的货车在高速公路的A 处加满油后,以每小时80千米的速度匀速行驶,前往与A 处相距636千米的B 地,下表记录的是货车一次加满油后油箱内余油量y (升)与行驶时间x (1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y 与x 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)(2)按照(1)中的变化规律,货车从A 处出发行驶4.2小时到达C 处,求此时油箱内余油多少升?(3)在(2)的前提下,C 处前方18千米的D 处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B 地.(货车在D 处加油过程中的时间和路程忽略不计)第23题图 一班竞赛成绩统计图 二班竞赛成绩统计图25.已知:如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AMN △是等腰三角形.(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立; (3)在(2)的条件下,请你在图②中延长ED 交线段BC 于点P .求证:PBD AMN △∽△.八、(本题14分) 26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,. (1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.2008年沈阳市中等学校招生统一考试C E ND A BM图① C A EM B D N图② 第25题图第26题图数学试题参考答案及评分标准一、选择题(每小题3分,共24分) 1.B 2.A 3.D 4.C 5.C 6.D7.A8.C二、填空题(每小题3分,共24分) 9.2010.2(2)(2)m m m +-11.12012.90BAD ∠=(或AD AB ⊥,AC BD =等)13.4x >14.1215.65 16.8 三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.解:原式1(2)5=+-+- ···························································· 4分125=-+- ··················································································· 5分6= ······································································································ 6分18.解:12(3)x x =-- ·················································································· 2分126x x =--7x = ··········································································································· 5分 检验:将7x =代入原方程,左边14==右边 ························································ 7分所以7x =是原方程的根 ·················································································· 8分 (将7x =代入最简公分母检验同样给分)19.解:原式2222222xy y x xy y x y =++-+-- ················································ 4分 xy =- ········································································································· 6分 当13x =-,3y =时,原式1313⎛⎫=--⨯= ⎪⎝⎭······················································································ 8分 20.解:(1)答案不唯一,如分割线为三角形的三条中位线中任意一条所在的直线等.································· 2分拼接的图形不唯一,例如下面给出的三种情况:图① 图② 图③ 图④图①~图④,图⑤~图⑦,图⑧~图⑨,画出其中一组图中的两个图形. ······················ 6分 (2)对应(1)中所给图①~图④的周长分别为4+8,4+4+ 图⑤~图⑦的周长分别为10,8+8+图⑧~图⑨的周长分别为2+4+ ···································· 10分 四、(每小题10分,共20分) 21.解:(1)OD AB ⊥,AD DB ∴= ··························································· 3分 11522622DEB AOD ∴∠=∠=⨯= ································································· 5分 (2)OD AB ⊥,AC BC ∴=,AOC △为直角三角形, 3OC =,5OA =,由勾股定理可得4AC == ·············································· 8分 28AB AC ∴== ························································································· 10分 22.解:(1)1()3P =一次出牌小刚出象牌“” ··················································· 4分(2)树状图(树形图):·············································································· 8分图⑤ 图⑥图⑦图⑧ 图⑨A 1B 1C 1 AA 1B 1C 1 BA 1B 1C 1C开始小刚 小明或列表···························································· 8分 由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种. ········································································ 9分1()3P ∴=一次出牌小刚胜小明. ····································································· 10分 五、(本题12分) 23.解:(1)21······························································································ 2分 (2)一班众数为90,二班中位数为80 ······························································· 6分 (3)①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班成绩好; ···································································································· 8分 ②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好; ················································································································· 10分 ③从B 级以上(包括B 级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班成绩好. ······························································································· 12分 六、(本题12分) 24.解:(1)设y 与x 之间的关系为一次函数,其函数表达式为y kx b =+ ················ 1分将(0100),,(180),代入上式得, 10080b k b =⎧⎨+=⎩ 解得20100k b =-⎧⎨=⎩20100y x ∴=-+ ·························································································· 4分验证:当2x =时,20210060y =-⨯+=,符合一次函数; 当 2.5x =时,20 2.510050y =-⨯+=,也符合一次函数.∴可用一次函数20100y x =-+表示其变化规律,而不用反比例函数、二次函数表示其变化规律. ··················································· 5分 y ∴与x 之间的关系是一次函数,其函数表达式为20100y x =-+ ··························· 6分 (2)当 4.2x =时,由20100y x =-+可得16y =即货车行驶到C 处时油箱内余油16升. ····························································· 8分 (3)方法不唯一,如:方法一:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 设在D 处至少加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯+=+, ··················································· 11分 解得,69a =(升) ····················································································· 12分方法二:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 汽车行驶18千米的耗油量:1820 4.580⨯=(升) D B ,之间路程为:63680 4.218282-⨯-=(千米)汽车行驶282千米的耗油量:2822070.580⨯=(升) ················································································· 11分 70.510(16 4.5)69+--=(升) ···································································· 12分 方法三:由(1)得,货车行驶中每小时耗油20升, ············································· 9分设在D 处加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯++≤,解得,69a ≥ ····························································································· 11分 ∴在D 处至少加油69升,货车才能到达B 地. ················································· 12分七、(本题12分) 25.证明:(1)①BAC DAE ∠=∠ BAE CAD ∴∠=∠AB AC =,AD AE = ABE ACD ∴△≌△BE CD ∴= ·································································································· 3分 ②由ABE ACD △≌△得ABE ACD ∠=∠,BE CD =M N ,分别是BE CD ,的中点,BM CN ∴= ················································· 4分 又AB AC = ABM ACN ∴△≌△AM AN ∴=,即AMN △为等腰三角形 ···························································· 6分 (2)(1)中的两个结论仍然成立. ···································································· 8分 (3)在图②中正确画出线段PD由(1)同理可证ABM ACN △≌△ CAN BAM ∴∠=∠ BAC MAN ∴∠=∠ 又BAC DAE ∠=∠MAN DAE BAC ∴∠=∠=∠AMN ∴△,ADE △和ABC △都是顶角相等的等腰三角形 ································· 10分 PBD AMN ∴∠=∠,PDB ADE ANM ∠=∠=∠PBD AMN ∴△∽△ ···················································································· 12分 八、(本题14分)26.解:(1)点E 在y 轴上 ·············································································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ································································· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=∴在Rt DOM △中,12DM =,2OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ················································································ 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ·················································································· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A ,12D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得32131242a a ⎧+=⎪⎨+=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:2829y x x =--+ ·················································· 9分(3)存在符合条件的点P ,点Q . ································································· 10分。
成都七中09年外招生考试数学模拟试题及答案

成都七中外地生招生考试数学模拟试题 第 1 页 共 13 页成都七中外地生招生考试数 学 模拟试题(考试时间120分钟,满分150分)第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
不能答在试卷纸上。
3.考试结束后,监考员将第Ⅰ卷、第Ⅱ卷和答题卡一并收回。
一、单项选择(共12小题,每小题5分,满分60分)每小题只有一个选项符合题意。
1.已知二次函数c bx ax y ++=2(0≠a )的图象如图所示, 则下列结论 ①0<++c b a ②0<+-c b a ③02<+a b ④0>abc 其中正确的个数是 A .1个 B .2个C .3个D .4个2.如图,O 是线段BC 的中点,A 、D 、C 到O 点的距离相等。
若30=∠ABC ,则ADC ∠的度数是 A .30°B .60°C .120°D .150°3.如图,△ACB 内接于⊙O ,D 为弧BC 的中点,ED 切⊙O 于D的延长线相交于E ,若AC =2,AB =6,ED +EB =6,那么A .2B .4C .6D .84.现有A 、B 两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6)用小丽掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P ),(y x 。
那么它们各掷一次所确定的点E DC成都七中外地生招生考试数学模拟试题 第 2 页 共 13 页P 落在已知抛物线x x y 42+-=上的概率为 A .118 B .112 C .19 D .165.不等式组4831531x x -≥--<- 的所有整数解的和是A .—1B .0C .1D .26.如果自然数a 是一个完全平方数,那么与a 之差最小且比a 大的一个完全平方数是A .1a +B .21a+ C .221a a ++ D .21a +7.如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a =1,则这个正方形的面积为A BC .2D .(21 8.对于两个数,200820092009M =⨯,200920082008N =⨯。
2008年四川省成都市七中外地生招生考试数学试卷及分析答案

2008年四川省成都市七中外地生招生考试数学试卷
,则
C.
.
是方程的两个根,
上一点,,若分)方程
的中点,的最小值为
,
2008年四川省成都市七中外地生招生考试数学试卷
参考答案与试题解析
一、选择题(每小题只有一个正确答案,共10个小题,满分60分)
222
2.(6分)已知abc=1,a+b+c=2,a2+b2+c2=3,则的值为(D)
3.(6分)设x﹣px+q=0的两实根为α,β,而以α,β为根的一元二次方程仍是x﹣px+q=0,则数对(p,q)的
顶点,并且面积为1的三角形有(D)
1234
直线上,则它的面积等于(B)
D.
11.(6分)(2012•驻马店二模)如图,正方体的每一面上都有一个正整数,已知相对的两个面上两数之和都相等,如果13、9、3的对面的数分别为a、b、c,则a2+b2+c2﹣ab﹣bc﹣ca的值等于76.
12.(6分)已知等边△ABC外有一点P,设P到BC、CA、AB的距离分别为h1,h2,h3,且h1﹣h2+h3=6,那么等边△ABC的面积为12.
13.(6分)Rt△ABC中,∠C=90°,若sinA和sinB是方程的两个根,则k=﹣.
14.(6分)在△ABC中,AC=2,D是AB的中点,E是CD上一点,,若,则BC=2.
15.(6分)方程的解为.
R=S=
,﹣)
(,﹣
的长为。
2008年成都市

成都市2008年高中阶段教育学校统一招生考试(含成都市初三毕业会考)数 学 试 题全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
A 卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷为选择题,第Ⅱ为其它类型的题。
第Ⅰ卷(选择题,共30分)注意事项:1.第Ⅰ卷共2页。
答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在试卷和答题卡上。
考试结束,监考人员将试卷和答题卡一并收回。
2.第Ⅰ卷全是选择题。
各题均有四个选项,只有一项符合题目要求。
每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动骼橡皮摖干净后,再先涂其他答案,选择题的答案不能答在试卷上。
请注意机读答题卡的横竖格式。
A 卷(共100分)一、选择题。
(每小题3分,共30分) 1.2cos45°的值等于 .................. ( )A .22B .2C .42D .222.化简(-3x 2)·2x 3的结果是 .................. ( ) A .-6x 5 B .-3x 5 C .2x 5 D .6x 53. 北京奥运会火炬传递以“和谐之旅”为主题,以“点燃激情 传递梦想”为口号进行,其传递总路程约为1370000千米,这个路程用科学记数法表示为 .............. ( ) A .13.7×104千米 B .13.7×105千米 C .1.37×105千米 D .1.37×106千米4. 用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是 .................. ( )A .4B .5C .6D .75.下列事件是必然事件的是 ..................( )A .打开电视机,任选一个频道,屏幕上正在播放天气预报B .到电影院任意买一张电影票,座位号是奇数C .在地球上,抛出去的篮球会下落D .掷一枚均匀的骰子,骰子停止转动后偶数点朝上6.在函数y=中,自变量x 的取值范围是.................. ( )A .x ≥ - 3B .x ≤ - 3C .x ≥ 3D .x ≤ 37. 如图,在△ABC 与△DEF 中,已有条件AB=DE ,还需添加两个条件才能使△ABC ≌△DEF ,不能添加的一组条件是 ( ) A .∠B=∠E,BC=EF B .BC=EF ,AC=DF C .∠A=∠D ,∠B=∠E D .∠A=∠D ,BC=EF8. 一交通管理人员星期天在市中心的某十字路口,对闯红灯的人次进行统计,根据上午7∶00 ~ 12∶00中各时间段(以1小时为一个时间段)闯红灯的人次,制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别为 ( ) A .15,15 B .10,15 C .15,20 D .10,209. 如图,小红同学要用纸板制作一个高4cm ,底面周长是6πcm 的圆锥形漏斗模型,若不计接 缝和损耗,则她所需纸板的面积是 ( ) A .12πcm 2 B .15πcm 2 C .18πcm 2 D .24πcm 210.有下列函数:①y = - 3x ;②y = x – 1:③y = -x1(x < 0);④y = x 2 + 2x + 1.其中当x 在各自的自变量取值范围内取值时,y 随着x 的增大而增大的函数有 ( )A .①②B .①④C .②③D .③④第Ⅱ卷(非选择题,共70分)注意事项:1.A 卷的第Ⅱ卷和B 卷共10页,用蓝、黑钢笔或圆珠笔直接答在试卷上。
四川省成都七中2008级高三年级上学期期中考试(数学理

四川省成都七中2008级高三年级上学期期中考试数学试卷(理)考试时间120分钟 满分150分第Ⅰ卷一、选择题(共60分,每小题5分)1.设{}210S x x =+>,{}350T x x =-<,则S T = ( )A .∅B .12x x ⎧⎫<-⎨⎬⎩⎭C .53x x ⎧⎫>⎨⎬⎩⎭D .1523x x ⎧⎫-<<⎨⎬⎩⎭2.设等差数列{}n a 的前n 项和为n S ,若357=S ,则=4a ( )A .8B .7C .6D . 53.设等比数列{}n a 的前10项和为10,前20项和为30,则它的前30项和为 ( )A .50B .70C .90D .1104.设函数)(x f y =的反函数为)(1x fy -=,且)12(-=x f y 的图象过点)1,21(,则)(1x fy -=的图象必过( )A .)1,21(B .)21,1( C .(1,0)D .(0,1)5.设等差数列{}n a 的前n 项和为n S ,已知,65S S <,876S S S >=则在下列结论中错误的是( )A .0<dB .07=aC .59S S >D .n S S S 均为76,中的最大值6.设1a >,函数()log a f x x =在区间[]2a a ,上的最大值与最小值之差为12,则a =( )AB .2C .D .47.若函数y =f (x )的图象可由函数y =lg(x +1)的图象绕坐标原点O 逆时针旋转2π得到, 则 f (x )=( )A .10-x -1B .10x -1C .1-10-xD .1-10x8.设等差数列{}n a 的前n 项和为n S ,,01>a 若,0,02004200320042003<⋅>+a a a a 则使0>n S 成立的最大自然数n 为( )A . 4005B .4006C .4007D .40089.已知数列{}n a 满足a 2+n =a 1+n -a n ,a 1=1,a 2=2,则2005S =( )A .1B .2C .3D .4 10.设)(),(x g x f 分别是定义在R 上的奇函数和偶函数,当0<x 时,,0)()()()(>'+'x g x f x g x f且,0)3(=-g 则不等式0)()(<x g x f 的解集是 ( )A .),3()0,3(+∞⋃-B .)3,0()0,3(⋃-C .),3()3,(+∞⋃--∞D .)3,0()3,(⋃--∞11.对于函数①()()12lg +-=x x f ,②()()22-=x x f ,③()()2cos +=x x f .判断如下三个命题的真假:命题甲:()2+x f 是偶函数;命题乙:()()2,∞-在区间x f 上是减函数,在区间()+∞,2 上是增函数;命题丙:()()x f x f -+2在()+∞∞-,上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是 ( ) A .①③ B .①② C .③ D .②12.设p :f (x )=e x +ln x +2x 2+mx +l 在(0,+∞)内单调递增,q :m ≥-5,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件第Ⅱ卷二、填空题(共16分,每小题4分)13.若0342<-+mx mx 恒成立,则实数m 的取值范围是____________14.已知函数)24(log )(3+=x x f ,则方程4)(1=-x f 的解=x __________.15.等差数列{}n a 的前n 项和为n S ,若 }{,75,7157nS T S S n n 为数列==的前n 项和,则n T =_____________。
四川成都市2008年高中阶段教育学校统一招生考试

四川成都市2008年高中阶段教育学校统一招生考试语文全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
A卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷为选择题,第Ⅱ卷为其他类型的题。
A 卷( 共100 分)注意事项:1. 第I卷共2页,答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在试卷和答题卡上。
考试结束后,监考人员将试卷和答题卡一并收回。
2. 第I卷各题均有四个选项,只有一项符合题目要求。
每小题选出答案后,用2B铅笔把答题卡对应题目的答案标号涂黑;如需改动,橡皮擦干净后,再选涂其他答案,不能答在试卷上。
请注意机读答题卡的横竖格式。
第I 卷一、基础知识(10分,每小题2分)1.下面语句中加点字的注音有误的一项是A.人类的智慧与大自然的智慧相比实在是相形见绌(zhuō),无论是令人厌恶(wù)的苍蝇蚊子,还是美丽可人的鲜花绿草,都是大自然精巧绝伦的艺术品。
B.我常常把手放在大地上,我会感到她在跳跃(yuè),和我的心的跳跃是一样的, 它们的热血一直在流,在热情的默契(qì)里它们彼此呼唤,终有一天它们要汇合在一起。
C.这是某种令人惊骇(hài)而不知名的杰作,在不可名状的晨曦(xī)中依稀可见,宛如在欧洲文明的地平线上瞥见的亚洲文明的剪影。
D.峰环水抱的萨尔茨堡,高高低低的房屋鳞次栉(zhì)比,庄严肃(sù)穆的修道院坐落在绿树浓阴中。
2.下面语句中书写准确无误的一项是A. 黄土高原啊,只有你,才能承受如此惊心动魄的博击!B. 因为我听到海依然在远方为我喧腾——那雪白的海潮啊,夜夜奔来一次次漫湿了枯干的心灵。
C. 读书的要决,全在于会意。
对于这一点,陶渊明尤其有独到的见解。
D. 不管扔进去什么东西,这个慷概大方的洞全部一视同仁,照收不误。
3.依次填入下列句子横线处的词语,最恰当的一项是①那时候,他已经诗兴不作而研究志趣正浓。
成都市2008年高中阶段教育学校统一招生考试

成都市2008年高中阶段教育学校统一招生考试英语(满分150分,考试时间120分钟)A卷(共100分)A卷第I卷(选择题,共90分)第一部分基础知识运用(共50小题,满分50分)一、选择填空(共30小题;每小题1分,满分30分)(A)从各题的A、B、C三个选项中,找出和画线部分意思相同或相近、并能替换画线部分的选项。
(共5小题;每小题1分,满分5分)1.A few minutes later,Paul and Nancy got to Center Street by bus.A.ran to B.arrived at C.went to2.Sam looks strong,but actually he is not in good health.A.in fact B.in all C.in general3.I found a supermarket close to my new house.A.in front of B.far from C.next to4.After the vacation,all the students returned to the school.A.gave back B.sent back C.went back5.Peter told me he loves China and he wants to travel all over China.A.around B.through C.in(B)从各题的A、B、C三个选项中选择正确答案。
(共25小题;每小题1分,满分25分)6.—Could you lend me the book you bought last week?—__________.A.Y es,here you are B.No,I can’t lend it to you C.It’s not interesting7.—Tom,shall we set up a student volunteer project in our school?—__________.A.I don’t want to join youB.Thank you for your helpC.That’s a good idea8.—Happy birthday to you,Jack.—________.A.With pleasure B.Thanks a lot C.The same to you9.We all feel ________ the disabled girl has made so much progress in music.A.worried B.lovely C.surprised10.The funny toy monkey ________ Sandy five dollars.A.cost B.spent C.used11.—Where is Mike? He asked me to go out for a walk this evening.—Maybe he ________ TV in the living room now.A.watched B.will watch C.is watching12.My friend Dave helped me a lot by giving me ________ on English learning.A.advices B.many advice C.some advice13.—I haven’t seen Bob for a long time.—I haven’t seen him,________.A.too B.either C.instead14.When Mary couldn’t see her mother,she began to cry and ________ her.A.look for B.look after C.look at15.—Please give this note to John.—OK,I’ll give it to him as soon as he ________.A.is coming back B.will come back C.comes back16.There is ________ big square in ________ center of our city.A.a;the B.the;a C.the;the17.Y ou ________ stay in bed any longer.Get up to work quickly!A.must B.won’t C.can’t18.Alice ran Lucy。
【VIP专享】2008年四川省成都市中考数学试卷答案

(C)1.37×105 千米
(B)13.7×105 千米
(D)1.37×106 千米
4. 用若干个大小相同,棱长为 1 的小正方体搭成一个几何体模型,其三视图如图所示,则
搭成这个
几何体模型所用的小正方体的个数是
(A)4
5. 下列事件是必然事件的是
(B)5
(A)打开电视机,任选一个频道,屏幕上正在播放天气预报
2008 年四川省成都市中考数学试卷 (含成都市初三毕业会考)
全卷分 A 卷和 B 卷,A 卷满分 100 分,B 卷满分 50 分;考试时间 120 分钟。A 卷分 第Ⅰ卷和第Ⅱ卷,第Ⅰ卷为选择题,第Ⅱ为其它类型的题。
A 卷(共 100 分) 第Ⅰ卷(选择题,共 30 分) 注意事项: 1. 第Ⅰ卷共 2 页。答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在试卷 和答题卡上。考试结束,监考人员将试卷和答题卡一并收回。 2. 第Ⅰ卷全是选择题。各题均有四个选项,只有一项符合题目要求。每小题选出答案后, 用 2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其 他答案,选择题的答案不能答在试卷上。请注意机读答题卡的横竖格式。 一、选择题:(每小题 3 分,共 30 分) 1. 2cos45°的值等于
(D)7
(D) 2 2
(D)6x5
(D )x≤ 3
8. 一交通管理人员星期天在市中心的某十字路口,对闯红灯的人次进行统计,根据上午
7∶00 ~ 12∶00 中各时间段(以 1 小时为一个时间段)闯红灯的人次,制作了如图所示的 条形统计图,则各时间段闯红灯人次的众数和中位数分别为
2 (A) 2
2. 化简( - 3x2)·2x3 的结果是
(A)- 6x5
成都2008年高中阶段教育学校统一招生考试

成都市2008年高中阶段教育学校统一招生考试化学(满分90分,考试时间60分钟)第Ⅰ卷(选择题,共36分)一、选择题(本题包括12个小题,每小题3分,共36分。
每小题只有一个选项符合题意。
)化学课上,每个学习小组各有一瓶无标签的无色透明液体。
请你和同学们一起对此液体进行探究,并完成下列1~4题。
1.某小组同学打开瓶盖后没有闻到特殊气味。
可推测该液体不可能是()A.食盐水B.纯净水C.澄清石灰水D.白醋2.从组成上看,这些液体不可能属于()A.混合物B.纯净物C.含有Cu2+的盐溶液D.氧化物3.几组同学分别取少量液体进行如下实验,其中一定发生化学变化的是()A.加热——有水汽产生B.通入CO2——产生白色沉淀C.加入活性炭——振荡后变浑浊D.滴加植物油——静置后分层4.若某小组的液体为只含有一种溶质的溶液,加入少量MnO2后产生能使带火星的木条复燃的气体。
则下列说法不正确的是()A.反应前后MnO2的化学性质不变B.该反应的化学方程式为2H2O2===H2O+O2C.产生的气体高温时能与磷、硫等发生氧化反应D.如果用右图装置收集该气体,则气体应从b端进入5.比较煤与石油,下列说法正确的是()A.都是化石燃料B.都是含有碳元素的有机物C.综合利用的途径相同D.都可直接用作家用燃料6.丙氨酸的结构简式为CH3—CH—COOH。
丙氨酸的说法不正确的是()NH2A.含有C、H、O、N四种元素B.每个分子中含有三个碳原子C.是一种离子化合物D.化学式可表示为C3H7O2N7.硫离子的结构示意图如右图所示,与硫原子比较,二者()A.核内质子数相同B.核外电子数相同C.化合价相同D.化学性质相同8.通过化学课的学习,成语“细水长流”可理解为()A.在家用细细的长流水洗衣服或刷牙B.节约每一滴水,形成“细水长流”的水资源C.地球淡水储量丰富,可供人类永久使用D.水龙头漏水可让其“细水长流”,方便使用9.某同学在实验室闻到类似碘酒的气味,寻“味”而去,发现实验台上棕色瓶内装有固体碘。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年四川省成都市七中外地生招生考试数学试卷一、选择题(每小题只有一个正确答案,共10个小题,满分60分)1、已知三个整数a,b,c的和为奇数,那么a2+b2﹣c2+2abc()A、一定是非零偶数B、等于零C、一定为奇数D、可能是奇数,也可能是偶数2、已知abc=1,a+b+c=2,a2+b2+c2=3,则的值为()A、﹣1B、C、2D、3、设x2﹣px+q=0的两实根为α,β,而以α2,β2为根的一元二次方程仍是x2﹣px+q=0,则数对(p,q)的个数是()A、2B、3C、4D、04、设函数y=﹣x2﹣2kx﹣3k2﹣4k﹣5的最大值为M,为使M最大,k=()A、﹣1B、1C、﹣3D、35、若3x2﹣x=1,则9x4+12x3﹣2x2﹣7x+2008=()A、2011B、2010C、2009D、20086、已知坐标原点O和点A(2,﹣2),B是坐标轴上的一点,若△AOB是等腰三角形,则这样的点B一共有多少个()A、4B、5C、6D、87、如图:有六个面积为1的正方形组成的长方形,其中有A、B、C、D、E、F、G 7个点,以这7个点为顶点,并且面积为1的三角形有()A、11个B、12个C、13个D、14个8、锐角△ABC的三边两两不等,D是BC边上的一点,∠BAD+∠C=90°,则AD一定过△ABC的()A、垂心B、内心C、外心D、重心9、有纯农药一桶,倒出20升后用水补满;然后又倒出10升,在用水补满,这是桶中纯农药与水的容积之比为3:5,则桶的容积为()A、30升B、40升C、50升D、60升10、如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于1,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于()A、4B、5C、D、二、填空题(每小题6分,满分48分)11、如图正方形的每一个面上都有一个自然数,已知相对的两个面上二数之和都相等,若13、9、3的对面的书分别为a,b,c,则a2+b2+c2﹣ab﹣ac﹣bc=_________.12、已知等边△ABC外有一点P,设P到BC、CA、AB的距离分别为h1,h2,h3,且h1﹣h2+h3=6,那么等边△ABC的面积为_________.13、Rt△ABC中,∠C=90°,若sinA和sinB是方程的两个根,则k=_________.14、在△ABC中,AC=2,D是AB的中点,E是CD上一点,,若,则BC=_________.15、方程的解为_________.16、在正八边形中,与所有边均不平行的对角线有_________条.17、若正整数n恰好有4个正约数,则称n为奇异数,例如6、8、10都是奇异数,那么在27、42、69、111、125、137、343、899、3599、7999这10个正整数中奇异数有_________个.18、如图,MN是半圆O的半径,A是半圆的一个三等分点,B是的中点,P是直径MN上的点,若AP+PB的最小值为厘米,则圆的半径r=_________厘米.三、解答题(每小题14分,满分42分)19、已知二次函数y=mx2+(m﹣3)x﹣3(m>0)的图象如图所示.(1)这条抛物线与x轴交于两点A(x1,0)、B(x2,0)(x1<x2),与y轴交于点C,且AB=4,⊙M过A、B、C三点,求扇形MAC的面积;(2)在(1)的条件下,抛物线上是否存在点P,使△PBD(PD垂直于x轴,垂足为D)被直线BC分成面积比为1:2的两部分?若存在,请求出P点坐标;若不存在,请说明理由.20、某校在向“希望工程”捐款活动中,甲班的m个男生和11个女生的捐款总数与乙班的9个男人和n个女生的捐款总数相等,都是(m•n+9m+11n+145)元,已知每人的捐款数相同,且都是整数元,求每人的捐款数.21、已知△ABC是圆O的内接三角形,∠BAC的平分线交BC于F交圆O于D,DE切圆O于D交AC的延长线于E,连BD,若BD=3,DE+EC=6,AB:AC=3:2,求BC的长.答案与评分标准一、选择题(每小题只有一个正确答案,共10个小题,满分60分)1、已知三个整数a,b,c的和为奇数,那么a2+b2﹣c2+2abc()A、一定是非零偶数B、等于零C、一定为奇数D、可能是奇数,也可能是偶数考点:因式分解的应用。
专题:计算题。
分析:先把代数式分解因式,再根据已知进行讨论得出正确选项.解答:解:a2+b2﹣c2+2abc=(a+b+c)(a+b﹣c)+2abc﹣2ab=(a+b+c)(a+b﹣c)+2(abc﹣ab),已知a+b+c为奇数,而改变加减运算符号,不改变奇偶性,∴a+b﹣c也为奇数,则(a+b+c)(a+b﹣c)也为奇数,2(abc﹣ab)是偶数,∴a2+b2﹣c2+2abc=(a+b+c)(a+b﹣c)+2(abc﹣ab)一定是奇数,故选:C.点评:本题考查了因式分解的应用,把式子分解因式是解题关键.2、已知abc=1,a+b+c=2,a2+b2+c2=3,则的值为()A、﹣1B、C、2D、考点:分式的化简求值。
分析:由a+b+c=2,a2+b2+c2=3,利用两个等式之间的平方关系得出ab+bc+ac=;再根据已知条件将各分母因式分解,通分,代入已知条件即可.解答:解:由a+b+c=2,两边平方,得a2+b2+c2+2ab+2bc+2ac=4,将已知代入,得ab+bc+ac=;由a+b+c=2得:c﹣1=1﹣a﹣b,∴ab+c﹣1=ab+1﹣a﹣b=(a﹣1)(b﹣1),同理,得bc+a﹣1=(b﹣1)(c﹣1),ca+b﹣1=(c﹣1)(a﹣1),∴原式=++=====﹣.故选D.点评:本题考查了分式的化简其中计算,解题时,充分运用已知条件变形,使分式能化简通分,得出结果.3、设x2﹣px+q=0的两实根为α,β,而以α2,β2为根的一元二次方程仍是x2﹣px+q=0,则数对(p,q)的个数是()A、2B、3C、4D、0考点:根与系数的关系;根的判别式。
专题:分类讨论。
分析:利用根与系数的关系把α,β之间的关系找出来,利用α,β之间的关系,解关于p,q的方程,然后再代入原方程检验即可.解答:解:根据题意得,α+β=p①,αβ=q②;α2+β2=p③,α2β2=q④.由②④可得α2β2﹣αβ=0,解之得αβ=1或0由①③可得α2+β2=(α+β)2﹣2αβ=p2﹣2q=p,即p2﹣p﹣2q=0,当q=0时,p2﹣p=0,解之得,p=0或p=1,即,,把它们代入原方程的△中可知符合题意.当q=1时,p2﹣p﹣2=0,解之得,p=﹣1或2,即,,把它们代入原方程的△中可知不合题意舍去,所以数对(p,q)的个数是3对.故本题选B.点评:将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2=﹣,x1•x2=.4、设函数y=﹣x2﹣2kx﹣3k2﹣4k﹣5的最大值为M,为使M最大,k=()A、﹣1B、1C、﹣3D、3考点:二次函数的最值。
专题:计算题。
分析:由于M是最大值,那么M=,即M=﹣2k2﹣4k﹣5,于是求k=﹣的值即可.解答:解:∵y=﹣x2﹣2kx+(﹣3k2﹣4k﹣5),∴M==∴M=﹣2k2﹣4k﹣5,又∵M最大,∴k=﹣=﹣=﹣1.故选A.点评:本题考查了函数的最值.注意y最大值=即可.5、若3x2﹣x=1,则9x4+12x3﹣2x2﹣7x+2008=()A、2011B、2010C、2009D、2008考点:因式分解的应用。
专题:计算题;整体思想。
分析:将3x2﹣x=1化简为3x2﹣x﹣1=0,整体代入9x4+12x3﹣2x2﹣7x+2008变形的式子3x2(3x2﹣x﹣1)+5x(3x2﹣x﹣1)+2(3x2﹣x﹣1)+2010,计算即可求解.解答:解:∵3x2﹣x=1,即3x2﹣x﹣1=0,∴9x4+12x3﹣2x2﹣7x+2008=3x2(3x2﹣x﹣1)+5x(3x2﹣x﹣1)+2(3x2﹣x﹣1)+2010=2010.故选B.点评:本题考查因式分解的运用,注意运用整体代入法求解.6、已知坐标原点O和点A(2,﹣2),B是坐标轴上的一点,若△AOB是等腰三角形,则这样的点B一共有多少个()A、4B、5C、6D、8考点:等腰三角形的判定;坐标与图形性质。
专题:应用题。
分析:根据等腰三角形的性质,要使△AOB等腰三角形,可以分两种情况考虑:当OA是底边时,作OA 的垂直平方线,和坐标轴出现交点,当OA是腰时,则分别以点O、点A为圆心,OA为半径画弧,和坐标轴出现交点.解答:解:①作OA的垂直平分线,交坐标轴于两个点;②以O为圆心,OA为半径画弧,交坐标轴于四个点;③以A为圆心,OA为半径画弧,交坐标轴于两个点.如图所示,显然这样的点有8个.故选D.点评:本题考查了等腰三角形的定义,运用数形结合的思想进行解决,难度适中.7、如图:有六个面积为1的正方形组成的长方形,其中有A、B、C、D、E、F、G 7个点,以这7个点为顶点,并且面积为1的三角形有()A、11个B、12个C、13个D、14个考点:面积及等积变换。
分析:由有六个面积为1的正方形组成的长方形,然后依据三角形的面积等于底乘以高,抓住底与高一个为2,一个为1,然后从一边开始,依次求解即可求得答案,小心别漏解.解答:解:∵如图是六个面积为1的正方形组成的长方形,∴以AB为边:△ABD,△ABE,△ABF,△ABG,以AC为边:△ACG,以AD为边:△ADE,以AE为边:△AEF,以AF为边:△AFG,以BC为边:△BCF,以BD为边:△BDE,以BE为边:△BEF,以BF为边:△BFG,以CD为边:△CDF,以CE为边:△CEG.故以这7个点为顶点,并且面积为1的三角形有14个.故选D.点评:此题考查了三角形的面积问题.此题属于易错题,难度较大,解题的关键是注意依次数得,小心别漏解.8、锐角△ABC的三边两两不等,D是BC边上的一点,∠BAD+∠C=90°,则AD一定过△ABC的()A、垂心B、内心C、外心D、重心考点:三角形的外接圆与外心;三角形内角和定理。
专题:证明题。
分析:作∠ABE=90°,BE交AD的延长线与E,根据三角形的内角和定理求出∠BAD+∠E=90°,推出∠C=∠E,根据三角形的外接圆的圆心的定义求出即可.解答:解:作∠ABE=90°,BE交AD的延长线与E,∴∠BAD+∠E=90°,∵∠C+∠BAD=90°,∴∠C=∠E,∴E在△ABC的外接圆上,∵∠ABE=90°,∴AD是直径,∴AD一定过△ABC的外心.故选C.点评:本题主要考查对三角形的外接圆与外心,三角形的内角和定理等知识点的理解和掌握,能求出∠E=∠C是解此题的关键.9、有纯农药一桶,倒出20升后用水补满;然后又倒出10升,在用水补满,这是桶中纯农药与水的容积之比为3:5,则桶的容积为()A、30升B、40升C、50升D、60升考点:分式方程的应用。
