蚂蚁行程模型

合集下载

蚁群算法及案例分析精选全文

问过的节点;另外,人工蚁
群在选择下一条路径的时
候并不是完全盲目的,而是
按一定的算法规律有意识
地寻找最短路径
自然界蚁群不具有记忆的
能力，它们的选路凭借外
激素，或者道路的残留信
息来选择，更多地体现正
反馈的过程
人工蚁群和自然界蚁群的相似之处在于,两者优先选择的都
是含“外激素”浓度较大的路径; 两者的工作单元(蚂蚁)都
正反馈、较强的鲁棒性、全
局性、普遍性
局部搜索能力较弱，易出现
停滞和局部收敛、收敛速度
慢等问题
优良的分布式并行计算机制
长时间花费在解的构造上，
导致搜索时间过长
Hale Waihona Puke 易于与其他方法相结合算法最先基于离散问题，不
能直接解决连续优化问题
蚁群算法的
特点
蚁群算法的特点及应用领域
由于蚁群算法对图的对称性以
及目标函数无特殊要求，因此
L_ave=zeros(NC_max,1);
%各代路线的平均长度
while NC<=NC_max
%停止条件之一：达到最大迭代次数
% 第二步：将m只蚂蚁放到n个城市上
Randpos=[];
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))';
scatter(C(:,1),C(:,2));
L(i)=L(i)+D(R(1),R(n));
hold on
end
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)])

模型46 勾股定理之蚂蚁行程、弦图模型(解析版)

1．平面展开-最短路径问题（1）平面展开﹣最短路径问题，先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．（2）关于数形结合的思想，勾股定理及其逆定理它们本身就是数和形的结合，所以我们在解决有关结合问题时的关键就是能从实际问题中抽象出数学模型．例．如图所示，有一正方体纸盒，在点C1处有一只小虫，它要爬到点A吃食物．应该沿着怎样的路线才能使行程最短？解：如图，把侧面或上面展开与正面组成一矩形，连接AC1，则AC1就是行程最短的路线．2.赵爽弦图模型我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成了一个大的正方形（如图1），这个正方形称为赵爽弦图，验证了一个非常重要的结论：在直角三角形中两直角边a、b与斜边c满足关系式a2+b2＝c2．称为勾股定理．把这四个全等的直角三角形拼成了另一个大的正方形（如图2），也能验证这个结论证明：由图2得，大正方形面积＝4×＝（a+b）2，整理得b2+c2+2ab＝2ab+c2，∴c2＝a2+b2，即直角三角形两直角边的平方和等于斜边的平方．例题精讲考点一：行程最短问题【例1】．如图，有一个圆柱，它的高等于16cm，底面半径等于4cm，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面上与A点相对的B点处的食物，需要爬行的最短路程是20 cm．（π取3）解：将圆柱体展开，连接A、B，根据两点之间线段最短，根据题意可得：AC是圆周的一半，∴AC＝×2×4π＝12，∴AB＝＝20cm．变式训练【变式1-1】．如图，圆锥的底面圆的半径为10cm，母线长为40cm，C为母线PA的中点，一只蚂蚁欲从点B处沿圆锥的侧面爬到点C处，则它爬行的最短距离是20cm．解：由题意知，底面圆的直径AB＝20，故底面周长等于20π设圆锥的侧面展开后的扇形圆心角为n°∵根据底面周长等于展开后扇形的弧长得，20π＝，解得n＝90°∴展开图中扇形圆心角＝90°，作CE⊥PB于E，则CE＝PE＝10，BE＝40﹣10，∵根据勾股定理求得它爬行的最短距离是＝20cm∴蚂蚁爬行的最短距离为20cm【变式1-2】．如图，一只蚂蚁从长为7cm、宽为5cm，高是9cm的长方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是15cm．解：由题意可得，当展开前面和右面时，最短路线长是：＝＝15（cm）；当展开前面和上面时，最短路线长是：＝＝7（cm）；当展开左面和上面时，最短路线长是：＝（cm）；∵15＜7＜，∴一只蚂蚁从长为7cm、宽为5cm，高是9cm的长方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是15cm，故答案为：15．【变式1-3】．如图是一个三级台阶，它的每一级长、宽、高分别是2米、0.3米、0.2米，A，B是这个台阶上两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿台阶面爬行到B点最短路程是 2.5米．解：三级台阶平面展开图为长方形，长为2，宽为（0.2+0.3）×3，则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长．可设蚂蚁沿台阶面爬行到B点最短路程为x，由勾股定理得：x2＝22+[（0.2+0.3）×3]2＝2.52，解得x＝2.5．考点二：弦图模型的应用【例2】．如图，“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形EFGH拼成的大正方形ABCD．若AE＝5，AB＝13，则中间小正方形EFGH的面积是49．解：∵AE＝5，AB＝13，∴BF＝AE＝5，在Rt△ABF中，AF＝＝12，∴小正方形的边长EF＝12﹣5＝7，∴小正方形EFGH的面积为7×7＝49．故答案为：49．变式训练【变式2-1】．如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成．若较短的直角边BC＝2.5，将四个直角三角形中较长的直角边分别向外延长一倍，得到图2所示的“数学风车”，若△BCD的周长是15，则这个风车的外围周长是38．解：依题意，设“数学风车”中的四个直角三角形的斜边长为x，AC＝y，则x2＝4y2+2.52，∵△BCD的周长是15，∴x+2y+2.5＝15则x＝6.5，y＝3．∴这个风车的外围周长是：4（x+y）＝4×9.5＝38．故答案是：38．【变式2-2】．如图，在弦图中，正方形ABCD的对角线AC与正方形EFHI的对角线EH交于点K，对角线AC交正方形EFHI于G，J两点，记△GKH面积为S1，△JIC面积为S2，若AE＝12，CD＝4，则S1+S2的值为16．解：由题意可得，AF＝CI，∠AFG＝∠CIJ＝90°，FH∥EI，∵∠AGF＝∠HGK，∠IJC＝∠KJE，∵FH∥EI，∴∠HGK＝∠KJE，∴∠AGF＝∠IJC，在△AFG和△CIJ中，，∴△AFG≌△CIJ（AAS），∴FG＝IJ，∵四边形EFHI为正方形，∴EI﹣IJ＝FH﹣FG，即HG＝EJ，在△GHK和△JEK中，，∴△GHK≌△JEK（AAS），∴HK＝EK，即点K为正方形EFHI的中心，如图，过点K作KM⊥FH于点M，∵AE＝12，CD＝4，∴BF＝12，AD＝，在Rt△ADE中，由勾股定理得DE＝＝4，∴AF＝DE＝4，EF＝AE﹣AF＝12﹣4＝8，则FH＝8，KM＝4，设GH＝a，FG＝b，则a+b＝FH＝8，∴＝，＝＝2b，∴S1+S2＝2a+2b＝2（a+b）＝16．故答案为：16．1．如图所示，一只小蚂蚁从棱长为1的正方体的顶点A出发，经过每个面的中心点后，又回到A点，蚂蚁爬行最短程S满足（）A．5＜S≤6B．6＜S≤7C．7＜S≤8D．8＜S≤9解：正方体展开图形为：则蚂蚁爬行最短程S＝5+＝5+．即6＜S≤7．故选：B．2．如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan ∠ADE的值为（）A．B．C．D．解：设小正方形EFGH面积是a2，则大正方形ABCD的面积是13a2，∴小正方形EFGH边长是a，则大正方形ABCD的边长是a，∵图中的四个直角三角形是全等的，∴AE＝DH，设AE＝DH＝x，在Rt△AED中，AD2＝AE2+DE2，即13a2＝x2+（x+a）2解得：x1＝2a，x2＝﹣3a（舍去），∴AE＝2a，DE＝3a，∴tan∠ADE＝＝，故选：C．3．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为S1、S2、S3．若S1+S2+S3＝60，则S2的值是（）A．12B．15C．20D．30解：设每个小直角三角形的面积为m，则S1＝4m+S2，S3＝S2﹣4m，因为S1+S2+S3＝60，所以4m+S2+S2+S2﹣4m＝60，即3S2＝60，解得S2＝20．故选：C．4．四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为4，大正方形面积为74，直角三角形中较小的锐角为θ，那么tanθ的值是（）A．B．C．D．解：由已知条件可知，小正方形的边长为2，大正方形的边长为．设直角三角形中较小边长为x，则有（x+2）2+x2＝（）2，解得x＝5．则较长边的边长为x+2＝5+2＝7．故tanθ＝＝．故选：B．5．赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形，中间是一个小正方形（如图所示）．某次课后服务拓展学习上，小浔绘制了一幅赵爽弦图，她将EG延长交CD于点I．记小正方形EFGH的面积为S1，大正方形ABCD的面积为S2，若DI＝2，CI＝1，S2＝5S1，则GI的值是（）A．B．C．D．解：如图，连接DG，∵赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形，中间是一个小正方形，∴AE＝BF＝CG＝DH，AF＝BG＝CH＝DE，CH⊥DE，∵DI＝2，CI＝1，∴CD＝DI+CI＝2+1＝3，∵大正方形ABCD的面积为S2，∴S2＝CD2＝32＝9，又∵小正方形EFGH的面积为S1，S2＝5S1，∴S1＝，∴EF＝FG＝GH＝HE＝，∵将EG延长交CD于点I，∴∠HGE＝45°，在Rt△EHG中，由勾股定理得：EG＝＝，设AE＝BF＝CG＝DH＝x，则AF＝BG＝CH＝DE＝x+，在Rt△CDH中，由勾股定理得：CD2＝DH2+CH2，即9＝x2+（x+）2，解得：x1＝，x2＝﹣（不合题意，舍去），即AE＝BF＝CG＝DH＝x＝，∴DH＝EH＝，∴CH垂直平分ED，∴DG＝EG＝，∴∠DGH＝∠HGE＝45°，∴∠DGE＝45°+45°＝90°，∴∠DGI＝90°，在Rt△DGI中，由勾股定理得：GI＝＝＝，故选：A．6．如图，一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1，若圆柱底面半径为，高为5，则蚂蚁爬行的最短距离为13．解：因为圆柱底面圆的周长为2π×＝12，高为5，所以将侧面展开为一长为12，宽为5的矩形，根据勾股定理，对角线长为＝13．故蚂蚁爬行的最短距离为13．7．如图，底面半径为1，母线长为4的圆锥，一只小蚂蚁若从A点出发，绕侧面一周又回到A点，它爬行的最短路线长是．解：由题意知，底面圆的直径为2，故底面周长等于2π．设圆锥的侧面展开后的扇形圆心角为n°，根据底面周长等于展开后扇形的弧长得，2π＝，解得n＝90°，所以展开图中圆心角为90°，根据勾股定理求得到点A的最短的路线长是：＝＝4．8．将四个全等的直角三角形分别拼成正方形（如图1，2），边长分别为6和2．若以一个直角三角形的两条直角边为边向外作正方形（如图3），其面积分别为S1，S2．则S1﹣S2＝12．解：设四个全等的直角三角形的两条直角边分别为a，b（a＞b），根据图1得：a+b＝6，根据图2得：a﹣b＝2，联立解得：，∴S1＝16，S2＝4，则S1﹣S2＝12．故答案为：12．9．如图1，四个全等的直角三角形围成一个大正方形，中间是一个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．连接四条线段得到如图2的新的图案，如果图1中的直角三角形的长直角边为5，短直角边为3，图2中阴影部分的面积为S，那么S的值为16．解：由题意作出如下图，得AC＝，BD＝2，AB＝CD，△ABD是直角三角形，则大正方形面积＝AC2＝34，△ADC面积＝（5×3﹣2×3）＝4.5，阴影部分的面积S＝34﹣4×4.5＝16，故答案为：16．10．如图所示一棱长为3cm的正方体，把所有的面均分成3×3个小正方形．其边长都为1cm，假设一只蚂蚁每秒爬行2cm，则它从下底面点A沿表面爬行至侧面的B点，最少要用2.5秒钟．解：因为爬行路径不唯一，故分情况分别计算，进行大、小比较，再从各个路线中确定最短的路线．（1）展开前面右面由勾股定理得AB＝＝cm；（2）展开底面右面由勾股定理得AB＝＝5cm；所以最短路径长为5cm，用时最少：5÷2＝2.5秒．11．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形E 的边长为7cm，则图中五个正方形A、B、C、D、E的面积和为98cm2．解：设正方形A、B、C、D的边长分别是a、b、c、d，则正方形A的面积＝a2，正方形B的面积＝b2，正方形C的面积＝c2，正方形D的面积＝d2，又∵a2+b2＝x2，c2+d2＝y2，∴正方形A、B、C、D、E的面积和＝（a2+b2）+（c2+d2）+72＝x2+y2+72＝72+72＝98（cm2）．即正方形A，B，C，D、E的面积的和为98cm2．故答案为：98．12．我国汉代数学家赵爽为了证明勾股定理，创制了一幅弦图，后人称其为赵爽弦图（如图1）．图2为小明同学根据弦图思路设计的，在正方形ABCD中，以点B为圆心，AB为半径作，再以CD为直径作半圆交于点E，若边长AB＝10，则△CDE的面积为20．解：如图，取CD的中点F，连接BF、BE、DE、EF，由题意可得，FE＝FC，BE＝BC，∴BF是EC的垂直平分线，∴∠FBC+∠BCE＝90°，∵∠BCD＝90°，∴∠DCE+∠BCE＝90°，∴∠FBC＝∠DCE，又∵∠BCF＝∠CED＝90°，∴△BCF∽△CED，∴＝＝，∵BC＝CD＝AB＝10，CF＝5，∠BCF＝90°，∴BF＝＝＝5，∴＝＝，解得：CE＝4，ED＝2，＝×CE×DE＝×4×2＝20，∴S△CDE故答案为：20．13．图1是一个勾股定理演示教具的正面示意图，当它倒过来时，大正方形中的全部墨水恰能注满两个小正方形．王老师有一个内长为11寸，内宽为9寸的木质盒子（如图2）．现要自制一个这样的教具（由三个正方形和一个直角三角形组成），使得教具恰好摆入这个盒子中，以便保护和携带（如图3所示，A，B，C，D，E五点均紧贴盒子边缘，教具的厚度等于木盒的内高）．此时盒子的空间利用率为．解：如图，过点A作AM⊥EG的延长线于点M，过点F作FR⊥GH于点R，过点B作BN⊥GH，过点F作FN∥GH，延长GH交CK于K，∵四边形AGFL、DEGH、BCHF均为正方形，∴AG＝FG，BF＝FH＝CH，EG＝GH，∠AGF＝∠BFH＝90°＝∠AMG＝∠FRG＝∠BNF ＝∠CKH，∴∠AGM+∠FGM＝∠FGR+∠FGM，∴∠AGM＝∠FGR，∴△AGM≌△FGR（AAS），∴AM＝FR，GM＝GR，同理，△BFN≌△HFR≌△CHK（AAS），∴FR＝FN＝HK＝AM，BN＝HR，设AM＝x，BN＝y，AM＝FR＝z，则FR＝FN＝HK＝AM＝x，BN＝HR＝y，由勾股定理得：FH2＝x2+y2，FG2＝x2+z2，GH＝y+z，根据题意，得：FH2+FG2＝GH2，∴x2+z2+x2+y2＝（y+z）2，∴x2＝yz①，∵AM+GR+RH+HK＝9，BN+FR+EG＝11，∴2x+y+z＝9②，x+2y+z＝11③，②﹣③，得：x﹣y＝﹣2，即y＝x+2④，②×2﹣③，得：3x+z＝7，即z＝7﹣3x⑤，将④⑤代入①，得：x2＝（x+2）（7﹣3x），解得：x1＝2，x2＝﹣（舍去），∴y＝4，z＝1，∴GH＝5，FG2＝5，FH2＝20，∴勾股定理演示教具的正面面积为：S＝25+5+20+××2＝55，∵教具的厚度等于木盒的内高，∴盒子的空间利用率为：＝，故答案为：．14．我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形，如图，若拼成的大正方形为正方形ABCD，面积为9，中间的小正方形为正方形EFGH，面积为2，连接AC，交BG于点P，交DE﹣S△CGP＝，③DH+HC＝4，④HC＝2+，于点M，①△CGP≌△AEM，②S△AFP以上说法正确的是①③④.（填写序号）解：∵Rt△BCG≌Rt△DAE，∴CG＝AE，∠CGP＝∠AEM，∵CH∥AF．∴∠GCP＝∠MAE，∴△CGP≌△AEM（ASA），＝S△AEM，CP＝ME，∴S△CGP﹣S△CGP＝S四边形MEFP∴S△AFP∵HE＝GF，∴HM＝PF，＝S四边形MHGP＝S正方形EFGH＝1，∴S四边形MEFP﹣S△CGP＝1，∴S△AFP∵DH2+CH2＝DC2＝9，∴（DH+CH）2＝DH2+CH2+2DH•CH＝9+2DH•CH，∵CH﹣DH＝HG，∴（CH﹣DH）2＝HG2＝2，∴CH2+DH2﹣2DH•CH＝2，∴2DH•CH＝7，∴（DH+CH）2＝9+7＝16，∴DH+CH＝4，∵CH﹣DH＝，∴HC＝＝2+，故答案为：①③④．15．一个长方体盒子，它的长是12dm，宽是4dm，高是3dm，（1）请问：长为12.5dm的铁棒能放进去吗？（1）如果有﹣只蚂蚁要想从D处爬到C处，求爬行的最短路程．解：（1）如图1，连接BD，∵AD＝12，AB＝4，∴BD2＝AD2+AB2＝122+42＝160，∴CD＝＝＝13（dm）．∵13dm＞12.5dm，∴长为12.5dm的铁棒能放进去；（2）如图2所示，CD＝＝dm．如图3所示，CD＝＝dm，如图4所示，CD＝＝dm，∵＞＞，∴爬行的最短路程是dm．16．如图①，美丽的弦图，蕴含着四个全等的直角三角形．（1）如图①弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a．较短的直角边为b，斜边长为c，可以验证勾股定理；（2）如图②，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1、2、S3，若S1+S2+S3＝16，则S2＝．（1）证明：，另一方面，即a2﹣2ab+b2＝c2﹣2ab，则a2+b2＝c2；（2）解：设正方形MNKT的面积为x，八个全等的直角三角形的面积均为y，∵S1+S2+S3＝16，∴S1＝8y+x，S2＝4y+x，S3＝x，∴S1+S2+S3＝12y+3x＝16，∴4y+x＝，∴S2＝4y+x＝．故答案为：．17．如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理，思路是：大正方形的面积有两种求法，一种是等于c2，另一种是等于四个直角三角形与一个小正方形的面积之和，即，从而得到等式c2＝，化简便得结论a2+b2＝c2．这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双求法”．现在，请你用“双求法”解决下面两个问题（1）如图2，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，AC＝3，BC＝4，求CD的长度．（2）如图3，在△ABC中，AD是BC边上的高，AB＝4，AC＝5，BC＝6，设BD＝x，求x的值．解：（1）在Rt△ABC中，由面积的两种算法可得：，解得：CD＝．（2）在Rt△ABD中AD2＝42﹣x2＝16﹣x2，在Rt△ADC中AD2＝52﹣（6﹣x）2＝﹣11+12x﹣x2，所以16﹣x2＝﹣11+12x﹣x2，解得＝．。

蚁群算法及其在移动机器人路径规划中应用剖析.pptx

第11页/共14页
第12页/共14页
•（1）近期对蚁群算法在移动机器人路径规划中的应用研究还处于初期探索阶段 , 研究重点主要集中在算法模型的建立与实例仿真方面,而对于算法的理论分析、与其他算法结合等方面的研究较少; • （2）近期对蚁群算法在移动机器人路径规划的研究主要集中于静态环境下的路径规划研究,而对动态环境下的路径规划研究相对较少。
allowed c tabu 蚂蚁间的协作性就越强；可称为期望k 启发式因子，k 在算法中代表能见度的相对重要性。是启发函数，在算
法中表示由节点i 转移到节点 j 的期望程度，通常可取
。在算法运行时每只蚂蚁将根据(2-1)式
进行搜索前进。
ij
ij 1/ dij
pikj
ij
(t
)ij
(t
第2页/共14页
• 2.蚁群算法的基本原理
Hale Waihona Puke 图1.1初始状态蚂蚁随机挑选路径寻找食物
图1.2经过一段时间后蚂蚁成功避开障碍物找到一条合适路径
第3页/共14页
• 3.蚁群算法的数学模型
• 设 m 表示蚂蚁总数量，用表示节点 i 和节点 j 之间的距离，表示在 t 时刻连线上的信息素浓度。在初始时刻，m只蚂蚁会被随机地放置，各路径上的初始信息素浓度是相同的。在 t 时刻，蚂蚁 k 从节点i转移到节点 j 的状态转移概率为
应用全局更新
找出最短路径
否
满足终止
条件？
是
结束
第9页/共14页
•6.机器人路径规划 •移动机器人导航的任务主要由定位、避障和路径规划组成, 其中路径规划是机器人控制最为关键的技术。移动机器人路径规划是指在有障碍物的工作环境中按照一定的评价标准(如工作代价最小、行走路线最短、行走时间最短等),寻找一条从起始状态(包括位置和姿态)到达目标状态(包括位置和姿态)的无碰路径。

蚂蚁怎样走最短

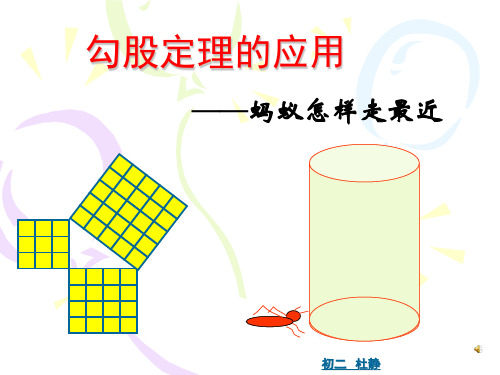
C
B
AC '2 AC 2 CC '2
C
C'
沿AB剪开，
展成长方形
A
A
其中AC是圆柱的高
CC'是圆柱的底面周长
变式2：
有一圆柱形油罐底面圆的周长为8m，高为6m，一只蚂蚁从A处爬行到BC中点E处吃食物，它爬行的最短路线长为多少？
C
D
D
C
D’
E
E
3
A
4
B
A’
A
B
变式3：
有一圆柱形油罐底面圆的周长为8m，高为4m，一只蚂蚁
从距底面1m的A处爬行到对角B处吃食物，它爬行的最短路线长为多少？
请同
C
B
C
B
学们
自
A
A
己独
立
解：AC=4 1 3，BC= 1 8=4 2
在RtABC中，由勾股定理得
完成过程
AB2 AC 2 BC 2
=32 +42
=25
所以AB （ 5 cm）
答：它爬行的最短路线长为5cm
蚂蚁爬行最短问题解题思路（5步走）
2
=20²+(5n)²
Ｂ
蚂蚁爬行最短路程问题小结：
• 1、转化思想的应用
（立体图形
平面图形）
• 2、得到最短路线的依据是平面内两点之间线段最短
• 3、构造出直角三角形从而利用勾股定理进行计算
如图：圆柱形玻璃杯,高为12cm,底面圆的周长为
18cm,在杯子内壁离杯底4cm的点C处有一滴蜂蜜，
将长方体的前面与上面展开放在同一平面上
H G
B F
12

专题24 勾股定理中的蚂蚁爬行模型--2024年中考数学核心几何模型重点突破(学生版)

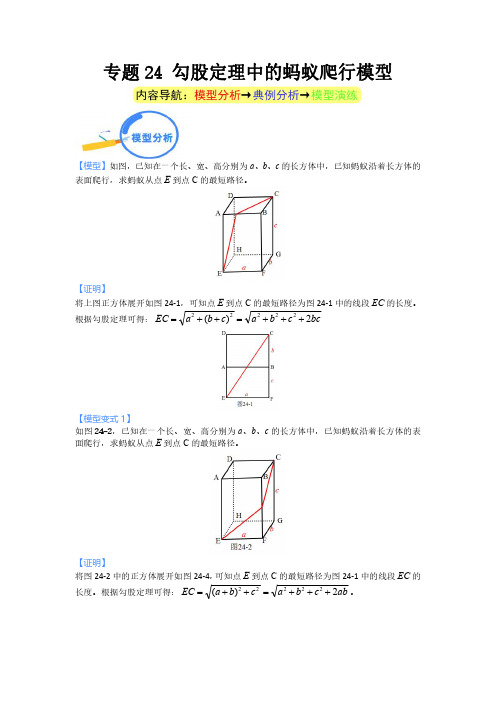
专题24勾股定理中的蚂蚁爬行模型【模型】如图，已知在一个长、宽、高分别为a 、b 、c 的长方体中，已知蚂蚁沿着长方体的表面爬行，求蚂蚁从点E 到点C 的最短路径。

【证明】将上图正方体展开如图24-1，可知点E 到点C 的最短路径为图24-1中的线段EC 的长度。

根据勾股定理可得：bcc b a c b a EC 2)(22222+++=++=【模型变式1】如图24-2，已知在一个长、宽、高分别为a 、b 、c 的长方体中，已知蚂蚁沿着长方体的表面爬行，求蚂蚁从点E 到点C 的最短路径。

【证明】将图24-2中的正方体展开如图24-4，可知点E 到点C 的最短路径为图24-1中的线段EC 的长度。

根据勾股定理可得：ab c b a c b a EC 2)(22222+++=++=。

【模型变式2】如图24-3，已知在一个长、宽、高分别为a 、b 、c 的长方体中，已知蚂蚁沿着长方体的表面爬行，求蚂蚁从点E 到点C 的最短路径。

【证明】将图24-3中的正方体展开如图24-5，可知点E 到点C 的最短路径为图24-1中的线段EC 的长度。

根据勾股定理可得：ac c b a b c a EC 2)(22222+++=++=。

【例1】如图，长方形的长为15，宽为10，高为20，点B 离点C 的距离为5，蚂蚁如果要沿着长方形的表面从点A 爬到点B ，需要爬行的最短距离是（）A ．35B ．1055C ．25D ．21【例2】如图，在圆柱的截面ABCD中，AB＝16，BC＝12，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离为_____．【例3】如图，一个长方体形盒子的长、宽、高分别为4cm，4cm，6cm(1)一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B，请你帮蚂蚁设计一条最短的路线，蚂蚁要爬行的最短路线是多少？(2)若将一根木棒放进盒子里并能盖上盖子，则能放入该盒子里的木棒的最大长度是多少cm?(结果可保留根号)一、单选题1．如图，一只蜘蛛在一块长方体木块的一个顶点A处，一只苍蝇在这个长方体的对角顶点G处，若AB＝3cm，BC＝5cm，BF＝6cm，则最短的爬行距离是（）A．10B．14C D2．如图，圆柱形玻璃板，高为12cm，底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm 与蜂蜜相对的A 处，则蚂蚁到达蜂蜜的最短距离是（）A ．15cmB ．16cmC ．17cmD ．18cm3．如图所示，圆柱的高AB ＝3，底面直径BC ＝6，现在有一只蚂蚁想要从A 处沿圆柱侧面爬到对角C 处捕食，则它爬行的最短距离是（）A ．B ．C ．9D ．4．如图是一个三级台阶，它的每一级的长，宽，高分别是20dm,3dm,2dm ，A 和B 是这个台阶相对的端点，点A 处有一只蚂蚁，想到B 处去吃食物，则这只蚂蚁爬行的最短距离为（）A ．25dmB ．26dmC ．24dmD ．27dm5．图，长方体的长为8，宽为10，高为6，点B 离点C 的距离为2，一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ，需要爬行的最短距离是（）A ．B ．C ．D ．6．如图，在长方体透明容器（无盖）内的点B 处有一滴糖浆，容器外A 点处的蚂蚁想沿容器壁爬到容器内吃糖浆，已知容器长为6cm ，宽为4cm ，高为3cm ，点A 距底部2cm ，请问蚂蚁需爬行的最短距离是（容器壁厚度不计）A ．B ．10cmC ．D ．二、填空题7．如图，长方体的长为15，宽为10，高为20，点B 离点C 的距离为5，一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ，需要爬行的最短距离是_____．8．如图，一只蚂蚁沿长方体的表面从顶点A 爬到另一顶点M ，已知AB ＝AD ＝2，BF ＝3．这只蚂蚁爬行的最短距离_____．9．如图，圆柱形容器外壁距离下底面3cm 的A 处有一只蚂蚁，它想吃到正对面外壁距离上底面3cm 的B 处的米粒，若圆柱的高为12cm ，底面周长为24cm ．则蚂蚁爬行的最短距离为_______．10．如图，圆柱形玻璃杯高为12cm 、底面周长为18cm ，在杯内离杯底4cm 的点C 处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm 与蜂蜜相对的点A 处，则蚂蚁到达蜂蜜的最短距离为_______cm ．11．如图一只蚂蚁从长为4cm ，宽为3cm ，高为2cm 的长方体纸箱A 点沿纸箱爬到B 点，那么它爬行的最短路线的长是_________cm12．在底面周长为6cm ，高为3cm 的圆柱体侧面上，用一条无弹性的丝带从A 至C 按如图所示的圈数缠绕，则丝带的最短长度为_________．三、解答题13．如图，长方体的透明玻璃鱼缸，假设其长80cm AD =，高60cm AB =，水深为40cm AE =，在水面上紧贴内壁G 处有一鱼饵，G 在水面线EF 上，且60cm EG =；一小虫想从鱼缸外的A 点沿壁爬进鱼缸内G 处吃鱼饵，求小动物爬行的最短距离．（鱼缸厚度忽略不计）14．(1)如图1，长方体的长、宽、高分别为3m ，2m ，1m ，如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点C ，那么所用细线最短需要______m ；(2)如图2，长方体的棱长分别为6cm AB BC ==，114cm AA =，假设昆虫甲从盒内顶点1C 开始以1cm/s 的速度在盒子的内部沿棱1C C 向下爬行，同时昆虫乙从盒内顶点A 以相同的速度在盒内壁的侧面上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？15．如图，长方体盒子（无盖）的长、宽、高分别是12cm ，8cm ，30cm ．(1)在AB 的中点C 处有一滴蜜糖，一只小虫从D 处爬到C 处去吃，有无数种走法，则最短路程是多少？(2)若此长方体盒子有盖，则能放入木棒的最大长度是多少？16．如图①，长方体长AB 为8cm ，宽BC 为6cm ，高BF 为4cm ．在该长体的表面上，蚂蚁怎样爬行路径最短？(1)蚂蚁从点A 爬行到点G ，且经过棱EF 上一点，画出其最短路径的平面图，并标出它的长．(2)设该长方体上底面对角线EG 、FH 相交于点O （如图②），则OE ＝OF ＝OG ＝OH ＝5cm ．①蚂蚁从点B 爬行到点O 的最短路径的长为cm ；②当点P 在BC 边上，设BP 长为a cm ，求蚂蚁从点P 爬行到点O 的最短路的长（用含a 的代数式表示）．17．如图，已知圆柱底面的周长为12，圆柱的高为8，在圆柱的侧面上，过点A ，C 嵌有一圈长度最短的金属丝．(1)现将圆柱侧面沿AB剪开，所得的圆柱侧面展开图是______．(2)如图①，求该长度最短的金属丝的长．(3)如图②，若将金属丝从点B绕四圈到达点A，则所需金属丝最短长度是多少？18．在每个小正方形的边长为1的网格中，每个小正方形的顶点称为格点．我们将从一个格5．．．．．（1）在图15（2）在图2中有一只电子小马从格点M出发，经过跳马变换到达与其相对的格点N，则最少需要跳马变换的次数是次．的正方形网格中，一只电子小马从格点S经过若干次跳马变换到达（3）如图3，在2020与其相对的格点T，则它跳过的最短路程为．19．如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，为了吃到蜂蜜，蚂蚁从外壁A处沿着最短路径到达内壁B处．（1）右图是杯子的侧面展开图，请在杯沿CD上确定一点P,使蚂蚁沿A-P-B路线爬行，距离最短．（2）结合右图，求出蚂蚁爬行的最短路径长．20．现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm)．(1)求线段BG的长；(2)现在箱外的点A处有一只蜘蛛，箱内的点C处有一只小虫正在午睡，保持不动．请你为蜘蛛设计一种捕虫方案，使得蜘蛛能以最短的路程捕捉到小虫．(木板的厚度忽略不计)。

初中数学解题模型专题讲解12---蚂蚁行程

初中数学解题模型专题讲解初中数学解题模型专题讲解专题12 12 蚂蚁行程蚂蚁行程蚂蚁行程模型模型 1 1 立体图形展开的最短路径立体图形展开的最短路径模型分析上图为无底的圆柱体侧面展开图，如图蚂蚁从点 A 沿圆柱表面爬行一周，到点 B 的最短路径就是展开图中 AB′的长。

做此类题目的关键就是，正确展开立体图形，利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。

模型实例模型实例例 1．有一圆柱体油罐，已知油罐底面周长是 12m，高 AB 是 5m，要从点 A 处开始绕油罐一周建造房子，正好到达 A 点的正上方 B 处，问梯子最短有多长？例 2．如图，一直圆锥的母线长为 QA=8，底面圆的半径r =2，若一只小蚂蚁从 A 点出发，绕圆锥的侧面爬行一周后又回到 A 点，则蚂蚁爬行的最短路线长是多少？例3．已知长方体的长、宽、高分别为 30cm、20cm、10cm，一只蚂蚁从 A处出发到 B 处觅食，求它所走的最短路径。

（结果保留根号）模型练习模型练习1．有一个圆锥体如图，高 4cm，底面半径 5cm，A 处有一蚂蚁，若蚂蚁欲沿侧面爬行到 C 处，求蚂蚁爬行的最短距离。

2．如图，圆锥体的高为 8cm，底面周长为 4cm，小蚂蚁在圆柱表面爬行，从 A 点到 B 点，路线如图，则最短路程是多少？3．桌上有一个圆柱形无盖玻璃杯，高为 12 厘米，底面周长 18 厘米，在杯口内壁离杯口距离 3 厘米的 A 处有一滴蜜糖，一只小虫 22 杯子外壁，当它正好在蜜糖相对方向离桌面 3 厘米的 B 处时，突然发现了蜜糖，问小虫至少爬多少厘米才能到达蜜糖所在的位置。

4．已知 O 为圆锥顶点，OA、OB 为圆锥的母线，C 为 OB 的中点，一只小蚂蚁从点 C 开始沿圆锥侧面爬行到点 A，另一只小蚂蚁也从 C 点出发绕着圆锥侧面爬行到点 B，它们所爬行的最短路线的痕迹如图所示，若沿 OA 剪开，则得到的圆锥侧面展开图为（）5．如图，一只蚂蚁沿着边长为到点 B，如果它运动的路径是6．如图是一个边长为 6 的正蚂蚁从 P 点出发沿木箱表面爬7．如图，是一个三级台阶，边长为 2 的正方体表面从点 A 出发，经过路径是最短的，则最短距离为多少？的正方体木箱，点 Q 在上底面的棱上，AQ=2表面爬行到点 Q，求蚂蚁爬行的最短路线。

中考数学复习满分突破(全国通用)：专题20 蚂蚁爬行模型(解析版)

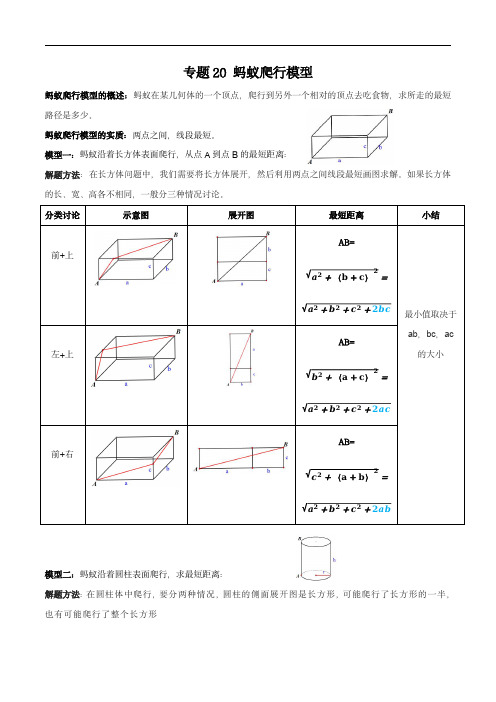
专题20蚂蚁爬行模型蚂蚁爬行模型的概述：蚂蚁在某几何体的一个顶点，爬行到另外一个相对的顶点去吃食物，求所走的最短路径是多少。

蚂蚁爬行模型的实质：两点之间，线段最短。

模型一：蚂蚁沿着长方体表面爬行，从点A到点B的最短距离：解题方法：在长方体问题中，我们需要将长方体展开，然后利用两点之间线段最短画图求解。

如果长方体的长、宽、高各不相同，一般分三种情况讨论。

模型二：蚂蚁沿着圆柱表面爬行，求最短距离：解题方法：在圆柱体中爬行，要分两种情况，圆柱的侧面展开图是长方形，可能爬行了长方形的一半，也有可能爬行了整个长方形模型三（蚂蚁吃蜂蜜问题）：求蚂蚁从点A沿着外壁爬行再沿着内壁爬行到点B 蜂蜜处的最短距离。

模型四：蚂蚁爬楼梯问题模型五：蚂蚁爬圆锥问题问题示意图展开图最短距离如图，现有一个圆锥，圆锥的底面直径为4cm，母线长为6cm，一只蚂蚁在点A 位置，食物在母线BC 的中点点D 处，蚂蚁沿着圆锥表面由点A 向点D 处爬行觅先利用扇形弧长公式求圆心角，再根据勾股定理求AD长食，路线如图所示，求最短距离【培优过关练】1．（2022秋·河北石家庄·九年级石家庄市第十七中学校考阶段练习）如图，有一圆锥形粮堆，其主视图是边长为4cm的正三角形ABC，母线AC的中点P处有一老鼠正在偷吃粮食，小猫从B处沿圆锥表面去偷袭老鼠，则小猫经过的最短路程是（）cm．A．B．4C．D．6故选：C ．【点睛】本题考查的是平面展开最短路线问题，根据题意画出圆锥的侧面展开图，利用勾股定理求解是解答此题的关键．2．（2022春·吉林长春·九年级校考阶段练习）如图，点A 是棱长为2的正方体的一个顶点，点B 是一条棱的中点，将正方体按图中所示展开，则在展开图中A B ，两点间的距离为（）AB C D3．（2022秋·广东惠州·九年级校考阶段练习）如图，圆锥的底面半径3dm R ，母线5dm l ，AB 为底面直径，C 为底面圆周上一点，150COB ，D 为VB 上一点，VD ，现在有一只蚂蚁，沿圆锥表面从点C 爬到点D ，则蚂蚁爬行的最短路程是（）A ．B ．C ．15dm 2D ．∵ 150351802BC，∴设弧BC 所对的圆心角的度数为∴552180n，4．（2022春·九年级课时练习）如图，圆柱的底面周长为12cm ，AB 是底面圆的直径，在圆柱表面的高BC 上有一点D ，且10cm BC ，2cm DC ．一只蚂蚁从点A 出发，沿着圆柱体的表面爬行到点D 的最短路程是（）cm ．A．14B．12C．10D．85．（2022·山东淄博·统考二模）如图，一只蚂蚁要从圆柱体下底面的A点，沿圆柱侧面爬到与A相对的上底面的B点，圆柱底面直径为4，母线为6，则蚂蚁爬行的最短路线长为（）AB CD ．10BC ＝6，AC 为底面半圆弧长，所以AB ＝226(2)36 故选：B ．6．（2022·山东东营·统考二模）如图一个圆柱，底圆周长10cm ，高4cm ，一只蚂蚁沿外壁爬行，要从A 点爬到B 点，则最少要爬行（）cm ．A ．9B ．14CD ．【答案】C【分析】要求蚂蚁爬行的最短距离，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果．7．（2022春·九年级课时练习）已知圆锥底面半径为1，母线长为4，地面圆周上有一点A，一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B，则蚂蚁爬行的最短路程为（）A． B C．D．2【答案】C【分析】要求蚂蚁爬行的最短距离，需将圆锥的侧面展开，连接AB，根据展开所得扇形的弧长等于圆锥底面圆的周长求得扇形的圆心角，进而解三角形即可求解．【详解】解：根据题意，将该圆锥展开如下图所示的扇形，则线段AB就是蚂蚁爬行的最短距离．∵点B是母线PA的中点，4PA ，∴2PB ，8．（2022·全国·九年级专题练习）如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离容器底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是（）A cm B．13cm C．cm D．cm故选：B．【点睛】本题考查立体图形平面展开的最短路径问题．了解“两点之间线段最短”并结合轴对称和勾股定理进行求解是解题的关键．9．（2022秋·安徽芜湖·九年级校考开学考试）如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）A．B．25C．5D．3510．（2022秋·浙江·九年级专题练习）如图所示是一个几何体的三视图，如果一只蚂蚁从这个几何体的点B 出发，沿表面爬到AC 的中点D 处，则最短路线长为（）A ．B ．332C ．D ．211．（2021春·广东肇庆·八年级统考期末）如图是一个三级台阶，它的每一级的长、宽和高分别为93、和1,A 和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物．则这只蚂蚁沿着台阶面爬行的最短路程是（）A．18B．15C．12D．8【答案】B【分析】此类题目只需要将其展开便可直观的得出解题思路．将台阶展开得到的是一个矩形，蚂蚁要从B 点到A点的最短距离，便是矩形的对角线，利用勾股定理即可解出答案．【详解】解：如图，将台阶展开，因为AC＝3×3＋1×3＝12，BC＝9，所以AB2＝AC2＋BC2＝225，所以AB＝15，所以蚂蚁爬行的最短线路为15．故选B．【点睛】本题考查了勾股定理的应用，掌握勾股定理的应用并能得出平面展开图是解题的关键．12．（2022秋·广东梅州·九年级校考阶段练习）如图，一只蚂蚁沿着边长为2的正方体表面从点A出发，经过3个面爬到点B，如果它运动的路径是最短的，则AC的长为____．13．（2022春·广东茂名·九年级统考期末）如图，圆柱形玻璃容器高12cm ，底面周长为24cm ，在容器外侧距下底1cm 的点A 处有一只蚂蚁，在蚂蚁正对面距容器上底2cm 的点B 处有一滴蜂蜜，则蚂蚁要吃到蜂蜜所爬行的最短距离为______cm ．∵底面周长为24cm ，∴12cm EC ，∵AF CD ，∴1AE CF cm ，故答案为：15．【点睛】本题主要考查勾股定理的应用，根据题意正确得到圆柱体的展开图是解题的关键．14．（2022秋·山东临沂·九年级统考期末）如图，已知长方体的长为5cm，宽为4cm，高为3cm．一只蚂蚁如果沿长方体的表面A点爬到C点，那么这只蚂蚁需要走的最短路程为___________．15．（2022·山东临沂·校考二模）如图，圆柱底面半径为4厘米，高18 厘米，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一棉线从A顺着圆柱侧面绕3圈到B，求棉线最短为__________．【答案】30π厘米【分析】要求圆柱体中两点之间的最短路径，最直接的作法，就是将圆柱体展开，然后利用两点之间线段最短解答．【详解】解：圆柱体的展开图如图所示：16．（2022·江苏扬州·统考一模）如图，已知长方体的三条棱AB、BC、BD分别为4，5，2，蚂蚁从A点出发沿长方体的表面爬行到M的最短路程的平方是_____.【答案】61【详解】解:如图①:AM2=AB2+BM2=16+(5+2)2=65;如图②:AM2=AC2+CM2=92+4=85;如图③:AM2=52+(4+2)2=61.∴蚂蚁从A点出发沿长方体的表面爬行到M的最短路程的平方是:61.故答案为:61.17．（2021·全国·九年级专题练习）如图所示的长方体的长、宽、高分别为3厘米、2厘米、4厘米．若一只蚂蚁从A点出发沿着长方体的表面爬行到棱BC的中点M处．则蚂蚁需爬行的最短路程是_______________厘米．18．（2022春·陕西西安·九年级校考期中）如图，有一个圆柱形食品盒，它的高为10cm，底面圆周长为24cm，如果在盒外AD的中点P处有一只蚂蚁，蚂蚁爬行的速度为2cm/s，它想吃到点B处（点A、B正好相对）的食物，那么它至少需要爬行_____s．根据题意有：AD=10，AB为底面圆周长的一半，即∵P点为AD中点，∴AP=5，在Rt△APB中，2PB AP∵蚂蚁的速度为2cm/s，∴蚂蚁需要的时间为：13÷2=6.5即此时蚂蚁需要6.5s；第二种情况：蚂蚁由P点直接到达∵底面圆的周长为24∴底面圆的直径AB=∵AP=5，∴此时蚂蚁行走的距离为19．（2023秋·广东佛山·八年级佛山市高明区沧江中学校考期末）如图，台阶A处的蚂蚁要爬到B处搬运食物，则它爬行的最短距离为_____．【答案】13m##13米【分析】先将图形平面展开，再用勾股定理根据两点之间线段最短进行解答．【详解】解：如图所示，台阶平面展开图为长方形，5AC ，9312BC ，则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长．由勾股定理得：222AB AC BC ，即222512169AB ，13AB ，故答案为：13m ．【点睛】本题主要考查了平面展开图—最短路径问题，用到台阶的平面展开图，只要根据题意判断出长方形的长和宽即可解答．20．（2022秋·河北邢台·九年级金华中学校考期末）一个几何体的三视图如图所示，如果一只蚂蚁要从这个几何体中的点B 出发，沿表面爬到CD 的中点E ，请你求出这条线路的最短路径．21．（2022秋·九年级单元测试）如图，是一块长、宽、高分别是6cm，4cm和3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径是多少？如图2，当爬的长方体的长是如图3，爬的长方体的长是∵1099785，它需要爬行的最短路径是【点睛】本题考查勾股定理的应用．解题的关键是将长方体展开成平面图形，利用勾股定理求出最短路径．22．（2022秋·浙江宁波·九年级校考期中）葛藤是一种刁钻的植物．它自己腰托不硬，为了争夺雨露阳光，常常绕着树干盘旋而上，它还有一手绝招，就是绕树盘旋上升的路段，总是沿着最短路线——盘旋前进的，难道植物也懂得数学吗？阅读以上信息，你能设计一种方法解决下列问题吗？(1)如图，如果树干的周长（即底面圆的周长）为30cm，从点A绕一圈到点B，葛藤升高40cm，则它爬行路程是多少厘米？(2)如果树干的周长（即底面圆的周长）为40cm，绕一圈爬行50cm，则爬行一圈升高多少厘米？如果爬行10圈到达树顶，则树干高多少厘米？【答案】(1)50cm(2)300cm【分析】（1）将圆柱展开，可知底面圆周长，即为AC的长，圆柱的高即为AB的长，求出BC的长即为葛藤绕树的最短路程．（2）先根据勾股定理求出绕行1圈的高度，再求出绕行10圈的高度，即为树干高．【详解】（1）解：如图，23．（2022秋·辽宁沈阳·九年级校考阶段练习）如图，两个一样的长方体礼品盒，其底面是边长为15cm的正方形，高为20cm；现有彩带若干（足够用），数学组的小明和小刚分别采用自己喜欢的方式用彩带装饰两个礼品盒（假设彩带完美贴合长方体礼品盒）.(1)如图1，小明从底面点A开始均匀缠绕长方体侧面，刚好缠绕2周到达点B，求所用彩带的长度；(2)如图2，小刚沿着长方体的表面从点C缠绕到点D，点D与点E的距离是5cm，请问小刚所需要的彩带最短是多少？（注：以上两问均要求画出平面展开示意图，再解答）将长方体的侧面沿AB展开，取A B 的中点则2为所求的彩带长，AM NB AM222∵，AM AA A M此时215CD 当右边的面与前面的面展成一个平面时，如图，此时22202020CD 当上面的面与左边的面展成一个平面时，如图，此时235CD 由上可知小刚所需要的彩带最短是【点睛】本题考查了平面展开用了数形结合思想．24．（2022秋·辽宁葫芦岛·九年级校考阶段练习）如图1，等腰三角形ABC 中，当顶角A 的大小确定时，它的对边（即底边BC ）与邻边（即腰AB 或AC ）的比值也就确定了，我们把这个比值记作 T A ，即 CT A A BC A A 的对边(底边)的邻边(腰)，当60A 时，如 601T ．(1) 90T ， 120T ， T A 的取值范围是；(2)如图2，圆锥的母线长为18，底面直径14PQ ，一只蚂蚁从点P 沿着圆锥的侧面爬行到点Q ，求蚂蚁爬行的最短路径长．（精确到0.1，参考数据： 1400.53T ， 700.8735 1.66T T ，）25．（2022·江苏·九年级专题练习）在几何体表面上，蚂蚁怎样爬行路径最短？（1）如图①，圆锥的母线长为12cm ，B 为母线OC 的中点，点A 在底面圆周上， AC 的长为4cm ．在图②所示的圆锥的侧面展开图中画出蚂蚁从点A 爬行到点B 的最短路径，并标出它的长（结果保留根号）．（2）图③中的几何体由底面半径相同的圆锥和圆柱组成．O 是圆锥的顶点，点A 在圆柱的底面圆周上．设圆锥的母线长为l ，圆柱的高为h ．①蚂蚁从点A爬行到点O的最短路径的长为________（用含l，h的代数式表示）．②设 AD的长为a，点B在母线OC上，OB b ．圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点A爬行到点B的最短路径的示意图，并写出求最短路径的长的思路．∴26．（2022秋·浙江·九年级专题练习）李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长．（1）如图1，正方体的棱长为5cm 一只蚂蚁欲从正方体底面上的点A 沿着正方体表面爬到点1C 处；（2）如图2，正四棱柱的底面边长为5cm ，侧棱长为6cm ，一只蚂蚁从正四棱柱底面上的点A 沿着棱柱表面爬到1C 处；（3）如图3，圆锥的母线长为4cm ，圆锥的侧面展开图如图4所示，且1120AOA ，一只蚂蚁欲从圆锥的底面上的点A 出发，沿圆锥侧面爬行一周回到点A ．27．（2023春·八年级课时练习）如图有一个四级台阶，它的每一级的长、宽分别为18分米、4分米．(1)如果给台阶表面8个矩形区域铺上定制红毯，需要定制红毯的面积为432平方分米，那么每一级台阶的高为多少分米？(2)A和C是这个台阶上两个相对的端点，台阶角落点A处有一只蚂蚁，想到台阶顶端点C处去吃美味的食物，则蚂蚁沿着台阶面从点A爬行到点C的最短路程为多少分米？。

蚂蚁行程模型绕球上的有关题目

蚂蚁行程模型绕球上的有关题目摘要：1.蚂蚁行程模型的概述2.蚂蚁行程模型在球面上的应用3.蚂蚁行程模型的优点和局限性正文：一、蚂蚁行程模型的概述蚂蚁行程模型是一种用来描述蚂蚁在寻找食物路径的算法模型。

在这个模型中，蚂蚁在平面上随机行走，通过释放信息素来标记路径，其他蚂蚁则通过感知信息素来选择最优路径。

这种模型在解决复杂的路径问题上具有很高的效率，被广泛应用于运筹学、人工智能等领域。

二、蚂蚁行程模型在球面上的应用将蚂蚁行程模型应用到球面上，可以为解决一些球面几何问题提供新的思路。

例如，在球面上寻找最短路径、最小生成树等问题，都可以借助蚂蚁行程模型来求解。

在球面上实现蚂蚁行程模型，需要对原有的算法进行一些改进。

首先，由于球面是一个闭合的曲面，蚂蚁在球面上行走时不能像在平面上那样无限延伸。

因此，需要为蚂蚁的行走范围设置一个边界，以确保模型的有效性。

其次，在球面上计算距离和角度时，需要采用球面几何的相关知识，以保证算法的准确性。

三、蚂蚁行程模型的优点和局限性蚂蚁行程模型在解决一些复杂问题上具有很多优点，例如：1.具有很强的鲁棒性：即使在存在干扰和不确定性的情况下，蚂蚁行程模型仍然可以找到较优解。

2.具有自适应性：随着问题的变化，蚂蚁行程模型可以自动调整算法，以适应不同的需求。

3.计算复杂度较低：蚂蚁行程模型的计算复杂度较低，可以在较短的时间内得到满意的结果。

然而，蚂蚁行程模型也存在一些局限性，例如：1.对初始条件敏感：蚂蚁行程模型的结果受到初始条件的影响较大，不同的初始条件可能导致不同的结果。

2.信息素的作用有限：在现实世界中，信息素的作用可能会受到环境等因素的影响，导致模型的准确性降低。

3.模型的扩展性有限：蚂蚁行程模型主要适用于一维和二维空间，对于高维空间问题，模型的扩展性较低。

总之，蚂蚁行程模型作为一种经典的算法模型，在球面上的应用具有很大的潜力。

初中数学31个几何模型之蚂蚁行程和中点四大模型

初中数学31个几何模型之蚂蚁行程和中点四大模型
蚂蚁行程就是求蚂蚁在杯壁中爬行觅食，求它爬行的最短距离，这种题型实际上是轴对称模型的一种变式应用。

这种题型有两种形式，一种是蚂蚁沿着立体图形的表面进行爬行，一种是从外表面爬行到内壁觅食。

第一种只需要把例题图形展开，沿对角线爬行即最短路径；第二钟是用轴对称的知识来找到最短路径，然后再计算。

这种题型在中考中考查的比较少，但是在刚学轴对称之后用的比较多，需要和“勾股定理”一起使用，求最短距离的长度。

中点的四大模型，包含中线倍长、等腰三角形三线合一、中位线定理、直角三角形斜边中线，这在八年级几何中非常的常见，也非常的重要，主要是构造全等三角形。

在九年级几何当中也是比较重要的，有的同学在刚学全等三角形的时候，老师由于这种类型讲的比较多，用起来还比较的顺手，但到了九年级这种题型讲的少了，遇到中点的问题就又忘了怎么做了。

所以我把几何模型归纳后，掌握几何模型比较重要的。

初中数学勾股定理之“蚂蚁爬行”模型 (解析版)

勾股定理之“蚂蚁爬行”模型【知识梳理】蚂蚁爬行的最值问题是非常经典的一类最值问题，我们如果能够记住最值的特点，那么解题将会更高效.【考点剖析】一、单选题1(2022秋·江苏·八年级专题练习)如图，圆柱的高为4cm，底面半径为3πcm，在圆柱下底面的A点处有一只蚂蚁，它想吃到上底面B处的食物，已知四边形ADBC的边AD、BC恰好是上、下底面的直径、问：蚂蚁食到食物爬行的最短距离是( )cm．A.5B.5πC.3+4πD.3+8π【答案】A【分析】如图，先把圆柱体沿着直线AC剪开，得到矩形如图示：可得线段AB的长度为所求的最短距离，再利用勾股定理可得答案.【详解】解：把圆柱体沿着直线AC剪开，得到矩形如下：则线段AB的长度为所求的最短距离.由题意得圆柱的高为：4cm, 底面半径为3πcm，∴AC=4,BC=12C底面圆=12×2π×3π=3,∴AB=AC2+BC2=32+42=5,所以蚂蚁至少要爬行5cm路程才能吃到食物.故选：A【点睛】本题考查平面展开最短路径问题，弄懂圆柱展开图是长方形，根据两点之间线段最短是解题的关键．2(2023春·山东济宁·八年级统考阶段练习)如图，长方体的高为9dm，底面是边长为6dm的正方形.一只蚂蚁从顶点A开始爬向顶点B，那么它爬行的最短路程为()A.10dmB.12dmC.15dmD.20dm【答案】C【分析】将立体图形展开，有三种不同的展法，连接AB，利用勾股定理求出AB的长，找出最短的即可．【详解】解：①如图，将长方体的正面和上面展开在同一平面内，则AD=6dm，BD=6+9=15dm，②如图，将长方体的正面和右面展开在同一平面内，AC=6+6=12dm，BC=9dm，AB=122+92=15dm；③将长方体的上面和左面展开在同一平面内，则DE=6dm，BE=6+9=15dm，DB=62+152=329dm；∵15<329，所以蚂蚁爬行的最短路程为15dm．故选：C．【点睛】本题考查的是平面展开--最短路径问题，此类问题先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径一般情况是利用两点之间，线段最短．关键是在平面图形上构造直角三角形解决问题．3(2022秋·浙江·九年级专题练习)如图，圆柱的底面周长为16，BC=12，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S，则移动的最短距离为()A.10B.12C.14D.20【答案】A【分析】由于圆柱的高为12cm，S为BC的中点，故BS=6cm，先把圆柱的侧面展开，连接AS，利用勾股定理即可得出AS的长．【详解】解：沿着S所在的母线展开，如图，连接AS，则AB=12×16=8，BS=12BC=6，在Rt△ABS中，根据勾股定理AB2+BS2=AS2，即82+62=AS2，解得AS=10．∵A，S两点之间线段AS最短，∴点A到点S移动的最短距离为AS=10cm．故选：A．【点睛】本题考查的是平面展开-最短路径问题，根据题意画出圆柱的侧面展开图，利用勾股定理求解是解答此题的关键．4(2022秋·江苏·八年级专题练习)如图，在长方体透明容器(无盖)内的点B处有一滴糖浆，容器外A 点处的蚂蚁想沿容器壁爬到容器内吃糖浆，已知容器长为6cm，宽为4cm，高为3cm，点A距底部2cm，请问蚂蚁需爬行的最短距离是(容器壁厚度不计)A.229cmB.10cmC.62cmD.45cm【答案】B【分析】沿着上面的棱将A点翻折至A'处，分三种情况讨论，利用化曲为直的思想和勾股定理求解即可．【详解】解：沿着上面的棱将A点翻折至A'处，则新长方体的长、宽、高依次为6cm，4cm，4cm，若蚂蚁的行走路线为后壁和下壁，则最短路径为：62+82=10cm，若蚂蚁的行走路线为左壁和下壁，则最短路径为：102+42=229cm，若蚂蚁的行走路线为左壁和前壁，则最短路径为：102+42=229cm，∵10<229，∴最短路径为：10cm．故选：B．【点睛】本题考查勾股定理的应用，求算术平方根．能分类讨论是解题关键．5(2022秋·江苏·八年级专题练习)如图是一个三级台阶，它的每一级的长，宽，高分别是20dm,3dm,2dm，A和B是这个台阶相对的端点，点A处有一只蚂蚁，想到B处去吃食物，则这只蚂蚁爬行的最短距离为()A.25dmB.26dmC.24dmD.27dm【答案】A【分析】先将图形平面展开，再由勾股定理根据两点之间线段最短进行解答．【详解】解：三级台阶平面展开图为长方形，长为20dm，宽为(2+3)×3dm，则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长．设蚂蚁沿台阶面爬行到B点最短路程为xdm，由勾股定理得：x2=202+[(2+3)×3]2=252，解得x=25．故选：A．【点睛】本题的是平面展开-最短路径问题，解答此类问题时要先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题6(2022秋·福建宁德·九年级校考期中)如图，有一个圆柱，底面圆的直径AB=16π，高BC=12cm，P为BC的中点，一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短距离为()A.9cmB.10cmC.11cmD.12cm【答案】B【分析】把圆柱的侧面展开，连接AP，利用勾股定理即可得出AP的长，即蚂蚁从A点爬到P点的最短距离．【详解】解：如图：展开后线段AB 的长度是圆柱中半圆AB 的周长，∵圆柱底面直径16πcm 、高BC =12cm ，P 为BC 的中点，∴BP =6cm ，∴AB =12×π×16π=8cm,在Rt △ABP 中，AP =AB 2+PB 2=82+62=10(cm )，∴蚂蚁从A 点爬到P 点的最短距离为10cm ，故选：B ．【点睛】本题考查的是平面展开-最短路径问题，根据题意画出圆柱的侧面展开图，利用勾股定理求解是解答此题的关键．7(2022秋·江苏·八年级专题练习)如图，一只蜘蛛在一块长方体木块的一个顶点A 处，一只苍蝇在这个长方体的对角顶点G 处，若AB =3cm ，BC =5cm ，BF =6cm ，则最短的爬行距离是()A.10B.14C.106D.130【答案】A 【分析】把长方体展开，根据两点之间线段最短得出最短路线AG ，根据勾股定理，即可求出AG 长度；【详解】把长方体展开有三种情况：当蜘蛛从A 出发到EF 上再到G 时，如下图所示∵BC=5cm，∴FG=BC=5cm，∴BG=5+6=11(cm)，在Rt△ABG中，AG=32+112=130(cm)；当蜘蛛从A出发到BF上再到G时，如下图所示∵AB=3cm，BC=5cm，∴AG=3+5=8(cm)，∵BF=6cm，∴CG=BF=6cm，在Rt△ABG中，AG=82+62=10(cm)，当蜘蛛从A出发到EH上再到G时，如下图所示∵AE=6cm，EF=3cm FG=5cm，∴AF=9cm，在Rt△AFG中，AG=92+52=106(cm)，∵130>106>10．故选：A．【点睛】本题考查勾股定理的应用，掌握两点之间线段最短是解题的关键．8(2022秋·江西萍乡·八年级统考期中)如图，长方体的长为20cm，宽为15cm，高为10cm，点B离点C 为5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖，需要爬行的最短距离是()A.529cmB.25cmC.537cmD.16cm【答案】B【分析】分三种情况讨论：把上面展开到左侧面上，连结AB，如图1；把上面展开到正面上，连结AB，如图2；把侧面展开到正面上，连结AB，如图3，然后利用勾股定理分别计算各情况下的AB，再进行大小比较．【详解】把上面展开到左侧面上，连结AB，如图1，AB=(10+20)2+52=925=537(cm)把上面展开到正面上，连结AB，如图2，把侧面展开到正面上，连结AB，如图3，AB=102+(20+5)2=725=529(cm)．∵925>725>25所以一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离为25cm．故选：B．【点睛】本题考查了平面展开-最短路径问题：先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．9(2023春·八年级课时练习)如图，桌上有一个圆柱形玻璃杯(无盖)高6厘米，底面周长16厘米，在杯口内壁离杯口1.5厘米的A处有一滴蜜糖，在玻璃杯的外壁，A的相对方向有一小虫P，小虫离杯底的垂直距离为1.5厘米，小虫爬到蜜糖A处的最短距离是()A.73厘米B.10厘米C.82厘米D.8厘米【答案】B【分析】把圆柱沿着点A所在母线展开，把圆柱上最短距离转化为将军饮马河型最短问题求解即可.【详解】把圆柱沿着点A所在母线展开，如图所示，作点A的对称点B，连接PB，则PB为所求，根据题意，得PC=8，BC=6，根据勾股定理，得PB=10，故选B.【点睛】本题考查了圆柱上的最短问题，利用圆柱展开，把问题转化为将军饮马河问题，灵活使用勾股定理是解题的关键.10(2021春·山东临沂·八年级统考期中)如图，圆柱形玻璃板，高为12cm，底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的A处，则蚂蚁到达蜂蜜的最短距离是()A.15cmB.16cmC.17cmD.18cm【答案】A【分析】在侧面展开图中，过C作CQ⊥EF于Q，作A关于EH的对称点A′，连接A′C交EH于P，连接AP，则AP+PC就是蚂蚁到达蜂蜜的最短距离，求出A′Q，CQ，根据勾股定理求出A′C即可．【详解】解：沿过A的圆柱的高剪开，得出矩形EFGH，过C作CQ⊥EF于Q，作A关于EH的对称点A′，连接A′C交EH于P，连接AP，则AP+PC就是蚂蚁到达蜂蜜的最短距离，∵AE=A′E，A′P=AP，∴AP+PC=A′P+PC=A′C，×18cm=9cm，A′Q=12cm-4cm+4cm=12cm，∵CQ=12在Rt△A′QC中，由勾股定理得：A′C=122+92=15cm，故选：A．【点睛】本题考查了平面展开-最短路径问题，同时也考查了学生的空间想象能力．将图形侧面展开，利用轴对称的性质和勾股定理进行计算是解题的关键．二、填空题11(2023秋·河南南阳·八年级统考期末)如图，圆柱形容器的高为0.9m，底面周长为1.2m，在容器内壁离容器底部0.3m处的点B处有一蚊子．此时，一只壁虎正好在容器外壁，离容器上沿0.2m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为m．【答案】1【分析】画出容器侧面展开图(见详解)，作点A关于EF的对称点A′，根据两点之间线段最短可知A′B的长度即为所求．【详解】解：如图，将容器侧面展开，作点A关于EF的对称点A′，连接A′B，则A′B为最短距离．由题意知，A′D=0.6m，A′E=AE=0.2m，∴BD=0.9-0.3+0.2=0.8m，∴A′B=A D2+BD2=0.62+0.82=1(m)．故答案为：1．【点睛】本题考查了勾股定理的应用最短路径问题，将圆柱的侧面展开，利用轴对称的性质和勾股定理进行计算是解题的关键．12(2022秋·江苏·八年级专题练习)如图是一个边长为6的正方体木箱，点Q在上底面的棱上，AQ= 2，一只蚂蚁从P点出发沿木箱表面爬行到点Q，则蚂蚁爬行的最短路程为．【答案】10【分析】将正方体上表面如图展开(见详解)，根据两点之间，线段最短，即可得到：连接PQ的线段是P到Q 的最短路程，再根据勾股定理计算即可．【详解】解：将正方体上表面展开，如图所示，∵PB=AB=6，AQ=2，∴BQ=6+2=8，∴PQ=PB2+BQ2=62+82=10．∴蚂蚁爬行的最短路程10．故答案为：10．【点睛】此题考查的是勾股定理之最短路径问题，掌握两点之间线段最短和利用勾股定理求边长是解决此题的关键.13(2023秋·江西宜春·八年级校考期末)如图，长方体的长BE=15cm，宽AB=10cm，高AD=20cm，点M在CH上，且CM=5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点M，需要爬行的最短距离是cm．【分析】首先将长方体沿CH、HE、BE剪开，向右翻折，使面ABCD和面BEHC在同一个平面内，连接AM；或将长方体沿CH、GD、GH剪开，向上翻折，使面ABCD和面DCHG在同一个平面内，连接AM，或将长方体沿AB、AF、EF剪开，向下翻折，使面CBEH和下面在同一个平面内，连接AM，然后分别在Rt△ADM与Rt△ABM与Rt△ACM，利用勾股定理求得AM的长，比较大小即可求得需要爬行的最短路程．【详解】解：将长方体沿CH、HE、BE剪开，向右翻折，使面ABCD和面BEHC在同一个平面内，连接AM，如图1，由题意可得：MD=MC+CD=5+10=15cm，AD=20cm，在Rt△ADM中，根据勾股定理得：AM=152+202=25cm；将长方体沿CH、GD、GH剪开，向上翻折，使面ABCD和面DCHG在同一个平面内，连接AM，如图2，由题意得：BM=BC+MC=20+5=25(cm)，AB=10cm,在Rt△ABM中，根据勾股定理得：AM=252+102=529cm,连接AM，如图3，由题意得：AC=AB+CB=10+20=30(cm)，MC=5cm,在Rt△ACM中，根据勾股定理得：AM=302+52=537cm,∵25<529<537，则需要爬行的最短距离是25．【点睛】此题考查了最短路径问题，利用了转化的思想，解题的关键是将立体图形展为平面图形，利用勾股定理的知识求解．14(2022秋·广东揭阳·八年级统考期末)如图，在圆柱的截面ABCD中，AB=16π，BC=12，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离为．【分析】先把圆柱的侧面展开，连接AS ，利用勾股定理即可得出AS 的长．【详解】如图所示，将其展开，∵在圆柱的截面ABCD 中：AB =16π，BC =12，∴AB =12×π×16π=8，BS =12BC =6，将其展开可得如下的矩形，在Rt ΔABS 中，∴AS =82+62=10．故答案为：10．【点睛】题目主要考查弧长公式、勾股定理及其在圆柱展开展开中的应用，能想到将圆柱展开应用勾股定理是解题关键．三、解答题15(2022秋·陕西咸阳·八年级校考阶段练习)如图，有一个高为10dm ，底面周长为48dm 的圆柱形水桶，水桶的底端A 处有一只蚂蚁，它准备沿水桶的侧面爬行到对角B 处去吃一滴蜂蜜，求蚂蚁爬行的最短路线长．【答案】蚂蚊爬行的最短路线长为26dm ．【分析】先把水桶的侧面展开图如图所示．确定AD 为半周长，然后利用勾股定理求解即可．【详解】解：水桶的侧面展开图如图所示．由题意，易得BD =10dm ，AD =24dm ，由勾股定理得，AB =AD 2+BD 2=242+102=26dm ，即蚂蚊爬行的最短路线长为26dm ．【点睛】本题考查最短路径问题，掌握圆柱侧面展开图，确定点B 是半周长的山边缘，用勾股定理求解是解题关键．16(2022秋·江苏·八年级专题练习)如图，一只螳螂在树干的点A 处，发现它的正上方点B 处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是就绕到虫子后面吃掉它，已知树干的半径为10cm ，A ，B 两点的距离为45cm，求螳螂爬行的最短距离(π取3)．【答案】75cm【分析】将圆柱形树干的侧面如图所示展开，根据两点之间线段最短，可得AB即为螳螂爬行的最短距离，利用勾股定理即可求出AB．【详解】解：将圆柱形树干的侧面如图所示展开，根据两点之间线段最短，可得AB即为螳螂爬行的最短距离AF=2π×10≈60cm，BF=45cm∴AB=AF2+BF2=602+452=75cm答：螳螂爬行的最短距离为75cm．【点睛】此题考查的是勾股定理的应用，掌握利用勾股定理解直角三角形和两点之间线段最短是解题关键．17(2022秋·江苏·八年级专题练习)如图，是用棱长为1cm的两个正方体拼成的新几何体，求一只蚂蚁从顶点A出发沿着新几何体的表面爬行到顶点B的最短路程是多少cm？【答案】22cm【分析】根据两点之间线段最短，将组合体图形转化为平面图形，进而勾股定理求解即可【详解】解：如图，将组合体的上底面展开，点B到了点B 的位置，蚂蚁沿A→D→B所在的直线运动到B 路程最短，∴AB=AC2+B C2=22+22=22．若按以下方式展开，则AB =1+32=10∵10>22即蚂蚁从顶点A出发到顶点B的最短路程是22cm．【点睛】本题考查了勾股定理的应用，将立体图形转化为平面图形是解题的关键．【过关检测】一．选择题(共7小题)18(2022秋•市中区期中)正方体盒子的棱长为2，BC的中点为M，一只蚂蚁从A点爬行到M点的最短距离为()A.13B.17C.5D.2+5【分析】把此正方体的点M所在的面展开，然后在平面内，利用勾股定理求点A和点M间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于2长，另一条直角边长等于3，利用勾股定理可求得．【解答】解：展开正方体的点M所在的面，∵BC的中点为M，所以MC=12BC=1，在直角三角形中AM=22+1+22=13．故选：A．【点评】本题考查了勾股定理的拓展应用．“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．19(2022秋•清新区期中)如图所示，一圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程(π取3)是()A.12cmB.10cmC.14cmD.无法确定【分析】根据两点之间，线段最短．先将图形展开，再根据勾股定理可知．【解答】解：如图所示：可以把A和B展开到一个平面内，即圆柱的半个侧面是矩形：矩形的长BC=4π2=2π=6，矩形的宽AC=8，在直角三角形ABC中，AC=8，BC=6，根据勾股定理得：AB=2π2+64≈10．故选：B．【点评】要求不在同一个平面内的两点之间的最短距离，需要把两个点展开到一个平面内，再计算．20(2022春•思明区校级期中)如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是()A.521B.25C.105+5D.35【分析】要求蚂蚁爬行的最短距离，需将长方体的侧面展开，进而根据“两点之间线段最短”得出结果．【解答】解：将长方体展开，连接A、B，根据两点之间线段最短，(1)如图，BD=10+5=15，AD=20，由勾股定理得：AB=AD2+BD2=152+202=625=25．(2)如图，BC=5，AC=20+10=30，由勾股定理得，AB=AC2+BC2=52+302=925=537．(3)只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图：∵长方体的宽为10，高为20，点B离点C的距离是5，∴BD=CD+BC=20+5=25，AD=10，在直角三角形ABD中，根据勾股定理得：∴AB=BD2+AD2=102+252=529；由于25<529<537，故选：B．【点评】本题是一道趣味题，将长方体展开，根据两点之间线段最短，运用勾股定理解答即可．21(2021秋•金水区校级月考)如图：有一圆柱，它的高等于8cm，底面直径等于4cm(π=3)，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面与A相对的B点处的食物，需要爬行的最短路程大约()A.10cmB.12cmC.19cmD.20cm【分析】根据两点之间，线段最短．首先把A和B展开到一个平面内，即展开圆柱的半个侧面，得到一个矩形，然后根据勾股定理，求得蚂蚁爬行的最短路程即展开矩形的对角线的长度．【解答】解：展开圆柱的半个侧面，得到一个矩形：矩形的长是圆柱底面周长的一半即2π=6，矩形的宽是圆柱的高即8．根据勾股定理得：蚂蚁爬行的最短路程即展开矩形的对角线长即10．故选：A．【点评】本题考查了勾股定理的拓展应用．“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．本题注意只需展开圆柱的半个侧面．22(2021春•宣化区期中)如图，一圆柱体的底面周长为24cm，高BD为5cm，BC是直径，一只蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程大约是()A.6cmB.12cmC.13cmD.16cm【分析】根据题意，先将圆柱体展开，再根据两点之间线段最短．【解答】解：将圆柱体展开，连接DC，圆柱体的底面周长为24cm，则DE=12cm，根据两点之间线段最短，CD=52+122=13(cm)．而走D-B-C的距离更短，∵BD=5，BC=24π，∴BD+BC≈13．故选：C．【点评】本题考查了平面展开--最短路径问题，将圆柱体展开，根据两点之间线段最短，运用勾股定理解答即可．23(2022春•璧山区期中)如图，一圆柱体的底面周长为10cm，高AB为12cm，BC是直径，一只蚂蚁从点A出发沿着圆柱的表面爬行到点C的最短路程为()A.17cmB.13cmC.12cmD.14cm【分析】将圆柱的侧面展开，得到一个长方形，再然后利用两点之间线段最短解答．【解答】解：如图所示：由于圆柱体的底面周长为10cm，则AD=10×12=5(cm)．又因为CD=AB=12cm，所以AC=52+122=13(cm)．故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是13cm．故选：B．【点评】此题主要考查了平面展开图的最短路径问题和勾股定理的计算，将圆柱的侧面展开，构造出直角三角形是解题的关键．24(2021秋•通川区校级月考)如图是一块长，宽，高分别是6cm，4cm和3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是()A.(3+213)cmB.97cmC.85cmD.109cm【分析】作此题要把这个长方体中，蚂蚁所走的路线放到一个平面内，在平面内线段最短，根据勾股定理即可计算．【解答】解：第一种情况：把我们所看到的前面和上面组成一个平面，则这个长方形的长和宽分别是9和4，则所走的最短线段是42+92=97；第二种情况：把我们看到的左面与上面组成一个长方形，则这个长方形的长和宽分别是7和6，所以走的最短线段是72+62=85；第三种情况：把我们所看到的前面和右面组成一个长方形，则这个长方形的长和宽分别是10和3，所以走的最短线段是32+102=109；三种情况比较而言，第二种情况最短．故选：C．【点评】此题的关键是明确线段最短这一知识点，然后把立体的长方体放到一个平面内，求出最短的线段．二．填空题(共8小题)25(2022春•凉州区期末)如图一只蚂蚁从长为5cm、宽为3cm，高是4cm的长方体纸箱的A点沿纸箱爬到B点，那么它所爬行的最短路线的长是74cm．【分析】把此长方体的一面展开，然后在平面内，利用勾股定理求点A和B点间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于长方体的高，另一条直角边长等于长方体的长宽之和，利用勾股定理可求得．【解答】解：因为平面展开图不唯一，故分情况分别计算，进行大、小比较，再从各个路线中确定最短的路线．(1)展开前面右面由勾股定理得AB2=(5+3)2+42=80；(2)展开前面上面由勾股定理得AB2=(4+3)2+52=74；(3)展开左面上面由勾股定理得AB2=(5+4)2+32=90．所以最短路径的长为AB=74(cm)．故答案为：74．【点评】本题考查了平面展开-最短路径问题及勾股定理的拓展应用．“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．26(2021秋•将乐县期中)如图，有一圆柱，其高为12cm，底面半径为3cm，在圆柱下底面A点处有一只蚂蚁，它想得到上底面B处的食物，则蚂蚁经过的最短距离为15cm．(π取3)【分析】本题应先把圆柱展开即得其平面展开图，则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πr，蚂蚁经过的最短距离为连接A，B的线段长，由勾股定理求得AB的长．【解答】解：圆柱展开图为长方形，则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πrcm，蚂蚁经过的最短距离为连接A，B的线段长，由勾股定理得AB=122+3π2=122+92=225=15cm．故蚂蚁经过的最短距离为15cm．【点评】解答本题的关键是计算出圆柱展开后所得长方形长和宽的值，然后用勾股定理计算即可．27(2021•南岗区校级开学)一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是10．【分析】根据”两点之间线段最短”，将点A和点B所在的两个面进行展开，展开为矩形，则AB为矩形的对角线，即蚂蚁所行的最短路线为AB．【解答】解：如图(1)所示：AB=32+8+32=130；如图(2)所示：AB=62+82=10．由于130>10，所以最短路径为10．【点评】本题的关键是将点A和点B所在的面展开，运用勾股定理求出矩形的对角线．28(2021秋•浚县期末)如图，一只蚂蚁从长为7cm、宽为5cm，高是9cm的长方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是15cm．【分析】根据题意，过A点和B点的平面展开图分三种情况，再根据两点之间线段最短和勾股定理可以分别求得三种情况下的最短路线，然后比较大小，即可得到A点到B点的最短路线，本题得以解决．【解答】解：由题意可得，当展开前面和右面时，最短路线长是：7+52+92=225=15(cm)；当展开前面和上面时，最短路线长是：72+9+52=245=75(cm)；当展开左面和上面时，最短路线长是：52+9+72=281(cm)；∵15<75<281，∴一只蚂蚁从长为7cm、宽为5cm，高是9cm的长方体纸箱的A点沿纸箱爬到B点，那么它所走的最短路线的长是15cm，故答案为：15．【点评】本题考查平面展开-最短路径问题，解题的关键是明确两点之间线段最短，利用分类讨论的方法解答．29(2022春•芙蓉区校级期末)如图是棱长为4cm的立方体木块，一只蚂蚁现在A点，若在B点处有一块糖，它想尽快吃到这块糖，则蚂蚁沿正方体表面爬行的最短路程是45cm．【分析】根据“两点之间线段最短”，将点A和点B所在的各面展开，展开为矩形，AB为矩形的对角线的长即为蚂蚁沿正方体表面爬行的最短距离．【解答】解：将点A和点B所在的面展开为矩形，AB为矩形对角线的长，∵矩形的长和宽分别为8cm和4cm，∴AB=82+42=45cm．故蚂蚁沿正方体的最短路程是45cm．【点评】本题的关键是将蚂蚁所走的最短路程转化为求矩形的对角线的长．30(2022春•重庆月考)如图，一只蚂蚁从长、宽都是4，高是6的长方体纸箱的A点沿纸箱表面爬到B 点，那么它所行的最短路线的长是10．【分析】根据题意画出图形，求出AC、BC的长，根据勾股定理求出AB即可．【解答】解：有两种情况，如图所示：连接AB，求出AB的长就可以，(1)由题意知AC=4，BC=6+4=10，由勾股定理得：AB=AC2+BC2=116；(2)由题意知：AC=4+4=8，BC=6，由勾股定理得：AB=AC2+BC2=100=10，(3)如图3，AC=8，BC=6，由勾股定理得：AB=100=10；∵116>100，∴最短是10．故答案为：10．【点评】本题主要考查对平面展开-最短路线问题，勾股定理等知识点的理解和掌握，知道求出AB的长度是本题的结果是解此题的关键．31(2022秋•薛城区校级月考)如图是一个三级台阶，它的每一级长、宽、高分别是2米、0.3米、0.2米，A，B是这个台阶上两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿台阶面爬行到B点最短路程是 2.5米．【分析】先将图形平面展开，再用勾股定理根据两点之间线段最短进行解答．【解答】解：三级台阶平面展开图为长方形，长为2，宽为(0.2+0.3)×3，则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长．可设蚂蚁沿台阶面爬行到B点最短路程为x，由勾股定理得：x2=22+[(0.2+0.3)×3]2=2.52，解得x=2.5．【点评】本题用到台阶的平面展开图，只要根据题意判断出长方形的长和宽即可解答．32(2021秋•城阳区校级月考)如图，有一个圆柱形仓库，它的高为10m，底面半径为4m，在圆柱形仓库下底面的A处有一只蚂蚁，它想吃相对一侧中点B处的食物，蚂蚁爬行的速度是50cm/min，那么蚂蚁吃到食物最少需要26min．(π取3)【分析】要想求得最少时间，则需要求得最短路程．首先展开圆柱的半个侧面，即是矩形．此时AB所在的三角形的直角边分别是5m，12m，根据勾股定理求得AB的长．再根据时间=路程÷速度，求得蚂蚁吃到食物最少需要的时间．【解答】解：首先展开圆柱的半个侧面，即是矩形．此时AB所在的三角形的直角边分别是5m，12m．根据勾股定理求得AB=13m=1300cm，故蚂蚁吃到食物最少需要的时间是1300÷50=26min．【点评】此题的难点在于求得最短路径．是中等题．三．解答题(共2小题)33(2021秋•七里河区校级期末)如图，长方体的底面是边长为1cm的正方形，高为3cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，请利用侧面展开图计算所用细线最短为多少．。

蚁群算法简述PPT课件

12
2.蚁群算法的特征
基本蚁群算法流程图（详细）
1. 在初始状态下，一群蚂蚁外出，此时没有信息素，那么各自会随机的选择一条路径。 2. 在下一个状态，每只蚂蚁到达了不同的点，从初始点到这些点之间留下了信息素，蚂蚁继续走，已经到达目标的蚂蚁开始返回，与此同时，下一批蚂蚁出动，它们都会按照各条路径上信息素的多少选择路线(selection)，更倾向于选择信息素多的路径走（当然也有随机性）。 3. 又到了再下一个状态，刚刚没有蚂蚁经过的路线上的信息素不同程度的挥发掉了(evaporation)，而刚刚经过了蚂蚁的路线信息素增强(reinforcement)。然后又出动一批蚂蚁，重复第2个步骤。每个状态到下一个状态的变化称为一次迭代，在迭代多次过后，就会有某一条路径上的信息素明显多于其它路径，这通常就是一条最优路径。
蚂蚁在运动过程中，能够在它所经过的路径上留下一种称之为外激素(pheromone)的物质进行信息传递，而且蚂蚁在运动过程中能够感知这种物质，并以此指导自己的运动方向，因此由大量蚂蚁组成的蚁群集体行为便表现出一种信息正反馈现象：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。
4
1.蚁群算法的提出
ACO），又称蚂蚁算法——一种用来在图中寻找优化路径的机率型算法。
它由Marco Dorigo于1992年在他的博士论文“Ant system: optimization by a colony of cooperating agents”中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。最早用于解决著名的旅行商问题(TSP , traveling salesman problem)。
式中，Q表示蚂蚁循环一周，且在一定程度上影响算法收敛速度的信息素总量；Lk表示本次循环中，蚂蚁k所走路段的长度。

蚁群算法应用(运输问题)

一、蚁群算法基本原理图表示蚂蚁觅食的线路，A 为蚁穴 , B 为食源，从A 到B 有两条线路可走，A C B --是长路径，A D B --是短路径.蚂蚁走过一条路线以后，在地面上会留下信息素气味，后来蚂蚁就是根据留在地面上这种气味的强度选择移动的方向.图（a ）表示起始情况，假定蚁穴中有4只蚂蚁，分别用1,2,3,4表示，Ｂ为食源.开始时蚁穴中蚂蚁1,2向食源移动，由于路线A C B --和A D B --上均没有蚂蚁通过，在这两条路线上都没有信息素气味，因此蚂蚁1,2选择这两条线路的机会均等.令蚁1选择A C B --线路，蚁2选择A D B --线路，假定蚂蚁移动的速度相同，当蚁2到达食源B 时，蚁1还在途中，如图（b ）.蚁2到达食源以后就返回，这时从B 返回也有两条线路选择，哪一条线路上信息素的气味重就选择哪一条.因为蚁1还在途中，没有到达终点，这时在B C A --线路上靠近B 端处，蚁1还没有留下信息素气味，所以蚁2返回蚁穴的线路只有一个选择，就是由原路返回.当蚁2返回A 时，蚁3开始出发，蚁3的线路选择必定是A D B --，因为这时A D B --上气味浓度比A C B --上重 (A D B --上已有蚂蚁两次通过 ) ，如图（c ）所示.当蚁1到达食源B 时 ,蚁1返回线路必然选择B D A --，如图（d ）所示.如此继续下去，沿A D B --线路上移动的蚂蚁越来越多，这就是巢穴到食源的最短路线，蚂蚁根据线路上留下信息素浓度的大小，确定在路线上移动的方向，蚁群向信息素浓度重的线路集聚的现象称为正反馈.蚂蚁算法正是基于正反馈原理的启发式算法.二、蚁群觅食中的简单规则每只蚂蚁并不是像我们想象的需要知道整个信息，他们其实只关心很小范围内的局部信息，而且根据这些局部信息利用几条简单的规则进行决策，这样，在蚁群这个集体里，复杂性的行为就会凸现出来.这就是人工生命、复杂性科学解释的规律.那么，这些简单规则是什么呢？下面给出比较详细的说明.（1）范围：蚂蚁观察到的范围是一个方格世界，蚂蚁有一个参数为速度半径（一般是3），那么它能观察到的范围就是33⨯个方格世界，并且能移动的距离也在这个范围之内.（2）环境：蚂蚁所在的环境是一个虚拟的世界，其中有障碍物，有别的蚂蚁，还有信息素，信息素有两种，一种是找到食物的蚂蚁洒下的食物信息素，一种是找到窝的蚂蚁洒下的窝的信息素.每个蚂蚁都仅仅能感知它范围内的环境信息.环境以一定的速率让信息素消失.（3）觅食规则：在每只蚂蚁能感知的范围内寻找是否有食物，如果有就直接过去.否则看是否有信息素，并且比较在能感知的范围内哪一点的信息素最多，这样，它就朝信息素多的地方走，并且每只蚂蚁多会以小概率犯错误，从而并不总是往信息素最多的点移动.蚂蚁找窝的规则和上面一样，只不过它对窝的信息素做出反应，而对食物信息素没反应.（4）移动规则：每只蚂蚁都朝向信息素最多的方向移，并且，当周围没有信息素指引的时候，蚂蚁会按照自己原来运动的方向惯性的运动下去，并且，在运动的方向有一个随机的小的扰动.为了防止蚂蚁原地转圈，它会记住最近刚走过了哪些点，如果发现要走的下一点已经在最近走过了，它就会尽量避开.（5）避障规则：如果蚂蚁要移动的方向有障碍物挡住，它会随机的选择另一个方向，并且有信息素指引的话，它会按照觅食的规则行为.（6）播撒信息素规则：每只蚂蚁在刚找到食物或者窝的时候散发的信息素最多，并随着它走的距离越远，播撒的信息素越来越少.在蚁群算法中，需要定义人工蚂蚁的概念，人工蚂蚁具有双重特性，首先，它们是真实蚂蚁行为特征的一种抽象，通过对真实蚂蚁行为的观察，将蚁群行为中的智能化因素赋予人工蚂蚁；另一方面，为了解决实际问题，人工蚂蚁必须具备真实蚂蚁一些所不具备的特性.归纳起来看，它有如下的主要特征.(1) 人工蚁与真实蚁一样，都是一个需要合作的群体问题的解决需要通过人工蚁的合作来完成，人工蚁群通过相互协调与合作从而有可能找到全局最优方案，而每只人工蚁的单独行动只可能找到局部最优解.(2) 人工蚁和真实蚁一样，都要完成一个共同的任务人工蚁与真实蚁一样，都要寻找一个从源节点（巢穴）到目的节点（食物源）之间的最短路径（或最小代价），人工蚂蚁与真实蚂蚁一样都不能跳跃，必须在相邻节点之间移动，直至遍历所有可能路径，为了减少计算复杂度并寻找出最短路径，需要记录当前路径.(3) 人工蚁与真实蚁一样都通过使用信息素进行间接通信真实蚂蚁在经过的路径上留下信息素，人工蚁则不断修改更新在其所经过的路径上存储的信息，是一种模拟自然界中的信息素轨迹更新的过程.(4) 人工蚁利用真实蚁觅食行为中的自催化机制—正反馈当一些路径上通过的蚂蚁越来越多时，路径上留下的信息素轨迹也越来越多，使得信息素强度变大，根据蚂蚁群倾向于选择信息强度大的特点，后来的蚂蚁选择该路径的概率也越高，从而增加了该路径的信息素强度，这称之为自催化过程，自催化机制利用信息素作为反馈，通过对系统演化过程中较优解的增强作用，使得问题的解向着全局最优的方向逐步接近.(5) 信息素的挥发机制在蚁群算法中设置一种挥发机制，类似于真实信息素的挥发，这种机制需要蚂蚁忘记过去，不受过去经验的过分约束，有利于指引蚂蚁朝着新的方向搜索，避免早熟收敛.(6)利用当前信息进行路径选择的随机选择策略人工蚁与真实蚁都是利用概率选择策略实现一个节点到相邻节点的移动，选择策略只利用当前的信息去预测未来的情况，而不能利用未来的信息，因此，人工蚁与真实蚁所使用的选择策略在时间和空间上都具有局部特性.三、蚁群算法与TSP 问题用()i b t 表示t 时刻位于城市i 的蚂蚁数目，m 为蚁群中蚂蚁的总数目，n 为TSP 问题的规模，即城市的个数.显然， 1()ni i m b t ==∑，()ij t τ表示t 时刻路径(,)i j 上的信息量，{()|,}ij i j t c c V τΓ=∈是t 时刻集合V 中元素（城市）两两连接ij l 上残留信息量的集合，在初始时刻各路径上的信息量都相等，即设(0)ij C τ=（常数），基本蚁群算法的寻优是通过有向图(,,)g V A =Γ来实现的.蚂蚁(1,2,3,,)k k m = 在运动过程中，根据各条路径上留下的信息量决定其转移方向.此处采用禁忌表(1,2,3,,)k tabu k m = 来记录蚂蚁k 当前所走过的城市.集合随着进化过程作动态调整，而k allowed 用来表示蚂蚁k 下一步允许访问的城市位置，显然k k allowed V tabu =-.若用ij d 表示城市i 和城市j 之间的距离，则t 时刻图中边(,)i j 反映由城市i 转移到城市j 的启发程度，即能见度，可以取为1()ij ij t d η=，这是一个与时间无关的常数.在搜索过程中，蚂蚁根据各条路径上的信息量以及路径的启发信息（主要是路径长度）来计算状态转移概率，如用()k ij p t 表示蚂蚁k 在 t 时刻由城市i 转移到城市j 的状态转移概率，则可以定义[()][()],[()][()]()0,k ij ij k k is sj ij s allowed t t j allowed t t p t αβαβτητη∈⎧∈⎪⎪=⎨⎪⎪⎩∑否则 (6.3.1)在上式中，α与β分别反映了路径轨迹与路径能见度的相对重要性. α作为信息启发式因子，反映了蚂蚁在运动过程中所积累的信息在蚂蚁运动时所起的作用，其值越大，则该蚂蚁越倾向于选择其他蚂蚁经过的路径，蚂蚁之间的协作性越强，β作为启发式因子，反映了蚂蚁在运动过程中启发因素在选择路径时的受重视程度，其值越大，则该状态转移越接近贪心规则.在两种极端情形：0α=与0β=下，则分别退化为传统的贪心算法与纯粹的正反馈启发式方法.上述状态转移概率的计算用到t 时刻各条路径上信息量的计算，下面我们讨论()ij t τ的计算方法.在初始时刻，0t =，可以选择(0)ij const τ=（常数），蚂蚁完成一次循环后各路径上的信息量更新方程设为1(1)()(,1)(,1)(,1)ij ij ij m k ij ij k t t t t t t t t τρττττ=+=+∆+∆+=∆+∑ (6.3.2)其中，ρ表示信息素的持久系数（即信息的挥发度），而1ρ-则表示信息素的衰减系数，因此一般选择01ρ<<比较合适.从上式可以看出，在已知(0)ij τ的情况下，为了计算()ij t τ，需要计算出全体蚂蚁在时刻t 到时刻1t +内留在路径(,)i j 上信息素量的增量(,1)ij t t τ∆+，因此，需要计算出每只蚂蚁k 在时刻t 到时刻1t +内留在路径(,)i j 上信息素量的增量(,1)k ij t t τ∆+.根据更新策略的不同，Dorigo M 提出了三种计算(,1)k ij t t τ∆+不同的方法，从而得到三种不同的蚁群算法模型，分别称之为Ant-Quantity （蚁量）模型、Ant-Density （蚁密）模型以及Ant-Cycle （蚁周）模型.在蚁量模型中,(,)(,1)0,k ij ij Q k i j d t t τ⎧⎪∆+=⎨⎪⎩若蚂蚁在时间t 到时间t+1内经过否则 (6.3.3)其中，Q 表示信息素强度，为蚂蚁循环一周释放的总信息量.在蚁密模型中,(,)(,1)0,k ij Q k i j t t τ⎧∆+=⎨⎩若蚂蚁在时间t 到时间t+1内经过否则 (6.3.4)从上面的定义不难看到，在蚁密模型中，一只蚂蚁从城市i 转移到城市j 的过程中路径(,)i j 上信息素的增量与边的长度ij d 无关，而在蚁量模型中，它与ij d 成反比，就是说，在蚁量模型终端路径对蚂蚁更具有吸引力，因此，更一步加强了状态转移概率方程中能见度因子ij η的值.在上述两种基本蚁群算法模型中，蚂蚁完成一步后即更新路径上的信息素，即在建立方案的同时释放信息素，采用的是局部信息，为了充分利用整体信息从而得到全局最优算法，下面介绍一种蚁周模型.蚁周模型与上述两种模型的主要区别在于k ij τ∆的不同，在蚁周模型中，(,)k ij t t n τ∆+表示蚂蚁经过n 步完成一次循环后更新蚂蚁k 所走过的路径，具体更新值满足,(,)(,)0,k k ij Q k i j L t t n τ⎧⎪∆+=⎨⎪⎩若蚂蚁在本次循环中经过否则（6.3.5）其中，k L 表示蚂蚁k 在本次循环中所走路径的长度.由于蚁周系统中，要求蚂蚁已经建立了完整的轨迹后再释放信息，信息素轨迹根据如下公式进行更新11()()(,)(,)(,)ij ij ij m k ij ij k t n t t t n t t n t t n τρττττ=+=+∆+∆+=∆+∑ （6.3.6）6.3.3 基本蚁群算法的实现以TSP 为例，基本蚁群算法的具体实现步骤描述如下：（1）参数初始化令时间0t =，循环次数计数器初值0c N =，轨迹强度增量的初值设为0，即(0)0ij τ∆=，初始阶段禁忌表设为空集，即k tabu =Φ，()ij t η由某种启发式算法规则确定，在TSP 中一般取为1ij d ，将m 只蚂蚁随机置于n 个元素（城市）上，并令有向图上每条边(,)i j 的初始信息量为常数，即(0)ij const τ=；（2）循环次数1;c c N N ←+蚂蚁禁忌表索引号1k =，蚂蚁数目1k k ←+；（3）蚂蚁个体根据状态转移概率公式(6.3.1)计算的概率并沿元素（城市）j 前进，{}k j V tabu ∈-；（4）修改禁忌指针表，即将选择好之后的蚂蚁移动到新的元素（城市），并将该元素（城市）移到该蚂蚁个体的禁忌表中；（5）信息素更新的计算在蚁密模型中， (,1):(,1)k k ij ij t t t t Q ττ∆+=∆++；在蚁量模型中，(,1):(,1)k k ij ij ij Q t t t t d ττ∆+=∆++；对于每一个路径(,)i j ，设置持久因子ρ，并按照（6.3.2）计算(1)ij t τ+.在蚁周模型中，对于1k m ≤≤，根据禁忌表的记录计算k L ，对于11s m ≤≤-，设(,):((),(1))k k h l tabu s tabu s =+，即(,)h l 为蚂蚁k 的禁忌表中连接城市(,1)s s +的路径，计算():()hl hl k Q t n t n L ττ∆+=∆++，对于每一条路径(,)i j ，按照（6.3.5）计算()ij t n τ+.（6）纪录到目前为止的最短路径，如果max c N N ≥，则计算终止，循环结束并输出计算结果，否则，清空禁忌表并返回步骤（2）.一系列仿真试验表明，在求解TSP 问题时，蚁周算法的性能优于蚁密与蚁量算法，因此，人们更多地关注于蚁周算法的研究.下面我们讨论基本蚁群算法的计算复杂度问题.算法计算复杂度由时间复杂度和空间复杂度构成.根据蚁群算法所列参数，以及每一步算法描述，其算法每一步运算量主要包括：初始化参数，含赋值运算量为2()O n m +，设置禁忌表赋值运算量为()O m ，每只蚂蚁单独求解需要算术运算量为2()O n m ，而信息素轨迹浓度的更新需要2()O n 次算术运算，因此，算法总的运算量为2max ()O N n m .基本蚁群算法的求解通过有向图来描述，因此需要一个n 阶二维距离矩阵来描述问题本身的特征；为了表示有向图上的信息量，需要用另外一个n 阶二维距离来表示图上的信息素浓度；同时，在求解TSP 问题的过程中，为了保证TSP 城市不出现重复的现象，需要为每只蚂蚁设置一个n 阶一维数组的禁忌表；为了保存蚂蚁寻找到的解，还需为每只蚂蚁设置一个数组；为了便于更新轨迹，需要利用二维数组保存每条边上的信息素更新量，等等.整个计算过程所耗的空间复杂度为2()O n nm +.由于蚁群算法是一种比较新的模拟进化智能算法，目前还没有形成非常严格的系统理论，包括算法中的许多参数设置、信息素量的更新策略等都仍然有许多值得研究的地方.另外，蚁群算法可以用来有效求解较小规模的TSP 问题，但是，对较大规模的TSP 问题，蚁群算法存在需要循环次数偏大等问题.针对这些问题，近年来研究者进行了大量深入的研究，提出了许多改进的蚁群优化算法，这些改进算法主要集中在性能的改进等方面.例如，精英策略，其思想是在算法开始后便对到目前为止所发现的最佳路径给以记录，并将随之得到的行程标记为全局最优行程，一旦对信息进行搜索更新，则对所得到的行程加权处理，而经过上述行程的蚂蚁记为“精英”，这样做的目的可以增加选择较好行程的机会，从而可能以更快的速度收敛到更好的解.在精英策略中，需要注意的是：若选择的精英过多，则算法可能因为陷入局部最优解的陷阱而过早出现搜索停滞现象.改进的蚁群算法一、具有变异特征的蚁群算法这是1999年吴庆洪等人针对TSP 问题的基本蚁群算法提出的一种改进方案.对于路径的选择采取逆转变异方式，设某个体所走路径：012(1){0,1,2,3,,1}n i i i i n -∈-如果距离满足12121122[(1)/][(1)/][(1)/][(1)/](,)(,)(,)(,)s s s n s n s s n s s n d i i d i i d i i d i i +++++<+其中[]x 表示对x 进行取整运算.则进行操作：inversion(12,,s s solution ),函数inversion()的功能是把个体solution 的11s +和2s 这一段颠倒过来，如：(2,5,0123456)0154326inversion =其中，变异的次数是随机的，这一过程涉及到的运算比蚁群算法中的循环过程要简单得多，因此只需较短的时间内便可完成相同次数的运算.另一方面，经过这种变异算子作用后，这一代解的性能产生明显的改善，从而也能改善整个群体的性能，减少计算时间.试验表明，上述具有变异特征的蚁群算法可以有效加快搜索速度.该算法的伪代码表示为：Begin {for (0;;1k k m k =<+++) }初始化过程： {以概率()k ij p t 选择城市j;Ncycle:=0;{0,1,2,,1}k j n tabu ∈--Bestcycle:=0; } :;ij C τ= 将所选城市的序号加到k tabu 中0;ij τ∆= /*（动态调整集合k tabu ）；*/ij η由某种启发式算法确定； }k tabu =Φ；计算()k ij index τ∆，()ij index n τ+While (not termination condition) 确定本次循环中找到的最佳路径{ncycle:=ncycle+1; }for (index=0;index<n;index++) 输出最佳路径与最佳结果/*index 表示已走过的城市*/ end选用M.Dorigo 最早使用过的O liver 30 TSP 作为实验例子进行实验，实验结果取10次实验的平均结果，得到下面三个图形：图6.11 最优解进化曲线图图6.12 最劣解进化曲线图图6.13最优路径为了便于比较，下面给出基本蚁群算法所对应最优解以及最裂解情形下得进化曲线图.图6.14 基本蚁群算法最优解进化曲线图图6.15 基本蚁群算法最劣解进化曲线图选取48座城市的TSP问题进行仿真，实验表明，在最优路径长度基本一致的条件下，具有变异特征蚁群算法所需要的进化代数约为基本蚁群算法的20%左右，这说明，具有变异特征的蚁群算法的高效特性.二、基于蚁群算法与遗传算法融合(GAAA)的改进方法上述GAAA算法是由丁建立等在2003年提出了的，其基本思想是吸取两种算法的优点，克服各自的缺陷，优势互补.在时间效率上优于遗传算法，在求解精度效率上优于遗传算法，是时间效率和求精解效率都比较好的启发式算法.其基本思路是算法前过程采用遗传算法，充分利用遗传算法的快速性、随机性、全局收敛性，其结果是产生有关问题的初始信息素分布. 算法后过程采用蚁群算法，在一定初始信息素分布的情况下，充分利用蚁群算法的并行性、正反馈性、求精解效率高登特点.总体框架如图6.16 所示：图6.16 GAAA 算法总体框架下面讨论GAAA 算法中遗传算法的定义与设置.在编码与适应值函数的涉及中，结合解决问题，采用十进制编码，适应值函数结合目标函数而定，如TSP 问题，以遍历城市次序作为遗传算法的编码，适应值函数取为哈密顿圈的长度的倒数.种群生成与染色体选择则利用rand 函数随机生成一定数量的十进制实数编码种群，根据适应值函数选择准备进行交配的一对染色体父串.交叉算子采用Davis 提出的顺序交叉法，先进行常规的双点交叉，再进行维持原有相对访问顺序的巡回路线修改，具体交叉如下：·随机在父串上选择一个交配区域，如两父串选定为112|3456|789298|7654|321old old ==·将2old 的交配区域加到1old 前面，将1old 的交配区域加到2old 的前面：''17654|123345678923456|987654321old old ==·依次删除''1,2old old 中与交配区域相同的数码，最后得到两字串：17654123892345698721new new ==变异算子采用逆转变异方法，所谓逆转，如染色体(123456)-----在区间23-和56-处发生断裂，断裂片断又以顺序插入，于是逆转后的染色体变为125436-----，其中，“进化”是指逆转算子的单方向性，只有经逆转后适应值有提高的才能接受下来，否则逆转无效.为了实现遗传算法和蚁群算法的有效结合，需要讨论GAAA 算法的改进与衔接问题.首先通过遗传算法得到一定的路径信息素，并把信息素的初值设置为S C G τττ=+，其中，c τ是根据具体求解问题规模给定的一个信息素常数，G τ是遗传算法求解结果转换得信息素值.信息素更新模型采用蚁群圈模型进行信息素更新，即一圈中只有最短路径的蚁群才进行信息素修改增加，而所有路径的轨迹更新方程均采用：(1)()()kij ij ij t t t τρττ+=+∆∑为了验证算法性能，采用典型的含遍历30个城市的TSP 问题进行仿真实验，GAAA 算法中迭代次数固定为30代，蚁群算法中各路径的信息素初始值c τ设为60，遗传算法求解结果转换的信息素值为经过路径加2，轨迹更新0.8,1000.Q ρ==表2.3.1反映GAAA 算法优化求解数据逼近过程，图6.17直观地说明了GAAA 算法中经过遗传算法求解结果在信息素初值设置的表现，不难看出GAAA 算法是一个逐步收敛的过程，从均值与分布的角度来看，具有非常高的求解精度，图6.18 是应用GAAA 算法得到的最优解，与采用其他方法得到的最优解结果一致.图6.19～图6.20找到的解与最优解非常接近，是其它算法容易陷入举步最优的几个值，由于在遗传阶段采用随机产生种群，因而有效避免了陷入举步最优.表6.6 GAAA 算法优化解数据逼近过程图6.17 GAAA算法一次随机遗传变异后产生的信息素分布图6.18 GAAA算法找到的最优路径（d 423.74）图6.19 GAAA算法一次随机迭代找到的最优路径(d=424.46)图6.20 GAAA算法一次随机迭代找到的最优路径(d=424.67) 下面的三个表则给出了GAAA算法与基本蚁群算法以及遗传算法与模拟退火算法结合方法的实验结果比较.表6.7 GAAA算法实验结果表6.8 基本蚁群算法实验结果表6.9 遗传算法与模拟退火算法结合方法实验结果通过仿真实验可以看出，GAAA 算法无论在优化性能还是时间性能上都能够取得好的效果，由于在遗传算法中使用随机生成种群，不仅加快了蚁群算法的速度还避免了求精解阶段陷入局部最优，另外，由于采用遗传算法与蚁群算法结合，对于蚁群算法中的参数调整有较大的减少，从而减少了盲目的实验次数.在蚁群算法的设计过程中，为了避免ρ过小导致收敛速度慢的缺陷，还可以通过设置自适应变化的ρ以提高收敛速度，例如，取初始值0()1t ρ=，当算法求得的最优值在规定的N 次循环后还没有明显改进时，取minmin (1),(1)(),t t t ϖρϖρρρρ--≥⎧=⎨⎩若其它其中ϖ为调解因子，一般取0.91ρ<<，而min ρ为ρ的最小值.仿真结果表明，与基本蚁群算法相比，最优解以及收敛性能等方面均有一定的提高.某城区有36 个垃圾集中点，每天都要从垃圾处理厂（第37 号节点）出发将垃圾运回.现有一种载重6 吨的运输车.每个垃圾点需要用10 分钟的时间装车，运输车平均速度为40/km h（夜里运输，不考虑塞车现象）；每台车每日平均工作 4 小时.运输车重载运费 1.8 元/ 吨公里；运输车和装垃圾用的铲车空载费用0.4 元/ 公里；并且假定纵、横整公里处均有街道，方向平行于坐标轴.请你给出满意的运输调度方案以及计算程序.考虑下列问题：（1）运输车应如何调度（需要投入多少台运输车，每台车的调度方案，总运营费用）?（2）铲车应如何调度（需要多少台铲车，每台铲车的行走路线，总运营费用）?(3) 如果有载重量为4 吨、6 吨、8 吨三种运输车，又如何调度？垃圾点地理坐标数据表问题分析（一）、目标分析本文将此问题视为多目标规划问题.这些目标主要包括：垃圾运输车的总运营费、矿铲车的总运营费、工作时间长度及安排的科学性和合理性、投入垃圾运输车的数量、投入矿铲车的数量等.在这些众多的目标中我们认为垃圾运输车的总运营费是最主要的目标，因为此项指标的优化空间是最大的，且与垃圾处理厂的经济效益的关系最大，其它各项因素包括车辆安排、路线的选择、工作时间的调度都是以运营费最小为出发点考虑的.因为每天的垃圾量固定，矿铲车铲起并装运垃圾所作的有用功是相同的，同时车辆在一段时期内的效率是稳定的，因此矿铲车的总运营费中的可变部分只与在路上的运费有关，在不引起混淆的情况下我们将此可变部分也成为矿铲车的总运营费.而矿铲车每公里的费用仅0.4￥，远小于运输车的重载费用1.8￥，所以矿铲车的运营费宜作为第二目标处理，即在运输车总运费最低的情况下在对矿铲车的行进路线、装运时间安排进行优化.垃圾运输车和矿铲车的投入数量也是一项与经济效益有很大关系的指标.车辆投入不足，严重影响工作效率；投入过多，会耗费过多的保养、维护费用.因此车辆的数量应以刚刚满足运输需求或略有剩余（作为备用）为宜.（二）、约束分析垃圾车的数量必须保证每天的垃圾都能在晚上规定的时间内及时运回，不会滞留至次日白天，还应使每台车每天的工作时间维持在4小时左右，在此约束下的理想调度方案应使垃圾处理厂投入最少的车辆、花费最少的成本完成每天的城市清洁任务.首先，在规定时间（题目假设中的18:004:00--）内能够完成垃圾的清理任务是必须要满足的基本要求.另外，由于是夜间行车，基于安全考虑，车速限为40/km h 、最大载重6Ton 的约束也定为必须严格执行的硬性约束.题目中要求每台车每日平均工作 4 小时，我们认为这个约束可以适当放宽一些，比如3.8 4.2-小时，且工作时间应当是针对驾驶员而言的，歇人不歇车的情况是允许的，垃圾处理厂可以通过轮换工作表、雇佣兼职人员等措施来使驾驶员的平均工作时间尽量为4小时.（三）、对题意的理解我们讨论一下有关空载费用与重载费用的两个不同的理解.一种理解认为空载费用就是空载时的计费方式，而重载费用就是车辆有负载时的计费方式，两种计费方式是互相独立没有交集的，认为汽车负载时费用只包含重载费用.这种理解方式的重要缺陷是夸大了车体本身的重量与负载的重量的区别，就本题而言，假如让一辆运输车负载0.1Ton ，那么该车以40/km h 的速度行进1km 的费用将是1.80.110.18⨯⨯=元，比空载运行还节省，显然是不合理的.另一种理解是将空载费用视为车体本身重量造成的费用，重载费用则是用来衡量负载的重量造成的费用，二者皆以重量为出发点，可以叠加.该理解方式认为运输车有负载时的费用应由空载费用和重载费用两部分组成.这种理解方式是比较自然，也是比较合理的.所以我们在模型中采取的是后一种理解方式，同时为了便于比较，我们给出了两种理解下的结果.模型的建立与求解我们首先抛开题目建立一个简单的代数系统,<ΩΘ>，其中Ω是一个二维空间，Ω的两维(),X Y 是自然数空间N 中的子空间，即X NY N⊂⎧⎨⊂⎩.关系集Θ包括两种序关系：{}, ，它们被定义为：。

蚂蚁行程模型绕球上的有关题目

蚂蚁行程模型绕球上的有关题目
以下是关于蚂蚁在球面上行程的相关题目：
1. 一只蚂蚁位于球面上的坐标为(θ1, φ1)，它向东行进了α角度，然后向北行进β角度，最后再向上行进γ角度。

请问蚂蚁的最终坐标是多少？
2. 在球的表面上，一只蚂蚁从点A沿短弧AB移动，然后再沿短弧BC移动，最后再沿短弧CD移动回到点D。

如果角度AB = β，角度BC = γ，角度CD = α，问蚂蚁在球面上行程的总角度是多少？
3. 在一个均匀的球体上有N只蚂蚁，每只蚂蚁同时从球面上某一点出发，且每只蚂蚁的行进速度相同。

蚂蚁沿球面的最短路径行程，如果它们同时从一个点出发，同时终止于一个点，问蚂蚁们的行程会有交叉吗？如果有交叉，交叉的情况会有多少种？
4. 在球面上有一只蚂蚁，它每秒钟能够随机选择球面上的一个方向（即从球面上随机选取一个单位切向矢量），并以单位速度前进。

问蚂蚁会在球面上停下来吗？为什么？
希望以上题目能够对您有所帮助！如果您还有其他问题，请随时提问。

基于蚁群优化算法的最优旅游路线模型设计

基于蚁群优化算法的最优旅游路线模型设计
假设我们有一系列的景点，每个景点都有其独特的吸引力和耗时。

我们需要设计一个模型来确定游客应该以怎样的顺序访问这些景点。

蚁群优化算法概述：蚁群优化算法模拟了蚂蚁在寻找食物时的行为。

每只蚂蚁通过释放信息素来引导其他蚂蚁找到更好的路径。

信息素浓度在路径选择中起到了重要的作用，蚂蚁会倾向于选择信息素浓度高的路径。

随着时间的推移，较短路径上的信息素浓度会增加，从而吸引更多的蚂蚁选择该路径，最终导致找到最优路径。

模型设计步骤：
a.初始化：随机放置一定数量的蚂蚁在起始景点。

b.路径选择：每只蚂蚁根据信息素浓度和启发式信息（如距离、吸引力等）选择下一个要访问的景点。

选择过程中，可以使用轮盘赌选择法，其中信息素浓度高的路径有更高的选择概率。

c.路径更新：每只蚂蚁完成一次路径选择后，根据其走过的路径长度和景点吸引力更新路径上的信息素浓度。

较短路径和吸引力更高的景点上的信息素浓度将增加，而较长路径上的信息素浓度将逐渐蒸发。

d.重复步骤b和c：重复执行路径选择和路径更新的步骤，直到达到指定的迭代次数或满足停止条件。

输出结果：在模型迭代完成后，选择具有最高信息素浓度的路径作为最优旅游路线。

中班科学活动：蚂蚁行进图

中班科学活动：蚂蚁行进图活动目的本次活动的目的是让中班幼儿通过观察蚂蚁行为，了解蚂蚁群体和行进规律，进一步培养幼儿的观察、探索和创新精神，提高幼儿的科学探究能力。

活动准备1.蚂蚁模型2.纸片3.涂色笔4.包装纸盒子5.高分子吸水材料6.水杯7.透明玻璃板活动过程第一步：了解蚂蚁群体1.师带领幼儿观察蚂蚁模型，引导幼儿讨论蚂蚁主要特征：身体呈长形，分头、胸、腹三部分，有六条腿，头上有一对触角和一对复眼。

2.师带领幼儿学习蚂蚁群体分工：有工蚁、兵蚁、术蚁、王蚁和雄蚁，不同种类的蚂蚁担负不同的职责，共同维护整个群体。

3.给幼儿分享蚂蚁群体的一些有趣行为：保存食物、寻找食物、护送同伴、筑巢等等。

第二步：观察蚂蚁行为1.师带领幼儿观察蚂蚁的行动，引导幼儿发现蚂蚁在行进时的规律和序列。

2.老师向幼儿们提出问题：蚂蚁在行进时是否会出现堵塞情况？出现堵塞的原因是什么？3.老师设置观察活动，让幼儿举起放在透明玻璃板上的纸盒子，并加入高分子吸水材料和水，观察蚂蚁行进的过程中，是否会因为材料的多少或者区域限制等待堵塞现象的发生。

4.师引导幼儿讨论蚂蚁堵塞产生的影响和对应规律。

第三步：绘制蚂蚁行进图1.指导幼儿使用涂色笔在纸片上画出蚂蚁行进的轨迹。

2.激励幼儿们对蚂蚁行进的规律和规则进行总结。

3.引导幼儿们一起绘制蚂蚁行进图，记录蚂蚁行进的路径和规律。

活动反思本次活动通过引导幼儿观察蚂蚁行为，了解蚂蚁群体和行进规律，培养幼儿的观察、探索和创新精神，提高幼儿的科学探究能力。

在活动过程中，我们还发现了幼儿们对事物的敏感性和探究精神，老师们也在其中收获了意想不到的启示。

更重要的是，通过这样一个有趣的活动，学习变得不再枯燥，蚂蚁这样普通的昆虫也因为幼儿们的观察和探究变得更加神奇。

相信这样的精彩科学活动能够为孩子们的成长和发展，铺就坚实的基础。