西安交通大学计算机图形学 6

合集下载

1063 理学专业介绍

理学专业介绍1．数学类：数学与应用数学、信息与计算科学2．物理学类：物理学、应用物理学3．化学类化学、应用化学、化学生物学、4.生物科学类生物科学、生物技术、5.地质学类地质学6.地理科学类地理学7.电子信息科学类电子信息科学与技术、光信息科学与技术、专业详细基本概况一，数学类1.数学与应用数学主干学科：数学主要课程：分析学、代数学、几何学、概率论、物理学、数学模型、数学实验、计算机基础、数值方法、数学史等，以及根据应用方向选择的基本课程。

教学实践包括计算机实习、生产实习、科研训练或毕业论文等，一般安排10～20周。

培养目标本专业培养掌握数学科学的基本理论与基本方法，具备运用数学知识、使用计算机解决实际问题的能力，受到科学研究的初步训练，能在科技、教育和经济部门从事研究、教学工作或在生产经营及管理部门从事实际应用、开发研究和管理工作的高级专门人才。

培养要求本专业学生主要学习数学和应用数学的基础理论、基本方法，受到数学模型、计算机和数学软件方面的基本训练，具有较好的科学素养，初步具备科学研究、教学、解决实际问题及开发软件等方面的基本能力。

就业方向1．具有扎实的数学基础，受到比较严格的科学思维训练，初步掌握数学科学的思想方法；2．具有应用数学知识去解决实际问题，特别是建立数学模型的初步能力，了解某一应用领域的基本知识；3．能熟练使用计算机（包括常用语言、工具及一些数学软件），具有编写简单应用程序的能力；4．了解国家科学技术等有关政策和法规；5．了解数学科学的某些新发展和应用前景；6．有较强的语言表达能力，掌握资料查询、文献检索及运用现代信息技术获取相关信息的基本方法，具有一定的科学研究和教学能力。

开设院校[北京]北京大学[广东]中山大学[上海]复旦大学[北京]北京理工大学[四川]西南交通大学[北京]中国人民大学[北京]中央财经大学[上海]上海交通大学[北京]北京邮电大学[吉林]吉林大学[广东]华南理工大学[北京]北京航空航天大学[江苏]苏州大学[重庆]重庆大学[陕西]西安交通大学[山东]山东科技大学[陕西]西北工业大学[天津]天津大学[辽宁]大连理工大学[湖南]湖南大学[重庆]西南大学[四川]西南财经大学[山东]中国海洋大学[四川]成都理工大学[辽宁]东北财经大学[北京]北京科技大学[山东]青岛科技大学[上海]华东理工大学[北京]北京师范大学[黑龙江]哈尔滨工业大学[四川]电子科技大学[广东]深圳大学[山东]烟台大学[广东]暨南大学[天津]天津工业大学[广东]广州大学[天津]天津理工大学[江苏]江南大学[江苏]南京理工大学[山东]山东经济学院[江苏]南京审计学院[海南]海南大学[北京]中国农业大学[辽宁]大连海事大学[上海]华东师范大学[甘肃]兰州大学[陕西]西安电子科技大学[广东]广东商学院[辽宁]东北大学[上海]上海理工大学2.信息与计算科学主干学科：数学、计算机科学与技术主要课程：数学基础课（分析、代数、几何）、概率统计、数学模型、物理学、计算机基础（计算概论、算法与数据结构、软件系统基础）、信息科学基础、理论计算机科学基础、数值计算方法、计算机图形学、运筹与优化等。

西安交通大学PPT课件

4) 操作系统
分时操作系统实时操作系统并行操作系统网络操作系统分布式操作系统
5) 数据库、集成开发环境
2021
9
4. 微型计算机
1) 处理器芯片
Intel 4004微处理器 8080-P4
2)微机的代表(PC)
ALTAIR 8800 第一台微机苹果机 IBM PC
通讯娱乐家用电器信息管理（学籍、图书馆、OA）信息检索
2021
20
1.3 计算机主要应用领域
计算机典型应用领域介绍
一. 科学与工程计算二. 信息管理三. 电子商务
2021
21
一. 科学和工程计算
计算数学+计算机科学计算
计算数学：研究数值计算方法计算机：计算数学强有力的工具
科学计算是第三种科学手段
理论研究：无法求得理论解科学实验：难以应用实验手段可以进行计算
计算机是人类计算能力的延伸
2021
22
科学和工程计算的步骤
建立数学模型探索有效的计算方法计算方法的理论分析编写程序进行计算数值模型问题的计算
2021
10
5.中国计算机的发展
1)科学计算
103机、104机、107机、109乙机、109丙机、 119机
2)高性能计算机
银河、曙光、神威系列
3) 微机：长城0520CH 4) 芯片：龙芯 5) 软件：CCDOS、WPS
2021
11
三. 未来的计算机
1. 电子计算机的发展方向
1) 微型化: LSI和VSI,走入千家万户 2) 巨型化: 速度高,容量大,功能完善 3) 网络化: 实现信息传递和资源共享 4) 智能化: 模拟人的思维活动

西安交通大学专业课程设置

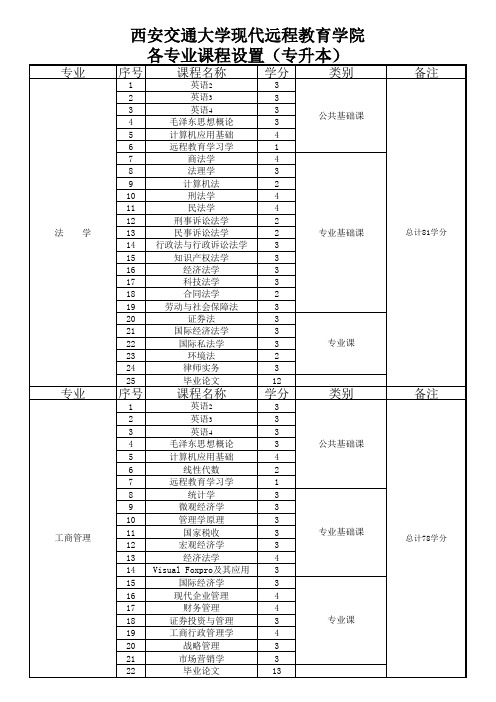
西安交通大学现代远程教育学院对于切削刀具生产商来说，最神圣的成就莫过于能满足客户在更高生产效率、更长切方面的要求，重要因素之一就是涂层技术和制造工艺上现代涂层技术已经使将不同材料一层层地加在硬质合金刀片上成为可能。

只要适当调配序，以及选用合适的涂层制造技术，就能大幅度改进性能，并可显著提高金属切削的生产何让步。

目前有两种基本涂层技术可供选择：一种是化学气相沉积法（简称CVD），另一种是物理良好的耐磨性时使用CVD；而需要获得最大限度的切削刃边缘韧性时则采用PVD。

现代刀片用作不同的涂层，并与几种中间体薄层作时效处理，以达到良好的附着力及其所需晶体和具有不同属性的晶粒结构存在。

CVD工艺在880～l000℃的温度中进行。

涂层在反应器中形成，做法是严格控制几种活性气应器中暴露于这些气体中。

不同的涂层就这样逐个原子地慢慢形成。

在如此高温下，所形料和硬质合金刀片的热膨胀系数不同，因此便开始形成扩张应力，当反应器冷却时逐步在层材料断裂韧性的水平时，涂层便开始龟裂，于是便形成冷却裂纹。

达到室温后，涂层也干旱的冷却裂纹。

裂纹和扩张应力降低了CVD涂层刀片的韧性。

但是，如果用适当的后处应力并使表面光滑。

另外，通过在靠近涂层表面将冷却裂纹闭合，也可另一种新的后处理技术是让涂层表面接受强烈的材料冲击，所产生的冲击波穿过涂层，改应力状态，这样就产生厚实的防磨涂层，其刀口边缘韧性可以达到与目前应用较多的CVD涂层是两层TiCN涂层加上Al2O3，较厚的TiCN涂层有助于改善两侧抗低月牙洼磨损，并可作为一道热屏障，保护热敏感的硬质合金材料。

如果Al2O3的厚度和并进一步改善耐磨性。

以前，增加Al2O3涂层厚度意味着降低其韧性，并增加出现涂层分是说，不同属性之间总要作出某种程度的牺牲）。

应用后处理技术，就有可能在切削刃升到能与PVD涂层媲美的水平，使其更适合于断续切削和更高速度的应用场合。

另外，在降低其它方面的属性。

此外使用超细晶粒硬质合金新材料也是新的突破，新的硬质合金材料带有一定含量的铬，独特的切削刃边缘韧性和安全性水平都显著高于普通更长切削时间，以及在多种切削条件下具有更佳性能等要因素之一就是涂层技术和制造工艺上的突破。

参数曲面三角网格生成的改进波前法

参数曲面三角网格生成的改进波前法王伟;樊宏周;席光【摘要】为了消除基于波前法的有限元三角网格算法在参数曲面网格剖分过程中单元形状映射畸变的问题,结合直接法和映射法各自的优点,提出了一种新的三角网格生成算法,即:对当前节点进行剖分,并在三维空间直接产生新节点且进行节点的合法性判断,再将物理网格映射到参数空间形成参数域网格;对相邻波前段形成的角度进行剖分,依据角度大小生成个数不等的单元,通过优先剖分锐角节点使波前段始终构成钝角多边形.经剖分算例表明:所提算法减少了节点合法性判断内容和判断次数,避免了重复剖分,取消了剖分结束算法,提高了网格剖分效率,生成了高质量的三角网格;仅需对网格排列情况的直观分析,便可定性判断三维曲面的空间曲率变化.该算法对叶片加工中振动分析、精密加工研究等具有指导意义.【期刊名称】《西安交通大学学报》【年(卷),期】2014(048)003【总页数】7页(P61-67)【关键词】有限元;曲面网格;波前法;三角剖分;映射畸变【作者】王伟;樊宏周;席光【作者单位】西安交通大学能源与动力工程学院,710049,西安;西安交通大学能源与动力工程学院,710049,西安;西安交通大学能源与动力工程学院,710049,西安【正文语种】中文【中图分类】TP391曲面网格生成是有限元分析中几何建模的关键,曲面网格可以直接作为膜结构、壳体等的有限元模型进行计算分析。

三维实体的表面是由各种曲面和平面组成,三维实体表面离散的数据点及曲面网格质量将直接影响剖分算法的可靠性和生成体网格的质量[1]。

所以,有限元、计算流体动力学和计算机图形学分析中获得高质量的曲面网格是必不可少的前提条件[2]。

曲面网格剖分算法中波前法(Advancing Front Technique,AFT)是曲面三角网格生成的重要方法,具有启发性、局部适应性和单元可控性[3]。

基于波前法的三角网格剖分算法涉及到映射法和直接法。

映射法是运用波前法将参数空间的参数域进行剖分,并映射到三维曲面上生成曲面网格,其研究重点是克服曲面参数化不均匀导致的网格映射畸变。

全国大学计算机专业排名 2011

全国大学计算机专业排名2011-11-13 20:20学校代码及名称排名得分10003 清华大学 1 100 90002 国防科学技术大学 2 94 10006 北京航空航天大学 3 88 10335 浙江大学 4 88 10213 哈尔滨工业大学 5 87 10001 北京大学 6 85 10248 上海交通大学7 85 10284 南京大学8 83 10145 东北大学9 82 10487 华中科技大学10 81 10358 中国科学技术大学11 81 10698 西安交通大学12 79 10013 北京邮电大学13 78 10183 吉林大学14 77 10246 复旦大学15 77 10286 东南大学16 77 10486 武汉大学17 77 10610 四川大学18 76 10007 北京理工大学19 74 10614 电子科技大学20 73 10699 西北工业大学21 73 10422 山东大学22 72 10533 中南大学23 74 10008 北京科技大学24 71 10005 北京工业大学25 70 10247 同济大学26 70 10561 华南理工大学27 70 10611 重庆大学28 70 10701 西安电子科技大学29 70 10004 北京交通大学30 69 10056 天津大学31 69 10269 华东师范大学32 69 10002 中国人民大学33 68 10141 大连理工大学34 68 10280 上海大学35 68 10288 南京理工大学36 68 10294 河海大学37 68 10217 哈尔滨工程大学38 67中国哪个大学的计算机科学与技术专业比较不错？给你提供个2006年大学计算机专业排行榜，供参考：1、计算机系统结构排名（1）清华大学（2）浙江大学（3）华中科技大学（4）北京大学（5）上海交通大学（6）东北大学（7）复旦大学（8）中国科学技术大学（9）哈尔滨工业大学（10）吉林大学（11）电子科技大学北京邮电大学西安电子科技大学西安交通大学西北工业大学武汉大学东南大学2、计算机软件与理论排名（1）北京大学（2）南京大学（3）上海交通大学（4）复旦大学（5）武汉大学（6）清华大学（7）浙江大学（8）中山大学（9）北京航空航天大学（10）吉林大学（11）山东大学（12）华中科技大学中国科学技术大学哈尔滨工业大学西北大学东北大学贵州大学西北工业大学西安交通大学3、计算机应用排名（1）清华大学（2）浙江大学（3）哈尔滨工业大学（4）华南理工大学（5）北京大学（6）南京大学（7）中国科学技术大学（8）西安电子科技大学（9）吉林大学（10）复旦大学（11）西北工业大学（12）东北大学（13）东南大学（14）南开大学（15）武汉大学（16）同济大学（17）上海交通大学（18）安徽大学（19）北京邮电大学（20）北京航空航天大学（21）大连理工大学（22）天津大学北京理工大学南京理工大学北京工业大学湖南大学四川大学南京航空航天大学哈尔滨工程大学华中科技大学电子科技大学北京科技大学计算机科学国家重点实验室（中国科学院软件研究所）简要概况计算机科学国家重点实验室依托中国科学院软件研究所，实验室成立于1993年，1994年由中国科学院批准成为中国科学院开放实验室，2001年改名为中国科学院重点实验室。

2022年计算机专业考研科目及学校排名

2022年计算机专业考研科目及学校排名2022年计算机专业考研学校排名：2022年计算机专业考研学校排名2022年计算机专业考研学校排名2022年计算机专业考研学校排名2022考研计算机三大专业高校排名及十大计算计算机应用技术前60名(总共271所高校)1.清华大学2.浙江大学3.哈尔滨工业大学4.北京大学5.东南大学6.东北大学7.西北工业大学8.安徽大学9.上海交通大学10.华中科技大学11.北京航空航天大学12.北京理工大学13.西安电子科技大学14.西安交通大学15.吉林大学16.西南交通学17.大连理工大学18.电子科技大学19.北京工业大学20.重庆大学21.复旦大学22.哈尔滨工程大学23.武汉理工大学24.武汉大学25.同济大学26.南京大学27.中国科学技术大学28.华南理工大学29.南京理工大学30.四川大学31.南京航空航天大学32.天津大学33.上海大学34.北京邮电大学35.北京科技大学36.北京交通大学37.中南大学38.合肥工业大学39.山东大学40.江苏大学41.湖南大学42.大连海事大学43.中山大学44.河北科技大学45.中国矿业大学46.南开大学47.华东师范大学48.太原理工大学49.苏州大学50.河海大学52.中国海洋大学53.中国人民大学54.华东理工大学55.山西大学56.重庆邮电大学57.新疆大学58.内蒙古大学59.哈尔滨理工大学60.南京邮电大学中国研究生教育计算机专业排名计算机系统结构前20名(总共47所高校)1.清华大学2.华中科技大学3.西安交通大学4.上海交通大学5.浙江大学6.西安电子科技大学7.武汉大学8.复旦大学9.哈尔滨工业大学10.东北大学11.北京大学12.东南大学13.北京航空航天大学14.中国科学技术大学15.电子科技大学16.吉林大学17.南京理工大学19.北京科技大学20.同济大学计算机软件与理论前40名(总共158所高校)1.上海交通大学2.南京大学3.北京大学4.北京航空航天大学5.吉林大学6.清华大学7.浙江大学8.西安交通大学9.东南大学10.电子科技大学11.中国科学技术大学12.哈尔滨工业大学13.大连理工大学14.华中科技大学15.武汉大学16.复旦大学17.中山大学18.西安电子科技大学19.东北大学20.西北工业大学21.北京理工大学22.北京交通大学23.南京理工大学24.重庆大学26.四川大学27.中南大学28.云南大学29.上海大学30.同济大学31.河海大学32.北京邮电大学33.山东科技大学34.中国人民大学35.南京邮电大学36.西北大学37.武汉理工大学38.贵州大学39.陕西师范大学40.天津大学吉林大学：十几年前，计算机系的创始人王湘浩院士和他的得力助手们还在的时候，吉林大学在软件方面的优势是相当大的。

信息与计算科学专业大学排名

信息与计算科学专业大学排名信息与计算科学专业介绍：信息与计算科学专业Information and Computing Science (原名：计算数学,1987年更名为计算数学及其应用软件，1998年教育部将其更名为信息与计算科学)信息与计算科学专业是以信息领域为背景。

数学与信息，计算机管理相结合的计算机科学与技术类专业。

该专业培养的学生具有良好的数学基础，能熟练地使用计算机,初步具备在信息与计算机科学领域的某个方向上从事科学研究，解决实际问题，设计开发有关计算机软件的能力。

本专业的课程体系和知识结构体现了在扎实的数学基础之上，合理架构信息科学与计算机科学的专业基础理论。

通过信息论、科学计算、运筹学等方面的基础知识教育和建立数学模型、数学实践课、专业实习各环节的训练，着重培养学生解决科学计算、软件开发和设计、信息处理与编码等实际问题的能力，培养能胜任信息处理、科学与工程计算部门工作的高级专门人才。

信息与计算科学专业方向：信息与计算科学专业为理科专业，包括信息科学与计算机科学两个方面。

方向一是以信息科学方面为主，计算数学方面为辅;方向二是以数学方面为主，信息科学方面为辅。

信息与计算科学专业课程：数学分析、高等代数、几何、概率统计、数学模型、离散数学、模糊数学、实变函数、复变函数、微分方程、物理学、信息处理、信息编码与信息安全、现代密码学教程、计算智能、计算机科学基础、数值计算方法、数据挖掘、最优化理论、运筹学、计算机组成原理、计算机网络、计算机图形学、c/c++语言、java 语言、汇编语言、算法与数据结构、数据库应用技术、软件系统、操作系统等。

信息与计算科学专业怎么样?(学长学姐评价)北京化工大学：信息与计算科学这个专业，属于数学系。

毋庸置疑，扎实的数学功底必不可缺。

因此，学号本专业的基础知识在大一大二阶段尤为重要。

既然有信息两字,就联系上了计算机，除非对数学有着特别的爱好，想搞数学方面的研究生(或者博士)，否则毕业找工作90%都是计算机相关的(至少我们这一届差不多)。

计算机图形学第一章基本知识

计算机图形学郑州大学信息工程学院
课程内容
• 第二篇实用图形编程技术第八章基于MFC的图形编程基础第九章基于MFC的交互绘图第十章 OpenGL基础知识和实验框架的建立第十一章 OpenGL的基本图形第十二章 OpenGL的组合图形及光照和贴图第十三章摄像漫游与OpenGL的坐标变换
1.2 计算机图形学的发展历史
时间五十年代特征 MIT 旋风一号，计算机驱动CRT+照相机， SAGE(交互式图形技术诞生)
六十年代
随机扫描显示器，图形学之父
六十年代至七十年代存储管显示器，应用的软件包初七十年代至八十年代光栅扫描显示器，新型的图形输入设备，图初形语言标准八十年代至九十年代图形工作站(Apollo,Sun,Hp) 初九十年代至今微机，交叉学科（多媒体等）
计算机图形学郑州大学信息工程学院
•按工作原理分为：1、阴极射线管(CRT)
1.4.3 显示器
控制栅
聚焦系统
荧光粉涂层
灯丝
阴极加速系统偏转系统
计算机图形学郑州大学信息工程学院
2、等离子屏幕显示器
• 由一个细小氖泡矩阵组成，由于氖泡有两种状态：开启(点燃)、关闭(熄灭)，且状态可保持。分为 1）前层：垂直导线 2）中层：细小氖泡 3）后层：水平导线
真实图形生成技术的发展
• 逼真地显示出该物体在现实世界中所观察到的形象，就需要采用适当的光照模型，尽可能准确地模拟物体在现实世界中受到各种光源照射时的效果 • 局部光照模型模拟漫反射和镜面反射，而将许多没有考虑到的因素用一个环境光来表示。 • 光线跟踪方法和辐射度方法为代表的全局光照模型，使得图像的逼真程度大为提高

计算机图形学、计算机视觉

0618302 Mobile Ad Hoc网络中安全感知路由协议增强方案刊,中/杨瑞君//计算机工程.2006,32(5).131 134(E)0618303基于开放源码的企业自建CA系统的研究与实现刊,中/许峰//计算机工程.2006,32(5).128130(E)分析了企业自建CA系统的必要性,通过一个PKI系统myCA的设计与实现,论证了在企事业单位内部建立专有CA的可行性,并提出了隐藏PKI 系统复杂性的具体方法。

参60618304 B级安全的轻量级内核BSK的设计与实现刊,中/冷健//计算机工程.2006,32(5).125127(E)0618305基于签名的近似垃圾邮件检测算法刊,中/詹川//计算机工程.2006,32(5).122124(E)0618306 IKE协议主模式认证机制的分析与改进刊,中//计算机工程与应用.2006,42(9).120128(C2)本部分报道了网络、通信与安全栏目的3篇文章,内容涉及IKE协议主模式认证机制的分析与改进(作者:陈艳红,汕头大学工学院);MANET网络中基于ID签名算法的安全路由协议研究(作者:戴紫珊,郑州解放军信息工程大学电子技术学院);KS分组密码算法的流水线实现(作者:许萍,北京电子科技学院通信工程系)。

0618307一个强前向安全的代理签名方案刊,中//计算机工程与应用.2006,42(9).109119(C2)本部分报道了网络、通信与安全栏目的3篇文章,内容涉及一个强前向安全的代理签名方案(作者:张波,山东大学南校区计算机科学与技术学院);网络课程中短消息平台的开发及应用(作者:杨晋吉,广州中山大学计算机科学系);基于P2P模型的网络入侵检测系统PeerI DS(作者:金舒,南京理工大学信息学院计算机技术系)。

0618308基于双线性对的可证明安全的环签名和代理环签名刊,中//计算机工程与应用.2006,42(8).107 117(L2)本部分报道了网络、通信与安全栏目的3篇文章,内容涉及基于双线性对的可证明安全的环签名和代理环签名(作者:王尚平,西安理工大学密码理论与网络安全研究室);大规模网络中I nternet蠕虫主动防治技术研究利用DNS服务抑制蠕虫传播(作者:郑辉,北京清华大学网络中心);基于主机的网络层访问控制机制设计与实现(作者李莉,南京邮电大学网络技术研究中心)。

高考专业：计算机科学与技术

⾼考专业：计算机科学与技术⾼考专业《计算机科学与技术》计算机科学与技术专业是研究计算机的设计与制造，并利⽤计算机进⾏有关的信息表⽰、收发、存储、处理、控制等的理论⽅法和技术的学科;包括计算机硬件和软件组成原理、计算机操作系统、计算机⽹络基础、算法与数据结构等，计算机的基本知识和基本技能与⽅法主⼲课程1.公共课程：数学（⾼等数学、线性代数、概率论与数理统计）、政治（马克思主义思想概论、⽑泽东思想概论与中国特⾊社会主义思想、思想道德修养与法律基础、中国近现代史纲要）、⼤学英语、体育、2.专业基础课程：电路原理、模拟电⼦技术、数字逻辑、数值分析、微型计算机技术、计算机系统结构、⾼级语⾔、汇编语⾔、编译原理、图形学、⼈⼯智能、计算⽅法、⼈机交互、⾯向对象⽅法、计算机英语等。

3.专业⽅向课程：离散数学、算法与数据结构、计算机组成原理、计算机操作系统、计算机⽹络基础、计算机编译原理、计算机数据库原理、C语⾔/c++语⾔、Java语⾔等这⾥涉及了⼤量的数学专业的发展:1.⽬前计算机的技术展现了以下特点:A.智能化:具有模拟⼈的感觉和思维过程的能⼒，使计算机成为智能计算机.研究领域包括模式识别、图像识别、⾃然语⾔的⽣成和理解、博弈、定理⾃动证明、⾃动程序设计、专家系统、学习系统和智能机器⼈B.⽹络化:⽤现代通信技术和计算机技术把分布在不同地点的计算机互联起来，组成⼀个规模⼤、功能强、可以互相通信的⽹络结构C.多媒体技术:使多种信息(包括⽂本、视频图像、图形、声⾳、⽂字等)建⽴了有机联系，并集成为⼀个具有⼈机交互性的系统。

就是利⽤计算机技术、通信技术和⼤众传播技术，来综合处理多种媒体信息的计算机。

2.未来的计算机A.量⼦计算机:遵循量⼦⼒学规律进⾏⾼速数学和逻辑运算、存储及处理的量⼦物理设备，当某个设备是由两⼦元件组装，处理和计算的是量⼦信息，运⾏的是量⼦算法时，它就是量⼦计算机B.神经⽹络计算机:⼈脑总体运⾏速度相当于每秒1000万亿次的电脑功能，可把⽣物⼤脑神经⽹络看做⼀个⼤规模并⾏处理的、紧密耦合的、能⾃⾏重组的计算⽹络。

具有保面积参数化的双二次Bézier曲面

第33卷第3期计算机辅助设计与图形学学报Vol.33No.3 2021年3月Journal of Computer-Aided Design & Computer Graphics Mar. 2021具有保面积参数化的双二次Bézier曲面李效伟1,2), 赵庆辉1), 杨义军3)*, 曾薇4), 孙黎1), 李缨1), 徐岗2)1) (山东女子学院数据科学与计算机学院济南 250300)2) (杭州电子科技大学计算机学院杭州 310018)3) (西安交通大学计算机科学与技术学院西安 710049)4) (西安交通大学数学与统计学院西安 710049)(********************)摘要: 为了构建具有保面积参数化的双二次Bézier曲面, 提出2种双二次Bézier曲面的构造算法. 首先根据曲面第一微分基本形式, 推导双线性和双二次Bézier曲面满足保面积参数化的约束条件, 得出具有保面积参数化的双线性有理Bézier曲面只能是平行四边形的结论; 然后根据双二次曲面的约束条件, 通过求解方程组的形式设计符合约束条件的双二次Bézier曲面构造算法, 并且给出并证明了严格满足保面积参数化约束条件的双二次Bézier曲面只能为平面曲面的结论; 再将保面积参数化约束条件松弛, 基于曲面拟合思想设计具有较强造型能力的双二次Bézier曲面构造算法, 构造满足用户指定容差范围的双二次Bézier曲面; 最后给出若干具有保面积参数化的双二次Bézier曲面, 验证了算法有效性和曲面造型能力. 使用C++语言实现的多个等参线分布和纹理映射的实例结果表明, 该算法生成的双二次Bézier曲面参数化能够保持面积拉伸.关键词: 保面积参数化; 双二次Bézier曲面; 曲面造型中图法分类号: TP391.41 DOI: 10.3724/SP.J.1089.2021.18501Biquadratic Bézier Surfaces with Area-Preservation ParameterizationLi Xiaowei1,2), Zhao Qinghui1), Yang Yijun3)*, Zeng Wei4), Sun Li1), Li Ying1), and Xu Gang2)1) (School of Data and Computer Science, Shandong Women’s University, Jinan 250300)2) (School of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou 310018)3) (School of Computer Science & Technology, Xi’an Jiaotong University, Xi’an 710049)4) (School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049)Abstract: Construction of Bézier surfaces with area-preservation parameterization constraints is one of the important topics in surface modeling. In order to construct biquadratic Bézier surfaces with area-preservation parameterization, two algorithms are proposed to automatically construct biquadratic Bézier surfaces in this paper. Firstly, the standard conditions of bilinear and biquadratic Bézier surfaces with area-preservation parameterization are obtained by using the first fundamental form, and the fact that the only bilinear rational Bézier surfaces satisfying area-preservation conditions are parallelograms is drawn. Next, according to the standard conditions, a method of surface construction is designed, and the conclusion that the only biquad-ratic Bézier surfaces with area-preservation parameterization are planar is drawn. Besides, a method of sur-收稿日期: 2020-07-17; 修回日期: 2020-08-17. 基金项目: 国家自然科学基金(61872224, 61772163); 山东省自然科学基金(ZR2017MF003); 国家自然科学基金-浙江两化融合联合基金(U1909210); 山东女子学院高水平科研项目培育基金(2019GSPSJ08). 李效伟(1989—), 男, 博士研究生, 讲师, CCF会员, 主要研究方向为CAD&CG; 赵庆辉(1998—), 女, 在校学生; 杨义军(1979—), 男, 博士, 教授, 博士生导师, CCF会员, 论文通讯作者, 主要研究方向为CAD&CG; 曾薇(1980—), 女, 博士, 教授, 博士生导师, 主要研究方向为计算机图形学; 孙黎(1985—), 女, 硕士, 讲师, CCF会员, 主要研究方向为人工智能; 李缨(1971—), 女, 硕士, 教授, 硕士生导师, CCF会员, 主要研究方向为人工智能; 徐岗(1981—), 男, 博士, 教授, 博士生导师, CCF会员, 主要研究方向为3D 建模与仿真.466 计算机辅助设计与图形学学报第33卷face construction with great modeling ability is designed, thanks to the fact that the standard conditions have been relaxed. Finally, some biquadratic Bézier surfaces satisfying the area-preserving criteria are given, which shown in the created Windows-based applications using C++. Several examples of tessellation and texture mapping demonstrate that surfaces generated by proposed algorithms are area-preserving.Key words: area-preservation parameterization; biquadratic Bézier surfaces; surface modeling保面积参数化是参数曲面的一种重要几何特征, 对曲面造型、纹理映射、等几何分析和四边形网格生成等算法或应用的质量起决定性作用. 保面积参数化保持面积拉伸, 对于曲面上的任意一个区域, 其曲面面积和参数面积相等, 在计算机辅助设计领域, 它经常被用作衡量曲面参数化质量的重要指标. 构造具有保面积参数化的曲面有着重要的理论意义与应用价值.近十余年, 网格曲面和自由曲面的保面积参数化得到了研究人员的广泛关注. Yang等[1]使用Möbius变换和有理双线性变换等方法优化非均匀有理B样条(non-uniform rational B-splines, NURBS)曲面的保面积能量, 以增加少量保角能量为代价, 生成较好的保面积参数化曲面, 提升曲面四边形网格生成效果. 在等几何分析应用中, Xu等[2]通过Bézier曲面扩展、细分和全局优化等步骤, 构建适合等几何分析的平面B样条曲面参数化, 该方法能够保证细分曲面边界具有一定的连续性. 除了在曲面四边形网格化和等几何分析中的应用, 保面积参数化还能够较为显著地提升曲面的纹理映射效果[3-5]. Dominitz等[3]针对三角网格形式的闭合曲面, 将保角参数化作为优化过程的初始解, 通过最优传输技术不断迭代优化保面积能量, 使曲面上的纹理映射效果接近最优. 根据Gu等[4]对离散曲面保面积的相关理论证明, Zhao等[5]依据Monge-Brenier定理, 构建比Monge-Kantorovich方法计算效率更高的优化算法, 将利用Ricci flow[6]获取的保角映射作为初始解, 使用最优传输技术优化三角网格曲面的保面积能量, 在零亏格三角网格曲面上实现了具有保面积纹理映射.1 相关工作目前, 大部分的研究工作主要集中在通过使用优化方法升网格曲面的保面积参数化[7-10], 试图建立一个适用于所有三角网格曲面的统一方法, 期望能够将其应用在医学工程、机械设计和艺术设计等领域. Lévy等[7]引入了柯西-黎曼方程的一阶有限元逼近, 算法在相似意义下的解唯一, 且不会产生三角形交叠的情况, 通过一个共形参数映射提升曲面纹理映射质量. Floater[8]引入平均值坐标来计算广义调和映射, 能够简化曲面参数化的计算复杂度. Yoshizawa等[9]将广义调和映射算法结果作为初始解, 通过若干次迭代优化, 生成了较为快速和鲁棒的保拉伸参数化方法. Zou等[10]通过使用最小二乘共形映射获取初始解, 利用等积参数化算法计算出了大脑模型(三角网格模型)的保面积参数化.除了构造适用于网格曲面的统一性算法, 研究人员对自由曲线和自由曲面的几何特征也进行了较深入的研究[11-14]. Farouki等[11]提出“完全满足弧长参数化特征的曲线只能是直线形式”的观点. Farin[12]使用极坐标法在复平面上构建可弦长参数化的有理二次Bézier曲线. Xu等[13]给出拉伸、弯曲和jerk能量极小低次Bézier曲线的构建方法. 杨义军等[14]给出具有正交参数特性的双二次Bézier 曲面的约束条件, 并提出相应的曲面构建算法. 针对自由曲面共形参数化[15-18]的研究较为成熟, 其能够提升基于导数的算法(如曲面采样、曲面相交、曲率计算等)的鲁棒性和稳定性. He等[15]提出了一种有理双三次重参数化方法来改进近似Gregory 曲面片的参数化, 以使新参数化更加符合给定细分曲面的参数化. Yang等[16]基于Möbius变换提出提升Bézier曲面参数化的方法, 在不改变曲面形状的前提下, 能够提升曲面的等参线分布的均匀性. 为了提升有理Bézier曲面等参线分布的正交性和均匀性, Yang等[17]提出使用有理双线性参数化的方法来优化衡量自由曲面均匀性和正交性的非线性能量函数. 为了更深入地提高自由曲面的共形参数化质量, Yang等[18]利用最小二乘法计算出一个近似共形参数化, 将其作为初始解, 最终使用列文伯格-马夸尔特(Levenberg-Marquardt, LM)非线性优化方法得到最优参数化结果. 然而, 关于自由曲面参数化的研究工作大多将重心放在共形参数第3期李效伟, 等: 具有保面积参数化的双二次Bézier 曲面 467化上, 并没有把保面积参数化作为主要的研究对象, 以上研究工作得到的最优参数化虽然能够逼近共形参数化, 但是对保面积参数化的优化还不能够达到共形的效果.虽然Yang 等[1]给出了NURBS 曲面的保面积参数化方法, 但是没有给出双二次Bézier 曲面保面积参数化约束条件和相应的曲面构造算法. 研究具有保面积参数化的双二次Bézier 曲面的约束条件和构造算法具有重要意义, 尤其在曲面造型、曲面细分、网格生成和纹理映射等实际应用中. 例如, 对于复杂形状的曲面, 可以使用具有保面积参数化的双二次Bézier 曲面替代自由曲面造型细分后的小面片, 从而使整个曲面都能具有良好的保面积参数化. 另外, 满足保面积参数化的自由曲面智能造型和参数化算法[19]能够为纹理映射、曲面细分和四边形网格生成等算法提供更加鲁棒和稳定的计算.本文根据自由曲面微分几何第一基本形式和保面积参数化条件, 首先探讨双线性Bézier 曲面的具有保面积参数化的约束条件, 得出“完全满足保面积参数化约束条件的双线性有理Bézier 曲面只能是平行四边形”的结论; 紧接着推导具有保面积参数化的双二次Bézier 曲面形式, 得出完全具有保面积参数化的双二次Bézier 曲面所满足的约束条件, 并据此设计了满足约束条件的双二次Bézier 曲面构造算法; 为了拓展具有保面积参数化Bézier 曲面的造型能力, 本文还将保面积参数化约束条件松弛, 设计了具有较强造型能力的双二次Bézier 曲面构造算法; 最后给出了若干个曲面等参线分布和纹理映射结果, 验证了本文结论、算法的有效性和曲面造型能力.2 保面积双二次Bézier 曲面2.1 Bézier 曲面的第一基本形式一张Bézier 曲面的微分几何形式[20]可以表示为00(,)()()m nm n i j iji j u v B u B v ===∑∑X P (1) 其中, u 和v 分别为曲面上2个方向的参数, 满足条件01u ≤≤, 01v ≤≤; P ij 为曲面的控制顶点;()m i B u 和()n j B v 为伯恩斯坦多项式.曲面的第一微分基本形式[21]可表示为 222d (d )2d d (d )u u u v v v s u u v v =⋅+⋅+⋅X X X X X X (2)其中, s 为曲线弧长; u u ∂=∂X X ,v v∂=∂XX , 即X u 和X v 分别为曲面X 在u 和v 方向的偏导数.令, 1,2, 1,2g αβαβαβ=⋅==X X , 则式(2)的参数可表示为矩阵形式, 即11121222gg g g ⎛⎫= ⎪⎝⎭I .其中, g 11和g 22给出了u 向和v 向偏导数点乘之后的平方值, g 12表示曲面任意点处的正交性度量. 式(2)可重新表示为矩阵相乘的形式2d d (d d )d u s u v v ⎛⎫= ⎪⎝⎭I .因为在正则性的假设条件下, 矩阵I 有一个恒为正的行列式[22], 即g 的值恒大于0, 其计算式为2112212det g g g g ==-I . 将g 开方, 得到[], ,0,1u v u v =⨯∈X X .假设变量A 表示曲面面积, 则其计算方式为111000d d d u v A u v u v ==⨯⎰⎰⎰⎰X X .如果给定曲面是保面积参数化曲面, 则曲面上的任意点处都必须满足条件u v A ⨯≡X X (3)2.2 具有保面积参数化的双线性Bézier 曲面双线性Bézier 曲面是一种公式表达极为简单的双线性插值曲面, 任意等参线也都是直线段, 它是直纹面, 其特点为只含有P 00, P 01, P 10和P 11等4个控制顶点, 并且曲面上的点均由其线性插值表示. 一张双线性Bézier 曲面可表示为00011011(,)(1)(1)(1) (1)u v u v u v u v uv =--+-+-+X P P P P(4)将式(4)分别对参数u 和v 求偏导数得到00011011(,)(1)(1)u v v v v v u ∂=--+-+∂X P P P P , 00011011(,)(1)(1)u v u u u u v∂=-+--+∂X P P P P . 根据曲面的第一基本形式, 要得到曲面满足保面积参数化的约束条件, 则必须要满足式(3). 为了便于计算, 本文将曲面面积设定为A , 得到条件式(,)(,)u v u v A u v∂∂⨯=∂∂X X . 经过公式推导, 求出双线性Bézier 曲面必须满足2组约束, 才能够满足式(3)所表示的保面积468计算机辅助设计与图形学学报第33卷参数化约束条件, 即 ()()10000100=A -⨯-P P P P (5)()()()()1000110111100100=-⨯-⎧⎨-⨯-=⎩P P P P P P P P 00 (6) 式(5)给出了在P 00点处法向量的模必须为A 的约束; 式(6)给出控制顶点所构成4条边界中的对边平行的约束. 根据式(6)和Bézier 曲面的端点性质, 即控制顶点P 00, P 01, P 10和P 11分别表示曲面的4个端点; 又根据边界线性质, 曲面的4条边界线()0,v X ,()1,v X ,(),0u X 和(),1u X 分别以0001,P P1011,P P 0010P P 和0111P P 为控制多边形. 由于2点所构成的控制多边形只能是直线, 并且00011011P P P P ∥, 00100111P P P P ∥, 因此曲面的4条边界曲线只能是直线; 又因为双线性Bézier 曲面只有4个控制顶点, 并且曲面上的点均由线性差插值产生, 所以严格满足保面积参数化约束条件的有理双线性Bézier 曲面只能是平行四边形. 根据双线性Bézier 曲面的定义以及式(5)(6)所示的保面积参数化约束条件, 给出如图1所示一般双线性曲面和具有保面积参数化的双线性曲面实例.a. 一般双线性曲面b. 具有保面积参数化双线性曲面图1 Bézier 形式双线性曲面由图1a 可以看出, 每个网格面积拉伸差异较大, 曲面参数化不保持面元; 由图1b 可以看出, 平行四边形和矩形图形的每个网格面积与参数面积拉伸一致, 其曲面参数化保持面元.2.3 双二次Bézier 曲面保面积参数化条件推导双二次Bézier 曲面的边界曲线和等参线均为抛物线, 9个控制顶点中的8个决定了曲面的4条边界曲线, 内部控制顶点11P 只影响曲面内部形状,对边界不产生影响. 根据式(1)和Bézier 曲面的微分几何形式, 双二次Bézier 曲面可表示为 ()()()()()()()()()()()()()()()()()()()222200000101222202021010222211111212222220202121222222,u v B u B v B u B v B u B v B u B v B u B v B u B v B u B v B u B v B u B v =++++++++X P P P P P P P P P (7)依据曲面的第一微分基本形式, 为了得到式(3)中曲面上任意一点的u 和v 向切向量的显式表示, 将式(7)分别对参数u 和v 求偏导, 即()()()()()()()()()()()()()()()20020102221011222122022122,=211 41121 21121 41141 21221 412,u v u v uu v v u v u v u v u v v u v v u v uv u v u v v uv ∂----∂----+⎡⎤----+⎣⎦----+⎡⎤⎣⎦⎡⎤--+-+⎣⎦-+X P P P P P P P P P()()()()()()()()()()()()()()()20022012021011212202222122,=211+ 21121 21411 41141 4121 2122u v u v vu v v u v u u u v u u v uv u uv u u v u v u v u v ∂---∂⎡⎤----+⎣⎦----+----+⎡⎤⎣⎦---+⎡⎤--+⎣⎦X P P P P P P P P P .首先将(),u v u∂∂X 和(),u v v∂∂X 作向量叉乘运算,得到曲面上(u ,v )点处的法向量; 然后将法向量取模, 依据式(3)和向量叉乘运算的加法分配率和反交换律等化简49个条件式, 包含441项多项式; 最后求出双二次Bézier 曲面必须满足4组约束条件.定义向前差分为1,0 1 ,i j i j i j Δ+=-P P P,01,01,01 , 1,2,3k k k i j i j i j ΔΔΔk --+=-=P P P ,0,11 ,i j i j i j Δ+=-P P P0,0,10,11 , 1,.,23l l l i j i j i j ΔΔΔl --+=-=P P P其中Δ为向前差分算子.1,00,10000 4AΔΔ⨯=P P (8)第3期李效伟, 等: 具有保面积参数化的双二次Bézier 曲面 4692,02,000012,02,000022,02,001020,20,220000,20,220100,20,21000 =ΔΔΔΔΔΔΔΔΔΔΔΔ⎧⨯⎪⨯=⎪⎪⨯=⎪⎨⨯=⎪⎪⨯=⎪⎪⨯=⎩0000P P P P P P P P P P P P (9) ()()()()()()1,00,10,10,20,10,21000100000101,01,00,11,00,100000010002,02,00,20,2010010000,20,20,20,1001020002,02,01,00100000,20,2102 4 2ΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔ-+⨯=⨯⨯=⨯--⨯-=-+⨯+-⨯=-0P P P P P P P P P P PP P P P P P P P P P P P P ()()1,00,1001000ΔΔ⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⨯-⎪⎩P P(10)()()()()()2,01,00,11,02,01,00010000101002,00,11,00,11,000001000001,02,02,02,0000001022,00,20,20010001,00,12,02,010*******,00,0022 2 2ΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔΔ⎡⎤⨯-+=⨯⎣⎦⨯=-⨯⨯-++⨯-=-⨯-⨯P P P P P P P P P P PP P P P P P P P P P P P ()()22,02,00,1000100000,20,21,01000002 2ΔΔΔΔΔΔ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪+-⨯=⎪⎪-⨯⎪⎩P P P P P P P (11)令2,02,01002012,2,ΔΔ==H P H P 2,03022,Δ=H P0,20,20,24205106002, 2, 2,ΔΔΔ===H P H P H P 曲面控制顶点和差分向量分布情况如图2所示.图2 式(8)~式(11)中控制顶点和向量的原理图2.4 具有保面积参数化的双二次Bézier 曲面的构造算法对于任意双二次Bézier 曲面, 只有同时满足式(8)~式(11)这4组约束条件, 才能够满足式(3)所表达的保面积参数化条件. 式(8)给出了在P 00点处法向量的模必须为A /4的约束; 式(9)给出了曲面同方向控制顶点所构成向量必须平行的约束条件, 即123////H H H , 456////H H H ; 式(10)(11)分别给出了横向和纵向控制顶点构成向量之间的关系, 且具有一定的对称性, 式(10)给出了456,,H H H 与12,,H H H 之间的约束关系; 式(11)给出了123,,H H H 与56,,H H H 之间的约束关系.算法1. 具有保面积参数化的双二次Bézier 曲面构造算法.输入. 控制顶点P 00, P 00点处u 和v 方向的偏导矢的方向(不共线)、模的比值和曲面面积A .输出. 具有保面积参数化的双二次Bézier 曲面.Step1. 将P 00点处u 和v 方向的偏导矢的方向、模的比值和曲面面积A 代入式(8), 计算控制顶点P 10和P 01.Step2. 根据式(9), 给出剩余6个控制顶点P 02, P 11, P 12, P 20, P 21和P 22坐标值的计算系数:Step2.1.由分类讨论得出约束=H 0, 则可令11011000=+-P P P P ;Step2.2. 根据约束条件()()()()100060100101001000125613220⎧-⨯=-⨯⎪⨯-=⨯-⎪⎪⨯=⎨⎪⨯=⎪⎪⨯=⎩P P H P P H H P P H P P H H H H H H , 1000,0-≠P P 0100,0-≠P P 当1≠0H 并且6≠0H 时,可将控制顶点P 02, P 20, P 21, P 12和P 22的坐标表示为0211000010020201001000213002010110112400020111102250020101202()2()2(2)2(2)2(2)2k k k k k =-+-⎧⎪=-+-⎪⎪=+-+-⎨⎪=+-+-⎪⎪=+-+-⎩P P P P P P P P P P P P P P P P P P P P P PP P P P P P (12) 其中, 12345,,,,k k k k k ⊂ . 类似地, 当1=0H 或6=0H 时, 这些控制顶点坐标也将得到形式如式(12)的表达式;Step2.3. 将P 02, P 20, P 21, P 12和P 22的坐标表示代入剩余约束条件()()()1110601005111012100021561000123156216540100216561621010056[2()]()[2()]()()()()(2)4() 4()(2)()4() 4()0+-⨯=-⨯⨯+-=⨯--⨯-=-⨯-++⨯-=⨯--+⨯-+-⨯=-⨯⨯+-⨯-=-⨯H P P H P P H H H P P H P P H H H H P P H H H H H H H H H H H H P P H H H H H HH H H H P P H H P ()1000⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪-⎩P,470计算机辅助设计与图形学学报第33卷得到方程组()()()()()()()()()()()()()()()()()()1401001000230100100012340100100023514110000100123010010001201001000111112221k k k k k k k k k k k k k k k k k k k ⎧--⨯-=⎪--⨯-=⎪⎪---⨯-=⎪⎨-+-+-⨯-=⎪⎪--⨯-=⎪⎪-⨯-=⎩000000P P P P P P P P P P P P P P P P P P P P P P P P . P 00, P 10和P 01必须构成三角形的前提条件, 得到约束()()01001000-⨯-≠0P P P P , 化简方程组得到一个便于求解的方程组()()()()()()1423123423514112312101011012220100k k k k k k k k k k k k k k k k k k k ⎧-=⎪-=⎪⎪--=⎪⎨-+-+=⎪⎪-=⎪⎪=⎩; Step2.4. 求解方程组, 得到约束123500==1k k k k =⎧⎪≠⎨⎪⎩. Step3. 给定自由变量k 2和k 4的值, 根据式(12)计算P 02, P 12, P 20, P 21, P 22的值, 输出9个控制顶点坐标所表示的双二次Bézier 曲面.2.5 具有保面积参数化的双二次Bézier 曲面只能为平面曲面对于具有保面积参数化的双二次Bézier 曲面, 必满足式(8)~式(11), 其表达的几何含义为曲面任意点处的一个法向量的模恒为常量. 根据双二次Bézier 曲面的微分几何含义, 由于向量0100-P P 和1000-P P 所构成的平面是曲面在P 00点处的切平面, 故能得到P 00, P 01和P 103点共面. 又因为, 从式(8)~式(11)中的4组约束条件出发, 根据分类讨论结果, 得出向量H 只能为零向量, 否则, 必有其中的一个约束条件不成立, 因此得到式11011000=+-P P P P . 根据向量共面定理[23]可知, P 00, P 01, P 10和P 11 4点共面. 由于控制顶点P 20, P 02, P 21, P 12和P 22可表示为式(12)的形式, 并且式(12)中每个控制顶点的表达式均满足向量共面定理, 即5个控制顶点均与点P 00, P 01和P 10共面, 可得曲面的9个控制顶点共面. 又根据Bézier 曲面的凸包性质, 由以上9个控制顶点生成的曲面为一平面片. 综上所述, 严格满足保面积参数化约束条件的双二次Bézier 曲面只能是平面曲面.3 松弛保面积参数化双二次Bézier 曲面3.1 问题描述对于双二次Bézier 曲面, 由于严格满足保面积参数化约束条件式(8)~式(11)的曲面只能是平面曲面, 在第2.5节给出了相关证明. 为了构造出具有丰富弯曲造型的真正意义上的曲面, 本文提出通过求解在不等式约束下的能量函数来生成逼近保面积参数化的Bézier 曲面.求解能量函数()()()()1100min ,s.t. ,,M N iji j u v u v A e u v u v A e--==⎧-⎪⎨⎪-∂⨯∂+⎩∑∑X Q X X ≤≤. 其中, u 和v 是采样点处的参数坐标, 不等式的个数由采样点密度决定, 优化参数是曲面的控制顶点坐标, 目标函数是希望生成的曲面尽量通过给定的逼近点ij Q , 同时要求约束采样点处的最大面积误差不得超过e . 上述优化问题是一个在非线性约束下的最小二乘优化问题, 本文使用fmincon 函数进行求解.3.2 松弛保面积参数化约束条件的双二次Bézier曲面构造算法本文提出通过松弛保面积参数化约束条件来构造具有保面积参数化的双二次Bézier 曲面的算法思路. 首先通过增加曲面的面积容差, 然后指定在曲面的m ×n 个采样点处满足面积容差约束, 最后使用最小二乘法[24]拟合所要构造的双二次Bézier 曲面, 以达到曲面接近或经过给定曲面逼近点的形状设计要求.算法2. 松弛保面积参数化约束条件的双二次Bézier 曲面构造算法.输入. M ×N 个逼近点Q 00, Q 01, , Q 0M ; Q 10, Q 11, , Q 1M ; ; Q N 0, Q N 1, , Q NM 坐标, 采样点的个数m 和n , 以及面积容差e .输出. 具有保面积参数化的双二次Bézier 曲面.Step1. 根据输入控制顶点计算曲面面积A . Step2. 根据曲面u 和v 向的采样点个数m 和n 确定采样点处的不等式约束.Step3. 拟合双二次Bézier 曲面, 更新曲面控制顶点P 00, P 01, P 02, P 10, P 11, P 12, P 20, P 21和P 22坐标, 重新计算曲面面积A ʹ.Step4. 迭代. 将Step1中的输入控制顶点替代为Step3重更新后的控制顶点. 重复执行Step1~Step3, 直到2||||10A A A -'-⋅≤.第3期李效伟, 等: 具有保面积参数化的双二次Bézier曲面 471Step5. 重新拟合双二次Bézier曲面, 输出控制顶点P00, P01, P02, P10, P11, P12, P20, P21和P22坐标.4 实例本文使用的实验平台是主频为 3.6 GHz的Intel Core I7处理器, 内存为16 GB的台式机, 运行系统为64位的Windows 7操作系统, 显卡为8 GB显存的英伟达GeForce GTX1080. 实验过程中, 使用Visual Studio 2018集成开发环境实现本文提出的构造算法, 使用C++语言和OpenGL图形库显示曲面的等参线分布和纹理映射效果. 实验内容包括:实例1. 具有保面积参数化的双二次Bézier曲面的构造实例, 所构造曲面严格满足式(8)~式(11)给出约束条件.实例2. 松弛保面积参数化约束条件的双二次Bézier曲面的构造实例, 设定面积容差, 使用曲面拟合方法构造, 所构造曲面在容差范围内满足保面积参数化.4.1实例1为了展示本文算法的有效性, 图3中给出了3个实验结果. 图3a给出了曲面的等参线分布实验结果, 展示了曲面细分和网格化效果, 图3b给出了曲面的纹理映射实验结果. 实验结果可以看出, 3个曲面的参数化保持面积拉伸, 即完全满足保面积约束条件式(8)~式(11), 在曲面细分实验中, 虽然细分曲面的形状不同, 但是任何一个细分曲面的面积均保持面积拉伸; 在纹理映射实验中, 分别用黑白棋盘格和圆盘格展示了本文算法1生成曲面的保面积参数化特性, 虽然小方格和小圆圈形状发生了拉伸, 但是其面积仍然保持拉伸. 从曲面构造角度看, 通过本文算法1找到的曲面均需要保证有一个方向的控制顶点构成直线, 即控制多边形P00P01P02, P10P11P12和P20P21P22均为直线, 也即H1=H2=H3或H4=H5=H6, 这种约束导致可生成的曲面形状的有限性; 曲面另外一个方向可以实现一定程度的弯曲, 为了检验是否满足条件, 最终生成的曲面需要代入式(10)(11)验证. 虽然保面积约束条件较为苛刻, 但是不局限于图3中展示的3个曲面, 通过本文算法1可以找到更多符合保面积参数化约束条件的双二次Bézier曲面, 一个可行的方法为: 以图3中的任意一个曲面为基础, 通过调整曲面弯曲方向的控制顶点坐标位置, 可以生成一簇保面积参数化曲面, 如图4所示, 可以看出, 虽然同一簇曲面的形状相似, 但其弯曲程度不同. 表1给出了图4中4个双二次Bézier曲面图形的3个输入控制顶点坐标和其余控制顶点的计算系数. 图3~图5所示的曲面图形中, P00, P01和P10为本文算法1的输入控制顶点; P02, P11, P12, P20, P21, P22为通过本文算法1计算得到的控制顶点.需要特殊说明的是, 只是通过输入计算出的3个输入控制顶点P00, P01和P10, 并不能唯一确定满足条件的其余控制顶点, 因为在本文算法1的执行过程中其余控制顶点的计算系数k2和k4是自由变量, 通过设定不同的k2和k4值可以生成不同形状的双二次Bézier曲面. 另外, 经过实验案例测试, 在3个输入控制顶点P00, P01和P10取值相同, 但k2和k4取值不同的情况下, 生成了2种不同形状的双二次Bézier曲面, 如图5所示, 2种曲面都满足式(8)~式(11).图3 等参线分布和纹理映射实验图4 一簇具有保面积参数化的双二次Bézier曲面472计算机辅助设计与图形学学报第33卷表1 图4中图形的部分控制顶点坐标和计算系数计算系数顶点坐标图序k 1k 2k 3k 4k 5P 00P 01P 104a 0.0 5.0 1.0 1.0 1.0 (2,0,0) (2.5,0,0) (0,0.5,0) 4b 0.0 4.0 1.0 2.0 1.0 (1.5,0,0) (2,0,0) (0,0.5,0) 4c 0.0 3.5 1.0 3.0 1.0 (1.25,0,0)(1.75,0,0) (0,0.5,0)4d 0.0 3.0 1.0 4.0 1.0 (1,0,0) (1.5,0,0) (0,0.5,0)图5 输入数据相同的双二次Bézier 曲面通过给定不同的输入数据计算出的3个输入控制顶点P 00, P 01和P 10坐标, 能够生成形状较为丰富的具有保面积参数化的双二次Bézier 曲面, 如图6所示. 表2给出了图6中6个曲面图形的3个由本文算法1的输入数据计算出的控制顶点坐标和其余控制顶点的计算系数.4.2 实例2由于严格满足保面积参数化约束条件的双二次曲面的造型能力较为有限, 只能生成平面空间中的曲面,难以生成造型丰富的曲面, 因此其在某些特殊的实际应用中具有一定的局限性. 为此, 本文提出了松弛保面积参数化约束的双二次Bézier 曲面的构造算法. 为了验证松弛保面积参数化约束的双二次Bézier 曲面的造型能力, 使用C++语言编写程序实现了基于不等式方程组约束的曲面拟合算法, 所生成曲面的等参线分布和纹理映射效果如图7所示. 可以看出, 通过本文算法2构造的双二次Bézier 曲面具有丰富的形状, 具有较强的造型能力.a. 曲面1b. 曲面2c. 曲面3d. 曲面4e. 曲面5f. 曲面6图6 不同的输入数据生成双二次Bézier 曲面表2 图6中图形的部分控制顶点坐标和计算系数计算系数顶点坐标图序k 1k 2k 3k 4k 5P 00P 01P 10 6a 0.0 1.0 1.0 0.4 1.0 (0,0,0) (0.5,0.5,0) (0,0.5,0) 6b 0.0 2.0 1.0 0.0 1.0 (0,0,0) (–0.25,0.2,0) (1,0.2,0) 6c 0.0 2.0 1.0 0.3 1.0 (0,0,0) (–0.25,0.4,0) (0.375,0.4,0) 6d 0.0 1.0 1.0 0.6 1.0 (0,0,0) (–0.25,0.333 3,0) (0.5,0.333 3,0)6e 0.0 1.0 1.0 0.9 1.0 (0,0,0) (–0.25,0.5,0) (0.25,0.5,0) 6f 0.0 1.0 1.0 1.0 1.0 (0,0,0) (–0.25,0.25,0)(0.75,0.25,0)表3给出的数据验证了本文算法2的有效性, 表中数据为采样数为104×104时图7中8个曲面的目标函数值f 、最大保面积能量J max 、迭代次数和给定的容差e . 其中, 目标函数值f 表示拟合生成的曲面与目标曲面的偏离程度, f 值越大, 表明拟合曲面越难以经过本文算法2中输入中的给定点, 从而更加偏离给定的曲面形状; 表3第4列表示在满足不等式约束的前提下优化过程的迭代次数. 相对于曲面2~曲面8, 曲面1的弯曲程度较小, 故将容差设置为其他曲面容差的1/10, 设定的容差第3期李效伟, 等: 具有保面积参数化的双二次Bézier曲面 473a. 曲面1b. 曲面2c.曲面3 d. 曲面4e. 曲面5f.曲面6 g.曲面7 h.曲面8图7 松弛后的双二次Bézier曲面表3图7曲面采样数为104×104的保面积能量与容差曲面 f J max迭代次数e曲面 f J max迭代次数e1 0.1457 0.00091450 0.00151.0247 0.008621 267 0.0102 0.8622 0.008502870.010 6 0.9875 0.00938268 0.0103 1.2457 0.009657 168 0.01071.5416 0.00933174 0.0104 1.3245 0.009355 171 0.01081.3142 0.00994459 0.010越小, 则生成的曲面越接近保面积参数化. 对于曲面造型, 如果预想生成弯曲幅度较大的曲面, 则可适当地将容差设定的更大一些. 例如, 本实验的曲面2~曲面8中, 将容差设置为0.010; 否则优化过程更新后的曲面不能很好地经过算法输入的给定点, 最终生成的曲面虽然能够将保面积容差限定在用户定义的范围, 但是其形状将会较大幅度地偏离初始曲面形状. 曲面上最大保面积能量J max表示的是曲面最坏处的保面积参数化偏离程度, 其值越大, 表明曲面在此位置处越偏离保面积参数化; 其值越小, 表明曲面在此位置处的保面积参数化效果越好. 曲面上采样点处最大保面积能量的。

一种快速求取空间任意两条曲线交点的算法

参考文献
! 戴葵等译 R（美）/5FA01 SR 85251" 86T5F> PR +CUBA=" /5FV 8R PC5WC 著 R
X 焦李成 R 神经网络的应用与实现 R 西安：西安电子科技大学出版社， !**YR
’ 孙靖民 R 机械优化设计 R 北京：机械工业出版社，!**%R % 许崎，李永生，威学成 R 梯度法与 PQ 神经网络的结合在机械优化设
2在两条曲线存在交点的区间内计算两条曲线的最短距离在两条曲线存在交点可能的参数区间内利用控制顶点正算出所对应的曲线段求两条曲线的最短距离
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!"
《机械设计与制造》 ,GAR #&&’ -6R % /5G=01CFM +C@021 _ /51BD5GABFC
所对应的两条曲线没有交点，如图 0 + ; , 和图 0 + < , 所示。
上述判断原理的算法步骤为：
%=*&06 分别选取两条曲线控制多边形的其中一条边。
%=*&"6 计算 !0 和 !"，如果 !0 与 !" 方向相反，计算 !! 与 !5，如果 !! 与 !5 方向相反，则所对应的两条曲线存在相交的可能性，分别记录所对应的控制顶点 + !" $ 0/ !"/ !" 7 0/ !" 7 " , 、+ -$ $ 0/ -$/ -$ 7 0/ -$ 7 " , 及参数区间，以备下一步处理。如果 !! 与 !5 方向相同，则所对应的两条曲线没有交点。如果 !0 与 !" 方向相同，则所对应的两条曲线也没有交点。

人工智能专业排名前50名大学有哪些学校

人工智能专业排名前50名大学有哪些学校全国人工智能专业学校排名排名院校名称专业名称专业排名等级1电子科技大学人工智能A+2西安电子科技大学人工智能A+3北京大学人工智能A4清华大学人工智能A5东南大学人工智能A6北京邮电大学人工智能A-7复旦大学人工智能A-8上海交通大学人工智能A-9南京大学人工智能A-10浙江大学人工智能A-11西安交通大学人工智能A-12北京航空航天大学人工智能B+13北京理工大学人工智能B+14天津大学人工智能B+16南京邮电大学人工智能B+17杭州电子科技大学人工智能B+ 18华中科技大学人工智能B+19西北工业大学人工智能B+20国防科技大学人工智能B+21空军工程大学人工智能B+22北京工业大学人工智能B23南开大学人工智能B24哈尔滨工业大学人工智能B25华东师范大学人工智能B26南京理工大学人工智能B27中国科学技术大学人工智能B 28厦门大学人工智能B29武汉大学人工智能B30中山大学人工智能B31华南理工大学人工智能B32北京交通大学人工智能B-33大连理工大学人工智能B-35合肥工业大学人工智能B-36福州大学人工智能B-37山东大学人工智能B-38湖南大学人工智能B-39重庆大学人工智能B-40西南交通大学人工智能B-41西安理工大学人工智能B-42陆军工程大学(原解放军理工大学)人工智能B- 43中国传媒大学人工智能C+44河北工业大学人工智能C+45太原理工大学人工智能C+46长春理工大学人工智能C+47黑龙江大学人工智能C+48燕山大学人工智能C+49上海大学人工智能C+50中南大学人工智能C+人工智能专业课程有哪些1.认知与神经科学课程群具体课程：认知心理学、神经科学基础、人类的记忆与学习、语言与思维、计算神经工程2.人工智能伦理课程群具体课程：《人工智能、社会与人文》、《人工智能哲学基础与伦理》3.科学和工程课程群新一代人工智能的发展需要脑科学、神经科学、认知心理学、信息科学等相关学科的实验科学家和理论科学家的共同努力，寻找人工智能的突破点，同时必须要以严谨的态度进行科学研究，让人工智能学科走在正确、健康的发展道路上。

第六章特征线法-西安交通大学

第六章特征线法
本章主要学习用特征线法求解一阶偏微分方程以及一维波动方程。

特征线法也是求解偏微分方程的一种基本方法。

其实质是沿偏微分方程的特征线积分以使方程的形式简化，从而使其求解成为可能。

它不仅适用于线性偏微分方程，而且也是求解非线性方程的一种有效方法。

特征方程。

t
c f
和
特征线法的基本思想就是将其转化为
定义6.1 考虑下面一阶线性微分方程
注：给出例1求解方法的一个几何解释。

在该例中，使用了参数c ，即为特征线的初始值()4t x au bu cu f ++=其中,,a b c ()05dx
a b dt
−=和f 均为自变量,x t 的函数。

方程称为(4)式的特征方程，其积分曲线称为(4)式的特征曲线。

(0)x 。

当参数(0)c x =在x 轴滑动时，(3)式的解曲线就织成了为了避免和常数c 混淆，下面用变量τ代替参数c 。

(1)(2)的解曲面。

(2024年)计算机图形学孙家广

计算机图形学孙家广CONTENTS •计算机图形学概述•图形生成技术•图形变换与裁剪•颜色模型与光照模型•图形用户界面设计•计算机动画技术•计算机图形学前沿技术01计算机图形学概述计算机图形学定义与发展定义计算机图形学是研究计算机生成、处理和显示图形的一门科学，它涉及计算机科学、数学、物理学、心理学等多个领域。

发展历程从20世纪50年代的简单图形绘制，到60、70年代的光栅扫描显示和三维图形技术，再到80、90年代的图形处理单元（GPU）和虚拟现实技术的发展，计算机图形学经历了飞速的发展。

计算机图形学应用领域计算机辅助设计与制造（CAD/CAM）利用计算机图形学技术进行产品设计、模拟和分析，提高生产效率和产品质量。

影视娱乐计算机图形学技术在电影、游戏等娱乐领域的应用，创造逼真的虚拟世界和角色。

数据可视化将大量数据通过图形的方式呈现出来，帮助人们更好地理解和分析数据。

虚拟现实与增强现实通过计算机图形学技术构建虚拟环境或增强现实场景，为用户提供沉浸式的交互体验。

包括图形处理器（GPU ）、显示设备（如显示器、投影仪等）和输入设备（如鼠标、键盘、触摸屏等）。

图形硬件包括操作系统中的图形子系统、图形库和图形应用程序等，提供图形生成、处理和显示的功能。

图形软件包括光栅化、纹理映射、光照模型、阴影生成等算法，用于实现各种图形效果。

图形算法包括二维图形、三维模型、图像等数据，作为计算机图形系统的输入和输出。

图形数据计算机图形系统组成02图形生成技术包括数值微分法（DDA）和Bresenham算法等，用于在像素网格上精确或近似地绘制点和直线。

涉及中点圆生成算法和参数化椭圆生成方法等，用于生成各种大小和位置的圆和椭圆。

包括扫描线填充算法、边界填充算法等，用于对多边形内部进行颜色填充。

点和直线的生成算法圆和椭圆的生成算法多边形的填充算法基本图形生成算法曲线曲面生成技术参数曲线曲面使用参数化表示方法，如Bezier曲线和曲面、B样条曲线和曲面等，能够描述复杂的曲线和曲面形状。