2015江西卷高考数学试题及答案或解析下载_2015高考真题抢先版
2015江西卷高考英语试题及答案或解析下载_2015高考真题抢先版

2015年高考将于6月6、7日举行,我们将在第一时间收录真题,现在就请先用这套权威预测解解渴吧江西省上饶市2015届高三第二次高考模拟英语试题第I卷(三部分,共115分)第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
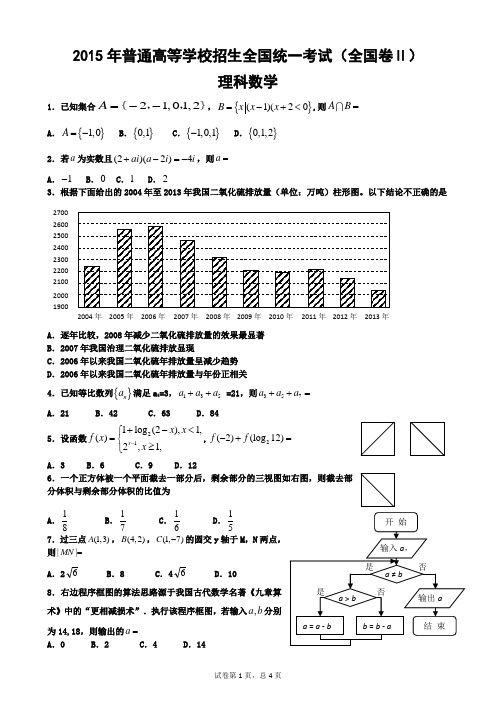
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在答题卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Who would like to change the time?A. Marty.B. Mrs. Martin.C. Sally.2. What happened to the speakers?A. They missed the bus.B. They were late for class.C. They took too long to put on their lies.3. On which floor does Rudolf live?A. The third floor.B. The second floor.C. The firstfloor.4. What did the man do on the weekend?A. He did some reading.B. He helped in the store.C. He went to theseaside.5. Why did the man change his mind?A. For cost.B. For safety.C. For weather.第二节(共15小题,每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
2015年高考理科数学全国卷1(含答案解析)

绝密★启用前 2015年普通高等学校招生全国统一考试(全国新课标卷1)数学(理科)使用地区:河南、山西、河北、江西本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足1+z1z-=i ,则|z|=( ) A .1B .2C .3D .2 2.sin20cos10cos160sin10︒︒︒︒-=( )A .32-B .32C .12-D .123.设命题:p n ∃∈Ν,22n n >,则⌝p 为( )A .2n n n ∀∈N 2,>B .2n n n ∃∈N 2,≤C .2n n n ∀∈N 2,≤D .=2n n n ∃∈N 2,4.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )A .0.648B .0.432C .0.36D .0.3125.已知00()M x y ,是双曲线2212x C y -=:上的一点,F 1,F 2是C 的两个焦点.若120MF MF <,则0y 的取值范围是( )A .33()33-, B .33()66-, C .2222()33-, D .2323()33-, 6. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A .14斛B .22斛C .36斛D .66斛 7.设D 为ABC △所在平面内一点,=3BC CD ,则( )A .1433AD AB AC =-+ B .1433AD AB AC =- C .4133AD AB AC =+ D .4133AD AB AC =-8.函数=cos(+)x f x ωϕ()的部分图象如图所示,则f x ()的单调递减区间为( )A .13π,π+44k k k -∈Z (),B .132π,2π+44k k k -∈Z (),C .13,+44k k k -∈Z (),D .132,2+44k k k -∈Z (),9.执行如图所示的程序框图,如果输入的0.01t =,则输出 的n =( )A .5B .6C .7D .810.25()x x y ++的展开式中,52x y 的系数为( )A .10B .20C .30D .6011.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r =( )A .1B .2C .4D .812.设函数()()21x f x e x ax a =--+,其中a<1,若存在唯一的整数0x 使得0()0f x <,则a 的取值范围是( )--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________A .3[)21,e-B .43[,)23e -C .3[,)234e D .3[,)21e第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.若函数2()=()ln f x x a x x ++为偶函数,则a =________. 14.一个圆经过椭圆22=1164x y+的三个顶点,且圆心在x 轴的正半轴上,则该圆的标准方程为________.15.若x ,y 满足约束条件10,0,40,x x y x y -⎧⎪-⎨⎪+-⎩≥≤≤则y x 的最大值为________.16.在平面四边形ABCD 中,==75=A B C ∠∠∠︒,=2BC ,则AB 的取值范围是________. 三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分)n S 为数列{}n a 的前n 项和.已知0n a >,2n n n +2=4+3a a S .(Ⅰ)求{}n a 的通项公式;(Ⅱ)设n n n+11=b a a ,求数列{}n b 的前n 项和.18.(本小题满分12分)如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC . (Ⅰ)证明:平面AEC ⊥平面AFC ; (Ⅱ)求直线AE 与直线CF 所成角的余弦值.19.(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z(单位:千元)的影响,对近8年的年宣传费i x 和年销售量i y (i =1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.xyω28i=1()ixx -∑28i=1()iωω∑-8i=1()()iiy x x y-∑-8i=1()()ii y y ωω--∑46.65636.8289.8 1.6 1 469108.8表中i ω=i x ,ω=188i i=1ω∑(Ⅰ)根据散点图判断,y a bx =+与y c d x =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)已知这种产品的年利率z 与x ,y 的关系为z=0.2y -x .根据(Ⅱ)的结果回答下列问题:(i )年宣传费x =49时,年销售量及年利润的预报值是多少? (ii )年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据11()u v ,,22(,)u v ,…,(,)n n u v ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为121()(),()nii i nii uu v v v u uu βαβ==--==--∑∑.20.(本小题满分12分)在直角坐标系xOy 中,曲线24C y x :=与直线)0(l y kx a a >:=+交于M ,N 两点.(Ⅰ)当k =0时,分别求C 在点M 和N 处的切线方程;(Ⅱ)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM =∠OPN ?说明理由.21.(本小题满分12分)已知函数31()4f x x ax =++,()ln g x x =-. (Ⅰ)当a 为何值时,x 轴为曲线()y f x =的切线;(Ⅱ)用min{,}m n 表示m ,n 中的最小值,设函数()min{(),()}h x f x g x =(0)x >,讨论()h x 零点的个数.请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4—1:几何证明选讲如图,AB 是O 的直径,AC 是O 的切线,BC 交O 于点E . (Ⅰ)若D 为AC 的中点,证明:DE 是O 的切线; (Ⅱ)若OA =3CE ,求∠ACB 的大小.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,直线1C :x =-2,圆2C :(x -1)2+(y -2)2=1,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (Ⅰ)求1C ,2C 的极坐标方程; (Ⅱ)若直线3C 的极坐标方程为()π4θρ=∈R ,设2C 与3C 的交点为M ,N ,求2C MN △的面积.24.(本小题满分10分)选修4—5:不等式选讲已知函数12f x =|||x |x a -+-(),0a >. (Ⅰ)当=1a 时,求不等式1f x >()的解集;(Ⅱ)若f x ()的图象与x 轴围成的三角形面积大于6,求a 的取值范围. 2015年普通高等学校招生全国统一考试(全国新课标卷1)数学(理科)答案解析第Ⅰ卷一、选择题 1.【答案】A 【解析】由1=i 1z z+-,得1i (1i)(1i)=i 1i (1i)(1i)z -+-+-===++-,故1z =,故选C . 【提示】先化简复数,再求模即可. 【考点】复数的运算. 2.【答案】D【解析】原式1sin 20cos10cos20sin10sin302=+==,故选D . 【提示】直接利用诱导公式以及两角和的正弦函数,化简求解即可. 【考点】三角函数的运算. 3.【答案】C【解析】命题的否定是:22n n n ∀∈≤N ,.【提示】根据特称命题的否定是全称命题即可得到结论. 【考点】命题. 4.【答案】A【解析】根据独立重复试验公式可得,该同学通过测试的概率为2233C 0.60.40.6=0.648.⨯+【提示】判断该同学投篮投中是独立重复试验,然后求解概率即可.【考点】概率. 5.【答案】A【解析】由题知12(F F ,,220012x y -=,所以222120000000(3,)(3,)331MF MF x y xy x y y =-----=+-=-<,解得0y <<,故选A . 【提示】利用向量的数量积公式,结合双曲线方程,即可确定0y 的取值范围. 【考点】双曲线. 6.【答案】B【解析】设圆锥底面半径为r ,则116238,43r r ⨯⨯=⇒=所以米堆的体积为 2111632035,4339⎛⎫⨯⨯⨯⨯= ⎪⎝⎭故堆放的米约为320 1.6222,9÷≈故选B . 【考点】圆锥体积.【提示】根据圆锥的体积公式计算出对应的体积即可. 7.【答案】A【解析】由题知1114()3333AD AC CD AC BC AC AC AB AB AC =+=+=+-=-+【提示】将向量AD 利用向量的三角形法则首先表示为AC CD +,然后结合已知表示为AC AC ,的形式.【考点】向量运算. 8.【答案】D【解析】由五点作图知,1π42,53π42ωϕωϕ⎧+=⎪⎪⎨⎪+=⎪⎩解得ππ,4ωϕ==,所以π()cos π,4f x x ⎛⎫=+ ⎪⎝⎭令2ππ2ππ,,4k x k k π<+<+∈Z 解得1322,,44k x k k -<<+∈Z故()f x 的单调递减区间为132,2,44k k k ⎛⎫-+∈ ⎪⎝⎭Z ,故选D .【提示】由周期求出ω,由五点法作图求出ϕ,可得()f x 的解析式,再根据余弦函数的单调性,求得()f x 的减区间. 【考点】三角函数运算. 9.【答案】C【解析】执行第1次,0.01,1,t S ==10,0.5,2n m === 0.5,0.25,2mS S m m =-===1,0.50.01n S t ==>=,是,循环,执行第2次, 0.25,0.125,2mS S m m =-===2,0.250.01n S t ==>=,是,循环,执行第3次,0.125,0.0625,2mS S m m =-===3,0.1250.01n S t ==>=,是,循环,执行第4次,0.0625,0.03125,2mS S m m =-===4,0.06250.01n S t ==>=,是,循环,执行第5次,0.03125,0.015625,2mS S m m =-===5,0.031250.01n S t ==>=,是,循环,执行第6次,0.015625,0.0078125,2mS S m m =-===6,0.0156250.01n S t ==>=,是,循环,执行第7次,0.0078125,S S m =-=2mm =0.00390625=, 7,0.00781250.01n S t ==>=,否,输出7,n =故选C .【提示】由题意依次计算,当7,0.00781250.01,n S t ==>=停止由此可得结论. 【考点】程序框图. 10.【答案】C【解析】在25()x x y ++的五个因式中,2个取因式中2x 剩余的3个因式中1个取x ,其余因式取y ,故52x y 的系数为212532C C C 30,=故选C .【提示】利用展开式的通项进行分析,即可得出结论. 【考点】二项式展开式. 11.【答案】B【解析】由正视图和俯视图知,该几何体是半球和半个圆柱的组合体,圆柱和球的半径都是r ,圆柱的高为2r ,其表面积为222214ππ2π225π41620π2r r r r r r r r ⨯+⨯++⨯=+=+,解得r=2,故选B .【提示】通过三视图可知该几何体是一个半球拼接半个圆柱,计算即可. 【考点】空间几何体的表面积. 12.【答案】D【解析】设()()e 21,,xg x x y ax a =-=-由题知存在唯一的整数0x ,使得0()g x 在直线y ax a =-的下方.因为()e (21)xg'x x =+,所以当12x <-时,'()0g x <,当12x >-,()0,g'x >所以当12x =-时,12min [()]2e g x -=-.当0x =时(0)1g =-,(1)e 0g =>,直线y ax a =-恒过(1,0)且斜率a ,故(0)1a g ->=-,且1(1)3e g a a --=-≥--,解得312ea ≤<,故选D .【提示】设()()e 21,,xg x x y ax a =-=-,问题转化为存在唯一的整数0x 使得0()g x 在直线y ax a =-的下方,由导数可得函数的极值,数形结合可得(0)1a g ->=-且1(1)3e g a a --=-≥--,解关于a 的不等式组可得.【考点】带参函数.第Ⅱ卷二、填空题 13.【答案】1【解析】由题知ln(y x =是奇函数,所以22ln(ln(ln()ln 0x x a x x a +-=+-==,解得 1.a =【提示】由题意可得,()()f x f x -=,代入根据对数的运算性质即可求解 【考点】函数奇偶性.14.【答案】2232524x y ⎛⎫±+= ⎪⎝⎭【解析】设圆心为(,0)a ,则半径为4a -,则222(4)2,a a -=+解得32a =±, 故圆的标准方程为2232524x y ⎛⎫±+= ⎪⎝⎭.【提示】利用椭圆的方程求出顶点坐标,然后求出圆心坐标,求出半径即可得到圆的方程. 【考点】圆的标准方程. 15.【答案】3【解析】做出可行域如图中阴影部分所示,由斜率的意义知,yx是可行域内一点与原点连线的斜率,由图可知,点(1,3)与原点连线的斜率最大,故yx的最大值3.【提示】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定y x的最大值.【考点】线性规划问题.16.【答案】【解析】如下图所示:延长BACD ,交于点E ,则可知在△ADE 中,105DAE ∠=︒,45ADE ∠=︒,30,E ∠=︒∴设12AD x =,2AE x =,4DE x =,CD m =,2BC =,sin151m ⎫∴+︒=⎪⎪⎝⎭⇒m +=∴04x <<,而2AB m x +-,2x∴AB的取值范围是.【提示】如图所示,延长BACD ,交于点,设12AD x =,2AE x =,4DE x =,CD m =m +=AB 的取值范围. 【考点】平面几何问题. 三.解答题17.【答案】(Ⅰ)21n + (Ⅱ)11646n -+ 【解析】(Ⅰ)当1n =时,211112434+3a a S a +=+=,因为0n a >,所以1a =3,当2n ≥时,221122n n n n a a a a --+--=14343n n S S -+--=4n a ,即111()()2()n n n n n n a a a a a a ---+-=+,因为0n a >,所以1n n a a --=2,所以数列{}n a 是首项为3,公差为2的等差数列,所以n a =21n +; (Ⅱ)由(1)知,1111(21)(23)22123n b n n n n ⎛⎫==- ⎪++++⎝⎭,所以数列{}n b 前n 项和为121111111=235572123n b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫+++-+-++- ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎣⎦=11646n -+. 【提示】(Ⅰ)根据数列的递推关系,利用作差法即可求{}n a 的通项公式:(Ⅱ)求出11n n n b a a +=,利用裂项法即可求数列{}n b 的前n 项和.【考点】数列前n 项和与第n 项的关系,等差数列定义与通项公式. 18.【答案】(Ⅰ)答案见解析 【解析】(Ⅰ)连接BD ,设,BDAC G =连接EG FG EF ,,,在菱形ABCD 中,不妨设1GB =,由∠ABC=120°,可得AG GC ==由BE ⊥平面ABCD ,AB BC =,可知AE EC =, 又∵AE EC ⊥,∴EG EG AC =⊥,在Rt EBG △中,可得BE,故DF =在Rt FDG △中,可得FG =在直角梯形BDEF 中,由2BD =,BE,2DF =,可得2EF =, ∴222EG FG EF +=, ∴EG FG ⊥, ∵ACFG G =,∴EG ⊥平面AFC , ∵EG ⊂平面AEC , ∴平面AFC ⊥平面AEC .(Ⅱ)如图,以G 为坐标原点,分别以,GB GC 的方向为x 轴,y 轴正方向,||GB 为单位长度,建立空间直角坐标系G xyz -,由(Ⅰ)可得0,A (,(E,2F ⎛- ⎝⎭,C ,∴AE =,1,CF ⎛=- ⎝⎭.故cos ,3||||AE CFAE CF AE CF <>==-,所以直线AE 与CF .【提示】(Ⅰ)连接BD ,设BD AC G =,连接EG EF FG ,,,运用线面垂直的判定定理得到EG ⊥平面AFC ,再由面面垂直的判定定理,即可得到.(Ⅱ)以G 为坐标原点,分别以GB GC ,为x 轴,y 轴,GB 为单位长度,建立空间直角坐标系G xyz -,求得AE F C ,,,的坐标,运用向量的数量积的定义,计算即可得到所求角的余弦值.【考点】空间垂直判定与性质,异面直线所成角的计算.19.【答案】(Ⅰ)答案见解析 (Ⅱ)答案见解析 (Ⅲ)(i )66.32 (ii )46.24【解析】(Ⅰ)由散点图可以判断,y c =+y 关于年宣传费用x 的回归方程类型.(Ⅱ)令w =先建立y 关于w 的线性回归方程,由于81821()()108.8=68,16()iii ii w w yy d w w ==--==-∑∑ ∴56368 6.8100.6.==c y d w -⨯=-∴y 关于w 的线性回归方程为=100.6+68y w ,y ∴关于x 的回归方程为y (Ⅲ)(i )由(Ⅱ)知,当49x =时,年销量y的预报值576.6y =, 年利润z 的预报值=576.60.249=66.32z ⨯-(ii )根据(Ⅱ)的结果知,年利润z 的预报值20.12z x =x +--,∴13.66.8,2=即46.24x =,z 取得最大值,故宣传费用为46.24千元时,年利润的预保值最大.【提示】(Ⅰ)根据散点图,即可判断出.(Ⅱ)先建立中间量w =y 关于w 的线性回归方程,根据公式求出w ,问题得以解决.(Ⅲ)(Ⅰ)年宣传费49x =时,代入到回归方程,计算即可. (ii )求出预报值得方程,根据函数的性质,即可求出.【考点】线性回归方程求法,利用回归方程进行预报预测. 20.【答案】0y a --=0y a ++=(Ⅱ)答案见解析【解析】(Ⅰ)由题设可得)Ma ,()N a -,或()M a-,)N a .∵12yx '=,故24x y =在x =C在)a 处的切线方程为y a x -=-0y a --=,故24x y =在x =-处的导数值为,C 在()a -处的切线方程为y a x -=+,0y a ++=0y a --=0y a ++=. (Ⅱ)存在符合题意的点,证明如下:设(0,)P b 为符合题意得点,11(,)M x y ,22(,)N x y ,直线PM PN ,的斜率分别为12k k ,.将y kx a =+代入C 得方程整理得2440x kx a --=.∴12124,4x x k x x a +==-.∴1212121212122()()()=y b y b kx x a b x x k a b k k x x x x a--+-+++=+. 当b a =-时,有12k k + =0,则直线PM 的倾斜角与直线PN 的倾斜角互补,故OPM OPN ∠=∠,所以(0,)P a -符合题意.【提示】(Ⅰ)求出C在)a 处的切线方程,故24x y =在x =-即可求出方程.(Ⅱ)存在符合条件的点(0,)P b ,11(,)M x y,22(,)N x y ,直线PM PN ,的斜率分别为12k k ,直线方程与抛物线方程联立化为2440x kx a --=,利用根与系数的关系,斜率计算公式可得12()=k a b k k a++=即可证明. 【考点】抛物线的切线,直线与抛物线位置关系. 21.【答案】(Ⅰ)34a =- (Ⅱ)答案见解析【解析】(Ⅰ)设曲线()y f x =与x 轴相切于点0(,0)x ,则0()0f x =,0()0f x '=,即3002010430x ax x a ⎧++=⎪⎨⎪+=⎩,解得013,24x a ==-,因此,当34a =-时,x 轴是曲线()y f x =的切线. (Ⅱ)当(1,)x ∈+∞时,()ln 0g x x =-<,从而()min{(),()}()0h x f x g x g x =≤<, ∴()h x 在(1,)+∞无零点. 当1x =时,若54a ≥-,则5(1)04f a =+≥,(1)min{(1),(1)}(1)0h f g g ===,故1x =是()h x 的零点;若54a <-,则5(1)04f a =+<,(1)min{(1),(1)}(1)0h f g f ==<,故x =1不是()h x 的零点.当(0,1)x ∈时,()ln 0g x x =->,所以只需考虑()f x 在(0,1)的零点个数.(ⅰ)若3a ≤-或0a ≥,则2()3f x x a '=+在(0,1)无零点,故()f x 在(0,1)单调,而1(0)4f =,5(1)4f a =+,所以当3a ≤-时,()f x 在(0,1)有一个零点;当a ≥0时,()f x 在(0,1)无零点.(ⅱ)若30a -<<,则()f x在⎛ ⎝单调递减,在⎫⎪⎪⎭单调递增,故当x =()f x取的最小值,最小值为14f =.①若0f >,即304x -<<,()f x 在(0,1)无零点.②若0f =,即34a =-,则()f x 在(0,1)有唯一零点;③若0f <,即334a -<<-,由于1(0)4f =,5(1)4f a =+,所以当5344a -<<-时, ()f x 在(0,1)有两个零点;当534a -<≤-时,()f x 在(0,1)有一个零点.综上,当34a >-或54a <-时,()h x 有一个零点;当34a =-或54a =-时,()h x 有两个零点;当5344a -<<-时,()h x 有三个零点.【提示】(Ⅰ)设曲线()y f x =与x 轴相切于点0(,0)x ,则0()0f x =,0()0f x '=解出即可. (Ⅱ)对x 分类讨论:当(1,)x ∈+∞时,()ln 0g x x =-<,可得函数(1)min{(1),(1)}(1)0h f g g ===,即可得出零点的个数.当1x =时,对a 分类讨论利用导数研究其单调性极值即可得出.【考点】利用导数研究曲线的切线,分段函数的零点. 22.【答案】(Ⅰ)答案见解析 (Ⅱ)60ACB ∠=【解析】(Ⅰ)连接AE ,由已知得,AE BC AC AB ⊥⊥,,在Rt AEC △中,由已知得DE DC =,∴DEC DCE ∠=∠,连接OE ,OBE OEB ∠=∠, ∵90ACB ABC ∠+∠=, ∴90DEC OEB ∠+∠=,∴90OED ∠=,∴DE 是圆O 的切线.(Ⅱ)设1CE AE x ==,,由已知得AB =,BE =,由射影定理可得,2AE CE BE =,∴2x =x = ∴60ACB ∠=.【提示】(Ⅰ)连接AE 和OE ,由三角形和圆的知识易得90OED ∠=,可得DE 是O 的切线.(Ⅱ)设1CE AE x ==,,由射影定理可得关于x的方程2x =,解方程可得x 值,可得所求角度.【考点】圆的切线判定与性质,圆周角定理,直角三角形射影定理. 23.【答案】(Ⅰ)22cos 4sin 40ρρθρθ--+= (Ⅱ)12【解析】(Ⅰ)因为cos ,sin x y ρθρθ==, ∴1C 的极坐标方程为cos 2ρθ=-,2C 的极坐标方程为22cos 4sin 40ρρθρθ--+=.(Ⅱ)将=4θπ代入22cos 4sin 40ρρθρθ--+=,得240ρ-+=,解得1ρ=2ρ12=MN ρρ-,因为2C 的半径为1,则2C MN △的面积111sin 45=22⨯.【提示】(Ⅰ)由条件根据cos sin x y ρθρθ==,求得12C C ,的极坐标方程.(Ⅱ)把直线3C 的极坐标方程代入22cos 4sin 40ρρθρθ--+=,求得12ρρ,的值,从而求出2C MN △的面积.【考点】直角坐标方程与极坐标互化,直线与圆的位置关系.24.【答案】(Ⅰ)22.3x x ⎧⎫<<⎨⎬⎩⎭(Ⅱ)(2)+∞,【解析】(Ⅰ)当1a =时,不等式()1f x >化为1211x x +-->,等价于11221x x x ≤⎧⎨--+->⎩或111221x x x -<<⎧⎨++->⎩或11221x x x ≥⎧⎨+-+>⎩,解得223x <<,∴不等式()1f x >的解集为22.3x x ⎧⎫<<⎨⎬⎩⎭(Ⅱ)由题设可得,12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--≤≤⎨⎪-++>⎩,所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21,03a A -⎛⎫⎪⎝⎭,(21,0)B a +,(,+1)C a a ,所以ABC △的面积为22(1)3a +, 由题设得22(1)63a +>,解得2a >,所以a 的取值范围为(2)+∞,. 【提示】(Ⅰ)当1a =时,把原不等式去掉绝对值,转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.(Ⅱ)化简函数()f x 的解析式,求得它的图像与x 轴围成的三角形的三个顶点的坐标,从而求得()f x 的图像与x 轴围成的三角形面积;再根据()f x 的图像与x 轴围成的三角形面积大于6,从而求得a 的取值范围.【考点】含绝对值不等式解法,分段函数,一元二次不等式解法.。
高考数学2015江西十校联考数学(理)试题及答案

江西省重点中学盟校2015届第一次联考数学(理)试卷景德镇一中 邱金龙 操军华 贵溪一中 何卫中 新余四中 何幼平第Ⅰ卷(选择题 共60分)一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知集合101x M xx +⎧⎫=≥⎨⎬-⎩⎭,则R M =C ( ).A {}11x x -<< .B {}11x x -<≤ .C {}11x x x <-≥或 .D {}11x x x ≤-≥或2、已知11abi i=-+,其中,a b 是实数,i 是虚数单位,则||a bi -=( ) .A 3 .B 2 .C 5 .D 3、函数3y x =的图象在原点处的切线方程为( ).A y x = .B 0x = .C 0y = .D 不存在4、函数2lg(2)y x x a =-+的值域不可能是( ).A (,0]-∞ .B [0,)+∞ .C [1,)+∞ .D R5、实数,x y 满足10(2)(26)0x y x y x y -+≥⎧⎨--+≤⎩,若2t y x ≤+恒成立,则t 的取值范围是( ).A 13t ≤ .B 5t ≤- .C 13t ≤- .D 5t ≤ 6、如图是某算法的程序框图,则程序运行后输出的T 是( ).A 1 .B 2 .C 3 .D 47、已知12F F 、分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,过点2F 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ,若点M 在以线段12F F 为直径的圆外,则双曲线离心率的取值范围是( ).A .B )+∞ .C .D (2,)+∞8、已知()3sin 2cos 2f x x a x =+,其中a 为常数.()f x 的图象关于直线6x =π对称,则()f x 在以下区间上是单调函数的是( ).A 31[,]56--ππ .B 71[,]123--ππ .C 11[,]63-ππ .D 1[0,]2π9、一个几何体的三视图如图所示,该几何体外接球的 表面积为( ).A 9π .B 283π .C 8π .D 7π2正视图10、已知焦点在x 轴上的椭圆方程为222141x y a a +=-, 随着a 的增大该椭圆的形状( ).A 越接近于圆 .B 越扁.C 先接近于圆后越扁 .D 先越扁后接近于圆11、坐标平面上的点集S 满足2442{(,)|log (2)2sin 2cos [,]}84S x y x x y y y =-+=+∈,-ππ,将点集S 中的所有点向x 轴作投影,所得投影线段的长度为( ).A 1 .B.C.D 212.已知函数1ln 1)(-+=x x x f ,*)()(N k xkx g ∈=,若对任意的1c >,存在实数b a ,满足0a b <<c <,使得)()()(b g a f c f ==,则k 的最大值为( ).A 2 .B 3 .C 4 .D 5第Ⅱ卷 (非选择题)二、填空题(本题共4小题,每小题5分,共20分.将答案填入答题纸相应位置) 13、在ABC 中,3,2,30a b A === ,则cos B = .14.已知()f x 是定义在R 上周期为4的奇函数,当(0,2]x ∈时,2()2log x f x x =+,则(2015)f = .15、从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行 位置调换,则经过两次这样的调换后,甲在乙左边的概率是 . 16、如图所示,在O 中,AB 与CD 是夹角为60°的两条直径,,E F 分别是O 与直径CD 上的动点,若0OE BF OA OC λ⋅+⋅=,则λ的取值范围是________.三、解答题(共6小题,共70分;要求写出必要的文字说明,解题过程和演算步骤) 17、(本小题满分12分)某校随机调查了80位学生,以研究学生中爱好羽毛球运动与性别的关系,得到下面的数据表: (1)将此样本的频率估计为总体的概率,随机调查了本校的3名学生.设这3人中爱好羽毛球运动的人数为X ,求X 的分布列和期望值; (2)根据表中数据,能否有充分证据判定爱好羽毛球运动与性别有关联?若有,有多大把握?ABCDO EF附:22()()()()()n ad bc a b c d a c b d χ-=++++18、(本小题满分12分)已知数列{}n a 为等差数列,首项11a =,公差0d ≠.若123,,,,,n b b b b a a a a 成等比数列,且11b =,22b =,35b =.(1)求数列{}n b 的通项公式n b ;(2)设3(21)n n c log b =-,求和12233445212221n n n n n T c c c c c c c c c c c c -+=-+-+⋅⋅⋅+-.19、(本小题满分12分)在三棱柱111ABC A B C -中,侧面11ABB A 为矩形,2AB =,1AA =D 是1AA 的中点,BD 与1AB 交于点O ,且CO ⊥平面11ABB A . (1)证明:1BC AB ⊥;(2)若OC OA =,求直线CD 与平面ABC 所成角的正弦值.20、(本小题满分12分)已知抛物线2:2(0)C x py p =>的焦点为F ,过F 的直线l 交抛物线C 于点,A B ,当直线l 的倾斜角是45 时,AB 的中垂线交y 轴于点(0,5)Q . (1)求p 的值;(2)以AB 为直径的圆交x 轴于点,M N ,记劣弧 MN 的 长度为S ,当直线l 绕F 旋转时,求SAB的最大值.21、(本小题满分12分)已知函数()ln ln ,(),()au x x x x v x x a w x x=-=-=,(1)若()()u x v x ≥恒成立,满足条件的实数a 组成的集合为B ,试判断集合A 与B 的关系,并说明理由;(2)记()()[()()][()]2w x G x u x w x v x =--,是否存在m N *∈,使得对任意的实数(,)a m ∈+∞,函数()G x 有且仅有两个零点?若存在,求出满足条件的最小正整数m ;若不存在,说明理由.(以下数据供参考:1)0.8814e ≈≈ )请考生在第22、23、24题中任选一题做答,如果多做,则按所做第一题记分.在答题卡选答相交于点E .BA C1A1B1O(1) 求BD 长; (2)当CE ⊥OD 时,求证:AO AD =.AEODCB(2)过点M 平行于直线l 的直线与曲线C 交于,A B两点,若83MA MB ⋅=,求点M 轨迹的直角坐标方程. . (1)解不等式()5g x <;(2)若对任意1x R ∈,都有2x R ∈,使得12()()f x g x =成立,求实数a 的取值范围.江西省重点中学盟校2015届第一次联考数学(理)试卷答 案一、CDCAB CDBBA DB12、分析:易知()()g()f c g b c =>,即lnc 1c c kc c+>-lnc 1c c k c +∴<-,1c >. 令ln ()1c c c p c c +=-,1c >,则()()()()2211ln 1ln 2ln ()11c c c c c c cp c c c ++-----'==--令()2ln 1q c c c c =-->,,1'()10q c c=->, ()q c 递增,()(1)1q c q ∴>=-.又()31ln30q =-<,()42ln40q =->, ,∴存在()03,4c ∈,使得0()0q c =,即002ln c c -=当()01,c c ∈时,()0q c <,()p c 递减,当()0,c c ∈+∞时,()0q c >,()p c 递增.000min 00ln ()()1c c c p c p c c +==- 002ln c c -=代入得000000min 000ln (2)()11c c c c c c p c c c c ++-===-- 03k c k ∴<≤易知10a e<<,当3k =时可证明()()()f a g b g a =< max 3k ∴=. 二、13 14.-2 15. 23 16. [-16、解:设圆的半径为r ,以O 为原点,OB 为x 轴建立直角坐标系,则1(,0),(,)2B r C r 设(cos ,sin )E r r αα,(,)(11)2OF OC r r μ=μ=-≤μ≤ 212OA OC r λ⋅=- 2[(1)c o s s i n ]2OE BF r μ⋅=-αα (2)cos sin ∴λ=μ-αα )3λ[∴λ∈-三、17、解:(1)任一学生爱好羽毛球的概率为38,故X ~3(3,)8B ………………2分 0335125(0)()8512P XC === 12335225(1)()88512P X C ===22335135(2)()88512P X C === 333327(3)()8512P X C ===X 的分布列为39388EX =⨯=…………8分(2)2280(20201030)800.3556 2.70630503050225χ⨯-⨯==≈<⨯⨯⨯……………………10分 故没有充分证据判定爱好羽毛球运动与性别有关联. ……………………12分 18、解:(1)222152(1)1(14)12142=0a a a d d d d d d d =⋅⇒+=⨯+++=+⇒=或(舍去)1211, 3.3b b a a a q ===∴=……………………3分11(1)22113n n b n n a b b -=+-⨯=-=⨯ , 1312n n b -+∴=……………………6分 (2)3(21)n n c log b =-1n =- ……………………7分 213435657221()()()()n nn nT c c c c c c c c c c c c -+=-+-+-+⋅⋅⋅+- 2422()n c c c =-++⋅⋅⋅+22[135(21)]2n n =-+++⋅⋅⋅+-=-……………………12分19、解:(1)由题意tan AD ABD AB ∠==11tan 2AB AB B BB ∠==, 又0ABD <∠,12AB B π∠<,1ABD AB B ∴∠=∠,1112AB B BAB ABD BAB π∴∠+∠=∠+∠=,2AOB π∠=,1AB BD ∴⊥.又11CO ABB A ⊥平面,1ABCO ∴⊥, BD 与CO 交于点O ,1AB CBD ∴⊥平面,又BC CBD ⊂平面,1AB BC ∴⊥.…6分(2)如图,分别以1,,OD OB OC 所在直线为,,x y z 轴,以O 为坐标原点,建立如图所示的空间直角坐标系O xyz -,则(0,(A B,C D ,(AB AC CD === ,设平面ABC 的法向量为(,,)n x y z =,则00n AB n AC ⎧⋅=⎪⎨⋅=⎪⎩,即0033x y y x ⎧+=⎪⎪⎨⎪+=⎪⎩, 令1y =,则1z =-,x =,所以1)n =-. 设直线CD 与平面ABC 所成角为α,则1)sin cos ,||||CD n CD n CD n α⋅-⋅===⋅0((1)++⨯-==,所以直线CD 与平面ABC……………………12分 20、解:(1)(0,)2p F 当l 的倾斜角为45 时,l 的方程为2p y x =+ 设1122(,),(,)A x y B x y 222p y x x py ⎧=+⎪⎨⎪=⎩得2220x px p --=1212122,3x x p y y x x p p +=+=++= 得AB 中点为3(,)2D p p …………3分 AB 中垂线为3()2y p x p -=-- 0x =代入得552y p == 2p ∴=……6分 (2)设l 的方程为1y kx =+,代入24x y =得2440x kx --=212122()444AB y y k x x k =++=++=+ AB 中点为2(2,21)D k k +令2MDN ∠=α 122S AB AB =α⋅=α⋅ SAB∴=α…………8分 D 到x 轴的距离221DE k =+222211cos 1122222DE k k k AB +α===-++…………10分 当20k =时cos α取最小值12α的最大值为3π 故SAB的最大值为3π.……………………12分 21.解:(1)()1()()ln ln ().()ln ,1,u x v x a x x x x m x m x x x x'≥⇒≥-+==-∈+∞. 易知1()ln m x x x'=-在(1,)+∞上递减,()(1)1m x m ''∴<=…………6分 存在0(1,)x ∈+∞,使得0()0m x '=,函数()m x 在()01,x x ∈递增,在()0+x x ∈∞,递减0()a m x ≥. 由0()0m x '=得001ln x x =0000000111()11m x x x x x x x =-⋅+=+-> 1a ∴> B A ⊆……………………6分(2)()()()()ln ln ,()(),(1,)22a w x a f x u x w x x x x g x v x x a x x x=-=--=-=--∈+∞令. ①21()ln 10,(1,)af x x x x x '=+-+>∈+∞,由于(),1,(1)0,a m a f a ∈+∞⇒>=-< ,()x f x →+∞→+∞,由零点存在性定理可知:()1,,a ∀∈+∞函数()f x 在定义域内有且仅有一个零点……………………8分②2()10,(1,)2a g x x x '=+>∈+∞,3(1)10,2a g =-<,()x g x →+∞→+∞,同理可 知()1,,a ∀∈+∞函数()g x 在定义域内有且仅有一个零点……………………9分③假设存在0x 使得()()000f x g x ==,2000000ln ln 2a x x x x a x a x⎧=-⎪⎨-=⎪⎩消a 得002002ln 021x x x x -=-- 令22()ln 21x h x x x x =--- 222142()0(21)x h x x x x +'=+>-- ()h x ∴递增44132(2)ln 2ln 01)0.88140553h h e =-=<=->()01x ∴∈此时200001181,21125422x a x x x ⎛⎫==++-∈ ⎪⎛⎫⎝⎭++ ⎪⎝⎭所以满足条件的最小整数2m =……………………12分22、解:(1)∵OC =OD ,∴∠OCD =∠ODC ,∴∠OAC =∠ODB .∵∠BOD =∠A ,∴△OBD ∽△AOC . ∴ACODOC BD =, ∵OC =OD =6,AC =4,∴466=BD ,∴BD=9.……………………5分 (2)证明:∵OC =OE ,CE ⊥OD .∴∠COD =∠BOD =∠A .∴∠AOD =180º–∠A –∠ODC=180º–∠COD –∠OCD=∠ADO . ∴AD =AO ……………………10分23、解:(1)直线:l y x = 曲线22:12x C y +=……………………4分(2)设点()00,M x y 及过点M的直线为0102:x x l y y ⎧=+⎪⎪⎨⎪=+⎪⎩由直线1l 与曲线C 相交可得:222000032202t x y +++-= 220022883332x y MA MB +-⋅=⇒=,即:220026x y +=2226x y +=表示一椭圆……………………8分取y x m =+代入2212x y +=得:2234220x mx m ++-= 由0∆≥得m ≤≤故点M 的轨迹是椭圆2226x y +=夹在平行直线y x =10分 24.解(1)由125x -+<得5125x -<-+<713x ∴-<-< 得不等式的解为24x -<<……………………5分(2)因为任意1x R ∈,都有2x R ∈,使得12()()f x g x =成立, 所以{|()}{|()}y y f x y y g x =⊆=,又()223|(2)(23)||3|f x x a x x a x a =-++≥--+=+,()|1|22g x x =-+≥,所以|3|2a +≥,解得1a ≥-或5a ≤-,所以实数a 的取值范围为1a ≥-或5a ≤-.……………………10分。
2015届高考江西九校联合体数学(文)试卷

数学试卷(文)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}1,0,1A =-,集合{}124xB x =≤<,则A B I 等于 ( )A .{}1,0,1-B . {}1C .{}1,1-D .{}0,12.设i 是虚数单位,若复数201a aiz i+=>-,则a 的值为 ( ) A .0或1- B .0或1 C .1- D .13.已知命题00:R,sin p x x ∃∈=2:R,10q x x x ∀∈-+>.则下列结论正确的是( )A .命题是p q ∨假命题B . 命题是p q ∧真命题C .命题是()()p q ⌝∨⌝真命题D .命题是()()p q ⌝∧⌝真命题 4. ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2a =,b =,6A π=,则ABC∆的面积为( )A.B. C.D5.对于下列表格所示的五个散点,已知求得的线性回归方程为ˆ0.7671yx =-.则实数m A .6.8 B .7 C .7.2 D .7.46. 在区域⎩⎨⎧≤≤≤≤1010y x 内任意取一点),(y x P ,则122>+y x 的概率是( )A. 244π-B. 24π-C. 4πD.44π-7. 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为 ( )A.πB.2πC.3πD.4π8.执行如图的程序框图,如果输入的352log 2,log 2,log 3a b c ===,那么输出m 的值是 ( )A.5log 2B. 3log 2C.2log 3D.都有可能9. 已知函数①sin cos y x x =+,②cos y x x =,则下列结论正确的是( )A. 两个函数的图象均关于点(,0)4π-成中心对称B. 两个函数的图象均关于直线4x π=-对称C. 两个函数在区间(,)44ππ-上都是单调递增函数D. 可以将函数②的图像向左平移4π个单位得到函数①的图像10. 已知直角ABC ∆中,斜边6=AB ,D为线段AB 的中点,P 为线段CD 上任意一点,则()PA PB PC +⋅u u u r u u u r u u u r的最小值为( )A. 92 B. 92- C.2 D.2-11. 中心在原点,焦点在x 轴上的双曲线C ,直线l 与双曲线C 交于,A B 两点,线段AB 中点M 在第一象限,并且在抛物线22(0)y px p =>上,且M 到抛物线焦点的距离为p ,则直线l 的斜率为( )A . 2 B.32C.1 D.112. 设函数32()2ln f x x ex mxx =-+-,记,若函数()g x 至少存在一个零A B C二、填空题:本大题共4小题,每小题5分,共20分.13.曲线(2ln 1)y x x =-在点(1,1)-处的切线方程为 .14. 已知过双曲线22221x y a b-=右焦点且倾斜角为45︒的直线与双曲线右支有两个交点,则双曲线的离心率e 的取值范围是.15.设直线210x y -+=的倾斜角为α,则2cos sin 2αα+的值为 .16.已知函数()f x 为R 上的增函数,函数图像关于点(3,0)对称,若实数,x y 满足侧视图俯视图7题图8题图22(9)(2)0f x f y y -++-≤,则yx的取值范围是 .三、解答题:本大题共5小题,共60分. 解答应写出文字说明、证明过程或演算步骤.17. (本小题满分12分)已知{}n a 为等差数列,数列{}n b 满足对于任意N n *∈,点1(,)n n b b +在直线2y x =上,且112a b ==,22a b =.(1) 求数列{}n a 与数列{}n b 的通项公式;(2)若 nn na n cb n ⎧⎪=⎨⎪⎩为奇数,为偶数,求数列{}n c 的前2n 项的和2n S .18. (本小题满分12分)两会结束后,房价问题仍是国民关注的热点问题,某高校金融学一班的学生对某城市居民对房价的承受能力(如能买每平方米6千元的房子即承受能力为6千元)的调查作为社会实践,进行调查统计,将承受能力数据按区间[2.5,3.5),[3.5,4.5),[4.5,5.5),[5.5,6.5),[6.5,7.5](千元)进行分组,得到如下统计图:(1) 求a 的值,并估计该城市居民的平均承受能力是多少元;(2)若用分层抽样的方法,从承受能力在[3.5,4.5)与[5.5,6.5)的居民中抽取5人,在抽取的5人中随机取2人,求2人的承受能力不同的概率.19. (本小题满分12分)如图1,ABC ∆,4AB AC ==,23BAC π∠=,D 为BC 的中点,DE AC ⊥,沿DE 将CDE ∆折起至'C DE ∆,如图2,且'C 在面ABDE 上的投影恰好是E ,连接'C B ,M是'C B 上的点,且1'2C M MB =. (1)求证:AM ∥面'C DE ; (2)求三棱锥'C AMD -的体积.20. (本小题满分12分)设椭圆222:12x y M a +=(a >的右焦点为1F ,直线2:22-=a a x l 与x 轴交于点A ,若1120OF AF +=u u u r u u u r r(其中O 为坐标原点). (1)求椭圆M 的方程;(2)设P 是椭圆M 上的任意一点,EF 为圆()12:22=-+y x N 的任意一条直径(E 、F 为直径的两个端点),求⋅的最大值.21.(本小题满分12 (1)若函数)(x f 在),1(+∞上为减函数,求实数(2)若存在212,[,]x x e e ∈,使成立,求正实数a 的取值范围.请考生从第(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,作答时请用B 2铅笔在答题卡上将所选题号后的方框涂黑.22.(本小题满分10分)选修4-1:几何证明选讲 如图,在ABC ∆中,ο90=∠ABC ,以AB 为直径的圆O 交AC 于点E ,点D 是BC 边的中点,连接OD 交圆O 于点M .(1)求证:DE 是圆O 的切线;(2)求证:AB DM AC DM BC DE ⋅+⋅=⋅.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xoy 中,直线l 的参数方程为)(226222为参数t t y t x ⎪⎪⎩⎪⎪⎨⎧+=-=.在极坐标系(与直角坐标系xoy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为θρcos 10=.(1)求圆C 的直角坐标方程;(2)设圆C 与直线l 交于点B A 、,若点P 的坐标为)6,2(,求||||PB PA +.24.(本小题满分10分)选修4—5:不等式选讲已知函数()-|-2|f x m x =,R m ∈,且(2)0f x +≥的解集为[1,1]-. (1)求m 的值;AB CDE图1 图2 AB'C EDMAB CD EMO(2)若,,R a b c +∈ 23z a b c =++ 的最小值.。
高考数学2015江西十校联考数学(理)试题和答案

江西省重点中学盟校2015届第一次联考数学(理)试卷第Ⅰ卷(选择题 共60分)一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知集合101x M xx +⎧⎫=≥⎨⎬-⎩⎭,则R M =C ( ).A {}11x x -<< .B {}11x x -<≤ .C {}11x x x <-≥或 .D {}11x x x ≤-≥或2、已知11abi i=-+,其中,a b 是实数,i 是虚数单位,则||a bi -=( ) .A 3 .B 2 .C 5 .D 3、函数3y x =的图象在原点处的切线方程为( ).A y x = .B 0x = .C 0y = .D 不存在4、函数2lg(2)y x x a =-+的值域不可能是( ).A (,0]-∞ .B [0,)+∞ .C [1,)+∞ .D R5、实数,x y 满足10(2)(26)0x y x y x y -+≥⎧⎨--+≤⎩,若2t y x ≤+恒成立,则t 的取值范围是( ).A 13t ≤ .B 5t ≤- .C 13t ≤- .D 5t ≤ 6、如图是某算法的程序框图,则程序运行后输出的T 是( ).A 1 .B 2 .C 3 .D 47、已知12F F 、分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,过点2F 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ,若点M 在以线段12F F 为直径的圆外,则双曲线离心率的取值范围是( ).A .B )+∞ .C 2) .D (2,)+∞8、已知()3sin 2cos 2f x x a x =+,其中a 为常数.()f x 的图象关于直线6x =π对称,则()f x 在以下区间上是单调函数的是( ).A 31[,]56--ππ .B 71[,]123--ππ .C 11[,]63-ππ .D 1[0,]2π9、一个几何体的三视图如图所示,该几何体外接球的表面积为( ).A 9π .B 283π .C 8π .D 7π10、已知焦点在x 轴上的椭圆方程为222141x y a a +=-,2正视图随着a 的增大该椭圆的形状( ).A 越接近于圆 .B 越扁.C 先接近于圆后越扁 .D 先越扁后接近于圆11、坐标平面上的点集S 满足2442{(,)|log (2)2sin 2cos [,]}84S x y x x y y y =-+=+∈,-ππ,将点集S 中的所有点向x 轴作投影,所得投影线段的长度为( ).A 1 .B2.C.D 212.已知函数1ln 1)(-+=x x x f ,*)()(N k xkx g ∈=,若对任意的1c >,存在实数b a ,满足0a b <<c <,使得)()()(b g a f c f ==,则k 的最大值为( ).A 2 .B 3 .C 4 .D 5第Ⅱ卷 (非选择题)二、填空题(本题共4小题,每小题5分,共20分.将答案填入答题纸相应位置) 13、在ABC 中,3,2,30a b A ===,则cos B = .14.已知()f x 是定义在R 上周期为4的奇函数,当(0,2]x ∈时,2()2log xf x x =+,则(2015)f = .15、从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行 位置调换,则经过两次这样的调换后,甲在乙左边的概率是 . 16、如图所示,在O 中,AB 与CD 是夹角为60°的两条直径,,E F 分别是O 与直径CD 上的动点,若0OE BF OA OC λ⋅+⋅=,则λ的取值范围是________.三、解答题(共6小题,共70分;要求写出必要的文字说明,解题过程和演算步骤) 17、(本小题满分12分)某校随机调查了80位学生,以研究学生中爱好羽毛球运动与性别的关系,得到下面的数据表: (1)将此样本的频率估计为总体的概率,随机调查了本校的3名学生.设这3人中爱好羽毛球运动的人数为X ,求X 的分布列和期望值; (2)根据表中数据,能否有充分证据判定爱好羽毛球运动与性别有关联?若有,有多大把握? 附:2()()()()()n ad bc a b c d a c b d χ-=++++18、(本小题满分12分)ABCDO EF已知数列{}n a 为等差数列,首项11a =,公差0d ≠.若123,,,,,n b b b b a a a a 成等比数列,且11b =,22b =,35b =.(1)求数列{}n b 的通项公式n b ;(2)设3(21)n n c log b =-,求和12233445212221n n n n n T c c c c c c c c c c c c -+=-+-+⋅⋅⋅+-.19、(本小题满分12分)在三棱柱111ABC A B C -中,侧面11ABB A 为矩形,2AB =,1AA =D 是1AA 的中点,BD 与1AB 交于点O ,且CO ⊥平面11ABB A . (1)证明:1BC AB ⊥;(2)若OC OA =,求直线CD 与平面ABC 所成角的正弦值.20、(本小题满分12分)已知抛物线2:2(0)C x py p =>的焦点为F ,过F 的直线l 交抛物线C 于点,A B ,当直线l 的倾斜角是45时,AB 的中垂线交y 轴于点(0,5)Q . (1)求p 的值;(2)以AB 为直径的圆交x 轴于点,M N ,记劣弧MN 的长度为S ,当直线l 绕F 旋转时,求SAB的最大值.21、(本小题满分12分)已知函数()ln ln ,(),()au x x x x v x x a w x x=-=-=,(1)若()()u x v x ≥恒成立,满足条件的实数a 组成的集合为B ,试判断集合A 与B 的关系,并说明理由;(2)记()()[()()][()]2w x G x u x w x v x =--,是否存在m N *∈,使得对任意的实数(,)a m ∈+∞,函数()G x 有且仅有两个零点?若存在,求出满足条件的最小正整数m ;若不存在,说明理由.(以下数据供参考:1)0.8814e ≈≈ )请考生在第22、23、24题中任选一题做答,如果多做,则按所做第一题记分.在答题卡选答相交于点E . (1) 求BD 长; (2)当CE ⊥OD 时,求证:AO AD =.BA CD1A1B1OAEODCB(2)过点M 平行于直线l 的直线与曲线C 交于,A B 两点,若83MA MB ⋅=,求点M 轨迹的直角坐标方程.24、(本小题满分10分)选修4-5:不等式选讲. 已知函数()223,()12f x x a x g x x =-++=-+. (1)解不等式()5g x <;(2)若对任意1x R ∈,都有2x R ∈,使得12()()f x g x =成立,求实数a 的取值范围.江西省重点中学盟校2015届第一次联考数学(理)试卷答 案一、CDCAB CDBBA DB12、分析:易知()()g()f c g b c =>,即lnc 1c c kc c+>-lnc 1c c k c +∴<-,1c >. 令ln ()1c c cp c c +=-,1c >, 则()()()()2211ln 1ln 2ln ()11c c c c c c c p c c c ++-----'==--令()2ln 1q c c c c =-->,,1'()10q c c=->, ()q c 递增,()(1)1q c q ∴>=-.又()31ln30q =-<,()42ln 40q =->, ,∴存在()03,4c ∈,使得0()0q c =,即002ln c c -=当()01,c c ∈时,()0q c <,()p c 递减,当()0,c c ∈+∞时,()0q c >,()p c 递增.000min 00ln ()()1c c c p c p c c +==- 002ln c c -=代入得000000min 000ln (2)()11c c c c c c p c c c c ++-===-- 03k c k ∴<≤易知10a e<<,当3k =时可证明()()()f a g b g a =< max 3k ∴=. 二、13.3 14.-2 15. 2316. [- 16、解:设圆的半径为r ,以O 为原点,OB 为x 轴建立直角坐标系,则1(,0),(,)22B rC r r -设(cos ,sin )E r r αα,(,)(11)2OF OC r r μ=μ=-≤μ≤ 212OA OC r λ⋅=- 2[(1)c o s s i n]2OE BF r μ⋅=-αα (2)cos sin ∴λ=μ-αα )3λ[∴λ∈-三、17、解:(1)任一学生爱好羽毛球的概率为38,故X ~3(3,)8B ………………2分 0335125(0)()8512P XC ===12335225(1)()88512P X C === 22335135(2)()88512P X C ===333327(3)()8512P X C === X 的分布列为39388EX =⨯=…………8分(2)2280(20201030)800.3556 2.70630503050225χ⨯-⨯==≈<⨯⨯⨯……………………10分 故没有充分证据判定爱好羽毛球运动与性别有关联. ……………………12分 18、解:(1)222152(1)1(14)12142=0a a a d d d d d d d =⋅⇒+=⨯+++=+⇒=或(舍去)1211, 3.3b b a a a q ===∴=……………………3分11(1)22113n n b n n a b b -=+-⨯=-=⨯ , 1312n n b -+∴=……………………6分(2)3(21)n n c log b =-1n =- ……………………7分213435657221()()()()n nn nT c c c c c c c c c c c c -+=-+-+-+⋅⋅⋅+- 2422()n c c c =-++⋅⋅⋅+22[135(21)]2n n =-+++⋅⋅⋅+-=-……………………12分19、解:(1)由题意tan 2AD ABD AB ∠==,11tan AB AB B BB ∠==, 又0ABD <∠,12AB B π∠<,1ABD AB B ∴∠=∠,1112AB B BAB ABD BAB π∴∠+∠=∠+∠=,2AOB π∠=,1AB BD ∴⊥.又11CO ABB A ⊥平面,1AB CO ∴⊥,BD 与CO 交于点O ,1AB CBD ∴⊥平面,又BC CBD ⊂平面,1AB BC ∴⊥.…6分(2)如图,分别以1,,OD OB OC 所在直线为,,x y z 轴,以O 为坐标原点,建立如图所示的空间直角坐标系O xyz -,则(0,(A B,C D ,262323236(,,0),(0,,),(,0,333333AB AC CD =-==-, 设平面ABC 的法向量为(,,)n x yz =,则0n AB n AC ⎧⋅=⎪⎨⋅=⎪⎩,即00x y y x ⎧+=⎪⎪+=, 令1y =,则1z =-,2x=,所以(1)2n =-. 设直线CD 与平面ABC 所成角为α,则1)sincos ,||||CD nCD n CD n α⋅-⋅===⋅0((1)++-⨯-==,所以直线CD 与平面ABC 所成角的正弦值为5.……………………12分 20、解:(1)(0,)2p F 当l 的倾斜角为45时,l 的方程为2p y x =+ 设1122(,),(,)A x y B x y 222p y x x py ⎧=+⎪⎨⎪=⎩得2220x px p --=1212122,3x x p y y x x p p +=+=++= 得AB 中点为3(,)2D p p …………3分 AB 中垂线为3()2y p x p -=-- 0x =代入得552y p == 2p ∴=……6分 (2)设l 的方程为1y kx =+,代入24x y =得2440x kx --=212122()444AB y y k x x k =++=++=+ AB 中点为2(2,21)D k k +令2MDN ∠=α 122S AB AB =α⋅=α⋅ S AB∴=α…………8分 D 到x 轴的距离221DE k =+222211cos 1122222DE k k k AB +α===-++…………10分 当20k =时cos α取最小值12α的最大值为3π 故S AB的最大值为3π.……………………12分 21.解:(1)()1()()ln ln ().()ln ,1,u x v x a x x x x m x m x x x x'≥⇒≥-+==-∈+∞. 易知1()ln m x x x'=-在(1,)+∞上递减,()(1)1m x m ''∴<=…………6分 存在0(1,)x ∈+∞,使得0()0m x '=,函数()m x 在()01,x x ∈递增,在()0+x x ∈∞,递减0()a m x ≥. 由0()0m x '=得001ln x x =0000000111()11m x x x x x x x =-⋅+=+-> 1a ∴> B A ⊆……………………6分(2)()()()()ln ln ,()(),(1,)22a w x af x u x w x x x xg x v x x a x x x=-=--=-=--∈+∞令. ①21()ln 10,(1,)af x x x x x '=+-+>∈+∞,由于(),1,(1)0,a m a f a ∈+∞⇒>=-< ,()x f x →+∞→+∞,由零点存在性定理可知:()1,,a ∀∈+∞函数()f x 在定义域内有且仅有一个零点……………………8分②2()10,(1,)2a g x x x'=+>∈+∞,3(1)10,2ag =-<,()x g x →+∞→+∞,同理可 知()1,,a ∀∈+∞函数()g x 在定义域内有且仅有一个零点……………………9分③假设存在0x 使得()()000f x g x ==,2000000ln ln 2a x x x x a x a x⎧=-⎪⎨-=⎪⎩消a 得002002ln 021x x x x -=-- 令22()ln 21x h x x x x =--- 222142()0(21)x h x x x x +'=+>-- ()h x ∴递增44132(2)ln 2ln 01)0.88140553h h e =-=<=->()01x ∴∈此时200001181,21125422x a x x x ⎛⎫==++-∈ ⎪⎛⎫⎝⎭++ ⎪⎝⎭所以满足条件的最小整数2m =……………………12分22、解:(1)∵OC =OD ,∴∠OCD =∠ODC ,∴∠OAC =∠ODB .∵∠BOD =∠A ,∴△OBD ∽△AOC . ∴ACODOC BD =, ∵OC =OD =6,AC =4,∴466=BD ,∴BD=9.……………………5分 (2)证明:∵OC =OE ,CE ⊥OD .∴∠COD =∠BOD =∠A .∴∠AOD =180º–∠A –∠ODC=180º–∠COD –∠OCD=∠ADO . ∴AD =AO ……………………10分23、解:(1)直线:l y x = 曲线22:12x C y +=……………………4分 (2)设点()00,M x y 及过点M的直线为0102:2x x l y y ⎧=+⎪⎪⎨⎪=+⎪⎩由直线1l 与曲线C 相交可得:222000032202t x y +++-= 220022883332x y MA MB +-⋅=⇒=,即:220026x y += 2226x y +=表示一椭圆……………………8分取y x m =+代入2212x y +=得:2234220x mx m ++-= 由0∆≥得m ≤≤故点M 的轨迹是椭圆2226x y +=夹在平行直线y x =±10分24.解(1)由125x -+<得5125x -<-+<713x ∴-<-< 得不等式的解为24x -<<……………………5分(2)因为任意1x R ∈,都有2x R ∈,使得12()()f x g x =成立, 所以{|()}{|()}y y f x y y g x =⊆=,又()223|(2)(23)||3|f x x a x x a x a =-++≥--+=+,()|1|22g x x =-+≥,所以|3|2a +≥,解得1a ≥-或5a ≤-,所以实数a 的取值范围为1a ≥-或5a ≤-.……………………10分。
2015届高考江西九校联合体数学(理)参考答案

江西省重点中学协作体2015届高三第二次联考数学(理)答案一、选择题:1-5: C D DAB 6-10:BACDC 11-12: DA 二、填空题:13.160- 14.2- 15. π5 16. 6 三、解答题:17.解:由题意可得1)62sin(2)(+-=πx x f(1)226222πππππ+≤-≤-k x k所以增区间为: ]3,6[ππππ+-k k Z k ∈.………………………………………6分(2)由511)122(=+πA f 得53sin =A ;………………………………………7分1323)32(=+πB f 得1312sin ,135cos ==B B ;………………………………………8分 由于,<simB simA 131253==则54,=ℑ⇒∠A CO b a ……………………………10分所以6563)sin(sin =+=B A C .……………………………………………………12分 18.解:(1)取AC 中点O ,连结BO PO ,, PC PA =,BC AB =,∴AC OB AC OP ⊥⊥,,又 平面⊥APC 平面ABC ,∴ABC OP 面⊥………2分,OB OP ⊥,∴222PB OB OP =+,即1641622=-+-OC OC ,得2=OC ,则14,2,2===OP OB OA ,22=AC ,………4分∴22222121=⋅⋅=⋅⋅=∆OB AC S ABC . ∴31421423131=⋅⋅=⋅⋅=∆-OP S V ABC ABC P .……………………6分 (2)方法一 :分别以OP OC OB 、、为z y x 、、得)14,0,0(),0,2,0(),0,0,2(),0,2,0(),0,0,0(P C B A O -,………8分∴)0,2,2(-=,)14,0,2(-=,设平面PBC 的法向量),,(z y x =.由0,0=⋅=⋅得方程组⎪⎩⎪⎨⎧=+-=+-0142022z x y x ,取1=z ,得)1,7,7(=.10分)0,2,2(=AB ,∴15210152142||||,cos ==⋅>=<n AB n AB . 故直线AB 与平面PBC 所成角的正弦值为15210.……………………12分 方法二 :设点A 到平面PBC 的距离为d ,作H BC BC PH 于点交⊥, 则15142222=-=-=HC PC PH ,151522121=⨯⨯=⋅=∆PH BC S PBC ∴151423142153131=⇒=⋅⋅=⋅⋅⇒=∆--d d d S V V PBC PBC A ABC P ∴直线AB 与平面PBC 所成角的正弦值为15210152142==AB d . 19.解:(1)4086531811325==C C C P …………………………5分 (2)X 可能的取值为0、1、2、3408143)0(318313===C C X P 408195)1(31821315===C C C X P 40865)2(31811325===C C C X P 4085)3(31835===C C X P………10分65=EX ……………………………………………………12分20.解:(1)连接QF ,∵|QE |+|QF |=|QE |+|QP |=|PE |=4>|EF |=32, ∴动点Q 的轨迹是以)0,3(-E 、)0,3(F 为焦点,长轴长42=a 的椭圆,即动点Q 的轨迹方程为:1422=+y x ;…………………4分(2)依题结合图形知直线l 的斜率不为零,所以设直线l 的方程为n my x +=(R m ∈). ∵直线l 即0=--n my x 与圆O :122=+y x 相切,∴11||2=+m n 得122+=m n .(5分) 又∵点B A ,的坐标),(),,(2211y x y x 满足:⎩⎨⎧=-++=04422y x n my x , 消去x 整理得042)4(222=-+++n mny y m ,由韦达定理得42221+-=+m mny y ,442221+-=m n y y .…………………6分又 ||1||212y y m AB -⋅+=,点O 到直线l 的距离11||2=+=mn d ,∴||||21||121||2121212y y n y y m AB d S AOB -⋅=-⋅+⋅=⋅=∆ 222222)4(132)4(32++⋅=+⋅=m m m n………8分∵21212121))((y y n my n my y y x x OB OA +++=+=⋅=λ414445)()1(22222221212++=+--=++++=m m m m n n y y mn y y m . ∵3221≤≤λ,令12+=m t ,则]6,3[]32,21[3∈⇒∈+=t t t λ ∴69326932)3(32)4(13222222++=++⋅=+⋅=++⋅=∆tt tt t t t m m S AOB,…………………10分 ∵]121,272[691]227,12[69]227,12[69]215,6[9∈++⇒∈++⇒∈++⇒∈+tt t t t t t t ∴]1,322[∈∆AOB S ,∴AOB S ∆的取值范围为:]1,322[.…………………12分21.解:(1)x ae x f -=1)(',由题意知01)0('=-=a f 1=∴a .…………3分(2)由题意知:11x ae x = ① 22x ae x = ② 不妨设21x x <①-②得 )(2121x x e ea x x -=- 2121x x ee x x a --=∴ ③ …………5分 又)(2121x x e ea x x +=+,欲证221>+x x 只需证2)(21>+x x e e a ④联立③④得2))((212121>--+x x x x e e x x e e…………7分 即21))(1(212121>--+--x x x x e x x e ,令21x x t -= (0<t ) 则上式等价于21)1(>-+tt e te ,即02)2(>++-t t e t ⑤…………9分 令2)2()(++-=t t e t tϕ (0<t ) 1)1()('+-=t e t t ϕ,0)(''<=t te t ϕ )('t ϕ∴在)0,(-∞上单调递减,从而0)0(')('=>ϕϕt )(t ϕ∴在)0,(-∞上单调递增,从而0)0()(=<ϕϕt即⑤式成立,221>+∴x x ……………………………………………………12分 22.解:(1)证明:连接OA , OB OA =,∴OBA OAB ∠=∠. PA 与圆O 相切于点A ,∴ 90=∠OAP . ∴OAB PAC ∠-=∠ 90. OP OB ⊥, ∴OBA BCO ∠-=∠ 90. ∴PAC BCO ∠=∠.又PCABCO ∠=∠,∴PCA PAC ∠=∠.∴PC PA =.…………………5分(2)假设PO 与圆O 相交于点M ,延长PO 交圆O 于点N .PA 与圆O 相切于点A ,PMN 是圆O 的割线, ∴)()(2ON PO OM PO PN PM PA +⋅-=⋅=.5=PO ,3==ON OM ,∴16)35()35(2=+⨯-=PA . ∴4=PA .∴由(1)知4==PA PC . ∴1=OC .在OAP Rt ∆中,53cos ==∠OP OA AOP . NC ABPMO∴5325313219cos 2222=⨯⨯⨯-+=∠⋅⋅⋅-+=AOP OC OA OC OA AC . ∴5104532==AC .…………………10分 23.解:(1)由θρcos 10=得01022=-+x y x ,即25)5(22=+-y x .…………4分(2)将l 的参数方程代入圆C 的直角坐标方程,得25)226()223(22=++--t t . 即020292=++t t ,…………6分由于082204)29(2>=⨯-=∆,可设21,t t 是上述方程的两个实根.所以⎩⎨⎧=⋅-=+20292121t t t t ,又直线l 过点)6,2(P ,可得:29)()()(||||||||212121=+-=-+-=+=+t t t t t t PB PA .…………10分 24.解:(1)原不等式等价于即不等式的解集为}21|{≤≤-x x …………………5分 (2)4|)32()12(||32||12|=--+≥-++x x x x4|1|>-∴a 3a ∴<-或5a > …………………10分。
2015年江西高考理科数学样卷

2015年江西省高考 理科数学 模拟样卷注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2. 回答第Ⅰ卷时.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动.用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答且卡一并交回.第I 卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|05}A x x =<<,2{|230}B x x x =-->,则A B =R ð A . (0,3) B . (3,5) C . (1,0)- D .(0,3] 2.复数1i (0)z a a a a=+∈≠R 且对应的点在复平面内位于 A .第一、二象限 B .第一、三象限 C .第二、四象限 D .第三、四象限 3.命题“2,x x x ∀∈≠R ”的否定是A .2,x x x ∀∉≠R B .2,x x x ∀∈=R C . 2,x x x ∃∉≠R D .2,x x x ∃∈=R 4.已知函数2()f x x -=,3()tan g x x x =+,那么 A. ()()f x g x ⋅是奇函数 B. ()()f x g x ⋅是偶函数 C. ()()f x g x +是奇函数 D. ()()f x g x +是偶函数 5.已知等比数列{}n a 中,2109a a =,则57a a +A. 有最小值6B. 有最大值6C. 有最小值6或最大值6-D.有最大值6- 6.下列程序框图中,则输出的A 值是A .128B .129C .131D .1347.已知函数()sin()f x x ωϕ=+(0,2πωϕ><)的部分图像如图所示,则()y f x = 的图象可由cos 2y x = 的图象A .向右平移3π个长度单位 B .向左平移3π个长度单位 C .向右平移6π个长度单位 D .向左平移6π个长度单位8.已知抛物线:C 24y x =,那么过抛物线C 的焦点,长度为不超过 2015的整数的弦条数是A . 4024B . 4023C .2012D .2015 9.学校组织同学参加社会调查,某小组共有5名男同学,4名女同学。
2015年江西卷理科综合高考试卷(原卷 答案)

绝密★启用前2015年普通高等学校招生全国统一考试(江西卷)理科综合能力测试本试卷共40题,共300分。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列叙述错误..的是A.DNA与ATP中所含元素的种类相同B.一个tRNA分子中只有一个反密码子C.T2噬菌体的核酸由脱氧核糖核苷酸组成D.控制细菌性状的基因位于拟核和线粒体中的DNA上2. 下列关于植物生长素的叙述,错误..的是A.植物幼嫩叶片中的色氨酸可转变为生长素B.成熟茎韧皮部中的生长素可以进行非极性运输C.幼嫩细胞和成熟细胞对生长素的敏感程度相同D.豌豆幼苗切段中乙烯的合成受生长素浓度的影响3. 某同学给健康实验兔静脉滴注0.9%的NaCl溶液(生理盐水)20mL后,会出现的现象是A. 细胞内液和细胞外液分别增加10mLB.输入的溶液会从血浆进入组织液C.细胞内液Na+的增加远大于细胞外液Na+的增加D.输入的Na+中50%进入细胞内液,50%分布在细胞外液4. 下列关于初生演替中草本阶段和灌木阶段的叙述,正确的是A.草本阶段与灌木阶段群落的丰富度相同B.草本阶段比灌木阶段的群落空间结构复杂C.草本阶段比灌木阶段的群落自我调节能力强D.草本阶段为灌木阶段的群落形成创造了适宜环境5. 人或动物PrP基因编码一种蛋白(PrP c),该蛋白无致病性。
PrP c的空间结构改变后成为PrP Bc (朊粒),就具有了致病性。
2015年高考全国2卷理科数学试题及答案(精校word解析版)
【解析】程序在执行过程中, , 的值依次为 , ; ; ; ; ; ,此时 程序结束,输出 的值为2,故选B.
9.C
【解析】如图所示,当点C位于垂直于面 的直径端点时,三棱锥 的体积最大,设球 的半径为 ,此时 ,故 ,则球 的表面积为 ,故选C.
10.B
【解析】由已知得,当点 在 边上运动时,即 时, ;当点 在 边上运动时,即 时, ,当 时, ;当点 在 边上运动时,即 时, ,从点 的运动过程可以看出,轨迹关于直线 对称,且 ,且轨迹非线型,故选B.
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量与年份正相关
4.已知等比数列 满足a1=3, =21,则
A.21 B.42 C.63D.84
5.设函数 ,
A.3 B.6 C.9 D.12
6.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);
6.D
【解析】由三视图得,在正方体 中,截去四面体 ,如图所示,,设正方体棱长为 ,则 ,故剩余几何体体积为 ,所以截去部分体积与剩余部分体积的比值为 ,故选D.
7.C
【解析】由已知得 , ,所以 ,所以 ,即 为直角三角形,其外接圆圆心为 ,半径为 ,所以外接圆方程为 ,令 ,得 ,所以 ,故选C.
2015江西十校高考数学联考文科试题(带答案)

2015江西十校高考数学联考文科试题(带答案)江西省重点中学盟校2015届高三第一次联考高三数学(文)试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、要从已编号()的枚最新研制的某型导弹中随机抽取枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的7枚导弹的编号可能是() A. B. C. D. 2、已知R是实数集,M={x| 2x<1},N={y|y=x-1},则 = ( ) A.(1,2) B.[1,2] C.[1,2) D.[0,2] 3、已知等比数列中,,且,则=( ) A.12 B.1 C.2 D.14 4、如下图,边长为2的正方形中有一阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为23 .则阴影区域的面积为 ( ) A.43 B.83 C.23 D.无法计算 5、已知向量、的夹角为120°,且| |=1,|2 + |=,则| |=( ) A.32 B.22 C.4 D.2 6、复数与复数在复平面上的对应点分别是、,则等于( ) A. B. C. D. 7、双曲线的左焦点在抛物线的准线上,则该双曲线的离心率为( )A. B. C. D. 8、已知函数是偶函数,当x∈(1,+∞)时,函数,设=,,,则、、的大小关系为( ) A. < < B. < < C. < < D. < < 9、已知某几何体的三视图如图所示,三个视图都为直角三角形,其中主视图是以2为直角边的等腰直角三角形,则该几何体的外接球的表面积为( ) A. B. C. D. 10、若函数在其定义域上只有一个零点,则实数的取值范围是( ) A. >16 B.≥16 C. <16 D.≤16 11、下列命题中, 其中是假命题的为( ) ① 若是异面直线,且,则与不会平行;②函数的最小正周期是;③命题“∀∈R,函数f(x)=(x-1) +1恒过定点(1,1)”为真;④“命题为真”是“命题为真”的必要不充分条件;A.0个 B.1个 C.2个 D.3个 12、坐标平面上的点集S满足S= ,将点集S中的所有点向轴作投影,所得投影图形的长度为() A.1 B. C. D.2 第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答,第22题~第24题为选考题,考生根据要求做答。
2015年高考理科数学试题全国卷2及解析word完美版

2015年高考全国新课标卷Ⅱ理科数学真题一、选择题1、已知集合A={–2,–1,0,1,2},B={x|(x –1)(x+2)<0},则A∩B=() A .{–1,0} B .{0,1} C .{–1,0,1} D .{0,1,2}2、若a 为实数,且(2+ai)(a –2i)=–4i ,则a=() A .–1 B .0 C .1 D .23、根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图,以下结论中不正确的是()A .逐年比较,2008年减少二氧化硫排放量的效果最显着B .2007年我国治理二氧化硫排放显现成效C .2006年以来我国二氧化硫排放量呈减少趋势D .20064、已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则A .21 B .42 C .63 D .84 5、设函数f(x)=,则f(–2)+f(log 212)=() A .3 B .6 C .9 D .12 6.一个正方体被一个平面截去一部分后,分体积的比值为()A .B .C .D .7、过三点A .2 8、如上左2a=() A .0 9、已知A ,C 为该球上的动点,若三棱锥O –ABC 的体积最大值为36A .36π.256π10、如上左O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记∠BOP=x x 的函数,则y=f(x)的图像大致为()A .B .C .D . 11、已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为()A .B .2C .D .12、设函数f’(x)是奇函数f(x)(x R)的导函数,f(–1)=0,当x>0时,xf’(x)–f(x)<0,则使得f(x)>0成立的x 的取值范围是() A .(–∞,–1)∪(0,1) B .(,0)∪(1,+∞)C .(–∞,–1)∪(–1,0) D .(,1)∪(1,+∞) 二、填空题13、设向量a,b 不平行,向量λa+b 与a+2b 平行,则实数λ=. 14、若x ,y 满足约束条件,则z=x+y 的最大值为.15、(a+x)(1+x)4的展开式中x 的奇数次幂项的系数之和为32,则a=.16、设S n 是数列{a n }的前n 项和,且a 1=–1,a n+1=S n S n+1,则S n =________________. 三、解答题17、△ABC 中,D 是BC 上的点,AD 平分∠BAC,△ABD 面积是△ADC 面积的2倍. (1)求.(2)若AD=1,DC=,求BD 和AC 的长.18.某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机抽查了20个用户,得到用户对产品的满意度评分如下: A 地区:62738192958574645376 78869566977888827689B 地区:73836251914653736482 93486581745654766579(1)均值及分散程度(记事件C :“A 地区用户的满意等级高于B 19、如图,长方形ABCD –A 1B 1C 1D 1中,AB=16,BC=101F=4.过点E ,F 的平面α(1)在途中画出这个正方形(不必说明画法和理由(2)求直线AF 与α平面所成角的正弦值.20、已知椭圆C :9x 2+y 2=M 2(m>0).直线l A ,B ,线段AB 的中点为M .(1)(2)若l l 的21、设函数(1)证明:(2)2)|≤e –1,求m 的取值范围.22、[选修4ABC 内一点,⊙O 与△ABC 的底边BC 交于M ,N E ,F 两点. (1)(2)若AG EBCF 的面积. 23、[选修4xOy 中,曲线C 1:(t 为参数,t≠0),其中0≤α<π. 在以O C 2:ρ=2sinθ,C 3:ρ=2cosθ. (1)求C 2与C (2)若C 1与C 2相交于点A ,C 1与C 3相交于点B ,求|AB|的最大值24、[选修4–5:不等式选讲]设a ,b ,c ,d 均为正数,且a+b=c+d ,证明: (1)若ab>cd ,则+>+;(2)+>+是|a –b|<|c –d|的充要条件. 2015年高考全国新课标卷Ⅱ理科数学真题 一、选择题1、答案:A .∵(x–1)(x+2)<0,解得–2<x<1,∴B={x|–2<x<1},∴A∩B={–1,0}.2、答案:B .∵(2+ai)(a–2i)=(2a+2a)+(a 2–4)i=–4i ,∴a 2–4=–4,解得a=0.3、答案:D .由柱形图得,从2006年以来,我国二氧化硫排放量呈下降趋势,故年排放量与年份负相关.4、答案:B .∵a 1+a 3+a 5=a 1+a 1q 2+a1q 4=3(1+q 2+q 4)=21,∴1+q 2+q 4=7,整理得(q 2+3)(q 2–2)=0.解得q 2=2,∴a 3+a 5+a 7=a 1q 2+a 1q 4+a 1q 6=a 1q 2(1+q 2+q 4)=3×2×7=42. 5、答案:C .∵f(–2)=1+log 2(2+2)=3,()222log 121log 3log 412log 1222f -+-==222log 3log 2log 6226+===,∴f(–2)+f(log 212)=9.6、答案:D .如图所示截面为ABC ,设边长为a ,则截取部分体积为S △ADC ·|DB|=a 3, 所以截去部分体积与剩余部分体积的比值为=.7、答案:C .由题可得,解得,所以圆方程为x 2+y 2–2x+4y –20=0,令x=0,解得y=–2±2, 所以|MN|=|–2+2–(–2–2)|=4. 8、答案:B .输入a=14,b=18.第一步a≠b 成立,执行a>b ,不成立执行b=b –a=18–14=4; 第二步a≠b第三步a≠b 第四步a≠b 第四步a≠b 第五步a≠b 9、答案:C 点C 到平面10、答案:当点P 在CD 当x=时,从点P B . 11、答案:过点M 作, 12、答案:因为当x>0 又因为函数且g(–, 二、填空题131415、答案:所以Ca+Ca+C+C+C=32,解得a=3.16、答案:–.∵a n+1=S n+1–S n =S n S n+1,∴–=1.即–=–1,∴{}是等差数列, ∴=–(n –1)=–1–n+1=–n ,即S n =–. 三、解答题17、答案:(1);(2)|BD|=,|AC|=1.(1)如图,由题意可得S △ABD =|AB||AD|sin ∠BAD,S △ADC =|AC||AD|sin ∠CAD, ∵S △ABD =2S △ADC ,∠BAD=∠DAC,∴|AB |=2|AC|,∴==. (2)设BC 边上的高为h ,则S △ABD =|BD|·h=2S △ADC =2××h ,解得|BD|=,设|AC|=x ,|AB|=2x ,则cos ∠BAD=,cos ∠DAC=.∵cos∠DAC=cos ∠BAD ,∴=,解得x=1或x=–1(舍去).∴|AC|=1. 18、(1)如图所示.通过茎叶图可知A 地区的平均值比B 地区的高,A地区的分散程度大于B地区.(2)记事件不满意为事件A1,B1,满意为事件A2,B2,非常满意为事件A3,B3.则由题意可得P(A1)=,P(A2)=,P(A3)=,P(B1)=,P(B2)=,P(B3)=,则P(C)=P(A2)P(B1)+P(A3)(P(B1)+P(B2))=×+×(+)=.19、(1)如图所示(2)建立空间直角坐标系.由题意和(1)可得A(10,0,0),F(0,4,8),E(10,4,8),G(10,10,0),则向量AF=(–10,4,8),EF=(–10,0,0),EG=(0,6,–8).设平面EFHG的一个法向量为n=(x,y,z),则,即,解得x=0,令y=4,z=3,则n=(0,4,3).所以直线AF与α平面所成角的正弦值为sinθ=|cos<AF,n>|===.20、(1)设直线l的方程为y=kx+b(k≠0),点A(x1,y1),B(x2,y2),则M(,),联立方程,消去y整理得(9+k2)x2+2kbx+b2–m2=0(*),∴x1+x2=–,y1+y2=k(–)+2b=,∴kOM ·kAB=·k=·(–)·k=–9.k=4±,有21∴∴,所以此时当令e–m–2m 在而.当当22则∵.在在Rt△AEO中,sin∠OAE===.∴∠OAE=60°,∵∠OAE=∠OAF=∠EAF,AE=AF,∴∠EAF=2∠OAE=60°,∴△AEF、△ABC是等边三角形.连接OM,∴OM=2.∵OD⊥MN,∴MD=ND=MN=.在Rt△ODM中,OD===1,∴AD=OA+AD=4+1=5.在Rt△ADB中,AB===.∴四边形EBCF的面积为S△ABC –S△AEF=×()2–×(2)2=.23、(1)将曲线C2,C3化为直角坐标系方程C2:x2+y2–2y=0,C3:x2+y2–2x=0.联立,解得或.所以交点坐标为(0,0),(,).(2)曲线C1的极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤α<π.∵A的极坐标为(2sinα,α),B的极坐标为(2cosα,α).∴|AB|=|2sinα–2 cosα|=4|sin(α–)|.当α=时,|AB|取得最大值,最大值为4.24、(1)由题意可得(+)2=a+b+2,(+)2=c+d+2,∵ab>cd,∴>,而a+b=c+d,∴(+)2>(+)2,即+>+.(2)+>+,即a+b+2>c+d+2,∴>,∴ab>cd,∴–4ab<–4cd,∴(a+b)2–4ab<(c+d)2–4cd,∴(a–b)2<(c–d)2,∴|a–b|<|c–d|.。
2015年高考数学试卷真题附详细解析

2015年高考数学试卷一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(真题卷)数学(理科)1.(5分)(2015•真题)已知集合P={x|x2﹣2x≥0},Q={x|1<x≤2},则(∁R P)∩Q=()A .[0,1)B.(0,2]C.(1,2)D.[1,2]2.(5分)(2015•真题)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A .8cm3B.12cm3C.D.3.(5分)(2015•真题)已知{a n}是等差数列,公差d不为零,前n项和是S n,若a3,a4,a8成等比数列,则()A .a1d>0,dS4>0B.a1d<0,dS4<0C.a1d>0,dS4<0D.a1d<0,dS4>04.(5分)(2015•真题)命题“∀n∈N*,f(n)∈N*且f(n)≤n”的否定形式是()A.∀n∈N*,f(n)∉N*且f(n)>n B.∀n∈N*,f(n)∉N*或f(n)>nC.∂n0∈N*,f(n0)∉N*且f(n0)>n0D.∂n0∈N*,f(n0)∉N*或f(n0)>n05.(5分)(2015•真题)如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是()A .B.C.D.6.(5分)(2015•真题)设A,B是有限集,定义:d(A,B)=card(A∪B)﹣card(A∩B),其中card(A)表示有限集A中的元素个数()命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)A.命题①和命题②都成立B.命题①和命题②都不成立C.命题①成立,命题②不成立D.命题①不成立,命题②成立7.(5分)(2015•真题)存在函数f(x)满足,对任意x∈R都有()A .f(sin2x)=sinx B.f(sin2x)=x2+xC.f(x2+1)=|x+1| D.f(x2+2x)=|x+1|8.(5分)(2015•真题)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′﹣CD﹣B的平面角为α,则()A .∠A′DB≤αB.∠A′DB≥αC.∠A′CB≤αD.∠A′CB≥α二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)(2015•真题)双曲线=1的焦距是,渐近线方程是.10.(6分)(2015•真题)已知函数f(x)=,则f(f(﹣3))=,f(x)的最小值是.11.(6分)(2015•真题)函数f(x)=sin2x+sinxcosx+1的最小正周期是,单调递减区间是.12.(4分)(2015•真题)若a=log43,则2a+2﹣a=.13.(4分)(2015•真题)如图,三棱锥A﹣BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是.14.(4分)(2015•真题)若实数x,y满足x2+y2≤1,则|2x+y﹣2|+|6﹣x﹣3y|的最小值是.15.(6分)(2015•真题)已知是空间单位向量,,若空间向量满足,且对于任意x,y∈R,,则x0=,y0=,|=.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)(2015•真题)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A=,b2﹣a2=c2.(1)求tanC的值;(2)若△ABC的面积为3,求b的值.17.(15分)(2015•真题)如图,在三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求二面角A1﹣BD﹣B1的平面角的余弦值.18.(15分)(2015•真题)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[﹣1,1]上的最大值.(1)证明:当|a|≥2时,M(a,b)≥2;(2)当a,b满足M(a,b)≤2时,求|a|+|b|的最大值.19.(15分)(2015•真题)已知椭圆上两个不同的点A,B关于直线y=mx+对称.(1)求实数m的取值范围;(2)求△AOB面积的最大值(O为坐标原点).20.(15分)(2015•真题)已知数列{a n}满足a1=且a n+1=a n﹣a n2(n∈N*)(1)证明:1≤≤2(n∈N*);(2)设数列{a n2}的前n项和为S n,证明(n∈N*).高考数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(真题卷)数学(理科)1.(5分)考点:交、并、补集的混合运算.专题:集合.分析:求出P中不等式的解集确定出P,求出P补集与Q的交集即可.解答:解:由P中不等式变形得:x(x﹣2)≥0,解得:x≤0或x≥2,即P=(﹣∞,0]∪[2,+∞),∴∁R P=(0,2),∵Q=(1,2],∴(∁R P)∩Q=(1,2),故选:C.点评:此题考查了交、并、补集的混合运算,熟练掌握运算法则是解本题的关键.2.(5分)考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:判断几何体的形状,利用三视图的数据,求几何体的体积即可.解答:解:由三视图可知几何体是下部为棱长为2的正方体,上部是底面为边长2的正方形奥为2的正四棱锥,所求几何体的体积为:23+×2×2×2=.故选:C.点评:本题考查三视图与直观图的关系的判断,几何体的体积的求法,考查计算能力.3.(5分)考点:等差数列与等比数列的综合.专题:等差数列与等比数列.分析:由a3,a4,a8成等比数列,得到首项和公差的关系,即可判断a1d和dS4的符号.解答:解:设等差数列{a n}的首项为a1,则a3=a1+2d,a4=a1+3d,a8=a1+7d,由a3,a4,a8成等比数列,得,整理得:.∵d≠0,∴,∴,=<0.故选:B.点评:本题考查了等差数列和等比数列的性质,考查了等差数列的前n项和,是基础题.4.(5分)考点:命题的否定.专题:简易逻辑.分析:根据全称命题的否定是特称命题即可得到结论.解答:解:命题为全称命题,则命题的否定为:∂n0∈N*,f(n0)∉N*或f(n0)>n0,故选:D.点评:本题主要考查含有量词的命题的否定,比较基础.5.(5分)考点:直线与圆锥曲线的关系.专题:圆锥曲线的定义、性质与方程.分析:根据抛物线的定义,将三角形的面积关系转化为的关系进行求解即可.解答:解:如图所示,抛物线的准线DE的方程为x=﹣1,过A,B分别作AE⊥DE于E,交y轴于N,BD⊥DE于E,交y轴于M,由抛物线的定义知BF=BD,AF=AE,则|BM|=|BD|﹣1=|BF|﹣1,|AN|=|AE|﹣1=|AF|﹣1,则===,故选:A点评:本题主要考查三角形的面积关系,利用抛物线的定义进行转化是解决本题的关键.6.(5分)考点:复合命题的真假.专题:集合;简易逻辑.分析:命题①根据充要条件分充分性和必要性判断即可,③借助新定义,根据集合的运算,判断即可.解答:解:命题①:对任意有限集A,B,若“A≠B”,则A∪B≠A∩B,则card(A∪B)>card(A∩B),故“d(A,B)>0”成立,若d(A,B)>0”,则card(A∪B)>card(A∩B),则A∪B≠A∩B,故A≠B成立,故命题①成立,命题②,d(A,B)=card(A∪B)﹣card(A∩B),d(B,C)=card(B∪C)﹣card(B∩C),∴d(A,B)+d(B,C)=card(A∪B)﹣card(A∩B)+card(B∪C)﹣card(B∩C)=[card (A∪B)+card(B∪C)]﹣[card(A∩B)+card(B∩C)]≥card(A∪C)﹣card(A∩C)=d(A,C),故命题②成立,故选:A点评:本题考查了,元素和集合的关系,以及逻辑关系,分清集合之间的关系与各集合元素个数之间的关系,注意本题对充要条件的考查.集合的元素个数,体现两个集合的关系,但仅凭借元素个数不能判断集合间的关系,属于基础题.7.(5分)考点:函数解析式的求解及常用方法.专题:函数的性质及应用.分析:利用x取特殊值,通过函数的定义判断正误即可.解答:解:A.取x=0,则sin2x=0,∴f(0)=0;取x=,则sin2x=0,∴f(0)=1;∴f(0)=0,和1,不符合函数的定义;∴不存在函数f(x),对任意x∈R都有f(sin2x)=sinx;B.取x=0,则f(0)=0;取x=π,则f(0)=π2+π;∴f(0)有两个值,不符合函数的定义;∴该选项错误;C.取x=1,则f(2)=2,取x=﹣1,则f(2)=0;这样f(2)有两个值,不符合函数的定义;∴该选项错误;D.令|x+1|=t,t≥0,则f(t2﹣1)=t;令t2﹣1=x,则t=;∴;即存在函数f(x)=,对任意x∈R,都有f(x2+2x)=|x+1|;∴该选项正确.故选:D.点评:本题考查函数的定义的应用,基本知识的考查,但是思考问题解决问题的方法比较难.8.(5分)考点:二面角的平面角及求法.专题:创新题型;空间角.分析:解:画出图形,分AC=BC,AC≠BC两种情况讨论即可.解答:解:①当AC=BC时,∠A′DB=α;②当AC≠BC时,如图,点A′投影在AE上,α=∠A′OE,连结AA′,易得∠ADA′<∠AOA′,∴∠A′DB>∠A′OE,即∠A′DB>α综上所述,∠A′DB≥α,故选:B.点评:本题考查空间角的大小比较,注意解题方法的积累,属于中档题.二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)双曲线的简单性质.考点:计算题;圆锥曲线的定义、性质与方程.专题:确定双曲线中的几何量,即可求出焦距、渐近线方程.分析:解解:双曲线=1中,a=,b=1,c=,答:∴焦距是2c=2,渐近线方程是y=±x.故答案为:2;y=±x.本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.点评:10.(6分)函数的值.考点:计算题;函数的性质及应用.专题:分根据已知函数可先求f(﹣3)=1,然后代入可求f(f(﹣3));由于x≥1时,f(x)=,析:当x<1时,f(x)=lg(x2+1),分别求出每段函数的取值范围,即可求解解答:解:∵f(x)=,∴f(﹣3)=lg10=1,则f(f(﹣3))=f(1)=0,当x≥1时,f(x)=,即最小值,当x<1时,x2+1≥1,(x)=lg(x2+1)≥0最小值0,故f(x)的最小值是.故答案为:0;.本题主要考查了分段函数的函数值的求解,属于基础试题.点评:11.(6分)两角和与差的正弦函数;三角函数的周期性及其求法;正弦函数的单调性.考点:专三角函数的求值.题:分由三角函数公式化简可得f(x)=sin(2x﹣)+,易得最小正周期,解不等析:式2kπ+≤2x﹣≤2kπ+可得函数的单调递减区间.解答:解:化简可得f(x)=sin2x+sinxcosx+1=(1﹣cos2x)+sin2x+1=sin(2x﹣)+,∴原函数的最小正周期为T==π,由2kπ+≤2x﹣≤2kπ+可得kπ+≤x≤kπ+,∴函数的单调递减区间为[kπ+,kπ+](k∈Z)故答案为:π;[kπ+,kπ+](k∈Z)点评:本题考查三角函数的化简,涉及三角函数的周期性和单调性,属基础题.12.(4分)考点:对数的运算性质.专题:函数的性质及应用.分析:直接把a代入2a+2﹣a,然后利用对数的运算性质得答案.解答:解:∵a=log43,可知4a=3,即2a=,所以2a+2﹣a=+=.故答案为:.点评:本题考查对数的运算性质,是基础的计算题.13.(4分)考点:异面直线及其所成的角.专题:空间角.分析:连结ND,取ND 的中点为:E,连结ME说明异面直线AN,CM所成的角就是∠EMC 通过解三角形,求解即可.解答:解:连结ND,取ND 的中点为:E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC,∵AN=2,∴ME==EN,MC=2,又∵EN⊥NC,∴EC==,∴cos∠EMC===.故答案为:.点评:本题考查异面直线所成角的求法,考查空间想象能力以及计算能力.14.(4分)考点:函数的最值及其几何意义.专题:不等式的解法及应用;直线与圆.分析:根据所给x,y的范围,可得|6﹣x﹣3y|=6﹣x﹣3y,再讨论直线2x+y﹣2=0将圆x2+y2=1分成两部分,分别去绝对值,运用线性规划的知识,平移即可得到最小值.解答:解:由x2+y2≤1,可得6﹣x﹣3y>0,即|6﹣x﹣3y|=6﹣x﹣3y,如图直线2x+y﹣2=0将圆x2+y2=1分成两部分,在直线的上方(含直线),即有2x+y﹣2≥0,即|2+y﹣2|=2x+y﹣2,此时|2x+y﹣2|+|6﹣x﹣3y|=(2x+y﹣2)+(6﹣x﹣3y)=x﹣2y+4,利用线性规划可得在A(,)处取得最小值3;在直线的下方(含直线),即有2x+y﹣2≤0,即|2+y﹣2|=﹣(2x+y﹣2),此时|2x+y﹣2|+|6﹣x﹣3y|=﹣(2x+y﹣2)+(6﹣x﹣3y)=8﹣3x﹣4y,利用线性规划可得在A(,)处取得最小值3.综上可得,当x=,y=时,|2x+y﹣2|+|6﹣x﹣3y|的最小值为3.故答案为:3.点本题考查直线和圆的位置关系,主要考查二元函数在可行域内取得最值的方法,属于中档题.评:15.(6分)空间向量的数量积运算;平面向量数量积的运算.考点:专创新题型;空间向量及应用.题:分由题意和数量积的运算可得<•>=,不妨设=(,,0),=(1,0,0),析:由已知可解=(,,t),可得|﹣(|2=(x+)2+(y﹣2)2+t2,由题意可得当x=x0=1,y=y0=2时,(x+)2+(y﹣2)2+t2取最小值1,由模长公式可得|.解解:∵•=||||cos<•>=cos<•>=,答:∴<•>=,不妨设=(,,0),=(1,0,0),=(m,n,t),则由题意可知=m+n=2,=m=,解得m=,n=,∴=(,,t),∵﹣()=(﹣x﹣y,,t),∴|﹣(|2=(﹣x﹣y)2+()2+t2=x2+xy+y2﹣4x﹣5y+t2+7=(x+)2+(y﹣2)2+t2,由题意当x=x0=1,y=y0=2时,(x+)2+(y﹣2)2+t2取最小值1,此时t2=1,故|==2故答案为:1;2;2点本题考查空间向量的数量积,涉及向量的模长公式,属中档题.评:三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)余弦定理.考点:解三角形.专题:分(1)由余弦定理可得:,已知b2﹣a2=c2.可得,a=.利析:用余弦定理可得cosC.可得sinC=,即可得出tanC=.(2)由=×=3,可得c,即可得出b.解解:(1)∵A=,∴由余弦定理可得:,∴b2﹣a2=bc﹣c2,答:又b2﹣a2=c2.∴bc﹣c2=c2.∴b=c.可得,∴a2=b2﹣=,即a=.∴cosC===.∵C∈(0,π),∴sinC==.∴tanC==2.(2)∵=×=3,解得c=2.∴=3.点评:本题考查了正弦定理余弦定理、同角三角形基本关系式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.17.(15分)考点:二面角的平面角及求法;直线与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(1)以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系,通过•=•=0及线面垂直的判定定理即得结论;(2)所求值即为平面A1BD的法向量与平面B1BD的法向量的夹角的余弦值的绝对值的相反数,计算即可.解答:(1)证明:如图,以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系.则BC=AC=2,A1O==,易知A1(0,0,),B(,0,0),C(﹣,0,0),A(0,,0),D(0,﹣,),B1(,﹣,),=(0,﹣,0),=(﹣,﹣,),=(﹣,0,0),=(﹣2,0,0),=(0,0,),∵•=0,∴A1D⊥OA1,又∵•=0,∴A1D⊥BC,又∵OA1∩BC=O,∴A1D⊥平面A1BC;(2)解:设平面A1BD的法向量为=(x,y,z),由,得,取z=1,得=(,0,1),设平面B1BD的法向量为=(x,y,z),由,得,取z=1,得=(0,,1),∴cos<,>===,又∵该二面角为钝角,∴二面角A1﹣BD﹣B1的平面角的余弦值为﹣.点评:本题考查空间中线面垂直的判定定理,考查求二面角的三角函数值,注意解题方法的积累,属于中档题.18.(15分)考点:二次函数在闭区间上的最值.专题:函数的性质及应用.分析:(1)明确二次函数的对称轴,区间的端点值,由a的范围明确函数的单调性,结合已知以及三角不等式变形所求得到证明;(2)讨论a=b=0以及分析M(a,b)≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1,进一步求出|a|+|b|的求值.解答:解:(1)由已知可得f(1)=1+a+b,f(﹣1)=1﹣a+b,对称轴为x=﹣,因为|a|≥2,所以或≥1,所以函数f(x)在[﹣1,1]上单调,所以M(a,b)=max{|f(1),|f(﹣1)|}=max{|1+a+b|,|1﹣a+b|},所以M(a,b)≥(|1+a+b|+|1﹣a+b|)≥|(1+a+b)﹣(1﹣a+b)|≥|2a|≥2;(2)当a=b=0时,|a|+|b|=0又|a|+|b|≥0,所以0为最小值,符合题意;又对任意x∈[﹣1,1].有﹣2≤x2+ax+b≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1,易知|a|+|b|=max{|a﹣b|,|a+b|}=3,在b=﹣1,a=2时符合题意,所以|a|+|b|的最大值为3.点评:本题考查了二次函数闭区间上的最值求法;解答本题的关键是正确理解M(a,b)是|f(x)|在区间[﹣1,1]上的最大值,以及利用三角不等式变形.19.(15分)考点:直线与圆锥曲线的关系.专题:创新题型;圆锥曲线中的最值与范围问题.分析:(1)由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程可得(m2+2)y2﹣2mny+n2﹣2=0,设A(x1,y1),B(x2,y2).可得△>0,设线段AB的中点P(x0,y0),利用中点坐标公式及其根与系数的可得P,代入直线y=mx+,可得,代入△>0,即可解出.(2)直线AB与x轴交点横坐标为n,可得S△OAB=,再利用均值不等式即可得出.解答:解:(1)由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程,可得(m2+2)y2﹣2mny+n2﹣2=0,设A(x1,y1),B(x2,y2).由题意,△=4m2n2﹣4(m2+2)(n2﹣2)=8(m2﹣n2+2)>0,设线段AB的中点P(x0,y0),则.x0=﹣m×+n=,由于点P在直线y=mx+上,∴=+,∴,代入△>0,可得3m4+4m2﹣4>0,解得m2,∴或m.(2)直线AB与x轴交点纵坐标为n,∴S△OAB==|n|•=,由均值不等式可得:n2(m2﹣n2+2)=,∴S△AOB=,当且仅当n2=m2﹣n2+2,即2n2=m2+2,又∵,解得m=,当且仅当m=时,S△AOB取得最大值为.点评:本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段垂直平分线的性质、三角形面积计算公式、弦长公式、均值不等式的性质,考查了推理能力与计算能力,属于难题.20.(15分)考点:数列的求和;数列与不等式的综合.专题:创新题型;点列、递归数列与数学归纳法.分析:(1)通过题意易得0<a n≤(n∈N*),利用a n﹣a n+1=可得≥1,利用==≤2,即得结论;(2)通过=a n﹣a n+1累加得S n=﹣a n+1,利用数学归纳法可证明≥a n≥(n≥2),从而≥≥,化简即得结论.解答:证明:(1)由题意可知:0<a n≤(n∈N*),又∵a2=a1﹣=,∴==2,又∵a n﹣a n+1=,∴a n>a n+1,∴≥1,∴==≤2,∴1≤≤2(n∈N*);(2)由已知,=a n﹣a n+1,=a n﹣1﹣a n,…,=a1﹣a2,累加,得S n=++…+=a1﹣a n+1=﹣a n+1,易知当n=1时,要证式子显然成立;当n≥2时,=.下面证明:≥a n≥(n≥2).易知当n=2时成立,假设当n=k时也成立,则a k+1=﹣+,由二次函数单调性知:a n+1≥﹣+=≥,a n+1≤﹣+=≤,∴≤≤,即当n=k+1时仍然成立,故对n≥2,均有≥a n≥,∴=≥≥=,即(n∈N*).点评:本题是一道数列与不等式的综合题,考查数学归纳法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.。
2015年江西省高考 .doc

2015年江西省高考 文科数学 模拟样卷注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2. 回答第Ⅰ卷时.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动.用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3.回答第Ⅱ卷时.将答案写在答题卡上.写在本试卷上无效.4.考试结束后.将本试卷和答且卡一并交回.第I 卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|05}A x x =<<,2{|230}B x x x =-->,则AB =R ðA. (0,3)B. (3,5)C. (1,0)-D.(0,3]2.复数1(i)(0)z a a a a=+∈≠R 且对应的点在复平面内位于A .第一、二象限B .第一、四象限C .第二、四象限D .第二、三象限 3.命题“2,x x x ∀∈≠R ”的否定是A .2,x x x ∀∉≠R B .2,x x x ∀∈=R C . 2,x x x ∃∉≠R D .2,x x x ∃∈=R4.已知函数2()f x x -=,3()tan g x x x =+,那么A. ()()f x g x ⋅是奇函数B. ()()f x g x ⋅是偶函数C. ()()f x g x +是奇函数D. ()()f x g x +是偶函数 5.已知等比数列{}n a 中,2109a a =,则57a a +A. 有最小值6B. 有最大值6C. 有最小值6或最大值-6D.有最大值-6 6.下列程序框图中,则输出的A 的值是A .128B .129C .131D .1347.已知数列{}n a 中,122,8a a ==,数列1{2}n n a a +-是公比为2的等比数列,则下列判断正确的是A. {}n a 是等差数列B. {}n a 是等比数列C. {}2n n a 是等差数列 D. {}2nna 是等比数列 8.已知抛物线:C 24y x =,那么过抛物线C 的焦点,长度为整数且不超过2015的弦的条数是A . 4024B . 4023C .2012D .2015 9.已知函数()sin()f x x ωϕ=+(0,2πωϕ><)的部分图像如图所示,则()y f x = 的图象可由cos 2y x = 的图象A .向右平移3π个长度单位B .向左平移3π个长度单位C .向右平移6π个长度单位D .向左平移6π个长度单位10.已知函数1()ln 2xf x x =-(),若实数x 0满足01188()log sinlog cos88f x ππ>+,则0x 的取值范围是A .(,1)-∞B .(0,1)C .(1,)+∞D .1(,)2+∞11.已知函数232,31,()1ln ,13x x x f x x x ⎧-+--≤≤⎪=⎨<≤⎪⎩,若()|()|g x ax f x =-的图像与x 轴有3个不同的交点,则实数a 的取值范围是A. ln 31[,)3eB. 1(0,)2eC. 1(0,)eD. ln 31[,)32e12.某几何体三视图如图所示,则该几何体的体积为 A .23 B .1 C .43 D .32第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22-2正视图侧视图俯视图ABCD A 1B 1C 1第24题为选考题,考生根据要求作答. 二.填空题:本大题共4小题,每小题5分.13. 已知回归直线斜率的估计值为2,样本点的中心为点(4,5),则回归直线的方程为 . 14.已知=a,)k =b ,且a 与b 的夹角为3π,则k = . 15.若变量y x ,满足约束条件1,,3215x y x x y ≥⎧⎪≥⎨⎪+≤⎩,则42x yw =⋅的最大值是 .16.对椭圆有结论一:椭圆2222:1(0)x y C a b a b +=>>的右焦点为(,0)F c ,过点2(,0)a P c的直线l交椭圆于,M N 两点,点M 关于x 轴的对称点为'M ,则直线'M N 过点F .类比该结论,对双曲线有结论二,根据结论二知道:双曲线22':13x C y -=的右焦点为F ,过点3(,0)2P 的直线与双曲线'C 右支有两交点,M N ,若点N的坐标是,则在直线NF 与双曲线的另一个交点坐标是__________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知函数2()sin cos sin f x a x x b x =+,x R ∈,且()112f π=,()16f π=. (Ⅰ)求函数()f x 的单调递增区间; (Ⅱ)若3()25f α=,(,)3παπ∈-,求sin α的值. 18.某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如下茎叶图(单位:cm ).男队员身高在180cm 以上定义为“高个子”,女队员身高在170cm 以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.(Ⅰ)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;(Ⅱ)求这5名队员中,恰好男女“高个子”各1名队员的概率.19.(本小题满分12分)如图,已知在直三棱柱111ABC A B C -中, 12AB AA ==,3ACB π∠=,点D 是线段BC 的中点.(Ⅰ)求证:1A C ∥平面1AB D ;(Ⅱ)当三棱柱111ABC A B C -的体积最大时,求三棱锥11A AB D -的体积.20.(本小题满分12分)FED CBA已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别是12(1,0),(1,0)F F -,直线l 的方程是4x =,点P 是椭圆C 上动点(不在x 轴上),过点2F 作直线2PF 的垂线交直线l 于点Q ,当1PF 垂直x 轴时,点Q 的坐标是(4,4). (Ⅰ)求椭圆C 的方程;(Ⅱ)判断点P 运动时,直线PQ 与椭圆C 的公共点个数,并证明你的结论. 21.(本小题满分12分) 已知函数ln ()a x bf x x+=(其中0a <),函数()f x 在点(1,(1))f 处的切线过点(3,0). (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若函数()f x 与函数2()2g x a x x=+--的图像在(0,2]有且只有一个交点,求实数a 的取值范围.请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分, 做答时请写清题号.22.(本小题满分10分)选修41-:几何证明选讲如图,圆内接四边形ABCD 的边BC 与AD 的延长线交于点E ,点F 在BA 的延长线上. (Ⅰ)若21,31==EA ED EB EC ,求ABDC的值; (Ⅱ)若CD EF //,证明:FB FA EF ⋅=2.23.(本小题满分10分)选修44-;坐标系与参数方程在直角坐标系xoy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:24cos 20ρρθ-+=. (Ⅰ)将极坐标方程化为普通方程;(Ⅱ)若点P (x ,y )在该圆上,求x +y 的最大值和最小值. 24.(本小题满分10分)选修45-:不等式选讲 已知函数()||f x x =,()|4|g x x m =--+ (Ⅰ)解关于x 的不等式[()]20g f x m +->;(Ⅱ)若函数()f x 的图像在函数()g x 图像的上方,求实数m 的取值范围.。
