2014年春季学期新版新人教版七年级数学下册9.1.2不等式的性质同步试卷3
人教版七年级下册数学 9.1.2不等式及性质 同步练习(含答案)

9.1.2不等式及其性质 同步练习一、选择题1. 在式子﹣3<0,x≥2,x=a ,x 2﹣2x ,x≠3,x+1>y 中,是不等式的有( )A .2个B .3个C .4个D .5个2.下列不等式表示正确的是( ).A .a 不是负数表示为a >0B .x 不大于5可表示为x >5C .x 与1的和是非负数可表示为x+1>0D .m 与4的差是负数可表示为m-4<03.式子“①x+y=1;②x >y ;③x+2y ;④x-y≥1;⑤x <0”属于不等式的有( )A .2个B .3个C .4个D .5个4.已知a <b ,则下列不等式一定成立的是( )A .a+3>b+3B .2a >2bC .-a <-bD .a-b <05.若图示的两架天平都保持平衡,则对a 、b 、c 三种物体的重量判断正确的是( ).A.a>cB.a<cC.a<bD.b<c6.下列变形中,错误的是( ).A .若3a+5>2,则3a >2-5B .若213x ->,则23x <- C .若115x -<,则x >-5 D .若1115x >,则511x > 二、填空题7.如果a <b ,则﹣3a ﹣3b (用“>”或“<”填空).8.用不等式表示“x 与a 的平方差不是正数”为 .9.在-l ,12-,0,23,2中,能使不等式5x >3x+3成立的x 的值是________;________是不等式-x >0的解.10.假设a >b ,请用“>”或“<”填空(1)a-1________b-1; (2)2a______2b ;(3)12a -_______12b -; (4)a+l________b+1. 11.已知a >b ,且c≠0,用“>”或“<”填空. (1)2a________a+b (2)2a c _______2b c (3)c-a_______c-b (4)-a|c|_______-b|c|12. k 的值大于-1且不大于3,则用不等式表示k 的取值范围是_______.(使用形如a≤x≤b 的类似式子填空.)13.现有不等式的性质:①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等式的方向改变.请解决以下两个问题:(1)利用性质①比较2a与a的大小(a≠0);(2)利用性质②比较2a与a的大小(a≠0).14. ①当a=3,b=5时用不等式表示a2+b2与2ab的大小是_______;②当a=-3,b=5时用不等式表示a2+b2与2ab的大小是__________;③当a=1,b=1时用不等式表示a2+b2与2ab的大小是________;④根据上述数学实验你猜想a2+b2与2ab的大小关系_______;⑤用a、b的其他值检验你的猜想______.15.已知x<y,比较下列各对数的大小.(1)8x-3和8y-3;(2)516x-+和516y-+;(3) x-2和y-1.一、选择题1. 【答案】C;【解析】解:﹣3<0是不等式,x≥2是不等式,x=a是等式,x2﹣2x是代数式,x≠3是不等式,x+1>y是不等式.不等式共有4个.故选C.2. 【答案】D;【解析】a不是负数应表示为a≥0,故A错误;x不大于5应表示为x≤5,故B错误;x与1的和是非负数应表示为x+1≥0,故C错误;m与4的差是负数应表示为m-4<0,故D正确。
9.1.2 不等式的性质 同步练习(含答案)数学人教版七年级下册

9.1.2 不等式的性质一、选择题1.已知a ,b ,c ,d 是实数,若a >b ,c =d ,则( )A .a +c>b +dB .a +b>c +dC .a +c>b -dD .a +b>c -d2.若m >n ,则下列不等式中正确的是( )A .m -2<n -2B .-12 m>-12 nC .n -m >0D .1-2m<1-2n3.利用不等式的性质可得不等式4x<3x +2的解集是( )A .x >-2B .x<-2C .x >2D .x<24.把不等式x -1<2的解集在数轴上表示出来,正确的是( )5.已知a >b ,则一定有-4a□-4b ,“□”中应填的符号是( )A .>B .<C .≥D .=6.小明的作业本上有四道利用不等式的性质解不等式的作业题:①由x +7>8解得x >1;②由x <2x +3解得x <3;③由3x -1>x +7解得x >4;④由-3x >-6解得x <-2.其中正确的有( )A .1题B .2题C .3题D .4题7.若a >b ,am <bm ,则一定有( )A .m =0B .m <0C .m >0D .m 为任何实数8.若a>b ,则下列不等式中正确的是( )A .a -1<b -1B .-3a <-3bC .5a<5bD .-2-a >-2-b9.下列说法中错误的是( )A .若a <b ,则a +2024<b +2024B .若-2024a >-2024b ,则a <bC .若a<b ,则ac<bcD .若a(c 2+1)<b(c 2+1),则a<b二、填空题10.若a -b <c -b ,则a_____c.(填“>”“<”或“=”)11.若关于x 的不等式x -n≥-1的解集如图所示,则n 等于 ____.12.如果点P(2n ,1-2m)在第四象限,那么m ,n 的取值范围分别是____________.13.如果不等式(b +1)x <b +1的解集是x >1,那么b 的范围是_________.三、解答题14.利用不等式的性质解下列不等式,并在数轴上表示解集:(1)3x≤5x -2; (2)2x -14 <1-x.15.判断命题“如果a >b ,那么5-2a <5-2b”是否正确,如果不正确,请说明理由;如果正确,说明变形的过程和依据.16.甲从一个鱼摊上买了三条鱼,平均每条a 元,又从另一个鱼摊上买了两条鱼,平均每条b 元,后来他又转手以每条a +b 2 的价格全部卖给了乙,结果发现赔了钱,你知道为什么吗?17.先阅读下面解题过程,然后解题.已知a >b ,试比较-2 024a +1与-2 024b +1的大小.解:因为a >b ,所以-2 024a >-2 024b.①故-2 024a +1>-2 024b +1.②(1)上述解题过程中,从第____步开始出现错误;(2)错误的原因是什么?(3)请写出正确的解题过程.18.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若a -b >0,则a >b ;若a -b =0,则a =b ;若a -b <0,则a <b .反之也成立.这种比较大小的方法称为“求差法比较大小”.请运用这种方法尝试解决下面的问题:(1)比较4+3a 2-2b +b 2与3a 2-2b +1的大小;(2)若2a +2b -1>3a +b ,请求出a 与b 的大小关系.参考答案一、选择题1.已知a ,b ,c ,d 是实数,若a >b ,c =d ,则( A )A .a +c>b +dB .a +b>c +dC .a +c>b -dD .a +b>c -d2.若m >n ,则下列不等式中正确的是( D )A .m -2<n -2B .-12 m>-12 nC .n -m >0D .1-2m<1-2n3.利用不等式的性质可得不等式4x<3x +2的解集是( D )A .x >-2B .x<-2C .x >2D .x<24.把不等式x -1<2的解集在数轴上表示出来,正确的是( D )5.已知a >b ,则一定有-4a□-4b ,“□”中应填的符号是( B )A .>B .<C .≥D .=6.小明的作业本上有四道利用不等式的性质解不等式的作业题:①由x +7>8解得x >1;②由x <2x +3解得x <3;③由3x -1>x +7解得x >4;④由-3x >-6解得x <-2.其中正确的有( B )A .1题B .2题C .3题D .4题7.若a >b ,am <bm ,则一定有( B )A .m =0B .m <0C .m >0D .m 为任何实数8.若a>b ,则下列不等式中正确的是( B )A .a -1<b -1B .-3a <-3bC .5a<5bD .-2-a >-2-b9.下列说法中错误的是( C )A .若a <b ,则a +2024<b +2024B .若-2024a >-2024b ,则a <bC .若a<b ,则ac<bcD .若a(c 2+1)<b(c 2+1),则a<b二、填空题10.若a -b <c -b ,则a_____c.(填“>”“<”或“=”)【答案】<11.若关于x 的不等式x -n≥-1的解集如图所示,则n 等于 ____.【答案】312.如果点P(2n ,1-2m)在第四象限,那么m ,n 的取值范围分别是____________.【答案】m >12 ,n >013.如果不等式(b +1)x <b +1的解集是x >1,那么b 的范围是_________.【答案】b <-1三、解答题14.利用不等式的性质解下列不等式,并在数轴上表示解集:(1)3x≤5x -2; (2)2x -14 <1-x.解:x≥1,数轴略 解:x <56 ,数轴略15.判断命题“如果a >b ,那么5-2a <5-2b”是否正确,如果不正确,请说明理由;如果正确,说明变形的过程和依据.解:命题是正确的.∵a >b ,∴-2a <-2b(不等式的性质3),∴-2a +5<-2b +5(不等式的性质1),即5-2a <5-2b16.甲从一个鱼摊上买了三条鱼,平均每条a 元,又从另一个鱼摊上买了两条鱼,平均每条b 元,后来他又转手以每条a +b 2 的价格全部卖给了乙,结果发现赔了钱,你知道为什么吗?解:由题意得a +b 2 ×5-(3a +2b)<0,∴b <a ,∵甲从第一个鱼摊买的鱼比从第二个鱼摊买的鱼贵,∴他后来赔了17.先阅读下面解题过程,然后解题.已知a >b ,试比较-2 024a +1与-2 024b +1的大小.解:因为a >b ,所以-2 024a >-2 024b.①故-2 024a +1>-2 024b +1.②(1)上述解题过程中,从第__①__步开始出现错误;(2)错误的原因是什么?(3)请写出正确的解题过程.解:(2)不等式两边乘同一个负数,不等号的方向要改变.(3)因为a >b ,所以-2 024a <-2 024b ,故-2 024a +1<-2 024b +1.18.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若a -b >0,则a >b ;若a -b =0,则a =b ;若a -b <0,则a <b .反之也成立.这种比较大小的方法称为“求差法比较大小”.请运用这种方法尝试解决下面的问题:(1)比较4+3a 2-2b +b 2与3a 2-2b +1的大小;(2)若2a +2b -1>3a +b ,请求出a 与b 的大小关系.解:(1)∵4+3a 2-2b +b 2-(3a 2-2b +1)=b 2+3>0,∴4+3a 2-2b +b 2>3a 2-2b +1.(2)不等式两边同时减(3a+b),得-a+b-1>0,∴b-a>1>0,∴a<b.。
9.1.2不等式的性质课课练习及答案(新人教版七年级下)pdf版

不等式两边加 或减 同一个数 或式子 不等号的方向不变.
( ) ( ),
不等式的性质
9ư1ư2
.掌握不等式的基本性质 体会不等式与等式性质的联系与区别.
1 ,
C. < D. >
. 2012Ű贵州六盘水 已知不等式x 则此不等式的解集在数轴上表示为 .
12 ( ) -1≥0, ( )
.若a b 则下列各式中一定成立的是 .
4 < , ( )
a b
a b
6 (1) <2 (2) < ,
4
. .m 1
7 C 8 <-
2
, !
. 2012Ű广东广州 已知a b 若c是任意实数 则下列不等式中总是成立的是 .
11 ( ) > , , ( )
.a 是任意有理数 下列各式正确的是 .
5 , ( )
a a
a a
试用 中的方法比较 x2 x 与 x2 x 的大小.
(3) (1) 3 -2 +7 4 -2 +7
瞧 中考曾经这么考
a
若|| 则a .
(3) a =-1, 0
.探究题
10 :
如果a b 那么a b
(1)① - <0, ;
在不等式两边同时乘以 或除以 同一个负数 不等号方向 .
(3) ( ) ,
. 要使不等式x 成立 则x 的取值范围是
.. 不等式的性质
912
. 不变 不变 改变
1 (1) (2) (3)
. x
2 (1) >-3 (2)> > <
.
3 B 4.A 5.D
. x x 5 在数轴上表示略.
【初中数学】人教版七年级下册9.1.2 不等式的性质(练习题)

人教版七年级下册9.1.2 不等式的性质(377)1.解不等式12x−3≤0时,两边都加,得,然后两边都除以,得.2.不等式−x>2的解集在数轴上表示为()A. B.C. D.3.利用不等式的性质解下列不等式:(1)x−9>25;(2)−3x>9;(3)12x+1>−24.用不等式的性质解下列不等式,并在数轴上表示其解集.(1)x+1>4;(2)3x<x−6.5.在括号里填上下列不等式变形的依据.(1)x>3⇒x+2>5;( )(2)12a<3⇒a<6( )(3)−2a>3⇒a<−32;( )(4)3a>2a+1⇒a>1.( )6.用“>”或“<”填空:(1)若m<n,则m−3n−3;(2)若−2a>1,则−4a2;(3)若−1.25y<10,则y−8;(4)若a>b,则a(m2+1)b(m2+1);(5)若a>b,则2a+12b+1;(6)若a>b,则−12a+c−12b+c.7.已知a>b>0,下列结论错误的是()A.a+m>b+mB.√a>√bC.−2a>−2bD.a2>b28.由a>b,得到am>bm的条件是()A.m>0B.m<0C.m≥0D.m≤0参考答案1.【答案】:3;12x≤3;12;x≤62.【答案】:D3(1)【答案】解:不等式两边同时加上9得:x−9+9>25+9,∴x>34.(2)【答案】不等式两边同时除以−3得:x<−3 .(3)【答案】不等式两边同时减去1得:12x>−3,不等式两边同时乘以2得:x>−6.4(1)【答案】解:不等式两边同时减去1得:不等式的解集为x>3,将解集表示在数轴上如图所示:(2)【答案】不等式两边同时减去x得:2x<−6,不等式两边同时除以2得:不等式的解集为x<−3.将解集表示在数轴上如图所示:5(1)【答案】不等式的性质1(2)【答案】不等式的性质2(3)【答案】不等式的性质3(4)【答案】不等式的性质16.【答案】:<;>;>;>;>;<7.【答案】:C8.【答案】:A。
人教七年级下册数学9.1.2不等式的性质同步练习(解析版)

9.1.2不等式的性质基础闯关全练1.如果a <b ,下列各式中不一定正确的是( )A .a-1<b-1B .-3a >-3bC .b a 11<D .44a b<2.若3x >-3y ,则下列不等式中一定成立的是( ) A .x+y >0 B .x-y >0 C .x+y <0 D .x-y <0 3.若m <n ,比较下列各式的大小:(1) m-3________n-3; (2) -5m_______-5n ;(3)3m -______3n -; (4) 3-m____2-n ; (5)0____m-n ; (6)423m --______423n--4.不等式1+x <0的解集在数轴上表示正确的是( )5.写出下列不等式的变形是根据不等式的哪一条性质: (1)由321->x ,得x >-6:___________; (2)由3+x ≤5,得x ≤2:____; (3)由-2x <6,得x >-3:____; (4)由3x ≥2x -4,得x ≥-4:________.6.若a <3,则不等式(a-3)x <2+a 的解集为____.7.利用不等式的性质求下列不等式的解集,并在数轴上表示出来.(1)x-3<2; (2)2141>-x ; (3)5x ≥3x-2.能力提升全练1.若不等式(a-3)x <1的解集是31->a x ,则a 的取值范围是( )A.a >3B.a <3C.a ≠3D.以上均不对2.实数a ,b ,c 在数轴上的对应点如图所示,则下列式子正确的是( )A .ac >bcB .|a-b| =a-bC .-a <-b <cD .-a-c >-b-c3.定义一种新运算“⊕”,其运算规则为a ⊕b= -2a+3b ,如:1⊕5= -2×1+3×5= 13,则不等式x ⊕4<0的解集为______.4.利用不等式的性质解下列不等式,并把解集在数轴上表示出来. (1)4x+3<3x ;(2) 4-x ≥4.三年模拟全练 一、选择题1.下列不等式变形正确的是( )A .由a >b 得ac >bcB .由a >b 得-2a >-2bC .由a >b 得-a <-bD .由a >b 得a-2<b-22.利用不等式的性质,把不等式2x-3<1的解集在数轴上表示为( )A B C D3.若实数a ,b ,c 在数轴上对应点的位置如图,则下列不等式成立的是( )A .ac >bcB .ab >cbC .a+c >b+cD .a+b >c+b 二、填空题 4.数轴上实数b 的对应点的位置如图所示,比较大小121+b ______0(用“<”或“>”填空).5.若关于x 的不等式(1-a) x >2可化为a x ->12,则a 的取值范围是_______.五年中考全练一、选择题1.若a <b ,则下列结论不一定成立的是( )A .a-1<b-1B .2a <2b C.33b a ->-D.a ²<b ² 2.已知实数a ,b 满足a+1>b+1,则下列选项可能错误的是( ) A .a >b B .a+2>b+2 C .-a <-b D .2a >3b 3.若x+5>0,则( )A .x+1<0B .x-1<0C .15-<xD.-2x <12二、填空题4.用一组a ,b ,c 的值说明命题“若a <b ,则ac <bc ”是错误的,这组值可以是a=_____.b=________.c=___________. 核心素养全练1.某商贩去蔬菜批发市场买黄瓜,上午,他买了30千克,价格为每千克x 元;下午,他又买了20千克,价格为每千克y 元.后来他以每千克2yx +元的价格卖完后,结果发现自己赔了钱,其原因是( )A .x <yB .x >yC .x ≤yD .x ≥y2.甲同学与乙同学讨论有关不等式的问题,甲说:当每个苹果的质量一样时,5个苹果的质量大于4个苹果的质量,设每个苹果的质量为x .则有5x >4x. 乙说:这肯定是正确的.甲又说:设a 为一个有理数,那么5a 一定大于4a ,对吗?乙同答:这与5x >4x 是一同事儿,当然也是正确的.请问:乙同学的回答正确吗?试说明理由.9.1.2不等式的性质1.C 根据不等式的性质可知A 、B 、D 均正确,而C 选项不一定正确.2.A 根据不等式的性质2,对3x >-3y 两边同除以3得x >-y ,再根据不等式的性质1,两边同加y 得x+y >0.3.答案(1)<(2)>(3)>(4)>(5)>(6)<4.A ∵1+x <0,∴根据不等式的性质1,两边同时减1,不等号方向不变,得x <-1,x <-1在数轴上表示如图.5.答案(1)不等式的性质2 (2)不等式的性质1 (3)不等式的性质3 (4)不等式的性质1 6.答案32-+>a ax解析 由于a <3,所以a-3<0,不等式(a-3)x <2+a 两边同除以(a-3),不等号方向改变.7.解析 (1)不等式两边同时加3,不等号方向不变,得x <5.(2)不等式两边同时乘-4,不等号方向改变,得x <-2.(3)不等式两边同时减去3x ,不等号方向不变,得5x-3x ≥3x-2-3x,即2x ≥-2.不等式2x ≥-2两边同时除以2,不等号方向不变,得x ≥-1.在数轴上表示各解集如图:能力提升全练1.B 由题意知不等号方向发生改变,由不等式的性质3,可知a-3<0,故a <3. 2.D 由题图可知,a <b <0<c ,∴ac <bc ,故A 选项错误;∵a <b ,∴a-b <0,∴|a-b | =b-a ,故B 选项错误;∵a <b,∴-a >-b ,故C 选项错误;∵-a >-b ,∴-a-c >-b-c ,故D 选项正确.故选D . 3.答案x >6解析 由题意得x ⊕4=-2x+3×4,所以原不等式可化为- 2x+12<0.所以-2x <-12,可得x >6.4.解析(1)原不等式可变形为4x+3-3x-3<3x-3x-3,整理得x <-3.数轴表示如图.(2)原不等式可变形为4-x-4≥4-4,整理得-x ≥0,在不等式的两边同时乘-1,不等号改变方向,得x ≤0.数轴表示如图.三年模拟全练一、选择题1.C 当c ≤0时,选项A 错误;根据不等式的性质,在不等式两边乘同一个负数时,不等号的方向改变,故选项B 错误,选项C 正确;在不等式两边加上(或减去)同一个数,不等号的方向不变,故选项D 错误,故选C .2.D 根据不等式的性质1,两边同加3,得2x <4,再根据不等式的性质2,两边同除以2,得x <2,从2向左画,且2处为空心圆圈,故选D . 3.B 由数轴知c >O >b >a ,再用不等式的性质进行判断. 二、填空题 4.答案>解析 由题图知-2<b <-1,所以21211-<<-b ,所以211210<+<b ,所以0121>+b .5.答案 a <1解析 由关于x 的不等式(1-a) x >2可化为a x ->12,得1-a >0.可得a <1.五年中考全练 一、选择题1.D A 选项,不等式a <b 两边同时减去1,不等号方向不变,故A 成立.B 选项,不等式a <b 两边同时乘2,不等号方向不变,故B 成立.c 选项,不等式a <b 两边同时乘31-,不等号方向改变,故C 成立,选项D ,举例:-5<-2,但(-5)²>(-2)²,故D 不一定成立,故选D .2.D 根据不等式的性质即可得到a >b ,a+2>b+2.-a <-b .因此可能错误的是D . 3.D 因为x+5>0,所以x >-5,所以- 2x <10,又因为10<12,所以-2x <12.此题选D . 二、填空题4.答案1;2;-1(答案不唯一)解析由不等式的性质2可知,当c >0时,命题才是真命题,所以当c ≤O 时,命题为假命题,答案不唯一,例如:1;2;-1.核心素养全练1.B 由题意得30x+20y >50×2yx +,变形可得x >y ,故选B .2.解析 乙同学的回答不正确,理由:a 为一个有理数,应分三种情况讨论:当a >0时,根据不等式的性质2,得5a >4a ;当a <0时,根据不等式的性质3,得5a <4a ;当a=0时.5a= 4a.。
人教版数学七年级下册:9.1.2《不等式的性质》同步练习题(2)及答案

c c1 1 1 136.若 x2x -113 y - 1 10 y + 59.1.2《不等式的性质》同步练习题知识点:1、不等式的性质 1:不等式的两边加上(或减去)同一个数(或式子),不等号 的方向不变,用式子表示:如果 a>b ,那么 a±c>b±c.2、不等式的性质 2:不等式的两边乘以(或除以)同一正数,不等号的方向不变,3、不等式的性质 3:不等式两边乘以(或除以)同一个负数,不等号的方向改变,a b 用式子表示:a>b ,c<0,那么,ac < bc或 <.同步练习:1、下列不等式变形正确的是 ()A.由 4x- 1≥0 得 4x>1B.由 5x>3 得 x>3C.由 y 2>0 得 y>0 D.由-2x<4 得 x<-22、图中表示的是不等式的解集,其中错误的是( )A 、x≥-2B 、x <1 -2 -1 00 1C 、x≠0D 、x <03.在平面直角坐标系中,点(-7,-2m+1)在第三象限,则 m 的取值范围是( )A.m <B.m> -C.m < -D.m >2 2 2 24.关于 x 的不等式(1-a )x> 3 解集为 x < ,则 a 的取值范围是 ( )1- aA.a >0B.a<0C.a > 1D.a < 15.不等式 2x> 3 - x 解集为- 的值不大于 1,则该不等式的负整数解是2 37.若关于 x 的方程 x +a =7 的解是非负数,则 a 的取值范围是8.解下列不等式,并将其解集在数轴上表示出来:(1)3x + 1 > x - 2(2) x - 3 ≤-2x + 3 (3) 5x – 1 >3x-22(4)-6x > -4x +2 (5) 1- x≥ x – 2 (6) 3x -2 ≥ x +43(7)5x – 3 > 2 (3-2x ) (8) ≥ - 12 69.1.2《不等式的性质》同步练习题(2)答案:1.C2.D3.D4.C5.X>16.-4;-3;-2;-17.a≤78.(1)x>-32(2)x≤2(3)x≤2(4)x<-1(5)x≤94(6)x≥3(7)x>1(8)y≤-2。
人教版数学七年级下册 9.1.2 不等式的性质 练习(含答案)

9.1.2 不等式的性质练习一、选择题1.已知x>y,则下列不等式成立的是()A. x−1<y−1B. 3x<3yC. −x<−yD. x2<y22.若x<y,且(a+5)x>(a+5)y,则a的取值范围()A. a>−5B. a≥−5C. a<−5D. a<53.已知a,b,c均为实数,a<b,那么下列不等式一定成立的是()A. a−b>0B. −3a<−3bC. a|c|<b|c|D. a(c2+1)<b(c2+1)4.若a<b,则下列各式中一定成立的是()A. a+1>b+1B. a−1>b−1C. −3a>−3bD. a2>b25.若a>b,则下列结论:①a+x>b+x;②ax >bx;③ax2>bx2;④ab<b2;⑤−|a|<−|b|.其中一定成立的个数是()A. 1B. 2C. 3D. 46.若a<b,则下列不等式变形错误的是()A. a+x<b+xB. 3−a<3−bC. 2a−1<2b−1D. a2−b2<07.下列说法不一定成立的是()A. 若a>b,则a+c>b+cB. 若a+c>b+c,则a>bC. 若a>b,则ac2>bc2D. 若ac2>bc2,则a>b8.若a<b,则下列各式中,错误的是()A. a−3<b−3B. −a<−bC. −2a>−2bD. 13a<13b9.已知a、b、c是有理数,下列不等式变形中,一定正确的是()A. 若ac>bc,则a>bB. 若a>b,则ac>bcC. 若ac2>bc2,则a>bD. 若a>b,则ac2>bc210.如果关于x的不等式(a+1)x>a+1的解集为x<1,则a的取值范围是()A. a<0B. a<−1C. a>1D. a>−1二、填空题11.若不等式(m−2)x>1的解集是x<1m−2,则m的取值范围是______.12.若关于x的不等式(1−a)x>2可化为x<21−a,则a的取值范围是______.13.若a>c,则当m______ 时,am<cm;当m______ 时,am=cm.14.如果x>y,且(a−1)x<(a−1)y,那么a的取值范围是______.15.用不等号填空:若a>b,则a−5______b−5,−4a______−4b,a3______b3.16.利用不等式的性质填“>”或“<”.(1)若a>b,则2a+1_______2b+1;(2)若−1.25y<−10,则y_______8;(3)若a<b,且c<0,则ac+c_______bc+c;三、计算题17.根据不等式的性质,将下列不等式化成“x>a”或“x<a”的形式.(1)10x−1>7x;(2)−12x>−1.18.根据不等式的基本性质,把下列各式化成“x>a”或“x<a”的形式.(1)x−2<3x−3;(2)−2x+1<x+4.19.已知x>y,请比较下列各组的大小,并说明理由.(1)x3−2与y3−2;(2)3−2x与3−2y.20.利用不等式的性质把不等式化为“x>a”或“x<a”的形式.(1)2x−1<3;(2)32x+6<2;(3)4x<6x−4;(4)2−13x<4.参考答案1.【答案】C2.【答案】C3.【答案】D4.【答案】C5.【答案】A6.【答案】B7.【答案】C8.【答案】B9.【答案】C10.【答案】B11.【答案】m<212.【答案】a>113.【答案】<0;=014.【答案】a<115.【答案】>;<;>16.【答案】(1)>;(2)>;(3)>;17.【答案】解:(1)10x−1>7x,两边都减7x、加1,得10x−7x+1−1>7x−7x+1,3x>1,两边都除以3,得x>13;(2)−12x>−1,两边都乘以−2,得x<2.18.【答案】解:(1)两边都减x,移项得3−2<2x,x>12;(2)不等式的两边都加2x,移项得1−4<3x,x>−1.19.【答案】解:(1)x3−2>y3−2,理由如下:∵x>y,∴x3>y3.∴x3−2>y3−2.(2)3−2x<3−2y,理由如下:∵x>y,∴−2x<−2y.∴3−2x<3−2y.20.【答案】(1)解:x<2;(2)解:x<−8;3(3)解:x>2;(4)解:x>−6.。
人教版七年级数学下册9.1.2不等式的性质同步测试

人教版七年级数学下册 9.1.2 不等式的性质同步测试一、选择题1. 以下 4种说法:① x = 5 是不等式 4x - 5> 0的解;② x = 5是不等式 4x -5>0的一个解;4 2③ x > 5是不等式 4x - 5> 0的解集;④ x >2中任何一个数都能够使不等式 4x4- 5> 0建立,因此 x >2也是它的解集,此中正确的有()A 、1个B 、2个C 、3个D 、4个2. 已知χ> y 且χ y <0,a 为随意有理数,以下式子中正确的选项是﹙﹚A. -χ>- yB.a 2χ> a 2yC. -χ+ a <- y +aD.χ>- y3. 以下说法中正确的选项是﹙﹚A. χ= 1是不等式- 2χ< 1的解集B. χ= 1是不等式- 2χ< 1的解C. χ=1是不等式- χ< 的解D.不等式- χ< 的解是χ=122 12 14. 在以下各不等式中,错误 的是()..A 、若 a b b c ,则 a cB 、若 a b ,则 a c b cC 、若 ab bc ,则 a c D、若 a b ,则 2c a 2c b5. 假如对于 x 的不等式 (a 1)x a 1 的解集为 x 1,那么 a 的取值范围是()A 、 a 0B 、 a 0C 、 a 1D 、 a16. 已知 b <a <0,以下不等式正确的选项是﹙ ﹚A.7 -a >bB.a>1C.1 > 1D.a2> b 2ba b7. 若a <b ,则以下结论不必定建立的是 ()A . a - b - 1B . a b1< 2 <2a b22C .- 3>-3D .a <b8. 有以下四个命题:①若 a > b ,则 a + 1>b +1;②若a >b ,则 a - 1> b - 1;③若 a19.若实数 a, b, c在数轴上的对应地点如下图,则以下不等式建立的是()A.ab> bc B.ac>bcC.a+c>b+c D.a+b>c+bx y获得 ax ay的条件应是()10.由 < >A.a≥0B.a≤ 0C.a>0D.a<0二、填空题11.假如 x>y,且( a-1 ) x<( a-1 )y,那么 a的取值范围是 ______.12. 若不等式(a-2 )x<1,两边除以 a-2 后变为 x<1 ,则 a的取值范围是 ______.a 213. 若a>0,c<0,则 ac________0。
人教版数学七年级下同步练习 9.1.2 不等式的性质(含答案)

第九章不等式与不等式组9.1.2 不等式的性质基础导练1.如果b>0,那么a+b与a的大小关系是( )A.a+b<aB.a+b>aC.a+b≥aD.不能确定2.下列变形不正确的是( )A.由b>5得4a+b>4a+5B.由a>b得b<aC.由-12x>2y得x<-4y D.-5x>-a得x>5a3.若a>b,am<bm,则一定有( )A.m=0B.m<0C.m>0D.m为任何实数4.在下列不等式的变形后面填上依据:(1)如果a-3>-3,那么a>0;______________________________.(2)如果3a<6,那么a<2;______________________________.(3)如果-a>4,那么a<-4.______________________________.5.利用不等式的性质填“>”或“<”.(1)若a>b,则2a+1__________2b+1;(2)若-1.25y<-10,则y__________8;(3)若a<b,且c<0,则ac+c__________bc+c;(4)若a>0,b<0,c<0,则(a-b)c__________0.6.利用不等式的性质,求下列不等式的解集.(1)x+13<12;(2)6x-4≥2;(3)3x-8>1;(4)3x-8<4-x.7.设“▲”、“●”、“■”分别表示三种不同的物体,现用天平秤两次,情况如图所示,那么▲、●、■这三种物体按质量从大到小排列应为( )A.■、●、▲B.▲、■、●C.■、▲、●D.●、▲、■8.某单位打算和一个体车主或一出租车公司签订月租合同.个体车主答应除去每月1 500元租金外,每千米收1元;出租车公司规定每千米收2元,不收其他费用.设该单位每月用车x 千米时,乘坐出租车合算,请写出x 的范围.能力提升9.若x >y ,则下列式子中错误的是( )A.x-3>y-3B.3x >3y C.x+3>y+3 D.-3x >-3y 10.不等式2x <-4的解集在数轴上表示为( )11.下列命题正确的是( )A.若a >b ,b <c ,则a >cB.若a >b ,则ac >bcC.若a >b ,则ac 2>bc 2D.若ac 2>bc 2,则a >b12.若式子3x+4的值不大于0,则x 的取值范围是( )A.x <-43B.x≥43C.x <43D.x≤-4313.利用不等式的基本性质求下列不等式的解集,并说出变形的依据.(1)若x+2 012>2 013,则x__________;(______________________________)(2)若2x>-13,则x__________;(______________________________) (3)若-2x>-13,则x__________;(______________________________) (4)若-7x >-1,则x__________.(______________________________) 14.指出下列各式成立的条件:(1)由mx<n,得x<n m; (2)由a<b,得ma>mb ;(3)由a>-5,得a 2≤-5a ;(4)由3x>4y ,得3x-m>4y-m.参考答案1.B2.D3.B4.(1)不等式的性质1(2)不等式的性质2(3)不等式的性质35.(1)> (2)> (3)> (4)<6.(1)x<16. (2)x≥1. (3)x>3. (4)x<3.7.C8.根据题意,得1 500+x>2x,x<1 500.又由于单位每月用车x(千米时)不能是负数.因此,x的取值范围是x>0且x<1 500.9.D 10.D 11.D 12.D13.(1)>1 不等式两边同时减去2 012,不等号方向不变(2)>-16不等式两边同时除以2,不等号方向不变(3)<16不等式两边同时除以-2,不等号方向改变(4)<7 不等式两边同时乘以-7,不等号方向改变14.(1)m>0.(2)m<0.(3)-5<a≤0.(4)m为任意实数.。
人教版七年级数学下9.1.2不等式的性质-同步练习(3).docx

9.1.2《不等式的性质》同步练习1.用a >b ,用“<”或“>”填空:⑴ a +2 b +2⑵ 3a 3b⑶ -2a -2b⑷ a -b 0⑸ -a -4 -b -4⑹ a -2 b -2;2. 用“<”或“>”填空:⑴若a -b <c -b ,则a c⑵若3a >3b ,则a b⑶若-a <-b ,则a b⑷若2a +1<2b +1,则a b3.已知a >b ,若a <0,则2a a b ;若a >0,则2a a b.4. 用“<”或“>”填空:⑴ 若a -b >a 则b 0⑵ 若2ac >2bc 则a b⑶ 若a <-b 则πa -πb⑷ 若a <b 则a -b 0⑸ 若a <0,b 0时,ab>05.若3a -<2a -,则a 一定满足 ( ) A 、a >0 B 、a <0 C 、a ≥0 D 、a ≤06.若x >-y ,则下列不等式中成立的有 ( )A 、x +y <0B 、x -y >0C 、2a x >2a -yD 、3x+3y >07.若0<x <1,则下列不等式成立的是 ( )A 、2x >x 1>xB 、x1>2x >x C 、x >x 1>2x D 、x1>x >2x8.若方程组⎩⎨⎧=++=+3313y x k y x 的解为x ,y ,且x+y >0,则k 的范围是 ( ) A 、k >4 B 、k >-4 C 、k <4 D 、k <-49.用不等式表示下列各式,并利用不等式性质解不等式。
⑴a 的31是非负数 ⑵m 的2倍与1的和小于7⑶a 与4的和的20%不大于-5⑷x 的61与x 的3倍的和是非负数。
9.1.2《不等式的性质》同步练习答案:1、(1)>;(2)>;(3)<;(4) >;(5)<;(6)>2、(1)<;(2)>;(3)>;(4)<3、< >4、(1)<;(2)>;(3)<;(4)<;(5)<5、B6、D7、 D8、B9、⑴ 31a ≥ 0 ⑵ 2m + 1 < 7 ⑶20%(a + 4 ) ≤ - 5 ⑷ 61x + 3x ≥ 0初中数学试卷马鸣风萧萧。
人教版七年级数学下《9.1.2不等式的性质》同步练习

9.12不等式的性质班级:___________姓名:___________得分:__________(满分:100分,考试时间:90分钟)一、选择题:(本大题7个小题,每小题5分,共35分)1、若x >y ,则下列式子错误的是( )A 、x ﹣3>y ﹣3B 、﹣3x >﹣3yC 、 x+3>y+3D 、 >2、已知a <b ,下列式子中,错误的是( )A 、4a <4bB 、-4a <-4b C.、a +4<b +4 D 、a -4<b -4 3、已知a>b ,则下列不等式中不一定成立的是( ) A. a -2>b -2B. 14a >14bC. -5a <-5bD. a 2>ab4、若a <b <0,有下列不等式:①a +1<b +2;②a b >1;③a +b <ab ;④1a <1b .其中正确的有( )A. 1个B. 2个C. 3个D. 4个5、 若实数abc 满足a 2+b 2+c 2=9,代数式(a ﹣b )2+(b ﹣c )2+(c ﹣a )2的最大值是( ) A .27B .18C .15D .126、 5名学生身高两两不同,把他们按从高到低排列,设前三名的平均身高为a 米,后两名的平均身高为b 米.又前两名的平均身高为c 米,后三名的平均身高为d 米,则( ) A .B .C .D .以上都不对A 、若a >b ,b <c ,则a >cB 、若a >b ,则ac >bcC 、若a >b ,则ac 2>bc 2D 、若ac 2>bc 2,则a >b 二、填空题:(本大题5个小题,每小题4分,共20分) 8. 如果a <b .那么3﹣2a 3﹣2b .(用不等号连接) 9. 设a >b ,则:(1)2a 2b ;(2)(x 2+1)a (x 2+1)b ; (3)3.5b +1 3.5a +1.10. 下边的框图表示解不等式的流程,其中“系数化为 ”这一步骤的依据是 .11. 如果且 是负数,那么 的取值范围是 .12. 若x <﹣y ,且x <0,y >0,则|x |﹣|y | 0.二、综合题:(本大题4个小题,共45分) 13. (12分)把下列不等式化成“”或“”或“”或“”的形式:Ⅰ ; Ⅱ ; Ⅲ; Ⅳ.14.(10分)已知a ,b ,c 是三角形的三边,求证:a b +c +b c +a +c a +b<2.15.(10分)已知a ,b ,c 在数轴上的位置如图所示.(1)求|ab|a +|b|-bc|bc|的值;(2)比较a +b ,b +c ,c -b 的大小,用“>”号将它们连接起来.16.(13分) 阅读下列材料:解答 “已知 ,且,,试确定的取值范围”有如下解法:解 ,又 ,..又,同理得:由得,的取值范围是.请按照上述方法,完成下列问题:Ⅰ已知,且,,则的取值范围是.Ⅱ已知,,若成立,求的取值范围(结果用含的式子表示).参考答案一、选择题1. B2. B3. D4. C【解析】 ①∵a <b ,∴a +1<b +1,b +1<b +2, ∴a +1<b +2. ②∵a <b <0,∴a b >bb ,即a b>1. ③∵a <b <0,∴a +b <0,ab >0, ∴a +b <ab .④∵a <b <0,∴ab >0, ∴a ab <b ab ,∴1b <1a . 5. A【解析】解:∵a 2+b 2+c 2=(a +b +c )2﹣2ab ﹣2ac ﹣2bc , ∴﹣2ab ﹣2ac ﹣2bc=a 2+b 2+c 2﹣(a +b +c )2①∵(a ﹣b )2+(b ﹣c )2+(c ﹣a )2=2a 2+2b 2+2c 2﹣2ab ﹣2ac ﹣2bc ; 又(a ﹣b )2+(b ﹣c )2+(c ﹣a )2 =3a 2+3b 2+3c 2﹣(a +b +c )2 =3(a 2+b 2+c 2)﹣(a +b +c )2②①代入②,得3(a 2+b 2+c 2)﹣(a +b +c )2=3×9﹣(a +b +c )2=27﹣(a +b +c )2, ∵(a +b +c )2≥0, ∴其值最小为0, 故原式最大值为27. 故选A . 6. B【解析】解:∵3a +2b=2c +3d ,∵a >d , ∴2a +2b <2c +2d , ∴a +b <c +d ,∴<,即>,故选:B.由图可得:S>P,R<P,PR>QS,故选D.7. D二、填空题8.>.【解析】解:∵a<b,两边同乘﹣2得:﹣2a>﹣2b,不等式两边同加3得:3﹣2a>3﹣2b,故答案为:>.9.(1)2a>2b;(2)(x2+1)a>(x2+1)b;(3)3.5b+1<3.5a+1.【解答】(1)根据不等式的基本性质2,不等式两边乘同一个正数2,不等号的方向不变,即2a>2b;(2)根据不等式的基本性质1,不等式两边加同一个式子(x2+1),不等号的方向不变,所以(x2+1)a>(x2+1)b;(3)a>b即b>a,不等式两边乘同一个正数3.5,不等号的方向不变,不等式两边加同一个数1,不等号的方向不变,所以3.5b+1<3.5a+1.10.不等式的两边同时乘以或除以一个负数,不等式方向改变;(或不等式的基本性质)11.12.>【解答】∵x<﹣y,且x<0,y>0,∴|x|>|y|,∴不等式的两边同时减去|y|,不等式仍成立,∴|x|﹣|y|>0.故答案是:>三、 综合题13、 (1)x −10+10<−6+10,x <4.(2)−13x ×(−3)>−2×(−3),x <6.(3)12x ×2>−3×2,x >−6.(4) 1−x −1−x ≥2+x −1−x,−2x ≥1,−2x ×(−12)≤1×(−12),x ≤−12.14、【解】 由“三角形两边之和大于第三边”可知,a b +c ,b c +a ,c a +b 均是真分数,再利用分数与不等式的性质,得a b +c <a +a b +c +a =2ab +c +a , 同理,b c +a <2b c +a +b ,c a +b <2c a +b +c .∴a b +c +b c +a +c a +b <2a b +c +a +2b c +a +b +2ca +b +c =2(a +b +c )a +b +c=2. 15、【解】 (1)由图知,a <0,b <0,c >0,a<b<c.∴|ab|a +|b|-bc |bc|=ab a -b -bc -bc =1. (2)c -b>b +c>a +b.(1)x >-1; (2)x <2; (3)x ≥6. 16、 (1)(2), ,,,,,同理得由得,的取值范围是.。
【初中数学】人教版七年级下册9.1.2 不等式的性质(练习题)

人教版七年级下册9.1.2 不等式的性质(181)1.二元一次方程组{2x +3y =10,4x −3y =2的解满足不等式ax >4−y ,求a 的取值范围.2.已知关于x 的不等式(1−a)x >2两边都除以(1−a),得x <21−a ,试化简:|a −1|+|a +2|. 3.现有不等式的性质:①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;②在不等式的两边都乘同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.请解决以下两个问题:(1)利用性质①比较2a 与a 的大小(a ≠0);(2)利用性质②比较2a 与a 的大小(a ≠0).4.若关于x 的方程x −a =3的解为负数,则a 的取值范围是 .5.根据不等式的性质,把下列各式化为x >a 或x <a 的形式.(1)−3x +2<2x +3;.(2)13x ≥13(6−3x).6.某棉布厂棉布的销售数量与销售价格如下表所示.若某人带了8000元,则他最多可以购买棉布多少米?7.利用不等式的性质解下列不等式:(1)x +12>10;(2)13x <43;(3)−8x ≥−16.8.黄石市某天的最高气温为+5℃,最低气温比最高气温低8℃,则这天此地气温t(℃)的取值范围是 .9.如图,x 克和5克分别是天平上两边的砝码质量,请你用“>”或“< ”填空:x −3 2.10.已知关于x 的不等式2x >m 的解集如图所示,则()A.m>6B.m<6C.m=6D.m>311.实数a,b,c在数轴上对应的点的位置如图所示,则下列式子中正确的是()A.a−c>b−cB.a+c<b+cC.ac>bcD.ab <cb12.若3x>−3y,则下列不等式中一定成立的是()A.x+y>0B.x−y>0C.x+y<0D.x−y<013.由m>n到km>kn成立的条件为()A.k>0B.k<0C.k≤0D.k≥014.若x>y,则下列不等式中不一定成立的是()A.x+1>y+1B.2x>2yC.x2>y2D.x2>y215.若−2x>y,则下列结论正确的是()A.2x>−yB.x>−y2C.x<−y2D.x<−2y16.若a>b,则4a4b(填“<”或“>”).17.如果不等式ax<b的解集是x>ba,那么a的取值范围是.18.根据不等式的基本性质,将不等式变形为x>a或x<a的形式.(1)x−14<34,根据不等式的性质,不等式两边都,得;(2)32x>−5,根据不等式的性质,不等式两边都,得;(3)−8x>16,根据不等式的性质,不等式两边都,得.19.把不等式x+2≤0的解集在数轴上表示出来,正确的是()A. B.C. D.20.不等式(3.14−π)x<π−3.14的解集是.21.若x>y,则下列式子中错误的是()A.x−3>y−3B.x+3>y+3C.−3x>−3yD.x3>y3参考答案1.【答案】:解方程组{2x +3y =10,4x −3y =2,得{x =2,y =2.把{x =2,y =2代入不等式ax >4−y ,得2a >4−2,不等式两边都除以2,得a >1.所以a 的取值范围是a >1【解析】:解方程组{2x +3y =10,4x −3y =2,得{x =2,y =2. 把{x =2,y =2代入不等式ax >4−y ,得2a >4−2, 不等式两边都除以2,得a >1. 所以a 的取值范围是a >12.【答案】:∵不等式(1−a)x >2两边都除以(1−a)后不等号方向发生了改变, ∴1−a <0,解得a >1,∴|a −1|+|a +2|=(a −1)+(a +2)=2a +1【解析】:∵不等式(1−a)x >2两边都除以(1−a)后不等号方向发生了改变, ∴1−a <0,解得a >1, ∴|a −1|+|a +2|=(a −1)+(a +2)=2a +13(1)【答案】若a >0,则a +a >a +0,即2a >a ;若a <0,则a +a <a +0,即2a <a(2)【答案】若a >0,∵2>1,∴2·a >1·a ,即2a >a ;若a <0,∵2>1,∴2·a <1·a ,即2a <a4.【答案】:a <−3【解析】:x =a +3<0,解得a <−35(1)【答案】−3x +2<2x +3.两边都减去2,得−3x <2x +1.两边都减去2x ,得−5x <1.两边都除以−5,得x >−15.(2)【答案】13x ≥13(6−3x).两边都乘3,得x ≥6−3x .两边都加上3x ,得4x ≥6.两边同时除以4,得x≥326.【答案】:设该人可以买x米棉布,根据题意,得8x≤8000.根据不等式的基本性质2,在不等式的两边同时除以8,得x≤1000,所以他最多可以购买棉布1000米【解析】:设该人可以买x米棉布,根据题意,得8x≤8000. 根据不等式的基本性质2,在不等式的两边同时除以8,得x≤1000,所以他最多可以购买棉布1000米7(1)【答案】根据不等式的基本性质1,不等式两边同时减去12,得x>−2,得x<4(2)【答案】根据不等式的基本性质2,不等式两边都除以13(3)【答案】根据不等式的基本性质3,不等式两边都除以−8,得x≤28.【答案】:−3℃≤t≤5℃【解析】:5−8=−3(℃),∴这天此地气温t(℃)的取值范围是−3℃≤t≤5℃9.【答案】: <10.【答案】:C.由数轴可看出该不等式的解集为x>3,所【解析】:由不等式2x>m,得x>m2=3,所以m=6以m211.【答案】:B12.【答案】:A【解析】:两边都除以3,得x>−y,两边都加y,得x+y>0,故选 A13.【答案】:A【解析】:根据“不等式的两边都乘同一个正数,不等号的方向不变”得k>014.【答案】:D【解析】:在不等式x >y 两边都加1,不等号的方向不变,故A 正确;在不等式x >y 两边都乘2,不等号的方向不变,故B 正确;在不等式x >y 两边都除以2,不等号的方向不变,故C 正确;当x =1,y =−2时,x >y ,但x 2<y 2,故D 错误15.【答案】:C16.【答案】:>17.【答案】:a <0【解析】:因为不等号的方向改变,所以不等式两边同时除以一个负数,所以a <018(1)【答案】1 ;加上14;x <1(2)【答案】2;乘23;x >−103(3)【答案】3;除以−8;x <−219.【答案】:D20.【答案】:x >−1【解析】:因为3.14−π<0,且π−3.143.14−π=−1,所以x >−121.【答案】:C。
人教版七年级数学下册9.1.2不等式的性质同步测试
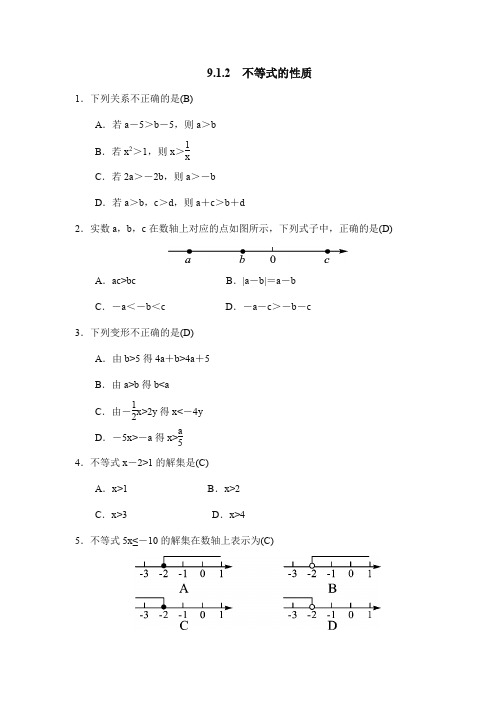
9.1.2 不等式的性质1.下列关系不正确的是(B)A .若a -5>b -5,则a >bB .若x 2>1,则x >1xC .若2a >-2b ,则a >-bD .若a >b ,c >d ,则a +c >b +d2.实数a ,b ,c 在数轴上对应的点如图所示,下列式子中,正确的是(D)A .ac>bcB .|a -b|=a -bC .-a <-b <cD .-a -c >-b -c3.下列变形不正确的是(D)A .由b>5得4a +b>4a +5B .由a>b 得b<aC .由-12x>2y 得x<-4yD .-5x>-a 得x>a 54.不等式x -2>1的解集是(C)A .x>1B .x>2C .x>3D .x>45.不等式5x≤-10的解集在数轴上表示为(C)6. a 、b 都是实数,且a<b ,则下列不等式的变形正确的是(C)A .a +x>b +xB .-a +1<-b +1C .3a<3b D.a 2>b 27.下列说法不一定成立的是(C)A .若a>b ,则a +c>b +cB .若a +c>b +c ,则a>bC .若a>b ,则ac 2>bc 2D .若ac 2>bc 2,则a>b8.若式子3x +4的值不大于0,则x 的取值范围是(D)A .x <-43B .x≥43C .x <43D .x≤-439.设“▲”、“●”、“■”分别表示三种不同的物体,现用天平秤两次,情况如图所示,那么▲、●、■这三种物体按质量从大到小排列应为(C)A .■、●、▲B .▲、■、●C .■、▲、●D .●、▲、■10.若不等式(a -2)x <1,两边除以a -2后变成x>1a -2,则a 的取值范围是a <2.11.若a <0,则不等式ax -b≥0的解集是x≤b a .12.利用不等式的性质填空(填“>”或“<”).(1)若a>b ,则2a +1>2b +1;(2)若-1.25y<-10,则y>8;(3)若a<b ,且c<0,则ac +c>bc +c ;(4)若a>0,b<0,c<0,则(a -b)c<0.13.利用不等式的性质解下列不等式,并把解集在数轴上表示出来.(1)12x≥-4;解:利用不等式性质2,两边都乘以2,得x≥-8.在数轴上表示为:(2)-10x≤5.解:利用不等式性质3,两边都除以-10,得x≥-12.在数轴上表示为:14.指出下列各式成立的条件:(1)由a<b ,得ma>mb ;(2)由a>-5,得a 2≤-5a ;解: (1)m<0.(2)-5<a≤0.15.利用不等式的性质解下列不等式.(1)2(x-1)<3(x+1)-2.解:去括号,得2x-2<3x+3-2.不等式两边加上2,得2x<3x+3.不等式两边减去3x,得-x<3.不等式两边乘以-1,得x>-3.(2)x-13≥12x-1.解:不等式两边都乘以6,得2(x-1)≥3x-6.去括号,得2x-2≥3x-6.不等式两边都加2,得2x≥3x-4.不等式两边都减去3x,得-x≥-4.不等式两边除以-1,得x≤4.16.现有不等式的两个性质:①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.请解决以下两个问题:(1)利用性质①比较2a与a的大小(a≠0);(2)利用性质②比较2a与a的大小(a≠0).解:(1)若a>0,则a+a>0+a,即2a>a.若a<0,则a+a<0+a,即2a<a.(2)若a>0,由2>1得2·a>1·a,即2a>a.若a<0,由2>1得2·a<1·a,即2a<a.。
人教版七年级数学下册9.1.2 不等式的性质(原卷版)

第九章不等式与不等式组9.1.2不等式的性质一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列变形不正确的是A.由b>5得4a+b>4a+5 B.由a>b得b<aC.由-12x>2y得x<-4y D.-5x>-a得x>5a2.已知关于x的不等式x>32a-表示在数轴上如图所示,则a的值为A.1 B.2 C.-1 D.-23.用不等式表示如图所示的解集,其中正确的是A.x>-2 B.x<-2C.x≥-2 D.x≤-24.小明的作业本上有四道利用不等式的性质,将不等式化为x>a或x<a的作业题:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2,其中正确的有A.1题B.2题C.3题D.4题5.不等式23x>-解集是A.23x>-B.23x<-C.32x>-D.32x<-二、填空题:请将答案填在题中横线上.6.已知数a、b的对应点在数轴上的位置如图所示,则a-3__________b-3.学-科网7.若关于x的不等式(1-a)x>2可化为x>21a-,则a的取值范围是__________.三、解答题:解答应写出文字说明、证明过程或演算步骤.8.直接写出下列各不等式的解集:(1)x+1>0;(2)3x<6.学+科网9.利用不等式的性质解下列不等式,并在数轴上表示其解集.(1)-3x+2>2x+7;(2)142 55x x≥--.。
永宁县四中七年级数学下册第九章不等式与不等式组9.1.2不等式的性质同步练习含解析新版新人教版

3.AD∥BC,AB∥DC
4.AB,CD,同位角相等,两直线平行
5. ∠1,∠4
∠2,∠3
6.AB,CD;CD,EF.
7. ∠DAC=45°
内错角相等两直线平行
C.平行公理D.平行于同一直线的两直线平行
4.如图所示,下列推理正确的是()
A.∵∠1=∠4(已知)∴AB∥CD(内错角相等,两直线平行)
B.∵∠2=∠3(已知)∴AE∥DF(内错角相等,两直线平行)
C.∵∠1=∠3(已知)∴AB∥DF(内错角相等,两直线平行)
D.∵∠2=∠2(已知)∴AE∥DC(内错角相等,两直线平行)
16.根据不等式的基本性质,把下列不等式化为“x>a”或“x<a”的形式.
(1)x-2<3;(2)6x<5x-1;
(3) x>5;(4)-4x>3;
(5)- x< ;(6) x>- x-6
答案
1.D
2.D
3.B
4.B
5.D
6.B
7.D
8.C
9.B
10.>
11.-1
12.>, >, >, <, >, <
(三)典例精析 , 掌握新知
.
例2计算 :
例3 已知-2x3m+1y2n与4xn-6y-3-m的积与-x4y是同类项 , 求m、n的值.
[教学说明]教师给出例题 , 学生独立自主完成 , 教师可让几个学生上台在黑板上演算 , 然后给予点评.
(四)运用新知 , 深化理解
1.计算 :
.
2.计算 :
3.〞勇气〞号探测器于北京时间2004年1月4日在火星上成功登陆.〞勇气〞号探测器是按第二宇宙速度〔11.2km/s〕飞行了6个月后到达火星的 , 此时 , 它飞行了多少千米 ?〔1个月按30天计算〕
人教版七年级数学下册《9.1.2不等式的性质》同步练习

9.1.2 不等式的性质关键问答①在处于不平衡状态下的天平左右两侧同时添加或去掉同质量的物体,天平的状态怎么 样?它对应不等式什么样的性质?②这个例子可以说明不等式的哪个性质?③解不等式,实际是把复杂的不等式化成什么形式?1.设“▲”“●”“■”分别表示三种不同的物体,现用天平称两次,情况如图 9-1-4,那么将“▲”“●”“■”这三种物体的质量按从大到小的顺序排列应为( )图 9-1-4A .■,●,▲B .▲,■,●C .■,▲,●D .●,▲,■2. 已知表示数 a ,b 的点在数轴上的位置如图 9-1-5 所示,则有 a ________b .结合 数轴,可得-a ________-b .图 9-1-53.用不等式的性质解下列不等式,并在数轴上表示其解集.1(1)x -17<-5; (2)- x >-3.2命题点 1 不等式的性质 [热度:97%]① ②③4.若 x >y ,则下列不等式中不一定成立的是( )1A .x +1>y +1B .2x >2yC. x > y D .x >y 2方法点拨④要说明不等式不成立,只需要找出一个反例即可.即条件成立,结论不成立.5. ⑤若-2a <-2b ,则 a >b ,其根据是()A .不等式的性质 1B .不等式的性质 2C .不等式的性质 3D .等式的性质 2易错警示⑤利用不等式的性质 3 时,要注意改变不等号的方向.6.若 x <y ,且(a +5)x >(a +5)y ,则 a 的取值范围为( )A .a >-5B .a ≥-5C .a <-5D .a <57.若数 a ,b ,c 在数轴上对应点的位置如图 9-1-6 所示,则下列不等式成立的是()图 9-1-6a cA .a -c >b -cB .a +c <b +cC .ac >bcD. <b b解题突破⑥由数轴上点的位置得到关于 a ,b ,c 的不等式,观察选项中的不等式是否可由这些不 等式变形得到.可利用不等式的性质进行判断.8.已知 x >y ,且 xy <0,|x |<|y |,a 为任意有理数,下列式子正确的是( )A .-x >-yB .a x >a yC .-x +a <-y +aD .x >-y 解题突破④ 2 2⑥ ⑦2 2⑦a 2的取值范围是什么?x +y 的值是正数还是负数?9.若 a <b <0,则 1,1-a ,1-b 这三个数之间的大小关系为______________(用“<” 连接).10.若 2a +3b -1>3a +2b ,则 a ,b 的大小关系为__________(用“<”连接).命题点 2 利用不等式的性质解简单的不等式 [热度:96%]11. 把不等式 2x +2≥0 的解集表示在数轴上,正确的是( )图 9-1-7方法点拨⑧大于向右画,小于向左画,有等于号是实心圆点. 12.按下列要求写出不等式.6 5(1) m > n ,两边都乘 15,得____________;5 37 8(2)- x ≤-5,两边都乘- ,得____________;(3)x -5≥-7,两边都加上 5,得____________.13. ⑨解下列不等式,并把它们的解集表示在数轴上.(1)2x -3>1;1 2(2) x >- x -2; 3 31(3)-4x ≤-2x + ;(4)2x -1≥10x +1.⑧ 8 7 2解题突破⑨这里要用到不等式的性质,利用不等式的性质3时,要注意不等号的方向要改变.命题点3不等式的简单应用[热度:98%]14.某种品牌的八宝粥的净含量为x g,外包装标明:净含量为(330±10)g,表明了x 的取值范围是( )A.320<x<340B.320≤x<340C.320<x≤340D.320≤x≤34015.⑩有3人携带装修材料乘坐电梯,这3人的体重共200kg,每捆材料重20kg,电梯最大载重负荷为1050kg,则该电梯在此3人乘坐的情况下最多还能搭载材料( ) A.41 捆B.42捆C.43捆D.44捆易错警示⑩注意不等式的解要符合实际意义.16.现有不等式的性质:①不等式两边加(或减)同一个数(或式子),不等号的方向不变;②不等式两边乘同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.请解决以下两个问题:(1)利用性质①比较2a与a的大小(a≠0);(2)利用性质②比较2a与a的大小(a≠0).易错警示⑪注意利用不等式的性质时,有可能需要分情况考虑问题.17.⑫【提出问题】已知x-y=2,且x>1,y<0,试确定x+y的取值范围.【分析问题】先根据已知条件用一个量如y表示另一个量如x,然后根据题中已知量x的取值范围,构建关于y的不等式,从而确定y的取值范围,同法再确定另一未知量x的取值范围,最后利用不等式的性质即可获解.【解决问题】解:∵x-y=2,∴x=y+2.又∵x>1,∴y+2>1,∴y>-1.又∵y<0,∴-1<y<0.①同理,得1<x<2.②由①+②,得-1+1<y+x<0+2.∴x+y 的取值范围是0<x+y<2.【尝试应用】已知x-y=-3,且x<-1,y>1,求x+y的取值范围.方法点拨若a>c,b>d,则有a+b>c+d,这也是不等式的一个重要性质典题讲评与答案详析1.C 2.< >3.解:(1)不等式的解集为 x <12.在数轴上表示如下:(2)不等式的解集为 x <6.在数轴上表示如下:4.D [解析] 由不等式的性质 1,可得 A 正确;由不等式的性质 2,可得 B ,C 正确; 选项 D 不一定成立.5.C [解析] 由-2a <-2b ,左右两边同时除以-2,由不等式的性质 3,可得 a >b . 6.C [解析]∵x <y ,且(a +5)x >(a +5)y ,∴a +5<0,即 a <-5.7.B [解析] 由数轴上点的位置可得,a <b <0,c >0,所以由不等式的性质 1,可得不 等式 a +c <b +c 是成立的.8.C [解析] 因为 x >y ,利用不等式的性质 3,两边都乘以-1,得-x <-y ,则 A 错误;因为-x <-y ,利用不等式的性质 1,两边都加上 a ,得-x +a <-y +a ,因此选项 C 正确;因为 x >y ,利用不等式的性质 2,两边都乘以 a 2(a ≠0),得 a x >a y ,而这里没有确定 a 是不等于 0 的,故 a x >a y 不一定成立,因此 B 错误;另外由 x >y ,xy <0,得 x >0,y <0,又|x |<|y |, 可得 x +y <0,即 x <-y ,故 D 错误.9.1<1-b <1-a[解析] 因为 a <b <0,所以-a >-b >0,所以 1-a >1-b >1,即 1<1-b <1-a .10.a <b [解析] 已知 2a +3b -1>3a +2b ,由不等式的性质 1,不等式的左右两边同时减去 2a ,得 3b -1>a +2b .再由不等式的性质 1,不等式的左右两边同时减去 2b ,得 b -2 2 221>a ,所以 a <b .11.C [解析] 不等式的 2x +2≥0 的解集为 x ≥-1.故选 C.4012.(1)18m >25n (2)x ≥ (3)x ≥-213.解:(1)不等式的解集为 x >2.把解集表示在数轴上如下:(2)不等式的解集为 x >-2.把解集表示在数轴上如下:1(3)不等式的解集为 x ≥- .把解集表示在数轴上如下:1(4)不等式的解集为 x ≤- .把解集表示在数轴上如下:14.D [解析 ] 净含量为 330±10 g ,表明了这罐八宝粥的净含量最大为 330+10= 340(g),最小为 330-10=320(g),所以 320≤x ≤340.15.B [解析] 设还能搭载 x 捆材料.依题意,得200+20x ≤1050,解得 x ≤42.5,所以最多还能搭载材料 42 捆.16.解:(1)当 a >0 时,a +a >a +0,即 2a >a ;当 a <0 时,a +a <a +0,即 2a <a .(2)当 a >0 时,由 2>1,得 2·a >1·a ,即 2a >a ;当 a <0 时,由 2>1,得 2·a <1·a ,即 2a <a .17.解:∵x -y =-3,∴x =y -3.又∵x <-1,∴y -3<-1,7 44∴y<2.又∵y>1,∴1<y<2.①同理,得-2<x<-1.②由①+②,得1-2<y+x<2-1.∴x+y 的取值范围是-1<x+y<1.【关键问答】①天平的状态保持不变,它对应不等式的性质1,即不等式两边加(或减)同一个数(或式子),不等号的方向不变.②不等式的性质3.③x>a或x<a.。
9.1.2不等式的性质课课练习及答案(新人教版七年级下)pdf版

9 1 2㊀不等式的性质㊀1.掌握不等式的基本性质,体会不等式与等式性质的联系与区别.2.能根据不等式的性质将不等式变形.3.能解数字系数的一元一次不等式,并能在数轴上表示出解集.㊀开心预习梳理,轻松搞定基础.1.(1)在不等式两边同时加上(或减去)同一个数或整式,不等号方向㊀㊀㊀㊀; (2)在不等式两边同时乘以(或除以)同一个正数,不等号方向㊀㊀㊀㊀; (3)在不等式两边同时乘以(或除以)同一个负数,不等号方向㊀㊀㊀㊀.2.(1)要使不等式x+3>0成立,则x的取值范围是㊀㊀㊀㊀;(2)若x>4,则x+3㊀㊀㊀㊀4+3;若-3x<9,则x㊀㊀㊀㊀-3;若x2<-y4,则2x ㊀㊀㊀㊀-y.㊀重难疑点,一网打尽.3.由不等式a x>b,得到x<b a,则(㊀㊀).A.a=0B.a<0C.a>0D.aʂ04.若a<b,则下列各式中一定成立的是(㊀㊀).A.a-1<b-1B.a3>b3C.-a<-b D.a c<b c5.a是任意有理数,下列各式正确的是(㊀㊀).A.3a>4a B.a3<a4C.a>-a D.1-a>12-a6.利用不等式的性质解下列不等式,并将解集在数轴上表示出来:(1)5x-1<9;(2)-45x>-1.不等式两边加(或减)同一个数(或式子),不等号的方向不变.㊀源于教材,宽于教材,举一反三显身手.7.若0<x<1,则x,1x,x2的大小关系是(㊀㊀).A.1x<x<x2B.x<1x<x2C.x2<x<1x D.1x<x2<x8.关于x的不等式(2m+1)x<2m+1的解集是x>1,则m的取值范围是㊀㊀㊀㊀.9.用 > < 或 = 填空.(1)若x>-2,则x-m㊀㊀㊀㊀-2-m;(2)若7m-5b<7n-5b,则7m㊀㊀㊀㊀7n,1-7m㊀㊀㊀㊀1-7n;(3)若|a|a=-1,则a㊀㊀㊀㊀0.10.探究题:(1)①如果a-b<0,那么a㊀㊀㊀㊀b;②如果a-b=0,那么a㊀㊀㊀㊀b;③如果a-b>0,那么a㊀㊀㊀㊀b.(2)由(1)中的结论你能归纳出比较a,b大小的方法吗?请你用文字语言叙述出来; (3)试用(1)中的方法比较3x2-2x+7与4x2-2x+7的大小.㊀瞧,中考曾经这么考!11.(2012 广东广州)已知a>b,若c是任意实数,则下列不等式中总是成立的是(㊀㊀).A.a+c<b+c B.a-c>b-cC.a c<b c D.a c>b c12.(2012 贵州六盘水)已知不等式x-1ȡ0,则此不等式的解集在数轴上表示为(㊀㊀).9.1.2㊀不等式的性质1.(1)不变㊀(2)不变㊀(3)改变2.(1)x>-3㊀(2)>㊀>㊀<3.B㊀4.A㊀5.D6.(1)x<2㊀(2)x<54,在数轴上表示略.7.C㊀8.m<-129.(1)>㊀(2)<㊀>㊀(3)<10.(1)<㊀=㊀>(2)比较a,b两数的大小,如果a与b的差大于0,则a>b;如果a与b的差等于0,则a=b;如果a与b的差小于0,则a<b.(3)(3x2-2x+7)-(4x2-2x+7)=-x2ɤ0,故3x2-2x+7ɤ4x2-2x+7.11.B㊀12.C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.1.2《不等式的性质》同步练习题(2)
知识点:
1、不等式的性质1:不等式的两边加上(或减去)同一个数(或式子),不等号的方向不变,用式子表示:如果a>b ,那么a ±c>b ±c.
2、不等式的性质2:不等式的两边乘以(或除以)同一正数,不等号的方向不变,
3、不等式的性质3:不等式两边乘以(或除以)同一个负数,不等号的方向改变,
用式子表示:a>b ,c<0,那么,ac < bc 或 a c < b c
. 同步练习:
1、下列不等式变形正确的是 ( )
A.由4x- 1≥0得4x>1
B.由5x>3 得 x>3
C.由
2
y >0得 y>0 D.由-2x<4得x<-2 2、图中表示的是不等式的解集,其中错误的是( ) A 、x ≥-
2 B 、x <1 C 、x ≠0 D 、x <0
3.在平面直角坐标系中,点(-7,-2m+1)在第三象限,则m 的取值范围是( )
A.m <
21 B.m> - 21 C.m < -21 D.m > 2
1 4.关于x 的不等式(1-a )x> 3 解集为x < a -13,则a 的取值范围是 ( ) A.a >0 B.a<0 C.a > 1 D.a < 1
5.不等式 2x> 3 - x 解集为
6.若 2x - 3
1-x 2的值不大于 1,则该不等式的负整数解是 7.若关于x 的方程x +a =7的解是非负数,则a 的取值范围是
8.解下列不等式,并将其解集在数轴上表示出来:
(1)3x + 1 > x - 2 (2) x - 3 ≤-2x + 3 (3)2
5x – 1 >3x-2 (4)-6x > -4x +2 (5) 1-3
1x ≥ x – 2 (6) 3x -2 ≥ x +4 (7)5x – 3 > 2 (3-2x ) (8) 213-y ≥ 6
510+y - 1 0
0010-1
-2
9.1.2《不等式的性质》同步练习题(2)答案:
1.C
2.D
3.D
4.C
5.X > 1
6. -4;-3;-2;-1
7.a ≤ 7
8.(1) x > -
23 (2)x ≤ 2 (3) x ≤ 2 (4)x < -1 (5)x ≤ 49 (6)x ≥ 3 (7)x >1 (8)y ≤-2。
