长江大学信号与系统7-4
长江大学信号与系统matlab实验答案

实验1 信号变换与系统非时变性质的波形绘制●用MA TLAB画出习题1-8的波形。
●用MA TLAB画出习题1-10的波形。
Eg 1.8代码如下:function [y]=zdyt(t) %定义函数zdyty=-2/3*(t-3).*(heaviside(-t+3)-heaviside(-t));endt0=-10;t1=4;dt=0.02;t=t0:dt:t1;f=zdyt(t);y=zdyt(t+3);x=zdyt(2*t-2);g=zdyt(2-2*t);h=zdyt(-0.5*t-1);fe=0.5*(zdyt(t)+zdyt(-t));fo=0.5*(zdyt(t)-zdyt(-t));subplot(7,1,1),plot(t,f);title('信号波形的变化')ylabel('f(t)')grid;line([t0 t1],[0 0]);subplot(7,1,2),plot(t,y);ylabel('y(t)')grid;line([t0 t1],[0 0]);subplot(7,1,3),plot(t,x);ylabel('x(t)')grid;line([t0 t1],[0 0]);subplot(7,1,4),plot(t,g);ylabel('g(t)')grid;line([t0 t1],[0 0]);subplot(7,1,5),plot(t,h);ylabel('h(t)')grid;line([t0 t1],[0 0]);subplot(7,1,6),plot(t,fe);ylabel('fe(t)')grid;line([t0 t1],[0 0]);subplot(7,1,7),plot(t,fo);ylabel('fo(t)')grid;line([t0 t1],[0 0]);xlabel('Time(sec)')结果:Eg1.10代码如下:function [u]=f(t) %定义函数f(t) u= heaviside(t)-heaviside(t-2); endfunction [u] =y(t) %定义函数y(t)u=2*(t.*heaviside(t)-2*(t-1).*heaviside(t-1)+(t-2).*heaviside(t-2)); endt0=-2;t1=5;dt=0.01; t=t0:dt:t1; f1=f(t); y1=y(t); f2=f(t)-f(t-2); y2=y(t)-y(t-2); f3=f(t)-f(t+1); y3=y(t)-y(t+1);subplot(3,2,1),plot(t,f1); title('激励——响应波形图') ylabel('f1(t)')grid;line([t0 t1],[0 0]);-10-8-6-4-2024012信号波形的变化f (t)-10-8-6-4-2024012y (t)-10-8-6-4-2024012x (t)-10-8-6-4-2024012g (t)-10-8-6-4-2024012h (t)-10-8-6-4-202400.51f e (t)-10-8-6-4-2024-101f o (t)Time(sec)subplot(3,2,2),plot(t,y1); ylabel('y1(t)')grid;line([t0 t1],[0 0]); subplot(3,2,3),plot(t,f2); ylabel('f2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,4),plot(t,y2); ylabel('y2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,5),plot(t,f3); ylabel('f3(t)')grid;line([t0 t1],[0 0]); subplot(3,2,6),plot(t,y3); ylabel('y3(t)')grid;line([t0 t1],[0 0]); xlabel('Time(sec)')结果:实验2 微分方程的符号计算和波形绘制上机内容用MA TLAB 计算习题2-1,并画出系统响应的波形。
《信号与系统(第四版)》习题详解图文

故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组{ξ1(t),ξ2(t),ξ3(t),ξ4(t)}在(0,4)区间上是否 为正交函数组,是否为归一化正交函数组,是否为完备正交函 数组,并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到:
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=-f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω),且 试在K≥ωm条件下化简下式:
72
第3章 连续信号与系统的频域分析 73
107
“信号与系统”课程教学中对分教学法的应用

101Internet Application互联网+应用引言:对方教学法是复旦大学张学新教授提出的新型的课堂教学模式,其核心就是将教学环节一分为二,让学生在设问和提问的过程当中产生自主学习的动机和欲望,养成自主学习习惯,而教师在解答疑问的过程当中与学生进行交流沟通,两者共同承担教学空间。
为了保障学生的学习效率和学习积极性,教师需要根据一定的思路来调整教学方法,强化学生对于基本知识的理解和掌握,也能够强化学生综合运用知识的工程应用能力。
一、对分教学法的基本流程对分课堂主体分为三个教学环节:教师讲解(Presentation),学生自学、内化吸收及作业(Assimilation),课堂讨论环节(Discussion),也称PAD 课堂。
在教学时间安排上,对分课堂强调,一半时间由教师讲解基本概念与重难点知识。
另一半时间学生以自学或者讨论的方式进行内化吸收,(一) 课前准备环节课前准备环节就将课堂划分为两个部分,一部分给教师进行讲课,另一部分让学生完成讨论进行互动学习,其中课堂对分就是最为主要的形式,让学生利用学习知识和讨论之间的时间差完成独立的探索和研究,并互相交流沟通,从而能够解决一些简单的问题,某些重难点问题可以交给教师进行处理。
该模式与传统教学最大的不同之处在于学生可以提前做好准备,进行讨论完成当堂对分,通过不同的教学方法实现教学目标。
(二)课堂讲授环节在课程讲授环节,教师不必将所有内容进行系统化和具体化讲解,对分课堂强调的是精讲,要求教师在缩短课堂时长的前提下,对某些主要学习内容和重难点进行针对性讲解,涵盖课程所涉及到的框架类知识结构。
这样一来,学生可以对所学概念有一个框架性的认识,并完成知识的内化和补充。
在后续的作业设计阶段,应该引导学生将所有知识进行综合整合,同时让学生在课堂对分当中有充足的时间用于将所有知识进行理解和深化,让所有的教学步骤在课堂上就能完成。
对于学生受益最大的知识和某些难以解决的问题,在蔡骁(1990.07——),男,汉族,湖南长沙,硕士研究生,助教,中国消防救援学院,研究方向:通信与信息系统教学,应急通信技术;通信作者:宋亚婷,女,硕士研究生,中国消防救援学院。
信号与系统第四版习题解答

《信号与系统》(第四版)习题解析高等教育2007年8月目录第1章习题解析1第2章习题解析5第3章习题解析14第4章习题解析21第5章习题解析29第6章习题解析39第7章习题解析47第8章习题解析52第1章习题解析1-1题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解(a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
](a) 2 f (t - 2 )(b) f ( 2t )(c)f (2t ) (d)f (-t +1 )题1-2图解以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图S R S L S C解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅=tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
题1-4图解系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) +f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有21显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
精品文档-信号与系统(第四版)(陈生潭)-第3章

An cos(nt n )
Fne jnt
n 1
n
F0 2 Fn cos(nt n )
其中:
n 1
an
2 T
t0 T t0
fT (t )cosntdt
bn
2 T
t0 T t0
fT (t )sin ntdt
n0,1,2...
1
n1,2...
Fn
T
t0 T t0
fT (t)e jnt dt
fT (t)sin ntdt
A0 a0 An an2 bn2
n 1,2...
n
arctg
bn an
说明:1.周期信号可分解表示为三角函数的线性组合。
2.物理意义:周期信号可分解为众多频率成整数倍
和正(余)弦函数或分量的线性组合。具体有:
a0 A0 直流分量cost, sin t 基波分量 22
fT (t)
Fne jnt
F e j (nt n ) n
F0
2 Fn cos(nt n )
n
n
n1
各谐波分量的角频率nΩ 是基波角频率Ω的n倍且有不同的
振幅和相位,均有傅立叶系数 Fn Fn e jn 反映出来。
为揭示各谐波振幅、初相随角频率变化情况,特画出振幅
及相位随w变化的曲线称其为频谱图。
的模
最小,(此时的C12称为最佳),当C12=0时,Ve的
模最小,此时V1和V2正交。
2.矢量分解
在平面空间里,相互正交的矢量
V1和V2构成一个正交矢量集,而且为
完备的正交矢量集。平面空间中的任
一矢量V都可表示为V1和V2的线性组合 (如上图)。即:
V=C1V1+C2 V2。式中V1、V2为单位矢量,且V1·V2=0。其中:
《信号与系统》教学改革思考与实践

…
…
…
…
…
…
…
…
…
国地一 -
《 信号与系统 》教学改革思考与实践
长江大学电信 学院 蔡 卫菊
【 摘要】 《 信 号与系统》是 电子信息类 的专业基础课 ,针对 《 信号 与系统》课 程的特 点,本 文从教 学方法和手段、讨论课 的教 学、课程实验环节等方面进行 思考
与 实 践 ,将MATL A B软 件 引入 教 学 和 实 验 中 ,更 好 地 培 养 了 学 生 思考 问题 、分 析 问 题 、 解 决 问 题 的 能 力 , 取 得 了 良好 的 教 学 效 果 。 【 关键 词 】 信 号 与 系 统 ;MAT L AB; 教 学 改 革
《 信 号 与 系 统 》 是 电 子 信 息 类 等 相 关 习题 是 对 课 堂 教 学 内容 的 延 伸 和 拓 展 , 专 业 的一 门重 要 专 业 基 础 课 ,所 涉 及 的概 念 能 够 帮 助 学 生 消 化 和 巩 固 所 学 知 识 , 培 养 学 和 分 析 方 法 已经 在 众 多 领 域 和 学 科 中 有 所 应 生 运 用 理 论 知 识 解 决 实 际 问题 的 能 力 。在 习 用 。 该 课 程 以高 等 数 学 、 工 程 数 学 等 课 程 为 题 的 挑 选 上 主 要 分 五 个 部 分 : 自测 题 ,每 节 基 础 ,是 后 继 的 数 字 信 号 处 理 、通 信 原 理 、 课 完 成 之 后 进 行 自 我 检 测 的 题 目 ; 基 本 习 自动控制 原理等 专业课程 的先修课 程 ,在教 题 , 要 求 绝 大 多 数 学 生 都 会 做 的 习 题 ; 复 学 环 节 中 起 着 承 上 启 下 的 作 用 , 由 于 该 课 程 习提 高题 ,针对 学 有 余 力 的学 生 ,特 别是 理 论 性 很 强 , 内容 比较 抽 象 , 公式 和 理 论 推导 要 考 研 的 学 生 , 为 此 本 课 程 配 备 了 考 研 指 导 多 , 具 有 一 定 的 教 学 难 度 。 同时 《 信 号 与 系 书 ; 学 习 指 导 书 中 的 阶 段 自测 题 , 在 一 阶 段 统 》是 一 门理论 与 实 践 相 结 合 、应 用 性 极 强 的 的相 关 课 程 完 成 之 后 要 求 学 生 进 行 阶 段 性 测 课 程 。 因 此 , 将 抽 象 的 理 论 变 为 学 生 可 接 受 试 ;M A T L A B 练 习 题 ;主 要 用 于 锻 炼 学 生 利 用 的感 性 认 识 ,如 何 与 实 际 工程 应 用 相 结 合 ,是 M A T L A B 对课程 中主要知 识点进行仿 真分析 , 《 信 号 与 系 统 》课 程 面 临 的挑 战 之 一 …。本 文 加 深 对 理 论 的理 解 , 同 时 本 书 还 配 套 了 《 信 针对 《 信 号 与 系 统 》 课 程 的 特 点 , 从 教 学 方 号 与 系 统 》 的实 验 教 程 供 学 生 参 考 。 在 习 题 法 和 手 段 、 讨 论 课 的 教 学 、 课 程 实 验 环 节 等 课 教 学 过 程 中 , 注 重 理 论 与 实 践 相 结 合 , 让 方面 进行 思考与实 践,将M A T L A B 软 件 引 入 教 学 生 掌 握 分 析 问题 解 决 问 题 的 方 法 , 从 而 进 学和 实验 中,更好地 培养 了学生思考 问题 、 步理解 和掌握 知识难 点,拓宽知识 面,锻 分 析 问 题 、解 决 问题 的 能 力 。 炼 思 维 能 力 “ 。 改 进教 学 方 法 和手 段 。实现 知 识 5 . 重 视 网 络 教 学 资 源 的 利 用 传授 与能力培 养结合 在长 江 大 学 精 品课 程 网站 上 , 《 信 号 1 . 把 握 教 学 的 核 心 内 容 与 系 统 》 作 为 省 级 精 品课 程 , 一 直 致 力 于 给 信 号 与 系 统 课 程 的 特 点 是 理 论 性 比 较 学 生 提 供 更 完 善 的 教 学 资源 , 从 理 论 课 的 课 强 , 内 容 比较 多 ,但 课 程 内容 之 间 有 着 非 常 件 到 课 后 习 题 解 答 , 从 理 论 讲 解 到 实 验 演 密 切 的 联 系 。 例 如 在 变 换 域 分 析 方 法 中 , 可 示 , 以及 在 线 答 疑 等 等 多 方 面 的 内容 ,有 利 以将 傅 里 叶 变 换 和 傅 里 叶 级 数 以 及 拉 普 拉 斯 于 提 高 学 生 的 学 习 积 极 性 , 帮 助 学 生 实 时 解 变 化 联 系 起 来 , 同时 系 统 的 傅 里 叶 分 析 与 系 决 学 习 中疑 问 。 统 的 拉 普 拉 斯 变 化 分 析 也 有 相 似 和 不 同 的 地 二 、加强信 号与系统 讨论课 的教 学 方 ,通 过 比较 分析 ,使 其成为 一个有机 的整 针 对 多 数 学 生 该 课 程 究 竟 有 何 用 处 很 体 。又如 ,连 续时 间系 统与离散 时 间系 统的 茫 然 的 情 况 , 以及 学 习 该 门课 程 的 困难 展 开 分 析 方 法 在 很 多 地 方 是 非 常 相 似 的 ,但 是 又 讨 论 ,意 在 激 发 学 生 的 积 极 性 , 讨 论 了信 号 有 各 自 的 特 点 。 在 教 学 中 , 突 出 了这 些 相 互 与 系 统 与 前 续 课 程 及 与 后 续 主 要 课 程 之 间 的 之 间 的 联 系 ,使 得 学 生 可 以从 更 高 层 面 上 整 关 系 , 让 学 生 了 解 到 学 习 《 信 号 与 系 统 》课 体 把 握 课 程 的 核 心 内容 。 程 的重要性 和专业知 识的应用情 况。讨论课 2 . 对 教 学 内容 的 授 课 顺 序 进 行 改 革 对 《 信号 与 系 统 》课 程 中涉 及 的频 域 分析 针 对 以 往 学 生 的 学 习 效 果 , 学 生 普 遍 方 法 作 了简 单 的 总 结 , 包 括 对 信 号 的 表 示 和 反 映 傅 里 叶 变 化 较 难 接 受 , 而 拉 普 拉 斯 变 化 系 统 的 分 析 方 法 ,其 中 对 重 要 的 公 式 作 了简 更 容 易接 受 , 因 此 在 教 学 过 程 首 先 讲 授 拉 普 单 的 回 顾 和 总 结 , 旨在 让 学 生 从 整 体 上 认 识 拉 斯 变 换 以 及 连 续 系 统 的 拉 普 拉 斯 变 化 分 频 域 分 析 方 法 。 并 对 频 域 分 析 的应 用 进 行 析 , 其 次 是 傅 里 叶 变 化 以及 系 统 的 分 析 , 这 举 例 , 通 过 频 域 分 析 的 实 例 加 深 学 生 对 频 域 样 让 原 本 复 杂 的过 程 变 得 更 加 循 序 渐 进 , 学 分 析 的 概 念 和 应 用 认 识 , 引 导 学 生将 这 些 分 生 学起来 更加轻松 。 析 问题 的 方 法 应 用 到 实 际 中 , 并 给 出 每 个 实 3 . 采用多种 教学形 式结合 例 相 应 的M A T L A B 程 序 ,通 过 仿 真 实 验 可 加 让 本 课 程 对 每 一 节 课 的 授 课 方 案 作 出 详 学 生 更 加 直 观 的 认 识 信 号 与 系 统 的理 论 知 识 细 的 安 排 。 如 授 课 方 式 、主 要 知 识 点 、 课 堂 与 实 践 工 程 有 何 关 联 等 。对 《 信号与 系统》 小 结 、 课 堂 提 问与 练 习 等 。 由 于 教 学 教 学 对 课 程 中 涉 及 的 复频 域 分 析 方 法 作 了简 单 的 总 象 的 个 体 差 异 和 多 样 性 ,不 存 在 单 一 的 最 佳 结 , 并 将 其 与 频 域 进 行 比 较 分 析 其 联 系 与 区 的 教 学 方 法 和 手 段 ,所 以在 教 学 的 过 程 中 , 别 , 加 深 了 学 生 对 复 频 域 的 理 解 。 同 时 , 对 要 勇 于 创 新 。 我 校 在 信 号 与 系 统 的 教 学 过 程 复 频 域 的应 用 进 行 举 例 ,通 过 仿 真 实 验 让 学 中 主 要 采 用 讲 授 、 演 示 、 讨 论 相 结 合 的 方 生 更 好 地 理 解 理 论 与 实 践 之 间 的 联 系 。 法 。 研 制 了 信 号 与 系 统 实 验 演 示 系 统 , 把 讨 论 课 是 师 生 互 动 的 主 要 方 式 , 通 过 M A T L A B 引 入 到 教 学 中 。 例 如 讲 解 卷 积 积 分 计 讨 论 课 可 以解 决 学 习 过 程 中 的 疑 问 ,帮 助 学 算 过 程 , 采 用 多 媒 体 动 画 演 示 卷 积 积 分 的 计 生 更 好 完 成 后 续 课 程 的 学 习 ,提 高 了学 生 的 算过程 ,使原本 枯燥 乏味的计 算过程变得 生 学 习 兴 趣 , 调 动 了学 生 的 积 极 性 , 同 时 讨 论 动 直 观 , 学 生 就 会 明 白 卷 积 的 图解 含 义 。 又 课 程 的 开 展 扩 展 了本 课 程 的应 用 , 培 养 学 生 如在z 变 化 和 拉 普 拉 斯 变 化 的 关 系 中 , 利 用 分 析 问 题 、 解 决 问题 的 能 力 。 动画演示 其Z 平面 和S 平 面 的 映 射 关 系 图 , 可 三 、加强信号 与系统仿真 实验环节 以 让 学 生 清 楚 两 者 之 间 的关 系 。 M A T L A B 软件 是 由M a t h W o r k 公司 于 l 9 8 4 4 . 重 视 习题 课 的 教 学 年 推 出 的 数 学 软 件 ,如 今 已成 为 各 种 系 统 仿
新版长江大学电子信息考研经验考研参考书考研真题

在很多年之前我从来不认为学习是一件多么重要的事情,那个时候我混迹于人群之中,跟大多数的人一样,做着这个时代青少年该做的事情,一切都井井有条,只不过,我不知做这些是为了什么,只因大家都这样做,所以我只是随众而已,虽然考上了一个不错的大学,但,我的人生目标一直以来都比较混乱。
但是后来,对世界有了进一步了解之后,我忽而发现,自己真的不过是这浩渺宇宙中的苍茫一粟,而我自身的存在可能根本不能由我自己来把握。
认识到个体的渺小之后,忽然有了争夺自己命运主导权的想法。
所以走到这个阶段,我选择了考研,考研只不过是万千道路中的一条。
不过我认为这是一条比较稳妥且便捷的道路。
而事到如今,我觉得我的选择是正确的,时隔一年之久,我终于涅槃重生得到了自己心仪院校抛来的橄榄枝。
自此之后也算是有了自己的方向,终于不再浑浑噩噩,不再在时代的浪潮中随波逐流。
而这一年的时间对于像我这样一个懒惰、闲散的人来讲实在是太漫长、太难熬了。
这期间我甚至想过不如放弃吧,得过且过又怎样呢,还不是一样活着。
可是最终,我内心对于自身价值探索的念头还是占了上峰。
我庆幸自己居然会有这样的觉悟,真是不枉我活了二十多个春秋。
在此写下我这一年来的心酸泪水供大家闲来翻阅,当然最重要的是,干货满满,包括备考经验,复习方法,复习资料,面试经验等等。
所以篇幅会比较长,还望大家耐心读完,结尾处会附上我的学习资料供大家下载,希望会对各位有所帮助,也不枉我码了这么多字吧。
长江大学电子信息的初试科目为:(101)思想政治理论(203)日语(302)数学二(852)信号与系统或(101)思想政治理论(203)日语(302)数学二(853)自动控制原理或(101)思想政治理论(204)英语二(302)数学二(852)信号与系统或(101)思想政治理论(204)英语二(302)数学二(853)自动控制原理参考书目为:(852)信号与系统《信号与系统》(第一版),金波,高等教育出版社,2011 (853)自动控制原理《自动控制原理》(第一版),吴怀宇、廖家平,华中科技大学出版社,2012;《现代控制理论》(第一版),赵明旺,华中科技大学出版社,2007先介绍一下英语现在就可以开始背单词了,识记为主(看着单词能想到其中文章即可,不需要能拼写)从前期复习到考试前每天坚持两到四篇阅读(至少也得一篇)11月到考试前一天背20篇英语范文(能默写的程度)。
长江大学地物院信号分析与处理考试试卷A和B

长江大学地物学院试卷班级姓名序号…………….…………………………….密………………………………………封………………..…………………..线……………………………………..2012—2013学年 第一学期 《信号分析与处理》课程考试试卷(B )参考答案 题号 一 二 三 四 五 总分 阅卷人 得分 注意:1、本试卷共 4 页 2、考试形式: 闭卷 3、考试时间: 110分钟 4、适用专业: 勘工、地物 5、班级、学号、姓名必须写在指定地方 一、 填空题 (每小题 2 分,共22 分) 1、功率有限信号通常是指 (1) 信号。
2、系统的时移不变性是指(2) 的性质。
3、反因果稳定系统()H Z 的收敛域为(3) 。
4、已知系统的单位冲激响应h(t),在输人信号x(t)作用下,当系统满足(4) 性质时,输人信号x(t)被分解为(5) 的线性组合。
5、最小相位信号时域特征是(6) ,其零、极点在 Z 平面的分布特征是(7) 。
6非周期信号的延续时间是2m t ,在频域被离散后,其时域信号与原时域信号的关系 是(8) ,当满足(9) 条件时,时域不会产生混叠现象。
7、DFT 的正交基kn N W 具有三种特性(10) 、(11) 和周期性。
二、简答题 (每小题 6 分,共 24 分) 1、 简述频谱混叠现象产生原因及导致的后果。
2、简述理想低通滤波器作为无失真传输系统,应满足的条件。
阅卷人 得分 阅卷人 得分3、简述何为栅栏效应及减小该效应的方法。
4、简述白噪声信号的特点。
三、 判断题[正确填√,错误填X] (每小题 2 分,共14分)1、设系统函数为()()n n H z h n z ∞-=-∞=∑,则图a 为最小相位的全通系统。
( ) 2、设系统函数为()()nn H z h n z ∞-=-∞=∑,则图b 为最小相位的高通滤波器。
( )3、将时域离散信号变换到频域后,其频域信号一定是离散的。
长江大学通信工程专业自评报告doc

湖北省普通高等学校本科专业教学合格评估自评报告学校名称:长江大学院系名称:电信学院专业名称:通信工程专业负责人:余厚全二○○九年十月十八日目录一、专业概况 (1)二、专业建设过程及成效 (2)1专业建设规划与培养方案 (2)1.1 专业设置 (2)1.2 专业建设规划 (3)1.3 人才培养方案 (4)2 专业基础条件 (5)2.1 教学科研仪器设备 (5)2.2 实践教学基地 (6)2.3 专业图书与网络资源 (6)2.4 教学经费 (7)3 师资队伍建设 (7)3.1 队伍建设状况 (7)3.2 主讲教师情况 (8)3.3 科学研究水平 (8)4 课程建设 (9)4.1 课程体系 (9)4.2 教材选用与建设 (11)4.3 教学方法与手段 (12)5 实践教学 (12)5.1 实践教学体系 (12)5.2 实验、实习和实训 (14)6 教学管理 (15)6.1 教学规章制度执行情况 (15)6.2 教学质量监控 (16)7 人才培养质量 (17)7.1 学生专业素质水平 (17)7.2 学生毕业论文(设计)质量 (19)7.3 社会评价 (19)三、存在问题与拟整改措施 (19)一、专业概况通信工程专业是在电子信息学院电子信息工程专业的基础上,根据IT行业对通信人才的巨大需求而设置的。
该专业隶属长江大学电子信息学院,以学院现有的“信号与信息处理”、“通信与信息系统”两个硕士学位点和一个“信号与信息处理”省级重点学科为依托,2003年被省教育厅批准立项建设,同年开始招收本科生74人。
本专业共有教师26人,其中教授2人,副教授和高级工程师10人,讲师12人,助教2人。
其中具有博士学位3人,具有硕士学位13人。
80%以上教师毕业于武汉大学、华中科技大学等国内著名重点大学,已形成了一支力量较雄厚的教学及科研队伍。
近三年来,本专业教师积极开展课程建设、教学改革及科学研究。
现有省级精品课程3门,校级精品课程2门;在教学改革与研究方面,获得国家级教学成果二等奖1项,湖北省教学成果一等奖和二等奖各1项;公开出版各类教材16部,发表教学研究论文14篇;完成教学研究项目5项,其中省级教研项目2项;在科研方面,先后承担省部级纵横向项目18项;发表学术论文60余篇,其中EI收录9篇,ISTP收录2篇。
《信号与系统(第四版)》习题详解 (1)

第1章 信号与系统的基本概念 解 此题练习离散信号的图形表示方法。要求熟悉常用指数 和正弦序列的图形表示、阶跃序列的定义和基本性质以及序列平 移和翻转操作对序列图形的影响。
7
第1章 信号与系统的基本概念
题解图 1.2 8
第1章 信号与系统的基本概念 1.3 试写出题图1.1各信号的解析表达式。
第1章 信号与系统的基本概念 24
第1章 信号与系统的基本概念
题解图 1.5-7 25
第1章 信号与系统的基本概念 26
第1章 信号与系统的基本概念
题解图 1.5-8 27
第1章 信号与系统的基本概念 (9) 两个连续信号相加,任一时刻的和信号值等于两信号在 该时刻的信号值之和。题(9)信号波形如题解图1.5-9所示。
3
第1章 信号与系统的基本概念 解 此题练习连续信号的波形图表示方法。除应熟悉常用连 续指数、正弦和斜升信号波形外,还应特别注意阶跃函数的基本 性质以及信号平移、翻转操作对信号波形的影响。
4
第1章 信号与系统的基本概念
题解图 1.1 5
第1章 信号与系统的基本概念 1.2 绘出下列信号的图形:
题图 1.1 9
第1章 信号与系统的基本概念 10
第1章 信号与系统的基本概念 11
第1章 信号与系统的基本概念 1.4 判定下列信号是否为周期信号。若是周期信号,则确
定信号周期T。
12
第1章 信号与系统的基本概念
解 (1) 若有两个周期分别为T1和T2的连续信号相加,当
T1/T2为有理数时,其和信号亦是周期信号,相应周期为T1和T2的最
题解图 1.5-9 28
第1章 信号与系统的基本概念 (10) 两个连续信号相乘,任一时刻的积信号值等于两信 号在该时刻的信号值之积。题(10)信号波形如题解图1.5-10 所示。
《信号与系统》精品课程建设实践探讨

加 速实 现与其 他技 术平 台课程 、计 算机技 术 间的相 互联 系及 迁移运 用 ;以多 媒体 技术 与信号 与 系统课 堂 教学 整合 问题 为切入 点 ,建构 了既 能发挥 教师 主导 作用 ,又 能体现 学生认 知 主体作 用 的教学 模式 ,培养
了学 生 的 自学 习惯 ,变传 统教 学 为创造性 教学 _ 。 1 ] 1 2 优 化重 组课 堂教学 内容 .
1 3 精 心编 制 多媒 体课 件 ,打造信 号与 系统 智能 化教 学平 台 . 精 品课程 建设 ,构 造智 能化教 学平 台是前 驱 。在 教学 中 ,多 角度 挖 掘 教材 内容 的启 发 性 、探 索性 、 开放 性 、实用 性与情 感 教育 功能 ,精心 编制 多媒体 课件 ,构 造智 能化课 程教 学平 台 。
精 品课程 建设 ,教 学 内容 更新 是 核 心 。在 教 学 中,本 着 “ 强基 础 、强化 致 用 、促 进 创新 ” 的原 加
则 ,对信 号与 系统 的教学 内容 大胆 进行 了清理 、调 整 和重 构 ,重新 编 写 了教学 大 纲 、教 材 和专 题讲 义 ,
精 简和整 合 了传统 教学 内容 ,补充 介 绍一 些 科 学 研究 前 沿 课 题 等 ,使 学 生掌 握 该 门课 程 的基 本 知 识框 架 、知识 间 的 内在 联系 ,培养 其创 新意识 和实践能 力 。
与 传 统 课 堂 教 学 的整 合 为 切 入 点 , 对整 合 后 的课 堂 教 学模 式 、 学 生 学 习辅 导 系 统 、教 学 质 量 科 学评 价 体 系 等进 行 了探 索 和 实 践 。
[ 键词]《 号与系统》 关 信 ;精 品课 程 ;建 设 ; 措 施 ; 实 践 ; 效 果 [ 图分 类 号 ] N4 中 [ 献标识码]A 文 [ 文章 编 号] 17 —10 (0 8 3 3 4 3 6 3 4 9 2 0 )0 一N 2 —0
长江大学研究生课程成绩登记表

长江大学研究生课程成绩登记表学年第学期专业:结构工程年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:地图学与地理信息系统年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:地质工程年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:矿产普查与勘探年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:矿物学、岩石学、矿床学年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:矿物学、岩石学、矿床学年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:矿物学、岩石学、矿床学年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:地球化学年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:地球探测与信息技术年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:固体地球物理学年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:通信与信息系统年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:信号与信息处理年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:企业管理年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:环境工程年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:应用化学年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:机械设计及理论年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:计算机应用技术年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:应用数学年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:油气井工程年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:油气田开发工程年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:农业经济管理年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:作物遗传育种年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日长江大学研究生课程成绩登记表学年第学期专业:年级: 05级课程名称:任课教师:课程类别:学时:学分:考试方式:考试时间:年月日系(教研室)主任:年月日院(系)主管领导:年月日。
信号与线性系统分析第四版(吴大正)习题答案
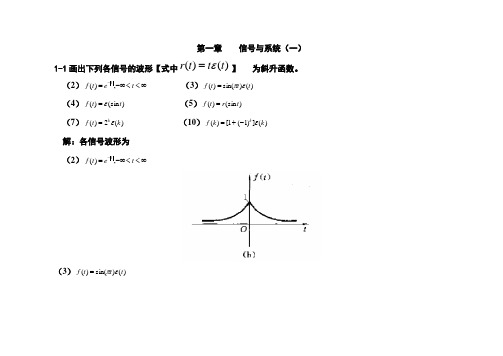
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】 为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))tf=r(sin)(t(7))tf kε(k=(2)(10))f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
长江大学电子信息学院研究生招生专业介绍及要求

长江大学电子信息学院研究生招生专业介绍及要求1长江大学电子信息学院研究生招生专业长江大学电子信息学院是长江大学的重要学院之一,拥有丰富的教学和科研资源。
作为一所综合性大学,长江大学电子信息学院在研究生招生专业方面也非常优秀。
根据2023年的招生计划,长江大学电子信息学院共开设了两个研究生专业,分别是电子信息和信息与通信工程。
电子信息专业是长江大学电子信息学院的一项核心专业,专业代码为085400。
该专业主要培养学生在电子信息领域的研究和应用能力,使学生能够在电子信息技术、电子产品设计与制造、电子信息系统集成与管理等方面具备较高的理论水平和实践能力。
学生在学习过程中将接受一系列的课程培训,包括电路与系统、数字信号处理、通信原理等。
毕业后,学生可以在电子信息领域的科研机构、高新技术企业、通信公司等单位从事科研、设计和管理等工作。
信息与通信工程是长江大学电子信息学院的另一项重要研究生专业,专业代码为081000。
该专业主要培养学生在信息与通信领域的研究和应用能力,使学生能够在通信技术、网络技术、无线通信等方面具备较高的理论水平和实践能力。
学生在学习过程中将接受一系列的课程培训,包括通信原理、网络编程、数字图像处理等。
毕业后,学生可以在通信领域的科研机构、电信运营商、互联网公司等单位从事科研、设计和管理等工作。
长江大学电子信息学院研究生招生专业的开设,为广大研究生提供了丰富多样的选择。
学院拥有一支优秀的师资队伍,教师们具有丰富的教学和科研经验,能够为学生提供高质量的教学和指导。
此外,学院还拥有先进的实验设备和实验室,为学生的实践能力培养提供了良好的条件。
如果你对电子信息或信息与通信工程感兴趣,并且想要深入研究相关领域,长江大学电子信息学院研究生招生专业将是你的不二选择。
通过系统的学习和培养,你将能够掌握先进的理论知识和实践技能,为未来的科研和工作打下坚实的基础。
如果你对长江大学电子信息学院研究生招生专业感兴趣,可以登录学院的官网了解更多详细信息。
信号与系统PPT电子书陈生谭版课后习题答案

1.22 在题 1.21 的基础上,若还已知 f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,有 y(t)=2+e-t+2e-3t,t≥0 试求当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统响应 y(t)。 解: 记,f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,系统响应 yf(t)=y(t)=2+e-t+2e-3t,t≥0 则当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统全响应 y(t)为: y(t)=3yf(t)+2y1(t)+5y2(t)
解:
(1)
is
(t)
=
i(t
)
+
ic
(t )
+
iR
(t )
=
i (t )
+
Cuc′
(t )
+
1 2
u (t )
----⑴
而 uC (t) = u(t)
对回路①,有:
⎧− ⎩⎨iL
3i(t) (t) =
+ is
LiL′ (t) + u(t) (t) − i(t)
=
0
⇒
u(t)
=
3i(t
)
−
Lis′
(t)
− p 1+ p
−1
3p 0
−p
− p 0 1+ p +1/ p
− p f (t) i2 (t) = 3 p − p
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y(t)
y (t )
t
t0
电信学院
t
3
无失真传输的条件
在频域中:
设激励频谱为F(j),
件是
响应频谱为Y(j), 无失真传输的条 Y(j)=K F(j)e-jt
0
其中:系统函数
H ( j )
K
H(j)= K e -jt
0
( )
0
0
t0
电信学院
4
相位失真的条件
其中:c为截止频率。称为理想低通滤波器的 通频 带,简称频带。
电信学院
8
冲激响应
已知: G (t ) Sa(
2
t ) ,根据对偶性: Sa( ) 2 G ( ) 2
c
C 将 换成2c,得: Sa(C t ) G2 ( ) 根据时移特性: C Sa[( C (t t0 )] G2 ( ) e j t K C h(t ) Sa[( C (t t0 )] h(t )
设输入为 则输出为
f (t ) A1 sin( 1t ) A2 sin( 21t )
y(t ) KA1 sin( 1t 1 ) KA2 sin( 21t 2 )
1 2 KA1 sin 1 (t ) KA2 sin 21 (t ) 1 21
H ( j )
1
0
通带
阻带
0 C 0 0 C 通带 阻带 通带
理想带阻滤波器
电信学院
17
补充例题(习题7-17)
图示是理想高通滤波器的幅频与相频特性,求该滤波器的 冲激响应。
H ( j )
1
( )
C
C
t0
解:由理想高通滤波器特性可知,其特性可用1-理想低通 特性(门函数)表示。 即:
电信学院
12
滤波器的概念
理想低通滤波器
信号通过系统时,系统使信号的某些频率分量通过,而
使其他频率的分量受到抑制,这样的系统称为滤波器。 若系统的幅频特性在某一频带内保持为常数而在该频带 外为零,相频特性始终为过原点的一条直线,则这样的 系统就称为理想滤波器。 理想低通滤波器在的频率范围内(称为通带),信号能 无衰减地通过,而对大于(称为阻带)的所有频率分量 则完全抑制。称为理想低通滤波器的截止频率。理想低 通滤波器的特性如图7-32所示。
电信学院
13
滤波器的概念
理想低通滤波器的频率特性可写为(设相角为0)
H Lp ( j ) G2C ( )
截止频率
H ( j )
1 1
H ( j )
C
1 0.707 2
C
C
C
C
阻带
通带
阻带
阻带
通带
阻带
理想低通滤波器
电信学院
非理想低通滤波器
14
滤波器的概念
c
0
K
C
0
电信学院
t0
C
t
9
阶跃响应
g (t ) h( )d
t
KC
t
Sa[C ( t0 )]d
令 x ( t0 )C S i ( x)
sin y 0 y dy K C (t t0 ) sin x g (t ) dx x K S i () S i [C (t t0 )] 1 1 K S i [C (t t0 )] 2
电信学院
25
解调
已调信号y (t)= f (t)cos0t
y (t )
c 0 c
g (t ) y (t ) s(t ) f (t ) s 2 (t ) f (t ) cos 2 0t 1 [ f (t ) f (t ) cos 2 0t ] 2
g (t )
电信学院
1
7.5.1 信号的无失真传输
失真与无失真:
系统的响应波形与激励波形不同,信号在传输过程
中将产生失真。
线性系统引起的信号失真有两个原因:幅度失真与
相位失真。称为线性失真。
幅度失真与相位失真都不产生新的频率分量;而非
线性失真可能产生新的频率分量。
无失真是指响应信号与激励信号相比,只是大小与
f 2 (t ) [sin( 2 (t 1)) sin( 5 (t 1))] [ (t 1) (t 2)]
f 3 (t ) [sin( 2 t 2 ) sin( 5 t 2 )] [ (t 1) (t 2)]
电信学院
x(t )
H2(j)
y (t)
cos9t
H1(j)
1
F(j)
1
H2(j)
2
-15
-9 -6
0
6 9
15
-9
0
9
-9
0
9
解:频谱图如下
X(j)
1 ½ 6 9 15
-15
-9 -6
0
电信学院
19
例 7.19
求y(t)的频谱
X(j)
½ -15 -9 -6 0 6 9 15
XS(j)
电信学院
人眼对相位失真敏感而对幅度失真不敏感。
7
7.5.2 理想低通滤波器
理想低通滤波器特性:
H ( j )
K
H ( j )
Ke
0
j t0
| | C | | C
C
C
H ( )
或: H ( j ) Ke j t0
G2C ( )
¼ -15 -9 -6 0 6 9 15
Y(j)
½ -9 -6 0 6 9
20
电信学院
信号与系统的二维视角
信号与系统都有双重属性:频域和时域。
为了较深入地观察它们之间的关系,应该对这两个属性
进行分析和理解,因为它们看问题的视角是互为补充的。 人们常常会本能地在两个域内思考问题。
当观察一个信号时,
出现的时间不同,而波形不变化。
电信学院
2
无失真传输的条件
在时域中:
设激励信号为f(t),
响应信号为y(t), 无失真传输的条 件是 y(t)=Kf(t-t0) 式中:K是一常数, t0为滞后 时间。若 f(t)=(t), 则 y(t)=h(t)=K(t-t0),
f(t)
f (t )
线性系统
6
幅度失真与相位失真的应用
人耳容易觉察幅度失真,而对于相位失真反应并不敏感
在音频信号中,每一个音节可以看成一个单独的信号,音节的持续 时间在0.01秒到0.1秒的数量级的范围内,音频系统具有非线性的相 位特性, 在实际系统中,()的斜率变化不大,而人耳对相位的失真不敏感。 因此,音频设备制造商主要关心音频系统的幅度特性。 在电视信号中的幅度失真只作为图像的相对黑白亮度的部分损坏显 露,这个影响对人眼不是很明显。 相位失真会在不同的图像像素上产生不同的延时。这会将一幅图像 变得模糊,其效果容易被人眼所觉察。 在数字通信中相位失真也是很重要的,因为信道的非线性相位特性 会引起脉冲扩散,它会带来与前后相邻脉冲间的干扰。这种干扰会 在接收端产生脉冲幅度上的误差,可能将二进制的1读成0,或将0 读成1。
电信学院
23
7.6 调制与解调
调制与解调:
所谓调制,就是用一个信号(原信号也称调制信号)去控制另 一个信号(载波信号)的某个参量,从而产生已调制信号, 解调则是相反的过程,即从已调制信号中恢复出原信号。 根据所控制的信号参量的不同,调制可分为: 调幅,使载波的幅度随着调制信号的大小变化而变化的调 制方式。 调频,使载波的瞬时频率随着调制信号的大小而变,而幅 度保持不变的调制方式。 调相,利用原始信号控制载波信号的相位。 这三种调制方式的实质都是对原始信号进行频谱搬移,将信号 的频谱搬移到所需要的较高频带上,从而满足信号传输的需要。
H Bp ( j ) G2C ( 0 ) G2C ( 0 )]
H ( j )
1
0
通带
0 C 0 0 C 阻带 通带
理想带通滤波器
电信学院
16
滤波器的概念
理想带阻滤波器的频率特性可写为
H BS ( j ) 1 H Bp ( )
傅里叶变换的应用
在分析连续系统时更多的是使用拉普拉斯变换分 析法。
傅里叶变换的运用一般要受绝对可积条件的约束,能适
用的信号有限。 傅里叶反变换往往不太容易。
傅里叶变换更广泛应用于通信系统中,如信号传 输过程中的调制与解调等。 三个典型的应用
无失真传输 理想滤波器 调制与解调
x
电信学院
10
阶跃响应
上升时间与频带的关系
g (t )
K
K 2
C C
0
t0 tr
t
上升时间tr ,定义为从阶跃响应的极小值上升到极大值 所经历的时间。它与频带c的关系为 2 tr
C
电信学院
11
阶跃响应
结论
tr 2
C
或 t rC 常数
阶跃响应的上升时间与系统的截止频率(频带) 成反比。这也是时间带宽积为常数。 此结论对各种实际的滤波器同样具有指导意义。 例如,一个一阶RC低通滤波器的阶跃响应为 指数上升波形,上升时间与RC时间常数成正 比,但从频域特性来看,此低通滤波器的带宽 却与RC乘积值成反比. 理想低通滤波器是非因果系统,是物理不可实 现的。
