《MATLAB语言》课程第五次作业

MATLAB语言基础与应用(第二版)第5章习题答案

第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答：>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答：>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布，用二次曲线拟合。

MATLAB习题及参考答案经典.doc

习题：1，计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2，对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3，已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4，角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5，将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵：（1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546，将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7，求解多项式x 3-7x 2+2x +40的根。

(应用roots)8，求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9，计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10，解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11，求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv) 12，矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

MATLAB上机内容及作业

MATLAB上机内容及作业无约束优化求解函数fminsearch和fminunc求解无约束非线性优化问题的函数有fminsearch 函数、fminunc 函数。

函数fminsearch和fminunc功能相同，但fminunc函数可以得到目标函数在最优解处的梯度和Hessian矩阵值。

无约束优化数学模型为：min f(X) X∈R n求解无约束非线性优化问题的步骤为：第一步：先编写目标函数的M文件；第二步：再在命令窗口中调用相应的优化函数。

1、fminsearch函数调用格式为[x, fval]=fminsearch(@myfun, x0)输出参数的含义：x：返回最优解的设计变量的值；fval：在最优设计变量值时，目标函数的最小值；exitflag：返回算法终止的标志，有以下几种情况，＞0 表示算法收敛于最优解处；＝0 表示算法已经达到迭代的最大次数；＜0 表示算法不收敛。

output：返回优化算法信息的一个数据结构，有以下信息：output.iteration 表示迭代次数output.algorithm 表示所采用的算法output.funcCount 表示函数评价次数输入参数的含义：@myfun：目标函数的M文件，在其前要加“@”，或表示为'myfun' ，myfun自己可以任意命名；x0：在调用该优化函数时，需要先对设计变量赋一个初始值；2、fminunc函数的调用格式[x, fval]=fminunc (@myfun, x0)grad：返回目标函数在最优解处的梯度信息；hessian：返回目标函数在最优解处的hessian矩阵信息。

其余含义同上。

3、实例已知某一优化问题的数学模型为：min f(X)=3x12+2x1x2+x22X∈R n用MA TLAB程序编写的代码为：第一步：首先编写目标函数的.m文件，并保存为examplefsearch.m文件（先单击file菜单，后点击New 命令中的M—file，即可打开M文件编辑窗口进行代码的编辑，在英文状态下输入程序代码），代码为：function f=examplefsearch（x）f=3*x(1)^ 2+2*x(1)*x(2)+x(2)^2;第二步：在Command窗口中调用fminsearch函数，代码为：x0=[1;1]; %赋初值[x,fval]=fminsearch(@examplefsearch,x0) %回车即可调用fminsearch函数，得到结果输出最优解结果为：x=1.0e-0.08* -0.7914 0.2260 %分别为x1和x2的最优点的值（近似为0）fval=1.5722e-016 %对应最优点的最优目标函数值（近似为0）4、作业已知几个优化问题的数学模型分别为：（1）min f(X)=0.1935x1 x22 x32(4+6x4) X∈R4（2）min f(X)= (x13+cos x2+log x3）/ e x1 X∈R3（3）min f(X)=2x13+4x1x23 -10x1x2+x33X∈R3试用MATLAB编程分别求解上述优化问题的最优解。

MATLAB作业5参考答案

MATLAB作业5参考答案1、试求出下面线性微分方程的通解。

543225432()()()()()136415217680()[sin(2)cos(3)]3t d y t d y t d y t d y t dy t y t e t t dt dt dt dt dt π-+++++=++假设上述微分方程满足已知条件(0)1,(1)3,()2,(0)1,(1)2y y y y y π=====，试求出满足该条件的微分方程的解析解。

【求解】先定义t 为符号变量，求出等号右侧的函数，则可以由下面命令求出方程的解析解，解的规模较大，经常能占数页。

>> syms texp(-2*t)*(sin(2*t+sym(pi)/3)+cos(3*t))ans =exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))>> y=dsolve(['D5y+13*D4y+64*D3y+152*D2y+176*Dy+80*y=',...'exp(-2*t)*(sin(2*t+1/3*pi)+cos(3*t))'],'y(0)=1','y(1)=3','y(pi)=2',...'Dy(0)=1','Dy(1)=2')略：事实上，仔细阅读求出的解析解就会发现，其中大部分表达式是关于系数的，所以如果能对系数进行近似则将大大减小解的复杂度。

>> vpa(y)ans =.20576131687242798353909465020576e-2*exp(-2.*t)*cos(3.*t)+.15538705805619602372728107411086e-1*exp(-2.*t)*sin(2.*t)+.76830587084294035590921611166287e-2*exp(-2.*t)*cos(2.*t)-106.24422608844727797303237726774*exp(-2.*t)*t^2+98.159206062620455331994871615083*exp(-2.*t)*t+59.405044899367325888329709780356*exp(-2.*t)*t^3-30.741892776456442808809983330755*exp(-2.*t)+.20576131687242798353909465020576e-2*exp(-2.*t)*sin(3.*t)+31.732152104579289125415500223136*exp(-5.*t)2、试求解下面微分方程的通解以及满足(0)1,()2,(0)0x x y π===条件下的解析解。

Matlab第五章答案

第一题（1）a=[1 9 8;7 2 5;3 -2 7] %产生矩阵det(a) %检验是否可逆ans=-442,非0，可逆div(a) %求逆矩阵（2）b=[1 0 -7 5;0 -26 7 2;7 4 3 5;8 -3 2 15]det(b)div(b)第二题(1)A=[1 2 3;2 2 5;3 5 1];B=[11 12 31];X=B/A(2) A=[3 1 0 5;0 6 7 3;0 4 3 0;2 -1 2 6];B=[2 4 7 8];X=B/A第三题（1）t=[1 2 3 4 5 6 7 8 9 10]';y=[4.842 4.362 3.754 3.368 3.169 3.083 3.034 3.016 3.012 3.005]';A=[ones(size(t)) exp(-t)];C=A\yT=[0:.1:10]';Y=[ones(size(T)) exp(-T)]*C;plot(T,Y,'-',t,y,'o')title( '采用y(t)≈c1+c2e–t的拟合' )xlabel('\itt'), ylabel('\ity')（2）t=[0 .3 .8 1.1 1.6 2.3]';y=[.82 .72 .63 .60 .55 .50]';A=[ones(size(t)) t.*exp(-t)];C=A\y;T=[0:.1:2.5]';Y=[ones(size(T)) T.*exp(-T)]*C;plot(T,Y,'-',t,y,'o')title('采用y(t)≈d1+d2te–t拟合')xlabel('\itt'), ylabel('\ity')第四题A=[11.59 12.81 15.66; 15.2 4.18 13.61; 10.597.59 9.22];[L,U]=lu(A)[Q R]=qr(A)B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35-23.9 10.34];[C,D]=lu(B)[E F]=qr(B)第五题（1）A=[5 -5 -6;3 -2 5;2 -1 -4];x0=[1;-4;5];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on(2)A=[1 2 -3 1;3 0 1 -2;1 -2 0 5;2 3 0 1];x0=[1;-1;2;1];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on第六题（1）A=[11.59 12.81 15.66; 15.2 4.18 13.61;10.59 7.59 9.22];lambda=eig(A)[V,D]=eig(A)（2）B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35 -23.9 10.34];lambda=eig(B)[V,D]=eig(B)第七题（1）x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,2);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('二阶多项式曲线拟合')(2)x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,3);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('三阶多项式曲线拟合')第八题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8,0];[L1,U1]=lu(p1)r1=roots(p1)[L2,U2]=lu(p2)r2=roots(p2)[L3,U3]=lu(p3)r3=roots(p3)[L4,U4]=lu(p4)r4=roots(p4)第九题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8];p1_x=polyval(p1,[-1.5,2.1,3.5]) p2_x=polyval(p2,[-1.5,2.1,3.5]) p3_x=polyval(p3,[-1.5,2.1,3.5]) p4_x=polyval(p4,[-1.5,2.1,3.5])第十题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];d1=conv(a,b)[d2,r2]=deconv(c,a)[d3,r3]=deconv(c,b)第十一题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];dao1=polyder(a,b)[dao2,r2]=polyder(c,a)[dao3,r3]=polyder(c,b)第十二题x=-5:.25:5;y=10*exp(-x);xi=-5:5;y1=interp1(x,y,xi,'nearest');y2=interp1(x,y,xi,'linear');y3=interp1(x,y,xi,'spline');y4=interp1(x,y,xi,'cubic'); figure(1);subplot(2,2,1)plot(x,y,'-',xi,y1,'o');title('最邻近内插');grid on;xlabel('x');ylabel('y');subplot(2,2,2)plot(x,y,'-',xi,y2,'o');title('线性内插');grid on;xlabel('x');ylabel('y');subplot(2,2,3)plot(x,y,'-',xi,y3,'o');title('三次样条内插');grid on;xlabel('x');ylabel('y');subplot(2,2,4)plot(x,y,'-',xi,y4,'o');title('三次曲线内插');grid on;xlabel('x');ylabel('y');第十三题x=rand(1,50);y=randn(1,50);minx=min(x)miny=min(y)maxx=max(x)maxy=max(y)avx=mean(x)avy=mean(y)Ex=(std(x)).^2Ey=(std(y)).^2第十四题t=[0 .2 .4 .6 .8 1.0 2.0 5.0 ]';y=[1.0 1.51 1.88 2.13 2.29 2.40 2.60 24.00]'; X1=[ones(size(t)) t t.^2];a=X1\y;X2=[ones(size(t)) exp(-t) t.*exp(-t)];b=X2\y;T=[0:.1:6]';Y1=[ones(size(T)) T T.^2]*a;Y2=[ones(size(T)) exp(-T) T.*exp(-T)]*b; figure(1)subplot(1,2,1)plot(T,Y1,'-',t,y,'o'),grid ontitle('多项式回归')subplot(1,2,2)plot(T,Y2,'-',t,y,'o'),grid ontitle('指数函数回归')第十五题t=0:1/119:1;x=3*sin(2*pi*20*t)+10*sin(2*pi*200*t+pi/4)+10*randn(size(t)); y=fft(x);m=abs(y);f=(0:length(y) -1)'*119/length(y);figure(1)subplot(2,1,1),plot(t,x),grid ontitle('被噪声污染的信号')ylabel('Input \itx'),xlabel('Time ')subplot(2,1,2),plot(f,m)ylabel('Abs. Magnitude'),grid onxlabel('Frequency (Hertz)')第十六题w=input('w=');t=0:1/119:1;x1=sin(w.*t)+randn(size(t));x2=cos(w.*t)+randn(size(t));x3=sin(w.*t)+randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)若没有正弦分量w=input('w=');t=0:1/119:1;x1=randn(size(t));x2=randn(size(t));x3=randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)第十七题z1=quad('exp(-2*t)',0,2)z2=quad('exp(2*t)',0,2)z3=quad('exp(t.^2-3*t+.5)',-1,1)第十八题function y=five(x)y=exp(-x)-1.5*exp(2*cos(2*x));%主函数x0=input('x0='); %执行时，按要求输入[-1,1]z=fzero('five',x0)第十九题function f=five(x,y)f=exp(-x.*y)-2*x.*y;%主函数z=dblquad('five',0,1,-1,1)第二十题function dy=five(t,y)dy=[0.5-y(1);y(1)-4*y(2)];%主函数X0=[1; -0.5];tspan=[0,25];[T,X]=ode45('five',tspan,X0);figure(1)subplot(2,1,1),plot(T,X(:,1),'r'),title('x_{1}'),grid onsubplot(2,1,2),plot(T,X(:,2),'k'),title('x_{2}'),grid onfigure(2)plot(X(:,1),X(:,2)),title('系统轨迹'),grid onxlabel('x_{1}'),ylabel('x_{2}')。

数学建模作业题+答案

数学建模MATLAB 语言及应用上机作业11. 在matlab 中建立一个矩阵135792468101234501234A ⎡⎤⎢⎥⎢⎥=⎢⎥-----⎢⎥⎣⎦答案：A = [1,3,5,7,9;2,4,6,8,10;-1,-2,-3,-4,-5;0,1,2,3,4]2. 试着利用matlab 求解出下列方程的解（线性代数22页例14）123412423412342583692254760x x x x x x x x x x x x x x +-+=⎧⎪--=⎪⎨-+=-⎪⎪+-+=⎩ 答案：A=[2 ,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6]; B=[8;9;-5;0]; X=A\B 或A=[2,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6] b=[8,9,-5,0]' X=inv(A)*b3. 生成一个5阶服从标准正态分布的随机方阵，并计算出其行列式的值，逆矩阵以及转置矩阵。

答案:A=randn(5) det(A) inv(A) A'4. 利用matlab 求解出110430002A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦的特征值和特征向量。

答案：A=[-1,1,0;-4,3,0;0,0,2] [V,D]=eig(A)5.画出衰减振荡曲线3sin3t y et -=在[0,4]π上的图像。

要求，画线颜色调整为黑色，画布底面为白色。

（在实际中，很多打印机时黑白的，因此大多数作图要考虑黑白打印机的效果。

）给出恰当的x ，y 坐标轴标题，图像x 轴的最大值为4π。

6. 生成一个0-1分布的具有10个元素的随机向量，试着编写程序挑选出向量中大于0.5的元素。

数学建模和Matlab 上机作业2（2016-9-20）跟老师做（不用整合进作业中）：上机演示讲解：函数，递归的两个例子的写法。

附：1. Fibonacci Sequence （斐波那契数列）在数学上，费波那西数列是以递归的方法来定义： F1= 1；F2= 1；F （n ）=F （n-1）+F （n-2） 2. 阶乘举例：数学描述：n!=1×2×……×n ；计算机描述：n!=n*(n-1)!自己做（需要整合进作业中，提交到系统中）：1. 写一个m 文件完成分值百分制到5分制的转换（即输入一个百分制，转换后输出一个5级对应的得分，联系条件控制语句）。

MATLAB教程2012a第5章习题解答-张志涌..

d=0.05;
%控制运动速度（0.01——0.5)
n=200;
x=[0:pi/30:4*pi]; %供画曲线用的横坐标
axis([-0.2,4*pi,-1,1]),axis off,
10
pause(0.1)
%足够迟延似乎不可缺。否则可能图形有误。
for tt=0:n
%决定画曲线的时刻
a=tt*pi/24-x;
3
y=(exp(-(zk-beta)*t)-exp(-(zk+beta)*t))/(2*beta); plot(t,y,'r') if zk>1.2
text(0.3,0.14,'\zeta = 1.4') end end end text(10,0.7,'\Delta\zeta=0.2') axis([0,18,-0.4,0.8]) hold off box on grid on
9
图 p5-9
10 在[0,4 ] 区间内，根据 y(t, x) e0.2x sin( t x) ，通过图形曲线表 24 现“行波”。做题前，请先运行 prob510.p 文件，观察演示。
图 p5-10
〖解答〗
function prob510
% prob510.m
clear all clf,shg
-0.9801 -0.9801 -0.9801 -0.9801 y0 =
0.2005 0.2005 0.2005 0.2005
CRROS-POINTS OF ' y/(1+x2+y2)-0.1 ' AND ' sin(x+cos(y)) '
0.8

MATLAb与数学实验第五章习题解答

i=
1 3 2 4 1 3 5 2 4 3 5
j=
1 1 2 2 3 3
3 4 4 5 5
s=
1 3 1 3 2 1 3 2 1 2 1 A1 =
10200 01020 30102 03010 00301 (2) n=nnz(A)
n=
13 ans =
1 2 -1 3 -2 4 1 -3 5 2
-4 3 -5
>> nx=nzmax(A)
nx =
35
>> [i,j,s]=find(A)
i=
1 2 1 3 2 4 1 3 5 2 4 3 5
j=
1 2 3 3 4 4 5 5 5 6 6 7 7
s=
1 2 -1 3 -2 4 1 -3 5 2 -4 3 -5
A1 =
1 0 -1 0 1 0 0
0 2 0 -2 0 2 0
C=
11 11 11
>> B=[3 5 7;0 1 0]
B=
357 010
>> D=[0 0 0;0 0 0]
D=
000 000
2.随机生成：（1）一个含有五个元素的列向量. （2）一个数值在 0~100 之间的三行四列的矩阵.
答 (1) rand(5,1)
ans =
0.9501
0.2311 0.6068 0.4860 0.8913
0 0 3 0 -3 0 3
0 3 0 1 0
0 0 0
4
0
4
0

0 0 3 0 1
0 0 0 0 5 0 5
答（1） n=nnz(A)
n=
11
>> nonzeros(A)

matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件，是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境，已被广泛应用于不同领域。

Matlab的基本功能包括：数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。

Matlab第二章1．创建double的变量，并进行计算。

(1)a=87，b=190，计算a+b、a-b、a*b。

(2)创建uint8 类型的变量，数值与(1)中相同，进行相同的计算。

>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =ans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2，v=3，计算：(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u) ans =15.4189>> sqrt(u-3*v)/(u*v) ans =0 + 0.4410i 4.计算如下表达式：(1)(2)>> (3-5*i)*(4+2*i)22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。

MATLAB教程课后实验报告题目及解答[第一至第五章]

MATLAB教程实验报告实验项目名称实验一 Matlab基本操作学生姓名汪德旺专业班级 09数教（1）班学号 0301090131实验成绩日期一. 实验目的和要求1、了解MATLAB 的开发环境。

2、熟悉Matlab的基本操作。

3、掌握建立矩阵的方法。

4、掌握MATLAB各种表达式的书写规则以及常用函数的使用。

5、填写实验报告，实验报告文件取名为report1.doc。

6、于邮件附件形式将实验报告文件report1.doc 发到邮箱*******************，邮件主题为班级学号姓名，如：09数教1班15号张三。

二、实验内容1、先求下列表达式的值，然后显示MATLAB工作空间的使用情况并保存全部变量。

（1）0 122sin851ze =+（2）2212 1ln(0.4552i z x x+⎡⎤==⎢⎥-⎣⎦其中（3）0.30.330.3sin(0.3)ln,22a ae e az a--+=++a=-3.0,-2.9,-2.8,…, 2.8, 2.9,3.0（4）2242,011,12,0:0.5:2.521,23t tz t tt t t⎧≤<⎪=-≤<=⎨⎪-+≤<⎩其中t2.已知：1234413134787,2033657327 A B--⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值：（1）A+6*B和A-B+I(其中I为单位矩阵) （2）A*B和A.*B（3）A^3和A.^3（4）A/B和B\A（5）[A,B]和[A([1,3],:);B^2]3、设有矩阵A 和B123453016678910A=,B=17-691112131415023-41617181920970212223242541311⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦（1）求它们的乘积C 。

（2）将矩阵C 的右下角3*2子矩阵赋给D 。

（3）查看MATLAB 工作空间的使用情况。

Matlab第五章答案

第一题（1）a=[1 9 8;7 2 5;3 -2 7] %产生矩阵det(a) %检验是否可逆ans=-442,非0，可逆div(a) %求逆矩阵（2）b=[1 0 -7 5;0 -26 7 2;7 4 3 5;8 -3 2 15]det(b)div(b)第二题(1)A=[1 2 3;2 2 5;3 5 1];B=[11 12 31];X=B/A(2) A=[3 1 0 5;0 6 7 3;0 4 3 0;2 -1 2 6];B=[2 4 7 8];X=B/A第三题（1）t=[1 2 3 4 5 6 7 8 9 10]';y=[4.842 4.362 3.754 3.368 3.169 3.083 3.034 3.016 3.012 3.005]';A=[ones(size(t)) exp(-t)];C=A\yT=[0:.1:10]';Y=[ones(size(T)) exp(-T)]*C;plot(T,Y,'-',t,y,'o')title( '采用y(t)≈c1+c2e–t的拟合' )xlabel('\itt'), ylabel('\ity')（2）t=[0 .3 .8 1.1 1.6 2.3]';y=[.82 .72 .63 .60 .55 .50]';A=[ones(size(t)) t.*exp(-t)];C=A\y;T=[0:.1:2.5]';Y=[ones(size(T)) T.*exp(-T)]*C;plot(T,Y,'-',t,y,'o')title('采用y(t)≈d1+d2te–t拟合')xlabel('\itt'), ylabel('\ity')第四题A=[11.59 12.81 15.66; 15.2 4.18 13.61; 10.597.59 9.22];[L,U]=lu(A)[Q R]=qr(A)B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35-23.9 10.34];[C,D]=lu(B)[E F]=qr(B)第五题（1）A=[5 -5 -6;3 -2 5;2 -1 -4];x0=[1;-4;5];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on(2)A=[1 2 -3 1;3 0 1 -2;1 -2 0 5;2 3 0 1];x0=[1;-1;2;1];X=[];for t=0:.01:1X=[X expm(t*A)*x0];endplot3(X(1,:),X(2,:),X(3,:),'-o')grid on第六题（1）A=[11.59 12.81 15.66; 15.2 4.18 13.61;10.59 7.59 9.22];lambda=eig(A)[V,D]=eig(A)（2）B=[16.00 4.41 -10.37 -21.61; 0.88 -20.04 12.86 8.56; -1.43 10.71 18.81 -5.99; -12.48 24.35 -23.9 10.34];lambda=eig(B)[V,D]=eig(B)第七题（1）x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,2);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('二阶多项式曲线拟合')(2)x=[1 2 3 4 5 6 7 8 9 10];y=[15.0 39.5 66.0 85.5 89.0 67.5 12.0 -86.4 -236.9 -448.4];p=polyfit(x,y,3);x2=1:.1:10;y2=polyval(p,x2);figure(1)plot(x,y,'o',x2,y2)grid ontitle('三阶多项式曲线拟合')第八题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8,0];[L1,U1]=lu(p1)r1=roots(p1)[L2,U2]=lu(p2)r2=roots(p2)[L3,U3]=lu(p3)r3=roots(p3)[L4,U4]=lu(p4)r4=roots(p4)第九题p1=[1,-2-3,4,2];p2=[1,-7,5,31,-30];p3=[1,-1,-25,25];p4=[-2,3,1,5,8];p1_x=polyval(p1,[-1.5,2.1,3.5]) p2_x=polyval(p2,[-1.5,2.1,3.5]) p3_x=polyval(p3,[-1.5,2.1,3.5]) p4_x=polyval(p4,[-1.5,2.1,3.5])第十题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];d1=conv(a,b)[d2,r2]=deconv(c,a)[d3,r3]=deconv(c,b)第十一题a=[2,3,-4];b=[4,-2,5];c=[3,0,-2,5,6];dao1=polyder(a,b)[dao2,r2]=polyder(c,a)[dao3,r3]=polyder(c,b)第十二题x=-5:.25:5;y=10*exp(-x);xi=-5:5;y1=interp1(x,y,xi,'nearest');y2=interp1(x,y,xi,'linear');y3=interp1(x,y,xi,'spline');y4=interp1(x,y,xi,'cubic'); figure(1);subplot(2,2,1)plot(x,y,'-',xi,y1,'o');title('最邻近内插');grid on;xlabel('x');ylabel('y');subplot(2,2,2)plot(x,y,'-',xi,y2,'o');title('线性内插');grid on;xlabel('x');ylabel('y');subplot(2,2,3)plot(x,y,'-',xi,y3,'o');title('三次样条内插');grid on;xlabel('x');ylabel('y');subplot(2,2,4)plot(x,y,'-',xi,y4,'o');title('三次曲线内插');grid on;xlabel('x');ylabel('y');第十三题x=rand(1,50);y=randn(1,50);minx=min(x)miny=min(y)maxx=max(x)maxy=max(y)avx=mean(x)avy=mean(y)Ex=(std(x)).^2Ey=(std(y)).^2第十四题t=[0 .2 .4 .6 .8 1.0 2.0 5.0 ]';y=[1.0 1.51 1.88 2.13 2.29 2.40 2.60 24.00]'; X1=[ones(size(t)) t t.^2];a=X1\y;X2=[ones(size(t)) exp(-t) t.*exp(-t)];b=X2\y;T=[0:.1:6]';Y1=[ones(size(T)) T T.^2]*a;Y2=[ones(size(T)) exp(-T) T.*exp(-T)]*b; figure(1)subplot(1,2,1)plot(T,Y1,'-',t,y,'o'),grid ontitle('多项式回归')subplot(1,2,2)plot(T,Y2,'-',t,y,'o'),grid ontitle('指数函数回归')第十五题t=0:1/119:1;x=3*sin(2*pi*20*t)+10*sin(2*pi*200*t+pi/4)+10*randn(size(t)); y=fft(x);m=abs(y);f=(0:length(y) -1)'*119/length(y);figure(1)subplot(2,1,1),plot(t,x),grid ontitle('被噪声污染的信号')ylabel('Input \itx'),xlabel('Time ')subplot(2,1,2),plot(f,m)ylabel('Abs. Magnitude'),grid onxlabel('Frequency (Hertz)')第十六题w=input('w=');t=0:1/119:1;x1=sin(w.*t)+randn(size(t));x2=cos(w.*t)+randn(size(t));x3=sin(w.*t)+randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)若没有正弦分量w=input('w=');t=0:1/119:1;x1=randn(size(t));x2=randn(size(t));x3=randn(size(t));a=corrcoef(x1,x2)b=corrcoef(x1,x3)第十七题z1=quad('exp(-2*t)',0,2)z2=quad('exp(2*t)',0,2)z3=quad('exp(t.^2-3*t+.5)',-1,1)第十八题function y=five(x)y=exp(-x)-1.5*exp(2*cos(2*x));%主函数x0=input('x0='); %执行时，按要求输入[-1,1]z=fzero('five',x0)第十九题function f=five(x,y)f=exp(-x.*y)-2*x.*y;%主函数z=dblquad('five',0,1,-1,1)第二十题function dy=five(t,y)dy=[0.5-y(1);y(1)-4*y(2)];%主函数X0=[1; -0.5];tspan=[0,25];[T,X]=ode45('five',tspan,X0);figure(1)subplot(2,1,1),plot(T,X(:,1),'r'),title('x_{1}'),grid onsubplot(2,1,2),plot(T,X(:,2),'k'),title('x_{2}'),grid onfigure(2)plot(X(:,1),X(:,2)),title('系统轨迹'),grid onxlabel('x_{1}'),ylabel('x_{2}')。

MATLAb与数学实验第五章习题解答

01 10 00 0 -2
(1,1)
1
(3,2)
1
(2,3)
2
(1,4)
-1
(3,5)
3
A2 =
1 0 0 -1 0 00200
01003 (3) A1 =
(1,1)
1
(5,1)
2
(4,2)
3
(3,3)
1
(2,4)
3
(1,5)
2
(5,5)
1
A2 =
10002 00030 00100 03000 20001 18．创建一个 4 阶稀疏矩阵，使副对角线上元素为 1 答 A=sparse(1:4,1:4,1)
B=
-2 0 0 010 004
C=
-2 1 4
14 47 7 10
D=
-2 0 0 -2 1 4 010147 0 0 4 4 7 10
F=
-2 1 4 147 4 7 10 -2 0 0 010 004
(4) C=[-2 1 4;1 4 7;4 7 10] C(:,1)=[]
C=
-2 1 4 147 4 7 10
A=
(1,1)
1
(2,2)
1
(3,3)
1
(4,4)
1
19．创建如下稀疏矩阵，查看其信息，并将其还原成全元素矩阵
1 0 2 0 0 1 0 1 0 1 0 0
0 1 0 2 0
0 2 0 2 0
2
0

（1） 3 0 1 0 2 (2) 0 0 3 0 3 0 3
工种
天数在木工家的工作天数在电工家的工作天数在油漆工家的工作天数
木工
2 4 4

MatLab语言及应用--习题及参考答案

MatLab语言及应用--习题1.产生一个1x10的随机矩阵，大小位于（-5 5），并且按照从大到小的顺序排列好！1.A = [21 2 3; 4 35 6; 7 8 49];B = [3; 2; 1];设求AB、BTA、A-1与A-1B，求A2、A的2次数幂，并求矩阵A的秩、转置和行列式。

2.请产生一个100*5的矩阵，矩阵的每一行都是[1 2 3 4 5]4. 请修改下面的程序，让他们没有for循环语句！A=[1 2 3; 4 5 6; 7 8 9];[r c]=size(A);for i=1:1:rfor j=1:1:cif (A(i,j)>8 | A(i,j)<2)A(i,j)=0;endendend5.a=[1 2 3 4 5],b=a(1)*a(5)+a(2)*a(4)+a(3)*a(3)+a(4)*a(2)+a(5)*a(1).试用MATLAB中最简单的方法计算b，注意最简单。

6. 求下列联立方程的解3x+4y-7z-12w=45x-7y+4z+ 2w=-3x +8z- 5w=9-6x+5y-2z+10w=-8求系数矩阵的秩；求出方程组的解。

7.设 y=cos[0.5+((3sinx)/(1+x^2))]把x=0~2π间分为101点，画出以x为横坐标，y为纵坐标的曲线；8. 设f(x)=x^5-4x^4+3x^2+2x+6取x=[-2,8]之间函数的值（取100个点），画出曲线，看它有几个零点。

9. 在[-10，10；-10，10]范围内画出函数的三维图形。

10.编写一个函数，使其能够产生如下的分段函数：⎪⎩⎪⎨⎧≤≤<-≤=x x x x x x f 65.0620.251.525.0)(，，，，并调用此函数，绘制曲线2)()(范围的2]，[0在+•+=x f x f x 。

（10分）11.将一个屏幕分4幅，选择合适的步长在右上幅与左下幅绘制出下列函数的图形。

matlab第四、五次作业

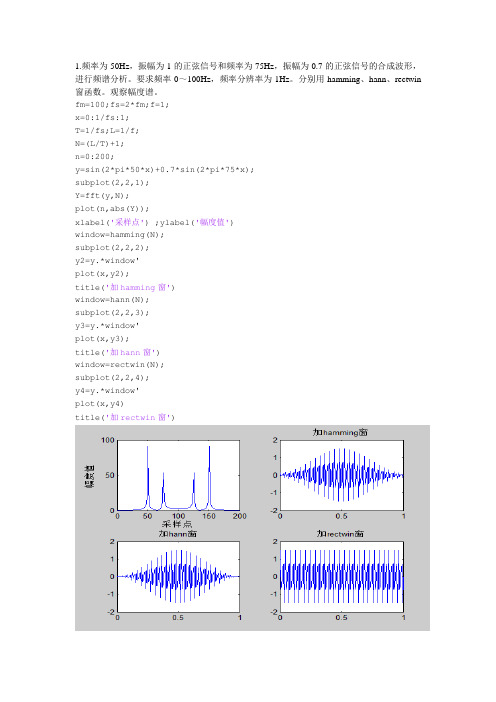
1.频率为50Hz，振幅为1的正弦信号和频率为75Hz，振幅为0.7的正弦信号的合成波形，进行频谱分析。

要求频率0～100Hz，频率分辨率为1Hz。

分别用hamming、hann、rectwin 窗函数。

观察幅度谱。

fm=100;fs=2*fm;f=1;x=0:1/fs:1;T=1/fs;L=1/f;N=(L/T)+1;n=0:200;y=sin(2*pi*50*x)+0.7*sin(2*pi*75*x);subplot(2,2,1);Y=fft(y,N);plot(n,abs(Y));xlabel('采样点') ;ylabel('幅度值')window=hamming(N);subplot(2,2,2);y2=y.*window'plot(x,y2);title('加hamming窗')window=hann(N);subplot(2,2,3);y3=y.*window'plot(x,y3);title('加hann窗')window=rectwin(N);subplot(2,2,4);y4=y.*window'plot(x,y4)title('加rectwin窗')2.x(t)=sin2*pi*60t+2*sin2*pi*110t+n(t),其中在n(t)为高斯噪声，求功率谱估计。

functiont = 0:.001:0.5;x = sin(2*pi*60*t) + 2*sin(2*pi*110*t);y = x + randn(size(t));subplot(1,2,1)plot(t,y)title('Noisy time domain signal')Y=fft(y,501);Pyy = Y.*conj(Y)/501;f = 1000/501*(0:500);subplot(1,2,2)plot(f,Pyy(1:501))title('Power spectral density')xlabel('Frequency (Hz)')endLevinson-Durbin算法:f1=20;f2=40;f=[f1;f2];B=[1 2];Fs=400;t=0:1/Fs:1;x=B*sin(2*pi*f*t);%产生噪声noise和被污染的信号xnrandn('state',0);noise=0.5*randn(size(t));%设置参数p=15;nfft=512;[Pxx1,f]=pyulear(xt,p,nfft,Fs);Pxx1=10*log10(Pxx1);plot(f,Pxx1);figure(1);title('Levinson-Durbin算法（阶数p=15）'); xlabel('频率（Hz）');ylabel('功率谱密度（dB/Hz）');grid onBurg算法:f0=20;f1=40;f=[f0;f1];B=[1 2];fs=500;t=0:1/fs:1;x=B*sin(2*pi*f*t);%产生噪声n和被污染的信号xnrandn('state',0);noise=0.1*randn(size(t));%设置参数p=15;nfft=512;[Pxx1,f]=pburg(xn,p,nfft,fs); Pxx1=10*log10(Pxx1);plot(f,Pxx1);xlabel('频率（Hz）');ylabel('功率谱密度（dB/Hz）'); title('Burg算法（阶数=15）'); grid on。

matlab参考答案matlab第5次作业至诚2013参考答案

1 将字符串’matlab’和’is string’合并。

1-1）直接水平合并，使用strcat水平合并。

str1='matlab’str2='is string'str3=strcat(str1,str2)str3 =matlabis string1-2）分别使用strvcat,char,str2mat等指令垂直合并。

>> str4=strvcat(str1,str2)>> str5=char(str1,str2)>> str6=str2mat(str1,str2)2 运行下列指令，写出执行结果，比较c和d的区别。

2-1）a={'abcdefg'}b={'hello',1:3}c={a,b}d=[a,b]c ={1x1 cell} {1x2 cell}d ='abcdefg' 'hello' [1x3 double]区别：C为1*2的元胞，包含两个元胞元素：元胞数组a和元胞数组bD为1*3的元胞，由元胞数组a和b的各个元胞单元组成新的一个元胞数组。

2-2) 分别从c，d元胞中提取a中的子串’cde’c{1}{1}(2:4)d{1}(2:4)33.1-1）将每个学生的姓名以字符串形式存储，并将所有的字符串存入一个元胞数组Namename={'Mike';'Nancy';'Emily'}3.1-2）将每个学生的学号以字符串形式存储，并将所有的字符串存入一个字符矩阵Idid=['1001';'1002';'1003']3.1-3）将学生的所有成绩存放在一个二维数组中ScorestuCell={name,id,score}3.1-5）从步骤4）创建的元胞中提取所有学生的数学成绩。

stuCell{3}(:,2)3.2 结构数组32-1) 创建结构数组，将表格信息保存在结构数组student中。

DSP Matlab作业(第5~10章)

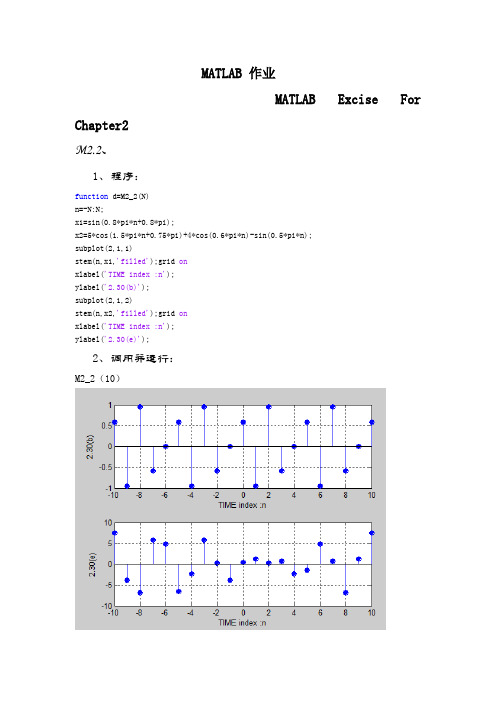
MATLAB 作业MATLAB Excise For Chapter2M2.2、1、程序：function d=M2_2(N)n=-N:N;x1=sin(0.8*pi*n+0.8*pi);x2=5*cos(1.5*pi*n+0.75*pi)+4*cos(0.6*pi*n)-sin(0.5*pi*n);subplot(2,1,1)stem(n,x1,'filled');grid onxlabel('TIME index :n');ylabel('2.30(b)');subplot(2,1,2)stem(n,x2,'filled');grid onxlabel('TIME index :n');ylabel('2.30(e)');2、调用并运行：M2_2（10）M2.3、1、程序：function s=M2_3(A,omega,fai,N)n=0:N;x=A*sin(omega*n+fai);stem(n,x,'fill');grid onaxis([0,N,-2,2]);xlabel('Time index n');ylabel('Amplitude');2、调用并运行(a)、M2_3(1.5,0,pi/2,40)、M2_3(1.5,0.1*pi,pi/2,40)、M2_3(1.5,0.2*pi,pi/2,40)、M2_3(1.5,0.8*pi,pi/2,40)、M2_3(1.5,0.9*pi,pi/2,40)、M2_3(1.5,pi,pi/2,40)、M2_3(1.5,1.1*pi,pi/2,40)、M2_3(1.5,1.2*pi,pi/2,40)(b)、（1）omega=0.6*pi周期T=10；理论上：T=10 （2）omega=0.28*pi周期T=50；；理论上：T=50；（3）omega=0.45*pi周期T=40；理论上：T=40；（4）omega=0.55*pi周期T=40；理论上：T=40；（4）omega=0.65*pi周期T=40；理论上：T=40；M2.9、MATLAB Excise For Chapter3M3.3、调用程序program 3-1运行M3_3Number of frequency points = [1000]Numerator coefficients = 0.2418*[1 0.139 -0.3519 0.139 1] Denominator coefficients = [1 0.2386 0.8258 0.1393 0.4153]The plot of the program are shown in below：运行M3_3Number of frequency points = [1000]Numerator coefficients = 0.1397*[1 -0.0911 0.0911 -1] Denominator coefficients = [1 1.1454 0.7275 0.1205]The plot of the program are shown in below：M3.7、h=input('Type in the target sequence= ');%输入要计算群延时的序列N=input('Type in the group delay frequency point=');%输入要计算的群延时点n=0:(length(h)-1);H=fft(h,N);K=fft(n.*h,N);tao=real(K./H)运行M3-7M3_7Type in the target sequence= [1 1 2 0 0 6 3]Type in the group delay frequency point=8tao =4.0769 7.7221 4.6923 4.0556 9.0000 4.05564.6923 7.7221MATLAB Excise For Chapter5 M5.11、程序function d=M5_1(N)k1=-N:N;x1=ones(1,2*N+1);omega=0:pi/500:2*pi;X1=freqz(x1,1,omega);X1dft=fft(x1);n1=0:1:2*N;figure(1),plot(omega/pi,abs(X1),2*n1/(2*N+1),abs(X1dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');k2=0:N;x2=ones(1,N+1);X2=freqz(x2,1,omega);X2dft=fft(x2);n2=0:1:N;figure(2),plot(omega/pi,abs(X2),2*n2/(N+1),abs(X2dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');k3=k1;x3=1-(abs(k3)/N);X3=freqz(x3,1,omega);X3dft=fft(x3);n3=n1;figure(3),plot(omega/pi,abs(X3),2*n3/(2*N+1),abs(X3dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');x4=N+1-abs(k3);X4=freqz(x4,1,omega);X4dft=fft(x4);figure(4),plot(omega/pi,abs(X4),2*n3/(2*N+1),abs(X4dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');x5=cos(pi*k3/(2*N));X5=freqz(x5,1,omega);X5dft=fft(x5);figure(5),plot(omega/pi,abs(X5),2*n3/(2*N+1),abs(X5dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');实现了problem3.19中5个序列的求DTFT和DFT2、调用程序运行结果M5_1（8）The red circles denote the DFT samples.当N=8时序列y1的DTFT和DFT采样当N=8时序列y2的DTFT和DFT采样当N=8时序列y3的DTFT和DFT采样当N=8时序列y4的DTFT和DFT采样当N=8时序列y5的DTFT和DFT采样M5.21、程序x=input('the sequence one to convolution;');y=input('the sequence two to convolution;');X=fft(x);Y=fft(y);S=X.*Y;s=ifft(S)2、调用程序M5_2the sequence one to convolution;[5,-2,2,0,4,3]the sequence two to convolution;[3,1,-2,2,4,4]s =10.0000 9.0000 16.0000 44.0000 36.0000 29.0000 M5_2M5_2the sequence one to convolution;[2-j,-1-j*3,4-j*3,1+j*2,3+j*2] the sequence two to convolution;[-3,2+j*4,-1+j*4,4+j*2,-3+j]s =11.0000 +25.0000i -9.0000 +48.0000i 3.0000 +17.0000i 29.0000 + 0.0000i -10.0000 +12.0000iProgram for （c）N=4;n=0:1:N;x=cos(pi*n/2);y=3.^n;X=fft(x);Y=fft(y);S=X.*Y;s=ifft(S)s =-23.0000 -69.0000 35.0000 105.0000 73.0000M5.81、程序X=[11 8-j*2 1-j*12 6+j*3 -3+j*2 2+j 15];k=8:12;XR(k)=conj(X(mod(-k+2,12)));XC=[X XR(k)];x=ifft(XC);n=0:1:11;x1=exp(i*2*pi*n/3);y=x1.*x;output=[x(1) x(7) sum(x) sum(y)];disp(output)disp(sum(x.*x))2、调用程序M5_84.5000 -0.8333 11.0000 -3.0000 - 2.0000i 74.8333MATLAB Excise For Chapter6M6.1(a)、The output of program6_1 by input the coefficient of problem （a）Numerator factors1.00000000000000 -2.10000000000000 5.000000000000001.00000000000000 -0.40000000000000 0.90000000000000Denominator factors1.000000000000002.00000000000000 4.999999999999991.00000000000000 -0.20000000000000 0.40000000000001Gain constant0.50000000000000Then ，The pole-zero plot of is given below:There are 3 ROCs associated with :R1,|z|<;R2,<|z|<; R3,|z|>The inverse –transform corresponding to the ROC is a left-sided sequence, the inverse–transform corresponding to the ROC is a two-sided sequence, and the inverse –transform corresponding to the ROC is a right-sided sequence.(b)、The output of program6_1 by input the coefficient of problem （b）Numerator factors1.00000000000000 1.20000000000000 3.999999999999991.00000000000000 -0.50000000000000 0.90000000000001Denominator factors1.000000000000002.10000000000000 4.000000000000011.00000000000000 0.60000000000003 01.00000000000000 0.39999999999997 0Gain constant1Then ，The pole-zero plot of is given below:There are 4 ROCs associated with :R1,|z|<R2,<|z|<; R3,<|z|<; R4,|z|>The inverse –transform corresponding to the ROC is a left-sided sequence, the inverse–transform corresponding to the ROC is a two-sided sequence, and the inverse –transform corresponding to the ROC is a right-sided sequence.M6.3The output of programme6_4 by type in：（a）M6_3Type in the residues = [-0.8,-7/6]Type in the poles = [-0.2,-1/6]Type in the constants = 3The output is as following：Numerator polynomial coefficients1.0333 0.7333 0.1000Denominator polynomial coefficients1.0000 0.3667 0.0333Hence（b）Rewrite X2（z）asM6_3Type in the residues = [3,-0.7+j*0.6454972243679,-0.7-j*0.6454972243679] Type in the poles = [-0.4,j*0.774596669,-j*0.774596669]Type in the constants = -2.5The output is as following：Numerator polynomial coefficients-0.9000 -2.5600 -0.1000 -0.6000Denominator polynomial coefficients1.0000 0.4000 0.6000 0.2400Hence，（c）M6_3Type in the residues = [5,1.5,-0.25]Type in the poles = [-0.64,-0.5,-0.5]Type in the constants = 0The output is as following：Numerator polynomial coefficients6.2500 6.5500 1.7300 0Denominator polynomial coefficients1.0000 1.6400 0.8900 0.1600Hence，（d）Rewrite X4（z）asM6_3Type in the residues = [-0.75,-0.375+j*0.2905,-0.375-j*0.2905] Type in the poles = [0.5,-j*0.4303,j*0.4303]Type in the constants = -5The output is as following：Numerator polynomial coefficients-4.5000 -6.8750 -3.6375 -0.8438Denominator polynomial coefficients1.0000 1.5000 0.7875 0.1688MATLAB Excise For Chapter7M7.31、程序k = input('Number of frequency points = ');num = input('Numerator coefficients = ');den = input('Denominator coefficients = ');w = 0:pi/(k-1):pi;h = freqz(num, den, w);plot (w,20*log10(abs(h)));gridxlabel('Normalized frequency'); ylabel('Gain, dB');2、调用M7_3运行结果如下M7_3Number of frequency points = 1000Numerator coefficients = [0,1,-2,1]Denominator coefficients = [1,-1.28,0.61+0.4*0.88,-(0.4*0.61)]From the gain response of the transfer function we can get that when the frequency become high and stable then we can conclude that this has a high pass responseM7.51、程序k = input('Number of frequency points = ');num = input('Numerator coefficients = ');den = input('Denominator coefficients = ');w = 0:pi/(k-1):pi;h = freqz(num, den, w);figure(1),plot(w/pi,abs(h));grid ontitle('Magnitude Spectrum')xlabel('\omega/\pi'); ylabel('Magnitude')figure(2),plot(w/pi,angle(h));grid ontitle('Phase Spectrum')xlabel('\omega/\pi'); ylabel('Phase, radians')2、调用M7_5运行结果如下M7_5Number of frequency points = 1000Numerator coefficients = 0.2031*[1,-(1+0.2743),1+0.2743,-1]Denominator coefficients =[1,0.487+0.1532,0.8351+0.83+0.1532*0.487+0.84,0.1532*0.84+0.487*0.8352,0.84*0.8351]Fro m the magnitude response plot given above it can be seen that represents a highpass filter. The difference equation representation of is given byy[n]+0.7074y[n-1]+0.7976y[n-2]+0.2004y[n-3]=0.2031x[n]-0.2588x[n-1]+0.2588x[n-2]-0.2031x[n-3]MATLAB Excise For Chapter9M9.21、程序Fp = input('Passband edge frequency in Hz = ');Fs = input('Stopband edge frequency in Hz = ');FT = input('Sampling frequency in Hz = ');Rp = input('Passband ripple in dB = ');Rs = input('Stopband minimum attenuation in dB = ');Wp = 2*Fp/FTWs = 2*Fs/FT[N, Wn] = buttord(Wp, Ws, Rp, Rs)[b, a] = butter(N, Wn);disp('Numerator polynomial');disp(b)disp('Denominator polynomial');disp(a)[h, w] = freqz(b, a, 512);figure（1），plot(w/pi, 20*log10(abs(h))); grid axis([0 1 -60 5]);xlabel('\omega/\pi'); ylabel('Magnitude, dB'); figure（2），plot(w/pi, unwrap(angle(h))); grid axis([0 1 -8 1]);xlabel('\omega/\pi'); ylabel('Phase, radians');2、调用M9_2运行结果如下M9_2Passband edge frequency in Hz = 10000Stopband edge frequency in Hz = 30000Sampling frequency in Hz = 100000Passband ripple in dB = 0.4Stopband minimum attenuation in dB = 50Wp =0.2000Ws =0.6000N =5Wn =0.2613Numerator polynomial0.0039 0.0197 0.0394 0.0394 0.0197 0.0039Denominator polynomial1.0000 -2.3611 2.6131 -1.5486 0.4864-0.0636M9.111、（a）TF=9kHZ，1pF=1.2kHZ，2pF=2.2kHZ，1sF=650HZ，2sF=3kHZ pα=0.8dB，sα=31dBThenTpp FF112πω==0.8378，Tpp FF222πω==1.536，Tss FF112πω==0.4538，Tss FF222πω==2.094According to bilinear transformation method ：)2tan(11ppω=ΩΛ=0.445，)2tan(22ppω=ΩΛ=0.996，)2tan(11ssω=ΩΛ=0.231，)2tan(22s s ω=ΩΛ=1.731. ωB =2p ΛΩ—1p ΛΩ=0.521，s Ω=3.13程序[N, Wn] = cheb1ord(1, 3.13, 0.8, 31, 's');[B, A] = cheby1(N, 0.8, Wn, 's');[BT, AT] = lp2bp(B, A, sqrt(0.43), 0.521);[num, den] = bilinear(BT, AT, 0.5);[h, omega] = freqz(num, den, 256);plot(omega/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi'); ylabel('Gain,in dB');title('Chebyshev I Bandpass Filter');axis([0 1 -60 5]);2、调用M9_11运行结果如下MATLAB Excise For Chapter10M10.11、程序M1= input('M1= ');M2= input('M2= ');n1=-M1:0.5:M1;n2=-M2:0.5:M2;num1=-0.4*sinc(0.4*n1);num2=-0.4*sinc(0.4*n2);num1(M1+1)=0.6;num2(M2+1)=0.6;w1= 0:pi/(4*M1):pi;w2= 0:pi/(4*M2):pi;h1= freqz(num1, 1, w1);h2= freqz(num2, 1, w2);plot(w1/pi,abs(h1),w2/pi,abs(h2));grid ontitle('Magnitude Spectrum')xlabel('\omega/\pi'); ylabel('Magnitude')2、调用程序运行结果M10.51、程序N = 36;fc = 0.2*pi;M = N/2;n = -M:1:M;t = fc*n;lp = fc*sinc(t);b = 2*[lp(1:M) (lp(M+1) - 0.5) lp((M+2):N+1)]; bw = b.*hamming(N+1)';[h2, w] = freqz(bw, 1, 512);plot(w/pi, abs(h2));axis([0 1 0 1.2]);xlabel('\omega/\pi');ylabel('Magnitude');title(['\omega_c = ', num2str(fc), ', N = ', num2str(N)]);grid on 2、运行结果M10.81、程序wp = 4*(2*pi)/18;ws = 6*(2*pi)/18;wc = (wp + ws)/2;dw = ws - wp;% HammingM = ceil(3.32*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = hamming(N)';b = num.*wh;figure(1);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(2);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h))); grid;xlabel('\omega/\pi'); ylabel('Gain, in dB');title('Lowpass filter designed using Hamming window');axis([0 1 -80 10]);% HannM = ceil(3.11*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = hann(N)';b = num.*wh;figure(3);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(4);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Hann window'); axis([0 1 -80 10]);% BlackmanM = ceil(5.56*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = blackman(N)';b = num.*wh;figure(5);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(6);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Blackman window'); axis([0 1 -80 10]);2、运行结果M10.91、程序beta = 3.631;N = 44;n = -N/2:N/2;num = (6/18)*sinc(6*n/18);wh = kaiser(N+1,beta)';b = num.*wh;figure(1);stem(b);title('Impulse Response Coefficients');xlabel('Time index n');ylabel('Amplitude')figure(2);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Kaiser window'); axis([0 1 -80 10]);2、运行结果。

MATLAB课程作业

注意：11月15日是交作业的最后期限。

（交word和MATLAB程序清单，word以“班级-学号-姓名”命名，每个MATLAB程序以”zuoye_题号”命名后，放在一个文件夹下（文件夹命名为“作业程序”），如zuoye_1_1.m），将word和“作业程序”文件夹放在一个文件夹（文件夹以“班级-学号-姓名”）交到班长处，班长统一交到教学办公室。

第一部分程序设计1.1、用MA TLAB可以识别的格式输入下面两个矩阵：(1) 矩阵A的维数；(2) 矩阵A中的元素a41的值；(3) 修改矩阵A的元素，使a41 =3.0；(4) 矩阵A中最后2行和最后3列交汇形成的子矩阵的值。

(5)求出A和B的乘积矩阵C，并将C矩阵的右下角2X 3子矩阵赋给D矩阵。

1.2、已知111121111,131,111214A B⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求(1)AB-2A，(2)A*B，(3)A﹒*B，(4) AB-BA 1.3、解线性方程：1.4、解方程组：1.5、用MA TLAB语言实现下面的分段函数：1.6、已知x=[1 2 3 ],y=[4 5 6 ]，试计算z=x.*y 、x.\y 和x./y.1.7、分别用for 和while 循环语句编写程序，求出1.8、已知在平面坐标中两点(x 1, y 1)和(x 2, y 2)之间的距离计算公式为 ()()222121y y x x L -+-=(1) 利用命令文件的形式，编写求解该距离的M 文件dis1.m ；(2) 利用函数文件的形式，编写求解该距离的M 文件dis2.m ；(3) 给定两点坐标的值(2,3)和(8, －5)，试分别调用命令文件dis1.m 和函数文件dis2.m 求解该两点间距离的值。

1.9、求解方程x 5+6x 3一3x 2＝10的5个根，并将其位置用五角星符号标记在复平面上，要求横纵坐标袖的刻度等长，注明虚轴和实轴，在title 位置上写㈩方程。

《MATLAB语言》课程第五次作业

MATLAB语言基础与应用(第二版)第5章 习题答案

MATLAB习题及参考答案经典.doc

MATLAB上机内容及作业

MATLAB作业5参考答案

Matlab第五章答案

数学建模作业题+答案

MATLAB教程2012a第5章习题解答-张志涌..

MATLAb与数学实验 第五章习题解答

matlab1-8章课后作业

MATLAB教程课后实验报告题目及解答[第一至第五章]

Matlab第五章答案

MATLAb与数学实验 第五章习题解答

MatLab语言及应用--习题及参考答案

matlab第四、五次作业

matlab参考答案matlab第5次作业至诚2013参考答案

DSP Matlab作业(第5~10章)

MATLAB课程作业

MATLAB语言基础与应用(第二版)第5章习题答案

MATLAb与数学实验第五章习题解答

MATLAb与数学实验第五章习题解答