美国数学建模竞赛第二次模拟赛题
数学建模美赛2024题目

数学建模美赛2024题目全文共四篇示例,供读者参考第一篇示例:今年的题目是关于气候变化和环境保护的议题。
题目涉及到了全球变暖对气候和环境的影响,以及如何通过有效的政策和措施来减缓这种影响。
参赛者需要结合大量的气象数据、环境数据和经济数据,建立数学模型来分析不同政策对环境的影响,并提出具体的政策建议。
题目要求参赛者首先了解全球变暖的背景和影响,包括气候变化对冰川、海平面和生态系统的影响。
然后需要收集大量的数据,包括气温、降水、二氧化碳排放量等信息,建立数学模型来模拟气候变化的趋势和影响。
在此基础上,参赛者需要分析不同政策对气候和环境的影响,比如减排政策、再生能源政策、森林保护政策等。
最终,他们需要提出具体的政策建议,用数学模型来验证这些政策的有效性和可行性。
这道题目不仅考验参赛者的数学建模能力,还要求他们具备丰富的跨学科知识和分析能力。
参赛者需要深入了解气候变化和环境问题的本质,同时还需要掌握大量的数据处理和模型建立技巧。
他们需要运用数学、统计学、计算机科学等知识,同时还要具备创新思维和团队合作能力。
通过参与这项挑战性的比赛,大学生们不仅可以提升自己的数学建模能力,还可以培养跨学科的综合能力和团队合作精神。
这对于他们未来从事科研、工程或管理等领域的工作都将大有裨益。
这也是一次展示自己才华和创造力的绝佳机会,可以让他们在学术界和工业界获得更多的认可和机会。
2024年美国大学生数学建模竞赛的题目涉及到了气候变化和环境保护这一全球性议题,要求参赛者建立数学模型来分析不同政策对环境的影响,并提出具体的政策建议。
这是一项极具挑战性和实践意义的比赛,将为参赛者提供一个全面发展和展示自己才华的平台。
希望所有参赛者都能在这场比赛中收获满满的成绩和经验!第二篇示例:2024年美国大学生数学建模竞赛(MCM/ICM)是一个全球性的高水平数学建模比赛。
在这个比赛中,参赛队伍需要在72小时内利用自己的数学建模技能解决提出的真实世界问题。
历年美国大学生数学建模竞赛试题MCM.翻译版doc

1985 年美国大学生数学建模竞赛MCM 试题1985年MCM:动物种群选择适宜的鱼类和哺乳动物数据准确模型。
模型动物的自然表达人口水平与环境相互作用的不同群体的环境的重要参数,然后调整账户获取表单模型符合实际的动物提取的方法。
包括任何食物或限制以外的空间限制,得到数据的支持。
考虑所涉及的各种数量的价值,收获数量和人口规模本身,为了设计一个数字量代表的整体价值收获。
找到一个收集政策的人口规模和时间优化的价值收获在很长一段时间。
检查政策优化价值在现实的环境条件。
1985年MCM B:战略储藏管理钴、不产生在美国,许多行业至关重要。
(国防占17%的钴生产。
1979年)钴大局部来自非洲中部,一个政治上不稳定的地区。
1946年的战略和关键材料储藏法案需要钴储藏,将美国政府通过一项为期三年的战争。
建立了库存在1950年代,出售大局部在1970年代初,然后决定在1970年代末建立起来,与8540万磅。
大约一半的库存目标的储藏已经在1982年收购了。
建立一个数学模型来管理储藏的战略金属钴。
你需要考虑这样的问题:库存应该有多大?以什么速度应该被收购?一个合理的代价是什么金属?你也要考虑这样的问题:什么时候库存应该画下来吗?以什么速度应该是画下来吗?在金属价格是合理出售什么?它应该如何分配?有用的信息在钴政府方案在2500万年需要2500万磅的钴。
美国大约有1亿磅的钴矿床。
生产变得经济可行当价格到达22美元/磅(如发生在1981年)。
要花四年滚动操作,和thsn六百万英镑每年可以生产。
1980年,120万磅的钴回收,总消费的7%。
1986 年美国大学生数学建模竞赛MCM 试题1986年MCM A:水文数据下表给出了Z的水深度尺外表点的直角坐标X,Y在码(14数据点表省略)。
深度测量在退潮。
你的船有一个五英尺的草案。
你应该防止什么地区的矩形(75200)X(-50、150)?1986年MCM B:Emergency-Facilities位置迄今为止,力拓的乡牧场没有自己的应急设施。
USACO 2024年2月黄金组试题

USACO2024F EBRUARY C ONTEST,G OLD P ROBLEM1.B ESSLA M OTORS**注意:本题的时间限制为3秒,通常限制的 1.5倍。
本题的内存限制为512MB,通常限制的2倍。
**为了推广他的贝斯拉(Bessla)电动拖拉机系列,Farmer John希望展示贝斯拉的充电网络。
他已标记了地图上N(2≤N≤5⋅104)个编号为1…N的兴趣点,其中前C(1≤C<N)个是充电站,其余为旅游目的地。
这些兴趣点之间由M(1≤M≤105)条双向道路连接,其中第i条连接不同的点ui和vi(1≤ui,vi≤N)且长度为ℓi英里(1≤ℓi≤109)。
贝斯拉一次充电最多可行驶2R英里(1≤R≤109),使之可以到达一个充电站R英里范围内的任何目的地。
一个目的地被称之为交通便利的,如果可以从至少K(1≤K≤10)个不同的充电站到达目的地。
你的任务是帮助Farmer John确定交通便利的旅游目的地的集合。
输入格式:输入的第一行包含五个空格分隔的整数N,M,C,R和K。
以下M行,每行包含三个空格分隔的整数ui,vi和ℓi,其中ui≠vi。
充电站的编号为1,2,…,C。
其余兴趣点均为旅游目的地。
输出格式:首先输出一行,包含交通便利的旅游目的地的数量。
然后升序输出所有交通便利的旅游目的地,每个一行。
输入样例:33141123135232输出样例:12我们在1有一个充电站。
从这个充电站出发,我们可以到达2(因为它与1的距离为3),但不能到达3(因为它与1的距离为5)。
因此,只有点2是交通便利的。
输入样例:4321012121231001410输出样例:234我们在1和2有充电站,点3和4均位于1和2的101距离内。
因此,点3和4都是交通便利的。
输入样例:4321002121231001410输出样例:14测试点性质:测试点4-5:K=2,N≤500且M≤1000。
测试点6-7:K=2。
第二次数学建模作业
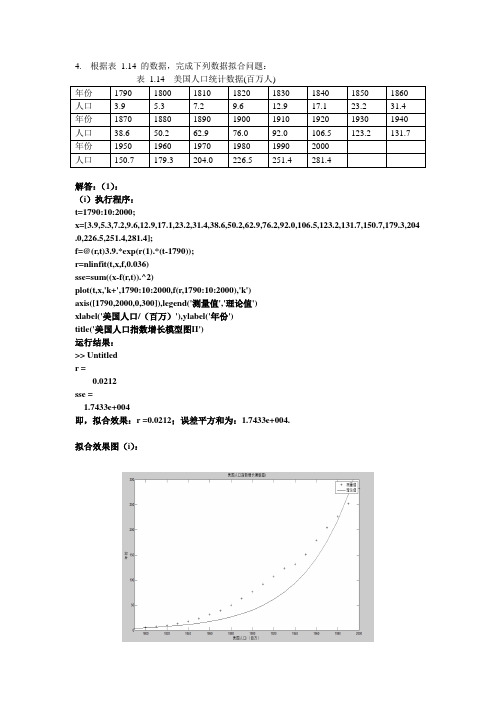
4. 根据表1.14 的数据,完成下列数据拟合问题:年份1790 1800 1810 1820 1830 1840 1850 1860 人口 3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4年份1870 1880 1890 1900 1910 1920 1930 1940 人口38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 年份1950 1960 1970 1980 1990 2000人口150.7 179.3 204.0 226.5 251.4 281.4解答:(1):(i)执行程序:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204 .0,226.5,251.4,281.4];f=@(r,t)3.9.*exp(r(1).*(t-1790));r=nlinfit(t,x,f,0.036)sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:10:2000,f(r,1790:10:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值')xlabel('美国人口/(百万)'),ylabel('年份')title('美国人口指数增长模型图II')运行结果:>> Untitledr =0.0212sse =1.7433e+004即,拟合效果:r =0.0212;误差平方和为:1.7433e+004.拟合效果图(i):(ii)由表1.14我们知道,当t=1800时,有5)101(0≈+r x ,所以我们可以猜测,r=0.1,x =2.5.对待定参数0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-1790)); r0=[2.5,0.1]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图II')命令窗口显示的计算的结果如下: >> Untitled r =15.0005 0.0142 sse =2.2657e+003即我们知道,拟合结果为:r=r(2)= 0.0142, 0x =r(1)= 15.0005;误差平方和为:2.2657e+003. 拟合效果图(ii ):(iii)由表1.14我们知道,当t=1900时,有()76)-t 1900101(00≈+r x ,所以我们可以猜测,r=0.03,x =19, 0t =1800.对待定参数0t ,0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-r(3))); r0=[19,0.03,1800]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图III')命令窗口显示的计算的结果如下:>> UntitledWarning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be estimated well (they are not identifiable). Use caution in making predictions. > In nlinfit at 224 In Untitled at 5 r =1.0e+003 *0.0159 0.0000 1.7939 sse =2.2657e+003即,拟合效果:r =0,0x =7.9,0t =1742.5;误差平方和为:2.2657e+003我们由MATLAB9给出的警告信息,知道这个拟合存在病态条件,所以数据可能拟合的不太好。
2012年美国数学建模题目中文版3篇

2012年美国数学建模题目中文版第一篇:2012年美国数学建模题目解析2012年美国数学建模竞赛题目分为3个部分:A、B、C 部分,其中A、B两部分每个题目都设计成了开放式问题,而C部分则是两道严谨的数学证明题目。
A部分共有四个问题,分别为:1、搜索引擎的自动补充功能对于使用者的输入进行了什么样的预测和补全?如果这种功能可以被改变,在搜索引擎中进行必要的优化,会对搜索引擎的使用产生什么影响?2、在一个公共交通的网络中,如何合理地分配车辆保证所有的车辆在一定时间内都能够按时到达各自的终点站?3、如何在餐馆排队时,给不同的桌子和不同的人分配最佳位置,以便让顾客在餐厅等待的时间最短?4、针对特定的树木,如何编写算法来找到该树生长的变化,在叶片的数量和大小、气孔的数量和大小等方面的特征?对于这四个问题,考生需要通过分析问题,理清思路,构思模型,进行数据分析,最后得出自己的结论。
需要注意的是,每个问题都是非常开放式的,没有标准答案,最终得分并不会仅仅取决于观点是否正确,具体的解题过程、数据展示和准确度也是非常关键的。
B部分共有三个问题,分别为:1、如何通过旅游者在社交网络上的信息,帮助旅游者更好地定制旅游计划?2、如何在残缺不全的传媒报道中,找到事实并从中解读该事件?3、针对滑雪者在滑雪过程中的各种情况,如何预测他们的滑雪技巧以及未来的滑雪表现?对于B部分的三个问题,其实也都是很自由的问题,可以根据自己所擅长领域进行分析,构思自己的模型和算法,注重细节和数据展示。
C部分共有两个题目:1、已知一个最小二乘问题,其正则化后的解为稀疏的,试设计一个迭代算法在有效的处理机制下对其进行数值求解。
2、已知一个对象向一条线段上匀速运动,在线段的中途,运动的对象突然重力下落,如果目标是在最短的时间内捕捉该运动的对象,该怎样运动才是最优策略?对于C部分两个题目,需要在数学基础扎实的基础上进行思考,深入分析,构建出严谨的证明过程,注重逻辑和方法。
美国数学建模竞赛1985-2013试题

1985~2013年美国大学生数学建模竞赛题目集锦目录1985 MCM A: Animal Populations (3)1985 MCM B: Strategic Reserve Management (3)1986 MCM A: Hydrographic Data (4)1986 MCM B: Emergency-Facilities Location (4)1987 MCM A: The Salt Storage Problem (5)1987 MCM B: Parking Lot Design (5)1988 MCM A: The Drug Runner Problem (5)1988 MCM B: Packing Railroad Flatcars (6)1989 MCM A: The Midge Classification Problem (6)1989 MCM B: Aircraft Queueing (6)1990 MCM A: The Brain-Drug Problem (6)1990 MCM B: Snowplow Routing (7)1991 MCM A: Water Tank Flow (8)1991 MCM B: The Steiner Tree Problem (8)1992 MCM A: Air-Traffic-Control Radar Power (8)1992 MCM B: Emergency Power Restoration (9)1993 MCM A: Optimal Composting (10)1993 MCM B: Coal-Tipple Operations (11)1994 MCM A: Concrete Slab Floors (11)1994 MCM B: Network Design (12)1995 MCM A: Helix Construction (13)1995 MCM B: Faculty Compensation (13)1996 MCM A: Submarine Tracking (13)1996 MCM B: Paper Judging (13)1997 MCM A: The Velociraptor Problem (14)1997 MCM B: Mix Well for Fruitful Discussions (15)1998 MCM A: MRI Scanners (16)1998 MCM B: Grade Inflation (17)1999 MCM A: Deep Impact (17)1999 MCM B: Unlawful Assembly (18)2000 MCM A: Air Traffic Control (18)2000 MCM B: Radio Channel Assignments (19)2001 MCM A: Choosing a Bicycle Wheel (20)2001 MCM B: Escaping a Hurricane's Wrath (An Ill Wind...). (21)2002 MCM A: Wind and Waterspray (23)2002 MCM B: Airline Overbooking (23)2003 MCM A: The Stunt Person (24)2003 MCM B: Gamma Knife Treatment Planning (24)2004 MCM A: Are Fingerprints Unique? (25)2004 MCM B: A Faster QuickPass System (25)2005 MCM A: Flood Planning (26)2005 MCM B: Tollbooths (26)2006 MCM A: Positioning and Moving Sprinkler Systems for Irrigation (27)2006 MCM B: Wheel Chair Access at Airports (28)2007 MCM A: Gerrymandering (29)2007 MCM B: The Airplane Seating Problem (29)2008 MCM A: Take a Bath (30)2008 MCM B: Creating Sudoku Puzzles (30)2009 MCM A: Designing a Traffic Circle (30)2009 MCM B: Energy and the Cell Phone (30)2010 MCM A: The Sweet Spot (32)2010 MCM B: Criminology (32)2011 MCM A: Snowboard Course (33)2011 MCM B: Repeater Coordination (33)2012 MCM A: The Leaves of a Tree (33)2012 MCM B: Camping along the Big Long River (34)2013 MCM A: The Ultimate Brownie Pan (34)2013 MCM B: Water, Water, Everywhere (35)1985 MCM A: Animal PopulationsChoose a fish or mammal for which appropriate data are available to model it accurately. Model the animal's natural interactions with its environment by expressing population levels of different groups in terms of the significant parameters of the environment. Then adjust the model to account for harvesting in a form consistent with the actual method by which the animal is harvested. Include any outside constraints imposed by food or space limitations that are supported by the data.Consider the value of the various quantities involved, the number harvested, and the population size itself, in order to devise a numerical quantity that represents the overall value of the harvest. Find a harvesting policy in terms of population size and time that optimizes the value of the harvest over a long period of time. Check that the policy optimizes that value over a realistic range of environmental conditions.1985 MCM B: Strategic Reserve ManagementCobalt, which is not produced in the US, is essential to a number of industries. (Defense accounted for 17% of the cobalt production in 1979.) Most cobalt comes from central Africa, a politically unstable region. The Strategic and Critical Materials Stockpiling Act of 1946 requires a cobalt reserve that will carry the US through a three-year war. The government built up a stockpile in the 1950s, sold most of it off in the early 1970s, and then decided to build it up again in the late 1970s, with a stockpile goal of 85.4 million pounds. About half of this stockpile had been acquired by 1982.Build a mathematical model for managing a stockpile of the strategic metal cobalt. You will need to consider such questions as:▪How big should the stockpile be?▪At what rate should it be acquired?▪What is a reasonable price to pay for the metal?You will also want to consider such questions as:▪At what point should the stockpile be drawn down?▪At what rate should it be drawn down?▪At what price is it reasonable to sell the metal?▪How should it be allocated?Useful Information on CobaltThe government has projected a need ot 25 million pounds of cobalt in 1985.The U.S. has about 100 million pounds of proven cobalt deposits. Production becomes economically feasible when the price reaches $22/lb (as occurred in 1981). It takes four years to get operations rolling, and thsn six million pounds per year can be produced.In 1980, 1.2 million pounds of cobalt were recycled, 7% of total consumption.1986 MCM A: Hydrographic DataThe table below gives the depth Z of water in feet for surface points with rectangular coordinates X, Y in yards [table of 14 data points omitted]. The depth measurements were taken at low tide. Your ship has a draft of five feet. What region should you avoid within the rectangle (75,200) x (-50, 150)?1986 MCM B: Emergency-Facilities LocationThe township of Rio Rancho has hitherto not had its own emergency facilities. It has secured funds to erect two emergency facilities in 1986, each of which will combine ambulance, fire, and police services. Figure 1 indicates the demand [figure omitted], or number of emergencies per square block, for 1985. The ―L‖ region in the north is an obstacle, while the rectangle in the south is a part with shallow pond. It takes an emergency vehicle an average of 15 seconds to go one block in the N-S direction and 20 seconds in the E-W direction. Your task is to locate the two facilities so as to minimize the total response time.Assume that the demand is concentrated at the center of the block and that the facilities will be located on corners.▪Assume that the demand is uniformly distributed on the streets bordering each block and that the facilities may be located anywhere on the streets.1987 MCM A: The Salt Storage ProblemFor approximately 15 years, a Midwestern state has stored salt used on roads in the winter in circular domes. Figure 1 shows how salt has been stored in the past. The salt is brought into and removed from the domes by driving front-end loaders up ramps of salt leading into the domes. The salt is piled 25 to 30 ft high, using the buckets on the front-end loaders.Recently, a panel determined that this practice is unsafe. If the front-end loader gets too close to the edge of the salt pile, the salt might shift, and the loader could be thrown against the retaining walls that reinforce the dome. The panel recommended that if the salt is to be piled with the use of the loaders, then the piles should be restricted to a matimum height of 15 ft.Construct a mathematical model for this situation and find a recommended maximum height for salt in the domes.1987 MCM B: Parking Lot DesignThe owner of a paved, 100' by 200' , corner parking lot in a New England town hires you to design the layout, that is, to design how the ``lines are to be painted. You realize that squeezing as many cars into the lot as possible leads to right-angle parking with the cars aligned side by side. However, inexperienced drivers have difficulty parking their cars this way, which can give rise to expensive insurance claims. To reduce the likelihood of damage to parked vehicles, the owner might then have to hire expert drivers for ``valet parking. On the other hand, most drivers seem to have little difficulty in parking in one attempt if there is a large enough ``turning radius'' from the access lane. Of course, the wider the access lane, the fewer cars can be accommodated in the lot, leading to less revenue for the parking lot owner.1988 MCM A: The Drug Runner ProblemTwo listening posts 5.43 miles apart pick up a brief radio signal. The sensing devices were oriented at 110 degrees and 119 degrees, respectively, when the signal was detected; and they are accurate to within 2 degrees. The signal came from a region of active drug exchange, and it is inferred that there is a powerboat waiting for someone to pick up drugs. it is dusk, the weather is calm, and there are no currents. A small helicopter leaves from Post 1 and is able to fly accurately along the 110 degree angle direction. The helicopter's speed is three times the speed of the boat. The helicopter will be heard when it gets within 500 ft of the boat. This helicopter has only one detection device, a searchlight. At 200 ft, it can just illuminate a circular region with a radius of 25 ft.▪Develop an optimal search method for the helicopter.▪Use a 95% confidence level in your calculations.1988 MCM B: Packing Railroad FlatcarsTwo railroad flatcars are to be loaded with seven types of packing crates. The crates have the same width and height but varying thickness (t, in cm) and weight (w, in kg). Table 1 gives, for each crate, the thickness, weight, and number available [table omitted]. Each car has 10.2 meters of length available for packing the crates (like slices of toast) and can carry up to 40 metric tons. There is a special constraint on the total number of C_5, C_6, and C_7 crates because of a subsequent local trucking restriction: The total space (thickness) occupied by these crates must not exceed 302.7 cm. Load the two flatcars (see Figure 1) so as to minimize the wasted floor space [figure omitted].1989 MCM A: The Midge Classification ProblemTwo species of midges, Af and Apf, have been identified by biologists Grogan and Wirth on the basis of antenna and wing length (see Figure 1). It is important to be able to classify a specimen as Af of Apf, given the antenna and wing length.1. Given a midge that you know is species Af or Apf, how would you go about classifying it?2. Apply your method to three specimens with (antenna, wing) lengths(1.24,1.80),(1.28,1.84),(1.40,2.04).3. Assume that the species is a valuable pollinator and species Apf is a carrier of adebilitating disease. Would you modify your classification scheme and if so, how?1989 MCM B: Aircraft QueueingA common procedure at airports is to assign aircraft (A/C) to runways on a first-come-first-served basis. That is, as soon as an A/C is ready to leave the gate (―push-back‖), the pilot calls ground control and is added to the queue. Suppose that a control tower has access to a fast online database with the following information for each A/C:▪the time it is scheduled for pushback;▪the time it actually pushes back; the number of passengers who are scheduled to make a connection at the next stop, as well as the time to make that connection; and▪the schedule time of arrival at its next stop Assume that there are seven types of A/C with passenger capacities varying from 100 to 400 in steps of 50. Develop and analyze amathematical model that takes into account both the travelers' and airlines' satisfaction.1990 MCM A: The Brain-Drug ProblemResearches on brain disorders test the effects of the new medical drugs – for example, dopamine against Parkinson's disease – with intracerebral injections. To this end, they must estimate the size and the sape of the spatial distribution of the drug after the injection, in order to estimate accurately the region of the brain that the drug has affected.The research data consist of the measurements of the amounts of drug in each of 50 cylindrical tissue samples (see Figure 1 and Table 1). Each cylinder has length 0.76 mm and diameter 0.66 mm. The centers of the parallel cylinders lie on a grid with mesh 1mm X 0.76mm X 1mm, so that the sylinders touch one another on their circular bases but not along their sides, as shown in the accompanying figure. The injection was made near the center of the cylinder with the highest scintillation count. Naturally, one expects that there is a drug also between the cylinders and outside the region covered by the samples.Estimate the distribution in the region affected by the drug.One unit represents a scintillation count, or 4.753e-13 mole of dopamine. For example, the table shows that the middle rear sylinder contails 28353 units.Table 1. Amounts of drug in each of 50 cylindrical tissue samples.Rear vertical sectionFront vertical section1990 MCM B: Snowplow RoutingThe solid lines of the map (see Figure 1) represent paved two-lane county roads in a snow removal district in Wicomico County, Maryland [figure omitted]. The broken lines are state highways. After a snowfall, two plow-trucks are dispatched from a garage that is about 4 miles west of each of the two points (*) marked on the map. Find an efficient way to use the two trucks to sweep snow from the county roads. The trucks may use the state highways to access the county roads. Assume that the trucks neither break down nor get stuck and that the road intersections require no special plowing techniques.1991 MCM A: Water Tank FlowSome state water-right agencies require from communities data on the rate of water use, in gallons per hour, and the total amount of water used each day. Many communities do not have equipment to measure the flow of water in or out of the municipal tank. Instead, they can measure only the level of water in the tank, within 0.5% accuracy, every hour. More importantly, whenever the level in the tank drops below some minimum level L, a pump fills the tank up to the maximum level, H; however, there is no measurement of the pump flow either. Thus, one cannot readily relate the level in the tank to the amount of water used while the pump is working, which occurs once or twice per day, for a couple of hours each time. Estimate the flow out of the tank f(t) at all times, even when the pump is working, and estimate the total amount of water used during the day. Table 1 gives real data, from an actual small town, for one day[ table omitted]. The table gives the time, in, since the first measurement, and the level of water in the tank, in hundredths of a foot. For example, after 3316 seconds, the depth of water in the tank reached 31.10 feet. The tank is a vertical circular cylinder, with a height of 40 feet and a diameter of 57 feet. Usually, the pump starts filling the tank when the level drops to about 27.00 feet, and the pump stops when the level rises back to about 35.50 feet.1991 MCM B: The Steiner Tree ProblemThe cost for a communication line between two stations is proportional to the length of the line. The cost for conventional minimal spanning trees of a set of stations can often be cut by introducing―phantom‖ stations and then constructing a new Steiner tree. This device allows costs to be cut by up to 13.4% (= 1- sqrt(3/4)). Moreover, a network with n stations never requires more than n-2 points to construct the cheapest Steiner tree. Two simple cases are shown in Figure 1.For local networks, it often is necessary to use rectilinear or ―checker-board‖ distances, instead of straight Euclidean lines. Distances in this metric are computed as shown in Figure 2.Suppose you wish to design a minimum costs spanning tree for a local network with 9 stations. Their rectangular coordinates are: a(0,15), b(5,20), c(16,24), d(20,20), e(33,25), f(23,11), g(35,7), h(25,0) i(10,3). You are restricted to using rectilinear lines. Moreover, all ―phantom‖ stations must be located at lattice points (i.e., the coordinates must be integers). The cost for each line is its length.1. Find a minimal cost tree for the network.2. Suppose each stations has a cost w*d^(3/2), where d=degree of the station. If w=1.2, find aminimal cost tree.3. Try to generalize this problem1992 MCM A: Air-Traffic-Control Radar PowerYou are to determine the power to be radiated by an air-traffic-control radar at a major metropolitan airport. The airport authority wants to minimize the power of the radar consistent with safety andcost. The authority is constrained to operate with its existing antennae and receiver circuitry. The only option that they are considering is upgrading the transmitter circuits to make the radar more powerful. The question that you are to answer is what power (in watts) must be released by the radar to ensure detection of standard passenger aircraft at a distance of 100 kilometers.1992 MCM B: Emergency Power RestorationPower companies serving coastal regions must have emergency response systems for power outages due to storms. Such systems require the input of data that allow the time and cost required for restoration to be estimated and the ―value‖ of the outage judged by objective criteria. In the past, Hypothetical Electric Company (HECO) has been criticized in the media for its lack of a prioritization scheme.You are a consultant to HECO power company. HECO possesses a computerized database with real time access to service calls that currently require the following information:▪time of report,▪type of requestor,▪estimated number of people affected, and▪location (x,y).Cre sites are located at coordinates (0,0) and (40,40), where x and y are in miles. The region serviced by HECO is within -65 < x < 60 and -50 < y < 50. The region is largely metropolitan with an excellent road network. Crews must return to their dispatch site only at the beginning and end of shift. Company policy requires that no work be initiated until the storm leaves the area, unless the facility is a commuter railroad or hospital, which may be processed immediately if crews are available.HECO has hired you to develop the objective criteria and schedule the work for the storm restoration requirements listed in Table 1 using their work force described in Table 2. Note that the first call was received at 4:20 A.M. and that the storm left the area at 6:00 A.M. Also note that many outages were not reported until much later in the day.HECO has asked for a technical report for their purposes and an ―executive summary‖ i n laymen's terms that can be presented to the media. Further, they would like recommendations for the future. To determine your prioritized scheduling system, you will have to make additional assumptions. Detail those assumptions. In the future, you may desire additional data. If so, detail the information desired.Table 1. Storm restoration requirements. (table incomplete)Table 2. Crew descriptions.1993 MCM A: Optimal CompostingAn environmentally conscious institutional cafeteria is recycling customers' uneaten food into compost by means of microorganisms. Each day, the cafeteria blends the leftover food into a slurry, mixes the slurry with crisp salad wastes from the kitchen and a small amount of shredded newspaper, and feeds the resulting mixture to a culture of fungi and soil bacteria, which digest slurry, greens, and papers into usable compost. The crisp green provide pockets of oxygen for the fungi culture, and the paper absorbs excess humidity. At times, however, the fungi culture is unable or unwilling to digest as much of the leftovers as customers leave; the cafeteria does not blame the chef for the fungi culture's lack of appetite. Also, the cafeteria has received offers for the purchase of large quantities of it compost. Therefore, the cafeteria is investigating ways to increase its production of compost. Since it cannot yet afford to build a new composting facility, the cafeteria seeks methods to accelerate the fungi culture's activity, for instance, by optimizing the fungiculture's environment (currently held at about 120 F and 100% humidity), or by optimizing the composition of the moisture fed to the fungi culture, or both.Determine whether any relation exists between the proportions of slurry, greens, and paper in the mixture fed to the fungi culture, and the rate at which the fungi culture composts the mixture. if no relation exists, state so. otherwise, determine what proportions would accelerate the fungi culture's activity. In addition to the technical report following the format prescribed in the contest instructions, provide a one-page nontechnical recommendation for implementation for the cafeteria manager. Table 1 shows the composition of various mixtures in pounds of each ingredient kept in separate bins, and the time that it took the fungi to culture to compost the mixtures, from the date fed to the date completely composted [table omitted].1993 MCM B: Coal-Tipple OperationsThe Aspen-Boulder Coal Company runs a loading facility consisting of a large coal tipple. When the coal trains arrive, they are loaded from the tipple. The standard coal train takes 3 hours to load, and the tipple's capacity is 1.5 standard trainloads of coal. Each day, the railroad sends three standard trains to the loading facility, and they arrive at any time between 5 A.M. and 8 P.M. local time. Each of the trains has three engines. If a train arrives and sits idle while waiting to be loaded, the railroad charges a special fee, called a demurrage. The fee is $5,000 per engine per hour. In addition, a high-capacity train arrives once a week every Thursday between 11 A.M. and 1 P.M. This special train has five engines and holds twice as much coal as a standard train. An empty tipple can be loaded directly from the mine to its capacity in six hours by a single loading crew. This crew (and its associated equipment) cost $9,000 per hour. A second crew can be called out to increase the loading rate by conducting an additional tipple-loading operation at the cost of $12,000 per hour. Because of safety requirements, during tipple loading no trains can be loaded. Whenever train loading is interrupted to load the tipple, demurrage charges are in effect.The management of the Coal Company has asked you to determine the expected annual costs of this tipple's loading operations. Your analysis should include the following considerations:▪How often should the second crew be called out?▪What are the expected monthly demurrage costs?▪If the standard trains could be scheduled to arrive at precise times, what daily schedule would minimize loading costs? Would a third tipple-loading crew at $12,000 per hour reduce annual operations costs?▪Can this tipple support a fourth standard train every day?1994 MCM A: Concrete Slab FloorsThe U.S. Dept. of Housing and Urban Development (HUD) is considering constructing dwellings of various sizes, ranging from individual houses to large apartment complexes. A principal concern is to minimize recurring costs to occupants, especially the costs of heating and cooling. The region inwhich the construction is to take place is temperate, with a moderate variation in temperature throughout the year.Through special construction techniques, HUD engineers can build dwellings that do not need to rely on convection- that is, there is no need to rely on opening doors or windows to assist in temperature variation. The dwellings will be single-story, with concrete slab floors as the only foundation. You have been hired as a consultant to analyze the temperature variation in the concrete slab floor to determine if the temperature averaged over the floor surface can be maintained within a prescribed comfort zone throughout the year. If so, what size/shape of slabs will permit this?Part 1, Floor Temperature: Consider the temperature variation in a concrete slab given that the ambient temperature varies daily within the ranges given Table 1. Assume that the high occurs at noon and the low at midnight. Determine if slabs can be designed to maintain a temperature averaged over the floor surface within the prescribed comfort zone considering radiation only. Initially, assume that the heat transfer into the dwelling is through the exposed perimeter of the slab and that the top and bottom of the slabs are insulated. Comment on the appropriateness and sensitivity of these assumptions. If you cannot find a solution that satisfies Table 1, can you find designs that satisfy a Table 1 that you propose?Part 2, Building Temperature: Analyze the practicality of the initial assumptions and extend the analysis to temperature variation within the single-story dwelling. Can the house be kept within the comfort zone?Part 3, Cost of Construction: Suggest a design that considers HUD's objective of reducing or eliminating heating and cooling costs, considering construction restrictions and costs.1994 MCM B: Network DesignIn your company, information is shared among departments on a daily basis. This information includes the previous day's sales statistics and current production guidance. It is important to get this information out as quickly as possible. [Network diagram (with 5 nodes and 7 capacitated edges) omitted.]We are interested in scheduling transfers in an optimal way to minimize the total time it takes to complete them all. This minimum total time is called the makespan. Consider the three following situations for your company: [Three more network diagrams (on roughly 20 nodes each) omitted.]1995 MCM A: Helix ConstructionA small biotechnological company must design, prove, program and test a mathematical algorithm to locate ―in real time‖ all the intersections of a helix and a plane in general positions in space. Design, justify, program and test a method to compute all the intersections of a plane and a helix, both in general positions (at any locations and with any orientations) in space. A segment of the helix may represent, for example, a helicoidal suspension spring or a piece of tubing in a chemical or medical apparatus. Theoretical justification of the proposed algorithm is necessary to verify the solution from several points of view, for instance, through mathematical proofs of parts of the algorithm, and through tests of the final program with known examples. Such documentation and tests will be required by government agencies for medical use.1995 MCM B: Faculty CompensationAluacha Balaclava College, and undergraduate facility, has just hired a new Provost whose first priority is the institution of a fair and reasonable faculty-compensation plan. She has hired your consulting team to design a compensation system that reflects the following circumstances and principles: [Three paragraphs of details omitted] Design a new pay system, first withoutcost-of-living increases. Incorporate cost-of-living increases, and then finally, design a transition process for current faculty that will move all salaries towards your system without reducing anyone's salary. The Provost requires a detailed compensation system plan for implementation, as well as a brief, clear, executive summary outlining the model, its assumptions, strengths, weaknesses and expected results, which she can present to the Board and faculty. [A detailed table of current salaries is omitted.]1996 MCM A: Submarine TrackingThe world's oceans contain an ambient noise field. Seismic disturbances, surface shipping, and marine mammals are sources that, in different frequency ranges, contribute to this field. We wish to consider how this ambient noise might be used to detect large maving objects, e.g., submarines located below the ocean surface. Assuming that a submarine makes no intrinsic noise, develop a method for detecting the presence of a moving submarine, its speed, its size, and its direction of travel, using only information obtained by measuring changes to the ambient noise field. Begin with noise at one fixed frequency and amplitude.1996 MCM B: Paper JudgingWhen determining the winner of a competition like the Mathematical Contest in Modeling, there are generally a large number of papers to judge. Let's say there are P=100 papers. A group of J judges is collected to accomplish the judging. Funding for the contest contrains both the number of judges that can be obtained and the amount of time they can judge. For example if P=100, then J=8 is typical.。
1999年美国大学生数学建模大赛赛题

1999年美国大学生数学建模大赛赛题1999 MCM Problem ADeep ImpactProblem:For some time, the National Aeronautics and Space Administration (NASA) has been considering the consequences of a large asteroid impact on the earth.As part of this effort, your team has been asked to consider the effects of such an impact were the asteroid to land in Antarctica. There are concerns that an impact there could have considerably different consequences than one striking elsewhere on the planet.You are to assume that an asteroid is on the order of 1000 m in diameter, and that it strikes the Antarctic continent directly at the South Pole.Your team has been asked to provide an assessment of the impact of such an asteroid. In particular, NASA would like an estimate of the amount and location of likely human casualties from this impact, an estimate of the damage done to the food production regions in the oceans of the southern hemisphere, and an estimate of possible coastal flooding caused by large-scale melting of the Antarctic polar ice sheet.1999 MCM Problem BUnlawful AssemblyProblem:Many public facilities have signs in rooms used for public gatherings which state that it is "unlawful" for the rooms to be occupied by more than a specified number of people. Presumably, this number is based on the speed with whichpeople in the room could be evacuated from the room's exits in case of an emergency. Similarly, elevators and other facilities often have"maximum capacities" posted.Develop a mathematical model for deciding what number to post on such a sign as being the "lawful capacity". As part of your solution discuss criteria, other than public safety in the case of a fire or other emergency, that might govern the number of people considered "unlawful" to occupy the room (or space). Also, for the model that you construct, consider the differences between a room with movable furniture such as a cafeteria (with tables and chairs), a gymnasium, a public swimming pool, and a lecture hall with a pattern of rows and aisles. You may wish to compare and contrast what might be done for a variety of different environments: elevator, lecture hall, swimming pool, cafeteria, or gymnasium. Gatherings such as rock concerts and soccer tournaments may present special conditions.Apply your model to one or more public facilities at your institution (or neighboring town). Compare your results with the stated capacity, if one is posted. If used, your model is likely to be challenged by parties with interests in increasing the capacity. Write an article for the local newspaper defending your analysis.1999 ICM ProblemGround Pollution Problem:BackgroundSeveral practically important but theoretically difficult mathematical problems pertain to the assessment of pollution. One such problem consists in deriving accurate estimates of the location and amount of pollutants seeping inaccessibly underground, and the location of their source, on the basis ofvery few measurements taken only around, but not necessarily directly in, the suspected polluted region.ExampleA data set is located at: procdata.xlsThe data set (an Excel file which can be downloaded into most spreadsheets) shows measurements of pollutants in underground water from 10 monitoring wells (MW) from 1990 to 1997. The units are micrograms per liter(μg/l). The location and elevation for eight of the wells is known and given below. The first two numbers are the coordinates of the location of the well on a Cartesian grid on a map. The third number is the altitude in feet above Mean Sea Level of the water level in the well.Well Number(ft)x-Coordinate(ft)y-Coordinate(ft)Elevation (ft)MW-14187.56375.01482.23MW-39062.54375.01387.92MW-77625.05812.51400.19MW-99125.04000.01384.53MW-119062.55187.51394.26MW-129062.54562.51388.94MW-139062.55000.01394.25MW-144750.02562.51412.00The locations and elevations of the other two wells in the data set (MW-27 and MW-33) are not known. In the data set you will also see the letter T, M or B after the well number, indicatingthe measurements were taken at the Top, Middle, or Bottom of the aquifer in the well. Thus, MW-7B and MW-7M are from the same well, but from the bottom and from the middle. Also, other measurements indicate that water tends to flow toward well MW-9 in this area.Problem OneBuild a mathematical model to determine whether any new pollution has begun during this time period in the area represented by the data set. If so, identify the new pollutants and estimate the location and time of their source.Problem TwoBefore the collection of any data, the question arises whether the intended type of data and model can yield the desired assessment of the location and amount of pollutants. Liquid chemicals may have leaked from one of the storage tanks among many similar tanks in a storage facility built over a homogeneous soil. Because probing under the many large tanks would be prohibitively expensive and dangerous, measuring only near the periphery of the storage facility or on the surface of the terrain seemspreferable. Determine what type and number of measurements, taken only outside the boundary or on the surface of the entire storage facility, can be used in a mathematical model to determine whether a leak has occurred, when it occurred, where (from which tank) it occurred, and how much liquid has leaked.。
美国(MCM)(ICM)试题(96年-09年)(英文版)

美国大学生数学建模竞赛试题1996 American MCM Problems Problem AThe world's oceans contain an ambient noise field. Seismic disturbances, surface shipping, and marine mammals are sources that, in different frequency ranges,contribute to this field. We wish to consider how this ambient noise might be used to detect large moving objects, e.g., submarines located below the ocean surface. Assuming that a submarine makes no intrinsic noise, developa method for detecting the presence of a moving submarine, its size, and its direction of travel, using only information obtained by measuring changes to the ambient noise field. Begin with noise at one fixed frequency and amplitude.Problem BWhen determining the winner of a competition like the Mathematical Contest inModeling, there are generally a large number of papers to judge. Let's saythere are P=100 papers.A group of J judges is collected to accomplish thejudging. Funding for the contest constains both the number of judges that canbe obtained and amount of time that they can judge. For eample if P=100, thenJ=8 is typical.Ideally, each judge would read paper and rank-order them, but there are toomany papers for this. Instead, there will be a number of screening rounds inwhich each judge will read some number of papers and give them scores. Thensome selection scheme is used to reduce the number of papers under consideration: If the papers are rank-ordered, then the bottom 30% that eachjudge rank-orders could be rejected. Alternatively, if the judges do not rank-order, but instead give them numerical score (say, from 1 to 100),then all papers below some cut-off level could be rejected.The new pool of papers is then passed back to the judges, and the process is repeated.A concern is then the total number of papers that judge reads must besubstantially less than P. The process is stopped when there are only W papersleft. There are the winners. Typically for P=100, W=3.Your task is to determine a selection scheme, using a combination of rank-ordering, numerical scoring, and other methods, by which the final Wpapers will include only papers from among the "best" 2W papers. (By "best",we assume that there is an absolute rank-ordering to which all judges wouldagree.) For example, the top three papers. Among all such methods, the one thatrequired each judge to read the least number of papers is desired.Note the possibility of systematic bias in a numerical scoring scheme. For example, for a specific collection of papers, one judge could average 70points, while another could average 80 points. How would you scale your schemeto accommodate for changes in the contest parameters (P, J, and W)?1997 American MCM ProblemsProblem A The Velociraptor ProblemThe velociraptor,Velociraptor mongoliensis, was a predatory dinosaur that lived during the late Cretaceous period, approximately 75 million years ago. Paleontologists think that it was a very tenacious hunter, and may have hunted in pairs or largerpacks .Unfortunately, there is no way to observe its hunting behavior in the wild as can be done with modern mammalian predators. A group of paleontologists has approached your team and asked for help in modeling the hunting behavior of the velociraptor. They hope to compare your results with field data reported by biologists studying the behaviors of lions, tigers, and similar predatory animals.The average adult velociraptor was 3 meters long with a hip height of 0.5 meters and an approximate mass of 45 kg. It is estimated that the animal could run extremely fast at speed of 60 km/hr for about 15 seconds. After the initial burst of speed ,the animal needed to stop and recover from a buildup of lactic acid in its muscles.Suppose that velociraptor preyed on Thescelosaurus neglectus, a herbivorous biped approximately the same size as the Velociraptor. A biomachanical analysis of a fossilized Thescelosaurus indicates that it could run at a speed of about 50 km/hr. for long period of time.Part1Assuming the velociraptor is a solitary hunter, design a mathematical model that describe a hunting strategy for a single velociraptor stalking and chasing a single Thescelosaurus as well as the evasive strategy of the prey. Assume that the Thescelosaurus can always detect the velociraptor when it comes within 15 meters .but may detect the predator at even greater ranges (up to 50 meters depending upon the habitat and weather conditions. Additionally ,due to its physical structure and strength, the velociraptorhas a limited turning radius when running at full speed. This radius is estimated to be three times the animal's hip height. On the other hand, the Thescelosaurus is extremely agile and has a turning radius of 0.5 meters.Part2Assuming more realistically that the velociraptor hunted in pairs, design a new model that describes a hunting strategy for two velociraptor stalking and chasing a single Thescelosaurus as well as the evasive strategy of the prey. Use the other assumptions and limitations given in Part 1.Problem B Mix Well For Fruitful DiscussionsSmall group meeting for the discussions of important issues, particular long-range planning ,are gaining popularity. It is believed that large groups discourage productive discussion and that a dominant personality will usually control and direct the discussion. Thus ,in corporate board meetings the board will meet in small groups to discuss issues before meeting as a whole, these smaller groups still tun the risk of control by a dominant personality. In an attempt to reduce this danger it is common to schedule several sessions with a different mix of people in each group.A meeting of An Tostal Corporation will be attended by 29 Board Members of which nine are in-house members(i.e., corporate employees).The meeting is to be an all-day affair with three sessions scheduled for the morning and four for the afternoon. Each session will take 45 minutes, beginning on the hour from 9:00 A.M. to 4:00 P.M., with lunch scheduled at noon. Each morning session will consist of six discussion groups with each discussion group led by one of the corporation's six senior officers. None of these officers are board members. Thus each senior officers will not be involved in the afternoon sessions and each of these sessions will consist of only four different discussion groups.The president of the corporation wants a list of board-member assignment to discussion groups for each of the seven sessions. The assignments should achieve as much of a mix of the members as much as possible. The ideal assignment would have each board member in a discussion group the same number of times while minimizing common membership of groups for the different sessions.The assignment should also satisfy the following criteria:1.For the morning sessions ,no board member should be in the same senior officer's discussion group twice.2.No discussion group should contain a disproportionate number of in-house members.Give a list of assignments for members 1-9 and 10-29 and officers 1-6.Indicate how well the criteria in the previous paragraphs are met. Since it is possible that some board members will cancel at the last minute or that some not scheduled will show up, an algorithm that the secretary could use to adjust the assignments with an hour's notice would be appreciated. It would be ideal if the algorithm could also be used to make assignments for future meetings involving different levels of participation for each type of attendee.1998 American MCM ProblemsProblem A MRI ScannersIntroductionIndustrial medical diagnostic machines known as Magnetic Resonance Imager (MRI) scan a three-dimensional object such as a brain, and deliver their results in the form of a three-dimensional array of pixel. Each pixel consists of one number indicating a color or a shade of gray that encodes a measure of water concentration in a small region of the scanned object at the location of the pixel .For instance,0 can picture high water concentration in black (ventricles, blood vessels),128 can picture a medium water concentration in gray(brain nuclei and gray matter),and 255 can picture a low water density in white (liquid-rich white matter consisting of myelinated axons).Such MRI scanners also include facilities to picture on a screen any horizontal or vertical slice through the three-dimensional array (slices are parallel to any of the three Cartesian coordinate axes ).Algorithms for picturing slices through oblique planes ,however ,are proprietary .Current algorithms are limited in terms of the angles and parameter options available ;are implemented only on heavily used dedicated workstations ;lack input capabilities for marking points in the picture before slicing; and tend to blur and "feather out" sharp boundaries between the original pixels.A more faithful, flexible algorithm implemented on a personal computer would be useful.(1)for planning minimally invasive treatments,(2)for calibrating the MRI machines,(3)for investigating structures oriented obliquely in space, such as post-mortem tissue sections in a animal research,(4)for enabling cross-sections at any angle through a brain atlas consisting (4)for enabling cross-sections at any angle through a brain atlas consistingof black-and-white line drawingTo design such an algorithm, one can access the value and locations of the pixels, but not the initial data gathered by the scanners.ProblemDesign and test an algorithm that produces sections of three-dimensional arrays by planes in any orientation in space, preserving the original gray-scale value as closely as possible.Data SetsThe typical data set consists of a three-dimensional array A of numbers A(i,j,k) which indicates the density A(i,j,k) of the object at the location (x,y,z)i,j,k. Typically A(i,j,k) can range from 0 to 255.In most applications the data set is quite large.Teams should design data sets to test and demonstrate their algorithms. The data sets should reflect conditions likely Teams should design data sets to test and demonstrate their algorithms. The data sets should reflect conditions likely to be of diagnostic interest. Teams should also characterize data sets the limit the effectiveness of their algorithms.SummaryThe algorithm must produce a picture of the slice of the three-dimensional array by a plane in space. The plane can have any orientation and any location in space.(The plane can miss some or all data points.)The result of the algorithm should be a model of the density of the scanned object over the selected plane.Problem B Grade InflationBackgroundSome college administrators are concerned about the grading at A Better Class(ABC) college. On average, the faculty at ABC have been giving out high grades(the average grade now given out is an A-),and it is impossible to distinguish between the good and mediocre students .The terms of a very generous scholarship only allow the top 10% of the students to be funded, so a class ranking is required.The dean had the thought of comparing each student to the other students in each class ,and using this information to build up a ranking. For example, if a student obtains an A in a class in which all students obtain an A, then this student is only "average" in this class. On the other hand, if a student obtain the only A in a class, then that student is clearly "above average". Combining information from several classes might allow students to be placed in deciles (top 10%,next 10%,ect.)across the college.ProblemAssuming that the grades given out are(A+,A-,B+,B-,...)can the dean's idea be made to work?Assuming that the grades given out are only (A,B,C,...)can the dean's idea be made to work?Can any other schemes produce a desired ranking?A concern is that the grade in a single class could change many student's deciles. Is this possible?Data SetsTeams should design data sets to test and demonstrate their algorithms. Teams should characterize data sets that limit the effectiveness of their algorithms.Mathematical Contest in Modeling 1999 ProblemsProblem A - Deep ImpactFor some time, the National Aeronautics and Space Administration (NASA) has been considering the consequences of a large asteroid impact on the earth.As part of this effort, your team has been asked to consider the effects of such an impact were the asteroid to land in Antarctica. There are concerns that an impact there could have considerably different consequences than one striking elsewhere on the planet.You are to assume that an asteroid is on the order of 1000 m in diameter, and that it strikes the Antarctic continent directly at the South Pole.Your team has been asked to provide an assessment of the impact of such an asteroid. In particular, NASA would like an estimate of the amount and location of likely human casualties from this impact, an estimate of the damage done to the food production regions in the oceans of the southern hemisphere, and an estimate of possible coastal flooding caused by large-scale melting of the Antarctic polar ice sheet.Problem B - Unlawful AssemblyMany public facilities have signs in rooms used for public gatherings which state that it is "unlawful" for the rooms to be occupied by more than a specified number of people. Presumably, this number is based on the speed with which people in the room could be evacuated from the room's exits in case of an emergency. Similarly, elevators and other facilities often have "maximum capacities" posted.Develop a mathematical model for deciding what number to post on such a sign as being the "lawful capacity". As part of your solution discuss criteria, other than public safety in the case of a fire or other emergency, that might govern the number of people considered "unlawful" to occupy the room (or space). Also, for the model that you construct, consider the differences between a room with movable furniture such as a cafeteria (with tables and chairs), a gymnasium, a public swimming pool, and a lecture hall with a pattern of rows and aisles. You may wish to compare and contrast what might be done for a variety of different environments: elevator, lecture hall, swimming pool, cafeteria, or gymnasium. Gatherings such as rock concerts and soccer tournaments may present special conditions.Apply your model to one or more public facilities at your institution (or neighboring town). Compare your results with the stated capacity, if one is posted. If used, your model is likely to be challenged by parties with interests in increasing the capacity. Write an article for the local newspaper defending your analysis.2000 Mathematical Contest in ModelingProblem A Air traffic ControlDedicated to the memory of Dr. Robert Machol, former chief scientist of the Federal Aviation Agency To improve safety and reduce air traffic controller workload, the Federal Aviation Agency (FAA) is considering adding software to the air traffic control system that would automatically detect potential aircraft flight path conflicts and alert the controller. To that end, an analyst at the FAA has posed the following problems.Requirement A: Given two airplanes flying in space, when should the air traffic controller consider the objects to be too close and to require intervention?Requirement B: An airspace sector is the section of three-dimensional airspace that one air traffic controller controls. Given any airspace sector, how do we measure how complex it is from an air traffic workload perspective? To what extent is complexity determined by the number of aircraft simultaneously passing through that sector (1) at any one instant?(2) during any given interval of time?(3) during a particular time of day? How does the number of potential conflicts arising during those periods affect complexity?Does the presence of additional software tools to automatically predict conflicts and alert the controller reduce or add to this complexity?In addition to the guidelines for your report, write a summary (no more than two pages) that the FAA analyst can present to Jane Garvey, the FAA Administrator, to defend your conclusions.Problem B Radio Channel AssignmentsWe seek to model the assignment of radio channels to a symmetric network of transmitter locations over a large planar area, so as to avoid interference. One basic approach is to partition the region into regular hexagons in a grid (honeycomb-style), as shown in Figure 1, where a transmitter is located at the center of each hexagon.Figure 1An interval of the frequency spectrum is to be allotted for transmitter frequencies. The interval will be divided into regularly spaced channels, which we represent by integers 1, 2, 3, ... . Each transmitter will be assigned one positive integer channel. The same channel can be used at many locations, provided that interference from nearby transmitters is avoided. Our goal is to minimize the width of the interval in the frequency spectrum that is needed to assign channels subject to some constraints. This is achieved with the concept of a span. The span is the minimum, over all assignments satisfying the constraints, of the largest channel used at any location. It is not required that every channel smallerthan the span be used in an assignment that attains the span.Let s be the length of a side of one of the hexagons. We concentrate on the case that there are two levels of interference.Requirement A: There are several constraints on frequency assignments. First, no two transmitters within distance of each other can be given the same channel. Second, due to spectral spreading, transmitters within distance 2s of each other must not be given the same or adjacent channels: Their channels must differ by at least 2. Under these constraints, what can we say about the span in,Requirement B: Repeat Requirement A, assuming the grid in the example spreads arbitrarily far in all directions.Requirement C: Repeat Requirements A and B, except assume now more generally that channels for transmitters within distance differ by at least some given integer k, while those at distance at most must still differ by at least one. What can we say about the span and about efficient strategies for designing assignments, as a function of k?Requirement D: Consider generalizations of the problem, such as several levels of interference or irregular transmitter placements. What other factors may be important to consider?Requirement E: Write an article (no more than 2 pages) for the local newspaper explaining your findings.2001 Mathematical Contest in Modeling (MCM)Problem A: Choosing a Bicycle WheelCyclists have different types of wheels they can use on their bicycles. The two basic typesof wheels are those constructed using wire spokes and those constructed of a solid disk (see Figure 1) The spoked wheels are lighter, but the solid wheels are more aerodynamic.A solid wheel is never used on the front for a road race but can be used on the rear of the bike.Professional cyclists look at a racecourse and make an educated guess as to what kind of wheels should be used. The decision is based on the number and steepness of the hills, the weather, wind speed, the competition,and other considerations. The director sportif of your favorite team would like to have a better system in place and has asked your team for information to help determine what kind of wheel should be used fora given course.Figure 1: A solid wheel is shown on the left and a spoked wheel is shown on the right. The director sportif needs specific information to help make a decision and has asked your team to accomplish the tasks listed below. For each of the tasks assume that the same spoked wheel will always be used on the front butthere is a choice of wheels for the rear.Task 1. Provide a table iving the wind peed at which the power required for a solid rear wheel is less than for a spoked rear wheel. The table should include the wind speeds for different road grades starting from zero percent to ten percent in one percent increments. (Road grade is defined to be the ratio of the total rise of a hill divided by the length of the road. If the hill is viewed as a triangle, the grade is the sine of the angle at the bottom of the hill.) A rider starts at the bottom of the hill at a speed of 45 kph, and the deceleration of the rider is proportional to the road grade.A rider will lose about 8 kph for a five percent grade over 100 meters.Task 2. Provide an example of how the table could be used for a specific time trial courseTask 3. Determine if the table is an adequate means for deciding on the wheel configuration and offer other suggestions as to how to make this decision.Problem B: Escaping a Hurricane's Wrath (An Ill Wind...)Evacuating the coast of South Carolina ahead of the predicted landfallof Hurricane Floydin 1999 led to a monumental traffic jam. Traffic slowed to a standstill on Interstate I-26, which is the principal route going inland from Charleston to the relatively safe haven of Columbia in the center of the state. What is normally an easy two-hour drive took up to 18 hours to complete. Many cars simply ran out of gas along the way.Fortunately, Floyd turned north and spared the state this time, but the public outcry is forcing state officials to find ways to avoid a repeat of this traffic nightmare.The principal proposal put forth to deal with this problem is the reversalof traffic onI-26, so that both sides, including the coastal-bound lanes,have traffic headed inland from Charleston to Columbia. Plans to carry this out have been prepared (and posted on the Web)by the South Carolina Emergency Preparedness Division. Traffic reversal on principal roads leading inland from Myrtle Beach and Hilton Head is also planned.A simplified map of South Carolina is shown. Charleston has approximately 500,000 people, Myrtle Beach has about 200,000 people, and another 250,000 people are spread out along the rest of the coastal strip. (More accurate data,if sought, are widely available.)The interstates have two lanes of traffic in each direction except in the metropolitan areas where they have three. Columbia, another metro area of around 500,000 people, does not have sufficient hotel space to accommodate the evacuees (including some coming from farther northby other routes), so some traffic continues outbound on I-26 towards Spartanburg; on I-77 north to Charlotte; and on I-20 east to Atlanta. In 1999, traffic leaving Columbia going northwest was moving only very slowly. Construct a model for the problem to investigate what strategies may reduce the congestion observed in 1999. Here are the questions that need to be addressed:1.Under what conditions does the plan for turning the two coastal-bound lanes of I-26 into two lanes of Columbia-bound traffic, essentially turning the entire I-26 into one-way traffic, significantly improve evacuation traffic flow?2.In 1999, the simultaneous evacuation of the state's entire coastal region was ordered. Would the evacuation traffic flow improve under an alternative strategy that staggers the evacuation, perhaps county-by-county over some time period consistent with the pattern of how hurricanes affect the coast?3.Several smaller highways besides I-26 extend inland from the coast. Under what conditions would it improve evacuation flow to turn around traffic on these?4.What effect would it have on evacuation flow to establish more temporary shelters in Columbia, to reduce the traffic leaving Columbia?5.In 1999, many families leaving the coast brought along their boats, campers, and motor homes. Many drove all of their cars. Under what conditions should there be restrictionson vehicle types or numbers of vehicles brought in order to guarantee timely evacuation? 6.It has been suggested that in 1999 some of the coastal residents of Georgia and Florida, who were fleeing the earlier predicted landfalls of Hurricane Floyd to the south, came upI-95 and compounded the traffic problems. How big an impact can they have on the evacuation traffic flow? Clearly identify what measures of performance are used to compare strategies. Required: Prepare a short newspaper article, not to exceed two pages,explaining the results and conclusions of your study to the public.问题 A: 选择自行车车轮骑自行车的人有几种不同类型的车轮可以用在他们的自行车上。
2012年美国数学邀请赛(AIMEⅡ)第二试试题(中文版)

2012年美国数学邀请赛(AIME Ⅱ)第二试试题1.求方程20122012m n +=的正整数解(),m n 的组数.2.设123,,a a a ⋅⋅⋅与123,,,b b b ⋅⋅⋅是拥有相同公比的两个等比数列,且11151127,99,,a b a b ===求9a .3.一个大学的数学科学学院有数学、统计学和计算机科学三个专业,每个专业有两个男教授和两个女教授. 现在每个专业选两名教授组成一个六人的委员会,并且委员会中男女各三人,求组成这个委员会所有可能的不同方法数.4.设,,A B C 三人骑单车的速度分别为8.6/,6.2/,5/m s m s m s .他们同时在一个长方形区域的东北角开始骑车(长方形区域两边长分别为南北向与东西向,且东西向的边比南北向的边要长).A 先向西沿着区域的边骑车;B 先向南沿着区域的边骑车;C 先沿着直线向区域南边上一点D 骑去.,,A B C 同时第一次到达D 点,且区域的长、宽、D 点到区域东南角距离三者的比为::p q r ,,,p q r 为正整数,且(),1p q =,求p q r ++的值.5.在右图中,外边的正方形S 边长为40,里面边长为15的正方形'S 的边与S的边都平行,且中心重合.从S 的每一边中点向两个最接近的'S 的顶点连线,得到一个星状的图像内切于S .裁出这个星状图形,以'S 为底面折成一个四棱锥,求这个四棱锥的体积.6.设复数,z a bi =+0,5b z >=,且满足点3(12)i z +到点5z 的距离最大,令4z c di =+,求c d +的值.7.设S 是在二进制中刚好有8个“1”的正整数从小到大排列而成的序列,N 是S 中的第1000个数.求N 被1000除的余数.8.设,z w 是复数,满足20512410i z i w i w i z⎧+=+⎪⎪⎨⎪+=-+⎪⎩.求2zw 的最小可能值.9.设,x y R ∈且满足sin cos 1sin 2cos 23,,sin cos 2sin 2cos 2x x x x p y y y y q==+=,,p q N +∈且(,)1p q =,求p q +的值. 10.设,1000n N n +∈< ,求所有满足存在x R +∈,使得[]n x x =的n 的个数.11.令123()331f x x =-+,当2n ≥时,11()(())n n f x f f x -=.已知x R ∈满足1001()3f x x =-,且m x n =(,m n 为互质的正整数),求m n +的值.12.对于一个正整数p ,定义正整数n 为“p -安全”:当且仅当n 与任意p 的整数倍的差的绝对值大于2.例如,满足“10-安全”的正整数集合为{}3,4,5,6,7,13,14,15,16,17,23,⋅⋅⋅.求同时满足“7-安全”,“11-安全”,“13-安全”不超过10000的正整数个数.13.正ABC ∆,11122324,,,AD E AD E AD E AD E ∆∆∆∆是与ABC ∆全等的不同的三角形,12BD BD ==()421k k CE =∑的值.14.在一个9人的集合中,每个人刚好与其它两人握手.求不同的握手方案的安排数(当一个人在一个安排中与另外一个人握手但在另一个安排中不握手,则称为两种不同的安排). 15.ABC ∆内接于圆ω,且5,7,3A B B C A C ===,A ∠的内角平分线交边BC 于点D ,交圆ω于另一点E .设以DE 为直径的圆为γ,两圆相交于,E F 两点.若2m AF n=(,m n 为互质的正整数),求m n +的值.。
历届美国数学建模竞赛赛题

? 对正常组织或器官的整个体积照射要剂量总和最小
对指定的正常组织点的剂量要限制在忍耐剂量以下?
使关键体积所需的最大剂量达到最小?
在Gamma单元治疗方案中,有以下限制:
禁止“shot”伸展到目标以外?
禁止“shot”交迭(避免热点)?
? 用有效的剂量覆盖尽可能多的目标体积,但至少90%目标体积要被“shot”覆盖
你的任务是设计一个算法,随着风力条件的变化,运用风速计给出的数据来调整由喷泉射出的水流。
AMCM2002问题-B航空公司超员订票
你备好行装准备去旅行,访问New York城的一位挚友。在检票处登记之后,航空公司职员告诉说,你的航班已经超员订票。乘客们应当马上登记以便确定他们是否还有一个座位。
任务1. 提供一个给出风速的表格,在这种速度下实体后轮所需要的体能少于辐条后轮。这个表格应当包括相应于从百分之零到百分之十增量为百分之一的不同公路陡度的风速。(公路陡度定义为一座山丘的总升高除以公路长度。如果把山丘看作一个三角形,它的陡度是指山脚处倾角的正弦。)一位骑手以初始速度45kph从山脚出发,他的减速度与公路陡度成正比。对于百分之五的陡度,骑上100米车速要下降8kph左右。
2005A.水灾计划
南卡罗来纳州中部的磨累河是由北部的一个巨大水坝形成的,这是在1930年为了发电而修建的,模拟一起洪水淹没下游的事件,这起事件是由于一次灾难性的地震损毁了水坝造成的。
两个问题:
Rawls Creek是水坝下游流入Saluda河的一条终年流动的河流,则当水坝损毁后在Rawls Creek将会出现多大的洪流,洪水的波及面将有多大?
AMCM2002问题-A风和喷水池
在一个楼群环绕的宽阔的露天广场上,装饰喷泉把水喷向高空。刮风的日子,风把水花从喷泉吹向过路行人。喷泉射出的水流受到一个与风速计(用于测量风的速度和方向)相连的机械装置控制,前者安装在一幢邻近楼房的顶上。这个控制的实际目标,是要为行人在赏心悦目的景象和淋水浸湿之间提供可以接受的平衡:风刮得越猛,水量和喷射高度就越低,从而较少的水花落在水池范围以外。
2024数学建模美赛a题

2024数学建模美赛a题全文共四篇示例,供读者参考第一篇示例:2024年数学建模美赛A题的题目是一个挑战性的问题,需要参赛选手在短时间内进行思考和分析,然后给出一个合理的解决方案。
这个题目涉及到了数学建模、数据分析和计算机编程等多个领域,需要选手具备较强的逻辑思维能力和解决问题的能力。
题目要求参赛选手利用给定的数据集,对某个特定问题进行建模和分析,然后给出解决方案。
选手需要根据现有的数据集进行数据清洗和预处理,然后利用统计学和数学建模的方法对数据进行分析和建模,最终提供一个可行的解决方案。
在解题过程中,选手需要运用各种数学工具和编程语言来处理数据和进行计算,例如Python、R语言等。
选手还需要结合实际问题的背景知识和专业知识,对数据进行合理的解释和分析。
在解题过程中,选手需要注意数据的质量和可靠性,同时还需要对模型的准确性和稳定性进行评估。
最终,选手需要给出一个详细的报告,说明解决问题的方法和步骤,以及给出相关的结论和建议。
参加数学建模比赛可以锻炼选手的团队合作能力和解决问题的能力,同时也能够提高选手的数学建模和数据分析能力。
希望参赛选手在比赛中能够充分发挥自己的潜力,充分展现出自己的优势和才华,最终取得优异的成绩。
【字数不足,正在努力补充中……】第二篇示例:2024数学建模美赛a题分析数学建模是一门涵盖数学、计算机科学和工程等多学科知识的综合性学科,应用广泛,涉及领域广泛。
每年举办的数学建模比赛更是为广大热爱数学和挑战智力的学生提供了一个展示自己才华的舞台。
今天我们就来分析一下2024年数学建模美赛的a题。
让我们来看一下2024年数学建模美赛a题的具体问题描述:根据指定信息,设计出最佳的实体投资组合。
实体投资组合包括个人、公司、政府、银行等单位所投资的资金和资产,投资的目的是为了获得更高的回报率。
在实际投资中,投资者需要根据市场行情、经济形势等因素来选择不同的投资产品,以实现最大化的利润。
我们需要通过收集数据来分析市场行情和经济形势,以确定合适的投资产品。
2000-2013美国数学建模竞赛(MCM、ICM)历年试题汇总(1)

目录2000 年美国大学生数学建模竞赛MCM、ICM 试题 (3)2000 MCM A: Air Traffic Control (3)2000 MCM B: Radio Channel Assignments (3)2000 ICM: Elephants: When is Enough, Enough? (5)2001 年美国大学生数学建模竞赛MCM、ICM 试题 (7)2001 MCM A: Choosing a Bicycle Wheel (7)2001 MCM B: Escaping a Hurricane's Wrath (An Ill Wind...). (8)2001 ICM: Our Waterways - An Uncertain Future (10)2002 年美国大学生数学建模竞赛MCM、ICM 试题 (14)2002 MCM A: Wind and Waterspray (14)2002 MCM B: Airline Overbooking (14)2002 ICM: Scrub Lizards (15)2003 年美国大学生数学建模竞赛MCM、ICM 试题 (19)2003 MCM A: The Stunt Person (19)2003 MCM B: Gamma Knife Treatment Planning (19)2003 ICM: Aviation Baggage Screening Strategies: To Screen or Not to Screen, that is the Question (20)2004 年美国大学生数学建模竞赛MCM、ICM 试题 (24)2004 MCM A: Are Fingerprints Unique? (24)2004 MCM B: A Faster QuickPass System (24)2004 ICM: To Be Secure or Not to Be? (24)2005 年美国大学生数学建模竞赛MCM、ICM 试题 (25)2005 MCM A: Flood Planning (25)2005 MCM B: Tollbooths (25)2005 ICM: Nonrenewable Resources (25)2006 年美国大学生数学建模竞赛MCM、ICM 试题 (27)2006 MCM A: Positioning and Moving Sprinkler Systems for Irrigation (27)2006 MCM B: Wheel Chair Access at Airports (27)2006 ICM: Trade-offs in the fight against HIV/AIDS (28)2007 年美国大学生数学建模竞赛MCM、ICM 试题 (32)2007 MCM A: Gerrymandering (32)2007 MCM B: The Airplane Seating Problem (32)2007 ICM: Organ Transplant: The Kidney Exchange Problem (33)2008 年美国大学生数学建模竞赛MCM、ICM 试题 (38)2008 MCM A: Take a Bath (38)2008 MCM B: Creating Sudoku Puzzles (38)2008 ICM: Finding the Good in Health Care Systems (38)2009 年美国大学生数学建模竞赛MCM、ICM 试题 (40)2009 MCM A: Designing a Traffic Circle (40)2009 MCM B: Energy and the Cell Phone (40)2009 ICM: Creating Food Systems: Re-Balancing Human-Influenced Ecosystems41 2010年美国大学生数学建模竞赛 MCM、ICM 试题 (42)2010 MCM A: The Sweet Spot (42)2010 MCM B: Criminology (43)2010 ICM: The Great Pacific Ocean Garbage Patch (44)2011年美国大学生数学建模竞赛 MCM、ICM 试题 (45)2011 MCM A: Snowboard Course (45)2011 MCM B: Repeater Coordination (45)2011 ICM: Environmentally and Economically Sound (46)2012年美国大学生数学建模竞赛 MCM、ICM 试题 (48)2012 MCM A: The Leaves of a Tree (48)2012 MCM B: Camping along the Big Long River (50)2012 ICM: Modeling for Crime Busting (51)2013年美国大学生数学建模竞赛 MCM、ICM 试题 (59)2013 MCM A: The Ultimate Brownie Pan (59)2013 MCM B: Water, Water, Everywhere (61)2013 ICM: NetworkModeling of Earth's Health (62)2000 年美国大学生数学建模竞赛MCM、ICM 试题2000 MCM A: Air Traffic ControlTo improve safety and reduce air traffic controller workload, the Federal Aviation Agency (FAA) is considering adding software to the air traffic control system that would automatically detect potential aircraft flight path conflicts and alert the controller. To that end, an analysit at the FAA has posed the following problems.Requirement A: Given two airplanes flying in space, when should the air traffic controller consider the objects to be too close and to require intervention? Requirement B: And airspace sector is the section of three-dimensional airspace that one air traffic controller controls. Given any airspace sector, how do we measure how complex it is from an air traffic workload perspective? To what extent is complexity determined by the number of aircraft simultaneously passing through that sector1.at any one instant?2.during any given interval of time?3.during a particular time of day?How does the number of potential conflicts arising during those periods affect complexity? Does the presence of additional software tools to automatically predict conflicts and alert the controller reduce or add to this complexity? In addition to the guidelines for your report, write a summary (no more than two pages) that the FAA analyst can present to Jane Garvey, the FAA Administrator, to defend your conclusions.2000 MCM B: Radio Channel AssignmentsWe seek to model the assignment of radio channels to a symmetric network of transmitter locations over a large planar area, so as to avoid interference. One basic approach is to partition the region into regular hexagons in a grix (honeycomb-style), as shown in Figure 1, where a transmitter is located at the center of each hexagon.An interval of the frequency spectrum is to be alloted for transmitter frequencies. The interval will be divided into regularly spaced channels, which we represent by integers 1,2,3, … . Each transmitter wil be assigned one positive integer channel. The same channel can be used at many locations, provided that interference from nearby transmitters is avoided.Our goal is to minimize the width of the interval in the frequency spectrum that is needed to assugn channels subject to some constraints. This is achieved with the concept of a span. The span is the minimum, over all assignments satisfying the constraints, of the largest channel used at any location. It is not required that every channel smaller than the span be used in an assignment that attains the span.Let s be the length of a side of one of the hexagons. We concentrate on the case that there are two levels of interference.Requirement A: There are several contrainsts on the frequency assignments. First, no two transmitters within distance 4s of each other can be given the same channel. Second, due to spectral spreading, transmitters within distance 2s of each other must not be given the same or adjacent channels: Their channels must differ by at least 2. Under these contraints, what can we say about the span in Figure 1?Requirement B: Repeat Requirement A, assuming the grid in the example spreads arbitrarily far in all directions.Requirement C: Repeat Requirements A and B, except assume now more generally that channels for transmitters within distance 2s differ by at least some given integer k, while those at distance at most 4s must still differ by at least one. What cna we say about the span and about efficient strategies for designing assignments, as a function of k?Requirement D: Consider generalizations of the problem, such as several levels of interference or irregular transmitter placements. What other factors may be important to consider?Requirement E: Write an article (no more than 2 pages) for the local newspaper explaining your findings.2000 ICM: Elephants: When is Enough, Enough?“Ultimately, if a habitat is undesirably changed by elephants, then their removal should be considered -even by culling.”National Geographic (Earth Almanac) –December 1999 A large National Park in South Africa contains approximately 11,000 elephants. Management policy requires a healthy environment that can maintain a stable herf of 11,000 elephants. Each year park rangers count the elephant population. During the past 20 years whole herds have been removed to keep the population as close to 11,000 as possible. The process involved shooting (for the most part) and occasionally relocating approximately 600 to 800 elephants per year.Recently, there has been a public outcry against the shooting of these elephants. In addition, it is no longer feasible to relocate even a small population of elephants each year. A contraceptive dart, however, has been developed that can prevent a mature elephant cow from conceiving for a period of two years.Here is some information about eh elephants in the Park:∙There is very little emigration of immigration of elephants.∙The gender ratio is very close to 1:1 and control measures have endeavored to maintain parity.∙The gender ratio of newborn calves is also about 1:1. Twins are bornaverage, a calf every 3.5 years until they reach an age of about 60.Gestation is approximately 22 months.∙The contraceptive dart causes an elephant cow to come into oestrus every month (but not conceiving). Elephants usually have courtship only once in 3.5 years, so the monthly cycle can cause additional stress.∙ A cow can be darted every year without additional detrimental effects. A mature elephant cow will not be able to conceive for 2 years after thelast darting.∙Between 70% and 80% of newborn calves survive to age 1 year.Thereafter, the survival rate is uniform across all ages and is very high(over 95%), until about age 60; it is a good assumption that elephantsdie before reading age 70.There is no hunting and negligible poaching in the Park.The park management has a rough data file of the approximate ages and2 years. This data is available on website: icm2000data.xls. Unfortunately no data is available for the elephants that have been shot or remain in the Park.Your overall task is to develop and use models to investigate how the contraceptive dart might be used for population control. Specifically:Task 1: Develop and use a model to speculate about the likely survival rate for elephants aged 2 to 60. Also speculate about the current age structure of the elephant population.Task 2: Estimate how many cows would need to be darted each year to keep the population fixed at approximately 11,000 elephants. Show how the uncertainty in the data at your disposal affects your estimate. Comment on any changes in the age structure of the population and how this might affect tourists. (You may want to look ahead about 30-60 years.)Task 3: If it were feasible to relocate between 50 and 300 elephants per year, how would this reduce the number of elephants to be darted? Comment on the trade-off between darting and relocation.large number of elephants (due to disease or uncontrolled poaching), even if darting stopped immediately, the ability of the population to grow again would be seriously impeded. Investigate and respond to this concer.Task 5: The management in the Park is skeptical about modeling. In particular, they argue that a lack of complete data makes a mockery of any attempt to use models to guide their decision. In addition to your technical report, include a carefully crafted report (3-page maximum) written explicitly for the park management that responds to their concerns and provides advice. Also suggest ways to increase the park managers confidence in your model and your conclusions.Task 6: If your model works, other elephant parks in Africa would be interested in using it. Prepare a darting plan for parks of various sizes (300-25,000 elephants), with slightly different survival rates and transportation possibilities.2001 年美国大学生数学建模竞赛MCM、ICM 试题2001 MCM A: Choosing a Bicycle WheelCyclists have different types of wheels they can use on their bicycles. The two basic types of wheels are those constructed using wire spokes and those constructed of a solid disk (see Figure 1) The spoked wheels are lighter, but the solid wheels are more aerodynamic. A solid wheel is never used on the front for a road race but can be used on the rear of the bike.Professional cyclists look at a racecourse and make an educated guess as to what kind of wheels should be used. The decision is based on the number and steepness of the hills, the weather, wind speed, the competition, and other considerations. The director sportif of your favorite team would like to have a better system in place and has asked your team for information to help determine what kind of wheel should be used for a given course.Figure 1: A solid wheel is shown on the left and a spoked wheel is shown on the right.The director sportif needs specific information to help make a decision and has asked your team to accomplish the tasks listed below. For each of the tasks assume that the same spoked wheel will always be used on the front but there is a choice of wheels for the rear.Task 1. Provide a table giving the wind speed at which the power required for a solid rear wheel is less than for a spoked rear wheel. The table should include the wind speeds for different road grades startingfrom zero percent to ten percent in one percent increments. (Roadgrade is defined to be the ratio of the total rise of a hill divided by thelength of the road. If the hill is viewed as a triangle, the grade is the sine of the angle at the bottom of the hill.) A rider starts at the bottom of the hill at a speed of 45 kph, and the deceleration of the rider is proportionalto the road grade. A rider will lose about 8 kph for a five percent grade over 100 meters.∙Task 2. Provide an example of how the table could be used for a specific time trial course.∙Task 3. Determine if the table is an adequate means for deciding on the wheel configuration and offer other suggestions as to how to make this decision.2001 MCM B: Escaping a Hurricane's Wrath (An Ill Wind...)Evacuating the coast of South Carolina ahead of the predicted landfall of Hurricane Floyd in 1999 led to a monumental traffic jam. Traffic slowed to a standstill on Interstate I-26, which is the principal route going inland from Charleston to the relatively safe haven of Columbia in the center of the state. What is normally an easy two-hour drive took up to 18 hours to complete. Many cars simply ran out of gas along the way. Fortunately, Floyd turned north and spared the state this time, but the public outcry is forcing state officials to find ways to avoid a repeat of this traffic nightmare.The principal proposal put forth to deal with this problem is the reversal of traffic on I-26, so that both sides, including the coastal-bound lanes, have traffic headed inland from Charleston to Columbia. Plans to carry this out have been prepared (and posted on the Web) by the South Carolina Emergency Preparedness Division. Traffic reversal on principal roads leading inland from Myrtle Beach and Hilton Head is also planned.A simplified map of South Carolina is shown. Charleston has approximately 500,000 people, Myrtle Beach has about 200,000 people, and another 250,000 people are spread out along the rest of the coastal strip. (More accurate data, if sought, are widely available.)The interstates have two lanes of traffic in each direction except in the metropolitan areas where they have three. Columbia, another metro area of around 500,000 people, does not have sufficient hotel space to accommodate the evacuees (including some coming from farther north by other routes), so some traffic continues outbound on I-26 towards Spartanburg; on I-77 north to Charlotte; and on I-20 east to Atlanta. In 1999, traffic leaving Columbia going northwest was moving only very slowly. Construct a model for the problem to investigate what strategies may reduce the congestion observed in 1999. Here are the questions that need to be addressed:1.Under what conditions does the plan for turning the two coastal-boundlanes of I-26 into two lanes of Columbia-bound traffic, essentiallyturning the entire I-26 into one-way traffic, significantly improveevacuation traffic flow?2.In 1999, the simultaneous evacuation of the state's entire coastal regionwas ordered. Would the evacuation traffic flow improve under analternative strategy that staggers the evacuation, perhapscounty-by-county over some time period consistent with the pattern of how hurricanes affect the coast?3.Several smaller highways besides I-26 extend inland from the coast.Under what conditions would it improve evacuation flow to turn around traffic on these?4.What effect would it have on evacuation flow to establish moretemporary shelters in Columbia, to reduce the traffic leaving Columbia?5.In 1999, many families leaving the coast brought along their boats,campers, and motor homes. Many drove all of their cars. Under whatconditions should there be restrictions on vehicle types or numbers ofvehicles brought in order to guarantee timely evacuation?6.It has been suggested that in 1999 some of the coastal residents ofGeorgia and Florida, who were fleeing the earlier predicted landfalls ofHurricane Floyd to the south, came up I-95 and compounded the traffic problems. How big an impact can they have on the evacuation trafficflow? Clearly identify what measures of performance are used tocompare strategies. Required: Prepare a short newspaper article, not to exceed two pages, explaining the results and conclusions of your study to the public.Clearly identify what measures of performance are used to compare strategies. Required: Prepare a short newspaper article, not to exceed two pages, explaining the results and conclusions of your study to the public.2001 ICM: Our Waterways - An Uncertain FutureZebra mussels, Dreissena polymorpha, are small, fingernail-sized, freshwater mollusks unintentionally introduced to North America via ballast water from a transoceanic vessel. Since their introduction in the mid 1980s, they have spread through all of the Great Lakes and to an increasing number of inland waterways in the United States and Canada. Zebra mussels colonize on various surfaces,such as docks, boat hulls, commercial fishing nets, water intake pipes and valves, native mollusks and other zebra mussels. Their only known predators, some diving ducks, freshwater drum, carp, and sturgeon, are not numerous enough to have a significant effect on them. Zebra mussels have significantly impacted the Great Lakes ecosystem and economy. Many communities are trying to control or eliminate these aquatic pests. SOURCE: Great Lakes Sea Grant Network /.Researchers are attempting to identify the environmental variables related to the zebra mussel infestation in North American waterways. The relevant factors that may limit or prevent the spread of the zebra mussel are uncertain. You will have access to some reference data to include listings of several chemicals and substances in the water system that may affect the spread of the zebra mussel throughout waterways. Additionally, you can assume individual zebra mussels grow at a rate of 15 millimeters per year with a life span between 4 - 6 years. The typical mussel can filter 1 liter of water each day.Requirement A: Discuss environmental factors that could influence the spread of zebra mussels.Requirement B: Utilizing the chemical data provided at:ap/undergraduate/contests/icm/imagesdata/LakeAChem1.xls, and the mussel population data provided at:ap/undergraduate/contests/icm/imagesdata/LakeAPopulation 1.xls model the population growth of zebra mussels in Lake A. Be sure to review the Information about the collection of the zebra mussel data. Requirement C: Utilizing additional data on Lake A from another scientist provided at :ap/undergraduate/contests/icm/imagesdata/LakeAChem2.xls and additional mussel population data provided at:ap/undergraduate/contests/icm/imagesdata/LakeAPopulation 2.xls corroborate the reasonableness of your model from Requirement B. As a result of this additional data, adjust your earlier model. Analyze the performance of your model. Discuss the sensitivity of your model. Requirement D: Utilizing the Chemical data from two lakes (Lake B and Lake C) in the United States provided atap/undergraduate/contests/icm/imagesdata/LakeB.xls and ap/undergraduate/contests/icm/imagesdata/LakeC.xls determine if these lakes are vulnerable to the spread of zebra mussels. Discuss your prediction.Requirement E: The community in the vicinity of Lake B (in requirement D) is considering specific policies for the de-icing of roadways near the lake duringthe winter season. Provide guidance to the local government officials regarding a policy on “de-icing agents.”In your guidance include predictions on the long-term impact of de-icing on the zebra mussel population. Requirement F: It has been recommended by a local community in the United States to introduce round goby fish. Zebra mussels are not often eaten by native fish species so they represent a dead end ecologically. However, round gobies greater than 100 mm feed almost exclusively on zebra mussels. Ironically, because of habitat destruction, the goby is endangered in its native habitat of the Black and Caspian Seas in Russia. In addition to your technical report, include a carefully crafted report (3-page maximum) written explicitly for the local community leaders that responds to their recommendation to introduce the round goby. Also suggest ways to help reduce the growth of the mussel within and among waterways.Information about the collection of the zebra mussel dataThe developmental state of the Zebra mussel is categorized by three stages: veligers (larvae), settling juveniles, and adults. Veligers (microscopic zebra mussel larvae) are free-swimming, suspended in the water for one to three weeks, after which they begin searching for a hard surface to attach to and begin their adult life. Looking for zebra mussel veligers is difficult because they are not easily visible by the naked eye. Settled juvenile zebra mussels can be felt on smooth surfaces like boats and motors. An advanced zebra mussel infestation can cover a surface, even forming thick mats sometimes reaching very high densities. The density of juveniles was determined along the lake using three 15×15 cm settling plates. The top plate remained in the water for the entire sampling season (S - seasonal) to estimate seasonal accumulation. The middle and bottom plates are collected after specific periods (A –alternating ) of time denoted by “Lake Days”in the data files.The settling plates are placed under the microscope and all juveniles on the undersides of the plate are counted and densities are reported as juveniles/m^2.2002 年美国大学生数学建模竞赛MCM、ICM 试题2002 MCM A: Wind and WatersprayAn ornamental fountain in a large open plaza surrounded by buildings squirts water high into the air. On gusty days, the wind blows spray from the fountain onto passersby. The water-flow from the fountain is controlled by a mechanism linked to an anemometer (which measures wind speed and direction) located on top of an adjacent building. The objective of this control is to provide passersby with an acceptable balance between an attractive spectacle and a soaking: The harder the wind blows, the lower the water volume and height to which the water is squirted, hence the less spray falls outside the pool area. Your task is to devise an algorithm which uses data provided by the anemometer to adjust the water-flow from the fountain as the wind conditions change.2002 MCM B: Airline OverbookingYou're all packed and ready to go on a trip to visit your best friend in New York City. After you check in at the ticket counter, the airline clerk announces that your flight has been overbooked. Passengers need to check in immediately to determine if they still have a seat.Historically, airlines know that only a certain percentage of passengers who have made reservations on a particular flight will actually take that flight. Consequently, most airlines overbook-that is, they take more reservations than the capacity of the aircraft. Occasionally, more passengers will want to take a flight than the capacity of the plane leading to one or more passengers being bumped and thus unable to take the flight for which they had reservations. Airlines deal with bumped passengers in various ways. Some are given nothing, some are booked on later flights on other airlines, and some are given some kind of cash or airline ticket incentive.Consider the overbooking issue in light of the current situation: Less flights by airlines from point A to point B Heightened security at and around airports Passengers' fear Loss of billions of dollars in revenue by airlines to dateBuild a mathematical model that examines the effects that different overbooking schemes have on the revenue received by an airline company in order to find an optimal overbooking strategy, i.e., the number of people by which an airline should overbook a particular flight so that the company's revenue is maximized. Insure that your model reflects the issues above, andconsider alternatives for handling “bumped”passengers. Additionally, write a short memorandum to the airline's CEO summarizing your findings and analysis.2002 ICM: Scrub LizardsThe Florida scrub lizard is a small, gray or gray-brown lizard that lives throughout upland sandy areas in the Central and Atlantic coast regions of Florida. The Florida Committee on Rare and Endangered Plants classified the scrub lizard as endangered.You will find a fact sheet on the Florida Scrub Lizard at/undergraduate/contests/mcm/contests/2002/problem s/icm2002data/scrublizard.pdfThe long-term survival of the Florida scrub lizard is dependent upon preservation of the proper spatial configuration and size of scrub habitat patches.Task 1: Discuss factors that may contribute to the loss of appropriate habitat for scrub lizards in Florida. What recommendations would you make to the state of Florida to preserve these habitats and discuss obstacles to the implementation of your recommendations?average fecundity of adult lizards); Sj (the survivorship of juvenile lizards- between birth and the first reproductive season); and Sa (the average adult survivorship).Table 1Summary data for a cohort of scrub lizards captured and followed for 4 consecutive years. Hatchling lizards (age 0) do not produce eggs during the summer they are born. Average clutch size for all other females is proportional to body size according to the function y = 0.21*(SVL)-7.5, where y is the clutch size and SVL is the snout-to-vent length in mm.Year Age Total NumberLivingNumber of LivingFemalesAvg. Female Size(mm)1 0 972 495 30.32 1 180 92 45.83 2 20 11 55.84 3 2 2 56.0Task 3: It has been conjectured that the parameters Fa , Sj , and Sa , are related to the size and amount of open sandy area of a scrub patch. Utilize the data provided in Table 2 to develop functions that estimate Fa, Sj , and Sa for different patches. In addition, develop a function that estimates C, the carrying capacity of scrub lizards for a given patch.Table 2Summary data for 8 scrub patches including vital rate data for scrub lizards. Annual female fecundity (Fa), juvenile survivorship (Sj), and adult survivorship (Sa) are presented for each patch along with patch size and the amount of open sandy habitat.Patch Patch Size (ha) Sandy Habitat (ha) Fa Sj Sa Density (lizards/ha)a 11.31 4.80 5.6 0.12 0.06 58b 35.54 11.31 6.6 0.16 0.10 60c 141.76 51.55 9.5 0.17 0.13 75d 14.65 7.55 4.8 0.15 0.09 55e 63.24 20.12 9.7 0.17 0.11 80f 132.35 54.14 9.9 0.18 0.14 82g 8.46 1.67 5.5 0.11 0.05 40h 278.26 84.32 11.0 0.19 0.15 115Task 4: There are many animal studies that indicate that food, space, shelter, or even reproductive partners may be limited within a habitat patch causing individuals to migrate between patches. There is no conclusive evidence on why scrub lizards migrate. However, about 10 percent of juvenile lizards do migrate between patches and this immigration can influence the size of the population within a patch. Adult lizards apparently do not migrate. Utilizing the data provided in the histogram below estimate the probability of lizards surviving the migration between any two patches i and patch j.Table 3HistogramMigration data for juvenile lizards marked, released, and recaptured up to 6 months later. Surveys for recapture were conducted up to 750m from release sites.Task 5: Develop a model to estimate the overall population size of scrub lizards for the landscape given in Table 3. Also, determine which patches are suitable for occupation by scrub lizards and which patches would not support a viable population.Patch size and amount of open sandy habitat for a landscape of 29 patches located on the Avon Park Air Force Range. See:/undergraduate/contests/icm/2002problem/map.jpg for a map of the landscape.Patch Identification Patch Size (ha) Sandy Habitat (ha)1 13.66 5.382 32.74 11.913 1.39 0.234 2.28 0.765 7.03 3.626 14.47 4.387 2.52 1.998 5.87 2.499 22.27 8.44。
2020年美赛试题

2020年美赛试题全文共四篇示例,供读者参考第一篇示例:2022020年美赛试题是一个国际性的数学建模比赛,是美国大学生数学建模竞赛的简称。
该比赛每年都吸引着全球众多优秀的大学生数学爱好者参与,旨在培养学生的团队合作能力、数学建模能力和解决实际问题的能力。
2020年美赛试题包括了多个实际问题,涉及到各种不同领域的知识和技能。
有关气候变化、交通拥堵、疾病传播等方面的问题,都是参赛选手需要解决的挑战。
参赛选手需要在规定的时间内,对所选题目进行深入分析、建立数学模型、进行模拟计算,并最终给出合理有效的解决方案。
本次比赛的试题设计十分考验参赛选手的综合能力,要求他们具备较强的数学建模能力、编程能力、数据分析能力等。
参赛选手需要充分发挥团队合作精神,共同分工协作,共同完成试题,最终得出科学合理的结论。
除了在数学建模能力上的要求,参赛选手还需要具备良好的逻辑思维能力、创新能力和团队精神。
在解决实际问题的过程中,需要他们不断挑战自我,勇于探索未知领域,寻找新的解决方案。
在本次比赛中,参赛选手将会面临着各种各样的挑战和困难。
他们需要面对未知的实际问题,需要分析复杂的数据,需要精确建立数学模型,需要进行大量的模拟计算。
只有克服了这些困难,才能最终给出可信的解决方案。
2020年美赛试题的设计十分贴近实际生活,涉及到了各种领域的知识,对参赛选手提出了很高的要求。
参赛选手需要在短时间内做出合理的数学建模、给出有效的解决方案,这不仅考验了他们的数学水平,更考验了他们的团队合作能力和解决问题的能力。
通过参与这样的数学建模比赛,不仅可以提高参赛选手的综合素质,更可以锻炼他们的团队合作精神和解决问题的能力。
希望更多的大学生能够参与到类似的比赛中,不断挑战自我,不断提高自己的能力,成为未来社会的栋梁之才。
第二篇示例:2020年美国大学生数学建模竞赛(简称美赛)是一项旨在提倡学生团队合作、数学建模和创新思维的竞赛活动。
该赛事已经成为全球最具影响力的数学建模比赛之一,吸引了来自世界各地的大学生参与。
历年美国数学建模竞赛题目

历年美国数学建模竞赛题目1985 A J 动物群体的常微分方程.pdf1985 A J 动物群体的管理.pdf1985 A O An Effective Method for Harvesting Salmon.pdf1985 A O Grizzly Bears in Yellowstone National Park.pdf1985 A O Population Dynamics of Deer.pdf1985 A O Population Dynamics of The Peruvian Anchovy.pdf1985 B J B题的若干知识.pdf1985 B J 战略物资的存贮管理.rar1985 B O Managing a Cobalt Stockpile.pdf1985 B O The Problem of Managing a Strategic Reserve.pdf1986 A O Contour Interpolation of Random Data.pdf1986 A O Contouring of Hydrographic Data.pdf1986 A O Interpolating a Topographical Map of The Ocean Floor.pdf 1986 A O Spline Analysis of Hydrographic Data.pdf1986 A O 水道测量数据.pdf1986 B J 应急设施位置.pdf1986 B J 应急设施的优化选址问题.pdf1986 B J 应急设施的位置.pdf1987 A J 盐的贮存.pdf1987 A O The Salt Problem—Making a Mountain Out of Molehills.pdf 1988 A J 关于毒品走私船位置问题的数学模型.pdf1988 B J 两辆平板车的装载问题.pdf1988 B J 两辆铁路平板车的装货问题.pdf1988 B O Locating a Drug Runner Miami Vice Style.pdf1989 A J 判别分析和蠓虫分类.pdf1989 A J 蠓的分类.pdf1989 A O Neural-Network Approach to Classification Problems.pdf 1989 B J 飞机起飞的最优次序.pdf1990 A J 扩散问题的偏微分方程模型.pdf1990 A J 精神病用药问题.pdf1990 A J 试题分析.pdf1990 A O Error-Function Diffusion A Dopamine–Fick’s Model.pdf 1990 B J 扫雪问题.pdf1990 B J 扫雪问题的数学模型.pdf1991 A J 估计水箱的水流量.pdf1991 A J 估计水箱的水流量模型.pdf1991 A J 水塔水流量估计.pdf1991 A J 逼近观察数据的一些样条模型.pdf1991 B J 可靠网络中生成树的优化模型.pdf1991 B J 最小Steiner生成树.pdf1991 B J 最小费用斯坦纳树的构造.pdf1991 B O Finding Optimal Steiner Trees.pdf1991 B P 水塔流量估计.rar1992 B J 应急电力修复系统的修复计划.pdf1992 B O Development of an Emergency-Response System.pdf1993 A J 通过数学建模解决混合物转化为有机肥最佳过程问题.pdf1993 A O Coal-Tipple Operations.pdf1993 B J 倒煤台的操作方案.pdf1993 B J 煤车装卸系统的优化操作.PDF1994 A J 房屋隔热经济效益核算.pdf1994 B J 计算机网络的最小接通时间.pdf1994 B J 计算机网络的最短传输时间.pdf1994 B M 信息传递最少用时的数学模型.pdf1994 B O Talking Fast Finding the Makespan of a Communications Network.pdf1995 A C Author’s Commentary The Outstanding Helix Intersections Papers.pdf1995 A JC 单个的螺旋线.pdf1995 A O A Specialized Root-Finding Method for Rapidly Determining the Intersections of a Plane and a Helix.pdf1995 A O Planes and Helices.pdf1995 A O The Single Helix.pdf1995 B H 学院教师的付薪方案.pdf1995 B L 工资调整系统.pdf1995 B L 教员工资分配调整方案.pdf1995 B O How to Keep Your Job as Provost.pdf1995 B O Long-Term and Transient Pay Scale for College Faculty.pdf1995 B O Paying Professors What They’re Worth.pdf1995 B O The World’s Most Complicated Payroll.pdf1996 A J The Outstanding Helix Intersections Papers.pdf1996 A M 利用环境噪声场探测无自噪声潜艇.pdf1996 A O Detection of a Silent Submarine.pdf1996 A O Gone Fishin.pdf1996 A O How to Locate a Submarine.pdf1996 A O Imaging Underwater Objects with Ambient Noise.pdf1996 A P The Outstanding Submarine Location Papers.pdf1996 B J The Outstanding Contest Judging Papers A.pdf1996 B J The Outstanding Contest Judging Papers B.pdf1996 B JC 竞赛择优问题.pdf1996 B JC 竞赛评卷仿真.pdf1996 B M 快速评卷的方案设计.pdf1996 B M 竞赛评判问题.pdf1996 B O Judging a Mathematics Contest.pdf1996 B O Modeling Better Modeling Judges.pdf1996 B O Select the Winners Fast.pdf1996 B O The Inconsistent Judge.pdf1996 B O The Paper Selection Scheme Simulation Analysis.pdf1997 A H 恐龙的追逐捕食模型.pdf1997 A J The Outstanding Velociraptor Papers.pdf1997 A O A Three-Phase Model for Predator–Prey Analysis.pdf1997 A O Lunch on the Run.pdf1997 A O Modeling Optimal Predator and Prey Strategies.pdf1997 A O Pursuit–Evasion Games in the Late Cretaceous.pdf1997 A O The Geometry and the Game Theory of Chases.pdf1997 B J The Outstanding Discussion Groups Papers.pdf1997 B M The Well-Mixed Assignments.pdf1997 B M 有效讨论的最优混合解.pdf1997 B O A Greedy Algorithm for Solving Meeting Mixing Problems.pdf1997 B O An Assignment Model for Fruitful Discussions.pdf1997 B O Meetings Bloody Meetings.pdf1997 B O Using Simulated Annealing.pdf1997 B P The Outstanding Discussion Groups Papers.pdf1998 A J Judge's Commentary The Outstanding Scanner Papers.pdf1998 A M A Quick Algorithm for MRI Problem.pdf1998 A M Image Reconstruction in MRI.pdf1998 A O A Method for Taking Cross Sections of Three-Dimensional Gridded Data.pdf1998 A O A Model for Arbitrary Plane Imaging, or the Brain in Pain Falls Mainly on the Plane.pdf1998 A O A Tricubic Interpolation Algorithm for MRI Image Cross Sections.pdf1998 A O MRI Slice Picturing.pdf1998 A P Proposer's Commentary The Outstanding Scanner Papers.pdf1998 B H Place Students in Deciles Reasonably.pdf1998 B O A Case for Stricter Grading.pdf1998 B O Alternatives to the Grade Point Average for Ranking Students.pdf1998 B O Grade Infation A Systematic Approach to Fair Achievement Indexing.pdf1998 B O Judge's Commentary The Outstanding Grade Inflation Papers.pdf1998 B P Practitioner's Commentary The Outstanding Grade Inflation Papers.pdf1999 A H The Assessment Metheod of Impact.pdf1999 A O Antarctic Asteroid Effects.pdf1999 A O Asteroid Impact at the South Pole A Model-Based Risk Assessment.pdf1999 A O Not an Armageddon.pdf1999 A O The Sky is Falling.pdf1999 B H How to Calculate the Lawful Capacity in the Constraied Condition.pdf1999 B H How to Calculate the Lawful Capcity in the Constrained Condition .pdf1999 B J Judge's Commentary The Outstanding Lawful Capacity Papers.pdf1999 B O Determining the People Capacity of a Structur.pdf1999 B O Don't Panic.pdf1999 B O Hexagonal Unpacking.pdf1999 B O Room Capacity Analysis Using a Pair of Evacuation Models.pdf1999 B O Standing Room Only.pdf2000 A J Judge's Commentary The Outstanding Air Traffic Control Papers.pdf2000 A M Channel Assignment Strategies for Cellular Phone Systems.pdf2000 A M The Model For Measuring Complexity of Air Traffic Control Predicting and Adjusting Path Conflicts.pdf2000 A O Air Traffic Control.pdf2000 A O The Iron Laws of Air Traffic Control.pdf2000 A O The Safe Distance Between Airplanes and the Complexity of an Airspace Sector.pdf 2000 A O You Make the Call Feasibility of Computerized Aircraft Control.pdf2000 B J Author Judge's Commentary The Outstanding Channel Assignment Papers.pdf2000 B O A Channel Assignment Model The Span Without a Face.pdf2000 B O Groovin'with the Big Band(width).pdf2000 B O Radio Channel Assignments.pdf2000 B O Utilize the Limited Frequency Resources Efficiently.pdf2000 B O We're Sorry,You're Outside the Coverage Area.pdf2000 C J Judge's Commentary The Outstanding Elephant Population Papers.pdf2000 C O A Computational Solution for Elephant Overpopulation.pdf2000 C O EigenElephants When Is Enough,Enough.pdf2000 C O Elephant Population A Linear Model.pdf2001 A J Author-Judge's Commentary The Outstanding Bicycle Wheel Papers.pdf2001 A O A Systematic Technique for Optimal Bicycle Wheel Selection.pdf2001 A O Can’t Quite Put Our Finger On It.pdf2001 A O Selection of a Bicycle Wheel Type.pdf2001 A O Spokes or Discs.pdf2001 A P Choosing a Bicycle Wheel.zip2001 B M Strategies for Escaping a Hurricane's Wrath.zip2001 B H Hurricane Evacuation .pdf2001 B J Judge's Commentary The Outstanding Hurricane Evacuation Papers.pdf2001 B M What If Another Floyd Escaping a Hurricane's Wrath.pdf2001 B M When a Hard Wind Blows the Traffic Slows.pdf2001 B O Jammin'with Floyd A Traffic Flow Analysis of South Carolina Hurricane Evacuation.pdf2001 B O Please Move Quickly and Quietly to the Nearest Freeway.pdf2001 B O Project H.E.R.O. Hurricane Evacuation Route Optimization.pdf2001 B O The Crowd Before the Storm.pdf2001 B O Traffic Flow Models and the Evacuation Problempdf.pdf2001 B P 飓风来临的最佳疏散方案.rar2001 C J Judge’s Commentary The Outstanding Zebra Mussel Papers.pdf2001 C O A Multiple Regression Model to Predict Zebra Mussel Population Growth.pdf 2001 C O Identifying Potential Zebra Mussel Colonization.pdf2001 C O Waging War Against the Zebra Mussel.pdf2002 A J Judge’s Commentary The Outstanding Wind and Waterspray Papers.pdf2002 A M Blowin'in the Wind.pdf2002 A M Fountain Spray as a Particle Model.pdf2002 A M Woner Control Beautiful Foutain.rar2002 A O A Foul Weather Fountain.pdf2002 A O Simulating a Fountain.pdf2002 A O The Fountain That Math Built.pdf2002 A O Wind and Waterspray.pdf2002 B H How much to overbook this flight.zip2002 B J Judge’s Commentary The Outstanding Airline Overbooking Papers.pdf2002 B M Whole.rar2002 B O ACE is High.pdf2002 B O Overbooking on Airlines.pdf2002 B O Probabilistically Optimized Airline Overbooking Strategies.pdf2002 B O The Airline Overbooking Problem.pdf2002 B O Things That Go Bump in the Flight.pdf2002 C M If we Scrub our land too much we may lose the LIZARDs.rar2002 C M Life Model of Florida Scrub Lizard.rar2002 C O Cleaning Up the Scrub Saving the Florida Scrub Lizard.pdf2002 C O Where's the Scrub Aye,There's the Rub.pdf2003 A H Shaken, not Stirred.pdf2003 A M The Stunt Person.rar2003 A O Cardboard Comfortable When it comes to Crashing.pdf2003 A O Safe Landings.pdf2003 A O Thinking Outside the Box and Over the Elephant.pdf2003 A O You Too Can Be James Bond.pdf2003 A P Design and Stack the Cardboard Boxes.pdf2003 A P The design of the buffer cardboard boxes.pdf2003 B M Optimization of Stereotactic Radiosurgery Treatment Planning.pdf2003 B O Shelling Tumors with Caution and Wiggles.pdf2003 B P Shelling Procedure and Optimization by Simulated Annealing For Sphere Packing.pdf 2003 C H Aviation Baggage Screening.pdf2003 C H Security Screening at Airport.pdf2003 C H To Screen or Not.pdf2003 C M Aviation Baggage Screening Smart Approach to Screen.rar2003 C P Aviation Baggage Screening.pdf2004 A J Editor's Commentary Fingerprint Identification .pdf2004 A J Judge's Commentary The Outstanding Fingerprints Papers.pdf2004 A J Publisher's Editorial The Good Fight.pdf2004 A M Are Fingerprints Unique.pdf2004 A M Are Fingerprints Unique.rar2004 A M Fe-Fi-Fo Thumb.pdf2004 A O Can't Quite Put Our Finger On It.pdf2004 A O Not Such a Small Whorl After All.pdf2004 A O The Myth of The Myth of Fingerprints.pdf2004 A O Z Rule of Thumb Prints Beat DNA.pdf2004 B H a Faster QuickPass System.pdf2004 B H Magic Regulation Scheme for QuickPass System.pdf2004 B J Editor's Commentary Fingerprint Identification .pdf2004 B J Judges' Commentary The Quick Pass Fusaro Award Paper.pdf2004 B M Virtual Lines in Topoland with these Designs.pdf2004 B O A Myopic Aggregate-Decision Model for Reservation Systems in Amusement Parks.pdf 2004 B O An Adaptive Approach to Virtual Queing.pdf2004 B O Developing Improved Algorithms for QuickPass Systems.pdf2004 B O Developing Improved Algorithms for QuickPass Systems.pdf .pdf2004 B O KalmanQueue An Adaptive Approach to Virtual Queueing.pdf2004 B O Theme-Park Queueing Systems.pdf2004 B O Z Theme Park Simulation with a Nash-Equilibrium-Based Visitor Behavior Model.pdf 2004 B P Make Your Way Faster.pdf2004 B P Optimized QuickPass System.pdf2004 B P You Must Be at Least This Tall to Ride This Paper.pdf2004 C H ?IT Security Keep Hackers and Virus Out.pdf2004 C J Authors' Commentary The Outstanding Information Technology Security Papers.pdf 2004 C J Judge's Commentary The Outstanding Information Technology Security Papers.pdf 2004 C O Catch Thieves Online IT Security.pdf2004 C O Firewalls and Beyond Engineering IT Security.pdf2004 C O It's All About the Bottom Line.pdf2004 C O Making the CIA Work for You.pdf2005 A J Judge's Commentary The Outstanding Flood Planning Papers.pdf2005 A M One Two Step .pdf2005 A O Analysis of Dam Failure in the Saluda River Valley.pdf2005 A O From Lake Murray to a Dam Slurry.pdf2005 A O Through the Breach Modeling Flooding from a Dam Failure in South Carolina.pdf 2005 A O Z Catastrophic Consequences of Earthquake Destruction of the Saluda Dam.pdf 2005 B H For Whom the Booth Tolls .pdf2005 B H Is the Number of Tollbooths Optimal.pdf2005 B H Modeling Toll Plaza Behavior Using.pdf2005 B H Optimal Design of Toll Plaza.pdf2005 B H ?Pass the Plaza more Quickly .pdf2005 B J Judge's Commentary The Outstanding Tollbooths Papers.pdf2005 B M Giving Queueing the Booth.pdf2005 B O A Quasi-Sequential Cellular-Automaton Approach to Traffic Modeling.pdf2005 B O A Single-Car Interaction Model of Traffic for a Highway Toll Plaza.pdf2005 B O For Whom the Booth Tolls.pdf2005 B O Lane Changes and Close Following Troublesome Tollbooth Traffic.pdf2005 B O The Booth Tolls for Thee .pdf2005 B O The Booth Tolls for Thee.pdf2005 B O The Multiple Single Server Queueing System.pdf2005 B O Two Tools for Tollbooth Optimization.pdf2005 C H A Projection of Southeast Alaskan Salmon Populations.pdf2005 C H Between a Rockfish and a Hard Plaice.pdf2005 C H The future of “black gold”.pdf2005 C H When will the oil run out.pdf2005 C J Author's Commentary The Outstanding Exhaustible Resource Papers.pdf2005 C J Editorial Where Else to Publish.pdf2005 C J Judge's Commentary The Outstanding Exhaustible Resource Papers.pdf2005 C O Preventing the Hydrocalypse A Model for Predicting and Managing Worldwide Water Resource.pdf2005 C O The Coming Oil Crisis.pdf2005 C O The Petroleum Armageddon.pdf2006 A H A Simulated Annealing Approach to Irrigation.pdf2006 A H Minimizing Maintenance Cost for Hand-Moved Irrigation Systems.pdf2006 A H On Portable Irrigation Systems .pdf2006 A H Optimal Design of Irrigation Schedule.pdf2006 A J Judge's Commentary The Outstanding Irrigation Problem Papers.pdf2006 A M Optimizing a Handmove Sprinkler System .pdf2006 A M Piping Hot Weather.pdf2006 A M Positioning and Moving Sprinkler Systems for Irrigation.rar2006 A O Fastidious Farmer Algorithms (FFA).pdf2006 A O Fastidious Farmer Algorithms.pdf2006 A O Optimization of Irrigation.pdf2006 A O Z A Schedule for Lazy but Smart Ranchers.pdf2006 A O Z Developing Improved Algorithms for Irrigation Systems.pdf2006 A O Z Optimization of Irrigation.pdf2006 A O Z Sprinkle, Sprinkle, Little Yard.pdf2006 A O Z Sprinkler Systems for Dummies Optimizing a Hand-Moved Sprinkler System.pdf 2006 A P Positioning and Moving Sprinkler Systems for Irrigation .pdf2006 B H The Scheme of the Wheelchair Dispatch and Cost Analysis for Epsilon Airlines.pdf 2006 B H Transfer Suffers NEVER.pdf2006 B J Judges' Commentary The Fusaro Award Wheelchair Paper.pdf2006 B J Special Section on the MCM Judges Commentary The Fusaro Award Wheelchair Paper.pdf 2006 B M Minimal Costs for Serving Disabilities.pdf2006 B M Operational Research for Wheelchair Service Provided by Epsilon Airlines.pdf 2006 B M sly_airport.rar2006 B M When the Model Hits the Runway.pdf2006 B O A Simulation-Driven Approach for a Cost-Efficient Airport Wheelchair Assistance Service.pdf2006 B O Application of Min-Cost Flow to Airline Accessibility Services.pdf2006 B O Z A Simulation-Driven Approach for a Cost-Efficient Airport Wheelchair Assistance Service.pdf2006 B O Z Cost Minimization of Providing a Wheelchair Escort Service.pdf2006 B O Z Minimization of Cost for Transfer Escorts in an Airport Terminal.pdf2006 B O Z Profit Maximizing Allocation of Wheelchairs in a Multi-Concourse Airport.pdf 2006 C H Fighting against AIDS.pdf2006 C H War of the World Fight against AIDS.pdf2006 C J Author's Commentary The Outstanding HIV AIDS Papers.pdf2006 C J HIV The Math..pdf2006 C M AIDS A Global Crisis.pdf2006 C O AIDS Modeling a Global Crisis and Australia.pdf2006 C O Managing the HIV AIDS Pandemic 2006-2055.pdf2006 C O Managing the HIVAIDS Pandemic.pdf2006 C O The Spreading HIV AIDS Problem.pdf2006 C O The United Nations and the Quest for the Holy Grail (of AIDS).pdf2006 C O The United Nations and the Quest for the Holy Grail.pdf2007 A H Genetic Algorithm for Non-Partisan Legislative Districting.pdf2007 A O A Cluster-Theoretic Approach to Political Districting.pdf2007 A O Applying Voronoi Diagrams to the Redistricting Problem.pdf2007 A O When Topologists Are Politicians.pdf2007 B H A Practical Approach to Boarding Deboarding an A380.pdf2007 B H The Airplane Seating Problem 2.pdf2007 B H The Airplane Seating Problem.pdf2007 B H 朱姝(自动化)、朱俊华(自动化)、丁金金(信息与计算科学).pdf2007 B H 陈侠航(数学与应用数学)何军(测控技术与仪器)杨水生(数学与应用数学).pdf 2007 B M A Quadrilateral Approach to Congressional Districting.pdf2007 B M An Analysis of the Kidney Transplant Network.pdf2007 B O Boarding at the Speed of Flight.pdf2007 B O Novel Approaches to Airplane Boarding.pdf2007 C C Organ Transplant The Kidney Exchange Problem.pdf2007 C H Kidney Exchange.pdf2007 C H Organ Transplant The Kidney Exchange Problem 2.pdf2007 C H Organ Transplant The Kidney Exchange Problem.pdf2007 C H 王教团(信息与计算科学)周朝卫(信息与计算科学)周龙飞(信息管理与信息系统).pdf 2007 C J Author's Commentary The Outstanding Kidney Exchange Papers.pdf2007 C J Judges' Commentary The Outstanding Kidney Exchange Papers.pdf2007 C J Write Your Own Contest Entry.pdf2007 C M More Kidney Donors More Lives Can Be Saved.pdf2007 C O Analysis of Kidney Transplant System Using Markov Process Models.pdf2007 C O Optimizing the Effectiveness of Organ Allocation.pdf2007 C P Practitioner's Commentary The Outstanding Kidney Exchange Papers.pdf。
美国数学建模比赛历年试题

2003 MCM ProblemsPROBLEM A: The Stunt PersonAn exciting action scene in a movie is going to be filmed, and you are the stunt coordinator! A stunt person on a motorcycle will jump over an elephant and land in a pile of cardboard boxes to cushion their fall. You need to protect the stunt person, and also use relatively few cardboard boxes (lower cost, not seen by camera, etc.).Your job is to:•determine what size boxes to use•determine how many boxes to use•determine how the boxes will be stacked•determine if any modifications to the boxes would help•generalize to different bined weights (stunt person & motorcycle) and different jump heightsNote that, in "Tomorrow Never Dies", the James Bond character on a motorcycle jumps over a helicopter.PROBLEM B: Gamma Knife Treatment PlanningStereotactic radiosurgery delivers a single high dose of ionizing radiation to a radiographicallywell-defined, small intracranial 3D brain tumor without delivering any significant fraction of the prescribed dose to the surrounding brain tissue. Three modalities are monly used in this area; they are the gamma knife unit, heavy charged particle beams, and external high-energy photon beams from linear accelerators.The gamma knife unit delivers a single high dose of ionizing radiation emanating from 201 cobalt-60 unit sources through a heavy helmet. All 201 beams simultaneously intersect at the isocenter, resulting in a spherical (approximately) dose distribution at the effective dose levels. Irradiating the isocenter to deliver dose is termed a “shot.” Shots can be represented as different spheres. Four interchangeable outer collimator helmets with beam channel diameters of 4, 8, 14, and 18 mm are available for irradiating different size volumes. For a target volume larger than one shot, multiple shots can be used to cover the entire target. In practice, most target volumes are treated with 1 to 15 shots. The target volume is a bounded, three-dimensional digital image that usually consists of millions of points.The goal of radiosurgery is to deplete tumor cells while preserving normal structures. Since there are physical limitations and biological uncertainties involved in this therapy process, a treatment plan needs to account for all those limitations and uncertainties. In general, an optimal treatment plan is designed to meet the following requirements.1.Minimize the dose gradient across the target volume.2.Match specified isodose contours to the target volumes.3.Match specified dose-volume constraints of the target and critical organ.4.Minimize the integral dose to the entire volume of normal tissues or organs.5.Constrain dose to specified normal tissue points below tolerance doses.6.Minimize the maximum dose to critical volumes.In gamma unit treatment planning, we have the following constraints:1.Prohibit shots from protruding outside the target.2.Prohibit shots from overlapping (to avoid hot spots).3.Cover the target volume with effective dosage as much as possible. But at least 90% of thetarget volume must be covered by shots.e as few shots as possible.Your tasks are to formulate the optimal treatment planning for a gamma knife unit as a sphere-packing problem, and propose an algorithm to find a solution. While designing your algorithm, you must keep in mind that your algorithm must be reasonably efficient.2002 Contest ProblemsProblem AAuthors: Tjalling YpmaTitle: Wind and WatersprayAn ornamental fountain in a large open plaza surrounded by buildings squirts water high into the air. On gusty days, the wind blows spray from the fountain onto passersby. The water-flow from the fountain is controlled by a mechanism linked to an anemometer (which measures wind speed and direction) located on top of an adjacent building. The objective of this control is to provide passersby with an acceptable balance between an attractive spectacle and a soaking: The harder the wind blows, the lower the water volume and height to which the water is squirted, hence the less spray falls outside the pool area.Your task is to devise an algorithm which uses data provided by the anemometer to adjust the water-flow from the fountain as the wind conditions change.Problem BAuthors: Bill Fox and Rich WestTitle: Airline OverbookingYou're all packed and ready to go on a trip to visit your best friend in New York City. After you check in at the ticket counter, the airline clerk announces that your flight has been overbooked. Passengers need to check in immediately to determine if they still have a seat.Historically, airlines know that only a certain percentage of passengers who have made reservations on a particular flight will actually take that flight. Consequently, most airlines overbook-that is, they take more reservations than the capacity of the aircraft. Occasionally, more passengers will want to take a flight than the capacity of the plane leading to one or more passengers being bumped and thus unable to take the flight for which they had reservations.Airlines deal with bumped passengers in various ways. Some are given nothing, some are booked on later flights on other airlines, and some are given some kind of cash or airline ticket incentive.Consider the overbooking issue in light of the current situation:Less flights by airlines from point A to point BHeightened security at and around airportsPassengers' fearLoss of billions of dollars in revenue by airlines to dateBuild a mathematical model that examines the effects that different overbooking schemes have on the revenue received by an airline pany in order to find an optimal overbooking strategy, i.e., the number of people by which an airline should overbook a particular flight so that the pany's revenue is maximized. Insure that your model reflects the issues above, and consider alternatives for handling "bumped" passengers. Additionally, write a short memorandum to the airline's CEO summarizing your findings and analysis.MCM2000Problem A Air traffic ControlTo improve safety and reduce air traffic controller workload, the Federal Aviation Agency (FAA) is considering adding software to the air traffic control system that would automatically detect potential aircraft flight path conflicts and alert the controller. To that end, an analyst at the FAA r traffic control system that would automatically detect potential aircraft flight path conflicts and alert the controller. To that end, an analyst at the FAA has posed the following problemsRequirement A: Given two airplanes flying in space, when should the air traffic controller ld the air traffic controller consider the objects to be too close and to require intervention?Requirement B: An airspace sector is the section of three-dimensional airspace that one air traffic controller controls. Given any airspace sector, how we measure how plex it is from an air traffic workload perspective? To what extent is plexity determined by the number of we measure how plex it is from an air traffic workload perspective? To what extent is plexity determined by the number of aircraft simultaneously passing through that sector (1) at any one instant? (2) During any given interval of time? (3) During particular time of day? How does the number of potential conflicts arising during those periods affect plexity?Does the presence of additional software tools to automatically predict conflicts and alert the controller reduce or add to this plexity?In addition to the guidelines for your report, write a summary (no more than two pages) that the FAA analyst can present to Jane Garvey, the FAA Administrator, to defend your conclusionsProblem B Radio Channel AssignmentsWe seek to model the assignment of radio channels to a symmetric network of transmitter locations over a large planar area, so as to avoid interference. One basic approach is to partition the region into regular hexagons in a grid (honeyb-style), as shown in Figure 1, where a transmitter is located at the center of each hexagon.An interval of the frequency spectrum is to be allotted for transmitter frequencies. The interval will be divided into regularly spaced channels, which we represent by integers 1, 2, 3, ... . Each transmitter will be assigned one positive integer channel. The same channel can be used at many locations, provided that interference from nearby transmitters is avoided. Our goal is to minimize the width of the interval in the frequency spectrum that is needed to assign channels subject to some constraints. This is achieved with the concept of a span. The span is the minimum, over all assignments satisfying the constraints, of the largest channel used at any location. It is not required that every channel smaller than the span be used in an assignment that attains the span.Let s be the length of a side of one of the hexagons. We concentrate on the case that there are two levels of interferenceRequirement A: There are several constraints on frequency assignments. First, no two transmitters within distance of each other can be given the same channel. Second, due to spectral spreading, transmitters within distance 2s of each other must not be given the same or adjacent channels: Their channels must differ by at least 2. Under these constraints, what can we say about the span in,Requirement B: Repeat Requirement A, assuming the grid in the example spreads arbitrarily far in all directions.Requirement C: Repeat Requirements A and B, except assume now more generally that channels for transmitters within distance differ by at least some given integer k, while those at distance at most must still differ by at least one. What can we say about the span and about efficient strategies for designing assignments, as a function of k?Requirement D: Consider generalizations of the problem, such as several levels of interference or irregular transmitter placements. What other factors may be important to consider?Requirement E: Write an article (no more than 2 pages) for the local newspaper explaining your findingsMCM2000问题A 空间交通管制为加强安全并减少空中交通指挥员的工作量,联邦航空局(FAA)考虑对空中交通管制系统添加软件,以便自动探测飞行器飞行路线可能的冲突,并提醒指挥员。
美国大学生数学建模竞赛试题Problem-E-结果成绩

2016 Interdisciplinary Contest in Modeling®Press Release—April 8, 2016COMAP is pleased to announce the results of the 18th annual Interdisciplinary Contest in Modeling (ICM). This year 5025 teams representing institutions from eight countries participated in the contest. Fourteen teams were designated as OUTSTANDING WINNERS representing the following schools:∙Brown University, USA∙Chongqing University, China∙Communication University of China, China∙Huazhong University of Science and Technology, China, (INFORMS winner)∙NC School of Science and Mathematics, USA,(Vilfredo Pareto Award)∙NC School of Science and Mathematics, USA,(INFORMS winner)∙Northwestern Polytechnical University, China∙Renmin University of China, China∙Rensselaer Polytechnic Institute, USA,(Leonhard Euler Award)∙Shandong University, China∙Sun Yat-Sen University, China, (INFORMS winner)∙United States Military Academy, USA,(Rachel Carson Award)∙University of Colorado Denver, USA∙Xiamen University, ChinaThis year’s conte st ran from Thursday, January 28 to Monday, February 1, 2016. During that time, teams of three students researched, modeled, and communicated a solution to an open-ended interdisciplinary modeling problem. The 2016 ICM was primarily an online contest, where teams registered and obtained contest materials through COMAP’s ICM W ebsite.ICM teams chose one of the following three problems: The D Problem involved measuring the evolution of so ciety’s information networks. By taking a historical perspective of flow of information relative to value of information, the modelers sought to understand the methodology, purpose, andfuncti onality of society’s networks. The E Problem focused on the theme of environmental science. The teams needed to understand the drivers of water scarcity to create intervention strategies for a region to mitigate the water crisis. The new F Problem introduced policy modeling to the ICM. The problem for this first-time topic of policy modeling focused on the Middle East-Europe refugee migration issues. Consistent with other ICM problems, the policy problem challenged teams to utilize a diverse set of disciplinary skills including science, mathematics, politics, government operations, data science, and analysis in their modeling and problem solving. In all three cases, teams searched for pertinent data and grappled with how phenomena internal and external to the system under study needed to be considered. The student teams came up with creative and relevant solutions.These problems also had the ever-present ICM requirements to use thorough data analysis, creative modeling, and scientific methodology, along with effective writing and visualization to communicate their teams' results in a 20-page report. A selection from the Outstanding solution papers will be featured in The UMAP Journal, along with commentaries from the problem authors and judges. This year’s judges remarked that due to the multi-disciplinary nature of the problems, teams were able to solve these problems using a variety of methods and tools. This allowed teams to showcase their strengths in many diverse areas including history, information science, networks, ecology, environmental sciences, health sciences, public policy, dynamical systems, and geo-spatial techniques.2016 ICM Statistics∙5025 Teams participated∙864 Problem D submissions∙3209 Problem E submissions∙952 Problem F submissions∙91 US Teams (2%)∙4934 Foreign Teams (98%) from Australia, Canada, China, Hong Kong SAR, Indonesia, Singapore andUnited Kingdom∙14 Outstanding Winners (1%)∙15 Finalist Winners (1%)∙935 Meritorious Winners (18%)∙2287 Honorable Mentions (45%)∙1649 Successful Participants (33%)∙125 Unsuccessful Participants (2%)ICM is associated with COMAP’s Mathematical Contest in Modeling (MCM), which was held during the same weekend. ICM is designed to develop and advance interdisciplinary problem-solving skills in science, technology, engineering, mathematics (STEM) and the humanities, as well as competence in data science and written communication. Over the years the ICM problems have included topics in environmental science, biology, chemistry, resource management, operations research, information science, public health, and network science. Each team is expected to include advisors and team members who represent a range of disciplinary and interdisciplinary interests in applied problem solving and modeling. To obtain additional information about the ICM and to obtain a complete listing of all the team designations, please visit the ICM Website at: .Major start-up funding for the ICM was provided by a grant from the National Science Foundation (through Project INTERMATH) and COMAP. Additional support is provided by The Institute for Operations Research and the Management Sciences (INFORMS). COMAP's Mathematical Contest in Modeling and Interdisciplinary Contest in Modeling are unique among modeling competitions in that they are the only international contests in which students work in teams to find a solution. Centering its educational philosophy on mathematical modeling, COMAP uses mathematical tools to explore real-world problems. It serves the educational community as well as the world of work by preparing students to become better informed—and prepared—citizens, consumers, workers, and community leaders.Administered byThe Consortium for Mathematicsand Its ApplicationsContest DirectorsChris Arney, United States Military Academy, NY Tina Hartley, United States Military Academy, NY Executive DirectorSolomon A. Garfunkel, COMAP, Inc., MA。
2015年美国数学建模竞赛第二次模拟赛题A题

Problem A Warmer Days or Sour Grapes ?The high quality of wines(葡萄酒)produced in the Finger Lakes Region(五指湖区)of upstate (北部)New York is widely known. Proximity(接近)to lakes tempers the climate and makes it more suitable for growing several varieties of premium(独特)grapes: R iesling(雷司令), G ewürztraminer(琼瑶浆), C hardonnay (霞多丽), M erlot(梅洛), P inot Noir(黑比诺), and Cabernet F ranc(品丽珠). (There are many more, but we will restrict(限制)the discussion to these six to simplify(简化)the modeling.) Each variety has its own preferred “average temperature” range but is also different in its susceptibility(感受性)to diseases and ability to withstand(抵抗)short periods of unusually cold temperature.As our local climate changes, the relative suitability of these varieties will be changing as well. A forward-looking winery(酒厂)has hired your team to help with the long-term planning. You will need to recommenda) the proportion(比例)of the total vineyard(葡萄园)to be used for growing each of the above six varieties;b) and when should these changes be implemented (实施)(based on observed temperatures and/or current market prices for each type of wine).Naturally, the winery is interested in maximizing its annual profit. But since the latter (后者)is weather-dependent, it might vary a lot year-to-year. You are also asked to evaluate the trade-offs (权衡)between optimizing the expected/average case versus the worst(-realistic-)scenario(情景).Things to keep in mind:(复杂)and predicting the rate of “global warming” is a hotly debated area. For the purposes of this problem, assume that the annual average temperature in Ithaca(伊萨卡), NY will increase by no more than 4°C by the end of this century.average temperature – a short snap(临时)of sub-zero (零度)temperature in late Ferburay or early March (after the vines already started getting used to warmer weather) is far more damaging than the same low temperature would be in the middle of the winter.start producing grapes suitable for winemaking.。
第二届Mathorcup全球数学建模挑战赛题目[试题]
![第二届Mathorcup全球数学建模挑战赛题目[试题]](https://img.taocdn.com/s3/m/bb259115df80d4d8d15abe23482fb4daa58d1ddd.png)
第二届Mathorcup全球数学建模挑战赛题目A题:最佳飞行队列常见的飞行队列有直线形,V字形等多种不同的排列方式。
在生活中,大雁每年都要以排队列的方式进行南北迁徙,而且会根据情况变换不同的排列方式;在电影中,战斗机飞行也要按照不同的队列飞行,每个战斗机需按照规定的飞行线路飞行,完成任务后返回营地。
现有研究表明大雁的飞行队列有利于节省体力,那么战机编队飞行是否也利于节省燃油呢?请你研究飞行队列的数模模型,回答如下问题:1、从宏观上给不同飞行队列建立数学模型,至少要求考虑直线形和V字形两种情况,说明不同队列在空气中的飞行情况;2、在不考虑碰撞的情况下,计算滑翔、煽动、螺旋桨战机的最佳飞行队列。
B题:公司业务数据分析某互联网公司推出一项服务,此项服务包括5个主要的业务,这5项业务共包含8个指标,某项业务可以含有1个或多个指标,在这8个指标中其中有一个指标是收入。
客户可以根据自己的需要选择开通某些业务,各个业务之间没有强制绑定关系,但是某些业务之间通过相互宣传有一定的促进作用。
附件中是本公司2012年第一季度的数据,包括各个业务的各个指标的数据:指标数据为0,说明该业务还没有这个指标;从0变为正数说明此项业务开始包含新的功能,新功能具有新的指标。
附件中还包括此项服务带来的收入数据。
请你根据各个服务的指标数据和收入数据,完成如下问题:1、其中某些业务的使用量接近饱和,请你建立模型计算哪些业务量接近饱和,饱和的指标估计值是多少;2、根据财务数据,你能判断出哪个指标是收入吗,请你说明收入主要和哪些业务相关;3、请你分析出各个业务之间的相关性,哪几个业务相互促进可以使得收入增加;4、假如你是本服务的项目经理,根据现有的数据和你所建立的模型,给公司总经理写一份季度分析报告,分析当前的状态以及以后发展的建议,如何扩大公司的盈利空间以及服务规模。
题目说明:本题是一个开放性题目,请参赛者自己选择研究方向写一篇论文。
C题:地质灾害预测地质灾害是指在自然或者人为因素的作用下形成的,对人类生命财产、环境造成破坏和损失的地质作用(现象)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Problem A Rotating Grill Design for oscillating fanOne common type of oscillating directional electronic fan is a rotate grill fan. The key technology is the shape and speed of the rotating grill. The special-designed grill rotates to direct air for wide circulation. The clockwise and counter clockwise motion changes airflow direction.Please consider the factors of natural breeze, and build a breeze mode to design the grill to make the air from the fan to be comfortable.一种用于振动风机的旋转格栅设计问题一种常见的振动定向电子风机是一种旋转式格栅风机。
关键技术是旋转格栅的形状和速度。
特别设计的烧烤炉旋转,以直接空气流通。
顺时针和逆时针方向运动改变气流方向。
请考虑自然因素的微风,并建立风模式设计的格栅,使空气从风扇舒适。
Problem B Red Sun in the Morning: find an exit strategyRed sun at night, sailors' delight. Red sun in the morning, sailors take warning.Ten years ago hurricane Katrina had a devastating effect on the economies of several states, causing many deaths and much suffering. Comprehensive evacuation plans have been developed since then, but the authorities still want to improve their effectiveness. Your team has been hired by the Mississippi Emergency Management Administration (MSEMA) to review their current evacuation strategies.Things to keep in mind: All hurricanes are assigned a category: from 1 (the weakest) to 5 (the strongest, like Katrina). The category and the location of landfall are first predicted about 4 days in advance. Predictions are revised using updated information 48 hours later, and the final (most accurate) predictions become available 24 hours ahead of the expected landfall. The category of the hurricane and the actual location of the landfall determine which counties will be flooded. In addition, driving conditions in surrounding counties might be seriously affected by the size of the hurricane.Build a model to advise MSEMA on an optimal strategy: which counties should be ordered to evacuate, when, and where to. The first page of your manuscript should be a one page non-technical, executive summary for the governor of Mississippi. It should describe your main recommendations, the criteria you used to evaluate their effectiveness, and any caveats you believe are important to mention.%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Time permitting, your model should also account for the fact that evacuations initiated in Louisiana, Alabama, and Mississippi affect each other. For example, a large portion of the New Orleans population will likely evacuate through Jackson, MS using highways 59 and 55. If the population of Jackson needs to evacuate, much of it will be directed North within MS or West toward Monroe, LA. Parts of coastal counties in MS will evacuate through Mobile, AL.Despite these interdependencies, the decisions in each state are rarely made collaboratively. So, if you are a governor in one of these states and you order the evacuation later than the others, the population of your state might be at disadvantage since the roads will be already clogged by then. If thehurricane turns out to be stronger than expected, your constituents might end up stuck in traffic in affected areas. On the other hand, if you order the evacuation too early, this disruption carries a high economic cost –coastal areas generate much revenue for your state and early predictions about the expected hurricane strength/landfall time/location might be inaccurate.夜晚的红太阳,水手们的喜悦。
早晨红太阳,水手们采取警告。
十年前,卡特丽娜飓风对几个州的经济造成了毁灭性的影响,导致许多人死亡,许多苦难。
自那时以来,已经制定了全面的疏散计划,但当局仍希望提高其有效性。
你的团队被密西西比急救管理聘用(msema)审查目前的疏散策略。
事情要记住:所有的飓风都被分配一个类别:从1(最弱)到5(最强的,像卡特丽娜)。
类别和登陆位置第一预测提前4天左右。
预测修订后的48小时后使用更新的信息,并最终(最准确)的预言变成未来的预期登陆24小时。
类的飓风和实际位置登陆确定县将被淹没。
此外,在周围的县的驾驶条件可能会受到严重影响的大小飓风。
建立一个模型的最优策略msema建议:各国应下令疏散,当,在哪里。
您的稿件的第一页应该是一一页的技术,为密西西比州州长执行概要。
它应该描述你的主要建议,你用来评估其有效性的标准,以及任何你认为重要的事项提。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%如果时间允许的话,你的模型应该考虑的事实,在路易斯安那,阿拉巴马州和密西西比州开始疏散,相互影响。
例如,新奥尔良的一大部分人口将有可能通过禅师撤离,使用高速公路59和55。
如果杰克逊的人口需要撤离,大部分将是朝着北西向梦露,拉。
沿海县的部分地区将通过移动,铝。
尽管这些相互依赖,每个州的决定很少合作。
因此,如果你是这些州中的一位州长,你要比其他国家晚一点的话,你的国家人口可能处于不利地位,因为那时道路已经被堵塞了。
如果飓风的结果是强于预期,你的选民可能会最终陷入受影响地区的交通。
另一方面,如果你为了疏散太早,这种破坏有很高的经济成本–沿海地区产生多少收入,你的状态和早期预测预计飓风的强度/登陆时间/地点可能不准确。
Problem C Refugee Quota PlanThe recent surge of migration into Europe has been unprecedented in scope, with an estimated 1 million migrants from the Middle East and North Africa, making for a massive humanitarian crisis, as well as a political and moral dilemma for European governments.European Union interior ministers have reached a deal to share out 120,000 refugees across the European Union bloc after holding an emergency meeting.The agreement was reached in Brussels on Tuesday despite fierce opposition from some central and eastern states that deepened rifts over Europe's worst refugee crisis in decades.Refugees queue to register at a camp after crossing the Greek-Macedonian border near GevgelijaRequirement 1: Predict the total number of refugees.Requirement 2: Provide optimal refugee quota plan.Requirement 3: What are the problems with the current plan.Requirement 4: Your suggestion.问题的难民配额计划最近移民潮在欧洲范围内是史无前例的,估计从中东和北非移民到100万,这是一次巨大的人道主义危机,也是欧洲各国政府的政治和道德困境。
