2016美国大学生数学建模比赛H奖

合集下载

美国大学生数学建模竞赛数据及评阅分析_吴孟达

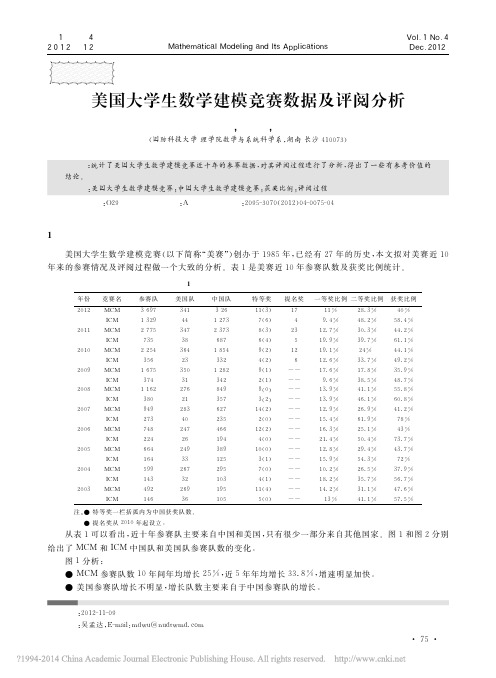
给出了ＭＣＭ和ＩＣＭ中国队和美国队参赛队数的变化。
图１分析：
● ＭＣＭ参赛队数１０年间年均增长２５％，近５年年均增长３３．８％，增速明显加快。
● 美国参赛队增长不明显，增长队数主要来自于中国参赛队的增长。
收稿日期：２０１２－１１－０９通讯作者：吴孟达，Ｅ－ｍａｉｌ：ｍｄｗｕ＠ｎｕｄｔｗｍｄ．ｃｏｍ
摘要：统计了美国大学生数学建模竞赛近十年的参赛数据，对其评阅过程进行了分析，得出了一些有参考价值的结论。关键词：美国大学生数学建模竞赛；中国大学生数学建模竞赛；获奖比例；评阅过程
中图分类号：Ｏ２９文献标志码：Ａ文章编号：２０９５－３０７０（２０１２）０４－００７５－０４
３２６１２７３２３７３６８７１８５４３３２１２８２３４２８４９３５７６２７２３５４６６１９４３８９１２５２９５１０３１９５１０５
１１（３）７（６）８（３）６（４）９（２）４（２）９（１）２（１）９（０）３（２）
图２ＩＣＭ参赛队数变化图图３ＭＣＭ获奖比例图４ＩＣＭ获奖比例
２评阅过程分析
据美赛 “评委评论 ”介绍，美赛评阅过程大致分为三轮。第一轮可以称为“淘汰轮（ｔｈｅＴｒｉａｇｅＲｏｕｎｄ）”。此轮评阅主要以摘要信息以及论文整体结构为评判依据，时间大约是５～１０分钟。每个评委以 “通过 ”、“不通过 ”计分，事先应当设置有大致的 “通过 ”比例（此轮与国内研赛的网评阶段相类似）。当两位评委意见不一致时可以协商达成一致意见，如果仍不能达成一致意见，则请第三位评委评阅。有 “评论 ”介绍说，这一轮的淘汰率大约为４５％，通过这一轮评审的参赛队大约有８０％的获奖概率。关于如何通过这一轮评审，评委给出的建议是：１）摘要至关重要，必须清晰且信息量充分。评委关心的是你对问题的理解是否准确，你建立的模型及使用的方法是否恰当，以及根据你所建模型得到的主要结果和主要结论是否合理。过于冗长的技术性描述将 · ７６ ·

历年美国大学生数学建模竞赛试题MCM.翻译版doc

1985 年美国大学生数学建模竞赛MCM 试题1985年MCM:动物种群选择适宜的鱼类和哺乳动物数据准确模型。

模型动物的自然表达人口水平与环境相互作用的不同群体的环境的重要参数,然后调整账户获取表单模型符合实际的动物提取的方法。

包括任何食物或限制以外的空间限制,得到数据的支持。

考虑所涉及的各种数量的价值,收获数量和人口规模本身,为了设计一个数字量代表的整体价值收获。

找到一个收集政策的人口规模和时间优化的价值收获在很长一段时间。

检查政策优化价值在现实的环境条件。

1985年MCM B:战略储藏管理钴、不产生在美国,许多行业至关重要。

(国防占17%的钴生产。

1979年)钴大局部来自非洲中部,一个政治上不稳定的地区。

1946年的战略和关键材料储藏法案需要钴储藏,将美国政府通过一项为期三年的战争。

建立了库存在1950年代,出售大局部在1970年代初,然后决定在1970年代末建立起来,与8540万磅。

大约一半的库存目标的储藏已经在1982年收购了。

建立一个数学模型来管理储藏的战略金属钴。

你需要考虑这样的问题:库存应该有多大?以什么速度应该被收购?一个合理的代价是什么金属?你也要考虑这样的问题:什么时候库存应该画下来吗?以什么速度应该是画下来吗?在金属价格是合理出售什么?它应该如何分配?有用的信息在钴政府方案在2500万年需要2500万磅的钴。

美国大约有1亿磅的钴矿床。

生产变得经济可行当价格到达22美元/磅(如发生在1981年)。

要花四年滚动操作,和thsn六百万英镑每年可以生产。

1980年,120万磅的钴回收,总消费的7%。

1986 年美国大学生数学建模竞赛MCM 试题1986年MCM A:水文数据下表给出了Z的水深度尺外表点的直角坐标X,Y在码(14数据点表省略)。

深度测量在退潮。

你的船有一个五英尺的草案。

你应该防止什么地区的矩形(75200)X(-50、150)?1986年MCM B:Emergency-Facilities位置迄今为止,力拓的乡牧场没有自己的应急设施。

2016全国大学生数学建模竞赛获奖名单

2016高教社杯全国大学生数学建模竞赛获奖名单（初稿）（异议期：2016年11月7日-2016年11月20日）
本科组高教社杯获得者：张滕翔、夏智康、郑安琪（东南大学）
专科组高教社杯获得者：吴伟龙、杨婷、段玲（湖南化工职业技术学院）
本科组MATLAB创新奖获得者：王毅然、纪昀红、张伟（中国人民大学）
专科组MATLAB创新奖获得者：刘苏生、祝王缘、王柏熙（海军蚌埠士官学校）
[注]以下每一获奖等级内，按赛区顺序排列（同一赛区内，按学校笔画顺序排列）。

本科组一等奖（共294名）
本科组二等奖（共1621名）
曹小
专科组一等奖（共60名）。

2016年美国大学生数学建模竞赛C题H奖论文

Contents1.Introduction (1)1.1 Background (1)1.2 Foundation & ROI (1)2 Task (1)3 Fundamental assumptions (2)4 Definitions and Notations (2)5 Models (3)5.1 Filter data (3)5.2 Object Selection Model (Grey Relational Analysis) (4)5.2.1 Model analysis (4)5.2.2 Model solution (4)5.3 ROI Model (Principal Component Analysis) (5)5.3.1 Model analysis (5)5.3.2 Model solution (6)5.4 Verify the possibility (9)5.4.1 Comparison (9)5.4.2 External factor (10)5.5 Investment Forecast Model (11)5.5.1 Linear Regression Forecasting Model (11)5.5.2 School potential Prediction (TOPSIS) (12)5.5.3 Final investment (TOPSIS) (13)6 Conclusions (16)7 Strengths and Weaknesses (18)7.1 Strengths (19)7.2 Weaknesses (20)8 Letter to Mr. Alpha Chiang (21)9 References (22)Team # 44952 Page 1 of 221 Introduction1.1 BackgroundThe Goodgrant Foundation is a charitable organization that wants to help improve educational performance of undergraduates attending colleges and universities in the United States. To do this, the foundation intends to donate a total of $100,000,000 (US100 million) to an appropriate group of schools per year, for five years, starting July 2016. In doing so, they do not want to duplicate the investments and focus of other large grant organizations such as the Gates Foundation and Lumina Foundation.Our team has been asked by the Goodgrant Foundation to develop a model to determine an optimal investment strategy that identifies the schools, the investment amount per school, the return on that investment, and the time duration that the organi zation’s money should be provided to have the highest likelihood of producing a strong positive effect on student performance. This strategy should contain a 1 to N optimized and prioritized candidate list of schools you are recommending for investment bas ed on each candidate school’s demonstrated potential for effective use of private funding, and an estimated return on investment (ROI) defined in a manner appropriate for a charitable organization such as the Goodgrant Foundation.1.2 Foundation & ROIFoundation (charitable foundation) refers to the nonprofit legal person who uses the property of the natural persons, legal persons or other organizations to engage in public welfare undertakings. In terms of its nature, foundation is a kind of folk non-profit organizations.ROI is a performance measure used to evaluate the efficiency of an investment or to compare the efficiency of a number of different investments. ROI measures the amount of return on an investment relative to the investment’s cost. To calculate ROI, the benefit (or return) of an investment is divided by the cost of the investment, and the result is expressed as a percentage or a ratio.2 Task●One-page summary for our MCM submission●Using our models to achieve the candidate list of schools●Calculate the time durati on that the organization’s money should be provided to have thehighest likelihood of producing a strong positive effect on student performance●Calculate the investment amount Goodgrant Foundation would pay for each school●Calculate the ROI of the Goodgrant Foundation●Forecast the development of this kind of investment mode●Write a letter to the CFO of the Goodgrant Foundation, Mr. Alpha Chiang, that describesthe optimal investment strategy。

2016全国大学生数学建模竞赛获奖名单

本科组一等奖（共294名）
本科组二等奖（共1621名）
曹小
专科组一等奖（共60名）。

2017年国际(美国)大学生数学建模竞赛获奖情况

曾璐（金融）
杨凯然（能建）
郭丽华
65243
成功参赛奖
鲁亮（外语）
牛付芝（计算机）
韩龄萱（计算机）
周庆欣
64797
成功参赛奖
孟凡宁（轻工）
刘思彤（轻工）
马心蕊（轻工）
刘义翔
张敬信
64326
国际二等奖
吴奇学（英才）
陈泓伊（英才）
钟逸（金融）
张敬信
65234
国际二等奖
闫舒（会计）
冯立花（计算机）
谢慧（基础）
曲国坤
65776
国际二等奖
刘瑞（金融）
涂人匀（会计）
梅锦标（计算机）
任中贵
64342
成功参赛奖
叶雪薇（基础）
王卓承（会计）
崔立龙（财政）
吴刚
64361
成功参赛奖
万丽君（经济）
张光倩（轻工）
陈立影（轻工）
周书琦（英才）
吴刚
64394
国际二等奖
李天翼（能建）
王偲雪（能建）
鲁慧敏（外语）
杨姗姗
64378
国际二等奖
卢水根（轻工）
丁浩珂（基础）
王莹（英才）
王勇
64384
国际二等奖
何佳琪（经济）
李奥（经济）
刘艺欣（会计）
王勇
64321
国际二等奖
王晓峰（英才）
徐帅（英才）
程实（金融）
65770
成功参赛奖
戴克宁（金融）
王寿年（计算机）
徐李珍（会计）
叶永刚
65781
成功参赛奖
丁宁（基础）
王降圣（基础）
李珺彤（英才）
任中贵

参加美国大学生数学建模竞赛 - 知乎

1.组队
我们队一个应用数学的学渣（就是我）一个化学院的女森加上一个计算机院物联网的男生一般组队都是数院电气电信经管这样我们一次模拟都没有做过，但是分析过大概10多篇08年一等奖的文章，当时觉得他们的模型都看不懂= =
2.场地
因为学校机房有限，都给了参加过过赛的同学的队，比赛的时候出去开了两间房，白天就在一起做题。酒店没有桌子，就坐在地上然后把电脑放床上= =
比赛：最理想是国赛前定下美国赛队伍，拿国赛练级攒经验比较恰当。其他如教工杯之类的比赛，鉴于真实比赛环境和练习的机会不多，建议当成美赛认真练。只要认真练，几次真赛历练之后，建模和配合方面问题就不应该太大了。学术论文写作：难点不是专业词汇或格式排版的问题，这些问题阅卷人可能会对外国参赛者宽容些，真正困难是表达如何逻辑清晰严密、符合学术规范了。有条件的最好找英语国家教授或学术期刊编辑帮忙不断改，找不到就只能是找海归教授、理工专业外国留学生将就了，再没条件的只能研读outstanding和英文经典论文了。
赛前准备程度基本决定了比赛的时间充裕度，赛前准备不足往往要靠比赛时不眠不休、争分夺秒拼命抢时间来弥补，这种情况下能做出多少创造性工作就难说了。
三、练级篇：
练习：练习的时候要根据队伍的特点有针对性的训练提高——模型方面，多积累实际问题产生背景，注意培养思考的深度，善用发散和逆向思维；实现方面，注意提升各种算法求解效率的方法，多积累算法调试、测试、参数调整、有效性检验等方面的经验；
大家要有信心一等奖不难加油噢~ 编辑于 2013-07-23 9 条评论
参加美国大学生数学建模竞赛 - 知乎
改名中，我的头像更适合做知乎吉祥物李曈、Steve Balaba、张镇麟等人赞同首先说一下自己的参赛经历：2013年S奖，2014年M奖，两次参赛是不同的队伍。

中国大学生数学建模竞赛发展史

2000.9.26～29
2000网易杯全国大学生数学建模竞赛举行，27省（市、自治区）517所院校的3210队参加，其中608队参加大专组竞赛，香港城市大学有1个队首次参赛
2000.12.6～8
2000年各赛区负责人工作会议暨颁奖仪式在中山大学珠海校区举行，119队获一等奖（其中大专组23队），245队获二等奖（其中大专组55队）。
1998年全国大学生数学建模竞赛举行，26省（市、自治区）400所院校的2103队参加。
1998.12.10～13
1998年各赛区负责人工作会议暨颁奖仪式在上海华东理工大学举行，79队获一等奖，153队获二等奖。
1999.2.6～8
1999年美国大学生数学建模竞赛举行，我国参赛院校43个，占总数的19%，参赛队155个，占总数的32%，浙江大学获一项特等奖。从1999年起增加交叉学科建模竞赛（作为C题）。
2003.2
2003年美国大学生数学建模竞赛（MCM）和交叉学科竞赛（ICM）举行，我国共参加300队，占总数的47%，浙江大学、北京大学、东南大学、东华大学各一队获特等奖。
2003.9.22~25
2003高教社杯全国大学生数学建模竞赛举行，30省（市、自治区）637所院校的5406队参加。
2003.12.6~7
2003年各赛区工作会议暨颁奖仪式在厦门举行，厦门大学承办，608队获全国奖，其中本科组一等奖151队，二等奖306队，大专组一等奖48队，二等奖103队。
2004.2
2004年美国大学生数学建模竞赛（MCM）和交叉学科竞赛（ICM）举行，我国共参加398队，占总数的54%，成都电子科技大学一队获特等奖。
数学建模发展史
1992.11.27～29
1992年部分城市大学生数学模型联赛举行，这是全国性的首届竞赛，10省（市）79所院校的314队参加。

正确写作美国大学生数学建模竞赛论文省名师优质课赛课获奖课件市赛课一等奖课件

论文旳主体是指导言之后及结论之前旳部分，用于描述模型旳设计，涉及列出和论证建立数学模型所做旳假设，以及对赛题所做旳分析。论文旳主体一般分为若干小节。
3.1）、假设条件和解释
合理旳数学模型应基于合理旳假设，所以在描述模型之前，参赛小组应该将模型设计所用旳假设条件一一列出并解释清楚。不要有未经阐明旳假设，以免读者自行猜测而造成误解。另外，还应该对建模旳初衷和动机合适旳加以讨论。
3、写作旳主要性
论文旳写作应尽早开始。根据以往旳经验，许多参赛小组往往低估了论文写作所需旳时间，不能及时写出条理清楚旳论文。所以，参赛小组能够考虑在竞赛开始后旳第二天开始写作，并约定一种时间结束手头旳建模工作，以便全力以赴写好参赛论文。
第二部分论文构造
1、小节划分
论文应该按内容划提成小节和子小节，并冠以恰当旳标题，使评委无需阅读细节就能把握论文旳根本。根据论文旳评审原则，MCM竞赛委员会提议参赛小组按下列构造将论文分节：
特级论文（0.5﹪）特级提名论文（0.5﹪）甲级论文（10﹪—15﹪）乙级论文（25-30﹪）合格论文（60﹪）不合格论文
2、论文评审
评审流程：
论文评审旳方式是盲审。全部参赛论文均使用唯一给定旳编号统一辨认，这个编号称为控制编号。论文旳作者姓名及其所在大学旳名称均不得在论文中出现。评审分为两个阶段：
1、小节划分
下列是该论文旳小节划分及标题： Summary
1 Restatement of the Problem 2 Assumptions 3 Justification of Our Approach 4 The Model
4.1 Dissatisfaction of a passenger needing a connection 4.2 Dissatisfaction of a passenger not needing a connection 4.3 Total dissatisfaction on an aircraft 5 Testing the Model 6 Results 7 Strengths and Weaknesses References

2016年美国大学生数学建模大赛A题获奖论文A Hot Bath

Part II Finding the best strategy ...................................................................12 VI. Results ........................................................................................................ 12
The first part has five sections: air’s heat radiation, bathtub wall’s heat radiation, person in, hot water in, bubble existed. We discuss some factors that affect water temperature, such as the shape and the volume of the bathtub and person, especially the motions made by the person in the bathtub because the temperature in the bathtub has a great connection with person. Finally, we get the water temperature variation and distribution model.
In this article, we establish two models. One is water temperature variation and distr one is finding best strategy model. We put forward some acceptable hypothesis to simplify the model. What’s more, we clear the meaning of the word “noticeably”.

2016美国大学生数学建模大赛C题特等奖(原版论文)C42939Tsinghua University, China

For ofﬁce use only T1T2T3T4T eam Control Number42939Problem ChosenCFor ofﬁce use onlyF1F2F3F42016Mathematical Contest in Modeling(MCM)Summary Sheet (Attach a copy of this page to each copy of your solution paper.)SummaryIn order to determine the optimal donation strategy,this paper proposes a data-motivated model based on an original deﬁnition of return on investment(ROI) appropriate for charitable organizations.First,after addressing missing data,we develop a composite index,called the performance index,to quantify students’educational performance.The perfor-mance index is a linear composition of several commonly used performance indi-cators,like graduation rate and graduates’earnings.And their weights are deter-mined by principal component analysis.Next,to deal with problems caused by high-dimensional data,we employ a lin-ear model and a selection method called post-LASSO to select variables that statis-tically signiﬁcantly affect the performance index and determine their effects(coef-ﬁcients).We call them performance contributing variables.In this case,5variables are selected.Among them,tuition&fees in2010and Carnegie High-Research-Activity classiﬁcation are insusceptible to donation amount.Thus we only con-sider percentage of students who receive a Pell Grant,share of students who are part-time and student-to-faculty ratio.Then,a generalized adaptive model is adopted to estimate the relation between these3variables and donation amount.Weﬁt the relation across all institutions and get aﬁtted function from donation amount to values of performance contributing variables.Then we divide the impact of donation amount into2parts:homogenous and heterogenous one.The homogenous inﬂuence is modeled as the change inﬁt-ted values of performance contributing variables over increase in donation amount, which can be predicted from theﬁtted curve.The heterogenous one is modeled as a tuning parameter which adjusts the homogenous inﬂuence based on deviation from theﬁtted curve.And their product is increase in true values of performance over increase in donation amount.Finally,we calculate ROI,deﬁned as increase in performance index over in-crease in donation amount.This ROI is institution-speciﬁc and dependent on in-crease in donation amount.By adopting a two-step ROI maximization algorithm, we determine the optimal investment strategy.Also,we propose an extended model to handle problems caused by time dura-tion and geographical distribution of donations.A Letter to the CFO of the Goodgrant FoundationDear Chiang,Our team has proposed a performance index quantifying the students’educational per-formance of each institution and deﬁned the return of investment(ROI)appropriately for a charitable organization like Goodgrant Foundation.A mathematical model is built to help predict the return of investment after identifying the mechanism through which the donation generates its impact on the performance.The optimal investment strategy is determined by maximizing the estimated return of investment.More speciﬁcally,the composite performance index is developed after taking all the pos-sible performance indicators into consideration,like graduation rate and graduates’earnings. The performance index is constructed to represents the performance of the school as well as the positive effect that a college brings to students and the community.From this point of view, our deﬁnition manages to capture social beneﬁts of donation.And then we adopt a variable selection method toﬁnd out performance contributing vari-ables,which are variables that strongly affect the performance index.Among all the perfor-mance contributing variables we select,three variables which can be directly affected by your generous donation are kept to predict ROI:percentage of students who receive a Pell Grant, share of students who are part-time and student-to-faculty ratio.Weﬁtted a relation between these three variables and the donation amount to predict change in value of each performance contributing variable over your donation amount.And we calculate ROI,deﬁned as increase in the performance index over your donation amount, by multiplying change in value of each performance contributing variable over your donation amount and each performance contributing variable’s effect on performance index,and then summing up the products of all performance contributing variables.The optimal investment strategy is decided after maximizing the return of investment according to an algorithm for selection.In conclusion,our model successfully produced an investment strategy including a list of target institutions and investment amount for each institution.(The list of year1is attached at the end of the letter).The time duration for the investment could also be determined based on our model.Since the model as well as the evaluation approach is fully data-motivated with no arbitrary criterion included,it is rather adaptable for solving future philanthropic educational investment problems.We have a strong belief that our model can effectively enhance the efﬁciency of philan-thropic educational investment and provides an appropriate as well as feasible way to best improve the educational performance of students.UNITID names ROI donation 197027United States Merchant Marine Academy21.85%2500000 102711AVTEC-Alaska’s Institute of Technology21.26%7500000 187745Institute of American Indian and Alaska Native Culture20.99%2000000 262129New College of Florida20.69%6500000 216296Thaddeus Stevens College of Technology20.66%3000000 229832Western Texas College20.26%10000000 196158SUNY at Fredonia20.24%5500000 234155Virginia State University20.04%10000000 196200SUNY College at Potsdam19.75%5000000 178615Truman State University19.60%3000000 199120University of North Carolina at Chapel Hill19.51%3000000 101648Marion Military Institute19.48%2500000187912New Mexico Military Institute19.31%500000 227386Panola College19.28%10000000 434584Ilisagvik College19.19%4500000 199184University of North Carolina School of the Arts19.15%500000 413802East San Gabriel Valley Regional Occupational Program19.09%6000000 174251University of Minnesota-Morris19.09%8000000 159391Louisiana State University and Agricultural&Mechanical Col-19.07%8500000lege403487Wabash Valley College19.05%1500000 Yours Sincerely,Team#42939An Optimal Strategy of Donation for Educational PurposeControl Number:#42939February,2016Contents1Introduction51.1Statement of the Problem (5)1.2Baseline Model (5)1.3Detailed Deﬁnitions&Assumptions (8)1.3.1Detailed Deﬁnitions: (8)1.3.2Assumptions: (9)1.4The Advantages of Our Model (9)2Addressing the Missing Values93Determining the Performance Index103.1Performance Indicators (10)3.2Performance Index via Principal-Component Factors (10)4Identifying Performance Contributing Variables via post-LASSO115Determining Investment Strategy based on ROI135.1Fitted Curve between Performance Contributing Variables and Donation Amount145.2ROI(Return on Investment) (15)5.2.1Model of Fitted ROIs of Performance Contributing Variables fROI i (15)5.2.2Model of the tuning parameter P i (16)5.2.3Calculation of ROI (17)5.3School Selection&Investment Strategy (18)6Extended Model186.1Time Duration (18)6.2Geographical Distribution (22)7Conclusions and Discussion22 8Reference23 9Appendix241Introduction1.1Statement of the ProblemThere exists no doubt in the signiﬁcance of postsecondary education to the development of society,especially with the ascending need for skilled employees capable of complex work. Nevertheless,U.S.ranks only11th in the higher education attachment worldwide,which makes theﬁnancial support from large charitable organizations necessary.As it’s essential for charitable organizations to maximize the effectiveness of donations,an objective and systematic assessment model is in demand to develop appropriate investment strategies.To achieve this goal,several large foundations like Gates Foundation and Lumina Foundation have developed different evaluation approaches,where they mainly focus on spe-ciﬁc indexes like attendance and graduation rate.In other empirical literature,a Forbes ap-proach(Shifrin and Chen,2015)proposes a new indicator called the Grateful Graduates Index, using the median amount of private donations per student over a10-year period to measure the return on investment.Also,performance funding indicators(Burke,2002,Cave,1997,Ser-ban and Burke,1998,Banta et al,1996),which include but are not limited to external indicators like graduates’employment rate and internal indicators like teaching quality,are one of the most prevailing methods to evaluate effectiveness of educational donations.However,those methods also arise with widely acknowledged concerns(Burke,1998).Most of them require subjective choice of indexes and are rather arbitrary than data-based.And they perform badly in a data environment where there is miscellaneous cross-section data but scarce time-series data.Besides,they lack quantiﬁed analysis in precisely predicting or measuring the social beneﬁts and the positive effect that the investment can generate,which serves as one of the targets for the Goodgrant Foundation.In accordance with Goodgrant Foundation’s request,this paper provides a prudent def-inition of return on investment(ROI)for charitable organizations,and develops an original data-motivated model,which is feasible even faced with tangled cross-section data and absent time-series data,to determine the optimal strategy for funding.The strategy contains selection of institutions and distribution of investment across institutions,time and regions.1.2Baseline ModelOur deﬁnition of ROI is similar to its usual meaning,which is the increase in students’educational performance over the amount Goodgrant Foundation donates(assuming other donationsﬁxed,it’s also the increase in total donation amount).First we cope with data missingness.Then,to quantify students’educational performance, we develop an index called performance index,which is a linear composition of commonly used performance indicators.Our major task is to build a model to predict the change of this index given a distribution of Goodgrant Foundation$100m donation.However,donation does not directly affect the performance index and we would encounter endogeneity problem or neglect effects of other variables if we solely focus on the relation between performance index and donation amount. Instead,we select several variables that are pivotal in predicting the performance index from many potential candidates,and determine their coefﬁcients/effects on the performance index. We call these variables performance contributing variables.Due to absence of time-series data,it becomes difﬁcult toﬁgure out how performance con-tributing variables are affected by donation amount for each institution respectively.Instead, weﬁt the relation between performance contributing variables and donation amount across all institutions and get aﬁtted function from donation amount to values of performance contribut-ing variables.Then we divide the impact of donation amount into2parts:homogenous and heteroge-nous one.The homogenous inﬂuence is modeled as the change inﬁtted values of performance contributing variables over increase in donation amount(We call these quotientsﬁtted ROI of performance contributing variable).The heterogenous one is modeled as a tuning parameter, which adjusts the homogenous inﬂuence based on deviation from theﬁtted function.And their product is the institution-speciﬁc increase in true values of performance contributing variables over increase in donation amount(We call these values ROI of performance contributing vari-able).The next step is to calculate the ROI of the performance index by adding the products of ROIs of performance contributing variables and their coefﬁcients on the performance index. This ROI is institution-speciﬁc and dependent on increase in donation amount.By adopting a two-step ROI maximization algorithm,we determine the optimal investment strategy.Also,we propose an extended model to handle problems caused by time duration and geographical distribution of donations.Note:we only use data from the provided excel table and that mentioned in the pdfﬁle.Table1:Data SourceVariable DatasetPerformance index Excel tablePerformance contributing variables Excel table and pdfﬁleDonation amount PdfﬁleTheﬂow chart of the whole model is presented below in Fig1:Figure1:Flow Chart Demonstration of the Model1.3Detailed Deﬁnitions&Assumptions 1.3.1Detailed Deﬁnitions:1.3.2Assumptions:A1.Stability.We assume data of any institution should be stable without the impact from outside.To be speciﬁc,the key factors like the donation amount and the performance index should remain unchanged if the college does not receive new donations.A2.Goodgrant Foundation’s donation(Increase in donation amount)is discrete rather than continuous.This is reasonable because each donation is usually an integer multiple of a minimum amount,like$1m.After referring to the data of other foundations like Lumina Foundation,we recommend donation amount should be one value in the set below:{500000,1000000,1500000, (10000000)A3.The performance index is a linear composition of all given performance indicators.A4.Performance contributing variables linearly affect the performance index.A5.Increase in donation amount affects the performance index through performance con-tributing variables.A6.The impact of increase in donation amount on performance contributing variables con-tains2parts:homogenous one and heterogenous one.The homogenous inﬂuence is repre-sented by a smooth function from donation amount to performance contributing variables.And the heterogenous one is represented by deviation from the function.1.4The Advantages of Our ModelOur model exhibits many advantages in application:•The evaluation model is fully data based with few subjective or arbitrary decision rules.•Our model successfully identiﬁes the underlying mechanism instead of merely focusing on the relation between donation amount and the performance index.•Our model takes both homogeneity and heterogeneity into consideration.•Our model makes full use of the cross-section data and does not need time-series data to produce reasonable outcomes.2Addressing the Missing ValuesThe provided datasets suffer from severe data missing,which could undermine the reliabil-ity and interpretability of any results.To cope with this problem,we adopt several different methods for data with varied missing rate.For data with missing rate over50%,any current prevailing method would fall victim to under-or over-randomization.As a result,we omit this kind of data for simplicity’s sake.For variables with missing rate between10%-50%,we use imputation techniques(Little and Rubin,2014)where a missing value was imputed from a randomly selected similar record,and model-based analysis where missing values are substituted with distribution diagrams.For variables with missing rate under10%,we address missingness by simply replace miss-ing value with mean of existing values.3Determining the Performance IndexIn this section,we derive a composite index,called the performance index,to evaluate the educational performance of students at every institution.3.1Performance IndicatorsFirst,we need to determine which variables from various institutional performance data are direct indicators of Goodgrant Foundation’s major concern–to enhance students’educational performance.In practice,other charitable foundations such as Gates Foundation place their focus on core indexes like attendance and graduation rate.Logically,we select performance indicators on the basis of its correlation with these core indexes.With this method,miscellaneous performance data from the excel table boils down to4crucial variables.C150_4_P OOLED_SUP P and C200_L4_P OOLED_SUP P,as completion rates for different types of institutions,are directly correlated with graduation rate.We combine them into one variable.Md_earn_wne_p10and gt_25k_p6,as different measures of graduates’earnings,are proved in empirical studies(Ehren-berg,2004)to be highly dependent on educational performance.And RP Y_3Y R_RT_SUP P, as repayment rate,is also considered valid in the same sense.Let them be Y1,Y2,Y3and Y4.For easy calculation and interpretation of the performance index,we apply uniformization to all4variables,as to make sure they’re on the same scale(from0to100).3.2Performance Index via Principal-Component FactorsAs the model assumes the performance index is a linear composition of all performance indicators,all we need to do is determine the weights of these variables.Here we apply the method of Customer Satisfaction Index model(Rogg et al,2001),where principal-component factors(pcf)are employed to determine weights of all aspects.The pcf procedure uses an orthogonal transformation to convert a set of observations of pos-sibly correlated variables into a set of values of linearly uncorrelated variables called principal-component factors,each of which carries part of the total variance.If the cumulative proportion of the variance exceeds80%,it’s viable to use corresponding pcfs(usually theﬁrst two pcfs)to determine weights of original variables.In this case,we’ll get4pcfs(named P CF1,P CF2,P CF3and P CF4).First,the procedure provides the linear coefﬁcients of Y m in the expression of P CF1and P CF2.We getP CF1=a11Y1+a12Y2+a13Y3+a14Y4P CF2=a21Y1+a22Y2+a23Y3+a24Y4(a km calculated as corresponding factor loadings over square root of factor k’s eigenvalue) Then,we calculate the rough weights c m for Y m.Let the variance proportions P CF1and P CF2 represent be N1and N2.We get c m=(a1m N1+a2m N2)/(N1+N2)(This formulation is justiﬁedbecause the variance proportions can be viewed as the signiﬁcance of pcfs).If we let perfor-mance index=(P CF 1N 1+P CF 2N 2)/(N 1+N 2),c m is indeed the rough weight of Y m in terms of variance)Next,we get the weights by adjusting the sum of rough weights to 1:c m =c m /(c 1+c 2+c 3+c 4)Finally,we get the performance index,which is the weighted sum of the 4performance indicator.Performance index= m (c m Y m )Table 2presents the 10institutions with largest values of the performance index.This rank-ing is highly consistent with widely acknowledged rankings,like QS ranking,which indicates the validity of the performance index.Table 2:The Top 10Institutions in Terms of Performance IndexInstitutionPerformance index Los Angeles County College of Nursing and Allied Health79.60372162Massachusetts Institute of Technology79.06066895University of Pennsylvania79.05044556Babson College78.99269867Georgetown University78.90468597Stanford University78.70586395Duke University78.27719116University of Notre Dame78.15843964Weill Cornell Medical College 78.143341064Identifying Performance Contributing Variables via post-LASSO The next step of our model requires identifying the factors that may exert an inﬂuence on the students’educational performance from a variety of variables mentioned in the excel table and the pdf ﬁle (108in total,some of which are dummy variables converted from categorical variables).To achieve this purpose,we used a model called LASSO.A linear model is adopted to describe the relationship between the endogenous variable –performance index –and all variables that are potentially inﬂuential to it.We assign appropriate coefﬁcient to each variable to minimize the square error between our model prediction and the actual value when ﬁtting the data.min β1J J j =1(y j −x T j β)2where J =2881,x j =(1,x 1j ,x 2j ,...,x pj )THowever,as the amount of the variables included in the model is increasing,the cost func-tion will naturally decrease.So the problem of over ﬁtting the data will arise,which make the model we come up with hard to predict the future performance of the students.Also,since there are hundreds of potential variables as candidates.We need a method to identify the variables that truly matter and have a strong effect on the performance index.Here we take the advantage of a method named post-LASSO (Tibshirani,1996).LASSO,also known as the least absolute shrinkage and selection operator,is a method used for variableselection and shrinkage in medium-or high-dimensional environment.And post-LASSO is to apply ordinary least squares(OLS)to the model selected byﬁrst-step LASSO procedure.In LASSO procedure,instead of using the cost function that merely focusing on the square error between the prediction and the actual value,a penalty term is also included into the objective function.We wish to minimize:min β1JJj=1(y j−x T jβ)2+λ||β||1whereλ||β||1is the penalty term.The penalty term takes the number of variables into con-sideration by penalizing on the absolute value of the coefﬁcients and forcing the coefﬁcients of many variables shrink to zero if this variable is of less importance.The penalty coefﬁcient lambda determines the degree of penalty for including variables into the model.After min-imizing the cost function plus the penalty term,we couldﬁgure out the variables of larger essence to include in the model.We utilize the LARS algorithm to implement the LASSO procedure and cross-validation MSE minimization(Usai et al,2009)to determine the optimal penalty coefﬁcient(represented by shrinkage factor in LARS algorithm).And then OLS is employed to complete the post-LASSO method.Figure2:LASSO path-coefﬁcients as a function of shrinkage factor sFigure3:Cross-validated MSEFig2.displays the results of LASSO procedure and Fig3displays the cross-validated MSE for different shrinkage factors.As speciﬁed above,the cross-validated MSE reaches minimum with shrinkage factor between0.4-0.8.We choose0.6andﬁnd in Fig2that6variables have nonzero coefﬁcients via the LASSO procedure,thus being selected as the performance con-tributing variables.Table3is a demonstration of these6variables and corresponding post-LASSO results.Table3:Post-LASSO resultsDependent variable:performance_indexPCTPELL−26.453∗∗∗(0.872)PPTUG_EF−14.819∗∗∗(0.781)StudentToFaculty_ratio−0.231∗∗∗(0.025)Tuition&Fees20100.0003∗∗∗(0.00002)Carnegie_HighResearchActivity 5.667∗∗∗(0.775)Constant61.326∗∗∗(0.783)Observations2,880R20.610Adjusted R20.609Note:PCTPELL is percentage of students who receive aPell Grant;PPTUG_EF is share of students who are part-time;Carnegie_HighResearchActivity is Carnegie classiﬁca-tion basic:High Research ActivityThe results presented in Table3are consistent with common sense.For instance,the pos-itive coefﬁcient of High Research Activity Carnegie classiﬁcation implies that active research activity helps student’s educational performance;and the negative coefﬁcient of Student-to-Faculty ratio suggests that decrease in faculty quantity undermines students’educational per-formance.Along with the large R square value and small p-value for each coefﬁcient,the post-LASSO procedure proves to select a valid set of performance contributing variables and describe well their contribution to the performance index.5Determining Investment Strategy based on ROIWe’ve identiﬁed5performance contributing variables via post-LASSO.Among them,tu-ition&fees in2010and Carnegie High-Research-Activity classiﬁcation are quite insusceptible to donation amount.So we only consider the effects of increase in donation amount on per-centage of students who receive a Pell Grant,share of students who are part-time and student-to-faculty ratio.We denote them with F1,F2and F3,their post-LASSO coefﬁcients withβ1,β2andβ3.In this section,weﬁrst introduce the procedure used toﬁt the relation between performance contributing variables and donation amount.Then we provide the model employed to calcu-lateﬁtted ROIs of performance contributing variables(the homogenous inﬂuence of increase in donation amount)and the tuning parameter(the heterogenous inﬂuence of increase in dona-tion amount).Next,we introduce how to determine stly,we show how the maximiza-tion determines the investment strategy,including selection of institutions and distribution of investments.5.1Fitted Curve between Performance Contributing Variables and Donation AmountSince we have already approximated the linear relation between the performance index with the3performance contributing variables,we want to know how increase in donation changes them.In this paper,we use Generalized Adaptive Model(GAM)to smoothlyﬁt the relations. Generalized Adaptive Model is a generalized linear model in which the dependent variable depends linearly on unknown smooth functions of independent variables.Theﬁtted curve of percentage of students who receive a Pell Grant is depicted below in Fig4(see the other two ﬁtted curves in Appendix):Figure4:GAM ApproximationA Pell Grant is money the U.S.federal government provides directly for students who needit to pay for college.Intuitively,if the amount of donation an institution receives from other sources such as private donation increases,the institution is likely to use these donations to alleviate students’ﬁnancial stress,resulting in percentage of students who receive a Pell Grant. Thus it is reasonable to see aﬁtted curve downward sloping at most part.Also,in commonsense,an increase in donation amount would lead to increase in the performance index.This downward sloping curve is consistent with the negative post-LASSO coefﬁcient of percentage of students who receive a Pell Grant(as two negatives make a positive).5.2ROI(Return on Investment)5.2.1Model of Fitted ROIs of Performance Contributing Variables fROI iFigure5:Demonstration of fROI1Again,we useﬁtted curve of percentage of students who receive a Pell Grant as an example. We modeled the blueﬁtted curve to represent the homogeneous relation between percentage of students who receive a Pell Grant and donation amount.Recallﬁtted ROI of percentage of students who receive a Pell Grant(fROI1)is change in ﬁtted values(∆f)over increase in donation amount(∆X).SofROI1=∆f/∆XAccording to assumption A2,the amount of each Goodgrant Foundation’s donation falls into a pre-speciﬁed set,namely,{500000,1000000,1500000,...,10000000}.So we get a set of possible ﬁtted ROI of percentage of students who receive a Pell Grant(fROI1).Clearly,fROI1is de-pendent on both donation amount(X)and increase in donation amount(∆X).Calculation of ﬁtted ROIs of other performance contributing variables is similar.5.2.2Model of the tuning parameter P iAlthough we’ve identiﬁed the homogenous inﬂuence of increase in donation amount,we shall not neglect the fact that institutions utilize donations differently.A proportion of do-nations might be appropriated by the university’s administration and different institutions allocate the donation differently.For example,university with a more convenient and well-maintained system of identifying students who needﬁnancial aid might be willing to use a larger portion of donations to directly aid students,resulting in a lower percentage of under-graduate students receiving Pell grant.Also,university facing lower cost of identifying and hiring suitable faculty members might be inclined to use a larger portion of donations in this direction,resulting in a lower student-to-faculty ratio.These above mentioned reasons make institutions deviate from the homogenousﬁtted func-tion and presents heterogeneous inﬂuence of increase in donation amount.Thus,while the homogenous inﬂuence only depends on donation amount and increase in donation amount, the heterogeneous inﬂuence is institution-speciﬁc.To account for this heterogeneous inﬂuence,we utilize a tuning parameter P i to adjust the homogenous inﬂuence.By multiplying the tuning parameter,ﬁtted ROIs of performance con-tributing variables(ﬁtted value changes)convert into ROI of performance contributing variable (true value changes).ROI i=fROI i·P iWe then argue that P i can be summarized by a function of deviation from theﬁtted curve (∆h),and the function has the shape shown in Fig6.The value of P i ranges from0to2,because P i can be viewed as an ampliﬁcation or shrinkage of the homogenous inﬂuence.For example,P i=2means that the homogeneous inﬂuence is ampliﬁed greatly.P i=0means that this homogeneous inﬂuence would be entirely wiped out. The shape of the function is as shown in Fig6because of the following reasons.Intuitively,if one institution locates above theﬁtted line,when deviation is small,the larger it is,the larger P i is.This is because the institution might be more inclined to utilize donations to change that factor.However,when deviation becomes even larger,the institution grows less willing to invest on this factor.This is because marginal utility decreases.The discussion is similar if one institution initially lies under theﬁtted line.Thus,we assume the function mapping deviation to P i is similar to Fig6.deviation is on the x-axis while P i is on the y-axis.Figure6:Function from Deviation to P iIn order to simplify calculation and without loss of generality,we approximate the function。

大学生数学建模竞赛介绍

ICM Problem D (operations research/network science) ICM Problem E (environmental science) ICM Problem F (policy) • Mark your calendars the 2016 MCM/ICM dates are set for January 28 – February 1, 2016
2015 OUTSTANDING WINNERS
• THE FIVE OUTSTANDING WINNERS OF THE CONTINUOUS MCM (A) PROBLEM ARE: • Northwestern Polytechnical University, China • State University of New York, University at Buffalo, NY — MAA Prize Recipient • Chongqing University, China — SIAM Prize RecipientCentral South University, China — Ben Fusaro Award • University of Adelaide, Australia — INFORMS Prize Recipient • THE FIVE OUTSTANDING WINNERS OF THE DISCRETE MCM (B) PROBLEM ARE: • University of Colorado Boulder, CO — SIAM Prize Recipient & Two Sigma Scholarship Award • Bethel University, MN — MAA Prize Recipient & Frank Giordano Award • University of Colorado Boulder, CO • Colorado College, CO — INFORMS Prize Recipient • Tsinghua University, China • THE FIVE OUTSTANDING WINNERS OF THE INTERDISCIPLINARY ICM (C) PROBLEM ARE: • Xidian University, China • Shanghai Jiao Tong University, China • Xi'an Jiaotong University, China — Leonhard Euler Award • Tsinghua University, China • National University of Defense Technology, China • Also winning as a FINALIST is: • University of Colorado Denver, CO — INFORMS Prize Recipient • THE FOUR OUTSTANDING WINNERS OF THE INTERDISCIPLINARY ICM (D) PROBLEM ARE: • NC School of Science and Mathematics, NC — INFORMS Prize Recipient • Xi'an Jiaotong University, China • Humboldt State University, CA — Rachel Carson Award & Two Sigma Scholarship Award • Zhejiang University, China

美国大学生数学建模竞赛经验分享

•
A B C 总
2012 美赛哈工大参赛及获奖具体统计
总数 F 百分比 181 2 1.1% 166 0 0.0% 144 0 0.0% 491 2 0.4% 该统计可能包括威海分区 M 28 16 12 56 百分比 15.5% 9.6% 8.3% 11.4% H 百分比 69 38.1% 62 37.3% 45 31.3% 176 35.8%
评阅过程
• 初评（triage)是否回答解决问题，重点看摘要，综述整篇文章，各节提供综述有帮助 • 甄别（screening)考察模型，清晰模型和坚实分析可得较高分，分析、结果和写作的一致性是重要的。 • 终评（final）目的挑选优秀论文，细节比较，最后若干篇每个评委都要看，讨论后遴选 outstanding, final list
准备工作
• • • • • • • • 竞赛时间确定仔细阅读竞赛规则论文格式及排版常备一些文献数据资料网址制定竞论文，多用英文练笔
赛前准备
1、根据自己的情况和圈子、渠道尽早完成组队和队员磨合工作； 2、访问官方网站，仔细研读参赛规则： /undergraduate/contests/mcm/inst ructions.php /thread-168106-1-1.html含中文参考翻译； 3、尽可能多的研读和实践历年获奖论文及其中的模型和求解算法，如有条件，每周都抽出一定时间进行组内队员的研讨，以有助于队员之间的磨合； 4、注册成为数学中国论坛/forum.php 的会员并通过各种手段获取尽可能多的体力值以保证赛前和比赛期生建议
• “建模的创造性”，表现出很好创造性的论文即使出现比较大的错误亦有可能获得一等奖。 • 注意离散和随机模型 • “模型的检验越多越好”。可以采用证明的方法，但更多的是对某些感兴趣的情形进行计算并分析结果、对重要参数的高中低水平进行计算并分析，考虑放松某些假设等。

2016年全国大学生数学建模竞赛获奖论文

小区开放对道路通行的影响评价模型摘要本文针对小区开放对道路的影响进行了研究，建立了层次分析模型、通行能力评价模型，使用了MATLAB、EXCEL等软件，得出小区开放在不同条件下会对道路交通产生不同的影响。

首先运用层次分析法，分析得出整体一般情况下小区开放有利于周边道路交通的结论。

之后构建了不同类型的小区，并分析得出小区开放的效果与小区结构及周边道路结构、车流量有关，因此小区开放不能盲目采取，要因地制宜。

最后根据分析结果，从交通通行的角度，向城市规划和交通管理部门提出了关于小区开放的合理化建议。

本文的突出特点是使用了层次分析法定量的比较了小区开放前后道路合理性，构建了对于研究该问题具有代表性的三种类型的小区，并建立了影响评估模型，客观的对不同小区结构及周边道路结构、车辆通行的影响进行评价。

针对问题一，首先查阅相关资料选取影响道路通行的指标，并对选取的指标进行筛选，然后运用各项指标进行层次分析，通过小区开放和小区封闭对道路交通和理性的判断来分析小区开放对道路通行的影响最后得出从整体看来，小区开放有利于道路通行。

针对问题二，通过查阅有关道路通行能力的相关资料建立了通行能力评价模型，首先根据模型求出道路基本通行能力的表达式，基本通行能力是理想状态下的通行能力，与实际情况分析对比存在差异。

因此基于差异，通过各实际因素对道路通行能力的影响进行修正，得到实际道路通行能力的数据。

最终计算出小区开放前后实际通行能力的相对系数。

针对问题三，构建了三种类型的小区，不同类型的小区具有不同的结构及不同的周边道路结构、车流量，应用问题二建立的模型分别对三种小区开放和封闭条件下周边道路的实际通行能力进行了计算，通过相对系数评价不同类型的小区开放对道路通行的影响，分析得出小区开放与地理位置、内部结构等因素有关，不能一概而论。

针对问题四，结合前述模型结果分析结果，从交通出行角度对城市规划部门和交通管理部门提出了合理化意见。

小区开放要合理的实施以体现小区开放的意义。

2018-2019信息科学与工程学院国家奖学金、校长奖学金拟

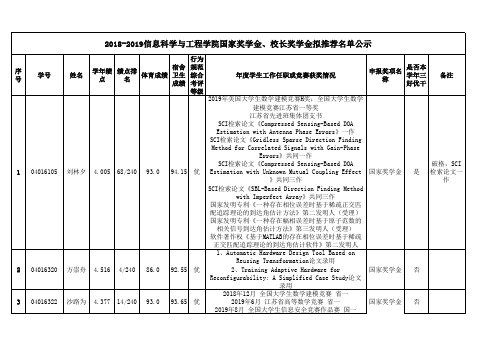
校长奖学金是
全国大学生英语竞赛校级三等奖
18 04017536 叶子文 4.342 11/306 87.5 90 优
040175支部副班长学生会社青部门副部长 IEEE Signal Cup国际比赛中获团体第九名数模竞赛校级三等奖创新体验竞赛校级三等奖；
校长奖学金是
040175班班长
院学生会主席
国家奖学金否
2019年8月全国大学生信息安全竞赛作品赛国一
040166班班长/2019年全国大学生电子设计竞赛江苏省
二等奖/2019年美国大学生数学建模竞赛国际级一等奖
4 04016640 薛家龙 4.389 11/240 88.0
93.5Biblioteka 优/2019年江苏省普通高等学校第十六届高等数学竞赛省（部、地区）级一等奖/东南大学2019年第二十一届电
SCI检索论文《Compressed Sensing-Based DOA
Estimation with Antenna Phase Errors》一作
SCI检索论文《Gridless Sparse Direction Finding
Method for Correlated Signals with Gain-Phase
3.东南大学本科生第十三届数学建模竞赛校级三等奖校长奖学金是
4.东南大学第十八届结构创新竞赛”暨“第八届南京高校结构创
新邀请赛”校级优秀奖
东南大学本科生第十三届数学建模竞赛校级二等奖；
2019年全国大学生英语竞赛（NECCS）国家级二等奖；
21
04018607
黄乐扬
3.83
33/214
100.0
级一等奖；2019年美国大学生数学建模竞赛国际二等奖；2018年Robocup机器人竞赛校级二等奖；2019年东

美国大学生数学建模竞赛赛20160719

美国大学生数学建模竞赛的命题与评阅
天津大学边馥萍 fpbian@
美国大学生数学建模竞赛
热烈祝贺山东大学荣获2016年美赛O奖
参赛命题评阅获奖培训
1. MCM/ICM 简介
美国大学生数学建模竞赛创始人 Ben Fusaro 1984年向美国教育部申请到一笔为期三年的基金，并于1985年开始正式举办。竞赛由COMAP组织和管理竞赛的命题、组织形式、宗旨、评审原则 MCM参赛情况：第1届：1985年参赛队158个队（美国），交卷90队，70所大学第32届：2016年参赛队7421个队，919所大学， 12个国家及地区，中国学生参赛队超过93.5%
初评标准
对题目的解读，赛题中没有明确给出的模糊概念是否澄清。建模所需的前提条件及假设及其合理性的说明。通过对赛题的分析论证建模的合理性。建立有效解答赛题的模型。对模型的稳定性、敏感性进行测试，检验。讨论模型的优缺点，给出清晰的结论。符合要求的摘要：应包含以下内容用自己的语言描述要解决的问题，强调建模所用的假设，指出所用的模型类型或构造的新模型，模型检验及误差分析和优缺点讨论。
2016 ICM Contest Outstanding Teams
2训资料（高教出版社出版）
美国大学生数学建模竞赛题解析与研究 2007-2008 第一册 2005-2006 第二册 Mathematical Modeling for the MCM/ICM Contest , Volume 1, 2 正确写作美国大学生数学建模竞赛论文 …..
UMAP数学建模案例精选1、2册，3册即将出版
UMAP 案例精选—1、2测已出版，3册即将出版特点：案例及习题有具体解法，有些适合做教学案例配套PPT正在制作中

西北工业大学竞赛获奖推荐免试名单

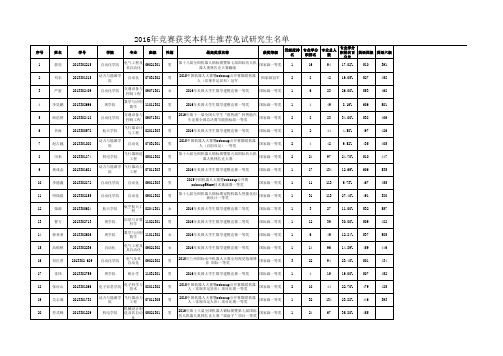
17
134
12.69%
606
535
10
11
113
9.73%
467
455
11 12 13
明瑞晨柴源
2013302155 2013300684
自动化学院航天学院
自动化
09011302
男女
第十七届全国机器人锦标赛宠物机器人智能化创国家级一等奖新设计一等奖 2016年美国大学生数学建模竞赛二等奖国际级二等奖
2
7 32 34
27 68 134
25.92% 47.00% 25.37%
565 500 590
457 413 548
郭靖韩昌富
2013300611 2013301659
航天学院
男男
1 2
41 42
动力与能源学飞行器动力 07011302 院工程电子信息学院电磁场与无 08051302 线技术
37
杨鸿杰苏秀中
2013300576 2012301054
航天学院机电学院
男男
1 3
14 47
44 97
31.80% 48.50%
476 525
437 464
38 39 40
张茜
2013300384
航空学院
女
中国国际飞行器设计挑战赛暨科研类全国航空航国家级一等奖天模型锦标赛限时载运空投项目 15、16年美国大学生数学建模竞赛二等奖 2015中国机器人大赛暨robocup公开赛（自创异形）一等奖冠军 2015中国机器人大赛暨robocup公开舞蹈机器人（自创多足异形）冠军国际级二等奖国家级冠军
6
27
22.20%

美国大学生数学建模竞赛概况及备战建议

楚含义即可。科技性的文章以陈述的句式为主，不需要华
・自２０１３年起，全国大学生数学建模竞赛组委会联合中国工业与应用数学学会数学模型专业委员会，将与美赛组织者通力合作，共同评阅美赛论文ｐ１。
３美赛备战参考建议
因为参加美赛绝大多数是中国队伍，美赛俨然已成为 “中国大学生数学建模竞赛”的春季赛。但其并不与“中国式数学建模＋中译英”画等号。如果不熟悉美赛的风格及相关注意事宜，难以在激烈的竞赛中脱颖而出。如何准备才能在美赛中取得佳绩？笔者结合自身实践与体会，从以下几方面阐述，抛砖引玉以飨读者。３．１培养检索英文文献能力通常情况下，数学建模是在对实际问题做适当简化和处理的基础上建立模型，这就需要选手熟悉问题的背景和特点。早期的美赛题目许多来自于美国的社会与生活，如２００５年的“水灾计划”和“收费亭”赛题。这对于不熟悉美国社会特点的外国选手，尤其是中国学生来说是很难找到切人点，故常常得到一些不切实际的结果。更糟糕的是，与赛题相关的中文文献往往寥寥无几，难以满足比赛的需要，这就要求参赛选手必须习惯检索英文文献。鉴于Ｇｏｏｇｌｅ学术搜索包括了世界上绝大部分出版的学术期刊且其功能强大、操作简单，所以我们建议选手优先熟悉Ｇｏｏｇｌｅ学术搜索功能及高级学术搜索技巧。３．２注重文献阅读技巧有针对地选择文献关键在于选准关键词，这样才能确保检索内容的全面性。阅读文献时的顺序是先看摘要，通
部时间１月３１日２０点至２月４１３２０点（北京时间２月１
１３
９点至２月５日９点）进行。今年的赛题延续了美赛以
参赛队伍数
Ｏｕｔｓｔａｎｄｉｎｇ
５６３６１１１３８５７１６５０３０９５
往的风格，与之同时也出现了一些新的亮点，在ＭＣＭ的
Ｗｉｎｎｅｒ

2016年美国数学建模竞赛选拔名单

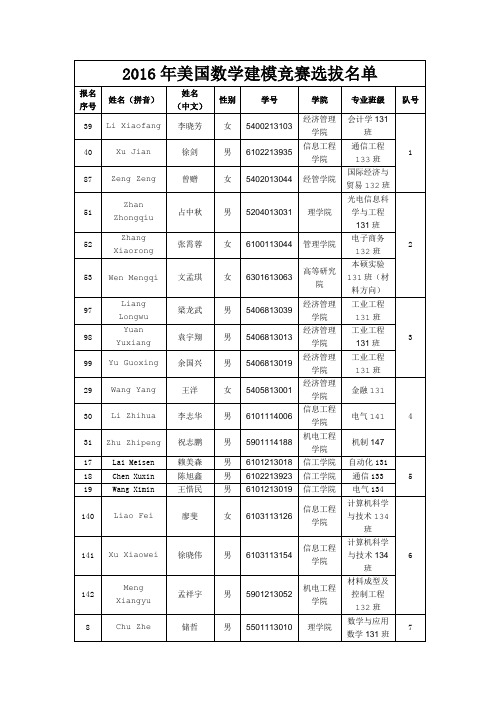
2016年美国数学建模竞赛选拔名单报名序号姓名（拼音）姓名（中文）性别学号学院专业班级队号39 Li Xiaofang 李晓芳女5400213103 经济管理学院会计学131班140 Xu Jian 徐剑男6102213935 信息工程学院通信工程133班87 Zeng Zeng 曾赠女5402013044 经管学院国际经济与贸易132班51ZhanZhongqiu占中秋男5204013031 理学院光电信息科学与工程131班252ZhangXiaorong张霄蓉女6100113044 管理学院电子商务132班53 Wen Mengqi 文孟琪女6301613063 高等研究院本硕实验131班（材料方向）97LiangLongwu梁龙武男5406813039经济管理学院工业工程131班398YuanYuxiang袁宇翔男5406813013经济管理学院工业工程131班99 Yu Guoxing 余国兴男5406813019 经济管理学院工业工程131班29 Wang Yang 王洋女5405813001 经济管理学院金融131430 Li Zhihua 李志华男6101114006 信息工程学院电气14131 Zhu Zhipeng 祝志鹏男5901114188 机电工程学院机制14717 Lai Meisen 赖美森男6101213018 信工学院自动化131518 Chen Xuxin 陈旭鑫男6102213923 信工学院通信13319 Wang Ximin 王惜民男6101213019 信工学院电气134140 Liao Fei 廖斐女6103113126 信息工程学院计算机科学与技术134班6141 Xu Xiaowei 徐晓伟男6103113154 信息工程学院计算机科学与技术134班142MengXiangyu孟祥宇男5901213052机电工程学院材料成型及控制工程132班8 Chu Zhe 储哲男5501113010 理学院数学与应用数学131班713 Zhao Yuan 赵远女 5501113004 理学院数学与应用数学131班 12 Yang Peng 杨朋男 7101313059理学院应用数学131班 41 Li linhai 李林海男 7301013001 材料学院新能源131 842 Tian Yue 田岳女 6100113018 管理学院电子商务131 43 Li Xuan 李轩男 5501313007 理学院金融数学132班 47 Li Ruixin李瑞欣男 6101113078 信息工程学院电气132班 112 Chen wenfeng 陈文枫男 5902613070 机电工程学院能动132 9 113 Zeng Liang曾良男 5902613035 机电工程学院能动131班 114 Liao Yangqin 廖洋琴女 5405813037 经济管理学院金融131 136 Deng Qi 邓祺男 6102113085 信息工程学院电子信息工程132班 137 Xu Zhijun徐志军男 6102113074 信息工程学院电子信息工程132班 10 138 Fu Tangyixun 付唐伊浔女 5405813024 经济管理学院金融131班 139 Qiu Yilan 邱祎岚女 5405813007 经济管理学院金融131班 103Nie Kaiwen聂凯文男5702113063高等研究院本硕131班 11104 Xiong Yifei 熊逸飞男 5702113122 材料学院材料132班（金属方向） 105 Wang Jing王静女 5405713051经济管理学院工商管理（中法实验班131） 2 Yang Xuefeng 杨雪峰男 5501213050 理学院信息与计算科学131班 123 Zhou Fang 周方男 5501213030理学院信息与计算科学131班 4 Cao Yunkai 曹允开男 5901113027 前湖学院本硕实验131班 48 Zhu Haiqing 朱海清男 5501213042 理学院信息与计算科学131班 1349Luo Tao罗涛男5501213001理学院信息与计算科学131班50 Peng Zhiyun彭志云男 6101213054信息工程学院电气工程及其自动化134班 33 Chen Mingqin 陈名钦男 5502113015 理学院物理131 1434 Gao Weiguang 高伟光男 5502113004 理学院物理131 35 Wang Zhongyi 王忠义男 5502113008 理学院物理学131 44Song Haiping 宋海平男5204010322理学院光电131班 15 54 Du XinPeng 杜鑫鹏男 5204013038 理学院光电信息科学与工程131班 26 He Jianwei何建伟男 5502113025理学院物理学131 1627 Wei Xiaoying 韦肖莹女 6100113027 管理学院电子商务131 28 Huang Yilin黄依琳女 6100113037 管理学院电子商务13284 YiXing 易行男 5405813100 经管学院金融131班 17 86 YanHong 燕洪女 5405813048 经管学院金融132班 59 Liu Yue 刘月男 5502213019 理学院应用物理132班 1860 Xiong WeiHong 熊为红男 5502213025 理学院应用物理132班 61 Li Yang 李阳男 5502213042 理学院应用物理131班 56 Liu Zan 刘赞女 6002313001 建筑工程学院工程管理131班 1957 Yu ruihao 于瑞昊男 5405713032 经济管理学院中法131 58 Li Ding 李丁女 5501113006 理学院数学与应用数学131班 20 He Chen 何晨男 5402013031 经济管理学院国际经济与贸易131 2021 Cui Xianghe崔祥鹤女 5405813022经济管理学院金融131 22 Wang Xiaoxia 王小霞女 6100113048 管理学院电子商务132 23 Cai Dakun 蔡大坤男 6102213903 信息工程学院通信133 2124 Zeng Liang 曾亮男 6102213883信息工程学院通信132 25Li Jiaman李佳蔓女6100113023 管理学院电子商务13145 Lin Zihuang 林子煌男6102113031 信息工程学院电子信息131班2246 Hu tao 胡涛男5406813066 经管学院工业工程132班66 ZengYuHang 曾宇航女5400213120 经管学院会计131班72JiangYangTing蒋杨婷女6102213916信息工程学院通信工程133班2364 Song Qiu Yun 宋秋韵女5405813046 经管学院金融学131班90 ZuoYue 左玥女5405813036 经管学院金融131班94 ChenYing 陈盈男6102213907 信息工程学院通信工程133班2495ZhangShuyun张舒云女6103113028信息工程学院计算机科学与技术131班96 Xu Zhenyang 徐振烊男5901213181 机电工程学院材料成型及控制工程134班124 Yao Jiang 姚江男6104113058 管理学院信息管理与信息系统132班25125 Li Xuan 李炫女信息工程学院通信工程131班126JiangYuTing蒋雨婷女6104113024 管理学院信息管理与信息系统132班132 Qin Qi 秦琪女6002113091 建筑工程学院土木工程13226133 Wan Zhaoyu 万兆宇男6101113096 信息工程学院电气工程及其自动化133班134 Wu Huicheng 伍惠铖男6101113100 信息工程学院电气工程及其自动化133班147 Qin Gang 秦刚男5502213046 信息工程学院电气工程及其自动化132班27148 Zeng Ya Min 曾亚敏女6101113138 信息工程学院电气工程及其自动化133班149 Li Yirui 李依蕊女6101113047 信息工程学院电气工程及其自动化131班120 Zhang Jun 张俊男5702113077 材料学院材料131班（金属方向）67 ZhongWeiJun 钟伟俊男5501213032 理学院信计131班68 SuWeizhong 苏伟中男5501213033 理学院信计131班88ZhongChongyu仲崇禹男5501213052 理学院信息与计算科学131班89MiaoLianhai缪莲海男5501213012 理学院信息与计算科学131班63 Wu Mengyuan 吴孟元男5501314016 理学院金融数学143班65 Li Xue Chen 李雪晨女5501114008 理学院应数141班116 wangxiao 王潇女5501213034 理学院信计131班10 Hu Yuhao 胡玉洁女5204013054 理学院光电信息科学与工程131班11ShanDanyang单丹阳男5502213060 理学院应用物理1329 Wang Hao 王昊男5502213040 理学院应用物理1321 Liu Heng 刘恒男5204013001 理学院光电信息科学与工程131班122 Huang Yun 黄云女5502113001 理学院物理学131班123 Zhong Qilan 钟琦岚女5502113018 理学院物理学131班62 Du Xinchen 杜鑫晨男5501314003 理学院金融数学142班133QiaoYanning乔燕凝女5501214039 理学院信计14169 HeQi 何柒女6103113164 信息工程学院计算机科学与技术134班78 Suo Jingwen 索婧雯女6103413020 信息工程学院中兴通信131班79 Gao wenhua 高文华女6103413003 信息工程学院中兴通信131班101 Liangkexin 梁可欣女6102213931 信息工程学院通信工程133班102 Du Jingxuan 杜靖瑄女6102213915 信息工程学院通信工程133班R1 tang zhenhao唐贞豪男 8000113225 软件学院嵌入式133班 35R2 ji kai 季凯男 8000113213 软件学院嵌入式134班 R3 song zheng bo 宋正博男 8000113235 软件学院嵌入式134班 R4 zhao run han 赵润翰男 8000114116 软件学院软工143 36 R5 huang yu peng 黄宇鹏男 8000114117 软件学院软工143R6 wu xi xiang 伍细香女 8000114146 软件学院软工143班 R7 liu hui 刘辉男 8000114137 软件学院软工143 37R8 lu si yu 鲁厶语女 8000114161 软件学院软工144 R9 ji yi yi 季义义女 8000114136 软件学院软工143 R10 zhao zi hao 赵子豪男 8001714024 软件学院信安141 38 R11 lv yin 吕垠女 8001714002 软件学院信安141 R12 ye meng 叶蒙女 8000114206 软件学院软工147 R13 zhang qian 张倩女 8000114032 软件学院软工141 39 R14 wang xiaoman 王潇蔓女 8000114251 软件学院软工145 R15 wang ze 王泽男 8001714030 软件学院信息安全141班 R16 lishijing 李世敬男 8000113036 软件学院嵌入式133班 40 R17 liuzhicheng 刘治成男 8000113003 软件学院嵌入式133班 R18 tangjisheng唐计生男 8000113050 软件学院嵌入式133班 R19zhangxiaodong 张小东男 8000113158软件学院嵌入式131班41R20 lijiacheng 李嘉诚男 8000113121 软件学院东软131班 R21liyongsheng李永胜男8000113233 软件学院嵌入式133班。