三角函数(课堂讲义和例题)
三角函数知识点及典型例题

三角函数知识点及典型例题三角函数知识点及典型例题§1.1.1、任意角1、正角、负角、零角、象限角的概念.2、与角α终边相同的角的集合:{}|360,S k k Z ββα==+?∈.§1.1.2、弧度制1、把长度等于半径长的弧所对的圆心角叫做1弧度的角.2、 rl =α.3、弧长公式: R4、扇形面积公式: S=21 lr=21αr 2.§1.2.1、任意角的三角函数1、设α是一个任意角,它的终边与单位圆交于点()y x P ,,那么:xyx y ===αααtan ,cos ,sin . 2、设点()00,y x A 为角α终边上任意一点,那么:(设2020y x r +=)_______sin r y =α,________cos rx=α,_____tan x y =α.3、αsin ,αcos ,αtan 在四个象限的符号一正二正弦三切四余和三角函数线的画法. 4、诱导公式一:()()()_tan _2tan _cos _2cos _sin _2sin απααπααπα=+=+=+kk k (Z k ∈)5、特殊角0°,30°,45°,60°,90°,180°,270°的三角函数值. §1.2.2、同角三角函数的基本关系式1、平方关系:22sin cos 1αα+=.2、商数关系:sin tan cos ααα=. §1.3、三角函数的诱导公式1、诱导公式二:()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ=+-=+-=+2、诱导公式三:()()()._tan _tan _____,cos _cos _,sin _sin αααααα-=-=--=-3、诱导公式四:()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ-=--=-=-4、诱导公式五:._sin _2cos _,cos _2sin ααπααπ=??-=-5、诱导公式六:._sin _2cos _,cos _2sin ααπααπ-=??+=+ §1.4.1、正弦、余弦函数的图象1、记住正弦、余弦函数图象:2、能够对照图象讲出正弦、余弦函数的相关性质:定义域、值域、最大最小值、对称轴、对称中心、奇偶性、单调性、周期性. 3、会用五点法作图.§1.4.2、正弦、余弦函数的性质1、周期函数定义:对于函数()x f ,如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有()()x f T x f =+,那么函数()x f 就叫做周期函数,非零常数T 叫做这个函数的周期.§1.4.3、正切函数的图象与性质 1、记住正切函数的图象:2、能够对照图象讲出正切函数的相关性质:定义域、值域、对称中心、奇偶性、单调性、周期性. §1.5、函数()?ω+=x A y sin 的图象1、能够讲出函数x y sin =的图象和函数()b x A y ++=?ωsin 的图象之间的平移伸缩变换关系.2、对于函数:()()0,0sin >>++=ω?ωA b x A y 有:振幅A ,周期ωπ2=T ,初相?,相位?ω+x ,频率πω21==f .第三章、三角恒等变换两角和与差的正弦、余弦、正切公式cos()cos cos sin sin αβαβαβ-=+cos()cos cos sin sin αβαβαβ+=-sin()αβ+=sin cos cos sin αβαβ+sin()sin cos cos sin αβαβαβ-=-tan()αβ-tan tan 1tan tan αβαβ-=+ . tan()αβ+tan tan 1tan tan αβαβ+=-二倍角的正弦、余弦、正切公式1、_cos sin 2_2sin ααα=,变形:cos α=ααsin 22sin .2、22cos2cossin ααα=-22cos 1α=-212sin α=-变形1:21cos 2cos 2αα+=,变形2:21cos 2sin 2αα-=. 3、22tan tan 21tan ααα=- 1、注意正切化弦、平方降次. 解三角形 1、正弦定理R CcB b A a 2sin sin sin === 2、余弦定理a A bc c b cos 222-+=变形 cosA=bca cb 2222-+b B ac c a cos 2222-+=变形 cosB=acb c a 2222-+c C ab b a cos 2222-+=变形cosC=abc b a 2222-+3、三角形面积公式: S =21absinC=21bcsinA=21acsinB 课本题(必修4)1.(P 11 习题13)若扇形的周长为定值l ,则该扇形的圆心角为多大时,扇形的面积最大?22.(P 23 练习4)已知sin (4π-x )=-51,且0<x<="">623.( P 24 习题9(2))设tan α=-21,计算αααα22cos 2cos sin sin 1--。
06第六章 三角函数【讲义】

x
x
注:以上两例用到了三角函数的单调性和有界性及辅助角公式,值得注意的是角的讨论。
用心 爱心 专心
3.最小正周期的确定。 例 4 求函数 y=sin(2cos|x|)的最小正周期。
4.三角最值问题。 例5 已知函数 y=sinx+ 1 cos x ,求函数的最大值与最小值。
2
例6
设 0< <π,求 sin
的图象先保持横坐标不变,纵坐标变为原来的 A 倍,再保持纵坐标不变,横坐标变为原来
个单位,得到 y=Asin( x+ )的图象。 例 10 例 10 已知 f(x)=sin( x+ )( >0, 0≤ ≤π)是 R 上的偶函数,其图象关于点 3 M ,0 对称,且在区间 0, 上是单调函数,求 和 的值。
是很容易的。
6.图象变换:y=sinx(x∈R)与 y=Asin( x+ )(A, , >0). 由 y=sinx 的图象向左平移 个单位,然后保持横坐标不变,纵坐标变为原来的 A 倍,然后 再保持纵坐标不变,横坐标变为原来的
1
,得到 y=Asin( x+ )的图象;也可以由 y=sinx
x 2 , 2 的反函数叫反正切函数。记作 y=arctanx(x∈[-∞, +∞]). y=cosx(x∈[0, π])的反
函数称为反余切函数,记作 y=arccotx(x∈[-∞, +∞]). 定理 15 三角方程的解集,如果 a∈(-1,1),方程 sinx=a 的解集是{x|x=nπ+(-1)narcsina, n∈Z}。 方程 cosx=a 的解集是{x|x=2kx arccosa, k∈Z}. 如果 a∈R,方程 tanx=a 的解集是 {x|x=kπ+arctana, k∈Z}。恒等式:arcsina+arccosa= 定理 16 若 x 0,
三角函数.讲义学生版

板块一 基础知识一、锐角三角函数的定义1. 锐角A 的正弦、余弦、正切、余切都叫做A ∠的锐角三角函数.2. 正弦:Rt ABC ∆中,锐角A 的对边与斜边的比叫做A ∠的正弦,记作sin A ,即sin a A c =.3. 余弦:Rt ABC ∆中,锐角A 的邻边与斜边的比叫做A ∠的余弦,记作cos A ,即cos b A c =.4. 正切:Rt ABC ∆中,锐角A 的对边与邻边的比叫做A ∠的正切,记作tan A ,即tan a A b =.5. 余切:Rt ABC ∆中,锐角A 的邻边与对边的比叫做A ∠的余切,记作cot A ,即cot b A a=. 从定义中可以看出,① 正弦、余弦、正切、余切都是在直角三角形中给出的,要避免应用时对任意三角形随便套用定义. ② sin A 、cos A 、tan A 、cot A 分别是正弦、余弦、正切、余切的数学表达符号,是一个整体,不能理解为sin 与A 、cos 与A 、tan 与A 、cot 与A 的乘积.③ 在直角三角形中,正弦、余弦、正切、余切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值,当这个锐角确定后,这些比值都是固定值.二、特殊角三角函数这些特殊角的三角函数值一定要牢牢记住.三、锐角三角函数的取值范围在Rt ABC ∆中,90C ∠=︒,000a b c a c b c >>><<,,,,,又s i n a A c =,cos b A c =,tan a A b =,cot b A a=,所以0sin 10cos 1tan 0cot 0A A A A <<<<>>,,,.四、三角函数关系1. 同角三角函数关系:三角函数 0︒ 30︒ 45︒ 60︒ 90︒ sin A 0 12 22 321 cos A 1 32 2212 0 tan A 0 331 3 - cot A - 3 1 330 例题精讲三角函数22sin cos 1A A +=,sin tan cos AA A=,tan cot 1A A ⋅= 2. 互余角三角函数关系:⑴ 任意锐角的正弦值等于它的余角的余弦值:()sin cos 90A A =︒-; ⑵ 任意锐角的余弦值等于它的余角的正弦值:()cos sin 90A A =︒-; ⑶ 任意锐角的正切值等于它的余角的余切值:()tan cot 90A A =︒-;⑷ 任意锐角的余切值等于它的余角的正切值:()cot tan 90A A =︒-.3. 锐角三角函数值的变化规律: 令1c =,锐角A ∠越小,则a 越小,则b 越大;当A ∠越大,则a 就越大,b 就越小,且a c b c <<,,所以当角度在0~90︒︒范围内变化时,正弦值随角度的增大(或减小)而增大(或减小);余弦值随角度的增大(或减小)而减小(或增大).而正切值也是随角度的增大(或减小)而增大(或减小);余切值随角度的增大(或减小)而减小(或增大).可以应用0~90︒︒间的正弦值、余弦值、正切值、余切值的增减性来比较角的正弦、余弦、正切、余切值的大小,其规律是:⑴A B 、为锐角且A B >,则sin sin A B >,cos cos A B <,tan tan A B >,cot cot A B <;⑵A B 、为锐角且A B <,则s in s in A B <,cos cos A B >,tan tan A B <,cot cot A B >.该规律反过来也成立.板块二 常用公式1. 和角公式:cos()cos cos sin sin αβαβαβ+=-,sin()sin cos cos sin αβαβαβ+=+,tan tan tan()1tan tan αβαβαβ++=-⋅;2. 差角公式:cos()cos cos sin sin αβαβαβ-=+,sin()sin cos cos sin αβαβαβ-=-,tan tan tan()1tan tan αβαβαβ--=+⋅;3. 倍角公式:2222cos2cos sin 2cos 112sin ααααα=-=-=-,sin22sin cos ααα=,22tan tan 21tan ααα=-;4. 半角公式:21cos cos 22αα+=,21cos sin 22αα-=,sin 1cos tan 21cos sin ααααα-==+; 5. 万能公式:22tan2sin 1tan 2ααα=+,221tan 2cos 1tan 2ααα-=+,22tan2tan 1tan 2ααα=-;6. 积化和差公式:1cos cos [cos()cos()]2αβαβαβ=++-,1cos sin [sin()sin()]2αβαβαβ=+--,1sin cos [sin()sin()]2αβαβαβ=++-,1sin sin [cos()cos()]2αβαβαβ=-+--.7. 和差化积公式:cos cos 2cos cos22αβαβαβ+-+=,cos cos 2sin sin22αβαβαβ+--=-,sin sin 2sin cos22αβαβαβ+-+=,sin sin 2cossin22αβαβαβ+--=.板块一、三角函数基础【例1】 已知如图:在Rt ABC ∆中,810BC AC ==,.求sin A 和sin B 的值。
三角函数的图像和性质知识点讲解+例题讲解(含解析)

三角函数的图像与性质一、知识梳理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝ ⎛⎭⎪⎫π2,1,(π,0),⎝ ⎛⎭⎪⎫3π2,-1,(2π,0).(2)余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )π3.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是14个周期. (2)正切曲线相邻两对称中心之间的距离是半个周期.(3).对于y =tan x 不能认为其在定义域上为增函数,而是在每个区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )内为增函数.二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”) (1)余弦函数y =cos x 的对称轴是y 轴.( ) (2)正切函数y =tan x 在定义域内是增函数.( ) (3)已知y =k sin x +1,x ∈R ,则y 的最大值为k +1.( ) (4)y =sin|x |是偶函数.( )解析 (1)余弦函数y =cos x 的对称轴有无穷多条,y 轴只是其中的一条. (2)正切函数y =tan x 在每一个区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )上都是增函数,但在定义域内不是单调函数,故不是增函数.(3)当k >0时,y max =k +1;当k <0时,y max =-k +1. 答案 (1)× (2)× (3)× (4)√2.若函数y =2sin 2x -1的最小正周期为T ,最大值为A ,则( ) A.T =π,A =1 B.T =2π,A =1 C.T =π,A =2D.T =2π,A =2解析 最小正周期T =2π2=π,最大值A =2-1=1.故选A. 答案 A3.函数y =-tan ⎝ ⎛⎭⎪⎫2x -3π4的单调递减区间为________.解析 由-π2+k π<2x -3π4<π2+k π(k ∈Z ), 得π8+k π2<x <5π8+k π2(k ∈Z ),所以y =-tan ⎝ ⎛⎭⎪⎫2x -3π4的单调递减区间为⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z ). 答案 ⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z )4.(2017·全国Ⅱ卷)函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3的最小正周期为( )A.4πB.2πC.πD.π2解析 由题意T =2π2=π. 答案 C5.(2017·全国Ⅲ卷)函数f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+cos ⎝ ⎛⎭⎪⎫x -π6的最大值为( )A.65B.1C.35D.15解析 cos ⎝ ⎛⎭⎪⎫x -π6=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫x +π3=sin ⎝ ⎛⎭⎪⎫x +π3,则f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+sin ⎝ ⎛⎭⎪⎫x +π3=65sin ⎝ ⎛⎭⎪⎫x +π3,函数的最大值为65. 答案 A6.(2018·江苏卷)已知函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫-π2<φ<π2 的图象关于直线x =π3对称,则φ的值是________.解析 由函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫-π2<φ<π2的图象关于直线x =π3对称,得sin ⎝ ⎛⎭⎪⎫2π3+φ=±1.所以2π3+φ=π2+k π(k ∈Z ),所以φ=-π6+k π(k ∈Z ),又-π2<φ<π2,所以φ=-π6. 答案 -π6考点一 三角函数的定义域【例1】 (1)函数f (x )=-2tan ⎝ ⎛⎭⎪⎫2x +π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x |x ≠π6 B.⎩⎨⎧⎭⎬⎫x |x ≠-π12 C.⎩⎨⎧⎭⎬⎫x |x ≠k π+π6(k ∈Z ) D.⎩⎨⎧⎭⎬⎫x |x ≠k π2+π6(k ∈Z ) (2)不等式3+2cos x ≥0的解集是________.(3)函数f (x )=64-x 2+log 2(2sin x -1)的定义域是________. 解析 (1)由2x +π6≠k π+π2(k ∈Z ),得x ≠k π2+π6(k ∈Z ).(2)由3+2cos x ≥0,得cos x ≥-32,由余弦函数的图象,得在一个周期[-π,π]上,不等式cos x ≥-32的解集为⎩⎨⎧⎭⎬⎫x |-5π6≤x ≤56π,故原不等式的解集为⎩⎨⎧⎭⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z .(3)由题意,得⎩⎨⎧64-x 2≥0,①2sin x -1>0,②由①得-8≤x ≤8,由②得sin x >12,由正弦曲线得π6+2k π<x <56 π+2k π(k ∈Z ).所以不等式组的解集为⎝ ⎛⎭⎪⎫-116π,-76π∪⎝ ⎛⎭⎪⎫π6,56π∪⎝ ⎛⎦⎥⎤13π6,8. 答案 (1)D (2)⎩⎨⎧⎭⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z (3)⎝ ⎛⎭⎪⎫-116π,-76π∪⎝ ⎛⎭⎪⎫π6,56π∪⎝ ⎛⎦⎥⎤13π6,8【训练1】 (1)函数y =sin x -cos x 的定义域为________. (2)函数y =lg(sin x )+cos x -12的定义域为______.解析 (1)要使函数有意义,必须使sin x -cos x ≥0.利用图象,在同一坐标系中画出[0,2π]上y =sin x 和y =cos x 的图象,如图所示.在[0,2π]上,满足sin x =cos x 的x 为π4,5π4再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x |π4+2k π≤x ≤54π+2k π,k ∈Z .(2)要使函数有意义必须有⎩⎪⎨⎪⎧sin x >0,cos x -12≥0, 即⎩⎪⎨⎪⎧sin x >0,cos x ≥12,解得⎩⎪⎨⎪⎧2k π<x <π+2k π,-π3+2k π≤x ≤π3+2k π(k ∈Z ),所以2k π<x ≤π3+2k π(k ∈Z ),所以函数的定义域为⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∈Z .答案(1)⎩⎨⎧⎭⎬⎫x |π4+2k π≤x ≤54π+2k π,k ∈Z (2)⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∈Z考点二 三角函数的值域与最值【例2】 (1)y =3sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤0,π2上的值域是________.(2)(2017·全国Ⅱ卷)函数f (x )=sin 2x +3cos x -34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0,π2的最大值是________. (3)函数y =sin x -cos x +sin x cos x 的值域为________.解析 (1)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-12,1,故3sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,3,即y =3sin ⎝ ⎛⎭⎪⎫2x -π6的值域为⎣⎢⎡⎦⎥⎤-32,3. (2)由题意可得f (x )=-cos 2x +3cos x +14=-(cos x -32)2+1.∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴cos x ∈[0,1].∴当cos x =32,即x =π6时,f (x )max =1. (3)设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x cos x ,sin x cos x =1-t22,且-2≤t ≤2,所以y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-2时,y min =-12- 2 .所以函数的值域为⎣⎢⎡⎦⎥⎤-12-2,1. 答案 (1)⎣⎢⎡⎦⎥⎤-32,3 (2)1 (3)⎣⎢⎡⎦⎥⎤-12-2,1【训练2】 (1)函数f (x )=cos 2x +6cos ⎝ ⎛⎭⎪⎫π2-x 的最大值为( )A.4B.5C.6D.7(2)(2019·临沂模拟)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫x +π6,其中x ∈⎣⎢⎡⎦⎥⎤-π3,a ,若f (x )的值域是⎣⎢⎡⎦⎥⎤-12,1,则实数a 的取值范围是________. 解析 (1)由f (x )=cos 2x +6cos ⎝ ⎛⎭⎪⎫π2-x =1-2sin 2x +6sin x =-2⎝ ⎛⎭⎪⎫sin x -322+112,又sin x ∈[-1,1],所以当sin x =1时函数的最大值为5.(2)由x ∈⎣⎢⎡⎦⎥⎤-π3,a ,知x +π6∈⎣⎢⎡⎦⎥⎤-π6,a +π6.因为x +π6∈⎣⎢⎡⎦⎥⎤-π6,π2时,f (x )的值域为⎣⎢⎡⎦⎥⎤-12,1,所以由函数的图象知π2≤a +π6≤7π6,所以π3≤a ≤π. 答案 (1)B(2)⎣⎢⎡⎦⎥⎤π3,π考点三 三角函数的单调性 角度1 求三角函数的单调区间【例3-1】 (1)函数f (x )=tan ⎝ ⎛⎭⎪⎫2x -π3的单调递增区间是( ) A.⎣⎢⎡⎦⎥⎤k π12-π12,k π2+5π12(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π12-π12,k π2+5π12(k ∈Z )C.⎝ ⎛⎭⎪⎫k π+π6,k π+2π3(k ∈Z )D.⎝ ⎛⎭⎪⎫k π-π12,k π+5π12(k ∈Z ) (2)函数y =sin ⎝ ⎛⎭⎪⎫-2x +π3的单调递减区间为________. 解析 (1)由k π-π2<2x -π3<k π+π2(k ∈Z ),得k π2-π12<x <k π2+5π12(k ∈Z ),所以函数f (x )=tan ⎝ ⎛⎭⎪⎫2x -π3的单调递增区间为⎝ ⎛⎭⎪⎫k π2-π12,k π2+5π12(k ∈Z ).(2)y =-sin ⎝ ⎛⎭⎪⎫2x -π3,它的减区间是y =sin ⎝ ⎛⎭⎪⎫2x -π3的增区间.令2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故其单调递减区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z . 答案 (1)B (2)⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z角度2 利用单调性比较大小【例3-2】 已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫x +π6,设a =f ⎝ ⎛⎭⎪⎫π7,b =f ⎝ ⎛⎭⎪⎫π6,c =f ⎝ ⎛⎭⎪⎫π4,则a ,b ,c 的大小关系是( ) A.a >b >c B.a >c >b C.c >a >bD.b >a >c解析 令2k π≤x +π6≤2k π+π,k ∈Z ,解得2k π-π6≤x ≤2k π+5π6,k ∈Z ,∴函数f (x )=2cos ⎝ ⎛⎭⎪⎫x +π6在⎣⎢⎡⎦⎥⎤-π6,5π6上是减函数,∵-π6<π7<π6<π4<5π6, ∴f ⎝ ⎛⎭⎪⎫π7>f ⎝ ⎛⎭⎪⎫π6>f ⎝ ⎛⎭⎪⎫π4. 答案 A角度3 利用单调性求参数【例3-3】 (2018·全国Ⅱ卷)若f (x )=cos x -sin x 在[-a ,a ]是减函数,则a 的最大值是( ) A.π4B.π2C.3π4D.π解析 f (x )=cos x -sin x =2cos ⎝ ⎛⎭⎪⎫x +π4,由题意得a >0,故-a +π4<π4,因为f (x )=2cos ⎝ ⎛⎭⎪⎫x +π4在[-a ,a ]是减函数,所以⎩⎪⎨⎪⎧-a +π4≥0,a +π4≤π,a >0,解得0<a ≤π4,所以a 的最大值是π4.答案 A【训练3】 (1)设函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈⎣⎢⎡⎦⎥⎤-π2,π,则以下结论正确的是( )A.函数f (x )在⎣⎢⎡⎦⎥⎤-π2,0上单调递减B.函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增 C.函数f (x )在⎣⎢⎡⎦⎥⎤π2,5π6上单调递减 D.函数f (x )在⎣⎢⎡⎦⎥⎤5π6,π上单调递增(2)cos 23°,sin 68°,cos 97°的大小关系是________.(3)若函数f (x )=sin ωx (ω>0)在⎣⎢⎡⎦⎥⎤0,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减,则ω=________.解析 (1)由x ∈⎣⎢⎡⎦⎥⎤-π2,0,得2x -π3∈⎣⎢⎡⎦⎥⎤-4π3,-π3,此时函数f (x )先减后增;由x ∈⎣⎢⎡⎦⎥⎤0,π2,得2x -π3∈⎣⎢⎡⎦⎥⎤-π3,2π3,此时函数f (x )先增后减;由x ∈⎣⎢⎡⎦⎥⎤π2,5π6,得2x -π3∈⎣⎢⎡⎦⎥⎤2π3,4π3,此时函数f (x )单调递减;由x ∈⎣⎢⎡⎦⎥⎤5π6,π,得2x -π3∈⎣⎢⎡⎦⎥⎤4π3,5π3,此时函数f (x )先减后增.(2)sin 68°=cos 22°,又y =cos x 在[0°,180°]上是减函数,∴sin 68°>cos 23°>cos 97°.(3)法一 由于函数f (x )=sin ωx (ω>0)的图象经过坐标原点,由已知并结合正弦函数的图象可知,π3为函数f (x )的14周期,故2πω=4π3,解得ω=32.法二 由题意,得f (x )max =f ⎝ ⎛⎭⎪⎫π3=sin π3ω=1.由已知并结合正弦函数图象可知,π3ω=π2+2k π(k ∈Z ),解得ω=32+6k (k ∈Z ),所以当k =0时,ω=32.答案 (1)C (2)sin 68°>cos 23°>cos 97° (3)32考点四 三角函数的周期性、奇偶性、对称性 角度1 三角函数奇偶性、周期性【例4-1】 (1)(2018·全国Ⅰ卷)已知函数f (x )=2cos 2x -sin 2x +2,则( ) A.f (x )的最小正周期为π,最大值为3 B.f (x )的最小正周期为π,最大值为4 C.f (x )的最小正周期为2π,最大值为3 D.f (x )的最小正周期为2π,最大值为4(2)(2019·杭州调研)设函数f (x )=sin ⎝ ⎛⎭⎪⎫12x +θ-3cos ⎝ ⎛⎭⎪⎫12x +θ⎝ ⎛⎭⎪⎫|θ|<π2的图象关于y 轴对称,则θ=( ) A.-π6 B.π6 C.-π3 D.π3解析 (1)易知f (x )=2cos 2x -sin 2x +2=3cos 2x +1=3cos 2x +12+1=32cos 2x +52,则f (x )的最小正周期为π,当2x =2k π,即x =k π(k ∈Z )时,f (x )取得最大值,最大值为4.(2)f (x )=sin ⎝ ⎛⎭⎪⎫12x +θ-3cos ⎝ ⎛⎭⎪⎫12x +θ=2sin ⎝ ⎛⎭⎪⎫12x +θ-π3, 由题意可得f (0)=2sin ⎝ ⎛⎭⎪⎫θ-π3=±2,即sin ⎝ ⎛⎭⎪⎫θ-π3=±1,∴θ-π3=π2+k π(k ∈Z ),∴θ=5π6+k π(k ∈Z ). ∵|θ|<π2,∴k =-1时,θ=-π6. 答案 (1)B (2)A角度2 三角函数图象的对称性【例4-2】 (1)已知函数f (x )=a sin x +cos x (a 为常数,x ∈R )的图象关于直线x =π6对称,则函数g (x )=sin x +a cos x 的图象( )A.关于点⎝ ⎛⎭⎪⎫π3,0对称B.关于点⎝ ⎛⎭⎪⎫2π3,0对称 C.关于直线x =π3对称 D.关于直线x =π6对称解析 (1)因为函数f (x )=a sin x +cos x (a 为常数,x ∈R )的图象关于直线x =π6对称,所以f (0)=f ⎝ ⎛⎭⎪⎫π3,所以1=32a +12,a =33,所以g (x )=sin x +33cos x =233sin ⎝ ⎛⎭⎪⎫x +π6,函数g (x )的对称轴方程为x +π6=k π+π2(k ∈Z ),即x =k π+π3(k ∈Z ),当k =0时,对称轴为直线x =π3,所以g (x )=sin x +a cos x 的图象关于直线x =π3对称. 规律方法 1.对于可化为f (x )=A sin(ωx +φ)形式的函数,如果求f (x )的对称轴,只需令ωx +φ=π2+k π(k ∈Z ),求x 即可;如果求f (x )的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z ),求x 即可.2.对于可化为f (x )=A cos(ωx +φ)形式的函数,如果求f (x )的对称轴,只需令ωx +φ=k π(k ∈Z ),求x ;如果求f (x )的对称中心的横坐标,只需令ωx +φ=π2+k π(k ∈Z ),求x 即可.【训练4】 (1)(2018·全国Ⅲ卷)函数f (x )=tan x1+tan 2x的最小正周期为( )A.π4B.π2C.πD.2π(2)设函数f (x )=cos ⎝ ⎛⎭⎪⎫x +π3,则下列结论错误的是( )A.f (x )的一个周期为-2πB.y =f (x )的图象关于直线x =8π3对称 C.f (x +π)的一个零点为x =π6 D.f (x )在⎝ ⎛⎭⎪⎫π2,π单调递减解析 (1)f (x )的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π+π2,k ∈Z .f (x )=sin x cos x 1+⎝ ⎛⎭⎪⎫sin x cos x 2=sin x ·cos x =12sin 2x ,∴f (x )的最小正周期T =2π2=π.(2)A 项,因为f (x )的周期为2k π(k ∈Z 且k ≠0),所以f (x )的一个周期为-2π,A 项正确.B 项,因为f (x )图象的对称轴为直线x =k π-π3(k ∈Z ),当k =3时,直线x =8π3是其对称轴,B 项正确.C 项,f (x +π)=cos ⎝ ⎛⎭⎪⎫x +4π3,将x =π6代入得到f ⎝ ⎛⎭⎪⎫7π6=cos 3π2=0,所以x =π6是f (x+π)的一个零点,C 项正确.D 项,因为f (x )=cos ⎝ ⎛⎭⎪⎫x +π3的递减区间为⎣⎢⎡⎦⎥⎤2k π-π3,2k π+2π3 (k ∈Z ),递增区间为⎣⎢⎡⎦⎥⎤2k π+2π3,2k π+5π3 (k ∈Z ),所以⎝ ⎛⎭⎪⎫π2,2π3是减区间,⎣⎢⎡⎭⎪⎫2π3,π是增区间,D 项错误.答案 (1)C (2)D三、课后练习1.若对于任意x ∈R 都有f (x )+2f (-x )=3cos x -sin x ,则函数f (2x )图象的对称中心为( )A.⎝ ⎛⎭⎪⎫k π-π4,0(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π-π8,0(k ∈Z ) C.⎝ ⎛⎭⎪⎫k π2-π4,0(k ∈Z ) D.⎝ ⎛⎭⎪⎫k π2-π8,0(k ∈Z ) 解析 因为f (x )+2f (-x )=3cos x -sin x ,所以f (-x )+2f (x )=3cos x +sin x .解得f (x )=cos x +sin x =2sin ⎝ ⎛⎭⎪⎫x +π4,所以f (2x )=2sin ⎝ ⎛⎭⎪⎫2x +π4. 令2x +π4=k π(k ∈Z ),得x =k π2-π8(k ∈Z ).所以f (2x )图象的对称中心为⎝ ⎛⎭⎪⎫k π2-π8,0(k ∈Z ). 答案 D2.(2017·天津卷)设函数f (x )=2sin(ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f ⎝ ⎛⎭⎪⎫5π8=2,f ⎝ ⎛⎭⎪⎫11π8=0,且f (x )的最小正周期大于2π,则( ) A.ω=23,φ=π12 B.ω=23,φ=-11π12C.ω=13,φ=-11π24D.ω=13,φ=7π24解析 ∵f ⎝ ⎛⎭⎪⎫5π8=2,f ⎝ ⎛⎭⎪⎫11π8=0,且f (x )的最小正周期大于2π, ∴f (x )的最小正周期为4⎝ ⎛⎭⎪⎫11π8-5π8=3π, ∴ω=2π3π=23,∴f (x )=2sin ⎝ ⎛⎭⎪⎫23x +φ. ∴2sin ⎝ ⎛⎭⎪⎫23×5π8+φ=2,得φ=2k π+π12(k ∈Z ), 又|φ|<π,∴取k =0,得φ=π12.答案 A3.已知x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,则f (x )的单调递减区间是________.解析 因为x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,所以sin ⎝ ⎛⎭⎪⎫2×π3+φ=1,解得φ=2k π-π6(k ∈Z ). 不妨取φ=-π6,此时f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6, 令2k π+π2≤2x -π6≤2k π+3π2(k ∈Z ),得f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤k π+π3,k π+56π(k ∈Z ). 答案 ⎣⎢⎡⎦⎥⎤k π+π3,k π+56π(k ∈Z )4.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫π2-x sin x -3cos 2x +32. (1)求f (x )的最大值及取得最大值时x 的值;(2)若方程f (x )=23在(0,π)上的解为x 1,x 2,求cos(x 1-x 2)的值.解 (1)f (x )=cos x sin x -32(2cos 2x -1) =12sin 2x -32cos 2x =sin ⎝ ⎛⎭⎪⎫2x -π3. 当2x -π3=π2+2k π(k ∈Z ),即x =512π+k π(k ∈Z )时,函数f (x )取最大值,且最大值为1.(2)由(1)知,函数f (x )图象的对称轴为x =512π+k π(k ∈Z ),∴当x ∈(0,π)时,对称轴为x =512π.又方程f (x )=23在(0,π)上的解为x 1,x 2.∴x 1+x 2=56π,则x 1=56π-x 2,∴cos(x 1-x 2)=cos ⎝ ⎛⎭⎪⎫56π-2x 2=sin ⎝ ⎛⎭⎪⎫2x 2-π3, 又f (x 2)=sin ⎝ ⎛⎭⎪⎫2x 2-π3=23, 故cos(x 1-x 2)=23.5.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫x -π6,若对任意的实数α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,都存在唯一的实数β∈[0,m ],使f (α)+f (β)=0,则实数m 的最小值是________.解析 因为α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,所以α-π6∈⎣⎢⎡⎦⎥⎤-π,-2π3,则f (α)=sin ⎝ ⎛⎭⎪⎫α-π6∈⎣⎢⎡⎦⎥⎤-32,0,因为对任意的实数α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,都存在唯一的实数β∈[0,m ],使f (α)+f (β)=0,所以f (β)在[0,m ]上单调,且f (β)∈⎣⎢⎡⎦⎥⎤0,32,则sin ⎝ ⎛⎭⎪⎫β-π6∈⎣⎢⎡⎦⎥⎤0,32,则β-π6∈⎣⎢⎡⎦⎥⎤0,π3,所以β∈⎣⎢⎡⎦⎥⎤π6,π2,即实数m 的最小值是π2. 答案 π26.(2017·山东卷)函数y =3sin 2x +cos 2x 的最小正周期为( )A.π2B.2π3C.πD.2π解析 ∵y =2⎝ ⎛⎭⎪⎫32sin 2x +12cos 2x =2sin ⎝ ⎛⎭⎪⎫2x +π6, ∴T =2π2=π.答案 C7.(2019·石家庄检测)若⎝ ⎛⎭⎪⎫π8,0是函数f (x )=sin ωx +cos ωx 图象的一个对称中心,则ω的一个取值是( )A.2B.4C.6D.8解析 因为f (x )=sin ωx +cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx +π4,由题意,知f ⎝ ⎛⎭⎪⎫π8=2sin ⎝ ⎛⎭⎪⎫ωπ8+π4=0,所以ωπ8+π4=k π(k ∈Z ),即ω=8k -2(k ∈Z ),当k =1时,ω=6.答案 C8.已知函数f (x )=2sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤-π3,π4上的最小值是-2,则ω的最小值等于( ) A.23 B.32 C.2 D.3解析 ∵ω>0,-π3≤x ≤π4,∴-ωπ3≤ωx ≤ωπ4.由已知条件知-ωπ3≤-π2,∴ω≥32.答案 B9.(2019·湖南十四校联考)已知函数f (x )=2sin ωx -cos ωx (ω>0),若f (x )的两个零点x 1,x 2满足|x 1-x 2|min =2,则f (1)的值为( ) A.102 B.-102 C.2 D.-2解析 依题意可得函数的最小正周期为2πω=2|x 1-x 2|min =2×2=4,即ω=π2,所以f (1)=2sin π2-cos π2=2.答案 C10.(2018·北京卷)设函数f (x )=cos ⎝ ⎛⎭⎪⎫ωx -π6(ω>0).若f (x )≤f ⎝ ⎛⎭⎪⎫π4对任意的实数x 都成立,则ω的最小值为________.解析 由于对任意的实数都有f (x )≤f ⎝ ⎛⎭⎪⎫π4成立,故当x =π4时,函数f (x )有最大值,故f ⎝ ⎛⎭⎪⎫π4=1,πω4-π6=2k π(k ∈Z ),∴ω=8k +23(k ∈Z ).又ω>0,∴ωmin =23. 答案 2311.(2019·北京通州区质检)已知函数f (x )=sin ωx -cos ωx (ω>0)的最小正周期为π.(1)求函数y =f (x )图象的对称轴方程;(2)讨论函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的单调性. 解 (1)∵f (x )=sin ωx -cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx -π4,且T =π, ∴ω=2,于是f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π4. 令2x -π4=k π+π2(k ∈Z ),得x =k π2+3π8(k ∈Z ).即函数f (x )图象的对称轴方程为x =k π2+3π8(k ∈Z ).(2)令2k π-π2≤2x -π4≤2k π+π2(k ∈Z ),得函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π8,k π+3π8(k ∈Z ). 注意到x ∈⎣⎢⎡⎦⎥⎤0,π2,所以令k =0,得函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的单调递增区间为⎣⎢⎡⎦⎥⎤0,3π8; 同理,其单调递减区间为⎣⎢⎡⎦⎥⎤3π8,π2.。
三角函数讲义

学生姓名年级授课时间教师姓名课时 2三角函数讲义(1)——任意角及任意角的三角函数,基本关系与诱导公式,两角和与差公式【高考会这样考】1.考查三角函数的定义及应用.2.考查三角函数值符号的确定.3.考查同角三角函数的基本关系式.4.考查诱导公式在三角函数化简求值中的运用.5.考查利用两角和与差的正弦、余弦、正切公式及倍角公式进行三角函数式的化简与求值.6.利用三角公式考查角的变换、角的范围基础梳理1.任意角(1)角的概念的推广①按旋转方向不同分为正角、负角、零角.②按终边位置不同分为象限角和轴线角.(2)终边相同的角终边与角α相同的角可写成α+k·360°(k∈Z).(3)弧度制①1弧度的角:把长度等于半径长的弧所对的圆心角叫做1弧度的角.②规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,|α|=lr,l是以角α作为圆心角时所对圆弧的长,r为半径.③用“弧度”做单位来度量角的制度叫做弧度制,比值lr与所取的r的大小无关,仅与角的大小有关.④弧度与角度的换算:360°=2π弧度;180°=π弧度.⑤弧长公式:l=|α|r,扇形面积公式:S扇形=12lr=12|α|r2.2.任意角的三角函数定义设α是一个任意角,角α的终边上任意一点P(x,y),它与原点的距离为r(r>0),那么角α的正弦、余弦、正切分别是:sin α=yr,cos α=xr,tan α=yx,它们都是以角为自变量,以比值为函数值的函数.3.三角函数线设角α的顶点在坐标原点,始边与x轴非负半轴重合,终边与单位圆相交于点P,过P作PM垂直于x轴于M,则点M是点P在x轴上的正射影.由三角函数的定义知,点P的坐标为(cos_α,sin_α),即P(cos_α,sin_α),其中cos α=OM,sin α=MP,单位圆与x轴的正半轴交于点A,单位圆在A点的切线与α的终边或其反向延长线相交于点T,则tan α=AT.我们把有向线段OM、MP、AT叫做α的余弦线、正弦线、正切线.三角函数线有向线段MP为正弦线有向线段OM为余弦线有向线段AT为正切线4.同角三角函数的基本关系5.诱导公式6.两角和与差的正弦、余弦、正切公式7.二倍角的正弦、余弦、正切公式及降幂公式8.辅助角公式函数f (α)=a cos α+b sin α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)或f (α)=a 2+b 2cos(α-φ),其中φ可由a ,b 的值唯一确定.考向探究 题型一:角的集合表示及象限角的判定【例题1】下列与9π4的终边相同的角的表达式中正确的是( ). A .2k π+45°(k ∈Z ) B .k ·360°+94π(k ∈Z ) C .k ·360°-315°(k ∈Z )D .k π+5π4(k ∈Z )【例题2】若α=k ·180°+45°(k ∈Z ),则α在( ). A .第一或第三象限 B .第一或第二象限 C .第二或第四象限D .第三或第四象限【变式1】若α 是第二象限的角,则2α所在的象限是( ) A .第一、二象限B .第一、三象限C .第二、四象限D .第二、三象限题型二:三角函数的定义【例题3】已知角α的终边过点(-1,2),则cos α的值为( ). A .-55 B.255 C .-255 D .-12【变式2】已知角θ的终边经过点P (-3,m )(m ≠0)且sin θ=24 m ,试判断角θ所在的象限,并求cos θ和tan θ的值.题型三:弧度制的应用【例题4】已知半径为10的圆O 中,弦AB 的长为10. (1)求弦AB 所对的圆心角α的大小;(2)求α所在的扇形的弧长l 及弧所在的弓形的面积S .【变式3】 已知扇形周长为40,当它的半径和圆心角取何值时,才使扇形面积最大?题型四:三角函数线及其应用【例题5】在单位圆中画出适合下列条件的角α的终边的范围.并由此写出角α的集合:sin α≥32;【例题6】下列不等式中正确的是( )A .π74sin π75sin> B .⎪⎭⎫⎝⎛->7πtan π815tanC .⎪⎭⎫⎝⎛->⎪⎭⎫ ⎝⎛-6πsin 5πsin D .⎪⎭⎫⎝⎛->⎪⎭⎫ ⎝⎛-π49cos π53cos 【变式4】求函数的定义域:y =2cos x -1;【变式5】若2ππ24ππ2+≤≤+k k α,k ∈Z ,则sin α 与cos α 的大小关系是( ) A .sin α >cos αB .sin α <cos αC .sin α ≥cos αD .sin α ≤cos α题型五:利用同角三角函数关系化简与求值【例题7】已知sin 45α=,并且α是第二象限的角,那么tan α的值等于( )A.43-B.34-C.34D.43【变式6】已知tan 13α=-,计算:sin 2cos (1)5cos sin αααα+-; 21(2)2sin cos cos ααα+.题型六:利用诱导公式化简与求值【例题8】.如果sin(π1)2α+=-,那么cos 3()2πα-等于 ( )A.12B.12- C.32-D.32【例题9】已知cos(π6-θ)=a (|a |≤1),则cos(56π+θ)的值是________. 【变式7】已知f (α)=sin (π-α)cos (2π-α)sin ⎝⎛⎭⎫π2+αtan (π+α),求f ⎝⎛⎭⎫31π3.题型七:诱导公式、同角三角函数关系式的综合应用【例题10】已知sin 3()25πα-=,则cos(π2)α-等于( )A.725B.2425C.725-D.2425-【变式8】记cos(-80)=k ,那么tan100等于( )A.21k k - B.21k k -- C.21k k - D.21k k--题型八:和差角公式的运用【例题11】计算sin105=( ) A .624--B .624-C .624+-D .624+【例题12】计算cos18cos42cos72cos48-=( )A .12-B .12C .32-D .32【例题13】已知,(,)4αβ3π∈π,3sin()5αβ+=-,12sin()413βπ-=,则c o s ()4απ+= .【变式9】已知1t a n 3α=-,5cos ,5β=,(0,)αβ∈π,则tan()αβ+的值等于 .题型九:二倍角公式的运用 【例题14】化简1sin8+=( )A .sin 4cos4+B .sin 4cos4--C .sin 4D .cos 4【例题15】已知3sin(),45x π-=则sin 2x 的值为( )A.1925B.1625C.1425D.725【变式10】已知(,0)2x π∈-,4cos 5x =,则=x 2tan ( )A .247 B .247- C .724 D .724-【变式11】cos10cos80sin 20⋅= .题型十:“22sin cos sin()a b a b θθθϕ+=++”的应用【例题16】函数3sin 4cos 5y x x =++的最小正周期是( )A.5π B.2πC.πD.2π【例题17】函数x x y cos 3sin +=在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为 .【变式12】函数2sin cos 3cos 3y x x x =+-的图象的一个对称中心是( ) A.23(,)32π- B.53(,)62π- C.23(,)32π- D.(,3)3π-巩固训练1.角α与角β的终边互为反向延长线,则( ).A .α=-βB .α=180°+βC .α=k ·360°+β(k ∈Z )D .α=k ·360°±180°+β(k ∈Z )2.若sin α<0且tan α>0,则α是( ). A .第一象限角 B .第二象限角 C .第三象限角D .第四象限角3.把405°化为弧度为( )A .π3683B .π47 C .π613 D .π49 4.已知α =2rad ,则α 是第( )象限角A .一B .二C .三D .四5.(2011·课标全国)已知角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边在直线y =2x 上,则cos 2θ=( ). A .-45 B .-35 C.35 D.456.(2011·江西)已知角θ的顶点为坐标原点,始边为x 轴非负半轴,若P (4,y )是角θ终边上一点,且sin θ=-255,则y =________. 7.已知角α的终边在直线3x +4y =0上,求sin α+cos α+45tan α.8.当x ∈[0,2π ]时,使得不等式22cos ≥x 成立的x 的取值范围是( ) A .⎥⎦⎤⎢⎣⎡π2,4πB .⎥⎦⎤⎢⎣⎡4π,0C .⎥⎦⎤⎢⎣⎡-4π,4πD .⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡π2,4π74π,09.(2012·东莞模拟)已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ=( )A .-43 B.54 C .-34 D.4510.若cos α+2sin α=-5,则tan α=( )A.12 B .2 C .-12 D .-211.已知角α终边上一点P (-4,3),则cos ⎝⎛⎭⎫π2+αsin (-π-α)cos ⎝⎛⎭⎫11π2-αsin ⎝⎛⎭⎫9π2+α的值为________..12.已知sin θ=2cos θ,则sin (π2+θ)-cos (π-θ)sin (π2-θ)-sin (π-θ)=( )A .2B .-2C .0 D.2313.(2010,广东文16)设函数()3sin()6f x x πω=+,0,(,)x ω>∈-∞+∞ ,且以2π为最小正周期. (1)求(0)f ; (2)求()f x 的解析式;(3)若94125f απ⎛⎫+= ⎪⎝⎭,求sin α的值.14.(2011铁一中三模16)已知:函数()2sin 2cos()f x x x π=++. (1)求函数()f x 的最小正周期和值域;(2)若函数()f x 的图象过点6(,)5α,344ππα<<.求()4f πα+的值.15.已知,αβ均为锐角,1cos 7α=,11cos()14αβ+=-,则cos β= . 16.已知24βαπ3π<<<,且12cos()13αβ-=,3sin()5αβ+=-. (1)求,αβαβ-+的取值范围; (2)求cos2β的值.17.(福建文)若a ∈(0, 2π),且sin 2a+cos2a=14,则tana 的值等于A .22B . 33C . 2D . 318.(上海文)函数2sin cos y x x =-的最大值为 。
(完整word版)三角函数专题讲义

三角函数专题一、核心知识点归纳:1、正弦函数、余弦函数和正切函数的图象与性质:sin y x =cos y x =tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =; 当22x k ππ=-()k ∈Z 时,min 1y =-. 当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+ ()k ∈Z 上是减函数. 在,22k k ππππ⎛⎫-+ ⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称中心对称中心函 数 性 质2。
正、余弦定理:在ABC ∆中有: ①正弦定理:2sin sin sin a b cR A B C===(R 为ABC ∆外接圆半径) 2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩⇒ sin 2sin 2sin 2a A Rb B Rc C R⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩注意变形应用 ②面积公式:111sin sin sin 222ABC S abs C ac B bc A ∆=== ③余弦定理: 2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩二、方法总结:1.三角函数恒等变形的基本策略。
(经典讲义)高一数学下必修四第一章三角函数

高一数学下必修四第一章三角函数第一讲:三角函数(1)⎧⎪⎨⎪⎩正角:按逆时针方向旋转形成的角1、任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角2、角α的顶点与原点重合,角的始边与x轴的非负半轴重合,终边落在第几象限,则称α为第几象限角.第一象限角的集合为{}36036090,k k kαα⋅<<⋅+∈Z第二象限角的集合为{}36090360180,k k kαα⋅+<<⋅+∈Z第三象限角的集合为{}360180360270,k k kαα⋅+<<⋅+∈Z第四象限角的集合为{}360270360360,k k kαα⋅+<<⋅+∈Z终边在x轴上的角的集合为{}180,k kαα=⋅∈Z终边在y轴上的角的集合为{}18090,k kαα=⋅+∈Z终边在坐标轴上的角的集合为{}90,k kαα=⋅∈Z3、与角α终边相同的角的集合为{}360,k kββα=⋅+∈Z4、已知α是第几象限角,确定()*nnα∈N所在象限的方法:先把各象限均分n 等份,再从x 轴的正半轴的上方起,依次将各区域标上一、二、三、四,则α原来是第几象限对应的标号即为nα终边所落在的区域.5、长度等于半径长的弧所对的圆心角叫做1弧度.6、半径为r 的圆的圆心角α所对弧的长为l ,则角α的弧度数的绝对值是l rα=.7、弧度制与角度制的换算公式:2360π=,1180π=,180157.3π⎛⎫=≈⎪⎝⎭.8、若扇形的圆心角为()αα为弧度制,半径为r ,弧长为l ,周长为C ,面积为S ,则l r α=,2C r l =+,21122S lr r α==.9、设α是一个任意大小的角,α的终边上任意一点P 的坐标是(),x y ,它与原点的距离是()0r r =>,则sin y r α=,cos x rα=,()tan 0yx xα=≠. 10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正.11、三角函数线:sin α=MP ,cos α=OM ,tan α=AT 12、同角三角函数的基本关系:()221sin cos 1αα+=()2222sin 1cos ,cos 1sin αααα=-=-;()sin 2tan cos ααα=sin sin tan cos ,cos tan αααααα⎛⎫== ⎪⎝⎭.13、三角函数的诱导公式:()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=.()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-. ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-.口诀:函数名称不变,符号看象限.()5sin cos 2παα⎛⎫-=⎪⎝⎭,cos sin 2παα⎛⎫-= ⎪⎝⎭. ()6sin cos 2παα⎛⎫+=⎪⎝⎭,cos sin 2παα⎛⎫+=- ⎪⎝⎭. 口诀:正弦与余弦互换,符号看象限.14、函数sin y x =的图象上所有点向左(右)平移ϕ个单位长度,得到函数()sin y x ϕ=+的图象;再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象.函数sin y x =的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数sin y x ω=的图象;再将函数sin y x ω=的图象上所有点向左(右)平移ϕω个单位长度,得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. 函数()()sin 0,0y x ωϕω=A +A >>的性质: ①振幅:A ;②周期:2πωT =;③频率:12f ωπ==T ;④相位:x ωϕ+;⑤初相:ϕ.函数()sin y x ωϕ=A ++B ,当1x x =时,取得最小值为min y ;当2x x =时,取得最大值为max y ,则()max min 12y y A =-,()max min 12y y B =+,()21122x x x x T=-<. 15、正弦函数、余弦函数和正切函数的图象与性质:sin y x =cos y x =tan y x =图象定义R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭问题1各是第几象限角问题:已知α角是第三象限角,则2α,2问题21.有向线段:坐标轴是规定了方向的直线,那么与之平行的线段亦可规定方向。
三角函数的概念(精讲)(解析版)
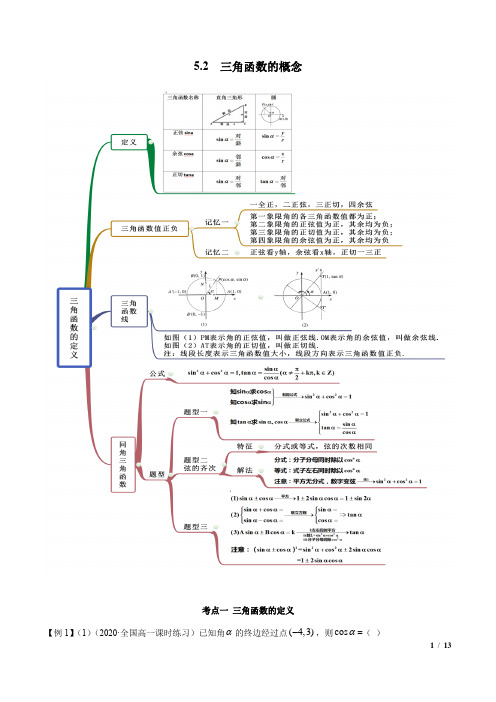
5.2 三角函数的概念考点一三角函数的定义-,则cosα=()【例1】(1)(2020·全国高一课时练习)已知角α的终边经过点(4,3)A .45B .35C .35D .45-(2)(2020·甘肃省岷县第一中学高二月考)若角600°的终边上有一点(-4,a ),则a 的值是( )A .B .±C .-D(3)(2020·应城市第一高级中学高一月考)已知角α的终边上一点的坐标为(sin 43π,cos 43π),则角α的最小正值为( ) A .76πB .116πC .56π D .43π 【答案】(1)D (2)C (3)A【解析】(1)∵已知角α的终边经过点(4,3)-,∴4,3,5x y r =-===.∴4cos 5x r α==-.故选:D .(2)∵角600︒的终边上有一点()4,a -,根据三角函数的定义可得tan 6004a︒=-,即()4tan 6004tan 540604tan 60a =-︒=-+=-︒=-,故选C.(3)由题意41sin cos32πα==-,又4sin 03π<,点(sin ,cos )33ππ44在第三象限,即α是第三象限角, ∴72,6k k Z παπ=+∈,最小正值为76π.故选:A .【一隅三反】1.(2020·辽宁沈河·沈阳二中高一期末)如果角α的终边过点(2sin 30,2cos30)P ︒︒-,那么sin α等于( )A .12-B .12C .D .【答案】C【解析】由题意得(1,P ,它与原点的距离为2,∴sin α=.故选:C.2.(2020·永州市第四中学高一月考)若一个α角的终边上有一点()4,P a -且sin cos αα⋅=,则a 的值为( )A .B .±C .-或D 【答案】C【解析】由已知,得()224sin44aaαα-==∴=-+,解得a=-C.3.(2020·河南高一期末)已知点()8,6cos60P m-在角α的终边上,且3tan4α=,则m的值为()A.2-B.2C.-D.【答案】A【解析】16cos60632m m m=⨯=,即点()8,3P m-,由三角函数的定义可得33tan84mα==-,解得2m=-.故选:A.考点二三角函数值正负判断【例3】(2020·辽宁高一期末)若sin tan0αα<,且costanαα<,则角α是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角【答案】C【解析】2sinsin tan0cosαααα=<,cos0α∴<,又2cos costan sinαααα=<,则sin0α<.因此,角α为第三象限角.故选:C.【一隅三反】1.(2020·大连市普兰店区第一中学高一月考)已知点()tan,sinPαα在第三象限,则角α的终边所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】点()tan,sinPαα在第三象限,∴tan0α<,sin0α<,由tan0α<,知角α的终边所在的象限为第二象限或第四象限,由sin 0α<,知角α的终边所在的象限为第三象限或第四象限, 综上,角α的终边所在的象限为第四象限.故选:D. 2.(2020·昆明市官渡区第一中学高一月考)若-2π<α<0,则点P(tanα,cosα)位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】B【解析】∵-2π<α<0,∴tanα<0,cosα>0,∴点P(tanα,cosα)位于第二象限,故选B 3.(2020·山东滨州·高二期末)“θ为第一或第四象限角”是“cos 0θ>”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】当θ为第一或第四象限角时,cos 0θ>,所以“θ为第一或第四象限角”是“cos 0θ>”的充分条件,当cos 0θ>时,θ为第一或第四象限角或x 轴正半轴上的角,所以“θ为第一或第四象限角”不是“cos 0θ>”的必要条件,所以“θ为第一或第四象限角”是“cos 0θ>”的充分不必要条件.故选:A考点三 三角函数线【例3】(1)(2020·辽宁沈阳·高一期中)下列关系式中,正确的是( ) A .sin1cos1tan1<< B .cos1sin1tan1<< C .tan1sin1cos1<<D .cos1tan1sin1<< (2)(2020·内蒙古通辽·高一期中(理))对于下列四个命题: ①sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭;②2517cos cos 44ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭; ③tan138tan143︒>︒; ④tan 40sin 40︒>︒. 其中正确命题的序号是( ) A .①③B .①④C .②③D .②④【答案】(1)B (2)B【解析】(1)画出1弧度的正弦线,余弦线和正切线,如图所示:则sin1,cos1,tan1MP OM AT ===,比较,,OM MP AT 的长度, 得cos1sin1tan1<< .故选:B.(2)根据正弦函数的性质,可知:sin y x =在,22ππ⎛⎫- ⎪⎝⎭上单调递增1810ππ->-,sin sin 1810ππ⎛⎫⎛⎫∴->- ⎪ ⎪⎝⎭⎝⎭,①正确; 由诱导公式,可得:2525cos cos 6cos 444ππππ⎛⎫⎛⎫⎛⎫-=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1717cos cos 4cos 444ππππ⎛⎫⎛⎫⎛⎫-=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2517cos cos 44ππ⎛⎫⎛⎫∴-=- ⎪ ⎪⎝⎭⎝⎭,②错误; 根据正切函数的性质,可知:tan y x =在,2ππ⎛⎫⎪⎝⎭上单调递增,138143︒<︒,tan138tan143∴<︒︒,③错误;画出2409πα==的正弦线和正切线,如下: ︒=tan 40AT ,︒=sin 40MP ,所以tan 40sin 40︒>︒,故④正确.故选:B【一隅三反】1.(2019·重庆)sin4,cos4,tan4a b c===则,,a b c的的大小关系是( )A.a b c<<B.b a c<<C.a c b<<D.c b a<<【答案】A【解析】设4α=,则5π3π42α<<,作出角α的三角函数线,如下图,则sin0MPα=<,cos0OMα=<,tan0ATα=>,又在OMP中,ππ,42MOP⎛⎫∠∈ ⎪⎝⎭,则MP OM>,故sin cos0tanααα<<<,即sin4cos40tan4<<<.故选:A.2.(2020·湖南长沙·高一月考)设sin1,cos1,tan1a b c===,则,,a b c的大小关系为()A.a b c>>B.a c b>>C.c a b>>D.c b a>>【答案】C【解析】以O 为圆心作单位圆,与x 轴正半轴交于点A ,作1POA ∠=交单位圆第一象限于点P ,做PB x ⊥轴,作AT x ⊥轴交OP 的延长线于点T ,如下图所示:由三角函数线的定义知,cos1OB =,sin1BP =,tan1AT =, 因为ππ124>>,AT BP OB ∴>>∴tan1sin1cos1>>∴c a b >>故选:C 3.(2019·伊美区第二中学高一月考)已知点(sin cos ,tan )P ααα-在第一象限,则在[0,2]π内α的取值范围是( ). A .35,,244ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭B .5,,424ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭C .353,,2442ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ D .3,,424ππππ⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭【答案】B【解析】由已知点(sin cos ,tan )P ααα-在第一象限得:sin cos 0αα->,tan 0α>,即sin cos αα>,tan 0α>,当sin cos αα>,可得52244k k πππαπ+<<+,k Z ∈. 当tan 0α>,可得222k k ππαπ<<+或3222k k πππαπ+<<+,k Z ∈. ∴2242k k πππαπ+<<+或5224k k πππαπ+<<+,k Z ∈. 当0k =时,42ππα<<或54ππα<<.02απ,∴42ππα<<或54ππα<<.故选:B .考点四 同角三角函数【例4】(1)(2020·镇原中学高一期末)若1sin 2α=,π(,π)2α∈,则cos α= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题1 三角函数基本概念1.角的有关概念(1)从运动的角度看,角可分为正角、负角和零角. (2)从终边位置来看,可分为象限角和轴线角.(3)若α与β是终边相同的角,则β可用α表示为{}Z k k S ∈⋅+==,360 αββ(或{}Z k k ∈+=,2παββ). 2.象限角3.弧度与角度的互化(1)1弧度的角:长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad 表示.(2)角α的弧度数:如果半径为r 的圆的圆心角α所对弧的长为l ,那么αr l =,角α的弧度数的绝对值是rl=α(3)角度与弧度的换算①;1801rad π=①π1801=rad(4)弧长、扇形面积的公式:设扇形的弧长为l ,圆心角大小为()rad α,半径为r ,又αr l =,则扇形的面积为22121r lr S α==.叫做叫做5.三角函数线设角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边与单位圆相交于点P ,过P 作PM 垂直于x 轴于M ,则点M 是点P 在x 轴上的正射影.由三角函数的定义知,点P 的坐标为()ααsin ,cos ,即()ααsin ,cos P ,其中,sin ,cos MP OM ==αα单位圆与x 轴的正半轴交于点A ,单位圆在A 点的切线与α的终边或其反向延长线相交于点T ,则AT =αtan .我们把有向线段AT MP OM 、、叫做α的余弦线、正弦线、正切线.6.对任意角的理解(1)不少同学往往容易把“小于 90的角”等同于“锐角”,把“ 90~0的角”等同于“第一象限的角”.其实锐角的集合是{}900<<αα,第一象限角的集合为{}Z k k k ∈+⋅<<⋅,90360360 αα.(2)终边相同的角不一定相等,相等的角终边一定相同,终边相同的角的同一三角函数值相等. 【例1】︒-870的终边在第几象限( ) A .一B .二C .三D .四【例2】已知角α的终边经过点)1-,则角α的最小正值是( )A .32π B .611πC .65π D .43π 【例3】若0sin <α且0tan >α,则α是( ) A .第一象限角 B .第二象限角C .第三象限角D .第四象限角【例4】若点P 在32π角的终边上,且P 的坐标为),1(y -,则y 等于________. 【例5】弧长为π3,圆心角为 135的扇形半径为________,面积为________. 【例6】(1)如果α是第三象限的角,那么α-,α2的终边落在何处? (2)写出终边在直线x y 3=上的角的集合.【例7】若角β的终边与 60角的终边相同,则在 360~0范围内,终边与角3β的终边相同的角为________.任意角三角函数求法1.三角函数的定义中,当()y x P ,是单位圆上的点时有y =αsin ,x =αcos ,xy=αtan ,但是若不是单位圆时,如圆的半径为r ,则r y =αsin ,r x =αcos ,xy =αtan . 2.若已知角α的终边上有异于原点的点的坐标()y x A ,,求角α的三角函数值时,则应先求r OA =,然后再利用定义r y =αsin ,r x =αcos ,xy=αtan 求解. 3. 同角三角函数的关系 平方关系:12cos 2sin =+αα 商数关系:αααcos sin tan = 常考模型一 已知一三角函数值,求另外两个三角函数值 【例8】(1)已知 31sin =α ,求αcos ,αtan 的值;(2)已知21cos -=α,且α 在第三象限,求αsin ,αtan 的值;(3)已知 2tan -=α ,且α 在第二象限,求αsin ,αcos 的值.【例9】已知角α的终边经过点()3,-m P ,且54cos -=α,则m 等于( )A .411-B .411 C .4- D .4 【例10】角θ的终边上有一点),(a a ,其中R a ∈且0≠a ,则θsin 的值是( ) A .22B .22-C .22或22- D .1常考模型二 已知正切值,求齐次分式的值 齐次分式:分子分母的正余弦次数相同,例如:222222sin cos sin cos +sin cos sin cos +sin cos sin cos sin cos a b a b c a b c c d αααααααααααααα+++⇒++或者 【例11】已知2tan =α,求:(1)ααααcos sin cos sin -+;(2)ααα222sin cos 32sin -+;(3)2cos sin sin 2++ααα.专题2 三角函数诱导公式一 六组诱导公式2αcos α对于角()Z k ∈±"2"α的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说()Z k ∈±α2的三角函数值等于“当k 为奇数时,正弦变余弦,余弦变正弦;当k 为偶数时,函数名不变,然后α的三角函数值前面加上当α为锐角时,原函数值的符号.【例1】 585sin 的值为( ) A .22-B .22 C .23-D .23 【例2】已知()()θπθπ--=+2cos 3sin ,2πθ<,则θ等于( )A .6π-B .3π-C .6π D .3π 【例3】如果()21sin =+A π,那么⎪⎭⎫⎝⎛-A 23cos π 的值是________. 【例4】如果(),cos sin 52sin tan x x x x f -=那么()5f =________. 【例5】若角α的终边落在第三象限,则αααα22cos 1sin 2sin 1cos -+-的值为( )A .3B .3-C .1D .1-【例6】已知)0,(πα-∈,31)3tan(=+απ,则⎪⎭⎫⎝⎛+απ23cos 的值为( ) A .1010B .1010-C .10103 D .10103-【例7】 240tan 600sin +的值等于( ) A .23-B .23 C .213-D .213+【例8】已知()()()4cos sin ++++=βπαπx b x a x f (a ,b ,α,β为非零实数),()52011=f ,则=)2012(f ( ) A .3B .5C .1D .不能确定1.诱导公式在三角形中经常应用,常用的变形结论有:.2222,2222;πππ=++=++-=+C B A C B A C B A 2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.【例9】在ABC ∆中,31cos =A ,则()=+C B sin ________.【例10】在ABC ∆中,若()()B A --=-ππsin 22sin ,()B A --=πcos 2cos 3,求ABC ∆的三个内角. 注意:(1)若t =+ααcos sin ,则21cos sin 2-=t αα;22cos sin t -±=-αα(2)若t =ααcos -sin ,则21sin cos 2t αα-=;22cos sin t -±=+αα(3)若t =ααcos sin ,则t 21cos sin +±=+αα;t 21cos sin -±=-αα 判断ααcos sin -与a cos sin +α的符号法则 根据r y =αsin , r x =αcos ,rx y -=-ααcos sin ,x y >∴时,0cos sin >-αα,反之亦然 52,244k k ππαππ⎛⎫∴∈++ ⎪⎝⎭,sin cos 0αα->;372,244k k ππαππ⎛⎫∈++ ⎪⎝⎭,sin cos 0αα+<. 32,244k k ππαππ⎛⎫∴∈-+⎪⎝⎭,sin cos 0αα+>;372,244k k ππαππ⎛⎫∈++⎪⎝⎭,sin cos 0αα+<. 【例11】已知),0(πθ∈,213cos sin -=+θθ,则θtan 的值为( ) A .3-或33- B .33-C .3-D .23-专题3 三角函数图像与性质正弦函数x ysin =与()ϕω+=x A y sin 的图像性质关系类比于研究sin y x =的性质,只需将()sin y A x ωϕ=+中的x ωϕ+看成x y sin =中的x ,但在求()sin y A x ωϕ=+的单调区间时,要特别注意A 和ω的符号,通过诱导公式先将ω化为正数.研究函数()cos y A x ωϕ=+,()n y Ata x ωϕ=+的性质的方法与其类似,也是类比、转化.【例1】函数2sin 36yx,x R 的最小正周期是()A .3B .23C .32D .π【例2】函数tan36xf x的最小正周期为( )A .π3B .π6 C.3D .23【例3】已知函数sin 4y A x πω⎛⎫=+ ⎪⎝⎭(0>ω)的最小正周期为π,则函数)(x f 的图象( )A .关于直线4x 对称 B .关于直线8x 对称C .关于点)0,4(π对称D .关于点)0,8(π对称【例4】设函数()()sin f x A x ωϕ=+(A ≠0,ω>0,22ππϕ-<<的图象关于直线23x对称,它的最小正周期为π,则( ) A .)(x f 的图象过点10,2B .)(x f 在2,123上是减函数C .)(x f 的一个对称中心是5,012D .)(x f 的一个对称中心是,06【例5】函数2sin 26y x π⎛⎫=+ ⎪⎝⎭在,22ππ⎡⎤-⎢⎥⎣⎦上对称轴的条数为( )A .1B .2C .3D .0【例6】函数)43sin(2π-=x y 的图象中两条相邻对称轴之间的距离是 .【例7】同时具有性质:①最小正周期是π;①图象关于直线3x 对称;①在,63ππ⎡⎤-⎢⎥⎣⎦上是增函数的一个函数是( ) A .sin26xy B .cos 23y xC .sin 26y xD .cos26xy【例8】函数sin26y x 的单调递增区间是( ) A .2,263k kkZB .52,236k k k ZC .,63k k k ZD .5,36k k k Z【例9】已知函数)sin(ϕω+=x A y (0>A ,πϕ<)的一段图象如下图所示, 求函数的解析式.【例10】已知函数sin()y A x ωϕ=+在同一周期内,当9π=x 时,取得最大值12,当94π=x 时,取得最小值21-,则该函数的解析式是( )2A .12sin()36y x π=-B .1sin(3)26y x π=+C .1sin(3)26y x π=-D .1sin(3)26y x π=-+【例11】若函数,求()2sin(2)6f x x π=+在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【例12】若函数()2sin()3f x x πω=+,且2f,0f ,βα-的最小值是2,则)(x f 的单调递增区间是( ) A .5,1212k k k Z B .,36k k k ZC .22,233k kk ZD .52,266k kkZ【例13】(1)若函数()3cos()f x wx θ=+对任意的,()()66x R f x f x 有ππ∈+=-,则()6f π等于( )A .3-B .0C .3D .3±(2)若m x x f ++=)cos(2)(ϕω,对任意实数t 都有)()4(t f t f -=+π,且()18f ,则实数m 的值为( ) A .1±B .3±C .3-或1D .1-或3【例14】函数()()sin f x A x ωϕ=+(ω,φ是常数,ω>0).若()f x 在区间]1,31[上具有单调性,且2(0)(1)3f f f ⎛⎫==- ⎪⎝⎭,则下列有关()f x 的每题正确的有 (请填上所有正确命题的序号).①()f x 的最小周期为2;①31=x 是 ()f x 的对称轴; ①()f x 在]35,1[上具有单调性;①56yf x为奇函数.函数)sin(ϕω+=x A y 的图象可以通过下列两种方式得到:1.−−−−−−−−−→−+=−−−−→−=倍横坐标缩短到原来的图象左移ωϕϕ1)sin(sin x y x y )sin(ϕω+=x y )sin(ϕω+=−−−−−−−−−→−x A y A 倍纵坐标伸长为原来的2.−−−−→−=−−−−−−−−−→−=ωϕωω图象左移倍横坐标缩短到原来的)sin(sin 1x y x y )sin(ϕω+=x y )sin(ϕω+=−−−−−−−−−→−x A y A 倍纵坐标伸长为原来的关键:把握先移后缩和先缩后移的区别。
