2010.07.01北京市西城区初一第二学期数学期末试题(B卷)
北京市西城区-学年七年级下期末数学试卷含标准答案

北京市西城区■学年七年级下期末数学试卷含答案作者: 日期:西城区2017-2018学年度第二学期期末试卷七年级数学2018.7 试卷满分:100分,考试时间:100分钟一、选择题(本题30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.8的立方根等于().A.-2B.2C.-4D.42.已知a<b,下列不等式中,正确的是().A. a+4>b+4B.a-3>b-3C. 1 a< 1 bD. -2a<-2 b2 23.下列计算中,正确的是()A.m2+m4 =m6B. m2• m4=m8C.(3m)2=3m2D. 2m4+m2=2 m24.如图,直线a//b,三角板的直角顶点放在直线b上,两直角边与直线a相交, 如果/ 1=600,那么/ 2等于().A. 300B. 400C. 500D. 6005.如果点P(5, y)在第四象限,那么y的取值范围是(A.y<0B.y>0C.y<0D.y>06.为了解游客对恭王府、北京大观园、北京动物园和景山公园四个旅游景区的满意率情况,某班实践活动小组的同学给出了以下几种调查方案:方案一:在多家旅游公司随机调查400名导游;方案二:在恭王府景区随机调查400名游客;方案三:在北京动物园景区随机调查400名游客;方案四:在上述四个景区各随机调查400名游客.在这四种调查方案中,最合理的是().A.方案一B.方案二C.方案三D.方案四7.下列运算中,正确的是().A. (a+b)2=a2+b2B.(a- 1)2=a2-a+ 1C. (a-b)2=a2+2ab-b2D.(2a+b)2=2a2+2ab+b28.下列命题中,是假命题的是()A.在同一平面内,过一点有且只有一条直线与已知直线垂直9.同旁内角互补,两直线平行C.两条直线被第三条直线所截,同位角相等D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行10某品牌电脑的成本为2400元,售价为2 800元,该商店准备举行打折促销活动,要求利润率不低于5%,如果将这种品牌的电脑打x折销售,则下列不等式中能正确表示该商店的促销方式的是().A. 2 800x >2400x5%B.2800X — 2400 >2400 x 5%C. 2 800 — > 2400 x 5%D. 2 800 —2400 >2400 x 5% 1010 1010.为倡导绿色发展,避免浪费能源,某市准备对居民用电量采用阶梯收费的方法,计划实施三档的阶梯电价:第一档、第二档和第三档的电价分别覆盖全市居民家庭的80% ,15 %和5%.为了合理确定各档之间的界限,相关部门在该市随机调查了20000户居民6月份的用电量(单位:kw? h),并将收集的样本数据进行排序整理(排序样本),绘制了如下频数分布直方图(每段用电量均含最小值,不含最大值).①抽样调查6月份的用电量,是因为6月份的用电量在一年12个月的用电量中处于中等偏上水平②在调查的20000户居民中,6月份的用电量的最大值与最小值的差小于500③月用电量小于160 kw? h的该市居民家庭按第一档电价交费,月用电量不小于310 kw? h的该市居民家庭按第三档电价交费④该市居民家庭月用电量的中间水平(50%的用户)为110 kw? h其中合理的是().A.①②③B.①②④C.①③④D.②③④二、填空题(本题共18分,第11-16题每小题2分,第17,18题每小题3分)xf 1 一.一.、一11.不等式组的解集是 _____________________ .xp 212.如图,点A,B,C,D,E在直线l上,点P在直线l外,PC,l于点C,在线段PA,PB,PC ,PD,PE中,最短的一条线段是 ,理由是14.如图,在Rt?ABC 中,/ C=900 ,AD 平分/ CAB 交BC 于点D, BE 上AD 于点E.若/ CAB=500,则/ DBE=15.如图,AB//CD, CE 交AB 于点F, /C=550, /AEC=150则/A=16.七巧板又称智慧板,是中国民间流传的智力玩具,它由七块板组成(如图1),用这七块板可拼出许多图形(1 600种以上).例如:三角形、平行四边形以及不规则的多边形,它还可以拼出各种人物、动物、建筑等.请你用七巧板中标号为①②③的三块板(如图2)经过平移、旋转拼出下列图形(相邻两块板之间无空隙,无重叠;示意图的顶点画在小方格顶点上):⑴拼成长方形,在图3中画出示意图;(2)拼成等腰直角三角形,在图4中画出示意图.17.如图,在平面直角坐标系xOy中,平行四边形ABCD的四个顶点A,B,C, D 是整点(横、纵坐标都是整数),则平行四边形ABCD的面积是_18.若一个整数能表示成a2+b2(a,b是整数)的形式,则称这个数为“完美数”例如,因为5=22+12,所以5是一个“完美数”.⑴请你再写一个大于10且小于20的“完美数”;(2)已知M是一个“完美数”,且M=x2 + 4xy+5y2-12y+ k(x,y是两个任意整数, k是常数),则k的值为三、解答题(本题共17分,第19题5分,第20,21题每小题6分)19.计算:3石电2拈| 2ml ( 3)0解:121 .先化间,再求值:(ab+2)(ab-2)+(a 2b 2+4ab) + ab,其中 a=10, b =-5四、解答题(本题共27分,第24题6分,其余每小题7分) 22 .在平面直角坐标系xOy 中,?ABC 的三个顶点分别是 A(-2,0) ,B(0,3) ,C(3,0).(1)在所给的图中,画出这个平面直角坐标系;(2)点A 经过平移后对应点为D(3, -3),将△ ABC 作同样的平移得到△ DEF , 画出平移后的△ DEF;⑶在(2)的条件下,点M 在直线CD 上,若CM=2DM ,直接写出点M 的坐标. 解:(3)点M 的坐标为23.如图,点 O 在直线AB 上,OC1OD, / EDO 与/ 1互余. (1)求证:ED// AB;⑵OF 平分/ COD 交DE 于点F,若/OFD=70°,补全图形,并求/ 1的度数.⑴证明:(2)解:20.解不等式:2^—2 竺」f 1,并把解集表示在数轴上.(3) 2012 2017年全国生活用水情况统计如下图所示, 根据统计图中提供的信24 .某地需要将一段长为180米的河道进行整修,整修任务由 A,B 两个工程队 先、后接力完成.已知A 工程队每天整修12米,B 工程队每天整修8米,共用 时20天.问A,B 两个工程队整修河道分别工作了多少大? (1)以下是甲同学的做法:设A 工程队整修河道工作了 x 天,B 工程队整修河道工作了 y 天.根据题意,得方程组: _________________________x X解得y X请将甲同学的上述做法补充完整;(2)乙同学说:本题还有另外一种解法,他列出了不完整的方程组如下: x y XA y X12 8①在乙同学的做法中,x 表示,y 表示;8②请将乙同学所列方程组补充完整.25 .阅读下列材料:2017年,我国全年水资源总量为 28675亿m 3..2016年,我国全年水资源 总量为32466.4亿m3, 2015年,我国全年水资源总量为 27 962. 6亿m3, 全年平均降水量为660. 8 mm.我国水资源的消费结构包含工业用水、农业用水、生态用水、生活用水四 类.2017年全国用水总量为6 040亿m 3,其中工业用水占用水总量的 22%, 农业用水占用水总量的62%,生态用水占用水总量的2%,生活用水844.5亿 m 3.根据上述材料,解答下列问题:(1)根据材料画适当的统计图,直观地表示 情况;(2) 2017年全国生活用水占用水总量的2017年全阳水资源消费情况统计图2015 — 2017年我国全年水资源总量%,并补全扇形统计图农业用水62%息①请你估计2018年全国生活用水量为 亿m3,你的预估理由是 ②谈谈节约用水如何从我做起?2012 ~ 2017年全国生活用水量统计图五、解答题(本题共8分)26.如图,在直角三角形 ABC 中,/ACB=90".(1)如图1,点M 在线段CB 上,在线段BC 的延长线上取一点N,使得/ NAC =/ MAC .过点B 作BD XAM ,交AM 延长线于点D,过点N 作NE//BD ,交 AB 于点E,交AM 于点F.判断/ ENB 与/ NAC 之间的数量关系,写出你的结 论,并加以证明; (2)如图2,点M 在线段CB 的延长线上,在线段BC 的延长线上取一点N,使 得/ NAC = / MAC .过点B 作BD XAM 于点D,过点N 作NE// BD ,交BA 延 长线于点E,交MA 延长线于点F. ①依题意补全图形;②若/CAB=45°,求证:/ NEA=/NAE.ktj J -8iiF u y/ -J- L —r hir 'I f VI* klj fc —r (/■fl fu- ( fl-54J 3 2 l rtf X 7h 5 4。
北京市七年级数学下册期末试题(带答案)

北京市七年级数学下册期末试题(带答案)聪明出于勤奋,天才在于积累。
尽快地掌握科学知识,迅速提高学习能力,接下来查字典数学网为大家提供的北京市七年级数学下册期末试题(带答案)一、选择题(本题共36分,每小题3分)1.不等式组3x-24的解集是( )A.xB.xC. xD. x22.某种流感病毒的直径是0.00 000 008米,用科学记数法表示0.00 000 008为( )A. B. C. D.3.若 ab,则下列结论中正确的是( )A.4 a4 bB.a+cb+cC.a-54.下列计算中,正确的是( )A. B. C. D.5.下列计算中,正确的是( )A.(m+2)2=m2+4B.(3+y)( 3-y)= 9-y2C.2x(x-1)= 2x2-1D.(m-3)(m+1)= m2-36.如图,AF是BAC的平分线,EF∥AC交AB于点E.若1=25,则的度数为( )A.15B.50C.25D.12.57.下列从左到右的变形正确进行因式分解的是( )A.(x+5)(x-5)=x2-25B.x2+x+1=x(x+1)+1C.-2x2-2xy=-2x(x+y)D.3x+6xy+9xz=3x(2y+9z)8.下列调查中,适合用普查方法的是( )A.了解某班学生对北京精神的知晓率B.了解某种奶制品中蛋白质的含量C.了解北京台《北京新闻》栏目的收视率D.了解一批科学计算器的使用寿命9.我市某一周的最高气温统计如下表:最高气温( )25262728天数1123则这组数据的中位数与众数分别是( )A.27,28B.27.5,28C.28,27D.26.5,2710. 如图所示,点在AC的延长线上,下列条件中能判断 ( )A.4B.C. D.11.不等式组无解,则m的取值范围是( )A.mB.mC.mD.m112.关于 , 的二元一次方程组的解满足 , 则的取值范围是( )A. B. C. D.二、填空题(本题共24分,每小题2分)13.把方程写成用含x的代数式表示y的形式,则y= .14如果一个角等于54,那么它的余角等于度.15.在方程中,当时,y= .16.分解因式 = .17.我市六月份连续五天的日最高气温(单位: )分别为35,33,37,34,39,则我市这五天的日最高气温的平均值为 .18.计算的结果是 .19.已知是关于x,y的方程组的解,那么的值是 .20.已知1与2互补,3与2互补,1=72,则3= 度.21.如图,直线AB,CD相交于点O,OEAB,O为垂足,EOD=26,则AOC= .22.若,,则的值是 .23.若多项式是完全平方公式,则k= .24. 右图为手的示意图,在各个手指间标记字母 .请你按图中箭头所指方向(即的方式)从开始数连续的正整数当字母第次出现时( 为正整数),恰好数到的数是_____________(用含的代数式表示).三、计算(本题共6分,每小题3分)1. 2.四、因式分解(本题共9分,每小题3分)1. 2. 3. .五、先化简,再求值(本题5分)其中, .六、解答题(本题共16分,每小题4分)1.解不等式,并把它的解集在数轴上表示出来.2. 解方程组3. 解不等式组并求它的所有整数解.4.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分BEF交CD于点G,1=50,求2的度数.七、在括号中填入适当的理由(本题共7分,每空1分)已知:如图,2,4. 求证:DF∥BC.证明:∵4(已知),又∵2(已知),DF∥BC. ( )八、解答题(本题5分)为了解某区2021年八年级学生的体育测试情况,随机抽取了该区若干名八年级学生的测试成绩进行了统计分析,并根据抽取的成绩等级绘制了如下的统计图表(不完整):图1 图2请根据以上统计图表提供的信息,解答下列问题:(1)本次抽查的学生有___________名,成绩为B类的学生人数为_________名,A类成绩所在扇形的圆心角度数为________;(2)请补全条形统计图;(3)根据抽样调查结果,请估计该区约5000名八年级学生体育测试成绩为D类的学生人数.九、列方程组解应用问题解答题(本题5分)如图,用火柴棍连续搭建三角形和正方形,公共边只用一根火柴棍. 如果搭建三角形和正方形共用了77根火柴棍,并且三角形形的个数比正方形的个数少5个,那么一共能连续搭建三角形、正方形各多少个?十、解答题(本题7分)如图,已知射线CB∥OA,OAB=120,E、F在CB上,且满足FOB=FBO,OE平分COF.(1) 求EOB的度数;(2) 若向右平行移动AB,其它条件不变,那么OBC:OFC的值是否发生变化?若变化,找出其中规律,若不变,求出这个比值;(3) 在向右平行移动AB的过程中,是否存在某种情况,使OEC=OBA?若存在,请直接写出OBA度数,若不存在,说明理由..以上就是查字典数学网为大家提供的北京市七年级数学下册期末试题(带答案).大家仔细阅读了吗?加油哦!。
西城B初一数学答案

北京市西城区2009–2010学年度第一学期期末测试初一数学试卷(B 卷) 2010.1(时间100分钟,满分100分)一、精心选一选(共10个小题,每小题3分,共30分) 1.15-的相反数是( A ). A .15 B .15- C .5 D .5-2.三峡工程是具有防洪、发电、航运、供水等巨大综合利用效益的特大型水利水电工程,其防洪库容量为22 150 000 0003m ,这个数用科学记数法表示为( C ). A .83221.510m ⨯ B .9322.1510m ⨯ C .1032.21510m ⨯ D .1132.21510m ⨯3.已知3a =-,则a 等于( D ).A .3B .3-C .0D .3±4.现规定一种运算:a b ab a b *=+-,其中a ,b 为有理数,则35*的值为( C ).A .11B .12C .13D .14 5.A 、B 两点的距离是( B ).A .连接A 、B 两点的线段 B .连接A 、B 两点间的线段的长度C .过A 、B 两点的直线D .过A 、B 两点的线段 6.如图所示,下列说法中错误..的是( D ). A .OA 的方向是北偏西15° B .OB 的方向是南偏西45°C .OC 的方向是南偏东60°D .OD 的方向是北偏东60° 7.甲、乙两人练习赛跑,甲每秒钟跑7米,乙每秒钟跑6.5米.他俩从同一地点起跑,乙先跑5米后,甲出发追赶乙.设甲出发x 秒后追上乙,则下列四个方程中正确的是( A ). A .55.67+=x x B .55.67-=x x C .x x 5.657=+ D .5)5.67(=+x8.一个无盖的正方体盒子的平面展开图可以是下列图形中的( B ).A .图①、图②B .图①、图③C .图②、图③D .只有图① 9.下列各式中去括号正确的是( D ).A .2222(2)2a a b b a a b b --+=--+B .2222(2)()2x y x y x y x y -+--+=-++-C .2223(5)235x x x x --=-+D .3232[4(13)]413a a a a a a ---+-=-+-+10.下列图形都是由边长为1厘米的小正方形连接组成的.按照图形的变化规律,第2009个图形的周长是( B )厘米.A .4018B .4020C .8036D .6027二、细心填一填(共10个小题,每小题2分,共20分) 11.将236875精确到万位的结果是_______5104.2⨯________.12.体校里男学生人数是m ,女学生人数是n ,教练人数和学生人数的比是1:20,则教练人数是__)(201n m +_______________. 13.观察右图中的数轴,a 、b 、c 表示的数由小到大的顺序为_______b<c<a__________. 14.一个角的余角比它的补角的29多1度,则这个角为____63____度. 15.若2222m ab +与3343-+-n m b a 是同类项,则m n +=____6____. 16.已知212=-mn m ,152-=-n mn ,则代数式22n m -=___6_____. 17.从下午13:15到当天下午13:54,时钟的分针转过的角度为___154_____度.18.已知线段AB=10cm ,C 是直线AB 上一点,且BC=6cm ,M 、N 分别是AB 、BC 的中点,则线段MN 的长为__8cm 或2cm ___________.19.如图,有4种4×4方格图案,其中阴影部分面积相同的图案是__ __(1)和(4)______________.(请填写序号)20.一个人先沿水平道路前进,继而爬山到达了山顶,之后又沿原路返回到出发点,全程共用了5小时.已知此人在水平路上每小时走4千米,上山每小时走3千米,下山每小时走6千米,则此人所走的全程是__20_______千米.三、用心算一算(共4个小题,每小题4分,共16分)21.计算:)()(2.385.98.7---+-.= —6.522.计算:)10()25()4()5.7(-÷+÷-⨯-. = 56-23.计算:)7(33)7(128)7(18-÷+-÷--÷. = 1124.计算:222172(3)(6)()3-+⨯-+-÷-. = —85四、先化简,再求值(本题4分)25.已知2a b -=,1ab =-.求(45)(235)a b ab a b ab ----+的值. =2(a-b )-6ab当2a b -=,1ab =-时,原式=10)1(622=-⨯-⨯五、解方程(本题5分) 26.14126110312-+=+--x x x . 解:61=x六、列方程解应用题(共2个小题,每小题5分,共10分)27.在暖气管线中装有甲、乙两种水管共25根,总长为155米.甲种水管每根长5米,乙种水管每根长8米.请问甲、乙两种水管各有多少根?解:设甲种水管有x 根,乙种水管有(25—x)根 5x+8(25-x)=155 x=15答:甲种水管有15根,乙种水管有10根。
北京市西城区七年级下学期期末历年数学试卷及解析汇总

2009-2010学年北京市西城区七年级(下)期末数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)下列四个算式中,正确的个数有()①a4•a3=a12;②a5+a5=a10;③a5÷a5=a;④(a3)3=a6.A.0个B.1个C.2个D.3个2.(3分)在数轴上表示不等式组的解集,正确的是()A.B.C.D.3.(3分)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是()A.相等B.互余C.互补D.互为对顶角4.(3分)已知一个样本:23,24,25,26,26,27,27,27,27,27,28,28,28,29,29,30,30,31,31,32,那么频数为8的范围是()A.24.5~26.5B.26.5~28.5C.28.5~30.5D.30.5~32.5 5.(3分)化简:(a+1)2﹣(a﹣1)2=()A.2B.4C.4a D.2a2+26.(3分)下列命题中是假命题的是()A.两直线被第三直线所截,同旁内角互补,两直线平行B.直线a⊥直线b,则a与b的夹角为直角C.如果两个角互补,那么这两个角一个是锐角,一个是钝角D.若a∥b,a⊥c,那么b⊥c7.(3分)下列变形不正确的是()A.若a>b,则b<a B.若﹣a>﹣b,则b>aC.由﹣2x>a,得x>D.由x>﹣y,得x>﹣2y8.(3分)下列变形是因式分解的是()A.xy(x+y)=x2y+xy2B.x2+2x+1=x(x+1)+1C.(a﹣b)(m﹣n)=(b﹣a)(n﹣m)D.ab﹣a﹣b+1=(a﹣1)(b﹣1)9.(3分)科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为()A.6米B.8米C.12米D.不能确定10.(3分)△ABC的三边a,b,c都是正整数,且满足a≤b≤c,如果c=4,那么这样的三角形共有()个.A.4B.6C.8D.10二、填空题(共10小题,每小题2分,满分20分)11.(2分)因式分解:a3+2a2+a=.12.(2分)如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2=度.13.(2分)若点P(2m+1,)在第四象限,则m的取值范围是.14.(2分)如图,一个顶角∠A为90°的直角三角形纸片,剪去这个角后得到一个四边形,则∠BEF+∠CFE的度数是度.15.(2分)用“※”定义新运算:对于任意有理数a、b,都有a※b=2a2+b.例如3※4=2×32+4=22,那么(﹣5)※2=;当m为有理数时,m※(m※2)=.16.(2分)已知方程组的解是,则a+b的值为.17.(2分)有一个多边形的内角和是它外角和的5倍,则这个多边形是边形.18.(2分)如果的值是非正数,则x的取值范围是.19.(2分)如图,△ABC中,AC=BC,∠BAC的外角平分线交BC的延长线于点D,若∠ADC=∠CAD,则∠ABC=度.20.(2分)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为25cm,宽为x cm,为了保证能折成图④的形状(即纸条两端均超出点P),那么x的取值范围是cm.三、解答题(共10小题,满分50分)21.(5分)先化简,再求值:(a﹣2b)(a+2b)+ab3÷(﹣ab),其中a=,b=﹣1.22.(5分)解方程组:.23.(5分)解不等式组:24.(5分)如图,CD平分∠ACB,DE∥BC,∠AED=80°.(1)求∠EDC;=30,求点E到BC的距离.(2)若BC=10,S△BCD25.(5分)在平面直角坐标系中有四个点,它们的坐标分别是A(0,3),B(﹣2,﹣1),C(3,﹣1),D(5,3).(1)在坐标系中描出这四个点,并依次连接它们,画出所得图形;(2)将所得的图形向下平移2个单位长度,画出平移后的图形,写出平移后对应的四点A′,B′,C′,D′的坐标.26.(5分)A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:A B C笔试859590口试8085(1)请将表一和图一中的空缺部分补充完整.(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.27.(5分)为改善办学条件,北海中学计划购买部分A品牌电脑和B品牌课桌.第一次,用9万元购买了A品牌电脑10台和B品牌课桌200张.第二次,用9万元购买了A品牌电脑12台和B品牌课桌120张.(1)每台A品牌电脑与每张B品牌课桌的价格各是多少元?(2)第三次购买时,销售商对一次购买量大的客户打折销售.规定:一次购买A品牌电脑35台以上(含35台),按九折销售,一次购买B品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?28.(5分)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.29.(5分)如果有理数x,y满足等式2x+x2+9y2+2=﹣6y,求x﹣3y的值.30.(5分)如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD =∠BCF.(1)求∠ECF+DAC+∠ECA的度数;(2)判断ED与FC的位置关系,并对你的结论加以证明.2009-2010学年北京市西城区七年级(下)期末数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)下列四个算式中,正确的个数有()①a4•a3=a12;②a5+a5=a10;③a5÷a5=a;④(a3)3=a6.A.0个B.1个C.2个D.3个【分析】根据同底数幂相乘,底数不变指数相加;同底数幂相除,底数不变指数相减;幂的乘方,底数不变指数相乘;对各选项计算后即可选取答案.【解答】解:①应为a4•a3=a7;②应为a5+a5=2a5;③应为a5÷a5=1;④应为(a3)3=a9;所以正确的个数是0个.故选:A.【点评】本题主要考查同底数幂的乘法,同底数幂的除法,幂的乘方,合并同类项,熟练掌握运算性质和法则是解题的关键.2.(3分)在数轴上表示不等式组的解集,正确的是()A.B.C.D.【分析】本题可根据数轴的性质,实心圆点包括该点用“≥”,“≤”表示,空心圆圈不包括该点用“<”,“>”表示,大于向右,小于向左.【解答】解:依题意得,数轴可表示为:故选:B.【点评】本题考查不等式组解集的表示方法.把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.3.(3分)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是()A.相等B.互余C.互补D.互为对顶角【分析】根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余.【解答】解:图中,∠2=∠COE(对顶角相等),又∵AB⊥CD,∴∠1+∠COE=90°,∴∠1+∠2=90°,∴两角互余.故选:B.【点评】本题考查了余角和垂线的定义以及对顶角相等的性质.4.(3分)已知一个样本:23,24,25,26,26,27,27,27,27,27,28,28,28,29,29,30,30,31,31,32,那么频数为8的范围是()A.24.5~26.5B.26.5~28.5C.28.5~30.5D.30.5~32.5【分析】根据题意可得:共20个数据,其中在26.5~28.5之间的有8个,故可以求得其频数.【解答】解:∵共20个数据,其中在26.5~28.5之间的有8个,∴频数为8的范围是26.5~28.5一组.故选:B.【点评】此题考查频率、频数的关系频率=频数÷数据总和.5.(3分)化简:(a+1)2﹣(a﹣1)2=()A.2B.4C.4a D.2a2+2【分析】将a+1和a﹣1看成一个整体,用平方差公式解答.【解答】解:(a+1)2﹣(a﹣1)2,=[(a+1)﹣(a﹣1)][(a+1)+(a﹣1)],=2×2a,=4a.故选:C.【点评】本题考查了平方差公式,关键是将a+1和a﹣1看成一个整体,并熟练掌握平方差公式:(a﹣b)(a+b)=a2﹣b2.6.(3分)下列命题中是假命题的是()A.两直线被第三直线所截,同旁内角互补,两直线平行B.直线a⊥直线b,则a与b的夹角为直角C.如果两个角互补,那么这两个角一个是锐角,一个是钝角D.若a∥b,a⊥c,那么b⊥c【分析】根据平行线的性质及常用的知识点对各个命题进行分析,从而得到正确答案.【解答】解:A,正确,符合平行线的判定;B,正确,符合垂线的性质;C,不正确,两个角也可能都是直角;D,正确,符合垂线的性质;故选:C.【点评】此题主要考查学生对平行线的判定及垂线的性质等知识点的综合运用.7.(3分)下列变形不正确的是()A.若a>b,则b<a B.若﹣a>﹣b,则b>aC.由﹣2x>a,得x>D.由x>﹣y,得x>﹣2y【分析】根据不等式的基本性质1和基本性质2以及基本性质3即可判定四个选项那个正确.【解答】解:∵﹣2x>a,根据不等式的基本性质3可得:x<;所以,C不正确;故选:C.【点评】不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.8.(3分)下列变形是因式分解的是()A.xy(x+y)=x2y+xy2B.x2+2x+1=x(x+1)+1C.(a﹣b)(m﹣n)=(b﹣a)(n﹣m)D.ab﹣a﹣b+1=(a﹣1)(b﹣1)【分析】因式分解就是把多项式变形成几个整式积的形式,根据定义即可判断.【解答】解:A、结果不是整式的积的形式,故错误;B、结果不是整式的积的形式,故错误;C、不是把多项式变形,故错误;D、正确.故选:D.【点评】因式分解与整式的乘法互为逆运算,并且因式分解是等式的恒等变形,变形前后一定相等.9.(3分)科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为()A.6米B.8米C.12米D.不能确定【分析】利用多边形的外角和即可解决问题.【解答】解:∵机器人从点A出发再回到点A时正好走了一个正多边形,∴多边形的边数为360°÷30=12,∴他第一次回到出发点O时一共走了12×1=12米.故选:C.【点评】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°,用外角和求正多边形的边数直接让360度除以一个外角即可.10.(3分)△ABC的三边a,b,c都是正整数,且满足a≤b≤c,如果c=4,那么这样的三角形共有()个.A.4B.6C.8D.10【分析】本题根据三角形的三边关系首先确定出a、b、c三边长,可直接得出有几个三角形.【解答】解:∵△ABC的三边a,b,c都是正整数,且满足a≤b≤c,c=4,∴a,b,c,三边长可以有以下几种情况:1、4、4,2、4、4,3、4、4,2、3、4,3、3、4,4、4、4.∴可知这样的三角形共有6个.【点评】本题主要考查一元一次不等式即三角形的三边关系,解题的关键是利用了在三角形中,任意两边之和大于第三边,任意两边之差小于第三边的三边关系.二、填空题(共10小题,每小题2分,满分20分)11.(2分)因式分解:a3+2a2+a=a(a+1)2.【分析】先提取公因式a,再对余下的项利用完全平方公式继续分解因式.完全平方公式:a2±2ab+b2=(a±b)2.【解答】解:a3+2a2+a,=a(a2+2a+1),…(提取公因式)=a(a+1)2.…(完全平方公式)故答案为:a(a+1)2.【点评】本题考查了提公因式法,公式法分解因式,难点在于对余下的项利用完全平方公式进行二次分解因式.12.(2分)如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2=133度.【分析】两直线平行,同位角、内错角相等,据此即可解答.【解答】解:过点B作BD∥l1,则BD∥l2,∴∠ABD=∠AOF=90°,∠1=∠EBD=43°,∴∠2=∠ABD+∠EBD=133°.故答案为:133.【点评】注意此类题中常见的辅助线,能够根据平行线的性质证明要求的角和已知角之间的关系.13.(2分)若点P(2m+1,)在第四象限,则m的取值范围是﹣<m<.【分析】让点P的横坐标大于0,纵坐标小于0列式求值即可.【解答】解:∵点P(2m+1,)在第四象限,∴,解得:﹣<m<.故答案为:﹣<m<.【点评】第四象限点的符号是(+,﹣).14.(2分)如图,一个顶角∠A为90°的直角三角形纸片,剪去这个角后得到一个四边形,则∠BEF+∠CFE的度数是270度.【分析】先根据直角三角形的性质求得两个锐角和是90°,再根据四边形的内角和是360°,即可求得∠BEF+∠CFE的值.【解答】解:∵∠A=90°,∴∠B+∠C=90°.∵∠B+∠C+∠BEF+∠CFE=360°,∴∠BEF+∠CFE=360°﹣90°=270°.故答案为:270.【点评】本题要知道剪去直角三角形这个角后得到一个四边形,可根据四边形的内角和来求解.要会灵活的运用直角三角形和四边形的相关性质.15.(2分)用“※”定义新运算:对于任意有理数a、b,都有a※b=2a2+b.例如3※4=2×32+4=22,那么(﹣5)※2=52;当m为有理数时,m※(m※2)=4m2+2.【分析】将新定义的运算按定义的规律转化为有理数的混合运算.【解答】解:由a※b=2a2+b,可得(﹣5)※2=2×(﹣5)2+2=52,m※(m※2)=m※(2m2+2)=2m2+(2m2+2)=4m2+2.【点评】本题是新定义问题,考查了有理数的运算方法和数学的综合能力.解题的关键是根据题意掌握新运算的规律.16.(2分)已知方程组的解是,则a+b的值为3.【分析】所谓“方程组”的解,指的是该数值满足方程组中的每一方程.在求解时,可以将代入方程得到a和b的关系式,然后求出a,b的值.【解答】解:将代入方程,得到2a+b=4,2b+a=5,解得a=1,b=2.∴a+b=1+2=3.【点评】本题不难,考查的是二元一次方程组的解的应用.17.(2分)有一个多边形的内角和是它外角和的5倍,则这个多边形是12边形.【分析】一个多边形的内角和等于它的外角和的5倍,任何多边形的外角和是360度,因而这个正多边形的内角和为5×360度.n边形的内角和是(n﹣2)•180°,代入就得到一个关于n的方程,就可以解得边数n.【解答】解:根据题意,得(n﹣2)•180=5×360,解得:n=12.所以此多边形的边数为12.【点评】已知多边形的内角和求边数,可以转化为解方程的问题解决.18.(2分)如果的值是非正数,则x的取值范围是x≤1.【分析】值是非正数,用小于等于0表示,列出不等式求解即可.【解答】解:根据题意,得≤0,两边都乘以,得﹣(1﹣x)≤0,去括号,得x﹣1≤0,移项,得x≤1.故答案为:x≤1.【点评】本题是简单的列不等式求解题,主要考查一元一次不等式的解法.19.(2分)如图,△ABC中,AC=BC,∠BAC的外角平分线交BC的延长线于点D,若∠ADC=∠CAD,则∠ABC=36度.【分析】设∠CDA=α,由∠ADC=∠CAD,根据角平分线定义得到∠CAD=∠DAE=2α,再根据三角形外角的性质得到∠B=2α﹣α=α,而AC=BC,得到∠BAC=∠B=α,然后根据三角形的内角和定理即可得到α.【解答】解:设∠CDA=α,∵∠ADC=∠CAD,∴∠CAD=2α,而AD平分∠CAE,∴∠CAD=∠DAE=2α,而∠EAD=∠B+∠ADC,∴∠B=2α﹣α=α,又∵AC=BC,∴∠BAC=∠B=α,在△ABD中,∴∠B+∠CAB+∠CAD+∠ADC=180°,即α+α+2α+α=180°,∴α=36°.故答案为:36.【点评】此题主要考查了学生的三角形的内角和定理:三角形的内角和为180°.也考查了角平分线定义以及三角形外角的性质.20.(2分)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为25cm,宽为x cm,为了保证能折成图④的形状(即纸条两端均超出点P),那么x的取值范围是0<x<5cm.【分析】立体图形问题可以转化为平面图形问题解决.将图形展开我们可看到,超出P 点的线段有两条与x相等,还有两条是以x为边长的正方形的对角线,列出不等式解答即可.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.【解答】解:展开后AP与BM之间的部分有五个边长为x的正方形,根据题意列不等式可得0<5x<25,解得0<x<5.故答案为:0<x<5.【点评】本题主要考查展开图折叠成几何体.通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们展开以后的形状.三、解答题(共10小题,满分50分)21.(5分)先化简,再求值:(a﹣2b)(a+2b)+ab3÷(﹣ab),其中a=,b=﹣1.【分析】根据平方差公式和单项式除单项式的法则化简,然后代入数据计算求值.【解答】解:(a﹣2b)(a+2b)+ab3÷(﹣ab),=a2﹣4b2﹣b2,=a2﹣5b2,当a=,b=﹣1时,原式=()2﹣5×(﹣1)2=2﹣5=﹣3.【点评】主要考查平方差公式和单项式的除法的运用,熟练掌握公式和运算法则是解题的关键.22.(5分)解方程组:.【分析】由于两个方程中y的系数相同,可以选择用加减消元法来解.【解答】解:,(2)﹣(1),得x=5,把x=5代入(1),得y=2.∴原方程组的解为:.【点评】解二元一次方程组体现了数学的转化思想,即二元方程一元化,本题也可以利用代入消元法求解,但是不如加减消元法简单,同学们不妨一试.23.(5分)解不等式组:【分析】分别解出两不等式的解集,再求其公共解.【解答】解:由①得2x﹣x<4﹣3∴x<1由②得x﹣3>2x∴﹣x>3即x<﹣3∴不等式组的解集为x<﹣3.【点评】求不等式组的解集应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.24.(5分)如图,CD平分∠ACB,DE∥BC,∠AED=80°.(1)求∠EDC;=30,求点E到BC的距离.(2)若BC=10,S△BCD【分析】(1)根据两直线平行,同位角相等可以得到∠ABC=∠AED,又CD平分∠ACB,所以∠BCD的度数可以求出,再根据两直线平行,内错角相等即可求出∠EDC的度数;(2)根据三角形的面积求出点D到BC边的距离,再根据平行线间的距离相等,点E到BC的距离就等于点D到边BC的距离.【解答】解:(1)∵DE∥BC,∴∠AED=∠ACB=80°,∠EDC=∠DCB,∵DC平分∠ACB,∴∠ECD=∠DCB=∠EDC=40°;=30,(2)∵BC=10,S△BCD∴点D到BC的距离是6,∵DE∥BC,∴点D到BC的距离=点E到BC的距离,∴点E到BC的距离是6.【点评】本题主要考查平行线的性质和两平行线间的距离相等的性质,熟练掌握性质是解题的关键.25.(5分)在平面直角坐标系中有四个点,它们的坐标分别是A(0,3),B(﹣2,﹣1),C(3,﹣1),D(5,3).(1)在坐标系中描出这四个点,并依次连接它们,画出所得图形;(2)将所得的图形向下平移2个单位长度,画出平移后的图形,写出平移后对应的四点A′,B′,C′,D′的坐标.【分析】(1)可先判断出各点所在象限或坐标轴,找到各点的位置,按题中所给坐标的顺序连接各点即可;(2)把所得图形的各顶点向下平移2个单位长度,按原来图形的顺序连接得到的各点即可.根据各点所在的象限和距离坐标轴的距离得到平移后相应各点的坐标即可.【解答】解:(1)如图:(2)平移后的图形如图:A′(0,1),B′(﹣2,﹣3),C′(3,﹣3),D′(5,1).【点评】用到的知识点为:图形的平移要归结为图形顶点的平移.平移作图的一般步骤为:①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.26.(5分)A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:A B C笔试859590口试8085(1)请将表一和图一中的空缺部分补充完整.(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.【分析】(1)结合表一和图一可以看出:A大学生的口试成绩为90分;(2)A的得票为300×35%=105(张),B的得票为300×40%=120(张),C的得票为:300×25%=75(张);(3)分别通过加权平均数的计算方法计算A的成绩,B的成绩,C的成绩,综合三人的得分,则B应当选.【解答】解:(1)A大学生的口试成绩为90;补充后的图如图所示:A B C笔试859590口试908085(2)A的票数为300×35%=105(张),B的票数为300×40%=120(张),C的票数为300×25%=75(张);(3)A的成绩为=92.5(分)B的成绩为=98(分)C的成绩为=84(分)故B学生成绩最高,能当选学生会主席.【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.27.(5分)为改善办学条件,北海中学计划购买部分A品牌电脑和B品牌课桌.第一次,用9万元购买了A品牌电脑10台和B品牌课桌200张.第二次,用9万元购买了A品牌电脑12台和B品牌课桌120张.(1)每台A品牌电脑与每张B品牌课桌的价格各是多少元?(2)第三次购买时,销售商对一次购买量大的客户打折销售.规定:一次购买A品牌电脑35台以上(含35台),按九折销售,一次购买B品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?【分析】(1)设每台A品牌电脑m元,每张B品牌课桌n元,列方程组即可求解;(2)设购电脑x台,课桌y张,列出方程组,解得x、y的取值范围,再确定购买方案.【解答】解:(1)设每台A品牌电脑m元,每张B品牌课桌n元,则有,解得.答:每台A品牌电脑6000元,每张B品牌课桌150元.(2)有两种方案.设购电脑x台,则课桌有张,则有,解得:35≤x≤36,则x=35或36.x=35时,=675(张);x=36时,=630(张).方案①:购电脑35台,课桌675张;方案②:购电脑36台,课桌630张.【点评】(1)是二元一次方程组的应用,找到两个等量关系式是关键;(2)考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式实关键.28.(5分)如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.【分析】通过分析条件可知,连接AD,构造四边形ABCD,利用内角和求出∠BAD+∠ADC=150°,再利用四边形ADEF中的内角和关系求出∠F=130°.【解答】解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.∵AB⊥BC,∴∠B=90°.又∵∠C=120°,∴∠BAD+∠ADC=150°.∵CD∥AF,∴∠CDA=∠DAF.在四边形ADEF中,∠DAF+∠EDA+∠F+∠E=360°,∴∠F+∠E=210°.又∵∠E=80°,∴∠F=130°.【点评】主要考查了四边形的内角和是360度的实际运用.解题关键是构造四边形利用已知条件结合四边形内角和求解.29.(5分)如果有理数x,y满足等式2x+x2+9y2+2=﹣6y,求x﹣3y的值.【分析】把等式2x+x2+9y2+2=﹣6y根据完全平方公式整理成两个平方和的形式,然后根据平方数非负数的性质列式求出x、y的值,再代入计算即可.【解答】解:由2x+x2+9y2+2=﹣6y,得x2+2x+1+9y2+6y+1=0,即(x+1)2+(3y+1)2=0,∴x+1=0,3y+1=0,解得x=﹣1,y=﹣∴x﹣3y=﹣1﹣3×(﹣)=﹣1+1=0.【点评】本题考查了完全平方公式,灵活运用完全平方公式简化计算,整理成平方和的形式然后利用非负数的性质是解题的关键.30.(5分)如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD =∠BCF.(1)求∠ECF+DAC+∠ECA的度数;(2)判断ED与FC的位置关系,并对你的结论加以证明.【分析】(1)由题意易得∠ECF+DAC+∠ECA=45°+∠BCF+45°﹣∠BCF=90°;(2)由凹四边形ADEC得内角和是360°以及已知易得∠ADE=90°,可得∠ECA+∠CED+∠CAD=∠EDA=90°,又(1)的结论是∠ECF+DAC+∠ECA=90°,∴∠CED =∠ECF,因此由内错角相等即知DE∥CF.【解答】解:(1)∵∠ECF=∠ECB+∠BCF,∴∠ECF+∠DAC+∠ECA=(∠ECB+∠BCF)+∠DAC+∠ECA(∠BCF=∠BAD)=(∠ECB+∠ECA)+(∠DAC+∠BAD)=∠BCA+∠BAC=45°+45°=90°即∠ECF+DAC+∠ECA=90°;(2)ED和FC平行,理由如下:∵∠EAD=∠AED=45°,∴∠EDA=90°,∴在C,E,D,A四点组成的凹四边形里,∠ECA+∠CED+∠CAD=∠EDA=90°又∵(1)的结论是∠ECF+DAC+∠ECA=90°,∴∠CED=∠ECF,∴DE∥CF(内错角相等,两直线平行).【点评】此题主要考查了角之间的和差关系、四边形的内角和、平行线的判定等知识点,有点难度,特别是凹四边形的应用不太常见.2010-2011学年北京市西城区(北区)七年级(下)期末数学试卷B卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)2x+3y=5,可以得到用含x的式子表示y,正确的是()A.y=B.y=C.y=D.y=5﹣2.(3分)下列计算正确的是()A.a3•a4=a12B.(a3)4=a7C.(a2b)3=a6b3D.a3÷a4=a(a≠0)3.(3分)已知x>y,下列不等式变形中错误的是()A.x+9>y+9B.x﹣9>y﹣9C.9x>9y D.9﹣x>9﹣y 4.(3分)如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是()A.95°B.85°C.75°D.65°5.(3分)等腰三角形的两边长分别是5cm和10cm,则它的周长是()A.15cm B.20cm C.25cm D.20cm或25cm 6.(3分)一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为()A.x>﹣2B.x≤3C.﹣2≤x<3D.﹣2<x≤3 7.(3分)一个正多边形的一个内角比它的一个外角大90°,则这个正多边形是()A.九边形B.八边形C.七边形D.六边形8.(3分)小明家从今年起使用了分时电表,即按“平时段”(6:00~22:00)和“谷时段”(22:00~次日6:00)分别计费,“平时段”电价0.60元/度,“谷时段”电价0.30元/度.小明把前五个月的月用电量及月交电费情况绘制成下面的部分统计图表:月份用电量(度)月电费(元)1月9051.02月9250.13月9848.64月10548.05月根据上述信息,下列说法中,正确的是()A.从1至5月,小明家“平时段”用电量呈上升趋势,“谷时段”用电量呈下降趋势B.从1至5月,小明家“平时段”用电量呈下降趋势,月用电量呈下降趋势C.从1至5月,小明家“谷时段”用电量呈上升趋势,月电费呈上升趋势D.从1至5月,小明家月用电量呈上升趋势,月电费呈下降趋势9.(3分)已知:a2﹣4b﹣4=0,a2+2b2=3,则的值为()A.﹣1B.0C.D.110.(3分)如图将六边形ABCDEF沿着直线GH折叠,使点A、B落在六边形CDEFGH的内部,则下列结论一定正确的是()A.∠1+∠2=900°﹣2(∠C+∠D+∠E+∠F)B.∠1+∠2=1080°﹣2(∠C+∠D+∠E+∠F)C.∠1+∠2=720°﹣(∠C+∠D+∠E+∠F)D.∠1+∠2=360°﹣(∠C+∠D+∠E+∠F)二、填空题(共10小题,每小题2分,满分20分)11.(2分)计算:(x+3y)(x﹣3y)=.12.(2分)点P是△ABC内一点,连接BP并延长交AC于点D,连接PC,则∠1,∠2的大小关系.13.(2分)如图,AB∥CD,DE交AB于点F,且CF⊥DE于点F,若∠EFB=125°,则∠C=°.14.(2分)点P(2a﹣12,3﹣a)位于第三象限,则a的取值范围是.15.(2分)下列命题中真命题的是(填写命题序号)①若a+b>0且ab>0,则a>0且b>0.②若a>b且ab>0,则a>b>0.③在同一平面内,垂直于同一直线的两直线平行.④一个锐角的补角比它的余角小90°.16.(2分)在平面直角坐标系中,A(﹣2,1),B(m,n)两点在平行x轴的同一直线上,且B到y轴的距离为3,则点B的坐标是.17.(2分)某超市在“六一节,大促销”活动中规定:一次购买的商品超过200元时,就可享受打折优惠.小红同学准备为班级购买奖品,需买6本影集和若干支钢笔,已知影集每本15元,钢笔每支8元,她至少买支钢笔才能享受打折优惠.18.(2分)我们知道,可以利用直观的几何图形形象的表示有些代数恒等式.例如:(2a+b)(a+b)=2a2+3ab+b2,可以用图1的面积关系来表示.还有许多代数恒等式也可以用几何图形面积来表示其正确性.(1)根据图2写出一个代数恒等式;(2)已知等式:(a+2b)2=a2+4ab+4b2,请你在图3的方框内画出一个相应的几何图形,利用这个图形的面积关系来表示等式的正确性.19.(2分)如图,在平行四边形ABCD中,M是BC边上一点,AM与对角线BD交于点N,=3,若S△ABNS△BMN=2,则S△DMN=,S△AND=.20.(2分)如果关于x不等式组的整数解仅为1,2,3,则a的取值范围是,b的取值范围是.三.解答题(本题共30分,每小题5分)21.(5分)解方程组:.22.(5分)解不等式:﹣,并把它的解集在数轴上表示出来.23.(5分)先化简,再求值:(x+2)(x﹣3)﹣3x(x﹣1)+(2x﹣1)2,其中x=.24.(5分)已知:如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF ∥AB,(1)求证:CE∥DF;(2)若∠DCE=130°,求∠DEF的度数.25.(5分)(1)请在下面的网格中建立平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,﹣2);(2)在(1)的条件下,过点B作x轴的垂线,垂足为点M,在BM的延长线上截取MC =BM.①写出点C的坐标;②平移线段AB使点A移动到点C,画出平移后的线段CD,并写出点D 的坐标.26.(5分)根据北京市统计局公布的2000年,2005年,2010年北京市常住人口相关数据,绘制部分统计图表如下:表12000年,2006年,2010年北京市全部常住人口中受教育程度情况统计表(人数单位:万人)年份大学程度人数(指大专及以上)高中程度人数(含中专)初中程度人数小学程度人数其他人数2000年233320475234120 2006年362372476212114。
北京市西城区2007数学期末试卷

北京市西城区2007—2008年学度第二学期抽样测试七年级数学试卷2008.7一、精心选一选(共10个小题,每小题3分,共30分)在下列各题的四个备选答案中,只有一个是正确的,请把正确结论的代号写在题后的括号内.1.计算(2ab)2的结果是( ).(A)4a2b2(B)4ab(C)2a2b(D)2ab22.不等式x+1≥2的解集在数轴上表示正确的是( ).3.已知三角形的两边的长分别为2cm和7cm,设第三边的长为x cm,则x的取值范围是( ).(A)2<x<7 (B)5<x<7 (C)5<x<9 (D)7<x<9 4.若a>b,则下列不等式中错误..的是( ).(A)a-1>b-1 (B)a+1>b+1(C)2a>2b(D)-2a>-2b5.如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( ).(A)同位角相等,两直线平行(B)两直线平行,同位角相等(C)内错角相等,两直线平行(D)两直线平行,内错角相等6.在下面四种正多边形的瓷砖中,用同一种瓷砖能镶嵌成一个平面图案的是( ).(A)①②③(B)①②④(C)①③④(D)②③④7.2008年5月4日,北京奥运圣火传入海南省三亚市,这是“祥云”火炬在境内传递的第一站.传递路线为:三亚—五指山—万宁—海口.如图,某校学生小红在海南省地图中用(-2,-1)表示火炬传递起点三亚市,用(-1,0)表示五指山,那么火炬传递终点海口市的位置可以表示为( ).(A)(3,4)(B)(4,5)(C)(4,2)(D)(2,4)8.下面的统计图分别反映的是甲、乙两班全体学生喜欢四种球类运动的情况,根据统计图,下列对喜欢乒乓球运动的人数占全班总人数的百分比做出的判断中,正确的是( ).(A)甲班大,乙班小(B)甲班小,乙班大(C)甲班、乙班一样大(D)无法确定哪个班大9.如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为( ).图①图②(A)70°(B)75°(C)80°(D)85°10.如图,正方形ABCD与正方形EFGH的边长分别a、b(a>b),若C与G重合,F在BC的延长线上,H在DC的延长线上,则△BDE的面积为( ).(A)22212121bab a++(B)aba 212+(C)2221ba + (D)ab a +221二、细心填一填(共8个小题,每小题3分,共24分)11.把命题“对顶角相等”改写为“如果……,那么……”的形式:__________________________________________________. 12.x 的21与3的差是负数,用不等式表示为__________.13.如图,AD ∥BC ,点E 在BD 的延长线上,若∠ADE =130°,则∠DBC 的度数为______°.14.一个多边形的内角和为900°,这个多边形为______边形.15.若已知点P (a -2,2a +3)在y 轴上,则点P 到原点的距离是______________.16.如图,每个小正方形的边长为1cm ,蚂蚁从A 点沿正方形的网格线,经过C 点,爬到B 点的最短路程是______cm .17.王强同学解方程组⎩⎨⎧=+=-824y x y x ●时,求得方程组的解为由于不慎,将一些墨水滴到了作业本上,刚好遮住了●处和◆处的数,那么●处表示的数应该是______,◆处表示的数应该是______.18.△ABC 中,∠B =20°,AD 为BC 边上的高,若∠DAC =30°,则∠BAC 的度数为______°.三、认真做一做(共5个小题,每小题6分,共30分)19.先化简,再求值:(3x +1)(3x -1)-10x (x +1)+(x +2)2,其中⋅-=31x20.解方程组:⎩⎨⎧=+=-.153,94y x y x21.解不等式组:⎪⎩⎪⎨⎧>++≤-.235,623x x x x22.如图,在四边形ABCD 中,AB ∥CD ,点E 、F 分别在AD 、BC 边上,连结AC 交EF 于G ,∠1=∠BAC .(1)求证:EF ∥CD ;(2)若∠CAF =15°,∠2=45°,∠3=20°,求∠B 和∠ACD 的度数.23.某校学生会要了解本校七年级学生周末进行体育锻炼的情况.在确定调查方式时,甲同学说:“我去七年级2班调查全体学生”;乙同学说:“我去七年级每个班随机调查一定数量的学生”;丙同学说:“我去市少年体育活动中心调查参加体育锻炼的学生”. (1)请你指出在以上三种调查方式中,哪位同学的调查方式最为合理?(2)该校学生会采用了最为合理的调查方式收集数据,并绘制了不完整的频数分布表和频数分布直方图.正正请你根据图表提供的信息,写出a 、b 的值,并补全频数分布直方图;(3)若该校七年级共有300名学生,请你估计在周末进行体育锻炼的时间少于1小时的学生人数,并根据调查情况向同学们提出一条建议. 四、解答题(共2个小题,每小题6分,共12分)24.如图,将△ABC 向右平移3个单位长度,然后再向上平移2个单位长度,可以得到△A 1B 1C1.(1)画出平移后的△A 1B 1C 1;(2)写出△A 1B 1C 1三个顶点的坐标;(3)已知点P 在x 轴上,以A 1、B 1、P 为顶点的三角形面积为4,求P 点的坐标. 解:25.某住宅小区将要举办“迎奥运”知识竞赛,物业的工作人员在购买奖品时,了解到如下信息:(1)求一盒“福娃”和一枚徽章各多少元?(2)物业公司公布本次活动奖品发放方案如下:元,设一、二、三等奖共20名,其中一等奖2名,那么二等奖和三等奖应各设多少名?五、解答题(本题4分)26.△ABC 中,AB =2,BC =4,CD ⊥AB 于D .(1)如图①,AE ⊥BC 于E ,求证:CD =2AE图①(2)如图②,P 是AC 上任意一点(P 不与A 、C 重合),过P 作PE ⊥BC 于E ,PF ⊥AB于F ,求证:2PE +PF =CD ;图②(3)在(2)中,若P 为AC 的延长线上任意一点,其它条件不变,请你在备用图中画出图形,并探究线段PE 、PF 、CD 之间的数量关系. (1)证明:(2)证明:(3)画图:备用图结论:B 卷 本卷满分20分六、归纳与猜想(本题6分)27.观察下面给出的图形,探究图形中的点的个数变化规律,并填表:七、解答题(本题7分)28.在平面直角坐标系中,已知x 轴上两个点A (2m -6,0),B (4,0)分别在原点两侧,且A 、B 两点间的距离小于7个单位长度.(1)求m 的取值范围;(2)C 是AB 的中点且为整点(横、纵坐标都为整数的点叫做整点),若D 为整点,当△BCD 为等腰直角三角形时,求出点D 的坐标.八、解答题(本题7分)29.△ABC 中,∠BAC =∠ACB .(1)如图,E 是AB 延长线上一点,连结CE ,∠BEC 的平分线交BC 于点D ,交AC 于点P .求证:∠CPD =90°-21∠BCE ;(2)若E 是射线BA 上一点(E 不与A 、B 重合),连结CE ,∠BEC 的平分线所在直线交BC 于点D ,交CA 所在直线于点P . ∠CPD 与∠BCE 有什么关系?请画出图形,给出你的结论,并说明理由. (1)证明:。
北京市西城区2009-2010年初一期末试题参考答案(B卷)
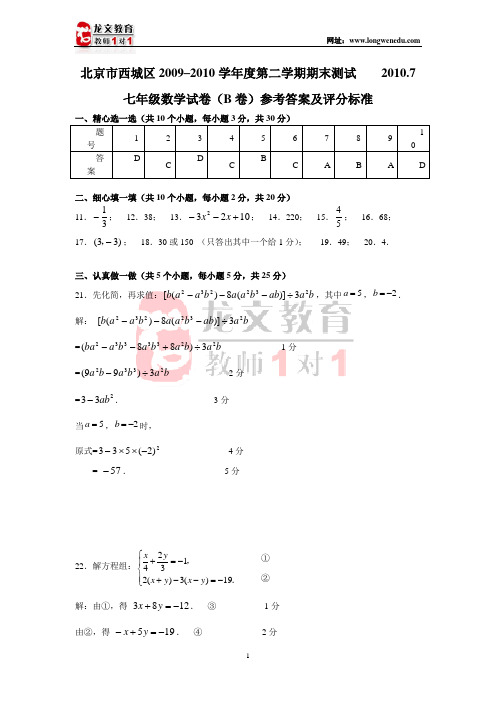
北京市西城区2009–2010学年度第二学期期末测试 2010.7七年级数学试卷(B 卷)参考答案及评分标准一、精心选一选(共10个小题,每小题3分,共30分)二、细心填一填(共10个小题,每小题2分,共20分) 11.31-; 12.38; 13.10232+--x x ; 14.220; 15.54; 16.68;17.)33(-,; 18.30或150 (只答出其中一个给1分); 19.49; 20.4.三、认真做一做(共5个小题,每小题5分,共25分)21.先化简,再求值:b a ab b a a b a a b 2322323)](8)([÷---,其中5a =,2b =-. 解: b a ab b a a b a a b 2322323)](8)([÷---=b a b a b a b a ba 22333323)88(÷+-- -----------------1分 =b a b a b a 23323)99(÷- -----------------2分 =233ab -. ----------------------------3分 当5a =,2b =-时,原式=2)2(533-⨯⨯- --------------------4分= 57-. -----------------------------5分22.解方程组:21432()3()19x y x y x y ⎧+=-⎪⎨⎪+--=-⎩,.解:由①,得 1283-=+y x . ③ ------------1分由②,得 195-=+-y x . ④ ----------------2分① ②④×3+③,得 6923-=y ,3-=y . -----------------------3分把3-=y 代入④,得 19)3(5-=-⨯+-x ,4=x . ------------------4分所以方程组的解为 ⎩⎨⎧-==34y x . -----------------------5分(其它正确解法相应给分)23.解不等式组:2(2)41213x x x x -->⎧⎪+⎨≤-⎪⎩,.解:解不等式①,得 2>x . ----------------------2分解不等式②,得 4≥x . ----------------------4分 把不等式①和②的解集在数轴上表示出来.所以不等式组的解集为4≥x .----------------------5分24.(1)表中m = 10 ,n = 50 ;--------2分(答对一个得1分)(2)如右图所示:----------------3分 (3)72度; ----------------------4分 (4))(4420050)110(人=⨯÷+答:估计该校初一年级女生掷实心球的成绩达到优秀的总人数约为44人.---------------5分25.(1)请写出图中下列地点的坐标: 牡丹园 (300,300) ;------------1分 游乐园 (200,-200) ;------------2分① ② 45O 123(2)如右图所示: -----------------4分 (3)问题(2)中湖心亭平移后的对应点 的坐标为 (-300, 0) . -------------5分四、解答题(共5个小题,每小题5分,共25分)26.解:设搭造A 种园艺造型x 个,则搭造B 种园艺造型)50(x -个.------1分 依题意,得 ⎩⎨⎧≤-+≤-+.,2900)50(100303600)50(4090x x x x ---------------2分由不等式①,得 32≤x .由不等式②,得 30≥x .因此,不等式组的解集为 3230≤≤x . ------------------3分根据题意,x 的值应是整数,所以323130或或=x . ----------------4分 当30=x 时,2050=-x ; 当31=x 时,1950=-x ; 当32=x 时,1850=-x . 答:符合要求的搭造方案有三种:① 搭造A 种园艺造型30个,搭造B 种园艺造型20个; ② 搭造A 种园艺造型31个,搭造B 种园艺造型19个;③ 搭造A 种园艺造型32个,搭造B 种园艺造型18个.-----------5分27.(1)可能的图形有:-------------3分 (画对一个图得1分)(2)周长的最大值为2b+2c ; -------------------4分周长的最小值为2a+2b . -------------------5分28.解:∵ 6=-b a , ∴ 6+=b a . -----------------1分∵ 2()90ab c a +-+=, ∴ 09)()6(2=+-++a c b b .∴ 0)()3(22=-++a c b . ---------------------------2分 ∴ a c b =-=且3. ---------------------------3分① ② acbc acbacb acb ab∴ 36)3(=+-=a ,3=c . -------------------------4分 ∴ 3333=+-=++c b a . -------------------------5分29.(1) 猜想: AF ∥ CD ;--------1分(2) 证明方法一:连接AD . -----------------2分 ∵在六边形ABCDEF 中,∠BAF+∠B+∠C+∠CDE+∠E+∠F=720180)26(=⨯-,而∠BAF +∠B+∠C=∠CDE +∠E+∠F , ∴∠BAF +∠B+∠C=21×720°=360°.即∠1+∠2+∠B+∠C=360°. ----------------3分 ∵在四边形ABCD 中,∠1+∠B+∠C+∠3=360°,∴∠2=∠3. ------------------4分 ∴AF ∥CD . ------------------5分证明方法二:连接AC . -----------------2分 ∵在六边形ABCDEF 中,∠BAF+∠B+∠BCD+∠D+∠E+∠F=720180)26(=⨯-,而∠BAF +∠B+∠BCD =∠D +∠E+∠F , ∴∠BAF +∠B+∠BCD =21×720°=360°.即∠1+∠2+∠B+∠3+∠4=360°. ----------------3分 ∵在三角形ABC 中,∠1+∠B+∠3=180°, ∴∠2+∠4=180°. ------------------4分 ∴AF ∥CD . ------------------5分证明方法三:延长AB 、DC 交于点G .-----------2分 ∵在六边形ABCDEF 中,∠A+∠ABC+∠BCD+∠D+∠E+∠F =720180)26(=⨯-,而∠A+∠ABC+∠BCD =∠D +∠E+∠F , ∴∠A +∠ABC+∠BCD =21×720°=360°.----------------3分∵∠ABC=∠G+∠2,∠BCD=∠G+∠1, ∴∠A+(∠G+∠2)+ (∠G+∠1)= 360°. ∵在三角形BCG 中,∠1+∠2+∠G=180°,EBBEE∴∠A+∠G=180°. ------------------4分 ∴AF ∥CD . ------------------5分(其它正确证明方法相应给分)30.(1) △DBF 的面积为 7 ; -----------------1分(2) 解:连接PA .∵在△PAB 中,D 、E 是AB 的三等分点, ∴PBE PBA ∆∆=S 3S ,PBE PAE ∆∆=S 2S . ∵在△PAC 中,F 、G 是AC 的三等分点, ∴PAF PAC ∆∆=S 3S .∵在△ABC 中,D 、E 是AB 的三等分点,F 、G 是AC 的三等分点, ∴284232S 32S =⨯==∆∆ABC CAE , 144231S 31S =⨯==∆∆A B C B A F .设x PEB =∆S ,y PFA=∆S ,则由题意得 ⎩⎨⎧=+=+.2823143x y y x , 解得 ⎩⎨⎧==.82y x ,∴2S =∆PEB . -----------------3分(3) 解:连接AM .∵在△MAB 中,D 、E 是AB 的三等分点, ∴MAD MAB ∆∆=S 3S .∵在△MAC 中,F 、G 是AC 的三等分点, ∴MAF MAC ∆∆=S 3S .∵在△ABC 中,D 、E 是AB 的三等分点,F 、G 是AC 的三等分点, ∴ =∆BAF S 144231S 31S =⨯==∆∆ABC CAD .设m MAD =∆S ,S M FA n ∆=,则由题意得 ⎩⎨⎧=+=+.143143m n n m , 解得 ⎩⎨⎧==.5.35.3n m ,∴5.3S =∆MAD . ∴7S 2S ==∆∆MAD MBD .图2B图3B由(2)可知 2S =∆PEB , ∴=EPMD四边形S 527S S =-=-∆∆PEB MBD . -------------5分。
20100701北京市西城区初一第二学期数学期末精彩试题B卷

实用文档学年度第二学期期末测试2009–2010北京市西城区卷)B 七年级数学试卷( 2010.7 分)100分钟,满分100(时间总分四二三题号一得分分)分,共30一、精心选一选(共10个小题,每小题3 .)1.下列计算正确的是(523333x(x)?x2x?x?. BA.444853y(xy)?xx??xx D.C.).2.下列命题中正确的有(c;,则a∥b若a∥,b∥c①相等的角是对顶角;②邻补角的平分线互相垂直.同位角相等;④③个.个 D3.1个 C.2A.0个 B .,则下列不等式一定成立的是()3.已知ba?b2a???25b?a?5? A. B.33b?a0?7b7a?.C. D22AD2可以得到的结论是().4.如图,由AD∥BC14 1=∠A.∠1=∠2 B.∠434 .∠2=∠3 D.∠3=∠C CB01?x??.的解集,正确的是()5.利用数轴确定不等式组?2?x?.. BA32O1-13O12-1-2-2C.. D-1O123-231O-12-26.下列调查中,适宜采用抽样调查的个数是().了解全国中学生的用眼卫生情况;① 30名成员订做比赛服装的尺寸大小;了解某校合唱团②了解某种电池的使用寿命;③④了解中央电视台直播上海世博会开幕式的全国收视率情况. 2个.A1 B.个4 D个3C..个大全.实用文档).7.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( 360°C.1620° D.A.1260° B.900°x)kxx?2)(1?(k化简后的结果中不含有)8.已知的一次项,则.的值为(11?1?1 D.A. C. B.22k4x?y??x y10?x?2y,的解也是二元一次方程9.若关于的二元一次方程组?k2x?y??k的解,则.的值为()0.5?0.52?2A. B.. DC.为三边的三角ca、b、c中,c的最大值为6且a<b<c,则以b10.已知正整数a、、形共有(). D.7个 B.5个 C.6个A.4个F2分,共20分)二、细心填一填(共10个小题,每小题m1m?2?m3x =________11.若点P()在.,轴上,则BAE CD,∠A=32°,∠C=70°,12.如图,AB∥则∠F=_______°.DC2)32?1)?(2x?3)(x?(x.计算:.=__________________13A14.如图,四边形ABCD 中,∠B=40°,沿直线MN剪去MDE1中,∠1+∠°.2=_________∠B,则所得五边形AEFCD2CBF2xx?1???N1ax?by?都是方程和的解,15.已知??12y?y??A???a?b _______.则BAC,B=30°,∠C=74°,AD平分∠16.如图,△ABC中,∠F°.,则∠AEF=_______⊥AD于F,AE⊥BC于E EF ECDB17.若点P在第四象限,且距离每个坐标轴都是3个单位长度,则点P的坐标为_______________.18.已知OA⊥OB,∠AOC:∠AOB=2:3,则∠BOC=_______________°.19.在一块边长为10米的正方形草坪上修了横竖各两条宽都为1.5米的长方形小路(图中阴影部分)将草坪分隔成如图所示的图案,则图中未被小路覆盖的草坪的总面积为_____________平方米.2252y??2xy?x2?y.多项式20__________的最小值是.大全.实用文档三、认真做一做(共5个小题,每小题5分,共25分)21.先化简,再求值:232232b3aab)]8a(a?([bab?a?b)?,其中,.2?b?a?5x2y????1,?.解方程组:2243??2(x?y)?3(x?y)??19.?2x?(x?2)?4,??1?2x?.解不等式组:23?x?1.?3?大全.实用文档24.李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).请你结合图表中所给信息回答下列问题:频<6<454%nm;=_________,(1)表中=_________ )请补全频数分布直方图;(2x____________度;≤7<这一组所占圆心角的度数为6 (3)在扇形统计图中,米以上为优秀,请你估计该校初一年级女664)如果掷实心球的成绩达到米或(生掷实心球的成绩达到优秀的总人数.大全.实用文档.如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北方25yx长.已知各轴正方向建立平面直角坐标系,规定一个单位长度代表向为1m轴、).建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0 )请写出图中下列地点的坐标:(1牡丹园__________________;;游乐园__________________(2)连接音乐台、湖心亭和望春亭这三个地点,画出所得的三角形.然200个单位后将所得三角形向下平移长度,画出平移后的图形;)中湖心亭平移后的对)问题((32 __________________.应点的坐标为四、解答题(共5个小题,每小题5分)分,共25盆乙种花,计划用甲、盆甲种花和290026.在一次活动中,主办方共准备了3600 50两种园艺造型共个,搭造要求的花盆数如下表所示:BA乙两种花搭造出、甲造型乙 30盆盆A 90 盆40B100盆请问符合要求的搭造方案有几种?请写出具体的方案.大全.实用文档沿ABCD,其中a<b<c.将长方形AC=cABCD中,AB =a,BC =b,27.如图,长方形剪开.AC形状不同但面积相等(即要ABCD(1)用所得的两个三角形可以拼出几个与长方形求没有缝隙,也不重叠)的凸四边形?请分别画出所有可能的图形;)拼接所得的四边形中,周长的最大值与最小值分别为多少?请用12)在问题((表示出来.、ca、b ADcaCBb20?a)?9?ab?(c c6??b?aba?,,求的值.28.已知:大全.实用文档,猜想可得六边形∠FE+C=∠D+∠A+29.已知:如图,六边形ABCDEF中,∠∠B+∠ ABCDEF中必有两条边是平行的. ________;)根据图形写出你的猜想:_______∥1()中写出的猜想.2()请证明你在(1 AFB ECD大全.实用文档A30.阅读理解S表示BC的中点.如果用如图a,在△ABC中,D是ABC?CBD的面积,则由等底等高的三角形的面积相等,可得△ABC a图1A SS?S?E、ABC中,D.同理,如图b,在△ABC???ABDACD21S?S??SS的三等分点,可得.是BC ABCABD???ADEAEC?3CBEDb图结论应用A,请利用上面的结论解42ABC的面积为已知:△决下列问题DE BECD与AB、AC的中点,、(1)如图1,若DE分别是F____________;F,则△DBF的面积为交于点CB1图类比推广BG、CD分别交BFF、G是AC的三等分点,D(2)如图2,若、E是AB的三等分点, BEP,求△的面积;于P、QBF于M、N,CE分别交、BG AD FM NEPG Q CB2图探究新知 EPMD的面积.3,问题(2)中的条件不变,求四边形)如图(3 ADF M NEGP QC B3图大全.实用文档大全.。
2010-2011学年北京市西城区(北区)七年级(下)期末数学试卷B卷

2010-2011学年北京市西城区(北区)七年级(下)期末数学试卷B卷2010-2011学年北京市西城区(北区)七年级(下)期末数学试卷B卷一、选择题(共10小题,每小题3分,满分30分)y=4.(3分)如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是()6.(3分)一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为()8.(3分)小明家从今年起使用了分时电表,即按“平时段”(6:00~22:00)和“谷时段”(22:00~次日6:00)分别计费,“平时段”电价0.60元/度,“谷时段”电价0.30元/度.小明把前五个月的月用电量及月交电费情况绘制成)9.(3分)已知:a2﹣4b﹣4=0,a2+2b2=3,则的值为()D10.(3分)如图将六边形ABCDEF沿着直线GH折叠,使点A、B落在六边形CDEFGH的内部,则下列结论一定正确的是()(∠二、填空题(共10小题,每小题2分,满分20分)11.(2分)计算:(x+3y)(x﹣3y)=_________.12.(2分)点P是△ABC内一点,连接BP并延长交AC于点D,连接PC,则∠1,∠2的大小关系_________.13.(2分)如图,AB∥CD,DE交AB于点F,且CF⊥DE于点F,若∠EFB=125°,则∠C=_________°.14.(2分)点P(2a﹣12,3﹣a)位于第三象限,则a的取值范围是_________.15.(2分)下列命题中真命题的是_________(填写命题序号)①若a+b>0且ab>0,则a>0且b>0.②若a>b且ab>0,则a>b>0.③在同一平面内,垂直于同一直线的两直线平行.④一个锐角的补角比它的余角小90°.16.(2分)在平面直角坐标系中,A(﹣2,1),B(m,n)两点在平行x轴的同一直线上,且B到y轴的距离为3,则点B的坐标是_________.17.(2分)某超市在“六一节,大促销”活动中规定:一次购买的商品超过200元时,就可享受打折优惠.小红同学准备为班级购买奖品,需买6本影集和若干支钢笔,已知影集每本15元,钢笔每支8元,她至少买_________支钢笔才能享受打折优惠.18.(2分)我们知道,可以利用直观的几何图形形象的表示有些代数恒等式.例如:(2a+b)(a+b)=2a2+3ab+b2,可以用图1的面积关系来表示.还有许多代数恒等式也可以用几何图形面积来表示其正确性.(1)根据图2写出一个代数恒等式_________;(2)已知等式:(a+2b)2=a2+4ab+4b2,请你在图3的方框内画出一个相应的几何图形,利用这个图形的面积关系来表示等式的正确性.19.(2分)如图,在平行四边形ABCD中,M是BC边上一点,AM与对角线BD交于点N,若S△ABN=3,S△BMN=2,则S△DMN=_________,S△AND=_________.20.(2分)如果关于x不等式组的整数解仅为1,2,3,则a的取值范围是_________,b的取值范围是_________.三.解答题(本题共30分,每小题5分)21.(5分)解方程组:.22.(5分)解不等式:﹣,并把它的解集在数轴上表示出来.23.(5分)先化简,再求值:(x+2)(x﹣3)﹣3x(x﹣1)+(2x﹣1)2,其中x=.24.(5分)已知:如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB,(1)求证:CE∥DF;(2)若∠DCE=130°,求∠DEF的度数.25.(5分)(1)请在下面的网格中建立平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,﹣2);(2)在(1)的条件下,过点B作x轴的垂线,垂足为点M,在BM的延长线上截取MC=BM.①写出点C的坐标;②平移线段AB使点A移动到点C,画出平移后的线段CD,并写出点D的坐标.26.(5分)根据北京市统计局公布的2000年,2005年,2010年北京市常住人口相关数据,绘制部分统计图表如下:(1)从2000年到2010年的十年中,北京市常住人口增加了_________万人;(2)2010年北京市常住人口中,大学程度人数占全部常住人口数的百分比是_________%(精确到1%,大学程度人数在扇形统计图中所对应的圆心角的度数是_________度(精确到1度),并补全上面的扇形图;(3)从2005年到2010年的五年中,结合统计图中的数据,对于北京市常住人口受教育程度的状况,谈谈你的看法.四.解答题(本题共10分,每小题5分)27.(5分)某工厂要用图1所示的长方形和正方形纸板,经过组合加工成竖式,横式两种长方体形状的无盖纸盒.张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完.(3)该厂在某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试问在这一天加工这两种纸盒时,a的所有可能的值.28.(5分)在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半轴上,且OB=OA=3.(1)求点A,B的坐标;(2)若点C(﹣2,2),求△BOC的面积;(3)点P是第一,三象限角平分线上一点,若S△ABP=,求点P的坐标.五.解答题(本题共10分,第29题6分,第30题4分)29.(6分)如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A 按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).(1)当α为_________度时,AD∥BC,并在图3中画出相应的图形;(2)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;(3)当0°<α<45°,连接BD,利用图4探究∠BDE+∠CAE+∠DBC的度数是否发生变化,并给出你的证明.30.(4分)(1)如图1,在△ABC中,BC=3,AC=4,AB=5.D为AB边上一点,且△ACD与△BCD的周长相等,则AD=_________.(2)如图2,在△ABC中,BC=a,AC=b,AB2=BC2+AC2.E为BC边上一点,且△ABE与△ACE的周长相等;F 为AC边上一点,且△ABF与△BCF的周长相等,求CE•CF(用含a,b的式子表示).2010-2011学年北京市西城区(北区)七年级(下)期末数学试卷B卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)y=y=.4.(3分)如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是()6.(3分)一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为()8.(3分)小明家从今年起使用了分时电表,即按“平时段”(6:00~22:00)和“谷时段”(22:00~次日6:00)分别计费,“平时段”电价0.60元/度,“谷时段”电价0.30元/度.小明把前五个月的月用电量及月交电费情况绘制成)9.(3分)已知:a2﹣4b﹣4=0,a2+2b2=3,则的值为()Dab+2b=(10.(3分)如图将六边形ABCDEF沿着直线GH折叠,使点A、B落在六边形CDEFGH的内部,则下列结论一定正确的是()(∠HGA=GHB=(+(∠二、填空题(共10小题,每小题2分,满分20分)11.(2分)计算:(x+3y)(x﹣3y)=x2﹣9y2.12.(2分)点P是△ABC内一点,连接BP并延长交AC于点D,连接PC,则∠1,∠2的大小关系∠1>∠2.13.(2分)如图,AB∥CD,DE交AB于点F,且CF⊥DE于点F,若∠EFB=125°,则∠C=35°.14.(2分)点P(2a﹣12,3﹣a)位于第三象限,则a的取值范围是3<a<6.解:根据题意得:15.(2分)下列命题中真命题的是①③(填写命题序号)①若a+b>0且ab>0,则a>0且b>0.②若a>b且ab>0,则a>b>0.③在同一平面内,垂直于同一直线的两直线平行.④一个锐角的补角比它的余角小90°.16.(2分)在平面直角坐标系中,A(﹣2,1),B(m,n)两点在平行x轴的同一直线上,且B到y轴的距离为3,则点B的坐标是(3,1)或(﹣3,1).17.(2分)某超市在“六一节,大促销”活动中规定:一次购买的商品超过200元时,就可享受打折优惠.小红同学准备为班级购买奖品,需买6本影集和若干支钢笔,已知影集每本15元,钢笔每支8元,她至少买14支钢笔才能享受打折优惠.,18.(2分)我们知道,可以利用直观的几何图形形象的表示有些代数恒等式.例如:(2a+b)(a+b)=2a+3ab+b,可以用图1的面积关系来表示.还有许多代数恒等式也可以用几何图形面积来表示其正确性.(1)根据图2写出一个代数恒等式(a+2b)(2a+b)=2a2+5ab+2b2;(2)已知等式:(a+2b)2=a2+4ab+4b2,请你在图3的方框内画出一个相应的几何图形,利用这个图形的面积关系来表示等式的正确性.19.(2分)如图,在平行四边形ABCD中,M是BC边上一点,AM与对角线BD交于点N,若S△ABN=3,S△BMN=2,则S△DMN=3,S△AND=.∴,∴=,.20.(2分)如果关于x不等式组的整数解仅为1,2,3,则a的取值范围是0<a≤9,b的取值范围是24<b≤32.≤<,≥<不等式组的解集是<≤<三.解答题(本题共30分,每小题5分)21.(5分)解方程组:.,代入②×﹣∴22.(5分)解不等式:﹣,并把它的解集在数轴上表示出来.23.(5分)先化简,再求值:(x+2)(x﹣3)﹣3x(x﹣1)+(2x﹣1)2,其中x=.代入求解即可求得答案.时,(×﹣524.(5分)已知:如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB,(1)求证:CE∥DF;(2)若∠DCE=130°,求∠DEF的度数.CDE=∠25.(5分)(1)请在下面的网格中建立平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,﹣2);(2)在(1)的条件下,过点B作x轴的垂线,垂足为点M,在BM的延长线上截取MC=BM.①写出点C的坐标;②平移线段AB使点A移动到点C,画出平移后的线段CD,并写出点D的坐标.26.(5分)根据北京市统计局公布的2000年,2005年,2010年北京市常住人口相关数据,绘制部分统计图表如下:(1)从2000年到2010年的十年中,北京市常住人口增加了579万人;(2)2010年北京市常住人口中,大学程度人数占全部常住人口数的百分比是32%(精确到1%,大学程度人数在扇形统计图中所对应的圆心角的度数是115度(精确到1度),并补全上面的扇形图;(3)从2005年到2010年的五年中,结合统计图中的数据,对于北京市常住人口受教育程度的状况,谈谈你的看法.四.解答题(本题共10分,每小题5分)27.(5分)某工厂要用图1所示的长方形和正方形纸板,经过组合加工成竖式,横式两种长方体形状的无盖纸盒.(2)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完.(3)该厂在某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试问在这一天加工这两种纸盒时,a的所有可能的值.依题意,得依题意得:,28.(5分)在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半轴上,且OB=OA=3.(1)求点A,B的坐标;(2)若点C(﹣2,2),求△BOC的面积;(3)点P是第一,三象限角平分线上一点,若S△ABP=,求点P的坐标.=<﹣•+•OA ∴3a+﹣.+S=•+•OA ∴•×3=五.解答题(本题共10分,第29题6分,第30题4分)29.(6分)如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A 按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).(1)当α为15度时,AD∥BC,并在图3中画出相应的图形;(2)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;(3)当0°<α<45°,连接BD,利用图4探究∠BDE+∠CAE+∠DBC的度数是否发生变化,并给出你的证明.30.(4分)(1)如图1,在△ABC中,BC=3,AC=4,AB=5.D为AB边上一点,且△ACD与△BCD的周长相等,则AD=2.(2)如图2,在△ABC中,BC=a,AC=b,AB2=BC2+AC2.E为BC边上一点,且△ABE与△ACE的周长相等;F 为AC边上一点,且△ABF与△BCF的周长相等,求CE•CF(用含a,b的式子表示).CE+AC=BE+AB=(CE+AC=BE+AB=(x+b=(x=(y+a=([c参与本试卷答题和审题的老师有:星期八;Liuzhx;sks;caicl;zhjh;lk;wangjc3;sd2011;cair。
北京市西城区七年级第二学期期末试题(附加题)答案(2021.7)

北京市西城区2020—2021学年度第二学期期末试卷 七年级数学附加题答案及评分参考 第1页(共2页)北京市西城区2020—2021学年度第二学期期末试卷 七年级数学附加题答案及评分参考 2021.7一、填空题(本题6分)1.(1)2,1; ························································································································ 4分(2)955H ≤≤. ··············································································································· 6分 二、解答题(本题共14分,第2题6分,第3题8分)2.解:(1)30;····················································································································· 1分(2)如图,过点P 作直线HQ ∥AB .∵ AB ∥CD ,∴ HQ ∥AB ∥CD .∴2FPQ CFP t ∠=∠=,3EPQ KEP t ∠=∠=.∴ EPF t ∠=. ………………………………2分∵ KP ⊥FN ,∴ o 90KPF ∠=.∴ o 90KPE t ∠=−. ··································································································· 3分(3)易知,当0<t ≤60时,EM 与FN 不平行. ……………………………………4分当60<t ≤90时,如图,EM ∥FN ,设FN 与AB 交于点G .∴ AGF MEB ∠=∠.根据题意得,o 3180MEB t ∠=−,∴ o 3180AGF t ∠=−.……………………………5分∵ AB ∥CD ,∴ o 180AGF CFN ∠+∠=.∵ 2CFN t ∠=,∴ o o 31802180t t −+=.∴ 72t =. ……………………………………………………………………6分3.解:(1)①5; ……………………………………………………………………… 1分北京市西城区2020—2021学年度第二学期期末试卷 七年级数学附加题答案及评分参考 第2页(共2页)②(30)−,,(50),.·························································································· 3分(2)①∵ 点P ,Q 在y 轴上,P 在Q 的上方,PQ =6,点Q 的坐标为(01),,∴点P 的坐标为(07),.设点T (0)t ,为线段PQ 上任意一点,则17t ≤≤.∵点M 的坐标为(50)−,,∴ 5x d =,y d t =.∴()5x y M T d d t μ=−=−,.………………………………………………4分由17t ≤≤,可得 254t -≤-≤,∴ 0()4M T μ≤,≤.∴ ()M T μ,的最大值是4.∴ ()4M PQ μ=,. ······························································································ 5分②()M PQ μ,的最小值是3,此时点P 的坐标是(08),或(02),-.························································································································· 8分。
西城初一数学下学期期末试卷

西城初一数学下学期期末试卷2019西城初一数学下学期期末试卷一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.9的平方根是().A. B. C. D.2.计算的结果是().A. B. C. D.3.下列调查中,适宜采用全面调查方式的是().A. 调查春节联欢晚会在北京地区的收视率B. 了解全班同学参加社会实践活动的情况C. 调查某品牌食品的蛋白质含量D. 了解一批手机电池的使用寿命4.若,则点P(,)所在的象限是().A.第一象限 B.第二象限 C.第三象限 D.第四象限5.下列各数中的无理数是().A. B. C. D.6.如图,直线a∥b,c是截线.若∠2=4∠1,则∠1的度数为().A.30° B.36° C.40° D.45°7.若,则下列不等式中,正确的是().A. B.AC,BC中,最长的边是.16.服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.(1)表中 = , = ;(2)身高满足的校服记为L号,则需要订购L号校服的学生占被调查学生的百分数为.17.在平面直角坐标系中,点A的坐标为(,).若线段AB∥x轴,且AB的长为4,则点B的坐标为.18.在平面直角坐标系xOy中,直线l经过点A(,),点A1,A2,A3,A4,A5,……按如图所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,则A8的坐标为;若点An(为正整数)的横坐标为2019,则 = .三、解答题(本题共18分,每小题6分)19.解不等式组解:20.已知:如图,AB∥DC,AC和BD相交于点O, E是CD 上一点,F是OD上一点,且∠1=∠A.(1)求证:FE∥OC;(2)若∠B=40°,∠1=60°,求∠OFE的度数.(1)证明:(2)解:21.先化简,再求值:,其中,.解:四、解答题(本题共11分,第22题5分,第23题6分)22.某校学生会为了解该校同学对乒乓球、羽毛球、排球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能从中选择一项),随机选取了若干名同学进行抽样调查,并将调查结果绘制成了如图1,图2所示的不完整的统计图.(1)参加调查的同学一共有______名,图2中乒乓球所在扇形的圆心角为_______°;(2)在图1中补全条形统计图(标上相应数据);(3)若该校共有2400名同学,请根据抽样调查数据估计该校同学中喜欢羽毛球运动的人数.(3)解:23.如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(,),B(,),C(,).将△ABC向右平移5个单位长度,再向下平移4个单位长度,得到△ ,其中点,,分别为点A,B,C的对应点.(1)请在所给坐标系中画出△ ,并直接写出点的坐标;(2)若AB边上一点P经过上述平移后的对应点为(,),用含,的式子表示点P的坐标;(直接写出结果即可)(3)求△ 的面积.解:(1)点的坐标为;(2)点 P的坐标为;(3)五、解答题(本题共19分,第25题5分,第24、26题每小题7分)24.在一次知识竞赛中,甲、乙两人进入了“必答题”环节.规则是:两人轮流答题,每人都要回答20个题,每个题回答正确得m分,回答错误或放弃回答扣n分.当甲、乙两人恰好都答完12个题时,甲答对了9个题,得分为39分;乙答对了10个题,得分为46分.(1)求m和n的值;(2)规定此环节得分不低于60分能晋级,甲在剩下的比赛中至少还要答对多少个题才能顺利晋级?解:25.阅读下列材料:某同学遇到这样一个问题:如图1,在△ABC中,AB=AC,BD 是△ABC的高.P是BC边上一点,PM,PN分别与直线AB,AC垂直,垂足分别为点M,N.求证:.他发现,连接AP,有,即.由AB=AC,可得.他又画出了当点P在CB的延长线上,且上面问题中其他条件不变时的图形,如图2所示.他猜想此时BD,PM,PN之间的数量关系是:.请回答:(1)请补全以下该同学证明猜想的过程;证明:连接AP.∵AB=AC,(2)参考该同学思考问题的方法,解决下列问题:在△ABC中,AB=AC=BC,BD是△ABC的高.P是△ABC 所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.①如图3,若点P在△ABC 的内部,则BD,PM,PN,PQ之间的数量关系是:;②若点P在如图4所示的位置,利用图4探究得出此时BD,PM,PN,PQ之间的数量关系是:.26.在△ABC中,BD,CE是它的两条角平分线,且BD,C E 相交于点M,MN⊥BC于点N.将∠MBN记为∠1,∠MCN记为∠2,∠CMN记为∠3.(1)如图1,若∠A=110°,∠BEC=130°,则∠2= °,∠3-∠1= °;(2)如图2,猜想∠3-∠1与∠A的数量关系,并证明你的结论;(3)若∠BEC= ,∠BDC= ,用含和的代数式表示∠3-∠1的度数.(直接写出结果即可)解:(2)∠3-∠1与∠A的数量关系是:.证明:(3)∠3-∠1= .北京市西城区2019— 2019学年度第二学期期末试卷七年级数学附加题试卷满分:20分一、填空题(本题6分)1.已知,是正整数.(1)若是整数,则满足条件的的值为;(2)若是整数,则满足条件的有序数对(,)为.二、解答题(本题7分)2.已知代数式.(1)若代数式M的值为零,求此时,,的值;(2)若,,满足不等式,其中,,都为非负整数,且为偶数,直接写出,,的值.解:三、解决问题(本题7分)3.在平面直角坐标系xOy中,点A在x轴的正半轴上,点B 的坐标为(0,4),BC平分∠ABO交x轴于点C(,0).点P是线段AB上一个动点(点P不与点A,B重合),过点P作AB的垂线分别与x轴交于点D,与y轴交于点E,DF平分∠PDO交y轴于点F.设点D的横坐标为t.(1)如图1,当时,求证:DF∥CB;(2)当时,在图2中补全图形,判断直线DF与CB的位置关系,并证明你的结论;(3)若点M的坐标为(,),在点P运动的过程中,当△MCE 的面积等于△BCO面积的倍时,直接写出此时点E的坐标.(1)证明:(2)直线DF与CB的位置关系是:.证明:(3)点E的坐标为.七年级数学参考答案及评分标准一、选择题(本题共30分,每小题3分)二、填空题(本题共22分,11~15题每小题2分,16~18题每小题4分)11.. 12.110. 13.九. 14.11. 15. AC.16.(1)15,5;(2)24%.(阅卷说明:第1个空1分,第2个空1分,第3个空2分)17.或.(阅卷说明:两个答案各2分)18.,4029.(阅卷说明:每空2分)三、解答题(本题共18分,每小题6分)19.解:解不等式①,得.…………………………………………………………………2分解不等式②,得.………………………………………………………………4分把不等式①和②的解集在数轴上表示出来.所以原不等式组的解集为.…………………………………………………6分20.(1)证明:∵AB∥DC,∴∠A=∠C.…………………………………1分∵∠1=∠A,∴∠1=∠C.…………………………………2分∴FE∥OC.…………………………………3分(2)解:∵AB∥DC,∴∠D=∠B.…………………………………………………………………4分∵∠B=40°,∴∠D=40°.∵∠OFE是△DEF的外角,∴∠OFE=∠D+∠1,…………………………………………………………5分∵∠1=60°,∴∠OFE=40°+60°=100°.……………………………………………………6分21.解:………………………………………………… 3分.…………………………………………………………………………… 4分当,时,原式…………………………………………………………………… 5分.…………………………………………………………………………6分四、解答题(本题共11分,第22题5分,第23题6分)22.解:(1)200,72;…………………… 2分(2)如右图所示;………………… 4分(3)(人).…………………… 5分答:估计该校2400名同学中喜欢羽毛球运动的有288人.23.解:(1)△ 如右图所示,………………… 2分点的坐标为(,);…………… 3分(2)点P的坐标为(,);……………………… 4分(3)过点作H⊥ 轴于点H,则点H的坐标为(,).∵ ,的坐标分别为(,),(,),. (6)分五、解答题(本题共19分,第25题5分,第24、26题每小题7分)24.解:(1)根据题意,得……………………………………… 2分解得………………………………………………………………… 3分答:m的值为5,n的值为2.(2)设甲在剩下的比赛中答对个题.………………………………………… 4分根据题意,得.……………………………… 5分解得.………………………………………………………………… 6分∵ 且为整数,∴ 最小取6.…………………………………… 7分而,符合题意.答:甲在剩下的比赛中至少还要答对6个题才能顺利晋级.25.解:(1)证明:连接AP.∵ ,…………………………………………… 1分∴ .………………………… 3分∵AB=AC ,(2)① ; (4)分② .………………………………………………… 5分26.解:(1)20,55;……………………………………………………………………… 2分(2)∠3-∠1与∠A的数量关系是:.……………… ……… 3分证明:∵在△ABC中,BD,CE是它的两条角平分线,∵MN⊥BC于点N,∴在△MNC中,.∵在△ABC中,,∴ ............................... 5分(3). (7)分北京市西城区2019— 2019学年度第二学期期末试卷七年级数学附加题参考答案及评分标准 2019.7一、填空题(本题6分)1.(1)7;…………………………………………………………………………………… 2分(2)(7,10)或(28,4 0). (6)分(阅卷说明:两个答案各2分)二、解答题(本题7分)2.解:(1)∵ ,∴ .………………………………………… 3分∴ ,. (5)分(2),,.……………………………………………………… 7分三、解决问题(本题7分)3.(1)证明:如图1.∵在平面直角坐标系xOy中,点A在x轴的正半轴上,点B 的坐标为(0,4),∵DP⊥AB于点P,∵在四边形DPBO中,,∴ .………………………………………………… 1分∵BC平分∠ABO,DF平分∠PDO,∵在△FDO中,,∴DF∥CB.………………………………………………………………… 2分(2)直线DF与CB的位置关系是:DF⊥CB.…………………………………… 3分证明:延长DF交CB于点Q,如图2.∵在△ABO中,,∵在△APD中,,∵BC平分∠ABO,DF平分∠PDO,∴ .……………………………………………………………… 4分∵在△CBO中,,∴在△QCD中,.∴DF⊥CB.………………………………………………………………… 5分(3)点E的坐标为(,)或(,).……………………………………… 7分(阅卷说明:两个答案各1分)。
北京市西城区七年级下期末数学试卷有答案

北京市西城区第二学期期末试卷七 年 级 数 学 试卷满分:100分,考试时间:100分钟一、选择题(本题共29分,第1~9题每小题3分,第10题2分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. 9的算术平方根是( ). A. 3-B. 3C. 3D.±32. 已知a b >,下列不等式中,不.正确的是( ). A. 44a b +>+ B. 88a b ->- C.55a b > D.66a b ->-3.下列计算,正确的是( ). A. 3412x x x ⋅=B.336()x x =C.22(3)9x x =D. 22x x x ÷=4. 若1,2x y =⎧⎨=-⎩是关于x 和y 的二元一次方程1ax y +=的解,则a 的值等于( ).A.3B. 1C. -1D. -35. 下列邮票中的多边形中,内角和等于540°的是( ).6.如图,在数轴上,与表示2的点最接近的点是( ).A.点AB. 点BC.点CD. 点D 7.下列命题中,不.正确的是( ). A. 两条直线相交形成的对顶角一定相等 B. 两条平行线被第三条直线所截,同旁内角一定相等 C. 三角形的第三边一定大于另两边之差并且小于另两边之和 D. 三角形一边上的高的长度一定不大于这条边上的中线的长度8. 如图,在△ABC 中,点D ,E ,F 分别是三条边上的点,EF ∥AC , DF ∥AB ,若∠B =45°,∠C =60°,则∠EFD =( ). A.80° B.75° C.70°D.65°9.若点(3,1)P m m --在第二象限,则m 的取值范围是( ). A. 3m > B. 1m >C. 1m <D. 13m <<10.对任意两个实数a ,b 定义两种运算: (), = (),a a b a b b a b ≥⎧⊕⎨<⎩若若 (),= (),b a b a b a a b ≥⎧⊗⎨<⎩若若 并且定义运算顺序仍然是先做括号内的,例如(2) 3=3-⊕,(2) 3=2-⊗-, ()(2) 32=2-⊕⊗. 那么3(52)27⊕⊗等于( ).A. 5B. 3C. 6D. 35二、填空题(本题共25分,第13题2分,第12、17题各4分,其余每小题3分) 11. 平面上直线a ,b 分别经过线段OK 的两个端点,所形成的角 的度数如图所示,则直线a ,b 相交所成的锐角等于______°. 12. ()223768--+-=_________(书写每项化简过程)=____.13. 右图中是德国现代建筑师丹尼尔·里伯斯金设计的“时间迷宫” 挂钟,它直观地表达出了设计师对时间的理解:时间是迷宫一般 的存在——“若干抽象的连接和颇具玩味的互动”.在挂钟所在 平面内,通过测量..、画图..等操作方式判断:AB ,CD 所在直线 的位置关系是________(填“相交”或“平行”),图中1∠与2∠ 的大小关系是1∠ 2∠.(填“>”或“=”或“<”)14. 写出一个解集为x >1的一元一次不等式: .15. 如图是建筑大师梁思成先生所做的“清代北平西山碧云寺金刚宝座塔” 手绘 建筑图.1925年孙中山先生在北京病逝 后,他的衣帽被封存于此塔内,因此也 被称为“孙中山先生衣冠冢”.在图中 右侧俯视图的示意图中建立如图所示 的平面直角坐标系,其中的小正方形 网格的宽度为1,那么图中塔的外围左 上角处点C 的坐标是______.16. 如图,直线AB ∥CD ,E 为直线AB 上一点,EH ,EM 分别交直线CD 于点F ,M ,EH 平分∠AEM ,MN ⊥AB ,垂足 为点N ,∠CFH =α .(1)MN ME (填“>”或 “=” 或“<”), 理由是 ; (2)∠EMN= (用含α的式子表示).17. 如图,在平面直角坐标系xOy 中,(1,0)A -,(3,3)B --,若BC ∥OA ,且BC =4OA ,(1)点C 的坐标为 ; (2)△ABC 的面积等于 = .18.下边横排有15个方格,每个方格中都只有一个数字,且 任何..相邻三个数字之和都是16.( = ,= ;(2)利用你在解决(1)时发现的规律,设计一个在本题背景下相关的拓展问题,或给出设计思路(可以增加条件,不用解答).(1分)三、解答题(本题共46分) 19.(本题6分) (1)解不等式254x -≤316x +-;(2)求(1)中不等式的正整数解. 解:20.(本题6分)小华同学在学习整式乘法时发现,如果合理地使用乘法公式可以简化运算,于是 如下计算题她是这样做的:你好好查一下.”小华仔细检查后自己找到了如下一处错误:(1)你认为小禹说的对吗?(对,不对)(2)如果小禹说的对,那小华还有哪些错误没有改出来?请你帮助小华把第一步中的 其它错误圈画出来并改正,再完成此题的解答过程........... 解:21.(本题6分)依语句画图并回答问题:已知:如图,△ABC .(1)请用符号或文字语言描述线段..CD 的特征; (2)画△ABC 的边BC 上的高AM ;(3)画BCD ∠的对顶角ECF ∠,使点E 在BC 的延长线上,CE=BC ,点F 在DC 的延长线上,CF=DC ,连接EF ,猜想线段EF 所在直线与DB 所在直线的位置关系;(4)连接AE ,过点F 画射线FN ,使FN ∥AE ,且FN 与线段AB 的交点为点N ,猜想 线段FN 与AE 的数量关系.解:(1)线段..CD 的特征是 .(2)画图.(3)画图,线段EF 所在直线与DB 所在直线的位置关系是EF DB . (4)画图,线段FN 与AE 的数量关系是FN AE .22.请从以下两题22.1、22.2中任选一题....做答,22.1题4分(此时卷面满分100分),22.2 题6分(卷面总分不超过100分).22.1 解方程组 263,+ 2.x y x y =-⎧⎨=⎩22.2 (1)阅读以下内容:已知实数x ,y 满足2x y +=,且3272,236,x y k x y +=-⎧⎨+=⎩求k 的值.三位同学分别提出了以下三种不同的解题思路:甲同学:先解关于x ,y 的方程组3272,236,x y k x y +=-⎧⎨+=⎩再求k 的值.乙同学:先将方程组中的两个方程相加,再求k 的值.丙同学:先解方程组2,236,x y x y +=⎧⎨+=⎩再求k 的值.(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题(5分),再对 你选择的思路进行简要评价....(1分). (评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才 能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等) 请先在以下相应方框内打勾,再解答相应题目. 解:23. (本题6分) 解决下列问题:甲、乙两所学校的同学一起去北京农业职业学院参加学农教育实践活动,活动结束时,两校各派出一些志愿者协助老师布置闭营成果展示会活动现场. 老师先派了9名甲校志愿者搬运物品,发现此时剩下的甲校志愿者是乙校志愿者的一半,根据需要又派了14名乙校志愿者也去搬运,这时剩下的甲校志愿者比剩下的乙校志愿者少7人. 问:甲、乙两所学校各有志愿者多少人?解:24. (本题6分)如图,在平面直角坐标系xOy中,几段14圆弧(占圆周的14的圆弧)首尾连接围成的封闭区域形如“宝瓶”,其中圆弧连接点都在正方形网格的格点处,点A的坐标是(0,6)A,点C的坐标是(6,0)C-.(1)点B的坐标为,点E的坐标为;(2)当点B向右平移个单位长度时,能与点E重合,如果圆弧BCD也依此规则平移,那么BCD上点(,)P x y的对应点P'的坐标为(用含x,y的式子表示),在图中画出点P'的位置和平移路径(线段PP');(3)结合画图过程说明求“宝瓶”所覆盖区域面积的思路.解:25.(本题6分)在学习“相交线与平行线”一章时,课本中有一道关于潜望镜的拓广探索题,老师倡议班上同学分组开展相关的实践活动.小钰所在组上网查阅资料,制作了相关PPT 介绍给同学(图1、图2);小宁所在组制作了如图所示的潜望镜模型并且观察成功(图3). 大家结合实践活动更好地理解了潜望镜的工作原理.(1)图4中,AB ,CD 代表镜子摆放的位置,动手制作模型时,应该保证AB 与CD平行,入射光线与反射光线满足1=2∠∠,3=4∠∠,这样离开潜望镜的光线MN 就与进入潜望镜的光线EF 平行,即MN ∥EF .请完成对此结论的以下填空及后续证明过程(后续证明无需标注理由).(2)在之后的实践活动总结中,老师进一步布置了一个任务:利用图5中的原理可以制 作一个新的装置进行观察,那么在图5中方框位置观察到的物体“影像”的示意图 为 . A.B.C.D.26. (本题6分)∵ AB ∥CD (已知),∴ 2= ∠∠( ). ∵ 1=2∠∠,3=4∠∠(已知), ∴ 1=234∠∠=∠=∠( ).如图,△ABC 中,D ,E ,F 三点分别在AB ,AC ,BC 三边上,过点D 的直线与线段EF 的交点为点H ,1+2=180∠∠︒,3=C ∠∠.(1)求证:DE ∥BC ;(2)在以上条件下,若△ABC 及D ,E 两点的位置不变,点F 在边BC 上运动使得∠DEF 的大小发生变化,保证点H 存在且不与点F 重合,记C α∠=,探究:要使∠1=∠BFH 成立,∠DEF 应满足何条件(可以是便于画出准确位置的条件).直接写出你探究得到的结果,并根据它画出符合题意的图形. (1)证明:(2)要使∠1=∠BFH 成立,∠DEF 应满足.北京市西城区第二学期期末试卷七年级数学附加题试卷满分:20分一、填空题(本题6分)1. 参加学校科普知识竞赛决赛的5名同学A,B,C,D,E在赛后知道了自己的成绩,想尽快得知比赛的名次,大家互相打听后得到了以下消息:(分别以相应字母来对应他们本人的成绩)(1(2)5位同学的比赛名次依次是 .(仿照第二条信息的数学表达式用“>”连接)二、解答题(本题共14分,每题7分)2.(1)阅读下列材料并填空:对于二元一次方程组4354,336,x yx y+=⎧⎨+=⎩我们可以将x,y的系数和相应的常数项排成一个数表4 3 541 3 36⎛⎫⎪⎝⎭,求得的一次方程组的解,x ay b=⎧⎨=⎩用数表可表示为1 00 1ab⎛⎫⎪⎝⎭.用数表可以简化表达解一次方程组的过程如下,请补全其中的空白:从而得到该方程组的解为 ,.x y =⎧⎨=⎩(2)仿照(1)中数表的书写格式写出解方程组236,+2x y x y +=⎧⎨=⎩的过程.3.(1)如图,在平面直角坐标系xOy 中,点A ,B 分别为x 轴正半轴和y 轴正半轴上的两 个定点,点C 为x 轴上的一个动点(与点O ,A 不重合),分别作∠OBC 和∠ACB的角平分线,两角平分线所在直线交于点E ,直接回答∠BEC 的度数及点C 所在的相应位置.解:(2)如图,在平面直角坐标系xOy 中,△FGH 的一个顶点F 在y 轴的负半轴上,射线FO 平分∠GFH ,过点H 的直线MN 交x 轴于点M ,满足∠MHF =∠GHN ,过点H 作HP ⊥MN 交x 轴于点P ,请探究∠MPH 与∠G 的数量关系,并写出简要证明思路.解:∠MPH 与∠G 的数量关系为 . 简要证明思路:北京市西城区第二学期期末试卷七年级数学参考答案及评分标准一、选择题(本题共29分,第1~9题每小题3分,第10题2分)19. (本题6分)解:(1)去分母,得 3(25)2(3)12x x -+-≤. …………………………………………… 1分去括号,得 6152612x x -+-≤. …………………………………………………2分 移项,合并,得 9x 4≤. ……………………………………………………………3分 系数化1,得 94x ≤. …………………………………………………………4分 所以此不等式的解集为94x ≤.(2)因为(1)中不等式的解集为94x ≤,所以它的正整数解为1,2. …………… 6分 20.(本题6分)解:(1)对;……………………………………………………………………………………1分 (2)……………………… 5分2(23)(2)(2)x y x y x y ---+=222241294x xy y x y -+-+=2231213x xy y -+.………………………………………………………………6分阅卷说明:两处圈画和改错各1分,结果1分. 21.(本题6分) 解:见图1.(1)CD ⊥BC ,垂足为点C ,与边AB 的交点为点D .………………………………………………1分(2)画图. …………………………………………2分 (3)画图. …………………………………………3分EF // DB . …………………………………4分(4)画图. ……………………………………………………………………………… 5分FN = AE . …………………………………………………………………… 6分22. (22.1题4分,22.2题6分)22.1 263,+ 2.x y x y =-⎧⎨=⎩解:由②得 2.x y =- ③ ………………………………………………………………… 1分将③代入①得 2(2)63.y y -=- …………………………………………………… 2分 解得 2.y = ………………………………………………………………………………3分 将2y =代入③ ,得 0.x =∴ 原方程组的解为0,2.x y =⎧⎨=⎩ …………………………………………………………… 4分22.2 解:甲同学:3272,23 6.x y k x y +=-⎧⎨+=⎩②⨯3-①⨯2,得 22145ky -=. ③…………………………………………… 2分把③代入②得 21185k x -=. ④ …………………………………………… 3分 把③、④代入2x y +=,得 21182214255k k--+=.………………………… 4分 解得 67k =. ……………………………………………………………………… 5分 乙同学:3272,23 6.x y k x y +=-⎧⎨+=⎩①+②,得 5574x y k +=+. ③ ……………………………………………… 3分将2x y +=整体代入③,得 7410k +=. ………………………………………4分 解得 67k =. ……………………………………………………………………… 5分 丙同学:先解2,23 6.x y x y +=⎧⎨+=⎩得0,2.x y =⎧⎨=⎩………………………………………… 4分再将x ,y 的值代入3272x y k +=-,解得67k =. …………………………… 5分 评价参考:甲同学是直接根据方程组的解的概念先解方程组,得到用含k 的式子表示x ,y 的表达式,再代入2x y +=得到关于k 的方程,没有经过更多的观察和思考,解法比较繁琐,计算量大;乙①②①②①②同学观察到了方程组中未知数x ,y 的系数,以及与2x y +=中的系数的特殊关系,利用整体代入简化计算,而且不用求出x ,y 的值就能解决问题,思路比较灵活,计算量小;丙同学将三个方程做为一个整体,看成关于x ,y ,k 的三元一次方程组,并且选择先解其中只含有两个未知数x ,y 的二元一次方程组,相对计算量较小,但不如乙同学的简洁、灵活. …………………………………………………………… 6分 23.(本题6分)解:设甲校有志愿者x 人,乙校有志愿者y 人. ………………………………………… 1分根据题意,得9,29(14)7.y x x y ⎧-=⎪⎨⎪-=--⎩………………………………………………………3分 解方程组,得30,42.x y =⎧⎨=⎩………………………………………………………………… 5分答:甲校有志愿者30人,乙校有志愿者42人. ……………………………………………6分 24. (本题6分)解:(1)(3,3)B -,(3,3)E .………………………………2分 (2)6,(6,)x y +. ………………………………… 4分画图见图2. ………………………………………5分 (3)将圆弧BCD 及线段BD 围成的区域向右平移6个单位长度,将AB 和AE 以及线段BE 围成的区域向下平移 6个单位长度,“宝瓶”所覆盖区域面积与正方形BDFE 面积相等,求正方形BDFE 面积即可.(面积为36)…………………………………………… 6分阅卷说明:不回答“面积为36”不扣分;其它思路相应给分. 25.(本题6分) 解:(1(2)C. ………………………………………………………………………………… 6分 26.(本题6分)(1)证明:如图3.∵ ∠1是△DEH 的外角, ∴ ∠1=∠3+∠4.又∵ ∠3=∠C ,∠1+∠2=180︒,∴ ∠C +∠4+∠2=180︒. ∵ ∠DEC =∠4+∠2, ∴ ∠DEC +∠C =180︒.∴ DE ∥BC . ……………………………………………………………… 4分(2)902DEF α∠=︒-,或者点F 运动到∠DEC 的角平分线与边BC 的交点位置(即EF平分∠DEC ). ……………………………………………………………………… 5分画图见图4. ……………………………………………………………………………6分北京市西城区第二学期期末试卷七年级数学附加题参考答案及评分标准一、填空题(本题6分) 1.解:(1)下行-上行1 0 60 1 10⎛⎫ ⎪⎝⎭4 D 的得分高于ED E >(2)B D E C A >>>>.………………………………………………………………6分阅卷说明:写对B D E >>得第4分,C ,A 的名次酌情给分.二、解答题(本题共14分,每题7分) 2.解:(1)………………………………………………………………………1分…………………………………………………………………… 2分…………………………………………………………………4分(2)所以方程组的解为0,2.x y =⎧⎨=⎩………………………………………………………7分3.解:(1)如图1,当点C 在x 轴负半轴上或x 轴正半轴上点A 右侧时,∠BEC=135︒; …………………………………………………………………2分 当点C 在线段OA 上(且与点O ,A 不重合)时,∠BEC=45︒.………………4分(2)12MPH G ∠=∠.………………………………………………………………5分简要证明思路:如图2,设射线FO 与y 轴的交点为点Q . 由∠MHF =∠GHN ,HP ⊥MN 可得12∠=∠,再由射线FO 平分∠GFH ,可知34∠=∠,点Q 是△FGH 的两条角平分线的交点,可得1118013180(180)9022FQH G G ∠=︒-∠-∠=︒-︒-∠=︒+∠.……………………………………………………………………………………………6分 又由∠FQH 是△OPQ 的外角可得90FQH MPH ∠=︒+∠. 可得12MPH G ∠=∠.……………………………………………………………7分 图1 x yO 11EBA CxO11E B A Cy O EB A C阅卷说明:其它证明思路相应给分.图2。
北京市西城区七年级下期末数学试卷有答案

北京市西城区第二学期期末试卷七年级数学试卷满分:100分,考试时间:100分钟、选择题(本题共29分,第1~9题每小题3分,第10题2分)F 面各题均有四个选项,其中只有一个是符合题意的.1.9的算术平方根是().2.已知a b ,下列不等式中,不 正确的是(5.下列邮票中的多边形中,内角和等于540。
的是A. 点AB.点BC.点CD.点D7.下列命题中,不.正确的是( ). A.两条直线相交形成的对顶角一定相等B. 两条平行线被第三条直线所截,同旁内角一定相等C. 三角形的第三边一定大于另两边之差并且小于另两边之和D.三角形一边上的高的长度一定不大于这条边上的中线的长度8. 如图,在厶ABC 中,点D ,E ,F 分别是三条边上的点, EF // AC ,DF // AB ,若/ B=45 ° / C=60 ° 则/ EFD=( ).A.80 °B.75 °C.70 °D.65 °9. 若点P (3 -m,m -1)在第二象限,则 m 的取值范围是().A. a +4 >b +4 B. a _8 >b _8 C. 5a . 5b D. -6a a —6b 3. 下列计算,正确的是( A 3 4 12 A. x x x x —14. 若x'是关于x 和y 的二元一次方程 7 = -23\3 6 B.(x ) x C. (3x)2 =9x 2ax • y =1的解,则a 的值等于( ). A.3 B. 1 C. -1 D. -3A. -3B. 3 c.D. ±AB).6.如图,在数 轴上,与表示 -2的点最接B. m . 1 D. 1 ::: m (3)a (右a _b ),b (右a _ b ),10.对任意两个实数a , b 定义两种运算:a 二b 二 卄a :b 二 卄 并且b (右a cb ),a (右a cb ),定义运算顺序仍然是先做括号内的,例如(-2)二3=3 , (-2) : 3= -2 ,(-2)二 3 : 2=2 .那么(店二 2) : 327 等于( )•A. . 5B. 3C. 6D. 3.5二、填空题(本题共25分,第13题2分,第12、17题各4分,其余每小题3 分)11. 平面上直线a ,b 分别经过线段 0K 的两个端点,所形成的角的度数如图所示,则直线 a ,b 相交所成的锐角等于 _________ 12. {-J 7 ) 一后 +7^8= __________ (书写每项化简过程) =—13. 右图中是德国现代建筑师丹尼尔 里伯斯金设计的时间迷宫”挂钟,它直观地表达出了设计师对时间的理解:时间是迷宫一般 的存在 ’右干抽象的连接和颇具玩味的互动”.在挂钟所在 平面内,通过测量.、画图等操作方式判断:AB ,CD 所在直线 的位置关系是 ________ (填 相交”或 平行”),图中与丛2的大小关系是.[.2.(填、”或二”或N”)14. 写出一个解集为x>1的一元一次不等式:15.如图是建筑大师梁思成先生所做的清代北平西山碧云寺金刚宝座塔”手绘 建筑图.1925年孙中山先生在北京病逝 后,他的衣帽被封存于此塔内,因此也 被称为孙中山先生衣冠冢”在图中 右侧俯视图的示意图中建立如图所示 的平面直角坐标系,其中的小正方形 网格的宽度为1,那么图中塔的外围左 上角处点C 的坐标是 ______________ .A. m . 3 C. m ::: 1■16. 如图,直线AB// CD,E为直线AB上一点,EH,EM分别交直线CD于点F,M,EH平分/ AEM,MN丄AB,垂足为点N,/ CFH = a.(1)MN ____ ME (填“>”“=”或“<),理由是________________________________(2) ________________ / EMN= (用含a的式子表示)17. 如图,在平面直角坐标系xOy中,A(_1,0),B(_3, _3),若BC // OA,且BC=4OA,(1)点C的坐标为__________________ ;(2)△ ABC的面积等于= _________ .18. 下边横排有15个方格,每个方格中都只有一个数字, 任何相邻三个数字之和都是16.6m n(1 )以上方格中3 m = , n = ; (2 分)(2)利用你在解决(1)时发现的规律,设计一个在本题背景下相关的拓展问题,或给出设计思路(可以增加条件,不用解答).(1分)你所设计的问题(或设计思路)是:三、解答题(本题共46分)19. (本题6分)2x— 5 x +3(1)解不等式------- <——-1 ; ( 2)求(1)中不等式的正整数解4 6解:20. (本题6分)小华同学在学习整式乘法时发现,如果合理地使用乘法公式可以简化运算,于是如下计算题她是这样做的:(2x-3y)2-(x-2y)(x 2y)2 2 2 2=4x -6xy 3y -x -2y 第一步=3x2^6xy ' y2第二步小禹看到小华的做法后,对她说: ---- 你做错了,在第步运用公式时出现了错误,你好好查一下•'小华仔细检查后自己找到了如下一处错误:(1 )你认为小禹说的对吗?________ (对,不对)(2 )如果小禹说的对,那小华还有哪些错误没有改出来?请你帮助小华把第一步中的其它错误圈画出来并改正,再完成此题的解答过程解:小禹看到小华的改错后说:你还有错没有改出来21. (本题6分)依语句画图并回答问题:已知:如图,△ ABC.(1 )请用符号或文字语言描述线段..CD的特征;(2 )画厶ABC的边BC上的高AM ;(3 )画.BCD的对顶角.ECF,使点E在BC的延长线上,CE=BC,点F在DC的延长线上,CF=DC,连接EF,猜想线段EF所在直线与DB所在直线的位置关系;(4)连接AE,过点F画射线FN,使FN // AE,且FN与线段AB的交点为点N,猜想线段FN与AE的数量关系.解:(1)线段CD的特征是______________________________________ .(2)画图.(3)________________________________________________________ 画图,线段EF所在直线与DB所在直线的位置关系是EF ___________________________________ DB.(4)画图,线段FN与AE的数量关系是FN ________ AE.22. 请从以下两题22.1、22.2中任选一题做答,22.1题4分(此时卷面满分100分),22.2题6分(卷面总分不超过100分).耳二6 _3y,22.1解方程组、x+y =2.22.2 (1)阅读以下内容:3x 2y = 7k - 2,已知实数x, y满足x ^2,且' 求k的值.[2x + 3y =6,三位同学分别提出了以下三种不同的解题思路:工3x 2y =7k -2,十,…甲同学:先解关于x, y的方程组再求k的值.I2x+3y=6,乙同学:先将方程组中的两个方程相加,再求k的值.x 十y =2丙同学:先解方程组'再求k的值.£x +3y =6,(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题( 5分),再对你选择的思路进行简要评价(1分).(评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等)请先在以下相应方框内打勾,再解答相应题目解:23. (本题6分)解决下列问题:甲、乙两所学校的同学一起去北京农业职业学院参加学农教育实践活动,活动结束时,两校各派出一些志愿者协助老师布置闭营成果展示会活动现场.老师先派了9名甲校志愿者搬运物品,发现此时剩下的甲校志愿者是乙校志愿者的一半,根据需要又派了14名乙校志愿者也去搬运,这时剩下的甲校志愿者比剩下的乙校志愿者少7人•问:甲、乙两所学校各有志愿者多少人?解:24. (本题6分)如图,在平面直角坐标系xOy中,几段1圆弧(占圆周的 -的圆弧)首尾连接围4 4成的封闭区域形如宝瓶”其中圆弧连接点都在正方形网格的格点处,点A的坐标是A(0,6),点C 的坐标是C(_6,0).(1 )点B的坐标为 _____ ,点E的坐标为________ ;(2)当点B向右平移____ 个单位长度时,能与点E重合,如果圆弧BCD也依此规则平移,那么BCD 上点P(x,y)的对应点P的坐标为 _______________ (用含x,y的式子表示),在图中画出点P的位置和平移路径(线段PP ');(3)结合画图过程说明求宝瓶”所覆盖区域面积的思路•解:25. (本题6分)在学习相交线与平行线”一章时,课本中有一道关于潜望镜的拓广探索题,老师倡议班上同学分组开展相关的实践活动•小钰所在组上网查阅资料,制作了相关PPT介绍给同学(图1、图2);小宁所在组制作了如图所示的潜望镜模型并且观察成功(图3).大家结合实践活动更好地理解了潜望镜的工作原理•(1)图4中,AB ,CD 代表镜子摆放的位置,动手制作模型时,应该保证 AB 与CD平行,入射光线与反射MN 就与 进入潜望镜的光 线EF 平行,即MN // EF.请完成 对此结论的以下 填空及后续证 明过程(后续证明 无需标注理由).世界上最平起魏瞥豐乾隊理的古书,是处元前二 世皑我H 的(淮奇万羊卓〉=书中記裁Tii ■畀晞一屣话:“取大曲書址’ ■木 ■于KT-則见四邻矣"”尹代,在我国一秦第山 古盛妁屋H 下,常常押蚪 地崔着一西耆划丸锐.如 聚在雇仃欲世界大战战壕潜审镜AB// CD (已知),2= _ ( ___________________________________ ).1= 2,3= 4 (已知),.仁.2=/3=/4 ( ).(2)在之后的实践活动总结中,老师进一步布置了一个任务:利用图5中的原理可以制作一个新的装置进行观察,那么在图5中方框位置观察到的物体影像”的示意图为 ______.A. B. C. D.26. (本题6分)如图,△ ABC中,D,E,F三点分别在AB,AC, BC三边上,过点D的直线与线段EF 的交点为点H,• 1 + . 2=180,. 3= C .(1)求证:DE // BC ;(2)在以上条件下,若△ ABC及D, E两点的位置不变,点F在边BC上运动使得/ DEF的大小发生变化,保证点H存在且不与点F重合,记.C =;:,探究:要使/仁/ BFH成立,•直接写出你探究得到的结果,并根据它画/ DEF应满足何条件(可以是便于画出准确位置的条件) 出符合题意的图形.(1)证明:(2)要使/ 1 = / BFH成立,/ DEF应满足北京市西城区第二学期期末试卷七年级数学附加题试卷满分:20分一、填空题(本题6分)1.参加学校科普知识竞赛决赛的5名同学A, B, C, D, E在赛后知道了自己的成绩,想尽快得知比赛的名次,大家互相打听后得到了以下消息:(分别以相应字母来对应他们本人的成绩)(1)请参照表中第二条文字信息的翻译方式,在表中写出其它三条文字信息的数学表达式;(2) ___________________________________________________ 5位同学的比赛名次依次是.(仿照第二条信息的数学表达式用“〉”连接)二、解答题(本题共14分,每题7分)2. (1)阅读下列材料并填空:4x 3y 二54,对于二元一次方程组我们可以将x, y的系数和相应的常数项排成一个数表2 +3y = 36,3 54 3 36丿求得的一次方程组的解x = at '用数表可表示为y 二b:0 : 用数表可以简化表达解一次1°1 b丿方程组的过程如下,请补全其中的空白:解:(2)如图,在平面直角坐标系 xOy 中,△ FGH 的一个顶点F 在y 轴的负半轴上,射线 FO 平分/ GFH,过点H 的直线 MN 交x 轴于点M ,满足/ MHF=/GHN ,过点H 作 HP 丄MN 交x 轴于点P ,请探究/ MPH 与/ G 的数量关系,并写出简要证明思路.解:/ MPH 与/ G 的数量关系为 _________________________ .上行卜3 54' 怖 11 3 361 0 6 1 P 3 3<*J从而得到该方程组的解为(2)仿照(1)中数表的书写格式写出解方程组2x 3^6,的过程.x+y =23. (1)如图,B 分别为x 轴正半轴和y 轴正半轴上的两 O , A 不重合),分别作/ OBC 和/ ACB E ,直接回答/ BEC 的度数及点C 所在的备用图简要证明思路:北京市西城区第二学期期末试卷七年级数学参考答案及评分标准、选择题(本题共29分,第1~9题每小题3分,第10题2分)、填空题(本题共25分,第13题2分,第12、17题各4分,其余每小题3分)19. (本题6分)解:(1)去分母,得3(2x-5)w2(x,3)-12. ............................................................... 1 分去括号,得6x -15< 2x 6-12. ....................................................................................... 2 分移项,合并,得4x W 9. .................................................................................. 3分9系数化 1,得 xW — .......................................................................... 4分4所以此不等式的解集为 xW -.4(2)因为(1)中不等式的解集为 x W —,所以它的正整数解为 1 , 2. ................. 6分420. (本题6分)解:(1)对; ................................................................ 1分(2)............................................... 5分2(2x_3y) _(x_2y)(x 2y)= 4x 2 -12xy 9y 2 -x 2 4y 222=3x -12xy 13y . ..................................................................................... 6 分 阅卷说明:两处圈画和改错各 1分,结果1分. 21. (本题6分)解:见图1.(1) CD 丄BC,垂足为点 C ,与边AB 的交点为点 D. 1分FN = AE. ........................................................................................................ 6 分22. (22.1 题 4 分,22.2 题 6 分) 2x =6「3y,① 22.1 ①K+y =2.②解:由②得 x = 2 -y.③ ....................................................... 1分将③代入①得2(2 -y) =6 -3y. ..........................................................................解得y =2. ..........................................................................................................将y = 2代入③,得x = 0.x = 0•••原方程组的解为x O,..................................................卜=2.工3x 2y =7k -2,22.2解:甲同学:① 、2x+3y=6.②② 3 —①2,得 y =22T 4k .③ ......................................(2) ....................................................................... 画图 .......................................... 2分(3) ....................................................................... 画图 .......................................... 3分2分 3分4分2分 3分(2 一呵刃仗+ 2刃那一步521k T8 .④ ...................................... 把③代入②得x=521k -18 22 -14k把③、④代入x • y =2,得2 ................................... 4分55解得k =6. ...................................................................................................... 5分7乙同学:3X 2^7k^,①2x +3y =6.②①+②,得5x 5y =7k 4 .③ ............................................ 3分 将x ,y=2整体代入③,得 7k 4 =10 . ................................................................ 4分 解得 k =6. ..................................................................................................... 5分7X y = 2,/口 X = 0,八丙同学:先解得 .............................. 4分J 2x 3y = 6.I y = 2.再将x , y 的值代入3x 2y =7k -2,解得k = 6 . ................................................ 5分7评价参考:甲同学是直接根据方程组的解的概念先解方程组,得到用含k 的式子表示x,y 的表达式,再代入x ^2得到关于k 的方程,没有经过更多的观察和思考,解法比较繁琐,计算量大;乙同学观 察到了方程组中未知数 x ,y 的系数,以及与x y 2中的系数的特殊关系,利用整体代入简化计算,而 且不用求出x ,y 的值就能解决问题,思路比较灵活,计算量小;丙同学将三个方程做为一个整体,看成 关于x , y ,k 的三元一次方程组,并且选择先解其中只含有两个未知数x , y 的二元一次方程组,相对计算量较小,但不如乙同学的简洁、灵活 . ..................................................................................... 6分 23. (本题6分)解:设甲校有志愿者 x 人,乙校有志愿者 y 人............................... 1分L —9 /根据题意,得 x 92,.................................................................... 3分x -9 =(y -14) -7. {x = 30,解方程组,得................................................. 5分卜=42.答:甲校有志愿者 30人,乙校有志愿者 42人. .................................... 6分 (本题6分)(1) B( -3,3),E(3,3). ............................................ 2 分(2) 6,(x 6,y). .................................................. 4 分画图见图2. ........................................................ 5分(3) 将圆弧BCD 及线段BD 围成的区域向右平移 6个单位 长度,将AB 和AE 以及线段BE 围成的区域向下平移 6个单位长度,“宝瓶”所覆盖区域面积与正方形 BDFE 面积相等,求正方形 BDFE 面积即可.(面积为36) ••• AB// CD (已知),••• Z 2=7 3 (两直线平行,内错角相等) . ••• 7 仁/ 2,7 3= 7 4 (已知), • 7 1 = 7 2=7 3=7 4 (等量代换) ..... .....24.解: 25. 解:........................................................... 6分阅卷说明:不回答“面积为 36 ”不扣分;其它思路相应给分 (本题6分)(1)图2(2) C. ................................................................................................................................. 6 分26.(本题6分) (1)证明:如图3.••• / 1是厶DEH的外角,••• / 仁/3+/ 4.又••• / 3=/ C,/ 1 + / 2=180 , •/ C+/ 4+/ 2=180 .•/ / DEC=/ 4+/ 2,•/ DEG/C =180 .•DE// BC ................................................................................................ 4 分⑺乙DEF =90 ,或者点F运动到/ DEC的角平分线与边BC的交点位置(即EF2平分/ DEC . ................................................................................................... 5分画图见图4. ......................................................................................................... 6分B FC H图3 图4北京市西城区第二学期期末试卷七年级数学附加题参考答案及评分标准(2) B D - E C A一、填空题(本题6分)1•解:(1)6分阅卷说明:写对 B . D . E 得第4分,C , A 的名次酌情给分. 二、解答题(本题共14分,每题7分) 2•解:(1)下行-上行0 6 ) I \0 1 10 y又由/ FQH 是厶OPQ 的外角可得• FQH =90 • • MPH .1可得 MPH G ............... ..................................2阅卷说明:其它证明思路相应给分.hff-Tfr <0 1 iI 1 2 下行-上行 7分 所以方程组的解为 交换上、rtf poo [oi 2 jx =0,…y =2•… 3•解:(1) 如图1,当点C 在x 轴负半轴上或 x 轴正半轴上点 A 右侧时,/ BEC= 135 ; 2分4分当点C 在线段OA 上 FO 与y 轴的交点为点Q .由/ MHF = / GHN , 再由射线FO 平分/ GFH ,可知 )…5分简要证明思路:如 图2,设射线(且与点 O , A 不重合)时,/ BEC=45 . 21 MPH G 2HP 丄 MN 可得.1 = • 2 ,.3- 4,点Q 是厶FGH 的两条角平分线的交点,可得11FQH =180 - 1 - 3 =180(180 - G) =90— G . (2)27分。
西城区七年级第二学期数学期末试卷

北京市西城区(北区)第二学期抽样测试七年级数学试卷一.选择题(本题共30分,每题3分)下面各题均有四个选项,其中只有一个符合题意1.计算23()a 的结果是( ) 6.A a 5.B a .5C a .D a2.已知a b <,下列不等式变形正确的是( ).22Aa b ->-.22a bB >.22C a b ->- .3131D a b +>+3.下列长度的三条线段能组成三角形的是( ).2,3,6A .4,4,8B .5,9,14C .6,12,13D4.已知一个多边形的内角和是它外角和的3倍,则这个多边形是( ) A.六边形 B.七边形 C.八边形 D.九边形5.如果点(4,)P a a -在y 轴上,则点P 的坐标是( )(4,0)A .(0,4)B .(4,0)C - .(0,4)D - 6.下列格式中,从左向右的变形是因式分解的是( )2.2(2)Aa ab a a a b ++=+ 2.1025(10)25B a a a a ++=++ 222.()C ax ay a x y +=+ 22.4(2)(2)D a b a b a b -=+-7.下列命题中,是真命题的是( )①两条直线被第三条直线所截,同位角相等;②在同一平面内,垂直于同一直线的两条直线互相平行 ③三角形的三条高中,必有一条在三角形的内部 ④三角形的三个外角一定都是锐角A.①②B.①③C.②③D.③④8.如图,在△ABC 中,将△ABC 沿射线BC 方向移动,使点B 移动到点C ,得到△DCF ,连接AF,若△ABC 的面积为4,则△ACF 的面积为( ) A. 2 B. 4 C. 8 D. 16F D CB A9.在平面直角坐标系中,定义两种新的变换:对于平面内任一点(,)P m n ,规定: ①(,)(,)f m n m n =-,例如:(2,1)(2,1);f =- ②(,)(,)g m n m n =-,例如:(2,1)(2,1)g =-. 按照以上变换有:[](3,4)(3,4)(3,4),g f g -=--=-那么[](5,2)f g 等于( ).(5,2)A -- .(5,2)B - .(5,2)C - .(5,2)D10.已知,a b 为非零有理数,下面四个不等式组中,解集有可能为22x -<<的不等式组是( )1.1ax A bx >⎧⎨>⎩ 1.1ax B bx >⎧⎨<⎩ 1.1ax C bx <⎧⎨>⎩1.1ax D bx <⎧⎨<⎩ 二.细心填一填(本题共20分,第1114题,每小题3分,第1518题,每小题2分) 11.分解因式:2242ax ax a -+= .12.关于x 的方程5336x x m =+-的解是负数,则m 的取值范围是 . 13.将一副直角三角尺如图放置,已知AB ∥DE ,则∠AFC= 度.14.抽取某校学生的一个容量为150的样本,测得学生身高后,得到身高频数分布直方图如图所示,已知该校有学生1500名,则可以估计出该校身高位于160 cm 至165cm 之间大约有 人.15.若3,1,a b ab +==则22a b += .16.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点(2,1)P m m -+在第二象限,则m 的值为 .17.点O 在直线AB 上,35AOC ∠=︒,射线,OD OC BOD ⊥∠的度数是 度.18.如图,一张长为20cm ,宽为5cm 的长方形纸片ABCD ,分别在边AB 、CD 上取点M 、N ,沿MN 折叠纸片,BM 与DN 交于点K ,得到△MNK.则△MNK 的面积的最小值是 cm 2.三.解答题(本题共25分,第1921题,每小题6分,第22小题7分)19.解不等式组20.先化简,再求值:231(1)(2)(2)63,.2x x x x x x +++--÷=其中21.已知:如图,四边形ABCD 中,AD ∥BC ,AC 为对角线,点E 在BC 边上,点F 在AB 边上,且∠1=∠2. (1)求证:EF ∥AC(2)若CA 平分∠BCD ,∠B=50︒,∠D=120︒,求∠BFE 的度数.523(2)12123x x x x +<+⎧⎪--⎨≤⎪⎩ A FEDCB22.在平面直角坐标系中,A 、B 、C 三点的坐标分别为(-6,7)、(-3,0)、(0,3) (1)画出△ABC ,并求出它的面积;(2)在△ABC 中,点C 经过平移后的对应点(5,4)C ',将△ABC 作同样的平移得到A B C '''∆,画出平移后的A B C '''∆,并写出A B ''、的坐标;(3)点-3P(,m)为△ABC 内一点,将点P 向右平移4个单位后,再向下平移6个单位得到点(,3)Q n -,则m= ,n= .四.解答题(本题共13分,第23题7分,第24题6分) 23.列方程组或不等式组解应用题: 某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元. (1)该小区新建1个地上停车位和1个地下停车位各需多少万元?(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?24.图①、图②反映是杭州银泰商场今年1-5月份的商品销售额统计情况.观察图①和图②,解答下面问题:(1)来自商场财务部的报告表明,商场1-5月份的销售总额一共是370万元,请你根据这一信息补全图①,并写出两条由上两图获得的信息;(2)商场服装部5月份的销售额是多少万元?(3)李强观察图②后认为,5月份服装部的销售额比4月份减少了.你同意他的看法吗?为什么?五.解答题(本题共12分,每小题6分) 25.阅读下列材料:小明同学遇到如下问题: 解方程他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的23x y +看作一个数,把23x y -看作一个数,通过换元,可以解决问题.以下是他的解题过程:令23,23.m x y n x y =+=- 这时方程组化为把60,23,23.24.m m x y n x y n =⎧=+=-⎨=-⎩代入 得2360,9,2324.14.x y x x y y +==⎧⎧⎨⎨-=-=⎩⎩解得请你参考小明同学的做法,解决下面的问题:(1)解方程组(2)若方程组23237,4323238.32x y x yx y x y +-⎧+=⎪⎪⎨+-⎪+=⎪⎩7,60,4324.8.32m nm m n n ⎧+=⎪=⎧⎪⎨⎨=-⎩⎪+=⎪⎩解得3,6101.610x y x yx y x y +-⎧+=⎪⎪⎨+-⎪-=-⎪⎩11111122222251,,3,63.. 2.51.63a x b y c a x b y c x a x b y c y a x b y c ⎧+=⎪+==⎧⎧⎪⎨⎨⎨+==⎩⎩⎪+=⎪⎩解得求方程组的解26.在Rt △ABC 中,∠ACB=90°,∠ABC=45°,点E 在线段BC 上,射线ED ⊥AB 于点D.(1)如图,点F 在线段DEA 上,过点F 作MN ∥BC ,分别交AB 、AC 于点M 、N ,点G 在线段AF 上,且∠GFN=∠GNF,∠GDF=∠GFD.①试判断线段DG 与NG 有怎样的位置关系,直接写出你的结论; ②求证:∠1=∠2;如图2,点F 在线段ED 的延长线上,过F 作FN ∥BC,分别交AB 、AC 于点M 、N ,点G 在线段AF 上,且∠GFN=∠GNF,∠GDF=∠GFD.探究线段DG 与NG 的位置关系,并图1B 图2 D G F MN EA 21E G FNMD C B A2012-2013学年北京市西城区七年级(下)期末数学试卷一、选择题(本题共10个小题,每小题3分,共30分.)1.(3分)点(﹣7,0)在()A.x轴正半轴上B.y轴负半轴上C.y轴正半轴上D.x轴负半轴上2.(3分)在数轴上表示不等式组的解集,正确的是()A.B.C.D.3.(3分)下列长度的三条线段,能组成三角形的是()A.1cm,2cm,3cm B.2cm,3cm,6cm C.4cm,6cm,8cm D.5cm,6cm,12cm4.(3分)下列四种调查:①了解一批炮弹的命中精度;②调查全国中学生的上网情况;③审查某文章中的错别字;④考查某种农作物的长势其中适合做抽样调查的个数有()A.1个B.2个C.3个D.4个5.(3分)已知a<b,则下列不等式一定成立的是()A.a+5>6+5 B.﹣2a<﹣2b C.D.7a﹣7b<06.(3分)下列图形中,由AB∥CD,能得到∠1=∠2的是()A.B.C.D.7.(3分)如果一个多边形的每一个外角都等于40°,那么这个多边形的边数为()A.9B.8C.7D.68.(3分)下列计算正确的是()A.a m﹣a2=a2m B.(a3)2=a5C.x3﹣x2﹣x=x5D.a3m﹣5÷a5﹣m=a4m-109.(3分)如图,用四个螺丝将四条不可弯曲的木条围成一个木框ABCD,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则现在A、C相对的螺丝的距离的最大值,以及现在B、D相对的螺丝的距离的最大值分别为()A.5和7 B.10和7 C.5和8 D.10和810.(3分)定义:平面内的两条直线l1与l2相交于点O,对于该平面内任意一点M,M点到直线l1,l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”.根据上述定义,“距离坐标”为(2,3)的点的个数是()A.1B.2C.3D.4二、填空题(本题共10个小题,每小题2分,共20分)11.(2分)因式分解:x2﹣x﹣12=_________.12.(2分)计算:(3m﹣2n)2=_________.13.(2分)图中x的值为_________.14.(2分)已知点P(3a﹣8,a﹣1),若点P在y轴上,则点P的坐标为_________.15.(2分)把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式:_________.16.(2分)将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是_________17.(2分)如果M(a﹣b)2=(a2﹣b2)3,那么整式M=_________.18.(2分)如图1,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图2所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为_________.19.(2分)已知x﹣y=1,xy=﹣2,则x3y﹣2x2y2+xy3的值是_________.20.(2分)对面积为1的△ABC进行以下操作:分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1(如图所示),记其面积为S1.现再分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C11A,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2,则S2=_________.三、解答题(共50分)21.(6分)分解因式(1)ax2﹣8ax+16a;(2)a2(x+y)﹣4b2(x+y).22.(5分)解不等式组,并写出该不等式组的整数解.23.(6分)先化简,再求值:[(a+b)(a﹣b)+(a﹣b)2+4a(a+1)]÷2a,其中a=﹣,b=﹣2.24.(6分)如图,在平面直角坐标系统中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).(1)求出△ABC的面积;(2)画出三角形ABC向右平移3个单位长度的三角形A1B1C1;(3)写出点A1、B1、C1的坐标.25.(5分)为了了解初一年级的学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了某校初一年级的学生一个学期参加综合实践活动的天数,并用得到的数据绘制了两幅不完整的统计图.请你根据图中提供的信息,回答下列问题:(1)求出扇形统计图中a的值和该校初一年级学生总数;(2)求出活动时间为5天的学生人数,并补全条形统计图;(3)如果某区初一年级的学生共有3000人,根据以上数据,试估计这3000人中“活动时间不少于4天”的百分比.26.(11分)几何解答题(1)如图1,直线l1、l2分别与直线l3、l4相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.(2)如图2,∠1+∠2=180.,∠3=∠B,试判断∠AED与∠ACB的大小关系,并对此结论进行证明.27.(6分)已知:A(0,1),B(2,0),C(4,3)(1)求△ABC的面积;(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.28.(5分)解答下列问题(1)如图,△ABC中,∠ABC=50°,∠ACB=70°,D为边BC上一点(D与B、C不重合),连接AD,∠ADB的平分线所在直线分别交直线AB、AC于点E、F.求证:2∠AED﹣∠CAD=170°;(2)若∠ABC=∠ACB=n°,且D为射线CB上一点,(1)中其他条件不变,请直接写出∠AED 与∠CAD的数量关系.(用含n的代数式表示)。
人教版北京市西城区七年级下数学期末检测卷附答案

北京市西城区七年级下学期数学期末检测试卷一、精心选一选(本题共10小题,每小题3分,共30分,每小题给出的4个选项只有一个符合题意,请将唯一正确答案的代号填在表格内) 1.下列方程组中,是二元一次方程组的是A .⎩⎨⎧==20y xB .⎩⎨⎧=+=+82z y y xC .⎩⎨⎧==12y xyD .⎩⎨⎧=+=-3012y x x2.如图所示,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,并且CD .BE 相交于点P ,若∠A =50°,则∠BPC 等于A .90°B .270°C .130°D .315°3.为了了解某校2000名学生的体重情况,从中抽取了150名学生的体重,就这个问题来说,下面说法正确的是A .2000名学生的体重是总体B .2000名学生是总体C .每个学生是个体D .150名学生是所抽取的一个样本4.设“○”、“口”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“口”、“△”这样的物体,按质量从小到大的顺序排列为A .○△口B .○口△C .△口○D .口○△5.点P (m+3,m+1)在直角坐标系中的x 轴上,则点p 坐标为A .(0,-2)B .(2,0)C .(4,0)D .(0,一4)6.下列图形中具有稳定性有① ② ③ ④ ⑤ ⑥A .2个B .3个C .4个D .5个7.等腰三角形两边长分别为4,8,则它的周长为A .20B .16C .20或16D .不能确定8.二元一次方程2534=+y x 的正整数解有A .1个B .2个C .3个D .4个9.如果p (a -3,a+1)在第二象限,那么a 的取值范围是A .a>-1B .a<3C .-3<a<3D .一1<a<310.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x 人,组数为y 组,则列方程组为A .⎩⎨⎧+=+=5837x y x yB .⎩⎨⎧=-+=xy x y 5837C .⎩⎨⎧=++=xy x y 5837D .⎩⎨⎧+=-=5837x y x y二、耐心填一填(本题共10小题,每小题3分,共30分,请将正确答案直接填在题中的横线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市西城区2009–2010学年度第二学期期末测试
七年级数学试卷(B 卷) 2010.7
一、精心选一选(共10个小题,每小题3分,共30分) 1.下列计算正确的是( ).
A .3
3
3
2x x x =⋅ B .532)(x x = C .3
5
8
x x x += D .444)(y x xy =
2.下列命题中正确的有( ).
① 相等的角是对顶角; ② 若a ∥b ,b ∥c ,则a ∥c ; ③ 同位角相等; ④ 邻补角的平分线互相垂直. A .0个 B .1个 C .2个 D .3个 3.已知a b <,则下列不等式一定成立的是( ).
A . 55a b +>+
B .22a b -<-
C .
33
22
a b > D .770a b -< 4.如图,由AD ∥BC 可以得到的结论是( ). A .∠1=∠2 B .∠1=∠4 C .∠2=∠3 D .∠3=∠4 5.利用数轴确定不等式组102
x x +≥⎧⎨<⎩的解集,正确的是( ).
A .
B
.
C .
D .
6.下列调查中,适宜采用抽样调查的个数是( ). ① 了解全国中学生的用眼卫生情况;
② 了解某校合唱团30名成员订做比赛服装的尺寸大小; ③ 了解某种电池的使用寿命;
④ 了解中央电视台直播上海世博会开幕式的全国收视率情况. A .1个 B .2个 C .3个 D .4个
34
A
B
C
D
1
2
7.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( ).
A .1260°
B .900°
C .1620°
D .360°
8.已知)1)(2(kx x --化简后的结果中不含有x 的一次项,则k 的值为( ).
A .1-
B .2
1-
C .21
D .1
9.若关于x ,y 的二元一次方程组42x y k
x y k
-=⎧⎨
+=⎩的解也是二元一次方程210x y -=
的解,则k 的值为( ).
A .2
B .2-
C .0.5
D .0.5-
10.已知正整数a 、b 、c 中,c 的最大值为6且a<b<c ,则以a 、b 、c 为三边的三角
形共有( ).
A .4个
B .5个
C .6个
D .7个
二、细心填一填(共10个小题,每小题2分,共20分) 11.若点P(m -2,13+m )在x 轴上,则m =________. 12.如图,AB ∥CD ,∠A=32°,∠C=70°,
则∠F=_______°.
13.计算:)32)(32()1(2
-+--x x x =__________________. 14.如图,四边形ABCD 中,∠B=40°,沿直线MN 剪去
∠B ,则所得五边形AEFCD 中,∠1+∠2=_________°.
15.已知⎩⎨⎧-==21y x 和2
1x y =⎧⎨=⎩
都是方程1=-by ax 的解,
则=+b a _______.
16.如图,△ABC 中,∠B=30°,∠C=74°,AD 平分∠BAC
,
AE ⊥BC 于E , EF ⊥AD 于F ,则∠AEF=_______°. 17.若点P 在第四象限,且距离每个坐标轴都是3个单位长度,则点P 的坐标为
_______________.
18.已知OA ⊥OB ,∠AOC :∠AOB=2:3,则∠BOC=_______________°.
19.在一块边长为10米的正方形草坪上修了横竖各两条宽都为1.5米
的长方形小路(图中阴影部分)将草坪分隔成如图所示的图案,则图中未被小路覆盖的草坪的总面积为_____________平方米. 20.多项式52222
2
+++-y y xy x 的最小值是__________.
A
B
C
D
E
F A
F B
E C D
M N
12A
B
D
F
三、认真做一做(共5个小题,每小题5分,共25分) 21.先化简,再求值:
b a ab b a a b a a b 2322323)](8)([÷---,其中5a =,2b =-.
22.解方程组:2143
2()3()19x y x y x y ⎧+=-⎪⎨⎪+--=-⎩,
.
23.解不等式组:2(2)41213
x x x x -->⎧⎪
+⎨≤-⎪⎩,.
24.李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).请你结合图表中所给信息回答下列问题:
(1)表中m =_________,n =_________; (2)请补全频数分布直方图;
(3)在扇形统计图中,6≤x <7这一组所占圆心角的度数为____________度; (4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.
频数
25.如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表1m长.已知各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).
(1)请写出图中下列地点的坐标:
牡丹园__________________;
游乐园__________________;
(2)连接音乐台、湖心亭和望春亭
这三个地点,画出所得的三角形.然
后将所得三角形向下平移200个单位
长度,画出平移后的图形;
(3)问题(2)中湖心亭平移后的对
应点的坐标为__________________.
四、解答题(共5个小题,每小题5分,共25分)
26.在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、
27.如图,长方形ABCD 中,AB =a ,BC =b ,AC=c ,其中a<b<c .将长方形ABCD 沿AC 剪开.
(1)用所得的两个三角形可以拼出几个与长方形ABCD 形状不同但面积相等(即要求没有缝隙,也不重叠)的凸四边形?请分别画出所有可能的图形;
(2)在问题(1)拼接所得的四边形中,周长的最大值与最小值分别为多少?请用a 、b 、c 表示出来.
28.已知:6a b -=,2()90ab c a +-+=,求a b c ++的值.
b c
a A B
C D
29.已知:如图,六边形ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F ,猜想可得六边形ABCDEF 中必有两条边是平行的.
(1)根据图形写出你的猜想:_______∥________; (2)请证明你在(1)中写出的猜想.
D B A
C E
F
30.阅读理解
如图a ,在△ABC 中,D 是BC 的中点.如果用ABC ∆S 表示△ABC 的面积,则由等底等高的三角形的面积相等,可得
ABC ACD ABD ∆∆∆=
=S 2
1
S S .同理,如图b ,在△ABC 中,D 、E 是BC 的三等分点,可得ABC AEC ADE ABD ∆∆∆∆===S 31
S S S .
结论应用 已知:△ABC 的面积为42,请利用上面的结论解决下列问题:
(1)如图1,若D 、E 分别是AB 、AC 的中点,CD
与BE 交于点F ,则△DBF 的面积为____________; 类比推广
(2)如图2,若D 、E 是AB 的三等分点,F 、G 是AC 的三等分点,CD 分别交BF 、BG 于M 、N ,CE 分别交BF 、BG 于P 、Q ,求△BEP 的面积;
探究新知
(3)如图3,问题(2)中的条件不变,求四边形EPMD 的面积.
E A
D C
B 图b
图a B
C
D
A
图1
图2
B 图3。
