RSA加密体制的密钥生成技术的研究
rsa公钥加密技术原理

rsa公钥加密技术原理RSA公钥加密技术原理一、引言随着信息技术的迅猛发展,数据的安全性问题日益凸显。
为了保护数据的机密性和完整性,人们提出了许多加密算法。
RSA公钥加密技术作为公认的加密算法之一,具有较高的安全性和广泛的应用范围。
本文将介绍RSA公钥加密技术的原理及其应用。
二、RSA公钥加密技术原理1. 概述RSA公钥加密技术采用了一种基于大数分解的数论问题,其安全性基于质因数分解的困难性。
其原理可以概括为以下几个步骤:密钥生成、加密和解密。
2. 密钥生成RSA公钥加密技术使用两个不同的大质数p和q作为私钥的一部分,并通过这两个质数计算得到公钥。
具体过程如下:(1)随机选择两个大质数p和q。
(2)计算n = p * q,其中n为公钥和私钥的一部分。
(3)计算φ(n) = (p-1) * (q-1),其中φ(n)为欧拉函数。
(4)选择一个整数e,使得1 < e < φ(n)且e与φ(n)互质,e为公钥的一部分。
(5)计算d,使得 d * e ≡ 1 (mod φ(n)),d为私钥的一部分。
3. 加密和解密(1)加密:假设明文为M,加密后的密文为C。
公式为:C ≡ M^e (mod n)。
(2)解密:假设解密后的明文为M',则有M' ≡ C^d (mod n)。
三、RSA公钥加密技术的应用1. 数据加密RSA公钥加密技术在数据传输过程中起到了重要作用。
发送方使用接收方的公钥对数据进行加密,只有拥有相应私钥的接收方才能解密并获取原始数据。
这种方式保证了数据在传输过程中的安全性。
2. 数字签名RSA公钥加密技术可以用于数字签名。
发送方使用自己的私钥对消息进行签名,接收方使用发送方的公钥对签名进行验证。
这种方式可以确保消息的真实性和完整性,防止被篡改。
3. 身份认证RSA公钥加密技术还可用于身份认证。
服务器发送一个随机数给客户端,客户端使用自己的私钥对该随机数进行加密,并将加密后的密文发送给服务器。
简述rsa加密算法

简述rsa加密算法一、引言RSA加密算法是公钥加密算法的代表,由Ron Rivest、Adi Shamir 和Leonard Adleman三位数学家于1977年发明。
RSA算法的安全性基于大数分解这一NP难题,被广泛应用于信息安全领域。
二、RSA加密算法原理1. 公钥和私钥的生成:RSA算法使用两个大素数p和q作为私钥,并根据p和q计算出n=p*q作为公钥。
同时,根据欧拉函数φ(n)=(p-1)*(q-1),选择一个整数e与φ(n)互质作为公钥,再计算d=e^-1 mod φ(n)作为私钥。
2. 加密过程:发送方使用接收方的公钥对明文进行加密,加密后的密文只能由接收方使用其私钥进行解密。
具体地,将明文m转换成整数M,并计算C=M^e mod n得到密文。
3. 解密过程:接收方使用自己的私钥对密文进行解密,还原出原始明文。
具体地,将密文C计算出明文M=C^d mod n。
三、RSA加密算法实现1. 公钥和私钥的生成:选择两个大素数p和q,并计算n=p*q、φ(n)=(p-1)*(q-1)。
选择一个整数e与φ(n)互质,计算d=e^-1 mod φ(n)。
公钥为(n,e),私钥为(n,d)。
2. 加密过程:将明文m转换成整数M,并计算C=M^e mod n得到密文。
3. 解密过程:将密文C计算出明文M=C^d mod n。
四、RSA加密算法的安全性RSA算法的安全性基于大数分解这一NP难题,即对于一个大整数n=p*q,要找到p和q是困难的。
目前最好的分解方法是基于数域筛法和多项式求解器的广义数域筛法,但其时间复杂度依然非常高。
RSA算法在实际应用中具有较高的安全性。
五、RSA加密算法的应用RSA算法被广泛应用于信息安全领域,如数字签名、数据加密、证书认证等。
其中,数字签名可以保证信息的完整性和真实性;数据加密可以保护敏感信息不被窃取;证书认证可以确定通信双方身份并建立可信任的通信渠道。
六、总结RSA加密算法是一种公钥加密算法,在信息安全领域得到了广泛应用。
RSA加密算法的实现调研报告

RSA加密算法的实现调研报告背景资料●RAS算法是一种基于大素数乘法和因式分解的加密算法,它是一种可以同时用于加密和数字签名的算法。
●RSA算法在1977年由LenAdleman、Ron Rivest以及RonRivest提出,它是基于一个很基本的数学公论,即计算两个大素数的乘积很容易,但将这个乘积进行因式分解则非常困难,因此可以将乘积作为公开密钥,来实现数字签名。
●RAS算法自提出以来,经历了各种攻击以及时间的考验,事实证明RSA算法是一种很优秀的加密算法,已被广泛接受及应用。
RSA算法的基本流程●密钥的产生:●选取两个保密的大素数p、q●计算N=p*q,并计算φ(N)=(p-1)(q-1)●取整数e,满足1<e<φ(N),且e与φ(N)的最大公约数为1●计算私钥d,满足ed ≡1(mod(φ(N))。
d是e在φ(N)下的乘法逆元加密过程:●加密时,每次加密的内容在数值上不能超过N,即比特长度不能超过logN。
所以需要对要加密的明文进行分组。
2●对分组后的明文做加密运算,算法为:密文C=明文M e mod N解密过程:●对密文进行如下运算得到明文:M=C d mod N●在具体应用时,由于使用的素数很大,还需要用其他算法来完成指数运算等。
芯片数据通路设计●加密芯片需要输入三个数据:明文M,指数e,模N。
由于加密密钥使用1024位,设计使用三个1024位的存储器,即图中的A,B,M。
●其中,模N在运算中会反复用到,将起存在寄存器M中,而明文M因为只用了一次,将其暂存在寄存器A中。
寄存器A、B的主要作用是存储幂模运算和SRT除法的中间结果。
蒙哥马利模乘器•模乘器是新片的主要模块,是进行幂模运算的核心部分。
其行为描述如图所示:•由于1024位的幂模匀速需要大量的时间,从图中可以看出,初始化时,模存在M中,被乘数存在A中,乘数装在B中,寄存器A中的迭代从最低有效位向最高有效位进行,每次迭代寄存器R的最低位即下一次迭代的q1,这样可以极大的缩短运算所需要的时间,提高了芯片的运算效率。
RSA加密算法的研究与实现

RSA加密算法的研究与实现摘要:在信息时代,如何保证信息的安全是个十分重要的问题。
在多年的发展中,人们提出了许多不同类型的加密算法。
其中RSA加密算法是公认的最经典的非对称密码算法之一。
本文首先介绍了课题研究的背景和意义,再介绍了使用的研究工具,然后使用Verilog 硬件描述语言设计了一个RSA的加密系统,最后通过Modelsim进行了仿真测试。
结果证明本文通过硬件实现的RSA加密算法可以有效的加密数据。
关键词:RSA;Verilog;Modelsim;硬件仿真;Abstract:In the information age, the security of information is a very important issue. In the years of development, people have proposed many different types of encryption algorithms. RSA encryption algorithm is one of the most classical asymmetric cryptographic algorithms. This paper first introduces the background and significance of the research, then introduces the research tools, then designs a RSA encryption system using Verilog hardware description language, and finally performs simulation tests through Modelsim. The result proves that the RSA encryption algorithm implemented in hardware can be effective and efficient.Keywords:RSA; Verilog; Modelsim; Hardware simulation;目录摘要 (Ⅰ)Abstract (Ⅰ)目录 (Ⅱ)1绪论 (1)1.1研究背景 (1)1.2研究意义 (1)2相关知识介绍 (2)2.1加密算法介绍 (2)2.1.1对称密钥密码体制 (2)2.1.2非对称密钥密码体制 (3)2.1.3 RSA的研究现状 (3)2.2开发工具介绍 (4)2.2.1 Verilog语言的介绍 (4)2.2.2 Modelsim介绍 (4)3 RSA加密系统的实现细节 (5)3.1 RSA参数的选择 (6)3.2 RSA加密系统 (8)4 RSA加密系统的实现 (10)4.1 RSA的乘法求模模块 (10)4.2 RSA加密系统顶层模块 (13)4.3仿真测试 (15)5总结 (16)5.1本文总结 (16)5.2未来展望 (17)参考文献 (17)致谢 (18)1 绪论1.1研究背景自20世纪以来,计算机网络技术得到了飞速发展和十分广泛的应用,但网络在带给我们便利的同时也给我们带来了很多问题。
RSA加密算法实验报告_2

现代密码学实验报告题目: RSA算法的实现过程
一、实验目的
二、简单实现RSA过程, 通过OpenSSL命令编辑器实现发送方对明文进行加
密, 签名, 接受方验证, 解密的简单过程。
三、实验原理
RSA加密算法的基本流程:
四、实验步骤
发送方对明文进行加密:
首先利用MD5对明文进行摘要操作:
然后生成秘钥文件:
再利用这个密钥对摘要进行加密:
然后对摘要进行签名操作:
发送方加密后要发送的东西是: 明文和摘要的签名传送到接收方后,接收方进行解密操作:
接收方进行验证:
通过比较可以发现所得摘要的结果是相同的, 则可以得到结论: 该明文没有被篡改。
五、实验心得
通过对RSA过程的简单模仿, 我们可以明白理论和现实是有一定差别的, 我们需要将明文利用MD5进行摘要处理, 然后在通过MD5对摘要进行验证, 从而判断密文是否经过修改, 达到数据的安全性, 完整性和保密性。
在使用OpenSSL进行RSA过程模仿时要注意文件名的对应, 这需要我们在命名文件时能做到见名之意, 方便我们后续的操作。
命令行的书写方式需要我们对字母有一定的敏感性, 经常会出现字母出现问题而导致错误的发生。
RSA加密算法的研究与实现

RSA加密算法的研究与实现摘要在新信息时代,信息的保密尤为重要。
公钥密码学的出现对现代保密体系起到了十分重要的作用,其中RSA算法是目前在理论和实际应用中最为成熟和完善的一种公钥密码体制。
它运用最多的地方是加密,还可用来进行身份验证和数字签名,是一种典型的公钥密码体制。
本文给出了RSA运算中的模幂乘速度上的改进,对RSA加解密变换、身份验证的基本原理进行了相应的分析,分析了当前针对RSA算法的攻击手段,归纳出提高RSA算法安全性应该考虑的几个因素。
此外,论文还通过实验方式对改进的RSA算法进行了验证,通过比对,得出改进的算法比原有算法在效率上有一定程度提高的结论。
论文还设计了一个加解密程序,并对其进行了验证。
关键词RSA,密码学,算法研究ABSTRACTIn the new information age, information confidential is particularly important.The emergence of modern public key cryptography to confidentiality system plays a very important role,including RSA algorithms are currently in theory and practical application of the most mature and perfect a public key cryptosystems.It utilizes most place is encrypted,also can be used for identity authentication and digital signature,is a kind of typical public key cryptosystems.This paper gives the mould by RSA operation speed of the power of RSA encryption improvement,transform,the basic principle of identity check the corresponding analysis,this article analyses the current according to the RSA algorithms attack methods, concludes improve safety should consider RSA algorithms of several factors.In addition,this paper also through experiments to improve RSA algorithms way is verified by comparing,concluded that the improved algorithm on efficiency than the original algorithm with a certain degree increase conclusion.This paper also designed a gal declassification procedures, and analyses the verification.Keywords:RSA,Cryptography,Algorithms第一章绪论 (1)1.1 问题的提出 (1)1.2 密码学概述 (3)1.3 国内外研究现状与水平及其意义 (4)第二章 RSA算法 (6)2.1 RSA算法 (6)2.2 RSA签名算法 (6)第三章 RSA的安全性 (8)3.1 RSA参数选择 (8)3.2 RSA的安全性分析 (10)第四章 RSA算法的研究 (12)4.1 RSA算法实现 (12)4.2 RSA改进算法 (13)4.3 结果分析 (16)第五章文件加密的设计 (17)5.1分析和设计 (17)5.2 对TXT文本加解密 (19)总结 (22)参考文献: (23)致谢 (24)第一章绪论随着时代在进步,科技的发展。
RSA实验报告2024

RSA实验报告(二)引言:RSA算法是一种公钥加密算法,被广泛应用于信息安全领域。
本次实验旨在通过实现RSA算法,深入理解其原理和实际应用。
本文将通过对RSA算法进行实验,并详细分析实验结果,探讨RSA算法的性能和安全性。
概述:RSA算法是由三位密学家Rivest、Shamir和Adleman于1977年共同提出的。
它基于数论中的大数分解问题,通过巧妙地利用素数和模幂运算的特性,实现了一种快速且安全的加密算法。
本次实验将从密钥对、加密和解密三个方面对RSA算法进行实验。
正文内容:一、密钥对1.选择素数:通过随机的方法选择两个大的素数p和q,保证其大小和位数的安全性。
2.计算n和φ(n):根据选择的p和q,计算出n和φ(n),其中n=pq,φ(n)为欧拉函数的值。
3.选择公钥:选择一个与φ(n)互质的整数e,作为公钥。
4.计算私钥:根据选择的公钥e和φ(n),通过扩展欧几里得算法计算出私钥d。
5.密钥完毕:将公钥(n,e)和私钥(n,d)存储起来,用于后续的加密和解密操作。
二、加密1.明文转化:将要加密的明文转化为对应的整数,使用ASCII 码或其他字符编码方式进行转化。
2.加密运算:使用公钥(n,e),对明文进行模幂运算,得到密文。
3.密文输出:将得到的密文输出。
三、解密1.密文转化:将接收到的密文转化为对应的整数。
2.解密运算:使用私钥(n,d),对密文进行模幂运算,得到解密后的明文。
3.明文输出:将得到的明文输出。
四、性能分析1.密钥长度:根据实验结果统计不同密钥长度下加密和解密的速度,比较性能差异。
2.加解密时间:通过实验测量不同明文长度下的加密和解密时间,分析RSA算法的执行效率。
3.密文大小:研究密文与明文的关联性,分析密文对明文的扩展效果。
4.安全性分析:基于已知攻击手段,分析RSA算法的安全性,包括素数选择、模幂运算等环节。
五、实验结果1.密钥:统计不同长度密钥所需时间,并分析其对RSA算法的影响。
RSA加密、解密原理及秘钥生成
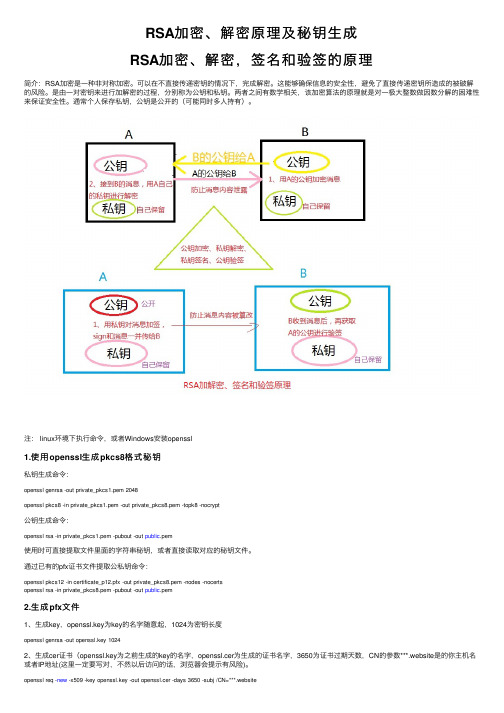
RSA加密、解密原理及秘钥⽣成RSA加密、解密,签名和验签的原理简介:RSA加密是⼀种⾮对称加密。
可以在不直接传递密钥的情况下,完成解密。
这能够确保信息的安全性,避免了直接传递密钥所造成的被破解的风险。
是由⼀对密钥来进⾏加解密的过程,分别称为公钥和私钥。
两者之间有数学相关,该加密算法的原理就是对⼀极⼤整数做因数分解的困难性来保证安全性。
通常个⼈保存私钥,公钥是公开的(可能同时多⼈持有)。
注: linux环境下执⾏命令,或者Windows安装openssl1.使⽤openssl⽣成pkcs8格式秘钥私钥⽣成命令:openssl genrsa -out private_pkcs1.pem 2048openssl pkcs8 -in private_pkcs1.pem -out private_pkcs8.pem -topk8 -nocrypt公钥⽣成命令:openssl rsa -in private_pkcs1.pem -pubout -out public.pem使⽤时可直接提取⽂件⾥⾯的字符串秘钥,或者直接读取对应的秘钥⽂件。
通过已有的pfx证书⽂件提取公私钥命令:openssl pkcs12 -in certificate_p12.pfx -out private_pkcs8.pem -nodes -nocertsopenssl rsa -in private_pkcs8.pem -pubout -out public.pem2.⽣成pfx⽂件1、⽣成key,openssl.key为key的名字随意起,1024为密钥长度openssl genrsa -out openssl.key 10242、⽣成cer证书(openssl.key为之前⽣成的key的名字,openssl.cer为⽣成的证书名字,3650为证书过期天数,CN的参数***.website是的你主机名或者IP地址(这⾥⼀定要写对,不然以后访问的话,浏览器会提⽰有风险)。
深入剖析RSA密钥原理及实践

深⼊剖析RSA密钥原理及实践⼀、前⾔在经历了⼈⽣的很多⾄暗时刻后,你读到了这篇⽂章,你会后悔甚⾄愤怒:为什么你没有早点写出这篇⽂章?!你的⾄暗时刻包括:1.你所在的项⽬需要对接银⾏,对⽅需要你提供⼀个加密证书。
你⼿上只有⼀个六级英语证书,不确定这个是否满⾜对⽅需求。
由于你迟迟⽆法提供正确的证书,项⽬因此延期,加薪计划泡汤,⽉供断了,⼥朋友分⼿了,你感觉⼈⽣完了。
2. 你⽼骥伏枥 2 个⽉,终于搞懂了.crt 格式证书。
加⼊到新项⽬,项⽬在进⾏证书托管改造。
哈哈,这题我会,就是把证书⽂件上传到托管系统。
你对项⽬组成员⼤喝⼀声,放开那些证书,让我来!挤进去⼀看,是陈年⽼项⽬了,根本没有证书,当时使⽤是公钥和私钥,如何公钥和私钥变成证书⋯⋯由于你迟迟⽆法提供正确的证书,项⽬因此延期,加薪计划泡汤,⽉供断了,⼥朋友分⼿了,你感觉⼈⽣完了。
3. 你卧薪尝胆 3 个⽉,摸清楚了 SSL 证书的来龙去脉。
踌躇满志加⼊到新项⽬,你向项⽬经理痛陈⾎泪史,经此⼀役,你已经成长为安全证书⽅⾯的专家。
项⽬经理喜出望外,正好项⽬在进⾏数据安全改造,数据库需要启⽤ SSL,来得正是时候,不着急,明天下班前提供⼏个密钥⽂件就⾏。
越明⽇,下班前半⼩时,你缓缓⾛向项⽬经理,“你要的货到了”,便排出三个证书,这个是 key ⽂件,这个是公钥⽂件,这个是证书⽂件。
项⽬经理点点头⼜摇摇头,我要的是JKS ⽂件呀。
你说,明天提供。
越明⽇,下班前的半个⼩时,你把 JKS 格式⽂件交给项⽬经理,项⽬经理点点头⼜摇摇头,密码呢?没有密码怎么⾏?由于你迟迟⽆法提供正确的证书,项⽬因此延期,加薪计划泡汤,⽉供断了,⼥朋友分⼿了,你感觉⼈⽣完了。
本⽂将从以下⼏部分来揭⽰ RSA 密钥⽂件的鲜为⼈知的秘密:RSA 算法数学基础RSA秘钥体系六层模型RSA ⼯具使⽤RSA密钥使⽤场景注:虽然密钥与证书严格意义上并不等同,但为了表述⽅便,没有特殊指定的话,本⽂中的密钥⼀词涵盖了公钥,私钥,证书等概念。
RSA加密算法的研究及系统级实现

RSA加密算法的研究及系统级实现RSA(Rivest–Shamir–Adleman)是一种非对称密码算法,广泛应用于数字签名、密钥交换和数据加密等领域。
RSA算法的研究和系统级实现主要包括RSA算法原理、RSA算法的安全性分析、实现RSA算法的关键技术和系统级应用等方面内容。
首先,研究RSA算法的原理是理解和掌握该算法的基础。
RSA算法基于数论中的一些基本性质,包括大素数因子分解困难性和模幂运算的唯一性等原理。
通过对这些原理的研究,可以理解RSA算法的加密和解密过程。
其次,RSA算法的安全性分析是研究RSA算法是否可以抵抗各种攻击的重要部分。
RSA算法的安全性主要建立在数论中的大素数因子分解困难性上。
研究者通过对RSA算法的数学模型分析和实验验证,对RSA算法的安全性进行评估和证明。
实现RSA算法涉及到一些关键技术,包括大素数的生成、模幂运算的实现、模逆运算的实现等。
大素数的生成是RSA算法的基础,需要选择足够大的素数作为RSA算法的关键参数。
模幂运算是RSA算法的主要运算,需要采用快速模幂算法来提高其计算效率。
模逆运算是解密运算中的关键,需要采用扩展欧几里得算法来求解模逆元素。
最后,将RSA算法应用于系统级实现中,可以实现数据的安全传输和保护。
例如,在网络通信中,可以使用RSA算法进行数据的加密和解密,以保障数据的机密性。
在数字签名中,可以使用RSA算法生成和验证数字签名,以保障文档的真实性和完整性。
综上所述,RSA加密算法的研究和系统级实现涉及多个方面,包括RSA算法原理的研究、安全性分析、实现RSA算法的关键技术和系统级应用等。
通过深入研究和实践,可以更好地理解和应用RSA算法,提高数据的安全性和保障信息的传输和保护。
rsa密钥生成方法

rsa密钥生成方法摘要:1.RSA加密算法简介2.密钥生成过程概述3.生成公钥和私钥的具体步骤4.应用场景和优势5.总结正文:**RSA加密算法简介**RSA(Rivest-Shamir-Adleman)加密算法是一种非对称加密算法,由麻省理工学院的Ronald L.Rivest、Adi Shamir和Whitfield Diffie于1977年发明。
RSA加密算法基于大数分解的困难性,使得加密和解密过程可以相互独立,从而提高了数据安全。
**密钥生成过程概述**在RSA加密算法中,首先需要生成一对非对称的密钥,即公钥和私钥。
公钥用于加密数据,私钥用于解密数据。
生成密钥的过程主要包括以下几个步骤:1.选择两个不同的大素数p和q。
2.计算n = p * q,其中n为模数。
3.计算欧拉函数f(n) = (p-1) * (q-1)。
4.选择一个与f(n)互质的整数e,作为加密指数。
5.计算e关于f(n)的模反元素d,作为解密指数。
6.公钥为(n,e),私钥为(n,d)。
**生成公钥和私钥的具体步骤**1.选择两个不同的大素数p和q。
例如,可以从中随机选择两个大于2的质数,如3和5。
2.计算n = p * q。
在这个例子中,n = 3 * 5 = 15。
3.计算欧拉函数f(n) = (p-1) * (q-1)。
在这个例子中,f(n) = (3-1) * (5-1) = 8。
4.选择一个与f(n)互质的整数e,作为加密指数。
在这个例子中,可以选择e = 11,因为11与8互质。
5.计算e关于f(n)的模反元素d,作为解密指数。
可以使用扩展欧几里得算法计算d,得到d = 2。
6.公钥为(n,e),私钥为(n,d)。
在这个例子中,公钥为(15,11),私钥为(15,2)。
**应用场景和优势**RSA加密算法广泛应用于数据传输、数字签名、安全认证等领域。
其优势主要体现在以下几点:1.非对称加密:RSA采用非对称加密,使得加密和解密过程可以相互独立,减轻了加密计算负担。
rsa公钥私钥生成原理

rsa公钥私钥生成原理RSA公钥私钥生成原理伟大的密码学家Rivest、Shamir和Adleman将数字签名大大简化,成为实用的工具。
RSA是非对称加密算法,可用于安全地传递信息。
这种加密技术使得在不暴露密钥的情况下加密和解密信息成为可能,从而更好地保护了数据的隐私和安全。
本文将介绍RSA公钥私钥生成原理。
公钥RSA算法中,定义了一个包括公钥和私钥两个部分的密钥对。
公钥是用于对消息进行加密的密钥。
公钥的生成包括以下步骤:(1)选取两个不同的质数p,q;(2)计算n=p*q;(3)选取与(p-1)×(q-1)互质的整数e,使得1<e<(p-1)×(q-1);(4)将n和e组合成的数作为公钥。
私钥私钥是用于对密文进行解密以及数字签名的密钥。
可以通过公钥计算私钥,计算方法如下:(1)根据p、q计算n=p*q;(2)计算λ(n)=lcm(p-1,q-1),其中lcm表示最小公倍数;(3)在[1,λ(n)]中选取一个整数d,使得ed≡1(mod λ(n));(4)将n和d组合成的数作为私钥。
加密假设Bob要向Alice发送一条信息,他首先需要得到Alice的公钥,公钥包含阶数和加密指数e。
然后Bob将消息m用公钥加密,产生一个密文c:c ≡ m^e (mod n)其中m为明文,n和e是Alice的公钥中的参数。
Bob将c发送给Alice,Alice使用私钥解密密文c:m ≡ c^d (mod n)其中d是Alice的私钥中的参数。
因为:c^d ≡ (m^e)^d ≡ m^(ed) (mod n)根据私钥的定义,ed≡1(mod λ(n)),所以上式右边可以化简为:m^1 (mod n) ≡ m所以,Alice成功解密出Bob发送的消息m。
总结RSA算法是一种安全的密码学算法。
该算法使用两个不同的密钥对,一个用于加密,另一个用于解密。
公钥由阶数和加密指数组成,私钥则由阶数和解密指数组成。
RSA公钥密码算法的研究

“网络对抗原理”技术报告题目关于RSA公钥密码算法的研究学生 X X X年级 2007级班级 0207XX 班学号 0207XXXX专业信息对抗技术学院电子工程学院西安电子科技大学2010年5月关于RAS公钥密码算法的研究作者:XXX摘要:分析RSA算法的应用现状,论证文件加密应用RSA算法的可行性和意义。
设计一套完整实用的RSA文件加密解决方案,具体编码实现。
对RSA算法进行研究,从常规RSA 算法出发,用C++实现RSA加密算法类库,并在32位windows平台封装成组件。
在.Net平台引用此组件,实现可以对任意文件进行RSA加密操作的窗体应用程序。
经过加密的文件以及密钥文件都是文本文件。
给出关键类类图、整个应用程序的结构描述文档、关键模块流程图、较详细的接口文档、所有源代码。
对应用程序进行测试,对测试结果进行分析研究,进而对应用程序进行改进,对关键算法进行尽可能的优化,最终得到一个在windows运行的可以用指定密钥对任意文件进行RSA加密并可解密的完整应用程序,和一些相关的可移植组件。
关键词: RSA RSA算法加密解密目录引言 (1)第一章RSA算法描述 (1)1.1密钥的生成 (1)1.2 加密 (1)1.3 解密 (1)第二章RSA算法实现的分析 (2)2.1素数的选取与测试 (2)2.2如何提高加解密算法的速度 (2)2.3加密幂次e和解密幂次d的选取 (3)第三章RSA算法代码及其运行结果分析 (3)3.1 RSA算法C++源代码 (3)3.2结果分析 (9)第四章RSA算法的安全性 (11)第五章RSA算法的缺点 (11)结论 (12)参考文献 (13)引言一个公开环境下的信息加密,在加密算法是公开的情况下,唯一能保证信息加密的是密钥。
在常规的对称加密算法中,如DES,加密解密密钥是相同的,如信息的发送者和合法接收者使用相同的密钥,意味前提条件为信息发送者和合法接收者互相认识或者互相信任,而且意味着密钥将分布在通信的的每一个节点,由此带来了密钥管理问题。
RSA加密算法的分析与实现实验指导书

信息安全技术实验指导二RSA加密算法的分析与实现(4学时)一、实验目的1、比较深入了解RSA算法的加密、解密原理;2、通过RSA算法加密、解密过程的学习,进一步了解通用的公开密钥加密、解密的一般过程与原理;3、用一种程序工具进行RSA加密算法代码的调试运行。
二、实验说明1、本实验分两次进行,一共4个学时。
调试RSA算法代码,并将算法实现的思路彻底搞清楚理清,进行注释。
2、写出实验报告。
三、实验指导1、RSA算法介绍:它是第一个既能用于数据加密也能用于数字签名的算法。
它易于理解和操作,也很流行。
算法的名字以发明者的名字命名:Ron Rivest, Adi Shamir 和Leonard Adleman。
但RSA的安全性一直未能得到理论上的证明。
它经历了各种攻击,至今未被完全攻破。
2、RSA算法加密、解密过程:第一步、密钥生成:选两个大素数(比如100位)p,q,N=pq,随机选取两个e,d ,使e,d与φ(N)互素(其中φ(N)表示小于N的所有数中与N互为质数的个数),且ed ≡1mod φ(n);公开N、e作为E 记E=(N,e);保密p,q,d与φ(n),作为D,记(p,q,d,φ(n))(其中p,q 可丢弃,但绝不可泄露)。
第二步、加密过程:查出E=(N,e);将明文分组x=x1x2x3……x r……;加密:y i=E(x i)=x i e mod N。
第三步、信息传递:将密文信息y=y1y2y3……y r……传送出去。
第四步、解密:x i=D(y i)= y i d mod N;合并得明文。
例:用RSA加密算法传送数据2。
第一步、密钥生成:p=5,q=7, φ(n)=24,e=11则:d=e-1mod 24=11 第二步、加密:211mod 35=18第三步、数据传输…………第四步、解密:1811 mod 35=2四、实验要求根据附件中的RSA算法代码调试运行程序。
五、实验报告要求1、在标有“注释”的地方,说明此段代码的作用;将运行结果抓2、对程序代码的错处,调试改正,并加以指出。
RSA加密体制的密钥生成技术的研究

RSA加密体制的密钥生成技术的研究
李倩
【期刊名称】《现代计算机(专业版)》
【年(卷),期】2006(000)010
【摘要】RSA是一种非对称加密算法,在公钥加密标准和电子商业中被广泛应用.RSA的可靠性基于大整数的分解难度.事实证明,因子分解的难度随着密钥长度的增加而增加.本文讨论密钥长度为1000位以上密钥生成技术,这种技术主要涉及通过素性检测生成一个大素数.运用Rabin-Miller算法检测素数,并在成功生成两个大素数之后,运用欧几里德算法在默认公钥的前提下求得私钥,然后就可运用公钥和私钥进行加密与解密了.
【总页数】5页(P4-7,20)
【作者】李倩
【作者单位】南京邮电大学计算机学院,南京,210003
【正文语种】中文
【中图分类】TP3
【相关文献】
1.海上基于超短波信道特征的密钥生成技术研究 [J], 欧敏晟;廖巍;袁志民;罗旬
2.RSA公开密钥密码体制的密钥生成研究 [J], 尹孟嘉
3.RAA公开密钥密码体制的密钥生成研究 [J], 王勇;易星
4.基于CIR的物理密钥生成技术的MAQ量化与VQ量化策略研究 [J], 陈钰洁
5.无线信道密钥生成技术综述 [J], 陈娲;李为;雷菁
因版权原因,仅展示原文概要,查看原文内容请购买。
rsa公钥私钥生成原理

rsa公钥私钥生成原理
RSA公钥私钥生成原理是一种基于大数质因数分解的加密算法。
其核心原理是利用两个大质数的乘积作为公钥进行加密,而私钥则是由这两个质数的乘积以及一些其他参数生成的。
在RSA算法中,公钥和私钥是一对密钥,其中公钥可以公开,而私钥则需要保密。
公钥由两个数字组成,一个是公钥指数e,一个是大数n,即n = p * q,其中p和q都是大素数。
私钥由两个数字组成,一个是私钥指数d,一个是大数n。
RSA算法的加密过程是利用公钥对明文进行加密,其中明文m必须是小于n的整数。
加密过程可以表示为:c = m^e mod n,其中c 是密文。
解密过程是利用私钥对密文进行解密,即m = c^d mod n。
RSA算法的安全性基于大数质因数分解的困难性,即将大数n分解为其两个素数因子p和q的乘积。
因为对大数进行质因数分解是一件非常困难的事情,所以RSA算法被广泛应用于加密通信、数字签名等领域,保护了信息安全。
- 1 -。
RSA算法研究及其安全性分析

RSA算法研究及其安全性分析1、前言随着Internet的迅猛发展,基于Internet的各种应用也日新月异,日益增长。
但是,由于Internet是一个极度开放的环境,任何人都可以在任何时间、任何地点接入Internet获取所需的信息,这也使得在Internet上信息传输及存储的安全问题成为影响Internet应用发展的重要因素。
正因为如此,信息安全技术也就成为了人们研究Internet应用的新热点。
信息安全的研究包括密码理论与技术、安全协议与技术、安全体系结构理论、信息对抗理论与技术、网络安全与安全产品等诸多领域。
在其中,密码算法的理论与实现研究是信息安全研究的基础。
而确保数据加密算法实现的可靠性和安全性对于算法理论应用到各种安全产品中起到了至关重要的作用。
对各类电子信息进行加密,以保证在其存储,处理,传送以及交换过程中不会泄露,是对其实施保护,保证信息安全的有效措施。
RSA公钥加密算法是1977年由Ron Rivest、Adi Shamirh和LenAdleman在(美国麻省理工)开发的。
RSA取名来自开发他们三者的名字。
RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的所有密码攻击,已被ISO推荐为公钥数据加密标准。
RSA 算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但那时想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
2、什么是RSARSA算法是第一个能同时用于加密和数字签名的算法,也易于理解和操作。
RSA是被研究得最广泛的公钥算法,从提出到现在已近二十年,经历了各种攻击的考验,逐渐为人们接受,普遍认为是目前最优秀的公钥方案之一。
RSA的安全性依赖于大数的因子分解,但并没有从理论上证明破译RSA的难度与大数分解难度等价。
即RSA的重大缺陷是无法从理论上把握它的保密性能如何,而且密码学界多数人士倾向于因子分解不是NPC问题。
RSA的缺点主要有:A)产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密。
rsa算法密钥生成过程

rsa算法密钥生成过程RSA算法是一种非对称加密算法,由Rivest、Shamir和Adleman三位数学家于1977年提出。
它的安全性基于大数质因数分解问题,应用广泛,包括数字签名、身份认证、数据加密等。
在RSA算法中,密钥的生成过程是非常重要的,下面介绍一下RSA算法密钥生成的过程。
选择两个大素数RSA算法的密钥生成过程始于选择两个大素数p和q,它们需要满足以下条件:p和q应当足够大,通常长度为1024或2048位;p和q应当相对较小的概率下互质。
这些条件的选择是为了保证RSA算法的安全性和可靠性。
因为大素数的质因数分解是一件困难的事情,所以要确保选择的p和q足够大。
同时,p和q需要保持机密性,因此需要满足相对较小的概率下互质。
计算n和欧拉函数将两个大素数p和q相乘得到n,即:n = p * q接着,计算欧拉函数φ(n),即:φ(n) = (p-1) * (q-1)欧拉函数φ(n)是n的正整数个数中与n互质的数的个数。
选择e选择一个与φ(n)互质的整数e(1<e<φ(n))。
e作为公钥中的一部分,用于加密明文。
计算d计算私钥d,使得d与e模φ(n)同余,即:d *e ≡1 (mod φ(n))可以使用扩展欧几里得算法求解d,扩展欧几里得算法是求解最大公约数的一种方法,可以求得d的值。
生成密钥对将n和e作为公钥,将n和d作为私钥,即:公钥:(n, e)私钥:(n, d)公钥是可公开的,用于加密明文。
私钥需要保持机密性,只有拥有私钥的人才能解密密文。
验证密钥对生成密钥对后,需要验证公钥和私钥是否合法。
验证的方法是:使用公钥加密一个明文,再使用私钥解密密文。
如果能够得到原始的明文,则表明密钥对是有效的。
以上就是RSA算法密钥生成的过程。
RSA算法的密钥生成过程是关键的一步,它的安全性和可靠性都依赖于素数的选择和密钥对的生成。
在实际应用中,在生成密钥对之后,还需要对密钥对进行安全性的评估和验证,确保密钥对的安全性和有效性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
难 度 也相 应 增 加 ,其安 全性 也 可 以得 到 进一 步 的保 证, 因而我 们需要 小 心地选 择 R A的密钥 大小 。在 目 S
前 看来 , 一个 12 0 4到 2 4 0 8比特 的密 钥大 小应 该 比较
合理。 如何 自动生成 有 可靠性 的 R A密钥呢 ? S 本文 就
二
mi ( dn o解 密时作 如下计算 : =cd( dn。 ^ mo e m。 i mo ) ^
() 数的存储 2大
大整数 的分 解难 度。事 实证 明 , 因子分 解的 难度 随着 密钥 长度的 增加 而增加 。本 文讨 论 密钥
长度 为 10 0 0位 以 上 密 钥 生 成 技 术 , 种 技 术 主 要 涉及 通 过 素 性 检 测 生 成 一 个 大 素 数 。 运 用 这
Pai- l r 法检 测 素数 , .bn Mie 算 l 并在 成功 生成 两个 大素 数之 后 . 用欧 几 里德 算 法在 默认 公钥 运
维普资讯
安全技术
李 倩
( 南京 邮电 大学计算 机 学 院 , 南京 2 0 0 ) 10 3
摘
要 :RS 是 一 种 非 对 称 加 密 算 法 , 公 钥 加 密 标 准 和 电 子 商 业 中被 广 泛 应 用 RS 的 可 靠 性 基 于 A 在 A
的算法 .那 么用 R A 加密 的信 息 的可 靠性 肯定 会极 S
度下 降。 实证 明 , 事 随着 密钥长 度 的增 加 , 因子 分解 的
数 组 , 于 目前 的 3 对 2位 系统 而 言 , 以取值 为 2的 n可
1 6次方 , O 10 0 假如将 一 个二 进制为 1 2 即 x00 。 0 4位 的 大 数转 化成 O l0 0进 制 . 就变 成 了 6 xO0 它 4位 , 每一 而 位 的取 值范 围就不 是二 进 制 0 1或 十进制 的 0 9 而 ~ ~. 是 0 0 脏 .我们 正 好可 以用 一个 无 符号 长 整数 来表 —x
一
数 在计算机 中是 如何被 保存 的 。目前 . 主流 的 R A算 S 法都 建立在 12 0 4位 以上 的大 数上 ,而大多 数 的编译 器 只能支 持到 6 4位 的整 数运 算 ,即在 运算 中使 用的
整 数必 须小 于 6 4位 , o【ff 即 )ff fl f
决 这 一 问题 。
^
10 0 0 0  ̄ 0000 1
位 . 一位 是 1其 他 四位是 0, 第 , 如此 等等 。 实 际应 用 在 中 .数 字 ” “ 数组采 用低位 在后 高位 在前 的方 式 , 样 , 这 大数 A就可 以方便地被表示 为 A=s m [ 一 o no ] u i 1dw to n ( [* x 0 0 * i 其 中 ,H 表 示求 和 , i A i 0 10 0 *), ] Si n A[表示 记 录 】 A 的数组 中第 i 元素 , 个 表示 乘积 , 表示 乘方 。 料 任何 整数 运 算最 终 都 能分 解 成数 字 与数 字之 间
的前提 下求得 私钥 . 然后 就 可 运 用 公 钥 和 私 钥 进 行 加 密 与 解 密 了 。
关键 词 :RS A;加 密 ;公开 密钥 密码 :Rai— l r bn Mie 算法 :欧几 里德 算法 l
引 言
随着 网络 的发 展和普 及 . 安全 问题越 来越 引起人 们 的关 注 。 尤其 当传送 一些 比较 机密或 是不 想 被他人 知道 的文件 时 , 们就 不得不 考虑 加密 技术 。R A 是 人 S
计 ③利 用 E c d ul 算法计 算解密密 钥 d i ,满足 e d = 算 1 mo(一 ) q 1 。其 中 n和 d也要 互质 。 ( dp 1 - ) ( ) 机 数 e和 n是 公钥 . 私钥 。加 密信息 m( d是 二进 制 表示) , 时 首先把 m 分成等长数 据块 m , .m , 长 m , i块 总 第 s 中 2s< , s 可能 的大 。对 应的 密文是 : : ,其 ^ :n 尽 c
是 ff 而 14 6 4 0 3 0 5 1 1 等 于 0 0 0 0 f. f 84 7 4 7 7 9 5 6 6 000 1
1ห้องสมุดไป่ตู้基 本 知 识
( ) A算 法 简介 1 RS
①选择两个大素数 P和 q, 计算 n=P q ; ②随机选择加密密钥 e要求 e和 ( 1 ( 1 , p ) q ) 一 - 现 代 互质 :
一
。这远 远 达不 到
种 比较 经 典 和实 用 的加 密算 法 ,既能 用于 数 据加
密 , 能用 于数 字 签 名 , 且 其可 靠性 与所 用 密钥 的 又 而 长度有很 大 关系 . 如有人 找到 一种 很快 的分 解 因子 假
需求 . 于是有 人提 出建立 一个 专 门的大数 运算 库来 解 个有 效 的方 法 是将 大数 表 示 为一 个 n进制 的
这一 问题进 行详细 探讨 。
示 这一 数 值 。所 以 .0 4位 的大数 就是 一 个有 6 12 4个
元 素 的 u s e dit 组 , 对 u s e dit 组进 行 ni n 数 g n 针 ni n 数 g n 各 种运算 所需 的循环 规模 至 多 6 4次 而 已 ,而 且 0 l0 0进 制 与 二 进制 , 于计算 机 来说 , 乎 是 一 x0 0 对 几 回事 . 转换 非常容 易 。 例 如 , 大 数 14 6 4 0 3 0 5 1 1 , 等 于 847 47 79 565 册mm . 相 当 于十进 制 的 9 9 有 四位 , 就 9 9: 每位 都 , 相 当于 十进 制的 10 0 有 5 就 00 :
