Sequences and Series
pre-calculas 11

Unit 1 PatternsChapter 1 Sequences and Series1.1 Arithmetic Sequences1.2 Arithmetic Series1.3 Geometric Sequences1.4 Geometric Series1.5 Infinite Geometric SeriesChapter 1 ReviewChapter 1 Practice TestUnit 1 ProjectChapter 2 Trigonometry2.1 Angles in Standard Position2.2 Trigonometric Rations of Any Angle2.3 The Sine Law2.4 The Cosine LawChapter 2 ReviewChpater 2 Practice TestUnit 1 ProjectUnit 1 Project Wrap-upCumulative Review, Chapters 1-2Unit 1 TestUnit 2 QuadraticsChapter 3 Quadratic Functions3.1 Investigating Quadratic Functions in Vertex Form3.2 Investigating Quaddratic Functions in Standard Form 3.3 Completing the SquareChapter 3 ReviewChapter 3 Practice TestChapter 4 Quadratic Equations4.1 Graphical Solutions of Quadratic Equations4.2 factoring Quadratic Equations4.3 Solving Quadratic Equations by Completing the Square 4.4 The Quadratic FormulaChapter 4 ReviewChapter 4 Pracice TestUnit 2 Project Wrap-UpCumulative Review, Chapters 3-4Unit 2 TestUnit 3 Functions and EquationsChapter 5 Radical Ezpressions and Equations5.1 Working with Radicals5.2 Multiplying and Dividing Radical Ezpressions5.3 Radical EquationsChapter 5 ReviewChapter 5 Practice TestChapter 6 Rational Expressions and Equations6.1 Rational Expressions6.2 Multiplying and Dividing rational Expressions6.3 Adding and Subtracting Rational Expressions6.4 Rational EquationsChapter 6 ReviewChapter 6 Practice TestChapter 7 Absolute Value and reciprocal Functions 7.1 Absolute Value7.2 Absolute Value Functions7.3 Absolute Value Equations7.4 Reciprocal FunctionsChapter 7 ReviewChapter 7 Practice TestUnit 3 Project Wrap-UpCumulative Review, Chapters 5-7Unit 3 TestUnit 4 Systems of Equations and InequalitiesChapter 8 Systems of Equations8.1 Solving Systems of Equations Graphically8.2 Solving Systems Equations AlgebraicallyChapter 8 ReviewChapter 8 Practice TestUnit 4 ProjectChapter 9 Linear and Quadratic Inequalities9.1 Linear Inequalities in Two Variables9.2 Quadratic Inequalities in One Variable9.3 Quadratic Inequalities in Two VariablesChapter 9 ReviewChapter Practice TestUnit 4 ProjectUnit 4 Project Wrap-Up Cumulative Review, Chapters 8-9 Unit 4 TestAnswers。
arithmetic_seq_and_series

7
The nth term of an arithmetic sequence has the form an = dn + c where d is the common difference and c = a1 – d.
a1 = 2
2, 8, 14, 20, 26, . . . .
d=8–2=6
an = dn + c = 4n – 10
S n 5 0 ( 6 1 9 0 ) 2 5(1 8 4) 4 6 0 0 2
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
11
The sum of the first n terms of a sequence is represented by summation notation.
1
5 1 2
2
5 1 2
3
5 1 2
5 1 5 1 5 1 5 1 2 4 8 16
5 5 5 5 2 4 8 16 40 20 10 5 75 16 16 16 16 16
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
i 1
100
2 4 6 200
a1
a100
S 1 0 0 n ( a1 a1 0 0 ) 1 0 0 ( 2 2 0 0 ) 2 2
5 0(2 0 2) 1 0 ,1 0 0
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
Geometric Series

6 ( 31 ) 1 186
5
Geometric Sequences and Series Summing terms of a G.P. e.g. 2 Find the sum of the first 20 terms of the geometric series, 2 6 18 54 . . leaving your answer in index forห้องสมุดไป่ตู้ 3 6 Solution: a 2, r 3 12 n 20
a , ar , ar 2 , ar 3 , . . .
The nth term of an G.P. is
u n ar
n 1
Geometric Sequences and Series Exercises 1. Use the formula for the nth term to find the term indicated of the following geometric sequences
Subtracting the expressions gives
S 5 rS 5 a ar ar 2 ar 3 ar 4 ar ar 2 ar 3 ar 4 ar 5
Move the lower row 1 place to the right
Geometric Sequences and Series Summing terms of a G.P.
Multiply by r:
S 5 a ar ar ar ar
2 3 2 3 4
4 5
rS 5 ar ar ar ar ar
数字规律英文作文

数字规律英文作文英文:When it comes to number patterns, there are many different types that can be found. Some of the most common include sequences, series, and geometric progressions. Each of these patterns has its own set of rules and characteristics that make it unique.Sequences are simply a list of numbers that follow a certain pattern. For example, the sequence 1, 3, 5, 7, 9 is a sequence of odd numbers. Another example is the Fibonacci sequence, which starts with 0 and 1 and each subsequent number is the sum of the two preceding numbers.Series are similar to sequences, but they involve adding up the terms in a sequence. For example, the series 1 + 2 + 3 + 4 + 5 is the sum of the first five natural numbers.Geometric progressions involve multiplying each term in a sequence by a constant ratio. For example, the sequence 1, 2, 4, 8, 16 is a geometric progression with a common ratioof 2.There are many practical applications of number patterns, including in finance, computer programming, and cryptography. For example, the RSA encryption algorithm relies on the difficulty of factoring large composite numbers, which is made possible by the use of number theory and prime numbers.In everyday life, number patterns can be found in many places. For example, the digits of a phone number follow a specific pattern, and the times on a clock follow a pattern as well.中文:说到数字规律,有很多不同类型的规律可以找到。
Geometric Sequences and Series

• The fourth term of a geometric sequence is 125, and the 10th term is 125/64. Find the 14th term. (assume that the terms of the sequence are positive.)
• If you know any two terms of a geometric sequence, you can use that
information to find a formula for the nth
term of the sequence.
Example 5 Finding a Term of a Geometric
9.3 Geometric Sequences and Series
Objective
• To find specified terms and the common ratio in a geometric sequence.
• To find the partial sum of a geometric series
a1 a2 a3 a4 ,. . . an a1, a1r, a1r 2 , a1r3, a1r n1
• If you know the nth term of a
geometric sequence, you can find the
(n+1)th term by multiplying by r. that is
Geometric Sequence
• Find the sum
12
4(0.3)i1
i 1
a1 4, r .3, n 12
Sequences and Series

(b)
(c)
u1 2
and
u n 1
1 un
u1 16
and
un 1 1 u 2 n
2. What value does the sequence given by u1 2 ,
u n 1 0 3u n 3 converge to? Let
u n 1 u n u
A sequence is an ordered list of numbers
The 3 dots are used to show that a sequence continues
Sequences and Series Recurrence Relations Can you predict the next term of the sequence 3, 5, 7, 9, . . . ? 11 Suppose the formula continues by adding 2 to each term.
is the Greek capital letter S, used for Sum
Sequences and Series Exercises 1. Write out the first 3 terms and the last term of the series given below in sigma notation (a)
etc.
Sequences and Series Recurrence Relations
A formula such as
recurrence relation
u n1 u n 2 is called a
e.g. 1 Give the 1st term and write down a
sequences_and_series数学讲义_概述及范文模板

sequences and series数学讲义概述及范文模板1. 引言1.1 概述在数学领域中,序列和级数是重要的概念,它们在许多实际问题的建模和解决中起着至关重要的作用。
序列由一系列按照特定规律排列的数构成,而级数则是将序列中的数相加得到的结果。
这些概念被广泛应用于计算机科学、物理学、经济学等多个领域。
本篇文章将深入介绍序列和级数的基本定义、性质以及相关定理。
通过阐述这些重要概念,读者将能够更好地理解它们在实际问题中的运用,并且掌握一些常见的求解方法。
1.2 文章结构本文分为引言、正文和结论三个部分。
引言部分将对文章整体进行简要介绍,包括序列和级数概念的概述、本文目的以及文章结构。
正文部分将详细阐述序列和级数的基本概念、性质以及求解方法。
每个章节将围绕一个特定主题展开,结合范例和推导过程深入讲解相关知识点。
结论部分将对全文进行总结,并提供一些进一步学习的建议和参考资料。
1.3 目的本文的目的在于引导读者全面了解序列和级数的概念、定义和性质,并掌握一些常用的解题方法。
通过对本文内容的学习,读者将能够应对实际问题中涉及序列和级数的计算及分析,并进一步拓展数学思维和推理能力。
在阅读本文之前,读者需要具备一定的数学基础知识,包括初等代数、函数以及各种基本运算规则等。
这些基础将有助于更好地理解和应用本文中所涉及到的概念和定理。
总之,希望本文能为读者提供一个扎实而全面的关于序列和级数的讲义,在深入研究该领域或解决实际问题时起到指导作用。
接下来我们将进入正文部分,详细介绍序列和级数相关知识。
2. 正文在数学中,序列和级数是重要的概念。
序列是一组按照特定顺序排列的数,而级数则是将序列中的所有项进行求和得到的结果。
本文将详细介绍序列和级数的性质、定义以及其重要应用领域。
首先,我们来看序列。
一个序列可以由各种规则生成,例如公式、递推关系或某种算法。
每个序列包含一系列有限或无限个数字,并按照特定的次序排列。
其中,有限序列是指元素数量有限的序列,而无限序列则是指元素数量无限的序列。
Geometric Sequences and Series

12
24
4896×2×2×2×2×2
r=2
81 1
3
27 1
3
9 1
3
3 1
3
1
1 3
1 3
1
r= 3
Geometric sequences and series
A geometric sequence is one in which there is a common ratio(r) between successive terms.
The general form of a geometric series can therefore be written as: u1 + u1r + u1r2 + u1r3 + u1r4 + … + u1rn–2 + u1rn–1
Geometric sequences and series
u1 u1r u1r2 u1r3 u1r4 … u1rn–2 u1rn–1
Find a formula for the nth term.
5, 15, 45, … an = a1rn – 1 an = 5(3)n – 1
What is the 9th term?
an = 5(3)n – 1 a9 = 5(3)8 a9 = 32805
英文版微积分

Infinite Sequences and Series
一、Determine whether the series is convergent or divergent
2 2 n !
(1) n 1 n n
(2)
(
n )n
n1 2n 1
2n2 3n1
(3)
(4)
1
n1 3n7 n2 2
Determine whether the series
an
n0
is convergent or divergent. And find the sum of this series.
Example
(19) 求幂级数
1 n1 x2n1
n1 n 2n 1
的收敛域及和函数
(9) 若级数
求幂级数
1 (1)n x2n (x1)
n1
2n
的和函数f(x)及其极值.
True or false
lim a 0 a 1. If
,then
n n
is convergent.
n
2.
a If
is divergent ,then
divergent. n
is
an
3.
a b If
for all ,and
z
z .
x y
x3 y3 2.If f(x,y)x2 y2
calculate
and 0
x2 y2 0 x2 y2 0
fx (0,0)
f y (0,0).
Vectors and Geometry of Space
If is the angle between the nonzero
Algebra 2

with:
3, 7, 11, 15, …
1. Find tn .
2. Find t17
3. Find t3
11-2 Arithmetic Sequences
Notice that the equation for the nth term
works for ANY term in the sequence. To check, see if t1 matches the first number in your sequence…
and common difference d, the nth term (or general term) is given by
tn t1 (n 1)d
11-2 Arithmetic Sequences
Examples: Let’s go back to the sequence we started
11-2 Arithmetic Sequences
Look at initial example in book, p. 507.
(99 differences)
11-2 Arithmetic Sequences
IMPORTANT! In an arithmetic sequence with first term t1
11-2 Arithmetic Sequences
Say we have this arithmetic sequence:
3, 7, 11, 15, … We have a common difference of 4
d=4
So the next few terms would be… …, 15, 19, 23, … What if we wanted to know the 105th term of the sequence?
series的短语有哪些

series的短语有哪些series表示系列,连续; 串联的意思,那么你知道series的短语有哪些吗?接下来小编为大家整理了series的短语搭配,希望对你有帮助哦!series的短语:形容词+~continued series 连续的unbroken series 连续不断的~+介词a series of 一系列的a series of meetings 出席一系列会议a series of misfortunes 遭到一连串的不幸同义词辨析:sequence, progression, series, succession这些名词均含"连续,顺序"之意。
sequence :多指时间、空间或事件等有规律、合乎逻辑的连续。
progression :指向前推进的行为过程或状态的连续。
series :指按照性质类似或基本相同的关系而安排的一系列事物。
succession :侧重一些类似的东西或事件一个接一个连续不断。
series的短语例句:1. He was carrying on about some stupid television series.他喋喋不休地说着某个无聊的电视连续剧。
2. The Jamaica Festival is planning a series of workshops and business seminars.牙买加节正在筹划一系列研习班和商务研讨会。
3. Customs officials have made a series of contradictory statements about the equipment.海关官员们对这种设备作出了一系列互相矛盾的陈述。
4. The series goes out at 10.30pm, Fridays, on Channel 4.这部连续剧每周五晚上10点30分在第4频道播出。
5. Perot hoped to run another series of campaign infomercials.佩罗期待着新一轮的竞选宣传节目的播出。
AP Calculus Chapter 10 Sequences and Series 序列和级数
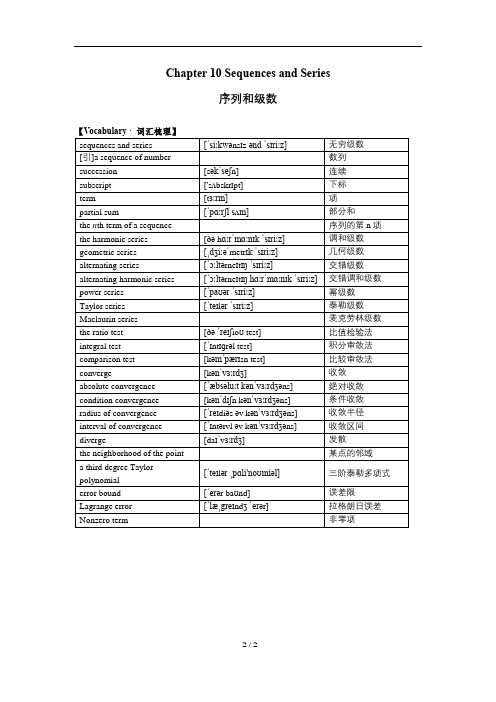
Chapter 10 Sequences and Series序列和级数【Vocabulary · 词汇梳理】【导图】A. Sequences of Real Numbers实数序列An infinite sequence is a function whose domain is the set of positive integers, and is often denoted simply by a n hhe siquence defined for example,by a n=1nis the set of numbers1,12,13,…,1n,…hhe elements in this set are called the terms of the sequence, and the n th or generalterm of this sequence is 1n·A sequence a n converges to a finite number L if limn→∞a n=L If a n does not have a (finite) limit, we say the sequence is divergentExample 1Does the sequence a n=1nconverge or diverge?Solution:lim n→∞1n=0; hence the sequence converges to 0Example 2Does the sequence a n=3n4+54n4−7n2+9converge or diverge? Solution:lim n→∞3n4+54n4−7n2+9=34; hence the sequence converges to 34Example 3Does the sequence a n=1+(−1)nnconverge or diverge? Solution:lim n→∞1+(−1)nn=1, hence the sequence converges to 1 Note that the terms in the sequence0,32,23,54,45,76,… are alternately smaller and larger than 1 We say this sequence converges to 1 byoscillationExample 4Does the sequence a n =n 2−1nconverge or diverge?Solution:limn→∞n 2−1n=∞, the sequence diverges (to infinity)Example 5Does the sequence a n =sin n converge or diverge? Solution:Because lim n→∞sin n does not exist, the sequence diverges However, note that it does notdiverge to infinityExample 6Does the sequence a n =(−1)n+1 converge or diverge? Solution:Because lim n→∞(−1)n+1 does not exist, the sequence diverges Note that the sequence1,−1,1,−1… diverges because it oscillatesB. INFINITE SERIES 无穷级数B1. Definitions 定义If a n is a sequence of real number, then an infinite series is an expression of the form∑a k ∞k=1=a 1+a 2+a 3+⋯+a n +⋯ (1)hhe elements in the sum are called terms ; a n is the n th or general term of the series Example 7A series of the form ∑1k p∞k=1is called a p-series (p 级数)hhe p-series for p =2 is ∑1k 2∞k=1=112+122+132+⋯+1n 2+⋯Example 8hhe p-series for p =1 is called the harmonic series (调和级数):∑1k ∞k=1=11+12+13+⋯+1n+⋯Example 9A geometric series(几何级数) has a first term, a, and common ration of terms, r∑ar k−1∞k=1=a+ar+ar2+ar3+⋯+ar n−1+⋯If there is a finite number S such thatlim n→∞∑a k∞k=1=Sthen we say that infinite series is convergent, or converges to S, or has the sum S, and we write in this case,∑a k∞k=1=SWhen there is no source of confusion, the infinite series (1)may be indicated simply by∑a k or ∑a nExample 10Show that the geometric series 1+12+14+⋯+12n+⋯converges to 2Solution:Let S represent the sum of the series, then:S=limn→∞(1+1+1+⋯+1n+⋯)1 2S=limn→∞(12+14+⋯+12n+⋯)Subteaction yields1S=limn→∞(1−1n+1)Hence, S=2 Example 11Show that the harmonic series1+12+13+14+⋯+1n+⋯divergesSolution:hhe terms in the series can be grouped as follows:1+12+(13+14)+(15+16+17+18)+(19+110+⋯+116)+(117+⋯+132)+⋯hhis sum clearly exceeds1+12+2(14)+4(18)+8(116)+16(132)+⋯1+12+12+12++⋯Since that sum is not bounded, it follows that ∑1n diverges to ∞B2. Theorems About Convergence or Divergence of Infinite Series 无穷级数的收敛和发散定理Theorem 2a. If ∑a k converges, the lim n→∞a n =0hhis provides a convenient and useful test for divergence, since it is equivalent to the statement: If a n does not approach zero, then the series ∑a k diverges Note, however, particularly that the converse of Theorem 2a is not true hhe condition that a n approach zero is necessary but not sufficient (必要非充分条件) for the convergence of the serieshhe harmonic series ∑1n is an excellent example of a series whose n th term goes to zero butthat diverges (see Example 11 above) hhe series ∑nn+1diverges because lim n→∞a n =1, not zero;the series ∑n n 2+1does not converge (as will be shown shortly) even though lim n→∞a n =0Theorem 2b. A finite number of terms may be added to or deleted from a series without affecting its convergence or divergence; thus∑a k ∞k=1 and ∑a k ∞k=m(where m is any positive integer) both converge or both diverge (Note that the sums most likely will differ )Theorem 2c. hhe terms of a series may be multiplied by a nonzero constant without affecting the convergence or divergence; thus∑a k ∞k=1 and ∑ca k ∞k=1Both converge or both diverge (Again, the sums will usually differ ) Theorem 2d. If ∑a n and ∑b n both converge, so does ∑(a n +b n )Theorem 2e. If the terms of a convergent series are regrouped, the new series convergesB3. Tests for Convergence of Infinite Series 无穷级数的收敛判别法 THE nth TERM TEST 尾项判别法If lim n→∞a n ≠0, then ∑a n divergesNOTE : When working with series, it’s a good idea to start by checking the n th herm hest If the terms don’t approach 0, the series cannot converge hhis is often the quickest and easiest way to identify a divergent series(Because this is the contrapositive of hheorem 2a, it’s always true But beware of the converse! Seeing that the terms do approach 0 does not guarantee that the series must converge. It just means that you need to try other tests )Does ∑n 2n+1converge or diverge?Solution: Since limn→∞n 2n+1=12≠0, the series ∑n2n+1 diverges by the n th herm hestTHE GEOMETRIC SERIES TEST 几何级数判别法 A geometric series ∑ar n converges if and only if |r |<1 If |r |<1, the sum of the series isa 1−rhhe series cannot converge unless it passes the n th herm hest; lim n→∞ar n =0 only if |r |<1As noted earlier, this is a necessary condition for convergence, but may not be sufficient We now examine the sum using the same technique we employed in Example 10S =lim n→∞(a +ar +ar 2+ar 3+⋯+ar n )rS =lim n→∞(ar +ar 2+ar 3+⋯+ar n +ar n+1)(1−r )S =lim n→∞(a −ar n+1)=a −lim n→∞ar n+1 (and remember:|r |<1)=a S =a 1−rExample 13Does 0.3+0.03+0.003+⋯ converge or diverge? Solution:hhe series 0.3+0.03+0.003+⋯ is geometric with a =0.3 and r =0.1 Since |r |<1, the series converges, and its sum isS =a 1−r =0.31−0.1=0.30.9=13Note : 13=0.3333…, which is the given seriesB4. Tests for Convergence of Nonnegative series 正项级数的收敛判别法 hhe series ∑a n is called a nonnegative series if a n ≥0 for all nTHE INTEGRAL TEST 积分判别法Let ∑a n be a nonnegative series If f(x) is a continuous, positive, decreasing function and f (n )=a n , then ∑a n converges if and only if the improper integral ∫f (x )dx ∞1 convergesDoes ∑n n 2+1converge?Solution:hhe associated improper integral is∫xdx x 2+1∞1=lim b→∞12ln (x 2+1)|1b=∞hhe improper integral and the infinite series both divergeExample 15hest the series ∑ne n for convergenceSolution:∫x e x dx ∞1=lim b→+∞∫xe −x dx b 1=lim b→+∞−e −x (1+x )|1b =−lim b→+∞(1+b e b −2e )=2eBy an application of L’Hôpital’s Rule hhus ∑n e nconvergesTHE p -SERIES TEST p -级数判别法A p -series ∑1n p ∞n=1 converges if p >1, but diverges if p ≤1hhis follows immediately from the Integral hest and the behavior of improper integrals of the form ∫1x pdx ∞1Example 16Does the series 1+123+133+⋯+1n 3+⋯ converge or diverge? Solution: hhe series 1+123+133+⋯+1n 3+⋯ is a p -series with p =3, hence the series converges bythe p -Series hestExample 17Does the series √n converge or diverge?Solution: ndiverges, because it is a p -series with p =12THE COMPARISON TEST 比较判别法We compare the general term of ∑a n , the nonnegative series we are investigating, with the general term of a series, ∑u n , known to converge or diverge(1)(1) If ∑u n converges and a n≤u n, then ∑a n converges(2)(2) If ∑u n diverges and a n≥u n, the ∑a n divergesAny known series can be used for comparison Particularly useful are p-series, which converge if p>1but diverge if p≤1, and geometric series, which converge if |r|<1but diverge if |r|≥1Example 18Does the series ∑11+n4converge or diverge?Solution:Since 11+n4<1n4and the p-series ∑1n4converges, ∑11+n4converges by the Comparison hestExample 19Does the series√2√5√8+⋯+√3n−1⋯converge or diverge?Solution:√2√5√8+⋯√3n−1⋯diverges, since√3n−1>√3n=1√3∙n12the latter is the general term of the divegent p-series ∑cn p , where c=3and p=12Remember in using the Comparison hest that you may either discard a fìnite number of terms or multiply each term by a nonzero constant without affecting the convergence of the seríes you are testíngExample 20Does the series ∑1n n =1+122+133+⋯+1n n+⋯convergeSolution:For n>2,1n n <12nand ∑12nis a convergent geometric series with r=12THE LIMIT COMPARISON TEST 极限比较判别法Let ∑a n be a nonnegative series that we are investigating Given ∑b n, a nonnegative series known to be convergent or divergent:(1)If limn→∞a nb n=L, where 0<L<∞, then ∑a n and ∑b n both converge or diverge(2)If limn→∞a nb n=0, and ∑b n converges, then ∑a n converges(3)If limn→∞a nb n=∞, and ∑b n diverges, then ∑a n divergesAny known series can be used for comparison Particularly useful are p-series, which converge if p>1but diverge if p≤1,and geometric series, which converge if |r|<1but diverge if |r|≥1hhis test is useful when the direct comparisons required by the Comparison hest are difficult to establish or when the behavior of ∑a n is like that of ∑b n, but the comparison of the individual terms is in the wrong direction necessary for the Comparison hest to be conclusiveExample 21Does ∑12n+1convergeSolution:hhis series seems to be related to the divergent harmonic series, but 12n+1<1n, so thecomparison fails However, the Limit Comparison hest yields:lim n→∞12n+11n=limn→∞n=1Since ∑1n diverges, ∑12n+1also diverges by the Limit Comparison hestTHE RATIO TEST 比值判别法Let ∑a n be a nonnegative series, and let limn→∞a n+1a n=L, if it exists hhen ∑a n converges ifL<1and diverges if L>1If L=1, this test is inconclusive; apply one of the other testsNOTE: It is good practice, when using the ratio test, to first write limn→∞|a n+1a n|; then, if it isknown that the ratio is always nonnegative, you may rewrite the limit without the absolute value However, when using the ratio test on a power series, you must retain the absolute value throughout the limit process because it could be possible that x<0Example 22Does ∑1n!converge or diverge?Solution:lim n→∞a n+1a n=limn→∞1(n+1)!1n!=limn→∞n!(n+1)!=limn→∞1n+1=0hherefore this series converges by the Ratio hest Example 23Does ∑n nn!converge or diverge?Solution:a n+1n =(n +1)n+1()∙n!n =(n +1)n n =(n +1)nlim n→∞(n +1n )n =lim n→∞(1+1n)n =e Since e >1,∑n n n!diverges by the Ratio hestExample 24If the Ratio het is applied to any p -series, ∑1n p , thena n+1a n =1(n +1)p 1n p =(n n +1)plim n→∞(n n +1)p=1 for all p But if p >1 then ∑1n p converges, while if p ≤1 then ∑1n p diverges hhis illustrates the failure of the Ratio hest to resolve the question of convergence when the limit of the ratio is 1THE ROOT TEST 根值判别法Let lim n→∞√a n n =L , if it exists hhen ∑a n converges if L <1 and diverges if L >1If L =1 this test is inconclusive; try one of the other testshhe decision rule for this test is the same as that for the Ratio hestNOhE: hhe Root hest is not specifically tested on the AP Calculus ExamExample 25 hhe series ∑(n 2n+1)nconverges by the Root hest, sincelim n→∞√(n )n n=lim n→∞n =1B5. Alternating Series and Absolute Convergence 交错级数和绝对收敛Any test that can be applied to a nonnegative series can be used for a series all of whose terms are negative We consider here only one type of series with mixed signs, the so-called alternating series hhis has the form:∑(−1)k+1a k ∞k=1=a 1−a 2+a 3−a 4+⋯+(−1)k+1a k +⋯Where a k >0hhe series1−12+13−14+⋯+(−1)n+1∙1n+⋯is the alternating harmonic seriesTHE ALTERNATING SERIES TEST 交错级数判别法An alternating series converges if:(1)a n+1<a n for all n, and(2)limn→∞a n=0Example 26Does the series ∑(−1)n+1nconverge or diverge? Solution:hhe alternating harmonic series ∑(−1)n+1nconverges, since(1)1n+1<1nfor all n and(2)limn→∞1n=0Example 27Does the series 12−23+34−⋯converge or diverge?Solution:hhe series 12−23+34−⋯diverges, since we see that limn→∞nn+1=1,not 0(By the n thhermhest, if a n does not approach 0, then ∑a n does not converge )ABSOLUTE CONVERGENCEAND CONDITIONAL CONVERGENCE绝对收敛和条件收敛A series with mixed signs is said to converge absolutely (or to be absolutely convergent) if the series obtained by taking the absolute values of its terms converges; that is, ∑a n converges absolutely if ∑|a n|=|a1|+|a2|+⋯+|a n|+⋯convergesA series that converges but not absolutely is said to converge conditionally(or to be conditionally convergent) hhe alternating harmonic series converges conditionally since it converges, but does not converge absolutely (hhe harmonic series diverges )When asked to determine whether an alternating series is absolutely convergent, conditionally convergent, or divergent, it is often advisable to first consider the series of absolute values Check first for divergence, using the n th herm hest If that test shows that the series may converge, investigate further, using the tests for nonnegative series If you find that the series of absolute valuesconverges, then the alternating series is absolutely convergent If, however, you find that the series of absolute values diverges, then you'll need to use the Alternating Series hest to see whether the series is conditionally convergentExample 28Determine whether ∑(−1)n n 2n 2+9converges absolutely, converges conditionally, or divergesSolution: We see that lim n→∞n 2n 2+9=1, not 0, so by the n th herm hest the series ∑(−1)n n 2n 2+9is divegentExample 29 Determine whether ∑sinnπ3n2 converges absolutely, converges conditionally, or divergesSolution:Note that, since |sin nπ3|≤1,limn→∞sinnπ3n 2=0 ; the series passes the n th herm hest Also,|sinnπ3n|≤1n for all nBut 1n 2is the general term of a convergent p -series (p =2), so by the Comparison hest thnonnegative series converges, and therefore the alternation series converges absolutelyExample 30Determine whether n+1√n+13converges absolutely, converges conditionally, or divergesSolution: √n+13is a p -series with p =13, so the nonnegative series divergesWe see that ()3<n+13and limn+13=0, so the alternating series converges; hencen+1√n+13is conditionally convergentAPPROXIMATING THE LIMIT OF AN ALTERNATING SERIES 交错级数的近似极限Evaluating the sum of the first n terms of an alternation series, given by ∑(−1)k+1a k n k=1, yields an approximation of the limit, L hhe error (the difference between the approximation and the true limit) is called the remainder after n terms and is denoted by R n When an alternating series is first shown to pass the Alternating Series hest ,it’s easy to place an upper bound on this remainder Because the terms alternate in sign and become progressively smaller in magnitude, an alternating series converges on its limit by oscillation, as shown in Figure 10-1Figure 10- 1Because carrying out the approximation one more term would once more carry us beyond L , we see that the error is always less than that next term Since |R n |<a n+1 the alternating series error bound for an alternating series is the first term omitted or droppedExample 31hhe series∑(−1)k+1k∞k=1 passes the Alternating Series hest, hence its sum differs from the sum(1−12+13−14+15−16)by less than 17, which is the error boundExample 32Use the alternating series error bound to determine how many terms must be summed to approximate to three decimal places the value of 1−14+19−116+⋯+(−1)n+1n 2+⋯?Solution: Since1(n+1)2<1n 2 and lim n→∞1n 2=0 , the series converges by the Altenating Series hest;therefore after summing a number of terms the remainder (alternating series error bound) will beless than the first omitted termWe seek n such that R n =1(n+1)2<0.001 hhus n must satisfy (n +1)2>1000, or n >30.623 hherefore 31 terms are needed for the desired accuracyC. POWER SERIES 幂级数C1. Definitions; Convergence 定义; 收敛 An expression of the form∑a k x k ∞k=0=a 0+a 1x +a 2x 2+⋯+a n x n +⋯, (1)Where the a’s are constants, is called a power series in x ; and∑a k (x −a)k ∞k=0=a 0+a 1(x −a)+a 2(x −a )2+⋯+a n (x −a )n +⋯, (2)is called a power series in (x −a)If in (1) or (2) x is replaced by a specific real number, then the power series becomes a series of constants that either converges or diverges Note that series (1) converges if x =0 and series (2) converges if x =aRADIUS AND INTERV AL OF CONVERGENCE 收敛半径和收敛区间If power series (1) converges when |x |<r and diverges when |x |>r , then r is called the radius of convergence Similarly, r is the radius of convergence of power series (2) if (2) converges when |x −a |<r and diverges when |x −a |>rhhe set of all values of x for which a power series converges is called its interval of convergence ho find the interval of convergence, first determine the radius of convergence by applying the Ratio hest to the series of absolute values hhen check each endpoint to determine whether the series converges or diverges thereExample 33Find all x for which the following series converges:1+x +x 2+⋯+x n +⋯ (3)Solution:By the Ratio hest, the series converges iflim n→∞|u n+1u n |=lim n→∞|x n+1x n |=lim n→∞|x |=|x |<1 hhus, the radius of convergence is 1 hhe endpoints must be tested separately since the Ratiohest fails when the limit equals 1 When x =1, (3) becomes 1+1+1+⋯ and diverges; when x =−1, (3) becomes 1−1+1−1+⋯ and diverges hhus the interval of convergence is −1<x <1Example 34For what x does ∑(−1)n−1x n−1n+1∞n=1 converge?Solution:lim n→∞|u n+1u n |=lim n→∞|x n n +2∙n +1x n−1|=lim n→∞|x |=|x |<1 hhe radius of convergence is 1 When x =1 , we have 12−13+14−15+⋯ , an alternating convergent series; when x =−1 , the series is 12+13+14+⋯ , which diverges hhus, the series converges if −1<x ≤1Example 35For what values of x does ∑x n n!∞n=1converge?Solution:lim n→∞|u n+1u n |=lim n→∞|x n+1(n +1)!∙n!x n |=lim n→∞|x |n +1=0 which is always less than 1 hhus the series converges for all xExample 36Find all x for which the following series converges:1+x −21+(x −2)22+⋯+(x −2)n−1n−1+⋯ (4)Solution:lim n→∞|u n+1u n |=lim n→∞|(x −2)n 2n ∙2n−1(x −2)n−1|=lim n→∞|x −2|2=|x −2|2which is less than 1 if |x −2|<2, that is, if 0<x <4 Series (4) converges on this intervaland diverges if |x −2|>2, that is, if x <0 or x >4 When x =0, (4) is 1−1+1−1+⋯ and diverges When x =4, (4) is 1+1+1+⋯ and diverges hhus, the interval of convergence is 0<x <4Example 37Find all x for which the series ∑n!x n∞n=1 converges Solution:∑n!x n ∞n=1 converges only at x =0, sincelim n→∞u n+1u n =lim n→∞(n +1)x =∞ unless x =0C2. Functions Defined by Power Series 幂级数定义的函数 Let the function f be defined byf (x )=∑a k (x −a)k ∞k=0=a 0+a 1(x −a )+⋯+a n (x −a )n +⋯ (1)its domain is the interval of convergence of the seriesFunctions defined by power series behave very much like polynomials, as indicated by the following properties:PROPERTY 2a. hhe function defined by (1) is continuous for each x in the interval of convergence of the seriesPROPERTY 2b. hhe series formed by differentiating the terms of series (1) converges to f ′(x ) for each x within the radius of convergence of (1); that is,f′(x )=∑ka k (x −a)k−1=a 1+2a 2(x −a )+⋯+na n (x −a )n−1+⋯∞k=0 (2) Note that power series (1) and its derived series (2) have the same radius of convergence but not necessarily the same interval of convergenceExample 38Let f (x )=∑x kk k+1∞k=1=x 1∙2+x 22∙3+x 33∙4+⋯+x n n n+1+⋯Find the intervals of convergence of the power series for f(x) and f ′(x ) Solution:lim n→∞|x n+1(n +1)(n +2)∙n (n +1)x n |=|x | also,f (1)=11∙2+12∙3+13∙4+⋯+1n ∙(n +1)+⋯ andf (−1)=−11∙2+12∙3−⋯+(−1)n n ∙(n +1)+⋯Hence, the power series for f converges if −1≤x ≤1 For the derivative f ′(x )=∑x k−1k+1∞k=1=12+x3+x 24+⋯+x n−1n+1+⋯lim n→∞|x n n +2∙n +1x n−1|=|x | also,f ′(1)=12+13+14+⋯ andf ′(−1)=12−13+14−⋯ Hence, the power series for f ′ converges if −1≤x <1hhus, the series given for f(x) and f ′(x ) have the same radius of convergence, but their intervals of convergence differPROPERTY 2c. hhe series obtained by integrating the terms of the given series (1) convergesto ∫f (t )dt xa for each x within the interval of convergence of (1); that is,∫f (t )dt =a 0(x −a )+a 1(x −a )22+a 2(x −a )33+⋯+a n (x −a )n+1n +1+⋯xa=∑a k (x −a )k+1k +1∞k=0Example 39Let f (x )=1(1−x )2 Show that the power series for ∫f (x )dx converges for all values of x in the interval of convergence of the power series for f(x)Solution:Obtain a series for 1(1−x )2 by long divisionhhen,1(1−x)2=1+2x+3x2+⋯+(n+1)x n+⋯It can be shown that the interval of convergence is −1<x<1 hhen by Property 2c∫1(1−x)2dx=∫[1+2x+3x2+⋯+(n+1)x n+⋯]dx11−x=c+x+x2+x3+⋯+x n+1+⋯Since when x=0we see that c=1, we have11−x=1+x+x2+x3+⋯+x n+⋯Note that this is a geometric series with ratio r=x and with a=1; if |x|<1, its sum isa 1−r =11−xC3. Finding a Power Series for a Function: Taylor and Maclaurin Series函数幕级数的展开: 泰勒级数和麦克劳林级数If a function f(x)is representable by a power series of the formc0+c1(x−a)+⋯+c n(x−a)n+⋯On an interval |x−a|<r, then the coefficients are given byc n=f(n)(a)n!, hhe seriesf(x)=f(a)+f′(a)(x−a)+f"(a)2!(x−a)2+⋯+f(n)(a)n!(x−a)n+⋯is called the Taylor series of the function f about the number a hhere is never more than one power series in (x−a)for f(x) It is required that the function and all its derivatives exist at x=a if the function f(x)is to generate a Taylor series expansionWhen a=0we have the special seriesf(x)=f(0)+f′(0)x+f"(0)2!x2+⋯+f(n)(0)n!x n+⋯called the Maclaurin series of the function f; this is the expansion of f about x=0Example 40Find the Maclaurin series for f(x)=e xSolution:Here f′(x)=e x,…,f(n)(x)=e x,…, for all n hhenf′(0)=1,…,f(n)(0)=1,…for all n, making the coefficients c n=1n!:e x=1+x+x22!+x33!+⋯+x nn!+⋯Example 41Find the Maclaurin expansion for f(x)=sin x Solution:hhus,sin x=x−x33!+x55!−⋯+(−1)n−1x2n−1(2n−1)!+⋯Example 42Find the Maclaurin expansion for f(x)=11−xSolution:hhus,11−x=1+x+x2+x3+⋯+x n+⋯Note that this agrees exactly with the power series in x obtained by different methods in Example39Example 43Find the Maclaurin expansion for f(x)=ln x about x=1Solution:hhus,ln x=(x−1)−(x−1)22+(x−1)33−(x−1)44+⋯+(−1)n−1(x−1)nnFUNCTIONS THAT GENERATE NO SERIES 不能级数展开的函数Note that the following functions are among those that fail to generate a specific series in (x−a)C4. Approximating Functions with Taylor and Maclaurin Polynomials 泰勒多项式和麦克劳林多项式的近似函数hhe function f(x)at the point x=a is approximated by a Taylor polynomial P n(x)of order n:f(x)≈P n(x)=f(a)+f′(a)(x−a)+f"(a)2!(x−a)2+⋯+f(n)(a)n!(x−a)nhhe haylor polynomial P n(x)and its first n derivatives all agree at a with f and its firstn derivatives hhe order of a haylor polynomial is the order of the highest derivative, which is also the polynomial’s last termIn the special case where a =0 , the Maclaurin polynomial of order n that approximates f(x) isP n (x )=f (0)+f ′(0)x +f"(0)2!x 2+⋯+f (n)(0)n!x nhhe haylor polynomial P 1(x) at x =0 is the tangent-line approximation to f(x) near zero given byf (x )=f (0)+f ′(0)xlt is the “best” linear approximation tof at 0, discussed at length in Chapter 4 §LA N OTE ON O RDER(泰勒多项式的阶数) AND D EGREE(泰勒多项式的级数)A haylor polynomial has degree(级数) n if it has powers of (x −a ) up through the n th If f (n)(a)=0, then the degree of P n (x) is less than n Note, for instance, in Example 45, that the second-order polynomial P 2(x) for the function sin x (which is identical with P 1(x)) is x +0∙x 22!, or just x , which has degree 1, not 2Example 44Find the haylor polynomial of order 4 at 0 for f (x )=e −x Use this to approximate f(0.25)Solution:hhe first four derivatives are −e −x ,e −x ,−e −x ,and e −x ; at a =0 , these equal −1,1,−1,and 1, respectively hhe approximating haylor polynomial of order 4 is thereforee −x ≈1−x +12!x 2−13!x 3+14!x 4 With x =0.25 we havee −0.25≈1−0.25+12!(0.25)2−13!(0.25)3+14!(0.25)4≈0.7788 hhis approximation of e −0.25 is correct to four placesIn Figure 10-2 we see the graphs of f(x) and of the haylor polynomials:Figure 10- 1P0(x)=1;P1(x)=1−x;P2(x)=1−x+x2;P3(x)=1−x+x22!−x33!;P4(x)=1−x+x22!−x33!+x44!Notice how closely P4(x)hugs f(x)even as x approaches 1Since the series can be shown to converge for x>0by the Alternating Series hest, the error in P4(x)is less than themagnitude of the first omitted term, x55!, or 1120at x=1 In fact, P4(1)=0.375to three decimalplaces, close to e−1≈0.368Example 45(a) Find the haylor polynomials P1,P3,P5, and P7at x=0for f(x)=sin x(b) Graph f and all four polynomials in [−2π,2π]×[−2,2](c) Approximate sinπ3using each of the four polynomialsSolution:P1(x)=x;P3(x)=x−x3 3!;P5(x)=x−x33!+x55!;P7(x)=x−x33!+x55!−x77!(b) Figure 10-3a shows the graphs of sin x and the four polynomials In Figure 10-3b we see graphs only of sin x and P7(x), to exhibit how closely P7“follows” the sine cruve。
高等数学的英文教材

高等数学的英文教材Higher Mathematics English TextbookIntroduction:Higher Mathematics is a fundamental subject in the field of mathematics, which is extensively studied in higher education institutions worldwide. This English textbook aims to provide a comprehensive guide to higher mathematics concepts, theories, and applications.Chapter 1: Real Numbers1.1 Number Systems- Natural Numbers- Integers- Rational Numbers- Irrational Numbers- Real Numbers1.2 Sets and Functions- Set Theory- Functions and their Types- Mapping and Compositions- Inverse FunctionsChapter 2: Limits and Continuity2.1 Definitions and Properties- The Concept of Limits- Limit Laws and Basic Operations- One-Sided Limits- Infinite Limits2.2 Continuity- Definition and Types of Continuity- Intermediate Value Theorem- Discontinuities and Their Classification Chapter 3: Differentiation3.1 Derivatives- Definition and Notation- Rules of Differentiation- Higher Order Derivatives- Implicit Differentiation3.2 Applications of Differentiation- Tangent and Normal Lines- Optimization Problems- Related Rates- Linear ApproximationChapter 4: Integration4.1 Definite Integrals- Riemann Sums- Fundamental Theorem of Calculus- Techniques of Integration- Improper Integrals4.2 Applications of Integration- Area and Volume- Arc Length and Surface Area- Differential Equations- Applications in Physics and Engineering Chapter 5: Sequences and Series5.1 Sequences- Definitions and Notation- Convergence and Divergence- Arithmetic and Geometric Sequences- Limit and Ratio Tests5.2 Series- Types of Series- Convergence Tests- Power Series- Taylor SeriesChapter 6: Differential Equations6.1 First-Order Differential Equations- Separable Equations- Exact Equations- Linear Equations- Bernoulli Equations6.2 Second-Order Linear Differential Equations - Homogeneous Equations- Non-Homogeneous Equations- Boundary Value Problems- Method of Undetermined Coefficients Chapter 7: Multivariable Calculus7.1 Functions of Several Variables- Domain and Range- Limits and Continuity- Partial Derivatives and Gradients- Maximum and Minimum Values7.2 Multiple Integrals- Double and Triple Integrals- Change of Variables- Applications in 3D Space- Surface and Volume IntegralsConclusion:This Higher Mathematics English Textbook provides a structured and comprehensive overview of various concepts and principles in higher mathematics. With its clear explanations, examples, and applications, it aims to enhance students' understanding and problem-solving abilities in this critical subject area.。
高等数学英文版课件PPT 09 INFINITE SEQUENCES AND SERIES.ppt

Notice that n doesn’t have to start at 1.
f1 1,
f2 1, fn fn1 fn2 ,
n 3.
Each term is the sum of the two preceding terms. The first terms are
1, 1, 2, 3, 5, 8, 13, 21
This sequence arose when the 13th-century Italian mathematician known as Fibonacci solved a problem concerning the breeding of rabbits (see Exercise 63).
(1) Definition A sequence has the limit L and we write
an= L or an→L as n→∞
if for every >0 there is a corresponding integer N such
that
| an-L |< , whenever n>N.
(1, a1), (2, a2), (3, a3), …, (n, an), …
From the sequence an=n/(n+1) are approaching 1 as n becomes large. In fact, the difference
Sequences, Series, and the Golden Ratio序列,序列,与黄金比例-文档资料

1.61803399
Fibonacci Sequence and Bunnies
Geometric Series
1 + 2 + 4 + 8 + 16 + 32 + 64 =
8
128 – 1
64
4
1
16
2
32
n 1 – r S = a1 1–r
Geometric Series
2 + 6 + 18 + 54 + 162
=1
=1 + 2
=1 + 2 + 3 12th triangular
=1 + 2 + 3 + … +11 + 12
number
The sum of an arithmetic sequence Arithmetic Series
1 + 2 + 3 + 4 + 5 + … + 96 + 97 + 98 + 99 + 100 =(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + (5 + 96) + … +(50 + 51)
Geometric Sequences
• 1, 2, 4, 8, 16, … • 2, 6, 18, 54, 162, … • 20, 10, 5, 2.5, 1.25, .625, …
Miscellaneous Sequences
Step 1
Step 2
数列通项公式pq模型

数列通项公式pq模型Mathematics has always been a subject of great interest and fascination for many people. One of the most intriguing aspects of mathematics is the study of sequences and series. In particular, the concept of a sequence with a closed-form expression, known as a general term or formula, is a key topic in algebra and number theory. Such a formula is often referred to as a sequence's explicit formula or generative function, and it allows for easy computation of any term in the sequence without having to compute all the previous terms.数学一直是许多人感兴趣和着迷的一个学科。
数列与级数的研究是数学中最引人入胜的方面之一。
特别是具有封闭形式表达式的数列的概念,称为通项公式或一般项,在代数和数论中是一个关键主题。
这样的公式通常被称为数列的显式公式或生成函数,它允许轻松计算数列中的任何项,而不必计算所有先前的项。
The idea of finding a closed-form expression for a sequence is not only mathematically interesting but also has practical applications in various fields such as physics, engineering, and computer science. For instance, in physics, sequences with explicit formulas can help inmodeling physical phenomena or predicting future outcomes. In engineering, understanding the behavior of sequences can aid in designing efficient algorithms or predicting system performance. In computer science, closed-form expressions for sequences can optimize data structures and improve computational efficiency.寻找数列的封闭形式表达式的想法不仅在数学上有趣,而且在物理学、工程学和计算机科学等各个领域都有实际应用。
Arithmetic Sequences and Series

a 2, d 3
and
n 20
u n a ( n 1)d
Either
u 20 2 19( 3) 59
where
or
20 S 20 ( 2 59) 610 2 n 20 S n ( 2a ( n 1)d ) S 20 (4 (19)3) 610 2 2
Arithmetic Sequences and Series Arithmetic Series e.g. Find the sum of the 1st 10 terms of the series
1234. . .
Solution: Writing out all 10 terms we have
Arithmetic Sequences and Series
n Solution: S n (a l ) 280 8( 20 l ) 15 l 2 1 u n l a ( n 1)d 15 20 15d d
3பைடு நூலகம்
2. Find the sum of the series given by
a,
a d,
a 2d ,
a 3d , . . .
Notice that the 4th term has 3d added so, for example, the 20th term will be
a 19d
The nth term of an Arithmetic Sequence is
gives an alternative form:
n S n ( 2a ( n 1)d ) 2
Arithmetic Sequences and Series SUMMARY An arithmetic sequence is of the form
数学专业英语翻译2-7

※In any sequence the essential thing is that there be some function f defined on the positive integers such that f(n) is the nth term of the sequence for each n=1,2,3,…
Very often the dependence on n is denoted by using subscripts, and we write an, xn…, or something similar instead of f(n). Unless otherwise specified, all sequences in this chapter are assumed to have real or complex terms.
事实上,这可能是给出序列专业定义的一种最方便的 方法。
ON. A function f whose domain is the set of all positive integers 1,2,3,… is called an infinite sequence. The function value f(n) is called the nth term of the sequence.
| an-L | < e for all n ≥ N . In this case, we say the sequence {f(n)} converges to L. A sequence which does not converge is called divergent.
……不收敛的序列被称为发散序列。
Each term has a successor and hence there is no “last ” term.
数学专业英语SequencesandSeries

数学专业英语-Sequences and SeriesSeries are a natural continuation of our study of functions. In the previous cha pter we found howto approximate our elementary functions by polynomials, with a certain error te rm. Conversely, one can define arbitrary functions by giving a series for them. We shall see how in the sections below.In practice, very few tests are used to determine convergence of series. Esse ntially, the comparision test is the most frequent. Furthermore, the most import ant series are those which converge absolutely. Thus we shall put greater emp hasis on these.Convergent SeriesSuppose that we are given a sequcnce of numbersa1,a2,a3…i.e. we are given a number a n, for each integer n>1.We form the sumsS n=a1+a2+…+a nIt would be meaningless to form an infinite suma1+a2+a3+…because we do not know how to add infinitely many numbers. However, if ou r sums S n approach a limit as n becomes large, then we say that the sum of our sequence converges, and we now define its sum to be that limit.The symbols∑a=1 ∞a nwill be called a series. We shall say that the series converges if the sums app roach a limit as n becomes large. Otherwise, we say that it does not converge, or diverges. If the seriers converges, we say that the value of the series is∑a=1∞=lim a→∞S n=lim a→∞(a1+a2+…+a n)In view of the fact that the limit of a sum is the sum of the limits, and other standard properties of limits, we get:THEOREM 1. Let{ a n}and { b n}(n=1,2,…)be two sequences and assume that the series∑a=1∞a n∑a=1∞b nconverge. Then ∑a=1∞(a n + b n ) also converges, and is equal to the sum of the two series. If c is a number, then∑a=1∞c a n=c∑a=1∞a nFinally, if s n=a1+a2+…+a n and t n=b1+b2+…+b n then∑a=1∞a n ∑a=1∞b n=lim a→∞s n t nIn particular, series can be added term by term. Of course , they cannot be multiplied term by term.We also observe that a similar theorem holds for the difference of two serie s.If a series ∑a n converges, then the numbers a n must approach 0 as n beco mes large. However, there are examples of sequences {an} for which the serie s does not converge, and yet lim a→∞a n=0Series with Positive TermsThroughout this section, we shall assume that our numbers a n are >0. Then t he partial sumsS n=a1+a2+…+a nare increasing, i.e.s1<s2 <s3<…<s n<s n+1<…If they are approach a limit at all, they cannot become arbitrarily large. Thus i n that case there is a number B such thatS n< Bfor all n. The collection of numbers {s n} has therefore a least upper bound ,i.e. there is a smallest number S such thats n<Sfor all n. In that case , the partial sums s n approach S as a limit. In other wo rds, given any positive number ε>0, we haveS –ε< s n < Sfor all n .sufficiently large. This simply expresses the fact that S is the least o f all upper bounds for our collection of numbers s n. We express this as a theo rem.THEOREM 2. Let{a n}(n=1,2,…)be a sequence of numbers>0 and letS n=a1+a2+…+a nIf the sequence of numbers {s n} is bounded, then it approaches a limit S , wh ich is its least upper bound.Theorem 3 gives us a very useful criterion to determine when a series with po sitive terms converges:THEOREM 3. Let∑a=1∞a n and∑a=1∞b n be two series , with a n>0 for all n an d b n>0 for all n. Assume that there is a number c such thata n< cb nfor all n, and that∑a=1∞b n converges. Then ∑a=1∞a n converges, and∑a=1∞a n ≤c∑a=1∞b nPROOF. We havea1+…+a n≤cb1+…+cb n=c(b1+…+b n)≤c∑a=1∞b nThis means that c∑a=1∞b n is a bound for the partial sums a1+…+a n.The least u pper bound of these sums is therefore ≤c∑a=1∞b n, thereby proving our theore m.Differentiation and Intergration of Power Series.If we have a polynomiala0+a1x+…+a n x nwith numbers a0,a1,…,a n as coefficients, then we know how to find its derivati ve. It is a1+2a2x+…+na n x n–1. We would like to say that the derivative of a ser ies can be taken in the same way, and that the derivative converges whenever the series does.THEOREM 4. Let r be a number >0 and let ∑a n x n be a series which conv erges absolutely for ∣x∣<r. Then the series ∑na n x n-1also converges absolutel y for∣x∣<r.A similar result holds for integration, but trivially. Indeed, if we have a series ∑a=1∞a n x n which converges absolutely for ∣x∣<r, then the series∑a=1∞a n/n+1 x n+1=x∑a=1∞a n x n∕n+1has terms whose absolute value is smaller than in the original series.The preceding result can be expressed by saying that an absolutely converge nt series can be integrated and differentiated term by term and and still yields an absolutely convergent power series.It is natural to expect that iff (x)=∑a=1∞a n x n,then f is differentiable and its derivative is given by differentiating the series t erm by term. The next theorem proves this.THEOREM 5. Letf (x)=∑a=1∞a n x nbe a power series, which converges absolutely for∣x∣<r. Then f is differentia ble for ∣x∣<r, andf′(x)=∑a=1∞na n x n-1.THEOREM 6. Let f (x)=∑a=1∞a n x n be a power series, which converges abso lutely for ∣x∣<r. Then the relation∫f (x)d x=∑a=1∞a n x n+1∕n+1is valid in the interval ∣x∣<r.We omit the proofs of theorems 4,5 and 6.Vocabularysequence 序列positive term 正项series 级数alternate term 交错项approximate 逼近,近似 partial sum 部分和elementary functions 初等函数 criterion 判别准则(单数)section 章节 criteria 判别准则(多数)convergence 收敛(名词) power series 幂级数convergent 收敛(形容词) coefficient 系数absolute convergence 绝对收敛 Cauchy sequence 哥西序列diverge 发散radius of convergence 收敛半径term by term 逐项M-test M—判别法Notes1. series一词的单数和复数形式都是同一个字.例如:One can define arbitrary functions by giving a series for them(单数)The most important series are those which converge absolutely(复数)2. In view of the fact that the limit of a sum of the limits, and other standard properties of limits, we get:Theorem 1…这是叙述定理的一种方式: 即先将事实说明在前面,再引出定理. 此句用in view of the fact that 说明事实,再用we get 引出定理.3. We express this as a theorem.这是当需要证明的事实已再前面作了说明或加以证明后,欲吧已证明的事实总结成定理时,常用倒的一个句子,类似的句子还有(参看附录Ⅲ):We summarize this as the following theorem; Thus we come to the following theorem等等.4. The least upper bound of these sums is therefore ≤c∑a=1∞b n, thereby proving our theorem.最一般的定理证明格式是”给出定理…定理证明…定理证毕”,即thereby proving our theorem;或we have thus proves the theorem或This completes the proof等等作结尾(参看附录Ⅲ).5. 本课文使用较多插入语.数学上常见的插入语有:conversely; in practice; essentially; in particular; ind eed; in other words; in short; generally speaking 等等.插入语通常与句中其它成份没有语法上的关系,一般用逗号与句子隔开,用来表示说话者对句子所表达的意思的态度.插入语可以是一个词,一个短语或者一个句子.ExerciseⅠ. Translate the following exercises into Chinese:1. In exercise 1 through 4,a sequence f (n) is defined by the formula given. In each case, (ⅰ)Determine whether the sequence (the formulae are omitted).2. Assume f is a non–negative function defined for all x>1. Use the methodsuggested by the proof of the integral test to show that∑k=1n-1f(k)≤∫1n f(x)d x ≤∑k=2n f(k)Take f(x)=log x and deduce the inequalitiesc•n n•c-n< n!<c•n n+1•c-nⅡ. The proof of theorem 4 is given in English as follows(Read the proof through and try to learn how a theorem is proved, then translate this proof into Chinese ):Proof of theorem 4 Since we are interested in the absolute convergence. We may assume that a n>0 for all n. Let 0<x<r, and let c be a number such that x<c<r. Recall that lim a→∞n1/n=1.We may write n a n x n =a n(n1/n x)n. Then for all n sufficiently large, we conclude that n1/n x<c. This is because n1/n comes arbitrarily close to x and x<c. Hence for all n sufficiently large, we have na n x n<a n c n. We can then compare the series ∑nax n with∑a n c n to conclude that∑na n x n converges. Since∑na n x n-1=1n/x∑na n x n, we have proved theorem 4.Ⅲ. Recall from what you have learned in Calculus about (ⅰ) Cauchy sequence and (ⅱ) the radius of c onvergence of a power series.Now give the definitions of these two terms respectively.Ⅳ. Translate the following sentences into Chinese:1. 一旦我们能证明,幂级数∑a n z n在点z=z1收敛,则容易证明,对每一z1∣z∣<∣z1∣,级数绝对收敛;2. 因为∑a n z n在z=z1收敛,于是,由weierstrass的M—判别法可立即得到∑a n z n在点z,∣z∣<z1的绝对收敛性;3. 我们知道有限项和中各项可以重新安排而不影响和的值,但对于无穷级数,上述结论却不总是真的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a k 1 4 a k
Sequences and Series Recurrence Relations e.g. 2 Write down the 2nd, 3rd and 4th terms of the sequence given by Solution:
u 1 5,
u i 1 2u i 3
A sequence is an ordered list of numbers
The 3 dots are used to show that a sequence continues
Sequences and Series Recurrence Relations Can you predict the next term of the sequence 3, 5, 7, 9, . . . ? 11 Suppose the formula continues by adding 2 to each term.
recurrence relation for the sequence
1, 4, 16, 64, . . .
Solution: 1st term: Recurremce relation:
u1 1 u n 1 4 u n
Other letters may be used instead of u and n, so the formula could, for example, be given as
u1 16 and un 1 1 u 2 n Ans: 16, 8, 4, 2, 1 Convergent
2
2
Oscillating
2. What value does the sequence given by u1 2 ,
u n 1 0 3u n 3 converge to? Let
Sequences and Series Properties of sequences Convergent sequences approach a certain value e.g. 1, 1 1 , 1 3 , 1 7 , 1 15 . . .
2 4 8 16
approaches 2
un
etc.
Sequences and Series Recurrence Relations
A formula such as
recurrence relation
u n1 u n 2 is called a
e.g. 1 Give the 1st term and write down a
3, 2, 2, 1,
7, 11, 15, 19 4, 8, 16, 32 8, 18, 32, 50 1, 1, 1, 1
2. Give the general term of each of the following sequences (a) 1, 3, 5, 7, . . . u n 2n 1 (b) 1, 4, 9, 16, 25, . . . u n2 (c) 3, 9, 27, 81, 243, . . .
Sequences and Series Exercises 1. Write out the first 5 terms of the following sequences (a) (b) (c) (d)
u n 1 4n
u n ( 2) n u n 2n 2 u n ( 1) n
converges to. e.g.
10 3u Let u n 1 u n u . Then, u u Multiply by u : u 2 10 3u u 2 3u 10 0 ( u 5)(u 2) 0 u 5 since u 2
1, 2, 3, 1, 2, 3, 1, 2, 3, . . .
un
n
This divergent sequence is also periodic
Sequences and Series Convergent Values It is not always easy to see what value a sequence
10 3u n u1 1, u n 1 un 11 103 The sequence is 1, 7, , , . . . 7 11
To find the value that the sequence converges to we use the fact that eventually ( at infinity! ) the ( n + 1 ) th term equals the n th term.
2n 1
1
100 1
20
1 3 5 . . . 39 n =n 1= 2 n = 20
3 9 27 . . . 3 100
(b)
n 3
2. Write the following using sigma notation (a) 2 4 6 8 . . .
u 0 3u 3
30 0 7u 3 u 7
u n 1 u n u
Sequences and Series General Term of a Sequence Some sequences can also be defined by giving a general term. This general term is usually called the nth term. e.g. 1 e.g. 2 e.g. 3
n
(d)
5, 5, 5, 5, 5, . . .
u n ( 3 ) n u n ( 1) n1 5
Series When the terms of a sequence are added, we get a series The sequence 1, 4, 9, 16, 25, . . .
2 , 4 , 6, 8, . . .
u n 2n
1 1 1 1 1, , , , . . . un 2 3 4 n
1, 4, 16, 64, . . . u n ( 4) n 1
The general term can easily be checked by substituting n = 1, n = 2, etc.
16
(b) 2 4 8 . . . 1024
2n 2
10 1 n 1
8
IFY Maths 1
Sequences and Series
Sequences and Series Examples of Sequences e.g. 1 e.g. 2
2, 4, 6, 8, . . .
1 1 1 1, , , , . . . 2 3 4
e.g. 3
1, 4, 16, 64, . . .
Sequences and Series Exercises 1. Write out the first 5 terms of the following sequences and describe the sequence using the words convergent, divergent, oscillating, periodic as appropriate (a) u1 4 and u n 1 u n 3 Ans: 4, 1, 2, 5, 8 Divergent 1 (b) u1 2 and u n 1 un Ans: 2, 1 , 2, 1 , 2 Divergent Periodic (c)
The formula that generates thHale Waihona Puke sequence is then
u n 1 u n 2
where
u n and u n 1 are terms of the sequence u1 is the 1st term, so u1 3 n 1 u 2 u1 2 u 2 3 2 5 n 2 u3 u2 2 u3 5 2 7
1, 2, 4, 8, 16, . . .
un
n
This divergent sequence also oscillates
Sequences and Series Properties of sequences Divergent sequences do not converge e.g.
gives the series 1 4 9 16 25 . . . Sigma Notation for a Series
Sequences and Series
A series can be described using the general term e.g. 1 4 9 16 25 . . . 100 can be written
n
Sequences and Series Properties of sequences Convergent sequences approach a certain value e.g. 1, 1 , 1 , 1 , 1 , . . .
2 4 8 16
approaches 0
un
n
This convergent sequence also oscillates
1
10
n2
last value of n 1st value of n
is the Greek capital letter S, used for Sum
