哈尔滨市2014南岗区一摸
赵一曼受刑记录(一)_高中作文

赵一曼受刑记录(一)本文是关于高中作文的赵一曼受刑记录(一),感谢您的阅读!档案解密:赵一曼受刑始末(本来想说是酷刑,但酷刑已经不能表达这些刑罚的残忍程度)此档案为当时对赵一曼用刑的日本鬼子的供词。
赵一曼出生在一个大地主家庭,“少女时代气质高雅,清纯美丽,天生喜欢朴素的生活,嗜书如命。
”加入中国共-产-党后成为我党“早期杰出的女军事人才之一。
”她率领抗日健儿转战于绥滨铁路以北的侯林乡、宋家店、黑龙宫一带,艰苦卓绝,奋勇杀敌,威镇敌胆。
给日伪以沉重的打击。
赵一曼的威名使敌人闻风丧胆,登报悬赏捉拿她这个“挎双枪,骑白马的密林女王”。
1935年11月15日,为掩护主力部队突围,赵一曼主动要求留下掩护,最后她率150多名战士被敌人包围在左撇子沟,经过一天浴血奋战,击毙日寇30余。
激战中,队伍被打散。
突围时,赵一曼左手腕受伤,后与4名同志潜入小西北沟窝棚里养伤,不幸行踪被特务探知。
3天后,在敌人抓捕她时,赵一曼腿上中了子弹,右腿被打断,露出了骨头。
她一头栽倒在雪地上,失去了知觉,不幸被敌人捉住了。
为了从赵一曼口中了解抗联的活动情报,滨江省公署警务厅派员把赵一曼从珠河县转到哈尔滨滨江省公署警务厅看押。
这是一座位于哈尔滨市南岗区一曼街的洁白、庄严的西欧古典式大楼。
在那里,滨江省警务厅特务科对赵一曼进行了“严刑拷问和人格污辱,”“甚至剥光全身进行羞辱,”特务科的日本宪兵为了逼迫赵一曼供出抗联的机密和党的地下组织,对她进行了残酷的拷问。
“用了多种手法,进行了各种尝试,甚至不顾她的伤势,施加残酷的拷打,可是她一直没有改变态度。
”据记载,刑讯前后进行过多次,采用的酷刑多达几十种,先采用包括鞭打、吊拷、老虎凳、竹筷夹手指、脚趾、拔牙齿、压杠子、扭胸肉、搓肋骨、……等“轻刑”。
轮番折磨赵一曼,让她长时间疼痛难忍、汗如雨下却不昏迷。
以此来迫使赵一曼开口,但得到的回答却是她对日本侵略者罪行的控诉和誓死抗日的决心,每次审讯,她总是坚定地回答说:“我没有什么共党身份,强迫一个人说自己不知道的事情,未免太蛮横了吧?你说我是共-产-党员,你把证据拿出来!”“你们不用多问了,我的主义就是抗日,正如你们的职责是以破坏抗日会逮捕我们为目的一样,我有我的目的,进行反满抗日并宣传其主义,就是我的目的,我的主义,我的信念。
王成、哈尔滨景阳物业管理有限公司物业服务合同纠纷二审民事判决书

王成、哈尔滨景阳物业管理有限公司物业服务合同纠纷二审民事判决书【案由】民事合同、无因管理、不当得利纠纷合同纠纷服务合同纠纷物业服务合同纠纷【审理法院】黑龙江省哈尔滨市中级人民法院【审理法院】黑龙江省哈尔滨市中级人民法院【审结日期】2020.08.18【案件字号】(2020)黑01民终2226号【审理程序】二审【审理法官】谢国丰潘雪梅李萌【审理法官】谢国丰潘雪梅李萌【文书类型】判决书【当事人】王成;哈尔滨景阳物业管理有限公司【当事人】王成哈尔滨景阳物业管理有限公司【当事人-个人】王成【当事人-公司】哈尔滨景阳物业管理有限公司【法院级别】中级人民法院【终审结果】二审维持原判二审改判【字号名称】民终字【原告】王成【被告】哈尔滨景阳物业管理有限公司【本院观点】王成于2014年8月14日进户时与景阳物业公司签订《物业管理服务合同》,并交纳了2014年7月1日至2015年6月30日的物业费5126.40元,足以说明王成对物业管理服务合同的认可。
【权责关键词】代理违约金新证据诉讼请求维持原判发回重审执行【指导案例标记】0【指导案例排序】0【本院认为】本院认为,王成于2014年8月14日进户时与景阳物业公司签订《物业管理服务合同》,并交纳了2014年7月1日至2015年6月30日的物业费5126.40元,足以说明王成对物业管理服务合同的认可。
二审期间,王成对拖欠的物业费数额亦认可,辩称应在另案生效的裁判文书中景阳物业公司赔偿王成各项损失中予以扣除,因法律关系不同,案件不同,调解不成,本院二审不作处理。
对于景阳物业公司服务存在不到位的问题,一审法院对景阳物业公司请求王成支付相应违约金未予支持,也是对景阳物业公司需要提高服务质量的变相处罚,业主和物业公司之间需要在服务过程中相互支持、加强理解与信任。
王成在接受物业服务的同时应及时履行交费的义务,王成拖欠物业费的事实客观存在,故对王成的上诉请求,本院不予支持。
综上所述,王成的上诉请求不能成立,应予驳回;一审判决认定事实清楚,适用法律正确,应予维持。
黑龙江省哈尔滨市南岗区20142015学年八年级上学期期末调研测试物理试题及答案

黑龙江省哈尔滨市南岗区2014-2015学年八年级上学期期末调研测试物理试题及答案一、选择题(1——12题,每小题2分,共计24分,每小题只有一个正确选项)1.神舟十号”飞船与“天宫一号”实施自动交会对接。
如图所示为即将对接时的模拟图。
成功对接后,“神舟十号”内的航天员看到“天宫一号”纹丝不动,地球在缓缓转动,则航天员选择的参照物是()A.太阳 B.地球C.“天宫一号” D.“神舟十号”2.雅安地震时,解放军及时赶到灾区进行救援。
被埋者也要积极采取措施配合,方法之一是不断敲击周围坚硬物体,其目的是()A.将周围物体砸开B.利用声传递能量C.利用声传递信息D.消除寂寞3.如图所示的现象中,属于光的反射现象的是()A.水中倒影 B.日食形成 C.小孔成像 D.铅笔“折断”4.电影院放映电影过程中涉及到很多光学知识,下列说法正确的是()A.光射到银幕上发生了镜面反射B.银幕上的像是正立放大的虚像C.从放映机射向银幕的光是沿直线传播的D.白色的银幕可以吸收所有的色光5.下列光路图中,正确表示了光从空气进入水中的是()A B C D6.如图所示,检查视力时平面镜、被测者和视力表的位置关系示意图。
若平面镜距视力表3m远,该视力表要求被测者在5m远处,则人到视力表的距离应该是()A.3m B.2mC.1m D.0.5m7.如图所示是用温度计测量液体温度的示意图,其中温度计使用正确的是()A B C D8.如图2所示的四种物态变化的实例中,属于液化的是()9.如图是“探究某物质熔化和凝固规律”的实验图像,下列说法正确的是()A.在t时=5min时,该物质处于固态B.在BC段,该物质不吸热C.该物质凝固过程持续了5min学科王D.该物质的凝固点是45℃10.有一体积为30cm3的均匀固体,用天平测得它的质量为237g,则()A.用天平测质量时,固体应放在天平右盘B.此固体的密度为7.9g/cm3C.把此固体截去一半,剩余部分密度减小D.只改变此固体形状,它的质量减少11.小伟同学利用天平和量筒测橙汁的密度,下列操作步骤中多余的是()A.用天平测量空烧杯的质量B.将橙汁倒入烧杯中,用天平测量烧杯和橙汁的总质量C.将烧杯中的橙汁倒入量筒中一部分,测出量筒中橙汁的体积D.用天平测量烧杯和剩余橙汁的总质量12.甲、乙两物体同时同地向东做匀速直线运动,它们的s-t图像如图所示。
【中考必做卷】哈尔滨市南岗区2014年中考调研测试(一)

哈尔滨市南岗区2014年中考调研测试(一)物理试卷一、选择题(1-12小题,每小题2分,共24分。
每小题只有一个正确选项)1.下列数据中最接近实际情况的是()A.一个中学生站立时对水平地面的压强约为100PaB.一标准大气压能支持约0.76m高水柱C.用分度值为1cm的刻度尺测量一个中学生的身高为1.762mD.考场内一盏日光灯正常发光时的电流约为2A2. 运动员百米赛跑情境如图所示,下列说法正确的是( )A.以地面为参照物,运动员是静止的B.运动员的鞋底花纹很深,可以减小摩擦C.运动员跑得越快,到达终点所用时间越长D.运动员冲刺到终点不能立即停下,是由于人具有惯性3.用图像表示一个物理量随另一个物理量的变化规律,可使物理规律更直观、形象。
如图所示,关于此图所表示的物理规律,下列分析错误..的是()A.物体所受重力与质量的关系B. 液体压强与深度的关系C. 做匀速直线运动的物体,速度与时间的关系D.通过定值电阻的电流与电压的关系4.如图是同学手拿重锤线匀速下坡、静止在水平地面和匀速上楼的情景,以下说法中不正确...的是()A三种情况对比可知重力的方向总是竖直向下的B三种情况下人受合力都为零C三种情况下绳对重锤的拉力相同D三种情况下重力都没对人做功5.人们生活所需的用品中涉及到很多物理知识,下列对应关系正确的是()A.移动电话——超声波B.超声加湿器——电磁波C.电热水器——电流的热效应D.筷子——省力杠杆6.晓彤在洗澡时发现自己学到的科学知识能解释很多现象,下列有关解释错误..的是()A.地面铺的防滑地砖是通过增大接触面的粗糙程度来增大摩擦的B.人在镜子中成像的原理是光的反射C.热水冲洗后皮肤温度升高主要是热传递的结果D.镜子上的水雾是水蒸气液化而成的7.如下图甲乙,分别演示的是电话的话筒和听筒的工作过程,下面有关这两幅图的说明中正确的是()A.甲图表现的是电话的听筒,它是利用电磁感应原理来工作的B.甲图表现的是电话的话筒,它工作时将电能转化为机械能C.乙图表现的是电话的听筒;它是利用磁场对电流的作用来工作的D.乙图表现的是电话的话筒,它工作时将机械能转化为电能8.小雪学习了“家庭电路”后,有如下几点认识,其中正确的是()A.电能表是用来测量电路消耗电能的仪表,应安装在总开关之前B.电热毯内的电阻丝断了,只需将断头接上后,仍可安全使用C.当电路因故障导致保险装置断开时,只需更换保险线或使空气开关复位D.家庭电器或电线着火时,首先应立即灭火9.南极是世界上最冷的地方,常年平均气温是﹣25℃,如图所示,一天企鹅妈妈与小企鹅之间发生了一次有趣的对话,他们的部分说法如下,其中正确的是()A.小企鹅:妈妈,这么冷,我都没温度了B.企鹅妈妈:不对,是没有内能C.小企鹅:冰天雪地的,可能连水蒸气都没有吧D.企鹅妈妈:呵呵,水蒸气倒肯定有,因为冰是可以升华的呀10.在如图所示的电路中,闭合开关,下列说法中正确的是( )A.电流表测的是通过灯L1的电流B.电流表测的是通过灯L1和L2的总电流C.取下灯L1后L2仍然会亮,电流表有读数D .取下灯L 2后L 1也不亮,电流表无读数11.同学们要应用如图所示的装置(R 1=R 2)、若干节干电池、开关、导线和停表探究“电热跟电流关系”,提出的下列说法错误..的是( ) A.实验时通过比较红色液柱上升的高度比较电热的大小B.实验时应该将1、2两装置并联接到电池节数不变的电源上C.实验时应该将1、2两装置分别接到电池节数不同的电源上D.只用装置1和给出的器材也能完成探究12.如图所示是已连接的一部分电路图,R 1=5Ω,R 2=20Ω。
2024年黑龙江省哈尔滨市南岗区虹桥中学中考数学一模试卷+答案解析
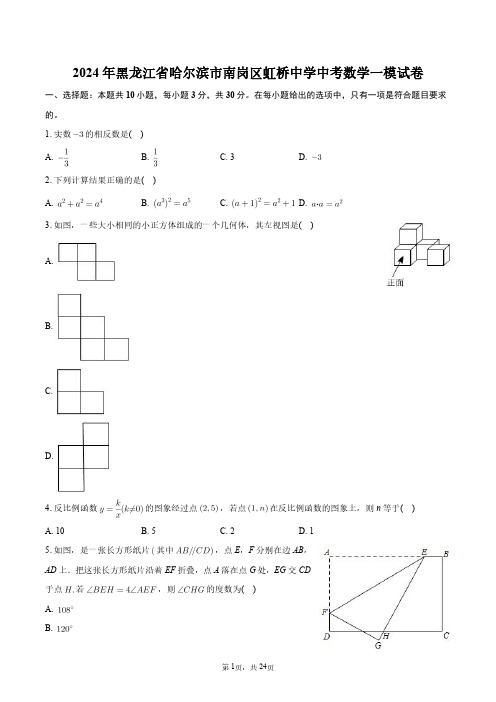
2024年黑龙江省哈尔滨市南岗区虹桥中学中考数学一模试卷一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.实数的相反数是()A. B. C.3 D.2.下列计算结果正确的是()A. B. C. D.3.如图,一些大小相同的小正方体组成的一个几何体,其左视图是()A.B.C.D.4.反比例函数的图象经过点,若点在反比例函数的图象上,则n等于()A.10B.5C.2D.15.如图,是一张长方形纸片其中,点E,F分别在边AB,AD上.把这张长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点若,则的度数为()A.B.C.D.6.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为()A. B.C. D.7.甲、乙两人加工某种机器零件,已知每小时甲比乙少加工6个这种零件,甲加工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等,设甲每小时加工x个零件,所列方程正确的是()A. B. C. D.8.如图,是的外接圆,半径为2cm,若,则的度数为() A.B.C.D.9.小王利用计算机设计了一个计算程序,输入和输出的数据如表:输入…12345…输出……那么,当输入数据为8时,输出的数据为()A. B. C. D.10.甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中,分别表示甲、乙两辆摩托车到A地的距离与行驶时间的函数关系.则下列说法错误的是()A.乙摩托车的速度较快B.经过小时甲摩托车行驶到A,B两地的中点C.经过小时两摩托车相遇D.当乙摩托车到达A地时,甲摩托车距离A地二、填空题:本题共10小题,每小题3分,共30分。
11.2017年5月18日,我国在南海北部神弧海域进行的可燃冰试开采成功,标志着我国成为全球第一个在海域可燃冰开采中获得连续稳定的国家.目前每日的天然气试开采量约为16000立方米,把16000立方米用科学记数法表示为______立方米.12.使在实数范围内有意义的x的取值范围是______.13.因式分解:______.14.不等式组的最小整数解为______.15.如图,边长为2的正方形ABCD中心与半径为2的的圆心重合,E、F分别是AD、BA的延长线与的交点,则图中阴影部分的面积是______结果保留16.如图,在中,已知,,垂足为D,若E是AD的中点,则______.17.在中考体育达标跳绳项目测试中,1分钟跳绳160次为达标,小敏记录了他预测时1分钟跳的次数分别为145,155,140,162,164,则他在该次测试中达标的概率是______.18.如图,已知是一个锐角,以点O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再分别以点A、B为圆心,大于长为半径画弧,两弧交于点C,画射线过点A作,交射线OC于点D,过点D作,交ON于点设,,则______.19.等腰内接于,若半径为10cm,底边长为12cm,则这个等腰三角形的腰长______20.如图,在四边形ABCD中,,AC、BD相交于点E,,且,若,,则CD边的长为______.三、解答题:本题共7小题,共60分。
赵一曼受刑记录(一)-高中作文

赵一曼受刑记录(一)本文是关于高中作文的赵一曼受刑记录(一),感谢您的阅读!档案解密:赵一曼受刑始末(本来想说是酷刑,但酷刑已经不能表达这些刑罚的残忍程度)此档案为当时对赵一曼用刑的日本鬼子的供词。
赵一曼出生在一个大地主家庭,“少女时代气质高雅,清纯美丽,天生喜欢朴素的生活,嗜书如命。
”加入中国共-产-党后成为我党“早期杰出的女军事人才之一。
”她率领抗日健儿转战于绥滨铁路以北的侯林乡、宋家店、黑龙宫一带,艰苦卓绝,奋勇杀敌,威镇敌胆。
给日伪以沉重的打击。
赵一曼的威名使敌人闻风丧胆,登报悬赏捉拿她这个“挎双枪,骑白马的密林女王”。
1935年11月15日,为掩护主力部队突围,赵一曼主动要求留下掩护,最后她率150多名战士被敌人包围在左撇子沟,经过一天浴血奋战,击毙日寇30余。
激战中,队伍被打散。
突围时,赵一曼左手腕受伤,后与4名同志潜入小西北沟窝棚里养伤,不幸行踪被特务探知。
3天后,在敌人抓捕她时,赵一曼腿上中了子弹,右腿被打断,露出了骨头。
她一头栽倒在雪地上,失去了知觉,不幸被敌人捉住了。
为了从赵一曼口中了解抗联的活动情报,滨江省公署警务厅派员把赵一曼从珠河县转到哈尔滨滨江省公署警务厅看押。
这是一座位于哈尔滨市南岗区一曼街的洁白、庄严的西欧古典式大楼。
在那里,滨江省警务厅特务科对赵一曼进行了“严刑拷问和人格污辱,”“甚至剥光全身进行羞辱,”特务科的日本宪兵为了逼迫赵一曼供出抗联的机密和党的地下组织,对她进行了残酷的拷问。
“用了多种手法,进行了各种尝试,甚至不顾她的伤势,施加残酷的拷打,可是她一直没有改变态度。
”据记载,刑讯前后进行过多次,采用的酷刑多达几十种,先采用包括鞭打、吊拷、老虎凳、竹筷夹手指、脚趾、拔牙齿、压杠子、扭胸肉、搓肋骨、……等“轻刑”。
轮番折磨赵一曼,让她长时间疼痛难忍、汗如雨下却不昏迷。
以此来迫使赵一曼开口,但得到的回答却是她对日本侵略者罪行的控诉和誓死抗日的决心,每次审讯,她总是坚定地回答说:“我没有什么共党身份,强迫一个人说自己不知道的事情,未免太蛮横了吧?你说我是共-产-党员,你把证据拿出来!”“你们不用多问了,我的主义就是抗日,正如你们的职责是以破坏抗日会逮捕我们为目的一样,我有我的目的,进行反满抗日并宣传其主义,就是我的目的,我的主义,我的信念。
2014年哈尔滨市中考调研测试南岗区一模(数学试卷及答案)

2014年中考调研测试(一)数学试卷参考答案与评分标准二、(每小题3分,共计30分) 三、解答题(共计60分)21.解:xx x -+-24224............22)2)(2(2424222'+=--+=--=---=x x x x x x x x x∵x =2sin 60°-2tan 45°=1 (23122)32'-=⨯-⨯∴1 (3223224)22'=+-=+=-+-x x x x 22. 解:(1)画图正确2....................' 1.....).........1,2(1'--C (2)画图正确1.....).........4,2(2....................2''C 23. 证明:过点A 作BG AM ⊥交GB 的延长线于M , 作DG AN ⊥于N ︒=∠=∠=∠∴90AND ANG AMG DE BG ⊥ ︒=∠∴90BGD∴四边形AMGN 为矩形 ︒=∠∴90MAN '2....................................∵四边形ABCD 为正方形MAN BAD ∠=︒=∠∴90 AD AB =BAN BAD BAN MAN ∠-∠=∠-∠∴即DAN BAM ∠=∠....................................1' DAN BAM ∆∆∴≌....................................1'\AN AM =∴ ....................................1'M∴GA 平分BGD ∠ ....................................1'24. 解:(1)1410616450=----=x ,图形略3....................................' (2)70分以上的频率为:64.05010616=++, 由样本估计总体可知:)(38460064.0人=⨯∴估计该校学生时事政治掌握情况良好的人数约为384人. 3....................................'25.(1)证明:连接OE ,在⊙O 中,OB OE OA ==,2.........,//,'∠=∠=∠=∠∴∠=∠∴EOD OEB OBE AOD BE OD OEB OBE1..................,,'∠=∠∴∆∆∴==OED OAD EOD AOD OD OD OE OA ≌又∵AM 是⊙O 的切线,切点为A , ∴AM ⊥BA , ∴DE OE OED OAD ⊥∴︒=∠=∠,90∵OE 是⊙O 的半径 是DE ∴⊙O 的切线.1................' (2)解:过点D 作BC 的垂线,垂足为H. ∵BN 切⊙O 于点B ,∴BHDBAD ABC ∠=∠=︒=∠90∴四边形ABHD是矩形,2........................................,1'===∴DH AB BH AD314=-=-=∴BH BC CH AD 、CB 、CD 分别切⊙O 于点A 、B 、E ,1...............541,4,1'=+=+=∴====∴CE DE DC CE BC ED AD在 DHC Rt ∆中,1.....................435,22222'=-==∴+=DH AB CH DH DC 26. 解:(1)设甲种商品每件的进价是x 元,则乙种商品每件的进价为x 3元.依题意可得8031200400=+xx ,解得'2........................................10=x 经检验10=x 为原分式方程的解,∴301033=⨯=x '2.................................................答:甲、乙两种商品的进价分别为每件10元、30元.(2)设六月份再次购进甲种商品a 件,则购进乙种商品)80(a -件,依题意可得3.............................................600)80)(3040()1015('≥--+-a a 解得40≤a ,a 的最大值是40答:该超市六月份最多购进甲种商品40件....................................1' 27. 解:(1) 令0=x ,则33,02=++==+=+-=bx ax y n n n x y,3n OC ==∴令,0=y 则1....................................).........0,3(,3,03'∴===+-B OB x x在AOC ∆中, 1.........).........0,1(,1,33t an ,90'-∴=∴===∠︒=∠A OA OAOA CO CAO AOC 将A(-1,0),B(3,0)代入32++=bx ax y , 得⎩⎨⎧=+-=++030339b a b a 解得:⎩⎨⎧=-=21b a∴抛物线的解析式:'1 (322)++-=x x y (2) 如图1,∵P 点的横坐标为t 且PQ 垂直于x 轴 ∴P 点的坐标为(t ,-t+3),Q 点的坐标为(t ,-t 2+2t+3).∴PQ=|(-t+3)-(-t 2+2t+3)|=| t 2-3t | ∴ d=-t 2+3t (0<t<3)2.............................' d=t 2-3t (t>3) 1........................................' (3) ∵e d ,是y 2-(m+3)y+41(5m 2-2m+13)=0(m 为常数)的两个实数根,∴△≥0,即△=(m+3)2-4×41(5m 2-2m+13)≥0 整理得:△= -4(m -1)2≥0,∵-4(m -1)2≤0,∴△=0,m=1,1.........................................' ∴ PQ 与PH 是y 2-4y+4=0的两个实数根,解得y 1=y 2=2∴ PQ=PH=2, ∴-t+3=2,∴t=1 ,1.....................................' ∴此时Q 是抛物线的顶点,延长MP 至L ,使LP=MP ,连接LQ 、LH ,如图2, ∵LP=MP ,PQ=PH ,∴四边形LQMH 是平行四边形, ∴LH ∥QM ,∴∠1=∠3,∵∠1=∠2,∴∠2=∠3, ∴LH=MH ,∴平行四边形LQMH 是菱形,∴PM ⊥QH ,∴点M 的纵坐标与P 点纵坐标相同,都是2,∴在y=-x 2+2x+3令y=2,得x 2-2x -1=0,∴x 1=1+2,x 2=1-2综上:t 值为1,M 点坐标为(1+2,2)和(1-2,2) 2...........................................' 28.(1)证明:如图1,延长AG 至M ,使得MG=AG∵DG=EG ,∠AGD=∠EGM∴△ADG ≌△MEG .............................................................................1' ∴∠DAG=∠M ,AD=EM..................................................................1' ∵∠DAG=∠B ∴∠M=∠B...............................................................1' ∵∠EAG=∠C ,∴△AME ∽△CBA.................................................1'∴54===AE AD AE EM AC AB ∴AB=54AC.................................................................1' (2)○1∵∠EAG=∠ACB ,∠DAG=∠B,∴∠EAD+∠BAC=180°,又∵∠EAD=∠AFD ∴∠AFD+∠BAC=180°∴DF ∥AB..................1'∴△CDF ∽△CKA ∴CD:CK=CF:AC=1:2,∴DQ ∥BC ,∴△KDQ ∽△KCB,KCKDBC DQ KB KQ ==∴∵CD=DK,∴QK=BQ BC=2QD ∴点Q 为BK 的中点LHM(如图2)(图1)M○2BE 与DQ 的数量关系为DQ BE 167= 延长BA 至R ,使AR=AB ,连接CR 、DR,∴AC ARAE AD = ∵∠EAD+∠BAC=180° ∠CAR+∠BAC=180° ∴∠EAD=∠CAR,∴∠EAD+∠CAD=∠CAD+∠CAR ,即∠EAC=∠DAR ∴△DAR ∽△EAC,∴∠DRA=∠ACB54==AE AD CE DR 即DR=54CE ∵DQ ∥BC ∴∠AQD=∠B,∴△ABC ∽△DQR54==∴AC AB DR DQ 即DR=45DQ.........................................1'∴54CE=45DQ ,∴CE=DQ 1625DQ BC 2= DQ DQ DQ CE BC BE 16716252=-=-=∴∴DQ BE 167=................1'(以上各解答题如有不同解法并且正确,请按相应步骤给分)。
2014年哈尔滨市中考南岗区二模理化综合试卷及答案

2014南岗(二)物理参考答案及评分标准一、选择题16.B 17.D 18.D 19.D 20.B 21.D 22.C 23.C 24.D25.A 26.C 27.D二、非选择题38.240 手离车轮更远些(或石块离车轮更近些)39.平衡力根据p=ρgh,当管内外液体对橡皮膜的压强相等时,ρ与h成反比,h不同,是由于ρ液不同造成的(强调:公式、反比、结论)40.像和物是关于平面镜为轴的对称关系光的反射定律41.拆下一个灯泡,若另一个灯泡发光,则两灯并联(1分),若另一个灯泡不发光,则两灯串联(1分)42.电饭锅,电热水器(合理即可)发生相(火)线与用电器金属外壳连通故障时,(故障电流)会使熔断器熔断(或使断路器、漏电保护器自动切断电源)43.电磁感应机械44.3.78××10525245.地面对鞋增大压力来增大摩擦46.管口下方的空气流动比管口上方慢,压强小,这个压强差使纸屑向管内运动,并从管口上方飞出47.(1)含盐冰比纯冰的熔点低,含盐浓度越高,熔点越低;(2)含盐冰比纯冰的比热容小,含盐浓度越高,比热容越小。
(1和2中说其中一句就可给分,其它论述,酌情给分)48.如图所示49.如图所示50.(1)④用电压表测量L1、L2两端的总电压并记录在表格中(1分,多答多次测量不扣分)表格:(1分,多次实验更好)(2)只将L1作为已经对象(1分),调节滑动变阻器的滑片P,用伏安法测出L1在不同亮度下的电阻(0.5分),并观察记录对应的亮度,分析比较即可(0.5分)。
(3)如图所示,实验中电压表示数不大于2.5V(1分,没有文字说明不扣分,没有电压表不得此分)51.(1)操作:将凸透镜和光屏向下调整,使烛焰中心、光心、光屏的中心在同一高度上(1分,没有调整过程不给分)目的:使烛焰的像成在光屏的中央(1分)(2)将光屏放在60~70cm之间移动,至像清晰为止(1分,“在1倍2倍焦距之间移动”的答法,不得此分)(3)倒立、放大(4)烛焰发出的光可以通过凸透镜的下半段成像(1分)(2)η=W有/W总=Gh/Fs (1分)=2×2N×2cm/2N×6cm=66.7%≠2×44.4% (0.5分)∴小雪的猜想不正确(0.5分)(3)同一滑轮组,机械效率随物重的增加而增大(1分,没有前提条件不得分)53.(1)∵P =UI , ∴I ==45×103/380V =118.42A (1分) ∵P =, ∴W =Pt =45×103W ×40s =1.8×106J (1分)(2)根据η=W 有W 总 ,在W 总相同时,η与W 有成正比(0.5分)∴η1η2 =W 有1W 有2 =m 1gh m 2gh =m 1m 2 =5×60kg 10×60kg =12(0.5分)电梯载客越少效率越低(或电梯载客越多效率越高) (1分)(3)生产电梯时,应使电梯的质量尽量减小;(1分)使用电梯时,应尽量满员载客(或尽量多载客) (1分)2014年区调研测试(二)化学卷参考答案及评分标准说明:化学式、化学方程式、化学用语、配平、条件错误不得分,沉淀符号、气体符号、错别字、字母书写不准确、漏字错3个扣1分。
2014年黑龙江省哈尔滨市南岗区中考一模数学试卷(解析版)

2014年黑龙江省哈尔滨市南岗区中考数学一模试卷一、选择题(每小题3分,共计30分)1.(3分)的相反数是()A.﹣B.C.﹣D.2.(3分)下列运算中,正确的是()A.2x+2y=2xy B.(x2y3)2=x4y5C.(xy)2÷=(xy)3D.2xy﹣3yx=xy3.(3分)下面的图案中,是轴对称图形而不是中心对称图形的是()A.B.C.D.4.(3分)如图所示的由六个小正方体组成的几何体的俯视图是()A.B.C.D.5.(3分)抛物线y=(x+3)2+4的对称轴是()A.直线x=3B.直线x=﹣3C.直线x=D.直线x=﹣6.(3分)在Rt△ABC中,∠C=90°,若AB=2,AC=1,则tan A的值为()A.B.C.D.7.(3分)圆锥的底面半径是1,侧面积是2π,则这个圆锥的侧面展开图的圆心角的度数为()A.180°B.150°C.120°D.60°8.(3分)下列命题正确的是()A.若两个三角形相似,则它们的面积之比等于相似比B.若三角形的两个内角互为余角,则这个三角形是直角三角形C.等腰三角形的角平分线既是高线也是中线D.矩形对角线的夹角是直角9.(3分)已知点P1(x1,y1),P2(x2,y2)均在双曲线y=上,当x1<x2<0时,y1<y2,那么m的取值范围是()A.m>B.m>﹣C.m<D.m<﹣10.(3分)小成从家出发,骑电动自行车到江北度假村办事,途中遇到从江北度假村步行锻炼回家的哥哥小军.小成在江北度假村办完事后,在返回家的途中又遇到哥哥小军,便用电动自行车载上哥哥小军,一同回到家中,结果小成比预计时间晚到1分钟.假设小成和哥哥小军都是沿直线行进的,且二人与家的距离S(千米)和小成从家出发后所用的时间t(分)之间的函数关系如图.有如下的结论:①小成出发时,哥哥小军已经离开江北度假村2千米;②小成去江北度假村的速度比返回时的速度快了千米/分;③小成返回途中载着哥哥小军返回家的速度是千米/分;④哥哥小军比预计时间早到15分钟.其中正确的结论有()A.1个B.2个C.3个D.4个二、填空题(每小题3分,共计30分)11.(3分)李克强总理在2014年政府工作报告中指出“今年要淘汰燃煤小锅炉5万台,推进燃煤电厂脱硫改造1500万千瓦、脱硝改造1.3亿千瓦、除尘改造180000000千瓦”.其中数字180000000用科学记数法可以表示为.12.(3分)函数y=中,自变量x的取值范围是.13.(3分)把3x3﹣6x2y+3xy2分解因式的结果是.14.(3分)化简:=.15.(3分)把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6厘米,DC=7厘米.把三角板DCE绕点C顺时针旋转15°得到△D1CE1,如图(2),这时AB与CD1相交于点O,与D1E1相交于点F.则AD1=cm.16.(3分)小红、小明在一起做游戏,需要确定做游戏的先后顺序,他们约定用“剪刀、包袱、锤子”的方式确定.在一个回合当中两个人都出“包袱”的概率是.17.(3分)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为.18.(3分)▱ABCD在平面直角坐标系中的位置如图,其中A(﹣4,O),B(2,0),C(3,m),反比例函数y=的图象经过点C.将▱ABCD沿x轴翻折得到□AD′C′B′,则点D′的坐标为.19.(3分)如图,△ABC中,AB=AC,AD⊥BC于点D,点E在AC上,CE=2AE,AD=9,BE=10,AD与BE交于点F,则△ABC的面积是.20.(3分)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图的直角梯形,其中三边长分别为2、3、3,则原直角三角形纸片的斜边长是.三、解答题(其中21-24题各6分,25~26题各8分,27~28题各10分,共计60分)21.(6分)先化简,再求代数式+的值,其中x=2sin60°﹣2tan45°.22.(6分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(﹣2,1),C(﹣2,4).(1)画出△ABC沿着y轴向下平移5个单位得到的△A1B1C1,并直接写出点C 的对应点C1的坐标;(2)画出△ABC关于y轴对称的△AB2C2,并直接写出点C的对应点C2的坐标.23.(6分)如图,点E是正方形ABCD边BC上的一点,连接DE,过点B作直线DE的垂线,垂足为G,连接GA.求证:GA平分∠BGD.24.(6分)某中学为了了解学校600名学生的时事政治的掌握情况,举行了一次“两会”时事政治知识测试,并随机抽取了部分学生的成绩作为样本,绘制了下面尚未完成的频数分布表和频数分布直方图.频数分布表请解答下列问题:(1)求出x的值,并补全频数分布直方图;(2)若成绩在70分以上(不含70分)为学生时事政治掌握情况良好,请估计该校学生时事政治掌握情况良好的人数.25.(8分)如图,已知AB是OD的直径,AM和BN是⊙O的两条切线,点E 是⊙O上一点,点D是AM上一点,连接DE并延长交BN于点C,连接OD、BE,且OD∥BE.(1)求证:DE是⊙O的切线;(2)若AD=l,BC=4,求直径AB的长.26.(8分)某超市销售甲、乙两种商品,五月份该超市同时购进甲、乙两种商品共80件,购进甲种商品用去400元,购进乙种商品用去1200元.(1)已知每件甲种商品的进价是每件乙种商品的进价的,求甲、乙两种商品每件的进价;(2)由于甲、乙这两种商品受到市民欢迎,六月份超市决定再次购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价15元,乙种商品每件的售价40元.要使六月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?(利润=售价一进价)27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.(1)求抛物线的解析式;(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y 为未知数的一元二次方程:y2﹣(m+3)y+(5m2﹣2m+13)=0(m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.28.(10分)在△ABC与△ADE中,点E在BC边上,AD=AE,AG为△ADE 的中线,且∠EAG=∠ACB,∠DAG=∠B.(1)如图1,求证:AB=AC;(2)如图2,点F是AC中点,连接DF,∠AFD=∠DAE,连接CD并延长交AB于点K,过点D作DQ∥BC交BK于点Q.①求证:点Q为BK的中点;②试探究线段BE与DQ的数量关系,并证明你的结论.2014年黑龙江省哈尔滨市南岗区中考数学一模试卷参考答案与试题解析一、选择题(每小题3分,共计30分)1.(3分)的相反数是()A.﹣B.C.﹣D.【解答】解:∵+(﹣)=0,∴的相反数是﹣.故选:A.2.(3分)下列运算中,正确的是()A.2x+2y=2xy B.(x2y3)2=x4y5C.(xy)2÷=(xy)3D.2xy﹣3yx=xy【解答】解:A、2x+2y无法计算,故此选项错误;B、(x2y3)2=x4y6,故此选项错误;C、此选项正确;D、2xy﹣3yx=﹣xy,故此选项错误;故选:C.3.(3分)下面的图案中,是轴对称图形而不是中心对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,也是中心对称图形,故本选项错误;B、不是轴对称图形,是中心对称图形,故本选项错误;C、是轴对称图形,不是中心对称图形,故本选项正确;D、是轴对称图形,也是中心对称图形,故本选项错误.故选:C.4.(3分)如图所示的由六个小正方体组成的几何体的俯视图是()A.B.C.D.【解答】解:从上面看易得左边第一列有3个正方形,中间第二列有1个正方形,最右边一列有1个正方形.故选:D.5.(3分)抛物线y=(x+3)2+4的对称轴是()A.直线x=3B.直线x=﹣3C.直线x=D.直线x=﹣【解答】解:∵抛物线的解析式为:y=(x+3)2+4,∴此抛物线的对称轴方程是直线x=﹣3.故选:B.6.(3分)在Rt△ABC中,∠C=90°,若AB=2,AC=1,则tan A的值为()A.B.C.D.【解答】解:∵AB=2,AC=1,∴CB==,∴tan A==,故选:D.7.(3分)圆锥的底面半径是1,侧面积是2π,则这个圆锥的侧面展开图的圆心角的度数为()A.180°B.150°C.120°D.60°【解答】解:如图:l=2π×1=2π,∵lR=2π,∴×2πR=2π,∴R=2,∴=2π,∴=2π,∴n=180°,故选:A.8.(3分)下列命题正确的是()A.若两个三角形相似,则它们的面积之比等于相似比B.若三角形的两个内角互为余角,则这个三角形是直角三角形C.等腰三角形的角平分线既是高线也是中线D.矩形对角线的夹角是直角【解答】解:A、相似三角形的面积的比等于相似比的平方,故错误;B、若三角形的两个内角互为直角,则这两个三角形是直角三角形,正确;C、等腰三角形的顶角的平分线既是底边的高也是底边的中线,故错误;D、矩形的对角线的夹角是直角时,矩形为正方形,故错误,故选:B.9.(3分)已知点P1(x1,y1),P2(x2,y2)均在双曲线y=上,当x1<x2<0时,y1<y2,那么m的取值范围是()A.m>B.m>﹣C.m<D.m<﹣【解答】解:∵x1<x2<0时,y1<y2,∴反比例函数图象分布在第二、四象限,∴2m+3<0,∴m<﹣.故选:D.10.(3分)小成从家出发,骑电动自行车到江北度假村办事,途中遇到从江北度假村步行锻炼回家的哥哥小军.小成在江北度假村办完事后,在返回家的途中又遇到哥哥小军,便用电动自行车载上哥哥小军,一同回到家中,结果小成比预计时间晚到1分钟.假设小成和哥哥小军都是沿直线行进的,且二人与家的距离S(千米)和小成从家出发后所用的时间t(分)之间的函数关系如图.有如下的结论:①小成出发时,哥哥小军已经离开江北度假村2千米;②小成去江北度假村的速度比返回时的速度快了千米/分;③小成返回途中载着哥哥小军返回家的速度是千米/分;④哥哥小军比预计时间早到15分钟.其中正确的结论有()A.1个B.2个C.3个D.4个【解答】解:①由图象可知,小成30分钟后离家6千米,所以两人相遇时,哥哥小军已经离开江北度假村6﹣20×=2千米,①错误;②由图象可知,小成去江北度假村用了30分钟,返回途中,在未遇见小军时小成回家1千米需=4分钟,预计需用6×4=24分钟,又因结果小成比预计时间晚到1分钟,所以返回时用了25分钟;因为去时的时间比返回时的时间多,而路程相同,所以去时的速度比返回时的速度慢,②错误;③小成返回途中载着哥哥小军返回家的速度是=千米/分,③错误;④由图象可知,小军80﹣20=60分钟步行4﹣1=3千米,所以小军步行的速度为=千米/分,步行1千米所用的时间为=20分,所以哥哥小军比预计时间早到20﹣5=15分钟,④正确.故选:A.二、填空题(每小题3分,共计30分)11.(3分)李克强总理在2014年政府工作报告中指出“今年要淘汰燃煤小锅炉5万台,推进燃煤电厂脱硫改造1500万千瓦、脱硝改造1.3亿千瓦、除尘改造180000000千瓦”.其中数字180000000用科学记数法可以表示为 1.8×108.【解答】解:180 000 000=1.8×108.故答案为:1.8×108.12.(3分)函数y=中,自变量x的取值范围是x≠﹣1.【解答】解:根据题意得:x+1≠0;解得x≠﹣1;故答案为x≠﹣1.13.(3分)把3x3﹣6x2y+3xy2分解因式的结果是3x(x﹣y)2.【解答】解:3x3﹣6x2y+3xy2=3x(x2﹣2xy+y2)=3x(x﹣y)2.故答案为:3x(x﹣y)2.14.(3分)化简:=.【解答】解:原式=3﹣2=.故答案为:.15.(3分)把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6厘米,DC=7厘米.把三角板DCE绕点C顺时针旋转15°得到△D1CE1,如图(2),这时AB与CD1相交于点O,与D1E1相交于点F.则AD1=5cm.【解答】解:由题意易知:∠CAB=45°,∠ACD=30°.若旋转角度为15°,则∠ACO=30°+15°=45°.∴∠AOC=180°﹣∠ACO﹣∠CAO=90°.在等腰Rt△ABC中,AB=6,则AC=BC=3.同理可求得:AO=OC=3.在Rt△AOD1中,OA=3,OD1=CD1﹣OC=4,由勾股定理得:AD1=5.16.(3分)小红、小明在一起做游戏,需要确定做游戏的先后顺序,他们约定用“剪刀、包袱、锤子”的方式确定.在一个回合当中两个人都出“包袱”的概率是.【解答】解:列表得:可以得出一共有27种情况,在一回合中两个人都出“布”的概率是:=.故答案为:.17.(3分)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为.【解答】解:在Rt△ABC中,AC=3,BC=4;根据勾股定理,得AB=5.过C作CM⊥AB,交AB于点M,如图所示,由垂径定理可得M为AE的中点,=AC•BC=AB•CM,且AC=3,BC=4,AB=5,∵S△ABC∴CM=,在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+()2,解得:AM=,∴AE=2AM=.故答案为:.18.(3分)▱ABCD在平面直角坐标系中的位置如图,其中A(﹣4,O),B(2,0),C(3,m),反比例函数y=的图象经过点C.将▱ABCD沿x轴翻折得到□AD′C′B′,则点D′的坐标为(﹣3,﹣3).【解答】解:∵反比例函数y=的图象经过点C(3,m),∴m==3,∴C点坐标为(3,3),∵A(﹣4,O),B(2,0),∴AB=2﹣(﹣4)=6,∴D点坐标为(﹣3,3),∵▱ABCD沿x轴翻折得到□AD′C′B′,即点D′和点D关于x轴对称,∴点D′的坐标为(﹣3,﹣3).故答案为(﹣3,﹣3).19.(3分)如图,△ABC中,AB=AC,AD⊥BC于点D,点E在AC上,CE=2AE,AD=9,BE=10,AD与BE交于点F,则△ABC的面积是54.【解答】解:如图,取CE的中点G,连接DG.∵△ABC中,AB=AC,AD⊥BC,∴BD=CD,即点D是BC的中点,∴GD是△BCE的中位线,∴DG∥BE,DG=BE=5.又∵CE=2AE,∴AE=GE,即点E是AG的中点,∴点F是AD的中点,∴AF=DF=4.5,EF是△ADG的中位线,∴EF=DG=2.5,∴BF=BE﹣EF=7.5.则在直角△BFD中,由勾股定理易求BD=6.∴BC=12.则△ABC的面积是:BC•AD=×12×9=54.故答案是:54.20.(3分)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图的直角梯形,其中三边长分别为2、3、3或.【解答】解:①如图所示:,连接CD,CD==,∵D为AB中点,∴AB=2CD=2;②如图所示:,连接EF,EF==3,∵E为AB中点,∴AB=2EF=6,故答案为:或.三、解答题(其中21-24题各6分,25~26题各8分,27~28题各10分,共计60分)21.(6分)先化简,再求代数式+的值,其中x=2sin60°﹣2tan45°.【解答】解:原式===x+2,∵x=2sin60°﹣2tan45°=2×﹣2×1=﹣2,∴原式=﹣2+2=.22.(6分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(﹣2,1),C(﹣2,4).(1)画出△ABC沿着y轴向下平移5个单位得到的△A1B1C1,并直接写出点C 的对应点C1的坐标;(2)画出△ABC关于y轴对称的△AB2C2,并直接写出点C的对应点C2的坐标.【解答】解:(1)△A1B1C1如图所示,C1(﹣2,﹣1);(2)△AB2C2如图所示,C2(2,4).23.(6分)如图,点E是正方形ABCD边BC上的一点,连接DE,过点B作直线DE的垂线,垂足为G,连接GA.求证:GA平分∠BGD.【解答】证明:如图,过点A作AM⊥BG交GB的延长线于M,作AN⊥DG于N,∴∠AMG=∠ANG=∠AND=90°∵BG⊥DE∴∠BGD=90°∴四边形AMGN为矩形∴∠MAN=90°∵四边形ABCD为正方形∴∠BAD=90°=∠MAN,AB=AD∴∠MAN﹣∠BAN=∠BAD﹣∠BAN即∠BAM=∠DAN∴△BAM≌△DAN∴AM=AN∴GA平分∠BGD.24.(6分)某中学为了了解学校600名学生的时事政治的掌握情况,举行了一次“两会”时事政治知识测试,并随机抽取了部分学生的成绩作为样本,绘制了下面尚未完成的频数分布表和频数分布直方图.频数分布表请解答下列问题:(1)求出x的值,并补全频数分布直方图;(2)若成绩在70分以上(不含70分)为学生时事政治掌握情况良好,请估计该校学生时事政治掌握情况良好的人数.【解答】解:(1)x=50﹣4﹣16﹣6﹣10=14(人),频率是:14÷10=1.4.;(2)70分以上的频率为:,由样本估计总体可知:0.64×600=384(人);∴估计该校学生时事政治掌握情况良好的人数约为384人.25.(8分)如图,已知AB是OD的直径,AM和BN是⊙O的两条切线,点E 是⊙O上一点,点D是AM上一点,连接DE并延长交BN于点C,连接OD、BE,且OD∥BE.(1)求证:DE是⊙O的切线;(2)若AD=l,BC=4,求直径AB的长.【解答】(1)证明:连接OE,在⊙O中,OA=OE=OB,∴∠OBE=∠OEB,∵OD∥BE,∴∠AOD=∠OBE=∠OEB=∠EOD,在△AOD和△EOD中,,∴△AOD≌△EOD(SAS),∴∠OAD=∠OED,∵AM是⊙O的切线,切点为A,∴BA⊥AM,∴∠OAD=∠OED=90°,∴OE⊥DE,∵OE是⊙O的半径,∴DE是⊙O的切线;(2)解:过点D作BC的垂线,垂足为H,∵BN切⊙O于点B,∴∠ABC=90°=∠BAD=∠BHD,∴四边形ABHD是矩形,∴AD=BH=1,AB=DH,∴CH=BC﹣BH=4﹣1=3,∵AD、CB、CD分别切⊙O于点A、B、E,∴AD=ED=1,BC=CE=4,∴DC=DE+CE=1+4=5,在Rt△DHC中,DC2=DH2+CH2,∴AB=DH==4.26.(8分)某超市销售甲、乙两种商品,五月份该超市同时购进甲、乙两种商品共80件,购进甲种商品用去400元,购进乙种商品用去1200元.(1)已知每件甲种商品的进价是每件乙种商品的进价的,求甲、乙两种商品每件的进价;(2)由于甲、乙这两种商品受到市民欢迎,六月份超市决定再次购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价15元,乙种商品每件的售价40元.要使六月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?(利润=售价一进价)【解答】解:(1)设甲种商品每件的进价是x元,则乙种商品每件的进价为3x 元,依题意可得:,解得:x=10,经检验:x=10为原分式方程的解,且符合题意,则3x=3×10=30,答:甲、乙两种商品的进价分别为每件10元、30元;(2)设六月份再次购进甲种商品a件,则购进乙种商品(80﹣a)件,依题意可得:(15﹣10)a+(40﹣30)(80﹣a)≥600,解得:a≤40,即a的最大值是40.答:该超市六月份最多购进甲种商品40件.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.(1)求抛物线的解析式;(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y 为未知数的一元二次方程:y2﹣(m+3)y+(5m2﹣2m+13)=0(m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.【解答】解:(1)当x=0,则y=﹣x+n=0+n=n,y=ax2+bx+3=3,∴OC=3=n.当y=0,∴﹣x+3=0,x=3=OB,∴B(3,0).在△AOC中,,∴OA=1,∴A(﹣1,0).将A(﹣1,0),B(3,0)代入y=ax2+bx+3,得,解得:∴抛物线的解析式:y=﹣x2+2x+3;(2)如图1,当点P在线段CB上时.∵P点的横坐标为t且PQ垂直于x轴,∴P点的坐标为(t,﹣t+3),Q点的坐标为(t,﹣t2+2t+3).∴PQ=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t.如图3,当点P在射线BN上时.∵P点的横坐标为t且PQ垂直于x轴,∴P点的坐标为(t,﹣t+3),Q点的坐标为(t,﹣t2+2t+3).∴PQ=﹣t+3﹣(﹣t2+2t+3)=t2﹣3t.∵BO=3,∴d=﹣t2+3t(0<t<3),d=t2﹣3t(t>3),答:当0<t<3时,d与t之间的函数关系式为:d=﹣t2+3t,当t>3时,d与t之间的函数关系式为:d=t2﹣3t;(3)∵d,e是y2﹣(m+3)y+(5m2﹣2m+13)=0(m为常数)的两个实数根,∴△≥0,即△=(m+3)2﹣4×(5m2﹣2m+13)≥0整理得:△=﹣4(m﹣1)2≥0.∵﹣4(m﹣1)2≤0,∴△=0,∴﹣4(m﹣1)2=0∴m=1,∴y2﹣4y+4=0.∵PQ与PH是y2﹣4y+4=0的两个实数根,解得:y1=y2=2∴PQ=PH=2,∴﹣t+3=2,∴t=1,∵y=﹣x2+2x+3,∴y=﹣(x﹣1)2+4,∴抛物线的顶点坐标是(1,4).∴此时Q是抛物线的顶点,延长MP至L,使LP=MP,连接LQ、LH,如图2,∵LP=MP,PQ=PH,∴四边形LQMH是平行四边形,∴LH∥QM,∴∠1=∠3.∵∠1=∠2,∴∠2=∠3,∴LH=MH,∴平行四边形LQMH是菱形,∴PM⊥QH,∴点M的纵坐标与P点纵坐标相同,都是2,∴在y=﹣x2+2x+3中,当y=2时,∴x2﹣2x﹣1=0,∴x1=1+,x2=1﹣.综上所述:t值为1,M点坐标为(1+,2)或(1﹣,2).28.(10分)在△ABC与△ADE中,点E在BC边上,AD=AE,AG为△ADE 的中线,且∠EAG=∠ACB,∠DAG=∠B.(1)如图1,求证:AB=AC;(2)如图2,点F是AC中点,连接DF,∠AFD=∠DAE,连接CD并延长交AB于点K,过点D作DQ∥BC交BK于点Q.①求证:点Q为BK的中点;②试探究线段BE与DQ的数量关系,并证明你的结论.【解答】解:(1)如图1,延长AG至M,使得MG=AG,在△ADG与△MEG中,,∴△ADG≌△MEG(SAS),∴∠DAG=∠M,AD=EM,∵∠DAG=∠B,∴∠M=∠B,∵∠EAG=∠C,∴△AME∽△CBA,∴===,∴AB=AC;(2)①∵∠EAG=∠ACB,∠DAG=∠B,∴∠EAD+∠BAC=180°,又∵∠EAD=∠AFD,∴∠AFD+∠BAC=180°,∴DF∥AB,∴△CDF∽△CKA,∴CD:CK=CF:AC=1:2,∴DK=CD,∵DQ∥BC,∴△KDQ∽△KCB,∴==,∵CD=DK,∴QK=BQ BC=2QD,∴点Q为BK的中点;②延长BA至R,使AR=AB,连接CR、DR,则=,∵∠EAD+∠BAC=180°∠CAR+∠BAC=180°,∴∠EAD=∠CAR,∴∠EAD+∠CAD=∠CAD+∠CAR,即∠EAC=∠DAR,∴△DAR∽△EAC,∴∠DRA=∠ACB,==,即DR=CE,∵DQ∥BC,∴∠AQD=∠B,∴△ABC∽△DQR,∴==,即DR=DQ,∴CE=DQ,∴CE=DQ,∵BC=2DQ,∴BE=BC﹣CE=2DQ﹣DQ=DQ,∴BE=DQ.。
2014年黑龙江哈尔滨语文中考试卷(试卷+答案)

哈尔滨市2014年初中升学考试语文试题(含答案全解全析)一、积累与运用(25分)1.下列词语中加点字注音完全正确的一项是(3分)( )A.追溯.(sù)取缔.(tì)广袤.无垠(mào)B.煞.白(sà)阔绰.(chuò)锋芒毕露.(lù)C.默契.(qì)贮.蓄(zhù)即物起兴.(xīng)D.拂.晓(fú)狡黠.(xiá)九曲.连环(qū)2.下列词语中没有错别字的一项是(3分)( )A.屏障隐秘通宵达旦B.阻遏慰籍周而复始C.炼达愧怍相得益彰D.预兆诀别闲情逸志3.下面句子没有语病的一项是(3分)( )A.由于安倍政府对历史的严重歪曲,使日本和东亚各国的关系不断恶化。
B.只要你悉心品读汉字,认读汉字,就会发现它的神奇之处。
C.柳宗元的山水游记在中国文学史上具有独特的地位。
D.心理学家认为,让孩子讲故事有助于培养孩子的语言表达水平。
4.下面名著中的人物和情节对应不正确的一项是(3分)( )A.宋江——私放晁盖(《水浒传》)B.华子良——狱中装疯(《红岩》)C.诸葛亮——火烧连营(《三国演义》)D.鲁滨逊——荒岛造船(《鲁滨逊漂流记》)5.下面情境下,表述准确、得体.....的一项是(3分)( )[情境]小明把从小刚那儿借的书弄脏了。
他不好意思直接把书还给小刚,就委托小亮代还,并且让小亮代他致歉。
小亮对小刚说:A.小明把你借给他的书弄脏了,他不好意思自己来,让我代还,并替他说声对不起。
B.我来替小明还书。
书被他不小心弄脏了,他不好意思自己来。
不就一本书嘛,你就别计较了。
C.这是向你借的书,现在还给你,但书不小心弄脏了,真是对不起。
D.这是你借给小明的书,他让我还给你,并让我转达他对你的谢意。
6.填入下面横线处最恰当的一项是(3分)( )2013年感动中国人物胡佩兰——退休后20年坚持每天出诊的仁医。
【数学】2014年黑龙江省哈尔滨市南岗区中考一模数学试卷含解析

16. (3 分)小红、小明在一起做游戏,需要确定做游戏的先后顺序,他们约定 用“剪刀、包袱、锤子”的方式确定.在一个回合当中两个人都出“包袱” 的概率是 .
17. (3 分)如图,在 Rt△ABC 中,∠C=90°,AC=3,BC=4,以点 C 为圆心, CA 为半径的圆与 AB、BC 分别交于点 E、D,则 AE 的长为 .
2. (3 分)下列运算中,正确的是( A.2x+2y=2xy C. (xy)2÷
3. (3 分)下面的图案中,是轴对称图形而不是中心对称图形的是(
A.
B.
C.
D. )
4. (3 分)如图所示的由六个小正方体ຫໍສະໝຸດ 成的几何体的俯视图是(A.
B.
C. )
D.
5. (3 分)抛物线 y=(x+3)2+4 的对称轴是( A.直线 x=3 B.直线 x=﹣3
B.150° )
C.120°
D.60°
8. (3 分)下列命题正确的是(
A.若两个三角形相似,则它们的面积之比等于相似比 B.若三角形的两个内角互为余角,则这个三角形是直角三角形 C.等腰三角形的角平分线既是高线也是中线 D.矩形对角线的夹角是直角 9. (3 分)已知点 P1(x1,y1) ,P2(x2,y2)均在双曲线 y= <0 时,y1<y2,那么 m 的取值范围是( A.m> B.m>﹣ ) D.m<﹣ 上,当 x1<x2
C.直线 x=
D.直线 x=﹣ )
6. (3 分) 在 Rt△ABC 中, ∠C=90°, 若 AB=2, AC=1, 则 tanA 的值为 ( A. B. C. D.
7. (3 分)圆锥的底面半径是 1,侧面积是 2π,则这个圆锥的侧面展开图的圆心 角的度数为( )
2014年黑龙江省哈尔滨市中考一模数学试卷(解析版)

2014年黑龙江省哈尔滨市中考数学一模试卷一、选择题(共10小题,每小题3分,共计30分)1.(3分)如果温泉河的水位升高0.8m时,水位变化记作+0.8m,那么水位下降0.5m时,水位变化记作()A.0m B.0.5m C.﹣0.8m D.﹣0.5m 2.(3分)用科学记数法表示537万正确的是()A.5.37×104B.5.37×105C.5.37×106D.5.37×107 3.(3分)下列各式中,计算正确的是()A.2x+3y=5xy B.x6÷x2=x3C.x2•x3=x5D.(﹣x3)3=x6 4.(3分)下列图形,既是轴对称图形,又是中心对称图形的是()A.B.C.D.5.(3分)已知一个圆锥形零件的母线长为5,底面半径为2,则这个圆锥形零件的侧面积为()A.5πB.10πC.3πD.6π6.(3分)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小7.(3分)六个大小一样的正方体搭成的几何体如图所示,则关于它的视图说法正确的是()A.正视图的面积最大B.俯视图的面积最大C.左视图的面积最大D.三个视图的面积一样大8.(3分)已知二次函数y=ax2﹣1的图象的开口向下,则直线y=ax﹣1的图象经过的象限是()A.第一、二、三象限B.第一、二、四象限C.第一、三、四象限D.第二、三、四象限9.(3分)如图,△ABC是一张直角三角形的纸片,∠C=90°,AC=6,BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为()A.B.3C.D.410.(3分)甲乙两人在同一条笔直的公路上骑自行车从A地去往B地.已知AB 两地的距离为40千米,乙比甲晚出发1小时,他们在途中均休息了0.5小时,甲出发2小时后,此时乙的速度是此时甲的速度的1.2倍,甲乙两人离A地的距离y(千米)与甲行驶是时间t(小时)的函数关系图象如图所示,下列说法中正确的个数为()①甲休息之前的速度为15千米/小时;②乙休息之前的速度为20千米/小时;③甲出发2小时的时候,甲乙两人的距离为千米;④乙比甲晚到B地0.5小时.A.1个B.2个C.3个D.4个二、填空题(共10小题,每小题3分,共计30分)11.(3分)计算:÷=.12.(3分)在函数y=中,自变量x的取值范围是.13.(3分)把多项式3x2y+12xy2+12y3分解因式的结果是.14.(3分)不等式组的解集为.15.(3分)如图,⊙O的直径AB过弦CD的中点M,∠ABD=27°,则∠AOC =度.16.(3分)方程﹣1=的解为.17.(3分)在一个不透明的袋子中装有红、绿各一个小球,它们只有颜色上的区别,从袋子中随机摸出一个小球记下颜色后放回,再随机摸出一个,则两次都摸到红球的概率为.18.(3分)等腰△ABC两边的长分别是一元二次方程x2﹣5x+6=0的两个解,则这个等腰三角形的周长是.19.(3分)如图,在矩形ABCD中,点E为BC边上一点,连接AE,DE,若AE平分∠BED,DE:AE=5:6,CD=4,则EC的长为.20.(3分)如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为,则线段DB的长为.三、解答题(其中21-24题各6分,25-26题各8分,27-28题各10分,共计60分)21.(6分)先化简,再求代数式的值,其中a=tan60°﹣6sin30°.22.(6分)图①,图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A,点B和点C在小正方形的顶点上,请在图①、图②中各画一个四边形,满足以下要求:(1)在图①中以AB和BC为边画四边形ABCD,点D在小正方形的顶点上,且此四边形只有一组角相等;(2)在图②中以AB和BC为边画四边形ABCE,点E在小正方形的顶点上,且此四边形有两组角相等;(3)图①所画的四边形与图②所画的四边形不全等.23.(6分)某中学生为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题:(1)将统计图补充完整;(2)若该校共有1800名学生,根据以上调查结果估计该校全体学生每天完成作业所用总时间.24.(6分)如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C80海里,轮船沿正南方向匀速航行一段时间后,到达灯塔C的东南方向上的B处.(1)求灯塔C到航线AB的距离;(2)若轮船的速度为20海里/时,求轮船从A处到B处所用的时间(结果仅保留根号).25.(8分)如图,在Rt△ABC中,∠C=90°,CB=CA=6,半径为2的⊙F 与射线BA相切于点G,且AG=4,将Rt△ABC绕点A顺时针旋转135°后得到Rt△ADE,点B,C的对应点分别是点D,E.(1)求证:DE为⊙F的切线;(2)求出Rt△ADE的斜边AD被⊙F截得的弦PQ的长度.26.(8分)某机械厂甲、乙两个生产车间承担生产同一种零件的任务.甲、乙两车间共有50人,甲车间平均每人每天生产零件30个,乙车间平均每人每天生产零件20个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个.(1)求甲、乙两车间各有多少人?(2)该机械厂改进了生产技术,在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间,调整后甲车间平均每人每天生产零件35个,乙车间平均每人每天生产零件25个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于1480个,求从甲车间最多调出多少人到乙车间?27.(10分)如图,在平面直角坐标系中,点O是坐标原点,抛物线y=x2+bx+c 与x轴交于A,B两点,与y轴交于点C,过点C的直线y=﹣x+2与x轴交于点D,与抛物线交于点E,且点E到x轴的距离为1.(1)求抛物线的解析式;(2)点P为第一象限线段CD上一点,点Q为线段CD延长线上一点,CP=DQ.点M为x轴下方抛物线上一点,当△PQM是以PQ为斜边的等腰直角三角形时,求点M的坐标;(3)在(2)的条件下,N(m,m)为平面直角坐标系内一点,直线MN交直线CD于点F,且NF=2FM,求出m的值,并判断点N是否在(1)中的抛物线上.28.(10分)在Rt△ABC中,∠ACB=90°,sin B=,作CH⊥AB于点H,D,K分别为边AB,AC上的点,连接CD,DK,在射线DK上取一点E,使∠DCE=∠B,且BC•CK=CD•CE.(1)如图,求证:∠CED=90°;(2)连接AE并延长交直线BC于点G,探究线段BC,BG,DH之间的数量关系,并证明你的结论.2014年黑龙江省哈尔滨市中考数学一模试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共计30分)1.(3分)如果温泉河的水位升高0.8m时,水位变化记作+0.8m,那么水位下降0.5m时,水位变化记作()A.0m B.0.5m C.﹣0.8m D.﹣0.5m【解答】解∵水位升高0.8 m时水位变化记作+0.8 m,∴水位下降0.5 m时水位变化记作﹣0.5 m,故选:D.2.(3分)用科学记数法表示537万正确的是()A.5.37×104B.5.37×105C.5.37×106D.5.37×107【解答】解:将537万用科学记数法表示为5.37×106.故选:C.3.(3分)下列各式中,计算正确的是()A.2x+3y=5xy B.x6÷x2=x3C.x2•x3=x5D.(﹣x3)3=x6【解答】解:A、由于2x和3y不是同类项,不能合并,故本选项错误;B、由于x6÷x2=x4≠x3,故本选项错误;C、由于x2•x3=x2+3=x5,故本选项正确;D、由于(﹣x3)3=﹣x9≠x6,故本选项错误.故选:C.4.(3分)下列图形,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误;B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;C、此图形旋转180°后能与原图形重合,此图形是中心对称图形,不是轴对称图形,故此选项错误;D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.故选:D.5.(3分)已知一个圆锥形零件的母线长为5,底面半径为2,则这个圆锥形零件的侧面积为()A.5πB.10πC.3πD.6π【解答】解:这个圆锥形零件的侧面积=•2π•2•5=10π.故选:B.6.(3分)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小【解答】解:设B(x,y).∴S=0A•y;△OAB∵OA是定值,点B是双曲线(x>0)上的一个动点,双曲线(x>0)在第一象限内是减函数,∴当点B的横坐标x逐渐增大时,点B的纵坐标y逐渐减小,∴S=0A•y会随着x的增大而逐渐减小.△OAB故选:C.7.(3分)六个大小一样的正方体搭成的几何体如图所示,则关于它的视图说法正确的是()A.正视图的面积最大B.俯视图的面积最大C.左视图的面积最大D.三个视图的面积一样大【解答】解:观察图形可知,几何体的正视图由4个正方形组成,俯视图由5个正方形组成,左视图由4个正方形组成,所以俯视图的面积最大.故选:B.8.(3分)已知二次函数y=ax2﹣1的图象的开口向下,则直线y=ax﹣1的图象经过的象限是()A.第一、二、三象限B.第一、二、四象限C.第一、三、四象限D.第二、三、四象限【解答】解:∵二次函数y=ax2﹣1的图象的开口向下,∴a<0,∴直线y=ax﹣1的图象经过的象限是第二、三、四象限.故选:D.9.(3分)如图,△ABC是一张直角三角形的纸片,∠C=90°,AC=6,BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为()A.B.3C.D.4【解答】解:∵AC=6,BC=8,∴AB==10,tan B=,由折叠的性质得,∠B=∠DAE,tan B=tan∠DAE=,AE=EB=AB=5,∴DE=AE tan∠DAE=.故选:C.10.(3分)甲乙两人在同一条笔直的公路上骑自行车从A地去往B地.已知AB 两地的距离为40千米,乙比甲晚出发1小时,他们在途中均休息了0.5小时,甲出发2小时后,此时乙的速度是此时甲的速度的1.2倍,甲乙两人离A地的距离y(千米)与甲行驶是时间t(小时)的函数关系图象如图所示,下列说法中正确的个数为()①甲休息之前的速度为15千米/小时;②乙休息之前的速度为20千米/小时;③甲出发2小时的时候,甲乙两人的距离为千米;④乙比甲晚到B地0.5小时.A.1个B.2个C.3个D.4个【解答】解:根据图象可得甲开始1小时行驶了15千米,15÷1=15(千米/小时),故①正确;根据图象可得乙开始0.5小时行驶了10千米,则10÷(1.5﹣1)=20(千米/小时),故②正确;甲休息0.5小时后的速度:(40﹣15)÷1.5=(千米/小时),×(2﹣1.5)=(千米),+15﹣10=千米,故③正确;乙休息0.5小时后的速度:×1.2=20(千米/小时),时间:(40﹣10)÷20=1.5(小时),乙比甲晚到B地时间:1.5+2﹣3=0.5(小时),故④正确,故选:D.二、填空题(共10小题,每小题3分,共计30分)11.(3分)计算:÷=3.【解答】解:÷==3.故答案为:3.12.(3分)在函数y=中,自变量x的取值范围是x≠2.【解答】解:由题意得,3x﹣6≠0,解得x≠2.故答案为:x≠2.13.(3分)把多项式3x2y+12xy2+12y3分解因式的结果是3y(x+2y)2.【解答】解:原式=3y(x2+4xy+4y2)=3y(x+2y)2.故答案是:3y(x+2y)2.14.(3分)不等式组的解集为2<x≤2.5.【解答】解:原不等式组可化简为:,∴解集为2<x≤2.5.15.(3分)如图,⊙O的直径AB过弦CD的中点M,∠ABD=27°,则∠AOC =54度.【解答】解:∵⊙O的直径AB过弦CD的中点M,由垂径定理知弧AC=弧AD,由圆周角定理知∠AOC=2∠B=54°.16.(3分)方程﹣1=的解为x=.【解答】解:方程的两边同乘2(3x﹣1),得4﹣2(3x﹣1)=3,解得x=.检验:把x=代入2(3x﹣1)=1≠0.∴原方程的解为:x=.故答案为x=.17.(3分)在一个不透明的袋子中装有红、绿各一个小球,它们只有颜色上的区别,从袋子中随机摸出一个小球记下颜色后放回,再随机摸出一个,则两次都摸到红球的概率为.【解答】解:列表如下:所有等可能的情况有4种,其中两次摸到红球的情况有1种,则P=.故答案为:18.(3分)等腰△ABC两边的长分别是一元二次方程x2﹣5x+6=0的两个解,则这个等腰三角形的周长是7或8.【解答】解:解方程x2﹣5x+6=0得x1=2,x2=3,当2是腰时,2+2>3,可以构成三角形,周长为7;当3是腰时,3+2>3,可以构成三角形,周长为8;所以周长是7或8.19.(3分)如图,在矩形ABCD中,点E为BC边上一点,连接AE,DE,若AE平分∠BED,DE:AE=5:6,CD=4,则EC的长为.【解答】解:如图,过点A作AF⊥DE于F,在矩形ABCD中,AB=CD=4,∵AE平分∠BED,∴AF=AB=4,设DE=5k,AE=6k,=DE•AF=×5k•4=10k,∵S△ADE=BC•CD=4BC=2•10k,∴S矩形ABCD解得BC=5k,由勾股定理得,BE==,EC==,∵BE=BC﹣EC,∴=5k﹣,解得k=,∴EC==.故答案为:.20.(3分)如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为,则线段DB的长为.【解答】解:如图,延长BE交AC边于点F,因为∠FCD+∠DCB=60°,∠DEB=∠EBC+∠ECB=60°,∴∠ACD=∠FBC,在△ACD和△CBF中,∴△ACD≌△CBF,∴BF=CD,S△ACD==S△CBF=CE•EF•sin60°+CE•BE•sin60°=CE•BF•sin60°,∴BF=7,则DE=2,∠DBE=∠DCB,∠DEB=∠DBC=90°,△BED∽△CBD,∴BD2=DE•CD=14,∴BD=.三、解答题(其中21-24题各6分,25-26题各8分,27-28题各10分,共计60分)21.(6分)先化简,再求代数式的值,其中a=tan60°﹣6sin30°.【解答】解:原式=÷(﹣)=÷=×=﹣,∵a=tan60°﹣6sin30°=﹣6×=﹣3,∴原式=﹣=﹣=﹣.22.(6分)图①,图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A,点B和点C在小正方形的顶点上,请在图①、图②中各画一个四边形,满足以下要求:(1)在图①中以AB和BC为边画四边形ABCD,点D在小正方形的顶点上,且此四边形只有一组角相等;(2)在图②中以AB和BC为边画四边形ABCE,点E在小正方形的顶点上,且此四边形有两组角相等;(3)图①所画的四边形与图②所画的四边形不全等.【解答】解:(1)如图所示:四边形ABCD即为所求;(2)如图所示:四边形ABCD即为所求.23.(6分)某中学生为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题:(1)将统计图补充完整;(2)若该校共有1800名学生,根据以上调查结果估计该校全体学生每天完成作业所用总时间.【解答】解:(1)正确补全(2)由图可知==3(小时)可以估计该校全体学生每天完成作业所用总时间=3×1800=5400(小时),所以该校全体学生每天完成作业所用总时间5400小时.24.(6分)如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C80海里,轮船沿正南方向匀速航行一段时间后,到达灯塔C的东南方向上的B处.(1)求灯塔C到航线AB的距离;(2)若轮船的速度为20海里/时,求轮船从A处到B处所用的时间(结果仅保留根号).【解答】解:(1)过C作CD⊥AB于D.∴∠A=30°,∠BCD=45°,在Rt△ACD中,AC=80,∠A=30°,∴CD=AC=40海里,答:灯塔C到AB的距离为40海里;(2)在Rt△ACD中,AD=AC•cos30°=80×=40.在Rt△BCD中,∠BCD=∠B=45°,∴BD=CD=40(海里).∴AB=AD+BD=40+40(海里).∴轮船所用的时间为:=2+2(小时).答:轮船从A处到B处所用的时间为(2+2)小时.25.(8分)如图,在Rt△ABC中,∠C=90°,CB=CA=6,半径为2的⊙F 与射线BA相切于点G,且AG=4,将Rt△ABC绕点A顺时针旋转135°后得到Rt△ADE,点B,C的对应点分别是点D,E.(1)求证:DE为⊙F的切线;(2)求出Rt△ADE的斜边AD被⊙F截得的弦PQ的长度.【解答】(1)证明:作FM⊥DE于M,连结FG,如图,∵∠C=90°,CB=CA=6,∴∠BAC=45°,∵将Rt△ABC绕点A顺时针旋转135°后得到Rt△ADE,点B,C的对应点分别是点D,E.∴∠CAE=135°,DE=EA=6,∠AED=∠ACB=90°∴∠ABC+∠CAE=180°,即点C、A、E共线,∵⊙F与射线BA相切于点G,∴FG⊥AE,∴四边形FGEM为矩形,∴FM=GE=AE﹣AG=6﹣4=2,∵⊙F的半径为2,即FM为⊙F的半径,∴DE为⊙F的切线;(2)解:延长EF交PQ于N,连结FP,如图,∵FM=FG=2,∴四边形FGEM为正方形,∴EF平分∠AED,EF=FM=2,而△EAD为等腰直角三角形,∴EN⊥PQ,EN=AB=×6=3∴PN=QN,在Rt△PFN中,FP=2,FN=EN﹣EF=3﹣2=,∴PN==,∴PQ=2PN=2.26.(8分)某机械厂甲、乙两个生产车间承担生产同一种零件的任务.甲、乙两车间共有50人,甲车间平均每人每天生产零件30个,乙车间平均每人每天生产零件20个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个.(1)求甲、乙两车间各有多少人?(2)该机械厂改进了生产技术,在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间,调整后甲车间平均每人每天生产零件35个,乙车间平均每人每天生产零件25个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于1480个,求从甲车间最多调出多少人到乙车间?【解答】解:(1)设甲车间有x人,乙车间有y人,由题意得,,解得:,答:甲车间有30人,乙车间有20人.(2)设从甲车间调出a人到乙车间,则甲车间有(30﹣a)人,乙车间有(20+a)人,35(30﹣a)+25(20+a)≥1480解得:a≤7答:从甲车间最多调出7人到乙车间.27.(10分)如图,在平面直角坐标系中,点O是坐标原点,抛物线y=x2+bx+c 与x轴交于A,B两点,与y轴交于点C,过点C的直线y=﹣x+2与x轴交于点D,与抛物线交于点E,且点E到x轴的距离为1.(1)求抛物线的解析式;(2)点P为第一象限线段CD上一点,点Q为线段CD延长线上一点,CP=DQ.点M为x轴下方抛物线上一点,当△PQM是以PQ为斜边的等腰直角三角形时,求点M的坐标;(3)在(2)的条件下,N(m,m)为平面直角坐标系内一点,直线MN交直线CD于点F,且NF=2FM,求出m的值,并判断点N是否在(1)中的抛物线上.【解答】解:(1)∵y=﹣x+2,∴C(0,2),由题意可得出:点E的纵坐标为:﹣1,∵y=﹣x+2,则﹣1=﹣x+2,解得;x=3,∴E(3,﹣1),又∵C(0,2),E(3,﹣1)在抛物线y=x2+bx+c上,∴,解得:,∴抛物线y=x2﹣4x+2;(2)如图1,∵y=﹣x+2,∴OC=OD=2,∴∠OCD=∠ODC=45°,∴CD=2,∵CP=DQ,∴PQ=CD=2,∵△PMQ是以PQ为斜边的等腰直角三角形,∴∠MPQ=45°,∴∠OCD=∠MPQ,∴PM∥y轴,设P(t,﹣t+2),由PQ=2得,PM=2,∴M点的坐标为:(t,﹣t),将M(t,﹣t)代入抛物线y=x2﹣4x+2,得﹣t=t2﹣4t+2,解得:t1=﹣1,t2=2,当t=2时,P与D点重合,故t2=2(舍去),∴M(1,﹣1);(3)过点N作NH∥PM交直线CD于H,则∠MPE=∠PHN,∠PMF=∠MNH,∴△FNH∽△FMP,∴=,∵NF=2MF,∴NH=2PM,∴NH=4,①如图2,当N在H点上方时,H(m,m﹣4),把点H(m,m﹣4)代入y=﹣x+2中,得m﹣4=﹣m+2,解得:m=4,∴N(4,2),抛物线y=x2﹣4x+2,∴N点在抛物线上;②如图3,当点N在H点下方时,同理可得出:H(m,m+4),把点H(m,m+4)代入y=﹣x+2中,m+4=﹣m+2,解得:m=﹣,∴N(﹣,﹣),抛物线y=x2﹣4x+2,当x=﹣时,y=≠﹣,∴N点不在抛物线上.综上所述N(4,2)在抛物线上.28.(10分)在Rt△ABC中,∠ACB=90°,sin B=,作CH⊥AB于点H,D,K分别为边AB,AC上的点,连接CD,DK,在射线DK上取一点E,使∠DCE=∠B,且BC•CK=CD•CE.(1)如图,求证:∠CED=90°;(2)连接AE并延长交直线BC于点G,探究线段BC,BG,DH之间的数量关系,并证明你的结论.【解答】(1)证明:如图1,∵CH⊥AB,∴∠BHC=90°.又∠ACB=90°,∴∠B=∠ACH,∴∠DCE=∠B,∴∠DCE=∠ACH,∴∠DCH=∠KCE.又sin B==,∵BC•CK=CD•CE,∴CH•CK=CD•CE,即=,∴△CEK∽△CHD,∴∠DEC=∠DHC=90°,∴∠CED=90°;(2)BG﹣BC=DH.理由如下:①如图2,当点D在线段BH上时.故点D作DC的垂线交CE的延长线于点M,连接AM.由(1)可知,∠DCM=∠ACH.∴cos∠DCN=cos∠ACH,∴=.又∵∠DCH=∠MCA,∴△CDH∽△CMA,∴==,∠MAC=∠DHC=90°,∴∠MAC+∠BCA=180°,∴MA∥BC,∴∠AME=∠GCE,又∠AEM=∠CEG.∴△AME∽△GCE,∴=.又tan∠DCE=tan∠MDE=,∴==,∴=,∴=,∴BG﹣BC=DH;②如图3,当点D在线段AH上时,同理可得BG﹣BC=DH.。
黑龙江省哈尔滨市南岗区初中数学毕业第一次模拟试题

南岗区 2013年中考调研测试(一) 数学试卷一、选择题(每小题3分,共计30分)1.-12的相反数是( ) (A)2 (B)-2 (C)12 (D)-122.下列运算中,正确的是( )(A)235a a a •= (B)235()a a = (C)623a a a ÷= (D)624a a a -=3.在下面由阴影组成的图案中,是轴对称图形的图案是( )4.下列的四个立体图形如图摆放,其中俯视图为矩形的立体图形是( )5.将抛物线2y x =经过下面的平移可得到抛物线2(3)4y x =++的是( )(A)向左平移3个单位,向上平移4个单位 (B)向左平移3个单位,向下平移4个单位 (C)向右平移3个单位,向上平移4个单位 (D)向右平移3个单位,向下平移4个单位6.在Rt △ABC 中,若∠C=900,BC=6,A=8,则tanA 的值为( ) (A)45 (B) 34 (C)35 (D) 437圆锥盼母线长是5cm ,侧面积是15π2cm ,则这个圆锥的底面圆半径是( ) (A)1 .5cm (B)3 cm (C)4 cm (D)6 cm8.如图,E 是AB 边上的中点,将△ABC 沿过E 的直线折叠,使点A 落在BC 上F 处,折痕交边AC 于点D,若BC=100,则折痕DE 的长度是( ) (A)50 (B)60 (C)70 (D)809.不等式组{ 2x-1≥0, x-1<0的解集是( ) (A)12<x≤ 2 (B) 12 ≤x<2 (c)-2<x ≤12 (D)-2≤x≤1210一如图,边长为1的正方形ABCD 中,点E 在CB 延长线上,连接ED 交A8于点F ,AF=x(0.2≤x≤0.8), EC=y .则在下面函数图象中,大致能反映y 与x 之闻函数关系的是( ).二、填空题(每小题3分,共计30分)11.2 013 000用科学记数法表示应为 . 12.函数11x x -+的自变量x 的取值范围是 . 13.把多项式2228x a -分解因式的结果是 . 14.计算2012⨯=15.分别写有一5,一9,0,5,9的五张外观形状完全相同的卡片,蒙上眼睛从中任抽一张,那么抽表示负数的卡片概率是.16.如图,⊙0中,弦AB 与弦CD 交于E,连接AC,OE,BD,若AE=BE ,AC ∥0E,则 ∠CDB= . 17.分式方程211x x=+的解是x= . 18.如图△ABC 中,DE ∥BC ,CD 、BE 交于点F ,若DF=l ,CF=3,.AD=2,则线段BD 的长等于 . 19.如图,平行四边形ABCD 中,连接AC,点0为对称中心,点P 在AC 上,若OP=5,tan ∠ DCA=12,∠ABC=1200,BC=23,则AP= . . 。
东北烈士纪念馆

东北烈士纪念馆作者:来源:《活力》2012年第21期东北烈士纪念馆隶属于黑龙江省文化厅,坐落于美丽的冰城夏都——哈尔滨市南岗区一曼街上,是全国首批“爱国主义教育示范基地”。
2004年被中宣部、教育部、人事部、文化部授予“全国爱国主义教育示范基地先进单位”;2007年被人事部、国家文物局授予“全国文物系统先进集体”;2008年被评为“国家一级博物馆”;2009年被评为国家国防教育示范基地;2010年被评为全国红色旅游工作先进集体;2011年被评为省级文明单位标兵。
东北烈士纪念馆是中国共产党领导下建立起来的第一个规模较大的纪念性博物馆,是在东省特别区图书馆馆址上改建而成,整体建筑始建于1928年6月1日,于1931年竣工。
通体呈白色,一排巨大的克林斯柱立于楼前,是典型的西欧古典主义建筑风格,典雅肃穆、雄伟壮观。
日本帝国主义武装侵占我国东北后,东省特别区图书馆于1933年被伪哈尔滨警察厅占用。
从此,这里成为日本侵略者残酷镇压中国人民的罪恶场所,不计其数的为反抗日本侵略者而进行英勇斗争的共产党员和爱国志士在这里被关押、折磨致死,著名抗日女英雄赵一曼烈士就曾在这里被关押和刑讯。
1946年哈尔滨解放后,为缅怀和纪念在东北抗日战争和解放战争初期牺牲的革命先烈,东北行政委员会将伪哈尔滨警察厅旧址辟为东北烈士纪念馆,1948年10月10日正式面向社会开放。
东北烈士纪念馆成立以来,一直受到党和国家领导人的关注和重视。
周恩来、刘少奇、彭真、罗荣桓、李济深、郭沫若等百余位老一辈革命家和社会各界知名人士曾来馆参谒并留下了珍贵的题诗、题词。
2009年,中共中央政治局常委、国家副主席习近平专程到东北烈士纪念馆参谒。
东北烈士纪念馆现有展区面积4280平方米,主要陈列在东北抗日战争和解放战争中牺牲的烈士事迹,承担着征集革命烈士史料、文物,进行陈列展览,对公民进行爱国主义和革命传统教育的任务。
东北烈士纪念馆于2005年8月15日推出新的基本陈列,陈列分为《黑土英魂——东北抗日战争时期烈士事迹陈列》和《伪满洲国哈尔滨警察厅罪恶及旧址复原陈列》两部分。
黑龙江省哈尔滨市南岗区2024届科目一模拟考试100题(及参考答案)

黑龙江省哈尔滨市南岗区2024届科目一模拟考试100题(及参考答案)1、以下哪种情形会被扣留车辆?A、车内装饰过多B、驾驶人开车打电话C、未放置检验合格标志D、未安装防撞装置正确答案:C分析:《道路交通安全法》第九十五条:上道路行驶的机动车未悬挂机动车号牌,未放置检验合格标志、保险标志,或者未随车携带行驶证、驾驶证的,公安机关交通管理部门应当扣留机动车。
2、准驾车型为小型汽车的,可以驾驶小型自动挡载客汽车。
A、正确B、错误正确答案:A分析:小型汽车(C1)准驾车型:小型、微型载客汽车以及轻型、微型载货汽车;轻型、微型专项作业车,小型、微型自动挡载客汽车以及轻型、微型自动挡载货汽车,低速载货汽车,三轮汽车。
3、通过漫水路时要谨慎慢行,不得空挡滑行。
A、正确B、错误正确答案:A分析:所有情况都不允许空挡滑行,空挡滑行是种坏习惯,无法利用发动机制动,以及无法保证牵引力。
手动档的老司机喜欢玩这种“节油”技术,现在的自动挡就绝不允许空挡滑行了,不然会烧变速箱。
4、驾驶人一边驾车,一边打手持电话是违法行为。
A、正确B、错误正确答案:A分析:以后所有“违章”行为变为“违法”行为。
5、车辆在高速公路发生故障不能移动时,驾驶人这种尝试排除故障的做法是否正确?A、正确B、错误正确答案:B分析:三处错误:1.应立即开启危险警报闪光灯,利用车辆惯性,将车驶入紧急停车带或右侧露肩听下,尽量不要占用行车道;2.车辆停放好后,驾驶人和乘车人从路外侧的车门尽快离开车辆,转移到右侧的露肩或者应急车道内,如需到车内或车下进行维修,也应由外侧的车门出入;3.要把故障车警告标志放置在来车方向150米处,并立即报警,如果是夜间,还必须开启示宽灯和尾灯6、图中圈内的白色半圆状标记是什么标线?A、减速行驶线B、车速确认线C、车距确认线D、路口减速线正确答案:C分析:当驾驶人所驾驶的车辆与路肩处在不安全的横向距离情况下行驶时会发出尖锐的声音,提醒驾驶人与路肩保持安全的横向距离,以免出轨.7、驾驶机动车准备驶离环岛时,应如何使用灯光?A、提前开启左转向灯B、不用指示灯提示C、开启危险报警闪光灯D、提前开启右转向灯正确答案:D分析:环岛的正式名称是“环形路口”,能使车辆按同一方向行驶,将冲突点转变为通行点,能有效地减少交通事故的发生。
纪实故事-归来的大哥要上位

纪实故事-归来的大哥要上位父亲临终前告诉刘炳昌,他是抱养的。
刘炳昌非常震惊,从此悄悄寻找亲生父母。
因为养父母对他特别好,所以他寻找亲生父母的目的只是想知道自己的身世。
当他找到亲生父母时,发现亲生父母竟然是拥有千万资产的大老板。
为了弥补20多年的亏欠,亲生父母不断满足刘炳昌的物质需求。
渐渐地,刘炳昌忘记了初衷,在利益驱使下,与弟弟竞争父亲接班人位置,上演了一场兄弟相残的悲剧……生父竟是千万富翁,穷小子骤变“富二代”“炳昌,你是我抱养的,我走后,你要好好孝敬妈妈。
”2013年3月6日上午,患肝癌晚期的刘军在临终前,将埋藏在心里的秘密告诉了26岁的儿子刘炳昌。
忙完了父亲的后事,刘炳昌找了个机会,详细向妈妈高艳询问,得知了真相……56岁的高艳是哈尔滨市南岗区一所小学的退休教师,比她大1岁的丈夫刘军是一家私企工人,两人1984年结婚,婚后高艳一直没能怀孕。
1987年初,高艳夫妇委托在医院做妇产科医生的邻居马芳留心帮忙,想收养一个孩子。
不久,在马芳的帮助下,高艳夫妇在松北区妇幼保健院抱养了一个男婴。
男婴的父母是一对大学刚毕业、尚未结婚的年轻男女,名叫马忠轩、吕欣。
那个时候,未婚先孕是件很麻烦的事,再加上前途茫茫,两人便商量着把孩子送给一户可靠的人家。
刘军夫妇不知道的是,这对年轻的情侣把孩子送人后,怕高艳后悔,便留给马芳一个名字和地址,拜托她如果孩子过得不好,就给他们捎个信儿。
几天后,高艳和刘军到民政部门顺利办理了领养手续,并给孩子起名刘炳昌。
从此,高艳和刘军视刘炳昌如己出,百般疼爱……高艳怎么也没想到,丈夫临终前会将这个秘密说出来。
据案发后刘炳昌交待,知道自己的身世后,他心里像长了草,出于好奇,他很想知道亲生父母到底是谁。
其实这个时候,刘炳昌只想知道自己的身世,并没有更多的想法,尤其,养父母对自己一直很好,他想好好报答养育之恩。
2013年4月,刘炳昌四处打听,找到了儿时常抱他玩的邻居阿姨马芳。
刘炳昌谎称自己早已知道了身世,现在得了白血病,需要亲生父母捐骨髓。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年中考调研测试(一)
数学试卷
第I 卷选择题(共30分)(涂卡)
一、选择题(每小题3分,共计30分) 1.2的相反数是( ) (A)2 (B)-2 (C)-
22 (D) 2
2 2.下列运算中,正确的是( )
(A)2x+2y=2xy (B)(x 2y 3)2=x 4y 5 (C)(xy)2÷
xy
1
=(xy)3 (D)2xy -3yx=xy 3.下面的图案中,是轴对称图形而不是中心对称图形的是( )
(A ) (B ) (C ) (D ) 4.如图所示的由六个小正方体组成的几何体的俯视图是( )
5.抛物线y=}(x+3)2+4的对称轴是( )
(A)直线x=3 (B)直线x=-3 (C)直线x=
31 (D)直线x=-3
1 6.在Rt △ABC 中,∠C=90°,若AB=2,AC=1,则tanA 的值为( )
(A)
21 (B) 23 (C) 3
3
(D) 3
7.圆锥的底面半径是1,侧面积是2π,则这个圆锥的侧面展开图的圆心角的度数为( )
(A)180° (B)150° (C)120° (D)60° 8.下列命题正确的是( )
(A)若两个三角形相似,则它们的面积之比等于相似比
(B)若三角形的两个内角互为余角,则这个三角形是直角三角形 (C)等腰三角形的角平分线既是高线也是中线
9.已知点P 1(x 1,y 1),P 2(x 2,y 2)均在双曲线y=
x
m 3
2+,当x 1<x 2<0时,y 1<y 2,那么m 的取值范围是( ) (A)m>
23 (B)m>-23 (C)m<23 (D)m<-2
3 lo .小成从家出发,骑电动自行车到江北度假村办事,途中遇到从江北度假村步行锻炼回家的哥哥小军.小成在江北度假村办完事后,在返回家的途中又遇到哥哥小军,便用电动自行车载上哥哥小军,一同回到家中,结果小成比预计时间晚到1分钟.假设小成和哥哥小军都是沿直线行进的,且二人与家的距离S(千米)和小成从家出发后所用的时间t(分)之间的函数关系如图所示.有如下
的结论: ①小成出发时,哥哥小军已经离开江北度假村2千米;
②小成去江北度假村的速度比返回时的速度快了20
1
千米/分; ③小成返回途中载着哥哥小军返回家的速度是
4
1
千米/分; ④哥哥小军比预计时间早到15分钟.其中正确的结论有( ) (A)1个 (B)2个 (C)3个 (D)4个
第Ⅱ卷非选择题(共90分)
二、填空题(每小题3分,共计30分)
11.李克强总理在2014年政府工作报告中指出“今年要淘汰燃煤小锅炉5万台,推进燃煤电厂脱硫改
造1500万千瓦、脱硝改造1.3亿千瓦、除尘改造180 000 000千瓦”.其中数字180 000 000用科学计数法可以表示为______________. 12.函数y=
x
x
+1的自变量x 的取值范围是_____________. 13.把多项式3x 3﹣6x 2y+3xy 2分解因式的结果是________________. 14.计算:18-8=__________.
15.把一副三角板如图甲放置,点E 在BC 上,其中 ∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边 AB=6,DC=7,把三角板DCE 绕着点C 顺时针旋转 15°得到△D 1CE 1(如图乙),此时AB 与CD 1交于 点O ,连接AD 1,则线段AD 1的长度为___________. 16.小红、小明在一起做游戏,需要确定做游戏的先后顺 序,他们约定用“剪刀、包袱、锤子”的方式确定.
在一个回合当中两个人都出“包袱”的概率是__________.
17.如图,在Rt △ABC 中,∠ACB=90°,AC=3,BC=4,以点C 为圆心,CA 为半径的圆与AB 交 于点D ,则AD 的长为___________.
18.□ABCD 在平面直角坐标系中的位置如图所示,其中A(﹣4,O),B(2,0),C(3,m),反比例函
数y=
x
9
的图象经过点C .将□ABCD 沿x 轴翻折得到□AD′C′B′,则点D′的坐标为__________. 19.如图,△ABC 中,AB=AC ,AD 上BC 于点D ,点E 在AC 上,CE=2AE ,AD=9,BE=10,AD
与BE 交于点F ,则△ABC 的面积是___________.
剩下的部分是如图所示的直角梯形,其中三边长分别为2、3、3,则原直角三角形纸片的斜边长是__________.
(第17题图) (第18题图) (第19题图) (第20题图) 三、解答题(其中21—24题各6分,25~26题各8分,27~28题各10分,共计60分) 21.(本题6分)
先化简,再求代数式22
-x x +x
-24的值,其中a =2sin60°-2tan45°.
22.(本题6分)
如图,在平面直角坐标系中,△ABC 的三个顶点的坐标分别为A(0,1),B(﹣2,1),C(﹣2,4). (1)画出△ABC 沿着y 轴向下平移5个单位得到的
△A 1B 1C 1,并直接写出点C 的对应点C 1的坐标; (2)画出△ABC 关于y 轴对称的△AB 2C 2,并直接写出点 C 的对应点C 2的坐标;
23.(本题6分)
如图,点E 是正方形ABCD 边BC 上的一点,连接DE ,过点B 作直线DE 的垂线,垂足为G ,连接GA .求证:GA 平分∠BGD .
(第23题图)
24.(本题6分)
某中学为了了解学校600名学生的时事政治的掌握情况,举行了一次“两会”时事政治知识测试,并随机抽取了部分学生的成绩(得分取正整数,满分为l00分)作为样本,绘制了下面尚未完成的频数分布表和频数分布直方图.
频数分布表 频数分布直方图
(第24题图)
请解答下列问题:
(1)求出x 的值,并补全频数分布直方图;
(2)若成绩在70分以上(不含70分)为学生时事政治掌握情况良好,请估计该校学生时 事政治掌握情况良好的人数. 25.(本题8分)
如图,已知AB 是OD 的直径,AM 和BN 是⊙O 的两条切线,点E 是⊙O 上一点,点D 是 AM 上一点,连接DE 并延长交BN 于点C ,连接OD 、BE ,且OD ∥BE. (1)求证:DE 是⊙O 的切线;
(2)若AD=l ,BC=4,求直径AB 的长.
26.(本题8分)
某超市销售甲、乙两种商品,五月份该超市同时购进甲、乙两种商品共80件,购进甲种商品用去400元,购进乙种商品用去1200元.
(1)已知每件甲种商品的进价是每件乙种商品的进价的
3
1
,求甲、乙两种商品每件的进价; (2)由于甲、乙这两种商品受到市民欢迎,六月份超市决定再次购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价15元,乙种商品每件的售价40元.要使六月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?(利润=售价一进价)
27.(本题lO 分)
如图,在平面直角坐标系中,点O 为坐标原点,直线y=﹣x+n 与x 轴、y 轴分别交于B 、c 两点,抛物线y=ax 2+bx+3(a ≠0)过C 、B 两点,交x 轴于另一点A ,连接AC ,且tan ∠CAO=3. (1)求抛物线的解析式;
(2)若点P 是射线CB 上一点,过点P 作x 轴的垂线,垂足为H ,交抛物线于Q ,设P 点横坐标为t ,线段PQ 的长为d ,求出d 与t 之间的函数关系式,并写出相应的自变量t 的取值范围; (3)在(2)的条件下,当点P 在线段BC 上时,设PH=e ,已知d ,e 是以y 为未知数的一元二次方程:y 2一(m+3)y+
4
1
(5m 2—2m+13)=0 (m 为常数)的两个实数根,点M 在抛物线上,连接MQ 、MH 、PM ,且.MP 平分∠QMH ,求出t 值及点M 的坐标.
(第27题图) (第27题备用图)
28.(本题10分)
在△ABC 与△ADE 中,点E 在BC 边上,AD=5
4
AE ,AG 为△ADE 的中线,且∠EAC=∠ACB ,∠DAG=∠B
(1)如图1,求证:AB=
5
4
AC ; (2)如图2,点F 是AC 中点,连接DF ,∠AFD=∠DAE ,连接CD 并延长交AB 于点K ,过点D 作DQ ∥BC 交BK 于点Q .
①求证:点Q 为BK 的中点;
②试探究线段BE 与DQ 的数量关系,并证明你的结论.
(第28题图1) ﹙第28题图2)。
