七年级数学下册5相交线与平行线周周练5.1_5.2新版10
人教版数学七年级下册 第五章 相交线与平行线 单元练习含答案

第五章相交线与平行线1.如图,下列各组角中,是对顶角的一组是( )A.∠1和∠2 B.∠3和∠5 C.∠3和∠4 D.∠1和∠52.如图,下列说法不正确的是( )A.∠1和∠2是同旁内角B.∠1和∠3是对顶角C.∠3和∠4是同位角D.∠1和∠4是内错角3. 下列选项中,哪个不可以得到l1∥l2( )A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°4. 如图所示,下列推理正确的有( )①因为∠1=∠4,所以BC∥AD;②因为∠2=∠3,所以AB∥CD;③因为∠BCD +∠ADC=180°,所以AD∥BC;④因为∠1+∠2+∠C=180°,所以BC∥AD. A.1个B.2个C.3个D.4个5. 在下列说法中:①三角形ABC在平移过程中,对应线段一定相等;②三角形ABC在平移过程中,对应线段一定平行;③三角形ABC在平移过程中,周长保持不变;④三角形ABC在平移过程中,面积不变.其中正确的有( )A.①②③ B.①②③④ C.①②④ D.①③④6. 如图是长方形花园,准备修建一条通往对边的小路,现有甲、乙、丙三种设计方案,三种方案的入口和出口宽都一样,而且每条小路的水平宽度始终也一样,则三种方案的小路中占地面积较大的是( )A.甲 B.乙 C.丙 D.甲、乙、丙一样大7. 如图,已知直线AB和CD相交于点O,∠BOE=90°,∠AOD=128°,则∠COA 的度数为,∠COE的度数为 .8. 命题“任意两个直角都相等”的题设是,结论是,它是 (填“真”或“假”)命题.9. (1)在图①中,过AB外一点M作AB的垂线;(2)在图②中,过A、B分别作OB、OA的垂线.10. 如图,若∠B=102°,∠1=78°,则AB与CD平行吗?11. 如图,∠E=∠B+∠D,猜想AB与CD有怎样的位置关系?并说明理由.12. 如图,AB∥CD,∠B=∠C.求证:BE∥CF.13. (1)如图,AB∥CD,若∠B=130°,∠C=30°,求∠BEC的度数;(2)如图,AB∥CD,探究∠B、∠C、∠BEC三者之间有怎样的数量关系?试说明理由.14. 完成下列证明,并在括号内填上理由.如图,BC∥AD,∠1=∠E,求证:∠A=∠C.证明:∵∠1=∠E(已知),∴AB∥ ( ),∴∠A+∠ADC=180°().∵BC∥AD(已知),∴∠ADC+∠=180°().∴∠A=∠C( ).15. 如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)AE与FC平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?16. 如图,在三角形ABC中,CE⊥AB于点E,DF⊥AB于点F,DE∥CA,CE平分∠ACB,试说明∠EDF=∠BDF.17. 如图所示,一个四边形纸片ABCD中,∠B=∠D=90°,把纸片沿AE折叠,使点B落在AD边上的B′点,AE是折痕.(1)试猜想B′E与DC的位置关系,并说明理由;(2)如果∠C=130°,求∠AEB的度数.18. (1)如图①,AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?请说明理由;(2)如图②,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7还有类似的数量关系吗?若有,请直接写出,并将它们推广到一般情况,用一句话写出你的结论.答案;1---6 BACAD D7. 52°38°8. 两个角都是直角这两个角相等真9. 解:如图:10. 解:AB∥CD.理由:∵∠BFC与∠1是对顶角,∴∠BFC=∠1=78°.又∵∠B=102°,∴∠BFC+∠B=78°+102°=180°.∴AB∥CD(同旁内角互补,两直线平行).11. 解:AB∥CD.理由如下:过E点作EF∥AB,∴∠B=∠BEF,又∵∠BED=∠B +∠D,∴∠BED=∠BEF+∠D,即∠BEF+∠DEF=∠BEF+∠D,∴∠DEF=∠D,∴EF∥CD,∴AB∥CD.12. 证明:作EM∥AB,作FN∥CD,则EM∥NF.∴∠BEM=∠B,∠CFN=∠C,∠MEF=∠EFN.∵∠B=∠C,∴∠BEM=∠CFN,∴∠BEF=∠EFC,∴BE∥CF.13. 解:(1)过E点向左侧作EF∥AB,∴∠B+∠BEF=180°,∴∠BEF=180°-∠B=50°,又∵AB∥CD,且EF∥AB,∴EF∥CD,∴∠FEC=∠C=30°,∴∠BEC=∠BEF+∠FEC=50°+30°=80°;(2)∠B+∠BEC-∠C=180°.理由如下:过E点向左侧作EF∥AB,又∵AB∥CD,∴EF∥CD,∴∠FEC=∠C,又∵∠BEF=∠BEC-∠FEC,∴∠BEF=∠BEC-∠C,∵AB∥EF,∴∠B+∠BEF=180°,∴∠B+∠BEC-∠C=180°.14. CE 内错角相等,两直线平行 两直线平行,同旁内角互补 C 两直线平行,同旁内角互补 同角的补角相等15. 解:(1)AE ∥FC.理由:∵∠1+∠2=180°,∠2+∠CDB =180°, ∴∠1=∠CDB ,∴AE ∥FC ;(2)AD ∥BC.理由:∵AE ∥CF ,∴∠C =∠CBE.又∠A =∠C ,∴∠A =∠CBE , ∴AD ∥BC ;(3)BC 平分∠DBE.理由:∵DA 平分∠BDF ,∴∠FDA =∠ADB.∵AE ∥CF ,AD ∥BC ,∴∠FDA =∠A =∠CBE ,∠ADB =∠CBD.∴∠CBE =∠CBD ,∴BC 平分∠DBE. 16. 解:∵DF ⊥AB ,CE ⊥AB ,∴DF ∥CE.∴∠BDF =∠DCE ,∠EDF =∠DEC. ∵DE ∥CA ,∴∠DEC =∠ACE.∵CE 平分∠ACB ,∴∠ACE =∠DCE ,∴∠DCE =∠DEC ,∴∠EDF =∠BDF.17. 解:(1)B′E∥DC ,理由如下:由折叠意义可知,∠AB′E=∠B =90°, 又∵∠D =90°,∴∠AB′E=∠D ,∴B′E∥DC ;(2)∵B′E∥DC ,∠C =130°,∴∠B′EB=∠C =130°,∵∠AEB′=∠AEB ,∴∠AEB =12∠B′EB=12×130°=65°.18. 解:(1)∠2+∠4=∠1+∠3+∠5.理由如下:分别过点E 、G 、M 作EF ∥AB ,GH ∥AB ,MN ∥AB.∵AB ∥CD ,∴AB ∥CD ∥EF ∥GH ∥MN ,∴∠1=∠BEF ,∠FEG =∠EGH ,∠HGM =∠GMN ,∠CMN =∠5,∴∠2+∠4=∠BEF +∠FEG +∠GMN +∠CMN =∠1+∠EGH +∠MGH +∠5=∠1+∠3+∠5;(2)∠2+∠4+∠6=∠1+∠3+∠5+∠7.结论:开口朝左的所有角的度数之和与开口朝右的所有角的度数之和相等.。
新版七下数学第五章相交线与平行线复习题五套

第五章相交线与平行线专题(一)相交线1.如图所示,直线AB与CD相交于点O,OE平分∠AOD,∠BOC=80°,求∠BOD和∠AOE的度数.2.如图,三条直线相交于点O,则∠1+∠2+∠3等于()A.90°B.120°C.180°D.360°,(第2题图)),(第3题图))3.如图,三条直线AB,CD,EF相交于点O,若∠BOE=4∠BOD,∠AOE=100°,则∠AOC 等于()A.30°B.20°C.15°D.10°4.如图,AB和CD相交于点O.(1)若∠1+∠3=50°,则∠3=__ __;(2)若∠1∶∠2=2∶3,则∠3=__ __;(3)若∠2-∠3=70°,则∠3=__ __.5.如图,两条直线AB,CD相交于点O,OE平分∠BOC,若∠1=30°,∠2=___ _,∠3=__ __.6.如图所示,直线AB,CD,EF相交于点O.(1)试写出∠AOC,∠AOE,∠EOC的对顶角;(2)试写出∠AOC,∠AOE,∠EOC的邻补角;(3)若∠AOC=40°,求∠BOD,∠BOC的度数.7.如图,一长方形纸片ABCD沿折痕EF对折,得到点D的对应点D′,点C的对应点C′,若∠BFE=50°,试求∠BFC′的度数.8.如图所示,已知直线AB,CD相交于点O,OE平分∠BOD,若∠3∶∠2=8∶1,求∠AOC 的度数.第五章相交线与平行线专题(二)平行线的判定1.如图所示,直线a ,b 被直线c 所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a ∥b 的条件为( )A .①②B .①③C .①④D .③④2.如图所示,要得到DE ∥BC ,则需要的条件为( )A .CD ⊥AB ,GF ⊥AB B .∠4+∠5=180°C .∠1=∠3D .∠2=∠33.对于图中标记的各角,下列条件能够推理得到a ∥b 的是( )A .∠1=∠2B .∠2=∠4C .∠3=∠4D .∠1+∠4=180°4.如图,在下列给出的条件中,不能判定AB ∥DF 的是( )A .∠A +∠2=180°B .∠3=∠AC .∠1=∠4D .∠1=∠A5.)如图所示,下列判断不正确的是( )A .∵∠1=∠2,∴AE ∥BDB .∵∠1=∠2,∴AB ∥EDC .∵∠3=∠4,∴AB ∥CD D .∵∠5=∠BDC ,∴AE ∥BD6.如图,能说明AB ∥DE 的有( )①∠1=∠D ;②∠CFB +∠D =180°;③∠B =∠D ;④∠D =∠BFD.A .1个B .2个C .3个D .4个(第1题图)(第2题图) (第5题图)(第6题图)7.如图,给出下面的推理:①因为∠B =∠BEF ,所以AB ∥EF ;②因为∠B =∠CDE , 所以AB ∥CD ;③因为∠B +∠BDC =180°,所以AB ∥EF ;④因为AB ∥CD ,CD ∥EF , 所以AB ∥EF.其中正确的推理是( )A .①②③B .①②④C .①③④D .②③④9.如图,下列推理正确的是( )A .∵∠1=∠2,∴AB ∥CD B .∵∠1+∠2=180°,∴AB ∥CDC .∵∠3=∠4,∴AB ∥CD D .∵∠3+∠4=180°,∴AB ∥CD10.如图,已知直线EF 分别交CD ,AB 于点M ,N ,且∠EMD =65°,∠MNB =115°,则下列结论正确的是( )A .AE ∥CFB .AB ∥CDC .∠A =∠D D .∠E =∠F11.如图,BD 平分∠ABC ,若∠1=∠2,则( )A .AB ∥CD B .AD ∥BC C .AD =BC D .AB =CD12.如图所示,AC ⊥BC ,垂足为C ,∠B =50°,∠ACD =40°,则AB 与CD 的位置关系是 AB ∥CD__.13.如图所示,下列条件中:(1)∠B +∠BCD =180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B =∠5.能判定AB ∥CD的条件有 .(填序号),(第9题图)) ,(第10题图)) ,(第11题图)) ,(第12题图))14.(8分)如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°,直线AB,CD有何位置关系?说明理由.16.(10分)如图,已知直线a,b,c被直线d,e所截,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?17.(12分)如图,AC⊥EC,B,C,D在同一直线上,∠A=∠1,∠E=∠2,直线AB与DE平行吗?试说明理由.第五章相交线与平行线专题(三)平行线的性质1.如图,直线m ∥n ,∠α为( )A .70 B .65° C .50° D .40°2.如图,AB ∥ED ,AG 平分∠BAC ,∠ECF =70°,则∠FAG 的度数是( )A .155°B .145°C .110°D .35°3.如图,已知AB ∥CD ,∠1=130°,则∠2=__ .4.如图,EF ∥BC ,AC 平分∠BAF ,∠B =80°,求∠C 的度数5.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( )A .60°B .50°C .40°D .30°6. 6.一张长方形的纸条,按如图方式折叠一下,已知∠3=120°,则∠1的度数为( )7.A .30° B .60° C .90° D .120°8.9. ,(第1题图)) ,(第2题图)) ,(第5题图)) ,(第6题图))10.7.(4分)如图,∠1=50°,∠2=140°,∠C =50°,则∠B =____.9.某次考古发掘出的一个梯形残缺玉片如下图,工作人员从玉片上量得∠A =115°,∠D =100°,已知梯形的两底AD ∥BC ,请你帮助工作人员求出另外两个角的度数,并说明理由.10.如图所示,点B 是△ADC 的边AD 的延长线上一点,DE ∥AC ,若∠C =50°, ∠BDE =60°,则∠CDB 的度数等于( )A .70°B .100°C .110°D .120°11.如图所示,已知AB ∥EF ∥DC ,EG ∥BD ,则图中与∠1相等的角共有( )A .6个B .5个C .4个D .2个12.如图所示,已知AB ∥CD ,BC ∥DE ,则∠B +∠D 的度数为____.13.如图,AC ∥BD ,AE 平分∠BAC 交BD 于点E ,若∠1=64°,则∠2=___ _.(第10题图) (第11题图), ( 第 7 题图 )14.(12分)如图所示,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC,求∠BOC的度数.15.(12分)如图,直线AD与AB,CD相交于A,D两点,EC,BF与AB,CD相交于点E,C,B,F,如果∠1=∠2,∠B=∠C.小明在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF,同桌的小慧说:“不光有这个发现,我还能得到∠A=∠D呢?”小明再深入其中,很快也明白了小慧是怎么得到∠A=∠D的了.你能帮助他们写出过程吗?16.(12分)如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.(1)试找出∠1,∠2,∠3之间的关系并说明理由;(2)如果点P在A,B两点之间运动时,问∠1,∠2,∠3之间的关系是否发生变化?(3)如果点P在A,B两点外侧运动时,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).第五章相交线与平行线专题(四)平行线的性质与判定的综合运用1.如图,直线AB ,CD 相交于点O ,OT ⊥AB 于点O ,CE ∥AB 交CD 于点C ,若∠ECO =30°,则∠DOT 的度数为( ) A .30° B .45° C .60° D .120°2.如图,AB ∥CD ,∠DFE =135°,则∠ABE 的度数是( )A .30°B .45C .60°D .90°3.如图,a ,b ,c 为三条直线,且a ⊥c ,b ⊥c ,若∠1=70°,则∠2的度数为( )A .70°B .90°C .110°D .80°4.如图所示,已知∠1=∠2=∠3=55°,则∠4的度数是( )A .110°B .115°C .120°D .125°5.(4分)如图所示,已知∠1=∠2,∠3=80°,则∠4等于( )A .80°B .70°C .60°D .50°6.(4分)如图,已知直线a ∥b ,∠1=40°,∠2=60°,则∠3等于( )A .100°B .60°C .40°D .20°(第1题图)(第2题图) (第3题图)(第4题图)7.将一副直角三角板如图所示放置,使含30°角的三角板短直角边和含45°角 的三角板的一条直角边重合,则∠1的度数为__.8.如图所示是一大门的栏杆,AE 为地面,BA ⊥AE 于点A ,CD ∥AE ,则∠ABC +∠BCD= _9.(8分)如图,直线AB ,CD 分别与直线AC 相交于点A ,C ,与直线BD 相交于点B ,D.若∠1=∠2,∠3=75°,求∠4的度数.10.如图,AB ∥CD ,AE 交CD 于C ,∠A =34°,∠DEC =90°,则∠D 的度数为() A .17° B .34° C .56° D .124°11.如图,已知AB ∥CD ,∠C =65°,∠E =30°,则∠A 的度数为( )A .30°B .32.5°C .35°D .37.5°12.如图所示,AB ∥CD ∥EF ,则∠BAD +∠ADE +∠DEF 等于( )A .180°B .270°C .360°D .540°13.如图所示,∠A =60°,∠4=45°,DE ∥BC ,EF ∥AB ,则∠1=___ _, ∠2=__ __, ∠3=__ _,∠B =__ _,∠C =___ _. (第5题图) (第6题图,(第10题图)) ,(第11题图)(第7题图) (第8题图)14.如图,直线l1∥l2∥l3,点A ,B ,C 分别在直线l1,l2,l3上.若∠1=70°,∠2=50°,则∠ABC =____.15.如图,l ∥m ,等边△ABC 的顶点A 在直线m 上,则∠α=__.16.(8分)如图,AD ⊥BC 于点D ,EG ⊥BC 于点G ,∠E =∠3.请问:AD 平分∠BAC 吗?若平分,请说明理由.17.(10分)如图所示,CD ⊥AB ,垂足为D ,F 是BC 上任意一点,EF ⊥AB ,垂足为E ,且∠1=∠2,∠3=80°,求∠BCA 的度数.18.(12分)如图所示,∠1+∠2=180°,∠3=∠B ,试判断∠AED 与∠C 的大小关系,并(第12题图)(第13题图) ,(第14题图)),(第15题图)说明你的理由.第五章相交线与平行线专题(五)平行线的性质与判定变式训练【教材母题】(教材P36第8题(2)改编)如图,∠1+∠2=180°,∠3=108°,求∠4的度数.变式1.(2014·菏泽)如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为()A.25°B.45°C.35°D.30°变式2.(2014·邵阳)如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是()A.45°B.54°C.40°D.50°,(第1题图)),(第2题图))变式3.(2014·聊城)如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=27°,那么∠2的度数为()A.53°B.55°C.57°D.60°变式4.(2014·遵义)如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=() A.30°B.35°C.36°D.40°,(第3题图)),(第4题图))变式5.如果一个角的两边分别与另一个角的两边平行,且一个角比另一个角的3倍少40°,则这两个角的度数分别为__变式6.填写推理理由:如图,CD∥EF,∠1=∠2.求证:∠3=∠ACB.变式7.如图所示,已知AD⊥BC于D,E是AB上一点,EF⊥BC于F,且∠1=∠2,试判断∠B与∠CDG的大小关系,并说明理由.变式8.如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.变式9.如图,∠BAP+∠APD=180°,∠1=∠2.求证:∠E=∠F.变式10.若AB∥CD,∠1=∠2,∠3=∠4,AD与BC平行吗?为什么?变式11.如图,已知∠1=∠2,∠MAE=45°,∠FEG=15°,∠NCE=75°,EG平分∠AEC,试说明AB∥EF∥CD.变式12.(探究题)(1)如图①,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?(3)若将点E移至图②的位置,此时∠B,∠D,∠E之间有什么关系?(4)若将点E移至图③的位置,此时∠B,∠D,∠E之间的关系又如何?(5)在图④中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?。
(精校版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案

(直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改)的全部内容。
初一数学人教版七年级下册第五章 相交线与平行线5.1 相交线同步练习题1. 下列说法中正确的是( )A.不相等的角一定不是对顶角B.互补的两个角是邻补角C.互补且有一条公共边的两个角是邻补角D.两条直线相交所成的角是对顶角2. 下列说法正确的是( )A.在同一平面内,过直线外一点向该直线画垂线,垂足一定在该直线上B.在同一平面内,过线段或射线外一点向该线段或射线画垂线,垂足一定在该线段或射线上C.过线段或射线外一点不一定能画出该线段或射线的垂线D.过直线外一点与直线上一点画的一条直线与该直线垂直3. 已知∠α和∠β的对顶角,若∠α=60°,则∠β的度数为( )A.30° B.60° C.70° D.150°4。
如图,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2,其推理依据是( )A.同角的余角相等 B.对顶角相等C.同角的补角相等 D.等角的补角相等5. 如图,OB⊥CD于点O,∠1=∠2,则∠2与∠3的关系是( )A.∠2=∠3 B.∠2与∠3互补C.∠2与∠3互余 D.不能确定6。
2024年第五章-相交线与平行线周测(5.1-5.2)及答案

A.125°
B.135°
C.65°
1
2
3
4
D.55°
5
6
7
8
9
10
周测(5.1~5.2)
填空题
选择题
解答题Leabharlann 8.[2023·沧州南皮县桂和中学模拟]如图,河道的一侧有甲、乙两个村庄,
现要铺设一条管道将水引向甲、乙两村,下列四种方案中最节省材料的
是( B )
A
B
C
1
2
3
4
D
5
6
7
8
9
10
周测(5.1~5.2)
∠BAG,FG平分∠AGC.请说明AE∥GF.给出了如下不完整的解答过程,
请将解答过程补充完整并在括号内填上推理的依据.
15
16
17
18
周测(5.1~5.2)
选择题
填空题
解答题
解:因为∠BAG+∠AGD=180°(已知),
∠AGC+∠AGD=180°(邻补角的性质),
所以∠BAG=∠AGC( 等量代换 ).
因为EA平分∠BAG,
所以∠1= ∠BAG(
角平分线的定义
因为FG平分∠AGC,所以∠2=
所以 AE∥GF (
).
∠AGC . 所以∠1=∠2(等量代换).
内错角相等,两直线平行
).
15
16
17
18
周测(5.1~5.2)
选择题
填空题
解答题
16.(6分)观察图形,回答下列问题:
(1)∠1的同位角是哪个角?
.
14.【推理能力】如图是某小区大门的道闸栏杆的示意图,立柱BA垂直
人教版七年级数学下册《5.1相交线》同步练习(含答案)

人教版七年级数学下册第五章相交线与平行线 5.1 相交线同步练习一、单选题(共10题;共30分)1.如图所示,∠1和∠2是对顶角的图形有( )A. 1个B. 2个C. 3个D. 4个2.如图,下列说法不正确的是()A. ∠1和∠2是同旁内角B. ∠1和∠3是对顶角C. ∠3和∠4是同位角D. ∠1和∠4是内错角3.如图所示,∠1和∠2是对顶角的是()A. B. C. D.4.下列说法中正确的个数为()①两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直;②两条直线相交成四个角,如果有一个角是直角,那么这两条直线垂直;③一条直线的垂线可以画无数条;④在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直.A. 1B. 2C. 3D. 45.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为()A. 75°B. 15°C. 105°D. 165°6.如图所示,下列说法错误的是()A. ∠A和∠B是同旁内角B. ∠A和∠3是内错角C. ∠1和∠3是内错角D. ∠C和∠3是同位角7.如图,三条直线相交于点O.若CO⊥AB,∠1=56°,则∠2等于()A. 30°B. 34°C. 45°D. 56°8.在下列语句中,正确的是().A. 在平面上,一条直线只有一条垂线;B. 过直线上一点的直线只有一条;C. 过直线上一点且垂直于这条直线的直线有且只有一条;D. 垂线段就是点到直线的距离9.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有( )A. 1个B. 2个C. 3个D. 4个10.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是()①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.A. ①②③B. ①②④C. ①③④D. ②③④二、填空题(共10题;共30分)11.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC=________12.如图,已知直线AB与CD相交于点O,OA平分∠COE,若∠DOE=70°,则∠BOD=________.13.如图,∠1和∠2是________角,∠2和∠3 是________角。
七年级数学下册第五章相交线与平行线5.1相交线5.1.2垂线同步练习含解析新版新人教版

5.1.2垂线基础闯关全练1.如图,直线AB、CD、EF相交于点O,且AB⊥CD,若∠BOE=35°,则∠DOF=( )A.65° B.45° C.35° D.55°2.如图,点O在直线AB上且OC⊥OD,若∠COA= 36°,则∠DOB的大小为( )A.36°B.54°C.55°D.44°3.下列选项中,过点P画AB的垂线CD,三角板放法正确的是( )A B C D4.在下图所示的各图中用三角板分别过点C画线段AB的垂线.(1)(2)(3)(4)5.如图,在立定跳远中,体育老师是这样测量运动员的成绩的,用一块直角三角板的一边附在起跳线上,另一边与拉直的皮尺重合,这样做的理由是( )A.两点之间,线段最短B.过两点有且只有一条直线C.垂线段最短D.过一点可以作无数条直线6.如图.想在河堤两岸搭建一座桥,图中四种搭建方式PA,PB,PC,PD中,最短的是_______. 7.下列图形中,线段PQ的长为点P到直线MN的距离的是( )A B C D8.如图.立定跳远比赛时,小明从点A起跳落在沙坑内B处,这次小明的跳远成绩是4.6米,则小明从起跳点到落脚点之间的距离( )A.大于4.6米 B.等于4.6米 C.小于4.6米 D.不能确定能力提升全练1.如图,∠ACB= 90°.CD⊥AB,垂足为点D,则下面的结论中,正确的有( )①BC与AC互相垂直②AC与CD互相垂直③点A到BC的垂线段是线段BC④点C到AB的垂线段是线段CD⑤线段BC是点B到AC的距离⑥线段AC的长度是点A到BC的距离A.2个 B.3个 C.4个 D.5个2.如图,已知直线CD、EF相交于点O.OA⊥OB,且OE平分∠AOC,若∠EOC= 60°,则∠BOF=______.3.如图,直线AB,CD相交于点O,∠DOE=∠BOD.OF平分∠AOE.(1)判断OF与OD的位置关系;(2)若∠AOC:∠AOD=1:5.求∠EOF的度数.三年模拟全练一、选择题1.如图所示,直线AB⊥CD于点D,直线EF经过点O.若∠1=26°,则∠2的度数是( )A.26° B.64° C.54° D.以上答案都不对2.如图,直线AB、CD相交于点O,OE⊥CD,∠AOE= 52°,则∠BOD等于( )A.24°B.26° C.36° D.38°二、填空题3.如图,已知AC⊥BC,CD⊥ AB.AC=3,BC=4,CD= 2.4,则点C到直线AB的距离等于______. 4.如图,当∠1与∠2满足_________条件时,OA⊥OB.三、解答题5.如图,直线AB与CD相交于点D,OP是∠BOC的平分线,OE ⊥AB,OF⊥ CD.(1)图中除直角外,写出三对相等的角:(2)已知∠EOC= 50°,求∠POF的度数,五年中考全练选择题.1.如图,直线AB,CD相交于点O,EO⊥CD.下列说法错误的是( ) A.∠AOD=∠BOC B.∠AOE+∠BOD=90°C.∠AOC=∠AOED.∠AOD+∠BOD= 180°2.如图,经过直线l外一点A画l的垂线,能画出( )A.1条B.2条C.3条D.4条3.如图所示,点P到直线l的距离是( )A.线段PA的长度 B.线段PB的长度C.线段PC的长度 D.线段PD的长度核心素养全练如图,随意画一个锐角∠MON和一个钝角∠M'O’N’,画出∠MON的平分线OP和∠M'O’N'的平分线O’P’.(1)在OP上任取一点A,画AB⊥OM,AC⊥ON,垂足分别为B,C;(2)在O'P’上任取一点A’,画A'B'⊥O'M’,A'C'⊥O'N',垂足分别是B’,C’;(3)通过度量线段AB,AC,A'B’,A'C'的长度,发现AB____AC,A'B'____ A'C’;(填“=”或“≠”)(4)通过上面的画图和度量,和同学们交流一下,有什么猜想?请用一句话表述出来.5.1.2垂线1.D∵AB⊥CD,∠BOE=35°,∴∠AOF=35°,∠AOD=∠BOC=90°,∴∠DOF= 90°-35°=55°.故选D.2.B∵OC⊥OD,∴∠COD= 90°,又∵∠AOC+∠COD+∠DOB= 180°.∴∠DOB= 180°-36°-90°= 54°.故选B. 3.C根据垂线的作法,将直角三角板的一条直角边与直线AB重合,另一条直角边过点P后沿该直角边画直线即可.4.解析5.C根据垂线段的性质:垂线段最短,故选C.6.答案PC解析根据“连接直线外一点与直线上各点的所有线段中,垂线段最短”与PC⊥AD.知PC最短.7.A对于选项A,PQ⊥MN,Q是垂足,故线段PQ的长为点P到直线MN的距离.8.A 跳远的成绩是点B 到起跳线的距离,即垂线段的长度为4.6米,结合题图知AB 的长大于4.6米.1.B .∵∠ACB=90°,∴AC ⊥BC,故①正确;AC 与DC 相交不垂直,故②错误;点A 到BC 的垂线段是线段AC .故③错误;点C 到AB 的垂线段是线段CD,故④正确;线段BC 的长度是点B 到AC 的距离,故⑤错误;线段AC 的长度是点A 到BC 的距离,故⑥正确.故选B . 2.答案30°解析∵OE 平分∠AOC,∠EOC=60°,∴∠AOE=∠COE= 60°,∠DOE= 180°-∠COE= 120°, ∴∠DOA= 60°,∵OA ⊥OB,∴∠DOA+∠BOD= 90°.∴∠DOB=30°, ∵∠DOF=∠EOC=60°,∴∠BOF=30°. 3.解析(1)因为OF 平分∠AOE,所以∠AOF=∠EOF=21∠AOE . 又因为∠DOE=∠BOD=21∠BOE,所以∠DOE+∠EOF=21(∠BOE+∠AOE)=21×180°=90°,即∠FOD=90°,所以OF ⊥OD.(2)设∠AOC=x .因为∠AOC:∠AOD=1:5, 所以∠AOD=5x,因为∠AOC+∠AOD= 180°, 所以x+5x= 180°,x=30°. 所以∠DOE=∠BOD=∠AOC=30°.又因为∠FOD= 90°.所以∠EOF= 90°-30°= 60°. 一、选择题1.B ∵∠1=26°,∠DOF 与∠1是对顶角, ∴∠DOF=∠1=26°,又∵AB ⊥CD.∴∠DOF+∠2=90°,∴∠2=90°-∠ DOF=90°-26°=64°.故选B.2.D 因为OE ⊥CD, ∠AOE =52°,所以∠AOC= 38°,则∠BOD=∠AOC= 38°,故选D . 二、填空题 3.答案2.4解析由题意得点C 到直线AB 的距离等于CD 的长,即点C 到直线AB 的距离等于2.4. 4.答案∠1+∠2= 90°解析当∠1+∠2= 90°时,∠AOB= 90°,根据垂直的定义得OA ⊥OB. 三、解答题5.解析(1)①∠AOD= ∠BOC,②∠COP= ∠BOP,③∠COE=∠ BOF 等. (2)∵OE ⊥AB,∴ ∠EOB=90°.∵∠ EOC= 50°,∴∠COB= ∠EOB- ∠EOC= 40°.∵OP 是∠BOC 的平分线,∴∠COP=21∠BOC=20°.∵OF ⊥CD, ∴∠COF=90°,∴∠POF= ∠COF-∠COP=70°. 选择题1.C 由对顶角相等知∠AOD=∠BOC,选项A 中说法正确;由对顶角相等知∠BOD=∠AOC .由EO ⊥CD 知∠AOE+∠AOC=90°,所以∠AOE+∠BOD=90°,选项B 中说法正确;由邻补角概念知∠AOD+∠BOD= 180°,选项D 中说法是正确的.只有选项C 中说法是错误的.2.A 同一平面内,过一点有且只有一条直线垂直于已知直线. 3.B 点P 到直线l 的距离就是点P 到直线l 的垂线段PB 的长度。
人教版数学七年级下册第五章《相交线与平行线》周练习含答案

人教版数学七年级下册第五章《相交线与平行线》周练习第五章相交线与平行线周周测1一选择题1. 如图:下列四个判断中,正确的个数是().①的内错角只有②的同位角是③的同旁内角是..④图中的同位角共有个A. 个B. 个C. 个D. 个2.如图,已知于点,点..在同一直线上,且,则为().A.B.C.D.3.如图,直线相交于点 ,射线平分 , ,若,则的度数为().A.B.C.D.4.如图,直线.被直线所截,则的同旁内角是()A.B.C.D.5.如图,与是内错角的是()A.B.C.D.6.如图,与是()A. 对顶角B. 同位角C. 内错角D. 同旁内角7.已知两条平行线被第三条直线所截,则以下说法不正确的是()A. 一对同位角的平分线互相平行B. 一对内错角的平分线互相平行C. 一对同旁内角的平分线互相平行D. 一对同旁内角的平分线互相垂直8.如图,直线相交于点,于,若,则不正确的结论是()A.B.C.D.9.如果点在直线上,也在直线上,但不在直线上,且直线..两两相交符合以上条件的图形是()A.B.C.D.10.如图两条非平行的直线被第三条直线所截,交点为,那么这条直线将所在平面分成()A. 个部分B. 个部分C. 个部分D. 个部分11.如图,若两条平行线,与直线,相交,则图中共有同旁内角的对数为()A.B.C.D.12.若点到直线的距离为,点到直线的距离为,则线段的长度为()A.B.C. 或D. 至少13.如图,在平面内,两条直线,相交于点,对于平面内任意一点,若,分别是点到直线,的距离,则称为点的“距离坐标”.根据上述规定,“距离坐标”是的点共有()个.A. 个B. 个C. 个D. 个14.如图,两条直线,交于点,射线是的平分线,若,则等于()A.B.C.D.15.如图,点是直线外的一点,点在直线上,且,垂足是,,则下列不正确的语句是()A. 线段的长是点到直线的距离B. 线段的长是点到直线的距离C. 三条线段中,最短D. 线段的长是点到直线的距离二填空题16.如图,与相交于点,,,则度.17.如图,在菱形中,点是对角线上的点,于点,若,则到的距离为.18.如图,标有角号的个角中共有对内错角,对同位角,对同旁内角.19.四条直线两两相交,至多会有个交点.20.如图,,,,则度.三解答题21.如图,图中共有多少对同位角,多少对内错角,多少对同旁内角.22.如图,用数字标出的八个角中,同位角.内错角.同旁内角分别有哪些?请把它们一一写出来.23.如图,直线..两两相交,射线平分,已知,,求的度数.第五章相交线与平行线周周测1 参考答案与解析一、选择题1.C2.B3.C4.C5.D6.B7.C8.C9.D 10.C 11.D 12.D13.D 解析:依题意,作与l1平行且距离为2的直线两条,作与l2平行且距离为1的直线两条,两组平行线的交点即为所求,共4个点符合题意.14.C 15.B二、填空题16.36 17.3 18.4 2 4 19.6 20.55三、解答题21.解:有6对同位角,4对内错角,4对同旁内角.22.解:同位角:∠2与∠8,∠3与∠7,∠4与∠6;内错角:∠1与∠4,∠2与∠6,∠3与∠5,∠4与∠8,;同旁内角:∠2与∠4,∠2与∠5,∠3与∠6,∠4与∠5.23.解:∵BE平分∠ABD,∠2=75°,∴∠ABE=∠2=75°,∴∠1=180°-∠ABE=∠2=180°-75°-75°=30°.∵∠1=3∠3,∴∠3=25°.∵∠3与∠4是对顶角,∴∠4=∠3=25°.第五章相交线与平行线周周测2一选择题1.如图,已知直线a,b被直线所截,那么的同位角是()A.B.C.D.2. 如图,已知三条直线,,相交于一点,则等于().A. °B. °C. °D. °3.将一副三角板按图中方式叠放,则角的度数是().A.B.C.D.4.如图,下列叙述正确的是().A. 和是内错角B. 和是同位角C. 和是同位角D. 和是同旁内角5.如图,直线,被直线所截,则的同旁内角是()A.B.C.D.6.如图:下列四个判断中,正确的个数是().①的内错角只有②的同位角是③的同旁内角是,,④图中的同位角共有个A. 个B. 个C. 个D. 个7.甲.乙.丙.丁四个学生在判断时钟的分针与时针互相垂直的时,他们每个人都说两个时间,说对的是()A. 丁说时整和时整B. 丙说时整和时分C. 乙说点分和点分D. 甲说时整和点分8.如图,直线相交于点,于,若,则不正确的结论是()A.B.C.D.9.如图,若两条平行线,与直线,相交,则图中共有内错角的对数为()A.B.C.D.10.如图,能表示点到直线的距离的线段共有()A. 条B. 条C. 条D. 条11.在一个平面上任意画条直线,最多可以把平面分成的部分是()A.B.C.D.12.如图,点是直线外的一点,点在直线上,且,垂足是,,则下列不正确的语句是()A. 线段的长是点到直线的距离B. 线段的长是点到直线的距离C. 三条线段中,最短D. 线段的长是点到直线的距离二填空题13.如图,与相交于点,,,则度.14.如图,,于,图中共有_______个直角,图中线段______的长表示点到的距离,线段_________的长表示点到的距离.15.如图,的内错角有个.16.如图,,,,则度.三解答题17.如图,图中共有多少对同位角,多少对内错角,多少对同旁内角.18.如图,用数字标出的八个角中,同位角.内错角.同旁内角分别有哪些?请把它们一一写出来.19.如图,直线,,相交于点,平分,,.求的度数.第五章相交线与平行线周周测2 参考答案与解析一、选择题1.A2.C3.D4.A5.C6.C7.A8.C9.D 10.D 11.C 12.B二、填空题13.36 14.3 CD AC 15.3 16.55三、解答题17.解:有6对同位角,4对内错角,4对同旁内角.18.解:同位角:∠2与∠8,∠3与∠7,∠4与∠6;内错角:∠1与∠4,∠2与∠6,∠3与∠5,∠4与∠8,;同旁内角:∠2与∠4,∠2与∠5,∠3与∠6,∠4与∠5.19.解:∵,,∴∠DOE=180°-∠1-∠2=180°-30°-45°=105°.∵∠DOE与∠COF是对顶角,∴∠COF=105°.∵平分,∴∠3=∠FOG=105°÷2=52.5°.第五章相交线与平行线周周测3一选择题1. 如图,已知∠1=∠2,则下列结论一定成立的是()A.AB//CD B.AD//BC C.∠B=∠D D.∠3=∠42. 下列图形中,能由∠1=∠2得到AB//CD的是()A.B. C.D.3. 如图,能判定的条件是()A.B.C.D.4. 对于图中标记的各角,下列条件能推理得到a∥b的是()A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180°5. 如图,下列条件中:(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.能判定AB∥CD的条件个数有()A.1个B.2个C.3个D.4个6. 如图,下列条件中,不能判断直线∥的是()A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°7. 如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件()A.∠2=70° B.∠2=100° C.∠2=110° D.∠3=110°8. 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的定理是()A.同位角相等两直线平行B.同旁内角互补,两直线平行C.内错角相等两直线平行D.平行于同一条直线的两直线平行9. 如图,能判定EC∥AB的条件是()A.∠B=∠ACE B.∠A+∠ACD=180°C.∠ACE=∠DCE D.∠A=∠ACE10. 如图,下列能判定AB∥CD的条件有().(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1个B.2个C.3个D.4个11. 过一点画已知直线的平行线,则( )A.有且只有一条B.有两条C.不存在D.不存在或只有一条12. 如图,能判断直线AB∥CD的条件是()A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180 o D.∠3+∠4=180 o二填空题13. 如图,两直线a.b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a.b的位置关系是____________ .14. 在同一平面内,_____________________叫作平行线.15. 如图,直线a、b被直线c所截,若满足,则a、b平行(写出一个即可).16. 已知为平面内三条不同直线,若,,则与的位置关系是.三解答题17. 看图填空:如图,∠1的同位角是,∠1的内错角是,如果∠1=∠BCD,那么,根据是;如果∠ACD=∠EGF,那么,根据是.18. 如图,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.19.已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.20.如图,已知:∠B=∠D+∠E,试说明:AB∥CD.第五章相交线与平行线周周测3 参考答案与解析一、选择题1.B2.D3.D4.D5.C6.B7.C8.C9.D 10. C 11.D 12.D二、填空题13.平行14.不相交的两条直线15.∠1=∠2(答案不唯一)16.平行三、解答题17.∠EFG ∠BCD,∠AED DE∥BC 内错角相等,两直线平行CD∥GF 同位角相等,两直线平行18. 解:∵AC平分∠DAB,,∴∠1=∠CAB.∵∠1=∠2,∴∠CAB=∠2,∴DC∥AB.19. 证明:∵∠A=∠F,∴AC∥DF,∴∠C=∠CEF.∵∠C=∠D,∴∠D=∠CEF,∴BD∥CE.20..解:过点E向右作EM//CD,则∠D=∠DEM.∵∠B=∠D+∠E,第五章相交线与平行线周周测4一选择题1.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等12第1题图第2题图第3题图2.如图,梯子的各条横档互相平行,若∠1=70°,则∠2的度数是()A.80°B.110°C.120°D.140°3.如图所示,点E 在AC 的延长线上,下列条件中能判断AB ∥CD 的是( ) A .∠3=∠4B .∠1=∠2C .∠D =∠DCE D .∠D +∠ACD =180°4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )A .第一次右拐50°,第二次左拐130°B .第一次左拐50°,第二次右拐130°C .第一次左拐50°,第二次左拐130°D .第一次右拐50°,第二次左拐50° 5.如图,下列说法中,正确的是( ) A .因为∠A +∠D =180°,所以AD ∥BC B .因为∠C +∠D =180°,所以AB ∥CD C .因为∠A +∠D =180°,所以AB ∥CDD .因为∠A +∠C =180°,所以AB ∥CD 第5题图 二 填空题6.在同一平面内,如果直线b 和c 都与直线a 垂直,那么直线b 和c的位置关系是 . 7.如图,已知∠1=∠2,由此可得 ∥ .第7题图 第8题图8.如图,已知直线、被直线所截,∠1=60°, 则当∠2= °时,∥. 9.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线和,这是根据________________,两直线平行.第9题图 第10题图10.如图,直线a 、b 与直线c 相交,给出下列条件:①∠1=∠2; ②∠4=∠6; ③∠4+∠7=180°; ④∠5+∠3=180°.其中能判断a ∥b 的条件是 (只填序号). 三 解答题11.如图,已知∠1=70°,∠2=110°,请用三种方法判定AB ∥DE.a b c a b AB CD12.已知:如图,CE平分∠ACD,∠1=∠2.求证:AB∥CD.第五章相交线与平行线周周测4 参考答案与解析一、选择题1.A2.B3.B4.D5.C二、填空题6.平行7.AD BC8.1209.内错角相等10.①③④三、解答题11. 解:(1)∵∠1=70°,∴∠AFC=180°-70°=110°.∵∠2=110°,∴∠AFC=∠2,∴AB//DE.(2)∵∠1=70°,∴∠BFD=180°-70°=110°.∵∠2=110°,∴∠BFD=∠2,∴AB//DE.(3)∵∠1=70°,∴∠AFD=70°.∵∠2=110°,∴∠AFD+∠2=180°,∴AB//DE.12.证明:∵CE平分∠ACD,,∴∠2=∠DCE.∵∠1=∠2,∴∠DCE=∠1,∴AB ∥CD.第五章 相交线与平行线周周测5一 选择题1.如果相等的两个角的一边在一条直线上,另一边互相平行,那么这两个角( ) A.相等 B.互补 C.相等或互补 D.不能确定2.如图,∠1和∠2互补,那么图中平行的直线是( ) A.b a // B.d c // C.e d // D.e c //第2题图 第4题图3.下列条件中,能得到互相垂直的是( )A.对顶角的平分线B.邻补角的平分线C.平行线的内错角的平分线D.平行线的同位角的平分线 4.如图,n m //,那么∠1.∠2.∠3的关系是( )A.∠1+∠2+∠3=360°B.∠1+∠2-∠3=180°C.∠1-∠2+∠3=180°D.∠1+∠2+∠3=180°5.一辆汽车在直路上行驶,两次拐弯后,仍按原来的方向行驶,那么这两次拐弯时( ) A.第一次向右拐30°,第二次向右拐30°B.第一次向右拐30°,第二次向右拐150°C.第一次向左拐30°,第二次向右拐150°D.第一次向左拐30°,第二次向右拐30° 6.下列命题中,是假命题的是( )A.同旁内角互补B.对顶角相等C.直角的补角仍然是直角D.两点之间,线段最短7.如图,在三角形ABC中,BC=5,∠A=70°,∠B=75°,把三角形ABC沿直线BC的方向平移到三角形DEF的位置.若CF=3,则下列结论中错误的是 ( ) A.DF=5 B.∠F=35°C.BE=3 D.AB∥DE8.如图,将周长为10个单位的三角形ABC沿边BC向右平移2个单位得到三角形DEF,则四边形ABFD周长为()A.12B.14C.16D.18第8题图第9题图第10题图9.如图是一块长方形ABCD的场地,AB=102m,AD=51m,从A.B两处入口中的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为()A.5050m2B.4900m2C.5000m2D.4998m210.如图,O是正六边形ABCDEF的中心,下列图形:三角形OCD;三角形ODE;三角形OEF;三角形OAF;三角形OAB.其中可由三角形OBC平移得到的有()A.1个B.2个C.3个D.4个二填空题11.如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC周长为16cm,则四边形ABFD周长为.第13题图第14题图第15题图12.如图,长方形ABCD的边AB=10,BC=6,则图中四个小长方形的周长和为.13.如图,在长方形ABCD中,AB=10cm,BC=6cm,若此长方形以2cm/s的速度沿着A→B方向移动,则经过 s,平移后的长方形与原来长方形重叠部分的面积为24 . 14.如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF= .15.“两数之和始终是正数”是________命题(填“真”或“假”).16.把命题“平行于同一条直线的两条直线互相平行”改写成“如果……,那么……”的形式为_______________________________________________.17.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上.下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=度.第17题图第18题图18.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有(只填序号).三解答题19.如图,点A在直线MN上,且MN//BC.求证:∠BAC+∠B+∠C=180°.M A NB C20.如图,M,N,T和P,Q,R分别在同一直线上,且∠1=∠3,∠P=∠T.求证:∠M=∠R.21.如图,直线m⊥l,n⊥l,∠1=∠2.求证:∠3=∠4.22.已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.第五章相交线与平行线周周测5 参考答案与解析一、选择题1.C2.D3.D4.B5.D6.A7.A8.B9.C 10.B二、填空题11.20 12.32 13.3 14.30°15.假16.如果两条直线平行于同一条直线,那么这两条直线互相平行17. 90 18.①②③三、解答题19.证明:∵MN∥BC,∴∠B=∠MAB,∠C=∠NAC.∵∠BAC+∠MAB+∠NAC=180°,∴∠BAC+∠B+∠C=180°.20.证明:∵∠1=∠3,∠1=∠2,∴∠2=∠3,∴PN∥QT,∴∠T=∠MNP.∵∠P=∠T,∴∠P=∠MNP,∴PR∥MT,∴∠M=∠R..21.证明:∵m⊥l,n⊥l,∴m∥n,∴∠1=∠4,∠,2=∠3.∵∠1=∠2,∴∠3=∠4.22.解:BF⊥AC.理由如下:∵∠AGF=∠ABC,∴FG∥BC,∴∠1=∠3.∵∠1+∠2=180°,∠3+∠2=180°,∴BF∥DE,∴∠BFC=∠DEC.∵DE⊥AC,∴∠DEC=90°,∴∠BFC=90°,∴BF⊥AC.第五章相交线与平行线周周测6一选择题1. 下列命题正确的是( )A.两直线与第三条直线相交,同位角相等B.两直线与第三条直线相交,内错角相等C.两直线平行,内错角相等D.两直线平行,同旁内角相等2.如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是()A.23°B.22°C.37°D.67°3.如图,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为()A.20°B.70°C.100°D.110°4.如图,∠B=∠C,AD∥BC,∠BAC=100°,则∠CAD的度数是()A.30°B.35°C.40°D.50°5.如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是()A.40°B.50°C.70°D.80°6.如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2=()A.40°B.45°C.50°D.60°7.如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于()A.30°B.45°C.60°D.75°8. 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=()A.70°B.100°C.140°D.170°9.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是()A.∠1=∠3 B.∠2+∠3=180°C.∠2+∠4<180°D.∠3+∠5=180°10.如图,已知AB∥CD,CE平分∠ACD,当∠A=120°时,∠ECD的度数是()A.45°B.40°C.35°D.30°11. 如图,点D是三角形ABC的边AB的延长线上一点,BE∥AC.若∠C=50°,∠DBE=60°,则∠CBD的度数等于()A.120°B.110°C.100°D.70°12.如图,AB∥ED,则∠A+∠C+∠D=( )A.180°B.270°C.360°D.540°二填空题13. 如图,已知AB//DE,∠ABC=75°,∠CDE=150°,则∠BCD的度数为.14.如图,已知AD∥BE,∠DAC=29°,∠EBC=45°,则∠ACB= °.15.如图,已知AB∥CD,∠1=130°,则∠2= .16.如图,AB∥CD,∠1=64°,FG平分∠EFD,则∠EGF= °.三解答题17. 如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H. ∠GFH+ ∠BHC=180°.求证:.18.如图,已知∠B=∠C,AD∥BC,求证:AD平分∠CAE.19.如图,已知AB//CD,分别写出下列四个图形中,∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以证明.20.如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.解:∵∠1=∠2(已知),∠2=∠DGF(),∴∠1=∠DGF,∴BD∥CE(),∴∠3+∠C=180º().又∵∠3=∠4(已知),∴∠4+∠C=180º,∴∥DF(同旁内角互补,两直线平行),∴∠A=∠F().第五章相交线与平行线周周测6 参考答案与解析一、选择题1.C2.C3.D4.C5.C6.C7.D8.C9.D 10.D 11.B 12.C二、填空题13.45°14.74 15.50°16.32三、解答题17.证明:∵BD平分∠ABC,∴∠2=∠ABD.∵∠GFH+∠BHC=180°,∠FHD=∠BHC,∴∠GFH+∠FHD=180°,∴FG∥BD,∴∠1=∠ABD.∵∠2=∠ABD,∴∠1=∠2.18.证明:∵AD∥BC,∴∠2=∠B,∠1=∠C.∵∠B=∠C,∴∠1=∠2,∴AD平分∠CAE.19.解:(1)∠P=360°-∠A-∠C.(2)∠P=∠A+∠C.(3)∠P=∠C-∠A.(4)∠P=∠A-∠C.若选(3),证明如下:过点P向左作PQ∥AB,则∠A=∠APQ.∵AB∥CD,∴PQ∥CD,∴∠C=∠CPQ,∴∠CPA=∠CPQ-∠APQ=∠C-∠A.20.对顶角相等同位角相等,两直线平行两直线平行,同旁内角互补AC 两直线平行,内错角相等第五章相交线与平行线周周测7一选择题1.将图①所示的图案通过平移后可以得到的图案是()A B C D 图①2.在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是()A. 先向下移动1格,再向左移动1格B. 先向下移动1格,再向左移动2格C. 先向下移动2格,再向左移动1格D. 先向下移动2格,再向左移动2格第2题图第3题图3.如图,已知三角形ABC的面积为8,将三角形ABC沿BC的方向平移到三角形A’B’C’的位置,使B’和C重合,连结AC’交A’C于D,则三角形CAC’的面积为()A.4B.6C.8D.164.四根火柴棒形成如图所示的“口”字,平移火柴棒后,原图形能变成的汉字是()5.如图,面积为12cm²的三角形ABC沿BC方向平移至三角形DEF的位置,平移的距离是边BC的2倍,则图中四边形ACFD的面积为()A.24cm²B.36cm²C.48cm²D.60cm²第5题图第6题图6.如图,小明从家到学校有①②③三条路可走,每条路的长分别为a,b,c,则()A. B. C. D.7.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积是()A.20 B.22 C.24 D.26第7题图第8题图8.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动()A.8格B.9格C.11格D.12格二填空题9.如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC周长为16cm,则四边形ABFD周长为.第9题图第10题图第11题图10.如图,将三角形ABC沿射线AC平移得到三角形DEF.若AF=17,DC=7,则AD= .11.如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为_________.12.某小区的一块长26米,宽15米的草坪内要修一条如图所示宽度相同的通道.当通道的宽度为2米时,剩下的草坪面积是通道面积的倍.第12题图第13题图第14题图13.鑫都大酒店在装修时,准备在主楼梯(如图)上铺上红地毯,已知这种地毯每平方米售价35元.楼梯宽2米,则购买这种地毯至少需元.14.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,WC=6cm,求阴影部分的面积为cm2.三解答题15.如图,已知,AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠AEF,∠1=40°,求∠2的度数.16.如图①是长方形纸带,将纸带沿EF折叠成图②,再沿BF折叠成图③.(1)若图①中∠DEF=20°,则图③中∠CFE的度数是多少?(2)若图①中∠DEF=α,把图③中∠CFE的度数用α表示是多少?17.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.求∠PAG的度数.第五章相交线与平行线周周测7 参考答案与解析一、选择题1.A2.C3.C4.B5.C6.C7.C8.A二、填空题9.20 10.5 11.24cm²12.4 13.630 14.168三、解答题15.解:∵AB∥CD,∠1=40°,∴∠AEG=∠1=40°.∵EG平分∠AEF,,∴∠AEF=2∠AEG=80°,∴∠2=180°-∠AEF=180°-80°=100°.16.解:图①中,∵AD∥BC,∴∠DEF=∠BFE,∴∠CFE=180°-∠DEF.图②中,由折叠得∠CEF=180°-∠DEF,∴∠CFB=∠CEF-∠BFE=180°-2∠DEF.图③中,由折叠得∠CFB=180°-2∠DEF,∴∠CFE=∠CFB-∠BFE=180°-3∠DEF.(1)若图①中∠DEF=20°,则图③中∠CFE=180°-3×20°=120°.(2)若图①中∠DEF=α,则图③中∠CFE=180°-3α.17.解:∵DB∥FG∥EC,∠ABD=60°,∠ACE=36°,∴∠BAG=∠ABD=60°,∠CAG=∠ACE=36°,∴∠BAC=∠BAG+∠CAG=60°+36°=96°.∵AP平分∠BAC,∴∠PAC=12∠BAC=12×96°=48°,∴∠PAG=∠PAC-∠CAG=48°-36°=12°.第五章相交线与平行线周周测8一选择题1.下列选项中能由左图平移得到的是()A. B. C. D.2.在四边形ABCD中,下列各图中∠1与∠2相等的是()3.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在()A.A点B.B点C.C点D.D点4.将命题“对顶角相等”写成“如果……,那么……”的形式,正确的是()A.如果两个角相等,那么它们是对顶角B.如果两个角是对顶角,那么它们相等C.如果对顶角,那么相等D.如果两个角不是对顶角,那么这两个角不相等5.如图,与∠1是同旁内角的是()A.∠2B.∠3C.∠4D.∠56.如图,AB//CD,∠AGE=128°,HM平分∠EHD,则∠MHD的度数是()A.46°B.23°C.26°D.24°7.如图,下列条件中,不能判断直线l1∥l2的是()A.∠1=∠3B.∠4=∠5C.∠2=∠3D.∠2+∠4=180°8.如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是()CA.60°B.65°C.70°D.80°9.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=()A.30°B.60°C.90°D.120°10.如图,已知AB∥DE,∠ABC=70º,∠CDE=140º,则∠BCD的值为( )A.70ºB.50ºC.40ºD.30º二填空题11.如图,将三角形ABC沿BC’方向平移4cm,得到三角形A’B’C’,那么CC’= cm.12.将一个直角三角板和一把长方形直尺按如图放置,若∠α=54°,则∠β的度数是______.13.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=40°,则∠AEF=.14.如图,直线a∥b,三角板的直角顶点A落在直线a上,两条直角边分别交直线b于B,C两点.若∠1=42°,则∠2的度数是.15.如图,AB∥CD,∠B=160°,∠D=120°,则∠E=_________16.如图①:MA1∥NA2,图②:MA1∥NA3,图③:MA1∥NA4,图④:MA1∥NA5,…,则第n个图中的∠A1+∠A2+∠A3+…+∠A n+1= °(用含n的代数式表示).三解答题17.完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.求证:∠EGF=90°.证明:∵HG∥AB(已知),∴∠1=∠3(______ ).又∵HG∥CD(已知),∴∠2=∠4.∵AB∥CD(已知),∴∠BEF+______=180°(______ ).又∵EG平分∠BEF(已知),∴∠1=∠______.又∵FG平分∠EFD(已知),∴∠2=∠______,∴∠1+∠2=(______ ),∴∠1+∠2=90°,∴∠3+∠4=90°(______ ),即∠EGF=90°.18.如图是一个汉字“互”字,其中,∥,∠1=∠2,∠=∠.求证:∠=∠.19.如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°. (1)证明:∠B=∠ADG;(2)求∠BCA的度数.20.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.21.如图,已知DC∥FP,∠1=∠2,∠FED=28º,∠AGF=80º,FH平分∠EFG.(1)证明:DC∥AB;(2)求∠PFH的度数.22.如图,已知AB∥CD,C在D的右侧,BM平分∠ABC,DN平分∠ADC,BM,DN所在直线交于点E,∠ADC =70°.(1)求∠EDC的度数;(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.第五章相交线与平行线周周测8参考答案与解析一、选择题1.C2.B3.A4.B5.A6.C7.C8.C9.B 10.D二、填空题11.4 12.36° 13.110° 14.48° 15.40° 16.180n三、解答题17.两直线平行,内错角相等∠EFD 两直线平行,同旁内角互补 BEF EFD ∠BEF+∠EFD 等量代换18.证明:如图,延长交于点.∵∥,∴∠1=∠3.又∵∠1=∠2,∴∠2=∠3,∴∥HN,∴∠=∠.又∵∠=∠,∴∠=∠.19.(1)证明:∵CD⊥AB,FE⊥AB,∴CD∥EF,∴∠2=∠BCD.∵∠1=∠2,∴∠1=∠BCD,∴BC∥DG,∴∠B=∠ADG.(2)解:∵DG∥BC,∴∠3=∠BCA.∵∠3=80°,∴∠BCA=80°.20.解:∵EF∥AD,AD∥BC,∴EF∥BC,∴∠ACB+∠DAC=180°.∵∠DAC=120°,∴∠ACB=60°.又∵∠ACF=20°,∴∠FCB=∠ACB﹣∠ACF=40°.∵CE平分∠BCF,∴∠BCE=20°.∵EF∥BC,∴∠FEC=∠BCE=20°.21.(1) 证明:∵∠1=∠2,∴AB∥FP.∵DC∥FP,∴DC∥AB.(2)解:∵DC∥FP,∴∠EFP=∠FED=28º.∵AB∥FP,∴∠GFP=∠AGF=80º.∴∠EFG=∠EFP+∠GFP=28°+80°=108°.∵FH平分∠EFG,∴∠EFH=∠EFG=×108°=54°,∴∠PFH=∠EFH-∠EFP=54°-28°=26 º.22.解:(1)∵DE平分∠ADC,∠ADC=70°,∴∠EDC=∠ADC=×70°=35°.(2)如图,过点E向左作EF∥AB.∵AB∥CD,∴AB∥CD∥EF,∴∠ABE=∠BEF,∠CDE=∠DEF.∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,∴∠BED=∠BEF+∠DEF=n°+35°.(3)如图①,过点E向左作EF∥AB.∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°.∵AB∥CD,∴AB∥CD∥EF,∴∠BEF=180°-∠ABE=180°-n°,∠CDE=∠DEF=35°,∴∠BED=∠BEF+∠DEF=180°-n°+35°=215°-n°.图①图②如图②,过点E向左作EF∥AB.∵BM平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,∴∠ABM=∠ABC=n°,∠CDE=∠ADC=35°.∵AB∥CD,∴AB∥CD∥EF,∴∠BEF=∠ABM=n°,∠CDE=∠DEF=35°,∴∠BED=∠BEF-∠DEF=n°-35°.综上所述,∠BED的度数发生了改为,改变为215°-n°或n°-35°.第五章相交线与平行线周周测9一选择题1.点P为直线l外一点,点A,B,C为直线l上三点,P A=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为()A.4cm B.5cmC.小于3cm D.不大于3cm2.如图,点E,F分别是AB,CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断中,错误的是()A.∠AEF=∠EFC B.∠A=∠BCFC.∠AEF=∠EBC D.∠BEF+∠EFC=180°第2题图第3题图3.如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,且∠ODE与∠ADC相等,则∠DEB的度数是()A.75°36′ B.75°12′ C.74°36′ D.74°12′4.下列图形中,可以由其中一个图形通过平移得到的是()5.如图①~④,其中∠1与∠2是同位角的有()A.①②③④B.①②③C.①③D.①第5题图第6题图6.如图,能判断直线AB∥CD的条件是()A.∠1=∠2 B.∠3=∠4C.∠1+∠3=180° D.∠3+∠4=180°7.有下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④内错角相等.其中假命题有()A.①②B.①③C.②④D.③④8.若∠1与∠2是对顶角且互补,则它们两边所在的直线()A.互相垂直B.互相平行C.既不垂直也不平行D.不能确定9.如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为() A.65° B.60° C.55° D.50°第9题图第10题图10.已知直线m∥n,将一块直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=20°,则∠2的度数为()A.20° B.30°C.45° D.50°二填空题11.如图,当剪刀口∠AOB增大21°时,∠COD增大________°.第11题图第12题图12.如图,平行线AB,CD被直线AE所截,∠1=50°,则∠A=________°.13.如图,在线段AC,BC,CD中,线段________最短,理由是____________________.第13题图第14题图14.如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD的度数为________.15.如图,直线l1∥l2,∠1=20°,则∠2+∠3=________°.第15题图第17题图16.平移变换不仅与几何图形有着密切的联系,而且在一些特殊结构的汉字中,也有平移变换的现象,如:“日”“朋”“森”等,请你再写两个具有平移变换现象的汉字_____ ___.17.如图是超市里购物车的侧面示意图,扶手AB与车底CD平行,∠2比∠3大10°,∠1是∠2的1911倍,则∠2的度数是________.18.以下三种沿AB折叠纸带的方法:(1)如图①,展开后测得∠1=∠2;(2)如图②,展开后测得∠1=∠2且∠3=∠4;(3)如图③,测得∠1=∠2.其中能判定纸带两条边线a,b互相平行的是________(填序号).三解答题19.如图,直线AB,CD相交于O,OE是∠AOD的平分线,∠AOC=28°,求∠AOE的度数.20.如图,在方格纸中,每个小方格的边长均为1个长度单位,三角形ABC的三个顶点和点P都在小方格的顶点上.要求:①将三角形ABC平移,使点P落在平移后的三角形内部;②平移后的三角形的顶点在方格的顶点上.请你在图甲和图乙中分别画出符合要求的一个示意图,并写出平移的方法.21.如图,已知AE⊥BC,FG⊥BC,∠1=∠2.求证:AB∥CD.22.如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.(1)直接写出图中∠AOC的对顶角为________,∠BOE的邻补角为________;(2)若∠AOC=70°,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.23.如图,现有以下3个论断:①AB∥CD;②∠B=∠C;③∠E=∠F.请以其中2个论断为条件,另一个论断为结论构造命题.(1)你构造的是哪几个命题?(2)你构造的命题是真命题还是假命题?请选择其中一个真命题加以证明.24.如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……第n次操作,分别作∠ABE n-1和∠DCE n-1的平分线,交点为E n.(1)如图①,求证:∠BEC=∠B+∠C;(2)如图②,求证:∠BE2C=14∠BEC;(3)猜想:若∠E n=b°,求∠BEC的度数.第五章相交线与平行线周周测9 参考答案与解析一、选择题1.D2.C3.B4.B5.C6.D7.D8.A9.A 10.D二、填空题11.21 12.50 13.CD 垂线段最短14.22°15.20016.林晶(答案不唯一)17.55°18.①②三、解答题19.解:∵∠AOC=28°,∴∠AOD=180°-∠AOC=180°-28°=152°.∵OE是∠AOD的平分线,∴∠AOE=12∠AOD=12×152°=76°.20.解:如图,共有3种情况:图甲图乙图丙图甲:将三角形ABC向右平移4个单位长度;图乙:将三角形ABC先向右平移4个单位长度,再向上平移1个单位长度;图丙:将三角形ABC先向右平移3个单位长度,再向上平移1个单位长度.21.证明:∵AE⊥BC,FG⊥BC,∴AE∥FG,∴∠1=∠A.∵∠1=∠2,∴∠2=∠A,∴AB∥CD.22.解:(1)∠BOD ∠AOE(2)∵∠AOC=70°,∴∠BOD=70°.∵∠BOE∶∠EOD=2∶3,∴∠BOE=25∠BOD=25×70°=28°,∴∠AOE=180°-∠BOE=180°-28°=152°.23.解:(1)命题一:如果AB∥CD,∠B=∠C,那么∠E=∠F.命题二:如果AB∥CD,∠E=∠F,那么∠B=∠C.命题三:如果∠B=∠C,∠E=∠F,那么AB∥CD.(2)三个命题都是真命题.若选择命题(1),证明如下:∵AB∥CD,∴∠B=∠CDF.∵∠B=∠C,∴∠CDF=∠C,∴AC∥BD,∴∠E=∠F.24.(1)证明:过点E向左作EF∥AB.∵AB∥CD,∴AB∥CD∥EF,∴∠BEC=∠B,∠CEF=∠C,∴∠BEC=∠BEF+∠CEF=∠B+∠C.(2)证明:同(1)理,可证∠BE1C=∠ABE1+∠DCE1,∠BE2C=∠ABE2+∠DCE2.∵∠ABE和∠DCE的平分线交于点E1,∠ABE1和∠DCE1交于点E2,∴∠ABE1=12∠ABE,∠DCE1=12∠DCE,∠ABE2=12∠ABE1,∠DCE2=12∠DCE1,∴∠BE1C=12∠ABE+12∠DCE=12∠BEC,∴∠BE2C=12×12∠ABE+12×12∠DCE=14∠BEC.(3)由(1)(2)知∠BE1C=12∠BEC,∠BE2C=14∠BEC,∴∠∠BE n C=12n⎛⎫⎪⎝⎭∠BEC,∴若∠E n=b°,∠BEC=2n。
数学七年级下册 第5章 《相交线与平行线》 常考题型训练(五)(含答案)

七年级下册《相交线与平行线》常考题型训练(五)1.如图,直线AB和直线CD相交于点O,OF平分∠COE,过点O作OG⊥OF.(1)若∠AOE=80°,∠COF=22°,则∠BOD=;(2)若∠COE=40°,试说明:OG平分∠DOE.2.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN 上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ 平分∠EPK,求∠HPQ的度数.3.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE 交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.(1)求证:BE∥CF;(2)若∠C=35°,求∠BED的度数.4.如图,已知AB∥CD,∠ABE的平分线与∠CDE的平分线相交于点F.(1)在图1中,求证:①∠ABE+∠CDE+∠E=360°;②∠ABF+∠CDF=∠BFD;(2)如图2,当∠ABM=∠ABF,∠CDM=∠CDF时,请你写出∠M与∠E之间的关系,并加以证明;(3)当∠ABM=∠ABF,∠CDM=∠CDF,且∠E=m°时,请你直接写出∠M的度数(用含m,n的式子表示)5.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.(1)求证:AB∥CD;(2)若FG⊥BC于点H,BC平分∠ABD,∠D=112°,求∠1的度数.6.将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.(1)①若∠DCE=45°,则∠ACB的度数为.②若∠ACB=140°,则∠DCE的度数为.(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<90°且点E在直线AC的上方时,当这两块角尺有一组边互相平行时,请写出∠ACE角度所有可能的值.并说明理由.7.已知,AB∥CD,点E为射线AB上一点,连接CE,∠ACE=n∠DCE,∠BAC=α.(1)如图1,若n=5,α=60°,则∠BEC=(直接写出结果);(2)如图2,点F为CE延长线上一点,连接AF,若n=3,试判断∠F,∠BAC,∠BAF 之间的数量关系,并说明理由;(3)点F为射线CE上一点(不与点C,E重合).若n=1,AM平分∠F AC,交CF于点M,∠BAM=20°,直接写出∠AFC的度数(用含α的式子表示).8.已知:∠BDG+∠EFG=180°,∠B=∠DEF.(1)如图1,求证:DE∥BC.(2)如图2,当∠A=∠EFG=90°时,请直接写出与∠C互余的角.9.已知直线BC∥ED.(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上,求证:∠ACG=∠BAC+∠ABC;(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.10.等角转化如图1,已知点A是BC外一点,连结AB、AC,求∠BAC+∠B+∠C的度数.(1)阅读并补充下面的推理过程解:过点A作ED∥BC,∴∠B=∠EAB,∠C=()又∵∠EAB+∠BAC+∠DAC=180°∴∠B+∠BAC+∠C=180°从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC、∠B、∠C “凑”在一起,得出角之间的关系,使问题得以解决.(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数(提示:过点C作CF∥AB);(3)如图3,已知AB∥CD,点C在点D的右侧,∠ADC=80°,点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,点E在两条平行线AB与CD之间,求∠BED的度数.参考答案1.解:(1)∵OF平分∠COE,∠COF=22°,∴∠COE=2∠COF=44°,∵若∠AOE=80°,∴∠AOC=∠AOE﹣∠COE=80°﹣44°=36°,∴∠BOD=∠AOC=36°;故答案为:36°;(2)∵∠COE=40°,OF平分∠COE,∴∠COF=∠EOF=COE=20°,∵OG⊥OF,∴∠FOG=90°,∴∠EOG=70°,∠COG=∠COF+∠FOG=20°+90°=110°,∴∠DOG=180°﹣∠COG=70°,∴∠EOG=∠DOG=70°,∴OG平分∠DOE.2.解:(1)AB∥CD,理由如下:∵∠1与∠2互补,∴∠1+∠2=180°,又∵∠1=∠AEF,∠2=∠CFE,∴∠AEF+∠CFE=180°,∴AB∥CD;(2)由(1)知,AB∥CD,∴∠BEF+∠EFD=180°.又∵∠BEF与∠EFD的角平分线交于点P,∴,∴∠EPF=90°,即EG⊥PF.∵GH⊥EG,(3)∵∠PHK=∠HPK,∴∠PKG=2∠HPK.又∵GH⊥EG,∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK.∴∠EPK=180°﹣∠KPG=90°+2∠HPK.∵PQ平分∠EPK,∴.∴∠HPQ=∠QPK﹣∠HPK=45°.答:∠HPQ的度数为45°.3.(1)证明:方法一:∵∠1=∠2,∠2=∠BFG,∴∠1=∠BFG,∴AC∥DG,∴∠ABF=∠BFG,∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,∴∠EBF=∠ABF,BFG,∴∠EBF=∠CFB,∴BE∥CF;方法二:∵∠1=∠2,∠1=∠ABF,∠2=∠BFG,∴∠ABF=∠BFG,∵∠ABF的平分线是BE,∠BFG的平分线是FC,∴∠EBF=∠ABF,BFG,∴∠EBF=∠CFB,∴BE∥CF;(2)解:∵AC∥DG,BE∥CF,∠C=35°,∴∠C=∠CFG=35°,∴∠CFG=∠BEG=35°,∴∠BED=180°﹣∠BEG=145°.4.解:(1)①如图1,过点E作EN∥AB,∴∠ABE+∠BEN=180°,∵AB∥CD,AB∥NE,∴NE∥CD,∴∠CDE+∠NED=180°,∴∠ABE+∠E+∠CDE=360°;②如图1,过点F作FG∥AB,∵FG∥AB,∴∠ABF=∠BFG,∵AB∥CD,FG∥AB,∴FG∥CD,∴∠CDF=∠GFD,∴∠ABF+∠CDF=∠BFG+∠GFD=∠BFD;(2)结论:∠E+∠M=360°,理由是:∵设∠ABM=x,∠CDM=y,则∠FBM=2x,∠EBF=3x,∠FDM=2y,∠EDF=3y,由(1)得:∠ABE+∠E+∠CDE=360°,∴6x+6y+∠E=360°,∵∠M+∠EBM+∠E+∠EDM=360°,∴6x+6y+∠E=∠M+5x+5y+∠E,∴∠M=x+y,∴∠E+6∠M=360°;(3)设∠ABM=x,∠CDM=y,则∠FBM=(n﹣1)x,∠EBF=nx,∠FDM=(n﹣1)y,∠EDF=ny,由(1)可得:∠ABE+∠E+∠CDE=360°,∴2nx+2ny+∠E=360°,∴x+y=,∵∠M+∠EBM+∠E+∠EDM=360°,∴2nx+2ny+∠E=∠M+(2n﹣1)x+(2n﹣1)y+∠E,∴∠M=.5.(1)证明:∵FG∥AE,∴∠2=∠3,∵∠1=∠2,∴∠1=∠3,∴AB∥CD.(2)解:∵AB∥CD,∴∠ABD+∠D=180°,∵∠D=112°,∴∠ABD=180°﹣∠D=68°,∵BC平分∠ABD,∴∠4=∠ABD=34°,∵FG⊥BC,∴∠1+∠4=90°,∴∠1=90°﹣34°=56°.6.解:(1)①∵∠DCE=45°,∠ACD=90°∴∠ACE=45°∵∠BCE=90°∴∠ACB=90°+45°=135°故答案为:135°;②∵∠ACB=140°,∠ECB=90°∴∠ACE=140°﹣90°=50°∴∠DCE=90°﹣∠ACE=90°﹣50°=40°故答案为:40°;(2)猜想:∠ACB+∠DCE=180°理由如下:∵∠ACE=90°﹣∠DCE又∵∠ACB=∠ACE+90°∴∠ACB=90°﹣∠DCE+90°=180°﹣∠DCE即∠ACB+∠DCE=180°;(3)30°、45°.理由:当CB∥AD时,∠ACE=30°;当EB∥AC时,∠ACE=45°.7.解:(1)如图1,∠ACE=5∠DCE,∠BAC=60°,∵AB∥CD,∴∠BAC+∠ACD=180°,∴∠ACD=180°﹣60°=120°,∵∠ACE=5∠DCE∴∠ACE=∠ACD=×120°=100°,∴∠BEC=∠A+∠ACE=60°+100°=160°;故答案为160°;(2)如图2,∠ACE=3∠DCE,∵AB∥CD,∴∠BAC+∠ACD=180°,∴∠ACD=180°﹣α,∵∠ACE=3∠DCE∴∠ACE=∠ACD=(180°﹣α)=135°﹣α∴∠BEC=∠A+∠ACE=α+135°﹣α=135°+α∵∠AEF=∠BEC,∴∠F+∠BAF+135°+α=180°,∴∠F+∠BAF+∠BAC=45°;(3)当AM在AB下方时,如图1,∵∠BAM=20°,∴∠CAM=α﹣20°,∵AB∥CD,∴∠BAC+∠ACD=180°,∴∠ACD=180°﹣α,∵∠ACE=∠DCE∴∠ACE=∠ACD=(180°﹣α)=90°﹣α∴∠AMC=180°﹣(90°﹣α)﹣(α﹣20°)=110°﹣α,∵AM平分∠F AC,∴∠F AM=∠CAM=α﹣20°,∵∠AMC=∠AFC+∠F AM,∴∠AFC=110°﹣α﹣(α﹣20°)=130°﹣α;当AM在AB上方,如图4,∵∠BAM=20°,∴∠CAM=α+20°,而∠ACE=∠ACD=90°﹣α∴∠AMC=180°﹣(90°﹣α)﹣(α+20°)=70°﹣α,∵AM平分∠F AC,∴∠F AM=∠CAM=α+20°,∵∠AMC=∠AFC+∠F AM,∴∠AFC=70°﹣α﹣(α+20°)=50°﹣α;综上所述,∠AFC的度数为50°﹣α或130°﹣α.故答案为50°﹣α或130°﹣α.8.(1)证明:∵∠EFD+∠EFG=180°,∠BDG+∠EFG=180°,∴∠BDG=∠EFD,∴BD∥EF,∴∠BDE+∠DEF=180°,又∵∠DEF=∠B,∴∠BDE+∠B=180°,∴DE∥BC;(2)解:∵∠A=∠EFG=90°,∴∠ADE+∠AED=90°,∠B+∠C=90°,∵DE∥BC,∴∠ADE=∠B,∵∠B=∠DEF,∴与∠C互余的角有∠B,∠ADE,∠DEF.9.解:(1)∵BC∥ED,∠B=44°,∴∠DAB=∠B=44°,∵∠BAC=180°﹣∠DAB﹣∠EAC∴∠BAC=180°﹣44°﹣57°=79°.(2)过点A作MN∥BG,∴∠ACG=∠MAC,∠ABC=∠MAB而∠MAC=∠MAB+∠BAC∴∠ACG=∠MAB+∠BAC=∠ABC+∠BAC.(3)如图,设AC与FH交于点P∵FH平分∠AFE,CH平分∠ACG∴∠AFH=∠EFH=∠AFE,∠ACH=∠HCG=∠ACG ∵BC∥ED∴∠AFE=∠B∴∠AFH=∠B∵∠A+∠B=∠ACG∴∠ACH=∠ACG=∠A+∠B在△APF和△CPH中∵∠APF=∠CPH∴∠A+∠B=∠A+∠B+∠FHC∴∠FHC=∠A∵∠FCH=2∠A﹣60°∴∠A=2∠A﹣60°∴∠A=40°.10.解:(1)∵ED∥BC,∴∠B=∠EAB,∠C=∠DAC(两直线平行,内错角相等);(2)过C作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠D=∠FCD,∵CF∥AB,∴∠B=∠BCF,∵∠BCF+∠BCD+∠DCF=360°,∴∠B+∠BCD+∠D=360°,(3)如图3,过点E作EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠ABE=∠BEF,∠CDE=∠DEF,∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=80°,∴∠ABE=∠ABC=30°,∠CDE=∠ADC=40°,∴∠BED=∠BEF+∠DEF=30°+40°=70°.故答案为:∠DAC;两直线平行,内错角相等.。
七年级下学期数学第五章相交线与平行线测试题(新人教版)

4321七年级下学期数学第五章相交线及平行线测试题(新人教版)班级 姓名 (时间100分,满分120分)一、选择题:(每题3分,共48分) 1、在同一平面内,如果两条直线不重合,那么它们( )。
A .平行B.相交C.相交、垂直 D.平行或相交2、如果两条平行线被第三条直线所截,那么其中一组同位角角平分线( )。
A.垂直B.相交C.平行D.不能确定3、一辆汽车在笔直公路上行驶,在两次转弯后,仍在原来方向上平行前进,那么这两次转弯角度可以是( )。
A 、先右转80°,再左转100°B 、先左转80°,再右转80°C 、先左转80°,再右转100°D 、先右转80°,再右转80°4、如右图AB ∥CD ,则∠1=( )。
A 、75°B 、80°C 、85°D 、95°5、已知:OA OC ⊥,:2:3AOB AOC ∠∠=,则BOC ∠度数为( )。
A.30︒B.60︒C.150︒D.30︒或150︒6、如图,已知12355∠=∠=∠=︒,则4∠度数是( )。
A.110︒ B.115︒ C.120︒D.125︒7、将一直角三角板及两边平行纸条如图所示放置,下列结论:(1)∠1=∠2; (2)∠3=∠4; (3)∠2+∠4=90°;(4)∠4+∠5=180° 其中正确个数是( )A.1B.2 C.3D.48、下列说法中,正确是( )。
A.不相交两条直线是平行线.B.过一点有且只有一条直线及已知直线平行.C.从直线外一点作这条直线垂线段叫做点到这条直线距离.D.在同一平面内,一条直线及两条平行线中一条垂直,则及另一条也垂直.9、1∠和2∠是两条直线1l ,2l 被第三条直线3l 所截同旁内角,如果12l l ∥,那么必有( ).A.∠1=∠2 B.∠1+∠2=90° C.D.∠1是钝角,∠2是锐角21EDC BA4321DCB A1()5()4()3()2()222211112121F E DCBA21EDCBAHGFEDBCA110、如右图,AB DE ∥,那么BCD ∠=( ).A.21∠-∠ B.12∠+∠ C.18012︒+∠-∠ D.180221︒+∠-∠ 11、如右图,在下列条件中:①∠1=∠2;②∠BAD =∠BCD ; ③∠ABC =∠ADC 且∠3=∠4;④∠BAD +∠ABC =180°, 能判定AB ∥CD 有( ).A.3个 B.2个 C.1个 D.0个12、下列说法错误是( )A.内错角相等,两直线平行. B.两直线平行,同旁内角互补. C.相等角是对顶角. D.等角补角相等. 13、下列图中∠1和∠2是同位角是( )A. ⑴、⑵、⑶,B. ⑵、⑶、⑷,C. ⑶、⑷、⑸,D. ⑴、⑵、⑸14、已知:如右图, 12∠∠=, 则有( )A.AB CD ∥B.AE DF ∥C. AB CD ∥且AE DF ∥D.以上都不对15、如图,直线AB 及CD 交于点O ,OE AB ⊥于O ,图1∠及2∠关系是( )A.对顶角B.互余C.互补 D 相等16、如图,DH EG BC ∥∥,且DC EF ∥,那么图中和∠1相等角个数是( )A.2,B. 4,C. 5,D. 6第15题 第16题 二、填空题(1-6题每题3分,7-13题每题4分,第14题5分,共51分) 1、小玮家在小强家北偏西75度,则小强家在小玮家坐标方向是 度 。
新人教版相交线与平行线经典练习5.1-5.2

相交线与平行线5.1-5.2(一)姓名一、选择题:1.如图,四个图形中的∠1和∠2,不是同位角的是()2.如图,在下列给出的条件中个,不能判断AB// FE的是()A.∠B+∠2=1800B.∠B=∠3C.∠1=∠4D.∠1=∠B3.图中有直线L截过两直线L1、L2后所形成的八个角,由下列哪一个选项中的条件可判断L1// L2?()A.∠2+∠4=180︒B.∠3+∠8=180︒C.∠5+∠6=180︒D.∠7+∠8=180︒4.如图,如果AC⊥BC,CD⊥AB,∠1=∠2,那么:①∠1=∠B;②∠A=∠B;③AC//DE;④∠2与∠A互余;⑤∠2=∠A;⑥A,C两点的距离是线段AC的长。
这六个结论中,正确的个数是()A.3B.4C.5第5题第6题5.如图、下列判断正确的是( )A.∵∠l=∠2,∴DE∥BFB.∵∠1=∠2,∴CE∥AFC.∵∠CEF+∠AFE=180°,∴DE∥BFD.∵∠CEF+∠AFE=180°,∴CE∥AF6、如图,∠1=∠2,则下列结论一定成立的是()A AB∥CDB AD∥BC C ∠B=∠D D ∠3=∠47、阅读下列推理过程,在括号中填写理由:已知:如图9,∠1=78°,∠2=78°,∠3=78°,∠4=102°。
1432图2A B CD∵∠1=∠2=78°∴AB ∥CD ( )∵∠2=∠3=78°∴AB ∥CD ( )∵∠2+∠4=78°+102°=180°∴AB ∥CD ( )8.在同一平面内的三条直线,如果要使其中两条且只有两条平行,那么它们( )A.有三个交点B.只有一个交点C.有两个交点D.没有交点9.在平面内有两两相交的3条直线,如果最多有m 个交点,最少有n 个交点,那么mn =() A.0 B.1 C.3 D.610.若∠α与∠β是同旁内角,∠α=50°,则∠β的度数是( )A.50°B.130°C.50°或130°D.不能确定11.如图,图中同旁内角的对数是( )A.2对B.3对C.4对D.5对12.如图,能与 构成同位角的有( )A. 1个B. 2个C. 3个D. 4个13、如图(13)∠EFB=∠GHD=550,∠IGA=1270 ,由这些条件,你能找到几对平行线? 说说你的理由。
七年级数学下册 第五章 相交线与平行线5.2 平行线及其判定 5.2.1平行线练习(含解析)(新版)

5。
2。
1平行线分卷I一、选择题(共27小题,每小题分,共0分) 1。
已知直线a、b、c在同一平面内,则下列说法错误的是() A.如果a∥b,b∥c,那么a∥cB.a⊥b,c⊥b,那么a∥cC.如果a与b相交,b与c相交,那么a与c一定相交D.如果a与b相交,b与c不相交,那么a与c一定相交2.己知直线AB及AB外一点P,若过点P作一直线与AB平行,那么这样的直线( )A.有且只有一条B.有两条C.不存在D.无数条3.下列画图方法,一定可以画出的是( )A.过点P画线段CD,使线段CD与已知线段AB相交B.过点P画线段CD,使线段CD与已知射线AB相交C.过射线AB外一点P画直线CD,使CD∥ABD.过直线AB外一点P画射线CD,使AB与CD相交4.下列说法中,正确的是()A.两条不相交的直线叫做平行线B.一条直线的平行线有且只有一条C.若直线a∥b,a∥c,则b∥cD.若两条线段不相交,则它们互相平行5.下列语句:①不相交的两条直线叫平行线;②在同一平面内,两条直线的位置关系只有两种:相交和平行;③如果线段AB和线段CD不相交,那么直线AB和直线CD平行;④如果两条直线都和第三条直线平行,那么这两条直线平行;⑤过一点有且只有一条直线与已知直线平行.正确的个数是( )A. 1B. 2C. 3D. 46.过一点画已知直线的平行线()A.有且只有一条B.不存在C.有两条D.不存在或有且只有一条7.下为说法中正确的个数是()①射线AB与射线BA是同一条射线;②两点确定一条直线;③对顶角相等;④不相交的两条直线叫做平行线;⑤过一点有只有一条直线与这条直线平行.A. 1B. 2C. 3D. 48.下列说法中正确的是()A.在同一平面内,两条直线的位置只有两种:相交和垂直B.有且只有一条直线垂直于已知直线C.如果两条直线都与第三条直线平行,那么这两条直线也互相平行D.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离9.已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是()A.相交B.平行C.垂直D.平行或相交10。
人教版初一数学七年级下册第5章相交线与平行线5.1相交线同步训练题含答案

人教版初一数学七年级下册第5章相交线与平行线5.1相交线同步训练题含答案1. 以下说法正确的选项是( )A.垂线最短B.对顶角相等C.两点之间直线最短D.过一点有且只要一条直线垂直于直线2. 如图,直线AB,CD相交于点O,假定∠1+∠2=100°,那么∠BOC等于( )A.130° B.140° C.150° D.160°3. 如图,能表示点到直线的距离的线段共有( )A.2条 B.3条 C.4条 D.5条4. 如图,直线a,b被直线c所截,那么以下说法中错误的选项是( ) A.∠1与∠2是邻补角 B.∠1与∠3是对顶角C.∠2与∠4是同位角 D.∠3与∠4是内错角5. 如图,直线AB,CD相交于点O,以下条件中,不能说明AB⊥CD的是( ) A.∠AOD=90° B.∠AOC=∠BOCC.∠BOC+∠BOD=180° D.∠AOC+∠BOD=180°6. 如图,∠F的内错角有_____________.7. 如下图,AB交CD于点O,∠AOC=60°,那么∠AOD的度数为_______.8. 如图,直线l1,l2被直线l3所截,那么图中同位角有_____对.9. 图所示,一个破损的扇形零件,应用图中的量角器可以量出这个扇形零件的圆心角的度数,测量的依据是_________.10. 如图,要把小河里的水引到田地A处,那么作AB⊥l,垂足为点B,沿AB 挖水沟,水沟最短,理由是______________.11. 如图,直线AB,CD相交于点O,OE平分∠BOC,∠COE=65°,那么∠BOD =________°.12. 两条直线都与第三条直线相交,∠1和∠2是内错角,∠3和∠2是邻补角.(1)依据上述条件,画出契合题意的图形;(2)假定∠1∶∠2∶∠3=1∶2∶3,求∠1,∠2,∠3的度数.13. 如图,直线AB,CD相交于点O,过点O作两条射线OM,ON,且∠AOM=∠CON=90°.(1)假定OC平分∠AOM,求∠AOD的度数;(2)假定∠1=∠BOC,求∠AOC和∠MOD.参考答案:1---11 BADDC6. ∠AEF和∠ADF7. 120°8. 49. 对顶角相等10. 垂线段最短11. 5012. 解:(1)如图:(2)由∠1∶∠2∶∠3=1∶2∶3,设∠1=x°,∠2=2x°,∠3=3x°.由∠2与∠3是邻补角,得∠2+∠3=2x°+3x°=180°,解得x=36,2x=72,3x=108.所以∠1=36°,∠2=72°,∠3=108°.13. 解:(1)由于∠AOM=∠CON=90°,OC平分∠AOM,所以∠1=∠AOC=45°,所以∠AOD=180°-∠AOC=180°-45°=135°.(2)由于∠AOM=90°,所以∠BOM=180°-90°=90°.由于∠1=∠BOC,所以∠1=∠BOM=30°,所以∠AOC=90°-30°=60°,∠MOD=180°-30°=150°.。
七年级数学下册5相交线与平行线周周练5.1_5.2新版10(1)

周周练(5.1~5.2)(时间:45分钟满分:100分)一、选择题(每小题4分,共32分)1.邻补角是指(D)A.和为180°的两个角B.有一条公共边且相等的两个角C.有公共顶点且互补的两个角D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角2.如图,∠1和∠2是对顶角的是(B)A B C D3.(宿迁中考)如图所示,直线a,b被直线c所截,∠1与∠2是(A)A.同位角B.内错角C.同旁内角D.邻补角4.(厦门中考改编)如图,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是(B) A.线段CA的长B.线段CD的长C.线段AD的长D.线段AB的长5.下列说法错误的是(C)A.两条直线相交,有一个角是直角,则两条直线互相垂直B.若两对顶角之和为180°,则两直线互相垂直C.两直线相交,所构成的四个角中,若有两个角相等,则两直线互相垂直D.在同一平面上,过点A作直线l的垂线,这样的垂线只有一条6.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是(C) A.20°B.40°C.50°D.80°7.(平顶山期末)如图,下列条件不能判断直线l1∥l2的是(A)A.∠1=∠3 B.∠1=∠4C.∠2+∠3=180°D.∠3=∠58.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是(B) A.先向左转130°,再向左转50°B.先向左转50°,再向右转50°C.先向左转50°,再向右转40°D.先向左转50°,再向左转40°二、填空题(每小题4分,共24分)9.如图,已知∠1+∠2=100°,则∠3=130°.10.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是153°.11.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.12.如图,在同一平面内,OA⊥l,OB⊥l,垂足为O,则OA与OB重合的理由是同一平面内,过一点有且只有一条直线与已知直线垂直.13.(浦东新区期中)如图,要使AD∥BC,需添加一个条件,这个条件可以是∠1=∠4.(只需写出一种情况)14.如图所示,AB与BC被AD所截得的内错角是∠1和∠3;DE与AC被直线AD所截得的内错角是∠2和∠4;图中∠4的内错角是∠5和∠2.三、解答题(共44分)15.(6分)如图,已知AB⊥AD,CD⊥AD,∠1=∠2,完成下列推理过程:∵AB⊥AD,CD⊥AD(已知),∴∠BAD=∠CDA=90°(垂直的定义).又∵∠1=∠2(已知),∴∠BAD-∠1=∠CDA-∠2,即∠DAE=∠ADF.∴DF∥AE(内错角相等,两直线平行).16.(6分)如图,直线AO,BO交于点O,过点P作PC⊥AO于C,PD⊥BO于D,画出图形.解:作∠ACP=90°,作∠PDB=90°,则直线PC、PD即为所求.17.(6分)如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明AB∥CD.解:∵OF平分∠EOD,∠FOD=25°,∴∠EOD=2∠FOD=50°.又∵∠OEB=130°,∴∠OEB+∠EOD=180°.∴AB∥CD.18.(8分)如图,已知∠1=∠2,∠3+∠4=180°,求证:AB∥EF.证明:∵∠1=∠2,∴AB∥C D.∵∠3+∠4=180°,∴CD∥EF.∴AB∥EF.19.(8分)如图,AB和CD交于O点,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.解:∵AB,CD相交于点O,∴∠BOD=∠AOC=40°.∵OD平分∠BOF,∴∠DOF=∠BOD=40°.∵OE⊥CD,∴∠EOD=90°.∴∠EOF=∠EOD+∠DOF=130°.20.(10分)我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气,同样会发生折射现象.如图所示是光线从空气射入水中,再从水中射入空气的示意图.由于折射率相同,已知∠1=∠4,∠2=∠3,请你用所学知识来判断光线c与光线d是否平行?并说明理由.解:c∥d.理由如下:∵∠1+∠5=180°,∠4+∠6=180°,∠1=∠4,∴∠5=∠6.∵∠2=∠3,∴∠2+∠5=∠3+∠6.∴c∥d.。
2019最新部编RJ人教版 初中七年级数学 下册第二学期(含解析答案) 第五章 相交线与平行线周周测4(5.2)

第五章 相交线与平行线周周测4(时限:100分钟 满分:100分)一 选择题1.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( ) A .同位角相等,两直线平行 B .内错角相等,两直线平行C .两直线平行,同位角相等D .两直线平行,内错角相等第1题图 第2题图 第3题图2.如图,梯子的各条横档互相平行,若∠1=70°,则∠2的度数是( ) A .80°B .110°C .120°D .140° 3.如图所示,点E 在AC 的延长线上,下列条件中能判断AB ∥CD 的是( ) A .∠3=∠4B .∠1=∠2C .∠D =∠DCE D .∠D +∠ACD =180°4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )A .第一次右拐50°,第二次左拐130°B .第一次左拐50°,第二次右拐130°C .第一次左拐50°,第二次左拐130°D .第一次右拐50°,第二次左拐50° 5.如图,下列说法中,正确的是( ) A .因为∠A +∠D =180°,所以AD ∥BC B .因为∠C +∠D =180°,所以AB ∥CD C .因为∠A +∠D =180°,所以AB ∥CDD .因为∠A +∠C =180°,所以AB ∥CD 第5题图 二 填空题6.在同一平面内,如果直线b 和c 都与直线a 垂直,那么直线b 和c 的位置关系是 .7.如图,已知∠1=∠2,由此可得 ∥ .第7题图第8题图8.如图,已知直线a、b被直线c所截,∠1=60°,则当∠2=°时,a∥b.9.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线AB和CD,这是根据________________,两直线平行.第9题图第10题图10.如图,直线a、b与直线c相交,给出下列条件:①∠1=∠2;②∠4=∠6;③∠4+∠7=180°;④∠5+∠3=180°.其中能判断a∥b的条件是(只填序号).三解答题11.如图,已知∠1=70°,∠2=110°,请用三种方法判定AB∥DE.12.已知:如图,CE平分∠ACD,∠1=∠2.求证:AB∥CD.第五章相交线与平行线周周测4 参考答案与解析一、选择题1.A2.B3.B4.D5.C二、填空题6.平行7.AD BC8.1209.内错角相等10.①③④三、解答题11. 解:(1)∵∠1=70°,∴∠AFC=180°-70°=110°.∵∠2=110°,∴∠AFC=∠2,∴AB//DE.(2)∵∠1=70°,∴∠BFD=180°-70°=110°.∵∠2=110°,∴∠BFD=∠2,∴AB//DE.(3)∵∠1=70°,∴∠AFD=70°.∵∠2=110°,∴∠AFD+∠2=180°,∴AB//DE.12.证明:∵CE平分∠ACD,,∴∠2=∠DCE.∵∠1=∠2,∴∠DCE=∠1,∴AB∥CD.。
七年级下册第五章相交线与平行线单元测试卷及答案.docx
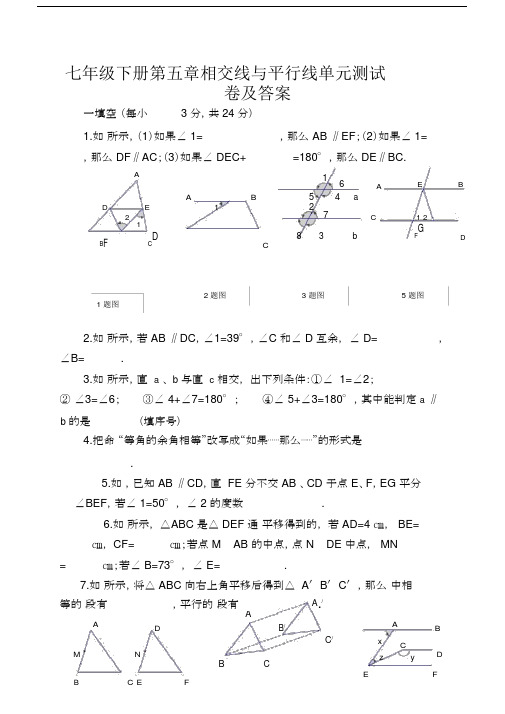
七年级下册第五章相交线与平行线单元测试卷及答案一填空 (每小 3 分,共 24 分)1.如 所示,(1)如果∠ 1=,那么 AB ∥EF ;(2)如果∠ 1=,那么 DF ∥AC ;(3)如果∠ DEC+=180°,那么 DE ∥BC.A16EBABDA5 4 aE 1271 2 21C83bFGDB FCDC2 题图3 题图 5 题图1 题图2.如 所示,若 AB ∥DC ,∠1=39°,∠C 和∠ D 互余, ∠ D=,∠B=.3.如 所示,直 a 、 b 与直 c 相交, 出下列条件:①∠ 1=∠2;② ∠3=∠6;③∠ 4+∠7=180°; ④∠ 5+∠3=180°,其中能判定 a ∥b 的是(填序号)4.把命 “等角的余角相等”改写成“如果⋯⋯那么⋯⋯”的形式是.5.如 ,已知 AB ∥CD ,直 FE 分不交 AB 、CD 于点 E 、F ,EG 平分∠BEF ,若∠ 1=50°, ∠ 2 的度数.6.如 所示, △ABC 是△ DEF 通 平移得到的, 若 AD=4 ㎝, BE=㎝, CF=㎝;若点 M AB 的中点,点 N DE 中点, MN=㎝;若∠ B=73°, ∠ E=.7.如 所示,将△ ABC 向右上角平移后得到△ A ′B ′C ′,那么 中相等的 段有,平行的 段有A ./AAADB /BxC /CMNDBCzyEFB C EF6 题图7 题图8 题图8.如图所示,已知AB ∥CD∥EF,则∠x、∠y、∠z三者之间的关系是.二、选择题(每小题 3 分,共 30 分)9.在同一平面内有三条直线,若有且只有两条直线平行,则它们()A. 没有交点只有一个交点有两个交点有三个交点10.两条直线相交所构成的四个角中:①有三个角都相等;② 有一对对顶角互补;③有一个角是直角;④有一对邻补角相等,其中能判定这两条直线垂直的有()A.1个B.2个C.3个D.4个11.如图所示,已知 AD ∥BC,则下列结论:①∠ 1=∠2;②∠ 2=∠3;③ ∠6=∠8;④∠ 5=∠8;⑤∠ 2=∠4,其中一定正确的是()A. ②B.②③⑤C.①③④D.②④12.如图所示,下列判定中错误的是()A. 因为∠ A+∠ADC=180 °,因此 AB ∥CDB.因为 AB ∥CD,因此∠A BC+ ∠C=180°C.因为∠ 1=∠2,因此 AD ∥BCD.因为 AD ∥BC,因此∠ 3=∠413.如图所示,把一个长方形纸片沿EF 折叠后,点 D、C 分不落在点 D′、C′位置,若∠ EFB=65°,则∠ AED′等于()A.50°B.55°C.60°D.65°14.如图所示,已知直线 AB ∥CD,当点 E 在直线 AB 与 CD 之间时,有∠ BED= ∠ABE+ ∠CDE 成立;而当点 E 在直线 AB 与 CD 之外时,下列关系成立的是()A. ∠BED= ∠ABE+∠CDE 或∠ BED=∠ ABE -∠ CDEB. ∠BED=∠ A BE -∠ CDEC. ∠BED=∠CDE -∠ ABE 或∠ BED= ∠ABE -∠ CDED. ∠ BED=∠CDE -∠ ABE15.在下列讲法中:(1)△ ABC 在平移过程中, 对应线段一定相等;(2)△ A BC 在平移过程中,对应线段一定平行; (3)△ABC 在平移过程中,周长保持不变;(4)△ ABC 在平移过程中,对应边中点的连线段的长等于平移的距离;(5)△ ABC 在平移过程中,面积不变,其中正确的有()A. (1)(2)(3)(4)B.( 1)(2)(3)(4)(5)C.(1)(2)(3)(5)D.(1)(3)(4)(5)16.如图所示, AB ⊥BC ,BC ⊥CD ,∠ EBC=∠BCF ,那么∠ ABE 与∠DCF的位置和大小关系是()A. 是同位角且相等B.不是同位角但相等C.是同位角但不等D.不是同位角也不等17.在俄罗斯方块游戏中,已拼成的图案如图所示,现又显现一小方块拼图向下运动,为了使所有图案消逝,你必须进行以下哪项操作,才能拼成一个完整的图案,使其自动消逝 .()A. 向右平移 1 格B.向左平移 1 格C.向右平移2 格 D.向右平移 3 格A1DADAEDAB5 2174E63D /65°8CD3BFC42BC BCC/11 题图 12 题图 13 题图 14 题图18.如果∠ 与∠ 的两边分不平行, ∠ 比∠ 的 3 倍少 36°,则∠的度数是( )A.18°B.126°C.18°或 126°D.以上都不对FEAECBCABOFDD16 题图 17 题图 19 题图三、解答题(共 46 分)19.(10 分)如图所示,直线 AB 、CD 相交于点 O ,OE ⊥AB ,点 O 为垂足, OF 平分∠ AOC ,且∠ COE= 2∠AOC ,求∠ DOF 的度数 .520.(8 分)如图所示,某地一条小河的两岸差不多上直的,为测定河岸两边是否平行,小明和小亮分不在河的两岸拉紧了一根细绳,并分不测出∠ 1=70°,∠ 2=70°,测出那个结果后,他们的同学小华讲河岸两边是平行的,那个讲法对不对?什么缘故?1220 题图21.(8 分)如图所示,已知∠ A= ∠1,∠ C=∠F ,请咨询 BC 与 EF 平行吗?C F121题图22.(10 分)如图所示,已知 AB//CD ,∠1:∠2:∠3=1:2:3,求证:BA 平分∠ EBF.下面给出证法1:证法 1:设∠ 1、∠ 2、∠ 3 的度数分不为x°、 2 x°、 3 x° .∵AB//CD ,∴ 2 x°+3 x°=180°,解得x°=36°.∴∠ 1=36°,∠ 2=72°,∠ 3=108°.∵∠ EBD=180°,∴∠ EBA=72 °.∴BA 平分∠ EBF.请阅读证法 1 后,找出与证法 1 不同的证法 2,并写出证明过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
周周练(5.1~5.2)
(时间:45分钟满分:100分)
一、选择题(每小题4分,共32分)
1.邻补角是指(D)
A.和为180°的两个角
B.有一条公共边且相等的两个角
C.有公共顶点且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.如图,∠1和∠2是对顶角的是(B)
A B C D
3.(宿迁中考)如图所示,直线a,b被直线c所截,∠1与∠2是(A)
A.同位角B.内错角
C.同旁内角D.邻补角
4.(厦门中考改编)如图,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是(B) A.线段CA的长B.线段CD的长
C.线段AD的长D.线段AB的长
5.下列说法错误的是(C)
A.两条直线相交,有一个角是直角,则两条直线互相垂直
B.若两对顶角之和为180°,则两直线互相垂直
C.两直线相交,所构成的四个角中,若有两个角相等,则两直线互相垂直
D.在同一平面上,过点A作直线l的垂线,这样的垂线只有一条
6.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是(C) A.20°B.40°
C.50°D.80°
7.(平顶山期末)如图,下列条件不能判断直线l1∥l2的是(A)
A.∠1=∠3 B.∠1=∠4
C.∠2+∠3=180°D.∠3=∠5
8.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是(B) A.先向左转130°,再向左转50°
B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40°
D.先向左转50°,再向左转40°
二、填空题(每小题4分,共24分)
9.如图,已知∠1+∠2=100°,则∠3=130°.
10.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是153°.
11.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短.
12.如图,在同一平面内,OA⊥l,OB⊥l,垂足为O,则OA与OB重合的理由是同一平面内,过一点有且只有一条直线与已知直线垂直.
13.(浦东新区期中)如图,要使AD∥BC,需添加一个条件,这个条件可以是∠1=∠4.(只需写出一种情况)
14.如图所示,AB与BC被AD所截得的内错角是∠1和∠3;DE与AC被直线AD所截得的内错角是∠2和∠4;图中∠4的内错角是∠5和∠2.
三、解答题(共44分)
15.(6分)如图,已知AB⊥AD,CD⊥AD,∠1=∠2,完成下列推理过程:
∵AB⊥AD,CD⊥AD(已知),
∴∠BAD=∠CDA=90°(垂直的定义).
又∵∠1=∠2(已知),
∴∠BAD-∠1=∠CDA-∠2,
即∠DAE=∠ADF.
∴DF∥AE(内错角相等,两直线平行).
16.(6分)如图,直线AO,BO交于点O,过点P作PC⊥AO于C,PD⊥BO于D,画出图形.
解:作∠ACP=90°,作∠PDB=90°,则直线PC、PD即为所求.
17.(6分)如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明AB∥CD.
解:∵OF平分∠EOD,
∠FOD=25°,
∴∠EOD=2∠FOD=50°.
又∵∠OEB=130°,
∴∠OEB+∠EOD=180°.
∴AB∥CD.
18.(8分)如图,已知∠1=∠2,∠3+∠4=180°,求证:AB∥EF.
证明:∵∠1=∠2,
∴AB∥C D.
∵∠3+∠4=180°,
∴CD∥EF.
∴AB∥EF.
19.(8分)如图,AB和CD交于O点,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.
解:∵AB,CD相交于点O,
∴∠BOD=∠AOC=40°.
∵OD平分∠BOF,
∴∠DOF=∠BOD=40°.
∵OE⊥CD,∴∠EOD=90°.
∴∠EOF=∠EOD+∠DOF=130°.
20.(10分)我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气,同样会发生折射现象.如图所示是光线从空气射入水中,再从水中射入空气的示意图.由于折射率相同,已知∠1=∠4,∠2=∠3,请你用所学知识来判断光线c与光线d是否平行?并说明理由.
解:c∥d.理由如下:
∵∠1+∠5=180°,∠4+∠6=180°,∠1=∠4,
∴∠5=∠6.
∵∠2=∠3,
∴∠2+∠5=∠3+∠6.
∴c∥d.。
