基于蚁群算法的钣金件数控切割路径规划
基于某蚁群算法地路径规划

MATLAB实现基于蚁群算法的机器人路径规划1、问题描述移动机器人路径规划是机器人学的一个重要研究领域。
它要求机器人依据某个或某些优化原则(如最小能量消耗,最短行走路线,最短行走时间等),在其工作空间中找到一条从起始状态到目标状态的能避开障碍物的最优路径。
机器人路径规划问题可以建模为一个有约束的优化问题,都要完成路径规划、定位和避障等任务。
2 算法理论蚁群算法(Ant Colony Algorithm,ACA),最初是由意大利学者Dorigo M. 博士于1991 年首次提出,其本质是一个复杂的智能系统,且具有较强的鲁棒性,优良的分布式计算机制等优点。
该算法经过十多年的发展,已被广大的科学研究人员应用于各种问题的研究,如旅行商问题,二次规划问题,生产调度问题等。
但是算法本身性能的评价等算法理论研究方面进展较慢。
Dorigo 提出了精英蚁群模型(EAS),在这一模型息素更新按照得到当前最优解的蚂蚁所构造的解来进行,但这样的策略往往使进化变得缓慢,并不能取得较好的效果。
次年Dorigo 博士给出改进模型(ACS),文中改进了转移概率模型,并且应用了全局搜索与局部搜索策略,来得进行深度搜索。
Stützle 与Hoos给出了最大-最小蚂蚁系统(MAX-MINAS),所谓最大-最小即是为信息素设定上限与下限,设定上限避免搜索陷入局部最优,设定下限鼓励深度搜索。
蚂蚁作为一个生物个体其自身的能力是十分有限的,比如蚂蚁个体是没有视觉的,蚂蚁自身体积又是那么渺小,但是由这些能力有限的蚂蚁组成的蚁群却可以做出超越个体蚂蚁能力的超常行为。
蚂蚁没有视觉却可以寻觅食物,蚂蚁体积渺小而蚁群却可以搬运比它们个体大十倍甚至百倍的昆虫。
这些都说明蚂蚁群体部的某种机制使得它们具有了群体智能,可以做到蚂蚁个体无法实现的事情。
经过生物学家的长时间观察发现,蚂蚁是通过分泌于空间中的信息素进行信息交流,进而实现群体行为的。
下面简要介绍蚁群通过信息素的交流找到最短路径的简化实例。
基于平滑蚂蚁算法的路径规划实现与仿真

2018年第5期【摘要】机器人的应用范围越来越广,但是它的路径规划问题还是具有明显的缺点,目前用于解决机器人路径规划的智能算法有很多,但是每种算法都有其缺陷,不能很好的解决路径规划问题。
基于此本文提出基于平滑蚂蚁算法的路径规划的研究。
【关键词】平滑蚂蚁算法;路径规划一、平滑蚁群算法蚁群算法作为一种新兴的仿生智能算法,在解决许多最优问题时具有一定的优势。
但是,任何事物都具有两面性。
蚁群算法在进行路径规划时,就有搜索时间长,容易陷入局部最优等缺点,并且蚁群算法规划的路径具有转折次数多,累计转折角大等问题。
这样,就造成了铸造机器人能量的浪费,在铸造机器人本身存储电能一定的情况下,铸造机器人完成的任务相对较少。
在此基础上,提出平滑蚁群算法,对蚁群算法规划出的最优路径进行平滑处理,缩短路径长度,改善路径质量。
通过蚁群算法得到的路径规划结果,铸造机器人所走的路径节点都是自由栅格中心点,受此约束,造成了铸造机器人出现不必要的转弯和行走一些多余的路径。
图1-1为利用蚁群算法在栅格规模为8×8简单地图中规划出的最优路径,从规划的路径图中可以看出路径规划的结果并不是机器人起始点与目标点之间的最短路径。
为了获得更好的路径规划效果,减少机器人不必要的能量消耗,对蚁群算法得到的最优路径进行平滑处理。
由于蚁群算法在进行路径规划时都是搜寻与当前节点连接的相邻节点,所以本节所做的优化就是路径中的相邻节点。
由图1-2可以看出减少一些路径中的不必要的节点,可以改善路径质量,但是怎样删除这些不必要节点是本节研究的重点。
本节所提出的平滑蚁群算法是在蚁群算法规划出来的最优路径的基础上,将路径中两个不在同一条直线上的两个节点连线,判断当前的连线是否穿过障碍区域,如果不穿过障碍区域,将当前连线作为新的路径,中间节点删除,否则对当前路径不作任何修改。
按此方法,依次操作路径中所有符合条件的节点,生成新路径,对图1-1进行平滑处理后的路径如图1-2所示,平滑处理后的路径更符合机器人的路径规划要求。
一种改进的蚁群算法在机器人路径规划中的应用

第 12 期
杨建勋.一种改进的蚁群算法在机器人路径规划中的应用
209
图1 蚁群避障碍物路径过程 Fig. 1 Ant colony optimization to avoid obstacles path process
到紧急突发情况的时候,能够迅速地反应,譬如移动机 器人在运动中遇到突发状况,会立即停止运动,但是这 种行为不具备智能性。
Abstract:With the modernization of the rapid development of science and technology, high technology has been more and more widely applied. Path planning of robot technology as research and artificial intelligence research is a very im- portant research field, to improve the robot function and the technical level and have a great role. Path planning of mo- bile robot can effectively help to realize the navigation technology used successfully, but also can better judge the degree of intelligent mobile robot. This paper mainly describes the technology of mobile robot path planning in the basic ant colony algorithm in the application, at the same time, improve and optimize the ant colony algorithm, through the three step way, helpα,β and Q to achieve the best combination of identified patterns, in order to improve the stability of the robot and the capability of optimization. Key words:ant colony optimization algorithms; robot;path planning; optimization and improvement
钣金件数控激光切割割嘴路径的优化

文中把按某种方法确定的内环loopi 上的打孔点记 为Pi,Oloop 上的打孔点记为PE. 显然,Pi∈{Vi1, Vi2,…,ViV(k)};PEE∈{OV1,OV2,…,OVw},并 设对所有打孔点 PE{P0,P1,P2,…,PM ,PE}的一 个访问顺序为 TE{P0,t1,t2,tM ,PE,P0},其中ti ∈{P0,P1,P2,…,PM ,PE},则切割路径的数学模 型为
量 的 影 响,并 纳 入 了 切 割 路 径 优 化 的 数 学 模 型 中. 文献[1-3]皆未涉及割嘴随动功能对切割路径的影 响.国内关于激光切割的自动编程系统的论文很少 有系统地 研 究 路 径 优 化 或 随 动 功 能 对 切 割 路 径 的
影响. 在单件小批量生产中,尺寸较大且内部包含多
圆等,定义直线的顶点是直线的首尾两端点,圆弧的
顶点是圆弧 的 起 点 与 终 点. 对 圆 而 言,定 义 一 个 顶 点,这个顶点是圆上的某一点,这点对切割过程而言
回程序零点. 在图 1 中假定程序 零 点 为 P0,内 环
loop1 打孔点为 V11,loop2 打孔点为 V21,loop3 打
Abstract Anhierarchicalthree-stepapproachispresentedtosolvetheoptimizationproblem.First, animprovednearestneighboralgorithmisappliedtoselectpiercepoints.Thenantsystemalgorithmis usedtosolvetheoptimalcuttingpath.Atlast,theformerpathisadjustedtoavoidthetorchfalling downintothefinishedcutcavityduringitsvacancycourse. Exampleandthefurtherresearchare discussed.
蚁群算法及其应用讲座文档

蚁群算法及其应用讲座文档蚁群算法的基本思想是通过蚂蚁在环境中留下信息素来进行信息交流和协作,从而找到最优解。
蚂蚁在移动过程中会释放一种叫作信息素的化学物质,这种信息素会留下路径上的浓度标记,其浓度越高代表路径越好。
蚂蚁会根据信息素浓度的大小选择移动路径,并在移动过程中不断更新路径上的信息素。
蚁群算法的应用十分广泛,下面介绍几个常见的应用领域:1.路径规划:蚁群算法可以用于寻找最优路径,例如在地理导航系统中寻找最短路径或最少拥堵路径。
2. 旅行商问题(Traveling Salesman Problem,简称TSP):TSP是一个经典的组合优化问题,要求在给定的城市中找到一条最短的路径,每个城市只能经过一次。
蚁群算法可以应用于TSP问题的求解,通过模拟蚂蚁的移动过程找到最优路径。
3.群集分析:蚁群算法可以用于群集分析,例如在数据挖掘中寻找数据集中的相关模式或聚类。
4.任务调度:在任务调度问题中,蚁群算法可以应用于寻找最优的任务分配和调度策略。
蚁群算法的优点在于其具有分布式计算和自适应性的特点。
由于蚁群算法模拟了蚂蚁的集体行为,它可以将空间分解成多个子问题,并利用信息素交流和协作来寻找全局最优解。
此外,蚁群算法还具有自适应性,可以根据环境的变化自动调整参数和策略。
然而,蚁群算法也存在一些限制。
由于蚁群算法的过程是基于概率的,它在处理大规模问题和高维问题时可能会受到计算资源和空间的限制。
此外,蚁群算法的性能也会受到参数选择、初始信息素浓度和信息素挥发速率等因素的影响。
总结起来,蚁群算法是一种基于蚂蚁集体行为的启发式算法,可以用于解决各种优化问题。
其应用领域广泛,包括路径规划、旅行商问题、群集分析和任务调度等。
蚁群算法具有分布式计算和自适应性的优点,但在处理大规模问题和高维问题时可能存在一些限制。
蚁群算法路径优化matlab代码

蚁群算法路径优化matlab代码蚁群算法是一种基于生物群体的智能算法,常用于路径优化等问题。
在这个问题中,蚂蚁在寻找食物时会根据周围的环境信息和食物的香味找到最短路径。
本文将介绍如何在 MATLAB 中使用蚁群算法进行路径优化,并提供一些拓展。
在 MATLAB 中实现蚁群算法需要用到三个主要函数:ants_logic.m、ants_move.m 和 ants_display.m。
以下是这三个函数的基本功能和代码实现。
1. ants_logic.m这个函数是蚁群算法的核心部分,负责计算蚂蚁的当前路径和更新路径搜索树。
函数的基本思路是每个蚂蚁根据当前环境和食物香味来选择前进方向,如果前方是死路或食物已经被其他蚂蚁找到,则蚂蚁会返回原路。
如果蚂蚁到达了食物位置,则它会将自己的信息传递给其他蚂蚁,并更新食物香味。
拓展:在路径优化问题中,通常会有多个不同的路径可供选择,而蚁群算法可以通过学习其他蚂蚁的路径来发现更短、更快的路径。
为了实现这一功能,可以在 ants_logic.m 函数中增加一个参数,指示当前蚂蚁应该学习其他哪个蚂蚁的路径。
2. ants_move.m这个函数负责控制蚂蚁的移动方向。
在函数中,我们需要给定蚂蚁的当前位置和食物位置,并计算蚂蚁应该移动到的新位置。
在MATLAB 中,我们可以使用 rand 函数生成一个随机数,然后将其作为新位置的坐标。
拓展:为了提高路径搜索的效率,我们可以在 ants_move.m 函数中加入一些随机因子。
例如,可以在蚂蚁移动方向上添加一个随机偏置,这样可以让蚂蚁更有可能探索新的区域。
3. ants_display.m这个函数用于可视化路径搜索的过程。
在函数中,我们可以给定蚂蚁的初始位置和食物位置,并使用 MATLAB 的图形处理函数绘制路径。
拓展:为了使路径搜索过程更加有趣,我们可以在ants_display.m 函数中添加一些动画效果。
例如,可以使用 MATLAB 的 animation 函数创建动画,让蚂蚁路径在屏幕上动态地显示。
基于蚁群算法下钣金件数控切割路径规划的分析

基于蚁群算法下钣金件数控切割路径规划的分析钣金件制造环节中,关键环节之一即为数控切割,成批制造环境下,后续加工若想顺利开展,要求数控切割能够快速、高效、合理的进行,为满足此种要求,本文在蚁群算法基础上,分析了科学规划钣金件数控切割路径的具体方法。
数控切割过程中,合理规划加工路径后,喷嘴空行程距离可以显著减少,机床加工效果得到提升,由此可见,本文利用蚁群算法优化切割路径具有十分重要的现实意义。
标签:蚁群算法;钣金件;数控切割;路径规划1 蚁群算法20世纪90年代,M.Dorigo等人首先提出蚁群算法,也叫蚁群系统。
旅行商问题利用蚁群算法成功求解后,其他领域中相继引入该算法。
蚁群中所有蚂蚁出现的集体行为就属于信息正反馈现象,即单位时间内越多的蚂蚁通过某条路径,越能证明该线路具有更好的可用性,后来者也就具备越大的该条路径选择概率。
基于蚂蚁群的集体行为,提出蚂蚁算法,能够良好的解决旅行商问题,而且蚂蚁算法鲁棒性比较强。
2 基于蚂蚁算法的钣金件数控切割路径规划方法2.1 建立切割路径数学模型钣金件数控切割时,为将切割效率提升,并达到节省钣金件的目的,通常会把多个零件排列在一块钣金件上,此时,要以零件具体情况、钣金件大小等相关因素为依据,对零件进行最优化排列。
实践证明,采取混排方式,钣金材料利用率、数控切割效率均可得到提升。
本文建立切割路径数学模型时,以图1为例,首先定义钣金零件轮廓。
图1中,零件有2种,共14个,划分其中几何元素后,层次分为3个:第一为内部共边层次,即蓝色实体部分,共有8个;第二为内轮廓层次,即红色实体部分,共有39个;第三为外轮廓层次,即黑色实体部分,共7个。
无论零件排列方式为何种,均必须要切割内部共边及封闭的内外环,因此,不管切割开始点为哪个位置,共边、内外环长度均不会发生变化,也就是路径优化问题不存在[1]。
因共边顶点有两个,打孔点可能会存在两个,站在切割工艺角度,内外环上并不具备唯一的打孔点,任一顶点都可能是打孔点。
[MCM]基于蚁群算法的三维路径规划
![[MCM]基于蚁群算法的三维路径规划](https://img.taocdn.com/s3/m/5464cf661fb91a37f111f18583d049649b660e60.png)
[MCM]基于蚁群算法的三维路径规划%% 该函数⽤于演⽰基于蚁群算法的三维路径规划算法%% 清空环境clcclear%% 数据初始化HeightData = [2000 1400 800 650 500 750 1000 950 900 800 700 900 1100 1050 1000 1150 1300 1250 1200 1350 1500;1100 900 700 625 550 825 1100 1150 1200 925 650 750 850 950 1050 1175 1300 1350 1400 1425 1450;200 400 600 600 600 900 1200 1350 1500 1050 600 600 600 850 1100 1200 1300 1450 1600 1500 1400;450 500 550 575 600 725 850 875 900 750 600 600 600 725 850 900 950 1150 1350 1400 1450;700 600 500 550 600 550 500 400 300 450 600 600 600 600 600 600 600 850 1100 1300 1500;500 525 550 575 600 575 550 450 350 475 600 650 700 650 600 600 600 725 850 1150 1450;300 450 600 600 600 600 600 500 400 500 600 700 800 700 600 600 600 600 600 1000 1400;550 525 500 550 600 875 1150 900 650 725 800 700 600 875 1150 1175 1200 975 750 875 1000;800 600 400 500 600 1150 1700 1300 900 950 1000 700 400 1050 1700 1750 1800 1350 900 750 600;650 600 550 625 700 1175 1650 1275 900 1100 1300 1275 1250 1475 1700 1525 1350 1200 1050 950 850;500 600 700 750 800 1200 1600 1250 900 1250 1600 1850 2100 1900 1700 1300 900 1050 1200 1150 1100;400 375 350 600 850 1200 1550 1250 950 1225 1500 1750 2000 1950 1900 1475 1050 975 900 1175 1450;300 150 0 450 900 1200 1500 1250 1000 1200 1400 1650 1900 2000 2100 1650 1200 900 600 1200 1800;600 575 550 750 950 1275 1600 1450 1300 1300 1300 1525 1750 1625 1500 1450 1400 1125 850 1200 1550;900 1000 1100 1050 1000 1350 1700 1650 1600 1400 1200 1400 1600 1250 900 1250 1600 1350 1100 1200 1300;750 850 950 900 850 1000 1150 1175 1200 1300 1400 1325 1250 1125 1000 1150 1300 1075 850 975 1100;600 700 800 750 700 650 600 700 800 1200 1600 1250 900 1000 1100 1050 1000 800 600 750 900;750 775 800 725 650 700 750 775 800 1000 1200 1025 850 975 1100 950 800 900 1000 1050 1100;900 850 800 700 600 750 900 850 800 800 800 800 800 950 1100 850 600 1000 1400 1350 1300;750 800 850 850 850 850 850 825 800 750 700 775 850 1000 1150 875 600 925 1250 1100 950;600 750 900 1000 1100 950 800 800 800 700 600 750 900 1050 1200 900 600 850 1100 850 600];%⽹格划分LevelGrid=10;PortGrid=21;%起点终点⽹格点starty=10;starth=4;endy=8;endh=5;m=10;%算法参数PopNumber=100; %种群个数BestFitness=[]; %最佳个体%初始信息素pheromone=ones(21,21,21);%% 初始搜索路径[path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone, HeightData,starty,starth,endy,endh);fitness=CacuFit(path); %适应度计算[bestfitness,bestindex]=min(fitness); %最佳适应度bestpath=path(bestindex,:); %最佳路径BestFitness=[BestFitness;bestfitness]; %适应度值记录%% 信息素更新rou=0.2;cfit=100/bestfitness;for i=2:PortGrid-1pheromone(i,bestpath(i*2-1),bestpath(i*2))= (1-rou)*pheromone(i,bestpath(i*2-1),bestpath(i*2))+rou*cfit;end%% 循环寻找最优路径for kk=1:200 %这⾥改迭代次数kk %迭代次数%% 路径搜索[path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone,HeightData,starty,starth,endy,endh);%% 适应度值计算更新fitness=CacuFit(path);[newbestfitness,newbestindex]=min(fitness);if newbestfitness<bestfitnessbestfitness=newbestfitness;bestpath=path(newbestindex,:);endBestFitness=[BestFitness;bestfitness];%% 更新信息素cfit=100/bestfitness;for i=2:PortGrid-1pheromone(i,bestpath(i*2-1),bestpath(i*2))=(1-rou)* pheromone(i,bestpath(i*2-1),bestpath(i*2))+rou*cfit;endend%% 最佳路径for i=1:21a(i,1)=bestpath(i*2-1);a(i,2)=bestpath(i*2);endfigure(1)x=1:21;y=1:21;[x1,y1]=meshgrid(x,y);mesh(x1,y1,HeightData)axis([1,21,1,21,0,2000])hold onk=1:21;plot3(k(1)',a(1,1)',a(1,2)'*200,'-o','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','r','MarkerSize',7)plot3(k(21)',a(21,1)',a(21,2)'*200,'-o','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','r','MarkerSize',7)text(k(1)',a(1,1)',a(1,2)'*200,'起点');text(k(21)',a(21,1)',a(21,2)'*200,'终点');xlabel('km','fontsize',12);ylabel('km','fontsize',12);zlabel('m','fontsize',12);title('三维路径规划空间','fontsize',12)set(gcf, 'Renderer', 'ZBuffer')hold onplot3(k',a(:,1)',a(:,2)'*200,'r-o')%% 适应度变化figure(2)plot(BestFitness)title('最佳个体适应度变化趋势')xlabel('迭代次数')ylabel('适应度值')main.mfunction [path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone,HeightData,starty,starth,endy,endh) %% 该函数⽤于蚂蚁蚁群算法的路径规划%LevelGrid input 横向划分格数%PortGrid input 纵向划分个数%pheromone input 信息素%HeightData input 地图⾼度%starty starth input 开始点%path output 规划路径%pheromone output 信息素%% 搜索参数ycMax=2; %蚂蚁横向最⼤变动hcMax=2; %蚂蚁纵向最⼤变动decr=0.9; %信息素衰减概率%% 循环搜索路径for ii=1:PopNumberpath(ii,1:2)=[starty,starth]; %记录路径NowPoint=[starty,starth]; %当前坐标点%% 计算点适应度值for abscissa=2:PortGrid-1%计算所有数据点对应的适应度值kk=1;for i=-ycMax:ycMaxfor j=-hcMax:hcMaxNextPoint(kk,:)=[NowPoint(1)+i,NowPoint(2)+j];if (NextPoint(kk,1)<20)&&(NextPoint(kk,1)>0)&&(NextPoint(kk,2)<20)&&(NextPoint(kk,2)>0)qfz(kk)=CacuQfz(NextPoint(kk,1),NextPoint(kk,2),NowPoint(1),NowPoint(2),endy,endh,abscissa,HeightData); qz(kk)=qfz(kk)*pheromone(abscissa,NextPoint(kk,1),NextPoint(kk,2));kk=kk+1;elseqz(kk)=0;kk=kk+1;endendend%选择下个点sumq=qz./sum(qz);pick=rand;while pick==0pick=rand;endfor i=1:25pick=pick-sumq(i);if pick<=0index=i;break;endendoldpoint=NextPoint(index,:);%更新信息素pheromone(abscissa+1,oldpoint(1),oldpoint(2))=0.5*pheromone(abscissa+1,oldpoint(1),oldpoint(2));%路径保存path(ii,abscissa*2-1:abscissa*2)=[oldpoint(1),oldpoint(2)];NowPoint=oldpoint;endpath(ii,41:42)=[endy,endh];endsearchpath.mfunction qfz=CacuQfz(Nexty,Nexth,Nowy,Nowh,endy,endh,abscissa,HeightData)%% 该函数⽤于计算各点的启发值%Nexty Nexth input 下个点坐标%Nowy Nowh input 当前点坐标%endy endh input 终点坐标%abscissa input 横坐标%HeightData input 地图⾼度%qfz output 启发值%% 判断下个点是否可达if HeightData(Nexty,abscissa)<Nexth*200S=1;elseS=0;end%% 计算启发值%D距离D=50/(sqrt(1+(Nowh*0.2-Nexth*0.2)^2+(Nexty-Nowy)^2)+sqrt((21-abscissa)^2 ...+(endh*0.2-Nexth*0.2)^2+(endy-Nowy)^2));%计算⾼度M=30/abs(Nexth+1);%计算启发值qfz=S*M*D;CacuQfz.mfunction fitness=CacuFit(path)%% 该函数⽤于计算个体适应度值%path input 路径%fitness input 路径[n,m]=size(path);for i=1:nfitness(i)=0;for j=2:m/2%适应度值为长度加⾼度fitness(i)=fitness(i)+sqrt(1+(path(i,j*2-1)-path(i,(j-1)*2-1))^2 +(path(i,j*2)-path(i,(j-1)*2))^2)+abs(path(i,j*2)); endendCacuFit.m改进clcclearh=[1800 2200 1900 2400 2300 2100 2500 2400 2700 2600 29001600 2000 2000 2600 2900 2000 2000 2500 2700 3000 28002100 1900 2000 1900 1700 2000 2000 2000 2000 2500 29001700 2000 2000 2000 1800 2000 2200 2000 2000 2000 28002200 1800 2000 3100 2300 2400 1800 3100 3200 2300 20001900 2100 2200 3000 2300 3000 3500 3100 2300 2600 25001700 1400 2300 2900 2400 2800 1800 3500 2600 2000 32002300 2500 2400 3100 3000 2600 3000 2300 3000 2500 27002000 2200 2100 2000 2200 3000 2300 2500 2400 2000 23002300 2200 2000 2300 2200 2200 2200 2500 2000 2800 27002000 2300 2500 2200 2200 2000 2300 2600 2000 2500 2000];h=h-1400;[n,m]=size(h);for i=3:n+2for j=3:n+2H(i,j)=h(i-2,j-2);endendH(3:m+2,2)=(290*H(3:m+2,3)-366*H(3:m+2,4)+198*H(3:m+2,5)-38*H(3:m+2,6))/84;H(3:m+2,1)=(7211*H(3:m+2,3)-12813*H(3:m+2,4)+8403*H(3:m+2,5)-1919*H(3:m+2,6))/882;H(3:m+2,n+3)=-(21*H(3:m+2,n-1)-101*H(3:m+2,n)+177*H(3:m+2,n+1)-135*H(3:m+2,n+2))/38;H(3:m+2,n+4)=-(2079*H(3:m+2,n-1)-8403*H(3:m+2,n)+12013*H(3:m+2,n+1)-6411*H(3:m+2,n+2))/722;H(2,:)=(290*H(3,:)-366*H(4,:)+198*H(5,:)-38*H(6,:))/84;H(1,:)=(7211*H(3,:)-12813*H(4,:)+8403*H(5,:)-1919*H(6,:))/882;H(n+3,:)=-(21*H(n-1,:)-101*H(n,:)+177*H(n+1,:)-135*H(n+2,:))/38;H(n+4,:)=-(2079*H(n-1,:)-8403*H(n,:)+12013*H(n+1,:)-6411*H(n+2,:))/722;%⼆维四次卷积插值[n,m]=size(h);D=[-21 59 -32 -48 61 -1963 -261 386 -222 15 19-63 366 -600 354 -57 021 -164 6 156 -19 00 0 240 0 0 0];for i=1:10*(n-1)for j=1:10*(m-1)indexi=floor(i/10)+3;indexj=floor(j/10)+3;s=mod(i,10)*0.1;if j==100indexj=indexj-1;endif i==100indexi=indexi-1;end% if s==0% indexi=indexi-1;% endt=mod(j,10)*0.1;% if t==0% indexj=indexj-1;% endS=[s^4,s^3,s^2,s 1];T=[t^4,t^3,t^2,t,1];C=[H(indexi-2,indexj-2) H(indexi-2,indexj-1) H(indexi-2,indexj) H(indexi-2,indexj+1) H(indexi-2,indexj+2) H(indexi-2,indexj+3)H(indexi-1,indexj-2) H(indexi-1,indexj-1) H(indexi-1,indexj) H(indexi-1,indexj+1) H(indexi-1,indexj+2) H(indexi-1,indexj+3)H(indexi ,indexj-2) H(indexi ,indexj-1) H(indexi ,indexj) H(indexi ,indexj+1) H(indexi ,indexj+2) H(indexi ,indexj+3)H(indexi+1,indexj-2) H(indexi+1,indexj-1) H(indexi+1,indexj) H(indexi+1,indexj+1) H(indexi+1,indexj+2) H(indexi+1,indexj+3) H(indexi+2,indexj-2) H(indexi+2,indexj-1) H(indexi+2,indexj) H(indexi+2,indexj+1) H(indexi+2,indexj+2) H(indexi+2,indexj+3) H(indexi+3,indexj-2) H(indexi+3,indexj-1) H(indexi+3,indexj) H(indexi+3,indexj+1) H(indexi+3,indexj+2) H(indexi+3,indexj+3)]; HH(i,j)=S*D*C*D'*T'/57600;endend[n,m]=size(HH);x=1:n;y=1:m[xx,yy]=meshgrid(x,y);mesh(xx,yy,HH)xlabel('km')ylabel('km')zlabel('m')a =[ 50 60065 60050 60040 60030 80030 60035 80035 60035 80025 80030 120015 120020 100015 100030 100035 120035 100040 100030 140035 160040 1000];b=[0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100]; hold onplot3(b',a(:,1)-2,a(:,2)+300,'r-o','linewidth',1)⾼程⼆维四次卷积插值后路径规划。
matlab基于蚁群算法的二维路径规划算法【matlab优化算法二十二】
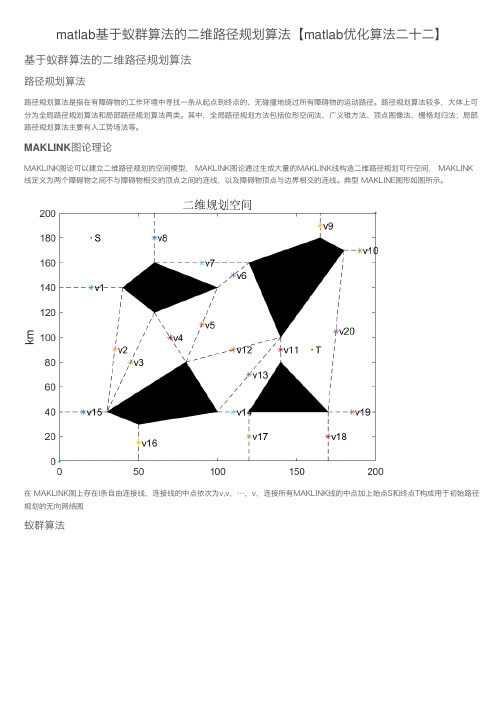
matlab基于蚁群算法的⼆维路径规划算法【matlab优化算法⼆⼗⼆】基于蚁群算法的⼆维路径规划算法路径规划算法路径规划算法是指在有障碍物的⼯作环境中寻找⼀条从起点到终点的、⽆碰撞地绕过所有障碍物的运动路径。
路径规划算法较多,⼤体上可分为全局路径规划算法和局部路径规划算法两类。
其中,全局路径规划⽅法包括位形空间法、⼴义锥⽅法、顶点图像法、栅格划归法;局部路径规划算法主要有⼈⼯势场法等。
MAKLINK图论理论MAKLINK图论可以建⽴⼆维路径规划的空间模型, MAKLINK图论通过⽣成⼤量的MAKLINK线构造⼆维路径规划可⾏空间, MAKLINK 线定义为两个障碍物之间不与障碍物相交的顶点之间的连线,以及障碍物顶点与边界相交的连线。
典型 MAKLINE图形如图所⽰。
在 MAKLINK图上存在l条⾃由连接线,连接线的中点依次为v,v,…,v,连接所有MAKLINK线的中点加上始点S和终点T构成⽤于初始路径规划的⽆向⽹络图蚁群算法蚁群算法是由 dorigo.M等⼈在20世纪90年代初提出的⼀种新型进化算法,它来源于对蚂蚁搜索问题的研究。
⼈们在观察蚂蚁搜索⾷物时发现,蚂蚁在寻找⾷物时,总在⾛过的路径上释放⼀种称为信息素的分泌物,信息素能够保留⼀段时间,使得在⼀定范围内的其他蚂蚁能够觉察到该信息素的存在。
后继蚂蚁在选择路径时,会选择信息素浓度较⾼的路径,并且在经过时留下⾃⼰的信息素这样该路径的信息素会不断增强,蚂蚁选择的概率也在不断增⼤蚁群算法最优路径寻找如图。
图表达了蚂蚁在觅⾷过程中的三个过程,其中点A是蚂蚁蚁巢,点D是⾷物所在地,四边形 EBFCE表⽰在蚁巢和⾷物之间的障碍物。
蚂蚁如果想从蚁巢点A达到点D,只能经过路径BFC或者路径BEC,假定从蚁巢中出来若⼲只蚂蚁去⾷物所在地D搬运⾷物,每只蚂蚁经过后留下的信息素为1,信息素保留的时间为1.⼀开始,路径BFC和BEC上都没有信息素,在点A的蚂蚁可以随机选择路径,蚂蚁以相同的概率选择路径BFC或BEC,如图(b)所⽰。
基于改进蚁群算法的AGV路径规划研究

基于改进蚁群算法的AGV路径规划研究目录一、内容概述 (2)1.1 研究背景与意义 (2)1.2 国内外研究现状综述 (3)1.3 主要研究内容与方法 (4)二、蚁群算法理论基础 (6)2.1 蚂蚁系统 (7)2.2 最大最小蚂蚁系统 (8)2.3 蚁群算法改进方向 (9)三、改进蚁群算法在AGV路径规划中的应用 (9)3.1 初始解的生成策略 (10)3.2 蚂蚁的转移规则 (12)3.3 动态信息素更新策略 (13)3.4 算法实现步骤 (14)四、仿真实验与结果分析 (15)4.1 实验环境与参数设置 (16)4.2 实验结果与对比分析 (17)4.3 结果讨论与优化建议 (18)五、结论与展望 (19)5.1 研究成果总结 (20)5.2 存在问题与不足 (22)5.3 后续研究方向与应用前景展望 (23)一、内容概述在当前制造业和物流领域,AGV路径规划对于提高生产效率、优化资源分配和降低成本等方面具有至关重要的作用。
由于复杂的生产环境和动态的任务需求,AGV路径规划面临诸多挑战,如路径选择、任务调度和避障等。
为了应对这些挑战,本文提出了一种基于改进蚁群算法的AGV路径规划方法。
本文将介绍研究背景和意义,阐述AGV路径规划的重要性和现有挑战。
概述研究的主要内容和目标,包括改进蚁群算法的设计和实现过程,以及该算法在AGV路径规划中的应用。
在此基础上,本文将详细阐述算法的具体实现过程,包括算法的关键步骤、参数设置和优化策略等。
还将讨论如何通过仿真实验验证算法的有效性和性能,总结研究成果,分析改进蚁群算法在AGV路径规划中的优势和潜在应用前景。
本文的研究对于提高AGV系统的智能化水平和实际应用的推广具有重要的理论意义和实践价值。
1.1 研究背景与意义传统方法在处理复杂环境下的路径规划时存在局限性,当环境发生变化时(如障碍物的增加或位置移动),传统方法往往难以快速适应并找到最优路径。
传统方法在计算效率方面有待提高,对于大规模的AGV网络,传统的路径规划算法需要耗费大量的计算资源和时间,这在实际应用中是不可接受的。
拖拉机零部件数控多加工路线优化——基于蚁群算法集成求解

拖拉机零部件数控多加工路线优化—基于蚁群算法集成求解刘 芹(山东商业职业技术学院,济南 250103)摘 要:数控加工路线是机床零部件加工编程的关键,针对计算机辅助设计中工艺路线规划问题,提出了一种基于蚁群算法集成求解的拖拉机零部件数控多加工路线优化算法,可根据加工元、加工方法及加工元约束条件,优化零部件加工机床路线,计算出机床最优的加工工艺路线。
通过实例验证,证实了该方法可以较大程度地优化加工路线,大大节省了加工时间,提高了作业效率。
关键词:数控加工;机床;蚁群算法;加工路线中图分类号:S219.03;TG659 文献标识码:A文章编号:1003-188X(2021)01-0196-050 引言工艺路线的合理性对产品结构功能性与外观影响重大。
数控加工是指在数控机床上进行零件加工的一种工艺方法,数控机床加工与传统机床加工的工艺规程从总体上说是一致的,主要是解决零件品种多变、批量小、形状复杂及精度高等问题和实现高效化和自动化加工。
对于一个复杂程度高、精度要求高、需要用数控机床来加工的零件,制定和优化零部件加工路线显得尤为重要。
1 蚁群算法近年来,科学界一直致力于分析和理解不同动物群体的集体智能行为,如昆虫。
这些动物用于相互交流或获得食物来源的技术被广泛进行建模研究并应用于各种科学学科,如各种模型优化问题。
其中,蚁群算法是以动物为灵感的优化算法中的一种,由Italy学者Dorigo等人提出,适用于解决复杂组合优化的问题,如旅行商问题、路径优化等。
蚂蚁是为了使用最短路径来获取食物来源,还能感知和适应自身周围的环境变化。
通过这种方式,当它们遵循的路径不是最短路径时,能够快速找到新的短路径。
蚂蚁沿直线路径行进,以便在开始时到达它们的食物来源,在使用化学物质的信息素沉积为其路径的障碍之后,使其他蚂蚁遵循相同的路径。
信息素被用作殖民地中收稿日期:2019-06-24基金项目:山东省教育教学研究课题(2018JXY1090)作者简介:刘 芹(1975-),女,济南人,工程师,硕士,(E-mail)liuqin1975sdsy@126.com。
基于蚁群算法的AGV路径规化的实现

或停车站当小车上的阅 读 器 对 准 下 面 的“电 子 标 牌”时,在阅 读 器 发 射 的 高 频 电 磁 波 的 激 励 下,“电 子标牌”对 其 产 生 调 制 作 用,阅 读 器 接 收 到 调 制 信 号后经高频放大,解调还原出“电子标牌”所携地址 编码,最后通过标准 RS - 232 串行口输出,可与微 电脑 RS - 232 串行口相接。
在各个节点上运行蚁群算法,然后将最优解传 给主程序。主程序将收到的最优解与前一次进行比 较,将最优解保留,如此反复,直到传给主程序的最 好结果不再改进为止。当最优解不再改变时,表明 已得不到更好的路径,此时满足终止条件。如表 1 所示,在第 35 至第 100 次最短路径的值几乎未再改 变则最短路径长度为 74. 2m。由此可见: 蚁群算法 具有多解性,在本质上具有分布性和并行性,易于分 布和并行实现,选择较好的实验参数,同时利用正反 馈的特性,往往能够得到好的实验结果。
表 1 蚁群算法仿真结果
α
β
ρ 最短路径长度 收敛所需的迭代次数
1
2
0. 5
74. 7
35
1
2
0. 5
74. 5
40
1
2
0. 5
74. 5
45
1
2
0. 5
74. 4
50
1
2
0. 5
74. 4
55
2
1
0. 5
74. 3
60
2
1
0. 5
74. 2
70
2
1
0. 5
74. 2
80
2
1
0. 5
74. 2
90
2
中图分类号:TP301 文献标识码:A 文章编号:1009 - 2552(2011)11 - 0103 - 04
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直 到切 割 完所 有 内轮 廓 3 、4 、5 、6 、7 ,再 关 光 、
快速空行程行进 到零件外轮廓8 上, 开 光 打 孔 并 切
割 ;最 后 从 零件 外 轮 廓8 的打 孔 点处 关 光 ,快 速 空
行程 返 回到 程序 零点 0。
判断实体类别
2 零件排样及切割工程 图的层次划分
、 l
. 8 化
基于蚁群算法 的钣金件数控切割 路径规 划
Sh eet m et al CNC cut t i ng pat h pl anni ng bas ed on ant col ony al gor i t hm
蒋麒麟 ,王宗荣 ,李翔英
高 压 水 图I 激光切割 原理 图
1 钣 金件数控切 割概述
钣 金 件 数 控 切 割 工 艺 一 般 由三 部 分组 成 ,分 别 是 预 热 打 孔 、 切 割 和 空 行 程 ,其 利 用数 控 切 割
机 ,根 据 不 同 的 零 件 、具 体 的 加 工 工艺 编 写数 控
代 码 ,对 已 在 整 块 钣 金 件上 排 样 好 的 零 件 轮 廓 进 行 自动 切 割 。 钣 金件 的数 控 切 割 主 要使 用 四种 切
关闭实体对象 获取块表 记录指针
遍历指针下移
创建块表记录 遍历器
N
情 况 对 零 件 进 行 优 化 排 样 。根 据 钣 金 件 上 零 件 种 类 的 个 数 ,零 件 排 样 的 基 本 方 式 有 单 排 、 联 排 和
混排 三 种 。混排 对 于提 高 钣金 件 的材 料利 用 率和
第3 6 卷
第2 期
2 0 1 4 - 0 2 ( 下) [ 9 1பைடு நூலகம்
1
一
訇 出
继 承 自Ad Db C u r v e 类 。提 取 切 割 工 程 图 中的 实 体
几 何信 息 的过程 如 图5 所示。
个零 件 内 轮廓 3 上 ,依次 重 复 前面 相 同 的步 骤 ,
割 完 内轮 廓 I ,回到 起 始打 孔 点 ;然 后 关光 、快 速 空 行程 行 进 到 下一 个 零 件 内轮 廓2 上 ,预 热 并 开光
打 孔 ,然 后 以该 打 孔 点 为起 点切 割 完 内轮 廓 2 , 回 到 起 始 打 孔 点 ;然 后 关 光 、快 速 空 行 程 行 进 到 下
割方法u 】 :I )气体火焰切割;2 )等离子弧切割 ;
3 )激 光切 割 ( 如 图l 所 示 );4 )高压 水 射流 切 割 ( 如 图2 所 示 )。
射 流
图2 高压水射流切剖原理 图
以数控激光切割为例 ,针对图3 中的简单零件
轮 廓 ,其 切 割 一般 过 程 为 : 首 先 割 嘴 从程 序 零 点 ( 即 对 刀 点 ) 0出 发 ,快 速 行 进 到 零 件 内轮 廓 I 上 , 预热 并 开 光 打 孔 ,然 后 以 该 打 孔 点 为 起 点 切
J l ANG Qi — I i n 。 一 ,W ANG Zo n g . r o n g ,L I Xi a n g . y i n g
( 1 . 南京航空航天大学 机 电学院 ,南京 2 1 0 0 1 6 ;2 . 南京工程学院 机械 学院,南京 2 1 1 1 6 7 ) 摘 要 :在熟悉钣金件数控切割方法与工 艺的基础上 , 根据 切割 工程图 ,提取工程图中的几何信息 ,将 几何信 息转化 为工艺信 息 ,建立钣 金件数控 切割加 工路径数 学模型 ,选择蚁群 算法 ,合 理规 划切割加工路径 ,为工 艺设计 、工时定额 与成 本估算提 供基 础。 关键 词 :钣金件 ;数控切割 ;O b J e c t A R X ; 蚁群算 法 ;路径 规划 中圈分类号 :T O 4 8 文献标识码 :A 文童 编号 ;1 0 0 9 - 0 1 3 4 ( 2 0 1 4 ) o 2 ( 下) -0 0 0 9 - 0 4
在 钣 金 件 切 割 过 程 中 , 为 了 节 约 钣 金 件 、提
获取 块表指针
保 存至链表
高 切 割 效 率 ,一 块 钣 金 件 上 往 往 排 列 若 干 个 相 同
或 者 不 同 的 零 件 , 此 时 ,需 要 根 据 钣 金 件 的 大 小 、零 件 的 形 状 与 尺 寸 ,切 割 的 方 便 程 度 等 具 体
D o i :1 0 . 3 9 6 9 / J . I s s n . 1 0 0 9 - 0 1 3 4 . 3 0 1 4 . o e ( 下) . 0 3
0 引言
数 控 切 割 是 钣 金 件 制 造 过 程 中一 个 极 其 重 要 的 环 节 ,在大 批 量 制 造 环境 下 ,对 钣 金 件 快 速 、 合理 、 高 效地 数 控切 剖 是 钣 金 件 后 续 加 工 工艺 的
重 要 前 提 , 同 时也 是钣 金 件 产 品制 造 过 程 中 工 时
定 额 与成 本 估 算 的一 个 重 要 基 础 。在 钣 金 件 数 控
切 割 过 程 中 ,加 工 路径 的合 理 规 划 可 以大 幅 度 减
动 方 向
少喷 嘴 空 行 程 的距 离 、节 省 机 床 的加 工 时 间 、提 高 机 床 的工 作 效 率 。 同时 加 工 路 径 的合 理 规 划 , 对 提 高 钣 金 件 的加 工 质 量 和 减 少 机 床 的故 障 率 还 具 有非 常积 极 的作 用 。
图3 钣金件数控切割一般过程
救稽日嗣:2 0 1 3 -I 1 -1 5 基盒项目:国家 自然基金 ( 5 1 2 7 5 2 2 7 );上海 飞机 制造 有限公司委托 关键技术攻关项 目 ( S A MC1 4 - J S 一 1 5 — 0 0 2 ) 作者俺介:蒋麒麟 ( 1 9 7 6一),男,安徽马鞍 山人,讲师,在职博士生 ,研究方向为数字化制造技术 。
