2015年苏州市中考数学复习模拟试卷(3)及答案
2015年苏州市中考数学试卷与答案

2015 年苏州市初中毕业暨升学考试试卷数学本试卷由选择题、填空题和解答题三大题组成,共28 小题,满分130 分,考试时间120 分钟.注意事项:1.答题前,考生务必将自己的姓名、考点名称、考场号、座位号用0.5 毫米黑色墨水签字笔填写在答题卡相应位置上,并认真核对条形码上的准考号、姓名是否与本人的相符;2.答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其他答案;答非选择题必须用0.5 毫米黑色墨水签字笔写在答题卡指定的位置上,不在答题区域内的答案一律无效,不得用其他笔答题;3.考生答题必须答在答题卡上,保持卡面清洁,不要折叠,不要弄破,答在试卷和草稿纸上一律无效.一、选择题:本大题共10 小题,每小题 3 分,共30 分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B 铅笔涂在答.题.卡.相.应.位.置.上..1.2 的相反数是A.2 B.12C. 2 D.122.有一组数据:3,5,5,6,7,这组数据的众数为A.3 B.5 C.6 D.73.月球的半径约为1 738 000m ,1 738 000 这个数用科学记数法可表示为6 B.1.738×107 C.0.1738×107 D.17.38×105A.1.738×104.若2m 2 ,则有2A.0<m<1 B.- 1<m<0 C.- 2<m<-1D.- 3<m<- 2 5.小明统计了他家今年 5 月份打电话的次数及通话时间,并列出了频数分布表:通话时间x/min 0<x≤ 5 5<x≤10 10<x≤15 15<x≤20频数(通话次数)20 16 9 5 则通话时间不超过15min 的频率为A.0.1 B.0.4 C.0.5 D.0.96.若点A(a,b)在反比例函数y 2x的图像上,则代数式a b- 4 的值为A .0 B.- 2 C. 2 D.- 67.如图,在△ABC 中,AB= A C,D 为BC 中点,∠BAD =35°,则∠ C 的度数为A.35°B.45°C.55°D.60°ABD C(第7 题)8.若二次函数y=x2+bx 的图像的对称轴是经过点(2,0)且平行于y 轴的直线,则关于x 的方程x2+ b x=5 的解为A .x1 0, x2 4 B.x1 1, x2 5 C.x1 1, x2 5 D.x1 1, x2 5 9.如图,AB 为⊙O 的切线,切点为B,连接AO,AO 与⊙O 交于点C,BD 为⊙O 的直径,连接CD.若∠A=30°,⊙O 的半径为2,则图中阴影部分的面积为A .433 B.432 3 C. 3 D.233北C B西东南22.5 °OC A45°lAB DD(第9 题)(第10 题)10.如图,在一笔直的海岸线l 上有A、B 两个观测站,AB=2km,从 A 测得船 C 在北偏东45°的方向,从 B 测得船 C 在北偏东22.5°的方向,则船 C 离海岸线l 的距离(即CD 的长)为A .4 km B. 2 2 km C.2 2 km D. 4 2 km二、填空题:本大题共8 小题,每小题 3 分,共24 分.把答案直接填在答题.卡.相.应.位.置.上...11.计算: 2a a = ▲.12.如图,直线a∥b,∠1=125°,则∠2 的度数为▲°.a1c羽毛球30%其他10%乒乓球篮球20% 240%b(第12 题)(第13 题)13.某学校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少 6 人,则该校被调查的学生总人数为▲名.14.因式分解: 2 4 2a b = ▲.15.如图,转盘中8 个扇形的面积都相等.任意转动转盘 1 次,当转盘停止转动时,指针指向大于 6 的数的概率为▲.1 82 73 64 5(第15 题)16.若a 2b 3 ,则9 2a 4b 的值为▲.17.如图,在△ABC 中,CD 是高,CE 是中线,CE=CB,点A、D 关于点 F 对称,过点 F 作FG∥CD,交AC 边于点G,连接GE.若AC =18,BC=12,则△CEG 的周长为▲.CA DGA B C F EF E D B(第18 题)(第17 题)18.如图,四边形ABCD 为矩形,过点 D 作对角线BD 的垂线,交BC 的延长线于点E,取BE 的中点F,连接DF ,DF =4.设AB= x,AD =y,则 22 4x y 的值为▲.三、解答题:本大题共10 小题,共76 分.把解答过程写在答题.卡.相.应.位.置.上..,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B 铅笔或黑色墨水签字笔.19.(本题满分5分)计算:0 9523.20.(本题满分5分)解不等式组:x12,3x1>x 5.21.(本题满分6分)先化简,再求值:121x2x1x2x2,其中x31.22.(本题满分6分)甲、乙两位同学同时为校文化艺术节制作彩旗.已知甲每小时比乙多做5面彩旗,甲做60面彩旗与乙做50面彩旗所用时间相等,问甲、乙每小时各做多少面彩旗?23.(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)从中任意摸出1个球,恰好摸到红球的概率是▲;(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.24.(本题满分8分)如图,在△ABC中,AB=A C.分别以B、C为圆心,BC长为半径在BC下方画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD.(1)求证:AD平分∠BAC;(2)若BC=6,∠BAC=50,求D?E、D?F的长度之和(结果保留).ABCED(第24题)F25.(本题满分8分)如图,已知函数y kx(x>0)的图像经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图像经过点A、D,与x轴的负半轴交于点E.(1)若AC=32OD,求a、b的值;y(2)若BC∥AE,求BC的长.AD F BxE OC(第25题)26.(本题满分10分)如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.(1)求证:ED∥AC;(2)若BD=2CD,设△EBD的面积为S,△ADC的面积为S2,且12S116S240,求△ABC的面积.EAOB D C(第26题)27.(本题满分10分)如图,已知二次函数21y x m x m(其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P 为对称轴l上的点,连接PA、PC,PA=PC.(1)∠ABC的度数为▲°;(2)求P点坐标(用含m的代数式表示);(3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.ylPxA O BC(第27题)28.(本题满分10分)如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm 的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B →C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).(1)如图①,点P从A→B→C→D,全程共移动了▲cm(用含a、b的代数式表示);(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.B P CPB CO O O1A D A D(图①)(图②)(第28题)2015 年苏州市初中毕业暨升学考试数学试题答案一、选择题1.C 2.B 3.A 4.C 5.D6.B 7.C 8.D 9.A 10.B二、填空题11. 3a 12.55 13.60 14. a 2b a 2b15.1416.3 17.27 18.16三、解答题22.6解:原式=3+5 1 =7.22.7解:由x 1 2,解得x 1,由 3 x 1 >x 5 ,解得x>4 ,∴不等式组的解集是x>4 .x1x 1 x 2 x 2 2=x 1 x 2 12x 2 x 1 x 122.8解:原式=.当x 3 1时,原式=1 1 33 1 1 3 3.22.9解:设乙每小时做x 面彩旗,则甲每小时做(x+5)面彩旗.根据题意,得60 50x 5 x.解这个方程,得x=25.经检验,x=25 是所列方程的解.∴x+5=30.答:甲每小时做30 面彩旗,乙每小时做25 面彩旗.22.10解:(1)12.(2)用表格列出所有可能的结果:第二次红球1 红球2 白球黑球第一次红球 1 (红球1,红球2)(红球1,白球)(红球1,黑球)红球 2 (红球2,红球1)(红球2,白球)(红球2,黑球)白球(白球,红球1)(白球,红球2)(白球,黑球)黑球(黑球,红球1)(黑球,红球2)(黑球,白球)由表格可知,共有12 种可能出现的结果,并且它们都是等可能的,其中“两次都摸到红球”有 2 种可能.∴P(两次都摸到红球)= 212 = 16 .22.11证明:(1)由作图可知B D =C D.在△ABD 和△ACD 中,AB AC,BD CD ,AD AD,∴△ABD≌△ACD(SSS).∴∠BAD=∠CAD,即AD 平分∠BAC.解:(2)∵AB=AC,BAC =50°,∴∠ABC=∠ACB= 65°.∵BD= CD = BC,∴△BDC 为等边三角形.∴∠DBC=∠DCB= 60°.∴∠DBE=∠DCF= 55°.∵BC=6,∴BD= CD =6.∴D?E的长度= D?F的长度= 55 6 11180 6 .∴D?E、D?F的长度之和为11 11 116 6 3 .25.解:(1)∵点B(2,2)在y kx的图像上,∴k=4,y 4x .∵BD⊥y 轴,∴D 点的坐标为(0,2),OD =2.∵AC⊥x 轴,AC= 32OD,∴AC =3,即 A 点的纵坐标为3.∵点A 在y 4x 的图像上,∴ A 点的坐标为(43,3).∵一次函数y=ax+b 的图像经过点A、D,∴43a b 3, a解得34, b 2. b 2.(2)设A点的坐标为(m, 4m ),则C点的坐标为(m,0).∵BD∥CE,且BC∥DE,∴四边形B CED 为平行四边形.∴CE= BD =2.∵BD∥CE,∴∠ADF =∠AEC.4AF m2∴在Rt△AFD 中,tan∠ADF =,DF m4在Rt△ACE 中,tan∠AEC= AC m EC 2,∴4 42m mm 2,解得m=1.∴C 点的坐标为(1,0),BC= 5 .26.证明:(1)∵AD 是△ABC 的角平分线,∴∠BAD =∠DAC.∵∠E=∠BAD,∴∠E =∠DAC.∵BE∥AD,∴∠E =∠EDA.∴∠EDA =∠DA C.∴ED∥AC.解:(2)∵BE∥AD,∴∠EBD =∠ADC.∵∠E =∠DAC,∴△EBD∽△ADC,且相似比k BD 2DC .··················∴S1S22k 4 ,即S1 4S2 .∵ 2S1 16 S2 4 0 ,∴216S 16S 4 0 ,即2 224S 2 0 .2∴ 1S .22∵S BC BD CD 3CDV ,∴ 3ABC3S V .ABCS CD CD CD 2 227.解:(1)45.理由如下:令x=0,则y=- m,C 点坐标为(0,- m).2 1 0令y=0,则x m x m ,解得x1 1 ,x2 m.∵0<m<1,点A 在点B 的左侧,∴B 点坐标为(m,0).∴OB =OC= m.∵∠BOC=90°,∴△BOC 是等腰直角三角形,∠OBC=45°.(2)解法一:如图①,作P D⊥y 轴,垂足为D,设l 与x 轴交于点E,由题意得,抛物线的对称轴为1 m x .2设点P 坐标为( 12m ,n).∵PA= PC,∴PA2= PC2,即AE2+ PE2=CD2+ PD2.∴2 21 m 1 m221 n n m .2 2解得1 mn .∴P 点的坐标为21 m 1 m,2 2.解法二:连接P B.由题意得,抛物线的对称轴为1 m x .2∵P 在对称轴l 上,∴PA=PB.∵PA=PC,∴PB=PC.∵△BOC 是等腰直角三角形,且OB=OC,∴P 在BC 的垂直平分线y x上.∴P 点即为对称轴 1 mx 与直线y x的交点.2∴P 点的坐标为1m 1 m,2 2.y yl lPDPQDx xA Q EB A E O BOC C图①图②(3)解法一:存在点Q 满足题意.∵P 点的坐标为1m 1 m,2 2,∴PA2+ PC2=AE2+ PE2+CD2+ PD2=2 2 2 21 m 1 m 1 m 1 m21 m 1 m .2 2 2 22∵AC2=1 m ,∴PA2+ PC2= A C2.∴∠APC=90°.∴△PAC 是等腰直角三角形.∵以Q、B、C 为顶点的三角形与△PAC 相似,∴△QBC 是等腰直角三角形.∴由题意知满足条件的点Q 的坐标为(- m,0)或(0,m).①如图①,当Q 点的坐标为(- m,0)时,若PQ 与x 轴垂直,则 1若PQ 与x 轴不垂直,2 mm ,解得1m ,PQ=313.则2 2 22 2 2 1 m 1 m 5 2 1 5 2 1 PQ PE EQ m m 2m m .2 2 2 2 2 5 10∵0<m<1,∴当2m 时,52PQ 取得最小值110,PQ 取得最小值1010.∵1010<13,∴当2m ,即Q 点的坐标为(525,0)时,PQ 的长度最小.②如图②,当Q 点的坐标为(0,m)时,若PQ 与y 轴垂直,则 1若PQ 与y 轴不垂直,2mm ,解得1m ,PQ=313.则2 2 22 2 2 1 m 1 m 5 2 1 5 2 1 PQ PD DQ m m 2m m .2 2 2 2 2 5 10∵0<m<1,∴当 2m 时,52PQ 取得最小值110,PQ 取得最小值1010.10 1 ∵<,10 3∴当2m ,即Q 点的坐标为(0,525)时,PQ 的长度最小.综上:当Q 点坐标为(25 ,0)或(0,25)时,PQ 的长度最小.解法二:如图①,由(2)知P 为△ABC 的外接圆的圆心.∵∠APC 与∠ABC 对应同一条弧A?C,且∠ABC=45°,∴∠APC=2∠ABC=90°.下面解题步骤同解法一.28.解:(1)a+2b.(2)∵在整个运动过程中,点P 移动的距离为 a 2b cm,圆心O 移动的距离为 2 a 4 cm,由题意,得 a 2b 2 a 4 .①∵点P 移动2s 到达B 点,即点P 用2s 移动了bcm,点P 继续移动3s,到达BC 的中点,即点P 用3s移动了12a cm.∴1ab22 3.②由①②解得ab24,22.12∵点P 移动的速度与⊙O 移动的速度相等,b∴⊙O 移动的速度为 42(cm/s).∴这5s时间内圆心O 移动的距离为5×4=20(cm).(3)存在这种情形.解法一:设点P 移动的速度为v1cm/s,⊙O 移动的速度为v2cm/s,由题意,得v a 2b 20 2 10 51v 2 a 4 2 20 4 42.PB CHEO O1FA DG如图,设直线OO1与AB 交于点E,与CD 交于点F,⊙O1 与AD 相切于点G.若PD 与⊙O1 相切,切点为H,则O1G=O1H.易得△DO1G≌△DO1H,∴∠ADB =∠BDP.∵BC∥AD,∴∠ADB =∠CBD.∴∠BDP =∠CBD .∴BP=DP.设BP=xcm,则D P =xcm,PC =(20- x)cm,在Rt△PCD 中,由勾股定理,可得 2 2 2PC CD PD ,即 2 2 220 x 10 x ,解得25 x .2∴此时点P 移动的距离为10 25 452 2∵EF ∥AD,∴△BEO1∽△BAD.(cm).∴EO1 BEAD BA ,即E O1 820 10.∴EO1=16cm.∴OO1=14cm.①当⊙O 首次到达⊙O1 的位置时,⊙O 移动的距离为14cm,45452∴此时点P 与⊙O 移动的速度比为14 28.∵45 528 4 ,∴此时PD 与⊙O1不可能相切.②当⊙O 在返回途中到达⊙O1 的位置时,⊙O 移动的距离为2×(20- 4)- 14=18 (cm),4545 52∴此时点P 与⊙O 移动的速度比为18 36 4.∴此时PD 与⊙O1恰好相切.解法二:∵点P 移动的距离为452 cm(见解法一),OO1=14cm(见解法一),v1v254,45 4 2 5∴⊙O 应该移动的距离为18(cm).①当⊙O 首次到达⊙O1 的位置时,⊙O 移动的距离为14cm≠18 cm,∴此时PD 与⊙O1不可能相切.②当⊙O 在返回途中到达⊙O1 的位置时,⊙O 移动的距离为2×(20- 4)- 14=18 (cm),∴此时PD 与⊙O1恰好相切.解法三:点P 移动的距离为452 cm,(见解法一)OO1=14cm,(见解法一)由v1v254可设点P 的移动速度为5k cm/s,⊙O 的移动速度为4k cm/s,45∴点P 移动的时间为925k 2k(s).①当⊙O 首次到达⊙O1 的位置时,⊙O 移动的时间为∴此时PD 与⊙O1不可能相切.14 7 94k 2k 2k,②当⊙O 在返回途中到达⊙O1 的位置时,⊙O 移动的时间为2 (20 4) 14 94k 2k,∴此时PD 与⊙O1 恰好相切.。
苏州市中考数学试卷及答案

2015年苏州市初中毕业暨升学考试试卷数 学一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B 铅笔涂在答题卡相应位置上......... 1.2的相反数是 A .2B .12C .-2D .-122.有一组数据:3,5,5,6,7,这组数据的众数为 A .3B .5C .6D .73.月球的半径约为1 738 000m ,1 738 000这个数用科学记数法可表示为A .1.738×106B .1.738×107C .0.1738×107D .17.38×1054.若()2m =-,则有 A .0<m <1 B .-1<m <0 C .-2<m <-1 D .-3<m <-25.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:则通话时间不超过15min 的频率为 A .0.1B .0.4C .0.5D .0.96.若点A (a ,b )在反比例函数2y x=的图像上,则代数式ab -4的值为 A .0 B .-2C . 2D .-67.如图,在△ABC 中,AB =AC ,D 为BC 中点,∠BAD =35°,则∠C 的度数为 A .35° B .45°C .55°D .60°DCBA8.若二次函数y =x 2+bx 的图像的对称轴是经过点(2,0)且平行于y 轴的直线,则关于x 的方程x 2+bx =5的解为 A .120,4x x ==B .121,5x x ==C .121,5x x ==-D .121,5x x =-=9.如图,AB 为⊙O 的切线,切点为B ,连接AO ,AO 与⊙O 交于点C ,BD 为⊙O 的直径,连接CD .若∠A =30°,⊙O 的半径为2,则图中阴影部分的面积为 A.43πB.43π-C.π D.23π10.如图,在一笔直的海岸线l 上有A 、B 两个观测站,AB =2km ,从A 测得船C 在北偏东45°的方向,从B 测得船C 在北偏东22.5°的方向,则船C 离海岸线l 的距离(即CD 的长)为 A .4kmB.(2+kmC.D.(4km二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相应位置上......... 11.计算:2a a ⋅= ▲ .12.如图,直线a ∥b ,∠1=125°,则∠2的度数为 ▲ °.13.某学校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛(第9题)(第10题)lba(第13题)20%10%30%40%其他乒乓球篮球羽毛球球的人数比最喜欢乒乓球的人数少6人,则该校被调查的学生总人数为 ▲ 名. 14.因式分解:224a b -= ▲ .15.如图,转盘中8个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,指针指向大于6的数的概率为 ▲ .16.若23a b -=,则924a b -+的值为 ▲ .17.如图,在△ABC 中,CD 是高,CE 是中线,CE =CB ,点A 、D 关于点F 对称,过点F作FG ∥CD ,交AC 边于点G ,连接GE .若AC =18,BC =12,则△CEG 的周长为 ▲ .18.如图,四边形ABCD 为矩形,过点D 作对角线BD 的垂线,交BC 的延长线于点E ,取BE 的中点F ,连接DF ,DF =4.设AB =x ,AD =y ,则()224x y +-的值为 ▲ . 三、解答题:本大题共10小题,共76分.把解答过程写在答题卡相应位置上........,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B 铅笔或黑色墨水签字笔. 19.(本题满分5分)(052---. 20.(本题满分5分)解不等式组:()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩>(第17题)GF E D CBA F EDC B A (第18题)(第15题)21.(本题满分6分)先化简,再求值:2121122x x x x ++⎛⎫-÷⎪++⎝⎭,其中1x .22.(本题满分6分)甲、乙两位同学同时为校文化艺术节制作彩旗.已知甲每小时比乙多做5面彩旗,甲做60面彩旗与乙做50面彩旗所用时间相等,问甲、乙每小时各做多少面彩旗?23.(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)从中任意摸出1个球,恰好摸到红球的概率是 ▲ ;(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.24.(本题满分8分)如图,在△ABC 中,AB =AC .分别以B 、C 为圆心,BC 长为半径在BC 下方画弧,设两弧交于点D ,与AB 、AC 的延长线分别交于点E 、F ,连接AD 、BD 、CD .(1)求证:AD 平分∠BAC ;(2)若BC =6,∠BAC =50︒,求DE 、DF 的长度之和(结果保留π).CBA25.(本题满分8分)如图,已知函数ky x=(x >0)的图像经过点A 、B ,点B 的坐标为(2,2).过点A 作AC ⊥x 轴,垂足为C ,过点B 作BD ⊥y 轴,垂足为D ,AC 与BD 交于点F .一次函数y=ax +b 的图像经过点A 、D ,与x 轴的负半轴交于点E . (1)若AC =32OD ,求a 、b 的值; (2)若BC ∥AE ,求BC 的长.26.(本题满分10分)如图,已知AD 是△ABC 的角平分线,⊙O 经过A 、B 、D 三点,过点B 作BE ∥AD ,交⊙O 于点E ,连接ED . (1)求证:ED ∥AC ;(2)若BD =2CD ,设△EBD 的面积为1S ,△ADC 的面积为2S ,且2121640S S -+=,求△ABC 的面积.27.(本题满分10分)如图,已知二次函数()21y x m x m =+--(其中0<m <1)的图像与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴为直线l .设P 为对称轴l 上的点,连接P A 、PC ,P A =PC . (1)∠ABC 的度数为 ▲ °;(2)求P 点坐标(用含m 的代数式表示);(3)在坐标轴上是否存在点Q (与原点O 不重合),使得以Q 、B 、C 为顶点的三角形与△P AC 相似,且线段PQ 的长度最小?如果存在,求出所有满足条件的点Q 的坐标;如果不存在,请说明理由.28.(本题满分10分)如图,在矩形ABCD 中,AD =a cm ,AB =b cm (a >b >4),半径为2cm的⊙O 在矩形内且与AB 、AD 均相切.现有动点P 从A 点出发,在矩形边上沿着A →B →C →D 的方向匀速移动,当点P 到达D 点时停止移动;⊙O 在矩形内部沿AD 向右匀速平移,移动到与CD 相切时立即沿原路按原速返回,当⊙O 回到出发时的位置(即再次与AB 相切)时停止移动.已知点P 与⊙O 同时开始移动,同时停止移动(即同时到达各自的终止位置).(1)如图①,点P 从A →B →C →D ,全程共移动了 ▲ cm (用含a 、b 的代数式表示); (2)如图①,已知点P 从A 点出发,移动2s 到达B 点,继续移动3s ,到达BC 的中点.若点P 与⊙O 的移动速度相等,求在这5s 时间内圆心O 移动的距离;(3)如图②,已知a =20,b =10.是否存在如下情形:当⊙O 到达⊙O 1的位置时(此时圆心O 1在矩形对角线BD 上),DP 与⊙O 1恰好相切?请说明理由.2015年苏州市初中毕业暨升学考试数学试题答案一、选择题 1.C2.B3.A4.C5.D(第28题)(图②)(图①)6.B7.C8.D9.A10.B 二、填空题 11.3a 12.55 13.60 14.()()22a b a b +- 15.1416.317.2718.16三、解答题19.解:原式 = 3+5-1 = 7. 20.解:由12x +≥,解得1x ≥,由()315x x -+>,解得4x >, ∴不等式组的解集是4x >.21.解:原式=()21122x x x x ++÷++ =()2121211x x x x x ++⨯=+++.当1x==. 22.解:设乙每小时做x 面彩旗,则甲每小时做(x +5)面彩旗.根据题意,得60505x x=+. 解这个方程,得x =25.经检验,x =25是所列方程的解. ∴x +5=30. 答:甲每小时做30面彩旗,乙每小时做25面彩旗. 23.解:(1)1. (2)用表格列出所有可能的结果: 到红球”有2种可能.∴P (两次都摸到红球)=212=16. 24.证明:(1)由作图可知BD =CD .在△ABD 和△ACD 中,,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩∴△ABD≌△ACD(SSS).∴∠BAD=∠CAD,即AD平分∠BAC.解:(2)∵AB=AC,∠BAC=50°,∴∠ABC=∠ACB=65°.∵BD= CD = BC,∴△BDC为等边三角形.∴∠DBC=∠DCB=60°.∴∠DBE=∠DCF=55°.∵BC=6,∴BD= CD =6.∴DE的长度=DF的长度=556111806ππ⨯⨯=.∴DE、DF的长度之和为111111 663πππ+=.25.解:(1)∵点B(2,2)在kyx=的图像上,∴k=4,4yx =.∵BD⊥y轴,∴D点的坐标为(0,2),OD=2.∵AC⊥x轴,AC=32OD,∴AC=3,即A点的纵坐标为3.∵点A在4yx=的图像上,∴A点的坐标为(43,3).∵一次函数y=ax+b的图像经过点A、D,∴43,32.a bb⎧+=⎪⎨⎪=⎩解得3,42.ab⎧=⎪⎨⎪=⎩(2)设A点的坐标为(m,4m),则C点的坐标为(m,0).∵BD∥CE,且BC∥DE,∴四边形BCED为平行四边形.∴CE= BD=2.∵BD∥CE,∴∠ADF=∠AEC.∴在Rt△AFD中,tan∠ADF=42 AF mDF m-=,在Rt△ACE中,tan∠AEC=42 AC m EC=,∴4422m mm-=,解得m=1.∴C点的坐标为(1,0),BC.26.证明:(1)∵AD是△ABC的角平分线,∴∠BAD =∠DAC.∵∠E=∠BAD,∴∠E =∠DAC.∵BE∥AD,∴∠E =∠EDA.∴∠EDA =∠DA C . ∴ED ∥AC .解:(2)∵BE ∥AD ,∴∠EBD =∠ADC .∵∠E =∠DAC ,∴△EBD ∽△ADC ,且相似比2BDk DC==. ··················· ∴2124S k S ==,即124S S =. ∵2121640S S -+=,∴222161640S S -+=,即()22420S -=.∴212S =. ∵233ABC S BC BD CD CD S CD CD CD +====,∴32ABCS=. 27.解:(1)45.理由如下:令x =0,则y =-m ,C 点坐标为(0,-m ).令y =0,则()210x m x m +--=,解得11x =-,2x m =.∵0<m <1,点A 在点B 的左侧,∴B 点坐标为(m ,0).∴OB =OC =m .∵∠BOC =90°,∴△BOC 是等腰直角三角形,∠OBC =45°. (2)解法一:如图①,作PD ⊥y 轴,垂足为D ,设l 与x 轴交于点E ,由题意得,抛物线的对称轴为12mx -+=. 设点P 坐标为(12m-+,n ). ∵P A = PC , ∴P A 2= PC 2,即AE 2+ PE 2=CD 2+ PD 2.∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭.解得12m n -=.∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭. 解法二:连接PB .由题意得,抛物线的对称轴为12m x -+=. ∵P 在对称轴l 上,∴P A =PB . ∵P A =PC ,∴PB =PC .∵△BOC 是等腰直角三角形,且OB =OC , ∴P 在BC 的垂直平分线y x =-上.∴P 点即为对称轴12mx -+=与直线y x =-的交点. ∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭.图①图②(3)解法一:存在点Q 满足题意.∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭, ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ∵AC 2=21m +,∴P A 2+ PC 2=AC 2.∴∠APC =90°. ∴△P AC 是等腰直角三角形.∵以Q 、B 、C 为顶点的三角形与△P AC 相似, ∴△QBC 是等腰直角三角形.∴由题意知满足条件的点Q 的坐标为(-m ,0)或(0,m ). ①如图①,当Q 点的坐标为(-m ,0)时,若PQ 与x 轴垂直,则12mm -+=-,解得13m =,PQ =13.若PQ 与x 轴不垂直, 则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. ∵0<m <1,∴当25m =时,2PQ 取得最小值110,PQ .<13, ∴当25m =,即Q 点的坐标为(25-,0)时, PQ 的长度最小.②如图②,当Q 点的坐标为(0,m )时,若PQ 与y 轴垂直,则12mm -=,解得13m =,PQ =13.若PQ 与y 轴不垂直, 则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.∵0<m <1,∴当25m =时,2PQ 取得最小值110,PQ.<13, ∴当25m =,即Q 点的坐标为(0,25)时, PQ 的长度最小.综上:当Q 点坐标为(25-,0)或(0,25)时,PQ 的长度最小.解法二: 如图①,由(2)知P 为△ABC 的外接圆的圆心. ∵∠APC 与∠ABC 对应同一条弧AC ,且∠ABC =45°,∴∠APC =2∠ABC =90°. 下面解题步骤同解法一.28.解:(1)a +2b .(2)∵在整个运动过程中,点P 移动的距离为()2a b +cm ,圆心O 移动的距离为()24a -cm , 由题意,得()224a b a +=-. ①∵点P 移动2s 到达B 点,即点P 用2s 移动了b cm ,点P 继续移动3s ,到达BC 的中点,即点P 用3s 移动了12a cm .∴1223a b =. ② 由①②解得24,8.a b =⎧⎨=⎩∵点P 移动的速度与⊙O 移动的速度相等, ∴⊙O 移动的速度为42b=(cm/s ).∴这5s 时间内圆心O 移动的距离为5×4=20(cm ). (3)存在这种情形.解法一:设点P 移动的速度为v 1cm/s ,⊙O 移动的速度为v 2cm/s ,由题意,得()()1222021052422044v a b v a ++⨯===--.FE如图,设直线OO 1与AB 交于点E ,与CD 交于点F ,⊙O 1与AD 相切于点G .若PD 与⊙O 1相切,切点为H ,则O 1G =O 1H .易得△DO 1G ≌△DO 1H ,∴∠ADB =∠BDP .∵BC ∥AD ,∴∠ADB =∠CBD .∴∠BDP =∠CBD .∴BP =DP .设BP =x cm ,则DP =x cm ,PC =(20-x )cm ,在Rt △PCD 中,由勾股定理,可得222PC CD PD +=,即()2222010x x -+=,解得252x =.∴此时点P 移动的距离为25451022+=(cm ). ∵EF ∥AD ,∴△BEO 1∽△BAD . ∴1EO BE AD BA =,即182010EO =. ∴EO 1=16cm .∴OO 1=14cm .①当⊙O 首次到达⊙O 1的位置时,⊙O 移动的距离为14cm , ∴此时点P 与⊙O 移动的速度比为454521428=.∵455284≠, ∴此时PD 与⊙O 1不可能相切.②当⊙O 在返回途中到达⊙O 1的位置时,⊙O 移动的距离为2×(20-4)-14=18(cm ), ∴此时点P 与⊙O 移动的速度比为45455218364==. ∴此时PD 与⊙O 1恰好相切. 解法二:∵点P 移动的距离为452cm (见解法一),OO 1=14cm (见解法一),1254v v =, ∴⊙O 应该移动的距离为4541825⨯=(cm ). ①当⊙O 首次到达⊙O 1的位置时,⊙O 移动的距离为14cm ≠18 cm , ∴此时PD 与⊙O 1不可能相切.②当⊙O 在返回途中到达⊙O 1的位置时,⊙O 移动的距离为2×(20-4)-14=18(cm ),∴此时PD 与⊙O 1恰好相切.解法三:点P 移动的距离为452cm ,(见解法一) OO 1=14cm ,(见解法一) 由1254v v =可设点P 的移动速度为5k cm/s ,⊙O 的移动速度为4k cm/s , ∴点P 移动的时间为459252k k=(s ).①当⊙O 首次到达⊙O 1的位置时,⊙O 移动的时间为1479422k k k=≠, ∴此时PD 与⊙O 1不可能相切.②当⊙O 在返回途中到达⊙O 1的位置时,⊙O 移动的时间为2(204)14942k k⨯--=, ∴此时PD 与⊙O 1恰好相切.。
江苏省苏州市2015届中考数学模拟试卷及答案(三)

2015年苏州市九年级数学中考模拟试卷(三)一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将选择题的答案用2B 铅笔涂在答题卡相对应的位置上........... 1. 如果a 与2互为相反数,则a 的值为 ( ) A. 2 B. -2 C. 21 D. - 212. 函数y =的自变量x 的取值范围是 ( ) A .x ≥-1且x ≠0 B .x >-1且x ≠0 C .x ≥0且x ≠-1 D .x >0且x ≠-13. 某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:则这11双鞋的尺码组成的一组数据中,众数和中位数分别是 ( ) A .25,25 B .24.5,25 C .25,24.5 D .24.5,24.54.一个不透明口袋中装着只有颜色不同的1个红球和2个白球,搅匀后从中摸出一个球,摸到白球的概率为( )(A )32 (B )21 (C )31 (D )15. 如图,△ABC 是⊙O 的内接三角形,AC 是⊙O 的直径,∠C=50°, ∠ABC 的平分线BD 交⊙O 于点D ,则∠BAD 的度数是( ) A .45° B.85° C.90° D.95°6. 已知方程x 2-5x +2=0的两个解分别为x 1、x 2,则2x 1-x 1x 2+2x 2的值为( ) A .8 B .-12 C .12 D .-87. 下列计算或化简正确的是 ( )A 3±B .235a a a += C +=.2()a ab ab a ---=- 8. 抛物线y=1(2)2x --2顶点坐标是 ( ) A .(-2 ,0) B .(2, 0) C .(0, 0) D .(0, 2)9. 如图,平面直角坐标系中,△ABC 的顶点坐标分别是A (1,1),B (3,1),C (2,2),当直线b x y +=21与△ABC 有交点时,b 的取值范围是( ) A.-1≤b ≤1 B. -21≤b ≤1 C. -21≤b ≤21 D. -1≤b ≤2110.如图(1)所示,E 为矩形ABCD 的边AD 上一点,动点P 、Q 同时从点B 出发,点P 以1cm/秒的速度沿折线BE —ED —DC 运动到点C 时停止,点Q 以2cm/秒的速度沿BC 运动到点C 时停止.设P 、Q 同时出发t 秒时,△BPQ 的面积为y cm 2.已知y 与t 的函数关系图象如图(2)(其中曲线OG 为抛物线的一部分,其余各部分均为线段),则下列结论: ①当0<t ≤5时,y =54t 2; ②当 t =6秒时,△ABE ≌△PQB ; ③cos ∠CBE =45④当t =292秒时,△ABE ∽△QBP ;其中正确的是( )A .①②B .①③④C .③④D .①②④二、填空题:本大题共8个小题,每小题3分,共24分.把答案直接填在答题卡相对应的.......位置。
2015年江苏省中考数学真题试卷(含答案解析)

【考点】扇形统计图. 【分析】设被调查的总人数是x人,根据最喜欢羽毛球的人数比最喜欢 乒乓球的人数少6人,即可列方程求解. 【解答】解:设被调查的总人数是x人,则40%x﹣30%x=6, 解得:x=60. 故答案是:60. 【点评】本题考查的是扇形统计图的综合运用,读懂统计图,从统计图 中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体 的百分比大小.
A.4km B.(2+ )km C.2 km D.(4﹣ )km 【考点】解直角三角形的应用-方向角问题. 【分析】根据题意在CD上取一点E,使BD=DE,进而得出EC=BE=2, 再利用勾股定理得出DE的长,即可得出答案. 【解答】解:在CD上取一点E,使BD=DE, 可得:∠EBD=45°,AD=DC, ∵从B测得船C在北偏东22.5°的方向, ∴∠BCE=∠CBE=22.5°, ∴BE=EC, ∵AB=2, ∴EC=BE=2, ∴BD=ED=
菁优网版权所有
=2,得b=﹣4,解x2﹣4x=5即可. 【解答】解:∵对称轴是经过点(2,0)且平行于y轴的直线, ∴﹣ =2, 解得:b=﹣4, 解方程x2﹣4x=5,
解得x1=﹣1,x2=5, 故选:D. 【点评】本题主要考查二次函数的对称轴和二次函数与一元二次方程的 关系,难度不大. 9.(3分)(2015•苏州)如图,AB为⊙O的切线,切点为B,连接AO,AO与 ⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2, 则图中阴影部分的面积为( )
频数(通话 20 16 9 5 次数) 则通话时间不超过15min的频率为( ) A.0.1 B.0.4 C.0.5 D.0.9 【考点】频数(率)分布表. 【分析】用不超过15分钟的通话时间除以所有的通话时间即可求得通话 时间不超过15分钟的频率. 【解答】解:∵不超过15分钟的通话次数为20+16+9=45次,通话总次数 为20+16+9+5=50次, ∴通话时间不超过15min的频率为
江苏省2015年苏州市中考数学复习模拟试卷(含答案) (2)

2015年苏州市中考数学复习模拟试卷(2)(满分:130分 考试时间:120分钟)一、选择题(本大题共10小题,每小题3分,共30分) 1.如果a 与-3互为倒数,则a 等于 ( ) A .-3B .-13C .13D .32.下列各等式成立的是 ( ) A .a 2+a 5=a 7 B .(-a 2)3=a 6 C .a 2-1=(a +1) (a -1) D .(a +b)2=a 2+b 2 3.国家统计局的统计数据显示:2013年全国粮食总产量达到6.0193亿吨,比上年增长2.1%,6.0193亿吨用科学记数法表示为 ( ) A .61.093×107吨 B .6.1093×107吨 C .0.61093×109吨 D .6.1093×108吨 4.使分式1xx 有意义的x 的取值范围是 ( ) A .x ≠-1 B .x ≠1 C .x =-1 D .x =15.若⊙O 的半径为4,圆心O 到直线l 的距离为5,则直线l 与⊙O 的位置关系是 ( ) A .相交 B .相切 C .相离 D .无法确定6.如图,将Rt △ABC 绕直角边AB 旋转一周,所得的几何体的主视图是 ( )7.某校篮球课外活动小组21名同学的身高如下表:则该篮球课外活动小组21名同学身高的众数和中位数分别是 ( ) A .176,176 B .176,177 C .176,178 D .184,1788.如图,数轴上的A 、B 、C 三点所表示的数分别为a 、b 、c ,AB =BC ,如果a >c >b ,那么该数轴的原点O 的位置应该在( )A .点A 的左边B .点A 与点B 之间C .点B 与点C 之间D .点C 的右边9.清明小长假某人驾车从A 地上高速公路前往B 地,中途在服务区休息了一段时间.出发时油箱中存油40 L ,到B 地后发现油箱中还剩油4 L ,则从出发后到B 地油箱中所剩油y(L)与时间t(h)之间函数的大致图像是 ( )10.如图,将边长为a 的正六边形A 1A 2A 3A 4A 5A 6在直线l 上由图①的位置按顺时针方向向右作元滑动滚动,当点A 1第一次滚动到图②位置时,顶点A 1所经过的路径的长为( )A 423a +B 843a +C 43a +D 23a + 二、填空题(本大题共8小题,每小题3分,共24分) 11.一组数据-2,1,0,-1,2的极差是_______.12.如图,已知AB ∥CD ,∠EFA =50°,则∠DCE =_______.13.已知a -b =1,则a 2-b 2-2b 的值是_______.14.在一个不透明的口袋中装有若干个只有颜色不同的球,如果口袋中装有5个红球,且摸出红球的概率为13,那么袋中其他颜色的球有_______个.15.如图,⊙O 为锐角三角形ABC 的外接圆,若∠BAO =18°,则∠C 的度数为_______. 16.已知一个圆锥底面圆的半径为5 cm ,高为12 cm ,则圆锥的侧面积为_______cm 2.17.关于x 的分式方程3111m x x+=--的解是正数,则m 的取值范围_______. 18.如图,反比例函数y =kx(x>0)的图像经过矩形OABC 对角线的交点M ,且分别与AB 、BC 交于点D 、E ,若四边形ODBE 的面积为12,则k 的值为_______. 三、解答题(本大题共11小题,共76分) 19.(本题满分5分)11272cos30232-⎛⎫︒+- ⎪⎝⎭.20.(本题满分5分)解方程组:33219x y x y -=⎧⎨+=⎩21.(本题满分5分)先化简,再求值:21111x x x ⎛⎫+÷ ⎪--⎝⎭,其中x 是方程x 2-2x =0的根.22.(本题满分6分)某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出第二组的频率是0.06,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题:(1)这次共抽调了多少人?(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少? (3)若该校九年级有800名学生,请估计该校九年级达到优秀的人数是多少.23.(本题满分6分)如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.①②(1)求格点三角形ABC的面积;(2)在网格图中画出△ABC先向右平移4个单位,再向上平移3个单位后的△A1B1C1;(3)画出格点三角形ABC绕点C逆时针旋转90°后的△A2B2C2.24.(本题满分7分)如图,在△ABC中,AB=AC.(1)作∠BAC的角平分线,交BC于点D;(尺规作图,保留痕迹)(2)在AD的延长线上任取一点E,连接BE、CE.求证:△BDE≌△CDE;(3)当AE=2AD时,四边形ABEC是什么图形?请说明理由.25.(本题满分7分)如图,有一电路AB是由图示的开关控制,闭合a、b、c、d、e五个开关中的任意两个开关.(1)请用列表或画树状图的方法,列出所有可能的情况;(2)求出使电路形成通路的概率.26.(本题满分8分)如图,小明在教学楼上的窗口A看地面上的B、C两个花坛,测得俯角∠EAB=30°,俯角∠EAC=45°.已知教学楼基点D与点C、B在同一条直线上;且B、C两花坛之间的距离为10 m,求窗口A到地面的高度AD.(结果保留根号)27.(本题满分8分)如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于点E,连接CE.(1)判断CD与⊙O的位置关系,并证明你的结论;(2)若E是AC的中点,⊙O的半径为2,求图中阴影部分的面积.28.(本题满分9分)某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)(1)写出每月的利润W(万元)与销售单价x(元)之间的函数关系式;(2)当销售单价为多少元时,厂商每月获得的利润为440万元?(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?29.(本题满分10分)如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于点A,交x轴于B、C两点(点B在点C的左侧),已知点A的坐标为A(0,-5).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.参考答案1—10 BCDAC DCCBA11.412.130°13.114.10 15.72°16.65π17.m>2且m≠3 18.419.320.52 xy=⎧⎨=⎩21.3.22.(1)200人.(2)43%.(3)344(人).23.(1)2.(2)~(3)略24.(1)略(2)略(3)菱形.25.(1)列表如下:(2)3 526.(5+3.27.(1)相切328.(1)W=-2x2+136x-1800.(2)当销售单价为28元或40元时,厂商每月获得的利润为440万元.(3)当销售单价为35元时,厂商每月获得的利润最大,为510万元.29.(1)y=-x2+6x-5.(2)相离.(3)存在.。
2015苏科版数学中考模拟试卷及答案
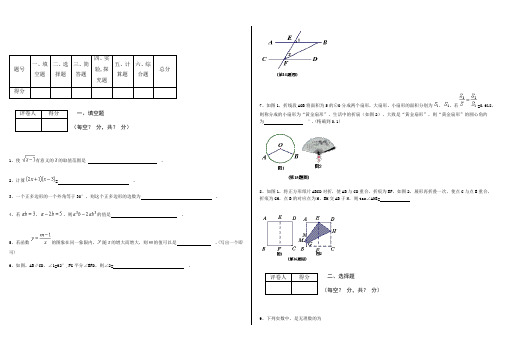
一、填空题(每空?分,共?分)1、使有意义的的取值范围是 .2、计算= .3、一个正多边形的一个外角等于30°,则这个正多边形的边数为 .4、若,,则的值是 .5、若函数的图象在同一象限内,随的增大而增大,则的值可以是 .(写出一个即可)6、如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2= .7、如图1,折线段AOB将面积为S的⊙O分成两个扇形,大扇形、小扇形的面积分别为、,若=0.618,则称分成的小扇形为“黄金扇形”,生活中的折扇(如图2),大致是“黄金扇形”,则“黄金扇形”的圆心角约为°.(精确到0.1)8、如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF,如图2,展形再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为M,EM交AB于N,则tan∠ANE=二、选择题(每空?分,共?分)9、下列实数中,是无理数的为A.-1 B. C. D.3.1410、计算的结果是A. -3 B.3 C.-9 D.911、在平面直角坐标系中,点P(-2,3)关于原点对称的点Q的坐标为A.(2,-3) B.(2,3) C.(3,-2) D.(-2,-3)12、“丝绸之路”经济带首个实体平台——中哈物流合作基地在我市投入使用,其最大装卸能力达410 000标箱,其中“410 000”用科学计数法表示为A.0.41×106 B. 4.1×105 C.41×104 D.4.1×10413、一组数据1,3,6,1,2的众数与中位数分别是A.1,6 B.1,1 C.2,1 D.1,214、如图,若△ABC和△DEF的面积分别为、,则A .B .C .D .15、如图,点P在以AB为直径的半圆内,连AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法正确的是:①AC垂直平分BF;②AC平分∠BAF;③PF⊥AB;④BD⊥AF.A.①② B.①④C.②④ D.③④16、如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数在第一象限内的图像与△ABC有交点,则的取值范围是A.2≤≤ B.6≤≤10C.2≤≤6 D.2≤≤三、简答题(每空?分,共?分)17、我市启动了第二届“美丽港城·美在悦读”全民阅读活动。
2015年苏州市中考数学试卷及答案

2015年苏州市初中毕业暨升学考试试卷数学一、选择题:本大题共 小题,每小题 分,共 分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用 铅笔涂在答题卡相应位置上......... . 的相反数是✌. .12 . . 12.有一组数据: , , , , ,这组数据的众数为✌. . . ..月球的半径约为 ❍, 这个数用科学记数法可表示为✌. × . × . × . × .若()2m=-,则有✌. <❍< . <❍< . <❍< . <❍< .小明统计了他家今年 月份打电话的次数及通话时间,并列出了频数分布表:则通话时间不超过 ❍♓⏹的频率为✌. . . . .若点✌(♋,♌)在反比例函数2yx=的图像上,则代数式♋♌ 的值为✌. . . . .如图,在△✌中,✌ ✌, 为 中点,∠ ✌ °,则∠ 的度数为✌. °. ° . ° . °.若二次函数⍓ ⌧ ♌⌧的图像的对称轴是经过点( , )且平行于⍓轴的直线,则关于⌧的方程⌧ ♌⌧ 的解为 ✌.120,4x x ==.121,5x x == .121,5x x ==- .121,5x x =-=.如图,✌为⊙ 的切线,切点为 ,连接✌,✌与⊙ 交于点 , 为⊙的直径,连接 .若∠✌ °,⊙ 的半径为 ,则图中阴影部分的面积为✌.43π..如图,在一笔直的海岸线●上有✌、 两个观测站,✌ ❍,从✌测得船 在北偏东 °的方向,从 测得船 在北偏东 °的方向,则船 离海岸线●的距离(即 的长)为 ✌.4 ❍.(2 ❍ . .(4 ❍二、填空题:本大题共 小题,每小题 分,共 分.把答案直接填在答题卡相应位置.......DCB A(第 题)(第 题)(第 题)l上.. .计算:2a a ⋅ ✧ ..如图,直线♋∥♌,∠ °,则∠ 的度数为 ✧ °..某学校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少 人,则该校被调查的学生总人数为 ✧ 名..因式分解:224a b - ✧ ..如图,转盘中 个扇形的面积都相等.任意转动转盘次,当转盘停止转动时,指针指向大于 的数的概率为 ✧ ..若23a b -=,则924a b -+的值为 ✧ ..如图,在△✌中, 是高, ☜是中线, ☜ ,点✌、 关于点☞GCDA ba(第 题)20%10%30%40%其他乒乓球篮球羽毛球(第 题)对称,过点☞作☞☝∥ ,交✌边于点☝,连接☝☜.若✌ , ,则△☜☝的周长为 ✧ ..如图,四边形✌为矩形,过点 作对角线 的垂线,交 的延长线于点☜,取 ☜的中点☞,连接 ☞, ☞ .设✌ ⌧,✌ ⍓,则()224x y +-的值为 ✧ .三、解答题:本大题共 小题,共 分.把解答过程写在答题卡相应位置上........,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用 铅笔或黑色墨水签字笔..(本题满分 分)(052--..(本题满分 分)解不等式组:()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩>.(本题满分 分)先化简,再求值:2121122x x x x ++⎛⎫-÷⎪++⎝⎭,其中1x =..(本题满分 分)甲、乙两位同学同时为校文化艺术节制作彩旗.已知甲每小时比乙多做 面彩旗,甲做 面彩旗与乙做 面彩旗所用时间相等,问甲、乙每小时各做多少面彩旗?.(本题满分 分)一个不透明的口袋中装有 个红球(记为红球 、红球 )、 个白球、 个黑球,这些球除颜色外都相同,将球摇匀.( )从中任意摸出 个球,恰好摸到红球的概率是 ✧ ;( )先从中任意摸出 个球,再从余下的 个球中任意摸出 个球,请用列举法(画树状图或列表)求两次都摸到红球的概率..(本题满分 分)如图,在△✌中,✌ ✌.分别以 、 为圆心, 长为半径在 下方画弧,设两弧交于点 ,与✌、✌的延长线分别交于点☜、☞,连接✌、 、 . ( )求证:✌平分∠ ✌;( )若 ,∠ ✌= ,求DE 、DF 的长度之和(结果保留π)..(本题满分 分)如图,已知函数ky x=(⌧> )的图像经过点✌、 ,点 的坐标为( , ).过点✌作✌⊥⌧轴,垂足为 ,过点 作 ⊥⍓轴,垂足为 ,✌与 交于点☞.一次函数⍓♋⌧ ♌的图像经过点✌、 ,与⌧轴的负半轴交于点☜.(第 题)FEDCBA( )若✌32,求♋、♌的值; ( )若 ∥✌☜,求 的长..(本题满分 分)如图,已知✌是△✌的角平分线,⊙ 经过✌、 、 三点,过点 作 ☜∥✌,交⊙ 于点☜,连接☜. ( )求证:☜∥✌;( )若 ,设△☜的面积为1S ,△✌的面积为2S ,且2121640S S -+=,求△✌的面积..(本题满分 分)如图,已知二次函数()21y x m x m =+--(其中 <❍< )的图像与⌧轴交于✌、 两点(点✌在点 的左侧),与⍓轴交于点 ,对称轴为直线●.设为对称轴●上的点,连接 ✌、 , ✌ .(第 题)( )∠✌的度数为 ✧ °; ( )求 点坐标(用含❍的代数式表示);( )在坐标轴上是否存在点✈(与原点 不重合),使得以✈、 、 为顶点的三角形与△ ✌相似,且线段 ✈的长度最小?如果存在,求出所有满足条件的点✈的坐标;如果不存在,请说明理由..(本题满分 分)如图,在矩形✌中,✌ ♋♍❍,✌ ♌♍❍(♋>♌> ),半径为 ♍❍的⊙ 在矩形内且与✌、✌均相切.现有动点 从✌点出发,在矩形边上沿着✌→ → → 的方向匀速移动,当点 到达 点时停止移动;⊙ 在矩形内部沿✌向右匀速平移,移动到与 相切时立即沿原路按原速返回,当⊙ 回到出发时的位置(即再次与✌相切)时停止移动.已知点 与⊙ 同时开始移动,同时停止移动(即同时到达各自的终止位置).( )如图①,点 从✌→ → → ,全程共移动了 ✧ ♍❍(用含♋、♌的代数式表示);( )如图①,已知点 从✌点出发,移动 ♦到达 点,继续移动 ♦,到达 的中点.若点 与⊙ 的移动速度相等,求在这 ♦时间内圆心 移动的距离;( )如图②,已知♋ ,♌ .是否存在如下情形:当⊙ 到达⊙ 的位置时(此时圆心 在矩形对角线 上), 与⊙ 恰好相切?请说明理由.年苏州市初中毕业暨升学考试数学试题答案一、选择题 . . .✌ . . . ...✌.二、填空题 .3a . . .()()22a b a b +- .14.. . 三、解答题解:原式 = = . 解:由12x +≥,解得1x ≥,由()315x x -+>,解得4x >, 不等式组的解集是4x >.解:原式=()21122x x x x ++÷++ =()2121211x x x x x ++⨯=+++.当1x ===. 解:设乙每小时做⌧面彩旗,则甲每小时做(⌧ )面彩旗.根据题意,得60505x x=+. 解这个方程,得⌧ .经检验,⌧ 是所列方程的解. ⌧ .答:甲每小时做 面彩旗,乙每小时做 面彩旗.解:( )1. ( )用表格列出所有可能的结果: 由表格可知,共有 种可能出现的结果,并且它们都是等可能的,其中“两次都摸到红球”有 种可能. ∴ (两次都摸到红球)212 16. 证明:( )由作图可知 .在 ✌和 ✌中, ,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩✌≌ ✌( ).✌= ✌,即✌平分 ✌.解:( ) ✌ ✌, ✌ , ✌= ✌ °. , 为等边三角形. = °. ☜= ☞ °. , .DE 的长度 DF 的长度 556111806ππ⨯⨯=. DE 、DF 的长度之和为111111663πππ+=. .解:( ) 点 ( , )在ky x=的图像上,∴ ,4y x=. ⊥⍓轴,∴ 点的坐标为( , ), .✌⊥⌧轴,✌32,∴✌ ,即✌点的纵坐标为 . 点✌在4y x=的图像上,∴✌点的坐标为(43, ).一次函数⍓ ♋⌧ ♌的图像经过点✌、 , ∴43,3 2.a b b ⎧+=⎪⎨⎪=⎩ 解得3,42.a b ⎧=⎪⎨⎪=⎩ ( )设✌点的坐标为(❍,4m),则 点的坐标为(❍, ). ∥ ☜,且 ∥ ☜,∴四边形 ☜为平行四边形.∴ ☜ .∥ ☜,∴∠✌☞ ∠✌☜.∴在 ♦✌☞中,♦♋⏹∠✌☞ 42AF mDF m -=, 在 ♦✌☜中,♦♋⏹∠✌☜ 42AC mEC =, ∴4422m m m -=,解得❍ .∴ 点的坐标为( , ), ..证明:( )∵✌是△✌的角平分线,∴∠ ✌ ∠ ✌.∵∠☜∠ ✌,∴∠☜ ∠ ✌. ∵ ☜∥✌,∴∠☜ ∠☜✌. ∴∠☜✌ ∠ ✌ . ∴☜∥✌.解:( )∵ ☜∥✌,∴∠☜ ∠✌.∵∠☜ ∠ ✌,∴△☜ △✌,且相似比2BDk DC==. ∴2124S k S ==,即124S S =. ∵2121640S S -+=,∴222161640S S -+=,即()22420S -=.∴212S =. ∵233ABC S BC BD CD CD S CD CD CD +====,∴32ABCS=. .解:( ) .理由如下:令⌧ ,则⍓ ❍, 点坐标为( , ❍). 令⍓ ,则()210x m x m +--=,解得11x =-,2x m =. ∵ <❍< ,点✌在点 的左侧, ∴ 点坐标为(❍, ).∴ ❍.∵∠ = °,∴△ 是等腰直角三角形,∠ = °.( )解法一:如图①,作 ⊥⍓轴,垂足为 ,设●与⌧轴交于点☜,由题意得,抛物线的对称轴为12mx -+=. 设点 坐标为(12m-+,⏹). ∵ ✌ , ∴ ✌ ,即✌☜ ☜ .∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭.解得12m n -=.∴ 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭.解法二:连接 .由题意得,抛物线的对称轴为12mx -+=. ∵ 在对称轴●上,∴ ✌ . ∵ ✌ ,∴ .∵△ 是等腰直角三角形,且 , ∴ 在 的垂直平分线y x =-上.∴ 点即为对称轴12mx -+=与直线y x =-的交点. ∴ 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭.图①图②( )解法一:存在点✈满足题意.∵ 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭, ∴ ✌ ✌☜ ☜ 222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ∵✌ 21m +,∴ ✌ ✌ .∴∠✌= °. ∴△ ✌是等腰直角三角形.∵以✈、 、 为顶点的三角形与△ ✌相似, ∴△✈是等腰直角三角形.∴由题意知满足条件的点✈的坐标为( ❍, )或( ,❍). ①如图①,当✈点的坐标为( ❍, )时, 若 ✈与⌧轴垂直,则12mm -+=-,解得13m =, ✈ 13.若 ✈与⌧轴不垂直, 则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+⎪⎪ ⎪⎝⎭⎝⎭⎝⎭.∵ <❍< ,∴当25m =时,2PQ 取得最小值110, ✈.<13, ∴当25m =,即✈点的坐标为(25-, )时, ✈的长度最小.②如图②,当✈点的坐标为( ,❍)时, 若 ✈与⍓轴垂直,则12mm -=,解得13m =, ✈ 13.若 ✈与⍓轴不垂直, 则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.∵ <❍< ,∴当25m =时,2PQ 取得最小值110, ✈.<13, ∴当25m =,即✈点的坐标为( ,25)时, ✈的长度最小.综上:当✈点坐标为(25-, )或( ,25)时, ✈的长度最小.解法二: 如图①,由( )知 为△✌的外接圆的圆心. ∵∠✌ 与∠✌对应同一条弧AC ,且∠✌= °, ∴∠✌= ∠✌= °. 下面解题步骤同解法一..解:( )♋ ♌.( )∵在整个运动过程中,点 移动的距离为()2a b +♍❍,圆心 移动的距离为()24a -♍❍, 由题意,得()224a b a +=-. ①∵点 移动 ♦到达 点,即点 用 ♦移动了♌♍❍,点 继续移动 ♦,到达 的中点,即点 用 ♦移动了12a ♍❍.∴1223a b =. ② 由①②解得24,8.a b =⎧⎨=⎩∵点 移动的速度与⊙ 移动的速度相等, ∴⊙ 移动的速度为42b=(♍❍♦). ∴这 ♦时间内圆心 移动的距离为 × (♍❍).( )存在这种情形.解法一:设点 移动的速度为❖ ♍❍♦,⊙ 移动的速度为❖ ♍❍♦, 由题意,得()()1222021052422044v a b v a ++⨯===--.FE如图,设直线 与✌交于点☜,与 交于点☞,⊙ 与✌相切于点☝. 若 与⊙ 相切,切点为☟,则 ☝ ☟. 易得 ☝≌ ☟,∴∠✌ ∠ . ∵ ∥✌,∴∠✌ ∠ . ∴∠ ∠ .∴ .设 ⌧♍❍,则 ⌧♍❍, ( ⌧)♍❍,在 ♦△ 中,由勾股定理,可得222PC CD PD +=, 即()2222010x x -+=,解得252x =. ∴此时点 移动的距离为25451022+=(♍❍). ∵☜☞∥✌,∴△ ☜ ∽△ ✌. ∴1EO BE AD BA =,即182010EO =.∴☜ ♍❍.∴ ♍❍.①当⊙ 首次到达⊙ 的位置时,⊙ 移动的距离为 ♍❍, ∴此时点 与⊙ 移动的速度比为454521428=.∵455284≠, ∴此时 与⊙ 不可能相切.②当⊙ 在返回途中到达⊙ 的位置时,⊙ 移动的距离为 ☎✆(♍❍),∴此时点 与⊙ 移动的速度比为45455218364==. ∴此时 与⊙ 恰好相切. 解法二:∵点 移动的距离为452♍❍(见解法一), ♍❍(见解法一),1254v v =,∴⊙ 应该移动的距离为4541825⨯=(♍❍). ①当⊙ 首次到达⊙ 的位置时,⊙ 移动的距离为 ♍❍≠ ♍❍, ∴此时 与⊙ 不可能相切.②当⊙ 在返回途中到达⊙ 的位置时,⊙ 移动的距离为 ☎✆(♍❍),∴此时 与⊙ 恰好相切. 解法三:点 移动的距离为452♍❍,(见解法一) ♍❍,(见解法一)由1254v v =可设点 的移动速度为 ♍❍♦,⊙ 的移动速度为 ♍❍♦, ∴点 移动的时间为459252k k=(♦).①当⊙ 首次到达⊙ 的位置时,⊙ 移动的时间为1479422k k k=≠, ∴此时 与⊙ 不可能相切.②当⊙ 在返回途中到达⊙ 的位置时,⊙ 移动的时间为2(204)14942k k⨯--=, ∴此时 与⊙ 恰好相切.。
2015年江苏省苏州市吴中、相城、吴江区中考一模数学试卷(解析版)

2015年江苏省苏州市吴中、相城、吴江区中考数学一模试卷一、选择题(本大题共有10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是符合题目要求的.)1.(3分)化简|﹣2|的结果是()A.一2B.2C.D.±22.(3分)下列腾讯QQ表情中,不是轴对称图形的是()A.B.C.D.3.(3分)下列运算正确的是()A.x3+x3=2x6B.(﹣x5)4=x20C.x m•x n=x mn D.x8÷x2=x4 4.(3分)如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是()A.17°B.34°C.56°D.68°5.(3分)在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为()A.y=x B.y=x﹣1C.y=x+1D.y=﹣x+1 6.(3分)我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)()A.36,8B.28,6C.28,8D.13,37.(3分)设函数y=x+5与的图象的两个交点的横坐标为a、b,则的值是()A.B.C.D.8.(3分)在△ABC中,∠C=90°,∠A=60°,AC=1,D在BC上,E在AB上,使得△ADE为等腰直角三角形,∠ADE=90°,则BE的长为()A.B.C.D.9.(3分)在平面直角坐标系中,一次函数y=x的图象、反比例函数y=图象以及二次函数y=x2﹣6x的对称轴围成一个封闭的平面区域(含边界),从该区域内所有格点(横、纵坐标均为整数的点称为格点)中任取3个,则该3点恰能作为一个三角形的三个顶点的概率是()A.B.C.D.10.(3分)定义一个新的运算:a⊕b=,则运算x⊕2的最小值为()A.﹣3B.﹣2C.2D.3二、填空题(本大题共8小题,每小题3分,共24分.)11.(3分)已知1nm等于0.000001mm,则0.000001用科学记数法可表示为•12.(3分)某班30位女生所穿鞋子的尺码.数据如下(单位:码):记众数为a,中位数为b,则a+b=.13.(3分)“两直线平行,内错角相等”的逆命题是.14.(3分)分解因式:2x2+x﹣6=.15.(3分)如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径为5,则图中阴影部分的面积是.16.(3分)若二次函数y=ax2+bx+c(a<0)的对称轴为直线x=﹣1,图象经过点(1,0),有下列结论:①abc<0;②2a﹣b=0;③a+b+c>0;④b2>5ac,则以上结论一定正确的个数是.17.(3分)若关于x,y的二元一次方程组的解满足2x+y≤2,则t的取值范围为.18.(3分)设抛物线y=﹣x2+2x+3的顶点为E,与y轴交于点C,EF⊥x轴于点,若点M(m,0)是x轴上的动点,且满足以MC为直径的圆与线段EF 有公共点,则实数m的取值范围是.三、解答题(本大题共11小题,共76分,把解答过程写在答题卷相应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.)19.(5分)计算:.20.(5分)解不等式组.21.(5分)先化简,再求值:,其中.22.(6分)现有甲、乙两种金属的合金10kg,如果加入甲种金属若干,那么重新熔炼后的合金中乙种金属占2份,甲种金属占3份,如果加入的甲种金属是第一次加入的2倍,那么重新熔炼后的合金中乙种金属占3份,甲种金属占7份,第一次加入的甲种金属多少?原来这块合金中甲种金属的百分比是多少?23.(6分)解分式方程:.24.(6分)苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:频率分布表:请结合图表完成下列各题:(1)求表中a的值:(2)请把频数分布直方图补充完整;(3)若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”25.(7分)某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,已知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:=1.73.)26.(8分)有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC =8.(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;(2)若将这两张矩形纸片交叉叠放(如图2),试判断四边形MNPQ的形状,并证明.27.(9分)如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.(1)求运动时间t的取值范围;(2)t为何值时,△POQ的面积最大?最大值是多少?(3)t为何值时,以点P、0、Q为顶点的三角形与Rt△AOB相似?28.(9分)如图所示,D是以AB为直径的半圆O上的一点,C是弧AD的中点,点M在AB上,AD与CM交于点N,CN=AN.(1)求证:CM⊥AB;(2)若AC=;,BD=2,求半圆的直径.29.(10分)如图所示,已知点C(﹣3,m),点D(m﹣3,0).直线CD交y 轴于点A.作CE与X轴垂直,垂足为E,以点B(﹣1,0)为顶点的抛物线恰好经过点A、C.(1)则∠CDE=;(2)求抛物线对应的函数关系式;(3)设P(x,y)为抛物线上一点(其中﹣3<x<﹣1或﹣1<x<1,连结BP并延长交直线CE于点N,记N点的纵坐标为y N,连结CP并延长交X 轴于点M.①试证明:EM•(EC+y N)为定值;②试判断EM+EC+y N是否有最小值,并说明理由.2015年江苏省苏州市吴中、相城、吴江区中考数学一模试卷参考答案与试题解析一、选择题(本大题共有10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是符合题目要求的.)1.(3分)化简|﹣2|的结果是()A.一2B.2C.D.±2【解答】解:|﹣2|=2,故选:B.2.(3分)下列腾讯QQ表情中,不是轴对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,故本选项错误;B、是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项正确;D、是轴对称图形,故本选项错误.故选:C.3.(3分)下列运算正确的是()A.x3+x3=2x6B.(﹣x5)4=x20C.x m•x n=x mn D.x8÷x2=x4【解答】解:A.x3+x3=2x3,故错误;B.正确;C.x m•x n=x m+n,故错误;D.x8÷x2=x6,故错误;故选:B.4.(3分)如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是()A.17°B.34°C.56°D.68°【解答】解:∵AB∥CD,∴∠ABC=∠C=34°,∵BC平分∠ABE,∴∠CBE=∠ABC=34°,∴∠BED=∠C+∠CBE=68°.故选:D.5.(3分)在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为()A.y=x B.y=x﹣1C.y=x+1D.y=﹣x+1【解答】解:∵直线x=0与x轴的夹角是90°,∴将直线x=0绕原点顺时针旋转45°后的直线与x轴的夹角为45°,∴此时的直线方程为y=x.∴再向上平移1个单位得到直线a的解析式为:y=x+1.故选:C.6.(3分)我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)()A.36,8B.28,6C.28,8D.13,3【解答】解:设绳长x米、井深y米,依题意有,解得.答:绳长36米、井深8米.故选:A.7.(3分)设函数y=x+5与的图象的两个交点的横坐标为a、b,则的值是()A.B.C.D.【解答】解:联立消掉y得,x2+5x﹣3=0,∵两个交点的横坐标为a、b,∴a+b=﹣5,ab=﹣3,∴===.故选:B.8.(3分)在△ABC中,∠C=90°,∠A=60°,AC=1,D在BC上,E在AB 上,使得△ADE为等腰直角三角形,∠ADE=90°,则BE的长为()A.B.C.D.【解答】解:过点E作EF作∥AC,交BC于点F,∴∠BFC=∠C=90°,∵∠C=90°,∠BAC=60°,∴∠B=30°∴AB=2AC=2,在Rt△ABC中,由勾股定理得:CB===,∵△ADE是等腰直角三角形,∴DE=DA,∵∠DAC+∠ADC=90°,∠EDF+∠ADC=90°,∴∠DAC=∠EDF在△ADC和△DEF中,,∴△ADC≌△DEF(AAS),∴DF=AC=1,设CD=x,所以EF=x,BF=﹣1﹣x∵EF∥AC∴=,即=,解得:x=2﹣,∴BE=2x=4﹣2.故选:A.9.(3分)在平面直角坐标系中,一次函数y=x的图象、反比例函数y=图象以及二次函数y=x2﹣6x的对称轴围成一个封闭的平面区域(含边界),从该区域内所有格点(横、纵坐标均为整数的点称为格点)中任取3个,则该3点恰能作为一个三角形的三个顶点的概率是()A.B.C.D.【解答】解:如图,二次函数y=x2﹣6x的对称轴为直线x==3,当x=,解得x=±,因为>1,所以封闭的平面区域(含边界)不含横坐标为1的点,当x=2时,y=x=2,而y==0.55,则点A(2,1)、点B(2,2)满足条件的点;当x=3时,y=x=3,而y=≈0.37,则点C(3,1)、点D(3,2)、点E(3,3)为满足条件的点;从5个点中任取3个点共有(ABC、ABD、ABE、ACD、ACE、ADE、BCD、BCE、BDE、CDE)10中等可能的结果数,其中有9种结果数作为一个三角形,所以3点恰能作为一个三角形的三个顶点的概率是.故选:D.10.(3分)定义一个新的运算:a⊕b=,则运算x⊕2的最小值为()A.﹣3B.﹣2C.2D.3【解答】解:当x≤2时,x⊕2=﹣2x+2,此时当x=2时有最小值﹣2;当x>2时,x⊕2==﹣,此时没有最小值,综上,最小值为﹣2,故选:B.二、填空题(本大题共8小题,每小题3分,共24分.)11.(3分)已知1nm等于0.000001mm,则0.000001用科学记数法可表示为1×10﹣6•【解答】解:0.000 001=1×10﹣6,故答案为:1×10﹣6.12.(3分)某班30位女生所穿鞋子的尺码.数据如下(单位:码):记众数为a ,中位数为b ,则a +b = 70 . 【解答】解:∵35出现的次数最多, ∴众数a =35,把这组数据从小到大排列,最中间两个数的平均数是=35,则中位数为b =35, 则a +b =35+35=70; 故答案为:70.13.(3分)“两直线平行,内错角相等”的逆命题是 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行 .【解答】解:“两直线平行,内错角相等”的条件是:两直线平行,结论是:内错角相等.将条件和结论互换得逆命题为:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.故答案为:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 14.(3分)分解因式:2x 2+x ﹣6= (2x ﹣3)(x +2) . 【解答】解:原式=(2x ﹣3)(x +2). 故答案为:(2x ﹣3)(x +2)15.(3分)如图,AB 是⊙O 的切线,切点为B ,AO 交⊙O 于点C ,且AC =OC ,若⊙O 的半径为5,则图中阴影部分的面积是.【解答】解:连接OB ,∵AB 是⊙O 的切线,切点为B , ∴∠OBBA =90°,∵AC =OC ,⊙O 的半径为5, ∴AC =5,AB =5,∴∠A =30°,则∠BOC =60°,∴图中阴影部分的面积为:S △OBA ﹣S 扇形BOC =×BO ×AB ﹣=﹣.故答案为:﹣.16.(3分)若二次函数y=ax2+bx+c(a<0)的对称轴为直线x=﹣1,图象经过点(1,0),有下列结论:①abc<0;②2a﹣b=0;③a+b+c>0;④b2>5ac,则以上结论一定正确的个数是2.【解答】解:①∵二次函数图象与y轴交于正半轴,∴c>0,∵二次函数图象的对称轴是直线x=﹣1,∴﹣=﹣1,∴b=2a,∵a<0,∴b<0,∴abc>0,∴①不正确;②∵b=2a,∴2a﹣b=0,②正确;③图象经过点(1,0),∴a+b+c=0,③不正确;④图象与x轴有两个交点,∴b2﹣4ac>0,∵ac<0,∴b2>5ac,④正确,故答案为:2.17.(3分)若关于x,y的二元一次方程组的解满足2x+y≤2,则t的取值范围为t≤0.【解答】解:,①+②得,4x+2y=4+t,∵2x+y≤2,∴4x+2y≤4,可得:4+t≤4,解得:t≤0,故答案为:t≤0.18.(3分)设抛物线y=﹣x2+2x+3的顶点为E,与y轴交于点C,EF⊥x轴于点,若点M(m,0)是x轴上的动点,且满足以MC为直径的圆与线段EF 有公共点,则实数m的取值范围是﹣≤m≤5.【解答】解:∵M(m,0),C(0,3),∴圆心N的坐标(,),圆N的半径为:,圆心到EF的距离为:|1﹣|,由题意得,|1﹣|≤≤,解得:﹣≤m≤5.故答案为:﹣≤m≤5.三、解答题(本大题共11小题,共76分,把解答过程写在答题卷相应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.)19.(5分)计算:.【解答】解:原式=3+1+3﹣2×=4+2.20.(5分)解不等式组.【解答】解(1)由①得,x≤4,由②得,x>2,∴不等式组的解集为:2<x≤4.21.(5分)先化简,再求值:,其中.【解答】解:原式=×﹣=﹣=﹣,把x=+2代入原式=﹣=﹣=﹣1﹣.22.(6分)现有甲、乙两种金属的合金10kg,如果加入甲种金属若干,那么重新熔炼后的合金中乙种金属占2份,甲种金属占3份,如果加入的甲种金属是第一次加入的2倍,那么重新熔炼后的合金中乙种金属占3份,甲种金属占7份,第一次加入的甲种金属多少?原来这块合金中甲种金属的百分比是多少?【解答】解:设原来这块合金中甲种金属的百分比是x,则甲种金属有10xkg,乙种金属有(10﹣10x)kg,根据题意得(10﹣10x)÷﹣10=2×[(10﹣10x)÷﹣10],解得x=40%.则(10﹣10×40%)÷﹣10=5(kg).答:第一次加入的甲种金属是5kg,原来这块合金中甲种金属的百分比是40%.23.(6分)解分式方程:.【解答】解:去分母得:15x﹣12=4x+10﹣6x+12,移项合并得:17x=34,解得:x=2,经检验x=2是增根,分式方程无解.24.(6分)苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:频率分布表:请结合图表完成下列各题:(1)求表中a的值:(2)请把频数分布直方图补充完整;(3)若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”【解答】解:(1)a=100﹣(8+16+32+20)=24;(2)根据题意补图如下:(3)根据题意得:600×=120(人),答:该校九年级有120人可以获得“乒宝”.25.(7分)某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,已知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:=1.73.)【解答】解:如图所示,作DM⊥AB于M,BN⊥CD于N,则DM=BN=24米,在Rt△ADM中,由题意∠DAM=60°,∴AM==8米,在Rt△BNC中,由题意∠NCB=45°,∴DN=DC﹣NC=45×5﹣24=201米,∴AB=AM+MB=8+201=214.8米,答:A、B两点的距离214.8米.26.(8分)有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC =8.(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;(2)若将这两张矩形纸片交叉叠放(如图2),试判断四边形MNPQ的形状,并证明.【解答】解:(1)由折叠得,∠ADB=∠EDB,∵矩形ABCD的对边AD∥BC,∴∠ADB=∠DBC,∴∠FBD=∠FDB,∴BF=DF,设BF=x,则CF=8﹣x,在Rt△CDF中,CD2+CF2=DF2即32+(8﹣x)2=x2,解得:x=,即BF=;(2)四边形MNPQ的形状是菱形,证明:∵矩形纸片ABCD和A′B′C′D′,∴MN∥PQ,MQ∥AP,∴四边形MNPQ是平行四边形,①如图2,过点N分别做NE⊥MQ,NF⊥QP,垂足分别为E、F,∴NF=NE,=NE•MQ=NF•PQ,∵S平行四边形MNPQ∴MQ=PQ,②由①②知,四边形MNPQ是菱形.27.(9分)如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.(1)求运动时间t的取值范围;(2)t为何值时,△POQ的面积最大?最大值是多少?(3)t为何值时,以点P、0、Q为顶点的三角形与Rt△AOB相似?【解答】解:(1)∵点A(0,6),B(8,0),∴OA=6,OB=8,∵点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动,∴2t=8,解得:t=4,∴0≤t≤4;(2)根据题意得:经过t秒后,AP=t,OQ=2t,∴OP=OA﹣AP=6﹣t,∵△POQ的面积=•OP•OQ,即△POQ的面积=(6﹣t)×2t=﹣t2+6t.∵a=﹣1<0,∴△POQ的面积有最大值,当t=﹣=3时,△POQ的面积的最大值==9,即当t=3时,△POQ的面积最大,最大值是9.(3)①若Rt△POQ∽Rt△AOB时,∵Rt△POQ∽Rt△AOB,∴,即=,解得:t=;②若Rt△QOP∽Rt△AOB时,∵Rt△QOP∽Rt△AOB,∴,即,解得:t=.所以当t为或时,以点P、0、Q为顶点的三角形与Rt△AOB相似.28.(9分)如图所示,D是以AB为直径的半圆O上的一点,C是弧AD的中点,点M在AB上,AD与CM交于点N,CN=AN.(1)求证:CM⊥AB;(2)若AC=;,BD=2,求半圆的直径.【解答】(1)证明:如图1,连接BC,则∠ACB=90°,∵CN=AN,∴∠NCA=∠NAC,∴∠MCA=∠DAC,∵C是弧AD的中点,∴∠ABC=∠DAC,∴∠MCA=∠ABC,∵∠CAB=∠BAC,∴△ABC∽△ACM,∴∠AMC=90°,∴CM⊥AB;(2)解:如图2,连接CD,作CE⊥BD,交BD的延长线于E,在△CMB与△BCE中,,∴△CMB≌△CEB,∴BM=BE,CM=CE,∵C是弧AD的中点,∴AC=CD,在R t△ACM与R t△CED中,,∴R t△ACM≌R t△CED,∴AM=DE,设AM=x,则BM=BE=BD+DE=2+x,∴AB=AM+BM=2+2x,∵∠ACB=∠AMC=90°,∴AC2=AM•AB,∴12=x(2+2x),解得:x=2,∴AB=6.29.(10分)如图所示,已知点C(﹣3,m),点D(m﹣3,0).直线CD交y 轴于点A.作CE与X轴垂直,垂足为E,以点B(﹣1,0)为顶点的抛物线恰好经过点A、C.(1)则∠CDE=45°;(2)求抛物线对应的函数关系式;(3)设P(x,y)为抛物线上一点(其中﹣3<x<﹣1或﹣1<x<1,连结BP并延长交直线CE于点N,记N点的纵坐标为y N,连结CP并延长交X 轴于点M.①试证明:EM•(EC+y N)为定值;②试判断EM+EC+y N是否有最小值,并说明理由.【解答】解:(1)∵AE=m﹣3﹣(﹣3)=m,CE=m,∴AE=CE,∴∠EAC=45°.(2)设E点横坐标为x E,D点横坐标为x D,则ED=x D﹣x E=m,又C(﹣3,m),∴EC=ED,即∠CDE=45°,∴OA=OD=m﹣3,即A(0,m﹣3),设抛物线的方程为y=a(x+1)2,则,解得,a=1,m=4,故抛物线方程为y=(x+1)2.(3)①设P(x,x2+2x+1),作PQ⊥x轴于Q,如图:由Rt△BPQ∽Rt△BNE,可得y N=﹣2(x+1),由Rt△MPQ∽Rt△MCE可得,EM=,∴EM•(EC+y N)=•(﹣2x﹣2+4)=8(为定值)(﹣3<x<﹣1和﹣1<x<1两种情况完全相同).②有最小值.记y=EM+EC+y N,s=EM,t=EC+y N,由①st=8,∴y=s+t=t+=(﹣)2+4,此时,(﹣)2=0,化简得t=2,即x=1﹣时,取到最小值.。
江苏省苏州市2015年中考模拟名校联考数学试题及答案

启用前绝密江苏省苏州市2015年中考中考模拟百校联考数学试题(时间:120分钟 总分:150分)一.选择题(每小题4分,共32分)1.于四条线段a 、b 、c 、d ,如果ab =cd ,那么( ).A. b a =d cB. a d =c bC. a c =b dD. b a =d c2.乙两人在相同的条件下各射靶 10 次,射击成绩的平均数都是 8 环,甲射击成绩的方差是 1.2,乙射击成绩的方差是 1.8.下列说法中不一定正确的是 ( ) A .甲、乙射击成绩的众数相同 B .甲射击成绩比乙稳定 C .乙射击成绩的波动比甲较大 D .甲、乙射中的总环数相同3.如图,DE ∥FG ∥BC ,且DE 、FG 把△ABC 的面积三等分,若BC =12,则FG 的长是( ). A .8 B .6 C .64 D .344.P 是Rt △ABC 的斜边BC 上异于点B 、C 的一点,过点P 作直线截△ABC ,使截得的三角形与△ABC 相似,满足这样条件的直线共有 ( ).A .1条B .2条C .3条D .4条5.为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年11月份用电量的调查结果:6.一个圆锥的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角等于( ).7.如图,在平面直角坐标系中,点A B C 、、的坐标为(1,4)、(5,4)、 (1、2-),则ABC △外接圆的圆心坐标是( ).A.(2,3)B.(3,2)C.(1,3)D.(3,1)8.已知正比例函数y =(k -2)x 的图经过第一、三象限,则一元二次方程x 2-(2k -1)x+k 2-1=0根的情况是( ).A. 有两个不等实根B. 有两个相等实根C. 没有实根D. 无法确定 二.填空题(每小题4分,共32分)9.如图,在△ABC 中,D 在AB 上,要说明△ACD ∽△ABC 相似, 需添加的条件是 .10.方程x 2=-2x 的根是 .11.点C 是线段AB 的黄金分割点,已知AB=4,则AC= .12.设a 、b 是方程x2+x-2014=0的两个不等的根,则a2+2a+b 的值为 .13.小明在一次以“四礼八仪”为主题的演讲比赛中,“演讲内容”、“语言表达”、“演讲技能”、“形象礼仪”的各项得分依次为9.8;9.4;9.2;9.3.若其“综合得分”按“演讲内容”50%,“语言表达”20%,“演讲技能”20%,“形象礼仪”10%的比例进行计算,则他的“综合得分”是 。
苏州市三区2015届中考模拟数学试题及答案

2015届初三中考模拟考试试卷数 学 2015. 5一、选择题(本大题共有10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是符合题目要求的.) 1.化简2-的结果是A .一2B .2C .12D .±2 2.下列腾讯QQ 表情中,不是轴对称图形的是3.下列运算正确的是A .3362x x x += B .5420()x x -= C .mnmnx x x⋅= D .824x x x ÷=4.如图,己知AB ∥CD ,BC 平分∠ABE ,∠C=34°, ∠BED 的大小为 A .17° B .34° C .56° D .68° 5.在平面直角坐标系中,将y 轴绕原点顺时针旋转45°,再向上平移1个单位后得到直线a ,则直线a 对应的函数表达式为A .y x =B .1y x =- C·1y x =+ D·1y x =-+ 6.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)A .36,8B .28,6C .28,8D .13,37.设函数5y x =+与3y x =的图象的两个交点的横坐标为a 、b ,则11a b+的值是 A .53- B .53 C .35- D·358.在△ABC 中,∠C=90°,∠A=60°,AC=1,D 在BC 上,E 在AB 上,使得△ADE 为等腰直角三角形,∠ADE=90。
,则BE 的长为A .4-B .2C 1D .11)29.在平面直角坐标系中,一次函数y x =图象、反比例函数 1.1y x=图象以及二次函数26y x x =-的对称轴围成一个封闭的平面区域(含边界),从该区域内所有的格点(横、纵坐标均为整数的点称为格点)中任取3个,则该3点恰能作为一个三角形的三个顶点的概率是A .12 B .35 C .710 D .91010.定义一个新的运算:2()2()a b a b a b b a b a-+≤⎧⎪⊕=+⎨>⎪-⎩则运算2x ⊕的最小值为A .一3B .一2C .2 D·3 二、填空题(本大题共8小题,每小题3分,共24分.)11.已知l nm 等于0.000001 mm ,则0.000001用科学记数法可表示为 ▲ ·记众数为a ,中位数为b ,则a+b= ▲ .13.命题“两直线平行,内错角相等”的逆命题是 ▲ . 14.分解因式:226x x +-= ▲ .15.如图,AB 是⊙O 的切线,切点为B ,AO 交⊙O 于点C , 且AC=OC ,若⊙O 的半径为5,则图中阴影部分的面积是 ▲ .16.若二次函数2(0)y ax bx c a =++<的对称轴为直线1x =-,图象经过点(1,0),有下列结论: ①0abc <;②20a b -=; ③0a b c ++> ④25b ac >则以上结论一定正确的个数是 ▲ .17.若关于,x y 的二元一次方程组 3133x y tx y -=+⎧⎨+=⎩的解满足22x y +≤,则t 的取值范围为▲.18.设抛物线223y x x =-++的顶点为E ,与y 轴交于点C ,EF ⊥x 轴于点,,若点M(m ,0)是x 轴上的动点,且满足以MC 为直径的圆与线段EF 有公共点,则实数m 的取值范围是 ▲ .三、解答题(本大题共11小题,共76分,把解答过程写在答题卷相应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.)19.(本题满分5分)计算:01012cos303-⎛⎫+⎪⎝⎭ 20.(本题满分5分)解不等式组31214x x x -≤⎧⎪⎨+->⎪⎩21.(本题满分5分)先化简,再求值:22244(2)244x x x x x x +-÷+---+其中2x =22.(本题满分6分)某工厂进行新材料实验,现有甲、乙两种金属合金共10KG.如果加入甲金属若干,那么重新熔炼后的合金中乙金属占2份,甲金属占3份;如果加入的甲金属是第一次加入的2倍,那么重新熔炼后的合金中乙种金属占3份,甲种金属占7份.(1)第一次加入的甲种金属有多少?(2)原来这块合金中含甲金属的百分比是多少?23.(本题满分6分)解分式方程:544102 236x xx x-+=---24.(本题满分6分)苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:请结合图表完成下列各题:(1)求表中a的值:(2)请把频数分布直方图补充完整;(3)若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?25.(本题满分7分)某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,己知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1 1.41 1.73==.)26.(本题满分8分)有两张相同的矩形纸片ABCD和A’B’C’D’,其中AB=3,BC=8·(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;(2)若将这两张矩形纸片交叉叠放(如图2),试判断四边形MNPQ 的形状,并证明·27.(本题满分9分)如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P 从A 点出发,以每秒1个单位的速度沿AO 运动;同时,点Q 从O 出发,以每秒2个单位的速度沿OB 运动,当Q 点到达B 点时,P 、Q 两点同时停止运动. (1)求运动时间t 的取值范围;(2)t 为何值时,△POQ 的面积最大?最大值是多少? (3)t 为何值时,以点P 、0、Q 为顶点的三角形 与Rt △AOB 相似?28.(本题满分9分)如图所示,D 是以AB 为直径的半圆O 上的一点,C 是弧AD 的中点,点M 在AB 上,AD 与CM 交于点N ,CN=AN . (1)求证CM ⊥AB ;(2)若AC=,BD=2,求半圆的直径.29.(本题满分10分)如图所示,已知点C(一3,m),点D(m 一3,0).直线CD 交y 轴于点A .作CE 与X 轴垂直,垂足为E ,以点B(一1,0)为顶点的抛物线恰好经过点A 、C . (1)则∠CDE= ▲ .(2)求抛物线对应的函数关系式;(3)设P(x ,y)为抛物线上一点(其中31x -<<-或11x -<<, 连结BP 并延长交直线CE 于点N,记N 点的纵坐标为N y , 连结CP 并延长交X 轴于点M . ①试证明:EM·(EC+N y )为定值;②试判断EM+EC+N y 是否有最小值,并说明理由.。
2015年苏州市初中毕业暨升学考试数学模拟试卷答案

2015年苏州市初中毕业暨升学考试数学模拟试卷答案佚名【期刊名称】《中学数学月刊》【年(卷),期】2015(000)005【总页数】2页(P59-60)【正文语种】中文ADCBC CBBAD11.2.45×106. 12.x≥-1. 13.y=2x2-1.14.800. 15.4. 16.10. 17.4.18.①②③④.19.原式=3+2-1=4.20.由①得x-3x+6≤6,故x≥0.由②得1+2x>3x-3,故x<4.因此0≤x<4.21.原式当时,原式22.两边同乘x(x-1),得x2-3(x-1)=x(x-1),x2-3x+3=x2-x,故经检验,是原方程的解.23.(1)因为AB∥DC,所以∠ABD=∠EDC.又因为∠1=∠2,BD=DC,所以△ABD≌△EDC. (2)因为△ABD≌△EDC,所以∠DEC=∠A.又∠A=135°,所以∠DEC=135°.又因为BD=DC,∠BDC=30°,所以∠DBC=∠BCD=75°,故∠BCE=∠DEC-∠DBC=60°.24.25.过C作CG⊥BE,CH⊥AB(图1).因为CD=6,∠CDE=60°,可得又BD=10,所以HC=BG=13.又因为∠ACF=45°,所以AH=13.故26.(1)因为E(3,a)在一次函数x+2的图象上,所以又因为在一次函数y=2x+m的图象上,所以(2)①方法1 解方程组得故又因为E在第一象限,所以故-8<m<2.方法2 如图2,数形结合法(略),由C(0,2),D(4,0), F(0,-8),可得-8<m<2.②方法1 如图3,过E作EG⊥x轴,易得,所以,故m=-3.方法2如图3,过D作DH⊥x轴,交y=2x+m于H,易得△AEC≌△HED,H(4,8+m),HD=8+m,CA=2-m,易得HD=CA,8+m=2-m,故m=-3.27.(1)①因为BG2=BD·BC,所以又∠GBD=∠CBG,所以△GBD∽△CBG,故∠BGD=∠BCG.② 连结ED.因为∠BGD=∠BED,且∠BGD=∠BCG,所以∠BCG=∠BED,故∠BCG+∠HBC=∠BED+∠HBC.因为BE为直径,所以∠BDE=90°,故∠BCG+∠HBC=∠BED +∠HBC=90°,所以∠BHC=90°,因此AB⊥CG.(2)① 连结OF,设⊙O的半径为r,因为AC为⊙O的切线,所以OF⊥AC.易证∠A=∠BED=∠BGD,因为,所以,故,解得r=4.② 易证∠CFI=∠HIB=∠CIF,故CI=CF.易求,所以28.(1)BM=t,CM=8- t,∠BMN=∠CDM.△BMN∽△CDM,故 (2)如图5,过Q作,故当t=4时,S的最大值为8. (3)分三种情况讨论.情况1 如图6,当P在AD边上时,BN+AN=6,通过△BMN∽△CDM,可得,可得AN=t.故,所以(舍),情况2 如图7,当Q在AD边上时,此时△BMN≌△MCD,可得BM=CD,故t=6.情况3 当N在AD边上时,或用根的判别式Δ<0无解,不成立.综上所述,当或6时,正方形MNPQ的一个顶点恰好落在矩形ABCD的边AD上.29.(1)A(m,0),D(1,-1+m), E(4,-16+4m).(2)①15.②分三种情况考虑,如图8.情况1 当∠ADE=90°时,可判断△HDE为等腰直角三角形.因为HD=EC-BD=4m-16-(m-1)=3m-15,根据HD=EH,易得3m-15=3,故m=6>4,成立.情况2 当∠AED=90°时,易得△HDE∽△CAE,所以,故,从而,成立.情况3 当∠EAD=90°时,因为∠EAD<∠EAC=90°,所以∠EAD不可能等于90°.综上所述,当△ADE为直角三角形时,m=6或 (3)方法1 易得AB=BD=2MB,即;同时NC=2AC,即因为△ABM与△AMN相似,所以△AMN必为直角三角形,接下来与第(2)小题类似,分情况讨论.情况1 当∠AMN=90°时,△ABM∽△MGN,易得GM=6,可求得从而求得,此时△ABM与△AMN不相似.情况2 当∠ANM=90°时,△ACN∽△MGN,易得,可求得m=6.从而求得,此时△ABM与△AMN不相似.情况3 ∠MAN不可能等于90°.综上所述,△ABM不可能与△AMN相似.方法2 易得△ABM∽△NCA,从而判断出∠BMA=∠CAN.∠MAN的对应角不可能是∠ABM,因为∠MAN<∠NAC<90°;∠MAN的对应角也不可能是∠AMB,因为BM与AN不可能平行.这样一来,∠MAN的对应角只可能是∠BAM,而当∠MAN=∠BAM时,必然有,易得∠BAM=30°,∠AMB=60°,此时,与矛盾.故△ABM不可能与△AMN相似.。
2015年苏州市中考数学预测试卷附答案

2015年中考数学本试卷由选择题、填空题和解答题三大题组成.共29小题,满分130分.考试时间120分钟.注意事项:1.答题前,考生务必将自己的姓名、考点名称、考场号、座位号用0.5毫米黑色墨水签字笔填写在答题卡相应位置上,并认真核对条形码上的准考号、姓名是否与本人的相符;2.答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其他答案;答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上,不在答题区域内的答案一律无效,不得用其他笔答题;3.考生答题须答在答题卡上,保持卡面清洁,不要折叠,不要弄破,答在试卷和草稿纸上一律无效.一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将选择题的答案用2B铅笔涂在答题卡相应位置上.1.(-3)×3的结果是()A.-9;B.0 ; C.9 ; D.-62.已知∠α和∠β是对顶角,若∠α=30°,则∠β的度数为()A.30°B.60°C.70°D.150°3.有一组数据:1,3.3,4,5,这组数据的众数为()A.1 B.3 C.4 D.54x的取值范围是()A.x≤-4 B.x≥-4 C.x≤4 D.x≥45.如图,一个圆形转盘被分成6个圆心角都为60°的扇形,任意转动这个转盘1次,当转盘停止转动时,指针指向阴影区域的概率是()A.14B.13C.12D.236.如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为()A.30°B.40°C.45°D.60°7.下列关于x的方程有实数根的是()A.x2-x+1=0 ;B.x2+x+1=0;C.(x-1)(x+2)=0 ;D.(x-1)2+l=0 8.一次函数y=ax2+bx-1(a≠0)的图象经过点(1,1).则代数式1-a-b的值为()A.-3 B.-1 C.2 D.59.如图,港口A在观测站O的正东方向,OA=4km.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为()A.4km B.23km C.22km D.(3+1)km10.如图,△AOB为等腰三角形,顶点A的坐标为(2,5,底边OB在x轴上.将△AOB 绕点B按顺时针方向旋转一定角度后得△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为()A.(203,103)B.(163,453)C.(203,453)D.(163,3二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相应位置上.11.32的倒数是▲ .12已知地球的表而积约为510000000km2.数510000000用科学记数法可以表示为▲ .13.已知正方形ABCD的对角线AC2,则正方形ABCD的周长为▲ .14.某学校计划开设A,B,C,D四门校本课程供全体学生选修,规定每人必须并且只能选修其中一门.为了了解各门课程的选修人数,现从全体学牛中随机抽取了部分学牛进行调查,并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名,由此可以估计选修C课程的学生有▲ 人.15.如图,在△ABC 中,AB =AC =5,BC =8.若∠BPC =12∠BAC ,则tan ∠BPC = ▲ .16.某地准备对一段长120m 的河道进行清淤疏通,若甲工程队先用4天单独完成其中一部分河道的疏通任务,则余下的任务由乙工程队单独完成需要9天;若甲工程队先单独工作8天,则余下的任务由乙工程队单独完成需要3天,设甲工程队平均每天疏通河道xm ,乙工程队平均每天疏通河道ym ,则(x +y )的值为 ▲ .17.如图,在矩形ABCD 中,35AB BC =,以点B 为圆心,BC 长为半径画弧,交边AD 于点E ,若AE·ED =43,则矩形ABCD 的面积为 ▲ .18.如图,直线l 与半径为4的⊙O 相切于点A ,P 是⊙O 上的一个动点(不与点A 重合),过点P 作PB ⊥l ,垂足为B ,连接PA .设PA =x ,PB =y ,则(x -y )的最大值是 ▲ .三、解答题:本大题共11小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要的计算过程、推演步骤或文字说明,作图时用2B 铅笔或黑色墨水签字笔.19.(本题满分5分)计算:2214+--.20.(本题满分5分)解不等式组:()12221x x x ->⎧⎪⎨+≥-⎪⎩. 21.(本题满分5分)先化简,再求值:21111x x x ⎛⎫÷+ ⎪--⎝⎭,其中x 21. 22.(本题满分6分)解分式方程:2311x x x+=--. 23.(本题满分6分)如图,在Rt △ABC 中,∠ACB =90°,点D ,F 分别在AB ,AC 上,CF =CB .连接CD ,将线段CD 绕点C 按顺时针方向旋转90°后得CE ,连接EF .(1)求证:△BCD ≌△FCE ; (2)若EF ∥CD .求∠BDC 的度数.24.(本题满分7分)如图,已知函数y =-12x +b 的图象与x 轴、y 轴分别交于点A ,B ,与函数y =x 的图象交于点M ,点M 的横坐标为2.在x 轴上有一点P (a ,0)(其中a>2),过点P 作x 轴的垂线,分别交函数y =-12x +b 和y =x 的图象于点C ,D . (1)求点A 的坐标; (2)若OB =CD ,求a 的值.25.(本题满分7分)如图,用红、蓝两种颜色随机地对A ,B ,C 三个区域分别进行涂色,每个区域必须涂色并且只能涂一种颜色,请用列举法(画树状图或列表)求A ,C 两个区域所涂颜色不相同的概率.26(本题满分8分)如图,已知函数y =k x(x>0)的图象经过点A ,B ,点A 的坐标为 (1,2).过点A 作AC ∥y 轴,AC =1(点C 位于点A 的下方),过点C 作CD ∥x 轴,与函数的图象交于点D ,过点B 作BE ⊥CD ,垂足E 在线段CD 上,连接OC ,OD .(1)求△OCD 的面积; (2)当BE =12AC 时,求CE 的长.27.(本题满分8分)如图,已知⊙O 上依次有A ,B ,C ,D 四个点,»»AD BC ,连接AB ,AD ,BD ,弦AB 不经过圆心O .延长AB 到E ,使BE =AB ,连接EC ,F 是EC 的中点,连接BF .(1)若⊙O的半径为3,∠DAB=120°,求劣弧»BD的长;(2)求证:BF=12BD;(3)设G是BD的中点探索:在⊙O上是否存在点P(小同于点B),使得PG=PF?并说明PB与AE 的位置关系.28.(本题满分9分)如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=43cm,AD=4cm.若⊙O与矩形ABCD沿l1同.时.向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).(1)如图①,连接OA,AC,则∠OAC的度数为▲ °;(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)29.(本题满分10分)如图,一次函数y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.(1)用含m的代数式表示a;(2)求证:ADAE为定值;(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.2015年苏州市中考数学预测试卷一、选择题:1.﹣的例数是()A.2B.C.﹣2 D.﹣2.下列运算正确的是()C.a•a=2a D.a3÷a=a2 A.π﹣3.14=0 B.+=3.为了丰富学生课余活动,我校开展的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:成绩(分)9.40 9.50 9.60 9.70 9.80 9.90人数 2 3 5 4 3 1则入围同学决赛成绩的中位数和众数分别是()A. 9.70,9.60 B.9.60,9.60 C.9.60,9.70 D.9.65,9.604.若在实数范围内有意义,则x的取值范围是()A.x>0 B.x>3 C.x≥3D.x≤35.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC 于E,则∠ADE的大小是()A.45°B.54°C.40°D.50°(第5题)(第7题)(第8题)6.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+1x(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是1x,矩形的周长是2(x+1x);当矩形成为正方形时,就有x=1x(0>0),解得x=1,这时矩形的周长2(x+1x)=4最小,因此x+1x(x>0)的最小值是2.模仿张华的推导,你求得式子(x>0)的最小值是()A.2B.1C.6D.107.如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于()A.140°B.150°C.160°D.120°8.如图,A、B两点在双曲线y=4x上,分别由A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=()A.3B.4C.5D.69.下列命题是假命题的是()A.对角线垂直的四边形是菱形B.对角线相等的平行四边形是矩形C.四个角相等的四边形是矩形D.对角线垂直的平行四边形是菱形10.如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE =CF;②线段EF的最小值为23;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=25;⑤当点D从点A运动到点B时,线段EF扫过的面积是163.其中正确结论个数是().A、4个;B、3个;C、2个;D、1个。
2015苏州中考数学试题及答案

2015苏州中考数学试题及答案2015年苏州市初中毕业暨升学考试试卷数学(2015年6月16日)一、选择题:(本大题共10小题,每小题3分,共30分)1. 2015年是抗日战争胜利70周年,下列年份中属于抗日战争胜利的年份是()A. 1945年B. 1937年C. 1931年D. 1949年答案:A2. 一个数的绝对值是3,这个数是()A. 3B. -3C. 3或-3D. 以上答案都不对答案:C3. 一个等腰三角形的两边长分别为5和8,这个三角形的周长是()A. 18B. 21C. 26D. 234. 将下列各数从小到大排列:-2,-1,0,1,2,3,4,5,6,7,8,9()A. -2<-1<0<1<2<3<4<5<6<7<8<9B. -2<-1<0<1<2<3<4<5<6<7<8<9C. -2<-1<0<1<2<3<4<5<6<7<8<9D. -2<-1<0<1<2<3<4<5<6<7<8<9答案:A5. 已知a,b,c是三个实数,且a>b,c>0,则下列不等式中一定成立的是()A. ac>bcB. a+c>b+cC. ac>bcD. a-c>b-c答案:B6. 已知a,b,c是三个实数,且a>b,c<0,则下列不等式中一定成立的是()A. ac>bcB. a+c>b+cC. ac>bcD. a-c>b-c7. 已知a,b,c是三个实数,且a>b,c>0,则下列不等式中一定成立的是()A. ac>bcB. a+c>b+cC. ac>bcD. a-c>b-c答案:A8. 已知a,b,c是三个实数,且a>b,c<0,则下列不等式中一定成立的是()A. ac>bcB. a+c>b+cC. ac>bcD. a-c>b-c答案:C9. 已知a,b,c是三个实数,且a>b,c>0,则下列不等式中一定成立的是()A. ac>bcB. a+c>b+cC. ac>bcD. a-c>b-c答案:B10. 已知a,b,c是三个实数,且a>b,c<0,则下列不等式中一定成立的是()A. ac>bcB. a+c>b+cC. ac>bcD. a-c>b-c答案:D二、填空题:(本大题共6小题,每小题3分,共18分)11. 已知一个角的补角是它的余角的3倍,则这个角的度数是60°。
苏州市2015-2016学年初三上期末数学模拟试卷(三)及答案

苏州市2015-2016学年第一学期期末初三数学模拟试卷三(范围:苏科版2013年九年级上下两册;分值:130分;时间:120分钟)2016年1月一、选择题(每小题3分,共24分)1.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这七名同学成绩的()A.众数 B.平均数C.中位数D.方差2.一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖).组员甲乙丙丁戊方差平均成绩得分81 79 ■80 82 ■80那么被遮盖的两个数据依次是()A.80,2 B.80,C.78,2 D.78,3.关于x的一元二次方程3x2﹣6x+m=0有两个不相等的实数根,则m的取值范围是()A.m<3 B.m≤3 C.m>3 D.m≥34.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为()A.2a2B.3a2C.4a2D.5a2(4题)(5题)(6题)5.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为()A.﹣3 B.3 C.﹣6 D.96.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为()A.4B.8C.2D.47.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP 的最大值是()A.30°B.45°C.60°D.90°8.如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为()A.2.5 B.1.6 C.1.5 D.1(7题)(8题)二、填空题(每小题3分,共30分)9.某校篮球班21名同学的身高如下表:身高/cm 180 185 187 190 201人数/名 4 6 5 4 2则该校篮球班21名同学身高的中位数是cm.10.某校从参加计算机测试的学生中抽取了60名学生的成绩(40~100分)进行分析,并将其分成了六段后绘制成如图所示的频数分布直方图(其中70~80段因故看不清),若60分以上(含60分)为及格,试根据图中信息来估计这次测试的及格率约为.(10题)(11题)11.已知如图所示的图形的面积为24,根据图中的条件,可列出方程:.12.已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根为x1和x2,且(x1﹣2)(x1﹣x2)=0,则k的值是.13.我市为了增强学生体质,开展了乒乓球比赛活动.部分同学进入了半决赛,赛制为单循环形式(即每两个选手之间都赛一场),半决赛共进行了6场,则共有人进入半决赛.14.在﹣1、3、﹣2这三个数中,任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的概率是.15.P为⊙O外一点,PA,PB分别切⊙O于点A,B,∠APB=50°,点C为⊙O上一点(不与A,B重合),则∠ACB的度数为.16.如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=米.(结果精确到1米)(参考数据:,)(16题)(18题)17.二次函数y=ax2+bx+c图象上部分点的对应值如下表:x ﹣3 ﹣2 ﹣1 0 1 2 3 4y 6 0 ﹣4 ﹣6 ﹣6 ﹣4 0 6则当y≤0时,x的取值范围为.18.如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置.若正六边形的边长为2cm,则正六边形的中心O运动的路程为cm.三、解答题(共76分)(19、20题5分)19.计算:﹣22﹣3×3﹣1+(﹣1)0+2sin30°.20.已知x是一元二次方程x2+3x﹣1=0的实数根,求代数式:的值.21.(6分)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)22.(6分)小英与她的父亲、母亲计划外出旅游,初步选择了延安、西安、汉中、安康四个城市,由于时间仓促,他们只能去其中一个城市,到底去哪一个城市三个人意见不统一,在这种情况下,小英父亲建议,用小英学过的摸球游戏来决定,规则如下:①在一个不透明的袋子中装一个红球(延安)、一个白球(西安)、一个黄球(汉中)和一个黑球(安康),这四个球除颜色不同外,其余完全相同;②小英父亲先将袋中球摇匀,让小英从袋中随机摸出一球,父亲记录下其颜色,并将这个球放回袋中摇匀,然后让小英母亲从袋中随机摸出一球,父亲记录下它的颜色;③若两人所摸出球的颜色相同,则去该球所表示的城市旅游,否则,前面的记录作废,按规则②重新摸球,直到两人所摸出求的颜色相同为止.按照上面的规则,请你解答下列问题:(1)已知小英的理想旅游城市是西安,小英和母亲随机各摸球一次,均摸出白球的概率是多少?(2)已知小英母亲的理想旅游城市是汉中,小英和母亲随机各摸球一次,至少有一人摸出黄球的概率是多少?23.(9分)2014年5月31日是世界卫生组织发起的第27个“世界无烟日”.为了更好地宣传吸烟的危害,某中学九年级(1)班数学兴趣小组设计了如下调查问卷,在东方广场随机调查了部分吸烟人群,并将调查结果绘制成如图所示的统计图.根据以上信息,解答下列问题:(1)本次接受调查的总人数是,并把条形统计图补充完整;(2)在扇形统计图中,C选项的人数所占百分比是,E选项所在扇形的圆心角的度数是.(3)若某区约有烟民38万人,试估计对吸烟有害持“无所谓”态度的人数,你对这部分人群有何建议?24.(8分)如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.(1)求证:△CDE∽△CAD;(2)若AB=2,AC=2,求AE的长.25.(6分)一学校为了绿化校园环境,向某园林公司购买了一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?26.(9分)如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P 过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.(1)求抛物线的解析式;(2)求证:ED是⊙P的切线;27.(10分)如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.(1)求证:OF∥BE;(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,求(2)中x和y的值;如果不存在,请说明理由.28.(12分)如图,二次函数y=a(x2﹣2mx﹣3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.(1)用含m的代数式表示a;(2)求证:为定值;(3)设该二次函数图象的顶点为F,探索:在x轴的负半轴上是否存在点G,连接GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.参考答案与试题解析一、选择题(每小题3分,共24分)1.解:由于总共有7个人,且他们的分数互不相同,第4的成绩是中位数,要判断是否进入前4名,故应知道中位数的多少.故选:C.2.解:根据题意得:80×5﹣(81+79+80+82)=78,方差=[(81﹣80)2+(79﹣80)2+(78﹣80)2+(80﹣80)2+(82﹣80)2]=2.故选C.3.解:根据题意得△=(﹣6)2﹣4×3×m>0,解得m<3.故选A.4.解:∵某小区将原来正方形地砖更换为如图所示的正八边形植草砖,设正八边形与其内部小正方形的边长都为a,∴AB=a,且∠CAB=∠CBA=45°,∴sin45°===,∴AC=BC=a,∴S△ABC=×a×a=,∴正八边形周围是四个全等三角形,面积和为:×4=a2.正八边形中间是边长为a的正方形,∴阴影部分的面积为:a2+a2=2a2,故选:A.5.解:(法1)∵抛物线的开口向上,顶点纵坐标为﹣3,∴a>0,=﹣3,即b2=12a,∵一元二次方程ax2+bx+m=0有实数根,∴△=b2﹣4am≥0,即12a﹣4am≥0,即12﹣4m≥0,解得m≤3,∴m的最大值为3.(法2)一元二次方程ax2+bx+m=0有实数根,可以理解为y=ax2+bx和y=﹣m有交点,可见﹣m≥﹣3,∴m≤3,∴m的最大值为3.故选B.(5题)(6题)6.解:∵⊙O的直径AB=12,∴OB=AB=6,∵BP:AP=1:5,∴BP=AB=×12=2,∴OP=OB﹣BP=6﹣2=4,∵CD⊥AB,∴CD=2PC.如图,连接OC,在Rt△OPC中,∵OC=6,OP=4,∴PC===2,∴CD=2PC=2×2=4.故选D.7.解:根据题意知,当∠OAP取最大值时,OP⊥AP;在Rt△AOP中,∵OP=OB,OB=AB,∴OA=2OP,∴∠OAP=30°.故选A.(7题)(8题)8.解:连接OD、OE,设AD=x,∵半圆分别与AC、BC相切,∴∠CDO=∠CEO=90°,∵∠C=90°,∴四边形ODCE是矩形,∴OD=CE,OE=CD,又∵OD=OE,∴CD=CE=4﹣x,BE=6﹣(4﹣x)=x+2,∵∠AOD+∠A=90°,∠AOD+∠BOE=90°,∴∠A=∠BOE,∴△AOD∽OBE,∴=,∴=,解得x=1.6,故选:B.二、填空题(每小题3分,共30分)9.187.10.解:∵频数=×组距,∴当40≤x<50时,频数=0.6×10=6,同理可得:50≤x<60,频数=9,60≤x<70,频数=9,80≤x<90,频数=15,90≤x<100,频数=3,∴70≤x<80,频数=60﹣6﹣9﹣9﹣15﹣3=18,∴这次测试的及格率=×100%=75%.11.解:根据题意得:(x+1)2﹣1=24,即:(x+1)2=25.故答案为:(x+1)2=25.12.解:∵(x1﹣2)(x1﹣x2)=0,∴x1﹣2=0或x1﹣x2=0.①如果x1﹣2=0,那么x1=2,将x=2代入x2+(2k+1)x+k2﹣2=0,得4+2(2k+1)+k2﹣2=0,整理,得k2+4k+4=0,解得k=﹣2;②如果x1﹣x2=0,那么(x1﹣x2)2=(x1+x2)2﹣4x1x2=[﹣(2k+1)]2﹣4(k2﹣2)=4k+9=0,解得k=﹣.又∵△=(2k+1)2﹣4(k2﹣2)≥0.解得:k≥﹣.所以k的值为﹣2或﹣.13.解:假设共有x人进入半决赛.∴x(x﹣1)=6,解得:x 1=4,x 2=﹣3(舍去),答:共有4人进入半决赛.故答案为:4.14.解:画树状图得:∵共有6种等可能的结果,任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的有2种情况,∴任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的概率是:=.故答案为:.15.解:连接OA、OB.∵PA,PB分别切⊙O于点A,B,∴OA⊥PA,OB⊥PB;∴∠PAO=∠PBO=90°;又∵∠APB=50°,∴在四边形AOBP中,∠AOB=360°﹣90°﹣90°﹣50°=130°,∴∠ADB=×∠AOB=×130°=65°,即当C在D处时,∠ACB=65°.在四边形ADBC中,∠ACB=180°﹣∠ADB=180°﹣65°=115°.于是∠ACB的度数为65°或115°.(15题)16.解:∵∠ABD=30°,∠ACD=60°,∴假设CD=x,AC=2x,∴AD=x,tanB==,∴=,解得:x=150,∴AD=x=×150≈260米.故答案为:260米.17.解:由表中数据可知抛物线y=ax2+bx+c与x轴的交点为(﹣2,0)、(3,0),根据表格确定y≤0的是x的取值范围﹣2≤x≤3,故答案为:﹣2≤x≤3.18.解:根据题意得:每次滚动正六边形的中心就以正六边形的半径为半径旋转60°,正六边形的中心O运动的路程∵正六边形的边长为2cm,∴运动的路径为:=;∵从图1运动到图2共重复进行了六次上述的移动,∴正六边形的中心O运动的路程6×=4πcm三、解答题(共76分)19.(5分)解:原式=﹣4﹣1+1+1=﹣3.20.(5分)解:∵x2+3x﹣1=0.∴x2+3x=1.x(x+3)=1∴原式=÷==.21.(6分)解:作EF⊥AC,根据题意,CE=18×15=270米,∵tan∠CED=1,∴∠CED=∠DCE=45°,∵∠ECF=90°﹣45°﹣15°=30°,∴EF=CE=135米,∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°﹣45°﹣60°﹣30°=45°,∴AE=135≈190.4米22.(6分)解:(1)画树状图得:∵共有16种等可能的结果,小英和母亲随机各摸球一次,均摸出白球的只有1种情况,∴小英和母亲随机各摸球一次,均摸出白球的概率是:;(2)由(1)得:共有16种等可能的结果,小英和母亲随机各摸球一次,至少有一人摸出黄球的有7种情况,∴小英和母亲随机各摸球一次,至少有一人摸出黄球的概率是:.23.(9分)(1)调查的总人数=126÷42%=300,决定戒烟,远离烟草危害的人数为300﹣12﹣126﹣78﹣30=54人,如图,故答案为:300人;(23答图)(26答图)(2)在扇形统计图中,C选项的人数所占百分比是78÷300=26%,×360°=36°,故答案为:26%,36°.(3)估计对吸烟有害持“无所谓”态度的人数为38×=1.52(万人)建议:吸烟有害身体健康.24.(8分)(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∴∠B+∠BAD=90°,∵AC为⊙O的切线,∴BA⊥AC,∴∠BAC=90°,即∠BAD+∠CAD=90°,∴∠B=∠CAD,∵OB=OD,∴∠B=∠ODB,而∠ODB=∠CDE,∴∠B=∠CDE,∴∠CAD=∠CDE,而∠ECD=∠DCA,∴△CDE∽△CAD;(2)解:∵AB=2,∴OA=1,在Rt△AOC中,AC=2,∴OC==3,∴CD=OC ﹣OD=3﹣1=2,∵△CDE∽△CAD,∴=,即=,∴CE=.∴AE=AC﹣CE=2﹣=.25.(6分)解:因为60棵树苗售价为120元×60=7200元<8800元,所以该校购买树苗超过60棵,设该校共购买了x棵树苗,由题意得:x[120﹣0.5(x﹣60)]=8800,解得:x1=220,x2=80.当x=220时,120﹣0.5×(220﹣60)=40<100,∴x=220(不合题意,舍去);当x=80时,120﹣0.5×(80﹣60)=110>100,∴x=80.答:该校共购买了80棵树苗.26.(9分)解:(1)∵C(2,0),BC=6,∴B(﹣4,0),在Rt△OCD中,∵tan∠OCD=,∴OD=2tan60°=2,∴D(0,2),设抛物线的解析式为y=a(x+4)(x﹣2),把D(0,2)代入得a•4•(﹣2)=2,解得a=﹣,∴抛物线的解析式为y=﹣(x+4)(x﹣2)=﹣x2﹣x+2;(2)在Rt△OCD中,CD=2OC=4,∵四边形ABCD为平行四边形,∴AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6,∵AE=3BE,∴AE=3,∴=,==,∴=,而∠DAE=∠DCB,∴△AED∽△COD,∴∠ADE=∠CDO,而∠ADE+∠ODE=90°∴∠CDO+∠ODE=90°,∴CD⊥DE,∵∠DOC=90°,∴CD为⊙P的直径,∴ED是⊙P的切线;27.(10分)(1)证明:连接OE。
历届中考数学一模卷

2015年苏州市区初三一模卷数 学一、选择题:(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B 铅笔涂在答题卡相对应的位置上...........) 1.2015(1)-的值是A .-1B .IC .2015D .-20152.下列计算正确的是A .224a a a +=B .235()a a =C .22a a -=D .222()ab a b = 3.一组数据1,3,2,0,3,0,2的中位数是A .0B .1C .2D .34.下列函数中,自变量的取值范围是x ≥2的是A .2y x =-B .12y x =-C .2y x =-D .2y x =- 5.若等腰三角形的两边长为2和5,则该等腰三角形的周长为A .9B .12C .9或12D .106.下列关于x 的一元二次方程中一定有实数根的是A .2240x x -+=B .2240x x ++=C .2240x x --=D .240x +=7.己知反比例函数(0)k y k x=≠的图象经过点p (2,3-),则这个函数的图象位于 A .第一、三象限 B .第二、四象限 C .第一、二象限 D .第三、四象限8. 如图,⊙O 上A 、B 、C 三点,若∠B=50,∠A=20°,则∠AOB 等于A .30°B .50°C .70°D .60°9.如图,△ABC 与△DEF 都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°, 则△ABC 与△DEF 的面积比为A .9:4B .3:2C 32D .33210.若二次函数2(0)y ax bx c a =++≠与x 轴交于两个不同点A(1x ,0),B(2x ,0);且二次函数化为顶点式是2()y a x h k =-+,则下列说法:①240b ac -> ②122x x h +=③二次函数 22(0)y ax bx c a =++≠化为顶点式为2()2y a x h k =-+ ④若c k =,则一定有h b = 正确的有A .①②B .①②③C .①②④D .①②③④二、填空题(本大题共8小题,每小题3分,共24分,把答案填在答题卷相应题中横线上.)11.若关于x 的方程25x a +=的解为1x =-,则 a = ▲ .12.2014年的一份调查报告显示,苏州城市人口(常驻人口加流动人口)跨入千万行列, 达到10460000人,数字10460000用科学记数法表示为 ▲ .13.己知m 是关于x 的方程2270x x --=的一个根,则22(2)m m -= ▲ . 14.在Rt △ABC 中,斜边AB=4cm ,∠B=60°,将△ABC 绕点B 旋转60°,顶点C 运动的路线长是 ▲ cm(保留π).15.某校在九年级的一次模拟考试中,随机抽取50名学生的数学成绩进行分析,其中有 10名学生的成绩达110分以上,据此估计该校九年级650名学生中这次模拟考试数学 成绩达110分以上的约有 ▲ 名学生.16.在3×3的方格中,A 、B 、C 、D 、E 、F 分别位于如图所示的小正方形的顶点上,从C 、D 、E 、F 四点中任意取一点,以所取得一点及点A 、B 为顶点画三角形,则所画三角形为等腰三角形的概率是 ▲ .17.如图,CA ⊥AB ,DB ⊥AB ,已知AC=2,AB=,点P 射线BD 上一动点,以CP 为直径作⊙O ,点P 运动时,若⊙O 与线段AB 有公共点,则BP 最大值为 ▲ .18.如图,在正方形ABCD 外作等腰直角△CDE ,.DE=CE ,连接AE ,则sin ∠AED= ▲ .三、解答题(本大题共11小题,共76分.把解答过程写在答题卷相对应的位置上,解答 时应写出必要的计算过程、推演步骤或文字说明.)19.(本题5分)0119(3)2()3π---+ 20.(本题5分)解不等式组:1334(1)1x x +≤⎧⎨--<⎩21.(本题5分)先化简,再求值:22121()122a a a a a a -+-÷---其中21a =22.(本题6分)解分式方程:221211x x x =--+ 23.(本题7分)如图,在四边形ABCD 中,AD ∥BC ,∠A=90°,CE ⊥BD 于E ,AB=EC·(1)求证:△ABD ≌△ECB ;(2)若∠EDC=65°,求∠ECB 的度数;3)若AD=3,AB=4,求DC 的长.24.(本题6分)某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开(1)用树状图表示,小明从进入到离开,对于入口和出口的选掉有多少种不同的结果?(2)小明从入口A 进入并从出口1离开的概率是多少?25.(本题6分)如图,在直角坐标系xOy 中,一直线2y x b =+经过点A(一1,O)与Y 轴 正半轴交于B 点,在X 轴正半轴上有一点D ,且OB=OD ,过D 点作DC ⊥X 轴交直线2y x b =+ 于c 点,反比例函数(0)k y x x=>经过点C . (1)求b ,k 的值; (2)求△BDC 的面积;(3)在反比例函数(0)k y x x=>的图像上找一点P(异于点C),使△BDP 与△BDC 的面积相等,求出P 点坐标.26.(本题8分)如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子,己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,.EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).27.(本题8分)如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC 交⊙O于C 点,过C点作CD⊥A E的延长线于D点,直线CD与射线AB交于P点.(1)求证:DC为⊙O切线;(2)若DC=1,5O半径长;②求PB的长.28.(本题10分)如图①,一个Rt△DEF直角边DE落在AB上,点D与点B重合,过A点作二射线AC与斜边EF平行,己知AB=12,DE=4,DF=3,点P从A点出发,沿射线AC方向以每秒2个单位的速度运动,Q为AP中点,设运动时间为t秒(t>0)·(1)当t=5时,连接QE,PF,判断四边形PQEF的形状;(2)如图②,若在点P运动时,Rt△DEF同时沿着BA方向以每秒1个单位的速度运动,当D点到A点时,两个运动都停止,M为EF中点,解答下列问题:①当D、M、Q三点在同一直线上时,求运动时间t;②运动中,是否存在以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切,若存在,求出此时的运动时间t,若不存在,说明理由.29.(本题10分)如图,己知抛物线(1)(3)(0y k x x k k =+->且)与x 轴分别交于A 、B 两点,A 点在B 点左边,与Y 轴交于C 点,连接BC ,过A 点作AE ∥CB 交抛物线于E 点,0为坐标原点.(1)用k 表示点C 的坐标(0, );(2)若k=1,连接BE ,①求出点E 的坐标;②在x 轴上找点P ,使以P 、B 、C 为顶点的三角形与△ABE 相似,求出P 点坐标;(3)若在直线AE 上存在唯一的一点Q ,连接OQ 、BQ ,使OQ ⊥BQ ,求K 的值·。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年苏州市中考数学复习模拟试卷(3)
(满分:130分考试时间:120分钟)
一、选择题(本大题共10小题,每小题3分,共30分)
1.2015的相反数是( )
A.2015 B.-2015 C.
1
2015
D.-
1
2015
2.下列计算错误的为( )
A.20=1 B.2-3=1
8
C.(a3)2=a5D.(-2a)2=4a2
3.下列各式中,是3a2b的同类项的是( )
A.2x2y B.-2ab2C.a2b D.3ab
4.下列说法正确的是( )
A.某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖B.为了解全国中学生的睡眠情况,应该采用普查的方式
C.-组数据3,5,4,5,5,6,10的众数和中位数都是5
D.若甲组数据的方差s2
甲=0.05,乙组数据的方差s2
乙
=0.1,则乙组数据比甲组数据稳定
5.一个几何体的三视图如图所示,则这个几何体可能是( )
6.一个多边形的每个外角都等于72°,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
7.如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,则∠2的度数为( )
A.35°B.65°C.85°D.95°
8.如图,∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,若MN=2,则OM等于( )
A.3 B.4.C.5 D.6
9.如图,Rt △OAB 的顶点O 与坐标原点重合,∠AOB =90°,AO =2BO ,当点A 在反
比例函数y =
2
x (x>0)的图像上移动时,点B 的坐标满足的函数解析式为 ( ) A .()10y x x =-< B .()102y x x =-< C .()104y x x =-< D .()1
08y x x
=-<
10.如图,已知点A 1、A 2、…、A 2014在函数y =2x 2
位于第二象限的图像上,点B 1、B 2、…、B 2014在函数y =2x 2位于第一象限的图像上,点C 1、C 2、…、C 2014在y 轴的正半轴上,若四边形OA 1C 1B 1、C 1A 2C 2B 2、…、C 2013A 2014C 2014B 2014都是正方形,则正方形C 2013A 2014C 2014B 2014的边长为 ( )
A .1007
B .
C .
2013
2
D .
20132
二、填空题(本大题共8小题,每小题3分,共24分) 11.2014年3月14日,“玉兔号”月球车成功在距地球约384 400公里远的月球上自主唤醒,将384 400精确到万位用科学记数法表示为_______.
12.函数y x 的取值范围是_______.
13.四张完全相同的卡片上分别画有圆、矩形、等边三角形、等腰梯形,现在从中随机抽取一张,卡片上画的恰好是中心对称图形的概率是_______.
14.两圆的半径分别为2 cm 、3 cm ,圆心距为2 cm ,这两个圆的位置关系是_______. 15.已知圆锥的底面圆的半径为3 cm ,母线长为5 cm ,则侧面展开图面积为_______cm 2.(结果保留π)
16.如图,△ABC 的三个顶点都在⊙O 上,AD 是直径,且∠CAD =56°,则∠B 的度数为_______°.
17.已知a +3a -2=0,a -b =2,则
12
1a b
++的值为_______.
18.如图,边长为2的正方形EFGH 在边长为6的正方形ABCD 所在平面上移动,始终保持EF ∥AB .线段CF 的中点为M ,DH 的中点为N ,则线段MN 的长为_______. 三、解答题(本大题共11小题,共76分) 19.(本题满分5分)
计算:2022cos302014-+︒+.
20.(本题满分5分)
先化简,再求值:22
2111
x x x x x
-∙++,其中x
21.(本题满分5分)
解不等式组:()2130
3112
x x x ⎧-+>⎪
⎨-+≥⎪
⎩
22.(本题满分6分)
甲、乙两校参加市教育局举办的初中生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
(1)在图①中,“7分”所在扇形的圆心角等于_______°; (2)请将图②的统计图和乙校成绩统计表补充完整;
(3)经计算,甲校的平均分是8.3分,中位数是8分,请写出乙校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
23.(本题满分6分)
小伟和小欣玩一种抽卡片游戏:将背面完全相同,正面分别写有1、2、3、4的四张卡片背面向上冼匀后,小伟和小欣各自随机抽取一张(不放回).将小伟的数字作为十位数字,小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否则小欣胜.
(1)请用树状图或表格分别求出小伟、小欣获胜的概率;
(2)当小伟抽取的卡片数字为2时,两人谁获胜的可能性大?为什么?
24.(本题满分6分)
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
25.(本题满分7分)
如图,小明在大楼30 m高(即PH=30 m)的窗口P处进行观测,测得山坡上A处的俯
角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1P、
H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于_______°;
(2)求A、B两点间的距离.(结果精确到0.1 m 1.73)
如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.
(1)求证:EF是⊙O的切线;
(2)若CE=1,sinF=3
5
,求⊙O的半径.
27.(本题满分8分)
某市从2014年3月起,居民生活用水按阶梯式计算水价,水价计算方式如图所示,每吨水需另加污水处理费0.80元.已知小张家2014年3月份用水20 t,交水费52元;4月份用水25 t,交水费69元.(温馨提示:水费=水价+污水处理费)
(1)求m、n的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小张计划把5月份的水费控制在不超过月收入的2%.若小张的月收人为6500元,则小张家5月份最多能用水多少吨?
如图,二次函数y =ax 2+
3
2
x +c (a ≠0)的图像与x 轴交于A 、B 两点,与y 轴交于点C ,已知点A (-1,0),点C(0,2).
(1)求抛物线的函数解析式,并求出该抛物线的顶点坐标; (2)若点D 是抛物线在第一象限的部分上的一动点, ①当四边形OCDB 的面积最大时,求点D 的坐标;
②若E 为BC 的中点,DE 的延长线交线段AB 于点F ,当△BEF 为钝角三角形时,请直接写出点D 的纵坐标y 的范围.
29.(本题满分10分)
对于平面直角坐标系xOy 中的点P(a ,b),若点P'的坐标为(a +
b
k
,ka +b )(其中k 为常数,且k ≠0),则称点P'为点P 的“k 属派生点”,例如:P(2,4)的“2属派生点”为P'(2+
4
2
,2×2+4),即P'(4,8). (1)①点P(2,-1)的“2属派生点”P'的坐标为_______;
②若点P 的“k 属派生点”P'的坐标为(-2,-2),请写出一个符合条件的点P 的坐标_______.
(2)若点P 在x 轴的正半轴上,点P 的“k 属派生点”为点P',且△OPP'为等腰直角三角形,则k 的值为_______.
(3)如图,点Q 的坐标为(0,,点A 在函数y =
(x<0)的图像上,且点A 是
点B ,当线段BQ 最短时,求点B 的坐标.
参考答案
1—10 BCCCD ADCBB
11.3.8×105
12.x≥-1
13.1 2
14.相交15.15π16.34
17.-3 4
18 19.-3.
20
21.-1≤x<5 2
22.(1)144°.(2)略(3)中位数是7分.甲校成绩较好.
23.(1)1
2
(2)小欣获胜的可能性大.
24.(1)略(2)正方形.25.(1) 30 (2)34.6 m.
26.(1)略(2)5 2
27.(1)m=1.80,n=2.60.(2)40 t.
28.(1)(3
2
,
25
8
)(2)
13
9
≤y≤
25
8
29.(1)①(3
2
,3)②答案不唯一(2)±1 (3)B(-
9
4
)。
