用递归方法求GCD和FIB

30个Python常用极简代码拿走就用

30个Python常用极简代码拿走就用Python是一种简洁高效的编程语言，广泛应用于各个领域。

作为Python程序员，熟悉并掌握一些常用的极简代码是非常重要的。

在本文中，将介绍30个Python常用极简代码，供大家使用。

1. 输出Hello, World!```print("Hello, World!")```这是Python入门必备的一行代码，用于输出"Hello, World!"这个经典的字符串。

2. 计算两个数字的和```num1 = 5num2 = 10sum = num1 + num2print("两个数字的和为：", sum)```通过定义两个变量，将它们相加，并打印结果。

3. 判断一个数字是否为偶数```num = 6if num % 2 == 0:print("这个数字是偶数")else:print("这个数字是奇数")```使用取模运算符判断数字是否能被2整除，若余数为0则是偶数，否则为奇数。

4. 计算列表中数字的平均值```numbers = [1, 2, 3, 4, 5]average = sum(numbers) / len(numbers)print("列表中数字的平均值为：", average)```使用sum()函数计算列表中数字的总和，然后除以列表长度得到平均值。

5. 判断一个字符串是否为回文```string = "level"if string == string[::-1]:print("这个字符串是回文")else:print("这个字符串不是回文")```通过将字符串反转并与原字符串比较，判断是否为回文。

6. 打开文件并统计其中的单词数```file = open("example.txt", "r")content = file.read()words = len(content.split())print("文件中的单词数为：", words)file.close()```通过打开文件，读取其内容，并使用split()函数将内容分割成单词进行统计。

数据结构递归算法例子

数据结构递归算法例子数据结构中的递归算法是指一个函数在其定义中调用自身的过程。

递归算法在解决一些问题时非常有效，因为它可以将复杂的问题分解为更小的子问题来解决。

在本文中，我将列举一些常见的数据结构递归算法的例子，来帮助读者更好地理解递归的概念和应用。

1. 阶乘算法：计算一个正整数的阶乘。

阶乘的定义是n! = n * (n-1) * (n-2) * ... * 1。

使用递归算法可以简洁地实现阶乘的计算，代码如下：```pythondef factorial(n):if n == 0:return 1else:return n * factorial(n-1)```2. 斐波那契数列：斐波那契数列是一个数列，其中每个数字是前两个数字之和。

使用递归算法可以很容易地计算斐波那契数列的第n 个数字，代码如下：```pythondef fibonacci(n):if n <= 1:return nelse:return fibonacci(n-1) + fibonacci(n-2)```3. 二叉树遍历：二叉树是一种常见的数据结构，它包含一个根节点和每个节点最多有两个子节点。

使用递归算法可以实现二叉树的前序、中序和后序遍历。

下面是一个中序遍历的例子：```pythonclass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef inorderTraversal(root):if root:inorderTraversal(root.left)print(root.val)inorderTraversal(root.right)```4. 链表反转：链表是一种常见的数据结构，通过指针将一组节点连接在一起。

使用递归算法可以反转一个链表，即将链表的指针方向改变。

输入两个正整数a、b,求a、b的最大公约数。要求采用递归函数实现。

输入两个正整数a、b，求a、b的最大公约数。

要求采
用递归函数实现。

求最大公约数的递归函数
1. 程序思路
欧几里得算法（辗转相除法）：如果两个数的最大公约数是d，那么a 可以表示成d的倍数，即a=md，同理可以表示b=nd，其中m和n都是整数。

可以采用如下方法求d：
1. 如果a能够被b整除，那么d=b；
2. 如果a不能被b整除，那么d等于b和a除以b的余数c的最大公约数。

即d=gcd(b,c)。

2. 代码实现
用函数gcd(a,b)表示a和b的最大公约数。

```python
def gcd(a,b):
if b==0:
return a
else:
return gcd(b,a%b)
```
3. 测试样例
输入a=12，b=18，输出6。

4. 复杂度分析
时间复杂度：O(log(max(a,b)))，即递归深度为log(max(a,b))。

空间复杂度：O(log(max(a,b)))，即递归深度为log(max(a,b))。

c语言递归试题及答案

c语言递归试题及答案递归是一种在函数中调用自身的编程技巧。

在学习C语言时，递归是一个重要的概念，掌握递归的用法对于解决问题非常有帮助。

本文将介绍一些常见的C语言递归试题，并提供详细的答案解析。

一、计算阶乘题目：编写一个递归函数，计算给定正整数n的阶乘。

答案：```c#include <stdio.h>int factorial(int n) {if (n == 0) {return 1;} else {return n * factorial(n - 1);}}int main() {int n;printf("请输入一个正整数：");scanf("%d", &n);printf("%d的阶乘为：%d\n", n, factorial(n));return 0;}```解析：该程序定义了一个递归函数factorial，当n为0时，递归结束，返回1；否则，返回n与factorial(n-1)的乘积。

在主函数中，用户输入一个正整数n，调用factorial函数进行阶乘计算并输出结果。

二、斐波那契数列题目：编写一个递归函数，计算给定正整数n的斐波那契数列值。

答案：```c#include <stdio.h>int fibonacci(int n) {if (n == 0 || n == 1) {return n;} else {return fibonacci(n - 1) + fibonacci(n - 2);}}int main() {int n;printf("请输入一个正整数：");scanf("%d", &n);printf("斐波那契数列第%d项的值为：%d\n", n, fibonacci(n));return 0;}```解析：该程序定义了一个递归函数fibonacci，当n为0或1时，递归结束，返回n；否则，返回fibonacci(n-1)与fibonacci(n-2)的和。

《用递归法解决问题》教学设计-最新文档

《用递归法解决问题》教学设计学习者分析本节课的教学对象为高中二年级的学生。

这个阶段的学生具有很强的自主意识，具备一定的探究能力，喜欢自己动手实践来获得新知。

多次经历从问题到程序的思考过程，在面对现有软件无法解决的问题时能够编写程序解决问题。

在此之前，学生已经掌握了循环、数组、自定义函数的使用，为本课的学习做好了充分的准备。

学习内容分析《用递归法解决问题》是高中选修教材《算法与程序设计》（科教版）第三章“算法的程序实现”第五小节的内容。

在本课学习之前，学生已经学会了用循环的方法来解决问题，然而循环的方法往往并不会那么清晰地描述解决问题的步骤，递归法则可以非常直白地描述一个问题的求解过程，因此递归法也是最容易实现的算法。

递归的基本思想是把规模大的问题转化为规模小的相类似的子问题来解决。

在函数实现时，因为解决大问题的方法和解决小问题的方法往往是同一种方法，所以就产生了调用自身的情况。

递归是利用系统的堆栈保存函数中的局部变量来解决问题的，因为函数调用的开销比较大，递归常常会带来效率问题。

本节课学生不仅要学会用递归法解决问题，更重要的是领会递归思想的精髓。

递归思想是计算机学科中的核心技术思想之一，其本质反映的是一种将复杂问题简单化的思维方法。

学习目标知识与技能目标：理解递归的含义，找出递归问题中缩小问题规模的递归处理方法及递归结束条件，了解递归算法的优缺点。

过程与方法目标：能用程序实现递归算法，学会用简单模式解决复杂问题的方法。

情感态度与价值观目标：领悟递归思想，体验递归思想在实际生活中的应用。

教学重点、难点重点：分析递归结束条件及缩小问题规模的方法，以及递归算法的程序实现。

难点：递归算法的程序实现。

教学策略呈现斐波那契数列问题，由学生比较熟悉的递推法入手，针对问题描述中的不严谨之处，引入递归定义及其关键因素――递归结束条件和缩小问题规模的递归处理。

在递归的学习过程中，学生通过阅读代码、尝试模仿、归纳提炼、拓展应用等环节逐渐完成知识的内化并达到应用、迁移的目的。

递归方法求斐波那契函数FIB（N）

递归⽅法求斐波那契函数FIB（N）《微机原理实践》课程设计报告题⽬：递归⽅法求斐波那契函数FIB(N)专业：计算机系班级：学号：姓名：指导教师：胡美娇完成⽇期：2013年 1 ⽉1⽇⼀、课程设计⽬的1、加深对汇编语⾔理论和基本知识的理解,掌握DOS和BIOS系统功能调⽤，掌握运⽤汇编语⾔设计具有⼀定功能的软件的基本⽅法.2、通过编写⼀定规模和难度的程序，进⾏⼀次较全⾯的汇编编程训练，提⾼分析问题和解决问题的能⼒3、提⾼调试程序的能⼒⼆、课程设计内容递归⽅法求斐波那契函数FIB(N)要求：从键盘输⼊数N, 当N=0,1时,FIB=1 ;当N>=2时，FIB=FIB（N-1）+FIB（N-2），结果⽤⼗进制输出。

要求：具有友好的交互界⾯，建⽴主菜单界⾯：'********************Display Program********************input number n: Array the FIBN=三、课程设计过程1、算法设计（画出算法流程图）2、程序代码清单DATA SEGMENTNUM DW ?GRADE DW 2(?)MESS1 DB ,0AH,0DH,,0AH,0DH,'***Display Program***'MESS2 DB ,0AH,0DH, 'INPUT NUMBER N:$',0AH,0DH,MESS3 DB 0AH,0DH,'FIB(N)=$'MESS4 DB 'INPUT ERROR! $'MESS5 DB ,0AH,0DH, 'INPUT NUMBER N:'PROGNAM SEGMENTMAIN PROC FAR ;主程序⼊⼝ASSUME CS:PROGNAM,DS:DATA START:PUSH DSSUB AX,AXPUSH AXMOV AX,DATAMOV DS,AXLEA DX,MESS1MOV AH,09INT 21HL1: LEA DX,MESS5MOV AH,09INT 21HMOV BX,0 ;显⽰欢迎主界⾯NEWCHAR:MOV AH,01H ;键盘输⼊，每个数据以回车结束INT 21HCMP AL,13JE LEE01SUB AL,30H ;转移JL ERRORCMP AL,9D ;AL中的数与取来的数据⽐较JG ERRORCBWXCHG AX,BX ;交换指令MOV CX,10DMUL CXXCHG AX,BXADD BX,AXJMP NEWCHAR ;⽆条件跳转ERROR:LEA DX,MESS4INT 21H ;中断JMP L1RETLEE01:MOV NUM,BXMOV SI,0MOV AX,0CALL FIB(N) ;段内直接过程调⽤LEA DX,MESS3MOV AH,09INT 21HPUSH BX ;将相关信息压⼊栈⾥PUSH CXPUSH SIPUSH DIMOV BX,GRADE[SI]MOV CX,10000DCALL DEC_DIVMOV CX,1000DCALL DEC_DIVMOV CX,100DCALL DEC_DIVMOV CX,10DCALL DEC_DIVMOV CX,1DCALL DEC_DIVPOP DIPOP SIPOP CX ;将相关信息弹出栈内POP BXJMP L1RETMAIN ENDPDEC_DIV PROC NEARMOV DX,0DIV CXMOV BX,DXMOV DL,AL ;结果要放在dl中ADD DL,30HMOV AH,02HINT 21HRETDEC_DIV ENDPFIB(N) PROC NEARCMP NUM,0 ;num为0转到L2JE LEE02CMP NUM,1 ;num⾃减1JE LEE02DEC NUMCALL FIB(N)MOV AX,GRADE[SI]MOV BX,GRADE[SI-2]MOV GRADE[SI-2],AXADD AX,BX ;进⾏加法运算MOV GRADE[SI],AXJMP LEE03LEE02:MOV GRADE[SI],1ADD SI,2MOV GRADE[SI],1LEE03: RETFIB(N) ENDPPROGNAM ENDSEND START3、调试过程(包括实验过程中实验步骤,出现的问题,解决的⽅法,使⽤的实验数据等)步骤：⾸先是先对递归函数的了解，然后分成三种情况，⼀种是输⼊的是0和1的情况，⼀种是输⼊的是其他数字，最后⼀种是输⼊的不是数字，最后对各种情况进⾏设计。

递归函数python例子

递归函数python例子递归是一种算法，它通过反复调用自身来解决问题。

在计算机科学中，递归函数是一种函数，它在其定义中调用自身。

递归函数可以用于解决许多问题，例如树的遍历、排序、搜索等。

Python是一种支持递归函数的编程语言，本文将介绍递归函数的基本原理和几个Python例子。

递归函数的原理递归函数的原理是将一个大问题分解成若干个小问题，然后通过递归解决每个小问题，最后将结果组合起来得到大问题的解。

递归函数需要满足两个条件：基本情况和递归情况。

基本情况是指递归函数能够直接得到答案的情况，不需要再次递归。

递归情况是指递归函数需要继续递归下去的情况。

在递归函数中，基本情况通常是通过if语句来实现的。

递归函数的基本结构如下：def function_name(parameters):if base_case:return base_case_solutionelse:recursive_case = function_name(modified_parameters)return recursive_case_solution递归函数Python例子下面将介绍几个常见的递归函数Python例子。

1. 阶乘阶乘是指从1到n的所有整数相乘的结果，通常用n!表示。

例如，5! = 5 x 4 x 3 x 2 x 1 = 120。

递归函数可以用于计算阶乘，其基本情况是n=1时，阶乘为1，递归情况是n>1时，阶乘为n乘以(n-1)的阶乘。

def factorial(n):if n == 1:return 1else:return n * factorial(n-1)2. 斐波那契数列斐波那契数列是指前两个数为1，之后每个数都是前两个数之和的数列。

例如，斐波那契数列的前10个数为1, 1, 2, 3, 5, 8, 13, 21, 34, 55。

递归函数可以用于计算斐波那契数列，其基本情况是第一个数和第二个数都是1，递归情况是第n个数等于第n-1个数和第n-2个数之和。

易语言编程案例

易语言编程案例1. 求解斐波那契数列题目描述：输入一个正整数n，求解斐波那契数列的第n个数。

实现思路：使用递归的方法实现斐波那契数列的求解。

代码示例：```// 定义递归函数function fib(n)if n <= 1 thenreturn nelsereturn fib(n-1) + fib(n-2)end ifend function// 输入正整数ninput "请输入一个正整数n："，n// 输出斐波那契数列的第n个数print "斐波那契数列的第" + n + "个数为：" + fib(n)```2. 判断一个数是否为素数题目描述：输入一个正整数n，判断n是否为素数。

实现思路：从2到n-1，逐个判断n是否能被这些数整除。

代码示例：```// 输入正整数ninput "请输入一个正整数n："，n// 初始化标志变量isPrime = true// 判断n是否为素数for i = 2 to n-1if n mod i = 0 thenisPrime = falseexit forend ifnext// 输出判断结果if isPrime thenprint n + "是素数"elseprint n + "不是素数"end if```3. 求解一元二次方程的根题目描述：输入一元二次方程的系数a、b、c，求解方程的根。

实现思路：根据一元二次方程的求解公式，计算方程的根。

代码示例：```// 输入一元二次方程的系数input "请输入一元二次方程的系数a："，ainput "请输入一元二次方程的系数b："，binput "请输入一元二次方程的系数c："，c// 计算方程的根delta = b^2 - 4*a*cif delta > 0 thenx1 = (-b + sqrt(delta)) / (2*a)x2 = (-b - sqrt(delta)) / (2*a)print "方程的根为：" + x1 + "和" + x2else if delta = 0 thenx = -b / (2*a)print "方程的根为：" + xelseprint "方程无实根"end if4. 求解阶乘题目描述：输入一个正整数n，求解n的阶乘。

实验2-8参考答案

实验二、选择结构参考答案1．修改下列程序，使之满足当x为10时输出“= =”，否则输出“！=”的条件。

#include"stdio.h"main(){int x;scanf("%d",&x);if(x==10)printf("==\n");else printf("!=\n");}2．修改下列程序，使之实现以下功能：#include “stdio.h”main( ){ int a,b,c;scanf(“%d%d%d”,&a,&b,&c);if (a==b)｛if(b==c)printf(“a==b==c”);｝elseprintf(“a!=b”);}3．程序填空。

从键盘输入任意一个字母，将其按小写字母输出。

#include <stdio.h>main(){ char c;scanf("%c",&c);if (c>='A'&&c<='Z')c=c+32;printf("\n%c",c);}7. 有一函数x (x<1)y = 2x–1 (1≤x<10)3x–11 (x≥10)编写程序输入x，输出y值。

#include "stdio.h"main(){int x,y;scanf ("%d",&x);if (x<1)y=x;else if(x<10)y=2*x-1;elsey=3*x-11;printf ("%d",y);}9．给一个不多于3位的正整数，要求：（1）求出它是几位数；（2）、分别打出每一位数字；（3）、按逆序打出各位数字，例如原数为321，应输出123。

#include "stdio.h"void main(){int a,b,c,x,n;scanf("%d",&x);a=x/100;b=(x-a*100)/10;c=x%10;if(a!=0)printf("%d为3位数,原数为%d，逆序数为%d\n",x,x,c*100+b*10+a);else if(b!=0)printf("%d为2位数,原数为%d，逆序数为%d\n",x,x,c*10+b);elseprintf("%d为1位数,原数为%d，逆序数为%d\n",x,x,c);}实验三、循环结构实验（1）1．分析并修改下面的程序，使该程序能正常结束运行。

斐波那契数列

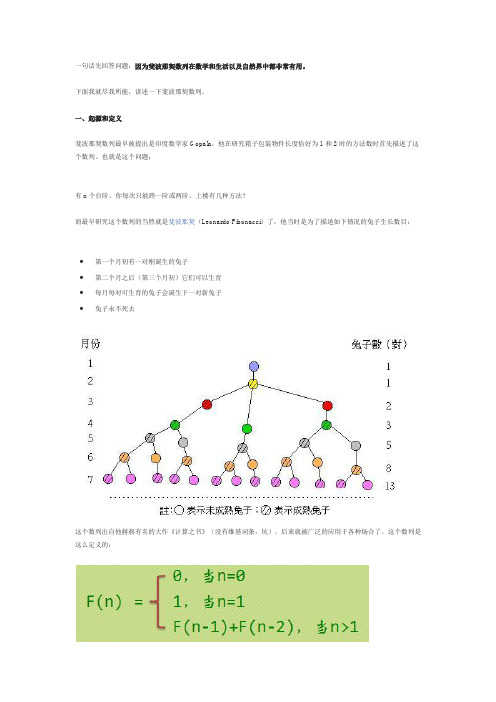
一句话先回答问题：因为斐波那契数列在数学和生活以及自然界中都非常有用。

下面我就尽我所能，讲述一下斐波那契数列。

一、起源和定义斐波那契数列最早被提出是印度数学家Gopala，他在研究箱子包装物件长度恰好为1和2时的方法数时首先描述了这个数列。

也就是这个问题：有n个台阶，你每次只能跨一阶或两阶，上楼有几种方法？而最早研究这个数列的当然就是斐波那契（Leonardo Fibonacci）了，他当时是为了描述如下情况的兔子生长数目：•第一个月初有一对刚诞生的兔子•第二个月之后（第三个月初）它们可以生育•每月每对可生育的兔子会诞生下一对新兔子•兔子永不死去这个数列出自他赫赫有名的大作《计算之书》（没有维基词条，坑），后来就被广泛的应用于各种场合了。

这个数列是这么定义的：The On-Line Encyclopedia of Integer Sequences® (OEIS®)序号为A000045 - OEIS（注意，并非满足第三条的都是斐波那契数列，卢卡斯数列（A000032 - OEIS）也满足这一特点，但初始项定义不同）二、求解方法讲完了定义，再来说一说如何求对应的项。

斐波那契数列是编程书中讲递归必提的，因为它是按照递归定义的。

所以我们就从递归开始讲起。

1.递归求解int Fib(int n){return n < 2 ? 1 : (Fib(n-1) + Fib(n-2));}这是编程最方便的解法，当然，也是效率最低的解法，原因是会出现大量的重复计算。

为了避免这种情况，可以采用递推的方式。

2.递推求解int Fib[1000];Fib[0] = 0;Fib[1] = 1;for(int i = 2;i < 1000;i++) Fib[i] = Fib[i-1] + Fib[i-2];递推的方法可以在O(n)的时间内求出Fib(n)的值。

但是这实际还是不够好，因为当n很大时这个算法还是无能为力的。

c语言直接递归和间接递归

c语言直接递归和间接递归递归是一种在函数内调用自身的编程技术。

递归分为直接递归和间接递归两种类型。

1. 直接递归（Direct Recursion）：在直接递归中，函数直接调用自身。

以下是一个简单的C 语言直接递归的例子，计算阶乘：```c#include <stdio.h>int factorial(int n) {if (n == 0 || n == 1) {return 1;} else {return n * factorial(n - 1);}}int main() {int num = 5;printf("Factorial of %d is %d\n", num, factorial(num));return 0;}```上述例子中，`factorial` 函数直接调用自身来计算阶乘。

2. 间接递归（Indirect Recursion）：在间接递归中，两个或多个函数相互调用，形成一个循环调用链。

以下是一个简单的 C 语言间接递归的例子，判断一个正整数是否为偶数：```c#include <stdio.h>// 声明函数isOdd，因为isEven 函数中会调用isOddint isOdd(int);int isEven(int n) {if (n == 0) {return 1; // 是偶数} else {return isOdd(n - 1);}}int isOdd(int n) {if (n == 0) {return 0; // 是奇数} else {return isEven(n - 1);}}int main() {int num = 6;if (isEven(num)) {printf("%d is even.\n", num);} else {printf("%d is odd.\n", num);}return 0;}```在上述例子中，`isEven` 函数调用`isOdd` 函数，而`isOdd` 函数又调用`isEven` 函数，形成了一个间接递归的关系。

[练习]C语言实验七、函数程序设计答案

实验七函数及程序结构（二）一、实验目的1．掌握函数的嵌套调用和递归调用2．掌握数组做函数参数的用法3．掌握全局变量和局部变量的用法。

？4．掌握变量的存储类别。

？二、实验内容1．[目的]掌握函数的嵌套调用方法。

[题目内容] 编写程序计算cb a 。

要求设计主函数main()读取a 、b 、c 的值，并调用ratio 函数计算a/(b-c)的值。

如果(b-c)=0那么ratio 就不能计算，因此，ratio 函数调用另一个函数dif ，以测试(b-c)的差是否为零，如果b 不等于c ，dif 返回1，否则返回0。

[输入] a 、b 、c 的值[输出] 计算结果[提示] main 函数调用ratio 函数，ratio 函数调用dif 函数。

三个函数平行定义，嵌套调用。

#include <stdio.h>void main(){float ratio(int x,int y ,int z);int dif(int x,int y);int a,b,c;float d;printf("请输入a,b,c:");scanf("%d%d%d",&a,&b,&c);d=ratio(a,b,c);if(d==0.0) printf("b-c 为零。

");else printf("%d/(%d-%d)=%f\n",a,b,c,d);}float ratio(int x,int y ,int z){if(dif(y ,z)==1) return (float)x/(float)(y-z);else return 0.0;}int dif(int x,int y){if(x==y) return 0;else return 1;}2．[目的]利用标准库提供的随机数功能。

[题目内容]编写程序，帮助小学生练习乘法计算。

C++第5章函数习题答案

第5章函数与预处理1．利用递归函数调用方式，将所输入的5个字符以相反顺序打印出来。

#include <iostream>using namespace std;int main(){ int i=5;void palin(int n);cout<<"请输入5个字符:";palin(i);cout<<endl;return 0;}void palin(int n){ char next;if(n<=1){ next=getchar();cout<<next;}else{ next=getchar();palin(n-1);cout<<next;}}2．编写递归函数求两个正整数a和b的最大公约数（GCD，Greatest Common Divisor），其中Euclid算法：（1）如果a除以b能整除，则最大公约数是b。

（2）否则，最大公约数等于b和a%b的最大公约数。

#include <iostream>using namespace std;int GCD(int a,int b){ if(a%b==0)return b;elsereturn GCD(b,a%b);}int main(){ i nt i,x,y;cout<<"请输入两个正整数,用空格隔开两个数:";cin>>x>>y;i=GCD(x,y);cout<<x<<"与"<<y<<"的最大公约数为:"<<i<<endl;return 0;}3．编写递归函数求Fibonacci数列的第n项，这个数列是这样定义的：fib(n)=fib(n-1)+fib(n-2)#include <iostream>using namespace std;int fib(int n){ if(n==0)return 1;else if (n==1)return 1;else{ int i;i=fib(n-1)+fib(n-2);return i;}}int main(void){ int i,z;cout<<"请输入要计算的第几项:";cin>>z;i=fib(z);cout<<"fibonacci数列的第"<<z<<"项为:"<<i<<endl;return 0;}4．编写函数，计算s=22！+32！。

c语言函数之递归函数

c语言函数之递归函数朱有鹏1、递归函数1.1、函数的调用机制C语言函数的调用一般在X86平台是用栈的方式来支持其操作的（也就是Calling Convention），栈是先进后出的数据结构，当函数发生调用的时候，函数以入栈的方式，将函数的返回地址、参数等进行压栈，C语言默认环境下的调用规范为，参数是从右向左依次压栈（如：printf函数），这就是函数的调用机制。

同时函数每调用一次，就会进行一次压栈，其所占的空间彼此独立，调用函数和被调用函数依靠传入参数和返回值彼此联系。

如: 一个main()函数调用函数sub（int a, int b）的简单的内存图形是：入栈int aInt bsub()返回地址main参数main()返回地址栈1.2、递归函数（1）什么是递归函数？通过简单的了解函数的调用机制，在程序设计中经常会用递归函数解决问题，此方法清晰易于理解。

那么什么是递归函数呢？递归函数的本质就是函数直接或间接调用其函数本身。

直接调用函数调用本身示例：求n的阶乘？factorial()函数直接调用其本身。

间接调用是函数调用其它函数，其它函数又调用其本身函数示例：func_1()函数中调用了func_2() 函数,func_2()函数又调用了func_1() 这样的方式就是间接递归，此示例，本身就是个错误，各位不要急后面一一道来（没有注意收敛性）。

（2）递归的调用的原理比如下例：#include<stdio.h>void recursion(int n) {printf("递归前：n = %d.\n", n); if (n > 1) {recursion(n-1);} else {printf("结束递归，n = %d.\n", n); }printf("递归后：n = %d.\n", n); }int main(void){void recursion(3);}执行结果为：递归前：n = 3.递归前：n = 2.递归前：n = 1.结束递归，n = 1.递归后：n = 1.递归后：n = 2.递归后：n = 3.函数的执行顺序，如图所示:解析：当程序执行时，通过主函数执行到void recursion(3);时，以n=3进入recursion函数中。

用递归的方法求斐波那契数列

用递归的方法求斐波那契数列嘿，朋友们！今天咱来聊聊用递归的方法求斐波那契数列这事儿。

啥是斐波那契数列呀？简单说，就是从 0 和 1 开始，后面每一项都是前两项的和。

就像兔子繁殖一样，一对兔子过一个月能长成大兔子，再过一个月就能生一对小兔子，然后小兔子又这样长大、繁殖，这数量的变化就有点像斐波那契数列呢！那用递归方法咋求呢？这就好像是在一个迷宫里找路。

递归呢，就是函数自己调用自己。

比如说，我们要求第 10 个斐波那契数，它就得先知道第 9 个和第 8 个是多少，那求第 9 个呢，又得知道第 8 个和第 7 个，就这么一层一层往里钻。

你想啊，这就好比你要去一个特别深的洞里找宝贝，你得先走过一段路，到了一个地方，发现还得继续往下走，就这样不断深入。

这过程中可能会有点晕头转向，但一旦找到了，哇，那成就感可不一般！用递归求斐波那契数列，代码写起来可能就那么几行，但这里面的学问可大着呢！就好像是一门神奇的魔法，能把看似复杂的问题变得简单又有趣。

每次函数调用自己的时候，就像是给自己挖了一个新的坑，然后又得想办法从这个坑里跳出来。

如果不小心掉进去出不来了，那可就麻烦啦！这就需要我们特别小心地处理，就像走钢丝一样，得保持平衡。

而且哦，递归有时候就像个调皮的小孩子，你得好好哄着它，不然它可能就给你闹别扭。

比如说，如果递归的次数太多了，那计算量可就大得吓人，电脑都得累得气喘吁吁呢！那怎么才能让这个调皮的小孩子乖乖听话呢？这就需要我们动动脑筋啦！我们可以设置一些条件，让它不要乱跑乱跳。

就像给小孩子立规矩一样，让它知道什么能做，什么不能做。

比如说，我们可以限制递归的深度，不让它无限制地往下跑。

或者我们可以用一些巧妙的算法来优化，让它跑得更快更稳。

哎呀呀，这用递归求斐波那契数列可真是个有趣的事儿！它就像一个神秘的宝盒，等着你去打开，去发现里面的奇妙世界。

总之呢，用递归的方法求斐波那契数列，既是一种挑战，也是一种乐趣。

它能让你感受到编程的魅力和数学的神奇。

斐波那契数列递归复杂度

斐波那契数列递归复杂度
斐波那契数列是一个经典的数列，其中每个数都是前两个数的和。

这个数列可以通过递归方式来计算，但是递归算法的时间复杂度是比较高的。

递归算法的时间复杂度可以通过递归树来分析。

对于斐波那契数列的递归算法，递归树如下所示：
fib(n)
/
fib(n-1) fib(n-2)
/ /
fib(n-2) fib(n-3) fib(n-3) fib(n-4)
... ... ...
在递归树中，每个节点代表一次函数调用，每个节点的子节点代表该节点调用的子函数。

在斐波那契数列递归算法中，每个节点会调用两个子函数fib(n-1)和fib(n-2)，因此每个节点会产生两个子节点。

递归算法的时间复杂度可以通过递归树中所有节点的数量来计算。

在斐波那契数列递归算法中，节点数量可以用斐波那契数列的第n个数来表示，即节点数量为fib(n+1)。

因此，递归算法的时间复杂度为O(fib(n+1))。

斐波那契数列的递归算法的时间复杂度非常高，随着n的增加，
时间复杂度增长得非常快。

因此，在实际应用中，一般使用非递归方式来计算斐波那契数列。

c语言编写递归函数,实现斐波那契数列前20项的和。

篇一：斐波那契数列是一组以2为首项、以5为公差值的等差数列。

在数学中,这个数列通常用符号斐波那契数列来表示,例如,1、1、2、3、5、8、13、21、34、55、89、144等等。

在C语言中,我们可以使用递归函数来计算斐波那契数列的前n项和。

递归函数是一种函数调用自身的函数,这种函数调用可以在程序中循环执行,从而实现复杂的计算。

下面是一个简单的C语言代码示例,用于计算斐波那契数列前20项的和: ```c#include <stdio.h>int fibonacci(int n) {if (n == 0) {return 0;} else if (n == 1) {return 1;} else {return fibonacci(n - 1) + fibonacci(n - 2);}}int main() {int n;printf("Enter the number of terms: ");scanf("%d", &n);printf("Fibonacci sum of %d terms: %d", n, fibonacci(n));return 0;}```在这个示例中,`fibonacci`函数是递归函数,用于计算斐波那契数列的前n 项和。

在函数中,如果n等于0,返回0;如果n等于1,返回1;否则,返回fibonacci(n-1)加上fibonacci(n-2)。

在`main`函数中,我们输入要计算的斐波那契数列项数n,然后调用`fibonacci`函数来计算前n项和,并将结果打印出来。

需要注意的是,递归函数的返回值是一个整数,如果需要使用浮点数,需要使用`double`类型来传递参数。

另外,在使用递归函数时,需要注意递归条件的设置,以避免无限递归导致程序崩溃。

斐波那契数列(fibonacci sequence),从1,1开始,后面每一项等于前面两项之和。输出

斐波那契数列(fibonacci sequence)斐波那契数列是一个非常有趣和有用的数学概念，它在自然界、艺术、计算机科学等领域都有广泛的应用。

本文将介绍斐波那契数列的定义、性质、算法和应用，希望能给你带来一些启发和乐趣。

定义斐波那契数列是由意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci）在1202年的著作《计算之书》中提出的，他以兔子繁殖为例子，发现了一个数列，即每个月的兔子对数等于前两个月的兔子对数之和。

这个数列就被称为斐波那契数列，或者兔子数列，又或者黄金分割数列。

斐波那契数列的前几项如下：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...可以看出，这个数列从第三项开始，每一项都等于前两项之和。

用数学符号表示，就是：F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2) (n >= 2)其中，F(n)表示第n项的值。

性质斐波那契数列有许多有趣和重要的性质，下面列举一些常见的：奇偶性：斐波那契数列中，从第三项开始，每三项中有两个奇数和一个偶数。

也就是说，F(n)是奇数当且仅当n是3的倍数或者比3的倍数大1。

相邻项之比：斐波那契数列中，相邻两项之比会逐渐接近一个常数值，这个常数值就是黄金分割比φ≈1.618。

也就是说，当n趋向于无穷大时，F(n+1)/F(n)趋向于φ。

前n项之和：斐波那契数列中，前n项之和等于第n+2项减去1。

也就是说，F(0)+F(1)+...+F(n) = F(n+2)-1。

奇偶项之和：斐波那契数列中，所有奇数项之和等于最后一个奇数项的下一项减去1；所有偶数项之和等于最后一个偶数项的下一项减去2。

也就是说，如果F(m)是最后一个奇数项，则F(1)+F(3)+...+F(m) = F(m+1)-1；如果F(m)是最后一个偶数项，则F(0)+F(2)+...+F(m) = F(m+1)-2。

迭代算法——精选推荐

迭代算法迭代算法军⼈在进攻时常采⽤交替掩护进攻的⽅式，若在数轴上的点表⽰A，B两⼈的位置，规定在前⾯的数⼤于后⾯的数，则是A>B，B>A交替出现。

但现在假设军中有⼀个胆⼩⿁，同时⼤家⼜都很照顾他，每次冲锋都是让他跟在后⾯，每当前⾯的⼈占据⼀个新的位置，就把位置交给他，然后其他⼈再往前占领新的位置。

也就是A始终在B的前⾯，A向前迈进，B跟上，A把⾃⼰的位置交给B（即执⾏B = A操作），然后A 再前进占领新的位置，B再跟上……直到占领所有的阵地，前进结束。

像这种两个数⼀前⼀后逐步向某个位置逼近的⽅法称之为迭代法。

迭代法也称辗转法，是⼀种不断⽤变量的旧值递推新值的过程,跟迭代法相对应的是直接法（或者称为⼀次解法），即⼀次性解决问题。

迭代算法是⽤计算机解决问题的⼀种基本⽅法。

它利⽤计算机运算速度快、适合做重复性操作的特点，让计算机对⼀组指令（或⼀定步骤）进⾏重复执⾏，在每次执⾏这组指令（或这些步骤）时，都从变量的原值推出它的⼀个新值。

利⽤迭代算法解决问题，需要做好以下三个⽅⾯的⼯作：⼀、确定迭代变量。

在可以⽤迭代算法解决的问题中，⾄少存在⼀个直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量。

⼆、建⽴迭代关系式。

所谓迭代关系式，指如何从变量的前⼀个值推出其下⼀个值的公式（或关系）。

迭代关系式的建⽴是解决迭代问题的关键，通常可以使⽤递推或倒推的⽅法来完成。

三、对迭代过程进⾏控制。

在什么时候结束迭代过程？这是编写迭代程序必须考虑的问题。

不能让迭代过程⽆休⽌地重复执⾏下去。

迭代过程的控制通常可分为两种情况：⼀种是所需的迭代次数是个确定的值，可以计算出来；另⼀种是所需的迭代次数⽆法确定。

对于前⼀种情况，可以构建⼀个固定次数的循环来实现对迭代过程的控制；对于后⼀种情况，需要进⼀步分析出⽤来结束迭代过程的条件。

最经典的迭代算法是欧⼏⾥德算法，⽤于计算两个整数a,b的最⼤公约数。

其计算原理依赖于下⾯的定理：定理：gcd(a, b) = gcd(b, a mod b)证明：a可以表⽰成a = kb + r，则r = a mod b 。

c语言斐波那契数列问题

c语言斐波那契数列问题斐波那契数列是一个非常经典的数学问题，也是计算机科学中常用的一个例子。

它的定义是：第一个和第二个数都是1，从第三个数开始，每个数都是前两个数的和。

也就是说，斐波那契数列的前几个数是1、1、2、3、5、8、13、21、34、55……以此类推。

在C语言中，我们可以通过编写代码来计算斐波那契数列。

下面是一个简单的示例代码：```c#include <stdio.h>int fibonacci(int n) {if (n <= 1) {return n;}return fibonacci(n-1) + fibonacci(n-2);}int main() {int n;printf("请输入要计算的斐波那契数列的项数：");scanf("%d", &n);printf("斐波那契数列的前%d项为：\n", n);for (int i = 0; i < n; i++) {printf("%d ", fibonacci(i));}printf("\n");return 0;}```在这段代码中，我们定义了一个名为`fibonacci`的函数，它接受一个整数参数`n`，并返回斐波那契数列的第`n`项。

在函数内部，我们使用递归的方式来计算斐波那契数列。

当`n`小于等于1时，直接返回`n`；否则，返回前两个数的和。

在`main`函数中，我们首先通过`scanf`函数获取用户输入的项数`n`，然后使用一个循环来打印出斐波那契数列的前`n`项。

最后，我们使用`printf`函数输出结果。

使用这段代码，我们可以方便地计算任意项数的斐波那契数列。

例如，如果用户输入的项数为10，那么程序将输出斐波那契数列的前10项：1 1 2 3 5 8 13 21 34 55。

需要注意的是，由于递归的方式计算斐波那契数列的效率较低，当项数较大时，程序可能会运行较慢。