Java算法最大公约数和最小公倍数
用辗转相除法求最大公约数java

用辗转相除法求最大公约数java用辗转相除法求最大公约数,是一种简单且常用的算法。
这个算法基于一个简单的道理,两个数的最大公约数也是其中较小数与两数的差的最大公约数。
首先,我们需要了解什么是最大公约数。
最大公约数,也叫最大公因数,指的是两个或多个整数共有的约数中最大的一个。
它在数学上具有很多应用,比如化简分数、求解线性方程等。
接下来,我们将以Java编程语言为例,详细介绍如何用辗转相除法求最大公约数。
步骤一:获取输入的两个整数我们首先需要从用户那里获取两个整数。
可以使用Java的Scanner类来实现用户输入的功能。
代码如下:javaimport java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);System.out.println("请输入第一个整数:");int num1 = scanner.nextInt();System.out.println("请输入第二个整数:");int num2 = scanner.nextInt();其他代码scanner.close();}}步骤二:实现辗转相除法辗转相除法基于一个简单的原理:两个数的最大公约数也是其中较小数与两数的差的最大公约数。
我们可以使用递归的方式来实现这个算法。
代码如下:javapublic class Main {辗转相除法计算最大公约数public static int gcd(int num1, int num2) {if (num2 == 0) {return num1;}return gcd(num2, num1 num2);}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);System.out.println("请输入第一个整数:");int num1 = scanner.nextInt();System.out.println("请输入第二个整数:");int num2 = scanner.nextInt();int result = gcd(num1, num2);System.out.println("最大公约数是:" + result);scanner.close();}}解释一下上面的代码。
JAVA算法编程题全集(50题及答案)

程序1。
题目:古典问题:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少?//这是一个菲波拉契数列问题public class lianxi01 {public static void main(String[] args) {System.out.println("第1个月的兔子对数: 1");System.out.println("第2个月的兔子对数: 1");int f1 = 1, f2 = 1, f, M=24;for(int i=3; i<=M; i++) {f = f2;f2 = f1 + f2;f1 = f;System.out.println("第" + i +"个月的兔子对数: "+f2);}}}。
程序2。
题目:判断101-200之间有多少个素数,并输出所有素数。
程序分析:判断素数的方法:用一个数分别去除2到sqrt(这个数),如果能被整除,则表明此数不是素数,反之是素数。
public class lianxi02 {public static void main(String[] args) {int count = 0;for(int i=101; i<200; i+=2) {boolean b = false;for(int j=2; j<=Math.sqrt(i); j++){if(i % j == 0) { b = false; break; }else { b = true; }}if(b == true) {count ++;System.out.println(i );}}System.out.println( "素数个数是: " + count);}}。
程序3。
题目:打印出所有的"水仙花数",所谓"水仙花数"是指一个三位数,其各位数字立方和等于该数本身。
最大公约数和最小公倍数Java源程序

//求长整型数a和长整型数b的最大公约数和最小公倍数,Test类为主类class GreatestCommonDivisor //求长整型数a和长整型数b的最大公约数,同时输出a和b的所有约数{private long a;private long b;private Divisor aDivisor;private Divisor bDivisor;GreatestCommonDivisor(){a = 1;b = 1;aDivisor = new Divisor();bDivisor = new Divisor();}GreatestCommonDivisor(long a,long b){this.a = a;this.b = b;aDivisor = new Divisor(a);bDivisor = new Divisor(b);}public void setA(long a){this.a = a;}public long getA(){return a;}public void setB(long b){this.b = b;}public long getB(){return b;}public void setADivisor(Divisor aDivisor){this.aDivisor = aDivisor;}public Divisor getADivisor(){return aDivisor;}public void setBDivisor(Divisor bDivisor){this.bDivisor = bDivisor;}public Divisor getBDivisor(){return bDivisor;}/** 直接求两个数a和b的最大公约数,用较大数依次除以较小数的所有约数,其中最大的约数即为最大公约数* 即用较小数的所有约数,包括较小数本身,按照从大到小的顺序依次去除较大数* 第一个能把较大数除尽的数就是最大公约数public long getGreatestCommonDivisor(){long result = 1;long n = 0;if(a==0){result = b;}else if(b==0){result = a;}else{long absA = 1;long absB = 1;long littleNumber = 1;long bigNumber = 1;absA = Math.abs(a);absB = Math.abs(b);if(absA<absB){littleNumber = absA;bigNumber = absB;}else{littleNumber = absB;bigNumber = absA;//System.out.println("littleNumber=" + littleNumber);//System.out.println("bigNumber=" + bigNumber);long i = littleNumber;while(i>1){if(bigNumber%i==0){break;}else{do{i--;}while(littleNumber%i!=0);if(bigNumber%i==0){break;}}}if(a<0 && b<0){result = -i;}else if(a>0 && b>0){result = i;}else{result = 1;}}return result;}*/public long getGreatestCommonDivisor(){long result = 1;if(getA()==0){if(getB()!=0){result = getB(); //定义0与另一个非零数a的最大公约数GCD(0,a)=a }elseresult = 1; //定义0与0的最大公约数GCD(0,0)=1}}else if(getB()==0){if(getA()!=0){result = getA(); //定义0与另一个非零数a的最大公约数GCD(0,a)=a }else{result = 1; //定义0与0的最大公约数GCD(0,0)=1}}else //求两个非零数的最大公约数{long commonDivisor[];commonDivisor=aDivisor.getCommonDivisor(bDivisor);for(int i = 1;i<(int)commonDivisor[0];i++){if(result<commonDivisor[i]){result = commonDivisor[i];}}if(getA()<0 && getB()<0){result = -result; //两个负数的最大公约数是负数}else if(getA()>0 && getB()>0) //两个正数的最大公约数已经求出,不做处理{}else{result = 1; //两个异号数的最大公约数是1}}return result;}public void displayGreatestCommonDivisor(){System.out.println(getA() + "和"+ getB() + "的最大公约数是:"+ getGreatestCommonDivisor());}}class Divisor //求长整型a的所有约数{private long a;private long divisor[];private final int MAXIMUMINDEXOFDIVISOR = 10000;Divisor(){a = 1;divisor = new long[MAXIMUMINDEXOFDIVISOR];divisor[0] = 1;divisor[1] = 1;for (int i = 2;i<MAXIMUMINDEXOFDIVISOR;i++){divisor[i] = 1;}}Divisor(long a){if(a>=0){a = a;}else{a = -a;}this.a = a;divisor = new long[MAXIMUMINDEXOFDIVISOR];divisor[0] = 1;divisor[1] = 1;int index = 2;//数字a的约数的顺序号for (long j = 2;j<=getA();j++){if(getA()%j==0){divisor[index] = j;System.out.printf("divisor[index]=%5d\t",divisor[index]);index++;}}index--;divisor[0] = index;System.out.printf("divisor[0]=%5d\n",divisor[0]);for(int j = index + 1;j<MAXIMUMINDEXOFDIVISOR;j++){divisor[j] = 1;}}public void setA(long a){if(a>=0){this.a = a;}else{this.a = -a;}}public long getA(){return a;}public void setDivisor(){divisor[0] = 1;divisor[1] = 1;int index = 1;//属性a的约数的顺序号for(long j = 2;j<=getA();j++){if(getA()%j==0){index++;divisor[index] = j;}}divisor[0] = index;for(int j = index + 1;j<MAXIMUMINDEXOFDIVISOR;j++){divisor[j] = 1;}}public long[] getDivisor(){return divisor;}public long[] getCommonDivisor(Divisor aDivisor) //求本对象的成员变量a和另一个类Divsior型对象中的成员变量a的所有公约数{long []result = new long[MAXIMUMINDEXOFDIVISOR];long otherDivisor[] = aDivisor.getDivisor();int littleIndex = (int)(divisor[0]<otherDivisor[0]?divisor[0]:otherDivisor[0]);int bigIndex = (int)(divisor[0]>otherDivisor[0]?divisor[0]:otherDivisor[0]);//System.out.printf("littleIndex=%5d\tbigIndex=%5d\t",littleIndex,bigIndex);int commonDivisorIndex = 1;result[0] = 1;result[1] =1;for(int i = 2;i<=littleIndex;i++){for(int j = 2;j<=bigIndex;j++){if(divisor[i]==otherDivisor[j]){commonDivisorIndex++;result[commonDivisorIndex] = divisor[i];}}}result[0] = commonDivisorIndex;for(int j = commonDivisorIndex + 1;j<MAXIMUMINDEXOFDIVISOR;j++){result[j] = 1;}return result;}public void displayDivisor(){long aDivisor[];aDivisor = getDivisor();System.out.println(getA() + "有" + aDivisor[0] + "个约数,分别是:");for(int i = 1;i<=aDivisor[0];i++){System.out.printf("\t%10d",aDivisor[i]);}}}class LeastCommonMultiple //求成员变量a和成员变量b的最小公倍数{private long a;private long b;LeastCommonMultiple(){a = 1;b = 1;}LeastCommonMultiple(long a,long b){this.a = a;this.b = b;}public void setA(long a){this.a = a;}public long getA(){return a;}public void setB(long b){this.b = b;}public long getB(){return b;}public long getLeastCommonMultiple(){GreatestCommonDivisor gCD = new GreatestCommonDivisor(a,b);long result = 1;if(a==0 && b==0) //定义0和一个数a的最小公倍数LCM(0,a)=0{result = 0;}else{result = a * b / gCD.getGreatestCommonDivisor();}return result;}public void displayLeastCommonMultiple(){System.out.println(getA() + "和"+ getB() + "的最小公倍数是:"+ getLeastCommonMultiple());}}public class Test{public static void main(String [] args){GreatestCommonDivisor gCD = new GreatestCommonDivisor(40,60);gCD.displayGreatestCommonDivisor();LeastCommonMultiple leastCommonMultiple = new LeastCommonMultiple(gCD.getA(),gCD.getB());leastCommonMultiple.displayLeastCommonMultiple();/*GreatestCommonDivisor greatestCommonDivisor = new GreatestCommonDivisor(40,0);SubGreatestCommonDivisor subGreatestCommonDivisor = new SubGreatestCommonDivisor(greatestCommonDivisor.getA(),greatestCommonDivisor.getB());System.out.println(greatestCommonDivisor.getA() + "和"+ greatestCommonDivisor.getB() + "的最大公约数是:"+ greatestCommonDivisor.getGreatestCommonDivisor());System.out.println(subGreatestCommonDivisor.getA() + "和"+ subGreatestCommonDivisor.getB() + "的最小公倍数是:"+ subGreatestCommonDivisor.getGreatestCommonDivisor());*/}}。
Java实现:求两个数的最大公约数

Java实现:求两个数的最⼤公约数title: Java实现:求两个数的最⼤公约数tags:java算法categories: 个⼈笔记copyright: trueabbrlink: f202date: 2019-12-07 16:44:58求解两个数的最⼤公约数的⼏种⽅法的⽐较1. 暴⼒枚举法优点:思路简单缺点:运算次数多,效率低极端例⼦:求1000和10001的最⼤公约数需要计算1000/2 - 1 = 4999次// 暴⼒枚举法public static int getGreatestCommonDivisor(int a,int b) {int big = a > b ? a : b;int small = a < b ? a : b;if (big % small == 0) {return small;}for (int i = small / 2; i > 1; i--) {if (big % i == 0 && small % i == 0) {return i;}}return 1;}2. 辗转相除法优点:运算次数少确定:模运算的开销较⼤// 辗转相除法public static int getGreatestCommonDivisor2(int a, int b) {int big = a > b ? a : b;int small = a < b ? a : b;if (big % small == 0) {return small;}return getGreatestCommonDivisor2(big % small, small);}3. 更相减损法优点:避免了取模运算,采⽤减法运算,开销较⼩缺点:算法性能不稳定,运算次数多极端例⼦:两数相差悬殊时,如求1和10001的最⼤公约数,需要递归9999次// 更相减损法public static int getGreatestCommonDivisor3(int a, int b) {if(a == b){return a;}int big = a > b ? a : b;int small = a < b ? a : b;return getGreatestCommonDivisor2(big - small, small);}4. 结合辗转相除法和更相减损法(位运算优化)当a和b均为偶数时,gcd(a,b) = 2×gcd(a/2,b/2) = 2×gcd(a >>1,b>>1)。
JAVA经典算法题目(含答案)

int N;
N=0;
try{
N=Integer.parseInt(str);
}
catch(NumberFormatException e){
e.printStackTrace();
}
str=(N>90?"A":(N>60?"B":"C"));
System.out.println(str);
}
}
【程序 6】 题目:输入两个正整数 m 和 n,求其最大公约数和最小公倍数。 1.程序分析:利用辗除法。 最大公约数:
public static void main(String args[]){ int i=0; for(i=1;i<=20;i++) System.out.println(f(i));
} public static int f(int x) {
if(x==1 || x==2) return 1;
else return f(x-1)+f(x-2);
System.exit(0);///不能少这句,否则结果会出错 } public static void main(String[] args){
String str=""; exp2 c=new exp2();
str=javax.swing.JOptionPane.showInputDialog("请输入N的值(输入exit退出):"); int N;
{
if(N<0||M<0)
{
System.out.println("ERROR!");
return -1;
java求最大公约数的方法_概述及解释说明

java求最大公约数的方法概述及解释说明1. 引言1.1 概述在计算机编程中,求最大公约数是一个常见且重要的问题。
最大公约数(Greatest Common Divisor,简称GCD)是指能同时整除给定两个或多个整数的最大正整数。
在解决实际问题时,求最大公约数可以帮助我们简化计算、优化算法,并提高程序的效率。
本文将介绍Java中求解最大公约数的方法。
1.2 文章结构本文分为以下几个部分来讨论Java中求解最大公约数的方法:- 引言:对本文进行概述和说明。
- 最大公约数的概念与性质:介绍最大公约数的定义、性质以及其意义与应用。
- Java中求最大公约数的方法:探讨目前常用的三种方法,包括辗转相除法、基于质因数分解的方法和比较法。
- 方法解释与实现示例:对每种方法进行详细描述,并给出具体实现示例。
- 结论:总结本文内容,并提供不同情景下选择和应用建议。
1.3 目的本文旨在全面介绍Java中求解最大公约数的常见方法,通过详细说明每种方法的原理和实现步骤,使读者能够理解不同方法之间的比较,从而在实际应用中选择合适的求解方法。
通过本文的学习,读者将能够掌握Java求最大公约数的技巧,并能够灵活运用于问题解决中。
2. 最大公约数的概念与性质2.1 基本定义:最大公约数(Greatest Common Divisor,简称GCD)指的是两个或多个整数共有的最大因数,即能够同时整除这些整数的最大正整数。
例如,对于整数30和45来说,它们的最大公约数为15,因为15既能整除30也能整除45。
2.2 公约数的性质:- 公约数必然是它所对应被求公约数的两个或多个整数的因子。
- 任意两个非零正整数一定存在一个共同的因子,即它们至少存在一个公约数。
- 若a和b是整数,则它们的绝对值之间的最小正值就是它们的最大公约数。
2.3 最大公约数的意义与应用:最大公约数在很多实际问题中都有着重要意义和广泛应用:- 通讯传输:在数据传输过程中需要保证数据正确无误地接收。
JAVA经典算法面试40题及答案

JAVA经典算法⾯试40题及答案现在是3⽉份,也是每年开年企业公司招聘的⾼峰期,同时有许多的朋友也出来找⼯作。
现在的招聘他们有时会给你出⼀套⾯试题或者智⼒测试题,也有的直接让你上机操作,写⼀段程序。
算法的计算不乏出现,基于这个原因我⾃⼰搜集了⼀些算法上的题型。
希望对于⼤家有所帮助。
【程序1】题⽬:古典问题:有⼀对兔⼦,从出⽣后第3个⽉起每个⽉都⽣⼀对兔⼦,⼩兔⼦长到第四个⽉后每个⽉⼜⽣⼀对兔⼦,假如兔⼦都不死,问每个⽉的兔⼦总数为多少?1.程序分析:兔⼦的规律为数列1,1,2,3,5,8,13,21….public class exp2{public static void main(String args[]){int i=0;for(i=1;i<=20;i++)System.out.println(f(i));}public static int f(int x){if(x==1 || x==2)return 1;elsereturn f(x-1)+f(x-2);}}或public class exp2{public static void main(String args[]){int i=0;math mymath = new math();for(i=1;i<=20;i++)System.out.println(mymath.f(i));}}class math{public int f(int x){if(x==1 || x==2)return 1;elsereturn f(x-1)+f(x-2);}}【程序2】题⽬:判断101-200之间有多少个素数,并输出所有素数。
1.程序分析:判断素数的⽅法:⽤⼀个数分别去除2到sqrt(这个数),如果能被整除,则表明此数不是素数,反之是素数。
public class exp2{public static void main(String args[]){int i=0;math mymath = new math();for(i=2;i<=200;i++)if(mymath.iszhishu(i)==true)System.out.println(i);}}class math{public int f(int x){if(x==1 || x==2)return 1;elsereturn f(x-1)+f(x-2);}public boolean iszhishu(int x){for(int i=2;i<=x/2;i++)if (x % 2==0 )return false;return true;}}【程序3】题⽬:打印出所有的 “⽔仙花数 “,所谓 “⽔仙花数 “是指⼀个三位数,其各位数字⽴⽅和等于该数本⾝。
输入两个正整数m和n,求其最大公约数和最小公倍数

输⼊两个正整数m和n,求其最⼤公约数和最⼩公倍数题⽬:输⼊两个正整数m和n,求其最⼤公约数和最⼩公倍数。
程序分析:利⽤辗除法。
在循环中,只要除数不等于0,⽤较⼤数除以较⼩的数,将⼩的⼀个数作为下⼀轮循环的⼤数,取得的余数作为下⼀轮循环的较⼩的数,如此循环直到较⼩的数的值为0,返回较⼤的数,此数即为最⼩公约数,最⼩公倍数为两数之积除以最⼩公倍数。
1package com.li.FiftyAlgorthm;23import java.util.Scanner;45/**b6 * 题⽬:输⼊两个正整数m和n,求其最⼤公约数和最⼩公倍数。
程序分析:利⽤辗除法。
7 * 在循环中,只要除数不等于0,⽤较⼤数除以较⼩的数,将⼩的⼀个数作为下⼀轮循环的⼤数,取得的余数作为下⼀轮循环的较⼩的数,如此循环直到较⼩的数的值为0,返回8 * 较⼤的数,此数即为最⼩公约数,最⼩公倍数为两数之积除以最⼩公倍数。
9 *10 * @author yejin11 *12*/13public class CommonDiviser {14public static void main(String[] args) {15int a, b;16 Scanner s1 = new Scanner(System.in);17 Scanner s2 = new Scanner(System.in);18 a = s1.nextInt();19 b = s2.nextInt();20 CommonDiviser cd = new CommonDiviser();21int m = cd.division(a, b);22int n = a * b / m;23 System.out.println("最⼤公约数: " + m);24 System.out.println("最⼩公倍数: " + n);25 }2627public int division(int x, int y) {28int t;29if (x < y) {30 t = x;31 x = y;32 y = t;33 }3435while (y != 0) {36if (x == y)37return 1;38else {39int k = x % y;40 x = y;41 y = k;42 }43 }44return x;45 }46 }。
求两个正整数的最大公约数和最小公倍数

算法还可以更精简只要求出最大公约数之后即可根据某两个数的乘积等于这两个数的最大公约数和最小公倍数之积即可求出他们的最小公倍数了
求两个正整数的最大公约数和最小公倍数
import java.util.Scanner; public class Gyb {
public static voi min=m; m=n; n=min; } int num1=Gongyue(m,n);//最大公约数 int num2=Gongbei(m,n);//最小公倍数为 System.out.println("最大公约数为:"+num1+"\n"+"最小公倍数为:"+num2); } public static int Gongyue(int m,int n)//求公约数 { while(m%n!=0) { int min = m % n; m=n; n=min; } return n;//递归调用将求余后的值作为下一个除数 } public static int Gongbei(int m,int n)//求最小公倍数 { return m*n/Gongyue(m,n);//最小公倍数=两个数的乘积/它们的最大公约数 } }
Java最大公约数(一般方法及辗转相除法)

Java最⼤公约数(⼀般⽅法及辗转相除法)挺简单的,就放下代码吧,都写了注释import java.util.Scanner;public class maxdivisor {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int a=sc.nextInt();int b=sc.nextInt();int gcd=1;for (int i=2;i<=a && i<=b;i++) {//最⼤公约数,⼩于等于两个数中的minif(a%i==0&&b%i==0) {//i对两个数取余都为零gcd=i;}}System.out.println(gcd);}}运⾏结果第⼆部分:⽤辗转相除法求最⼤公约数辗转相除法:对于给定的两个数,⽤较⼤的数除以较⼩的数。
若余数不为零,则将余数和较⼩的数构成新的⼀对数,继续上⾯的除法,直到⼤数被⼩数除尽,则这时较⼩的数就是原来两个数的最⼤公约数。
代码import java.util.Scanner;public class maxdivisor1 {public static void main(String []args) {Scanner sc = new Scanner (System.in);int a=sc.nextInt();int b=sc.nextInt();int oa=a;int ob=b;while(b!=0) {int i=a%b;a=b;b=i;}System.out.println(oa+"和"+ob+"的最⼤公约数为"+a);}}运⾏结果。
JAVA经典算法题目(含答案)

JAVA经典算法题目(含答案)【程序1】题目:古典问题:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第四个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少?1.程序分析:兔子的规律为数列1,1,2,3,5,8,13,21....publicclae某p2{publictaticvoidmain(Stringarg[]){inti=0;for(i=1;i<=20;i++)Sytem.out.println(f(i));}publictaticintf(int某){if(某==1||某==2)return1;elereturnf(某-1)+f(某-2);}}或publicclae某p2{publictaticvoidmain(Stringarg[]){inti=0;mathmymath=newmath();for(i=1;i<=20;i++)Sytem.out.println(mymath.f(i));}}clamath{publicintf(int某){if(某==1||某==2)return1;elereturnf(某-1)+f(某-2);}}【程序2】题目:打印出所有的\水仙花数\,所谓\水仙花数\是指一个三位数,其各位数字立方和等于该数本身。
例如:153是一个\水仙花数\,因为153=1的三次方+5的三次方+3的三次方。
1.程序分析:利用for循环控制100-999个数,每个数分解出个位,十位,百位。
publicclae某p2{publictaticvoidmain(Stringarg[]){inti=0;mathmymath=newmath();for(i=100;i<=999;i++)if(mymath.hui某ianhua(i)==true)Sytem.out.println(i);}}clamath{publicintf(int某){if(某==1||某==2)return1;elereturnf(某-1)+f(某-2);}publicbooleanizhihu(int某){for(inti=2;i<=某/2;i++)if(某%2==0)returnfale;returntrue;}publicbooleanhui某ianhua(int某){inti=0,j=0,k=0;i=某/100;j=(某%100)/10;k=某%10;if(某==i某i某i+j某j某j+k某k某k)returntrue;elereturnfale;}}【程序3】题目:判断101-200之间有多少个素数,并输出所有素数。
n范围内最大公约数 java算法

n范围内最大公约数 java算法
最大公约数,也成为最大公因数或者最大公测量,是指两个或多个整
数的公共因数中最大的一个。
在java中,求取两个整数的最大公约数的算法可以使用辗转相除法。
辗转相除法是一种古老的求取最大公约数的方法,也是一种递归算法。
该算法的核心思想是,两个整数的最大公约数等于其中较小数与两数
的差值的最大公约数。
因此,我们可以通过递归不断求解两数之差的
最大公约数,直到两数之差为0,此时递归结束,较小的数即为最大公约数。
下面是java代码实现:
public static int gcd(int a, int b){
if(b == 0){
return a;
}else{
return gcd(b, a%b);
}
}
在Java中,递归过程中会消耗一定的内存,因此,我们也可以选择非递归的方式来实现最大公约数的求解。
具体方法是,用较小的数除以
较大的数,得到余数,再用余数去除较小的数,得到余数,依次类推,直到余数为0时,则停止操作。
最后一次操作的除数即为最大公约数。
下面是Java代码实现:
public static int gcd(int a, int b){
if(a < b){
int temp = a;
a = b;
b = temp;
}
while(b != 0){
int temp = a % b;
a = b;
b = temp;
}
return a;
}
最后,需要注意的是,除以0是不合法的操作,因此在代码实现时,
需要对输入参数进行边界检查。
最大公约数算法复杂度 java

最大公约数算法复杂度分析与Java实现一、概述最大公约数(Greatest Common Divisor,简称GCD)是数论中的一个重要概念,常用于对两个整数的约数进行求解。
在实际应用中,对于两个数的最大公约数的求解经常会涉及到性能优化和算法复杂度的分析。
本文将对最大公约数算法的复杂度进行详细分析,并通过Java语言实现最大公约数算法。
二、最大公约数算法复杂度分析1. 暴力枚举法暴力枚举法是求解最大公约数的一种基本方法,其思想是通过遍历从1到两个整数中较小的一个数,找出它们的公共约数中的最大值。
该方法的时间复杂度为O(min(a, b)),其中a和b分别为两个整数。
2. 辗转相除法辗转相除法,又称欧几里德算法,是一种更有效的求解最大公约数的方法。
其基本思想是用较大的数除以较小的数,然后用上一步得到的余数再去除上一步的除数,一直重复这个过程,直到余数为0。
这时,除数就是最大公约数。
该方法的时间复杂度为O(log(max(a, b)))。
3. Stein算法Stein算法是一种更优化的求解最大公约数的方法,它结合了辗转相除法和位运算的思想。
该方法的时间复杂度为O(log(min(a, b)))。
4. 更优化的算法除了上述提到的算法,还有其他一些更为优化的最大公约数算法,比如质因数分解法、线性时间复杂度算法等。
辗转相除法和Stein算法是较为常用且性能较优的最大公约数算法,对于大整数的最大公约数求解,采用这两种算法能够更好地平衡性能和时间复杂度的需求。
三、Java实现最大公约数算法下面通过Java语言分别对辗转相除法和Stein算法进行实现。
1. 辗转相除法的Java实现```javapublic int gcd(int a, int b) {while (b != 0) {int temp = a b;a = b;b = temp;}return a;}```2. Stein算法的Java实现```javapublic int gcd(int a, int b) {if (a == b) {return a;}if (a == 0) {return b;}if (b == 0) {return a;}if ((~a 1) != 0) {if ((b 1) != 0) {return gcd(a >> 1, b);} else {return gcd(a >> 1, b >> 1) << 1; }}if ((~b 1) != 0) {return gcd(a, b >> 1);}if (a > b) {return gcd((a - b) >> 1, b);}return gcd((b - a) >> 1, a);}```四、总结最大公约数算法的性能对于整数处理和数论计算有着重要的影响。
java 数组最小公约数

java 数组最小公约数摘要:1.了解Java数组和最小公约数的概念2.分析求解数组最小公约数的算法3.给出代码示例及解析4.总结与拓展正文:在我们了解如何用Java求解数组最小公约数之前,我们先来了解一下数组和最小公约数的概念。
1.数组数组是一种用来存储多个相同类型数据的方法。
在Java中,数组是一种基本的数据结构,可以存储任何类型的数据,如整数、字符、对象等。
2.最小公约数最小公约数(也称最大公约数)是指两个或多个整数公有的最大公约数。
在数学中,求最小公约数是一种常见的计算问题,可以用辗转相除法、欧几里得算法等方法求解。
接下来,我们来分析如何用Java求解数组最小公约数。
3.求解数组最小公约数的算法对于一个数组,我们可以通过以下步骤求解其最小公约数:- 首先,计算数组中所有元素的最大公约数。
- 然后,将数组中的每个元素依次除以最大公约数,得到一个新的数组。
- 重复上述过程,直到数组中的所有元素互质。
根据这个思路,我们可以编写一个Java程序来求解数组的最小公约数。
4.代码示例及解析```javapublic class ArrayGCD {public static void main(String[] args) {int[] arr = {12, 24, 36, 48};System.out.println("数组最小公约数:" + findArrayGCD(arr));}public static int findArrayGCD(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int gcd = arr[0];for (int i = 1; i < arr.length; i++) {gcd = gcd(gcd, arr[i]);}return gcd;}public static int gcd(int a, int b) {if (b == 0) {return a;}return gcd(b, a % b);}}```在这个示例中,我们首先定义了一个名为`findArrayGCD`的方法,用于求解数组的最小公约数。
使用Java代码进行因数分解和求最小公倍数的示例

使⽤Java代码进⾏因数分解和求最⼩公倍数的⽰例因数分解/*因数分解是⼗分基本的数学运算,应⽤⼴泛。
下⾯的程序对整数n(n>1)进⾏因数分解。
⽐如,n=60, 则输出:2 2 3 5。
请补充缺失的部分。
*/public class 因数分解 {public static void f(int n) {for (int i = 2; i < n / 2; i++) {while(n%i==0){ // 填空System.out.printf("%d ", i);n = n / i;}}if (n > 1)System.out.printf("%d\n", n);}public static void main(String[] args) {f(60);}}运⾏结果:2 23 5最⼩公倍数/*求两个数字的最⼩公倍数是很常见的运算。
⽐如,3和5的最⼩公倍是15。
6和8的最⼩公倍数是24。
下⾯的代码对给定的两个正整数求它的最⼩公倍数。
请填写缺少的代码,使程序尽量⾼效地运⾏。
把填空的答案(仅填空处的答案,不包括题⾯)存⼊考⽣⽂件夹下对应题号的“解答.txt”中即可。
*/public class 最⼩公倍数 {public static int f(int a, int b){int i;for(i=a;;i+=a){ // 填空if(i%b==0) return i;}}public static void main(String[] args){System.out.println(f(6,8));}}运⾏结果:复制代码代码如下:24。
利用递归求最大公约数和最小公倍数
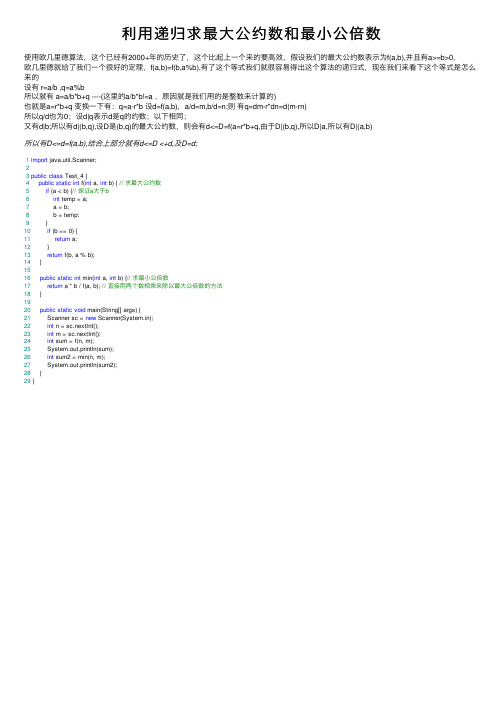
利⽤递归求最⼤公约数和最⼩公倍数使⽤欧⼏⾥德算法,这个已经有2000+年的历史了,这个⽐起上⼀个来的要⾼效,假设我们的最⼤公约数表⽰为f(a,b),并且有a>=b>0,欧⼏⾥德就给了我们⼀个很好的定理,f(a,b)=f(b,a%b),有了这个等式我们就很容易得出这个算法的递归式,现在我们来看下这个等式是怎么来的设有 r=a/b ,q=a%b所以就有 a=a/b*b+q ----(这⾥的a/b*b!=a ,原因就是我们⽤的是整数来计算的)也就是a=r*b+q 变换⼀下有:q=a-r*b 设d=f(a,b),a/d=m,b/d=n;则有q=dm-r*dn=d(m-rn)所以q/d也为0;设d|q表⽰d是q的约数;以下相同;⼜有d|b;所以有d|(b,q),设D是(b,q)的最⼤公约数,则会有d<=D=f(a=r*b+q,由于D|(b,q),所以D|a,所以有D|(a,b)所以有D<=d=f(a,b),结合上部分就有d<=D <+d,及D=d;1import java.util.Scanner;23public class Test_4 {4public static int f(int a, int b) { // 求最⼤公约数5if (a < b) {// 保证a⼤于b6int temp = a;7 a = b;8 b = temp;9 }10if (b == 0) {11return a;12 }13return f(b, a % b);14 }1516public static int min(int a, int b) {// 求最⼩公倍数17return a * b / f(a, b); // 直接⽤两个数相乘来除以最⼤公倍数的⽅法18 }1920public static void main(String[] args) {21 Scanner sc = new Scanner(System.in);22int n = sc.nextInt();23int m = sc.nextInt();24int sum = f(n, m);25 System.out.println(sum);26int sum2 = min(n, m);27 System.out.println(sum2);28 }29 }。
java最小公约数

java最小公约数Java是一种面向对象的编程语言,广泛应用于各种开发领域。
在Java中,求解最小公约数是一个常见的需求。
最小公约数,也叫做最大公因数,是指能够同时整除两个或多个数的最大正整数。
在Java中,我们可以使用欧几里得算法来求解最小公约数。
欧几里得算法,也叫做辗转相除法,是一种通过逐次取余的方式求解最大公约数的方法。
下面我们就来看一下如何在Java中实现这个算法。
我们需要定义一个方法来计算两个数的最小公约数。
这个方法的输入参数是两个整数,输出结果是它们的最小公约数。
我们可以使用递归的方式来实现这个方法。
具体的实现代码如下所示:```public static int gcd(int a, int b) {if (b == 0) {return a;}return gcd(b, a % b);}```在这个方法中,我们首先判断b是否等于0,如果是的话,就返回a。
否则,我们将a除以b的余数作为新的a,将b作为新的b,然后递归调用gcd方法。
通过不断递归调用,直到b等于0,我们就可以得到a和b的最小公约数。
接下来,我们可以在主函数中调用这个方法来求解最小公约数。
例如,我们想求解12和18的最小公约数,可以使用如下代码:```int a = 12;int b = 18;int result = gcd(a, b);System.out.println("最小公约数是:" + result);```运行这段代码,我们可以得到输出结果为6,即12和18的最小公约数是6。
除了求解两个数的最小公约数,我们还可以求解多个数的最小公约数。
我们可以先求解前两个数的最小公约数,然后再将结果与第三个数求最小公约数,依次类推,直到所有的数都求解完毕。
具体的实现代码如下所示:```public static int gcd(int[] nums) {int result = nums[0];for (int i = 1; i < nums.length; i++) {result = gcd(result, nums[i]);}return result;}```在这个方法中,我们首先将第一个数作为初始的最小公约数,然后通过循环依次求解剩下的数与最小公约数的最小公约数,直到所有的数都求解完毕。
