切线长定理课件20141021
合集下载
切线长定理PPT

人教版/数学/九年级
作者: 镇初级中学
学习目标
1 进一步了解过一点画圆切线的方法 2 探索并证明切线长定理 3 了解三角形的内心 4 会利用基本作图作三角形的内切圆
学习准备 三角尺、圆说切:点“给A所我连一线个段支即点圆,心我O就到能直撬线起l的整距个离地,球恰。好”
∵经过PA圆和外P一B是点的圆O的两 条∴又∴的切长的引们一∵线∴切点,切PPOR切O圆的点,AAAtA线之叫线=,线⊥△=从P的和切切上间做PO长BB,AAB圆两圆点线,的这是PO,,∠切P,外这 线 点条 心 分长A≌O点段到点OPP一O切 的 别相RB=O和的圆的为t⊥O点=线 连 为等△P∠两AB.可, 线, AB,PB,条P.O以B它这平BOP.切... ∴分P两A=条PB切,线∠的AP夹O=角∠.BPO.
巩固提高
如图,是一个三角形的卡片,如何在它上 面截下一个圆形,并且使截下来的圆与三角形 的三边都相切?
与三角形各边都相切的圆叫做三角形的内切圆, 内切圆的圆心是三角形三条角平分线的交点,叫做三 角形的内心.
等把于地圆球O和的杠半杆径抽,象所成以圆经和过直半线径,的那外么端这并条且直垂线直是于圆这的条切半线 径的直线是圆的切线
O
l
A
温故知新
画一画:
如图,经过一点P画圆O的切线,你会吗?请你试一试
O P
O
P
探索新知
PA,PB是 O的两条切线,切点分别为A,B。 则PA=PB,∠APO=∠BPO.
如切图线资,料长连卡接定O理A和:OB.
作者: 镇初级中学
学习目标
1 进一步了解过一点画圆切线的方法 2 探索并证明切线长定理 3 了解三角形的内心 4 会利用基本作图作三角形的内切圆
学习准备 三角尺、圆说切:点“给A所我连一线个段支即点圆,心我O就到能直撬线起l的整距个离地,球恰。好”
∵经过PA圆和外P一B是点的圆O的两 条∴又∴的切长的引们一∵线∴切点,切PPOR切O圆的点,AAAtA线之叫线=,线⊥△=从P的和切切上间做PO长BB,AAB圆两圆点线,的这是PO,,∠切P,外这 线 点条 心 分长A≌O点段到点OPP一O切 的 别相RB=O和的圆的为t⊥O点=线 连 为等△P∠两AB.可, 线, AB,PB,条P.O以B它这平BOP.切... ∴分P两A=条PB切,线∠的AP夹O=角∠.BPO.
巩固提高
如图,是一个三角形的卡片,如何在它上 面截下一个圆形,并且使截下来的圆与三角形 的三边都相切?
与三角形各边都相切的圆叫做三角形的内切圆, 内切圆的圆心是三角形三条角平分线的交点,叫做三 角形的内心.
等把于地圆球O和的杠半杆径抽,象所成以圆经和过直半线径,的那外么端这并条且直垂线直是于圆这的条切半线 径的直线是圆的切线
O
l
A
温故知新
画一画:
如图,经过一点P画圆O的切线,你会吗?请你试一试
O P
O
P
探索新知
PA,PB是 O的两条切线,切点分别为A,B。 则PA=PB,∠APO=∠BPO.
如切图线资,料长连卡接定O理A和:OB.
切线长定理 -课件

CE=4cm,则BC= 11 cm , AC= 6 cm, AB= 9 cm .
A
2
F
E
4
C
B
7
D
切线长 定理
温故知新 新知探究 学以致用
实践运用 总结梳理
5、已知:如图,PA、PB是⊙O的切线,切
点分别是A、B.Q为AB上一点,过Q点作
⊙O的切线,交PA、PB于E、F点,已知
PA=12cm,△PEF的周长是(
由 BD+CD=BC 可得
总结梳理 B9-x D 13-x C
(13-x)+(9-x)=14.
解得 x=4.
因此 AF=4,BD=5,CE=9.
切线长 定理
温故知新 新知探究 学以致用
实践运用 总结梳理
1、如图,Δ ABC的内切圆分别和BC,AC, AB切于D,E,F;如果AF=2cm,BD=7cm,
.
切线长 定理
温故知新 新知探究 学以致用 实践运用
总结梳理
1
切线长 定理
4
连接圆心和切点
是我们解决切线长 定理相关问题时常 用的辅助线
2
切线与切 线长区别
3 三角形的外 心和三角形 的内心
敬请指导
WELCOME TO GUIDE
)cm.
A. 12cm B. 24cm C.14cm
D. 8cm
A EO
Q
P
FB
切线长 定理
温故知新 新知探究 学以致用
实践运用
课后练习
总结梳理
1.如图,△ABC中,∠ABC=50°, ∠ACB=75°,点O是△ABC的内心,求 ∠BOC的度数.
A
·O
B
C
A
2
F
E
4
C
B
7
D
切线长 定理
温故知新 新知探究 学以致用
实践运用 总结梳理
5、已知:如图,PA、PB是⊙O的切线,切
点分别是A、B.Q为AB上一点,过Q点作
⊙O的切线,交PA、PB于E、F点,已知
PA=12cm,△PEF的周长是(
由 BD+CD=BC 可得
总结梳理 B9-x D 13-x C
(13-x)+(9-x)=14.
解得 x=4.
因此 AF=4,BD=5,CE=9.
切线长 定理
温故知新 新知探究 学以致用
实践运用 总结梳理
1、如图,Δ ABC的内切圆分别和BC,AC, AB切于D,E,F;如果AF=2cm,BD=7cm,
.
切线长 定理
温故知新 新知探究 学以致用 实践运用
总结梳理
1
切线长 定理
4
连接圆心和切点
是我们解决切线长 定理相关问题时常 用的辅助线
2
切线与切 线长区别
3 三角形的外 心和三角形 的内心
敬请指导
WELCOME TO GUIDE
)cm.
A. 12cm B. 24cm C.14cm
D. 8cm
A EO
Q
P
FB
切线长 定理
温故知新 新知探究 学以致用
实践运用
课后练习
总结梳理
1.如图,△ABC中,∠ABC=50°, ∠ACB=75°,点O是△ABC的内心,求 ∠BOC的度数.
A
·O
B
C
切线长定理(共33张)PPT课件

a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:
Rt△ABC的内切圆的半径 r.
解:设Rt△ABC的内切圆与三边相切于D、E、F,
连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
A
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
F
设AD= x , BE= y ,CE= r
∠OAC=∠OBC=∠APC=∠BPC
(3)写出图中所有相等的线段
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
-
12
例题1
已知:如图,PA、PB是⊙O的切线,切点分别是
A、B,Q为AB上一点,过Q点作⊙O的切线,交
PA、PB于E、F点,已知PA=12CM,求△PEF的周
长。
易证EQ=EA, FQ=FB,
OP垂直平分AB
切线长定理为证明线段相等,角
相等,弧相等,垂直关系提供了理论
依据。必须掌握并能- 灵活应用。
21
练习.如图,△ABC中,∠C =90º,它的
内切圆O分别与边AB、BC、CA相切
于点D、E、F,且BD=12,AD=8,
求⊙O的半径r.
A
D
F O
B
EC
-
22
思考
三角形的内切圆的有关计算
OP垂直平分AB
OM
P
A 证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB
-
10
若延长PO交⊙O于点C,连结CA、CB,你又 能得出什么新的结论?并给出证明.
切线长定理九年级数学课件(与“切线”相关文档共6张)

切切线线长:经长过:圆经外一过点作圆圆的外切一线, 点作圆的切线,
_______是一种智力游戏.
这点和切点之间的距离 已知:PA,PB是圆O的两条切线,
(4)若AF是直径,连结BF,求证OP∥BF
这点和切点之间的距离
(2)若PA=PB=4,则△PDE的周长?
(PA,PB) 考一考:你的观察能力,
切线长:经过圆外一点作圆的切线,
? 切 线 长 定 理
(2)写出图中所有的全等三角形.
B
F
=
(1)写出图中所有的垂直关系; 考一考:你的观察能力,
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。 (2)若PA=PB=4,则△PDE的周长?
成
∠APO=∠BPO.
(2)写出图中所有的全等三角形.
功
(3)若PA=4,PD=2,求半径OA的长
切线长定理
无棣县第二实验学校
第1页,共6页。
你准备 好了吗?
数学 _______是一种智力游戏.
________思维的体操
第2页,共6页。
考一考:你的观察能力,
请注意图形的变化
A
Pห้องสมุดไป่ตู้
O
B
你看清楚了吗?你 可要认真啊!
第3页,共6页。
切线长 定理: 从圆外一点引圆的两条切线,它们的切线 长相等,这一点和圆心的连线平分两条切 线的夹角。
(4)若AF是直径,连结BF,求证OP∥BF
第5页,共6页。
挑战自我
其
实
A
每 个
D
人
都 差
P
C
O
不
多
E
可 能 就 是 只 差 一 步
切线长定理课件PPT
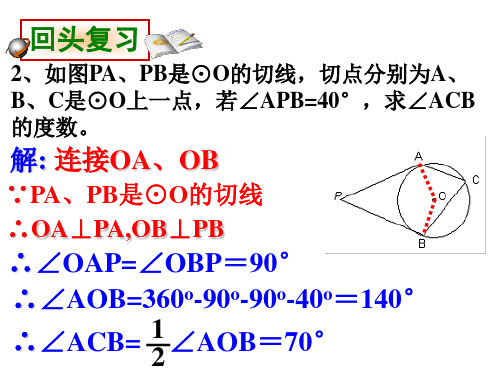
回头复习
2、如图PA、PB是⊙O的切线,切点分别为A、 B、C是⊙O上一点,若∠APB=40°,求∠ACB 的度数。
解: 连接OA、OB
∵PA、PB是⊙O的切线 ∴OA⊥PA,OB⊥PB
∴∠OAP=∠OBP=90° ∴∠AOB=360o-90o-90o-40o=140° 1 ∴∠ACB= ∠AOB=70° 2
课堂练习
4、如图:在△ABC中,AB=AC,内切圆O 与边BC,AC,AB分别相切于点D,E,F. 求证:BF=CE
如图,P为⊙O 外一点,PA、PB分别切⊙O于A、B两点, OP交 ⊙O于C,若PA=6,PC=2 ,求⊙ O的半径OA 3 及两切线PA、PB的夹角。
解:连接OA、AC,则OA⊥AP
5 10
学习新课
如图,PA、PB是⊙O的切线,A、B为切点。如 果连结OA、OB、OP,图中的PA与PB,∠APO A 与∠BPO有什么关系?
从圆外一点可以 引圆的两条切线, 切线长相等,这一 点和圆心的连线平 分两条切线的夹角
B 几何语言:
∵ PA、PB是⊙O 的切线 ∴PA=PB ∠APO=∠BPO
解:(1)∵PA、PB是⊙O的切线 ∴OA⊥PA, OB⊥PB
∴∠OAP=∠OBP=90° ∵OA=OB ∴∠OBA=∠OAB=30o ∴∠PAB=∠PBA=60o ∴∠APB=180o-60o-60o=60°
课堂练习
5、如图,PA,PB是⊙O的切线,A,B为切点, ∠OAB=30°. (1)求∠APB的度数;(2)当OA=3时,求AP的长.
3 4 2
C
O
1
D F
如图所示是一张三角形的铁皮,如何 在它上面剪下一块圆形的用料,并且 使圆的面积尽可能大呢? A A
2、如图PA、PB是⊙O的切线,切点分别为A、 B、C是⊙O上一点,若∠APB=40°,求∠ACB 的度数。
解: 连接OA、OB
∵PA、PB是⊙O的切线 ∴OA⊥PA,OB⊥PB
∴∠OAP=∠OBP=90° ∴∠AOB=360o-90o-90o-40o=140° 1 ∴∠ACB= ∠AOB=70° 2
课堂练习
4、如图:在△ABC中,AB=AC,内切圆O 与边BC,AC,AB分别相切于点D,E,F. 求证:BF=CE
如图,P为⊙O 外一点,PA、PB分别切⊙O于A、B两点, OP交 ⊙O于C,若PA=6,PC=2 ,求⊙ O的半径OA 3 及两切线PA、PB的夹角。
解:连接OA、AC,则OA⊥AP
5 10
学习新课
如图,PA、PB是⊙O的切线,A、B为切点。如 果连结OA、OB、OP,图中的PA与PB,∠APO A 与∠BPO有什么关系?
从圆外一点可以 引圆的两条切线, 切线长相等,这一 点和圆心的连线平 分两条切线的夹角
B 几何语言:
∵ PA、PB是⊙O 的切线 ∴PA=PB ∠APO=∠BPO
解:(1)∵PA、PB是⊙O的切线 ∴OA⊥PA, OB⊥PB
∴∠OAP=∠OBP=90° ∵OA=OB ∴∠OBA=∠OAB=30o ∴∠PAB=∠PBA=60o ∴∠APB=180o-60o-60o=60°
课堂练习
5、如图,PA,PB是⊙O的切线,A,B为切点, ∠OAB=30°. (1)求∠APB的度数;(2)当OA=3时,求AP的长.
3 4 2
C
O
1
D F
如图所示是一张三角形的铁皮,如何 在它上面剪下一块圆形的用料,并且 使圆的面积尽可能大呢? A A
切线长定理课件 (上课)

24.2.2直线和圆的位置关系(三)
问题1、经过平面上一个已知点,作已知 圆的切线会有怎样的情形?
P· · O
P·
· O
P·
· O
问题2、经过圆外一点P,如何作已知⊙O的 切线?
问题2、经过圆外一点P,如何作已知⊙O的 切线? A
。
P
O
B
一、切线长定义 经过圆外一点做圆的切线,这点和切点之间的 线段的长叫做这点到圆的切线长。
A D P E ·O
C B
选做题:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
C E C
E
D
D
A · O
F
B
A
· O
B
练一练
已知:两个同心圆PA、PB是大圆的两条切线, PC、PD是小圆的两条切线,A、B、C、D为切点。 求证:AC=BD
A
O·
P
切线与切线长的区 别与联系:
B
(1)切线是一条与圆相切的直线; (2)切线长是指切线上某一点与切点间的线段的长。
若从⊙O外的一点引两条切线PA,PB,切点 分别是A、B,连结OA、OB、OP,你能发现什么结 论?并证明你所发现的结论。
B
PA = PB
∠OPA=∠OPB
。
P A
O
已知PA、PB是⊙O的两条切线,A、B为切点,
归纳:在解决有
关圆的切线长的问 题时,往往需要我 们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点 (3)连结圆心和圆外一点
A
。
O
P B
例2.如图所示PA、PB分别切圆O于A、B, 并与圆O的切线分别相交于C、D,• 已知 PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD的度数
问题1、经过平面上一个已知点,作已知 圆的切线会有怎样的情形?
P· · O
P·
· O
P·
· O
问题2、经过圆外一点P,如何作已知⊙O的 切线?
问题2、经过圆外一点P,如何作已知⊙O的 切线? A
。
P
O
B
一、切线长定义 经过圆外一点做圆的切线,这点和切点之间的 线段的长叫做这点到圆的切线长。
A D P E ·O
C B
选做题:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
C E C
E
D
D
A · O
F
B
A
· O
B
练一练
已知:两个同心圆PA、PB是大圆的两条切线, PC、PD是小圆的两条切线,A、B、C、D为切点。 求证:AC=BD
A
O·
P
切线与切线长的区 别与联系:
B
(1)切线是一条与圆相切的直线; (2)切线长是指切线上某一点与切点间的线段的长。
若从⊙O外的一点引两条切线PA,PB,切点 分别是A、B,连结OA、OB、OP,你能发现什么结 论?并证明你所发现的结论。
B
PA = PB
∠OPA=∠OPB
。
P A
O
已知PA、PB是⊙O的两条切线,A、B为切点,
归纳:在解决有
关圆的切线长的问 题时,往往需要我 们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点 (3)连结圆心和圆外一点
A
。
O
P B
例2.如图所示PA、PB分别切圆O于A、B, 并与圆O的切线分别相交于C、D,• 已知 PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD的度数
切线长定理_课件

练习 如图,已知⊙O的半径为3厘米,PO=6厘米,PA,PB分别切 ⊙O于A,B,则PA=_______,∠APB=_____.
(1)3 厘米
练习 答案:25°
练习
补充题
如图:从⊙O外的定点P作⊙O的两条切线,分别切⊙O于点A和 B,在弧AB上任取一点C,过点C作⊙O的切线,分别交PA、PB 于点D、E. 试证: ⑴ △PDE 的周长是定值; ⑵ ∠DOE 的大小是定值. 答案: (1)PA+PB;
根据这个性质,你能确定圆心吗?
思考
如图,是一块三角形的铁皮,如何在它上面截下一块圆形的用 料,并且使截下来的圆与三角形的三条边都相切? 我们以前学过,三角形的三条角平分线交于一点, 并且这个点到三条边的距离相等. 所以圆心I是角平分线的交点.
I
三角形的内切圆
与三角形各边都相切的圆叫做三角形的内切圆. 内切圆的圆心是三角形三条角平分线的交点, 叫做三角形的内心.
练习 如图,AE、AD、BC分别切⊙O于E、D、F,若AD=20cm,则 △ABC的周长为_4__0_c_m___.
提示:BD=BF,CE=CF
练习 如图,四边形ABCD四条边都与圆O相切,切点分别为E、F、 G、H,且AD=8,BC=18,求四边形ABCD的周长_5__2_____.
提示:切线长相等
经过圆外一点的圆的切线上,这点和切点之间线段的长, 叫做这点到圆的切线长.
思考
如图,已知直线PA,PB分别与⊙O相切,切点分别是A,B.在 半透明的纸上画出这个图形,沿着直线OP将图形对折. 猜想:线段 PA 与 PB 有什么关系? ∠APO和∠BPO有什么关系?
思考
如图,已知直线PA,PB分别与⊙O相切,切点分别是A,B.在 半透明的纸上画出这个图形,沿着直线OP将图形对折.
切线长定理课件(人教版)

活动五、归纳、小结、反思
1、通过本节课的学习,你有什么收获? 2、在运用切线长定理进行计算时,应该注意 哪些问题? 3、本节课用到哪些数学方法?
意图:让学生对本节所学内容进行系 统回顾,加深理解记忆。
作业延展:
设计意图:让学生课后复习温故本节的学 习的内容,对相应的数学学习方法,数学 知识进行巩固。
说课流程
教材分析 教法分析 学法分析 教学过程
• 教材分析:
地位作用
本节课要研究的切线长定理,是
在学了直线与圆的位置关系;切线的 定义、性质以及判定之后进行的;它 既是前面知识的应用,又是后面学习 的基础,在证明线段相等、角相等、 线段成比例等起着重要的作用。
• 教材分析:
了解切线长的定义,掌握切线长定理,并利 用它进行有关的计算。
教学目标
经历画图、度量、猜想、证明等数学活动过 程,培养学生推理能力和阐述自己的观点的 能力。
引发学生对数学的好奇心与求知欲,在数学学 习活动中获得成功的体验,并培养学生良好的 学习习惯和严谨的思维品质。
• 教材分析:
教学重点
掌握切线长定理,利用定理进行 相关的计算和证明。
教学难点
灵活运用切线长定理解决实际问 题
教学过程:
(一)旧知联想、创设情境
1、直线和圆有几种位置关系,分别是什么? 2、什么是直线与圆相切? 3、切线的判定定理、性质定理内容是什么? 4、过圆上一点作圆的切线,能作几条?过圆外 一点作圆的切线能作几条?
设计意图以提问的情势创设情境,使学生对旧知识 产生设疑,把学生带入下一环节—发现问题,探求 新知
∴PA=PB,∠1=∠2
A
师生归纳:文字语言、 符号语言。
O
1
⌒⌒
切线长定理课件

A
BD=BF=AB﹣AF=9﹣x ∵ BD+CD=BC ∴(13﹣x)+(9﹣x)=14
解得
因此
x
x
F
9
9﹣x
13
E O 9﹣x D 13﹣x B
X=4 AE=4 cm BD=5 cm CE=9 cm
13﹣x
14
C
例题:如图, △ABC的内切圆⊙O与BC、CA、AB分别
相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求 AE、BD、CE的长。
O
B
C
(∠ABC +
∠ACB)
=180°-
2 1 (180°- ∠A)=180°- 70°=110° 2
小 结
1. 切线长定理
回 顾
2.如何作三角形的内切圆? 3.三角形的内心的性质 4.区分三角形的内切圆和外接圆,三角 形的内心和外心。
作业本:第103页第12、15题
练习册:做完第89页第3课时
垂直平分线的交点。
外接圆的半径:交点到三角形 任意一个顶点的距离
三角形的外心到三角形三个顶点 三角形的内心到三角形三边的距 的距离相等。 离相等。
例题:如图, △ABC的内切圆⊙O与BC、CA、AB分别
相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求 AE、BD、CE的长。
解:设AE=x (cm), 则AF=x (cm) CD=CE=AC﹣AE=13﹣x
反思:在解决有
关圆的切线长的问 题时,往往需要我 们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点 (3)连结圆心和圆外一点
A
。
OPBiblioteka B一张三角形的铁皮,如何在它上面 截下一块圆形的用料,并且使圆的 面积尽可能大呢?
BD=BF=AB﹣AF=9﹣x ∵ BD+CD=BC ∴(13﹣x)+(9﹣x)=14
解得
因此
x
x
F
9
9﹣x
13
E O 9﹣x D 13﹣x B
X=4 AE=4 cm BD=5 cm CE=9 cm
13﹣x
14
C
例题:如图, △ABC的内切圆⊙O与BC、CA、AB分别
相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求 AE、BD、CE的长。
O
B
C
(∠ABC +
∠ACB)
=180°-
2 1 (180°- ∠A)=180°- 70°=110° 2
小 结
1. 切线长定理
回 顾
2.如何作三角形的内切圆? 3.三角形的内心的性质 4.区分三角形的内切圆和外接圆,三角 形的内心和外心。
作业本:第103页第12、15题
练习册:做完第89页第3课时
垂直平分线的交点。
外接圆的半径:交点到三角形 任意一个顶点的距离
三角形的外心到三角形三个顶点 三角形的内心到三角形三边的距 的距离相等。 离相等。
例题:如图, △ABC的内切圆⊙O与BC、CA、AB分别
相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求 AE、BD、CE的长。
解:设AE=x (cm), 则AF=x (cm) CD=CE=AC﹣AE=13﹣x
反思:在解决有
关圆的切线长的问 题时,往往需要我 们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点 (3)连结圆心和圆外一点
A
。
OPBiblioteka B一张三角形的铁皮,如何在它上面 截下一块圆形的用料,并且使圆的 面积尽可能大呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
O P
M B
C
小结:在解决有关圆的 切线长问题时,往往需 要我们构建基本图形。
反思:在解决有关圆 A 的切线长的问题时, 往往需要我们构建基 本图形。 。
O
P
B
(1)分别连结圆心和切点
(2)连结两切点 (3)连结圆心和圆外一点
数学探究 三角形的内切圆: 与三角形各边都相切的圆叫做三角形的内切圆 三角形的内心: 三角形的内切圆的圆心叫 做三角形的内心
切于D、E、F,连结OD、OE、OF则 OA⊥AC,OE⊥BC,OF⊥AB。 在Rt△ABC中,BC=3,AC=4, ∴AB=5 ∵ ⊙O与Rt△ABC的三边都相切 ∴AD=AF,BE=BF,CE=CD
A
F D O
·
B
C E 由已知可得四边形ODCE为正方形,∴CD=CE=OD
设AD= x , BE= y ,CE= r x+r=4 则有 y+r=3 解得 r=1 ∴ Rt△ABC的内切圆的 半径为1。 x+ y= 5
(2)如图所示,设与BC、AC 相切的最大圆与BC、AC的切 点分别为B、D,连结OB、OD, 则四边形BODC为正方形。
A
∴OB=BC=3 ∴半径r的取值范围为0<r≤3
D
O ·
几何问题代数化是 解决几何问题的一 种重要方法。
C
B
同学们要好好学习!
老师期盼你们快快进步!
反思:切线长定理为证明线段相等、角相 等提 供了新的方法
回顾我们学过的切线,常有 四个 三个 性质:
1、切线和圆只有一个公共点;
2、圆心到切线的距离等于圆的半径;
3、(1)过圆心(2)过切点(3)垂直于切线
任选两个为题设,另一个为结论都成立。
4、从圆外一点引圆的两条切线,它们的切线长相等, 圆心和这一点的连线平分两条切线的夹角。
圆的内接四边形:角的关系
圆的外切四边形:边的关系
例1:△ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm, 求AF、BD、CE的长.
解: ∵ ⊙O与△ABC的三边都相切
∴AF=AE,BD=BF,CE=CD
设AF=x(cm), BD=y(cm),CE=z(cm) 则有 x+ y = 9 y+z=14 x+z=13 x= 4 解得 y=5 z=9
A
D
O
E
三角形的内心是三角形三 条角平分线的交点,它到 三角形三边的距离相等。 B
F
C
三角形外接圆
C
三角形内切圆
C
. o
A B B
. o
A
外接圆圆心:三角形三边 垂直平分线的交点。
内切圆圆心:三角形三个 内角平分线的交点。 内切圆的半径:交点到三 角形任意一边的垂直距离。
外接圆的半径:交点到三 角形任意一个定点的距离。
(1)找出图中所有相等的线段 N D C DN=DP,AP=AL,BL=BM,CN=CM P O M
A
已知:四边形ABCD的边 AB,BC,CD,DA和圆O 分别相切于L,M,N,P。探索圆外切四边形边 的关系。
(2)填空:AB+CD = AD+BC B L (>,<,=) 结论:圆的外切四边形的两组对边和相等。 比较圆的内接四边形的性质:
问题:经过圆外一点P,可以作几条直线与圆 数学探究 相切?如何作已知⊙ A O的切线?
。
P
O
B
思考:假设切线PA已作出,A为切点, 则∠OAP=90°,连接OP,可知A在怎样 的圆上?
过⊙O外一点作⊙O的切线
A
O O·
P
B
一、切线长定义 经过圆外一点作圆的切线,这点和切点之间的 线段的长叫做这点到圆的切线长。
试用文字语言 叙述你所发现 的结论
∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB ∠OPA=∠OPB
二、切线长定理 从圆外一点引圆的两条切线, 它们的切线长相等,圆心和这一点的连线平分 两条切线的夹角。 B
。
O
P
A
几何语言: PA、PB分别切⊙O于A、B
PA = PB ∠OPA=∠OPB
∴ AF=4(cm), BD=5(cm),
CE=9(cm).
(1)Rt△的三边长与其内切圆半径间的关系
已知:如图,⊙O是Rt△ABC的内切圆,∠C 是直角,三边长分别是a,b,c. 求⊙O的半径r.
D
A
abc r . 2
●
O
┓
┗ F
B
E
C
(2)已知:如图,△ABC的面积为S,三边长分别为 a,b,c. A 求内切圆⊙O的半径r. D F
A· OP切线与切线长的区 别与联系:
B
(1)切线是一条与圆相切的直线; (2)切线长是指切线上某一点与切点间的线段的长。
若从⊙O外的一点引两条切线PA,PB,切点 分别是A、B,连结OA、OB、OP,你能发现什么结 论?并证明你所发现的结论。
B
PA = PB
∠OPA=∠OPB
O
。
P
A 证明:∵PA,PB与⊙O相切,点A,B是切点 ∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
1 则S△ABC= lr 2
r B r O r C
如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙O为 Rt△ABC的内切圆. (1)求Rt△ABC的内切圆的半径 . (2)若移动点O的位置,使⊙O保持与△ABC的边AC、 BC都相切,求⊙O的半径r的取值范围。
解:(1)设Rt△ABC的内切圆与三边相
例:如图所示PA、PB分别切圆O于A、B, CD与圆O切于点E,与PA、PB分别相交 于C、D,已知PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD的度数
A D P E ·O
C
B
随堂训练 如图,AC为⊙O的直径,PA、PB分别切⊙O于 点A、B,OP交⊙O于点M,连结BC。 (1)若OA=3cm, ∠APB=60°,则PO=______. (2)观察OP与BC的位置关系,并给予证明。
●
O
2S r . abc
1 S r a b c . 2
B
E
┓
C
试一试:如图△ABC中,∠C=90,AC=6, BC=8,三角形三边与⊙O均相切,切点分别 是D、E、F,求⊙O的半径。
A F
D C E O B
这节课你学到了什么?
小结一下吧!
知识拓展
2、△ABC的内切圆半径为 r , △ABC的周长为 l , 求△ABC的面积。(提示:设内心为O,连接OA、 OB、OC。) 若△ABC的内切圆半径为 r , 周长为 l , A
