第一章集合单元测试卷

合集下载

数学高一必修1 第一章集合单元测试

(时间：100分钟，满分：120分)一、选择题(本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知集合A ＝{x |x (x ＋1)＝0}，那么下列结论正确的是( )A ．0∈AB ．1∈AC ．－1∉AD ．0∉A解析：选A.由于A ＝{0，－1}，故选A.2．下列四种说法：①“所有很小的正数”能构成一个集合；②方程(x －1)2＝0的解的集合是{1，1}；③{1，3，5，7}与{3，7，5，1}表示同一个集合；④集合{(x ，y )|y ＝x 2－1}与{y |y ＝x 2－1}表示同一个集合，其中正确的是( )A ．①④B ．②③C ．③D ．③④解析：选C.对①，“很小的正数”无客观标准，不能构成集合，②不满足互异性，③中两集合所含元素完全相同，是同一个集合，④中一个集合为点集，一个为数集，两集合不同．3．设集合U ＝{1，2，3，4}，S ＝{1，3}，则∁U S ＝( )A ．∅B ．RC ．UD ．{2，4}解析：选D.因为U ＝{1，2，3，4}，S ＝{1，3}，所以∁U S ＝{2，4}．4．方程组⎩⎪⎨⎪⎧x ＋y ＝1，x －y ＝3的解集是( ) A ．{2，－1} B ．{x ＝2，y ＝－1}C ．{(x ，y )|(2，－1)}D ．{(2，－1)}解析：选D.由⎩⎪⎨⎪⎧x ＋y ＝1，x －y ＝3得⎩⎪⎨⎪⎧x ＝2，y ＝－1，所以方程组⎩⎪⎨⎪⎧x ＋y ＝1，x －y ＝3的解集为{(2，－1)}． 5．若集合M ＝{0，1，2，3，4}，N ＝{1，3，5}，P ＝M ∩N ，则P 的子集共有( )A ．2个B ．4个C ．6个D ．8个解析：选B.因为P ＝M ∩N ＝{1，3}，所以P 的子集有22＝4个．6.下列表示图形中的阴影部分的是( )A ．(A ∪C )∩(B ∪C )B ．(A ∪B )∩(A ∪C )C ．(A ∪B )∩(B ∪C )D ．(A ∪B )∩C解析：选A.阴影部分可表示为(A ∩B )∪C ＝(A ∪C )∩(B ∪C )．7．如果S ＝{1，2，3，4，5}，M ＝{1，3，4}，N ＝{2，4，5}，那么(∁S M )∩(∁S N )等于( )A．∅B．{1，3}C．{4} D．{2，5}解析：选A.法一：∁S M＝{2，5}，∁S N＝{1，3}，(∁S M)∩(∁S N)＝{2，5}∩{1，3}＝∅.法二：M∪N＝{1，2，3，4，5}，(∁S M)∩(∁S N)＝∁S(M∪N)＝∅.8．在集合{a，b，c，d}上定义两种运算⊕和⊗如下：那么d⊗(a⊕c)＝()A．a B．bC．c D．d解析：选A.由⊕定义知a⊕c＝c，由⊗定义知d⊗c＝a，即d⊗(a⊕c)＝d⊗c＝a.9．已知全集为U，集合M，N是U的子集，若M∩N＝N，则()A．(∁U M)⊇(∁U N) B．M⊆(∁U N)C．(∁U M)⊆(∁U N) D．M⊇(∁U N)解析：选C.因为M∩N＝N，所以N⊆M，借助Venn图易知∁U N⊇∁U M.10．已知全集U＝A∪B中有m个元素，(∁U A)∪(∁U B)中有n个元素．若A∩B非空，则A∩B的元素个数为()A．mn B．m＋nC．n－m D．m－n解析：选D.画出Venn图(图略)．因为U＝A∪B中有m个元素．(∁U A)∪(∁U B)＝∁U(A∩B)中有n个元素，所以A∩B中有m－n个元素，故选D.二、填空题(本大题共5小题，每小题5分，共25分．把答案填在题中的横线上)11．已知A＝{x|－4≤x≤4}，B＝{0，2，4，6}，则A∪B＝________．解析：A∪B＝{x|－4≤x≤4或x＝6}．答案：{x|－4≤x≤4或x＝6}12．已知全集U＝{1，2，3，4}，集合A＝{1，2}，B＝{2，3}，则A∩(∁U B)等于________．解析：因为∁U B＝{1，4}，所以A∩(∁U B)＝{1}．答案：{1}13．设集合A＝{1，2，3}，B＝{4，5}，M＝{x|x＝a＋b，a∈A，b∈B}，则M中元素的个数为________．解析：由题意可知，集合M＝{5，6，7，8}，共4个元素．答案：414．设集合M＝{x|x＝3k，k∈Z}，P＝{x|x＝3k＋1，k∈Z}，Q＝{x|x＝3k－1，k∈Z}，若a∈M，b∈P，c∈Q，则a＋b－c∈________(填M，P，Q中的一个)．解析：依据题意设a＝3k，b＝3t＋1，c＝3m－1(k，t，m∈Z)，则a＋b－c＝3(k＋t－m)＋2，所以该元素具有集合Q中元素的特征性质，应属于集合Q.答案：Q15．已知－5∈{x |x 2－ax －5＝0}，则集合{x |x 2＋ax ＋3＝0}中所有元素之和为________．解析：由题意知－5是方程x 2－ax －5＝0的一个根，所以(－5)2＋5·a －5＝0，解得a ＝－4，则方程x 2＋ax ＋3＝0，即为x 2－4x ＋3＝0，解得x 1＝1，x 2＝3，所以{x |x 2－4x ＋3＝0}＝{1，3}．即所有元素之和为1＋3＝4.答案：4三、解答题(本大题共5小题，共55分．解答应写出必要的文字说明、证明过程或演算步骤)16．(本小题满分10分)设A ＝{x ∈Z |－6≤x ≤6}，B ＝{1，2，3}，C ＝{3，4，5，6}，求：(1)A ∪(B ∩C )；(2)A ∩∁A (B ∪C )．解：因为A ＝{x ∈Z |－6≤x ≤6}＝{－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6}，B ＝{1，2，3}，C ＝{3，4，5，6}，所以B ∩C ＝{3}，B ∪C ＝{1，2，3，4，5，6}．(1)A ∪(B ∩C )＝A ＝{－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6}．(2)∁A (B ∪C )＝{－6，－5，－4，－3，－2，－1，0}，所以A ∩∁A (B ∪C )＝∁A (B ∪C )＝{－6，－5，－4，－3，－2，－1，0}．17．(本小题满分10分)已知集合A ＝{3，4，4a 2－6a －1}，B ＝{4a ，－3}，A ∩B ＝{－3}，求实数a 的值及此时的A ∪B .解：由题意得4a 2－6a －1＝－3，解得a ＝1或a ＝12，当a ＝12时，A ＝{3，4，－3}，B ＝{2，－3}，满足要求，此时A ∪B ＝{2，3，4，－3}；当a ＝1时，A ＝{3，4，－3}，B ＝{4，－3}，不满足要求，综上得，a ＝12，A ∪B ＝{2，3，4，－3}． 18．(本小题满分10分)设全集I ＝R ，已知集合M ＝{x |(x ＋3)2≤0}，N ＝{x |x 2＋x －6＝0}．(1)求(∁I M )∩N ；(2)记集合A ＝(∁I M )∩N ，已知集合B ＝{x |a －1≤x ≤5－a ，a ∈R }，若A ∪B ＝A ，求实数a 的取值范围．解：(1)因为M ＝{x |(x ＋3)2≤0}＝{－3}，N ＝{x |x 2＋x －6＝0}＝{－3，2}，所以∁I M ＝{x |x ∈R 且x ≠－3}，所以(∁I M )∩N ＝{2}．(2)A ＝(∁I M )∩N ＝{2}，因为A ∪B ＝A ，所以B ⊆A ，所以B ＝∅或B ＝{2}，当B ＝∅时，a －1>5－a ，得a >3；当B ＝{2}时，⎩⎪⎨⎪⎧a －1＝25－a ＝2，解得a ＝3，综上所述，所求a 的取值范围为{a |a ≥3}．19．(本小题满分12分)设集合A ＝{x |x 是小于6的正整数}，B ＝{x |(x －1)(x －2)＝0}，C ＝{x |(m －1)x －1＝0}．(1)求A ∩B ，A ∪B ；(2)若B ∩C ＝C ，求由实数m 为元素所构成的集合M .解：(1)A ＝{x |x 是小于6的正整数}＝{1，2，3，4，5}，B ＝{1，2}，A ∩B ＝{1，2}，A ∪B ＝{1，2，3，4，5}．(2)因为B ∩C ＝C ，所以C ⊆B ，当C ＝∅时，此时m ＝1，符合题意；当C ≠∅时，m ≠1，此时C ＝{x |x ＝1m －1}，因为C ⊆B ，所以1m －1＝1或2，解得m ＝2或32. 综上所述：由实数m 为元素所构成的集合M ＝{1，2，32}． 20．(本小题满分13分)已知全集U ＝R ，A ＝{x ∈R |x 2－3x ＋b ＝0}，B ＝{x ∈R |(x －2)(x 2＋3x －4)＝0}．(1)若b ＝4时，存在集合M 使得A M B ，求出所有这样的集合M ；(2)集合A ，B 是否能满足(∁U B )∩A ＝∅？若能，求实数b 的取值范围；若不能，请说明理由．解：(1)易知A ＝∅且B ＝{－4，1，2}，由已知M 应该是一个非空集合，且是B 的一个真子集，所以用列举法可得这样的M 共有如下6个：{－4}、{1}、{2}、{－4，1}、{－4，2}、{1，2}．(2)由(∁U B )∩A ＝∅得A ⊆B ，当A ＝∅时，A 是B 的一个子集，此时Δ＝9－4b <0，所以b >94；当A ≠∅时，因为B ＝{－4，1，2}，当－4∈A 时，b ＝－28，则得到A ＝{－4，7}，不可能为B 的一个子集．当1∈A 时，b ＝2，此时A ＝{1，2}，是B 的子集；当2∈A 时，b ＝2，此时A ＝{1，2}，是B 的子集．综上可知：当且仅当A ＝∅或A ＝{1，2}时，(∁U B )∩A ＝∅，所以实数b 的取值范围是⎩⎨⎧b ⎪⎪⎭⎬⎫b >94或b ＝2.。

第一章集合与常用逻辑用语单元测试卷(Word版含答案)

《第一章集合与常用逻辑用语》单元测试卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合U={1,2,3,4,5,6},A={1,3,4},B={1,3,5},则(∁U A)∪B=()A.{5}B.{1,3}C.{1,2,3,5,6}D.⌀2.命题“∀x∈Q,3x2+2x+1∈Q”的否定为()A.∀x∉Q,3x2+2x+1∉QB.∀x∈Q,3x2+2x+1∉QC.∃x∉Q,3x2+2x+1∉QD.∃x∈Q,3x2+2x+1∉Q3.已知集合A={0,1,2},B={1,m}.若B⊆A,则m=()A.0B.0或1C.0或2D.1或24.设全集U=R,M={x|x<-3或x>3},N={x|2≤x≤4},如图,阴影部分所表示的集合为()A.{x|-3≤x<2}B.{x|-3≤x≤4}C.{x|x≤2或x>3}D.{x|-3≤x≤3}5. “|x|≠|y|”是“x≠y”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.设集合A={x|2a<x<a+2},B={x|x<-3或x>5},若A∩B=⌀,则实数a的取值范围为()A.{a|a≥-32} B.{a|a>-32}C.{a|a≤-32} D.{a|a<-32}7.若p:x2+x-6=0是q:ax-1=0(a≠0)的必要不充分条件,则实数a的值为()A.-12B.-12或13C.-13D.12或-138.已知集合A中有10个元素,B中有6个元素,全集U有18个元素,A∩B≠⌀.设集合(∁U A)∩(∁U B)中有x个元素,则x的取值范围是()A.{x|3≤x≤8,且x∈N}B.{x|2≤x≤8,且x∈N}C.{x|8≤x≤12,且x∈N}D.{x|10≤x≤15,且x∈N}二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知命题p:∃x∈R,x2+2x+2-a=0为真命题,则实数a的值可以是()A.1B.0C.3D.-310.图中阴影部分表示的集合是()A.N∩(∁U M)B.M∩(∁U N)C.[∁U(M∩N)]∩ND.(∁U M)∩(∁U N)11.设全集为U,下列选项中,是“B⊆A”的充要条件的是()A.A∪B=AB.A∩B=AC.(∁U A)⊆(∁U B)D.A∪(∁U B)=U12.整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},其中k∈{0,1,2,3,4}.以下判断正确的是()A.2 022∈[2]B.-2∈[2]C.Z=[0]∪[1]∪[2]∪[3]∪[4]D.若a-b∈[0],则整数a,b属于同一“类”三、填空题:本题共4小题,每小题5分,共20分.13.设集合M={2,3,a2+1},N={a2+a,a+2,-1},且M∩N={2},则实数a的值为.14.写出一个使得命题“∀x∈R,ax2-2x+3>0恒成立”是假命题的实数a的值:.15.若p:m-1≤x≤2m+1,q:2≤x≤3,q是p的充分不必要条件,则实数m的取值范围是.16.已知有限集合A={a1,a2,a3,…,a n},定义集合B={a i+a j|1≤i<j≤n,i,j∈N*}中的元素的个数为集合A的“容量”,记为L(A).若集合A={x∈N*|1≤x≤3},则L(A)=;若集合A={x∈N*|1≤x≤n},且L(A)=4 041,则正整数n的值是.(本题第一空2分,第二空3分.)四、解答题:本题共2小题,共20分.解答应写出文字说明、证明过程或演算步骤.≤x≤2}.17.(10分)已知集合A={x|2-b≤ax≤2b-2}(a>0),B={x|-12(1)当a=1,b=3时,求A∪B和∁R B.(2)是否存在实数a,b,使得A=B?若存在,求出a,b的值;若不存在,请说明理由.18.(10分)在①A∪B=B,②“x∈A”是“x∈B”的充分条件,③“x∈∁R A”是“x∈∁R B”的必要条件这三个条件中任选一个,补充到本题第(2)问的横线处,并求解下列问题.问题:已知集合A={x|a≤x≤a+2},B={x|-1<x<3}.(1)当a=2时,求A∩B;(2)若,求实数a的取值范围.注:如果选择多个条件分别解答,按第一个解答计分.参考答案一、单项选择题1.C2.D3.C4.A5.A6.A7.D8.A二、多项选择题9.AC 10.AC 11.ACD 12.ACD三、填空题13.-2或014.-1(答案不唯一)15.{m|1≤m≤3}16.3 2 022四、解答题17. 解：(1)当a =1,b =3时,A ={x |-1≤x ≤4}.又B ={x |-12≤x ≤2},所以 A ∪B ={x |-1≤x ≤4},(2分) ∁R B ={x |x <-12或x >2}.(4分)(2)假设存在实数a ,b 满足条件.因为a >0,所以由2-b ≤ax ≤2b -2,得2−b a ≤x ≤2b−2a .(6分) 由A =B ,得{2−b a =−12,2b−2a =2, 解得{a =2,b =3.(9分) 故存在a =2,b =3,使得A =B.(10分)18. 解：(1)当a =2时,A ={x |2≤x ≤4}, 所以A ∩B ={x |2≤x <3}.(4分)(2)方案一选条件①.因为A ∪B =B ,所以A ⊆B ,(7分)所以{a >−1,a +2<3,解得-1<a <1.(10分) 方案二选条件②.因为“x ∈A ”是“x ∈B ”的充分条件, 所以A ⊆B ,(7分)所以{a >−1,a +2<3,解得-1<a <1.(10分) 方案三选条件③.因为“x ∈∁R A ”是“x ∈∁R B ”的必要条件,所以A ⊆B ,(7分)所以{a >−1,a +2<3,解得-1<a <1.(10分)。

【高一】高一数学上册第一章集合单元测试题(附答案)

【高一】高一数学上册第一章集合单元测试题（附答案）第一单元集合1、头衔1．集合{1，2，3}的真子集共有______________。

（a） 5（b）6（c）7（d）82．已知集合a={}b={}则a=______________。

3.如果a={1,2，a2-3a-1}，B={1,3}，a{3,1}，那么。

（a）-4或1（b）-1或4（c）-1（d）44.设u={0,1,2,3,4}，a={0,1,2,3}，B={2,3,4}，然后（CUA）（cub）=。

5．设s、t是两个非空集合，且st，ts，令x=s那么sx=____________。

6.设a={x}和B={x}。

如果AB={2,3,5}，那么a和B是。

7．设一元二次方程ax2+bx+c=0(a<0)的根的判别式，则不等式ax2+bx+c0的解集为____________。

8.如果={}，n={Z}，那么n=_______;。

9．已知u=n，a={}，则cua等于_______________。

10.如果二次函数的图像与x轴不相交，则的值范围为______。

11．不等式<x2-4的解集是_______________。

12.将整组设为，并使用集合a、B和C的交集、并集和补集在表中阴影部分签名。

（1）（2）（3）13．若方程8x2+(k+1)x+k-7=0有两个负根，则k的取值范围是14.设a={}，B={x}，AB，则实数k的取值范围为。

三、解答题15.让完整的集合u={1,2,3,4}，和={x2-5x+=0，Xu}如果CUA={1,4}，则找到的值。

16．已知集合a={a关于x的方程x2-ax+1=0,有实根}，b={a不等式ax2-x+1>0对一切xr成立},求ab。

17.如果你知道集合a={A2，a+1，-3}，B={a-3，2a-1，A2+1}，如果AB={3}，找到实数a。

18．设a={x,其中xr,如果ab=b，求实数a的取值范围。

第一章：集合与常用逻辑用语单元测试

第一章：集合与常用逻辑用语小结与测试一、单选题(共40分)1．已知集合{}0,1,2,3A =，{}2,3,4,5B =，记集合Q A B =⋂，则（） A ．4Q ∉B ．1Q ∈C ．5Q ∈D ．3Q ∉2．已知全集{}0,1,2,3U =，集合{}{}0,1,3,0,2,3A B ==，则()UA B =（）A ．{}0,1B ．{}1,2C ．{}0,2D ．{}0,33．已知集合{}13A x x =∈-<<N ，2,1,0,1,2U ，则U A（）A ．{}0,1,2B ．{}1,2C ．{}2,1,0--D ．{}2,1--4．用图形直观表示集合的运算关系，最早是由瑞士数学家欧拉所创，故将表示集合运算关系的图形称为“欧拉图”．后来，英国逻辑学家约翰•韦恩在欧拉图的基础上创建了世人所熟知的“韦恩图”．则图中的阴影部分表示的集合为（） A ．A B C ⋂⋂ B ．()U A B C C ．()U A B C ⋂⋂D ．()UA BC5．已知集合{1,0,1,2}A =-，{}*2N 90B x x =∈-≥，则A B ⋃=（）A ．{1,2}B ．{0,1,2}C ．{1,0,1,2}-D ．{1,0,1,2,3}- 6．“1m ≥-”是“2m ≥-”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件7．命题“x ∀∈R ，210x -<”的否定是（） A ．x ∀∈R ，210x - B ．x ∃∈R ，210x - C ．x ∃∈R ，210x -D ．x ∀∈R ，210x -<8．王昌龄是盛唐著名的边塞诗人，被誉为“七绝圣手”，其《从军行》传诵至今"青海长云暗雪山，孤城遥望玉门关黄沙百战穿金甲，不破楼兰终不还"，由此推断，最后一句“不返家乡"是“不破楼兰"的（） A ．必要条件 B ．充分条件C ．充要条件D ．既不充分也不必要二、多选题(共20分)9．设全集{1,2,3,4,5}U =，集合{1,2,3,4}S =，则U S 的子集为（） A ．{5}B ．{1,2,5}C ．{2,3,4}D ．∅10．(多选)已知集合{}21,3,A m =，{}1,B m =．若A B A ⋃=，则实数m 的值为（） A ．0 B ．1 C ．2D ．311．下列四个命题中，是真命题的有（） A ．没有一个无理数不是实数 B ．空集是任何一个集合的真子集C ．112+≤D ．至少存在一个正数x ，使得21x x -+是正数12．下列命题中，真命题是（）A ．若,R x y ∈且2x y +>，则,x y 至少有一个大于1B ．2R,2x x x ∀∈<C ．0a b +=的充要条件是1ab=- D ．命题“21,1x x ∀<<”的否定形式是“2001,1x x ∃<≥” 三、填空题(共20分)13．“R x ∃∈，210ax ax -+<”是假命题，则实数a 的取值范围为 _________ .14．已知集合[)3,6A =-，(),B a =-∞，若A B =∅是假命题，则实数a 的取值范围是______．15．若“11x -<<”是“11x m -<-<”的充要条件，则实数m 的取值是_________．16．有下列各组对象：（1）某校的年轻教师；（2）被5除余数是2的所有整数；（3）著名数学家；（4）直线l 上的所有点；（5）大于1且小于2的所有有理数．其中能构成集合的对象有_________（填写序号）四、解答题(共70分)(10分)17．已知集合{}42A x x =-<<，{5B x x =<-或}1x >．求A B ，()RA B ；(12分)18．设A ＝{x |x 是小于11的正整数}，{}1,2,3,4B =，{}3,4,5,6,7C =．求A C ，A B ，()AB C ，()AB C ．(12分)19．判断下列命题是全称量词命题还是存在量词命题，并判断其真假． (1)至少有一个整数，既能被11整除，又能被9整除； (2)R x ∀∈，2460x x -+>； (3)N x ∃∈，2x x ≤；(4)N x *∃∈，使x 为29的约数； (5)N x ∀∈，20x >．(12分)20．已知集合{}|310A x x =≤<，集合{}|(2)(4)0B x x x =--<， (1)求A B ； (2)求()A B R ∩．(12分)21．已知集合A ＝{x |2≤x ＜4}，B ＝{x |a +2≤x ≤3a }．(1)当a ＝2时，求A ∩B ；(2)若B ⊆A ，求实数a 的取值范围．(12分)22．已知集合{}121A x a x a =-≤≤+，集合{}2310B x x x =-<.(1)若x A ∈是x B ∈的必要条件，求实数a 的取值范围； (2)若A B A =，求实数a 的取值范围.第一章：集合与常用逻辑用语小结与测试参考答案：1．A 【分析】根据集合的交集运算求出Q ，再由元素与集合的关系求解. 【详解】由{2,3}Q A B ==知，4Q ∉正确，1Q ∈，5Q ∈，3Q ∉均是错误的，故选：A2．B 【分析】先求出A B ，再求其补集【详解】因为{}0,3A B ⋂=，又全集{}0,1,2,3U =，所以(){}1,2UA B ⋂=.故选：B3．D 【分析】先求出集合A ，再由补集的定义即可得出答案. 【详解】因为{}N 13A x x =∈-<< {}0,1,2=，所以UA ={}2,1--.故选：D.4．D 【分析】根据阴影部分在集合AB 的公共部分，且不在集合C 中可得答案. 【详解】解：由图可知，阴影部分在集合AB 的公共部分，且不在集合C 中，故图中的阴影部分表示的集合为()UA B C .故选：D.5．D 【分析】先确定集合B ，再根据集合并集的定义计算．【详解】{1,0,1,2}A =-，{N*|33}{1,2,3}B x x =∈-≤≤=，A B ⋃={1,0,1,2,3}-．故选：D ．6．A 【分析】根据“1m ≥-”和“2m ≥-”的逻辑推理关系，即可判断答案.【详解】由1m ≥-可以推出2m ≥-，但反之不成立，故“1m ≥-”是“2m ≥-”的充分不必要条件，故选:A7．B 【分析】全称量词命题的否定，是把全称量词改成存在量词，并把后面的结论否定. 【详解】根据全称命题的否定是特称命题可得，命题“x ∀∈R ，210x -<”的否定是“x ∃∈R ，210x -”.故选：B.8．A 【分析】先阅读理解题意，再利用充分条件、必要条件的判定方法，即可求解. 【详解】由题意知，“不破楼兰”则可推得“不返家乡”，即必要条件成立，反之“不返家乡”不一定是“不破楼兰”，即充分条件不成立，故“不返家乡"是“不破楼兰"的必要不充分条件. 故选：A.9．AD 【分析】根据补集和子集的定义即可求出答案. 【详解】因为{}5U C S =，集合{}5的子集有：∅，{5}. 故选：AD.10．AD 【分析】依题意可得B A ⊆，即可得到2m m =或3m =，即可求出m ，再代入检验即可；【详解】解：因为A B A ⋃=，所以B A ⊆．因为{}21,3,A m =，{}1,B m =，所以2m m =或3m =，解得0m =或1m =或3m =.当0m =时，{}1,3,0A =，{}1,0B =，符合题意；当1m =时，集合A 不满足集合元素的互异性，不符合题意；当3m =时，{}1,3,9A =，{}1,3B =，符合题意．综上，0m =或3；故选：AD11．ACD 【分析】根据命题的等价性可判断A ；由真子集的概念可判断B ；由“或”命题真假判断方法可判断C ；由特称命题的真假判断方法可判断D. 【详解】A,该命题等价于所有无理数都是实数，为真命题； B,该命题为假命题，空集是任何非空集合的真子集； C,该命题显然成立，为真命题；D,取1x =，能使21x x -+是正数，为真命题. 故选：ACD12．AD 【分析】根据不等式的性质，以及实数的运算性质，以及含有一个量词的否定的概念，逐项判定，即可求解.【详解】对于A 中，若实数,x y 都小于等于1，那么可以推出2x y +≤，所以A 正确；对于B 中，当2x =时，22x x =，所以B 错误；对于C 中，当0a b 时，满足0a b +=，但1ab=-不成立，所以C 错误；对于D 中，由含有一个量词的否定的概念，可得命题“21,1x x ∀<<”的否定形式是“2001,1x x ∃<≥”，所以D 是正确的. 故选：AD.13．04a ≤≤【分析】存在量词命题是假命题，则其否定全称量词命题是真命题，写出其全称量词命题，是一个二次不等式恒成立问题，分情况讨论，求a 的范围. 【详解】由题意可知，“R x ∃∈，210ax ax -+<”的否定是真命题，即“R x ∀∈，210ax ax +≥-”是真命题，当0a =时，10≥，不等式显然成立，当0a ≠时，由二次函数的图像及性质可知，2Δ40a a a >⎧⎨=-≤⎩，解得04a <≤，综上，实数a 的取值范围为04a ≤≤. 故答案为：04a ≤≤.14．()3,-+∞【分析】考虑A B =∅是真命题，列不等式求实数a 的取值范围，取其在R 中的补集可得实数a 的取值范围.【详解】若A B =∅是真命题，则3a ≤-， ∴当A B =∅是假命题时，3a >-．故答案为：()3,-+∞.15．0【分析】根据充要条件的定义即可求解. 【详解】1111x m m x m -<-<⇒-<<+，则{x |11x -<<}＝{x |11m x m -<<+}，即11011m m m -=-⎧⇒=⎨+=⎩. 故答案为：0.16．（2）（4）（5）．【分析】可看出（1）所说的“某校”和（3）所说的“著名”都不能确定，从而都不能构成集合的对象．而（2）（4）（5）所说的对象是可确定的，能构成集合的对象．【详解】（1）“某校”不确定，不能构成集合的对象；（2）”被5除余数是2的所有整数”是确定的，可以构成集合的对象；（3）“著名”是不确定的，不能构成集合的对象；（4）“直线l 上的所有点”是确定的，能构成集合的对象；（5）“大于1且小于2的所有有理数”是确定的，能构成集合的对象．故答案为：（2）（4）（5）．【点睛】本题考查元素是否可以构成集合的判断，注意确定性的应用，属简单题.17．{5A B x x ⋃=<-或}4x >-；(){}41A B x x ⋂=-<≤R 【分析】由并集、补集和交集定义直接求解即可.【详解】由并集定义知：{5A B x x ⋃=<-或}4x >-； {}51B x x =-≤≤R ，(){}41A B x x ∴⋂=-<≤R .18．{}3,4,5,6,7A C ⋂=，{}5,6,7,8,9,10A B =，(){}8,9,10AB C ⋃=，(){}1,2,3,4,5,6,7,8,9,10A B C ⋃⋂=【分析】先得出{}1,2,3,4,5,6,7,8,9,10A =，再利用集合的交集，并集，和补集的运算公式进行求解.【详解】{}1,2,3,4,5,6,7,8,9,10A =，则{}3,4,5,6,7A C ⋂=；{}5,6,7,8,9,10AB =；{}1,2,3,4,5,6,7B C ⋃=，故(){}8,9,10AB C ⋃=；{}3,4B C=⋂，所以(){}1,2,3,4,5,6,7,8,9,10A B C ⋃⋂=19．(1)存在量词命题，真命题 (2)全称量词命题，真命题 (3)存在量词命题，真命题 (4)存在量词命题，真命题 (5)全称量词命题，假命题【分析】利用全称量词命题与存在量词命题的概念，及不等式的性质，举例子分别判断各命题. （1）命题中含有存在量词“至少有一个”，因此是存在量词命题，99既能被11整除，又能被9整除，故该命题为真命题．（2）命题中含有全称量词“∀”，故是全称量词命题，因为()2246222x x x -+=-+≥，所以2460x x -+>恒成立，故该命题为真命题．（3）命题中含有存在量词“∃”，故是存在量词命题，当0x =或1x =时，2x x =，故该命题为真命题．（4）命题中含有存在量词“∃”，故是存在量词命题，当1x =时，x 为29的约数，所以该命题为真命题．（5）命题中含有全称量词“∀”，故是全称量词命题，当0x =时，20x =，所以该命题为假命题． 20．(1){}0|21x x << (2){}|23x x <<【分析】（1）由一元二次不等式的解法可求得集合B ，再由集合的并集定义，计算即可；（2）先根据全集R 和集合A 求出集合A 的补集，然后再求出集合A 的补集与B 的交集. (1)由题意得，{}|24B x x =<<，{}|210A B x x ∴=<<．(2){}310A x x =<≥R或，∴(){}|23A B x x =<<R ． 21．(1)A ∩B ＝∅(2)（﹣∞，43）【分析】（1）利用交集及其运算求解即可．（2）利用集合间的关系列出不等式组，求解即可．（1）当a ＝2时，B ＝{x |a +2≤x ≤3a }＝{x |4≤x ≤6}， ∵A ＝{x |2≤x ＜4}，∴A ∩B ＝∅．（2）若B ⊆A ，①当B ＝∅时，则a +2＞3a ，∴a ＜1， ②当B ≠∅时，则232234a aa a +≤⎧⎪+≥⎨⎪<⎩，∴1≤a 43＜，综上，实数a 的取值范围为（﹣∞，43）．22．(1)3a ≥； (2)2a <.【分析】（1）解一元二次不等式求集合B ，由题设有B A ⊆可得12{215a a -≤-+≥求范围即可. （2）由题设有A B ⊆，讨论A =∅、A ≠∅求a 的取值范围. (1)由2310x x -<，有2310(5)(2)0x x x x --=-+<，解得25x -<<， ∴{|25}B x x =-<<，又{}121A x a x a =-≤≤+，由题设，易知B A ⊆，则12{215a a -≤-+≥，解得3a ≥.(2)由题设，A B ⊆，当A =∅时，121a a ->+，可得0a <；当A ≠∅时，12112215a a a a -≤+⎧⎪->-⎨⎪+<⎩，可得02a ≤<；综上，2a <.。

完整版第一章集合单元测试题

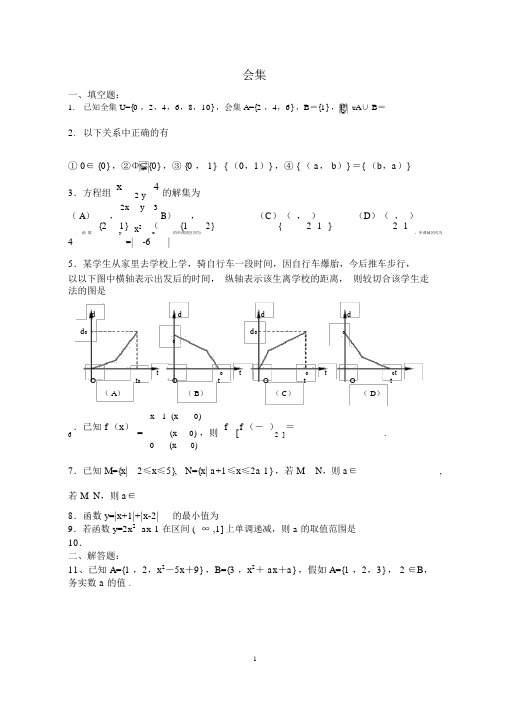
会集一、填空题：1.已知全集 U={0 ，2，4，6，8，10} ，会集 A={2 ，4，6} ，B＝{1} ，则U A∪ B＝ ____________2.以下关系中正确的有 ________________________① 0∈ {0} ，②Φ{0} ，③ {0 ， 1}{ （0，1）} ，④ { （ a， b）} ＝{ （b，a）}3．方程组x2 y4的解集为 _________________________ 2x y3（ A）{2，1}（B）{1，2}（C）（，）（D）（，）x2{ 2 1 } 2 14．函数y=|-6x|的单调增区间为，单调减区间为____________________________________5．某学生从家里去学校上学，骑自行车一段时间，因自行车爆胎，今后推车步行，以以下图中横轴表示出发后的时间，纵轴表示该生离学校的距离，则较切合该学生走法的图是d d d dd0d00d dO t0tO0tO0tO0tt t t（ A）（ B）（ C）（ D）x 1 (x0)．已知 f （x）=(x0) ，则f[f （－）＝________________.6 2 ]0(x0)7．已知 M={x|2≤x≤5},N={x| a+1≤x≤2a 1} ，若 M N，则 a∈________________,若 M N，则 a∈________________8．函数 y=|x+1|+|x-2|的最小值为__________9．若函数 y=2x2 -ax-1 在区间 (- ∞ ,1] 上单调递减，则 a 的取值范围是 ________________ 10．二、解答题：11、已知 A={1 ，2，x2－5x＋9} ，B={3 ，x2＋ ax＋a} ，假如 A={1 ，2，3} ， 2 ∈B，务实数 a 的值 .17．已知会集 A { x | x 2 3x 2 0}, B { x | x 2 2x m 0} 且 A BA, 求 m 的取值范围。

高一数学第一章集合单元测试题

高一数学第一章集合单元测试题（一）班级__________ 学号___________姓名_____________一、选择题1、己知A= {x | x > - 1},那么正确的是（）（A ）0⊆A (B){0}⊆A (C)A={0} (D)Φ∈A2、设U ={1，2，3，4，5，6，7，8}，A={3，4，5}，B={1，3，6} 则集合 {2，7，8}是（）（A ）A B （B ）A B（C ）（C U A ）（C U B ）（D ）（C U A ）（C U B ）3、下列四个命题：①空集没有子集 ②空集是任何一个集合的真子集 ③空集中元素个数为0 ④任一集合必有两个或两个以上的子集。

其中正确的有（）（A ）0 （B ）1 （C ）2 （D ）34、设A={y | y = -1 + x –2 x 2} ，若m∈A 则必有 ( ) （A ）m∈{正有理数} （B ）m ∈{负有理数} （C ）m ∈{正实数} （D ）m ∈{负实数}5、已知=>+-==M C x x x M R U U 则},044{,2（）（A ） R （B ）Φ （C ） {2} （D ） {0}6、已知全集},4{},,2{,+++∈==∈===N n n x x B N n n x x A N U 则(A) B A U = (B) B A C U U =(C) )(B C A U U = (D) )()(B C A C U U U =7、已知集合N M y x y x N y x y x M 那么}4),{(},2),{(=-==+=为( )(A)1,3-==y x (B) (3,-1) (C) {3,-1} (D) {(3,-1)}8、已知集合}1{},3,2,1{==A B A 则B 的子集最多可能有( )(A) 5个 (B) 6个 (C) 7个 (D) 8个9、已知},,1{},4,3,2,1{A x x y y B A ∈-===则{0}与B 的关系是( )(A) B ∈}0{ (B) B ⊂}0{ (C) B ⊄}0{ (D) B ⊇}0{10、已知},,14{},,1{22+∈+-==∈+==N m m m x x Q N n n x x P 则P 与Q 的关系是( )(A) Q P = (B) Q P ⊂ (C) P Q ⊂ (D)以上答案都不对11、已知则},,1{},,1{22R x x y y N R x x y y M ∈+-==∈+== N M 是( )(A) {0,1} (B) {(0,1)} (C) {1} (D)C 以上答案均不对12、符合条件{a ,b ,c} ⊆ P ⊆ {a ,b ,c ,d ,e}的集合P 的个数是（）（A ）2 （B ）3 （C ）4 （D ）8二、填空题13、{（1，2），（-3，4）}的所有真子集是；14、设直线的32+=x y 点集为P =___________________,则点(2,7)与P 的关系为(2,7)____ P15、已知},{b a P =又P 的所有子集组成集合Q ,用列举法表示Q ,则Q =_____________________16、如图所示，阴影部分表示的集合为17、已知,.,},3),{(},12),{(B a A a x y y x B x y y x A ∈∈+==-==则______=a18、若},,34{},,42{22R b b b y y B R a a a x x A ∈+-==∈++==试确定A 与B 的关系为 __________.三、解答题19、已知B A b b B a a A ==++=若},,1{},21,1,1{2,求b a ,20、已知,}1{},62{P Q a x a x Q x x P ⊆+≤≤=≤≤=若求a 的范围21、已知集合},02{2=+-=k x x x P 若集合P 中的元素少于两个,求.k22、已知全集}4{≤=x x U 集合},33{},32{≤<-=<<-=x x B x x A 求B A C B A C B A U U )(),(,23、设A 是数集，满足A a ∈时，必有A a∈-11, (1)若A ∈2,问:①A 中至少有几个元素?并把它列举出来? ② A 中还可以有其它元素吗?(2)若A 中只能有一个元素且A ∉2,实数a 是否存在?。

高一数学第一章集合单元测试卷

高一数学集合单元测试卷（时间45分钟满分100分）一、选择题（每小题有且只有一个正确答案，8×4分=32分）１．下列各项中不能组成集合的是 ( ) A ．所有正三角形 B ．《数学》教材中所有的习题 C ．所有数学难题 D ．所有无理数 2．若集合M =}{6|≤x x ，a =5，则下面结论中正确的是 ( ) A ．}{M a ⊆ B ．M a ⊆ C ．}{M a ∈ D ．M a ∉ 3．设集合S ={0，1，2，3，4}，集合A ={1，2，3}，集合B ={2，3}，则 ( ) A ．B A C S ⊆ B ．A C B C S S ⊆ C ．B C A C S S ⊆ D ．A C S =B C S 4．已知集合A 中有10个元素，集合B 中有8个元素，集合A ∩B 中共有4个元素，则集合A ∪B 中共有（）个元素 ( ) A ． 14 B ． 16 C ． 18 D ．不确定 5．已知a ∈R ，集A =}{1|2=x x 与B =}{1|=ax x 若A B A ⋃=则实数a 所能取值为A ．1B ．-1C ．-1或1D ．-1或0或1 ( ) 6．如果集合A ={x |ax 2＋2x ＋1=0}中只有一个元素，则a 的值是 ( ) A ．0 B ．0 或1 C ．1 D ．不能确定 7．满足{1，2，3} ⊆M ⊆{1，2，3，4，5，6}的集合M 的个数是 ( ) A ．8 B ．7 C ．6 D ．5 8．集合A ={x |x =2n ＋1，n ∈Z }，B ={y |y =4k ±1，k ∈Z }，则A 与B 的关系为 ( ) A ．A =B B ．A ⊆B C ．A =B D ．A ≠B 二．填空题（5×4分=20分） 9．集合{}23*<-∈x N x 用列举法表示应是； 10．设集合{}12|)(-==x y y x A ，，{}3|)(+==x y y x B ，，则A ∩B ＝． 11．某班有学生55人，其中音乐爱好者34人，体育爱好者43人，还有4人既不爱好体育也不爱好音乐，则班级中即爱好体育又爱好音乐的有人．12．已知全集{}{}=∈>-=≤≤-=A C U x x x A x x U U ，则，，31281________．姓名________________班级______________得分__________________ ———————————————————————————————————————————————————三．解答题(4⨯13分=52分)13．设集合A ={2，4，6，8，10}，=A C U {1，3，5，7，9}，=B C U {1，4，7，9}，求集合B ．14．若集合{}{}{}213113A x B x A B x ==⋃=，，，，，，，，求满足上述条件的实数x ．15．设U ={1，2，3，4，5}，若A ∩B ={2}，(C U A )∩B ={4}，(C U A )∩(C U B )={1，5}，求A ，B ．16．设集合A ={x |x 2＋4x =0}，B ={x |x 2＋2(a ＋1)x ＋a 2－1=0}，A ∩B =B ，求实数a 的值．。

高一数学必修1第一章集合与函数的概念单元测试题(含答案)

一、选择题(本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．设集合M＝{x|x2＋2x＝0，x∈R}，N＝{x|x2－2x＝0，x∈R}，则M∪N＝()A．{0} B．{0,2}C．{－2,0} D．{－2,0,2}解析M＝{x|x(x＋2)＝0.，x∈R}＝{0，－2}，N＝{x|x(x－2)＝0，x∈R}＝{0,2}，所以M ∪N＝{－2,0,2}．答案 D2．设f：x→|x|是集合A到集合B的映射，若A＝{－2,0,2}，则A∩B＝()A．{0} B．{2}C．{0,2} D．{－2,0}解析依题意，得B＝{0,2}，∴A∩B＝{0,2}．答案 C3．f(x)是定义在R上的奇函数，f(－3)＝2，则下列各点在函数f(x)图象上的是() A．(3，－2) B．(3,2)C．(－3，－2) D．(2，－3)解析∵f(x)是奇函数，∴f(－3)＝－f(3)．又f(－3)＝2，∴f(3)＝－2，∴点(3，－2)在函数f(x)的图象上．答案 A4．已知集合A＝{0,1,2}，则集合B＝{x－y|x∈A，y∈A}中元素的个数是()A．1 B．3C．5 D．9解析逐个列举可得．x＝0，y＝0,1,2时，x－y＝0，－1，－2；x＝1，y＝0,1,2时，x－y＝1,0，－1；x＝2，y＝0,1,2时，x－y＝2,1,0.根据集合中元素的互异性可知集合B的元素为－2，－1,0,1,2.共5个．答案 C6．设f(x)＝x＋3(x>10)，f(x＋5)(x≤10)，则f(5)的值为()A．16 B．18C．21 D．24解析f(5)＝f(5＋5)＝f(10)＝f(15)＝15＋3＝18.答案 B7．设T＝{(x，y)|ax＋y－3＝0}，S＝{(x，y)|x－y－b＝0}，若S∩T＝{(2,1)}，则a，b的值为()A．a＝1，b＝－1 B．a＝－1，b＝1C．a＝1，b＝1 D．a＝－1，b＝－1解析依题意可得方程组2a＋1－3＝0，2－1－b＝0，⇒a＝1，b＝1.答案 C8．已知函数f(x)的定义域为(－1,0)，则函数f(2x＋1)的定义域为()A．(－1,1) B.－1，－12C．(－1,0) D.12，1解析由－1<2x＋1<0，解得－1<x<－12，故函数f(2x＋1)的定义域为－1，－12.答案 B9．已知A＝{0,1}，B＝{－1,0,1}，f是从A到B映射的对应关系，则满足f(0)>f(1)的映射有()A．3个B．4个C．5个D．6个解析当f(0)＝1时，f(1)的值为0或－1都能满足f(0)>f(1)；当f(0)＝0时，只有f(1)＝－1满足f(0)>f(1)；当f(0)＝－1时，没有f(1)的值满足f(0)>f(1)，故有3个．答案 A10．定义在R上的偶函数f(x)满足：对任意的x1，x2∈(－∞，0](x1≠x2)，有(x2－x1)[f(x2)－f(x1)]>0，则当n∈N*时，有()A．f(－n)<f(n－1)<f(n＋1)B．f(n－1)<f(－n)<f(n＋1)C．f(n＋1)<f(－n)<f(n－1)D．f(n＋1)<f(n－1)<f(－n)解析由题设知，f(x)在(－∞，0]上是增函数，又f(x)为偶函数，∴f(x)在[0，＋∞)上为减函数．∴f(n＋1)<f(n)<f(n－1)．又f(－n)＝f(n)，∴f(n＋1)<f(－n)<f(n－1)．答案 C11．函数f(x)是定义在R上的奇函数，下列说法：①f(0)＝0；②若f(x)在[0，＋∞)上有最小值为－1，则f(x)在(－∞，0]上有最大值为1；③若f(x)在[1，＋∞)上为增函数，则f(x)在(－∞，－1]上为减函数；④若x>0时，f(x)＝x2－2x，则x<0时，f(x)＝－x2－2x.其中正确说法的个数是()A．1个B．2个C．3个D．4个解析①f(0)＝0正确；②也正确；③不正确，奇函数在对称区间上具有相同的单调性；④正确．12．f(x)满足对任意的实数a，b都有f(a＋b)＝f(a)•f(b)且f(1)＝2，则f(2)f(1)＋f(4)f(3)＋f(6)f(5)＋…＋f(2014)f(2013)＝()A．1006 B．2014C．2012 D．1007解析因为对任意的实数a，b都有f(a＋b)＝f(a)•f(b)且f(1)＝2，由f(2)＝f(1)•f(1)，得f(2)f(1)＝f(1)＝2，由f(4)＝f(3)•f(1)，得f(4)f(3)＝f(1)＝2，……由f(2014)＝f(2013)•f(1)，得f(2014)f(2013)＝f(1)＝2，∴f(2)f(1)＋f(4)f(3)＋f(6)f(5)＋…＋f(2014)f(2013)＝1007×2＝2014.答案 B二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．函数y＝x＋1x的定义域为________．解析由x＋1≥1，x≠0得函数的定义域为{x|x≥－1，且x≠0}．答案{x|x≥－1，且x≠0}14．f(x)＝x2＋1(x≤0)，－2x(x>0)，若f(x)＝10，则x＝________.解析当x≤0时，x2＋1＝10，∴x2＝9，∴x＝－3.当x>0时，－2x＝10，x＝－5(不合题意，舍去)．∴x＝－3.答案－315．若函数f(x)＝(x＋a)(bx＋2a)(常数a，b∈R)是偶函数，且它的值域为(－∞，4]，则该函数的解析式f(x)＝________.解析f(x)＝(x＋a)(bx＋2a)＝bx2＋(2a＋ab)x＋2a2为偶函数，则2a＋ab＝0，∴a＝0，或b＝－2.又f(x)的值域为(－∞，4]，∴a≠0，b＝－2，∴2a2＝4.∴f(x)＝－2x2＋4.答案－2x2＋416．在一定范围内，某种产品的购买量y吨与单价x元之间满足一次函数关系，如果购买1000吨，每吨为800元，购买2000吨，每吨为700元，那么客户购买400吨，单价应该是________元．解析设一次函数y＝ax＋b(a≠0)，把x＝800，y＝1000，和x＝700，y＝2000，代入求得a＝－10，b＝9000.∴y＝－10x＋9000，于是当y＝400时，x＝860.三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)已知集合A＝{x|2≤x≤8}，B＝{x|1<x<6}，C＝{x|x>a}，U＝R.(1)求A∪B，(∁UA)∩B；(2)若A∩C≠∅，求a的取值范围．解(1)A∪B＝{x|2≤x≤8}∪{x|1<x<6}＝{x|1<x≤8}．∁UA＝{x|x<2，或x>8}．∴(∁UA)∩B＝{x|1<x<2}．(2)∵A∩C≠∅，∴a<8.18．(本小题满分12分)设函数f(x)＝1＋x21－x2.(1)求f(x)的定义域；(2)判断f(x)的奇偶性；(3)求证：f1x＋f(x)＝0.解(1)由解析式知，函数应满足1－x2≠0，即x≠±1.∴函数f(x)的定义域为{x∈R|x≠±1}．(2)由(1)知定义域关于原点对称，f(－x)＝1＋(－x)21－(－x)2＝1＋x21－x2＝f(x)．∴f(x)为偶函数．(3)证明：∵f1x＝1＋1x21－1x2＝x2＋1x2－1，f(x)＝1＋x21－x2，∴f1x＋f(x)＝x2＋1x2－1＋1＋x21－x2＝x2＋1x2－1－x2＋1x2－1＝0.19．(本小题满分12分)已知y＝f(x)是定义在R上的偶函数，当x≥0时，f(x)＝x2－2x.(1)求当x<0时，f(x)的解析式；(2)作出函数f(x)的图象，并指出其单调区间．解(1)当x<0时，－x>0，∴f(－x)＝(－x)2－2(－x)＝x2＋2x.又f(x)是定义在R上的偶函数，∴f(－x)＝f(x)．∴当x<0时，f(x)＝x2＋2x.(2)由(1)知，f(x)＝x2－2x(x≥0)，x2＋2x(x<0).作出f(x)的图象如图所示：由图得函数f(x)的递减区间是(－∞，－1]，[0,1]．f(x)的递增区间是[－1,0]，[1，＋∞)．20．(本小题满分12分)已知函数f(x)＝2x＋1x＋1，(1)判断函数在区间[1，＋∞)上的单调性，并用定义证明你的结论．(2)求该函数在区间[1,4]上的最大值与最小值．解(1)函数f(x)在[1，＋∞)上是增函数．证明如下：任取x1，x2∈[1，＋∞)，且x1<x2，f(x1)－f(x2)＝2x1＋1x1＋1－2x2＋1x2＋1＝x1－x2(x1＋1)(x2＋1)，∵x1－x2<0，(x1＋1)(x2＋1)>0，所以f(x1)－f(x2)<0，即f(x1)<f(x2)，所以函数f(x)在[1，＋∞)上是增函数．(2)由(1)知函数f(x)在[1,4]上是增函数，最大值f(4)＝95，最小值f(1)＝32.21．(本小题满分12分)已知函数f(x)的定义域为(0，＋∞)，且f(x)为增函数，f(x•y)＝f(x)＋f(y)．(1)求证：fxy＝f(x)－f(y)；(2)若f(3)＝1，且f(a)>f(a－1)＋2，求a的取值范围．解(1)证明：∵f(x)＝fxy•y＝fxy＋f(y)，(y≠0)∴fxy＝f(x)－f(y)．(2)∵f(3)＝1，∴f(9)＝f(3•3)＝f(3)＋f(3)＝2.∴f(a)>f(a－1)＋2＝f(a－1)＋f(9)＝f[9(a－1)]．又f(x)在定义域(0，＋∞)上为增函数，∴a>0，a－1>0，a>9(a－1)，∴1<a<98.22．(本小题满分12分)某商场经销一批进价为每件30元的商品，在市场试销中发现，此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系：x 30 40 45 50y 60 30 15 0(1)在所给的坐标图纸中，根据表中提供的数据，描出实数对(x，y)的对应点，并确定y与x的一个函数关系式．(2)设经营此商品的日销售利润为P元，根据上述关系，写出P关于x的函数关系式，并指出销售单价x为多少元时，才能获得最大日销售利润？解(1)由题表作出(30,60)，(40,30)，(45,15)，(50,0)的对应点，它们近似地分布在一条直线上，如图所示．设它们共线于直线y＝kx＋b，则50k＋b＝0，45k＋b＝15，⇒k＝－3，b＝150.∴y＝－3x＋150(0≤x≤50，且x∈N*)，经检验(30,60)，(40,30)也在此直线上．∴所求函数解析式为y＝－3x＋150(0≤x≤50，且x∈N*)．(2)依题意P＝y(x－30)＝(－3x＋150)(x－30)＝－3(x－40)2＋300.∴当x＝40时，P有最大值300，故销售单价为40元时，才能获得最大日销售利润．。

高一数学第1章集合单元测试题

集合单元测试题（时间90分钟；满分150分）一、选择题：（每小题5分；共计60分）1、如果集合{}8,7,6,5,4,3,2,1=U ；{}8,5,2=A ；{}7,5,3,1=B ；那么(A U)B 等于（）(A){}5 (B) {}8,7,6,5,4,3,1 (C) {}8,2 (D) {}7,3,1 2、如果U 是全集；M ；P ；S 是U 的三个子集；则阴影部分所表示的集合为（）（A ）（M ∩P ）∩S ；（B ）（M ∩P ）∪S ；（C ）（M ∩P ）∩（C U S ）（D ）（M ∩P ）∪（C U S ）3、已知集合{(,)|2},{(,)|4}M x y x y N x y x y =+==-=；那么集合MN 为（）A 、3,1x y ==-B 、(3,1)-C 、{3,1}-D 、{(3,1)}- 4. 2{4,21,}A a a =--；B={5,1,9},a a --且{9}A B ⋂=；则a 的值是 ( ) A. 3a = B. 3a =- C. 3a =± D. 53a a ==±或2{440,}A x kx x x R =++=∈中只有一个元素；则实数k 的值为 ( )A.0B. 1C. 0或1D. 1k < 6. 集合2{4,,}A y y x x N y N ==-+∈∈的真子集的个数为 ( ) A. 9 B. 8 C. 7 D. 67. 符号{}a ⊂≠{,,}P a b c ⊆的集合P 的个数是 ( ) A. 2 B. 3 C. 4 D. 58. 已知2{1,},{1,}M y y x x R P x x a a R ==-∈==-∈；则集合M 与P 的关系是( )A. M=PB. P R ∈ C . M ⊂≠P D. M ⊃≠P9. 设P 、Q 为两个非空实数集合；定义集合P+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ；则P+Q 中元素的个数是（）A ．9B ．8C ．7D ．610. 设全集{(,),},I x y x y R =∈集合3{(,)1},{(,)1}2y M x y N x y y x x -===≠+-；那么()()I I C M C N ⋂等于 ( )A. ∅B.{(2,3)}C. (2；3)D. {(,)1}x y y x ≠+ 11. 2{60},{10}A x x x B x mx =+-==+=；且A B A ⋃=；则m 的取值范围是( )A.11{,}32-B. 11{0,,}32--C. 11{0,,}32-D. 11{,}32二、选择题：（每小题5分；满分20分）13. 设集合{=M 小于5的质数}；则M 的真子集的个数为 .14. 设{1,2,3,4,5,6,7,8}U =；{3,4,5},{4,7,8}.A B ==则:()()U U C A C B ⋂= ； ()()U U C A C B ⋃= .15. 已知{15},{4}A x x x B x a x a =<->=≤<+或；若A ⊃≠B ；则实数a 的取值范围是 .16. 已知集合22{31},{31}P x x m m T x x n n ==++==-+；有下列判断:①5{}4P T y y ⋂=≥- ②5{}4P T y y ⋃=≥- ③ P T ⋂=∅ ④P T = 其中正确的是 . 三、解答题17. （本题满分15分）已知含有三个元素的集合2{,,1}{,,0},ba a ab a=+求20082007b a +的值.18. （本题满分15分）若集合}10{的正整数小于=S ；S B S A ⊆⊆,；且}8,6,4{)()(},2{},9,1{)(=⋂=⋂=⋂B C A C B A B A C S S S ；求A 和B 。

高中数学必修一第一章测试题(含答案)

必修一第一章集合与简易逻辑单元测试学校:___________姓名：___________班级：___________考号：___________一、单选题 1．已知全集U ={1,2,3,4,5,6,7}，A ={2,3,5,7}，B ={1,3,6,7}，则∁U (A ∩B )=（） A ．{4}B ．∅C ．{1,2,4,5,6}D ．{1,2,3,5,6}2．A ={2,3}，B ={x ∈N|x 2−3x <0}，则A ∪B =（） A ．{1,2,3}B ．{0,1,2,}C ．{0,2,3}D ．{0,1,2,3}3．下列各组集合表示同一集合的是（） A ．M ={(3,2)},N ={(2,3)} B ．M ={(x,y)|x +y =1},N ={y |x +y =1} C ．M ={4,5}，N ={5,4}D ．M ={1,2},N ={(1,2)}4．已知全集U =Z ，集合M ={x|−1<x <2,x ∈Z}，N ={−1,0,1,2}，则()C U M N ⋂=（） A ．{−1,2}B ．{−1,0}C ．{0,1}D ．{1,2}5．设集合U ={1,2,3,4}，M ={1,2,3}，N ={2,3}，则∁U (M ∩N )=（） A ．{4}B ．{1,2}C ．{}2,3D ．{1,4}6．下列各式中：①{0}∈{0,1,2}；②{0,1,2}⊆{2,1,0}；③∅⊆{0,1,2}；④∅={0}；⑤{0,1}={(0,1)}；⑥0={0}.正确的个数是（） A ．1B ．2C ．3D ．47．命题“∃x ∈R ，x 2−2x +2≤0”的否定是（） A ．∃x ∈R ，x 2−2x +2≥0 B ．∃x ∈R ，2220x x -+> C ．∀x ∈R ，2220x x -+>D ．∀x ∈R ，x 2−2x +2≤08．王昌龄《从军行》中两句诗为“黄沙百战穿金甲，不破楼兰终不还”，其中后一句中“攻破楼兰”是“返回家乡”的（） A ．充分条件 B ．必要条件C ．充要条件D ．既不充分也不必要条件9．若命题：“∃x ∈R ，使x 2−x −m =0”是真命题，则实数m 的取值范围是（） A ．[−14,0]B ．10,4⎡⎤⎢⎥⎣⎦C ．1,4⎡⎫-+∞⎪⎢⎣⎭D ．1,4⎛⎤-∞ ⎥⎝⎦10．命题“∀x ∈[1，2]，x 2－a ≤0”为真命题的一个充分不必要条件是（） A ．a ≥4B ．a ≤4C ．a ≥5D ．a ≤511．已知集合A ={x|ax =x 2}，B ={0，1，2}，若A ⊆B ，则实数a 的值为（） A ．1或2B ．0或1C ．0或2D ．0或1或212．已知集合A ={x|−2≤x ≤5}，B ={x|m +1≤x ≤2m −1}．若B ⊆A ，则实数m 的取值范围为（） A ．m ≥3B ．2≤m ≤3C ．3m ≤D ．m ≥2二、填空题 13．已知集合A ={−1,0,1}，B ={0,a,a 2}，若A =B ，则a =______.14．已知集合M ={(x,y)|x +y =2}、N ={(x,y)|x −y =4}，那么集合M ∩N= 15．“方程220x x a --=没有实数根”的充要条件是________.16．已知A ，B 是两个集合，定义A −B ={x|x ∈A,x ∉B}，若A ={x|−1<x <4}，B ={x|x >2}，则A −B =_______________.三、解答题 17．已知A ={a −1,2a 2+5a +1,a 2+1}, −2∈A ,求实数a 的值.18．已知集合A ={x |−4<x <2}，B ={x |x <−5或x >1}．求A ∪B ，A ∩(∁R B )； 19．已知集合U ={1,2,3,4,5,6,7,8,9}，A ={x|3≤x ≤7且x ∈U}，B ={x|x =3n,n ∈Z 且x ∈U}.（1）写出集合B 的所有子集；（2）求A ∩B ，A ∪∁U B .20．已知全集U =R ,集合A ={x|−1≤x ≤3}. (1)求C U A ;(2)若集合B ={x |2x −a >0},且B ⊆(C U A ),求实数a 的取值范围.21．已知集合{}|123A x a x a =-≤≤+，{}|14B x x =-≤≤，全集U =R ．(1)当a=1时，求(C U A)∩B；(2)若“x∈B”是“x∈A”的必要条件，求实数a的取值范围．22．命题p：“∀x∈[1,2]，x2+x−a≥0”，命题q：“∃x∈R，x2+3x+2−a=0”.(1)写出命题p的否定命题¬p，并求当命题¬p为真时，实数a的取值范围；(2)若p和q中有且只有一个是真命题，求实数a的取值范围．参考答案：1．C【分析】先求交集，再求补集，即得答案.【详解】因为A={2,3,5,7}，B={1,3,6,7}，所以A∩B={3,7}，A B={1,2,4,5,6}.又全集U={1,2,3,4,5,6,7}，所以()U故选：C2．A【分析】根据一元二次不等式的运算求出集合B，再根据并集运算即可求出结果.【详解】因为B={x∈N|x2−3x<0}，所以B={1,2}，所以A∪B={1,2,3}.故选：A.【点睛】本题主要考查了集合的并集运算，属于基础题.3．C【分析】根据集合的表示法一一判断即可；【详解】解：对于A：集合M={(3,2)}表示含有点(3,2)的集合，N={(2,3)}表示含有点(2,3)的集合，显然不是同一集合，故A错误；对于B：集合M表示的是直线x+y=1上的点组成的集合，集合N=R为数集，故B错误；对于C：集合M、N均表示含有4,5两个元素组成的集合，故是同一集合，故C正确；对于D：集合M表示的是数集，集合N为点集，故D错误；故选：C4．A【解析】根据集合M，求出C U M，然后再根据交集运算即可求出结果.【详解】M={x|−1<x<2,x∈Z}={0,1}∴()C {1,2}U M N ⋂=-. 故选:A.【点睛】本题主要考查集合的交集和补集运算，属于基础题. 5．D【分析】根据交集、补集的定义计算可得；【详解】解：∵集合U ={1,2,3,4}，M ={1,2,3}，N ={2,3} ∴M ∩N ={2,3}，则∁U (M ∩N)={1,4}．故选：D ． 6．B【分析】根据相等集合的概念，元素与集合、集合与集合之间的关系，空集的性质判断各项的正误.【详解】∈集合之间只有包含、被包含关系，故错误；②两集合中元素完全相同，它们为同一集合，则{0,1,2}⊆{2,1,0}，正确； ③空集是任意集合的子集，故∅⊆{0,1,2}，正确； ④空集没有任何元素，故∅≠{0}，错误；⑤两个集合所研究的对象不同，故{0,1},{(0,1)}为不同集合，错误； ⑥元素与集合之间只有属于、不属于关系，故错误； ∈∈∈正确. 故选：B. 7．C【分析】根据存在量词命题的否定为全称量词命题判断即可；【详解】解：命题“∃x ∈R ，2220x x -+”为存在量词命题，其否定为：∀x ∈R ，2220x x -+>；故选：C 8．B【分析】“返回家乡”的前提条件是“攻破楼兰”，即可判断出结论. 【详解】“返回家乡”的前提条件是“攻破楼兰”，故“攻破楼兰”是“返回家乡”的必要不充分条件故选：B9．C【分析】利用判别式即可得到结果.【详解】∵“∃x∈R，使x2−x−m=0”是真命题，∴Δ=(−1)2+4m≥0，解得m≥−14.故选：C10．C【分析】先要找出命题为真命题的充要条件{a|a≥4}，从集合的角度充分不必要条件应为{a|a≥4}的真子集，由选择项不难得出答案【详解】命题“∀x∈[1，2]，x2－a≤0”为真命题，可化为∀x∈[1，2]，a≥x2恒成立即只需a ≥(x2)max，即命题“∀x∈[1，2]，x2－a≤0”为真命题的的充要条件为a≥4，而要找的一个充分不必要条件即为集合{a|a≥4}的真子集，由选择项可知C 符合题意.故选：C11．D【解析】先求出集合A，再根据A⊆B，即可求解.【详解】解：当a=0时，A={0}，满足A⊆B，当a≠0时，A{0,a}，若A⊆B，∴a=1或a=2，综上所述：a=0,1或a=2．故选：D．12．C【分析】讨论B=∅,B≠∅两种情况，分别计算得到答案.【详解】当B=∅时：m+1>2m−1∴m<2成立；当B≠∅时：{m+1≤2m−1m+1≥−22m−1≤5解得：2≤m≤3.综上所述：3m 故选C【点睛】本题考查了集合的关系，忽略掉空集的情况是容易发生的错误. 13．1-【分析】根据集合相等，元素相同，即可求得a 的值. 【详解】∵集合A ={−1,0,1}，B ={0,a,a 2}，A =B ，1a ∴=-，a 2=1.故答案是：1-. 14．{(3,1)}-【分析】确定集合中的元素，得出求交集就是由求得方程组的解所得．【详解】因为M ={(x,y)|x +y =2}、N ={(x,y)|x −y =4}，所以M ∩N ={(x,y)|{x +y =2x −y =4}={(3,−1)}.故答案为：{(3,1)}-． 15．a <−1【解析】利用判别式求出条件，再由充要条件的定义说明．【详解】解析因为方程220x x a --=没有实数根，所以有440a ∆=+<，解得a <−1，因此“方程220x x a --=没有实数根”的必要条件是a <−1.反之，若a <−1，则Δ<0，方程220x x a --=无实根，从而充分性成立.故“方程220x x a --=没有实数根”的充要条件是“a <−1”. 故答案为：a <−1【点睛】本题考查充要条件，掌握充要条件的定义是解题关键． 16．{x|−1<x ≤2}【分析】根据集合的新定义，结合集合A 、B 求A −B 即可.【详解】由题设，A −B ={x|x ∈A,x ∉B}，又A ={x|−1<x <4}，B ={x|x >2}， ∴A −B ={x|−1<x ≤2}. 故答案为：{x|−1<x ≤2} 17．−32【分析】由−2∈A ,有a −1=−2,或2a 2+5a +1=−2，显然a 2+1≠−2，解方程求出实数a 的值，但要注意集合元素的互异性.【详解】因为−2∈A ，所以有a −1=−2,或2a 2+5a +1=−2，显然a 2+1≠−2，当a −1=−2时，a =−1，此时a −1=2a 2+5a +1=−2不符合集合元素的互异性，故舍去；当2a2+5a+1=−2时，解得a=−32，a=−1由上可知不符合集合元素的互异性，舍去，故a=−32.【点睛】本题考查了元素与集合之间的关系，考查了集合元素的互异性，考查了解方程、分类讨论思想.18．A∪B={x|x<−5或x>−4}；A∩(∁R B)={x|−4<x≤1}【分析】由并集、补集和交集定义直接求解即可.【详解】由并集定义知：A∪B={x|x<−5或x>−4}；∵∁R B={x|−5≤x≤1}，∴A∩(∁R B)={x|−4<x≤1}.19．（1）∅，{3}，{6}，{9}，{3,6}，{3,9}，{}6,9，{3,6,9}；（2）A∩B={3,6}，A∪∁U B={1,2,3,4,5,6,7,8}.【分析】（1）根据题意写出集合B，然后根据子集的定义写出集合B的子集；（2）求出集合A，利用交集的定义求出集合A∩B，利用补集和并集的定义求出集合A∪∁U B.【详解】（1）∵B={x|x=3n,n∈Z且x∈U}，∴B={3,6,9}，因此，B的子集有：∅，{3}，{6}，{9}，{3,6}，{3,9}，{}6,9，{3,6,9}；（2）由（1）知B={3,6,9}，则∁U B={1,2,4,5,7,8}，∵A={x|3≤x≤7且x∈U}={3,4,5,6,7}，因此，A∩B={3,6}，A∪∁U B={1,2,3,4,5,6,7,8}.【点睛】本题考查有限集合的子集，以及补集、交集和并集的运算，考查计算能力，属于基础题.20．(1) {x|x>3或x<−1}；(2) a≥6.【分析】(1)利用数轴,根据补集的定义直接求出C U A;(2)解不等式化简集合B的表示,利用数轴根据B⊆(C U A),可得到不等式,解这个不等式即可求出实数a的取值范围.【详解】(1)因为集合A={x|−1≤x≤3}.所以C U A={x|x>3或x<−1}；(2) B={x|2x−a>0}={x|x>a2}.因为B⊆(C U A),所以有362aa≤⇒≥.【点睛】本题考查了补集的定义,考查了已知集合的关系求参数问题,运用数轴是解题的关键. 21．(1)(C U A)∩B={x|−1≤x<0}(2)a <−4或0≤a ≤12【分析】（1）根据补集与交集的运算性质运算即可得出答案.（2）若“x ∈B ”是“x ∈A ”的必要条件等价于A ⊆B .讨论A 是否为空集，即可求出实数a 的取值范围.（1）当a =1时，集合{}|05A x x =≤≤，C U A ={x|x <0或x >5}， (C U A)∩B ={x|−1≤x <0}．（2）若“x ∈B ”是“x ∈A ”的必要条件，则A ⊆B ， ①当A =∅时，a −1>2a +3,∴a <−4；②A ≠∅，则a ≥−4且a −1≥−1,2a +3≤4，∴0≤a ≤12. 综上所述，a <−4或0≤a ≤12． 22．(1)a >2 (2)a >2或a <−14【分析】（1）根据全称命题的否定形式写出¬p ，当命题¬p 为真时，可转化为(x 2+x −a)min ，当x ∈[1,2]，利用二次函数的性质求解即可；（2）由（1）可得p 为真命题时a 的取值范围，再求解q 为真命题时a 的取值范围，分p 真和q 假，p 假和q 真两种情况讨论，求解即可（1）由题意，命题p ：“∀x ∈[1,2]，x 2+x −a ≥0”，根据全称命题的否定形式，¬p ：“∃x ∈[1,2]，x 2+x −a <0” 当命题¬p 为真时，(x 2+x −a)min ，当x ∈[1,2]二次函数y =x 2+x −a 为开口向上的二次函数，对称轴为x =−12 故当x =1时，函数取得最小值，即(x 2+x −a)min 故实数a 的取值范围是a >2 （2）由（1）若p 为真命题a ≤2，若p 为假命题a >2 若命题q ：“∃x ∈R ，x 2+3x +2−a =0” 为真命题则Δ=9−4(2−a)≥0，解得14a ≥-故若q 为假命题a <−14由题意，p 和q 中有且只有一个是真命题，当p 真和q 假时，a ≤2且a <−14，故a <−14；当p 假和q 真时，a >2且14a ≥-，故a >2；综上：实数a 的取值范围是a >2或a <−14。

人教A版数学必修一第一章《集合》单元测试卷.docx

& 鑫达捷致力于精品文档精心制作仅供参考 &鑫达捷必修一第一章《集合》单元测试卷一、选择题：（共12小题，每小题5分，合计60分）1.方程组⎩⎨⎧-=-=+13y x y x ，的解集不可表示为（）A.()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎩⎨⎧-=-=+13,y x y x y xB.()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎩⎨⎧==21,y x y xC.{1，2}D.{（1，2）} 2.若A ={0,2,4,6},B ={0,3,6,9},则A ∩B=（）A ．{0}B ．{6}C ．{0,6}D ．{0,3,6} 3.已知集合A ={x |-3≤x ＜3},B ={ x |2＜x ≤5}，则A ∪B ＝（） A ．{ x |2＜x ＜3} B ．{ x |-3≤x ≤5} C ．{ x |-3＜x ＜5} D ．{ x |-3＜x ≤5}4.设集合U ＝{1,2,3,4,5,6,7}，M ＝{1,2,4,7}，则 U M ð＝（） A ．U B ．{1,3,5} C ．{3,5,6} D ．{2,4,6}5.已知I ＝{0,1,2,3,4,5,6,7,8}，M ＝{1,2,4,5}，N ＝{0,3,5,7}，则()I M N U ð＝（） A.{6,8} B.{5,7} C.{4,6,7} D.{1,3,5,6,8}6.已知集合{}20,,33A m m m =-+且1A ∈，则实数m 的值为（）A.2B.1 C ．1或2 D.0，1，2均可 7若{1,2,3}⊆ A ⊆{1,2,3,4,5}，则集合A 的个数为（） A ．2 B ．3 C ．4 D ．58.已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R}，B ＝{x |0＜x ＜5，x ∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为（）A.1B.2C.3D.4 9.已知集合A={2,9},B={m 2,2}，若A=B,则实数m 的值为（） A.3 B.－3 C.9 D.±3 10.已知集合P ={1,3}，则满足P ∪Q ={1,2,3,4}的集合Q 的个数是（） A.1 B.2 C.3 D.411．已知全集R U =，{}{}1,0)3(-<=<+=x x M x x x N ，则图中阴影部分表示的集合是（）A.{}13-<<-x x Ｂ.{}03<<-x xＣ.{}01<≤-x x Ｄ.{}3-<x12.已知集合A ＝{x |a －1≤x ≤a ＋2}，B ＝{x |3＜x ＜5}，则能使A ⊇B 成立的实数a 的取值范围是（） A ．{a |3＜a ≤4} B ．{a |3≤a ≤4} C ．{a |3＜a ＜4} D ．∅ 二、填空题（共4小题，每小题5分，合计20分）13.已知集合{}{}2104M x x ,N x x ,=+≥=<则M N =I ____.14．已知全集{}2,1,0,1,2,3U =--，{}1,0,1,3M =-，{}2,0,2,3N =-，则(∁U M )N I 为____. 15．设集合{}1,2,4A =,集合{},,B x x a b a A b A ==+∈∈，则集合B 中有___个元素16.含有三个实数的集合既可表示成,,1b a a ⎧⎫⎨⎬⎩⎭，又可表示成{}2,,0a a b +，则20172018a b += .三、解答题(每题10分，合计40分)17.已知集合2{|2390}A x N x x =∈--<,{101}B =-，， 2{|320}C x x x =-+= 求A B I ,()A B C I U ,()Z C A C I .18．已知集合2{|0}A x ax ax =-= 中有且只有一个元素，求实数a 的取值范围.19．已知集合P ＝{x |x 2＋4x ＋3＝0}，Q ＝{x |x 2＋6x ＋a ＝0}，若P ∪Q ＝P ，求实数a 的取值范围．20.已知集合2{|340}A x x x =--> ，{|3}B x a x a =≤≤+ 且A B A =U ,求实数a 的取值范围.。

高中数学第一章集合与常用逻辑用语单元测试卷精品练习(含解析)新人教A版必修第一册-新人教A版高一

第一章单元测试卷一、单项选择题(本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只有一个是符合题目要求的)1．已知集合A ＝{－1,0,1,2}，B ＝{x |0≤x <2}，则A ∩B ＝( ) A ．{－1,0,1} B ．{0,1,2} C ．{0,1} D ．{1,2}2．已知集合A ＝{1,2,3,4}，B ＝{y |y ＝3x －2，x ∈A }，则A ∩B ＝( ) A ．{1} B ．{4} C ．{1,3} D ．{1,4}3．命题“∃x 0∈(0，＋∞)，x 20＋1≤2x 0”的否定为( ) A ．∀x ∈(0，＋∞)，x 2＋1>2x B ．∀x ∈(0，＋∞)，x 2＋1≤2x C ．∀x ∈(－∞，0]，x 2＋1≤2x D ．∀x ∈(－∞，0]，x 2＋1>2x4．集合A ＝{(x ，y )|y ＝3x －2}，B ＝{(x ，y )|y ＝x ＋4}，则A ∩B ＝( ) A ．{3,7} B ．{(3,7)} C ．(3,7) D ．{x ＝3，y ＝7}5．已知全集U ＝{0,1,2,3}，∁U A ＝{0,2}，则集合A 的真子集共有( ) A ．3个 B ．4个 C ．5个 D ．6个6．设x ∈R ，则“x >1”是“x 3>1”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件7．已知集合P ＝{x |x 2≤1}，M ＝{a }．若P ∪M ＝P ，则a 的取值X 围是( ) A ．{a |a ≤－1} B ．{a |a ≥1}C ．{a |－1≤a ≤1} D．{a |a ≤－1或a ≥1}8．已知a ，b ∈R ，若⎩⎨⎧⎭⎬⎫a ，b a，1＝{a 2，a ＋b,0}，则a 2 019＋b 2 019的值为( )A ．1B ．0C ．－1D ．±1二、多项选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)9．下面四个说法中错误的是( )18．(本小题满分12分)已知集合A＝{x|－2<x<4}，B＝{x|－1<x≤5}，U＝R.(1)求A∩B，A∪B；(2)求(∁R A)∩B.19.(本小题满分12分)设集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}．(1)若A＝{x∈Z|－2≤x≤5}，求A的非空真子集的个数；(2)若A∩B＝B，某某数m的取值X围．20．(本小题满分12分)设集合A＝{x|x2－3x＋2＝0}，B＝{x|ax＝1}．“x∈B”是“x∈A”的充分不必要条件，试求满足条件的实数a组成的集合．21．(本小题满分12分)是否存在实数p，使“4x＋p<0”是“x2－x－2>0”的充分条件？如果存在，求出p的取值X围．22．(本小题满分12分)设集合A＝{x|x2＋4x＝0}，B＝{x|x2＋2(a＋1)x＋a2－1＝0}．(1)若－1∈B，求a的值；(2)若B⊆A，求a的值．第一章单元测试卷1．解析：A ＝{－1,0,1,2}，B ＝{x |0≤x <2}，∴A ∩B ＝{0,1}．故选C. 答案：C2．解析：由题意得，B ＝{1,4,7,10}，所以A ∩B ＝{1,4}．答案：D3．解析：由存在量词命题的否定为全称量词命题，可得命题“∃x 0∈(0，＋∞)，x 20＋1≤2x 0”的否定为“∀x ∈(0，＋∞)，x 2＋1>2x ”，故选A.答案：A4．解析：联立A 与B 中方程得：⎩⎪⎨⎪⎧y ＝3x －2，y ＝x ＋4，消去y 得：3x －2＝x ＋4，解得：x ＝3，把x ＝3代入得：y ＝9－2＝7，∴方程组的解为⎩⎪⎨⎪⎧x ＝3，y ＝7，∵A ＝{(x ，y )|y ＝3x －2}，B ＝{(x ，y )|y ＝x ＋4}， ∴A ∩B ＝{(3,7)}，故选B. 答案：B5．解析：全集U ＝{0,1,2,3}，∁U A ＝{0,2}，则A ＝{1,3}，故集合A 的真子集共有22－1＝3个．故选A.答案：A6．解析：∵x >1，∴x 3>1.又x 3－1>0，即(x －1)(x 2＋x ＋1)>0，解得x >1，∴“x >1”是“x 3>1”的充要条件，故选C.答案：C7．解析：由P ∪M ＝P ，可知M ⊆P ，即a ∈P ，因为集合P ＝{x |－1≤x ≤1}，所以－1≤a ≤1. 答案：C8．解析：∵ba为分式，∴a ≠0，∵⎩⎨⎧⎭⎬⎫a ，b a，1＝{a 2，a ＋b,0}，∴b a＝0，即b ＝0，∴{a,0,1}＝{a 2，a,0}，∴当⎩⎪⎨⎪⎧a 2＝1，a ＝a 时，a ＝－1或a ＝1，当a ＝1时，即得集合{1,0,1}，不符合元素的互异性，故舍去，当a ＝－1时，即得集合{－1,0,1}，满足．当⎩⎪⎨⎪⎧a ＝1a 2＝a 时，a ＝1，即得集合{1,0,1}，不符合元素的互异性，故舍去，综上，a ＝－1, b ＝0.∴a2 019＋b2 019＝(－1)2 019＋02 019＝－1，故选C.答案：C9．解析：10以内的质数组成的集合是{2,3,5,7}，故A 正确；由集合中元素的无序性知{1,2,3}和{3,1,2}表示同一集合，故B 正确；方程x 2－2x ＋1＝0的所有解组成的集合是{1}，故C 错误；由集合的表示方法知0不是集合，故D 错误．故选CD.答案：CD10．解析：∵A ⊆B ，A ⊆C ，B ＝{2,0,1,8}，C ＝{1,9,3,8}， ∴B ∩C ＝{1,8}∴A ⊆(B ∩C )⇒A ⊆(1,8)，故选AC. 答案：AC11．解析：根据venn 图，可直接得出结果．由venn 图可知，ABCD 都是充要条件．故选ABCD. 答案：ABCD12．解析：A 中，－1∈B,1∈B ，但是－1－1＝－2∉B ，B 不是“完美集”，故A 说法不正确；B 中，有理数集满足“完美集”的定义，故B 说法正确；C 中，0∈A ，x 、y ∈A ，∴0－y ＝－y ∈A ，那么x －(－y )＝x ＋y ∈A ，故C 说法正确；D 中，对任意一个“完美集”A ，任取x 、y ∈A ，若x 、y 中有0或1时，显然xy ∈A ，若x 、y 均不为0、1，而1xy ＝12xy ＋12xy＝1x ＋y2－x 2－y2＋1x ＋y2－x 2－y2，x 、x －1∈A ，那么1x －1－1x ＝1x x －1∈A ，∴x (x －1)∈A ，进而x (x －1)＋x ＝x 2∈A .同理，y 2∈A ，则x 2＋y 2∈A ，(x ＋y )2∈A ， ∴2xy ＝(x ＋y )2－(x 2＋y 2)∈A .∴1x ＋y2－x 2－y2∈A ，结合前面的算式，知xy ∈A ，故D 说法正确；故选：BCD. 答案：BCD13．解析：因为A ＝{x |－1<x <2}，B ＝{x |x >0}，所以A ∩B ＝{x |0<x <2}，(∁R B )∪A ＝{x |x <2}．答案：{x |0<x <2} {x |x <2} 14．答案：必要不充分15．解析：因为集合A ＝{m ＋2,2m 2＋m }，且3∈A ，所以⎩⎪⎨⎪⎧m ＋2＝3，2m 2＋m ≠3，或⎩⎪⎨⎪⎧2m 2＋m ＝3，m ＋2≠3.解得m ＝－32.答案：－3216．解析：由M ∪N ＝M 得N ⊆M ，当N ＝∅时，2t ＋1≤2－t ，即t ≤13，此时M ∪N ＝M 成立．当N ≠∅时，由下图可得⎩⎪⎨⎪⎧2－t <2t ＋1，2t ＋1≤5，2－t ≥－2，解得13<t ≤2.综上可知，实数t 的取值X 围是{t |t ≤2}．答案：{t |t ≤2}17．解析：(1)由于命题中含有全称量词“任意的”，因而是全称量词命题；又由于“任意的”的否定为“存在一个”，因此，綈p ：存在一个x ∈R ，使x 2＋x ＋1≠0成立，即“∃x ∈R ，使x 2＋x ＋1≠0成立”；(2)由于“∃x ∈R ”表示存在一个实数x ，即命题中含有存在量词“存在一个”，因而是存在量词命题；又由于“存在一个”的否定为“任意一个”，因此，綈p ：对任意一个x 都有x 2＋2x ＋5≤0，即“∀x ∈R ，x 2＋2x ＋5≤0”． 18．解析：(1)由题意，集合A ＝{x |－2<x <4}，B ＝{x |－1<x ≤5}，所以A ∩B ＝{x |－1<x <4}，A ∪B ＝{x |－2<x ≤5}．(2)由题意，可得∁R A ＝{x |x ≤－2或x ≥4}，所以(∁R A )∩B ＝{x |4≤x ≤5}．19．解析：(1)∵A ＝{－2，－1,0,1,2,3,4,5}，∴A 的非空真子集有28－2＝254(个)． (2)∵A ∩B ＝B ，∴B ⊆A .当B ＝∅时，m ＋1>2m －1，∴m <2；当B ≠∅时，⎩⎪⎨⎪⎧m ＋1≤2m －1，m ＋1≥－2，2m －1≤5，∴⎩⎪⎨⎪⎧m ≥2，m ≥－3，m ≤3，∴2≤m ≤3.综上可知，实数m 的取值X 围是{m |m ≤3}． 20．解析：∵A ＝{x |x 2－3x ＋2＝0}＝{1,2}，又“x ∈B ”是“x ∈A ”的充分不必要条件，∴B A .当B ＝∅时，得a ＝0；当B ≠∅时，由题意得B ＝{1}或B ＝{2}．则当B ＝{1}时，得a ＝1；当B ＝{2}时，得a ＝12.综上所述，实数a 组成的集合是⎩⎨⎧⎭⎬⎫0，1，12.21．解析：x 2－x －2>0的解集是{x |x >2或x <－1}，由4x ＋p <0得x <－p4.要想使x <－p4时，x >2或x <－1成立，必须有－p4≤－1，即p ≥4.所以p ≥4时，“4x ＋p <0”是“x 2－x －2>0”的充分条件．22．解析：(1)由题意，因为－1∈B ，即x ＝－1是方程x 2＋2(a ＋1)x ＋a 2－1＝0的根，可得1－2(a ＋1)＋a 2－1＝0，即a 2－2a －2＝0，解得a ＝1±3； (2)由题意，集合A ＝{x |x 2＋4x ＝0}＝{0，－4}，因为B ⊆A ，可得①当B ＝∅时，则Δ＝4(a ＋1)2－4(a 2－1)<0，解得a <－1； ②当B ＝{0}或{－4}时，则Δ＝4(a ＋1)2－4(a 2－1)＝0，解得a ＝－1，此时B ＝{x |x 2＝0}＝{0}满足题意；③当B ＝{0，－4}时，则⎩⎪⎨⎪⎧－2a ＋1＝－4a 2－1＝0，解得a ＝1，综上可得，a ＝1或a ≤－1.。

新课程北师大版高中数学必修1第一章《集合》单元测试题(含解答)

高中数学必修1第一章《集合》单元测试题一、选择题（本大题共12小题，每小题5分，共60分）1.设集合A ={}|12,x x x N -<≤∈，集合B ={}3,2，则A B 等于（）A.{}1,2,3B.{}0,1,2,3C.{}2D.{}1,0,1,2,3-2.设集合U ={}1,2,3,4,5，A {}1,2,3=，B {}2,3,4=，则U (A B )等于（）A.{}2,3B.{}1,4,5C.{}4,5D.{}1,53.设全集U ={}1,3,5,7,集合M ={}1,|5|a -,M ⊆U ，U M ={}5,7，则a 的值为（）A.2或-8B.-8或-2C.-2或8D.2或84.满足M ⊆{}1234,,,a a a a ,且M {}{}12312,,,a a a a a =的集合M 的个数是（）A.1B.2C.3D.45.已知全集U =R ，集合A ={x |-2≤x ≤3}，B ={x |x <-1或x >4}，那么集合A ∩(u B )等于（）A.{}|24x x -≤<B. {}|34x x x ≤≥或C. {}|21x x -≤<-D. {}|13x x -≤≤6.设集合S ={x |15x x <->或},T ={x |a <x <a +8}, S ∪T =R ,则a 的取值范围是（）A. -3<a <-1B. -3≤a ≤-1C. a ≤-3或a ≥-1D. a <-3或a >-17.已知U =R ，A ={x |x >0},B ={x |x ≤-1}，则(A ∩U B )∪(BU A )等于（） A.∅ B.{x |x ≤0} C.{x |x >-1} D.{x |x >0或x ≤-1}8. 已知集合 },61|{Z m m x x M ∈+==，},312|{Z n n x x N ∈-==， =P x x |{+=2p },61Z p ∈，则P N M ,,的关系（） A ．N M =P B ．M P N = C ．M N P D ． N P M9.设全集U =R ，集合M ={x |x ≤1或x ≥3}，集合P ={}|1,R x k x k k <<+∈，且 U M P ≠∅，则实数k 的取值范围是（）A.k ＜0或k ＞3B.1＜k ＜2C.0＜k ＜3D.-1＜k ＜310.定义集合运算：A *B ={}|,,.z z xy x A y B =∈∈设A ={},2,1B {},2,0=则集合 A *B 的所有元素之和为（）A.0 B.2 C.3 D.611.设U 为全集，非空集合A 、B 满足A B ，则下列集合为空集的是（）A.A BB.A ( U B )C.B ( U A )D.(U A ) (U B )12. 下面关于集合的表示正确的个数是（）①}2,3{}3,2{≠；②}1|{}1|),{(=+==+y x y y x y x ；③}1|{>x x =}1|{>y y ； ④}1|{}1|{=+==+y x y y x x ； A ．0 B ．1 C ．2 D ．3二、填空题（本大题共4小题，每小题5分，共20分）13．已知A ={a +2，(a +1)2，a 2+3a +3}，若1∈A ，则a = ；14．集合P =(){},0x y x y +=，Q =(){},2x y x y -=，则P ∩Q = ；15．已知集合A =126x NN x ⎧⎫∈∈⎨⎬-⎩⎭，用列举法表示集合A = ； 16．设P 是一个数集，且至少含有两个数.若对任意a 、b ∈P ，都有a +b 、a -b 、ab 、a b∈P (除数b ≠0)，则称P 是一个数域。

人教版高一上学期数学第一章《集合》单元测试卷

个数为（）
A．1
B．2
C．3
D．4
7．（5 分）已知集合 A＝{x|x＜a}，B＝{x|x2﹣3x+2＜0}，若 A∩B＝B，则实数 a 的取值范围是（）
A．（﹣∞，1]
B．（﹣∞，1）
C．[2，+∞）
ቤተ መጻሕፍቲ ባይዱ
D．（2，+∞）
8．（5 分）已知集合 A＝{x|x2﹣2tx+t+6＝0}，B＝{x|x＜0}，若 A∩B≠∅，则实数 t 的取值范围是（）
A．0
B．1
C．2
D．0 或 1 或 2
10．（5 分）已知 A＝{x|2x2﹣ax+b＝0}，B＝{x|6x2+（a+2）x+5+b＝0}，且
，则 A∪B 中的元素
是（）
第 1页（共 2页）
A．﹣4
B．1
C．
D．
11．（5 分）已知集合 A＝{x∈Z|x2﹣x﹣2≥0}，则∁ZA 中的元素是（）
20．已知集合 A＝{x∈R|ax2﹣3x﹣4＝0}．（1）若 A 中有两个元素，求实数 a 的取值范围；（2）若 A 中至多有一个元素，求实数 a 的取值范围．
21．设集合 A＝{x|x2+4x＝0}，B＝{x|x2+2（a+1）x+a2﹣1＝0}．（1）若 A∩B＝B，求实数 a 的值；（2）若 A∪B＝B，求实数 a 的值．
A．（﹣6，﹣2） B．[﹣6，﹣2]
C．（﹣∞，﹣2] D．（﹣∞，﹣6]
二、多项选择题：（本题共 4 小题，每小题 5 分，共 20 分。在每小题给出的选项中，有多项符合题目要求。
全部选对的得 5 分，有选错的得 0 分，部分选对的得 3 分。）

苏教版数学必修一《第1章集合》单元测试(附详细答案)

(时间：120分钟；满分：160分)一、填空题(本大题共14小题，每小题5分，共70分，请把答案填在题中横线上)1.下列六个关系式：①{a ，b }⊆{b ，a }；②{a ，b }＝{b ，a }；③{0}＝∅；④0∈{0}；⑤∅∈{0}；⑥∅⊆{0}．其中正确的个数为________．解析：①②④⑥是正确的．答案：42.下列各对象可以组成集合的是________．①与1非常接近的全体实数；②某校2013～2014学年度第一学期全体高一学生；③高一年级视力比较好的同学；④与无理数π相差很小的全体实数．解析：据集合的概念判断，只有②可以组成集合．答案：②3.已知全集U ＝{－1，0，1，2}，集合A ＝{－1，2}，B ＝{0，2}，则(∁U A )∩B ＝________.解析：∁U A ＝{0，1}，故(∁U A )∩B ＝{0}．答案：{0}4.集合A ＝{0，2，a }，B ＝{1，a 2}．若A ∪B ＝{0，1，2，4，16}，则a 的值为________．解析：∵A ∪B ＝{0，1，2，a ，a 2}，又A ∪B ＝{0，1，2，4，6}，∴{a ，a 2}＝{4，16}，∴a ＝4.答案：45.设集合A ＝{－1，4，8}，B ＝{－1，a ＋2，a 2＋4}，若A ＝B ，则实数a 的值为________．解析：∵A ＝B ，∴①⎩⎨⎧a ＋2＝4a 2＋4＝8或②⎩⎨⎧a ＋2＝8a 2＋4＝4，由①得a ＝2，此时B ＝{－1，4，8}满足题意，②无解，∴a ＝2.答案：26.已知集合A ＝{3，m 2}，B ＝{－1，3，2m －1}，若A ⊆B ，则实数m 的值为________．解析：∵A ⊆B ，∴A 中元素都是B 的元素，即m 2＝2m －1，解得m ＝1.答案：17.若集合A ＝{x |x ≥3}，B ＝{x |x <m }满足A ∪B ＝R ，A ∩B ＝∅，则实数m ＝________.解析：结合数轴知，当且仅当m ＝3时满足A ∪B ＝R ，A ∩B ＝∅.答案：38.设集合A ＝{1，4，x }，B ＝{1，x 2}，且A ∪B ＝{1，4，x }，则满足条件的实数x 的个数是________．解析：由题意知x 2＝4或x 2＝x ，所以x ＝0，1，2，－2，经检验知x ＝0，2，－2符合题意，x ＝1不符合题意，故有3个．答案：39.已知集合M ⊆{4，7，8}，且M 中至多有一个偶数，则这样的集合共有________个．解析：M 可以为∅，{4}，{4，7}，{8}，{8，7}，{7}．答案：610.已知集合A ＝{x |y ＝ 1－x 2，x ∈Z }，B ＝{y |y ＝x 2＋1，x ∈A }，则A ∩B 为________．解析：由1－x 2≥0得，－1≤x ≤1，∵x ∈Z ，∴A ＝{－1，0，1}．当x ∈A 时，y ＝x 2＋1∈{2，1}，即B ＝{1，2}，∴A ∩B ＝{1}．答案：{1}11.集合P ＝{(x ，y )|x ＋y ＝0}，Q ＝{(x ，y )|x －y ＝2}，则P ∩Q ＝________.解析：P∩Q＝{(x ，y )|⎩⎨⎧x ＋y ＝0，x －y ＝2，}＝{(x ，y )|⎩⎨⎧x ＝1，y ＝－1，}＝{(1，－1)}．答案：{(1，－1)}12.设P 和Q 是两个集合，定义集合P －Q ＝{x |x ∈P，且x ∉Q}，若P ＝{1，2，3，4}，Q ＝{x |x ＋12<2，x ∈R }，则P －Q ＝________.解析：由定义P －Q ＝{x |x ∈P，且x ∉Q}，求P －Q 可检验P ＝{1，2，3，4}中的元素在不在Q ＝{x |x ＋12<2，x ∈R }中，所有在P 中不在Q 中的元素即为P －Q 中的元素，故P －Q ＝{4}．答案：{4}13.设P 、Q 为两个非空实数集合，定义集合P*Q ＝{z |z ＝ab ，a ∈P ，b ∈Q}，若P ＝{－1，0，1}，Q ＝{－2，2}，则集合P*Q 中元素的个数是________．解析：按P*Q 的定义，P*Q 中元素为2，－2，0，共3个．答案：314.设A 是整数集的一个非空子集，对于k ∈A ，如果k －1∉A 且k ＋1∉A ，那么k 是A 的一个“孤立元”，给定S ＝{1，2，3，4，5，6，7，8}，由S 的3个元素构成的所有集合中，不含“孤立元”的集合共有________个．解析：不含“孤立元”的集合就是在集合中有与k 相邻的元素，故符合题意的集合有：{1，2，3}，{2，3，4}，{3，4，5}，{4，5，6}，{5，6，7}，{6，7，8}，共6个．答案：6二、解答题(本大题共6小题，共90分，解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)已知全集U ＝R ，A ＝{x |2≤x <5}，集合B ＝{x |3<x <9}．求(1)∁U (A ∪B )；(2)A ∩∁U B .解：(1)∵A ∪B ＝{x |2≤x <9}，∴∁U (A ∪B )＝{x |x <2或x ≥9}．(2)∵∁U B ＝{x |x ≤3或x ≥9}，∴A ∩∁U B ＝{x |2≤x ≤3}．16.(本小题满分14分)设全集U ＝{2，4，－(a －3)2}，集合A ＝{2，a 2－a ＋2}，若∁U A ＝{－1}，求实数a 的值．解：由∁U A ＝{－1}，可得⎩⎨⎧－1∈U ，－1∉A ，所以⎩⎨⎧－（a －3）2＝－1，a 2－a ＋2≠－1，解得a ＝4或a ＝2. 当a ＝2时，A ＝{2，4}，满足A ⊆U ，符合题意；当a ＝4时，A ＝{2，14}，不满足A ⊆U ，故舍去．综上，a 的值为2.17.(本小题满分14分)已知集合A ＝{x |x 2－3x －10≤0}，集合B ＝{x |p ＋1≤x ≤2p －1}．若B ⊆A ，求实数p 的取值范围．解：由x 2－3x －10≤0得－2≤x ≤5，故A ＝{x |－2≤x ≤5}．①当B ≠∅时，即p ＋1≤2p －1⇒p ≥2.由B ⊆A 得：－2≤p ＋1且2p －1≤5，解得－3≤p ≤3.∴2≤p ≤3.②当B ＝∅时，即p ＋1>2p －1⇒p <2.由①②得p 的取值范围是p ≤3.18.(本小题满分16分)已知集合A ＝{x ∈R |ax 2－3x ＋2＝0，a ∈R }．(1)若A 是空集，求a 的取值范围；(2)若A 中只有一个元素，求a 的值；(3)若A 中至多只有一个元素，求a 的取值范围．解：(1)若A 是空集，则方程ax 2－3x ＋2＝0没有根，则a ≠0且Δ＝9－8a <0，即a >98. (2)若A 中只有一个元素，则方程ax 2－3x ＋2＝0有一个根，①当a ≠0且Δ＝9－8a ＝0时，则a ＝98； ②当a ＝0时，方程为－3x ＋2＝0，只有一个根．综上，a ＝0或98. (3)若A 中至多只有一个元素，则A 是空集或A 只有一个元素，故a ＝0或a ≥98. 19.(本小题满分16分)某班50名学生中，会讲英语的有36人，会讲日语的有20人，既会讲英语又会讲日语的有14人，问既不会讲英语又不会讲日语的有多少人？解：设全集U ＝{某班50名学生}，A ＝{会讲英语的学生}，B ＝{会讲日语的学生}，A ∩B ＝{既会讲英语又会讲日语的学生}，则由韦恩图知，既不会英语又不会日语的学生有：50－22－14－6＝8(人)．20.(本小题满分16分)已知集合A ＝{x |x 2－2x －8＝0}，B ＝{x |x 2＋ax ＋a 2－12＝0}，若A ∪B ≠A ，求实数a 的取值范围．解：若B ∪A ＝A ，则B ⊆A ，又A ＝{x |x 2－2x －8＝0}＝{－2，4}，所以集合B 有以下三种情况：①当B ＝∅，有Δ＝a 2－4(a 2－12)<0⇒a 2>16⇒a <－4或a >4；②当B 是单元素集合时，有Δ＝0⇒a 2＝16⇒a ＝－4或a ＝4.若a ＝－4，则B ＝{2}⊄A ，若a ＝4，则B ＝{－2}⊆A ；③当B ＝{－2，4}时，有－2，4是关于x 的方程x 2＋ax ＋a 2－12＝0的两根 ⇒⎩⎨⎧－2＋4＝－a （－2）×4＝a 2－12⇒a ＝－2. 此时，B ＝{x |x 2－2x －8＝0}＝{－2，4}⊆A .综上可知，B ∪A ＝A 时，实数a 的取值范围是a <－4或a ≥4或a ＝－2. 所以B ∪A ≠A 时，实数a 的取值范围为－4≤a <4，且a ≠－2.。

高中数学单元测试题必修1第一章《集合》

高中数学单元测试题必修1第一章《集合》一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）.1．下列集合的表示法正确的是（ A ）A ．}1|{}1|{=+==+y x y y x xB ．第二、四象限内的点集可表示为{}(,)0,,x y xy x R y R ≤∈∈；C ．集合{}1,2,2,5,7；D ．不等式14x -<的解集为{}5x <2．已知集合}1,1{-=A ，}1|{==mx x B ，且A B A = ，则m 的值为A ．1B ．1-C ．1或1-D ．1或1-或0 3．设全集}7,6,5,4,3,2,1{=U ，集合}5,3,1{=A ，集合}5,3{=B ，则A ．U AB = B ．()U U A B = ðC ．()U U A B = ðD ．()()U U U A B = 痧4．设U ＝{1，2，3，4} ，若A B ＝{2}，(){4}U A B = ð，()(){1,5}U U A B = 痧，则下列结论正确的是A ．A ∉3且B ∉3 B ．A ∈3且B ∉3C ．A ∉3且B ∈3D ．A ∈3且B ∈35．设全集是实数集R ，{|22}M x x =-≤≤，N x x =<{|}1，则R M N ð等于A ．{|}x x <-2B ．{|}x x -<<21C ．{|}x x <1D ．{|}x x -≤<216．设U 为全集，Q P ,为非空集合，且P ÜQ ÜU ,下面结论中不正确．．．的是 A ．()U P Q U = ð B ．()U P Q = ðφ C ．P Q Q =D ．()U Q P = ðφ7．下列四个集合中，是空集的是 A ．}33|{=+x x B ．},,|),{(22R y x x y y x ∈-=C ．}0|{2≤x x D ．}01|{2=+-x x x8．设集合},412|{Z k k x x M ∈+==，},214|{Z k k x x N ∈+==，则 A ．M N = B ．M ÜNC ．N ÜMD ．M N ϕ=9．表示图形中的阴影部分A ．()()A CBC B ．()()A B A CC ．()()A B B CD ．()A B C 10．已知全集{1,2,3,4,5,6,7},{3,4,5},{1,3,6}U M N ===，则集合{2,7}等于A ．M NB ．U U M N 痧C ．U U M N 痧D ．M N 11．满足{1，2，3} ÜM Ü{1，2，3，4，5，6}的集合M 的个数是A ．8B ．7C ．6D ．512．下列命题之中，U 为全集时，不正确的是A ．若AB = φ，则()()U U A B U = 痧 B ．若A B = φ，则A = φ或B = φC ．若A B = U ，则()()U U A B = 痧φD ．若A B = φ，则==B A φ 二、填空题：请把答案填在题中横线上（每小题5分，共20分）.13．若集合{(,)|20240}{(,)|3}x y x y x y x y y x b +-=-+=⊆=+且，则b = ．14．设集合}0|),{(111=++=c x b x a y x A ，}0|),{(222=++=c x b x a y x B ，则方程)(111c x b x a ++0)(222=++c x b x a 的解集为 .15．已知集合}023|{2=+-=x ax x A 至多有一个元素，则a 的取值范围 .16．设集合{|12},{|}M x x N x x a =-≤<=≤，若M N ≠∅ ，则a 范围是 .三、解答题：解答应写出文字说明、证明过程或演算步骤(共70分).17．（10分）已知集合A ＝{x |x ＝m 2－n 2,m ∈Z ,n ∈Z},求证：（1）3∈A ；（2）偶数4k -2 (k ∈Z)不属于A.CB A18．（12分）（1）P ＝{x |x 2－2x －3＝0}，S ＝{x |ax ＋2＝0}，S ⊆P ，求a 取值.（2）A ＝{－2≤x ≤5} ，B ＝{x |m ＋1≤x ≤2m －1}，B ⊆A,求m 的取值范围.19．（12分）在1到100的自然数中有多少个能被2或3整除的数？20．（12分）已知集合22{|320},{|20}A x x x B x x x m =-+==-+=且=B A ,A 求m的取值范围.21．设}019|{22=-+-=a ax x x A ，}065|{2=+-=x x x B ，}082|{2=-+=x x x C .①当A B =A B 时，求a 的值；②当φÜA B ，且A C =φ时，求a 的值； ③当A B =A C ≠φ时，求a 的值；（12分）22．（12分）设1a ，2a ，3a ，4a ，5a 为自然数，A={1a ，2a ，3a ，4a ，5a }， B={21a ，22a ，23a ，24a ，25a }，且1a <2a <3a <4a <5a ，并满足A ∩B={1a ，4a }， 1a ＋4a =10，A ∪B 中各元素之和为256，求集合A ？高中数学单元测试题必修1第一章《集合》一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）.1．下列集合的表示法正确的是（ A ）A ．}1|{}1|{=+==+y x y y x xB ．第二、四象限内的点集可表示为{}(,)0,,x y xy x R y R ≤∈∈；C ．集合{}1,2,2,5,7；D ．不等式14x -<的解集为{}5x <已知集合{(,)|2},{(,)|4}M x y x y N x y x y =+==-=，那么集合M N 为（D ）A ．3,1x y ==-B ．(3,1)-C ．{3,1}-D ．{(3,1)}-2．已知集合}1,1{-=A ，}1|{==mx x B ，且A B A = ，则m 的值为（D ） A ．1 B ．1- C ．1或1- D ．1或1-或03．设全集}7,6,5,4,3,2,1{=U ，集合}5,3,1{=A ，集合}5,3{=B ，则（C ） A ．U A B = B ．()U U A B = ð C ．()U U A B = ð D ．()()U U U A B = 痧4．设U ＝{1，2，3，4} ，若A B ＝{2}，(){4}U A B = ð，()(){1,5}U U A B = 痧，则下列结论正确的是（ B ）A ．A ∉3且B ∉3 B ．A ∈3且B ∉3C ．A ∉3且B ∈3D ．A ∈3且B ∈35．设全集是实数集R ，{|22}M x x =-≤≤，N x x =<{|}1，则R M N ð等于（A ）A ．{|}x x <-2B ．{|}x x -<<21C ．{|}x x <1D ．{|}x x -≤<21 设集合{1,2,3,4,5,6},{|26}P Q x R x ==∈≤≤，那么下列结论正确的是（D ）A ．P Q P =B ．P Q Q ÝC ．P Q Q =D ．P Q P Ü 集合{|22},{|13}A x x B x x =-<<=-≤<，那么A B = （A ）A ．{|23}x x -<<B ．{|12}x x ≤<C ．{|21}x x -<≤D ．{|23}x x <<以下四个关系：φ}0{∈，∈0φ，{φ}}0{⊆，φÜ}0{,其中正确的个数是（ A ）A ．1B ．2C ．3D ．4 下列五个写法：①{}{}00,1,2;∈②{}0;∅⊆③{}{}0,1,21,2,0;⊆④0;∈∅⑤0 ∅.=∅ 其中错误．．写法的个数为（C ） A ．1 B ．2 C ．3 D ．4 如果集合{}1->=x x P ，那么（D ）A ．P ⊆0B ．{}P ∈0C ．P ∈∅D ．{}P ⊆06．设U 为全集，Q P ,为非空集合，且P ÜQ ÜU ,下面结论中不正确．．．的是（ B ） A ．()U P Q U = ð B ．()U P Q = ðφ C ．P Q Q =D ．()U Q P = ðφ 7．下列四个集合中，是空集的是（ D ）A ．}33|{=+x xB ．},,|),{(22R y x x y y x ∈-=C ．}0|{2≤x xD ．}01|{2=+-x x x8．设集合},412|{Z k k x x M ∈+==，},214|{Z k k x x N ∈+==，则（ B ） A ．M N = B ．M ÜNC ．N ÜMD ．M N ϕ= 已知集合 },61|{Z m m x x M ∈+==，},312|{Z n n x x N ∈-==， =P x x |{+=2p },61Z p ∈，则P N M ,,的关系（B ） A ．N M =ÜP B ．M ÜP N = C ．M ÜN ÜP D ． N ÜP ÜM设集合},3|{Z k k x x M ∈==，},13|{Z k k x x P ∈+==，},13|{Z k k x x Q ∈-==，若Q c P b M a ∈∈∈,,，则∈-+c b a（ C ） A ．M B ． P C ．Q D ．P M ⋃9．表示图形中的阴影部分（ A ）A ．()()A CBC B ．()()A B A CC ．()()A B B CD ．()A B CB A10．已知全集{1,2,3,4,5,6,7},{3,4,5},{1,3,6}U M N ===，则集合{2,7}等于（ B ）A ．M NB ．U U M N 痧C ．U U M N 痧D ．M N 11．满足{1，2，3} ÜM Ü{1，2，3，4，5，6}的集合M 的个数是（C ） A ．8 B ．7 C ．6 D ．5满足{,}M N a b = 的集合N M ,共有（C ）A ．7组B ．8组C ．9组D ．10组满足条件{1}{1,2,3}M = 的集合M 的个数是（ C ）A ．4B ．3C ．2D ．112．下列命题之中，U 为全集时，不正确的是（B ）A ．若AB = φ，则()()U U A B U = 痧 B ．若A B = φ，则A = φ或B = φC ．若A B = U ，则()()U U A B = 痧φD ．若A B = φ，则==B A φ 二、填空题：请把答案填在题中横线上（每小题5分，共20分）.13．若集合{(,)|20240}{(,)|3}x y x y x y x y y x b +-=-+=⊆=+且，则b =2．14．设集合}0|),{(111=++=c x b x a y x A ，}0|),{(222=++=c x b x a y x B ，则方程)(111c x b x a ++0)(222=++c x b x a 的解集为A ∪B.15．已知集合}023|{2=+-=x ax x A 至多有一个元素，则a 的取值范围a =0或89≥a . 16．设集合{|12},{|}M x x N x x a =-≤<=≤，若M N ≠∅ ，则a 范围是{|1}a a -?设集合(]{}2,,|1,M m P y y x x R =-∞==-∈，若M P =∅ ，则实数m 范围是(D ) A ．1m ≥- B ．1m >- C ．1m ≤- D ．1m <-三、解答题：解答应写出文字说明、证明过程或演算步骤(共70分).17．（10分）已知集合A ＝{x |x ＝m 2－n 2,m ∈Z ,n ∈Z},求证：（1）3∈A ；（2）偶数4k -2 (k ∈Z)不属于A.证明：（1）3＝22－12 ∴3∈A ；（2）设4k －2∈A,得存在m,n ∈Z,使4k －2＝m 2－n 2成立.（m －n ）(m ＋n )＝4k －2，当m,n 同奇或同偶时，m －n,m ＋n 均为偶数.∴（m －n ）(m ＋n )为4的倍数，与4k －2不是4 倍数矛盾.当m,n 同分别为奇，偶数时，m －n,m ＋n 均为奇数.(m －n)(m ＋n )为奇数，与4k －2是偶数矛盾.∴4k －2∉A18．（12分）（1）P ＝{x |x 2－2x －3＝0}，S ＝{x |ax ＋2＝0}，S ⊆P ，求a 取值.（2）A ＝{－2≤x ≤5} ，B ＝{x |m ＋1≤x ≤2m －1}，B ⊆A,求m 的取值范围.解：（1）a ＝0,S ＝φ，φ⊆P 成立 a ≠0，S ≠φ，由S ⊆P ，P ＝{3，－1}得3a ＋2＝0，a ＝23-或－a ＋2＝0，a ＝2； ∴a 值为0或23-或2. （2）B ＝φ，即m ＋1>2m －1,m <2 φ⊆A 成立.B≠φ，由题得121,21,215m m m m +≤-⎧⎪-≤+⎨⎪-≤⎩得2≤m ≤3，∴m <2或2≤m ≤3 ，即m ≤3为取值范围.注：（1）特殊集合φ作用，常易漏掉；（2合思想常使集合问题简捷比. 用描述法表示图中的阴影部分（包括边界）解：}0,121,231|),{(≥≤≤-≤≤-xy y x y x19．（12分）在1到100的自然数中有多少个能被2或3整除的数？解：设集合A 为能被2整除的数组成的集合，集合B 为能被3整除的数组成的集合，则A B 为能被2或3整除的数组成的集合，A B 为能被2和3（也即6）整除的数组成的集合.显然集合A 中元素的个数为50，集合B 中元素的个数为33，集合A B 中元素的个数为16，可得集合A B 中元素的个数为50+33-16=67.某市数、理、化竞赛时，高一某班有24名学生参加数学竞赛，28名学生参加物理竞赛，19名学生参加化学竞赛，其中参加数、理、化三科竞赛的有7名，只参加数、物两科的有5名，只参加物、化两科的有3名，只参加数、化两科的有4名。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

集合单元测试题一、选择题 1．下列表示①②③ ④中,正确的个数为 ( )A 、 1 B 、 2 C 、 3 D 、 4
2 50名同学参加跳远和铅球测验，跳远和铅球测验成绩分别为及格40人和31人，2项测验成绩均不及格的有4人，2项测验成绩都及格的人数是（）A 35 B 25 C 28 D 15
3．满足
的集合的个数为（）（A ）6 （B ） 7 （C ） 8 （D ）9 4．方程组⎩⎨⎧=-=+91
22y x y x 的解集是（）A ．()5,4 B ．()4,5- C ．(){}4,5- D ．(){}4,5-
5 设全集U ＝R ，集合A ＝(1，＋∞)，集合B ＝(－∞，2)。

则CU (A ∩B)＝（）
A ．(－∞，1)∪(2，＋∞)
B ．(－∞，1)∪[2，＋∞)
C ．(－∞，1]∪(2，＋∞)
D ．(－∞，1]∪[2，＋∞)
6.设集合},412|{Z k k x x M ∈+=
=，},214|{Z k k x x N ∈+==，则（）
A N M =
B M N
C N M
D M N φ= 7．设
，，若，则实数的取值范围是（）（A ）
（B ）（C ）（D ） 8．如图所示，
，，是的三个子集，则阴影部分所表示的集合是（）（A ）（B ）
（C ）（D ）
9.设I 为全集，S 1、S 2、S 3是I 上的三个非空子集，且S 1∪S 2∪S 3=I ，则下列论断正确
的是（）A 、 C I S 1∩（S 2∪S 3）=∅ B 、 S 1⊆（C I S 2∩C I S 3）
C 、 C I S 1∩C I S 2∩C I S 3=∅
D 、 S 1⊆（C I S 2∪C I S 3）
10. 设全集
，若，，，则下列结论正确的是（）（A ）且（B ）且（C ）且（D ）
且 11.设P 、Q 为两个非空实数集合，定义集合p+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若
}6,2,1{=Q ，则P+Q 中元素的个数是（） A ．9 B ．8 C ．7 D ．6
12．设⊕是R 上的一个运算,A 是R 上的非空子集,若对任意的a 、b ∈A ，
有a ⊕b ∈A ，则称A 对运算⊕封闭，下列数集对加法、减法、乘法和除法（除数不等于0）四则运算都封闭的是（） A 自然数集 B 整数集 C 有理数集 D 无理数集
二、填空题
13.Ａ＝｛a ²,a+1,－3｝，Ｂ＝｛a －3,2a －1,a ²+1｝，若Ａ∩Ｂ＝｛－３｝，那么a ＝_______.
14.已知{}R x x x y y M ∈+-==,34|2，{}
R x x x y y N ∈++-==,82|2则__________=N M
15．若集合只有一个元素，则实数的值为 16.设全集{}(,),U x y x y R =∈,集合
2(,)12y M x y x ⎧+⎫==⎨⎬-⎩⎭，{}(,)4N x y y x =≠-, 那么
()()U U C M C N 等于________________ 三、解答题
17．设全集合
，，，
求
，，，
18．已知集合{}2|0A x x px q =-+=，{}2|0B x x x r =++=，{}1A
B =，{}1,2A B =-，求,,p q r 的
值．
19.已知,}221{},102{P Q a x a x Q x x P ⊆+≤≤-=≤≤=若求a 的范围。

20.已知集合
，，，求实数的取值范围。

21．集合{}22|190A x x ax a =-+-=，{}2|560B x x x =-+=，{}2|280C x x x =+-=
满足,A B φ≠，,A C φ=求实数a 的值。

22．设S 为满足下列两个条件的实数所构成的集合：
①S 内不含1； ②若a S ∈，则11S a
∈- 解答下列问题：（Ⅰ）若2S ∈，则S 中必有其他两个元素，求出这时的集合S ；
（Ⅱ）有人断定集合S 可以是单元素的集合，请你判断他的断言是否正确，说明理由；
（III ）若集合S ≠∅，试证集合S 中的元素个数必为3的整数倍，并给出除（Ⅰ）中以外的一个集合S ．。