工程力学习题答案5廖明成教材
大学《工程力学》课后习题解答-精品
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
工程力学习题册第五章-答案

第五章拉伸和压缩一、填空题1•轴向拉伸或压缩的受力特点是作用于杆件两端的外力大小相等—和方向相反,作用线与—杆件轴线重合_。
其变形特点是杆件沿_轴线方向伸长或缩短—。
其构件特点是_等截面直杆_。
2•图5-1所示各杆件中受拉伸的杆件有AB、BC、AD、DC,受压缩的杆件有BE、BD 。
3•内力是外力作用引起的,不同的__外力—引起不同的内力,轴向拉、压变形时的内力称为_轴力__。
剪切变形时的内力称为剪力__,扭转变形时的内力称为—扭矩__,弯曲变形时的内力称为__剪力与弯矩。
4•构件在外力作用下,单位面积上的内力称为应力。
轴向拉、压时,由于应力与横截面垂直, 故称为—正应力___;计算公式彷=F N/A ;单位是_N/怦_或___ __。
1MPa= _106N/m2= _1__N/mm。
5•杆件受拉、压时的应力,在截面上是一均匀一分布的。
6•正应力的正负号规定与轴力相同, 拉伸时的应力为—拉应力__,符号为正。
压缩时的应力为__压应力-,符号位负。
7•为了消除杆件长度的影响,通常以绝对变形除以原长得到单位长度上的变形量,称为相对变形_,又称为线应变,用符号邑表示,其表达式是E= △ L/L。
8. 实验证明:在杆件轴力不超过某一限度时,杆的绝对变形与_轴力__和杆长__成正比,而与一横截面面积成反比。
9. 胡克定律的两种数学表达式为= E s 和△ L= F N L O/EA E称为材料的_弹性模量_。
它是衡量材料抵抗弹性变形能力的一个指标。
10. 实验时通常用低碳钢代表塑性材料,用灰铸铁代表脆性材料。
11. 应力变化不大,应变显着增大,从而产生明显的塑性变形—的现象,称为屈服_ 。
12. 衡量材料强度的两个重要指标是_屈服极限一和_抗拉强度_。
13. 采用—退火___的热处理方法可以消除冷作硬化现象。
14. 由于铸铁等脆性材料的—抗拉强度一很低,因此,不宜作为承拉零件的材料。
15. 工程上把材料丧失—工作能力—时的应力称为危险应力或—极限应力—,以符号仃°表示。
(建筑工程管理)工程力学习题廖明成

(建筑工程管理)工程力学习题廖明成*第十五章能量法简介习题15.1试计算图标结构的变形能。
略去剪切影响,为已知。
对于只受拉压变形的杆件,需要考虑拉压的变形能。
解:(a)如图a所示,因结构和载荷均对此,所以利用静力学平衡条件,可很容易地得到约束反力并且只取梁的一般进行计算。
AB段梁任一截面上的弯矩方程为梁的应变能为(b)如图b所示,利用静力学平衡条件,求的约束反力为梁各段的弯矩方程为BA段AC段应变能为(c)如图c所示,各杆段的弯矩方程为AB段BC段刚架的应变能为(d)如图d所示利用静力学平衡条件求得梁AC的支座反力和杆BD的轴力为(拉)梁各段的弯矩方程为CB段BA段结构的应变能为(e)如图e所示利用静力学平衡条件,得刚架的支座反力和轴力为,刚架各段的弯矩方程为AB段BC段结构的应变能为15.2试用卡氏定理计算习题15-1中各结构中截面A的铅垂位移以及B截面((e)图)的转角。
解:(a)受力分析如下图所示,有分析可得在x方向是不受力,只受y方向的力由于在A处并无垂直外力,为此,设想在A处加一垂直外力,这时求解共同作用下的支座反力,A受力分析如图所示,由平衡条件求得弯矩及对的偏导数为BA段AC段截面A的铅垂位移为(2)由于在A处并无垂直外力,为此,设想在A处加一垂直外力,这时求解共同作用下的支座反力,A受力分析如图所示,由平衡条件求得弯矩及对的偏导数为BA段AC段将以上结果代入得截面A的铅垂位移为(3)由于在A处并无垂直集中外力,为此,设想在A处加一垂直外力,这时求解共同作用下的支座反力,A受力分析如图所示,由平衡条件求得弯矩及对的偏导数为AB段BC段将以上结果代入得截面A的铅垂位移为(4)题中受力分析如图所示,由平衡条件求得弯矩及对的偏导数为AB段BC段同时求出BD轴力及偏导数为将以上结果代入得(5)1.题中受力分析如图所示,由平衡条件求得弯矩及对的偏导数为AB段BC段将以上结果代入得截面A的铅垂位移为2.由于在截面B处并无弯矩,设想在截面B处加一个弯矩,在杆件截面B上加了,如图所示,这时求共同作用下的支座反力,由平衡条件求得弯矩及对的偏导数为AB段BC段将以上结果代入得即15.3图示桁架,在节点B处承受铅垂载荷作用,试用卡氏定理计算点节B的水平位移。
《工程力学》课后习题答案全集

(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章 刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
解:如图示,车轮在A点打滑, m/s, =rad/s,车轮作平面运动,以O为基点。
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
解: 是四杆机构。速度分析如图。点P是AB杆和轮Ⅱ的速度瞬心,故:
杆 的角速度为: rad/s
两轮齿合点M的速度和轮Ⅰ的角速度分别为:
, rad/s
6.在图所示星齿轮结构中,齿轮半径均为 cm。试求当杆OA的角速度 rad/s、角加速度 时,齿轮Ⅰ上B和C两点的加速度。
解:(1)B为轮Ⅰ的速度瞬心,
即
以轮为研究对象列方程
⑦
;
将①和③代入②得
由于轮做纯滚动
8.如图所示两等长杆AB与BC在点B用铰链连接,又在杆的D、E两点连一弹簧。弹簧的刚度系数为k,当距离AC等于a时,弹簧内拉力为零,不计各构件自重与各处摩擦。如在点C作用一水平力F,杆系处于平衡,求距离AC之值。
解:(图)
弹簧力如图:为
各力作用点横向坐标及其变分为
解:火箭在空中飞行时,若只研究它的运行轨道问题,可将火箭作为质点处理。这时画出其受力和坐标轴 、 如下图所示,可列出平衡方程。
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触.(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1—2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1—3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计.(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0.如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图第二章 平面力系 9所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m.电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力.题2—3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
工程力学课后题答案3 廖明成

第三章力偶系习题3.1 如图3.1A、B、C、D均为滑轮,绕过B、D两轮的绳子两端的拉力为400N,绕过A、C两轮的绳子两端的拉力F为300N,α=30°。
求这两力偶的合力偶的大小和转向。
滑轮大小忽略不计。
题3.1图解:两力偶的矩分别为1400sin60240400cos60200123138M N mm =•+•=•2300sin30480300cos30200123962M N mm =•+•=•合力偶矩为12247.1M M M N m=+=•(逆时针转向)3.2 已知粱AB上作用一力偶,力偶矩为M,粱长为L,粱重不计。
求在图3.2中a,b,c三种情况下,支座A和B的约束力。
题3.2图解:AB 梁受力如个图所示, 由0iM=∑,对图(a )(b)有0RA F l M -=得RA NB M F F l==对图(c )有cos 0RA F l M θ-=得cos RA NBMF F l θ==3.3 齿轮箱的两个轴上作用的力偶如图所示,它们的力偶矩的大小分别为M 1=500 N ·m ,M 2=125N ·m 。
求两螺栓处的铅垂约束力。
图中长度单位为cm 。
题3.3图FF 'NBF RAF RA F F 3l NBF RAF解:1200M Fd M M =+-=合, 750F N =-力的方向与假设方向相反3.4 汽锤在锻打工件时,由于工件偏置使锤头受力偏心而发生偏斜,它将在导轨DA 和BE 上产生很大的压力,从而加速导轨的磨损并影响锻件的精度。
已知锻打力F=1000kN ,偏心距e =20mm ,试求锻锤给两侧导轨的压力。
题3.4图N1F N2F解:锤头受力如图,这是个力偶系的平衡问题, 由10,0iN MF e F h =-=∑解得1220N N F F h==KN3.5四连杆机构在图示位置平衡,已知OA =60 m ,BC =40 cm , 作用在BC 上力偶的力偶矩大小M 1=1 N ·m ,试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力F AB 。
工程力学课后题答案廖明成
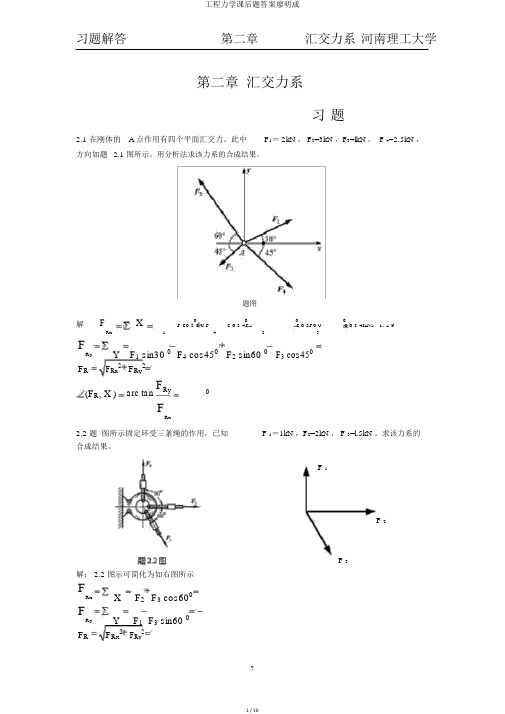
习题解答 第二章 汇交力系 河南理工大学第二章 汇交力系习 题2.1 在刚体的 A 点作用有四个平面汇交力。
此中 F 1= 2kN , F 2=3kN ,F 3=lkN , F 4=2.5kN ,方向如题 2.1 图所示。
用分析法求该力系的合成结果。
题图解FX0 0RxF co s 3 0 F4 c o s 4F52c o sF6 0c o s 4KN5 1. 2 913FRyY F 1 sin30 0 F 4 cos450 F 2 sin60 0 F 3 cos450F RF Rx 2 F Ry 2(F R , X ) arc tanF Ry 0FRx2.2 题 图所示固定环受三条绳的作用,已知 F 1=1kN ,F 2=2kN , F 3=l.5kN 。
求该力系的合成结果。
F 1F 2F 3解: 2.2 图示可简化为如右图所示F RxX F 2 F 3 cos600 FRyYF 1 F 3 sin60 0F RF Rx 2 F Ry 2(F R , X ) arc tanF RyF Rx2.3 力系如题 2.3 图所示。
已知: F 1= 100N ,F 2=50N , F 3=50N ,求力系的协力。
F 1F 2F 3解: 2.3 图示可简化为如右图所示BACarctan8053060F RxX F 3 F 2 cos 80KNFRyYF 1 F 2 sin 140KNF RF Rx 2 F Ry 2 161.25 KN(F R , X ) arc tanF Ry 0FRx2.4 球重为 W = 100N ,悬挂于绳上,并与圆滑墙相接触,如题 2.4 图所示。
已知 30 ,试求绳所受的拉力及墙所受的压力。
F 拉F 推OW题图解: 2.4 图示可简化为如右图所示X F 推 F 拉 sinY F 拉 cos WF拉,F推墙所受的压力2.5 均质杆AB重为W、长为l ,两头置于互相垂直的两圆滑斜面上,如题 2.5 图所示。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 31-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5(b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7(f)(g)8第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F FBC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学第五版习题册答案

工程力学第五版习题册答案工程力学第五版习题册答案工程力学是一门研究物体在受力作用下的力学性质和变形规律的学科。
它是工程学的基础课程之一,对于工程师的培养具有重要的意义。
而工程力学第五版习题册则是帮助学生巩固和应用所学知识的重要辅助教材。
本文将为大家提供一些工程力学第五版习题册的答案,希望对大家的学习有所帮助。
第一章:静力学1. 题目:一个质量为10kg的物体静止在水平地面上,受到一个水平方向的15N的力作用。
求地面对物体的支持力。
答案:根据牛顿第一定律,物体静止时合力为零。
因此,地面对物体的支持力大小为15N。
2. 题目:一个质量为5kg的物体静止在斜面上,斜面的倾角为30°。
求物体沿斜面方向的受力大小。
答案:物体沿斜面方向的受力可以分解为两个分力,一个是物体的重力沿斜面方向的分力,另一个是斜面对物体的支持力。
根据三角函数的关系,物体沿斜面方向的受力大小为5kg * 9.8m/s^2 * sin30° = 24.5N。
第二章:动力学1. 题目:一个质量为2kg的物体受到一个水平方向的5N的力作用,开始时静止,求物体在2s内的速度变化。
答案:根据牛顿第二定律,物体的加速度等于合力除以物体的质量。
物体的加速度为5N / 2kg = 2.5m/s^2。
由于物体开始时静止,所以物体在2s内的速度变化为2.5m/s^2 * 2s = 5m/s。
2. 题目:一个质量为3kg的物体受到一个水平方向的10N的力作用,开始时速度为2m/s,求物体在5s内的位移。
答案:根据牛顿第二定律,物体的加速度等于合力除以物体的质量。
物体的加速度为10N / 3kg = 3.33m/s^2。
由于物体开始时速度为2m/s,所以物体在5s内的位移为2m/s * 5s + (1/2) * 3.33m/s^2 * (5s)^2 = 10m + 41.67m = 51.67m。
第三章:力的分解与合成1. 题目:一个力的大小为20N,方向与x轴夹角为30°,求该力在x轴和y轴上的分力大小。
2021年工程力学第六章答案 梁的变形-工程力学梁的弯曲答案

第五章梁的变形欧阳光明(2021.03.07)测试练习1.判断改错题5-1-1梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零.()5-1-2两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。
()5-1-3悬臂梁受力如图所示,若A点上作用的集中力P在A B段上作等效平移,则A截面的转角及挠度都不变。
()5-1-4图示均质等直杆(总重量为W),放置在水平刚性平面上,若A端有一集中力P作用,使AC B部分仍与刚性平面贴剪力和)5-1-5挠曲线近似微分方程不能用于求截面直梁的位移。
()5-1-6等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。
()5-1-7两简支梁的抗刚度E I及跨长2a均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的。
题5-1-3图题5-1-4图( )5-1-8 简支梁在图示任意荷载作用下,截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用,则梁的截面C 的挠度要改变,而转角不变。
( )5-下别按放截面同。
( )5-1-10 图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有6个积分常量。
( )5-2-1 挠曲线近似微分方程y "。
5-2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等,则=21P P 5-2-3 应用叠加原理求梁的变形时应满足的条件是:。
5-2-4 在梁的变形中挠度和转角之间的关系是。
5-2-5 用积分法求图示的外伸梁(B D 为拉杆)的挠曲线方程时,求解积分常量所用到的边界条件是,连续条件是。
5-2-6 用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是,连续条件是。
5-2-7 图示结构为次超静定梁。
题5-1-8图题5-1-7图题5-1-9图 题5-2-2图5-2-8形后曲线为5-2-9 两根E I 值相同、跨度之比为1:2的简支梁,当承受相同的均布荷载q 作用时,它们的挠度之比为。
《工程力学》课后习题解答

M A(F ) 0 : 2 0.8 0.5 1.6 0.4 0.7 FB 2 0
FB 0.26 kN
Fy 0 :
约束力的方向如图所示。
FAy 2 0.5 FB 0 FAy 1.24 kN
14
《工程力学》习题选解
(c):(1) 研究 AB 杆,受力分析,画出受力图(平面任意力系);
(d)
A F
D
FC
A
D
F
C B FB
E
F C F’C E
FC B
FE
FF
FE
FF
FB
(e)
A
OB
FOx W
FB FOy
FB B
FC C
G D
A
OB
D
FOx
G
FOy
C’ C
W FC’
4
《工程力学》习题选解
2-2 杆 AC、BC 在 C 处铰接,另一端均与墙面铰接,如图所示,F1 和 F2 作用在销钉 C 上, F1=445 N,F2=535 N,不计杆重,试求两杆所受的力。
1-1 试画出以下各题中圆柱或圆盘的受力图。与其它物体接触处的摩擦力均略去。
B
OWA
F OWA
A O
B
(a)
(b)
W (c)
B
解:
OW A
(d)
BO FB
W (a)
FB
B OWA (e)
F
O W
A
FA
B
FA
FB
(b)
FB
FA
A OW
FA (d)
B OWA (e)
FO A
O
FA
W (c)
1-2 试画出以下各题中 AB 杆的受力图。
工程力学练习册习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)2 第一章静力学基础(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图第一章静力学基础 3(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
4 第一章静力学基础(a)(b)第一章静力学基础 5 (c)(d)6 第一章静力学基础(e)(f)第一章静力学基础7(g)第二章平面力系2-1 电动机重P=5000N,放在水平梁AC的中央,如图所示。
梁的A端以铰链固定,另一端以撑杆BC支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A、B处的约束反力。
8 第一章 静力学基础题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
第四章 材料力学基本概念 9题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学习题-答案4-廖明成

第四章 平面任意力系习 题4.1 重W ,半径为r 的均匀圆球,用长为L 的软绳AB 及半径为R 的固定光滑圆柱面支持如图,A 与圆柱面的距离为d 。
求绳子的拉力T F 及固定面对圆球的作用力N F 。
题4.1图F TyxOF N解:软绳AB 的延长线必过球的中心,力N F 在两个圆球圆心线连线上N F 和T F 的关系如图所示:AB 于y 轴夹角为θ 对小球的球心O 进行受力分析:0,sin cos TNX F F θθ==∑ 0,cos sin T NY F F W θθ=+=∑sin R rR d θ+=+ cos L rR dθ+=+ ()()()()22T R d L r F W R r L r ++=+++()()()()22NR d R r F W R r L r ++=+++4.2 吊桥AB 长L ,重1W ,重心在中心。
A 端由铰链支于地面,B 端由绳拉住,绳绕过小滑轮C 挂重物,重量2W 已知。
重力作用线沿铅垂线AC ,AC =AB 。
问吊桥与铅垂线的交角θ为多大方能平衡,并求此时铰链A 对吊桥的约束力A F 。
题4.2图A yF A xF解:对AB 杆件进行受力分析:120,sin cos 022A L M W W L θθ=-=∑ 解得:212arcsinW W θ= 对整体进行受力分析,由:20,cos02Ax X F W θ=-=∑2cos2Ax F W θ=210,sin02Ay Y F W W θ=+-=∑22121Ay W W F W +=4.3 试求图示各梁支座的约束力。
设力的单位为kN ,力偶矩的单位为kN ·m ,长度单位为m ,分布载荷集度为kN /m 。
(提示:计算非均布载荷的投影和与力矩和时需应用积分。
)题4.3图解:AyF AxF ByAxF AyF ByFBAxF AyF AyF Ax F AM(a )受力如图所示0,0.8cos300AxX F =-=∑ 0,0.110.80.150.20AByM F=⨯+⨯-=∑0,10.8sin300Ay By Y F F =+--=∑0.43, 1.1,0.3Ax By Ay F KN F KN F KN ===(b )受力如图所示0,0.40AxX F =+=∑0,0.820.5 1.60.40.720AByM F=⨯-⨯-⨯-=∑0,20.50Ay By Y F F =+-+=∑0.4,0.26,0.24Ax By Ay F KN F KN F KN =-==(c )受力如图所示0,sin300AxBX F F =-=∑ 0,383cos300ABM F =+-=∑ 0,cos3040AyBY F F =+-=∑2.12, 4.23,0.3Ax By Ay F KN F KN F KN ===(d )受力如图所示()()133q x x =- 0,0AxX F==∑()()33010,3 1.53Ay Y F q x dx x dx KN ===-=∑⎰⎰()30,0A A M M xq x dx =+=∑⎰()3013 1.53A M x x dx KN m =-=-•⎰4.4 露天厂房立柱的底部是杯形基础。
参考资料(答案)-《工程力学(第五版)习题册》-A02-9111

F1y=F1 ·cos60°=20 N F2x=0 F2y= -F2= -40 N F3x= -F3= -40 N F3y=0 F4x=F4·cos135°= -28.28 N F4y=F4 ·cos45°=28.28 N 2. 解:F1x=F1=100N F1y=0 N F2x=0 N F2y=F2 =100 N F3x=F3 ·cos30°=129.9 N F3y=F3 ·cos60°=75 N F4x=F4 ·cos60°=50 N F4y=F4·cos150°= -86.6 N F5x=F5 ·cos60°=75 N F5y=F5·cos150°= -129.9 N F6x=F6·cos120°= -100 N
FDX =FD
FDY =0
FBX=FB·cos135°=-0.866FB FBY=FB·cos60°=0.5FB (3) 列 方 程
由 ∑Fix=0:FX +FDX +FBX =0 由 ∑Fiy=0:FY +FDY +FBY =0 (4) 解 方 程
解方程得到:FD=193.2 (N)(方向如图所示)
· 154 ·
F6y=F6·cos150°= -173.2 N 3. 解:MO(F1)=F1×1=F1
MA (F1)= -F1 ×1= -F1 MO (F2)= -F2 ×2= -2F2 MA (F2)= -F2 ×4= -4F2 MO(F3)=F3×0=0 MA(F3)=F3×1×sin45°=0.707F3 MO(F4)=F4×3=3F4 MA(F4)=F4×4=4F4 MO(F5)=F5×1.414=1.414F5 MA (F5)= -F5 ×1×sin45°= -0.707F5 4. 解: (a)MB(F)=F·la=50×0.6=30 N·m
工程力学课后题答案2廖明成

第二章 汇交力系习 题2.1 在刚体的A 点作用有四个平面汇交力。
其中F 1=2kN ,F 2=3kN ,F 3=lkN , F 4=2.5kN ,方向如题2.1图所示。
用解析法求该力系的合成结果。
题2.1图解 00001423cos30cos45cos60cos45 1.29Rx F X F F F F KN ==+--=∑ 00001423sin30cos45sin60cos45 2.54Ry F Y F F F F KN ==-+-=∑2.85R F KN ==0(,)tan63.07Ry R RxF F X arc F ∠==2.2 题2.2图所示固定环受三条绳的作用,已知F 1=1kN ,F 2=2kN ,F 3=l.5kN 。
求该力系的合成结果。
23解:2.2图示可简化为如右图所示023cos60 2.75Rx F X F F KN ==+=∑ 013sin600.3Ry F Y F F KN ==-=-∑2.77R F KN ==0(,)tan6.2Ry R RxF F X arc F ∠==-2.3 力系如题2.3图所示。
已知:F 1=100N ,F 2=50N ,F 3=50N ,求力系的合力。
32F 1解:2.3图示可简化为如右图所示080arctan5360BAC θ∠=== 32cos 80Rx F X F F KN θ==-=∑ 12sin 140Ry F Y F F KN θ==+=∑161.25R F KN ==0(,)tan60.25Ry R RxF F X arc F ∠==2.4 球重为W =100N ,悬挂于绳上,并与光滑墙相接触,如题2.4 图所示。
已知30α=,试求绳所受的拉力及墙所受的压力。
题2.4图解:2.4图示可简化为如右图所示sin 0X F F α=-=∑拉推 cos W 0Y Fα=-=∑拉115.47N 57.74N F F ∴==拉推,∴墙所受的压力F=57.74N2.5 均质杆AB 重为W 、长为 l ,两端置于相互垂直的两光滑斜面上,如题2.5图所示。
工程力学习题 答案 廖明成

第四章 平面任意力系习 题4.1 重W ,半径为r 的均匀圆球,用长为L 的软绳AB 及半径为R 的固定光滑圆柱面支持如图,A 与圆柱面的距离为d 。
求绳子的拉力T F 及固定面对圆球的作用力N F 。
题4.1图F TyxOF N解:软绳AB 的延长线必过球的中心,力N F 在两个圆球圆心线连线上N F 和T F 的关系如图所示:AB 于y 轴夹角为θ 对小球的球心O 进行受力分析:0,sin cos TNX F F θθ==∑ 0,cos sin T NY F F W θθ=+=∑sin R rR d θ+=+ cos L rR dθ+=+ ()()()()22T R d L r F W R r L r ++=+++()()()()22NR d R r F W R r L r ++=+++4.2 吊桥AB 长L ,重1W ,重心在中心。
A 端由铰链支于地面,B 端由绳拉住,绳绕过小滑轮C 挂重物,重量2W 已知。
重力作用线沿铅垂线AC ,AC =AB 。
问吊桥与铅垂线的交角θ为多大方能平衡,并求此时铰链A 对吊桥的约束力A F 。
题4.2图A yF A xF解:对AB 杆件进行受力分析:120,sin cos 022A L M W W L θθ=-=∑ 解得:212arcsinW W θ= 对整体进行受力分析,由:20,cos02Ax X F W θ=-=∑2cos2Ax F W θ=210,sin02Ay Y F W W θ=+-=∑22121Ay W W F W +=4.3 试求图示各梁支座的约束力。
设力的单位为kN ,力偶矩的单位为kN ·m ,长度单位为m ,分布载荷集度为kN /m 。
(提示:计算非均布载荷的投影和与力矩和时需应用积分。
)题4.3图解:AyF AxF ByAxF AyF ByFBAxF AyF AyF Ax F AM(a )受力如图所示0,0.8cos300AxX F =-=∑ 0,0.110.80.150.20AByM F=⨯+⨯-=∑0,10.8sin300Ay By Y F F =+--=∑, 1.1,0.3Ax By Ay F F KN F KN ===(b )受力如图所示0,0.40AxX F =+=∑0,0.820.5 1.60.40.720A ByM F=⨯-⨯-⨯-=∑0,20.50Ay By Y F F =+-+=∑0.4,0.26,0.24Ax By Ay F KN F KN F KN =-==(c )受力如图所示0,sin300AxBX F F =-=∑ 0,383cos300ABM F =+-=∑ 0,cos3040AyBY F F =+-=∑2.12, 4.23,0.3Ax By Ay F KN F KN F KN ===(d )受力如图所示()()133q x x =- 0,0AxX F==∑()()33010,3 1.53Ay Y F q x dx x dx KN ===-=∑⎰⎰()30,0A A M M xq x dx =+=∑⎰()3013 1.53A M x x dx KN m =-=-•⎰4.4 露天厂房立柱的底部是杯形基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 空间任意力系习 题5.1 托架A 套在转轴z 上,在点C 作用一力F = 2000 N 。
图中点C 在Oxy 平面内,尺寸如图所示,试求力F 对x ,y ,z 轴之矩。
题5.1图解:cos 45sin 60 1.22x F F KN ==cos45cos600.7y F F KN ==sin 45 1.4z F F KN ==6084.85x z M F mm KN mm ==⋅5070.71y z M F mm KN mm ==⋅ 6050108.84z x y M F mm F mm KN mm =+=⋅5.2 正方体的边长为a ,在其顶角A 和B 处分别作用着力F 1和F 2,如图所示。
求此两力在轴x ,y ,z 上的投影和对轴x ,y ,z 的矩。
xyzOaaa ABF 1 F 2 αβα题5.2图F F zF xyF yF x解:21sin cos sin x F F F αβα=-1cos cos y F F βα=-12sin cos z F F F βα=+12sin cos x z M F a aF aF βα==+ 1sin y M aF β=121cos cos sin cos sin z y x MF a F a aF aF aF βααβα=-=---5.3 如图所示正方体的表面ABFE内作用一力偶,其矩M = 50 kN·m ,转向如图。
又沿GA 、BH 作用两力F 、F ′,F = F ′,a = 1 m 。
试求该力系向C 点的简化结果。
解:两力F 、F ′能形成力矩1M1M Fa m ==⋅11cos 45x M M =10y M = 11sin 45z MM =1cos4550x M M KN m ==⋅11sin 4550100z z M M M M KN m =+=+=⋅C M m ==⋅63.4α= 90β= 26.56γ=5.4 如图所示,置于水平面上的网格,每格边长a = 1m ,力系如图所示,选O 点为简化中心,坐标如图所示。
已知:F 1 = 5 N ,F 2 = 4 N ,F 3 = 3 N ;M 1 = 4 N·m ,M 2 = 2 N·m ,求力系向O 点简化所得的主矢'R F 和主矩M O 。
题5.4图解:'1236R F F F F N =+-=方向为Z 轴正方向21232248x M M F F F N m =++-=⋅ 1123312y M M F F F N m =--+=-⋅2214.42O y x M M M N m =+=⋅56.63α= 33.9β=-90γ=5.5 如图所示圆柱重W =10kN ,用电机链条传动而匀速提升。
链条两边都和水平方向成300角。
已知鼓轮半径r =10cm ,链轮半径1r =20cm ,链条主动边(紧边)的拉力T 1大小是从动边(松边)拉力T 2大小的两倍。
若不计其余物体重量,求向心轴承A 和B 的约束力和链的拉力大小(图中长度单位cm )。
题5.5图解:120,cos30cos300AxBx X F F T T =+++=∑210,sin30sin300AzBz Z F F T T W =+-+-=∑120,60cos3060cos301000zBx M T T F =---=∑ 120,3060sin3060sin301000xBz M W T T F =-+-+=∑ 21110,0yMWr T r T r =+-=∑20.78,13Ax Az F KN F KN =-= 7.79, 4.5Bx Bz F KN F KN == 1210,5T KN T KN ==5.6 如图所示均质矩形板ABCD 重为W = 200 N ,用球铰链A 和蝶形铰链B 固定在墙上,并用绳索CE 维持在水平位置。
试求绳索所受张力及支座A ,B 处的约束力。
解:取长方形板ABCD 为研究对象,受力如图所示重力W 作用于板的型心上。
选坐标系Axyz ,设AD 长题5.6图2a ,AB 长为2b ,列出平衡方程并求解F AxF AzF BxF BzWBzF=100AzF N=5.7 如图所示,水平轴上装有两个凸轮,凸轮上分别作用已知力F1=800N和未知力F。
如轴平衡,求力F和轴承约束力的大小。
xyzBAFF140cm60cm40cm2cm20cmBxFBzFAzFAxF题5.7图解:10,0Ax BxX F F F=++=∑0,0Az BzZ F F F=++=∑10,1401000z BxM F F=--=∑10,20200yM F F =-=∑ 0,401000xBz MF F =+=∑320,480Ax Az F N F N ==- 1120,320Bx Bz F N F N =-=-800F N =5.8 扒杆如图所示,立柱 AB 用 BG 和 BH 两根缆风绳拉住,并在 A 点用球铰约束,A 、H 、G 三点位于Oxy 平面内,G 、H 两点的位置对称于y 轴,臂杆的D 端吊悬的重物重W = 20 kN ;求两绳的拉力和支座A 的约束反力。
题5.8图解:G 、H 两点的位置对称于y 轴BG BH F F =0,sin 45cos60sin 45cos600BGBH Ax X F F F =-++=∑ 0,cos45cos60cos45cos600BGBH Ay Y F F F =--+=∑0,sin60sin600AzBG BH Z F F F W =---=∑0,5sin 45cos605sin 45cos6050xBG BH MF F W =+-=∑28.28,0,20,68.99BG BH Ax Ay Az F F KN F F KN F KN =====5.9 如图所示,一重量W = 1000N 的均质薄板用止推轴承A 、B 和绳索CE 支持在水平面上,可以绕水平轴AB 转动,今在板上作用一力偶,其力偶矩为M ,并设薄板平衡。
已知a = 3 m ,b = 4 m ,h = 5 m ,M = 2000 N·m ,试求绳子的拉力和轴承A 、B 的约束力。
5.10 如图所示作用在踏板上的铅垂力F 1使得位于铅垂位置的连杆上产生的拉力F = 400 N ,o 30α=,a = 60 mm ,b = 100 mm ,c = 120 mm 。
求轴承A 、B 处的约束力和主动力F 1。
题5.10图解:0,0ByAy Y F F =+=∑ 10,0AzBz Z FF F F =+--=∑10,2cos 0xM bF cF α=-=∑ 0,0yBz Az M aF bF bF =-+=∑ 0,0zBy Ay MbF bF =-=∑0Ay By F F ==,423.92Az F N =, 183.92Bz F N =1207.84F N =5.11 如图所示为一均质薄板,其尺寸单位为mm 并标示于图中,求该薄板的重心。
x题 5.11图解:三角形OAB 的中心为:()15,6.6721300A mm =小圆重心为:()6,6216A π=该薄板的重心:5.12 如图所示,从 R = 120 mm 的均质圆板中挖去一个等腰三角形。
求板的重心位置。
x题5.12图解:圆重心:()0,011221216.8x A x A x A A -==-1122120.4y A y A y A A -==--2114400A mm π=三角形重心:()0,30228100A mm =板的重心位置:5.13 试求图所示均质板OABCD 的重心位置(图中尺寸的单位为mm )。
x题5.13图题5.14图解:I 部分重心:()45,20 212700A mm =∏部分重心:()105,20 22900A mm =I∏部分重心:()60,20- 234800A mm =均质板OABCD 的重心:1122120x A x A x A A -==-1122126.54y A y A y A A -==--11223312360x A x A x A x mm A A A ++==++1122331232.86y A y A y A y mmA A A ++==-++5.14 试求图所示均质等厚板的重心位置(图中尺寸的单位为mm )。
x解:I 部分重心:()2145,60,10800A mm =∏部分重心:()2273,60,800A mm π= I∏部分重心:()2345,20,2700A mm -=均质等厚板的重心:11223312349.4x A x A x A x mmA A A ++==++11223312346.5y A y A y A y mmA A A ++==++。
