2013甘肃第五章同步考点强训

合集下载

2019-2020年中考化学二轮复习考点突击步步为赢(解析版)(II).doc (2)

A．H2
B．N2
C．NH3
D．N2H4
2.（2013 福建莆田）有关治疗 H7N9 禽流感的新药帕拉米韦（C15H28N4O4）的下列说法，正确的是（） A. 帕拉米韦是由 C、H、N、O 四种元素组成 B. 帕拉米韦的相对分子质量为 328g C. 帕拉米韦中含有 15 个碳原子 D. 帕拉米韦分子中 C、H、N、O 的原子质量比为 15：28：4：4
化合价为+4，则 N 的化合价是（）
A．+5
B．+3
C．+1
D．﹣3
12．（2013 辽宁大连）下列关于甲烷（CH4）的说法错误的是（）
A．甲烷由碳、氢两种元素组成
B．甲烷由碳原子和氢原子构成
C．甲烷中碳、氢元素质量比是 3：1
D．甲烷的相对分子质量是 16
13．（2013 江西南昌）帕拉米布是一种新型的抗流感病毒药物．对其主要成分（化学式为 C15H28N4O4）描述正确的是（）
A．属于无机物
B．由碳、氢、氮、氧四种元素组成
C．其中碳、氢元素的质量比为 15：28
D．它的 1 个分子中含有 2 个氧分子
14．（2013 江苏苏州）下列符号表示氧气化学式的是（）
A．O2﹣
B．O2
C．O
【答案】B
D．MnO2
15．（2013湖北黄冈）写出符合下列要求的物质（或主要成分）的化学式。（1）植物光合作用得到的单质__________；（2）碘酒中的溶剂_________；（3）厨房中的酸性调味剂_________；（4）菱铁矿的主要成分________；（5）不含金属元素的碱__________。
（5）化合价与化学式相结合的计算利用化合物中正、负化合价的代数和为零的原则来计算。

中考九年级语文上册专题6古诗词赏析(考点串讲统编版)

羊·骊山怀古》（张养浩）、《朝天子·咏喇叭》（王磐）
考试题型
常见的考查方向： 1.把握内容，体会情感 2.诵读语句，分析风格 3.品味词语，赏析名句 4.描述画面，分析意境填空题、选择题、简答题古诗词曲阅读是主要考查题型。
考试题型
题型一：分析意象、意境型要分析意象、意境，先要明确两个概念一意象与意境。中国古典诗歌
强化训练
【答案】C 【解析】本题考查诗歌的内容、意境、思想感情等多个方面能力。C．有误，“闲来”两句连用两个历史典故，表现诗人渴望重新得到重用而不是对乘舟垂钓悠闲生活的渴望、向往。故选C。
强化训练
（2023·广东省广州市期末）2.阅读下面这首诗，然后回答问题。长沙过贾谊宅刘长卿
三年谪宦此栖迟，万古惟留楚客悲。秋草独寻人去后，寒林空见日斜时。汉文有道恩犹薄，湘水无情吊岂知？寂寂江山摇落处，怜君何事到天涯！（1）诗句“秋草独寻人去后，寒林空见日斜时”描绘了一幅什么样的画面？
（2）尾联抒发了诗人怎样的感情？请简要分析。
强化训练
（1）诗句“秋草独寻人去后，寒林空见日斜时”描绘了一幅什么样的画面？【答案】我在秋草中独自寻觅你的足迹，人迹不在，只有黯淡的斜阳映照着翰林。【解析】本题考查诗歌画面描绘。描绘诗歌展示的画面时，首先理解诗歌的内容。然后在翻译句子的基础上，发挥想象，用优美的语言描述。“秋草独寻人去后，寒林空见日斜时” 是围题中的“过”字展开描写的。“秋草”，“寒林”，“人去”，“日斜”，渲染出故宅一片萧条冷落的景色，而在这样的氛围中，诗人还要去“独寻”，一种景仰向慕、寂寞兴叹的心情，油然而生。寒林日斜，不仅是眼前所见，也是贾谊当时的实际处境，也正是李唐王朝危殆形势的写照。由此我们可以提取出几种景物进行描述。

2013年甘肃省高考试题解读

2013年甘肃省高考试题解读名师点评甘肃省高考试题：语文难易适度作文题关注现实今年是甘肃省第一次在新课标教学背景下首次参加新课标命题原则下的高考。

今年的新课标卷总体上体现了高考命题保持稳定，稳中求变的原则。

试题特点稳定仍是最大的特点。

今年的试卷结构和试题设置完全按照近三年全国普通高等院校招生考试新课标卷的体式命制，整体试卷分为第Ⅰ卷阅读题，第Ⅱ卷表达题。

阅读题由必考题和选考题两部分构成，包括一至四大题；表达题包括五、六两个大题。

全卷共六个大题，18个小题，共计150分，考试时间150分钟。

考生实际完成五个大题，17个小题。

试卷的能力考查及考点的涉及体现了新课标考试大纲精神。

今年所考的《三峡》(初中篇目)《劝学》《琵琶行》(高中篇目)均在考纲所给定的参考篇目范围内，也符合“诸子”“诗歌”“散文”，“初中少量考，高中侧重考”的内容及数量方面的设置原则。

作文仍然采取了给材料作文，延续了材料作文这一命题形式。

细微变化体现了新课标教学可发展性。

据学生反映，今年的高考语文试卷与我们的复习方向、诊断试题、模拟试卷在命题思路及命题形式上吻合度颇高，作为高考的第一门“实战”科目，这是最令人欣慰的地方。

当然试题也有一些很有意思的变化，值得新一届高三老师思量。

(1)选考题部分的实用文本出现了“知识链接”部分，这是以往的试卷从未出现过的，对学生答最后一道8分试题会有一定的借鉴意义。

但也正因为如此，大量学生反映今年高考的文学类读本(小说)与实用类文本(人物评传)在文本及试题命制的难度分布及区分度设置上仍出现了“一边倒”现象，显然实用文本的试题更易上手。

学生均反映试题因此对绝大多数考生失去了“选考”意义。

从“考什么就教什么”的应试策略上看，小说的教学地位和学生的学习热情恐怕会受到进一步影响。

(2)从宁海卷到全国新课标卷一直没有缺席的“仿写”题今年终于“变脸”了。

今年的16、17小题分别是缺句填充与图文转换，这充分证明新课标试卷的命制对甘肃考生而言是全新的，当年大纲卷上的“试验田”在新课标卷的命制上也将进入两道试题同时交叉变化的命题阶段。

2013年高考物理高频考点模拟新题精选训练专题30 带电粒子在电场、磁场中的运动

1 高考物理高频考点2013模拟新题精选训练专题30 带电粒子在电场、磁
场中的运动
1．(2013北京朝阳区期末)如图所示，一个静止的质量为m 、电荷量为q 的粒子（重力忽略不计），经加速电压U 加速后，垂直进入磁感应强度为B 的匀强磁场中，粒子打到P 点，OP =x ，能正确反映x 与U 之间关系的是
A ．x 与U 成正比
B ．x 与U 成反比
C ．x
与成正比
D ．x
与成反比
答案：C
解析：由x=2R=2mv/qB ，qU=1
2mv 2，可得x
成正比，选项C 正确。

2．(18分) （2013甘肃省张掖市一诊）如图所示，在xoy 坐标系中，y>0的范围内存在着沿y 轴正方向的匀强电场，在y<0的范围内存在着垂直纸面的匀强磁场（方向未画出）。

已知oa=oc=cd=L, ob=L/4。

现有一群带电粒子，质量为m ，电荷量大小为q (重力不计），分布在y 轴的a 、b 之间。

t=0时刻，这群带电粒子以相同的初速度v 0沿x 轴正方向开始运动。

观察到从a 点出发的带电粒子
恰好从d 点第一次进入磁场，然后从O 点第—次离开磁场。

试回答：
(1) 判断匀强磁场的方向；
(2) 带电粒子第一次进入磁场的位置坐标x 与出发点的位置坐标y 的关系式；
(3) 带电粒子第一次离开磁场的位置坐标x 1与出发点的位置坐标y 的关系式。

第五章第24讲考点一交通运输方式的选择

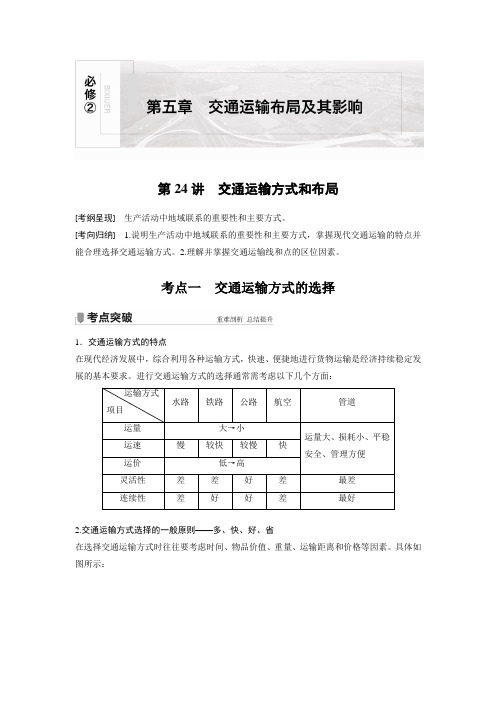
第24讲交通运输方式和布局[考纲呈现]生产活动中地域联系的重要性和主要方式。

[考向归纳] 1.说明生产活动中地域联系的重要性和主要方式，掌握现代交通运输的特点并能合理选择交通运输方式。

2.理解并掌握交通运输线和点的区位因素。

考点一交通运输方式的选择1．交通运输方式的特点在现代经济发展中，综合利用各种运输方式，快速、便捷地进行货物运输是经济持续稳定发展的基本要求。

进行交通运输方式的选择通常需考虑以下几个方面：运输方式水路铁路公路航空管道项目运量大→小运量大、损耗小、平稳运速慢较快较慢快安全、管理方便运价低→高灵活性差差好差最差连续性差好好差最好2.交通运输方式选择的一般原则——多、快、好、省在选择交通运输方式时往往要考虑时间、物品价值、重量、运输距离和价格等因素。

具体如图所示：经济性、迅速性、安全性和通达性是运输方式的四大评价指标。

因此交通运输方式的选择除了上述要求外，还应考虑运输起点与终点之间的实际交通状况，即现有交通条件；尽量减少调运过程中不必要的中间环节，避免重复运输。

3．采用优选法确定货运方式根据货运的需要，先看运距是远还是近，再看运量是多还是少，运费是贵还是便宜，最终用优选法来确定运输方式。

“绿色出行”新理念已为我国许多城市市民所接受。

下图为“1986～2015年某城市市民主要出行方式变化图”。

读图回答1～2题。

1．新理念对市民出行方式产生明显影响的年份开始于()A．2000年B．2005年C．2007年D．2011年2．市民出行方式变化对该城市产生的主要影响是()A．优化城市空间结构B．改善城市交通状况C．改变城市服务功能D．扩大城市地域范围答案 1.D 2.B解析第1题，读图可知，小汽车出行方式自2011年后快速下降，而同期公共交通出行方式占比快速上升，自行车出行方式占比呈现首次上升，由此可以看出绿色出行新理念对市民出行方式产生明显影响的年份开始于2011年，故选D。

第2题，市民出行方式变化主要表现为小汽车出行方式占比下降，公共交通和自行车出行方式占比上升，出行方式的变化对城市空间结构、服务功能和地域范围没有影响，而公共交通运输效率高，公共交通和自行车占比的提高可有效改善城市交通状况，故选B。

甘肃省选拔万名普通高校毕业生到基层工作考试专用教材公共基础知识考前15天终极密押试卷

严格依据最新甘肃省选拔万名普通高校毕业生到基层工作考试大纲编写主编李永新中公教育甘肃公职考试研究院审定公共基础知识考前15天终极密押试卷甘肃省选拔万名普通高校毕业生到基层工作考试专用教材图书在版编目(CIP)数据公共基础知识考前15天终极密押试卷/李永新主编.—北京:人民日报出版社,2013.3(2014.3重印)甘肃省选拔万名普通高校毕业生到基层工作考试专用教材ISBN978⁃7⁃5115⁃1705⁃0Ⅰ.①公...Ⅱ.①李...Ⅲ.①基层干部-招聘-考试-中国-习题集Ⅳ.①D630.3-44中国版本图书馆CIP数据核字(2013)第048789号书名:甘肃省选拔万名普通高校毕业生到基层工作考试专用教材·公共基础知识·考前15天终极密押试卷作者:李永新出版人:董伟责任编辑:李英封面设计:中公教育设计中心出版发行:社址:北京金台西路2号邮政编码:100733发行热线:(010)65369527653698466536950965369510邮购热线:(010)6536953065363527编辑热线:(010)65369511网址:经销:新华书店印刷:三河市宇通印刷装订厂开本:787mm×1092mm1/16字数:115千字印张:6印次:2013年4月第1版2014年3月第1版第2次印刷书号:ISBN978⁃7⁃5115⁃1705⁃0定价:30.00元前言甘肃省选拔万名普通高校毕业生到基层工作考试已经成为甘肃省高校毕业生最为关注的考试之一。

这一考试有两大特点,一是名额较多。

甘肃省每年都会定期地举行考试,且招聘人数每年都是一万名,给高校毕业生提供了广阔的就业机会。

二是待遇较高。

被录用的人员工资待遇与当地事业单位工资持平,且纳入省财政转移支付。

因此,每年有十余万考生参与这一万个名额的角逐。

为帮助广大考生迅速掌握考试内容、精准把握考试脉搏,中公教育依十余年公职类考试研究之积淀,携数百名业内专家及一线名师之团队,编写了本套《甘肃省选拔万名普通高校毕业生到基层工作考试专用教材》。

高考数学考点与题型知识点5平面向量

平面向量平面向量 (2)第一节平面向量的概念及线性运算 (2)考点一平面向量的有关概念 (3)考点二平面向量的线性运算 (5)考点三共线向量定理的应用 (7)第二节平面向量基本定理及坐标表示 (13)考点一平面向量基本定理及其应用 (14)考点二平面向量的坐标运算 (15)考点三平面向量共线的坐标表示 (16)第三节平面向量的数量积 (22)考点一平面向量的数量积的运算 (23)考点二平面向量数量积的性质 (26)第四节平面向量的综合应用 (33)考点一平面向量与平面几何 (33)考点二平面向量与解析几何 (34)考点三平面向量与三角函数 (35)第五章平面向量第一节平面向量的概念及线性运算一、基础知识1．向量的有关概念(1)向量的定义及表示：既有大小又有方向的量叫做向量．以A 为起点、B 为终点的向量记作AB ―→，也可用黑体的单个小写字母a ，b ，c ，…来表示向量．(2)向量的长度(模)：向量AB ―→的大小即向量AB ―→的长度(模)，记为|AB ―→|. 2．几种特殊向量单位向量有无数个，它们大小相等，但方向不一定相同；与向量a 平行的单位向量有两个，即向量a|a |和－a|a |.3．向量的线性运算三角形法则平行四边形法则三角形法则多个向量相加，利用三角形法则，应首尾顺次连接，a＋b＋c表示从始点指向终点的向量，只关心始点、终点.4．共线向量定理向量a(a≠0)与b共线，当且仅当有唯一一个实数λ，使得b＝λa.只有a≠0才保证实数λ的存在性和唯一性.二、常用结论(1)若P为线段AB的中点，O为平面内任一点，则OP―→＝12(OA―→＋OB―→)．(2)OA―→＝λOB―→＋μOC―→(λ，μ为实数)，若点A，B，C三点共线，则λ＋μ＝1.考点一平面向量的有关概念[典例]给出下列命题：①若a＝b，b＝c，则a＝c；②若A，B，C，D是不共线的四点，则AB―→＝DC―→是四边形ABCD为平行四边形的充要条件；③a ＝b 的充要条件是|a |＝|b |且a ∥b ； ④若a ∥b ，b ∥c ，则a ∥c . 其中正确命题的序号是________．[解析] ①正确．∵a ＝b ，∴a ，b 的长度相等且方向相同，又b ＝c ，∴b ，c 的长度相等且方向相同， ∴a ，c 的长度相等且方向相同，故a ＝c .②正确．∵AB ―→＝DC ―→，∴|AB ―→|＝|DC ―→|且AB ―→∥DC ―→，又A ，B ，C ，D 是不共线的四点， ∴四边形ABCD 为平行四边形；反之，若四边形ABCD 为平行四边形，则AB ―→∥DC ―→且|AB ―→|＝|DC ―→|，因此，AB ―→＝DC ―→.③不正确．当a ∥b 且方向相反时，即使|a |＝|b |，也不能得到a ＝b ，故|a |＝|b |且a ∥b 不是a ＝b 的充要条件，而是必要不充分条件．④不正确．考虑b ＝0这种特殊情况．综上所述，正确命题的序号是①②. [答案] ①②[解题技法] 向量有关概念的关键点 (1)向量定义的关键是方向和长度．(2)非零共线向量的关键是方向相同或相反，长度没有限制． (3)相等向量的关键是方向相同且长度相等． (4)单位向量的关键是长度都是一个单位长度．(5)零向量的关键是长度是0，规定零向量与任意向量共线． [题组训练] 1．给出下列命题：①两个具有公共终点的向量，一定是共线向量； ②λa ＝0(λ为实数)，则λ必为零；③λ，μ为实数，若λa ＝μb ，则a 与b 共线．其中错误的命题的个数为( ) A ．0B ．1C ．2D ．3解析：选D ①错误，两向量共线要看其方向而不是起点或终点．②错误，当a ＝0时，不论λ为何值，λa ＝0.③错误，当λ＝μ＝0时，λa ＝μb ＝0，此时，a 与b 可以是任意向量．故错误的命题有3个，故选D.2．设a 0为单位向量，下列命题中：①若a 为平面内的某个向量，则a ＝|a |·a 0；②若a 与a 0平行，则a ＝|a |a 0；③若a 与a 0平行且|a |＝1，则a ＝a 0，假命题的个数是( )A ．0B ．1C ．2D ．3解析：选D 向量是既有大小又有方向的量，a 与|a |a 0的模相同，但方向不一定相同，故①是假命题；若a 与a 0平行，则a 与a 0的方向有两种情况：一是同向，二是反向，反向时a ＝－|a |a 0，故②③也是假命题．综上所述，假命题的个数是3.考点二平面向量的线性运算[典例] (1)(2018·全国卷Ⅰ)在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB ―→＝( )A.34AB ―→－14AC ―→B.14AB ―→－34AC ―→C.34AB ―→＋14AC ―→ D.14AB ―→＋34AC ―→(2)如图，在直角梯形ABCD 中，DC ―→＝14AB ―→，BE ―→＝2EC ―→，且AE ―→＝r AB ―→＋s AD ―→，则2r ＋3s ＝( )A ．1B ．2C ．3D ．4[解析] (1)作出示意图如图所示．EB ―→＝ED ―→＋DB ―→＝12AD ―→＋12CB ―→＝12×12(AB ―→＋AC ―→)＋12(AB ―→－AC ―→)＝34AB ―→－14AC ―→.故选A. (2)根据图形，由题意可得AE ―→＝AB ―→＋BE ―→＝AB ―→＋23BC ―→＝AB ―→＋23(BA ―→＋AD ―→＋DC ―→)＝13AB ―→＋23(AD ―→＋DC ―→)＝13AB ―→＋23⎝⎛⎭⎫AD ―→＋14AB ―→＝12AB ―→＋23AD ―→. 因为AE ―→＝r AB ―→＋s AD ―→，所以r ＝12，s ＝23，则2r ＋3s ＝1＋2＝3.[答案] (1)A (2)C[解题技法] 向量线性运算的解题策略(1)常用的法则是平行四边形法则和三角形法则，一般共起点的向量求和用平行四边形法则，求差用三角形法则，求首尾相连的向量的和用三角形法则．(2)找出图形中的相等向量、共线向量，将所求向量与已知向量转化到同一个平行四边形或三角形中求解．(3)用几个基本向量表示某个向量问题的基本技巧：①观察各向量的位置；②寻找相应的三角形或多边形；③运用法则找关系；④化简结果． (4)与向量的线性运算有关的参数问题，一般是构造三角形，利用向量运算的三角形法则进行加法或减法运算，然后通过建立方程组即可求得相关参数的值．[题组训练]1．设D 为△ABC 所在平面内一点，BC ―→＝3CD ―→，则( ) A ．AD ―→＝－13AB ―→＋43AC ―→B ．AD ―→＝13AB ―→－43AC ―→C ．AD ―→＝43AB ―→＋13AC ―→D ．AD ―→＝43AB ―→－13AC ―→解析：选A 由题意得AD ―→＝AC ―→＋CD ―→＝AC ―→＋13BC ―→＝AC ―→＋13AC ―→－13AB ―→＝－13AB ―→＋43AC ―→. 2．(2019·太原模拟)在正方形ABCD 中，M ，N 分别是BC ，CD 的中点，若AC ―→＝λAM ―→＋μAN ―→，则实数λ＋μ＝________.解析：如图，∵AM ―→＝AB ―→＋BM ―→＝AB ―→＋12BC ―→＝DC ―→＋12BC ―→，①AN ―→＝AD ―→＋DN ―→＝BC ―→＋12DC ―→，②由①②得BC ―→＝43AN ―→－23AM ―→，DC ―→＝43AM ―→－23AN ―→，∴AC ―→＝AB ―→＋BC ―→＝DC ―→＋BC ―→＝43AM ―→－23AN ―→＋43AN ―→－23AM ―→＝23AM ―→＋23AN ―→，∵AC ―→＝λAM ―→＋μAN ―→，∴λ＝23，μ＝23，λ＋μ＝43.答案：43考点三共线向量定理的应用[典例] 设两个非零向量a 与b 不共线，(1)若AB ―→＝a ＋b ，BC ―→＝2a ＋8b ，CD ―→＝3a －3b ，求证：A ，B ，D 三点共线；(2)试确定实数k ，使k a ＋b 和a ＋k b 同向．[解] (1)证明：∵AB ―→＝a ＋b ，BC ―→＝2a ＋8b ，CD ―→＝3a －3b ， ∴BD ―→＝BC ―→＋CD ―→＝2a ＋8b ＋3a －3b ＝5(a ＋b )＝5AB ―→， ∴AB ―→，BD ―→共线．又∵它们有公共点B ， ∴A ，B ，D 三点共线． (2)∵k a ＋b 与a ＋k b 同向，∴存在实数λ(λ>0)，使k a ＋b ＝λ(a ＋k b )，即k a ＋b ＝λa ＋λk b . ∴(k －λ)a ＝(λk －1)b .∵a ，b 是不共线的非零向量，∴⎩⎪⎨⎪⎧ k －λ＝0，λk －1＝0，解得⎩⎪⎨⎪⎧ k ＝1，λ＝1或⎩⎪⎨⎪⎧k ＝－1，λ＝－1，又∵λ>0，∴k ＝1.1.向量共线问题的注意事项(1)向量共线的充要条件中，当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，注意待定系数法和方程思想的运用．(2)证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得到三点共线．[题组训练]1．在四边形ABCD 中，AB ―→＝a ＋2b ，BC ―→＝－4a －b ，CD ―→＝－5a －3b ，则四边形ABCD 的形状是( )A ．矩形B ．平行四边形C ．梯形D ．以上都不对解析：选C 由已知，得AD ―→＝AB ―→＋BC ―→＋CD ―→＝－8a －2b ＝2(－4a －b )＝2BC ―→，故AD ―→∥BC ―→.又因为AB ―→与CD ―→不平行，所以四边形ABCD 是梯形．2．已知向量e 1≠0，λ∈R ，a ＝e 1＋λe 2，b ＝2e 1，若向量a 与向量b 共线，则( ) A ．λ＝0 B ．e 2＝0 C ．e 1∥e 2D ．e 1∥e 2或λ＝0解析：选D 因为向量e 1≠0，λ∈R ，a ＝e 1＋λe 2，b ＝2e 1，又因为向量a 和b 共线，存在实数k ，使得a ＝k b ，所以e 1＋λe 2＝2k e 1，所以λe 2＝(2k －1)e 1，所以e 1∥e 2或λ＝0.3．已知O 为△ABC 内一点，且AO ―→＝12(OB ―→＋OC ―→)，AD ―→＝t AC ―→，若B ，O ，D 三点共线，则t ＝( )A.14B.13C.12D.23解析：选B 设E 是BC 边的中点，则12(OB ―→＋OC ―→)＝OE ―→，由题意得AO ―→＝OE ―→，所以AO ―→＝12AE ―→＝14(AB ―→＋AC ―→)＝14AB ―→＋14t AD ―→，又因为B ，O ，D 三点共线，所以14＋14t ＝1，解得t ＝13，故选B.4．已知O ，A ，B 三点不共线，P 为该平面内一点，且OP ―→＝OA ―→＋AB―→|AB ―→|，则( )A ．点P 在线段AB 上 B ．点P 在线段AB 的延长线上C ．点P 在线段AB 的反向延长线上D ．点P 在射线AB 上解析：选D 由OP ―→＝OA ―→＋AB ―→|AB ―→|，得OP ―→－OA ―→＝AB ―→|AB ―→|，∴AP ―→＝1|AB ―→|·AB ―→，∴点P在射线AB 上，故选D.[课时跟踪检测]1．设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB ―→＋FC ―→＝( ) A ．AD ―→B.12AD ―→C.12BC ―→ D ．BC ―→解析：选A 由题意得EB ―→＋FC ―→＝12(AB ―→＋CB ―→)＋12(AC ―→＋BC ―→)＝12(AB ―→＋AC ―→)＝AD ―→.2．已知向量a ，b 不共线，且c ＝λa ＋b ，d ＝a ＋(2λ－1)b ，若c 与d 共线反向，则实数λ的值为( )A ．1B ．－12C ．1或－12D ．－1或－12解析：选B 由于c 与d 共线反向，则存在实数k 使c ＝kd (k ＜0)，于是λa ＋b ＝k []a ＋(2λ－1)b . 整理得λa ＋b ＝k a ＋(2λk －k )b .由于a ，b 不共线，所以有⎩⎪⎨⎪⎧λ＝k ，2λk －k ＝1，整理得2λ2－λ－1＝0，解得λ＝1或λ＝－12.又因为k ＜0，所以λ＜0，故λ＝－12.3．设向量a ，b 不共线，AB ―→＝2a ＋p b ，BC ―→＝a ＋b ，CD ―→＝a －2b ，若A ，B ，D 三点共线，则实数p 的值为( )A ．－2B ．－1C ．1D ．2解析：选B 因为BC ―→＝a ＋b ，CD ―→＝a －2b ，所以BD ―→＝BC ―→＋CD ―→＝2a －b .又因为A ，B ，D 三点共线，所以AB ―→，BD ―→共线．设AB ―→＝λBD ―→，所以2a ＋p b ＝λ(2a －b )，所以2＝2λ，p ＝－λ，即λ＝1，p ＝－1.4．(2019·甘肃诊断)设D 为△ABC 所在平面内一点，BC ―→＝－4CD ―→，则AD ―→＝( ) A.14AB ―→－34AC ―→ B.14AB ―→＋34AC ―→C.34AB ―→－14AC ―→ D.34AB ―→＋14AC ―→解析：选B 法一：设AD ―→＝x AB ―→＋y AC ―→，由BC ―→＝－4CD ―→可得，BA ―→＋AC ―→＝－4CA―→－4AD ―→，即－AB ―→－3AC ―→＝－4x AB ―→－4y AC ―→，则⎩⎪⎨⎪⎧－4x ＝－1，－4y ＝－3，解得⎩⎨⎧x ＝14，y ＝34，即AD ―→＝14AB ―→＋34AC ―→，故选B.法二：在△ABC 中，BC ―→＝－4CD ―→，即－14BC ―→＝CD ―→，则AD ―→＝AC ―→＋CD ―→＝AC ―→－14BC―→＝AC ―→－14(BA ―→＋AC ―→)＝14AB ―→＋34AC ―→，故选B.5．在平面直角坐标系中，O 为坐标原点，A ，B ，C 三点满足OC ―→＝34OA ―→＋14OB ―→，则|BC ―→||AC ―→|等于( )A ．1B ．2C ．3D.32解析：选C 因为BC ―→＝OC ―→－OB ―→＝34OA ―→＋14OB ―→－OB ―→＝34BA ―→，AC ―→＝OC ―→－OA ―→＝34OA ―→＋14OB ―→－OA ―→＝14AB ―→，所以|BC ―→||AC ―→|＝3.故选C.6．已知△ABC 的边BC 的中点为D ，点G 满足GA ―→＋BG ―→＋CG ―→＝0，且AG ―→＝λGD ―→，则λ的值是( )A.12 B ．2 C ．－2D ．－12解析：选C 由GA ―→＋BG ―→＋CG ―→＝0，得G 为以AB ，AC 为邻边的平行四边形的第四个顶点，因此AG ―→＝－2GD ―→，则λ＝－2.故选C.7．下列四个结论：①AB ―→＋BC ―→＋CA ―→＝0；②AB ―→＋MB ―→＋BO ―→＋OM ―→＝0； ③AB ―→－AC ―→＋BD ―→－CD ―→＝0；④N Q ―→＋Q P ―→＋MN ―→－MP ―→＝0，其中一定正确的结论个数是( ) A ．1 B ．2 C ．3D ．4解析：选C ①AB ―→＋BC ―→＋CA ―→＝AC ―→＋CA ―→＝0，①正确；②AB ―→＋MB ―→＋BO ―→＋OM ―→＝AB ―→＋MO ―→＋OM ―→＝AB ―→，②错误；③AB ―→－AC ―→＋BD ―→－CD ―→＝CB ―→＋BD ―→＋DC ―→＝CD ―→＋DC ―→＝0，③正确；④N Q ―→＋Q P ―→＋MN ―→－MP ―→＝NP ―→＋PN ―→＝0，④正确．故①③④正确．8.如图，在平行四边形ABCD 中，M ，N 分别为AB ，AD 上的点，且AM ―→＝34AB ―→，AN ―→＝23AD ―→，AC ，MN 交于点P .若AP ―→＝λAC ―→，则λ的值为( ) A.35 B.37C.316D.617解析：选D ∵AM ―→＝34AB ―→，AN ―→＝23AD ―→，∴AP ―→＝λAC ―→＝λ(AB ―→＋AD ―→)＝λ⎝⎛⎭⎫43AM ―→＋32AN ―→＝43λAM ―→＋32λAN ―→.∵点M ，N ，P 三点共线，∴43λ＋32λ＝1，则λ＝617.故选D. 9．设向量a ，b 不平行，向量λa ＋b 与a ＋2b 平行，则实数λ＝________. 解析：因为向量λa ＋b 与a ＋2b 平行，所以可设λa ＋b ＝k (a ＋2b )，则⎩⎪⎨⎪⎧λ＝k ，1＝2k ，所以λ＝12.答案：1210．若AP ―→＝12PB ―→，AB ―→＝(λ＋1)BP ―→，则λ＝________.解析：如图，由AP ―→＝12PB ―→，可知点P 是线段AB 上靠近点A 的三等分点，则AB ―→＝－32BP ―→，结合题意可得λ＋1＝－32，所以λ＝－52.答案：－5211．已知平行四边形ABCD 的对角线AC 和BD 相交于O ，且OA ―→＝a ，OB ―→＝b ，则DC ―→＝________，BC ―→＝________.(用a ，b 表示)解析：如图，DC ―→＝AB ―→＝OB ―→－OA ―→＝b －a ，BC ―→＝OC ―→－OB ―→＝－OA ―→－OB ―→＝－a －b .答案：b －a －a －b12．(2019·长沙模拟)在平行四边形ABCD 中，M 为BC 的中点．若AB ―→＝λAM ―→＋μDB ―→，则λ－μ＝________.解析：如图，在平行四边形ABCD 中，AB ―→＝DC ―→，所以AB ―→＝AM ―→＋MB ―→＝AM ―→＋12CB ―→＝AM ―→＋12(DB ―→－DC ―→)＝AM ―→＋12(DB ―→－AB ―→)＝AM ―→＋12DB ―→－12AB ―→，所以32AB ―→＝AM ―→＋12DB ―→，所以AB ―→＝23AM ―→＋13DB ―→，所以λ＝23，μ＝13，所以λ－μ＝13.答案：1313．设e 1，e 2是两个不共线的向量，已知AB ―→＝2e 1－8e 2，CB ―→＝e 1＋3e 2，CD ―→＝2e 1－e 2.(1)求证：A ，B ，D 三点共线；(2)若BF ―→＝3e 1－k e 2，且B ，D ，F 三点共线，求k 的值．解：(1)证明：由已知得BD ―→＝CD ―→－CB ―→＝(2e 1－e 2)－(e 1＋3e 2)＝e 1－4e 2， ∵AB ―→＝2e 1－8e 2， ∴AB ―→＝2BD ―→.又∵AB ―→与BD ―→有公共点B ， ∴A ，B ，D 三点共线． (2)由(1)可知BD ―→＝e 1－4e 2，∵BF ―→＝3e 1－ke 2，且B ，D ，F 三点共线， ∴存在实数λ，使BF ―→＝λBD ―→，即3e 1－ke 2＝λe 1－4λe 2，得⎩⎪⎨⎪⎧λ＝3，－k ＝－4λ.解得k ＝12.第二节平面向量基本定理及坐标表示一、基础知识1．平面向量基本定理(1)定理：如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2.(2)基底：不共线的向量e 1e 2叫做表示这一平面内所有向量的一组基底． (1)基底e 1，e 2必须是同一平面内的两个不共线向量，零向量不能作为基底； (2)基底给定，同一向量的分解形式唯一；(3)如果对于一组基底e 1，e 2，有a ＝λ1e 1＋λ2e 2＝μ1e 1＋μ2e 2，则可以得到⎩⎪⎨⎪⎧λ1＝μ1，λ2＝μ2.2．平面向量的坐标运算(1)向量的加法、减法、数乘向量及向量的模：设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ＋b ＝(x 1＋x 2，y 1＋y 2)， a －b ＝(x 1－x 2，y 1－y 2)，λa ＝(λx 1，λy 1)，|a |＝x 21＋y 21.若a ＝b ，则x 1＝x 2且y 1＝y 2. (2)向量坐标的求法：①若向量的起点是坐标原点，则终点坐标即为向量的坐标． ②设A (x 1，y 1)，B (x 2，y 2)，则AB ―→＝(x 2－x 1，y 2－y 1)， |AB ―→|＝(x 2－x 1)2＋(y 2－y 1)2. 3．平面向量共线的坐标表示设a ＝(x 1，y 1)，b ＝(x 2，y 2)，其中b ≠0，则a ∥b ⇔x 1y 2－x 2y 1＝0.当且仅当x 2y 2≠0时，a ∥b 与x 1x 2＝y 1y 2等价．即两个不平行于坐标轴的共线向量的对应坐标成比例．考点一平面向量基本定理及其应用[典例] 如图，以向量OA ―→＝a ，OB ―→＝b 为邻边作平行四边形OADB ，BM ―→＝13BC ―→，CN ―→＝13CD ―→，用a ，b 表示OM ―→，ON ―→，MN ―→.[解] ∵BA ―→＝OA ―→－OB ―→＝a －b ， BM ―→＝16BA ―→＝16a －16b ，∴OM ―→＝OB ―→＋BM ―→＝16a ＋56b .∵OD ―→＝a ＋b ， ∴ON ―→＝OC ―→＋13CD ―→＝12OD ―→＋16OD ―→ ＝23OD ―→＝23a ＋23b ， ∴MN ―→＝ON ―→－OM ―→＝23a ＋23b －16a －56b ＝12a －16b .综上，OM ―→＝16a ＋56b ，ON ―→＝23a ＋23b ，MN ―→＝12a －16b .[解题技法]1．平面向量基本定理解决问题的一般思路(1)先选择一组基底，并运用该基底将条件和结论表示为向量的形式，再通过向量的运算来解决．(2)在基底未给出的情况下，合理地选取基底会给解题带来方便．另外，要熟练运用平面几何的一些性质定理．2．应用平面向量基本定理应注意的问题(1)只要两个向量不共线，就可以作为平面向量的一组基底，基底可以有无穷多组． (2)利用已知向量表示未知向量，实质就是利用平行四边形法则或三角形法则进行向量的加减运算或数乘运算．[题组训练]1．在△ABC 中，P ，Q 分别是AB ，BC 的三等分点，且AP ＝13AB ，BQ ＝13BC ，若AB ―→＝a ，AC ―→＝b ，则P Q ―→＝( )A.13a ＋13b B ．－13a ＋13bC.13a －13b D ．－13a －13b解析：选A 由题意知P Q ―→＝PB ―→＋B Q ―→＝23AB ―→＋13BC ―→＝23AB ―→＋13(AC ―→－AB ―→)＝13AB ―→＋13AC ―→＝13a ＋13b . 2．已知在△ABC 中，点O 满足OA ―→＋OB ―→＋OC ―→＝0，点P 是OC 上异于端点的任意一点，且OP ―→＝m OA ―→＋n OB ―→，则m ＋n 的取值范围是________．解析：依题意，设OP ―→＝λOC ―→(0<λ<1)，由OA ―→＋OB ―→＋OC ―→＝0，知OC ―→＝－(OA ―→＋OB ―→)，所以OP ―→＝－λOA ―→－λOB ―→，由平面向量基本定理可知， m ＋n ＝－2λ，所以m ＋n ∈(－2,0)．答案：(－2,0)考点二平面向量的坐标运算[典例] 已知A (－2,4)，B (3，－1)，C (－3，－4)．设AB ―→＝a ，BC ―→＝b ，CA ―→＝c ，且CM ―→＝3c ，CN ―→＝－2b ，(1)求3a ＋b －3c ；(2)求M ，N 的坐标及向量MN ―→的坐标．[解] 由已知得a ＝(5，－5)，b ＝(－6，－3)，c ＝(1,8)． (1)3a ＋b －3c ＝3(5，－5)＋(－6，－3)－3(1,8) ＝(15－6－3，－15－3－24)＝(6，－42)． (2)设O 为坐标原点，∵CM ―→＝OM ―→－OC ―→＝3c ， ∴OM ―→＝3c ＋OC ―→＝(3,24)＋(－3，－4)＝(0,20)． ∴M (0,20)．又∵CN ―→＝ON ―→－OC ―→＝－2b ， ∴ON ―→＝－2b ＋OC ―→＝(12,6)＋(－3，－4)＝(9,2)， ∴N (9,2)，∴MN ―→＝(9，－18)．[变透练清]1.(变结论)本例条件不变，若a ＝m b ＋n c ，则m ＝________，n ＝________. 解析：∵m b ＋n c ＝(－6m ＋n ，－3m ＋8n )，a ＝(5，－5)，∴⎩⎪⎨⎪⎧－6m ＋n ＝5，－3m ＋8n ＝－5，解得⎩⎪⎨⎪⎧m ＝－1，n ＝－1.答案：－1 －12．已知O 为坐标原点，向量OA ―→＝(2,3)，OB ―→＝(4，－1)，且AP ―→＝3PB ―→，则|OP ―→|＝________.解析：设P (x ，y )，由题意可得A ，B 两点的坐标分别为(2,3)，(4，－1)，由AP ―→＝3PB ―→，可得⎩⎪⎨⎪⎧x －2＝12－3x ，y －3＝－3y －3，解得⎩⎪⎨⎪⎧x ＝72，y ＝0，故|OP ―→|＝72.答案：72[解题技法]1．平面向量坐标运算的技巧(1)向量的坐标运算主要是利用向量加、减、数乘运算的法则来进行求解的，若已知有向线段两端点的坐标，则应先求向量的坐标．(2)解题过程中，常利用“向量相等，则其坐标相同”这一原则，通过列方程(组)来进行求解．2．向量坐标运算的注意事项(1)向量坐标与点的坐标形式相似，实质不同． (2)向量坐标形式的线性运算类似多项式的运算．(3)向量平行与垂直的坐标表达形式易混淆，需清楚结论推导过程与结果，加以区分．考点三平面向量共线的坐标表示[典例] 已知a ＝(1,0)，b ＝(2,1)． (1)当k 为何值时，k a －b 与a ＋2b 共线；(2)若AB ―→＝2a ＋3b ，BC ―→＝a ＋m b ，且A ，B ，C 三点共线，求m 的值． [解] (1)∵a ＝(1,0)，b ＝(2,1)， ∴k a －b ＝k (1,0)－(2,1)＝(k －2，－1)， a ＋2b ＝(1,0)＋2(2,1)＝(5,2)， ∵k a －b 与a ＋2b 共线，∴2(k －2)－(－1)×5＝0，∴k ＝－12.(2)AB ―→＝2(1,0)＋3(2,1)＝(8,3)， BC ―→＝(1,0)＋m (2,1)＝(2m ＋1，m )． ∵A ，B ，C 三点共线，∴AB ―→∥BC ―→， ∴8m －3(2m ＋1)＝0，∴m ＝32.[解题技法]1．平面向量共线的充要条件的2种形式(1)若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件是x 1y 2－x 2y 1＝0. (2)若a ∥b (b ≠0)，则a ＝λb . 2．两个向量共线的充要条件的作用判断两个向量是否共线(或平行)，可解决三点共线的问题；另外，利用两个向量共线的充要条件可以列出方程(组)，求参数的值．[题组训练]1．已知向量a ＝(1,2)，b ＝(－3,2)，若(k a ＋b )∥(a －3b )，则实数k 的取值为( ) A ．－13B.13C ．－3D ．3解析：选A k a ＋b ＝k (1,2)＋(－3,2)＝(k －3,2k ＋2)． a －3b ＝(1,2)－3(－3,2)＝(10，－4)，则由(k a ＋b )∥(a －3b )得(k －3)×(－4)－10×(2k ＋2)＝0，所以k ＝－13.2．(2019·唐山模拟)已知在平面直角坐标系xOy 中，P 1(3,1)，P 2(－1,3)，P 1，P 2，P 3三点共线且向量OP 3―→与向量a ＝(1，－1)共线，若OP 3―→＝λOP 1―→＋(1－λ)OP 2―→，则λ＝( )A ．－3B ．3C ．1D ．－1解析：选D 设OP 3―→＝(x ，y )，则由OP 3―→∥a 知x ＋y ＝0，于是OP 3―→＝(x ，－x )．若OP 3―→＝λOP 1―→＋(1－λ)OP 2―→，则有(x ，－x )＝λ(3,1)＋(1－λ)(－1,3)＝(4λ－1,3－2λ)，即⎩⎪⎨⎪⎧4λ－1＝x ，3－2λ＝－x ，所以4λ－1＋3－2λ＝0，解得λ＝－1，故选D.3．在梯形ABCD 中，AB ∥CD ，且DC ＝2AB ，三个顶点A (1,2)，B (2,1)，C (4,2)，则点D 的坐标为________．解析：∵在梯形ABCD 中，DC ＝2AB ，AB ∥CD ， ∴DC ―→＝2AB ―→.设点D 的坐标为(x ，y )，则DC ―→＝(4－x,2－y )，AB ―→＝(1，－1)， ∴(4－x,2－y )＝2(1，－1)，即(4－x,2－y )＝(2，－2)，∴⎩⎪⎨⎪⎧ 4－x ＝2，2－y ＝－2，解得⎩⎪⎨⎪⎧x ＝2，y ＝4，故点D 的坐标为(2,4)．答案：(2,4)[课时跟踪检测]1．(2019·昆明调研)已知向量a ＝(－1,2)，b ＝(1,3)，则|2a －b |＝( ) A.2 B ．2 C.10D ．10解析：选C 由已知，易得2a －b ＝2(－1,2)－(1,3)＝(－3,1)，所以|2a －b |＝(－3)2＋12＝10.故选C.2．已知向量a ＝(5,2)，b ＝(－4，－3)，c ＝(x ，y )，若3a －2b ＋c ＝0，则c ＝( ) A ．(－23，－12) B ．(23,12) C ．(7,0)D ．(－7,0)解析：选A 由题意可得3a －2b ＋c ＝3(5,2)－2(－4，－3)＋(x ，y )＝(23＋x,12＋y )＝(0,0)，所以⎩⎪⎨⎪⎧ 23＋x ＝0，12＋y ＝0，解得⎩⎪⎨⎪⎧x ＝－23，y ＝－12，所以c ＝(－23，－12)．3．(2018·石家庄模拟)已知向量a ＝(1，m )，b ＝(m,1)，则“m ＝1”是“a ∥b ”成立的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：选A 若a ∥b ，则m 2＝1，即m ＝±1，故“m ＝1”是“a ∥b ”的充分不必要条件，选A.4．已知点M 是△ABC 的边BC 的中点，点E 在边AC 上，且EC ―→＝2AE ―→，则EM ―→＝( ) A.12AC ―→＋13AB ―→ B.12AC ―→＋16AB ―→C.16AC ―→＋12AB ―→ D.16AC ―→＋32AB ―→解析：选C 如图，因为EC ―→＝2AE ―→，所以EC ―→＝23AC ―→，所以EM ―→＝EC ―→＋CM ―→＝23AC ―→＋12CB ―→＝23AC ―→＋12(AB ―→－AC ―→)＝12AB ―→＋16AC ―→.5．已知点A (8，－1)，B (1，－3)，若点C (2m －1，m ＋2)在直线AB 上，则实数m ＝( ) A ．－12 B ．13 C ．－13D ．12解析：选C 因为点C 在直线AB 上，所以AC ―→与AB ―→同向．又AB ―→＝(－7，－2)，AC ―→＝(2m －9，m ＋3)，故2m －9－7＝m ＋3－2，所以m ＝－13.故选C.6．在平面直角坐标系xOy 中，已知A (1,0)，B (0,1)，C 为坐标平面内第一象限的点，且∠AOC ＝π4，|OC |＝2，若OC ―→＝λOA ―→＋μOB ―→，则λ＋μ＝( )A ．22 B.2 C ．2 D ．42解析：选A 因为|OC |＝2，∠AOC ＝π4，所以C (2，2)，又因为OC ―→＝λOA ―→＋μOB ―→，所以(2，2)＝λ(1,0)＋μ(0,1)＝(λ，μ)，所以λ＝μ＝2，λ＋μ＝2 2.7．已知|OA ―→|＝1，|OB ―→|＝3，OA ―→⊥OB ―→，点C 在线段AB 上，∠AOC ＝30°.设OC ―→＝m OA ―→＋n OB ―→(m ，n ∈R )，则m n等于( )A.13 B ．3 C.33D.3 解析：选B 如图，由已知|OA ―→|＝1，|OB ―→|＝3，OA ―→⊥OB ―→，可得AB ＝2，∠A ＝60°，因为点C 在线段AB 上，∠AOC ＝30°，所以OC ⊥AB ，过点C 作CD ⊥OA ，垂足为点D ，则OD ＝34，CD ＝34，所以OD ―→＝34OA ―→，DC ―→＝ 14OB ―→，即OC ―→＝34OA ―→＋14OB ―→，所以mn＝3.8.(2019·深圳模拟)如图，在正方形ABCD 中，M 是BC 的中点，若AC ―→＝λAM ―→＋μBD ―→，则λ＋μ＝( )A.43B.53C.158D ．2解析：选B 以点A 为坐标原点，分别以AB ―→，AD ―→的方向为x 轴，y 轴的正方向，建立平面直角坐标系(图略)．设正方形的边长为2，则A (0,0)，C (2,2)，M (2,1)，B (2,0)，D (0,2)，所以AC ―→＝(2,2)，AM ―→＝(2,1)，BD ―→＝(－2,2)，所以λAM ―→＋μBD ―→＝(2λ－2μ，λ＋2μ)，因为AC―→＝λAM ―→＋μBD ―→，所以⎩⎪⎨⎪⎧2λ－2μ＝2，λ＋2μ＝2，解得⎩⎨⎧λ＝43，μ＝13，所以λ＋μ＝53.9．已知向量a ＝(2,1)，b ＝(1，－2)，若m a ＋n b ＝(9，－8)(m ，n ∈R )，则m －n 的值为________．解析：∵m a ＋n b ＝(2m ＋n ，m －2n )＝(9，－8)，∴⎩⎪⎨⎪⎧ 2m ＋n ＝9，m －2n ＝－8，∴⎩⎪⎨⎪⎧m ＝2，n ＝5， ∴m －n ＝2－5＝－3. 答案：－310．已知向量a ＝(1，m )，b ＝(4，m )，若有(2|a |－|b |)(a ＋b )＝0，则实数m ＝________. 解析：因为a ＋b ＝(5,2m )≠0，所以由(2|a |－|b |)(a ＋b )＝0得2|a |－|b |＝0，所以|b |＝2|a |，所以42＋m 2＝212＋m 2，解得m ＝±2. 答案：±211．(2019·南昌模拟)已知向量a ＝(m ，n )，b ＝(1，－2)，若|a |＝25，a ＝λb (λ<0)，则m －n ＝________.解析：∵a ＝(m ，n )，b ＝(1，－2)， ∴由|a |＝25，得m 2＋n 2＝20， ① 由a ＝λb (λ<0)，得⎩⎪⎨⎪⎧m <0，n >0，－2m －n ＝0， ②由①②，解得m ＝－2，n ＝4. ∴m －n ＝－6. 答案：－612．已知向量a ＝(1,2)，b ＝(x,1)，u ＝a ＋2b ，v ＝2a －b ，且u ∥v ，则实数x 的值为________．解析：因为a ＝(1,2)，b ＝(x,1)，u ＝a ＋2b ，v ＝2a －b ，所以u ＝(1,2)＋2(x,1)＝(2x ＋1,4)， v ＝2(1,2)－(x,1)＝(2－x,3)．又因为u ∥v ，所以3(2x ＋1)－4(2－x )＝0，即10x ＝5，解得x ＝12.答案：1213．在平面直角坐标系xOy 中，已知点A (1,1)，B (2,3)，C (3,2)，点P (x ，y )在△ABC 三边围成的区域(含边界)上．(1)若P A ―→＋PB ―→＋PC ―→＝0，求|OP ―→|；(2)设OP ―→＝m AB ―→＋n AC ―→(m ，n ∈R )，用x ，y 表示m －n .解：(1)∵P A ―→＋PB ―→＋PC ―→＝0，P A ―→＋PB ―→＋PC ―→＝(1－x,1－y )＋(2－x,3－y )＋(3－x,2－y )＝(6－3x,6－3y )，∴⎩⎪⎨⎪⎧6－3x ＝0，6－3y ＝0，解得x ＝2，y ＝2，即OP ―→＝(2,2)，故|OP ―→|＝2 2.(2)∵OP ―→＝m AB ―→＋n AC ―→，AB ―→＝(1,2)，AC ―→＝(2,1)． ∴(x ，y )＝(m ＋2n,2m ＋n )，即⎩⎪⎨⎪⎧x ＝m ＋2n ，y ＝2m ＋n ，两式相减，得m －n ＝y －x .第三节平面向量的数量积一、基础知识1．向量的夹角(1)定义：已知两个非零向量a 和b ，如图所示，作OA ―→＝a ，OB ―→＝b ，则∠AOB ＝θ(0°≤θ≤180°)叫做向量a 与b 的夹角，记作〈a ，b 〉．只有两个向量的起点重合时所对应的角才是两向量的夹角． (2)范围：夹角θ的范围是[0，π]．当θ＝0时，两向量a ，b 共线且同向；当θ＝π2时，两向量a ，b 相互垂直，记作a ⊥b ；当θ＝π时，两向量a ，b 共线但反向． 2．平面向量数量积的定义已知两个非零向量a 与b ，我们把数量|a ||b | cos θ叫做a 与b 的数量积(或内积)，记作a ·b ，即a ·b ＝|a ||b |cos θ，其中θ是a 与b 的夹角．规定：零向量与任一向量的数量积为零． 3．平面向量数量积的几何意义 (1)一个向量在另一个向量方向上的投影设θ是a ，b 的夹角，则|b |cos θ叫做向量b 在向量a 的方向上的投影，|a |cos θ叫做向量a 在向量b 的方向上的投影．(2)a ·b 的几何意义数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos θ的乘积．投影和两向量的数量积都是数量，不是向量. 4．向量数量积的运算律 (1)交换律：a ·b ＝b ·a .(2)数乘结合律：(λa )·b ＝λ(a ·b )＝a ·(λb )． (3)分配律：(a ＋b )·c ＝a ·c ＋b ·c .向量数量积的运算不满足乘法结合律，即(a ·b )·c 不一定等于a ·(b ·c )，这是由于(a ·b )·c表示一个与c共线的向量，a·(b·c)表示一个与a共线的向量，而c与a不一定共线．5．平面向量数量积的性质设a，b为两个非零向量，e是与b同向的单位向量，θ是a与e的夹角，则(1)e·a＝a·e＝|a|cos θ.(2)a⊥b⇔a·b＝0.(3)当a与b同向时，a·b＝|a||b|；当a与b反向时，a·b＝－|a||b|.特别地，a·a＝|a|2或|a|＝a·a.(4)cos θ＝a·b|a||b|.(5)|a·b|≤|a||b|.6．平面向量数量积的坐标表示已知两个非零向量a＝(x1，y1)，b＝(x2，y2)，θ为a与b的夹角，则(1)|a|＝x21＋y21；(3)a⊥b⇔x1x2＋y1y2＝0；(2)a·b＝x1x2＋y1y2;_ (4)cos θ＝x1x2＋y1y2x21＋y21x22＋y22.二、常用结论汇总1．平面向量数量积运算的常用公式(1)(a＋b)·(a－b)＝a2－b2；(2)(a±b)2＝a2±2a·b＋b2.2．有关向量夹角的两个结论(1)两个向量a与b的夹角为锐角，则有a·b>0，反之不成立(因为夹角为0时不成立)；(2)两个向量a与b的夹角为钝角，则有a·b<0，反之不成立(因为夹角为π时不成立)．考点一平面向量的数量积的运算[典例](1)(2018·新乡二模)若向量m＝(2k－1，k)与向量n＝(4,1)共线，则m·n＝()A ．0B ．4C ．－92D ．－172(2)(2018·天津高考)在如图所示的平面图形中，已知OM ＝1，ON ＝2，∠MON ＝120°，BM ―→＝2MA ―→，CN ―→＝2NA ―→，则BC ―→·OM ―→的值为( )A ．－15B ．－9C ．－6D ．0[解析] (1)∵向量m ＝(2k －1，k )与向量n ＝(4,1)共线，∴2k －1－4k ＝0，解得k ＝－12，∴m ＝⎝⎛⎭⎫－2，－12， ∴m ·n ＝－2×4＋⎝⎛⎭⎫－12×1＝－172. (2)法一：如图，连接MN . ∵BM ―→＝2MA ―→，CN ―→＝2NA ―→， ∴AM AB ＝AN AC ＝13. ∴MN ∥BC ，且MN BC ＝13.∴BC ―→＝3MN ―→＝3(ON ―→－OM ―→)． ∴BC ―→·OM ―→＝3(ON ―→·OM ―→－OM ―→2) ＝3(2×1×cos 120°－12)＝－6.法二：在△ABC 中，不妨设∠A ＝90°，取特殊情况ON ⊥AC ，以A 为坐标原点，AB ，AC 所在直线分别为x 轴，y 轴建立如图所示的平面直角坐标系，因为∠MON ＝120°，ON ＝2，OM ＝1，所以O ⎝⎛⎭⎫2，32，C ⎝⎛⎭⎫0，332，M ⎝⎛⎭⎫52，0，B ⎝⎛⎭⎫152，0. 故BC ―→·OM ―→＝⎝⎛⎭⎫－152，332·⎝⎛⎭⎫12，－32＝－154－94＝－6.[答案] (1)D (2)C[解题技法] 求非零向量a ，b 的数量积的策略(1)若两向量共起点，则两向量的夹角直接可得，根据定义即可求得数量积；若两向量的起点不同，则需要通过平移使它们的起点重合，再计算．(2)根据图形之间的关系，用长度和相互之间的夹角都已知的向量分别表示出向量a ，b ，然后根据平面向量的数量积的定义进行计算求解．(3)若图形适合建立平面直角坐标系，可建立坐标系，求出a ，b 的坐标，通过坐标运算求解．[题组训练]1．(2019·济南模拟)已知矩形ABCD 中，AB ＝2，BC ＝1，则AC ―→·CB ―→＝( ) A ．1 B ．－1 C.6D ．22解析：选B 设AB ―→＝a ，AD ―→＝b ，则a ·b ＝0， ∵|a |＝2，|b |＝1，∴AC ―→·CB ―→＝(a ＋b )·(－b )＝－a ·b －b 2＝－1.2．(2019·南昌调研)已知向量a ，b 满足a ·(b ＋a )＝2，且a ＝(1,2)，则向量b 在a 方向上的投影为( )A.55B ．－55C ．－255D ．－355解析：选D 由a ＝(1,2)，可得|a |＝5，由a ·(b ＋a )＝2，可得a ·b ＋a 2＝2， ∴a ·b ＝－3，∴向量b 在a 方向上的投影为a ·b |a |＝－355.3．(2018·石家庄质检)在△ABC 中，已知AB ―→与AC ―→的夹角为90°，|AB ―→|＝2，|AC ―→|＝1，M 为BC 上的一点，且AM ―→＝λAB ―→＋μAC ―→ (λ，μ∈R)，且AM ―→·BC ―→＝0，则 λμ的值为________．解析：法一：∵BC ―→＝AC ―→－AB ―→，AM ―→·BC ―→＝0， ∴(λAB ―→＋μAC ―→)·(AC ―→－AB ―→)＝0，∵AB ―→与AC ―→的夹角为90°，|AB ―→|＝2，|AC ―→|＝1， ∴－λ|AB ―→|2＋μ|AC ―→|2＝0，即－4λ＋μ＝0，∴λμ＝14.法二：根据题意，建立如图所示的平面直角坐标系，则A (0,0)，B (0,2)，C (1,0)，所以AB ―→＝(0,2)，AC ―→＝(1,0)，BC ―→＝(1，－2)．设M (x ，y )，则AM ―→＝(x ，y )，所以AM ―→·BC ―→＝(x ，y )·(1，－2)＝x －2y ＝0，所以x ＝2y ，又AM ―→＝λAB ―→＋μAC ―→，即(x ，y )＝λ(0,2)＋μ(1,0)＝(μ，2λ)，所以x ＝μ，y ＝2λ，所以λμ＝12y 2y ＝14.答案：14考点二平面向量数量积的性质考法(一) 平面向量的模[典例] (1)(2019·昆明适应性检测)已知非零向量a ，b 满足a ·b ＝0，|a |＝3，且a 与a ＋b 的夹角为π4，则|b |＝( )A ．6B ．32C ．22D ．3(2)(2019·福州四校联考)已知向量a ，b 为单位向量，且a ·b ＝－12，向量c 与a ＋b 共线，则|a ＋c |的最小值为( )A ．1 B.12C.34D.32[解析] (1)∵a ·b ＝0，|a |＝3，∴a ·(a ＋b )＝a 2＋a ·b ＝|a ||a ＋b |cos π4，∴|a ＋b |＝32，将|a ＋b |＝32两边平方可得，a 2＋2a ·b ＋b 2＝18，解得|b |＝3，故选D.(2)∵向量c 与a ＋b 共线，∴可设c ＝t (a ＋b )(t ∈R)，∴a ＋c ＝(t ＋1)a ＋t b ，∴(a ＋c )2＝(t ＋1)2a 2＋2t (t ＋1)·a ·b ＋t 2b 2， ∵向量a ，b 为单位向量，且a ·b ＝－12，∴(a ＋c )2＝(t ＋1)2－t (t ＋1)＋t 2＝t 2＋t ＋1≥34，∴|a ＋c |≥32，∴|a ＋c |的最小值为32，故选D. [答案] (1)D (2)D考法(二) 平面向量的夹角[典例] (1)已知平面向量a ，b 的夹角为π3，且|a |＝1，|b |＝12，则a ＋2b 与b 的夹角是( )A.π6 B.5π6C.π4D.3π4(2)已知向量a ＝(1，3)，b ＝(3，m )且b 在a 方向上的投影为－3，则向量a 与b 的夹角为________．[解析] (1)因为|a ＋2b |2＝|a |2＋4|b |2＋4a ·b ＝1＋1＋4×1×12×cos π3＝3，所以|a ＋2b |＝ 3.又(a ＋2b )·b ＝a ·b ＋2|b |2＝1×12×cos π3＋2×14＝14＋12＝34，所以cos 〈a ＋2b ，b 〉＝(a ＋2b )·b |a ＋2b ||b |＝343×12＝32，所以a ＋2b 与b 的夹角为π6.(2)因为b 在a 方向上的投影为－3，所以|b |cos 〈a ，b 〉＝－3，又|a |＝12＋(3)2＝2，所以a ·b ＝|a ||b |cos 〈a ，b 〉＝－6，又a ·b ＝3＋3m ，所以3＋3m ＝－6，解得m ＝－33，则b ＝(3，－33)，所以|b |＝32＋(－33)2＝6，所以cos 〈a ，b 〉＝a ·b |a ||b |＝－62×6＝－12，因为0≤〈a ，b 〉≤π，所以a 与b 的夹角为2π3. [答案] (1)A (2)2π3考法(三) 平面向量的垂直[典例] (1)若非零向量a ，b 满足|a |＝223|b |，且(a －b )⊥(3a ＋2b )，则a 与b 的夹角为( )A.π4B.π2C.3π4D ．π(2)已知向量AB ―→与AC ―→的夹角为120°，且|AB ―→|＝3，|AC ―→|＝2.若AP ―→＝λAB ―→＋AC ―→，且AP―→⊥BC ―→，则实数λ的值为________．[解析] (1)设a 与b 的夹角为θ，因为|a |＝223|b |，(a －b )⊥(3a ＋2b )，所以(a －b )·(3a ＋2b )＝3|a |2－2|b |2－a ·b ＝83|b |2－2|b |2－223|b |2cos θ＝0，解得cos θ＝22，因为θ∈[0，π]，所以θ＝π4. (2)由AP ―→⊥BC ―→，知AP ―→·BC ―→＝0，即AP ―→·BC ―→＝(λAB ―→＋AC ―→)·(AC ―→－AB ―→)＝(λ－1)AB ―→·AC ―→－λAB ―→2＋AC ―→2＝(λ－1)×3×2×⎝⎛⎭⎫－12－λ×9＋4＝0，解得λ＝712. [答案] (1)A (2)712[解题技法]1．利用坐标运算证明两个向量的垂直问题若证明两个向量垂直，先根据共线、夹角等条件计算出这两个向量的坐标；然后根据数量积的坐标运算公式，计算出这两个向量的数量积为0即可．2．已知两个向量的垂直关系，求解相关参数的值根据两个向量垂直的充要条件，列出相应的关系式，进而求解参数．[题组训练]1．(2018·深圳高级中学期中)已知向量m ＝(λ＋1,1)，n ＝(λ＋2,2)，若(m ＋n )⊥(m －n )，则λ＝( )A ．－4B ．－3C ．－2D ．－1解析：选B ∵(m ＋n )⊥(m －n )，∴(m ＋n )·(m －n )＝m 2－n 2＝(λ＋1)2＋1－(λ＋2)2－4＝0，解得λ＝－3.故选B.2．(2018·永州二模)已知非零向量a ，b 的夹角为60°，且|b |＝1，|2a －b |＝1，则|a |＝( ) A.12 B ．1 C.2D ．2解析：选A ∵非零向量a ，b 的夹角为60°，且|b |＝1，∴a ·b ＝|a |×1×12＝|a |2，∵|2a－b |＝1，∴|2a －b |2＝4a 2－4a ·b ＋b 2＝4|a |2－2|a |＋1＝1，∴4|a |2－2|a |＝0，∴|a |＝12，故选A.3．(2019·益阳、湘潭调研)已知向量a ，b 满足|a |＝1，|b |＝2，a ＋b ＝(1，3)，记向量a ，b 的夹角为θ，则t a n θ＝________.解析：∵|a |＝1，|b |＝2，a ＋b ＝(1，3)，∴(a ＋b )2＝|a |2＋|b |2＋2a ·b ＝5＋2a ·b ＝1＋3，∴a ·b ＝－12，∴cos θ＝a ·b |a |·|b |＝－14，∴sin θ＝1－⎝⎛⎭⎫－142＝154，∴t a n θ＝sin θc os θ＝－15. 答案：－15[课时跟踪检测]1．已知向量a ，b 满足|a |＝1，|b |＝23，a 与b 的夹角的余弦值为sin 17π3，则b ·(2a－b )等于( )A ．2B ．－1C ．－6D ．－18解析：选D ∵a 与b 的夹角的余弦值为sin 17π3＝－32， ∴a ·b ＝－3，b ·(2a －b )＝2a ·b －b 2＝－18.2．已知平面向量a ＝(－2,3)，b ＝(1,2)，向量λa ＋b 与b 垂直，则实数λ的值为( ) A.413 B ．－413C.54D ．－54解析：选D ∵a ＝(－2,3)，b ＝(1,2)，∴λa ＋b ＝(－2λ＋1,3λ＋2)．∵λa ＋b 与b 垂直，∴(λa ＋b )·b ＝0，∴(－2λ＋1,3λ＋2)·(1,2)＝0，即－2λ＋1＋6λ＋4＝0，解得λ＝－54.3．已知向量a ，b 满足|a |＝1，b ＝(2,1)，且a ·b ＝0，则|a －b |＝( ) A.6 B.5 C ．2D.3解析：选A 因为|a |＝1，b ＝(2,1)，且a ·b ＝0，所以|a －b |2＝a 2＋b 2－2a ·b ＝1＋5－0＝6，所以|a －b |＝ 6.故选A.4．已知向量a ＝(1,2)，b ＝(2，－3)．若向量c 满足(a ＋c )∥b ，c ⊥(a ＋b )，则c ＝( ) A.⎝⎛⎭⎫79，73B.⎝⎛⎭⎫－73，－79C.⎝⎛⎭⎫73，79D.⎝⎛⎭⎫－79，－73 解析：选D 设c ＝(m ，n )，则a ＋c ＝(1＋m,2＋n )，a ＋b ＝(3，－1)，因为(a ＋c )∥b ，则有－3(1＋m )＝2(2＋n )，即3m ＋2n ＝－7，又c ⊥(a ＋b )，则有3m －n ＝0，联立⎩⎪⎨⎪⎧3m ＋2n ＝－7，3m －n ＝0.解得⎩⎨⎧m ＝－79，n ＝－73.所以c ＝⎝⎛⎭⎫－79，－73. 5．(2018·襄阳调研)已知i ，j 为互相垂直的单位向量，a ＝i －2j ，b ＝i ＋λj ，且a 与b 的夹角为锐角，则实数λ的取值范围是( )A.⎝⎛⎭⎫－2，23∪⎝⎛⎭⎫23，＋∞B.⎝⎛⎭⎫12，＋∞ C ．(－∞，－2)∪⎝⎛⎭⎫－2，12D.⎝⎛⎭⎫－∞，12解析：选C 不妨令i ＝(1,0)，j ＝(0,1)，则a ＝(1，－2)，b ＝(1，λ)，因为它们的夹角为锐角，所以a ·b ＝1－2λ>0且a ，b 不共线，所以λ<12且λ≠－2，故选C.6．(2019·石家庄质检)若两个非零向量a ，b 满足|a ＋b |＝|a －b |＝2|b |，则向量a ＋b 与a 的夹角为( )A.π6B.π3C.2π3D.5π6解析：选A ∵|a ＋b |＝|a －b |，∴|a ＋b |2＝|a －b |2，∴a ·b ＝0.又|a ＋b |＝2|b |，∴|a ＋b |2＝4|b |2，|a |2＝3|b |2，∴|a |＝3|b |，cos 〈a ＋b ，a 〉＝(a ＋b )·a |a ＋b ||a |＝a 2＋a ·b |a ＋b ||a |＝|a |22|b ||a |＝|a |2|b |＝32，故a ＋b 与a 的夹角为π6. 7．(2018·宝鸡质检)在直角三角形ABC 中，角C 为直角，且AC ＝BC ＝1，点P 是斜边上的一个三等分点，则CP ―→·CB ―→＋CP ―→·CA ―→＝( )A ．0B ．1 C.94D ．－94解析：选B 以点C 为坐标原点，分别以CA ―→，CB ―→的方向为x 轴，y 轴的正方向建立平面直角坐标系(图略)，则C (0,0)，A (1，0)，B (0,1)，不妨设P ⎝⎛⎭⎫13，23，所以CP ―→·CB ―→＋CP ―→·CA ―→＝CP ―→·(CB ―→＋CA ―→)＝13＋23＝1.故选B.8．(2019·武汉调研)已知平面向量a ，b ，e 满足|e |＝1，a ·e ＝1，b ·e ＝－2，|a ＋b |＝2，则a ·b 的最大值为( )A ．－1B ．－2C ．－52D ．－54解析：选D 不妨设e ＝(1,0)，则a ＝(1，m )，b ＝(－2，n )(m ，n ∈R)，则a ＋b ＝(－1，m ＋n )，所以|a ＋b |＝1＋(m ＋n )2＝2，所以(m ＋n )2＝3，即3＝m 2＋n 2＋2mn ≥2mn ＋2mn ＝4mn ，当且仅当m ＝n 时等号成立，所以mn ≤34，所以a ·b ＝－2＋mn ≤－54，综上可得a ·b的最大值为－54.9．已知平面向量a ，b 满足a ·(a ＋b )＝3，且|a |＝2，|b |＝1，则向量a 与b 的夹角的正弦值为________．解析：∵a ·(a ＋b )＝a 2＋a ·b ＝22＋2×1×cos 〈a ，b 〉＝4＋2cos 〈a ，b 〉＝3， ∴cos 〈a ，b 〉＝－12，又〈a ，b 〉∈[0，π]，∴sin 〈a ，b 〉＝1－c os 2〈a ，b 〉＝32. 答案：3210．(2018·湖北八校联考)已知平面向量a ，b 的夹角为2π3，且|a |＝1，|b |＝2，若(λa ＋b )⊥(a －2b )，则λ＝________.解析：∵|a |＝1，|b |＝2，且a ，b 的夹角为2π3，∴a ·b ＝1×2×⎝⎛⎭⎫－12＝－1，又∵(λa ＋b )⊥(a －2b )，∴(λa ＋b )·(a －2b )＝0，即(λa ＋b )·(a －2b )＝λa 2－2b 2＋(1－2λ)a ·b ＝λ－8－(1－2λ)＝0，解得λ＝3.答案：311．(2018·合肥一检)已知平面向量a ，b 满足|a |＝1，|b |＝2，|a ＋b |＝3，则a 在b 方向上的投影等于________．解析：∵|a |＝1，|b |＝2，|a ＋b |＝3， ∴(a ＋b )2＝|a |2＋|b |2＋2a ·b ＝5＋2a ·b ＝3， ∴a ·b ＝－1，∴a 在b 方向上的投影为a ·b |b |＝－12.答案：－1212.如图所示，在等腰直角三角形AOB 中，OA ＝OB ＝1，AB ―→＝4AC ―→，则OC ―→·(OB ―→－OA ―→)＝________.解析：由已知得|AB ―→|＝2，|AC ―→|＝24，则OC ―→·(OB ―→－OA ―→)＝(OA ―→＋AC ―→)·AB ―→＝OA ―→·AB ―→＋AC ―→·AB ―→＝2cos 3π4＋24×2＝－12. 答案：－1213．(2019·南昌质检)设向量a ，b 满足|a |＝|b |＝1，且|2a －b |＝ 5. (1)求|2a －3b |的值；(2)求向量3a －b 与a －2b 的夹角θ.解：(1)∵|2a －b |2＝4a 2－4a ·b ＋b 2＝4－4a ·b ＋1＝5，∴a ·b ＝0， ∴|2a －3b |＝4a 2－12a ·b ＋9b 2＝4＋9＝13.(2)cos θ＝(3a －b )·(a －2b )|3a －b ||a －2b |＝3a 2＋2b 29a 2＋b 2×a 2＋4b 2＝510×5＝22，∵θ∈[0，π]，∴θ＝π4.。

2013年高考政治第一轮复习第五单元第13课

考点突破·深度剖析
第十三课
①人民群众参与国家政治生活增强和政治素养的提高
②人民群众民主意识的 ④决策
本课栏目开关
③政府决策更加科学
机关和公民共同制定政府的重大决策 A．①②④ B．②③④ C．①③④ D．①②③
解析本题易错选④，公民不能制定政府的决策。
答案 D
考点突破·深度剖析
高频考点二核心突破 1．公民进行民主监督的合法渠道信访举报制度公民通过给国家机含区义别关写信、打电话或当面向有关人员反映自己的意见，提出批评、建议人大代表联系群众制度公民将自己的意见、建议和要求反映给人大代表，形成人大代表的议案，上传到国家权力机关民主监督
本课概览
本课栏目开关
知识整合·有序识记
第十三课
知识整合〃有序识记
一、我国的选举制度及选举方式 1．我国的选举方式直接选举和间接选举、等额选举和差额选举。注意直接选举和间接选举、等额选举和差额选举，都是民主选举的方式，都各有自己的利弊，不能认为哪种选举会更优越或更民主。
本课栏目开关
本课栏目开关
知识整合·有序识记
第十三课
提示
民主决策、民主监督具体的参与方式中有些是相
本课栏目开关
同的，如写信、打电话、听证会等。如何区分两者关键是看该行为是一种“事前”行为还是“事后”行为。 “事前”行为属于民主决策，“事后”行为属于民主监督。如，向有关部门提建议，在决策之前，就应该是民主决策的具体途径；在执行过程中，应该是决策之后，就应该是民主监督的具体途径。
意；重大事项社会公示制度一般是公布一个决策草稿，然后有针对性地征求意见；专家咨询制度征求的是专家的意见；社会听证制度征求的是各方面代表的意见。

2013年甘肃省事业单位类招聘行政能力测试真题及答案

2013年甘肃省事业单位类招聘行政能力测试真题及答案（说明：本卷共100题，考试时间90分钟，满分100分）一、单选题1.依照法律规定冻结存款、汇款的，作出决定的行政机关应当在（）日内向当事人交付冻结决定书。

A、3B、5C、7D、15【答案】A2.引起法律关系产生、变更、消灭的法律事件（）是不依人的意志为转移的。

A、必须B、可以C、不能D、可能【答案】A3.依照法律规定冻结存款、汇款的，作出决定的行政机关应当在（）日内向当事人交付冻结决定书。

A、3B、5C、7D、15【答案】A4.纪某因为运输毒品罪被判处有期徒刑7年，刑满释放后7年，禁不住朋友的再三恳求，帮助朋友贩卖了30克毒品。

纪某的行为（）。

A、属于毒品犯罪的累犯，应当从重处罚B、属于毒品犯罪的惯犯，应当从重处罚C、属于毒品犯罪的再犯，应当从重处罚D、定贩卖毒品罪，加重处罚【答案】C5.通报情况使用（）。

A、通知B、通告C、通报D、情况报告【答案】C6.纪某因为运输毒品罪被判处有期徒刑7年，刑满释放后7年，禁不住朋友的再三恳求，帮助朋友贩卖了30克毒品。

纪某的行为（）。

A、属于毒品犯罪的累犯，应当从重处罚B、属于毒品犯罪的惯犯，应当从重处罚C、属于毒品犯罪的再犯，应当从重处罚D、定贩卖毒品罪，加重处罚【答案】C7.法与统治阶级的道德的关系是（）。

A、决定与被决定的关系B、相互对立的关系C、法决定道德，道德服从法D、相互渗透、相辅相成【答案】D8.马克思主义政治经济学的理论基础是（）。

A、英国古典经济学B、劳动价值论C、剩余价值理论D、辩证唯物主义和历史唯物主义【答案】A9.法与统治阶级的道德的关系是（）。

A、决定与被决定的关系B、相互对立的关系C、法决定道德，道德服从法D、相互渗透、相辅相成【答案】D10.“任何组织或者个人都不得有超越宪法和法律的特权”，这一规则不属于（）。

A、义务性规则B、强行性规则C、授权性规则D、禁止性规则【答案】C11.行政案件当事人要求听证的，行政机关应当组织听证，当事人（）行政机关组织听证的费用。

第五章中国的地理差异复习2013-4-8

“橘生淮南则为橘，橘生淮北则为枳。”意思是说南方的橘树移栽到淮河以北，就会变成小灌木，橘子也会变成不能吃的“枳”。 ——结合本课的知识，请你解释这种现象。
橘树是喜温作物，移栽到淮河以北，因地理环境发生了变化，热量不足，所以树木本身及果实发生了变化。
“秦岭—淮河”一线的地理意义一月均温图
-32℃ -24℃
-16℃ -8℃
0℃等温线
8℃
16℃
返回表格
中国温度带划分图
暖温带
亚热带
返回表格
400mm年等降水量线 800mm年等降水量线
1600mm年等降水量线
返回表格
我国干湿地区划分图
半湿润地区
湿润地区
返回表格
返回表格
温带针阔混交林
一、温度带的分界线
二、湿润地区和半湿润地区的分界线
三、河流有差异的分界线
四、不同土壤和植被的分界线五、农业生产差异的分界线
返回目录
五、练习巩固
1、我国某山脉以北以旱地为主、以南以水田为主。关于此山脉的走向正确的叙述是 A 南北走向 B 东北-西南走向 C 东西走向 D 东西-西南走向 C
2 、秦岭——淮河一线大致是 A 400毫米等降水量线通过的地方 B 一月0℃等温线通过的地方 B C 季风区和非季风区的分界线 D 内流区和外流区分界线
·人教版
[解析] 本题考查了我国四大地理区域的位置、范围和各区域分界线，以及各个区域分界的主要因素。南北方区域的差异主要是受气候的影响，北方地区和西北地区的差异主要是受海陆因素影响造成的降水的差异。A区域作为一个独立的单元，是因为它的地势较高。
·人教版
例2 【2011· 石家庄】我国北方地区、南方地区在自然、人文等方面均有较大差异。据此回答下列问题。 (1)北方地区与南方地区的分界线是( D ) A．太行山 B．昆仑山 C．祁连山 D．秦岭 (2)下列自然地理状况，属于南方地区的是( A ) ①1月平均气温在0℃以上 ②植被类型主要是常绿阔叶林 ③年降水量在800mm以下 ④河流数量少，含沙量大 A．①② B．②③ C．①③ D．②④

2014年中考总复习提能训练课件_第五章第1讲圆的基本性质

第五章
圆
第1讲
圆的基本性质
1．理解圆及其有关概念、了解弧、弦、圆心角的关系． 2．了解圆周角与圆心角的关系、直径所对圆周角的特征．
考点1
圆的有关概念及性质
1．圆．
定点定长的所有点组 (1) 平面上到__________ 的距离等于________
成的图形叫做圆．
轴对称图形，也是__________ 中心对称图形． (2)圆是________ 三点可确定一个圆． (3)不共线的________
)
A．10
B．4 30
C．10 或 4 30
D．10 或 2 165
解析：如图 22，连接 OA，OC.作直线 EF⊥CD 于 E，交 AB
1 于 F，则 EF⊥AB.∵OF⊥AB，OE⊥CD，∴AF＝2AB＝12，CE 1 ＝2CD.在 Rt△AOF 中，根据勾股定理，得 OF＝ 132－122＝5.
OA，CE⊥OB，点 D，E 分别是垂足，试判断 CD，CE 的大小
关系，并证明你的结论．
解：CD＝CE.理由：连接 CO.
∵C 是弧 AB 的中点，
，∴∠COD＝∠COE. AC ＝ BC ∴
图5-1-4
∵CD⊥AO，CE⊥BO，∴∠CDO＝∠CEO＝90°. 又∵CO＝CO，∴△COD≌△COE. ∴CD＝CE.
题用它最常见．
1．如图 5-1-1，AB 是⊙O 的直径，CD 为⊙O 的弦，CD⊥
AB 于 E，则下列结论不成立的是( D )
A．∠A＝∠D
B．CE＝DE
C. ∠ACB＝90°
D．BD＝CE
图 5-1-1
2．如图 5-1-2，⊙O 的弦AB垂直平分半径OC，若 AB＝则⊙O 的半径为( A )

七下地理_第五章地方文化特色与旅游(B卷真题重组卷)七年级下册分层训练AB卷(原卷版)

2022-2023学年七年级地理下册单元考点梳理分层卷（中图版）第五章地方文化特色与旅游（B卷·真题重组卷）一、选择题（本大题共25小题，每小题2分，共50分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）（2022·山东济宁·统考中考真题）济宁市位于华北平原与鲁中南山地交界地带，是孔孟之乡、礼仪之邦。

读济宁市地形图，完成下面小题。

1．山地、丘陵主要分布在邹城市和（）A．泗水县B．微山县C．梁山县D．汶上县2．东部山区符合因地制宜、可持续发展理念的项目是（）A．大规模放牧，散养牛、羊B．积极发展生态旅游C．持续扩种小麦、玉米，提高粮食产量D．发挥资源优势，大力开采石材3．济宁市地势低平、有“鱼米之乡”之称的县（市、区）是（）A．金乡县B．嘉祥县C．鱼台县D．任城区4．抗日战争时期，铁道游击队队员曾战斗过的县（市、区）是（）A．金乡县B．兖州区C．微山县D．汶上县5．尼山位于曲阜市东南部，有著名的孔子出生地夫子洞，研修学习的尼山书院、气势恢宏的孔子像、烟波浩渺的孔子湖，幽静舒适的步道等场所和景观。

我们来这里研学旅行的意义有（）①置身圣境，感悟自然之美②瞻仰圣人遗迹，礼拜先师③学习儒学，弘扬传统文化④学传统礼仪，树儒雅之风A．①②③B．②③④C．①②④D．①②③④（2022·山东青岛·统考中考真题）“山之东，日初升。

始东夷，生文明。

衍千秋，出圣人。

行仁礼，传盛名。

”齐鲁文化是在原东夷文化的基础上发展而来的，依托优越的地理位置和自然条件，形成了丰富多彩的各类文化资源。

读山东省示意图，完成下面6-8小题。

克己复礼为仁。

一日克己复礼，天下归仁焉！为仁由己，而由人乎哉？——《论语·颜渊》6．“齐鲁大地”——山东省（）A．位于中国的西部B．北、东、南三面濒临黄海C．位于低纬度地区D．位于黄河下游地区7．有利于齐鲁文化形成与发展的自然条件有（）①海陆兼备，海岸线曲折漫长②亚热带季风气候，四季分明③平原丘陵地形，地貌类型多样④河流稀疏，湖泊较少A．①②B．①③C．②③D．②④8．最能体现“仁”和“礼”文化特点的旅游资源是（）A．济南千佛山B．青岛太清宫C．烟台蓬莱阁D．济宁曲阜三孔（2022·四川绵阳·统考中考真题）溜索是一种古老的交通工具。

2013年甘肃事业单位招考《公共科目》综合基础知识冲刺资料

2013甘肃省事业单位招考《公共科目》考试综合基础知识复冲刺资料（含答案）参考答案一、单项选择题1．B 2.D 3.A 4.A 5.C6.B7.B8.C9.D 10.C11.C 12.D 13.B 14.B 15.C16.D 17.C 18.C 19.D 20.D21.B 22.A 23.A 24.C 25.A26.C 27.A 28.A 29.B 30.C31.A 32.D 33.D 34.A 35.A36.A 37.D 38.D 39.B 40.B41.D 42.C 43.B 44.A 45.D46.D 47.C 48.C 49.D 50.D51.B 52.B 53.B 54.A 55.D二、公文实务题56.D 57.C 58.D 59.C 60.C三、案例分析题61．B 62.D 63.C 64.A 65.B四、综合分析题66.C 67.A 68.C 69.B 70.A五、简析题（一）1、社会主义核心价值体系的基本内容？答：社会主义核心价值体系是党的十六届六中全会首次明确提出的一个科学命题，是和谐社会的灵魂,是建设和谐文化的根本。

社会主义核心价值体系的基本内容包括：马克思主义指导思想，中国特色社会主义共同理想，以爱国主义为核心的民族精神和以改革创新为核心的时代精神，社会主义荣辱观。

2、怎样建立社会主义核心价值体系？答：（1）必须坚持马克思主义在意识形态领域的指导地位。

（2）牢牢把握社会主义先进文化的前进方向。

（3）大力弘扬民族优秀文化传统，积极借鉴人类先进文明成果答题须知一、单项选择题（在下列选项中选择最恰当的1项，并用2B铅笔在答题卡相应题号下涂黑所选答案项的信息点，在试卷上作答一律无效。

本大题每题1分，共55题。

）1．党的十七大报告指出，推进社会主义新农村建设的首要任务是（）A．建立以工促农、以城带乡长效机制B．发展现代农业、繁荣农村经济C．严格保护耕地，增加农业投入D．发展乡镇企业，壮大县域经济，多渠道转移农民就业2．社会主义核心价值体系的精髓是（）A．时代文化和民族精神B．民族文化和时代精神C．民族精神和民族文化D．民族精神和时代精神3．社会主义和谐社会的建设目标是（）A．民主法治、公平正义、诚信友爱、充满活力、安定有序、人与自然和谐相处的社会B．社会各阶层各尽所能、各取所需的和谐社会C．充分保障劳动者的就业权利，实现劳动力资源的合理利用D．保持经济总量基本平衡，促进经济结构优化，引导国民经济持续、快速、健康发展。

甘肃省2013届高考理综适应性训练试题

甘肃省2013届高三新课改高考适应性训练理科综合能力试题注意事项：1．本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第33～40题为选考题，其他题为必考题。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．答第I卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案方框涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案方框。

写在本试卷上无效。

3．答第Ⅱ卷时，将答案写在答题卡上，在本试卷上答题无效。

4．考试结束后，将本试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 C 12 O 16 Si 28 S 32 Cu 64 Ag 108第I卷一、选择题：本题共1 3小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列关于生物膜的说法，正确的是A．细胞间信息交流体现了膜具有选择透过性B．细胞呼吸过程中ATP的产生均在膜上进行’C．Na+通过主动运输进入突触后膜使后膜产生兴奋D．膜功能的复杂程度取决于膜蛋白的种类和数量2．下列有关细胞生命历程的说法，不正确的是A．细胞生长，物质运输效率会增强B．细胞分化，核遗传物质不会改变C．细胞癌变导致癌细胞膜上糖蛋白减少D．细胞凋亡是由基因控制的细胞编程性死亡3．人在紧张、恐惧的时候，甲状腺激素分泌增加，甲状腺激素可以作用于多种器官，使机体产生出汗、心率加快、呼吸急促等生理现象。

下列叙述错误的是A．该实例中神经调节的神经中枢是下丘脑B．该激素可使神经系统兴奋性提高，使人反应灵敏C．体内几乎所有细胞都是该激素的靶细胞D．该激素的分泌与垂体有密切的关系4．下图表示某绿色植物的非绿色器官在氧浓度为a、b、c、d时，CO2释放量和O2吸收量的变化。

下列相关叙述正确的是A．氧浓度为a时，最适于贮藏该植物器官B．氧浓度为b时，无氧呼吸消耗的葡萄糖是有氧呼吸的5倍C．氧浓度为c时，无氧呼吸最弱D．氧浓度为d时，无氧呼吸的强度与有氧呼吸相等5．右图表示某种小鼠的进化过程，X、Y、Z表示物种形成的基本环节。

夯实考点,注重基础 -----兰州高考y语文研讨会心得体会

夯实考点，注重基础-----兰州高考研讨会心得体会王海龙2014年高考备考研讨会心得王海龙10月26日，我们高三教师一行60多人赴兰州参加高考备考研讨会：短短一天的培训时间，我非常珍惜这种学习机会并在本次会议中受益匪浅。

本次会议分为两个部分。

第一部分是原国家命题组调研员张银华老师做的关于2013年高考命题特点及变化趋势的解析。

其中给我感觉最为重要的内容就是高考语文应对策略。

高考语文应对策略主要.，高考复习必须按效率最优化原则选择对策。

高考复习对策必须有普遍的优势，有最高的效率且对全体有效。

所谓面向全体，不是指面向一个笼统的班级，而是指承认个性，通过面向每一个个体来实现面向全体。

长期以来，我们的复习强调得更多的是共性而非个性，因此，不少学生的潜能并没有得到最大限度的发挥，而一些学生的薄弱点也并没有得到真正的突破。

研究性复习由于其个性化特征而具有很强的针对性。

每个学生找出自己的位置，分析自己的需要，明确自己的方向，选择自己解决问题的方法，在成功中获得经验，在失败中吸取教训，把整个复习变成一次次对知识的体验和对困难的征服，这样在复习过程中才会突破弱点，巩固知识，形成能力;从另一方面说，高三学生经过近三年高中学习，已具备展开初级研究的能力和独自探究的欲望，研究性复习给了他们一个观望自身的窗口。

对高考成功者进行分析，有一点是相通的：他们有自己的复习方案，思路和方法，也就是自发地采用了研究性复习这一策略。

第二部分是西北师大附中彭亚娟老师做的2013年甘肃省高考语文试卷（全国新课标卷Ⅱ）分析及考生答卷质量分析。

主要内容有三个方面：一、试卷结构及总体特点。

二、试卷各题分析及考生答卷质量分析。

三、对2014年高三复习备考工作的建议。

我感受最深刻的是彭老师对于2014年高三复习备考工作的建议，主要有一下六方面：1．研究《考试大纲》，明确考试方向。

研究《普通高中语文课程标准》和《考试大纲》，明确高考改革的方向。

要随时关注《考试大纲》与《考试说明》可能出现的调整，关注是否会加大改革力度，以提高复习的针对性。

2013年新课标高考物理考纲解读

2013年新课标高考物理考纲解读1、全国高考物理卷新课标高考：（宁夏、辽宁、陕西、湖南、湖北、黑龙江、吉林、江西、山西、河南、新疆、云南、河北、内蒙古14）全国卷：（青海、贵州、甘肃、广西、西藏5）地方卷：（北京、广东、山东、浙江、福建、安徽、天津、重庆、四川、江苏、海南、上海12）2、2013年高考新动向考试的性质（无变化）考试的形式与试卷结构（有变化）单选还是多选在题号中有明确的指示。

各科考核目标、内容及题型示例（无变化）Ⅰ. 2010-2012全国新课标高考物理试题特点分析一、选择题部分2010年选择题所考知识点情况题号答案考查的知识点范围要求14 A C 物理学史Ⅰ15 C 胡克定律Ⅰ16 A D 功和功率以及动能定理ⅡⅡ17 A 电场力方向和曲线运动所受合外力与轨迹的关系Ⅱ18 B 力的平衡Ⅱ19 D 电源的效率Ⅱ20 B 开普勒第三定律Ⅰ21 D 右手定则和法拉第电磁感应定律ⅡⅡ2011年选择题所考知识点情况题号答案考查的知识点范围要求14 B 安培定则和地磁场分布Ⅰ15 ABD 力和运动关系Ⅱ16 ABC 功和能的关系ⅡⅠ17 A 主要考查交流电的有效值、功率及理想变压器的有关知识。

18 BD 动能定理和安培力Ⅱ19 B 开普勒第三定律Ⅰ20 D 电场力方向和曲线运动所受合外力与轨迹的关系Ⅱ21 A 摩擦力和牛顿第二定律ⅡⅡ2012年选择题所考知识点情况题号答案考查的知识点范围要求14 AD 物理学史、惯性概念Ⅰ15 BD 抛体运动Ⅱ16 B 力的合成与分解Ⅱ17 B 交流电、变压器Ⅰ18 BD 电容器、匀强电场、电势差Ⅱ19 C 电磁感应Ⅰ20 A 电磁感应安培力Ⅱ21 A 万有引力定律Ⅱ近三年选择题部分命题点的分析1、10年试题涉及到对物理学史知识的考查，力求体现新课改的三维目标要求。

11年未考。

12年又考。

2、质点的运动是历年高考的必考内容，可以与其它知识点相结合，也可以单独考查。