概率第一章历年考研真题(数学一、三、四)

合集下载

历年数学一概率(1987-2015)..

历年考研数学一真题1987-2014（经典珍藏版）1987年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在一次实验中,事件A 发生的概率为,p 现进行n 次独立试验,则A 至少发生一次的概率为____________;而事件A 至多发生一次的概率为____________.(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________. (3)已知连续随机变量X 的概率密度函数为221(),xx f x-+-=则X 的数学期望为____________,X 的方差为____________.十一、（本题满分6分）设随机变量,X Y 相互独立,其概率密度函数分别为()X f x = 1001x ≤≤其它,()Y f y = e 0y- 00y y >≤, 求2Z X Y =+的概率密度函数.1988年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在三次独立试验中,事件A出现的概率相等,若已知A至少出现一次的概率等于19,27则事件A在一次试验中出现的概率是____________.(2)若在区间(0,1)内任取两个数,则事件”两数之和小于65”的概率为____________.(3)设随机变量X服从均值为10,均方差为0.02的正态分布,已知22(),(2.5)0.9938,uxx duφφ-==⎰则X落在区间(9.95,10.05)内的概率为____________.十一、（本题满分6分）设随机变量X的概率密度函数为21(),(1)Xf xxπ=-求随机变量1Y=-的概率密度函数().Yf y1989年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机事件A的概率()0.5,P A=随机事件B的概率()0.6P B=及条件概率(|)0.8,P B A=则和事件A B的概率()P A B=____________.(2)甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为____________.(3)若随机变量ξ在(1,6)上服从均匀分布,则方程210x xξ++=有实根的概率是____________.十一、（本题满分6分）设随机变量X与Y独立,且X服从均值为1、标准差(均方差)的正态分布,而Y服从标准正态分布.试求随机变量23Z X Y=-+的概率密度函数.1990年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机变量X 的概率密度函数1()e ,2xf x x -=-∞<<+∞ 则X 的概率分布函数()F x =____________.(2)设随机事件A 、B 及其和事件的概率分别是0.4、0.3和0.6,若B 表示B 的对立事件,那么积事件AB 的概率()P AB =____________.(3)已知离散型随机变量X 服从参数为2的泊松()Poisson 分布,即22e {},0,1,2,,!k P X k k k -===则随机变量32Z X =-的数学期望()E Z =____________.十一、（本题满分6分）设二维随机变量(,)X Y 在区域:01,D x y x <<<内服从均匀分布,求关于X 的边缘概率密度函数及随机变量21Z X =+的方差().D Z1991年全国硕士研究生入学统一考试十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)若随机变量X 服从均值为2、方差为2σ的正态分布,且{24}0.3,P X <<=则{0}P X <=____________.(2)随机地向半圆0y a <<为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与x 轴的夹角小于4π的概率为____________.十一、（本题满分6分）设二维随机变量(,)X Y 的密度函数为(,)f x y =(2)2e 0,00 x y x y -+>>其它求随机变量2Z X Y =+的分布函数.1992年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上) (1)已知11()()(),()0,()(),46P A P B P C P AB P AC P BC ======则事件A、B 、C 全不发生的概率为____________.(2)设随机变量X 服从参数为1的指数分布,则数学期望2{e }X E X -+=____________. 十一、（本题满分6分）设随机变量X 与Y 独立,X 服从正态分布2(,),N Y μσ服从[,]ππ-上的均匀分布,试求Z X Y =+的概率分布密度(计算结果用标准正态分布函数Φ表示,其中22()e)t xx dt --∞Φ=.1993年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为____________.(2)设随机变量X 服从(0,2)上的均匀分布,则随机变量2Y X =在(0,4)内的概率分布密度()Y f y =____________.十一、（本题满分6分）设随机变量X的概率分布密度为1()e ,.2xf x x -=-∞<<+∞ (1)求X 的数学期望EX 和方差.DX(2)求X 与X 的协方差,并问X 与X 是否不相关? (3)问X 与X 是否相互独立?为什么?1994年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分. (1)已知A 、B 两个事件满足条件()(),P AB P AB =且(),P A p =则()P B =____________.(2)设相互独立的两个随机变量,X Y 具有同一分布率,且X 的分布率为则随机变量max{,}Z X Y =的分布率为____________. 十一、（本题满分6分）设随机变量X和Y 分别服从正态分布2(1,3)N 和2(0,4),N 且X 与Y 的相关系数1,2xy ρ=-设,32X Y Z =+(1)求Z 的数学期望EZ 和DZ 方差. (2)求X 与Z 的相关系数.xz ρ (3)问X 与Y 是否相互独立?为什么?1995年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设X 表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则2X 的数学期望2()E X =____________.(2)设X 和Y 为两个随机变量,且34{0,0},{0}{0},77P X Y P X P Y ≥≥=≥=≥= 则{max(,)0}P X Y ≥=____________. 十一、（本题满分6分）设随机变量X 的概率密度为()X f x = e 0x- 00x x ≥<,求随机变量e XY =的概率密度().Y f y1996年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设工厂A 和工厂B 的产品的次品率分别为1%和2%,现从由A 和B 的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属A 生产的概率是____________.(2)设,ξη是两个相互独立且均服从正态分布2)N 的随机变量,则随机变量ξη-的数学期望()E ξη-=____________.十一、（本题满分6分）设,ξη是两个相互独立且服从同一分布的两个随机变量,已知ξ的分布率为1(),1,2,3.3P i i ξ===又设max(,),min(,).X Y ξηξη==(1)写出二维随机变量的分布率:(2)求随机变量X 的数学期望().E X 1997年全国硕士研究生入学统一考试数学(一)试卷(5)袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是_____________. (5)设两个相互独立的随机变量X 和Y 的方差分别为4和2,则随机变量32X Y -的方差是(A)8 (B)16 (C)28 (D)44 九、（本题满分7分）从学校乘汽车到火车站的途中有3个交通岗,假设再各个交通岗遇到红灯的事件是相互独立的,并且概率都是2.5设X 为途中遇到红灯的次数,求随机变量X 的分布律、分布函数和数学期望. 十、（本题满分5分）设总体X 的概率密度为()f x =(1)0x θθ+ 01x <<其它其中1θ>-是未知参数12,,,,n X X X 是来自总体X 的一个容量为n 的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.1998年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (5)设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成,二维随机变量(,)X Y 在区域D 上服从均匀分布,则(,)X Y 关于X的边缘概率密度在2x =处的值为_____________. (5)设,A B是两个随机事件,且0()1,()0,(|)(|),P A P B P B A P B A <<>=则必有(A)(|)(|)P A B P A B = (B)(|)(|)P A B P A B ≠(C)()()()P AB P A P B = (D)()()()P AB P A P B ≠ 十三、（本题满分6分）设两个随机变量,X Y 相互独立,且都服从均值为0、方差为12的正态分布,求随机变量X Y -的方差.十四、（本题满分4分）从正态总体2(3.4,6)N 中抽取容量为n 的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n 至少应取多大? 附:标准正态分布表22()t zx dt -Φ=⎰十五、（本题满分4分）设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生地成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70 分?并给出检验过程. 附:t 分布表{()()}p P t n t n p ≤=1999年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(5)设两两相互独立的三事件,A B和C 满足条件:1,()()(),2ABC P A P B P C =∅==<且已知9(),16P A B C =则()P A =_____________.二、选择题(5)设两个相互独立的随机变量X 和Y 分别服从正态分布(0,1)N 和(1,1)N ,则 (A)1{0}2P X Y +≤=(B)1{1}2P X Y +≤=(C)1{0}2P X Y -≤=(D)1{1}2P X Y -≤=十二、(本题满分8分)设随机变量X 与Y 相互独立,下表列出了二维随机变量(,)X Y 联合分布率及关于X 和关于Y 的边缘分布率中的部分数值,试将其余数值填入表中的空白处.十三、(本题满分6分)设X 的概率密度为36() 0< ()0 其它xx x f x θθθ⎧-<⎪=⎨⎪⎩,12,,,n X X X 是取自总体X 的简单随机样本 (1)求θ的矩估计量ˆθ. (2)求ˆθ的方差ˆ().D θ2000年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(5)设两个相互独立的事件A和B都不发生的概率为19,A发生B不发生的概率与B发生A不发生的概率相等,则()P A=_____________.二、选择题(5)设二维随机变量(,)X Y服从二维正态分布,则随机变量X Yξ=+与X Yη=-不相关的充分必要条件为(A)()()E X E Y=(B)2222()[()]()[()]E X E X E Y E Y-=-(C)22()()E X E Y=(D)2222()[()]()[()]E X E X E Y E Y+=+十二、(本题满分8分)某流水线上每个产品不合格的概率为(01)p p<<,各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为X,求X的数学期望()E X和方差()D X.十三、(本题满分6分)设某种元件的使用寿命X的概率密度为2()2e(;)x xf xxθθθθ-->⎧=⎨≤⎩,其中0θ>为未知参数.又设12,,,nx x x是X的一组样本观测值,求参数θ的最大似然估计值.2001年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把(5)()2D X=,则根据车贝晓夫不等式有估计≤≥-}2)({XEXP _____________.二、选择题(5)将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上的次数, 则X和Y相关系数为(A) -1 (B)0(C)12(D)1十一、(本题满分7分)设某班车起点站上客人数X服从参数为(0)λλ>的泊松分布,每位乘客在中途下车的概率为(01),p p<<且中途下车与否相互独立.Y为中途下车的人数,求:(1)在发车时有n个乘客的条件下,中途有m人下车的概率.(2)二维随机变量(,)X Y的概率分布.十二、(本题满分7分)设2~(,)X Nμσ抽取简单随机样本122,,,(2),nX X X n ≥样本均值∑==niiXnX2121,∑=+-+=niiniXXXY12)2(,求().E Y2002年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(5)设随机变量),(~2σμN X ,且二次方程42=++X y y 无实根的概率为0.5,则μ=_____________.二、选择题(5)设X 和Y 是相互独立的连续型随机变量,它们的密度函数分别为)(x f X 和)(y f Y ,分布函数分别为)(x F X 和)(y F Y ,则(A))(x f X ＋)(y f Y 必为密度函数 (B))(x f X )(y f Y 必为密度函数(C))(x F X ＋)(y F Y 必为某一随机变量的分布函数 (D))(x F X )(y F Y 必为某一随机变量的分布函数.十一、(本题满分7分)设维随机变量X 的概率密度为()f x =1cos 0220 xx x≤≤其它对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分) 设总体X 的概率分布为其中θ(102θ<<)是未知参数,利用总体X 的如下样本值 3,1,3,0,3,1,2,3.求θ的矩估计和最大似然估计值.2003年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (5)设二维随机变量(,)X Y 的概率密度为(,)f x y =60x01x y ≤≤≤其它,则=≤+}1{Y X P .(6)已知一批零件的长度X (单位:cm)服从正态分布)1,(μN ,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则μ的置信度为0.95的置信区间是 . (注:标准正态分布函数值.)95.0)645.1(,975.0)96.1(=Φ=Φ 二、选择题(6)设随机变量21),1)((~X Y n n t X =>,则 (A)2~()Y n χ (B)2~(1)Y n χ- (C)~(,1)Y F n (D)~(1,)Y F n 十一、(本题满分10分)已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:(1)乙箱中次品件数的数学期望.(2)从乙箱中任取一件产品是次品的概率. 十二、(本题满分8分) 设总体X 的概率密度为()f x =2()2e 0x θ-- 0x x θ>≤ 其中0>θ是未知参数. 从总体X 中抽取简单随机样本n X X X ,,,21 ,记).,,,min(ˆ21nX X X =θ (1)求总体X 的分布函数()F x .(2)求统计量θˆ的分布函数)(ˆx F θ.(3)如果用θˆ作为θ的估计量,讨论它是否具有无偏性.2004年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (6)设随机变量X 服从参数为λ的指数分布,则}{DX X P >= __________ . 二、选择题(本题共8小题,每小题4分,满分32分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(13)设随机变量X 服从正态分布(0,1),N 对给定的)10(<<αα,数αu 满足αα=>}{u X P ,若α=<}{x X P ,则x 等于(A)2αu (B)21α-u(C)21α-u (D) α-1u(14)设随机变量)1(,,,21>n X X X n 独立同分布,且其方差为.02>σ 令∑==ni i X n Y 11,则(A)21Cov(,)X Y nσ= (B)21Cov(,)X Y σ=(C)212)(σnn Y X D +=+ (D)211)(σnn Y X D +=- (22)(本题满分9分)设,A B 为随机事件,且111(),(|),(|)432P A P B A P A B ===,令;,,0,1不发生发生A A X ⎩⎨⎧= .,,0,1不发生发生B B Y ⎩⎨⎧= 求:(1)二维随机变量(,)X Y 的概率分布. (2)X 和Y 的相关系数.XY ρ (23)(本题满分9分)设总体X 的分布函数为,1,1,0,11),(≤>⎪⎩⎪⎨⎧-=x x x x F ββ其中未知参数n X X X ,,,,121 >β为来自总体X 的简单随机样本,求:(1)β的矩估计量. (2)β的最大似然估计量.2005年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (6)从数1,2,3,4中任取一个数,记为X , 再从X ,,2,1 中任取一个数,记为Y , 则}2{=Y P =____________.二、选择题(13)设二维随机变量(,)X Y 的概率分布为已知随机事件}0{=X 与}1{=+Y X 相互独立,则(A)0.2,0.3a b == (B)0.4,0.1a b == (C)0.3,0.2a b == (D)0.1,0.4a b ==(14)设)2(,,,21≥n X X X n 为来自总体(0,1)N 的简单随机样本,X 为样本均值,2S 为样本方差,则(A))1,0(~N X n (B)22~()nS n χ(C))1(~)1(--n t SXn (D)2122(1)~(1,1)nii n X F n X=--∑(22)(本题满分9分)设二维随机变量(,)X Y 的概率密度为(,)f x y = 10 01,02x y x<<<<其它求:(1)(,)X Y 的边缘概率密度)(),(y f x f Y X . (2)YX Z-=2的概率密度).(z f Z(23)(本题满分9分)设)2(,,,21>n X X X n 为来自总体(0,1)N 的简单随机样本,为样本均值,记.,,2,1,n i X X Y i i =-=求:(1)i Y 的方差n i DY i ,,2,1, =. (2)1Y 与n Y 的协方差1Cov(,).n Y Y数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (6)设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,则{}max{,}1P X Y ≤= .二、选择题(13)设,A B 为随机事件,且()0,(|)1P B P A B >=,则必有(A)()()P A B P A > (B)()()P A B P B > (C)()()P A B P A = (D)()()P A B P B = (14)设随机变量X 服从正态分布211(,)N μσ,Y 服从正态分布222(,)N μσ, 且12{||1}{||1},P X P Y μμ-<>-<则(A)12σσ< (B)12σσ> (C)12μμ< (D)12μμ>(22)随机变量x 的概率密度为()()21,1021,02,,40,令其它x x f x x y x F x y ⎧-<<⎪⎪⎪=≤<=⎨⎪⎪⎪⎩为二维随机变量(,)X Y 的分布函数.(1)求Y 的概率密度()Y f y .(2)1,42F ⎛⎫- ⎪⎝⎭. (23)(本题满分9分)设总体X 的概率密度为(,0)F X = 10θθ- 0112x x <<≤<其它,其中θ是未知参数(01)θ<<,12n ,...,X X X 为来自总体X 的简单随机样本,记N 为样本值12,...,n x x x 中小于1的个数,求θ的最大似然估计.数学(一)试卷一、选择题(9)某人向同一目标独立重复射击,每次射击命中目标的概率为()01p p <<,则此人第4次射击恰好第2次命中目标的概率为(A)23(1)p p - (B)26(1)p p - (C)223(1)p p - (D)226(1)p p -(10)设随即变量(,)X Y 服从二维正态分布,且X 与Y 不相关,()X f x ,()Y f y 分别表示,X Y的概率密度,则在Y y =的条件下,X 的条件概率密度|(|)X Y f x y 为(A)()X f x (B)()Y f y (C)()X f x ()Y f y (D)()()X Y f x f y 二、填空题(16)在区间(0,1)中随机地取两个数,则这两个数之差的绝对值小于12的概率为________.(23)设二维随机变量(,)X Y 的概率密度为2,01,01(,)0,x y x y f x y --<<<<⎧=⎨⎩其他(1)求{2}.P X Y > (2)求Z X Y =+的概率密度.(24)设总体X 的概率密度为1,021(;),12(1)0,x f x x θθθθθ⎧<<⎪⎪⎪=≤<⎨-⎪⎪⎪⎩其他 12,,n X X X 是来自总体x 的简单随机样本,X 是样本均值(1)求参数θ的矩估计量ˆθ.(2)判断24X 是否为2θ的无偏估计量,并说明理由.2008年全国硕士研究生入学统一考试数学(一)试卷一、选择题(7)设随机变量,X Y 独立同分布且X 分布函数为()F x ,则{}max ,Z X Y =分布函数为 (A)()2F x (B) ()()F x F y (C) ()211F x --⎡⎤⎣⎦ (D) ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦ (8)设随机变量()~0,1X N ,()~1,4Y N 且相关系数1XY ρ=,则 (A){}211P Y X =--= (B){}211P Y X =-= (C){}211P Y X =-+= (D){}211P Y X =+= 二、填空题(14)设随机变量X 服从参数为1的泊松分布,则{}2P X EX == .(22)设随机变量X 与Y 相互独立,X 的概率分布为{}()11,0,13P X i i ===-,Y 的概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它,记Z X Y =+,(1)求102P Z X ⎧⎫≤=⎨⎬⎩⎭.(2)求Z 的概率密度. (23)设12,,,n X X X 是总体为2(,)N μσ的简单随机样本.记11n i i X X n ==∑,2211()1n ii S X X n ==--∑,221T X S n =- (1)证明T 是2μ的无偏估计量. (2)当0,1μσ==时 ,求DT .2009年全国硕士研究生入学统一考试数学(一)试卷一、选择题(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =(A)0 (B)0.3 (C)0.7 (D)1(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为(A)0 (B)1 (C)2 (D)3 二、填空题(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .(22)袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(1)求{}10p X Z ==. (2)求二维随机变量(),X Y 概率分布(23)设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,1X ,2X ,…n X 是来自总体X 的简单随机样本.(1)求参数λ的矩估计量. (2)求参数λ的最大似然估计量.2010年全国硕士研究生入学统一考试数学(一)试卷一、选择题(7)设随机变量X的分布函数()F x = 00101,21e 2x x x x -<≤≤->则{1}P X ==(A)0 (B)1 (C)11e 2-- (D)11e --(8)设1()f x 为标准正态分布的概率密度2,()f x 为[1,3]-上均匀分布的概率密度,()f x =12()()af x bf xx x ≤> (0,0)a b >>为概率密度,则,a b 应满足(A)234a b += (B)324a b += (C)1a b += (D)2a b +=二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.) (14)设随机变量X 概率分布为{}(0,1,2,),!CP X k k k ===则2EX = . (22)(本题满分11分)设二维随机变量()X Y +的概率密度为2222(,)e ,,,x xy y f x y A x y -+-=-∞<<∞-∞<<∞求常数及A 条件概率密度|(|).Y X f y x(23)(本题满分11 分) 设总体X 的概率分布为其中(0,1)θ∈未知,以i N 来表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3),i =试求常数123,,,a a a 使31i i i T a N ==∑为θ的无偏估计量,并求T 的方差.212011年全国硕士研究生入学统一考试数学(一)试卷一、选择题7、设)()(21x F x F 为两个分布函数，且连续函数)()(21x f x f 为相应的概率密度，则必为概率密度的是（）A )()(21x f x fB )()(212x F x fC )()(21x F x fD )()(21x F x f +)()(12x F x f8、设随机变量Y X ,相互独立，且EY EX ,都存在，记{}Y X U ,max ={}Y X V ,min =，则=EUV （）A EV EU ⋅B EY EX ⋅C EY EU ⋅D EV EX ⋅二、填空题14、设二维随机变量)0,,,,(~),(22σσμμN Y X ，则____________)(2=XY E22、设随机变量X 与Y 的概率分布分别为且{}122==Y X P求（1）二维随机变量（X ，Y ）的概率分布；（2）XYZ=的概率分布（3）X 与Y 的相关系数XY ρ23、（本题满分11分）设n X X X 21,是来自正态总体),(20σμN 的简单随机样本，其中0μ已知，02>σ未知.2,S X 为样本均值和样本方差. 求（1）求参数2σ的最大似然估计Λ2σ(2) 计算E Λ2σ和D Λ2σ222012年全国硕士研究生入学统一考试数学(一)试卷一、选择题：（7）设随机变量x 与y 相互独立，且分别服从参数为1与参数为4的指数分布，则{}=<y x p （）1124()()() ()5355A B C D（8）将长度为1m 的木棒随机地截成两段，则两段长度的相关系数为（）1)(21)(21)(1)(--D C B A二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸．．．指定位置上. （14）设,,A B C 是随机事件，,A C 互不相容，1()2P AB =,1()3P C =,则()P AB C -=________。

考研数学(三)题库概率论与数理统计(第一章随机事件和概率)打印版【圣才出品】

A．P（A）－P（B）
B．P（A）－P（B）＋P（AB）
C．P（A）－P（AB）
＿
＿
D．P（A）＋P（A）－P（AB）
4 / 29
圣才电子书十万种考研考证电子书、题库视频学习平台

【答案】C
＿
＿
【解析】P（A）＝P[A（B∪B）]＝P（AB）＋P（AB）＝P（A－B）＋P（AB），故 P
9．假设事件 A 和 B 满足 P（B|A）＝1，0＜P（A），则（）。 A．A 是必然事件 B．P（A|B）＝0 C．A 包含事件 B D．P（A－B）＝0 【答案】D 【解析】因为 P（B|A）＝1 且 P（A）＞0，故 P（AB）＝P（A），P（A－B）＝P（A）－P（AB）＝0。
10．对于任意两事件 A 和 B，P（A－B）＝（）。
＿＿
P（A∪B）＝1。
1 / 29
圣才电子书十万种考研考证电子书、题库视频学习平台

3．若 A、B 互斥，且 P（A）＞0，P（B）＞0，则下列式子成立的是（）。 A．P（A|B）＝P（A） B．P（B|A）＞0 C．P（AB）＝P（A）P（B） D．P（B|A）＝0 【答案】D 【解析】因为 A，B 互斥，故 AB＝∅，P（AB）＝0，P（B|A）＝P（AB）/P（A）＝0。
14．对于事件 A、B、C，如果 A B C ，则（）。
＿＿＿
A．A∪B⊂C
＿＿＿
B．AB⊃C
＿
C．A∪B⊂C
D．AB⊂C
【答案】C
＿
【解析】∵ A B C ∴ A B C ，即 A∪B⊂C。
15．对于事件 A、B，如果 A⊃B，P（B）＞0，则（）。
A．P（B|A）＝P（B）

概率与数理统计历年考研试题及解答(数一、数三、数四)

概率与数理统计历届真题第一章随机事件和概率数学一：1〔87，2分〕设在一次试验中A 发生的概率为p ，现进展n 次独立试验，如此A 至少发生一次的概率为；而事件A 至多发生一次的概率为。

2〔87，2〕三个箱子，第一个箱子中有4个黑球1个白球，第二个箱子中有3个黑球3个白球，第三个箱子中有3个黑球5个白球。

现随机地取一个箱子，再从这个箱子中取出1个球，这个球为白球的概率等于。

取出的球是白球，此球属于第二个箱子的概率为。

3〔88，2分〕设三次独立试验中，事件A 出现的概率相等，假如A 至少出现一次的概率等于2719，如此事件A 在一次试验中出现的概率为。

4〔88，2分〕在区间〔0，1〕中随机地取两个数，如此事件“两数之和小于56〞的概率为。

5〔89，2分〕随机事件A 的概率P 〔A 〕=0.5，随机事件B 的概率P 〔BP 〔B | A 〕=0.8，如此和事件A B 的概率P 〔A B 〕=。

6〔89，2分〕甲、乙两人独立地对同一目标射击一次，其命中率分别为0.6和0.5，现目标被命中，如此它是甲射中的概率为。

7〔90，2分〕设随机事件A ，B 与其和事件A B 的概率分别是0.4, 0.3和0.6，假如B 表示B 的对立事件，那么积事件A B 的概率P 〔A B 〕=。

8〔91，3分〕随机地向半圆0<y <22x ax -(a 为正常数)内掷一点，点落在半圆内任何区域的概率与该区域的面积成正比。

如此原点与该点的连线与x 轴的夹角小于4π的概率为。

9〔92，3分〕P 〔A 〕=P 〔B 〕=P 〔C 〕=161)()(,0)(,41===BC P AC P AB P ，如此事件A 、B 、C 全不发生的概率为。

10〔93，3分〕一批产品有10个正品和2个次品，任意抽取两次，每次抽一个，抽出后不再放回，如此第二次抽出的是次品的概率为。

11〔94，3分〕A 、B 两个事件满足条件P 〔AB 〕=P 〔A B 〕，且P 〔A 〕=p ，如此P 〔B 〕=。

历年考研概率真题集锦(2000-2019)-精品推荐

历年考研概率真题集锦（2000-2019） ——对应茆诗松高教出版社“概率论与数理统计”第一章§1.11、（2001数学四）（4）对于任意二事件A 和B ，与A B B ⋃=不等价的是（） A 、A B ⊂ B 、B A ⊂ C 、AB =Φ D 、AB =Φ2、（2000数学三、四）（5）在电炉上安装4 个温控器，其显示温度的误差是随机的，在使用过程中，只要有两个温控器显示的温度不低于临界温度0t ，电炉就断电。

以E 表示事件“电炉断电”，而(1)(2)(3)(4)T T T T ≤≤≤为4 个温控器显示的按递增顺序排列的温度值，则事件E 等于（）(A ) {}(1)0T t ≥ (B ) {}(2)0T t ≥ (C ) {}(3)0T t ≥ (D ) {}(4)0T t ≥ §1.21、（2007数学一、三）(16)在区间(0,1)中随机地取两个数,这两数之差的绝对值小于12的概率为________. §1.31、（2009数学三）（7）设事件A 与事件B 互不相容，则( ) (A )()0P AB = (B )()()()P AB P A P B =(C )()1()P A P B =-(D )()1P A B ⋃=2、（2015数学一、三）(7) 若A ,B 为任意两个随机事件，则( ) (A ) ()()()≤P AB P A P B (B ) ()()()≥P AB P A P B (C ) ()()()+2≤P A P B P AB (D ) ()()()+2≥P A P B P AB3、（2019数学一、三）（7）设A 、B 为随机事件，则()()P A P B =的充分必要条件是（）（A ）()()()P AB P A P B =+ （B ） ()()()P AB P A P B =（C ）()()P AB P B A = （D ）()()P AB P AB = §1.41、（2005数学一、三）（6）从数1，2，3，4中任取一个数，记为X ，再从X ,,2,1 中任取一个数，记为Y ，则}2{=Y P =____________.2、（2006数学一）(13) 设,A B 为随机事件，且()0,(|)1P B P A B >=，则必有( ) (A )()()P A B P A ⋃>(B )()()P A B P B ⋃> (C )()()P A B P A ⋃= (D )()()P A B P B ⋃=3、（2012数学一、三）(14)设A ,B ,C 是随机变量，A 与C 互不相容，()()()11,,23p AB P C p AB C === 。

概率论与数理统计历年考研真题(数一)1995--2012年

å sˆ 2 = 1
n
z2
3n i i=1
å å （3） E(sˆ 2 ) = 1 n E(z 2 ) = 1 n [(Ez)2 + Dz] = 1 (3ns 2 ) = s 2
3n i=1
i
3n i=1
3n
因此sˆ 2 是s 2 的无偏估计
3
2011 年（数一）
（7）设 F1 (x), F2 (x) 为两个分布函数，其相应的概率密度 f1 (x), f 2 (x) 是连续函数，则必为
（ 14 ）设 A, B, C 是随机事件， A 与 C 互不相容， P( AB) = 1 ， P(C) = 1 ，则
2
3
P( AB C) = ________
【答案】 3 4
【解析】 P( AB C) = P( ABC) = P( ABC)
P(C )
1- 1
3
而 P( ABC) + P( ABC) = P( AB) = 1 ，而 0 £ P( ABC) < P( AC) = 0 ，故 P( ABC) = 1
ò ò EX =
+¥
0.3xj(x)dx +
4
X
Y
-1
0
1
0
Hale Waihona Puke 0010
再由 X 和 Y 的概率分布可得 ( X ,Y ) 的概率分布为
X
Y
-1
0
1
0
0
13
0
1
13
0
13
（2） XY 的可能取值为 -1,0,1 Z = XY 的概率分布为
XY -1
0
1

数理统计与概率论--历年考研真题汇总

第一章概率论基础1、（2002，数四，8分）设B A 、是任意二事件，其中A 的概率不等于0和1，证明)()(A B p A B p =是事件A 与B 独立的充分必要条件。

2、（2003，数三，4分）将一枚硬币独立地掷两次，引进事件=1A “掷第一次出现正面”，=2A “掷第二次出现正面”， =3A “正、反面各出现一次”， =4A “正面出现两次”，则事件（）（A ）321,,A A A 相互独立。

（B ）432,,A A A 相互独立。

（C ）321,,A A A 两两独立。

（D ）432,,A A A 两两独立。

3、（2003，数四，4分）对于任意二事件A 和B ，则（A ）若φ≠AB ,则B A 、一定独立；（B ）若φ≠AB ,则B A 、有可能独立；（C ）若φ=AB ,则B A 、一定独立；（D ）若φ=AB ,则B A 、一定不独立；4、（2006，数一，4分）设B A 、为两个随机事件,且,1)(,0)(=>B A p B p 则必有（A ）)()(A p B A p >⋃ （B ）)()(B p B A p >⋃（C ）)()(A p B A p =⋃ （D ）)()(A p B A p =⋃第二章随机变量及其分布1、（2005，数一，4分）从数1，2，3，4中任取一个数，记为X ，再从X ,,1 中任取一个数，记为Y ，则==}2{Y p 。

2、（2003，数三，13分）设随机变量X 的概率密度为⎪⎩⎪⎨⎧∈=其它,0]8,1[ ,31)(32x x x f ，)(x F 是X 的分布函数。

求随机变量)(X F Y =的分布函数。

3、（2006，数一，4分）随机变量X 与Y 相互独立，且均服从区间[0,3]上的均匀分布，则=≤)1},(max{Y X P 。

20、（2007，数一，4分）在区间（0，1）中随机地取两个数，则这两个数之差的绝对值小于21的概率为。

考研数学概率论和数理统计第一章测试题(卷)(含答案解析)

考研数学概率论与数理统计第一章测试题（含答案）一、单项选择题（每小题2分，共20分）1.对于任意二事件A 和B ，与B BA不等价．．．的是（）(A)B A (B)A B(C)BA (D)BA 2.设事件A 与事件B 互不相容，则（）(A)0)(B A P (B))()()(B P A P AB P (C))(1)(B P A P (D)1)(B AP 3.对于任意二事件A 和B ，则以下选项必然成立的是（）(A)若AB ，则B A,一定独立 (B)若AB ，则B A,有可能独立(C)若AB ，则B A,一定独立 (D)若AB，则B A,一定不独立4.设A 和B 是任意两个概率不为零的不相容事件，则下列结论中肯定正确的是（）(A)A 与B 互不相容(B)A 与B 相容(C))()()(B P A P AB P (D))()(A P B AP 5.设B A,为任意两个事件，且B A ，0)(B P ，则下列选项必然成立的是（）(A))|()(B A P A P (B))|()(B A P A P (C))|()(B A P A P (D))|()(B A P A P 6.设B A,为两个随机事件，且0)(B P ，1)|(B A P ，则必有（）(A))()(A P B A P (B))()(B P B A P (C))()(A P B A P (D))()(B P B AP 7.已知1)(0B P ，且)|()|(]|)[(2121B A P B A P B A A P ，则下列选项成立的是（）(A))|()|(]|)[(2121B A P B A P B A A P (B))()()(2121B A P B A P B A BA P (C))|()|()(2121B A P B A P A A P (D))|()()|()()(2211A B P A P A B P A P B P 8.将一枚硬币独立地掷两次，引进事件：1A {掷第一次出现正面}，2A {掷第二次出现正面}，3A {正、反面各出现一次}，4A {正面出现两次}，则事件（）(A)321,,A A A 相互独立 (B)432,,A A A 相互独立(C)321,,A A A 两两独立 (D)432,,A A A 两两独立9.某人向同一目标独立重复射击，每次射击命中目标的概率为p （10p ），则此人第4射击恰好第2次命中目标的概率为（）(A)2)1(3p p (B)2)1(6p p (C)22)1(3p p (D)22)1(6p p 10.设C B A ,,是三个相互独立的随机事件，且1)()(0C P AC P ，则在下列给定的四对事件中不．相互独立的是（）(A)B A与C (B)AC 与C (C)B A与C (D)AB 与C二、填空题（每小题2分，共14分）1.“C B A ,,三个事件中至少有两个发生”，这一事件可以表示为___2.若事件B A ，满足1BP A P ，则A 与B 一定____________3.在区间)1,0(中随机地取两个数，则两数之差的绝对值小于21的概率为4.在一次试验中，事件A 发生的概率为p 。

概率考研真题

概率考研真题一、简答题1. 什么是概率？概率是描述随机事件发生可能性的一种数学工具。

它用来表示某个事件发生的可能性大小，通常以0到1之间的数值表示，0表示事件不可能发生，1表示事件一定会发生。

2. 什么是条件概率？条件概率是指在一定条件下，某个事件发生的概率。

如果事件B已经发生，那么在B发生的前提下，事件A发生的概率就是条件概率。

3. 什么是独立事件？独立事件是指两个或多个事件之间互不影响，一个事件的发生与否不会对其他事件的发生概率产生影响。

4. 什么是贝叶斯公式？贝叶斯公式是概率论中的一个重要公式，用于计算在某个事件已经发生的条件下，另一个事件发生的概率。

公式表达为：P(A|B) = P(B|A) * P(A) / P(B)其中，P(A)和P(B)分别表示事件A和事件B的概率，P(A|B)表示在事件B发生的条件下，事件A发生的概率，P(B|A)表示在事件A发生的条件下，事件B发生的概率。

二、计算题1. 有一个标准52张扑克牌的扑克牌组合，请计算从中随机抽取5张牌，得到一个顺子（即五张牌的大小连续）的概率。

解：首先计算顺子可能的情况数。

顺子包含10种可能的组合，即A2345、23456、34567、45678、56789、678910、78910J、8910JQ、910JQK、10JQKA。

然后计算从52张扑克牌中随机抽取5张的组合数。

由于每张扑克牌只能抽取一次，故组合数为C(52, 5)。

所以，顺子的概率为10 / C(52, 5) ≈ 0.0039。

2. 甲、乙两个商店在同一天同时举行促销活动，吸引了大量顾客。

调查显示，70%的顾客参加了甲店的促销活动，60%的顾客参加了乙店的促销活动，50%的顾客同时参加了两家店的促销活动。

请计算一个顾客是通过甲店购物的概率。

解：设事件A表示顾客通过甲店购物，事件B表示顾客通过乙店购物。

根据题意，已知P(A∩B) = 0.5，P(A∪B) = 0.7，P(B) = 0.6，我们的目标是计算P(A)。

考研概率论真题汇总1

求 (I) P(X=2Y) (II) CoV(X-Y,Y)与 X,Y的相关系数XY
(12111) 设随机变量X,Y相互独立, 且分别服从正态总体 N(,σ 2)与 N(,2σ 2),其中σ 2>0是未知参数,设Z=X-Y, (I) 求z的概率密度f(z,σ 2) (II) 设z1,z2,……,zn是来自Z的简单随机样本,求σ 2的最大似然估计量 ˆ2 (III)证明
6(09304). 设事件A与事件B互不相容，则
(A) P( AB) 0 (C) P(A)=1-P(B) (B)P(AB)=P(A)P(B) (D)
P( A B) 1
7（94403，94503）设0<P(A)<1, 0<P(B)<1,
P(A|B)+ P（A | B ） 1，则( ).
2 X 1 令随机变量 Y X 1 X 2 1 X 2
(1)求Y的分布函数 (2)求概率P(X≤Y)
(13311) 设随机变量(X,Y)关于X的边缘概率密度为
3 x 2 f ( x) 0
0 x 1 其它
在给定X=x(0<x<1)的条件下,Y的条件概率密度为
(11311) 设二维随机变量(X,Y)在G上服从均匀分布， G由x-y=0,x+y=2,y=0围成，求（1）边缘概率密度fX(x) （2）条件概率密度fX|Y(x|y)
(11111分) 设 X1 , X 2 ,
, Xn
是来自正态总体N(0,σ 2) 的简单随机样本, 其中0已知，σ 2>0未知，
2(07104,07304.07404). 在区间(0,1)中随机的取两个数, 则这两个数之差的绝对值小于1/2的概率为_____.

历届考研概率试题及答案

历届考研概率试题及答案模拟试题：历届考研概率试题及答案一、选择题（每题2分，共10分）1. 设随机变量X服从参数为λ的泊松分布，那么P(X=2)等于：A. λ^2B. λ^2e^(-λ)C. e^(-λ)λ^2/2!D. e^(-λ)λ^2/3!答案：C2. 某工厂生产的零件长度服从正态分布N(50, 25)，那么长度在45到55之间的零件所占的百分比是：A. 68%B. 95%C. 99%D. 86.6%答案：B3. 设随机变量Y服从二项分布B(n, p)，若n=15，p=0.4，那么E(Y)等于：A. 4.8B. 6C. 3D. 5.2答案：B4. 从一副不含大小王的扑克牌中随机抽取一张，抽到红心的概率是：A. 1/2B. 1/4C. 1/3D. 13/52答案：B5. 设随机变量Z服从标准正态分布，那么P(Z > 1.5)的值是：A. 0.0668B. 0.1C. 0.2D. 0.05答案：A二、填空题（每题3分，共15分）6. 设随机变量X服从均匀分布U(0, 4)，则P(X > 2) = ___________。

答案：1/27. 某地一年内发生地震的次数X服从泊松分布，若该地区一年内发生地震的平均次数为3次，则该地区一个月内发生至少一次地震的概率是 ___________。

答案：1 - e^(-3/12)8. 设随机变量Y服从二项分布B(16, 1/4)，则P(Y ≥ 5) =___________。

答案：1 - C(16, 0)(1/4)^0(3/4)^16 - C(16,1)(1/4)^1(3/4)^15 - ... - C(16, 4)(1/4)^4(3/4)^129. 从10件产品中随机抽取3件进行检测，其中2件次品，8件正品，抽到至少1件次品的概率是 ___________。

答案：1 - C(8, 3)/C(10, 3)10. 设随机变量Z服从标准正态分布，那么P(-2 < Z < 2)的值是___________。

概率与数理统计历届考研真题（数一、数三、数四）

概率与数理统计历届考研真题（数⼀、数三、数四）概率与数理统计历届真题第⼀章随机事件和概率数学⼀：15（99，3分）设两两相互独⽴的三事件A ，B 和C 满⾜条件；ABC =Ф，P （A ）=P （B ）=P （C ）<21，且已知169)(=C B A P ，则P （A ）= 。

16（00，3分）设两个相互独⽴的事件A 和B 都不发⽣的概率为91，A 发⽣B 不发⽣的概率与B 发⽣A 不发⽣的概率相等，则P （A ）=。

17（06，4分）设,A B 为随机事件，且()0,(|)1P B P A B >=，则必有（A ）()().P A B P A ?> （B ）()().P A B P B ?>（C ）()().P A B P A ?=（D ）()().P A B P B ?=数学三：19（00，3分）在电炉上安装了4个温控器，其显⽰温度的误差是随机的。

在使⽤过程中，只要有两个温控器显⽰的温度不低于临界温度t 0，电炉就断电。

以E 表⽰事件“电炉断电”，⽽)4()3()2()1(T T T T ≤≤≤为4个温控器显⽰的按递增顺序排列的温度值，则事件E 等于（A ）}{0)1(t T ≥ （B ）}{0)2(t T ≥ （C ）}{0)3(t T ≥（D ）}{0)4(t T ≥[]20（03，4分）将⼀枚硬币独⽴地掷两次，引进事件：1A ={掷第⼀次出现正⾯}，2A ={掷第⼆次出现正⾯}，3A ={正、反⾯各出现⼀次}，4A ={正⾯出现两次}，则事件（A ）321,,A A A 相互独⽴。

（B ）432,,A A A 相互独⽴。

（C ）321,,A A A 两两独⽴。

（D ）432,,A A A 两两独⽴。

第⼆章随机变量及其分布数学⼀：7（02，3分）设随机变量X 服从正态分布)0)(,(2>σσµN ，且⼆次⽅程042=++X y y ⽆实根的概率为21。

概率论考研题目及答案

概率论考研题目及答案题目一：概率论基本概念问题：某工厂生产的零件，合格率为0.95。

求：1. 随机抽取一个零件，它是合格品的概率。

2. 随机抽取两个零件，至少有一个是合格品的概率。

答案：1. 由于合格率为0.95，随机抽取一个零件是合格品的概率即为合格率，即 P(合格) = 0.95。

2. 抽取两个零件至少有一个是合格品的概率可以通过计算两个零件都不合格的概率，然后用1减去这个概率来得到。

两个零件都不合格的概率是 (1 - 0.95) * (1 - 0.95) = 0.0025。

因此，至少有一个是合格品的概率为 1 - 0.0025 = 0.9975。

题目二：条件概率问题：某地区有两家医院，A医院的产妇数量占70%，B医院占30%。

在A医院出生的婴儿中，男孩的比例是60%，在B医院出生的婴儿中，男孩的比例是70%。

现在随机选择了一个男孩，求这个男孩是在A医院出生的概率。

答案：设事件A为在A医院出生，事件B为在B医院出生，事件M为是男孩。

使用贝叶斯公式：\[ P(A|M) = \frac{P(M|A)P(A)}{P(M)} = \frac{0.6 \times0.7}{0.63} \approx 0.6985 \]题目三：随机变量及其分布问题：一个随机变量X服从参数为λ的泊松分布。

求：1. X的期望值和方差。

2. X=k的概率，其中k是一个给定的正整数。

答案：1. 泊松分布的期望值（E[X]）和方差（Var(X)）都等于参数λ。

近年考研数学三概率论部分题目整合及其答案

7．（03）对于任意二事件 A 和 B ，（
）
1
（A）若 AB ≠ ∅，则 A, B 一定独立．
（B）若 AB ≠ ∅，则 A, B 有可能独立．
（C）若 AB = ∅，则 A, B 一定独立．
（D）若 AB = ∅，则 A, B 一定不独立．
解：设 AB = ∅，有 P( AB) = 0 ；设 A, B 独立，则 P( AB) = P( A)P(B) ，二者之间没有推导关系．
（D） A2 , A3 , A4 两两独立．
解：因 A3 A4 = ∅，且显然 P( A3 ) > 0, P( A4 ) > 0 ，有 P( A3 A4 ) = 0 ≠ P( A3 )P( A4 ) ，可知 A3 , A4 不独立，
故（B）、（D）是错误的；
又因为
P( A1)
=
1 2
=
P( A2 )
解：因 A ⊂ B ，有 P( A | B) = P( AB) = P( A) ≥ P( A) ， P(B) P(B)
选择：（B）．
3．（98）设 A, B, C 是三个相互独立的随机事件，且 0 < P(C) < 1 ，则在下列给定的四对事件中不相互独
立的是（
）
（A） A + B 与 C ．（B） AC 与 C ．
选择：（D）．
注：此题有误，不能由 P( A − B) = 0 推出 A − B = ∅．
2．（96）设 A, B 为任意两个事件且 A ⊂ B ， P(B) > 0 ，则下列选项必然成立的是（
）
（A） P( A) < P( A | B) ．（B） P( A) ≤ P( A | B) ．（C） P( A) > P( A | B) ．（D） P( A) ≥ P( A | B) ．

历年数学一概率(1987-2015)

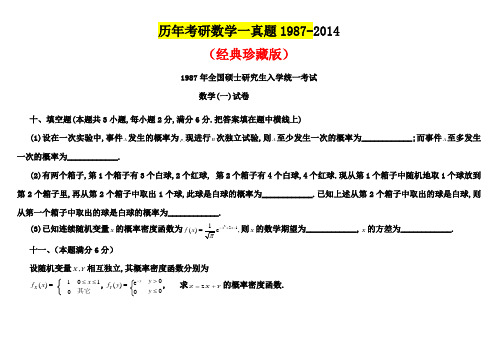
历年考研数学一真题1987-2014（经典珍藏版）1987年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在一次实验中,事件A 发生的概率为,p 现进行n 次独立试验,则A 至少发生一次的概率为____________;而事件A 至多发生一次的概率为____________.(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________. (3)已知连续随机变量X 的概率密度函数为221(),xx f x-+-=则X 的数学期望为____________,X 的方差为____________.十一、（本题满分6分）设随机变量,X Y 相互独立,其概率密度函数分别为()X f x = 1001x ≤≤其它,()Y f y = e 0y- 00y y >≤, 求2Z X Y =+的概率密度函数.1988年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在三次独立试验中,事件A出现的概率相等,若已知A至少出现一次的概率等于19,27则事件A在一次试验中出现的概率是____________.(2)若在区间(0,1)内任取两个数,则事件”两数之和小于65”的概率为____________.(3)设随机变量X服从均值为10,均方差为0.02的正态分布,已知22(),(2.5)0.9938,uxx duφφ-==⎰则X落在区间(9.95,10.05)内的概率为____________.十一、（本题满分6分）设随机变量X的概率密度函数为21(),(1)Xf xxπ=-求随机变量1Y=-的概率密度函数().Yf y1989年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机事件A的概率()0.5,P A=随机事件B的概率()0.6P B=及条件概率(|)0.8,P B A=则和事件A B的概率()P A B=____________.(2)甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为____________.(3)若随机变量ξ在(1,6)上服从均匀分布,则方程210x xξ++=有实根的概率是____________.十一、（本题满分6分）设随机变量X与Y独立,且X服从均值为1、标准差(均方差)的正态分布,而Y服从标准正态分布.试求随机变量23Z X Y=-+的概率密度函数.1990年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机变量X 的概率密度函数1()e ,2xf x x -=-∞<<+∞ 则X 的概率分布函数()F x =____________.(2)设随机事件A 、B 及其和事件的概率分别是0.4、0.3和0.6,若B 表示B 的对立事件,那么积事件AB 的概率()P AB =____________.(3)已知离散型随机变量X 服从参数为2的泊松()Poisson 分布,即22e {},0,1,2,,!k P X k k k -=== 则随机变量32Z X =-的数学期望()E Z =____________.十一、（本题满分6分）设二维随机变量(,)X Y 在区域:01,D x y x <<<内服从均匀分布,求关于X 的边缘概率密度函数及随机变量21Z X =+的方差().D Z1991年全国硕士研究生入学统一考试十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)若随机变量X 服从均值为2、方差为2σ的正态分布,且{24}0.3,P X <<=则{0}P X <=____________.(2)随机地向半圆0y a <<为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与x 轴的夹角小于4π的概率为____________.十一、（本题满分6分）设二维随机变量(,)X Y 的密度函数为(,)f x y =(2)2e 0,00 x y x y -+>>其它求随机变量2Z X Y =+的分布函数.1992年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上) (1)已知11()()(),()0,()(),46P A P B P C P AB P AC P BC ======则事件A、B 、C 全不发生的概率为____________.(2)设随机变量X 服从参数为1的指数分布,则数学期望2{e }X E X -+=____________. 十一、（本题满分6分）设随机变量X 与Y 独立,X 服从正态分布2(,),N Y μσ服从[,]ππ-上的均匀分布,试求Z X Y =+的概率分布密度(计算结果用标准正态分布函数Φ表示,其中22()e)t xx dt --∞Φ=.1993年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为____________.(2)设随机变量X 服从(0,2)上的均匀分布,则随机变量2Y X =在(0,4)内的概率分布密度()Y f y =____________.十一、（本题满分6分）设随机变量X的概率分布密度为1()e ,.2xf x x -=-∞<<+∞ (1)求X 的数学期望EX 和方差.DX(2)求X 与X 的协方差,并问X 与X 是否不相关? (3)问X 与X 是否相互独立?为什么?1994年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分. (1)已知A 、B 两个事件满足条件()(),P AB P AB =且(),P A p =则()P B =____________.(2)设相互独立的两个随机变量,X Y 具有同一分布率,且X 的分布率为则随机变量max{,}Z X Y =的分布率为____________. 十一、（本题满分6分）设随机变量X和Y 分别服从正态分布2(1,3)N 和2(0,4),N 且X 与Y 的相关系数1,2xy ρ=-设,32X Y Z =+(1)求Z 的数学期望EZ 和DZ 方差. (2)求X 与Z 的相关系数.xz ρ (3)问X 与Y 是否相互独立?为什么?1995年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设X 表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则2X 的数学期望2()E X =____________.(2)设X 和Y 为两个随机变量,且34{0,0},{0}{0},77P X Y P X P Y ≥≥=≥=≥= 则{max(,)0}P X Y ≥=____________. 十一、（本题满分6分）设随机变量X 的概率密度为()X f x = e 0x- 00x x ≥<,求随机变量e XY =的概率密度().Y f y1996年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设工厂A 和工厂B 的产品的次品率分别为1%和2%,现从由A 和B 的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属A 生产的概率是____________.(2)设,ξη是两个相互独立且均服从正态分布2)N 的随机变量,则随机变量ξη-的数学期望()E ξη-=____________.十一、（本题满分6分）设,ξη是两个相互独立且服从同一分布的两个随机变量,已知ξ的分布率为1(),1,2,3.3P i i ξ===又设max(,),min(,).X Y ξηξη==(1)写出二维随机变量的分布率:(2)求随机变量X 的数学期望().E X 1997年全国硕士研究生入学统一考试数学(一)试卷(5)袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是_____________. (5)设两个相互独立的随机变量X 和Y 的方差分别为4和2,则随机变量32X Y -的方差是(A)8 (B)16 (C)28 (D)44 九、（本题满分7分）从学校乘汽车到火车站的途中有3个交通岗,假设再各个交通岗遇到红灯的事件是相互独立的,并且概率都是2.5设X 为途中遇到红灯的次数,求随机变量X 的分布律、分布函数和数学期望. 十、（本题满分5分）设总体X 的概率密度为()f x =(1)0x θθ+ 01x <<其它其中1θ>-是未知参数12,,,,n X X X 是来自总体X 的一个容量为n 的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.1998年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (5)设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成,二维随机变量(,)X Y 在区域D 上服从均匀分布,则(,)X Y 关于X的边缘概率密度在2x =处的值为_____________. (5)设,A B是两个随机事件,且0()1,()0,(|)(|),P A P B P B A P B A <<>=则必有(A)(|)(|)P A B P A B = (B)(|)(|)P A B P A B ≠(C)()()()P AB P A P B = (D)()()()P AB P A P B ≠ 十三、（本题满分6分）设两个随机变量,X Y 相互独立,且都服从均值为0、方差为12的正态分布,求随机变量X Y -的方差.十四、（本题满分4分）从正态总体2(3.4,6)N 中抽取容量为n 的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n 至少应取多大? 附:标准正态分布表22()t zx dt -Φ=⎰十五、（本题满分4分）设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生地成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70 分?并给出检验过程. 附:t 分布表{()()}p P t n t n p ≤=1999年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(5)设两两相互独立的三事件,A B和C 满足条件:1,()()(),2ABC P A P B P C =∅==<且已知9(),16P A B C = 则()P A =_____________.二、选择题(5)设两个相互独立的随机变量X 和Y 分别服从正态分布(0,1)N 和(1,1)N ,则 (A)1{0}2P X Y +≤=(B)1{1}2P X Y +≤=(C)1{0}2P X Y -≤=(D)1{1}2P X Y -≤=十二、(本题满分8分)设随机变量X 与Y 相互独立,下表列出了二维随机变量(,)X Y 联合分布率及关于X 和关于Y 的边缘分布率中的部分数值,试将其余数值填入表中的空白处.十三、(本题满分6分)设X 的概率密度为36() 0< ()0 其它xx x f x θθθ⎧-<⎪=⎨⎪⎩,12,,,n X X X 是取自总体X 的简单随机样本 (1)求θ的矩估计量ˆθ. (2)求ˆθ的方差ˆ().D θ2000年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(5)设两个相互独立的事件A和B都不发生的概率为19,A发生B不发生的概率与B发生A不发生的概率相等,则()P A=_____________.二、选择题(5)设二维随机变量(,)X Y服从二维正态分布,则随机变量X Yξ=+与X Yη=-不相关的充分必要条件为(A)()()E X E Y=(B)2222()[()]()[()]E X E X E Y E Y-=-(C)22()()E X E Y=(D)2222()[()]()[()]E X E X E Y E Y+=+十二、(本题满分8分)某流水线上每个产品不合格的概率为(01)p p<<,各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为X,求X的数学期望()E X和方差()D X.十三、(本题满分6分)设某种元件的使用寿命X的概率密度为2()2e(;)x xf xxθθθθ-->⎧=⎨≤⎩,其中0θ>为未知参数.又设12,,,nx x x是X的一组样本观测值,求参数θ的最大似然估计值.2001年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把(5)()2D X=,则根据车贝晓夫不等式有估计≤≥-}2)({XEXP _____________.二、选择题(5)将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上的次数, 则X和Y相关系数为(A) -1 (B)0(C)12(D)1十一、(本题满分7分)设某班车起点站上客人数X服从参数为(0)λλ>的泊松分布,每位乘客在中途下车的概率为(01),p p<<且中途下车与否相互独立.Y为中途下车的人数,求:(1)在发车时有n个乘客的条件下,中途有m人下车的概率.(2)二维随机变量(,)X Y的概率分布.十二、(本题满分7分)设2~(,)X Nμσ抽取简单随机样本122,,,(2),nX X X n≥样本均值∑==niiXnX2121,∑=+-+=niiniXXXY12)2(,求().E Y2002年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(5)设随机变量),(~2σμN X ,且二次方程42=++X y y 无实根的概率为0.5,则μ=_____________.二、选择题(5)设X 和Y 是相互独立的连续型随机变量,它们的密度函数分别为)(x f X 和)(y f Y ,分布函数分别为)(x F X 和)(y F Y ,则(A))(x f X ＋)(y f Y 必为密度函数 (B))(x f X )(y f Y 必为密度函数(C))(x F X ＋)(y F Y 必为某一随机变量的分布函数 (D))(x F X )(y F Y 必为某一随机变量的分布函数.十一、(本题满分7分)设维随机变量X 的概率密度为()f x =1cos 0220 xx x≤≤其它对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y 的数学期望.十二、(本题满分7分) 设总体X 的概率分布为其中θ(102θ<<)是未知参数,利用总体X 的如下样本值 3,1,3,0,3,1,2,3.求θ的矩估计和最大似然估计值.2003年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (5)设二维随机变量(,)X Y 的概率密度为(,)f x y =60x01x y ≤≤≤其它,则=≤+}1{Y X P .(6)已知一批零件的长度X (单位:cm)服从正态分布)1,(μN ,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则μ的置信度为0.95的置信区间是 . (注:标准正态分布函数值.)95.0)645.1(,975.0)96.1(=Φ=Φ 二、选择题(6)设随机变量21),1)((~X Y n n t X =>,则 (A)2~()Y n χ (B)2~(1)Y n χ- (C)~(,1)Y F n (D)~(1,)Y F n 十一、(本题满分10分)已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:(1)乙箱中次品件数的数学期望.(2)从乙箱中任取一件产品是次品的概率. 十二、(本题满分8分) 设总体X 的概率密度为()f x =2()2e 0x θ-- 0x x θ>≤ 其中0>θ是未知参数. 从总体X 中抽取简单随机样本n X X X ,,,21 ,记).,,,min(ˆ21nX X X =θ (1)求总体X 的分布函数()F x .(2)求统计量θˆ的分布函数)(ˆx F θ.(3)如果用θˆ作为θ的估计量,讨论它是否具有无偏性.2004年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (6)设随机变量X 服从参数为λ的指数分布,则}{DX X P >= __________ . 二、选择题(本题共8小题,每小题4分,满分32分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(13)设随机变量X 服从正态分布(0,1),N 对给定的)10(<<αα,数αu 满足αα=>}{u X P ,若α=<}{x X P ,则x 等于(A)2αu (B)21α-u(C)21α-u (D) α-1u(14)设随机变量)1(,,,21>n X X X n 独立同分布,且其方差为.02>σ 令∑==ni i X n Y 11,则(A)21Cov(,)X Y nσ= (B)21Cov(,)X Y σ=(C)212)(σnn Y X D +=+ (D)211)(σnn Y X D +=- (22)(本题满分9分)设,A B 为随机事件,且111(),(|),(|)432P A P B A P A B ===,令;,,0,1不发生发生A A X ⎩⎨⎧= .,,0,1不发生发生B B Y ⎩⎨⎧= 求:(1)二维随机变量(,)X Y 的概率分布. (2)X 和Y 的相关系数.XY ρ (23)(本题满分9分)设总体X 的分布函数为,1,1,0,11),(≤>⎪⎩⎪⎨⎧-=x x x x F ββ其中未知参数n X X X ,,,,121 >β为来自总体X 的简单随机样本,求:(1)β的矩估计量. (2)β的最大似然估计量.2005年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (6)从数1,2,3,4中任取一个数,记为X , 再从X ,,2,1 中任取一个数,记为Y , 则}2{=Y P =____________.二、选择题(13)设二维随机变量(,)X Y 的概率分布为已知随机事件}0{=X 与}1{=+Y X 相互独立,则(A)0.2,0.3a b == (B)0.4,0.1a b == (C)0.3,0.2a b == (D)0.1,0.4a b ==(14)设)2(,,,21≥n X X X n 为来自总体(0,1)N 的简单随机样本,X 为样本均值,2S 为样本方差,则(A))1,0(~N X n (B)22~()nS n χ(C))1(~)1(--n t SXn (D)2122(1)~(1,1)nii n X F n X=--∑(22)(本题满分9分)设二维随机变量(,)X Y 的概率密度为(,)f x y = 10 01,02x y x<<<<其它求:(1)(,)X Y 的边缘概率密度)(),(y f x f Y X . (2)YX Z-=2的概率密度).(z f Z(23)(本题满分9分)设)2(,,,21>n X X X n 为来自总体(0,1)N 的简单随机样本,为样本均值,记.,,2,1,n i X X Y i i =-=求:(1)i Y 的方差n i DY i ,,2,1, =. (2)1Y 与n Y 的协方差1Cov(,).n Y Y数学(一)试卷一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上) (6)设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,则{}max{,}1P X Y ≤= .二、选择题(13)设,A B 为随机事件,且()0,(|)1P B P A B >=,则必有(A)()()P A B P A > (B)()()P A B P B > (C)()()P A B P A = (D)()()P A B P B = (14)设随机变量X 服从正态分布211(,)N μσ,Y 服从正态分布222(,)N μσ, 且12{||1}{||1},P X P Y μμ-<>-<则(A)12σσ< (B)12σσ> (C)12μμ< (D)12μμ>(22)随机变量x 的概率密度为()()21,1021,02,,40,令其它x x f x x y x F x y ⎧-<<⎪⎪⎪=≤<=⎨⎪⎪⎪⎩为二维随机变量(,)X Y 的分布函数.(1)求Y 的概率密度()Y f y .(2)1,42F ⎛⎫- ⎪⎝⎭. (23)(本题满分9分)设总体X 的概率密度为(,0)F X = 10θθ- 0112x x <<≤<其它,其中θ是未知参数(01)θ<<,12n ,...,X X X 为来自总体X 的简单随机样本,记N 为样本值12,...,n x x x 中小于1的个数,求θ的最大似然估计.数学(一)试卷一、选择题(9)某人向同一目标独立重复射击,每次射击命中目标的概率为()01p p <<,则此人第4次射击恰好第2次命中目标的概率为(A)23(1)p p - (B)26(1)p p - (C)223(1)p p - (D)226(1)p p -(10)设随即变量(,)X Y 服从二维正态分布,且X 与Y 不相关,()X f x ,()Y f y 分别表示,X Y的概率密度,则在Y y =的条件下,X 的条件概率密度|(|)X Y f x y 为(A)()X f x (B)()Y f y (C)()X f x ()Y f y (D)()()X Y f x f y 二、填空题(16)在区间(0,1)中随机地取两个数,则这两个数之差的绝对值小于12的概率为________.(23)设二维随机变量(,)X Y 的概率密度为2,01,01(,)0,x y x y f x y --<<<<⎧=⎨⎩其他(1)求{2}.P X Y > (2)求Z X Y =+的概率密度.(24)设总体X 的概率密度为1,021(;),12(1)0,x f x x θθθθθ⎧<<⎪⎪⎪=≤<⎨-⎪⎪⎪⎩其他 12,,n X X X 是来自总体x 的简单随机样本,X 是样本均值(1)求参数θ的矩估计量ˆθ.(2)判断24X 是否为2θ的无偏估计量,并说明理由.2008年全国硕士研究生入学统一考试数学(一)试卷一、选择题(7)设随机变量,X Y 独立同分布且X 分布函数为()F x ,则{}max ,Z X Y =分布函数为 (A)()2F x (B) ()()F x F y (C) ()211F x --⎡⎤⎣⎦ (D) ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦ (8)设随机变量()~0,1X N ,()~1,4Y N 且相关系数1XY ρ=,则 (A){}211P Y X =--= (B){}211P Y X =-= (C){}211P Y X =-+= (D){}211P Y X =+= 二、填空题(14)设随机变量X 服从参数为1的泊松分布,则{}2P X EX == .(22)设随机变量X 与Y 相互独立,X 的概率分布为{}()11,0,13P X i i ===-,Y 的概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它,记Z X Y =+,(1)求102P Z X ⎧⎫≤=⎨⎬⎩⎭.(2)求Z 的概率密度. (23)设12,,,n X X X 是总体为2(,)N μσ的简单随机样本.记11n i i X X n ==∑,2211()1n ii S X X n ==--∑,221T X S n =- (1)证明T 是2μ的无偏估计量. (2)当0,1μσ==时 ,求DT .2009年全国硕士研究生入学统一考试数学(一)试卷一、选择题(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =(A)0 (B)0.3 (C)0.7 (D)1(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为(A)0 (B)1 (C)2 (D)3 二、填空题(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .(22)袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(1)求{}10p X Z ==. (2)求二维随机变量(),X Y 概率分布(23)设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,1X ,2X ,…n X 是来自总体X 的简单随机样本.(1)求参数λ的矩估计量. (2)求参数λ的最大似然估计量.2010年全国硕士研究生入学统一考试数学(一)试卷一、选择题(7)设随机变量X的分布函数()F x = 00101,21e 2x x x x -<≤≤->则{1}P X ==(A)0 (B)1 (C)11e 2-- (D)11e --(8)设1()f x 为标准正态分布的概率密度2,()f x 为[1,3]-上均匀分布的概率密度,()f x =12()()af x bf xx x ≤> (0,0)a b >>为概率密度,则,a b 应满足(A)234a b += (B)324a b += (C)1a b += (D)2a b +=二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.) (14)设随机变量X 概率分布为{}(0,1,2,),!CP X k k k === 则2EX = . (22)(本题满分11分)设二维随机变量()X Y +的概率密度为2222(,)e ,,,x xy y f x y A x y -+-=-∞<<∞-∞<<∞求常数及A 条件概率密度|(|).Y X f y x(23)(本题满分11 分) 设总体X 的概率分布为其中(0,1)θ∈未知,以i N 来表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3),i =试求常数123,,,a a a 使31i i i T a N ==∑为θ的无偏估计量,并求T 的方差.212011年全国硕士研究生入学统一考试数学(一)试卷一、选择题7、设)()(21x F x F 为两个分布函数，且连续函数)()(21x f x f 为相应的概率密度，则必为概率密度的是（）A )()(21x f x fB )()(212x F x fC )()(21x F x fD )()(21x F x f +)()(12x F x f8、设随机变量Y X ,相互独立，且EY EX ,都存在，记{}Y X U ,max ={}Y X V ,min =，则=EUV （）A EV EU ⋅B EY EX ⋅C EY EU ⋅D EV EX ⋅二、填空题14、设二维随机变量)0,,,,(~),(22σσμμN Y X ，则____________)(2=XY E22、设随机变量X 与Y 的概率分布分别为且{}122==Y X P求（1）二维随机变量（X ，Y ）的概率分布；（2）XYZ=的概率分布（3）X 与Y 的相关系数XY ρ23、（本题满分11分）设n X X X 21,是来自正态总体),(20σμN 的简单随机样本，其中0μ已知，02>σ未知.2,S X 为样本均值和样本方差. 求（1）求参数2σ的最大似然估计Λ2σ(2) 计算E Λ2σ和D Λ2σ222012年全国硕士研究生入学统一考试数学(一)试卷一、选择题：（7）设随机变量x 与y 相互独立，且分别服从参数为1与参数为4的指数分布，则{}=<y x p （）1124()()() ()5355A B C D（8）将长度为1m 的木棒随机地截成两段，则两段长度的相关系数为（）1)(21)(21)(1)(--D C B A二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸．．．指定位置上. （14）设,,A B C 是随机事件，,A C 互不相容，1()2P AB =,1()3P C =,则()P AB C -=________。

考研数学一(概率论与数理统计)历年真题试卷汇编4(题后含答案及解析)

考研数学一（概率论与数理统计）历年真题试卷汇编4(题后含答案及解析)题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

应选C。

知识模块：概率论与数理统计2．设A，B为随机事件，且P(B)＞0，P(A | B)=1，则必有( )A．P(A∪B)＞P(A)B．P(A∪B)＞P(B)C．P(A∪B)=P(A)D．P(A∪B)=P(B)正确答案：C解析：由题设，知P(A|B)==1，即P(AB)=P(B)。

又P(A∪B)=P(A)+P(B) —P(AB)=P(A)。

故应选C。

知识模块：概率论与数理统计3．设A，B为随机事件，若0＜P(A)＜1，0＜P(B)＜1，则P(A|B)＞P(A|)的充要条件是( )A．B．C．D．正确答案：A解析：知识模块：概率论与数理统计4．设随机事件A与B相互独立，且P(B)=0．5，P(A —B)=0．3，则P(B—A)=( )A．0.1B．0.2C．0.3D．0.4正确答案：B解析：P(A —B)=0．3，则P(A) —P(AB)=0．3。

又随机事件A与B相互独立，则有P（AB）=P(A)P(B)，因此有P(A) —P(A) P(B)=0．3。

又P(B)=0．5，故P(A)=0．6，且P(AB)=P(A)P(B)=0．3。

因此P(B—A)=P(B) —P(AB)=P(B)一P(A)P(B)=0．2。

答案为B。

知识模块：概率论与数理统计5．若A，B为任意两个随机事件，则( )A．P(AB)≤P(A)P(B)B．P(AB)≥P(A)P(B)C．D．正确答案：C解析：P(A)+P(B)=P(A∪B)+P(AB)≥2P(AB)，故选C。

概率论第一章测试题及答案考研

概率论第一章测试题及答案考研### 概率论第一章测试题及答案#### 一、选择题1. 某事件A的概率为0.5，那么事件A的补事件的概率是多少？A. 0.5B. 0.3C. 0.2D. 0.72. 以下哪个不是概率论的公理？A. 非负性B. 归一性C. 互斥性D. 可加性#### 二、填空题1. 概率论中，一个事件的概率范围在_________之间。

2. 如果事件A和事件B是互斥的，那么P(A∪B) = __________。

#### 三、简答题1. 简述什么是条件概率，并给出一个条件概率的计算公式。

2. 解释什么是独立事件，并给出两个事件独立性的判断条件。

#### 四、计算题1. 已知事件A和事件B的概率分别为P(A)=0.3，P(B)=0.4，且P(A∩B)=0.1。

求：- P(A|B)- P(B|A)#### 五、论述题1. 论述随机试验与随机事件的区别，并给出一个生活中的例子。

#### 答案#### 一、选择题1. 答案：A. 0.5解析：事件A的补事件概率等于1减去事件A的概率，即P(A') = 1 - P(A) = 1 - 0.5 = 0.5。

2. 答案：C. 互斥性解析：概率论的三个公理是：非负性（每个事件的概率非负），归一性（所有事件的概率之和为1），可加性（互斥事件的概率之和等于它们各自概率的和）。

互斥性不是概率论的公理，而是可加性的应用条件。

#### 二、填空题1. 答案：[0,1]解析：概率论中，任何事件的概率值都在0和1之间。

2. 答案：P(A) + P(B)解析：如果事件A和事件B是互斥的，那么它们不会同时发生，所以它们的并事件概率等于它们各自概率的和。

#### 三、简答题1. 条件概率是指在已知某个事件B发生的条件下，事件A发生的相对概率，计算公式为P(A|B) = P(A∩B) / P(B)。

2. 独立事件是指两个事件的发生互不影响，它们的独立性判断条件是P(A∩B) = P(A)P(B)。

考研概率论试题（数一,数三）（2）

考研概率论试题（数一,数三）（2）考研概率论试题（数一，数三）题目：(87,2分)设在一次试验中A 发生的概率为p ,现进行n 次独立试验,则A 至少发生一次的概率为1(1);n p --而事件A 至多发生一次的概率为。

知识点：伯努利概型解答：根据伯努利概型的概率计算公式，A 至少发生一次的概率1-P{A 发生0次}=11111553353238120+?+?= 而P{A 至多发生1次}= P{A 发生0次}+P{A 恰发生1次}= 000111(1)(1)n n n n C p p C p p ---+-= 1(1)(1)n n p np p --+-题目：(87,2) 三个箱子,第一个箱子中有4个黑球1个白球,第二个箱子中有3个黑球3个白球,第三个箱子中有3个黑球5个白球.现随机地取一个箱子,再从这个箱子中取出1个球,这个球为白000111(1)(1)n n n n C p p C p p ---+-球的概率等于53120，已知取出的球是白球,此球属于第二个箱子的概率为2053.知识点：全概率公式和贝叶斯公式的应用解答：记i A ={取的是第i 个箱子)(i=1，2，3)，B={从箱子中取出的是白球)，那么1231()()()3P A P A P A ===112233()()()()()()()P B P A P B A P A P B A P A P B A =++,22()()()P A B P A B P B =,35()8P B A =第一问由全概率公式，得112233()()()()()()()P B P A P B A P A P B A P A P B A =++ =11111553353238120+?+?=第二问由贝叶斯公式，得22()()()P A B P A B P B ==22112233()()()()()()()()P A P B A P A P B A P A P B A P A P B A ++=1120325353120?= 1120325353120=题目：(87,6分)设随机变量X,Y 相互独立,其概率密度函数分别为1,01()0,X x f x ≤≤?=?其他 ,0()0,y Y e y f y y -?>=?≤?求随机变量Z=2X+Y 的概率密度函数.知识点：二维随机变量（连续型）函数的分布答案：2001()(1)0221(1)22z Z ZZ f Z e Z e e Z --??∞-∞-∞+?=11202(2)()yz x xdx h x y e dy dx h z e e dz +∞+∞--+==2122202(())(())z zx z x h z ee dx dz h z e e dx dz +∞--+??=2202(()(1)()(1)22z z ze e h z e dz h z e dz --+∞--+-?? 所以2001()(1)0221(1)22z Z Z Z f Z e Z e e Z --??<-≥??题目：(87,2分) 已知连续型随机变量X的概率密度为221()xx f x -+-=,则EX =1,DX =12知识点：正态分布的密度，期望和方差解答：因2(1)1221()()1x f x e x R --=∈ , 可见1(1,)2X N ,故1()1,()2E X D X == .题目：(88,2分)设三次独立试验中,事件A 出现的概率相等,若已知A 至少出现一次的概率等于1927,则事件A 在一次试验中出现的概率为1 3.知识点：伯努利概型解答：设在每次试验中A 出现的概率为户．则1927= 1927=P{A 至少出现1次)= 1一P{A 出现0次}=0030331(1)1(1)C p p p ---=--，解答：得13p =。

考研概率论真题汇总1-精品文档

X
为样本均值，
S
2
为样本方差，
(I) 求参数σ
2的最大似然估计量
ˆ
2
(II) 计算 E ˆ 2 和
D ˆ
2
(12111,12311) 设随机变量X,Y,XY的概率分布分别为
0 X P Y P XY P 1/2 0 1/3 0 7/12 1 1/3 1/3 1 1/3 2 0 1/6 2 1/3 4 1/12 1 2
（14111）设总体X的分布函数
0, x 0 F(x) x2 1e , x 0
其中θ>0为未知参数，
X ,X ,X 1 2, n 为来自总体X的简单随机样本。
（I）求EX及EX2
（II）求θ的最大似然估计量
ˆ
（III）是否存在实数a，使得对任意的ε >0，都有 ˆ lim P {| a | } 0 n (14311) .设随机变量X和Y的概率分布相同， X的概率分布为P(X=0)=1/3,P(X=1)=2/3, 且X和Y的相关系数为1/2 (1)求(X,Y)的概率分布 (2) 求P(X+Y<1)
3y2 3 0 y x fY|X (y| x) x 0 其它
(1)求(X,Y)的概率密度f(x,y) (2)求Y的边缘概率密度fY(y)
(13111,13311) 设总体X的概率密度为
2 3 e x x0 f (x) x 0 其它
(θ为未知参数)
求 (I) P(X=2Y) (II) CoV(X-Y,Y)与 X,Y的相关系数XY
(12111) 设随机变量X,Y相互独立, 且分别服从正态总体 N(,σ 2)与 N(,2σ 2),其中σ 2>0是未知参数,设Z=X-Y, (I) 求z的概率密度f(z,σ 2) (II) 设z1,z2,……,zn是来自Z的简单随机样本,求σ 2的最大似然估计量 ˆ 2 (III)证明 ˆ