matlab第5.1章
MATLAB语言及其应用教案

MATLAB语言及其应用教案第一章:MATLAB简介1.1 课程目标让学生了解MATLAB的发展历程及其在工程领域的应用让学生熟悉MATLAB的工作环境让学生掌握MATLAB的基本命令和操作1.2 教学内容MATLAB的发展历程MATLAB的工作环境MATLAB的基本命令和操作1.3 教学方法讲授结合实例演示学生上机操作练习1.4 课后作业熟悉MATLAB的工作环境掌握MATLAB的基本命令和操作第二章:MATLAB基本语法2.1 课程目标让学生了解MATLAB的基本语法规则让学生掌握MATLAB的数据类型和变量让学生熟悉MATLAB的数学运算2.2 教学内容MATLAB的基本语法规则MATLAB的数据类型和变量MATLAB的数学运算2.3 教学方法讲授结合实例演示学生上机操作练习2.4 课后作业熟悉MATLAB的基本语法规则掌握MATLAB的数据类型和变量熟练运用MATLAB的数学运算第三章:MATLAB编程技巧3.1 课程目标让学生了解MATLAB的编程技巧让学生掌握MATLAB的循环和条件语句让学生熟悉MATLAB的函数编程3.2 教学内容MATLAB的编程技巧MATLAB的循环和条件语句MATLAB的函数编程3.3 教学方法讲授结合实例演示学生上机操作练习3.4 课后作业熟悉MATLAB的编程技巧掌握MATLAB的循环和条件语句熟练运用MATLAB的函数编程第四章:MATLAB绘图功能4.1 课程目标让学生了解MATLAB的绘图功能让学生掌握MATLAB的基本绘图命令让学生熟悉MATLAB的绘图技巧4.2 教学内容MATLAB的绘图功能MATLAB的基本绘图命令MATLAB的绘图技巧4.3 教学方法讲授结合实例演示学生上机操作练习4.4 课后作业熟悉MATLAB的绘图功能掌握MATLAB的基本绘图命令熟练运用MATLAB的绘图技巧第五章:MATLAB在信号处理中的应用5.1 课程目标让学生了解MATLAB在信号处理领域的应用让学生掌握MATLAB信号处理的基本方法让学生熟悉MATLAB信号处理的实例5.2 教学内容MATLAB在信号处理领域的应用MATLAB信号处理的基本方法MATLAB信号处理的实例5.3 教学方法讲授结合实例演示学生上机操作练习5.4 课后作业熟悉MATLAB在信号处理领域的应用掌握MATLAB信号处理的基本方法熟练运用MATLAB信号处理的实例第六章:MATLAB在控制系统设计中的应用6.1 课程目标让学生了解MATLAB在控制系统设计领域的应用让学生掌握MATLAB控制系统设计的基本方法让学生熟悉MATLAB控制系统设计的实例6.2 教学内容MATLAB在控制系统设计领域的应用MATLAB控制系统设计的基本方法MATLAB控制系统设计的实例6.3 教学方法讲授结合实例演示学生上机操作练习6.4 课后作业熟悉MATLAB在控制系统设计领域的应用掌握MATLAB控制系统设计的基本方法熟练运用MATLAB控制系统设计的实例第七章:MATLAB在图像处理中的应用7.1 课程目标让学生了解MATLAB在图像处理领域的应用让学生掌握MATLAB图像处理的基本方法让学生熟悉MATLAB图像处理的实例7.2 教学内容MATLAB在图像处理领域的应用MATLAB图像处理的基本方法MATLAB图像处理的实例7.3 教学方法讲授结合实例演示学生上机操作练习7.4 课后作业熟悉MATLAB在图像处理领域的应用掌握MATLAB图像处理的基本方法熟练运用MATLAB图像处理的实例第八章:MATLAB在仿真建模中的应用8.1 课程目标让学生了解MATLAB在仿真建模领域的应用让学生掌握MATLAB仿真建模的基本方法让学生熟悉MATLAB仿真建模的实例8.2 教学内容MATLAB在仿真建模领域的应用MATLAB仿真建模的基本方法MATLAB仿真建模的实例8.3 教学方法讲授结合实例演示学生上机操作练习8.4 课后作业熟悉MATLAB在仿真建模领域的应用掌握MATLAB仿真建模的基本方法熟练运用MATLAB仿真建模的实例第九章:MATLAB在优化计算中的应用9.1 课程目标让学生了解MATLAB在优化计算领域的应用让学生掌握MATLAB优化计算的基本方法让学生熟悉MATLAB优化计算的实例9.2 教学内容MATLAB在优化计算领域的应用MATLAB优化计算的基本方法MATLAB优化计算的实例9.3 教学方法讲授结合实例演示学生上机操作练习9.4 课后作业熟悉MATLAB在优化计算领域的应用掌握MATLAB优化计算的基本方法熟练运用MATLAB优化计算的实例第十章:MATLAB在工程实践中的应用10.1 课程目标让学生了解MATLAB在工程实践领域的应用让学生掌握MATLAB工程实践的基本方法让学生熟悉MATLAB工程实践的实例10.2 教学内容MATLAB在工程实践领域的应用MATLAB工程实践的基本方法MATLAB工程实践的实例10.3 教学方法讲授结合实例演示学生上机操作练习10.4 课后作业熟悉MATLAB在工程实践领域的应用掌握MATLAB工程实践的基本方法熟练运用MATLAB工程实践的实例重点解析本文教案主要介绍了MATLAB语言及其在各个领域的应用。
matlab教程(完整版)-matlab教程

授课教师:刘晨晨 单位:网络工程与信息安全系 email: lcczzm@ Application of Matlab Language
课程的作用 课程的目的 课程的特点 课程安排
2019/12/23
Application of Matlab Language
Jack Little
2019/12/23
Application of Matlab Language
10
• 在公司初创的五年,Jack Little非常辛苦,常常身兼数职(董事长、总经理、推销、 程序开发等),但公司一直稳定发展,从当初的一人公司,到1993年的200人,到2000年的 500余人,到2005年公司员工达到了1300人,不但打败其他竞争软件,而且前景一片欣欣向 荣。根据Jack Little个人说法,MATLAB早期成功的两大因素是:选用了C语言及选定PC为 主要平台,这似乎和微软的成功有相互呼应之妙。
MATLAB软件功能之强大、应用之广泛,已成为为21世纪最为重要的科学计算 语言。可见学习掌握这一工具的重要性。
2019/12/23
Application of Matlab Language
13
1.2 MATLAB产品的体系结构
围绕着MATLAB这个计算核心,形成了诸多针对不同 习使M实用A际MMTA上LATATMLBLAA产ABTBS间 的呢品LimA或核?由uB围 称 专 Bl离心这若本ilnoM序 的 器 运用绕 为k散。c就干身M核 数是Ak文编标 行模着 模s时AT有模就心 据e窗件译准 效块块StLT间、必块是i与 可Am口L编生的率集集AB的S要组一u基视图i译成C。lB,(mCi动n成了个/础化是形oP生函k如BCm态o仿,解极,于M应(用的位而领l+方ow成数Cp系c+真A不这其ei是一开用工且域详To式kl标库r文eTmosS统核同一丰r集体e发领具新,见的Loy这m准或t件slA建s心的软富bt高的提域箱的可Mu)、种e的可Bo可nm模所模件的Ax性高产供的大工以i,专编cM执C)以TB、a开块产资/能效品的算概具首门tAL译l行,i被Coo分A发T完品源数编家工法有箱先c+用n器文这B任Lk析+的成的库Bs值程族具A程还到在4于可e件些何语0lB和to应不体,多计语的箱序在网线、连以c产,工一言k仿用同系那个算言计,包不上帮S续s将品以具种文ie真g程的结么t,与。算这,断查助时nM、提提箱C件a序功构应另些被增找文A/lD供高的,CT包能该外工称加是档S。+许程L列而P,,从+A还具为。否。多序表生编B其哪有箱专如已M程的以成译中一A其的用 果 有及T有部他总工 你 相L每A:分公数具 有 关个B开司已箱 特 的本工始或有别 工身具着研1的 具所箱0手0究应 箱提的多、单用 ,供使个学,
MATLAB学习课件第五章

4
5.1 概述
根据程序运行方式的不同,可以将MATLAB程序设计分为
两种方式:
一种是在命令窗口中逐条输入命令,另一种是将相关
的命令存储在一个M文件中。
前者称为命令行方式,又称为指令驱动模式。后者称
为M文件的程序运行方式。
命令行方式 M文件编程方式 命令逐条解释执行 自动一次执行完文件中所有命令 简单,直观 不直观 速度慢,执行过程不能保留, 速度快,可以重复执行文件 不能重复执行
25
2、while语句
while语句的一般格式为: while 表达式 循环体语句 end while语句为条件循环语句,循环次数不确定,只要循环条件
表达式的结果非零,语句体就重复执行,直到循环条件表达 式的结果为零,则跳出循环
26
5.3.4 程序流的控制
与控制程序执行过程相关的语句主要有break语句、
5.3 MATLAB程序结构
MATLAB程序的控制结构有3种:
顺序结构、选择结构和循环结构。
按照程序设计的观点, 任何算法功能都可以通过由程序模
块组成的三种基本程序结构的组合来实现。
11
5.3.1 顺序结构
顺序结构是指程序按程序语句或模块在执行流中的顺序逐
个执行,直到执行到程序的最后一个语句。
函数式M文件 接受输入参数,有返回值 文件中定义变量为局部变量, 文件执行完毕时,局部变量 清除,不保留在工作空间
要通过函数调用的方式调用 才能运行 用户需要自定义某种具体算 法时使用
5.2.3 M文件操作
对M文件常用的操作有:打开M文件、新建M文件、编辑
M文件、保存M文件和运行M文件等。
10
例5.8:判断读取矩阵是否正确。 解:程序如下 n=4; a=magic(3) try a_n=a(n,:), %取a的第n 行元素 catch a_n=a(end, : ), %如取a的第n 行出错,则改取a的最后一行 end lasterr %显示出错原因 执行结果如下; a= 8 1 6 3 5 7 4 9 2 a_n = 9 2 ans = Attempted to access a(4,:); index out of bounds because size(a)=[3,3].
matlab 程序设计

【例5.8】用try... catch... end结构来进行矩阵相乘运算. 例
% EX0508 try结构 n=4; a=magic(n); m=3; b=eye(3); try c=a*b catch c=a(1:m,1:m)*b end lasterr
5.2.6 流程控制语句
break, continue, return, pause, keyboard, input 1. break命令 命令 break命令可以使包含break的最内层的for或while 语句强制终止,立即跳出该结构,执行end后面的命令, break命令一般和if结构结合使用.
5.2.4 switch…case开关结构
语法: switch 开关表达式 case 表达式 表达式1 语句段1 语句段 case表达式2 case表达式2 表达式 语句段2 语句段 ... otherwise 语句段n 语句段 end
说明: (1) 将开关表达式依次与case后面的表达式进行比较,如 果表达式1不满足,则与下一个表达式2比较,如果都不 满足则执行otherwise后面的语句段n;一旦开关表达式 与某个表达式相等,则执行其后面的语句段. (2) 开关表达式只能是标量或字符串. (3) case后面的表达式可以是标量,字符串或元胞数组, 如果是元胞数组则将开关表达式与元胞数组的所有元素 进行比较,只要某个元素与开关表达式相等,就执行其 后的语句段.
(2) 将函数文件保存为"Ex0502.m". (3) 在MATLAB命令窗口输入以下命令,则会出现f的计算值 注意: 注意:M脚本文件和M函数文件的文件名及函数名的命名规 和绘制的曲线:f=Ex0502(0.3) 则与MATLAB变量的命名规则相同.
《Matlab教案》课件

《MATLAB教案》PPT课件第一章:MATLAB概述1.1 MATLAB简介介绍MATLAB的历史和发展解释MATLAB的含义(Matrix Laboratory)强调MATLAB在工程和科学计算中的应用1.2 MATLAB界面介绍MATLAB的工作空间解释MATLAB的菜单栏和工具栏演示如何创建、打开和关闭MATLAB文件1.3 MATLAB的基本操作介绍MATLAB的数据类型演示如何进行矩阵运算解释MATLAB中的向量和矩阵运算规则第二章:MATLAB编程基础2.1 MATLAB脚本编程解释MATLAB脚本文件的结构演示如何编写和运行MATLAB脚本强调注释和代码的可读性2.2 MATLAB函数编程介绍MATLAB函数的定义和结构演示如何创建和使用MATLAB函数强调函数的重用性和模块化编程2.3 MATLAB编程技巧介绍变量和函数的命名规则演示如何进行错误处理和调试强调代码的优化和性能提升第三章:MATLAB数值计算3.1 MATLAB数值解算介绍MATLAB中的数值解算工具演示如何解线性方程组和不等式解释MATLAB中的符号解算和数值解算的区别3.2 MATLAB数值分析介绍MATLAB中的数值分析工具演示如何进行插值、拟合和数值积分解释MATLAB中的误差估计和数值稳定性3.3 MATLAB优化工具箱介绍MATLAB优化工具箱的功能演示如何使用优化工具箱进行无约束和约束优化问题解释MATLAB中的优化算法和参数设置第四章:MATLAB绘图和可视化4.1 MATLAB绘图基础介绍MATLAB中的绘图命令和函数演示如何绘制二维和三维图形解释MATLAB中的图形属性设置和自定义4.2 MATLAB数据可视化介绍MATLAB中的数据可视化工具演示如何绘制统计图表和散点图解释MATLAB中的数据过滤和转换4.3 MATLAB动画和交互式图形介绍MATLAB中的动画和交互式图形功能演示如何创建动画和交互式图形解释MATLAB中的图形交互和数据探索第五章:MATLAB应用案例5.1 MATLAB在信号处理中的应用介绍MATLAB在信号处理中的基本概念演示如何使用MATLAB进行信号处理操作解释MATLAB在信号处理中的优势和应用场景5.2 MATLAB在控制系统中的应用介绍MATLAB在控制系统中的基本概念演示如何使用MATLAB进行控制系统分析和设计解释MATLAB在控制系统中的优势和应用场景5.3 MATLAB在图像处理中的应用介绍MATLAB在图像处理中的基本概念演示如何使用MATLAB进行图像处理操作解释MATLAB在图像处理中的优势和应用场景《MATLAB教案》PPT课件第六章:MATLAB Simulink基础6.1 Simulink简介介绍Simulink作为MATLAB的一个集成组件解释Simulink的作用:模型化、仿真和分析动态系统强调Simulink在系统级设计和多领域仿真中的优势6.2 Simulink界面介绍Simulink库浏览器和模型窗口演示如何创建、编辑和运行Simulink模型解释Simulink中的块和连接的概念6.3 Simulink仿真介绍Simulink仿真的基本过程演示如何设置仿真参数和启动仿真解释Simulink仿真结果的查看和分析第七章:MATLAB Simulink高级应用7.1 Simulink设计模式介绍Simulink的设计模式,包括连续、离散、混合和事件驱动模式演示如何根据系统特性选择合适的设计模式解释不同设计模式对系统性能的影响7.2 Simulink子系统介绍Simulink子系统的概念和用途演示如何创建和管理Simulink子系统解释子系统在模块化和层次化设计中的作用7.3 Simulink Real-Time Workshop介绍Simulink Real-Time Workshop的功能演示如何使用Real-Time Workshop进行代码解释代码对于硬件在环仿真和嵌入式系统开发的重要性第八章:MATLAB Simulink库和工具箱8.1 Simulink库介绍Simulink库的结构和分类演示如何访问和使用Simulink库中的块解释Simulink库对于模型构建和功能复用的意义8.2 Simulink工具箱介绍Simulink工具箱的概念和功能演示如何安装和使用Simulink工具箱解释Simulink工具箱在特定领域仿真和分析中的作用8.3 自定义Simulink库介绍如何创建和维护自定义Simulink库演示如何将自定义块添加到库中解释自定义库对于个人和组织级模型共享的重要性第九章:MATLAB Simulink案例分析9.1 Simulink在控制系统中的应用介绍控制系统模型在Simulink中的构建演示如何使用Simulink进行控制系统设计和分析解释Simulink在控制系统教育和研究中的应用9.2 Simulink在信号处理中的应用介绍信号处理模型在Simulink中的构建演示如何使用Simulink进行信号处理仿真解释Simulink在信号处理领域中的优势和实际应用9.3 Simulink在图像处理中的应用介绍图像处理模型在Simulink中的构建演示如何使用Simulink进行图像处理仿真解释Simulink在图像处理领域中的优势和实际应用第十章:MATLAB Simulink项目实践10.1 Simulink项目实践流程介绍从需求分析到模型验证的Simulink项目实践流程演示如何使用Simulink进行项目规划和实施解释Simulink在项目管理和协作中的作用10.2 Simulink与MATLAB的交互介绍Simulink与MATLAB之间的数据交互方式演示如何在Simulink中使用MATLAB函数和脚本解释混合仿真模式对于复杂系统仿真的优势10.3 Simulink项目案例分析具体的Simulink项目案例演示如何解决实际工程问题解释Simulink在工程教育和项目开发中的应用价值《MATLAB教案》PPT课件第十一章:MATLAB App Designer入门11.1 App Designer简介介绍App Designer作为MATLAB中的应用程序开发环境解释App Designer的作用:快速创建跨平台的MATLAB应用程序强调App Designer在简化MATLAB代码部署和用户交互中的优势11.2 App Designer界面介绍App Designer的用户界面和工作流程演示如何创建新应用和编辑应用界面解释App Designer中的组件和布局的概念11.3 App Designer编程介绍App Designer中的MATLAB编程模式演示如何使用App Designer中的MATLAB代码块解释App Designer中事件处理和应用程序生命周期管理的重要性第十二章:MATLAB App Designer高级功能12.1 App Designer用户界面设计介绍App Designer中用户界面的定制方法演示如何使用样式、颜色和主题来美化应用界面解释用户界面设计对于提升用户体验的重要性12.2 App Designer数据模型介绍App Designer中的数据模型和模型视图概念演示如何创建、使用和绑定数据模型和视图解释数据模型在应用程序中的作用和重要性12.3 App Designer部署和分发介绍App Designer应用程序的部署和分发流程演示如何打包和发布应用程序解释如何为不同平台安装和运行App Designer应用程序第十三章:MATLAB App Designer案例研究13.1 图形用户界面(GUI)应用程序设计介绍使用App Designer设计的GUI应用程序案例演示如何创建交互式GUI应用程序来简化MATLAB脚本解释GUI应用程序在数据输入和结果显示中的作用13.2 数据分析和可视化应用程序设计介绍使用App Designer进行数据分析和可视化的案例演示如何创建应用程序来处理和显示大型数据集解释App Designer在数据分析和决策支持中的优势13.3 机器学习和深度学习应用程序设计介绍使用App Designer实现机器学习和深度学习模型的案例演示如何将MATLAB中的机器学习和深度学习算法集成到应用程序中解释App Designer在机器学习和深度学习应用部署中的作用第十四章:MATLAB App Designer实战项目14.1 App Designer项目规划和管理介绍App Designer项目的规划和管理方法演示如何组织和维护大型应用程序项目解释项目管理和版本控制对于团队协作的重要性14.2 App Designer与MATLAB的集成介绍App Designer与MATLAB之间的数据和功能集成演示如何在App Designer中调用MATLAB函数和脚本解释集成MATLAB强大计算和分析能力的重要性14.3 App Designer项目案例实现分析具体的App Designer项目案例实现过程演示如何解决实际工程项目中的问题解释App Designer在工程项目实践中的应用价值第十五章:MATLAB App Designer的未来趋势15.1 App Designer的新功能和技术介绍App Designer的最新功能和技术发展演示如何利用新功能和技术提升应用程序的性能和用户体验强调持续学习和适应新技术的重要性15.2 App Designer在跨平台开发中的应用介绍App Designer在跨平台应用程序开发中的优势演示如何创建适用于不同操作系统的应用程序解释跨平台开发对于扩大应用程序市场的重要性15.3 App Designer的未来趋势和展望讨论App Designer在未来的发展趋势和潜在应用领域激发学生对于应用程序开发和创新的兴趣强调持续探索和创造新应用的重要性重点和难点解析本文档为您提供了一份详尽的《MATLAB教案》PPT课件,内容涵盖了MATLAB 的基本概念、编程基础、数值计算、绘图和可视化、应用案例、Simulink的基础知识、高级应用、库和工具箱的使用、案例分析以及项目实践、App Designer 的基础知识、高级功能、案例研究、实战项目和未来趋势等方面的内容。
Matlab 电力电子仿真教程.

第5章 电力电子电路仿真分析
SimPowerSystems库提供的二极管模块图标如图5-3所示。
图5-3 二极管模块图标
第5章 电力电子电路仿真分析
2. 外部接口
二极管模块有2个电气接口和1个输出接口。2个电气接 口(a,k)分别对应于二极管的阳极和阴极。输出接口(m)输 出二极管的电流和电压测量值[Iak,Vak],其中电流单位为A, 电压单位为V。 3. 参数设置 双击二极管模块,弹出该模块的参数对话框,如图5-4 所示。在该对话框中含有如下参数: (1) “导通电阻”(Resistance Ron)文本框:单位为Ω,当 电感值为0时,电阻值不能为0。 (2) “电感”(Inductance Lon)文本框:单位为H,当电阻
第5章 电力电子Байду номын сангаас路仿真分析
(7) “缓冲电路阻值”(Snubber resistance Rs)文本框:并
联缓冲电路中的电阻值,单位为Ω。缓冲电阻值设为inf时将 取消缓冲电阻。 (8) “缓冲电路电容值”(Snubber capacitance Cs)文本框: 并联缓冲电路中的电容值,单位为F。缓冲电容值设为0时, 将取消缓冲电容;缓冲电容值设为inf时,缓冲电路为纯电 阻性电路。 (9) “测量输出端”(Show measurement port)复选框:选 中该复选框,出现测量输出端口m,可以观测晶闸管的电流 和电压值。 【例5.2】如图5-10所示,构建单相桥式可控整流电路,
MATLAB第五部分-统计函数

第5章MATLAB统计函数5.1 数据统计处理5.1.1 最大值和最小值MATLAB提供的求数据序列的最大值和最小值的函数分别为max和min,两个函数的调用格式和操作过程类似。
1.求向量的最大值和最小值求一个向量X的最大值的函数有两种调用格式,分别是:(1) y=max(X):返回向量X的最大值存入y,如果X中包含复数元素,则按模取最大值。
(2) [y,I]=max(X):返回向量X的最大值存入y,最大值的序号存入I,如果X中包含复数元素,则按模取最大值。
求向量X的最小值的函数是min(X),用法和max(X)完全相同。
例5-1 求向量x的最大值。
命令如下:x=[-53,72,9,15,23,57];y=max(x) %求向量x中的最大值[y,l]=max(x) %求向量x中的最大值及其该元素的位置2.求矩阵的最大值和最小值求矩阵A的最大值的函数有3种调用格式,分别是:(1) max(A):返回一个行向量,向量的第i个元素是矩阵A的第i列上的最大值。
(2) [Y,U]=max(A):返回行向量Y和U,Y向量记录A的每列的最大值,U向量记录每列最大值的行号。
(3) max(A,[],dim):dim取1或2。
dim取1时,该函数和max(A)完全相同;dim取2时,该函数返回一个列向量,其第i个元素是A矩阵的第i行上的最大值。
求最小值的函数是min,其用法和max完全相同。
例5-2 分别求3×5矩阵x中各列和各行元素中的最大值,并求整个矩阵的最大值和最小值。
3.两个向量或矩阵对应元素的比较函数max和min还能对两个同型的向量或矩阵进行比较,调用格式为:(1) U=max(A,B):A,B是两个同型的向量或矩阵,结果U是与A,B同型的向量或矩阵,U的每个元素等于A,B对应元素的较大者。
(2) U=max(A,n):n是一个标量,结果U是与A同型的向量或矩阵,U的每个元素等于A对应元素和n中的较大者。
MATLAB实用教程第郑阿奇

MATLAB 实用教程
返回
5.2.4 switch…case开关结构
0011 0010 1010 1101 0001 0100 1011
switch 开关表达式
case 表达式1
说明: (1) 如果表达式1不满足,则与下一
语句段1 case表达式2
语句段2 ...
otherwise 语句段n
end
个表达式2比较,如果都不满足则执 行otherwise后面的语句段n。 (2) 开关表达式只能是标量或字符
1 串。
(3) case后面的表达式可以是标量、
2 字符串或元胞数组,如果是元胞数
组则将开关表达式与元胞数组的所
4 有元素进行比较。
MATLAB 实用教程
返回
5.2.5 try... catch... End 试探结构(Trapping Errors)
for 循环变量=array
循环体
end
例:
for n=1:2:10
循环五次
说明:执行的次数就是 array 的 列 数 , array 可 以 是 向量也可以是矩阵,循环变 量依次取array的各列,每取
412 一次循环体执行一次。
MATLAB 实用教程
返回
5.2.2 while ... end循环结构
返回
5.2.3 If…else…end条件转移结构
if 条件式1 0011 0010 1010 1101 0001 0100 1011 语句段1
elseif 条件式2 语句段2 ...
else 语句段n+1
end
说明:If…else…end 结构也可以是没有 elseif和else的简单结 构。
微分方程模型-药物中毒急救模型(附matlab编程)

100μg/ml浓度会出现严重中毒, 200μg/ml浓度可致命.
医生需要判断:
(1)孩子的血药浓度会不会达到100~200 μg/ml?
(2)如果会达到,应采取怎样的紧急施救方案?
调查与分析
口服药物
胃肠道 药量x(t)
转移速率
和x成正比
血液系统
体外
了解药物的半衰期,可以帮助制定合理的用药 间隔,并且可以预知药物在体内的变化趋势。
调查与分析
通常,血液总量约为人体体重的7 % ~8%,体重 50~60 kg的成年人有4000ml左右的血液. 目测这个孩子的体重约为成年人的一半,可认为 其血液总量约为2000ml.
调查与分析
临床施救的办法
• 口服活性炭来吸附药物,可使药物的排除率 增加到原来(人体自身)的2倍.
在t=0瞬间进入胃肠道.
dx x, x(0) 1100
dt
y(t)由吸收而增长的速度是λx,由排除而减少的速度与y(t)
成正比(比例系数μ) , t=0时血液中无药物.
dy x y, y(0) 0
dt
模型求解
dx x, x(0) 1100
dt
药物吸收的半衰期为5 h
x(t) 1100et
2. 血液系统中药物的排除速率与y(t) 成正比,比例系数 μ(>0),t=0时血液中无药物.
3. 氨茶碱被吸收的半衰期为5 h,排除的半衰期为6 h.
4. 孩子的血液总量为2000 ml.
模型建立
口服药物
胃肠道 药量x(t)
转移率和
x成正比
血液系统
体外
药量y(t)
排除速率 和y成正比
Matlab 电力电子仿真教程

降到0到晶闸管能重新施加正向电压而不会误导通的时间。
第5章 电力电子电路仿真分析
(a)
(b)
图5-7 晶闸管模块的电路符号和静态伏安特性 (a) 电路符号;(b) 静态伏安特性
第5章 电力电子电路仿真分析
SimPowerSystems库提供的晶闸管模块一共有两种:一
种是详细的模块(Detailed Thyristor),需要设置的参数较多; 另一种是简化的模块(Thyristor),参数设置较简单。晶闸管 模块的图标如图5-8。
电感Lon、直流电压源Vf组成的串联电路和开关逻辑单元来 描述。电力电子元件开关特性的区别在于开关逻辑和串联电 路参数的不同,其中开关逻辑决定了各种器件的开关特征; 模块的串联电阻Ron和直流电压源Vf分别用来反映电力电子 器件的导通电阻和导通时的电压降;串联电感Lon限制了器 件开关过程中的电流升降速度,同时对器件导通或关断时的 变化过程进行模拟。
第5章 电力电子电路仿真分析
图5-6 例5.1的仿真波形图
第5章 电力电子电路仿真分析
5.1.2 晶闸管模块
1. 原理与图标 晶闸管是一种由门极信号触发导通的半导体器件,图57所示为晶闸管模块的电路符号和静态伏安特性。当晶闸管 承受正向电压(Vak>0)且门极有正的触发脉冲(g>0)时,晶闸 管导通。触发脉冲必须足够宽,才能使阳极电流Iak大于设定 的晶闸管擎住电流I1,否则晶闸管仍要转向关断。导通的晶 闸管在阳极电流下降到0(Iak=0)或者承受反向电压时关断, 同样晶闸管承受反向电压的时间应大于设置的关断时间,否 则,尽管门极信号为0,晶闸管也可能导通。这是因为关断 时间是表示晶闸管内载流子复合的时间,是晶闸管阳极电流
第5章 电力电子电路仿真分析
Matlab 讲义ch5-1

第五章 数据和函数的可视化视觉是人们感受世界、认识自然的最重要依靠。
数据可视化的目的在于:通过图形,从一堆杂乱的离散数据中观察数据间的内在关系,感受由图形所传递的内在本质。
MATLAB 一向注重数据的图形表示,并不断地采用新技术改进和完备其可视化功能。
本章将系统地阐述:曲线、曲面绘制的基本技法和指令;如何使用线型、色彩、数据点标记凸现不同数据的特征;如何利用着色、灯光照明、烘托表现高维函数的性状;如何生成和运用标识,画龙点睛般地注释图形等。
本章的图形指令只涉及MATLAB 的“高层”绘图指令。
这种指令的形态和格式友善,易于理解和使用。
整章内容遵循由浅入深、由基础到高级、由算例带归纳的原则。
所有算例都是运行实例,易于读者实践试验,并从中掌握一般规律。
引导5.1.1 离散数据和离散函数的可视化众所周知:一对实数标量),(y x 可表示为平面上的一个点;进而,一对实数“向量”),(y x 可表现为平面上的一组点。
MATLAB 就是利用这种几何比拟法实现了离散数据可视化。
至于离散函数可视化的步骤是:先根据离散函数特征选定一组自变量TN x x x ],,,[21 =x ;再根据所给离散函数)(n n x f y =算得相应的T N y y y ],,,[21 =y ,然后在平面上几何地表现这组向量对),(y x 。
【例5.1-1】图形表示离散函数n y =。
(图5.1-1)n=(-10:10)';y=abs(n);plot(n,y,'r.','MarkerSize',20) axis equalgrid on xlabel('n')图 5.1-1 离散函数的可视化5.1.2 连续函数的可视化连续函数可视化包含三个重要环节:一,从连续函数获得一组采样数据,即选定一组自变量采样点(包括采样的起点、终点和采样步长),并计算相应的函数值;二,离散数据的可视化;三,图形上离散点的连续化。
Matlab原理与工程应用第二版第五章(函数)

14
非线性方程数值求解
函数fzero()求一元函数的零点,其具体使用方法如下:
x = fzero(@fun,x0,options,p1,p2,…) , 在 x0 点 附 x = fzero(@fun,[x0,x1]) ,在 [x0,x1] 区间内寻找函
近寻找函数的零点;
数的零点;
x = fzero(@fun,x0,options) ,用 options 指定寻找零
subplot(1,3,1); plot(x,y,'ro',xi,yi_nearest,'b-'); title(‘最邻近插值'); subplot(1,3,2); plot(x,y,'ro',xi,yi_linear,'b-'); title(‘线性插值'); subplot(1,3,3); plot(x,y,'ro',xi,yi_spline,'b-'); title(‘三次样条插值');
23
8.1.2 数值积分的实现方法 1.变步长辛普生法 基于变步长辛普生法,MATLAB给出了quad函数来求定积 分。该函数的调用格式为: [I,n]=quad('fname',a,b,tol,trace) 其中fname是被积函数名。a和b分别是定积分的下限和 上限。tol用来控制积分精度,缺省时取tol=0.001。 trace控制是否展现积分过程,若取非0则展现积分过程, 取0则不展现,缺省时取trace=0。返回参数I即定积分 值,n为被积函数的调用次数。
19
将求得的解代回原方程,可以检验结果是否正确, 命令如下: q=myfun(x) q = 1.0e-009 * 0.2375 0.2957 可见得到了较高精度的结果。
MATLAB基础教程 第5章 符号运算

第五章 符号运算
5.1 符号运算基础
2. 符号表达式的转换
(2)expand:该函数用于符号表达式的展开。其操作对象可以是多种类型,如多项 式、三角函数、指数函数等。
例5-6 符号表达式的展开。 >>syms x y; >>f=(x+y)^3; >>expand(f) ans= x^3+3*x^2*y+3*x*y^2+y^3 >>expand(sin(x+y)) ans= sin(x)*cos(y)+cos(x)*sin(y) >>expand(exp(x+y)) ans= exp(x)*exp(y)
第五章 符号运算
5.1 符号运算基础
例5-2 符号运算和数值运算之间的差别 >>sym(2)/sym(5) ans= 2/5 >>2/5+1/3 ans=0.7333 >>sym(2)/sym(5)+sym(1)/sym(3) ans= 11/15 >>double(sym(2)/sym(5)+sym(1)/sym(3)) ans= 0.7333 由上例可以看出,当进行数值运算时,得到的结果为double型数据;采用符号进 行运算时,输出的结果为分数形式。
第五章 符号运算
5.1 符号运算基础
2. 符号表达式的转换
(4)simplify:该函数实现表达式的化简。 例5-8 simplify函数的应用。 >>simplify(sin(x)^2+cos(x)^2) ans= 1 >>syms a b c; >>simplify(exp(c*log(sqrt(a+b)))) ans= (a+b)^(1/2*c) >>S=[(x^2+5*x+6)/(x+2),sqrt(16)]; >>R=simplify(S) R= [3+x, 4]
第5章 MATLAB绘图

例5-7 在0≤x≤2区间内,绘制曲线y1=2e-0.5x和 y2=cos(4πx),并给图形添加图形标注。
程序如下:
x=0:pi/100:2*pi;
y坐标数据。
例5-1 在0≤x≤2区间内,绘制曲线 y=2e-0.5xcos(4πx)
程序如下: x=0:pi/100:2*pi; y=2*exp(-0.5*x).*cos(4*pi*x); plot(x,y)
例5-2 绘制曲线。 程序如下: t=0:0.1:2*pi; x=t.*sin(3*t); y=t.*sin(t).*sin(t); plot(x,y);
例5-9 用fplot函数绘制f(x)=cos(tan(πx))的曲线。 命令如下: fplot('cos(tan(pi*x))',[ 0,1],1e-4)
5.1.7 图形窗口的分割
subplot函数的调用格式为:
subplot(m,n,p)
该函数将当前图形窗口分成m×n个绘图区, 即每行n个,共m行,区号按行优先编号, 且选定第p个区为当前活动区。在每一个绘 图区允许以不同的坐标系单独绘制图形。
第5章 MATLAB绘图 5.1 二维数据曲线图 5.2 其他二维图形 5.3 隐函数绘图 5.4 三维图形 5.5 图形修饰处理 5.6 图像处理与动画制作
5.1 二维数据曲线图 5.1.1 绘制单根二维曲线 plot函数的基本调用格式为:
plot(x,y) 其中x和y为长度相同的向量,分别用于存储x坐标和
(2) 当x,y是同维矩阵时,则以x,y对应列元素为横、 纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
Matlab_plot
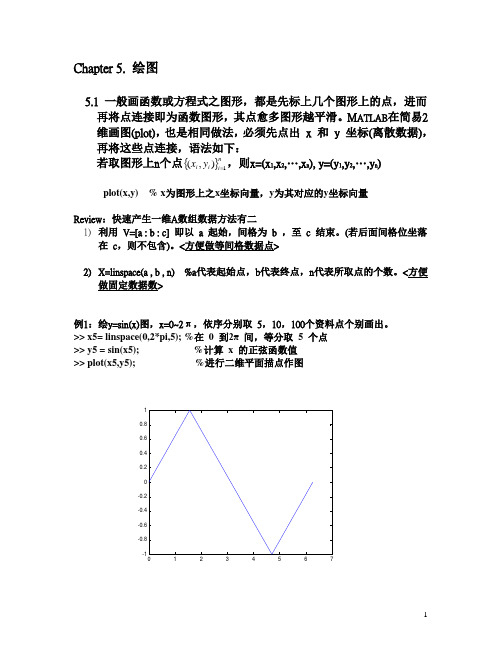
Chapter 5. 绘图5.1 一般画函数或方程式之图形,都是先标上几个图形上的点,进而再将点连接即为函数图形,其点愈多图形越平滑。
M ATLAB 在简易2维画图(plot),也是相同做法,必须先点出 x 和 y 坐标(离散数据),再将这些点连接,语法如下:若取图形上n 个点{}n i i i y x 1),(=,则x=(x 1,x 2,…,x n ), y=(y 1,y 2,…,y n )plot(x,y) % x 为图形上之x 坐标向量,y 为其对应的y 坐标向量Review :快速产生一维A 数组数据方法有二1) 利用 V=[a : b : c] 即以 a 起始,间格为 b ,至 c 结束。
(若后面间格位坐落在 c ,则不包含)。
<方便做等间格数据点>2) X=linspace(a , b , n) %a 代表起始点,b 代表终点,n 代表所取点的个数。
<方便做固定数据数>例1:绘y=sin(x)图,x=0~2π,依序分别取 5,10,100个资料点个别画出。
>> x5= linspace(0,2*pi,5); %在 0 到2π 间,等分取 5 个点>> y5 = sin(x5); %计算 x 的正弦函数值>> plot(x5,y5); %进行二维平面描点作图>> figure; % 开新画图窗口>> x10= linspace(0,2*pi,10); %在0 到2π 间,等分取10 个点>> y10 = sin(x10); %计算x 的正弦函数值>> plot(x10,y10);>> figure; % 开新画图窗口>> x100= linspace(0,2*pi,100); %在0 到2π 间,等分取100 个点>> y1000 = sin(x10); %计算x 的正弦函数值>> plot(x100,y100);>> plot(x, sin(x), x, cos(x)) %进行多条曲线作图,输入依序为各曲线的x ,%y 值提示:>> figure % 开另一窗口绘图5.2 快速方程式画图(fplot ,ezplot)5.2.1 fplot :单纯画方程式图形,图形上之(x,y)坐标值会自动取,但必须输入x 坐标的范围,其指令如下:fplot(‘函式’,[xmin,xmax,ymin,ymax]) %绘出函式图形,x 轴的范围取xmin到%xmax ,y 轴的范围取ymin 到ymax例1:绘出)2sin()cos(23x x x y --=图形>> fplot('x-cos(x^3)-sin(2*x^2)',[-3,3]) %绘出)2sin()cos(23x x x y --=图形x x2yx 2-y = 05.2.2 ezplot :类似fplot ,可以绘出y=f(x)显函数,也可绘出f(x ,y)=0隐函数以及参数式。
离散系统Matlab仿真

G1 (s)
s
1
1,G2
(
s)
s
1
, 2
采样周期T=1s,求该系统的脉冲传递函数G(z)。
G1=tf(1,[1 1]); G2=tf(1,[1 2]); G=G1*G2 Gd=c2d(G,1, 'imp')
14
2、闭环离散系统
例:闭环采样系统结构如图所示,其中
G(s) 1
H (s) 1
s(s 1)
20
例:闭环采样=1s,试求其单位阶跃响应。
sys=tf(1,[1 1 0]); sysd=c2d(sysc,1, 'zoh'); closysd=feedback(sysd,1); [num,den]=tfdata(closysd) dstep (num,den,25 )
25
Ts=1; dtime=(0:Ts:50) ; R1=dtime; R2=0.5*dtime.*dtime; subplot(2,1,1);dlsim(num,den,R1) subplot(2,1,2); dlsim(num,den,R2)
26
例:闭环采样系统结构如图所示,其中 G(s) 1
试用MATLAB创建系统的数学模型。
num=[0.01 0.03 -0.07]; den=[1 -2.7 2.42 -0.72]; G=filt(num,den) printsys (num, den, 'z')
5
二、数学模型旳互相转换
这两种数学模型之间是可以互相转换旳,其调用格式分别为: tf (sys) ——将零极点增益模型转换成传递函数模型; zpk (sys)——将传递函数模型转换成零极点增益模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
digits(n) 功能: 功能:设定计算精度和改变默认的有效位数 函数。其中n 为所期望的有效位数, 函数 。 其中 n 为所期望的有效位数 , 默认 值为32 32位 值为32位。 的格式为: vpa 的格式为: S=vpa(s,n) 功能: 表示为n位有效位数的符号对象。 功能:将s表示为n位有效位数的符号对象。
2
5.1 符号计算基础
5.1.1 概述 号计算的特点: 符号计算的特点: 1)符号运算对象可以是没赋值的符号 符 运算对象可以是没赋值的符号, ) 号表达式计算前必须定义符号变量。 号表达式计算前必须定义符号变量。 2)符号计算是精确计算。 )符号计算是精确计算 3)符号计算的计算速度较慢。 )符号计算的计算速度较慢。 4)符号计算的运算符和基本数学函数与数 ) 值计算中的几乎完全相同。 的几乎完全相同 值计算中的几乎完全相同。
5
2.创建符号变量 sym(‘变量 变量’ 参数) sym( 变量’,参数) 功能: 把变量定义为符号对象。 功能 : 把变量定义为符号对象 。 其中参 数用来设置限定符号变量的数学特性, 数用来设置限定符号变量的数学特性 , 有三种选择: 有三种选择: positive’ 表示为“ ’ positive 表示为 “ 正 、 实 ” 符号变 量, ’real’ 表示为“实”符号变量, real 表示为“ 符号变量, unreal’ 表示为“非实”符号变量。 ’unreal 表示为“非实”符号变量。
20
f4=subs(f,'sin(x)',sym('y')) 以符号变量y替换符号表达式sin(x) %以符号变量y替换符号表达式sin(x) f5=subs(f,{a,b,x},{2,2,sym(pi/3)}) 分别以标量2 替换符号变量a % 分别以标量 2 、 3 替换符号变量 a、b, 以符号常量 pi/3替换符号变量x pi/3替换符号变量x f6=subs(f,{a,b,x},{2,2,pi/3}) pi/3替换符号变量a %分别以标量2、3 、pi/3替换符号变量a、b、x 分别以标量2
3
与数值运算的区别 数值运算中必须先对变量赋值, 数值运算中必须先对变量赋值,然后才 能参与运算。 能参与运算。 符号运算无须事先对独立变量赋值, 符号运算无须事先对独立变量赋值,运 算结果以标准的符号形式表达。 算结果以标准的符号形式表达。
4
5.1.2 符号常量和符号变量 建符号常量 1.创建符号常量 sym函数的格 函数的格式 a=sym(‘常量 常量’ sym函数的格式1为:a=sym( 常量’) sym函数的格式 函数的格式2 sym(常量 参数) 常量, sym函数的格式2为: sym(常量,参数) 创建符号常量。 例5 - 1 创建符号常量。 b=sym(‘pi') %创建符号常量 c=sym(2 ,‘d’)% c=sym(2/3,‘d’)% 返 回 最 接 近 的 32 位 的十进制数值
22
f=x 的反函数。 例5-10 求f= 2的反函数。 syms x;f=x^2;g=finverse(f) fg=compose(g,f) %验算g(f(x))是否等于x 验算g(f(x))是否等于x g(f(x))是否等于 例5-11 求tex的反函数。 反函数。 f=sym('t*e^x')%原函数 % g=finverse(f) %对默认自由变量x求反函数 对默认自由变量x g=finverse(f,'t')%对t求反函数 %
15
5.2.4 自由变量的确定 符号表达式确定自由变量的原则: 符号表达式确定自由变量的原则: 小写字母i 不能作为自由变量。 1)小写字母i和j不能作为自由变量。 符号表达式中如果有多个字符变量, 2)符号表达式中如果有多个字符变量,则按 照以下顺序选择自由变量: 照以下顺序选择自由变量: 首先选择x作为自由变量;如果没有x 首先选择 x 作为自由变量 ;如果没有 x,则 选择在字母顺序中最接近x 的字符变量; 选择在字母顺序中最接近 x 的字符变量 ; 如果与x相同距离,则在x后面的优先。 如果与x相同距离,则在x后面的优先。 大写字母比所有的小写字母都靠后。 3)大写字母比所有的小写字母都靠后。
19
根据subs的置换规则,分析下列语句的功能。 的置换规则, 例5-9 根据 的置换规则 分析下列语句的功能。 syms a b x; %创建符号变量 , b,和 x 创建符号变量a, , 创建符号变量 f=a*sin(x)+b; %创建符号表达式 f1=subs(f,'a',sym('2')) %以符号常量2替换符号变量a 以符号常量2替换符号变量a f2=subs(f,{a,b},{sym('2'),sym('3')}) %分别以符号常量2、3替换符号变量a、b 分别以符号常量2 替换符号变量a f3=subs(f,{a,b},{3,2}) 分别以标量2 替换符号变量a %分别以标量2、3替换符号变量a、b
7
3.符号矩阵的创建 3.符号矩阵的创建 数值矩阵A=[1,2;3,4] A=[a,b;c,d] —— 不识别 命令格式:A=sym('[ ※ 需用sym指令定义 ※ 需用' '标识
8
]')
※ 符号矩阵内容同数值矩阵
建立符号常数矩阵,并转换为数值矩阵 例5-7建立符号常数矩阵 并转换为数值矩阵。 - 建立符号常数矩阵 并转换为数值矩阵。 s=sym('[1/3 5/7;sqrt(3) 8/9]') %建立符号常数矩阵 建立符号常数矩阵s 建立符号常数矩阵 single(s) %把s转换为数值矩阵 如何创建符号矩阵A=[a,b;c,d]? 注意:符号矩阵的每一行的两端都有方括号, 这是与 Matlab数值矩阵的一个重要区别。
11
5.2.2 符号数值精度控制 三种不同的算术运算: 三种不同的算术运算: MATLAB的浮点运算 的浮点运算。 1) 数值型 MATLAB的浮点运算。 Maple的精确符号运算 的精确符号运算。 2) 有理数型 Maple的精确符号运算。 VPA型 Maple的任意精度运算 的任意精度运算。 3) VPA型 Maple的任意精度运算。 种运算的精度可以任意设置, 第3种运算的精度可以任意设置,由digits vpa函数实现 函数实现。 和vpa函数实现。
21
5.2.6 反函数和复合函数 finverse(f,v) finverse(f,v) 功能:对指定自变量v的函数f(v)求反函数。 功能: 指定自变量v的函数f(v)求反函数。 f(v)求反函数 省略时, 当v省略时,则对默认的自由符号变量求反 函数。 函数。 compose(f,g,x,z) compose 功能:返回值为f(g(z))。其中f 功能:返回值为f(g(z))。其中f和g是符号表 f(g(z)) 达式, 是符号变量。 达式,x和z是符号变量。
14
5.2.3 符号对象转换为数值对象 double(S) 功能:把符号矩阵S转换为双精度浮点数矩阵 转换为双精度浮点数矩阵。 功能:把符号矩阵 转换为双精度浮点数矩阵。 single(S) 功能:把符号矩阵S转换为单精度浮点数矩阵 转换为单精度浮点数矩阵。 功能:把符号矩阵 转换为单精度浮点数矩阵。
13
应用digits vpa函数设置运算精度 digits和 函数设置运算精度。 例5-6 应用digits和vpa函数设置运算精度。 a=sym('2*sqrt(5 a=sym('2*sqrt(5)+pi') %创建符号对象 digits %显示默认的有效位数 vpa(a) %用默认的位数计算并显示 vpa(a,20 20) vpa(a,20) %按指定的精度计算并显示 digits(15 15) digits(15) %改变默认的有效位数 digits指定的精度计算并显示 vpa(a) %按digits指定的精度计算并显示
9
5.2 符号表达式的基本操作
5.2.1 符号表达式的基本运算 算术运算、 1.算术运算、关系运算 2.常用的函数 1) 三角函数和双曲函数 2) 指数和对数函数 3) 矩阵分析函数 4) 取整函数 5)复数函数
10
符号表达式的语法: 符号表达式的语法: 1) syms x;f1= sin(x)+5*x f1 —— 符号变量名 sin(x)+5*x—— 符号表达式 =‘sin(x)+5*x’ 2) f2 =‘sin(x)+5*x’ sym(‘sin(x)+5*x’) 3) f2 = sym(‘sin(x)+5*x’) 三者表达式之间有区别吗?
16
findsym的格式为: findsym的格式为: 的格式为 findsym(S,n) 功能:确定S中的自由变量。 功能:确定S中的自由变量。 其中S可以是符号表达式或符号矩阵; 其中S可以是符号表达式或符号矩阵;n为按 顺序得出符号变量的个数, 省略时, 顺序得出符号变量的个数,当n省略时, 则不按顺序给出S中所有的符号变量。 则不按顺序给出S中所有的符号变量。
第5章 符号计算 (1) 章 Nhomakorabea主要内容: 主要内容:
①创建符号常量和变量; 创建符号常量和变量; 符号多项式的四则运算; ②符号多项式的四则运算; 符号表达式的化简; ③符号表达式的化简; 符号微分和积分变换的计算; ④符号微分和积分变换的计算; 符号微分方程和代数方程的求解。 ⑤符号微分方程和代数方程的求解。
5.3.1 合并同类项 collect (S,v) 功能:合并多项式S的同类项。其中S是符号表 功能:合并多项式 的同类项。其中 是符号表 的同类项 达式, 是合并同类项的变量 是合并同类项的变量。 达式,v是合并同类项的变量。 collect (S) 功能: 确定的变量合并多项式S的同 功能:以findsym确定的变量合并多项式 的同 确定的变量合并多项式 类项。 类项。 函数pretty可给出多项式的易读形式。 pretty可给出多项式的易读形式 函数pretty可给出多项式的易读形式。
