内力调幅计算表
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
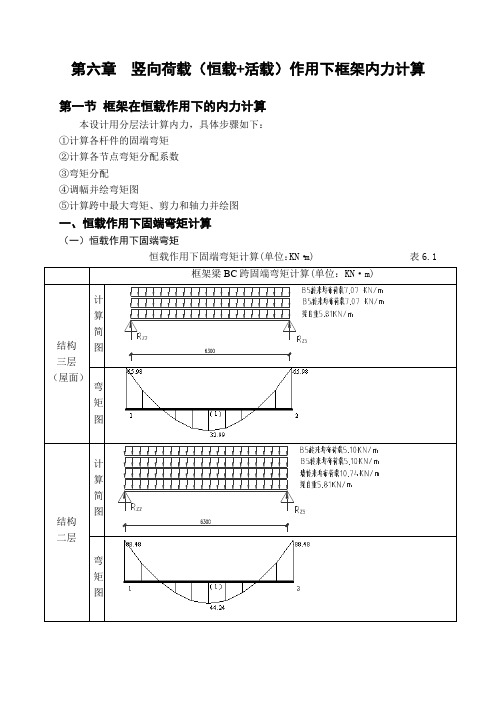
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
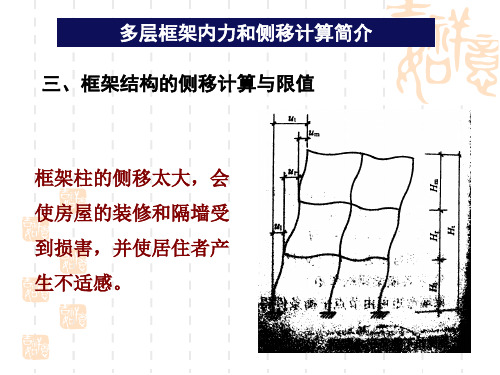
第五章多层框架内力和侧移计算简介
120
100(80)50
2、结构的抗震等级 地震作用下,钢筋混凝土结构的地震反应有下列特点:
(1)、地震作用越大,房屋的抗震要求越高; (2)、结构的抗震能力主要取决于主要抗侧力构件的性 能,结构形式不同,抗震要求也不同。 (3)、房屋越高,地震反应越大,抗震要求越高。
抗震等级是确定结构构件抗震计算和抗震措施的标准。 根据设防烈度、房屋高度、建筑类别、结构类型及构件在 结构中的重要程度确定,共分四个等级,一级最高。
9
≤ 25
一 一
≤ 50
一 一
注:①.建筑场地为Ⅰ类时,除6度外可按表内降低一度所对应的 抗震等级采取抗震构造措施,但相应的计算要求不应降低;
②.接近或等于高度分界时,应允许结合房屋不规则程度及场 地、地基条件确定抗震等级。
3、防震缝与抗撞墙布置
➢高层建筑避免采用不规则的建筑结构方案,尽量 不设防震缝。
(c) min 见下表
抗震等级
类别
一
二
三
四
中柱和边柱
1.0
4)框架梁下部纵向钢筋在端节点的锚固要求与中间 节点相同。
3 框架柱纵向钢筋在顶层节点的锚固 (1)框架柱纵筋在中间节点的锚固
梁高足够时
梁高不够时
板厚>80mm时
(2)框架柱纵筋在顶层端节点的锚固
三、箍筋
1.在框架节点内应设置水平箍筋,箍筋应符合柱箍 筋的构造规定,但间距不宜大于250mm。
2.对四边均有梁与之相连的中间节点,节点内可只 设置沿周边的矩形箍筋,不必设置复合箍筋。
2)框架-抗震墙结构房屋的防震缝宽度可采用
框架规定数值的50%,且不宜小于70mm。
3)防震缝两侧结构类型不同时,按需要较 宽防震缝的结构类型考虑和按低的房屋高 度计算缝宽。
2-3内力计算

3)塑性铰与理想铰的区别:前者能承受弯矩,并只 能沿弯矩作用发生一定限度的转动,而后者则不能 承受弯矩,但可自由转动。
4)塑性内力重分布的概念:塑性铰的出现将引起构 件各截面间的内力分布发生变化的现象,称为塑性内 力重分布。
5)塑性内力重分布的经济效应:按一般力学方法计 算出来的内力,其跨中与支座截面的弯矩比值为M1: MB=1:1.2,经过塑性内力重分布后,使其跨中与 支座截面的弯矩比值改变为M1:MB=1:1,从而 利用了跨中截面潜在的承载能力而取得经济效益。
项目二:肋梁楼盖设计 任务1 结构平面布置方案 任务2 计算简图及荷载计算 任务3 内力计算
任务4 正截面配筋计算
任务5 斜截面配筋计算 任务6 楼盖设计与构造要求 任务7 楼梯 单向板楼盖设计实例
双向板楼盖设计实例
任务3 单向板楼盖的内力计算
1.内力计算两种方法
钢筋混凝土连续板、梁的内力计算方法有两种: 即弹性计算法和塑性计算法。
剪力计算 : V ( g q )l n
0.4
0.5
0.5
0.5
0.6
-0.6
-0.5
-0.5
-0.5
-0.4
连 续 梁 的 剪 力 系 数
5、内力值的确定
1)单向板中内力值的确定
⑴支承在次梁或砖墙上的连续板,一般可按考虑塑性内 力重分布的方法计算。 ⑵板一般均能满足斜截面抗剪要求,设计时可不进行受 剪承载力计算。 ⑶一般规定,对四周与梁整体连接时,其中间跨板带的 跨中截面及中间支座截面的计算弯矩可折减20%,其他 截面则不予减少。
1)按弹性理论方法计算是假定结构构件为理想弹性材料,选 取计算简图后,其内力按结构力学的原理分析计算,一般 常用力矩分配法来求连续板、梁的内力。为计算方便,对 于常用荷载作用下的等跨连续梁板,均已编制成计算表格 可直接查用。 其计算结果比实际情况偏大,可靠度大。但其求得的支 座弯矩远大于跨中弯矩,这使得支座配筋拥挤,构造复杂, 施工不便。
结构设计各种调整系数

第i层框架柱剪力之和。
地震作用调整系数CE
又称地震力调整系数,
用于放大或缩小地震作用
一般CE=1.0。
特可取0.85-1.5
梁端弯矩调幅系数BT
考虑塑性内力重分布,调整减小梁端负弯矩,相应增加跨中弯矩
使梁上下配筋比较均匀,框架梁调幅后跨中按平衡条件相应增大。
装配式
0.7~0.8
实际工程中悬调梁负弯矩不调幅
1.8注3
一级
1.5(1.65=1.1×1.5)
2.1=1.4×1.5
(2.31=1.1×2.1)
1.5注3
二级
1.25(1.375=1.1×1.25)
1.5=1.2×1.25
(1.65=1.1×1.5)
1.25注3
结构类别
构件类型
部位
抗震等级
内力增大系数及其表达式
弯矩
剪力
轴力
框支结构
框支柱及框架柱
1.265=1.15×1.1
(1.392=1.1×1.265)
其他
特一级
1.68=1.2×1.4
(1.848=1.1×1.68)
2.352=1.2×1.96
(2.587=1.1×2.352)
1.0
9度及特一级
1.452=1.2×1.1×1.1
(1.597=1.1×1.452)
2.108=1.2×1.1×1.1×1.452
(1.584=1.1×1.4)
1.2
混凝土剪力墙结构构件设计内力的调整
普通高层结构
连梁
全部连梁
特一级
1.0
1.3
9度及特一级
1.3
一级
1.3
二级
1.2
内力组合及内力调整

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
1)、在恒载和活载作用下,跨间max M 可以近似取跨中的M 代替,在重力荷载代表值和水平地震作用下,跨内最大弯矩max M 采用解析法计算:先确定跨内最大弯矩max M 的位置,再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时,按公式7-1计算。
计算方式见图7-1、7-2括号内数值,字母C 、D 仅代表公式推导,不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = (7-1) 式中:q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值;M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值;l ——梁的计算跨度。
2)、在重力荷载代表值和地震作用组合时,左震时取梁的隔离体受力图,见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中:GC M 、GD M ——重力荷载作用下梁端的弯矩; EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力:()C 1=2GD GC EC ED ql R M M M M l--++;由0M ddx=,可求得跨间max M 的位置为:1C /X R q = ; 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为: 弯矩最大点位置距左端的距离为1X ,1=/E X R q ;()101X ≤≤; 最大组合弯矩值:2max 1/2GE EF M qX M M =-+;当10X <或11X >时,表示最大弯矩发生在支座处,取1=0X 或1=X l ,最大弯矩组合设计值的计算式为:2max C 11/2GE EF M R X qX M M =--+; 右震作用时,上式中的GE M 、EF M 应该反号。
计算书 4 内力

第四章 内力计算4.1 恒荷载作用下的内力计算恒荷载(竖向荷载)作用下的内力计算采用分层法,并进行以下修正:①除底层外其它层柱的线刚度均乘以0.9的折减系数;②底层柱传递系数取为1/2,其他各层取为1/3。
对各层用弯矩分配法进行计算,并可利用结构对称性取二分之一结构计算。
远端固定,传递系数为0.5;远端滑动支承,传递系数为-1。
4.1.1固端弯矩计算(1)第5层恒荷载作用下的内力计算梯形荷载等效系数2.0624.21=÷=α 25312115'AB 5)21(g AB AB g g αα+-+==4.84+(1-0.08+0.008)×9.94=14.06kN/mg 5BC =2.2kN/mM AB =121×14.06×62=42.18kN •mM BC =31×2.2×1.22=1.06kN •mM CB =61×2.2×1.22=0.53kN •m(2)第4层恒荷载作用下的内力计算'A 4g B =18.48+(1-0.08+0.008)×7.78=25.70kN/m g 4BC =2.2kN/mM AB =121×25.70×62=77.1kN •mM BC =31×2.2×1.22=1.06kN •mM CB =61×2.2×1.22=0.53kN •m(3)第1~3层恒荷载作用下的内力计算'A g B =4.84+(1-0.08+0.008)×7.78=12.06kN/mg BC =2.2kN/mM AB =121×12.06×62=36.18kN •mM BC =31×2.2×1.22=1.06kN •mM CB =61×2.2×1.22=0.53kN •m4.1.2 弯矩分配法计算内力4底层柱线刚度为2.16×1010N ·mm ,其他各层柱线刚度为3.2×0.9=2.88×1010N ·mm 。
一榀框架计算(土木工程毕业设计手算全过程)

合计
92.79KN
3.2 活荷载标准值计算 1)①屋面板活荷载标准值(不上人):
0.5KN/M²
②顶层次梁受板传递的活荷载标准值(计算简图见图 2) 0.5×3=1.5KN/M
③框架梁受次梁传递的活荷载标准值
1.5×9=13.5KN
④屋面板传递给边柱的集中荷载: 中柱的集中荷载:
0.5×1.5×9=6.75KN 0.5×3×9=13.5KN
图 4-4 恒载弯矩分配图
在竖向荷载作用下,梁端截面有较大的负弯矩,设计时应进行弯矩调幅,降低负 弯矩,以减少配筋面积。对于现浇框架,支座弯矩调幅系数为 0.85(在内力组合 的表中进行梁端调幅计算)
图 4-5 恒载作用下的框架弯矩图(等效为集中荷载时)
楼 层 AB 跨
荷载引起的弯矩 BC 跨
VA
VB
VB
VC
表 4-1 恒载作用下内力
CD 跨
VC
VD
AB 跨 VA
弯矩引起的内力
BC 跨 CD 跨
VB
VB VC VC
VD
顶 层 194.67 -194.67 194.67 -194.67 194.67 -194.67 -16.52 -16.52 0 0 16.52 16.52
5
180.6 -180.6 180.6 -180.6 180.6 -180.6 -6.07 -6.07 0 0 6.07 6.07
0.6 KN/M 2 0.02×20=0.4 KN/M 2
0.12×25=3 KN/M 2 0.2 KN/M 2 4.2 KN/M 2
楼面板传递给边柱的集中荷载: 中柱的集中荷载:
4.2×1.5×9=56.7KN 4.2×3×9=113.4KN
框架计算简图及梁柱线刚度

一、框架梁柱线刚度初估梁柱截面尺寸:⑴、梁:493010104254103010604.2500250121,500250·1093.4780010373.1108.2,10373.165030012122300,2173273121(,650,65097512181(,7800mm I mm mm h b mmN l EI i C mm I I mmb mm ~ h ~b mm h mm mm ~l ~h mm l b ⨯=⨯⨯=⨯=⨯⨯=⨯⨯⨯==⨯=⨯⨯⨯=========次梁取级,混凝土用取)取)⑵、柱:混凝土用30C 级按层高确定截面尺寸:底层取mm H 71006504506000=++=,mmN i mm mm h b mm mm ~H ~b c ·10896.15400/100.3800121800800,355473201151(1144⨯=⨯⨯⨯=⨯=⨯==取)底层mm N i c ·10442.17100/100.38001211144⨯=⨯⨯⨯=取梁的线刚度值为基准值1,则柱为:846.3,底层柱为:925.2,见下图2:双向板板厚:mm h mm ~l ~h 100,785.97501401(===取) 1、恒荷载计算:(标准值)⑴、屋面恒载:屋10 KN/ m 2 100厚现浇混凝土屋面板 ×25= KN/ m 2 10厚水泥砂浆抹灰 ×20= KN/ m 2 合计: KN/ m 2⑵、楼面恒载:楼10 KN/ m 2结合层一道100厚现浇混凝土屋面板 ×25= KN/ m 2 10厚水泥砂浆抹灰 ×20= KN/ m 2 合计: KN/ m 2⑶、梁自重:主梁mm mm h b 650300⨯=⨯主梁自重 25×× KN/m 10厚水泥砂浆抹灰 × ×2×20=m合计: KN/m 次梁自重 25××( )= KN/m 10厚水泥砂浆抹灰 ×()×2×20=m合计: m⑷、柱自重:mm mm h b 800800⨯=⨯柱自重 25××=16KN/m10厚水泥砂浆抹灰 ××4×20=m合计: m⑸、外墙自重:粉煤灰轻渣空心砌块:自重取 KN/ m 3标准层 8××()=m水刷石外墙面 ×=m 水泥粉刷内墙面 ()×=m合计: m 底层 8××()=m水刷石外墙面 ×= KN/m 水泥粉刷内墙面 ()×= KN/m合计: KN/m⑹、内墙自重:(同外墙)标准层 8××()= KN/m 水泥粉刷墙面 ()×2×= KN/m合计: KN/m 底层 8××()= KN/m 水泥粉刷墙面 ()×2×= KN/m合计: KN/m 2、恒载作用下框架受力分析:板传到次梁以及次梁传到主梁的荷载按三角形和梯形进行传递,计算时折算为均布荷载。
(整理)弯矩调幅法

调幅法弯矩调幅法简称调幅法,它是在弹性弯矩的基础上,根据需要适当调整某些截面的弯矩值。
通常是对那些弯矩绝对值较大的截面弯矩进行调整,然后,按调整后的内力进行截面设计和配筋构造,是一种实用的设计方法。
弯矩调幅法的一个基本原则是,在确定调幅后的跨内弯矩时,应满足静力平衡条件,即连续梁任一跨调幅后的两端支座弯矩MA、MB(绝对值)的平均值,加上调整后的跨度中点的弯矩M1’ 之和,应不小于该跨按简支梁计算的跨度中点弯矩Mo,即:另外还要考虑塑性内力重分布后应取得的效果-----⑴为了节约钢筋,应考虑弯矩包络图的面积为最小,⑵为了便于浇筑混凝土应减少支座上部承受负弯矩的钢筋,⑶为了便于钢筋布置,应力求使各跨跨中最大正弯矩与支座弯矩值接近相等。
按弯矩调幅法进行结构承载能力极限状态计算时,应遵循的下述规定:1)钢材宜采用I、II级和III级热轧钢筋,也可采用I级和Ⅱ级冷拉钢筋;宜采用强度等级为C20~C45的混凝土;2)截面的弯矩调幅系数δ不宜超过25%;3)调幅截面的相对受压区高度ϕ不应超过0.35。
当采用I级和Ⅱ级冷拉钢筋时,ϕ值不宜大于0. 3,调幅不宜超过15%;4)连续梁、单向连续板各跨两支座弯矩的平均值加跨度中点弯矩,不得小于该跨简支梁的弯矩。
任意计算截面的弯矩不宜小于简支弯矩的1/3;5)考虑内力重分布后,结构构件必须有足够的抗剪能力。
并且应注意,经过弯矩调幅以后,结构在正常使用极限状态下不应出现塑性铰。
截面弯矩的调幅用下式表示δ——弯矩调幅系数;Me——按弹性方法计算得的弯矩;Ma——调幅后的弯矩。
例有一承受均布荷载的五跨等跨连续梁,如图1-20,两端搁置在墙上,其活荷载与恒荷载之比q/g=3,用调幅法确定各跨的跨中和支座截面的弯矩设计值。
图1-20 五跨连续梁解:(1)折算荷载3=gq,()()qgqgg+=+=25.041,()()qgqgq+=+=75.043)1011(/)(--=eaeMMMδ)1111()(211-≥++'MMMMBA折算恒荷载 ()q g q g g +=+='4375.04 折算活荷载()q g q q +=='5625.043 (2)支座B 弯矩连续梁按弹性理论计算,当支座B 产生最大负弯矩时,活荷载应布置在1,2,4跨,故:()()()22222m ax 1129.05625.0119.04375.0105.0119.0105.0l q g l q g l q g l q l g M B +-=+⨯-+⨯-='-'-=考虑调幅20%,即β=0.2 ,则: ()()[]()22m ax m ax 3.09.01129.08.08.01l q g l q g M M M B B B +-=+-==-=β实际取()()220909.0111l q g l q g M B +-=+-= ∴111-=MB α (3)边跨跨中弯矩 对应于()2111l q g M B +-=,边支座A 的反力为()l q g +409.0,边跨跨内最大弯矩在离A 支座l x 409.0=处,其值为:()()210836.0409.0409.021l q g l l q g M +=⨯+⨯=按弹性理论计算,当活荷载布置在1,3,5跨时,边跨跨内出现最大弯矩,则:()()21222m ax 10836.00904.01.0078.0l q g M l q g l q l g M +=>+='+'=说明按()2m ax 10904.0l q g M +=计算是安全的。
内力组合及内力调整

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
1)、在恒载和活载作用下,跨间max M 可以近似取跨中的M 代替,在重力荷载代表值和水平地震作用下,跨内最大弯矩max M 采用解析法计算:先确定跨内最大弯矩max M 的位置,再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时,按公式7-1计算。
计算方式见图7-1、7-2括号内数值,字母C 、D 仅代表公式推导,不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = (7-1) 式中:q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值;M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值;l ——梁的计算跨度。
2)、在重力荷载代表值和地震作用组合时,左震时取梁的隔离体受力图,见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中:GC M 、GD M ——重力荷载作用下梁端的弯矩; EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力:()C 1=2GD GC EC ED ql R M M M M l--++;由0M ddx=,可求得跨间max M 的位置为:1C /X R q = ; 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为: 弯矩最大点位置距左端的距离为1X ,1=/E X R q ;()101X ≤≤; 最大组合弯矩值:2max 1/2GE EF M qX M M =-+;当10X <或11X >时,表示最大弯矩发生在支座处,取1=0X 或1=X l ,最大弯矩组合设计值的计算式为:2max C 11/2GE EF M R X qX M M =--+; 右震作用时,上式中的GE M 、EF M 应该反号。
框架梁调幅,规范

框架梁调幅,规范篇一:高规-听课笔记《高层建筑混凝土结构技术规程》JGJ3-2002培训班(主讲人:副主编黄小坤)听课笔记(规程及条文说明中没有的部分)1.本规程较原规程已适当提高安全度5~10%(其余新规范、新规程亦然)2.第3.2.3条中的D类地面粗糙度慎用!3.第3.2.7条中的相互干扰增大系数约为1.1~1.3。
4.根据第3.3.1条第2款规定,6度高层也要算地震作用。
5.第3.3.2条规定会使截面较原规程增加。
6.7度建筑要用100年,计算时大约可取7.5度。
7.第3.3.13条规定为剪重比的限值。
8.第3.3.16条(强制性条文)只是原则规定结构自重周期应考虑非承重墙体的刚度影响应予折减,但具体数值在第3.3.17条并不强制。
对于剪力墙结构,开间、进深大时才折减,短肢墙也可折减。
9.根据第4.1.3条规定,单跨框架不允许做。
10.注意楼盖的重要性(各章均有体现)。
11.建设部部长令中已没有关于最大高宽比的超限审查。
12.第4.3.6条规定的楼板在任一方向最小净宽度不宜小于5m已近危险。
13.第4.4节中违反其中一条,即为不规则结构,要专家审查。
14.第4.4.2条规定主要是限制下部刚度比上部小。
15.第4.4.6条限制外挑主要是考虑竖向地震的影响,实际上7度时竖向地震的影响已是比较大了。
16.第4.5.2条限制砼不高于C40,主要是考虑高于C40时易开裂。
17.第4.6.3条注意取层间最大位移,而不是质心位移。
18.第4.6.3条第2款规定1/500,主要是考虑下层位移引起的上层无害位移。
19.表4.8.2中筒体应分为框架-核心筒和筒中筒。
20.对特一级的要求大多在第4.9.2条规定了,另外在第11章中对特一级框支梁有规定,还有在第10.2.14条也有特一级的规定。
21.第5.1.4条中的薄壁杆系是指墙高/厚大于5。
22.第5.1.9条施工过程的模拟理论上应分析n个结构(从1层到n层),但现有计算软件值计算一个n层的结构,荷载分层添加。
塑性铰内力重分布弯矩调幅等概念

(5)应在可能产生塑性铰的区段适当增加箍筋数量 受剪配箍率:(防斜拉)
(6)必须满足正常使用阶段变形及裂缝宽度的要求,在使用阶段不应
出现塑性铰
混凝土结构设计
▪ 弯矩调幅法
第10章
《钢筋混凝土连续梁和 框架考虑内力重分布设 计规程》(CECS51:93) 规定:调幅系数一般为 0.2,且不宜超过0.25。
3. 掌握整体式(现浇)双向板结构的内力按弹性及按塑性
理论的设计方法;掌握其配筋构造要求。
4. 熟悉梁式楼梯和板式楼梯的受力特点、内力计算和配筋 构造要求。
混凝土结构设计
第10章
§10.1 概述 §10.2 整体式(现浇)单向板梁板结构设计 §10.3 整体式(现浇)双向板梁板结构设计 §10.4 整体式楼梯和雨篷设计
混凝土结构设计
▪ 内力计算及组合
内力按结构力学方法计 算。2~5跨等跨梁板内 力见教材附录13。内力 要根据荷载最不利布置 组合计算,画出内力包 络图。
恒载一次布置,活 载分跨布置再组合
第10章
混凝土结构设计
第10章
▪ 配筋计算
配筋计算方法按《混凝土结构设计原理》(第二 版)有关章节。 配筋时用的弯矩和剪力值按如下方法确定:
主页 目录 上一章 下一章 帮助
混凝土结构设计
▪ 计算跨度
第10章
对单跨梁和板
l0lnalnh 两端搁置在砖墙上的板
l0 ln b
两端与梁整体连接的板
l0lna1.05ln 单跨梁
混凝土结构设计
▪ 计算跨度
第10章
对多跨连续梁板
l0
ln
a 2
b,且 2
边 跨
l0
ln
h 2
11.2.5 连续梁、板按调幅法的内力计

立板带计算出的弯矩乘以小于 1的修正系数来考虑扭矩的影 响
14
l 2、四边支承板的主要试验结果
• 板底:跨中出现裂缝—— 相对角线方向延伸——板 底裂缝处钢筋屈服
• 板面:四角垂直对角线方向出现裂缝— —环状裂缝
15
11.3.2 双向板按弹性理论的内力计算
11.2.5 连续梁、板按调幅法的内力计 算
• 楼板设计时,板和次梁采用塑性法,主梁采用弹性法: 1.板和次梁的跨度计算见表11-5;
1
11.2.5 连续梁、板按调幅法的内力计 算
• 楼板设计时,板和次梁采用塑性法,主梁采用弹性法: 2.板和次梁的弯矩计算见表11-2;Mm(gq)l
2 0
M m (G Q )l0
(1)跨中最大正弯矩:活荷载按棋盘式布置。
(2)支座最大负弯矩:满布活荷载。相邻板支座负弯矩不等时,取绝对值较 大值。
17
ü四边固端 ü四边简支
18
4
l1、用调幅法计算不等跨连续梁、板 (1)不等跨连续梁:(前面讲过)
弹性法求出各截面最大弯矩——支座弯矩调幅——验算跨 中弯矩——静力平衡求剪力
Ø 1(1.22).不6 等单跨向连板续肋板梁:选楼取盖跨的中截弯面矩设——计静与力构平造衡求支座
l 1、弯单矩向板的(截剪面力设计?与)构造
(1)设计要点 a、板厚:(P49)考虑因素:跨度、荷载、刚度、施工、经济
8
Ø11.2.6 单向板肋梁楼盖的截面设计与构造
l1、单向板的截面设计与构造
②防裂构造钢筋:板面 ③与主梁垂直的附加负筋
④与承重墙体垂直的附加负筋 ⑤板角附加短钢筋
9
• 2、次梁 • (1)设计要点 • a、梁跨 :一般4~6m,梁高h=l/18~l/12跨度,梁宽b=h/3~h/2 • b、纵筋配筋率:0.6%~1.5% • c、正弯矩区段按T形截面计算;负弯矩区段按矩形截面计算 • d、塑性调幅时ξ ≤ 0.35 ,并增加箍筋面积20% • (2)配筋构造
(整理)弯矩调幅法

调幅法弯矩调幅法简称调幅法,它是在弹性弯矩的基础上,根据需要适当调整某些截面的弯矩值。
通常是对那些弯矩绝对值较大的截面弯矩进行调整,然后,按调整后的内力进行截面设计和配筋构造,是一种实用的设计方法。
弯矩调幅法的一个基本原则是,在确定调幅后的跨内弯矩时,应满足静力平衡条件,即连续梁任一跨调幅后的两端支座弯矩MA、MB(绝对值)的平均值,加上调整后的跨度中点的弯矩M1’ 之和,应不小于该跨按简支梁计算的跨度中点弯矩Mo,即:另外还要考虑塑性内力重分布后应取得的效果-----⑴为了节约钢筋,应考虑弯矩包络图的面积为最小,⑵为了便于浇筑混凝土应减少支座上部承受负弯矩的钢筋,⑶为了便于钢筋布置,应力求使各跨跨中最大正弯矩与支座弯矩值接近相等。
按弯矩调幅法进行结构承载能力极限状态计算时,应遵循的下述规定:1)钢材宜采用I、II级和III级热轧钢筋,也可采用I级和Ⅱ级冷拉钢筋;宜采用强度等级为C20~C45的混凝土;2)截面的弯矩调幅系数δ不宜超过25%;3)调幅截面的相对受压区高度ϕ不应超过0.35。
当采用I级和Ⅱ级冷拉钢筋时,ϕ值不宜大于0. 3,调幅不宜超过15%;4)连续梁、单向连续板各跨两支座弯矩的平均值加跨度中点弯矩,不得小于该跨简支梁的弯矩。
任意计算截面的弯矩不宜小于简支弯矩的1/3;5)考虑内力重分布后,结构构件必须有足够的抗剪能力。
并且应注意,经过弯矩调幅以后,结构在正常使用极限状态下不应出现塑性铰。
截面弯矩的调幅用下式表示δ——弯矩调幅系数;Me——按弹性方法计算得的弯矩;Ma——调幅后的弯矩。
例有一承受均布荷载的五跨等跨连续梁,如图1-20,两端搁置在墙上,其活荷载与恒荷载之比q/g=3,用调幅法确定各跨的跨中和支座截面的弯矩设计值。
图1-20 五跨连续梁解:(1)折算荷载3=gq,()()qgqgg+=+=25.041,()()qgqgq+=+=75.043)1011(/)(--=eaeMMMδ)1111()(211-≥++'MMMMBA折算恒荷载 ()q g q g g +=+='4375.04 折算活荷载()q g q q +=='5625.043 (2)支座B 弯矩连续梁按弹性理论计算,当支座B 产生最大负弯矩时,活荷载应布置在1,2,4跨,故:()()()22222m ax 1129.05625.0119.04375.0105.0119.0105.0l q g l q g l q g l q l g M B +-=+⨯-+⨯-='-'-=考虑调幅20%,即β=0.2 ,则: ()()[]()22m ax m ax 3.09.01129.08.08.01l q g l q g M M M B B B +-=+-==-=β实际取()()220909.0111l q g l q g M B +-=+-= ∴111-=MB α (3)边跨跨中弯矩 对应于()2111l q g M B +-=,边支座A 的反力为()l q g +409.0,边跨跨内最大弯矩在离A 支座l x 409.0=处,其值为:()()210836.0409.0409.021l q g l l q g M +=⨯+⨯=按弹性理论计算,当活荷载布置在1,3,5跨时,边跨跨内出现最大弯矩,则:()()21222m ax 10836.00904.01.0078.0l q g M l q g l q l g M +=>+='+'=说明按()2m ax 10904.0l q g M +=计算是安全的。
恒荷载内力计算

四恒荷载内力计算(一)恒荷载计算1.屋面框架梁线荷载标准值20厚水泥混凝土找平0.02×20=0.46kN/m240~120厚(1%找坡)膨胀珍珠岩(0.08+0.16)÷2×7=0.546kN/m2四层作法防水层0.36kN/m2100mm厚钢筋混凝土楼板0.1×25=2.56kN/m220mm厚石灰砂浆抹底0.02×17=0.34kN/m2屋面恒荷载 4.08 kN/m2边框架梁自重0.3×0.8×25=6kN/m边框架梁粉刷2×(0.8-0.1)×0.02×17=0.48kN/m中框架梁自重0.3×0.6×25=4.5kN/m2边框架梁粉刷2×(0.6-0.1)×0.03×17=0.34kN/m则作用于屋面框架梁上线荷载标准值为:g5AB1=6.48kN/mg5BC1=4.85kN/mg5AB2=4.08×3.9=15.91kN/mg5BC2=4.08×3=12.24kN/m2.楼面框架梁线荷载标准值20mm厚水泥砂浆找平0.02×20=0.46kN/m2100mm厚钢筋混凝土楼板0.1×25=2.5kN/m220mm厚石灰砂浆抹底0.02×17=0.34kN/m2水磨石面层0.65 kN/m2楼面恒荷载 3.89 kN/m2边框架梁自重及粉刷 6.48kN/m中框架梁自重及粉刷 4.85kN/m边跨填充墙自重0.24×3.6×18=15.55kN/m填充墙粉刷2×0.02×2×17=2.45kN/m则作用于楼面框架梁上线荷载标准值为:g AB1=6.48+15.55+2.45=24.48kN/mg BC1=4.85kN/mg AB2=3.89×3.9=15.17kN/mg BC2=3.89×3=11.67kN/m3.屋面框架节点集中荷载标准值纵向框架梁自重0.3×0.8×7.8×25=46.8kN纵向框架梁粉刷2×(0.8-0.1)×0.02×7.8×17=3.71kN纵向框架梁传来的屋面恒荷载2×(3.9/2)2×4.08=31.02kN次梁自重及粉刷0.6×0.2×25×7.2/2+2×0.02×(0.6-0.1)×7.2/2=10.87kN次梁传来的屋面恒荷载(1-2×0.272+0.273)×4.08×3.9×7.2/2=50.06kN1m高女儿墙自重及粉刷1×7.8×0.24×18+2×1×7.8×0.02×17=39kN则顶层边节点集中荷载为:G5A=181.46kN纵向框架梁自重及粉刷46.8+3.71=50.51kN纵向框架梁传来的屋面恒荷载31.02+(1-2×0.192+0.193)×4.08×7.8×3/2=75.64kN 次梁自重、粉刷及传来的屋面恒荷载10.87+50.06=60.93kN则顶层中节点集中荷载为:G5B=187.08kN4.楼面框架节点集中荷载标准值纵向框架梁自重及粉刷51.51kN纵向框架梁传来的楼面恒荷载2×(3.9/2)2×3.89=29.44kN次梁自重及粉刷10.87kN次梁传来的楼面恒荷载(1-2×0.272+0.273)×3.89×3.9×7.2/2=47.73kN钢窗自重2×2.3×1.8×0.4=3.31kN墙体自重(3.6×7.8-2×2.3×1.8)×0.24×18=85.54kN墙面粉刷2×(3.6×7.8-2×2.3×1.8)×0.02×1.7=13.46kN框架柱自重0.602×3.6×25=32.4kN柱面粉刷4×0.6×0.02×17=0.82kN中间层边柱节点集中荷载为:G A=274.08kN纵向框架梁自重及粉刷50.51kN纵向框架梁传来的楼面恒荷载29.44+(1-2×0.192+0.1923)×3.89×7.8×3/2=71.98kN 次梁粉刷、自重及传来的楼面恒荷载10.87+47.73=58.6kN木门自重2×1.0×2.6×0.2=1.04Kn墙体自重(3.6×7.8-2×1.0×2.6)×0.24×18=98.84kN墙面粉刷2×0.02×()×17=15.56kN框架主自重及粉刷32.4+0.82=33.22kN中间层中柱节点集中荷载为:G B=329.75kN(二)恒荷载作用下内力计算1.计算简图计算简图2.荷载等效27.02.729.31=⨯=α 顶层边跨 m /38kN .2048.691.15)27.027.021('g 325=+⨯+⨯-=边顶层中跨 m /12.5kN 4.8512.2485'g 5=+⨯=中中间层边跨 m /37.74kN 48.2417.15)27.027.021('g 32=+⨯+⨯-=边中间层中跨 m /11.97kN 4.6867.1185'g =+⨯=中荷载等效后的计算简图如下GD3.固端弯矩计算顶层边跨 m 88.04kN 2.738.20121M 25AB ⋅=⨯⨯=顶层中跨 m 38kN .95.15.1231M 25BC ⋅=⨯⨯=中间层边跨 m 04kN .1632.774.37121M 2AB ⋅=⨯⨯=中间层中跨 m 98kN .85.197.1131M 25BC ⋅=⨯⨯=4.分层计算弯矩(取半结构计算) 1)顶层分配系数计算如下569.040.39.0456.3456.312=⨯⨯+⨯⨯=μ431.0569.0111214=-=-=μμ442.023.640.39.0456.3456.321=⨯+⨯⨯+⨯⨯=μ223.023.640.39.0456.326.323=⨯+⨯⨯+⨯⨯=μ335.0223.0442.011232125=--=--=μμμ内力计算过程如下(单位:kN ∙m )1-4 1-2 2-1 2-5 2-3 0.431 0.569 0.442 0.335 0.223 -88.04 88.04 -9.38 37.95 50.09 → 25.05 -22.92 ← -45.84 -34.74 -23.13 9.88 13.04 → 6.52 -1.44 ← -2.88 -2.19 -1.45 0.62 0.82 → 0.41 -0.18 -0.14 -0.09 48.45 -48.4571.12-37.07-34.05M 图见下页(单位:kN ∙m )2)中间层分配系数计算如下301.056.3420.39.040.39.043631=⨯+⨯⨯⨯⨯⨯==μμ398.0301.0301.011363134=--=--=μμμ251.03.6256.3420.39.040.39.044742=⨯+⨯+⨯⨯⨯⨯⨯==μμ331.03.6256.3420.39.0456.3443=⨯+⨯+⨯⨯⨯⨯=μ167.0331.0251.0251.01143474234=---=---=μμμμ内力计算过程如下(单位:kN ∙m )3-6 3-1 3-4 4-3 4-2 4-7 4-5 0.301 0.301 0.398 0.331 0.251 0.251 0.167 -163.04 163.04 -8.98 49.08 49.08 64.88 → 32.44 -30.87 ← -61.73 -46.81 -46.81 -31.15 9.29 9.29 12.29 → 6.15 -1.02 ← -2.04 -1.54 -1.54 -1.03 0.31 0.31 0.40 → 0.20 -0.07 -0.05 -0.05 -0.03 58.68 58.68-117.36137.99-48.4-48.4-41.19M 图见下页(单位:kN ∙m )37.0734.0571.1212.3616.1548.4548.45(1)(2)(3)(4)(5)3)底层分配系数计算如下307.056.342.8140.39.040.39.0431=⨯+⨯+⨯⨯⨯⨯=μ32.056.342.8140.39.0481.2436=⨯+⨯+⨯⨯⨯=μ373.032.0307.011363134=--=--=μμμ248.03.6256.342.8140.39.040.39.0442=⨯+⨯+⨯+⨯⨯⨯⨯=μ259.03.6256.342.8140.39.0481.2447=⨯+⨯+⨯+⨯⨯⨯=μ328.03.6256.342.8140.39.0456.3443=⨯+⨯+⨯+⨯⨯⨯=μ0.165328.0259.0248.01143474234=---=---=μμμμ内力计算过程如下(单位:kN ∙m )3-6 3-1 3-4 4-3 4-2 4-7 4-5 0.32 0.307 0.373 0.328 0.248 0.259 0.165 -163.04 163.04 -8.98 52.17 50.05 60.82 → 30.41 -30.26 ← -60.51 -45.75 -47.78 -30.439.68 9.29 11.29 → 5.65 -0.93 ← -1,85 -1.40 -1.47 -0.93 0.30 0.29 0.34 → 0.17 -0.06 -0.04 -0.04 -0.03 62.1559.63121.78136.85-47.19-49.29-40.3748.4117.3619.5616.1348.4137.9941.1916.1319.5658.6858.68(1)(2)(3)(4)(5)(6)(7)M 图如下(单位:kN ∙m )5.不平衡弯矩分配计算过程见如下(单位:kN ∙m ),方框内为原不平衡弯矩7.13不平衡弯矩调整之后即可得出恒荷载作用下框架弯矩图,见第29页(单位:kN ∙m ,括号内为调幅后的弯矩值)15.7340.37136.8549.2947.1924.6531.0859.6362.15121.7819.88(1)(2)(3)(4)(5)(6)(7)6.跨中弯矩计算m 94kN .62225.7858.592.728.2081M 25AB ⋅=+-⨯⨯=m 81kN .1545.300.324.121210.385.481M 225BC ⋅-=-⨯⨯+⨯⨯=m 104.91kN 139.65-244.56272.14757.1312.737.7481M 24AB ⋅==+-⨯⨯=m 41kN .2243.3602.1436.430.311.671210.368.481M 224BC ⋅-=-=-⨯⨯+⨯⨯=m 77kN .103267.14892.13256.244M 3AB ⋅=+-=m 79kN .2181.3502.14M 3BC ⋅-=-=m 77kN .1032148.67133.0656.244M 2AB ⋅=+-=m 85kN .2187.3502.14M 2BC ⋅-=-=m 108.95kN 2142.14129.0856.244M 1AB ⋅=+-=m 23.69kN 37.7102.14M 1BC ⋅-=-=7.剪力计算5kN .62130.182159.221)]29.32.7(91.152.748.6[7.225.6858.59V 5AB =⨯+-=⨯-⨯+⨯+-=67.68kN 62.5-18.130V 5BA ==46kN .16)5.124.120.385.4(21V 5BC =⨯+⨯⨯=255.92124.221)]29.32.7(17.152.724.48[7.222.14757.131V 4AB ⨯+-=⨯-⨯+⨯+-=71kN .125=130.19kN 71.1259.255V 4BA =-=77kN .15)5.111.670.368.4(21V V V V 1BC 2BC 3BC 4BC =⨯+⨯⨯==== 125.76kN 255.9217.2148.67-132.92V 3AB =⨯+=130.14kN 76.1259.255V 3BA =-=125.8kN 255.9217.2148.52-133.06V 2AB =⨯+=130.1kN 8.1259.255V 2BA =-=M 图(单位:kN ∙m )126.14kN 255.9217.2142.14-129.08V 1AB =⨯+=129.76kN 126.149.255V 1BA =-=8.轴力计算96kN .2435.6246.181N 5At =+=24.65(109.72)(113.10)(112.98)(111.83)(50.64)(120.82)(126.25)(126.37)(125.56)(66.51)23.69(21.32)21.85(19.67)21.79(19.61)22.41(20.17)(14.23)15.81(32.05)37.71(30.49)35.87(30.44)35.81(30.97)36.43(25.88)30.45(130.74)(124.52)(124.52)(125.89)(75.53)108.95103.77103.77104.9162.9445.1156.1347.857.3856.4359.3256.5356.4353.61142.14148.53148.67142.4778.2531.0873.1955.89129.0866.6966.69133.0666.4666.46132.9764.0867.49131.5759.5859.5818kN .27782.04.3296.243N 5Ab =++= 75kN .64371.12508.27496.243N 4At =++= 97kN .67633.2275.643N 4Ab =+=59kN .104376.12508.274643.75N 3At =++= 81kN .107622.3359.1043N 3Ab =+= 1443.47kN 125.8274.081043.59N 2At =++= 69kN .147622.3347.1443N 2Ab =+=1843.69kN 126.14274.081443.47N 1At =++=56kN .190087.5669.18431702.03.5465.0253.565.0(69.1843N 21Ab =+=⨯⨯⨯⨯+⨯⨯+=271.22kN 16.4667.68187.08N 5Bt =++= 44kN .30422.3322.271N 5Bb =+=93kN .74615.77130.19329.7522.271N 4Bt =+++= 15kN .78022.3393.746N 4Bb =+=1222.59kN 130.14345.52746.93N 3Bt =++= 81kN .125522.3359.1222N 3Bb =+= 21kN .16981.13052.34559.1222N 2Bt =++= 43kN .173122.3321.1698N 2Bb =+=2173.49kN 129.76345.521698.21N 1Bt =++= 36kN .223087.5649.2173N 1Bb =+=框架结构的剪力图和轴力图如下(单位:kN )V NV ,M 图(单位:kN )9.弯矩调幅边跨:端部弯矩值乘以0.85,跨中弯矩值乘以1.2 中跨:端部弯矩值乘以0.85,跨中弯矩值乘以0.9 将调幅后的弯矩值表于框架弯矩图的()内1443.471043.59643.751900.561843.691476.691076.81676.97227.18243.962230.362173.491731.431698.211255.811222.59780.15746.93304.44271.2215.7715.7715.7715.7716.46129.76126.14130.19130.14130.10125.80125.76125.7167.6862.5010.梁端柱边剪力与弯矩V (kN)M (kN∙m)60.19 -65.37 13.55。
2010版混凝土规范关于弯矩调幅解析

考虑调幅20%(不超过允许最大调幅值25%), 则:
M B 0.8M Bmax 0.8 0.1129(g q)l 2 0.09032(g q)l 2
支座B弯矩 ——按查表
表11—1中取MB1( 11边跨内最大弯矩 ——按不利布置
可知,第一跨跨内 弯矩最大值仍应按 M1max计算,为便 于记忆,取,
M1max
1 11
(
g
q)l
2
MBmax
曲线1
曲线2
M1max 0.093(g q)l2
0.195MBmax
例题
已知:
l0 4.5m g 8kN / m
q1 24kN / m q2 q3 18kN / m
0.50
距端第二支座 外侧Bex 内侧Bn
0.60 0.55
0.55
中间支座 外侧Cex 内侧Cin
0.55 0.55
不等跨或不等荷载连续梁:
(1)先按弹性方法求出弯矩包罗图,再调幅, 剪力仍取弹性剪力值;
(2)根据平衡条件求跨中最大弯矩,取与弹性 计算的最大值.
不等跨或不等荷载连续板:
(1)从较大跨度开始,按下式计算跨中弯矩最 大值,
0.195MBmax
边跨内最大弯矩 ——按不利布置
MBmax
按弹性方法,边跨跨 内的最大正弯矩出现 于活荷载布置在一、 三、五跨(兰色曲线), 其值为:
曲线1
曲线2
M1max 0.093(g q)l2
M1max 0.078gl2 0.1ql2 0.093(g q)l2 M1 0.0836(g q)l2 ——按平衡方法
❖ 6.3.6 计算弯起钢筋时,截面剪力设计值可按 下列规定取用(图6.3.2a):
内力组合与塑性调幅

★★★内力组合与xx弯矩调幅一、控制截面1.柱:上、下端截面2.xx:左、中、右截面3.截面配筋设计时,应取梁端内力,而不是计算简图中的轴线处内力!P67图4-18: M’=M-V*b/2V’=V-(g+p)*b/2g、p:xxxx分布的恒载和活载。
当计算水平荷载或竖向集中荷载产生的内力时,则V’=V。
二、荷载效应组合——按第三章第二节要求(七种可能,实际多余七种计算)P36-39三、最不利内力组合1.xx截面:+Mmax—配置底筋-Mmax—配置支座面筋Vmax—配置箍筋2.跨中截面:+Mmax—配置底筋3.柱端截面:(1)|M|max及相应的N,V(2) Nmax及相应的M,V(3) Vmax及相应的M,N四、竖向最不利位置按P70第四种方法:不考虑活荷载的最不利布置,按均布处理,对梁跨中弯矩M乘扩大系数1.1-1.2***JGJ3-2010第5.1.8条/p455.1.8高层建筑结构内力计算中,当楼面活荷载大于4kN/m2时,应考虑楼面活荷载不利布置引起的结构内力的增大;当整体计算中未考虑楼面活荷载不利布置时,应适当增大楼面梁的计算弯矩。
对应条文说明:5.1.8目前国内钢筋混凝土结构高层建筑由恒载和活载引起的单位面积重力,框架与框架-剪力墙结构约为12kN/m2~14kN/m2,剪力墙和筒体结构约为13kN/m2~16kN/m2,而其中活荷载部分约为2kN/m2~3kN/m2,只占全部重力的15%~20%,活载不利分布的影响较小。
另一方面,高层建筑结构层数很多,每层的房间也很多,活载在各层间的分布情况极其繁多,难以一一计算。
如果活荷载较大,其不利分布对梁弯矩的影响会比较明显,计算时应予考虑。
除进行活荷载不利分布的详细计算分析外,也可将未考虑活荷载不利分布计算的框架梁弯矩乘以放大系数予以近似考虑,该放大系数通常可取为1.1~1.3,活载大时可选用较大数值。
近似考虑活荷载不利分布影响时,梁正、负弯矩应同时予以放大。
单向板与双向板

单向板和双向板的一些区别当梁突出于板的上表面,为反梁,在板的介绍中有这样的介绍,主要用楼面,屋面防水.四边支承板长短边长度比大于等于3.0时,板可按沿短边方向受力的单向板计算;此时,沿长边方向配置规范第10.1.8 条规定的分布钢筋已经足够。
当长短边长度比在2~3 之间时,板虽仍可按沿短边方向受力的单向板计算,但沿长边方向按分布钢筋配筋尚不足以承担该方向弯矩,应适度增大配筋量。
当长短边长度比小于等于 2 时,应按双向板计算和配筋。
第12章楼盖§12.1 概述一.单向板与双向板单向板:主要在一个方向弯曲;双向板:两个方向弯曲.如图12-1:某四边支撑板,受均布荷载作用.有关系: (a)沿两个方向划分条带后,板中间挠度应相等,即有关系:(b) 化简上式得: ,即(c)将(c)代入(a)式可得: (d);同理由(a)式可得:(e)讨论:当时,由(d)和(e)式可求得:上述关系说明,此时荷载主要沿短边方向传递到长边上;沿长边方向传递到短边上的荷载可忽略不计.基于以上原理,规范规定:对于四边支撑的板,当长边与短边之比大于或等于2时,按单向板计算;其他情况需要讨论确定.二.楼盖的结构类型1.按结构类型:肋梁楼盖图12-2(1)单向板楼盖(2)双向板楼盖(3)井式楼盖(4)密肋楼盖无梁楼盖(板柱结构)2.按预应力情况:(1)RC楼盖(2)PC楼盖3.按施工方法:(1)现浇楼盖(2)装配式楼盖(3)装配整体式§12.2现浇单向板肋梁楼盖设计步骤:平面布置,计算简图,内力分析(计算),配筋及构造和绘制施工图.一.结构平面布置(见附图)原则:计算方便(尽量对称,等跨,等截面和同材料),符合模数1. 柱网尺寸或承重墙间距:(1)考虑建筑使用要求(2)柱(墙)间距=梁的跨度.主梁:(5~8)米;次梁:(4~6)米2. 主梁的间距=次梁的跨度3. 次梁的间距=板的跨度4. 主梁的布置方向:类型:(1)主梁横向布置12-3(a)-横向刚度大,可布置较大门窗;(2)主梁纵向布置12-3(b)-横向刚度小,但室内净高大;(3)无主梁布置12-3(c)-适合砌体结构,中间可设走道.5. 截面尺寸:(1) 板: 刚度要求:h l/40(连续);h l/35(简支);h l/12(悬臂).使用要求:民用h=70mm(最小);工业h=80mm(最小).(2)梁:次梁:h/l=1/18~1/12;主梁:h/l=1/14~1/8;h/b=2~3二.计算简图墙体基础1.计算模型及简化假定主梁一般传力路径(见附图):板次梁柱基础墙体基础计算模型(简图):板:以次梁为中间支座和以墙体为边支座的多跨连续梁(梁宽为1 米);次梁:以主梁为中间支座和以墙体为边支座的多跨连续梁;主梁:以柱为中间支座和以墙体为边支座的多跨连续梁;小结:单向板楼盖结构可简化为三种不同的多跨连续梁.简化假定:(1)梁在支座处可以自由转动,支座无竖向位移;(2)不考虑薄膜效应(即假定为薄板);(3)按简支构件计算支座竖向反力;(4)实际跨数小于和等于五跨时,按实际跨数计算;实际跨数大于五跨且跨差小于10%时,按五跨计算.上述假定的物理意义:对于(1):忽略了次梁对板,主梁对次梁和柱对主梁的扭转刚见图12-4 度;忽略了次梁,主梁和柱的相对竖向变形;由此带来的误差通过"折算荷载"加以消除.对于(2):由于支座约束作用将在板内产生轴向压力,称为薄膜见图12-5 力或薄膜效应,它将减少竖向荷载产生的弯矩,这种有利作用在计算内力时忽略,但在配筋计算时通过折减计算弯矩加以调整.对于(3):主要为计算简单.对于(4):方便查表计算,可由结构力学证明.2.计算单元和从属面积(1)计算单元:板—取1米宽板带;(见附图) 次梁和主梁—取具有代表性的一根梁.(2)从属面积:板—取1米宽板带的矩形计算均布荷载;(见附图) 次梁和主梁—取相应的矩形计算均布和集中荷载.3.计算跨度(见附图)次梁的间距就是板的跨长;主梁的间距就是次梁的跨长;跨长不一定等于计算跨度;计算跨度是指用于内力计算的长度.计算跨度的取值原则:(1)中间跨取支承中心线之间的距离;(2)边跨与支承情况有关,参见图12-7.4.荷载取值(1)楼盖荷载类型:恒载(自重)和活载(人群,设备)(2)荷载分项系数恒载一般取1.2;活载取1.4;特殊情况下查阅规范.(3)折算荷载A.折算意义:消除由于前述假定(1)所带来的计算误差;B.折算原则:保持总的荷载大小不变,增大恒载,减小活载;板或梁搁置在砖墙或钢结构上时不折算;C.折算方法:见书上P.7公式(12-1)和(12-2)及其符号说明.注意:主梁不作折减三.连续梁,板按弹性理论的内力计算(方法)1.活荷载的最不利布置(1)原则:A.活荷载按满布一跨考虑,即不考虑某一跨中作用有部分荷载的情况;B.在此布置下,相应内力最大(绝对值).(2)活荷载最不利布置规律由结构力学可证明(参见图12-8):A.求某跨跨内最大正弯矩时,应在该跨布置活荷载,然后隔跨布置;B.求某跨跨内最大负弯矩时,应在该跨不布置活荷载,而在该跨左右邻跨布置,然后隔跨布置;C.求某支座最大负弯矩或该支座左右截面最大剪力时,应在该支座左右两跨布置活荷载,然后隔跨布置.2.内力计算(1)对于相应的荷载及其布置,当等跨或跨差小于等于10%时,可直接查表用相应公式计算(如查附录7,P.519);(2)公式(12-3)和(12-4)中的荷载应为折算荷载,其他相同.3.内力包络图(1)意义:确定非控制截面的内力,以便布置这些截面的钢筋.(2)内力包络图的作法:见附图,以五跨连续梁为例加以说明.步骤1:由于对称性,取梁的一半作图;步骤2:分别作组合A~D情况下的弯矩图;步骤3:取上述弯矩图的外包线即为所求弯矩包络图.(3)剪力包络图的作法同理.4.支座弯矩和剪力设计值(计算值)(1)问题的提出:由于将实际结构简化为直线,故所求得的支座弯矩和剪力是支座中心线处的数值,实际最危险的截面应该在支座边缘,所以应将所求得的数值加以调整,见附图.(2)具体作法:P.9公式(12-5)~(12-7)及其说明.讨论:关于弹性法的缺陷四.超静定结构塑性内力重分布的概念1.应力重分布与内力重分布(1)应力重分布:在弹性阶段,钢筋与混凝土承担的应力是按各自的初始弹性模量分配的,例如,轴心受压构件某截面的应变为,则钢筋承担的应力为,混凝土承担的应为;在弹塑性阶段钢筋与混凝土承担的应力是按各自的变形模量分配的,例如,钢筋承担的应力仍然为,混凝土承担的应力为: .由于,混凝土分配到的应力发生了变化,这种现象称为"应力重分布".应力重分布在静定结构和超静定结构中都可能发生.(2)内力重分布:超静定结构存在多余联系,其内力是按刚度分配的.在多余联系处,由于应力较大,材料进入弹塑性,产生塑性铰,改变了结构的刚度,内力不再按原有刚度分配,这种现象称为"内力重分布"."内力重分布" 只会在超静定结构中发生且内力不符合结构力学的规律.2.混凝土受弯构件的塑性铰(1)塑性铰的概念:适筋截面在钢筋屈服到混凝土压碎过程中形成的铰称为"塑性铰".参见P.11,图12-10.(2)塑性铰的特点:通过与理想铰比较可看出如下几点塑性铰理想铰A:能承受(基本不变的)弯矩不能承受弯矩B:具有一定长度集中于一点C:只能沿弯矩方向转动任意转动(3)塑性铰的分类钢筋铰—受拉钢筋先屈服,适筋截面;(转动大,延性好);混凝土铰—混凝土先压碎,超筋截面;(转动小,脆性).(4)塑性铰对结构的影响A:使超静定结构超静定次数减少,产生内力重分布;B:塑性铰出现时,只要结构不产生机动,仍可承受荷载;或者说,当出现足够的塑性铰,使结构产生机动时,结构才失效.3.内力重分布的过程P.12的两跨连续梁的情况自学.为进一步了解,现补充两端固定梁说明.由于MA>MC,所以将会在A或B处先产生塑性饺,使原有两端固定梁变成两端简支梁. 假定当g作用时,恰好支座出现塑性铰,此时支座和跨中弯矩分别为:A BL此时若在梁上再作用q,此时支座弯矩不增加,跨中弯矩增加为:4.影响内力重分布的因素充分的内力重分布:出现足够的塑性铰使结构成为机动.主要影响因素(1)塑性铰的转动能力:取决于纵向钢筋的配筋率,钢筋的品种和混凝土的极限压应变值;(2)斜截面承载力:在出现足够的塑性铰之前不能产生斜截面破坏,否则不能形成充分的内力重分布;(3)正常使用条件:控制内力重分布的幅度,一般要求在正常使用条件下不应出现塑性铰,以防止出现裂缝过宽或挠度过大.5.考虑内力重分布的意义和适用范围问题:目前的内力计算方法与配筋计算方法不相协调解决办法(之一):考虑塑性内力重分布考虑结构内力重分布的计算方法具有如下优点:(1)能正确估计结构的裂缝和变形;(2)能合理调整钢筋用量,方便施工;(3)可人为控制弯矩分布,简化结构计算;(4)充分发挥材料的作用,提高经济性.下列情况不宜考虑塑性内力重分布的方法:(1)裂缝宽度和挠度要求较严格的构件;(2)直接承受动荷载和重复荷载的构件;(3)预应力和二次受力构件;(4)重要的或可靠性要求较高的构件.五.连续梁,板按调幅法的内力计算1.调幅法的概念和原则(1)调幅法的概念:对按结构力学方法计算得出的内力(人为)进行调整,然后按调整后的内力进行配筋计算,是一种实用计算方法,为大多数国家采用.(2)弯矩调幅法的做法:引入弯矩调幅系数,其计算公式为为结构力学计算的弯矩; 为调幅后的弯矩;因为,所以有关系: ,即有结论:调幅弯矩值小于等于结构力学计算值.例P.15一两跨连梁(图12-14)(3)调幅法的原则A.应验算调幅后的内力(即平衡)和正常使用状态,并有相应构造措施;B.不宜采用高强材料,且相对受压区高度应满足下列条件:(4)调幅法的计算步骤A.用结构力学方法计算荷载最不利布置下若干控制截面(通常为支座截面)的弯矩最大值;B.采用调幅系数(不超过0.2)降低该弯矩值,采用公式(12-11);C.跨中弯矩值取结力计算值和(12-12)式计算值的较大者;D.调整后的各弯矩值应大于等于简支梁跨中弯矩的1/3;E.剪力设计值按荷载最不利布置和调整后的支座弯矩由静力平衡条件确定.2.用调幅法计算等跨连续梁,板(1)等跨连续梁计算条件:各跨均布荷载相等,集中荷载的大小和间距相等.计算方法:查表并用下式计算A.弯矩:均布荷载时:集中荷载时:B.剪力:均布荷载时: ;集中荷载时:上述公式中各符号的物理意义见P.16-17的说明.为方便记忆,将表12-1中各系数的位置表示在附图中.(2)等跨连续板表12-1中系数的推导,见P.18(自学)3.用调幅法计算不等跨连续梁,板采用前述原则和步骤进行,但不能直接使用上述表格,各内力的调幅值应根据实际情况计算. 例(12-1)自学.六.单向板肋梁楼盖的截面设计与构造1.单向板的截面设计与构造(1)设计要点:A.板厚的要求;B.区分端区格单向板和中间区格单向板,前者的内支座弯矩和中间跨的跨中弯矩可折减20%(解释P.21及图12-24或附图).C.板一般不进行抗剪计算,因混凝土的能力足够且板上仅考虑均布荷载;D.一般采用考虑塑性内力重分布的方法计算.(2)配筋构造1)受力筋:与板的短边平行,直径在6到12毫米之间,直径不一多于两种;布置形式有弯起式和分离式,见图12-18;满足一定条件时(等跨,等厚度,活载与恒载之比小于3等),可直接按该图进行钢筋的弯起或截断,否则应作包络图.2)板中构造钢筋:A.分布筋,平行于长跨,布置于板底部,受力筋之上,如下图: 受力筋分布筋B.与主梁垂直的附加负筋:如下图:C.与墙体垂直的附加负筋:见图12-20;D.板角附加短钢筋:见图12-20.2.次梁(1)设计要点1)可采用考虑塑性内力重分布的方法计算;2)配筋时,支座按矩形,跨中按T形截面计算;3)当考虑塑性内力重分布时,为防止过早出现斜截面破坏,可将计算得到的箍筋用量提高20%.(2)配筋构造当等跨,等截面和活载与恒载之比小于等于3时,纵筋的弯起和截断可按图12-21布置,否则按包络图布置.3.主梁(1)设计要点1)内力计算时,一般不考虑塑性内力重分布;2)配筋计算时,支座按矩形,跨中按T形截面计算.(2)构造特点1)主梁与次梁相交处上部钢筋布置按下图:2)对于主梁与次梁相交处的主梁上,由于间接加载,为防止主梁腹部产生局部破坏,应设置附加横向钢筋,如下图:附加横向钢筋具体计算方法和布置范围P.26,一般情况下优先考虑箍筋加密以方便施工.介绍例题P.27.§12.3 双向板肋梁楼盖一.双向板的受力特点和主要试验结果1.四边支承板弹性工作阶段的受力特点(见图12-33和12-34)(1)理论依据:弹性力学薄板理论;(2)主要结论:相邻板带之间存在剪力,构成扭矩;主弯矩作用下板底部将产生45度方向的裂缝.2.四边支承板的主要试验结果(见图12-35)特点:板底部裂缝沿45度方向;板顶裂缝沿支承边发展呈椭圆形.二.双向板按弹性理论的内力计算对于非规则的双向板,一般按薄板理论直接计算内力;对于规则的双向板,根据薄板理论制成表格后,查表计算.现加以讨论.1.单跨(单区格)双向板计算公式:几点说明(强调):(1)上式中各符号的意义见P.40;(2)表中系数的数值与板的四边支承条件和所求弯矩的位置有关,见附录8,P.527;(3)上式未考虑泊松比的影响,实际计算时必须考虑,此时混凝土的泊松比近似取0.2;(4)上式所求弯矩是单位长度的弯矩.2.多跨(多区格)双向板实际工程中单区格较少,一般为多区格楼盖.实用做法:将多区格楼盖简化为单区格板,然后按单区格查表计算.(1)跨中最大弯矩由薄板理论可知,跨中产生最大弯矩时,荷载为棋盘布置,可将多跨双向板楼盖分解为单跨板查表计算,将荷载重新组合,如附图所示.显然,产生的内力= 产生的内力+ 产生的内力.对于,中间的板块,按四边固定荷载为g+q/2的情况查表;端部的板块,按三边固定一边简支荷载为g+q/2的情况查表;对于,按四边简支荷载为q/2的情况查表;设按查表求得的x方向的弯矩为(未考虑泊松比);y方向的弯矩为(未考虑泊松比);则考虑(泊松比时),产生的x方向的弯矩为:产生的y方向的弯矩为:设按查表求得的x方向的弯矩为(未考虑泊松比);y方向的弯矩为(未考虑泊松比);则考虑(泊松比时),产生的x方向的弯矩为:产生的y方向的弯矩为:将,分别产生的x及y方向的弯矩叠加,即得跨中最大弯矩为:按上述计算值进行配筋计算.(2)支座最大负弯矩最不利活荷载的布置形式为全部楼盖满布.中间板块按四边固定的情况查表;端部板块按三边固定一边简支(若搁置在砖墙上)查表;角部板块按二边固定二边简支(若搁置在砖墙上)查表;相邻支承边上的负弯矩取绝对值较大者.三.双向板按塑性铰线法的计算(自学)四.双向板的截面设计与构造要求1.截面设计由于板四周受到梁的约束,将使实际弯矩有所减少.所以规范允许将计算弯矩值折减.(1)中间跨的跨中弯矩,中间支座弯矩可减少20%;(2)其余部位视情况确定;(3)角部板块不折减.2.构造要求配筋形式:弯起式和分离式;如图12-42,中间板带按计算配筋;边缘板带取一半;其余构造筋同单向板.五.双向板支承梁的设计1.支承梁承担的荷载板上作用的均布荷载按就近原则传递给支承梁,见附图.2.支承梁的结构模型:多跨连续梁3.设计步骤(1)荷载简化:采用支座弯矩等效的原则将T形和三角形荷载分布简化为均布分布.现以三角形分布为例加以说明.均布荷载下两端固定梁的支座弯矩为:(a)假定三角形荷载下两端固定梁的支座弯矩:采用结构力学解出,再令,即可解得等效荷载: (b)对于T形分布的均布荷载作类似的计算,也可求得相应等效荷载.于是,求解三角形荷载下两端固定梁的内力时,不须解超静定结构.先根据(b)式求等效荷载,再代入(a)式求支座弯矩;原超静定结构转化为三角形荷载和支座弯矩作用下的静定结构.各种类型分布荷载下两端固定梁的等效弯矩可查有关计算手册.(2)按最不利活荷载求控制截面的内力,原则同单向板楼盖梁.(3)作包络图进行配筋计算.六.双向板设计例题(简介)§12.4 无梁楼盖(自学)§12.5 装配式与装配整体式楼盖一.概述1.装配式:所有构件均在工厂或现场预制,然后起吊安装;整体性差,不利与抗震,仅适用于混合结构的多层房屋.2.装配整体式:部分构件(板)在工厂或现场预制,部分构件(柱)现浇,整体性强于装配式,适用于框架等小高层结构.3.一般采用标准化构件生产.二.预制板与预制梁1.预制板的形式:普通混凝土预制板,预应力混凝土预制板,轻质混凝土预制板和其他新型材料预制板(墙体).各种形状的预制板见图12-54.2.预制板的尺寸:标准化,一般根据开间或进深,柱距和施工方便确定,可查表准图选用.3.预制梁:普通混凝土预制梁,预应力混凝土预制梁;简支梁,连续梁,矩形截面,T形截面和花篮梁,见图12-55.三.预制构件的计算特点1.使用阶段承载力计算;2.正常使用极限状态验算;3.吊装验算(自重乘以1.5,吊环验算).四.铺板式楼盖的连接1.连接的目的:加强各构件的联系,确保结构的整体性.2.连接的方法:见P.65-67的标准图.。
