初一平面直角坐标系动点问题经典难题

(完整版)初一平面直角坐标系动点问题(经典难题)

(1)求点C，D的坐标及四边形ABDC的面积
(2)在y轴上是否存在一点P，连接PA，PB，使＝，
若存在这样一点，求出点P的坐标，若不存在，试说明理由．
(3)点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）给出下列结论：的值不变，的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．
5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣ ）（﹣9，）…根据你发现的规律，第100个有序数对是．
6、观察下列有规律的点的坐标：
依此规律，A11的坐标为，A12的坐标为．
7、以0为原点，正东，正北方向为x轴，y轴正方向建立平面直角坐标系，一个机器人从原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2，再向正西方向走9米到达A3，再向正南方向走12米到达A4，再向正东方向走15米到达A5，按此规律走下去，当机器人走到A6时，A6的坐标是．
平面直角坐标系动点问题
（一）找规律
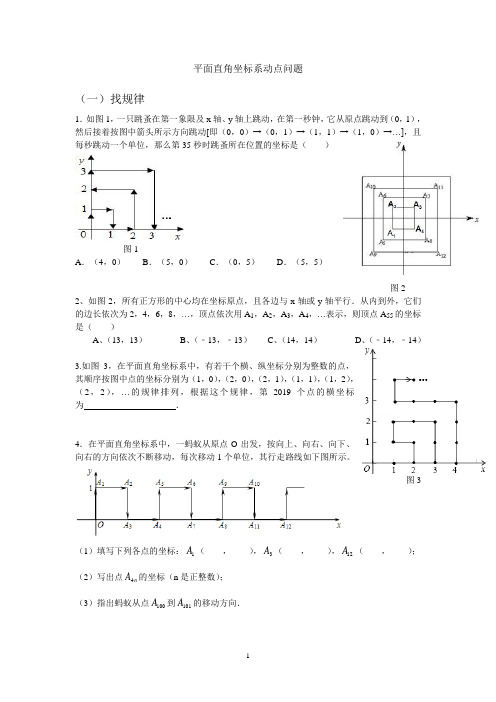
1．如图1，一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）
图1
A．（4，0）B．（5，0）C．（0，5）D．（5，5）
（1）汽车行驶到什么位置时离A村最近？写出此点的坐标．
（2）汽车行驶到什么位置时离B村最近？写出此点的坐标．
（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？
4．如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．

七年级平面直角坐标系动点规律问题(经典难题)

平面直角坐标系动点问题（一）找规律1．如图1，一只跳蚤在第一象限及x 轴、y 轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）图1A ．（4，0）B ．（5，0）C ．（0，5）D ．（5，5）图22、如图2，所有正方形的中心均在坐标原点，且各边与x 轴或y 轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A 1，A 2，A 3，A 4，…表示，则顶点A 55的坐标是（） A 、（13，13） B 、（﹣13，﹣13） C 、（14，14） D 、（﹣14，﹣14）3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列，根据这个规律，第2019个点的横坐标为．4．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。

图3（1）填写下列各点的坐标：1A （____，____），3A （____，____），12A （____，____）；（2）写出点n A 4的坐标（n 是正整数）；（3）指出蚂蚁从点100A 到101A 的移动方向．5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣）（﹣9，）…根据你发现的规律，第100个有序数对是．6、观察下列有规律的点的坐标：依此规律，A 11的坐标为，A 12的坐标为．7、以0为原点，正东，正北方向为x 轴，y 轴正方向建立平面直角坐标系，一个机器人从原点O 点出发，向正东方向走3米到达A 1点，再向正北方向走6米到达A 2，再向正西方向走9米到达A 3，再向正南方向走12米到达A 4，再向正东方向走15米到达A 5，按此规律走下去，当机器人走到A 6时，A 6的坐标是．8、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2019次，点P 依次落在点201921,,,P P P 的位置，则点2019P 的横坐标为 .9、如图，在平面直角坐标系上有个点P （1，0），点P 第1次向上跳动1个单位至点P 1（1，1），紧接着第2次向左跳动2个单位至点P 2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P 第100次跳动至点P 100的坐标是．点P 第2019次跳动至点P 2019的坐标是．图4 图5 10、如图5，已知A l （1，0），A 2（1，1），A 3（﹣1，1），A 4（﹣1，﹣1），A 5（2，﹣1），…．则点A 2019的坐标为．1PAOyxP1. 如图，一个粒子在第一象限内及x 、y 轴上运动，在第一分钟内它从原点运动到()1,0，而后它接着按图所示在x 轴、y 轴平行的方向上来回运动，且每分钟移动1个长度单位，那么，在1989分钟后这个粒子所处的位置是（）．A ．()35,44B ．()36,45C ．()37,45D ．()44,352. 如果将点P 绕定点M 旋转180︒后与点Q 重合，那么称点P 与点Q 关于点M 对称，定点M 叫做对称中心，此时，点M 是线段PQ 的中点，如图，在直角坐标系中，ABO △的顶点A 、B 、O 的坐标分别为()1,0、()0,1、()0,0，点1P ，2P ，3P ，…中相邻两点都关于ABO △的一个顶点对称，点1P 与点2P 关于点A 对称，点2P 与点3P 关于点B 对称，点3P 与点4P 关于点O 对称，点4P 与点5P 关于点A 对称，点5P 与点6P 关于点B 对称，点6P 与点7P 关于点O 对称，…对称中心分别是A ，B ，O ，A ，B ，O ，…且这些对称中心依次循环，已知1P 的坐标是()1,1．试写出点2P 、7P 、100P 的坐标．3. 如图，在平面直角坐标系中，四边形各顶点的坐标分别为：()0,0A ，()7,0B ，()9,5C ，()2,7D ．（1）求此四边形的面积．（2）在坐标轴上，你能否找到一点P ，使50PBC S =△?若能，求出P 点坐标；若不能，请说明理由．4. 如图①，已知OABC 是一个长方形，其中顶点A 、B 的坐标分别为()0,a 和()9,a ，点E在AB 上，且13AE AB =，点F 在OC 上，且13OF OC =．点G 在OA 上，且使GEC △的面积为20，GFB △的面积为16，试求a 的值．图②5. 如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如()1,0，()2,0，()2,1，()1,1，()1,2，()2,2……根据这个规律，第2019个点的横坐标为_______．6. 在平面直角坐标系xOy 中，我们把横、纵坐标都是整数的点叫做整点．已知点()0,4A ，点B 是x 轴正半轴上的整点，记AOB △内部（不包括边界）的整点个数为m ，当3m =时，点B 的横坐标的所有可能值是_______；当点B 的横坐标为4n （n 为正整数）时，m =________（用含n 的代数式表示）．7. 如图，把自然数按图的次序排在直角坐标系中，每个自然数都对应着一个坐标．如1的对应点是原点()0,0，3的对应点是()1,1，16的对应点是()1,2-，那么2019的对应点的坐标是_______．8．如图，长方形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙由点()2,0A 同时出发，沿长方形BCDE 的边作环绕运动，物体甲按逆时针方向以每秒1个单位长度的速度匀速运动，物体乙按顺时针方向以每秒2个单位长度的速度匀速运动，求两个物体开始运动后的第2019次相遇地点的坐标．9. 在平面直角坐标系中，如图①，将线段AB 平移至线段CD ，连接AC 、BD ．（1）直接写出图中相等的线段、平行的线段；（2）已知()3,0A -、()2,2B --，点C 在y 轴的正半轴上．点D 在第一象限内，且5ACD S =△，求点C 、D 的坐标；（3）如图②，在平面直角坐标系中，已知一定点，()1,0M ，两个动点(),21E a a +、(),23F b b -+，请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM ．若存在，求以点O 、M 、E 、F 为顶点的四边形的面积，若不存在，请说明理由．图②10 . 如图，AOCD 是放置在平面直角坐标系内的梯形，其中O 是坐标原点．点A 、C 、D 的坐标分别为()0,8，()5,0，()3,8，若点P 在梯形内，且PAD POC S S =△△，PAO PCD S S =△△，求P 点的坐标．11. 操作与研究（1）对数轴上的点P 进行如下操作：先把点P 表示的数乘以13，再把所得数对应的点向右平移1个单位，得到点P 的对应点'P B ．点A ，B 在数轴上，对线段AB 上的每个点进行上述操作后得到线段''A B ，其中点A ，B 的对应点分别为'A ，'B ．如图①，若点A 表示的数是3-，则点'A 表示的数是______；若点'B 表示的数是2，则点表示的数是______；已知线段AB 上的点E 经过上述操作后得到的对应点'E 与点E 重合，则点E 表示的数是_________．（2）如图②，在平面直角坐标系xOy 中，对正方形ABCD 及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a ，将得到的点先向右平移m 个单位，再向上平移n 个单位()0,0m n >>，得到正方形''''A B C D 及其内部的点，其中点A ，B 的对应点分别为'A ，'B ．已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点'F 与点F 重合，求点F 的坐标．图①A B'-1-2-3-412340图②（二）几何综合问题1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB//y 轴时、求点B 的坐标2、如图，已知A 、B 两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O 出发．（1）汽车行驶到什么位置时离A 村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B 村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？4．如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形D C 3-1BA O x y PDCBAOx y (2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ∆＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．(3)点P 是线段BD 上的一个动点，连接PC ，PO ，当点P 在BD 上移动时（不与B ，D 重合）给出下列结论：①DCP BOP CPO ∠+∠∠的值不变，②DCP CPOBOP∠+∠∠的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．5.已知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°，AB ∥CD ,AB =CD =8cm ，AD =BC =6cm ，D 点与原点重合，坐标为(0,0). （1）写出点B 的坐标.（2）动点P 从点A 出发以每秒3个单位长度的速度向终点B 匀速运动, 动点Q 从点C 出发以每秒4个单位长度的速度沿射线CD 方向匀速运动,若P ,Q 两点同时出发,设运动时间为t 秒,当t 为何值时,PQ ∥BC ?（3）在Q 的运动过程中,当Q 运动到什么位置时,使△ADQ 的面积为9? 求出此时Q 点的坐标.6．如图在平面直角坐标系中，A（a，0），B（b，0），（﹣1，2）．且|2a+b+1|+=0．（1）求a、b的值；（2）①在y轴的正半轴上存在一点M，使S△COM=S△ABC，求点M的坐标．②在坐标轴的其他位置是否存在点M，使S△COM=S△ABC仍成立？若存在，请直接写出符合条件的点M的坐标．7.如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b 满足关系式．（1）求a，b的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．8．在平面直角坐标系中，点A（a，b）是第四象限内一点，AB⊥y轴于B，且B（0，b）是y轴负半轴上一点，b2=16，S△AOB=12．（1）求点A和点B的坐标；（2）如图1，点D为线段OA（端点除外）上某一点，过点D作AO垂线交x轴于E，交直线AB于F，∠EOD、∠AFD的平分线相交于N，求∠ONF的度数．（3）如图2，点D为线段OA（端点除外）上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E，交直线AB于F，∠EOD，∠AFD的平分线相交于点N．若记∠ODF=α，请用α的式子表示∠ONF的大小，并说明理由．。

平面直角坐标系重难点题型(四大题型)(原卷版)

专题05 平面直角坐标系重难点题型（四大题型）【题型1 两点间距离】【题型2 求平面直角坐标系中动点问题的面积】【题型3 平面直角坐标系中规律题探究】【题型4 等腰三角形个数讨论问题】【题型1 两点间距离】1．在平面直角坐标系中，有A（﹣2，a+1），B（a﹣1，4），C（b﹣2，b）三点．（1）当AB∥x轴时，求A、B两点间的距离；（2）当CD⊥x轴于点D，且CD＝1时，求点C的坐标．2．已知平面直角坐标系内的三点：A（a﹣1，﹣2），B（﹣3，a+2），C（b﹣6，2b）．（1）当直线AB∥x轴时，求A，B两点间的距离；（2）当直线AC⊥x轴，点C在第二、四象限的角平分线上时，求点A和点C 的坐标．3．先阅读一段文字，再回答下列问题：已知在平面内两点坐标P1（x1，y1），P2（x2，y2），其两点间距离公式为P1P2＝，同时，当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴时，两点距离公式可简化成|x1﹣x2|或|y2﹣y1|．（1）已知A（3，5），B（﹣2，﹣1），试求A，B两点的距离；（2）已知A，B在平行于y轴的直线上，点A的纵坐标为6，点B的纵坐标为﹣4，试求A，B两点的距离；（3）已知一个三角形各顶点坐标为A（0，6），B（﹣3，2），C（3，2），找出三角形中相等的边？说明理由．4.先阅读一段文字，再回答下列问题：已知在平面内两点坐标P1（x1，y1），P2（x2，y2），其两点间距离公式为：p1p2＝，例如：点（3，2）和（4，0）的距离为．同时，当两点所在的直线在坐标轴上或平行于x轴或平行于y轴距离公式可简化成：p1p2＝|x1﹣x2|或p1p2＝|y1﹣y2|．（1）已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为2，则A，B两点的距离为；（2）线段AB平行于x轴，且AB＝3，若点B的坐标为（2，4），则点A的坐标是；（3）已知A（3，5），B（﹣4，4），A，B两点的距离为；（4）已知△ABC三个顶点坐标为A（3，4），B（0，5），C（﹣1，2），请判断此三角形的形状，并说明理由．5．先阅读下列一段文字，再解答问题：已知在平面内有两点P1（x1，y1），P2（x2，y2），其两点间的距离公式为；同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知点A（2，4），B（﹣2，1），则AB＝；（2）已知点C，D在平行于y的直线上，点C的纵坐标为3，点D的纵坐标为﹣2，则CD＝；（3）已知点M和（1）中的点A有MA∥x轴，且MA＝3，则点M的坐标为；（4）已知点P（3，1）和（1）中的点A，B，则线段P A，PB，AB中相等的两条线段是．6．先阅读下列一段文字，再回答后面的问题：已知在平面直角坐标系内两点P1（x1，y1），P2（x2，y2），其两点间的距离P1P2＝，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知A（1，3），B（﹣3，﹣5），试求A，B两点间的距离；（2）已知线段MN∥y轴，MN＝4，若点M的坐标为（2，﹣1），试求点N 的坐标．7．先阅读下列一段文字，再回答后面的问题．已知在平面内两点P1（x1，y1），P2（x2，y2），这两点间的距离P1P2＝，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知A（2，4），B（﹣3，﹣8），试求A，B两点间的距离；（2）已知A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A，B两点间的距离．8．阅读材料：两点间的距离公式：如果平面直角坐标系内有两点A（x1，y1）、B（x2，y2），那么A、B两点的距离AB＝，则AB2＝（x1﹣x2）2+（y1﹣y2）2．例如：若点A（4，1），B（3，2），则AB＝，若点A（a，1），B（3，2），且AB＝，则．根据实数章节所学的开方运算即可求出满足条件的a的值．根据上面材料完成下列各题：（1）若点A（﹣2，3），B（1，2），则A、B两点间的距离是．（2）若点A（﹣2，3），点B在x轴上，且A、B两点间的距离是5，求B 点坐标．9．在平面直角坐标系中，有A（﹣2，a+1），B（a﹣1，4），C（b﹣2，b）三点．（1）当点C在y轴上时，求点C的坐标；（2）当AB∥x轴时，求A，B两点间的距离；（3）当CD⊥x轴于点D，且CD＝1时，求点C的坐标．10．先阅读下列一段文字，在回答后面的问题．已知在平面内两点P1（x1，y1）、P2（x2，y2），其两点间的距离公式，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知A（2，4）、B（﹣3，﹣8），试求A、B两点间的距离；（2）已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A、B两点间的距离．（3）已知一个三角形各顶点坐标为A（0，6）、B（﹣3，2）、C（3，2），你能判定此三角形的形状吗？说明理由．【题型2 求平面直角坐标系中动点问题的面积】11．如图所示，在平面直角坐标系中，已知A（0，1），B（2，0），C（4，3）．（1）在平面直角坐标系中画出△ABC，则△ABC的面积是；（2）若点D与点C关于原点对称，则点D的坐标为；（3）已知P为x轴上一点，若△ABP的面积为4，求点P的坐标．12．如图，在平面直角坐标系中，已知A（a，0），B（b，0），其中a，b满足．（1）填空：a＝，b＝；（2）若在第三象限内有一点M（﹣2，m），用含m的式子表示△ABM的面积；（3）在（2）条件下，线段BM与y轴相交于C（0，﹣），当时，点P是y轴上的动点，当满足△PBM的面积是△ABM的面积的2倍时，求点P的坐标．13．如图，在平面直角坐标系内，已知点A的坐标为（3，2），点B的坐标为（3，﹣4），点P为直线AB上任意一点（不与A、B重合），点Q是点P 关于x轴的对称点．（1）在方格纸中标出A、B，并求出△ABO的面积；（2）设点P的纵坐标为a，求点Q的坐标；（3）设△OP A和△OPQ的面积相等，且点P在点Q的上方，求出此时P点坐标．14．如图，在平面直角坐标系中，已知A（a，0），B（b，0），其中a，b满足a2+2a+1+|3a+b|＝0．（1）填空：a＝，b＝；（2）若存在一点M（﹣2，m）（m＜0），点M到x轴距离，到y轴距离，求△ABM的面积（用含m的式子表示）；（3）在（2）条件下，当m＝﹣1.5时，在y轴上有一点P，使得△MOP的面积与△ABM的面积相等，请求出点P的坐标．15．如图，在平面直角坐标系中，已知A（0，a），B（b，0），C（3，c）三点，其中a、b、c满足关系式：|a﹣2|+（b﹣3）2+＝0．（1）求a、b、c的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP 的面积；（3）在（2）的条件下，是否存在负整数m，使四边形ABOP的面积不小于△AOP面积的两倍？若存在，求出所有满足条件的点P的坐标，若不存在，请说明理由．16．如图，已知在平面直角坐标系中，点A在y轴上，点B、C在x轴上，S△ABO ＝8，OA＝OB，BC＝10，点P的坐标是（﹣6，a），（1）求△ABC三个顶点A、B、C的坐标；（2）连接P A、PB，并用含字母a的式子表示△P AB的面积（a≠2）；（3）在（2）问的条件下，是否存在点P，使△P AB的面积等于△ABC的面积？如果存在，请求出点P的坐标；若不存在，请说明理由．17．如图，在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，2），且|a+2|+＝0．（1）求a，b的值；（2）①在x轴的正半轴上存在一点M，使△COM的面积＝△ABC的面积，求出点M的坐标；②在坐标轴的其它位置是否存在点M，使△COM的面积＝△ABC的面积恒成立？若存在，请直接写出符合条件的点M的坐标．18．如图，直线AB与x轴，y轴分别相交于点A（6，0），B（0，8），M是OB上一点，若将△ABM沿AM折叠，则点B恰好落在x轴上的点B'处．求：（1）点B'的坐标；（2）△ABM的面积．19．如图在直角坐标系中，已知A（0，a），B（b，0）C（3，c）三点，若a，b，c满足关系式：|a﹣2|+（b﹣3）2+＝0．（1）求a，b，c的值．（2）求四边形AOBC的面积．（3）是否存在点P（x，﹣x），使△AOP的面积为四边形AOBC的面积的两倍？若存在，求出点P的坐标，若不存在，请说明理由．20．已知：在平面直角坐标系中，A（0，1），B（2，0），C（4，3）（1）求△ABC的面积；（2）设点P在x轴上，且△ABP与△ABC的面积相等，求点P的坐标．21．如图，在平面直角坐标系中，A（2，2），B（﹣1，0），C（3，0）（1）求△ABC面积；（2）在y轴上存在一点D，使得△AOD的面积是△ABC面积的2倍，求出点D的坐标；（3）在平面内有点P（3，m），是否存在m值，使△AOP的面积等于△ABC 面积的2倍？若存在，直接写出m的值；若不存在，请说明理由．22．在平面直角坐标系中，△ABC的顶点坐标分别为A（2，0），B（0，4），C（﹣3，2）．（1）如图1，求△ABC的面积．（2）若点P的坐标为（m，0），①请直接写出线段AP的长为（用含m的式子表示）；②当S△P AB ＝2S△ABC时，求m的值．（3）如图2，若AC交y轴于点D，直接写出点D的坐标为．23．如图，在平面直角坐标系中，点A（﹣3b，0）为x轴负半轴上一点，点B （0，4b）为y轴正半轴上一点，其中b满足方程：3（b+1）＝6．（1）求点A、B的坐标；（2）点C为y轴负半轴上一点，且△ABC的面积为12，求点C的坐标；（3）在（2）的条件下，在x轴上是否存在点P，使得△PBC的面积等于△ABC的面积的一半？若存在，求出相应的点P的坐标；若不存在，请说明理由．【题型3 平面直角坐标系中规律题探究】24．如图，动点P按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次运动到点（2，0），第3次运动到点（3，2），…，按这样的运动规律，则第2021次运动到点（）A．（2021，1）B．（2021，2）C．（2020，1）D．（2021，0）25．有一组数，按照下列规律排列：1，2，3，6，5，4，7，8，9，10，15，14，13，12，11，16，17，18，19，20，21，……数字5在第三行左数第二个，我们用（3，2）点示5的位置，那点这组成数里的数字100的位置可以表示为（）A．（14，9）B．（14，10）C．（14，11）D．（14，12）26．如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2）．把一条长为2012个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（）A．（1，﹣1）B．（﹣1，1）C．（﹣1，﹣2）D．（1，﹣2）27．如图，在平面直角坐标系上有个点P（1，0），点P第一次向上跳动1个单位至P1（1，1），紧接着第二次向左跳动2个单位至点P2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P第100次跳动至点P100的坐标是（）A．（﹣24，49）B．（﹣25，50）C．（26，50）D．（26，51）28．如图，一个机器人从O点出发，向正东方向走3m到达A1点，再向正北方向走6m到达A2点，再向正西方向走9m到达A3点，再向正南方向走12m到达A4点，再向正东方向走15m到达A5点．按如此规律走下去，当机器人走到A6点时，离O点的距离是（）A．10m B．12m C．15m D．20m29．如图，将正整数按有图所示规律排列下去，若用有序数对（n，m）表示n 排从左到右第m个数．如（4，3）表示9，则（10，3）表示．30．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（0，1），（0，2），（1，2），（1，3），（0，3），（﹣1，3）…，根据这个规律探索可得，第90个点的坐标为．31．如图所示点A0（0，0），A1（1，2），A2（2，0），A3（3，﹣2），A4（4，0），…根据这个规律，探究可得点A2017坐标是．32．如图所示，一个机器人从O点出发，向正东方向走3m到达A1点，再向正北方向走6m到达A2点，再向正西方向走9m到达A3点，再向正南方向走12m 到达A4点，再向正东方向走15m到达A5点，按如此规律走下去，相对于点O，机器人走到A6时是位置．33．如图，在平面直角坐标系上有点A（1，0），点A第一次跳动至点A1（﹣1，1），第四次向右跳动5个单位至点A4（3，2），…，依此规律跳动下去，点A第100次跳动至点A100的坐标是．【题型4 等腰三角形个数讨论问题】34．如图，在平面直角坐标系中，点A的坐标是（6，6），点B在坐标轴上，且△OAB是等腰直角三角形，则点B的坐标不可能是（）A．（0，6）B．（6，0）C．（12，0）D．（0，﹣6）35．如图，在平面直角坐标系中，A，B两点的坐标分别为（﹣4，0），（0，3），连接AB，点P在第二象限，以点P，A，B为顶点的等腰直角三角形有个，任意写出其中一个点P坐标为．36．如图，在平面直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3．（1）观察每次变换前后的三角形的变化规律，若将△OA3B3变换成△OA4B4，则A4的坐标是，B4的坐标是．（2）若按第（1）题找到的规律将△OAB进行n次变换，得到△OA n B n，比较每次变换中三角形顶点坐标有何变化，找出规律，推测A n的坐标是，B n的坐标是．（3）若按第（1）题找到的规律将△OAB进行n次变换，得到△OA n B n，则△OA n B n的面积S为37．如图，方格纸中小正方形的边长均为1个单位长度，A、B均为格点．（1）在图中建立直角坐标系，使点A、B的坐标分别为（3，3）和（﹣1，0）；（2）在（1）中x轴上是否存在点C，使△ABC为等腰三角形（其中AB为腰）？若存在，请直接写出所有满足条件的点C的坐标．38．如图，在平面直角坐标系中，已知点A（﹣2，0），B（2，0）．（1）画出等腰三角形ABC（画一个即可）；（2）写出（1）中画出的三角形ABC的顶点C的坐标．。

七年级期中平面直角坐标系动点问题专项练习

平面直角坐标系动点问题
1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB//y 轴时、求点B 的坐标
2、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次，点P 依次落在点
1232008P P P P ，，，
，的位置，则点2008P 的横坐标为？
3、如图6－7，已知A 、B 两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O 出发．
（1）汽车行驶到什么位置时离A 村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B 村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？
4．如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．
(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形
(2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．
(3)点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）
给出下列结论：①
DCP BOP
CPO
∠+∠
∠
的值不变，②
DCP CPO
BOP
∠+∠
∠
的值不变，其中有且只
有一个是正确的，请你找出这个结论并求其值．。

初一-平面直角坐标系动点问题(经典难题)

初一-平面直角坐标系动点问题(经典难题)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN平面直角坐标系动点问题（一）找规律1．如图1，一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）图1A．（4，0） B．（5，0） C．（0，5） D．（5，5）图2 2、如图2，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示，则顶点A55的坐标是（）A、（13，13）B、（﹣13，﹣13）C、（14，14）D、（﹣14，﹣14）3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列，根据这个规律，第2015个点的横坐标为．4．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。

图3（1）填写下列各点的坐标：1A （____，____），3A （____，____），12A （____，____）；（2）写出点n A 4的坐标（n 是正整数）；（3）指出蚂蚁从点100A 到101A 的移动方向．5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣）（﹣9，）…根据你发现的规律，第100个有序数对是． 6、观察下列有规律的点的坐标：依此规律，A 11的坐标为，A 12的坐标为．7、以0为原点，正东，正北方向为x 轴，y 轴正方向建立平面直角坐标系，一个机器人从原点O 点出发，向正东方向走3米到达A 1点，再向正北方向走6米到达A 2，再向正西方向走9米到达A 3，再向正南方向走12米到达A 4，再向正东方向走15米到达A 5，按此规律走下去，当机器人走到A 6时，A 6的坐标是．8、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次，点P 依次落在点1232008P P P P ，，，，的位置，则点2008P的横坐标为 .9、如图，在平面直角坐标系上有个点P （1，0），点P 第1次向上跳动1个单位至点P 1（1，1），紧接着第2次向左跳动2个单位至点P 2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P 第100次跳动至点P 100的坐标是．点P 第2009次跳动至点P 2009的坐标是．图4 图510、如图5，已知A l （1，0），A 2（1，1），A 3（﹣1，1），A 4（﹣1，﹣1），A 5（2，﹣1），…．则点A 2007的坐标为．1PAOy xP（二）几何综合问题1、已知点A的坐标是（3，0）、AB=5，（1）当点B在X轴上时、求点B的坐标、（2）当AB//y轴时、求点B的坐标2、如图，已知A、B两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O出发．（1）汽车行驶到什么位置时离A村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？4．如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ∆＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．(3)点P 是线段BD 上的一个动点，连接PC ，PO ，当点P 在BD 上移动时（不与B ，D 重合）给出下列结论：①DCP BOPCPO∠+∠∠②DCP CPOBOP∠+∠∠你找出这个结论并求其值．5.已知:在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°，AB∥CD,AB=CD=8cm，AD=BC=6cm，D点与原点重合，坐标为(0,0).（1）写出点B的坐标.（2）动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥BC（3）在Q的运动过程中,当Q运动到什么位置时,使△ADQ的面积为9求出此时Q点的坐标.6．如图在平面直角坐标系中，A（a，0），B（b，0），（﹣1，2）．且|2a+b+1|+=0．（1）求a、b的值；（2）①在y轴的正半轴上存在一点M，使S△COM=S△ABC，求点M的坐标．②在坐标轴的其他位置是否存在点M，使S△COM=S△ABC仍成立？若存在，请直接写出符合条件的点M的坐标．7.如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b满足关系式．（1）求a，b的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．8．在平面直角坐标系中，点A（a，b）是第四象限内一点，AB⊥y轴于B，且B（0，b）是y轴负半轴上一点，b2=16，S△AOB=12．（1）求点A和点B的坐标；（2）如图1，点D为线段OA（端点除外）上某一点，过点D作AO垂线交x轴于E，交直线AB于F，∠EOD、∠AFD的平分线相交于N，求∠ONF的度数．（3）如图2，点D为线段OA（端点除外）上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E，交直线AB于F，∠EOD，∠AFD的平分线相交于点N．若记∠ODF=α，请用α的式子表示∠ONF的大小，并说明理由．。

初一平面直角坐标系动点问题(经典难题)

平面直角坐标系动点问题（一）找规律1．如图1，一只跳蚤在第一象限及x 轴、y 轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）图1A ．（4，0）B ．（5，0）C ．（0，5）D ．（5，5）图22、如图2，所有正方形的中心均在坐标原点，且各边与x 轴或y 轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A 1，A 2，A 3，A 4，…表示，则顶点A 55的坐标是（） A 、（13，13） B 、（﹣13，﹣13） C 、（14，14） D 、（﹣14，﹣14）3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列，根据这个规律，第2015个点的横坐标为．4．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。

图3（1）填写下列各点的坐标：1A （____，____），3A （____，____），12A （____，____）；（2）写出点n A 4的坐标（n 是正整数）；（3）指出蚂蚁从点100A 到101A 的移动方向．5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣）（﹣9，）…根据你发现的规律，第100个有序数对是．6、观察下列有规律的点的坐标：依此规律，A 11的坐标为，A 12的坐标为．7、以0为原点，正东，正北方向为x 轴，y 轴正方向建立平面直角坐标系，一个机器人从原点O 点出发，向正东方向走3米到达A 1点，再向正北方向走6米到达A 2，再向正西方向走9米到达A 3，再向正南方向走12米到达A 4，再向正东方向走15米到达A 5，按此规律走下去，当机器人走到A 6时，A 6的坐标是．8、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次，点P 依次落在点1232008P P P P ，，，，的位置，则点2008P 的横坐标为 .9、如图，在平面直角坐标系上有个点P （1，0），点P 第1次向上跳动1个单位至点P 1（1，1），紧接着第2次向左跳动2个单位至点P 2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P 第100次跳动至点P 100的坐标是．点P 第2009次跳动至点P 2009的坐标是．图4 图5 10、如图5，已知A l （1，0），A 2（1，1），A 3（﹣1，1），A 4（﹣1，﹣1），A 5（2，﹣1），…．则点A 2007的坐标为．1PAOyxP（二）几何综合问题1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB//y 轴时、求点B 的坐标2、如图，已知A 、B 两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O 出发．（1）汽车行驶到什么位置时离A 村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B 村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？4．如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形D C 3-1BA O x y PDCBAOx y (2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ∆＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．(3)点P 是线段BD 上的一个动点，连接PC ，PO ，当点P 在BD 上移动时（不与B ，D 重合）给出下列结论：①DCP BOP CPO ∠+∠∠的值不变，②DCP CPOBOP∠+∠∠的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．5.已知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°，AB ∥CD ,AB =CD =8cm ，AD =BC =6cm ，D 点与原点重合，坐标为(0,0). （1）写出点B 的坐标.（2）动点P 从点A 出发以每秒3个单位长度的速度向终点B 匀速运动, 动点Q 从点C 出发以每秒4个单位长度的速度沿射线CD 方向匀速运动,若P ,Q 两点同时出发,设运动时间为t 秒,当t 为何值时,PQ ∥BC ?（3）在Q 的运动过程中,当Q 运动到什么位置时,使△ADQ 的面积为9? 求出此时Q 点的坐标.6．如图在平面直角坐标系中，A（a，0），B（b，0），（﹣1，2）．且|2a+b+1|+=0．（1）求a、b的值；（2）①在y轴的正半轴上存在一点M，使S△COM=S△ABC，求点M的坐标．②在坐标轴的其他位置是否存在点M，使S△COM=S△ABC仍成立？若存在，请直接写出符合条件的点M的坐标．7.如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b 满足关系式．（1）求a，b的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．8．在平面直角坐标系中，点A（a，b）是第四象限内一点，AB⊥y轴于B，且B（0，b）是y轴负半轴上一点，b2=16，S△AOB=12．（1）求点A和点B的坐标；（2）如图1，点D为线段OA（端点除外）上某一点，过点D作AO垂线交x轴于E，交直线AB于F，∠EOD、∠AFD的平分线相交于N，求∠ONF的度数．（3）如图2，点D为线段OA（端点除外）上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E，交直线AB于F，∠EOD，∠AFD的平分线相交于点N．若记∠ODF=α，请用α的式子表示∠ONF的大小，并说明理由．。

七年级数学平面直角坐标系动点问题(二)

七年级数学平面直角坐标系动点问题(二)七年级数学平面直角坐标系动点问题1. 直线上的动点问题•问题：已知直线上两点A(x1, y1)和B(x2, y2)，求动点P在直线上的坐标。

•解释：通过已知的点A和B，可以确定一条直线。

求动点P在直线上的坐标，则需要满足直线上的点坐标满足某个特定的关系式。

2. 两条直线的交点问题•问题：已知直线L1和L2的方程，求两条直线的交点坐标。

•解释：根据直线L1和L2的方程，可以得到两个方程组，通过求解这个方程组，找到两条直线的交点坐标。

3. 线段上的动点问题•问题：已知线段AB的端点坐标，求动点P在线段AB上的坐标。

•解释：线段AB可以看作是两点A和B之间的所有点的集合。

求动点P在线段AB上的坐标，则需要满足P的坐标满足某个特定的关系式，并且P在线段之内。

4. 圆上的动点问题•问题：已知圆的圆心坐标和半径，求动点P在圆上的坐标。

•解释：圆可以看作是圆心到圆上所有点的距离都相等的集合。

求动点P在圆上的坐标，则需要满足P到圆心的距离等于圆的半径。

5. 平移和旋转的动点问题•问题：已知初始点的坐标和平移/旋转的规则，求平移/旋转后的动点坐标。

•解释：通过平移和旋转的规则，可以确定新点与初始点之间的位置关系。

根据这个关系，可以求得平移/旋转后的新点坐标。

6. 垂直/平行线段问题•问题：已知两个线段的坐标，判断其是否垂直或平行。

•解释：垂直线段的斜率之积为-1，平行线段的斜率相等。

通过求解两个线段的斜率，可以判断其是否垂直或平行。

7. 镜面对称点问题•问题：已知点关于某条直线的镜面对称点的坐标，求原点的坐标。

•解释：镜面对称点与原点关于某条直线对称。

通过已知的镜面对称点坐标，可以求得原点的坐标。

8. 解析几何计算问题•问题：已知一些点和计算公式，求解一些几何性质或计算结果。

•解释：解析几何通过坐标系和方程表达几何问题，通过已知条件和计算公式，可以求解一些几何性质或计算结果。

完整版)初一平面直角坐标系动点问题(经典难题)

完整版)初一平面直角坐标系动点问题(经典难题)一）找规律1.如图1，一只跳蚤在第一象限及x轴、y轴上跳动。

在第一秒钟，它从原点跳动到（0，1），然后按照箭头所示方向跳动（即（0，0）→（0，1）→（1，1）→（1，0）→…），每秒跳动一个单位。

那么第35秒时跳蚤所在位置的坐标是（4，1），因此答案为A。

2.如图2，所有正方形的中心都在坐标原点，且各边与x轴或y轴平行。

从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示。

顶点A55的坐标是（54，54），因此答案为A。

3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列。

根据这个规律，第2015个点的横坐标为1，因此答案为A。

4.在平面直角坐标系中，一只蚂蚁从原点O出发，按照向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如图3所示。

1）填写下列各点的坐标：A1（0，1），A3（2，1），A12（6，﹣2）；2）点A4n的坐标为（2n，﹣2n+1）；3）蚂蚁从点A100到A101的移动方向为向上。

5.观察下列有序数对：（3，﹣1），（﹣5，0），（7，﹣1），（﹣9，0），…根据你发现的规律，第100个有序数对是（195，﹣1）。

6.观察下列有规律的点的坐标：A1（1，0），A2（2，1），A3（4，0），A4（8，1），…依照规律，A11的坐标为（1024，1），A12的坐标为（2048，0）。

7.以原点为起点，正东，正北方向为x轴，y轴正方向建立平面直角坐标系。

一个机器人从原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2，再向正西方向走9米到达A3，再向XXX方向走12米到达A4，再向正东方向走15米到达A5，按此规律走下去，当机器人走到A6时，A6的坐标是（﹣3，﹣3）。

初一年级平面直角坐标系动点问题(经典难题)

平面直角坐标系动点问题(一)找规律1. 如图1，一只跳蚤在第一象限及x 轴、y轴上跳动，在第一秒钟，它从原点跳动到(0，1), 然后接着按图中箭头所示方向跳动［即(0, 0)T( 0, 1)^( 1, 1)T( 1 , 0)T…］，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是( ) 7*A.( 4, 0) B . (5, 0) C . (0, 5) D . (5, 5)图2 2、如图2,所有正方形的中心均在坐标原点，且各边与x轴或y轴平行.从内到外，它们的边长依次为2, 4, 6, 8,…，顶点依次用A1, A2, A B,A4,…表示，则顶点A55的坐标是3. 如图3,在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为(1, 0),( 2, 0),(2,1),( 1 ,1),( 1 , 2),(2 , 2)，…的规律排列，根据这个规律，第2015个点的横坐标为 .4. 在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。

A (13, 13)B (—13,—13)C (14, 14)A,__A3D、(—14, —14)图3(1 )填写下列各点的坐标：Ai ( _____ , ____ ), A3 ( ______ , ____ ), A2 ( ______ , ___ );(2)写出点A4n的坐标(n是正整数)；(3)指出蚂蚁从点Aoo到Aoi的移动方向.5、观察下列有序数对：(3, - 1) (- 5,寺)(7,-寺)(-9,壬)…根据你发现的规律，第100个有序数对是_______ .6、观察下列有规律的点的坐标：Ai (b 1) 扣Q “ 4) A. (4, 2) 去6 7) A s临-->3 A*(7, 10) A3 (S s4).......................... ,依此规律，A ii的坐标为_______________ , A i2的坐标为_______________ .7、以0为原点，正东，正北方向为x轴，y轴正方向建立平面直角坐标系，一个机器人从原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2,再向正西方向走9米到达A3,再向正南方向走12米到达A4,再向正东方向走15米到达A5,按此规律走下去，当机器人走到A6时，A6的坐标是_______________.8、如图，将边长为1的正三角形OAP沿x轴正方向连续翻转2008次，点P依次落在点9、如图，在平面直角坐标系上有个点P (1, 0),点P第1次向上跳动1个单位至点Pi ( 1, 1),紧接着第2次向左跳动2个单位至点(-1, 1),第3次向上跳动1个单位，第向右跳动3个单位，第5次又向上跳动1 单位，第6次向左跳动4个单位，…，依规律跳动下去，点P第100次跳动至点Pi oo的坐标是P24次个此___________________________________________________________ .点P第2009次跳动至点F2QQ9的坐标是_____________ .-3 ^2~7 2 3 t图4 图510、如图5，已知A( 1，0)，A2( 1，1)，A3 (- 1, 1), A4 (- 1,—1), A s (2,—1),….则点A2007的坐标为______________(二)几何综合问题1、已知点A的坐标是(3, 0)、AB=5,( 1)当点B在X轴上时、求点B的坐标、(2)当AB//y轴时、求点B的坐标2、如图，已知A、B两村庄的坐标分别为(2, 2)、( 7, 4), 一辆汽车在X轴上行驶，从原点O出发.(1)汽车行驶到什么位置时离A村最近？写出此点的坐标.(2)汽车行驶到什么位置时离B村最近？写出此点的坐标.(3 )请在图中画出汽车行驶到什么位置时，距离两村的和最短？8 164B2A» 1 | 1 11111111-512115111114. 如图，在平面直角坐标系中，点A, B的坐标分别为(一1 , 0) , ( 3, 0),现同时将点A, B分别向上平移2个单位，再向右平移1个单位，分别得到点A B的对应点C, D,连接AC, BD CD(1) 求点C, D的坐标及四边形ABDC勺面积绻边形ABDC⑵在y轴上是否存在一点P,连接PA, PB,使S PAB =S四边形ABDC ,若存在这样一点，求出点P的坐标，若不存在，试说明理由.⑶点P是线段BD上的一个动点，连接PC PO当点P在DCP BOP DCP 给出下列结论：①的值不变，②BD上移动时(不与CPO的值不变,B, D重合）CPO BOP有一个是正确的，请你找出这个结论并求其值.其中有且只5. 已知：在平面直角坐标系中，四边形ABCD是长方形，/ A=Z B=Z C=/ D=90°, AB// CDAB=CD=8cm, AD=BC=6cm D点与原点重合，坐标为(0,0).(1)写出点B的坐标.(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动，动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动，若P,Q两点同时出发，设运动时间为t秒，当t为何值时，PQ/ BC?(3)在Q的运动过程中，当Q运动到什么位置时，使厶ADC的面积为9?求出此时Q点的坐6.如图在平面直角坐标系中, A (a, 0), B ( b, 0),( Y P—>BAX0(D) W --------- CQ7: X1, 2).且|2a+b+1|+ Q时乱-4=0.(1) 求a、b 的值；(2) ①在y轴的正半轴上存在一点②在坐标轴的其他位置是否存在点M使“C^&ABC仍成立？若存在，请直接写出符M,使S AABC,求点M的坐标.合条件的点M的坐标.7.如图，在下面的直角坐标系中，已知 A (0, a), B ( b, 0), C(b, 4)三点，其中a, b满足关系式(1 )求a，b的值;(2)如果在第二象限内有一点P(m式子表示四边形ABOP勺面积；(3)在(2)的条件下，是否存在点的面积与厶ABC的面积相等？若存在, 若不存在，请说明理由.&在平面直角坐标系中，点 A ( a, b)是第四象限内一点，AB丄y轴于B,且B (0, b)是2y轴负半轴上一点，b =16, S^AOE=12.(1)求点A和点B的坐标；(2)如图1,点D为线段0A (端点除外)上某一点，过点D作A0垂线交x轴于E,交直线AB于F,/ EOD Z AFD的平分线相交于N,求/ ONF的度数.(3)如图2,点D为线段0A(端点除外)上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E,交直线AB于F, / EOD /AFD的平分线相交于点N若记/ ODF a, 请用a的式子表示/ ONF的大小，并说明理由.。

初一平面直角坐标系动点问题经典难题

平面直角坐标系动点问题（一）找规律1．如图1，一只跳蚤在第一象限及x 轴、y 轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（）图1A ．（4，0）B ．（5，0）C ．（0，5）D ．（5，5）图22、如图2，所有正方形的中心均在坐标原点，且各边与x 轴或y 轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A 1，A 2，A 3，A 4，…表示，则顶点A 55的坐标是（） A 、（13，13） B 、（﹣13，﹣13） C 、（14，14） D 、（﹣14，﹣14）3.如图3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），（1，2），（2，2），…的规律排列，根据这个规律，第2015个点的横坐标为．4．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示。

图3 （1）填写下列各点的坐标：1A （____，____），3A （____，____），12A （____，____）；（2）写出点n A 4的坐标（n 是正整数）；（3）指出蚂蚁从点100A 到101A 的移动方向．5.观察下列有序数对：（3，﹣1）（﹣5，）（7，﹣）（﹣9，）…根据你发现的规律，第100个有序数对是．6、观察下列有规律的点的坐标：依此规律，A 11的坐标为，A 12的坐标为．7、以0为原点，正东，正北方向为x 轴，y 轴正方向建立平面直角坐标系，一个机器人从原点O 点出发，向正东方向走3米到达A 1点，再向正北方向走6米到达A 2，再向正西方向走9米到达A 3，再向正南方向走12米到达A 4，再向正东方向走15米到达A 5，按此规D C y DCyDC3-1BA O xy律走下去，当机器人走到A 6时，A 6的坐标是．8、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次，点P 依次落在点1232008P P P P ，，，，的位置，则点2008P 的横坐标为 .9、如图，在平面直角坐标系上有个点P （1，0），点P 第1次向上跳动1个单位至点P 1（1，1），紧接着第2次向左跳动2个单位至点P 2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P 第100次跳动至点P 100的坐标是．点P 第2009次跳动至点P 2009的坐标是．图 4 图5 A 310、如图5，已知A l （1，0），A 2（1，1），（﹣1，1），A 4（﹣1，﹣1），A 5（2，﹣1），…．则点A 2007的坐标为．（二）几何综合问题1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB//y 轴时、求点B 的坐标2、如图，已知A 、B 两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O 出发．（1）汽车行驶到什么位置时离A 村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B 村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？4．如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形 (2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由． (3)点P 是线段BD 上的一个动点，连接PC ，PO ，当点P 在PBD上移动时（不与B，D重合）给出下列结论：①DCP BOPCPO∠+∠∠的值不变，②DCP CPOBOP∠+∠∠的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．5.已知:在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°，AB∥CD,AB=CD=8cm，AD=BC=6cm，D点与原点重合，坐标为(0,0).（1）写出点B的坐标.（2）动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥BC?（3）在Q的运动过程中,当Q运动到什么位置时,使△ADQ的面积为9? 求出此时Q点的坐标.6．如图在平面直角坐标系中，A（a，0），B（b，0），（﹣1，2）．且|2a+b+1|+=0．（1）求a、b的值；（2）①在y轴的正半轴上存在一点M，使S△COM=S△ABC，求点M的坐标．②在坐标轴的其他位置是否存在点M，使S△COM=S△ABC仍成立？若存在，请直接写出符合条件的点M的坐标．7.如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b满足关系式．（1）求a，b的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．8．在平面直角坐标系中，点A（a，b）是第四象限内一点，AB⊥y轴于B，且B（0，b）是y轴负半轴上一点，b2=16，S△AOB=12．（1）求点A和点B的坐标；（2）如图1，点D为线段OA（端点除外）上某一点，过点D作AO垂线交x轴于E，交直线AB于F，∠EOD、∠AFD的平分线相交于N，求∠ONF的度数．（3）如图2，点D为线段OA（端点除外）上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E，交直线AB于F，∠EOD，∠AFD的平分线相交于点N．若记∠ODF=α，请用α的式子表示∠ONF的大小，并说明理由．。

初一平面直角坐标系动点问题

平面直角坐标系动点问题（一）找规律1．如 1，一只跳蚤在第一象限及x 、y 上跳，在第一秒，它从原点跳到（ 0，1），而后接着按中箭所示方向跳[ 即（ 0，0）→（ 0，1）→（ 1，1）→（ 1，0）→⋯ ] ，且每秒跳一个位，那么第35 秒跳蚤所在地点的坐是（）1A．（ 4， 0） B ．（ 5， 0） C ．（ 0， 5） D ．（ 5， 5）22、如2，全部正方形的中心均在座原点，且各与x 或 y 平行．从内到外，它的挨次2， 4，6， 8，⋯，点挨次用A1，A2， A3， A4，⋯表示，点A55的坐是（）A、（ 13， 13）B、（ 13， 13）C、（ 14， 14）D、（ 14， 14）3.如 3，在平面直角坐系中，有若干个横、坐分整数的点，其序按中点的坐分（ 1，0），（ 2，0），（ 2，1），（1，1），（ 1，2），（ 2 ， 2 ），⋯的律摆列，依据个律，第2015 个点的横坐．4．在平面直角坐系中，一从原点O 出，按向上、向右、向下、向右的方向挨次不停移，每次移 1 个位，其行走路以下所示。

3（1）填写以下各点的坐：A1（____，____），A3（____，____）， A12（____，____）；（2）写出点A4n的坐（n是正整数）；（3）指出从点A100到 A101的移方向．5.察以下有序数：（ 3， 1）（ 5，）（ 7，）（ 9，）⋯依据你的律，第100 个有序数是．6、察以下有律的点的坐：依此律， A11的坐，A12的坐．7、以 0 原点，正，正北方向x ， y 正方向成立平面直角坐系，一个机器人从原点 O点出，向正方向走 3 米抵达 A1点，再向正北方向走 6 米抵达 A2，再向正西方向走 9 米抵达 A3，再向正南方向走12 米抵达 A4，再向正方向走15 米抵达 A5，按此律走下去，当机器人走到A6， A6的坐是．8、如，将 1 的正三角形OAP 沿x正方向翻2008 次，点P挨次落在点P， P ， P，， P的地点，点P的横坐.12320082008yPA O P1x9、如，在平面直角坐系上有个点P（1，0），点 P 第 1 次向上跳 1 个位至点P1（ 1，1），接着第 2 次向左跳 2 个位至点P2（ 1， 1），第 3 次向上跳 1 个位，第 4 次向右跳 3 个位，第 5 次又向上跳 1 个位，第 6 次向左跳 4 个位，⋯，依此律跳下去，点P 第 100 次跳至点P100的坐是．点P第2009次跳至点P2009的坐是．4510、如 5，已知 A l（ 1，0），A2（ 1，1），A3（ 1，1），A4（ 1， 1），A5（ 2， 1），⋯．点 A2007的坐．（二）几何综合问题1、已知点 A 的坐标是（ 3，0）、AB=5，（ 1）当点 B 在 X 轴上时、求点 B 的坐标、（ 2 ）当ABxyyy8C CCDDD 6AOPBBAAOB B4-13xx-1O3x2A-5510-2S四边形ABDCS PABS四边形ABDC DCPBOPDCPCPO知 :在平面直角坐标系CPOBOP中 , 四边形 ABCD 是长方形 , ∠ A =∠ B =∠ C =∠D =90°， AB ∥ CD , AB =CD =8cm ， AD =BC =6cm ，D 点与原点重合，坐标为 (0,0).（ 1）写出点 B 的坐标 .（ 2）动点 P 从点 A 出发以每秒3 个单位长度的速度向终点 B 匀速运动 , 动点 Q 从点 C 出发以每秒 4 个单位长度的速度沿射线CD 方向匀速运动 , 若 P , Q 两点同时出发 , 设运动时间为t 秒 , 当 t 为什么值时 , PQ ∥ BC ?（ 3）在 Q 的运动过程中 , 当 Q 运动到什么地点时 , 使△ ADQ 的面积为 9? 求出此时 Q 点的坐标.6．如图在平面直角坐标系中，A （ a ，0），B （ b ，0），（﹣1， 2）．且 |2a+b+1|+ =0．（1）求 a 、 b 的值；（2）①在 y 轴的正半轴上存在一点M，使 S△COM=S△ABC，求点 M的坐标．②在座标轴的其余地点能否存在点M，使 S△COM=S△ABC仍成立？若存在，请直接写出符合条件的点M的坐标．7.如图，在下边的直角坐标系中，已知A（ 0， a）， B（ b，0）， C（ b， 4）三点，此中 a， b知足关系式．（1）求 a， b 的值；（2）假如在第二象限内有一点P（ m，），请用含 m的式子表示四边形 ABOP的面积；（3）在（ 2）的条件下，能否存在点P，使四边形 ABOP的面积与△ ABC 的面积相等？若存在，求出点 P 的坐标；若不存在，请说明原因．8．在平面直角坐标系中，点 A（ a， b）是第四象限内一点， AB⊥y轴于 B，且 B（ 0， b）是 y 轴负半轴上一点， b2=16， S△AOB=12．（1）求点 A 和点 B 的坐标；（2）如图 1，点 D 为线段 OA（端点除外）上某一点，过点 D 作 AO垂线交 x 轴于 E，交直线AB于 F，∠ EOD、∠ AFD 的均分线订交于N，求∠ ONF的度数．（3）如图 2，点 D为线段 OA（端点除外）上某一点，当点 D 在线段上运动时，过点 D 作直线 EF 交 x 轴正半轴于 E，交直线 AB 于 F，∠EOD，∠AFD的均分线订交于点 N．若记∠ ODF=α，请用α的式子表示∠ ONF 的大小，并说明原因．。

七年级平面直角坐标系动点规律问题(经典难题)(可编辑修改word版)

点 A 、 B 、 O 的坐标分别为 1, 0 、 0 , 1 、 0 , 0，点 P1 ， P2 ， P3 ，…中相邻两点都关
于 △ ABO 的一个顶点对称，点 P1 与点 P2 关于点 A 对称，点 P2 与点 P3 关于点 B 对称，点 P3 与点 P4 关于点 O 对称，点 P4 与点 P5 关于点 A 对称，点 P5 与点 P6 关于点 B 对称，点 P6 与点 P7 关于点 O 对称，…对称中心分别是 A ， B ， O ， A ， B ， O ，…且这些对称中心依次
律走下去，当机器人走到 A6 时，A6 的坐标是
．
8、如图，将边长为 1 的正三角形 OAP 沿 x 轴正方向连续翻转 2019 次，点 P 依次落在点
P1, P2 ,, P2019 的位置，则点 P2019 的横坐标为
.
y
P
AO
P1
x
9、如图，在平面直角坐标系上有个点 P（1，0），点 P 第 1 次向上跳动 1 个单位至点
3.如图 3，在平面直角坐标系中，有若干个横、纵坐标分别为整数的点，
其顺序按图中点的坐标分别为（1，0），（2，0），（2，1），（1，1），
（1，2），（2，2），…的规律排列，根据这个规律，第 2019 个点的横坐
标为
．
4．在平面直角坐标系中，一蚂蚁从原点 O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动 1 个单位，其行走路线如下图所示。
C．（0，5）
D．（5，5）
图2 2、如图 2，所有正方形的中心均在坐标原点，且各边与 x 轴或 y 轴平行．从内到外，它们的边长依次为 2，4，6，8，…，顶点依次用 A1，A2，A3，A4，…表示，则顶点 A55 的坐标是（）

平面直角坐标系中的动点问题初一

平面直角坐标系中的动点问题初一
在平面直角坐标系中，动点问题涉及到描述物体运动轨迹和位置变化的问题。

一般情况下，我们使用x轴和y轴来表示平面直角坐标系。

在动点问题中，通常我们需要给出动点的起始位置和速度等运动参数，然后根据问题要求来分析动点的运动轨迹。

举例来说，如果一个物体的起始位置在坐标原点（0,0），它以每秒1单位的速度沿着x轴正方向运动，那么可以通过速度×时间的公式来计算物体在t秒后的位置，即(x,y) = (1t, 0)。

还有一些常见的动点问题，比如：
1. 若动点A在t时刻的位置为(x,y)，那么在t+1时刻的位置是多少？
2. 若动点A在t=0时刻的位置为(0, 0)，它以每秒2单位的速度沿着x轴正方向运动，那么在t秒后的位置是多少？
3. 若动点A在t=0时刻的位置为(0, 2)，它以每秒3单位的速度沿着y轴负方向运动，那么在t秒后的位置是多少？
这些问题的解答需要根据给定的运动参数和问题要求来确定物体的位置变化。

在解答过程中，我们可以运用坐标系中的几何概念和运动学知识来分析和计算。

希望以上内容对你有所帮助！。

七年级期中平面直角坐标系动点问题专项练习

平面直角坐标系动点问题
1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB//y 轴时、求点B 的坐标
二、如图，将边长为1的正三角形OAP 沿x 轴正方向持续翻转2020次，点P 依次落在点
1232008P P P P ，，，
，的位置，那么点2008P 的横坐标为？
3、如图6－7，已知A 、B 两村落的坐标别离为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O 动身．
（1）汽车行驶到什么位置时离A 村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B 村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？
4．如图，在平面直角坐标系中，点A ，B 的坐标别离为（－1，0），（3，0），现同时将点A ，B 别离向上平移2个单位，再向右平移1个单位，别离取得点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．
(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形
(2)在y 轴上是不是存在一点P ，连接PA ，PB ，使PAB S ＝ABDC S 四边形，假设存在如此一点，求出点P 的坐标，假设不存在，试说明理由．
(3)点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）
给出以下结论：①
DCP BOP
CPO
∠+∠
∠
的值不变，②
DCP CPO
BOP
∠+∠
∠
的值不
变，其中有且只有一个是正确的，请你找出那个结论并求其值．。

动点问题经典例题

动点问题经典例题在数轴上，点A从原点出发，以每秒2个单位长度的速度向右运动，同时点B也从原点出发，以每秒3个单位长度的速度向左运动。

经过5秒，A、B两点之间的距离是多少？A. 5个单位长度B. 10个单位长度C. 15个单位长度D. 25个单位长度在一条直线上，甲车以每小时40千米的速度从A地出发向B地行驶，同时乙车以每小时60千米的速度从B地出发向A地行驶。

若A、B两地相距200千米，则两车相遇时，它们各自行驶了多少千米？A. 甲车100千米，乙车100千米B. 甲车80千米，乙车120千米C. 甲车120千米，乙车80千米D. 甲车60千米，乙车140千米在平面直角坐标系中，点P从原点出发，沿x轴正方向以每秒1个单位长度的速度移动。

同时，点Q从点(0,4)出发，沿y轴负方向以每秒2个单位长度的速度移动。

当P、Q两点之间的距离达到5个单位长度时，它们各自移动了多少秒？A. 1秒B. 2秒C. 3秒D. 4秒在一条环形跑道上，甲、乙两人同时同地同向出发进行跑步比赛。

甲的速度是每分钟400米，乙的速度是每分钟500米。

经过多少分钟，两人会再次相遇？A. 1分钟B. 5分钟C. 10分钟D. 无法确定在数轴上，点A和点B分别表示-3和7。

点A以每秒2个单位长度的速度向右移动，同时点B以每秒1个单位长度的速度向左移动。

经过多少秒，A、B两点之间的距离为15个单位长度？A. 2秒B. 4秒C. 6秒D. 8秒在平面直角坐标系中，点A从(0,0)出发，沿x轴正方向以每秒1个单位长度的速度移动。

同时，点B从(4,0)出发，沿x轴负方向以每秒2个单位长度的速度移动。

当A、B两点之间的距离为2个单位长度时，它们各自移动了多少秒？A. 1秒B. 1.5秒C. 2秒D. 2.5秒在一条直线上，甲、乙两人相距100米，甲以每秒6米的速度向乙走去，乙以每秒4米的速度向甲走来。

经过多少秒，甲、乙两人会相遇？A. 5秒B. 10秒C. 15秒D. 20秒在平面直角坐标系中，点P从原点出发，沿x轴正方向以每秒2个单位长度的速度移动。

七年级期中平面直角坐标系动点问题专项练习

平面直角坐标系动点问题
1、已知点A 的坐标是（3，0）、AB=5，（1）当点B 在X 轴上时、求点B 的坐标、（2）当AB//y 轴时、求点B 的坐标
2、如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次，点P 依次落在点
1232008P P P P ，，，
，的位置，则点2008P 的横坐标为？
3、如图6－7，已知A 、B 两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x 轴上行驶，从原点O 出发．
（1）汽车行驶到什么位置时离A 村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B 村最近？写出此点的坐标．（3）请在图中画出汽车行驶到什么位置时，距离两村的和最短？
4．如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．
(1)求点C ，D 的坐标及四边形ABDC 的面积ABDC S 四边形
(2)在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ＝ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．
(3)点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）
给出下列结论：①
DCP BOP
CPO
∠+∠
∠
的值不变，②
DCP CPO
BOP
∠+∠
∠
的值不变，其中有且只
有一个是正确的，请你找出这个结论并求其值．。