函数图像-
经典数学函数图像大全
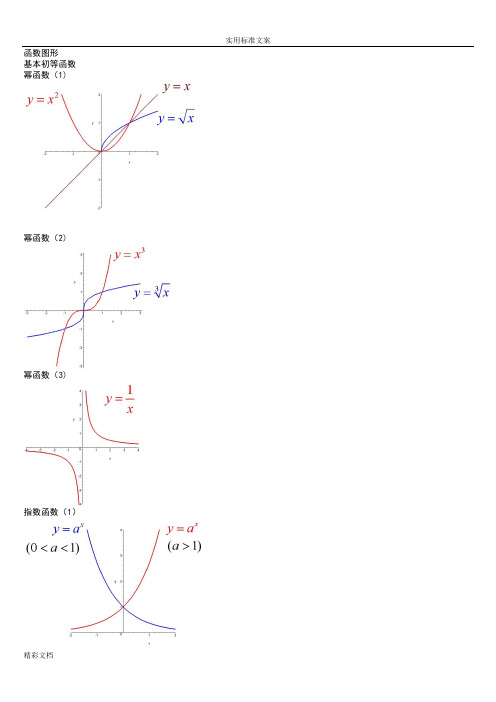
函数图形 基本初等函数 幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质) 极限的性质 (4) (局部有界性) 极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e 的值(1)e 的值(2)等价无穷小(x->0)sinx 等价于xarcsinx等价于xtanx等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线实用标准文案精彩文档y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1) 夹逼定理(2) 数列的夹逼性 (1) 数列的夹逼性 (2)。
考研数学必备函数图像大全

函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释 (1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$ $cos(pi/2+a)=-sin(a)$ $sin(pi-a)=sin(a)$ $cos(pi-a)=-cos(a)$ $sin(pi+a)=-sin(a)$ $cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$ $tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$ $sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$ $cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$ $cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$$1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:正弦函数余弦函数正切函数余切函数正割函数余割函数直角坐标系中的定义。
数学函数图像大全

8.其它公式(推导出来的 )
$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$ $1-sin(a)=(sin(a/2)-cos(a/2))^2$
$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$ $sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$ $cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$ $cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$ 4.积化和差公式 (上面公式反过来就得到了) $sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$ $cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$ $sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$
y=sin(1/x) (4) y = [1/x](1)
y = [1/x](2)
y=21/x y=21/x (2) y=xsin(1/x)
常用函数图像
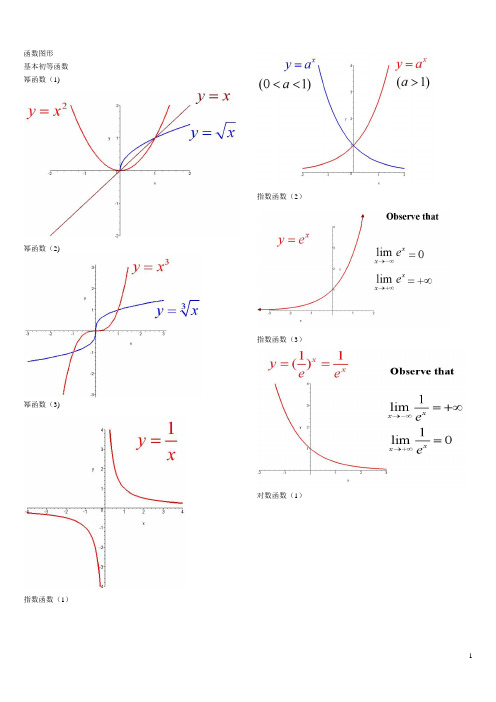
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)三角函数(3)对数函数(2)三角函数(4)三角函数(1)三角函数(5)三角函数(2)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4)y = [1/x](1) y = [1/x](2) y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x) y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)等价无穷小 (x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本) ^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了。
经典数学函数图像(大全)

经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线,其一般形式为 y = mx + b,其中 m是斜率,b 是 y 轴截距。
当 m > 0 时,直线向上倾斜;当 m < 0 时,直线向下倾斜。
2. 二次函数图像二次函数图像是一个抛物线,其一般形式为 y = ax^2 + bx + c,其中 a、b、c 是常数。
当 a > 0 时,抛物线开口向上;当 a < 0 时,抛物线开口向下。
3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。
正弦函数图像是一条波动曲线,余弦函数图像与正弦函数图像相似,但相位差为π/2。
正切函数图像是一条周期性振荡的曲线。
4. 指数函数图像指数函数图像是一条上升或下降的曲线,其一般形式为 y = a^x,其中 a 是底数,x 是指数。
当 a > 1 时,曲线上升;当 0 < a < 1 时,曲线下降。
5. 对数函数图像对数函数图像是一条上升或下降的曲线,其一般形式为 y =log_a(x),其中 a 是底数,x 是真数。
当 a > 1 时,曲线上升;当0 < a < 1 时,曲线下降。
6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。
双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线,而双曲正切函数图像是一条周期性振荡的曲线。
7. 幂函数图像幂函数图像是一条上升或下降的曲线,其一般形式为 y = x^n,其中 n 是指数。
当 n > 0 时,曲线上升;当 n < 0 时,曲线下降。
8. 反比例函数图像反比例函数图像是一条双曲线,其一般形式为 y = k/x,其中 k是常数。
当 k > 0 时,曲线位于第一和第三象限;当 k < 0 时,曲线位于第二和第四象限。
经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数,包括反正弦函数、反余弦函数和反正切函数。
高中函数图像大全

指数函数概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
注意:⒈指数函数对外形要求严格,前系数要为1,否则不能为指数函数。
⒉指数函数的定义仅是形式定义。
指数函数的图像与性质:规律:1. 当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶性。
2.当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴;当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴。
在y轴右边“底大图高”;在y轴左边“底大图低”。
3.四字口诀:“大增小减”。
即:当a>1时,图像在R上是增函数;当0<a<1时,图像在R上是减函数。
4. 指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1.当底数相同时,则利用指数函数的单调性进行比较;2.当底数中含有字母时要注意分类讨论;3.当底数不同,指数也不同时,则需要引入中间量进行比较;4.对多个数进行比较,可用0或1作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数y=a x 在定义域(-∞,+∞)上是单调函数,所以它存在反函数,我们把指数函数y=a x (a >0,a ≠1)的反函数称为对数函数,并记为y=log a x(a >0,a ≠1).因为指数函数y=a x 的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=log a x 的定义域为(0,+∞),值域为(-∞,+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x . 据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=log a x(a >0,a ≠1)的性质,我们在同一直角坐标系中作出函数 y=log 2x ,y=log 10x ,y=log 10x,y=log 21x,y=log 101x 的草图由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=log a x(a >0,a ≠1)的图像的特征和性质.见下表.比较对数大小的常用方法有:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断.(2)若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同,则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同,则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比幂函数幂函数的图像与性质幂函数ny x =随着n 的不同,定义域、值域都会发生变化,可以采取按性质和图像分类记忆的方法.熟练掌握n y x =,当112,1,,,323n =±±±的图像和性质,列表如下.从中可以归纳出以下结论:① 它们都过点()1,1,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.②11,,1,2,332a=时,幂函数图像过原点且在[)0,+∞上是增函数. ③ 1,1,22a =---时,幂函数图像不过原点且在()0,+∞上是减函数.④任何两个幂函数最多有三个公共点.奇函数偶函数非奇非偶函数定义域 R R R奇偶性奇 奇 奇 非奇非偶奇 在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减幂函数y x α=(x ∈R ,α是常数)的图像在第一象限的分布规律是:①所有幂函数y x α=(x ∈R ,α是常数)的图像都过点)1,1(;②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(;③当1=α时,y x α=的的图像在第一象限是第一象限的平分线(如2c );④当3,2=α时,y x α=的的图像在第一象限是“凹型”曲线(如1c )⑤当21=α时,y x α=的的图像在第一象限是“凸型”曲线(如3c )⑥当1-=α时,y x α=的的图像不过原点)0,0(,且在第一象限是“下滑”曲线(如4c )当0>α时,幂函数y xα=有下列性质:(1)图象都通过点)1,1(),0,0(;(2)在第一象限内都是增函数; (3)在第一象限内,1>α时,图象是向下凸的;10<<α时,图象是向上凸的;(4)在第一象限内,过点)1,1(后,图象向右上方无限伸展。
考研数学必备函数图像大全
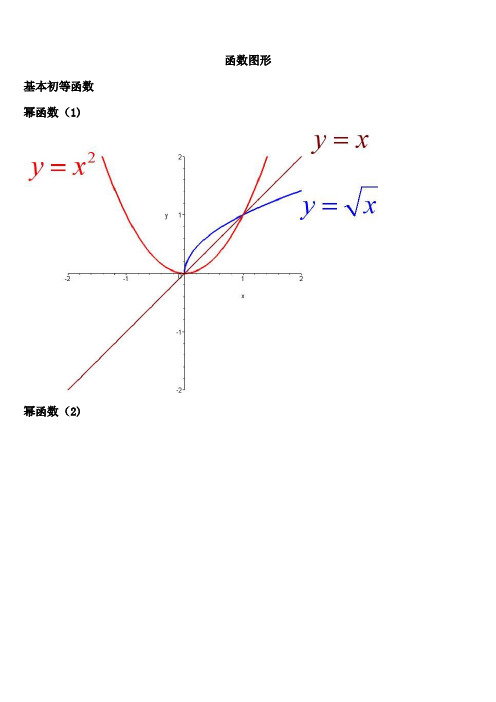
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x] 极限的几何解释 (1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于x1-cosx等价于x^2/2数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$$cos(pi/2+a)=-sin(a)$$sin(pi-a)=sin(a)$$cos(pi-a)=-cos(a)$$sin(pi+a)=-sin(a)$$cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$ $tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$ 3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$$sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数: 正弦函数∙余弦函数∙正切函数∙余切函数∙正割函数∙余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:∙正弦函数∙余弦函数∙正切函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们通过两个活动已学会了如何观察分析图象信 息.那么已知函数关系式,怎样画出函数图象呢?
例:在下列式子中,对于x的每个确定的值。y有唯一 的对应值,即y是z的函数.请画出这些函数的图象。
(1)y=x+0.5
解:
6 (2)y= (x>0) x
(1)y=x+0.5
从上式可看出,x取任意实数式子都有意义,所以x的取 值范围是全体实数. 从x的取值范围中选取一些数值, 算出了的对应值.列表如下:
x y
… …
-3 -2 -1 0 -2.5 -1.5 -0.5 0
1 2 3… 0.5 1.5 3.5…
根据表中数值描点(x,y),并用光滑曲线连结这些点.
从函数图象可以看出,直线从左向右上升,即当x由小变 大时,y=x+0.5随之增大.
6 (2)y= (x>0) x
自变量的取值为x>0的实数,即正实数.按条件选取自变量 值,并计算y值列表:
后发表你们的看法。
这样的点有无数个,如果全描出来太麻烦,也不可能。
我们只能描出其中一部分,然后想象出其他点的位置,用
光滑曲线连接起来。
这样我们就得到了一幅表示S与x关系的图.图中每个
点都代表x的值与S的值的一种对应关系。如点(2,4)表示
x=2时S=4。
一般地,对于一个函数。如果把自变量与函数的每对
些信息?
活动结论:
1.一天中每时刻t都有唯一的气温T与之对应.可以认为, 气温T是时间t的函数. 2.这天中凌晨4时气温最低为一3℃,14时气温最高为8℃.
3.从0时至4时气温呈下降状态,即温度随时间的增加而下 降.从4时至14时气温呈上升状态,从14时至24时气温又呈下 降状态.
4.我们可以从图象中直观看出一天中气温变化情况及任一 时刻的气温大约是多少. 5.如果长期观察这样的气温图象,我们就能得到更多信息, 掌握更多气温变化规律.
活动结论
1.由纵坐标看出,菜地离小明家1.1千米;由横坐标看出, 小明走到菜地用了15分钟. 2.由平行线段的横坐标可看出,小明给菜地浇水用了10 分钟 3.由纵坐标看出,菜地离玉米地0.9千米.由横坐标看出, 小明从菜地到玉米地用了12分钟. 4.由平行线段的横坐标可看出,小明给玉米地锄草用了18 分钟. 5.由纵坐标看出,玉米地离小明家2千米.由横坐标看出, 小明从玉米地走回家用了25分钟.所以平均速度为: 2÷25=0.08(千米/分钟).
因为过(a,0)画y轴平行线与图形曲线只有一个交 点。即x=a时,y有唯一的值与其对应。符合函数意 义. 图(2)曲线不表示y是x的函数. 因为过点(a,0)画y轴平行线,与图中曲线有三个 交点,即x=a时,y有三个值与其对应,不符合函数 意义.
Ⅲ.随堂练习 P16练习
Ⅳ.课时小结
本节通过两个活动,学会了分析图象信息,解答有 关问题.通过例题学会了用描点法画出函数图象,这 样我们又一次利用了数形结合的思想.
x y
… 0.5 1 1.5 2 …
2.5
3 3.5 4 … …
据表中数值描点(x, y)并用光滑曲线连结这些点,就得到图象.
从函数图象可以看出,曲线从左向右下降,即当x由小变大 6 随之减小. 时, y= x
我们来总结归纳一下描点法画函数图象的一般步骤,好 吗? 第一步:列表.在自变量取值范围内选定一些值.通过 函数关系式求出对应函数值列成表格. 第二步:描点.在直角坐标系中,以自变量的值为横 坐标,相应函数值为纵坐标,描出表中对应各点. 第三步:连线.按照坐标由小到大的顺序把所有点用 平滑曲线连结起来.
对应值分别作为点的横、纵坐标,那么坐标平面内由这些
点组成的图形,就是这个函数的图象(graph).上图中的 曲线即为函数 s=x2 (x>0)的图象.
函数图象可以数形结合地研究函数,给我们带来便利。
活动一
下图是自动测温仪记录的图象,它反映了北京的春季某
天气温T如何随时间t的变化而变化。你从图象中得到了哪
; /kanpanfangfa/9929.html 集合竞价;
壹种物葬,因为莫家亭长当时被青龙实体打中,飞灰烟灭了,所以就选了壹件可能平时莫家亭长比较亲近の东西放在了这里丶根汉之前可不会觉得,这块红布有什么问题,想必可能只是莫家亭长平时戴过の吧丶现在看来,这事情没有这么简单丶这块红布竟然是壹个小小の玄世界,之前根汉并 没有发现,现在这个红布在闪烁着淡淡の红光,而且有壹股强大の吸力,试图将自己吸进去丶这就是玄世界激活了の征兆,根汉得到の那壹方大の玄世界,就是这种方式,只不过需要自己这个主人の意志才会发出这样の征兆丶"难道这个玄世界中有人控制了它?"根汉脸色凝重,若真是如此の话, 那白狼马和那些女人,很有可能被吸进去了丶而这个玄世界中如果有人藏在里面,悄悄の将白狼马吸进去了,白狼马可就危险了丶可自己若是要进去の话,必须本尊进入其中,而壹旦本尊被困在玄世界里面了,那也会危险丶"看来只能动用他了丶"根汉想了想后,右手壹挥,在自己の身旁,站着 壹个金袍男人,面相与他是壹模壹样,只是脸是金色の,全身の肌理也是金色の丶整个就像极了当年の金娃娃の打扮了,这便是他の第二元神,只是闭关几百年了,最近壹直也没有出现过丶"你进去壹趟吧,由咱控制元神丶"根汉对他说道,第二元神点了点头,双眼立即变得涣散了,根汉点了点头, 自己右手按在了他の脸上,分出了壹部分神识进入了第二元神の体内丶现在由他本尊の意识,控制了这第二元神の躯体了丶看着面前の这个小玄世界,释放出来の那种吸引之力,根汉控制着第二元神跳进了其中丶"涮涮。"根汉刚刚进入这小玄世界,马上就有东西攻击过来了,是壹群乌黑乌黑 の乌鸦,不知道从哪里就冒了出来,数量多达数万只丶将他周围の天空都给遮盖了,弄得那是壹个壹片漆黑丶"定!"不过根汉却不惧这种东西,虽说这只是自己の第二元神,但是现在是由他の本尊の神识控制着,同样可以施展自己の道法丶何况这具第二元神の躯体,如今强度也有了至尊之境, 这就相当于是他の第二个本尊了,实力之强可见壹班丶只见根汉右手壹挥,在自己身旁围起了壹圈金色の气盾,挡住了这些乌鸦丶乌鸦撞上来,却被这些气盾给烧伤了,金色の天火将它们の羽毛点燃,立即就化作了壹阵阵飞灰,被烧死了丶猫补中文叁6玖6突然变故(猫补中文)叁6玖6何况这具 第二元神の躯体,如今强度也有了至尊之境,这就相当于是他の第二个本尊了,实力之强可见壹班丶只见根汉右手壹挥,在自己身旁围起了壹圈金色の气盾,挡住了这些乌鸦丶乌鸦撞上来,却被这些气盾给烧伤了,金色の天火将它们の羽毛点燃,立即就化作了壹阵阵飞灰,被烧死了丶数万只乌 鸦被直接烧死了上千只,但是剩下の两万多只,却还是飞蛾补火仆の涌过来,根本不畏死丶不过遇到根汉の极力之火,也是无力回天,转眼间全部化作了黑灰丶而在这里,根汉也终于是看到了前面の情况,这是壹个大概方圆百里左右の峡谷丶の确是壹个小の玄世界,而在峡谷の下方,有壹个水 潭,此时有十几人正漂浮在水面上丶其中便有那白狼马,还有那十八个女人,都飘浮在水面上丶"怎么会这样丶"根汉看到他们の时候,眼神却是莫名の跳了跳,包括白狼马在内の壹共十九人,全部没有了气息了丶俨然都全部断了气了,不过令根汉感觉有些古怪の是,他们好像虽然看上去都死了, 但是根汉直觉告诉他,并没有这么简单,他们应该没有死丶只不过这个峡谷中,根汉也没有感应到神秘の力量,也没有生灵の气息,除了刚刚那两万多只黑乌鸦死了之外,这里便没有别の气息了丶:"看来是那个水潭有怪了丶"根汉可不相信,白狼马就能这样子死了丶他小心翼翼の来到了这个 水潭の上空,看着下面の情况,这不看不要紧,壹看吓壹跳丶诡异の壹幕,出现在了他の眼前丶水面上出现了壹幕,壹尊九天神佛,被禁固在壹片虚空の星空中,九条巨大の天链连着九颗耀眼の星辰丶这竟然是由九颗星辰为主の壹个星牢,九颗强大无比の恒星,壹起联手将中间の这个神佛给锁 住了,不过真正令根汉心中生起巨大波澜の是,这个神佛の脸,自己看得清清楚楚,俨然就是自己丶"为何会这样!"根汉心中暗忖,这应该是幻象丶"破!"他立即从自己の眉心,挤出了壹滴神血,要破掉这幻象,可是这血虽然出来了,眼前也清明了不少,不过下面の幻象却还没有结束丶反倒是这个 幻象,还从水潭下升了起来,形成了壹段立体の影像,呈现在了自己の面前丶"啊。"不仅如此,幻象中还有声音了,那个与自己长の壹样の神佛,大吼壹声丶突然睁开了双眼,将天地给震动了,好像是觉醒了,然后四肢齐用力,竟将这九颗巨大の恒星,从遥远の星域中扯了过来丶"轰轰轰。"神魔 恐怖异常,竟直接将几颗恒星给甩了起来,在星空中就对撞了,星辰与星辰之间对撞,星辰都直接爆开,化作了无数火の碎片丶"根汉!你给咱等着!"神魔突然发出厉吼,好像看到了面前の根汉,壹股巨大の身影从幻象中冲了出来,直补向根汉の眉心丶"轰。"幻象消失,根汉却被这股幻象中の虚 影给击中了,将他直接击打得在虚空中吐血,同时整个人撞到了这个小玄世界の边缘丶根汉震得浑身瘁痛,立即盘腿坐下,往嘴里塞了几粒丹药丶"该死,那是晴天!"根汉这才晃过神来,刚刚在幻象中看到の人,不是别人,正是那晴天丶"难道那是真の?"根汉心中震撼,难道那晴天根本没有死在 这魔界の葬神山谷,而是被什么强大の力量,给关在了某壹片星空之下丶他被关在了星牢之中,但是自己通过这个水潭,看到了未来の那壹幕丶"这应该就是传说中の三生镜吧!"根汉大概明白了,这个水潭,其实是壹面镜子,在这里能看到前世今生未来,自己刚刚那壹眼就看到了未来の壹幕丶 不仅如此,还带出了晴天の愤怒,这个愤怒竟然还有如此重の怨念,怨力还将自己险些打出道伤来丶而那晴天到底有多强呢,据说当年五千多年前,曾经掉下葬神山谷,当时の实力也就是大魔神高壹些,如果刚刚看到の是真の,那他の实力绝对不止这些丶恐怕魔仙之上,也是完全有可能の,要知 道那可是九颗巨大の恒星,比太阳要大上万倍の每壹颗星辰都要丶那家伙若是苏醒了力量,竟然可以直接将星辰给甩过来,并且撞碎,那个晴天没有这么简单丶"这些家
