高数基本初等函数图像及性质 (1)

六大基本初等函数图像及其性质

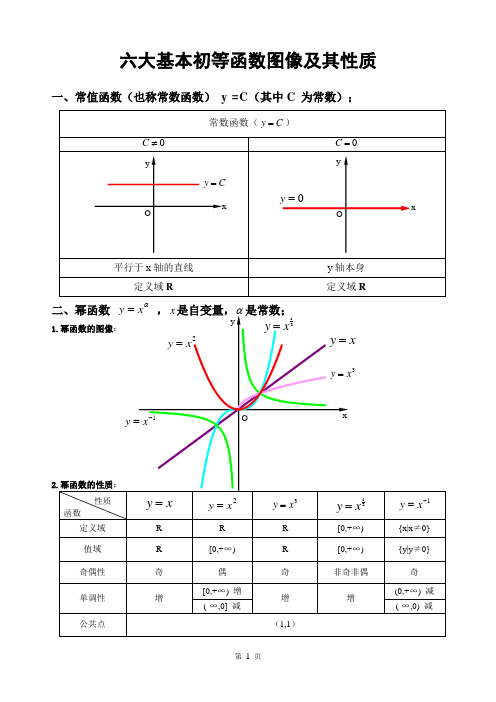
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

(完整版)基本初等函数的图形及性质

初等函数1、基本初等函数及图形基本初等函数为以下五类函数：(1)幂函数y x，是常数；1. 当 u 为正整数时，函数的定义域为区间x ( , )，他们的图形都经过原点，并当u>1 时在原点处与 X 轴相切。

且 u 为奇数时，图形对于原点对称；u 为偶数时图形对于 Y 轴对称；2. 当 u 为负整数时。

函数的定义域为除掉x=0 的全部实数。

3. 当 u 为正有理数 m/n 时， n 为偶数时函数的定义域为（0, + ）， n 为奇数时函数的定义域为（- + ）。

函数的图形均经过原点和（ 1 ,1）.假如 m>n 图形于 x 轴相切 ,假如 m<n,图形于 y 轴相切 ,且 m 为偶数时 ,还跟 y 轴对称 ;m,n 均为奇数时 ,跟原点对称.4.当 u 为负有理数时 ,n 为偶数时除 x=0 之外的一确实数.,函数的定义域为大于零的一确实数;n 为奇数时,定义域为去(2)指数函数y ax(a是常数且a 0，a 1)，x ( , )；1.当 a>1 时函数为单一增 ,当 a<1 时函数为单一减 .2.无论 x 为什么值 ,y 老是正的 ,图形在 x 轴上方 .3.当 x=0 时,y=1, 因此他的图形经过 (0,1)点 .(3)对数函数y logax(a是常数且a 0，a 1)，x (0, )；1.他的图形为于 y 轴的右方 .并经过点 (1,0)2.当 a>1 时在区间 (0,1),y 的值为负 .图形位于 x 的下方 ,在区间(1, + ),y 值为正 ,图形位于 x 轴上方 .在定义域是单一增函数 .a<1 在适用中极少用到 /(4)三角函数正弦函数y sin x ， x ( , ) ， y[ 1,1] ，余弦函数y cos x ，x( , ) ， y[ 1,1] ，x kZ ，y (, ) ，正切函数y tan x ， 2 ，k余切函数y cot x，x k，k Z，y ( , )；(5)反三角函数y arcsin x ，x [ 1,1] y [ , ]反正弦函数， 2 2 ，反余弦函数y arccosx ，x[ 1,1] ， y [0,] ，y arctan x ，x ( , ) y ( , )反正切函数， 2 2 ，反余切函数y arc cot x ，x(, ) ， y (0,) ．函数名称函数的记号函数的图形指数函数对数函数幂函数a 为随意实数这里只画出部分函数图形的一部分。

高数总结：基本初等函数图像及其性质

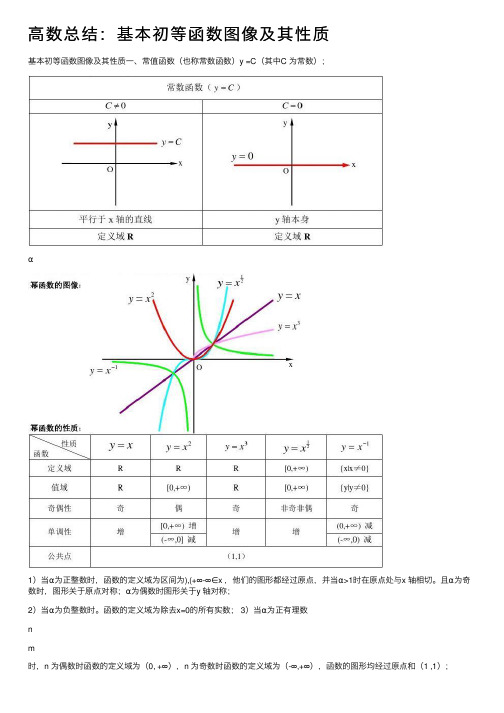
⾼数总结：基本初等函数图像及其性质基本初等函数图像及其性质⼀、常值函数（也称常数函数）y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数n4）如果m>n 图形于x 轴相切，如果m5）当α为负有理数时，n 为偶数时，函数的定义域为⼤于零的⼀切实数；n 为奇数时，定义域为去除x=0以外的⼀切实数。

三、指数函数xa y =(x 是⾃变量,a 是常数且0>a ，1≠a )，定义域是R ；[⽆界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上⽅； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的⼤⼩⽐较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ?=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越⼤，xa y =的图像越靠近y 轴；b.2.当10<的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=?m n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m n m(2))1,,,0(11*>∈>==-n Z n m a a amnm nm yxf x xxx g ?=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [⽆界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式⼦N a log 叫做对数式。

五大基本初等函数性质及其图像

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。

如，，，都是幂函数。

没有统一的定义域，定义域由值确定。

如,。

但在内总是有定义的，且都经过（1,1）点。

当时，函数在上是单调增加的，当时，函数在内是单调减少的。

下面给出几个常用的幂函数：的图形，如图1-1-2、图1-1-3。

图1-1-2图1-1-32.指数函数函数称为指数函数，定义域，值域；当时函数为单调增加的；当时为单调减少的，曲线过点。

高等数学中常用的指数函数是时，即。

以与为例绘出图形，如图1-1-4。

图1-1-43.对数函数函数称为对数函数，其定义域，值域。

当时单调增加，当时单调减少，曲线过（1，0）点，都在右半平面内。

与互为反函数。

当时的对数函数称为自然对数，当时，称为常用对数。

以为例绘出图形，如图1-1-5。

图1-1-54.三角函数有，它们都是周期函数。

对三角函数作简要的叙述：（１）正弦函数与余弦函数：与定义域都是，值域都是。

它们都是有界函数，周期都是，为奇函数，为偶函数。

图形为图1-1-6、图1-1-7。

图1-1-6 正弦函数图形图1-1-7 余弦函数图形（２）正切函数，定义域，值域为。

周期，在其定义域内单调增加的奇函数，图形为图1-1-8图1-1-8（３）余切函数，定义域，值域为，周期。

在定义域内是单调减少的奇函数，图形如图1-1-9。

图1-1-9（４）正割函数，定义域，值域为，为无界函数，周期的偶函数，图形如图1-1-10。

图1-1-10（５）余割函数，定义域，值域为，为无界函数，周期在定义域为奇函数，图形如图1-1-11。

图1-1-115.反三角函数反正弦函数，定义域，值域，为有界函数，在其定义域内是单调增加的奇函数，图形如图1-1-12；图1-1-12，为有界函数，在其定义域内为单调减少的非奇非偶函数，图形如图1-1-13；图1-1-13反正切函数，定义域，值域为，为有界函数，在定义域内是单调增加的奇函数，图形如图1-1-14；图1-1-14为有界函数，在其定义域内单调减少的非奇非偶函数。

高数第一章初等函数

2）反余弦函数余弦函数
反余弦函数
y cos x
y
1
0

2
x [0, ]
y arccos x x [1,1]
y

y [1,1]
y [0, ]

x
1
1
0
x 1
余弦函数 y cos x 在 [0, ] 上的反函数，称为
反余弦函数，记为 y arccos x x [1,1] y [0, ]
10
例2 判断函数 f ( x) ln ( x 2 1 x) 的奇偶性. 解
f x f x
ln [ x 2 1 x] [ x 2 1 x]

ln1 0
则此函数为奇函数
11
（4）三角函数 1）正弦函数的性质
y sin x
x ,
解：
x e ln x , x 0

ln x 1 0 e 1 f ln x ln x ln x e e 1
ye
y
x
1 f x x e
0 e 1
x
e 1
x
0,1
x
1 x 0 f x x e 0 x
22
反余弦函数的性质
y arccos x
x [1,1]
y

y [0, ]
（1）在[ -1, 1 ]是有界函数；
0 arccos x
（2）是非奇非偶函数；
1
0
x 1
（3）在 [1, 1] 上是单调减函数。
23
3）反正切函数正切函数 y tan x 在 (

六大基本初等函数图像及其性质

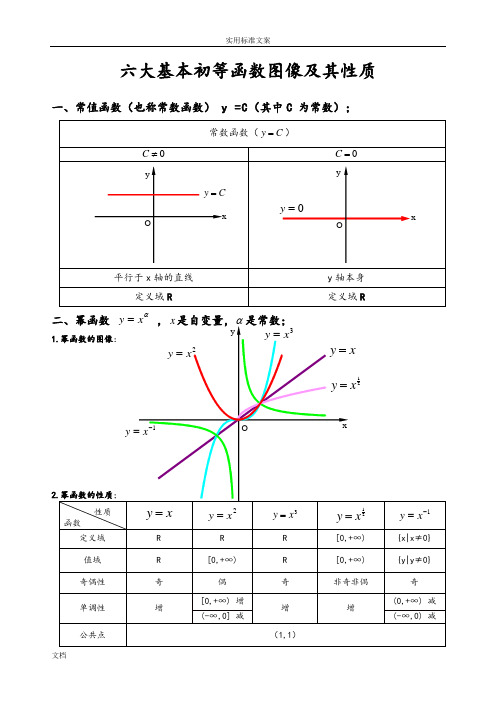
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

基本初等函数图像及性质小结

为高等数学小结的——基本初等函数1.函数的五个要素：自变量，因变量，定义域，值域，对应法则2.函数的四种特性：有界限，单调性，奇偶性，周期性复习的时候一定要从这四个方面去研究函数。

3.每个函数的图像很重要. 幂函数(a为实数)定义域：随a的不同而不同，但无论a取什么值，x^a在内总有定义。

值域：随a的不同而不同有界性：单调性：若a>0,函数在内单调增加；若a<0,函数在内单调减少。

奇偶性：要知道这些函数那些事奇函数，那些是偶函数周期性：每种函数的图像.. 指数函数定义域：值域：有界性：单调性：若a>1 函数单调增加；若0<a<1 函数单调减少奇偶性：周期性：注意：图形过（0，1）点暨 a^0=1 直线y=0为函数图形的水平渐近线今后用的较多这个函数的图形，性质要记清楚1、. 对数函数1、定义域：值域：有界性：单调性：a>1时，函数单调增加；0<a<1时，函数单调减少奇偶性：周期性：主要性质：与指数函数互为反函数，图形过（1，0）点，直线x=0为函数图形的铅直渐近线e=2.7182……，无理数经常用到以e为底的对数. 三角函数强调：图像定义域：值域：[-1,1]有界性：[-1,1] 有界函数单调性：（-T/2,T/2）单调递增奇偶性：奇函数周期性：以为周期的周期函数；定义域：值域：[-1,1] 有界性：[-1,1] 有界函数单调性：奇偶性：偶函数周期性：定义域：值域：有界性：单调性：奇偶性：奇函数周期性：，定义域：值域：有界性：单调性：奇偶性：奇函数周期性：，. 反三角函数定义域： [-1,1] 值域：有界性：单调性：单调增加奇偶性：奇函数周期性：---定义域值域：定义域： [-1,1] 值域：有界性：单调性：单调减少奇偶性：周期性：---定义域定义域：值域：有界性：单调性：单调增加奇偶性：奇函数周期性：---定义域定义域：值域：有界性：单调性：单调减少；奇偶性：周期性：以上是五种基本初等函数，关于它们的常用运算公式都应掌握。

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

六大基本初等函数图像及其性质

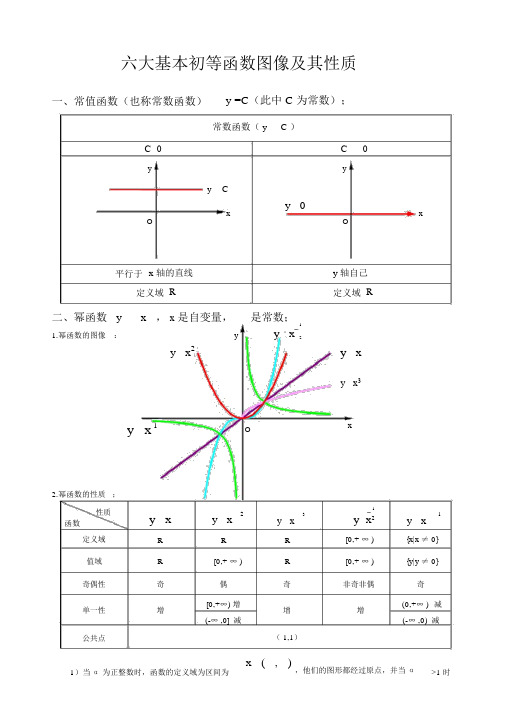
六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（此中 C 为常数）；常数函数（ y C ）C 0C0y yy Cx y 0xO O平行于x 轴的直线y 轴自己定义域R定义域R 二、幂函数 y x ，x是自变量，是常数；1y y x1.幂函数的图像：2y x2y xy x3y x1O x2.幂函数的性质；性质y x y x231y x1y x y x2函数定义域R R R[0,+ ∞ ){x|x ≠ 0}值域R[0,+ ∞ )R[0,+ ∞ ){y|y ≠ 0}奇偶性奇偶奇非奇非偶奇单一性增[0,+∞) 增增增(0,+∞ )减(-∞ ,0] 减(-∞ ,0)减公共点（ 1,1）1）当α为正整数时，函数的定义域为区间为x ( , )，他们的图形都经过原点，并当α>1 时在原点处与x 轴相切。

且α为奇数时，图形对于原点对称；α为偶数时图形对于y 轴对称；2）当α为负整数时。

函数的定义域为除掉x=0 的全部实数；3）当α为正有理数m时，n为偶数时函数的定义域为（0, +∞），n为奇数时函数的定义域为（-n∞ ,+∞），函数的图形均经过原点和（ 1 ,1）；4）假如 m>n 图形于 x 轴相切，假如m<n,图形于 y 轴相切，且m 为偶数时，还跟y 轴对称； m， n均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一确实数；n 为奇数时，定义域为去除 x=0 之外的一确实数。

三、指数函数 y a x(x是自变量,a是常数且a0， a1)，定义域是 R ；[ 无界函数 ]1.指数函数的图象：yy a x y a xy(a 1)(0a1)(0,1)y1(0,1)y1 O x O x2.指数函数的性质；性质y a x(a1)y a x(0 a 1)函数定义域R值域(0，+∞)奇偶性非奇非偶公共点过点 (0，1)，即 x0 时，y 1单一性在（，）是增函数在（，）是减函数1 ）当a 1时函数为单调增 , 当0a 1时函数为单调减；2 ）不论x为何值 ,y 总是正的,图形在 x 轴上方；3 ）当x 0时 , y 1, 所以它的图形通过 (0,1) 点。

(完整版)六大基本初等函数图像与性质

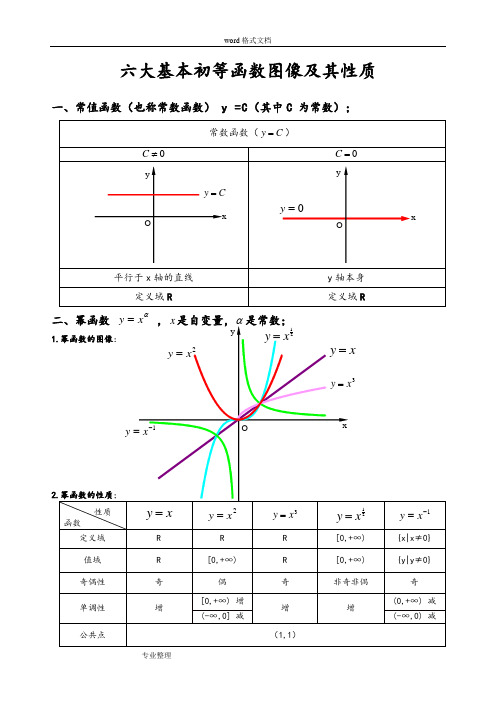
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

五大基本初等函数性质及其图像

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。

如，，，都是幂函数。

没有统一的定义域，定义域由值确定。

如,。

但在内总是有定义的，且都经过（1,1）点。

当时，函数在上是单调增加的，当时，函数在内是单调减少的。

下面给出几个常用的幂函数：的图形，如图1-1-2、图1-1-3。

图1-1-2图1-1-32.指数函数函数称为指数函数，定义域，值域；当时函数为单调增加的；当时为单调减少的，曲线过点。

高等数学中常用的指数函数是时，即。

以与为例绘出图形，如图1-1-4。

图1-1-43.对数函数函数称为对数函数，其定义域，值域。

当时单调增加，当时单调减少，曲线过（1，0）点，都在右半平面内。

与互为反函数。

当时的对数函数称为自然对数，当时，称为常用对数。

以为例绘出图形，如图1-1-5。

图1-1-54.三角函数有，它们都是周期函数。

对三角函数作简要的叙述：（１）正弦函数与余弦函数：与定义域都是，值域都是。

它们都是有界函数，周期都是，为奇函数，为偶函数。

图形为图1-1-6、图1-1-7。

图1-1-6 正弦函数图形图1-1-7 余弦函数图形（２）正切函数，定义域，值域为。

周期，在其定义域内单调增加的奇函数，图形为图1-1-8图1-1-8（３）余切函数，定义域，值域为，周期。

在定义域内是单调减少的奇函数，图形如图1-1-9。

图1-1-9（４）正割函数，定义域，值域为，为无界函数，周期的偶函数，图形如图1-1-10。

图1-1-10（５）余割函数，定义域，值域为，为无界函数，周期在定义域为奇函数，图形如图1-1-11。

图1-1-115.反三角函数反正弦函数，定义域，值域，为有界函数，在其定义域内是单调增加的奇函数，图形如图1-1-12；图1-1-12，为有界函数，在其定义域内为单调减少的非奇非偶函数，图形如图1-1-13；图1-1-13反正切函数，定义域，值域为，为有界函数，在定义域内是单调增加的奇函数，图形如图1-1-14；图1-1-14为有界函数，在其定义域内单调减少的非奇非偶函数。

初等函数图像知识点总结

初等函数图像知识点总结在学习初等函数的过程中，图像是一个非常重要的概念。

初等函数的图像可以帮助我们更直观地理解函数的性质和特点。

在本文中，我们将总结初等函数图像的相关知识点，包括函数图像的基本形状、对称性质、特殊点以及常见的初等函数图像等内容。

一、函数图像的基本形状1. 直线函数的图像直线函数的图像是一条直线，其一般方程为y = kx + b，其中k和b分别代表斜率和截距。

斜率k决定了直线的倾斜方向和程度，当k>0时，直线向右上方倾斜；当k<0时，直线向右下方倾斜。

截距b决定了直线与y轴的交点，当b>0时，直线与y轴的交点在y轴上方；当b<0时，直线与y轴的交点在y轴下方。

2. 平方函数的图像平方函数的图像是一个开口向上或向下的抛物线，其一般方程为y = ax^2 + bx + c，其中a决定了抛物线的开口方向和程度。

当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

二次函数的顶点坐标为(-b/2a, c)，可以通过顶点坐标确定抛物线的位置。

3. 绝对值函数的图像绝对值函数的图像是一条V形的折线，其一般方程为y = |x|，表示x的绝对值。

函数图像在原点处有一个拐点，称为折点，折点是函数图像的特殊点之一。

4. 根号函数的图像根号函数的图像是一条从原点开始的曲线，其一般方程为y = √x，函数图像在x轴的正半轴上。

根号函数的图像是一个开口向右的半圆形曲线。

5. 指数函数的图像指数函数的图像是一条增长或衰减的曲线，其一般方程为y = a^x，其中a>0且a≠1。

指数函数的图像在坐标轴之间没有交点，增长函数的图像是向上的曲线，衰减函数的图像是向下的曲线。

6. 对数函数的图像对数函数的图像是一条先增后减的曲线，其一般方程为y = log_ax，其中a>0且a≠1。

对数函数的图像在x轴的正半轴上，对数函数的图像与指数函数的图像是关于y=x对称的。

二、函数图像的对称性质1. 奇偶性奇函数的图像关于原点对称，即f(-x)=-f(x)，即图像关于原点对称。

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（此中 C 为常数）；常数函数（ y C ）C 0C0y yy Cx y 0xO O平行于x 轴的直线y 轴自己定义域R定义域R 二、幂函数 y x ，x是自变量，是常数；1y y x1.幂函数的图像：2y x2y xy x3y x1O x2.幂函数的性质；性质y x y x231y x1y x y x2函数定义域R R R[0,+ ∞ ){x|x ≠ 0}值域R[0,+ ∞ )R[0,+ ∞ ){y|y ≠ 0}奇偶性奇偶奇非奇非偶奇单一性增[0,+∞) 增增增(0,+∞ )减(-∞ ,0] 减(-∞ ,0)减公共点（ 1,1）1）当α为正整数时，函数的定义域为区间为x ( , )，他们的图形都经过原点，并当α>1 时在原点处与x 轴相切。

且α为奇数时，图形对于原点对称；α为偶数时图形对于y 轴对称；2）当α为负整数时。

函数的定义域为除掉x=0 的全部实数；3）当α为正有理数m时，n为偶数时函数的定义域为（0, +∞），n为奇数时函数的定义域为（-n∞ ,+∞），函数的图形均经过原点和（ 1 ,1）；4）假如 m>n 图形于 x 轴相切，假如m<n,图形于 y 轴相切，且m 为偶数时，还跟y 轴对称； m， n均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一确实数；n 为奇数时，定义域为去除 x=0 之外的一确实数。

三、指数函数 y a x(x是自变量,a是常数且a0， a1)，定义域是 R ；[ 无界函数 ]1.指数函数的图象：yy a x y a xy(a 1)(0a1)(0,1)y1(0,1)y1 O x O x2.指数函数的性质；性质y a x(a1)y a x(0 a 1)函数定义域R值域(0，+∞)奇偶性非奇非偶公共点过点 (0，1)，即 x0 时，y 1单一性在（，）是增函数在（，）是减函数1 ）当a 1时函数为单调增 , 当0a 1时函数为单调减；2 ）不论x为何值 ,y 总是正的,图形在 x 轴上方；3 ）当x 0时 , y 1, 所以它的图形通过 (0,1) 点。

六大基本初等函数图像与其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C （其中 C 为常数）；常数函数（ y C ）C 0yy Cy 0xO平行于 x 轴的直线定义域 R二、幂函数 y x， x 是自变量，是常数；1. 幂函数的图像：y y x3y x2y x1O2.幂函数的性质；性质y x y x2y x3函数定义域R R R值域R[0,+ ∞ )R奇偶性奇偶奇单调性增[0,+ ∞) 增增(-∞ ,0]减公共点（ 1,1）C 0yOy轴本身定义域 Ry x1y x 2x1y x 2[0,+ ∞ )[0,+ ∞ )非奇非偶增xy x 1{x|x ≠ 0}{y|y ≠ 0}奇(0,+∞) 减(-∞ ,0) 减第 1 页1）当 α 为正整数时，函数的定义域为区间为x ( ,)，他们的图形都经过原点，并当α >1 时在原点处与 x 轴相切。

且 α为奇数时，图形关于原点对称；α 为偶数时图形关于 y 轴对称；2）当 α 为负整数时。

函数的定义域为除去 x=0 的所有实数；3）当 α 为正有理数m时， n 为偶数时函数的定义域为（0, +∞）， n 为奇数时函数的定义域为（ -n∞ ,+∞），函数的图形均经过原点和（ 1 ,1）；4）如果 m>n 图形于 x 轴相切，如果m<n,图形于 y 轴相切，且 m 为偶数时，还跟y 轴对称； m ， n均为奇数时，跟原点对称；5）当 α 为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数ya x(x 是自变量,a 是常数且a0 ， a1 )，定义域是R ；[ 无界函数 ]1. 指数函数的图象：yaxyyy ax(a 1)(0 a1)(0,1)y 1(0,1)y 1OxOx2. 指数函数的性质；性质y a x(a 1)y a x(0 a 1)函数定义域 R值域(0，+∞)奇偶性非奇非偶公共点过点 (0，1)，即 x 0 时， y1单调性在（，）是增函数（，）在是减函数1 ）当 a1时函数为单调增 , 当 0 a 1时函数为单调减；2 ）不论 x 为何值 , y 总是正的 , 图形在 x 轴上方；3 ）当 x 0 时 , y1,所以它的图形通过(0,1)点。

（完整）六大基本初等函数图像及其性质

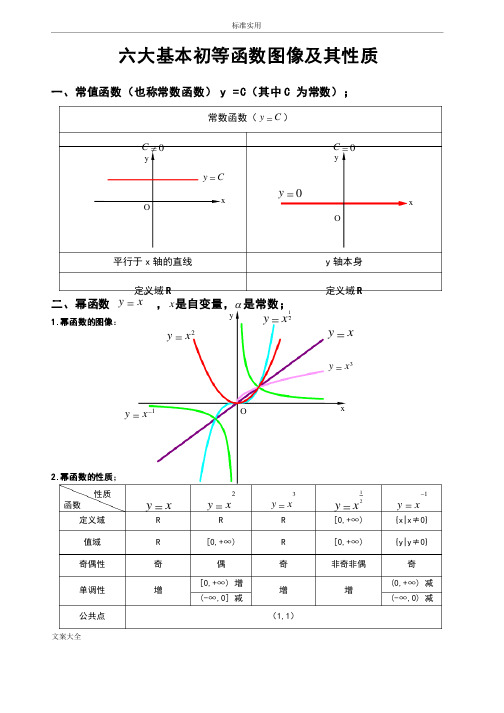
标准实用文案大全六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）≠C 0=C 平行于x 轴的直线y 轴本身定义域R 定义域R二、幂函数αx y=，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数xy =2xy =3xy =21x y =1-=xy 定义域R R R [0,+[0,+∞∞) {x|x {x|x≠≠0} 值域R [0,+[0,+∞∞) R [0,+[0,+∞∞) {y|y {y|y≠≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+[0,+∞∞) ) 增增增增(0,+(0,+∞∞) ) 减减(-(-∞∞,0] ,0] 减减(-(-∞∞,0) ,0) 减减公共点（1,11,1））xyOxy =2x y =3x y =1-=x y 21x y =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α，他们的图形都经过原点，并当α>1>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm 时，时，n n 为偶数时函数的定义域为（为偶数时函数的定义域为（0, +0, +0, +∞），∞），∞），n n 为奇数时函数的定义域为（为奇数时函数的定义域为（--∞,+,+∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（1 ,11 ,11 ,1）；）；4）如果m>n 图形于x 轴相切，如果m<n,m<n,图形于图形于y 轴相切，且m 为偶数时，还跟y 轴对称；轴对称；m m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，）当α为负有理数时，n n 为偶数时，函数的定义域为大于零的一切实数；为偶数时，函数的定义域为大于零的一切实数；n n 为奇数时，定义域为去除x=0以外的一切实数。

4、基本初等函数图像及其性质

基本初等函数图像以及性质一、指数函数的图象及性质函数y ＝a x (a >0，且a ≠1)图象0<a <1a >1图象特征在x 轴上方，过定点(0，1)当x 逐渐增大时，图象逐渐下降当x 逐渐增大时，图象逐渐上升性质定义域 R 值域(0，＋∞)单调性减增函数值变化规律当x ＝0时，y ＝1当x <0时，y >1；当x >0时，0<y <1当x <0时，0<y <1；当x >0时，y >1在同一平面直角坐标系中，分别作出指数函数y ＝a x ，y ＝b x ，y ＝c x ，y ＝d x (a ＞1，b ＞1，0＜c ＜1，0＜d ＜1)的图象，如图所示．作出直线x ＝1，分别与四个图象自上而下交于点A (1，a )，B (1，b )，C (1，c )，D (1，d )，得到底数的大小关系是：a ＞b ＞1＞c ＞d ＞0.根据y 轴右侧的图象，也可以利用口诀：“底大图高”来记忆．考点一指数函数的图像例1、如果函数在R 上是减函数，那么实数a 的取值范围是（） A ．｜a ｜＞ B ．＜｜a ｜＜ C ．｜a ｜＞ D ．｜a ｜＜3x a x f )2()(2-=22331、已知指数函数(0,1)x y a a a =>≠在[]1,2上的最大值比最小值大2a，则a =例2、函数y ＝a x －a －1(a >0且a ≠1)的图象可能是( )A BC D1、函数f (x )＝21－x 的大致图象为( )2、函数y＝xa x|x|(a>1)的图象大致是()例3、若函数f(x)＝|2x－2|－b有两个零点，则实数b的取值范围是________．1、若方程|3x－1|＝k有一解，则k的取值范围为________．2、若函数y＝21－x＋m的图象不经过第一象限，则m的取值范围为________．考点二指数函数单调性的应用例4、设a＝0.60.6，b＝0.61.5，c＝1.50.6，则a，b，c的大小关系是() A．a<b<c B．a<c<bC．b<a<c D．b<c<a1、已知函数f(x)＝a x＋b(a＞0，a≠1)的定义域和值域都是[－1，0]，则a＋b＝________．2、如果函数y＝a2x＋2a x－1(a>0，a≠1)在区间[－1，1]上的最大值是14，则a 的值为()A.13B．1C．3 D.13或33、(2017·合肥模拟)若2x＋5y≤2－y＋5－x，则有() A．x＋y≥0 B．x＋y≤0C．x－y≤0 D．x－y≥0 对数函数的图象与性质定义域：(0，＋∞)在同一平面直角坐标系中，分别作出对数函数y＝log a x，y＝log b x，y＝log c x，y＝log d x(a＞1，b＞1，0＜c＜1，0＜d＜1)的图象，如图所示．作出直线y＝1，分别与四个图象自左向右交于点A(c，1)，B(d，1)，C(a，1)，D(b，1)，得到底数的大小关系是：b＞a＞1＞d＞c＞0.根据直线x＝1右侧的图象，单调性相同时也可以利用口诀：“底大图低”来记忆．考点三对数的图像例5、函数y＝2log4(1－x)的图象大致是()1、【2019年高考浙江】在同一直角坐标系中，函数1xya=，1(2log)ay x=+(a>0，且a≠1)的图象可能是2、已知函数y＝log a(x＋c)(a，c为常数，其中a>0，a≠1)的图象如图所示，则下列结论成立的是()A．a>1，c>1B．a>1，0<c<1C．0<a<1，c>1D．0<a<1，0<c<13、(2018·张家界三模)在同一直角坐标系中，函数f(x)＝2－ax，g(x)＝log a(x＋2)(a>0，且a≠1)的图象大致为()A BC D例6、函数y ＝log a (x ＋4)－1(a >0，a ≠1)的图象恒过定点A ，若点A 在直线x m ＋yn ＝－1上，且m >0，n >0，则3m ＋n 的最小值为( )A ．13B ．16C ．11＋6 2D ．281、(2017·河北五校质监)函数y ＝log a (x ＋3)－1(a >0，且a ≠1)的图象恒过定点A ，若点A 在直线mx ＋n y ＋2＝0上，其中m >0，n>0，则2m ＋1n 的最小值为 ( )A ．2 2B ．4 C.52 D.92 考点六解不等式以及定义域例7、求不等式的解集（1）()113log 3<+x （2） 0log )12(21≥-x1、已知集合=⋂>-=<=N M x x N x M x x 则},0)1(log |{},33|{21322A ．)23,0(B ．)2,23(C ．)23,1(D ．(0,1)2、设函数f (x )＝⎩⎨⎧21－x ，x ≤1，1－log 2x ，x >1，则满足f (x )≤2的x 的取值范围是( )A ．[－1，2]B ．[0，2]C ．[1，＋∞)D ．[0，＋∞)例8、求下列函数的定义域（1）)1(log 121-=x y （2）y =1、【2018年江苏卷】函数f (x )＝log 13（4x －5）的定义域为( )A.⎝ ⎛⎭⎪⎫54，＋∞ B.⎝ ⎛⎭⎪⎫－∞，54 C.⎝ ⎛⎦⎥⎤54，32 D.⎝ ⎛⎭⎪⎫54，32 2、（2016年全国II 卷高考）下列函数中，其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是（）（A ）y =x （B ）y =lg x （C ）y =2x （D）y =考点七复合函数的定义域例9、求下列函数的单调区间（1） xx y 2221-⎪⎭⎫⎝⎛= （2）20.2()log (45)f x x x =-++1、【2017课标II ，文8】函数2()ln(28)f x x x =-- 的单调递增区间是 A.(,2)-∞- B. (,1)-∞- C. (1,)+∞ D. (4,)+∞2、【2014江苏高考】若f (x )＝lg(x 2－2ax ＋1＋a )在区间(－∞，1]上递减，则a 的取值范围为( )A ．[1,2)B ．[1,2]C ．[1，＋∞)D ．[2，＋∞)3、(2016·青海平安一中月考)已知函数f (x )＝log 12(x 2－ax ＋a )在区间(2，＋∞)上是减函数，则实数a 的取值范围是________．考点八比较大小例10、(2017·天津一模)已知a ＝log 25，b ＝log 5(log 25)，c ＝⎝ ⎛⎭⎪⎫12－0.52，则a ，b ，c的大小关系为( )A ．a ＜b ＜cB ．b ＜c ＜aC ．c ＜b ＜aD ．b ＜a ＜c1、【2019年高考全国Ⅰ卷理数】已知0.20.32log 0.220.2a b c ===，，，则 A ．a b c << B ．a c b << C ．c a b <<D ．b c a <<2、【2019年高考天津理数】已知5log 2a =，0.5og 2.l 0b =，0.20.5c =，则,,a b c 的大小关系为 A ．a c b << B ．a b c << C ．b c a <<D ．c a b <<3、已知奇函数f (x )在R 上是增函数．若a ＝－f (log 215)，b ＝f (log 24.1)，c ＝f (20.8)，则a ，b ，c 的大小关系为( )A ．a <b <cB ．b <a <cC ．c <b <aD ．c <a <b考点九数形结合例11、已知函数f (x )＝log a (2x －a )(a >0且a ≠1)在区间[12，23]上恒有f (x )>0，则实数a 的取值范围是( )A ．(13，1) B ．[13，1) C ．(23，1) D ．[23，1)1、(2017·合肥月考)当0<x ≤12时，4x <log a x ，则a 的取值范围是（）A.⎝ ⎛⎭⎪⎫0，22 B.⎝ ⎛⎭⎪⎫22，1C ．(1，2)D ．(2，2)2、(2016·南京师大附中等四校联考)若函数 f (x )＝⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫12x －3，x ≤2，log a x ，x ＞2(a >0且a ≠1)的值域是[2，＋∞)，则实数a 的取值范围是________．。

大学数学(高数微积分)专题一第2函数基本初等函数的图像性质(课堂讲义)

本讲栏目开关
主干知识梳理
5．与周期函数有关的结论 (1)若f(x＋a)＝f(x＋b)(a≠b)，则f(x)是周期函数，其中一个周期是T＝|a－b|.
本讲栏目开关
(2)若f(x＋a)＝－f(x)，则f(x)是周期函数，其中一个周期是T＝2a. 1 1 (3)若f(x＋a)＝或f(x＋a)＝－，则f(x)是周期函数， fx fx 其中一个周期是T＝2a. 提醒：若f(x＋a)＝f(－x＋b)(a≠b)，则函数f(x)关于直线x a＋b ＝对称. 2
热点分类突破
解析
(1)f(log23)＝f(log23＋3)
log2 24 2 ＝f(log224)＝＝24.
(2)依题意得，y＝(2＋log3x)2＋2＋log3x2
本 2 讲＝log2 3x＋6log3x＋6＝(log3x＋3) －3，栏目 2 因为 1 ≤ x ≤ 9 ，且 1 ≤ x ≤9，所以1≤x≤3，开关
3 1 1 －＝f ＝－ . 4 2 2
热点分类突破
函数的性质主要是函数的奇偶性、单调性和周期性
本讲栏目开关
以及函数图象的对称性，在解题中根据问题的条件通过变换函数的解析式或者已知的函数关系，推证函数的性质，根据函数的性质解决问题．
热点分类突破
(1)(2013· 天津)已知函数f(x)是定义在R上的偶函数，且在区间[0，＋∞)上单调递增．若实数a满足f(log2a)＋
热点分类突破
(1)函数 y＝xln(－x)与 y＝xln x 的图象关于 ( A．直线 y＝x 对称 B．x 轴对称 ( C．y 轴对称 D．原点对称 log2|x| (2)函数 y＝ x 的大致图象是

六大基本初等函数图像及其性质

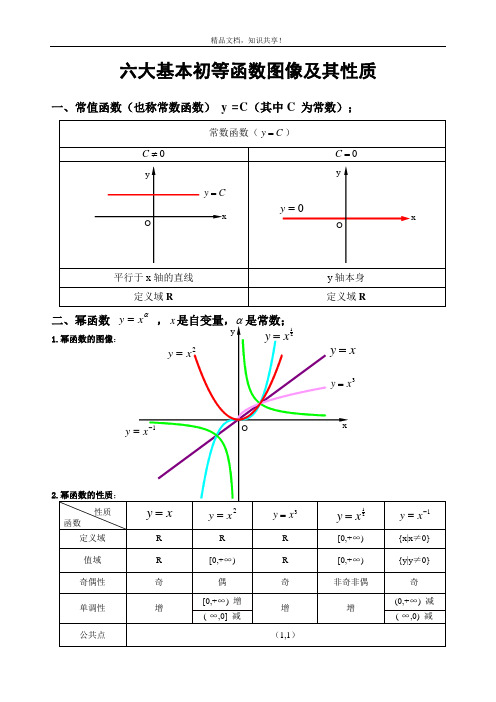
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

基本初等函数图像及性质大全之欧阳生创编

欧阳生创编一、一次函数与二次函数（一）一次函数（二）二次函数（1）二次函数解析式的三种形式 ①一般式：2()(0)f x ax bx c a =++≠ ②极点式：2()()(0)f x a x h k a =-+≠ ③两根式：12()()()(0)f x a x x x x a =--≠ （2）求二次函数解析式的办法欧阳生创编 ①已知三个点坐标时，宜用一般式．②已知抛物线的极点坐标或与对称轴有关或与最年夜（小）值有关时，常使用极点式．③若已知抛物线与x 轴有两个交点，且横线坐标已知时，选用两根式求()f x 更便利．（3）二次函数图象的性质①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线，对称轴方程为,2bx a=-极点坐标是24(,)24b ac b a a --欧阳生创编 ②那时0a >，抛物线开口向上，函数在(,]2ba-∞-上递加，在[,)2b a-+∞上递增，那时2bx a =-，2min 4()4ac b f x a -=；那时0a <，抛物线开口向下，函数在(,]2b a -∞-上递增，在[,)2ba-+∞上递加，那时2bx a=-，2max 4()4ac b f x a -=．二、幂函数（1）幂函数的界说一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数．（2）幂函数的图象过定点：所有的幂函数在(0,)+∞都有界说，并且图象都通过点(1,1)．三、指数函数（1）根式的概念：如果,,,1n x a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．（2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,mnaa m n N +=>∈且欧阳生创编1)n >．0的正分数指数幂即是0．②正数的负分数指数幂的意义是：1()0,,,m m nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．（3）运算性质①(0,,)r s r s a a a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈ （4）指数函数欧阳生创编四、对数函数（1）对数的界说①若(0,1)x a N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．②正数和零没有对数．③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =⇔=>≠>．（2）几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．（3）经常使用对数与自然对数经常使用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．（4）对数的运算性质如果0,1,0,0a a M N >≠>>，那么欧阳生创编 ①加法：log log log ()a a a M N MN +=②减法：log log log a a aMM N N-= ③数乘：log log ()n a a n M M n R =∈④log aN a N =⑤log log (0,)bn a anM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b N N b b a=>≠且（5）对数函数欧阳生创编五、反函数（1）反函数的概念设函数()y f x =的界说域为A ，值域为C ，从式子()y f x =中解出x ，得式子()x y ϕ=．如果对y 在C 中的任何一个值，通过式子()x y ϕ=，x在A 中都有唯一确定的值和它对应，那么式子()x y ϕ=暗示x 是y 的函数，函数()x y ϕ=叫做函数()y f x =的反函数，记作1()x f y -=，习惯上改写成1()y f x -=．（2）反函数的求法①确定反函数的界说域，即原函数的值域； ②从原函数式()y f x =中反解出1()x f y -=；③将1()x f y -=改写成1()y f x -=，并注明反函数的界说域．（3）反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称．欧阳生创编 ②函数()y f x =的界说域、值域辨别是其反函数1()y f x -=的值域、界说域．③若(,)P a b 在原函数()y f x =的图象上，则'(,)P b a 在反函数1()y f x -=的图象上．④一般地，函数()y f x =要有反函数则它必须为单调函数．六、三角函数的图像和性质（一）正弦与余函数的图像与性质函数x y sin =x y cos =图像定域义 RR值域[]1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时，时，2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时，时，单调性[2,2]223[2,2]22Zk k k k k ππππππππ-++++∈在每个上递增在每个上递减[2,2][2,2] Zk k k k k ππππππ-++∈在每个上递增在每个上递减奇偶性奇函数偶函数周期性是周期函数，2π为最小正周期是周期函数，2π为最小正周期欧阳生创编对称性对称中心(,0)k π，:,()2x k k Z ππ=+∈对称轴对称中心(,0)2k ππ+，:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质函数 x y tan = x y cot =图像定域义{|,}2x x R x k k Z ππ∈≠+∈且 {|,}x x R x k k Z ππ∈≠+∈且值域 RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,) Zk k k πππ+∈在每个上递减奇偶性奇函数奇函数周期性是周期函数，π为最小正周期是周期函数，π为最小正周期对称性对称中心(,0)2k π 对称中心(,0)2k π 七、反三角函数的图像与性质 1. 归正弦与反余函数的图像与性质函数归正弦函数arcsin y x =反余弦函数arccos y x =是[]cos 0,y x x π=∈，的反函数欧阳生创编是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦，的反函数图像定域义[]1,1-[]1,1-值域,22ππ⎡⎤-⎢⎥⎣⎦[]0,π单调性 [1,1]-+在上递增[1,1]-+在上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0)对称中心(0,)2π2. 归正切与反余切函数的图像与性质函数归正切函数arctan y x = 是tan (,)22y x x ππ=∈-，的反函数反余切函数arccot y x = 是()cot 0,y x x π=∈，的反函数图像定域义(,,)-∞+∞ (,,)-∞+∞欧阳生创编2021.02.08欧阳生创编2021.02.08。