讲义 (12)
第12讲 切线放缩

第12讲切线放缩本讲义由作业帮周永亮老师(白哥)独家编撰,侵权必究知识导航1.两个常见的切线放缩公式(1) ;(2)2.切线放缩在求导过程中的应用在求导的过程中,我们很多时候需要求二次导,乃至三次或多次,其实,对于几乎所有的问题,如果我们能够很好的利用放缩的技巧的话,我们最多只需要求二次导就可以了.3.切线放缩在数列不等式中的应用数列不等式有很多种,其中有一种最常见的叫做“拆和之函数放缩”,而这个函数,一般都是由我们这两个最常见的切线放缩公式演变而来的.知识札记例2(★★★☆☆)(2018·河北石家庄市一模)已知函数()在处的切线方程为.(1)求,.(2)若,证明:.例1(★★★☆☆)(2018·河北保定市模拟【文】)已知函数,函数,证明:当且时,.考点1 切线放缩的基础应用注:本讲对于切线放缩公式的应用,都写了易证,但在正常考试中,需要同学们证明.经典例题例5(★★★★☆)(2017·黑龙江大庆市期中【文】)已知,求证:当时,恒成立.例4(★★★★☆)已知函数,在点处的切线方程为.(1)求,;(2)证明:.例3(★★★★☆)证明:.考点2 切线放缩拓展应用例8(★★★★☆)证明:当,时,.考点3 切线放缩在数列不等式中的应用例7(★★★★★)证明:.例6(★★★★★)(2018·江苏泰州市期末【文】)已知函数,(,),当,时,求证:.例11(★★★★☆)(2013·安徽合肥市月考【理】)设函数(),数列满足:,().(1)求数列的通项公式;(2)求证:.例10(★★★★☆)(2018·辽宁月考【文】)求证:().例9(★★★★☆)(2016·湖南模拟【理】)证明不等式:().课后练习练1(★★★☆☆)(2017·贵州一模【文】)已知函数,证明:对任意,成立.练2(★★★★★)(2017·重庆渝中区模拟【理】)已知函数(为实数,为自然对数的底数),曲线在处的切线与直线平行.(1)求实数的值;(2)证明:当时,.练3(★★★★☆)(2016·全国卷)求证:当且时,.。
2014年10月自考《英语一》讲义 Unit 12_(含课文、生词表、课后练习及答案)
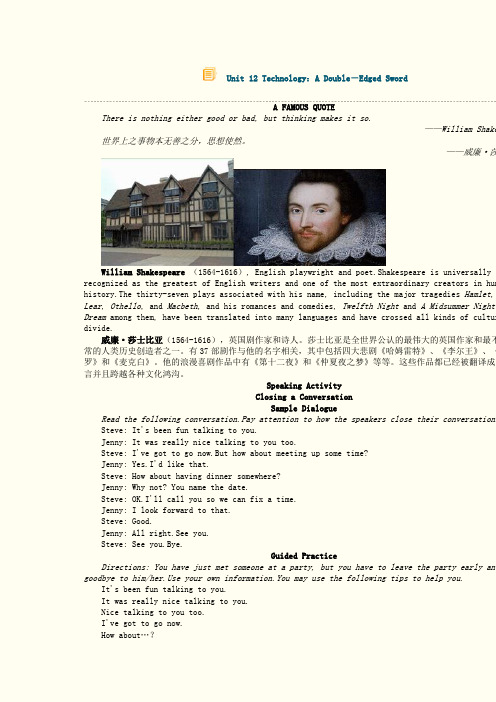
Unit 12 Technology:A Double-Edged SwordA FAMOUS QUOTEThere is nothing either good or bad, but thinking makes it so.——William Shake 世界上之事物本无善之分,思想使然。
——威廉·莎William Shakespeare(1564-1616), English playwright and poet.Shakespeare is universally recognized as the greatest of English writers and one of the most extraordinary creators in hum history.The thirty-seven plays associated with his name, including the major tragedies Hamlet, Lear, Othello, and Macbeth, and his romances and comedies, Twelfth Night and A Midsummer Night' Dream among them, have been translated into many languages and have crossed all kinds of cultur divide.威廉·莎士比亚(1564-1616),英国剧作家和诗人。
莎士比亚是全世界公认的最伟大的英国作家和最不常的人类历史创造者之一。
有37部剧作与他的名字相关,其中包括四大悲剧《哈姆雷特》、《李尔王》、《罗》和《麦克白》。
他的浪漫喜剧作品中有《第十二夜》和《仲夏夜之梦》等等。
这些作品都已经被翻译成多言并且跨越各种文化鸿沟。
Speaking ActivityClosing a ConversationSample DialogueRead the following conversation.Pay attention to how the speakers close their conversation.Steve: It's been fun talking to you.Jenny: It was really nice talking to you too.Steve: I've got to go now.But how about meeting up some time?Jenny: Yes.I'd like that.Steve: How about having dinner somewhere?Jenny: Why not? You name the date.Steve: OK.I'll call you so we can fix a time.Jenny: I look forward to that.Steve: Good.Jenny: All right.See you.Steve: See you.Bye.Guided PracticeDirections: You have just met someone at a party, but you have to leave the party early and goodbye to him/e your own information.You may use the following tips to help you.It's been fun talking to you.It was really nice talking to you.Nice talking to you too.I've got to go now.How about…?I look forward to that.All right.See you.Bye.New words1.privacy n.the state of being alone and not watched or disturbed by other people 隐私;私密2.feature v.to include a particular person or thing as a special feature 以……为特色;以…主要组成3.transparent adj.(of glass, plastic, etc.)allowing you to see through it 透明的4.isolate v.to separate somebody/something physically or socially from other people or thin (使)隔离,孤立5.coin v.to invent a new word or phrase that other people then begin to use 创造(新词语)6.cell n.a room for one or more prisoners in a prison or police station单间牢房;牢房7.unobserved adj.without being seen 不被看见(或发现)的8.behave v.to do things in a particular way 表现9.wired adj.connected to a system of computers 联机的10.metaphor n.a word or phrase used to describe somebody/something else, in a way that is different from its normal use 暗喻;隐喻11.surveillance n.the act of carefully watching a person suspected of a crime or a place wh crime may be committed 监视12.enormous adj.extremely large 巨大的;庞大的;极大的13.ubiquitous adj.seeming to be everywhere or in several places at the same time 似乎无所不的;十分普遍的14.whereabouts n.the place where somebody/something is 下落;行踪15.track v.to find somebody/something by following the marks, signs, information, etc., tha they have left behind them 跟踪;追踪16.survey n.an investigation of the opinions, behaviour, etc.of a particular group of peopl which is usually done by asking them questions 民意调查;民意测验17.scale n.the size or extent of something, especially when compared with something else 规范围,程度18.exchange n.an act of giving something to somebody or doing something for somebody and receiving something in return 交换;互换;交流19.expand v.to become greater in size, number or importance 扩大,增加,增强20.decade n.a period of ten years 十年,十年期21.electronic adj.relating to computers or something that is done by computers 电子的22.profile n.a description of somebody/something that gives useful information 概述;简介23.cyberspace n.the imaginary place where electronic messages, etc.exist while they are bei sent between computers 网络空间24.grant v.to agree to give somebody what they ask for, especially formal or legal permissi do something (尤指正式地或法律上)同意,准予,允许25.damage n.harmful effect 损害;伤害promise v.to do something that is against your principles or does not reach standards you have set 违背(原则);达不到(标准)27.increasingly adv.more and more all the time 越来越多地;不断增加地28.maintain v.to make something continue at the same level , standard, etc.维持;保持29.defend v.to protect somebody/something from attack 保护;保卫30.expose v.to show something that is usually hidden 暴露;显露;露出Phrases and Expressions1.or rather used to correct something you have said, or to give more accurate information 确说2.in addition (to) used when you want to mention another person or thing after somethin else 除……以外(还)3.apply for to make a formal request, usually in writing, for something such as a job, a pl at college, university, etc.(通常以书面形式)申请,请求4.beyond one's control impossible for someone to control 无法控制5.call (one's)attention to to make people notice and be concerned or think about somethin 起(某人)对……的注意Proper namesThe New York Times《纽约时报》Jeremy Bentham 杰里米?边沁(英国哲学家、法学家)Text A Privacy in Our High-Tech SocietyText APre-reading Questions1.Do you worry about safety on the Internet? What problems have you encountered on the inte2.How do you protect yourself in today's high-tech society?Privacy in Our High-Tech SocietyA recent New York Times "House and Home" article featured the story of a man who lived in a glass house.Every wall in his home was transparent; he had no walls to hide behind, not even in bathroom.Of course, he lived in an isolated area, so he didn't exactly have neighbors peering i watching his every move.But he had chosen to live without any physical privacy in a home that allowed every action to be seen.He had created his own panopticon, a place in which everything open to view.The term panopticon was coined by Jeremy Bentham in the late eighteenth century when he was describing an idea for how prisons should be designed.The prisoner's cells would be placed in a circle with a guard tower in the middle.All walls facing the center of the circle would be glas that way, every prisoner's cell would be in full view of the guards.The prisoners could do noth unobserved, but would not be able to see the guard tower.They would know they were being watche or rather, they would know that they could be being watched — but because they could not see t guard tower, they would never know when the guard was actually monitoring their actions.It is common knowledge that people behave differently when they know they are being watched act differently when we know someone is looking; we act differently when we think someone else be looking.In these situations, we are less likely to be ourselves; instead, we will act the wa think we should act when we are being observed by others.In our wired society, many talk of the panopticon as a metaphor for the future.But in many the panopticon is already here.Surveillance cameras are everywhere, and we often don't even kno actions are being recorded.In fact, the surveillance camera industry is enormous, and these cam keep getting smaller and smaller to make surveillance easier and more ubiquitous.In addition, w leave a record of everything we do online; our cyber-whereabouts can be tracked and that inform can be used for various purposes.Every time we use a credit card, make a major purchase, answer survey, apply for a loan, or join a mailing list, our actions are observed and recorded.And mos us have no idea just how much information about us has been recorded and how much data is avail to various sources.The scale of information gathering and the scale of exchange have both expan so rapidly in the last decade that there are now millions of electronic profiles of individuals existing in cyberspace, profiles that are bought and sold, traded, and often used for important decisions, such as whether or not to grant someone a loan.① However, that information is essentially beyond our control.We can do little to stop the information gathering and exchange can only hope to be able to control the damage if something goes wrong.With so much information floating about in cyberspace, and so much technology that can reco and observe, our privacy has been deeply compromised.There are those who argue that information be gathered for the social good.However, I find it truly amazing that anyone would want to live transparent house at any time, especially in an age when individual privacy is becoming increas difficult to maintain and defend.② Perhaps the story of the man who lived in a glass house isattempt to call our attention to the fact that the panopticon is already here, and that we are just as exposed as he is.Key Sentences1.The scale of information gathering and the scale of exchange have both expanded so rapidl the last decade that there are now millions of electronic profiles of individuals existing in cyberspace, profiles that are bought and sold, traded, and often used for important decisions, as whether or not to grant someone a loan.过去十年间,信息收集以及信息交换的规模迅速扩展,网络空间存有无数个人电子档案,这些档案被买卖易,经常用于重要决策,如是否给某人发放贷款等。
第12课 醉翁亭记-九年级语文上册课文全解讲义(统编版)

第12课醉翁亭记-九年级语文上册课文全解讲义(统编版)部编人教版九年级上册课文全解第三单元第12课醉翁亭记登亭台楼阁,观湖光山色,游目骋怀,纵情山水,可以让人感受自然之美,领略历史文化的底蕴。
本单元所选的诗文在描写景物、抒发感情的同时,也表达了作者的政治理想、志趣抱负。
学习时,要注意体会古人寄托于山水名胜中的思想情感,感受他们的忧乐情怀。
学习这个单元,要在理解课文内容的基础上,熟读成诵,积累、掌握课文中的文言实词和名言警句,并体会文言虚词在关联文意、传达语气等方面的作用。
《岳阳楼记》是一篇游记散文,以“记"为名,先叙事后写景,进而由景入情,生发议论《醉翁亭记》是一篇美文,应注重语言的品味与诵读,积累文言词句,掌握“也”和“而"字的语气了解本文语言骈散相融,节奏富于变化的写法。
《湖心亭看雪》以精炼的笔墨,记叙了作者自己湖心亭看雪的经过,描绘了所看到的幽静深远、洁白广阔的雪景图,表达他幽远脱俗的闲情雅致。
《行路难(其一)》描写了诗人在政治上遭遇挫折后内心的强烈苦闷和抑郁不平之情,同时又表现了诗人的倔强、自信和对理想的执着追求,展示了诗人力图从苦闷中挣脱出来的强大精神力量。
《酬乐天扬州初逢席上见赠》这首诗写了诗人被贬的不幸遭遇,抒发了诗人二十多年转徙巴山楚水的悲愤心情,同时也表现了诗人的坚定意志和乐观精神。
《水调歌头(明月几时有)》这首词借赏月抒发了丰富而乐观的思想情感,写出了作者以理遣情,以超然的思想排解政治上的失意,以积极的人生态度战胜抑郁惆怅之情的心理过程。
《诗词三首》是继八年级上册第六单元第25课《诗词五首》之后的第二个多种诗歌样式组合,其中词作苏轼的《水调歌头(明月几时有)》是继李清照《渔家傲(天接云涛连晓雾)》之后的第二首,为九下第三单元第12课《词四首》作好铺垫和储备。
李白的《行路难》(其一)以食难举箸的窘境倾诉前路不通的茫然,又以吕尚、伊尹的奇幻之思重振奋起的豪情壮志,情感迂回扭结又有一股无法阻遏的冲天信念,当真是“诗仙”之气气贯长虹。
讲义-数学-七年级上册-第12讲-几何图形与线

讲义表示方法:(1)用一个小写字母表示直线,如直线l .(2)用直线上的两点来表示直线,如直线AB ,如图1.点与直线的位置关系:(1)一个点在直线上,也可以说这条直线经过这个点;(2)一个点在直线外,也可以说直线不经过这个点.相交:当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点. 7.射线、线段射线和线段是直线的一部分.表示方法:(1)线段AB 或线段a ,如图2. (2)射线OA 或射线l ,如图3.注意:1.把线段向一方无限延伸所形成的图形叫做射线. 2.把线段向两方无限延伸所形成的图形叫做直线. 3.把射段反向延长就得到了一条直线. 【例题精讲】例1. 正方体有 个面, 个顶点,经过每个顶点有 条棱.这些棱的长度 (填相同或不同).棱长为a cm 的正方体的表面积为 cm 2 【考点】图形的点、线、面、体的计算.【解析】通过图形进行观察面、顶点、棱的个数,然后根据表面积公式进行计算. 【答案】6,8,3,相同, 26a【教学建议】根据所给条件,画出图形进行观察,然后将图形展开计算表面积. 例2. 下面图形中叫圆柱的是( )【考点】几何图形的分类判断.【解析】观察图形,通过圆柱性质来判断. 【答案】D【教学建议】熟悉掌握几何图形的分类和性质,然后根据题目要求进行判断.AB图1ABa图2 OA图3【巩固测试】1.观察下图,分别得它的主视图、左视图和俯视图,请写在对应图的下边.【考点】几何图形的三视图.【解析】对于一些立体图形的问题,常转化为平面图形来研究和处理,一般从立体图形的正面、左面、和上面看立体图形所得到的平面图形.【答案】俯视图左视图主视图【教学建议】根据已知几何体的形状,分别从它的正面、左面和上面看立体图形,从而观察出它的三视图. 2.下列图形中,是正方体表面展开图的是()(A)(B)(C)(D)【考点】几何图形的展开图.【解析】将正方体的表面适当剪开,可以展开成平面图形,通过观察选项可以判断出来.【答案】C【教学建议】根据已知几何体的形状,将它的表面剪开,从而观察出它的展开图.二、尺规作图【知识梳理】8.用圆规作一条线段等于已知线段步骤:1、作一条射线AB;2、用圆规量出已知线段的长度(记作a);3、以A为圆心,在射线AB上截取AC=a,则线段AC就是所求的线段.9.线段的概念及表示:如右图,表示的是一条线段.我们可以用两个大写的英文字母来表示一条线段的两个端点.线段可以用表示端点的两个字母A、B来表示,记作线段AB.我们也可以用一个小写的英文字母来表示,如a ,表示一条线段,记作线段a . 10.线段大小的比较及其方法:通常,把两条线段的长短称作两条“线段的大小的比较”.那么,线段大小的比较方法有:(1)叠合法:比较两条线段AB 、CD 的长短,可把它们移到同一条直线上,使一个端点A 和C 重合,另一端点B 和D 落在直线上A 和C 的同侧,如果点B 和D 重合.则AB CD =;如果点D 在线段AB 上,则AB CD >;如果点D 在线段AB 外,则AB CD <(如下图所示).(2)度量法:分别度量出每条线段的长度,再按长度的大小,比较线段的大小,线段的大小关系和它们长度的大小关系是一致的.【注意】线段是一个几何图形,而线段的长度是一个非负数,二者是有区别的,不能混为一谈. 11.线段的性质:两点之间的所有连线中,线段最短.【注意】(1)线段的这条性质是人们在日常生活中总结得出的,是一条基本事实,也称之为线段公理,所谓“公理”,简而言之就是“公认的真理”.(2)线段的性质在求最短路线问题时是一个重要的依据,在以后我们学习三角形时.还会用它来研究三角形三边关系,是一个很重要的性质. 12.两点之间的距离:两点之间的连线有无数条,它们的长度不一,两点之间线段的长度,叫做这两点之间的距离.【注意】(1)距离是指线段的长度,是一个数值,而不是指线段本身.(2)线段的长度可用刻度尺度量,如图所示,线段AB 的长度是2.2厘米;线段的长度也可以借助于圆规来度量,如图所示,线段AB 的长度也是2.2厘米.13.两条线段的和、差:两条线段可以相加(或相减),它们的和(或差)也是一条线段,其长度等于这两条线段的和(或差). 14.线段的倍分:(1)线段的倍:na (1n >为正整数,a 是一条线段)就是求n 条线段a 相加所得和的意义.na 也可以理1. 如图所示,比较线段AB 与AC ,AD 与AE ,AE 与AC 的大小. 【解析】解法一:用圆规截取可得:,,AB AC AD AE AE AC ><=解法二:用刻度尺测量长度,,,AB AC AD AE AE AC ><=【答案】,,AB AC AD AE AE AC ><=.【教学建议】根据线段的定义,只要两个线段的端点确定了,线段就可以确定. 在两条线段长度相差不大的情况下,目测法不一定可靠.比较线段的长短有两种方法:一是把它们放在同一条直线上比较,先把两条线段的一端重合,再看另一端的位置,从而确定两条线段的长短,这是从“形”的角度来进行比较;二是用刻度尺分别测量每条线段的长度,再根据度量的结果确定两条线段的长短,这是从“数”的角度进行比较.2. 在线段AB 上有一点M ,若6AB =厘米,2AM =厘米,则点M 与点B 之间的距离是多少?【考点】线段长度的计算. 【解析】因为6AB =厘米,2AM =厘米,所以624MB AB AM =-=-=(厘米).即点M 、B 之间的距离为4厘米. 【答案】4厘米.【教学建议】题中要求的是点M 与点B 之间距离,即线段BM 的距离,是指线段BM 的长度,它是一个数值. 3. 已知线段a 、b ,利用尺规比较a 、b 的大小.【考点】用尺规作图比较两条线段的大小. 【解析】如图所示,画图:(1)画射线AH .(2)以点A 为圆心,线段a 的长度为半径画弧,交AH 于B . (3)以点A 为圆心,线段b 的长度为半径画弧,交AH 于C .(4)在射线AH 上截取线段AB =a ,在射线AH 上截取线段AC =b .线段AB 的端点B 落在线段AC外,∴线段a 大于线段b ,即a b >.【答案】a b >.【教学建议】本题是利用叠合法比较线段的大小,若端点B 与C 重合,则a b =;若端点B 落在C 内,则a b <;若端点B 落在C 外,则 a b >.4. 如图所示,已知线段a 、b .(1)画出一条线段,使它的长度等于a b +. (2)画出一条线段,使它的长度等于a b -.【考点】画线段的和、差.【解析】解法一:(1)①画射线OP .①在射线OP 上顺次截取,OA a AB b ==.线段OB 就是所画的线段.(2) ①画射线OP ;①在射线OP 上截取OC a =,在射线CO 上截取CD b =.线段OD 就是所画的线段.解法二:(1)量得线段 2.6a =厘米, 1.5b =厘米, 4.1a b +=厘米. 画线段 4.1OA =厘米.(2)量得线段 2.6a =厘米, 1.5b =厘米. 1.1a b -=厘米.画线段 1.1OB =厘米.【答案】略.【教学建议】引导学生回顾线段和与差的基本画法,并通过本题让学生进一步熟悉用尺规画线段的和与差.课堂练习。
人教版初二下册数学第18章《平行四边形》讲义第12讲平行四边形-复习训练(有答案)
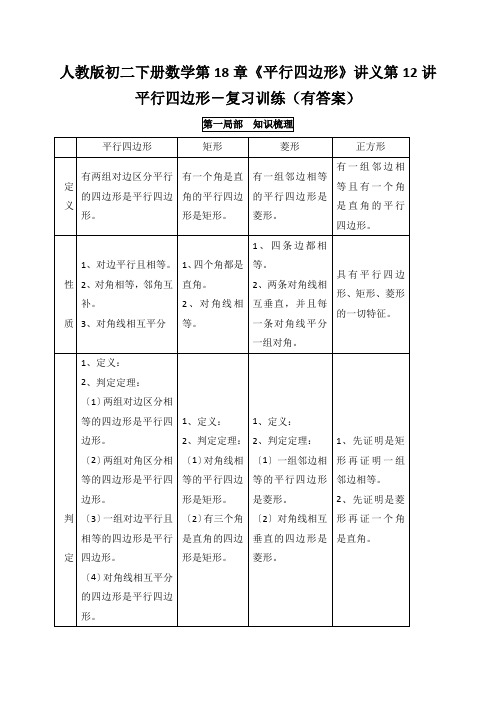
人教版初二下册数学第18章《平行四边形》讲义第12讲平行四边形-复习训练(有答案)对称 中心对称 中心对称轴对称图形 中心对称 轴对称图形 中心对称 轴对称图形第二局部 考点精讲精练考点一、平行四边形的性质及判定【知识要点】〔1〕、平行四边形的边、角、对角线性质, 对称性〔2〕、平行四边形判定方法〔3〕、三角形中位线【典型例题】例1、以下图形中是中心对称图形,但不是轴对称图形的是〔 〕A 、菱形B 、矩形C 、正方形D 、平行四边形例2、如图,□ABCD 与□DCFE 的周长相等,且∠BAD=60°,∠F=110°,那么∠DAE 的度数为 例3、如图,在平行四边形ABCD 中,AB=4,∠BAD 的平分线与BC 的延伸线交于点E,与DC 交于点F,且点F 为边DC 的中点,DG ⊥AE,垂足为G,假定DG=1,那么AE 的长为〔 〕 A 、2 B 、4 C 、4 D 、8例4、平面直角坐标系中,□ABCD 的顶点,A ,B ,D 的坐标区分是〔0,0〕〔5,0〕,〔2,3〕,那么顶点C 的坐标是〔 〕A 、〔3,7〕B 、(5,3)C 、(7,3)D 、 (8,2)〔例2〕 〔例3〕 〔例4〕例5、如图,E 是平行四边形内任一点, 假定S平行四边形ABCD =8,那么图中阴影局部的面积是〔 〕A 、3B 、4C 、5D 、6 例6、如图,将平行四边形ABCD 纸片沿EF 折叠,使点C 与点A 重合,点D 落在点G A yB CD处。
〔1〕求证:AE =AF〔2〕求证:△ABE ≌△AGF例7、如下图:四边形ABCD 是平行四边形,DE 平分BF ADC ,∠平分ABC ∠.试证明四边形BFDE 是平行四边形.例8、如图,在△ABC 中,AB =4,AC =3,BC =5,以三边为边,在BC 的同侧区分作三个等边三角形即△ABD 、△BCE 、△ACF 。
〔1〕求证:四边形EFAD 是平行四边形;〔2〕求四边形EFAD 的面积。
第12讲 均值不等式 拔高难度 讲义

均值不等式引入22.ab?b?2a?R,b?R,a、利用作差法证明:1 =(a-b)2≥0证明:∵a2+b2-2ab .=”a2∴+b2≥2ab,当且仅当a=b时,取“ab. a+=b≥2(a)2,b=,(b)2.据此证明:a>0b>0时,,2、当a>0b>0时,ab≥2ab. ∴aa++-(b)2-b2)2≥0.a·b=证明:∵a+b-ab2=((a)2解读1、等号成立条件对于任意实数,b,a,当且仅当时,等号成立.22ab?b2?aba?证明:,当时,;当时,.,当且仅当时,等号成立.2220)ba?=(ab?a??b2ba?2、基本2220)??2ab((baab?b?a?)?ba?b?a不等式a?b,是正数,那么如果ba,,当且仅当时,有等号成立.此结论又ba?ab≥2称均值不等式或基本不等式.a?b证明:,所以即,2220b?(b)(ab??ab2?a?()?a)?aa?≥2bbab≥23、均值不等式的理解a?b叫做,的算术平均值,叫做的几何(1)对于任意两个实数b,ba,b,aaab 2平均值.此定理可以叙述为:两个正数的算术平均数不小于他们的几何平均数.a?b的充要条件.也就是如果的理解应为是,则(2)对于ba?ba?”=“=ab2ba?.ab?2a?b)注意(3,后者是和成立的条件不同.前者是4、极值定理22abb2a??a?R,bab?2+Ra,b?(1)若(和为定值),则当时,取得最大值是;xyy?xsy??x42s?xyx?y证明:都2s是正数,yx,,有,当且仅当,2xy)??(y?xsy?x?xy?242时,取得最大值是;xy2s4(2)若(积为定值),则当时,取得最小值是;yx?pxy=p2y?x x?y都是正数,证明:yx,当且仅当时,等号成立.又,,??yxpx?yxy=xy?2.p2【注意】利用极值定理求最大值或最小值是应注意:①注意均值不等式的前提条件:函数式中的各项必须都是正数,在异号时不能运用均值不等式,在同负时可以先进行转化,再运用均值不等式;②求积最大值时,应看和是否是定值;求和最小值时,看是否为xyxyy?xyx?定值.③通过加减的方法配凑成使用算术平均数与几何平均数定理的形式;④注意“1”的代换;⑤等号是否成立: 只有具备了不等式中等号成立的条件,才能使函数式取到最大或最小值.否则不能由均值不等式求最值,只能用函数的单调性求最值.5、运用均值不等式的前提有口诀:一正二定三相等.探究a?b的一种几何解释,请你补充完整.下面是基本不等式ab≥2ABOACaCBb⊙,如图所示,=为=,的直径,CCDABODAD⊙⊥,上半圆于点连接作交,过点BD.CD OD ,由射影定理可知,==,而a?b CD OD ,所以因为, ab_____2CO ,等号成立.与时当且仅当,即a?ba?b OD?CD,OD.=答案:,ab=CD,当且仅当点C与圆心O ab≥22重合,即时,等号成立.b?a典例精讲一.选择题(共15小题)2+3xy﹣2=0,则2x+y的最小值是,且?周口期末)已知x>0,y>0x1.(2017秋().CBA...D【分析】由x代入2x+y化简之后利用基本不等式可求出2得+3xy﹣2=02x+y的最小值.【解答】解:由x,所以,,22x﹣﹣2=0,得3xy=2+3xy,由基本不等式可得当且仅当时,等号成立,>,即当因此,2x+y的最小值为,故选:C.2.(2018春?齐齐哈尔期末)若等边△ABC的边长为3,N为AB的中点,且AB 取得最小值时,上一点M满足:>>,,则当)(D.6 C.B.A.【分析】根据N为AB的中点,且AB上一点M满足M,A,B三点共线:>>,与基本不等式的”“+y=1,利用乘1法x,可知,性质求解xy.的值,即可求满足:AB上一点M【解答】解:由题意:N为AB的中点,且>>,y=1,,可知x+时()(x+y)=10+,y=,则x=,当且仅当=16取等号.由>,>,,则AM=3,MB=1.,CM=1,则CM=CN=N为AB的中点,正△ABC,那么的边长为3.=NCM=cos∠.则NCM=∠|?cos=|CN|×|CM故选:C.)(的最小值为则x+y=1,3.(2018春?重庆期末)已知正数x,y满足D.B.2 C.A.然后利用基本不等式计算14y+)=5,【分析】由x+y=1得4x+(=的最小值.的最小值,即可得到4y+1=5,∵x+y=1,∴4x+【解答】解:所以,==,,所以,时,等号成立,当且仅当,即当因此,的最小值为,.C故选:4.(2018春?柯桥区期末)已知正实数x,y满足x+y+3=xy,若对任意满足条件的正实数x,y都有不等式(x+y)﹣a(x+y)+1≥0恒成立,则实数a的取2值范围为()]B.(﹣∞A.(﹣∞,],,++∞)∞),D.(﹣∞,﹣C.]∪[[≤6,由题意可得axy≤,由二次不等式的解法可得x+y≥【分析】运用的最小值,运用对勾函数的单调性,可得最小值,进而得到所y)+(x+求范围.,3=xy≤【解答】解:x+y+可得(x+y)﹣4(x+y)﹣12≥0,2由x>0,y>0,解得x+y≥6,对任意满足条件的正实数x,y都有不等式(x+y)﹣a(x+y)+1≥0恒成立,2+的最小值,+y)可得a≤(x+的最小值为,t≥6递增,可得t+可令t=x+y,则t在≤,则aB.故选:)的是(张家界期末)下列函数中,最小值为5.(2018春?2x y=2.+ B.Ay=lgx+<<)(0+.Dy=.Cy=sinx【分析】A项中lgx不能保证>0;B项运用基本不等式可得答案;C项中等号不成立;D项中无解.sinx=,不满足正数条件;lgx∈R【解答】解:A中x运用基本不等式可知成立;>0B选项中2无解不满足三能等条件,不对;=中C无解.sinx=D中故选:B.),(,0,1),则,6.(2018春?石家庄期末)设a,bc∈(A.都不大于2 B.都不小于2D.至少有一个不大于2.至少有一个大于2C【分析】先利用基本不等式判断()+()+()>6,再用反证法证明,,中至少有一个大于2.【解答】解:a,b,c∈(0,1),2≥c+)(=a+)+(b+)+()则()+(+()=6,++22当且仅当a=b=c=1时取“=”;)+()+()>6,∴(假设,,都不大于2,则()+()+()≤6,这与()+()+()>6矛盾,,,中至少有一个大于2.∴假设不成立,即.D故选:则b),lga+lgb=lg(a+7.(2018春?沙坪坝区校级期末)若正数a,b满足:)的最小值为(1..4DA.16B.9C【分析】由对数运算得到ab=a+b,通过因式分解得到(a﹣1)(b﹣1)=1,再利用基本不等式即可求出的最小值.【解答】解:由lga+lgb=lg(a+b),可得lg(ab)=lg(a+b),所以,ab=a+b,则ab﹣a﹣b+1=1,即a(b﹣1)﹣(b﹣1)=1,所以,(a﹣1)(b﹣1)=1,由基本不等式可得,时,等号成立,,即当当且仅当的最小值为因此,4,故选:C.的则,+b=1,c+d=1,2018秋?越城区校级月考)已知实数a,b,cd满足a8.()最小值是(.9.43DC.A.10B【分析】利用基本不等式求得的最小值.再利用基本不等式求得,≥4【解答】解:∵a+b=1,c+d=1,∴ab≤,∴时,a=b=,当且仅当≥=4取等号.+)则=5=92+,≥+5+)(≥4+=c+d?(当且仅当a=b=时,且c=,d=时,的最小值为9,.B故选:的最小值y=且x+y=1,函数?城关区校级期末)设x>0,y>09.(2018春为()D8.A.10B.9C.【分析】将代数式x+y与代数式相乘,展开,然后利用基本不等式可求出答案.【解答】解:∵x>0,y>0且x+y=1,所以,,当且仅当,即当时,等号成立,因此,函数y=的最小值为9,故选:B.10.(2018春?金安区校级期末)下列说法正确的是()的最小值为2 A.的最小值为4,x∈(0,π)B.2+1的最小值为2x C.xD.4x(1﹣x)的最大值为1【分析】利用基本不等式或函数的基本性质来得出各代数式的最值,利用基本不等式时需注意“一正、二定、三相等”这三个条件要满足.<,A选项不符合题意!【解答】解:对于A选项,当x<0时,对于B选项,当x∈(0,π)时,0<sinx≤1,由基本不等式可得,即当sinx=2时,等号成立,这与0,当且仅当矛盾!1≤sinx<对于C选项,∵x222+1的最小值为1,所以,xC选项不合乎题意!≥0,x,+1≥1对于D选项,由基本不等式可得,当且仅当x=1﹣x时,即当x=时,等号成立,D选项正确!故选:D.中最22b+,a,>1则a+b2ab,2(11.2018春?平罗县校级期末)若a>1,b大的一个是()22+D.abB.2abC.2A.a+b【分析】利用基本不等式与重要不等式的性质、作差法即可得出.【解答】解:∵a>1,b>1,22≥2ab,+bb≥2,a ∴a+又(a)﹣(a+b)=﹣﹣22=0++b,>22>a+b+b,∴a因此:a+b,2ab,2,a中最大的一个是:a,2222b++b 故选:D.的解集为()萍乡期末)不等式春?12.(2018B.(]A.[0,1 0,1]D.(﹣,](﹣C.∞,0∪[1+∞)∞,0)∪[1,+∞)【分析】根据题意,原不等式可以转化为(1﹣x)x≥0且x≠0,解可得x的取值范围,即可得答案.解:根据题意,【解答】,0≠x且0≥x)x﹣1(?,1x<0解可得:≤,]1,0即不等式的解集为(.故选:B.<恒成立,则实数a的取值范怀化期末)若不等式13.(2017秋?围是(),,C.,.D A.(0,1B .)【分析】不等式恒成立化为x﹣2ax>﹣(3x+a)恒成立,即△<0,从而求出a22的取值范围.<恒成立,【解答】解:不等式即恒成立,<即x﹣2ax>﹣(3x+a)恒成立,22即x﹣(2a﹣3)x+a22>0恒成立,﹣4a22<02a﹣3),∴△=(即(2a﹣3+2a)(2a﹣3﹣2a)<0,解得a>;,+∞).的取值范围是(∴实数a故选:B.14.(2018春?道里区校级期末)若a>0,b>0,ab=a+b+1,则a+2b的最小值为()D.73C.3+A.3+3B.3﹣【分析】由ab=a+b+1得,代入a+2b得,然后利用基本不等式可求出该代数式的最小值.【解答】解:由ab=a+b+1,可得a(b﹣1)=b+1,得,由于a>0,b>0,,1>b则.所以,=,时,即当b=2时,等号成立,因此,a+2b的最小值为当且仅当>7,故选:D.)的最大值为(则.a+b=2a,b∈R,15+.(2018春?台州期末)已知2.D.A.1 B.C﹣1=2,令化简配方可得t=ab﹣1=a(﹣a)﹣【分析】=+,再由基t=≥4),即(,令(a﹣1)4﹣2t=ss2=≤0,则本不等式计算可得最大值.【解答】解:a,b∈R,a+b=2.则+=,===令t=ab﹣1=a(2﹣a)﹣1=﹣(a﹣1)2≤0,则,=令4﹣2t=s(s≥4),即t=,可得,==+由s,=8≥2当且仅当s=4,t=2﹣2 时上式取得等号,,可得=≤则的最大值为,+故选:C.二.填空题(共5小题)16.(2018春?定州市校级期末)已知实数x,y满足3x﹣y≤ln(x+2y﹣3)+ln(2x﹣3y+5),则x+y=.【分析】构造函数f(t)=lnt﹣t+1,求得导数和单调性,可得最值,再由条件可得等号成立的条件,解方程可得x,y,进而得到所求和.【解答】解:由f(t)=lnt﹣t+1的导数为:﹣1=,=f′(t)当t>1时,f′(t)<0,f(t)递减,当0<t<1时,f′(t)>0,f(t)递增,可得f(t)的最大值为f(1)=0,即有lnt≤t﹣1,则ln(x+2y﹣3)+ln(2x﹣3y+5)≤x+2y﹣3﹣1+2x﹣3y+5﹣1=3x﹣y,当且仅当x+2y﹣3=2x﹣3y+5=1时,取得等号,则x=,y=,可得x+y=,故答案为:.的,则xy=4y+++∞),x春?南京期中)若x,y∈(0,201817.(取值范围是(,].+由基本不等式可得x【分析】2+xy,可得()﹣4≤y+xy≥20,+可得0<xy≤2,即有1<xy+1≤3,化简所求式子,运用对勾函数的单调性,可得所求范围.【解答】解:x,y∈(0,+∞),x+y+xy=4,+x可得+xy,2xy≥y+可得()2﹣4≤+0,﹣2≤≤,可得0<xy≤2,即有1<xy+1≤3,则=,=t=xy+1,可令递减,可得]1)+在(1,3由(xy++=t+,,17)(xy+1)[∈,的取值范围是(则],,(故答案为:].的取值范2222yxy满足x+y=2x,则,东湖区校级期末)已知实数秋(18.2016?x围是[0,].【分析】由x﹣x,构造函数f(x)42223222=2x≥0?0≤x≤2,x+yy=2x,得y=2x﹣x ﹣x(0≤x≤2),利用导数法可求得函数的单调区间与极值,从而可求其43=2x 值域.【解答】解:由x2222≥0x,,得y =2x+y﹣=2x(2x﹣x)=2x﹣x.422223=xy2,x ∴0≤x≤设f(x)=2x﹣x(0≤x≤2),43则f′(x)=6x﹣4x(3﹣2x),232=2x当0<x<时,f′(x)>0,函数f(x)在(0,)上单调递增;当,2)上单调递减,)在(xf(f′(x)<0,函数<x<2时,时,函数取得极大值,也是最大值,f()=,x=∴当当x=0、x=2时,f(x)=0,],0,函数f(x)的值域为[∴.0≤x即22≤y,[0故答案为:].19.(2014?监利县校级模拟)若实数a,b,c,d满足ab=2,c+2d=0,则(a﹣c)的最小值为.22)+(b﹣d相切与曲线﹣的图象,设直线y=2x+ty=【分析】分别画出函数,y=﹣2x于第一象限内的点P(m,n),则点P到直线y=﹣2x的距离即为所求.2x的图象,﹣解:分别画出函数y=,y=【解答】n),相切于第一象限内的点P(m,ty=设直线﹣2x+与曲线∴,n=m=1,∴,解得=2∵..)2,1切点为(∴..d= 由点到直线的距离公式可得=的最小值为,化为.22)﹣db∴(a﹣c)+(故答案为:.的部分图象如图所示,)(x,6]上的偶函数,f﹣20.已知函数f(x)是定义在[6 .x <3}0﹣6<x<﹣3或<>则不等式xf(x)0的解集为{x|分别求出不等式的解.<0,0结合函数的性质,函数的图象,对x>和x【分析】<3,>0,可得0<xx【解答】解:当x>0时,不等式xf()]上的偶函数,[﹣6,6)是定义在因为函数f(x3 ﹣6<x<x<0时,不等式xf()>0,解得﹣所以x }<0x<3﹣6{>)0的解集为x|﹣<x<3或xxf不等式(<3}x03<<﹣x故答案为:{|6x﹣或<小题)3三.解答题(共.的最小值.,求1a>1,b+>21.(2018?南通一模)已知即可得出>1>1,b【分析】根据a,的最小值.,两式相加便可求出;b>1a【解答】解:∵>1,;1>0∴a﹣1>0,b﹣,;∴两式相加:;;∴当且仅当,且时成立;“=”8取得最小值.即a=b=2时,的≥2|,m∈R,且f(x+2)0|2018?22.(德阳模拟)已知函数f(x)=m﹣x﹣解集为[﹣1,1].(1)求m的值;,且+∞)∈b,c(0,(2)若a,9.3ca+2b+≥++=m,证明:【分析】(1)运用绝对值的解法,即可得到所求值;(2)运用乘1法和基本不等式,即可得到证明.【解答】解:(1)函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,1],可得m﹣|x|≥0的解集为[﹣1,1],即有[﹣m,m}={﹣1,1],可得m=1;(2)证明:a,b,c∈(0,+∞),且++=1,则a+2b+3c=(a+2b+3c)()++)+()+()=3++++(++≥3+222=3+2+2+2=9,当且仅当a=2b=3c=3,取得等号.23.(2018?杨浦区一模)如图所示,用总长为定值l的篱笆围成长方形的场地,以墙为一边,并用平行于一边的篱笆隔开.(1)设场地面积为y,垂直于墙的边长为x,试用解析式将y表示成x的函数,并确定这个函数的定义域;(2)怎样围才能使得场地的面积最大?最大面积是多少?;由,表示出面积y,则长为L﹣3x【分析】(1)由题意设长方形场地的宽为x 0,可得函数的定义域;﹣3x>lx>0,且2)对其运用基本不等式求出函数的最值即场地的面积最大值,从而求解.(,y)设场地面积为,垂直于墙的边长为x 【解答】解:(1 ;﹣3x)它的面积y=x(l,00,可得函数的定义域为(,且l ﹣3x>由x>0 ;l)))=,(2)y=xl﹣3x(2=3x)≤×((×3x1﹣时,这块长方形场地的面积最大,当x=.l ﹣3x=这时的长为,最大面积为l归纳总结1、,则(1)若abab2Ra,b?22??22ba?b?a )(2)若,则(当且仅当时取“=”R?a,b?ab2、2ba?)若1(*Ra,?b,则ab?2)若(2*ba?ab?2a?bRb?a,时取“(当且仅当=,则”)2b?a??)若(3*b?a ,则时取“( 当且仅当=”)R?a,b?ab??2??11x?x?0”时取“= 3、若(当且仅当,则)2x??x10x?,则若1??x”当且仅当时取“= )(2??x?x1110x?,则若b?a )时取“= (当且仅当”-2?x?即?2x???2或x xxxba b?0aab?)(4.若当且仅当时取“=,则”2??ab ababab0ab?,则若22-2a?b时取“(当且仅当=)”?即???或??bababa22bba?a?a?b时取“=”)(当且仅当,则5.若R?ba,2)(?22注意:(1)当两个正数的积为定植时,可以求它们的和的最小值,当两个正数的和为定植时,可以求它们的积的最小值,正所谓“积定和最小,和定积最大”.(2)求最值的条件“一正,二定,三取等”(3)均值定理在求最值、比较大小、求变量的取值范围、证明不等式、解决实际问题方面有广泛的应用。
09年自考“英语(二)”完整讲义(121)

09年自考“英语(二)”完整讲义(121)Unit 12 练习一、词汇英译汉:1. symptom2. intellectual3. detail4. initial5. inventor6. confront7. sensitivity8. reflection9. creativity 10. character 11. trace 12. modest词组:13. investment 14. to substitute … for 15. be contrary to 16. to put off17. be confronted with 18. to gaze at19. be unaware of 20. to impress…on21. be free from 22. be beneficial to二、句子英译汉:1. At its best,daydreaming was considered a compensatory substitute for the real things in life.(para.1)2. There are always those who would substitute fantasy lives for the rewards of real activity.(para.2)3. Most people suffer from a lack of daydreaming rather than an excess of it . (para. 2)4. Not only are they less able to deal with the pressure of day-to-day existence,but also their self -control and self-direction become endangered. (para.2)5. But its beneficial effects go beyond this . (para. 3)Go beyond 表示“超越…,不仅仅是…”6. Historically ,scientists and inventors are one group that seems to take full advantage of relaxed moments. (para.7)Take advantage of 利用7.Whenever confronted with a task which seemed too hard to be dealt with ,he would stretch out on his laboratory sofa and let fantasies flood his mind. (para.7)8.Picture yourself as winning and that will contribute remarkably to success.9.The important thing to remember is to picture these desired objectives as if you had already attained them .三、汉译英1.比来的研究成果表白,白日做梦是日常生活的一部分。
新高一数学暑假提升讲义12 集合的概念、表示、常用数集、空集(解析版)

新高一数学暑假提升讲义12 集合的概念、表示、常用数集、空集1.下列各组对象中能构成集合的是()A .充分接近3的实数的全体B .数学成绩比较好的同学C .小于20的所有自然数D .未来世界的高科技产品【答案】C【解析】选项A 、B 、D 中集合的元素均不满足确定性,只有C 中的元素是确定的,满足集合的定义,故选:C.2.设不等式2280x x --<的解集为M ,下列正确的是()A .1,4M M -∉∉B .1,4M M -∈∉C .1,4M M -∉∈D .1,4M M -∈∈【答案】B【解析】解不等式:2280x x --<,可得:24x -<<,所以{}=|-2<4M x x <,显然1,4M M -∈∉,故选:B.3.直线2y x =与3y x 的交点组成的集合是()A .{}3,6B .36,C .3,6x y ==D .{}(3,6) 【答案】D【解析】联立23y x y x =⎧⎨=+⎩,可得3x =,6y =,写成点集为{}(3,6).故选:D. 4.已知集合{}2|ln 1A x N x =∈<,则A =()A .1|x x e e ⎧⎫<<⎨⎬⎩⎭B .{}1C .{}2D .{}1,2【答案】D【解析】由2ln 1x <,可得:1ln 1x -<<,所以1x e e<<, 又因为:x ∈N ,所以{}1,2A =,故选:D5.已知集合M ={1,m +2,m 2+4},且5∈M ,则m 的值为A .1或-1B .1或3C .-1或3D .1,-1或3【答案】B【解析】因为5∈{1,m +2,m 2+4},所以m +2=5或m 2+4=5,即m =3或m =±1.当m =3时,M ={1,5,13};当m =1时,M ={1,3,5};当m =-1时,不满足互异性.所以m 的值为3或1.6.方程的解集为{}2|2320x R x x ∈--=,用列举法表示为____________. 【答案】1{,2}2-. 【解析】方程22320x x --=得12x =-或2x =,故答案为1{,2}2-. 【点睛】本题考查集合的表示方法,属于基础题.7.已知集合{}2320A x ax x =-+=,若A 中至少有一个元素,则a 的取值范围是______; 【答案】98a ≤[来源:学*科*网Z*X*X*K] 【解析】若A 中至少有一个元素,则方程2320ax x -+=至少有一个解. 当0a =时,方程2320ax x -+=等价为320x -+=,即23x =,满足条件. 当0a ≠,判别式980a ∆=-,解得98a ≤且0a ≠. 综上所述,a 的取值范围为98a ≤,即9,8a ⎛⎤∈-∞ ⎥⎝⎦ 故答案为:9,8⎛⎤-∞ ⎥⎝⎦【点睛】本题主要考查元素和集合之间关系的应用,利用一元二次方程根与判别式之间的关系是解决本题的关键,属于基础题.8.已知集合A 含有两个元素a 和a 2,若1∈A,求实数a 的值.【答案】a =-1.【解析】若1∈A,则a =1或a 2=1,即a =±1.当a =1时,集合A 有重复元素,∴a≠1;当a =-1时,集合A 含有两个元素1,-1,符合互异性.∴a=-1.9.设集合{|4},11M x x a =≥=,则下列关系中正确的是( )A .a M ∈B .a M ∉C .{}a M ∈D .{}a M ∉【答案】B【解析】411,a M >∴∉,故选B.【点睛】本题考查了元素与集合的关系,属于简单题..10.已知集合{}1,0,1A =-,(),|,,x B x y x A y A y ⎧⎫=∈∈∈⎨⎬⎩⎭N ,则集合B 中所含元素的个数为() A .3B .4C .6D .9【答案】B【解析】因为x A ∈,y A ,x y∈N , 所以满足条件的有序实数对为()1,1--,()0,1-,()0,1,()1,1.故选:B.11.已知集合{}1,2,3A =,集合{},,B z z x y x A y A ==-∈∈,则集合B 中元素的个数为( )A .4B .5C .6D .7【答案】B【解析】{}1,2,3A =,{},,B z z x y x A y A ==-∈∈,[来源:学&科&网]1,2,3x ∴=,1,2,3y =当1x =时,0,1,2x y -=--当2x =时,1,0,1x y -=-当3x =时,2,1,0x y -=即2,1,0,1,2x y -=--,即{}2,1,0,1,2B =--共有5个元素本题正确选项:B【点睛】本题主要考查集合元素个数的判断,利用条件求出x y -的值是解决本题的关键.12.已知集合2{2,25,12}A a a a =-+,且3A -∈,则a 等于( )A .-1B .23-C .32-D .32-或-1 【答案】C【解析】332A a -∈∴-=- 或2325a a -=+1a ∴=- 或32a =-∴当1a =- 时,223253a a a -=-+=-, ,不符合集合中元素的互异性, 故1a =-应舍去当32a =-时,2722532a a a -=-+=-,,满足题意32a ∴=-. 故选C . 【点睛】本题主要考察了集合中元素的互异性,较难.解题的关键是求出a 的值后要回代到集合中利用集合中元素的互异性进行检验.13.方程组2040x y x +=⎧⎨-=⎩的解组成的集合为_________. 【答案】()(){}2,2,2,2--【解析】由240x -=,解得2x =或2x =-,代入0x y +=,解得22x y =⎧⎨=-⎩或22x y =-⎧⎨=⎩,所以方程组2040x y x +=⎧⎨-=⎩的解组成的集合为{}(2,2),(2,2)--,故答案为{}(2,2),(2,2)--. 14.甲、乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.【答案】{48,51,54,57,60}【解析】因为20道选择题每题3分,甲最终的得分为54分,所以甲答错了2道题,又因为甲和乙有两道题的选项不同,则他们最少有16道题的答案相同,设剩下的4道题正确答案为AAAA ,甲的答案为BBAA ,因为甲和乙有两道题的选项不同,所以乙可能的答案为BBCC ,BCBA ,CCAA ,CAAA ,AAAA 等,所以乙的所有可能的得分值组成的集合为{48,51,54,57,60},故答案为{48,51,54,57,60}.【点睛】本题考查了集合的性质、分类讨论方法,考查了推理能力与计算能力,属于基础题.15.含有三个实数的集合既可表示成,,1b a a ⎧⎫⎨⎬⎩⎭又可表示成{}2,,0a a b +,20142015a b +=______. 【答案】1 【解析】由题意可知,两个集合相等,{}2,,1,,0b a a a b a ⎧⎫=+⎨⎬⎩⎭, 由0a ≠所以只能是0b a=,即0b =,所以{}{}2,0,1,,0a a a =, 由集合互异性可知1a ≠,则21a =,解得1a =-,符合题意,所以20142015101a b +=+=,故答案为:1.16.已知集合(){}21,1A m m =+-,若1A ∈,则m =______.【答案】2【解析】依题意11m +=或()211m -=,解得0m =或2m =;由集合中元素的互异性可知当0m =时,集合的两个元素相等,不合题意;所以2m =.故答案为:2.17.已知22{1,251,1}A a a a a =-+++, 2A -∈,求实数a 的值.【解析】因为2A -∈,所以有12,a -=-或22512a a ++=-,显然212a +≠-,当12a -=-时,1a =-,此时212512a a a -=++=-不符合集合元素的互异性,故舍去;当22512a a ++=-时,解得32a =-,1a =-由上可知不符合集合元素的互异性,舍去,故32a =-. 【点睛】本题考查了元素与集合之间的关系,考查了集合元素的互异性,考查了解方程、分类讨论思想.18.若集合2{|320,}A x ax x a R =-+=∈有且仅有两个子集,求实数a 的取值范围.【解析】依题意A 中只有一个元素.(1)当0a =时,方程320x -+=只有一解,∴0a =,(2)当0a ≠时,由00a ≠⎧⎨∆=⎩得98a =,综上,0a =或98a =. 19.求下列方程或方程组的解集.(1)42617120x x -+=(2)221321x y x y ⎧+=⎨-=⎩【解析】(1)422261712(34)(23)0x x x x -+=--=2340x ∴-=或223=0x -243x ∴=或23=2x 1234232366x x x x ∴====解集为232366{}(2)21x y -=即122x y =-代入2213x y += 2221()1352510(3)(517)022x x x x x x +-=∴--=∴+-= 21121735265x x y y ⎧=⎪=-⎧⎪∴⎨⎨=-⎩⎪=⎪⎩,,解集为: 176{(3,2),(,)}55-- 【点睛】本题考查了二次方程和方程组的解法,考查了学生转化与划归,数学运算的能力,属于中档题.20.用合适的方法表示下列集合,并说明是有限集还是无限集.(1)到A 、B 两点距离相等的点的集合(2)满足不等式21x >的x 的集合(3)全体偶数(4)被5除余1的数(5)20以内的质数(6){(,)|6,,}x y x y x N y N **+=∈∈(7)方程()0,x x a a R -=∈的解集【解析】(1)因为到A 、B 两点距离相等的点P 满足PA PB =,所以集合{A =点}P PA PB =,无限集.(2)由题意可知,集合{}21B x x =>,无限集.(3)因为偶数x 能被2整除,所以集合{}2,C x x k k Z ==∈,无限集.(4)由题意可知,集合{}51,D x x k k Z ==+∈,无限集.(5)因为20以内的质数有2,3,5,7,11,13,17,19.所以集合{}2,3,5,7,11,13,17,19E =,有限集.(6)因为6,,x y x N y N **+=∈∈,所以方程的解为15x y =⎧⎨=⎩,24x y =⎧⎨=⎩,33x y =⎧⎨=⎩,42x y =⎧⎨=⎩,51x y =⎧⎨=⎩,所以集合()()()()(){}1,5,2,4,3,3,4,2,5,1F =,有限集.(7)由题意可知,集合{}()0,G x x x a a R =-=∈,有限集.【点睛】本题考查集合的表示方法,属于较易题.21.用列举法表示下列集合:(1){}2|9A x x ==;(2){|12}B x N x =∈≤≤;[来源:](3){}2|320C x x x =-+=.【答案】(1){3,3}-(2){1,2}(3){1,2}【解析】 (1)由29x =得3x =±,因此{}2|9{3,3}A x x ===-.(2)由x ∈N ,且12x ≤≤,得1,2x =,因此{|12}{1,2}B x N x =∈≤≤=(3)由2320x x -+=得1,2x =.因此{}2|320{1,2}C x x x =-+==.。
12饮酒-2022年中考语文复习“决胜古诗文”专题讲义

【诗歌原文】饮酒(晋:陶渊明)结庐在人境,而无车马喧。
问君何能尔?心远地自偏。
采菊东篱下,悠然见南山。
山气日夕佳,飞鸟相与还。
此中有真意,欲辨已忘言。
【诵读点拨】饮酒(晋:陶渊明)结庐/在人境,而无/车马喧。
问君/何能尔?心远/地自偏。
采菊/东篱下,悠然/见南山。
山气/日夕佳,飞鸟/相与还。
此中/有真意,欲辨/已忘言。
【作家作品】陶渊明(约365~427年),字元亮,晚年更名潜,字渊明。
别号五柳先生,私谥靖节,世称靖节先生。
浔阳柴桑(今江西九江)人。
东晋杰出的诗人、辞赋家、散文家。
被誉为“田园诗派之鼻祖”。
他是中国第一位田园诗人,被称为“古今隐逸诗人之宗”,有《陶渊明集》。
代表作有《归田园居》《桃花源记》《饮酒》《五柳先生传》等。
【译文】住在喧嚣扰攘的尘世,却没有车马的喧闹。
问我为何能如此?因为心远离了尘世,住地就自然显得僻静了。
在东篱附近采摘野菊,抬头就可以悠闲地南山的景色。
暮色山中的云气很好,鸟儿结伴归来。
这里面蕴含着人生的真意,想要分辨清楚,却已忘了怎样表达。
[句析]1.结庐在人境,而无车马喧。
写诗人虽身居闹市,却不受世俗烦扰,表达了诗人陶醉于自然,恬淡愉悦的心情。
2.问君何能尔?心远地自偏。
运用设问的修辞,一问一答,回答了“无车马喧”的原因。
“心远”一词,反映了诗人超尘脱俗,毫无名利之念的精神世界。
3.采菊东篱下,悠然见南山。
以客观景物的描写衬托出诗人的闲适心情,“悠然”形象地写出了诗人远离世俗后心灵的自得、闲适、恬淡。
“见”写出了诗人看到南山美景时的随意自然,体现了作者心灵的自由和惬意。
心与山融为一体,悠然自得。
4.山气日夕佳,飞鸟相与还。
以飞鸟自喻,借飞鸟结伴飞返山林,万物自由自在,适性而动的景象,表达出诗人弃官归隐的情怀。
5.此中有真意,欲辨已忘言。
“真意”指自然之趣和人生真谛。
这两句哲理性的小结给读者言有尽而意无穷的想象余地。
[赏析]本诗是晋朝大诗人陶渊明创作的组诗《饮酒二十首》的第五首诗。
第12讲 初识家用电器和电路(教师版) 2024年新九年级物理暑假提升讲义(苏科版)

第12讲 初识家用电器和电路模块一思维导图串知识 模块二基础知识全梳理(吃透教材)模块三教材习题学解题 模块四核心考点精准练(6大考点)模块五 小试牛刀过关测1.理解电流的形成,及电流方向。
2.知道电路的构成、电路元件符号。
3.掌握电路图的画法和实物图的连接。
4.能够识别电路的三种状态。
5.能进行简单的故障判断。
1、电路的组成(2)电路各部分的作用(3)电源:提供电能的装置,将其他形式的能转化为电能。
的遥控器,都需用干电池为它们提供电能。
用于汽车、摩托车、通讯等。
能的转化:蓄电池在充电时,电能转化为化学能,放电时化学能又转化为电能。
2、电路图及元件符号(1)电路图:用规定的符号表示电路连接情况的图叫做电路图。
(2)几种常见的元件符号如下:3、电路的三种状态(1)通路:正常连接的电路,即用电器能够工作的电路。
通路特征:电路中有电流,用电器正常工作。
(2)断路(开路):断开的电路。
断路特征:电路中无电流,用电器不工作.原因有开关没闭合,接线处松动,导线断了,用电器损坏等。
(3)短路:不经过用电器而直接跟电源的两极相连的电路。
短路特征:用电器不工作,电路有很大电流,会损坏电源甚至烧坏导线的绝缘皮,引起火灾。
4、根据实物图画电路图(1)画好电路图的方法①应完整地反映电路的组成,即有电源、用电器、开关和导线。
②规范地使用电路元件符号,不能自选符号。
③交叉相连的点要画粗黑圆点。
④合理地安排电路元件符号的位置,尽可能让这些元件符号均匀地分布在电路中,使电路图清楚美观,并注意元件符号绝不能画在拐角处。
⑤导线要横平竖直,转弯画成直角,电路图一般呈长方形。
⑥最好从电源的正极开始,沿着电流的方向依次画电路元件,且知道在电路图中导线无长短之分的原则。
(2)根据实物图画出电路图的方法①先理清电流的路径,可从电源正极开始,沿着电流的方向逐个寻找,直到电源负极。
②所画出的电路图中各元件的顺序应与实物图保持一致。
教材习题01设法用一段导线、一节干电池使一个小灯泡发光。
12中医外科学讲义 泌尿男性疾病
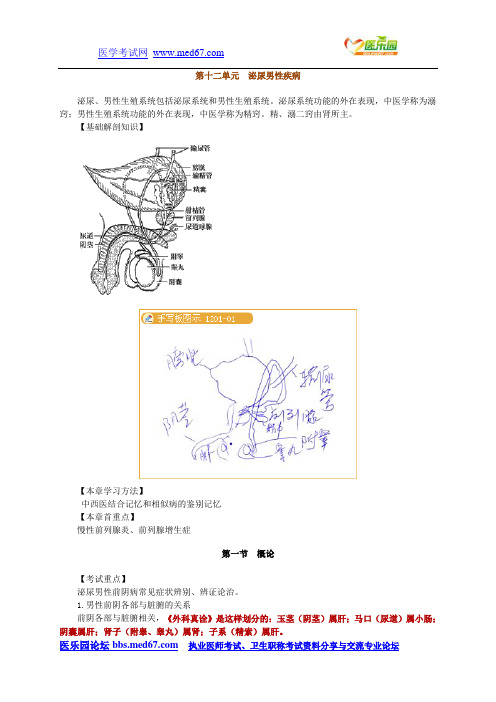
第十二单元泌尿男性疾病泌尿、男性生殖系统包括泌尿系统和男性生殖系统。
泌尿系统功能的外在表现,中医学称为溺窍;男性生殖系统功能的外在表现,中医学称为精窍。
精、溺二窍由肾所主。
【基础解剖知识】【本章学习方法】中西医结合记忆和相似病的鉴别记忆【本章首重点】慢性前列腺炎、前列腺增生症第一节概论【考试重点】泌尿男性前阴病常见症状辨别、辨证论治。
1.男性前阴各部与脏腑的关系前阴各部与脏腑相关,《外科真诠》是这样划分的:玉茎(阴茎)属肝;马口(尿道)属小肠;阴囊属肝;肾子(附睾、睾丸)属肾;子系(精索)属肝。
2.泌尿男性疾病常见证型及治法(1)湿热下注证:表现为尿频、尿急,茎中热痛,尿液黄赤,血淋,白浊,阴囊红肿热痛,附睾、睾丸肿痛,囊内积液,外阴多汗味臊等。
治疗法则为清利湿热。
溺窍异常多为膀胱漫热,用八正散、导赤散等加减;精窍异常多为脾肾湿热,用程氏萆薢分清饮加减;肝经湿热用龙胆泻肝汤加减。
(2)气血瘀滞证:表现为睾丸硬结,少腹、会阴、睾丸胀痛或刺痛,排尿困难或闭塞不通,或尿有血块等。
治疗大法为行气活血。
气滞为主者,用橘核丸、枸橘汤加减;血瘀为主者,用代抵挡丸、活血散瘀汤加减。
(3)浊痰凝结证:表现为附睾慢性肿块或阴茎结节,皮色不变,不痛或微痛;若浊痰化热,局部可发红发热,伴有疼痛,或化脓破溃;浊痰滞于溺窍,可出现排尿淋沥不畅,尿线变细;浊痰阻于精窍,可致不射精。
治疗法则为化痰散结。
寒痰凝结者,当温阳化痰散结,用阳和汤、橘核丸、化坚二陈汤加减;浊痰化热者,当清热化痰散结,用消核丸加减;精窍痰凝者,当通窍化痰散结,甩苍附导痰汤加减。
(4)肾阴不足证:表现为腰膝酸痛、头目眩晕、盗汗失眠、五心烦热、血精、精浊等。
治疗法则为滋补肾阴,常用方剂为六味地黄丸、知柏地黄丸、大补阴丸等。
(5)肾阳虚衰证:表现为形寒肢冷,腰膝酸痛,小便清长,夜尿频多,阳痿不举,精冷不育等。
治疗法则为温补肾阳,常用方剂为金匮肾气丸、右归丸、济生肾气丸等。
教师职业道德与专业发展,讲义第十二章 教师专业发展的途径

第十二章教师专业发展的途径第一节职前教师教育教育的核心任务是提高教育质量,而提高教育质量的核心是提高教师素质,教师职前教育承担着培养未来教师的重任。
教师专业化已经成为国际大趋势,教师的素质主要体现在专业化的程度上。
职前教师教育是教师教育的起点,也是教师专业发展的起点和基础,在教师教育过程中具有举足轻重的地位。
一、职前教师教育的概念职前教师教育就是教师的资格教育,是教师的专业预备教育。
广义的职前教育指所有准备从事教师职业的大学生在高校接受教育的过程,狭义的职前教师教育就是指职前师范教育阶段,其主要任务是为毕业后从事教师职业打下必要的思想和业务基础。
二、职前教师教育的主要内容及目标职前教师教育要为未来教师的专业发展奠定良好的基础,教育内容的选择至关重要。
1.职前教师教育的主要内容教育内容通过教育课程表现出来,教育课程是教师专业化发展的主要保障,职前教师教育课程主要包括四个部分:(1)普通教育普通教育课程,又称公共基础课、通识课程等,是教师教育课程体系的重要组成部分。
在教师教育课程体系中处于基础学科的地位,其主要目的是:培养学生形成正确的人生观和世界观;培养学生的人文精神,塑造健全人格与教师气质特征;塑造认识事物、观察事物和解决问题的能力;增强处理社会关系以及交流、协作的能力。
(2)专门学科教育专门学科教育是为教师在学校系统能承担一门学科的教学工作、传授该学科的基本原理和方法而设计的教育。
每一位教师应该熟悉所教学科的知识领域,掌握学科的基本原理及教学该学科的独特方法。
(3)专业教育专业教育是以教师在学校能有效地组织、开展教育教学活动,全面促进学生的身心发展为目的而设计的学习内容。
在职前教育阶段,专业教育的重心是学习系统化的教育理论,训练基本的教学技能,确立坚定的从教志向。
(4)教育实践课程各国师范教育中都设有教育实践课程,在教学实践中为学生提供了大量机会,运用掌握的知识和技能于实际教学,通过自身的努力充分将理论和实践结合。
小学数学6年级培优奥数讲义 第12讲-浓度应用题(教师版)

第12讲 浓度应用题①明确溶液的质量,溶质的质量,溶剂的质量之间的关系;②浓度三角的应用;③会将复杂分数应用题及其他类型题目转化成浓度三角形式来解;④利用方程解复杂浓度问题。
一、浓度问题中的基本量溶质:通常为盐水中的“盐”,糖水中的“糖”,酒精溶液中的“酒精”等;溶剂:一般为水,部分题目中也会出现煤油等;溶液:溶质和溶液的混合液体;浓度:溶质质量与溶液质量的比值。
二、几个基本量之间的运算关系1、溶液=溶质+溶剂;2、=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液。
三、解浓度问题的一般方法1、寻找溶液配比前后的不变量,依靠不变量建立等量关系列方程2、十字交叉法:(甲溶液浓度大于乙溶液浓度)形象表达:A B =甲溶液质量乙溶液质量B A =甲溶液与混合溶液的浓度差混合溶液与乙溶液的浓度差注:十字交叉法在浓度问题中的运用也称之为浓度三角,浓度三角与十字交叉法实质上是相同的.浓度三角的表示方法如下:教学目标知识梳理::乙溶液质量甲溶液质量z-y x-z z-y x-z乙溶液浓度y %甲溶液浓度x %混合浓度z%3、列方程解应用题也是解决浓度问题的重要方法.考点一:简单的溶液浓度问题例1、某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到,那么这种溶液的食盐浓度为多少?【解析】两种配置溶液共含食盐40×15%+60×10%=12克,而溶液质量为40+60-50=50克,所以这种溶液的浓度为12÷50=24%.例2、买来蘑菇10千克,含水量为99%,晾晒一会儿后,含水量为98%,问蒸发掉多少水份?【解析】方法一:做蒸发的题目,要改变思考角度,本题就应该考虑成“98%的干蘑菇加水后得到99%的湿蘑菇”,这样求出加入多少水份即为蒸发掉的水份,就又转变成“混合配比”的问题了。
但要注意,10千克的标注应该是含水量为99%的重量。
将10千克按1∶1分配,10÷2=5,蒸发掉5千克水份。
【独家】五年级上册语文讲义-预习与讲练:第12课《古诗三首》-部编版

第 周 第 天 星期教学目标:1.体会诗人的爱国主义情感,激发学生爱国意识。
2.会认“喑、擞”等6个生字,会写“祭、乃”等8个生字。
(重点)3.有感情地朗读并背诵这三首诗,理解这三首诗的意思。
(难点)12 古诗三首背诵课文示儿 [宋]陆 游死去元知万事空,但悲不见九州同。
王师北定中原日,家祭无忘告乃n ǎi翁。
题临安邸d ǐ[宋]林 升山外青山楼外楼,西湖歌舞几时休? 暖风熏x ūn得游人醉,直把杭州作汴bi àn州。
己亥h ài杂诗[清]龚ɡōn ɡ自珍九州生气恃sh ì风雷,万马齐喑y īn究可哀。
我劝天公重抖擞s ǒu,不拘一格降人才。
作者介绍:陆游,南宋诗人。
字务观,号放翁,一生坚持抗金,在仕途上一直受到当权派的排斥打击。
诗歌洋溢着爱国主义精神。
林升,字云友,又名梦屏,是一位擅长诗文的士人。
龚自珍,由于力主改革弊政,受当局排挤,48岁愤然辞官南归。
生字新词(给生字注音并组词。
)()()()()()()()()()()()()()()()()知识归纳生字组词:祭:祭拜祭祀祭奠祭天祭坛祭文乃:乃父乃至乃至于有容乃大熏:熏风熏陶熏肉熏染臭气熏人杭:杭州苏杭杭绸亥:亥时恃:自恃有恃无恐恃强凌弱恃才傲物哀:哀伤悲哀哀悼哀怜哀兵必胜拘:拘束拘谨拘禁拘管不拘一格多音字:几:jǐ几个 jī茶几降:jiàng降落 xiáng投降xūn:熏(熏陶)薰(薰衣草)shì:恃(有恃无恐)侍(侍候)形近字:祭:(祭拜)察(观察)杭:(杭州)抗(抗争)恃:(自恃)待(等待)课文主题《示儿》是诗人临终前写给儿子的一首诗,诗人痛惜自己无法亲眼看到国家统一,希望儿子以后家祭的时候能将这一好消息告诉自己,表达了他渴望收复失地、祖国统一的爱国情怀。
《题临安邸》描写了诗人对苟且偏安、一味寻欢作乐的达官贵人们的讽刺和愤慨,以乐景写哀情,表达了诗人的愤激之情。
《己亥杂诗》写了诗人对死气沉沉、缺乏生机的社会现状深感痛心,希望巨大的社会变革迅速到来,表达了诗人对国家未来命运的关切和对当政者能够广纳人才的渴望。
二年级语文暑假讲义(12)——修改符号

★ 调换符号 当我们把字词或者短语写错位置时,相比删除再改正的方法,更简单的方法是使 用调换符号,使它们回到正确的位置。
【典例分析】 1、我们好好学习应该。 2、哥哥今年十岁,我今年八岁,我比哥哥大。 3、我认真检查作业并完成了作业。 4、语文喜欢我。 5、一年四季:春、夏、冬、秋,是按照顺序更替的。
yǔ
sài pǎo yì
dào lù
biān zhī
jiǎn dān
yuàn
(二)用“ ”画出下列加点字的正确读音。 1.尽.(jǐn jìn)管我已经尽.(jǐn jìn)力了,但还是没有完成任务。 2.演出时,姑娘们扇.(shān shàn)动着手中的扇.(shān shàn)子,太迷
人了。 3.他吆喝.(he hē)道:“喝.(hè hē)了这种饮料,保你能量十足。” 4.我的.(dí de)妈妈的.(dí de)确是心灵手巧啊!
(四)用修改符号修改下面一段话。 我养了小猫一只。他的眼睛像黑色珍珠。小猫长得肥肥的,脖子有一圈毛白色的。 我十分酷爱小猫!
能标出物体在那个时间的时空位置。举例来说,地球的公转轨道是宇宙中一个近 乎圆形的三维封闭曲线,地球每年都会转回同一个点,但时间却不一样。地球的 世界线会在四维时空中循环(像弹簧的形状那样沿螺旋式轨迹延伸),而不会回 到同一点上。
时空是称为“事件”的“点”,与标有事件的持续、稳定坐标系之集合。四 维时空的每个事件都有三个空间维度和一个时间维度,在数学上这称为流形。若 将此概念应用于高阶空间,为了方便在平面上作图,其中两个空间维度会被省略。 每个事件都是闵可夫斯基图上的一个点,图上的坐标系纵坐标为时间轴,横坐标 为空间轴。粒子在闵可夫斯基图上的连续轨迹即为世界线。
12《野望》王绩上课讲义

小结
• 这首诗首尾两联抒情言事,中间两联 写景,经过情──景──情这一反复, 诗的意思更深化了一层。
• 这首诗写的是山野秋景,表达了作者 辞官隐居后闲逸、彷徨和苦闷的复杂 心情。
全诗于萧瑟怡静的景色描写中 流露出孤独抑郁的心情,抒发了 惆怅、孤寂的情怀。
• 王绩《野望》作品取境开阔,风 格清新,属对工整,格律谐和,是 唐初最早的五言律诗之一。王尧衢 曰:此诗格调最清,宜取以压卷。 视此,则律中起承转合了然矣。
作者简介
王绩(585—644),唐代医生、著 名诗人。字无功,号东皋子,绛州 (今属山西.河津市)人。其兄王通亦 是当时名医,绩尝任秘书正字,后借 故辞归,专心以医药济人。出身官宦 世家,是隋末大儒王通之弟,唐初诗 人王勃是他的侄孙。王绩一生郁郁不 得志,在隋唐之际,曾三仕三隐。心 念仕途,却又自知难以显达,故归隐 山林田园,以琴酒诗歌自娱。曾在隋 代任秘书省正字,初唐时,以原官待 召门下头纵目远眺,(我)徘徊不定, 不知归依何方。
• 树树皆秋色,山山唯落晖。
• 层层树林都染上秋天的色彩,重重山岭披覆着落日的余 光。
• 牧人驱犊返,猎马带禽归。
• 牧人驱赶着那牛群返回家园,猎人骑着马带着猎物回去。
• 相顾无相识,长歌怀采薇。
• 我看到这些人又并不认识,咏一曲长歌来怀念古代采薇 而食的隐士。
王绩还不能像陶渊明那样从田园中找到慰藉所以最后以相顾无相识长歌怀采薇结尾诉说自己在现实中孤独无依只好追怀古代的隐士过隐居生活和伯夷叔齐那样的人交朋友了
理解题意
• 结合注释,说说题目的意思 • 明确:“野望”意即眺望原野,是唐
代诗人王绩的诗作,是一首五言律诗。
写作背景
• 王绩入唐后以秘书省正字待诏门下省, 不久辞官还乡。贞观中出为太乐丞, 旋又告归。此诗当作于诗人辞官隐居 东皋(在今山西河津)时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
神奇的11
电脑前的小朋友们,你们都是2000年后出生的吧!现在呢,用你的出生年份的最后两个数字加上你今年的年龄,我将能预测到你算出的数字哦!不信吗?让咱们试试吧! 我看到了,你心中算出的数字是11,哈哈!我说对了吧!
想知道这是怎么回事吗?这就是数学的神奇哦!道理其实很简单,让咱们一块儿来看看吧!
为什么你的出生年份的最后两个数字加上你今年的年龄,正好是11呢?
思考:
爸爸妈妈的年龄加上出生年份的末两位数字也等于11吗?
数字黑洞
其实在数学世界里面,也有数字黑洞哦!它们就是:6 1 7 4
为什么把这几个数字叫做“数字黑洞”呢?让咱们一起来看看这几个数字的神奇之处吧!
选择四个数字(不能完全相同),把所有的数字从小到大排列;再把所有的数字从大往小排列。
分别得到两个数字,将两个数字做差之后得到一个新数。
重复刚才的操作,7步之内必然得到6174!
失踪的“1”
64=65?
孩子们,想知道“面积骗子”里的神奇吗?不要着急,让我们先来看一段动画吧!(温馨提示:动画见视频)
透视眼
为什么呢?为什么呢?快揭秘吧!(温馨提示:动画见视频)
其实这个魔术的原理非常非常简单,它仅仅是一个数学上的小把戏!赶紧来看看吧!
其实这个魔术的原理很简单,表演者只需要记住牌的数量,想办法让两叠牌的数量都是26张就可以啦!
读心术
电脑前的小朋友,我能知道你在想什么,你信吗?
当然不信啦~~~怎么可能嘛……
你要不信,那咱们就试试看吧!
现在呢,从1到10选一个数字记在心里。
用这个数乘以2,加上三,再乘以5,最后减去25,得到结果。
把结果告诉我,我就把你想的数告诉你哦!我们来试试!
结果是90!你倒是猜猜我心里想的数字是多少呀~
嘿嘿,你心里想的是10
啊?!你怎么知道的…
其实很简单,就是一个还原问题!让咱们一起看看吧!
用选出的数乘以2,加上三,再乘以5,最后减去25,得到结果。
通过这个结果,求出原来的数是多少。
