2020南充二诊试题及答案
四川省南充市2019-2020学年中考二诊数学试题含解析

四川省南充市2019-2020学年中考二诊数学试题一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.如图,⊙O 的半径OD ⊥弦AB 于点C ,连接AO 并延长交⊙O 于点E ,连接EC ,若AB=8,CD=2,则cos ∠ECB 为( )A .35B .313C .23D .213 2.二次函数y=x 2+bx –1的图象如图,对称轴为直线x=1,若关于x 的一元二次方程x 2–2x –1–t=0(t 为实数)在–1<x<4的范围内有实数解,则t 的取值范围是A .t≥–2B .–2≤t<7C .–2≤t<2D .2<t<73.如图,在Y ABCD 中,E 为CD 上一点,连接AE 、BD ,且AE 、BD 交于点F ,DEF ABF S S 425∆∆=::,则DE :EC=( )A .2:5B .2:3C .3:5D .3:24.某城2014年底已有绿化面积300公顷,经过两年绿化,到2016年底增加到363公顷,设绿化面积平均每年的增长率为x ,由题意所列方程正确的是( ).A .300(1)363x +=B .2300(1)363x +=C .300(12)363x +=D .2300(1)363x -= 5.下列运算正确的是( )A .(a 2)4=a 6B .a 2•a 3=a 6C 236=D 235=6.二次函数y=ax 2+bx+c(a≠0)的图象如图,则反比例函数y=a x与一次函数y=bx ﹣c 在同一坐标系内的图象大致是( )A.B.C.D.7.如图,这是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积为()A.9πB.10πC.11πD.12π8.反比例函数y=mx的图象如图所示,以下结论:①常数m<﹣1;②在每个象限内,y随x的增大而增大;③若点A(﹣1,h),B(2,k)在图象上,则h<k;④若点P(x,y)在上,则点P′(﹣x,﹣y)也在图象.其中正确结论的个数是( )A.1 B.2 C.3 D.49.如右图是用八块完全相同的小正方体搭成的几何体,从正面看几何体得到的图形是()A.B.C .D .10.某种商品每件的标价是270元,按标价的八折销售时,仍可获利20%,则这种商品每件的进价为( ) A .180元 B .200元 C .225元 D .259.2元11.下列计算正确的是( )A .a 4+a 5=a 9B .(2a 2b 3)2=4a 4b 6C .﹣2a (a+3)=﹣2a 2+6aD .(2a ﹣b )2=4a 2﹣b 212.下列各式正确的是( )A .0.360.6±=±B .93=±C .33(3)3-=D .2(2)2-=-二、填空题:(本大题共6个小题,每小题4分,共24分.)13.已知关于X 的一元二次方程()2m 2x 2x 10-++=有实数根,则m 的取值范围是____________________14.边长分别为a 和2a 的两个正方形按如图的样式摆放,则图中阴影部分的面积为_________.15.如图,在矩形ABCD 中,过点A 的圆O 交边AB 于点E ,交边AD 于点F ,已知AD=5,AE=2,AF=1.如果以点D 为圆心,r 为半径的圆D 与圆O 有两个公共点,那么r 的取值范围是______.16.若实数a 、b 在数轴上的位置如图所示,则代数式|b ﹣a|+2a 化简为_____.17.如图,△ABC ∽△ADE ,∠BAC=∠DAE=90°,AB=6,AC=8,F 为DE 中点,若点D 在直线BC 上运动,连接CF ,则在点D 运动过程中,线段CF 的最小值是_____.18.如图所示是一组有规律的图案,第l 个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n (n 是正整数)个图案中的基础图形个数为_______ (用含n 的式子表示).三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)反比例函数k y x =在第一象限的图象如图所示,过点A (2,0)作x 轴的垂线,交反比例函数k y x=的图象于点M ,△AOM 的面积为2. 求反比例函数的解析式;设点B 的坐标为(t ,0),其中t >2.若以AB 为一边的正方形有一个顶点在反比例函数k y x=的图象上,求t 的值. 20.(6分)如图,AB 为半圆O 的直径,AC 是⊙O 的一条弦,D 为»BC的中点,作DE ⊥AC ,交AB 的延长线于点F ,连接DA .求证:EF 为半圆O 的切线;若DA =DF =63,求阴影区域的面积.(结果保留根号和π)21.(6分)解方程组:222232()x y x y x y ⎧-=⎨-=+⎩. 22.(8分)如图,在ABC ∆中,AB AC =,以AC 边为直径作⊙O 交BC 边于点D ,过点D 作DE AB ⊥于点E ,ED 、AC 的延长线交于点F .求证:EF是⊙O的切线;若,且,求⊙O的半径与线段的长.23.(8分)由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)24.(10分)某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.求y关于x的函数关系式;该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.25.(10分)菏泽市牡丹区中学生运动会即将举行,各个学校都在积极地做准备,某校为奖励在运动会上取得好成绩的学生,计划购买甲、乙两种奖品共100件,已知甲种奖品的单价是30元,乙种奖品的单价是20元.(1)若购买这批奖品共用2800元,求甲、乙两种奖品各购买了多少件?(2)若购买这批奖品的总费用不超过2900元,则最多购买甲种奖品多少件?26.(12分)如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD、CD.(1)求证:AD=CD;(2)若AB=10,OE=3,求tan∠DBC的值.27.(12分)如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)(1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为m.(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.D【解析】【分析】连接EB,设圆O半径为r,根据勾股定理可求出半径r=4,从而可求出EB的长度,最后勾股定理即可求出CE的长度.利用锐角三角函数的定义即可求出答案.【详解】解:连接EB,由圆周角定理可知:∠B=90°,设⊙O 的半径为r ,由垂径定理可知:AC=BC=4,∵CD=2,∴OC=r-2,∴由勾股定理可知:r 2=(r-2)2+42,∴r=5,BCE 中,由勾股定理可知:13∴cos ∠ECB=CB CE =1313, 故选D .【点睛】本题考查垂径定理,涉及勾股定理,垂直定理,解方程等知识,综合程度较高,属于中等题型. 2.B【解析】【分析】利用对称性方程求出b 得到抛物线解析式为y=x 2﹣2x ﹣1,则顶点坐标为(1,﹣2),再计算当﹣1<x <4时对应的函数值的范围为﹣2≤y <7,由于关于x 的一元二次方程x 2﹣2x ﹣1﹣t=0(t 为实数)在﹣1<x <4的范围内有实数解可看作二次函数y=x 2﹣2x ﹣1与直线y=t 有交点,然后利用函数图象可得到t 的范围.【详解】抛物线的对称轴为直线x=﹣2b =1,解得b=﹣2, ∴抛物线解析式为y=x 2﹣2x ﹣1,则顶点坐标为(1,﹣2),当x=﹣1时,y=x 2﹣2x ﹣1=2;当x=4时,y=x 2﹣2x ﹣1=7,当﹣1<x <4时,﹣2≤y <7,而关于x 的一元二次方程x 2﹣2x ﹣1﹣t=0(t 为实数)在﹣1<x <4的范围内有实数解可看作二次函数y=x 2﹣2x ﹣1与直线y=t 有交点,∴﹣2≤t <7,故选B .【点睛】本题考查了二次函数的性质、抛物线与x 轴的交点、二次函数与一元二次方程,把求二次函数y=ax 2+bx+c (a ,b ,c 是常数,a≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程是解题的关键. 3.B【解析】【详解】∵四边形ABCD 是平行四边形,∴AB ∥CD∴∠EAB=∠DEF ,∠AFB=∠DFE∴△DEF ∽△BAF∴()2DEF ABF S S DE AB ∆∆=:: ∵DEF ABF S S 425∆∆=::, ∴DE :AB=2:5∵AB=CD ,∴DE :EC=2:3故选B4.B【解析】【分析】先用含有x 的式子表示2015年的绿化面积,进而用含有x 的式子表示2016年的绿化面积,根据等式关系列方程即可.【详解】由题意得,绿化面积平均每年的增长率为x ,则2015年的绿化面积为300(1+x ),2016年的绿化面积为300(1+x )(1+x ),经过两年的增长,绿化面积由300公顷变为363公顷.可列出方程:300(1+x )2=363.故选B.【点睛】本题主要考查一元二次方程的应用,找准其中的等式关系式解答此题的关键.5.C【解析】【分析】根据幂的乘方、同底数幂的乘法、二次根式的乘法、二次根式的加法计算即可.【详解】A 、原式=a 8,所以A 选项错误;B 、原式=a 5,所以B 选项错误;C 、原式= ==C 选项正确;D D 选项错误.故选:C .【点睛】本题考查了幂的乘方、同底数幂的乘法、二次根式的乘法、二次根式的加法,熟练掌握它们的运算法则是解答本题的关键.6.C【解析】【分析】根据二次函数的图象找出a 、b 、c 的正负,再结合反比例函数、一次函数系数与图象的关系即可得出结论.【详解】解:观察二次函数图象可知:开口向上,a >1;对称轴大于1,2b a->1,b <1;二次函数图象与y 轴交点在y 轴的正半轴,c >1. ∵反比例函数中k =﹣a <1,∴反比例函数图象在第二、四象限内;∵一次函数y =bx ﹣c 中,b <1,﹣c <1,∴一次函数图象经过第二、三、四象限.故选C .【点睛】本题考查了二次函数的图象、反比例函数的图象以及一次函数的图象,解题的关键是根据二次函数的图象找出a 、b 、c 的正负.本题属于基础题,难度不大,解决该题型题目时,根据二次函数图象找出a 、b 、c 的正负,再结合反比例函数、一次函数系数与图象的关系即可得出结论.7.B【解析】【分析】由三视图可判断出几何体的形状,进而利用圆锥的侧面积公式求出答案.【详解】由题意可得此几何体是圆锥,底面圆的半径为:2,母线长为:5,故这个几何体的侧面积为:π×2×5=10π,故选B .【点睛】本题考查了由三视图判断几何体的形状以及圆锥侧面积求法,正确得出几何体的形状是解题关键.8.B【解析】【分析】根据反比例函数的图象的位置确定其比例系数的符号,利用反比例函数的性质进行判断即可.【详解】解:∵反比例函数的图象位于一三象限,∴m >0故①错误;当反比例函数的图象位于一三象限时,在每一象限内,y 随x 的增大而减小,故②错误;将A(﹣1,h),B(2,k)代入y =x m ,得到h =﹣m ,2k =m , ∵m >0∴h <k故③正确;将P(x ,y)代入y =x m 得到m =xy ,将P′(﹣x ,﹣y)代入y =xm 得到m =xy , 故P(x ,y)在图象上,则P′(﹣x ,﹣y)也在图象上故④正确,故选:B .【点睛】本题考查了反比例函数的性质,牢记反比例函数的比例系数的符号与其图象的关系是解决本题的关键. 9.B【解析】【分析】找到从正面看所得到的图形即可,注意所有从正面看到的棱都应表现在主视图中.【详解】解:从正面看该几何体,有3列正方形,分别有:2个,2个,2个,如图.故选B .【点睛】本题考查了三视图的知识,主视图是从物体的正面看到的视图,属于基础题型.10.A【解析】【分析】设这种商品每件进价为x 元,根据题中的等量关系列方程求解.【详解】设这种商品每件进价为x 元,则根据题意可列方程270×0.8-x =0.2x ,解得x =180.故选A. 【点睛】本题主要考查一元一次方程的应用,解题的关键是确定未知数,根据题中的等量关系列出正确的方程. 11.B【解析】分析:根据合并同类项、幂的乘方与积的乘方、单项式乘多项式法则以及完全平方公式进行计算.详解:A 、a 4与a 5不是同类项,不能合并,故本选项错误;B 、(2a 2b 3)2=4a 4b 6,故本选项正确;C 、-2a (a+3)=-2a 2-6a ,故本选项错误;D 、(2a-b )2=4a 2-4ab+b 2,故本选项错误;故选:B .点睛:本题主要考查了合并同类项的法则、幂的乘方与积的乘方、单项式乘多项式法则以及完全平方公式,熟练掌握运算法则是解题的关键.12.A【解析】3=,则B 3=-,则C 2=,则D 错,故选A .二、填空题:(本大题共6个小题,每小题4分,共24分.)13.m≤3且m≠2【解析】试题解析:∵一元二次方程()22210m x x -++=有实数根 ∴4-4(m-2)≥0且m-2≠0解得:m≤3且m≠2.14.1a 1.【解析】【分析】结合图形,发现:阴影部分的面积=大正方形的面积的+小正方形的面积-直角三角形的面积.【详解】阴影部分的面积=大正方形的面积+小正方形的面积-直角三角形的面积=(1a )1+a 1-12×1a×3a =4a 1+a 1-3a 1=1a 1.故答案为:1a 1.此题考查了整式的混合运算,关键是列出求阴影部分面积的式子.15.105105r -<<+ 【解析】 【分析】因为以点D 为圆心,r 为半径的圆D 与圆O 有两个公共点,则圆D 与圆O 相交,圆心距满足关系式:|R-r|<d<R+r ,求得圆D 与圆O 的半径代入计算即可.【详解】连接OA 、OD ,过O 点作ON ⊥AE ,OM ⊥AF.AN=12AE=1,AM=12AF=2,MD=AD-AM=3 ∵四边形ABCD 是矩形∴∠BAD=∠ANO=∠AMO=90°,∴四边形OMAN 是矩形∴OM=AN=1∴OA=22215+=,OD=221310+=∵以点D 为圆心,r 为半径的圆D 与圆O 有两个公共点,则圆D 与圆O 相交∴105105r -<<+【点睛】本题考查了圆与圆相交的条件,熟记圆与圆相交时圆的半径与圆心距的关系是关键.16.2a ﹣b .【解析】【分析】直接利用数轴上a ,b 的位置进而得出b ﹣a <0,a >0,再化简得出答案.【详解】解:由数轴可得:b ﹣a <0,a >0,则|b ﹣2a=2a﹣b.故答案为2a﹣b.【点睛】此题主要考查了二次根式的性质与化简,正确得出各项符号是解题关键.17.1【解析】试题分析:当点A、点C和点F三点共线的时候,线段CF的长度最小,点F在AC的中点,则CF=1.18.3n+1【解析】试题分析:由图可知每个图案一次增加3个基本图形,第一个图案有4个基本图形,则第n个图案的基础图形有4+3(n-1)=3n+1个考点:规律型三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(2)6yx(2)7或2.【解析】试题分析:(2)根据反比例函数k的几何意义得到12|k|=2,可得到满足条件的k=6,于是得到反比例函数解析式为y=6x;(2)分类讨论:当以AB为一边的正方形ABCD的顶点D在反比例函数y=6x的图象上,则D点与M点重合,即AB=AM,再利用反比例函数图象上点的坐标特征确定M点坐标为(2,6),则AB=AM=6,所以t=2+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数y=6x的图象上,根据正方形的性质得AB=BC=t-2,则C点坐标为(t,t-2),然后利用反比例函数图象上点的坐标特征得到t(t-2)=6,再解方程得到满足条件的t的值.试题解析:(2)∵△AOM的面积为2,∴12|k|=2,而k>0,∴k=6,∴反比例函数解析式为y=6x;(2)当以AB为一边的正方形ABCD的顶点D在反比例函数y=6x的图象上,则D点与M点重合,即AB=AM,把x=2代入y=6x得y=6,∴M点坐标为(2,6),∴AB=AM=6,∴t=2+6=7;当以AB为一边的正方形ABCD的顶点C在反比例函数y=6x的图象上,则AB=BC=t-2,∴C点坐标为(t,t-2),∴t(t-2)=6,整理为t2-t-6=0,解得t2=2,t2=-2(舍去),∴t=2,∴以AB为一边的正方形有一个顶点在反比例函数y=kx的图象上时,t的值为7或2.考点:反比例函数综合题.20.(1)证明见解析(2﹣6π【解析】【分析】(1)直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF,即可得出答案;(2)直接利用得出S△ACD=S△COD,再利用S阴影=S△AED﹣S扇形COD,求出答案.【详解】(1)证明:连接OD,∵D为弧BC的中点,∴∠CAD=∠BAD,∵OA=OD,∴∠BAD=∠ADO,∴∠CAD=∠ADO,∵DE⊥AC,∴∠E=90°,∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,∴OD⊥EF,∴EF为半圆O的切线;(2)解:连接OC与CD,∵DA=DF,∴∠BAD =∠F ,∴∠BAD =∠F =∠CAD ,又∵∠BAD+∠CAD+∠F =90°,∴∠F =30°,∠BAC =60°,∵OC =OA ,∴△AOC 为等边三角形,∴∠AOC =60°,∠COB =120°,∵OD ⊥EF ,∠F =30°,∴∠DOF =60°,在Rt △ODF 中,DF =63, ∴OD =DF•tan30°=6,在Rt △AED 中,DA =63,∠CAD =30°,∴DE =DA •sin30°=33,EA =DA•cos30°=9,∵∠COD =180°﹣∠AOC ﹣∠DOF =60°,由CO =DO ,∴△COD 是等边三角形,∴∠OCD =60°,∴∠DCO =∠AOC =60°,∴CD ∥AB ,故S △ACD =S △COD ,∴S 阴影=S △AED ﹣S 扇形COD =216093362360π⨯⨯-⨯=27362π-.【点睛】此题主要考查了切线的判定,圆周角定理,等边三角形的判定与性质,解直角三角形及扇形面积求法等知识,得出S △ACD =S △COD 是解题关键.21.111,1x y =⎧⎨=-⎩;223232x y ⎧=-⎪⎪⎨⎪=⎪⎩;331252x y ⎧=-⎪⎪⎨⎪=-⎪⎩. 【解析】分析:把原方程组中的第二个方程通过分解因式降次,转化为两个一次方程,再分别和第一方程组合成两个新的方程组,分别解这两个新的方程组即可求得原方程组的解.详解:由方程222()x y x y -=+可得,0x y +=,2x y -=;则原方程组转化为223,0.x y x y ⎧-=⎨+=⎩(Ⅰ)或 223,2.x y x y ⎧-=⎨-=⎩ (Ⅱ), 解方程组(Ⅰ)得21123,1,21;3.2x x y y ⎧=-⎪=⎧⎪⎨⎨=-⎩⎪=⎪⎩, 解方程组(Ⅱ)得43341,1,21;5.2x x y y ⎧=-⎪=⎧⎪⎨⎨=-⎩⎪=-⎪⎩, ∴原方程组的解是21123,1,21;3.2x x y y ⎧=-⎪=⎧⎪⎨⎨=-⎩⎪=⎪⎩ 331,25.2x y ⎧=-⎪⎪⎨⎪=-⎪⎩. 点睛:本题考查的是二元二次方程组的解法,解题的要点有两点:(1)把原方程组中的第2个方程通过分解因式降次转化为两个二元一次方程,并分别和第1个方程组合成两个新的方程组;(2)将两个新的方程组消去y ,即可得到关于x 的一元二次方程.22.(1)证明参见解析;(2)半径长为154,AE =6. 【解析】【分析】(1)已知点D 在圆上,要连半径证垂直,连结OD ,则OC OD =,所以ODC OCD ∠=∠,∵AB AC =,∴B ACD ∠=∠.∴B ODC ∠=∠,∴OD ∥AB .由DE AB ⊥得出OD EF ⊥,于是得出结论;(2)由35OD AE OF AF ==得到35OD AE OF AF ==,设3OD x =,则5OF x =.26AB AC OD x ===,358AF x x x =+=,362AE x =-,由363285x x -=,解得x 值,进而求出圆的半径及AE 长. 【详解】解:(1)已知点D 在圆上,要连半径证垂直,如图2所示,连结OD ,∵AB AC =,∴B ACD ∠=∠.∵OC OD =,∴ODC OCD ∠=∠.∴B ODC ∠=∠,∴OD ∥AB .∵DE AB ⊥,∴OD EF ⊥.∴EF 是⊙O 的切线;(2)在Rt ODF ∆和Rt AEF ∆中,∵35OD AE OF AF ==,∴35 OD AEOF AF==. 设3OD x=,则5OF x=.∴26AB AC OD x===,358AF x x x=+=.∵32EB=,∴362AE x=-.∴363285xx-=,解得x=54,则3x=154,AE=6×54-32=6,∴⊙O的半径长为154,AE=6.【点睛】1.圆的切线的判定;2.锐角三角函数的应用.23.(1)甲型号的产品有10万只,则乙型号的产品有10万只;(2)安排甲型号产品生产15万只,乙型号产品生产5万只,可获得最大利润91万元.【解析】【分析】(1)设甲型号的产品有x万只,则乙型号的产品有(20﹣x)万只,根据销售收入为300万元可列方程18x+12(20﹣x)=300,解方程即可;(2)设安排甲型号产品生产y万只,则乙型号产品生产(20﹣y)万只,根据公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元列出不等式,求出不等式的解集确定出y的范围,再根据利润=售价﹣成本列出W与y的一次函数,根据y的范围确定出W的最大值即可.【详解】(1)设甲型号的产品有x万只,则乙型号的产品有(20﹣x)万只,根据题意得:18x+12(20﹣x)=300,解得:x=10,则20﹣x=20﹣10=10,则甲、乙两种型号的产品分别为10万只,10万只;(2)设安排甲型号产品生产y万只,则乙型号产品生产(20﹣y)万只,根据题意得:13y+8.8(20﹣y)≤239,解得:y≤15,根据题意得:利润W=(18﹣12﹣1)y+(12﹣8﹣0.8)(20﹣y)=1.8y+64,当y=15时,W最大,最大值为91万元.所以安排甲型号产品生产15万只,乙型号产品生产5万只时,可获得最大利润为91万元.考点:一元一次方程的应用;一元一次不等式的应用;一次函数的应用.24.(1) =﹣100x+50000;(2) 该商店购进A型34台、B型电脑66台,才能使销售总利润最大,最大利润是46600元;(3)见解析.【解析】【分析】(1)根据“总利润=A型电脑每台利润×A电脑数量+B型电脑每台利润×B电脑数量”可得函数解析式;(2)根据“B型电脑的进货量不超过A型电脑的2倍且电脑数量为整数”求得x的范围,再结合(1)所求函数解析式及一次函数的性质求解可得;(3)据题意得y=(400+a)x+500(100﹣x),即y=(a﹣100)x+50000,分三种情况讨论,①当0<a<100时,y随x的增大而减小,②a=100时,y=50000,③当100<m<200时,a﹣100>0,y随x的增大而增大,分别进行求解.【详解】(1)根据题意,y=400x+500(100﹣x)=﹣100x+50000;(2)∵100﹣x≤2x,∴x≥1003,∵y=﹣100x+50000中k=﹣100<0,∴y随x的增大而减小,∵x为正数,∴x=34时,y取得最大值,最大值为46600,答:该商店购进A型34台、B型电脑66台,才能使销售总利润最大,最大利润是46600元;(3)据题意得,y=(400+a)x+500(100﹣x),即y=(a﹣100)x+50000,3313≤x≤60,①当0<a<100时,y随x的增大而减小,∴当x=34时,y取最大值,即商店购进34台A型电脑和66台B型电脑的销售利润最大.②a=100时,a﹣100=0,y=50000,即商店购进A型电脑数量满足3313≤x≤60的整数时,均获得最大利润;③当100<a<200时,a﹣100>0,y随x的增大而增大,∴当x=60时,y取得最大值.即商店购进60台A型电脑和40台B型电脑的销售利润最大.【点睛】本题考查了一次函数的应用及一元一次不等式的应用,弄清题意,找出题中的数量关系列出函数关系式、找出不等关系列出不等式是解题的关键.25.(1)甲80件,乙20件;(2)x≤90【解析】【分析】(1)甲种奖品购买了x件,乙种奖品购买了(100﹣x)件,利用共用2800元,列出方程后求解即可;(2) 设甲种奖品购买了x件,乙种奖品购买了(100﹣x)件,根据购买这批奖品的总费用不超过2900元列不等式求解即可.【详解】解:(1)设甲种奖品购买了x件,乙种奖品购买了(100﹣x)件,根据题意得30x+20(100﹣x)=2800,解得x=80,则100﹣x=20,答:甲种奖品购买了80件,乙种奖品购买了20件;(2)设甲种奖品购买了x件,乙种奖品购买了(100﹣x)件,根据题意得:30x+20(100﹣x)≤2900,解得:x≤90,【点睛】本题主要考查一元一次方程与一元一次不等式的应用,根据已知条件正确列出方程与不等式是解题的关键.26.(1)见解析;(2)tan∠DBC=12.【解析】【分析】(1)先利用圆周角定理得到∠ACB=90°,再利用平行线的性质得∠AEO=90°,则根据垂径定理得到¼¼AD DC=,从而有AD=CD;(2)先在Rt△OAE中利用勾股定理计算出AE,则根据正切的定义得到tan∠DAE的值,然后根据圆周角定理得到∠DAC=∠DBC,从而可确定tan∠DBC的值.【详解】(1)证明:∵AB为直径,∴∠ACB=90°,∵OD∥BC,∴∠AEO=∠ACB=90°,∴OE⊥AC,∴¼¼AD DC=,∴AD=CD;(2)解:∵AB=10,∴OA=OD=5,∴DE=OD﹣OE=5﹣3=2,在Rt△OAE中,AE=225-3=4,∴tan∠DAE=2142 DEAE==,∵∠DAC=∠DBC,∴tan∠DBC=12.【点睛】垂径定理及圆周角定理是本题的考点,熟练掌握垂径定理及圆周角定理是解题的关键. 27.(1)11.4;(2)19.5m.【解析】【分析】(1)根据直角三角形的性质和三角函数解答即可;(2)过点D作DH⊥地面于H,利用直角三角形的性质和三角函数解答即可.【详解】解:(1)在Rt△ABC中,∵∠BAC=64°,AC=5m,∴AB=5÷0.4411.4 (m);故答案为:11.4;(2)过点D作DH⊥地面于H,交水平线于点E,在Rt△ADE中,∵AD=20m,∠DAE=64°,EH=1.5m,∴DE=sin64°×AD≈20×0.9≈18(m),即DH=DE+EH=18+1.5=19.5(m),答:如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是19.5m.【点睛】本题考查解直角三角形、锐角三角函数等知识,解题的关键是添加辅助线,构造直角三角形.。
2023年4月四川省南充市2020级2023届初中毕业班第二次诊断性检测(南充二诊)英语参考答案

2020级初中毕业班第二次诊断性测试英语参考答案及评分意见第一部分听力(每小题1.5分,满分30分)1~5ACACC6~10ABCAA11~15CABBC16~20AABCA第二部分读(满分70分)第一节完形填空(每小题2分,满分30分)21~25CDCBB26~30ADCDA31~35DACAB第二节阅读理解(每小题2分,满分30分)36~40DBBBC41~45CBDCA46~50CDACA第三节补全短文(每小题2分,满分10分)51~55CEABF第三部分写(满分50分)第一节语法填空(每小题1.5分,满分15分)56.was used57.instruments58.led59.their60.an61.successfully62.until63.When64.to hold65.who第二节阅读填空(每小题2分,满分10分)66.unhappy67.Reasons68.easily69.cheering70.certainly/surely/definitely/undoubtedly第三节书面表达(满分25分)A school did a survey among the Junior3students about how often they practice speaking English and how they practice English.Here are the results.17%of the students hardly ever practice speaking English and45%of the students usually practice speaking English.38%of the students practice speaking English sometimes.How do these students practice speaking English?Most students speak more in class and some of the students talk with friends.Over half of the students practice English in other ways.I have difficulty expressing myself in English fluently,so I practice every day.In my opinion, we can learn English songs.With the help of melody,it won’t be boring to practice.And we can also practice by repeating the actors’dialogues in the film.In this way,we can get lots of expressions which native speakers use every day.评分标准一档20~25分包含了所有要点,能围绕内容适当发挥,内容具体、丰富。
2020年4月7日四川省南充市高2020届高2017级高三南充二诊语文试题参考答案

息 在 第 ⑦段 第 一 、 二 句 , 原 文 表 述 为 “也 许 就 是 普 通 所 谓 “人 治 ”。
(二)实用类文本阅读(本题共 3小题,12分)
4. (3分)B【解析】偷换概念,曲解文意。原文是“共享经济”的概念首次由马科斯·费
9.(6分)【答案示例】
(1)联系上下文理解:在面临丈夫去世,没有孩子,没有家人,也没有钱去旅 游等厄运降临时,(1分)店员经过很长一段时间的反思后认识到,遭遇不幸也 是人生的一笔财富,(1分)在感恩生活中的美好的同时,也要感恩生活中的不 幸。(1分) (2)联系现实生活理解:(示例)生活中的麻烦、挫折、不幸和苦难等,也是我 们人生的一部分。我们应该勇敢面对,积极应对,学会反思,乐观生活。(联系 现实谈认识,1分)比如:2003年的非典,尽管给人民的生命和财产造成了无 法弥补的重大损失,但它也让我们提高了对突发性公共事件和自然灾害的认识和 应对能力,引发了我们治国理政理念的转变和一系列重大经济社会政策的调整。 所以,我们应该以积极的心态来看待非典,感恩为抗击非典默默付出、无私奉献 的所有人。(联系现实举例并分析,2分)。
A项 , 原 文 相 关 信 息 在 第 ③段 第 一 句 和 第 三 句 最 后 一 个 分 句 ; B项 , 原 文 相 关 信 息 在
第 ③段 第 七 、 八 句 ; C项 , 原 文 相 关 信 息 在 第 ④ 段 第 三 、 五 、 七 句 。
2. (3分)C【解析】C项,文章没有采用“不破不立”的写法,第①段先摆出错误观
诊 二 充 南
南充市高 2020届第二次高考适应性考试
2020年四川省南充市高考数学二诊试卷(文科) (含答案解析)

2020年四川省南充市高考数学二诊试卷(文科)一、单项选择题(本大题共12小题,共60.0分)1.复数3−ii=()A. 1+3iB. −1−3iC. −1+3iD. 1−3i2.设集合A={1,3,4},B={2,3,6},则A∪B等于()A. {3}B. {1,2,3,4}C. {1,2,3,6}D. {1,2,3,4,6}3.现有历史、政治、数学、物理、化学共有5本书,从中任取2本,取出的书至少有一本文科书的概率为()A. 310B. 12C. 710D. 454.已知α∈[π,3π2],sinα=−35,则tanα=()A. −43B. 43C. −34D. 345.在ΔABC中,AB=3,BC=√13,AC=4,则边AC上的高为()A. 3√22B. 32C. 3√32D. 3√36.已知函数y=2sin(2x+π4),则它的一条对称轴方程为()A. x=−π8B. x=0 C. x=π8D. x=π47.过圆x2+y2=2外一点P(1,3)向该圆引两条切线,M,N为切点,则MN的直线方程为()A. 2x+y−1=0B. x+3y−2=0C. x+2y−3=0D. 2x−3y+2=08.已知函数f(x)的定义域[−3,+∞)且f(6)=2,f′(x)为f(x)的导函数,f′(x)的图象如图所示,若正数a,b满足f(2a+b)<2,则b+3a−2的取值范围是()A. (−∞,−32)∪(3,+∞) B. (−92,3) C. (−∞,−92)∪(3,+∞)D. (−32,3)9. 某几何体的三视图如图所示,其中正视图是边长为4的正三角形,俯视图是由边长为4的正三角形和一个半圆构成,则该几何体的体积为( )A. 8+4√3π3B. 8+2√3π3C. 4+4√3π3D. 4+8√3π310. △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,b =2√2,A =30∘,C =105∘,则a =( )A. 1B. √2C. 2D. √311. 已知正三棱柱ABC −A 1B1C1(底面是正三角形,且侧棱垂直于底面)的底面边长为4,侧棱长为2√3,则该正三棱柱外接球的表面积为( )A.253πB.1003π C. 25π D. 100π12. 如图,F 1、F 2分别是双曲线的左、右焦点,过F 1的直线与双曲线的左、右两支分别交于A 、B 两点,若△ABF 2为等边三角形,则该双曲线的离心率为( )A. √3B. √5C. √7D. 3二、填空题(本大题共4小题,共20.0分)13. 已知|b ⃗ |=1,a ⃗ ⋅b ⃗ =2,则向量(2a ⃗ −b⃗ )⋅b ⃗ =______. 14. 已知某班有女生20人,男生30人,一次考试女生的平均分为75分,全班的平均分为72分,则男生的平均分为______.15. 已知函数f(x)=lnx +x ,则函数y =f(x)图象在点(1,f(1))处的切线方程为______. 16. 过抛物线C :y 2=2px(p >0)的焦点F 的直线与抛物线交于M ,N 两点,若MF ⃗⃗⃗⃗⃗⃗ =4FN⃗⃗⃗⃗⃗⃗ ,则直线l 的斜率为______.三、解答题(本大题共7小题,共82.0分)17. 在等差数列{a n }中,a 2+a 3=7,a 4+a 5+a 6=18.(1)求数列{a n }的通项公式;(2)设数列{a n }的前n 项和为S n ,求1S 3+1S 6+⋯+1S 3n.18. 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A ,B 两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如图.记成绩不低于90分者为“成绩优秀”. (1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个均“成绩优秀”的概率;(2)由以上统计数据作出列联表,并判断能否在犯错误的概率不超过0.1的前提下认为:“成绩优秀”与教学方式有关. P(K 2≥k 0)0.400 0.250 0.150 0.100 0.050 0.025 k 00.7081.3232.0722.7063.8415.024参考公式:K 2=n(ad−bc)2(a+c)(b+d)(a+b)(c+d)(n =a +b +c +d)19.如图,四棱锥P−ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=√6,E为PA的中点,(1)证明:PC//面BCE;(2)求三棱锥P−BCE的体积.20.如图,椭圆C:x24+y23=1的右焦点为F,过点F的直线l与椭圆交于A,B两点,直线n:x=4与x轴相交于点E,点M在直线n上,且满足BM//x轴.(1)当直线l与x轴垂直时,求直线AM的方程;(2)证明:直线AM经过线段EF的中点.21.已知函数f(x)=xlnx+2x−1.(1)求f(x)的极值;(2)若对任意的x>1,都有f(x)−k(x−1)>0(k∈Z)恒成立,求k的最大值.22.在平面直角坐标系xOy中,曲线C1:x2+y2−2y=0,倾斜角为π的直线l过点M(−2,0),以原6点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为.(1)求C1和C2交点的直角坐标;(2)若直线l与C1交于A,B两点,求|MA|+|MB|的值.23.已知函数F(x)=|3x−1|+ax(Ⅰ)当a=3时,解关于x的不等式f(x)≥|x−3|;(Ⅱ)若f(x)≥x−1在R上恒成立,求实数a的取值范围.2【答案与解析】1.答案:B解析:解:3−ii =−i(3−i)−i2=−1−3i,故选:B.直接由复数代数形式的乘除运算化简复数3−ii,则答案可求.本题考查了复数代数形式的乘除运算,是基础题.2.答案:D解析:解:由已知集合A={1,3,4},B={2,3,6},则A∪B={1,2,3,4,6};故选D.找出两个集合的公共元素组成的集合.本题考查了集合的并集运算;属于基础题.3.答案:C解析:分析:本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.历史、政治、数学、物理、化学共有5本书,从中任取两本,基本事件总数有10种,取出的书至少有一本文科书有7种,根据概率公式计算即可.解:历史、政治、数学、物理、化学共有5本书,从中任取两本,基本事件有:(历史,政治),(历史,数学),(历史,物理),(历史,化学),(政治,数学),(政治,物理),(政治,化学),(数学,物理),(数学,化学),(物理,化学),共10种,取出的书至少有一本文科书有7种情况,∴取出的书至少有一本文科书的概率p=710,故选C.4.答案:D解析:由条件利用同角三角函数的基本关系,求得tanα的值.本题主要考查同角三角函数的基本关系的应用,以及三角函数在各个象限中的符号,属于基础题.解:∵已知α∈[π,3π2],sinα=−35,∴cosα=√1−sin2α=−45,则tanα=sinαcosα=34,故选:D.5.答案:C解析:本题考查了解三角形的应用.由点B向AC作垂线,交点为D,设AD=x,则CD=4−x,利用勾股定理可知BD=√AB2−AD2=√BC2−CD2,进而解得x的值,再利用勾股定理求得BD.解:由点B向AC作垂线,交点为D.设AD=x,则CD=4−x,∴BD=√9−x2=√13−(4−x)2,解得x=32,因此BD=√9−x2=32√3.故选C.6.答案:C解析:解:由2x+π4=kπ+π2,得x=kπ2+π8(k∈Z),令k=0,得x=π8,∴它的一条对称轴方程为x=π8,故选:C.利用正弦函数的对称性,可知2x+π4=kπ+π2(k∈Z),k赋值为0即可求得答案.本题考查正弦函数的对称性,熟练掌握正弦函数的对称轴方程是解决问题的关键,属于基础题.7.答案:B解析:本题考查切线方程,和切点弦方程,基础题. 求出切线方程,得出切点弦方程. 解:M(a,b),N(m,n),由y−bx−a ⋅ba =−1, 得:直线PM :ax +by =2, 同理:直线PN :mx +ny =2,P(1,3)代入,所以a +3b =2,m +3n =2, 则x +3y −2=0是过M ,N 的直线, 也就是MN 的直线方程, 故选:B .8.答案:A解析:如图所示,f′(x)≥0在[0,+∞)上恒成立,∴函数f(x)在[−3,0)是减函数,(0,+∞)上是增函数,又∵f(2a +b)<2=f(6),∴{2a +b >02a +b <6,画出平面区域,令t =b+3a−2表示过定点(2,−3)的直线的斜率如图所示,故选A .9.答案:A解析:本题考查由三视图求空间组合体的体积,解决本题的关键是得到该几何体的形状,属于中档题.由已知中的三视图可得该几何体是一个半圆锥和三棱锥的组合体,计算出底面面积和高,代入锥体体积公式,可得答案.解:由已知中的三视图可得该几何体是一个半圆锥和三棱锥的组合体,半圆锥的底面半径为2,高为√42−22=2√3,三棱锥的底面为边长为4的正三角形,高为2√3,其体积为:1 3×[12×(π×22)+12×(4×2√3)]×2√3.故选A.10.答案:C解析:本题考查正弦定理,考查了推理能力与计算能力,属于基础题.利用正弦定理即可得出.解:∵A=30∘,C=105∘,∴B=45°,∵asinA =bsinB,∴a=bsinAsinB=2√2sin30∘sin45∘=2,故选C.11.答案:B解析:如图,取ΔABC的重心E,ΔA1B1C1的重心E1,取AC中点D,则EE1的中点O是该正三棱柱外接球的球心,OA为球半径,∵正三棱柱ABC−A1B1C1的底面边长为4,侧棱长为2√3,∴OE=√3,AE=BE=23BD=23√42−22=4√33,∴R =OA =√(√3)2+(4√33)2=√253, ∴该正三棱柱外接球的表面积:S =4πR 2=4π×(√253)2=100π3.故选:B .12.答案:C解析:本题考查双曲线的定义和余弦定理,双曲线离心率的求法,属于中档题.根据双曲线的定义算出△AF 1F 2中,|AF 1|=2a ,|AF 2|=4a ,由△ABF 2是等边三角形得∠F 1AF 2=120°,利用余弦定理算出c =√7a ,结合双曲线离心率公式即可算出双曲线C 的离心率.解:根据双曲线的定义,可得|BF 1|−|BF 2|=2a ,∵△ABF 2是等边三角形,即|BF 2|=|AB|,∴|BF 1|−|BF 2|=2a ,即|BF 1|−|AB|=|AF 1|=2a ,又∵|AF 2|−|AF 1|=2a ,∴|AF 2|=|AF 1|+2a =4a ,∵△AF 1F 2中,|AF 1|=2a ,|AF 2|=4a ,∠F 1AF 2=120°,∴|F 1F 2|2=|AF 1|2+|AF 2|2−2|AF 1|⋅|AF 2|cos120°,即4c 2=4a 2+16a 2−2×2a ×4a ×(−12)=28a 2,解得c =√7a ,由此可得双曲线C 的离心率e =c a =√7.故选C .13.答案:3解析:本题主要考查了向量数量积的性质的简单应用属于容易试题.直接利用向量数量积的性质进行求解即可.解:∵|b⃗ |=1,a⃗⋅b⃗ =2,则向量(2a⃗−b⃗ )⋅b⃗ =2a⃗⋅b⃗ −b⃗ 2=4−1=3.故答案为3.14.答案:70分解析:本题主要考查平均分的概念、运算以及应用,根据题意列出关系式可得解.解:设男生的平均分为x,则30x+75×20=(20+30)×72,解得x=70.即男生的平均分为70分.故答案为70分.15.答案:y=2x−1解析:本题考查利用导数计算函数的切线方程,注意导数的几何意义,属于基础题.根据题意,由函数的解析式求出其导数,计算可得f(1)与f′(1)的值,由直线的点斜式方程可得切线的方程,变形即可得答案.+1,解:根据题意,f(x)=lnx+x,则f′(x)=1x+1=2,则f(1)=ln1+1=1,f′(1)=11则切线的方程为y−1=2(x−1),即y=2x−1;故答案为:y=2x−1.16.答案:±43 解析: 作MB 垂直准线于B ,作NC 垂直准线于C ,作NA 垂直MB 于A ,根据抛物线定义,可得tan∠NMA 就是直线l 的斜率.本题考查了抛物线的定义的应用,利用平面几何知识,结合直线斜率与倾斜角的关系求解,属于中档题.解:如图,作MB 垂直准线于B ,作NC 垂直准线于C ,根据抛物线定义,可得MB =MF ,NC =NF .作NA 垂直MB 于A ,设FN =m ,则MN =5m ,NA =MF −NF =3m . 在直角三角形AMN 中,tan∠NMA =AN AM =43,∴直线l 的斜率为±43,故答案为:±43. 17.答案:解:(1)设等差数列{a n }的公差为d ,依题意,{a 1+d +a 1+2d =7a 1+3d +a 1+4d +a 1+5d =18,解得a 1=2,d =1, ∴a n =2+(n −1)×1=n +1(2)S 3n =3n(a 1+a 3n )2=3n(2+3n+1)2=9n(n+1)2,∴1S 3n =29n(n +1)=29(1n −1n +1) ∴1S 3+1S 6+⋯+1S 3n =29[(1−12)+(12−13)+⋯+(1n −1n +1)]=2n 9(n +1)解析:本题考查数列的求和,考查等差数列的通项公式与求和公式,考查裂项法,考查转化与分析运算的能力,属于中档题.(1)由等差数列{a n }中的a 2+a 3=7,a 4+a 5+a 6=18,即可求得其首项与公差,从而可得数列{a n }的通项公式;(2)可先求得S 3n ,再用裂项法即可求得答案.18.答案:解:(1)由题意知本题是一个等可能事件的概率,记该事件为A ,根据等可能事件的概率得到P(A)=C 52C 62=1015=23;-----------------(4分) (2)由已知数据,填写列联表得甲班 乙班 总计 成绩优秀1 5 6 成绩不优秀19 15 34 总计 20 20 40----------------------(6分)根据列联表中的数据,计算得随机变量K 2的观测值为k =40×(1×15−5×19)220×20×6×34≈3.137,-----------------------(9分)由于3.137>2.706,所以在犯错误的概率不超过0.1的前提下认为“成绩优秀”与教学方式有关.-----------------------(10分)解析:(1)由题意根据等可能事件的概率计算即可;(2)由已知数据填写列联表,计算得K 2的观测值,对照临界值得出结论.本题考查了古典概型的概率计算问题,也考查了独立性检验的应用问题,是基础题.19.答案:(1)证明:如图所示,连接AC 交BD 于点O .∵底面ABCD 是菱形,∴OA =OC ,又∵E 为PA 的中点,∴EO//PC ,而PC ⊄平面BED ,EO ⊂平面BED ,∴PC//平面EBD .(2)∵点E 是PA 的中点,∴V 三棱锥P−BCE ═12V 三棱锥A−PBC .由O 点是AC 的中点,可得V 三棱锥A−PBC =2V 三棱锥A−POB =13×12×OP ×OB ×OA =13×√3×1×√3=1.∴得V 三棱锥P−BCE =12V 三棱锥A−PBC =12解析:(1)如图所示,连接AC 交BD 于点O.由底面ABCD 是菱形,可得OA =OC ,利用三角形的中位线定理可得OE//PC ,再利用线面平行的判定定理即可证明PC//平面EBD .(2)由于点E 是PA 的中点,可得V 三棱锥P−BCE =12V 三棱锥A−PBC .由O 点是AC 的中点,可得V 三棱锥A−PBC =2V 三棱锥A−POB =13×12×OP ×OB ×OA ,即可得出.题考查了菱形的性质、三角形的中位线定理、线面平行的判定定理、三棱锥的体积计算公式,考查了了推理能力与计算能力,属于中档题 20.答案:解:(1)由c =√4−3=1,∴F(1,0),∵直线l 与x 轴垂直,∴x =1,由{x =1x 24+y 23=1得{x =1,y =32,或{x =1,y =−32, ∴A(1,32),M(4,−32)∴直线AM 的方程为y =−x +52.证明(2)设直线l 的方程为x =my +1,由{x 24+y 23=1x =my +1得3(my +1)2+4y 2=12, 即(3m 2+4)y 2+6my −9=0,设A(x 1,y 1),B(x 2,y 2),则y 1+y 2=−6m 3m 2+4,y 1y 2=−93m 2+4,∵EF 的中点N(52,0),点M(4,y 2),∴NA ⃗⃗⃗⃗⃗⃗ =(x 1−52,y 1)═(my 1−32,y 1),NM ⃗⃗⃗⃗⃗⃗⃗ =(32,y 2), ∴NA ⃗⃗⃗⃗⃗⃗ ⋅NM ⃗⃗⃗⃗⃗⃗⃗ =my 1y 2−32(y 1+y 2)=−9m 3m 2+4−32×−6m 3m 2+4=0.∴A ,N ,M 三点共线,∴直线AM 经过线段EF 的中点.解析:(1)由题意求出点A ,M 的坐标,即可求出直线AM 的方程,(2)设直线l 的方程为x =my +1,与椭圆联立,根据韦达定理和向量的运算即可证明A ,N ,M 三点共线,可得直线AM 经过线段EF 的中点本题主要考查了椭圆的标准方程.涉及了直线与椭圆的关系,考查了运算能力和转化能力,属于中档题21.答案:解:(1)函数f(x)的定义域为(0,+∞),f′(x)=lnx +3,令f′(x)=0,解得x =e −3,当x ∈(0,e −3)时,f′(x)<0,函数f(x)递减;当x ∈(e −3,+∞)时,f′(x)>0,函数f(x)递增;故f(x)的极小值为f(e −3)=−e −3−1,无极大值;(2)原式可化为k <f(x)x−1=xlnx+2x−1x−1, 令g(x)=xlnx+2x−1x−1(x >1),则g′(x)=x−2−lnx (x−1)2, 令ℎ(x)=x −2−lnx(x >1),则ℎ′(x)=1−1x >0,故ℎ(x)在(1,+∞)上递增,且ℎ(3)=1−ln3<0;ℎ(4)=2−ln4>0;故存在唯一的x 0∈(3,4),使得ℎ(x 0)=0,即lnx 0=x 0−2,且当x ∈(1,x 0)时,ℎ(x)<0,g′(x)<0,g(x)递减;当x ∈(x 0,+∞)时,ℎ(x)>0,g′(x)>0,g(x)递增;故g(x)min =g(x 0)=x 0+1,故k <x 0+1∈(4,5),所以整数k 的最大值为4.解析:(1)求导判断函数的单调性,由极值定义得解;(2)问题转化为k <f(x)x−1=xlnx+2x−1x−1在(1,+∞)上恒成立,构造函数g(x)=xlnx+2x−1x−1(x >1),利用导数求函数g(x)的范围,进而得到实数k 的范围,由此得到答案.本题考查利用导数研究函数的单调性,极值及最值,考查不等式的恒成立问题,考查分离参数法及转化思想,考查逻辑推理能力,属于常规题目.22.答案:解:(1)曲线C 2的极坐标方程为,化为直角坐标系的方程为x +y −2=0,联立{x +y −2=0x 2+y 2−2y =0, 消去x 得,y 2−3y +2=0,解得y =1或2,故C 1和C 2交点的坐标为(0,2),(1,1).(2)依题意,直线l 的参数方程为为参数),把直线l 的参数方程{x =−2+√32t y =12t 代入x 2+y 2−2y =0, 得(−2+√32t)2+(12t)2−t =0, 即t 2−(2√3+1)t +4=0,设A ,B 对应得参数分别为t 1,t 2,则t 1+t 2=2√3+1,t 1·t 2=4.易知点M 在圆x 2+y 2−2y =0外,所以|MA|+|MB|=|t 1+t 2|=2√3+1.解析:本题主要考查由直线极坐标方程求直角坐标方程,由直线直角坐标方程求其参数方程,考查参数的几何意义,属于中档题.(1)将曲线C 2的极坐标方程化成直角坐标方程,联立方程即可求解;(2)通过设直线l 的参数方程,联立方程,利用参数的几何意义求解.23.答案:解:(Ⅰ)当a =3时,关于x 的不等式f(x)≥|x −3|即|3x −1|+3x ≥|x −3|, 即|3x −1|−|x −3|+3x ≥0. ∴{x ≥33x −1−(x −3)+3x ≥0①,或{13≤x <33x −1−(3−x)+3x ≥0②,或 {x <131−3x −3+x +3x ≥0. 解①求得x ≥3,解②求得47≤x <3,解③求得x ∈⌀.综上可得,不等式的解集为[47,+∞).(Ⅱ)若f(x)≥x −12在R 上恒成立,即|3x −1|+ax ≥x −12在R 上恒成立,即|3x −1|+12≥(1−a)x .故函数ℎ(x)=|3x −1|+12的图象应该在直线y =(1−a)x 的上方或重合.如图所示:∴0≤1−a≤3,或−3≤1−a<0,解得−2≤a≤1,或1<a≤4,即a的范围是[−2,4]解析:(Ⅰ)当a=3时,关于x的不等式即|3x−1|−|x−3|+3x≥0,转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(Ⅱ)由题意可得函数ℎ(x)=|3x−1|+1的图象应该在直线y=(1−a)x的上方或重合,可得0≤1−2a≤1,或−2≤1−a<0,由此求得a的范围.本题主要考查绝对值不等式的解法,很熟的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.。
2020年四川省南充市高考数学二诊试卷(理科)(有答案解析)

2020年四川省南充市高考数学二诊试卷(理科)一、选择题(本大题共12小题,共60.0分)1.复数i+1i=()A. −2iB. 0C. 12i D. 2i2.已知集合A={1,3,√m},B={1,m},A∪B=A,则m=()A. 0或√3B. 0或3C. 1或√3D. 1或33.已知tanα=−12,π2<α<π,则sinα=()A. 2√55B. −√55C. −2√55D. √554.如图,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:有一根竹子,原高一丈(1丈=10尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子三尺远,问折断处离地面的高?()A. 4.55尺B. 5.45尺C. 4.2尺D. 5.8尺5.已知等式(1−x+x2)3⋅(1−2x2)4=a0+a1x+a2x2+⋯+a14x14成立,则a2+a4+⋯+a14=()A. 0B. 5C. 7D. 146.过圆x2+y2=4外一点M(4,−1)引圆的两条切线,则经过两切点的直线方程是()A. 4x−y−4=0B. 4x+y−4=0C. 4x+y+4=0D. 4x−y+4=07.定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)<1,则b+1a+1的取值范围是()A. (15,13) B. (−∞,13)∪(5,+∞)C. (13,5) D. (−∞,3)8.一个空间几何体的正视图是长为4,宽为√3的长方形,侧视图是边长为2的等边三角形,俯视图如图所示,则该几何体的体积为()A. 4√33B. 4√3 C. 2√33D.2√39.△ABC的内角A,B,C的对边分别为a,b,c,若(2a−b)cosC=ccosB,则内角C=()A. π6B. π4C. π3D. π210.正三棱锥底面边长为3,侧棱与底面成60°角,则正三棱锥的外接球的体积为()A. 4πB. 16πC.16π3D.32π311. 设双曲线C :x 29−y 216=1的右顶点为A ,右焦点为F ,过点F 作平行C 的一条渐近线的直线与C交于点B ,则△AFB 的面积为( )A. 15B. 3215C. 1532 D. 641512. 已知函数f(x)=x +e x−a ,g(x)=ln(x +2)−4e a−x ,其中e 为自然对数的底数,若存在实数x 0,使f(x 0)−g(x 0)=3成立,则实数a 的值为( ) A. −ln2−1 B. −1+ln2 C. −ln2 D. ln2 二、填空题(本大题共4小题,共20.0分)13. 已知向量a ⃗ ,b ⃗ 满足(a ⃗ +2b ⃗ )⋅(a ⃗ −b ⃗ )=−6,且|a ⃗ |=1,|b ⃗ |=2,则cos <a ⃗ ,b ⃗ >=______.14. 函数f(x)=cosx −√x 在[0,+∞)的零点个数为______.15. 已知函数f(x)=alnx −bx 2图象上一点(2,f(2))处的切线方程为y =−3x +2ln2+2,则a +b =______.16. 设F 为抛物线C :y 2=4x 的焦点,A ,B ,D 为C 上互相不重合的三点,且|AF ⃗⃗⃗⃗⃗ |、|BF ⃗⃗⃗⃗⃗ |、|DF⃗⃗⃗⃗⃗ |成等差数列,若线段AD 的垂直平分线与x 轴交于E(3,0),则B 的坐标为______. 三、解答题(本大题共7小题,共82.0分) 17. 等差数列{a n }中,a 1=1,a 6=2a 3.(1)求{a n }的通项公式;(2)设b n =2a n ,记S n 为数列{b n }前n 项的和,若S m =62,求m .18. 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米. (1)求出易倒伏玉米茎高的中位数m ;的前提下,认为抗倒伏与玉米矮茎有关?附:K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),19. 在四棱锥P −ABCD 中,底面ABCD 是边长为2的菱形,∠BAD =120°,PA =2,PB =PC =PD ,E 是PB 的中点. (1)证明:PA ⊥平面ABCD ; (2)设F 是直线BC 上的动点,当点E 到平面PAF 距离最大时,求面PAF 与面EAC 所成二面角的正弦值.20. 设点F 1(−c,0),F 2(c,0)分别是椭圆C :x 2a 2+y 2=1(a >1)的左、右焦点,P 为椭圆C 上任意一点,且PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 的最小值为0.(1)求椭圆C 的方程;(2)如图,动直线l :y =kx +m 与椭圆C 有且仅有一个公共点,点M ,N 是直线l 上的两点,且F 1M ⊥l ,F 2N ⊥l ,求四边形F 1MNF 2面积S 的最大值.21. 已知函数f(x)=12x 2+mx +lnx .(1)若函数f(x)不存在单调递减区间,求实数m 的取值范围; (2)若y =f(x)的两个极值点为x 1,x 2(x 1<x 2),m ≤−3√22,求f(x 1)−f(x 2)的最小值.22. 在平面直角坐标系xOy 中,直线l 的参数方程为{x =3−√22ty =√5+√22t(t 为参数).在以原点O 为极点,x 轴正半轴为极轴的极坐标中,圆C 的方程为ρ=2√5sinθ. (Ⅰ)写出直线l 的普通方程和圆C 的直角坐标方程;(Ⅱ)若点P 坐标为(3,√5),圆C 与直线l 交于A ,B 两点,求|PA|+|PB|的值.23. 设函数f(x)=|x −1|+|x −a|,a ∈R .(1)当a =4时,求不等式f(x)≥5的解集;(2)若f(x)≥4对x∈R恒成立,求a的取值范围.-------- 答案与解析 --------1.答案:B解析:解:i +1i =i +ii⋅i =i −i =0故选:B .直接对复数的分母、分子同乘i ,然后化简即可求出所求.本题主要考查了复数代数形式的混合运算,解题的关键i 2=−1,属于容易题. 2.答案:B解析:解:A ∪B =A ⇔B ⊆A . ∴{1,m}⊆{1,3,√m},∴m =3或m =√m ,解得m =0或m =1(与集合中元素的互异性矛盾,舍去). 综上所述,m =0或m =3. 故选:B .由两集合的并集为A ,得到B 为A 的子集,转化为集合间的基本关系,再利用子集的定义,转化为元素与集合,元素与元素的关系.此题考查了并集及其运算,以及集合间的包含关系,是一道基础题. 3.答案:D解析:解:已知tanα=−12,∴cos 2α=11+tan 2α=45,∴sin 2α=15.又π2<α<π,∴sinα=√55,故选:D .利用同角三角函数的基本关系,求出cos 2α 和sin 2α的值,再由π2<α<π,求出sinα的值. 本题考查同角三角函数的基本关系的应用,是一道基础题. 4.答案:A解析:解:如图,已知AC +AB =10(尺),BC =3(尺),AB 2−AC 2=BC 2=9,所以(AB +AC)(AB −AC)=9,解得AB −AC =0.9, 因此{AB +AC =10AB −AC =0.9,解得{AB =5.45AC =4.55,故折断后的竹干高为4.55尺, 故选:A .由题意可得AC +AB =10(尺),BC =3(尺),运用勾股定理和解方程可得AB ,AC ,即可得到所求值.本题考查三角形的勾股定理的运用,考查方程思想和运算能力,属于基础题. 5.答案:D解析:解:由(1−x+x2)3⋅(1−2x2)4=a0+a1x+a2x2+⋯+a14x14成立,令x=1,代入得1=a0+a1+a2+⋯+a14,令x=−1,代入得27=a0−a1+a2−⋯+a14,相加得28=2(a2+a4+⋯+a14),则a2+a4+⋯+a14=14故选:D.先令x=1,x=−1,联立可得.本题考查二项式赋值及其系数之间的关系,属于基础题.6.答案:A解析:解:设切点是P(x1,y1)、Q(x2,y2),则以P为切点的切线方程是:x1x+y1y=4,以Q为切点的切线方程是:x2x+y2y=4,∵点M(4,−1)在两条切线上,则4x1−y1=4,4x2−y2=4∴点P、Q的坐标满足方程:4x−y=4∴过两切点P、Q的直线方程是:4x−y−4=0.故选:A.设切点是P(x1,y1)、Q(x2,y2),则以P为切点的切线方程是:x1x+y1y=4,以Q为切点的切线方程是:x2x+y2y=4,由此能求出过两切点P、Q的直线方程.本题考查经过两个切点的直线方程的求法,是中档题,解题时要认真审题,注意圆的切线方程的性质的合理运用.7.答案:C解析:解:由图可知,当x>0时,导函数f′(x)>0,原函数单调递增∵两正数a,b满足f(2a+b)<1,∴0<2a+b<4,∴b<4−2a,由0<b<4−2a,可得0<a<2,画出可行域如图.k=b+1表示点Q(−1,−1)与点P(x,y)连线的斜率,a+1;当P点在A(2,0)时,k最小,最小值为:13当P点在B(0,4)时,k最大,最大值为:5.取值范围是C.故选C.先根据导函数的图象判断原函数的单调性,从而确定a、b的范围得到答案.本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.8.答案:B解析:解:由题意可知,三视图复原的几何体是放倒的正三棱柱,如图所示:,正三角形的边长为2,高为√3,正三棱柱的高为4,所以正三棱柱的体积为:12×2×√3×4=4√3,故选:B.通过三视图复原的几何体的特征,结合三视图的数据,求出几何体的体积即可.本题主要考查了根据三视图还原实物图,考查了几何体体积的求法,是基础题.9.答案:C解析:解:由正弦定理得:2sinAcosC−sinBcosC=sinCcosB,即2sinAcosC=sinBcosC+sinCcosB,即2sinAcosC=sin(B+C)=sinA,由于sinA≠0,故cosC=12,又0<C<π,所以C=π3.故选:C.由已知及正弦定理,三角函数恒等变换的应用可得2sinAcosC=sinA,结合sinA≠0,可求cos C,根据范围0<C<π,可求C的值.本题主要考查了正弦定理,三角函数恒等变换的应用,考查了运算求解能力和转化思想,属于基础题.10.答案:D解析:解:如图所示,过A作AE⊥平面BCD,垂足为E,则E为三角形BCD的外心,由题意可知,BE=√3,因为侧棱与底面成60°角,即∠ABE=60°,所以AE=3,Rt△OBE中,R2=3+(3−R)2,解可得R=2,则正三棱锥的外接球的体积V=4πR33=32π3.故选:D.由已知及线面角可求BE,AE,然后结合球的性质可求R,结合球体积公式可求.本题主要考查了三棱锥的外接球的体积的求解,解题的关键是球心的确定,属于中档试题.11.答案:B解析:解:a2=9,b2=16,故c=5,∴A(3,0),F(5,0),渐近线方程为y=±43x,不妨设BF的方程为y=43(x−5),代入双曲线x29−y216=1,解得:B(175,−3215).∴S△AFB=12|AF|⋅|y B|=12×2×3215=3215.故选:B.根据题意,由双曲线的方程可得a、b的值,进而可得c的值,可以确定A、F的坐标,设BF的方程为y=43(x−5),代入双曲线方程解得B的坐标,计算可得答案.本题考查双曲线方程的运用,注意关键在求出B的坐标;解此类面积的题目时,注意要使三角形的底或高与坐标轴平行或重合,以简化计算.12.答案:A解析:解:令f(x)−g(x)=x+e x−a−1n(x+2)+4e a−x,令y=x−ln(x+2),y′=1−1x+2=x+1x+2,故y=x−ln(x+2)在(−2,−1)上是减函数,(−1,+∞)上是增函数,故当x=−1时,y有最小值−1−0=−1,而e x−a+4e a−x≥4,(当且仅当e x−a=4e a−x,即x=a+ln2时,等号成立);故f(x)−g(x)≥3(当且仅当等号同时成立时,等号成立);故x=a+ln2=−1,即a=−1−ln2.故选:A.令f(x)−g(x)=x+e x−a−1n(x+2)+4e a−x,运用导数求出y=x−ln(x+2)的最小值;运用基本不等式可得e x−a+4e a−x≥4,从而可证明f(x)−g(x)≥3,由等号成立的条件,从而解得a.本题考查了导数的综合应用及基本不等式的应用,同时考查了方程的根与函数的零点的关系应用,属于中档题.13.答案:12解析:解:根据题意,向量a⃗,b⃗ 满足(a⃗+2b⃗ )⋅(a⃗−b⃗ )=−6,且|a⃗|=1,|b⃗ |=2,则有(a⃗+2b⃗ )⋅(a⃗−b⃗ )=a⃗2+a⃗⋅b⃗ −2b⃗ 2=−7+2cos<a⃗,b⃗ >=−6,解可得:cos<a⃗,b⃗ >=12;故答案为:12根据题意,由数量积的计算公式可得(a ⃗ +2b ⃗ )⋅(a ⃗ −b ⃗ )=a ⃗ 2+a ⃗ ⋅b ⃗ −2b ⃗ 2=−7+2cos <a ⃗ ,b ⃗>=−6,变形分析可得答案.本题考查向量数量积的计算,涉及向量夹角的计算,属于基础题. 14.答案:1解析:解:函数f(x)=cosx −√x 在[0,+∞)的零点的个数,即函数y =cosx 的图象(红线部分)和函数y =√x 的图象(蓝线部分)的交点个数, 如图所示:显然,函数y =cosx 的图象(红线部分)和函数y =√x 的图象(蓝线部分)在[0,+∞)的交点个数为1, 故答案为:1.方程转化为2个函数的图象的交点个数,数形结合可得结论.本题主要考查函数的两点个数的判断方法,体现了转化以及数形结合的数学思想,属于中档题. 15.答案:3解析:解:将x =2代入切线得f(2)=2ln2−4. 所以2ln2−4=aln2−4b①, 又f′(x)=ax −2bx , ∴f′(2)=a 2−4b =−3②,联立①②解得a =2,b =1. 所以a +b =3. 故答案为:3.将(2,f(2))代入切线求出f(2),再将切点坐标代入f(x)得方程①,再对原函数求导,进一步求出切点处导数并令其为−3,得方程②,联立①②求出a ,b 即可解决问题.本题考查了导数的几何意义,本题的关键在于利用切点满足曲线与切线方程,切点处的导数等于切线斜率列方程求解,注意计算要准确.属于基础题. 16.答案:(1,2)或(1,−2)解析:解:由抛物线的方程可得焦点F(1,0),准线方程为:x =−1设A(x 1,y 1),B(x 2,y 2),D(x 3,y 3),|AF|=x 1+1,|BF|=x 2+1,|DF|=x 3+1, 由|AF ⃗⃗⃗⃗⃗ |、|BF ⃗⃗⃗⃗⃗ |、|DF ⃗⃗⃗⃗⃗ |成等差数列可得2(x 2+1)=x 1+x 3+2,所以x 2=x 1+x 32,所以线段AD 的中点的坐标(x 1+x 32,y 1+y 32),因为线段AD 的垂直平分线与x 轴交于E(3,0), 所以线段AD 的垂直平分线的斜率为k =y 1+y 32x 1+x 22−3=y 1+y 3x 1+x 3−6,又k AD =y 3−y1x 3−x 1, 所以y 3−y 1x 3−x 1⋅y 1+y 3x 1+x 3−6=−1,即4x 3−4x 1(x3−x 1)2−6(x 3−x 1)=−1,因为x 1≠x 3,所以可得x 1+x 3=2,所以x 2=x 1+x 32=1,B 在抛物线上,代入抛物线的方程可得y 22=4×1,焦点y 2=±2,所以B 的坐标为:(1,2)或(1,−2). 故答案为:(1,−2)或(1,2).设A ,B ,D 的坐标,由|AF ⃗⃗⃗⃗⃗ |、|BF ⃗⃗⃗⃗⃗ |、|DF ⃗⃗⃗⃗⃗ |成等差数列可得三者的坐标之间的关系,进而可得线段AD 的中点坐标,由题意求出线段AD 的中垂线的斜率即AD 的斜率,由斜率之积为−1可得B 的横坐标代入抛物线的方程可得B 的纵坐标.本题考查等差数列的性质及抛物线的性质,属于中档题. 17.答案:解:(1)由题意,设等差数列{a n }的公差为d ,则 a n =1+(n −1)d , ∵a 6=2a 3,∴1+5d =2(1+2d), 解得d =1,∴a n =n ,n ∈N ∗.(2)由(1)知,b n =2n =2⋅2n−1,∴数列{b n }是以2为首项,2为公比的等比数列,∴S n =2−2n+11−2=2n+1−2,由S m =62,可得2m+1−2=62, 解得m =5.解析:本题第(1)题先设等差数列{a n }的公差为d ,然后根据等差数列的通项公式代入a 6=2a 3,可得关于公差d 的方程,解出d 的值,即可得到数列{a n }的通项公式;第(2)题先根据第(1)题的结果计算出数列{b n }的通项公式,可发现数列{b n }是以2为首项,2为公比的等比数列,根据等比数列的求和公式可得S n 的表达式,代入S m =62进行计算可得m 的值.本题主要考查等差数列和等比数列基本量的计算.考查了转化思想,方程思想,指数的运算,逻辑思维能力和数学运算能力.本题属中档题.18.答案:解:(1)m =190+1902=190;(3)由于k 2=45×(15×16−4×10)219×26×25×20=7.287>6.635,因此可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关.解析:(1)根据茎叶图可求易倒伏玉米茎高的中位数; (2)根据茎叶图的数据,即可完成列联表:(3)计算K 的观测值K 2,对照题目中的表格,得出统计结论.本题主要考查了中位数的求法,考查了独立性检验的应用问题,也考查了计算能力的应用问题,是基础题目.19.答案:(1)证明:取BC 中点M ,连接PM ,AM , 因为四边形ABCD 为菱形且∠BAD =120°. 所以AM ⊥BC ,因为PB =PC ,所以PM ⊥BC , 又AM ∩PM =M ,所以BC ⊥平面PAM ,因为PA ⊂平面PAM , 所以PA ⊥BC .同理可证PA ⊥DC , 因为DC ∩BC =C , 所以PA ⊥平面ABCD .(2)解:由(1)得PA ⊥平面ABCD ,所以平面PAF ⊥平面ABCD ,平面PAF ∩平面ABCD =AF . 所以点B 到直线AF 的距离即为点B 到平面PAF 的距离.过B 作AF 的垂线段,在所有的垂线段中长度最大的为AB =2,此时AF 必过DC 的中点, 因为E 为PB 中点,所以此时,点E 到平面PAF 的距离最大,最大值为1.以A 为坐标原点,直线AF ,AB ,AP 分别为x ,y ,z 轴建立空间直角坐标系A −xyz . 则A(0,0,0),C(√3,1,0),E(0,1,1),B(0,2,0),所以AC ⃗⃗⃗⃗⃗ =(√3,1,0),AE ⃗⃗⃗⃗⃗ =(0,1,1),AB ⃗⃗⃗⃗⃗ =(0,2,0), 平面PAF 的一个法向量为AB ⃗⃗⃗⃗⃗ =(0,2,0),设平面AEC 的法向量为n⃗ =(x,y,z), 则{AC ⃗⃗⃗⃗⃗ ⋅n ⃗ =√3x +y =0AE ⃗⃗⃗⃗⃗ ⋅n ⃗ =y +z =0, 取y =1,则n ⃗ =(−√33,1,−1),cos <n ⃗ ,AB ⃗⃗⃗⃗⃗ >=n ⃗⃗ ⋅AB ⃗⃗⃗⃗⃗⃗ |n ⃗⃗ |⋅|AB ⃗⃗⃗⃗⃗⃗ |=√217, 所以sin <n ⃗ ,AB ⃗⃗⃗⃗⃗ >=2√77,所以面PAF 与面EAC 所成二面角的正弦值为2√77.解析:(1)先证明BC ⊥平面PAM ,可得PA ⊥BC ,同理可证PA ⊥DC ,进而可证PA ⊥平面ABCD ; (2)依题意,以A 为坐标原点,直线AF ,AB ,AP 分别为x ,y ,z 轴建立空间直角坐标系,求出两平面的法向量,利用向量公式即可得解.本题考查线面垂直的判定以及利用空间向量求解二面角的正弦值,考查推理能力及计算能力,属于中档题.20.答案:解:(1)设P(x,y),则F 1P ⃗⃗⃗⃗⃗⃗⃗ =(x +c,y),F 2P⃗⃗⃗⃗⃗⃗⃗ =(x −c,y),∴PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ =x 2+y 2−c 2=a 2−1a 2x 2+1−c 2,x ∈[−a,a],由题意得,1−c 2=0⇒c =1⇒a 2=2, ∴椭圆C 的方程为x 22+y 2=1;(2)将直线l 的方程y =kx +m 代入椭圆C 的方程x 2+2y 2=2中,得(2k 2+1)x 2+4kmx +2m 2−2=0. 由直线l 与椭圆C 仅有一个公共点知,△=16k 2m 2−4(2k 2+1)(2m 2−2)=0,化简得:m 2=2k 2+1. 设d 1=|F 1M|=√k 2+1,d 2=|F 2N|=√k 2+1, 当k ≠0时,设直线l 的倾斜角为θ,则|d 1−d 2|=|MN|×|tanθ|, ∴|MN|=1|k|⋅|d 1−d 2|, ∴S =12⋅1|k|⋅d 1−d 2|⋅(d 1+d 2)=2|m|k 2+1=4|m|m 2+1=4|m|+1|m|,∵m 2=2k 2+1,∴当k ≠0时,|m|>1,|m|+1|m|>2, ∴S <2.当k =0时,四边形F 1MNF 2是矩形,S =2. 所以四边形F 1MNF 2面积S 的最大值为2.解析:(1)利用PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 的最小值为0,可得PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ =x 2+y 2−c 2=a 2−1a 2x 2+1−c 2,x ∈[−a,a],即可求椭圆C 的方程;(2)将直线l 的方程y =kx +m 代入椭圆C 的方程中,得到关于x 的一元二次方程,由直线l 与椭圆C仅有一个公共点知,△=0,即可得到m ,k 的关系式,利用点到直线的距离公式即可得到d 1=|F 1M|,d 2=|F 2N|.当k ≠0时,设直线l 的倾斜角为θ,则|d 1−d 2|=|MN|×|tanθ|,即可得到四边形F 1MNF 2面积S 的表达式,利用基本不等式的性质,结合当k =0时,四边形F 1MNF 2是矩形,即可得出S 的最大值.本题主要考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系、向量知识、二次函数的单调性、基本不等式的性质等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合、化归与转化思想.21.答案:解:(1)依题意,x >0,且f′(x)=x +m +1x =x 2+mx+1x,记g(x)=x 2+mx +1,①若△=m 2−4≤0,即−2≤m ≤2,则g(x)≥0恒成立,f′(x)≥0恒成立,符合题意; ②若△=m 2−4>0,即m >2或m <−2,当m >2时,x 2+mx +1=0有两个不等的负根,符合题意, 当m <−2时,x 2+mx +1=0有两个不等的正根, 则在两根之间函数f(x)单调递减,不符合题意. 综上可得m ≥−2.(2)由题意得x 1,x 2为g(x)=x 2+mx +1的两个零点,由(1)得x 1+x 2=−m ,x 1x 2=1,则f(x 1)−f(x 2)=12x 12+mx 1+ln x 1−(12x 22+mx 2+ln x 2) =12(x 12−x 22)+m(x 1−x 2)+ln x 1−ln x 2 =12(x 12−x 22)−(x 1+x 2)(x 1−x 2)+ln x 1−ln x 2 =lnx 1x 2−12(x 12−x 22) =ln x 1x 2−12⋅x 12⋅x 22x 1x 2 =ln x 1x 2−12(x 1x 2−x 2x 1).记x 1x 2=t ,由x 1<x 2且m ≤−3√22,知0<t <1,且f(x 1)−f(x 2)=ln t −12(t −1t ), 记φ(t)=ln t −12(t −1t ), 则φ′(t)=2t−t 2−12t 2=−(t−1)22t 2<0,故φ(t)在(0,1)上单调递减. 由m ≤−3√22,知(x 1+x 2)2≥92,从而x 12+x 22≥52,即x 12+x 22x1x 2≥52,故t +1t ≥52,结合0<t <1,解得0<t ≤12,从而φ(t)的最小值为φ(12)=34−ln2,即f(x 1)−f(x 2)的最小值为34−ln 2.解析:(1)先求出导数,再利用导数性质对m 分情况讨论来求解;(2)可先对f(x 1)−f(x 2)进行变形,再将问题转化为单变量函数问题来解决.本题考查导数知识的运用,考查函数的单调性、极值,导数在研究函数性质中的应用,正确求导,确定函数的最值是关键,考查运算求解能力,考查函数与方程思想,是中档题. 22.答案:解:(Ⅰ)由{x =3−√22ty =√5+√22t 得直线l 的普通方程为x +y −3−√5=0--------2分 又由ρ=2√5sinθ得ρ2=2√5ρsinθ,化为直角坐标方程为x 2+(y −√5)2=5;---------5分 (Ⅱ)把直线l 的参数方程代入圆C 的直角坐标方程,得(3−√22t)2+(√22t)2=5,即t 2−3√2t +4=0设t 1,t 2是上述方程的两实数根,所以t 1+t 2=3√2又直线l 过点P(3,√5),A 、B 两点对应的参数分别为t 1,t 2,所以|PA|+|PB|=|t 1|+|t 2|=t 1+t 2=3√2.------------------10分.解析:(Ⅰ)先利用两方程相加,消去参数t 即可得到l 的普通方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x ,ρsinθ=y ,ρ2=x 2+y 2,进行代换即得圆C 的直角坐标方程.(Ⅱ)把直线l 的参数方程代入圆C 的直角坐标方程,利用参数的几何意义,求|PA|+|PB|的值. 本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化. 23.答案:解:(1)当a =4时,不等式f(x)≥5,即|x −1|+|x −4|≥5, 等价于{x <1−2x +5≥5,或{1≤x ≤43≥5,或 {x >42x −5≥5,解得:x ≤0或x ≥5.故不等式f(x)≥5的解集为{x|x ≤0,或x ≥5 }. …(5分)(2)因为f(x)=|x −1|+|x −a|≥|(x −1)−(x −a)|=|a −1|.(当x =1时等号成立) 所以:f(x)min =|a −1|.…(8分) 由题意得:|a −1|≥4,解得 a ≤−3,或a ≥5. …(10分)解析:(1)不等式即|x −1|+|x −4|≥5,等价于{x <1−2x +5≥5,或{1≤x ≤43≥5,或 {x >42x −5≥5,分别求出每个不等式组的解集,再取并集即得所求.(2)因为f(x)=|x −1|+|x −a|≥|a −1|,由题意可得|a −1|≥4,与偶此解得 a 的值. 本题主要考查绝对值不等式的解法,函数的恒成立问题,属于中档题。
2020年四川省南充市高考数学二诊试卷(文科)(含答案解析)

2020年四川省南充市高考数学二诊试卷(文科)一、选择题(本大题共12小题,共60.0分)1.复数i+1i=()A. −2iB. 0C. 12i D. 2i2.已知集合A={1,3,√m},B={1,m},A∪B=A,则m=()A. 0或√3B. 0或3C. 1或√3D. 1或33.3本不同的语文书,2本不同的数学书,从中任意取出2本,取出的书恰好都是数学书的概率是()A. 12B. 14C. 15D. 1104.已知tanα=−12,π2<α<π,则sinα=()A. 2√55B. −√55C. −2√55D. √555.如图,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:有一根竹子,原高一丈(1丈=10尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子三尺远,问折断处离地面的高?()A. 4.55尺B. 5.45尺C. 4.2尺D. 5.8尺6.若函数y=2sin(2x+φ)的图象过点(π6,1),则它的一条对称轴方程可能是()A. x=π6B. x=π3C. x=π12D. x=5π127.过圆x2+y2=4外一点M(4,−1)引圆的两条切线,则经过两切点的直线方程是()A. 4x−y−4=0B. 4x+y−4=0C. 4x+y+4=0D. 4x−y+4=08.定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)<1,则b+1a+1的取值范围是()A. (15,13) B. (−∞,13)∪(5,+∞)C. (13,5) D. (−∞,3)9.一个空间几何体的正视图是长为4,宽为√3的长方形,侧视图是边长为2的等边三角形,俯视图如图所示,则该几何体的体积为()A. 4√33B. 4√3 C. 2√33D.2√310. △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若(2a −b)cosC =ccosB ,则内角C =( )A. π6B. π4C. π3D. π2 11. 正三棱锥底面边长为3,侧棱与底面成60°角,则正三棱锥的外接球的体积为( )A. 4πB. 16πC. 16π3D.32π312. 设F 1,F 2分别是双曲线x 2a 2−y 2b 2=1的左、右焦点.若双曲线上存在点M ,使∠F 1MF 2=60°,且|MF 1|=2|MF 2|,则双曲线离心率为( )A. √2B. √3C. 2D. √5二、填空题(本大题共4小题,共20.0分)13. 已知向量a ⃗ ,b ⃗ 满足(a ⃗ +2b ⃗ )⋅(a ⃗ −b ⃗ )=−6,且|a ⃗ |=1,|b ⃗ |=2,则cos <a ⃗ ,b ⃗ >=______.14. 一次考试后,某班全班50个人数学成绩的平均分为正数M ,若把M 当成一个同学的分数,与原来的50个分数一起,算出这51个分数的平均值为N ,则MN =______.15. 已知函数f(x)=alnx −bx 2图象上一点(2,f(2))处的切线方程为y =−3x +2ln2+2,则a +b =______.16. 已知F 是抛物线C :y 2=2px(p >0)的焦点,过F 作直线与C 相交于P ,Q 两点,且Q 在第一象限,若2PF ⃗⃗⃗⃗⃗ =FQ ⃗⃗⃗⃗⃗ ,则直线PQ 的斜率是______.三、解答题(本大题共7小题,共82.0分) 17. 等差数列{a n }中,a 1=1,a 6=2a 3.(1)求{a n }的通项公式;(2)设b n =2a n ,记S n 为数列{b n }前n 项的和,若S m =62,求m .18. 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米. (1)求出易倒伏玉米茎高的中位数m ;的前提下,认为抗倒伏与玉米矮茎有关?附:K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),K 3.841 6.635 10.82819. 在四棱锥P −ABCD 中,底面ABCD 是边长为2的菱形,∠BAD =120°,PA =2,PB =PC =PD ,E 是PB 的中点. (1)证明:PD//平面AEC ;(2)设F 是线段DC 上的动点,当点E 到平面PAF 距离最大时,求三棱锥P −AFE 的体积.20. 设点F 1(−c,0),F 2(c,0)分别是椭圆C :x 2a 2+y 24=1(a >2)的左,右焦点,P 为椭圆C 上任意一点,且PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 的最小值为3.(1)求椭圆C 的方程;(2)如图,直线l :x =5与x 轴交于点E ,过点F 2且斜率k ≠0的直线l 1与椭圆交于A ,B 两点,M 为线段EF 2的中点,直线AM 交直线l 于点N ,证明:直线BN ⊥l .21. 已知两数f(x)=lnx +kx .(1)当k =−1时,求函数f(x)的极值点;(2)当k =0时,若f(x)+bx −a ≥0(a,b ∈R)恒成立,求e a−1−b +1的最大值.22. 在平面直角坐标系xOy 中,直线l 的参数方程为{x =3−√22ty =√5+√22t(t 为参数).在以原点O 为极点,x 轴正半轴为极轴的极坐标中,圆C 的方程为ρ=2√5sinθ. (Ⅰ)写出直线l 的普通方程和圆C 的直角坐标方程;(Ⅱ)若点P 坐标为(3,√5),圆C 与直线l 交于A ,B 两点,求|PA|+|PB|的值.23. 设函数f(x)=|x −1|+|x −a|,a ∈R .(1)当a =4时,求不等式f(x)≥5的解集;(2)若f(x)≥4对x ∈R 恒成立,求a 的取值范围.-------- 答案与解析 --------1.答案:B解析:解:i+1i =i+ii⋅i=i−i=0故选:B.直接对复数的分母、分子同乘i,然后化简即可求出所求.本题主要考查了复数代数形式的混合运算,解题的关键i2=−1,属于容易题.2.答案:B解析:解:A∪B=A⇔B⊆A.∴{1,m}⊆{1,3,√m},∴m=3或m=√m,解得m=0或m=1(与集合中元素的互异性矛盾,舍去).综上所述,m=0或m=3.故选:B.由两集合的并集为A,得到B为A的子集,转化为集合间的基本关系,再利用子集的定义,转化为元素与集合,元素与元素的关系.此题考查了并集及其运算,以及集合间的包含关系,是一道基础题.3.答案:D解析:解:从中任意取出2本共有10种,取出的书恰好都是数学书有1种,从中任意取出2本,取出的书恰好都是数学书的概率为110,故选:D.求出总的事件个数,再求出符合题意的事件,求出概率.本题考查概率,属于基础题.4.答案:D解析:解:已知tanα=−12,∴cos2α=11+tan2α=45,∴sin2α=15.又π2<α<π,∴sinα=√55,故选:D.利用同角三角函数的基本关系,求出cos2α和sin2α的值,再由π2<α<π,求出sinα的值.本题考查同角三角函数的基本关系的应用,是一道基础题.5.答案:A解析:解:如图,已知AC+AB=10(尺),BC=3(尺),AB2−AC2=BC2=9,所以(AB+AC)(AB−AC)=9,解得AB−AC=0.9,因此{AB +AC =10AB −AC =0.9,解得{AB =5.45AC =4.55,故折断后的竹干高为4.55尺, 故选:A .由题意可得AC +AB =10(尺),BC =3(尺),运用勾股定理和解方程可得AB ,AC ,即可得到所求值.本题考查三角形的勾股定理的运用,考查方程思想和运算能力,属于基础题. 6.答案:B解析:解:∵函数y =2sin(2x +φ)的图象过点(π6,1),∴1=2sin(2×π6+φ),∴φ=2kπ+π6或2kπ+5π6(k ∈z)①.又∵对称轴方程为:2x +φ=k′π+π2,∴x =k′π2+π2−φ(k′∈z)②.将①代入②得 x =k′π2−kπ+π3(,k′∈z,k ∈z).当k′=0,k =0时,x =π3. 故选:B .由于函数过点(π6,1),代入函数得φ=2kπ+π6或2kπ+5π6,又可知对称轴方程为x =k′π2+π2−φ,将φ代入对称轴方程,对k ,k′赋值即可得出答案.本题考察三角函数图象和性质,属于中档题. 7.答案:A解析:解:设切点是P(x 1,y 1)、Q(x 2,y 2), 则以P 为切点的切线方程是:x 1x +y 1y =4, 以Q 为切点的切线方程是:x 2x +y 2y =4,∵点M(4,−1)在两条切线上,则4x 1−y 1=4,4x 2−y 2=4 ∴点P 、Q 的坐标满足方程:4x −y =4∴过两切点P 、Q 的直线方程是:4x −y −4=0. 故选:A .设切点是P(x 1,y 1)、Q(x 2,y 2),则以P 为切点的切线方程是:x 1x +y 1y =4,以Q 为切点的切线方程是:x 2x +y 2y =4,由此能求出过两切点P 、Q 的直线方程.本题考查经过两个切点的直线方程的求法,是中档题,解题时要认真审题,注意圆的切线方程的性质的合理运用.8.答案:C解析:解:由图可知,当x >0时,导函数f′(x)>0,原函数单调递增∵两正数a,b满足f(2a+b)<1,∴0<2a+b<4,∴b<4−2a,由0<b<4−2a,可得0<a<2,画出可行域如图.k=b+1表示点Q(−1,−1)与点P(x,y)连线的斜率,a+1当P点在A(2,0)时,k最小,最小值为:1;3当P点在B(0,4)时,k最大,最大值为:5.取值范围是C.故选C.先根据导函数的图象判断原函数的单调性,从而确定a、b的范围得到答案.本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.9.答案:B解析:解:由题意可知,三视图复原的几何体是放倒的正三棱柱,如图所示:,正三角形的边长为2,高为√3,正三棱柱的高为4,×2×√3×4=4√3,所以正三棱柱的体积为:12故选:B.通过三视图复原的几何体的特征,结合三视图的数据,求出几何体的体积即可.本题主要考查了根据三视图还原实物图,考查了几何体体积的求法,是基础题.10.答案:C解析:解:由正弦定理得:2sinAcosC−sinBcosC=sinCcosB,即2sinAcosC=sinBcosC+sinCcosB,即2sinAcosC=sin(B+C)=sinA,由于sinA≠0,,故cosC=12又0<C<π,.所以C=π3故选:C.由已知及正弦定理,三角函数恒等变换的应用可得2sinAcosC=sinA,结合sinA≠0,可求cos C,根据范围0<C<π,可求C的值.本题主要考查了正弦定理,三角函数恒等变换的应用,考查了运算求解能力和转化思想,属于基础题.11.答案:D解析:解:如图所示,过A作AE⊥平面BCD,垂足为E,则E为三角形BCD的外心,由题意可知,BE=√3,因为侧棱与底面成60°角,即∠ABE=60°,所以AE=3,Rt△OBE中,R2=3+(3−R)2,解可得R=2,则正三棱锥的外接球的体积V=4πR33=32π3.故选:D.由已知及线面角可求BE,AE,然后结合球的性质可求R,结合球体积公式可求.本题主要考查了三棱锥的外接球的体积的求解,解题的关键是球心的确定,属于中档试题.12.答案:B解析:【分析】本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.由双曲线的定义知|MF1|=4a,|MF2|=2a,由余弦定理得c=√3a,由此能求出双曲线的离心率.【解答】解:∵点M在双曲线x2a2−y2b2=1上,且|MF1|=2|MF2|,∴由双曲线的定义知|MF1|=4a,|MF2|=2a,又∵∠F1MF2=60°,∴在△MF1F2中,由余弦定理得:16a2+4a2−2⋅4a⋅2a⋅cos60°=4c2,解得c=√3a,∴e=ca=√3.故选:B.13.答案:12解析:解:根据题意,向量a⃗,b⃗ 满足(a⃗+2b⃗ )⋅(a⃗−b⃗ )=−6,且|a⃗|=1,|b⃗ |=2,则有(a⃗+2b⃗ )⋅(a⃗−b⃗ )=a⃗2+a⃗⋅b⃗ −2b⃗ 2=−7+2cos<a⃗,b⃗ >=−6,解可得:cos<a⃗,b⃗ >=12;故答案为:12根据题意,由数量积的计算公式可得(a⃗+2b⃗ )⋅(a⃗−b⃗ )=a⃗2+a⃗⋅b⃗ −2b⃗ 2=−7+2cos<a⃗,b⃗ >=−6,变形分析可得答案.本题考查向量数量积的计算,涉及向量夹角的计算,属于基础题. 14.答案:1解析:解:全班50个人数学成绩的平均分为正数M , 把M 当成一个同学的分数,则班中有51名同学,总成绩为51M , 这51人的平均分为N =51M 51=M ,所以MN =1.故答案为:1.全班50个人的平均分为M ,把M 当成一个同学的分数,则班中有51人,计算这51人的平均值N ,求出M N 的值即可.本题考查了平均数的计算问题,也考查了运算求解能力,是基础题. 15.答案:3解析:解:将x =2代入切线得f(2)=2ln2−4. 所以2ln2−4=aln2−4b①, 又f′(x)=ax −2bx , ∴f′(2)=a 2−4b =−3②,联立①②解得a =2,b =1. 所以a +b =3. 故答案为:3.将(2,f(2))代入切线求出f(2),再将切点坐标代入f(x)得方程①,再对原函数求导,进一步求出切点处导数并令其为−3,得方程②,联立①②求出a ,b 即可解决问题.本题考查了导数的几何意义,本题的关键在于利用切点满足曲线与切线方程,切点处的导数等于切线斜率列方程求解,注意计算要准确.属于基础题. 16.答案:2√2解析:解:过点P ,Q 分别作抛物线的准线l :x =−1的垂线,垂足分别是P 1、Q 1,由抛物线的定义可知,|Q 1Q|=|QF|,|P 1P|=|FP|, 设|PF|=k(k >0),2PF ⃗⃗⃗⃗⃗ =FQ ⃗⃗⃗⃗⃗ ,则|FQ|=2k ,|PQ|=3k ,又过点Q 作QR ⊥P 1P 于点R , 则在直角△PRQ 中,|RR|=k ,|PQ|=3k , |QR|=2√2k ,由∠PQR 与直线QP 的倾斜角相等,则直线PQ 的斜率k =tan∠QPR =2√2, ∴直线PQ 的斜率是2√2, 故答案为:2√2.过点P,Q分别作抛物线的准线l:x=−p的垂线,垂足分别是P1、Q1,由抛物线的|Q1Q|=|QF|定2义可知,|P1P|=|FP|,设|QF|=k(k>0),则|FP|=2k,在直角△PRQ中求解直线PQ的倾斜角即可求得直线PQ斜率.本题考查抛物线的简单几何性质及抛物线定义的应用,考查数形结合思想以及计算能力,属于中档题.17.答案:解:(1)由题意,设等差数列{a n}的公差为d,则a n=1+(n−1)d,∵a6=2a3,∴1+5d=2(1+2d),解得d=1,∴a n=n,n∈N∗.(2)由(1)知,b n=2n=2⋅2n−1,∴数列{b n}是以2为首项,2为公比的等比数列,=2n+1−2,∴S n=2−2n+11−2由S m=62,可得2m+1−2=62,解得m=5.解析:本题第(1)题先设等差数列{a n}的公差为d,然后根据等差数列的通项公式代入a6=2a3,可得关于公差d的方程,解出d的值,即可得到数列{a n}的通项公式;第(2)题先根据第(1)题的结果计算出数列{b n}的通项公式,可发现数列{b n}是以2为首项,2为公比的等比数列,根据等比数列的求和公式可得S n的表达式,代入S m=62进行计算可得m的值.本题主要考查等差数列和等比数列基本量的计算.考查了转化思想,方程思想,指数的运算,逻辑思维能力和数学运算能力.本题属中档题.=190;18.答案:解:(1)m=190+1902(2)抗倒伏易倒伏矮茎154高茎1016(3)由于k2=45×(15×16−4×10)2=7.287>6.635,19×26×25×20因此可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关.解析:(1)根据茎叶图可求易倒伏玉米茎高的中位数;(2)根据茎叶图的数据,即可完成列联表:(3)计算K的观测值K2,对照题目中的表格,得出统计结论.本题主要考查了中位数的求法,考查了独立性检验的应用问题,也考查了计算能力的应用问题,是基础题目.19.答案:(1)证明:连接DB与AC交于O,连接OE,∵ABCD是菱形,∴O为DB的中点,又∵E为PB的中点,∴PD//OE,∵PD⊄平面AEC,OE⊂平面AEC,∴PD//平面AEC ;(2)解:取BC 中点M ,连接AM ,PM ,∵四边形ABCD 是菱形,∠BAD =120°,且PC =PB ,∴BC ⊥AM ,BC ⊥PM ,又AM ∩PM =M ,∴BC ⊥平面APM ,又AP ⊂平面APM ,∴C ⊥PA .同理可证:DC ⊥PA ,又BC ∩DC =C ,∴PA ⊥平面ABCD ,则平面PAF ⊥平面ABCD ,又平面PAF ∩平面ABCD =AF ,∴点B 到直线AF 的距离即为点B 到平面PAF 的距离,过B 作直线AF 的垂线段,在所有垂线段中长度最大为AB =2,∵E 为PB 的中点,故点E 到平面PAF 的最大距离为1,此时,F 为DC 的中点,即AF =√3,∴S △PAF =12PA ⋅AF =12×2×√3=√3, ∴V p−AFE =V E−PAF =13×√3×1=√33.解析:(1)连接DB 与AC 交于O ,连接OE ,由三角形中位线定理证明PD//OE ,再由线面平行的判定可得PD//平面AEC ;(2)取BC 中点M ,连接AM ,PM ,证明PA ⊥平面ABCD ,则平面PAF ⊥平面ABCD ,又平面PAF ∩平面ABCD =AF ,可得点B 到直线AF 的距离即为点B 到平面PAF 的距离,过B 作直线AF 的垂线段,在所有垂线段中长度最大为AB =2,由此可得点E 到平面PAF 的最大距离为1,求得AF ,则三棱锥P −AFE 的体积可求.本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了多面体体积的求法,是中档题.20.答案:解:(1)设P(x,y),则PF 1⃗⃗⃗⃗⃗⃗⃗ =(−c −x,−y),PF 2⃗⃗⃗⃗⃗⃗⃗ =(c −x,−y),所以PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ =x 2+y 2−c 2=a 2−4a 2x 2+4−c 2, 因为a >2,x ∈[−a,a].所以当x =0时,PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 值最小,所以4−c 2=3,解得c =1,(舍负)所以a 2=5,所以椭圆C 的方程为x 25+y 24=1,(2)设直线l 1的方程为y =k(x −1),k ≠0,联立{y =k(x −1)x 25+y 24=1,得(4+5k 2)x 2−10k 2x +5k 2−20=0. 设A(x 1,y 1),B(x 2,y 2),则x 1+x 2=10k 24+5k 2,x 1x 2=5k 2−204+5k 2, 设N(5,y 0),因为A ,M ,N 三点共线,又M(3,0)所以−y 13−x 1=y 02,解得y 0=2y 1x 1−3.而y 0−y 2=2y 1x 1−3−y 2=2k(x 1−1)x 1−3−k(x 2−1)=3k(x 1+x 2)−kx 1x 2−5kx 1−3=3k⋅10k 24+5k 2−k⋅5k 2−204+5k 2−5k x 1−3=0所以直线BN//x 轴,即BN ⊥l .解析:(1)设P(x,y),求出PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ 的表达式,利用最小值,转化求解即可.(2)设直线l 1的方程为y =k(x −1),k ≠0,联立{y =k(x −1)x 25+y 24=1,得(4+5k 2)x 2−10k 2x +5k 2−20=0.设A(x 1,y 1),B(x 2,y 2),通过韦达定理,设N(5,y 0),因结合A ,M ,N 三点共线,解得y 0=2y 1x 1−3.计算y 0−y 2=0,即可说明直线BN//x 轴,即BN ⊥l .本题考查直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力,是难题. 21.答案:解:(1)f′(x)定义域为(0,+∞),当k =−1时,f(x)=lnx −x,f′(x)=1x −1, 令f′(x)=0得x =1,所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)有唯一的极大值点x =1,无极小值点.(2)当k =0时,f(x)+b x −a =lnx +b x −a .若f(x)+b x −a ≥0,(a,b ∈R)恒成立,则lnx +b x −a ≥0(a,b ∈R)恒成立,所以a ≤lnx +b x 恒成立,令y =lnx +b x ,则y′=x−bx 2,由题意b >0,函数在(0,b)上单调递减,在(b,+∞)上单调递增,所以a ≤lnb +1,所以a −1≤lnb所以e a−1≤b ,所以e a−1−b +1≤1,故e a−1−b +1的最大值为1.解析:(1)把k =−1代入后对函数求导,然后结合导数与单调性及极值关系即可求解;(2)由已知不等式恒成立,分离参数a 可得a ≤lnx +b x 恒成立,构造函数,转化为求解相应函数的范围,结合导数可求.本题主要考查了利用导数求解函数的极值,证明不等式,体现了转化思想的应用,属于中档试题.22.答案:解:(Ⅰ)由{x =3−√22t y =√5+√22t得直线l 的普通方程为x +y −3−√5=0--------2分 又由ρ=2√5sinθ得ρ2=2√5ρsinθ,化为直角坐标方程为x 2+(y −√5)2=5;---------5分 (Ⅱ)把直线l 的参数方程代入圆C 的直角坐标方程,得(3−√22t)2+(√22t)2=5,即t 2−3√2t +4=0 设t 1,t 2是上述方程的两实数根,所以t 1+t 2=3√2又直线l 过点P(3,√5),A 、B 两点对应的参数分别为t 1,t 2,所以|PA|+|PB|=|t 1|+|t 2|=t 1+t 2=3√2.------------------10分.解析:(Ⅰ)先利用两方程相加,消去参数t 即可得到l 的普通方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x ,ρsinθ=y ,ρ2=x 2+y 2,进行代换即得圆C 的直角坐标方程. (Ⅱ)把直线l 的参数方程代入圆C 的直角坐标方程,利用参数的几何意义,求|PA|+|PB|的值. 本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.23.答案:解:(1)当a =4时,不等式f(x)≥5,即|x −1|+|x −4|≥5,等价于{x <1−2x +5≥5,或{1≤x ≤43≥5,或 {x >42x −5≥5, 解得:x ≤0或x ≥5.故不等式f(x)≥5的解集为{x|x ≤0,或x ≥5 }. …(5分)(2)因为f(x)=|x −1|+|x −a|≥|(x −1)−(x −a)|=|a −1|.(当x =1时等号成立)所以:f(x)min =|a −1|.…(8分)由题意得:|a −1|≥4,解得 a ≤−3,或a ≥5. …(10分)解析:(1)不等式即|x −1|+|x −4|≥5,等价于{x <1−2x +5≥5,或{1≤x ≤43≥5,或 {x >42x −5≥5,分别求出每个不等式组的解集,再取并集即得所求.(2)因为f(x)=|x −1|+|x −a|≥|a −1|,由题意可得|a −1|≥4,与偶此解得 a 的值. 本题主要考查绝对值不等式的解法,函数的恒成立问题,属于中档题。
2020年四川省南充市中考数学二诊试卷及答案解析

2020年四川省南充市中考数学二诊试卷一、选择题(每小题5分,共50分)1.(5分)“瓦当”是中国古建筑装饰檐头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是()A.B.C.D.2.(5分)2017年国内生产总值达到827 000亿元,稳居世界第二.将数827 000用科学记数法表示为()A.82.7×104B.8.27×105C.0.827×106D.8.27×1063.(5分)下列事件属于必然事件的是()A.经过有交通信号的路口,遇到红灯B.任意买一张电影票,座位号是双号C.向空中抛一枚硬币,不向地面掉落D.三角形中,任意两边之和大于第三边4.(5分)如图,数轴上的点A,B,O,C,D分别表示数﹣2,﹣1,0,1,2,则表示数2﹣的点P应落在()A.线段AB上B.线段BO上C.线段OC上D.线段CD上5.(5分)关于x的分式方程=1的解为负数,则a的取值范围是()A.a>1B.a<1C.a<1且a≠﹣2D.a>1且a≠2 6.(5分)如图,△ABC的顶点A在反比例函数y=(x>0)的图象上,顶点C在x轴上,AB∥x轴,若点B的坐标为(1,3),S△ABC=2,则k的值为()A.4B.﹣4C.7D.﹣77.(5分)在反比例函数y=﹣图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是()A.y3<y2<y1B.y1<y3<y2C.y2<y3<y1D.y3<y1<y2 8.(5分)如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为()A.6π﹣B.6π﹣9C.12π﹣D.9.(5分)如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为()A.102°B.112°C.122°D.92°10.(5分)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>﹣c;⑤a+b>m(am+b)(m≠1的实数).其中正确结论的有()A.①②③B.②③⑤C.②③④D.③④⑤二、填空题(每小题5分,共40分)11.(5分)分解因式:2a2﹣8ab+8b2=.12.(5分)若关于x的一元二次方程x2﹣2mx﹣4m+1=0有两个相等的实数根,则(m﹣2)2﹣2m(m﹣1)的值为.13.(5分)不等式组的解集为14.(5分)如图,△ABC的外接圆O的半径为3,∠C=55°,则劣弧的长是.(结果保留π)15.(5分)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC 交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF的最小值是.16.(5分)如图,矩形OABC的顶点A,C分别在坐标轴上,B(8,7),D(5,0),点P 是边AB或边BC上的一点,连接OP,DP,当△ODP为等腰三角形时,点P的坐标为.17.(5分)在平面直角坐标系xOy中,已知A(2t,0),B(0,﹣2t),C(2t,4t)三点,其中t>0,函数y=的图象分别与线段BC,AC交于点P,Q.若S△P AB﹣S△PQB=t,则t的值为.18.(5分)如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=;④矩形EFGH的面积是4.其中一定成立的是.(把所有正确结论的序号填在横线上)三、解答题(本大题共6小题,共60分.解答时应写出文字说明、证明过程或演算步骤)19.(10分)计算:(1)(﹣)﹣2+(π﹣3)0+|1﹣|+tan45°(2)=+120.(10分)某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.请结合图中所给信息,解答下列问题:(1)本次调查的学生共有人;(2)补全条形统计图;(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.21.(10分)如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D 相距1000m,E在BD的中点处.(1)求景点B,E之间的距离;(2)求景点B,A之间的距离.(结果保留根号)22.(10分)如图,直线y=ax+2与x轴交于点A(1,0),与y轴交于点B(0,b).将线段AB先向右平移1个单位长度,再向上平移t(t>0)个单位长度,得到对应线段CD,反比例函数y=(x>0)的图象恰好经过C、D两点,连接AC、BD.(1)请直接写出a和b的值;(2)求反比例函数的表达式及四边形ABDC的面积.23.(10分)如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠P AC =∠B.(1)求证:P A是⊙O的切线;(2)弦CE⊥AD交AB于点F,若AF•AB=12,求AC的长.24.(10分)如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.(1)求该抛物线的函数解析式.(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC 于点F,当S△COF:S△CDF=3:2时,求点D的坐标.(3)如图2,点E的坐标为(0,),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.2020年四川省南充市中考数学二诊试卷参考答案与试题解析一、选择题(每小题5分,共50分)1.(5分)“瓦当”是中国古建筑装饰檐头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、不是轴对称图形,也不是中心对称图形;B、不是轴对称图形,是中心对称图形;C、是轴对称图形,不是中心对称图形;D、是轴对称图形,是中心对称图形.故选:D.【点评】本题主要考查轴对称图形和中心对称图形的概念,以及对轴对称图形和中心对称图形的认识.2.(5分)2017年国内生产总值达到827 000亿元,稳居世界第二.将数827 000用科学记数法表示为()A.82.7×104B.8.27×105C.0.827×106D.8.27×106【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:827 000=8.27×105.故选:B.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(5分)下列事件属于必然事件的是()A.经过有交通信号的路口,遇到红灯B.任意买一张电影票,座位号是双号C.向空中抛一枚硬币,不向地面掉落D.三角形中,任意两边之和大于第三边【分析】必然事件就是一定发生的事件,根据定义即可判断.【解答】解:A、经过有交通信号的路口,遇到红灯是随机事件,故选项错误;B、任意买一张电影票,座位号是双号,是随机事件,故选项错误;C、向空中抛一枚硬币,不向地面掉落,是不可能事件,故此选项错误;D、三角形中,任意两边之和大于第三边是必然事件,正确;故选:D.【点评】本题考查了必然事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.4.(5分)如图,数轴上的点A,B,O,C,D分别表示数﹣2,﹣1,0,1,2,则表示数2﹣的点P应落在()A.线段AB上B.线段BO上C.线段OC上D.线段CD上【分析】根据2<<3,得到﹣1<2﹣<0,根据数轴与实数的关系解答.【解答】解:2<<3,∴﹣1<2﹣<0,∴表示数2﹣的点P应落在线段BO上,故选:B.【点评】本题考查的是无理数的估算、实数与数轴,正确估算无理数的大小是解题的关键.5.(5分)关于x的分式方程=1的解为负数,则a的取值范围是()A.a>1B.a<1C.a<1且a≠﹣2D.a>1且a≠2【分析】分式方程去分母转化为整式方程,表示出整式方程的解,根据分式方程解为负数列出关于a的不等式,求出不等式的解集即可确定出a的范围.【解答】解:分式方程去分母得:x+1=2x+a,即x=1﹣a,根据分式方程解为负数,得到1﹣a<0,且1﹣a≠﹣1,解得:a>1且a≠2.故选:D.【点评】此题考查了分式方程的解,注意在任何时候都要考虑分母不为0.6.(5分)如图,△ABC的顶点A在反比例函数y=(x>0)的图象上,顶点C在x轴上,AB∥x轴,若点B的坐标为(1,3),S△ABC=2,则k的值为()A.4B.﹣4C.7D.﹣7【分析】设点A(a,3),根据题意可得:a=,即可求点A坐标,代入解析式可求k 的值.【解答】解:∵AB∥x轴,若点B的坐标为(1,3),∴设点A(a,3)∵S△ABC=(a﹣1)×3=2∴a=∴点A(,3)∵点A在反比例函数y=(x>0)的图象上,∴k=7故选:C.【点评】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,熟练运用反比例函数的性质解决问题是本题的关键.7.(5分)在反比例函数y=﹣图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是()A.y3<y2<y1B.y1<y3<y2C.y2<y3<y1D.y3<y1<y2【分析】根据反比例函数图象上点的坐标特征解答.【解答】解:∵A(x1,y1)在反比例函数y=﹣图象上,x1<0,∴y1>0,对于反比例函数y=﹣,在第二象限,y随x的增大而增大,∵0<x2<x3,∴y2<y3<0,∴y2<y3<y1故选:C.【点评】本题考查的是反比例函数图象上点的坐标特征,掌握反比例函数的性质、反比例函数的增减性是解题的关键.8.(5分)如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为()A.6π﹣B.6π﹣9C.12π﹣D.【分析】连接OD,如图,利用折叠性质得由弧AD、线段AC和CD所围成的图形的面积等于阴影部分的面积,AC=OC,则OD=2OC=6,CD=3,从而得到∠CDO=30°,∠COD=60°,然后根据扇形面积公式,利用由弧AD、线段AC和CD所围成的图形的面积=S扇形AOD﹣S△COD,进行计算即可.【解答】解:连接OD,如图,∵扇形纸片折叠,使点A与点O恰好重合,折痕为CD,∴AC=OC,∴OD=2OC=6,∴CD==3,∴∠CDO=30°,∠COD=60°,∴由弧AD、线段AC和CD所围成的图形的面积=S扇形AOD﹣S△COD=﹣•3•3=6π﹣,∴阴影部分的面积为6π﹣.故选:A.【点评】本题考查了扇形面积的计算:阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.记住扇形面积的计算公式.也考查了折叠性质.9.(5分)如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为()A.102°B.112°C.122°D.92°【分析】由平行四边形的性质和折叠的性质,得出∠ADB=∠BDF=∠DBC,由三角形的外角性质求出∠BDF=∠DBC=∠DFC=20°,再由三角形内角和定理求出∠A,即可得到结果.【解答】解:∵AD∥BC,∴∠ADB=∠DBC,由折叠可得∠ADB=∠BDF,∴∠DBC=∠BDF,又∵∠DFC=40°,∴∠DBC=∠BDF=∠ADB=20°,又∵∠ABD=48°,∴△ABD中,∠A=180°﹣20°﹣48°=112°,∴∠E=∠A=112°,故选:B.【点评】本题主要考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理的综合应用,熟练掌握平行四边形的性质,求出∠ADB的度数是解决问题的关键.10.(5分)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>﹣c;⑤a+b>m(am+b)(m≠1的实数).其中正确结论的有()A.①②③B.②③⑤C.②③④D.③④⑤【分析】由抛物线对称轴的位置判断ab的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.【解答】解:①∵对称轴在y轴的右侧,∴ab<0,由图象可知:c>0,∴abc<0,故①不正确;②当x=﹣1时,y=a﹣b+c<0,∴b﹣a>c,故②正确;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故③正确;④∵x=﹣=1,∴b=﹣2a,∵a﹣b+c<0,∴a+2a+c<0,3a<﹣c,故④不正确;⑤当x=1时,y的值最大.此时,y=a+b+c,而当x=m时,y=am2+bm+c,所以a+b+c>am2+bm+c(m≠1),故a+b>am2+bm,即a+b>m(am+b),故⑤正确.故②③⑤正确.故选:B.【点评】本题主要考查了图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定,熟练掌握二次函数的性质是关键.二、填空题(每小题5分,共40分)11.(5分)分解因式:2a2﹣8ab+8b2=2(a﹣2b)2.【分析】原式提取2,再利用完全平方公式分解即可.【解答】解:原式=2(a2﹣4ab+4b2)=2(a﹣2b)2,故答案为:2(a﹣2b)2【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.12.(5分)若关于x的一元二次方程x2﹣2mx﹣4m+1=0有两个相等的实数根,则(m﹣2)2﹣2m(m﹣1)的值为.【分析】根据根的判别式即可求出答案.【解答】解:由题意可知:△=4m2﹣2(1﹣4m)=4m2+8m﹣2=0,∴m2+2m=∴(m﹣2)2﹣2m(m﹣1)=﹣m2﹣2m+4=+4=故答案为:【点评】本题考查根的判别式,解题的关键是正确理解根的判别式的作用,本题属于基础题型.13.(5分)不等式组的解集为﹣1<x<3【分析】先求出每个不等式的解集,再求出不等式组的解集即可.【解答】解:∵解不等式①得:x<3,解不等式②得:x>﹣1,∴不等式组的解集为﹣1<x<3,故答案为:﹣1<x<3.【点评】本题考查了解一元一次不等式组,能根据不等式的解集找出不等式组的解集是解此题的关键.14.(5分)如图,△ABC的外接圆O的半径为3,∠C=55°,则劣弧的长是.(结果保留π)【分析】根据同弧所对的圆心角是圆周角的2倍,可求∠AOB=110°,根据弧长公式可求劣弧的长.【解答】解:∵∠AOB=2∠C且∠C=55°∴∠AOB=110°根据弧长公式的长==故答案为【点评】本题考查了三角形的外接圆与外心,同弧所对的圆心角是圆周角的2倍,弧长公式,关键是熟练运用弧长公式解决问题.15.(5分)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC 交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF的最小值是3﹣3.【分析】先判断出Rt△ADM≌Rt△BCN(HL),得出∠DAM=∠CBN,进而判断出△DCE ≌△BCE(SAS),得出∠CDE=∠CBE,即可判断出∠AFD=90°,根据直角三角形斜边上的中线等于斜边的一半可得OF=AD=3,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.【解答】解:如图,在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,,∴Rt△ADM≌Rt△BCN(HL),∴∠DAM=∠CBN,在△DCE和△BCE中,,∴△DCE≌△BCE(SAS),∴∠CDE=∠CBE∴∠DAM=∠CDE,∵∠ADF+∠CDE=∠ADC=90°,∴∠DAM+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO=AD=3,在Rt△ODC中,OC==3根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=3﹣3.故答案为:3﹣3.【点评】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出CF最小时点F的位置是解题关键.16.(5分)如图,矩形OABC的顶点A,C分别在坐标轴上,B(8,7),D(5,0),点P 是边AB或边BC上的一点,连接OP,DP,当△ODP为等腰三角形时,点P的坐标为(8,4)或(,7).【分析】分两种情形分别讨论即可解决问题;【解答】解:∵四边形OABC是矩形,B(8,7),∴OA=BC=8,OC=AB=7,∵D(5,0),∴OD=5,∵点P是边AB或边BC上的一点,∴当点P在AB边时,OD=DP=5,∵AD=3,∴P A==4,∴P(8,4).当点P在边BC上时,只有PO=PD,此时P(,7).综上所述,满足条件的点P坐标为(8,4)或(,7).故答案为(8,4)或(,7).【点评】本题考查矩形的性质、坐标与图形性质、等腰三角形的判定等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.17.(5分)在平面直角坐标系xOy中,已知A(2t,0),B(0,﹣2t),C(2t,4t)三点,其中t>0,函数y=的图象分别与线段BC,AC交于点P,Q.若S△P AB﹣S△PQB=t,则t的值为4.【分析】先根据题意画出,因为函数y=的图象分别与线段BC,AC交于点P,Q.可确定P和Q在第一象限,根据Q在AC上可得Q的坐标,根据反比例函数和直线BC的解析式列方程可得P的坐标,根据S△P AB﹣S△PQB=t,列关于t的方程可得结论.【解答】解:如图所示,∵A(2t,0),C(2t,4t),∴AC⊥x轴,当x=2t时,y==,∴Q(2t,),∵B(0,﹣2t),C(2t,4t),易得直线BC的解析式为:y=3x﹣2t,则3x﹣2t=,解得:x1=t,x2=﹣t(舍),∴P(t,t),∵S△P AB=S△BAC﹣S△APC,S△PQB=S△BAC﹣S△ABQ﹣S△PQC,∵S△P AB﹣S△PQB=t,∴(S△BAC﹣S△APC)﹣(S△BAC﹣S△ABQ﹣S△PQC)=t,S△ABQ+S△PQC﹣S△APC=+﹣=t,t=4,故答案为:4.【点评】本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数的解析式及计算图形面积的问题.解题的关键是确定交点P的坐标.18.(5分)如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=;④矩形EFGH的面积是4.其中一定成立的是①②④.(把所有正确结论的序号填在横线上)【分析】根据矩形的性质和全等三角形的判定分析各小题即可;【解答】解:∵∠FGH=90°,∴∠BGF+∠CGH=90°.又∵∠CGH+∠CHG=90°,∴∠BGF=∠CHG,故①正确.同理可得∠DEH=∠CHG.∴∠BGF=∠DEH.又∵∠B=∠D=90°,FG=EH,∴△BFG≌△DHE,故②正确.同理可得△AFE≌△CHG.∴AF=CH.易得△BFG∽△CGH.设GH、EF为a,∴=.∴=.∴BF=.∴AF=AB﹣BF=a﹣.∴CH=AF=a﹣.在Rt△CGH中,∵CG2+CH2=GH2,∴32+(a﹣)2=a2.解得a=2.∴GH=2.∴BF=a﹣=.在Rt△BFG中,∵cos∠BFG==,∴∠BFG=30°.∴tan∠BFG=tan30°=,故③错误.矩形EFGH的面积=FG×GH=2×2=4,故④正确.故答案为:①②④【点评】此题是几何变换综合题,主要考查了全等三角形的判定和性质,矩形的判定和性质,属于基础题.三、解答题(本大题共6小题,共60分.解答时应写出文字说明、证明过程或演算步骤)19.(10分)计算:(1)(﹣)﹣2+(π﹣3)0+|1﹣|+tan45°(2)=+1【分析】(1)原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可求出值;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)原式=4+1+﹣1+1=5+;(2)去分母得:3x=2x+3x+3,解得:x=﹣,经检验x=﹣是分式方程的解.【点评】此题考查了解分式方程,以及实数的运算,熟练掌握分式方程的解法以及运算法则是解本题的关键.20.(10分)某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.请结合图中所给信息,解答下列问题:(1)本次调查的学生共有100人;(2)补全条形统计图;(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.【分析】(1)根据A项目的人数和所占的百分比求出总人数即可;(2)用总人数减去A、C、D项目的人数,求出B项目的人数,从而补全统计图;(3)用该校的总人数乘以选择“唱歌”的学生所占的百分比即可;(4)根据题意先画出树状图,得出所有等情况数和选取的两人恰好是甲和乙的情况数,然后根据概率公式即可得出答案.【解答】解:(1)本次调查的学生共有:30÷30%=100(人);故答案为:100;(2)喜欢B类项目的人数有:100﹣30﹣10﹣40=20(人),补图如下:(3)选择“唱歌”的学生有:1200×=480(人);(4)根据题意画树形图:共有12种情况,被选取的两人恰好是甲和乙有2种情况,则被选取的两人恰好是甲和乙的概率是=.【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.21.(10分)如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D 相距1000m,E在BD的中点处.(1)求景点B,E之间的距离;(2)求景点B,A之间的距离.(结果保留根号)【分析】(1)根据已知条件得到∠C=90°,∠CBD=60°,∠CAE=45°,解直角三角形即可得到结论;(2)过E作EF⊥AB与F,在Rt△AEF中,求得EF,在Rt△BEF中,求得BF,于是得到结论.【解答】解:(1)由题意得,∠C=90°,∠CBD=60°,∠CAE=45°,∵CD=1000,∴BC==1000,∴BD=2BC=2000,∵E在BD的中点处,∴BE=BD=1000(米);(2)过E作EF⊥AB与F,在Rt△AEF中,EF=AF=BE•sin60°=1000×=500,在Rt△BEF中,BF=BE•cos60°=500,∴AB=AF﹣BF=500(﹣1)(米).【点评】此题考查直角三角形的问题,将已知条件和所求结论转化到同一个直角三角形中求解是解直角三角形的常规思路.22.(10分)如图,直线y=ax+2与x轴交于点A(1,0),与y轴交于点B(0,b).将线段AB先向右平移1个单位长度,再向上平移t(t>0)个单位长度,得到对应线段CD,反比例函数y=(x>0)的图象恰好经过C、D两点,连接AC、BD.(1)请直接写出a和b的值;(2)求反比例函数的表达式及四边形ABDC的面积.【分析】(1)利用坐标轴上的点的特点即可得出结论;(2)先表示出点C,D坐标,进而代入反比例函数解析式中求解得出k,再判断出BC ⊥AD,最后用对角线积的一半即可求出四边形的面积;【解答】解:(1)将点A(1,0)代入y=ax+2,得0=a+2.∴a=﹣2.∴直线的解析式为y=﹣2x+2.将x=0代入上式,得y=2.∴b=2.(2)由(1)知,b=2,∴B(0,2),由平移可得:点C(2,t)、D(1,2+t).将点C(2,t)、D(1,2+t)分别代入y=,得,∴,∴反比例函数的解析式为y=,点C(2,2)、点D(1,4).如图1,连接BC、AD.∵B(0,2)、C(2,2),∴BC∥x轴,BC=2.∵A(1,0)、D(1,4),∴AD⊥x轴,AD=4.∴BC⊥AD.∴S四边形ABDC=×BC×AD=×2×4=4.【点评】此题是反比例函数综合题,主要考查了待定系数法,全等三角形的判定和性质,四边形的面积的计算方法,构造出全等三角形是解本题的关键.23.(10分)如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,且满足∠P AC =∠B.(1)求证:P A是⊙O的切线;(2)弦CE⊥AD交AB于点F,若AF•AB=12,求AC的长.【分析】(1)先判断出∠CAD+∠D=90°,进而判断出∠CAD+∠P AC=90°,即可得出结论;(2)先判断出∠B=∠ACF,进而判断出△ABC∽△ACF,得出比例式即可得出结论.【解答】(1)∵AD是⊙O的直径∴∠ACD=90°;∴∠CAD+∠D=90°∵∠P AC=∠PBA,∠D=∠PBA,∴∠CAD+∠P AC=90°,∴∠P AD=90°,∴P A⊥AD,∵点A在⊙O上,∴P A是⊙O的切线(2)∵CF⊥AD,∴∠ACF+∠CAD=90°,∵∠CAD+∠D=90°,∴∠D=∠ACF,∴∠B=∠ACF,∵∠BAC=∠CAF,∴△ABC∽△ACF,∴,∴AC2=AF•AB∵AF•AB=12,∴AC2=12,∴AC=2.【点评】此题主要考查了圆的切线的判定,圆周角定理,相似三角形的判定和性质,判断出∠B=∠ACF是解本题的关键.24.(10分)如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.(1)求该抛物线的函数解析式.(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC 于点F,当S△COF:S△CDF=3:2时,求点D的坐标.(3)如图2,点E的坐标为(0,),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.【分析】(1)OB=OC=3,则:B(3,0),C(0,3),把B、C坐标代入抛物线方程,解得抛物线方程为:y=﹣x2+2x+3…①;(2)S△COF:S△CDF=3:2,则S△COF=S△COD,即:x D=x F,即可求解;(3)分∠PBE或∠PEB等于2∠OBE两种情况分别求解即可.【解答】解:(1)OB=OC=3,则:B(3,0),C(0,3),把B、C坐标代入抛物线方程,解得抛物线方程为:y=﹣x2+2x+3…①;(2)∵S△COF:S△CDF=3:2,∴S△COF=S△COD,即:x D=x F,设:F点横坐标为3t,则D点横坐标为5t,点F在直线BC上,而BC所在的直线表达式为:y=﹣x+3,则F(3t,3﹣3t),则:直线OF所在的直线表达式为:y=x=x,则点D(5t,5﹣5t),把D点坐标代入①,解得:t=或,则点D的坐标为(1,4)或(2,3);(3)①当∠PEB=2∠OBE时,当BP在x轴上方时,如图2,设BP1交y轴于点E′,∴∠P1BE=2∠OBE,∴∠E′BO=∠EBO,又∠E′OB=∠EBO=60°,BO=BO,∴E′BO△≌△EBO(AAS),∴EO=EO=,∴点E′(0,),直线BP1过点B、E′,则其直线方程为:y=﹣x+…②,联立①②并解得:x=﹣,故点P1的坐标为(﹣,);当BP在x轴下方时,如图2,过点E作EF∥BE′交BP2于点F,则∠FEB=∠EBE′,∴∠E′BE=2∠OBE,∠EBP2=2∠OBE,∴∠FEB=∠EBF,∴FE=BF,直线EF可以看成直线BE′平移而得,其k值为﹣,则其直线表达式为:y=﹣x﹣,设点F(m,﹣m﹣),过点F作FH⊥y轴交于点H,作BK⊥HF于点K,则点H(0,﹣m﹣),K(3,﹣m﹣),∵EF=BF,则FE2=BF2,即:m2+(﹣+m+)2=(3﹣m)2+(m+)2,解得:m=,则点F(,﹣),则直线BF的表达式为:y=x﹣…③,联立①③并解得:x=﹣或3(舍去3),则点P2(﹣,﹣);②当∠PBE=2∠OBE时,当EP在BE上方时,如图3,点E′为图2所求,设BE′交EP3于点F,∵∠EBE′=2∠OBE,∴∠EBE′=∠P3EB,∴FE=BF,由①知,直线BE′的表达式为:y=﹣x+,设点F(n,﹣n+),K(3,﹣n+),由FE=BF,同理可得:n=,故点F(,),则直线EF的表达式为:y=x﹣…④,联立①④并解得:n=1或﹣(舍去负值),∴P3(1,4);当EP在BE下方时,同理可得:x=(舍去负值),故点P4(,﹣),故点P的坐标为:(1,4)或(﹣,)或(﹣,﹣)或(,﹣).【点评】本题是二次函数综合题,涉及到三角形相似、勾股定理运用等诸多知识点,是一道难度较大的题目.。
2020年四川省南充市高考数学二诊试卷(文科)

2020年四川省南充市高考数学二诊试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)复数1(i i+= )A .2i -B .0C .12iD .2i2.(5分)已知集合{1A =,3,}m ,{1B =,}m ,A B A =,则(m = )A .0或3B .0或3C .1或3D .1或33.(5分)3本不同的语文书,2本不同的数学书,从中任意取出2本,取出的书恰好都是数学书的概率是( ) A .12B .14 C .15D .1104.(5分)已知1tan ,22πααπ=-<<,则sin (α= )A .255B .55-C .255-D .555.(5分)如图,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:有一根竹子,原高一丈(1丈10=尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子三尺远,问折断处离地面的高?( )A .4.55尺B .5.45尺C .4.2尺D .5.8尺6.(5分)若函数2sin(2)y x ϕ=+的图象过点(6π,1),则它的一条对称轴方程可能是()A .6x π=B .3x π=C .12x π=D .512x π=7.(5分)过圆224x y +=外一点(4,1)M -引圆的两条切线,则经过两切点的直线方程是()A .440x y --=B .440x y +-=C .440x y ++=D .440x y -+=8.(5分)定义在R 上的函数()f x 满足f (4)1=,()f x '为()f x 的导函数,已知()y f x ='的图象如图所示,若两个正数a ,b 满足()121,1b f a b a ++<+则的取值范围是( )A .11(,)53B .1(,)(5,)3-∞+∞C .1(,5)3D .(,3)-∞9.(5分)一个空间几何体的正视图是长为4,宽为3的长方形,侧视图是边长为2的等边三角形,俯视图如图所示,则该几何体的体积为( )A 43B .43C 23D .2310.(5分)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,若(2)cos cos a b C c B -=,则内角(C = ) A .6πB .4π C .3π D .2π 11.(5分)正三棱锥底面边长为3,侧棱与底面成60︒角,则正三棱锥的外接球的体积为()A .4πB .16πC .163πD .323π12.(5分)设1F ,2F 分别是双曲线22221x y a b-=的左、右焦点.若双曲线上存在点M ,使1260F MF ∠=︒,且12||2||MF MF =,则双曲线离心率为( )A 2B 3C .2D 5二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)已知向量,a b 满足(2)()6a b a b +-=-,且||1a =,||2b =,则cos a <,b >= . 14.(5分)一次考试后,某班全班50个人数学成绩的平均分为正数M ,若把M 当成一个同学的分数,与原来的50个分数一起,算出这51个分数的平均值为N ,则MN= . 15.(5分)已知函数2()f x alnx bx =-图象上一点(2,f (2))处的切线方程为3222y x ln =-++,则a b += .16.(5分)已知F 是抛物线2:2(0)C y px p =>的焦点,过F 作直线与C 相交于P ,Q 两点,且Q 在第一象限,若2PF FQ =,则直线PQ 的斜率是 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.(12分)等差数列{}n a 中,11a =,632a a =. (1)求{}n a 的通项公式;(2)设2n a n b =,记n S 为数列{}n b 前n 项的和,若62m S =,求m .18.(12分)为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米. (1)求出易倒伏玉米茎高的中位数m ; (2)根据茎叶图的数据,完成下面的列联表:(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?附:22()()()()()n ad bc K a b c d a c b d -=++++,)KK3.841 6.635 10.82819.(12分)在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,120BAD ∠=︒,2PA =,PB PC PD ==,E 是PB 的中点.(1)证明://PD 平面AEC ;(2)设F 是线段DC 上的动点,当点E 到平面PAF 距离最大时,求三棱锥P AFE -的体积.20.(12分)设点1(,0)F c -,2(,0)F c 分别是椭圆222:1(2)4x y C a a +=>的左,右焦点,P 为椭圆C 上任意一点,且12PF PF 的最小值为3. (1)求椭圆C 的方程;(2)如图,直线:5l x =与x 轴交于点E ,过点2F 且斜率0k ≠的直线1l 与椭圆交于A ,B 两点,M 为线段2EF 的中点,直线AM 交直线l 于点N ,证明:直线BN l ⊥.。
2020年四川省南充市高考(理科)数学二诊试卷含解析

2020 年高考(理科)数学二诊试卷三尺,问折者高几何?意思是:有一根竹子,原高一丈(阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子三尺远,问折断处离地面的高?()A .4.55 尺B . 5.45 尺C .4.2 尺D .5.8 尺5.已知等式(1﹣x+x 2)3?( 1﹣2x 2)4=a 0+a 1x+a 2x 2+⋯ +a 14x 14成立,则 a 2+a 4+⋯+a 14=( A . 0B . 5C .7D . 146.过圆 x 2+y 2=4 外一点 M (4,﹣1)引圆的两条切线, 则经过两切点的直线方程是( A .4x ﹣y ﹣4=0 B .4x+y ﹣4=0 C .4x+y+4=0 D .4x ﹣ y+4=07.定义在 R 上的函数 f (x )满足 f (4)= 1,f ′(x )为 f (x )的导函数,已知 y =、选择题(共 12 小题) .A .﹣ 2iB .0C .D . 2i2.已知集合 A = {1,3, } ,B ={1,m},A ∪B =A ,则 m =( )A . 0 或B . 0或3C .1或 D . 1或 3.已知 tan α=﹣α< π,则<sin α=()A .B .﹣ ﹣C .﹣﹣D .4.如图,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,31.复数 = )末折抵地,去本1 丈= 10 尺),虫伤有病,x )f′的图象如图所示,若两个正数a,b 满足的取值范围是(C . B .D .(﹣∞, 3) 8.一个空间几何体的正视图是长为 4,宽为 的长方形, 侧视图是边长为 2 的等边三角形, 俯视图如图所示,则该几何体的体积为( A . B .4 C.D .29.△ ABC 的内角 A , B , C 的对边分别为 a ,b , c ,若( 2a ﹣b ) cosC = ccosB ,则内角 C=( ) A .B .C .D .10.正三棱锥底面边长为 3,侧棱与底面成 60° 角,则正三棱锥的外接球的体积为( A . 4π B .16π D .C .==1 的右顶点为 11.设双曲线 C : A , 右焦点为 F ,过点 F 作平行 C 的一条渐近 线的直线与 C 交于点 B ,则△ AFB 的面积为 A .15 B . C . D .12.已知函数 f x )= x+e x ﹣a ,g (x )= ln (x+2)﹣ 4e a x,其中 e 为自然对数的底数,若 存在实数 x 0, 使 f (x 0)﹣ g (x 0)= 3 成立,则实数 a 的值为( A .﹣ ln2﹣1 B .﹣ 1+ln 2 C .﹣ ln 2 D .ln2二、填空题:共4 小题,每小题5 分,共 20 分.13.已知向量 满足( +2 )? ( ﹣ )=﹣ 6,且 | |=1,| |=2,则 cos <,>14.函数 f (x)=cosx﹣在[0,+∞)的零点个数为.15.已知函数f(x)=alnx ﹣bx2图象上一点(2,f(2))处的切线方程为y=﹣3x+2ln 2+2 ,则a+b =.16.设 F 为抛物线C:y2=4x的焦点,A,B,D为C上互相不重合的三点,且| |、| |、| |成等差数列,若线段AD 的垂直平分线与x 轴交于E(3,0),则 B 的坐标为.三、解答题:共70 分.解答应写出文字说明、证明过程或演算步骤.第17~21 题为必考题,每个试题考生都必须作答.第22、23 题为选考题,考生根据要求作答.(一)必考题:共60 分17.等差数列{a n}中,a1=1,a6=2a3.(1)求{a n}的通项公式;(2)设b n=2 ,记S n为数列{b n}前n 项的和,若S m=62,求m.18.为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180 厘米的玉米为高茎玉米,否则为矮茎玉米.(1)求出易倒伏玉米茎高的中位数m;(2)根据茎叶图的数据,完成下面的列联表:抗倒伏易倒伏矮茎高茎(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1% 的前提下,认为抗倒伏与玉米矮茎有关?附:K2=,附:=,P(K 2≥K )0.050 0.010 0.0013.841 6.635 10.828=PC=PD ,E 是 PB 的中点.1)证PA ⊥平面 ABCD ;20.设点 F 1(﹣ c ,0),F 2(c ,0)分别是椭圆为椭圆 C 上任意一点,且 ? 的最小值为 0. ( 1)求椭圆 C 的方程;( 2)如图,动直线 l :y =kx+m 与椭圆 C 有且仅有一个公共点,点 M ,N 是直线 l 上的 两点,且 F 1M ⊥l ,F 2N ⊥ l ,求四边形 F 1MNF 2面积 S 的最大值.19.在四棱锥 2 的菱形,∠ BAD = 120°,P A =2,PB 2)设 F 是直线 BC 上的动点,当点 E 到平面 PAF 距离最大时,求面 PAF 与面 EAC =1( a > 1)的左、右焦点, P ﹣ ABCD 中,底面 ABCD 是边长为 所成二面角的正弦值.1)若函数 f (x )不存在单调递减区间,求实数 m 的取值范围; ,求 f ( x 1)﹣ f ( x 2)的最小值.二)选考题:共 10 分.请考生在 22、 23 题中任选一题作答,如果多做,则按所做的第 题计分. [选修 4-4:坐标系与参数方程 ]点 O 为极点, x 轴正半轴为极轴的极坐标中,圆 C 的方程为 . Ⅰ)写出直线 l 的普通方程和圆 C 的直角坐标方程;Ⅱ)若点 P 坐标为 ,圆 C 与直线 l 交于 A , B 两点,求 |PA|+|PB|的值.[ 选修 4-5:不等式选讲 ]23.设函数 f ( x )= |x ﹣ 1|+|x ﹣a|,a ∈R .(1)当 a =4 时,求不等式 f (x )≥ 5的解集; (2)若 f (x )≥4对 x ∈R 恒成立,求 a 的取值范围.2)若 y = f ( x )的两个极值点为 x 1,x 2(x 1<x 2), m ≤﹣22.在平面直角坐标系 xOy 中,直线 l 的参数方程为t 为参数).在以原参考答案、选择题:共12 小题,每小题 5 分,共60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数=()A.﹣2i B.0C.D.2i【分析】直接对复数的分母、分子同乘i,然后化简即可求出所求.解:=i+ =i ﹣i=0故选: B .2.已知集合A={1,3,} ,B={1,m},A∪B=A,则m=()A.0 或B.0 或3C.1或D.1或3【分析】由两集合的并集为 A ,得到B 为 A 的子集,转化为集合间的基本关系,再利用子集的定义,转化为元素与集合,元素与元素的关系.解:A∪B=A? B? A.∴{1,m}? {1,3,},∴ m = 3或m=,解得m=0 或m=1(与集合中元素的互异性矛盾,舍去)综上所述,m=0 或m=3.故选: B .3.已知tan α=﹣<α<π,则sinα=A.B.﹣【分析】利用同角三角函数的基本关系,求出求出sin α的值.故选: D .cos2α 和sin2α的值,再由,α=.C.解:已知,又,∴2 sin24.如图,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:有一根竹子,原高一丈( 1 丈= 10 尺),虫伤有病, 阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子三尺远,问折断处离地面的高?A .4.55 尺B . 5.45 尺C .4.2 尺D .5.8 尺【分析】由题意可得 AC+AB =10(尺), BC =3(尺),运用勾股定理和解方程可得AB ,AC ,即可得到所求值.解:如图,已知 AC+AB =10(尺), BC =3(尺), AB 2﹣AC 2=BC 2=9, 所以( AB+AC )( AB ﹣ AC )= 9,解得 AB ﹣ AC = 0.9,,解得 ,故折断后的竹干高为 4.55 尺,5.已知等式(1﹣x+x 2)3?( 1﹣2x 2)4=a 0+a 1x+a 2x 2+⋯ +a 14x 14成立,则 a 2+a 4+⋯+a 14=( ) A . 0B . 5C .7D . 14【分析】先令 x = 1, x =﹣ 1,联立可得.解:由( 1﹣x+x 2)3? (1﹣2x 2) 4=a 0+a 1x+a 2x 2+⋯+a 14x 14成立, 令 x = 1,代入得 1=a 0+a 1+a 2+⋯ +a 14,令 x =﹣ 1,代入得 27=a 0﹣a 1+a 2﹣⋯ +a 14, 相加得 28=2( a 2+a 4+⋯+a 14),因此)则a2+a4+⋯+a14=14故选: D .6.过圆x2+y2=4 外一点M(4,﹣1)引圆的两条切线,则经过两切点的直线方程是()A.4x﹣y﹣4=0 B.4x+y﹣4=0 C.4x+y+4=0 D.4x﹣y+4=0【分析】设切点是P(x1,y1)、Q(x2,y2),则以P 为切点的切线方程是:x1x+y1y=4,以Q为切点的切线方程是:x2x+y2y=4,由此能求出过两切点P、Q 的直线方程.解:设切点是P(x1,y1)、Q(x2,y2),则以P 为切点的切线方程是:x1x+y1y=4,以Q 为切点的切线方程是:x2x+y2y=4,∵点M (4,﹣1)在两条切线上,则4x1﹣y1=4,4x2﹣y2=4∴点P、Q 的坐标满足方程:4x﹣y=4∴过两切点P、Q 的直线方程是:4x﹣y﹣4=0.故选: A .7.定义在R 上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′分析】先根据导函数的图象判断原函数的单调性,从而确定解:由图可知,当x>0时,导函数f'(x)> 0,原函数单调递增∵两正数a,b 满足f(2a+b)< 1,∴0<2a+b<4,∴ b< 4﹣2a,由0<b<4﹣2a,可得0<a< 2,画出可行域如图.k=表示点Q(﹣1,﹣1)与点P(x,y)连线的斜率,x))b 满足B.D.(﹣∞,3)的取值范围是(a、b 的范围得到答案.当 P 点在 A ( 2,0)时, k 最小,最小值为:当 P 点在 B ( 0,4)时, k 最大,最大值为:取值范围是 C .故选: C .8.一个空间几何体的正视图是长为 4,宽为 的长方形, 侧视图是边长为 2 的等边三角形,俯视图如图所示,则该几何体的体积为( )A .B . 4C .D . 2【分析】 通过三视图复原的几何体的特征, 结合三视图的数据, 求出几何体的体积即可. 解:由题意可知,三视图复原的几何体是放倒的正三棱柱,如图所示:5.正三角形的边长为 2,高为 ,正三棱柱的高为 4,所以正三棱柱的体积为:,故选: B .9.△ ABC 的内角A,B, C 的对边分别为a,b,c,若(2a﹣b)cosC =ccosB ,则内角 C =()D .分析】 由已知及正弦定理, 三角函数恒等变换的应用可得 2sin AcosC = sinA ,结合 sinA ≠0,可求 cosC ,根据范围 0<C <π,可求 C 的值. 解:由正弦定理得: 2sinAcosC ﹣ sin BcosC = sinCcosB , 即 2sinA cosC = sin B cosC+sin CcosB , 即 2sin A cosC = sin ( B +C )= sinA , 由于 sin A ≠0, 故 cosC= , 又 0<C <π, 所以 C故选: C .10.正三棱锥底面边长为A .4πB .16πC .D .R ,结合球体积公式可求.解:如图所示,过 A 作 AE ⊥平面 BCD ,垂足为 E ,则 E 为三角形 BCD 的外心, 由题意可知, BE = ,因为侧棱与底面成 60°角,即∠ ABE =60°, 所以 AE = 3,Rt △OBE 中, R 2=3+(3﹣R )2, 解可得 R = 2,则正三棱锥的外接球的体积 V = = .故选: D .3,侧棱与底面成60°角,则正三棱锥的外接球的体积为(分析】由已知及线面角可求 BE ,AE ,然后结合球的性质可求线的直线与 C 交于点B,则△ AFB 的面积为()A.15B.C.D.F 作平行 C 的一条渐近【分析】根据题意,由双曲线的方程可得a、b的值,进而可得 c 的值,可以确定A、F的坐标,设BF 的方程为y=(x﹣5),代入双曲线方程解得 B 的坐标,计算可得答案.解:a2=9,b2=16,故c=5,∴ A(3,0), F (5,0),渐近线方程为y=x,不妨设BF 的方程为y=(x﹣5),代入双曲线﹣=1,解得:B(,﹣).∴ S△AFB =|AF |? |y B|=×2× =.故选: B .12.已知函数x)=x+e x﹣a,g(x)=ln(x+2)﹣4e a﹣x,其中 e 为自然对数的底数,若存在实数x0,使f(x0)﹣g(x0)=3 成立,则实数a的值为()A .﹣ln 2﹣ 1 B.﹣1+ln 2 C.﹣ln2 D.ln2【分析】令f(x)﹣g(x)=x+ e x﹣a﹣1n(x +2)+4e a ﹣x,运用导数求出y=x﹣ln(x+2)的最小值;运用基本不等式可得e x﹣a+4e a﹣x≥4,从而可证明f(x)﹣g(x)≥3,由等号成立的条件,从而解得a.解:令f(x)﹣g(x)=x+e x﹣a﹣1n(x+2)+4e a﹣x令y=x﹣ln (x+2 ),y′=1﹣故y=x﹣ln (x+2 )在(﹣2,﹣1)上是减函数,x=﹣ 1 时,y 有最小值﹣1﹣0=﹣1,而e x﹣a+4e a﹣x≥4,(当且仅当e x﹣a=4e a﹣x,即x=a+ln2 时,等号成立);故f(x)﹣g(x)≥3(当且仅当等号同时成立时,等号成立);故x =a+ln 2=﹣1,即a=﹣1﹣ln 2.故选: A .、填空题:共4小题,每小题5分,共20 分.=.=.【分析】根据题意,由数量积的计算公式可得(+2 )? (﹣)=2+ ? ﹣ 2 2 =﹣7+2cos< , >=﹣6,变形分析可得答案.解:根据题意,向量满足(+2 )? (﹣)=﹣6,且| |=1,| |=2,则有(+2 )?(﹣)=2+ ? ﹣2 2=﹣7+2cos< , >=﹣6,解可得:cos< , >=;故答案为:14.函数 f (x)=cosx﹣在[0,+∞)的零点个数为 1 .【分析】方程转化为 2 个函数的图象的交点个数,数形结合可得结论.解:函数f(x)=cosx﹣在[0,+∞)的零点的个数,即函数y=cosx 的图象(红线部分)和函数y=的图象(蓝线部分)的交点个数,如图所示:1,+∞)上是增函数,故当13.已知向量满足(+2 )?﹣)=﹣ 6 ,且| |=1,| |=2,则cos< , >显然,函数y=cosx 的图象(红线部分)和函数y=的图象(蓝线部分)在[0,+∞)的交点个数为1,故答案为:1.15.已知函数f(x)=alnx ﹣bx2图象上一点(2,f(2))处的切线方程为y=﹣3x+2ln2+2,则a+b = 3 .【分析】将(2,f(2))代入切线求出f(2),再将切点坐标代入f(x)得方程① ,再对原函数求导,进一步求出切点处导数并令其为﹣3,得方程② ,联立①② 求出a,b 即可解决问题.解:将x=2 代入切线得f(2)=2ln 2﹣4.所以2ln 2﹣4=aln 2﹣4b① ,又,∴,联立①② 解得a=2,b=1.所以a+b=3.故答案为:3.16.设 F 为抛物线C:y2=4x的焦点,A,B,D 为C上互相不重合的三点,且| |、| |、| |成等差数列,若线段AD 的垂直平分线与x 轴交于E(3,0),则 B 的坐标为(1,2)或(1,﹣2).【分析】设A,B, D 的坐标,由| |、| |、| |成等差数列可得三者的坐标之间的关系,进而可得线段AD 的中点坐标,由题意求出线段AD 的中垂线的斜率即AD 的斜率,由斜率之积为﹣ 1 可得 B 的横坐标代入抛物线的方程可得 B 的纵坐标.解:由抛物线的方程可得焦点F(1,0),准线方程为:x=﹣1设A(x1,y1), B (x 2,y2),D(x3,y3),|AF |=x 1+1,|BF | =x2 +1,|DF |=x 3+1,由| |、| |、| |成等差数列可得 2(x 2+1)= x 1+x 3+2,所以 x 2=,所以线段即 =﹣ 1,因为 x 1≠ x 3,所以可得 x 1+x 3= 2,所以 x 2= = 1,B 在抛物线上,代入抛物线的方程可得 y 22=4×1,焦点 y 2=± 2,所以 B 的坐标为:( 1,2)或( 1,﹣ 2) 故答案为:1,﹣ 2)或( 1,三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 题,每个试题考生都必须作答.第 22、23 题为选考题,考生根据要求作答. (一)必考题: 共 60 分17.等差数列 {a n }中, a 1=1,a 6=2a 3.(1)求{a n }的通项公式;(2)设 b n =2 ,记 S n 为数列 {b n }前 n 项的和,若 S m =62,求 m .【分析】本题第( 1)题先设等差数列 {a n } 的公差为 d ,然后根据等差数列的通项公式代 入 a 6=2a 3,可得关于公差 d 的方程,解出 d 的值,即可得到数列 {a n }的通项公式; 第(2) 题先根据第( 1)题的结果计算出数列 {b n }的通项公式,可发现数列 {b n }是以 2 为首项, 2 为公比的等比数列,根据等比数列的求和公式可得 S n 的表达式,代入 S m =62 进行计算可得 m 的值.解:( 1)由题意,设等差数列 { a n }的公差为 d ,则a n = 1+( n ﹣1) d ,a 6= 2a 3,因为线段 AD 的垂直平分线与 x 轴交于 E ( 3,0),所以线段 AD 的垂直平分线的斜率为17~ 21 题为必考AD 的中点的坐标所以 ?∴1+5d=2(1+2d),解得d=1,∴ a n=n,n ∈N* .(2)由(1)知,=2? 2n﹣1∴数列{b n}是以2为首项,2为公比的等比数列,由S m=62,可得2m+1﹣2=62,解得m=5.18.为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180 厘米的玉米为高茎玉米,否则为矮茎玉米.(1)求出易倒伏玉米茎高的中位数m;(2)根据茎叶图的数据,完成下面的列联表:抗倒伏易倒伏矮茎高茎(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1% 的前提下,认为抗倒伏与玉米矮茎有关?附:K2=P(K2≥K)0.050 0.010 0.0013.841 6.635 10.828分析】( 1)根据茎叶图可求易倒伏玉米茎高的中位数;2)根据茎叶图的数据,即可完成列联表:3)计算 K 的观测值 K 2,对照题目中的表格,得出统计结论.抗倒伏矮茎高茎因此可以在犯错误的概率不超过 1% 的前提下,认为抗倒伏与玉米矮茎有关.19.在四棱锥 P ﹣ABCD 中,底面 ABCD 是边长为 2 的菱形,∠ BAD =120°,PA =2,PB =PC =PD ,E 是 PB 的中点.( 1)证明: PA ⊥平面 ABCD ;( 2)设 F 是直线 BC 上的动点,当点 E 到平面 PAF 距离最大时,求面 PAF 与面 EAC 所成二面角的正弦值.【分析】 (1)先证明 BC ⊥平面 PAM ,可得 PA ⊥ BC ,同理可证 PA ⊥DC ,进而可证PA ⊥平面 ABCD ;(2)依题意,以 A 为坐标原点,直线 AF ,AB ,AP 分别为 x ,y ,z 轴建立空间直角坐 标系,求出两平面的法向量,利用向量公式即可得解. 【解答】( 1)证明:取 BC 中点 M ,连接 PM ,AM , 因为四边形 ABCD 为菱形且∠ BAD =120° 所以 AM ⊥BC ,因为 PB =PC ,所以 PM ⊥BC ,解: 1)易倒伏15 1016由于又AM ∩PM =M,所以BC⊥平面PAM ,因为PA? 平面PAM,所以PA ⊥ BC .同理可证PA⊥DC ,因为DC∩BC =C,所以PA⊥平面ABCD .(2)解:由(1)得PA⊥平面ABCD ,所以平面PAF ⊥平面ABCD ,平面PAF ∩平面ABCD =AF.所以点 B 到直线AF 的距离即为点 B 到平面PAF 的距离.过 B 作AF 的垂线段,在所有的垂线段中长度最大的为AB =2,此时AF 必过DC 的中点,因为 E 为PB 中点,所以此时,点 E 到平面PAF 的距离最大,最大值为1.以 A 为坐标原点,直线AF ,AB ,AP 分别为x,y,z 轴建立空间直角坐标系A﹣xyz.则,所以,平面PAF 的一个法向量为,设平面AEC 的法向量为,取y=1,则所以所以面PAF 与面EAC 所成二面角的正弦值为20.设点F1(﹣c,0),F2(c,0)分别是椭圆C:=1(a>1)的左、右焦点,为椭圆 C 上任意一点,且? 的最小值为0.1)求椭圆 C 的方程;2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N 是直线l上的两点,且F1M⊥l,F2N⊥ l,求四边形F1MNF 2面积S 的最大值.分析】1)利用? 的最小值为0,可得? =x2+y2﹣c2,x∈[﹣a,a],即可求椭圆 C 的方程;(2)将直线l 的方程y=kx+m 代入椭圆C的方程中,得到关于x 的一元二次方程,由直线l 与椭圆 C 仅有一个公共点知,△=0,即可得到m,k 的关系式,利用点到直线的距离公式即可得到d1=|F1M|,d2=|F2N|.当k≠ 0时,设直线l 的倾斜角为θ,则|d1﹣d2| =|MN |×|tan θ|,即可得到四边形F1MNF 2面积S的表达式,利用基本不等式的性质,结合当k=0时,四边形F1MNF 2是矩形,即可得出S的最大值.解:(1)设P(x,y),则=(x+c,y),=(x﹣c,y),∴ ? =x2+y2﹣c2=x2+1﹣c2,x∈[﹣a,a],由题意得,1﹣c2=0? c=1? a2=2,∴椭圆 C 的方程为;(2)将直线l 的方程y=kx+m 代入椭圆 C 的方程x2+2y2=2 中,得(2k2+1)x2+4kmx +2m2 ﹣2=0.由直线l与椭圆 C 仅有一个公共点知,△=16k2m2﹣4(2k2+1)(2m2﹣2)=0,化简得:m2=2k2+1 .设d1=|F1M|=,d2=|F 2N|=当k≠ 0时,设直线l 的倾斜角为θ,则|d1﹣d2|=|MN |×|tanθ|,∴|MN |=? |d1﹣d2|,∵m2=2k2+1,∴当k≠0时,|m|>1,|m|+ >2,∴S<2.当k=0 时,四边形F1MNF 2是矩形,S=2.所以四边形F1MNF 2面积S 的最大值为2.x2+mx+lnx.21 .已知函数f(x )=1)若函数f(x)不存在单调递减区间,求实数m 的取值范围;,求f(x1)﹣f(x2)2)若y=f(x )的两个极值点为x1,x2(x1<x2),m≤﹣的最小值.分析】(1)先求出导数,再利用导数性质对m 分情况讨论来求解;(2)可先对f(x1)﹣f(x2)进行变形,再将问题转化为单变量函数问题来解决.解:(1)依题意,x> 0,且 f '(x)=x+m+ =,记g(x)=x2+mx+1,① 若△=m 2﹣4≤0,即﹣2≤m≤2,则g(x)≥0恒成立,f'(x)≥0 恒成立,符合题意;② 若△=m2﹣4>0,即m> 2 或m<﹣2,当m>2时,x2+mx+1=0 有两个不等的负根,符合题意,当m<﹣ 2 时,x2+mx +1=0 有两个不等的正根,则在两根之间函数 f (x)单调递减,不符合题意.综上可得m≥﹣2.2)由题意得x1,x2 为g(x)=x2+mx+1 的两个零点,由(1)得x1+x2=﹣m,x1x2=1,则f(x1)﹣f(x2)=+mx1+ln x1﹣(+mx2+ln x 2))+m(x1﹣x2)+ln x1﹣ln x2)﹣(x1+x2)(x1﹣x2)+ln x1﹣ln x2ln=ln=ln=t,由x1<x2 且m≤﹣,知0< t<1,2φ( t )在( 0,1)上单调递减.点 O 为极点, x 轴正半轴为极轴的极坐标中,圆 C 的方程为Ⅰ)写出直线 l 的普通方程和圆 C 的直角坐标方程;Ⅱ)若点 P 坐标为 ,圆 C 与直线 l 交于 A ,B 两点,求 |PA|+|PB|的值.分析】 (Ⅰ)先利用两方程相加,消去参数 t 即可得到 l 的普通方程,再利用直角坐标 与极坐标间的关系,即利用 ρcos θ=x ,ρsin θ=y ,ρ2=x 2+y 2,进行代换即得圆 C 的直角 坐标方程.Ⅱ)把直线 l 的参数方程代入圆 C 的直角坐标方程, 利用参数的几何意义, 求 |PA|+|PB|的值.且 f ( x 1)﹣ f (x 2)= ln t ﹣ (t ﹣ ), = = φ'(t ) <0,(t ﹣ ),= ln t ﹣ m ≤﹣ ,知( x 1+x 2) 2≥ , 从而 ,即故 t+ ≥ ,结合 0<t < 1,解得 0< t ≤ ,从而 φ( t )的最小值为 φ( )= ﹣ ln 2,即 f ( x 1)﹣ f ( x 2)的最小值为 ﹣ ln 2.二)选考题:共 10 分.请考生在 22、 23 题中任选一题作答,如果多做,则按所做的第 题计分. [选修 4-4:坐标系与参数方程 ]22.在平面直角坐标系 在以原xOy 中,直线 t 为参数)又由 得 ρ2=2 ρsin θ,化为直角坐标方程为x 2+( y ﹣ )2= 5;5分 Ⅱ)把直线 l 的参数方程代入圆 C 的直角坐标方程, 得直线 l 的普通方程为 x+y ﹣3﹣ = 0解:(Ⅰ)2得( 3﹣ t )2+( t ) 2=5,即 t 2﹣ 3 t+4= 0设 t 1,t 2 是上述方程的两实数根,所以 t 1+t 2= 3又直线 l 过点 P ,A 、 B 两点对应的参数分别为 t 1, t 2,所以 |PA |+|PB| = |t 1|+|t 2|=t 1+t 2= 3 .﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣ 10 分.[ 选修 4-5:不等式选讲 ] 23.设函数 f ( x )= |x ﹣ 1|+|x ﹣a|,a ∈R .1)当 a =4 时,求不等式 f (x )≥ 5的解集;2)若 f (x )≥4对 x ∈R 恒成立,求 a 的取值范围.解得: x ≤ 0 或 x ≥ 5.故不等式 f (x )≥5 的解集为 {x|x ≤0,或 x ≥5 }. ⋯( 2)因为 f ( x )= |x ﹣1|+|x ﹣a|≥ |( x ﹣ 1)﹣( x ﹣a )|=|a ﹣ 1|.(当 x = 1 时等号成立) 所以: f (x )min =|a ﹣1|.⋯由题意得: |a ﹣ 1|≥ 4,解得 a ≤﹣ 3,或 a ≥ 5. ⋯分析】( 1 )不等式即 |x ﹣ 1|+|x ﹣ 4| ≥ 5,等价于,或 ,或 , 2)因为 f分别求出每个不等式组的解集,再取并集即得所求.x )= |x ﹣ 1|+|x ﹣ a|≥ |a ﹣ 1|,由题意可得 |a ﹣1|≥4,与偶此解得 a 的值. 解:( 1)当 a = 4时,不等式 f (x )≥ 5,即 |x ﹣1|+|x ﹣4|≥5,等价于 ,或 ,或。
2020届四川省南充高三二诊理综试卷及答案

sin i
s1 s12 h12 …………2 分
sin r
s2 s22 h22 …………2 分
根据光的折射定律可知: n sin i …………1 分 sin r
联立并代入数据得:h2=2.4 m
…………1 分
(ii)当鱼饵灯离水面深度为 h3 时,水面 PQ 间恰好无光射出,此时鱼饵灯与浮标的连线
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
南充市高中 2020 届第二次适应性考试
物理试卷参考答案及评分意见
题号
14
15
16
17
…………1 分
(3)粒子在磁场中运动的周期为: T
2 r v
2 m qB
…………2 分
所求时间为: t T m 2 qB
…………2 分
25.(20 分)【参考解答】
(1)设小球运动到最低点的速率为 v0,由机械能守恒定律得:
mgL
1 2
mv02
…………2 分
解得: v0 2gL …………1 分
小球在圆周运动最低点,由牛顿第二定律: T mg m v02 …………2 分 R
由牛顿第三定律可知,小球对细绳的拉力:T´=T 解得:T´=3mg
…………1 分 …………1 分
(2)小球碰撞后平抛运动.竖直方向: h 1 gt2 2
…………2 分
水平方向:L= v0 t 2
…………2 分
解得:h=L
四川省南充市2020届高三二诊英语试题(含答案)

四川省南充市高2020届第二次高考适应性考试英语第I卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例: How much is the shirt?A. 19.15.B. 9.18.C. 9.15.答案是C。
1. Where does the conversation probably take place?A. In a library.B. In a bookstore.C. In a classroom.2. How does the woman feel now?A. Relaxed.B. Excited.C. Tired.3. How much will the man pay?A. $20.B. $ 80.C. S 100.4. What does the man tell Jane to do?A. Postpone his appointment.B. Meet Mr. Douglas.C. Return at 3 o'clock.5. Why would David quit his job?A. To go back to school.B. To start his own firm.C. To work for his friend.第二节(共15小题;每小题1.5分,满分2.5分)听下面5段对话或独白。
每段对话话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. What does the man want the woman to do?A. Check the cupboard.B. Clean the balcony.C. Buy an umbrella.7. What is the probable relationship between the speakers?A. Husband and wife.B. Employer and employee.C. Shop assistant and customer.听第7段材料,回答第8至10题8. Where did the woman go at the weekend?A. The city center.B. The forest park.C. The man's home.9. How did the man spend his weekend?A. Packing for a move.B. Going out with Jenny.C. Looking for a new house.10. What will the woman do for the man?A. Take Henry to hospital.B. Stay with his kid.C. Look after his pet.听第8段材料,回答第11至13题。
2020年四川省南充市高考地理二诊试卷(有答案解析)

2020年四川省南充市高考地理二诊试卷一、单选题(本大题共11小题,共22.0分)1.餐饮业是城市商业的重要“引流业态”,其布局与城市居住、交通、公共服务等空间功能密切相关。
如图为我国某直辖市城市餐饮业空间分布图。
据此完成1-2题。
该城市餐饮业空间集聚特征是()A. 围绕一个核心向四周扩展B. 沿河流呈条带状延展C. 围绕多个核心向四周扩展D. 沿交通线呈条带状延展2.餐饮业是城市商业的重要“引流业态”,其布局与城市居住、交通、公共服务等空间功能密切相关。
如图为我国某直辖市城市餐饮业空间分布图。
据此完成1-2题。
推测图中甲、乙、丙、丁处餐饮业密度最高的是()A. 甲处B. 乙处C. 丙处D. 丁处3.地名作为对地表特定地域空间的指称,有的可以反映特定时期地域的自然环境特征。
如图所示区域年均降雨量320.8-432.4mm,且70%以上的降水集中在7-9月。
据此完成3-5题。
推测图示区域聚落空间分布特征为()A. 集中西南最密B. 分散东北最稀C. 集中东南最密D. 分散西北最稀4.地名作为对地表特定地域空间的指称,有的可以反映特定时期地域的自然环境特征。
如图所示区域年均降雨量320.8-432.4mm,且70%以上的降水集中在7-9月。
据此完成3-5题。
影响图示区域聚落分布的主导因素为()A. 气候B. 地貌C. 河流D. 植被5.地名作为对地表特定地域空间的指称,有的可以反映特定时期地域的自然环境特征。
如图所示区域年均降雨量320.8-432.4mm,且70%以上的降水集中在7-9月。
据此完成3-5题。
图示甲区域众多聚落以“沟”、“湾”、“井”为名,这表明该区域()A. 现代风沙活动频繁B. 历史时期气候干旱C. 现代河流湖泊众多D. 历史时期温暖湿润6.热浪通常是指持续数天甚至数周,影响范围较大的极端酷热天气,城市地区由于城市热岛效应在热浪事件中易出现更大的风险。
如图示意上海市2016-2017年7月城、郊在热浪和非热浪期间的2m气温(离地2m高度的气温)平均日变化。
2020年四川省南充市高考(文科)数学第二次诊断测试试卷 含解析

2020年高考(文科)数学二诊试卷一、选择题(共12小题)1.复数=()A.﹣2i B.0C.D.2i2.已知集合A={1,3,},B={1,m},A∪B=A,则m=()A.0或B.0或3C.1或D.1或33.3本不同的语文书,2本不同的数学书,从中任意取出2本,取出的书恰好都是数学书的概率是()A.B.C.D.4.已知tanα=﹣<α<π,则sinα=()A.B.﹣C.﹣D.5.如图,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:有一根竹子,原高一丈(1丈=10尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子三尺远,问折断处离地面的高?()A.4.55尺B.5.45尺C.4.2尺D.5.8尺6.若函数y=2sin(2x+φ)的图象过点(,1),则它的一条对称轴方程可能是()A.x=B.x=C.x=D.x=7.过圆x2+y2=4外一点M(4,﹣1)引圆的两条切线,则经过两切点的直线方程是()A.4x﹣y﹣4=0B.4x+y﹣4=0C.4x+y+4=0D.4x﹣y+4=0 8.定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a,b满足的取值范围是()A.B.C.D.(﹣∞,3)9.一个空间几何体的正视图是长为4,宽为的长方形,侧视图是边长为2的等边三角形,俯视图如图所示,则该几何体的体积为()A.B.4C.D.210.△ABC的内角A,B,C的对边分别为a,b,c,若(2a﹣b)cos C=c cos B,则内角C =()A.B.C.D.11.正三棱锥底面边长为3,侧棱与底面成60°角,则正三棱锥的外接球的体积为()A.4πB.16πC.D.12.设F1,F2分别是双曲线﹣=1的左、右焦点.若双曲线上存在点M,使∠F1MF2=60°,且|MF1|=2|MF2|,则双曲线离心率为()A.B.C.2D.二、填空题13.已知向量满足(+2)•(﹣)=﹣6,且||=1,||=2,则cos<,>=.14.一次考试后,某班全班50个人数学成绩的平均分为正数M,若把M当成一个同学的分数,与原来的50个分数一起,算出这51个分数的平均值为N,则=.15.已知函数f(x)=alnx﹣bx2图象上一点(2,f(2))处的切线方程为y=﹣3x+2ln2+2,则a+b=.16.已知F是抛物线C:y2=2px(p>0)的焦点,过F作直线与C相交于P,Q两点,且Q在第一象限,若2=,则直线PQ的斜率是.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.等差数列{a n}中,a1=1,a6=2a3.(1)求{a n}的通项公式;(2)设b n=2,记S n为数列{b n}前n项的和,若S m=62,求m.18.为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)求出易倒伏玉米茎高的中位数m;(2)根据茎叶图的数据,完成下面的列联表:抗倒伏易倒伏矮茎高茎(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?附:K2=,P(K2≥K)0.0500.0100.001K 3.841 6.63510.82819.在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠BAD=120°,PA=2,PB =PC=PD,E是PB的中点.(1)证明:PD∥平面AEC;(2)设F是线段DC上的动点,当点E到平面PAF距离最大时,求三棱锥P﹣AFE的体积.20.设点F1(﹣c,0),F2(c,0)分别是椭圆C:+=1(a>2)的左,右焦点,P 为椭圆C上任意一点,且•的最小值为3.(1)求椭圆C的方程;(2)如图,直线l:x=5与x轴交于点E,过点F2且斜率k≠0的直线l1与椭圆交于A,B两点,M为线段EF2的中点,直线AM交直线l于点N,证明:直线BN⊥l.21.已知两数f(x)=lnx+kx.(1)当k=﹣1时,求函数f(x)的极值点;(2)当k=0时,若f(x)+﹣a≥0(a,b∈R)恒成立,求e a﹣1﹣b+1的最大值.(二)选考题共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在平面直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标中,圆C的方程为.(Ⅰ)写出直线l的普通方程和圆C的直角坐标方程;(Ⅱ)若点P坐标为,圆C与直线l交于A,B两点,求|PA|+|PB|的值.[选修4-5:不等式选讲]23.设函数f(x)=|x﹣1|+|x﹣a|,a∈R.(1)当a=4时,求不等式f(x)≥5的解集;(2)若f(x)≥4对x∈R恒成立,求a的取值范围.参考答案一、选择题(共12小题)1.复数=()A.﹣2i B.0C.D.2i【分析】直接对复数的分母、分子同乘i,然后化简即可求出所求.解:=i+=i﹣i=0故选:B.2.已知集合A={1,3,},B={1,m},A∪B=A,则m=()A.0或B.0或3C.1或D.1或3【分析】由两集合的并集为A,得到B为A的子集,转化为集合间的基本关系,再利用子集的定义,转化为元素与集合,元素与元素的关系.解:A∪B=A⇔B⊆A.∴{1,m}⊆{1,3,},∴m=3或m=,解得m=0或m=1(与集合中元素的互异性矛盾,舍去).综上所述,m=0或m=3.故选:B.3.3本不同的语文书,2本不同的数学书,从中任意取出2本,取出的书恰好都是数学书的概率是()A.B.C.D.【分析】求出总的事件个数,再求出符合题意的事件,求出概率.解:从中任意取出2本共有10种,取出的书恰好都是数学书有1种,从中任意取出2本,取出的书恰好都是数学书的概率为,故选:D.4.已知tanα=﹣<α<π,则sinα=()A.B.﹣C.﹣D.【分析】利用同角三角函数的基本关系,求出cos2α和sin2α的值,再由,求出sinα的值.解:已知,∴cos2α==,∴sin2α=.又,∴sinα=,故选:D.5.如图,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:有一根竹子,原高一丈(1丈=10尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子三尺远,问折断处离地面的高?()A.4.55尺B.5.45尺C.4.2尺D.5.8尺【分析】由题意可得AC+AB=10(尺),BC=3(尺),运用勾股定理和解方程可得AB,AC,即可得到所求值.解:如图,已知AC+AB=10(尺),BC=3(尺),AB2﹣AC2=BC2=9,所以(AB+AC)(AB﹣AC)=9,解得AB﹣AC=0.9,因此,解得,故折断后的竹干高为4.55尺,故选:A.6.若函数y=2sin(2x+φ)的图象过点(,1),则它的一条对称轴方程可能是()A.x=B.x=C.x=D.x=【分析】由于函数过点(,1),代入函数得φ=2kπ+或2kπ+,又可知对称轴方程为x=+﹣φ,将φ代入对称轴方程,对k,k'赋值即可得出答案.解:∵函数y=2sin(2x+φ)的图象过点(,1),∴1=2sin(2×+φ),∴φ=2kπ+或2kπ+(k∈z)①.又∵对称轴方程为:2x+φ=k'π+,∴x=+﹣φ(k'∈z)②.将①代入②得x=﹣kπ+(,k'∈z,k∈z).当k'=0,k=0时,x=.故选:B.7.过圆x2+y2=4外一点M(4,﹣1)引圆的两条切线,则经过两切点的直线方程是()A.4x﹣y﹣4=0B.4x+y﹣4=0C.4x+y+4=0D.4x﹣y+4=0【分析】设切点是P(x1,y1)、Q(x2,y2),则以P为切点的切线方程是:x1x+y1y=4,以Q为切点的切线方程是:x2x+y2y=4,由此能求出过两切点P、Q的直线方程.解:设切点是P(x1,y1)、Q(x2,y2),则以P为切点的切线方程是:x1x+y1y=4,以Q为切点的切线方程是:x2x+y2y=4,∵点M(4,﹣1)在两条切线上,则4x1﹣y1=4,4x2﹣y2=4∴点P、Q的坐标满足方程:4x﹣y=4∴过两切点P、Q的直线方程是:4x﹣y﹣4=0.故选:A.8.定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a,b满足的取值范围是()A.B.C.D.(﹣∞,3)【分析】先根据导函数的图象判断原函数的单调性,从而确定a、b的范围得到答案.解:由图可知,当x>0时,导函数f'(x)>0,原函数单调递增∵两正数a,b满足f(2a+b)<1,∴0<2a+b<4,∴b<4﹣2a,由0<b<4﹣2a,可得0<a<2,画出可行域如图.k=表示点Q(﹣1,﹣1)与点P(x,y)连线的斜率,当P点在A(2,0)时,k最小,最小值为:;当P点在B(0,4)时,k最大,最大值为:5.取值范围是C.故选:C.9.一个空间几何体的正视图是长为4,宽为的长方形,侧视图是边长为2的等边三角形,俯视图如图所示,则该几何体的体积为()A.B.4C.D.2【分析】通过三视图复原的几何体的特征,结合三视图的数据,求出几何体的体积即可.解:由题意可知,三视图复原的几何体是放倒的正三棱柱,如图所示:,正三角形的边长为2,高为,正三棱柱的高为4,所以正三棱柱的体积为:,故选:B.10.△ABC的内角A,B,C的对边分别为a,b,c,若(2a﹣b)cos C=c cos B,则内角C =()A.B.C.D.【分析】由已知及正弦定理,三角函数恒等变换的应用可得2sin A cos C=sin A,结合sin A ≠0,可求cos C,根据范围0<C<π,可求C的值.解:由正弦定理得:2sin A cos C﹣sin B cos C=sin C cos B,即2sin A cos C=sin B cos C+sin C cos B,即2sin A cos C=sin(B+C)=sin A,由于sin A≠0,故cos C=,又0<C<π,所以C=.故选:C.11.正三棱锥底面边长为3,侧棱与底面成60°角,则正三棱锥的外接球的体积为()A.4πB.16πC.D.【分析】由已知及线面角可求BE,AE,然后结合球的性质可求R,结合球体积公式可求.解:如图所示,过A作AE⊥平面BCD,垂足为E,则E为三角形BCD的外心,由题意可知,BE=,因为侧棱与底面成60°角,即∠ABE=60°,所以AE=3,Rt△OBE中,R2=3+(3﹣R)2,解可得R=2,则正三棱锥的外接球的体积V==.故选:D.12.设F1,F2分别是双曲线﹣=1的左、右焦点.若双曲线上存在点M,使∠F1MF2=60°,且|MF1|=2|MF2|,则双曲线离心率为()A.B.C.2D.【分析】由双曲线的定义知|MF1|=4a,|MF2|=2a,由余弦定理得c=,由此能求出双曲线的离心率.解:∵点M在双曲线﹣=1上,且|MF1|=2|MF2|,∴由双曲线的定义知|MF1|=4a,|MF2|=2a,又∵∠F1MF2=60°,∴在△MF1F2中,由余弦定理得16a2+4a2﹣2•4a•2a•cos60°=4c2,解得c=,∴e==.故选:B.二、填空题:共4小题,每小题5分,共20分.13.已知向量满足(+2)•(﹣)=﹣6,且||=1,||=2,则cos<,>=.【分析】根据题意,由数量积的计算公式可得(+2)•(﹣)=2+•﹣22=﹣7+2cos<,>=﹣6,变形分析可得答案.解:根据题意,向量满足(+2)•(﹣)=﹣6,且||=1,||=2,则有(+2)•(﹣)=2+•﹣22=﹣7+2cos<,>=﹣6,解可得:cos<,>=;故答案为:14.一次考试后,某班全班50个人数学成绩的平均分为正数M,若把M当成一个同学的分数,与原来的50个分数一起,算出这51个分数的平均值为N,则=1.【分析】全班50个人的平均分为M,把M当成一个同学的分数,则班中有51人,计算这51人的平均值N,求出的值即可.解:全班50个人数学成绩的平均分为正数M,把M当成一个同学的分数,则班中有51名同学,总成绩为51M,这51人的平均分为N==M,所以=1.故答案为:1.15.已知函数f(x)=alnx﹣bx2图象上一点(2,f(2))处的切线方程为y=﹣3x+2ln2+2,则a+b=3.【分析】将(2,f(2))代入切线求出f(2),再将切点坐标代入f(x)得方程①,再对原函数求导,进一步求出切点处导数并令其为﹣3,得方程②,联立①②求出a,b 即可解决问题.解:将x=2代入切线得f(2)=2ln2﹣4.所以2ln2﹣4=aln2﹣4b①,又,∴,联立①②解得a=2,b=1.所以a+b=3.故答案为:3.16.已知F是抛物线C:y2=2px(p>0)的焦点,过F作直线与C相交于P,Q两点,且Q在第一象限,若2=,则直线PQ的斜率是.【分析】过点P,Q分别作抛物线的准线l:x=﹣的垂线,垂足分别是P1、Q1,由抛物线的|Q1Q|=|QF|定义可知,|P1P|=|FP|,设|QF|=k(k>0),则|FP|=2k,在直角△PRQ中求解直线PQ的倾斜角即可求得直线PQ斜率.解:过点P,Q分别作抛物线的准线l:x=﹣1的垂线,垂足分别是P1、Q1,由抛物线的定义可知,|Q1Q|=|QF|,|P1P|=|FP|,设|PF|=k(k>0),2=,则|FQ|=2k,|PQ|=3k,又过点Q作QR⊥P1P于点R,则在直角△PRQ中,|RR|=k,|PQ|=3k,|QR|=2k,由∠PQR与直线QP的倾斜角相等,则直线PQ的斜率k=tan∠QPR=2,∴直线PQ的斜率是2,故答案为:2.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.等差数列{a n}中,a1=1,a6=2a3.(1)求{a n}的通项公式;(2)设b n=2,记S n为数列{b n}前n项的和,若S m=62,求m.【分析】本题第(1)题先设等差数列{a n}的公差为d,然后根据等差数列的通项公式代入a6=2a3,可得关于公差d的方程,解出d的值,即可得到数列{a n}的通项公式;第(2)题先根据第(1)题的结果计算出数列{b n}的通项公式,可发现数列{b n}是以2为首项,2为公比的等比数列,根据等比数列的求和公式可得S n的表达式,代入S m=62进行计算可得m的值.解:(1)由题意,设等差数列{a n}的公差为d,则a n=1+(n﹣1)d,∵a6=2a3,∴1+5d=2(1+2d),解得d=1,∴a n=n,n∈N*.(2)由(1)知,=2•2n﹣1,∴数列{b n}是以2为首项,2为公比的等比数列,∴,由S m=62,可得2m+1﹣2=62,解得m=5.18.为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)求出易倒伏玉米茎高的中位数m;(2)根据茎叶图的数据,完成下面的列联表:抗倒伏易倒伏矮茎高茎(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?附:K2=,P(K2≥K)0.0500.0100.001K 3.841 6.63510.828【分析】(1)根据茎叶图可求易倒伏玉米茎高的中位数;(2)根据茎叶图的数据,即可完成列联表:(3)计算K的观测值K2,对照题目中的表格,得出统计结论.解:(1);(2)抗倒伏易倒伏矮茎154高茎1016(3)由于,因此可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关.19.在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠BAD=120°,PA=2,PB =PC=PD,E是PB的中点.(1)证明:PD∥平面AEC;(2)设F是线段DC上的动点,当点E到平面PAF距离最大时,求三棱锥P﹣AFE的体积.【分析】(1)连接DB与AC交于O,连接OE,由三角形中位线定理证明PD∥OE,再由线面平行的判定可得PD∥平面AEC;(2)取BC中点M,连接AM,PM,证明PA⊥平面ABCD,则平面PAF⊥平面ABCD,又平面PAF∩平面ABCD=AF,可得点B到直线AF的距离即为点B到平面PAF的距离,过B作直线AF的垂线段,在所有垂线段中长度最大为AB=2,由此可得点E到平面PAF的最大距离为1,求得AF,则三棱锥P﹣AFE的体积可求.【解答】(1)证明:连接DB与AC交于O,连接OE,∵ABCD是菱形,∴O为DB的中点,又∵E为PB的中点,∴PD∥OE,∵PD⊄平面AEC,OE⊂平面AEC,∴PD∥平面AEC;(2)解:取BC中点M,连接AM,PM,∵四边形ABCD是菱形,∠BAD=120°,且PC=PB,∴BC⊥AM,BC⊥PM,又AM∩PM=M,∴BC⊥平面APM,又AP⊂平面APM,∴C⊥PA.同理可证:DC⊥PA,又BC∩DC=C,∴PA⊥平面ABCD,则平面PAF⊥平面ABCD,又平面PAF∩平面ABCD=AF,∴点B到直线AF的距离即为点B到平面PAF的距离,过B作直线AF的垂线段,在所有垂线段中长度最大为AB=2,∵E为PB的中点,故点E到平面PAF的最大距离为1,此时,F为DC的中点,即,∴,∴.20.设点F1(﹣c,0),F2(c,0)分别是椭圆C:+=1(a>2)的左,右焦点,P 为椭圆C上任意一点,且•的最小值为3.(1)求椭圆C的方程;(2)如图,直线l:x=5与x轴交于点E,过点F2且斜率k≠0的直线l1与椭圆交于A,B两点,M为线段EF2的中点,直线AM交直线l于点N,证明:直线BN⊥l.【分析】(1)设P(x,y),求出的表达式,利用最小值,转化求解即可.(2)设直线l1的方程为y=k(x﹣1),k≠0,联立,得(4+5k2)x2﹣10k2x+5k2﹣20=0.设A(x1,y1),B(x2,y2),通过韦达定理,设N(5,y0),因结合A,M,N三点共线,解得.计算y0﹣y2=0,即可说明直线BN∥x轴,即BN⊥l.解:(1)设P(x,y),则=(c﹣x,﹣y),所以=x2+y2﹣c2=,因为a>2,x∈[﹣a,a].所以当x=0时,值最小,所以4﹣c2=3,解得c=1,(舍负)所以a2=5,所以椭圆C的方程为,(2)设直线l1的方程为y=k(x﹣1),k≠0,联立,得(4+5k2)x2﹣10k2x+5k2﹣20=0.设A(x1,y1),B(x2,y2),则,设N(5,y0),因为A,M,N三点共线,又M(3,0)所以,解得.而y0﹣y2====所以直线BN∥x轴,即BN⊥l.21.已知两数f(x)=lnx+kx.(1)当k=﹣1时,求函数f(x)的极值点;(2)当k=0时,若f(x)+﹣a≥0(a,b∈R)恒成立,求e a﹣1﹣b+1的最大值.【分析】(1)把k=﹣1代入后对函数求导,然后结合导数与单调性及极值关系即可求解;(2)由已知不等式恒成立,分离参数a可得恒成立,构造函数,转化为求解相应函数的范围,结合导数可求.解:(1)f'(x)定义域为(0,+∞),当k=﹣1时,,令f'(x)=0得x=1,所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)有唯一的极大值点x=1,无极小值点.(2)当k=0时,.若恒成立,则恒成立,所以恒成立,令,则,由题意b>0,函数在(0,b)上单调递减,在(b,+∞)上单调递增,所以a≤lnb+1,所以a﹣1≤lnb所以e a﹣1≤b,所以e a﹣1﹣b+1≤1,故e a﹣1﹣b+1的最大值为1.(二)选考题共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在平面直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴正半轴为极轴的极坐标中,圆C的方程为.(Ⅰ)写出直线l的普通方程和圆C的直角坐标方程;(Ⅱ)若点P坐标为,圆C与直线l交于A,B两点,求|PA|+|PB|的值.【分析】(Ⅰ)先利用两方程相加,消去参数t即可得到l的普通方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得圆C的直角坐标方程.(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,利用参数的几何意义,求|PA|+|PB|的值.解:(Ⅰ)由得直线l的普通方程为x+y﹣3﹣=0﹣﹣﹣﹣﹣﹣﹣﹣2分又由得ρ2=2ρsinθ,化为直角坐标方程为x2+(y﹣)2=5;﹣﹣﹣﹣﹣﹣﹣﹣﹣5分(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,得(3﹣t)2+(t)2=5,即t2﹣3t+4=0设t1,t2是上述方程的两实数根,所以t1+t2=3又直线l过点P,A、B两点对应的参数分别为t1,t2,所以|PA|+|PB|=|t1|+|t2|=t1+t2=3.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣10分.[选修4-5:不等式选讲]23.设函数f(x)=|x﹣1|+|x﹣a|,a∈R.(1)当a=4时,求不等式f(x)≥5的解集;(2)若f(x)≥4对x∈R恒成立,求a的取值范围.【分析】(1)不等式即|x﹣1|+|x﹣4|≥5,等价于,或,或,分别求出每个不等式组的解集,再取并集即得所求.(2)因为f(x)=|x﹣1|+|x﹣a|≥|a﹣1|,由题意可得|a﹣1|≥4,与偶此解得a的值.解:(1)当a=4时,不等式f(x)≥5,即|x﹣1|+|x﹣4|≥5,等价于,或,或,解得:x≤0或x≥5.故不等式f(x)≥5的解集为{x|x≤0,或x≥5 }.…(2)因为f(x)=|x﹣1|+|x﹣a|≥|(x﹣1)﹣(x﹣a)|=|a﹣1|.(当x=1时等号成立)所以:f(x)min=|a﹣1|.…由题意得:|a﹣1|≥4,解得a≤﹣3,或a≥5.。
2020年四川省南充市高考生物二诊试卷 (含答案解析)

2020年四川省南充市高考生物二诊试卷一、单选题(本大题共6小题,共6.0分)1.下列有关化合物的叙述,正确的是()A. 构成蛋白质、核酸、淀粉等生物大分子的单体在排列顺序上具有多样性B. 淀粉、纤维素和糖原经彻底水解后,都能为细胞的生命活动提供能量C. 胆固醇是动植物细胞膜的重要成分,在人体内参与肠道中钙、磷的吸收D. 摄入人体的N元素可用于构成脂肪2.下列有关细胞器的叙述中正确的是A. 光合作用一定在叶绿体中进行B. 线粒体是有氧呼吸的场所C. 叶绿体是绿色植物进行光合作用的场所,含有DNA、RNA、蛋白质和磷脂等成分D. 脂质的合成是在高尔基体中完成3.下列有关免疫系统组成的叙述,正确的是()A. 免疫系统包括免疫器官、免疫细胞B. 免疫器官是免疫细胞生成、成熟或集中分布的场所C. 免疫细胞只包括T细胞和B细胞,分别在胸腺和骨髓中成熟D. 免疫活性物质是由免疫细胞产生的发挥作用的物质4.在探索外星空间是否存在生命的过程中,科学家始终把寻找水作为最关键的一环.这是因为水在生命中的意义是()A. 水在生物体内可以流动B. 生化反应必须在水中进行C. 水是细胞内含量最多的化合物D. 水具有缓和温度变化的作用5.下列相关实验中涉及“分离”的叙述,错误的是()A. 在“观察DNA和RNA在细胞中的分布”的实验中,盐酸能够使染色质中的蛋白质与DNA分离B. 在“绿叶中色素的提取和分离”的实验中,色素分离是因它们在层析液中的溶解度不同C. 在“探究植物细胞的吸水和失水”的实验中,滴加蔗糖溶液的目的是使细胞质与细胞壁分离D. 在“观察根尖分生组织细胞有丝分裂”的实验中,解离的目的是使组织细胞相互分离开6.下图为某单基因遗传病的系谱图,有关判断正确的是()A. 该遗传病为隐性性状B. 致病基因位于X染色体上C. Ⅱ3和Ⅱ4的基因型相同D. Ⅱ3和Ⅱ4的基因型不同二、识图作答题(本大题共1小题,共5.0分)7.利用基因编辑技术将病毒外壳蛋白基因导入猪细胞中,然后通过核移植技术培育基因编辑猪,可用于生产基因工程疫苗。
2020年四川省南充市高考化学二诊试卷 (含解析)

2020年四川省南充市高考化学二诊试卷一、单选题(本大题共7小题,共39.0分)1.生活中的很多问题都涉及了化学知识。
下列过程不涉及化学变化的是()A. 用食醋或醋精除去暖瓶内胆上的水垢B. 用四氯化碳擦去圆珠笔油渍C. 用糯米饭、酒曲等自制甜酒酿D. 用福尔马林浸制动物标本2.2010年“绿色”世博会上采用了“玉米塑料”替代传统塑料制成了一次性饭盒,并制成了世博会胸卡、证件等。
它是用“玉米”经生物发酵生产的乳酸为原料,通过直接缩聚技术或开环聚合技术制备而成的一种低成本、可自然降解的聚乳酸生物材料。
既解决了传统从石油中炼化出的塑料带来的“白色污染”问题,又节省了不可再生的石油资源。
这种“玉米塑料”属于()A. 金属材料B. 生物材料C. 无机材料D. 天然材料3.原子的核电荷数小于18个某元素X,其原子的电子层数为n,最外层电子数为2n+1,原子核内质子数为2n2−1.下列有关X的说法中不正确的是()A. X能形成化学式为X(OH)3的碱B. X能与某些金属元素形成的化合物C. X原子的最外层电子数和核电荷数肯定为奇数D. X可能形成化学式为KXO3的盐4.下列表达式中,属于水解反应的是()A. CO32−+H2O⇌HCO3−+OH−B. CO2+H2O⇌H2CO3C. HCO3−+OH−⇌CO32−+H2OD. H2O+H2O⇌H3O++OH−5.设N A为阿伏加德罗常数的值,下列说法正确的是()A. 密闭容器中2molSO2和1molO2催化反应后分子数为2N AB. 标准状况下,5.6LCO2气体中含有的氧原子数目为0.5N AC. 1mol重水与1mol水中中子数比为2:1D. 标准状况下,2.24LN2和O2的混合气体中分子数为0.2N A6.用如图所示装置和相应试剂能达到实验目的是()选项实验目的试剂a试剂b试剂c装置A验证非金属性:S>C>Si稀硫酸Na2CO3Na2SiO3溶液B制备纯净的NO浓硝酸Cu水C检验溶液X中含有CO32−盐酸溶液X澄清石灰水D除去Na2SO3中的Na2SO4氯水混合物NaOH溶液A. AB. BC. CD. D7.微生物脱盐电池是一种高效、经济的能源装置,利用微生物处理有机废水获得电能,同时可实现海水淡化。
2020南充二诊试题及答案
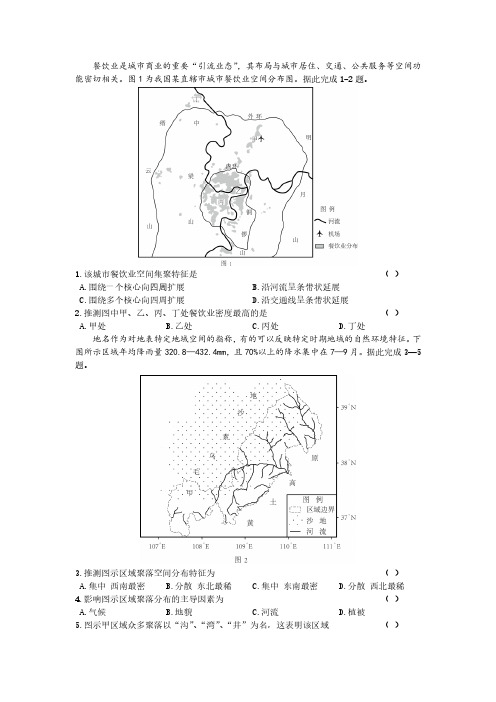
餐饮业是城市商业的重要“引流业态”,其布局与城市居住、交通、公共服务等空间功能密切相关。
图1为我国某直辖市城市餐饮业空间分布图。
据此完成1-2题。
1.该城市餐饮业空间集聚特征是()A.围绕一个核心向四周扩展B.沿河流呈条带状延展C.围绕多个核心向四周扩展D.沿交通线呈条带状延展2.推测图中甲、乙、丙、丁处餐饮业密度最高的是()A.甲处B.乙处C.丙处D.丁处地名作为对地表特定地域空间的指称,有的可以反映特定时期地域的自然环境特征。
下图所示区域年均降雨量320.8—432.4mm,且70%以上的降水集中在7—9月。
据此完成3—5题。
3.推测图示区域聚落空间分布特征为()A.集中西南最密B.分散东北最稀C.集中东南最密D.分散西北最稀4.影响图示区域聚落分布的主导因素为()A.气候B.地貌C.河流D.植被5.图示甲区域众多聚落以“沟”、“湾”、“井”为名,这表明该区域()A.现代风沙活动频繁B.历史时期气候干旱C.现代河流湖泊众多D.历史时期温暖湿润热浪通常是指持续数天甚至数周,影响范围较大的极端酷热天气,城市地区由于城市热岛效应在热浪事件中易出现更大的风险。
图3示意上海市2016-2017年7月城、郊在热浪和非热浪期间的2m气温(离地2m高度的气温)平均日变化。
据此完成6-8题。
6.表示该月非热浪期间上海市郊区2m气温的是()A.①B.②C.③D.④7.热浪期间,下列城市中与上海热岛效应强度昼夜变化一致最接近的是()A.乌鲁木齐B.雅典C.伦敦D.北京8.热浪期间,上海()A.城市风增强,海陆风减弱B.城市风增强,海陆风增强C.城市风减弱,海陆风增强D.城市风减弱,海陆风减弱勘察加半岛是世界著名的火山区。
某科考队8月考察勘察加半岛中东部三座活火山(见下图4)。
图示区域火山泥石流频发,其中最大的几次火山泥石流都是由舍维留奇火山爆发导致。
图5示意舍维留奇火山剖面。
据此完成9-11题。
9.影响图示区域火山泥石流形成的主导因素是()A.水源B.坡度C.物源D.植被覆盖度10.与我国西南山区的暴雨泥石流相比,图示区域火山喷发引起的泥石流()①气体较多②碎屑物颗粒较大③温度较高④运动速度慢A.①③B.①④C.②③D.②④11.舍维留奇火山泥石流形成后的流向最可能为()A.东北方向B.东南方向C.西北方向D.西南方向36.(22分)阅读图文材料,完成下列要求。
2023年4月四川省南充市2020级2023届初中毕业班第二次诊断性检测(南充二诊)语文答案解析

2020级初中毕业班第二次诊断性检测语文参考答案及评分意见1.(3分)C(A.劲jìnɡ怏yànɡ;B.稽qǐ戚qī;D.挈qiè禅shàn)2.(3分)D(A.暄碧;B.惘末;C.戮联)3.(3分)B(豁然:通达的样子;贯通:前后贯穿通晓。
指一下了弄通了某个道理。
首当其冲:当:承当,承受;冲:要冲,交通要道。
比喻最先受到攻击或遭到灾难。
川流不息:形容行人、车马等向水流一样连续不断。
此处用来形容降水不恰当,对象错误。
苦心孤诣:指苦心钻研,到了别人所达不到的地步。
也指为寻求解决问题的办法而煞费苦心。
)4.(3分)B(A.燕雀:代指没有宏大志向的人;C.“表”是中国古代向帝王上书陈情言事的一种特殊文体,也是封建社会下臣对皇帝有所陈述、请求、建议时用的一种文体,不属于议论性文体。
D.“雅”是宫廷乐歌,“颂”是祭祀乐歌。
)5.(3分)D(语言清新典雅,直白婉约,富有诗意之美。
)6.(3分)B(A.应为举例论证;C.应为豁达乐观地应对生活的苦难;D.原句为“爱诗之人,更容易捕捉到生活中那些稍纵即逝的美。
”)7.(3分)C(由“与岁月长河中的智者相遇;亦能视通万里,与辽远宇宙间的知己相拥。
”推论而来)8.(3分)D(应为时间顺序)9.(3分)C(A项原文为“人工智能绘画本质是计算。
人工智能绘画是一个从文本到图像的生成过程,输入一段话,生成一幅画,本质是计算。
”;B项原文为“可能是预训练大模型的兴起、大数据的训练和扩散模型的出现3方面共同作用的结果。
”;D项业界专家的推测有理有据,并非期望过高。
)10.(3分)①不能;②“几乎”表示估计、预测,并不是所有人工智能的技术发展都受益于这两方面的进展,如果删去,与事实不符;③同时“几乎”二字体现了说明文语言的准确性。
(每点1分,共3分,第②③点意思相近即可)11.(3分)①“刚……就”:指“才……就或一……就”,即第一时间发生某事,文中指作者刚到家就接到娜娜问候的微信;②说明娜娜一直在默默关注着作者,表达了娜娜对作者的在意。
2023年4月四川省南充市2020级2023届初中毕业班第二次诊断性检测(南充二诊)数学答案解析

第1页(共4页)2020级初中毕业班第二次诊断性检测数学参考答案及评分意见说明:(1)阅卷前务必认真阅读参考答案和评分意见,明确评分标准,不得随意拔高或降低标准.(2)全卷满分150分,参考答案和评分意见所给分数表示考生正确完成当前步骤时应得的累加分数.(3)参考答案和评分意见仅是解答的一种,如果考生的解答与参考答案不同,只要正确就应该参照评分意见给分.合理精简解答步骤,其简化部分不影响评分.(4)要坚持每题评阅到底.如果考生解答过程发生错误,只要不降低后继部分的难度且后继部分再无新的错误,可得不超过后继部分应得分数的一半,如果发生第二次错误,后面部分不予得分;若是相对独立的得分点,其中一处错误不影响其它得分点的评分.一、1.A ;2.C ;3.C ;4.B ;5.D ;6.D ;7.A ;8.C ;9.C ;10.B .7.解析:用枚举法.组成的两位数有23,24,25,32,34,35,42,43,45,52,53,54,共12个.是3的倍数的有24,42,45,54,共4个.∴概率P =412=13.8.解析:连接BC ,OC .则CE ⊥OC ,∠D =∠ABC =∠OCB .∴2∠ABC +∠BOC =180°,∠BOC +∠E =90°.∴2∠D -∠E =90°.9.解析:Δ=(a +1)2-4a =(a -1)2≥0.10.解析:(1)∵DE ︰CE ︰CD =3︰4︰5,∴∠CED =90°.∴△ADE ∽△BEC .∴选项A 正确.(2)设DE =3k ,则CE =4k ,CD =5k .设AD =3a ,AE =3b ,则BE =4a ,BC =4b .∴a 2+b 2=k 2.若CD 与⊙O 相离,则OH >OA ,OH >OB .∴AD >DH ,BC >CH .∴AD +BC >CD .∴3a +4b >5k .∴9a 2+16b 2+24ab >25k 2.∴9a 2+16b 2+24ab >25a 2+25b 2.∴16a 2+9b 2-24ab <0.即(4a -3b )2<0.∴CD 与⊙O 不可能相离.∴选项B 错误.(3)⊙O 为定圆.由(2),⊙O 与CD 只可能相交或相切.相切时OH 更大.作EF ⊥CD 于F .OH ≤EF .∴当点E 与点O 重合时,OH 取到最大值.OH 最大为半径,即52.∴选项C 正确.(4)由5k ·OH =3k ·4k =2S ,得OH =125k .由125k =52,得k =2524.∴CD =5k =12524.∴选项D正确.。
2023年4月四川省南充市2020级2023届初中毕业班第二次诊断性检测(南充二诊)化学参考答案

2020级初中毕业班第二次诊断性检测化学参考答案及评分意见一、选择题:每小题3分,共36分。
1.B2.A 3.C 4.D 5.D 6.A 7.C 8.B 9.C 10.B 11.C 12.B二、生活现象解释:本大题共4个小题,每空2分,共30分。
13.(1)H +(2)354O N NH +14.(1)肥皂水(2)CH 4+2O 2点燃====CO 2+2H 2O ;隔离可燃物(或将可燃物与火源隔离,合理即可)(3)B (4)2NaCl+2H 2O 通电====2NaOH+H 2↑+Cl 2↑15.(1)丙<乙<甲(2)75g (3)乙>甲=丙(或乙>丙=甲)(4)CD 16.(1)延展性;CO 2;Ca(OH)2+K 2CO 3=CaCO 3↓+2KOH(2)AgNO 3和Cu(NO 3)2三、科普材料阅读:本大题共1个小题,每空2分,共10分。
17.(1)汽油田、咸水层(每个1分,共2分)(2)物理变化(3)2NaOH+CO 2=Na 2CO 3+H 2O (4)BD (5)在所研究的压力范围内,不同的煤在相同条件下对CO 2的吸附能力随压强增大而增大(或在所研究的压力范围内,在相同压强时,无烟煤对CO 2的吸附能力最强)四、实验探究:本大题共2个小题,每空2分,共14分。
18.(1)锥形瓶(2)A (3)g→f→e19.(1)FeO 3+6HCl=2FeCl 3+3H 2O(2)CaCl 2和HCl ;③;④五、定量分析:本大题共2个小题,共10分。
20.(1)145(2)32:121.(1)Na 2SO 4;H 2SO 4(2)解:设消耗H 2SO 4质量为x...........................(0.5分)2NaOH+H 2SO 4=Na 2SO 4+2H 2O...........................(1分)809889×15%xx%15899880⨯=...........................(1分)x=1.47g ∴该硫酸溶液的溶质质量分数为%1003047.1⨯g g =4.9%...........................(1分)答:该硫酸溶液的溶质质量分数为4.9%。
2023年4月四川省南充市2020级2023届初中毕业班第二次诊断性检测(南充二诊)政治参考答案

2020级初中毕业班第二次诊断性检测道德与法治参考答案及评分意见一、单项选择题:(每题4分,共40分)1.D2.C3.D4.B5.B6.A7.B8.A9.C10.D二、非选择题(60分)11.(12分)(1)宗旨:为人民服务(2分)发展思想:以人民为中心(2分)(2)①衡量一个社会的文明程度,不仅要看经济发展状况,而且要看发展成果是否惠及全体人民,人民的合法权益是否得到切实保障;(4分)②人民对美好生活的向往,就是党的奋斗目标;(2分)③发展的根本目的就是增进民生福祉。
(2分)12.(11分)(1)对国家有认同、对文化有底气、对发展有信心(每点1分,共3分)(2)①开辟了中国特色社会主义道路;②形成了中国特色社会主义理论体系;③确立了中国特色社会主义制度;④发展了中国特色社会主义文化。
(每点2分;共8分)13.(9分)①我们要学习和借鉴人类文明的一切优秀成果,坚持以我为主,兼收并蓄;②积极主动地与世界各国交往,从不同文明中寻求智慧、吸取营养;③对其他文明的学习,我们不能只满足于欣赏物件的精美,更应该领略其中蕴含的人文精神。
(每点3分,共9分)14.(28分)(1)科教兴国、人才强国、创新驱动发展(每空2分,共6分)(2)①科技创新能力已经成为综合国力竞争的决定性因素;②创新是推动人类社会向前发展的重要力量;③创新已经成为世界上主要国家发展战略的重心;④创新驱动是国家命运所系;⑤创新是改革开放的生命;⑥在激烈的国际竞争中,唯创新者进,唯创新者强,唯创新者胜。
(每点2分,答对任意四点即可得8分)(3)必须坚持以马克思主义为指导,(1分)推动中华优秀传统文化创造性转化、创新性发展,(2分)继承革命文化,(1分)发展社会主义先进文化,(1分)不忘本来,(1分)吸收外来,(1分)面向未来,(1分)不断铸就中华文化新辉煌。
(共8分)(4)①要与日常生活紧密联系起来,做到落细、落小、落实;②应自觉做到勤于学习、敏于思考,注重修养、勇于实践;③明辨是非、善于选择,认真做事、踏实做人;④从身边小事做起,身体力行,积极参加社会公益活动等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
餐饮业是城市商业的重要“引流业态”,其布局与城市居住、交通、公共服务等空间功能密切相关。
图1为我国某直辖市城市餐饮业空间分布图。
据此完成1-2题。
1.该城市餐饮业空间集聚特征是()
A.围绕一个核心向四周扩展
B.沿河流呈条带状延展
C.围绕多个核心向四周扩展
D.沿交通线呈条带状延展
2.推测图中甲、乙、丙、丁处餐饮业密度最高的是()
A.甲处
B.乙处
C.丙处
D.丁处
地名作为对地表特定地域空间的指称,有的可以反映特定时期地域的自然环境特征。
下图所示区域年均降雨量320.8—432.4mm,且70%以上的降水集中在7—9月。
据此完成3—5题。
3.推测图示区域聚落空间分布特征为()
A.集中西南最密
B.分散东北最稀
C.集中东南最密
D.分散西北最稀
4.影响图示区域聚落分布的主导因素为()
A.气候
B.地貌
C.河流
D.植被
5.图示甲区域众多聚落以“沟”、“湾”、“井”为名,这表明该区域()
A.现代风沙活动频繁
B.历史时期气候干旱
C.现代河流湖泊众多
D.历史时期温暖湿润
热浪通常是指持续数天甚至数周,影响范围较大的极端酷热天气,城市地区由于城市热岛效应在热浪事件中易出现更大的风险。
图3示意上海市2016-2017年7月城、郊在热浪和非热浪期间的2m气温(离地2m高度的气温)平均日变化。
据此完成6-8题。
6.表示该月非热浪期间上海市郊区2m气温的是()
A.①
B.②
C.③
D.④
7.热浪期间,下列城市中与上海热岛效应强度昼夜变化一致最接近的是()
A.乌鲁木齐
B.雅典
C.伦敦
D.北京
8.热浪期间,上海()
A.城市风增强,海陆风减弱
B.城市风增强,海陆风增强
C.城市风减弱,海陆风增强
D.城市风减弱,海陆风减弱
勘察加半岛是世界著名的火山区。
某科考队8月考察勘察加半岛中东部三座活火山(见下图4)。
图示区域火山泥石流频发,其中最大的几次火山泥石流都是由舍维留奇火山爆发导致。
图5示意舍维留奇火山剖面。
据此完成9-11题。
9.影响图示区域火山泥石流形成的主导因素是()
A.水源
B.坡度
C.物源
D.植被覆盖度
10.与我国西南山区的暴雨泥石流相比,图示区域火山喷发引起的泥石流()
①气体较多②碎屑物颗粒较大③温度较高④运动速度慢
A.①③
B.①④
C.②③
D.②④
11.舍维留奇火山泥石流形成后的流向最可能为()
A.东北方向
B.东南方向
C.西北方向
D.西南方向
36.(22分)阅读图文材料,完成下列要求。
传统钢铁工业是大规模原料投入、高能耗、高排放的复杂流程工业,企业主要以铁矿石为原料,采取高炉炼铁—转炉炼钢工艺流程(长流程),生产规模大,往往形成全产业链的钢铁联合企业。
随着工业化和城市化的发展,1960年代以来,以废钢为主要原料的短流程钢铁企业(采用电炉炼钢技术)在发达国家首先兴起。
总部设在北卡罗来纳州夏洛特的美国N钢铁公司,采取以废钢为主要原料的电炉炼钢工艺,成为“小钢厂”的典型代表。
图6示意该公司发展历程。
(1)分析1960年代以来,短流程钢铁企业在发达国家首先兴起的条件。
(6分)
(2)推测短流程炼钢厂的布局特点,并说明理由。
(8分)
(3)在全球性钢铁过剩下,与全美其它钢铁企业相比,N公司利润最高的原因。
(8分)
37.(24分)阅读图文材料,完成下列要求。
冰川是冰冻圈的重要组成部分,冰川进退与气候变化关系密切,被视作气候变化的灵敏指示器。
冈底斯山横贯西藏自治区西南部,山体呈西北—东南走向,大致与喜马拉雅山平行,东西延伸长约1600km,东段宽于西段。
平均海拔约6000m,地势西高东低,山体陡峭,印度
洋水系与高原内流水系的重要分水岭。
图7示意2015—2016年冈底斯山不同面积等级的冰川数量和面积。
(1)描述冈底斯山2015-2016年冰川数量和面积特征。
(6分)
(2)与我国同纬度地区相比,分析冈底斯山雪线较高的原因。
(6分)
(3)推测近年来冈底斯山面积<0.1km2的冰川变化趋势,并说明理由。
(6分)
(4)据实际观测,西段冰川变化较东段慢。
依据材料及有关知识,试分析出现这种现象的原因(6分)
42.(10分)【旅游地理】
小七孔景区位于贵州省黔南布依族苗族自治州,为国家5A级风景名胜区,世界自然遗产,是贵州旅游业的新晋“网红”。
景区坐落在宽仅1公里、长12公里的狭长幽谷里,喀斯特地貌发育。
景区内地势起伏,各景点间用新能源观光车连接。
图为小七孔景区观光车站点示意图。
说明新能源观光车对促进景区旅游业健康发展的作用。
43.(10分)【环境保护】
随着我国经济的发展,农村生活污水排放量显著增加。
由于农村环保基础设施落后,解决环境问题的相关投入不足,近九成的村镇没有建设污水收集渠道和处理设施,加剧了农村环境污染的程度。
贵州喀斯特山区生态脆弱,经济水平较低,农村地区外出务工者多。
分析贵州喀斯特农村地区建立污水管网处理面临的困难。
(10分)
参考答案
36题(22分)
(1)(发达国家)工业化和城市化起步早,(汽车、机器等)进入报废期,废钢资源增加,废钢价格下降(2分);工艺流程短,生产规模较小,投资小(2分);短流程钢铁企业环境污染较轻,(政府)对环境保护意识增强(2分)。
(2)以废钢为主要原料,需靠近钢铁消费市场/靠近大城市,人口较稠密地区(2分),以电力为动力,需靠近拥有丰富廉价电力资源的地方/靠近能源成本较低地区(2分),废钢运输及产品运出,需靠近水陆交通便利的地区;生产过程较清洁,需水量大,可靠近城区、河流布局(2分)。
(前两点必答,每点2分,共4分,后两点任答一点即可得2分,只有结论无原因分析得1分)
(3)生产规模小,占地面积小,土地成本较低;(不需要投资焦炉、高炉及相应辅助设备,)固定投资少,建设周期短;原料投入、能耗低,生产效率高;生产过程绿色、清洁,环保设施投入少(或不需要环保设施投入);生产灵活,可小批量、定制化生产,市场需求量大/市场竞争力强;技术进步,工艺流程先进,产品附加值高。
(每点2分,任答4点得8分)
37题(24分)
(1)面积以介于0.1-5km2的冰川为主,(2分)数量以<0.5km2的冰川为主,(2分)以小冰川为主。
(2分)(①面积等级越高的冰川,数量越少;②面积等级<0.5km2的冰川,占绝大多数;③面积等级0.1-5km2的冰川,占冰川总面积比重最高。
)
(2)①海拔更高,高差更突出;②受喜马拉雅山的阻挡,降水较少;③山体陡峭,地形破碎(积雪容易下滑消融);④(位于我国第一阶梯上),地势高,大气稀薄,光热强,最热月0℃等温线分布较高。
(每点2分,共6分)
(3)数量增多,分布范围扩大。
(2分)理由:冈底斯山以小冰川为主(面积较小冰川数量多/基数大,分布面积广);(2分)全球气候变暖,小冰川对气候变化响应更敏感(环境温度变化对小型冰川影响更大),0.1-1km2冰川退缩强烈,面积缩小或分化为<0.1km2。
(2分)(4)西段,受喜马拉雅山的屏障作用/居于高原腹地/深居高原内部,降水较少,(2分)且山体较窄,雪线以上面积较小,(冰川积累较少)(2分);地势较高,能维持低温条件,退缩较慢;(①冈底斯山地区冰川的形成与发育受降水的影响较大;②全球变暖会对各地气温和降水产生影响,)(2分)
42题(旅游地理)
景区狭长,(采用新能源观光车接驳,)可提高景区游客承载量,减少拥堵,增加景区收入;(游客在固定站点集中上下车,)可集中配置(洗手间、餐饮点等)基础设施,减少非景点
地区的人类活动(适度开发),且新能源电动车绿色、节能、环保,易于保护景区生态环境;峡谷地形,喀斯特地貌发育,(采用新能源观光车接驳,)可减少非景点停留时间,提升(游客)旅游体验;可提高旅游活动的安全性,提升旅游质量。
43题(环境保护)
喀斯特地区地形起伏大/地表崎岖,村落和人口分布分散,不利于集中处理/污水处理成本高;道路崎岖,沟壑纵横,地形复杂,管道施工难度大;难以靠自流收集污水,(需要在低洼处设置泵站提升污水,或加大管线的埋深),污水处理成本高;污水处理费用付费意愿低,(后期)管理维护困难,难以持续/难以形成市场机制;(经济水平落后,)外出务工人员多,且村民生活习惯短时间难以改变,污水收集量小且波动大,(污水收集和处理)效率低;(每点2分,任答五点得10分)。
