chapter3 MATLAB数值运算
matlab学习3-数值计算

六、矩阵元素之间的逻辑运算
一、矩阵的构造
1、向量的构造
向量是1×N( N×1 )的特殊矩阵,称为N维向量。
是一种特殊的矩阵 (1)逐个输入法:x=[ ] 行向量:数据元素之间均用空格(或逗号)隔开; 例:x1=[2 3 sqrt(3) 5] 列向量:数据元素之间均用分号隔开 例:x2=[2;3;sqrt(3);5] 注:行向量和列向量之间的转换“ ’ ”
第二章
基本数值计算
第一节 简单的数学运算
第二节 MATLAB数值计算基础
第三节 MATLAB数值分析与多项式计算
第一节 简单的数学运算 一、常用的数学运算符 二、Matlab 语言规则 三、常用操作命令和键盘技巧 四、常量和变量 五、函数
一、常用的数学运算符
1、Matlab 的数学运算定义在复数域上。
example3
2、矩阵的基本运算: (1)标量与矩阵的数运算和数学函数对矩阵的运算等 于对矩阵的每一个元素的运算。 a=[1 2 3];b=a+100 b= 101 102 103 (2)进行矩阵加减时,参与运算的矩阵必须同维。 (3)进行矩阵乘法时, A的行数=B列数。 左乘与右乘不同:一般A*B不等于B*A 若A*B等于B*A,则称A,B对易 (4)幂运算A^n
2、对矩阵(A)的部分操作:
函数
Fliplr(A)
功能
矩阵左右翻转
函数
Tiag(A,k)
功能
取矩阵对角线 元素
Flipud(A)
Flipdim(A, m) Rot(A,k)
矩阵上下翻转
矩阵沿特定 维(m)翻转 矩阵逆时针旋 转k*90度
Tril(A,k)
Triu(A,k)
取矩阵的下三 角部分
matlab数值运算和符号运算

《深度探讨:从数值运算到符号运算的MATLAB应用》在科学计算领域中,MATLAB无疑是一个不可或缺的工具。
它被广泛应用于数学建模、数据分析、图形可视化和算法开发等领域。
在MATLAB中,数值运算和符号运算是两个核心概念,它们分别在不同的领域中发挥着重要作用。
本文将从数值运算和符号运算两个方面展开讨论,带您深入探索MATLAB的应用价值。
一、数值运算1. MATLAB中的数值数据类型在MATLAB中,常见的数值数据类型包括整数、浮点数和复数等。
它们在科学计算中有着广泛的应用,例如在矩阵运算、微分方程求解和优化算法中。
2. 数值计算函数的应用MATLAB提供了丰富的数值计算函数,包括线性代数运算、插值和拟合、统计分布和随机数生成等。
这些函数为科学计算提供了强大的支持,使得复杂的数值计算变得更加简单高效。
3. 数值方法在实际问题中的应用通过具体的案例,我们可以深入了解MATLAB在实际问题中的数值计算方法。
通过有限元分析解决结构力学问题、通过数值积分求解物理方程、通过数值微分求解工程问题等。
二、符号运算1. MATLAB中的符号计算工具MATLAB提供了符号计算工具包,可以进行符号变量的定义、代数运算、微分积分和方程求解等。
这为数学建模、符号推导和精确计算提供了强大的支持。
2. 符号计算函数的应用通过具体的例子,我们可以深入了解MATLAB中符号计算函数的应用。
利用符号计算求解微分方程、利用符号变量定义复杂的代数表达式等。
3. 符号计算在科学研究中的应用通过详细的案例,我们可以了解符号计算在科学研究中的应用。
利用符号计算推导物理模型、利用符号运算求解工程问题等。
总结与展望:通过本文的深度探讨,我们对MATLAB中的数值运算和符号运算有了全面的了解。
数值运算为我们提供了高效的数值计算工具,而符号运算则为我们提供了精确的符号计算工具。
这两者相辅相成,在不同的领域中发挥着重要的作用。
希望通过本文的阐述,读者可以更加深入地理解MATLAB中数值运算和符号运算的应用,提升科学计算的能力和水平。
matlab第3章 matlab3-数值计算

4. 矩阵的其它运算
inv —— 矩阵求逆 det —— 行列式的值 eig —— 矩阵的特征值 diag —— 对角矩阵
’ —— 矩阵转置 sqrt —— 矩阵开方
关系运算
关系符号 < <= > >= == ~= 意义 小于 小于或等于 大于 大于或等于 等于 不等于
5. 矩阵的数组运算(点运算)
d=[-1;0;2];f=pi*d f = -3.1416 0 6.2832 矩阵除的运算在线性代数中没有, 有矩阵逆的运算,在matlab中有两 种矩阵除运算
3. 矩阵乘方—— a^n,a^p,p^a
a ^ p —— a 自乘p次幂
方阵 >1的整数 的整数
如果a是矩阵,p是标量,a^p使用特征值 和特征向量自乘到p次幂;如a,p都是矩 阵,a^p则无意义。
3. 矩阵的修改
直接修改 可用↑键找到所要修改的矩阵,用←键 移动到要修改的矩阵元素上即可修改。 指令修改 可以用A(∗,∗)= ∗ 来修改。
例如 a=[1 2 0;3 0 5;7 8 9] a =1 2 0 3 0 5 7 8 9 a(3,3)=0 a =1 2 0 3 0 5 7 8 0
二、矩阵运算
1. 矩阵加、减(+,-)运算
规则: 相加、减的两矩阵必须有相同的行和 列两矩阵对应元素相加减。 允许参与运算的两矩阵之一是标量。 标量与矩阵的所有元素分别进行加 减操作。
2. 矩阵乘(∗)运算
规则: A矩阵的列数必须等于B矩阵的行数 标量可与任何矩阵相乘。 a=[1 2 3;4 5 6;7 8 0];b=[1;2;3];c=a*b c =14 32 23
矩阵元素
矩阵元素可以是任何matlab表达 式 ,可以是实数 ,也可以是复 数,复数可用特殊函数I,j 输入 a=[1 2 3;4 5 6] x=[2 pi/2;sqrt(3) 3+5i]
matlab数值计算方法

Matlab提供了多种数值计算方法,以下是其中一些常用的方法:
1. 整数计算:Matlab中的计算方式和计算器类似,可以直接输入数值然后加上运算符进行运算。
2. 小数计算:小数计算的方式和整数相似。
3. 分数计算:Matlab可以切换至分数模式,这一点较计算器等具有较大优势。
4. 赋值运算:Matlab中除了和计算器一样直接运算,还能进行赋值运算,直接将其中一个值赋值后,带入运算即可。
5. 多重赋值运算:Matlab在数值计算的时候,还支持多重赋值计算。
这样可以很方便的求解列出的问题。
以上内容仅供参考,建议查阅Matlab官方文档获取更全面和准确的信息。
matlab数值运算基础

§3.1 多项式 一、多项式的建立 1、多项式的表示 (1)一般都是按未知量的降幂排列各项之 和 f ( x ) = a x n + a x n −1 + L +
0 1
教案
a n −1 x + a n
(2)在MATLAB中,用它的系数矢量来表示多项式:
P = [ a 0 , a 1 , L , a n −1 , a n ]
rj (x − p j)
+
r j +1 (x − p j)
2
+L +
r j + m −1 (x − p j )m
在MATLAB中,利用函数residue( ),调用格式为 [r, p, k]=residue(b, a) 留数 极点 直项 分子 分母 逆函数: [b,a]=residue(r,p,k)
2、corrcoef(x,y)——求两随机变量的相关系数矩阵 2 corrcoef x y ——
2 3* 7
5 2 5 2 5 + 2 * 7 9 + 7 9 9
2
1
0
2、求多项式的根 求多项式p(x)的根的函数是roots(P),这里,P是p(x)的 教案 系数向量,该函数返回方程p(x)=0的全部根(含重根,复根)。 例、求多项式x3-27的根 》A=[1 0 0 -27]; 》r=roots(A) 在MATLAB中约定:
注意:若ai中有的为0,这个0不能省略,必须在系数矢量中。 2、创建多项式的方法 (1)系数矢量直接输入法 在命令窗口直接输入多项式的系数矢量,再利用转换函 数Poly2sym将多项式由系数矢量形式转换为符号形式。 例、》A=[1 -3 5 27 -9]; 》f=poly2sym(A)
MATLAB数值运算.pdf

第3章 MATLAB 数值运算教学提示:每当难以对一个函数进行积分或者微分以确定一些特殊的值时,可以借助计算机在数值上近似所需的结果,从而生成其他方法无法求解的问题的近似解。
这在计算机科学和数学领域,称为数值分析。
本章涉及的数值分析的主要内容有插值与多项式拟合、数值微积分、线性方程组的数值求解、微分方程的求解等,掌握这些主要内容及相应的基本算法有助于分析、理解、改进甚至构造新的数值算法。
教学要求:本章主要是让学生掌握数值分析中多项式插值和拟合、牛顿-科茨系列数值求积公式、3种迭代方法求解线性方程组、解常微分方程的欧拉法和龙格-库塔法等具体的数值算法,并要求这些数值算法能在MATLAB 中实现。
3.1 多 项 式在工程及科学分析上,多项式常被用来模拟一个物理现象的解析函数。
之所以采用多项式,是因为它很容易计算,多项式运算是数学中最基本的运算之一。
在高等数学中,多项式一般可表示为以下形式:120121()n n n n n f x a x a x a x a x a −−−=+++++…。
当x 是矩阵形式时,代表矩阵多项式,矩阵多项式是矩阵分析的一个重要组成部分,也是控制论和系统工程的一个重要工具。
3.1.1 多项式的表达和创建在MATLAB 中,多项式表示成向量的形式,它的系数是按降序排列的。
只需将按降幂次序的多项式的每个系数填入向量中,就可以在MATLAB 中建立一个多项式。
例如,多项式43231529s s s s +−−+在MATLAB 中,按下面方式组成一个向量x = [1 3 -15 -2 9]MATLAB 会将长度为n +1的向量解释成一个n 阶多项式。
因此,若多项式某些项系数为零,则必须在向量中相应位置补零。
例如多项式41s +在MATLAB 环境下表示为y = [1 0 0 0 1]3.1.2 多项式的四则运算多项式的四则运算包括多项式的加、减、乘、除运算。
下面以对两个同阶次多项式MATLAB 基础及其应用教程·66··66·32()234a x x x x =+++,32()4916b x x x x =+++做加减乘除运算为例,说明多项式的四则运算过程。
matlab 第3章 数值运算基础

HYIT
8
说明: 1.N阶方阵特征多项式系数矢量一定是n+1阶的 2.特征多项式系数矢量的第一个元素必须为1。
1 A 2 2
2 2 1 2 的特征多项式 2
1
2 2
2 2
2 ( )( 1) 3 9 5
HYIT
12
3.1.2 多项式运算
求多项式的值 求多项式的根 多项式的乘除运算 多项式的微积分 多项式的部分分式展开 多项式拟合
HYIT
13
求多项式的值
方法:函数polyval:按数组运算规则求值 函数polyvalm:按矩阵运算规则求值 格式: y=polyval(p,x) p为多项式,x可为标量/数组/矩阵 y=polyvalm(p,x) x可为标量/方阵
注:系数中的零不能省!
HYIT
4
创建多项式的方法
系数矢量直接输入法 特征多项式输入法 由根矢量创建多项式
HYIT
5
系数矢量直接输入法
适用于: 已知系数 → 表达式
方法: 函数poly2sym +系数矢量
例: 例: >> poly2sym([1 2 3 4]) >> poly2str([1 2 3 4],‘y') ans = ans = x^3+2*x^2+3*x+4 y^3 + 2 y^2 + 3 y + 4 说明: poly2str 以习惯方式显示多项式 poly2sym 双精度多项式系数转为符号多项式
HYIT
14
例: p=[1 1 1]; x=[0 1 2 3]; xm=[0 1; 2 3]; y1=polyval(p,x) y2=polyval(p,xm) ym=polyvalm(p,xm)
如何在MATLAB中进行数值计算

如何在MATLAB中进行数值计算1.基本数学操作:-加法、减法、乘法、除法:使用+、-、*、/操作符进行基本算术运算。
-幂运算:使用^或.^(点乘)操作符进行幂运算。
- 开平方/立方:可以使用sqrt(或power(函数进行开平方和立方运算。
2.矩阵操作:- 创建矩阵:可以使用矩阵构造函数如zeros(、ones(、rand(等创建矩阵。
- 矩阵运算:使用*操作符进行矩阵相乘,使用transpose(函数进行矩阵转置。
- 矩阵求逆和求解线性方程组:使用inv(函数求矩阵的逆,使用\操作符求解线性方程组。
3.数值积分和微分:- 数值积分:使用integral(函数进行数值积分。
可以指定积分函数、积分上下限和积分方法。
- 数值微分:使用diff(函数进行数值微分。
可以指定微分函数和微分变量。
4.解方程:- 一元方程:使用solve(函数可以解一元方程。
该函数会尝试找到方程的精确解。
- 非线性方程组:使用fsolve(函数可以求解非线性方程组。
需要提供初始值来开始求解过程。
-数值方法:可以使用牛顿法、二分法等数学方法来求解方程。
可以自定义函数来实现这些方法。
5.统计分析:- 统计函数:MATLAB提供了丰富的统计分析函数,如mean(、std(、var(等用于计算均值、标准差、方差等统计量。
- 直方图和密度估计:使用histogram(函数可以绘制直方图,并使用ksdensity(函数进行核密度估计。
- 假设检验:使用ttest(或anova(函数可以进行假设检验,用于比较多组数据之间的差异。
6.数值优化:- 非线性最小化:使用fminunc(函数可以进行非线性最小化。
需要提供目标函数和初始点。
- 线性规划:使用linprog(函数可以进行线性规划。
需要提供目标函数和限制条件。
- 整数规划:使用intlinprog(函数可以进行整数规划。
需要提供目标函数和整数约束。
7.拟合曲线:- 线性拟合:使用polyfit(函数进行线性拟合。
matlab的数值运算

matlab的数值运算当使用MATLAB 进行数值运算时,可以使用各种内置函数和运算符进行计算。
下面是一些常见的数值运算操作的详细说明:基本数学运算:加法:使用"+" 运算符进行两个数的相加。
例如,计算2 和3 的和:2 + 3。
减法:使用"-" 运算符进行两个数的相减。
例如,计算5 减去2 的结果:5 - 2。
乘法:使用"*" 运算符进行两个数的相乘。
例如,计算4 乘以3 的结果:4 * 3。
除法:使用"/" 运算符进行两个数的相除。
例如,计算10 除以2 的结果:10 / 2。
取余数:使用"mod" 函数或"%" 运算符计算两个数的余数。
例如,计算11 除以3 的余数:mod(11, 3) 或11 % 3。
幂运算:使用"^" 运算符进行幂运算。
例如,计算2 的3 次幂:2^3。
数学函数:MATLAB 提供了许多内置的数学函数,可以进行各种数值计算和分析操作。
这些函数包括但不限于:abs(x):返回x 的绝对值。
sin(x):返回x 的正弦值。
cos(x):返回x 的余弦值。
exp(x):返回e 的x 次幂,其中e 是自然对数的底数。
log(x):返回x 的自然对数。
sqrt(x):返回x 的平方根。
round(x):返回x 的四舍五入值。
floor(x):返回不大于x 的最大整数。
ceil(x):返回不小于x 的最小整数。
max(x, y):返回x 和y 中的较大值。
min(x, y):返回x 和y 中的较小值。
数组运算:MATLAB 中的数值计算通常涉及数组操作。
可以对向量、矩阵和多维数组执行各种运算,例如:矩阵相加:使用"+" 运算符对两个相同大小的矩阵进行元素级别的相加。
矩阵相乘:使用"" 运算符对两个矩阵进行乘法运算。
matlab的数值运算

matlab的数值运算Matlab的数值运算Matlab是一种强大的数值计算软件,它可以进行各种数值运算,包括基本的算术运算、矩阵运算、微积分、常微分方程求解、统计分析等。
在本文中,我们将介绍Matlab的数值运算功能,并且通过实例来说明如何使用Matlab进行数值计算。
基本的算术运算Matlab可以进行基本的算术运算,包括加、减、乘、除、幂等运算。
例如,我们可以使用Matlab计算以下表达式:a = 2 + 3; % 加法运算b = 5 - 2; % 减法运算c = 4 * 6; % 乘法运算d = 8 / 4; % 除法运算e = 2 ^ 3; % 幂运算在上面的代码中,我们使用了加、减、乘、除、幂等运算符来进行基本的算术运算。
在Matlab中,加、减、乘、除、幂等运算符分别为“+”、“-”、“*”、“/”、“^”。
矩阵运算Matlab是一种强大的矩阵计算软件,它可以进行各种矩阵运算,包括矩阵加、矩阵减、矩阵乘、矩阵转置、矩阵求逆等。
例如,我们可以使用Matlab计算以下矩阵运算:A = [1 2 3; 4 5 6; 7 8 9]; % 定义一个3x3的矩阵B = [2 3 4; 5 6 7; 8 9 10]; % 定义一个3x3的矩阵C = A + B; % 矩阵加法D = A - B; % 矩阵减法E = A * B; % 矩阵乘法F = A'; % 矩阵转置G = inv(A); % 矩阵求逆在上面的代码中,我们使用了矩阵加、矩阵减、矩阵乘、矩阵转置、矩阵求逆等运算符来进行矩阵运算。
在Matlab中,矩阵加、矩阵减、矩阵乘、矩阵转置、矩阵求逆等运算符分别为“+”、“-”、“*”、“'”、“inv”。
微积分Matlab可以进行微积分运算,包括求导、积分等。
例如,我们可以使用Matlab计算以下微积分运算:syms x; % 定义符号变量xf = x^2 + 2*x + 1; % 定义函数f(x)df = diff(f, x); % 求导intf = int(f, x); % 积分在上面的代码中,我们使用了符号变量x来定义函数f(x),然后使用diff函数来求导,使用int函数来积分。
数值分析--chapter3 多项式插值与样条插值

其中Ak 为待定系数。
由条件lk (xk ) = 1 可定Ak ,于是
lk=(xj)=n0=xx(k−x−k(xx−xjj−x0x)0()x(kx−−xx11))······((xxk−−xxkk−−11))((xx−k −xkx+k1+)1·)···(··x(−xkx−n)xn)
(6)
j =k
§3.2 拉格朗日(Lagrange)插值−−拉格朗日插值多项式
基函数法:由线性空间的基出发,构造满足插值条件的多项式方 法。
用基函数法求插值多项式分两步:
(1)定义n + 1个线性无关的特殊代数多项式(插值基函数), 用ϕ0(x), · · · , ϕn(x)表示;
(2)利用插值条件,确定插值基函数的线性组合表示的n次插值多
项式
p(x) = a0ϕ0(x) + a1ϕ1(x) + · · · + anϕn(x)
− −
x0 x0
y1
(8)
用L1(x)近似代替f (x)称为线性插值,公式(8)称为线性插值多项 式或一次插值多项式。
§3.2 拉格朗日(Lagrange)插值−−拉格朗日插值多项式
当n = 2时,拉格朗日插值多项式(7)为
【Matlab 参考教程】第三章 数值数组及其运算
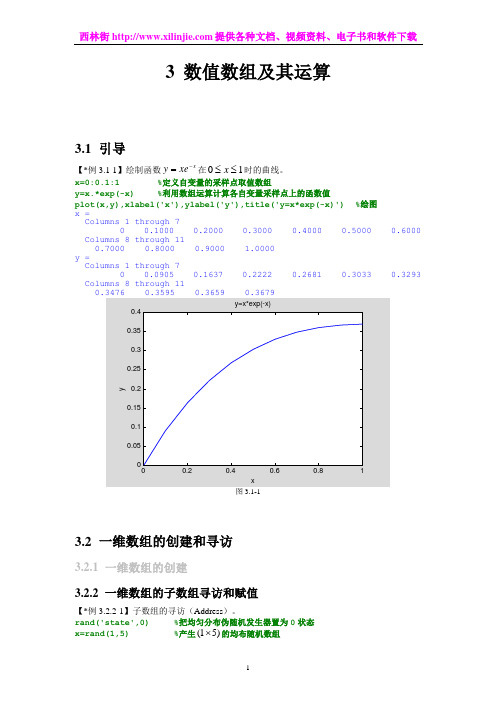
3 数值数组及其运算3.1 引导【*例3.1-1】绘制函数x xe y -=在10≤≤x 时的曲线。
x=0:0.1:1 %定义自变量的采样点取值数组y=x.*exp(-x) %利用数组运算计算各自变量采样点上的函数值plot(x,y),xlabel('x'),ylabel('y'),title('y=x*exp(-x)') %绘图 x =Columns 1 through 70 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 Columns 8 through 110.7000 0.8000 0.9000 1.0000y =Columns 1 through 70 0.0905 0.1637 0.2222 0.2681 0.3033 0.3293 Columns 8 through 113.2 一维数组的创建和寻访3.2.1 一维数组的创建3.2.2 一维数组的子数组寻访和赋值【*例3.2.2-1】子数组的寻访(Address )。
rand('state',0)%把均匀分布伪随机发生器置为0状态 x=rand(1,5) %产生)51(⨯的均布随机数组x =0.9501 0.2311 0.6068 0.4860 0.8913x(3) %寻访数组x的第三个元素。
ans =0.6068x([1 2 5]) %寻访数组x的第一、二、五个元素组成的子数组。
ans =0.9501 0.2311 0.8913x(1:3) %寻访前三个元素组成的子数组ans =0.9501 0.2311 0.6068x(3:end) %寻访除前2个元素外的全部其他元素。
end是最后一个元素的下标。
ans =0.6068 0.4860 0.8913x(3:-1:1) %由前三个元素倒排构成的子数组ans =0.6068 0.2311 0.9501x(find(x>0.5)) %由大于0.5的元素构成的子数组ans =0.9501 0.6068 0.8913x([1 2 3 4 4 3 2 1]) %对元素可以重复寻访,使所得数组长度允许大于原数组。
第三章 MATLAB数值运算

• cumsum(X):返回向量X累加和向量。 • cumsum(A,dim):当dim为1时,该函数等同于 cumsum(A),其第I列是A的第I列的累加和向量。 ;当 dim为2时,返回一个矩阵,其第i行是A的第i行的累加 和向量。
3.5稀疏矩阵
稀疏矩阵: 当一个矩阵只含一部分非零元素,而其余均为0元 素. 优点: 节省存储空间和计算时间,提高工作效率. 3.5.1 稀疏矩阵的建立 s=sparse(A) s=sparse(i,j,s,m,n,nzmax) ind1=[1 2 3 3 4 2] ind2=[1 2 1 4 5 3] n=[0 1 2 3 0 5] sparse(ind1,ind2,n)
用spdiags创建对角稀疏矩阵 [B,d]=spdiags(A) B=spdiags(A,d) A=spdiags(B,d,A)
计算多项式y=x5-3x4-8x3+7x2+3x-5在[-4 5]区间的微分 x=linspace(-4 5); p=[1 –3 –8 7 3 -5]; f=polyval(p,x);
计算方程式s1=6x3-4x2+bx-5,s2=sin(a),s3=(1-t3)/(1+t4)的微分
设x由[0,2π]间均匀分布的10个点组成,求sinx的 1~3阶差分。
• 3.1.4 多项式的构造 poly2sym(p) 利用函数poly2sym构造多项式s4+3s3-15s2-2s+9 利用多项式的根构造多项式s4+3s3-15s2-2s+9
3.2 插值和拟合
多项式插值函数 Y1=interp1(X,Y,X1,'method') 函数根据X,Y的值,计算函数在X1处的值。X,Y是两个等 长的已知向量,分别描述采样点和样本值,X1是一个 向量或标量,描述欲插值的点,Y1是一个与X1等长的 插值结果。method是插值方法,允许的取值有 ‘linear’、‘nearest’、‘cubic’、‘spline’。
MATLAB的数值运算

第三节 多项式运算
一、多项式的建立与表示方法
多项式 → 一个行向量
元素按多项式降幂排列
f(x)=anxn+an-1xn-1+……+a0
p=[an an-1 …… a1 a0]
x4 12x3 0x2 25x 116 p=[1 -12 0 25 116]
roots 多项式等于0的根,列向量
polynomial 已知多项式等于0的根,求 出相应多项式
4.矩阵乘方—— a^n,a^p,p^a
a ^ p —— a 自乘p次幂
方阵 >1的整数
a=[1,2,3;4,5,6;7,8,9]; a^2
ans =30 36 42
➢如果p是矩阵,a是标量:
66 81 96
a^p使用特征值和特征向量自乘到1p0次2 幂12;6 150
➢如a,p都是矩阵,则a^p无意义。
1、多项式乘运算
conv(P1,P2)
conv(conv(a,b),c)
多项式系数向量 conv指令嵌套使用
a(x)=x2+2x+3;b(x)=4x2+5x+6; a=[1 2 3];b=[4 5 6];
c = (x2+2x+3)(4x2+5x+6) c=conv(a,b)=conv([1 2 3],[4 5 6]) c = 4.00 13.00 28.00 27.00 18.00 p=poly2str(c,'x') p = 4 x^4 + 13 x^3 + 28 x^2 + 27 x + 18
a =1 2 0 305 780
1.转置
二、矩阵的运算
如何在MATLAB中进行数值计算

如何在MATLAB中进行数值计算MATLAB是一种用于数值计算和科学计算的程序设计语言和环境。
它提供了各种函数和工具箱,用于处理数值计算问题,包括线性代数、数值积分、数值微分、常微分方程求解、优化、插值等。
下面将介绍如何在MATLAB中进行数值计算的基本步骤和常用函数。
首先,启动MATLAB软件,创建一个新的脚本文件(.m文件),用于编写和保存MATLAB代码。
1.数值计算基础在MATLAB中进行数值计算的基本单位是矩阵和向量。
可以使用MATLAB提供的各种函数来创建和操作矩阵和向量。
例如,可以使用"zeros"函数创建一个全零的矩阵,使用"ones"函数创建一个全一的矩阵,使用"rand"函数生成一个随机矩阵。
2.线性代数计算MATLAB提供了丰富的线性代数函数,用于处理线性方程组、矩阵运算和特征值计算等问题。
例如,可以使用"inv"函数计算矩阵的逆,使用"det"函数计算矩阵的行列式,使用"eig"函数计算矩阵的特征值和特征向量。
3.数值积分MATLAB提供了多种数值积分方法,用于计算函数的定积分。
可以使用"quad"函数进行一维数值积分,使用"quad2d"函数进行二维数值积分,使用"quad3d"函数进行三维数值积分。
4.数值微分MATLAB提供了多种数值微分方法,用于计算函数的导数和偏导数。
可以使用"diff"函数计算函数的导数,使用"gradient"函数计算函数的梯度,使用"hessian"函数计算函数的Hessian矩阵。
5.常微分方程求解MATLAB提供了多种数值方法,用于求解常微分方程组。
可以使用"ode45"函数求解一阶常微分方程,使用"ode15s"函数求解刚性常微分方程。
第3章 MATLAB数值运算

2020/5/2
第三章 数值运算基础
§3.2 线性代数 3.2.4 欠定系统
定义:未知数的个数比方程式的个数多的系统。 调用格式:系统的解不唯一,能计算通解的基解。 特解由QR法求解。 格式如下: 最小元素解:a\b 最小范数解:pinv(a)*b
p=polyfit(x,y,n)
polyint
[p,S]=polyfit(x,y,n)
2020/5/2
[p,S,mu]=polyfit(x,y,n)
例3.13 求误差分式的6阶拟合多项式
>>x = (0: 0.1: 2.5)'; >>y = erf(x); >>p = polyfit(x,y,6) >>x = (0: 0.1: 5)'; >>y = erf(x); >>f = polyval(p,x); >>plot(x,y,'o',x,f,'-') >>axis([0 5 0 2])
2020/5/2
总结:
①假如方阵a的各个行矢量线性相关,则方阵a为奇异 阵,这也使线性方阵ax=b有无穷多组解。 ②假如方阵a近似奇异矩阵,则反斜线运算因子将发出 警告信息。 假如方阵a确定是奇异矩阵,则反斜线运算因子将发出 警告信息。
2020/5/2
第三章 数值运算基础
§3.2 线性代数 3.2.3 超定系统
2020/5/2
第三章 数值运算基础
§3.1 多项式 3.1.1 创建多项式 1.创建矢量的方法 (1)系数矢量法 例3.1 输入系数矢量,创建多项式 x3-4x2+3x+2 例3.2 创建多项式x3+3x+2
第3章MATLAB的数值运算与符号运算

3.1.3 数组与矩阵的输出
一般地,在命令窗口输入的函数语句执 行完毕后,即在工作空间产生其运行结 果。将来可以在命令窗口输入变量名查 看该变量值,也可以直接在工作空间中 打开进行查看或编辑。 如果用户需要将其保存到文件中,一是 可以保存整个工作空间,一是可以将变 量保存为数据文件,供将来调用。
MATLAB中有不同的方法生成矩阵。 概括起来,可以直接赋值输入,以快捷 方式输入,通过提示语句交互输入、通 过内建函数产生、加载外部数据文件等
3.1.1 数组与矩阵的输入
直接赋值输入矩阵或数组 这种方式是最基本且最直接的输入方式。
注:例1 >> A=[1 3 4] >> B=[1;3;4] >> E=[] 以直接赋值方式输入矩阵或数组。
MATLAB还提供了大量函数用于逻辑判断, 可以通过“is*”搜索MATLAB帮助文档查 询更多的状态测试函数及其帮助。
注:状态测试函数及其帮助文档导读
3.2.3 逻辑运算
注:例16 >> A=[1 0 2;3 0 5] >> B=[2 6 1; 0 0 8] >> A&B >> A|B >> ~A >> xor(A,B) 进行数组逻辑运算。
load -ascii filename load -mat filename
%加载ascii码数据文件 %加载二进制数据文件
3.1.1 数组与矩阵的输入
注:例5 >> load -ascii mydata.dat >> mydata
设从其它程序产生了ascii码数据文件。将其保 存在当前工作路径下,名为mydata.dat。通过 文件加载的方式将其导入工作空间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13
基于MATLAB的控制系统计算机辅助设计与仿真
例:
>> A=[1 12 7;3 8 5;4 3 6] A= 1 12 7 3 8 5 4 3 6 >> B=flipud(A) % 矩阵B由矩阵A上下翻转得到 B= 4 3 6 3 8 5 1 12 7 >> A/B ans = 0 0 1 0 1 0
基于MATLAB的控制系统计算机辅助设计与仿真
第 3 章 MATLAB数值运算
2016/1/15
1
基于MATLAB的控制系统计算机辅助设计与仿真
3.1 矩阵和数组
MATLAB具有强大的数值运算能力。数值运算主要指数组、 矩阵和多项式的运算。 MATLAB数值运算的表达式变量中不允许有未定义的自由 变量。 在MATLAB语言中,二维矩阵和数组在形式上一致,但它 们的运算规则不同 。矩阵运算是按照线性代数的规则进行 运算。数组运算是两个数组按元素位置进行的逐元运算, 即元素对元素的运算,数组中的元素都是平等的,要求被 操作的两个数组中元素的行数和列数必须相等。数组运算 符是在矩阵运算符前面加一点“. ”(加减法除外),如 “.* ” 、“./”和“.^”等。向量是数组的一种特例,一行 多列的数组为行向量,一列多行的数组为列向量。
2016/1/15
12
基于MATLAB的控制系统计算机辅助设计与仿真
例:
>> A=[1 12 7;3 8 5;4 3 6]; >> B=[4;9;13];C=[A;1 1 1]; >> D=[B;5]; >> X1=A\B %求解欠定方程 X1 = 2.6442 -0.1731 0.4904 >> X2=C\D %求解超定方程 X2 = 2.9536 -0.0847 0.2639
C(i,j ) A(i,k )B(k ,j ) k
1
n
矩阵乘法不满足交换律,即A*B≠B*A。 例:
>>A=[1 2 3;4 5 6;7 8 9];B=[4 1;7 5;0 3];C=3; >>D=A*B % A*B≠B*A >>E=A*C
2016/1/15
8
基于MATLAB的控制系统计算机辅助设计与仿真
D=rot90(A)
例:
>>A=[1 2 3;4 5 6;7 8 9];B=fliplr(A),C=flipud(A)
2016/1/15
18
基于MATLAB的控制系统计算机辅助设计与仿真
3.1.2 矩阵的特殊运算 1. 矩阵行列式(determinant) 矩阵A={aij}的行列式定义为
19
基于MATLAB的控制系统计算机辅助设计与仿真
计算矩阵的行列式有多种算法,在MATLAB 中采用的 方法为三角分解法(LU分解),将方阵分解为一个上 三角矩阵U和一个下三角矩阵L的积,即A=LU,这样 求得L矩阵的行列式即可得到原矩阵的行列式的值。L 矩阵形式特殊,其行列式计算方法非常简单:
4. 矩阵的除法 在线性代数中,只有矩阵的逆运算,而没有矩阵的除 法运算。在MATLAB中,矩阵的除法用来求线性方程 的解。MATLAB定义了矩阵的左除“\”和右除“/” 两种除法运算,表示了两种不同的除数矩阵和被除数 矩阵的关系。对于标量,两种除法运算的结果相同, 如1/4和4\1有相同的值0.25。2016/1/15inv函数求矩 阵的逆
基于MATLAB的控制系统计算机辅助设计与仿真
10
附录1:奇异矩阵
定义:
行列式等于0的矩阵称为奇异矩阵。
奇异矩阵的判断方法: 首先,看这个矩阵是不是方阵(方阵是行数和列数相等的矩 阵)。若不是方阵,那就谈不上奇异矩阵和非奇异矩阵。然 后,再看此方阵的行列式|A|是否等于0。若等于0,称矩阵A 为奇异矩阵;若不等于0,称矩阵A为非奇异矩阵。 同时,由 |A|≠0可知矩阵A可逆,这样可以得出另外一个重要结论:可 逆矩阵就是非奇异矩阵,非奇异矩阵也是可逆矩阵。如果A为 奇异矩阵,则AX=0有无穷解。如果A为非奇异矩阵,则AX=0有 且只有唯一零解。
P
2016/1/15
16
基于MATLAB的控制系统计算机辅助设计与仿真
② 底数A为标量,指数P为方阵,A^P由特征值和特性 向量计算得到。 ③ 底数A和指数P均为方阵,或者A和P两个矩阵中有一 个不是方阵,则MATLAB显示出错信息。
例:ex3_1.m
2016/1/15
17
基于MATLAB的控制系统计算机辅助设计与仿真
>> a=[2+3i 4-4i 5-2i;7+5i 6-9i 4+3i] >> b=a' %矩阵转置 >> c=a.' %数组转置 >> d=[2 4 5;7 6 4] >> e=d' %矩阵转置 >> f=d.' %数组转置
2016/1/15
6
基于MATLAB的控制系统计算机辅助设计与仿真
2. 矩阵的加、减 运算符:+、- 只有同阶的两个矩阵或者一个矩阵和一个标量才能进 行加减运算。两个同阶矩阵的加减运算是将对应元素 相加减,而矩阵和标量的加减运算是将矩阵中每一个 元素与标量进行加减运算。如果两个矩阵维数不匹配 将提示出错信息 例:
2016/1/15
14
基于MATLAB的控制系统计算机辅助设计与仿真
MATLAB计算矩阵的除法遇到不定方程(未知数的个 数多于方程个数,且解为整数、正整数、有理数或代 数整数的方程或方程组)或超定方程(方程个数大于 未知量个数的方程组)时,有时会无法给出一个确定 解(方程无解或有无穷多组解)。对于无解的情况, MATLAB采用最小二乘法给出一个误差最小的解。
2016/1/15
15
基于MATLAB的控制系统计算机辅助设计与仿真
5. 矩阵的乘方 A^P(幂) 运算符:^ 前提条件:矩阵必须为方阵,即只有方阵才能进行乘 方运算,但A和P不能同时为矩阵。 MATLAB中矩阵的幂运算有三种情况:
① 底数A为方阵,幂指数P为标量,表示A的P次幂。
2016/1/15
5
基于MATLAB的控制系统计算机辅助设计与仿真
1. 矩阵转置(共轭转置) 运算符: ' n×m矩阵A的转置矩阵B定义为bji=aij,i=1, …,n, j=1, …,m,B为m×n矩阵,记为B=AT。如果A为复数 矩阵,则 A '为复数矩阵的共轭转置(Hermit转置)。 例:
L i 1 lii
n
MATLAB求矩阵行列式函数的调用格式为
det(A)
例:ex3_2.m
2016/1/15
20
基于MATLAB的控制系统计算机辅助设计与仿真
如果矩阵A为数值矩阵,则det(A)得到行列式数值计算 结果;如果A为符号矩阵,则det(A)将得出解析解。二 者的区别是,对于接近奇异的系统,解析解的结果更 精确。
2016/1/15
21
基于MATLAB的控制系统计算机辅助设计与仿真
例:求Vandermonde矩阵A=[1 1 1;a b c;a2 b2 c2]的特征 多项式。 解: ex3_3_1.m 例:求状态矩阵A的特征多项式。
解:ex3_3_2.m
2016/1/15
22
基于MATLAB的控制系统计算机辅助设计与仿真
6. 矩阵翻转 MATLAB提供了一些处理矩阵翻转的特殊命令。对 n×m维矩阵A
B=fliplr(A) C=flipud(A)
%将矩阵A左右翻转再赋给B,即bij=ai,m+1-j %将矩阵A上下翻转再赋给C,即cij=an+1-i,j
%将矩阵A逆时针旋转90度后赋给D,即dij=aj,m+1-i
例:计算 10 阶 Hilbert 矩阵的行列式。 解: Hilbert 矩阵的通项为hij=1/(i+j-1),MATLAB中生 成Hilbert 矩阵的函数是hilb(n) ,用sym( )函数可以得出 其符号表达式。
>> H=hilb(10);det(H) %求数值解,不精确 ans = 2.1644e-053 >> H1=sym(H);det(H1) %先将矩阵变换为符号矩阵,再求解析解 ans = 1/46206893947914691316295628839036278726983680000000000
2016/1/15
9
基于MATLAB的控制系统计算机辅助设计与仿真
(1)矩阵左除 运算符:\ X= A\B是线性方程组A*X=B的解。若A为非奇异方阵, 则X=A\B=A-1*B=inv(A)*B ;当方程是欠定或超定情况 时,A\B所对应的是方程最小二乘解;若X不存在或不 唯一,则产生一警告信息。矩阵A可以是矩形矩阵(即 非方形矩阵),但此时方程组必须相容。 (2)矩阵右除 运算符:/ X=B/A是线性方程组X*A=B的解。A为非奇异方阵时, X=B/A= B*A-1 =B*inv(A) 。 通常A\B≠B/A
2016/1/15
3
基于MATLAB的控制系统计算机辅助设计与仿真
2016/1/15
4
基于MATLAB的控制系统计算机辅助设计与仿真
常用的十进制符号如小数点、负号等,在MATLAB中 也可以同样使用。 表示10的幂次用符号e或E,如:3、-99、0.0001、1.6e20、6.2e23。
A det(A) (1)k a1k1 a2k2 ...ankn
式中k1,k2,…,kn是将序列1,2,…,n的元素交换k次所得出 的序列,每个序列称为一个置换(permutation);∑表 示对k1,k2,…,kn取遍1,2,…,n的所有的排列求和。
