曲靖一中高考复习质量监测卷五理数-答案
2023届云南省曲靖市第一中学高三下学期教学质量监测试卷(五)理科综合试题

【考试时间:2022年12月25日9:00—11:30】曲靖市第一中学2023届第五次诊断性考试理科综合能力测试注意事项:1.答卷前,考生务必将自己的班级、姓名、考号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮檫干净后,再选涂其它答案标号。
回答非选择题时。
将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将答题卡交回。
可能用到的相对原子质量:H-1 N-14 O-16 Fe-56一、选择题:本题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 核糖核酸酶是由一条肽链折叠形成的蛋白质分子,加入尿素会导致其变性并失去活性,当去除尿素后,它又会重新折叠并再次获得活性。
下列叙述中正确的是()A.氨基酸通过脱水缩合就能形成具有活性的核糖核酸酶B.尿素的作用是使核糖核酸酶肽链中的氢键和肽键断裂C.决定核糖核酸酶结构的信息储存于基因的碱基序列中D.高温对核糖核酸酶结构的影响与尿素的影响完全相同2.人体正常细胞中的P53蛋白能促进丙酮酸进入线粒体,以维持正常的代谢途径。
癌细胞中的P53蛋白功能异常,从而影响了细胞呼吸过程。
下列说法错误的是()A.丙酮酸在细胞质基质中转化为乳酸的过程不会生成ATPB.人体细胞中的丙酮酸只有进入线粒体才能被氧化分解产生CO2C.P53蛋白功能异常会导致癌细胞从内环境中摄取更多的葡萄糖D.与正常细胞相比,癌细胞分解等质量的葡萄糖会产生更多热能3.细胞中的RNA主要有三大类,mRNA、tRNA和rRNA。
下列有关RNA的相关叙述,正确的是()A.在真核细胞中含有的三大类RNA,它们都是在细胞核中由DNA转录形成的B.如果mRNA上的密码子是5′AUG3′,那么tRNA上的反密码子是5′UAC3′C.tRNA是细胞中转运氨基酸的工具,氨基酸连接在tRNA的5′端的磷酸基团上D.有的RNA具有降低化学反应活化能的作用,这种RNA最可能是rRNA4.在神经调节过程中,兴奋会在神经纤维上传导和神经元之间传递。
曲靖一中高考复习质量监测卷五理综-答案

理科综合参考答案·第1页(共17页)曲靖一中高考复习质量监测卷五理科综合参考答案一、选择题:本题共13小题,每小题6分。
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 答案 D B C B C D D D B A B A C二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求;第19~21题有多项符合题目要求,全部选对的给6分,选对但不全的给3分,有选错的给0分。
题号 14 15 16 17 18 19 20 21 答案 D A C B C BC AC BD 【解析】1.A 项,酵母菌为真核生物,没有拟核;B 项,植物叶肉细胞内能够发生碱基互补配对的细胞器除了线粒体和叶绿体外,核糖体合成多肽链的过程中也发生碱基互补配对;C 项,神经递质与突触后膜相应受体结合后发挥作用,没有进入突触后膜内。
2.无氧呼吸第二阶段释放能量未储存到ATP 中,所以a 叙述中⑤⑤过程没有将能量储存到ATP 中;证明②过程释放的氧气来自水的科学家是鲁宾和卡门,b 错;如图是某植物细胞的细胞代谢过程,②过程产生氧气的速率和⑨过程中消耗氧气的速率相等时,只能说明该细胞光合作用速率等于呼吸作用速率,而不是植株;植株暗处理后,光反应产生的ATP 和[H ]减少,C 3还原受到影响,导致C 3含量增加;类胡萝卜素不吸收红光,所以e 错;光合作用暗反应所需[H ]和呼吸作用产生的[H ]不是同一物质。
理科综合参考答案·第2页(共17页)3.A 项,基因突变可以发生在生物个体发育的任何时期,描述的是基因突变的随机性;B 项,基因重组是指生物体进行有性生殖的过程中,控制不同性状的基因重新组合,发生在减数第一次分裂前期,同源染色体上的非姐妹染色单体交叉互换,或发生在减数第一次分裂后期,非同源染色体上的非等位基因自由组合;C 项,三倍体植株在减数分裂产生配子时,由于联会紊乱,产生无籽西瓜;D 项,新物种产生的标志是产生生殖隔离。
曲靖一中2018届高三12月高考复习质量监测卷(五)理科数学(2017.12)(含解析)

第 1 页 共 11 页
第 2 页 共 11 页
第 3 页 共 11 页
第 4 页 共 11 页
曲靖一中高考复习质量监测卷五 理科数学参考答案
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分) 题号 答案 1 B 2 A 3 D 4 D 5 A 6 C 7 C 8 B 9 B 10 C 11 A 12 D
代入得 zmax 2 ,故选 C.
图1
7.第一次循环 i 4 , S 100 4 96 ,不满足 i 30 ;第二次循环 i 8 , S 96 8 88 , 不满足 i 30 ;第三次循环 i 16 , S 88 16 72 ,不满足 i 30 ;第四次循环 i 32 ,
S 72 32 40 ,满足 i 30 ,输出 S 40 ,故选 C.
8.∵ a4 a6 0 ,∴ a5 0 , a5 a1 4d ,∴ 4d 16 , d 4 , S10 10a1
10 16 90 ( 4) 20 ,故选 B. 2
T2 (1)1 C1 5 5 ,故选 D.
4 .根据题意是求一个等比数列 {an } 的通项,第五天准备分割时线的长度为第四项,即
a4 1 1 1 ,故盒子外面线的长度为 米,故选 D. 4 2 16 16 2 cos 2 2sin cos 2 2 tan 1 1 1 , 2 2 2 sin cos tan 1 5
图2
m m ,故直线 x 经过双曲线 x 2 y 2 1 的左 4 4
m 故焦点到准线的距离为 p 2 2 , 2, m4 2, 2p 4 2 , 4
云南省曲靖市第一中学高三上学期第五次月考理数试题 Word版含答案

曲靖一中高考复习质量监测卷五理科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知m 为实数,i 为虚数单位,若0)1(2>-+i m m ,则=-+iim 1( ) A .1- B .1 C .i - D .i2.已知集合{}{}a y y B x y x A xln 2,1+==-==,且B C A R ⊆,则实数a 的取值范围是( )A .),[+∞eB .],0(eC .]1,(-∞D .]1,0(3.《九章算术》“竹九节”问题:现有一根九节的竹子,自上而下各节的容积成等比数列,上面3节的容积共9升,下面3节的容积共45升,则第五节的容积为( ) A .7升 B .8升 C .9升 D . 11升4.下表是y x ,的对应数据,由表中数据得线性回归方程为∧∧-=a x y 8.0.那么,当60=x 时,相应的∧y 为( )A .38B .43 C.48 D .52 5.下列说法中正确的是( )A .“b a >”是“b log a 2>2log ”的充要条件B .若函数x y 2sin =的图象向左平移4π个单位得到的函数图象关于y 轴对称C.命题“在ABC ∆中,3π>A ,则23sin >A ”的逆否命题为真命题 D .若数列{}n a 的前n 项和为n n S 2=,则数列{}n a 是等比数列6.若双曲线)0,0(1:2222>>=-b a by a x C 的一条渐近线的倾斜角是直线012:=+-y x l 倾斜角的两倍,则双曲线的离心率为( ) A .35 B .37 C. 45 D .347.由5,3,2,1,0组成的无重复数字的五位偶数共有( )A .36个B .42个 C.48个 D .120个 8.阅读如图所示的程序框图,若输入2110=a ,则输出的k 值是( )A .9B .10 C.11 D .129.已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≥≤+≥++040122xy y x y x ,则y x z +=2的取值范围是( )A .]52,2[-B .]0,2[- C.]252[,- D .]1,552[10.已知直线1l 是抛物线x y C 8:2=的准线,P 是C 上的一动点,则P 到直线1l 与直线02443:2=+-y x l 的距离之和的最小值为( )A .524 B .526 C.6 D .532 11.函数)257sin()17sin(+-+=x x y 的最大值为( ) A .1 B .2 C.2 D .3 12.设定义在区间],[k k -上的函数x mx x f +-=11lg)(是奇函数,且)21()21(f f ≠-.若][x 表示不超过x 的最大整数,0x 是函数62ln )(-++=k x x x g 的零点,则=][0x ( ) A .1 B .1或2 C.2 D .3第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量),1(),1,0(),2,1(m -===.若∥(2+,则实数=m . 14.已知]1,1[,-∈b a ,则不等式022≥+-b ax x 在R x ∈上恒成立的概率为 . 15.核算某项税率,需用公式)()71(*∈-=N n x K n.现已知K 的展开式中各项的二项式系数之和是64,用四舍五入的方法计算当7003=x 时K 的值.若精确到001.0,其千分位上的数字应是 .16.四棱锥ABCD P -的底面ABCD 为正方形,⊥PA 底面ABCD ,2=AB ,若该四棱锥的所有顶点都在表面积为π16的同一球面上,则=PA .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)在ABC ∆中,角C B A ,,的对边分别是c b a ,,,且A c b Ca cos )32()2sin 21(32-=-. (1)求角A 的大小;(2)若4,32==c b ,D 是BC 的中点,求AD 的长. 18. (本小题满分12分)如图所示,某班一次数学测试成绩的茎叶图(如图甲)和频率分布直方图(如图乙)都受到不同程度的污损,其中,频率分布直方图的分组区间分别为]100,90[),90,80[),80,70[),70,60[),60,50[,据此解答如下问题.(注:直方图中)60,50[与]100,90[对应的长方形的高度一样)(1)若按题中的分组情况进行分层抽样,共抽取16人,那么成绩在)90,80[之间应抽取多少人?(2)现从分数在]100,80[之间的试卷中任取2份分析学生失分情况,设抽取的试卷分数在]100,90[之间 份数为ξ,求ξ的分布列和数学期望.19. (本小题满分12分)如图是一几何体的直观图、主观图、俯视图、左视图.(1)求该几何体的体积V ; (2)证明:∥BD 平面PEC ;(3)求平面PEC 与平面PDA 所成的二面角(锐角)的余弦值. 20. (本小题满分12分)设非零向量,,规定:θ⊗(其中>=<,θ),21F F 、是椭圆)0(1:2222>>=+b a by a x C 的左、右焦点,点B A ,分别是椭圆C 的右顶点、上顶点,若32=⊗,椭圆C 的长轴的长为4.(1)求椭圆C 的方程;(2)过点2F 的直线l 交椭圆C 于点N M ,,若7212=⊗,求直线l 的方程.21. (本小题满分12分) 已知函数)1(24341ln )2(16)(f xx x f x f ++-'=. (1)求函数)(x f 的解析式和单调区间;(2)设42)(2-+-=bx x x g ,若对任意]2,1[),2,0(21∈∈x x ,不等式)()(21x g x f ≥恒成立,求实数b 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22. (本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴,建立极坐标系.已知曲线C 的及坐标方程为:θρcos 4=,直线l 的参数方程为:⎪⎪⎩⎪⎪⎨⎧=+=ty t x 21233(t 为参数),直线l 与C 交于21,P P 两点.(1)求曲线C 的直角坐标方程及直线l 的普通方程; (2)已知)0,3(Q ,求Q P Q P 21-的值. 23. (本小题满分10分)选修4-5:不等式选讲 已知函数11)(-++=x x x f .(1)若R x ∈∃0,使得不等式m x f ≤)(0成立,求实数m 的最小值M ; (2)在(1)的条件下,若正数b a ,满足m b a =+3,求ba a ++121的最小值.曲靖一中高考复习质量监测卷五理科数学参考答案一、选择题1-5:DACBB 6-10:ABDAC 11、12:DC 12.∵x mx x f +-=11lg )(是],[k k -上的奇函数可求得1±=m ,∵)21()21(f f ≠-,∴1=m ,ze11011<<-⇒>+-x x x ,∴)1,1(],[-⊆-k k 且],[21k k -∈±,∴121<-≤k , ∵)0(021)(>>+='x xx g ,即)(x g 为),0(+∞上的增函数(若)(x g 有零点,则只有一个),∵03ln )3(,022ln )2(>+=<-+=k g k g ,∴函数)(x g 的零点)3,2(0∈x ,则2][0=x .二、填空题13.4- 14.3115.3 16.22 三、解答题17.解:(1)由正弦定理可得,A C A B C A cos sin 3cos sin 2cos sin 3-=, 从而可得A B B A B C A cos sin 2sin 3,cos sin 2)sin(3==+.又B 为三角形的内角,所以0≠B sin ,于是23cos =A ,又A 为三角形内角,∴6A π=. (2)解法一:由余弦定理得:24cos 2222=⇒=-+=a A bc c b a ,又∵2222216)32(2c b a ==+=+,∴ABC ∆是直角三角形,2π=C ,∴1313222222=+=+=)(CD AC AD ,∴13=AD .解法二:∵)(21+=, ∴13)cos 2(41)(412222=++=+=b A bc c ,∴13=AD .18.解:(1)由茎叶图知分数在)60,50[的人数为4,)70,60[的人数为8,)80,70[的人数为10,由频率分布直方图知:)60,50[与]100,90[的人数都为4,故总人数为32100125.04=⨯,∴分数在)90,80[的人数为:64108432=----,∴成绩在)90,80[之间应抽:316326=⨯人.(2)∵分数在)90,80[的人数为6,分数在]100,90[的人数为4, ∴ξ的可能取值为:2,1,0,∵,,,152)2(158)1(31)0(21024210141621026=========C C P C C C P C C P ξξξ ∴ξ的分布列为∴515215130)(=⨯+⨯+⨯=ξE . 19.(1)解:由三视图可知,底面ABCD 是边长为4的正方形,四边形APEB 是直角梯形,⊥PA 平面ABCD ,⊥B C 平面APEB ,4,42====CB EB AB PA .连接AC ,∴CB S PA S V V V APEB ACD APED C ACD P ⋅+⋅=+=∆--3131 380)21312131=⋅⋅+⋅+⋅⋅=CB AB PA EB PA AD (. (2)证明:如图,取PC 的中点F ,连接BD 与AC 交于点M ,连接EF FM ,. ∴PA FM PA FM 21=,∥,∴EB FM EB FM =,∥,故四边形BMFE 为平行四边形,∴BM EF ∥,又⊂EF 平面PEC ,⊄BD 平面PEC ,∴∥BD 平面PEC.(3)解:如图,分别以BE BA BC ,,为z y x ,,轴建立空间直角坐标系, 则)4,4,0(),0,4,0(),2,0,0(),0,0,4(p A E C , ∴)0,4,0(=为平面PDA 的一个法向量.设平面PEC 的法向量为),,(z y x =,则⎩⎨⎧=++-=∴⎪⎩⎪⎨⎧=⋅=⋅0,20,0z y x x z CP n , 令1=x ,∴)2,11(-n ,=,∴66,cos -<, ∴平面PEC 与平面PDA 所成的二面角(锐角)的余弦值为66. 20.解:(1)由题意:242=⇒=a a ,3290sin ===⊗ab ab ,∴3=b ,∴所求椭圆C 为:13422=+y x .(2)①当直线l 为:0=y ,即在x 轴上时,72120180≠=⊗ 不符合题意; ②当直线l 不在x 轴上时,由(1)知2F 为)0,1(,设l 为:1+=my x ,将其代入椭圆C 的方程得:096)43(22=-++my x m ,∴⎪⎩⎪⎨⎧+-=+-=+439436221221m y y m m y y ,∴431124336)43(364)2222222122121++=+++=-+=-m m m m m y y y y y y (,又OAB S ∆>=<⊗2,7212431122122221212=++=-=-⨯⨯⨯=m m y y y y OF ,解得:12=m 或18172-=m (舍去),即1±=m . 综上,直线l 的方程为:1-=x y 或1+-=x y .21.解:(1))0(4341)2(16)(2>--'='x xx f x f , ∴161)2(163412)2(16)2(='⇒--'='f f f ,∴21)1()1(243411ln )1()1(24341ln )(-=⇒++=⇒++-=f f -f f x x x x f ,∴)0(14341ln )(>+-=x -xx x x f ,∴22243443411)(x x x x x x f --=--=', 由0>x 及0)(>'x f 得31<<x ;由0>x 及0)(<'x f 得10<<x 或3>x , 故函数)(x f 的单调递增区间是)3,1(,单调递减区间是),3(),1,0(+∞. (3)若对任意]2,1[),2,0(21∈∈x x ,不等式)()(21x g x f ≥恒成立, 问题等价于max min )()(x g x f ≥,由(1)可知,在)2,0(上,1=x 是函数)(x f 的极小值点,这个极小值点是唯一的极值点,故也是最小点,所以21)1()(min -==f x f ,]2,1[,42)(2∈-+-=x bx x x g , 当1<b 时,52)1()(max -==b g x g ; 当21≤≤b 时,4)()(2max -==b b g x g ; 当2>b 时,84)2()(max -b g x g ==;问题等价于⎪⎩⎪⎨⎧-≥-<5221,1b b 或⎪⎩⎪⎨⎧-≥-≤≤421212b b 或⎪⎩⎪⎨⎧-≥->84212b b , 解得1<b 或2141≤≤b 或φ∉b ,即214≤b ,所以实数b 的取值范围是]214,(-∞. 22.解:(1)∵θρρθρcos cos 442=⇒=,由⎩⎨⎧=+=xy x θρρcos 222得x y x 422=+,即C 的直角坐标方程为:4)2(22=+-y x , 直线l 消去参数t 得:033=--y x .(2)将直线l 的参数方程代入x y x 422=+,得:0332=-+t t , 设21,P P 的对应参数分别为21,t t ,∴3,32121-=-=+t t t t , 而40)23(22<+-,即点)0,3(Q 在圆C 的内部, ∴3212121=+=-=-t t t t Q P Q P . 23.解:(1)由题意,不等式m x x ≤-++11有解,即M x x m =-++≥min )11(. ∵2)1()1(11=--+≥-++x x x x ,当且仅当110)1)(1(≤≤-⇒≤-+x x x 时取等号, ∴2=M .(2)由(1)得23=+b a ,∴)121)](2[21)121)(321121b a a b a a b a a b a b a a ++++=+++=++(( 2)122(21)1221(21=+≥+++++=a b a b a a , 当且仅当2122==⇒+=+b a a b a b a a 时取等号,故2)121(min =++ba a .。
云南省曲靖市一中2025届高三一诊考试数学试卷含解析

云南省曲靖市一中2025届高三一诊考试数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知正项等比数列{}n a 的前n 项和为n S ,且2474S S =,则公比q 的值为( ) A .1B .1或12C .32D .32±2.已知函数()2xf x x a =+⋅,()ln 42xg x x a -=-⋅,若存在实数0x ,使()()005f x g x -=成立,则正数a 的取值范围为( )A .(]01,B .(]04,C .[)1+∞,D .(]0,ln2 3.函数()()1ln 12f x x x=++-的定义域为( ) A .()2,+∞B .()()1,22,-⋃+∞C .()1,2-D .1,24.若双曲线()222210,0x y a b a b-=>>的渐近线与圆()2221x y -+=相切,则双曲线的离心率为( )A .2B .32C .233D .35.双曲线﹣y 2=1的渐近线方程是( )A .x±2y=0B .2x±y=0C .4x±y=0D .x±4y=06.已知函数有三个不同的零点(其中),则 的值为( )A .B .C .D .7.如图所示是某年第一季度五省GDP 情况图,则下列说法中不正确的是( )A .该年第一季度GDP 增速由高到低排位第3的是山东省B .与去年同期相比,该年第一季度的GDP 总量实现了增长C .该年第一季度GDP 总量和增速由高到低排位均居同一位的省份有2个D .去年同期浙江省的GDP 总量超过了4500亿元8.已知数列{}n a 是公差为()d d ≠0的等差数列,且136,,a a a 成等比数列,则1a d=( ) A .4B .3C .2D .19.已知()22log 217y x x =-+的值域为[),m +∞,当正数a ,b 满足2132m a b a b+=++时,则74a b +的最小值为( ) A .94B .5C .524+ D .910.已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边经过点()1,2P ,则cos2θ=( ) A .35B .45-C .35D .4511.ABC 中,点D 在边AB 上,CD 平分ACB ∠,若CB a =,CA b =,2a =,1b =,则CD =( ) A .2133a b + B .1233a b +C .3455a b + D .4355a b + 12.设()'f x 函数()()0f x x >的导函数,且满足()()2'f x f x x>,若在ABC ∆中,34A π∠=,则( )A .()()22sin sin sin sin f A B f B A <B .()()22sinC sin sin sin f B f B C<C .()()22cos sin sin cos f A B f B A > D .()()22cosC sin sin cos f B f B C >二、填空题:本题共4小题,每小题5分,共20分。
云南省曲靖市2023-2024学年高三第一次教学质量监测数学答案
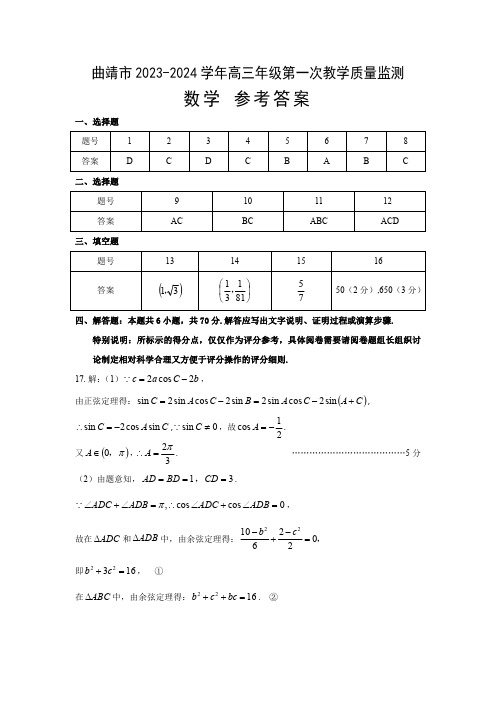
曲靖市2023-2024学年高三年级第一次教学质量监测数学参考答案一、选择题题号12345678答案DCDCBABC二、选择题题号9101112答案ACBCABCACD三、填空题题号13141516答案()31,⎪⎭⎫ ⎝⎛81131,7550(2分),650(3分)四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.特别说明:所标示的得分点,仅仅作为评分参考,具体阅卷需要请阅卷题组长组织讨论制定相对科学合理又方便于评分操作的评分细则.17.解:(1)b C a c 2cos 2-= ,由正弦定理得:()C A C A B C A C +-=-=sin 2cos sin 2sin 2cos sin 2sin ,C A C sin cos 2sin -=∴,0sin ≠C ,故21cos -=A .又()π,0∈A ,32π=∴A .…………………………………5分(2)由题意知,31===CD BD AD ,.0cos cos ,=∠+∠∴=∠+∠ADB ADC ADB ADC π ,故在ADC ∆和ADB ∆中,由余弦定理得:,02261022=-+-c b 即16322=+c b ,①在ABC ∆中,由余弦定理得:1622=++bc c b .②联立①②,解得774=c ,即774=AB .……………………………10分18.解:(1)n a S n n -=2 ,()()21211≥--=∴--n n a S n n ,两式相减,得121+=-n n a a ,故()()21211≥+=+-n a a n n .又当1=n 时,1211-=a a ,故11=a ,∴数列{}1+n a 是以2为首项,2为公比的等比数列,故n n n a 22211=⨯=+-,所以12-=nn a .…………………………………6分(2)()()121121*********---=--=+=+++n n n n nn n n n a a a b ,121112112171313111121--=⎪⎭⎫ ⎝⎛---++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+++=∴++n n nn n b b b T .由2024202312111>--+n ,得202411211<-+n ,2024121>-∴+n ,解得10≥n ,故n 的最小值是10.…………………………………12分19.解:(1)221==n p ,,即采用3局2胜制,故X 的所有可能取值为2,3,()212121222=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛==X P ,()21212121213212212=⋅⎪⎭⎫ ⎝⎛⋅+⋅⎪⎭⎫ ⎝⎛⋅==C C X P ,X ∴的分布列为:X 23P2121X ∴的数学期望()25213212=⨯+⨯=X E .…………………………………6分(2)当采用3局2胜制时,设甲获胜时比赛的总局数为ξ,则甲最终获胜的概率:()()()()p p p p p C p P P P 2313221222-=⋅-⋅⋅+==+==ξξ.当采用5局3胜制时,设甲获胜时比赛的总局数为η,则甲最终获胜的概率:()()()()()().101561154323222422333+-=⋅-⋅⋅+⋅-⋅⋅+==+=+==p p p p p p C p p p C p P P P P ηηη23P P > ,即()()p p p p p 2310156223->+-,0145223>-+-∴p p p ,即()()01212>-⋅-p p 121<<∴p .…………………………………12分20.解:(1)证明:由题意可知,BCE ∆为等边三角形,在图2中,取BE 的中点为F ,连接AF F C ,1,则BE F C ⊥1,且31=F C .在图1中,取BE 的中点为F ,则2160===∠AB BF ABF ,,,由余弦定理得,3=AF ,21212AC F C AF =+∴,故AF F C ⊥1,又F BE AF = ,ABED F C 平面⊥∴1,又E BC F C 11平面⊂,ABED E BC 平面平面⊥∴1.…………………………………5分(2)满足题设条件的点P 存在.如图所示,建立空间直角坐标系,则()()()().32323023230100230030001⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛,,,,,,,,,,,,,,,,,C F E B AD 由(1)知,平面EB C 1的一个法向量为()031321,,-==AF n ,设()101≤≤=λλDC DP ,则()⎪⎪⎭⎫ ⎝⎛+-+-=⎪⎪⎭⎫ ⎝⎛+--=+=λλλλλ3232233323230231,,,,,,DC BD BP ,又()013,,--=BE ,设平面PEB 的一个法向量为()z y x n ,,=2,由⎪⎩⎪⎨⎧=⋅=⋅022BE n BP n ,得()132--=λλλ,,n .由二面角1C EB P --的大小为45,得()22142322=-+--λλλλ,解得[]1031,∈=λ,所以在棱1DC 上存在点P ,使得二面角1C EB P --的大小为45,此时36311==DC DP .…………………………………12分21.解:(1)设()()2211y x B y x A ,,,,则⎪⎩⎪⎨⎧==22212122py x py x ,()()()2121212y y p x x x x -=-+∴,故p x x x x y y 2212121+=--,由题意,得124=p,所以2=p ,所以抛物线E 的方程为y x 42=.…………………………………4分(2)由(1)知,()10,F ,易知直线2l 的斜率必存在,设直线2l 的方程为1+=kx y ,()().4433y x N y x M ,,,由⎩⎨⎧+==142kx y y x ,得0442=--kx x ,440161643432-==+>+=∆∴x x k x x k ,,.且()22243214161611k k k x x kMN +=+⋅+=-+=.由42x y =,得2x y =',所以切线PM 的方程为:()3332x x x y y -=-,即()422333x x x x y +-=,①同理,切线PN 的方程为:()422444x x x x y +-=,②联立①②,得⎪⎪⎩⎪⎪⎨⎧-===+=14224343x x y k x x x ,()12-∴,k P ,∴点P 到直线2l 的距离22212122k k k d +=++=,()()41412142123222≥+=+⋅+⋅=∴∆k k k S PMN,当且仅当0=k 时取等号,综上,PMN ∆的面积存在最小值4,此时直线2l 的方程为1=y .…………………12分22.解:(1)()()14141+='∴+='a f ax x x f , ,由题意可知,()2141211-=+-='a f ,即,83-=∴a .…………………………………3分(2)()x f 的定义域为()∞+,0,且()x ax ax x x f 14412+=+=',∴当0≥a 时,()0>'x f ,()x f 在()∞+,0上单调递增;当0<a 时,令()0>'x f ,得a x 410-<<,令()0<'x f ,得ax 41->,所以()x f 在⎪⎪⎭⎫⎝⎛-a 410,上单调递增,在⎪⎪⎭⎫ ⎝⎛∞+-,a 41上单调递减.综上所述,当0≥a 时,()x f 在()∞+,0上单调递增;当0<a 时,()x f 在⎪⎪⎭⎫⎝⎛-a 410,上单调递增,在⎪⎪⎭⎫ ⎝⎛∞+-,a 41上单调递减.…………………………………6分(3)令()()()x g x f x F -=()12ln 2++++=x a ax x .函数()x f 的图象在函数()x g 的图象的下方,()0<∴x F 在()∞+,0上恒成立.当0≥a 时,()0321>+=a F ,不满足()0<x F 在()∞+,0上恒成立.当0<a 时,因为()()()()x ax x a ax xx F 112221++=+++='且0>x ,()()01010<'⎪⎭⎫ ⎝⎛∞+-∈>'⎪⎭⎫ ⎝⎛-∈∴x F ax x F a x 时,,,时,,,故()x F 在⎪⎭⎫ ⎝⎛-a 10,上单调递增,在⎪⎭⎫ ⎝⎛∞+-,a1上单调递减,()aa a F x F 11ln 1max -⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=∴.又()0<x F 恒成立,∴()0011ln <<-⎪⎭⎫ ⎝⎛-a aa 恒成立.令()()0ln >+=x x x x h ,则()0111>+=+='xx x x h ,()x h ∴在()+∞,0上单调递增,又0212ln 21<+-=⎪⎭⎫⎝⎛h ,()011>=h ,∴存在唯一的⎪⎭⎫⎝⎛∈1210,x ,使()00=x h ,且当()00x x ,∈时,()0<x h ,当()∞+∈,0x x 时,()0>x h ,010x a <-<∴,即01x a -<,又()121--∈-,x ,Z a ∈,a ∴的最大值为2-.…………………………………12分。
2025届云南省曲靖一中高考仿真模拟数学试卷含解析

2025届云南省曲靖一中高考仿真模拟数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数()2f x ax =-与()xg x e =的图象上存在关于直线y x =对称的点,则a 的取值范围是( )A .,4e ⎛⎤-∞ ⎥⎝⎦B .,2e ⎛⎤-∞ ⎥⎝⎦C .(],e -∞ D .(2,e ⎤-∞⎦2.若424log 3,log 7,0.7a b c ===,则实数,,a b c 的大小关系为( ) A .a b c >>B .c a b >>C .b a c >>D .c b a >>3.已知等比数列{}n a 的前n 项和为n S ,且满足122n n S λ+=+,则λ的值是( )A .4B .2C .2-D .4-4.下列四个图象可能是函数35log |1|1x y x +=+图象的是( )A .B .C .D .5.若23455012345(21)(21)(21)(21)(21)a a x a x a x a x a x x +-+-+-+-+-=,则2a 的值为( ) A .54B .58C .516D .5326.如图,四面体ABCD 中,面ABD 和面BCD 都是等腰直角三角形,2AB ,2BAD CBD π∠=∠=,且二面角A BD C --的大小为23π,若四面体ABCD 的顶点都在球O 上,则球O 的表面积为( )A .223πB .283πC .2π D .23π 7.若等差数列{}n a 的前n 项和为n S ,且130S =,3421a a +=,则7S 的值为( ). A .21B .63C .13D .848.阿基米德(公元前287年—公元前212年)是古希腊伟大的哲学家、数学家和物理学家,他和高斯、牛顿并列被称为世界三大数学家.据说,他自己觉得最为满意的一个数学发现就是“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”.他特别喜欢这个结论,要求后人在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,表面积为54π的圆柱的底面直径与高都等于球的直径,则该球的体积为 ( )A .4πB .16πC .36πD .643π9.已知函数31()sin ln 1x f x x x x +⎛⎫=++ ⎪-⎝⎭,若(21)(0)f a f ->,则a 的取值范围为( )A .1,2⎛⎫+∞ ⎪⎝⎭B .()0,1C .1,12⎛⎫ ⎪⎝⎭D .10,2⎛⎫ ⎪⎝⎭10.若2m >2n >1,则( ) A .11m n> B .πm ﹣n >1 C .ln (m ﹣n )>0D .1122log m log n >11.已知集合A={x|y=lg (4﹣x 2)},B={y|y=3x ,x >0}时,A∩B=( ) A .{x|x >﹣2} B .{x|1<x <2} C .{x|1≤x≤2} D .∅ 12.由曲线3,y x y x = )A .512B .13C .14D .12二、填空题:本题共4小题,每小题5分,共20分。
云南省曲靖市第一中学2024届高三上学期教学质量监测数学试题(五)试题含答案解析

曲靖一中2024届高三教学质量监测试卷(五)数学一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2,,0A a a =,{}2B x xx =-=,且B A ⊆,则a 的值为().A.1 B.1- C.1± D.22.已知221813iiz +=,则z 的虚部为().A.13- B.13i- C.13 D.18-3.已知πcos()3αα=-,则tan 2α=().A.3 B.3-C. D.4.已知F 是双曲线2213x y -=的左焦点,()1,3M ,P 是双曲线右支上的一动点,则PF PM +的最小值为().A.B. C.+ D.5.根据曲靖一中食堂人脸识别支付系统后台数据分析发现,高三年级小孔同学一周只去食堂一楼和二楼吃饭.周一去食堂一楼和二楼的概率分别为13和23,若他周一去了食堂一楼,那么周二去食堂二楼的概率为34,若他周一去了食堂二楼,那么周二去食堂一楼的概率为12,现已知小孔同学周二去了食堂二楼,则周一去食堂一楼的概率为().A.37 B.47C.15D.456.过点()0,2P 作圆22:430C x x y -++=的两条切线,设切点为A ,B ,则切点弦AB 的长度为()A.B.142C.4D.77.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若2C A =,a ,b ,c 成等差数列,则cos C =().A.18B.34C.12-D.458.已知函数()f x 及其导函数()f x '的定义域均为R ,及()()g x f x '=,若()12f x -,()2g x +均为偶函数,则下列说法正确的是().A.()10f =B.()g x 的周期为2C.()()13f f -= D.()()02g g =二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知x ,y 都是正数,且22x y +=,则下列说法正确的是().A.xy 的最大值为12B.12x y +的最小值为92C.224x y +的最小值为4D.+的最大值为210.已知抛物线2:4C y x =,O 为坐标原点,直线l 经过抛物线的焦点F ,与抛物线C 交于点A ,B 两点,设()11,A x y ,()22,B x y ,抛物线C 的准线与x 轴的交点为G .则下列说法正确的是()A.124x x = B.当8AB =时,直线l 的斜率为1±C.GF 始终平分AGB∠ D.()min 8AGB S = 11.已知函数()()sin f x x ωϕ=+,如图,A ,B 是直线12y =与曲线()y f x =的两个交点,若π3AB =,则下列说法正确的是().A.2ω=,π3ϕ=-B.()f x 在ππ,66⎡⎤-⎢⎥⎣⎦上单调递增 C.5π12x =-是()f x 的一条对称轴 D.32y x =-是曲线()f x 的一条切线12.远看曲靖一中文昌校区紫光楼主楼,一顶巨大的“博士帽”屹立在爨园之中.其基础主体结构可以看做是一个倒扣的正四棱台ABCD A B C D -''''.如图所示,过B '作底面ABCD 的垂线,垂足为G .记B BG α'∠=,B BC γ∠'=,GBC θ∠=,面BB C C ''与面ABCD 所成角为β,面BB C C ''与面BB G '所成角为x ,B C a ''=,BC b =,B G h '=,则()A.正四棱台ABCD A B C D -''''的体积为()2213h a b ab ++B.tan 2tan βα=C.sin sin sin αβγ=D.cos cos cos cos sin sin x θαγαγ-=三、填空题:本题共4小题,每小题5分,共20分.13.已知向量()2,2a b += ,()1,3a b -= ,则22a b -= __________.14.已知等差数列{}n a 中,19a =-,33a =-.记()121,2,3,n n T a a a n == ,则数列{}n T 中的最小项为__________.15.若函数()πsin 3y x ωω*⎛⎫=+∈ ⎪⎝⎭N 的图象在π0,2⎡⎤⎢⎥⎣⎦内恰好有两条对称轴,则实数ω的值可以是__________(写出一个满足题意的ω即可).16.已知函数()22e 18xf x a x =-+,其中0a >且1a ≠.若()f x 存在两个极值点1x ,2x ,则实数a 的取值范围为__________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知在ABC 中,5A B C +=,()3sin sin B C A -=,2AB =.(1)求ABC 的外接圆半径R ;(2)求sin A .18.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 为梯形,且//AD BC ,AB AD ⊥,22PA AB BC AD ====,E 为PB 边上的一点,满足2BE EP =.(1)求证:直线//PD 面ACE ;(2)F 为线段BC 的中点,求直线PF 与平面ACE 所成角的余弦值.19.某兴趣小组利用所学统计与概率知识解决实际问题.(1)现有甲池塘,已知小池塘里有10条鲤鱼,其中红鲤鱼有4条.若兴趣小组捉取3次,每次从甲池塘中有放回地捉取一条鱼记录相关数据.用X 表示其中捉取到红鲤鱼的条数,请写出X 的分布列,并求出X 的数学期望()E X .(2)现有乙池塘,已知池塘中有形状大小相同的红鲤鱼与黑鲤鱼共10条,其中红鲤鱼有()010,a a a *<<∈N 条,身为兴趣小组队长的骆同学每次从池塘中捉了1条鱼,做好记录后放回池塘,设事件A 为“从池塘中捉取鱼3次,其中恰有2次捉到红鲤鱼”.当0a a =时,事件A 发生的概率最大,求0a 的值.20.已知数列{}n a 是公差为()0d d ≠的等差数列,n S 是{}n a 的前n 项和,n *∈N .(1)若11a =,且22n n a a =,求数列{}n a 的通项公式;(2)若13a d =,数列{}n b a 的首项为1a ,满足13n n b b a a +=,记数列{}n b 的前n 项和为n T ,求5T .21.已知抛物线()2:20O x py p =>,其顶点在坐标原点,直线1y =与抛物线交于M ,N 两点,且OM ON ⊥.(1)求抛物线O 的方程.(2)已知()22:21C x y +-= ,1A ,2A ,3A 是抛物线O 上的三个点,且任意两点连线斜率都存在.其中12A A ,13A A 均与C 相切,请判断此时圆心C 到直线23A A 的距离是否为定值,如果是定值,请求出定值;若不是定值,请说明理由.22.已知函数()e xax f x =和ln ()xg x ax=有相同的最大值.(1)求a ;(2)证明:存在直线y =b ,其与两条曲线()y f x =和()y g x =共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.曲靖一中2024届高三教学质量监测试卷(五)数学一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2,,0A a a =,{}2B x xx =-=,且B A ⊆,则a 的值为().A.1 B.1- C.1± D.2【答案】B 【解析】【分析】解二次方程化简集合B ,再由集合的包含关系求得a ,进而利用元素的互异性即可得解.【详解】因为{}{}200,1B x x x =-==且B A ⊆,则集合A 中必含元素0,1,所以21a =或1a =,得1a =±,根据集合中元素的互异性可知:1a =-.故选:B .2.已知221813iiz +=,则z 的虚部为().A.13-B.13i- C.13D.18-【答案】C 【解析】【分析】应用复数运算法则化简式子求z ,根据i z a b =+求出i z a b =-即可知z 的共轭复数,求出z 的虚部即可.【详解】4i 1n =,所以224522i i i i 1⨯===⋅-,1813i z =--,1813i z =-+,所以z 的虚部为13.故选:C .3.已知πcos()3αα=-,则tan 2α=().A.33 B.33-C.D.【答案】D 【解析】【分析】综合应用两角和与差的正弦、余弦和正切公式即可解决.πcos()3αα=-1cos sin 22αα=+,即31sin cos 22αα=,可得3tan 3α=,由正切的倍角公式可得233tan 2113α==-故选:D .4.已知F 是双曲线2213x y -=的左焦点,()1,3M ,P 是双曲线右支上的一动点,则PF PM +的最小值为().A.B.C.+D.【答案】C 【解析】【分析】利用双曲线定义得到2PF PF a '-=,进而根据PM PF MF '+≥',即可求解【详解】设双曲线的右焦点为F ',由2213x y -=可知a =2c =,则()2,0F ',因为P是双曲线右支上的一动点,根据双曲线的定义可知:2PF PF a '-==所以PF PM PF PM +=+',因为PF PM MF +'≥',当且仅当F ',P ,M 三点共线时,达到最小值MF ',因为()1,3M ,()2,0F ',所以MF '=,即PF PM +的最小值为MF +='故选:C .5.根据曲靖一中食堂人脸识别支付系统后台数据分析发现,高三年级小孔同学一周只去食堂一楼和二楼吃饭.周一去食堂一楼和二楼的概率分别为13和23,若他周一去了食堂一楼,那么周二去食堂二楼的概率为34,若他周一去了食堂二楼,那么周二去食堂一楼的概率为12,现已知小孔同学周二去了食堂二楼,则周一去食堂一楼的概率为().A.37 B.47C.15D.45【答案】A 【解析】【分析】利用贝叶斯概率公式求解即可.【详解】记小赵同学周一去食堂一楼为事件A ,周二去食堂一楼为事件B ,则本题所求()()()()()()()13334132173432P B A P A P A B P B A P A P B A P A ⨯⋅===⋅+⋅⨯+⨯.故选:A .6.过点()0,2P 作圆22:430C xx y -++=的两条切线,设切点为A ,B ,则切点弦AB 的长度为()A.B.142C.144D.147【答案】B 【解析】【分析】先求PC 以及切线长,再根据等面积法即可得结果.【详解】圆22:430C x x y -++=,即()2221x y -+=,易知PC =C 的半径1r =,所以切线长PA PB ==.所以四边形PACB 的面积为1212PACB S =⨯=.所以根据等面积法知:12PACB S PC AB ==⨯⨯,所以142AB =.故选:B .7.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若2C A =,a ,b ,c 成等差数列,则cos C =().A.18B.34C.12-D.45【答案】A 【解析】【分析】根据等差中项性质并结合正弦定理及正弦函数两角和差公式,倍角公式即可求解.【详解】因为2C A =,所以π3B A =-.又因为a ,b ,c 成等差数列,则2b a c =+.根据正弦定理可得:2sin sin sin B A C =+,即()2sin 3sin sin A A C =+,展开得:2sin 2cos 2cos 2sin sin sin A A A A A C +=+,进一步得:()()sin 22cos 1sin 12cos 2A A A A -=-,因为sin 0A ≠,可得28cos 2cos 30A A --=,又易知A 为锐角,所以3cos 4A =,则231cos 2148C ⎛⎫=⨯-= ⎪⎝⎭,故A 正确.故选:A .8.已知函数()f x 及其导函数()f x '的定义域均为R ,及()()g x f x '=,若()12f x -,()2g x +均为偶函数,则下列说法正确的是().A.()10f =B.()g x 的周期为2C.()()13f f -=D.()()02g g =【答案】C 【解析】【分析】根据奇函数和偶函数的定义,结合函数的周期性和对称性,即可判断.【详解】因为()12f x -是偶函数,则()()1212f x f x -=+,即()f x 关于1x =对称,对()()1212f x f x -=+两边同时求导可得:()()212212f x f x --=+'',即()()12120g x g x -++=,所以()g x 关于()1,0对称,又因为()2g x +是偶函数可得()()22g x g x +=-,即()g x 关于2x =对称.从而得()g x 的周期为4.所以()f x 的周期也为4.对于选项A ,因为若()f x 满足题意,则()f x c +也满足题意.故()f x 的值不确定,所以A 错;对于选项B ,()g x 的周期为4,所以B 错;对于选项C ,()f x 的周期也为4,所以()()13f f -=,所以C 对;对于选项D ,()g x 关于()1,0对称,所以()()02g g =-,所以D 错.故选:C .二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知x ,y 都是正数,且22x y +=,则下列说法正确的是().A.xy 的最大值为12B.12x y +的最小值为92C.224x y +的最小值为4D.+的最大值为2【答案】ABD 【解析】【分析】利用基本不等式可对A ,C 、D 判断;利用基本不等式“1”的应用可对B 判断;【详解】对A :22x y +=≥可得12xy ≤,当且仅当21x y ==,即1x =,12y =时成立,故A 选项正确;对B :由22x y +=,得12xy +=,所以()12222559y x x y x y x y ⎛⎫++=++≥+=⎪⎝⎭,故1292x y +≥,当且仅当23x y ==时成立,故B 选项正确;对C :()2222444x y x xy y +=++=,由A 知12xy ≤,所以2214444422x y xy +=-≥-⨯=,仅当21x y ==,即1x =,12y =时成立,故C 选项错误;对D :由A 知12xy ≤,所以22224x y =++=+≤+=,当且仅当21x y ==,即1x =,12y =时成立,故D 选项正确.故选:ABD .10.已知抛物线2:4C y x =,O 为坐标原点,直线l 经过抛物线的焦点F ,与抛物线C 交于点A ,B 两点,设()11,A x y ,()22,B x y ,抛物线C 的准线与x 轴的交点为G .则下列说法正确的是()A.124x x = B.当8AB =时,直线l 的斜率为1±C.GF 始终平分AGB ∠ D.()min 8AGB S = 【答案】BC 【解析】【分析】设直线l 的方程为:1x ny =+,联立直线与抛物线的方程通过韦达定理可判断A ,通过弦长公式可判断B ,通过0AG BG k k =+可判断C ,由三角形面积公式可判断D.【详解】显然直线l 的斜率不为0,设直线l 的方程为:1x ny =+,联立直线与抛物线得2440y ny --=,则124y y =-,所以221212116y y x x ==,所以A 选项错误;又因为()212124448AB x x p n y y n =++=++=+=,可得21n =,即11n k==±,所以1k =±,所以B 选项正确;即证0AG BG k k =+,即()()()12121212221212121212122288011222424ny y y y y y y y n nx x ny ny n y y n y y n y y n y y ++-++=+===++++++++++,所以C 选项正确;由上述知:12AGB S AB d =⋅ ,已知直线方程为:10x ny --=,则d =,所以()214442AGB S n =+=≥ ,当且仅当0n =时成立,所以()min 4AGB S = ,所以D 选项错误.故选:BC .11.已知函数()()sin f x x ωϕ=+,如图,A ,B 是直线12y =与曲线()y f x =的两个交点,若π3AB =,则下列说法正确的是().A.2ω=,π3ϕ=-B.()f x 在ππ,66⎡⎤-⎢⎥⎣⎦上单调递增C.5π12x =-是()f x 的一条对称轴 D.32y x =-是曲线()f x 的一条切线【答案】AD 【解析】【分析】由函数的图象可确定ω,ϕ的值,从而确定单调性和对称性,再通过求导得到切线方程.【详解】设11,2A x ⎛⎫ ⎪⎝⎭,21,2B x ⎛⎫⎪⎝⎭,则21π3x x -=.因为()112sin x ωϕ+=,()212sin x ωϕ+=,所以1π2π6x k ωϕ+=+,25π2π6x k ωϕ+=+,Z k ∈,所以()212π3x x ωϕωϕ+-+=,即()212π3x x ω-=,即2ω=.又因为2π2πsin 033f ωϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,且2π,03⎛⎫⎪⎝⎭为下降零点,所以2ππ2π3k ωϕ+=+,Z k ∈,即π2π3k ϕ=-+,Z k ∈,故取π3ϕ=-.故()πsin 23f x x ⎛⎫=- ⎪⎝⎭.所以A 选项正确;当ππ,66x ⎡⎤∈-⎢⎥⎣⎦,π2π2,033x ⎡⎤-∈-⎢⎥⎣⎦,显然不是单调增区间,所以B 选项错误;将5π12x =-代入方程得()5ππ7πsin 2sin 11236f x -⎛⎫⎛⎫=⨯-=-≠± ⎪ ⎪⎝⎭⎝⎭,显然不是对称轴,所以C 选项错误;令()π2cos 213f x x ⎛⎫'=-= ⎪⎝⎭得ππ3x k =+或πx k =,取点30,2⎛- ⎝⎭得其中一条切线为32y x =-,所以D 选项正确.故选:AD .12.远看曲靖一中文昌校区紫光楼主楼,一顶巨大的“博士帽”屹立在爨园之中.其基础主体结构可以看做是一个倒扣的正四棱台ABCD A B C D -''''.如图所示,过B '作底面ABCD 的垂线,垂足为G .记B BG α'∠=,B BC γ∠'=,GBC θ∠=,面BB C C ''与面ABCD 所成角为β,面BB C C ''与面BB G '所成角为x ,B C a ''=,BC b =,B G h '=,则()A.正四棱台ABCD A B C D -''''的体积为()2213h a b ab ++B.tan 2tan βα=C.sin sin sin αβγ=D .cos cos cos cos sin sin x θαγαγ-=【答案】ACD 【解析】【分析】根据正四棱台的体积计算公式即可判断A 选项;作出面BB C C ''与面ABCD 的二面角β,分别写出tan ,tan βα的表达式,即可判断B 选项;根据B GB ' ,B GH ' ,B HB ' ,BHG 均为直角三角形.得到sin sin sin BB B H BB αγβ'''==,即可判断C 选项;作出面BB C C ''与面BB G '的二面角,通过余弦定理即可判断D 选项.【详解】对于A ,根据正四棱台体积计算公式:(()221133V h S S h a b ab =++=++下上台,所以A 正确;对于B ,过G 点作BC 边的垂线交BC 于H 点,因为GH BC ⊥,B G '⊥面ABCD ,BC ⊂面ABCD ,所以B G BC '⊥,又,HG B G '⊂面B HG ',所以BC ⊥面B HG ',所以B HG '∠就为面BB C C ''与面ABCD 所成角的二面角β,则tan B H BB α'=',2tan B GGHGBGβ''==,则tan tan βα=.所以B 错误;对于C ,因为B G '⊥面ABCD ,BC ⊥面B HG ',所以B GB ' ,B GH ' ,B HB ' ,BHG 均为直角三角形.所以sin sin sin BB B H BB αγβ'''==,即sin sin sin αβγ=.所以C 正确;对于D ,过H 点作BB '的垂线,交BB '于I ,再在平面BB G '内过I 作BB '的垂线交BG 于J .易知此时面BB C C ''与面BB G '所成角的二面角就为HIJ x ∠=.设BJ m =,则sin IJ m α=,cos sin cos m IH αγγ=.cos sin cos IH m BH αγγ==,22222222cos cos cos 2cos 2cos cos m m JH BJ BH BJ BH m ααθθγγ=+-⋅=+,由余弦定理可知:222cos 2IJ IH JH x IJ IH+-=⋅,222222222222cos sin cos 2cos cos sin cos cos cos 2sin cos sin cos m m m m m m αγααθαγγγααγγ+--+=,222222sin cos cos sin cos cos 2cos cos cos 2sin cos sin cos αγαγγααθγααγγ+--+=,2cos cos cos cos cos cos cos sin cos sin sin sin αθαγθαγααγαγ--==,所以D 正确.故选:ACD .三、填空题:本题共4小题,每小题5分,共20分.13.已知向量()2,2a b += ,()1,3a b -= ,则22a b -= __________.【答案】8【解析】【分析】利用向量数量积及平方差公式可得答案.【详解】()()2221238a b a b a b -=+⋅-=⨯+⨯=.故答案为:8.14.已知等差数列{}n a 中,19a =-,33a =-.记()121,2,3,n n T a a a n == ,则数列{}n T 中的最小项为__________.【答案】162-【解析】【分析】先求出数列的通项公式,求出n T ,观察可得答案.【详解】因为等差数列{}n a ,所以公差3132a a d -==,即()913312n a n n =-+-⨯=-.由于19a =-,26a =-,33a =-,40a =,所以19T =-,254T =,3162T =-,450n T T T ==== ,所以()3min 162n T T ==-.故答案为:162-15.若函数()πsin 3y x ωω*⎛⎫=+∈ ⎪⎝⎭N 的图象在π0,2⎡⎤⎢⎥⎣⎦内恰好有两条对称轴,则实数ω的值可以是__________(写出一个满足题意的ω即可).【答案】3或4(只写一个即可)【解析】【分析】根据π0,2⎡⎤∈⎢⎣⎦x 求得ππππ,3323x ωω⎡⎤+∈+⎢⎥⎣⎦,结合已知条件图象在π0,2⎡⎤⎢⎥⎣⎦内恰好有两条对称轴,求得关于ω的不等式解出ω范围,因ω*∈N 确定ω的值.【详解】因为π0,2⎡⎤∈⎢⎣⎦x ,则ππππ,3323x ωω⎡⎤+∈+⎢⎥⎣⎦,因为需要包含两条相邻的对称轴,因为π3在区间内,则有3πππ5π2232ω≤+<,即71333ω≤<,所以3ω=或4.故答案为:3或4(只写一个即可)16.已知函数()22e 18xf x a x =-+,其中0a >且1a ≠.若()f x 存在两个极值点1x ,2x ,则实数a 的取值范围为__________.【答案】()1,11,e e ⎛⎫⎪⎝⎭【解析】【分析】根据函数存在两个极值点,得出导函数存在两个不同的变号零点,研究导函数的零点,()0f x '=即ln e x a a x =,令()ln xh x a a =,()e g x x =,分1a >和01a <<两种情况讨论,根据()h x 与()g x 有两个交点,求出()h x 过原点的切线,比较()h x 过原点的切线的斜率与()g x 斜率,得出关于两斜率的不等式求解a 即可.【详解】对函数()22e 18xf x a x =-+求导得:()()2ln 2e 2ln e xxf x a a x a a x =-=-',因为()f x 存在两个极值点,所以()f x '有两个不同的变号零点.令()0f x '=,有ln e x a a x =,令()ln xh x a a =,()e g x x =,所以()h x 与()g x 有两个交点;当1a >时,()ln xh x a a =,()2ln xh x a a '=,设过原点的直线与()ln x h x a a =的切点坐标为()00,ln xx a a ,切线斜率为02ln x k a a =,所以切线方程为:()0020ln ln xxy a a a a x x -=-,将原点坐标带入切线方程得01ln x a=.此时切线的斜率为:122ln ln eln ak aa a==,现在需要ln e x a a x =有两个交点,即2eln e k a =<,因为1a >,有ln 0a >,所以0ln 1a <<,所以1e a <<;同理知当01a <<时,ln 0a <,2eln e k a =<,即1ln 0a -<<,所以11ea <<.综上知:a 的取值范围为()1,11,e e ⎛⎫ ⎪⎝⎭.故答案为:()1,11,e e ⎛⎫ ⎪⎝⎭四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知在ABC 中,5A B C +=,()3sin sin B C A -=,2AB =.(1)求ABC 的外接圆半径R ;(2)求sin A .【答案】(1)2R =(2)14【解析】【分析】(1)根据内角和求出C ,由正弦定理即可得结果;(2)通过两角和与差的正弦公式可得tan B ,即得sin B ,cos B ,最后根据()sin sin A B C =+即可得结果.【小问1详解】因为5A B C +=,πA B C ++=,所以π6C =.又因为2AB c ==,所以根据正弦定理得:24sin cR C==,所以2R =.【小问2详解】因为()()3sin sin sin B C A B C -==+,展开可得:sin cos 2cos sin B C B C =,即23tan 3B =,所以sin 7B =,cos 7B =,因为πA BC ++=,所以()273211321sin sin sin cos cos sin 727214A B C B C B C =+=+=⋅+⋅=.18.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 为梯形,且//AD BC ,AB AD ⊥,22PA AB BC AD ====,E 为PB 边上的一点,满足2BE EP =.(1)求证:直线//PD 面ACE ;(2)F 为线段BC 的中点,求直线PF 与平面ACE 所成角的余弦值.【答案】(1)证明见解析(2)659【解析】【分析】(1)连接BD 交AC 于G ,再连接EG ,证明出AGD CGB △∽△,可得出BG BEDG EP=,可证明出//PD AG ,再利用线面平行的判定定理可证得结论成立;(2)以点A 为坐标原点,AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法可求得直线PF 与平面ACE 所成角的余弦值.【小问1详解】证明:连接BD 交AC 于G ,再连接EG.因为//AD BC ,则DAG BCG ∠=∠,ADG CBG ∠=∠,则AGD CGB △∽△,所以,2BG BCDG AD ==,又因为2BE EP = ,则2BEEP =,所以,BG BE DG EP=,所以,//PD AG ,因为PD ⊄平面ACE ,AG ⊂平面ACE ,因此,//PD 平面ACE .【小问2详解】解:由题可得:PA ⊥平面ABCD ,AB AD ⊥,以点A 为坐标原点,AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系A xyz -.则()0,0,0A ,()0,0,2P ,24,0,33E ⎛⎫⎪⎝⎭,()2,2,0C ,因为F 为线段BC 的中点,则()2,1,0F ,所以,24,0,33AE ⎛⎫= ⎪⎝⎭,()2,2,0AC =.设面ACE 的法向量为(),,m x y z = ,则22024033m AC x y m AE x z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取2x =,可得()2,2,1m =--,又因为()2,1,2PF =-,设直线PF 与平面ACE 所成角为θ,则44sin cos ,339PF m PF m PF m θ⋅====⨯⋅,则65cos 9θ===,因此,直线PF 与平面ACE 所成角的余弦值为659.19.某兴趣小组利用所学统计与概率知识解决实际问题.(1)现有甲池塘,已知小池塘里有10条鲤鱼,其中红鲤鱼有4条.若兴趣小组捉取3次,每次从甲池塘中有放回地捉取一条鱼记录相关数据.用X 表示其中捉取到红鲤鱼的条数,请写出X 的分布列,并求出X 的数学期望()E X .(2)现有乙池塘,已知池塘中有形状大小相同的红鲤鱼与黑鲤鱼共10条,其中红鲤鱼有()010,a a a *<<∈N 条,身为兴趣小组队长的骆同学每次从池塘中捉了1条鱼,做好记录后放回池塘,设事件A 为“从池塘中捉取鱼3次,其中恰有2次捉到红鲤鱼”.当0a a =时,事件A 发生的概率最大,求0a 的值.【答案】19.分布列见解析,()65E X =20.07a =【解析】【分析】(1)根据已知条件求出每次捉到红鲤鱼的概率,23,5X B ⎛⎫~ ⎪⎝⎭,根据二项分布的公式可以求出分布列期望.(2)根据已知条件求出()P A 的表达式,求导判断函数的单调性,求出函数最值,结合010a <<且a *∈N ,比较()6P ,()7P 大小确定a 值.【小问1详解】由题可得:X 0=,1,2,3,可得:每次捉到红鲤鱼的概率为42105p ==.易知23,5X B ⎛⎫~ ⎪⎝⎭,()332705125P X ⎛⎫=== ⎪⎝⎭;()21323541C 55125P X ⎛⎫⎛⎫==⋅= ⎪ ⎪⎝⎭⎝⎭;()22323362C 55125P X ⎛⎫⎛⎫==⋅= ⎪⎪⎝⎭⎝⎭;()32835125P X ⎛⎫===⎪⎝⎭.分布列如表所示:X123()P X 2712554125361258125所以()26355E X np ==⨯=.【小问2详解】每次捉鱼,捉到红鲤鱼的概率为10a,则捉到黑鲤鱼的概率为110a -.所以()()223233C 11010101000a a P A a a ⎛⎫⎛⎫=⋅-=-+ ⎪⎪⎝⎭⎝⎭,其中010a <<且a *∈N ,令()3210h a a a =-+,则()2320h a a a '=-+,()0h a '=解得0a =或203a =,故在200,3⎛⎫ ⎪⎝⎭上()0h a '>,()h a 为增函数,在20,103⎛⎫⎪⎝⎭上()0h a '<,()h a 为减函数,所以()max 203h a h ⎛⎫=⎪⎝⎭.又因为010a <<且a *∈N ,所以验证()546125P =,()44171000P =,所以()()max 7P A P =,所以07a =,综上所述:事件A 发生的概率最大时07a =.20.已知数列{}n a 是公差为()0d d ≠的等差数列,n S 是{}n a 的前n 项和,n *∈N .(1)若11a =,且22n n a a =,求数列{}n a 的通项公式;(2)若13a d =,数列{}n b a 的首项为1a ,满足13n n b b a a +=,记数列{}n b 的前n 项和为n T ,求5T .【答案】(1)n a n =;(2)5353T =.【解析】【分析】(1)根据给定条件,利用等差数列通项列式,求出公差d 即可求出通项公式.(2)利用等差数列通项列式,求出1,n n b b +的关系,利用构造法求出数列{}n b 的通项,再借助分组求和即得.【小问1详解】由数列{}n a 是等差数列,22n n a a =,得()()()()1112121221a n d a n d a n d +-=+-=+-,则11d a ==,所以数列{}n a 的通项公式为:()11n a n n =+-=.【小问2详解】因为数列{}n a 是等差数列,且满足13n n b b a a +=,则()()()()1111131331n n n a b d a b d a b d ++-=+-=+-,又13a d =,则化简得:134n n b b +=+,于是()1232n n b b ++=+,由11b a a =,得11b =,因此数列{}2n b +是以3为首项,3为公比的等比数列,则23n n b +=,即32n n b =-,所以()553131035313T -=-=-.21.已知抛物线()2:20O x py p =>,其顶点在坐标原点,直线1y =与抛物线交于M ,N 两点,且OM ON ⊥.(1)求抛物线O 的方程.(2)已知()22:21C x y +-= ,1A ,2A ,3A 是抛物线O 上的三个点,且任意两点连线斜率都存在.其中12A A ,13A A 均与C 相切,请判断此时圆心C 到直线23A A 的距离是否为定值,如果是定值,请求出定值;若不是定值,请说明理由.【答案】(1)2x y=(2)是定值,定值为1【解析】【分析】(1)先由题意求得,M N 的坐标,从而利用向量数量积的坐标表示求得p ,由此得解;(2)充分利用()21,2,3i i x y i ==,得到直线12A A 与13A A 的方程,利用与圆相切的性质同构出直线23A A 的方程,从而得解.【小问1详解】因为1y =与抛物线相交,联立212y x py =⎧⎨=⎩,解得1y x =⎧⎪⎨=⎪⎩()M,)N .因为OM ON ⊥,所以210OM ON p ⋅=-+= ,所以21p =,则抛物线的方程为2x y =.【小问2详解】由题易知直线12A A ,13A A ,23A A 斜率一定存在,设()111,A x y ,()222,A x y ,()333,A x y ,则()21,2,3i i x y i ==,则直线12A A 的方程为:()211121y y y y x x x x --=--,即()()1211y y x x x x -=+-,即()21120x x x y x x +--=,因为()22:21C x y +-= 的圆心为()0,2C ,半径为1r =,因为直线12A A 与圆C1=,平方化简得:2222121212230x x x x x x --++=,看成关于2x ,2y 为变量的式子得:()121211230y y x x y -++-=,同理得直线13A A 与圆C 相切,化简式子后得:()131311230y y x x y -++-=,所以可以同构出直线23A A 的方程为:()1111230y y x x y -++-=,则所以圆心()0,2C 到直线23A A 的距离为:11111y d y +===+,此时圆心C 到直线23A A 的距离为定值,定值为1.【点睛】关键点睛:本题解决的关键是同构出直线23A A 的方程,从而得解.22.已知函数()e x ax f x =和ln ()x g x ax=有相同的最大值.(1)求a ;(2)证明:存在直线y =b ,其与两条曲线()y f x =和()y g x =共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.【答案】(1)1a =(2)证明见解析【解析】【分析】(1)由导数确定函数的单调性,得最大值,由最大值相等得参数值;(2)设()()h x f x b =-,由(1)确定10eb <<,结合(1)中所得单调性,利用零点存在定理证明函数存在两个零点,得y b =与()y f x =的图象有两个交点,同理得y b =与()()ln y f x g x ==也有两个交点,于是为满足题意有两个交点重合,结合()(ln )g x f x =可得出三个交战的横坐标之间的关系,从而证得结论成立.【小问1详解】()f x 定义域是(,)-∞+∞,()g x 的定义域是(0,)+∞,因为()()()211ln ,e x a x x f x g x ax''--==,当a<0时,()01f x x '<⇒<,()01f x x '>⇒>,()00e g x x '<⇒<<,()0e g x x '>⇒>,则()f x 在(),1-∞上单调递减,在()1,+∞单调递增,不存在最大值,()g x 在()0,e 上单调递减,在()e,+∞单调递增,也不存在最大值;同理知当0a >时,()f x 在(),1-∞上单调递增,在()1,+∞单调递减,()g x 在()0,e 上单调递增,在()e,+∞单调递减,所以()f x 有极大值()1ea f =,即()f x 的最大值,()g x 有极大值()1e e g a =,即()g x 的最大值,所以1e ea a =,即1a =;【小问2详解】由(1)知()()()ln ,ln e x x x f x g x f x x===,由于0x >时,()0f x >,1x >时,()0g x >,因此只有10e b <<才可能满足题意,记()e xx h x b =-,且10e b <<,由(1)得()h x 在(),1-∞上单调递增,在()1,+∞单调递减,且()()110,00eh b h b =->=-<,所以存在()10,1x ∈,使得()10h x =,设2()e x x x ϕ=-,则()e 2x x x ϕ'=-,设()()m x x ϕ'=,则()e 2x m x =-',0ln 2x <<时,()0m x '<,()m x 递减,ln 2x >时,()0m x '>,()m x 递增,所以min ()(ln 2)22ln 20m x m ==->,所以()(ln 2)0x ϕϕ''≥>,()ϕx 是增函数,0x >时,()(0)10x ϕϕ>=>,1211(e 0bb b ϕ=->,11e b b b <又1110eb b h b b ⎛⎫=-< ⎪⎝⎭,所以存在011,x b ⎛⎫∈ ⎪⎝⎭,使得()00h x =,即此时y b =与()y f x =有两个交点,其中一个交点在()0,1内,另一个交点在()1,+∞内,同理y b =与()()ln y f x g x ==也有两个交点,其中一个交点在()0,e 内,另一个交点在()e,+∞内,若y b =与()y f x =和()y g x =共有三个不同的交点,则其中一个交点为两条曲线()y f x =和()y g x =的公共点,记其横坐标为2x ,令()()()222ln f x g x f x ==,则()()221,e ,ln 0,1x x ∈∈,记y b =与()(),y f x y g x ==的三个交点的横坐标从左到右依次为324,,x x x ,且满足()()()()32432241e ,x x x f x f x g x g x <<<<===,且2222ln e x x x x =,即2222e ln x x x =,又()()()()3224ln ,ln f x f x f x f x ==,且()()3224,ln 0,1,,ln 1,e x x x x ∈∈,且()f x 在()0,1和()1,e 上分别单调,所以3224ln ,ln x x x x ==,即24e x x =,所以22342,x x x x =为34,x x 的等比中项,所以从左到右的三个交点的横坐标324,,x x x 成等比数列.【点睛】本题考查用导数求函数的最值,用导数研究方程的根的问题,属于难题.对于方程的根的问题,难点在于寻找两个方程的根之间的关系,首先第一步由零点存在定理证明存在两个零点(方程有两个根),其次通过函数式关系()(ln )g x f x =找到两个方程的根之间的关系,再根据等比数列的性质证明结论成立.。
云南省曲靖市第一中学2016届高三高考复习质量监测(五)理数试题 含解析

一、选择题(本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{|31}M x x =-<<,{|0}N x x =≤,则集合{|1}x x ≥=( ) A .M N B .M N C .()RCMND .()RCM N【答案】C 【解析】 试题分析:{}30MN x x =-<≤,{}1MN x x =<,{}()0R C MN x x =≥,故选C 。
考点:集合的运算. 2。
函数212()log(1)f x x =-的单调递增区间为( )A .(0,)+∞B .(,0)-∞C .(1,)+∞D .(,1)-∞- 【答案】D考点:函数的单调性. 3。
圆22(1)1xy +-=被直线0x y +=分成两段圆弧,则较长弧长与较短弧长之比为( )A .1:1B .2:1C .3:1D .4:1【解析】试题分析:圆心)1,0(到直线0x y +=的距离为22,半径为1,则0x y +=截圆的弦所对的劣弧的圆心角为090,则较长弧长与较短弧长之比439090360=-.故选C.考点:直线与圆的位置关系.4。
设,m n 是空间两条直线,,αβ是空间两个平面,则下列命题中不正确的是( )A .若,//m n αα⊂,则//n mB .若,m m αβ⊂⊥,则αβ⊥C .若,n n αβ⊥⊥,则//αβD .若,m n αα⊂⊥,则m n ⊥ 【答案】A考点:点线面的位置关系。
5。
已知()f x 是定义在R 上的奇函数,对x R ∀∈恒有(2)()(2)f x f x f -=+,当(0,1)x ∈时,2()f x x x =-,则3()2f =( )A .34B .34- C .14-D .14【答案】D试题分析:()f x 是定义在R 上的奇函数,则(0)0f =,由(2)()(2)f x f x f -=+得(0)(2)(2),(2)0f f f f =+∴=,又13()()(2)22f f f -=+,231111()()()[()()]22222f f f ∴=-=-=--14=,故选D 。
云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(1)

一、单选题1. 若定义在上的函数满足,且<0,,,,则的大小关系为( )A.B.C.D.2. 函数(,常数,,)的部分图象如图所示,为得到函数的图象,只需将函数的图象()A .向右平移个长度单位B .向右平移个长度单位C.向左平移个长度单位D .向左平移个长度单位3. 已知两个单位向量的夹角为,则下列向量是单位向量的是( )A.B.C.D.4. 赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成的),类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设,则()A.B.C.D.5.已知,则( )A.B .4C.D.6. 已知集合,,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.如图,圆锥的底面直径和高均是,过的中点作平行于底面的截面,以该截面为底面挖去一个圆柱,则剩下的几何体的表面积为()A.B.C.D.云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(1)云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(1)二、多选题8. 已知是定义在R 上的偶函数,其导函数为,且,则不等式的解集为( )A.B.C.D.9. 定义平面向量的一种运算“”如下:对任意的两个向量,,令,下面说法一定正确的是( )A .对任意的,有B.存在唯一确定的向量使得对于任意向量,都有成立C.若与垂直,则与共线D.若与共线,则与的模相等10.已知圆锥的侧面积为,底面圆的周长为,则( )A .圆锥的母线长为4B.圆锥的母线与底面所成角的正弦值为C.圆锥的体积为D.沿着圆锥母线的中点截圆锥所得圆台的体积为11. 面对新冠肺炎疫情冲击,我国各地区各部门统筹疫情防控和经济社会发展均取得显著成效.下表显示的是年月份到月份中国社会消费品零售总额数据,其中同比增长率是指和去年同期相比较的增长率,环比增长率是指与上个月份相比较的增长率,则下列说法正确的是( )中国社会消费品零售总额月份零售总额(亿元)同比增长环比增长累计(亿元)428178-7.50% 6.53%106758531973-2.80%13.47%138730633526-1.80% 4.86%172256732203-1.10%-3.95%2044598335710.50% 4.25%238029935295 3.30% 5.14%2733241038576 4.30%9.30%3119011139514 5.00% 2.43%35141512405664.60%2.66%391981A .年月份到月份,社会消费品零售总额逐月上升B .年月份到月份,月份同比增长率最大C .年月份到月份,月份环比增长率最大D .第季度的月消费品零售总额相比第季度的月消费品零售总额,方差更小12. 已知圆锥的底面圆的半径与球的半径相等,且圆锥,与球的表面积相等,则( )A .圆锥的母线与底面所成角的余弦值为B.圆锥的高与母线长之比为C.圆锥的侧面积与底面积之比为3三、填空题四、解答题D .球的体积与圆锥的体积之比为13. 从5名男医生名女医生中选3名医生组成一个医疗小分队,要求其中男女医生都有,则不同的组队方案共有______种数字回答.14. 已知一组数据8.6,8.9,9.1,9.6,9.7,9.8,9.9,10.2,10.6,10.8,11.2,11.7,则该组数据的第80百分位数为__________.15.若,,且,,则的值是______.16.已知数列的前项和为,满足.(1)求证:数列为等比数列;(2)设的前项和为,求.17.已知数列的前项积为,且满足.(1)求的值;(2)试猜想数列的通项公式,并给予证明;(3)若,记数列的前项和为,证明:.18.如图,某污水处理厂要在一正方形污水处理池内修建一个三角形隔离区以投放净化物质,其形状为三角形,其中位于边上,位于边上.已知米,,设,记,当越大,则污水净化效果越好.(1)求关于的函数解析式,并求定义域;(2)求最大值,并指出等号成立条件?19. 已知函数.(1)求的单调递增区间;(2)在中,a ,b ,c 为角A ,B ,C 的对边,且满足,且,求角A 的值,进而再求的取值范围.20.已知数列的前项和满足.(1)求证:是等差数列;(2)若当且仅当时,最大,比较与的大小.21. 已知是个正整数组成的行列的数表,当时,记.设,若满足如下两个性质:①;②对任意,存在,使得,则称为数表.(1)判断是否为数表,并求的值;(2)若数表满足,求中各数之和的最小值;(3)证明:对任意数表,存在,使得.。
云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(1)

一、单选题二、多选题1.将函数的图像向右平移个单位长度后得到曲线,若关于轴对称,则的最小值是( )A.B.C.D.2.双曲线的焦点坐标为( )A.B.C.D.3. 宫灯又称宫廷花灯,是中国彩灯中富有特色的汉民族传统手工艺品之一,如图为一件三层六角宫灯,三层均为正六棱柱,其中上、下层正棱柱的底面周长均为60cm ,高为6cm ,中间一层的正棱柱高为18cm.设计一个装该宫灯的可从中间打开的球形盒子,则该盒子的表面积至少为()A.B.C.D.4.已知函数A.B.C.D.5. 设是半径为1的圆上的三点,且,则的最大值是( )A.B.C.D .16. 已知各项均为正数的等比数列,则的值A.B.C.D.7. 已知双曲线的焦距为,过双曲线的右焦点的直线与双曲线的两条渐近线分别交于、两点,为坐标原点,若且,则双曲线的离心率为( )A.B.C.D.8. 下列函数中,既是偶函数又在上单调递增的函数是( )A.B.C.D.9. 如图,已知四棱锥的底面是直角梯形,,,,平面,,下列说法正确的是()A .与所成的角是B.与平面所成的角的正弦值是C .平面与平面所成的锐二面角余弦值是云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(1)云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(1)三、填空题四、解答题D.是线段上动点,为中点,则点到平面距离最大值为10. “杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广,创建了超级杂交稻技术体系,为我国粮食安全、农业科学发展和世界粮食供给作出了杰出贡献.某杂交水稻种植研究所调查某地水稻的株高,得出株高(单位:)近似服从正态分布.已知时,有,,.下列说法正确的是( )A.该地水稻的平均株高约为B .该地水稻株高的方差约为100C .该地株高超过的水稻约占68.27%D .该地株高低于的水稻约占99.87%11. 已知事件A ,B满足,,则下列选项正确的是( )A .若,则B .若A 与B互斥,则C .若A 与B相互独立,则D .若,则A 与B 相互独立12. 小王于2016年底贷款购置了一套房子,根据家庭收入情况,小王选择了10年期每月还款数额相同的还贷方式,且截止2020年底,他没有再购买第二套房子.下图是2017年和2020年小王的家庭收入用于各项支出的比例分配图:根据以上信息,判断下列结论中不正确的是()A .小王一家2020年用于饮食的支出费用跟2017年相同B .小王一家2020年用于其他方面的支出费用是2017年的3倍C .小王一家2020年的家庭收入比2017年增加了1倍D .小王一家2020年用于房贷的支出费用比2017年减少了13. 已知三棱锥的外接球O 的半径为,为等边三角形,若顶点P 到底面ABC 的距离为4,且三棱锥的体积为4,则满足上述条件的顶点P 的轨迹长度是___________.14. 祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为,高皆为的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面上.以平行于平面的平面于距平面任意高处可横截得到及两截面,可以证明知总成立.据此,短轴长为,长轴为的椭球体的体积是__________.15. 已知抛物线C :x 2=2py的焦点为F ,过F 且垂直于y 轴的直线与C 相交于A ,B 两点,若△AOB (O 为坐标原点)的面积为18,则p =________.16.设函数(1)设,,证明:在区间内存在唯一的零点;(2)设,若对任意,有,求的取值范围.17.如图,在四棱锥中,平面平面,,,,,,.(1)求证:平面;(2)求四面体的体积.18. 已知函数的最小正周期为.(1)求的值,并写出的对称轴方程;(2)在中角的对边分别是满足,求函数的取值范围.19. 如图,已知正方体的棱长为4,点E满足,点F是的中点,点G满足(1)求证:四点共面;(2)求平面与平面夹角的余弦值.20. 已知函数.(1)求的最小值;(2)证明:方程有三个不等实根.21. 已知函数,.(1)求的单调性;(2)若,且的最小值小于,求的取值范围.。
云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题

一、单选题1.已知,其中为虚数单位,则( )A.B.C.D.2. 某班会课上,班主任拟从甲、乙,丙、丁、戊五名同学选3人以新冠疫情为主题分享体会,则甲没被选中的概率为( )A.B.C.D.3.已知集合,,则中元素的个数是( )A .0B .1C .2D .34. 已知函数的导函数为,且满足关系式,则的值等于A.B.C.D.5. 已知是定义在上的奇函数,且;当时,,则A .-1B .0C .1D .26. 若向量,,则A.B.C .3D.7. 已知集合M ={-1,0,1},N ={x |x =ab ,a ,b ∈M ,且a ≠b },则集合M 与集合N 的关系是( )A .M =NB .M ∩N =NC .M ∪N =ND .M ∩N =∅8. 已知定义在实数集上的函数满足,则的最大值为( )A.B.C.D.9. 若复数满足,则其共轭复数在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限10. 已知集合A ={x |(x +2)(x +3)≥0},B ={x |x <0},则A ∩B =( )A .[﹣3,﹣2]B .(﹣∞,﹣3]∪[﹣2,+∞)C .(﹣∞,﹣3]D .(﹣∞,﹣3]∪[﹣2,0)11.中,角A 、B 、C 的对边分别为a 、b 、c ,且,,则面积的最大值为A.B .4C.D.12. 下列函数中,既是偶函数又在上单调递减的是( )A.B.C.D.13.设命题,,则是( )A .,B .,C .,D .,云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题二、多选题14.已知函数 的图象过点,若对恒成立,则的最小值为A.B.C.D.15. 双曲线,则此双曲线的离心率为( )A.B.C.D.16.圆与圆的公切线共有A .1条B .2条C .3条D .4条17. 若,则( )A.B.C.D.18. 已知正实数,满足,则下列结论中正确的是( )A.B .的最小值为36C.D.的最小值为1619.在中,为中点,且,则( )A.B.C .∥D.20. 经研究,变量y 与变量x 具有线性相关关系,数据统计如下表,并且根据表中数据,求得y 关于x的线性回归方程为,下列正确的是( )x 247101522y8.19.41214.418.524A .变量y 与x 呈正相关B .样本点的中心为(10,14.4)C.D .当时,y 的估计值为1321. 已知正方体的展开图如图所示,则下列说法正确的有()A.B .平面C .平面D.22.对于给定的,其外心为,重心为,垂心为,则下列结论正确的是( )A.B.C.过点的直线交于,若,,则三、填空题D .与共线23. 下列命题中,错误的是( )A.B.C.D.24. (多选)2020年12月26日太原地铁2号线开通,在一定程度上缓解了市内交通的拥堵状况,为了了解市民对地铁2号线开通的关注情况,某调查机构在地铁开通后两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构.并制作出如下等高堆积条形图:根据图中信息,下列结论正确的是( )A .样本中男性比女性更关注地铁2号线开通B .样本中多数女性是35岁及以上C .样本中35岁以下的男性人数比35岁及以上的女性人数多D .样本中35岁及以上的人对地铁2号线的开通关注度更高25.函数(是正实数)只有一个零点,则的最大值为_______.26. 如图(1)为陀螺实物体,图(2)为陀螺的直观图,已知,分别为圆柱两个底面圆心,设一个陀螺的外接球(圆柱上、下底面圆周与圆锥顶点均在球面上)的半径为2,球心为,点为圆锥顶点,若圆锥与圆柱的体积比为1:6,则圆柱的体积为___________________.27. 已知函数则的值是________.28. 已知,则曲线在点处的切线方程为__________.29.在中,,,,,求_________.30. 已知函数的部分图象如图所示,若函数在上的最大值等于1,则的取值范围是___________.四、解答题五、解答题31. 已知函数在上不单调,则实数的取值范围是____.32.已知集合,集合,若,则实数的取值范围为___________.33. 在长方体中,,.(1)在边上是否存在点,使得,为什么?(2)当存在点,使时,求的最小值,并求出此时二面角的正弦值.34.在中,,,.(1)求A 的大小;(2)求外接圆的半径与内切圆的半径.35.已知椭圆的两个焦点与短轴的一个端点连线构成等边三角形,且椭圆的短轴长为.(1)求椭圆的标准方程;(2)是否存在过点的直线与椭圆相交于不同的两点,且满足(为坐标原点)若存在,求出直线的方程;若不存在,请说明理由.36. ChatGPT 是由人工智能研究实验室OpenAI 于2022年11月30日发布的一款全新聊天机器人模型,它能够通过学习和理解人类的语言来进行对话,ChatGPT 的开发主要采用RLHF (人类反馈强化学习)技术.在测试ChatGPT 时,如果输入的问题没有语法错误,则ChatGPT 的回答被采纳的概率为85%,当出现语法错误时,ChatGPT 的回答被采纳的概率为50%.(1)在某次测试中输入了8个问题,ChatGPT 的回答有5个被采纳.现从这8个问题中抽取3个,以表示抽取的问题中回答被采纳的问题个数,求的分布列和数学期望;(2)已知输入的问题出现语法错误的概率为10%,(i )求ChatGPT 的回答被采纳的概率;(ii )若已知ChatGPT 的回答被采纳,求该问题的输入没有语法错误的概率.37. 已知函数,,.(1)将函数化简成,(,,),的形式;(2)求函数的值域.38. 已知圆.(1)证明:圆C 过定点;(2)当时,点P 为直线上的动点,过P 作圆C 的两条切线,切点分别为A ,B,求四边形面积最小值,并写出此时直线AB 的方程.39. 随着全球经济一体化进程的不断加快,机械零件的加工质量决定了制造工厂的生存,零件加工精度逐渐成为供应商判断制造公司产品的标准.已知某公司生产不同规格的一种产品,根据检测精度的标准,其合格产品的质量y()与尺寸x ()之间近似满足关系式(b ,c 为大于0的常数).现随机从中抽取6件合格产品,测得数据如下:尺寸x(〕384858687888质量y(〕16.818.820.722.42425.5根据测得数据作出如下处理:令,得相关统计量的值如下表:75.324.618.3101.4(1)根据所给统计数据,求y关于x的回归方程;(2)若从一批该产品中抽取n件进行检测,已知检测结果的误差满足,求至少需要抽取多少件该产品,才能使误差在(-0.1,0.1)的概率不少于0.9545?附:①对于样本,i)(i=1,2,…,n),其回归直线的斜率和截距的最小二乘估计公式分别为:,,.②,则40. 2020年1月15日教育部制定出台了《关于在部分高校开展基础学科招生改革试点工作的意见》(也称“强基计划”),《意见》宣布:2020年起不再组织开展高校自主招生工作,改为实行强基计划.强基计划主要选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.据悉强基计划的校考由试点高校自主命题,校考过程中通过笔试后才能进入面试环节.已知甲、乙两所大学的笔试环节都设有三门考试科目且每门科目是否通过相互独立.若某考生报考甲大学,每门科目通过的概率均为,该考生报考乙大学,每门科目通过的概率依次为,,,其中.(1)若,分别求出该考生报考甲、乙两所大学在笔试环节恰好通过一门科目的概率;(2)强基计划规定每名考生只能报考一所试点高校,若以笔试过程中通过科目数的数学期望为依据作出决策,当该考生更希望通过甲大学的笔试时,求的范围.41. 植物生长调节剂是一种对植物的生长发育有调节作用的化学物质,它在生活中的应用非常广泛.例如,在蔬菜贮藏前或者贮藏期间,使用一定浓度的植物生长调节剂,可抑制萌芽,保持蔬菜新鲜,延长贮藏期.但在蔬菜上残留的一些植物生长调节剂会损害人体健康.某机构研发了一种新型植物生长调节剂A,它能延长种子、块茎的休眠,进而达到抑制萌芽的作用.为了测试它的抑制效果,高三某班进行了一次数学建模活动,研究该植物生长调节剂A对甲种子萌芽的具体影响,通过实验,收集到A的浓度u()与甲种子发芽率Y的数据.表(一)A浓度u()发芽率Y0.940.760.460.240.10若直接采用实验数据画出散点图,(如图1所示)除了最后一个数据点外,其他各数据点均紧临坐标轴,这样的散点图给我们观察数据背后的规律造成很大的障碍,为了能够更好的观察现有数据,将其进行等价变形是一种有效的途径,通过统计研究我们引进一个中间量x,令,通过,将A浓度变量变换为A的浓度级变量,得到新的数据.表(二)A浓度u()A浓度级x12345发芽率Y0.940.760.460.240.10(1)如图2所示新数据的散点图,散点的分布呈现出很强的线性相关特征.请根据表中数据,建立Y关于x的经验回归方程;(2)根据得到的经验回归方程,要想使得甲种子的发芽率不高于0.4,估计A浓度至少要达到多少?附:对于一组数据,…,,其经验回归方程中斜率和截距的最小二乘估计公式分别为:,.42. 某城市在进行创建文明城市的活动中,为了解居民对“创文”的满意程度,组织居民给活动打分(分数为整数.满分为100分).从中随机抽取一个容量为120的样本.发现所有数据均在内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:(1)算出第三组的频数.并补全频率分布直方图;(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)43. 某省2019年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等,同时认定A,B,C等为合格,D等为不合格,已知甲、乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校样本的频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.(1)求图中x的值,并根据样本数据比较甲、乙两校的合格率;(2)在乙校的样本中,从成绩等级为C,D的学生中随机抽取2名学生进行调研,求抽出的2名学生中至少有1名学生成绩等级为D的概率.44. 为了参加某数学竞赛,某高级中学对高二年级理科、文科两个数学兴趣小组的同学进行了赛前模拟测试,成绩(单位:分)记录如下.理科:79,81,81,79,94,92,85,89文科:94,80,90,81,73,84,90,80(1)画出理科、文科两组同学成绩的茎叶图;六、解答题(2)计算理科、文科两组同学成绩的平均数和方差,并从统计学的角度分析,哪组同学在此次模拟测试中发挥比较好;(3)若在成绩不低于90分的同学中随机抽出3人进行培训,求抽出的3人中既有理科组同学又有文科组同学的概率.(参考公式:样本数据的方差:,其中为样本平均数)45. 已知椭圆E 的中心为坐标原点,对称轴为x 轴、y 轴,且过两点.(1)求E 的方程;(2)设过点的直线交E 于M ,N 两点,过M 且平行于x 轴的直线与线段AB 交于点T ,点H 满足.证明:直线HN 过定点.46. 如图,在斜三棱柱中,底面是边长为的正三角形,为棱的中点,,,.(1)求证:平面;(2)求斜三棱柱的体积.47. 如图,为圆柱的轴截面,是圆柱上异于的母线.(1)证明:平面;(2)若,当三棱锥的体积最大时,求二面角的正弦值.48. 如图,四棱柱的底面是正方形,侧面是菱形,,平面平面,E ,F分别为的中点.(1)求证:平面;(2)求与平面所成角的正切值.七、解答题49.如图,在三棱柱中,直线平面,平面平面.(1)求证:;(2)若,在棱上是否存在一点,使得四棱锥的体积为?若存在,指出点的位置;若不存在,请说明理由.50.如图,已知长方形中,,,为的中点.将沿折起,使得平面平面.(1)求证:;(2)若点是线段上的一动点,问点在何位置时,二面角的余弦值为.51. 当今社会面临职业选择时,越来越多的青年人选择通过创业、创新的方式实现人生价值.小明是一名刚毕业的大学生,通过直播带货的方式售卖自己家乡的特产,下面是他近5个月的家乡特产收入y (单位:万元)情况,如表所示.月份56789时间代号t 12345家乡特产收入y32.42.221.8(1)根据5月至9月的数据,求y 与t 之间的线性相关系数(精确到0.001),并判断相关性;(2)求出y 关于t的回归直线方程(结果中保留两位小数),并预测10月收入能否突破1.5万元,请说明理由.附:相关系数公式:.(若,则线性相关程度很强,可用线性回归模型拟合)②一组数据,,…,,其回归直线方程的斜率和截距的最小二乘估计公式分别为,.③参考数据:.52. 3月14日为国际数学日,也称为节,为庆祝该节日,某中学举办了数学文化节活动,其中一项活动是“数学知识竞赛”,初赛采用“两轮制”方式进行,要求每个班级派出两个小组,且每个小组都要参加两轮比赛,两轮比赛都通过的小组才具备参与决赛的资格.高三(6)班派出甲、乙两个小组参赛,在初赛中,若甲、乙两组通过第一轮比赛的概率分别是,通过第二轮比赛的概率分别是,且各个小组所有轮次比赛的结果互不影响.(1)若高三(6)班获得决赛资格的小组个数为,求的数学期望;(2)已知甲、乙两个小组在决赛中相遇,决赛以三道抢答题形式进行,抢到并答对一题得100分,答错一题扣100分,得分高的获胜.假设这两组在决赛中对每个问题回答正确的概率恰好是各自获得决赛资格的概率,且甲、乙两个小组抢到该题的可能性分别是,假设每道题抢与答的结果均互不影响,求乙已在第一道题中得100分的情况下甲获胜的概率.53. 某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量(件)与单价(元)之间的关系如图所示,该网店与这种商品有关的周开支均为25元.(1)根据周销售量图写出(件)与单价(元)之间的函数关系式;(2)写出利润(元)与单价(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.54. 某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图:(1)求直方图中的值;(2)由频率分布直方图可以认为,这种产品的质量指标值服从正态分布,试计算数据落在上的概率.参考数据:若,则,.(3)设生产成本为,质量指标为,生产成本与质量指标之间满足函数关系,假设同组中的每个数据用该组区间的右端点值代替,试计算生产该食品的平均成本.55. 随着科技发展的日新月异,人工智能融入了各个行业,促进了社会的快速发展.其中利用人工智能生成的虚拟角色因为拥有更低的人工成本,正逐步取代传统的真人直播带货.某公司使用虚拟角色直播带货销售金额得到逐步提升,以下为该公司自2023年8月使用虚拟角色直播带货后的销售金额情况统计.年月2023年8月2023年9月2023年10月2023年11月2023年12月2024年1月月份编号12345615.425.435.485.4155.4195.4销售金额/万元若与的相关关系拟用线性回归模型表示,回答如下问题:(1)试求变量与的样本相关系数(结果精确到0.01);(2)试求关于的经验回归方程,并据此预测2024年2月份该公司的销售金额.八、解答题附:经验回归方程,其中,,样本相关系数;参考数据:,.56. “一带一路”为世界经济增长开辟了新空间,为国际贸易投资搭建了新平台,为完善全球经济治理拓展了新实践.某企业为抓住机遇,计划在某地建立猕猴桃饮品基地,进行饮品,,的开发.(1)在对三种饮品市场投放的前期调研中,对100名试饮人员进行抽样调查,得到对三种饮品选择情况的条形图.若饮品的百件利润为400元,饮品的百件利润为300元,饮品的百件利润为700元,请估计三种饮品的平均百件利润;(2)为进一步提高企业利润,企业决定对饮品进行加工工艺的改进和饮品的研发.已知工艺改进成功的概率为,开发新饮品成功的概率为,且工艺改进与饮品研发相互独立;(ⅰ)求工艺改进和新品研发恰有一项成功的概率;(ⅱ)若工艺改进成功则可为企业获利80万元,不成功则亏损30万元,若饮品研发成功则获利150万元,不成功则亏损70万元,求该企业获利的数学期望.57. 已知函数(其中,,,均为常数,且,,)的部分图像如图所示.(1)求的解析式;(2)若,,求的值域.58. 如图,四边形ABCD 为矩形,△BCF 为等腰三角形,且∠BAE =∠DAE =90°,EA //FC.(1)证明:BF //平面ADE .(2)设,问是否存在正实数,使得三棱锥A ﹣BDF的高恰好等于BC?若存在,求出的值;若不存在,请说明理由.59.在①,②,③这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,判断的形状;若问题中的三角形不存在,说明理由.问题:是否存在,它的内角A,B,C的对边分别为a,b,c,且a,b,c成等差数列,﹐__________?注:如果选择多个条件分别解答,按第一个解答计分.60. 已知函数,为常数,.(1)讨论函数的单调性;(2),不等式恒成立,求的取值范围.61. 为落实食品安全的“两个责任”,某市的食品药品监督管理部门和卫生监督管理部门在市人民代表大会召开之际特别邀请相关代表建言献策.为保证政策制定的公平合理性,两个部门将首先征求相关专家的意见和建议,已知专家库中共有5位成员,两个部门分别独立地发出批建邀请的名单从专家库中随机产生,两个部门均邀请2位专家,收到食品药品监督管理部门或卫生监督管理部门的邀请后,专家如约参加会议.(1)设参加会议的专家代表共X名,求X的分布列与数学期望.(2)为增强政策的普适性及可行性,在征求专家建议后,这两个部门从网络评选出的100位热心市民中抽取部分市民作为群众代表开展座谈会,以便为政策提供支持和补充意见.已知这两个部门的邀请相互独立,邀请的名单从这100名热心市民中随机产生,食品药品监督管理部门邀请了名代表,卫生监督管理部门邀请了名代表,假设收到食品药品监督管理部门或卫生监督管理部门的邀请后,群众代表如约参加座谈会,且,请利用最大似然估计法估计参加会议的群众代表的人数.(备注:最大似然估计即最大概率估计,即当P(X=k)取值最大时,X的估计值为k)62. 已知双曲线的右焦点为,左、右顶点分别为,且为上不与重合的一点,直线的斜率之积为3.(1)求双曲线的方程;(2)平面一点且不在上,过的两条直线分别交的右支于两点和两点,若四点在同一圆上,求直线的斜率与直线的斜率之和.。
云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(高频考点版)

一、单选题二、多选题三、填空题1.若不等式的解集为,则实数的值分别是( )A.B.C.D.2. 已知幂函数为偶函数,若函数在[2,4]上单调,则实数a 的取值范围为( )A.B.C.D.3. 已知集合M ={x|0<x<1},集合N ={x|-2<x<1},那么“a ∈N”是“a ∈M”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4. 设函数,则,则( )A .0B.C.D .15.已知,,则的值为( )A .2B.C.D.6.设是定义域为的偶函数,且在区间上单调递减,则( )A.B.C.D.7. 下列各函数中,最小值为2的是( )A.B.C.D.8. 下列4个说法中正确的有( )①命题“若,则”的逆否命题为“若则”;②若,则;③若复合命题:“”为假命题,则p ,q 均为假命题;④“”是“”的充分不必要条件.A .①B .②C .③D .④9. 已知随机变量的分布列如下:1230.10.70.2则数学期望______.10. 已知a 为实数,并且的实部和虚部相等,则___________.11.在的展开式中,的系数为______.云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(高频考点版)云南省曲靖市第一中学2023届高三教学质量监测(五)数学试题(高频考点版)四、解答题12.二项式的展开式中的系数为________.13.如图,在四棱锥中,四边形是直角梯形,,,底面,, ,是的中点.(1)求证:平面;(2)若二面角的余弦值为,求直线与平面 所成角的正弦值.14. 某种水果按照果径大小可分为四类:标准果,优质果,精品果,礼品果.某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:等级标准果优质果精品果礼品果个数10304020(1)用样本估计总体,果园老板提出两种购销方案给采购商参考:方案1:不分类卖出,单价为20元/.方案2:分类卖出,分类后的水果售价如下表:等级标准果优质果精品果礼品果售价(元/)16182224从采购商的角度考虑,应该采用哪种方案较好?并说明理由.(2)从这100个水果中用分层抽样的方法抽取10个,再从抽取的10个水果中随机抽取3个,表示抽取到精品果的数量,求的分布列及数学期望.15. 已知,集合,.(1),能否相等?若能,求的值;若不能,试说明理由;(2)若命题,命题,且是的充分不必要条件,求的取值范围.16. 已知函数.(1)解关于x 的不等式;(2)若对,都有成立,求a 的最大值.。
2023届云南省曲靖市第一中学高三下学期教学质量监测试卷(五)数学答案

曲靖一中2023届高三教学质量监测卷(五)数学参考答案一、选择题题号123456789101112答案BADDBDCABCDABDACDBCD1.【答案】B【解析】因为{}{}2R12,R A x x B x x A =∈-≤≤=∈∉∣∣,所以{}{}2222-<>∈=>∈=x x R x x R x B 或,所以{}|2A B x x =<≤ .故选B2.【答案】A【详解】因为复数z 在复平面内对应的点为(1,-2),所以12z i =-,则12i z =+,所以()()()212i 12i 34i 34i.12i 12i 12i 555z z ++-+====-+--⨯+故选:A.3.【答案】D【详解】对于A,方差反映一组数据的波动大小,将一组数据中的每个数据都加上或减去同一个常数后,方差不变,但平均数变化,故A 错误,对于B,具有线性相关关系的两个变量x ,y 的相关系数为r ,则r 越接近于1,x 和y 之间的线性相关程度越强,故B 错误,对于C,在一个22⨯列联表中,由计算得2χ的值,则2χ的值越大,判断两个变量有关的把握越大,故C 错误,对于D ,()2~1,X N σ ,(01)(12)P X P X ∴<<=<<(1)(2)0.50.20.3P X P X =>->=-=.故D 正确.4.【答案】D【详解】设弧AD 所在圆的半径为R ,弧BC 所在圆的半径为r ,弧AD 长度是弧BC 长度的3倍,ππ322R r ∴=⨯,即3R r =,22CD R r r ∴=-==,解得:1r =,3R =,∴该曲池的体积221119ππππ510π4444V R r AA ⎛⎫⎛⎫=-⨯=-⨯= ⎪⎪⎝⎭⎝⎭.故选:D.5.【答案】B【解析】函数π()2sin(0)3f x x ωω=->的图象向左平移3ωπ个单位得到函数()y g x =的图象,则()ππ2sin 2sin 33g x x x ωωω⎡⎤⎛⎫=+-= ⎪⎢⎝⎭⎣⎦,又因为()y g x =在ππ[,64-上为增函数,所以ππ62ω⎛⎫⋅-≥- ⎪⎝⎭,且ππ42ω⋅≤,解得:2ω≤,故ω的最大值为2.故选:B.6.【答案】D【详解】若乙和丙在相邻两天参加服务,不同的排法种数为2525A A 240=,若乙和丙在相邻两天且甲安排在第一天参加服务,不同的排法种数为2424A A 48=,由间接法可知,满足条件的排法种数为24048192-=种.故选:D.7.【答案】C 【详解】设:bl y x a=,则点M 位于第四象限,由双曲线定义知:1222222MF MF MF MF MF a -=-==,14MF a ∴=;设过点2F 且与l 平行的直线的倾斜角为α,则tan ba α=,cos a cα∴=,12cos aF F M c∴∠=;在12F F M △中,由余弦定理得:222122112122cos 2F F MF MF F F M F F MF +-∠=⋅,即22244168a c a a c ac +-=,整理可得:225c a =,e ∴==故选:C.8.【答案】A【详解】设()e 1xf x x =--.因为()e 1xf x '=-,所以当0x <时,()0f x '<,()f x 在(),0∞-上单调递减,当0x >时,()0f x '<,()f x 在()0,∞+上单调递增,所以当x ∈R ,且0x ≠时,()()00f x f >=,即e 1x x >+.所以()0.33e30.31 2.1a --+>=⨯=,0.6e 0.61 1.6b =>+=,所以 1.6c =最小,又因为0.60.90.3e e e13e 33b a -==<<,所以b a <.综上可知,c b a <<.故选:A 二、多选题9.【答案】BCD【详解】A 选项,由()227a b-=,以及||||1a b == ,可得1447a b +-⋅=,则1=||||cos ,2a b a b a b ⋅<>=- ,即1cos ,2a b <>=- ,又,[0,180]a b <>∈ ,所以夹角,=a b <>120°.对于B ,因为()1,1a x =- ,()1,3b x =+ ,且,a b共线,则()()1311x x ⨯=-+解得2x =±.所以B 正确.C 选项,a 在b方向上的投影向量为282cos ,,171717b a b b a a b b b b b ⋅⎛⎫⨯=⨯==-=-- ⎪⎝⎭,故C 正确,对于D ,因为22b a ==,所以2a b -==5==所以2a b -的最大值是5,所以D 正确,10.【答案】ABD【详解】∵224120x y y +--=即22(2)16x y +-=,∴圆心()0,2C ,半径4r =()1,0P -在圆C内,PC =设圆心C 到直线AB 的距离为d,由题意得0d ≤≤∵AB =min AB ==,故A正确;1122ABC S AB d d =⋅=⨯==△∵205d ≤≤,∴当25d =时,()max ABC S =△,故B 正确C 错误,.取MN 的中点E ,则CE MN ⊥,又MN =3CE =,∴点E 的轨迹是以()0,2C 为圆心,半径为3的圆.因为2PM PN PE +=,且min 33PE PC =-= ,所以||PM PN +的最小值为65-D 正确.故选:ABD .11.【答案】ACD【解析】取11B C 、1C C 中点E F 、,连接11D E D F 、、EF 、PF ,由PF ∥1BC ∥11A D 且PF =111BC A D =知11A PFD 是平行四边形,∴1D F ∥1A P ,∵1D F ⊄平面1A PD ,1A P ⊂平面1APD ,1D F ∥平面1A PD ,同理可得EF ∥平面1A PD ,∵EF ∩1D F =F ,∴平面1A PD ∥平面1D EF ,则Q 点的轨迹为线段EF ,A 选项正确;如图,建立空间直角坐标系,则()11,0,0A ,11,1,2P ⎛⎫⎪⎝⎭,()0,0,1D ,设)z x Q ,1,(,1,0≤≤z x ,则()11,0,1A D =- ,110,1,2A P ⎛⎫= ⎪⎝⎭ ,()1,1,.D Q x z =设(),,m a b c=为平面1A PD 的一个法向量,则110,0.m A D m A P ⎧⋅=⎪⎨⋅=⎪⎩ 即0,0,2a c c b -+=⎧⎪⎨+=⎪⎩得,.2a c c b =⎧⎪⎨=-⎪⎩取1c =,则11,,12m ⎛⎫=-⎪⎝⎭ .若1D Q ⊥平面1A PD ,则1D Q ∥m ,即存在R λ∈,使得1D Q m λ=,则12x z λλλ=⎧⎪⎪=-⎨⎪=⎪⎩,解得[]20,1x z ==-∉,故不存在点Q 使得1D Q ⊥平面1A PD ,B 选项错误;1A PD △的面积为定值,∴当且仅当Q 到平面1A PD 的距离d 最大时,三棱锥1Q A PD -的体积最大.12332A Q m d x z m ⋅==+-,①23≤+z x ,()213d x z =-+,则当0x z +=时,d 有最大值1;②32x z +>,()213d x z =+-,则当2x z +=时,d 有最大值13;综上,当0x z +=,即Q 和1C 重合时,三棱锥1Q A PD -的体积最大,C 选项正确;11D C ⊥平面11BB C C ,111D C C Q ∴⊥,12D Q,12C Q ∴=,Q点的轨迹是半径为2,圆心角为2π的圆弧,轨迹长度为4,D 选项正确.故选:ACD.12.【答案】BCD【详解】令x =0,则()()f y f y -=-,所以()f x 为奇函数,故A 错误.令x =y =0,得()00f =,故B 正确.任取()12,1,1x x ∈-,且12x x <,则()()2121121x x f x f x f x x ⎛⎫--= ⎪-⎝⎭.因为()()1221121110x x x x x x +-=-+->,所以21121x x x x -<-,所以2112011x x x x -<<-.因为()0,1x ∈,()0f x >,所以211201x x f x x ⎛⎫-> ⎪-⎝⎭,()()12f x f x <,即()f x 在()1,1-上单调递增.因为A ,B 是锐角ABC 的内角,所以π2A B +>,所以π2A B >-,所以πsin sin cos 2A B B ⎛⎫>-= ⎪⎝⎭.因为sin A ,()cos 0,1B ∈,所以()()A f B f sin cos <,故C 正确.因为0n x >,且21112n n nx x x ++=,所以122(0,1)1n n n x x x +=∈+.令y =-x ,则222()1x f x f x ⎛⎫= ⎪+⎝⎭,令n x x =,则()()12221nn n nx f x f f x x +⎛⎫== ⎪+⎝⎭,所以()()12n n f x f x +=.因为()11f x =,所以(){}n f x 是首项为1,公比为2的等比数列,所以()12n n f x -=,故D 正确.故选:BCD 三、填空题13.34【详解】依题意()()432340123412x x a a x a x a x a x +++=++++,令0=x ,得90=a ,令1x =,得43012342343a a a a a ++++=+=.故=+++4321a a a a 3414.16π【详解】如图1所示,连接PO ,则222PO OB PB +=,解得2PO =即2PO OB ==,此圆锥外接球的球心为O ,半径为2,表面积为24π216πS =⨯=15.32+【详解】(1sin )(1cos )1sin cos sin cos ()f x x x x x x x ++=+++=,2(sin cos )11sin cos 2x x x x +-=+++,令πsin cos 4t x x x ⎛⎫=+=+ ⎪⎝⎭,因为π0,2x ⎛⎫∈ ⎪⎝⎭,所以ππ3π,444x ⎛⎫+∈ ⎪⎝⎭,所以πsin 4x ⎤⎛⎫+∈⎥ ⎪⎝⎭⎝⎦,所以(π4t x ⎛⎫=+∈ ⎪⎝⎭,所以(211(),22g t t t t =++∈,对称轴011t =-<,所以211()22g t t t =++在(单调递增,所以当0t =max 3()2g t g ==+,即当πsin 14x ⎛⎫+= ⎪⎝⎭,π4x =时,()(1sin )(1cos )f x x x =++32.故答案为:32.16.32【详解】设过点0,2p F ⎛⎫ ⎪⎝⎭的直线l 为2py kx =+,()()1122,,,A x y B x y联立方程222x py p y kx ⎧=⎪⎨=+⎪⎩消去x 得()2222104p y k py -++=,可得2124p y y =∵33AF BF ==,则可得:211232p y p y ⎧+=⎪⎪⎨⎪+=⎪⎩,可得231224p p p ⎛⎫⎛--= ⎪⎝⎭⎝⎭,解得32p =过点M 作准线的垂线,垂足为D ,则可得1sin MFMDMN MN MND==∠若MN MF取到最大值即MND ∠最小,此时直线MN 与抛物线C 相切23x y =,即23x y =,则23y x'=设200,3x M x ⎛⎫ ⎪⎝⎭,则切线斜率023k x =,切线方程为()2000233x y x x x -=-切线过30,4N ⎛⎫- ⎪⎝⎭,代入得220023433x x --=-,解得032x =±,即33,24M ⎛⎫± ⎪⎝⎭则33,22MD ND ==,即π4MND ∠=则1sin MFMDMN MN MND==∠2故答案为:322四、解答题.17.【详解】(1)因为422n n n S a -=…①,故111422n n n S a +++-=…②,()*n N ∈②-①可得11142222n n n n n a a a +++-+=-.整理可得112n n n a a -++=,即12n n b -=,()*n N ∈.因为11222nn n n b b +-==,()*n N ∈.故{}n b 是等比数列.(2)当1n =时,111422S a -=,解得11a =,又112n n n a a -++=,)()()()(2126543212n n n a a a a a a a a S ++++++++=- 12531-++++=n b b b b 4141--=n 314-=n .18.【详解】(13sin cos b A b A a c -=-,由正弦定理,3sin sin sin cos sin sin B A B A C A -+=,()3sin sin sin cos sin sin B A B A A B A -++=,3sin sin cos sin sin B A B A A +=.因为sin 0A >3cos 1B B +=,即1sin 62B π⎛⎫+= ⎪⎝⎭.因为()0,B π∈,所以7,666B πππ⎛⎫+∈ ⎪⎝⎭,所以566B ππ+=,即23B π=.(2)法一:因为点D 在AC 边上,满足AC 3AD =,所以2133BD BA BC =+ ,所以22222141433999BD BA BC BA BC BA BC ⎛⎫=+=++⋅ ⎪⎝⎭,因为3AB =,2BD =,23ABC π∠=,所以241414939992BC BC =⨯+-⨯⨯⨯,即260BC BC -=,解得6BC = ,即BC=6.法二:由已知得DC=2AD,设x AD =,x DC 2=.∵BDCADB ∠-=∠π∴BDCCOS ADB COS ∠-=∠∴x x 22942⨯-+=xa x 2224422⨯⨯-+-,即()1622-=x a ………①又∵120=∠ABC ∴21329922-=⨯⨯-+a x a ,即()19322=--+x a a ………②由方程①②解得6=a ,即BC=6.19.【详解】(1)11//BB CC ,且1BB ⊄平面11ACC A ,1CC ⊂平面11ACC A ,1//BB ∴平面11ACC A ,又1BB ⊂ 平面1B BD ,且平面1B BD 平面11ACC A DE =,1//BB DE ∴;(2)连结1A C ,取AC 中点O ,连结1AO ,BO ,在菱形11ACC A中,160A AC ∠= ,∴AC A 1∆是等边三角形,又O 为AC 中点,1A O AC ∴⊥,平面ABC ⊥平面11ACC A ,平面ABC 平面11ACC A AC =,1A O ⊂平面11ACC A ,且1A O AC ⊥,1A O ∴⊥平面ABC ,OB ⊂平面ABC ,1A O OB ∴⊥,又AB BC = ,BO AC ∴⊥,以点O 为原点,1,,OB OC OA 为x 轴,y 轴,z 轴,建立空间直角坐标系,假设存在点D,满足题意,设)0,0a D ,(()22≤≤-a ,)0,00,(O ,()0,2,0A -,(10,0,A ,()3,0,0B ,()0,,3a BD -=,(10,2,DE AA ==,设平面1B BDE 的一个法向量为),,(z y x n =,则00n BD n DE ⎧⋅=⎨⋅=⎩ ,所以⎩⎨⎧=+=+-032203z y ay x,令z =,则3=y ,a x =,故)3,3,(-=a n ,设平面11ABB A 的法向量为),,(111z y x m =()32,2,01=AA ,()0,2,3=AB ⎪⎩⎪⎨⎧=⋅=⋅001m AB m AA ,⎩⎨⎧=+=+0230322y x z y ,令3-=y ,则2=x ,3=z ,故)3,3,2(-=m,211612122cos 2=+-==a a ,解2=a ,所以点D 在点C 的位置时,平面11ABB A 与平面1B BDE 所成锐角为3π.由于D 不与A 、C 重合,故AC 上不存满足题意的点.20.【详解】(1)由题可知10个学校,参与“自由式滑雪”的人数依次为27,15,43,41,32,26,56,36,49,20,参与“单板滑雪”的人数依次为46,52,26,37,58,18,25,48,33,30,其中参与“单板滑雪”的人数超过30人的学校有6个,参与“单板滑雪”的人数超过30人,且“自由式滑雪”的人数超过30人的学校有4个,记“这10所学校中随机选取2所学校参与“单板滑雪”的人数超过30人”为事件A ,“这10所学校中随机选取2所学校参与“自由式滑雪”的人数超过30人”为事件B ,则()26210C 1C 3P A ==,()24210C 2C 15P AB ==,所以,()()()25P AB P B A P A ==.(2)参与“自由式滑雪”人数在40人以上的学校共4所,X 的所有可能取值为0,1,2,3,所以()0346310C C 2010C 1206P X ⋅====,()1246310C C 6011C 1202P X ⋅====,()2146310C C 3632C 12010P X ⋅====,()3046310C C 413C 12030P X ⋅====,所以X 的分布列如下表:X0123P1612310130所以()131623210305E X =+⨯+⨯=(3)记“甲同学在一轮测试中获得“优秀””为事件C ,则23233322220C 1C 33327P ⎛⎫⎛⎫⎛⎫=⨯-+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由题意,甲同学在集训测试中获得“优秀”的次数服从二项分布20,27B n ⎛⎫⎪⎝⎭,由题意列式20827n ≥,得545n ≥,因为*N n ∈,所以n 的最小值为11,故至少要进行11轮测试21【详解】(1)设动圆P 的半径为R ,圆心P 的坐标为(),x y 由题意可知:圆1C 的圆心为()11,0C -,半径为72;圆2C 的圆心为()21,0C ,半径为12. 动圆P 与圆1C 内切,且与圆2C 外切,112122724212PC R PC PC C C PC R ⎧=-⎪⎪∴⇒+=>=⎨⎪=+⎪⎩∴动圆P 的圆心的轨迹E 是以12,C C 为焦点的椭圆,设其方程为:22221(0)x y a b a b+=>>,其中224,22,2,3a c a b ==∴==,从而轨迹E 的方程为:22143x y +=证明:(2)由题意可知1(2,0)A -,2(2,0)A ,(4T ,)(0)t t ≠,设1(M x ,1)y ,2(N x ,2)y ,如图所示,直线1AT 的方程为(2)6t y x =+,直线2A T 的方程为(2)2t y x =-,联立方程22(2)6143t y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩,消去y 得2222(27)441080t x t x t +++-=,2124108227t x t -∴-⋅=+,即21254227t x t -=+,则2112254218(2)(2)662727t t t t y x t t -=+=+=++,22254218(,)2727t t M t t -∴++,联立方程22(2)2143t y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩,消去y 得2222(3)44120t x t x t +-+-=,∴22241223t x t -=+,即222263t x t -=+,则22222266(2)(2)2233t t t t y x t t --=-=-=++,2226(3t N t -∴+,26)3t t -+,22222221866273542269273MN t t t t t k t t t t t +++∴==-----++,∴直线MN 的方程为22226626()393t t t y x t t t -+=--+-+,即222666(1)999t t t y x x t t t =-+=-----,3t ≠±,故直线MN 过定点(1,0),所以FMN ∆的周长为定值8,当3t =±时,3(1,)2M ,3(1,)2N -或3(1,)2M -,3(1,)2N ,MN ∴过焦点(1,0),此时FMN ∆的周长为定值48a =,综上所述,FMN ∆的周长为定值8.22.【详解】(1)1=a ,x e x f x -=)(,1)(-='x e x f ,∴0)0(='f 又∵1)0(=f ,∴在))0(,0(f 处的切线方程为1=y .(2) ()f x 有两个零点,∴关于x 的方程e ax x =有两个相异实根, e 0ax >,∴0,x >)(x f 有两个零点即ln x a x=有两个相异实根.令()ln x G x x =,则()21ln x G x x -'=, ()0G x '>得0e x <<,()0G x '<得e,x >()G x ∴在()0,e 单调递增,在()e,+∞单调递减,()max 1()e e G x G ∴==,又()10,G = ∴当01x <<时,()0G x <,当1x >时,()0G x >,当x →+∞时,()0,G x →)(x f 有两个零点时,实数a 的取值范围为10,e ⎛⎫ ⎪⎝⎭;(3) 1,0a x ≥>,所以e e ax x x x ≥∴原命题等价于e ln 1x x x bx ≥++对一切()0,x ∞∈+恒成立,ln 1e x x b x x∴≤--对一切()0,x ∞∈+恒成立,令()ln 1e (0)x x F x x x x =-->,min (),b F x ∴≤()222ln e ln e x x x x x F x x x+=+='令()()2e ln ,0,x h x x x x ∞=+∈+,则()x 212e e 0,x h x x x x+'=+>()h x ∴在()0,+∞上单增,又()120e 11e 0,e 1e 10e h h -⎛⎫=>=-<-= ⎪⎝⎭,01,1e x ⎛⎫∴∃∈ ⎪⎝⎭使()00h x =,即0200e ln 0x x x +=①,当()00,x x ∈时,()0h x <,即()F x 在()00,x 递减当()0,x x ∈+∞时,()0h x >,即()F x 在()0,x +∞递增,()00min 000ln 1()e x x F x F x x x ∴==--由①知0200e ln x x x =-,001ln 000000ln 111e ln ln e x x x x x x x x ⎛⎫∴=-== ⎪⎝⎭, 函数()e x x x ϕ=在()0,+∞单调递增,001ln x x ∴=即00ln ,x x =-0ln 0min 0000111()e 11,x x F x x x x x --∴=--=+-=1,b ∴≤∴实数b 的取值范围为(],1-∞.。
