八年级数学上册三角形全等证明题专项练习
八年级数学上册第12章全等三角形证明经典50题(含答案)

3. 已知:∠ 1=∠2,CD=DE,EF//AB ,求证: EF=AC
A 12
F
C D E B
过 C 作 CG∥EF 交 AD 的延长线于点 G
CG∥EF,可得,∠ EFD=CGD
DE= DC
第 3 页 共 46 页
∠FDE=∠ GDC(对顶角) ∴△EFD≌△ CGD EF=CG ∠CGD=∠ EFD 又, EF∥AB ∴,∠ EFD=∠ 1 ∠1= ∠2 ∴∠ CGD=∠2 ∴△AGC 为等腰三角形, AC= CG 又 EF=CG ∴EF= AC
∵∠ EAB= ∠ BDE,
∴∠ AED= ∠ABD ,
∴四边形 ABDE 是平行四边形。
∴得: AE=BD ,
∵AF=CD,EF=BC ,
∴三角形 AEF 全等于三角形 DBC,
∴∠ F=∠C。
14.已知: AB=CD ,∠ A= ∠D,求证:∠ B=∠C
第 14 页 共 46 页
A
D
B
C
证明:设线段 AB,CD 所在的直线交于 E,(当 AD<BC 时,E 点是射 线 BA,CD 的交点, 当 AD>BC 时,E 点是射线 AB,DC 的交点) 。则: △AED 是等腰三角形。 ∴ AE=DE 而 AB=CD ∴BE=CE (等量加等量,或等量减等量) ∴△ BEC 是等腰三角形 ∴∠ B=∠C.
AE=AD+BE
第 11 页 共 46 页
在 AE 上取 F,使 EF=EB,连接 CF ∵ CE⊥AB ∴∠ CEB=∠CEF=90° ∵ EB=EF, CE=CE, ∴△ CEB≌△CEF ∴∠ B=∠ CFE ∵∠ B+∠ D=180°,∠ CFE+∠ CFA=180° ∴∠ D=∠ CFA ∵AC 平分∠ BAD ∴∠ DAC =∠ FAC 又∵ AC=AC ∴△ ADC ≌△ AFC(SAS) ∴AD =AF ∴AE=AF+FE=AD +BE
八年级数学上册 第12章 全等三角形证明经典50题(含答案)

八年级数学上册第12章 全等三角形证明经典50道含答案1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2ABAD B CDA B C3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGAB C D EF 2 1 B ACDF21 E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE。
人教版八年级上册数学第十二章全等三角形证明题训练

人教版八年级上册数学第十二章全等三角形证明题训练1.如图,已知:AB =AD ,BC =DE ,AC =AE ,试说明:∠1=∠2.2.如图,∠B =∠C =90°,E 是BC 的中点,DE 平分∠ADC .求证:AE 是∠DAB 的平分线.3.如图:A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF .求证:∠ABE ∠∠DCF .4.已知,在∠ABC 中,∠ACB =2∠B .当AD 为∠BAC 的角平分线时,求证:AB =AC +CD5.如图,点D ,E 分别在OA ,OB 上,点P 在OC 上,且PD PE =.若180ODP OEP ∠+∠=︒,求证:OC 平分AOB ∠.6.已知:如图,AD 、BF 相交于O 点,OA OD =,AB DF ∥,点E 、C 在BF 上,BE CF =.(1)求证:ABO ∠DFO ;(2)判断线段AC 、DE 的关系,并说明理由.7.如图,在ABC 中,D 是BC 边上的一点,AB DB =,BE 平分ABC ∠交AC 边于点E ,连接DE .(1)A ∠与BDE ∠相等吗?为什么?(2)若100A ∠=︒,50C ∠=︒,求AEB ∠的度数.8.如图,∠ABC 的两条高BE 、CD 相交于点O ,BD =CE .(1)求证:BE =CD ;(2)判断点O 是否在∠BAC 的平分线上,并说明理由.9.如图,A 、B 、C 、D 在同一直线上,且∠ABF ∠△DCE ,求证:(1)AF DE ∥、BF ∠CE ;(2)AC =BD10.如图,∠ABC 中,点D 在边BC 延长线上,100ACB ∠=︒,∠ABC 的平分线交AD 于点E ,过点E 作EH ∠BD ,垂足为H ,且50CEH ∠=︒.(1)求∠ACE 的度数;(2)求证:AE 平分∠CAF ;(3)若AC+CD =14,AB =8.5,且21ACD S =,求∠ABE 的面积.11.如图,DE ∠AB 于E ,DF ∠AC 于F ,若BD =CD 、BE =CF .(1)求证:∠BDE ∠△CDF(2)求证:AD 平分∠BAC ;(3)直接写出AB+AC与AE之间的等量关系.12.已知如图,B是CE的中点,AD=BC,AB=DC.DE交AB于F点.求证:(1)AD BC∥(2)AF=BF.13.如图,已知点B,E,C,F在一条直线上,BE=CF,AC DE∥,A D∠=∠.(1)求证:∠ABC ∠∠DFE;(2)若BF=12,EC=4,求BC的长.14.如图所示,E、F分别为线段AC上的两个点,且DE∠AC于点E,BF∠AC于点F,若AB=CD,AE=CF,BD交AC于点M.(1)试猜想DE与BF的关系,并证明你的结论;(2)求证:MB=MD.15.如图,已知点C,F在直线AD上,且有BC=EF,AB=DE,CD=AF.求证:∆ABC∠∆DEF.16.如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF∠AE,垂足为F,过B作BD∠BC交CF的延长线于D.(1)求证:AE=CD;(2)若AC=12cm,求BD的长17.如图,在∠ABC中,AB=AC,BD∠AC于D,CE∠AB于E,BD、CE相交于F.求证:(1)∠ABD∠∠ACE;(2)AF平分∠BAC.18.如图,在△ABC中,∠ACB=90°,AC=BC,点D在AC上,点E在BC的延长线上,CE=CD,BD的延长线交AE于点F.(1)求证:△ACE∠∠BCD;(2)求证:BF∠AE;(3)若BD=8,DF=2,直接写出△ABE的面积.19.已知:如图,AB=AD,∠C=∠E,∠1=∠2,求证:BC=DE.20.如图,A、E、F、C在一条直线上,AF=CE,过E、F分别作DE∠AC,BF∠AC,AB=CD,求证:(1)∠ABF∠∠CDE(2)BG=DG。
人教版八年级数学上册全等三角形的证明习题(大题)

全等三角形的证明1、如图,AB =AD ,∠BAD =∠CAE ,AC=AE ,求证:BC=DE2、如图,AF=DB ,BC=EF ,AC=DE ,求证:BC∠EF 。
3、已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线. 求证:AB =DC .4、如图,∠DCE =90°,CD =CE ,AD∠AC ,BE∠AC ,垂足分别为A 、B . 求证:AD +AB =BE .ABCDE5、已知,AC∠CE ,AC=CE , ∠ABC=∠EDC=900,证明:BD=AB+ED 。
6、如图,在∠ABC 中,D 为BC 边的中点,过D 点分别作DE ∠AB 交AC 于点E , DF ∠AC 交AB 于点F .求证:BF=DE 。
7、如图,点E 在AB 上,AC=AD ,请你添加一个条件,使图中存在全等三角形,并给予证明。
所添条件为 ,你得到的一对全等三角形是∆ ∆≅ .证明:ABCDE8、如图,AD 平分∠BAC ,DE∠AB 于E ,DF∠AC 于F ,且DB=DC ,求证:EB=FC.9、如图,AE 是∠BAC 的平分线,AB=AC 。
若点D 是AE 上任意一点,请证明:∠ABD∠∠ACD ;10、(1)把一大一小两个等腰直角三角板(即EC=CD,AC=BC )如图1放置,点D 在BC上,连结BE ,AD ,AD 的延长线交BE 于点F . 求证:(1)ΔACD∠ΔBCE (2)AF∠BE .FE D CB AECDBABACDEFB DE A(2)把左边的小三角板逆时针旋转一定的角度如图2放置,问AF与BE是否垂直?并说明理由.图2。
八年级上册数学全等三角形证明题

八年级上册数学全等三角形证明题一、全等三角形证明题1 20题及解析。
(一)题目1。
1. 题目。
已知:如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE = AC,延长BE交AC于F。
求证:AF = EF。
2. 解析。
证明:延长AD到G,使DG = AD,连接BG。
因为AD是BC边上的中线,所以BD = CD。
在△BDG和△CDA中,BD = CD,∠BDG = ∠CDA(对顶角相等),DG = DA。
根据SAS(边角边)全等判定定理,可得△BDG≌△CDA。
所以BG = AC,∠G = ∠CAD。
又因为BE = AC,所以BG = BE。
所以∠G = ∠BEG。
因为∠BEG = ∠AEF(对顶角相等),所以∠AEF = ∠CAD。
所以AF = EF。
(二)题目2。
1. 题目。
如图,在△ABC和△DEF中,AB = DE,BE = CF,∠B = ∠DEF。
求证:AC = DF。
2. 解析。
因为BE = CF,所以BE + EC = CF+EC,即BC = EF。
在△ABC和△DEF中,AB = DE,∠B = ∠DEF,BC = EF。
根据SAS全等判定定理,可得△ABC≌△DEF。
所以AC = DF。
(三)题目3。
1. 题目。
已知:如图,AB = CD,AE = DF,CE = FB。
求证:AF = DE。
2. 解析。
因为CE = FB,所以CE + EF = FB + EF,即CF = BE。
在△AEB和△DFC中,AB = CD,AE = DF,BE = CF。
根据SSS(边边边)全等判定定理,可得△AEB≌△DFC。
所以∠B = ∠C。
在△ABF和△DCE中,AB = CD,∠B = ∠C,BF = CE。
根据SAS全等判定定理,可得△ABF≌△DCE。
所以AF = DE。
(四)题目4。
1. 题目。
如图,在Rt△ABC中,∠ACB = 90°,CA = CB,D是AC上一点,E在BC的延长线上,且AE = BD,BD的延长线与AE交于点F。
八年级全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD B C证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴∠EBF=∠BEF 。
∵∠ABC=∠AED 。
∴∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点GCG∥EF,可得,∠EFD=CGDDE =DC∠FDE=∠GDC(对顶角)∴△EFD ≌△CGDEF =CG∠CGD=∠EFDBACDF21 E又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又 EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
人教版八年级上册数学第十二章全等三角形证明题练习

人教版八年级上册数学第十二章全等三角形证明题练习1.如图,点B,F,C,E在一条直线上,AB DE∥.=,AB ED∥,AC FD△≌△;(1)试说明ABC DEF(2)FB CE=吗?为什么?2.如图,△ADE的顶点D在△ABC的BC边上,且△ABD=△ADB,△BAD=△CAE,AC=AE.求证:BC=DE.3.己知:如图,点E,F是BD上的点,△AED=△CFB,AE=CF,BE=DF.求证:AB△CD,AB=CD.4.已知:如图,AB CD,B C=.求证:AF DE∠=∠,点E,F在线段AD上,BE CF=.5.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,△A=△EDF=60°.(1)求证:△ABC△△DEF;(2)若△B=100°,求△F的度数.6.如图,已知点C、点D都在线段AF上,AC=DF,BC△EF,△B=△E.求证:(1)△ABC△△DEF;(2)AB∥DE.=,M,N分别是AE,CD上的7.如图,在ADC中,DB是高,点E是DB上一点,AB DB=,EB CB=;点,且AM DN(1)试说明:ABE DBC ≅;(2)探索BM 和BN 的位置关系和数量关系,并说明理由.8.如图,已知点E ,D ,A ,B 在一条直线上,BC //EF ,△C =△F ,AD =1,AE =2.5,AB =1.5.(1)△ABC 和△DEF 全等吗?请说明理由.(2)小颖同学认为DF 与AC 相等,而小亮同学认为DF 与AC 平行,你认为谁的说法正确,并说明理由.9.如图,点D ,E 分别在AC ,AB 上,AD AE =,BE CD =.(1)求证:BD CE =.(2)若55A ∠=︒,30C ∠=︒,求COD ∠的度数.10.如图,已知,AB =AD ,BC =CD .(1)求证:△ABC △△ADC ;(2)若△1=30°,△2=50°,求△D 的度数.11.如图,AC △BD ,连接AD ,BC 交于点O ,若O 为BC 中点.(1)求证:AOC DOB ≌;(2)连接AB ,若2AB =,4AC =,若AD 的长是偶数,则AD 长为_______.12.如图,已知1B ∠=∠,BE CD =,BF CA =.(1)求证:D 2∠=∠;(2)若EF AC ∥,80BAC ∠=︒,求D ∠的度数.13.如图,在ABC 和AEF 中,点E 在BC 边上,AE AB =,AC AF =,CAF BAE ∠=∠,EF 与AC 交于点G .(1)求证:EF BC =;(2)若62B ∠=︒,24ACB ∠=︒,求FGC ∠的度数.14.已知:如图,,,12AB AD AC AE ==∠=∠.求证:.BC DE =15.如图所示,已知等腰Rt ABC △中,AC BC =,90ACB ∠=︒,点D 是AB 上一点,且AD BD <,AE CD ⊥于E ,BF CE ⊥于F .(1)试说明:ACE CBF ≌△△;(2)若2cm AE =,6cm BF =,求EF 的长度.16.如图,已知AB AD AM AN BM DN ===,,.(1)ABM 与ADN △全等吗?请说明理由:(2)请说明AC AE =.17.如图,△ABC 中,AD 平分BAC ∠,DG BC ⊥且平分BC ,DE AB ⊥于E ,DF AC ⊥于F .(1)证明:BE CF =;(2)如果5AB =,3AC =,求AE 、BE 的长.18.如图,已知AD 是ABC 的角平分线,且D 为BC 的中点,DE AB ⊥,DF AC ⊥.(1)写出图中所有的全等三角形;(2)求证:BE CF =.19.如图,AB AE=,AC DE∥.=,AB DE(1)求证:AD BC=;(2)若70DAB∠=︒,AE平分DAB∠,求B的度数.20.已知:如图,在△ABC,△ADE中,△BAC=△DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一直线上,连接BD.求证:(1)△BAD△△CAE;(2)试猜想BD,CE有何特殊位置关系,并证明.。
(完整版)八年级上册——全等三角形证明题题型归类训练
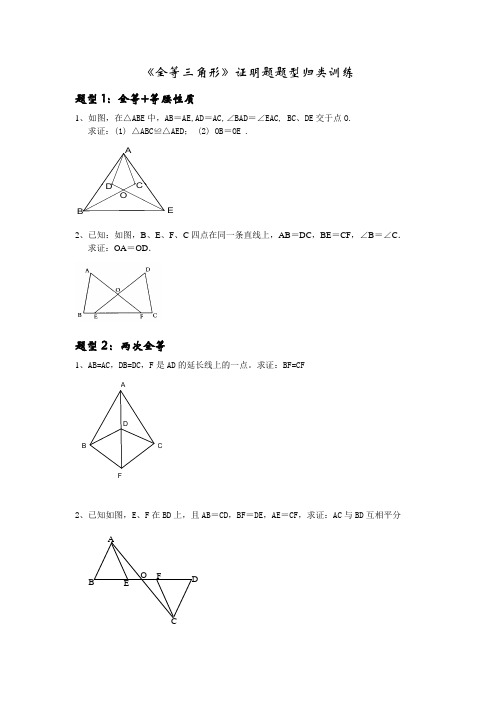
《全等三角形》证明题题型归类训练题型1:全等+等腰性质1、如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O. 求证:(1) △ABC ≌△AED ; (2) OB =OE .2、已知:如图,B 、E 、F 、C 四点在同一条直线上,AB =DC ,BE =CF ,∠B =∠C . 求证:OA =OD .题型2:两次全等1、AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CFFDCBA2、已知如图,E 、F 在BD 上,且AB =CD ,BF =DE ,AE =CF ,求证:AC 与BD 互相平分O C E BDAA B E O F D C3、如图,在四边形ABCD 中,AD ∥BC ,∠ABC=90°DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE=AC.求证:BG=FG题型3:直角三角形全等(余角性质)1、如图,在等腰Rt △ABC 中,∠C =90°,D 是斜边上AB 上任一点,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F ,CH ⊥AB 于H 点,交AE 于G . 求证:BD =CG .2、如图,将等腰直角三角形ABC 的直角顶点置于直线l 上,且过A ,B 两点分别作直线的垂线,垂足分别为D ,E ,请你在图中找出一对全等三角形,并写出证明它们全等的过程.AFCBDEG3、如图,∠ABC =90°,AB =BC ,D 为AC 上一点,分别过A 、C 作BD 的垂线,垂足分别为E 、F 求证:EF =CF -AE4、在△ABC 中,=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时, 求证: ①ADC ∆≌CEB ∆;②BE AD DE +=; (2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.5、如图:BE ⊥AC ,CF ⊥AB ,BM=AC ,CN=AB 。
八年级数学上册《三角形全等的判定》精选练习(8份)

23. 如图,已知 AB=AE,BC=ED,AC=AD. (1) ∠B=∠E 吗?为什么? (2)若点 F 为 CD 的中点,那么 AF 与 CD 有怎样的位置关系?请说明理由.
22. 证明:(1)在△EAD 和△FCB 中 AD=CB,AE=CF,DE=BF ∴△EAD≌△FCB(SSS) ∴∠D=∠B (2)由(1)知:△EAD≌△FCB ∴∠DEA=∠BFC ∵∠AEO=180-∠DEA,
∠CFO=180-∠BFC, ∴∠AEO=∠CFO
∴ AE∥CF
23. 解:(1)∠B=∠E 理由如下:在△ABC 和△AED 中 AB=AE,BC=ED,AC=AD. ∴△ABC≌△AED(SSS) ∴∠B=∠E.
∴△EAC≌△EBC(SSS) ∴∠A=∠C(全等三角形的对应角相等)
9 / 47
八年级数学上册《三角形全等的判定》精选练习
21. 解:(1) BD = DC (或点 D 是线段 BC 的中点), FD = ED , CF = BE 中 任选一个即可﹒ (2)以 BD = DC 为例进行证明: ∵CF∥BE, ∴∠FCD﹦∠EBD. 又∵ BD = DC ,∠ FDC﹦∠EDB, ∴△BDE≌△CDF.
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.AC=DC,∠A=∠D
5.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有
()
A.1对
B.2对
C.3对
D.4对
6.在△ABC 和 ∆A′B′C′ 中,∠C= ∠C′ ,b-a= b′ − a′ ,b+a= b′ + a′ ,则这两个三角形( )
八上全等三角形证明经典50题含答案(供参考)

1.已知:AB=4, AC=2, D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DEYD是BC中点ABD=DC在4ACD和4BDE中AD=DEZBDE=ZADCBD=DCAAACD^ABDEAAC=BE=2;在△ ABE中AB-BE<AE<AB+BEVAB=4即4・2V2ADV4+2KADOAAD=22.已知:D 是AB 中点,ZACB=90° ,求证,CD = -AB延长CD与P,使D为CP中点。
连接AP,BPVDP=DC,DA=DB•・・ACBP为平行四边形又NACB=90••・平行四边形ACBP为矩形/.AB=CP=1/2AB3.已知:BC=DE, ZB=ZE, ZC=ZD, F 是CD 中点,求证:Z1=Z25.证明:连接BF和EFV BC=ED,CF=DF, ZBCF= ZEDF.・・三角形BCF全等于三角形EDF(边角边)A BF=EF,ZCBF=ZDEF连接BE在三角形BEF中,BF=EF,ZEBF=ZBEF0V ZABC=ZAEDoA ZABE=ZAEB QA AB=AE O在三角形ABF和三角形AEF中AB=AE,BF=EF,ZABF=ZABE+ZEBF=ZAEB+ZBEF=ZAEF••・三角形ABF和三角形AEF全等。
A ZBAF=ZEAF(Z1=Z2)O6.已知:N1=N2, CD=DE, EF//AB,求证:EF=AC过C作CG〃EF交AD的延长线于点GCG//EF,可得,ZEFD=CGDDE=DCZFDE=ZGDC (对顶角)A A EFD^ACGDEF=CGZCGD=ZEFD又,EF/7AB••.,ZEFD=Z1Z1=Z2• .NCGD=N2.,.△AGC为等腰三角形,AC=CG又EF=CGAEF=AC7.已知:AD 平分NBAC, AC=AB+BD,求证:NB=2NCA证明:延长AB取点E,使AE=AC,连接DEVAD 平分NBACAZEAD = ZCADVAE=AC, AD=ADAAAED^AACD (SAS)AZE=ZCVAC=AB+BDAAE=AB+BDVAE=AB+BEABD=BEAZBDE=ZEV NABC = NE+NBDEA ZABC=2ZE:.ZABC=2ZC8.已知:AC 平分NBAD, CE±AB, ZB+ZD=180° ,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF VCE1ABAZCEB = ZCEF=90oVEB=EF, CE=CE, AACEB^ACEF AZB = ZCFEVZB + ZD=180" , ZCFE+ZCFA=180° ,ND=NCFAVAC 平分NBAD AZDAC=ZFACVAC=AC AAADC^AAFC (SAS) AAD=AFAAE=AF+FE=AD+BE9.已知:AB=4, AC=2, D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE・・・D是BC中点ABD=DC在4 ACD^O A BDE 中AD=DEAAC=BE=2二•在△ ABE中AB-BE<AE<AB+BEVAB=4BP4-2<2AD<4+21<AD<3:.AD=211.已知:BC=DE, NB=NE, NC=ND, F 是CD 中点,求证:N1=N2证明:连接BF和EF。
八年级上册典型题

八年级上册典型题一、三角形全等证明类(5题)1. 如图,在△ABC和△DEF中,AB = DE,BC = EF,∠A = ∠D。
求证:△ABC≌△DEF。
- 解析:- 在△ABC和△DEF中,已知AB = DE,BC = EF,∠A = ∠D。
- 但是“SSA”(边 - 边 - 角)不能判定三角形全等,所以这两个三角形不全等。
这是一个易错点,让学生明确全等三角形的判定定理中没有“SSA”。
2. 已知:如图,AC = BD,∠CAB=∠DBA。
求证:△CAB≌△DBA。
- 解析:- 在△CAB和△DBA中,AC = BD,∠CAB = ∠DBA,AB是公共边。
- 根据三角形全等判定定理中的“SAS”(边角边),因为AC = BD,∠CAB = ∠DBA,AB = BA,所以△CAB≌△DBA。
3. 如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE = AC,延长BE交AC于F。
求证:△AEF≌△DEB。
- 解析:- 因为AD是BC边上的中线,所以BD = CD。
- 在△AEF和△DEB中,- 对顶角∠AEF = ∠DEB。
- 因为BD = CD,AD是中线,∠BDE = ∠CDA(对顶角相等),可证△BDE≌△CDA (SAS),所以∠BED = ∠CAD,又因为BE = AC。
- 根据“AAS”(角角边),所以△AEF≌△DEB。
4. 如图,AB = AC,AD = AE,∠1 = ∠2。
求证:△ABD≌△ACE。
- 解析:- 因为∠1 = ∠2,所以∠1+∠CAD = ∠2 + ∠CAD,即∠BAD = ∠CAE。
- 在△ABD和△ACE中,AB = AC,AD = AE,∠BAD = ∠CAE。
- 根据“SAS”(边角边),所以△ABD≌△ACE。
5. 如图,点B、F、C、E在一条直线上,FB = CE,AB∥ED,AC∥FD。
求证:△ABC≌△DEF。
- 解析:- 因为FB = CE,所以FB+FC = CE + FC,即BC = EF。
八年级全等三角形简单证明题及解答(5道)

汇报人:XX
目 录
• 题目一:基本的全等三角形证明 • 题目二:利用角平分线性质证明 • 题目三:通过边边边条件证明 • 题目四:结合中线性质进行证明 • 题目五:综合应用多种性质证明 • 总结与拓展
01
题目一:基本的全等三角形证明
题目描述
• 已知三角形$ABC$和三角形$DEF$,其中$AB = DE$,$AC = DF$,$\angle BAC = \angle EDF$。求证:$\triangle ABC \cong \triangle DEF$。
由第二步可知,△BDE∽△CFD。
详细解答
4. 第四步,根据相似三角形的性质,对应边成比例,所以BD/CF=DE/DF。
5. 第五步,因为BD=AD(已知),所以AD/CF=DE/DF。又因为AE/EC=DE/EF(已知), 所以AD/CF=AE/EC。
6. 第六步,交叉相乘得AD*EC=AE*CF,即AE/AD=EC/CF。又因为∠A=∠ACF(对顶角相 等),所以△ADE∽△ACF。
第三步,根据相似三 角形的性质,有 AB/AC = BD/DC。
综上,我们证明了 AB/AC = BD/DC。
03
题目三:通过边边边条件证明
题目描述
已知
△ABC和△DEF中,AB = DE,BC = EF,AC = DF。
求证
△ABC ≌ △DEF。
题目描述
【分析】
本题主要考察全等三角形的判定方法——边边边条件。根据已知条件,我们可以 直接应用边边边定理来证明两个三角形全等。
题目描述
01
【解答】
02
证明
03
04
∵ 在△ABC和△DEF中,AB = DE,BC = EF,AC = DF(已
人教版八年级上册数学《全等三角形》证明题专项训练-最新

BA DC 人教版八年级上册数学《全等三角形》证明题专项训练·最新全等三角形证明习题(1)1.在△ABC 中,AB=AC ,AD 是三角形的中线.求证:△ABD ≌△ACD2. 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .3.已知,如图BD 平分∠ABC ,AB = BC 。
求证:AD = CD4.如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:AB=AC 。
CBABDC E A5. 如图,点E, F 在BC 上,BE=CF, AB=DC, ∠B=∠C. 求证: ∠A=∠D6. 如图,AB=AD, BC=DE, ∠B=∠D . 问∠BAE 与∠DAC 相等吗?为什么?7. 已知:如图,∠1=∠2,BD=CD,求证:AD 是∠BAC 的平分线.8.如图所示在△ABC 中,AB=AC , D 是BD 的中点,求证:△9.如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
CO ED BA FC10.已知:如图 , AB=AE , AC=AD , BC=DE , C , D 在BE 边上. 求证:∠CAE=∠DAB .11.已知:点D 在AB 上,点E 在AC 上,BE 和CD 相交于点O ,AB=AC , ∠B=∠C 。
求证: △ABE ≌△ACD12.如图:AC=DF ,AD=BE ,BC=EF 。
求证:∠C=∠F 。
13.如图:AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF 。
DBEA OC FEB DADA14.如图,CE ⊥AB 于E , DF ⊥AB 于F , AF=BE , 且AC=BD , 求证:AC ∥BD15.如图,已知AB=DE ,BC=EF ,AF=DC ,则∠EFD=∠BCA ,请说明理由。
16.如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
人教版八年级数学上册三角形全等的证明培优综合训练(含答案)

人教版八年级数学上册三角形全等的证明培优综合训练(含答案)考点1 利用SSS求证三角形全等1.如图,点B,F,C,E在同一条直线上,点A,D在直线BC的异侧,AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)若∠BFD=150°,求∠ACB的度数.2.如图,C是AB的中点,AD=CE,CD=BE.求证:(1)△DCA≌△EBC;(2)AD//CE.3.已知:如图,已知线段AB、CD相交于点O、AD、CB的延长线交于点E、OA=OC、EA=EC,求证:∠A=∠C、考点2 利用SAS求证三角形全等4.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,AB=DE,BF=CE,AB‖DE,求证:△ABC≅△DEF.5.在△ABC中,AD为边BC上的中线,延长AD到点E,使DE=AD,连接BE.△ABC的面积与△ABE的面积相等吗?说明理由6.两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC =DC,AC,BD相交于点O.(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;(2)如果AC=6,BD=4,求筝形ABCD的面积.考点3 利用AAS 或ASA 求证三角形全等7.已知:在ABC 中,90BAC ∠=︒,AB AC =,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .(1)证明:BDA AEC ≌;(2)3BD =,4CE =,求DE 的长.8.如图,已知AD 为ABC ∆的中线,延长AD ,分别过点B ,C 作BE AD ⊥,CF AD ⊥.求证:BED CFD ∆≅∆.9.如右图,已知,90AB AC BAC BE CE =∠=︒,⊥于点E ,延长BE CA 、相交于点F ,求证:ADC AFB ≌10.如图,已知E 、F 在AC 上,AD //CB ,且∠D=∠B ,AE=CF .求证:DF=BE .考点4 利用HL 求证三角形全等11.在ABC 中,AB CB =,90ABC ∠=︒,F 为AB 延长线上一点,点E 在BC 上,且AE CF =.(1)求证:ABE CBF ≌;(2)若30CAE ∠=︒,求ACF ∠度数.12.如图,已知AE =DE ,AB ⊥BC ,DC ⊥BC ,且AB =EC .求证:BC =AB +DC .13.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.(1)证明:Rt△BCE≌Rt△DCF;(2)若AB=21,AD=9,求AE的长.14.如图:AD是ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD、求 .证:BE AC考点5 全等三角形综合15.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M、N分别是射线AE、AF上的点,(1)如图1,当点M在线段AB上,点N在线段AC的延长线上,且PM=PN,求证:BM=CN;(2)在(1)的条件下,直接写出线段AM、CN与AC之间的数量关系_______.(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,∠MAN+MPN=180°,若AC:PC=2:1,PC=4,求四边形ANPM的面积.16.如图,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点.(1)如图1,若P为AB的中点,点M、N分别是OA、OB边上的动点,且保持AM=ON,则在点M、N运动的过程中,探究线段PM、PN之间的位置关系与数量关系,并说明理由.(2)如图2,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP,交OP、OA分别于F、D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.答案1.解:(1)证明:BF EC =∵,BF FC EC FC ∴+=+,BC EF ∴=,在ABC ∆和DEF ∆中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩,()ABC DEF SSS ≅∆∆∴;(2)150BFD ∠=︒,180BFD DFE ∠+∠=︒, 30DFE ∴∠=︒,由(1)知,ABC DEF ∆≅∆,ACB DFE ∴∠=∠,30ACB ∴∠=︒.2.(1)证明:点C 是AB 的中点,AC BC ∴=;在DCA ∆与EBC ∆中,AD CE CD BE AC BC =⎧⎪=⎨⎪=⎩,()DCA EBC SSS ∴∆≅∆,(2)证明:DCA EBC ∆≅∆,A BCE ∴∠=∠,//AD CE ∴.3.如图,连结OE在、OEA 和、OEC 中OA OC EA EC OE OE =⎧⎪=⎨⎪=⎩、、OEA、、OEC (SSS )、、A =、C (全等三角形的对应角相等)4.∵BF=CE ,∴BF+FC=CE+FC ,即BC=EF .∵AB ∥DE ,∴∠B=∠E .在△ABC 和△DEF 中AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (SAS )5.△ABC 与△ABE 的面积相等.理由:∵AD 为边BC 上的中线,∴BD=CD ,在△BDE 和△CAD 中,BD DC BDE CDA DE AD =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△CAD、SAS、,BDE ABD CAD ABD S S S S +=+,即△ABC 与△ABE 的面积相等.6.(1)证明:①在△ABC 和△ADC 中,AB=AD ,BC=DC ,AC=AC ,∴△ABC ≌△ADC (SSS ).②∵△ABC ≌△ADC ,∴∠BAO=∠DAO.∵AB=AD ,∠BAO=∠DAO ,OA=OA ,∴△ABO ≌△ADO (SAS ).∴OB=OD ,AC ⊥BD.(2)筝形ABCD 的面积=△ABC 的面积+△ACD 的面积=12×AC×BO+12×AC×DO=12×AC×(BO+DO)=12×AC×BD=12×6×4=12. 7.(1)证明:∵BD m ⊥,CE m ⊥,∴90ADB CEA ∠=∠=︒,∴90ABD BAD ∠+∠=︒,∵AB AC ⊥,∴90BAD CAE ∠+∠=︒,∴ABD CAE ∠=∠,在BDA 和AEC 中,90ADB CEA ABD CAEAB AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴()BDA AEC AAS ≅;(2)∵BDA AEC ≅△△,∴BD AE =,AD CE =,∴7DE DA AE BD CE =+=+=.8.证明:∵AD 是△ABC 的中线,∴ BD =CD ,∵ BE ⊥AD ,CF ⊥AD ,∴∠E =∠CFD =90°在Rt △BDE 和Rt △CDF 中,90BDE CDF E CFD BD CD ∠=∠⎧⎪∠=∠=⎨⎪=⎩,∴ Rt △BDE ≌Rt △CDF (AA S )9.、、BAC=90°,、、BAF=180°-、BAC=90°,、、BAF=、CAD ,、F+、ABF=90°,∵CE ⊥BE ,、、CEF=90°,、、F+、ACD=90°,、、ABF=、ACD ,在、ADC 和、AFB 中,BAF CAD AC ABACD ABF ∠=∠⎧⎪=⎨⎪∠=∠⎩, 、、ADC ≌、AFB (ASA ).10.解:证明:∵AE=CF ,∴AE -EF=CF -EF即AF=CE ,∵AD ∥CB ,∴∠A=∠C ,在△ADF 和△CBE 中,A C AF CE DB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADF ≌△CBE (ASA ),∴DF=BE .11.(1)证明:∵∠ABC=90°,∴∠CBF=∠ABE=90°,在Rt △ABE 和Rt △CBF 中,AE CF AB BC=⎧⎨=⎩, ∴Rt △ABE ≌Rt △CBF (HL );(2)解:∵AB=BC ,∠ABC=90°,∴∠CAB=∠ACB=45°,又∵∠BAE=∠CAB -∠CAE=45°-30°=15°,由(1)知:Rt △ABE ≌Rt △CBF ,∴∠BCF=∠BAE=15°,∴∠ACF=∠BCF+∠ACB=15°+45°=60°.12.∵AB ⊥BC ,DC ⊥BC ,∴∠B=∠C=90°,在Rt △AEB 和Rt △EDC 中,AB EC AE DE =⎧⎨=⎩, ∴Rt △AEB ≌Rt △EDC (HL ),∴DC=BE ,∵BC=BE+CE ,∴AB+DC=BC .13.(1)∵AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F , ∴CF=CE ,∠DFC=∠BEC=90°,在Rt △BCE 和Rt △DCF 中,CE CF BC CD =⎧⎨=⎩, ∴Rt △BCE ≌Rt △DCF (HL );(2)∵AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F , ∴CF=CE ,∠CFA=∠CEA=90°,在Rt △AFC 和Rt △AEC 中,CF CE AC AC =⎧⎨=⎩,∴Rt △AFC ≌Rt △AEC (HL ),∴AF=AE ,由(1)知Rt △BCE ≌Rt △DCF ,则BE=DF ,∵AB=21,AD=9,∴AB=AE+EB=AF+EB=AD+DF+ DF =AD+2DF=9+2DF=21, 解得,DF=6,∴AE=AF=AD+DF=9+6=15,即AE 的长是15.14.证明: ∵AD ⊥BC ,∴∠BDF =∠ADC =90°.又∵BF =AC ,FD =CD ,∴△RtADC ≌Rt △BDF (HL ).∴∠EBC =∠DAC .又∵∠DAC +∠ACD =90°,∴∠EBC +∠ACD =90°.∴BE ⊥AC .15.(1)证明:点P 为EAF ∠平分线上一点,PB AE ⊥于B ,PC AF ⊥于C , PB PC ∴=,在Rt PBM ∆和Rt PCN ∆中,PB PC PM PN =⎧⎨=⎩, Rt PBM Rt PCN ∴∆≅∆,BM CN ∴=;(2)AM CN AC +=,理由如下:在Rt PBA ∆和Rt PCA ∆中,PB PC AP AP =⎧⎨=⎩, Rt PBA Rt PCA ∴∆≅∆,AB AC ∴=,AM CN AM BM AB AC ∴+=+==,故答案为:AM CN AC +=;(3):2:1AC PC =,4PC =,8AC ∴=,PB AE ⊥,PC AF ⊥,90ABP ACP ∴∠=∠=︒,180MAN BPC ∴∠+∠=︒,又180MAN MPN ∠+∠=︒, MPB NPC ∴∠=∠,在PBM ∆和PCN ∆中,BPM CPN PB PCPBM PCN ∠=∠⎧⎪=⎨⎪∠=∠⎩, PBM PCN ∴∆≅∆,∴四边形ANPM 的面积=四边形ABPC 的面积1842322=⨯⨯⨯=. 16.解:(1)结论:PM =PN ,PM ⊥PN .理由如下:如图1中,连接OP .∵A 、B 坐标为(6,0)、(0,6),∴OB =OA =6,∠AOB =90°,∵P为AB的中点,∴OP=12AB=PB=P A,OP⊥AB,∠PON=∠P AM=45°,∴∠OP A=90°,在△PON和△P AM中,ON AMPON PAMOP AP=⎧⎪∠=∠⎨⎪=⎩,∴△PON≌△P AM(SAS),∴PN=PM,∠OPN=∠APM,∴∠NPM=∠OP A=90°,∴PM⊥PN,PM=PN.(2)结论:OD=AE.理由如下:如图2中,作AG⊥x轴交OP的延长线于G.∵BD⊥OP,∴∠OAG=∠BOD=∠OFD=90°,∴∠ODF+∠AOG=90°,∠ODF+∠OBD=90°,∴∠AOG=∠DBO,∵OB=OA,∴△DBO≌△GOA,∴OD=AG,∠BDO=∠G,∵∠BDO=∠PEA,∴∠G=∠AEP,在△P AE和△P AG中,AEP GPAE PAGAP AP∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△P AE≌△P AG(AAS),∴AE=AG,∴OD=AE.。
人教版八年级上册数学全等三角形证明题训练
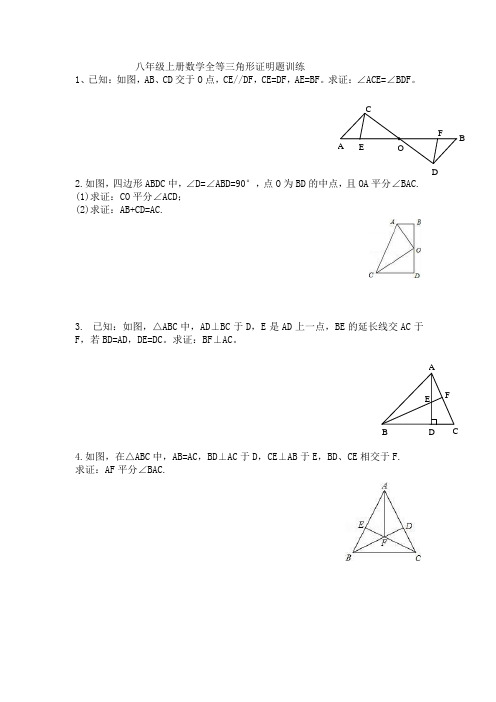
八年级上册数学全等三角形证明题训练1、已知:如图,AB、CD交于O点,CE//DF,CE=DF,AE=BF。
求证:∠ACE=∠BDF。
2.如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.(1)求证:CO平分∠ACD;(2)求证:AB+CD=AC.3. 已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
求证:BF⊥AC。
4.如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC.AB CDEFOAB CDE F5.已知:如图,AB=CD ,AD=BC ,O 是AC 中点,OE ⊥AB 于E ,OF ⊥D 于F 。
求证:OE=OF 。
6.如图,已知△ABC 中,∠1=∠2,AE=AD ,求证:DF=EF .7.如图,已知AB=AE ,BC=ED ,∠B=∠E ,AF ⊥CD ,F 为垂足,求证:①AC=AD ; ②CF=DF.8.如图,已知在四边形ABCD 中,点E 在AD 上,∠BCE=∠ACD=90°,∠BAC=∠D ,BC=CE.(1)求证:AC=CD ;(2)若AC=AE ,求∠DEC 的度数.A C D E F O9.已知:如图,AC ⊥OB ,BD ⊥OA ,AC 与BD 交于E 点,若OA=OB ,求证:AE=BE 。
10.如图,在△ABC 中,∠ACB=90°,AC=BC,BE ⊥CE 于E ,AD ⊥CE 于D. 求证:(1)△ADC ≌△CEB. (2)AD=5cm,DE=3cm ,求BE 的长度.11.已知:如图,AB//DE ,AE//BD ,AF=DC ,EF=BC 。
求证:△AEF ≌△DBC 。
A B CDEF12.已知:如图,PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线,•它们交于点P ,PD ⊥BM 于D ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.O B A C D E13.如图,已知AB=AD ,AC=AE ,∠BAD=∠CAE=90°,试判断CD 与BE 的大小关系和位置关系,并进行证明.14.在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE =AD +BE ;(2)当直线MN 绕点C 旋转到图2的位置时,求证:DE =AD -BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.15.如图,已知AD 是△ABC 的中线, DE ⊥AB 于E , DF ⊥AC 于F , 且BE=CF , 求证:(1)AD 是∠BAC 的平分线;(2)AB=AC .CB AE D图1 N M A B CDE M N 图2A C BE D N M 图3F A 1 2 E CDB16.如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F. (1)若∠ABE=60°,求∠CDA的度数.(2)若AE=2,BE=1,CD=4.求四边形AECD的面积.17.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.。
人教版八年级上学期数学《全等三角形证明》专题练习
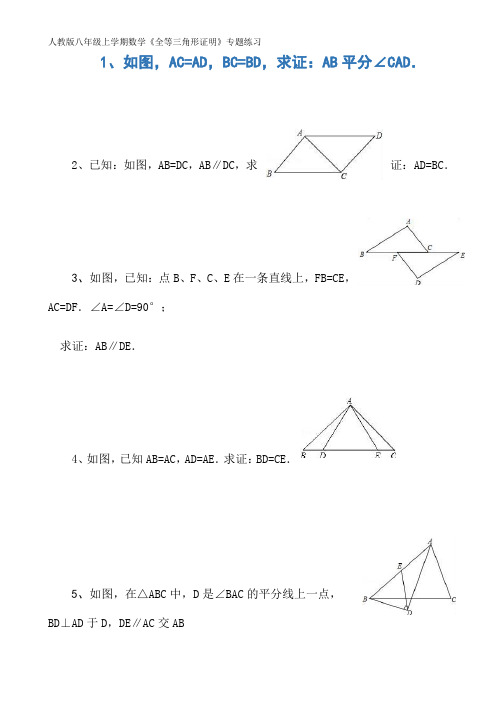
1、如图,AC=AD,BC=BD,求证:AB平分∠CAD.2、已知:如图,AB=DC,AB∥DC,求证:AD=BC.3、如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.4、如图,已知AB=AC,AD=AE.求证:BD=CE.5、如图,在△ABC中,D是∠BAC的平分线上一点,BD⊥AD于D,DE∥AC交AB于E,请说明AE=BE.6、一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:∠BAC=∠DAC.7、如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.8、如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.9、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:EC=BF.10、如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.试说明:AD垂直平分EF.11、已知:如图,点E、F在AD上,且AF=DE,∠B=∠C,AB∥DC.求证:AB=DC.12、已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.13、如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.试说明:AD垂直平分EF.14、如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:(1)MD=MB;(2)MN平分∠DMB.15、如图,已知,△ABC和△ADE均为等边三角形,BD、CE交于点F.(1)求证:BD=CE;(2)求锐角∠BFC的度数.16、如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数;(3)△DEF可能是等腰直角三角形吗?为什么?17、已知:如图,AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C.求证:(1)AE=CF;(2)AE∥CF.18、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:(1)CF=EB.(2)AB=AF+2EB.19、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.20、如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.(1)求证:△ACD≌△CBE;(2)猜想线段AD、BE、DE之间的关系,并说明理由.21、在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.(1)求BC的长;(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.22、(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN 的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F 在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.23、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN 于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,AD=5,BE=2,求线段DE的长.24、如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过后,点P与点Q第一次在△ABC的边上相遇?(直接写出答案,不必书写解题过程)25、如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:(1)△ABF与△AGF全等吗?说明理由;(2)求∠EAF的度数;(3)若AG=4,△AEF的面积是6,求△CEF的面积.26、已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC 于点F.求证:BF+EF=DE;(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学上册三角形全等证明题专项练习
1、如图,已知: AD是BC上的中线,且DF=DE.求证:BE∥CF.
2、已知:点A、F、E、C在同一条直线上,AF=CE,BE∥DF,BE=DF.求证:△ABE ≌△CDF.
3、如图:AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。
求证:AM是△ABC的中线。
4、已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:△ABC≌
△DE F.5、如图:AB=AC,ME⊥AB,MF⊥AC,垂足分别为E、F,ME=MF。
求证:AE=AF
6、如图:DF=CE,AD=BC,∠D=∠C。
求证:△AED≌△BFC。
7、如图:在△ABC中,BA=BC,D是AC的中点。
求证:BD⊥AC。
8、已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE BF
.
求证:AB CD
∥.
A
D
E
C
B
F
M F
E C
B A
D
C
B
A
C
M
F
E
F
E
D C
B
A
9、如图,已知∠1=∠2,∠3=∠4,求证:AB=CD
10、如图,已知AC ⊥AB ,DB ⊥AB ,AC =BE ,AE =BD ,试猜想线段CE 与DE 的大小与位置关系,并证明你的结论.
11、如图,已知AB =DC ,AC =DB ,BE =CE ,求证:AE =DE.
12、如图9所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .
13、已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C
14、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C
15、P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB
16、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE
17、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC
D
C
B
A F
E
A B
C D
P D
A
C
B
A
C
E
D
B
A
B
E
C
D
.
3
4
21
D
C
B
A
A
B
C D
E F
图9
18、如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.
19、如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA
20. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
21、如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求
证:AD+BC=AB.
22、如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,
AF=CE,BD交AC于点M.
(1)求证:MB=MD,ME=MF
(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.
23、已知:如图,DC∥AB,且DC=AE,E为AB的中点,
(1)求证:△AED≌△EBC.
F A
E D
C
B
P
E
D
C
B
A
(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):
24、如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C
点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .
25、AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF
26、如图:AB=CD ,AE=DF ,CE=FB 。
求证:AF=DE 。
27、公园里有一条“Z”字形道路ABCD ,如图所示,其中AB ∥CD ,在AB ,CD ,BC 三段路旁各有一只小石凳E ,F ,M ,且BE =CF ,M 在BC 的中点,试说明三只石凳E ,F ,M 恰好在一条直线上.
28、已知:如图所示,AB =AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证: AE =AF 。
29、如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.
30、已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F ,求证:BE =CD .
O
E
D
C
B
A
F
E D
C
B A
F D
C
B
A
F
E D
C
B A
D
A
F
E
654
32
1E D
C
B
A
A
C B D
E F
D
C
B
A
E
31、如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F 。
求证:DE =DF .
32、已知:如图, AC ⊥BC 于C , DE ⊥AC 于E , AD ⊥AB 于A , BC =AE .若AB = 5 ,求AD 的长?
33、如图,给出五个等量关系:①
AD BC = ②AC BD = ③CE DE = ④D C ∠=∠
⑤DAB CBA ∠=∠.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明. 已知: 求证: 证明:
34、在△ABC 中,︒=∠90ACB ,BC AC =
,直线MN 经过点C ,且MN AD ⊥于D ,
MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,
求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;
(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;
若不成立,说明理由.
35、如图所示,已知AE ⊥AB ,AF ⊥AC ,AE=AB ,AF=AC 。
求证:(1)EC=BF ;(2)EC ⊥BF
36、如图:BE ⊥AC ,CF ⊥AB ,BM=AC ,CN=AB 。
求证:(1)AM=AN ;(2)AM ⊥AN 。
A
E
B F B
C
D
E
F
M
N
E
123
4
A
E B
M C
F
37、如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相
等吗?请说明理由
38、已知:AB=4,AC=2,D是BC中点,AD是整数,求AD长
39、已知:D是AB中点,∠ACB=90°,求证:
1
2
CD AB
40、已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC
41、已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C
42、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
A
D
B C
D
C B
A
C
D
F
2
1
E
C
D
B
A。
