高中数学(北师大版必修2)1.3三视图

合集下载

高中数学 1.3 三视图课件北师大版必修2

[规范解答] 由三视图可知，左视图中 2 为正三棱柱的高，俯视图中 2 3为底面正三角形的高，所以正三棱柱的底面边长为 2 3÷ 23＝4，即这个正三棱柱的高是 2，底面边长是 4.左视图中矩形的宽为 2，长即为底面正三角形的高，等于 2 3.因此，左视图面积 S＝2×2 3＝4 3.
第三十四页，共42页。
第四十二页，共42页。
第三十二页，共42页。
• 由三视图求几何体的相关 (xiāngguān)量
若一个正三棱柱的三视图如图所示，求这个三棱柱的高和底面边长以及左视图的面积．
第三十三页，共42页。
• [思路(sīlù)分析] 根据三视图提供的信息，可得正三棱柱的高和底面正三角形的高，从而可求底面边长以及左视图的面积．
• (2014·北京(běi jīnɡ)文，11)某三棱锥的三视图如图所示，则该三棱锥最长棱的棱长为 ________．
[答案] 2 2
第三十六页，共42页。
[解析] 本题考查三视图．几何体示意图如下：
PA⊥底面 ABC，BO＝1，则 AB＝BC＝ 2，AC＝2，PA＝2， PB＝ 6，PC＝2 2，∴最长棱长为 2 2.
第十三页，共42页。
• 4．某物体的实物图如图(甲)所示，在其三视图中，图①是____________；图②是 ____________；图③是____________．
• [答案(dáàn)] 主视图俯视图左视图
第十四页，共42页。
• 5．一个几何体的主视图与左视图一样 (yīyàng)，请你写出这个几何体是 ____________________．(要求写出至少两种)
• 首先，确定主视、俯视、左视的
________．同一物体放置的位置不同，所画

2019-2020高中北师版数学必修2 目录课件PPT

第1课时直线方程的点斜式第2课时直线方程的两点式和一般式
1.3 两条直线的位置关系 1.4 两条直线的交点 1.5 平面直角坐标系中的距离公式阶段复习课专题强化训练(二)
§2 圆与圆的方程 2.1 圆的标准方程 2.2 圆的一般方程 2.3 直线与圆、圆与圆的位置关系
第1课时直线与圆的位置关系第2课时圆与圆的位置关系
Thank you for watching !
5.1 平行关系的判定 5.2 平行关系的性质
§6 垂直关系 6.1 垂直关系的判定 6.2 垂直关系的性质
§7 简单几何体的再认识 7.1 柱、锥、台的侧面展开与面积 7.2 柱、锥、台的体积 7.3 球
阶段复习课专题强化训练(一) 章末综合测评(一)
§1 直线与直线的方程 1.1 直线的倾斜角和斜率 1.2 直线的方程
§1 简单几何体 1.1 简单旋转体 1.2 简单多面体
§2 直观图 §3 三视图
3.1 简单组合体的三视图 3.2 由三视图还原成实物图
§4 空间图形的基本关系与公理 4.1 空间图形基Hale Waihona Puke 关系的认识 4.2 空间图形的公理
第1课时空间图形的公理(公理1、2、3) 第2课时空间图形的公理4及等角定理 §5 平行关系

2019-2020学年高中数学北师大版必修2一课三测：1.3 三视图含解析

§3三视图填一填1。

三视图的概念三视图包括主视图（又称正视图）、俯视图，侧视图（通常选择左侧视图,简称左视图)．2．三视图的画法规则(1)主、俯视图反映物体的长度—-“长对正”．(2)主、左视图反映物体的高度-—“高平齐"．（3)俯、左视图反映物体的宽度-—“宽相等”．3．由基本几何体形成的组合体的两种基本形式(1）将基本几何体拼接．(2)从基本几何体中切掉或挖掉部分.判一判1。

任何一个几何体都可画出三视图．（√）2．主视图和左视图都是矩形的几何体一定是长方体．（×)3．主视图的高就是看到的几何体的高．（×)4．画三视图时应保证光线与投射面垂直．（√)5．同一个物体的主视图可能不同．（√)6．画三视图时,被遮住的部分可不画．(×)7．圆柱的三视图都是矩形．（×）8．三视图可以是全等的三角形．（√）想一想1.提示：常见几何体正视图侧视图俯视图长方体矩形矩形矩形正方体正方形正方形正方形圆柱矩形矩形圆圆锥等腰三角形等腰三角形圆圆台等腰梯形等腰梯形两个同心的圆球圆圆圆2.画组合体三视图的“四个步骤”是什么?提示：（1)析：分析组合体的组成形式；(2)分：把组合体分解成简单几何体；(3）画：画分解后的简单几何体的三视图；（4)拼：将各个三视图拼合成组合体的三视图．3．画三视图时要注意避免出现哪些问题？提示：(1)没有确定主视方向直接画图；（2)三个视图摆放位置混乱；（3）未遵循长、宽、高的画图原则；（4）看不见的边界轮廓线未画成虚线．4．由三视图还原几何体的步骤是什么？提示：思考感悟:练一练1。

以下说法正确的是( )A．任何物体的三视图都与物体摆放位置有关B．任何物体的三视图都与物体摆放位置无关C．有的物体的三视图与物体的摆放位置无关D．正方体的三视图一定是三个全等的正方形答案：C2．有一个几何体的三视图如图所示，这个几何体应是一个________．答案:四棱台3．水平放置的下列几何体，主视图是长方形的是________．(填序号)答案：①③④4．一个圆柱的三视图中，一定没有的图形是（)A．矩形B．圆C．三角形D．正方形答案:C5．根据如图所示的俯视图，找出对应的物体．（1）对应________；(2)对应________；(3）对应________；(4）对应________；(5)对应________．答案：(1)（D) （2）(A) （3)（E) （4)（C)(5)（B）知识点一简单几何体的三视图1。

北师大版高中数学必修2课件1.3简单组合体的三视图课件(北师大版)

平行投影
把在一束平行光线照射下形成的投影，叫平行投影
投影线平行
投影法分类投影法
中心投影法平行投影法正投影斜投影
一、三视图相关概念
视图
正投影
从上面看
主视图
正面
主视图高长
左视图宽宽
从左面看
俯视图
从正面看
你能总结出三视图的概念吗
三视图概念：
将空间图形分别从正面，左面和上面向三个两两垂直的平面作正投影，然后把这三个投影按一定的布
作业
1.预习下一节“三视图的还原” 2.课本P22 习题1.2 A组 1、2
4.检查。
我相信你一定能画出这个复杂几何体的三视图！
巩固提高
10 6 12 8
组合体的三视图
归纳总结
1.三视图主视图——从正面看到的图左视图——从左面看到的图
俯视图——从上面看到的图
2.画物体的三视图时,要符合如下原则: 位置：主视图左视图俯视图大小：长对正,高平齐,宽相等。
北京师范大学出版社 | 必修二
第一章 · 立体几何初步
简单组合体的三视图
横看成岭侧成峰，远近高低各不同。不识庐山真面目，只缘身在此山中。 ——苏轼
新课导入
中心投影
把光由一点向外散射形成的投影，叫做中心投影
投影线交于一点，随着物体距离光源（屏幕）的远近，形成的投影大小不同，相似图形。
局放在一个平面内，这样构成的图形叫做空间图形的
三视图。
三视图的形成及其投影规则(1)
三视图的形成及其投影规则(2)
二、三视图的作图规则主—俯：长对正主—左：高平齐左—俯：宽相等
主视图左视图
俯视图

北师大版数学高一必修二三视图

研一研·问题探究、课堂更高效
例 3 根据三视图想象物体原形，并画出物体的实物草图： (1)三视图 1；(2)三视图 2.
本
课
时
栏
目
开
关
图1
图2
研一研·问题探究、课堂更高效
解 (1)由俯视图并结合其他两个视图可以看出，这个物体由
一个圆柱和一个正四棱柱组合而成．圆柱的下底面圆和正四
棱柱的上底面正方形内切．它的实物草图如图 1；
时栏
与主视图一样，左视图放在主视图的右面，高度与主视图一
目
样，宽度与俯视图的宽度一样．为了便于记忆，通常说：“长
开
关
对正，高平齐，宽相等”或说“主俯一样长，主左一样高，
俯左一样宽”．
研一研·问题探究、课堂更高效
问题 4 如何画出下图中正五棱锥的主视图．
本
课
时栏
解从主视方向看，该五棱锥有一条侧棱不可见，在主视图
征，你能画出几何体的直观图吗？
栏
目
开
关
答由几何体的三视图可知，几何体是一个倒立的三棱台，即上底面面积大，下底面面积小，直观图如右图．
研一研·问题探究、课堂更高效
问题 2 下图是简单组合体的三视图，想象它们表示的组合体的结构特征，并作适当描述．
本课时栏目开关
答举重运动员举重时用的体育器材．
本
课
时
栏
目
开关
(2)由三视图知，该物体下部分是一个长方体，上部分的表面
是两个等腰梯形和两个等腰三角形，它的实物草图如图 2.
研一研·问题探究、课堂更高效
小结在由组合体的三视图还原它的实物图时，应着重考虑
本课

北师大版必修2高中数学1.3《三视图》ppt课件

6.(2011·镇江模拟)用单位立方块搭一个几何体，使它的主视图和俯视图如图所示，则它的体积的最小值为_____，最大值为__________.
【解题提示】解答本题可先由俯视图确定“基座”再分析各列有几层，找出单位立方块个数的最小值和最大值. 【解析】综合分析俯视图和主视图可知单位立方块最少的情况如图(1)(不唯一)，共10个. 单位立方块最多的情况如图(2)，共16个.
3.如图是一个几何体的三视图，由图可以判断此几何体是 __________.
【解析】由三视图可知此几何体是正六棱台. 答案：正六棱台
4.主视图为一个三角形的几何体可以是__________．(写出三种) 【解析】由几何体的三视图可知，主视图为三角形的几何体可以是三棱锥、圆锥、四棱锥等. 答案：三棱锥、圆锥、四棱锥(不唯一)
【挑战能力】 (10分)如图(1)是由8个小正方体构成的大正方体，如图(2) 是由7个小正方体构成的组合体. (1)试画出这两个几何体的三视图. (2)你能想到还有哪些组合体(由6个小正方体构成)的三视图与以上两个几何体的三视图相同吗？
【解析】(1)这两个几何体的三视图相同，三视图如下：
(2)与以上两个几何体的三视图相同的几何体还有(不唯一)：
二、填空题(每题4分，共8分) 5.(2011·杭州高一检测)一个几何体的三视图如图所示，其中主视图和左视图是腰长为6的两个全等的等腰直角三角形，用__________个这样的几何体可以拼成一个棱长为6的正方体.
【解析】如图所示，该几何体是一个四棱锥，记作四棱锥P—ABCD，由图可见，用3个这样的几何体可以拼成一个棱长为6的正方体. 答案：3
④ 紧跟老师的推导过程抓住老师的思路。老师在课堂上讲解某一结论时，一般有一个推导过程，如数学问题的来龙去脉、物理概念的抽象归纳、语文课的分析等。感悟和理解推导过程是一个投入思维、感悟方法的过程，这有助于理解记忆结论，也有助于提高分析问题和运用知识的能力。

北师大版高中数学必修2课件1.3简单多组合体的三视图课件(数学北师大必修二)

一、概念： 2.三视图
一、概念： 3.三视图之间的投影规律正视图反映了物体的高度和长度；侧视图反映了物体的高度和宽度；俯视图反映了物体的长度和宽度.
主、俯视图长相等；
主、左视图高相等；左、俯视图宽相等；记作“长对正，高平齐，宽相等”.
二、知识应用：题型一画出几何体的三视图
例 1. 画出下列几何体的三视图.
一、概念： 1.投影 ⑴ 中心投影:
一、概念： 1.投影 ⑵ 平行投影: 在一束平行光线照射下形成的投影.
一、概念： 2.三视图一个物体在三个投影面内同时进行正称为正视图.
侧视图: 光线自物体的左面向右面正投影得到的投影图称为侧视图.
俯视图: 光线自物体的上面向下面正投影得到的投影图称为俯视图.
第三节· 三视图
3.1 简单组合体的三视图
请同学观察以下图片，你能还原对应的实际物体吗？
请同学观察以下图片，你能还原对应的实际物体吗？
请回忆已经学过的正方体、长方体、圆柱、圆锥、球的三视图，然后围绕以下三个问题展开讨论，给出答案.
一、概念： 1.投影 ⑴ 中心投影: 光由一点向外散射形成的投影. ⑵ 平行投影: 在一束平行光线照射下形成的投影.
二、知识应用：题型一画出几何体的三视图
例2. 请同学们画下面这两个圆台的三视图，如果你认为这两个圆台的三视图一样，画一个就可以；如果你认为不一样，请分别画出来.
二、知识应用：题型一画出几何体的三视图
例3.画出六角螺栓的三视图.
二、知识应用：
题型二
几何体的三视图应用问题
例 4.如图所示的正方体中,M,N 分别为 A1A,C1C 的中点,作四边形 D1MBN,则四边形 D1MBN 在正方体各个面上的正投影图形中,不可能出现的是( )

高中数学北师大版必修二 1.3 三视图课件(36张)

探究 1 根据如图 135 所给出的物体的三视图，请说出它们的名称.
图 135
上一页返回首页下一页
【提示】几何体的名称.
从观察三视图的特征入手，联想简单几何性三视图，从而确定
上一页
返回首页
下一页
探究 2 如图 136 是某一几何体的三视图，你能想象几何体的结构特征，
并画出几何体的直观图吗？
下一页
[基础· 初探]
教材整理 1 组合体
阅读教材 P13 至 P14“三、简单组合体的三视图”以上部分，完成下列问题. 1.定义：由基本几何体生成的几何体叫作组合体. 2.基本形式：有两种，一种是将基本几何体拼接成组合体；另一种是从基本几何体中切掉或挖掉部分构成组合体.
上一页
返回首页
下一页
以钝角三角形的较小边所在的直线为轴，其他两边旋转一周所得到的几何体是( )
A.两个圆锥拼接而成的组合体 B.一个圆台 C.一个圆锥 D.一个大圆锥挖去一个同底的小圆锥
上一页
返回首页
下一页
【解析】如图以 AB 为轴所得的几何体是一个大圆锥挖去一个同底的小圆锥.
【答案】 D
上一页
返回首页
下一页
上一页
返回首页
下一页
[再练一题] 1.画出如图 132 所示的空间几何体的三视图.(阴影面为主视面，尺寸不作严格要求)
图 132
上一页返回首页下一页
【解】三视图如下.
上一页
返回首页
下一页
简上形成的组合体，画出它的三视图.
图 133
【精彩点拨】观察图形，分析结构，画出组合体的三视图.
左视图放在主视图的右面，高度与主视图一样，宽度与俯视图的宽度一样.

2019-2020学年北师大版高中数学必修二教师用书：1-3 三视图 Word版含答案

姓名，年级：时间：§3三视图1．由基本几何体形成的组合体有两种基本的组成形式：(1)将基本几何体拼接成组合体；(2)从基本几何体中切掉或挖掉部分构成组合体．2．绘制三视图时的注意点（1）主、俯视图长对正；主、左视图高平齐；俯、左视图宽相等，前后对应．(2)在三视图中，需要画出所有的轮廓线,其中，视线所见的轮廓线画实线，看不见的轮廓线画虚线．(3)同一物体放置的位置不同,所画的三视图可能不同．（4）清楚简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置．判断正误(正确的打“√”，错误的打“×”)(1）任何几何体的三视图都与其摆放的位置有关．( )(2）任何几何体的三视图都与其摆放的位置无关．（)(3)有的几何体的三视图与其摆放的位置无关．（）（4)正方体的三视图一定是三个全等的正方形．( )[答案] （1）×(2）×(3)√（4)×题型一简单几何体的三视图【典例1】画出如图所示几何体的三视图．[思路导引］图①为正六棱柱,可按棱柱的画法画出，图②为一个圆锥与一个圆台的组合体,按圆锥、圆台的三视图画出它们的组合形状．[解] 按正六棱柱、圆锥、圆台的三视图画法如图所示．(1)画三视图时，首先确定主视、左视、俯视的方向,同一物体放置的位置不同，所画的三视图可能不同．一般主视方向确定了，则左视与俯视的方向也就确定了，在有的问题里，直接给出主视图，也是确定主视方向的一个方法．(2)一个物体的三视图的排列规则是:俯视图放在主视图的下面，左视图放在主视图的右面．［针对训练1］如下图所示，图（1)是底面边长和侧棱长都是2 cm 的四棱锥，图（2）是上、下底面半径分别为1 cm,2 cm，高为2 cm的圆台，分别画出它们的三视图．［解］(1)四棱锥的三视图如下图所示:(2)圆台的三视图如下图所示：题型二简单组合体的三视图【典例2】画出如图所示的几何体的三视图．[思路导引］画三视图之前,先把几何体的结构弄清楚，图为两个圆柱的组合体．［解] 如图所示．画简单组合体的三视图时要注意的问题（1)分清简单组合体是由哪些简单几何体组成的,是组合型还是切挖型．（2)先画主体部分，后画次要部分．（3)几个视图要配合着画．一般是先画主视图再确定左视图和俯视图．（4）组合体的各部分之间要画出分界线．［针对训练2］画出如图所示几何体的三视图．[解] 如图所示(1)(2）题型三由三视图还原成实物图【典例3】如图是一个物体的三视图，则此三视图所描述的物体是下列哪个几何体( )[思路导引］（1）通过主视图和左视图确定是柱体、锥体还是台体．若主视图和左视图为矩形，则原几何体为柱体；若主视图和左视图为等腰三角形,则原几何体为锥体；若主视图和左视图为等腰梯形，则原几何体为台体．（2)通过俯视图确定是多面体还是旋转体，若俯视图为多边形，则原几何体为多面体；若俯视图为圆,则原几何体为旋转体．[解析] 由俯视图可知该几何体为旋转体,由主视图、左视图、俯视图可知该几何体是由圆锥、圆柱组合而成．［答案] D由三视图还原成实物图时，一般先由俯视图确定底面，由主视图与左视图确定几何体的高及位置，同时想象视图中每一部分对应实物部分的形状．［针对训练3］根据三视图（如图所示）想象物体原形，指出其结构特征,并画出物体的实物草图．[解］由俯视图知,该几何体的底面是一直角梯形；再由主视图和左视图知，该几何体是一四棱锥，且有一侧棱与底面垂直，所以该几何体如图所示．1．如图，甲、乙、丙是三个立体图形的三视图，与甲、乙、丙相对应的标号是（）①长方体;②圆锥；③三棱锥；④圆柱．A．③①② B．①②③ C．③②④ D．④②③［答案] D2．已知三棱柱ABC—A1B1C1如右图所示，以BCC1B1的前面为正前方，画出的三视图正确的是( )[解析］主视图是矩形，左视图是三角形，俯视图是矩形,中间有一条线．[答案] A3．已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的主视图的面积不可能等于（）A．1 B. 2 C。

高中数学第1章立体几何初步3三视图3.1简单组合体的三视图3.2由三视图还原成实物图课件北师大版必修2

2．一几何体的直观图如图，下列给出的四个俯视图中正确的是 ()
B [由直观图可知，该几何体由一个长方体和一个截角三棱柱组成．从上往下看，外层轮廓线是一个矩形，矩形内部有一条线段连接的两个三角形．]
由三视图还原成实物图 [探究问题] 1．根据如图所给出的物体的三视图，请说出它们的名称．
提示：从观察三视图的特征入手，联想简单几何体三视图，从而确定几何体的名称，所以①是圆锥，②是三棱柱．
2．如图是某一几何体的三视图，你能想象几何体的结构特征，并画出几何体的直观图吗？
提示：由几何体的三视图可知，几何体是一个倒立的三棱台，即上底面面积大，下底面面积小，直观图如图．
【例3】根据三视图想象物体原形，并画出物体的实物草图．
[思路探究] 观察三视图时可将该几何体分解为上下两部分进行判断，易知该物体是由一个圆柱和一个长方体组合而成的．
1．三视图的主视图、左视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线，画几何体三视图的要求是主视图、俯视图长对正，主视图、左视图高平齐，俯视图、左视图宽相等，前后对应，画出的三视图要检验是否符合“长对正、高平齐、宽相等”的基本特征．
2．画组合体的三视图的步骤
特别提醒：画几何体的三视图时，能看见的轮廓线和棱用实线表示，看不见的轮廓线和棱用虚线表示．
1.通过了解组合体的概念培养数学抽象素养． 2．由三视图的成图原理，绘制三视图的规律，提升直观想象素养.
自主预习探新知
1．组合体 (1)定义：由基本几何体生成的几何体叫作组合体． (2)基本形式：有两种，一种是将基本几何体拼接成组合体；另一种是从基本几何体中切掉或挖掉部分构成组合体．
2．如图，该几何体的上半部分为正三棱柱，下半部分为圆柱，其俯视图是( )

【全优设计】高中数学第一章1.3.2 由三视图还原成实物图目标导学北师大版必修2

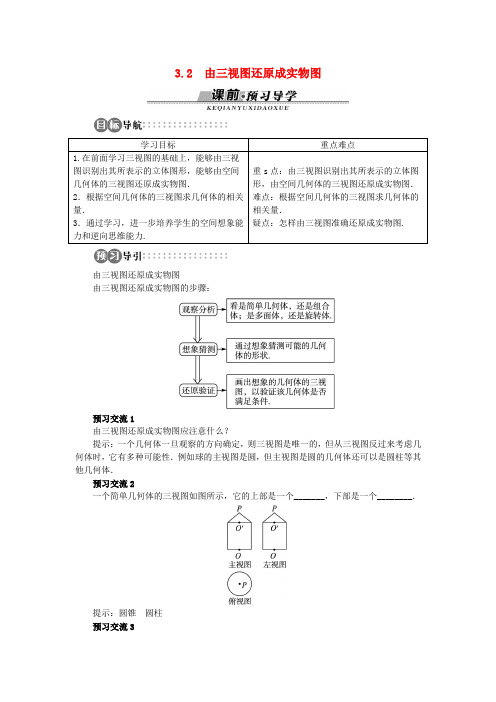
3.2 由三视图还原成实物图由三视图还原成实物图由三视图还原成实物图的步骤：预习交流1由三视图还原成实物图应注意什么？提示：一个几何体一旦观察的方向确定，则三视图是唯一的，但从三视图反过来考虑几何体时，它有多种可能性．例如球的主视图是圆，但主视图是圆的几何体还可以是圆柱等其他几何体．预习交流2一个简单几何体的三视图如图所示，它的上部是一个_______，下部是一个________．提示：圆锥圆柱预习交流3一个几何体的主视图为一个三角形，则这个几何体可能是下列几何体中的______．(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱提示：只要判断主视图是不是三角形就行了，画出图形容易知道三棱锥、四棱锥、圆锥一定可以，对于三棱柱，只需要横着放就可以了，所以①②③⑤均符合题目要求．1．由三视图还原成实物图一个几何体的三视图如图所示，请画出它的实物图．思路分析：解答本题可先根据三视图所提供的信息，应用三视图的相关概念，再进行逆推还原，从而使问题得解．解：由三视图可知，该几何体由正方体和四棱柱组成，如图所示．1．如图所示，甲、乙、丙是三个立体图形的三视图，甲、乙、丙对应的标号正确的是( )．①长方体②圆锥③三棱锥④圆柱A．④③②B．②①③C．①②③D．③②④解析：由于甲的俯视图是圆，则该几何体是旋转体，又因主视图和左视图均是矩形，则甲是圆柱；由于乙的俯视图是三角形，则该几何体是多面体，又因主视图和左视图均是三角形，则该多面体的各个面都是三角形，则乙是三棱锥；由于丙的俯视图是圆，则该几何体是旋转体，又因主视图和左视图均是三角形，则丙是圆锥．答案：A2．请根据三视图想象原物体图形，并画出它的直观图．解：由三视图可知，该几何体为三棱柱，如图所示．由三视图到立体图形，要仔细分析和认真观察三视图，充分想象实物图的样子，看图和想图是两个重要步骤．“想”于“看”中，形体分析的看图方法是解决此类还原问题的常用方法．2．由三视图求几何体的相关量若一个正三棱柱的三视图如图所示，求这个三棱柱的高和底面边长．思路分析：根据三视图提供的信息，确定正三棱柱的高和底面正三角形的高，再求底面边长．解：由三视图可知，左视图中2为正三棱柱的高，俯视图中所以正三棱柱的底面边长为＝4，即这个正三棱柱的高是2，底面边长是4.2如图，水平放置的三棱柱的侧棱长和底面边长均为2，且侧棱AA1⊥底面A1B1C1，主视图是边长为2的正方形，俯视图是边长为2的正三角形，求此三棱柱的左视图面积．解：据实物图及题意可作下视图如图：其中一边长与侧棱长相等，另一边长与底面三角形的高相等．∴面积S＝2×(2sin 60°)＝解决此类问题的关键是根据所给的三视图画出正确的直观图，这就要求熟悉三视图的画法，具有逆向思维能力和空间想象能力．1．一几何体的三视图如图，这个几何体是( )．A．三棱柱B．圆柱C．三棱锥D．圆锥答案：A2．如图所示是一个立体图形的三视图，该立体图形的名称为( )．A．圆柱B．棱锥C．长方体D．棱台答案：C3．如图①、②、③为三个几何体的三视图，根据三视图可以判断这三个几何体依次分别为( )．A．三棱台、三棱柱、圆台B．三棱锥、圆锥、圆台C．四棱锥、圆锥、圆台D．四棱锥、圆台、圆锥答案：C4．主视图为一个三角形的几何体可以是__________．(写出三种)答案：三棱锥、圆锥、四棱锥(不唯一)5．三视图如下图所示，想象物体原形，并画出物体的实物草图．解：由三视图可以看出，这个物体是由一个圆柱和一个正四棱柱组合而成，圆柱的下底面圆和正四棱柱的上底面正方形内切．它的实物草图如图所示．。