13.Fundamentals of SemiconductorMaterials & Devices
材料科学基础作业

Fundamentals of Materials Science 1. Determine the Miller indices for the planes shown in the following unit cell:A:(2 1 -1) B:(0 2 -1)2. Show that the atomic packing factor for HCP is 0.74.Solution:This problem calls for a demonstration that the APF for HCP is 0.74. Again, the APF is just the total sphere-unit cell volume ratio. For HCP, there are the equivalent of six spheres per unit cell, and thusNow, the unit cell volume is just the product of the base area times the cell height, c. This base area is just three times the area of the parallelepiped ACDE shown below.The area of ACDE is just the length of CD times the height BC. But CD is just a or 2R, and3. For both FCC and BCC crystal structures, the Burgers vector b may be expressed aswhere a is the unit cell edge length and [hkl] is the crystallographic direction having the greatest linear atomic density.(a) Compute and compare the linear densities of the [100], [110], and [111] directions for FCC and BCC.(b) What are the Burgers vector representations for FCC, BCC?(c) If the magnitude of the Burgers vector b isdetermine the values of b for aluminum, For Al which has an FCC crystal structure, R=0.1431nm.solutions:(a) In this problem we are to compute the linear densities of several crystallographic planes for the face-centered cubic crystal structure. For FCC the linear density of the [100] direction is computed as follows:The linear density, LD, is defined by the ratiowhere L l is the line length within the unit cell along the [100] direction, and Lc is line length passing through intersection circles. Now, L l is just the unit cell edge length, a which, for FCC is related to the atomic radius R according to a = 2R√2 [Equation (3.1)]. Also for this situation, Lc = 2R and therefore4. Show that the minimum cation-to-anion radius ratio for a coordination number of 6 is 0.414.solutions:In this problem we are asked to show that the minimum cation-to-anion radius ratio for a coordination number of six is 0.414. Below is shown one of the faces of the rock salt crystal structure in which anions and cations just touch along the edges, and also the face diagonals.5. The number-average molecular weight of a polypropylene is 1,000,000 g/mol. Compute the number-average degree of polymerization. Solution:We are asked to compute the number-average degree of polymerization for polypropylene, given that the number-average molecular weight is 1,000,000 g/mol.The mer molecular weight of polypropylene is justm = 3(A C) + 6(A H)= (3)(12.01 g/mol) + (6)(1.008 g/mol) = 42.08 g/molIf we let n n represent the number-average degree of polymerization, then from Equation (4.4a)6. A sheet of BCC iron 1mm thick was exposed to a carburizing gas atmosphere on one side and a decarburizing atmosphere on the other side at 725o C. After having reached steady state, the iron was quickly cooled to room temperature. The carbon concentrations at the two surfaces of the sheet were determined to be 0.012 and 0.0075 wt%. Compute the diffusion coefficient if the diffusion flux is 1.4 ×10-8 kg/m2-s. Hint: Use Equation 5.9 to convert the concentrations from weight percent to kilograms of carbon per cubic meter of iron.7. For a steel alloy it has been determined that a carburizing heat treatment of 10 h duration will raise the carbon concentration to 0.45 wt% at a point 2.5 mm from the surface. Estimate the time necessary to achieve the same concentration at a 5.0-mm position for an identical steel and at the same carburizing temperature.8. The diffusion coefficients for iron in nickel are given at two temperatures:(a) Determine the values of D0 and the activation energy Qd .(b) What is the magnitude of D at 1100 o C (1373 K)?9. A load of 44,500 N (10,000 lbf ) is applied to a cylindrical specimen of steel (displaying the stress–strain behavior shown in Figure 7.33) that has a cross-sectional diameter of 10 mm (0.40 in.).(a) Will the specimen experience elastic or plastic deformation? Why?(b) If the original specimen length is 500 mm (20 in.), how much will it increase in length when this load is applied?Solution:This problem asks us to determine the deformation characteristics of a steel specimen, the stress-strain behavior of which is shown in Figure7.33.(a)In order to ascertain whether the deformation is elastic or plastic, wemust first compute the stress, then locate it on the stress-strain curve, and, finally, note whether this point is on the elastic or plastic region.Thus,10. Consider a single crystal of silver oriented such that a tensile stress is applied along a [001] direction. If slip occurs on a (111) plane and in a[101] direction, and is initiated at an applied tensile stress of 1.1 MPa (160 psi), compute the critical resolved shear stress.Solution: λφστcos cos =11. For alloys of two hypothetical metals A and B, there exist an α, A-rich phase and a β, B-rich phase. From the mass fractions of both phases for two different alloys, which are at the same temperature,determine the composition of the phase boundary (or solubility limit) for both α and βphases at this temperature.12. What is the carbon concentration of an iron–carbon alloy for which the fraction of total ferrite is 0.94?Solution:This problem asks that we compute the carbon concentration of an iron-carbon alloy for which the fraction of total ferrite is 0.94. Application of the lever rule [of the form of Equation (10.12)] yields13. Is it possible to have an iron–carbon alloy for which the mass fractions of total ferrite and proeutectoid cementite are 0.846 and 0.049, respectively? Why or why not?Solution:This problem asks if it is possible to have an iron-carbon alloy for which Wα= 0.846 and W Fe3C = 0.049. In order to make this determination, it isnecessary to set up lever rule expressions for these two mass fractions in terms of the alloy composition, then to solve for the alloy composition of each; if both alloy composition values are equal, then such an alloy is possible. The expression for the mass fraction of total ferrite is14. The fatigue data for a brass alloy are given as follows:(a) Make an S–N plot (stress amplitude versus logarithm cycles to failure) using these data.(b) Determine the fatigue strength at 5×105 cycles.(c) Determine the fatigue life for 200 MPa.Solution:This problem first provides a tabulation of fatigue data (i.e., stress amplitude and cycles to failure) for a brass alloy.(a)These fatigue data are plotted below.(b) As indicated by one set of dashed lines on the plot, the fatigue strength at 5×105 cycles [log (5×105) = 5.7] is about 250 MPa.(c) As noted by the other set of dashed lines, the fatigue life for 200 MPa is about 2×106 cycles (i.e., the log of the lifetime is about 6.3).15. Is it possible to produce a continuous and oriented aramid fiber(芳香尼龙纤维)-epoxy matrix composite having longitudinal and transverse moduli of elasticity of 57.1 GPa and 4.12 GPa, respectively? Why or why not? Assume that the modulus of elasticity of the epoxy is 2.4 GPa. Solution:This problem asks for us to determine if it is possible to produce a continuous and oriented aramid fiber-epoxy matrix composite having longitudinal and transverse moduli of elasticity of 57.1 GPa and 4.12 GPa,respectively, given that the modulus of elasticity for the epoxy is 2.4 GPa. Also, from Table 15.4 the value of E for aramid fibers is 131 GPa. The approach to solving this problem is to calculate two values of Vf using the data and Equations (15.10b) and (15.16); if they are the same then this composite is possible.16. Below, weight gain-time data for the oxidation of copper at an elevated temperature are tabulated.(a) Determine whether the oxidation kinetics obey a linear, parabolic, or logarithmic rate expression.(b) Now compute W after a total time of 450 min.Solution:For this problem we are given weight gain-time data for the oxidation ofCu at an elevated temperature.(a)We are first asked to determine whether the oxidation kinetics obey aparabolic, linear, or logarithmic rate expression, expressions which are described by Equations (16.34), (16.35), and (16.36), respectively.One way to make this determination is by trial and error. Let us assume that the parabolic relationship is valid; that is, from Equation(16.34)which means that we may establish three simultaneous equations using the three sets of given W and t values, then using two combinations of two pairs of equations, solve for K1 and K2; if K1 and K2 have the same values for both solutions, then the kinetics are parabolic. If the values are not identical then the other kinetic relationships need to be explored. Thus, the three equations are。
Fundamentals of Materials Science and Engineering

材料科学导论 Fundamentals of Materials Science andEngineering(教案)青岛科技大学材料科学与工程学院1. IntroductionClasses of MaterialsIt is convenient to classify materials into broad categories for study. Many of the common characteristics of materials within a category arise from the lowest level of structure, the nature of the atomic bond that holds them together, and these similarities are aids to organizing our knowledge. The traditional classifications are:• Metals•Ceramics (and glasses, which are usually made up of the same elements but with a different atomic arrangement)•Polymers (or plastics, to use the more common name)•Composites (which combine several materials to achieve unique or economical combinations of properties)Some people (mostly those who use them) also distinguish electronic materials (semiconductors) as a separate class. The properties of these various classes of materials are usually rather distinct. For instance, metals are opaque to light and reflective. They are (usually) ductile, meaning that they can be bent before they break. They are electrically and thermally conducting. On the other hand, ceramics and glasses are usually brittle, can be transparent to light, and are good insulators. They are particularly useful at high temperatures or in corrosive environments, since they retain their properties. Most polymers, on the other hand, cannot withstand high temperatures. Most are insulators, and many are highly deformable (which is the real meaning of the word, "plastic"), and some have unique elastic properties (rubber bands). Semiconductors, of course, are distinguished by their electrical behavior. All of these property characteristics, and the reasons they exist, are discussed in some detail in the chapters that follow.It will be important to understand the differences between these classes of materials and how they arise from the nature of the atomic bonds and the microstructure. But it will also be important to recognize that comparisons are only meaningful based on similar measurement procedures. For example, mechanical strength and ductility, sensitivity to the presence of cracks, and creep at high temperatures are measured in the same ways for all classes of materials (of course, a high temperature for a polymer is much lower than it is for a ceramic). The response of the materials to these tests is described in a consistent way, using the same mathematical relationships and the same procedures for calculation.One recurring theme in this course will be the Arrhenius relationship which describes the change in many properties and characteristics with temperature. It applies to diffusion rates, creep at high temperatures, viscosity of fluids, electrical conductivity in insulators and semiconductors, and more. It will obviously be to the student's advantage to master the arithmetic of dealing with this relationship. But it will also be important to understand that the reason this same expression appears so many times is that there is an idea behind it that has a general validity. There is an activation energy needed to cause many processes to occur, and the energy to overcome that barrier is obtained from thermal energy.2.Atomic Structure and Interatomic Bonding2.1 Atoms and ElectronsAtoms and ElectronsThere are 92 naturally occurring elements, each identified by the atomic number (number of protons) and atomic weight (which includes the weight of the neutrons) and represents an average over the various isotopes that may exist). The atomic weight has units of grams per mole.A mole is the amount of material that corresponds to the atomic weight. Avogadro's number is the number of atoms in one gram mole. Most of this chapter's numeric problems involve calculating numbers of atoms.There are four principal kinds of bonds that form between atoms: metallic, ionic, covalent, and Van der Waals. The first three are "strong" bonds, roughly equal in magnitude, while the fourth is "weak" (about 1/100th as strong). The forces between atoms are electrostatic, and for the strong bonds, dependent directly on the electrons that surround the atoms. This section explains the origins of these forces and the relevant aspects of the atomic structure that are important to understanding them.2.2 Atoms and ElectronsBohr AtomThe Bohr Model represents the atomic energy levels with discrete levels much like the orbits of planets around the sun. A more complete picture of the electrons would show them asprobability clouds where the "orbit" is merely the most likely distance from the nucleus. For most purposes of chemistry and materials science, this quantum-mechanical view of theatom is not necessary, and the simple orbital model with its discrete energy levels is quiteadequate.2.3 Atoms and ElectronsElectron StatesThe complete description of the electron arrangement around an atom is given by aseries of numbers that describe the shell ("orbit") and the number of electrons in theshell. The filling of the shells is based on quantum number and energy levels.Thus, iron (atomic number 26) is 1s22s22p63s23p63d64s2:•There are 2 electrons in the first shell, 2 in the s level.•There is a total of 8 electrons in the second shell, 2 in the s and 6 in the plevels.•There is a total of 14 electrons in the third shell, 2 in the s, 6 in the p and 6 in the d levels.•There are 2 electrons in the fourth shell, 2 in the s level.These two sequences of diagrams show the process of filling the various quantumstates (electron shells and levels) as a function of atomic number, starting at Hydrogenand proceeding up through the periodic table. The filling of the various quantum states,either in terms of electron shells or energy levels as a function of atomic number,shows how, for instance, there are electrons in the 4s level before the 3d level is filled.The animation showing how the electron shells are filled emphasizes the pairs ofelectrons in each shell and level, with opposite spins.2.4 Atoms and ElectronsElectronegativityElectronegativity is the quantitative description of an atom's desire to gain or lose an electron. It is a function of the number of electrons in an atom's valence shell (nearly filled shells would like to become filled; nearly empty shells readily give up their electrons), and the distance of the shell from the nucleus (where the positive charge in the atom resides). For example, chlorine, with 7 valence electrons, is very eager to gain an electron to fill its outer shell, while sodium will easily give up its 1 valence electron.Electronegativity increases as you go right and up on the periodic table.•It is the electronegativities of atoms that determine what bond type forms.•If the atoms have high electronegativity, they share atoms in a covalent bond between individual pairs of atoms.•If the atoms have low electronegativity, they share atoms among all of the atoms in a metallic bond.•If some of the atoms have high and some low electronegativity, the electrons aretransferred from one atom to another, resulting in an ionic bond.2.5 Bond TypesBond TypesThe different bond types are characterized by how electrons are shared which controls the geometry of the atom packing, and by the relative strength of the bond (revealed in the temperature needed to melt the material and break the bonds).• The Metallic bond: shared valence electrons forming a highly mobile electron sea.• The Covalent bond: valence electrons shared between two atoms.• The Ionic bond: valence electrons transferred between two atoms.• The Van der Waals bond: polarization due to bond structure causes attractive and repulsive force between molecules.2.6 Bond TypesMetallic BondThe Metallic bond is formed between atoms that have a low value of electronegativity and easily give up their outer (valence) electrons. These form an "electron sea" that glues the positive ion cores (nuclei and inner electrons) together and shields the positive cores from each other. The electrons are not bound to any particular atom and so are free to move when an electrical field is applied. This accounts for the electrical conductivity of metals and also their thermalconductivity, since the moving electrons carry thermal vibration energy from place to place as they move. The animation is of this electron sea (in a real metal, there are many more electrons, and instead of being particle-like, they are actually very spread-out wave functions).The Metallic bond is non-directional, so atoms pack around each other densely. The Metallic bond is a strong bond, requiring only slightly less heat energy to cause melting than covalent or ionic bonds.2.7 Bond TypesCovalent BondThe Covalent bond is formed by a sharing of electrons between two adjacent atoms.Convention shows this as discrete electrons in their respective orbits located between the atoms. A more realistic model shows the electrons as a cloud of negative charge between the atoms. Since they are negative, the Covalent bonds repel each other, and this results in their staying as far apart as possible, producing the characteristic dihedral angle in 3D.2.8 Bond TypesIonic BondThe Ionic bond is an electrostatic attraction between positively and negatively chargedions. These bonds are formed by the transfer of electrons from one atom with a lowelectronegativity to a different atom with a high electronegativity.The example shows sodium (Na 11) and chlorine (Cl 17). The Na atom has a singleelectron in the valence shell which it easily gives up, while the Cl atom needs one more electron to complete its outer shell.Transferring the electron from Na to Cl produces positive and negatively charged ionswhich are smaller and larger, respectively, than the original neutral atoms.The electrostatic attractive force between the atoms is non-directional, and so the atom packing in an ionic material attempts to arrange as many positive ions around eachnegative one as possible, and vice versa. The magnitude of the force obeys Coulomb's law (inverse r-squared).Most real ionic bonds contain some degree of covalent nature as well, a mixture oftransferring and sharing the electrons.2.9 Bond TypesVan der Waals BondThe Van der Waals bond is a weak bond that forms by electrostatic attraction between molecules. A molecule with covalent bonds between the atoms localizes the electrons in the region of the bond. This produces polarization of the charge around the atoms so that there are residual positive and negative charges in various locations. The fractional amount of the charge is much less than produced by ionization that removes or adds a whole electron. The Hydrogen bond is a common example of a Van der Waals bond. The H2O molecules in water have polarization charge that is positive on the exposed tips of the hydrogen atomsand negative where the valence electrons are localized. This produces a Van der Waals force between the molecules that causes them to try to line up with the fractional + charges near the - charges. Since the bond angle is 109.5 degrees, close to 120 degrees, this results in a roughly hexagonal arrangement of molecules. Indeed, when water freezes to make ice,it has a hexagonal structure due to these same bond forces. The hexagonal geometry of the ice has a lower density than the water which is why ice floats.2.10 Bond DistanceBond Distance•The distance between atoms is determined by a balance between two forces.• The attractive force varies inversely with the square of the distance between the atoms for all of the various types of bonds (metallic, ionic, covalent, Van derWaals). This force pulls the atoms together with a greater force as they get closertogether.• A repulsive force arises when the electron clouds of negative charge meet. This force increases much faster with distance, with an exponent in the range 6-9 thatdepends on the particular atom and its electron shells.• When the sum of these forces is zero, the distance between the atoms is at the equilibrium value2.11 Bond DistanceBond ForceThe sum of the attractive and repulsive forces is the net force between atoms.Both the attractive and repulsive forces increase as the atoms are brought closertogether, but the repulsive force increases faster, and the sum of the two is zero at the equilibrium point.The slope of the force vs. distance curve at the equilibrium point defines the force needed to pull the atoms slightly apart and is the slope of the stress vs. strain curve. This slope is the modulus of elasticity.2.12 Bond DistanceBond EnergyThe Bond energy vs. distance curve is the integral of the bond force curve. Thelowest energy is the equilibrium point. The depth of the minimum is the total bondstrength which reflects the energy required to pull the atoms completely apart. Thedeeper the potential minimum, the higher the melting temperature. Because therepulsive force increases faster with distance than the attractive force, the bond energy curve is asymmetric. This is why most materials expand when heated. As energy isadded to a material, the thermal vibration of the atoms causes them to oscillate about the equilibrium distance. Because of the asymmetry of the bond energy curve, theaverage distance between atoms increases with temperature. The narrower thepotential minimum, the lower the expansion coefficient.3. Structure of Metals and CeramicsIntroductionThe first level of structure above atomic structure involves the arrangement of atoms. This level can have varying degrees of order or periodicity in the arrangements, from no order to long range order. A monatomic gas at high temperature and low pressure is anexample of disorder or no order. An atom could be anywhere within the enclosing volume and have no particular spatial relationship with any of the other atoms. Single crystals have long range order throughout (except at the surface) and are characterized by arepeating (periodic) arrangement of several atoms or molecules.Most solid materials have structures somewhere in between, having regions of short or long range order. Amorphous solids have structures similar to liquids and generally have isotropic (the same in all directions) properties while crystalline solids usually haveanisotropic (not the same in all directions) properties. Although it may seem to beadvantageous to have isotropic properties, the properties of an amorphous material may not be sufficient for a given application. Designing with anisotropic materials requires the consideration of the directional nature of the material's properties.Time, temperature, and bonding all have important roles in the development of atomic arrangement. As a simple example, a molten unary (one element or component) metal will freeze (solidify) below its melting temperature which depends on the strength of the bonds between atoms. The form of the solid will depend on the bonding between atoms as well as the cooling rate at which the melt solidifies. If the rate is very fast the atoms will not have time to form a periodic arrangement resulting in an amorphous structure. If the cooling rate is slow enough a single crystal can form.The periodic arrangement of atoms or molecules in solids is referred to as crystalstructure and will be the main focus of this topic.3.1 Atomic ArrangementsAtomic ArrangementsIn a liquid, the average interatomic distance is fixed (liquids do not expand to fill theavailable volume as gases do), and there is often local order due to polarization andVan der Waals forces {A&P Figure 3-1}. They may produce a short-range, or local,order. In some cases, rapid cooling of the liquid can lock this atom arrangement into a rigid solid, producing an amorphous, or glassy structure.In most solids (particularly metals and ceramics), the atoms are arranged in regularpatterns that surround each atom with the same number of neighbors as other similar atoms with the same interatomic distances and directions. These are determined bythe types of bonds that hold the atoms together and by the atomic or ionic radii.The long-range repetition of the same atomic arrangement is conveniently describedby a regular grid-like pattern called a lattice . This array of points provides astructure that repeats endlessly through space with the same atom or group of atoms associated with each point.The basic repetitive unit of structure in the three-dimensional grid is called the unit cell.The shapes of unit cells that occur in nature are those that can be stacked together to fill three-dimensional space. Just as equally sized five-sided polygons or equally sized seven-sided polygons cannot be used to tile a plane, only a few specific shapes canbe stacked together to fill three-dimensional space, and these are the basis for thestudy of crystal structures.3.2 Atomic ArrangementsUnit CellsThe simplest repeating unit of any structure that can be stacked to fill space is the unit cell. Consider this as a mathematical or geometric object and ignore for now just how the atoms are arranged within each unit cell, but the SAME arrangement of atoms must be present in each and every unit cell. There are seven such shapes that can be repeated to fill space, all based on the geometry shown at the right with various constraints on the sides and angles. The cubic shape has, of course, the highest symmetry. By adding additional lattice points to some of these seven basic shapes, the 14 Bravais lattices are generated which compactly describe all of the possible geometric packing arrangements with the greatest symmetry and simplicity.3.3Atomic ArrangementsCubic Unit CellsCubic unit cells come in three flavors {A&P Figure 3-7} - simple cubic (SC),body-centered cubic (BCC) , and face-centered cubic (FCC) . Since alldirections and faces are the same, this geometry has the most symmetry and thecalculations are the most straightforward. Many atoms bond in ways that utilize thecubic structure. In the sections on ionic and covalent bonding, we will see examples in which groups of atoms are associated with each lattice point. However, for manycommon metals, the "basis" of the unit cell (the number of atoms per lattice point) isone, and the simplicity of the cubic arrangement is particularly apparent.If all of the atoms are identical, then the coordination number (number of touchingneighbors) is 6 for SC, 8 for BCC {A&P Figure 3-9}, and 12 for FCC. Animations show the arrangement of atoms in the BCC and FCC unit cells and the relationship between the lattice points and the space-filling atoms. Problem 1 shows the relationshipbetween the size of the unit cell (the "lattice parameter") and the radius of the atom{A&P Figure 3-8}.3.4 Atomic ArrangementsPacking Factor and DensityCounting the atoms in a cell (for packing factor or density calculations) can be done by keeping track of just the portions of the atom spheres that lie within the boundaries, as shown for the case of (BCC) and (FCC) , where atoms at corners, edges, and faces belong partially to neighboring cells {A&P Figure 3-7}. Alternatively, any atom with center point coordinates x, y, and z that are greater than or equal to 0 and strictly less than 1 should be counted as part of the cell. If x, y, or z is equal to 1, the atom belongs to the next unit cell in that direction. The packing factor of a unit cell is the fraction of the cell volume that is occupied by the atoms, calculated assuming that each atom (or ion) is a sphere. The equation isFor the cubic unit cells with a single uniform atom at each lattice point, the packing factors are 0.524 for simple cubic, 0.680 for BCC, and 0.740 for FCC. For more complex unit cells, including ones with more than one kind of atom (the reason for the summation sign), the calculation requires understanding the geometry of the unit cell and correctly determining the number of atoms (the number of lattice points times the basis).The calculation of material density (mass/volume) is almost identical to the packing factor except that the atomic weights of the atoms are used instead of their volumes.3.5 Atomic ArrangementsHexagonal PackingQuite a few metals have the hexagonal close-packed (HCP) structure {A&P Figure 3-10}. To build up this atom arrangement, start with a hexagonal close-packed array of atoms in a plane. Place another layer of similarly arranged atoms on top so that they nestle into the valleys between the atoms in the first layer.Then place a third layer on top, in line with the first. Within this hexagonal array lies the unit cell ; the top and side views show that this cell contains two atoms (one inside plus one from the shared corners) and has the 90- and 120-degree angles expected for a hexagonal unit cell.If the same stacking of hexagonal close-packed layers is performed in a slightly different order so that the third layer goes into the third possible position instead of above the first,the surprising result is an FCC structure. The animation shows the construction of the stack, followed by the removal of some atoms to leave just the unit cell. The hexagonal planes run diagonally through the cube. The two stacking arrangements are called ABABAB (HCP) and ABCABC (FCC) {A&P Figures 3-20 and 3-21}. Although the two arrangements have the same density and coordination number, the FCC geometry has many more directions in which the hexagonal close-packed planes can be found, with important consequences for mechanical properties.3.6 Atomic ArrangementsAllotropic TransformationsQuite a few materials of engineering interest have more than one crystal structure, depending upon temperature. Iron is FCC at temperatures above 910°C and changes to BCC at lower temperatures. This is because the rather weak secondary forces between atoms that produce the BCC arrangement are overcome by thermal energy, and as the temperature is raised, the tendency of the metal atoms to form a close-packed array with 12-atom coordination is favored. Similarly, SiO2 changes structure several times as it is heated because of the change in proportion of the bond due to ionic and covalent bonding. This type of transformation is called a polymorphic, or allotropic, transformation. It is usually accompanied by a change in volume. For instance, in iron, the volume increases abruptly by more than 1% with cooling below 910°C. This produces residual stresses in the materials, and especially for brittle materials, can cause cracking.3.7 Coordinate SystemsCoordinate SystemsLocating points within the unit cell can be accomplished with Arraythree x, y, and z values. Rather than limiting these to orthogonalCartesian axes, it is more natural to align them with the edges ofthe unit cell (of course, these are still perpendicular for the cubicsystems). Instead of measuring distances in real units such asAngstroms or nanometers, we scale the values according to thelength of each side so that coordinates within each unit cell rangefrom 0,0,0 to 1,1,1 (this helps to see the similarity of atompositions in unit cells with the same arrangement of differentsized atoms) {A&P Figure 3-11}.3.8 Coordinate SystemsDirections and Linear DensityDirections in a unit cell are described using three integers in the form [a b c]. These are obtained by subtracting the coordinates of the base of the vector from its tip and clearing fractions. A direction parallel to one edge is a simple example. If the difference is negative, that is shown by inserting an over-bar on the value. If the base of the vector is at the origin, the subtraction is simplified, of course. Any fractions in the values are cleared.For a cubic unit cell, the symmetry of the geometry means that many equivalent directions can be combined into a family such as the <100> for all edge directions {A&P Figure3-13}, <110> for all face diagonals, and <111> for all body diagonals. For example, the equivalent directions of <100> are:.The importance of these directions is the atom or linear density along them. For instance, deformation (studied in subsequent chapters) occurs in directions with the highest density. The linear density in a given direction equals the inverse of the repeat distance (the distance between atom centers) in that direction. Problem 8 shows the calculationsfor the [111] direction in FCC. The directions in which atoms touch are directions of maximum linear density. In FCC, the atoms touch only along the face diagonal which isthe <110> family of directions {A&P Figure 3-14}. In BCC, the atoms touch along the body diagonal which is the <111> family of directions.3.9 Coordinate SystemsPlanes and Planar DensityPlanes in unit cells are also defined by three integer numbers called the Miller indices and written (hkl). These values can be determined by finding the intersection of the plane with the x, y, and z axes (shifting the origin, if necessary, so that the plane does not pass through it). These three values are then inverted and fractions cleared (a plane parallel to an axis has an "intersection" with it at infinity, whose inverse is zero). A sequence of planes is shown (you can use the movie controller bar to examine them at your own pace) that are parallel to a face, parallel to one axis, or cut across the unit cell in three dimensions.The symmetry of the cubic unit cell means that families of planes will have the same atom arrangements and densities. Planes of the family {100} are parallel to a face, while the family {110} is parallel to one axis, and the family {111} intersects all three axes. The series of images shows the members of the {110} and {111} families. Note that for a plane, the negative of all three indices produces the same plane. The Detail button shows the atomdensities of these planes in FCC and BCC metals.3.10 Interstitial SitesInterstitial SitesEven in structures comprised of identical atoms with the highest possible packing factors (FCC and HCP are 74% dense), there are some holes. Small atoms can sometimes fit into these holes and are called interstitials. Interstitial sites are characterized by thenumber of neighbors around each. For instance, in FCC, there are tetrahedral sites (four neighbors) and octahedral sites (six neighbors). Likewise, in the BCC structure, there are both tetrahedral and octahedral sites. (Note that for some of thesecases, some of the neighbors are in adjacent unit cells.) {A&P Figure 3-22}In the animations, all of the interstitial sites of each type are shown. In most cases, only a tiny fraction of these sites would be occupied because most interstitial atoms do notexactly fit into the site and cause some lattice deformation, as discussed in Chapter 4.However, the relationship between atom size and coordination number also applies to structures in which a large fraction or all of the sites are occupied in compounds of two or more elements. Notice that only quite small atoms can fit into the tetrahedral sites, while somewhat larger atoms can fit into the octahedral sites. The radius ratio of the small atom to the larger neighbor defines the ability of the atom to fit in, and consequently, thecoordination number (number of neighbors). Problem 11 gives an example of anoctahedral interstitial site in FCC copper.3.11 Interstitial SitesRadius RatioThe size of an atom that can fit into a site varies according to the number of neighbors. In compounds such as ceramics, where different atoms are combined and the packing obeys these rules, the ratio of atomic or ionic radii determines the kind of crystal structure. In most of these structures, either all of the available sites or a fraction of them (determined by the atom stoichiometry) are occupied by another atom type, so the packing must be exact and regular. An atom that is too small for a site allows the neighboring atoms to touch each other, which in the case of ionic bonding, would be undesirable as they have the same sign. An atom that is too large for a site would push the atoms further apart and create enough space for more neighbor atoms so that the rearrangement to a different geometry and coordination number can occur.Packing and coordination number depend on the radius ratio, the interstitial atom radius over the lattice atom radius. Regular packing with four , six , eight , and twelve。
14.Fundamentals of SemiconductorMaterials & Devices

Non-ideal MOSFET
Subthreshold regime
Subtreshold current MOS structure in weak inversion regime (below threshold). Inversion charge depends exponentially on VGS:
Non-ideal MOSFET
Subthreshold regime
Subthreshold regime important because it determines off current, Ioff:
To get Ioff ↓: • L ↑⇒ performance ↓ • VT↑⇒ performance ↓ • n ↓⇒ NA ↓⇒ ” short-channel” effects ↑ ⇒ xox ↓⇒ field in oxide ↑ Ioff: key goal in logic device design Ioff important because it contributes to DC power dissipation in CMOS.
Non-ideal MOSFET
Short-channel effects
Several comments: •Since ID ∼ µ e, mobility degradation more severe as VGS increases ⇒ ID won’t rise as fast with VGS. •Since µe depends on |ξav| ⇒ µ eff depends on y. Disregard to first order ⇒ use same µ eff everywhere. •Mobility degradation considered ” short-channel effect” because as L ↓⇒ xox ↓ and µ degradation becomes important.
The Fundamentals of Materials Science

The Fundamentals of Materials ScienceMaterials science is a branch of science that deals with the properties of materials. It is an interdisciplinary field that combines physics, chemistry, and engineering to gain an understanding of the behavior of materials at the atomic and molecular levels. Materials science plays a vital role in the development of new materials and products that have multiple applications in various fields such as electronics, healthcare, and construction. In this article, we will discuss the fundamentals of materials science, including the structure of materials, properties of materials, and various types of materials.Structure of Materials:The structure of materials at the atomic level determines their macroscopic properties. Atoms are the building blocks of matter, and they arrange themselves in various configurations depending on the element. The arrangement of atoms or molecules in a material determines its properties. For example, metals have a crystalline structure, which gives them strength, ductility, and toughness. On the other hand, glass has an amorphous structure, which makes it brittle.Properties of Materials:The properties of materials are determined by their chemical composition, structure, and processing techniques. Some of the important properties of materials include mechanical, optical, electrical, and thermal properties. Mechanical properties include strength, hardness, toughness, and ductility. Optical properties include the ability to transmit, absorb, or reflect light. Electrical properties include conductivity and resistivity, and thermal properties include the ability to conduct or insulate heat.Types of Materials:Materials are classified into various categories based on their properties and applications. Some of the common types of materials include metals, ceramics, polymers, composites, and semiconductors.Metals:Metals are materials that have high electrical conductivity and ductility. They are commonly used in the production of wires, electronic components, and structural materials. Aluminum, copper, and iron are some examples of metals.Ceramics:Ceramics are inorganic materials that have excellent thermal and electrical insulation properties. They are commonly used in the production of pottery, bricks, and tiles. Examples of ceramics include alumina, silica, and zirconia.Polymers:Polymers are organic materials that have high elasticity and flexibility. They are commonly used in the production of plastics, fibers, and rubbers. Examples of polymers include polyethylene, polystyrene, and polyvinyl chloride.Composites:Composites are materials that are made up of two or more materials to create a new material with superior properties. They are commonly used in the production of aircraft parts, boat hulls, and sports equipment. Carbon fiber reinforced polymers and fiberglass are examples of composites.Semiconductors:Semiconductors are materials that have electrical conductivity between insulators and conductors. They are commonly used in the production of electronic devices such as transistors, diodes, and solar cells. Silicon, gallium arsenide, and germanium are examples of semiconductors.Conclusion:Materials science is a fascinating field that plays a critical role in the development of new technologies. Understanding the structure, properties, and types of materials is essential for the production of new materials with superior properties and applications.The field of materials science is continually evolving, and new materials and processes are being developed every day. As we move forward, the development of new materials is expected to have a significant impact on our daily lives, the economy, and the environment.。
重庆理工大学材料科学基础双语翻译第3章modified翻译

Fundamentals of Materials Science and Engineering
Parallelism (平行, 对应, 类似) axe(轴) projection(投影) divide v. (除) multiply v.(乘) integer(整数) comma(逗点, 逗号) Enclose v.(装入) bracket(括弧) reduced(简化的)
Fundamentals of Materials Science and Engineering
be devoted to专心于: be dedicated to/ dealing with, being used for only one thing. 专于 Entity实体本质 n. pl. entities [c] something that exists as a single and complete unit 实体、整体
This Chapter will be devoted to (专于) the next level of 的等级 the structure of materials, specifically特别的, to some of the arrangements 安排that may be assumed 假定的 by atoms in the solid state固态. All metals金属, many ceramic materials陶瓷材料, and certain某些 polymers 聚合物form crystalline structures晶体结构 under normal 正常solidification 凝固 conditions条件. For those that do not crystallize使晶体, this longrange atomic order命令 is absent缺少; these noncrystalline非晶体 or amorphous非晶体物质 materials are discussed讨论 briefly 短暂at the end of this chapter.
Fundamentals of Materials Science and Engineering(上海交大最新版)

Fundamentals of Materials Science and Engineering第一章原子结构一. 波尔原子模型:1.在任意轨道上绕核运动,在一些符合一定量化的轨道上运动2.电子离核越远,原子所含能量越高,电子尽可能在离核较近的轨道上3.电子只有从较高能级跃迁到较低能级才以光子形式释放能量波动力学模型:量子力学模型量子力学是建立在微观世界的量子性和微粒运动统计性基本特征上,在量子力学处理氢原子核外电子的理论模型中,最基本的方程叫做薛定谔方程,是由奥地利科学家薛定谔(E.Schrödinger 1887-1961)在1926年提出来的。
薛定谔方程是一个二阶偏微分方程,它的自变量是核外电子的坐标,它的因变量是电子波的振幅(ψ)。
给定电子在符合原子核外稳定存在的必要、合理的条件时,薛定谔方程得到的每一个解就是核外电子的一个定态,它具有一定的能量,具有一个电子波的振幅随坐标改变的的函数关系式ψ=f(x,y,z),称为振幅方程或波动方程。
二. 能量最低原理:电子的排布总是尽可能使体系的能量最低三. 泡利不相容原理:在一个原子中不可能有运动状态完全相同的两个电子四. 洪德原则:在同一个亚层中,各个能级中,电子的排布尽可能分占不同的能级,而且自旋方向相同。
五. 原子键合:1.金属键:定义:金属中的电子与金属正离子相互间结合构成的键合特点:1.无方向性无饱和性2.电子公有化3.良好的延展性4.导电导热性,金属光泽2.离子键:定义: 金属将最外层的电子给予非金属原子,是自己成为带正电的正离子,而得到价电子的非金属成为带负电的负离子,正负离子靠静电引力相互结合在一起构的键合特点:1.以离子为结合单元,而不是原子2.无方向性无饱和性3.配位数高,熔点硬度高,绝缘体3.共价键:定义:由两个或多个电负性相差不大的原子相互结合在一起形成共用电子对而形成的键合特点:1.方向性,饱和性2.共用电子对3.熔点高,质硬脆,结构稳定,导电能力差。
《The Fundamentals Of Digital Semiconductor Testing》_中文版C
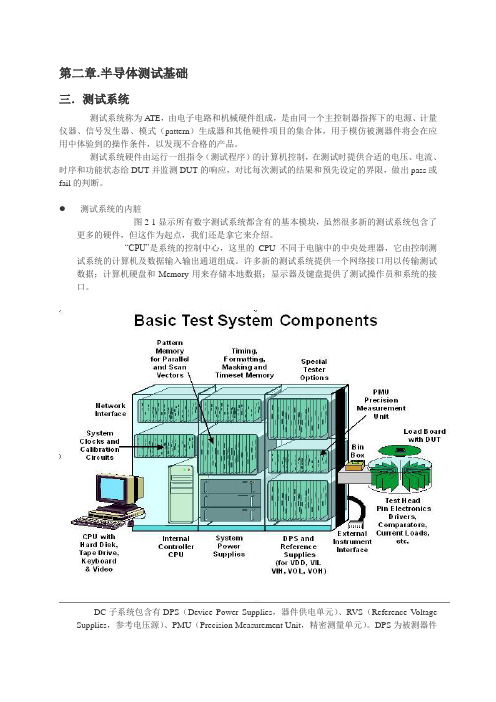
第二章.半导体测试基础三.测试系统测试系统称为ATE,由电子电路和机械硬件组成,是由同一个主控制器指挥下的电源、计量仪器、信号发生器、模式(pattern)生成器和其他硬件项目的集合体,用于模仿被测器件将会在应用中体验到的操作条件,以发现不合格的产品。
测试系统硬件由运行一组指令(测试程序)的计算机控制,在测试时提供合适的电压、电流、时序和功能状态给DUT并监测DUT的响应,对比每次测试的结果和预先设定的界限,做出pass或fail的判断。
测试系统的内脏图2-1显示所有数字测试系统都含有的基本模块,虽然很多新的测试系统包含了更多的硬件,但这作为起点,我们还是拿它来介绍。
“CPU”是系统的控制中心,这里的CPU不同于电脑中的中央处理器,它由控制测试系统的计算机及数据输入输出通道组成。
许多新的测试系统提供一个网络接口用以传输测试数据;计算机硬盘和Memory用来存储本地数据;显示器及键盘提供了测试操作员和系统的接口。
DC子系统包含有DPS(Device Power Supplies,器件供电单元)、RVS(Reference V oltage Supplies,参考电压源)、PMU(Precision Measurement Unit,精密测量单元)。
DPS为被测器件的电源管脚提供电压和电流;RVS为系统内部管脚测试单元的驱动和比较电路提供逻辑0和逻辑1电平提供参考电压,这些电压设置包括:VIL、VIH、VOL和VOH。
性能稍逊的或者老一点的测试系统只有有限的RVS,因而同一时间测试程序只能提供少量的输入和输出电平。
这里先提及一个概念,“tester pin”,也叫做“tester channel”,它是一种探针,和Loadboard背面的Pad接触为被测器件的管脚提供信号。
当测试机的pins共享某一资源,比如RVS,则此资源称为“Shared Resource”。
一些测试系统称拥有“per pin”的结构,就是说它们可以为每一个pin 独立地设置输入及输出信号的电平和时序。
Fundamental Studies of Molecular Electronics

Fundamental Studies of MolecularElectronics近年来,分子电子学已经成为纳米科技领域中备受关注的重要方向。
作为一种新型电学现象的研究,分子电子学探究的是分子的电学性质,以及这些性质如何在实际应用中实现。
分子电子学的基础研究是分子电子学的前沿领域。
在这个领域中,研究者们使用理论计算和实验方法来研究分子的电学性质,探究其在电子器件中的运用。
分子电子学的基础研究有两个主要方向:一是探究分子的导电性质,即分子的电导率;二是研究分子与电子器件之间的相互作用,以便更好地了解分子与电子器件之间的联系。
在探究分子的导电性质方面,研究者们需要考虑分子的内部结构、分子间的相互作用力、分子的电子结构等。
这些因素将直接影响分子的导电性质。
利用这些知识,研究者们可以设计出一些新型的分子结构,帮助改善分子的导电性能。
在研究分子与电子器件之间的相互作用方面,研究人员需要关注分子与电子器件之间的界面性质。
他们需要研究分子在不同界面下的电学行为,并探究这些行为对电子器件的性能产生的影响。
探究有助于更好地了解分子与电子器件的相互作用。
分子电子学的基础研究还包括探究分子的光电性质。
这些性质有助于我们更好地理解分子在光学电子器件中的应用,例如光电效应。
光电效应是光在分子中引起电子运动的现象。
研究者们通过探究分子的光电性质,可以寻找更合适的分子材料,以提高光电器件的效率。
分子电子学的基础研究在未来的纳米技术领域发挥着不可替代的作用。
他们不仅有助于我们了解分子电子学的基本原理,还有助于我们设计更加高效、灵活的分子电子器件。
在未来,研究者们将继续探究基础研究,为纳米技术的研究提供更多的可能。
材料科学基础专有名词英文翻译

Fundamentals of Materials Science 材料科学基础名词与术语第一章绪论metal: 金属ceramic:陶瓷polymer:聚合物Composites:复合材料Semiconductors: 半导体Biomaterials: 生物材料Processing:加工过程Structure: 组织结构Properties:性质Performance:使用性能Mechanical properties: 力学性能Electrical properties:电性能Thermal behavior:热性能Magnetic properties:磁性能Optical properties:光性能Deteriorative characteristics:老化特性第二章原子结构与原子键Atomic mass unit (amu):原子质量单位Atomic number:原子数Atomic weight:原子量Bohr atomic model: 波尔原子模型Bonding energy: 键能Coulombic force: 库仑力Covalent bond:共价键Dipole (electric):偶极子electronic configuration:电子构型electron state:电位Electronegative: 负电的Electropositive:正电的Ground state:基态Hydrogen bond: 氢键Ionic bond: 离子键Isotope: 同位素Metallic bond:金属键Mole:摩尔Molecule:分子Pauli exclusion principle:泡利不相容原理Periodic table:元素周期表Polar molecule:极性分子Primary bonding: 强键Quantum mechanics:量子力学Quantum number:量子数Secondary bonding:弱键valence electron:价电子van der waals bond:范德华键Wave—mechanical model: 波粒二象性模型第三章金属与陶瓷的结构Allotropy:同素异形现象Amorphous:无定形Anion: 阴离子Anisotropy: 各向异性atomic packing factor(APF): 原子堆积因数body—centered cubic (BCC): 体心立方结构Bragg’s law:布拉格定律Cation:阳离子coordination number:配位数crystal structure:晶体结构crystal system:晶系crystalline: 晶体的diffraction: 衍射face—centered cubic (FCC):面心立方结构第五章晶体缺陷Alloy:合金A metallic substance that is composed of two or more elements。
4 《材料科学基础》第四章 非晶态结构

了解
一、熔体形成过程 (以Na2O—SiO2熔体为例) 石英的分化
低聚物的缩聚
Onb
Ob
初期:主要是石英颗粒的分化; 中期:缩聚反应并伴随聚合物的变形;
后期:在一定温度(高温)和一定时间(足够长)下 达到聚合 解聚平衡。
石英分化过程示意图
[SiO4]Na4+ [SiO4]Na4 = [Si2O7]Na6+Na2O [SiO4]Na4+[Si2O7]Na6 =[Si3O10]Na8+ Na2O
1 2 1 2
由非熔融法形成玻璃的物质
原始物质 固体 (结晶) 形成原因 剪切应力 放射线照射 形成络合物 获得方法 冲击波 磨 碎 高速中子线 a 粒子线 金属醇盐 水解 真空蒸发 沉积 气 升 华 阴极飞溅和 氧化反应 气相反应 气相反应 体 电 解 辉光放电 实 例
石英、长石等晶体,通过爆炸的冲击波而非晶化 晶体通过磨碎,粒子表面层逐渐非晶化 石英晶体经高速中子线或 a 粒子线的照射后转变为非晶 体石英 Si、B、P、Al、Na、K 等醇盐酒精溶液加水分解得到胶 体,加热形成单组分或多组分氧化物玻璃 在低温基板上用蒸发沉积形成非晶质薄膜,如 Bi、Si、 Ge、B、M gO、Al2O 3、TiO 2、SiC 等化合物 在低压氧化气氛中,把金属或合金做成阴极,飞溅在基 极上形成非晶态氧化物薄膜,有 SiO 2、PbO-TeO 2、Pb -SiO2 系统薄膜等 SiCl4 水解或 SiH 4 氧化形成 SiO 2 玻璃。在真空中加热 B(OC2H 3)3 到 700℃~900℃形成 B2O 3 玻璃 利用辉光放电形成原子态氧和低压中金属有机化合物 分解,在基极上形成非晶态氧化物薄膜,如 Si(OC2H 5)4 →SiO 2 及其它例子 利用电介质溶液的电解反应,在阴极上析出非晶质氧化 物,如 Ta2O 3、Al2O 3、ZrO 2、Nb2O 3 等
Fundamentals of Materials Science

不全位错:柏氏矢量不等于点阵矢量整数倍的位错称为不全位错。
表面能:表面原子处于不均匀的力场之中,所以其能量大大升高,高出的能量称为表面自由能(或表面能)包晶转变:在二元相图中,包晶转变就是已结晶的固相与剩余液相反应形成另一固相的恒温转变。
固溶体:是以某一组元为溶剂,在其晶体点阵中溶入其他组元原子(溶剂原子)所形成的均匀混合的固态溶体,它保持溶剂的晶体结构类型。
固溶强化:由于合金元素(杂质)的加入,导致的以金属为基体的合金的强度得到加强的现象。
原因:由于溶质原子与位错相互作用的结果,溶质原子不仅使晶格发生畸变,而且易被吸附在位错附近形成柯氏气团,使位错被钉扎住,位错要脱钉,则必须增加外力,从而使变形抗力提高。
成分过冷;界面前沿液体中的实际温度低于由溶质分布所决定的凝固温度时产生的过冷。
过冷度:相变过程中冷却到相变点以下某个温度后发生转变,平衡相变温度与该实际转变温度之差称过冷度。
共晶转变:合金系中某一定化学成分的合金在一定温度下,同时由液相中结晶出两种不同成分和不同晶体结构的固相的过程称为共晶转变。
合金:两种或两种以上的金属或金属与非金属经熔炼、烧结或其他方法组合而成并具有金属特性的物质。
近程有序:在非晶态结构中,原子排列没有规律周期性,原子排列从总体上是无规则的,但是,近邻的原子排列是有一定的规律的这就是“短程有序”。
结构起伏:液态结构的原子排列为长程无序,短程有序,并且短程有序原子集团不是固定不变的,它是一种此消彼长、瞬息万变、尺寸不稳定的结构,这种现象称为结构起伏。
晶粒长大:是指再结晶结束后晶粒的长大过程,在晶界界面能的驱动下,新晶粒会发生合并长大,最终达到一个相对稳定的尺寸。
结晶:物质从液态(溶液或熔融状态)或气态凝出具有一定的几何形状的固体(晶体)的过程加工硬化:金属经冷塑性变形后,其强度和硬度上升,塑性和韧性下降,这种现象称为加工硬化。
原因:随变形量增加, 位错密度增加,由于位错之间的交互作用(堆积、缠结),使得位错难以继续运动,从而使变形抗力增加;这是最本质的原因。
材料科学基础专有名词英文翻译

材料科学基础专有名词英文翻译Fundamentals of Materials Science 材料科学基础名词与术语第一章绪论metal: 金属ceramic: 陶瓷polymer: 聚合物Composites: 复合材料Semiconductors: 半导体Biomaterials: 生物材料Processing: 加工过程Structure: 组织结构Properties: 性质Performance: 使用性能Mechanical properties: 力学性能Electrical properties: 电性能Thermal behavior: 热性能Magnetic properties: 磁性能Optical properties: 光性能Deteriorativecharacteristics: 老化特性第二章原子结构与原子键Atomic mass unit (amu): 原子质量单位Atomic number: 原子数Atomic weight: 原子量Bohr atomic model: 波尔原子模型Bonding energy: 键能Coulombic force: 库仑力Covalent bond: 共价键Dipole (electric): 偶极子electronic configuration: 电子构型electron state: 电位Electronegative: 负电的Electropositive: 正电的Ground state: 基态Hydrogen bond: 氢键Ionic bond: 离子键Isotope: 同位素Metallic bond: 金属键Mole: 摩尔Molecule: 分子Pauli exclusion principle: 泡利不相容原理Periodic table: 元素周期表Polar molecule: 极性分子Primary bonding: 强键Quantum mechanics: 量子力学Quantum number: 量子数Secondary bonding: 弱键valence electron: 价电子van der waals bond: 范德华键Wave-mechanical model: 波粒二象性模型第三章金属与陶瓷的结构Allotropy: 同素异形现象Amorphous: 无定形Anion: 阴离子Anisotropy: 各向异性atomic packing factor(APF): 原子堆积因数body-centered cubic (BCC): 体心立方结构Bragg’s law: 布拉格定律Cation: 阳离子coordination number: 配位数crystal structure: 晶体结构crystal system: 晶系crystalline: 晶体的diffraction: 衍射face-centered cubic (FCC): 面心立方结构第五章晶体缺陷Alloy: 合金A metallic substance that is composed of two or more elements.由两种及以上元素组成的金属材料。
ch03Fundamentals of Semiconductors

Chapter 3 Fundamentals ofSemiconductors第三章 半导体的基础知识§3.1 Energy band 能带结构§3.2 Intrinsic semiconductors and doped semiconductors 本征半导体和掺杂半导体§3.3 Carrier concentration under thermodynamic equilibrium 平衡状态下载流子浓度§3.4 Absorption of light in semiconductors 光在半导体中的吸收§3.5 3.5 Nonequilibrium Nonequilibrium Nonequilibrium carrier concentrationcarrier concentration 非平衡状态下载流子浓度§3.6 Transport of carriers 载流子的输运§3.1 Energy band 能带结构Conduction BandValence BandBand Gap E gE cE v§3.2 Intrinsic semiconductors and doped semiconductors 本征半导体和掺杂半导体Intrinsic semiconductorsDoped semiconductorsFermi energy of n-type and p-type silicon, E F,n and E F,p, as a function of doping density at 100, 200, 300, 400 and 500 K.Shown are the conduction and valence band edges, E c and E v.The midgap energy is set to zero.§3.4 Absorption of light in semiconductors光在半导体中的吸收Intrinsic absorption本征吸收g E h ≥νExtrinsic absorption 非本征吸收Impurity absorptionImpurity absorption 杂质吸收 Carrier absorptionCarrier absorption 载流子吸收 Exciton Exciton Exciton absorptionabsorption 激子吸收 Crystal lattice absorptionCrystal lattice absorption 晶格吸收§3.5 3.5 Nonequilibrium Nonequilibrium Nonequilibrium carrier concentrationcarrier concentration 非平衡状态下载流子浓度1 Equilibrium, 1 Equilibrium, NonequilibriumNonequilibrium 2 Generation and recombinationGeneration can be caused by an applied electric field, achange in temperature or exposure to light. Recombination is part of a process to restore equilibrium to a semiconductor that has been perturbed, or disturbed out of equilibrium.3 3 Nonequilibrium Nonequilibrium Nonequilibrium carrier concentration carrier concentration4 Majority carriers, minority carriers5 Lifetime of 5 Lifetime of NonequilibriumNonequilibrium§3.6 Transport of carriers载流子的输运Drift: When an electric field is applied across a semiconductor, the carriers start moving, producing a current. The positively charged holes move with the electric field, whereas the negatively charged electrons move against the electric field.Diffusion: Diffusion is the process of particles distributing themselves from regions of high concentration to regions of low concentration.。
The Chemistry and Physics of Semiconductor Devices

The Chemistry and Physics ofSemiconductor DevicesIntroductionSemiconductor devices are a vital part of modern-day electronics, and they have revolutionized several industries, including telecommunications and computing. These devices are made up of materials such as silicon, germanium, and gallium arsenide, which have unique properties that make them suitable for electronic applications. The chemical and physical properties of semiconductors are at the core of how these devices operate, and understanding them is crucial to unlock the full potential of these technologies.Semiconductor MaterialsSemiconductors are materials whose electrical conductivity lies between conductors and insulators. They have a unique property in that their conductivity can be altered by adding impurities to their crystal structure, a process called doping. The two most common elements used in doping are boron (for p-type doping) and phosphorus (for n-type doping).In p-type silicon, the boron atoms introduce holes into the crystal structure, which can accept electrons, leading to positive charge carriers. Meanwhile, in n-type silicon, the extra electrons from the phosphorus atoms create negative charge carriers. When a p-type and an n-type layer are placed next to each other, an interface is formed, where electrons are transferred from the n-type layer to the p-type layer. This process creates a depletion region, where no current can flow, making the interface act like a one-way valve, the basis of a diode.The p-n JunctionThe p-n junction, formed by placing a p-type and an n-type material together, is the most basic type of semiconductor device. When a voltage is applied across a p-n junction,electrons from the n-type region migrate to the p-type region, while holes from the p-type region migrate to the n-type region. Eventually, the zones deplete, creating a highly resistive barrier that prevents current from flowing in the reverse direction. This phenomenon is known as the rectifying property of a diode, and it is the basis for technologies such as LED lights, solar cells, and rectifiers.TransistorsTransistors are the fundamental building blocks of digital circuits. They are three-terminal devices that can amplify or switch electronic signals and were invented in 1947 by John Bardeen and Walter Brattain at Bell Labs. The transistor is essentially a switch with three sections in a sandwich formation: a collector, a base, and an emitter. The current between the collector and the emitter is controlled by the current flowing into the base.When no voltage is applied to the base, the transistor is off, and no current flows through it. However, introducing a small current in the base triggers a much larger current between the collector and the emitter, effectively turning the transistor on. Transistors paved the way for the creation of both analog and digital circuits, making them important for several technologies, including radios, computers, and microprocessors.Integrated CircuitsWhile transistors were a significant improvement over vacuum tubes, their widespread use was limited by their size. By etching transistors and other components directly onto a single crystal of semiconductor material, researchers were able to greatly reduce the size of electronic devices, leading to the development of integrated circuits (ICs). ICs paved the way for the development of computers, and they are now a critical component in many technologies, including smartphones, gaming consoles, and smart TVs. The miniaturization of ICs has also facilitated the development of wearable technology, providing solutions for healthcare, fitness, and entertainment.ConclusionSemiconductor devices have transformed society by enabling the development of technologies that we now take for granted. Understanding the chemistry and physics of semiconductor devices has led to the development of new electronic applications, making our lives easier, safer, and more enjoyable. Future advancements will undoubtedly continue to build upon the foundation laid by researchers and engineers who have contributed to the evolution of semiconductor technology.。
《材料化学专业英语》

To sum up, by learning this course, you could
Improve your English, learning new phrases or terms and concepts of materials science.
Expand your knowledge on the Principal of Materials Science and Engineering.
Unique[’ju:ni:k]太监 Unique [ju:’ni:k] usually good and special.
e.g., a unique opportunity
Attendance and class involvement (出勤与课堂表现)
Regular attendance is expected. In-class discussion of the writing assignments will be crucial to being able to complete them adequately by yourself. You are also expected to show up to class on time and asked for a leave or absense if you do being sick or have something to do.
Transpire: pass through the tissue or substance or its pores or interstices, as of gas
Prior to publication, the editorial office had consulted a German sinologist (汉学家)for a translation of the relevant text. The sinologist concluded that the text in question depicted classical Chinese characters in a noncontroversial (有争议的)context. To our sincere regret, however, it has now emerged that the text contains deeper levels of meaning, which are not immediately accessible to a non-native speaker.
(完整word版)TheFundamentalsofDigitalSemiconductorTesting(chinese)

目录第一章.认识半导体和测试设备 (3)一、晶圆、晶片和封装 (3)二、自动测试设备 (6)三、半导体技术 (7)四、数字和模拟电路 (7)五、测试系统的种类 (8)六、测试负载板(LoadBoard) (11)七、探针卡(ProbeCard) (12)第二章.半导体测试基础 (13)一、基础术语 (13)二、正确的测试方法 (14)三、测试系统 (16)四、PMU (18)五、管脚电路 (21)第三章.基于PMU的开短路测试 (25)一、测试目的 (25)二、测试方法 (25)第四章.DC参数测试 (29)一、基本术语 (29)二、Binning (29)三、Program Flow (30)四、Test Summary (31)五、DC测试与隐藏电阻 (32)六、VOH/IOH (33)七、VOL/IOL (36)八、IDD Gross Current (39)九、IDD Static Current (42)十、IDDQ (44)十一、IDD Dynamic Current (45)十二、入电流(IIL/IIH)测试 (48)十三、输入结构-高阻/上拉/下拉 (54)十四、输出扇出 (55)十五、高阻电流(High Impedance Currents, IOZH/IOZL) (57)十六、输出短路电流(output short circuit current) (60)第五章.功能测试 (63)一、基础术语 (64)二、功能测试 (64)三、测试周期 (65)四、输入数据 (65)五、输出数据 (68)六、功能测试参数定义 (72)七、总功能测试(Gross Function Test) (73)八、功能测试实例 (77)九、标准功能测试 (80)第六章.AC参数测试 (91)第一章.认识半导体和测试设备本章节包括以下内容,●晶圆(Wafers)、晶片(Dice)和封装(Packages)●自动测试设备(ATE)的总体认识●模拟、数字和存储器测试等系统的介绍●负载板(Loadboards)、探测机(Probers)、机械手(Handlers)和温度控制单元(Temperature units)一、晶圆、晶片和封装1947年,第一只晶体管的诞生标志着半导体工业的开始,从那时起,半导体生产和制造技术变得越来越重要。
fundamentals of materials science nbool -回复

fundamentals of materials science nbool -回复题为“材料科学基础”的文章。
材料科学基础材料科学是研究物质的结构、特性、制备和应用的学科。
作为一门跨学科的学科,材料科学综合了化学、物理学、工程学和生物学等多个学科的知识。
本文将一步一步地回答关于材料科学基础的问题。
一、什么是材料?材料是构成物体的原料。
它可以是固体、液体或气体,可以用于制造不同种类的产品,如电子设备、汽车、建筑物等。
材料的选择取决于其特性和所需应用的要求。
二、材料的分类有哪些?材料可以根据其组成、结构和性质进行分类。
常见的材料分类包括金属、陶瓷、聚合物和复合材料。
1. 金属材料:金属材料具有良好的导电性和导热性,常见的金属材料有铝、铁、钢等。
金属材料可用于制造结构件、电子器件等。
2. 陶瓷材料:陶瓷材料具有高硬度和耐磨性,常见的陶瓷材料有陶瓷砖、瓷器等。
陶瓷材料可用于制造绝缘体和耐高温环境的部件。
3. 聚合物材料:聚合物材料具有良好的绝缘性和可塑性,常见的聚合物材料有聚乙烯、聚氯乙烯等。
聚合物材料可用于制造塑料制品、纤维等。
4. 复合材料:复合材料是由两种或多种不同类型的材料组成的,以提高材料的性能。
常见的复合材料有纤维增强复合材料、混凝土等。
复合材料可用于制造航空航天器、汽车零部件等。
三、材料的性质如何评估?材料的性质包括物理性质、化学性质和机械性质等。
1. 物理性质:物理性质包括密度、熔点、导电性、导热性等。
这些性质可以通过实验方法进行测量和评估。
2. 化学性质:化学性质包括材料在不同环境下的化学反应、腐蚀性等。
这些性质可以通过化学实验来评估。
3. 机械性质:机械性质包括强度、硬度、韧性等。
这些性质可以通过拉伸、压缩、扭转等实验来评估。
四、材料的制备方法有哪些?材料的制备方法根据材料的类型和应用需求而定。
常见的制备方法包括熔融法、化学合成法、沉积法等。
1. 熔融法:熔融法是将材料加热至熔点,使其变为液态,并通过冷却使其凝固。
施敏 半导体元件物理 英文

施敏半导体元件物理英文Title: Semiconductor Device Physics by Shi MinIn the realm of semiconductor technology, the study of semiconductor device physics holds paramount importance. It is a field that explores the fundamental principles governing the behavior of semiconductor materials and devices, enabling the design and optimization of electronic components that are the building blocks of modern electronics. Shi Min, a renowned expert in this field, has made significant contributions to our understanding of semiconductor device physics.The foundation of semiconductor device physics lies in the quantum mechanical properties of semiconductors. These materials, unlike metals or insulators, have a unique electronic structure that allows them to conductelectricity under certain conditions. Shi Min's research has focused on elucidating these properties, particularlyin the context of device applications.One of the key aspects of Shi Min's work is the study of doping in semiconductors. Doping involves theintroduction of impurity atoms into the semiconductor crystal, which alters its electrical properties. Bycarefully controlling the type and concentration of dopants, it is possible to create semiconductors with desired characteristics, such as enhanced conductivity or specific band structures. Shi Min has developed novel doping techniques and analyzed their impact on device performance, paving the way for more efficient and reliable electronic components.Another area of expertise for Shi Min is the study of carrier transport in semiconductors. Carriers, which are electrons or holes in the semiconductor lattice, are responsible for the conduction of electricity. Shi Min has delved deeply into the mechanisms governing carrier transport, including diffusion, drift, and quantum tunneling. His insights into these processes have been crucial for understanding and improving the performance of semiconductor devices such as transistors and diodes.In addition to these fundamental aspects, Shi Min has also contributed to the development of advanced semiconductor devices. He has worked on the design andoptimization of various device structures, such as metal-oxide-semiconductor (MOS) transistors and heterostructure devices. His research has focused on enhancing device performance by improving carrier mobility, reducing leakage currents, and increasing breakdown voltages. These efforts have led to the development of faster, more efficient, and more reliable electronic components that are crucial for modern electronics applications.Moreover, Shi Min's work has also addressed the challenges associated with scaling down semiconductor devices. As the demand for smaller, faster, and moreenergy-efficient electronic devices continues to grow, the need for nanoscale semiconductors has become increasingly urgent. Shi Min has investigated the physical limitations of scaling down semiconductor devices and proposed innovative solutions to overcome these challenges. His research has focused on developing new materials, device structures, and fabrication techniques that can enable the continued miniaturization of electronic components while maintaining their performance and reliability.In conclusion, Shi Min's contributions to the field of semiconductor device physics are significant and diverse. His research has deepened our understanding of the fundamental properties of semiconductors and has led to the development of advanced electronic devices that are essential for modern electronics applications. His insights and innovations have been instrumental in pushing the boundaries of semiconductor technology and will continue to influence the development of future electronic systems.。
10.The Fundamentals ofSemiconductor Materials & Devices

Ideal MOS structure under bias
Semiconductor surface
Ideal semiconductor surface
Semiconductor comes to an end, but bulk properties unaffected →bonding arrangement at surface unchanged from bulk. Zero carrier current normal to surface; other than that, carriers unaffected by surface.
Semiconductor surface
Passivated surface
Ideal MOS structure at zero bias
MOS structures pervasive in modern microelectronics: • heart of MOSFETs (from which CMOS is made) • heart of DRAMs, Flash memories
Semiconductor surface
Real surface
7╳7 Reconstruction of Si(111)
Semiconductor surface
Passivated surface
“ Coating” of semiconductor surface with passivating layer so that bulk bonding prevails for surface atoms.
Ideal MOS structure at zero bias
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Dependence of VT(y) further debiases transistor: ⇒ ID lower than ideal ⇒ VDSsat lower than ideal
Non-ideal MOSFET
Voltage dependence of VT:
VTo is VT for VSB = 0. Charge control relation becomes:
channel current unchanged →MOSFET in saturation.
I-V characteristics of ideal MOSFET
Lateral electrostatics in saturation:
I-V characteristics of ideal MOSFET
• For VDS > 0 and VGS > VT: VGS ↑ ⇒ ID ↑. • For VGS = VT ⇒ ID = 0
I-V characteristics of ideal MOSFET
Study lateral electrostatics:
Along channel from source to drain: V ↑ ⇒ VGS − V(y) − VT ↓ ⇒ |Qi| ↓ ⇒ |ξy(x = 0)| ↑ Local overdrive on gate reduced the closer to the drain.
Gradual-channel approximation becomes invalid.
Sheet-charge approximation becomes invalid. Lateral field so large that linearity between field and
At the source end:
Qi at source end is set entirely by VGS: Qi(0) = −Cox(VG − VT) Qi is independent of what happens down the channel. VDS dependence in current equation comes entirely from vey(0). In mobility regime: At high VDS, channel debiasing implies that the rise of ξy(0) with VDS slows down and eventually, it does not increase anymore.
Insert into current equation:
Integrate from y = 0 to y = L ⇒ MOSFET current in linear regime:
Note new terms multiplied by γ ⇒ if γ → 0, body effect → 0.
Energy band Diagrams
Non-ideal MOSFET
Simplifying assumptions for ideal MOSFET: Carrier flow is one dimensional and uniform doping levels Electron transport in inversion layer takes place by drift (i.e., neglect diffusion). Electrons drift along the inversion layer in the mobility regime, i.e., the electron velocity is proportional to the lateral electric field along the inversion layer. Neglect body effect and no parasitic resistances. Ignore junction sidewall effects. No three-dimensional effects (device scales perfectly with its width). Neglect impact of substrate that surrounds the transistor.
How close can VDS get to VGS-VT before simple model fails? Answer: up to about 80% of VGS- VT which means up to about 96% of IDmax. Hence, simple model is pretty good up to VDS = VGS-VT.
I-V characteristics of ideal MOSFET
If VDS reaches or exceeds VGS- VT? Electron concentration at y = L drops to very small concentrations → depletion region appears at y = L: pinch-off. Depletion region is no barrier to electron flow: field "pulls” electrons into drain.
I-V characteristics of ideal MOSFET
If VDS reaches or exceeds VGS- VT? As VDS exceeds VGS- VT, depletion region widens into channel underneath gate; all extra voltage consumed in depletion region; electrostatics of channel, to first order, unperturbed;
I-V characteristics of ideal MOSFET
Develop first-order model
Separate variables:
Integrate from y=0(V=0) to y=L(V=VDS):
To get:
Terminal drain current:
I-V characteristics of ideal MOSFET
Current in saturation regime:
Non-ideal MOSFET
Body effect
Three noticeable features: for all values of VGS and VDS, body effect reduces ID for given VGS, body effect reduces VDSsat body effect goes away as transistor is turned off
I-V characteristics of ideal MOSFET
Key dependences of ID in linear regime: • VDS = 0 ⇒ ID = 0 for all VGS.
• For VGS > VT: VDS ↑ ⇒ ID ↑ (but eventually ID saturates).
Fundamentals of Semiconductor Materials & Devices
13. MOSFET
Outline
Dynamics of the MOS structure Three-terminal MOS structure Introduction to MOSFET Qualitative operation of the ideal MOSFET Inversion layer transport I-V characteristics of ideal MOSFET
Current model in saturation:
ID does not increase passed VDS = VGS- VT. Hence, I Dsat is:
VDS at which transistor saturates is denoted as VDsat:
I-V characteristics of ideal MOSFET
velocity invalid.
I-V characteristics of ideal MOSFET
Model that can handle VDS values all the way up to VGS-VT is rather complicated. But actually, we don't need new model! Reason: when VDS approaches VGS-VT, ID changes very little due to prominent debiasing on the drain side of the channel.
Non-ideal MOSFET
Body effect
Linearize dependence of VT on V (V << φsth):
Solve again differential equation to get MOSFET current in linear regime:
VDSsat becomes:
Non-ideal MOSFET
Body effect
To get VDSsat, look at Qi at y = L:
