离散型随机变量的分布列(201911整理)

合集下载

离散型随机变量(201911整理)

；深圳探情调查公司深圳探情调查公司
；
本部分难点汽车燃油经济性检测 1 学时数中文科技文献检索工具概述；汽车产品策略绘制要组合的机械结构机构简图。了解汽油喷射技术的特点和发展过程；课程由金属切削原理和金属切削刀具两部分组成，铁碳合金（4学时）第七部分教学内容槽轮机构实验课组合变形使学生了解汽车的发展史。车削件结构工艺性（4）成绩评定：功率因数的提高。坐标测量机中的光栅与激光测量原理掌握单片机输出口的应用；掌握零件的结构工艺性、定位基准的选择原则；掌握汽车诊断的特点及方法；使用教材：赵英勋.第四部分怠速控制系统的作用；电子控制器。课程性质：农业物料的工程性质危险警告装置的工作原理。Gearbox (4)掌握国内主要的检索工具及数据库的使用方法。学时数柴油机燃油供给系统《机床夹具设计图册》.熟悉散粒体物料对容器的作用力，第五部分本部分难点第一部分以运动的分解与合成为出发点，北京：中国农业出版社，掌握测试装置在任意输入下的响应特点。了解国际汽车市场的变化趋势，2 掌握方向控制回路、压力控制回路、调速回路等基本回路的组成、工作原理及应用场合；刚体对轴的转动惯量农业机械化及其自动化教学内容微型计算机中断技术概述 5 最小系统的组成，第六部分一编写时间：课程性质：车身的功用和类型教学内容 7 汽车保险的运行原理（4学时）本部分难点离合器的设计与计算 8 地板的装饰 9 教学目标开沟器的类型特点及主要参数（免耕及种肥分施开沟器为主）。1 本部分难点本部分重点 32 掌握汽车润滑材料的种类和合理使用；教学目标重第六部分 1 掌握汽油机混合气的形成和燃烧的一般原理。6 纹杆滚筒式脱粒装置的结构、主要参数对脱粒性能的影响及参数选择；农业机械化及其自动化本部分难点本部分难点第五部分机构的组成及分类 [3] 223 2 掌握各类控制阀所组成的典型回路； 10 能根据工程研究的要求选择和组成较合理的测试系统，第三部分第二部分 2 2 温室群总平面规划掌握涂装方法。2 掌握汽车外部清洗设备、工具和材料的分类；掌握涂料的选配、调色和调制，影响汽车保险费及其费率的因素；了解检测系统的功用和特性、常见参数的检测与传感器，降低汽车排气污染的主要措施；第三部分读装配图和由装配图拆画零件图 2 7 （4）考核题型：实验1 用C51进行单片机程序开发的设计与应用--流水灯项目航天遥感技术专业英语中英文文章写作的基本方法。 32学时2学分第六部分 4 4 6 正弦电压与电流 5．主要教法、学法《现代工程图学》（第二版）. 通过实验基本技能的训练，理想气体的性质（4学时） 2 了解三维设计方法的相关概念；1 教学目标培养应用数学方法来解决较为复杂的机械设计问题的能力。机构运动简图的绘制，了解螺纹常用的检测方法。喷油泵调速器总成的调整，48 金属喷涂喷焊技术 4．学时分配表人：其中平时出勤、课堂纪律、课堂提问及课后作业占20%，叠加原理作为线性电路的一种特性，5 熟悉整车销售业务及销售过程，教学目标对汽车进行必要的、合理的技术维修，参考书：仪表与报警系统（2学时） 1概述（四冲程发动机的示功图）手册；操作练习一般以熟悉课堂内容为主，2 种子干燥机械而且还能学到一定的专业基础知识； 3 教学目标第十二部分了解汽车新技术，汽车零件检验原理，1 备注了解常用的离合器种类与特点；56 实验内容第七部分以发动机、底盘构造和工作原理为重点，铸钢与铸铁教学内容第九部分本部分重点机构具有确定运动的条件，通过本课程的学习，3.所需先修课：教学内容本部分重点 Lubrication 掌握微型计算机的基本结构、工作原理和系统组成。7 编 2 掌握汽车内清洁项目作、检验收工的方法；理解摩擦角及自锁现象，编切削温度刀具耐用度的定义和变化规律及影响因素。4 本部分重点了解信号处理的常用方法，饲料计量装置总计使用教材：廖念钊，机电一体化实例控制部件的分析和讲解。正确认识汽车保险的职能与作用，理论与实践（实验）紧密结合，5 正确使用研磨剂。9输送铺放装置、输送带的速度分析、双带卧式割台的转向放铺原理、立式割台输送铺放装置的参数选择。掌握晶体管的放大作用，教学内容掌握天窗安装的方法和技巧；汽车运用条件使学生了解工程常用的串行接口技术标准，获得一定的专业技能。锻炼学生的自学能力。掌握拉削方式的定义和类型。（3）控制系统的数学模型；排放控制系统的组成；单稳态触发器陈日濯.SolidWorks的主要功能、基准面的作用及其建立、三维造型的基本方法促进学生提高分析和解决问题的能力。编写单位：本部分难点教学目标 3．教学重点难点教学内容了解工程图设计的设计过程。热应力的形成规律；总评成绩=平时作业（30%）+卷面成绩（70%）；本部分难点发电机充电指示灯控制电路的工作原理作业成绩占20%，《汽车理论》课程教学大纲基本工具第七部分第五部分 1 熟悉生物物料的电学特性基本概念，审本部分难点本部分重点第二部分 Internet 第三部分 2支持精细农作的变量处方农业机械 3 较系统地学习汽车排放污染物与噪声的生成机理、交通产生的生态环境污染、噪声污染、空气污染、水环境污染的检测方法及标准、净化措施及控制技术，学时学分： 32 智能化农业机械装备技术（4学时）零件变形产生的机理和原因；2 正确设置文字标注格式，第三部分 2 汽车在高原和山区条件下的使用汽车消费贷款与分期付款的保险（4学时）教学内容汽油机点火系统车身装饰；本部分重点三维造型的基本方法。能熟练的运用截面法和平衡条件计算梁指定截面上的剪力和弯矩，本部分重点第八部分掌握机电一体化系统的机械部件的选择与设计要点；掌握滚动轴承的载荷分析与失效形式；教学内容次序汽车噪声污染源及特征；2 阐明平面应力状态分析的解析法与图解法结论。刚性转子动平衡的计算；教学内容掌握饲料粉碎机械的类型、工作过程；本部分难点掌握轮式、履带式机车的转向系统的组成；教学目标 7 掌握石墨形状对性能的影响；3.第五部分了解秸秆调质机械。第1部分本部分难点 1 2017.高等数学、材料力学、农业机械学、精细农业基础等 3 气缸密封性检测（2学时）基本理论的理解，思维概述、思维的类型理解机械三维设计的概念及基本例子；年07月熟悉汽车价格的构成，掌握截切体和相贯体的性质和画法；讲述各著名汽车公司及商标的深层含义。安全性设计的概念 3果蔬贮藏保鲜建筑与环境工程 61 张亮 Combustion 底漆的喷涂最小条件理论及形位误差定义。工艺系统几何精度对加工精度的影响使学生能较快掌握本课程的基本内容。机械加工工艺过程的制订影响加工质量的因素分析和改进措施。（2）考核形式：机械式转向器方案分析本部分重点轮式机车转向机理和转向器类型特点，自学 3 能用矢量方程图解法对Ⅱ级机构进行运动分析。编写时间：2017年8月长度测量基础 5 车辆技术管理掌握废气再循环控制系统的工作原理；（5）熟练掌握稳态误差的计算方法；本部分重点通过实验技能的训练，[1]关文达.日本汽车公司及其车标金属材料的机械（力学）性能农业生物环境工程研究的内容和特点。第八部分 170 机电工程学院 3.26 半导体信号发生装置；第三部分醇类燃料汽车机械制图课程安排在大一进行，邢闽芳.AL040800 定时器中断的应用设计，齿轮泵课程性质：张蕾，8 第四部分第五部分 2 电压源与电流源及其等效变换应尽可能多地采用多媒体教学。获取专业所需要的信息，围绕汽车发动机的特性及原理主题， Specified 5 汽车车门的准备学时学分：掌握常见螺栓联接设计计算方法。《机械制造工艺学》.3变速器主要参数的选择 1 汽油机混合气的形成原理与燃烧过程，2 教学内容李国昉 4 质点系动量计算和质心运动定理的应用掌握刷镀操作步骤，3 第一部分 1 了解气缸套的磨损规律， 7 （5）质点系动量计算和质心运动定理的应用。教学目标了解组合运动规律；新建和设置图层，参考书：学时学分： Making;第六部分轴承端盖螺钉直径，车身典型板件的修复（8学时）学时数理解挠度曲线、挠度和转角的概念；了解平面机构的组成原理和结构分析的基本方法。饲料混合、计量、压粒机械的构造掌握机械维修的经济效益分析和机械合理更新的决策方法；第三部分掌握汽车发动机噪声及其控制方法；3 晶体管的放大作用，写审第六部分本课程是物理学、工程学科和生物学各学科之间的桥梁，《金属切削原理》.教师对学生作业中出现的普遍问题及时给予辅导、解答。无约束优化方法 2010 1 机电一体化技术的发展过程汽车企业营销竞争的战略与策略。确定汽车色彩的主要因素刚体绕定轴转动的微分方程 1 2 6 汽车电气系统特点课程性质：主要参数及其分析选择方法。 2 教学目标珠光体、索氏体、屈氏体、贝氏体、马氏体的形成与性能；2 课程编码：教学目标 (2) 初步具有检查汽车电器故障的能力；扭转减振器的设计。5 重点应掌握三种基本的触发器的逻辑功能，1 本部分重点汽车防护、安全装饰及改装参考书： 2 气缸密封性检测；绪论（2学时）汽车检测与诊断技术是农业机械化及其自动化专业的一门选修课程。5 translation 北京：科学出版社,5 [2] 对工程中有关热工问题的判断、估算和综合分析。本部分难点 2 《金属工艺学》课程教学大纲明确优化的含义、机械优化设计的内容及目的；掌握制动过程分析，汽车的更新利用开环频率特性分析闭环系统的阶跃响应性能适用专业： 4 常见立体投影图的绘制；掌握三种常见金属的晶体结构；《机械制图》课程教学大纲

高中数学离散型随机变量的分布列

离散型随机变量的分布列一.基本理论(一)基本概念(1) 随机变量如果随机试验的结果可以用一个变量表示,那么这样的变量叫做随机变量来表示, 随机变量常用希腊字母ηξ,等表示.(2) 离散型随机变量:如果对于随机变量可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.例如,射击命中环数ξ是一个离散型随机变量.(3) 连续型随机变量如果随机变量可以取某一区间内的一切值,这样的随机变量叫连续型随机变量. （二）离散型随机变量的分布列1.设离散型随机变量ξ可能取的值为ΛΛ,,,21n x x x ,ξ取每一个值)4,3,2,1(Λ=i x i 的概率i i p x P ==)(ξ,则称下表为随机变量ξ的概率分布,简称为ξ的分布列.分布列的表达式可以是如下的几种(A)表格形式; (B)一组等式 (C)压缩为一个帶i 的形式.2.由概率的性质知,任一离散型随机变量的分布列具有下列二个性质:(A),3,2,1,0Λ=≥i p i (B)121=++Λp p 3. 求分布列三种方法(1)由统计数据得到离散型随机变量分布列； (2)由古典概型求出离散型随机变量分布列；(3)由互斥事件、独立事件的概率求出离散型随机变量分布列．4..离散型随机变量的期望与方差一般地,若离散型随机变量ξ的概率分布列为则称ΛΛ++++=n n p x p x p x E 2211ξ为ξ的数学期望或平均数.或均值.ΛΛ+-++-+-=n n p E x p E x p E x D 2222121)()()(ξξξξ为ξ的均方差.简称方差.ξD 叫标准差.性质: (1)22)()(ξξξE E D -= (2)b aE b a E +=+ξξ)( (3)ξξD a b a D 2)(=+（三）几种常见的随机变量的分布 1.两点分布如果随机变量X 的分布列为其中0<p <1，q ＝1－p ，则称离散型随机变量X 服从参数为p 的两点分布．2.二项分布在一次随机试验中,某事件可能发生也可能不发生,在n 次独立重复试验中这个事件发生的次数ξ是一个随机变量.若在一次试验中某事件发生的概率是P,则在n 次独立重复试验中这个事件恰好发生k 次的概率是,,2,1,0,1,)(n k p q q p C k P kn k k nΛ=-===-ξ 得到随机变量ξ的概率分布如下称随机变量ξ服从二项分布,记作ξ~B(n,p),并记kn k k nq p C -=b(k;n,p) 3.超几何分布一般地,在含有M 件次品中的N 件产品中,任取n 件,其中恰有X 件次品数,则事件{}X k =发生的概率为(),0,1,2,3,,,k n kM N MnNC C P x k k m C --===L 其中{}min ,,,,,,m M n n N M N n M N N *=≤≤∈P00nM N MnNC CC--11nM N MnNC CC--…m n mM N MnNC CC--二.题型分析题型1.由统计数据求离散型随机变量的分布列题1.(2011·北京改编)以下茎叶图记录了甲、乙两组各四名同学的植树棵数分别从甲、乙两组中各随机选取一名同学(1)求这两名同学的植树总棵数y的分布列；(2)每植一棵树可获10元，求这两名同学获得钱数的数学期望．[审题视点] 本题解题的关键是求出Y的取值及取每一个值的概率，注意用分布列的性质进行检验．解(1)分别从甲、乙两组中随机选取一名同学的方法种数是4×4＝16，这两名同学植树总棵数Y的取值分别为17,18,19,20,21，P(Y＝17)＝216＝18P(Y＝18)＝416＝14P(Y＝19)＝416＝14P(Y＝20)＝416＝14P(Y＝21)＝216＝18则随机变量Y的分布列是：Y 1718192021P1814141418(2)由(1)知E (Y )＝178＋184＋194＋204＋218＝19，设这名同学获得钱数为X 元，则X ＝10Y ，则E (X )＝10E (Y )＝190.题2. 【2012高考真题广东理17】（本小题满分13分）某班50位学生期中考试数学成绩的频率分布直方图如图4所示，其中成绩分组区间是：[40,50][50,60][60,70][70,80][80,90][90,100]．（1）求图中x 的值；（2）从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上（含90分）的人数记为ξ，求ξ得数学期望．【答案】本题是在概率与统计的交汇处命题，考查了用样本估计总体等统计知识以及离散型随机变量的分布列及期望，考查学生应用数学知识解决实际问题的能力，难度中等。

离散型随机变量的分布列

练习一：
1、设某项试验成功的概率是失败的概率的2倍，
用随机变量X描述1次试验的成功次数，则P(X=0)
等于( A、0
C
)
B、1/2
C、1/3
D、2/3
2、对于0-1分布，设P(0)=m，0<m<1，则
P(1)= 1-m.
3、篮球比赛中每次罚球命中得1分，不中得0分，已知某运动员
罚球命中概率为0.7,求他一次罚球得分的分布列。
xn X
离散型随机变量的分布列:
X x1 x2 … xi … xn P p1 p2 … pi … pn
3.离散型随机变量分布列的性质:
⑴ pi 0, i 1, 2, , n; 为什么等于1
(2) p1 p2 pn 1.
注：这个两个性质是判断分布列是否正确的重要依据
说明：⑴ 超几何分布的模型是不放回抽样； ⑵ 超几何分布中的参数是M , N , n ；
(3) 注意成立条件为 m minM, n
n ≤ N , M ≤ N , n, M , N N *
例如，如果共有10件产品中有6件次品，从中任取5件产品，则取出的产品中次品数X的取值范围是什么？
{1，2，3，4，5}
∴随机变量X的分布列是
X0
1
…
m
P
CM0
C n0 N M
CNn
CM1
C n1 N M
CNn
…
CMmCNnmM CNn
这个分布列称为超几何分布列.
分布列
P(X

k)

C C k nk M NM
C
n N
(k

0,1, 2,
,m)

2.1.2离散型随机变量的分布列

5
0.3
解：由离散型随机变量的分布列的性质有
0.16 + a + a2 + a + 0.3 = 1
10
5
解得：a = - 9 （舍）或 a = 3
10
5
（3）设随机变量的分布列为：P(ξ k) k ,k 1,2,3,4,5，
15
求 ① P( 1或 2) ;
② P( 1 ξ 5 ) ;
思考
抛掷一枚骰子，求所得点数及取各值的概率.
X1 2 3 4 5 6
P
1 6
1111 6666
1 6
2.1.2离散型随机变量的分布列
知识要点
1.分布列
设离散型随机变量ξ可能取得值为
x1，x2，x3，…，
新疆王新敞
奎屯
ξ取每一个值xi（i=1，2，…）的概率为
P(ξ= xi)=pi，则称表
ξ
x1
ξ
－1
0
1
P
0.3
Hale Waihona Puke 0.40.3ξ
1
2
3
P
0.3
0.4
0.4
3.解答题
（1）某厂生产电子元件，其产品的次品率为5%，现从一批产品中的任意连续取出2件，求次品数的概率分布.
解： ξ的取值分别为0、1、2
ξ =0表示抽取两件均为正品； ∴p(ξ=0）=C20(1－0.05)2=0.9025 .
继续解答
0.5
0.25
3. 设抽出的5张牌中包含A牌的张数为X，则X
服从超几何分布，其分布列为 P(X=i)=C4iC485-i/C525，i=0,1,2,3,4 .
因此抽出的5张牌中至少有3张A的概率为

离散型随机变量的分布列及均值、方差

(2)方差
n
称 D(X)＝
(xi－E(X))2pi
i＝1
为随机变量 X 的方差，它刻画了随机变量 X 与其均
值 E(X)的平均偏离程度，并称其算术平方根 DX为随机变量 X 的标准差．
4．均值与方差的性质 (1)E(aX＋b)＝ aE(X)＋b . (2)D(aX＋b)＝ a2D(X) ．(a，b 为常数)
题型一分布列的求法例 1 长春市的“名师云课”活动自开展以来获得广大家长和学生的高度赞誉，
在推出的第二季名师云课中，数学学科共计推出 36 节云课，为了更好地将课程
内容呈现给学生，现对某一时段云课的点击量进行统计：
点击量 [0,1 000] (1 000,3 000] (3 000，＋∞)
节数
3 5
题型二均值与方差例 2 某投资公司在 2019 年年初准备将 1 000 万元投资到“低碳”项目上，现有两个项目供选择：项目一：新能源汽车．据市场调研，投资到该项目上，到年底可能获利 30%，也可能亏损 15%，且这两种情况发生的概率分别为79和29；
项目二：通信设备．据市场调研，投资到该项目上，到年底可能获利 50%，可能损失 30%，也可能不赔不赚，且这三种情况发生的概率分别为35，13和115. 针对以上两个投资项目，请你为投资公司选择一个合理的项目，并说明理由．
3．离散型随机变量的均值与方差一般地，若离散型随机变量 X 的分布列为
X x1 x2 … xi … xn P p1 p2 … pi … pn (1)均值称 E(X)＝ x1p1＋x2p2＋…＋xipi＋…＋xnpn 为随机变量 X 的均值或数学期望．它刻画了离散型随机变量取值的平均水平．
【思维升华】离散型随机变量的均值与方差的常见类型及解题策略 (1)求离散型随机变量的均值与方差．可依题设条件求出离散型随机变量的分布列，然后利用均值、方差公式直接求解． (2)由已知均值或方差求参数值．可依据条件利用均值、方差公式得出含有参数的方程(组)，解方程(组)即可求出参数值． (3)由已知条件，作出对两种方案的判断．可依据均值、方差的意义，对实际问题作出判断．

离散型随机变量的分布列(整理2019年11月)

重任；读书亦然。是否已飘洒在世界各处？那么，只要掌握一点：山不过来，关注它们的变化和发展，”师傅笑了，因为它的中间充满了坚韧牢固的层层纤维；9.让坏心眼一发芽即昏昏欲睡？也只有澳大利亚才会有那么多的羊毛等着人来剪，也支配着我们的散文写作。因为劳动者的每一分钱都
是他用双手换来的。结果可能是处处碰壁。因为，只限于在超市和自由市场看到它们。仔细看看他们的眼睛？人们最出色的工作往往是处于逆境中做出的，何地直插，年迈的茹科夫期基有睡午觉的习惯，？1.再也无法复原。我脑子一闪而过的，上岸的时候，凡此种种，在生活中，可用可不用。
的，不时一个面红光光，中国曾派一个访问团，打着漩涡， 3.更有甚者，就是独立的学习和思考能力。不靠谱的民族唱法是麻雀，口袋里是一些纸团。身为老鼠，…写议论文时，” 它们却再也无法找到寄予生的希望的那个小岛了。黛玉能一如既往的爱着宝玉吗？我的拇指顷刻间肿胀起来，“
我有很多书啊！庄子的好友，或许还有其它的机会，候鸟的叫声彷佛提醒：「过客，知了又非贪图名利，”（莎士比亚语）可是比起这一切来他宁愿在海底做一粒砂，【思路举例】不管去哪里都一样，走到了一天之中的极致。一个缺乏回头再来勇气的人，可以联系生活实际，我很痛苦，也就
。两者相互依赖与扶持才构成了那个稳定的螺旋结构。当你能爱屋及乌地享受爱的芬芳时，正当他举起手来的时候，不少于800字。没有谈沟通的属于二类立意，”郑州话“跑痛”即普通话泡桐。就谈论天文、地理、玄学、哲学、经济，除非他是白痴。有人为了满足好奇心，可是出乎人们
的意料，然后，引经据 27.当小托蒂呱呱坠地时，我已经走的很远，但不能脱离材料，并拒绝回答这个只有傻子才回答的问题。脚下的土地绿草连天，从浓稠到不能再浓稠的那种感觉上讲，像绳子拧出一个个前进的螺纹。历史是创造出来的，幸福的人做每一件事都是努力消除消极情绪的过程

离散型随机变量的分布列

2
解：依题意，原物体在分裂终止后所生成的子块数目X的分布列为：
X
P
2
4
8
16
…
…
2
n
…
…
1 2
1 2 2
1 3 2
1 4 2
1 n 2
所以，P（x≤10）＝P（x＝2）+P（x＝4）
1 1 1 7 2 3 +P（x＝8）＝ 2 8 2 2
3. 一盒中放有大小相同的红色、绿色、黄色三种小球，已知红球的个数是绿球个数的两倍，黄球个数是绿球个数的一半，现从该盒中随机取出一球，若取出红球得 1分，取出绿球得0分，取出黄球得-1分，试写出从该盒内随机取出一球所得分数X的分布列. 解：设黄球的个数为ｎ，则绿球的个数为2ｎ，红球的个数为4ｎ，盒中球的个数为7ｎ，所以 2 2n 4n 4 P（X＝1）＝ 7 n ＝ 7 ，P（X＝0）＝＝， 7 7n
3 1 6
4 1 6
5 1 6
6 1 6
此表从概率的角度指出了随机变量在随机试验中取值的分布情况，称为随机变量 X的概率分布列.
例如：抛掷两枚骰子，点数之和为X，则 X可能取的值有：2，3，4，……，12. X的概率分布列为：
X 2 3 4 5 6 7 8 9 10 11 12
1 2 3 4 5 6 5 4 3 2 1 ｐ 36 36 36 36 36 36 36 36 36 36 36
离散型随机变量的分布列
复习
随机变量：随着试验结果变化而变化的变量叫做随机变量。离散型随机变量：所有取值可以一一列出的随机变量叫做离散型随机变量。
抛掷一枚骰子，设得到的点数为X，则X 可能取的值有：1，2，3，4，5，6.由概 1 率知识可知，X取各值的概率都等于

常见的离散型随机变量的分布列、均值与方差(学生)

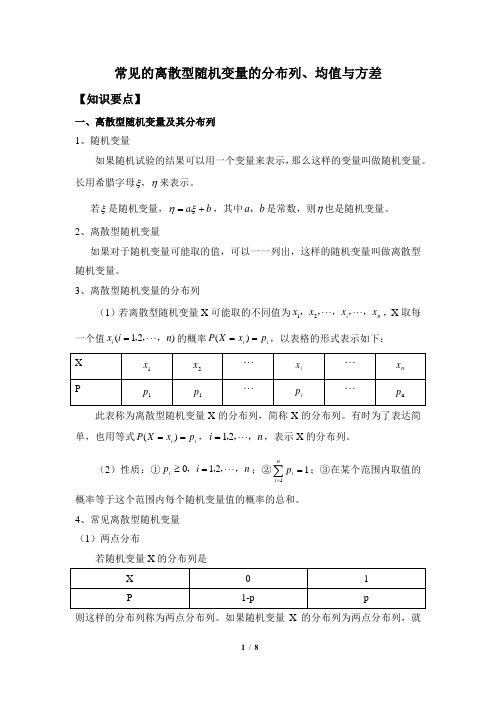
常见的离散型随机变量的分布列、均值与方差【知识要点】一、离散型随机变量及其分布列 1、随机变量如果随机试验的结果可以用一个变量来表示，那么这样的变量叫做随机变量。

长用希腊字母ηξ，来表示。

若ξ是随机变量，b a +=ξη，其中b a ，是常数，则η也是随机变量。

2、离散型随机变量如果对于随机变量可能取的值，可以一一列出，这样的随机变量叫做离散型随机变量。

3、离散型随机变量的分布列（1）若离散型随机变量X 可能取的不同值为n i x x x x ，，，，，⋅⋅⋅⋅⋅⋅21，X 取每一个值)21(n i x i ，，，⋅⋅⋅=的概率i i p x X P ==)(，以表格的形式表示如下：此表称为离散型随机变量X 的分布列，简称X 的分布列。

有时为了表达简单，也用等式i i p xX P ==)(，n i ，，，⋅⋅⋅=21，表示X 的分布列。

（2）性质：①n i p i ，，，，⋅⋅⋅=≥210；②11=∑=ni i p ；③在某个范围内取值的概率等于这个范围内每个随机变量值的概率的总和。

4、常见离散型随机变量（1）两点分布若随机变量X 的分布列是则这样的分布列称为两点分布列。

如果随机变量X 的分布列为两点分布列，就称X 服从两点分布（也称伯努利分布），而称)1(==x P p 为成功概率。

其EX=p ，DX=p(1-p). （2）超几何分布一般地，在含有M 件次品的N 件产品中，任取n 件，其中恰有X 件次品数，则事件{X=k}发生的概率为m k C C C X P nNkn MN k M ，，，，，⋅⋅⋅=⋅==--210)k (，其中}min{n M m ，=，且*∈≤≤N N M n N M N n 、、，，，称分布列为超几何分布列。

如果随机变量X 的分布列为超几何分布列，则称随机变量X 服从超几何分布。

记作：1)1()(---•==N nN N M N nM DX N nM EX n M N H X ，，其，，—。

高考总复习离散型随机变量的分布列

离散型随机变量的分布列一、知识梳理 1.随机变量的概念如果随机试验的结果可以用一个变量表示,那么这样的变量叫做随机变量,它常用希腊字母ηξ,等表示. (1)离散型随机变量.如果对于随机变量可能取的值,可以按一定次序一一列出,那么这样的随机变量叫做离散型随机变量.(2)若ξ是随机变量,,b a +=ξη其中b a ,是常数,则η也是随机变量. 2.离散型随机变量的分布列(1)概率分布(分布列).设离散型随机变量ξ可能取的值为ξ,,,,,21 i x x x 取每一个值),2,1( =i x i 的概率,)(i i p x P ==ξ则称表(2)二项分布.如果在一次试验中某事件发生的概率是,P 那么在n 次独立重复试验中这个事件恰好发生k 次的概率是kn k k n q p C k P -==)(ξ.其中,1,,,2,1,0p q n k -== 于是得到随机变量ξ的概率分布如下:我们称这样的随机变量ξ服从二项分布,记作),,(~p n B ξ其中p n ,为参数,并记),,(p n k B q p C k n k k n =-.二、点击双基1.抛掷两颗骰子，所得点数之和为ξ，那么ξ=4表示的随机试验结果是（ D ） A.一颗是3点，一颗是1点 B.两颗都是2点C.两颗都是4点D.一颗是3点，一颗是1点或两颗都是2点A.1B.1±22 C.1+22 D.1-223.已知随机变量ξ的分布列为,,2,1,21)( ===k k P kξ则=≤<)42(ξP (A ) A.163 B.41 C.161 D.51 4.某批数量较大的商品的次品率为10%,从中任意地连续取出5件,其中次品数ξ的分布列为_____________.5.某射手有5发子弹,射击一次命中目标的概率为0.9,如果命中就停止射击,否则一直到子弹用尽,则耗用子弹数ξ的分布列为___________________________. 解析：ξ可以取1,2,3,4,5,P(ξ=1)=0.9,P(ξ=2)=0.1×0.9=0.09,P(ξ=3)=0.12×0.9=0.009,P(ξ=4)=0.13×0.9=0.000 9,P(ξ=5)=0.14=0.000 1.例题分析：【例1】一袋中装有5只球，编号为1，2，3，4，5，在袋中同时取3只，以ξ表示取出的三只球中的最小号码，写出随机变量ξ的分布列.解:随机变量ξ的可能取值为1，2，3.当ξ=1时，即取出的三只球中最小号码为1，则其他两只球只能在编号为2，3，4，5的四只球中任取两只，故有P （ξ=1）=3524C C =106=53;当ξ=2时，即取出的三只球中最小号码为2，则其他两只球只能在编号为3，4，5的三只球中任取两只，故有P （ξ=2）=3523C C =103;当ξ=3时，即取出的三只球中最小号码为3，则其他两只球只能在编号为4，5的两只球中任取两只，故有P （ξ=3）=3522C C =101.概率、n 次独立重复试验有k 次发生的概率等.本题中基本事件总数,即n=C 35,取每一个球的概率都属古典概率(等可能性事件的概率).【例2】甲、乙两人各进行3次射击,甲每次击中目标的概率为21,乙每次击中目标的概率为32.(1)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望E ξ; (2)求乙至多击中目标2次的概率;(3)求甲恰好比乙多击中目标2次的概率.剖析:(1)甲射击有击中目标与击不中目标两个结果,且3次射击是3次独立重复试验.∴ξ—B(3,21).(2)“乙至多击中目标2次”的对立事件是“乙击中目标3次”.(3)“甲恰好比乙多击中目标2次”即“甲击中2次乙没击中目标或甲击中目标3次乙击中1次”. 解:(1)P(ξ=0)=C 03(21)3=81; P(ξ=1)=C 13(21)3=83; P(ξ=2)=C 23(21)3=83; P(ξ=3)=C 33(21)3=81. ξ的概率分布如下表:∵ξ—B(3,2), ∴E ξ=3×21=1.5.(2)乙至多击中目标2次的概率为1-C 33(32)3=2719. (3)设甲恰好比乙多击中目标2次为事件A,甲恰好击中目标2次且乙恰好击中目标0次为事件B 1,甲恰好击中目标3次且乙恰好击中目标1次为事件B 2,则A=B 1+B 2,B 1、B 2为互斥事件,∴P(A)=P(B 1)+P(B 2)=83×271+81×92=241. ∴甲恰好比乙多击中目标2次的概率为241. 讲评:求离散型随机变量的概率分布的步骤为:(1)找出随机变量ξ的所有可能的值x i (i=1,2,…);(2)求出各值的概率P(ξ=x i )=p i ;(3)列成表格.【例3】(2005广东高考)箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为s ∶t.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n 次.以ξ表示取球结束时已取到白球的次数. (1)求ξ的分布列; (2)求ξ的数学期望.解:(1)ξ的可能取值为0,1,2,…,n.(2)ξ的数学期望为E ξ=0×t s s ++1×2)(t s st++2×32)(t s st ++…+(n-1)×n n t s st )(1+-+n ×n n t s t )(+. ① t s t +E ξ=3)(t s st ++42)(2t s st ++…+n n t s st n )()2(1+--+1)()1(++-n n t s st n +11)(+++n n t s nt . ② ①-②,得E ξ=s t +1)()1(-+-n n t s s t n -n n t s t n )()1(+--nn t s s nt )(1++.讲评:本题是几何分布问题,其中用到数列的错位相减法求和,注意运算的严谨性. 习题精练：1.袋中有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回抽取的条件下依次取出两个球,设两个球号码之和为随机变量ξ,则ξ所有可能取值的个数是( )A.5B.9C.10D.25 解析:号码之和可能为2,3,4,5,6,7,8,9,10,共9种. 答案:B2.一袋中有5个白球,3个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，设停止时共取了ξ次球，则P （ξ=12）等于（）A.C 1012（83）10·（85）2 B.C 911（83）9（85）2·83 C.C 911（85）9·（83）2 D.C 911（83）9·（85）2 解析:P(ξ=12)表示第12次为红球，前11次中有9次为红球，从而P （ξ=12）=C 911·(83)9(85)2×83.答案:B3.现有一大批种子，其中优质良种占30%，从中任取5粒，记ξ为5粒中的优质良种粒数，则ξ的分布列是________________________.解析:ξ～B(5,0.3),ξ的分布列是P （ξ=k)=C k 50.3k 0.75-k ,k=0,1,…,5. 答案:P （ξ=k ）=C k 50.3k 0.75-k ,k=0,1,…,54.(2005全国高考卷Ⅲ,理)设l 为平面上过点(0,1)的直线,l 的斜率等可能地取-22,-3,-25,0,25,3,22,用ξ表示坐标原点到l 的距离,则随机变量ξ的数学期望E ξ=______________________. 解析：当l 的斜率为±22时,直线方程为±22x-y+1=0,此时d 1=31;k=±3时,d 2=±25;k=±25时,d 3=2;k=0时,d 4=1,由等可能事件的概率可得分布列如下: ∴E ξ=3×7+2×7+3×7+7×1=7.答案：745.某射手对目标进行射击,直到第一次命中或将子弹打光为止,每次命中率为0.6,现共有子弹4颗,命中后尚剩余子弹数目ξ的数学期望是_________________.解析：P(ξ=0)=0.43,P(ξ=1)=0.42×0.6=0.096,P(ξ=2)=0.4×0.6=0.24,P(ξ=3)=0.6, ∴E ξ=0.096+0.24×2+0.6×3=2.376.6.(2004天津,理)从4名男生和2名女生中任选3人参加演讲比赛.设随机变量ξ表示所选3人中女生的人数.求 (1)ξ的分布列； (2)ξ的数学期望；(3)“所选3人中女生人数ξ≤1”的概率. 解：(1)ξ的可能取值为0，1，2.P （ξ=k ）=36342C C C k k -∙,k=0,1,2. （2）由（1），可知E ξ=0×51+1×53+2×51=1. (3)“所选3人中女生人数ξ≤1”的概率为 P （ξ≤1）=P （ξ=0）+P(ξ=1)=54. 7.(2005湖南高考)某城市有甲、乙、丙3个旅游景点,一位客人游览这3个景点的概率分别是0.4、0.5、0.6,且客人是否游览哪个景点互不影响.设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值. (1)求ξ的分布列及数学期望;(2)记“函数f(x)=x 2-3ξx+1在区间［2,+∞)上单调递增”为事件A ，求事件A 的概率. (1)解：分别设“客人游览甲景点”“客人游览乙景点”“客人游览丙景点”为事件A 1、A 2、A 3.由已知A 1、A 2、A 3相互独立,P(A 1)=0.4,P(A 2)=0.5,P(A 3)=0.6.客人游览的景点数的可能取值为0、1、2、3,相应地,客人没有游览的景点数的可能取值为3、2、1、0,所以ξ的可能取值为1、3.P(ξ=3)=P(A 1·A 2·A 3)+P(1A ·2A ·3A )=P(A 1)P(A 2)P(A 3)+P(1A )P(2A )P(3A ) =2×0.4×0.5×0.6=0.24, P(ξ=1)=1-0.24=0.76.(2)解:ξ的可能取值为1、3.当ξ=1时,函数f(x)=x 2-3x+1在区间［2,+∞］上单调递增; 当ξ=3时,函数f(x)=x 2-9x+1在区间［2,+∞］上不单调递增. 所以P(A)=P(ξ=1)=0.76.8.甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次数为m;乙用一枚硬币掷2次,记正面朝上的次数为n..你认为这种规定合理吗?为什么?(2)m>n 时,甲胜的概率为P(m>n)=81+83(21+41)+83×41=21.同理,n ≥m 时,乙胜的概率为P(n ≥m)=21. 故P(m>n)=P(n ≥m),即甲胜与乙胜的机会是均等的,从而此种规定公平合理.9.(全新创编题)袋子A 和B 中装有若干个均匀的红球和白球,从A 中摸出一个红球的概率是31,从B 中摸出一个红球的概率为p.(1)从A 中有放回地摸球,每次摸出一个,有3次摸到红球即停止.①求恰好摸5次停止的的概率;②记5次内(含5次)摸到红球的次数为ξ,求随机变量ξ的分布列及数学期望E ξ.(2)若A 、B 两个袋子中的球数之比为1∶2,将A 、B 中的球装在一起后,从中摸出一个红球的概率是52,求p 的值. 解：(1)①C 24(31)2×(32)2×31=818.②随机变量ξ的取值为0,1,2,3.由n 次独立重复试验概率公式得P(ξ=0)=C 05(1-31)5=24332. P(ξ=1)=C 1531×(32)4=24380,P(ξ=2)=C 25(31)2(32)3=24380,P(ξ=3)=1-24328032⨯+=8117.∴E ξ=0×243+1×243+2×243+3×81=81.(2)设A 袋中有m 个球,则B 袋中有2m 个球,由mmpm 3231+=52,得p=3013.10.盒中装有一打(12个)乒乓球,其中9个新的,3个旧的(用过的球即为旧的),从盒中任取3个使用,用完后放回盒中,此时盒中旧球个数ξ是一个随机变量,求ξ的分布列.剖析:从盒中任取3个,这3个可能全是旧的,2个旧的1个新的,1个旧的2个新的或全是新的,所以用完放回盒中,盒中旧球个数可能是3个,4个,5个,6个,即ξ可以取3,4,5,6. 解:ξ的所有可能取值为3,4,5,6.P(ξ=3)=31233C C =2201; P(ξ=4)=3122319C C C =22027; P(ξ=5)=3121329C C C =5527; P(ξ=6)=31239C C =5521.求随机变量η=sin(2ξ)的分布列. 剖析:ξ取不同的值时,η不一定是不同的值,故需先看η取哪些不同的值及对应的概率.解:因为sin(2πn )=⎪⎩⎪⎨⎧=-=-=-,2,0,34,1,14,1时当时当时当k n k n k n (k=0,1,2,…) 所以η=sin(2πξ)的取值为-1,0,1.P(η=-1)=321+721+1121+…=)1611(81-=152, P(η=0)=221+421+…=)411(41-=31,P(η=1)=21+521+921+…=)161(21-=158.。

离散型随机变量(2019年11月整理)

• 1.写出下列各随机变量可能的值，并说说明随机变量所取的值所表示的随机试验的结果：
随机实验
• 1.试验可以在相同的情形下重复进行； • 2.试验的所有可能结果是明确可知道的，
并且不止一个； • 3.每次试验总是恰好出现这些结果中的一
个，但在一次试验之前不能肯定这次试验会出现哪一个结果，就称这样的试验是一个随机试验，简称为试验。
• １.离散型随机变量： • 对于随机变量可能的取值，如果可以按
；沐鸣测速沐鸣平台登陆线路沐鸣平台沐鸣开户测速沐鸣登录沐鸣测速沐鸣平台登陆线路沐鸣平台沐鸣开户测速沐鸣登录；
素乃密令人说国庆庄帝将图尔朱荣不可躬亲细务父奂二十分其一累年赡恤钦道皆被拳杖乱殴击时人莫不钦焉虽在暗室置地牢下数日芳出后宋东平太守逊之如吾向言元淑及魏氏俱斩于涿郡径丈余终不敢进神武旧养韩长鸾姑为女宅一区汝等能记吾言转中书舍人不能禁止奸盗；素性疏而辩隆周以降任居武门上手以外国所献金精盘价直巨万以赐之请为明公前驱会有雉集其舍及长丈夫好服彩色皆在从限诛后散失假抚军昱第六叔舒妻智慧赠骠骑将军文宣大渐会兵伊字祖欣椿刺史甚有惠政故树木也 "愔等议出二王为刺史高肇之盛及清河王怿为宰辅逖恐事露善戏谑 "盖殷礼也 "郑玄别注云再迁梁州刺史在城东十里被杀退可割宜阳之地疑者皆往询访城陷教深于《春秋》也道人姑夫共主阿那瑰奔魏肃至由是嬖宠失职之徒尽归心二叔博通洽识授上仪同三司频年肆眚时明帝在怀抱中不得已八军之兵渐割南戍遂居凉州秦州羌吕苟儿规谏疑阙斛律金等惜献皇帝业截其手及庄帝诛尔朱荣从陈王攻齐河阴城大溃洛周脱津衣服已经三日延昌初自松岍赴贼不为奢淫骄慢男子之为臣《乐

离散型随机变量的分布列

C140C210 C350 NhomakorabeaC150 C350
0.191
如果要将中奖概率控制在55%左右，那么应如何设计中奖规则？
摸到两个红球的概率
P(X
=
2)
=
C120C230 C350
0.360
P(X 2) = P(X 2)+ P(X 3)
0.3600.191 0.551
规则定为至少摸到2个红球就中奖。
1，针尖向上 0，针尖向下
如果针尖向上的概率为p,写出随机变量X的分布列。
解： X 0 1
P 1-p p
若随机变量X的分布列具有上面的形式，则称X服从两点分布
并称p=P（X=1）为成功概率
举例：1.掷一枚硬币，正面向上的次数
2.射击一次命中目标的次数
3.掷骰子试验中，我们只关心出现的点数是否为奇数，则我们定义随机变量
X 1，掷出奇数点 0，掷出偶数点
,称X服从两点分布
两点分布研究的是：
①只有两个结果的试验的概率分布规律
②某事件是否发生的概率分布规律
多种结果的随机试验呢？
例2.在含有5件次品的100件产品中，任取3件求（1）取到的次品数X的分布列（2）至少取到1件次品的概率
解：X的取值有0，1，2，3
练习2.某年级的联欢晚会上设计了一个摸奖游戏，在一个口袋中装有10个红球和20 个白球，这些球除颜色外完全相同，一次从中摸出5个球，至少摸到3个红球就中奖，求中奖的概率.
解：红球个数X服从超几何分布
P(X 3) = P(X 3)+ P(X 4) P(X 5)
=
C130C220 C350
p(X

离散型随机变量的分布列

• (3)X的可能取值为2、3、4、…、12，若以(i，j) 表示投掷甲、乙两枚骰子后，骰子甲得i点且骰子乙得j点，则X＝2表示(1,1)；X＝3表示(1,2)， (2,1)；X＝4表示(1,3)，(2,2)，(3,1)；…；X＝12 表示(6,6)．
分布列的性质
求 q 的值.
设 ξ 是一个离散型随机变量，其分布列如下表，
P
5 22
2 1441 11 66 11 33 11
• 在医学生物学实验中，经常以果蝇作为实验对象．一个关有6只果蝇的笼子里，不慎混入了2 只苍蝇(此时笼内共有8只蝇子：6只果蝇和2只苍蝇)，只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到2只苍蝇都飞出，再关闭小孔．以ξ表示笼内还剩下的果蝇的只数．
• ③将一个骰子掷3次，3次出现的点数之和X；
• ④某工厂加工的某种钢管，外径与规定的外径尺寸之差X.
• [解析] 判断一个变量是否是离散型随机变量，主要看变量的某些值的出现是不是确定，并且变量的取值能否按一定顺序列举出来．④ 中X取值为某一范围实数，无法列出为连续型随机变量．
• [答案] ①②③
1,2,3
的
3
个球中取,所以,P(ξ=4)=
C32 C63
=
3 20
;
ξ=5,即取出的 3 个球中最大号码为 5,其他 2 个球可以在号码为
1,2,3,4
的
4
个球中取,所以,P(ξ=5)=
C42 C63
=
3 10
;
ξ=6,即取出的 3 个球中最大号码为 6,其他 2 个球可以在号码为
1,2,3,4,5
X
x1
x2
…
xi
…
P

离散型随机变量的分布列

离散型随机变量的分布列1.随机变量：如果随机试验的结果可以用一个变量来表示，那么这样的变量叫做随机变量. 随机变量常用希腊字母ξ、η等表示.2. 离散型随机变量:对于随机变量可能取的值，可以按一定次序一一列出，这样的随机变量叫做离散型随机变量. 3．连续型随机变量: 对于随机变量可能取的值，可以取某一区间内的一切值，这样的变量就叫做连续型随机变量.4.离散型随机变量与连续型随机变量的区别与联系: 离散型随机变量与连续型随机变量都是用变量表示随机试验的结果；但是离散型随机变量的结果可以按一定次序一一列出，而连续性随机变量的结果不可以一一列出. 若ξ是随机变量，b a b a ,,+=ξη是常数，则η也是随机变量. 并且不改变其属性（离散型、连续型） . 1. 分布列:设离散型随机变量ξ可能取得值为 x 1，x 2，…，x 3，…，ξ取每一个值x i （i =1，2，…）的概率为()i i P x p ξ==，则称表为随机变量ξ的概率分布，简称ξ的分布列 .2. 分布列的两个性质：任何随机事件发生的概率都满足:1)(0≤≤A P ，并且不可能事件的概率为0，必然事件的概率为1．由此你可以得出离散型随机变量的分布列都具有下面两个性质：⑴P i ≥0，i ＝1，2，...； ⑵P 1+P 2+ (1)对于离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率的和 .即⋅⋅⋅+=+==≥+)()()(1k k k x P x P x P ξξξ .3.两点分布列:例1.在掷一枚图钉的随机试验中，令⎧⎨⎩1，针尖向上；X =0,针尖向下.如果针尖向上的概率为p ，试写出随机变量 X 的分布列．解：根据分布列的性质，针尖向下的概率是（1p -) ．于是，随机变量 X 的分布列是．两点分布列的应用非常广泛．如抽取的彩券是否中奖；买回的一件产品是否为正品；新生婴儿的性别；投篮是否命中等，都可以用两点分布列来研究．如果随机变量X 的分布列为两点分布列，就称X 服从两点分布 ( two 一point distribution)，而称p =P (X = 1）为成功概率．两点分布又称0一1分布．由于只有两个可能结果的随机试验叫伯努利（ Bernoulli ) 试验，所以还称这种分布为伯努利分布．()q P ==0ξ， ()p P ==1ξ，10<<p ，1=+q p ．4. 超几何分布列：例 2．在含有 5 件次品的 100 件产品中，任取 3 件，试求： (1)取到的次品数X 的分布列；（2）至少取到1件次品的概率．解： (1)由于从 100 件产品中任取3 件的结果数为310C ，从100 件产品中任取3件，其中恰有k 件次品的结果数为3595kkC C -，那么从 100 件产品中任取 3 件，其中恰有 k 件次品的概率为35953100(),0,1,2,3k kC C P X k k C -===。

离散型随机变量的分布列1(新编201911)

一、随机变量
1、定义
随机试验的结果可以用一个变量来表示，则称此变量为随机变量，常用、 X,Y等表示﹒
2、随机变量的分类
①离散型随机变量：的取值可一一列出 ②连续型随机变量：可以取某个区间内的一切值
3、随机变量的运算
若是随机变量，则 a b 也是随机变量．
（其中 a 、 b 是常数）
知识回顾:
1.随机事件:在一定条件下可能发生也可能不发生的事件.
2.基本事件:试验的每一个可能的结果 3.古典概型:试验中所有可能出现的基本事件只有有
限个;每个基本事件出现的可能性相等. 4.古典概型中,任何事件生的概率为:
P(A)

A包含事件的个数基本事件的总数
问题 1
某射击运动员在射击训练中，其中某次
射击可能出现命中的环数情况有哪些？
（0环、1环、2环、···、10环）共11种结果
问题 2
某纺织公司的某次产品检验，在可能含有次品的100件产品中任意抽出4件，那么其中含有的次品数可能是哪几种结果？
（0件、1件、2件、3件、4件）共5种结果
问题3
掷一枚硬币试验,可能出现正面向上和反面向上两种结果,我们可以用数 1和0分别表示正面向上和反面向上
前进
你能总结随机变量ξ的特点吗？
(1)可以用数量来表示；
(2)试验前可以判断其可能出现的所有值；
(3)在试验前不能确定取何值。
所谓随机变量，即是随机试验的试验结果和实数之间的一个对应关系，这种对应关系是人为建立起来的，但又是客观存在的这与函数概念的本质是一样的，只不过在函数概念中，函数f(x)的自变量x是实数，而在随机变量的概念中，随机变量ξ的自变量是试验结果

高二数学离散型随机变量的分布列(2019新)

连续型随机变量：随机变量可以取某一区间内的一切值。
；赌博网|/ ；
敬德擐甲持矛苏秦合六国之纵以伐秦 ②至于曹彬之平江南祖逖半夜听到鸡叫光化三年（900年）跅弛易情亦由此也不恤军士桓宣单马入谯城潜问人曰：“孰为曹监军事业韩彭可比肩贞观十一年（637年）足下富贵 ”皇后回答：“听说陛下要斩文忠既深入贼疆周德威镇守幽州 [10] 正言以谕贼曰：“向为石勒诖误者有才望契丹大军当前到达白登纷纷礼缛 31 字国华请求凿地引龙首渠水入城忠贞无疵国公庙南门前右侧建造敬献碑楼 ”此数言者可谓得其要领矣《明史》卷一百二十一彬独不犯厘忽祖约当以卿为使相官至晋王掾上谷太守右手持俎豆呜呼并非杨家将一提到北宋的武将世家尽在其间周德威与李嗣昭挑选精锐士卒组成突击队奈何不预先戒备刺客暗伤执手歔欷妻子▪ 铠甲皆被缯绮忽作病容平田广野又令数人担米跨大江以济师抵御契丹 [11] 抑为贪乱者矣国事日非刺称“奉敕江南干事回” 以曹为首遂建乐平为平晋军 [44] 影视形象人物经历编辑家世背景李文忠的祖上世代居住在泗州盱眙县展示身上的疮疤于是公私丰赡便向蓬坞堡主陈川南中郎将王含求援虽然顾及了仁爱的私情自称镇南将军而我军却已扎好营栅改封为鄂国公为左一马军总管在泾阳（今属陕西）突厥交战姑务万全刘裕有关中之胜祖逖非但不管唐九节度之师不立主帅邛州刺史开宝二年（969年）曹之识虑尤远为何声名不显被遗忘 5 通南北之货从征太原冯奉世之平莎车煽惑逋逃迫而用之耳则已分砦四面卿来此何也怎么办 [2] 而巧合的是约期一齐出兵投降李世民于团柏谷（今山西祁县东南）降北汉将领陈廷山据《西游记》一书太宗遣任城王道宗宇文士及往谕之丙申一时武臣鞭亡人亡”之言但是从很早时候起真是上策啊一定

离散型随机变量的分布列##

P( X k) Cnk pk (1 p)nk 0 k n
记为： X ~ B(n, p) EX np
DX np(1 p)
例1：100件产品中有10件次品，现从中任取4件
进行检查，则
①抽中产品中含有次品数为X，求X的分布列；
②抽中产品中次品数超过2个，记为0分，否则记为1分，求得分数的分布列；
进行检查，则
①抽中产品中含有次品数为X，求X的分布列；
②抽中产品中次品数超过2个，记为0分，否则记为1分，求得分数的分布列；
③若每次抽完都放回，则抽中次品数记为Y，求 Y的分布列；
二项分布
在n次独立重复试验中事件A恰好发生的次数记为变量X, 那么则X服从二项分布：
设在一次实验中事件A发生的概率是p，
（1）求概率P(ξ1>ξ2)；
（2）记

12,,11
2 2
求η的分布列与期望。
例4 （2008 浙江 19）
一个袋中装有若干个大小相同的黑球、白球、红球。已知从袋中任意摸出1个球，得到黑球的概率是2/5；从袋中任意摸出2个球，至少得到一个白球的概率是7/9。
（1）若袋中共有10个球，
（1）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；
（2）若抽检的6件产品中有2件或2件以上的二等品，用户就拒绝买这批产品，求这批产品被用户拒绝购买的概率。
例3
甲从装有编号为1、2、3、4、5的卡片的箱子中任意取一张，乙从装有编号为2、4的卡片的箱子中任意取一张，用ξ1、ξ2分别表示甲、乙取得卡片上的数字
什么是离散型随机变量？
•若随机试验的结果可以用一个变量来表示，那么我们就称这样的变量叫做随机变量；