辽宁师大附中2015届高三上学期期中考试文科6份

合集下载

辽宁师大附中高三上学期10月月考试卷语文 Word版含答案.pdf

辽师大附中2015—2016学年度学期考试满分：100分一、论述类文本阅读阅读下面文字，完成1—3题映射是一种独特的小说艺术，它决定于作家对生活的丰富性和复杂性的整体认识。

曹雪芹是一位最注意完整地把握和表现生活的作家，他从不孤立地写一个人、一件事，而总是着眼于生活的丰富性和复杂性，从生活的内在联系中去把握和表现生活。

映射就是指作家透过生活的表层，从内在关联中揭示出发人深思的底蕴。

他写一个人、一件事，其意义并不只是孤立地表现这个人、这件事本身，而是映射到其他人、其他事上面，在互相关联中从整体上显现出多方面的深刻丰富的含义。

第三十三回，写宝玉挨打之前，正在紧急之际，宝玉盼望有一个人去报信，以免皮肉之苦。

这时恰好来了一个聋老婆子。

宝玉急切地对她说：“快进去告诉，老爷要打我呢！快去，快去！要紧，要紧！”可因这老婆子耳聋，把“要紧”听成了“跳井”，便以为是说金钏儿跳井的事，立即回答说：“跳井让他跳去，二爷怕什么？”又说：“有什么不了的事？老早的完了，太太赏了衣服，又赏了银子。

”金钏儿的死，在贾府里只算得一件小事，可是曹雪芹写来却颇具匠心。

写金钏儿受辱在第三十回，写她悲愤跳井自杀在第三十二回末，此后又在好几处描写相关人物时多次提及这件事。

这里，作者特意写这么一个聋老婆子的出现和她说的这番话，就是着眼于生活内在的相互关联，映射出多方面的意义。

当然，安排这么一个微不足道的人物上场，首先是出于情节发展上的需要，即为下文写王夫人和贾母的出场，写这场轩然大波的收束作铺垫；其次，是在人物描写上的多层映射。

这个聋老婆子，作为贾府中的一个老仆妇，同是奴隶，其身份地位同金钏儿是一样的，却对金钏儿被逼惨死表现得极其冷漠。

这就自然映射到贾政身上，体现贾政的虚伪。

贾政在刚听说金钏儿跳井自杀时，曾说：“好端端的，谁去跳井？我家从无这样事情，我家自祖宗以来，皆是宽柔以待下人。

”聋老婆子那番话和所表现出的冷漠态度，就暗示读者，在贾府这类事件必然是经常发生，这才使聋老婆子这样的仆人也不以为奇，以至于麻木不仁了。

辽宁省辽宁师大附中高三上学期期中考试语文试题 Word版含答案.pdf

2013-2014辽师大附中期中考试高三语文试题命题人：高三备课组校对：高三备课组考试时间：150分钟满分：150分注意事项: 1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.作答时，将答案写在答题纸上。

写在本试卷上无效。

第Ⅰ卷阅读题现代文阅读（9分）阅读下面的文章，完成1到3题（每题3分）青铜时代是人类文明的开始。

中国青铜文化之源一直是学者们的研究热点。

1973年，陕西临潼姜寨遗址出土的一个距今6500年以上的黄铜片是我国目前已知最早的铜制品。

而中国最早的青铜器是1977年在甘肃东乡出土的一把公元前3000年的铜刀，据激光光谱分析为锡青铜。

在广泛分布于黄河流域的龙山文化遗址中，铜器发现较多，有红铜器、黄铜器及青铜器，还有与熔铜有关的遗物。

这些都可以表明，我国铜文化在开始就体现出以中原地带为中心的多元发展形式，一直延续至更后期。

1885年，英国伦敦大学的拉古别里提出了中国文明“西来说”。

1921年，瑞典人安特生根据他发现的仰韶文化彩陶，指出中国史前彩陶与中亚、东欧史前彩陶类似，于是“西来说”获得了考古资料的支持。

但不久之后，中国考古学者在山东龙山城子崖和河南安阳殷墟发掘出了中国本土文化史前时代的遗物。

这时若再说中国史前时代皆一片空白，人口和文化都是自西方输入的，便很难成立了。

所以1930年以后，许多外国学者多采用折衷的说法，即中国本土有人长期居住，但远在史前时代就受了西方文明的影响，而产生文化的进展，这其中当然也即包括我国古代文化重项：青铜文化。

“西来说”，多是外国学者提出，而其主要支持力量也来自于中国域外，他们对于中国文化的认识不会比中国本土的多数学者深厚，多数也未亲见国内有关文明起源的第一手考古材料，学说建立的基础也难免不扎实。

他们起初抱有一个结论，但是新的考古材料的出现完全否定了他们的论断后，他们很快就作出了调整，大意不变，只是很识时务的避开了矛盾，这就显得有点可笑，他们的论断是否有较多的主观成分呢？对“西来说”我们有两点学术上的质疑。

【恒心】2015届辽宁师大附中高三高考考前精品卷数学(文科)试题及参考答案【word版】

2015年辽师大附中高三年级模拟考试（精品卷）数学文科试卷命题人：高三数学文科备课组一．选择题（每题5分，共60分） 1.设集合}0{,},{,}ln ,2{=⋂==B A y x B x A 若，则y 的值为（）A ．eB ．1C ．e1D ．0 2.若复数Z 满足（1+i ）Z=i ，则Z 的虚部为（） A ．i 21-B ．21-C ． 21D ． i 21 3．下列结论正确的是（）A ．若向量b a // ，则存在唯一实数b a λλ=使B ．已知向量b a ,为非零向量，则“b a ,的夹角为钝角”的充要条件是“0<⋅b a ”C ．“若21cos ,3==θπθ则”的否命题为“若21cos ,3≠≠θπθ则” D ．若命题01,:,01,:22>+-∈∀⌝<+-∈∃x x R x p x x R x p 则 4．将函数f(x)＝sin ωx(其中ω>0)的图像向右平移π4个单位长度，所得图像经过点⎝⎛⎭⎫3π4，0，则ω的最小值是( ) A.13B ．1 C.53D ．25．已知向量c b a c b k a ⊥-===)32,)1,2(,)4,1(,)3,(且（，则实数k 的值为（） A ．29-B ．0C ．3D ．2156.执行如图所示的程序框图，输出的S 值为（）A.9B.16C.25D.367．某几何体的三视图如图所示，则该几何体中，面积最大的侧面的面积为（）（A ）22（B ）52（C ）62（D ）3 8.已知不等式组⎪⎩⎪⎨⎧≤-≥-≥+224x y x y x ，表示的平面区域为D ，点)0,1(),0,0(A O .若点M 是D 上的动点，则||OM OM OA ⋅的最小值是（）A.22 B.55 C.1010 D.101039．在△ABC 中，cos 2B 2＝a ＋c2c (a 、b 、c 分别为角A 、B 、C 的对边)，则△ABC 的形状为( )A ．直角三角形B ．等边三角形C ．等腰三角形或直角三角形D ．等腰直角三角形10.已知数列{a n }的通项公式a n ＝log 2n ＋1n ＋2(n ∈N *)，设{a n }的前n 项和为S n ，则使S n ＜－5成立的自然数n ( )A ．有最大值63B ．有最小值63C ．有最大值31D ．有最小值3111.已知F 2，F 1是双曲线)0,0(12222>>=-b a by a y 的上，下两个焦点，点F 2关于渐近线的对称点恰好落在以F 1为圆心，|OF 1|为半径的圆上，则双曲线的离心率为（）A ． 2B ．3C ． 3D ．212．已知)(x f 的定义域为),0(+∞，)()(x f x f 为'的导函数，且满足)()(x f x x f '-<，则不等式)1()1()1(2-->+x f x x f 的解集是（）A ．)1,0(B ．),1(+∞C ．（1，2）D ．),2(+∞ 二．填空题（每题5分，共20分） 13一元二次不等式)(022b a b x ax >>++的解集为⎭⎬⎫⎩⎨⎧-≠a x x 1|，则b a b a -+22的最小值为__________14. 已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上，若13,4,,12,A B A C A B A C A A ==⊥=，则球O 的半径为 __________.15．设S n 是数列{a n }的前n 项和，若S 2nS n (n ∈N *)是非零常数，则称数列{a n }为“和等比数列”．若数列{2b n }是首项为2，公比为4的等比数列，则数列{b n }__________(填“是”或“不是”)“和等比数列”．16数()2log 1f x a x =+（0a ≠），定义函数()()(),0F ,0f x x x f x x >⎧⎪=⎨-<⎪⎩，给出下列命题：①()()F x f x =；②函数()F x 是偶函数；③当0a <时，若01m n <<<，则有()()F F 0m n -<成立；④当0a >时，函数()F 2y x =-有4个零点．其中正确命题的个数为 .三．解答题17.(本题12分) 设n S 为数列{n a }的前项和，已知01≠a ，2n n S S a a ∙=-11，∈n N *（Ⅰ）求1a ，2a ，并求数列｛n a ｝的通项公式； (Ⅱ) 求数列｛n na ｝的前n 项和。

辽宁省师大附中2015届高三数学上学期期中试卷文(含解析)

辽宁师大附中2015届高三上学期期中数学试卷（文科）一．选择题（每题5分共60分）1．（5分）对于非0向量，“”是“”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件2．（5分）设，则的定义域为（）A．（﹣4，0）∪（0，4）B．（﹣4，﹣1）∪（1，4）C．（﹣2，﹣1）∪（1，2）D．（﹣4，﹣2）∪（2，4）3．（5分）设m，n是两条不同直线，α，β是两个不同的平面，下列命题正确的是（）A．m∥α，n∥β且α∥β，则m∥n B．m⊥α，n⊥β且α⊥β，则m⊥nC．m⊥α，n⊂β，m⊥n，则α⊥βD．m⊂α，n⊂α，m∥β，n∥β，则α∥β4．（5分）已知向量=（λ+1，1），=（λ+2，2），若（+）⊥（﹣），则λ=（）A．﹣4 B．﹣3 C．﹣2 D．﹣15．（5分）函数f（x）=sin（ωx+φ）（x∈R）（ω＞0，|φ|＜）的部分图象如图所示，如果，且f（x1）=f（x2），则f（x1+x2）=（）A．B．C．D．16．（5分）设数列{a n}是公差d＜0的等差数列，S n为其前n项和，若S6=5a1+10d，则S n取最大值时，n=（）A．5 B．6 C．5或6 D．6或77．（5分）设x，y∈R，且x+4y=40，则lgx+lgy的最大值是（）A．40 B．10 C．4 D．28．（5分）已知实数x，y满足不等式组，若目标函数z=y﹣ax取得最大值时的唯一最优解是（1，3），则实数a的取值范围为（）A．（﹣∞，﹣1）B．（0，1）C．[1，+∞）D．（1，+∞）9．（5分）一个几何体的三视图如图所示，其中主视图和左视图是腰长为4的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球的表面积是（）A．12πB．24πC．32πD．48π10．（5分）在等差数列{a n}中，a1＞0，a10•a11＜0，若此数列的前10项和S10=36，前18项和S18=12，则数列{|a n|}的前18项和T18的值是（）A．24 B．48 C．60 D．8411．（5分）已知：x＞0，y＞0，且，若x+2y＞m2+2m恒成立，则实数m的取值范围是（）A．（﹣∞，﹣2]∪[4，+∞）B．（﹣∞，﹣4]∪[2，+∞）C．（﹣2，4）D．（﹣4，2）12．（5分）设函数f（x）=x3+x2+tanθ，其中θ∈[0，]，则导数f′（1）的取值范围是（）A．[﹣2，2] B．[，] C．[，2] D．[，2]二．填空题（每题5分共20分）13．（5分）函数y=sin2x+2sin2x的最小正周期T为．14．（5分）等差数列{a n}前n项和为S n．已知a m﹣1+a m+1﹣a m2=0，S2m﹣1=38，则m=．15．（5分）已知x＞0，y＞0，x+3y+xy=9，则x+3y的最小值为．16．（5分）已知，是单位向量，•=0．若向量满足|﹣﹣|=1，则||的取值范围是．三．解答题17．（10分）设函数f（x）=mx2﹣mx﹣1．（1）若对一切实数x，f（x）＜0恒成立，求m的取值范围；（2）对于x∈[1，3]，f（x）＜﹣m+5恒成立，求m的取值范围．18．（12分）已知向量=（sin，1），=（cos，cos2）．（Ⅰ）若•=1，求cos（﹣x）的值；（Ⅱ）记f（x）=•，在△ABC中，A、B、C的对边分别为a、b、c，且满足（2a﹣c）cosB=bcosC，求函数f（A）的取值范围．19．（12分）已知在等比数列{a n}中，a1=1，且a2是a1和a3﹣1的等差中项．（1）求数列{a n}的通项公式；（2）若数列{b n}满足b1+2b2+3b3+…+nb n=a n（n∈N*），求{b n}的通项公式b n．20．（12分）21、设的大小，并证明你的结论．21．（12分）如图，在四棱锥P﹣ABCD中，AB∥CD，A B⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E和F分别是CD和PC的中点，求证：（Ⅰ）PA⊥底面ABCD；（Ⅱ）BE∥平面PAD；（Ⅲ）平面BEF⊥平面PCD．22．（12分）已知函数f（x）=kx，（1）求函数的单调递增区间；（2）若不等式f（x）≥g（x）在区间（0，+∞）上恒成立，求k的取值范围；（3）求证：．辽宁师大附中2015届高三上学期期中数学试卷（文科）参考答案与试题解析一．选择题（每题5分共60分）1．（5分）对于非0向量，“”是“”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件考点：向量的共线定理；充要条件．专题：常规题型．分析：利用向量垂直的充要条件，得到由前者推出后者；通过举反例得到后者推不出前者；利用充要条件的定义得到选项．解答：解：∵⇒⇒反之，推不出，例如满足两个向量平行但得到所以是的充分不必要条件故选A点评：本题考查向量共线的充要条件、考查说明一个命题不成立只要举一个反例即可、考查条件判断条件的方法．2．（5分）设，则的定义域为（）A．（﹣4，0）∪（0，4）B．（﹣4，﹣1）∪（1，4）C．（﹣2，﹣1）∪（1，2）D．（﹣4，﹣2）∪（2，4）考点：对数的运算性质．分析：根据对数函数的真数大于0且分式中的分母不为0可得f（x）的定义域，再由f（x）中的x、f（）中的、f（）的满足的条件相同求出x的取值答案．解答：解：由题意知，＞0，∴f（x）的定义域是（﹣2，2），故：﹣2＜＜2且﹣2＜＜2解得﹣4＜x＜﹣1或1＜x＜4故选B．点评：本题主要靠求对数函数定义域的问题．这里注意对数函数的真数一定要大于0，分式中分母不为0．3．（5分）设m，n是两条不同直线，α，β是两个不同的平面，下列命题正确的是（）A．m∥α，n∥β且α∥β，则m∥n B．m⊥α，n⊥β且α⊥β，则m⊥nC．m⊥α，n⊂β，m⊥n，则α⊥βD．m⊂α，n⊂α，m∥β，n∥β，则α∥β考点：平面与平面垂直的性质．专题：证明题；空间位置关系与距离．分析：对于A、由面面平行的判定定理，得A是假命题对于B、由m⊥α，n⊥β且α⊥β，可知m与n不平行，借助于直线平移先得到一个与m或n都平行的平面，则所得平面与α、β都相交，根据m与n所成角与二面角平面角互补的结论．对于C、通过直线与平面平行的判定定理以及平面与平面平行的性质定理，判断正误即可；对于D、利用平面与平面平行的判定定理推出结果即可．解答：解：对于A，若m∥α，n∥β且α∥β，说明m、n是分别在平行平面内的直线，它们的位置关系应该是平行或异面，故A错；对于B，由m⊥α，n⊥β且α⊥β，则m与n一定不平行，否则有α∥β，与已知α⊥β矛盾，通过平移使得m与n相交，且设m与n确定的平面为γ，则γ与α和β的交线所成的角即为α与β所成的角，因为α⊥β，所以m与n所成的角为90°，故命题B正确．对于C，根据面面垂直的性质，可知m⊥α，n⊂β，m⊥n，∴n∥α，∴α∥β也可能α∩β=l，也可能α⊥β，故C不正确；对于D，若“m⊂α，n⊂α，m∥β，n∥β”，则“α∥β”也可能α∩β=l，所以D不成立．故选B．点评：本题考查直线与平面平行与垂直，面面垂直的性质和判断的应用，考查逻辑推理能力，基本知识的应用题目．4．（5分）已知向量=（λ+1，1），=（λ+2，2），若（+）⊥（﹣），则λ=（）A．﹣4 B．﹣3 C．﹣2 D．﹣1考点：数量积判断两个平面向量的垂直关系．专题：平面向量及应用．分析：利用向量的运算法则、向量垂直与数量积的关系即可得出．解答：解：∵，．∴=（2λ+3，3），．∵，∴=0，∴﹣（2λ+3）﹣3=0，解得λ=﹣3．故选B．点评：熟练掌握向量的运算法则、向量垂直与数量积的关系是解题的关键．5．（5分）函数f（x）=sin（ωx+φ）（x∈R）（ω＞0，|φ|＜）的部分图象如图所示，如果，且f（x1）=f（x2），则f（x1+x2）=（）A．B．C．D．1考点：由y=Asin（ωx+φ）的部分图象确定其解析式；正弦函数的对称性．专题：计算题；三角函数的图像与性质．分析：通过函数的图象求出函数的周期，利用函数的图象经过的特殊点求出函数的初相，得到函数的解析式，利用函数的图象与函数的对称性求出f（x1+x2）即可．解答：解：由图知，T=2×=π，∴ω=2，因为函数的图象经过（﹣），0=sin（﹣+ϕ）∵，所以ϕ=，∴，，所以．故选C．点评：本题考查三角函数的解析式的求法，函数的图象的应用，函数的对称性，考查计算能力．6．（5分）设数列{a n}是公差d＜0的等差数列，S n为其前n项和，若S6=5a1+10d，则S n取最大值时，n=（）A．5 B．6 C．5或6 D．6或7考点：等差数列的性质．专题：计算题；等差数列与等比数列．分析：利用S6=5a1+10d，可得a6=0，根据数列{a n}是公差d＜0的等差数列，即可得出结论．解答：解：∵S6=5a1+10d，∴6a1+15d=5a1+10d得到a1+5d=0即a6=0，∵数列{a n}是公差d＜0的等差数列，∴n=5或6，S n取最大值．故选：C．点评：本题考查等差数列的性质，考查等差数列的通项与求和，比较基础．7．（5分）设x，y∈R，且x+4y=40，则lgx+lgy的最大值是（）A．40 B．10 C．4 D．2考点：基本不等式；对数的运算性质．专题：不等式的解法及应用．分析：利用基本不等式的性质和对数的运算性质即可求出．解答：解：∵x＞0，y＞0，x+4y=40，∴40，化为xy≤100，当且仅当x=4y=，即x=20，y=5时取等号，∴lgx+lgy=lg（xy）≤lg100=2．故选D．点评：熟练掌握基本不等式的性质和对数的运算性质是解题的关键．8．（5分）已知实数x，y满足不等式组，若目标函数z=y﹣ax取得最大值时的唯一最优解是（1，3），则实数a的取值范围为（）A．（﹣∞，﹣1）B．（0，1）C．[1，+∞）D．（1，+∞）考点：简单线性规划的应用．专题：计算题；作图题；不等式的解法及应用．分析：由题意作出其平面区域，将z=y﹣ax化为y=ax+z，z相当于直线y=ax+z的纵截距，由几何意义可得．解答：解：由题意作出其平面区域，将z=y﹣ax化为y=ax+z，z相当于直线y=ax+z的纵截距，则由图可知，若使目标函数z=y﹣ax取得最大值时的唯一最优解是B（1，3），则a＞1，故选D．点评：本题考查了简单线性规划，作图要细致认真，属于中档题．9．（5分）一个几何体的三视图如图所示，其中主视图和左视图是腰长为4的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球的表面积是（）A．12πB．24πC．32πD．48π考点：球内接多面体；由三视图求面积、体积．专题：空间位置关系与距离．分析：该几何体的直观图如图所示，它是有一条侧棱垂直于底面的四棱锥．其中底面ABCD 是边长为4的正方形，高为CC1=4，故可求结论．解答：解：由三视图可知该几何体是有一条侧棱垂直于底面的四棱锥．其中底面ABCD是边长为4的正方形，高为4，该几何体的所有顶点在同一球面上，则球的直径为，即球的半径为，所以该球的表面积是．故选D．点评：本题考查三视图与直观图的关系，考查空间想象能力，考查学生的计算能力．10．（5分）在等差数列{a n}中，a1＞0，a10•a11＜0，若此数列的前10项和S10=36，前18项和S18=12，则数列{|a n|}的前18项和T18的值是（）A．24 B．48 C．60 D．84考点：等差数列的性质．专题：计算题．分析：根据已知条件，求出其正负转折项，然后再求数列{|a n|}的前18项和．解答：解：∵a1＞0，a10•a11＜0，∴d＜0，a10＞0，a11＜0，∴T18=a1+…+a10﹣a11﹣…﹣a18=S10﹣（S18﹣S10）=60．故选C．点评：求数列{|a n|}的前n项和，关键是求出其正负转折项，然后转化成等差数列求和．11．（5分）已知：x＞0，y＞0，且，若x+2y＞m2+2m恒成立，则实数m的取值范围是（）A．（﹣∞，﹣2]∪[4，+∞）B．（﹣∞，﹣4]∪[2，+∞）C．（﹣2，4）D．（﹣4，2）考点：基本不等式；函数恒成立问题．专题：计算题．分析：x+2y＞m2+2m恒成立，即m2+2m＜x+2y恒成立，只需求得x+2y的最小值即可．解答：解：∵x＞0，y＞0，且，∴x+2y=（x+2y）（）=2+++2≥8（当且仅当x=4，y=2时取到等号）．∴（x+2y）min=8．∴x+2y＞m2+2m恒成立，即m2+2m＜（x+2y）min=8，解得：﹣4＜m＜2．故选D．点评：本题考查基本不等式与函数恒成立问题，将问题转化为求x+2y的最小值是关键，考查学生分析转化与应用基本不等式的能力，属于中档题．12．（5分）设函数f（x）=x3+x2+tanθ，其中θ∈[0，]，则导数f′（1）的取值范围是（）A．[﹣2，2] B．[，] C．[，2] D．[，2]考点：导数的运算．专题：压轴题．分析：利用基本求导公式先求出f′（x），然后令x=1，求出f′（1）的表达式，从而转化为三角函数求值域问题，求解即可．解答：解：∵f′（x）=sinθ•x2+cosθ•x，∴f′（1）=sinθ+cosθ=2sin（θ+）．∵θ∈[0，]，∴θ+∈[，]．∴sin（θ+）∈[，1]．∴2sin（θ+）∈[，2]．故选D．点评：本题综合考查了导数的运算和三角函数求值域问题，熟记公式是解题的关键．二．填空题（每题5分共20分）13．（5分）函数y=sin2x+2sin2x的最小正周期T为π．考点：二倍角的余弦；三角函数的周期性及其求法．专题：三角函数的求值．分析：函数解析式利用二倍角的余弦函数公式化简，再利用两角和与差的正弦函数公式化为一个角的正弦函数，找出ω的值，代入周期公式即可求出最小正周期T．解答：解：函数y=sin2x+2sin2x=sin2x+1﹣cos2x=sin（2x﹣）+1，∵ω=2，∴T=π．故答案为：π点评：此题考查了二倍角的余弦函数公式，熟练掌握公式是解本题的关键．14．（5分）等差数列{a n}前n项和为S n．已知a m﹣1+a m+1﹣a m2=0，S2m﹣1=38，则m=10．考点：等比数列的性质．专题：计算题；等差数列与等比数列．分析：利用等差数列的性质a n﹣1+a n+1=2a n，我们易求出a m的值，再根据a m为等差数列{a n}的前2m﹣1项的中间项（平均项），我们可以构造一个关于m的方程，解方程即可得到m的值．解答：解：∵数列{a n}为等差数列，∴a n﹣1+a n+1=2a n，∵a m﹣1+a m+1﹣a m2=0，∴2a m﹣a m2=0解得：a m=2，又∵S2m﹣1=（2m﹣1）a m=38，解得m=10故答案为10．点评：本题考查差数列的性质，关键利用等差数列项的性质：当m+n=p+q时，a m+a n=a p+a q，同时利用了等差数列的前n和公式．15．（5分）已知x＞0，y＞0，x+3y+xy=9，则x+3y的最小值为6．考点：基本不等式．专题：计算题．分析：由于要求x+3y的最小值，故在解题时注意把x+3y看为一个整体，需将已知方程中的xy利用基本不等式转化为x+3y的形式．解答：解：由于x＞0，y＞0，x+3y+xy=9，则9﹣（x+3y）=xy=，当且仅当x=3y时，取“=”则此时，由于x＞0，y＞0，解得，故x+3y=6故答案为6．点评：本题考查利用基本不等式求解式子的最值问题，属于基础题，可以训练答题者灵活变形及选用知识的能力．16．（5分）已知，是单位向量，•=0．若向量满足|﹣﹣|=1，则||的取值范围是．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由，是单位向量，•=0．可设=（1，0），=（0，1），=（x，y）．由向量满足|﹣﹣|=1，可得（x﹣1）2+（y﹣1）2=1．其圆心C（1，1），半径r=1．利用|OC|﹣r≤||=≤|OC|+r即可得出．解答：解：由，是单位向量，•=0．可设=（1，0），=（0，1），=（x，y）．∵向量满足|﹣﹣|=1，∴|（x﹣1，y﹣1）|=1，∴=1，即（x﹣1）2+（y﹣1）2=1．其圆心C（1，1），半径r=1．∴|OC|=．∴≤||=．∴||的取值范围是．故答案为：．点评：本题考查了向量的垂直与数量积的关系、数量积的运算性质、点与圆上的点的距离大小关系，考查了推理能力和计算能力，属于中档题．三．解答题17．（10分）设函数f（x）=mx2﹣mx﹣1．（1）若对一切实数x，f（x）＜0恒成立，求m的取值范围；（2）对于x∈[1，3]，f（x）＜﹣m+5恒成立，求m的取值范围．考点：函数恒成立问题；函数最值的应用．专题：函数的性质及应用．分析：（1）若f（x）＜0恒成立，则m=0或，分别求出m的范围后，综合讨论结果，可得答案．（2）若对于x∈[1，3]，f（x）＜﹣m+5恒成立，则恒成立，结合二次函数的图象和性质分类讨论，综合讨论结果，可得答案．解答：解：（1）当m=0时，f（x）=﹣1＜0恒成立，当m≠0时，若f（x）＜0恒成立，则解得﹣4＜m＜0综上所述m的取值范围为（﹣4，0]﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）（2）要x∈[1，3]，f（x）＜﹣m+5恒成立，即恒成立．令﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）当 m＞0时，g（x）是增函数，所以g（x）max=g（3）=7m﹣6＜0，解得．所以当m=0时，﹣6＜0恒成立．当m＜0时，g（x）是减函数．所以g（x）max=g（1）=m﹣6＜0，解得m＜6．所以m＜0．综上所述，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）点评：本题考查的知识点是函数恒成立问题，函数的最值，其中将恒成立问题转化为最值问题是解答此类问题的关键．18．（12分）已知向量=（sin，1），=（cos，cos2）．（Ⅰ）若•=1，求cos（﹣x）的值；（Ⅱ）记f（x）=•，在△ABC中，A、B、C的对边分别为a、b、c，且满足（2a﹣c）cosB=bcosC，求函数f（A）的取值范围．考点：数量积的坐标表达式；两角和与差的余弦函数；正弦定理．专题：平面向量及应用．分析：（1）利用向量的数量积公式列出方程求出，利用二倍角的余弦公式求出要求的式子的值．（2）利用三角形中的正弦定理将等式中的边转化为角的正弦值，利用三角形的内角和为180°化简等式，求出角B，求出角A的范围，求出三角函数值的范围．解答：解：（1）∵∴∵（2）∵（2a﹣c）cosB=bcosC∴2sinAcosB=sinCcosB+sinBcosC=sin（B+C）=sinA∵sinA＞0∴cosB=∵B∈（0，π），∴∴∵∴∵∴∴点评：本题考查向量的数量积公式、考查三角形的正弦定理、考查三角形的内角和为180°、考查利用三角函数的单调性求三角函数值的范围．19．（12分）已知在等比数列{a n}中，a1=1，且a2是a1和a3﹣1的等差中项．（1）求数列{a n}的通项公式；（2）若数列{b n}满足b1+2b2+3b3+…+nb n=a n（n∈N*），求{b n}的通项公式b n．考点：等比数列的通项公式；等差数列的通项公式；数列的求和．专题：等差数列与等比数列．分析：（1）设出等比数列的公比，直接利用a2是a1和a3﹣1的等差中项列式求出公比，则等比数列的通项公式可求；（2）当n=1时由递推式求出b1，模仿递推式写出n=n﹣1时的递推式，作差后代入a n即可求出b n．解答：解：（1）设等比数列{a n}的公比为q，由a2是a1和a3﹣1的等差中项得：2a2=a1+a3﹣1，∴，∴2q=q2，∵q≠0，∴q=2，∴；（2）n=1时，由b1+2b2+3b3+…+nb n=a n，得b1=a1=1．n≥2时，由b1+2b2+3b3+…+nb n=a n ①b1+2b2+3b3+…+（n﹣1）b n﹣1=a n﹣1②①﹣②得：．，∴．点评：本题考查等差数列和等比数列的通项公式，考查了数列的递推式，解答的关键是想到错位相减，是基础题．20．（12分）21、设的大小，并证明你的结论．考点：对数的运算性质；对数值大小的比较．专题：压轴题．分析：先判断与的大小，再由对数函数的单调性可得到答案．解答：解：当t＞0时，由基本不等式可得，当且仅当t=1时取“=”号∴t≠1时，当0＜a＜1时，y=log a x是单调减函数，∴，即当a＞1时，y=log a x是单调增函数，∴＞，即＞点评：本题主要考查对数函数的单调性，即当底数大于1时函数单调递增，当底数大于0小于1时函数单调递减．21．（12分）如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD．E和F分别是CD和PC的中点，求证：（Ⅰ）PA⊥底面ABCD；（Ⅱ）BE∥平面PAD；（Ⅲ）平面BEF⊥平面PCD．考点：直线与平面平行的判定；直线与平面垂直的判定；平面与平面垂直的判定．专题：空间位置关系与距离；立体几何．分析：（Ⅰ）根据条件，利用平面和平面垂直的性质定理可得PA⊥平面ABCD．（Ⅱ）根据已知条件判断ABED为平行四边形，故有BE∥AD，再利用直线和平面平行的判定定理证得BE∥平面PAD．（Ⅲ）先证明ABED为矩形，可得BE⊥CD ①．现证CD⊥平面PAD，可得CD⊥PD，再由三角形中位线的性质可得EF∥PD，从而证得CD⊥EF ②．结合①②利用直线和平面垂直的判定定理证得CD⊥平面BEF，再由平面和平面垂直的判定定理证得平面BEF⊥平面PCD．解答：解：（Ⅰ）∵PA⊥AD，平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，由平面和平面垂直的性质定理可得PA⊥平面ABCD．（Ⅱ）∵AB∥CD，AB⊥AD，CD=2AB，E和F分别是CD和PC的中点，故四边形ABED为平行四边形，故有BE∥AD．又AD⊂平面PAD，BE不在平面PAD内，故有BE∥平面PAD．（Ⅲ）平行四边形ABED中，由AB⊥AD可得，ABED为矩形，故有BE⊥CD ①．由PA⊥平面ABCD，可得PA⊥AB，再由AB⊥AD可得AB⊥平面PAD，∴CD⊥平面PAD，故有CD⊥PD．再由E、F分别为CD和PC的中点，可得EF∥PD，∴CD⊥EF ②．而EF和BE是平面BEF内的两条相交直线，故有CD⊥平面BEF．由于CD⊂平面PCD，∴平面BEF⊥平面PCD．点评：本题主要考查直线和平面垂直的判定定理，直线和平面平行的判定定理，平面和平面垂直的判定定理、性质定理的应用，属于中档题．22．（12分）已知函数f（x）=kx，（1）求函数的单调递增区间；（2）若不等式f（x）≥g（x）在区间（0，+∞）上恒成立，求k的取值范围；（3）求证：．考点：不等式的证明；利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：计算题；综合题．分析：（1）由g'（x）＞0，解得x的范围，就是函数的增区间．（2）问题转化为k大于等于h（x）的最大值，利用导数求得函数h（x）有最大值，且最大值为，得到k≥．（3）先判断＜（x≥2），得＜，用放缩法证明＜1，即得要证的不等式．解答：解：（1）∵（x＞0），∴，令g'（x）＞0，得0＜x＜e，故函数的单调递增区间为（0，e）．（2）由，则问题转化为k大于等于h（x）的最大值．又，令．当x在区间（0，+∞）内变化时，h'（x）、h（x）变化情况如下表：x （0，）（，+∞）h'（x）+ 0 ﹣h（x）↗↘由表知当时，函数h（x）有最大值，且最大值为，因此k≥．（3）由≤，∴＜（x≥2），∴＜．又∵＜=1﹣+++…+=1﹣＜1，∴＜．点评：本题考查利用导数研究函数的单调性，求函数极值，用放缩法证明不等式，放缩不等式是解题的难点．。

辽宁师大附中2014-2015学年上学期期中考试高三历史试题

辽师大附中2014-2015学年上学期期中考试高三历史试题第Ⅰ卷选择题（共60分）一、选择题(本题包括30小题，每小题2分，共60分。

每小题只有一个选项符合题意)1、下面是某电视专题片中出现的三组镜头，分别反映了不同朝代为解决洪水灾害，中央政府的运作情况：①蜀郡洪水为患，丞相与诸卿拿出治理方案，交给皇帝裁决。

②渝州发生洪灾，中书省按皇帝旨意起草文件，交门下省审核，皇帝裁定后，再交尚书省，尚书省交工部、户部办理。

③徐州府爆发洪灾，阁臣据皇帝旨意写成诏书，直送工部、户部执行赈灾。

据所学知识判断，上述历史场景最早出现的朝代分别是A、秦、唐、元B、汉、宋、明C、秦、元、清D、秦、唐、明2、余秋雨在《十万进士》中指出，科举制度选拔的“十万进士”，“其中包括着一大批极为出色的、有着高度文化素养的政治家和行政管理专家。

”这说明科举制度A、是行之有效的选官用人制度B、导致了“重文轻武”的现象C、已经成为束缚人们思想的工具D、有利于维护官僚队伍的廉洁高效3、古罗马的法学家说：“人类的正义，是要求同样的事情，按同样的规则来处理，而且，这种规则应能适用于一切人，适合于一切人与生俱来的本性。

”对这句话理解准确的是A、主张法律面前人人平等B、保护所有人的私有财产C、反对私有制基础上的人人平等D、主张消除阶级压迫4、古往今来，无论是东方古国，还是西方近代国家，都以建章立制来强化中央对地方的关系。

下列具有此类性质的文献和制度有①秦汉郡县制②《十二铜表法》③英国《权利法案》④美国《1787年宪法》A、①②B、①④C、③④D、②③5、据2008年7月1日《广州日报》报道，6月27日，英国王室官员“哭穷”，说王室缺乏足够的资金维持白金汉宫和温莎堡的日常维护。

根据英国的政治体制，英国王室解决经费问题应通过A、直接向全国征税B、向英联邦国家募集C、向政府申请拨款D、要求首相资助6、某史学家说：“对于西方的挑战，中国的反应之所以迟钝，是由于中国社会在19世纪中叶面临很不平常的历史环境。

东北三省三校2015届高三第一次高考模拟考试-文科综合

哈尔滨师大附中 2015年高三第一次联合模拟考试文科综合能力测试东北师大附中辽宁省实验中学12．中国人民银行决定，自2014年11月22日起下调金融机构人民币贷款和存款基准利率。

当前我国经济运行总体平稳，此次下调贷款和存款基准利率，重点是发挥基准利率对企业和居民的引导作用。

下列选项符合央行此举目的的是A ．促进货币回笼，释放通货膨胀压力B ．降低融资成本，激发企业投资需求C ．增加货币投放，促进经济快速增长D ．拓宽投资渠道，促进居民收入增长13．图5是“环境库兹涅茨曲线”，它指出在后工业化阶段，技术效应和结构效应超过规模效应，环境质量随着经济增长逐步改善。

为加速拐点到来，我国可以采取的措施是①加快转变经济发展方式，促进经济结构升级 ②推动中西部地区快速发展，增强发展持续性 ③实施创新驱动战略，提高科技自主创新能力 ④扩大能源和资源投入，进一步扩大生产规模 A ．①② B ．①③ C ．②④ D ．②③14．粮食是关系国家经济安全的重要战略物资，粮食安全与社会的和谐、政治的稳定、经济的持续发展息息相关。

为保障粮食安全，需要增加粮食供给，下列选项中正确的是①加大科技投入→大力发展转基因技术→提高谷物生产能力→增加粮食供给 ②降低人民币汇率→降低粮食进口成本→提高粮食进口量→增加粮食供给③加大对农业的财政补贴→增加神粮农民收入→提高粮食生产积极性→增加粮食供给④深化农村土地制度改革→引导土地承包经营权有序流转→发展农业适度规模经营→增加粮食供给A ．①③B ．②③C ．②④D ．③④15．领导人借出访之机推销产品，为双方签署大单提供支持，是和平发展时代的一种国际惯例。

李克强总理2014年五次出访签定近1400亿美元大单。

其中“铁路单唱主角，中土集团获得的尼日利亚131亿美元铁路大单，刷新了我国对外承包工程单体合同额最高记录；“能源单”金额高，其中英国石油公司与中国海洋石油总公司签署的液化天然气供应协议，达200亿美元。

辽宁师范大学附属中学2015届高三下学期高考考前精品卷高三语文试题及答案测试高三试题及答案

一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1～3题。

①节日无论今古，它们有一个共同的文化功能，就是调节民众生活。

由于古今社会文化背景的不同，古今节日形态又有着明显的差异。

②古今节日都注意节日在一年中的适度分布，如一、三、五、七、九月的节日排列，以适应个人与社会的需要，但节期选择的观念古今有着根本的区别。

古代社会以农耕为主，人们靠天吃饭，人们注意自然时序与人文节序的对应，节日是人们划分时间段落的特定标志，人们依据它安排自己的生产与生活。

现代节日以现代社会文化体系为基础，在节期选择上已很少或不再考虑自然物候变化，是一种纯粹的社会选择。

现在，即使是传统节日，人们也只是继承了它的形式以及它与当代社会能够适应的内容。

③古今节日也注重人们的身心调节。

但传统节日主要在于协调人与自然的关系，人们希望通过各种节日庆典与仪式取得与自然的沟通。

因为在传统观念中，自然属特定神灵的支配，人们生产是否丰收，身体是否康健，事业是否发达，子嗣是否兴旺，都仰靠神灵的荫庇。

中国传统节日从其起源看几乎都与神灵信仰有关，如元日驱山臊恶鬼、五月五祭水神等，神灵信仰成为传统节俗的中心项目。

人们通过传统节俗活动密切了人神之间的联系，获得一种身心的放松和精神自足。

④而现代，人们面对的是社会，人们需要调节的是人与人之间的关系，因此现代节日的主题是以公共活动的方式，实现人们之间的情感沟通。

通过节日这个人们共享的文化“平台”，密切社区成员乃至民族成员的联系，并展示民众的生命活力。

很多节日还保留了传统形式，但其民俗内容已演化为一般娱乐性质，娱乐是当代节日的主导原则。

如壮族的三月三，蒙古族的那达慕大会等，都成为欢乐的群众集会。

⑤古今节日还是社会生活中不可缺少的一环。

而在传统社会中，节日不仅是民众生活时段切分转换的标志，而且总表现为一种新旧的沟通与过渡，节日是一道道隐形的关口，过节与“度厄”成为节日形态的一体两面。

诸多节俗都是为了在关键时日给人们以精神的抚慰与生理的放松，祈求顺利过关与争取未来的幸运。

辽宁省五校协作体2015届高三上学期期中考试语文试卷 Word版含答案.pdf

辽宁省五校协作体2015届高三上学期期中考试语文试题考试时间150分钟分数：150分第Ⅰ卷阅读题甲必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1~3题。

“腾笼换鸟”是几年前我国一些沿海地区根据当地经济发展状况和国家转变经济发展方式大战略提出的区域经济战略。

由于国际金融危机冲击和经济形势变化，这一战略没有得及全面实施。

有人质疑“腾笼换鸟”脱离我国的优势，迟滞地区经济发展。

近年，有关议论并未停止。

对于“腾笼换鸟”的不同看法，实质上是对于是按照既有模式追求较高经济增长速度还是让经济转入新的增长轨道而宁可牺牲一部分增长速度的不同看法，也就是对于如何正确处理眼前利益与长远利益关系的不同看法。

一般地讲要兼顾眼前利益与长远利益没有多少实际意义，关键是怎么兼顾、怎么把握好时机。

经济学界最近兴起的关于刘易斯拐点的讨论，有助于厘清对于“腾笼换鸟”的不同看法。

刘易斯拐点是发展经济学的一个著名命题，由诺贝尔经济学奖获得者阿瑟·刘易斯提出。

该理论认为，在二元经济实现工业化的过程中，随着农村劳动力向非农产业转移，农村富余劳动力逐渐减少，最终将走向枯竭，出现一个从劳动力过剩转向劳动力短缺的转折点。

这个转折点就是刘易斯拐点。

当然，所谓的劳动力短缺并不是绝对短缺，而是相对短缺，表现为劳动力成本大幅度上升，不涨工资就招不到合适的员工。

这个工资成本明显上升的时点就是刘易斯拐点。

刘易斯拐点的存在，在日本和“亚洲四小龙”工业化的过程中都得到过验证。

不过，对于人口众多的我国说是否已经到了刘易斯拐点尚有争议，因为我国还有约1亿农村劳动力需要转移到非农产业，劳动力并不缺乏。

如果尚未到达刘易斯拐点，则仍然可以而且应该继续发挥低成本劳动力的优势，发展相关产业，“腾笼换鸟”似可缓行；如果刘易斯拐点已经到，“腾笼换鸟”则势在必行。

这里的关键在于怎样理解刘易斯拐点。

刘易斯拐点并非意味着劳动力绝对短缺，而是表现为工资大幅度上涨。

辽宁师大附中高三上学期期中考试语文 Word版含答案.pdf

辽师附中2015-2016学年上学期期中考试高三语文试题命题：高三备课组满分：150分考试时间：150分钟第Ⅰ卷阅读题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1～336分）（一）文言文阅读（19分）阅读下面的文言文，完成4～7题。

曾巩，字子固，建昌南丰人。

生而警敏，读书数百言，脱口辄诵。

年十二，试作《六论》，援笔而成，辞甚伟。

甫冠，名闻四方。

欧阳修见其文，奇之。

中嘉二年进士第，出通判越州。

岁饥，度常平不足赡，而田野之民，不能皆至城邑。

谕告属县，讽富人自实粟，总十五万石，视常平价稍增以予民。

民得从便受粟，不出田里，而食有余。

又贷之种粮，使随秋赋以偿，农事不乏。

知齐州，其治以疾奸急盗为本。

章邱民聚党村落间，号“霸王社”，椎剽夺囚，无不如志。

巩配三十一人，又属民为保伍，使几察其出入，有盗则鸣鼓相援，每发辄得盗。

有葛友者，自出首。

巩饮食冠裳之，假以骑从，辇所购金帛随之，夸徇四境。

盗闻，多出自首。

自是外户不闭。

河北发民浚河，调及它路，齐当给夫二万，县初按籍三丁出夫一，巩括其隐漏，至于九而取一，省费数倍。

知洪州。

会江西岁大疫，巩命县镇亭传，悉储药待求，军民不能自养者，来食息官舍，资其食饮衣衾之具，分医视诊。

书其全失、多寡为殿最。

师征安南，所过州为万人备。

他吏暴诛亟敛，民不堪。

巩先期区处猝集，师去，市里不知。

加直龙图阁、知福州。

南剑将乐盗廖恩既赦罪出降余众溃复合阴相结附旁连数州尤桀者呼之不至居人慑恐。

巩以计罗致之，继自归者二百辈。

福多佛寺，僧利其富饶，争欲为主守，赇请公行。

巩俾其徒相推择，识诸籍，以次补之。

授帖于府庭，却其私谢，以绝左右徼求之弊。

福州无职田，岁鬻园蔬收其直，自入常三四十万。

巩曰“太守与民争利，可乎？”罢之。

后至者亦不复取也。

徙明、亳、沧三州。

巩负才名，久外徙，世颇谓偃蹇不偶。

一时后生辈锋出，巩视之泊如也。

拜中书舍人。

甫数月，丁母艰去。

又数月而卒，年六十五。

【政治】辽宁师大附中2015届高三上学期期中考试

辽宁师大附中2015届高三上学期期中考试政治试题第Ⅰ卷选择题（共49分）一、选择题(本题包括26小题，每小题2分，共52分。

每小题只有一个选项符合题意) 【题文】1．下表为2014年10月1日—26日期间人民币对美元汇率基准价(人民币元/100美元)李某即将去美国旅游，他准备了一定数量的人民币、美元现金，以及一张同时具有人民币、美元结算账户的双币信用卡。

假如此后一段时间人民币汇率仍将维持上述趋势，不考虑其他因素,他在美国购物后，既方便又划算的结算方式是A．直接使用美元现金结算B.直接用人民币现金结算C．使用双币信用卡人民币账户透支消费, 免息期结束前用美元还款D.使用双币信用卡美元账户透支消费，免息期结束前用人民币还款【知识点】A1本题考查汇率。

【答案解析】 D 解析：依题意可知，人民币呈升值趋势美元贬值，因而答案为D。

A应为直接使用人民币现金结算；B划算但不方便；C方便，但不划算，应该用人民币还款。

【思路点拨】注意“既方便又划算”的要求。

【题文】2．右图是某种商品从产生到退出市场的价格波动图，当该商品价格从A点运行到B点，说明A．该商品生产者的个别劳动生产率降低B．该商品的生产者从赚钱到保本经营C.该商品的社会劳动生产率提高D.生产该商品已无盈利空间【知识点】A2本题考查价值规律。

【答案解析】 C 解析：A表述错误，个别劳动生产率并不影响商品的价格；B表述不合理，只有该生产者的个别劳动生产率与社会劳动生产率一致才可能保本经营，如果低于社会劳动生产率也可能是亏本经营，反之可能是盈利；D表述不合理，当个别劳动生产率高于社会劳动生产率，是存在盈利空间的。

【思路点拨】注意价值量由社会必要劳动时间决定；注意商品生产者之间的劳动生产率是不一样的。

【题文】3．“闪付”（QuickPass)作为一种消费新时尚，是针对单笔金额不超过lOOO元的消费，无需输入密码和签名，只需要在POS机上轻松一挥便可快速支付的方式。

辽宁省辽宁师大附中高三上学期期中考试数学文试题含答案

v2013-2014学年度上学期高三期中数学(文)试卷命题人:王红校对人：潘巍一选择题：(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求)1.在空间，下列命题正确的是（） A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行2.已知两条直线2-=ax y 和01)2(3=++-y a x 互相平行，则a 等于( ) A ．1或-3 B ．-1或3 C ．1或3 D ． -1或-33.直线l ：x －2y ＋2＝0过椭圆的左焦点F 1和上顶点B ，该椭圆的离心率为( )．A.15B.25C.55 D.2554.设b a ,是两条直线，βα,是两个平面，则b a ⊥的一个充分条件是（）A ．βαβα⊥⊥,//,b aB ．βαβα//,,⊥⊥b aC ．βαβα//,,⊥⊂b aD ．βαβα⊥⊂,//,b a5.过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点，它们的横坐标之和等于5，则这样的直线（） A ．有且仅有一条 B ．有且仅有两条 C ．有无穷多条 D ．不存在6 .如图，AB 是圆O 的直径，PA 垂直圆O 所在的平面于A ，点C 是圆上的任意一点，图中有（）对平面与平面垂直 A ．1 B ．2 C ．3 D ． 47.过抛物线y 2＝4x 的焦点F 的直线交该抛物线于A ，B 两点，O 为坐标原点．若|AF |＝3，则△AOB 的面积为( )． A.22 B. 2 C.322D ．2 2 8.已知F 1、F 2为双曲线C ：x 2－y 2＝2的左、右焦点，点P 在C 上，|PF 1|＝2|PF 2|，则cos ∠F 1PF 2＝( )A.14B.35C.34D.459.已知椭圆x 23＋y 24＝1的上焦点为F ，直线x ＋y －1＝0和x ＋y ＋1＝0与椭圆分别相交于点A ，PC BAB 和C ，D ，则AF ＋BF ＋CF ＋DF ＝( )．A ．2 3B ．4 3C ．4D ．810. 已知椭圆C ：x 22＋y 2＝1的右焦点为F ，直线l ：x ＝2，点A ∈l ，线段AF 交C 于点B ，若F A→＝3FB →，则|AF →|＝( )．A. 2 B ．2 C. 3 D ．3 11.已知双曲线x 2－y 23＝1的左顶点为A 1，右焦点为F 2，P 为双曲线右支上一点，则P A 1→·PF 2→的最小值为( )． A ．－2B ．－8116C ．1D ．012. 棱长为1的正方体ABCD －A 1B 1C 1D 1中，点P 1，P 2分别是线段AB ，BD 1(不包括端点)上的动点，且线段P 1P 2平行于平面A 1ADD 1，则四面体P 1P 2AB 1的体积的最大值是( )A.124B.112C.16D.12二、填空题：(本大题共4小题；每小题5分，共20分，把答案填在题中的横线上.) 13．若双曲线8kx 2－ky 2＝8的一个焦点坐标是(0，3)，则实数k 的值为________． 14．某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．图1－315. 已知＝，＝,＝,…。

辽宁师大附中高三上学期10月模块考试——数学(文)数学文

辽宁师大附中2015届高三上学期10月模块考试数学（文）试题注意：本试卷包含Ⅰ、Ⅱ两卷。

第Ⅰ卷为选择题，所有答案必须用2B 铅笔涂在答题卡中相应的位置。

第Ⅱ卷为非选择题，所有答案必须填在答题纸的相应位置。

第I 卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，选择一个符合题目要求的选项.1、已知集合B A x xx B x x x A 则},02|{},034|{2≤-=>+-=等于（） A ． B ． C ． D ． 2、已知数列为等差数列，且，则的值为（）A 、B 、C 、D 、 3、已知是两个非零向量，给定命题，命题，使得，则是的（）A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件 4、函数的一个单调减区间是（） A 、 B 、 C 、 D 、5、设等比数列{ }的前n 项和为，若 =3 ，则 =（） A 、 2 B 、 C 、 D 、36、已知某等差数列共有10项，其奇数项之和为15，偶数项之和为30，则其公差为( ) A 、3B 、4C 、5D 、27、已知向量，向量，且，则实数等于（）A 、B 、C 、D 、8、已知，log log a a x =，log log a a z =，则（） A ．B ．C ．D ．9、在中，内角所对的边长分别是。

若A A B C 2sin )sin(sin =-+，则的形状为（） A 、等腰三角形 B 、直角三角形 C 、等腰直角三角形 D 、等腰或直角三角形 10、函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是（）11、已知，则的值是（）A 、B 、C 、D 、12、已知实数33,,,,x x y d c b a -=且曲线成等比数列的极大值点坐标为（b,c ）则等于（）A ．2B ．1C ．—1D ．—2第Ⅱ卷（共60分）二、填空题：本大题共4小题，每小题4分，共16分.将正确答案填在相应位置上。

2015届高三上数学文科期中试卷(含答案)

2015届高三上数学文科期中试卷(含答案) 2014-2015学年度沈阳铁路实验学校11月月考卷高三数学（文）考试时间：120分钟；总分：150第I卷（选择题）一、选择题（每小题5分，共60分）1.集合，，,则集合的元素个数为（）A.B.C.D.2.已知，其中为虚数单位，则（）A、B、C、D、3.若变量满足约束条件，则目标函数的最小值为（）A.B.C.D.4.若，则的值为（）A.B.C.D.5.若向量的夹角为，且，则与的夹角为（）A.B.C.D.6.若按右侧算法流程图运行后，输出的结果是,则输入的的值为（）A.B.C.D.7.直线截圆所得劣弧所对圆心角为（）A.B.C.D.8、在同一个坐标系中画出函数，的部分图象，其中且，则下列所给图象中可能正确的是（）9、一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则该几何体的体积为（）ABCD10、设定义在上的奇函数，满足对任意都有，且时，，则的值等于（）ABCD11、已知球的直径SC=4，A，B是该球球面上的两点，AB=2．∠ASC=∠BSC=45°则棱锥S—ABC的体积为A．B．C．D．12、在平面直角坐标系中，已知是函数的图象上的动点，该图象在点处的切线交轴于点，过点作的垂线交轴于点.则的范围是A．B.C.D.第II卷（非选择题）二、填空题（（每小题5分，共20分））13、从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离小于该正方形边长的概率为14在等差数列中，，公差为，前项和为，当且仅当时取最大值，则的取值范围_________.15、若不等式对任意恒成立，则实数的取值范围为16、已知,动点满足,则的最大值为三、解答题（（第17-21每小题12分，选做题10，共70分））17、中内角所对的边分别是，且（1）若，求；（2）求函数的值域。

18、在如图所示的几何体中，四边形是菱形，是矩形，平面平面，为的中点.(Ⅰ)求证：;(Ⅱ)在线段是是否存在点，使得//平面，若存在，说明其位置，并加以证明；若不存在，请说明理由.19、某车间名工人年龄数据如下表：年龄（岁）工人数（人）合计（1）求这名工人年龄的众数与极差；（2）以十位数为茎，个位数为叶，作出这名工人年龄的茎叶图；（3）求这名工人年龄的方差.20、设数列的前项和为，点在直线上.(Ⅰ)求数列的通项公式；(Ⅱ)在与之间插入个数，使这个数组成公差为的等差数列，求数列的前项和.21、设，函数．（I）当时，求的极值；（II）设，若对于任意的，不等式恒成立，求实数的取值范围．请考生在22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分。

辽宁师大附中高三数学上学期10月模块考试试题文(含解

辽宁师大附中2015届高三上学期10月模块考试数学（文）试题（解析版）【试卷综析】试卷的题型着眼于考查现阶段学生的基础知识及基本技能掌握情况。

整份试卷难易适中，没有偏、难、怪题，保护了学生的学习信心并激励学生继续学习的热情；在选题和确定测试重点上都认真贯彻了“注重基础，突出知识体系中的重点，培养能力”的命题原则，重视对学生运用所学的基础知识和技能分析问题、解决问题能力的考查。

第I 卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，选择一个符合题目要求的选项. 【题文】1、已知集合B A x xx B x x x A 则},02|{},034|{2等于（） A ．}21|{ x x B ．}321|{ x x x 或C ．}10|{ x xD ．}310|{ x x x 或【知识点】交集及其运算.A1【答案解析】C 解析：由题意解出A ，B ，然后根据交集的定义和运算法则进行计算．【思路点拨】∵集合A={x|x 2﹣4x+3＞0}，∴A={x|x＞3或x ＜1}， ∵B={x|≤0}，∴B={x|0≤x＜2}，∴A∩B={x|0≤x＜1}，故选C ．【题文】2、已知数列}{n a 为等差数列，且 41371 a a a ，则)tan(122a a 的值为（）A 3B 、3C 、3、3【知识点】等差数列的性质；运用诱导公式化简求值；两角和与差的正切函数．C2 C5 D2 【答案解析】B 解析：∵ 41371 a a a ，则a 7=43， ∴tan（a 2+a 12）=tan2a 7=tan83=3 B. 【思路点拨】因为 41371 a a a ，则a 7=43 ，所以tan （a 2+a 12）=tan2a 7=tan 83，由诱导公式计算可得答案．【题文】3、已知b a ,是两个非零向量，给定命题b a b a p:，命题R t q :，使得b t a，则p 是q 的（）A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件【知识点】必要条件、充分条件与充要条件的判断；向量的几何表示．A2 F2【答案解析】C 解析：（1）若命题p 成立，∵，是两个非零向量，|•|=||||，即|||||•cos＜，＞|=||||，∴cos＜，＞=±1，＜，＞=00或＜，＞=1800∴，共线，即；∃t ∈R ，使得=t ，∴由命题p 成立能推出命题q 成立．（2）若命题p 成立，即∃t ∈R ，使得=t ，则，两个非零向量共线，∴＜，＞=00或＜，＞=1800，∴cos＜，＞=±1，即|||||•cos＜，＞|=||||， ∴|•|=||||，∴由命题q 成立能推出命题p 成立．∴p 是q 的充要条件．故选C ．【思路点拨】利用两个向量的数量积公式，由命题p 成立能推出命题q 成立，由命题q 成立能推出命题p 成立，p 是q 的充要条件．【题文】4、函数)42sin(2)(x x f 的一个单调减区间是（）A 、 ]89,85[B 、 ]83,8[C 、 ]87,83[D 、 ]85,8[ 【知识点】复合三角函数的单调性．C3 【答案解析】C 解析：由2kπ+≤2x﹣≤2kπ+（k ∈Z ）得：kπ+≤x≤kπ+，∴函数)42sin(2)(x x f 的单调递减区间为[kπ+，kπ+]．当k=0时，函数)42sin(2)(x x f 的一个单调递减区间是]87,83[．故选C ．【思路点拨】由正弦函数的单调性可求得正弦函数的递减区间，继而可得答案．【题文】5、设等比数列{ n a }的前n 项和为n S ，若63S S =3 ，则 69SS =（） A 、 2 B 、73 C 、 83D 、3 【知识点】等比数列的前n 项和.D3【答案解析】B 解析：设公比为q ，则63S S ===1+q 3=3，所以q 3=2，所以69S S ===．故选B ．【思路点拨】首先由等比数列前n 项和公式列方程，并解得q 3，然后再次利用等比数列前n项和公式则求得答案．【题文】6、已知某等差数列共有10项，其奇数项之和为15，偶数项之和为30，则其公差为( ) A 、3B 、4C 、5D 、2【知识点】等差数列的通项公式．D2 【答案解析】A 解析：根据题意得：115201552530a d a d，解得：3d ，故选A ．【思路点拨】写出数列的第一、三、五、七、九项的和，写出数列的第二、四、六、八、十项的和，都用首项和公差表示，两式相减，得到结果．【题文】7、已知向量(1,2)a r ，向量(,2)b x r，且()a a b r r r ，则实数x 等于（）A 、4B 、4C 、0D 、9 【知识点】数量积判断两个平面向量的垂直关系．F3【答案解析】D 解析：由向量(1,2)a r ，向量(,2)b x r，∴a b r r =（1﹣x ，4），又()a a b r r r，∴1×（1﹣x ）+2×4=0，解得x=9．故选D ．【思路点拨】由给出的向量的坐标求出a b r r的坐标，然后直接利用向量垂直的坐标表示列式求解x 的值．【题文】8、已知01a ，log 2log 3aa x ，1log 52a y ，log 21log 3a a z ，则（） A ．x y z B ．z y x C ．y x z D ．z x y【知识点】对数值大小的比较。

中学分校2015届高三上学期期中数学试卷(文科)(解析版)

辽宁省实验中学分校2015届高三上学期期中数学试卷（文科）一、选择题：本大题12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）已知集合M={0，1，2，3}，N={x|x2﹣3x＜0}，则M∩N=（）A．{0} B．{x|x＜0} C．{x|0＜x＜3} D．{1，2}2．（5分）已知复数是虚数单位，则复数z的虚部是（）A．B．C．D．3．（5分）设a=，b=，c=，则a，b，c的大小关系是（）A．c＞b＞a B．c＞a＞b C．a＞b＞c D．b＞c＞a4．（5分）函数f（x）=1﹣xlnx的零点所在区间是（）A．（0，）B．（，1）C．（1，2）D．（2，3）5．（5分）下列选项叙述错误的是（）A．命题“若x≠l，则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0，则x=1”B．若p∨q为真命题，则p，q均为真命题C．若命题p：∀x∈R，x2+x+1≠0，则¬p：∃x∈R，x2+x+1=0D．“x＞2”是“x2﹣3x+2＞0”的充分不必要条件6．（5分）要得到函数f（x）=sin（2x+）的图象，只需将函数g（x）=sin（2x+）的图象（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度7．（5分）若实数x，y满足条件，则2x+y的最大值是（）A．8B．2C．4D．78．（5分）已知tanα=2，则sin2α﹣sinαcosα的值是（）A．B．C．﹣2 D．29．（5分）已知两个不同的平面α，β和两条不重合的直线m，n，下列四个命题：①若m∥n，m⊥α，则n⊥α；②若m⊥α，m⊥β，则α∥β；③若m⊥α，m∥n，n⊂β，则α⊥β；④若m∥α，α∩β=n，则m∥n．其中正确命题的个数是（）A．0个B．1个C．2个D．3个10．（5分）执行如图所示的程序框图，如果输入的t∈[﹣2，2]，则输出的S属于（）A．[﹣6，﹣2] B．[﹣5，﹣1] C．[﹣4，5] D．[﹣3，6] 11．（5分）已知函数f（x）是定义在R上的奇函数，f（1）=0，当x＞0时，有＞0成立，则不等式f（x）＞0的解集是（）A．（﹣1，0）∪（1，+∞）B．（﹣1，0）C．（1，+∞）D．（﹣∞，﹣1）∪（1，+∞）12．（5分）已知函数f（x）=，若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（）A．（16，21）B．（16，24）C．（17，21）D．（18，24）第Ⅱ卷非选择题（共90分）注意事项：第Ⅱ卷全部是非选择题，必须在答题卡非选择题答题区域内，用黑色钢笔或签字笔作答，不能答在试卷上，否则答案无效二、填空题：本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上．13．（5分）已知f（x+1）的定义域为[﹣2，3]，则f（x）的定义域是．14．（5分）如图水平放置的三棱柱的侧棱长为1，且侧棱AA1⊥平面A1B1C1，主视图是边长为1的正方形，俯视图为一个等边三角形，则该三棱柱的左视图面积为．15．（5分）已知A，B，C点在球O的球面上，∠BAC=90°AB=AC=2．球心O到平面ABC 的距离为1，则球O的表面积为．16．（5分）已知函数f（x）=sin，x∈R，将函数y=f（x）图象上所有点的横坐标缩短为原来的倍（纵坐不变），得到函数g（x）的图象，则关于f（x）•g（x）有下列命题：①函数y=f（x）•g（x）是奇函数；②函数y=f（x）•g（x）不是周期函数；③函数y=f（x）•g（x）的图象关于点（π，0）中心对称；④函数y=f（x）•g（x）的最大值为．其中真命题为．三、解答题：本大题共6个小题，总分70分．解答应写出文字说明、证明过程或演算步骤. 17．（12分）在△ABC中，角A，B，C的对边分别为．（Ⅰ）求cosB的值；（Ⅱ）若，求a和c的值．18．直三棱柱ABC﹣A1B1C1中，，∠ABC=90°，N、F分别为A1C1、B1C1的中点．（Ⅰ）求证：CF⊥平面NFB；（Ⅱ）求四面体F﹣BCN的体积．19．（12分）函数f（x）=6cos2sinωx﹣3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．（Ⅰ）求ω的值及函数f（x）的值域；（Ⅱ）若f（x0）=，且x0∈（﹣），求f（x0+1）的值．20．（12分）已知函数f（x）=lnx﹣，g（x）=f（x）+ax﹣6lnx，其中a∈R．（Ⅰ）讨论f（x）的单调性；（Ⅱ）若g（x）在其定义域内为增函数，求正实数a的取值范围；（Ⅲ）设函数h（x）=x2﹣mx+4，当a=2时，若∃x1∈（0，1），∀x2∈[1，2]，总有g（x1）≥h（x2）成立，求实数m的取值范围．21．（12分）已知函数．（1）求函数f（x）的单调区间和极值；（2）若函数y=g（x）对任意x满足g（x）=f（4﹣x），求证：当x＞2，f（x）＞g（x）；（3）若x1≠x2，且f（x1）=f（x2），求证：x1+x2＞4．请考生在第22、23、24三题中任选一题作答，如果多做，则安所做的第一题记分.【选修4-1：几何证明选讲】22．（12分）如图，AB是⊙O的直径，弦CA、BD的延长线相交于点E，EF垂直BA的延长线于点F．求证：（1）∠DEA=∠DFA；（2）AB2=BE•BD﹣AE•AC．【选修4-4：坐标系与参数方程】23．（10分）在直角坐标系xOy中，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系、设曲线C参数方程为（θ为参数），直线l的极坐标方程为．（1）写出曲线C的普通方程和直线l的直角坐标方程；（2）求曲线C上的点到直线l的最大距离．【选修4-5：不等式选讲】24．已知函数f（x）=log2（|x﹣1|+|x﹣5|﹣a）．（1）当a=2时，求函数f（x）的最小值；（2）当函数f（x）的定义域为R时，求实数a的取值范围．辽宁省实验中学分校2015届高三上学期期中数学试卷（文科）参考答案与试题解析一、选择题：本大题12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）已知集合M={0，1，2，3}，N={x|x2﹣3x＜0}，则M∩N=（）A．{0} B．{x|x＜0} C．{x|0＜x＜3} D．{1，2}考点：交集及其运算．专题：计算题；集合．分析：求出N中不等式的解集确定出N，再找出两集合的交集即可．解答：解：由N中的不等式变形得：x（x﹣3）＜0，解得：0＜x＜3，即N=（0，3），∵M={0，1，2，3}，∴M∩N=[1，2}．故选：D．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．（5分）已知复数是虚数单位，则复数z的虚部是（）A．B．C．D．考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：根据复数的基本运算进行化简即可得到结论．解答：解：z=，故z的虚部为，故选：D点评：本题主要考查复数的基本运算，比较基础．3．（5分）设a=，b=，c=，则a，b，c的大小关系是（）A．c＞b＞a B．c＞a＞b C．a＞b＞c D．b＞c＞a考点：指数函数的图像与性质．专题：函数的性质及应用．分析：根据指数函数，对数函数的性质分别判断a，b，c的大小即可得到结论．解答：解：a=＜0，b=∈（0，1），c=＞1，∴c＞b＞a，故选：A．点评：本题主要考查函数值的大小比较，利用指数函数和对数函数的性质是解决本题的关键，比较基础．4．（5分）函数f（x）=1﹣xlnx的零点所在区间是（）A．（0，）B．（，1）C．（1，2）D．（2，3）考点：函数零点的判定定理．专题：函数的性质及应用．分析：利用根的存在定理分别判断端点值的符合关系．解答：解：∵f（1）=1＞0，f（2）=1﹣2ln2=ln＜0，∴函数f（x）=1﹣xlnx的零点所在区间是（1，2）．故选：C．点评：本题主要考查函数零点区间的判断，判断的主要方法是利用根的存在性定理，判断函数在给定区间端点处的符号是否相反．5．（5分）下列选项叙述错误的是（）A．命题“若x≠l，则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0，则x=1”B．若p∨q为真命题，则p，q均为真命题C．若命题p：∀x∈R，x2+x+1≠0，则¬p：∃x∈R，x2+x+1=0D．“x＞2”是“x2﹣3x+2＞0”的充分不必要条件考点：命题的真假判断与应用．专题：规律型．分析：A“若p则q，“的逆否命题为“若﹣p则﹣q“．故A正确；B p∨q为真命题说明p和q中至少有一个为真；C是全称命题与存在性命题的转化；D从充要条件方面判断．解答：解：A原命题为“若p则q，“，则它的逆否命题为“若﹣p则﹣q“．故正确；B当p，q中至少有一个为真命题时，则p∨q为真命题．故错误．C正确．D 由x2一3x+2＞0解得x＜1或x＞2显然x＞2⇒x＜1或x＞2但x＜1或x＞2不能得到x＞2故“x＞2”是“x2一3x+2＞0”的充分不必要条件，故正确．故选B点评：本题主要考查了四种命题的关系、充要条件的转化、全称命题与存在性命题的相互转化．6．（5分）要得到函数f（x）=sin（2x+）的图象，只需将函数g（x）=sin（2x+）的图象（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：由条件根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．解答：解：将函数g（x）=sin（2x+）的图象向左平移个单位长度，可得有y=sin[2（x+）+]=sin（2x+）的图象，故选：C．点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．7．（5分）若实数x，y满足条件，则2x+y的最大值是（）A．8B．2C．4D．7考点：简单线性规划．专题：计算题；作图题；不等式的解法及应用．分析：由题意作出其平面区域，将z=2x+y化为y=﹣2x+z，z相当于直线y=﹣2x+z的纵截距，由几何意义可得．解答：解：由题意作出其平面区域，令z=2x+y，化为y=﹣2x+z，z相当于直线y=﹣2x+z的纵截距，则解得，x=3，y=1；则2x+y的最大值是为6+1=7，故选D．点评：本题考查了简单线性规划，作图要细致认真，属于中档题．8．（5分）已知tanα=2，则sin2α﹣sinαcosα的值是（）A．B．C．﹣2 D．2考点：三角函数的化简求值．分析：先在sin2α﹣sinαcosα加上分母1，即，然后分子分母同时除以cos2α即可得到关于tanα的关系式，进而得到答案．解答：解：因为sin2α﹣sinαcosα====．故选A．点评：本题是基础题，考查三角函数的值的求法，注意齐次式的应用，考查计算能力．9．（5分）已知两个不同的平面α，β和两条不重合的直线m，n，下列四个命题：①若m∥n，m⊥α，则n⊥α；②若m⊥α，m⊥β，则α∥β；③若m⊥α，m∥n，n⊂β，则α⊥β；④若m∥α，α∩β=n，则m∥n．其中正确命题的个数是（）A．0个B．1个C．2个D．3个考点：平面的基本性质及推论．专题：阅读型．分析：由线面平行的性质定理判断出④不对，对于选项①②③用平行和垂直的结论以及面面垂直的判定定理判断解答：解：①正确，课本例题的结论；②正确，同垂直与一条直线的两个平面平行；③正确，由m⊥α，m∥n得，n⊥α，又因n⊂β，所以α⊥β．④不对，由线面平行的性质定理得，当m⊂β时成立；否则不一定成立．即正确的有①②③．故选D．点评：本题考查了空间中的线面位置关系，用了线面平行的性质定理，平行和垂直的结论以及面面垂直的判定定理判断．做这一类型题目的关键在于对知识的熟练掌握程度．10．（5分）执行如图所示的程序框图，如果输入的t∈[﹣2，2]，则输出的S属于（）A．[﹣6，﹣2] B．[﹣5，﹣1] C．[﹣4，5] D．[﹣3，6]考点：程序框图．专题：算法和程序框图．分析：根据程序框图，结合条件，利用函数的性质即可得到结论．解答：解：若0≤t≤2，则不满足条件输出S=t﹣3∈[﹣3，﹣1]，若﹣2≤t＜0，则满足条件，此时t=2t2+1∈（1，9]，此时不满足条件，输出S=t﹣3∈（﹣2，6]，综上：S=t﹣3∈[﹣3，6]，点评：本题主要考查程序框图的识别和判断，利用函数的取值范围是解决本题的关键，比较基础．11．（5分）已知函数f（x）是定义在R上的奇函数，f（1）=0，当x＞0时，有＞0成立，则不等式f（x）＞0的解集是（）A．（﹣1，0）∪（1，+∞）B．（﹣1，0）C．（1，+∞）D．（﹣∞，﹣1）∪（1，+∞）考点：函数奇偶性的性质．专题：函数的性质及应用；导数的概念及应用．分析：根据当x＞0时，有＞0成立，可得为增函数，结合函数f（x）是定义在R上的奇函数，f（1）=0，可分析出在各个区间上，和f（x）的符号，进而可得不等式f（x）＞0的解集．解答：解：∵当x＞0时，有＞0成立，∴当x＞0时，为增函数，又∵f（1）=0，∴当x＞1时，＞0，f（x）＞0，当0＜x＜1时，＜0，f（x）＜0，又∵函数f（x）是定义在R上的奇函数，∴是定义在（﹣∞，0）∪（0，+∞）上的偶函数，故当x＜﹣1时，＞0，f（x）＜0，当﹣1＜x＜0时，＜0，f（x）＞0，故f（x）＞0的解集是（﹣1，0）∪（1，+∞），点评：本题考查的知识点是函数奇偶性的性质，函数的单调性，是函数图象和性质与导函数的综合应用，难度中档．12．（5分）已知函数f（x）=，若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（）A．（16，21）B．（16，24）C．（17，21）D．（18，24）考点：对数函数图象与性质的综合应用．专题：数形结合；函数的性质及应用．分析：根据图象可判断：，1＜b＜2，2＜c＜4，6＜d＜8，当直线y=t，0＜t＜4，可以有4个交点，通过图象运动可以判断1×1×4×6=24，=16，直线越往上走abcd的积越小，越往下abcd的积越大，即可求出答案．解答：解：若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b ＞a＞0根据图象可判断：，1＜b＜2，2＜c＜4，6＜d＜8，当直线y=t，0＜t＜4，可以有4个交点，把直线向上平移，向下平移，可判断：直线越往上走abcd的积越小，越往下abcd的积越大，当t=0时1×1×4×6=24，当t=4时，=16，abcd的取值范围是（16，24），故选：B点评：本题综合考查了函数图象的运用，求解两个图象的交点问题，运用动的观点解决，理解好题意是解题关键．第Ⅱ卷非选择题（共90分）注意事项：第Ⅱ卷全部是非选择题，必须在答题卡非选择题答题区域内，用黑色钢笔或签字笔作答，不能答在试卷上，否则答案无效二、填空题：本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上．13．（5分）已知f（x+1）的定义域为[﹣2，3]，则f（x）的定义域是[﹣1，4]．考点：函数的定义域及其求法．专题：函数的性质及应用．分析：由已知f（x+1）的定义域为[﹣2，3]，可得﹣1≤x+1≤4，从而求得f（x）的定义域．解答：解：∵已知f（x+1）的定义域为[﹣2，3]，∴﹣1≤x+1≤4，则f（x）的定义域为[﹣1，4]，故答案为[﹣1，4]．点评：本题主要考查求抽象函数的定义域的方法，属于基础题．14．（5分）如图水平放置的三棱柱的侧棱长为1，且侧棱AA1⊥平面A1B1C1，主视图是边长为1的正方形，俯视图为一个等边三角形，则该三棱柱的左视图面积为．考点：简单空间图形的三视图．专题：计算题；空间位置关系与距离．分析：三棱柱的左视图是一个矩形，矩形的长是三棱柱的侧棱长，宽是底面三角形的一条边上的高，在边长是1的等边三角形中做出底边上的高的长度，得到结果．解答：解：由题意知三棱柱的左视图是一个矩形，矩形的长是三棱柱的侧棱长，宽是底面三角形的一条边上的高，在边长是1的等边三角形中，底边上的高是，∴侧视图的面积是．故答案为：．点评：本题考查简单的空间图形三视图，考查三视图的面积的计算，考查通过原图观察三视图的大小，本题是一个易错题，易错点在侧视图的宽，错成底边的边长．15．（5分）已知A，B，C点在球O的球面上，∠BAC=90°AB=AC=2．球心O到平面ABC 的距离为1，则球O的表面积为12π．考点：球的体积和表面积．专题：计算题；空间位置关系与距离；球．分析：由∠BAC=90°，AB=AC=2，得到BC，即为A、B、C三点所在圆的直径，取BC的中点M，连接OM，则OM即为球心到平面ABC的距离，在Rt△OMB中，OM=1，MB=，则OA可求，再由球的表面积公式即可得到．解答：解：如图所示：取BC的中点M，则球面上A、B、C三点所在的圆即为⊙M，连接OM，则OM即为球心到平面ABC的距离，在Rt△OMB中，OM=1，MB=，∴OA==，即球的半径R为，∴球O的表面积为S=4πR2=12π．故答案为：12π．点评：本题考查球的表面积计算问题，考查球的截面性质，考查运算能力，是基础题．16．（5分）已知函数f（x）=sin，x∈R，将函数y=f（x）图象上所有点的横坐标缩短为原来的倍（纵坐不变），得到函数g（x）的图象，则关于f（x）•g（x）有下列命题：①函数y=f（x）•g（x）是奇函数；②函数y=f（x）•g（x）不是周期函数；③函数y=f（x）•g（x）的图象关于点（π，0）中心对称；④函数y=f（x）•g（x）的最大值为．其中真命题为③．考点：命题的真假判断与应用．专题：函数的性质及应用．分析：本题可先根据图象平移的规律求出g（x）的解析式，再研究函数f（x）•g（x）的奇偶性、周期性、对称性和最值，从而选出正确选项．解答：解：∵函数f（x）=sin，x∈R，∴将函数y=f（x）图象上所有点的横坐标缩短为原来的倍（纵坐不变），函数g（x）=sinx．∴f（x）•g（x）=sinx•sin．记h（x）=sinx•sin．（1）h（﹣x）=sin（﹣x）•sin（﹣）=（﹣sinx）•（﹣sin）=sinx•sin．∴h（﹣x）=h（x）．∴h（x）是偶函数．假设h（x）是奇函数，则h（x）=0恒成立，与h（x）=sinx•sin矛盾．故假设不成立．∴h（x）不是奇函数．即①不成立．（2）∵==h （x），∴h（x）是周期函数．故②不成立．（3）设P（x，y）是函数y=h（x）图象上任意一点，则y=sinx•sin．点P（x，y）关于点（π，0）的对称点是P′（2π﹣x，﹣y），∵∴点是P′（2π﹣x，﹣y）也在函数y=sinx•sin的图象上．∴函数y=f（x）•g（x）的图象关于点（π，0）中心对称．∴③成立．（4）h（x）=sinx•sin=．令，则．H（x）=2（1﹣t2）t=﹣2t3+2t，（﹣1≤t≤1）．当时，H′（x）＜0，H（x）单调递减；当时，H′（x）＞0，H（x）单调递增；当时，H′（x）＜0，H（x）单调递减．∵H（﹣1）=2﹣2=0，，∴H（x）的最大值为．∴④不成立．故答案为③．点评：本题考查了函数的图象平移、函数的单调性、函数的奇偶性、函数的周期性、函数的最值，用到了换元法化简，导数法求最值．本题虽然是填空题，但计算量较大，思维要求高，属于中档题．三、解答题：本大题共6个小题，总分70分．解答应写出文字说明、证明过程或演算步骤.17．（12分）在△ABC中，角A，B，C的对边分别为．（Ⅰ）求cosB的值；（Ⅱ）若，求a和c的值．考点：余弦定理；同角三角函数基本关系的运用．专题：计算题．分析：（1）利用诱导公式求出sin的值，从而利用二倍角的余弦公式求得cosB．（2）由两个向量的数量积的定义求出ac的值，再利用余弦定理求出a和c的值．解答：解：（1）∵cos=，∴sin=sin（﹣）=，∴cosB=1﹣2sin2=．（2）由•=2可得a•c•cosB=2，又cosB=，故ac=6，由b2=a2+c2﹣2accosB 可得a2+c2=12，∴（a﹣c）2=0，故a=c，∴a=c=．点评：本题考查同角三角函数的基本关系，诱导公式和二倍角的余弦公式，两个向量的数量积的定义，以及余弦定理的应用．18．直三棱柱ABC﹣A1B1C1中，，∠ABC=90°，N、F分别为A1C1、B1C1的中点．（Ⅰ）求证：CF⊥平面NFB；（Ⅱ）求四面体F﹣BCN的体积．考点：直线与平面垂直的判定；棱柱、棱锥、棱台的体积．专题：空间位置关系与距离．分析：（I）根据直棱柱的性质及AB⊥BC，判定NF与平面BC1的垂直关系，再由线面垂直的性质判断线线垂直，然后由线线垂直⇒线面垂直．（II）根据三棱锥的换底性求解即可．解答：证明：（Ⅰ）直三棱柱ABC﹣A1B1C1中，B1B⊥AB，BC⊥AB，又B1B∩BC=B，∴AB⊥平面BB1C1C．又N、F分别为A1 C1、B1 C1的中点∴AB∥A1B1∥NF．∴NF⊥平面BB1C1C．∵FC⊂平面BB1C1C．∴NF⊥FC．∵BB1=B1F=C1F=a，∴BF=CF=a，BC=2a，∴BF2+CF2=BC2．∴BF⊥FC，又NF∩FB=F，∴FC⊥平面NFB．（Ⅱ）由（Ⅰ）知，NF⊥平面BCC1B1，，=．点评：本题考查线面垂直的判定及四面体的体积．19．（12分）函数f（x）=6cos2sinωx﹣3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．（Ⅰ）求ω的值及函数f（x）的值域；（Ⅱ）若f（x0）=，且x0∈（﹣），求f（x0+1）的值．考点：由y=Asin（ωx+φ）的部分图象确定其解析式；三角函数的化简求值；正弦函数的定义域和值域．专题：计算题；综合题．分析：（Ⅰ）将f（x）化简为f（x）=2sin（ωx+），利用正弦函数的周期公式与性质可求ω的值及函数f（x）的值域；（Ⅱ）由，知x0+∈（﹣，），由，可求得即sin（x0+）=，利用两角和的正弦公式即可求得f（x0+1）．解答：解：（Ⅰ）由已知可得，f（x）=3cosωx+sinωx=2sin（ωx+），又正三角形ABC的高为2，从而BC=4，∴函数f（x）的周期T=4×2=8，即=8，ω=，∴函数f（x）的值域为[﹣2，2]．（Ⅱ）∵f（x0）=，由（Ⅰ）有f（x0）=2sin（x0+）=，即sin（x0+）=，由，知x0+∈（﹣，），∴cos（x0+）==．∴f（x0+1）=2sin（x0++）=2sin[（x0+）+]=2[sin（x0+）cos+cos（x0+）sin]=2（×+×）=．点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，着重考查三角函数的化简求值与正弦函数的性质，考查分析转化与运算能力，属于中档题．20．（12分）已知函数f（x）=lnx﹣，g（x）=f（x）+ax﹣6lnx，其中a∈R．（Ⅰ）讨论f（x）的单调性；（Ⅱ）若g（x）在其定义域内为增函数，求正实数a的取值范围；（Ⅲ）设函数h（x）=x2﹣mx+4，当a=2时，若∃x1∈（0，1），∀x2∈[1，2]，总有g（x1）≥h（x2）成立，求实数m的取值范围．考点：利用导数求闭区间上函数的最值；函数恒成立问题；利用导数研究函数的单调性．专题：综合题；压轴题．分析：（Ⅰ）f（x）的定义域为（0，+∞），且，当a≥0时，f′（x）＞0，f（x）在（x，+∞）上单调递增；当a＞0时，由f′（x）＞0，得x＞﹣a；由f′（x）＜0，得x＜﹣a．由此能够判断f（x）的单调性．（Ⅱ）由g（x）=ax﹣，定义域为（0，+∞），知﹣=，因为g（x）在其定义域内为增函数，所以∀x∈（0，+∞），g′（x）≥0，由此能够求出正实数a的取值范围．（Ⅲ）当a=2时，g（x）=2x﹣，，由g′（x）=0，得x=或x=2．当时，g′（x）≥0当x时，g′（x）＜0．所以在（0，1）上，，由此能求出实数m的取值范围．解答：解：（Ⅰ）f（x）的定义域为（0，+∞），且，①当a≥0时，f′（x）＞0，f（x）在（x，+∞）上单调递增；②当a＜0时，由f′（x）＞0，得x＞﹣a；由f′（x）＜0，得x＜﹣a；故f（x）在（0，﹣a）上单调递减，在（﹣a，+∞）上单调递增．（Ⅱ）g（x）=ax﹣，g（x）的定义域为（0，+∞），﹣=，因为g（x）在其定义域内为增函数，所以∀x∈（0，+∞），g′（x）≥0，∴ax2﹣5x+a≥0，∴a（x2+1）≥5x，即，∴．∵，当且仅当x=1时取等号，所以a．（Ⅲ）当a=2时，g（x）=2x﹣，，由g′（x）=0，得x=或x=2．当时，g′（x）≥0；当x时，g′（x）＜0．所以在（0，1）上，，而“∃x1∈（0，1），∀x2∈[1，2]，总有g（x1）≥h（x2）成立”等价于“g（x）在（0，1）上的最大值不小于h（x）在[1，2]上的最大值”而h（x）在[1，2]上的最大值为max{h（1），h（2）}，所以有，∴，∴，解得m≥8﹣5ln2，所以实数m的取值范围是[8﹣5ln2，+∞）．点评：本题考查在闭区间上求函数最值的应用，考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．综合性强，难度大，有一定的探索性，对数学思维能力要求较高，是2015届高考的重点．解题时要认真审题，仔细解答．21．（12分）已知函数．（1）求函数f（x）的单调区间和极值；（2）若函数y=g（x）对任意x满足g（x）=f（4﹣x），求证：当x＞2，f（x）＞g（x）；（3）若x1≠x2，且f（x1）=f（x2），求证：x1+x2＞4．考点：利用导数研究函数的极值；利用导数研究函数的单调性．专题：计算题；压轴题．分析：（1）先求出其导函数，利用导函数值的正负对应的区间即可求出原函数的单调区间进而求出极值；（2），求出其导函数利用导函数的值来判断其在（2，+∞）上的单调性，进而证得结论．（3）先由（1）得f（x）在（﹣∞，2）内是增函数，在（2，+∞）内是减函数，故x1、x2不可能在同一单调区间内；设x1＜2＜x2，由（2）可知f（x2）＞g（x2），即f（x1）＞f（4﹣x2）．再结合单调性即可证明结论．解答：解：（1）∵f（x）=，∴f'（x）=．（2分）令f'（x）=0，解得x=2．x （﹣∞，2） 2 （2，+∞）f'（x）+ 0 ﹣f（x）↗极大值↘∴f（x）在（﹣∞，2）内是增函数，在（2，+∞）内是减函数．（3分）∴当x=2时，f（x）取得极大值f（2）=．（4分）（2）证明：，，∴F'（x）=．（6分）当x＞2时，2﹣x＜0，2x＞4，从而e4﹣e2x＜0，∴F'（x）＞0，F（x）在（2，+∞）是增函数．∴．（8分）（3）证明：∵f（x）在（﹣∞，2）内是增函数，在（2，+∞）内是减函数．∴当x1≠x2，且f（x1）=f（x2），x1、x2不可能在同一单调区间内．不妨设x1＜2＜x2，由（2）可知f（x2）＞g（x2），又g（x2）=f（4﹣x2），∴f（x2）＞f（4﹣x2）．∵f（x1）=f（x2），∴f（x1）＞f（4﹣x2）．∵x2＞2，4﹣x2＜2，x1＜2，且f（x）在区间（﹣∞，2）内为增函数，∴x1＞4﹣x2，即x1+x2＞4．（12分）点评：本小题主要考查函数与导数的综合应用能力，具体涉及到用导数来研究函数的单调性、极值，并考查数学证明．利用导数研究函数的单调性，求解函数的单调区间、极值、最值问题，是函数这一章最基本的知识，也是．教学中的重点和难点，学生应熟练掌握．请考生在第22、23、24三题中任选一题作答，如果多做，则安所做的第一题记分.【选修4-1：几何证明选讲】22．（12分）如图，AB是⊙O的直径，弦CA、BD的延长线相交于点E，EF垂直BA的延长线于点F．求证：（1）∠DEA=∠DFA；（2）AB2=BE•BD﹣AE•AC．考点：与圆有关的比例线段．专题：证明题；压轴题．分析：（1）连接AD，利用AB为圆的直径结合EF与AB的垂直关系，通过证明A，D，E，F四点共圆即可证得结论；（2）由（1）知，BD•BE=BA•BF，再利用△ABC∽△AEF得到比例式，最后利用线段间的关系即求得AB2=BE•BD﹣AE•AC．解答：证明：（1）连接AD，因为AB为圆的直径，所以∠ADB=90°，（1分）又EF⊥AB，∠AFE=90°，（1分）则A，D，E，F四点共圆（2分）∴∠DEA=∠DFA（1分）（2）由（1）知，BD•BE=BA•BF，（1分）又△ABC∽△AEF∴，即AB•AF=AE•AC（2分）∴BE•BD﹣AE•AC=BA•BF﹣AB•AF=AB•（BF﹣AF）=AB2（2分）点评：本小题主要考查与圆有关的比例线段、四点共圆的证明方法、三角形相似等基础知识，考查运算求解能力、化归与转化思想．属于基础题．【选修4-4：坐标系与参数方程】23．（10分）在直角坐标系xOy中，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系、设曲线C参数方程为（θ为参数），直线l的极坐标方程为．（1）写出曲线C的普通方程和直线l的直角坐标方程；（2）求曲线C上的点到直线l的最大距离．考点：椭圆的参数方程；点到直线的距离公式；参数方程化成普通方程；直线的参数方程．专题：直线与圆．分析：（1）利用两角差的余弦公式及极坐标与直角坐标的互化公式可得直线l的普通方程；利用同角三角函数的基本关系，消去θ可得曲线C的普通方程．（2）由点到直线的距离公式、两角和的正弦公式，及正弦函数的有界性求得点P到直线l的距离的最大值．解答：解：（1）由得ρ（cosθ+sinθ）=4，∴直线l：x+y﹣4=0．由得C：．（2）在C：上任取一点，则点P到直线l的距离为d==≤=3．∴当=﹣1，即+2kπ，k∈z 时，d max=3．点评：本小题主要考查坐标系与参数方程的相关知识，具体涉及到极坐标方程、参数方程与普通方程的互化，点到直线距离公式、三角变换等内容，属于中档题．【选修4-5：不等式选讲】24．已知函数f（x）=log2（|x﹣1|+|x﹣5|﹣a）．（1）当a=2时，求函数f（x）的最小值；（2）当函数f（x）的定义域为R时，求实数a的取值范围．考点：对数函数的定义域；对数函数的单调性与特殊点．专题：压轴题．分析：（1）设g（x）=|x﹣1|+|x﹣5|，则．由此可知g（x）min．（2）由题意知，g（x）=|x﹣1|+|x﹣5|的最小值为4，|x﹣1|+|x﹣5|﹣a＞0，由此可知a的取值范围．解答：解：函数的定义域满足|x﹣1|+|x﹣5|﹣a＞0，即|x﹣1|+|x﹣5|＞a，（1）当a=2时，f（x）=log2（|x﹣1|+|x﹣5|﹣2）设g（x）=|x﹣1|+|x﹣5|，则．（3分）g（x）min=4，f（x）min=log2（4﹣2）=1．（5分）（2）由（I）知，g（x）=|x﹣1|+|x﹣5|的最小值为4，7分|x﹣1|+|x﹣5|﹣a＞0，∴a＜4∴a的取值范围是（﹣∞，4）．（10分）点评：本题考查对数函数的性质和应用，解题时要注意公式的灵活运用．欢迎下载，资料仅供参考!!!。

辽宁省实验中学分校2015届高三上学期期中考试语文试题及答案

辽宁省实验中学分校2015届高三上学期期中考试语文试题第I卷阅读题必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1—3题。

论“不折腾”“不折腾”，一句百姓俚语，成为国际国内热议的新的政治词语，似在意料之外，实乃情理之中。

这句最寻常的老百姓自己的话，却最不寻常地反映了历史演进的规律，道出了人民大众的心声，凝练了为实现伟大目标而持守真理的坚强决心！百姓俚语用于政治领域，也使得“不折腾”成为汉译英的难题，在现代英语词汇中，确实找不到能够达意又传神的对应的词语，于是不得不将“不折腾”的汉语拼音“buzheteng”直接用于英译，人们甚至预言，“buzheteng”将成为一个新的英语词语收入英文词典。

“中国因素”在世界的显现，这又是一个鲜活的例证。

其实，在中文的语境中，特别是在中文的政治语境中，“不折腾”的含义，干部群众和政治家一样，都是心领神会的，人们相互的会心一笑，表达的是高度一致的政治认同。

这就是胡锦涛总书记所说的：“我们要始终坚持党的基本路线不动摇，做到思想上坚信不疑、行动上坚定不移，决不走封闭僵化的老路，也决不走改旗易帜的邪路，而是坚定不移地走中国特色社会主义道路。

”铿锵有力，掷地有声！积近代以的历史教训，中国之所以在近代落伍，从先进国家一步步衰败为落后国家，一个重要的原因，就是饱受内忧外患的“折腾”，百余年间没有获得安稳和平的发展环境，生产力遭到毁灭性破坏，中国人民在被“折腾”中从根本上丧失了使自己的国家实现现代化的权利和机会。

新中国建立后，人民当家作主，共和国赢得了解放和发展生产力的历史机遇，革命和建设的进程，一扫内忧外患的衰败国运，国家的发展进步欣欣向荣、蒸蒸日上。

然而，“文革”十年内乱的“折腾”，使中国又一次中断了快速发展前进的步伐，又一次与经济起飞的历史机遇擦肩而过，又一次延缓了实现现代化的时间表。

“文革”结束以后，十一届三中全会以实行改革开放的三十年，是近代以中国最少“折腾”的时期，从而成为生产力发展最迅速的时期，人民得实惠最丰厚的时期，综合国力增长最快捷的时期，国际地位提高最显著的时期。

辽宁省五校协作体2015届高三上学期期中数学试卷(文科)(解析版)

辽宁省五校协作体2015届高三上学期期中数学试卷（文科）一、选择题：本大题共有12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x||x|＜3}，B={x|y=lg（x﹣1）}，则集合A∩B为（）A．[0，3）B．[1，3）C．（1，3）D．（﹣3，1]2．（5分）下列函数中周期为π且为偶函数的是（）A．y=cos（2x﹣）B．y=sin（2x+）C．y=sin（x+）D．y=cos（x﹣）3．（5分）下列有关命题的说法正确的是（）A．命题“∀x∈R，均有x2﹣x+1＞0”的否定是：“∃x∈R，使得x2﹣x+1＜0”B．“x=3”是“2x2﹣7x+3=0”成立的充分不必要条件C．线性回归方程=x+对应的直线一定经过其样本数据点（x1，y1），（x2，y2），…，（x n，y n）中的一个点D．若“p∨（¬q）”为真命题，则“p∧q”也为真命题4．（5分）已知平面向量=（2m+1，3），=（2，m），且与反向，则||等于（）A．B．或2C．D．25．（5分）设偶函数f（x）对任意x∈R，都有f（x+3）=﹣，且当x∈[﹣3，﹣2]时，f（x）=4x，则f（107.5）=（）A．10 B．C．﹣10 D．﹣6．（5分）设l为直线，α，β是两个不同的平面，下列命题中正确的是（）A．若l∥α，l∥β，则α∥βB．若α⊥β，l∥α，则l⊥βC．若l⊥α，l∥β，则α∥βD．若l⊥α，l⊥β，则α∥β7．（5分）已知f（x）=sin+cos的最大值为A，若存在实数x1，x2，使得对任意实数x总有f（x1）≤f（x）≤f（x2）成立，则A|x1﹣x2|的最小值为（）A．B．C．D．8．（5分）已知向量=（2，1），•=10，|+|=5，则||=（）A．5B．25 C．D．9．（5分）某三棱锥的三视图如图所示，则该三棱锥的体积是（）A．1B．C．D．10．（5分）已知数列{a n}，定直线l：（m+3）x﹣（2m+4）y﹣m﹣9=0，若（n，a n）在直线l上，则数列{a n}的前13项和为（）A．10 B．21 C．39 D．7811．（5分）已知{a n}为等差数列，0＜d＜1，a5≠，sin2a3+2sina5cosa5=sin2a7，S n为数列{a n}的前n项和，若S n≥S10对一切n∈N*都成立，则首项a1的取值范围是（）A．[﹣π，﹣π）B．[﹣π，﹣π]C．（﹣π，﹣π） D．[﹣π，﹣π]12．（5分）已知函数f（x）在[0，+∞）上可导，其导函数记作f′（x），f（0）=﹣2，且f （x+π）=f（x），当x∈[0，π）时，f′（x）•cos2x＞f（x）•sin2x﹣f′（x），若方程f（x）+k n secx=0在[0，+∞）上有n个解，则数列{}的前n项和为（）A．（n﹣1）•2n+1 B．（n﹣1）•2n+1+2 C．n•2n﹣1D．二、填空题：本大题共4小题，每小题5分．13．（5分）设正实数x，y，z满足x2﹣3xy+4y2﹣z=0，则当取得最小值时，x+2y﹣z的最大值为．14．（5分）平面上三个向量，，，满足||=1，||=，||=1，•=0，则•的最大值是．15．（5分）在数列{a n}中，a1≠0，a n+1=a n，S n为{a n}的前n项和．记R n=，则数列{R n}的最大项为第项．16．（5分）设f（x）是定义在R上的函数，且对任意x，y∈R，均有f（x+y）=f（x）+f （y）+2014成立，若函数g（x）=f（x）+2014x2013有最大值M和最小值m，则M+m=．三、解答题：本大题共5小题，总计70分，解答应写出文字说明、证明过程或演算步骤．17．（12分）在△ABC中，角A、B、C所对的边分别为a，b，c，且a=1，c=，cosC=．（1）求sinA的值；（2）求△ABC的面积．18．（12分）如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=，AA1=2．（1）证明：AA1⊥BD（2）证明：平面A1BD∥平面CD1B1；（3）求三棱柱ABD﹣A1B1D1的体积．19．（12分）等差数列{a n}中，a7=4，a19=2a9，（Ⅰ）求{a n}的通项公式；（Ⅱ）设b n=，求数列{b n}的前n项和S n．20．（12分）数列{a n}的前n项和为S n，且S n+a n=1，数列{b n}满足b1=4，b n+1=3b n﹣2；（1）求数列{a n}和{b n}的通项公式；（2）设数列{c n}满足c n=a n log3（b2n﹣1﹣1），其前n项和为T n，求T n．21．（12分）设f（x）=xlnx，g（x）=x2﹣1．（1）令h（x）=f（x）﹣g（x），求h（x）的单调区间；（2）若当x≥1时，f（x）﹣mg（x）≤0恒成立，求实数m的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做第一题计分.选修4-1：几何证明选讲22．（10分）如图，CD为△A BC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BC•AE=DC•AF，B，E，F，C四点共圆．（Ⅰ）证明：CA是△ABC外接圆的直径；（Ⅱ）若DB=BE=EA，求过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值．选修4-4：坐标系与参数方程23．在直角坐标系xOy中，曲线C1的参数方程为（α为参数）M是C1上的动点，P点满足=2，P点的轨迹为曲线C2（Ⅰ）求C2的方程；（Ⅱ）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线θ=与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|．选修4-5：不等式选讲24．已知函数f（x）=|x+a|+|x﹣2|（1）当a=﹣3时，求不等式f（x）≥3的解集；（2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．辽宁省五校协作体2015届高三上学期期中数学试卷（文科）参考答案与试题解析一、选择题：本大题共有12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x||x|＜3}，B={x|y=lg（x﹣1）}，则集合A∩B为（）A．[0，3）B．[1，3）C．（1，3）D．（﹣3，1]考点：对数函数的定义域；交集及其运算．专题：集合．分析：根据绝对值和对数函数求出集合A和B，然后由交集的定义求出结果．解答：解：∵|x|＜3∴﹣3＜x＜3故A=（﹣3，3）∵y=lg（x﹣1）∴x﹣1＞0，解得x＞1故B=（1，+∞）∴A∩B=（1，3）故选：C．点评：本题考查交集的定义的运算，是基础题．解题时要认真审题，注意含绝对值不等式和对数函数的性质的灵活运用．2．（5分）下列函数中周期为π且为偶函数的是（）A．y=cos（2x﹣）B．y=sin（2x+）C．y=sin（x+）D．y=cos（x﹣）考点：三角函数的周期性及其求法．专题：计算题；三角函数的图像与性质．分析：先利用函数的周期性排除C，D，再利用诱导公式与函数的奇偶性可排除A，从而可得答案．解答：解：A：令g（x）=cos（2x﹣）=sin2x，则g（﹣x）=sin（﹣2x）=﹣sin2x=﹣g（x），∴g（x）=cos（2x+）为奇函数，故可排除A；B：∵y=f（x）=sin（2x+）=cos2x，∴其周期T==π，f（﹣x）=cos（﹣2x）=cos2x=f（x），∴y=sin（2x+）是偶函数，∴y=sin（2x+）是周期为π的偶函数，故B正确；C：∵y=sin（x+）其周期T=2π，故可排除C；D：同理可得y=cos（x﹣）的周期为2π，故可排除D；故选：B．点评：本题考查正弦函数与余弦函数的周期性与奇偶性，考查诱导公式的应用，属于中档题．3．（5分）下列有关命题的说法正确的是（）A．命题“∀x∈R，均有x2﹣x+1＞0”的否定是：“∃x∈R，使得x2﹣x+1＜0”B．“x=3”是“2x2﹣7x+3=0”成立的充分不必要条件C．线性回归方程=x+对应的直线一定经过其样本数据点（x1，y1），（x2，y2），…，（x n，y n）中的一个点D．若“p∨（¬q）”为真命题，则“p∧q”也为真命题考点：命题的真假判断与应用；特称命题；命题的否定．分析：利用全称命题与特称命题的否定关系判断A的正误；充要条件判断B的正误；回归直线方程判断C的正误；复合命题的真假判断D的正误；解答：解：对于A，命题“∀x∈R，均有x2﹣x+1＞0”的否定是：“∃x∈R，使得x2﹣x+1＜0”，不满足命题的否定形式，所以A不正确．对于B，“x=3”是“2x2﹣7x+3=0”成立的充分不必要条件，正确，前者推出后者，后者不能说明前者一定成立，所以B正确；对于C，线性回归方程=x+对应的直线一定经过其样本数据点（x1，y1），（x2，y2），…，（x n，y n）中的一个点，显然不正确，一定经过样本中心，所以C不正确；对于D，若“p∨（¬q）”为真命题，则“p∧q”也为真命题，不正确，所以D不正确．故选：B．点评：本题考查命题的真假的判断与应用，充要条件以及全称命题特称命题的否定关系，回归直线方程的应用，基本知识的考查．4．（5分）已知平面向量=（2m+1，3），=（2，m），且与反向，则||等于（）A．B．或2C．D．2考点：平面向量数量积的坐标表示、模、夹角．专题：平面向量及应用．分析：根据题意，平面向量、共线且反向，求m的值，即可得出||．解答：解：∵平面向量=（2m+1，3），=（2，m），且与反向，∴m（2m+1）﹣3×2=0，解得m=﹣2，或m=；验证m=时不满足题意，∴=（2，﹣2）；∴||==2．故选：D．点评：本题考查了平面向量的应用问题，解题时应用平面向量的坐标表示求向量共线问题，是基础题．5．（5分）设偶函数f（x）对任意x∈R，都有f（x+3）=﹣，且当x∈[﹣3，﹣2]时，f（x）=4x，则f（107.5）=（）A．10 B．C．﹣10 D．﹣考点：函数的周期性．专题：计算题．分析：先通过有f（x+3）=﹣，且可推断函数f（x）是以6为周期的函数．进而可求得f（107.5）=f（5.5），再利用f（x+3）=﹣以及偶函数f（x）和x∈[﹣3，﹣2]时，f（x）=4x即可求得f（107.5）的值．解答：解：因为f（x+3）=﹣，故有f（x+6）=﹣=﹣=f（x）．函数f（x）是以6为周期的函数．f（107.5）=f（6×17+5.5）=f（5.5）=﹣=﹣=﹣=．故选B点评：本题主要考查了函数的周期性．要特别利用好题中有f（x+3）=﹣的关系式．在解题过程中，条件f（x+a）=﹣通常是告诉我们函数的周期为2a．6．（5分）设l为直线，α，β是两个不同的平面，下列命题中正确的是（）A．若l∥α，l∥β，则α∥βB．若α⊥β，l∥α，则l⊥βC．若l⊥α，l∥β，则α∥βD．若l⊥α，l⊥β，则α∥β考点：空间中直线与直线之间的位置关系．专题：空间位置关系与距离．分析：利用空间中线线、线面、面面间的位置关系求解．解答：解：若l∥α，l∥β，则α与β相交或平行，故A错误；若α⊥β，l∥α，则l与β相交、平行或l⊂β，故B错误；若α⊥β，l∥α，则l与β相交、平行或l⊂β，故C错误；若l⊥α，l⊥β，则由平面与平面平行的判定定理知α∥β，故D正确．故选：D．点评：本题考查命题真假的判断，是基础题，解题时要注意空间思维能力的培养．7．（5分）已知f（x）=sin+cos的最大值为A，若存在实数x1，x2，使得对任意实数x总有f（x1）≤f（x）≤f（x2）成立，则A|x1﹣x2|的最小值为（）A．B．C．D．考点：三角函数的最值．专题：三角函数的图像与性质．分析：利用三角恒等变换可得f（x）=2sin，依题意可知A=2，|x1﹣x2|的最小值为T=，从而可得答案．解答：解：∵f（x）=sin+cos=sin2014x+cos2014x+cos2014x+sin2014x=sin2014x+cos2014x=2sin，∴A=f（x）max=2，周期T==，又存在实数x1，x2，对任意实数x总有f（x1）≤f（x）≤f（x2）成立，∴f（x2）=f（x）max=2，f（x1）=f（x）min=﹣2，|x1﹣x2|的最小值为T=，又A=2，∴A|x1﹣x2|的最小值为．故选：A．点评：本题考查三角函数的最值，着重考查两角和与差的正弦与余弦，考查三角恒等变换，突出正弦函数的周期性的考查，属于中档题．8．（5分）已知向量=（2，1），•=10，|+|=5，则||=（）A．5B．25 C．D．考点：平面向量数量积的坐标表示、模、夹角．专题：平面向量及应用．分析：根据平面向量的数量积的运算，结合题意，求出的模长．解答：解：∵向量=（2，1），•=10，|+|=5，∴||==，∴=+2•+=+2×10+=；解得=25，∴||=5．故选：A．点评：本题考查了平面向量的应用问题，解题时应根据平面向量的数量积，求向量的模长，是基础题．9．（5分）某三棱锥的三视图如图所示，则该三棱锥的体积是（）A．1B．C．D．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：由三视图可知：该几何体是一个以俯视图为底面的三棱锥，求出底面面积和高，进而可得该几何体的体积．解答：解：由三视图可知：该几何体是一个以俯视图为底面的三棱锥，底面的两条直角边均为1，底面面积S=×1×1=，高h=2，故棱锥的体积V=Sh=，故选：D点评：本题考查的知识点是由三视图求几何体的体积或表面积，由三视图正确恢复原几何体是解题的关键．10．（5分）已知数列{a n}，定直线l：（m+3）x﹣（2m+4）y﹣m﹣9=0，若（n，a n）在直线l上，则数列{a n}的前13项和为（）A．10 B．21 C．39 D．78考点：数列与解析几何的综合．专题：计算题；等差数列与等比数列．分析：由点（n，a n）（n∈N*）在直线l：（m+3）x﹣（2m+4）y﹣m﹣9=0上，可得a n=n ﹣，即可得到数列{a n}的前13项和．解答：解：∵点（n，a n）（n∈N*）在直线l：（m+3）x﹣（2m+4）y﹣m﹣9=0上，∴（m+3）n﹣（2m+4）a n﹣m﹣9=0，∴a n=n﹣．∴数列{a n}的前13项和S13==39．故选C．点评：本题考查数列与解析几何的综合，考查了等差数列的前n项和公式，属于基础题．11．（5分）已知{a n}为等差数列，0＜d＜1，a5≠，sin2a3+2sina5cosa5=sin2a7，S n为数列{a n}的前n项和，若S n≥S10对一切n∈N*都成立，则首项a1的取值范围是（）A．[﹣π，﹣π）B．[﹣π，﹣π]C．（﹣π，﹣π） D．[﹣π，﹣π]考点：数列与三角函数的综合．专题：综合题；等差数列与等比数列；三角函数的求值．分析：先确定d=，可得S n=，对称轴n=，利用S n≥S10对一切n∈N*都成立，可得9.5≤≤10.5，即可求出首项a1的取值范围．解答：解：∵sin2a3+2sina5cosa5=sin2a7，∴2s ina5cosa5=2sin cos•2cos sin，∴sin4d=1，∴d=，∴S n=．对称轴n=．∵S n≥S10对一切n∈N*都成立，∴9.5≤≤10.5，∴﹣π≤a1≤﹣．故选：D．点评：熟练掌握等差数列的前n项和公式和配方法、二次函数的单调性是解题的关键．12．（5分）已知函数f（x）在[0，+∞）上可导，其导函数记作f′（x），f（0）=﹣2，且f （x+π）=f（x），当x∈[0，π）时，f′（x）•cos2x＞f（x）•sin2x﹣f′（x），若方程f（x）+k n secx=0在[0，+∞）上有n个解，则数列{}的前n项和为（）A．（n﹣1）•2n+1 B．（n﹣1）•2n+1+2 C．n•2n﹣1D．考点：数列的求和．专题：计算题；函数的性质及应用；导数的综合应用；等差数列与等比数列．分析：由于f（0）=﹣2，且f（x+π）=f（x），则f（π）=f（0）=﹣1，f（2π）==﹣，f（3π）=﹣，…，f（nπ）=﹣（）n﹣1．再由导数的积的运算法则和二倍角公式，得到f（x）cosx的单调性和极值，由条件可得，k n=﹣f（x）cosx在[0，+∞）上有n个解，k1=﹣f（0）cos0=2，k2=﹣f（π）cosπ=﹣1，…，k n=﹣f（（n﹣1）π）cos（n﹣1）π，则有k2n=（）n﹣1，即有=n•2n﹣1，再运用错位相减法，即可得到前n项和．解答：解：由于f（0）=﹣2，且f（x+π）=f（x），则f（π）=f（0）=﹣1，f（2π）==﹣，f（3π）=﹣，…，f（nπ）=﹣（）n﹣1．由于当x∈[0，π）时，f′（x）•cos2x＞f（x）•sin2x﹣f′（x），则有f′（x）（1+cos2x）﹣f（x）sin2x＞0，即有2cosx（f′（x）cosx﹣f（x）sinx）＞0，则2cosx•（f（x）cosx）′＞0，则有cosx＞0，（f（x）cosx）′＞0，f（x）cosx在（0，）递增，cosx＜0，（f（x）cosx）′＜0，f（x）cosx在（，π）递减，由于方程f（x）+k n secx=0在[0，+∞）上有n个解，即有k n=﹣f（x）cosx在[0，+∞）上有n个解，则k1=﹣f（0）cos0=2，k2=﹣f（π）cosπ=﹣1，k3=﹣f（2π）cos2π=，k4=﹣f（3π）cos3π=﹣，…，k n=﹣f（（n﹣1）π）cos（n﹣1）π，则有k2n=（）n﹣1，即有=n•2n﹣1，令S=1+2•2+3•22+…+n•2n﹣1，则2S=1•2+2•22+3•23+…+n•2n，两式相减得，﹣S=1+2+22+23+…+2n﹣1﹣n•2n=﹣n•2n则S=（n﹣1）•2n+1．故选A．点评：本题考查导数的运用：求单调区间和极值，考查函数的零点问题，考查等比数列的通项和求和公式，考查错位相减法求数列的和，考查运算能力，属于中档题．二、填空题：本大题共4小题，每小题5分．13．（5分）设正实数x，y，z满足x2﹣3xy+4y2﹣z=0，则当取得最小值时，x+2y﹣z的最大值为2．考点：基本不等式．专题：综合题．分析：将z=x2﹣3xy+4y2代入，利用基本不等式化简即可得到当取得最小值时的条件，用x，z表示y后利用配方法求得x+2y﹣z的最大值．解答：解：∵x2﹣3xy+4y2﹣z=0，∴z=x2﹣3xy+4y2，又x，y，z为正实数，∴=+﹣3≥2﹣3=1（当且仅当x=2y时取“=”），即x=2y（y＞0），∴x+2y﹣z=2y+2y﹣（x2﹣3xy+4y2）=4y﹣2y2=﹣2（y﹣1）2+2≤2．∴x+2y﹣z的最大值为2．故答案为：2．点评：本题考查基本不等式，将z=x2﹣3xy+4y2代入，求得取得最小值时x=2y是关键，考查配方法求最值，属于中档题．14．（5分）平面上三个向量，，，满足||=1，||=，||=1，•=0，则•的最大值是3．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由于满足||=1，||=，||=1，•=0，建立如图所示的直角坐标系，可得A（1，0），B（0，），可设C（cosθ，sinθ），θ∈[0，2π）．再利用向量的坐标运算、数量积运算、两角和差的正弦公式、正弦函数的单调性有界性即可得出．解答：解：∵满足||=1，||=，||=1，•=0，如图所示，∴A（1，0），B（0，），可设C（cosθ，sinθ），θ∈[0，2π）．∴=（1﹣cosθ，﹣sinθ），=（﹣cosθ，﹣sinθ），∴•=﹣cosθ（1﹣cosθ）﹣sinθ（）=﹣cosθ﹣+1=﹣2sin （）+1≤3，当且仅当θ=时取等号．∴•最大值是3．故答案为：3．点评：本题考查了向量的坐标运算、数量积运算、两角和差的正弦公式、正弦函数的单调性有界性，属于中档题．15．（5分）在数列{a n}中，a1≠0，a n+1=a n，S n为{a n}的前n项和．记R n=，则数列{R n}的最大项为第4项．考点：数列的函数特性．专题：等差数列与等比数列．分析：利用等比数列的通项公式及其前n项和公式可得R n=，再利用基本不等式的性质即可得出．解答：解：∵a1≠0，a n+1=a n，∴=，．S n=，S2n=．∴R n===≤，比较R3，R4，R5可得当n=4时，R n取得最大值．故答案为：4．点评：本题考查了等比数列的通项公式及其前n项和公式、基本不等式的性质，考查了计算能力，属于中档题．16．（5分）设f（x）是定义在R上的函数，且对任意x，y∈R，均有f（x+y）=f（x）+f （y）+2014成立，若函数g（x）=f（x）+2014x2013有最大值M和最小值m，则M+m=﹣4028．考点：函数奇偶性的性质；函数的最值及其几何意义．专题：函数的性质及应用．分析：本题可先研究函数f（x）的特征，构造与f（x）、g（x）相关的奇函数，利用奇函数的图象对称性，得到相应的最值关系，从而得到g（x）的最大值M与最小值m的和，得到本题结论．解答：解：∵f（x）是定义在R上的函数，且对任意x，y∈R，均有f（x+y）=f（x）+f （y）+2014成立，∴取x=y=0，得：f（0）=f（0）+f（0）+2014，f（0）=﹣2014，取y=﹣x，得到：f（0）=f（x）+f（﹣x）+2014，∴f（x）+f（﹣x）=﹣4028．记h（x）=f（x）+2014x2013+2014，则h（﹣x）+h（x）=[f（﹣x）+2014（﹣x）2013+2014]+f（x）+2014x2013+2014=f（x）+f（﹣x）+2014x2013﹣2014x2013+4028=f（x）+f（﹣x）+4028=0，∴y=h（x）为奇函数．记h（x）的最大值为A，则最小值为﹣A．∴﹣A≤f（x）+2014x2013+2014≤A，∴﹣A﹣2014≤f（x）+2014x2013≤A﹣2014，∵g（x）=f（x）+2014x2013，∴∴﹣A﹣2014≤g（x）≤A﹣2014，∵函数g（x）有最大值M和最小值m，∴M=A﹣2014，m=﹣A﹣2014，∴M+m=A﹣2014+（﹣A﹣2014）=﹣4028．故答案为：﹣4028．点评：本题考查了函数奇偶性及其应用，还考查了抽象函数和构造法，本题难度适中，属于中档题．三、解答题：本大题共5小题，总计70分，解答应写出文字说明、证明过程或演算步骤．17．（12分）在△ABC中，角A、B、C所对的边分别为a，b，c，且a=1，c=，cosC=．（1）求sinA的值；（2）求△ABC的面积．考点：余弦定理；正弦定理．专题：解三角形．分析：（1）根据正弦定理即可求sinA的值；（2）根据余弦定理和是三角形的面积公式即可求△ABC的面积．解答：解：（1）∵cosC=，∴sinC=，∵，∴，即．（2）∵c2=a2+b2﹣2abcos⁡C，∴，即2b2﹣3b﹣2=0，解得b=2，∴三角形的面积S=．点评：本题主要考查三角形的面积公式的计算以及正弦定理和余弦定理的应用，涉及的公式较多．18．（12分）如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=，AA1=2．（1）证明：AA1⊥BD（2）证明：平面A1BD∥平面CD1B1；（3）求三棱柱ABD﹣A1B1D1的体积．考点：直线与平面垂直的性质；平面与平面平行的判定．专题：空间位置关系与距离．分析：（1）首先，得到BD⊥AC，然后，得到A1O⊥BD，最后，得到BD⊥面A1AC即可；（2）首先，得到A1B1∥AB AB∥CD，然后，得到四边形A1B1CD是平行四边形，从而得到证明结论；（3）直接根据体积公式进行求解即可．解答：解：（1）证明：∵底面ABCD是正方形，∴BD⊥AC，又∵A1O⊥平面ABCD且BD⊂面ABCD，∴A1O⊥BD，又∵A1O∩AC=O，A1O⊂面A1AC，AC⊂面A1AC，∴BD⊥面A1AC，AA1⊂面A1AC，∴AA1⊥BD．（2）∵A1B1∥AB，AB∥CD，∴A1B1∥CD，又A1B1=CD，∴四边形A1B1CD是平行四边形，∴A1D∥B1C，同理A1B∥CD1，∵A1B⊂平面A1BD，A1D⊂平面A1BD，CD1⊂平面CD1B1，B1C⊂平面CD1B，且A1B∩A1D=A1，CD1∩B1C=C，∴平面A1BD∥平面CD1B1．（3）∵A1O⊥面ABCD，∴A1O是三棱柱A1B1D1﹣ABD的高，在正方形ABCD中，AO=1．在Rt△A1OA中，AA1=2，AO=1，∴A1O=，∴V三棱柱ABD﹣A1B1D1=S△ABD•A1O=•（）2•=∴三棱柱ABD﹣A1B1D1的体积为．点评：本题考查了空间中点线面的位置关系，例如直线与平面平行、垂直，平面和平面平行等知识，属于中档题．19．（12分）等差数列{a n}中，a7=4，a19=2a9，（Ⅰ）求{a n}的通项公式；（Ⅱ）设b n=，求数列{b n}的前n项和S n．考点：数列的求和；等差数列的通项公式．专题：计算题；等差数列与等比数列．分析：（I）由a7=4，a19=2a9，结合等差数列的通项公式可求a1，d，进而可求a n （II）由==，利用裂项求和即可求解解答：解：（I）设等差数列{a n}的公差为d∵a7=4，a19=2a9，∴解得，a1=1，d=∴=（II）∵==∴s n===点评：本题主要考查了等差数列的通项公式及裂项求和方法的应用，试题比较容易20．（12分）数列{a n}的前n项和为S n，且S n+a n=1，数列{b n}满足b1=4，b n+1=3b n﹣2；（1）求数列{a n}和{b n}的通项公式；（2）设数列{c n}满足c n=a n log3（b2n﹣1﹣1），其前n项和为T n，求T n．考点：等差数列与等比数列的综合．专题：点列、递归数列与数学归纳法．分析：（1）根据递推公式分别求出{a n}和{b n}的通项公式；（2）由错位相减求和法求出数列{c n}的前n项和T n．解答：解：（1）①当n=1时，a1+S1=1∴a1=②当n≥2时，a n=S n﹣S n﹣1=（1﹣a n）﹣（1﹣a n﹣1）=a n﹣1﹣a n，∴a n=a n﹣1∴数列{a n}是以a1=为首项，公比为的等比数列；∴a n=•（）n﹣1=（）n∵b n+1=3b n﹣2∴b n+1﹣1=3（b n﹣1）又∵b1﹣1=3∴{b n﹣1}是以3为首项，3为公比的等比数列∴b n﹣1=3n、∴b n=3n+1（2）∵c n=（）n•log332n﹣1=（2n﹣1）•（）n∴S n=1×+3×（）2+5×（）3+…+（2n﹣3）•（）n﹣1+（2n﹣1）•（）n∴S n=1×（）2+3×（）3+5×（）4+…+（2n﹣3）•（）n+（2n﹣1）•（）n+1∴（1﹣）S n=1×+2[（）2+（）3+…+（）n﹣1+（）n]﹣（2n﹣1）•（）n+1 =﹣4×（）n+1﹣（2n﹣1）•（）n+1=﹣（2n+3）（）n+1∴S n=3﹣点评：本题考查数列的通项公式的求法和数列求和，解题时要注意公式的灵活运用，特别是错位相减求和法的合理运用．21．（12分）设f（x）=xlnx，g（x）=x2﹣1．（1）令h（x）=f（x）﹣g（x），求h（x）的单调区间；（2）若当x≥1时，f（x）﹣mg（x）≤0恒成立，求实数m的取值范围．考点：利用导数求闭区间上函数的最值；利用导数研究函数的单调性．专题：计算题；压轴题；导数的综合应用．分析：（1）由题意h（x）=xlnx﹣x2+1，二阶求导以确定导数的正负，从而求函数的单调区间；（2）令F（x）=xlnx﹣m（x2﹣1），对其二阶求导以确定导数的正负，从而求函数的最值，将恒成立问题化为最值问题，从而求解．解答：解：（1）h（x）=xlnx﹣x2+1h′（x）=lnx+1﹣2x令t（x）=lnx+1﹣2x t′（x）=﹣2=∴t（x）在（0，）上单调递增，在（，+∞）上单调递减，∴t（x）≤t（）=﹣ln2＜0，即h′（x）＜0，∴h（x）在（0，+∞）上单调递减．（2）令F（x）=xlnx﹣m（x2﹣1），则F′（x）=lnx+1﹣2mx，令G（x）=lnx+1﹣2mx，则G′（x）=﹣2m，①当m≥时，∵x≥1，∴≤1，∴﹣2m≤0，即G′（x）≤0；∴G（x）在[1，+∞）上单调递减，∴G（x）≤G（1）=1﹣2m≤0，即F′（x）≤0，∴F（x）在[1，+∞）上单调递减，∴F（x）≤F（1）=0，∴f（x）﹣mg（x）≤0，∴m≥符合题意；②当m≤0时，显然有F′（x）=lnx+1﹣2mx≥0，∴F（x）在（1，+∞）上单调递增，∴F（x）＞F（1）=0，即f（x）﹣mg（x）＞0，不符合题意；③当0＜m＜时，令G′（x）=﹣2m＞0解得：1＜x＜，G′（x）=﹣2m＜0解得：x＞；∴G（x）在[1，]上单调递增，∴G（x）≥G（1）=1﹣2m＞0，即F′（x）＞0；∴F（x）在[1，]上单调递增；∴当x∈（0，）时，F（x）＞F（0）=0，即f（x）﹣mg（x）＞0，不符合题意；综合①②③可知，m≥符合题意，∴m的取值范围是[，+∞）．点评：本题考查了导数的综合应用，难在二阶求导以判断函数的单调性与最值，同时考查了恒成立问题化成最值问题的处理方法，属于难题．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做第一题计分.选修4-1：几何证明选讲22．（10分）如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BC•AE=DC•AF，B，E，F，C四点共圆．（Ⅰ）证明：CA是△ABC外接圆的直径；（Ⅱ）若DB=BE=EA，求过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值．考点：与圆有关的比例线段．专题：立体几何．分析：（I）由已知与圆的切线的性质可得△CDB∽△AEF，∠DBC=∠EFA．利用B，E，F，C 四点共圆，可得∠CFE=∠DBC，∠EFA=∠CFE=90°，即可证明．（II）连接CE，由于∠CBE=90°，可得过B，E，F，C四点的圆的直径为CE，由DB=BE，有CE=DC，又BC2DB•BA=2DB2，可得CA2=4DB2+BC2=6DB2，而DC2=DB•DA=3DB2，即可得出．解答：（I）证明：∵CD为△ABC外接圆的切线，∴∠BCD=∠A，由题设知：=，故△CDB∽△AEF，∴∠DBC=∠EFA．∵B，E，F，C四点共圆，∴∠CFE=∠DBC，故∠EFA=∠CFE=90°∴∠CBA=90°，因此CA是△ABC外接圆的直径．（2）解：连接CE，∵∠CBE=90°，∴过B，E，F，C四点的圆的直径为CE，由DB=BE，有CE=DC，又BC2DB•BA=2DB2，∴CA2=4DB2+BC2=6DB2，而DC2=DB•DA=3DB2，故B，E，F，C四点的圆的面积与△ABC的外接圆面积的比值为．点评：本题考查了圆的切线的性质、四点共圆的性质、勾股定理、圆的面积与三角形的面积计算公式，考查了推理能力与计算能力，属于中档题．选修4-4：坐标系与参数方程23．在直角坐标系xOy中，曲线C1的参数方程为（α为参数）M是C1上的动点，P点满足=2，P点的轨迹为曲线C2（Ⅰ）求C2的方程；（Ⅱ）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线θ=与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|．考点：简单曲线的极坐标方程；轨迹方程．专题：计算题；压轴题．分析：（I）先设出点P的坐标，然后根据点P满足的条件代入曲线C1的方程即可求出曲线C2的方程；（II）根据（I）将求出曲线C1的极坐标方程，分别求出射线θ=与C1的交点A的极径为ρ1，以及射线θ=与C2的交点B的极径为ρ2，最后根据|AB|=|ρ2﹣ρ1|求出所求．解答：解：（I）设P（x，y），则由条件知M（，）．由于M点在C1上，所以即从而C2的参数方程为（α为参数）（Ⅱ）曲线C1的极坐标方程为ρ=4sinθ，曲线C2的极坐标方程为ρ=8sinθ．射线θ=与C1的交点A的极径为ρ1=4sin，射线θ=与C2的交点B的极径为ρ2=8sin．所以|AB|=|ρ2﹣ρ1|=．点评：本题考查点的极坐标和直角坐标的互化，以及轨迹方程的求解和线段的度量，属于中档题．选修4-5：不等式选讲24．已知函数f（x）=|x+a|+|x﹣2|（1）当a=﹣3时，求不等式f（x）≥3的解集；（2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．考点：绝对值不等式的解法；带绝对值的函数．专题：计算题；压轴题．分析：（1）不等式等价于，或，或，求出每个不等式组的解集，再取并集即得所求．（2）原命题等价于﹣2﹣x≤a≤2﹣x在[1，2]上恒成立，由此求得求a的取值范围．解答：解：（1）当a=﹣3时，f（x）≥3 即|x﹣3|+|x﹣2|≥3，即①，或②，或③．解①可得x≤1，解②可得x∈∅，解③可得x≥4．把①、②、③的解集取并集可得不等式的解集为{x|x≤1或x≥4}．（2）原命题即f（x）≤|x﹣4|在[1，2]上恒成立，等价于|x+a|+2﹣x≤4﹣x在[1，2]上恒成立，等价于|x+a|≤2，等价于﹣2≤x+a≤2，﹣2﹣x≤a≤2﹣x在[1，2]上恒成立．故当1≤x≤2时，﹣2﹣x的最大值为﹣2﹣1=﹣3，2﹣x的最小值为0，故a的取值范围为[﹣3，0]．点评：本题主要考查绝对值不等式的解法，关键是去掉绝对值，化为与之等价的不等式组来解，体现了分类讨论的数学思想，属于中档题．欢迎下载，资料仅供参考!!!。

辽宁师大附中2015届高三上学期期中考试语文试题及答案

辽师大附中2014-2015学年度（上学期）高三期中试题语文第I卷阅读卷一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1-3题。

神话“是人类心理在最基层水平上的象征和形象的表现”，西方神话学理论认为，神话中最早出现的是创世神话，这是神话发展的第一个阶段。

这个时期人尚未完全意识到自己的存在，自我意识刚刚萌芽，与客观世界混沌为一的动物意识还占着上风，主宰着人类。

英雄神话的产生是神话发展的第二个阶段，“在英雄神话中，世界作为宇宙的中心，而人则处于世界的中心”。

可以看出，有些西方神话学理论对于神话的分类，主要不是根据神话的内容，而是根据神话所体现的人类意识和精神的成长历程，也就是根据神话所蕴含的哲学观念。

这种植根于以希腊神话为代表的西方神话和历史文化土壤中的西方神话理论，未必适用于中国神话。

产生于自然崇拜观念基础上的希腊神话，其新神、旧神之间不但界限清楚，而且由于自然崇拜观念的统一性，具有一个内在统一的普遍的神系以及处于神系统治地位的主神。

具有内在统一性和系统性的神话便于容纳和展示系统的东西，所以，人类意识和精神的发展能够在其中比较清晰地反映出来。

正因为如此，希腊神话在被哲学家、思想家批判、扬弃之后，才能被希腊哲学吸收，成为希腊精神的原型。

与希腊神话不同，主要是产生于祖先崇拜观念基础上的中国神话，不但新神、旧神之间的界限不清楚，而且由于祖先所崇拜的对象不同，所以始终没有形成一个内在统一的普遍的神系以及处于核心地位上的主神。

中华民族形成和发展的历史道路与古希腊根本不同。

夏、商、周三个王朝的前身分别是以原始氏族血缘关系为基础的夏部族、商部族和周部族。

他们各自生息、发展于一隅，后来才先后入主中原，成为天下的共主。

地位虽然变了，但是，在统治阶级内部仍然保持着原先的那种血缘亲族关系。

不同血缘、不同祖先的夏、商、周三朝不但在政治上相互排斥，而且在文化上也难于相容。

一旦推翻旧王朝，前朝一切统统废弃，一切重新开始。

辽宁师大附中届高三上学期期中考试数学(文)含答案

辽师附中2017—2018上学期期中考试高三数学（文)试卷命题与校对:高三数学（文）备课组满分：150分时间:120分钟第Ⅰ卷（选择题共60分）一、选择题（本题共12道小题,每题5分，共60分。

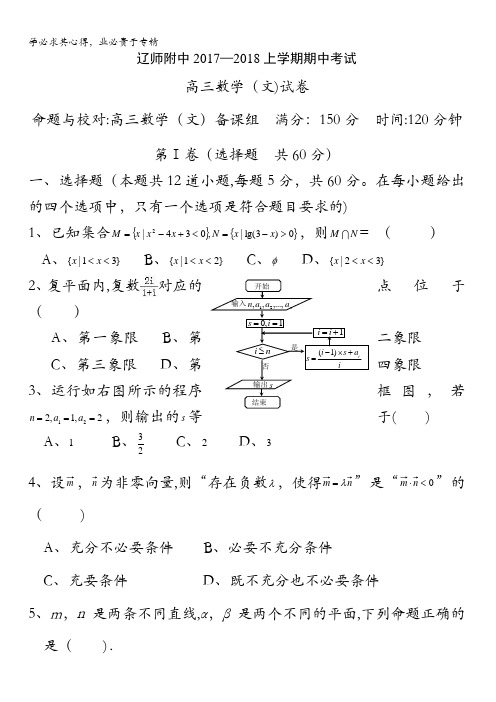
在每小题给出的四个选项中，只有一个选项是符合题目要求的) 1、已知集合{}{}0)3lg(|,034|2>-=<+-=x x N x x x M ，则MN = （） A 、}31|{<<x x B 、}21|{<<x x C 、φ D 、}32|{<<x x2、复平面内,复数对应的点位于（）A 、第一象限B 、第二象限C 、第三象限D 、第四象限3、运行如右图所示的程序框图，若122,1,2n a a ===，则输出的s 等于( )A 、1B 、23 C 、2 D 、34、设m ，n 为非零向量,则“存在负数λ，使得n m λ=”是“0<⋅n m ”的（ )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件5、m ，n 是两条不同直线,α，β是两个不同的平面,下列命题正确的是（ )．是否开始结束输入n a a a n ,...,,,211,0==i sia s i s i+⨯-=)1(输出s 1+=i ini ≤A 、m ∥α，n ∥β，且α∥β，则m ∥nB 、m ⊥α，n ⊂β，m ⊥n ，则α⊥βC 、m ⊥α,n ⊥β，且α⊥β,则m ⊥nD 、m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β6、设函数)1ln()1ln()(x x x f --+=,则)(x f 是（ )A 、偶函数，且在()1,0上是减函数B 、奇函数，且在()1,0上是减函数C 、偶函数，且在()1,0上是增函数D 、奇函数，且在()1,0上是增函数7、设函数f (x ）＝错误!x 3＋错误!x 2＋tan θ，θ∈错误!，则导数f ′(1)的取值范围为( )A 、［－2，2］B 、[错误!，错误!]C 、［错误!,2］D 、［错误!,2］8、我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式"，设△ABC 三个内角A 、B 、C 所对的边分别为a 、b 、c ，面积为S ，则“三斜求积"公式为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛-+-=222222241b c a c a S 。