多重线性回归分析
SPSS—回归—多元线性回归结果分析

SPSS—回归—多元线性回归结果分析(二),最近一直很忙,公司的潮起潮落,就好比人生的跌岩起伏,眼看着一步步走向衰弱,却无能为力,也许要学习“步步惊心”里面“四阿哥”的座右铭:“行到水穷处”,”坐看云起时“。
接着上一期的“多元线性回归解析”里面的内容,上一次,没有写结果分析,这次补上,结果分析如下所示:结果分析1:由于开始选择的是“逐步”法,逐步法是“向前”和“向后”的结合体,从结果可以看出,最先进入“线性回归模型”的是“price in thousands"建立了模型1,紧随其后的是“Wheelbase"建立了模型2,所以,模型中有此方法有个概率值,当小于等于0.05时,进入“线性回归模型”(最先进入模型的,相关性最强,关系最为密切)当大于等0.1时,从“线性模型中”剔除结果分析:1:从“模型汇总”中可以看出,有两个模型,(模型1和模型2)从R2 拟合优度来看,模型2的拟合优度明显比模型1要好一些(0.422>0.300)2:从“Anova"表中,可以看出“模型2”中的“回归平方和”为115.311,“残差平方和”为153.072,由于总平方和=回归平方和+残差平方和,由于残差平方和(即指随即误差,不可解释的误差)由于“回归平方和”跟“残差平方和”几乎接近,所有,此线性回归模型只解释了总平方和的一半,3:根据后面的“F统计量”的概率值为0.00,由于0.00<0.01,随着“自变量”的引入,其显著性概率值均远小于0.01,所以可以显著地拒绝总体回归系数为0的原假设,通过ANOVA方差分析表可以看出“销售量”与“价格”和“轴距”之间存在着线性关系,至于线性关系的强弱,需要进一步进行分析。
结果分析:1:从“已排除的变量”表中,可以看出:“模型2”中各变量的T检的概率值都大于“0.05”所以,不能够引入“线性回归模型”必须剔除。
从“系数a” 表中可以看出:1:多元线性回归方程应该为:销售量=-1.822-0.055*价格+0.061*轴距但是,由于常数项的sig为(0.116>0.1) 所以常数项不具备显著性,所以,我们再看后面的“标准系数”,在标准系数一列中,可以看到“常数项”没有数值,已经被剔除所以:标准化的回归方程为:销售量=-0.59*价格+0.356*轴距2:再看最后一列“共线性统计量”,其中“价格”和“轴距”两个容差和“vif都一样,而且VIF 都为1.012,且都小于5,所以两个自变量之间没有出现共线性,容忍度和膨胀因子是互为倒数关系,容忍度越小,膨胀因子越大,发生共线性的可能性也越大从“共线性诊断”表中可以看出:1:共线性诊断采用的是“特征值”的方式,特征值主要用来刻画自变量的方差,诊断自变量间是否存在较强多重共线性的另一种方法是利用主成分分析法,基本思想是:如果自变量间确实存在较强的相关关系,那么它们之间必然存在信息重叠,于是就可以从这些自变量中提取出既能反应自变量信息(方差),而且有相互独立的因素(成分)来,该方法主要从自变量间的相关系数矩阵出发,计算相关系数矩阵的特征值,得到相应的若干成分。
线性相关与回归(简单线性相关与回归、多重线性回归、Spearman等级相关)

4.剔除强影响点(Influential cases;或称为突出点, outliers)
通过标准化残差(Standardized Residuals)、学生氏残 差(Studentlized Residuals)来判断强影响点 。当指标 的绝对值大于3时,可以认为样本存在强影响点。
删除强影响点应该慎重,需要结合专业知识。以下两种情 况可以考虑删除强影响点:1.强影响点是由于数据记录错 误造成的;2.强影响点来自不同的总体。
r r t sr 1 r2 n2
只有当0时,才能根据|r|的大小判断相关 的密切程度。
4.相关与回归的区别和联系 (1)相关与回归的意义不同 相关表达两个变量 之间相互关系的密切程度和方向。回归表达两个变 量之间的数量关系,已知X值可以预测Y值。从散点 图上,散点围绕回归直线的分布越密集,则两变量 相关系数越大;回归直线的斜率越大,则回归系数 越大。 (2)r与b的符号一致 同正同负。
5.自变量之间不应存在共线性(Collinear)
当一个(或几个)自变量可以由其他自变量线性表示时,称 该自变量与其他自变量间存在共线性关系。常见于:1.一个 变量是由其他变量派生出来的,如:BMI由身高和体重计算 得出 ;2.一个变量与其他变量存在很强的相关性。 当自变量之间存在共线性时,会使回归系数的估计不确定、 预测值的精度降低以及对y有影响的重要自变量不能选入模 型。
P值
截距a 回归系数b sb 标准化回归系数 t值 P值
3.直线回归的预测及置信区间估计
给定X=X0, 预测Y
3.直线回归的预测及置信区间估计
因变量
自变量
保存(产生新变量,保 存在当前数据库) 统计
3.直线回归的预测及置信区间估计
多重线性回归的假设

多重线性回归的假设多重线性回归是一种常见的统计分析方法,可以处理多个自变量与相关因素之间的关系。
它是利用一个或多个变量对另一个变量进行线性回归分析。
它是一种综合性的分析技术,可以广泛应用于生物统计、经济学、数理统计和管理科学等领域的研究。
本文将详细论述多重线性回归的假设以及假设检验的步骤,以期为读者提供更深入了解多重线性回归假设检骤的概念。
一、多重线性回归的假设多重线性回归模型的基本假设包括线性关系假设、独立同分布假设、残差常态性假设、多重共线性假设以及外生自变量假设。
(1)线性关系假设。
即被解释变量Y与自变量X之间存在着线性关系,并且Y与X之间的关系可以用回归方程的形式表示。
(2)独立同分布假设。
即每个观测值的误差项i都是独立同分布的,服从正态分布,其样本和总体均值均为0,而方差σ^2是几乎相等的。
(3)残差常态性假设。
即被解释变量Y与自变量Xi之间的残差εi服从正态分布,均值为0,且其方差σ^2是几乎相等的。
(4)多重共线性假设。
即自变量之间不存在相关性,否则它们之间的变异性会混淆我们对被解释变量变量的理解和分析。
(5)外生自变量假设。
即自变量和被解释变量是独立的,不受外界因素的影响。
二、多重线性回归的假设检骤多重线性回归分析需要检验假设,以确定模型是否满足上述假设。
(1)数据预处理。
首先要对原始数据进行预处理,分析每个变量的分布特征,检测是否存在缺失值和异常值等。
如果存在缺失值和异常值,则必须进行合理的处理。
(2)回归分析。
回归分析是对数据进行多元线性回归的过程,可以用统计软件SPSS、SAS等进行分析,以求出每个变量的系数,并计算R、R2等统计量,以进行检验。
(3)残差分析。
残差的分析是检查模型预测结果的有效性的重要步骤。
通常,残差的分析以正态分布图、直方图等图形来表示。
(4)多重共线性检骤。
多重共线性可分为两种:一种是检查变量间是否存在共线性,另一种是检查系数是否收敛。
(5)假设检骤。
多元线性回归模型检验

多元线性回归模型检验引言多元线性回归是一种常用的统计分析方法,用于研究两个或多个自变量对目标变量的影响。
在应用多元线性回归前,我们需要确保所建立的模型符合一定的假设,并进行模型检验,以保证结果的可靠性和准确性。
本文将介绍多元线性回归模型的几个常见检验方法,并通过实例进行说明。
一、多元线性回归模型多元线性回归模型的一般形式可以表示为:$$Y = \\beta_0 + \\beta_1X_1 + \\beta_2X_2 + \\ldots + \\beta_pX_p +\\varepsilon$$其中,Y为目标变量,$X_1,X_2,\\ldots,X_p$为自变量,$\\beta_0,\\beta_1,\\beta_2,\\ldots,\\beta_p$为模型的回归系数,$\\varepsilon$为误差项。
多元线性回归模型的目标是通过调整回归系数,使得模型预测值和实际观测值之间的误差最小化。
二、多元线性回归模型检验在进行多元线性回归分析时,我们需要对所建立的模型进行检验,以验证假设是否成立。
常用的多元线性回归模型检验方法包括:1. 假设检验多元线性回归模型的假设包括:线性关系假设、误差项独立同分布假设、误差项方差齐性假设和误差项正态分布假设。
我们可以通过假设检验来验证这些假设的成立情况。
•线性关系假设检验:通过F检验或t检验对回归系数的显著性进行检验,以确定自变量与目标变量之间是否存在线性关系。
•误差项独立同分布假设检验:通过Durbin-Watson检验、Ljung-Box 检验等统计检验,判断误差项是否具有自相关性。
•误差项方差齐性假设检验:通过Cochrane-Orcutt检验、White检验等统计检验,判断误差项的方差是否齐性。
•误差项正态分布假设检验:通过残差的正态概率图和Shapiro-Wilk 检验等方法,检验误差项是否满足正态分布假设。
2. 多重共线性检验多重共线性是指在多元线性回归模型中,自变量之间存在高度相关性的情况。
多重线性回归

x1
x2
2.989 1.292
4.647
F0.05,(1,37)=4.11
23
评价回归方程的标准
• 复相关系数 • 校正复相关系数 • 剩余标准差
24
复相关系数
(multiple correlation coefficient)
• 0≤R≤1
R R2 SS回归 SS总
• R反映的是因变量与所有自变量的总的相关关 系,当方程中自变量个数增加时,R总是增加的。 当只有一个因变量y与一个自变量x时,R就等 于y与x的简单相关系数之绝对值:R= | ryx |。
SS (n k 1) 剩余
1
20
例20-1
总胆固醇和甘油三酯对空腹血糖的影响
• 模型检验结果
A NOVAb
Model 1
R egre ssio n R esidua l To t al
Sum of Sq ua re s
4. 2 81 10 . 293 14 . 574
df 2
37 39
Mean Square 2. 1 40 . 27 8
1 R2
1 MS误差 MS总
26
剩余标准差
• 剩余标准差 小则估计值与实测值接近,反 之则估计值与实测值相差较大,它是反映回 归方程精度的指标
s y,x1x2 xk
n
yi yˆi 2
i 1
n m 1
SS剩余 n m 1
MS剩余
27
自变量的筛选
• 全面分析法 • 前进法 • 后退法 • 逐步回归法
P3=0.223
• Y与x2 , x5
P4=0.635
• 选入X3 方程中有二个变量
•
多元线性回归分析预测法

多元线性回归分析预测法(重定向自多元线性回归预测法)多元线性回归分析预测法(Multi factor line regression method,多元线性回归分析法)[编辑]多元线性回归分析预测法概述在市场的经济活动中,经常会遇到某一市场现象的发展和变化取决于几个影响因素的情况,也就是一个因变量和几个自变量有依存关系的情况。
而且有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用。
例如,某一商品的销售量既与人口的增长变化有关,也与商品价格变化有关。
这时采用一元回归分析预测法进行预测是难以奏效的,需要采用多元回归分析预测法。
多元回归分析预测法,是指通过对两上或两个以上的自变量与一个因变量的相关分析,建立预测模型进行预测的方法。
当自变量与因变量之间存在线性关系时,称为多元线性回归分析。
[编辑]多元线性回归的计算模型[1]一元线性回归是一个主要影响因素作为自变量来解释因变量的变化,在现实问题研究中,因变量的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归。
当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元性回归。
设y为因变量,为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:其中,b0为常数项,为回归系数,b1为固定时,x1每增加一个单位对y的效应,即x1对y的偏回归系数;同理b2为固定时,x2每增加一个单位对y的效应,即,x2对y的偏回归系数,等等。
如果两个自变量x1,x2同一个因变量y呈线相关时,可用二元线性回归模型描述为:其中,b0为常数项,为回归系数,b1为固定时,x2每增加一个单位对y的效应,即x2对y的偏回归系数,等等。
如果两个自变量x1,x2同一个因变量y呈线相关时,可用二元线性回归模型描述为:y = b0 + b1x1 + b2x2 + e建立多元性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意自变量的选择,其准则是:(1)自变量对因变量必须有显著的影响,并呈密切的线性相关;(2)自变量与因变量之间的线性相关必须是真实的,而不是形式上的;(3)自变量之彰应具有一定的互斥性,即自变量之彰的相关程度不应高于自变量与因变量之因的相关程度;(4)自变量应具有完整的统计数据,其预测值容易确定。
多重线性回归分析

NTU Civil Engineering
4
研究流程
經系統誤差改正後之一 等水準網往返閉合差
方差分析法
檢驗水準網是否 有殘留系統誤差
時間序列分析法
檢驗殘留系統隱 藏在哪些測線內
多重線性迴歸分析法
找出可能造成系 NTU 統誤差的原因
Civil Engineering
5
二、變異數分析法
假設有個n條測線所組成的水準網,其中每條測線 中有Ki 個測段數,N為水準網中所有測段數, Sij 為各測段長度(km),其中ij表第i條測線中第j個 測段。
NTU Civil Engineering
7
二、變異數分析法 - 續
假設所有的測段閉合差dij為互相獨立的隨機變數呈常 態分佈,則每測線平均之閉合差d1 ,d2 ,d3 ,…,dn 2 2 其變異數期望值分別為 1 , 2 ,…, n2 。設定一 零假說進行統計檢驗:
2 2 H 0 : 12 2 ... n 2 2 2 2 2 H 1 : 1 2 ... n
D
i 1 k
ni npi
npi
2
i 1
k
oi ei
ei
2
(8)
應為一近似於自由度為k-1之χ2分佈。
NTU Civil Engineering
13
三、時間序列分析法
假設測量水準網內各測段之閉合差屬於互相獨立不相關 之隨機序列,為了描述此隨機序列,必須假設此序列為 穩定隨機,即其平均值及變異數為一固定常數,則自我 相關係數可由下式算得:
1
台灣一等一級水準網測量殘留之 系統誤差研究
第11章 多重线性回归分析案例辨析及参考答案
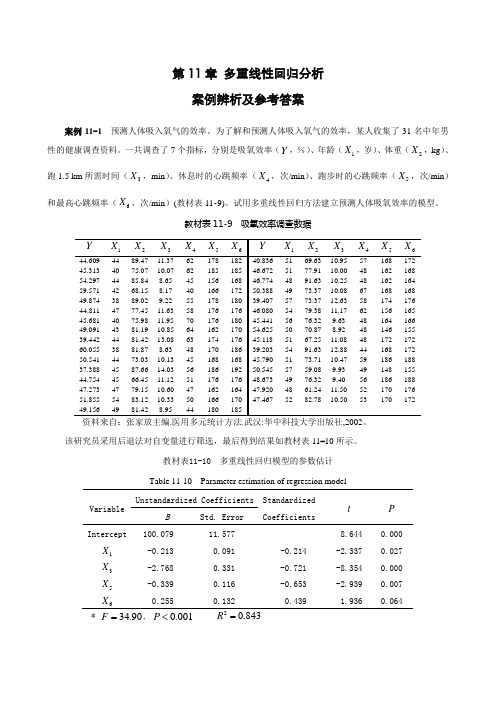
第11章 多重线性回归分析案例辨析及参考答案案例11-1 预测人体吸入氧气的效率。
为了解和预测人体吸入氧气的效率,某人收集了31名中年男性的健康调查资料。
一共调查了7个指标,分别是吸氧效率(Y ,%)、年龄(1X ,岁)、体重(2X ,kg )、跑1.5 km 所需时间(3X ,min )、休息时的心跳频率(4X ,次/min )、跑步时的心跳频率(5X ,次/min )和最高心跳频率(6X ,次/min )(教材表11-9)。
试用多重线性回归方法建立预测人体吸氧效率的模型。
教材表11-9 吸氧效率调查数据该研究员采用后退法对自变量进行筛选,最后得到结果如教材表11-10所示。
教材表11-10 多重线性回归模型的参数估计 Table 11-10 Parameter estimation of regression modelVariable Unstandardized Coefficients Standardized CoefficientstPB Std. Error Intercept100.079 11.577 8.644 0.000 1X -0.213 0.091 -0.214-2.337 0.027 3X -2.768 0.331 -0.721 -8.354 0.000 5X -0.339 0.116 -0.653 -2.939 0.007 6X0.2550.1320.4391.9360.064* 90.34=F , 001.0<P 843.02=R对模型进行方差分析的结果认为模型有统计学意义(P <0.05),确定系数的数值(0.843)也说明模型拟合的效果较好。
考察各个自变量的偏回归系数,研究者发现,6X 的偏回归系数符号为正,认为最高心跳频率越大,人的吸氧效率就越高,这与专业结论相反。
出现这种悖论的原因是什么呢?案例辨析 我们先分析一下各个自变量之间的简单相关系数,结果发现5X 和6X 存在有较强的相关(r =0.930, P <0.001), 对回归模型进行共线性诊断,结果发现自变量5X 的容忍度为0.122,方差膨胀因子等于8.188,自变量6X 的容忍度为0.117,方差膨胀因子等于8.522,说明自变量之间存在多重共线性,所以出现了与专业结论相反的现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
M
2 B
M
2 W
(6)
在零假說
H0
下,
M
2 B
應該不會特別大過於
M
2 W
,因
其估值均來自於同一個母體方差σ2,在p%的信心水
準下:
若 F ,則 f p,n1,N n H0 將不被接受
(7)
當滿足此條件時則我們可判定此網形仍殘留系統性誤 差。
11
二、變異數分析法 - 續
閉合差之常態分佈檢定
d ij d i 2
j
(3)
測lin線es與)測: 線間(di)之變異數(Mean squares between
M
2 B
1 n 1
i
K i d i d 2
(4)
dij N
其中d為平均值 i j
9
二、變異數分析法 - 續
由於
測段。
令 Dij為為第i測線中第j測段的閉合差(mm),則測 段之每公里閉合差為dij(= Dij /Sij),各測線中之 每公里閉合差其平均值為di(=Σdij /Ki),則可
將水準網中之各閉合差列如表1:
6
二、變異數分析法 - 續 表1 各測線及線段之每公里閉合差
7
二、變異數分析法 - 續
oi ei 2
i 1
npi
i 1
ei
(8)
應為一近似於自由度為k-1之χ2分佈。
13
三、時間序列分析法
假設測量水準網內各測段之閉合差屬於互相獨立不相關 之隨機序列,為了描述此隨機序列,必須假設此序列為 穩定隨機,即其平均值及變異數為一固定常數,則自我 相關係數可由下式算得:
(s)i
先假設所有的閉合差均為互相獨立不相關,設
定間隔Ai(i=1,2,…,k) ,紀錄閉合差落入各區間 之個數ni(i=1,2,…,k),算出各區間理論期望值 出現之機率p(Ai)= pi。 當n (=n1+ n2+…+ nk) 夠大時,則
k
D
ni npi 2 k
假設所有的測段閉合差dij為互相獨立的隨機變數呈常 態分佈,則每測線平均之閉合差d1 ,d2 ,d3 ,…, dn 其變異數期望值分別為 12 ,22 ,…,n2 。設定
一零假說進行統計檢驗:
H0
:
2 1
2 2
...
2 n
2
H1
:
2 1
2 2
.
.
.
2 n
4
研究流程
經系統誤差改正後之一 等水準網往返閉合差
方差分析法
檢驗水準網是否 有殘留系統誤差
時間序列分析法
檢驗殘留系統隱 藏在哪些測線內
多重線性迴歸分析法
找出可能造成系 統誤差的原因
5
二、變異數分析法
假設有個n條測線所組成的水準網,其中每條測線 中有Ki 個測段數,N為水準網中所有測段數, Sij 為各測段長度(km),其中ij表第i條測線中第j個
Sum of squares
SSB SSW SST
Degree of freedom
n-1 N-n N-1
Mean squares
M
2 B
SSB /(n 1)
M
2 W
SSW /(N n)
M
2 T
SST
/(N
1)
10
二、變異數分析法 - 續
Ftest 以F統計檢驗進行零假說測試,其自由度為n-1, N-n:
dij d 2
dij di 2 Ki di d 2
ij
ij
i
上式改寫成 SST = SSW + SSB
(5)
表2 ANOVA (analysis of variance) table
Source of variance
Between lines Within lines Total
三、時間序列分析法-續
自我相關係數之統計檢定
當測線的測段數Ki夠大時,自我相關係數會大致呈常
態分佈,將自我相關係數除以其標準差 1,其Ki 值 越偏離0則為越顯著,將其設定為零假說。
因此在95% 的信賴區間下,當 Z0 (s)i (s)i Ki >1.96或 <-1.96我們拒絕零假說,認為自我相關係 數檢定為顯著,表明諸測段閉合差間受某系統性誤 差影響。
cov(Dij , Dil )
1
[var(Dij ) var(Dil )] 2
, j 1,2,....Ki
l js
(10)
其中i表第i條測線,j表第j個測段,每條測線共有Ki個測 段,Dij表第i條測線第j個測段之閉合差。 s為lag數,表示
在測線i中之某j線段與下s個線段之相關係數。
14
台灣一等一級水準網測1 量殘 留之
系統誤差研究
Detecting Systematic Errors Remained In The FirstOrder ClassⅠLeveling Network of Taiwan By Using
Statistical Techniques
2
報告大綱
研究動機與目的及研究流程 方法介紹:變異數分析法
15
四、多重線性迴歸分析
將多重線性迴歸分析應用於台灣一等一級(2001)水準網, 其中以就有資料中可用來當成迴歸的資料包括高差(m)、
長度(m)、溫度、正高改正量共4項,分別以X1、X2、X3 及X4 代表。
(1) 整體迴歸模式建立及統計測試 假設模型 :
L i + vi =β1X1+β2X2+β3X3+β4X4
16
四、多重線性迴歸分析-續
在迴歸分析中,欲知係數項β對觀測量Y有無解釋能力, 及β之值是否會對Y造成改變,則必須對模式建立一統計
檢驗:
H 0 : 1 2 ... i 0 (11) H1 : i 0 at least one
時間序列分析法 多重線性迴歸分析法 實驗研究與成果 結論與建議 參考文獻
3
一、研究動機與目的
系統性誤差很難完全移除而留下殘餘之系統誤差, 以往是將殘留的系統誤差直接當成偶然誤差計算, 但系統誤差仍影響到整個網形之精度。
本研究旨在找出經由系統誤差改正分析後之台灣一 等一級水準網是否仍有測量殘留之系統誤差及分析 可能造成之原因。
2
(1)
8
二、變異數分析法 - 續
全網變異數(Grand mean squares):
M
2 T
1 N 1
i
d ij d 2
j
(2)
每條測線(Li)之變異數(Mean squares within lines) :
M
2 W
1 N n
i
