四年级奥林匹克数学竞赛专题应用题(无答案)

合集下载

四年级奥林匹克数学试卷(1)(无答案)

小学四年级奥数试卷
1．从10000里面连续减25，减多少次差是0？
2.在一道没有余数的除法算式里，被除数（不为零）加上除数和商的积，得到的和，除以被除数，所得的商是多少？
3.明明和花花用同一个数做除法，明明用12去除，花花用15去除。

明明除得商是32余数是6，花花计算的结果应是多少？
4.三棵树上停着24只鸟。

如果从第一棵树上飞4只鸟到第二棵树上去，再从第二棵树飞5只鸟到第三树上去，那么三棵树上的小鸟的只数都相等，第二棵树上原有几只？
5.两袋糖，一袋是84粒，一袋是20粒，每次从多的一袋里拿出8粒糖放到少的一袋里去，拿几次才能使两袋糖的粒数同样多。

6.小强、小清、小玲、小红四人中，小强不是最矮的，小红不是最高的，但比小强高，小玲不比大家高。

请按从高到矮的顺序，把名子写出来。

7.有10把不同的锁，开这10把锁的10把钥匙混在一起了，最多要试多少次，才能把这10把锁和钥匙全部配对。

8.用0、6、7、8、9这五个数字组成各个数位上数字不相同的两位数共有多少个？
9.五个同学参加乒乓球赛，每两人都要赛一场，一共要赛多少场？
10.2把小刀与3本笔记本的价钱相等，3本笔记本与6支铅笔的价钱相等，一把小刀1角8分，一支铅笔多少钱？。

四年级数学奥林匹克竞赛练习题1

四年级数学奥林匹克竞赛练习题1
1、如下图所示，图中的数是按规律排列的，那么A= ，B= 。

2、一次数学考试后，李军问于昆数学考试得多少分，于昆说：“用我得的分数减去8加上10，再除以
7，最后乘以4，得5”，于昆得了多少分？
3、阿凡提去赶集，他用钱的一半买肉，再用余下钱的一半买鱼，又用剩下的钱买菜。

别
人问他带多少钱，他说：“买菜的钱是1、2、3；3、2、
1；1、2、3、4、5、6、7的和；加7加8；加8加7；加9加10加11。

”阿凡提一共带了多少钱？买鱼用了多少钱？
4、有27个大小形状相同的小珠，其中26个珠的质量相同，另一个珠比其余26个都轻，给你一架天平（没有砝码），至少要称多少次一定能找出这个比较轻的小珠？
5、猴王给一群小猴子分一堆桃子，若每只小猴分8个，还剩14个；若每只小猴分9个，最后一只小猴只分得6个。

这堆桃子有多少个，小猴有多少只？
6、有一串数：188428……，这一串数从左边第3个数字起，每个数字都是它前面两个数字之积的个位数字，这串数从左边数起第168个数字是几？。

四年级数学竞赛应用题题

四年级数学竞赛练习题（应用题) 姓名：1．祖父今年75岁，3个孙子的年龄分别是17岁、15岁和13岁,多少年后3个孙子的年龄和等于祖父的年龄？2．王雪读一本故事书，第一天读了8页，以后每天都比前一天多读3页，最后一天读了32页正好读完。

她一共读了多少天?3．学校买来一些毽子,分给全校各班。

如果每班16个，恰好分完；如果少给2个班，每个班多分1个，还剩10个。

班级和毽子各多少个？4．从甲城往乙城运58吨货物，如果用载重5吨的大卡车运一趟，运费150元；用载重2吨的中卡车运一趟，运费80元；用载重1吨的小卡车运一趟,运费50元。

要想用最少的钱一次运完这批货物，需大、中、小卡车各多少辆？(只填写得数,不写算式）大卡车（）辆,中卡车（）辆小卡车（）辆5、体育老师买了3个排球和5个篮球,共用了345元，每个排球40元,每个篮球多少？6、某工厂第一车间有150人，第二车间有工人90人，要使第一车间的人数是第二车间的2倍，需要从第二车间调多少人到第一车间？7、一个球从100米的高处自由落下,每次着地后又跳回原来高度的一半又落下，当它第三次着地时，它共经过多少路程？8、在一条长200米公路的两侧栽树,每隔5米栽一棵，一共要栽多少棵树？9、小明读一本事故书,第一天读了8页，以后每天比前一天多读3页，最后一天读了32页，正好读完，这本书一共有多少页？10、从北京运至天津63吨货物，如果用载重5吨的大卡车运一趟，运费150元；用载重2吨的中卡车运一趟,运费80元；用载重1吨的小卡车运一趟，运费50元，要想用最少的钱一次运完这批货物,需大、中、小车各多少辆？答案1．（75—17—15—13）÷（3-1）=30÷2=15（年）2、(32-8)÷3+1=24÷3+1=9（天）3．（16×2-10）+2=（32—10)+2=24(个）16×24=384(个）4、用大卡车（11)辆,中卡车（1)辆,小卡车（1）辆。

小学奥林匹克数学一般应用题练习(2)(无答案)

一般应用题练习1．用汽车运一堆煤，原计划9小时运完。

实际每小时比原计划多运2吨，这样运了7小时就比原计划多运了4吨，原计划9小时运多少吨煤？2．汽车从甲地开往乙地，原计划8小时到达。

实际每小时比原计划多行10千米，行了6小时后，发现已超过乙地20千米。

甲、乙两地相距多少千米？3.甲、乙二人加工零件。

甲比乙每天多加工8个零件，乙中途停了10天没有加工。

40天后，乙所加工的零件个数正好是甲的一半。

求甲、乙二人每天各加工多少个零件？4.甲、乙二人加工一批帽子，甲每天比乙多加工15个。

途中乙因事休息了8天，18天后，甲加工的帽子正好是乙加工的2倍，求甲、乙二人每天各加工多少个帽子？5.甲、乙两车同时从A、B两地相对开出，甲车每小时比乙车多行15千米。

途中乙因修车用了2小时，6小时后甲车到达两地中点，而乙车才行了甲车所行路程的一半。

问：A、B 两地相距多少千米？6.加工一批零件，原计划每天加工60个，正好如期完成任务。

由于改进了生产技术，实际每天加工80个。

这样，不仅提前5天完成任务，而且还多加工了80个。

他们实际加工零件多少个？7.某车间按计划每天应加工40个零件，实际每天加工50个零件。

这样，不仅提前4天完成原计划加工零件的任务，而且还多加工了100个零件。

这个车间实际加工了多少个零件？8.王师傅原计划每天做80个零件，实际每天比原计划多做20个，结果提前5天完成任务。

王师傅一共做了多少个零件？9.一列火车3小时行驶240千米，照这样计算，再行6小时后，这列火车一共可以行使多少千米？10.挖一条水渠，原计划20人工作10天完成，工作4天后，又增加4人，剩下的任务多少天能完成？11.某化肥厂生产一批化肥，原计划每天生产60吨，实际每天比原计划多生产15吨，结果提前6天完成了任务。

这批化肥有多少吨？12.某物流公司运800个花瓶，按合同每个运费5元，每损坏一个除扣除5元运费外，还要赔偿花瓶价格的一半，结果运送中损坏花瓶4个，实收运费3780元。

小学奥林匹克数学倍数问题练习试卷(4)(无答案)

倍数问题练习1.甲站有公共汽车32辆，乙站有公共汽车36辆。

每小时由甲站向乙站开出汽车12辆，乙站向甲站开出汽车7辆，都是经过1小时到达。

几小时后乙站的公共汽车数是甲站的3倍？2.A有邮票42张，B有邮票48张。

每次A给B两张，而B又给A 四张，这样交换多少次后，A的邮票张数是B的2倍？3.甲仓库有大米700袋，乙仓库有大米280袋。

每天从甲、乙仓库各运出30袋，多少天后甲仓的大米袋数是乙仓的7倍？4.A、B、C三数的和是78，A比B的2倍多4，B比C的3倍少2.求这三个数。

5.有三个小组，甲组的人数比乙组的2倍多6人，乙组的人数是丙组的2倍。

三个小组一共有90人，求三个小组各有多少人？6.某学校共有学生600人，其中男生比女生的3倍少80人，男生和女生各有多少人？7.竹苑小学共有学生1050人，一至五年级人数是六年级人数的5倍还多30人。

求六年级有多少人？8.有两堆棋子，第一堆有87个，第二堆有69个，要从第一堆拿出多少个到第二堆，才能使第二堆棋子数是第一堆的3倍？9.饲养场的白兔是黑兔的6倍，后来卖掉了15只黑兔，买回来20只白兔，现在白兔的只数是黑兔的8倍。

饲养场原来养白兔和黑兔各多少只？10.把666本书放在书架的三层里，下层放的本数比上层的3倍多4本，中层放的本数是上层的2倍多2本。

问：上、中、下三层各放书多少本？11.有两堆煤，甲堆有6.4吨，已知甲堆重量的四分之一和乙堆重量的五分之一相等，乙堆有煤多少吨？12.有两杯水，一杯有水100毫升，另一杯有水20毫升，每次往两只杯中各倒进5毫升水，倒几次后，一只杯中的水是另一杯的3倍？13.三种水果共132个，已知苹果的个数比梨的3倍少6个，梨的个数比橘子的3倍多2个，三种水果各多少个？。

奥林匹克数学小学竞赛试卷

一、选择题（每题3分，共15分）1. 小明有10个苹果，小红有15个苹果，他们一共有多少个苹果？A. 20个B. 25个C. 30个D. 35个2. 下列哪个数是质数？A. 18B. 19C. 20D. 213. 一个长方形的长是8厘米，宽是4厘米，它的周长是多少厘米？A. 16厘米B. 24厘米C. 32厘米D. 40厘米4. 下列哪个图形的面积最大？A. 正方形B. 长方形C. 三角形D. 梯形5. 下列哪个数是偶数？A. 23B. 24C. 25D. 26二、填空题（每题5分，共20分）6. 7 + 5 = ________，减去4后等于 ________。

7. 12 ÷ 3 = ________，加上6后等于 ________。

8. 3 × 4 = ________，再减去5后等于 ________。

9. 20 - 8 = ________，再乘以2后等于 ________。

10. 下列数列中，下一个数是 ________。

2, 4, 6, 8, 10, ________三、解答题（每题10分，共30分）11. 小华有25个铅笔，每天用掉3个，几天后小华的铅笔用完了？12. 小明有一些铅笔，小红有比小明多10个铅笔，如果小明再买5个铅笔，那么小明和小红一共有多少个铅笔？13. 小红的储蓄罐里有50元，小红每天存入5元，几天后小红的储蓄罐里的钱可以买一本书（书的价格是120元）？四、应用题（每题15分，共30分）14. 小明和小红一起摘了30个苹果，小明摘了其中的12个，小红摘了剩下的苹果。

请计算小红摘了多少个苹果？15. 一辆汽车从甲地出发前往乙地，甲乙两地相距120千米。

汽车每小时行驶50千米，请问汽车从甲地出发，几小时后可以到达乙地？注意：本试卷满分为100分，考试时间为60分钟。

请认真审题，仔细作答。

祝各位同学取得优异成绩！。

小学奥林匹克数学钟面上的行程问题练习(3)(无答案)

钟面上的行程问题练习
1.现在是下午3点，从现在起时针和分针什么时候第一次重合？
2.分针和时针每隔多少时间重合一次？一个钟面上分针和时针一昼夜重合几次？
3.钟面上5点零8分时，时针与分针的夹角是多少度？
4.在4点与5点之间，时针与分针什么时候成直角？
5.8点整后时针与分针第一次成一条直线是在什么时刻？
6．10点整后时针与分针第一次成一条直线是什么时候？
7.在5点和6点之间，什么时刻分针与时针车位那个直角？
8.在3点和4点之间，什么时刻分针和时针成60度角？
9. 9点过多少分时，时针和分针离“9”的距离相等，并且在“9”的两边？
10.有一只钟，每小时比标准时间慢1分钟，中午12点调整，下午当中指向6点时，标准时间是几时几分？
11.钟面上的指针指在3点的哪一刻时，时针与分针的位置与3的距离相等？
12. 小明5点多起床，一看钟，6字恰好在时针和分针的正中间（即两针到6的距离相等），这时是5点几分？。

四年级奥林匹克数学综合训练题(五)(无答案)

四年级奥数综合训练题五
1. 852×7×11×13=（）
560-557+554-551+…+500-497=（）
2．已知数列5，7，11，17，… ，按照前几项规律，写出第十五项的数，应该是多少？（）
3.自然数中所有的两位奇数之和是多少？（）
4．用三辆卡车运910吨水泥到工地去，已知第一辆比第二辆多运30吨，第三辆运的是第二辆的一半。

问：第三辆卡车运（）吨。

5.农户有鸡和兔共290只，鸡的腿数比兔的腿少20只，那么共有兔子（），鸡有（）只。

6.60个苹果分给8个小朋友，每人分的的个数都不一样，那么最多能分得的个数是（）个。

7.平面上有7条直线，最多有（）交点，最少有（）个。

8.杭州到上海的列车途中除起点和终点外，还要停*7个大站，火车站要准备（）种不同的车票。

（从甲地到乙地用一种票，从乙地到甲地用另外一种票）
9.一艘轮船每小时行15千米，它逆水6小时行了72千米，如果它顺水行驶同样长的航程需要（）小时。

10.商店运来水果，运费花了1000元，水果报顺损了100千克，若按2元1千克卖出，则要亏损300元；若按3元1千克，则盈利500元，问原来进货多少千克？（）进货的金额是多少元？（）。

四年级奥林匹克数学竞赛试卷(无答案)

小学四年级数学竞赛试卷1.找规律填数1、2、4、7、11、16、22、（）2.被减数、减数、差相加的和是100，被减数是（）。

3.连续5个自然数的和是50，从小到大排列，第三个数是（）。

4.两个数相除，商是5，余数是20，除数最大是（）。

5.小强今年11岁，小军今年17岁，当两人的年龄和是38岁时，小强（）岁。

6.小华上体育课，站队时，从前向后数他是第10个，从后向前数他是第15个，问这队共有（）人。

7.小于10000而又与10000最接近的自然数是（）。

8.一个六位数，它的十万位、千位和百位上都是5，其余各位都是0，这个数是（）。

9.一个八位数，高位是7，任意相邻的数位上的数字相差3，最低位上是（）。

10.一个因数缩小倍，另一个因数也缩小3倍，积是120，原来的积是（）。

11.从2100里减去50，再加上20，这称作一次操作，经过（）次操作，所得的结果是0。

12.□600÷450，要使商是一位数，且没有余数，方框里应是（）。

13.一次智力测验有10道判断题，每答对一题得3分，答错一题扣2分，小红答完10题，只得20分，她答错（）题。

14.有8颗珠子，其中7颗一样重，一颗较轻，用一架天平称，最少称（）次能找到那颗轻的。

15.把一根木头锯断要2分钟，把这根木头锯成4段要（）分钟。

16.在一条长100米公路的两侧栽树，每隔10米栽一棵，一共栽（）棵。

17.跳绳比赛规定每人跳5分钟，王平共跳337下，张华平均每分钟比王平多跳12下，张华一共跳（）下。

18.甲船从A港出发，每小时行16千米，3小时后，乙船也从A港出发，行了12小时追上甲船，求乙船每小时行（）千米。

19.小华买1支钢笔和2支圆珠笔共用5元钱，小红买同样的钢笔2支，圆珠笔1支共用7元钱，每支钢笔（）元。

20.小军家距外婆家600米，一天他带一条狗，从家去外婆家，一出发狗就跑向外婆家，到外婆家后又立即回，回来遇到小军时，它又跑向外婆家，狗就这样来回不停的跑，已知小军每分钟走50米，狗每分钟跑200米，问小军到外婆家时，狗共跑了（）米路。

四年级奥林匹克数学竞赛题目完整版

四年级奥林匹克数学竞赛题目HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】四年级奥林匹克数学竞赛题目一、计算题 (4分)1、11×40＋39×48＋8×11 ＝2、1996＋1997＋1998＋1999＋2000＋2001＋2002＋2003＋2004＝二、填空题 (27分)1、找规律填数: 21 26 19 24 ( ) ( ) 15 202、用0--4五个数字组成的最大的五位数与最小的五位数相差( )。

3、用0、5、8、7这四个数字，可以组成（）个不同的四位数。

4、小明每天晚上9时30分睡觉，早晨6时30分起床，那么他的睡眠时间是（）小时。

5、甲、乙、丙三人站成一排照相，有（）种排法。

6、从午夜零时到中午12时，时针和分针共重叠（）次。

7、环形运动场上正在进行长跑比赛。

在每位参加赛跑的运动员前面有7个人在跑着，在每位运动员的后面，也有7个人在跑着，现在运动场上一共有（）名运动员。

8、一块豆腐，要想切成八块，最少的（）刀就可以完成。

9、妈妈使用一个平底锅烙饼，这个平底锅每次只能放2张饼，1张饼要烙两面，烙熟一面要3分钟，烙熟3张饼至少需要（）分钟。

三、选择题 (21分)1、公园要建一个正方形花坛,并在花坛四周铺上2米宽的草坪,草坪的面积是96平方米,花坛和草坪的面积总和是( )平方米.(A)204 (B)190 (C)196 (D)1002、小明每分钟走50米,小红每分钟走60 米,两人从相距660米的两村同时沿一条公路相对出发,8分钟后两人相距( )米.(A)75 (B)200 (C)220 (D)1103、右图的周长是（）分米.。

4分米 5分米（A）22 （B）20 （C）18 （D）284、500张白纸的厚度为50毫米，那么（）张白纸的厚度是 750毫米。

C. 75005、6个男生的平均体重是40千克，4个女生的平均体重是 30千克，这10个同学的平均体重是（）千克。

四年级奥林匹克数学竞赛题目

四年级奥林匹克数学竞赛题目一、数字规律类1. 题目：找规律填数：1，4，9，16，（），36。

解析：观察这组数字，1 = 1×1，4 = 2×2，9 = 3×3，16 = 4×4，所以括号里的数应该是5×5 = 25。

2. 题目：2，3，5，8，13，（）。

解析：从第三项起，每一项都是前两项之和。

2+3 = 5，3 + 5=8，5+8 = 13，那么8+13 = 21，括号里应填21。

二、简单运算类1. 题目：计算：125×32×25。

解析：把32分解成8×4，原式就变为125×8×4×25。

因为125×8 = 1000，4×25 = 100，所以结果为1000×100 = 100000。

2. 题目：99×99+99。

解析：根据乘法分配律，可以把式子转化为99×(99 + 1)=99×100 = 9900。

三、几何图形类1. 题目：一个长方形的长是12厘米，宽是8厘米，如果长增加4厘米，宽不变，这个长方形的面积增加了多少平方厘米？解析：原来长方形的面积是12×8 = 96平方厘米。

长增加4厘米后变为12 + 4 = 16厘米，新的面积是16×8 = 128平方厘米。

面积增加了128 96 = 32平方厘米。

2. 题目：一个等腰三角形的顶角是70°，那么它的底角是多少度？解析：等腰三角形的两个底角相等，三角形的内角和是180°。

所以底角的度数为(180°-70°)÷2 = 55°。

四、应用题类1. 题目：学校有图书1200本，其中故事书占30%，科技书占25%，其余的是文艺书，文艺书有多少本？解析：首先算出故事书的数量为1200×30% = 360本，科技书的数量为1200×25% = 300本。

小学四年级数学奥林匹克竞赛试题

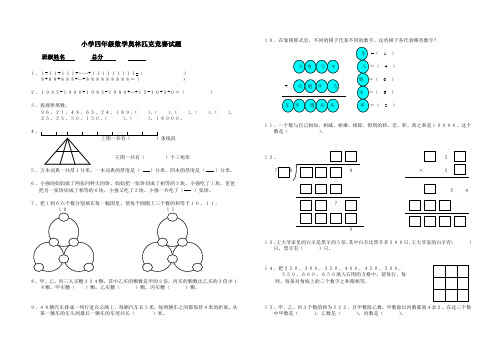
小学四年级数学奥林匹克竞赛试题班级姓名总分１、１+１１+１１１+……+１１１１１１１１１=（）８+８８+８８８+…+８８８８８８８８８＝（）２、１９９５-１９９０+１９８５-１９８０+…+１５-１０+５-０＝（）３、找规律填数。

９６、２１、４８、６３、２４、１８９、（）、（）、（）、（）、（）。

２５、２５、５０、１５０、（）、（）、１８０００。

４、上图一共有（）条线段左图一共有（）个三角形５、五本词典一共厚１分米，一本词典的厚度是（）分米。

６、小强的妈妈做了两张同样大的饼。

妈妈把一张饼切成了相等的３块，小强吃了１块。

爸爸把另一张饼切成了相等的６块，小强又吃了２块。

小强一共吃了（）张饼。

７、把１到６六个数分别填在每一幅图里，使每个圆圈上三个数的和等于１０、１１。

８、甲、乙、丙三人买糖３２４颗，其中乙买的颗数是甲的２倍，丙买的颗数比乙买的３倍少１８颗。

甲买糖（）颗，乙买糖（）颗，丙买糖（）颗。

９、４８辆汽车排成一列行进在公路上，每辆汽车长５米，每两辆车之间都保持４米的距离。

从第一辆车的车头到最后一辆车的车尾共长（）米。

１０、在象棋算式里，不同的棋子代表不同的数字。

这些棋子各代表哪些数字？=（ 1 ）＝（4）0）+6）＝（2）１１、一个数与自己相加、相减、相乘、相除，得到的和、差、积、商之和是１００００。

这个数是（）。

１２、５×２２４７０１３、王大爷家里的白羊是黑羊的５倍，其中白羊比黑羊多３００只，王大爷家的白羊有（）只，黑羊有（）只。

１４、把２５０、３００、３５０、４００、４５０、５００、５５０、６００、６５０填入右图的方格中，使每行、每列、每条对角线上的三个数字之和都相等。

１５、甲、乙、丙３个数的和为２２２，且甲数除乙数，甲数除以丙数都商４余２。

在这三个数中甲数是（），乙数是（），丙数是（）。

四年级奥林匹克数学题

四年级奥林匹克数学题
以下是一些适合四年级学生的奥林匹克数学题目，这些题目旨在培养学生的逻辑思维、问题解决和数学推理能力：
1.数字谜题：
将一个三位数的数字重新排列后得到一个新的三位数，将这两个三位数相加得到一个和。

例如，123 和321 相加得到444。

求证：所得的和一定可以被111 整除。

2.逻辑推理：
甲、乙、丙、丁四人参加数学竞赛，赛后他们四人预测名次的谈话如下：
甲说：“丙第一，我第三。

”
乙说：“我第一，丁第四。

”
丙说：“丁第二，我第三。

”
丁没有说话。

最后公布结果时，发现他们每人都只说对了一半，请说出四人这次竞赛的名次。

3.图形计数：
一个正方形的内部有1996 个点，以正方形的 4 个顶点和内部的1996 个点为顶点，将它剪成一些三角形。

问：一共可以剪成多少个三角形？如果沿上述这些点中某两点之间所连的线段剪开算作一刀，那么共需剪多少刀？
4.算式求值：
若A△B = A × B - (A + B)，求12△(6△8)的值。

5.最优化问题：
小悦、冬冬和阿奇三个人去吃雪糕，如果小悦吃 2 个，冬冬就吃 3 个，阿奇吃 5 个；
如果小悦吃4 个，冬冬就吃 5 个，阿奇就吃9 个。

已知阿奇共吃了119 个雪糕，请问：冬冬共吃了多少个雪糕？
6.年龄问题：
爸爸、妈妈今年的年龄和是78 岁。

6 年后，爸爸比妈妈大 4 岁。

爸爸今年多少岁？
这些问题旨在激发学生的数学兴趣和挑战他们的思维能力。

在解决这些问题时，学生可能需要应用数学知识，同时发展他们的逻辑和创造性思维。

小学奥林匹克数学周期问题练习(1)(无答案)

周期问题练习
1.根据下面的排列规律，算出第30个图形是什么？第60个呢？
△△○□△△○□△△……
2.王明把平时存起来的硬币按3个壹角，2个伍角，一个壹元……的顺序排列，请问：第150
枚是什么面值的硬币？
3.把1~160号卡片，依次发给小赵、小钱、小孙、小李四个人，已知1号发给小赵，问16号发给谁？99号呢？
4.30个7连乘的积得个位数是几？
5.42个8连乘，积的个位数字是几？
6.99个999连乘，积的个位数字是几？
7.有255朵花，按5朵红花，8朵黄花，11朵绿花的顺序轮流排列，最后一朵是什么颜色的
花？这255朵花中，红花、黄花、绿花各有多少朵？
8.
7
1=0.142857142857……小数点后面第120个数字是多少？
9.有56盏彩灯，按三盏红灯、四盏蓝灯、五盏黄灯的顺序排列着。

最后一盏灯是什么颜色的？三种颜色的灯各有多少盏？
10.下面是一个11位数，每3个相邻数字之和都是18，你知道“？”表示的数字是几吗？
11.下面是一个八位数，每3个相邻数字之和都是16，你知道问号表示的数字是几吗？
12.下面是一个11位数，每3个相邻数字之和都是15，你知道“？”表示的数是几吗？这个11位数是多少？
13.2001年10月1日是星期一，那么，2002年3月1日，是星期几？
14.2002年1月1日是星期二，2002年的5月1日是星期几？
15.如果今天是星期五，再过30天是星期几？。

四年级奥林匹克数学竞赛试题(无答案)

小学数学奥林匹克竞赛试题(四年级)姓名:__________ 班级:__________ 成绩:__________1.100-98+96-94+92-90+……8-6+4-2=( ).A.46B.48C.50D.522.四年级的同学参加“六一”儿童节的团体操表演,每横排人数同样多,每竖排人数也同样多。

王箐的位置是从左数第10人,从右数第8人,从前数第9人,从后数第7人。

则参加表演的同学有( )人。

A.272B.255C.245D.2103.一个挂钟,一点钟敲一下,两点钟敲两下,三点钟敲三下……十二点钟敲十二下,每逢半点敲一下。

这个挂钟一昼夜共敲( )下。

A.78B.102C.156D.1804.移动一根火柴,使下式成立:5.用24根火柴棒摆成下面的图形,请你移动四根火柴棒,使它变成两个大小相等的正方形。

6.请你将下面的图形改成能一笔画成的图形:7.如图,有8条线段,至少要分别测量编号为( )的三条线段的长度,才能求出这个图形的周长。

③⑧①A.①②⑤B.①②③C.①②⑦D.②③⑦8.排球、足球、篮球共90个,排球比足球的2倍多1个,篮球比足球的3倍少13个。

求排球、足球和篮球各有多少个?( )A.13、27、26B.17、33、64C.17、35、38D.13、25、529.一个除法算式,商是5,余数是1,被除数、除数、商和余数的和是109,除数是( )。

A.15B.16C.17D.1810.一根木头长24分米,要锯成4分米长的木棍。

若每锯一次要3分钟,锯完一段休息2分钟,则全部锯完需要( )分钟。

A.23B.25C.28D.3011.小洁比妈妈小24岁,5年以后妈妈的年龄是小洁的3倍,今年小洁( )岁。

A.6B.7C.8D.912.公共汽车共有男、女乘客100人,车到甲站后下车27个男的,9个女的,又上来3个男的,9个女的。

车到乙站后,上来8个女的,这时车上的男乘客正好是女乘客的3倍。

问原来男乘客比女乘客多多少人?( )A.66B.68C.72D.74。

四年级奥林匹克数学练习题(1)(无答案)

四年级奥数练习题1.甲、乙二人从相距60千米的两地同时相向而行,6时相遇。

如果二人的速度各增加1千米/时,那么相遇地点距前相遇地点1千米。

求甲乙二人的速度?2.某人沿着电车道旁的便道以4.5千米/时的速度步行,每0.12时有一辆电车迎面开过,每0.2时有一辆电车从后面追过。

如果电车按相等的时间间隔以同一速度不停地往返而行,那么电车的速度是多少?电车之间的时间间隔是多少?3.甲乙二人练习跑步,若甲让乙先跑10米,则甲跑5秒可追上乙;若乙比甲先跑2秒,则甲跑4秒能追上乙。

问:两人每秒各跑多少米?4.甲乙二人同时从A地出发去60千米外的B地，路上二人或者骑车或者步行。

由于仅有一辆自行车，所以途中任一时刻至多有一人骑车。

骑车的人可以随时将车放在路上继续步行前进，步行的人看到路上有自行车可以骑上车前进，也可以不骑车继续步行。

结果甲比乙晚到2小时，若步行速度为5千米／小时，骑车速度为15千米／小时，则甲至少步行多少千米。

5.有一艘船从甲港顺水而下行到乙港,马上又从乙港逆水返回甲港,共用8小时。

水流速度是每小时5千米,这样前4小时比后4小时多行60千米，甲乙两港相距多少千米。

6.张、李两人骑自行车同时从甲地出发,向同一方向进行,张的速度比李的速度每小时快4千米,张比李早2小时通过途中乙地,当李到达乙地时,张又前进了80千米, 那么甲、乙两地距离是多少千米？7.某单位沿着围墙外面的小路形成一个边长300米的正方形。

甲、乙两人分别从两个对角处沿逆时针方向同时出发。

如果甲每分走80米,乙每分走65米,经过多少时间甲才能看到乙?8.龟兔赛跑,全程2000米。

龟每分钟爬25米,兔每分钟跑320米。

兔子在途中睡了一觉,结果龟到终点时,兔离终点还有400米。

兔子在途中睡了几分钟?9.张、李两人骑自行车同时从甲地出发,向同一方向进行,张的速度比李的速度每小时快4千米,张比李早2小时通过途中乙地,当李到达乙地时,张又前进了80千米, 那么甲、乙两地距离是多少千米？10.一个自行车选手在相距950千米的甲、乙两地之间训练,从甲地出发,去时每90千米休息一次;到达乙地并休息一天后再沿原路返回,每100千米休息一次。

奥数四年级竞赛题

奥数四年级竞赛题一、计算类。

1. 计算：1 + 2 + 3+…+99 + 100。

解析：这是一个等差数列求和的问题。

等差数列求和公式为：（首项+末项）×项数÷2。

首项是1，末项是100，项数是100。

所以原式=(1 + 100)×100÷2=5050。

2. 99999×77778+33333×66666.解析：33333×66666 = 33333×3×22222=99999×22222.原式=99999×77778+99999×22222。

=99999×(77778 + 22222)=99999×100000.=9999900000.3. 2019×20202020 - 2020×20192019.解析：20202020=2020×10001.20192019 = 2019×10001.原式=2019×2020×10001-2020×2019×10001 = 0。

二、数字规律类。

4. 找规律填数：1，1，2，3，5，8，（），21，34。

解析：这是斐波那契数列，从第三项开始，每一项都等于前两项之和。

所以括号里的数是5 + 8=13。

5. 观察下面数列的规律，在括号内填上适当的数：3，5，9，15，23，33，45，（）解析：相邻两个数的差依次是2、4、6、8、10、12，下一个差应该是14。

所以括号里的数是45+14 = 59。

三、数论类。

6. 一个数除以5余3，除以6余4，除以7余5。

这个数最小是多少?解析：这个数加上2就能被5、6、7整除。

5、6、7的最小公倍数是5×6×7 = 210。

所以这个数最小是210 - 2=208。

7. 有一个三位数，它的各位数字之和是15，百位上的数字比十位上的数字大1，个位上的数字比十位上的数字大2，这个三位数是多少?解析：设十位上的数字为x，则百位上的数字为x + 1，个位上的数字为x+2。

小学数学奥林匹克竞赛试题(四年级)

小学数学奥林匹克竞赛试题(四年级) {骑大象的蚂蚁}1.找规律填数:（在横线上写出你发现的规律）21 26 19 24 ( ) ( ) 15 20 .(1)15,34 (2)17,18 (3)17,22 (4)23,25 2.甲乙两个数的和是218,如果再加上丙数,这时三个数的平均数比甲乙两数的平均数多5,丙数是( ).(1)124 (2) 122 (3)140 (4)1273.设X和Y是选自前500个自然数中的两个不同的数,那么(X+Y)?(X-Y)的最大值是( ).(1)1000 (2) 990 (3)999 (4)9984.选择: 8746×7576 的积的末四位数字是 ( ).(1) 6797 (3) 7669 (4) 67695. 现有1分,2分和5分的硬币各四枚,用其中的一些硬币支付2角3分钱,一共有多少种不同的支付方法？(1)4 (2) 5 (3)10 (4)8 6.右图中,所有正方形的个数是( )个.(1)10 (2)8 (3)11 (4)97.用0--4五个数字组成的最大的五位数与最小的五位数相差( ). (1)30870 (2)32900 (3)32976 (4)100008. 用0、5、8、7这四个数字，可以组成（）个不同的四位数？(1)10 (2)18 (3)11 (4)99. 学校进行乒乓球选拔赛，每个参赛选手都要和其他所有选手各赛一场，一共进行了21场比赛，有多少人参加了选拔赛？(1)7 (2)8 (3)11 (4)910 一个长方形的纸对折成三等份后变成了一个正方形，正方形的周长是40厘米，那么原来长方形的周长是多少？(1)70 (2)80 (3)100 (4)9611.小明每分钟走50米,小红每分钟走60 米,两人从相距660米的两村同时沿一条公路相对出发,8分钟后两人相距( )米.(1)75 (2)200 (3)220 (4)9012甲、乙、丙、丁四位同学的运动衫上印有不同的号码。