单种分析型_1839140

合集下载

16种统计分析方法

16种常用的数据分析方法汇总2015-11-10 分类：数据分析评论(0)经常会有朋友问到一个朋友，数据分析常用的分析方法有哪些，我需要学习哪个等等之类的问题，今天数据分析精选给大家整理了十六种常用的数据分析方法，供大家参考学习。

一、描述统计描述性统计是指运用制表和分类，图形以及计筠概括性数据来描述数据的集中趋势、离散趋势、偏度、峰度。

1、缺失值填充：常用方法：剔除法、均值法、最小邻居法、比率回归法、决策树法。

2、正态性检验：很多统计方法都要求数值服从或近似服从正态分布，所以之前需要进行正态性检验。

常用方法：非参数检验的K-量检验、P-P图、Q-Q图、W 检验、动差法。

二、假设检验1、参数检验参数检验是在已知总体分布的条件下（一股要求总体服从正态分布）对一些主要的参数(如均值、百分数、方差、相关系数等）进行的检验。

1）U验使用条件：当样本含量n较大时，样本值符合正态分布2）T检验使用条件：当样本含量n较小时，样本值符合正态分布A 单样本t检验：推断该样本来自的总体均数μ与已知的某一总体均数μ0 (常为理论值或标准值)有无差别；B 配对样本t检验：当总体均数未知时，且两个样本可以配对，同对中的两者在可能会影响处理效果的各种条件方面扱为相似；C 两独立样本t检验：无法找到在各方面极为相似的两样本作配对比较时使用。

2、非参数检验非参数检验则不考虑总体分布是否已知，常常也不是针对总体参数，而是针对总体的某些一股性假设（如总体分布的位罝是否相同，总体分布是否正态）进行检验。

适用情况：顺序类型的数据资料，这类数据的分布形态一般是未知的。

A 虽然是连续数据，但总体分布形态未知或者非正态；B 体分布虽然正态，数据也是连续类型，但样本容量极小，如10以下；主要方法包括：卡方检验、秩和检验、二项检验、游程检验、K-量检验等。

三、信度分析检査测量的可信度，例如调查问卷的真实性。

分类：1、外在信度：不同时间测量时量表的一致性程度，常用方法重测信度2、内在信度；每个量表是否测量到单一的概念，同时组成两表的内在体项一致性如何，常用方法分半信度。

单种分析型_1834077

Ⅰ. ADD A CHAPTER TITLE
Asadal has been running one of the biggest domain and web hosting sites in Korea since March 1998. More than 3,000,000 people have visited our website, for domain registration and web hosting.
Asadal has been running one of the biggest domain and web hosting sites in Korea since March 1998. More than 3,000,000 people have visited our website, for domain registration and web hosting.
Asadal has been running one of the biggest domain and web hosting sites in Korea since March 1998. More than 3,000,000 people have visited our website, for domain registration and web hosting.
Asadal has been running one of the biggest domain and web hosting sites in Korea since March 1998. More than 3,000,000 people have visited our website, for domain registration and web hosting.

单变量分析

某校三个系各选5名同学参加某校三个系各选名同学参加竞赛.他们的成绩分别如下他们的成绩分别如下: 竞赛他们的成绩分别如下
中文系:78, 79, 80, 81. 82 X = 80 数学系:65, 72, 80, 88, 95 X = 80 外语系:35, 78, 89, 98, 100 X = 80
当数据为偶数时中位数处于中间两个数值之间, 两个数值之间,这时一般以中间两个数值的平均数作为中位数. 个数值的平均数作为中位数.
六个工厂的职工人数, 规模依次为300 六个工厂的职工人数, 规模依次为300 200人 800人 500人 400、人, 200人, 800人, 500人, 400、 1000人求中位数。 1000人.求中位数。
思考：频率分布适用于哪些变量的测量？思考：频率分布适用于哪些变量的测量？
例：某班学生年龄分布
年龄（年龄（岁） 17 18 19 20 21 合计百分比 8 20 40 20 12 100（ 25） 100（n＝25）
期望收入分布频率表
期望收入（元） 1000及以下 1001-1500 1501－2500 2501以上合计百分比 0 0 75 25 100（n＝8）
标准差(Standand Deviation) 标准差
标准差是指一组数据对其平均数的偏差平方的算术平均数的平方根.它是用得最多的, 算术平均数的平方根.它是用得最多的,也是最重要的离散量数统计量. 重要的离散量数统计量.
原始资料计算标准差
中文系:78, 中文系:78, 79, 80, 81. 82 数学系:65, 数学系:65, 72, 80, 88, 95 外语系:35, 外语系:35, 78, 89, 98, 100

10大经典数据分析模型

10大经典数据分析模型模型分析法就是依据各种成熟的、经过实践论证的管理模型对问题进行分析的方法。

在长时间的企业管理理论研究和实践过程中，将企业经营管理中一些经典的相关关系以一个固定模型的方式描述出来，揭示企业系统内部很多本质性的关系，供企业用来分析自己的经营管理状况，针对企业管理出现的不同问题，能采用最行之有效的模型分析往往可以事半功倍。

1、波特五种竞争力分析模型XXX的五种竞争力分析模型被广泛应用于很多行业的战略制定。

XXX认为在任何行业中，无论是国内还是国际，无论是提供产品还是提供服务，竞争的规则都包括在五种竞争力量内。

这五种竞争力就是1.企业间的竞争2.潜在新竞争者的进入3.潜在替代品的开发4.供应商的议价能力5.购买者的议价能力这五种竞争力量决定了企业的盈利能力和水平。

竞争对手企业间的竞争是五种力量中最主要的一种。

只要那些比竞争对手的战略更具上风的战略才可能获得成功。

为此，公司必须在市场、价格、质量、产量、功用、服务、研发等方面建立自己的核心竞争上风。

影响行业内企业竞争的因素有：产业增加、固定（存储）成本/附加价值周期性生产过剩、产品差异、商标专有、转换成本、集中与平衡、信息复杂性、竞争者的多样性、公司的风险、退出壁垒等。

新进入者企业必须对新的市场进入者保持足够的警惕，他们的存在将使企业做出相应的反应，而这样又不可避免地需要公司投入相应的资源。

影响潜在新竞争者进入的因素有：经济规模、专卖产品的差别、商标专有、资本需求、分销渠道、绝对成本优势、政府政策、行业内企业的预期反击等。

购买者当用户分布集中、规模较大或大批量购货时，他们的议价能力将成为影响产业竞争强度的一个主要因素。

决定购买者力量的因素又：买方的集中程度相对于企业的集中程度、买方的数量、买方转换成底细对企业转换成本、买方信息、后向整合本领、替代品、克服危机的本领、价格/购买总量、产物差异、品牌专有、质量/机能影响、买方利润、决策者的激励。

单因素分析-定性资料2013.3.26

四格表χ2统计量的校正
R× C列联表χ2统计量的校正
1≤T<5格子数不超过1/5 且没有格子T<1
超过1/5格子数1≤T<5，或有格子T<1: 1) 增加样本量； 2) 专业允许情况下，将理论频数过小的行或列与性质相近的邻行或邻列合并； 3) 删除理论频数过小的行/列； 4) 无序R×C表用确切概率法。
正确输出的表格
未使用weight语句
proc freq; weight count; tables smoke*low; run;
proc freq order=data; weight count; tables smoke*low; run;
data a1; input smoke low count @@; cards; 1 1 30 1 0 44 0 1 29 0 0 86 ; run;
SAS过程步
proc freq data=lx2; tables a*b / agree; weight count; run;
/*b+c<40 校正公式*/ proc freq data=lx2; tables a*b; exact MCNEM; weight count; run;
精确概率法 (R×C表)
关联强度的计算
队列研究：相对危险度 (Relative Risk, RR)
暴露组发病率与非暴露组发病率之比
RR
a /(a b) c/(c d)
病例-对照研究：比值比 (Odds Ratio, OR )
病例组的暴露比值= 对照组的暴露比值=
a/(a c) a/c c /(a c)
或
0
0 1 0
0

主成分分析法例子

x7 0.79 0.009 -0.93 -0.046 0.672 0.658 1 -0.03 0.89
x8 0.156 -0.078 -0.109 -0.031 0.098 0.222 -0.03 1
0.29
x9 0.744 0.094 -0.924 0.073 0.747 0.707 0.89 0.29
▲贡献率:
i
p
k
k 1
(i 1,2,, p)
▲合计贡献率:
i
k
k 1
p
k
k 1
(i 1,2,, p)
一般取合计贡献率达85—95%旳特征值 1, 2 ,, m
所相应旳第一、第二、…、第m（m≤p）个主成份。
④各主成份旳得分
l11 l12 l1p x1
Z
l21
l22
l2
p
x2
二主成份z2代表了人均资源量。
③第三主成份z3，与x8呈显出旳正有关程度最高，其次是x6，而与x7呈负有关，所以能够以为第三主成份在一定程度上代表了农业经济构造。
显然，用三个主成份z1、z2、z3替代原来9个变量（x1， x2，…，x9），描述农业生态经济系统，能够使问题更进
一步简化、明了。
x4
0.0042
0.868
0.0037
75.346
x5
0.813
0.444
-0.0011
85.811
x6
0.819
0.179
0.125
71.843
x7
0.933
-0.133
-0.251
95.118
x8
0.197
-0.1
0.97
98.971

单变量变异数分析

Post Hoc Tests 事后比较
事后比较结果，采两两配对组别比较。从 Scheffe 方法作事后比较可以看出以适用度而言，国外品牌显着高于国内品牌，国外品牌与组装电脑没有显着差异，国内品牌与组装电脑没有显着差异。
范例结果整理如下：
1.叙述性统计量
2.变异数分析统计表
*P<.05 事后比较：事后比较结果，以适用度而言，国外品牌显着高于国内品牌，国外品牌与组装电脑没有显着差异，国内品牌与组装电脑没有显着差异。
2.相依样本,有二种情形 (1)重复量数：同一组受测者, 重复接受多次(k)的测试以比较之间的差异 (2)配对组法：选择一个与依变数有关控制配对条件完全相同, 以比较k组受测者在依变数的差异
10-3 变异数分析的基本假设条件
变异数分析的基本假设条件有常态、线性、变异数同质性。我们介绍如下：
常态：直方图, 偏度(skewness)和峰度(kcat osis), 检定, 改正 (非常态可以透过资料转型来改正)
计算t值 t值 = u1 (平均数) - u2 (平均数) / 组的平均数标准差 u1 是第一组的平均数 u2 是第二组的平均数
查t crit标准值在研究者指定可接受t分配型态 I (type I) 错误机率a (例如： 0.05或0.01) 样本1和样本2的degree of freedm = (N1+N2) – 2 我们可以透过查表, 得到 t crit标准值
➢F检定除了t检定外，我们也常用F值来检定单变量多组平均数是否颢着
10-5 单变量变异数分析范例
我们想了解不同年龄层 A组20 ~29岁，B组30 ~39岁，C组 40~49岁，对笔记型Bubble喜好程度是否有差异，随机抽取年龄层各5个人，以1 – 10的分数请他们评分如下：

spss方差分析实例

SPSS——单因素方差分析实例单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOV A过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1所示。

表1-1不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中，变量格式如图1-1。

分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOV A”项，系统打开单因素方差分析设置窗口如图1-2。

3）设置分析变量因变量: 选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量: 选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

单因素方差分析的“0ne-Way ANOV A”过程允许进行高达5次的均值多项式比较。

多项式的系数需要由读者自己根据研究的需要输入。

具体的操作步骤如下：①选中“Polynomial”复选项，该操作激活其右面的“Degree”参数框。

SPSS单因素方差分析

SPSS单因素方差分析单因素方差分析单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOVA过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measu re过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1所示。

表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数水稻品种重复12345141333837312393735393434035353834数据保存在“data1.sav”文件中，变量格式如图1-1。

图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

1）准备分析数据在数据编辑窗口中输入数据。

建立因变量“幼虫”和因素水平变量“品种”，然后输入对应的数值，如图1-1所示。

或者打开已存在的数据文件“dat a1.sav”。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOVA”项，系统打开单因素方差分析设置窗口如图1-2。

图1-2 单因素方差分析窗口3）设置分析变量因变量: 选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量: 选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

图1-3 “Contrasts”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

SPSS常用分析方法操作步骤之欧阳与创编

SPSS常用分析方法操作步骤一、单变量单因素方差分析例题：某个年级有三个班，现在对他们的一次数学考试成绩进行随机抽（见下表），试在显著性水平0.005下检验各班级的平均分数有无显著差异（数据文件：数学考试成绩.sav）。

（1）建立数学成绩数据文件。

（2）选择“分析”→“比较均值”→“单因素方差”，打开单因素方差分析窗口，将“数学成绩”移入因变量列表框，将“班级”移入因子列表框。

（3）单击“两两比较”按钮，打开“单因素ANOVA两两比较”窗口。

（4）在假定方差齐性选项栏中选择常用的LSD 检验法，在未假定方差齐性选项栏中选择Tamhane’s检验法。

在显著性水平框中输入0.05，点击继续，回到方差分析窗口。

（5）单击“选项”按钮，打开“单因素ANOVA选项”窗口，在统计量选项框中勾选“描述性”和“方差同质性检验”。

并勾选均值图复选框，点击“继续”，回到“单因素ANOVA选项”窗口，点击确定，就会在输出窗口中输出分析结果。

二、单变量多因素方差分析研究不同温度与不同湿度对粘虫发育历期的影响，得试验数据如表5-7。

分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异（数据文件：粘虫.sav）。

（1）建立数据文件“粘虫.sav”。

（2）选择“分析”→“一般线性模型”→“单变量”，打开单变量设置窗口。

（3）分析模型选择：此处我们选用默认；（4）比较方法选择：在窗口中单击“对比”按钮，打开“单变量：对比”窗口进行设置，单击“继续”返回；（5）均值轮廓图选择：单击“绘制”按钮，设置比较模型中的边际均值轮廓图，单击“继续”返回；（6）“两两比较”选择，用于设置两两比较检验，本例中设置为“温度”和“湿度”。

三、相关分析调查了29人身高、体重和肺活量的数据见下表，试分析这三者之间的相互关系。

（1）建立数据文件“学生生理数据.sav”。

（2）选择“分析”→“相关”→“双变量”，打开双变量相关分析对话框。

（3）选择分析变量：将“身高”、“体重”和“肺活量”分别移入分析变量框中。

具有局部和全局注意力机制的图注意力网络学习单样本组学数据表征

第61卷第6期吉林大学学报(理学版)V o l .61 N o .62023年11月J o u r n a l o f J i l i nU n i v e r s i t y (S c i e n c eE d i t i o n )N o v 2023d o i :10.13413/j .c n k i .jd x b l x b .2023047具有局部和全局注意力机制的图注意力网络学习单样本组学数据表征周丰丰1,2,张金楷1(1.吉林大学计算机科学与技术学院,长春130012;2.吉林大学符号计算与知识工程教育部重点实验室,长春130012)摘要:针对生物组学数据中基因数目远大于样本数目的高维大p 小n 问题,提出一种具有局部和全局注意力机制的图注意力网络G A T O r .该模型首先在组学数据上利用P e a r s o n 相关系数计算特征之间的相关性,构建组学数据的单样本网络;然后提出一种结合局部和全局注意力机制的图注意力网络从单样本网络中学习基于图的组学特征表示,从而将组学数据的高维特性转化为低维表示.实验结果表明,G A T O r 与其他传统分类算法相比,在分类任务的准确率及其他指标上均取得了较优性能.关键词:组学数据;单样本网络;注意力机制;图注意力网络中图分类号:T P 391 文献标志码:A 文章编号:1671-5489(2023)06-1351-07G r a phA t t e n t i o nN e t w o r kw i t hL o c a l a n dG l o b a lA t t e n t i o n M e c h a n i s mt oL e a r nS i n g l e -S a m p l eO m i cD a t aR e pr e s e n t a t i o n Z HO U F e n g f e n g 1,2,Z H A N GJ i n k a i 1(1.C o l l e g e o f C o m p u t e rS c i e n c e a n dT e c h n o l o g y ,J i l i nU n i v e r s i t y ,C h a n gc h u n 130012,C h i n a ;2.K e y L a b o r a t o r y o f S y m b o lC o m p u t a t i o na n dK n o w l ed g eE n g i ne e r i n g of M i n i s t r y o f Ed u c a t i o n ,J i l i nU n i ve r s i t y ,C h a n gc h u n 130012,C h i n a )收稿日期:2023-02-14.第一作者简介:周丰丰(1977 ),男,汉族,博士,教授,博士生导师,从事健康大数据的研究,E -m a i l :F e n g f e n g Z h o u @g m a i l .c o m.基金项目:国家自然科学基金(批准号:62072212;U 19A 2061)㊁吉林省中青年科技创新创业卓越人才(团队)项目(创新类)(批准号:20210509055R Q )和吉林省大数据智能计算实验室项目(批准号:20180622002J C ).A b s t r a c t :A i m i n g a t t h eh i g h -d i m e n s i o n a l b i g p s m a l l n p r o b l e m w h e r et h en u m b e ro f g e n e s i n b i o m i c s d a t a (d e n o t e da s p )w a s f a rm o r e t h a n t h en u m b e r o f s a m p l e s (d e n o t e d a s n ),w e p r o po s da g r a p ha t t e n t i o nn e t w o r kG A T O rw i t h l o c a l a n d g l o b a l a t t e n t i o nm e c h a n i s m s .F i r s t l y,t h em o d e l u s e d P e a r s o nc o r r e l a t i o nc o e f f i c i e n tt oc a l c u l a t et h ec o r r e l a t i o nb e t w e e nf e a t u r e so nt h eo m i cd a t a ,a n dc o n s t r u c t e das i n g l es a m p l en e t w o r ko ft h eo m i cd a t a .Se c o n d l y ,w e p r o p o s e da g r a pha t t e n t i o n n e t w o r kw h i c hc o m b i n e dl o c a l a n d g l o b a l a t t e n t i o n m e c h a n i s m st ol e a r n g r a p h -b a s e do m i c sf e a t u r e r e p r e s e n t a t i o n f r o ma s i n g l e -s a m p l e n e t w o r k ,t h e r e b y t r a n s f o r m i n g t h e h i g h -d i me n s i o n a l c h a r a c t e r i s t i c s of t h e o m i c sd a t a i n t ol o w -d i m e n s i o n a l r e p r e s e n t a t i o n s .T h ee x p e r i m e n t a l r e s u l t ss h o wt h a tc o m p a r e d w i t ho t h e r t r a d i t i o n a l c l a s s i f i c a t i o na lg o r i th m s ,G A T O r a c hi e v e sb e t t e r p e r f o r m a n c e i nc l a s s i f i c a t i o n t a s ka c c u r a c y an do t h e r i n d e x e s .K e y w o r d s :o m i c d a t a ;s i n g l e -s a m p l en e t w o r k ;a t t e n t i o nm e c h a n i s m ;g r a p ha t t e n t i o nn e t w o r k2531吉林大学学报(理学版)第61卷近年来,现代高通量生物医学技术得到快速创新和发展,生物数据积累加速[1].这些数据极大促进了许多生物学过程的潜在机制研究,包括衰老过程和复杂的疾病发病机制[2].但大多数生物组学数据集具有高噪声㊁多维度和多维异质性的特点.此外,生物组学的许多特征与表型无关,特征之间存在冗余.高通量技术生产的生物组学大多存在大p小n 的维度灾难问题,其中p指特征数量,n指样本数量.因此,组学数据存在高维问题.特征选择是克服高维组学数据维数灾难的有效方法.特征选择方法在生物信息学领域被广泛应用于生物标记物识别和数据降维.而现有的应用于组学数据的特征选择算法,基本都是使用传统的分类学习算法对数据进行分类,即在组学数据降维的研究中,很少考虑深度特征选择算法,导致组学数据分类精度较低.目前基于深度学习的方法有许多尝试采用基于图的混合策略,在分析前将每个组学建模为一个单独的图,利用图嵌入方法从每个网络中学习节点及其周围环境的低维表示.然后将新的基于图的特征组合并输入其他机器学习模型进行预测㊁分类等.在组学数据上构建网络的常用方法包括蛋白质相互作用网络㊁基于相关性的网络㊁比值网络等.J o n s s o n等[3]通过分析蛋白质相互作用网络,发现与癌变相关的蛋白质特征常具有更密切的相关性,表明功能相似的特征或特征集通常以模块化的形式反应有机体功能的表型.W a n g等[4]通过分析蛋白质相互作用网络揭示了肝脏特异性蛋白㊁肝脏疾病蛋白和重要信号通路分子之间的相互作用特征.L i u等[5]利用P e a r s o n相关系数计算特征之间的相关性,建立相应的生物网络,利用有特定样本和无特定样本时特征之间的相关性变化构建单个样本网络,为疾病的个性化治疗提供了帮助.N e t z e r等[6]使用配对生物标记标识符(p a i r e db i o m a r k e r i d e n t i f i e r s, P B I)作为指标,测量不同群体特征比的变化,并构建了相应的生物网络.将单个特征作为网络节点,通过特征之间比值关系的变化构建网络的方法首先应用于代谢组学数据,之后推广到基因组学数据[7].因此,选择合适的网络并找到高效的分类学习算法尤为重要.本文在从组学数据的单样本网络中学习有用信息的基础上,提出一种具有局部和全局注意力机制的图注意力网络(G A T O r).首先,从每个样本的组学数据中构建一个图,以一个组学特征作为一个节点,两两特征之间的相关性作为边的权值;由于构建图的时间复杂度为平方,因此对无关特征进行预筛选,以减少单样本图中组学特征的数量.其次,提取图注意力网络中集成的局部和全局注意模块的有用信息作为工程特征,并从该单样本网络中学习到的特征进行类预测任务.实验结果表明,与现有的组学分类方法相比,G A T O r具有更好的分类性能.1算法设计1.1单样本网络单样本网络是一种基于参考数据集的利用单样本数据构建的生物分子网络,它是一种将复杂网络的理论和方法应用于疾病研究和药物开发的方法,可从系统的角度识别个体疾病所涉及的相互作用或功能失调[8].L i u等[5]提出了基于P e a r s o n相关性的单样本网络,在疾病表征基因调控网络的背景下获得个体特异性或样本特异性网络.对于节点网络,其构建需要多个样本,但在临床实践中通常无法获得.在单样本[9]的基础上对节点网络进行表征或推断是必要的.这种方法的优点是网络只依赖于从每个模型中学习基于图的变量,这些变量可用于其他机器学习模型的输入,用于聚类㊁子类型发现或生存预测.1.2图注意力网络图神经网络通过聚合网络中多层邻居节点对当前节点的影响,更新节点的嵌入式表示,然后用更新的嵌入式表示完成后续任务,如节点分类和链接预测等[10].B r u n a等[11]提出了一种基于谱域的图卷积神经网络(G C N),谱域的卷积需要在L a p l a c e矩阵上进行特征分解,每次都需进行节点的聚合,非常耗费算力.D e f f e r r a r d等[12]对卷积核进行近似操作,提出了C h e b y s h e v网络,该网络避免了L a p l a c e矩阵的特征分解,降低了运算的复杂度.K i p f等[13]对其进行了进一步优化,提出了最初的图卷积网络模型,在谱域上的图卷积网络可以发挥其最大的效能.图注意力网络(G A T)先在各节点间采用消息传递的方式聚合邻居节点[14],然后更新自身节点的信息,通过学习注意力权值,放大更重要的节点和边的权重,使用注意力机制定义聚合函数,从而计算并更新节点的特征信息,得到节点局部结构新的特征.G A T 网络由堆叠简单的图注意力层(g r a p ha t t e n t i o n l a y e r )实现,每个注意力层对节点对(i ,j ),注意力系数计算方式为a i j =e x p {L e a k y R e L U (a [W h i ] [W h j ])}ðj ɪN ie x p {L e a k y R e L U (a [W h i ] [W h j ])},(1)其中a i j 为节点j 到i 的注意力系数,N i 表示节点i 的邻居节点.节点输入特征为h ={h 1,h 2, ,h N },h i ɪℝF ,节点特征的输出为h ᶄ={h ᶄ1,h ᶄ2, ,h ᶄN },h ᶄi ɪℝF,其中N ,F 分别表示节点个数和输入特征维数;W ɪℝF ᶄˑF 表示在每个节点上应用的线性变换权重矩阵;a ɪℝ2F ᶄ为权重向量,可以将输入映射到ℝ.最终使用S o f t m a x 进行归一化并加入L e a k yR e L U 以提供非线性.最终节点的特征输出可表示为h ᶄi =σðj ɪN ia i j W h ()j ,(2)其中σ表示非线性激活函数,如S i gm o i d 和R e L U.1.3 G A T O r 网络本文提出的基于局部和全局注意力机制学习组学特征表示的图注意力网络(G A T O r)整体结构如图1所示.由图1可见,其主要包含两部分:1)单样本网络,将每个组学数据样本建模为一个单样本网络,将特征作为节点,每对特征之间的相关性作为边;2)具有局部和全局注意力机制的图注意力网图1 基于局部和全局注意力机制学习组学特征表示的图注意力网络F i g .1G r a pha t t e n t i o nn e t w o r kb a s e do n l o c a l a n d gl o b a l a t t e n t i o nm e c h a n i s mt o l e a r no m i c s f e a t u r e r e pr e s e n t a t i o n 络,用于从单样本网络中学习表征特征向量进行分类任务.G A T O r 网络的优化目标是评估中心节点附近某个邻居节点的重要性,从而为其邻居节点分配不同权重.中心节点的局部注意力只关注其一阶邻居,而全局注意力则关注图中所有节点,局部与全局注意力机制的融合优化了特征提取能力,使下游的分类性能得到提高.G A T O r 网络引入了注意力机制,用于解决G C N 对邻居节点一视同仁的局限性,通过分配不同的权重给不同的邻居,赋予模型更强的特征表示能力,将原始图数据转换到低维空间并保留关键信息,生成保留原始图中某些重要信息的低维向量,同时也提高了节点分类等下游任务的分类性能.1.3.1 构建单样本网络本文将组学数据的样本作为单样本网络训练基于图的G A T O r 模型.考虑到现实情况,仅利用一个样本数据检测复杂疾病恶性突变的临界状态和预警信号至关重要.虽然表达数据或测序数据在单个样本的基础上提供了关于分子谱的信息,但由于数据集每个病人只有一个样本数据,无法利用传统方法计算出基因的相似性网络,因此需给出足量的参考样本表征正常时期基因之间的相关性,通过对比单个样本与参考样本之间的差异反应单样本特征[5,15].首先基于基因共表达网络构建出参考网络,通常用无向图表示,网络中的节点表示特征,边表示特征之间的相关性.给定n 个参考样本,参考样本数据中任意一对特征x 和y 之间的相关性可使用P e a r s o n 相关系数(P C C )计算,用公式表示为P C C n (x ,y )=ðni =1(x i-x )(y i-y )ðni =1(x i-x )2ðni =1(y i-y )2,(3)3531 第6期周丰丰,等:具有局部和全局注意力机制的图注意力网络学习单样本组学数据表征其中x i 和y i 分别为参考样本中第i 个样本特征x 和y 的值,x 和y 分别为参考样本组中特征x 和y 的平均值.Y u 等[16]检索了查询样本中每个组学特征相对于参考样本子集的方差,并计算了查询样本中两个组学特征方差向量之间的P C C .在查询样本中,这两个组学特征之间的P C C 值被定义为基于参考的变异P C C (r v P C C ).r v P C C 取值范围为-1~1,当r v P C C 接近-1或1时,将两个查询特征定义为正相关或负相关[17].组学数据集通常具有数千个甚至更多的特征,使得构建单样本网络的平方时间复杂性变得不切实际.本文使用t 检验衡量每个特征与类标签的关联,并选择排名靠前的k 个特征(本文中k =800)[18]进行进一步分析.采用P C C 测量特征间的冗余度.至此已构建出一个完整的单样本网络,该网络为一个加权无向图,可用于各种基于图的深度神经网络,为在网络层面表征个性化特征并分析生物系统开辟了新途径.1.3.2 局部与全局注意力机制G A T 使用特征向量a 学习节点及其邻居的相对重要性,可能无法捕获分类任务的有用信息.假设与节点本身相似的邻居节点可能更重要,则可通过直接计算两个相连节点之间的相似度得到节点的相对重要性[19].节点的局部注意力只关注其邻居,而节点的全局注意力从图中所有节点中提取信息.基于双重注意力机制的网络,通过对低层详细信息和高层语义信息的注意获取高质量㊁独特并可鉴别的特征[20].局部注意力系数计算公式为a (L)i j =e x p {β㊃c o s (W h i ,W h j )}ðj ɪN iex p {β㊃c o s (W h i ,W h j )},(4)式中β表示标准偏差,c o s (㊃)用于计算余弦相似度.为聚合来自节点邻域的信息,式(2)可表示为h ᶄ(L )i=σðj ɪN (v i)a(L )i jW h ()j .(5) 局部注意力模块与图注意力模块的区别:本文显式地使用c o s (㊃)计算节点之间的相似度作为相对重要性权重,而传统方法使用可学习参数a 学习节点之间的相对重要性.局部注意力是在图上一个节点的邻居上计算的,而本文在所有实体的集合上构造局部注意力.本文还实现了全局注意力机制,其中节点可有选择地聚合图中任何其他节点的信息.扩展图注意力层以进行全局操作.M o s t a f a 等[21]提出了一种基于欧氏距离的注意力系数.全局注意力系数可表示为a (G)i j =e x p {-λ ΦW h i -ΦW h j 2}ðNj =1e x p {-λ ΦW h i -ΦW h j 2},(6)其中:ΦɪℝD ˑF ᶄ为嵌入矩阵,它将节点特征转换到d 维节点相似度空间;λ表示标准差的逆, ㊃ 2表示2范数.节点i 的全局加权注意力为h ᶄ(G )i=σðNj =1a (G)i j W h ()j .(7)将局部聚集的特征向量和全局聚集的特征向量相连接,得到最终的特征向量h ᶄi 为h ᶄi =(h ᶄ(L )i h ᶄ(G )i),(8)其中为串联运算符.式(8)也可视为将不同注意力头的输出相连接.使用A 个注意力头,输出特征向量的维数为2A F ᶄ,最终的特征向量也可表示为h ᶄi = Aa =1g (G ,[h 1,h N ];W a ,Φa ),(9)4531 吉林大学学报(理学版) 第61卷其中G 表示单样本网络的无向图,注意力头数A =2,g 表示进行注意力操作的过程.2 实验2.1 数据集使用4个数据集评估G A T O r 特征工程算法,这4个数据集均选自文献[22]中整理的组学数据集:数据集R O S MA P 提供了阿尔茨海默病(A D )患者与正常对照组(N C )的组学数据;数据集L G G 用于低级别胶质瘤(L G G )的分级分类;数据集K I P A N 用于肾癌类型分类;数据集B R C A 用于乳腺癌P AM 50亚型的分型任务.每个数据集的预处理包括排除缺失值的特征以及随机选择参考样本.各数据集信息列于表1,其中第四列给出了每个数据集中两个或多个类的详细信息,最后一列给出了3种类型组学数据的特征数量,即m R N A 表达(m R N A )㊁D N A 甲基化(M e t h y )和m i R N A 表达(m i R N A ).数据缺失的特征被排除在进一步分析外.由于本文不讨论多组学整合分析,因此3种类型组学数据混在一起进行计算.表1 各数据集信息T a b l e 1 I n f o r m a t i o no f e a c hd a t a s e t数据集样本数特征数数据集类别m R N A ,M e t h y,m i R N A 特征数量R O S MA P 35179986N C (169),A D (182)55889,23788,309L G G51041193G r a d e 2(246),G r a d e 3(264)20531,20114,548K I P A N 65841087K I C H (66),K I R C (318),K I R P (274)20531,20111,445B R C A 87541140N o r m a l -l i k e (115),B a s a l -l i k e (131),H E R 2-e n r i c h e d (46),L u m i n a lA (436),L u m i n a l B (147)20531,20106,5032.2 评价指标在进行构建单样本网络等时间复杂度较高的任务前,先通过特征预筛选降低特征维度.由表1可见,4个数据集的特征数量都远大于样本数量.考虑到构建单样本网络的平方时间复杂度,因此仅对有限数量的原始组学(OM I C )特征设计G A T O r 特征.通过分层策略将每个数据集随机分为80%的训练数据集和20%的测试数据集,即保持训练数据集和测试数据集的类分布.二分类任务的评价指标为分类精度(A C C )和R O C 曲线下面积(A U C ).对于多分类任务,只计算A C C .2.3 实验结果及分析2.3.1 对比实验本文将G A T O r 的分类性能与以下7种组学数据基线方法进行比较.1)k 近邻分类器(K N N ):基于查询样本的k 个近邻的类别实现投票策略.2)支持向量机分类器(S VM ):一种流行的基于最大间隔分割平面的分类器.3)L 1正则化训练的线性回归(L a s s o ):L a s s o 回归是线性回归模型的一种收缩和变量选择方法,用于获取定量响应变量的预测误差最小的预测变量子集.4)随机森林分类器(R F ):融合多棵随机树的决策.5)朴素B a y e s 分类器(N B ):基于B a y e s 定义和特征条件独立假设的分类器方法.6)极限梯度提升算法(X G B o o s t ):提供了一种可扩展的快速梯度提升分类系统.7)全连接神经网络分类器(N N ):使用具有交叉熵损失的全连接神经网络作为基线神经网络分类器.G A T O r 算法与7种基线方法在4个数据集分类任务上的性能评估列于表2.由表2可见,G A T O r 框架在4个数据集上的A C C 和A U C 指标均优于其他基线分类器.与传统的组学分类方法相比,G A T O r 还获得了相对较小的标准差,具有更好的分类性能.5531 第6期周丰丰,等:具有局部和全局注意力机制的图注意力网络学习单样本组学数据表征表2 G A T O r 算法与7种基线方法在4个数据集分类任务上的性能评估T a b l e 2 P e r f o r m a n c e e v a l u a t i o no fG A T O r a l g o r i t h ma n d 7b a s e l i n em e t h o d s f o r c l a s s i f i c a t i o n t a s k s o n4d a t a s e t s 方法A C CR O S MA PL G GK I P A NB RC AA U CR O S MA PL G GK N N0.657ʃ0.0360.729ʃ0.0340.967ʃ0.0110.742ʃ0.0240.709ʃ0.0450.799ʃ0.038S VM0.770ʃ0.0240.754ʃ0.0460.995ʃ0.0030.729ʃ0.0180.770ʃ0.0260.754ʃ0.046L a s s o 0.694ʃ0.0370.761ʃ0.0180.974ʃ0.0020.732ʃ0.0120.770ʃ0.0350.823ʃ0.010R F 0.726ʃ0.0290.748ʃ0.0120.981ʃ0.0060.754ʃ0.0090.811ʃ0.0190.823ʃ0.023N B0.742ʃ0.0310.753ʃ0.0280.993ʃ0.0060.765ʃ0.0110.817ʃ0.0230.829ʃ0.028X G B o o s t 0.760ʃ0.0460.756ʃ0.0400.993ʃ0.0080.781ʃ0.0080.837ʃ0.0300.840ʃ0.037N N0.755ʃ0.0210.737ʃ0.0230.991ʃ0.0050.745ʃ0.0280.827ʃ0.0250.810ʃ0.044G A T O r 0.838ʃ0.0190.831ʃ0.0150.999ʃ0.0020.835ʃ0.0100.884ʃ0.0240.848ʃ0.0212.3.2 消融实验首先,实验评估了由单样本网络(S S N )学习到的嵌入特征的贡献度.将没有S S N 模块的G A T O r 过程表示为G A T O r -S S N ,即直接将预处理后的特征加载到下一个模块中,而不使用S S N 模块.实验结果列于表3.由表3可见,完整的G A T O r 过程在4个数据集上的两个性能指标A C C 和A U C 都优于G A T O r -S S N 版本.因此,有必要将单样本网络引入到OM I C 数据的特征工程任务中.表3单样本网络(S S N )嵌入特征的分类贡献T a b l e 3 C l a s s i f i c a t i o n c o n t r i b u t i o no f f e a t u r e s e m b e d d e db y s i n g l e -s a m pl e n e t w o r k (S S N )网络A C CR O S MA PL G GK I P A NB RC AA U CR O S MA PL G GG A T O r -S S N 0.713ʃ0.0150.728ʃ0.0180.970ʃ0.0090.742ʃ0.0130.723ʃ0.0150.798ʃ0.011G A T O r0.838ʃ0.0190.831ʃ0.0150.999ʃ0.0020.835ʃ0.0100.884ʃ0.0240.848ʃ0.015其次,通过消融实验评估G A T O r 主要模块的贡献.基线模型为图注意力网络G A T.将没有局部和全局注意力机制的G A T O r 网络分别表示为G A T O r -L o c a l 和G A T O r -G l o b a l .将这3种图网络与完整的G A T O r 网络根据其提取的特征进行分类性能比较.G A T O r 图注意力网络主要模块的分类贡献列于表4.由表4可见,移除任何一个模块都会降低分类A C C 和A U C 值.去掉局部注意力机制导致的性能下降最大,表明在G A T 网络中仅包含全局注意力可能会使提取的特征分类性能恶化.而全局注意力机制和局部注意力机制的引入对基线G A T 网络具有积极贡献,即使是基线G A T 网络也比表3中G A T O r -S S N 过程提取了有用的信息,以获得更好的分类性能.表4 G A T O r 图注意力网络主要模块的分类贡献T a b l e 4 C l a s s i f i c a t i o n c o n t r i b u t i o no fm a j o rm o d u l e s o fG A T O r g r a pha t t e n t i o nn e t w o r k 网络A C CR O S MA PL G GK I P A NB RC AA U CR O S MA PL G GG A T O r -L o c a l 0.735ʃ0.0100.760ʃ0.0180.965ʃ0.0100.748ʃ0.0090.818ʃ0.0220.791ʃ0.024G A T O r -G l o b a l0.752ʃ0.0120.782ʃ0.0140.997ʃ0.0020.756ʃ0.0120.865ʃ0.0120.838ʃ0.012G A T0.757ʃ0.0130.782ʃ0.0220.997ʃ0.0020.752ʃ0.0150.840ʃ0.0180.825ʃ0.023G A T O r 0.838ʃ0.0190.831ʃ0.0150.999ʃ0.0020.835ʃ0.0100.884ʃ0.0240.848ʃ0.021综上所述,本文提出了一种结合局部和全局注意力机制的图注意力网络,用于从组学数据的单样本网络中学习有用信息.本文对组学数据所有的样本构建其对应的单样本网络,通过具有局部和全局注意机制的图注意力网络从单样本网络中学习基于图的组学特征表示进行类预测任务.实验结果表明,即使是基线图注意力网络在分类任务上的性能也优于原始的组学特征,并且局部注意力和全局注意力的融合可以进一步提高数据分类性能.参考文献[1] M I S R ABB ,L A N G E F E L DC ,O L I V I E R M ,e t a l .I n t e g r a t e dO m i c s :T o o l s ,A d v a n c e s a n dF u t u r eA a p pr o a c h e s 6531 吉林大学学报(理学版)第61卷[J ].J o u r n a l o fM o l e c u l a rE n d o c r i n o l o g y,2019,62(1):R 21-R 45.[2] Z HA N G Y ,S U N H ,MA N D A V A A ,e t a l .F a s t M i x :A V e r s a t i l eD a t a I n t e g r a t i o nP i p e l i n e f o r C e l l T y p e -S p e c i f i c B i o m a r k e r I n f e r e n c e [J ].B i o i n f o r m a t i c s ,2022,38(20):4735-4744.[3] J O N S S O NPF ,B A T E SP A.G l o b a lT o p o l o g i c a lF e a t u r e so fC a n c e rP r o t e i n s i nt h e H u m a nI n t e r a c t o m e [J ].B i o i n f o r m a t i c s ,2006,22(18):2291-2297.[4] WA N GJ ,HU O K K ,MA L X ,e ta l .T o w a r da n U n d e r s t a n d i n g o ft h eP r o t e i nI n t e r a c t i o n N e t w o r ko ft h e H u m a nL i v e r [J ].M o l e c u l a r S y s t e m sB i o l o g y ,2011,7(1):536-1-536-10.[5] L I U XP ,WA N G Y T ,J IH B ,e t a l .P e r s o n a l i z e dC h a r a c t e r i z a t i o no fD i s e a s e sU s i n g S a m p l e -S p e c i f i cN e t w o r k s [J ].N u c l e i cA c i d sR e s e a r c h ,2016,44(22):e 164-1-e 164-18.[6] N E T Z E R M ,W E I N B E R G E RK M ,HA N D L E R M ,e t a l .P r o f i l i n g t h eH u m a nR e s p o n s e t oP h ys i c a l E x e r c i s e :A C o m p u t a t i o n a l S t r a t e g y f o r t h e I d e n t i f i c a t i o n a n dK i n e t i cA n a l ys i s o fM e t a b o l i cB i o m a r k e r s [J ].J o u r n a l o f C l i n i c a l B i o i n f o r m a t i c s ,2011,1:1-6.[7] F A N G XC ,N E T Z E R M ,B A UMG A R T N E R C ,e t a l .G e n e t i cN e t w o r ka n dG e n eS e tE n r i c h m e n tA n a l ys i s t o I d e n t i f y B i o m a r k e r s R e l a t e dt o C i g a r e t t eS m o k i n g a n d L u n g Ca n c e r [J ].C a n c e r T r e a t m e n t R e v i e w s ,2013,39(1):77-88.[8] Z HO U Y Y ,Z HO U B ,P A C H EL ,e t a l .M e t a s c a p eP r o v i d e s aB i o l o g i s t -O r i e n t e dR e s o u r c e f o r t h eA n a l y s i so f S y s t e m s -L e v e lD a t a s e t s [J ].N a t u r eC o mm u n i c a t i o n s ,2019,10(1):1523-1-1523-10.[9] Z E N G T ,Z HA N G W W ,Y U XT ,e t a l .B i g -D a t a -B a s e dE d g eB i o m a r k e r s :S t u d y o nD y n a m i c a l D r u g S e n s i t i v i t y a n dR e s i s t a n c e i n I n d i v i d u a l s [J ].B r i e f i n g s i nB i o i n f o r m a t i c s ,2016,17(4):576-592.[10] HAM I L T O N W L ,Y I N G R ,L E S K O V E CJ .R e p r e s e n t a t i o nL e a r n i n g o n G r a p h s :M e t h o d sa n d A p p l i c a t i o n s [E B /O L ].(2017-09-17)[2022-10-10].h t t p s ://a r x i v .o r g/a b s /1709.05584.[11] B R U N AJ ,Z A R E M B A W ,S Z L AM A ,e ta l .S p e c t r a lN e t w o r k sa n dL o c a l l y C o n n e c t e d N e t w o r k so n G r a p h s [E B /O L ].(2013-12-21)[2022-11-08].h t t p s ://a r x i v .o r g /a b s /1312.6203.[12] D E F F E R R A R D M ,B R E S S O N X ,V A N D E R G H E Y N S TP .C o n v o l u t i o n a lN e u r a lN e t w o r k s o nG r a p h sw i t hF a s t L o c a l i z e dS p e c t r a l F i l t e r i n g [J ].A d v a n c e s i nN e u r a l I n f o r m a t i o nP r o c e s s i n g S y s t e m s ,2016,29:3844-3852.[13] K I P F T N ,W E L L I N G M.S e m i -s u p e r v i s e d C l a s s i f i c a t i o n w i t h G r a p h C o n v o l u t i o n a l N e t w o r k s [E B /O L ].(2016-09-09)[2022-11-12].h t t p s ://a r x i v .o r g/a b s /1609.02907.[14] V E L I ㊅C K O V I C 'P ,C U C U R U L LG ,C A S A N O V A A ,e t a l .G r a p hA t t e n t i o nN e t w o r k s [E B /O L ].(2017-10-30)[2022-08-21].h t t p s ://a r x i v .o r g/a b s /1710.10903.[15] L I U X P ,C HA N G X ,L I U R ,e ta l .Q u a n t i f y i n g C r i t i c a lS t a t e so fC o m p l e x D i s e a s e s U s i n g S i n g l e -S a m p l e D y n a m i cN e t w o r kB i o m a r k e r s [J ].P L o SC o m p u t a t i o n a l B i o l o g y ,2017,13(7):e 1005633-1-e 1005633-10.[16] Y U XT ,Z HA N GJS ,S U NSY ,e t a l .I n d i v i d u a l -S p e c i f i cE d g e -N e t w o r kA n a l y s i s f o rD i s e a s eP r e d i c t i o n [J ].N u c l e i cA c i d sR e s e a r c h ,2017,45(20):e 170-1-e 170-11.[17] WA L D MA N N P .O nt h e U s eo ft h e P e a r s o n C o r r e l a t i o n C o e f f i c i e n tf o r M o d e lE v a l u a t i o ni n G e n o m e -W i d e P r e d i c t i o n [J ].F r o n t i e r s i nG e n e t i c s ,2019,10:899-1-899-4.[18] HA R I D A SV ,N I J ,M E A G E R A ,e t a l .C u t t i n g E d g e :T R A N K ,aN o v e lC yt o k i n eT h a tA c t i v a t e sN F -κBa n d c -J u n N -T e r m i n a lK i n a s e [J ].T h e J o u r n a l o f I mm u n o l o g y ,1998,161(1):1-6.[19] T H E K UM P A R AM P I L K K ,WA N G C ,OH S ,e t a l .A t t e n t i o n -B a s e d G r a p h N e u r a l N e t w o r k f o r S e m i -s u p e r v i s e dL e a r n i n g [E B /O L ].(2018-05-10)[2022-11-28].h t t p s ://a r x i v .o r g /a b s /1803.03735.[20] 孙俊,才华,朱新丽,等.基于双重注意力机制的深度人脸表示算法[J ].吉林大学学报(理学版),2021,59(4):883-890.(S U NJ ,C A I H ,Z HU X L ,e ta l .D e e p F a c e R e p r e s e n t a t i o n A l g o r i t h m B a s e do n D u a lA t t e n t i o n M e c h a n i s m [J ].J o u r n a l o f J i l i nU n i v e r s i t y (S c i e n c eE d i t i o n ),2021,59(4):883-890.)[21] MO S T A F A H ,N A S S A R M.P e r m u t o h e d r a l -g c n :G r a p h C o n v o l u t i o n a l N e t w o r k s w i t h G l o b a l A t t e n t i o n [E B /O L ].(2020-05-02)[2022-12-03].h t t p s ://a r x i v .o r g/a b s /2003.00635.[22] WA N G T X ,S HA O W ,HU A N GZ ,e t a l .MO G O N E TI n t e g r a t e sM u l t i -o m i c sD a t aU s i n g G r a p hC o n v o l u t i o n a l N e t w o r k s A l l o w i n g Pa t i e n t C l a s s i f i c a t i o n a n d B i o m a r k e rI d e n t i f i c a t i o n [J ].N a t u r e C o mm u n i c a t i o n s ,2021,12(1):3445-1-3445-13.(责任编辑:韩啸)7531 第6期周丰丰,等:具有局部和全局注意力机制的图注意力网络学习单样本组学数据表征。

单标记分析法

则其差异显著性测验可通过 t - 测验：
H 0 :1 0 = 0 v sH 1 :1 0 0
t ˆ1ˆ0
s2(n11
1 n0
)
t(n1n02)
其中 s2(n11)s12(n01)s02 n1n02
一、单标记QTL作图
1. T–测验
例如
标记
MiMi
n 1 1 s 1 2
D5 41 54.2 111.8
H14 42 55.2 104.1
Mimi
n 2 2 s 2 2
62 47.3 63.7
61 46.5 56.1
tp
3.75 0.0001 4.99 0.000001
一、单标记QTL作图
1. T–测验
F2群体
标记基因型 M i/M i M i/m i m i/m i
平均数
ˆ 2
ˆ 1
ˆ 0
样本方差
➢ 确定不同标记基因型内数量性状的概率分布 ➢ 构建拟然函数 ➢ 最大拟然估计
➢ 进行拟然比检验
拟然法分析详情后述
一、单标记QTL作图
4. 单标记分析所存在的问题
1. 不能识别标记是同一个还是多个QTL连锁； 2. 不能估计可能存在的QTL的位置； 3. 由于重组率的混淆，有可能低估了QTL的效应； 4. 容易出现假阳性； 5. 功效较低，需要较多的个体观测值
mimi n0 μ0 s02
t 1 t2
86 4.3 2.93 42 3.1 2.76 6.10 0.38
92 4.1 3.2 37 3.6 2.68 3.71 -0.05
一、单标记QTL作图
1. T–测验
统计上，t 测验等同于对简单回归模型的假设测验

单因素分析(一)-定量资料

问：慢性支气管炎患者与正常人的平均乙酰胆碱脂酶之间的差别有无显著性意义？
data aa; input x @@; d=x-1.44; cards; 1.50 2.19 2.32 2.41 2.11 2.54 2.20 2.36 1.42 2.17 1.84 1.96 2.39 ; run;
proc univariate data=aa ; var d; run;
因变量(Dependent variable)：反应变量、结局变量自变量 (Independent variable): 效应变量、处理因素根据研究假设中自变量的数目，可分为：
单因素分析多因素分析根据研究变量的资料类型，可分为：定量资料分析定性资料分析
单因素分析—母亲是否吸烟对婴儿出生体重的影响
proc univariate data=aa normal; var d; run;
proc means data=aa ; var d; run;
proc means data=aa n mean std t prt; var d; run;
data aa; input x @@; cards; 1.50 2.19 2.32 2.41 2.11 2.54 2.20 2.36 1.42 2.17 1.84 1.96 2.39 ; run;
适用：配对设计计量资料均数的比较，包括：
同一受试对象处理前后；同一受试对象接受两种不同的处理；两个同质受试对象分别接受两种不同的处理。
举例：拟研究某种药物的降压效果。
研究方法：确定研究对象；研究开始的时候，测量并记录血压水平；服用某种降压药一年；研究结束的时候，测量并记录血压水平；评价该药物的降压效果。
患者：
0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11

常用数据分析方法有那些

常用数据分析方法有那些文章来源：ECP数据分析时间：2013/6/28 13:35:06发布者：常用数据分析（关注：554）标签：本文包括：常用数据分析方法：聚类分析、因子分析、相关分析、对应分析、回归分析、方差分析；问卷调查常用数据分析方法：描述性统计分析、探索性因素分析、Cronbach’a 信度系数分析、结构方程模型分析(structural equations modeling) 。

数据分析常用的图表方法：柏拉图(排列图)、直方图(Histogram)、散点图(scatter diagram)、鱼骨图（Ishikawa）、FMEA、点图、柱状图、雷达图、趋势图。

数据分析统计工具：SPSS、minitab、JMP。

常用数据分析方法:1、聚类分析（Cluster Analysis）聚类分析指将物理或抽象对象的集合分组成为由类似的对象组成的多个类的分析过程。

聚类是将数据分类到不同的类或者簇这样的一个过程，所以同一个簇中的对象有很大的相似性，而不同簇间的对象有很大的相异性。

聚类分析是一种探索性的分析，在分类的过程中，人们不必事先给出一个分类的标准，聚类分析能够从样本数据出发，自动进行分类。

聚类分析所使用方法的不同，常常会得到不同的结论。

不同研究者对于同一组数据进行聚类分析，所得到的聚类数未必一致。

2、因子分析（Factor Analysis）因子分析是指研究从变量群中提取共性因子的统计技术。

因子分析就是从大量的数据中寻找内在的联系，减少决策的困难。

因子分析的方法约有10多种，如重心法、影像分析法，最大似然解、最小平方法、阿尔发抽因法、拉奥典型抽因法等等。

这些方法本质上大都属近似方法，是以相关系数矩阵为基础的，所不同的是相关系数矩阵对角线上的值，采用不同的共同性□2估值。

在社会学研究中，因子分析常采用以主成分分析为基础的反覆法。

3、相关分析（Correlation Analysis）相关分析（correlation analysis），相关分析是研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度。

SPSS实现析因设计资料单独效应分析的四种方法及比较

表3
Source of Variation WITHIN CELLS A WITHIN B （ 1 ） A WITHIN B （ 2 ） A WITHIN B （ 3 ）
A 药的单独效应分析结果
SS 6983. 33 1155. 56 650. 00 12638. 89 DF 18 2 2 2 MS 387. 96 577. 78 325. 00 6319. 44 1. 49 0. 84 16. 29 0. 252 0. 449 0. 000 F P
A 药、 B 药单独效应的多重比较结果（ LSD 法）
Std. Error P
16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082 16. 082
1. 南昌大学公共卫生学院（ 330006 ） 2. 江西师范大学科学技术学院 3. 南昌大学抚州医学分院 Email： liyue0803@ 126. com △通讯作者：李悦，
Chinese Journal of Health Statistics， Jun 2011 ， Vol． 28 ， No． 3
SPSS 实现析因设计资料单独效应分析的四种方法 1. 巧用 OneWay ANOVA 菜单实现法依次为上述实例的设计中因素 A 有三个水平， 1mg 、 2. 5mg 、 3mg ， 2、 3 表示；因分别用阿拉伯数字 1 、 15 μg 、 30 μg ，同样分素 B 也有三个水平，依次为 5 μg 、 2、 3 表示，别用 1 、两因素的组合数为 3 × 3 = 9 。为了 Way ANOVA 子菜单分析各因素能用 SPSS 中的 One的单独效应，把每种组合看作 1 组，这样该资料共 9 B =1 时组。建立一个组别变量（ group ），因素 A = 1 、 group = 1 ， B = 1 时 group = 2 ， B 因素 A = 2 、因素 A = 3 、 = 1 时 group = 3 ， B = 2 时 group = 4 ，因素 A = 1 、依次 B = 3 时 group = 9 ，因素 A = 3 、可手工输入组别类推，代码，也可用 transform 菜单实现组别代码。然后利用 OneWay ANOVA 子菜单实现单独效应分析。部分输出结果见表 2 。

SPSS常用分析方法操作步骤之欧阳育创编

（1）建立数学成绩数据文件。

（2）选择“分析”→“比较均值”→“单因素方差”，打开单因素方差分析窗口，将“数学成绩”移入因变量列表框，将“班级”移入因子列表框。

（3）单击“两两比较”按钮，打开“单因素ANOVA两两比较”窗口。

（4）在假定方差齐性选项栏中选择常用的LSD检验法，在未假定方差齐性选项栏中选择Tamhane’s检验法。

在显著性水平框中输入0.05，点击继续，回到方差分析窗口。

（5）单击“选项”按钮，打开“单因素ANOVA选项”窗口，在统计量选项框中勾选“描述性”和“方差同质性检验”。

并勾选均值图复选框，点击“继续”，回到“单因素ANOVA选项”窗口，点击确定，就会在输出窗口中输出分析结果。

二、单变量多因素方差分析研究不同温度与不同湿度对粘虫发育历期的影响，得试验数据如表5-7。

分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异（数据文件：粘虫.sav）。

（1）建立数据文件“粘虫.sav”。

（2）选择“分析”→“一般线性模型”→“单变量”，打开单变量设置窗口。

三、相关分析调查了29人身高、体重和肺活量的数据见下表，试分析这三者之间的相互关系。

（1）建立数据文件“学生生理数据.sav”。

（2）选择“分析”→“相关”→“双变量”，打开双变量相关分析对话框。

（3）选择分析变量：将“身高”、“体重”和“肺活量”分别移入分析变量框中。

spss数据类型对照表

spss数据类型与分析对照表
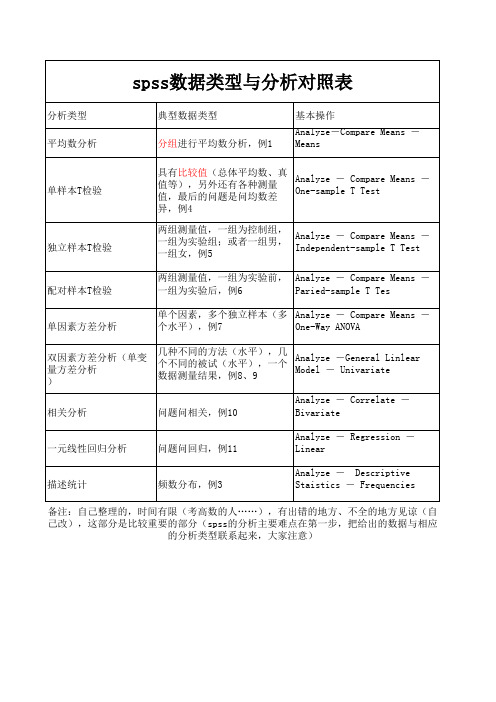
分析类型平均数分析典型数据类型分组进行平均数分析，例1 基本操作 Analyze－Compare Means － Means
单样本T检验
具有比较值（总体平均数、真 Analyze － Compare Means －值等），另外还有各种测量 One-sample T Test 值，最后的问题是问均数差异，例4 两组测量值，一组为控制组， Analyze － Compare Means －一组为实验组；或者一组男， Independent-sample T Test 一组女，例5 两组测量值，一组为实验前， Analyze － Compare Means －一组为实验后，例6 Paried-sample T Tes 单个因素，多个独立样本（多 Analyze － Compare Means －个水平），例7 One-Way ANOVA 几种不同的方法（水平），几 Analyze －General Linlear 个不同的被试（水平），一个 Model － Univariate 数据测量结果，例8、9 Analyze － Correlate － Bivariate Analyze － Regression － Linear Analyze － Descriptive Staistics － Frequencies
独立样本T检验
配对样本T检验
单因素方差分析双因素方差分析（单变量方差分析）相关分析
问题问相关，例10
一元线性回归分析问题问回归，例11源自描述统计频数分布，例3
备注：自己整理的，时间有限（考高数的人……），有出错的地方、不全的地方见谅（自己改），这部分是比较重要的部分（spss的分析主要难点在第一步，把给出的数据与相应的分析类型联系起来，大家注意）