模拟频率、数字频率、模拟角频率
傅立叶变换

信号:我们人类得到的从自己感知中得到消息,并通过大脑分析得出我们要的信息。
而其中消息的传递就需要信号,信号可以是图像、声音还有其他感觉,但是所有信号都是以波的形式在介质中传播。
而机械中的消息则是通过电信号的形式而传播。
最基本的波:正弦波,因为只有一个周期;而理论证明所有的波,都可以用正弦波叠加而成。
我们把这种周期性的波的周期倒数称为频率,这样我们就可以不用在时间上分析波的形态而可以在频率上做研究来分析波的性质。
而不同的信号形式把分解成正弦波的方法不同。
模拟频率f :每秒经历多少个周期,单位Hz ,即1/s ;周期:经过2*pi 需多长时间,单位s 。
模拟角频率Ω:每秒经历多少弧度,单位rad/s ; 数字频率w :每个采样点间隔之间的弧度,单位rad ;周期:经过2*pi 需多少个点,单位1。
关系:Ω=2pi*f ;w = Ω*T = 2π/N 。
(T 为采样间隔时间,N 为一个周期的采样点) 各种函数的关系FS (离散非周期函数)通过Ω = 2πf 将时域信号联系到频域中,它是研究连续周期信号在n Ω角频率处的分量的大小(频谱) FT (连续非周期函数)通过Ω = 2πf 将时域信号联系到频域中,它是研究连续非周期信号在各个角频率处的分量的大小(频谱)的密度函数(因为离散信号是连续信号的取样而成,这导致频谱周期性搬移,所以离散信号的频谱是周 期函数,如果信号时周期信号,因为这相当于我们把一个周期内信号进行搬移,也就是我 们在频域中进行采样,所以频谱是离散的)DFS (离散周期函数) 通过w = Ω*T (T 为采样间隔时间),它是研究离散周期信号,在nw 数字角频率处的分量的大小(频谱)(周期:s ω=2π/T)DTFT (连续周期函数)通过w = Ω*T (T 为采样间隔时间),它是研究离散非周期信号,在各个数字角频率处的分量的大小(频谱)的密度函数(周期:s ω=2π/T)(为了方便计算机运算,引入运算DFT )DFT (离散函数) 通过在DFS 中取主值区间,我们会在下面详细介绍DFT 及FFT 因为这是我们实际处理的工具周期信号的傅里叶级数(FS ) 三角形式: 设 是一个周期为 的波,在一定条件下可以把它写成()f t T ()()01cos 2n n n A f t A n t φ∞==+Ω+∑01cos sin 2n n n A a n t b n t∞==+Ω+Ω∑其中 是 阶谐波, 角频率 (Ω为离散时的角频率形式) 我们称上式右端的级数是由 所确定的傅里叶级数 指数形式:系数Fn 称复傅里叶系数(以证明只要周期信号满足狄里赫利(Dirichlet)条件,就可以分解成傅里叶级数)从上面两个公式,我们可以得出其中的信号的频谱和周期信号的功率(Parseval 等式 , 其中我们也可以得出频率的幅度大小决定信号的功率,这就给我们提供研究信号功率的方法,n F 称为频谱图) 非周期信号的傅里叶变换(FT )为了研究非周期信号的频谱特性,我们引入了傅里叶变换()()d j t F j f t e t +∞-Ω-∞Ω=⎰()1()d 2πj tf t F j e +∞Ω-∞ΩΩ=⎰()F j Ω是频谱密度函数 (Ω为连续时的角频率形式) (从上面公式可以得出,信号的能量谱2()()F j ξΩ=Ω)(上面都是讲的是连续的信号,信号离散也是我们用计算机处理的唯一方法,必须对信号进行采样变成离散的,只要满足采样定理2s m f f >,就能从离散的信号恢复出原来的信号,我们对离散信号的分析和处理也会对原来的连续信号有作用。
matlab信号处理学习总结

常用函数1 图形化信号处理工具,fdatool(滤波器设计),fvtool(图形化滤波器参数查看)sptool (信号处理),fvtool(b,a),wintool窗函数设计.或者使用工具箱 filter design设计。
当使用离散的福利叶变换方法分析频域中的信号时,傅里叶变换时可能引起漏谱,因此需要采用平滑窗,2数字滤波器和采样频率的关系。
如果一个数字滤波器的采样率为 FS,那么这个滤波器的分析带宽为Fs/2。
也就是说这个滤波器只可以分析[0,Fs/2]的信号.举个例字:有两个信号,S1频率为20KHz,S2频率为40KHz,要通过数字方法滤除S2。
你的滤波器的采样率至少要为Fs=80HKz,否则就分析不到 S2了,更不可能将它滤掉了!(当然根据采样定理,你的采样率 F0也必须大于80HK,,Fs和 F0之间没关系不大,可以任取,只要满足上述关系就行。
)3 两组数据的相关性分析 r=corrcoef(x,y)4 expm 求矩阵的整体的 exp4 离散快速傅里叶 fft信号处理中,傅里叶变换的典型用途是将信号分解成幅值分量和频率分量)。
Ft为连续傅里叶变换。
反傅里叶 ifft5 ztrans(),Z变换是把离散的数字信号从时域转为频率6 laplace()拉普拉斯变换是把连续的的信号从时域转为频域7 sound(x)会在音响里产生 x所对应的声音8 norm求范数,det行列式,rank求秩9 模拟频率,数字频率,模拟角频率关系模拟频率f:每秒经历多少个周期,单位Hz,即1/s;模拟角频率Ω是指每秒经历多少弧度,单位rad/s;数字频率w:每个采样点间隔之间的弧度,单位rad。
Ω=2pi*f; w = Ω*T10 RMS求法Rms = sqrt(sum(P.^2))或者norm(x)/sqrt(length(x) var方差的开方是std标准差,RMS应该是norm(x)/sqrt(length(x))吧. 求矩阵的RMS:std(A(:))11 ftshift 作用:将零频点移到频谱的中间12 filtfilt零相位滤波,采用两次滤波消除系统的非线性相位,y = filtfilt(b,a,x);注意x的长度必须是滤波器阶数的3倍以上,滤波器的阶数由max(length(b)-1,length(a)-1)确定。
数字信号处理实验报告

《数字信号处理》实验报告课程名称:《数字信号处理》学院:信息科学与工程学院专业班级:通信1502班学生姓名:侯子强学号:02指导教师:李宏2017年5月28日实验一离散时间信号和系统响应一. 实验目的1. 熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解2. 掌握时域离散系统的时域特性3. 利用卷积方法观察分析系统的时域特性4. 掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对离散信号及系统响应进行频域分析二、实验原理1. 采样是连续信号数字化处理的第一个关键环节。
对采样过程的研究不仅可以了解采样前后信号时域和频域特性的变化以及信号信息不丢失的条件,而且可以加深对离散傅里叶变换、Z 变换和序列傅里叶变换之间关系式的理解。
对连续信号()a x t 以T 为采样间隔进行时域等间隔理想采样,形成采样信号:ˆ()()()a a xt x t p t = 式中()p t 为周期冲激脉冲,$()a x t 为()a x t 的理想采样。
()a x t 的傅里叶变换为µ()a X j Ω: 上式表明将连续信号()a x t 采样后其频谱将变为周期的,周期为Ωs=2π/T。
也即采样信号的频谱µ()a X j Ω是原连续信号xa(t)的频谱Xa(jΩ)在频率轴上以Ωs 为周期,周期延拓而成的。
因此,若对连续信号()a x t 进行采样,要保证采样频率fs ≥2fm ,fm 为信号的最高频率,才可能由采样信号无失真地恢复出原模拟信号计算机实现时,利用计算机计算上式并不方便,因此我们利用采样序列的傅里叶变换来实现,即而()()j j n n X e x n e ωω∞-=-∞=∑为采样序列的傅里叶变换()()n P t t nT δ∞=-∞=-∑µ1()()*()21()n a a a s X j X j P j X j jn T π∞=-∞Ω=ΩΩ=Ω-Ω∑µ()()|j a TX j X e ωω=ΩΩ=2. 时域中,描述系统特性的方法是差分方程和单位脉冲响应,频域中可用系统函数描述系统特性。
基于Matlab的信号分析与数字滤波器设计
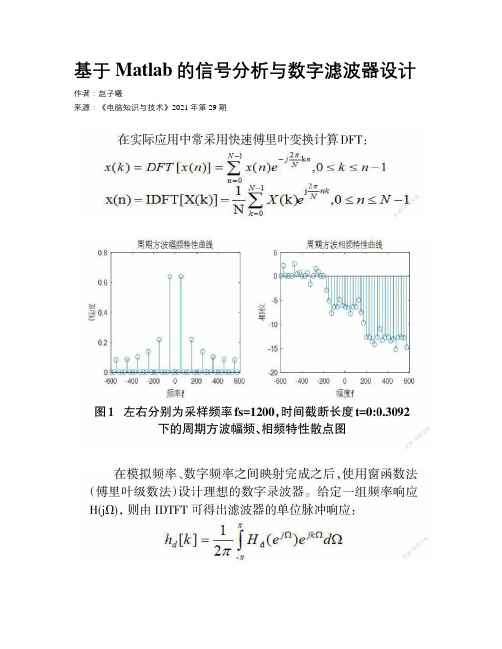
基于Matlab的信号分析与数字滤波器设计作者:赵子曦来源:《电脑知识与技术》2021年第29期摘要:对于信号的时域分析只能获取部分信息,因此在频域作出信号频谱以辅助分析显得十分重要。
在进行频谱分析后,会发现信号包含复杂噪声,因此使用软件设计滤波器去噪。
在Matlab的基础上,本文首先采用经典的傅里叶变换对各类信号进行频谱分析,然后用窗函数法设计FIR数字滤波器。
在声音信号上的实验证明,本文设计的FIR数字滤波器可以有效压制噪声,提取良好声音信号。
关键词:信号频谱分析; Matlab;滤波器;信号去噪中图分类号:TP311 文献标识码:A文章编号:1009-3044(2021)29-0114-02进入21世纪以来,计算机技术飞速发展,大数据、物联网、人工智能(AI:Artificial Intelligence)成为学界、工业界的研究热点,随之对信号分析技术提出了更高的要求,也带来了新的机遇。
在摩尔定律的基础上,计算机有限的算力在复杂数据的处理上显得吃力,而现代数据处理又十分追求更高的效率、更快的速度和更准确的结果。
Matlab是工程领域应用广泛的一款成熟软件,它拥有强大的矩阵运算能力和科学数据处理能力,可以处理十分微小的电路信号,因此使用Matlab进行信号分析与处理、数字滤波器设计等对于电路分析、小信号分析、波形重整具有十分重要的意义。
1信号频域分析1.1离散傅里叶变换与窗函数实际上,计算机存储的所有数据都是离散的,它们需要运用时域和频域都是离散的离散傅里叶变换(Discrete Fourier Transform,DFT)进行处理。
TD(Time-Domain)连续信号经采样后,通过快速傅里叶变换成为FD(Frequency-Domain)采样。
通过数学表达式绘图,不难看出输入DFT进行变换的时域信号和变换后输出的频域信号均为有限长序列,即主值序列。
在实际应用中常采用快速傅里叶变换计算DFT:连续周期、连续非周期、离散周期、离散非周期信号的频谱与 DFT之间的关系:时域上的信号是非周期的,则频域上的信号是连续的;时域上的信号是周期的,则频域上的信号是离散的;反之亦然。
数字信号处理作业-2012

《数字信号处理Ⅰ》作业姓名:学号:学院:2012 年春季学期第一章 时域离散信号和时域离散系统月 日一 、判断:1、数字信号处理和模拟信号处理在方法上是一样的。
( )2、如果信号的取值和自变量都离散,则称其为模拟信号。
( )3、如果信号的取值和自变量都离散,则称其为数字信号。
( )4、时域离散信号就是数字信号。
( )5、正弦序列都是周期的。
( )6、序列)n (h )n (x 和的长度分别为N 和M 时,则)n (h )n (x *的长度为N+M 。
( )7、如果离散系统的单位取样响应绝对可和,则该系统稳定。
( )8、若满足采样定理,则理想采样信号的频谱是原模拟信号频谱以s Ω(采样频率)为周期进行周期延拓的结果。
( )9、序列)n (h )n (x 和的元素个数分别为21n n 和,则)n (h )n (x *有(1n n 21-+)个元素。
( )二、选择1、R N (n)和u(n)的关系为( ):A. R N (n)=u(n)-u(n-N)B. R N (n)=u(n)+u(n-N)C. R N (n)=u(n)-u(n-N-1)D. R N (n)=u(n)-u(n-N+1)2、若f(n)和h(n)的长度为别为N 、M ,则f(n)*h(n)的长度为 ( ): A.N+M B.N+M-1 C.N-M D.N-M+13、若模拟信号的频率范围为[0,1kHz],对其采样,则奈奎斯特速率为( ): A.4kHz B. 3kHz C.2kHz D.1kHz4、LTIS 的零状态响应等于激励信号和单位序列响应的( ): A.相乘 B. 相加 C.相减 D.卷积5、线性系统需满足的条件是( ):A.因果性B.稳定性C.齐次性和叠加性D.时不变性 6、系统y(n)=f(n)+2f(n-1)(初始状态为0)是( ): A. 线性时不变系统 B. 非线性时不变系统 C. 线性时变系统 D. 非线性时变系统7、、若模拟信号的频率范围为[0,Fs],对其采样,则奈奎斯特间隔为( ):A.1/4FsB. 1/3FsC.1/2FsD.1/Fs 三、填空题1、连续信号的( )和( )都取连续变量。
对DFT(FFT)的一些理解
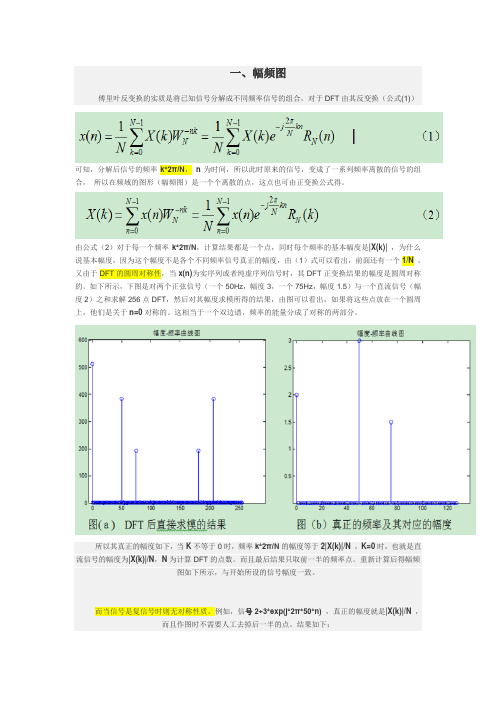
一、幅频图傅里叶反变换的实质是将已知信号分解成不同频率信号的组合,对于DFT由其反变换(公式(1))可知,分解后信号的频率k*2π/N,n为时间,所以此时原来的信号,变成了一系列频率离散的信号的组合,所以在频域的图形(幅频图)是一个个离散的点,这点也可由正变换公式得。
由公式(2)对于每一个频率k*2π/N,计算结果都是一个点,同时每个频率的基本幅度是|X(k)|,为什么说基本幅度,因为这个幅度不是各个不同频率信号真正的幅度,由(1)式可以看出,前面还有一个1/N,又由于DFT的圆周对称性,当x(n)为实序列或者纯虚序列信号时,其DFT正变换结果的幅度是圆周对称的。
如下所示,下图是对两个正弦信号(一个50Hz,幅度3,一个75Hz,幅度1.5)与一个直流信号(幅度2)之和求解256点DFT,然后对其幅度求模所得的结果,由图可以看出,如果将这些点放在一个圆周上,他们是关于n=0对称的。
这相当于一个双边谱,频率的能量分成了对称的两部分。
所以其真正的幅度如下,当K不等于0时,频率k*2π/N的幅度等于2|X(k)|/N,K=0时,也就是直流信号的幅度为|X(k)|/N,N为计算DFT的点数。
而且最后结果只取前一半的频率点。
重新计算后得幅频图如下所示,与开始所设的信号幅度一致。
而当信号是复信号时则无对称性质。
例如,信号2+3*exp(j*2π*50*n),真正的幅度就是|X(k)|/N,而且作图时不需要人工去掉后一半的点。
结果如下:另外,本人认为双边谱的结果只是计算的结果,并无实际物理意义,这与用虚指数信号表示的连续周期信号的傅里叶级数出现负频率类似,频率关于ω=0对称。
计算能量也就是真正的幅度时,要考虑到与真频率相对应的负频率。
对于对称性可以有以下的解释。
在傅里叶变换的层面上,总体的来说,因为傅里叶反变换就是把信号分解成以exp(jω)或者exp(jk*2π/N)为基本信号的组合,所以一个复指数信号就代表一个频率(其它复杂复信号可以由复指数信号合成),所以信号是复信号的时候没有对称性。
时域离散信号和离散系统试题

1.1 填空题1、数字频率ω是模拟频率Ω对 的归一化,其值是 (连续还是离散?)。
解:采样频率s f ;连续2 、线性时不变系统的性质有 律、 律、 律。
解:交换律,结合律、分配律3、序列()sin(3/5)x n n π=的周期为 。
解:104、数字信号处理是采用 的方法完成对信号的处理。
解:数值计算5、信号处理包括数据的采集以及对信号进行 、 、 、 等。
解:分析、变换、综合、估值与识别6、连续信号的 和 都取连续变量。
解:幅度;时间7、时域离散信号是 信号。
解: 幅度取连续变量,时间取离散值8、数字域频率ω与模拟角频率Ω之间的关系是 。
解:T ω=Ω9、对于任意序列x(n),可以用单位采样序列的移位加权表示,即 。
解:()()()m x n x m n m δ∞=-∞=-∑10、系统的输入、输出之间满足 原理的系统称为线性系统。
解:线性叠加11、线性时不变系统具有因果性的充分必要条件是 。
解:()0,0h n n =<12、系统稳定的充分必要条件是 。
解:系统的单位脉冲响应绝对可和。
(或()n h n ∞=∞<∞∑)13、模拟信号数字化的三个步骤是 、 、 。
解:采样、量化、编码 1.2 选择题1.信号通常是时间的函数,数字信号的主要特征是:信号幅度取 ;时间取 。
A.离散值;连续值 B.离散值;离散值 C.连续值;离散值 D.连续值;连续值 解:B2.数字信号的特征是( ) A .时间离散、幅值连续 B .时间离散、幅值量化 C .时间连续、幅值量化 D .时间连续、幅值连续 解:B3.下列序列中属周期序列的为( )A .x(n) = δ(n)B .x(n) = u(n)C .x(n) = R 4(n)D .x(n) = 1解:D 4.序列x(n)=sin ⎪⎭⎫⎝⎛n 311的周期为( ) A .3 B .6 C .11D .∞解:D5. 离散时间序列x (n )=cos(n 73π-8π)的周期是 ( ) A. 7 B. 14/3C. 14D. 非周期解:C6.以下序列中( )的周期为5。
角频率Ω和数字频率w的物理含义

角频率Ω和数字频率w的物理含义频率f,角频率Ω和数字频率w的物理含义--附MATLAB 仿真古人云:基础不牢,地动山摇。
勿在浮沙筑高台。
此话真不假,比如MATLAB中下标从1开始而物理概念t从0开始,结果往往会差一点,做FFT后结果会莫名其妙的差一点,做仿真的时候经常会因为这样一些基本概念不清而导致对结果无法正确的解释。
盲目的追求多学习,不求甚解是得不偿失的,最后无知的还是你自己。
一定要动脑子想想,把知识消化了才能灵活运用。
本文是数字信号处理的基本功,是本人学习思考后的总结,网上没有发现有人讲此很基本的内容,相信肯定有不懂的,所以贴出来希望大家能受益。
最后,原大家得大智慧,断贪嗔痴,阿弥陀佛。
1。
模拟角频率Ω:单位rad/s大OMEGA的物理含义是2*pi的时间段里面包含y=sin(OMEGA*t)正弦信号的个数。
Ω = 2*pi/T ,现象下手指头绕原点做圆周运动,经过一个周期T的时间,我们绕了Ω 圈,则在2*pi的时间段内,正弦y=sin(OMEGA*t)就会有Ω个完整的波形。
我们往往看到Ω = 2*pi/T每秒经历多少弧度,单位rad/s,你想想到Ω 当初其实就是刻画你绕原点画圆圈的快慢了吗?正弦信号和余弦信号实际上是绕圆周运动的点在x轴和y轴上的投影。
Ω=2*pi*ft=0:pi/50:2*pi;for OMEGA = 1:4y(:,OMEGA) = sin(OMEGA*t).';str{OMEGA}=['OMEGA=',num2str(OMEGA)];endh=plot(t',y);legend(h,str);2. 频率f:单位Hz,频率f的物理含义是1s的时间段内包含有f个y=sin(f*t)完整周期的信号波形。
根据f = 1/T 可以看出f 表征的是1s时间段内振动了多少次。
频率f不同于角频率Ω是绕着一个周期T时间间隔内物体绕原点转的圈数。
由Ω = 2*pi*f ,看出f已经和圆周2*pi脱离关系了,手指头绕原点画圆圈投影到x轴或者y轴上的情况是指尖左右移动,或者上下振动的情况,这就是f 的物理含义:在周期T内上下振动的次数,或者左右移动的次数。
专业名词专业英语信号处理导论

专业名词总结部分1.A/D conversion [eɪ] [diː][kən'vɜːʃ(ə)n]模数转换指为把数字信号转换为信息基本相同的模拟信号而设计的处理过程。
2.adder ['ædə]加法器加法器是产生数的和的装置。
加数和被加数为输入,和数与进位为输出的装置为半加器。
若加数、被加数与低位的进位数为输入,而和数与进位为输出则为全加器。
3.additive gauss white noise ['ædɪtɪv][gaʊs] [waɪt] [nɒɪz]加性高斯白噪声加性高斯白噪声指的是一种各频谱分量服从均匀分布(即白噪声),且幅度服从高斯分布的噪声信号。
因其可加性、幅度服从高斯分布且为白噪声的一种而得名。
4.aliasing ['eliəsɪŋ] 混叠频混现象又称为频谱混叠效应,它是指由于采样信号频谱发生变化,而出现高、低频成分发生混淆的一种现象。
5.all-pass function ['ɔl,pæs] ['fʌŋ(k)ʃ(ə)n] 全通函数全通函数是凡极点位于左半开平面,零点位于右半开平面,并且所有零点与极点对于虚轴为一一镜像对称的系统函数。
6.amplifier ['æmplɪfaɪə] 放大器是指能够使用较小的能量来控制较大能量的任何器件。
7.amplitude ['æmplɪtjuːd] 振幅指振动物体离开平衡位置的最大距离。
8.analog signal ['ænəlɒɡ] ['sɪgn(ə)l]模拟信号指信息参数在给定范围内表现为连续的信号。
或在一段连续的时间间隔内,其代表信息的特征量可以在任意瞬间呈现为任意数值的信号。
9.antialiasing profiler [,ænti'eliəsɪŋ] ['prəufailə] 抗混叠预滤波器指一种用以在输出电平中把混叠频率分量降低到微不足道的程度的低通滤波器。
模拟频率、数字频率、模拟角频率

模拟频率、数字频率、模拟角频率概念:模拟频率f:每秒经历多少个周期,单位Hz,即1/s;模拟角频率Ω:每秒经历多少弧度,单位rad/s;数字频率w:每个采样点间隔之间的弧度,单位rad。
表达式:模拟频率f:cos(2pi*f*t)模拟角频率Ω: cos(Ω*t);数字频率w:cos(w*n)=cos(Ω*n*T) [T为采样间隔时间]。
关系:Ω=2pi*f;w =Ω*T。
推导:cos(2pi*f*t) = cos(Ω*t) = cos(Ω*n*T) = cos(Ω*T*n) = cos(w*n)。
举例:x(n)=sin(n*4*PI/7)的数字频率=4*PI/7关键点:t = n*T:从时域角度理解:模拟信号周期:经过2*pi需多长时间,单位s;ex:f = 10Hz,则周期0.1s;数字信号周期:经过2*pi需多少个点,单位1;ex:f = 10Hz,fs = 20Hz,则周期2;基准关系是2*pi:从频域角度理解:站在这一角度,重新理解上述变量补充:在模拟信号中 f是模拟频率;Ω是模拟角频率,比如sin(Ωt)其中Ω=2*pi*f 当对模拟信号进行抽样后t=n*Ts,其中Ts为抽样周期,Ts=1/fs,fs为抽样频率。
把t=n*Ts回带入式子中,这时sin(Ωt)就变成了sin(Ω*Ts*n),此时的角频率称为数字角频率w,w=Ω*Ts,即sin(Ω*Ts*n)=sin(wn)。
w=Ω/fs=2*pi*f/fs。
此时w也称为数字频率,因为它是一个相对频率(仅仅是一种称呼),这时的w就不能简单的用w=2*pi*f来计算了,因为此时f是谁?不过当把f/fs当做一个新的f时也是可以等效为w=2*pi*f 的。
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
数字信号处理_笔记

T[x(n)]侧重点在于 x(n) , x(n) 变为 x(n k) ,则将 x(n k) 替换为 x(n)* 带入原式。
而 y(n) 的侧重点在 n 。举例说明:有T[x(n)] g(n)x(n) 则:T[x(n k)] g(n)x(n k)
0 w 2 是偶对成的,相位响应 arg[H (e jw )] 是奇对称的。
当输入为复指数序列 e jw0n 时,对应输出为 y(n) e jw0n H (e jw0 ) 。
另外,输入为正弦序列时,也可以先将其转换为复指数序列,再根据此方法求得输出。 对于不绝对可和的序列,如周期序列,其傅里叶变换可用冲激函数的形式表示出来。 具体解法:先求傅里叶级数,将原式变换为复指数形式,再求其离散傅里叶变换。 ??? 复指数序列与正弦序列的关系:
Y (e jw )
1
X (e jw ) H (e jw )
1
X (e j )H (e j(w ) )d
2
2
五:帕斯维尔(Parseval)定理
知识点:散时间傅里叶变换与模拟信号傅里叶变换之间的关系 ???查资料,比较多就不写了
频谱进行周期延拓,乘以系数乘以 1 T
混叠现象:当采样频率小于信号最大频率的两倍时,对连续时间信号采样后的离散时间信号 的频谱将会重叠,重叠部分的频率成分的幅值与原信号不同。原信号不是带限信号,混叠现 象一定存在。解决措施:采样频率应该足够高,如实际工程应用中,采样频率应为输入信号 最大频率的 3-5 倍。
但是, y(n k) g(n k)x(n k) ,既有T[x(n k)] y(n k) 。所以,系统不具有移不
变性。 线性非移变系统:既满足叠加原理,又,满足非移变条件的系统。 线性非移变系统输入为单位取样序列时,输出为单位取样响应。该系统的输出
数字信号处理的一般过程及研究内容数字信号处理的特点及应用

2、可靠性高: 模拟系统信号容易受干扰,产生失真;
二进制的数字信号在传输、存储、处理中不容易丢失信息。
3、灵活性强: 模拟系统要改变系统特性一般要改变元件值、或改变电路连接,比较困难。 数字系统中,特别是计算机数字信号处理系统可以通过修改信号处理软件参
线性系统的输出 y(t) = h (t ) ∗ x (t )
Y( Ω ) = H (Ω ) X (Ω )
傅立叶反变换即可 得到输出响应
时域卷积特性从频域角度分析系统和求解系统响应。
傅立叶变换及性质
频域卷积特性:在时域中两信号相乘的频谱等于两信号频谱的卷 积乘以1/2π。
若 x1 (t ) ⎯⎯FT → X 1 (Ω ) x 2 (t ) ⎯⎯FT → X 2 (Ω )
则
x1 (t ) x 2 (t ) ⎯⎯FT →
1
2π
X (Ω ) ∗ X 2 (Ω )
频域卷积特性应用:
进行信号处理时,往往要将无限长的信号(数据)截短成有限 长,即进行“有限化”处理——相当于无限长的信号与一矩形脉冲 信号相乘;抽样信号——连续信号与周期冲激信号相乘,因此, 利用频域卷积特性可计算截短后的有限长信号的频谱和抽样信号 的频谱等。
)
频域卷积特性
理想采样信号的频谱是连续信号频谱的周期延拓, 重复周期为Ωs(采样频率)。
抽样技术
X(Ω)
理
原连续时间信号的频谱
想 抽
-
Ω
m
Ω
m
Ω
(带限信号)
样
Xδ(Ω)
信
号 的
周期冲激序列的频谱
频
谱
Xδ(Ω)
抽样信号的频谱
巴特沃斯数字带阻滤波器讲解

《数字信号处理》课程设计报告设计课题滤波器设计与实现专业班级姓名学号报告日期 2012年12月目录1. 课题描述 (2)2. 设计原理 (2)2.1 滤波器的分类 (3)2.2 数字滤波器的设计指标 (3)2.3 巴特沃斯数字带阻模拟滤波器 (3)2.3.1 巴特沃斯数字带阻滤波器的设计原理 (4)2.3.2 巴特沃斯数字带阻滤波器的设计步骤 (7)3. 设计内容 (8)3.1 用MATLAB编程实现 (10)3.2 设计结果分析 (10)4. 总结 (10)5. 参考文献 (11)课程设计任务书题目滤波器设计与实现学生姓名学号专业班级设计内容与要求一、设计内容:设计巴特沃斯数字带阻滤波器,阻带频率200~500hz,通带上限频率600hz, 通带下限频率150hz,通带衰减为0.5dB,阻带最大衰减20dB,采样频率2000hz,画出幅频、相频响应曲线,并设计信号验证滤波器设计的正确性二、设计要求1 设计报告一律按照规定的格式,使用A4纸,格式、封面统一给出模版。
2 报告内容(1)设计题目及要求(2)设计原理 (包括滤波器工作原理、涉及到的MATLAB函数的说明)(3)设计内容(设计思路,设计流程、仿真结果)(4)设计总结(收获和体会)(5)参考文献(6)程序清单起止时间2012年 12 月 3日至 2011年 12月11 日指导教师签名2011年 12月 2日系(教研室)主任签名年月日学生签名年月日1 .课题描述数字滤波器是由数字乘法器、加法器和延时单元组成的一种算法或装置。
数字滤波器的功能是对输入离散信号的数字代码进行运算处理,以达到改变信号频谱的目的。
由于电子计算机技术和大规模集成电路的发展,数字滤波器已可用计算机软件实现,也可用大规模集成数字硬件实时实现。
使用MATLAB信号处理箱和BW(巴特沃斯)设计低通数字滤波器。
2.设计原理2.1 滤波器的分类数字滤波器有低通、高通、带通、带阻和全通等类型。
数字信号处理试卷及详细答案(三套)

数字信号处理试卷答案完整版一、填空题:(每空1分,共18分)1、 数字频率ω是模拟频率Ω对采样频率s f 的归一化,其值是连续(连续还是离散?)。
2、 双边序列z 变换的收敛域形状为圆环或空集。
3、 某序列的DFT 表达式为∑-==1)()(N n knMWn x k X ,由此可以看出,该序列时域的长度为N ,变换后数字频域上相邻两个频率样点之间的间隔是Mπ2。
4、 线性时不变系统离散时间因果系统的系统函数为252)1(8)(22++--=z z z z z H ,则系统的极点为2,2121-=-=z z ;系统的稳定性为不稳定。
系统单位冲激响应)(n h 的初值4)0(=h ;终值)(∞h 不存在。
5、 如果序列)(n x 是一长度为64点的有限长序列)630(≤≤n ,序列)(n h 是一长度为128点的有限长序列)1270(≤≤n ,记)()()(n h n x n y *=(线性卷积),则)(n y 为64+128-1=191点点的序列,如果采用基FFT2算法以快速卷积的方式实现线性卷积,则FFT 的点数至少为256点。
6、 用冲激响应不变法将一模拟滤波器映射为数字滤波器时,模拟频率Ω与数字频率ω之间的映射变换关系为Tω=Ω。
用双线性变换法将一模拟滤波器映射为数字滤波器时,模拟频率Ω与数字频率ω之间的映射变换关系为)2tan(2ωT =Ω或)2arctan(2T Ω=ω。
7、当线性相位FIR 数字滤波器满足偶对称条件时,其单位冲激响应)(n h 满足的条件为)1()(n N h n h --=,此时对应系统的频率响应)()()(ωϕωωj j e H eH =,则其对应的相位函数为ωωϕ21)(--=N 。
8、请写出三种常用低通原型模拟滤波器巴特沃什滤波器、切比雪夫滤波器、 椭圆滤波器。
二、判断题(每题2分,共10分)1、 模拟信号也可以与数字信号一样在计算机上进行数字信号处理,只要加一道采样的工序就可以了。
人声浊音基频测量谱分析算法

人声浊音基频测量谱分析算法作者:刘卫来源:《现代电子技术》2008年第04期摘要:人声基频检测是一个普遍关心的技术问题,目前所采用的方法也很多。
利用数字信号处理的方法,通过对人声的浊音部分进行功率谱分析的方式,采用一种检查共振峰位置,进而遏止共振峰,在频域中凸显基波频率的方法,在频域确定信号的频率,从而自动检查出信号的基频。
关键词:浊音;基频;DSP;功率谱;共振峰中图分类号:TN912文献标识码:B文章编号:1004—373X(2008)04—113—021算法概述一般来说,声音信号浊音部分,去其头尾,可以看作是平稳的随机信号。
当然,可以用频谱分析仪来观察信号频谱,在频谱图上寻找频率最低的谱峰来确定该段频率的基频。
同样,用时域分析的方法,比如相关函数。
类似这样的方法还有很多。
但是,如果用一种算法实现功率谱中基频的自动测量有一定的困难,无法用功率谱中某一个特征值(与其谐波有着明显的数值差距)。
由于共振峰影响,其功率谱表现出基频分量大小并不一定为其频率分量中的最大值。
所以,很难依靠一种功率谱值比较的方法来估计其基频。
这里提供一种相对较容易实现,算法简单的检波滤波的方法,利用数字信号处理的基本理论,依靠经典功率谱分析方法,其具体思路如下:首先,截取一段录制好的声音文件(这里采用,WAV格式的文件,采样频率为22.05 kHz),取2 048个采样点(便于进行FFT),大约100 ms。
如果信号的噪声干扰不大,可以采用周期图谱法。
如果噪声比较大,可以考虑用现代谱分析的方法,比如AR模型,以及类似的方法(普通话筒近距离录音,噪声影响不大)。
其次,在对这段数据进行谱分析前进行预处理,之后进行周期图谱分析,在该图谱中找出最大值,找出该最大值对应的数据位置。
根据数据位置和数字频率与模拟频率的对应关系,容易算出该谱峰对应的频率,这个频率通常是该信号的谐波频率,在声音信号中一般来说,其主要的谐波分量为其第二或第三次谐波。
医学信号处理_河南科技大学中国大学mooc课后章节答案期末考试题库2023年

医学信号处理_河南科技大学中国大学mooc课后章节答案期末考试题库2023年1.有限长序列z变换的收敛区域为()。
参考答案:有限z平面2.某FIR系统单位冲冲激响应h(n)={1,2,1,0,-1,-2,-1};抽样频率为100Hz;该关于滤波器的延时说法正确是()。
参考答案:0.03s加一个90相移3.已知FIR滤波器的系统函数H(z)=1+2z-1+4z-2+2z-3+z-4,则该滤波器的单位冲激响应h(n)的特点是( )参考答案:偶对称,N为奇数4.双线性变换法实现模拟滤波器数字化能够消除多值映射的原理是()。
参考答案:取了中间平面S1平面,将S平面非线性压缩到S1平面2π/T的水平条带,再映射到z平面5.窗函数法设计FIR滤波器时,下列()方法能减少滤波器通带、阻带的肩峰和波纹振荡。
参考答案:选择缓慢截断的窗函数6.系统只能是物理设备。
参考答案:错误7.右边序列z变换的收敛区域为()。
参考答案:在某一个圆的圆外8.主瓣宽度为8π/N的窗函数是()。
参考答案:三角窗_汉宁窗_海明窗9.关于脑电信号,错误的说法是().参考答案:被动信号10.生物医学信号的特点错误的有( )。
参考答案:功率高11.模拟信号在A/D转换之前最好是经过一个模拟的前置滤波器,该滤波器的功能是()。
参考答案:滤除信号中高于某一频率(折叠频率)的分量12.一个LSI系统因果稳定的充分必要条件是系统的所有极点分布于单位圆内。
参考答案:正确13.用窗函数设计法设计线性相位FIR数字滤波器. 若采用矩形窗,则改变窗函数的长度N值对矩形窗函数频谱不产生影响是()参考答案:幅度大小14.双线性变换法实现模拟滤波器数字化时,原模拟滤波器的模拟角频率Ω和数字滤波器的数字角频率ω的关系,下列说法错误的是()。
参考答案:Ω与ω的关系是真实的正确关系15.双线性变换法实现模拟滤波器数字化能够消除多值映射的原理是取了中间平面S1平面,将S平面非线性压缩到S1平面2π/T的水平条带,再映射到z 平面,关于S平面到S1平面映射下列说法错误的()。
数字信号处理辅导第一章

1.2 离散时间信号
离散时间信号的产生 设连续时间信号为x , 设连续时间信号为 a(t),对它进行等间隔采 采样周期为T, 样,采样周期为 ,则 样本值: xa (nT ) = xa (t ) t =nT n 为整数 样本值: 记为: 记为: x ( n) = xa ( nT ) 序列的三种表示方法: 序列的三种表示方法: 1、数学表示式表示法 、 2、图形表示法 、 3、样本集合符号表示法 、
y (n) = T [x(n)]
y (n − N ) = T [x(n − N )]
1.3 离散时间系统
3、因果性 、 响应信号总是在激励信号作用于系统之后才产 生。或者说,激励信号是响应信号产生的原 或者说, 这种系统称为因果系统。 因,这种系统称为因果系统。物理上能够实 现的系统都是因果系统。 现的系统都是因果系统。 我们在分析系统的特性时, 我们在分析系统的特性时,有时要分析一些 具有理想特性的系统, 具有理想特性的系统,比如理想低通滤波器 这类系统就不具有因果性。 等。这类系统就不具有因果性。因而是不可 以实现的系统。 以实现的系统。
∞
1.2.2 序列的基本运算 1、两序列之间的乘法运算: 、两序列之间的乘法运算: y (n) = x1 (n) ⋅ x2 (n) 指对应序号的两个样本值之间的乘法运算
1.2 离散时间信号
2、两序列的加法 、 指的是两个序列的对应序号的样本值相加运算: 指的是两个序列的对应序号的样本值相加运算:
y (n) = x1 (n) + x2 (n)
1.2 离散时间信号
5、正弦序列 、
xa (t ) = sin(Ωt ) xa (nT ) = sin( nΩT )
x(n) = sin(ωn)
IIR滤波器设计

fc
fs / 2 fs
1
2 f s 2
(2)
fs
T / f s 2 f / f s
an
5
数字信号处理
回顾
滤波器 性能参数 归一化模拟滤 反归一化H(s) 波器Han(s) =Han(s/Ωc) 频带变换 低通 H( z)
Rp
As
N
Ωc 查表an
双线性变换
N
[bz,az]=impinvar(b,a,Fs)
Y ( z) H ( z) X ( z)
12
b z
k 0 N k k 1
M
k
Fs:采样频率 单位:
k
1 ak z
Hz
数字信号处理
APDP
• 双线性变换法
畸变:
[bz,az]=bilinear(b,a,Fs)
1 1 / T Fs:采样频率 ! 1 1 单位: 1 2 tg 1 c OmegaP1=2*Fs*tan(wp/2)
1 z 1 sc 1 1 z
Hz
预畸变:P454 例7.23 第五行
2 tg c
! 1 1
13
OmegaS1=2*Fs*tan(ws/2) ! 1 !1 2 Fs tg(1 /2 ) c 2/T 2 F s
1
数字信号处理
for(i=0;i<IIRN;i++)
{
fSum+=(fXn[i]*fBn[i]);//输入乘累加 fSum+=(fYn[i]*fAn[i]);//输出乘累加
//数据的延时处理: for(i=IIRNUMBER-1;i>0;i--) {
频率角频率和数字频率的物理含义

古人云:基础不牢,地动山摇。
勿在浮沙筑高台。
此话真不假,比如MATLAB中下标从1开始而物理概念t从0开始,结果往往会差一点,做FFT后结果会莫名其妙的差一点,做仿真的时候经常会因为这样一些基本概念不清而导致对结果无法正确的解释。
盲目的追求多学习,不求甚解是得不偿失的,最后无知的还是你自己。
一定要动脑子想想,把知识消化了才能灵活运用。
本文是数字信号处理的基本功,是本人学习思考后的总结,网上没有发现有人讲此很基本的内容,相信肯定有不懂的,所以贴出来希望大家能受益。
最后,原大家得大智慧,断贪嗔痴,阿弥陀佛。
1。
模拟角频率Q:单位rad/s大OMEGA的物理含义是2*pi的时间段里面包含y=sin(0MEGA*t)正弦信号的个数。
Q = 2*pi/T,现象下手指头绕原点做圆周运动,经过一个周期T的时间,我们绕了Q圈,则在2*pi的时间段内,正弦y=sin(OMEGA*t)就会有◎个完整的波形。
我们往往看到Q = 2*pi/T每秒经历多少弧度,单位rad/s,你想想到Q当初其实就是刻画你绕原点画圆圈的快慢了吗?正弦信号和余弦信号实际上是绕圆周运动的点在x轴和y轴上的投影。
Q =2*pi*fI妙{* 11厂£00°0A(―i t o)J ho0:1 .%匕近t=0:pi/50:2*pi;for OMEGA = 1:4y(:,OMEGA) = sin (OMEGA*t).'; str{OMEGA}=['OMEGA=', nu m2str(OMEGA)]; endh=plot(t',y);lege nd(h,str);2. 频率f :单位Hz ,频率f 的物理含义是1s 的时间段内包含有f 个y=sin(f*t)完整周 期的信号波形。
根据f = 1/T 可以看出f 表征的是1s 时间段内振动了多少次。
频率f不同于角频率 ◎是绕着一个周期T 时间间隔内物体绕原点转的圈数。
北京邮电大学数字信号处理第4章答案

习题解答4.1 根据给定的模拟滤波器的幅度响应平方,确定模拟滤波器的系统函数 H(s)。
(1) 261|()|164H j Ω=+Ω(2) 2222216(25)|()|(49)(36)H j -ΩΩ=+Ω+Ω分析:在模拟滤波器设计中,由各种逼近方法确定了幅度响应,通过下列步骤求出滤波器的系统函数H(s)。
更进一步,通过脉冲响应不变法或双线性变换法,可以得到数字滤波器的传输函数 H(z)。
(1)考虑s j =Ω,将幅度响应表达式整理为s 为变量的表达式,求 ()()a a H s H s - 表达式的零极点;(2)为了系统稳定,选择左半平面的极点构成 H(s);(3)如果没有特殊要求,可以选择取 ()()a a H s H s -以虚轴为对称轴的对称零点的任意一半(应是共轭对)作为 H a (s) 的零点。
但如果要求是最小相位延时滤波器,则应取左半平面零点作为 H a (s) 的零点。
(4)对比()a H s 和()a H j Ω 的低频特性或高频特性,从而确定增益常数K 0。
解:(1)由于2)(Ωj H a 是非负有理函数,它在Ωj 轴上的零点是偶次的,所以满足幅度平方函数的条件,先求2321()()()164()22H s H s H j a a as s -=Ω=+-Ω=-其极点为0.50.250.4330.50.250.433j j --±±我们选出左半平面极点s=0.5和 0.250.433j -± 为)(s H a 的极点,并设增益常数为0K ,则得)(s H a 为:002()(0.5)(0.250.433)(0.250.433)(0.5)(0.50.25)K K H s a s s j s j s s s ==++-+++++ 按着()a H s 和()a H j Ω的低频特性或高频特性的对比可以确定增益常数。
在这里我们采用低频特性,即由00()|()|a s a H s H j =Ω==Ω的条件可得增益常数0K 为:018K =最后得到)(s H a 为:21()8(0.5)(0.50.25)H s a s s s =+++(2)由于2)(Ωj H a 是非负有理函数,它在Ωj 轴上的零点是偶次的,所以满足幅度平方函数的条件,得)36)(49()25(16222)()()(222s s s s j aH s a H s a H --+=-=ΩΩ=- 其极点为:6,7±=±=s s其零点为:5j s ±=(皆为二阶,位于虚轴上)j Ω虚轴上的零点或极点一定是二阶的,其中一半(应为共轭对)属于 H a (s)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟频率、数字频率、模拟角频率
概念:
模拟频率f:每秒经历多少个周期,单位Hz,即1/s;
模拟角频率Ω:每秒经历多少弧度,单位rad/s;
数字频率w:每个采样点间隔之间的弧度,单位rad。
表达式:
模拟频率f: cos(2pi*f*t)
模拟角频率Ω:cos(Ω*t);
数字频率w: cos(w*n)=cos(Ω*n*T) [T为采样间隔时间]。
关系:
Ω=2pi*f;
w =Ω*T。
推导:
cos(2pi*f*t) = cos(Ω*t) = cos(Ω*n*T) = cos(Ω*T*n) = cos(w*n)。
举例:
x(n)=sin(n*4*PI/7)的数字频率=4*PI/7
关键点:
t = n*T:
从时域角度理解:
模拟信号周期:经过2*pi需多长时间,单位s;
ex:f = 10Hz,则周期;
数字信号周期:经过2*pi需多少个点,单位1;
ex:f = 10Hz,fs = 20Hz,则周期2;
基准关系是2*pi:
从频域角度理解:站在这一角度,重新理解上述变量
补充:
在模拟信号中f是模拟频率;Ω是模拟角频率,比如sin(Ωt)其中Ω=2*pi*f 当对模拟信号进行抽样后
t=n*Ts,其中Ts为抽样周期,Ts=1/fs,fs为抽样频率。
把t=n*Ts回带入式子中,这时sin(Ωt)就变成了sin(Ω*Ts*n),此时的角频率称为数字角频率w,w=Ω*Ts,即sin(Ω*Ts*n)=sin(wn)。
w=Ω/fs=2*pi*f/fs。
此时w也称为数字频率,因为它是一个相对频率(仅仅是一种称呼),这时的w就不能简单的用w=2*pi*f 来计算了,因为此时f是谁不过当把f/fs当做一个新的f时也是可以等效为w=2*pi*f的。
