第5课时 求一次函数的关系式
(完整版)一次函数待定系数法经典专题

一次函数待定系数法专题学习目标1.理解待定系数法;2.能用待定系数法求一次函数,用一次函数表达式解决有关现实问题.3、体会用“数形结合”思想解决数学问题.学习过程一、课前准备☆导学问题一次函数关系式y=kx+b(k≠0),如果知道了k与b的值,函数解析式就确定了,那么有怎样的条件才能求出k和b呢?二、新课导学☆学习探究探究任务:待定系数法问题1 已知一个一次函数当自变量x=-2时,函数值y=-1,当x=3时,y=-3.能否写出这个一次函数的解析式呢?这种先设待求函数关系式(其中含有未知的常数系数),再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法。
☆☆点对点训练1已知一次函数y=kx+b的图象经过点(3,5)和点(-4,-9),求当x=5时,函数y的值.2 已知一次函数的图象如下图,写出它的关系式.3 若直线y=-kx+b与直线y=-x平行,且与y轴交点的纵坐标为-2;求直线的表达式.@@@链接中考1.点A,B,C,D的坐标如图,求直线AB与直线CD的交点坐标.2.已知:一次函数y kx b=+的图象经过M(0,2),(1,3)两点.(l) 求k、b的值;(2) 若一次函数y kx b=+的图象与x轴的交点为A(a,0),求a的值.3.如图6,在平面直角坐标系中,直线434:+-=x y l 分别交x 轴、y 轴于点A 、B ,将△AOB 绕点O 顺时针旋转90°后 得到△A ′OB ′(1)求直线A ′B ′的解析式;(2)若直线A ′B ′与直线l 相交于点,求△ABC 的面积。
三、总结提升 ☆学习小结本节课,我们讨论了一次函数解析式的求法。
求一次函数的解析式往往用待定系数法,即根据题目中给出的两个条件确定一次函数解析式y =kx +b (k ≠0)中两个待定系数k 和b 的值。
☆☆☆☆当堂测试(限时:8分钟)1.已知一次函数4-=kx y ,当2=x 时,3-=y(1)求一次函数的解析式;(2)将该函数的图象向上平移6个单位,求平移后的图象与x 轴交点的坐标.2.正比例函数y=kx 和一次函数y=ax+b 的图象都经过点A (1,2),且一次函数的图象交x 轴于点B (4,0).求正比例函数和一次函数的表达式.。
初三数学复习计划PPT课件

知识技能
数学思考 问题解决 情感态度
知识技能
1.体验从具体情境中抽象出数学符号的过程,理 解有理数、实数、代数式、方程、不等式、函数; 掌握必要的运算(包括估算)技能;探索具体问 题中的数量关系和变化规律,掌握用代数式、方 程、不等式、函数进行表述的方法。 2.探索并掌握相交线、平行线、三角形、四边 形和圆的基本性质与判定,掌握基本的证明方法 和基本的作图技能;探索并理解平面图形的平移、 旋转、轴对称;认识投影与视图;探索并理解平 面直角坐标系,能确定位置。 3.体验数据收集、处理、分析和推断过程,理 解抽样方法,体验用样本估计总体的过程;进一 步认识随机现象,能计算一些简单事件的概率。
情感态度
1.积极参与数学活动,对数学有好奇心和求知 欲。 2.感受成功的快乐,体验独自克服困难、解决 数学问题的过程,有克服困难的勇气,具备学 好数学的信心。 3.在运用数学表述和解决问题的过程中,认识 数学具有抽象、严谨和应用广泛的特点,体会 数学的价值。 4.敢于发表自己的想法、勇于质疑,养成认真 勤奋、独立思考、合作交流等学习习惯,形成 实事求是的科学态度。
12课时序号复习内容课时过关测试内容时间第1课时实数第2课时二次根式第3课时代数式整式运算第4课时因式分解分式第5课时一次方程分式方程一次方程组方程与不等式1课时第6课时一元二次方程第7课时一元一次不等式组1第8课时不等式的应用第9课时函数概念一次函数函数及其图像1课时第10课时反比例函数第11课时二次函数第12课时函数的应用第13课时平行线三角形与证图形的性质1课时第14课时特殊三角形第15课时多边形平行四边形与证明第16课时特殊平行四边形梯形与证明第19课时投影与视图图形与变换第20课时图形的变换图形与变换1课时第21课时相似形第22课时解直角三角形图形与坐标第23课时图形变换与坐标图形与坐标1课时14概率与统3课时第24课时统计概率测试1课时第5课时概率151620201217重视模块之间的联系
2022年中考数学人教版一轮复习课件:第5课 一次方程(组)的解法及应用

19.(2021·青海)已知 a,b 是等腰三角形的两边长,且 a,b 满足
2a-3b+5+(2a+3b-13)2=0,则此等腰三角形的周长为
A.8
( D)
B.6 或 8
C.7
D.7 或 8
20.(2021·眉山)解方程组:32xx- +21y5+y-203= =00① ②, .
解:方程组整理,得23xx+-125y=y=-3②20.①, ①×15+②×2,得 49x=-294, 解得 x=-6, 把 x=-6 代入②,得 y=1, ∴这个方程组的解为xy==1-. 6,
个肉粽和 5 个素粽共用去 70 元,设每个肉粽 x 元,则可列方
程为
( A)
A.10x+5(x-1)=70
B.10x+5(x+1)=70
C.10(x-1)+5x=70
D.10(x+1)+5x=70
15.(2021·东营)某玩具商店周年店庆,全场八折促销,持会员卡
可在促销活动的基础上再打六折.某电动汽车原价 300 元,
圆在该快递公司寄一件 8 千克的物品,需要付费
( B)
A.17 元
B.19 元
C.21 元
D.23 元
18.(2021·大连)某校为实现垃圾分类投放,准备在校园内摆放大、 小两种垃圾桶.购买 2 个大垃圾桶和 4 个小垃圾桶共需 600 元;购买 6 个大垃圾桶和 8 个小垃圾桶共需 1 560 元. (1)求大、小两种垃圾桶的单价; (2)该校购买 8 个大垃圾桶和 24 个小垃圾桶共需多少元?
26.(2020·绍兴)若关于 x,y 的二元一次方程组 xA+=y0=2,的解为
xy==11,,则多项式 A 可以是 xx--y(答yx案-不y唯x-一)(写出一个即可).
华师大版数学八年级下册17.3《一次函数》(第5课时)教学设计

华师大版数学八年级下册17.3《一次函数》(第5课时)教学设计一. 教材分析《一次函数》是华师大版数学八年级下册第17.3节的内容,本节主要让学生了解一次函数的定义、性质及图像,能运用一次函数解决实际问题。
教材通过丰富的实例,引导学生探究一次函数的规律,培养学生的动手操作能力和抽象思维能力。
二. 学情分析八年级的学生已经学习了代数和几何的基础知识,具备一定的逻辑思维和抽象思维能力。
但对于一次函数的图像和实际应用,可能还有一定的困惑。
因此,在教学过程中,要注重引导学生通过实例去发现一次函数的规律,提高他们解决实际问题的能力。
三. 教学目标1.了解一次函数的定义、性质及图像;2.学会运用一次函数解决实际问题;3.培养学生的动手操作能力和抽象思维能力。
四. 教学重难点1.一次函数的定义和性质;2.一次函数图像的特点;3.运用一次函数解决实际问题。
五. 教学方法1.实例教学:通过丰富的实例,让学生直观地感受一次函数的图像和性质;2.小组讨论:引导学生分组讨论,发现一次函数的规律,提高学生的合作能力;3.问题驱动:设置问题引导学生思考,培养学生的抽象思维能力;4.实践操作:让学生动手绘制一次函数的图像,提高学生的动手操作能力。
六. 教学准备1.教学PPT:制作包含一次函数定义、性质、图像及实际应用的PPT;2.实例:准备一些与生活息息相关的一次函数实例;3.练习题:准备一些针对一次函数的练习题,以便课后巩固。
七. 教学过程1.导入(5分钟)利用生活实例引入一次函数的概念,如“某商品的原价是80元,打8折后的价格是多少?”引导学生思考,激发学生的学习兴趣。
2.呈现(10分钟)通过PPT展示一次函数的定义、性质和图像,让学生直观地了解一次函数的基本知识。
3.操练(10分钟)让学生动手绘制一次函数的图像,观察图像的特点,加深对一次函数的理解。
同时,引导学生发现一次函数与实际问题的联系。
4.巩固(10分钟)分组讨论一次函数的性质,让学生通过合作交流,进一步掌握一次函数的知识。
人教版八年级数学下册《19.2.5 一次函数解析式的求法》课件

知2-练
3 若一次函数y=kx+b的图象经过点(0,2)和(1, 0),则这个函数的解析式是( D )
A.y=2x+3
C.y=x+2
B.y=3x+2
D.y=-2x+2
知1-讲
知识点
1
用待定系数法求正比例函数的解析式
由于正比例函数的解析式y=kx(k≠0)中,只有一个基
本量k(我们也称待定系数),因此只需要一个条件就可以求 得k的值,从而确定正比例函数的解析式.比如已知满足函
数解析式y=kx的一组x,y的值或已知直线y=kx上的一个
点等都可以确定正比例函数的解析式. 注意:先假定解析式中的未知系数,然后根据已知条件求 出待定的系数,从而确定出该解析式的方法是数学上常用 的方法,这种方法称为待定系数法.
C.b<2
D.b<-2
知2-练
6 【 2017· 怀化】一次函数y=-2x+m的图象经 过点P(-2,3),且与x轴,y轴分别交于点A, B,则△AOB的面积是( B )
1 2 C.4 1 4 D.8
A.
B.
2 7 【2017· 枣庄】如图,直线y= x+4与x轴,y轴分 3 别交于点A和点B,点C,D分别是线段AB,OB的
A.2
C.-2
B.8
D.-8
知2-讲
知识点
2 用待定系数法求一次函数的解析式
小明在有40元钱,每个月长攒5元钱, x个月小明有的 钱数为y元,请写出x与y的关系. 我们想:要想写出小明的钱数,先想到一个月5元, 那么x个月共攒多少元,则得到5x元,又因为原来有40元, 所以此时有(40+5x),即y=40+5x,这样我们看到,列 出一次函数的表达式,首先要分析题意,然后找出等量
人教版八年级数学下册课件:19.2一次函数--2.3 一次函数与方程、不等式(2)一次函数与二元一次方程组

24
知识点三:二元一次方程组与一次函数的关系
学以致用
3.已知坐标平面上有两直线相交于一点(2,a),且两直线的方
程式分别为2x+3y=7,3x-2y=b,其中a,b为两数,求a+b之值
为何?( C)A.1 B.-1 C.5 D.-5
4.若一次函数y=k1x+b1与y=k2x+b2的图象没有交点,则关于x
∴OA=3,OB=1,∴AB=4.∴S△ABC=
1 2
×4×1=2.
27
知识点四:一次函数与方程(组)与几何图形的综合问题
典例讲评
解:(3)能,理由如下:设点P的横坐标为x, y
则
S△APB=
1 2
×4×|x|=6,
A C
解得x=±3.
O
x
B
把x=3代入y=-2x-1,得y=-7;
把x=-3代入y=-2x-1,得y=5;
情景引入
大家观察一次函数的解析式y=x+1,是否有过这样的 疑问:为什么一次函数的解析式与二元一次方程非常相似呢? 是的,你没有猜错,如果我们将一次函数的解析式看作为 一个元一次方程,那么,一次函数y=x+1上的每一个点坐 标就对应二元一次方程x-y+1=0上的一个解.一次函数图象 上有无数个点,二元一次方程也有无数个解.本节课,我们 就来看看一次函数与二元一次方程的关系.
y y=kx-1
A
O Bx C
31
知识点四:一次函数与方程(组)与几何图形的综合问题
学以致用
2.(3)①当点A运动到什么位置时, △AOB的面积是 ? ②在①成立的情况下,在两条坐标轴上是
否存在一定P,使△POA是等腰直角三角 形?若存在,请写出满足条件的所有点P 的坐标;若不存在,请说明理由.
2024-2025学年初中数学八年级上册(沪科版)教案第12章一次函数12.2一次函数(第5课时)

第12章一次函数12.2一次函数第5课时利用一次函数进行方案决策教学反思教学目标1.能根据实际问题中变量之间的关系,确定一次函数关系式.2.培养学生用“数形结合”的思想方法解决数学问题的能力.教学重难点重点:根据实际问题中变量之间的关系,确定一次函数关系式.难点:根据实际情况,用数学语言选择出最优方案.教学过程知识回顾提问:1.已知一次函数y=90x+5,则当x=2时,y=,当y=365时,x= .2.某校办工厂现年产值是30万元,如果每增加1000元投资,一年可增加2500元产值.那么总产值y(万元)与增加的投资额x(万元)之间的函数关系式为.学生独立完成,展示答案,教师纠正,得出正确答案:1.1854;2.y=30+2.5x典型例题例1某单位有职工几十人,想在节假日期间组织到外地H地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到H地旅游的价格都是每人100元,经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1 000元后,给予每位游客六折优惠.问该单位选择哪家旅行社,使其支付的旅游总费用较少?分析:假设该单位参加旅游人数为x,按甲旅行社的优惠条件,应付费用80x元;按乙旅行社的优惠条件,应付费用(60x +1000)元.问题变为比较80x与60x+1000的大小了.解法一:设该单位参加旅游人数为x.那么如选甲旅行社,应付80x元,选乙旅行社,应付(60x +1000)元.记y1=80x,y2=60x+1000.在同一直角坐标系中作出两个函数的图象y1与y2的图象交于点(50,4000).观察图象,可得:当人数为50时,选择甲或乙旅行社费用都一样;当人数为0-49时,选择甲旅行社费用较少;当人数为51-100时,选择乙旅行社费用较少.解法二:设选择甲、乙旅行社所需费用之差为y,则y=y1-y2=80x-(60x+1000)=20x-1000.画一次函数y=20x-1000的图象观察可得一次函数y=20x-1000的图象与x轴的交点是(50,0).(1)当x=50时,y=0,即y1=y2,甲、乙两家旅行社的费用一样;(2)当x>50时,y>0,即y1>y2,乙旅行社的费用较低;(3)当x<50时y<0.,即y1<y2,甲旅行社的费用较低.例2某工程机械厂根据市场要求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:(2)该厂如何生产获得最大利润?(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?教学反思解:(1)设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台.由题意知200240(100)22400200240(100)22500x xx x+-≥⎧⎨+-≤⎩解得37.5≤x≤40.∵x取正整数,∴x为38、39、40.∴有三种生产方案:A型38台,B型62台;A型39台,B型61台;A 型40台,B型60台.(2)设获得利润为W(万元).由题意知:W=50x+60(100-x)=-10x+6 000.∴当x=38时,W最大=5 620,即生产A型挖掘机38台,B型挖掘机62台时,获得利润最大,最大利润为5 620万元.(3)由题意知W=(50+m)x+60(100-x)=(m-10)x+6 000.∴①当0<m<10时,取x=38,W最大,即生产A型挖掘机38台,B型挖掘机62台;②当m=10时,三种生产方案获得利润相等;③当m>10时,取x=40,W最大,即生产A型挖掘机40台,B型挖掘机60台.课堂练习1.电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )A.方案AB.方案BC.两种方案一样优惠D.不能确定2.某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,每副球拍配x(x≥2)个羽毛球,供社区居民免费借用.该社区附近A,B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价均为3元,目前两家超市同时在做促销活动:A超市:所有商品均打九折(按标价的90%)销售;B超市:买一副羽毛球拍送2个羽毛球.设在A超市购买羽毛球拍和羽毛球的费用为y A (元),在B超市购买羽毛球拍和羽毛球的费用为y B (元).请解答下列问题:(1)分别写出y A和y B与x之间的关系式;(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?(3)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.3.某县区大力发展猕猴桃产业,预计今年A地将采摘200吨,B地将采摘300教学反思吨.若要将这些猕猴桃运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的猕猴桃为x吨,A、B两地运往两仓库的猕猴桃运输费用分别为y A元和y B元.(1)分别求出y A、y B与x之间的函数关系式;(2)试讨论A、B两地中,哪个的运费较少;(3)考虑B地的经济承受能力,B地的猕猴桃运费不得超过4 830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.参考答案1.B解析:由图可知,通话时间为500分钟时,方案A的费用是230元,方案B的费用是168元,∵230>168,∴选择方案B更优惠.故选B.2.解:(1)y A=27x+270,y B=30x+240.(2)当y A=y B时,27x+270=30x+240,解得x=10;当y A>y B时,27x+270>30x+240,解得x<10;当y A<y B时,27x+270<30x+240,解得x>10.∴当2≤x<10时,到B超市购买划算;当x=10时,两家超市都一样;当x>10时,到A超市购买划算.(3)∵x=15>10,∴①选择在A超市购买,y A=27×15+270=675(元);②可先在B超市购买10副羽毛球拍,送20个羽毛球,后在A超市购买剩下的羽毛球10×15-20=130(个),则共需费用10×30+130×3×0.9=651(元).∵651<675,∴最省钱的购买方案是:先在B超市购买10副羽毛球拍,后在A超市购买130个羽毛球.3.解:(1)y A=20x+25(200-x)=-5x+5000,y B=15(240-x)+18(60+x)=3x+4 680.(2)∵y A-y B=(-5x+5000)-(3x+4680)=-8x+320,∴当-8x+320>0,即x<40时,B地的运费较少;当-8x+320=0,即x=40时,两地的运费一样多;当-8x+320<0,即x>40时,A地的运费较少.(3)设两地运费之和为y元,则y=y A+y B=(-5x+5000)+(3x+4680)=-2x +9 680.由题意得y B=3x+4680≤4830,解得x≤50.∵y随x的增大而减小,x 最大为50,∴y最小=-2×50+9680=9580.∴在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之和最少,最少是9580元.课堂小结利用一次函数解决方案选择问题第一步:根据实际情况确定函数关系式,并确定自变量的取值范围;第二步:画出函数图象;第三步:根据函数的性质和自变量的取值确定函数值的最大或最小值,从而选择最优方案.布置作业教材44页练习1,2题; 教材48页习题12.2中16题.板书设计第5课时 利用一次函数进行方案决策例 某工程机械厂根据市场要求,计划生产A 、B 两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:(2)该厂如何生产获得最大利润?(3)根据市场调查,每台B 型挖掘机的售价不会改变,每台A 型挖掘机的售价将会提高m 万元(m >0),该厂如何生产可以获得最大利润?解:(1)设生产A 型挖掘机x 台,则B 型挖掘机可生产(100-x )台. 由题意知200240(100)22400200240(100)22500x x x x +-≥⎧⎨+-≤⎩解得37.5≤x ≤40. ∵ x 取正整数, ∴ x 为38、39、40.∴ 有三种生产方案:A 型38台,B 型62台;A 型39台,B 型61台;A 型40台,B 型60台.(2)设获得利润为W (万元).由题意知:W =50x +60(100-x )=-10x +6 000. ∴ 当x =38时,W 最大=5 620 ,即生产A 型挖掘机38台,B 型挖掘机62台时,获得利润最大,最大利润为5 620万元. (3)由题意知W =(50+m )x +60(100-x )=(m -10)x +6 000.∴ ①当0<m <10时,取x =38,W 最大 ,即生产A 型挖掘机38台,B 型挖掘机62台;教学反思②当m=10时,三种生产方案获得利润相等;③当m>10时,取x=40,W最大,即生产A型挖掘机40台,B型挖掘机60台.。
第五章一次函数第5课时一次函数的图象一
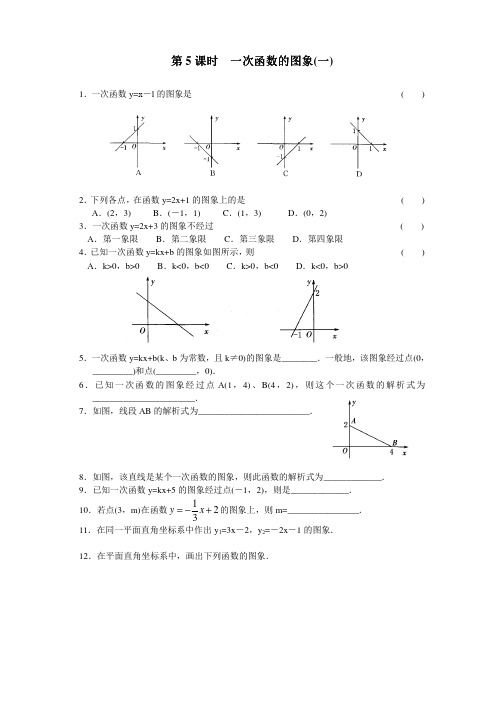
第5课时一次函数的图象(一)1.一次函数y=x-l 的图象是()2.下列各点,在函数y=2x+1的图象上的是()A .(2,3)B .(-1,1)C .(1,3)D .(0,2)3.一次函数y=2x+3的图象不经过()A .第一象限B .第二象限C .第三象限D .第四象限4.已知一次函数y=kx+b 的图象如图所示,则()A .k>0,b>0B .k<0,b<0C .k>0,b<0D .k<0,b>05.一次函数y=kx+b(k 、b 为常数,且k ≠0)的图象是________.一般地,该图象经过点(0,_________)和点(_________,0).6.已知一次函数的图象经过点A(1,4)、B(4,2),则这个一次函数的解析式为_______________________.7.如图,线段AB 的解析式为_________________________.8.如图,该直线是某个一次函数的图象,则此函数的解析式为_____________.9.已知一次函数y=kx+5的图象经过点(-1,2),则是_____________.10.若点(3,m)在函数123y x =−+的图象上,则m=________________.11.在同一平面直角坐标系中作出y 1=3x -2,y 2=-2x -1的图象.12.在平面直角坐标系中,画出下列函数的图象.(1)21y x =−+;(2)122y x =−.13.画出函数y=2x+3的图象,并解答下列问题:(1)求已知直线与y 轴交点A 的坐标.(2)点.A(一2,一1)是否在所画图象上?请说明理由.(3)在同一平面直角坐标系中画出函数y=2x 一1的图象,试判断这两个图象的位置关系.14.已知函数y=2x -4.(1)画出它的图象.(2)写出这条直线与x 轴、y 轴的交点的坐标.(3)求这条直线与两坐标轴所围成的三角形的面积.15.如图,正方形ABCD 的边长为4,点P 在边DC 上,点P 从点D 运动到点C .设PD=x ,梯形APCB 的面积为S .(1)写出S 与x 之间的函数关系式.(2)求自变量x 的取值范围.(3)画出函数的图象.参考答案1.C2.C3.D4.D5.直线bbk−6.21433y x=−+7.12(04)2y x x=−+≤≤8.y=2x+29.310.111.略12.略13.图略(1)A(0,3)(2)在理由略(3)略14.(1)略(2)(2,0),(0,一4)(3)4 15.(1)S=16—2x(2)0<x<4(3)略。
初中数学《一次函数》单元教学设计以及思维导图

强调数形结合,强调函数方程思想,强调与日常生活的关系。
主题单元规划思维导图
主题单元学习目标
知识与技能:1、理解并掌握函数的概念、函数的表示形式、函数的图象。
2、根据实际问题中的条件确定一次函数解析式
3、能判断一个函数是否为பைடு நூலகம்次函数
4、能用描点法、两点法、平移法画一次函数图象
5、会用待定系数法求一次函数的解析式
1、一次函数的图象及其性质是什么?
2、怎样求函数表达式?
所需教学环境和教学资源
信息化资源:几何画板,课件
常规资源:作图工具
教学支持环境:多媒体教室
其它:纸笔
学习活动设计
活动一:一次函数图象
1、给出函数图象的概念。
2、具体活动
(1)作出一次函数y=2x+1的图像。
注意:小组合作,共同完成,教师提示:线是有什么构成?找那些点合适?需要画很多点吗?有了点怎么办?
所需教学环境和教学资源
信息化资源:几何画板,课件
常规资源:作图工具
教学支持环境:多媒体教室
其它:纸笔
学习活动设计
1、利用所学知识,给出课本所列实例的结果。(可以小组内交流)
2、教师根据学生对课本前例的认识程度和存在的问题,指导学生试做课本例1,并考虑多种解法,在组内交流,班内展示。教师要鼓励学生发散思维,多种解法,但要认识到:本节的设计目的在于培养学生良好的识图能力,因而要防止学生过多的用代数方法解题。
第5课时 一次函数的图像和性质

1、一次函数的一般形式:y kx b(k , b为常数,k 0) 正比例函数的一般形式:y kx(k是常数,k 0)
两者有什么联系?
Байду номын сангаас
正比例函数是一次函数b=0时的 特殊情况
2、根据正比例函数表达式画函数的图象,有哪几步? 列表 描点 连线
一 次 函 数 y=kx+b
6、已知一次函数y=(3m+12)x+(5-n) (1)m、n为何值时?y随x的增大而增大。 (2)m、n为何值时?函数图像与y轴的交点在x轴 的下方。 (3)m、n为何值时?函数图像与y轴的交点在x轴 下方。 (4)当m=2,n=-1时,求此一次函数的图像与两 坐标轴的交点坐标。
2
本节课你学习了哪些知识?
1、一次函数的图像是经过(0,___),(____,0)的一条 _______ 2、b叫做一次函数在轴上________,它表示图像与 Y轴交点的_____坐标
m -4的图像过原点,则m 1、已知一次函数y=2mx+ 的值为( ) A、0, B、2, C、-1, D、 2 2、已知一次函数y=kx+b的图像不经过第三象限, 也不经过原点,那么k、b的取值范围( ) A、k>0,b>0.B、k>0,b<0,C、k<0,b>0,D、 k<0,b<0 3、一次函数y=kx+b的图像与y=2x-3平行,则 k=____, 若该直线经过第二象限,则b的取值范围是______
y O x x
y
y=x+1
y=-x+1 y
y=x-2 y x O x
O
O
即时练习
12.2 第5课时 一次函数的简单应用——分段函数问题练习题—2022学年沪科版八年级数学上册

第5课时 一次函数的简单应用——分段函数问题【基础练习】知识点 1 一次函数的简单应用1.摄氏度(℃)与华氏度(℉)都是用来表示物体温度的.用x 与y 分别表示华氏度(℉)与摄氏度(℃),y 是x 的一次函数,其表达式为y=59x -1609.在疫情期间,使用额温枪测某同学体温显示为96.8℉,调回摄氏度模式下测量,其温度大约是 ℃.2.[教材练习第3题变式题] 某航空公司规定每位旅客可以免费托运一定质量的行李,超过部分则需缴纳行李托运费,行李托运费y (元)与行李质量x (千克)之间的函数关系为y=15x -2,则乘客最多可以携带 千克行李而不需要缴纳行李托运费.3.[2020·金华] 某地区山峰的高度每增加1百米,气温大约降低0.6 ℃,气温T (℃)和高度h (百米)的函数关系图象如图1所示.请根据图象回答下列问题:(1)求高度为5百米时的气温;(2)求T 关于h 的函数表达式;(3)测得山顶的气温为6 ℃,求该山峰的高度.图1知识点 2 分段函数图象的应用4.如图2,折线ABC是某市区出租车所收费用y(元)与出租车行驶路程x(km)之间的函数关系图象,某人支付车费15.6元,则出租车走了km.图25.[教材练习第2题变式题]为了鼓励公民节约用电,某市采用分段计费的方法按月计算每户家庭的电费.每户家庭每月电费y(元)与用电量x(kW·h)之间的函数图象如图3所示.(1)求y与x之间的函数表达式;(2)若乙用户某月需缴电费132元,求乙用户该月的用电量.图3【能力提升】6.一个有进水管与出水管的容器,从某时刻开始的4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图4所示.根据图象提供的信息,下列结论中错误的是()A.第4 min时,容器内的水量为20 LB.每分钟的进水量为5 LC.每分钟的出水量为1.25 LD.第8 min时,容器内的水量为25 L图47.[2019·辽阳]一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图5所示,有下列结论:图5①A,B两村相距10 km;②出发1.25 h后两人相遇;③甲每小时比乙多骑行8 km;④相遇后,乙又骑行了15 min或65 min时两人相距2 km.其中正确的有()A.1个B.2个C.3个D.4个8.[2019·绥化]甲、乙两台机器共同加工一批零件,一共用了6 h.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数y(个)与甲加工时间x(h)之间的函数图象为折线OA-AB-BC,如图6所示.(1)这批零件一共有个,甲机器每小时加工个零件,乙机器排除故障后每小时加工个零件;(2)当3≤x≤6时,求y与x之间的函数表达式;(3)在整个加工过程中,甲机器加工多长时间时,甲与乙机器加工的零件个数相等?图69.某城市居民用水实行阶梯收费,每户每月用水量若未超过20吨,则按每吨1.9元收费;每户每月用水量若超过20吨,未超过的部分仍按每吨1.9元收费,超过的部分则按每吨2.8元收费.设每户每月用水量为x吨,应收水费为y元.(1)分别写出每户每月用水量未超过20吨和超过20吨时,y与x之间的函数表达式;(2)若该城市某用户5月份水费为平均每吨2.2元,求该用户5月份用水多少吨.10.[2020·合肥肥东县期末]为加强校园文化建设,某校准备打造校园文化墙,需用甲、乙两种石材.经市场调查,甲种石材的费用y(元)与使用面积x(m2)之间的函数关系如图7所示,乙种石材的价格为每平方米50元.(1)求y 与x 之间的函数表达式;(2)若校园文化墙的总面积为600 m 2,其中使用甲种石材x m 2,购买两种石材的总费用为w 元,请直接写出w 与x 之间的函数表达式;(3)在(2)的前提下,若甲种石材的使用面积多于300 m 2,且不超过乙种石材面积的2倍,则应该怎样分配甲、乙两种石材的面积才能使总费用最少?最少总费用为多少元?图7答案1.36 [解析] 当x=96.8时,y=59x -1609=59×96.8-1609=36. 2.10 [解析] 当y=0时,15x -2=0,解得x=10.3.解:(1)由题意,得高度增加2百米,气温降低2×0.6=1.2(℃),13.2-1.2=12(℃).所以高度为5百米时的气温大约是12 ℃.(2)设T 关于h 的函数表达式为T=kh+b.由题意,得{3k +b =13.2,5k +b =12,解得{k =-0.6,b =15.所以T 关于h 的函数表达式为T=-0.6h+15(h>0).(3)当T=6时,6=-0.6h+15,解得h=15.所以该山峰的高度大约为15百米,即1500米.4.105.解:(1)当0≤x<200时,y=0.5x.当x ≥200时,设y 与x 之间的函数表达式为y=mx+b.则{100=200m +b ,180=300m +b ,解得{m =0.8,b =-60.所以当x ≥200时,y=0.8x -60.综上可得,y 与x 之间的函数表达式为y={0.5x (0≤x <200),0.8x -60(x ≥200).(2)由图可知乙用户该月用电量超过200 kW·h,将y=132代入y=0.8x -60,得x=240.即乙用户该月的用电量是240 kW·h .6.C [解析] 由图象可得,第4 min 时,容器内的水量为20 L,故选项A 正确;每分钟的进水量为20÷4=5(L),故选项B 正确;每分钟的出水量为5-(30-20)÷(12-4)=3.75(L),故选项C 错误;第8 min 时,容器内的水量为20+(8-4)×(5-3.75)=25(L),故选项D 正确.7.D [解析] 由图象可知A 村、B 村相距10 km,故①正确;当1.25 h 时,甲、乙相距为0 km,故在此时相遇,故②正确;当0≤t ≤1.25时,易得一次函数的表达式为s=-8t+10,故甲的速度比乙的速度快8 km/h .故③正确;当1.25≤t ≤2时,函数图象经过点(1.25,0),(2,6).设一次函数的表达式为s=kt+b ,则{0=1.25k +b ,6=2k +b ,解得{k =8,b =-10,所以s=8t -10.当s=2时,2=8t -10,解得t=1.5,1.5-1.25=0.25(h)=15 min .同理当2≤t ≤2.5时,设函数表达式为s=mt+n.将点(2,6)和(2.5,0)代入,得{6=2m +n ,0=2.5m +n ,解得{m =-12,n =30,所以s=-12t+30.当s=2时,-12t+30=2,解得t=73, 73-1.25=1312(h)=65(min). 故相遇后,乙又骑行了15 min 或65 min 时两人相距2 km,故④正确.故选D .8.解:(1)由题图可知这批零件一共有270个.甲机器每小时加工零件:(90-50)÷(3-1)=20(个),乙机器排除故障后每小时加工零件:(270-90-20×3)÷3=40(个).故答案为270;20;40.(2)设当3≤x ≤6时,y 与x 之间的函数表达式为y=kx+b.把B (3,90),C (6,270)代入函数表达式,得{3k +b =90,6k +b =270,解得{k =60,b =-90,所以y 与x 之间的函数表达式为y=60x -90(3≤x ≤6).(3)由题意可知乙机器故障前每小时加工50-20=30(个).设甲加工x h 时,甲与乙机器加工的零件个数相等.①故障排除前:20x=30,解得x=1.5;②故障排除后:20x=30+40(x -3),解得x=4.5.答:甲机器加工1.5 h 或4.5 h 时,甲与乙机器加工的零件个数相等.9.[解析] (1)当0≤x ≤20时按1.9元/吨收费;当x>20时,其中20吨按1.9元/吨收费,其余(x -20)吨按2.8元/吨收费;(2)先确定该用户5月份的用水量的范围,然后代入函数表达式,求得用水量.解:(1)y={1.9x (0≤x ≤20),2.8x -18(x >20).(2)因为2.2>1.9,所以可以确定该用户5月份用水超过20吨.故设该用户5月份用水a 吨.由题意,得2.8a -18=2.2a ,解得a=30.答:该用户5月份用水30吨.10.解:(1)①当0≤x<300时,y=80x.②当x ≥300时,设y=kx+b.将(300,24000),(500,30000)代入y=kx+b ,得{300k +b =24000,500k +b =30000,解得{k =30,b =15000.故y 与x 之间的函数表达式为y={80x (0≤x <300),30x +15000(x ≥300).(2)当0≤x<300时,w=80x+50(600-x ),即w=30x+30000.当x ≥300时,w=30x+15000+50(600-x ),即w=-20x+45000.故w 与x 之间的函数表达式为w={30x +30000(0≤x <300),-20x +45000(x ≥300).(3)由题意,得{x >300,x ≤2(600-x ),解得300<x ≤400.由(2)知w=-20x+45000.因为-20<0,所以w 随x 的增大而减小.故当甲种石材的使用面积为400 m 2,乙种石材的使用面积为200 m 2时,总费用最少. w min =-20×400+45000=37000.答:甲种石材的使用面积为400 m 2,乙种石材的使用面积为200 m 2时,总费用最少,最少总费用为37000元.。
《第5课时 解一元二次方程—配方法》教案

第5课时解一元二次方程—配方法预设目标1、使学生进一步会用配方法解数字系数的一元二次方程。
2、使学生掌握配方法和推导过程,能使用配方法解一元二次方程。
3、渗透转化思想,掌握一些转化的技能。
教学重难点重点:掌握配方法解一元二次方程。
难点:把一元二次方程转化为形如〔x-a〕2=b的过程。
教具准备教法学法合作,探究,讨论教学过程一、自主学习感受新知【问题1】填上适当的数,使以下各式成立,并总结其中的规律。
⑴x2+ 6x+ =(x+3)2⑵x2+8x+ =(x+ )2⑶x2-12x+ =(x- )2⑷x2-x52+=(x- )2⑸a2+2ab+ =(a+ )2 ⑹a2-2ab+ =(a- )2【问题2】解以下方程:⑴x2-4x+7=0 ⑵2x2-8x+1=0二、自主交流探究新知【探究】利用配方法解以下方程,你能从中得到在配方时具有的规律吗?⑴3x2-6x + 4 = 0;⑵2x2+1=3x ⑶(2x-1)(x+3)=5.【归纳】利用配方法解方程时应该遵循的步骤:〔1〕把方程化为一般形式ax2+bx+c=0;〔2〕把方程的常数项通过移项移到方程的右边;〔3〕方程两边同时除以二次项系数a;〔4〕方程两边同时加上一次项系数一半的平方;〔5〕此时方程的左边是一个完全平方式,然后利用平方根的定义把一元二次方程化为两个一元一次方程来解.三、自主应用稳固新知【例1】用配方法解以下方程:⑴x(2x-5)=4x-10 ⑵4x2-12x-1=0四、当堂练习:教材P35练习题五、自主总结拓展新知〔1〕把方程化为一般形式ax2+bx+c=0;〔2〕把方程的常数项通过移项移到方程的右边;〔3〕方程两边同时除以二次项系数a;〔4〕方程两边同时加上一次项系数一半的平方;〔5〕此时方程的左边是一个完全平方式,然后利用平方根的定义把一元二次方程化为两个一元一次方程来解.〔6〕如果方程右边是非负数,两边直接开平方求解,如果方程右边是负数,那么原方程无解。
《一次函数》经典例题剖析(附练习及答案)

《一次函数》复习课知识点1 一次函数和正比例函数的概念若两个变量x ,y 间的关系式可以表示成y=kx+b (k ,b 为常数,k ≠0)的形式,则称y 是x 的一次函数(x 为自变量),特别地,当b=0时,称y 是x 的正比例函数.例如:y=2x+3,y=-x+2,y=21x 等都是一次函数,y=21x ,y=-x 都是正比例函数.【说明】 (1)一次函数的自变量的取值范围是一切实数,但在实际问题中要根据函数的实际意义来确定.(2)一次函数y=kx+b (k ,b 为常数,b ≠0)中的“一次”和一元一次方程、一元一次不等式中的“一次”意义相同,即自变量x 的次数为1,一次项系数k 必须是不为零的常数,b 可为任意常数.(3)当b=0,k ≠0时,y= kx 仍是一次函数. (4)当b=0,k=0时,它不是一次函数. 知识点2 函数的图象把一个函数的自变量x 与所对应的y 的值分别作为点的横坐标和纵坐标在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.画函数图象一般分为三步:列表、描点、连线.知识点 3一次函数的图象由于一次函数y=kx+b (k ,b 为常数,k ≠0)的图象是一条直线,所以一次函数y=kx+b 的图象也称为直线y=kx+b .由于两点确定一条直线,因此在今后作一次函数图象时,只要描出适合关系式的两点,再连成直线即可,一般选取两个特殊点:直线与y 轴的交点(0,b ),直线与x 轴的交点(-kb,0).但也不必一定选取这两个特殊点.画正比例函数y=kx 的图象时,只要描出点(0,0),(1,k )即可.知识点4 一次函数y=kx+b (k ,b 为常数,k ≠0)的性质 (1)k 的正负决定直线的倾斜方向; ①k >0时,y 的值随x 值的增大而增大; ②k ﹤O 时,y 的值随x 值的增大而减小.(2)|k|大小决定直线的倾斜程度,即|k|越大,直线与x 轴相交的锐角度数越大(直线陡),|k|越小,直线与x 轴相交的锐角度数越小(直线缓);(3)b 的正、负决定直线与y 轴交点的位置; ①当b >0时,直线与y 轴交于正半轴上; ②当b <0时,直线与y 轴交于负半轴上; ③当b=0时,直线经过原点,是正比例函数.(4)由于k ,b 的符号不同,直线所经过的象限也不同;①如图11-18(l )所示,当k >0,b >0时,直线经过第一、二、三象限(直线不经过第四象限); ②如图11-18(2)所示,当k >0,b ﹥O 时,直线经过第一、三、四象限(直线不经过第二象限); ③如图11-18(3)所示,当k ﹤O ,b >0时,直线经过第一、二、四象限(直线不经过第三象限); ④如图11-18(4)所示,当k ﹤O ,b ﹤O 时,直线经过第二、三、四象限(直线不经过第一象限). (5)由于|k|决定直线与x 轴相交的锐角的大小,k 相同,说明这两个锐角的大小相等,且它们是同位角,因此,它们是平行的.另外,从平移的角度也可以分析,例如:直线y=x +1可以看作是正比例函数y=x 向上平移一个单位得到的.知识点3 正比例函数y=kx (k ≠0)的性质 (1)正比例函数y=kx 的图象必经过原点;(2)当k >0时,图象经过第一、三象限,y 随x 的增大而增大; (3)当k <0时,图象经过第二、四象限,y 随x 的增大而减小. 知识点4 点P (x 0,y 0)与直线y=kx+b 的图象的关系(1)如果点P (x 0,y 0)在直线y=kx+b 的图象上,那么x 0,y 0的值必满足解析式y=kx+b ; (2)如果x 0,y 0是满足函数解析式的一对对应值,那么以x 0,y 0为坐标的点P (1,2)必在函数的图象上.例如:点P (1,2)满足直线y=x+1,即x=1时,y=2,则点P (1,2)在直线y=x+l 的图象上;点P ′(2,1)不满足解析式y=x+1,因为当x=2时,y=3,所以点P ′(2,1)不在直线y=x+l 的图象上.知识点5 确定正比例函数及一次函数表达式的条件(1)由于正比例函数y=kx (k ≠0)中只有一个待定系数k ,故只需一个条件(如一对x ,y 的值或一个点)就可求得k 的值.(2)由于一次函数y=kx+b (k ≠0)中有两个待定系数k ,b ,需要两个独立的条件确定两个关于k ,b 的方程,求得k ,b 的值,这两个条件通常是两个点或两对x ,y 的值.知识点6 待定系数法先设待求函数关系式(其中含有未知常数系数),再根据条件列出方程(或方程组),求出未知系数,从而得到所求结果的方法,叫做待定系数法.其中未知系数也叫待定系数.例如:函数y=kx+b 中,k ,b 就是待定系数.知识点7 用待定系数法确定一次函数表达式的一般步骤 (1)设函数表达式为y=kx+b ; (2)将已知点的坐标代入函数表达式,解方程(组);(3)求出k 与b 的值,得到函数表达式.例如:已知一次函数的图象经过点(2,1)和(-1,-3)求此一次函数的关系式. 解:设一次函数的关系式为y =kx+b (k ≠0), 由题意可知,⎩⎨⎧+-=-+=,3,21b k b k 解⎪⎪⎩⎪⎪⎨⎧-==.35,34b k ∴此函数的关系式为y=3534-x . 【说明】 本题是用待定系数法求一次函数的关系式,具体步骤如下:第一步,设(根据题中要求的函数“设”关系式y=kx+b ,其中k ,b 是未知的常量,且k ≠0);第二步,代(根据题目中的已知条件,列出方程(或方程组),解这个方程(或方程组),求出待定系数k ,b );第三步,求(把求得的k ,b 的值代回到“设”的关系式y=kx+b 中);第四步,写(写出函数关系式).思想方法小结 (1)函数方法.函数方法就是用运动、变化的观点来分析题中的数量关系,抽象、升华为函数的模型,进而解决有关问题的方法.函数的实质是研究两个变量之间的对应关系,灵活运用函数方法可以解决许多数学问题.(2)数形结合法.数形结合法是指将数与形结合,分析、研究、解决问题的一种思想方法,数形结合法在解决与函数有关的问题时,能起到事半功倍的作用.知识规律小结 (1)常数k ,b 对直线y=kx+b(k ≠0)位置的影响. ①当b >0时,直线与y 轴的正半轴相交; 当b=0时,直线经过原点;当b ﹤0时,直线与y 轴的负半轴相交.②当k ,b 异号时,即-kb>0时,直线与x 轴正半轴相交;当b=0时,即-kb=0时,直线经过原点;当k ,b 同号时,即-kb﹤0时,直线与x 轴负半轴相交.③当k >O ,b >O 时,图象经过第一、二、三象限; 当k >0,b=0时,图象经过第一、三象限; 当b >O ,b <O 时,图象经过第一、三、四象限; 当k ﹤O ,b >0时,图象经过第一、二、四象限; 当k ﹤O ,b=0时,图象经过第二、四象限; 当b <O ,b <O 时,图象经过第二、三、四象限.(2)直线y=kx+b (k ≠0)与直线y=kx(k ≠0)的位置关系. 直线y=kx+b(k ≠0)平行于直线y=kx(k ≠0)当b >0时,把直线y=kx 向上平移b 个单位,可得直线y=kx+b ; 当b ﹤O 时,把直线y=kx 向下平移|b|个单位,可得直线y=kx+b . (3)直线b 1=k 1x+b 1与直线y 2=k 2x+b 2(k 1≠0 ,k 2≠0)的位置关系. ①k 1≠k 2⇔y 1与y 2相交;②⎩⎨⎧=≠2121b b k k ⇔y 1与y 2相交于y 轴上同一点(0,b 1)或(0,b 2); ③⎩⎨⎧≠=2121,b b k k ⇔y 1与y 2平行; ④⎩⎨⎧==2121,b b k k ⇔y 1与y 2重合.典例剖析基本概念题本节有关基本概念的题目主要是一次函数、正比例函数的概念及它们之间的关系,以及构成一次函数及正比例函数的条件.例1 下列函数中,哪些是一次函数?哪些是正比例函数?(1)y=-21x ; (2)y=-x2; (3)y=-3-5x ;(4)y=-5x 2; (5)y=6x-21(6)y=x(x-4)-x 2.例2 当m 为何值时,函数y=-(m-2)x 32m+(m-4)是一次函数?基础知识应用题本节基础知识的应用主要包括:(1)会确定函数关系式及求函数值;(2)会画一次函数(正比例函数)图象及根据图象收集相关的信息;(3)利用一次函数的图象和性质解决实际问题;(4)利用待定系数法求函数的表达式.例3 一根弹簧长15cm ,它所挂物体的质量不能超过18kg ,并且每挂1kg 的物体,弹簧就伸长0.5cm ,写出挂上物体后,弹簧的长度y (cm )与所挂物体的质量x(kg )之间的函数关系式,写出自变量x 的取值范围,并判断y 是否是x 的一次函数.例4 某物体从上午7时至下午4时的温度M (℃)是时间t (时)的函数:M=t 2-5t+100(其中t=0表示中午12时,t=1表示下午1时),则上午10时此物体的温度为 ℃.例5 已知y-3与x 成正比例,且x=2时,y=7. (1)写出y 与x 之间的函数关系式; (2)当x=4时,求y 的值; (3)当y=4时,求x 的值.例6 若正比例函数y=(1-2m )x 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1﹤x 2时,y 1>y 2,则m 的取值范围是( )A .m ﹤OB .m >0C .m ﹤21D .m >M例7 已知一次函数y=kx+b 的图象如图11-22所示,求函数表达式.例8 求图象经过点(2,-1),且与直线y=2x+1平行的一次函数的表达式.综合应用题本节知识的综合应用包括:(1)与方程知识的综合应用;(2)与不等式知识的综合应用;(3)与实际生活相联系,通过函数解决生活中的实际问题.例9 已知y+a与x+b(a,b为是常数)成正比例.(1)y是x的一次函数吗?请说明理由;(2)在什么条件下,y是x的正比例函数?例10 某移动通讯公司开设了两种通讯业务:“全球通”使用者先交50元月租费,然后每通话1分,再付电话费0.4元;“神州行”使用者不交月租费,每通话1分,付话费0.6元(均指市内通话)若1个月内通话x分,两种通讯方式的费用分别为y1元和y2元.(1)写出y1,y2与x之间的关系;(2)一个月内通话多少分时,两种通讯方式的费用相同?(3)某人预计一个月内使用话费200元,则选择哪种通讯方式较合算?例11 已知y+2与x成正比例,且x=-2时,y=0.(1)求y与x之间的函数关系式;(2)画出函数的图象;(3)观察图象,当x取何值时,y≥0?(4)若点(m,6)在该函数的图象上,求m的值;(5)设点P在y轴负半轴上,(2)中的图象与x轴、y轴分别交于A,B两点,且S△ABP=4,求P点的坐标.例12 已知一次函数y=(3-k)x-2k2+18.(1)k为何值时,它的图象经过原点?(2)k为何值时,它的图象经过点(0,-2)?(3)k为何值时,它的图象平行于直线y=-x?(4)k为何值时,y随x的增大而减小?例13 判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.学生做一做判断三点A(3,5),B(0,-1),C(1,3)是否在同一条直线上.探索与创新题主要考查学生运用知识的灵活性和创新性,体现分类讨论思想、数形结合思想在数学问题中的广泛应用.例14 老师讲完“一次函数”这节课后,让同学们讨论下列问题:(1)x从0开始逐渐增大时,y=2x+8和y=6x哪一个的函数值先达到30?这说明了什么?(2)直线y=-x与y=-x+6的位置关系如何?甲生说:“y=6x的函数值先达到30,说明y=6x比y=2x+8的值增长得快.”乙生说:“直线y=-x与y=-x+6是互相平行的.”你认为这两个同学的说法正确吗?例15 某校一名老师将在假期带领学生去北京旅游,用旅行社说:“如果老师买全票,其他人全部半价优惠.”乙旅行社说:“所有人按全票价的6折优惠.”已知全票价为240元.(1)设学生人数为x,甲旅行社的收费为y甲元,乙旅行社的收费为y乙元,分别表示两家旅行社的收费;(2)就学生人数讨论哪家旅行社更优惠.学生做一做某公司到果园基地购买某种优质水果,慰问医务工作者.果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案.甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果量x(千克)之间的函数关系式,并写出自变量X的取值范围;(2)当购买量在什么范围时,选择哪种购买方案付款少?并说明理由.例16 一次函数y=kx+b的自变量x的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,则这个函数的解析式为 .基础训练习题:1.某地举办乒乓球比赛的费用y(元)包括两部分:一部分是租用比赛场地等固定不变的费用b(元),另一部分与参加比赛的人数x(人)成正比例,当x=20时y=160O;当x=3O时,y=200O.(1)求y与x之间的函数关系式;(2)动果有50名运动员参加比赛,且全部费用由运动员分摊,那么每名运动员需要支付多少元?2.已知一次函数y=kx+b,当x=-4时,y的值为9;当x=2时,y的值为-3.(1)求这个函数的解析式。
第5课时一次函数与行程培优专题
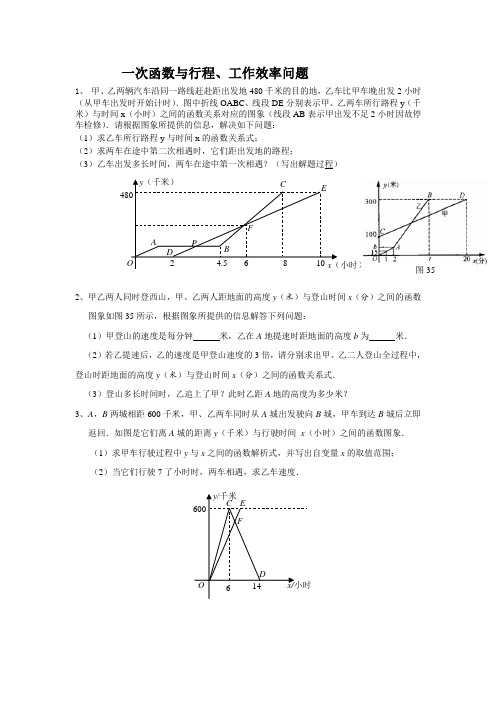
一次函数与行程、工作效率问题1、 甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线OABC 、线段DE 分别表示甲、乙两车所行路程y (千米)与时间x (小时)之间的函数关系对应的图象(线段AB 表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题: (1)求乙车所行路程y 与时间x 的函数关系式;(2)求两车在途中第二次相遇时,它们距出发地的路程;(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)2、甲乙两人同时登西山,甲、乙两人距地面的高度y (米)与登山时间x (分)之间的函数图象如图35所示,根据图象所提供的信息解答下列问题:(1)甲登山的速度是每分钟______米,乙在A 地提速时距地面的高度b 为______米. (2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y (米)与登山时间x (分)之间的函数关系式. (3)登山多长时间时,乙追上了甲?此时乙距A 地的高度为多少米?3、A ,B 两城相距600千米,甲、乙两车同时从A 城出发驶向B 城,甲车到达B 城后立即返回.如图是它们离A 城的距离y (千米)与行驶时间 x (小时)之间的函数图象. (1)求甲车行驶过程中y 与x 之间的函数解析式,并写出自变量x 的取值范围; (2)当它们行驶7了小时时,两车相遇,求乙车速度.x/小时y /千米600146OFEC DA OD PB F CE y (千米) x (小时)4806810 24.5图354、一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水.至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y (单位:升)与时间x (单位:分钟)之间的函数关系如图所示.关停进水管后,经过_____分钟,容器中的水恰好放完.5、某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s 与时间t 之间的图象.请回答下列问题: (1)求师生何时回到学校?(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半个小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s 与时间t 之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回学校,往返平均速度分别为每小时10km 、8km.现有A 、B 、C 、D 四个植树点与学校的路程分别是13km ,15km 、17km 、19km ,试通过计算说明哪几个植树点符合要求.t (时)s (km)86432141312111098O6、有两段长度相等的河渠挖掘任务,分别交给甲乙两个工程队同时进行挖掘,如图是反映所挖河渠长度y(米)与挖掘时间x(时)之间的关系的部分图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数的图象是 直线
我们在画函数y=2x,y=3x-1的图像时,至少应 选取几个点?为什么? 前面我们学习了给定一次函数解析式,可以说 出它的性质,反过来给出有关的信息,能否
求出解析式呢?
确定正比例函数的表达式,就是要确定哪个值?
K的值
(自变量的系数)
需要 (原点除外)几个点坐标呢?
K、b 的值 总结:在确定函数表达式时,要求几个系 数就需要知道几个点的坐标。
一次函数呢?
求函数解关系的一般步骤是怎样的呢? 可归纳为:“一设、二列、三解、四写”
一设:设出函数关系式的一般形式y=kx+b;
30 60 80
x
9.已知直线y=kx+b,经过点A(0,6),B(3,0)
1)写出表示这条直线的函数解析式。
2)如果这条直线经过点P(m,2), 求m的值。
3)求这条直线与x 轴,y 轴所围成的图形的 面积。
y A(0,6) 2 -2 -2 02
B(3,0)
x
求下图中直线的解析式:
解:图像是经过原点的直线, 因此是正比例函数,设解析 式为y=kx,把(1,2)代入,得 k=2,所以解析式为y=2x.
2
1
如图所示,已知直线 AB和x轴交于点B,和y 轴交于点A
y 5 4 3 2 1
①写出A、B两点 的坐标 ②求直线AB的 表达式
-3 -2 -1
A B
0 1 2 3 4
根同规格的碗整齐地放在桌面上,请根据图 中的数据信息,解答下列问题:
(1)求整齐摆放在桌面上的碗的高度y(cm)与碗的个数x(个) 之间的函数关系式;(y与x成一次函数关系)
(2)把这两摞碗整齐地摆成一摞时,碗的高度是多少?
11cm
14cm
2.在弹性限度内,弹簧的长度 y(厘米)是 所挂物体质量 x(千克)的一次函数。一 根弹簧不挂物体时长14.5厘米;当所挂物体 的质量为3千克时,弹簧长16厘米。请写出 y 与x之间的关系式,并求当所挂物体的质 量为4千克时弹簧的长度。
二列:根据已知两点的坐标列出关于k、b的二元 一次方程组; 三解:解这个方程组,求出k、b的值; 四写:把求得的k、b的值代入y=kx+b,写出函数 关系式.
小结:求一次函数关系式常见题型
1.利用图像求函数关系式
2.利用点的坐标求函数关系式
3.利用表格信息确定函数关系式
4.根据实际情况收集信息求函数关 系式
①若一次函数图像y=ax+3的图象经 过A(1,-2),则a= ( ) ②直线y=2x+b过点(1,-2),则它 与y轴交点坐标为( ) ③某函数具有下列两条性质:它的 图像经过原点(0,0)的一条直线; y值随x的增大而减小。 请你写出满足上述条件的函数(用 关系式表示)
B组练习题
y
某地长途汽车客运公司规 定旅客可随身携带一定质 量的行李,如果超过规定, 10 则需要购买行李票,行李 6 票费用y元是行李质量x (千克)的一次函数,其 0 图象如下图所示: ①写出y与x之间的函数关 系式; ②旅客最多可免费携带多 少千克行李?
x
-1 -2 -3
像这样先设出函数解析式,再根据条件确定解析 式中未知的系数,从而具体写出这个式子的方法, 叫做待定系数法.
函数解析式和函数图象如何相互转化呢?
从数到形
函数解析 式 y=kx+b(k ≠0)
选取
满足条件的 两点(x1,y1) 与(x2,y2)
画出
一次函数的 图象直线L
解出
从形到数
利用表格信息确定函数关系式
1.某型号汽车进行耗油实验,y(耗油量)是t(时间)的 一次函数,函数关系如下表,请确定函数表达式。
t (时 间) y(耗油量) 0 100 1 84 2 68 3 52 … …
2. 小明根据某个一次函数关系式填写了下表:
x y -2 3 -1 0 1 1 0
其中有一格不慎被墨汁遮住了,想想看,该空 格里原来填的数是多少?解释你的理由。
选取
体现了“数形结合”的数学思想
利用图像求函数关系式
某物体沿一个斜坡下 滑,它的速度 v (米/ 秒)与其下滑时间 t (秒)的关系如右图 所示:请写出 v 与 t 的关系式;
V/(米/秒)
O
t/秒
利用点的坐标求函数关系式
1.已知一次函数y=kx+b,当x =0时, y =2;当x =4时,y =6.求这个一次函 数的解析式. 2.已知一次函数的图象经过点(3,5)与 (-4,-9).求这个一次函数的解析 式.
