高考数学一轮复习 第4章 三角函数 第4课时 二倍角公式练习 理
4.3 两角和与差的正弦、余弦和正切公式、二倍角公式

αsin αsin
γγ=1t-antαan+αttaannγγ.
时 作 业
报
所以tan αtan β+tan βtan γ=1-tan αtan γ,
告
二
即tan αtan β+tan βtan γ+tan αtan γ=1.
第4章 第3节
第20页
名师伴你行 ·高考一轮总复习 ·数学(理)
报
告
一
课
告
二
∴ sin αcos β+cos αsin β=-12,
∴ sin(α+β)=-12.
第4章 第3节
第24页
名师伴你行 ·高考一轮总复习 ·数学(理)
报
告
Ⅱ.两角和与差公式的逆用
一
3.函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为
课 时
作
________.
业
报
告 二
[答案] 1
所以β=90°-(α+γ),
第4章 第3节
第19页
名师伴你行 ·高考一轮总复习 ·数学(理)
报 告 一
故tan β=tan[90°-(α+γ)]=csoins[[9900°°--αα++γγ]]=csoinsαα++γγ=
课
cos αcos γ-sin sin αcos γ+cos
二
β).
第4章 第3节
第29页
名师伴你行 ·高考一轮总复习 ·数学(理)
三角形中的常见变形
报 告 一
报 告 二
课 时 作 业
第4章 第3节
第30页
名师伴你行 ·高考一轮总复习 ·数学(理)
报 告
Ⅲ.辅助角公式:asin α+bcos α= a2+b2sin(α+φ)的应用
第4章第四章三角函数、解三角形第4节二倍角公式及应用课件(共35张PPT) 高考数学一轮复习

=12-co2s2α+12+14cos2α- 43sin2α+ 43sin2α-12sin2α=1-14cos2α-12 sin2α
=1-14(1-2sin2α)-12sin2α=34.
内容索引
思考1►►► 如何利用二倍角公式进行三角函数式的化简及恒等式的证明?要注 意什么?
内容索引
要充分观察角与角之间的联系,看角是否有倍数关系?能否用二倍 角公式化简?有切有弦要弦切互化.
sin15°cos15°=12sin30°=14,故 D 不正确.
【答案】 C
内容索引
2. 已知角α的顶点为坐标原点 ,始边与x轴的非负半轴重合 ,且
P(8,3cosα)为α终边上一点,则cos2α等于( )
A. -79
B. -89
7
8
C. 9
D. 9
【分析】 根据三角函数定义和同角三角函数关系求出sinα,再由二
=cos2αcsoinsαα2cosα2=cosαsinα2cosα2=12sinαcosα=14sin2α=右边, 所以原式成立.
内容索引
某同学在一次研究性学习中发现,以下四个式子的值都等于同 一个常数:
①sin212°+cos242°+sin12°cos42°; ②sin215°+cos245°+sin15°cos45°; ③sin220°+cos250°+sin20°cos50°; ④sin230°+cos260°+sin30°cos60°. (1) 试从上述式子中选择一个,求出这个常数; (2) 根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明 你的结论.
倍角公式可求cos2α.
内容索引
【解析】 由三角函数定义可知 tanα=3c8osα=csoinsαα,则 3cos2α=8sinα =3-3sin2α,解得 sinα=13或 sinα=-3(舍去),则 cos2α=1-2sin2α=79.
最新高考第一轮复习数学:4.4两角和与差、二倍角的公式(三)教案(含习题及答案)

关系: 2α+β =( α+β ) +α ,( α +β )- α =β可证得结论 .
证明: sin( 2α +β )- 2cos( α +β) sinα
=sin[( α +β) +α ]- 2cos( α +β) sinα
=sin( α +β )cosα +cos( α +β ) sinα - 2cos(α +β ) sinα =sin( α +β )cosα - cos( α+β ) sinα =sin[( α +β )- α ]=sin β. 两边同除以 sinα 得
为简、左右归一、变更命题等方法,使等式两端的“异”化为“同”
.
2.条件等式的证明,通过认真观察,发现已知条件和待证等式之间的关系,选择适当的 途径把条件用上去 .常用方法有代入法、消去法、综合法(即从已知条件出发,以待证式为 目标进行代数或三角恒等变形,逐步推出待证式) 、分析法等 .
4.4 两角和与差、二倍角的公式(三)
●知识梳理
1.化简要求 ( 1)能求出值的应求出值 . (2)使三角函数种数、 项数尽量少; 分母尽量不含三角函数; 被开方式尽量不含三角函数 .
2.化简常用方法 ( 1)活用公式(包括正用、逆用、变形用) . ( 2)切割化弦、异名化同名、异角化同角等 .
3.常用技巧
2 sin 20
sin 10
sin 10
cos(30 =
3 cos 20 20 ) 2 sin 20 = 2 sin 10
1 sin 20 2 sin 10
2 sin 20
3
3
cos 20 =2
2024届高三数学一轮复习-三角函数与解三角形 第4练 二倍角公式及应用(解析版)

B. cos A cos B
C. sin 2A sin 2B
D. cos 2A cos 2B
12.(2023·全国·高三专题练习)给出下列说法,其中正确的是( )
A.若 cos 1 ,则 cos 2 7
3
9
C.若 x 1 ,则 x 1 的最小值为 2
2
x
B.若 tan 2 4 ,则 tan 1
D. 5 或
5
5
)
D. 24 25
7.(2023·全国·高三专题练习)下列四个函数中,最小正周期与其余三个函数不同的是( )
A. f x cos2 x sin x cos x
B. f x 1 cos 2 x
2sin x cos x
C.
f
x
cos
x
π 3
cos
x
π 3
D.
f
x
sin
D
不
正确,
故选:BC.
10.AD
【分析】根据二倍角正弦公式、辅助角公式,结合正弦型函数的单调性、平移的性质、对称
性、换元法逐一判断即可.
【详解】 f (x) sin x cos x 1 sin 2x, g(x) sin x cos x 2 sin(x π ) ,
2
4
当
x
0,
π 4
时,
3 5 8
2
5 1 5 1.
16
4
故选:D.
2.B 【分析】根据三角恒等变换公式求解.
【详解】
sin
π 6
cos
3 sin 1 cos cos 3 ,
2
2
5
所以 3 sin 1 cos 3 ,
2024届新高考一轮总复习人教版 第四章 第2节 同角三角函数的基本关系式及诱导公式 课件(35张)

所以 cos2α=190,由 α 为第二象限角,易知 cosα<0,所以 cos α=-31010,sin α= 1100,
C.sin 54π+α=12
B.cos π4-α=12 D.cos 54π-α=-12
解析:由 sin π4+α=12,可得 cos (π4+α)=± 23,sin 54π+α=sin π+π4+α=-sin π4+α=-12,cos π4-α=cos [π2-π4+α]=sin π4+α=12,cos 54π-α=cos π+π4-α= -cos π4-α=-12.
(sin α+cos α)2-(sin α-cos α)2=4sin αcos α;
sin α=tan αcos αα≠π2+kπ,k∈Z;
sin
2α=sin
sin 2α 2α+cos
2α=tanta2nα2+α 1;
cos2α=sin
cos 2α 2α+cos
2α=tan21α+1.
【小题热身】 1.思考辨析(在括号内打“√”或“×”) (1)若 α,β 为锐角,则 sin2α+cos2β=1.( ) (2)sin(π+α)=-sin α 成立的条件是 α 为锐角.( ) (3)若 α∈R,则 tan α=csoins αα恒成立.( ) (4)若 sin (kπ-α)=13(k∈Z),则 sin α=13.( ) 答案:(1)× (2)× (3)× (4)×
2.三角函数的诱导公式
组数
一
二
三
四
角 2kπ+α(k∈Z) π+α
-α
π-α
正弦 余弦 正切
口诀
__s_in__α__ __c_o_s_α__ __ta_n__α__
__-__s_i_n_α__ __-__s_in__α__ __s_in__α__ __-__c_o_s_α__ __co_s__α__ _-___co_s__α__ __t_an__α__ __-__t_a_n_α__ _-___ta_n_α___
高考数学一轮复习第四章三角函数解三角形4.1任意角蝗制及任意角的三角函数课件理

(2)已知角α的终边在如图所示阴影表示的范围内(不包括边界),则角α 用集合可表示为_(2_k_π_+__π4_,__2_k_π_+__56_π_)_(k_∈__Z__) . 答案 解析
在[0,2π)内,终边落在阴影部分角的集合为π4,56π, ∴所求角的集合为2kπ+4π,2kπ+56π(k∈Z).
弧度数是 答案 解析
π
π
A.3
B.6
C.-π3
D.-π6
将表的分针拨快应按顺时针方向旋转,为负角,故A、B不正确;
又因为拨快10分钟,故应转过的角为圆周的 1 . 6
即为-16×2π=-π3.
(2)若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为
π
π
A.6
B.3
C.3
D. 3
答案
解析
如图,等边三角形ABC是半径为r的圆O的内接三角形,
2.弧度制
(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号
rad表示,读作弧度.正角的弧度数是一个 正数 ,负角的弧度数是一个
负数 ,零角的弧度数是 0 .
π
180
(2)角度制和弧度制的互化:180°= π
rad,1°=180 rad,1 rad=
π
.
1 (3)扇形的弧长公式:l= |α|·r ,扇形的面积公式:S= 2lr =
②若扇形的周长为20,求扇形面积的最大值,并求此时扇形圆心角的 弧度数. 解答
由题意知l+2r=20,即l=20-2r, S=12l·r=12(20-2r)·r=-(r-5)2+25, 当r=5时,S的最大值为25. 当 r=5 时,l=20-2×5=10,α=rl=2(rad). 即扇形面积的最大值为25,此时扇形圆心角的弧度数为2 rad.
高考数学大一轮复习 第四章 三角函数、解三角形 4.5 两角和与差及二倍角的三角函数 第1课时学案

§4.5三角恒等变形最新考纲考情考向分析1.会用向量的数量积推导出两角差的余弦公式.2.会用两角差的余弦公式推导出两角差的正弦、正切公式.3.会用两角差的余弦公式推导出两角和的正弦、余弦、正切公式,推导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.4.能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).三角恒等变换是三角变换的工具,主要考查利用两角和与差的三角函数公式、二倍角公式进行三角函数的化简与求值,重在考查化简、求值,公式的正用、逆用以及变式运用,可单独考查,也可与三角函数的图象和性质、向量等知识综合考查,加强转化与化归思想的应用意识.选择、填空、解答题均有可能出现,中低档难度.1.两角和与差的余弦、正弦、正切公式cos(α-β)=cos αcos β+sin αsin β(C(α-β))cos(α+β)=cos αcos β-sin αsin β(C(α+β))sin(α-β)=sin αcos β-cos αsin β(S(α-β))sin(α+β)=sin αcos β+cos αsin β(S(α+β))tan(α-β)=tan α-tan β1+tan αtan β(T(α-β))tan(α+β)=tan α+tan β1-tan αtan β(T(α+β))2.二倍角公式sin 2α=2sin αcos α;cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α;tan 2α=2tan α1-tan2α.知识拓展1.降幂公式:cos 2α=1+cos 2α2,sin 2α=1-cos 2α2.2.升幂公式:1+cos 2α=2cos 2α,1-cos 2α=2sin 2α.3.辅助角公式:a sin x +b cos x =a 2+b 2sin(x +φ),其中sin φ=b a 2+b 2,cos φ=a a 2+b 2.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)存在实数α,β,使等式sin(α+β)=sin α+sin β成立.( √ )(2)对任意角α都有1+sin α=⎝⎛⎭⎪⎫sin α2+cos α22.( √ )(3)y =3sin x +4cos x 的最大值是7.( × )(4)公式tan(α+β)=tan α+tan β1-tan αtan β可以变形为tan α+tan β=tan(α+β)(1-tanαtan β),且对任意角α,β都成立.( × )题组二 教材改编2.若cos α=-45,α是第三象限的角,则sin ⎝ ⎛⎭⎪⎫α+π4等于( ) A .-210 B.210 C .-7210 D.7210答案 C解析 ∵α是第三象限角, ∴sin α=-1-cos 2α=-35,∴sin ⎝ ⎛⎭⎪⎫α+π4=-35×22+⎝ ⎛⎭⎪⎫-45×22=-7210. 3.sin 347°cos 148°+sin 77°cos 58°= . 答案22解析 sin 347°cos 148°+sin 77°cos 58°=sin(270°+77°)cos(90°+58°)+sin 77°cos 58° =(-cos 77°)·(-sin 58°)+sin 77°cos 58° =sin 58°cos 77°+cos 58°sin 77° =sin(58°+77°)=sin 135°=22. 4.tan 20°+tan 40°+3tan 20°tan 40°= . 答案3解析 ∵tan 60°=tan(20°+40°)=tan 20°+tan 40°1-tan 20°tan 40°,∴tan 20°+tan 40°=tan 60°(1-tan 20°tan 40°) =3-3tan 20°tan 40°,∴原式=3-3tan 20°tan 40°+3tan 20°tan 40°= 3. 题组三 易错自纠5.化简:cos 40°cos 25°·1-sin 40°= .答案2解析 原式=cos 40°cos 25°1-cos 50°=cos 40°cos 25°·2sin 25°=cos 40°22sin 50°= 2. 6.(2018·昆明模拟)若tan α=13,tan(α+β)=12,则tan β= .答案 17解析 tan β=tan[(α+β)-α]=tan (α+β)-tan α1+tan (α+β)tan α=12-131+12×13=17.7.(2018·烟台模拟)已知θ∈⎝ ⎛⎭⎪⎫0,π2,且sin ⎝ ⎛⎭⎪⎫θ-π4=210,则tan 2θ= .答案 -247解析 方法一 sin ⎝⎛⎭⎪⎫θ-π4=210,得sin θ-cos θ=15,① θ∈⎝⎛⎭⎪⎫0,π2,①平方得2sin θcos θ=2425,可求得sin θ+cos θ=75,∴sin θ=45,cos θ=35,∴tan θ=43,tan 2θ=2tan θ1-tan 2θ=-247. 方法二 ∵θ∈⎝ ⎛⎭⎪⎫0,π2且sin ⎝ ⎛⎭⎪⎫θ-π4=210,∴cos ⎝⎛⎭⎪⎫θ-π4=7210,∴tan ⎝ ⎛⎭⎪⎫θ-π4=17=tan θ-11+tan θ,∴tan θ=43. 故tan 2θ=2tan θ1-tan 2θ=-247.第1课时 两角和与差的正弦、余弦和正切公式题型一 和差公式的直接应用1.(2018·青岛调研)已知sin α=35,α∈⎝ ⎛⎭⎪⎫π2,π,tan(π-β)=12,则tan(α-β)的值为( )A .-211 B.211 C.112 D .-112答案 A解析 ∵α∈⎝ ⎛⎭⎪⎫π2,π,∴tan α=-34,又tan β=-12,∴tan(α-β)=tan α-tan β1+tan α·tan β=-34+121+⎝ ⎛⎭⎪⎫-12×⎝ ⎛⎭⎪⎫-34=-211.2.(2017·山西太原五中模拟)已知角α为锐角,若sin ⎝ ⎛⎭⎪⎫α-π6=13,则cos ⎝⎛⎭⎪⎫α-π3等于( ) A.26+16B.3-28 C.3+28D.23-16答案 A解析 由于角α为锐角,且sin ⎝ ⎛⎭⎪⎫α-π6=13, 则cos ⎝⎛⎭⎪⎫α-π6=223,则cos ⎝ ⎛⎭⎪⎫α-π3=cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-π6-π6=cos ⎝ ⎛⎭⎪⎫α-π6cos π6+sin ⎝ ⎛⎭⎪⎫α-π6sin π6=223×32+13×12=26+16, 故选A.3.计算sin 110°sin 20°cos 2155°-sin 2155°的值为 . 答案 12解析sin 110°sin 20°cos 2155°-sin 2155°=sin 70°sin 20°co s 310°=cos 20°sin 20°cos 50°=12sin 40°sin 40°=12.思维升华 (1)使用两角和与差的三角函数公式,首先要记住公式的结构特征. (2)使用公式求值,应先求出相关角的函数值,再代入公式求值.题型二 和差公式的灵活应用命题点1 角的变换典例 (1)设α,β都是锐角,且cos α=55,sin(α+β)=35,则cos β= . 答案2525解析 依题意得sin α=1-cos 2α=255, 因为sin(α+β)=35<sin α且α+β>α,所以α+β∈⎝ ⎛⎭⎪⎫π2,π,所以cos(α+β)=-45. 于是cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α =-45×55+35×255=2525.(2)(2017·泰安模拟)已知cos(75°+α)=13,则cos(30°-2α)的值为 .答案 79解析 cos(75°+α)=sin(15°-α)=13,∴cos(30°-2α)=1-2sin 2(15°-α)=1-29=79.命题点2 三角函数式的变换典例 (1)化简:(1+sin θ+cos θ)⎝⎛⎭⎪⎫sin θ2-cos θ22+2cos θ (0<θ<π);(2)求值:1+cos 20°2sin 20°-sin 10°⎝ ⎛⎭⎪⎫1tan 5°-tan 5°.解 (1)由θ∈(0,π),得0<θ2<π2,∴cos θ2>0,∴2+2cos θ=4cos2θ2=2cos θ2. 又(1+sin θ+cos θ)⎝ ⎛⎭⎪⎫sin θ2-cos θ2 =⎝⎛⎭⎪⎫2sin θ2cos θ2+2cos 2θ2⎝ ⎛⎭⎪⎫sin θ2-cos θ2=2cos θ2⎝ ⎛⎭⎪⎫sin 2θ2-cos 2θ2=-2cos θ2cos θ.故原式=-2cos θ2cos θ2cosθ2=-cos θ.(2)原式=2cos 210°2×2sin 10°cos 10°-s in 10°⎝ ⎛⎭⎪⎫cos 5°sin 5°-sin 5°cos 5°=cos 10°2sin 10°-sin 10°·cos 25°-sin 25°sin 5°cos 5° =cos 10°2sin 10°-sin 10°·cos 10°12sin 10° =cos 10°2sin 10°-2cos 10°=cos 10°-2sin 20°2sin 10° =cos 10°-2sin (30°-10°)2sin 10°=cos 10°-2⎝ ⎛⎭⎪⎫12cos 10°-32sin 10°2sin 10°=3sin 10°2sin 10°=32.引申探究化简:(1+sin θ-cos θ)⎝ ⎛⎭⎪⎫sin θ2-cos θ22-2cos θ(0<θ<π).解 ∵0<θ2<π2,∴2-2cos θ=2sin θ2,又1+sin θ-cos θ=2sin θ2cos θ2+2sin 2θ2=2sin θ2⎝⎛⎭⎪⎫sin θ2+cos θ2∴原式=2sin θ2⎝⎛⎭⎪⎫sin θ2+cos θ2⎝ ⎛⎭⎪⎫sin θ2-cos θ22sinθ2=-cos θ.思维升华 (1)解决三角函数的求值问题的关键是把“所求角”用“已知角”表示.①当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;②当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系. (2)常见的配角技巧:2α=(α+β)+(α-β),α=(α+β)-β,β=α+β2-α-β2,α=α+β2+α-β2,α-β2=⎝ ⎛⎭⎪⎫α+β2-⎝ ⎛⎭⎪⎫α2+β等.跟踪训练 (1)(2017·豫北名校联考)计算:cos 10°-3cos (-100°)1-sin 10°= .(用数字作答)答案 2解析cos 10°-3cos (-100°)1-sin 10°=cos 10°+3cos 80°1-cos 80°=cos 10°+3sin 10°2·sin 40°=2sin (10°+30°)2·sin 40°= 2.(2)(2017·南充模拟)已知α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫0,π2,且cos α=17,cos(α+β)=-1114,则sin β= . 答案32解析 由已知可得sin α=437,sin(α+β)=5314, ∴sin β=sin[(α+β)-α]=sin(α+β)·cos α-cos(α+β)sin α=5314×17-⎝ ⎛⎭⎪⎫-1114×437=32.用联系的观点进行三角变形典例 (1)设α为锐角,若cos ⎝ ⎛⎭⎪⎫α+π6=45,则sin ⎝ ⎛⎭⎪⎫2α+π12 的值为 .(2)(1+tan 17°)·(1+tan 28°)的值为 . (3)已知sin α=35,α∈⎝ ⎛⎭⎪⎫π2,π,则cos 2α2sin ⎝ ⎛⎭⎪⎫α+π4= .思想方法指导 三角变形的关键是找到条件和结论中的角和式子结构之间的联系.变形中可以通过适当地拆角、凑角或对式子整体变形达到目的.解析 (1)∵α为锐角且cos ⎝ ⎛⎭⎪⎫α+π6=45>0, ∴α+π6∈⎝ ⎛⎭⎪⎫π6,π2,∴s in⎝ ⎛⎭⎪⎫α+π6=35.∴sin ⎝ ⎛⎭⎪⎫2α+π12=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫α+π6-π4=sin 2⎝ ⎛⎭⎪⎫α+π6cos π4-cos 2⎝ ⎛⎭⎪⎫α+π6sin π4=2sin ⎝ ⎛⎭⎪⎫α+π6cos ⎝ ⎛⎭⎪⎫α+π6-22⎣⎢⎡⎦⎥⎤2cos 2⎝ ⎛⎭⎪⎫α+π6-1 =2×35×45-22⎣⎢⎡⎦⎥⎤2×⎝ ⎛⎭⎪⎫452-1=12225-7250=17250.(2)原式=1+tan 17°+tan 28°+tan 17°·tan 28° =1+tan 45°(1-tan 17°·tan 28°)+tan 17°·tan 28° =1+1=2. (3)cos 2α2sin ⎝⎛⎭⎪⎫α+π4=cos 2α-sin 2α2⎝ ⎛⎭⎪⎫22sin α+22cos α=cos α-sin α,∵sin α=35,α∈⎝ ⎛⎭⎪⎫π2,π,∴cos α=-45,∴原式=-75.答案 (1)17250 (2)2 (3)-751.(2017·山西五校联考)若cos θ=23,θ为第四象限角,则cos ⎝ ⎛⎭⎪⎫θ+π4的值为( )A.2+106 B.22+106 C.2-106D.22-106答案 B解析 由cos θ=23,θ为第四象限角,得sin θ=-53, 故cos ⎝ ⎛⎭⎪⎫θ+π4=22(cos θ-sin θ)=22×⎝ ⎛⎭⎪⎫23+53=22+106.故选B. 2.(2018·成都模拟)若sin α=45,则sin ⎝ ⎛⎭⎪⎫α+π4-22cos α等于( )A.225B .-225C.425D .-425答案 A解析 sin ⎝ ⎛⎭⎪⎫α+π4-22cos α=sin αcos π4+cos αsin π4-22cos α=45×22=225. 3.(2017·西安检测)已知α是第二象限角,且tan α=-13,则sin 2α等于( )A .-31010B.31010 C .-35D.35答案 C解析 因为α是第二象限角,且tan α=-13,所以sin α=1010,cos α=-31010, 所以sin 2α=2sin αcos α=2×1010×⎝ ⎛⎭⎪⎫-31010=-35, 故选C.4.(2017·河南洛阳一模)设a =cos 50°cos 127°+cos 40°sin 127°,b =22(sin 56°-cos 56°),c =1-tan 239°1+tan 239°,则a ,b ,c 的大小关系是( ) A .a >b >cB .b >a >cC .c >a >bD .a >c >b答案 D 解析 a =sin 40°cos 127°+cos 40°sin 127°=sin(40°+127°)=sin 167°=sin 13°,b =22(sin 56°-cos 56°)=22sin 56°-22cos 56° =sin(56°-45°)=sin 11°,c =cos 239°-sin 239°cos 239°sin 239°+cos 239°cos 239°=cos 239°-sin 239°=cos 78°=sin 12°, ∵sin 13°>sin 12°>sin 11°,∴a >c >b .5.已知sin α=35且α为第二象限角,则tan ⎝⎛⎭⎪⎫2α+π4等于( ) A .-195 B .-519 C .-3117 D .-1731答案 D解析 由题意得cos α=-45,则sin 2α=-2425, cos 2α=2cos 2α-1=725. ∴tan 2α=-247, ∴tan ⎝ ⎛⎭⎪⎫2α+π4=tan 2α+tan π41-tan 2αtan π4=-247+11-⎝ ⎛⎭⎪⎫-247×1 =-1731. 6.已知sin 2α=23,则cos 2⎝⎛⎭⎪⎫α+π4等于( ) A.16B.13C.12D.23 答案 A解析 因为cos 2⎝⎛⎭⎪⎫α+π4=1+cos 2⎝ ⎛⎭⎪⎫α+π42 =1+cos ⎝ ⎛⎭⎪⎫2α+π22=1-sin 2α2, 所以cos 2⎝⎛⎭⎪⎫α+π4=1-sin 2α2=1-232=16,故选A. 7.(2018·新疆乌鲁木齐一诊)2cos 10°-sin 20°sin 70°的值是( ) A.12B.32C. 3D. 2答案 C解析 原式=2cos (30°-20°)-sin 20°sin 70°=2(cos 30°·cos 20°+sin 30°·sin 20°)-sin 20°sin 70°=3cos 20°cos 20°= 3. 8.已知锐角α,β满足sin α-cos α=16,tan α+tan β+3tan αtan β=3,则α,β的大小关系是( )A .α<π4<β B .β<π4<α C.π4<α<β D.π4<β<α 答案 B解析 ∵α为锐角,sin α-cos α=16>0,∴π4<α<π2. 又tan α+tan β+3tan αtan β=3,∴tan(α+β)=tan α+tan β1-tan αtan β=3, ∴α+β=π3,又α>π4,∴β<π4<α.9.(2017·江苏)若tan ⎝⎛⎭⎪⎫α-π4=16,则tan α= . 答案 75解析 方法一 ∵tan ⎝ ⎛⎭⎪⎫α-π4=tan α-tan π41+tan αtan π4=tan α-11+tan α=16, ∴6tan α-6=1+tan α(tan α≠-1),∴tan α=75. 方法二 tan α=tan ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫α-π4+π4 =tan ⎝ ⎛⎭⎪⎫α-π4+tan π41-tan ⎝⎛⎭⎪⎫α-π4tan π4=16+11-16=75. 10.(2018·河南八市质检)化简:2tan (45°-α)1-tan 2(45°-α)·sin αcos αcos 2α-sin 2α= . 答案 12解析 原式=tan(90°-2α)·12sin 2αcos 2α=sin (90°-2α)cos (90°-2α)·12·sin 2αcos 2α=cos 2αsin 2α·12·sin 2αcos 2α=12. 11.已知sin α+cos α=13,则sin 2⎝ ⎛⎭⎪⎫π4-α= . 答案 1718解析 由sin α+cos α=13,两边平方得1+sin 2α=19, 解得sin 2α=-89,所以sin 2⎝ ⎛⎭⎪⎫π4-α=1-cos ⎝ ⎛⎭⎪⎫π2-2α2 =1-sin 2α2=1+892=1718. 12.(2018·吉林模拟)已知sin(α-β)cos α-cos(β-α)sin α=35,β是第三象限角,则sin ⎝⎛⎭⎪⎫β+5π4= . 答案 7210解析 依题意可将已知条件变形为sin[(α-β)-α]=-sin β=35,sin β=-35. 又β是第三象限角,所以cos β=-45. 所以sin ⎝ ⎛⎭⎪⎫β+5π4=-sin ⎝⎛⎭⎪⎫β+π4 =-sin βcos π4-cos βsin π4=35×22+45×22=7210.13.(2017·河北衡水中学调研)若α∈⎝ ⎛⎭⎪⎫π2,π,且3cos 2α=sin ⎝ ⎛⎭⎪⎫π4-α,则sin 2α的值为( )A .-118 B.118 C .-1718 D.1718答案 C解析 由3cos 2α=sin ⎝⎛⎭⎪⎫π4-α可得 3(cos 2α-sin 2α)=22(cos α-sin α), 又由α∈⎝ ⎛⎭⎪⎫π2,π可知cos α-sin α≠0, 于是3(cos α+sin α)=22, 所以1+2sin α·cos α=118,故sin 2α=-1718.故选C. 14.已知cos ⎝ ⎛⎭⎪⎫π4+θcos ⎝ ⎛⎭⎪⎫π4-θ=14,则sin 4θ+cos 4θ的值为 . 答案 58解析 因为cos ⎝⎛⎭⎪⎫π4+θcos ⎝ ⎛⎭⎪⎫π4-θ =⎝ ⎛⎭⎪⎫22cos θ-22sin θ⎝ ⎛⎭⎪⎫22cos θ+22sin θ =12(cos 2θ-sin 2θ)=12cos 2θ=14. 所以cos 2θ=12. 故sin 4θ+cos 4θ=⎝⎛⎭⎪⎫1-cos 2θ22+⎝ ⎛⎭⎪⎫1+cos 2θ22 =116+916=58.15.(2017·武汉调研)设α,β∈[0,π],且满足sin αcos β-cos αsin β=1,则sin(2α-β)+sin(α-2β)的取值范围为 .答案 [-1,1]解析 由sin αcos β-cos αsin β=1,得sin(α-β)=1,又α,β∈[0,π],∴α-β=π2, ∴⎩⎪⎨⎪⎧ 0≤α≤π,0≤β=α-π2≤π,即π2≤α≤π, ∴sin(2α-β)+sin(α-2β)=sin ⎝⎛⎭⎪⎫2α-α+π2+sin(α-2α+π) =cos α+sin α=2sin ⎝⎛⎭⎪⎫α+π4. ∵π2≤α≤π,∴3π4≤α+π4≤5π4, ∴-1≤2sin ⎝⎛⎭⎪⎫α+π4≤1, 即取值范围为[-1,1].16.(2017·合肥模拟)已知函数f (x )=(2cos 2x -1)·sin 2x +12cos 4x . (1)求f (x )的最小正周期及递减区间;(2)若α∈(0,π),且f ⎝ ⎛⎭⎪⎫α4-π8=22,求tan ⎝⎛⎭⎪⎫α+π3 的值. 解 (1)f (x )=(2cos 2x -1)sin 2x +12cos 4x =cos 2x sin 2x +12cos 4x =12(sin 4x +cos 4x )=22sin ⎝⎛⎭⎪⎫4x +π4, ∴f (x )的最小正周期T =π2. 令2k π+π2≤4x +π4≤2k π+3π2,k ∈Z , 得k π2+π16≤x ≤k π2+5π16,k ∈Z .∴f (x )的递减区间为⎣⎢⎡⎦⎥⎤k π2+π16,k π2+5π16,k ∈Z . (2)∵f ⎝ ⎛⎭⎪⎫α4-π8=22,∴sin ⎝ ⎛⎭⎪⎫α-π4=1. ∵α∈(0,π),-π4<α-π4<3π4, ∴α-π4=π2,故α=3π4. 因此tan ⎝ ⎛⎭⎪⎫α+π3=tan 3π4+tan π31-tan 3π4tan π3=-1+31+3=2- 3.。
高考数学(理)一轮总复习课件:第四章 三角函数 4-2

49 120 ∴(sinθ+ cosθ) = .∴2sinθcosθ=- . 169 169 又 θ∈(0,π),∴sinθ>0,cosθ<0. ∴sinθ- cosθ= (sinθ-cosθ)2 17 = sin θ-2sinθcosθ+ cos θ=13.
2 2
(2)sin3θ+cos3θ=(sinθ+cosθ)(sin2θ-sinθcosθ+cos2θ)= 7 60 1 603 13×(1+169)=2 197.
答案 6 19 10
sin2α 2si nαcosα 解析 = =2tanα=2×3=6. 2 2 cos α cos α
授 人 以 渔
题型一
诱导公式 )
π 1 7 (1)已知 sin(α+12)=3,则 cos(α+12π )的值为( 1 A. 3 2 C.- 2 3 1 B.-3 2 D. 2 3
2
1 2 2 2 1-( ) =- . 3 3
1 (2)∵sinα=3,∴α是第一或第二象限角. 当 α 是第一象限角时, ∴cosα= 1-sin α= sinα 2 ∴tanα= cosα= 4 ; 当 α 是第二象限角时,tanα=- 2 . 4
2
1 2 2 2 1-( ) = . 3 3
(3)∵sinα= m(m≠0, m≠±1), ∴cosα=± 1-sin2α=± 1- m2 (当 α 为第一、四象限角时 取正号,当 α 为第二、三象限角时取负号). m ∴当 α 为第一、四象限角时,tanα= 2; 1- m m 当 α 为第二、三象限角时,tanα=- 2. 1- m 【答案】 2 (1)- 4 2 2 (2) 或- 4 4
3π 3π sin(-α- )sin( -α)tan2(2π-α) 2 2 (2)化简: ; π π cos( 2-α)cos( 2+α)sin(π+α) sin( nπ-α)· cos(nπ+α) (3)若 n∈Z,化简: . sin[(n+1)π+α]·cos[( n+1)π-α]
2019高考数学一轮复习 第4章 三角函数 第4课时 二倍角公式练习 理

第4课时 二倍角公式1.已知cos78°约等于0.20,那么sin66°约等于( ) A .0.92 B .0.85 C .0.88 D .0.95答案 A2.sin20°cos20°cos50°=( )A .2 B.22C. 2D.12答案 D3.计算tan15°+1tan15°的值为( )A. 2 B .2 C .4 D .2 2答案 C解析 tan15°+1tan15°=sin15°cos15°+cos15°sin15°=sin 215°+cos 215°sin15°cos15°=2sin30°=4.故选C.4.若sin α2=33,则cos α的值为( )A .-23B .-13C.13D.23答案 C解析 cos α=1-2sin2α2=1-23=13.故选C. 5.已知cos(π4-x)=35,则sin2x 的值为( )A.1825 B.725C .-725D .-1625答案 C解析 因为sin2x =cos(π2-2x)=cos2(π4-x)=2cos 2(π4-x)-1,所以sin2x =2×(35)2-1=1825-1=-725.6.(2018·遵义第一次联考)2002年在北京召开国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么sin2θ的值为( ) A.13 B.32 C.2324 D.2425答案 D解析 设锐角θ所对的直角边长为x ,由题意得x 2+(x +1)2=25,解得x =3,所以sin θ=35,cos θ=45,sin2θ=2425.故选D.7.(2018·河北保定中学期末)已知sin2α=2425,0<α<π2,则2cos(π4-α)的值为( )A .-15B.15 C .-75D.75答案 D解析 ∵sin2α=2425,0<α<π2,∴sin αcos α=1225,sin α>0,cos α>0.又∵sin 2α+cos 2α=1,∴(sin α+cos α)2=1+2sin αcos α=4925,∴sin α+cos α=75.∴2cos(π4-α)=2(22cos α+22sin α)=cos α+sin α=75.8.化简2+2cos8+21-sin8的结果是( ) A .4cos4-2sin4 B .2sin4 C .2sin4-4cos4 D .-2sin4答案 D解析 原式=4cos 24+2(sin4-cos4)2=|2cos4|+2|sin4-cos4|=-2sin4.故选D. 9.若α∈(0,π2),且sin 2α+cos2α=14,则tan α的值为( )A.22B.33C. 2D. 3答案 D解析 因为cos2α=cos 2α-sin 2α,所以sin 2α+cos2α=cos 2α,所以cos 2α=14.又α∈(0,π2),所以cos α=12,所以α=π3,故tan α= 3.故选D.10.(2017·长沙雅礼中学模拟)已知sin2α=23,则cos 2(α+π4)=( )A.16B.13C.12D.23答案 A解析 方法一:cos 2(α+π4)=12[1+cos(2α+π2)]=12(1-sin2α)=16.方法二:cos(α+π4)=22cos α-22sin α,所以cos 2(α+π4)=12(cos α-sin α)2=12(1-2sin αcos α)=12(1-sin2α)=16.11.已知tan(α+π4)=-12,且π2<α<π,则sin2α-2cos 2αsin (α-π4)的值等于( )A.255B .-3510C .-255D .-31010答案 C解析 sin2α-2cos 2αsin (α-π4)=2sin αcos α-2cos 2α22(sin α-cos α)=22cos α,由tan(α+π4)=-12,得tan α+11-tan α=-12,解得tan α=-3.因为π2<α<π,所以cos α=-1tan 2α+1=-1010.所以原式=22cos α=22×(-1010)=-255.故选C.12.(2018·江西抚州七校联考)若sin(x +π6)=13,则tan(2x +π3)=( )A.79 B .±79C.427D .±427答案 D解析 由sin(x +π6)=13,得cos(x +π6)=±1-sin 2(x +π6)=±223,tan(x +π6)=±24,tan(2x +π3)=tan2(x +π6)=2tan (x +π6)1-tan 2(x +π6)=±427.13.(2018·山西临汾五校联考)若tan α-1tan α=32,α∈(π4,π2),则sin(2α+π4)的值为( )A .-25 B.25 C .-210D.210答案 D解析 ∵tan α-1tan α=32,α∈(π4,π2),∴sin αcos α-cos αsin α=32,∴cos2αsin2α=-34.∵π4<α<π2,∴π2<2α<π,∴cos2α=-35,sin2α=45,∴sin(2α+π4)=sin2α×22+cos2α×22=210.14.(2018·广西百色一模)已知x∈(0,π),且cos(2x -π2)=sin 2x ,则tan(x -π4)=( )A.13 B .-13C .3D .-3答案 A解析 ∵cos(2x -π2)=sin 2x ,∴sin2x =sin 2x ,∴2sinxcosx =sin 2x.∵x ∈(0,π),∴sinx>0,∴2cosx =sinx ,∴tanx =2.∴tan(x -π4)=tanx -tanπ41+tanxtanπ4=2-11+2×1=13.故选A.15.(1)(2018·山东烟台期中)若cos(75°-α)=13,则cos(30°+2α)=________.答案 79解析 ∵cos(75°-α)=sin(15°+α)=13,∴cos(30°+2α)=1-2sin 2(15°+α)=1-2×19=79.(2)(2017·保定模拟)计算:3-sin70°2-cos 210°=________. 答案 2解析 3-sin70°2-cos 210°=3-cos20°2-cos 210°=3-(2cos 210°-1)2-cos 210°=2. 16.若sin(x -34π)cos(x -π4)=-14,则cos4x =________.答案 12解析 ∵sin(x -34π)=-cos(π2+x -34π)=-cos(x -π4),∴cos 2(x -π4)=14,∴1+cos (2x -π2)2=14.∴cos(2x -π2)=-12,即sin2x =-12.∴cos4x =1-2sin 22x =12.17.设α为第四象限的角,若sin3αsin α=135,则tan2α=________.答案 -34解析sin3αsin α=sin (2α+α)sin α=sin2αcos α+cos2αsin αsin α=135.∴2cos 2α+cos2α=135,cos2α+1+cos2α=135.∴cos2α=45.∵2k π-π2<α<2k π,∴4k π-π<2α<4k π(k∈Z ).又∵cos2α=45>0,∴2α为第四象限的角.sin2α=-1-cos 22α=-35,∴tan2α=-34.18.(2018·湖北百校联考)设α∈(0,π3),满足6sin α+2cos α= 3.(1)求cos(α+π6)的值;(2)求cos(2α+π12)的值.答案 (1)104 (2)30+28解析 (1)∵6sin α+2cos α=3,∴sin(α+π6)=64.∵α∈(0,π3),∴α+π6∈(π6,π2),∴cos(α+π6)=104. (2)由(1)可得cos(2α+π3)=2cos 2(α+π6)-1=2×(104)2-1=14.∵α∈(0,π3),∴2α+π3∈(π3,π),∴sin(2α+π3)=154.∴cos(2α+π12)=cos[(2α+π3)-π4]=cos(2α+π3)cos π4+sin(2α+π3)sin π4=30+28.若sin76°=m ,用含m 的式子表示cos7°为( ) A.1+m 2B.1-m2C .± 1+m2D.1+m2答案 D解析 ∵sin76°=cos14°=2cos 27°-1=m , ∴cos 27°=1+m 2,∴cos7°=1+m2.。
高考数学一轮总复习第4章三角函数第4节函数y=Asinωx+φ的图象及简单应用教师用书
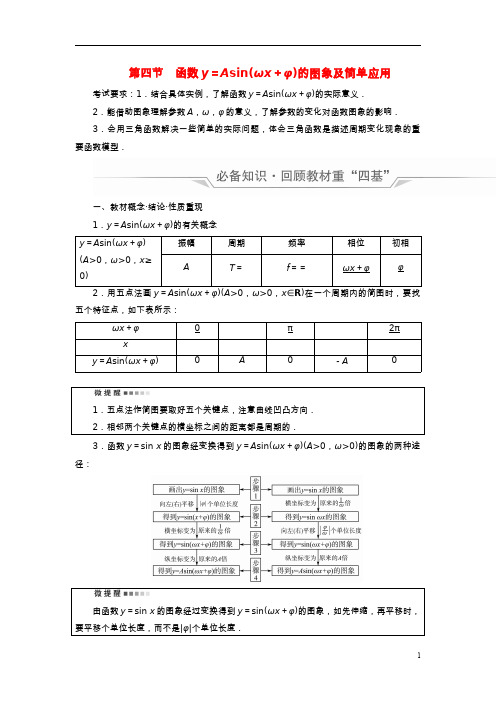
第四节 函数y =A sin(ωx +φ)的图象及简单应用考试要求:1.结合具体实例,了解函数y =A sin(ωx +φ)的实际意义.2.能借助图象理解参数A ,ω,φ的意义,了解参数的变化对函数图象的影响.3.会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型.一、教材概念·结论·性质重现1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0,x ≥0)振幅周期频率相位初相A T =f ==ωx + φ φ2.用五点法画y =A sin(ωx +φ)(A >0,ω>0,x ∈R )在一个周期内的简图时,要找五个特征点,如下表所示:ωx +φ0π2πxy =A sin(ωx+φ)0A 0-A 01.五点法作简图要取好五个关键点,注意曲线凹凸方向.3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)(A >0,ω>0)的图象的两种途径:由函数y =sin x 的图象经过变换得到y =sin(ωx +φ)的图象,如先伸缩,再平移时,要平移个单位长度,而不是|φ|个单位长度.二、基本技能·思想·活动经验1.判断下列说法的正误,对的打“√”,错的打“×”.(1)将y=sin 2x的图象向右平移个单位长度,得到y=sin的图象.( × )(2)函数f(x)=A sin(ωx+φ)(A≠0)的最大值为A,最小值为-A.( × )(3)若函数y=A sin(ωx+φ)(A≠0)为偶函数,则φ=kπ+(k∈Z).( √ )(4)函数y=A cos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为.( √ ) 2.(2021·常州一模)已知函数f(x)=2sin x,为了得到函数g(x)=2sin的图象,只需( )A.先将函数f(x)图象上所有点的横坐标变为原来的2倍,再向右平移个单位长度B.先将函数f(x)图象上所有点的横坐标变为原来的,再向右平移个单位长度C.先将函数f(x)的图象向右平移个单位长度,再将所有点的横坐标变为原来的D.先将函数f(x)的图象向右平移个单位长度,再将所有点的横坐标变为原来的2倍B 解析:将f(x)=2sin x的图象上各点的横坐标缩短到原来的,纵坐标不变,得到的函数解析式为f(x)=2sin 2x;再将函数f(x)=2sin 2x图象上所有的点向右平移个单位长度,得到函数f(x)=2sin.3.函数f(x)=cos(ω>0)的最小正周期是π,则其图象向右平移个单位长度后得到的图象对应函数的单调递减区间是( )A.(k∈Z)B.(k∈Z)C.(k∈Z)D.(k∈Z)B 解析:由题意知ω==2,将函数f(x)的图象向右平移个单位长度后得到函数g(x)=cos=cos=sin 2x的图象,由2kπ+≤2x≤2kπ+(k∈Z),解得函数的单调递减区间为(k∈Z).4.(2021·东城区一模)已知函数f(x)=A sin(2x+φ),其中x和f(x)部分对应值如表所示:x-0f(x)-2-2-222那么A=________.4 解析:由题意得f(0)=A sin φ=-2,f=-A cos φ=-2,所以A2(sin2φ+cos2φ)=16,因为A>0,所以A=4.5.函数y=A sin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω= .3 解析:观察函数图象可得周期T=,故T==,所以ω=3.考点1 由图象确定y=A sin ωx+φ 的解析式——基础性1.(2022·银川模拟)已知函数y=sin(ωx+φ)的图象如图所示,则此函数的解析式可以是( )A.y=sinB.y=sinC.y=sinD.y=sinC 解析:由函数y=sin(ωx+φ)的图象知,T=2×=π,ω==2,由五点法画图知,是函数图象的第三个关键点,即2×+φ=π,解得φ=,所以此函数的解析式是y=sin.2.若函数f(x)=sin(ωx+φ)满足f=f(x),且f(x)的图象如图所示,则φ=( )A. B.-C. D.-D 解析:因为函数f(x)=sin(ωx+φ)满足f=f(x),所以函数f(x)的图象关于直线x=对称,结合图象,-=×,所以ω=2.结合五点法作图可得,2×+φ=,所以φ=-.3.(2021·全国甲卷)已知函数f(x)=2cos(ωx+φ)的部分图象如图所示,则f =________.- 解析:由题意可得T=-=,所以T=π,ω==2,当x=时,ωx+φ=2×+φ=2kπ,所以φ=2kπ-π(k∈Z),令k=1可得φ=-,据此有f(x)=2cos,f =2cos=2cos=-.4.如图,某地一天6~14时的温度变化曲线近似满足函数T=A sin(ωt+φ)+b,则这段曲线对应的函数解析式为____________.y=10sin+20,x∈[6,14] 解析:从题图中可以看出,6~14时是函数y=A sin(ωx+φ)+b的半个周期,所以A=×(30-10)=10,b=×(30+10)=20.又×=14-6,所以ω=.又×10+φ=2π+2kπ,k∈Z,取φ=,所以y=10sin+20,x∈[6,14].1.由图象求解析式问题,求①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b 的交点求解(此时要注意交点在上升区间上还是在下降区间上).②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:“最大值点”(即图象的“峰点”)时ωx+φ=+kπ,k∈Z;“最小值点”(即图象的“谷点”)时ωx+φ=+kπ,k∈Z.考点2 函数y=A sin ωx+φ 的图象变换——综合性(1)(2021 ·全国乙卷)把函数y=f(x)图象上所有点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向右平移个单位长度,得到函数y=sin的图象,则f(x)=( )A.sin B.sinC.sin D.sinB 解析:由已知的函数y=sin逆向变换,第一步:向左平移个单位长度,得到y=sin=sin的图象,第二步:图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,得到y=sin的图象,即为y=f(x)的图象,所以f(x)=sin.(2)(2021·山西二模)将函数y=sin的图象沿x轴向右平移φ(φ>0)个单位长度得到y =cos 2x的图象,则φ的值可能为( )A. B.C. D.A 解析:将函数y=sin的图象沿x轴向右平移φ(φ>0)个单位长度,得到y=sin=sin=cos=cos=cos.若要得到y=cos 2x的图象,则-2φ-=2kπ,即φ=-kπ-,k∈Z.因为φ>0,所以当k=-1时,φ=.本例(1)若改为:函数y=sin的图象上所有点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向右平移个单位长度得到函数y=f(x)的图象,则f(x)=________.sin 解析:函数y=sin的图象上所有点的横坐标缩短到原来的倍,纵坐标不变,得到函数y=sin,向右平移个单位长度得到函数f(x)=sin=sin.1.由函数y移后伸缩”与“先伸缩后平移”.要特别注意这两种情况下平移的单位长度.2.当变换前后解析式三角函数名称不同时,要注意利用诱导公式转化.1.(2022·泰安模拟)已知函数f(x)=4sin的图象为C,为了得到函数g(x)=4sin的图象,只要把C上所有点的( )A.横坐标伸长到原来的2倍,纵坐标不变B.纵坐标缩短到原来的倍,横坐标不变C.纵坐标伸长到原来的2倍,横坐标不变D.横坐标缩短到原来的倍,纵坐标不变D 解析:函数f(x)=4sin的图象为C,为了得到函数g(x)=4sin的图象,只要把C 上所有点横坐标缩短到原来的倍,纵坐标不变,即可.2.已知函数f(x)=cos是偶函数,要得到函数g(x)=sin 2x的图象,只需将函数f(x)的图象( )A.向左平移个单位长度B.向右平移个单位长度C.向右平移个单位长度D.向左平移个单位长度C 解析:因为函数f(x)=cos是偶函数,所以φ-=kπ(k∈Z).因为|φ|<,所以φ=,所以f(x)=cos 2x,要得到函数g(x)=sin 2x=cos的图象,只需将函数f(x)=cos 2x的图象向右平移个单位长度.考点3 三角函数模型及其应用——应用性(2021·上海模拟)如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到点A的距离与点P的高度之和为( )A.5米B.(4+)米C.(4+)米D.(4+)米D 解析:以圆心O1为原点,以水平方向为x轴正方向,以竖直方向为y轴正方向建立平面直角坐标系,则根据大风车的半径为2米,圆上最低点O离地面1米,12秒转动一圈.设∠OO1P=θ,运动t(秒)后与地面的距离为f(t).又T=12,所以θ=t,所以f(t)=3-2cos t,t≥0;风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达点P,θ=6π+,P(,1),所以点P的高度为3-2×=4(米).因为A(0,-3),所以AP==,所以点P到点A的距离与点P的高度之和为(4+)米.三角函数模型的应用体现在两方面:一是已知函数模型求解数模型,再利用三角函数的有关知1.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中使用.假设在水流量稳定的情况下,筒车上的每一个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆O的半径为4 m,P0在水平面上,盛水筒M 从点P0处开始运动,OP0与水平面所成角为30°,且2分钟恰好转动1圈,则盛水筒M距离水面的高度H(单位:m)与时间t(单位:s)之间的函数关系式是( )A.H=4sin+2B.H=4sin+2C.H=4sin+2D.H=4sin+2A 解析:以O为原点,过点O的水平直线为x轴,建立如图所示平面直角坐标系,因为∠xOP0=30°=,所以OM在 t(s) 内转过的角度为t=t,所以以x轴为始边,以OM为终边的角为t-,则点M的纵坐标为4sin,所以点M距水面的高度H(m)表示为时间 t(s) 的函数是H=4sin+2.2.据市场调查,某种商品一年内每件出厂价在7 000元的基础上,按月呈f(x)=A sin(ωx+φ)+B的模型波动(x为月份).已知3月份达到最高价9 000元,9月份价格最低,为5 000元,则7月份的出厂价格为________元.6 000 解析:作出函数简图如图:三角函数模型为y=A sin(ωx+φ)+B,由题意知A=(9 000-5 000)=2 000,B=7 000,T=2×(9-3)=12,所以ω==.将(3,9 000)看成函数图象的第二个特殊点,则有×3+φ=,所以φ=0,故f(x)=2 000sin x+7 000(1≤x≤12,x∈N*).所以f(7)=2 000×sin+7 000=6 000(元).故7月份的出厂价格为6 000元.考点4 三角函数图象与性质的综合问题——综合性(1)(多选题)将函数f(x)=2sin的图象向右平移个单位长度后,所得图象对应的函数为y=g(x),则下列结论正确的是( )A.函数g(x)的图象关于直线x=对称B.函数g(x)的图象关于点对称C.函数g(x)在上单调递减D.函数g(x)在[0,2π]上恰有4个极值点AD 解析:函数f(x)=2sin的图象向右平移个单位长度后,所得图象对应的函数为y=g(x)=2sin的图象,对于A:当x=时,g=2,故A正确.对于B:当x=时,g=2sin=,故B错误.对于C:当x∈时,2x-∈,故函数在该区间上单调递增,故C错误.对于D:令2x-=kπ+(k∈Z),解得x=+(k∈Z),当k=0,1,2,3时,x=,,,,正好有4个极值点,故D正确.(2)已知关于x的方程2sin2x-sin 2x+m-1=0在上有两个不同的实数根,则m的取值范围是( )A. B.(-2,2)C.(-2,-) D.(-2,-1)D 解析:方程2sin2x-sin 2x+m-1=0可转化为m=1-2sin2x+sin 2x=cos 2x+sin 2x=2sin,x∈.设2x+=t,则t∈,题目条件可转化为=sin t,t∈,有两个不同的实数根.所以y=和y=sin t,t∈的图象有两个不同交点,如图:由图象观察知,的范围为,故m的取值范围是(-2,-1).已知关于x的方程2sin2x-sin 2x+m-1=0在x∈上有两个不同的实数根,则实数m的取值范围是________.1≤m<2 解析:2sin2x-sin 2x+m-1=-cos 2x-sin 2x+m=-2sin+m.因为x∈,所以2x+∈.要使方程2sin2x-sin 2x+m-1=0在x∈上有两个不同的实数根,则2x+∈且2x +≠,此时2sin∈[1,2),所以1≤m<2.1.研究y=1.(2021·运城模拟)函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则下列结论错误的是( )A.f(x)=2sinB.若把f(x)的横坐标缩短为原来的,纵坐标不变,则得到的函数在[-π,π]上是增函数C.若把函数f(x)的图象向左平移个单位长度,则所得图象对应的函数是奇函数D.函数y=f(x)的图象关于直线x=-4π对称B 解析:由图象可得T=-2π=,所以T=6π,所以ω==.因为f(2π)=2,所以f(2π)=2sin=2,即sin=1,所以+φ=2kπ+(k∈Z),所以φ=2kπ-(k∈Z).因为|φ|<π,所以φ=-.所以f(x)=2sin,故A正确.把f(x)的横坐标缩短为原来的,纵坐标不变,得到的函数为y=2sin.因为x∈[-π,π],所以-≤x-≤,所以y=2sin在[-π,π]上不单调递增,故B错误.把函数f(x)的图象向左平移个单位长度,得到的函数为y=2sin=2sin x,是奇函数,故C正确.f(-4π)=2sin=2,是最值,故x=-4π是f(x)的对称轴,故D正确.2.若将函数f(x)=2sin(2x+φ)的图象向左平移个单位长度后得到的图象关于y轴对称,则函数f(x)在上的最大值为( )A.2 B.C.1 D.A 解析:将函数f(x)=2sin(2x+φ)的图象向左平移个单位长度后,得到的y=2sin的图象关于y轴对称,所以φ=,函数f(x)=2sin.因为x∈,所以2x+∈,则当2x+=时,函数f(x)在上的最大值为2.将函数y=cos x+sin x(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( )A .B .C .D .[四字程序]思路参考:构造正弦型函数的解析式.B 解析:y =cos x +sin x =2sin ,函数的图象向左平移m (m >0)个单位长度,得y =2sin 的图象.由x +m +=k π+(k ∈Z ),得函数y =2sin 的图象的对称轴为x =-m +k π(k ∈Z ).因为所得的图象关于y 轴对称,所以-m +k π=0(k ∈Z ),即m =k π+(k ∈Z ),则m 的最小值为.思路参考:构造余弦型函数的解析式.B 解析:函数y =cos x +sin x =2cos 的图象向左平移m (m >0)个单位长度得到y =2cos 的图象.因为此函数图象关于y 轴对称,所以y =2cos 为偶函数,易知m 的最小值为.思路参考:根据图象对称轴与函数最值的关系.B 解析:由解法1,得y =2sin .因为所得的图象关于y 轴对称,可得当x =0时,y =±2,进而sin =±1,易知m 的最小值为.思路参考:利用函数图象.B 解析:y=cos x+sin x=2sin,可得此函数图象的对称轴为x=kπ+(k∈Z),可知离y轴最近的对称轴为x=和x=-.由图象向左平移m(m>0)个单位长度后关于y轴对称,易知m的最小值为.1.基于课程标准,解答本题一般需要提升运算求解能力、逻辑推理能力,体现逻辑推理、数学运算的核心素养.2.基于高考数学评价体系,本题涉及三角恒等变换、三角函数的图象与性质等知识,渗透了转化与化归思想方法,有一定的综合性,属于中低档难度题.将函数f(x)=sin(2x+φ)的图象向左平移个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在上的最大值为( )A.0 B.C. D.1D 解析:将函数f(x)=sin(2x+φ)的图象向左平移个单位长度后,可得函数g(x)=sin的图象.根据所得图象关于原点对称,可得+φ=kπ.因为|φ|<,所以φ=,f(x)=sin.在上,2x+∈,故当2x+=时,f(x)取得最大值为1.。
高考数学一轮复习第四章三角函数与解三角形第二节同角三角函数的基本关系与诱导公式课件理

[探究 3] 在本例(3)的条件下,求 sin2α+2sin αcos α 的值. 解:sin2α+2sin αcos α=sin2sαin+2α2+sincoαsc2αos α =tan12+α+ta2nt2aαn α=1196+-19836=-285.
第十五页,共29页。
(1)利用 sin2α+cos2α=1 可以实现角 α 的正弦、余弦的互化, 利用csions αα=tan α 可以实现角 α 的弦切互化.
第七页,共29页。
[典题 1] (1)(2015·福建高考)若 sin α=-153,且 α 为第四
象限角,则 tan α 的值等于( )
A.152
B.-152
C.152
D.-152
(2)sin21°+sin22°+…+sin289°=________.
(3)已知 α 为三角形的内角,且 sin α+cos α=15,则 tan α
第二十二页,共29页。
利用诱导公式化简三角函数的思路和要求 (1)思路方法:①分析结构特点,选择恰当公式;②利用公式 化成单角三角函数;③整理得最简形式. (2)化简要求:①化简过程是恒等变形;②结果要求项数尽可 能少,次数尽可能低,结构尽可能简单,能求值的要求出值.
第二十三页,共29页。
1.已知 sinα+1π2=13,则 cosα+71π2的值为________.
第二十五页,共29页。
解:(1)f(α)=sintαa-nπ-2·αco-sπ32π·s+inα-·taαn-ππ- α
=-cos-αta·sninαα··si-n αtan α=-cos α.
(2)∵cosα-32π=15,∴-sin α=15,从而 sin α=-15.
【学海导航】高考数学第1轮总复习 全国统编教材 4

上一个把α看成
角时原函锐数值的符号.
2. ±α, ±α的三角函数值等于α的 函数值,2 前面加上2 3一个把α看成
互余 角时原函数值的符号.记忆口诀为:
奇变锐偶不变,符号看象限.(注:奇、偶指 的
奇数倍或偶数倍.)
2
1已知△ABC中,cotA 12,则cosA=(
A. 12
5
B.
5
D)
13
13
5
由α是第二象限的角,知sinα>0
>cosα,所以sinα-cosα>0.
由条件可得(sincos)212sincos1,
则2sinαcosα= - 2 .4
25
所以(sin-cos)2 2 51-2sincos49,
得sinα-cosα= 7.
25
5
参考题
题型 :“1”的妙用
化简 1 - c o s 4
sin
2
sin 2 (1 (1 cos2
cos2
- sin cos4
2
-
)
sin
4
)
2 cos2
1 cos2 (cos2 sin 2 )(cos2 - sin 2 )
1
2 cos2 cos2 cos2
- sin 2
2 cos2 3cos2
2. 3
题型:切割化弦与齐次式的应用 2. 已知 tan -1,求下列各式的值:
所以结论成立.
【点评】:解决有关三角函数式的化简与证 明的问题,关键是合理选择公式和变形方向,如 异名化同名、整体代换、切化弦,等等.
化简 原c o s 式4 = sic n o 2 s 4 s in si2 n 2c o s 2 s in -2 c o s 1 c 4 o s2 ta -n c 4 o s 1 .4 c so in s4 4 .
【精编】2020年高考数学一轮复习对点提分专题4.3 两角和与差的正弦、余弦、正切公式 (文理科通用)(学

第四篇 三角函数与解三角形专题4.03 两角和与差的正弦、余弦和正切公式【考试要求】1.经历推导两角差余弦公式的过程,知道两角差余弦公式的意义;2.能从两角差的余弦公式推导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系;3.能运用上述公式进行简单的恒等变换(包括推导出积化和差、和差化积、半角公式,这三组公式不要求记忆). 【知识梳理】1.两角和与差的正弦、余弦和正切公式 sin(α±β)=sin αcos β±cos αsin β. cos(α∓β)=cos αcos β±sin αsin β. tan(α±β)=tan α±tan β1∓tan αtan β.2.二倍角的正弦、余弦、正切公式 sin 2α=2sin__αcos α.cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α. tan 2α=2tan α1-tan 2α.3.函数f (α)=a sin α+b cos α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)⎝⎛⎭⎫其中tan φ=ba 或f (α)=a 2+b 2·cos(α-φ)⎝⎛⎭⎫其中tan φ=ab . 【微点提醒】1.tan α±tan β=tan(α±β)(1∓tan αtan β).2.cos 2α=1+cos 2α2,sin 2α=1-cos 2α2.3.1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2, sin α±cos α=2sin ⎝⎛⎭⎫α±π4. 【疑误辨析】1.判断下列结论正误(在括号内打“√”或“×”)(1)两角和与差的正弦、余弦公式中的角α,β是任意的.( ) (2)存在实数α,β,使等式sin(α+β)=sin α+sin β成立.( )(3)公式tan(α+β)=tan α+tan β1-tan αtan β可以变形为tan α+tan β=tan(α+β)(1-tan αtan β),且对任意角α,β都成立.( ) (4)存在实数α,使tan 2α=2tan α.( )【教材衍化】2.(必修4P127T2改编)若cos α=-45,α是第三象限的角,则sin ⎝⎛⎭⎫α+π4等于( ) A.-210B.210 C.-7210D.72103.(必修4P146A4(2)改编)tan 20°+tan 40°+3tan 20°·tan 40°=________.【真题体验】4.(2018·全国Ⅲ卷)若sin α=13,则cos 2α=( )A.89B.79C.-79D.-895.(2019·青岛一模)已知角α是终边经过点P (sin 47°,cos 47°),则sin(α-13°)=( ) A.12 B.32 C.-12D.-326.(2018·全国Ⅱ卷)已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)=________.【考点聚焦】考点一 三角函数式的化简【例1】 (1)化简:sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)=________.(2)化简:(1+sin α+cos α)·⎝⎛⎭⎫cos α2-sin α22+2cos α(0<α<π)=________.【规律方法】 1.三角函数式的化简要遵循“三看”原则:一看角之间的差别与联系,把角进行合理的拆分,正确使用公式;二看函数名称之间的差异,确定使用的公式,常见的有“切化弦”;三看结构特征,找到变形的方向,常见的有“遇到分式要通分”、“遇到根式一般要升幂”等. 2.化简三角函数式的常见方法有弦切互化,异名化同名,异角化同角,降幂与升幂等. 【训练1】 (1)cos(α+β)cos β+sin(α+β)sin β=( ) A.sin(α+2β) B.sin α C.cos(α+2β)D.cos α(2)化简:2cos 4α-2cos 2α+122tan ⎝⎛⎭⎫π4-αsin 2⎝⎛⎭⎫π4+α=________.考点二 三角函数式的求值角度1 给角(值)求值【例2-1】 (1)计算:cos 10°-3cos (-100°)1-sin 10°=________.(2)(2018·江苏卷)已知α,β为锐角,tan α=43,cos(α+β)=-55.①求cos 2α的值; ②求tan(α-β)的值.角度2 给值求角【例2-2】 (1)(2019·河南六市联考)已知cos α=17,cos(α-β)=1314,若0<β<α<π2,则β=________.(2)已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,则2α-β的值为________.【规律方法】 1.“给角求值”、“给值求值”问题求解的关键在于“变角”,使其角相同或具有某种关系,借助角之间的联系寻找转化方法.2.“给值求角”:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,最后确定角.遵照以下原则:(1)已知正切函数值,选正切函数;(2)已知正、余弦函数值,选正弦或余弦函数;若角的范围是⎝⎛⎭⎫0,π2,选正、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为⎝⎛⎭⎫-π2,π2,选正弦较好. 【训练2】 (1)(2019·天津河西区模拟)tan 70°·cos 10°(3tan 20°-1)等于( ) A.1B.2C.-1D.-2(2)已知α,β为锐角,cos α=17,且sin(α+β)=5314,则角β=________.(3)若2cos 2θcos ⎝⎛⎭⎫π4+θ=3·sin 2θ,则sin 2θ=( ) A.13 B.23C.-23D.-13考点三 三角恒等变换的简单应用【例3】 (2019·杭州模拟)设函数f (x )=sin 2ωx -cos 2ωx +23sin ωx cos ωx +λ的图象关于直线x =π对称,其中ω,λ为常数,且ω∈⎝⎛⎭⎫12,1. (1)求函数f (x )的最小正周期;(2)若y =f (x )的图象经过点⎝⎛⎭⎫π4,0,求函数f (x )在区间⎣⎡⎦⎤0,3π5上的最值.【规律方法】 1.进行三角恒等变换要抓住:变角、变函数名称、变结构,尤其是角之间的关系;注意公式的逆用和变形使用.2.把形如y =a sin x +b cos x 化为y =a 2+b 2sin(x +φ),可进一步研究函数的周期、单调性、最值与对称性.【训练3】 (2017·北京卷)已知函数f (x )=3cos ⎝⎛⎭⎫2x -π3-2sin x cos x . (1)求f (x )的最小正周期;(2)求证:当x ∈⎣⎡⎦⎤-π4,π4时,f (x )≥-12.【反思与感悟】1.重视三角函数的“三变”:“三变”是指“变角、变名、变式”.(1)变角:对角的分拆要尽可能化成同角、特殊角;(2)变名:尽可能减少函数名称;(3)变式:对式子变形一般要尽可能有理化、整式化、降低次数等.2.在解决求值、化简、证明问题时,一般是观察角、函数名、所求(或所证明)问题的整体形式中的差异,再选择适当的三角公式恒等变形. 【易错防范】1.运用公式时要注意审查公式成立的条件,要注意和、差、倍角的相对性,要注意升幂、降幂的灵活运用,要注意“1”的各种变通.2.在(0,π)范围内,sin α=22所对应的角α不是唯一的. 3.在三角求值时,往往要借助角的范围确定三角函数值的符号或所求角的三角函数的名称. 【核心素养提升】【逻辑推理与数学运算】——缩小角的范围常用策略在运用平方关系和由三角函数值求角时都要注意角的范围.如果条件中角的范围恰好能够使用,那么就能顺势求解题目.但绝大部分题目都会设置一定的障碍,特别是角的范围,往往所给的范围较大,需要根据条件缩小范围.类型1 由三角函数值的符号缩小角的范围【例1】 (一题多解)已知α,β∈(0,π),tan α=2,cos β=-7210,求2α-β的值.【评析】 三角函数值的符号与角的范围有直接关系,借助三角函数值的符号可有效缩小角的范围.本题缩小角的范围分为两层:先由条件中tan α,cos β的符号缩小α,β的范围,得到α-β的范围,再由α-β的范围,结合tan(α-β)的符号进而缩小α-β的范围,得到2α-β的范围.难点是想到缩小α-β的范围. 另外,本题还可以采用缩小三角函数值的范围来缩小角的范围.法二较法一在求角的范围上运算量小了许多,这也显示出运用三角函数值的范围缩小角的范围的优势. 类型2 由三角函数值及特殊角的三角函数值缩小范围【例2】 设α,β∈(0,π),sin(α+β)=513,tan α2=12,则cos β=________.【评析】 本题缩小角的范围分为两层:(1)由cos α=35∈⎝⎛⎭⎫12,22,结合α∈(0,π),缩小角α的范围,得到α+β的范围;(2)由sin(α+β)=513∈⎝⎛⎭⎫0,12,结合α+β∈⎝⎛⎭⎫π4,4π3上不单调,解决办法是画图. 【分层训练】【基础巩固题组】(建议用时:40分钟) 一、选择题1.若tan θ=-13,则cos 2θ=( )A.-45B.-15C.15D.452.(2019·北京海淀区)若cos ⎝⎛⎭⎫α+π3=45,则cos ⎝⎛⎭⎫π3-2α=( ) A.2325 B.-2325C.725D.-7253.(2019·日照调研)sin 10°1-3tan 10°=( )A.14B.12C.32D.14.(2019·信阳一模)函数f (x )=3sin x 2cos x 2+4cos 2x2(x ∈R )的最大值等于( )A.5B.92C.52D.25.(2019·济南模拟)若sin ⎝⎛⎭⎫A +π4=7210,A ∈⎝⎛⎭⎫π4,π,则sin A 的值为( )A.35B.45C.35或45D.34二、填空题6.(2017·江苏卷)若tan ⎝⎛⎭⎫α-π4=16,则tan α=________.7.化简:2sin (π-α)+sin 2α2cos 2α2=________.8.(2017·全国Ⅰ卷)已知α∈⎝⎛⎭⎫0,π2,tan α=2,则cos ⎝⎛⎭⎫α-π4=________.三、解答题9.(2018·浙江卷)已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点P ⎝⎛⎭⎫-35,-45. (1)求sin(α+π)的值;(2)若角β满足sin(α+β)=513,求cos β的值.10.已知函数f (x )=(2cos 2x -1)·sin 2x +12cos 4x .(1)求f (x )的最小正周期及单调递减区间;(2)若α∈(0,π),且f ⎝⎛⎭⎫α4-π8=22,求tan ⎝⎛⎭⎫α+π3的值.【能力提升题组】(建议用时:20分钟)11.若点(θ,0)是函数f (x )=sin x +2cos x 图象的一个对称中心,则cos 2θ+sin θcos θ=( ) A.1110 B.-1110C.1D.-112.(一题多解)已知θ是第四象限角,且sin ⎝⎛⎭⎫θ+π4=35,则tan ⎝⎛⎭⎫θ-π4=( ) A.43 B.-43C.-34D.3413.(2019·广东七校联考)已知sin ⎝⎛⎭⎫α+π6+cos α=-33,则cos ⎝⎛⎭⎫π6-α=________.14.(2019·烟台二中月考)已知函数f (x )=⎝⎛⎭⎫a +2cos 2x 2·cos(x +θ)为奇函数,且f ⎝⎛⎭⎫π2=0,其中a ∈R ,θ∈(0,π). (1)求a ,θ的值;(2)若α∈⎝⎛⎭⎫π2,π,f ⎝⎛⎭⎫α2+π8+25cos ⎝⎛⎭⎫α+π4cos 2α=0,求cos α-sin α的值.【新高考创新预测】15.(试题创新)设α,β∈[0,π],且满足sin αcos β-cos αsin β=1,则sin(2α-β)+sin(α-2β)的取值范围为( ) A.[-2,1]B.[-1,2]C.[-1,1]D.[1,2]。
高三数学一轮复习课件 第四章 4.2 同角三角函数基本关系式及诱导公式

A.{1,-1,2,-2}
B.{-1,1}
√C.{2,-2}
D.{1,-1,0,2,-2}
解析 当 k 为偶数时,A=ssiinn αα+ccooss αα=2;
当 k 为奇数时,A=-sisninαα-ccooss αα=-2.
(2)(2018·太原质检)化简:tanπ+αcos2π+αsinα-32π= -1 . cos-α-3πsin-3π-α
A.-
2 6
B.
2 6
C.-23
√D.23
(2)已知 sin α=25 5,则 tan(π+α)+csoins5522ππ+-αα=
52或-52
.
3 课时作业
PART THREE
基础保分练
1.已知 α 是第四象限角,tan α=-152,则 sin α 等于
1 A.5
(2)商数关系:
sin cos
αα=tan
αα≠π2+kπ,k∈Z
.
2.三角函数的诱导公式
公式
一
角 2kπ+α(k∈Z)
二 π+α
三
四
-α π-α
正弦
sin α
-__s_i_n_α_ _-__s_in__α_ __s_in__α_
五 π2-α
_c_o_s__α_
六 π2+α
__c_o_s_α__
α=tan
-sin α α·cos α·tan
α=-tan1
α=2
1
6=
6 12 .
1 2 3 4 5 67
2 题型分类 深度剖析
PART TWO
自主演练
题型一 同角三角函数基本关系式的应用
1.已知 α 是第四象限角,sin α=-1123,则 tan α 等于
《三角恒等变换》三角函数PPT教学课件(第4课时二倍角的正弦、余弦、正切公式)

19
[解] (1)∵π2≤α<32π,∴34π≤α+π4<74π.
∵cosα+π4>0,∴32π<α+π4<74π,
∴sinα+π4=- 1-cos2α+π4=- 1-532=-45,
∴cos 2α=sin2α+π2=2sinα+π4cosα+π4=2×-45×35=-2245,
sin 2α=-cos2α+π2=1-2cos2α+π4=1-2×352=275,
() A.2sin 15°cos 15°
2sin215°=1-cos 30°=1- 23;
B.cos215°-sin215°
sin215°+cos215°=1,故选B.]
C.2sin215°
D.sin215°+cos215°
栏目导航
7
2.sin 15°cos 15°=________.
1 4
[sin 15°cos 15°=12×2sin
栏目导航
1.求下列各式的值 (1)cos 72°cos 36°; (2)sin150°+cos 530°.
16
栏目导航
17
[解]
(1)cos
36°cos
72°=2sin
36°cos 2sin
36°cos 36°
72°=2sin47si2n°c3o6s°72°=
s4isnin14346°°=14.
栏目导航
(2)法一:左边=cos2θ1-csoins22θθ =cos2θ-sin2θ=cos 2θ=右边. 法二:右边=cos 2θ=cos2θ-sin2θ =cos2θ1-csoins22θθ=cos2θ(1-tan2θ)=左边.
35
栏目导航
36
1.对于“二倍角”应该有广义上的理解,如:
2019届高考数学一轮复习 第四章 三角函数 解三角形 4-4 三角恒等变换讲义 文

π4+α=π2-π4-α等;2.将三角变换与代数变换密切结合:三角变 换主要是灵活应用相应的三角公式,对于代数变换主要有因式分 解、通分、提取公因式、利用相应的代数公式等,例如,sin4x+ cos4x=(sin2x+cos2x)2-2sin2xcos2x=1-12sin22x.
考点突破 提能力
5 5.
因为 A 为钝角,所以
cosA=- 1-sin2A=-
1-
552=-2
5
5 .
由 sinB= 1100,且 B 为钝角,可得
cosB=- 1-sin2B=-
1-
11002=-3
10 10 .
所以 cos(A+B)=cosAcosB-sinAsinB
=-2 5 5×-3 1010-
(2)三角函数求值的方法策略
类型
要点
给角 关键是正确地选用公式,以便把非特殊角的三角
求值 函数相约或相消,从而化为特殊角的三角函数
类型
要点
给出某些角的三角函数值,求另外一些角的 给值
三角函数值,解题关键在于“变角”,使其 求值
角相同或具有某种关系
给值 实质是转化为给值求值,关键是变角,把所
求角 求角用含已知角的式子表示,由所得的函数
解法二:原式=
cos2α
2tanπ4-αcos2π4-α
=
cos2α
= cos2α
2sinπ4-αcosπ4-α sinπ2-2α
=ccooss22αα=1.
考点二 三角函数式的求值——常考点 角度解读:三角函数的化简求值是三角函数的基本考点之 一,各种题型都有,有时也与解三角形联合起来综合考查.
(1)本例在寻找选项中的正确命题时,从两个角度进行了证 明,一是根据角之间的关系——α+β,α-β 与 2α,2β 之间的关 系,利用所证角表示已知角,代入已知等式进行化简;二是利用 选项的共性——两个角的正切值之间的比例关系,直接作商,然 后根据已知等式进行化简.解决此类问题要抓住两个方面 :一 是角,二是三角函数值.
5.5.1 第4课时 二倍角的正弦、余弦、正切公式

第4课时二倍角的正弦、余弦、正切公式学习目标1.会用两角和(差)的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.2.能熟练运用二倍角的公式进行简单的三角恒等变换并能灵活地将公式变形运用.知识点二倍角公式公式简记正弦sin 2α=□12sin_αcos_αS2α余弦cos 2α=cos2α-sin2α=□22cos2α-1=□31-2sin2αC2α正切tan 2α=□42tan α1-tan2αT2α(1)倍角公式不仅可运用于2α是α的二倍的情况,还可运用于4α作为2α的二倍,α作为α2的二倍,3α作为3α2的二倍,α+β作为α+β2的二倍等情况,这里蕴含着换元的思想;(2)常见二倍角公式的变形:cos 2α=(cos α+sin α)(cos α-sin α);1±sin 2α=sin2α+cos2α±2sin αcos α=(sin α±cos α)2;降幂公式:sin αcos α=12sin 2α;cos2α=1+cos 2α2;sin2α=1-cos 2α2.[微练1]计算1-2sin222.5°的结果等于()A.12B.22C.33D.32答案:B[微练2]已知tan α=43,则tan 2α=________.答案:-24 7[微练3]已知sin α+cos α=13,则sin 2α=________.答案:-8 9题型一给角求值(链接教材P223练习T5)求下列各式的值.(1)sin π8cosπ8;(2)cos2π6-sin 2π6;(3)2tan 150°1-tan2150°;(4)cos π5cos2π5cos45πcos85π[解](1)sin π8cosπ8=12×2sinπ8cosπ8=12×sinπ4=12×22=24.(2)cos2π6-sin 2π6=cos(2×π6)=cosπ3=12.(3)原式=tan(2×150°)=tan 300°=tan(360°-60°)=-tan 60°=- 3.(4)原式=2sinπ5cosπ5cos2π5cos45πcos85π2sinπ5=sin2π5cos2π5cos45πcos85π2sinπ5=sin45πcos45πcos85π4sinπ5=sin85πcos85π8sinπ5=sin165π16sinπ5=-116.给角求值问题的两类解法(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式进行转化,一般可以化为特殊角.(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.1.求下列各式的值.(1)tan 30°1-tan230°;(2)1sin 10°-3cos 10°.解:(1)tan 30°1-tan230°=12×2tan 30°1-tan230°=12tan 60°=32.(2)原式=cos 10°-3sin 10°sin 10°cos 10°=2(12cos 10°-32sin 10°)sin 10°cos 10°=4(sin 30°cos 10°-cos 30°sin 10°)2sin 10°cos 10°=4sin(30°-10°)sin(2×10°)=4sin 20°sin 20°=4.题型二给值求值(1)已知α∈(0,π2),2sin 2α=cos 2α+1,则sin α=()A.15B.55C.33D.255(2)若cos(π4-α)=35,则sin 2α=()A .725B .15C .-15D .-725(3)若tan θ=-13,则cos 2θ=( ) A .-45 B .-15 C .15D .45[解析] (1)由2sin 2α=cos 2α+1,得4sin αcos α=1-2sin 2α+1,即2sin αcos α=1-sin 2α.因为α∈(0,π2),所以2sin α=cos α,与sin 2α+cos 2α=1联立,解得sin α=55.(2)法一:因为cos (π4-α)=cos π4cos α+sin π4sin α=22(sin α+cos α)=35,所以sin α+cos α=325,所以1+sin 2α=1825,所以sin 2α=-725.法二:因为2(π4-α)=π2-2α,所以sin 2α=cos (π2-2α)=2cos 2(π4-α)-1=-725. (3)法一:由tan θ=-13,cos 2θ+sin 2θ=1,得sin 2θ=110,cos 2θ=910, 所以cos 2θ=cos 2θ-sin 2θ=45.法二:cos 2θ=cos 2θ-sin 2θcos 2θ+sin 2θ=1-tan 2θ1+tan 2θ=1-(-13)21+(-13)2=45. [答案] (1)B (2)D (3)D解决给值求值问题的方法(1)给值求值问题,注意寻找已知式与未知式之间的联系,有两个观察方向: ①有方向地将已知式或未知式化简,使关系明朗化;②寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.(2)注意几种公式的灵活应用,如: ①sin 2x =cos(π2-2x )=cos[2(π4-x )] =2cos 2(π4-x )-1=1-2sin 2(π4-x ); ②cos 2x =sin(π2-2x )=sin[2(π4-x )] =2sin(π4-x )cos(π4-x ).2.(1)已知sin (x +π6)=m ,则cos (2x -2π3)=( ) A .1-2m 2 B .2m 2-1 C .mD .2m -1(2)已知tan (α-π3)=33,则tan 2α=( ) A .-4 3 B .-32 C .4 3D .32解析:(1)B cos (2x -2π3)=cos [2(x +π6)-π]=-cos 2(x +π6)=2sin 2(x +π6)-1 =2m 2-1.(2)A 已知tan (α-π3)=tan α-tan π31+tan αtan π3=33,解得tan α=-32,则tan 2α=2tan α1-tan 2α=-4 3.题型三 化简与证明问题(1)化简:11-tan θ-11+tan θ;(2)求证:3-4cos 2A +cos 4A3+4cos 2A +cos 4A=tan 4A .[解] (1)原式=(1+tan θ)-(1-tan θ)(1-tan θ)(1+tan θ)=2tan θ1-tan 2θ=tan 2θ.(2)证明:因为左边=3-4cos 2A +2cos 22A -13+4cos 2A +2cos 22A -1=(1-cos 2A 1+cos 2A )2=(2sin 2A 2cos 2A )2=(tan 2A )2 =tan 4A =右边, 所以3-4cos 2A +cos 4A3+4cos 2A +cos 4A=tan 4A .1.化简问题的解题策略(1)着手点:从“幂”的差异、“名”的差异、“角”的差异这三个方面,结合所给“形”的特征入手解决.(2)化简方法:①弦切互化,异名化同名,异角化同角;②降幂或升幂;③一个重要结论:(sin θ±cos θ)2=1±sin 2θ.2.证明三角恒等式的方法(1)从复杂的一边入手,证明一边等于另一边; (2)比较法,左边-右边=0,左边右边=1;(3)分析法,从要证明的等式出发,一步步寻找等式成立的条件.3.(1)设α∈(2π,3π),2+2+2cos α的化简结果为________. 解析:∵α∈(2π,3π),∴π<α2<3π2,π2<α4<3π4, ∴cos α2<0,sin α4>0, ∴ 2+2+2cos α= 2+2(1+cos α) = 2+2×2cos 2α2=2(1-cos α2)=2×2sin 2α4=2sin α4.答案:2sin α4(2)求证:cos 2(A +B )-sin 2(A -B )=cos 2A cos 2B .证明:左边=1+cos (2A +2B )2-1-cos (2A -2B )2=cos (2A +2B )+cos (2A -2B )2=12(cos 2A cos 2B -sin 2A sin 2B +cos 2A ·cos 2B +sin 2A sin 2B )=cos 2A cos 2B =右边,∴原等式成立.1.知识网络2.特别提醒(1)二倍角的余弦公式的三种形式容易混淆,尤其是后两种.若对后两种形式不确定,可以记住第一种,再结合同角三角函数的平方关系推导出后两种.(2)一般情况下,sin 2α≠2sin α,cos 2α≠2cos α,tan 2α≠2tan α.课时规范训练 A 基础巩固练1.sin 110°sin 20°cos 2155°-sin 2155°=( )A .-12 B .12 C .32D .-32解析:B 原式=cos 20°sin 20°cos 310°=12sin 40°cos 50°=12×sin 40°sin 40°=12.2.已知sin(π4-x )=35,则cos(π2-2x )的值为( ) A .1925 B .1625 C .1425D .725解析:D 因为sin(π4-x )=35, 所以cos(π2-2x )=cos[2(π4-x )] =1-2sin 2(π4-x )=725.3.已知α∈(0,π),且3cos 2α-8cos α=5,则sin α=( ) A .53 B .23 C .13D .59解析:A 因为3cos 2α-8cos α=5,所以3(2cos 2α-1)-8cos α=5,所以6cos 2α-8cos α-8=0,所以3cos 2α-4cos α-4=0,解得cos α=2(舍去)或cos α=-23,因为α∈(0,π),所以sin α=1-cos 2α=53.故选A .4.设-3π<α<-5π2,化简1-cos (α-π)2的结果是( )A .sin α2 B .cos α2 C .-cos α2D .-sin α2解析:C 因为-3π<α<-5π2,-3π2<α2<-5π4,所以1-cos (α-π)2=1+cos α2=⎪⎪⎪⎪⎪⎪cos α2=-cos α2. 5.(多选题)下列式子的值为-32的是( ) A .2sin 15°cos 15° B .sin 215°-cos 215° C .2sin 215°-1D .1-2cos 215°解析:BCD 2sin 15°cos 15°=sin 30°=12,A 不正确,B 、C 、D 项所得值都是-cos 30°=-32.6.(多选题)函数y =2cos 2(x -π4)-1( )A.最小正周期为πB.最小正周期为π2C.是奇函数D.是偶函数解析:AC y=2cos2(x-π4)-1=cos 2(x-π4)=cos(2x-π2)=sin 2x,故T=π,且为奇函数.故选AC.7.4tanπ81-tan2π8=________.解析:原式=2×2tanπ81-tan2π8=2tan(2×π8)=2tan π4=2.答案:28.1-2sin 20°cos 20°2cos210°-1-cos2160°-1=________.解析:1-2sin 20°cos 20°2cos210°-1-cos2160°-1=(cos 20°-sin 20°)2 cos 20°-sin 20°=cos 20°-sin 20°cos 20°-sin 20°=1.答案:19.已知α为第二象限角,且sin α=154,求sin(α+π4)sin 2α+cos 2α+1的值.解:原式=22(sin α+cos α)2sin αcos α+2cos2α=2(sin α+cos α)4cos α(sin α+cos α). 因为α为第二象限角,且sin α=154, 所以sin α+cos α≠0,cos α=-14. 所以原式=24cos α=- 2.B 能力进阶练10.函数f (x )=sin 2x +3sin x cos x 在区间[π4,π2]上的最大值是( ) A .32 B .1 C .1+32D .1+ 3解析:A f (x )=1-cos 2x 2+32sin 2x =12+sin(2x -π6).∵π4≤x ≤π2,∴π3≤2x -π6≤5π6, ∴f (x )max =12+1=32.11.(多选题)已知函数f (x )=cos 2x -1sin 2x ,则下列说法正确的是( ) A .函数f (x )的图象关于直线x =π2对称 B .函数f (x )的图象关于点(π2,0)对称 C .函数f (x )是奇函数 D .函数f (x )的最小正周期为π解析:BCD 因为f (x )=cos 2x -1sin 2x =-2sin 2x 2sin x cos x =-tan x (x ≠k π2(k ∈Z )), 所以函数f (x )是周期为π的奇函数,图象关于点(π2,0)对称,故选BCD .12.若α∈(0,π),cos α,sin α是一元二次方程x2+13x-49=0的两个实根,则cos 2α等于()A.179B.±179C.-179D.173解析:A∵cos α,sin α是一元二次方程x2+13x-49=0的两个实根,∴cos α+sin α=-1 3,cos α·sin α=-4 9.又α∈(0,π),cos α·sin α=-49<0,∴sin α>0,cos α<0,∴cos α-sin α<0,∴cos α-sin α=-(cos α-sin α)2=-(cos α+sin α)2-4cos α·sin α=-(-13)2-4×(-49)=-173,∴cos 2α=cos2α-sin2α=(cos α+sin α)(cos α-sin α)=(-13)×(-173)=179.13.已知sin θ2+cosθ2=233,那么sinθ=________,cos 2θ=________.解析:因为sin θ2+cosθ2=233,所以(sin θ2+cosθ2)2=43,即1+2sin θ2cosθ2=43,所以sin θ=1 3,所以cos 2θ=1-2sin 2θ=1-2×(13)2=79. 答案:13 7914.已知sin x 2-2cos x 2=0.(1)求tan x 的值;(2)求cos 2xcos (5π4+x )sin (π+x )的值. 解:(1)由sin x 2-2cos x 2=0,知cos x 2≠0,所以tan x 2=2,所以tan x =2tan x 21-tan 2x 2=2×21-22=-43. (2)由(1)知tan x =-43,所以cos 2x cos (5π4+x )sin (π+x )=cos 2x -cos (π4+x )(-sin x )=cos 2x -sin 2x (22cos x -22sin x )sin x=(cos x -sin x )(cos x +sin x )22(cos x -sin x )sin x=2·cos x +sin x sin x=2·1+tan x tan x=24.C探索创新练15.数学家华罗庚倡导的“0.618优选法”在各领域都应用广泛,0.618就是黄金分割比m=5-12的近似值,黄金分割比还可以表示成2sin 18°,则m4-m22cos227°-1等于()A.4 B.5+1 C.2 D.5-1解析:C由题意可知2sin 18°=m=5-1 2,所以m2=4sin218°,则m4-m22cos227°-1=2sin 18°4-4sin218°2cos227°-1=2sin 18°·2cos 18°cos 54°=2sin 36°cos 54°=2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4课时 二倍角公式1.已知cos78°约等于0.20,那么sin66°约等于( ) A .0.92 B .0.85 C .0.88 D .0.95答案 A2.sin20°cos20°cos50°=( )A .2 B.22C. 2D.12答案 D3.计算tan15°+1tan15°的值为( )A. 2 B .2 C .4 D .2 2答案 C解析 tan15°+1tan15°=sin15°cos15°+cos15°sin15°=sin 215°+cos 215°sin15°cos15°=2sin30°=4.故选C.4.若sin α2=33,则cos α的值为( )A .-23B .-13C.13D.23答案 C解析 cos α=1-2sin2α2=1-23=13.故选C. 5.已知cos(π4-x)=35,则sin2x 的值为( )A.1825 B.725C .-725D .-1625答案 C解析 因为sin2x =cos(π2-2x)=cos2(π4-x)=2cos 2(π4-x)-1,所以sin2x =2×(35)2-1=1825-1=-725.6.(2018·遵义第一次联考)2002年在北京召开国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么sin2θ的值为( ) A.13 B.32 C.2324 D.2425答案 D解析 设锐角θ所对的直角边长为x ,由题意得x 2+(x +1)2=25,解得x =3,所以sin θ=35,cos θ=45,sin2θ=2425.故选D.7.(2018·河北保定中学期末)已知sin2α=2425,0<α<π2,则2cos(π4-α)的值为( )A .-15B.15 C .-75D.75答案 D解析 ∵sin2α=2425,0<α<π2,∴sin αcos α=1225,sin α>0,cos α>0.又∵sin 2α+cos 2α=1,∴(sin α+cos α)2=1+2sin αcos α=4925,∴sin α+cos α=75.∴2cos(π4-α)=2(22cos α+22sin α)=cos α+sin α=75.8.化简2+2cos8+21-sin8的结果是( ) A .4cos4-2sin4 B .2sin4 C .2sin4-4cos4 D .-2sin4答案 D解析 原式=4cos 24+2(sin4-cos4)2=|2cos4|+2|sin4-cos4|=-2sin4.故选D. 9.若α∈(0,π2),且sin 2α+cos2α=14,则tan α的值为( )A.22B.33C. 2D. 3答案 D解析 因为cos2α=cos 2α-sin 2α,所以sin 2α+cos2α=cos 2α,所以cos 2α=14.又α∈(0,π2),所以cos α=12,所以α=π3,故tan α= 3.故选D.10.(2017·长沙雅礼中学模拟)已知sin2α=23,则cos 2(α+π4)=( )A.16B.13C.12D.23答案 A解析 方法一:cos 2(α+π4)=12[1+cos(2α+π2)]=12(1-sin2α)=16.方法二:cos(α+π4)=22cos α-22sin α,所以cos 2(α+π4)=12(cos α-sin α)2=12(1-2sin αcos α)=12(1-sin2α)=16.11.已知tan(α+π4)=-12,且π2<α<π,则sin2α-2cos 2αsin (α-π4)的值等于( )A.255B .-3510C .-255D .-31010答案 C解析 sin2α-2cos 2αsin (α-π4)=2sin αcos α-2cos 2α22(sin α-cos α)=22cos α,由tan(α+π4)=-12,得tan α+11-tan α=-12,解得tan α=-3.因为π2<α<π,所以cos α=-1tan 2α+1=-1010.所以原式=22cos α=22×(-1010)=-255.故选C.12.(2018·江西抚州七校联考)若sin(x +π6)=13,则tan(2x +π3)=( )A.79 B .±79C.427D .±427答案 D解析 由sin(x +π6)=13,得cos(x +π6)=±1-sin 2(x +π6)=±223,tan(x +π6)=±24,tan(2x +π3)=tan2(x +π6)=2tan (x +π6)1-tan 2(x +π6)=±427.13.(2018·山西临汾五校联考)若tan α-1tan α=32,α∈(π4,π2),则sin(2α+π4)的值为( )C .-210D.210答案 D解析 ∵tan α-1tan α=32,α∈(π4,π2),∴sin αcos α-cos αsin α=32,∴cos2αsin2α=-34.∵π4<α<π2,∴π2<2α<π,∴cos2α=-35,sin2α=45,∴sin(2α+π4)=sin2α×22+cos2α×22=210.14.(2018·广西百色一模)已知x∈(0,π),且cos(2x -π2)=sin 2x ,则tan(x -π4)=( )A.13 B .-13C .3D .-3答案 A解析 ∵cos(2x -π2)=sin 2x ,∴sin2x =sin 2x ,∴2sinxcosx =sin 2x.∵x ∈(0,π),∴sinx>0,∴2cosx =sinx ,∴tanx =2.∴tan(x -π4)=tanx -tanπ41+tanxtanπ4=2-11+2×1=13.故选A.15.(1)(2018·山东烟台期中)若cos(75°-α)=13,则cos(30°+2α)=________.答案 79解析 ∵cos(75°-α)=sin(15°+α)=13,∴cos(30°+2α)=1-2sin 2(15°+α)=1-2×19=79.(2)(2017·保定模拟)计算:3-sin70°2-cos 210°=________. 答案 2解析 3-sin70°2-cos 210°=3-cos20°2-cos 210°=3-(2cos 210°-1)2-cos 210°=2. 16.若sin(x -34π)cos(x -π4)=-14,则cos4x =________.答案 12解析 ∵sin(x -34π)=-cos(π2+x -34π)=-cos(x -π4),∴cos 2(x -π4)=14,∴1+cos (2x -π2)2=14.∴cos(2x -π2)=-12,即sin2x =-12.∴cos4x =1-2sin 22x =12.17.设α为第四象限的角,若sin3αsin α=135,则tan2α=________.答案 -34解析sin3αsin α=sin (2α+α)sin α=sin2αcos α+cos2αsin αsin α=135.∴2cos 2α+cos2α=135,cos2α+1+cos2α=135.∴cos2α=45.∵2k π-π2<α<2k π,∴4k π-π<2α<4k π(k∈Z ).又∵cos2α=45>0,∴2α为第四象限的角.sin2α=-1-cos 22α=-35,∴tan2α=-34.18.(2018·湖北百校联考)设α∈(0,π3),满足6sin α+2cos α= 3.(1)求cos(α+π6)的值;(2)求cos(2α+π12)的值.答案 (1)104 (2)30+28解析 (1)∵6sin α+2cos α=3,∴sin(α+π6)=64.∵α∈(0,π3),∴α+π6∈(π6,π2),∴cos(α+π6)=104. (2)由(1)可得cos(2α+π3)=2cos 2(α+π6)-1=2×(104)2-1=14.∵α∈(0,π3),∴2α+π3∈(π3,π),∴sin(2α+π3)=154.∴cos(2α+π12)=cos[(2α+π3)-π4]=cos(2α+π3)cos π4+sin(2α+π3)sin π4=30+28.若sin76°=m ,用含m 的式子表示cos7°为( ) A.1+m 2B.1-m2C .± 1+m2D.1+m2答案 D解析 ∵sin76°=cos14°=2cos 27°-1=m , ∴cos 27°=1+m 2,∴cos7°=1+m2.。
