simple algebras
GMAT数学概念和名词 Algebra

GMAT数学概念和名词Algebra & arithmetic Absolute value 绝对值Add (addition) 加Average value 算术平均值Algebra 代数Algebraic expression 代数式Arithmetic mean 算术平均值Arithmetic progression (sequence)等差数列Approximate 近似Abscissa 横坐标Ordinate 纵坐标Binomial 二项式Common factor 公因子Common multiple 公倍数Common divisor 公约数Simple fractionCommon fraction 简分数Complex fraction 繁分数Common logarithm 常用对数Common ratio 公比Complex number 复数Complex conjugate 复共轭Composite number 合数Prime number 质数Consecutive number 连续整数Consecutive even(odd) integer 连续偶(奇)数Cross multiply 交叉相乘Coefficient 系数Complete quadratic equation 完全二次方程Complementary function 余函数Constant 常数Coordinate system 坐标系Decimal 小数Decimal point 小数点Decimal fraction 纯小数Decimal arithmetic 十进制运算Decimal system/decimal scale 十进制Denominator 分母Difference 差Direct proportion 正比Divide 除Divided evenly 被整除Differential 微分Distinct 不同的Dividend 被除数,红利Division 除法Division sign 除号Divisor 因子,除数Divisible 可被整除的Equivalent fractions 等值分数Equivalent equation 等价方程式Equivalence relation 等价关系Even integer/number 偶数Exponent 指数,幂Equation 方程Equation of the first degree 一次方程Endpoint 端点Estimation 近似Factor 因子Factorable quadratic equation 可因式分解的二次方程Incomplete quadratic equation 不完全二次方程Factorial 阶乘Factorization 因式分解Geometric mean 几何平均数Graph theory 图论Inequality 不等式Improper fraction 假分数Infinite decimal 无穷小数Inverse proportion 反比Irrational number 无理数Infinitesimal calculus 微积分Infinity 无穷大Infinitesimal 无穷小Integerable 可积分的Integral 积分Integral domain 整域Integrand 被积函数Integrating factor 积分因子Inverse function 反函数Inverse/reciprocal 倒数Least common denominator 最小公分母Least common multiple 最小公倍数Literal coefficient 字母系数Like terms 同类项Linear 线*的Minuend 被减数Subtrahend 被减数Mixed decimal 混合小数Mixed number 带分数Minor 子行列式Multiplicand 被乘数Multiplication 乘法Multiplier 乘数Monomial 单项式Mean 平均数Mode 众数Median 中数Negative (positive) number 负(正)数Numerator 分子Null set (empty set) 空集Number theory 数论Number line 数轴Numerical analysis 数值分析Natural logarithm 自然对数Natural number 自然数Nonnegative 非负数Original equation 原方程Ordinary scale 十进制Ordinal 序数Percentage 百分比Parentheses 括号Polynomial 多项式Power 乘方Product 积Proper fraction 真分数Proportion 比例Permutation 排列Proper subset 真子集Prime factor 质因子Progression 数列Quadrant 象限Quadratic equation 二次方程Quarter 四分之一Ratio 比率Real number 实数Round off 四舍五入Round to 四舍五入Root 根Radical sign 根号Root sign 根号Recurring decimal 循环小数Sequence 数列Similar terms 同类项Tens 十位Tenths 十分位Trinomial 三相式Units 个位Unit 单位Weighted average 加权平均值Union 并集Yard 码Whole number 整数Mutually exclusive 互相排斥Independent events 相互独立事件Probability 概率Combination 组合Standard deviation 标准方差Range 值域Frequency distribution 频率分布Domain 定义域Bar graph 柱图Geometry terms:Angle bisector 角平分线Adjacent angle 邻角Alternate angel 内错角Acute angle 锐角Obtuse angle 钝角Bisect 角平分线Adjacent vertices 相邻顶点Arc 弧Altitude 高Arm 直角三角形的股Complex plane 复平面Convex (concave) polygon 凸(凹)多边形Complementary angle 余角Cube 立方体Central angle 圆心角Circle 圆Clockwise 顺时钟方向Counterclockwise 逆时钟方向Chord 弦Circular cylinder 圆柱体Congruent 全等的Corresponding angle 同位角Circumference (perimeter) 周长Concentric circles 同心圆Circle graph 扇面图Cone (V =pai * r^2 * h/3) 圆锥Circumscribe 外切Inscribe 内切Diagonal 对角线Decagon 十边形Hexagon 六边形Nonagon 九边形Octagon 八边形Pentagon 五边形Quadrilateral 四边形Polygon 多边形Diameter 直径Edge 棱Equilateral triangle 等边三角形Exterior (interior) angle 外角/内角Extent 维数Exterior angles on the same side of the transversal同旁外角Hypotenuse 三角形的斜边Intercept 截距Included angle 夹角Intersect 相交Inscribed triangle 内接三角形Isosceles triangle 等腰三角形Midpoint 中点Minor axis 短轴Origin 原点Oblique 斜三角形Plane geometry 平面几何Oblateness (ellipse) 椭圆Parallelogram 平行四边形Parallel lines 平行线Perpendicular 垂直的Pythagorean theorem 勾股定理Pie chart 扇图Quadrihedron 三角锥Radius 半径Rectangle 长方形Regular polygon 正多边形Rhombus 菱形Right circular cylinder 直圆柱体Right triangle 直角三角形Right angle 直角Rectangular solid 正多面体Regular prism 正棱柱Regular pyramid 正棱锥Regular solid/polyhedron 正多面体Slope 斜率Sphere ( surface area=4 pai r^2, V=4 pai r^3 / 3) Side 边长Segment of a circle 弧形Semicircle 半圆Solid 立体Square 正方形,平方Straight angle 平角(180度)Supplementary angle 补角Scalene cylinder 斜柱体Scalene triangle 不等边三角形Trapezoid 梯形V olume 体积Width 宽Vertical angle 对顶角Word problem terms:Apiece 每人Per capita 每人Decrease to 减少到Decrease by 减少了Brace 双Cardinal 基数Cent 美分Nickel 五美分Dime 一角Penny 一美分Down payment 定金,预付金Simple interest 单利Compounded interest 复利Foot 英尺Dozen 打Gross = 12 dozen 罗Gallon = 4 quart 加仑Fahrenheit 华氏温度Depth 深度Discount 折扣Cumulative graph 累计图Interest 利息Margin 利润Profit 利润Retail price 零售价Pint 品脱Score 二十Common year 平年Intercalary year(leap year) 闰年Quarter 夸脱GMA T数学概念和名词大全quartile就是小于median的所有数的median, hehe就是将所有的统计标本按顺序排列,再从头到尾分为个数相同的4堆quartile就是第一堆的最后一个,或是第二堆的第一个题目中,50个数,一定知道median是第25个或第26个同样,quartile是第12或是13个,the third quartile当然是37或是38个至于到底是37还是38,GRE不会为难你的,这两个数肯定一样对Quartile的说明:Quartile(四分位数):第0个Quartile实际为通常所说的最小值(MINimum)第1个Quartile(En:1st Quartile)第2个Quartile实际为通常所说的中分位数(中数、二分位分、中位数:Median)第3个Quartile(En:3rd Quartile)第4个Quartile实际为通常所说的最大值(MAXimum)我想大家除了对1st、3rd Quartile不了解外,对其他几个统计量的求法都是比较熟悉的了,而求1st、3rd是比较麻烦的,下面以求1rd为例:设样本数为n(即共有n个数),可以按下列步骤求1st Quartile:(1)将n个数从小到大排列,求(n-1)/4,设商为i,余数为j(2)则可求得1st Quartile为:(第i+1个数)*(4-j)/4+(第i+2个数)*j/4例(已经排过序啦!):1.设序列为{5},只有一个样本则:(1-1)/4 商0,余数01st=第1个数*4/4+第2个数*0/4=52.设序列为{1,4},有两个样本则:(2-1)/4 商0,余数11st=第1个数*3/4+第2个数*1/4=1.753.设序列为{1,5,7},有三个样本则:(3-1)/4 商0,余数21st=第1个数*2/4+第2个数*2/4=34.设序列为{1,3,6,10},四个样本:(4-1)/4 商0,余数21st=第1个数*1/4+第2个数*3/4=2.55.其他类推!因为3rd与1rd的位置对称,这是可以将序列从大到小排(即倒过来排),再用1rd 的公式即可求得:例(各序列同上各列,只是逆排):1.序列{5},3rd=52.{4,1},3rd=4*3/4+1*1/4=3.253.{7,5,1},3rd=7*2/4+5*2/4=64.{10,6,3,1},3rd=10*1/4+6*3/4=7ETS明确规定Percentile是一定要求的一个统计量,不知道有没有G友遇到过关于Percentile的数学题,因为Percentile的计算比较复杂,所以我在此对Percentile的求法详述,以方便G友:Percentile: percent below用概念来说没什么用,而且易让人糊涂,所以在此我归纳出一个公式以供G友参考。
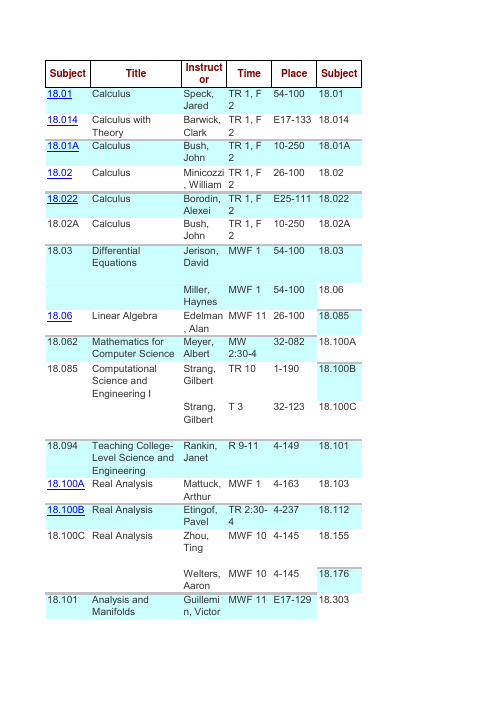
麻省理工学院数学系课表及教材
E17-122
Mathematics
Ankur 9:30-11
18.S997 Special Subject in Schlank, W 3-5 66-154
Mathematics
Tomer
Book
Author
* Calculus with Analytic Geometry, George
2nd ed.
E17-139 18.396
Advanced Analytic Cheng, MWF 11 E17-128 18.396 Methods in Science Hung and Engineering
Principles of Discrete Applied Mathematics
Goeman MWF 12 4-163 s, Michel
Topics in Lie Theory Introduction to Arithmetric Geometry Number Theory I
Topics in Number Theory
Charles, MW
E17-122 18.782
François 2:30-4
Bezrukav TR 1- 4-146 18.785
in Mathematics Larry
Introduction to Topology
Munkres, TR 11- 4-159 18.787 James 12:30
Algebraic Topology Tabuada TR 9:30- E17-122 18.787 , Gonç 11
alo
Graduate Topology Behrens, TR 2:30- E17-128 18.787
矩阵的迹

Trace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal (the diagonal from the upper left to the lower right) of A, i.e.,where aiirepresents the entry on the i th row and i th column of A. Equivalently, the trace of a matrix is the sum of its eigenvalues, making it an invariant with respect to a change of basis. This characterization can be used to define the trace for a linear operator in general. Note that the trace is only defined for a square matrix (i.e. n×n). Geometrically, the trace can be interpreted as the infinitesimal change in volume (as the derivative of the determinant), which is made precise in Jacobi's formula.The use of the term trace arises from the German term Spur (cognate with the English spoor), which, as a function in mathematics, is often abbreviated to "Sp".ExamplesLet T be a linear operator represented by the matrixThen tr(T) = −2 + 1 − 1 = −2.The trace of the identity matrix is the dimension of the space; this leads to generalizations of dimension using trace. The trace of a projection (i.e., P2 = P) is the rank of the projection. The trace of a nilpotent matrix is zero. The product of a symmetric matrix and a skew-symmetric matrix has zero trace.More generally, if f(x) = (x− λ1)d1···(x− λk)d k is the characteristic polynomial of a matrix A, thenIf A and B are positive semi-definite matrices of the same order then[1]PropertiesThe trace is a linear map. That is,for all square matrices A and B, and all scalars c.If A is an m×n matrix and B is an n×m matrix, then[2]Conversely, the above properties characterize the trace completely in the sense as follows. Let be a linear functional on the space of square matrices satisfying . Then and tr are proportional.[3]The trace is similarity-invariant, which means that A and P−1AP have the same trace. This is becauseA matrix and its transpose have the same trace:.Let A be a symmetric matrix, and B an anti-symmetric matrix. Then.When both A and B are n by n, the trace of the (ring-theoretic) commutator of A and B vanishes: tr([A, B]) = 0; one can state this as "the trace is a map of Lie algebras from operators to scalars", as the commutator of scalars is trivial (it is an abelian Lie algebra). In particular, using similarity invariance, it follows that the identity matrix is never similar to the commutator of any pair of matrices.Conversely, any square matrix with zero trace is the commutator of some pair of matrices.[4] Moreover, any square matrix with zero trace is unitarily equivalent to a square matrix with diagonal consisting of all zeros.The trace of any power of a nilpotent matrix is zero. When the characteristic of the base field is zero, the conversealso holds: if for all , then is nilpotent.Note that order does matter in taking traces: in general,In other words, we can only interchange the two halves of the expression, albeit repeatedly. This means that the trace is invariant under cyclic permutations, i.e.,However, if products of three symmetric matrices are considered, any permutation is allowed. (Proof: tr(ABC) = tr(A T B T C T) = tr((CBA)T) = tr(CBA).) For more than three factors this is not true. This is known as the cyclic property.Unlike the determinant, the trace of the product is not the product of traces. What is true is that the trace of the tensor product of two matrices is the product of their traces:The trace of a product can be rewritten as the sum of all elements from a Hadamard product (entry-wise product):.This should be more computationally efficient, since the matrix product of an matrix with an one(first and last dimensions must match to give a square matrix for the trace) has multiplications and additions, whereas the computation of the Hadamard version (entry-wise product) requires only multiplications followed by additions.The exponential traceExpressions like , where A is a square matrix, occur so often in some fields (e.g. multivariate statistical theory), that a shorthand notation has become common:This is sometimes referred to as the exponential trace function.Trace of a linear operatorGiven some linear map f : V→ V (V is a finite-dimensional vector space) generally, we can define the trace of this map by considering the trace of matrix representation of f, that is, choosing a basis for V and describing f as a matrix relative to this basis, and taking the trace of this square matrix. The result will not depend on the basis chosen, since different bases will give rise to similar matrices, allowing for the possibility of a basis independent definition for the trace of a linear map.Such a definition can be given using the canonical isomorphism between the space End(V) of linear maps on V and V⊗V*, where V* is the dual space of V. Let v be in V and let f be in V*. Then the trace of the decomposable elementv⊗f is defined to be f(v); the trace of a general element is defined by linearity. Using an explicit basis for V and the corresponding dual basis for V*, one can show that this gives the same definition of the trace as given above.Eigenvalue relationshipsIf A is a square n-by-n matrix with real or complex entries and if λ1,...,λnare the (complex and distinct) eigenvaluesof A (listed according to their algebraic multiplicities), thenThis follows from the fact that A is always similar to its Jordan form, an upper triangular matrix having λ1,...,λnonthe main diagonal. In contrast, the determinant of is the product of its eigenvalues; i.e.,More generally,DerivativesThe trace is the derivative of the determinant: it is the Lie algebra analog of the (Lie group) map of the determinant. This is made precise in Jacobi's formula for the derivative of the determinant (see under determinant). As a particular case, : the trace is the derivative of the determinant at the identity. From this (or from the connection between the trace and the eigenvalues), one can derive a connection between the trace function, the exponential map between a Lie algebra and its Lie group (or concretely, the matrix exponential function), and the determinant: det(exp(A)) = exp(tr(A)).For example, consider the one-parameter family of linear transformations given by rotation through angle θ,These transformations all have determinant 1, so they preserve area. The derivative of this family at θ = 0 is the antisymmetric matrixwhich clearly has trace zero, indicating that this matrix represents an infinitesimal transformation which preserves area.A related characterization of the trace applies to linear vector fields. Given a matrix A, define a vector field F on R n by F(x) = A x. The components of this vector field are linear functions (given by the rows of A). The divergence div F is a constant function, whose value is equal to tr(A). By the divergence theorem, one can interpret this in terms of flows: if F(x) represents the velocity of a fluid at the location x, and U is a region in R n, the net flow of the fluid out of U is given by tr(A)· vol(U), where vol(U) is the volume of U.The trace is a linear operator, hence its derivative is constant:ApplicationsThe trace is used to define characters of group representations. Two representations of agroup are equivalent (up to change of basis on ) if for all .The trace also plays a central role in the distribution of quadratic forms.Lie algebraThe trace is a map of Lie algebras from the Lie algebra glof operators on a n-dimensional space (nmatrices) to the Lie algebra k of scalars; as k is abelian (the Lie bracket vanishes), the fact that this is a mapof Lie algebras is exactly the statement that the trace of a bracket vanishes:The kernel of this map, a matrix whose trace is zero, is said to be traceless or tracefree, and these matrices form the simple Lie algebra sl, which is the Lie algebra of the special linear group of matrices with determinant 1. Thenspecial linear group consists of the matrices which do not change volume, while the special linear algebra is the matrices which infinitesimally do not change volume.In fact, there is a internal direct sum decomposition of operators/matrices into traceless operators/matrices and scalars operators/matrices. The projection map onto scalar operators can be expressed in terms of the trace, concretely as:Formally, one can compose the trace (the counit map) with the unit map of "inclusion of scalars" toobtain a map mapping onto scalars, and multiplying by n. Dividing by n makes this a projection, yielding the formula above.In terms of short exact sequences, one haswhich is analogous tofor Lie groups. However, the trace splits naturally (via times scalars) so but the splitting of the determinant would be as the n th root times scalars, and this does not in general define a function, so the determinant does not split and the general linear group does not decompose:Bilinear formsThe bilinear formis called the Killing form, which is used for the classification of Lie algebras.The trace defines a bilinear form:(x, y square matrices).The form is symmetric, non-degenerate[5] and associative in the sense that:In a simple Lie algebra (e.g., ), every such bilinear form is proportional to each other; in particular, to the Killing form.Two matrices x and y are said to be trace orthogonal ifInner productFor an m-by-n matrix A with complex (or real) entries and * being the conjugate transpose, we havewith equality if and only if A = 0. The assignmentyields an inner product on the space of all complex (or real) m-by-n matrices.The norm induced by the above inner product is called the Frobenius norm. Indeed it is simply the Euclidean norm if the matrix is considered as a vector of length mn.GeneralizationThe concept of trace of a matrix is generalised to the trace class of compact operators on Hilbert spaces, and the analog of the Frobenius norm is called the Hilbert-Schmidt norm.The partial trace is another generalization of the trace that is operator-valued.If A is a general associative algebra over a field k, then a trace on A is often defined to be any map tr: A→ k which vanishes on commutators: tr([a, b]) = 0 for all a, b in A. Such a trace is not uniquely defined; it can always at least be modified by multiplication by a nonzero scalar.A supertrace is the generalization of a trace to the setting of superalgebras.The operation of tensor contraction generalizes the trace to arbitrary tensors.Coordinate-free definitionWe can identify the space of linear operators on a vector space V with the space , where . We also have a canonical bilinear function that consists of applying an element of to an element of to get an element of in symbolsThis induces a linear function on the tensor product (by its universal property) which, as it turns out, when that tensor product is viewed as the space of operators, is equal to the trace.This also clarifies why and why as composition of operators (multiplication of matrices) and trace can be interpreted as the same pairing. Viewing one may interpret the composition map ascoming from the pairing on the middle terms. Taking the trace of the product then comes from pairing on the outer terms, while taking the product in the opposite order and then taking the trace just switches which pairing is applied first. On the other hand, taking the trace of A and the trace of B corresponds to applying the pairing on the left terms and on the right terms (rather than on inner and outer), and is thus different.In coordinates, this corresponds to indexes: multiplication is given by soand which is the same, whilewhich is different.For V finite-dimensional, with basis and dual basis , then is the entry of the matrix of the operator with respect to that basis. Any operator is therefore a sum of the form . Withdefined as above, . The latter, however, is just the Kronecker delta, being 1 if i=j and 0 otherwise. This shows that is simply the sum of the coefficients along the diagonal. This method, however, makes coordinate invariance an immediate consequence of the definition.DualFurther, one may dualize this map, obtaining a map This map is precisely the inclusion of scalars, sending to the identity matrix: "trace is dual to scalars". In the language of bialgebras,scalars are the unit, while trace is the counit.One can then compose these, which yields multiplication by n, as the trace of the identity is the dimension of the vector space.Notes[1]Can be proven with the Cauchy-Schwarz inequality.[2]This is immediate from the definition of matrix multiplication.[3]Proof:if and only if and (with the standard basis ),and thus.More abstractly, this corresponds to the decomposition as tr(AB)=tr(BA) (equivalently,, which has complement the scalar matrices, and leaves one degree of ) defines the trace on slnfreedom: any such map is determined by its value on scalars, which is one scalar parameter and hence all are multiple of the trace, a non-zero such map.[4]Proof: is a semisimple Lie algebra and thus every element in it is the commutator of some pair of elements, otherwise the derivedalgebra would be a proper ideal.[5]This follows from the fact that if and only ifArticle Sources and Contributors7 Article Sources and ContributorsTrace (linear algebra) Source: /w/index.php?oldid=402560193 Contributors: Achab, Adiel, Aetheling, Algebraist, Archelon, AxelBoldt, BenFrantzDale, Berland,Btyner, CYD, Calc rulz, CattleGirl, Charles Matthews, Chochopk, Dima373, Dysprosia, Edinborgarstefan, Egriffin, Email4mobile, Eranb, Eric Olson, Fropuff, Ged.R, Giftlite, Haseldon,JabberWok, Japanese Searobin, Jewbacca, Jshadias, Kaarebrandt, Kan8eDie, Katzmik, Keyi, Kruusamägi, Ksyrie, Laurentius, Lethe, Lukpank, MER-C, MarSch, Mct mht, Melchoir, MichaelHardy, Mon4, Nathanielvirgo, Nbarth, Nineteen O'Clock, Octahedron80, Oleg Alexandrov, Oyz, Phe, Phys, Pokipsy76, Pt, Robinh, Salgueiro, Saretakis, Sciyoshi, Spiel496, Spireguy,StradivariusTV, Sullivan.t.j, TakuyaMurata, Tarquin, Tercer, Tffff, Thehotelambush, Tsirel, V1adis1av, Whaa?, WhiteHatLurker, Wpoely86, Wshun, 84 anonymous edits LicenseCreative Commons Attribution-Share Alike 3.0 Unported/licenses/by-sa/3.0/。
丘成桐大学生数学竞赛数学专业大纲(英汉对照版)

modelica的simple算法

一、简介Modelica是一种面向物理建模和工程仿真的开放式建模语言,它的简单算法(simple algorithm)是其中的一种常用算法。
本文将介绍simple算法的基本原理、应用场景和优缺点。
二、简单算法的基本原理简单算法是一种基本的隐式数值积分方法,它通过迭代求解微分方程的数值解。
简单算法的基本原理如下:1. 对微分方程进行离散化处理,将微分方程转化为差分方程;2. 利用初始条件,采用迭代方法求解差分方程的数值解;3. 判断数值解的精度是否满足要求,如果不满足则继续迭代,直到满足要求为止。
简单算法的求解过程相对直观,易于理解和实现,因此在一些工程仿真软件中被广泛应用。
三、简单算法的应用场景简单算法适用于一些简单的动态系统仿真,特别是对于非刚性系统和非线性系统的仿真。
由于简单算法的迭代过程较为稳定,因此对于一些求解较为复杂的微分方程而言,简单算法可以提供较为可靠的数值解。
简单算法在电力系统、控制系统和热力系统等领域有着广泛的应用。
在这些系统中,通常涉及到复杂的微分方程,而简单算法可以提供较为准确的数值解,为工程设计和分析提供重要的支持。
四、简单算法的优缺点简单算法作为一种常用的数值积分方法,具有以下优缺点:1. 优点:(1)易于实现:简单算法的迭代过程相对简单,易于理解和实现;(2)稳定性较好:简单算法的迭代过程相对稳定,适用于一些复杂的微分方程的求解。
2. 缺点:(1)收敛速度较慢:简单算法的迭代过程需要较多的迭代次数,收敛速度较慢;(2)对刚性系统和高阶系统的适应性较差:简单算法在处理一些刚性系统和高阶系统时,可能会出现数值不稳定的情况。
简单算法作为一种常用的数值积分方法,适用于一些简单的动态系统仿真,具有易于实现、稳定性较好的特点,但在收敛速度和对复杂系统的适应性上存在一定的局限性。
五、结语简单算法作为Modelica建模语言的一种常用算法,在工程仿真和系统分析中有着重要的应用价值。
通过深入理解简单算法的基本原理和应用场景,可以更好地利用该算法进行系统建模和仿真,为工程设计和分析提供可靠的数值支持。
代数英语

(0,2) 插值||(0,2) interpolation0#||zero-sharp; 读作零井或零开。
0+||zero-dagger; 读作零正。
1-因子||1-factor3-流形||3-manifold; 又称“三维流形”。
AIC准则||AIC criterion, Akaike information criterionAp 权||Ap-weightA稳定性||A-stability, absolute stabilityA最优设计||A-optimal designBCH 码||BCH code, Bose-Chaudhuri-Hocquenghem codeBIC准则||BIC criterion, Bayesian modification of the AICBMOA函数||analytic function of bounded mean oscillation; 全称“有界平均振动解析函数”。
BMO鞅||BMO martingaleBSD猜想||Birch and Swinnerton-Dyer conjecture; 全称“伯奇与斯温纳顿-戴尔猜想”。
B样条||B-splineC*代数||C*-algebra; 读作“C星代数”。
C0 类函数||function of class C0; 又称“连续函数类”。
CA T准则||CAT criterion, criterion for autoregressiveCM域||CM fieldCN 群||CN-groupCW 复形的同调||homology of CW complexCW复形||CW complexCW复形的同伦群||homotopy group of CW complexesCW剖分||CW decompositionCn 类函数||function of class Cn; 又称“n次连续可微函数类”。
Cp统计量||Cp-statisticC。
浅谈Galois理论

Galois上同调是有限群上同调理论的推广,与二次型理论,中心单代数理论、代数群等数学分支都有着广泛的联系,下面我就来简单介绍一下它的基本理论及其应用概况。
先从投射有限群(profinite group)讲起,它实际上就是有限群的投射极限,等价于紧完全不连通的拓扑群。
对于交换投射有限群,可以通过Poincare对偶Hom(-,Q/Z)对应于挠Abel群。
为什么要考虑投射有限群呢?那是因为Galois群都是投射有限群。
具体来说,假若Ω/k 是Galois扩张,那么其Galois群同构于Ω/k的所有有限子扩张L/k的Galois群的投射极限,这里的同构是建立在拓扑群的意义上的。
实际上,我们已经有了抽象群的上同调,那么投射有限群与它有什么差别呢?主要就是加上了拓扑概念,对应的G-模A是要求连续,因此有时也被称为连续上同调。
接下来来我们自然可以问,是否存在一个投射有限群,它的上同调与它作为抽象群的上同调是不同的?这对于有限群是成立的,这是因为有限群的拓扑是离散的;对于零阶上同调群,两者也是相同的,它们都等于群作用的不动点集。
但假若我们取Z^为Z生成的投射有限群,它平凡的作用在Q上,那么对于连续上同调H^1(Z^,Q)=lim H^1(Z/n,Q)=0,但对于一般上同调H^1(Z,Q)=Hom(Z^,Q)≠0,这是因为由于Q的可除性,我们可以扩张Hom(Z,Q)的非零元。
投射有限群的上同调的代数构造与抽象群的上同调完全类似,这里我就不再重复了。
下面看相应的上同调序列,假若我们已经有投射有限群G-模的短正合列1→A→B→C→1,我们可以期盼这样的长正合列:1→H^0(G,A)→H^0(G,B)→H^0(G,C)→H^1(G,A)→H^1(G,B)→H^1(G,C)→H^2(G,A)→…其具体结论是逐步递进的:1)A是B的普通子群时,序列可以连到H^1(G,B)2)A是B的正规子群时,序列可以连到H^1(G,C)3)A是B的中心子群时,序列可以连到H^2(G,A)同时有两个连通同态也很值得注意:记上述正合列中f:A→B,1)δ_0:H^0(G,C)→H^1(G,A). 对任何c∈C^G,有拉回元素b∈B^G,定义δ_0(c)=[α},使得f(α_σ)=b^(-1)σ·b.2)δ_1:H^1(G,C)→H^2(G,A). 对任何[γ]∈H^1(G,C),各γ_σ均有拉回元素β_σ,定义δ_1([γ])=[α},使得f(α_σ,τ)=β_σ(σ·β_τ)(β_σ,τ)^(-1).这样的符号看似比较杂乱,但实际上就是群元素σ作用后带来的“交换障碍”,同时一阶连续上同调H^1(G,A)还可以被解释为A上的G-挠子(torsor)或主齐性空间,即带与G-作用一致的单可迁右作用的G-集。
The fine gradings of sl(3,C) and their symmetries

Introduction
— Admissible gradings of a simple Lie algebra L over the complex or real number field are basic structural properties of each L. Examples of exploitation of coarse gradings like Z2 are easy to find in the physics literature. Here we are interested in the opposite extreme: the fine gradings of L which only recently were described [8,9]. Our aim is to point out the interesting symmetries of the fine gradings on the example of sl(3, C ). Such symmetries can be used in the study of graded contractions of L. Indeed, they are the symmetries of the system of quadratic equations for the contraction parameters. Graded contractions are a systematic way of forming from L a family of equidimensional Lie algebras which are not isomorphic to L. An insight into such parameter–dependent families of Lie algebras provides a group theoretical tool for investigating relations between different physical theories through their symmetries. In this contribution we consider finite dimensional L and announce specific results for sl(3, C ) only. The decomposition Γ : L = i∈I Li is called a grading if, for any pair of indices i, j ∈ I , there exists an index k ∈ I such that 0 = [Li , Lj ] ⊆ Lk . There are infinitely many gradings of a given Lie algebra. We do not need to distinguish those gradings which can be transformed into each other. More precisely, if Γ : L = i∈I Li is a ˜ : L = i∈I g (Li ) is also a grading. grading and g is an automorphism of L, then Γ Two such gradings are called equivalent. A grading Γ : L = i∈I Li is a refinement of the grading Γ : L = i∈J Lj if for any i ∈ I there exists j ∈ J such that Li ⊆ Lj . A grading which cannot be properly refined is called fine. For construction of a grading of L, one can use any diagonalizable automorphism g from Aut L. It is easy to see that decomposition of L into eigenspaces of g is a
形式三角矩阵环的自同构

湘潭大学硕士学位论文形式三角矩阵环的自同构姓名:***申请学位级别:硕士专业:基础数学指导教师:***20030501摘要设A,B是两个有单位元的环,并且他们都只有平凡的幂等元,M为非零的口,回一双模。
记Tri∽,M,口)为所有以A,口中元为对角元,M中元为上三角元的2阶三角矩阵构成的环。
本文的研究是在Wai-shunCheung([16]),A.HaghangandK.Varadardjan([1]),You’gnCao([5])andLepingXie.Etc([18])等的研究基础上进行的,主要结论是:形式三角矩阵环(,一Tri(4,M,B)的映射妒是一个自同构的充分必要条件是存在环A的自同构g,环B的自同构h,似,口)一双模M的一个乜,.11).半线性同构七,M中的一个元素d,使妒(4州如h㈨一≯坳’)o关键词:环,双模,自同构,半线性同构AbstractThroughoutthispaper,weassumethatAandBareringswithidentitiesandtheonlyidempotentsinAandBare1and0.LetMisanonzeroleftArightBbimodule.Thefomattriangu-armatriX订ngTrt。
,M,动2(彳答)hasasitselementsformatmatrices(4:)wherea∈A,bCBanam…Weundertakeafurtherinvestigationofauto-morphismsonuppertriangularmatricesstudiedbyWai—shunCheung([16])A.HaghangandK.Varadardjan([1]),You’anCao([5])andLepingXie.etc([18]).Themainresultofthispaperisasfollows:assumeA,BandMaredefinedabove,themap∞onTri似,M,B)isanautomorphismifandonlyifthereareanautomorphismgofA,anautomorphismhofB,a(g,h)一semilinearautomorphismkofMandanelementdofMsuchthat妒㈡2P如卜≯坳’)-Keywords:ring,bimodule,automorphism,semiIinearautomorphism形式三角矩阵环的自同构引言代数和环上的映射一直是基础数学的一个非常重要的研究部分,矩阵代数和矩阵环上的自同构和Lie自同构的研究就是其中之一,人们在这一方面做了大量的研究。
数学中的123就跟英语中的ABC一样平凡和简单然而,按

Simple arithmetic problems using 123 can help develop basic problem-solving abilitcepts
By using numbers, students can begin to understand abstract ideas such as relationships and patterns.
06
Proficient in ABC in English can lead to opportunities in international business, diplomacy, teaching, and more.
Learning difficulty and practicality
• Learning ABC in English can be challenging due to the vast vocabulary and complex grammar rules.
Learning difficulty and practicality
The Application of 123 in Mathematics
Foundation for higher mathematics
123 is the starting point for more complex mathematical concepts such as fractions, algebra, and geometry.
It consists of 26 letters, each representing a unique sound in the English language.
simple算法适用条件

simple算法适用条件Simple算法适用条件简洁的算法(Simple Algorithm)是一种简单、直观、易于理解和实现的计算机算法。
它在一些特定的应用场景中具有一定的适用条件。
本文将从不同的角度探讨Simple算法的适用条件。
一、输入规模小Simple算法适用于输入规模较小的问题。
由于Simple算法的实现简单,通常不需要复杂的数据结构和算法,因此对于规模较小的问题,Simple算法能够快速得出解决方案。
例如,对于一个包含少量元素的数组进行排序,可以使用简单的冒泡排序算法,而不必使用更复杂的快速排序或归并排序。
二、问题的复杂性低Simple算法适用于问题的复杂性低的情况。
复杂性低意味着问题本身的结构简单,不涉及复杂的逻辑和计算。
在这种情况下,Simple 算法能够直接、简单地解决问题,而无需引入复杂的算法和数据结构。
例如,计算两个整数的和、差、积和商的问题,可以使用简单的加法、减法、乘法和除法运算符来解决。
三、数据分布均匀Simple算法适用于数据分布均匀的情况。
数据分布均匀意味着数据的取值范围较小,且各个取值的出现频率相似。
在这种情况下,Simple算法能够快速地找到问题的解决方案。
例如,计算数组中元素的平均值,如果数组中的元素取值分布均匀,可以直接将所有元素相加再除以元素个数来得到平均值。
四、问题具有局部性Simple算法适用于问题具有局部性的情况。
局部性指的是问题的解决只需要考虑一部分数据,而不需要考虑所有数据。
在这种情况下,Simple算法可以通过直接访问和处理局部数据来解决问题,而无需对整个数据集进行操作。
例如,查找数组中最小值的问题,只需要遍历数组一次,记录当前最小值即可,无需对整个数组进行排序或比较。
五、问题具有单一目标Simple算法适用于问题具有单一目标的情况。
单一目标意味着问题的解决只需要考虑一个优化目标,而不需要考虑多个目标的权衡。
在这种情况下,Simple算法可以通过直接追求单一目标来解决问题,而无需考虑复杂的权衡和调整。
全球数学网址大全

全球数学网址大全数理逻辑、数学理论AILAhttp://www.disi.unige.it/aila/eindex.html意大利逻辑及其应用协会的主页,包括意大利数理逻辑领域的相关内容。
Algebra and Logic/title.cgi?2110《代数与逻辑》,《西伯利亚代数与逻辑期刊》的翻译版,荷兰的Kluwer学术出版社提供其在线服务。
alt.math.undergrad-Math Forum/epigone/alt.math.undergradMsth Forum上的大学生和研究生数学论坛,提供档案文件、论题等信息。
Annals of Pure and Applied Logic/~dmjones/hbp/apal/《纯逻辑与应用逻辑学年鉴》,麻省理工大学计算理论小组主页提供其过刊的浏览,荷兰的Elservier出版社提供其电子刊的在线服务。
Archive for Mathematical Logichttp://link.springer.de/link/service/journ...00153/index.htm《数学逻辑档案》,属于德国Springer出版公司在线电子期刊的一种。
Aristotle and the Paradoxes of Logic-Gilbert Voeten/nilog/files/arist...adoxes_of_l.htm亚里士多德及其逻辑理论研究。
BLC/~exr/blc/不列颠逻辑研讨会的主页,包括数学逻辑的相关研究,如相关网站及电子期刊。
Books:Professional&Technical:Professional Science: /exec/obidos/tg/brows...3600008-7001844浏览亚马逊网上专业和技术店中的数学畅销书,提供应用范畴,混沌与系统化;几何与拓扑;数学分析;数学物理学;数字规律;纯数学;数学变换等领域,包括数理逻辑方面的畅销书的在线预览。
Unifying W-Algebras

Physikalisches Institut der Universit¨ at Bonn Nußallee 12, 53115 Bonn, Germany INFN, Sezione di Torino Via Pietro Giuria 1, 10125 Torinoct We show that quantum Casimir W -algebras truncate at degenerate values of the central charge c to a smaller algebra if the rank is high enough: Choosing a suitable parametrization of the central charge in terms of the rank of the underlying simple Lie algebra, the field content does not change with the rank of the Casimir algebra any more. This leads to identifications between the Casimir algebras themselves but also gives rise to new, ‘unifying’ W -algebras. For example, the k th unitary minimal model of WAn has a unifying W -algebra of type W (2, 3, . . . , k2 + 3k + 1). These unifying W -algebras are non-freely generated on the quantum level and belong to a recently discovered class of W -algebras with infinitely, non-freely generated classical counterparts. Some of the identifications are indicated by level-rank-duality leading to a coset realization of these unifying W -algebras. Other unifying W -algebras are new, including e.g. algebras of type WD −n . We point out that all unifying quantum W -algebras are finitely, but non-freely generated.
simple方法

simple方法
SIMPLE算法全称为Semi-Implicit Method for Pressure-Linked Equations,意思是压力耦合方程组的半隐式方法,是一种计算流体力学中常用的数值方法,用于求解不可压缩流动的Navier-Stokes方程。
SIMPLE算法的原理是将动量方程和连续性方程分别离散化为矩阵形式,然后通过对角线分解和逆运算,得到压力泊松方程和速度修正方程。
通过迭代求解这两个方程,可以得到压力场和速度场。
SIMPLE算法自1972年问世以来在世界各国计算流体力学及计算传热学界得到了广泛的应用,这种算法提出不久很快就成为计算不可压流场的主要方法,随后这一算法以及其后的各种改进方案成功的推广到可压缩流场计算中,已成为一种可以计算任何流速的流动的数值方法。
关于半代数若干问题的研究

广西师范大学硕士学位论文关于半代数若干问题的研究姓名:***申请学位级别:硕士专业:基础数学指导教师:***20090401关于半代数若干问题的研究研究生: 康德恒 导师: 易忠 学科专业: 基础数学 研究方向: 代数及其应用 年级: 2006级摘 要本文共分三部分,每部分为一章.第一章是关于半代数的零化子同余及忠实性的讨论.本章引入半代数零化子同余的概念,这一概念的提出为研究半代数的忠实性提供了有效的工具.我们揭示了零化子同余在半代数单态、满态、同构下的变化规律,得到了零化子同余的一些性质.随后以零化子同余为工具讨论了半代数的忠实性,给出了忠实半代数的几个等价条件.证明了每个自由半代数都是忠实的;并证明了交换半环R 是单的当且仅当R 作为R -半代数时的每个非零商半代数都是忠实的.本章主要结论有:定理1.3.6 设R 是交换半环,则R 是单的当且仅当R 作为R -半代数时的每个非零商半代数都是忠实的.第二章是关于半代数正合序列的讨论.本章中我们证明了半代数的序列有类似于模论中的图追踪,五引理,马蹄引理等命题.本章的主要结论有:定理2.2.1 设,,A B C ,,,A B C ′′′为半代数, ,,,,,,f g f g αβγ′′为半代数同态,且下图交换 f g f g AB A B CC αβ′′⎯⎯→⎯⎯→↓↓γ↓′′′⎯⎯→⎯⎯→若上图中行在B B ′和处都是正合的,则下面4条结论成立: (1)若,,f αγ′是单同态,且,B B ′加法可消,则β是单同态;(2)若,,g αγ是满同态,且()B B β′为的加法可消子半代数,则β是满同态; (3)若β是单同态,,g α是满同态,则γ是单同态;(4)若β是满同态,,f γ′是单同态,且()A A α′是的加法可消子半代数,则α是满同态. 在第三章中我们引入了半代数局部化的定义,讨论了该定义意义下局部化的若干性质,并证明了半代数局部化的泛性质.关键词: 零化子同余; 忠实半代数; 图追踪; 半代数的局部化Some Studies on Semi-algebrasGraduate student: Kang De-heng Supervisor: Professor Yi ZhongSubject: Basic Mathematics Direction: Algebra and its Applications Grade: 2006AbstractThis paper is composed of three parts. Each part is a chapter.In chapter 1, we discuss the annihilator congruence and faithfulness of semi-algebras. In this chapter, we introduce the concept of the annihilator congruence of semi-algebras. It is an effective tool for the study of semi-algebras. We show the relationships between annihilator congruence and the semi-algebra monomorphisms, epimorphisms and isomorphisms; obtain some properties of annihilator congruence. Then we discuss the faithfulness of semi-algebra by the annihilator congruence, and some equivalent conditions of faithful semi-algebra are given. At last we prove that every free semi-algebra is faithful; and a sufficient and necessary condition that a commutative semi-ring R is simple is also given.One of the main result of chapter 1 is as follows:Theorem 1.3.6 Let R be a commutative semi-ring, then R is simple if and only if each non-zero quotient left R-semi-algebra R M is faithful.In chapter 2, we discuss the exactness of semi-algebras, the Five lemma, Horseshoe lemma to the exact sequence of semi-algebra are proved.The main results of chapter 2 are as follows:Theorem 2.2.1 Let ,,A B C ,,,A B C ′′′be semi-algebras, and ,,,,,,f g f g αβγ′′be semi-algebra homomorphisms. Suppose the following diagram is commutativef g f g AB A B CC αβγ′′⎯⎯→⎯⎯→↓↓′′⎯⎯→⎯⎯→↓′In the diagram, if rows are exact at ,B B ′, then the following statements hold:(1) If ,,f αγ′ are monomorphisms, and ,B B ′are addition cancellative, then β is a monomorphism;(2) If ,,g αγ are epimorphisms, and ()B β is the addition cancellative subsemi-algebra of B ′, then β is an epimorphism;(3) If β is a monomorphism, ,g αare epimorphisms, then γ is a monomorphism; (4) If β is an epimorphism, ,f γ′ are monomorphisms, and ()A α is a addition cancellative subsemi-algebra of A ′, then α is an epimorphism.In chapter 3, we introduce the definition of localization of semi-algebras, some properties of localization are discussed, and the universal property of the localization of semi-algebras is alsoproved.Keywords: Annihilator congruence; Faithful semi-algebra; Diagram chasing; Localization of semi-algebra论文独创性声明本人郑重声明:所提交的学位论文是本人在导师的指导下进行的研究工作及取得的成果。
WEA

WEAK EFFECT ALGEBRASTHOMAS VETTERLEINAbstract.Weak effect algebras are based on a commutative,associative andcancellative partial addition;they are moreover endowed with a partial orderwhich is compatible with the addition,but in general not determined by it.Every BL-algebra,i.e.the Lindenbaum algebra of a theory of Basic Logic,givesrise to a weak effect algebra;to this end,the monoidal operation is restrictedto a partial cancellative operation.We examine in this paper BL-effect algebras,a subclass of the weak effect algebras which properly contains all weak effect algebras arising from BL-algebras.We describe the structure of BL-effect algebras in detail.We thusgeneralise the well-known structure theory of BL-algebras.Namely,we show that BL-effect algebras are subdirect products of linearly ordered ones and that linearly ordered BL-effect algebras are ordinal sums ofgeneralised effect algebras.The latter are representable by means of linearlyordered groups.1.IntroductionBL-algebras are the algebraic counterpart of H´a jek’s Basic Logic,the many-valued logic based on continuous t-norms and their residua[Haj,CEGT].The structure of BL-algebras is well-known:They are subdirect products of linearly ordered BL-algebras,and the latter are,in a certain transparent way,composed from MV-and product algebras(see[AgMo]).Interestingly,BL-algebras may be identified with a certain kind of partial algebra, which very much reminds of effect algebras[Vet1].Effect algebras have been studied in a completely different context;they describe the inner structure of the set of effects in quantum mechanics[FoBe].They are based on a partial addition,which is cancellative and which determines a bounded partial order in the natural way.In[Vet1],weak effect algebra were introduced as a common generalisation of effect algebras and BL-algebras.To this end,the effect algebra’s partial order was added as an own relation,and the assumption was dropped that this order is uniquely determined by the partial addition.So in a weak effect algebra,from a≤b it does in general not follow that a+x=b for some element x,although the converse is true.The prototypical examples of weak effect algebras arise from BL-algebras;the construction is,roughly speaking,the following.BL-algebras are based on two operations,a conjunction and an implication→.First of all,there is no loss of information when we drop one of them,for example→.Second, is in general 2000Mathematics Subject Classification.03B52,03G12,06F05.Key words and phrases.Weak effect algebras,BL-algebras,effect algebras,subdirect product representation,ordinal sum decomposition.This research was partially supported by the German Science Foundation(DFG)as part of the Collaborative Research Center“Computational Intelligence”(SFB531).12THOMAS VETTERLEINnot cancellative;but we may restrict to a partial operation which is defined only for the extremal cases;the resulting operation is then cancellative,and the original operation may easily be recovered.Now,putting the“cancellative part”of ,the partial order,and the constants together,we get a weak effect algebra.The aim of this paper is to examine BL-effect algebras,which are special weak effect algebras.Among them,wefind in particular all the algebras which correspond to BL-algebras.However,a simple example shows that BL-effect algebras are still strictly more general than BL-algebras.We proceed as follows.We show in afirst step that BL-effect algebras are subdirect products of linearly ordered BL-effect algebras.To this end,we introduce the necessary concepts of congruences and ideals of weak effect algebras.We then turn to the linear case.We prove that linearly ordered BL-effect algebras are ordinal sums of generalised effect algebras[HePu].The latter are known to be isomorphically embeddable into the positive cone of linearly ordered abelian groups (see[DvPu]).So the picture is in the end similar to case of BL-algebras,whose structure theory is contained as a special case.We note that in the present case,the hard step is thefirst one:the subdirect representation theorem;the second one,which caused so much trouble in the case of BL-algebras,is rather easy.In a concluding section,we point out the significance of our results with respect to the general problem how to classify residuated lattices(that is,integral,commu-tative residuated -monoids).We outline a possible approach to the latter problem, an approach which is exemplified by the procedure in this paper.2.Weak effect algebrasEffect algebras were originally introduced to describe the internal structure of the set of Hilbert space effects,which in turn model possibly unsharp quantum-physical propositions[FoBe].As opposed to that,BL-algebras are algebras of propositions of Basic Logic,the logic of continuous t-norms and their residua,introduced by H´a jek [Haj].In[Vet1],we combined both notions;we generalised effect algebras so as to get a class of partial algebras which is large enough to comprise also BL-algebras. Definition2.1.A weak effect algebra is a structure(E;≤,+,0,1)such that the following conditions hold:(E1)(E;≤,0,1)is a poset with the smallest element0and the largest element 1.(E2)+is a partial binary operation such that for any a,b,c∈E(a)(a+b)+c is defined iffa+(b+c)is defined,and in this case(a+b)+c=a+(b+c);(b)a+0is always defined and equals a;(c)a+b is defined iffb+a is defined,and in this case a+b=b+a. (E3)If,for a,b,c∈E,a+c and b+c are defined,then a≤b if and only if a+c≤b+c.(E4)If,for a,b∈E,a≤b,then there is a largest element¯a≤a such that ¯a+x=b for some x∈L.WEAK EFFECT ALGEBRAS3 It is easily seen that effect algebras are identifiable with those weak effect algebras for which the following holds:For any a,b such that a≤b,there is an x such that a+x=b.Note that(E3)implies the cancellativity of the partial addition.So if for some pair a,b of elements of a weak effect algebra such that a≤b,there is an element x such that a+x=b,then x is uniquely determined;we will denote this element by b−a.In the sequel,we will make use of the usual convention that a statement con-taining some partial operation is to be read as:The involved terms are defined, and the statement holds.We next recall how we may associate a BL-effect algebras with a BL-algebra. For a more intuitive presentation of this construction,see[Vet2].Definition2.2.Let(L;≤BL, ,⇒,0BL,1BL)be a BL-algebra.Seta≤b if b≤BL a,a⊕b=a b,a b=b⇒a,0=1BL,1=0BL.Then we call(L;≤,⊕, ,0,1)a dual BL-algebra.Furthermore,we define a partial addition+on L as follows:For a,b∈L,let a+b=a⊕b if a is the smallest element x such that x⊕b=a⊕b and b is the smallest element y such that a⊕y=a⊕b;else,we let a+b undefined.We call+ the partial addition associated to⊕.So what we do with a BL-algebra is:The order is reversed,which means just a change of notation;and the total operation⊕,which corresponds to the original ,is restricted to the pairs of elements which are minimal among those whose sum is the same.We next describe the transition from a partial algebra to a total one.Definition2.3.Let(E;≤,+,0,1)be a weak effect algebra.Let us call the partial addition+extendible to the total operation⊕if(1)a⊕b def=max{a +b :a ≤a,b ≤b and a +b is defined}exists for any a,b∈L.In this case,we call⊕the total addition associated to+.We will establish the exact connection between BL-algebras and weak effect algebras;Theorem2.5is a slightly modified version of[Vet1,Theorems4.2,4.3]. Definition2.4.A BL-effect algebra is a weak effect algebra(E;≤,+,0,1)such that the following conditions hold:(E5)(E;≤)is a lower semilattice.(E6)For any a,b,c∈E such that c≤a+b,there are a1≤a and b1≤b such that(α)c=a1+b1and(β)a1=a in case c≥a.(E7)For any a,b∈E,there are a1,a2,b1,b2such that a=a1+a2,b=b1+b2 and a1≤b,b1≤a and a2∧b2=0.(E8)For any a,b,c,x,y such that a+x=b+y=c,there is a z such that (a∧b)+z=c.Theorem2.5.(I)Let(L;≤,⊕, ,0,1)be a dual BL-algebra,and let+be the associated partial addition.Then(L;≤,+,0,1)is a BL-effect algebra.Moreover,the total addition associated to+exists and coincides with⊕.4THOMAS VETTERLEIN(II)Let(L;≤,+,0,1)be a BL-effect algebra,and let+be extendible to⊕.Let be the residual of⊕.Then(L;≤,⊕, ,0,1)is a dual BL-algebra.Moreover, the partial addition associated to⊕coincides with+.The following example shows that there are BL-effect algebras not arising from BL-algebras.Example2.6.Letπbe any irrational positive real number,and let E={a∈R: a∈Q and0≤a<π,or a=π}.Let+on E be the addition of real numbers whenever the sum is in E.Then(E;+,0,π)is a weak effect algebra.The partial addition on E is not extendible;the maximum(1)does not exist if the sum of the two elements a,b∈E exceedsπ.So E does not arise from a(dual) BL-algebra.We conclude the section by establishing some basic properties of BL-effect alge-bras.The key property assumed in[Rav]to represent effect algebras in the positive cone of partially ordered groups,is the Riesz decomposition property.We will use it in the present context formally unchanged.Definition 2.7.A weak effect algebra is said to fulfil the Riesz decomposition property,or(RDP)for short,if for all a,b,c,d such that a+b=c+d there are e1,e2,e3,e4such that the scheme(2)e1e2→a e3e4→b ↓↓c dholds.Here,by the scheme(2)to hold,we mean that any column or line adds up to what the arrow points to.Proposition2.8.Every BL-effect algebra fulfils(RDP).Proof.Assume a+b=c+d.Because c≤a+b,there are by(E6)e1≤a and e3≤b such that c=e1+e3.From e1≤a≤e1+e3+d,we conclude also by(E6) that a=e1+e2for some e2;and similarly,wefind an e4such that b=e3+e4.It follows c=e2+e4by cancellation. Lemma2.9.In a BL-effect algebra,the following holds.(i)Let a+b=c+d.Then a≤c if and only if b≥d.(ii)Let c−a and c−b exist.Then also c−(a∧b)exists,and c−(a∧b)= (c−a)∨(c−b).Proof.(i)If a≤c,it follows by(E6)that c=a+b1for some b1≤b.So d≤b follows by cancellation.(ii)By(E8),c−(a∧b)exists.By(i),we have c−(a∧b)≥c−a,c−b.Let x≥c−a,c−b.Let x =x∧c,and let x ≤x be the largest element such that x +y=c for some y;then x≥x ≥c−a,c−b.By(i),we further conclude y≤a,b,so y≤a∧b,hence x≥x =c−y≥c−(a∧b).WEAK EFFECT ALGEBRAS53.Congruences of weak effect algebrasEven for an effect algebra,it is difficult to give the exact conditions that an equivalence relation does not only allow the formation of a quotient algebra,but that this quotient is also again an effect algebra;see e.g.[GuPu].For weak effect algebras,the various special properties related to the partial order cause further difficulties.Like in the case of effect algebras,our definition of a congruence is such that we may at least form a quotient algebra;this quotient algebra,however,is in general not again a weak effect algebra.Definition3.1.Let(E;≤,+,0,1)be a weak effect algebra.Then an equivalence relation∼is called a congruence of E if the following holds:(C1)For all a,a ,b,b such that a∼a ,b∼b and a+b,a +b exist,a+b∼a +b . (C2)For all a,b,b such that a≤b and b∼b ,there is an a ∼a such that a ≤b . (C3)For all a,a ,b such that a∼a and a≤b≤a ,we have b∼a.∼being a congruence of E,we set[a]∼def={a :a ∼a}for a∈E,and[E]∼def= {[a]∼:a∈E}.We define[a]∼≤[b]∼if a ≤b for some a ∼a,b ∼bfor a,b∈E,and we let+be the partial binary operation on[E]∼such that[a]∼+[b]∼is definedand equals[c]∼ifffor some a ∼a and b ∼b,a +b is defined and a +b ∼c.Then([E]∼;≤,+,[0]∼,[1]∼)is called the quotient algebra of E induced by the con-gruence∼.Note that only(C1)in this definition makes sure that the quotient algebra’s partial operation+is defined unambigously.Moreover,(C2)and(C3)guarantee that the quotient algebra is by≤partially ordered:Lemma3.2.Let(E;≤,+,0,1)be a weak effect algebra,and let∼be a congruence of E.Then[E]∼is by≤partially ordered,and bounded by[0]∼and[1]∼.Proof.Let a,b,c∈E such that[a]∼≤[b]∼and[b]∼≤[c]∼.Then by(C2),there are b ∼b and a ∼a such that b ≤c and a ≤b ;it follows[a]∼≤[c]∼.Similarly, from[a]∼≤[b]∼and[b]∼≤[a]∼it follows a ≤b and b ≤a for some a ∼a,b ∼b; so[a]∼=[b]∼by(C3).Reflexivity of≤is obvious.So≤is a partial order on E, and[0]∼is clearly the smallest element and[1]∼the largest element.The numerous conditions needed to ensure that a congruence is structure-preserv-ing are listed in the following theorem.Fortunately,the situation will not remain that complicated when we will have to do with BL-effect algebras.Theorem3.3.Let(E;≤,+,0,1)be a weak effect algebra,and let∼be a congruence of E fulfilling the following conditions:(C4)For a,b,c∈E such that c∼a+b,there are a∼a and b∼b such that c=a +b .(C5)For a,a ,b,b ,c,c such that a∼a ,b∼b ,c∼c ,if a≤b and a +c,b +c exist,then there are a ∼a,c ∼c such that a ≤b and a +c and b +cexist.6THOMAS VETTERLEIN(C6)For a,b,c,c such that c∼c ,if a+c≤b+c ,then a ≤b for some a ∼a and b ∼b.(C7)Let a≤b,and let¯a≤a be largest such that¯a+x=b for some x.Then from c≤a and c +y=b for c ∼c,it follows c ≤¯a for some c ∼c. Then the quotient algebra([E]∼;≤,+,[0]∼,[1]∼)is again a weak effect algebra.Proof.(E1)holds by Lemma3.2.To show(E2),assume that([a]∼+[b]∼)+[c]∼exists.Then by(C4),this sum equals[(a +b )+c ]∼for some a ∼a,b ∼b,c ∼c,so(E2)(a)follows.(E2)(b)and (E2)(c)are obvious.For the proof of(E3),let us assume that[a]∼+[c]∼and[b]∼+[c]∼exist.We may further assume that a+c and b+c exist for some c ∼c.If now[a]∼≤[b]∼, then a ≤b for some a ∼a,b ∼b,and it follows by(C5)that a +c ≤b+c for some a ∼a,c ∼c;thus,we have[a]∼+[c]∼≤[b]∼+[c]∼.Conversely,from[a]∼+[c]∼≤[b]∼+[c]∼it follows by(C4)that a +c ≤b +c for some a ∼a,b ∼b,c ,c ∼c,and further by(C6)that a ≤b for some a ∼a and b ∼b;thus, [a]∼≤[b]∼.Finally,let[a]∼≤[b]∼;we may assume a≤b.Let¯a be the largest element below a such that¯a+x=b for some x.Assume further[c]∼≤[a]∼and[c]∼+[y]∼=[b]∼for some c,y;we claim that then[c]∼≤[¯a]∼,which proves(E4).Indeed,by(C4), c +y =b for some c ∼c,y ∼y,so by(C2)and(C7),c ≤¯a for some c ∼c.The notion of a homomorphism of partial algebras is used here as follows[Gra].Definition3.4.Let(E;≤,+,0E,1E)and(F;≤,+,0F,1F)be weak effect algebras.A mappingϕ:E→F is called a homomorphism if,for all a,b∈E,the following holds:(i)if a≤b,thenϕ(a)≤ϕ(b);(ii)if a+b is defined,then so isϕ(a)+ϕ(b), andϕ(a+b)=ϕ(a)+ϕ(b);(iii)ϕ(0E)=0F andϕ(1E)=1F.Moreover,a homomorphismϕ:E→F is called full if,for all a,b∈E,ϕ(a)+ϕ(b) is defined if and only if a +b is defined for some a ,b ∈E such thatϕ(a )=ϕ(a) andϕ(b )=ϕ(b).Proposition3.5.Let(E;≤,+,0E,1E)be a weak effect algebra,and let∼be a con-gruence such that[E]∼is again a weak effect algebra.Then the canonical embedding ι:E→[E]∼,a→[a]∼is a full homomorphism.4.The subdirect representation of BL-effect algebrasWe show in this section that any BL-effect algebra is a subdirect product of linearly ordered BL-effect algebras.Although certain modifications are necessary, it is possible to proceed in the standard way.Definition4.1.Let(E;≤,+,0,1)be a weak effect algebra.We call I⊆E an ideal of E if(α)a≤r and r∈I imply a∈I and(β)r,s∈I such that r+s exists implies r+s∈I.I being an ideal of E,we seta∼I b if a−r=b−s for some r,s∈I.Remarkably,we do not have to make any further assumption on an ideal of a BL-effect algebra that it induces a congruence preserving all axioms.We divide the proof into two parts.WEAK EFFECT ALGEBRAS7 Lemma4.2.Let I be an ideal of a BL-effect algebra E.Then∼I is a congruenceof E,and the quotient algebra([E]∼I ;≤,+,[0]∼I,[1]∼I)is a weak effect algebra.Proof.The relation∼I is clearly reflexive and symmetric.To see that it is transi-tive,let a∼I b and b∼I c,that is,let a−r=b−s and b−t=c−u for r,s,t,u∈I. Then we have(a−r)+s=(c−u)+t;applying(RDP)to this equation givens (a−r)−e2=(c−u)−e3for certain e2≤t,e3≤s,which means e2,e3∈I.We conclude a−(r+e2)=c−(u+e3),so a∼I c.We next show that all the properties(C1)–(C7)hold for∼I.By Theorem3.3,[E]∼I will then be proved to be a weak effect algebra.From a∼I a ,b∼I b and the existence of a+b,a +b ,it easily follows a+b∼I a +b ,which is(C1).From a≤b and b−r=b −s for r,s∈I,it follows a≤(b −s)+r,so by(E6) a=a +a r for a ≤b −s and a r≤r;so a ∼I a and a ≤b .This is(C2).Let a−r=a −s for r,s∈I,and a≤b≤a .Then a−r≤b≤(a−r)+s,and it follows by(E6)that b=(a−r)+t for some t≤s.So b∼I a,and(C3)is proved.Let now c∼I a+b,that is,c−s=(a+b)−r for some r,s∈I.Then we have a+b=r+(c−s),and by(RDP)we conclude that c−s=a +b for a ∼I a, b ∼I b.So c=a +b +s;this proves(C4).To see(C5),let a≤b and let a +c,b +c exist,where a∼I a ,b∼I b ,c∼I c . Then by(C2)a ≤b for an a ∼I a .Let a −r=a −s,b−t=b −u,c−v=c −w for r,s,t,u,v,w∈I.Then a −r≤b ,and(a −r)+(c −w)as well as b +(c −w) exist;(C5)is shown.Let now c∼I c and a+c≤b+c .Let c−r=c −s for r,s∈I;then a+(c −s)≤b+c ,so a≤b+s.This proves(C6).Finally,let a≤b,let¯a≤a be largest such that¯a+x=b for some x,and let c≤a and c +y=b for some c ∼I c.From c−r=c −s for r,s∈I,we get (c−r)+s+y=b,so c−r≤¯a,and also(C7)is proved. Theorem4.3.Let I be an ideal of a BL-effect algebra E.Then∼I is a congruenceof E,and the quotient algebra([E]∼I ;≤,+,[0]∼I,[1]∼I)is again a BL-effect algebra.Proof.By Lemma4.2,∼I is a congruence of E such that[E]∼I is a weak effectalgebra.To see that[E]∼I is actually a BL-effect algebra,it remains to prove theaxioms(E5)–(E8).Wefirst show that any equivalence class is closed under infima.Indeed,let a∼I a ,that is,a−r=a −s for r,s∈I.Then a−r≤a∧a ≤a =(a−r)+s; so because(E6)holds in E,a∧a =(a−r)+t for some t∈I.We next show that,for a,b,(3)[a∧b]∼=[a]∼∧[b]∼,which implies(E5).We clearly have[a∧b]∼≤[a]∼,[b]∼.Let c be such that [c]∼≤[a]∼,[b]∼;then by(C2),c ≤a and c ≤b for some c ,c ∼I c,so c ∧c ≤a∧b and[c]∼=[c ∧c ]∼≤[a∧b]∼.So(3)follows.To see(E6),let[c]∼≤[a]∼+[b]∼.We may assume that a+b exists and also, by(C2)and(C4),that c≤a+b holds.Thefirst part of(E6)now easily follows. If even[a]∼≤[c]∼,then we have a ≤c≤a+b for a ∼I a.From a−r=a −s, r,s∈I,we get a−r≤c≤(a−r)+r+b,from which c=(a−r)+b1for some b1≤b+r follows.This proves the second part of(E6).Finally,for any pair of elements a,b,there are a1,a2,b1,b2such that a=a1+a2, b=b1+b2,a1≤b,b2≤a,a2∧b2=0.We then have the same relations among the8THOMAS VETTERLEINrespective equivalence classes;this follows in the last case from(3).So also(E7) holds.(E8)follows from(C4)and(3). Definition4.4.An ideal I of a weak effect algebra E is called prime if for any a,b∈E such that a∧b=0,either a∈I or b∈I.Lemma4.5.Let E be a BL-effect algebra.(i)Let I be a prime ideal.Then[E]∼Iis linearly ordered.(ii)For any a=b,there is a prime ideal I such that a∼I b.Proof.(i)Let a,b∈E,and let a=a1+a2,b=b1+b2be decomposed according to (E7).Then either a2∈I,implying a∼I a1≤b and[a]∼≤[b]∼;or b2∈I,implying [b]∼≤[a]∼.(ii)I={0}is an ideal such that a∼I b.Let I be an ideal which is maximal w.r.t.the property a∼I b.Assume c∧d=0and c,d∈I.In view of(E6), I c={c1+...+c k+e:c1,...,c k≤c,e∈I}is the ideal generated by I and c;similarly,also I d is given.By the maximality of I,we have a∼Ic b and a∼Idb;this means that a−r=b−s and a−t=b−u for r,s∈I c and t,u∈I d.By Lemma 2.9,we have a−(r∧t)=(a−r)∨(a−t)=(b−s)∨(b−u)=b−(s∧u).But r=c1+...+c k+e and t=d1+...+d l+f for certain c1,...,c k≤c,d1,...,d l≤d, e,f∈I,and by(E6)we conclude r∧t∈I.Similarly,also s∧u∈I.So a∼I b,a contradiction.We have the following notions of subalgebras and subdirect representations of weak effect algebras[Gra].Definition4.6.Let(E;≤,+,0,1)and(F;≤ ,+ ,0,1)be weak effect algebras such that F is a subset of E containing the constants and≤ is the order of E restricted to F.Assume furthermore that if a+ b is defined in F,then also a+b is defined in E,in which case a+ b=a+b.Then(F;≤,+ ,0,1)is called a weak subalgebra of E.If,in addition,for a,b∈F,a+ b is defined in F if and only if a+b is defined in E and lies in F,then(F;≤,+ ,0,1)is called a relative subalgebra of E.Definition4.7.Let(Eι;≤ι,+ι,0ι,1ι),ι∈I,be weak effect algebras.Let E=ΠιEιbe the cardinal product of the Eι,ι∈I,endowed with the pointwise order ≤,with the partial addition+defined whenever performable in all components, and with the constants0=(0ι)ιand1=(1ι)ι.Then the weak effect algebra (E;≤,+,0,1)is called the direct product of the Eι,ι∈I.Moreover,a relative subalgebra F of E such that the projectionsπι:F→Eιare surjective,is called a subdirect product of the Eι.Theorem4.8.Any BL-effect algebra is the subdirect product of linearly ordered BL-effect algebras.Proof.Let E be a BL-effect algebra,and letϕbe the canonical mapping from E to the direct product of all quotient algebras arising from prime ideals.The latter are linearly ordered by Lemma4.5(i).Thenϕis by Theorem4.3and Proposition 3.5a homomorphism,which,by Lemma4.5(ii),is furthermore injective.It follows that E is a weak subalgebra of the direct product of the linearly ordered quotients induced by the prime ideals.WEAK EFFECT ALGEBRAS9 It remains to show that E even a relative subalgebra.So assume that,for a,b,c∈E,[a]I+[b]I=[c]I holds for all prime ideals I;we have to show that then,in E,a+b exists and equals c.Now,for an ideal I,[a]I+[b]I=[c]I means a +b ∼I c for some a ∼I a and b ∼I b.By(C4),we may even assume equality here,that is,a +b =c.Thus there are r,s∈I such that a =(a−r)+s,whence we may replace a by an element below a.So,for any prime ideal I,there is an a I≤a such that a I∼I a and c=a I+b I for some b I.Let now¯a≤a be the maximal element such that¯a+¯b=c for some¯b∈E.Thena I≤¯a≤a and hence,by(C3),¯a∼I a for all I.It follows¯a=a and¯b=b.5.Linearly ordered BL-effect algebrasOur next question is if linearly ordered BL-effect algebras are constructed in a similar way from simpler algebras,as this is the case for BL-algebras.The answer is positive.The constituents are,as to be expected,of a more general nature than in the case of BL-algebras.However,they may be described neatly in a uniform way:as generalised effect algebras.The latter were introduced in[HePu];they resemble effect algebras,but they are not assumed to have a largest element.Definition5.1.A generalised effect algebra is a structure(E;≤,+,0)with the following properties:(GE1)(E;≤,0)is a poset with a smallest element0.(GE2)+is a partial binary operation such that for any a,b,c∈E(a)(a+b)+c is defined iffa+(b+c)is defined,and in this case(a+b)+c=a+(b+c);(b)a+0is always defined and equals a;(c)a+b is defined iffb+a is defined,and in this case a+b=b+a. (GE3)If,for a,b,c∈E,a+c and b+c are defined,then a+c=b+c implies a=b.(GE4)For any a,b∈E,a≤b if and only if a+c=b for some c∈E.A generalised effect algebra with a largest element is called an effect algebra.So effect algebras are exactly the weak effect algebras in which(GE4)holds;note that this is in accordance with the remark following Definition2.1.Furthermore,a generalised effect algebra without largest element may be enlarged by a new such element,and becomes then also a weak effect algebra fulfilling(GE4).We conclude that the essential new condition in Definition5.1is the axiom(GE4),saying that the partial order is determined by the addition.We recall the following fact about the structure of generalised effect algebras; see[DvGr]or[DvVe].Definition5.2.Let(E;≤,+,0)be a generalised effect algebras and(G;≤,+,0) a po-group.A mappingϕ:E→G+is called a homomorphism if,for all a,b∈E, the following holds:(i)if a≤b,thenϕ(a)≤ϕ(b);(ii)if a+b is defined,then ϕ(a+b)=ϕ(a)+ϕ(b);(iii)ϕ(0)=0.In case that,moreover,a≤b if and only if ϕ(a)≤ϕ(b),we callϕan isomorphic embedding of E into G.Theorem5.3.Let(E;≤,+,0)be a generalised effect algebra;let(E;≤)be a lower semilattice;and assume that for any a,b,c such that c≤a+b,we have c=a1+b110THOMAS VETTERLEINfor some a 1≤a and b 1≤b .Then E may be isomorphically embedded into an abelian -group (G ;≤,+,0),such that the image of E is a convex subset of G +containing 0.In particular,any linearly ordered generalised effect algebra may be isomorphi-cally embedded into a linearly ordered abelian group (G ;≤,+,0),such that the image is a convex subset of G +containing 0.We next describe how BL-effect algebras may be constructed from a collection of generalised effect algebras.This construction is completely analogous to the ordinal sum construction linearly ordered BL-algebra are based on;cf.e.g.[AgMo].Definition 5.4.Let (I ;≤)be a linear order with a largest element κ;for any ι∈I ,let E ιbe a generalised effect algebra,and let E κbe an effect algebra.Let E ι=E ι\{0}for any ι,and let E =˙ ιE ι∪{¯0},where ¯0is a new element.Fora,b ∈E ,set a ≤b if either a,b ∈E ιfor some ιand a ≤b holds in E ι,or a ∈E ι1and b ∈E ι2such that ι1<ι2,or a =¯0.Let ¯1be the one element of E κ.We finally define the partial binary operation +as follows;let a,b ∈E .Ifa,b ∈E ιfor some ιsuch that a +b exists,let a +b be defined as in E ι;let a +¯0=¯0+a =a for any a ∈E ;and let a +b in other cases undefined.Then thestructure (E ;≤,+,¯0,¯1)is called the ordinal sum of the algebras E ι,ι∈I .Lemma 5.5.An ordinal sum of generalised effect algebras is a weak effect algebra.An ordinal sum of linearly ordered generalised effect algebras is a BL-effect al-gebra,which is also linear ordered.Proof.This is a simple check of the axioms.Now we are ready to formulate the main result of this section.Theorem 5.6.Every linearly ordered BL-effect algebra is the ordinal sum of lin-early ordered generalised effect algebras.Proof.Let E be a linearly ordered BL-effect algebra.For a,b ∈E such that 0<a ≤b ,set z (a,b )in case that there is some x such that a +x =b .We will show that (i)from 0<a ≤b ≤c and z (a,b )as well as z (b,c ),it follows z (a,c );and (ii)from 0<a ≤b ≤c and z (a,c ),it follows z (a,b )and z (b,c ).It will then follows that E \{0}consists of disjunct convex subsets which are,together the zero element,generalised effect algebras and such that addition is undefined between elements from different such subsets.So taking into account that the generalised effect algebra containing the 1element will necessarily be an effect algebra,the assertion will be proved.(i)holds trivially.To see (ii),assume 0<a ≤b ≤c and z (a,c ),say c =a +x .Then by (E6),b =a +y for some y ≤x ,whence z (a,b ).Now,we have either x ≤b ;in this case,y ≤x ≤a +y ,whence x =y +z for some z ,and so c =b +z ,that is,z (b,c ).Or we have b ≤x .Then let a ≤b be the largest element such that a +x =c for some x ;we have a ≥a >0.If then x ≤b ,we proceed as above to conclude z (b,c ).Else we have a ≤b ≤x ≤c =a +x .So x =a +z for some z ,hence c =a +a +z ;but a +a >a ,and a +a sums up with z to c ,so a ≤b <a +a .This in turn means b =a +t for some t ≤a ≤a +t ,so a =t +u for some u ,and a +a =a +t +u =b +u ,so c =b +u +z ,that is,z (b,c ).WEAK EFFECT ALGEBRAS11 As a corollary,we may describe the exact relation between linearly ordered BL-algebras and linearly ordered BL-effect algebras.Call a generalised effect algebra (E;≤,+,0)standard if it is isomorphic to a group interval,that is,if it is either of the form(G[0,u];≤,+,0),where+is defined whenever the sum is below u,or of the form(G+;≤,+,0),where+is always defined.Theorem5.7.A linearly ordered BL-effect algebra E corresponds to a dual BL-algebra(in the way described in Theorem2.5)if and only if E is the ordinal sum of standard generalised effect algebras.Proof.By Theorem2.5,a BL-effect algebra E corresponds to a(dual)BL-algebra iffthe partial addition on E is extendible according to(1).Let E be a linearly ordered.By Theorem5.6,E is then the ordinal sum of linearly ordered generalised effect algebras Eι,ι∈I.So E obviously corresponds to a BL-algebra iff,for each ι∈I,the partial addition on Eιis extendible to a total addition.If Eιis standard,then clearly,the addition is extendible.Assume that Eιis not standard.We may identify Eιwith a subset of the positive cone of an abelian partially ordered group G.In G,Eιis upper bounded,but has no maximal element; so for all pairs a,b∈Eιsuch that a+b>c for all c∈Eι,the maximum(1)does not exist.So in this case,the addition is not extendible.6.Outlook:Representation of residuated lattices by means ofpo-groupsIn the concluding section,we address the general problem how to characterise residuated lattices in general.We assume that the latter are bounded and com-mutative;recall that we could also talk about integral,commutative residuated -monoids.For general information on these algebras,see e.g.[JiTs]and the refer-ences given there.Dual BL-algebras are special residuated lattices,and we will describe the mean-ing of the results of the present paper for the analysis of the more general algebras. We will keep the exposition short;missing details are easily added.Definition6.1.Let(L;≤,⊕, ,0,1)be a residuated lattice,that is,let(L;≤,0,1) be a bounded lattice,let(L;⊕,0)be a commutative monoid,and for any a,b,c,∈L, assume a≤b⊕c iffa b≤c.Derive the partial addition+from⊕as described in Definition2.2.We then call(L;≤,+,0,1)the partial algebra associated to L.If (L;≤,+,0)is isomorphically embeddable into a partially ordered group(G;≤,+,0), we call L po-group representable.Theorem6.2.Any dual BL-algebra is po-group representable.Proof.Let(L;≤,+,0)be the partial algebra associated to a dual BL-algebra.Then L is a BL-effect algebra,which is,by Theorem4.8,a subdirect product of linearly ordered ones.So we may restrict to the linear case.If L is linearly ordered,then,by Theorem 5.7,L is the ordinal sum of generalised effect algebras Eι,ι∈I,where I is endowed with a linear order.Each Eιis in turn isomorphically embeddable into the positive cone of a linearly ordered group Gι.Let G be the lexicographical product of Gι,ι∈I,based on the linear order of I.Identifying each Gιwith a subgroup of G in the natural way,we see that(L;≤,+,0)is isomorphically embeddable into (G;≤,+,0).。
含幺元的二维交换结合代数的分类

含幺元的二维交换结合代数的分类李长洲;李海洋【摘要】为刻画实数域R上的二维交换结合代数的结构,给出了实数域R上含幺元的二维交换结合代数的分类,证明了在同构意义下实数域R上只有3类含幺元交换结合代数,即在该结合代数上存在一组基底{e,u},e是幺元,满足u2=u或u2=0或是复数域.%In order to describe the structure of 2-dimensional commutative algebras over the field of real numbers,the classification of 2-dimensional commutative associative algebras containing identity over the field of real numbers are studied,and it is proved that there are exactly three 2-dimensional real commutative algebras up to isomorphisms,there exist bases {e,u }such that e is unitary,either u2 =u or u2 =0 and the last case is nothing but the field of real numbers.【期刊名称】《纺织高校基础科学学报》【年(卷),期】2016(029)004【总页数】4页(P424-427)【关键词】幺元;二维交换结合代数;同构【作者】李长洲;李海洋【作者单位】西安工程大学理学院,陕西西安710048;西安工程大学理学院,陕西西安710048【正文语种】中文【中图分类】O153代数学的一个中心问题是研究各种代数结构在同构意义下的分类[1-4], 一旦得出代数结构的分类结果, 就可从中推出这个结构所具有的性质等, 而不必从这个代数结构所满足的公理来推导[5]. 早在凯莱提出矩阵代数时就已经有人开始研究结合代数[6-9], 目的是刻画各种结合代数的结构和表示.低维结合代数[10-16]是研究者们广泛关注的一个热门课题.文献[11]研究了有限维齐次单结合代数, 证明了在代数闭域上的有限维的结合除环同构于群代数;文献[12]研究了代数闭域K上的二维结合代数的分类,得出在该结合代数上存在一组基底{e,u}, 满足u2=u或u2=0.但文献[12]的分类结果还不够精细,未区分出代数闭域K上的不同的二维结合代数, 本文研究了实数域上含幺元的二维交换结合代数在同构意义下的分类.证明了实数域上含幺元的二维交换结合代数在同构意义下只有三类:在该结合代数上存在一组基底{e,u}, e是幺元, 满足u2=u或u2=0或是复数域.定义1[7] 设A是域K上的向量空间, 又在A上定义了一个乘法运算, 称A是域K 上的结合代数, 当A满足∀α,β,γ∈A,k∈K,有当A中乘法运算满足交换律时,即∀α,β∈A时有αβ=βα,称A是交换结合代数. 当存在元素e∈A,∀α∈A,有eα=αe=α,称e是A中的幺元,A是含幺元的结合代数.定义2[7] 向量空间A的维数称为域K上的结合代数A的维数.定义3[7] 设A是域K上的含幺元e的结合代数, 称A是可除结合代数, 当A满足∀α∈A-{0},∃β∈A,有αβ=βα=e.定义4[7] 设A是域K上的n维结合代数, α1,α2,…,αn是A的一组基底,于是有,称为A对于基底α1,α2,…,αn的结构常数.定义5[7] 设A1和A2是域K上的结合代数, 称A1同构于A2, 记为A1≅A2,如果存在一个从A1到A2的双映φ, 满足∀k1,k2∈K,α,β∈A,则有定义6[7] 设A是域R上的含幺元e的二维交换结合代数,e,u是A的一组基底, 则有称为A对于基底e,u的结构常数矩阵.注 a,b的不同取值决定向量空间A上的不同的结合代数.为了证明本文的结论,需要如下引理.引理1 设A1和A2是域K上的维数相同的有限维结合代数, 则A1≅A2当且仅当存在A1和A2的一组基底α1,α2,…,αn和β1,β2,…,βn,满足A1对于α1,α2,…,αn 的结构常数和A2对于β1,β2,…,βn的结构常数对应相等.证明 (必要性)当f:A1→A2是一个结合代数同构,则设f(αi)=βj, i=1,2,…n, 由于f是结合代数同构,则故结论成立.(充分性)当时,构造,显然f是一个同构线性映射,令,则故结论成立.引理2[8] (弗罗贝尼乌斯定理)实数域上的有限维可除结合代数只有实数域, 复数域, 四元数代数.定理1 设A是域K上的含幺元e的二维交换结合代数, 当结构常数矩阵中a=0,b≠0或a>0,b=0或a,b≠0,a+b2/4>0, 则A是一种同构型, 记为A1.证明当a=0,b≠0时有u2=bu, 从而易知也是A的一组基底, 由引理1知这是一种同构型.当a>0,b=0时有u2=ae, 设存在一个元素k1e+k2u与e线性无关, 且满足(k1e+k2u)2=k1e+k2u.化简得由于e,u是A的基底,则,可得,由引理1知A也是这种同构型.当时,有u2=ae+bu, 设存在一个元素k1e+k2u, k1,k2≠0,则令,则.由于故,由引理1得结论成立.定理2 设A是域K上的含幺元e的二维交换结合代数, 当结构常数矩阵中a<0,b=0或者时, 则A是一种同构型, 记为A2.证明当a<0,b=0时,设k1,k2≠0,由(k1e+k2u)(k3e+k4u)=e得(k1k3+k2k4a-1)e+(k1k4+k2k3)u=0,由于e,u是A的一组基底,从而有k1k3+k2k4a-1=0,k1k4+k2k3=0.由于故这个方程有解, 从而A是域, 由引理2知A同构型是复数域C.当,类似a<0,b=0时的情况,结论成立.定理3 设A是域K上的含幺元e的二维交换结合代数, 当结构常数矩阵中a=b=0或时,A是一种同构型, 记为A3.证明当同定理2一样知结论成立.定理4 A1, A2, A3彼此不同构.证明由于A2是域, 所以显然A2与A1和A3不同构. 只需证明A1和A3不同构即可. 由于A1中除幺元e外还有幂等元, 而A3中除幺元e外没有幂等元. 假设A3存在非幺元e的幂等元k1e+k2u,k2≠0, 那么有(k1e+k2u)2=k1e+k2u, 该等式无解, 从而A1和A3不同构.LI Changzhou,LI Haiyang.The classification of 2-dimensional commutative associative algebras containing identity over the field of realnumbers[J].Basic Sciences Journal of Textile Universities,2016,29(4):424-427.【相关文献】[1] WEI Changguo.Classification of extensions torus algebra II[J].Science China Mathematics,2012,55(1):179-186.[2] SHEN Shoufeng,QU Changzheng,HUANG Qing,et al.Lie group classification of the N-th-order nonlinear evolution equations[J].Science China Mathematics,2011,54(22):2553-2572.[3] ZHANG Xiaoxia.On the classification of compact quantum groups Uθ(2)[J].Scienc eChina Mathematics,2010,53(5):1293-1306.[4] KIRTLAND J.On two classes of finite inseparable p-groups[J].Acta Mathematica Sinica,2015,31(7):1203-1214.[5] TIMOTHY G.The princeton company to mathematics[M].New Jersey:The Princeton University Press,2008:78-83.[6] AUSLANDER M.Representation theory of artin algebra[M].Cambridge:Cambridge University Press,1993.[7] 孟道骥,王立云,史毅茜,等.抽象代数II-结合代数[M].北京:科学出版社,2011:1-4.MENG Daoji,WANG Liyun,SHI Yiqian,et al.Abstract algebra II-Associativealgebra[M].Beijing:Science Press,2011:1-4.[8] 陈辉.群的结构与对称性[M].杭州:浙江大学出版社,2008:85-86.CHEN Hui.Structure and symmetry of groups[M].Hangzhou:Zhejiang University Press,2008:85-86.[9] AUSLANDER M.Representation theory of artin algebra II[J].Communications in Algebra,1974,1(4):269-310.[10] WILLS-TORO Luis A.Classification of some graded not necessarily associative division algebras I[J].Communications in Algebra,2014,42(12):5019-5049.[11] KORESHKOV N.A.Finite-dimensional homogeneously simple algebras of associative type[J].Russian Mathematica,2010,54(9):30-35.[12] DROZD Y A,KIRICHENKO V V.Finite dimensional algebras[M].NewYork:Springer-Verlag,1993.[13] BAI R P,WANG X L,XIAO W Y,et al.The structure of low dimensional n-lie algebras over a field of characteristic 2[J].Linear Algebra and its Application,2008,428:1912-1920.[14] BARNES D W.On (n+2) dimensional n-lie algebras[J].Mathematics,arXiv:0704.1892.[15] De GRAAF W A.Classification of solvable lie algebras[J].Experimental Mathematics,2004,14(1):15-25.[16] 陈维新.纯量结合代数中的链条件和幂零理想[J].浙江大学学报,1985,19(2):112-115. CHEN Weixin.Chain conditions and nilpotent ideals in the scalar associativealgebras[J].Journal of Zhejiang University,1985,19(2):112-115.。
Algebra

AlgebraWhat is Algebra?Algebra is any type of math in which letters or other symbols(符号)represent numbers in a formula.A simple example of that is x+5=10.In this case,it’s easy to see that x represents the number5.As you already know,algebra gets far more complicated(复杂)than this. Why is Algebra Important?Thanks to our qualified math tutors,we’ve come up with ten reasons as to why algebra is important.These reasons go far beyond the walls of the classroom as math is used more often in everyday life than most people realize.1.Apply(应用)it to Other SubjectsThe first and most important reason algebra is important is that it can be applied to other subjects.These include:·Chemistry·Biology(生物)·Social sciences·Engineering·Physics·Food science·Psychology(心理学)·Computer scienceOther math classes like geometry(几何学),calculus(微积分),and trigonometry (三角学)also use algebra as a base,making it an essential(基本的)skill to master.For this reason,you’ll find that grades can improve across the board(全面的)by improving math skills.e Formulas(公式)Without algebra,we wouldn’t have an easy way to figure out(计算出)the area of a shape.Algebra allows you to take any formula,plug in numbers,and solve an equation.This is also a huge(巨大的)part of why algebra is used in so many other subjects.For example,if you need to figure out how much paint(油漆)is needed to cover a triangular-shaped(三角形的)wall,you need algebra to figure it out.Rather than guessing and buying way too little paint,you’ll know exactly(准确的)what you need.3.Solve Problems SimplyImagine(想象一下)if we didn’t have multiplication(乘法表).Multiplication is a shortcut that allows you to simply figure out5x10.If you couldn’t multiply,you’d have to add all those numbers together,or count out a grid with50points on it.In the same way,algebra simplifies problems so that they’re more easily solved.As we mentioned before(正如我们之前提到的),this is usually done with formulas. 4.Solve Problems QuicklyAs you can already imagine(正如你已经想的那样),being able to solve problems with a simple algebraic formula is far faster than other methods.Let’s go back to the example of a triangular-shaped wall.If you know the formula,you know all you have to do is multiply the height by the length of the base and then divide (划分)by two.5.Better Understand NumbersAlgebra teaches you to follow a logical(逻辑的)path to solve a problem.allows you to have a better understanding of how numbers function and work together in an equation(方程式).6.It’s Part of HistoryMath has been around since humans could count and started bartering(以物换物). Without math,humans might not be at the top of the food chain(链条).So,by learning algebra,you can gain a better appreciation(了解)for our human history.7.More Career OptionsThere are countless(无数的)careers that require an understanding of math and algebra in particular(尤其).These include:·Computer programmers(计算机程序员)·Statisticians(统计学家)·Teachers·Doctors·Scientists·Mathematicians(数学家)For that reason alone(仅仅因为这个原因),it’s vital(至关重要的)to understand algebra at an early age.判断奇偶数""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""in_x=int(input('输入整数:'))if in_x%2==0:print('偶数')else:print('奇数') """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""8.Improve TechnologySpeaking of careers,if you want to do anything to improve technology(技术),you need algebra.This and other similar types of maths will give you the base necessary to help make technological advances.For example,it was the use of maths that allowed us to put astronauts(宇航员)on the moon.Without it,the astronauts wouldn’t have been able to calculate the angle (角度)at which to leave the earth’s atmosphere(大气层).Today,algebra is used in nearly every aspect(方面)of technology,which includes how smartphones and computers operate.9.Save MoneyThis is a great example of how algebra can help you in your everyday life.By applying (应用)algebra to your budget(预算)and spending habits(习惯),you can make wiser(更明智的)decisions with your spending.10.Challenge YourselfThe final reason why learning algebra is important is that it challenges you.It will teach you how to face struggles(困难)and to overcome(克服)them.When you overcome a challenge(挑战),it helps build your confidence(信心)so you’re ready to face the next one.There are many challenges in life you’ll face that are more difficult than algebra,but it’s a good place to start.Teach Your Child AlgebraNow you know ten reasons that answer the question of why is algebra important.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Definition: Let K be a field. A quadratic invariant of ´ etale algebras of rank n over K (resp. of central simple algebras of degree n over K ) is a function E → qE (resp. A → qA ), which maps every ´ etale F -algebra of rank n (resp. every central simple F -algebra of degree n) to a non-degenerate quadratic form over F for every field extension F/K , and which commutes with scalar extensions. For example, E → TE , E → T2,E , A → TA and A → T2,A are quadratic invariants as soon as these forms are non-degenerate. If char K = 2, the trace form invariants have been studied extensively, and the second trace form of central simple algebras has been studied by T. Unger in [U]. The second trace form of ´ etale algebras does not have been studied in characteristic not two, but it is easy to show as in [U] that T2,E ≃ T2,F ⇐⇒ TE ≃ TF Moreover, we have the following result, proved by J.-P. Serre (unpublished): Theorem 1: Let K be a field of characteristic not two and let E → qE be a quadratic invariant of ´ etale algebras of rank n over K . Then
On the second trace form of central simple algebras in characteristic two
Gr´ egory Berhuy, Christoph Frings
U.M.R.6623 du C.N.R.S., Laboratoire de Math´ ematiques, Bureau 401B, 16 route de Gray, F-25030 Besan¸ con cedeБайду номын сангаас, France
chapter 8, §5 for example). If PrdA (a) = X n − s1 X n−1 + s2 X n−2 + . . . , then TrdA (a) := s1 and T2,A (a) := s2 are called respectively the reduced trace and the reduced second trace of a. If x1 , · · · , xn are the roots of PrdA (a) in an algebraic closure, we have TrdA (a) = x1 + · · · + xn and T2,A (a) = xi xj .
Introduction: Let K be a field and let A be a central simple algebra over K . The quadratic forms TA : x ∈ A → TrdA (x2 ) and T2,A : x ∈ A → T2,A (x) are called respectively the trace form and the second trace form of A. If K has characteristic not two, the trace form has been studied by many authors (see [B1], [B2], [L], [LM], [Se], [Ti] for example). In particular, its classical invariants are well-known (see [L], [LM], [Se] and [Ti]). The second trace form has also been studied in [U] when K has characteristic not two, but it is shown that this form does not give much more information than the trace form. When K has characteristic two, the trace form has rank zero. In this article, we show that the second trace form of a central simple algebra A of even degree over a field of characteristic two is non-degenerate and we compute its classical invariants. In the first part, we compute the second trace form of a split algebra. In the second one, we consider the case of cyclic algebras. Finally, we compute the Arf invariant and the Clifford invariant of the second trace form in the general case. The reader will also find in Appendix the proof of an unpublished result of Saltman which is the main ingredient of our work. This work is supported by the TMR research network (ERB FMRX CT97-0107) on “K-theory and algebraic groups. ” Preliminaries: Let A be a central simple algebra over a field K of arbitrary characteristic. If a ∈ A, the reduced characteristic polynomial of a, denoted by PrdA (a), is defined as follows: let L be a splitting field of A and ϕ : A ⊗ L → Mn (L) a K -isomorphism. Then PrdA (a) := det(XIn − ϕ(a ⊗ 1)) is an element of K [X ] and is independent of the choice of L and ϕ (cf.[Sc], 1
i<j
This easily implies the following equality for the bilinear form b2,A associated to the second trace form when the ground field has characteristic two: b2,A (x, y ) := T2,A (x + y ) + T2,A (x) + T2,A (y ) = TrdA (x)Trd(y ) + TrdA (xy ) Finally, if L is a maximal commutative subfield of A (if there is any), then it is well-known that A can be endowed with a structure of right L-vector space and that the map A ⊗ L → EndL (A), a ⊗ λ → (z → azλ) is an isomorphism. In particular, PrdA (a) is the characteristic polynomial of the left multiplication by a in the right L-vector space A. Assume that char K = 2. We denote by ℘(K ) the set {x2 + x, x ∈ K }. If α ∈ K ∗ and β ∈ K , we denote by (α, β ] the class of the corresponding quaternion algebra in the Brauer group. This algebra has a K -basis 1, e, f, ef satisfying the relations e2 = α, f 2 + f = β and ef + f e = f . Moreover, the map (α, β ) ∈ K ∗ /K ∗2 × K/℘(K ) → (α, β ] ∈ Br(K ) is well defined and bilinear. If a, b ∈ K , we denote by Pa,b the quadratic form (x, y ) ∈ K 2 → ax2 + xy + by 2 . The class of the Clifford algebra of Pa,b in Br(K ) is denoted by ((a, b)). It is easy to see that ((a, b)) = 0 if a = 0 and ((a, b)) = (a, ab] if a = 0. A non-degenerate quadratic form over K has even rank and is isomorphic to an orthogonal sum of some Pa,b . If q ≃ Pa1 ,b1 ⊥ · · · ⊥ Par ,br , then the Arf invariant of q is the element of K/℘(K ) defined by Arf(q ) := a1 b1 + · · · + ar br . We also define the Clifford invariant of q , denoted by c(q ), to be the class of the Clifford algebra of q in the Brauer group. It is easy to see that c(q ) := ((a1 , b1 )) + · · · + ((ar , br )) ∈ Br(K ) if q ≃ Pa1 ,b1 ⊥ · · · ⊥ Par ,br . If L/K is any field extension, ResL/K denotes the homomorphism [A] ∈ Br(K ) → [A ⊗ L] ∈ Br(L). Then c(qL ) = ResL/K (c(q )). 1. Motivations For any real number x, denote by [x] its integral part. Let K be a field of any characteristic. There are two interesting structures of K -algebras, namely ´ etale algebras and central simple algebras. In order to classify these algebras up to isomorphism, we need invariants. Since it is relatively simple to deal with quadratic forms, one even search quadratic invariants. Let us recall their definition. 2
