实验五 箱子装载问题
装载问题5种项目解决方案

.. . .. . ..算法分析与设计2016/2017(2)实验题目装载问题5种解法学生姓名学生学号. 专业学习资料... . .. . ..学生班级任课教师提交日期2017计算机科学与技术学目录一问题定义 (4)二解决方案 (4)1优先队列式分支限界法求解 (4)1.1算法分析 (4)1.2代码 (4)1.3运行结果 (17)2队列式分支限界法求解 (17)2.1算法分析 (17)2.2代码 (18)2.3测试截图 (30)3回朔法-迭代 (30)3.1算法分析 (30)3.2代码 (30)3.3测试截图 (35)4回朔法-递归 (35)4.1算法分析 (35)4.2代码 (35). 专业学习资料... . .. . ..4.3测试截图 (41)5贪心算法 (42)5.1算法分析 (42)5.2代码 (42)5.3测试截图 (46). 专业学习资料.一问题定义有一批共有n 个集装箱要装上两艘载重量分别为c1 和c2 的轮船,其中集装箱i 的重量为w[i], 且重量之和小于(c1 + c2)。
装载问题要求确定是否存在一个合理的装载方案可将这n 个集装箱装上这两艘轮船。
如果有,找出一种装载方案。
二解决方案1优先队列式分支限界法求解1.1算法分析活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。
以结点x为根的子树中所有结点相应的路径的载重量不超过它的优先级。
子集树中叶结点所相应的载重量与其优先级相同。
在优先队列式分支限界法中,一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解。
此时可终止算法。
1.2代码1.2-1////MaxHeap.htemplate<class T>class MaxHeap{public:MaxHeap(int MaxHeapSize = 10);~MaxHeap() {delete [] heap;}int Size() const {return CurrentSize;}T Max(){ //查找if (CurrentSize == 0){throw OutOfBounds();}return heap[1];}MaxHeap<T>& Insert(const T& x); //增MaxHeap<T>& DeleteMax(T& x); //删void Initialize(T a[], int size, int ArraySize);private:int CurrentSize, MaxSize;T *heap; // element array};template<class T>MaxHeap<T>::MaxHeap(int MaxHeapSize){// Max heap constructor.MaxSize = MaxHeapSize;heap = new T[MaxSize+1];CurrentSize = 0;}template<class T>MaxHeap<T>& MaxHeap<T>::Insert(const T& x){// Insert x into the max heap.if (CurrentSize == MaxSize){cout<<"no space!"<<endl;return *this;}// 寻找新元素x的位置// i——初始为新叶节点的位置,逐层向上,寻找最终位置int i = ++CurrentSize;while (i != 1 && x > heap[i/2]){// i不是根节点,且其值大于父节点的值,需要继续调整heap[i] = heap[i/2]; // 父节点下降i /= 2; // 继续向上,搜寻正确位置}heap[i] = x;return *this;}template<class T>MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x){// Set x to max element and delete max element from heap. // check if heap is emptyif (CurrentSize == 0){cout<<"Empty heap!"<<endl;return *this;}x = heap[1]; // 删除最大元素// 重整堆T y = heap[CurrentSize--]; // 取最后一个节点,从根开始重整// find place for y starting at rootint i = 1, // current node of heapci = 2; // child of iwhile (ci <= CurrentSize){// 使ci指向i的两个孩子中较大者if (ci < CurrentSize && heap[ci] < heap[ci+1]){ci++;}// y的值大于等于孩子节点吗?if (y >= heap[ci]){break; // 是,i就是y的正确位置,退出}// 否,需要继续向下,重整堆heap[i] = heap[ci]; // 大于父节点的孩子节点上升i = ci; // 向下一层,继续搜索正确位置ci *= 2;}heap[i] = y;return *this;}template<class T>void MaxHeap<T>::Initialize(T a[], int size,int ArraySize){// Initialize max heap to array a.delete [] heap;heap = a;CurrentSize = size;MaxSize = ArraySize;// 从最后一个内部节点开始,一直到根,对每个子树进行堆重整 for (int i = CurrentSize/2; i >= 1; i--){T y = heap[i]; // 子树根节点元素// find place to put yint c = 2*i; // parent of c is target// location for ywhile (c <= CurrentSize){// heap[c] should be larger siblingif (c < CurrentSize && heap[c] < heap[c+1]) {c++;}// can we put y in heap[c/2]?if (y >= heap[c]){break; // yes}// noheap[c/2] = heap[c]; // move child upc *= 2; // move down a level}heap[c/2] = y;}}1.2-2///6d3-2.cpp//装载问题优先队列式分支限界法求解#include "stdafx.h"#include "MaxHeap.h"#include <iostream>using namespace std;const int N = 4;class bbnode;template<class Type>class HeapNode{template<class Type>friend void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bo ol ch,int lev);template<class Type>friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);public:operator Type() const{return uweight;}private:bbnode *ptr; //指向活节点在子集树中相应节点的指针Type uweight; //活节点优先级(上界)int level; //活节点在子集树中所处的层序号};class bbnode{template<class Type>friend void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bo ol ch,int lev);template<class Type>friend Type MaxLoading(Type w[],Type c,int n,int bestx[]);friend class AdjacencyGraph;private:bbnode *parent; //指向父节点的指针bool LChild; //左儿子节点标识};template<class Type>void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,int l ev);template<class Type>Type MaxLoading(Type w[],Type c,int n,int bestx[]);int main(){float c = 70;float w[] = {0,20,10,26,15};//下标从1开始int x[N+1];float bestw;cout<<"轮船载重为:"<<c<<endl;cout<<"待装物品的重量分别为:"<<endl;for(int i=1; i<=N; i++){cout<<w[i]<<" ";}cout<<endl;bestw = MaxLoading(w,c,N,x);cout<<"分支限界选择结果为:"<<endl;for(int i=1; i<=4; i++){cout<<x[i]<<" ";}cout<<endl;cout<<"最优装载重量为:"<<bestw<<endl;return 0;}//将活节点加入到表示活节点优先队列的最大堆H中template<class Type>void AddLiveNode(MaxHeap<HeapNode<Type>>& H,bbnode *E,Type wt,bool ch,int l ev){bbnode *b = new bbnode;b->parent = E;b->LChild = ch;HeapNode<Type> N;N.uweight = wt;N.level = lev;N.ptr = b;H.Insert(N);}//优先队列式分支限界法,返回最优载重量,bestx返回最优解template<class Type>Type MaxLoading(Type w[],Type c,int n,int bestx[]){//定义最大的容量为1000MaxHeap<HeapNode<Type>> H(1000);//定义剩余容量数组Type *r = new Type[n+1];r[n] = 0;for(int j=n-1; j>0; j--){r[j] = r[j+1] + w[j+1];}//初始化int i = 1;//当前扩展节点所处的层bbnode *E = 0;//当前扩展节点Type Ew = 0; //扩展节点所相应的载重量//搜索子集空间树while(i!=n+1)//非叶子节点{//检查当前扩展节点的儿子节点if(Ew+w[i]<=c){AddLiveNode(H,E,Ew+w[i]+r[i],true,i+1); }//右儿子节点AddLiveNode(H,E,Ew+r[i],false,i+1);//取下一扩展节点HeapNode<Type> N;H.DeleteMax(N);//非空i = N.level;E = N.ptr;Ew = N.uweight - r[i-1];}//构造当前最优解for(int j=n; j>0; j--){bestx[j] = E->LChild;E = E->parent;}return Ew;}1.3运行结果2队列式分支限界法求解2.1算法分析在算法的循环体中,首先检测当前扩展结点的左儿子结点是否为可行结点。
集装箱货物实训实验报告

一、实验目的本次集装箱货物实训实验旨在使学生深入了解集装箱货物的相关知识,掌握集装箱货物的装卸、搬运、储存等操作技能,提高学生的实践操作能力和安全意识。
通过实验,使学生能够:1. 熟悉集装箱的结构、类型及特点;2. 掌握集装箱货物的装卸、搬运、储存等操作流程;3. 了解集装箱货物的安全注意事项;4. 培养学生的团队合作精神和沟通能力。
二、实验内容1. 集装箱的基本知识2. 集装箱货物的装卸操作3. 集装箱货物的搬运操作4. 集装箱货物的储存操作5. 集装箱货物的安全注意事项三、实验器材1. 集装箱2. 货物3. 起重机4. 搬运工具5. 安全防护用品四、实验步骤1. 集装箱的基本知识(1)观察集装箱的外观,了解其结构、类型及特点;(2)学习集装箱的编号、尺寸、自重等参数;(3)了解集装箱的装载限制和装载方法。
2. 集装箱货物的装卸操作(1)观察货物情况,了解货物的类型、体积、重量等;(2)制定装卸方案,包括装卸工具、人员安排、安全措施等;(3)进行货物装卸操作,注意操作规范和安全;(4)完成装卸后,检查货物是否完好。
3. 集装箱货物的搬运操作(1)观察货物在集装箱内的摆放情况,了解货物的摆放要求;(2)制定搬运方案,包括搬运工具、人员安排、安全措施等;(3)进行货物搬运操作,注意操作规范和安全;(4)完成搬运后,检查货物是否完好。
4. 集装箱货物的储存操作(1)观察集装箱内部情况,了解储存要求;(2)制定储存方案,包括储存位置、安全措施等;(3)进行货物储存操作,注意操作规范和安全;(4)完成储存后,检查货物是否完好。
5. 集装箱货物的安全注意事项(1)了解货物在装卸、搬运、储存过程中可能存在的安全隐患;(2)掌握安全操作规范,确保操作人员的人身安全;(3)加强安全意识,提高应急处理能力。
五、实验结果与分析1. 通过实验,学生对集装箱的结构、类型及特点有了更深入的了解;2. 学生掌握了集装箱货物的装卸、搬运、储存等操作技能,提高了实践操作能力;3. 学生了解了集装箱货物的安全注意事项,增强了安全意识;4. 学生在实验过程中培养了团队合作精神和沟通能力。
回溯法 装载问题
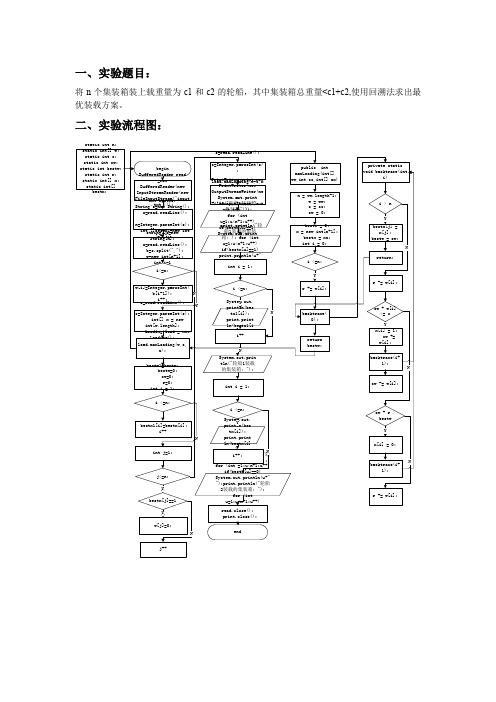
将n个集装箱装上载重量为c1和c2的轮船,其中集装箱总重量<c1+c2,使用回溯法求出最优装载方案。
二、实验流程图:input.txtoutput.txt四、源程序:package javaapplication1; import java.io.*;public class Main { static int n;static int []w;static int c1,c2;static int cw;static int bestw;static int r;static int []x;static int []bestx;public static int maxloading(int[]ww,int cc,int[]xx){w=ww;c1=cc;bestw=0;cw=0;x=new int[n+1];bestx=xx;r=0;for(int i=1;i<=n;i++)r+=w[i];backtrack(1);return bestw;}private static void backtrack(int i){if(i>n){ if(cw>bestw){for(int j=1;j<=n;j++)bestx[j]=x[j];bestw=cw; }return;}r-=w[i];if(cw+w[i]<=c1){x[i]=1;cw+=w[i];backtrack(i+1);cw-=w[i];}if(cw+r>bestw){x[i]=0;backtrack(i+1);}r+=w[i]; }public static void main(String[] args) throws IOException {BufferedReader read =new BufferedReader(new InputStreamReader(new FileInputStream("input.txt")));String a=new String();a=read.readLine();n=Integer.parseInt(a);System.out.println("集装箱个数: "+n);x=new int[n+1];String[]b=new String[n];a=read.readLine();System.out.println("集装箱重量: "+a);b=a.split(",");w=new int[n+1];for(int i=1;i<=n;i++){w[i]=Integer.parseInt(b[i-1]);}a=read.readLine();c1=Integer.parseInt(a);a=read.readLine();c2=Integer.parseInt(a);System.out.println("轮船载重量: "+c1+","+c2);int result= maxloading(w,c1,x);int max,temp;for(int i=1;i<3;i++){for(int j=2;j<3;j++){if(w[i]>w[j]){temp=w[i];w[i]=w[j];w[j]=temp;}}}if((w[3]>c1)&&(w[3]>c2)){System.out.println("都不可装");}else{System.out.println("轮船1装载的集装箱:");for (int u=1;u<n+1;u++)if(bestx[u]==1)System.out.println(u+" ");if(r>(result+c2))System.out.println("轮船1可装:"+result+" "+"轮船2装不完.");else{System.out.println("轮船2装载的集装箱:");for (int u=1;u<n+1;u++)if(bestx[u]==0)System.out.println(u+" ");System.out.println("最优装载--轮船1:"+result+" "+"轮船2:"+(r-result));}}PrintWriter print=new PrintWriter(new OutputStreamWriter(new FileOutputStream("output.txt")));if((w[3]>c1)&&(w[3]>c2)){print.println("都不可装。
实验5--平板车的装货问题

平板车的装货问题一、问题重述:有七种规格的包装箱有装到两辆铁路平板车上(如图所示).包装箱的高和宽相同,但厚度及重量不同,具体如表所示.每辆平板车载重40吨,并有10.2米的地方用来装箱.由于当地货物的限制,对x5,x6,x7类包装箱要求其总共所占空间(厚度)不能超过302.7厘米,试把包装箱装到平板车上使得浪费的空间最小.二、模型分析:本模型属于优化问题。
包装箱的长和宽均相等,厚度不一,本题假设厚度一定时(小于等于302.7厘米),求所装货物所占的最小空间。
三、符号说明:四、模型建立:目标函数:MIN=(2040-(48.7*x1+52*x2+61.3*x3+72*x4+48.7*x5+52*x6+64*x7+48.7*y1+52 *y2+61.3*y3+72*y4+48.7*y5+52*y6+64*y7));约束条件:两辆平板车的载重限制:2*x1+3*x2+x3+.5*x4+4*x5+2*x6+x7<=40;2*y1+3*y2+x3+.5*y4+4*y5+2*y6+y7<=40;平板车长度的限制:48.7*y1+52*y2+61.3*y3+72*y4+48.7*y5+52*y6+64*y7<=1020;48.7*x1+52*x2+61.3*x3+72*x4+48.7*x5+52*x6+64*x7<=1020; 对处,x5,x6,x7三类包装箱所占空间的限制:48.7*y5+52*y6+64*y7+48.7*x5+52*x6+64*x7<=302.7;且各变量均为整数。
五、模型求解运用lingo软件进行模型求解,所编程序如下:MIN=(2040-(48.7*x1+52*x2+61.3*x3+72*x4+48.7*x5+52*x6+64*x7+48.7*y1+52 *y2+61.3*y3+72*y4+48.7*y5+52*y6+64*y7));48.7*y5+52*y6+64*y7+48.7*x5+52*x6+64*x7<=302.7;48.7*y1+52*y2+61.3*y3+72*y4+48.7*y5+52*y6+64*y7<=1020;48.7*x1+52*x2+61.3*x3+72*x4+48.7*x5+52*x6+64*x7<=1020;2*x1+3*x2+x3+.5*x4+4*x5+2*x6+x7<=40;2*y1+3*y2+x3+.5*y4+4*y5+2*y6+y7<=40;x1+y1<=8;x2+y2<=7;x3+y3<=9;x4+y4<=6;x5+y5<=6;x6+y6<=4;x7+y7<=8;@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x5);@gin(x6);@gin(x7);@gin(y1);@gin(y2);@gin(y3);@gin(y4);@gin(y5);@gin(y6);@gin(y7);运行结果:Global optimal solution founy at iteration: 213097Objextive value: 0.6000000Variable Value Reyuxey XostX1 6.000000 -48.70000X2 2.000000 -52.00000X3 5.000000 -61.30000X4 3.000000 -72.00000X5 1.000000 -48.70000X6 1.000000 -52.00000X7 0.000000 -64.00000Y1 2.000000 -48.70000Y2 5.000000 -52.00000Y3 4.000000 -61.30000Y4 3.000000 -72.00000Y5 2.000000 -48.70000Y6 2.000000 -52.00000Y7 0.000000 -64.00000Row Slaxk or Surplus Yual Prixe1 2039.400 1.0000002 0.6000000 0.0000003 0.000000 0.0000004 0.6000000 0.0000005 9.500000 0.0000006 2.500000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 3.000000 0.00000012 1.000000 0.00000013 8.000000 0.000000 最优解为:平板车1的装货数量为:6 2 5 3 1 1 0平板车2的装货数量为:2 5 4 3 2 2 0此时平板车所浪费的空间最小。
【数据结构】--C++实现箱子装箱问题

【数据结构】--C++实现箱⼦装箱问题⼀、问题描述①在箱⼦装载问题中,有若⼲个容量为c的箱⼦和n个待装载⼊箱⼦中的物品。
物品i需占是s[i]个单元(0<s[i]<=c)。
所谓成功装载(feasible packing),是指能把所有物品都装⼊箱⼦⽽不溢出,⽽最优装载(optimal packing)是指使⽤了最少箱⼦的成功装载。
对于箱⼦装载问题,有4种流⾏的求解算法。
②基本要求:->n依次取100,200,500,1000,⽐较以上四种⽅法(在时间上和所⽤箱⼦的数量上)的性能。
->FF,FFD⽅法使⽤竞赛树结构,BF,BFD使⽤⼆叉搜索树结构。
⼆、需求描述1.4种流⾏的求解算法:<1>最先匹配法(FF):物品按1,2...,n的顺序装⼊箱⼦。
假设箱⼦从左⾄右排列,每⼀物品i放⼊可盛载它的最左箱⼦。
<2>最先匹配递减法(FFD):⽅法与FF类似,区别在于各物品⾸先按容量递减的次序排列,即对于1<=i<n,有s[i]>=s[i+1].<3>最优匹配法(BF):设c[j]为箱⼦j的可⽤容量,初始时,所有箱⼦的可负载容量为c。
物品i放⼊具有最⼩c且容量⼤于s[i]的箱⼦中。
<4>最优匹配递减法(BFD):⽅法与BF相似,区别在于各物品⾸先按容量递减的次序排列,即对于1<=i<n,有s[i]>=s[i+1].2.输⼊要求:①第⼀种输⼊⽅式:n在程序中固定读⼊100,200,500,1000个数,这些数预先在⽂本中⼿动输⼊为固定的⽆序正整数。
②第⼆种输⼊⽅式:n为程序运⾏后,⼈为输⼊的数n,并且⽣成n个随机数,⽤作程序所需要测试的物品⼤⼩数。
3.输出要求:输出的要求为:直观的分析排列出在不同的箱⼦数量、不同的物品数量以及不同的物品⼤⼩的情况下,上述四种⽅法在时间上和所⽤的箱⼦的数量上的不同。
⽐较四种⽅法的性能。
物流管理中的装载问题

物流管理中的装载问题第一章:概述装载问题是物流管理中的一个重要问题。
在物流过程中,物品的装载方式直接影响着物品的安全性、运输效率以及运输费用。
因此,物流管理中的装载问题需要得到重视。
本文将从不同角度探讨装载问题。
第二章:装载方式的分类装载方式可以分为手工装载、机械装载和自动化装载三种。
手工装载是最为原始的装载方式,需要劳动力的参与。
机械装载需要机器和设备的帮助,具有一定的效率和安全性。
自动化装载则使用智能化设备,实现货物的自动化装载与卸载,运输效率高、安全性强。
第三章:装载问题的影响因素物流管理中的装载问题受到诸多因素的影响。
包括所运输的物品的体积、重量、产品形态、运输距离、运输方式、运输工具等等。
而装载方案的选择需要考虑到这些因素的影响,以便更好地保障整个运输过程的高效、安全。
第四章:解决方法针对装载问题,需要采取一些有效的解决方法,以确保物品的安全和运输效率。
可以通过合理规划装载方案,减少物品运输途中的碰撞、摆动等情况。
同时也可以使用专业的装卸设备和物流包装材料,使物品能够更好的保护并降低对货车等运输工具的损害。
第五章:流程优化针对物流管理中装载问题,需要进行流程优化。
有些装载环节可以优化或省略,减少空间浪费和运输时间、能降低物流成本。
优化流程可以缩短整个运输时长,提高物流服务水平,降低成本。
第六章:可持续发展物流管理中有很多的问题需要我们去解决,所谓的可持续发展也是其中之一。
要实现可持续发展,提高物流管理的可持续性,那么在装载问题上能取得一定成效是非常必要的。
通过减少对环境的影响,在保证物品安全的前提下,最大化的降低物流运输的成本,从而推动可持续发展。
结语:物流管理中的装载问题需要得到重视,敬请各个方面对其予以关注。
通过优化装载方式、流程与环节,实现可持续发展的上升,从根源上减少对环境的影响,提高物流管理的效率和水平。
推箱子实验报告

推箱子实验报告推箱子实验报告引言:推箱子是一种经典的益智游戏,通过移动箱子将它们推到指定位置,是一项考验智力和策略的活动。
本次实验旨在通过推箱子游戏,探讨人类思维的规律和策略,并分析不同因素对游戏结果的影响。
实验方法:本次实验采用了电脑版推箱子游戏,共设置了10个关卡。
每个关卡都有不同的地图布局和箱子数量,参与者需要通过键盘控制人物移动,将所有箱子推到指定的目标位置。
实验过程中记录了每个参与者完成每个关卡所用时间,并进行了数据统计和分析。
实验结果:通过对实验数据的统计和分析,我们发现参与者在不同关卡中的表现存在明显差异。
在较简单的关卡中,参与者往往能够快速找到解决方案,并在较短的时间内完成任务。
然而,在难度较高的关卡中,参与者往往需要花费更多的时间来思考和尝试不同的策略。
这表明推箱子游戏的难度与参与者的思维能力和策略选择密切相关。
进一步分析发现,参与者在解决问题时往往会采用一定的规律和策略。
例如,他们倾向于先将箱子推向墙壁或角落,以便在后续的移动中有更多的空间和选择。
此外,参与者还会尝试不同的路径和移动顺序,以找到最佳的解决方案。
这些策略的使用表明了人类思维的灵活性和创造性。
讨论:推箱子游戏作为一种益智游戏,不仅能够锻炼参与者的思维能力和逻辑思维,还能够培养他们的耐心和坚持不懈的精神。
通过实验,我们不仅可以了解人类思维的规律和策略,还可以为教育和培训领域提供一些启示。
首先,推箱子游戏可以被应用于教育中,帮助学生培养解决问题的能力和创造性思维。
通过让学生参与推箱子游戏,他们可以在游戏中体验到思维的乐趣,学会分析问题、制定策略,并在尝试中不断提高自己的能力。
其次,推箱子游戏还可以被应用于团队建设和合作学习中。
在推箱子游戏中,参与者需要与其他队员密切合作,共同制定策略和解决问题。
这种合作学习的方式可以培养学生的团队合作精神和沟通能力,提高他们的协作能力。
结论:通过本次推箱子实验,我们深入了解了人类思维的规律和策略,并发现了推箱子游戏在教育和培训中的潜力。
5个箱子里放着同样个数的铅笔盒类似题

5个箱子里放着同样个数的铅笔盒类似题
摘要:
1.题目描述
2.解题思路
3.解决方案
4.总结
正文:
一、题目描述
有5 个箱子,每个箱子里都放着相同数量的铅笔盒。
现在需要计算出这些铅笔盒的总数量。
已知每个箱子里的铅笔盒数量是整数,并且至少有一个箱子里的铅笔盒数量不为0。
二、解题思路
假设每个箱子里的铅笔盒数量为x,那么5 个箱子里的铅笔盒总数量为5x。
由于题目已知至少有一个箱子里的铅笔盒数量不为0,所以x 不可能为0。
因此,我们可以通过计算5 个箱子里铅笔盒总数量的因数来确定x 的值。
三、解决方案
1.计算5 的因数:5 的因数有1 和5。
2.计算1 的因数:1 的因数有1。
3.计算5x 的因数:5x 的因数有1、5 和5x。
4.根据题目描述,5 个箱子里的铅笔盒总数量为5x,所以5x 必须是5
的因数。
因此,5x 只能是5。
5.根据步骤4,得出x=1。
所以每个箱子里的铅笔盒数量为1。
四、总结
通过计算5 个箱子里铅笔盒总数量的因数,我们得出每个箱子里的铅笔盒数量为1。
卡车运苹果箱的数学题

卡车运苹果箱的数学题
当卡车运输苹果箱时,可以涉及到一些数学问题。
首先,我们
可以考虑以下几个方面:
1. 容量问题,如果我们知道每个苹果箱的尺寸和卡车的容量,
我们可以计算出卡车能够装载多少个苹果箱。
这涉及到体积和容积
的计算,以及可能的空间浪费问题。
2. 重量问题,苹果箱的重量会影响卡车的负载能力。
我们需要
考虑苹果箱的重量以及卡车的最大承重量,以确保运输过程中安全
稳定。
3. 路程和时间问题,如果我们知道卡车的速度和行驶距离,我
们可以计算出运输整个批次苹果所需的时间。
这可能涉及到速度、
时间和距离的关系,以及可能的中途休息或加油时间。
4. 成本问题,运输苹果箱也会涉及到成本计算,包括燃料成本、人工成本、运输保险等方面的考量。
5. 路况和安全问题,在运输过程中,需要考虑到路况、交通和
安全等因素,以确保苹果箱能够安全到达目的地。
综上所述,运输苹果箱涉及到容量、重量、时间、成本以及安全等多个方面的数学问题。
针对不同的具体情况,我们可以采取不同的数学方法和计算公式来解决相关问题。
集装箱货物装载实训报告

一、实训目的本次实训旨在通过对集装箱货物装载过程的学习和实践,提高学生对集装箱运输的认识,掌握货物装载的基本原则和方法,增强安全意识和实际操作能力。
二、实训时间与地点实训时间:2023年10月25日实训地点:XX集装箱码头三、实训内容1. 理论学习首先,我们学习了集装箱运输的基本知识,包括集装箱的种类、尺寸、载重能力等。
然后,详细了解了货物装载的基本原则,如重量分配、货物固定、货物混装等。
2. 实操训练(1)货物分类与分配在实训过程中,我们根据货物的体积、重量、外包装的强度以及货物的性质进行分类。
将外包装坚固和重量较重的货物装在下面,轻货和易碎货物装在上面,确保货物的重量在箱底上形成均匀分布。
(2)货物衬垫针对外包装脆弱的货物和易碎货物,我们使用缓冲材料进行夹衬,防止货物相互碰撞挤压。
同时,在货物之间和货物与集装箱侧壁之间插入垫板、覆盖物等隔货材料,填补空隙。
(3)货物固定装箱后,我们对箱内货物进行固定处理,防止运输途中货物坍塌与破损。
采用方形木条等支撑,使货物固定;用方木等支柱在水平方向加以固定,或者插入塞物、缓冲垫、楔子等防止货物移动;用绳索、带子等索具捆绑货物。
(4)货物混装在混装货物时,我们注意避免相互污染或引起事故。
干、湿货物不混装,不与强臭货物、活气味强烈的货物混装,不与粉末货物混装。
危险货物之间应采取相应的安全措施。
(5)大件货物装载针对大件货物,我们了解了非标集装箱的使用方法,如侧面开门可以使用叉车,顶部开门可以使用吊车。
对于标准集装箱,我们推荐使用欧洲技术EZLOAD易载或Joloda大件货物整箱装载系统。
四、实训心得1. 安全意识通过本次实训,我们深刻认识到安全在集装箱运输中的重要性。
在装载过程中,我们要严格遵守操作规程,确保货物和人员的安全。
2. 团队协作集装箱装载工作需要多人协作完成,我们学会了如何与团队成员沟通、配合,提高工作效率。
3. 实际操作能力通过本次实训,我们掌握了货物装载的基本方法和技巧,提高了实际操作能力。
华电校赛B题 托盘装载问题

华电校赛B题托盘装载问题
B 托盘装载问题随着我国经济的发展,物资流动日益频繁,以散装、人工搬运为主
的传统运输方式已远远不能满足现代物流的需要。
现今托盘已成为衡量一个国家物流效率
水平的重要标志之一,中国作为世界制造业中心,物流托盘应用前景广阔,预计今后我国
托盘的总量将会以惊人的速度增长,因此研究如何在一个托盘中放置数目最多的长方体箱子,即托盘装载问题(Pallet loading problem,PLP),对降低物流运输成本,提高托盘
的使用效率具有重要的现实意义。
现有一些长方体箱子(具体尺寸及重量信息见附件1),考虑目前应用较为广泛的1210托盘(1200mm×1000mm),完成以下问题:
1. 考虑将编码为“1”的箱子水平且不重叠的摆放在1210托盘上,给出摆放方案使
得托盘面积的利用率尽可能高。
探讨建立一般模型,以此求出将某一任意规格的箱子放到
某一任意规格的托盘上使其利用率达到最大的摆放方式。
2. 考虑编码为“1”和“5”两
种规格的箱子,试着完成问题1。
3. 若考虑箱子的重量因素,综合考虑托盘面积的利用率和托盘的承重的均匀程度,
问题1和问题2所建立的模型是否适用,若不适用请建立模型对问题进行讨论。
4. 若托
盘可以重叠摆放箱子,并且叠放的高度不超过1000mm,附件中给出的30种箱子随机给出,每次给出三个,完成装载后再给出下一组箱子。
综合考虑托盘的空间利用率和稳定性,试
着完成装载问题。
- 1 -
感谢您的阅读,祝您生活愉快。
货物装载问题

x
取
ij
非负整
数
i 1,2,3; j 1,2,3,4,5
6
xij 12 i 1,2,3
j1
4、计算
sets: dianti/1..3/:t; louceng/1..5/:; link(dianti,louceng):x; endsets min=w; @for(dianti:w>=t); @for(louceng(j):10*@sum(dianti(i):x(i,j))=60); @for(dianti(i):t(i)=@sum(louceng(j):(10+20)*x(i,j)+(3+3)*(j +5)*x(i,j))); @for(link:@gin(x)); @for(dianti(i):@sum(louceng(j):x(i,j))<=12);
1、问题分析:
该问题要求设计运载方案,满足硬件要求:货物数量约束、 三个舱位载重量约束、三个舱位体积约束、货物不可分割约束、 三个舱位比例偏差约束。
2、变量设置:
xij:表示第i种货物装入第j舱位的件数,i=1,2,3;j=1,2,3; ai:表示第i种货物的件数; vi:表示第i种货物的单件体积;
二、回答问题2
1、分析:显然,电梯每次混合运输各层楼的员工比每 次只运输一层楼的员工需要多停几次,即所花费的时 间多。所以运输最佳方案一定在后面的方案中产生。 2、变量设置:
xij: 第i电梯运送的j层楼员工的次数;i=1,2,3表示 A,B,C电梯,
j=1,2,3,4,5表示第7,8,9,10,11层楼,其中,xij取整 数,且
575000 3000 y3 1500 y2 575000
前后舱位比例平衡
最优装载问题

代码实现—完整代码
#include <stdio.h> #include <stdlib.h> // 集装箱 结构体 } typedef struct box{ int weight;//重量 int index; //初始序号 }; //比较子函数 int cmp (const void *a, const void *b){ if(((struct box*)a)->weight > ((struct box*)b)->weight) return 1; else return 0; int main(){ //初始化集装箱集合 struct box boxes[8] = {100,0,200,0,50,0,90,0,150,0,50,0,20,0,80,0 }; int flag[8] = {0};//集装箱装载标志 int i ; int quantity; //可装载集装箱数量 int maxLoad; //船只最大载重 int countLoad;//已经装载重量 //输出集装箱初始数据 printf("集装箱初始数据"); printf("\n"); for(i=0;i<8;i++){ printf("b[%d]:%d \t",i,boxes[i].weight);} printf("\n"); //初始化 集装箱序号 for(i=0;i<8;i++){ boxes[i].index = i;} printf("\n"); printf("快速排序之后:"); printf("\n");
箱子的摆放问题

箱子的摆放问题(总15页) -CAL-FENGHAI.-(YICAI)-Company One 1■CAL■本页仅作为文档封面,使用请直接删除箱子的摆放策摘要关键词:利用率最高循环嵌套式算法线性加权评价一、问题重述义车是指对成件托盘货物进行装卸、堆垛和短距离运输作业的各种轮式搬运车辆。
如何摆放箱子,使得义车能将最多的货物从生产车间运输至仓库是众多企业关心的问题。
现将箱子的底面统一简化为形状、尺寸相同的长方形,义车底板设定为一个边长为米的正方形。
要求建立一个通用的优化模型,在给定长方形箱子的长和宽之后,就能利用这个模型算岀使得箱子数量最多的摆放方法。
本题需要解决的问题有:问题一:在不允许箱子超出义车底板,也不允许箱子相互重叠的情况下,构建一个优化模型,并根据题H中提供的三种型号箱子的数据,确定可以摆放的个数及摆放示意图。
问题二:假设箱子密度均匀,允许箱子在正方形底板的上方,左边,右边部分超出底板,但不至于掉落出义车底板。
重建优化模型,考虑问题一中三种规格的箱子的摆放方式。
问题三:在不允许箱子相互重叠的条件下,另外设计出一种摆放方案,再将设计的方案与问题一中的摆放方案的进行优劣性对比。
二、模型假设 1.假设箱子的密度都是均匀的,若允许箱子在正方形底板的上方,左边,右边部分超岀底板(下方紧靠义车壁,不能超出),只要重心不超岀底板,就不至于掉落出义车底板。
2•假设箱子表面光滑,箱子间摆放无缝隙,即把箱子当做小矩形进行分析。
3•假设义车的承重能力无限大,能承载足够多的箱子。
三.符号说明符号解释说明a小矩形箱的长b小矩形箱的宽c长边向上叠加的矩形箱个数d宽边向上叠加的矩形箱个数m底边上矩形箱的长边个数n底边上矩形箱的宽边个数sum小矩形的总个数Wj摆放指标的权重系数Xj摆放指标无量纲化后的数值四、问题分析本文研究的是在一个边长为的正方形义车底板上堆放长方体箱子的问题。
不同规格的箱子最佳堆放方式是不同的,要尽量多的满足各种型号箱子摆放数量最多,就要设计一个通用的优化方案。
算法装载问题实验报告

一、实验背景算法装载问题(Bin Packing Problem)是组合优化领域中的一个经典问题,主要研究如何将一组物品装入有限数量的容器中,使得容器中的物品总重量不超过容器的容量,同时尽可能减少容器的数量。
该问题在实际应用中具有广泛的意义,如物流运输、资源分配、生产计划等领域。
二、实验目的1. 了解算法装载问题的基本概念和特点;2. 掌握几种常用的算法装载问题的解决方法;3. 通过实验验证不同算法在解决算法装载问题时的性能;4. 分析算法的优缺点,为实际应用提供参考。
三、实验内容1. 实验环境操作系统:Windows 10编程语言:Python 3.8实验工具:Pandas、Numpy、Scipy2. 实验方法(1)遗传算法遗传算法是一种模拟自然选择和遗传学原理的搜索启发式算法。
在算法装载问题中,可以将物品和容器看作基因,通过交叉、变异等操作,不断优化解的质量。
(2)贪心算法贪心算法是一种在每一步选择中都采取当前最优策略的算法。
在算法装载问题中,可以根据物品的重量或容器的容量,对物品进行排序,然后依次将物品装入容器。
(3)动态规划动态规划是一种将复杂问题分解为子问题,并存储子问题的解的方法。
在算法装载问题中,可以根据物品的重量和容器的容量,计算最优解。
3. 实验数据实验数据来源于一组具有不同重量和数量的物品,以及不同容量和数量的容器。
四、实验结果与分析1. 遗传算法实验结果表明,遗传算法在解决算法装载问题时具有较高的求解能力。
随着迭代次数的增加,解的质量逐渐提高,但求解时间较长。
2. 贪心算法贪心算法在解决算法装载问题时具有较快的求解速度,但解的质量相对较差。
在部分情况下,贪心算法得到的解甚至无法满足所有容器的容量要求。
3. 动态规划动态规划在解决算法装载问题时具有较高的求解质量,但求解时间较长。
对于大型问题,动态规划可能无法在合理时间内得到最优解。
五、结论通过对遗传算法、贪心算法和动态规划在算法装载问题中的应用实验,得出以下结论:1. 遗传算法具有较高的求解能力,但求解时间较长;2. 贪心算法求解速度快,但解的质量较差;3. 动态规划求解质量高,但求解时间较长。
货车装货实验报告范文

货车装货实验报告范文
实验目的:
通过对货车装货进行实验,探究不同装货方式对货车运输的影响。
实验材料:
1. 一辆货车
2. 不同形状和重量的货物
实验步骤:
1. 准备不同形状和重量的货物,并记录它们的质量和体积。
2. 将货车清空,并记录货车的自重和载重能力。
3. 将第一种货物以一种方式装载到货车上,尽量利用货车的空间。
4. 在装载完第一种货物后,记录货车的载重量和体积利用率。
5. 依次重复步骤3和4,将所有货物按照不同方式装载到货车上。
实验结果:
1. 不同形状和重量的货物对货车的载重量和体积利用率有不同的影响。
2. 合理地利用货车空间可以提高载重量和体积利用率。
讨论与分析:
1. 装载方式的选择对于货车的载重量和体积利用率有重要影响。
需要根据货物的形状和重量来选择最佳的装载方式,例如使用货架或分层装载等。
2. 货车的载重量和体积利用率直接影响货车的运输效率和经济效益,因此合理地利用货车空间非常重要。
实验结论:
通过本次实验,我们发现货车装货时,选择合适的装载方式可以最大限度地提高货车的载重量和体积利用率,从而提高货车的运输效率和经济效益。
因此,在实际货物运输中,需要根据货物的特性合理组织货车的装货,以提高运输的效率和效益。
最佳平板车装载安排

最佳平板车装载安排由于要使平板车浪费的空间最小,等价于使装载货物箱的厚度和达到最大。
模型假设装载时相邻的量货物箱之间的间隙可以忽略。
首先,对符号进行说明,其中,,i i i t w n 分别表示第i 种货物箱的厚度、重量和库存量,i i x x '分别表示第i 种货物箱在两平板车上的装载数s 表示装载两车上的货物箱的厚度和()71i i i i s t x x ='=+∑由两辆车装载空间的限制和载重量的限制可得771177111020,102040,40i ii i i i i ii i i i t xt x w xw x ===='≤≤'≤≤∑∑∑∑货物箱库存量的限制为()1,2,3,4,5,6,7i i i x x n i '+≤= 关于第5、6、7这3种货物箱的限制可写为:71()302.7iiii t x x ='+≤∑又由题知,i i x x '为非负整数,故这是一个整数规划模型。
故此整数规划模型为:max ()71i i i i s t x x ='=+∑s.t. ()1,2,3,4,5,6,7i i i x x n i '+≤=7140i ii w x=≤∑7140i i i w x ='≤∑711020i ii t x=≤∑711020i i i t x ='≤∑71()302.7iiii t x x ='+≤∑同时,,i i x x '为非负整数即,0i i x x '≥()1,2,3,4,5,6,7i = 通过lingo 求解可知,{}{}4,7,4,3,0,0,0,4,0,5,3,3,3,1x x '== 同时2039.4s =,则此时浪费0.6cm 。
此时应在其中一辆平板车上装第一种箱子4箱,第二种箱子7箱,第三种箱子4箱,第四种箱子3箱,其余三种不装。
三年级数学装箱应用题

三年级数学装箱应用题小明的班级要进行一次春游活动,老师要求每位同学带一些水果和零食。
老师给每位同学发了一个小箱子,每个箱子的容量是10升。
现在小明需要将苹果、香蕉和橙子装进箱子里。
问题一:如果小明要带5个苹果,每个苹果的体积是0.8升,他能否将所有苹果装进箱子里?解答:首先,我们需要计算5个苹果的总体积。
每个苹果的体积是0.8升,所以5个苹果的总体积是5 × 0.8 = 4升。
因为箱子的容量是10升,而5个苹果的总体积是4升,小于箱子的容量,所以小明可以将所有苹果装进箱子里。
问题二:小明还想要带一些香蕉和橙子,香蕉每个的体积是0.5升,橙子每个的体积是1.2升。
如果小明的箱子已经装了苹果,他还想要带3个香蕉和2个橙子,他能否将这些水果全部装进箱子里?解答:首先,我们需要计算3个香蕉的总体积。
每个香蕉的体积是0.5升,所以3个香蕉的总体积是3 × 0.5 = 1.5升。
接着,我们计算2个橙子的总体积。
每个橙子的体积是1.2升,所以2个橙子的总体积是2 × 1.2 = 2.4升。
现在,我们需要将这些水果的体积加到已经装了苹果的箱子里。
箱子里已经有4升的苹果,加上香蕉和橙子的体积,总体积是 4 + 1.5 + 2.4 = 7.9升。
因为箱子的容量是10升,而7.9升小于箱子的容量,所以小明可以将这些水果全部装进箱子里。
问题三:如果小明想要将所有的水果平均分给5位同学,每个同学能分到多少升的水果?解答:首先,我们需要计算所有水果的总体积。
根据问题二的解答,我们知道总体积是7.9升。
然后,我们将这个总体积除以5(因为要分给5位同学),得到每个同学能分到的水果体积:7.9 ÷ 5 = 1.58升。
所以,每个同学能分到大约1.58升的水果。
问题四:如果小明想要将水果分成小包装,每个小包装的体积是1升,他需要多少个小包装?解答:根据问题三的解答,我们知道每个同学能分到1.58升的水果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验五箱子装载问题
一、实验目的:
1、理解和复习所学各种算法的概念;
2、掌握和复习所学各种算法的基本要素;
3、掌握各种算法的优点和区别;
4、通过应用范例掌握选择最佳算法的设计技巧与策略;
二、实验内容及要求:
1、使用贪心算法、回溯法、分支限界法解决箱子装载问题。
(任选两种)
2、通过上机实验进行算法实现。
3、保存和打印出程序的运行结果,并结合程序进行分析,上交实验报告。
三、实验原理:
贪心算法原理:
贪心算法通过一系列的选择来得到问题的解。
他所做的每一个选择都是当前状态下局部最好选择,即贪心选择。
回溯法原理:
从开始结点出发,以深度优先方式搜索整个解空间。
这个结点成为活结点,同时也成为当前的扩展结点。
在当前的扩展结点处,搜索向纵深方向一致一个新结点。
四、程序代码:
1、贪心算法:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1000;
int w[maxn];
int x[maxn];
int main()
{
int n,c;
printf("输入集装箱数量和轮船载重量:");
while(~scanf("%d %d",&n,&c))
{
printf("输入集装箱的重量:");
memset(x,0,sizeof(x));
for(int i=0;i<n;i++)
scanf("%d",&w[i]);
sort(w,w+n);
int ans = 0;
for(int i=0;i<n;i++) if(ans+w[i]<=c)
{
ans+=w[i];
x[i]=1;
}
printf("最大装载为 %d\n",ans);
printf("选中的集装箱重量分别为:\n");
for(int i=0;i<n;i++) if(x[i]) printf("%d ",w[i]);
}
}
2、回溯法
#include<iostream>
using namespace std;
class Loading
{
friend float MaxLoading(float[],float,int);
public:
void Backtrack(int i);
int n;
int *x,*bestx;
float *w,c,cw,bestw,r;
};
float Maxloading(float w1[],float c1,float c2,int n1,int bestx1[]) {
Loading k;
int j;
float MAXLoad;
k.x= new int [n1+1];
k.bestx=bestx1;
k.w = w1;
k.c = c1;
k.n = n1;
k.cw = 0;
k.bestw = 0;
k.r = 0;
for(int i=1;i<=n1;i++)
k.r+=w1[i];
k.Backtrack(1);
delete [] k.x;
cout<<"船1最优装载:"<<k.bestw<<endl; MAXLoad=k.bestw;
for( j=1;j<=n1;j++)
{
if(k.bestx[j]==0)
{
MAXLoad+=w1[j];
c2-=w1[j];
if(c2<0)
{
cout<<"找不到合理装载方法"<<endl; return -1;
}
}
cout<<"船1中的箱子:";
for( j=1;j<=n1;j++)
if(k.bestx[j]==1)
cout<<j<<" ";
cout<<endl;
cout<<"船2中的箱子:";
for( j=1;j<=n1;j++)
if(k.bestx[j]==0)
cout<<j<<" ";
cout<<endl;
return MAXLoad;
}
void Loading::Backtrack(int i) {
if(i>n)
{
if(cw>bestw)
{
for(int j=1;j<=n;j++)
bestx[j]=x[j];
bestw = cw;
}
return;
r-=w[i];
if(cw+w[i]<=c)
{
x[i]=1;
cw+=w[i];
Backtrack(i+1);
cw-=w[i];
}
if(cw+r>bestw)
{
x[i] = 0;
Backtrack(i+1);
}
r+=w[i];
}
int main()
{
float w[20];
float c1,c2,k;
int n,bestx[20];
cout<<"输入箱子数量:\n"; cin>>n;
cout<<"输入各箱子重量:\n";
for(int i=1;i<=n;i++)
cin>>w[i];
cout<<"分别输入船1,船2载重量:\n";
cin>>c1>>c2;
k=Maxloading(w,c1,c2,n,bestx);
if(k!=-1)cout<<"最优装载量:"<<k<<endl; return 1;
}
五、结果运行与分析:
贪心算法:
回溯法:
六、心得与体会:
通过本次实验,重新复习了贪心算法和回溯法的原理,在温故的同时,对这两种算法的区别和各自的优势也有了进一步的理解。
